10 Potenz- und Fourierreihen
|
|
|
- Emil Waldfogel
- vor 7 Jahren
- Abrufe
Transkript
1 10 Potenz- und Fourierreihen 10.1 Konvergenzbegriffe für Funktionenfolgen Im letzten Kapitel soll es noch einmal um eindimensionale Analysis gehen. Speziell werden wir uns mit Folgen und Reihen reeller Funktionen auseinandersetzen. Definition Eine unendliche Folge f 1, f 2, f 3,..., f n,... von Funktionen f n : I R auf einem Intervall I R nennen wir Funktionenfolge auf I. Notation: (f n ) n N oder kürzer (f n ), analog zu Zahlenfolgen. Funktionenreihen TU Bergakademie Freiberg 823 Punktweise Konvergenz Wir suchen nach geeigneten Konvergenzbegriffen für Funktionenfolgen. Das Naheliegendste ist: Definition Eine Funktionenfolge (f n ) auf I R heißt punktweise konvergent gegen die Funktion f : I R wenn lim f n(x) = f(x) für alle x I, (1) n d. h. wenn für jedes x I die Zahlenfolge (f n (x)) n gegen f(x) konvergiert. Die Funktion f heißt Grenzfunktion von (f n ). Äquivalent zu (1) ist die Aussage, dass f n (x) f(x) 0 für n für alle x I. Funktionenreihen TU Bergakademie Freiberg 824 Beispiele und Probleme Die Funktionenfolgen f n (x) = nx(1 x) n (links) und f n (x) = x(1 x) n (rechts) konvergieren auf [0, 1] beide punktweise gegen f(x) = 0. 1/e 1/e f 2 f 5 f 2 f 5 f 11 f 11 1/12 1/6 1/3 1 1/12 1/6 1/3 1 Am Beispiel der Funktionenfolge links erkennen wir bereits, dass trotz punktweiser Konvergenz auch für große n nicht alle Funktionswerte von f n beliebig nahe bei Null liegen müssen. Funktionenreihen TU Bergakademie Freiberg 825
2 Punktweise Konvergenz ist generell eine recht schwache Eigenschaft, z. B. kann auch folgendes passieren: die Grenzfunktion f ist nicht stetig, obwohl es alle Folgenglieder f n sind, die Folge der Integrale I f n(x) dx konvergiert, aber nicht gegen das Integral I f(x) dx über die Grenzfunktion. Illustrieren Sie dies an folgenden Beispielen: f n : [0, 1] R, f n (x) = x n, f n : [0, 1] R, { n 2 x, 0 x < 1 f n (x) = n ; 1 0, n x 1. Funktionenreihen TU Bergakademie Freiberg 826 Gleichmäßige Konvergenz Die Problemfälle von S. 826 haben gemeinsam, dass die Funktionswerte f n (x) auch für große n nicht gleichmäßig nahe bei f(x) liegen. Wir formulieren daher einen strengeren Konvergenzbegriff: Definition Eine Funktionenfolge (f n ) auf einem Intervall I R heißt gleichmäßig konvergent gegen f : I R, wenn sup f n (x) f(x) 0 für n. (2) x I Erinnerung: Das Supremum sup M einer beschränkten Menge M R ist deren kleinste obere Schranke. Falls das Maximum existiert, gilt sup M = max M. Funktionenreihen TU Bergakademie Freiberg 827 Beispiel Die Funktionenfolge f n (x) = sin x + 1 n sin(3x + n) konvergiert auf R gleichmäßig gegen f(x) = sin x, denn 1 sup f n (x) f(x) = sup x R x R n sin(3x + n) = 1 n 0 (n ). Gezeichnet sind einige Glieder der Funktionenfolge sowie deren Grenzfunktion. Man beachte, dass ab einem bestimmten n (hier z. B. n 5) alle Funktionsgraphen komplett innerhalb eines beliebig dünnen ε-schlauchs um die Grenzfunktion f verlaufen (blau gestrichelt). Funktionenreihen TU Bergakademie Freiberg 828
3 Eigenschaften gleichmäßig konvergenter Funktionenfolgen Satz Konvergiert eine Funktionenfolge (f n ) auf einem Intervall I gleichmäßig gegen f, dann konvergiert sie auch punktweise gegen f. Gleichmäßige Konvergenz ist also stärker als punktweise. Satz Konvergieren zwei Funktionenfolgen (f n ) und (g n ) auf einem Intervall I gleichmäßig gegen f bzw. g, so konvergieren die Funktionenfolge (f n ± g n ) gleichmäßig gegen f ± g, die Funktionenfolge (λf n ), λ R, gleichmäßig gegen λf. Funktionenreihen TU Bergakademie Freiberg 829 Die gleichmäßige Konvergenz behebt auch die Mängel von S. 826: Satz Ist (f n ) eine auf dem Intervall I gleichmäßig konvergente Folge stetiger Funktionen, so ist auch die Grenzfunktion f auf I stetig. Satz Ist (f n ) eine auf dem Intervall [a, b] gleichmäßig konvergente Folge integrierbarer Funktionen, so ist auch die Grenzfunktion f integrierbar, und es gilt b a f(x) dx = lim n b a f n (x) dx. Funktionenreihen TU Bergakademie Freiberg 830 Schließlich formulieren wir noch ein Ergebnis für die Ableitung bei gleichmäßiger Konvergenz: Satz Ist (f n ) eine auf dem Intervall [a, b] gleichmäßig konvergente Folge differenzierbarer Funktionen mit Grenzfunktion f, und ist die abgeleitete Funktionenfolge (f n) auf [a, b] ebenfalls gleichmäßig konvergent, so ist f differenzierbar mit f (x) = lim n f n(x) (für alle x [a, b]). Funktionenreihen TU Bergakademie Freiberg 831
4 Funktionenreihen Wie bei Zahlenfolgen kann man zu einer Funktionenfolge (f n ) n 0 eine Partialsummenfolge definieren: f 0, f 0 + f 1, f 0 + f 1 + f 2,..., n f k,... Diese Partialsummenfolge nennen wir auch Reihe der Funktionen f k. Die Funktionen f k heißen Glieder der Funktionenreihe. Notation: f k oder f k(x), sowohl für die Reihe selbst als auch für deren Grenzwert, genau wie bei reellen Reihen. Beispiel: Bereits bekannt ist die Funktionenreihe e x = xk k!. Funktionenreihen TU Bergakademie Freiberg 832 Gliedweises Integrieren und Differenzieren Da Funktionenreihen spezielle Funktionenfolgen sind, kann man unsere Konvergenzbegriffe wie auch die Sätze direkt übertragen. Sei f k gleichmäßig konvergent auf [a, b] mit f k = f. Dann gelten: Sind alle Reihenglieder f k stetig, so ist auch die Summenfunktion f stetig, und es gilt b [ b ] b f(x) dx = f k (x) dx = f k (x)dx. a a Sind alle f k differenzierbar, und konvergiert die abgeleitete Reihe f k gleichmäßig auf [a, b], dann ist auch die Summe f differenzierbar und [ f (x) = f k (x)] = f k (x). Funktionenreihen TU Bergakademie Freiberg 833 a 10.2 Potenzreihen Bei diesen Funktionenreihen wählt man als Glieder Funktionen vom Typ f k (x) = a k (x x 0 ) k. Als Partialsummen entstehen Polynome n-ten Grades: s n (x) = n a k(x x 0 ) k. Definition Eine Reihe der Form a k (x x 0 ) k (x, x 0, a k R) (3) heißt Potenzreihe mit Entwicklungspunkt x 0 und Koeffizienten a k. Die berühmteste Potenzreihe kennen Sie bereits: e x = 1 k! xk. Sie hat den Entwicklungspunkt x 0 = 0, die Koeffizienten a k = 1 k! und konvergiert für alle x R. Funktionenreihen TU Bergakademie Freiberg 834
5 Konvergenzverhalten Wir untersuchen nun das Konvergenzverhalten von (3) in Abhängigkeit von x, während a k und x 0 fest gehalten werden. Satz (von Cauchy-Hadamard ). Zu jeder Potenzreihe a k(x x 0 ) k gibt es einen Konvergenzradius R [0, ) {} mit folgenden Eigenschaften: Die Potenzreihe konvergiert (absolut) für x (x 0 R, x 0 + R). Die Potenzreihe konvergiert gleichmäßig auf jedem abgeschlossenen Intervall I (x 0 R, x 0 + R). Die Potenzreihe divergiert außerhalb [x 0 R, x 0 + R] (nur sinnvoll für R ). Jacques Hadamard, , französischer Mathematiker Funktionenreihen TU Bergakademie Freiberg 835 Prinzipskizze zum Konvergenzverhalten Divergenz?? Konvergenz Divergenz x 0 R x 0 x 0 +R Anmerkungen Das Intervall (x 0 R, x 0 + R) wird auch Konvergenzintervall der Potenzreihe genannt. Das Konvergenzverhalten an den kritischen Punkten x 0 R und x 0 + R muss immer gesondert untersucht werden. Funktionenreihen TU Bergakademie Freiberg 836 Berechnung des Konvergenzradius Satz Sei a k(x x 0 ) k eine Potenzreihe mit Konvergenzradius R. Dann gilt: R = lim a k, k a k+1 falls fast alle ak von Null verschieden sind, und dieser Grenzwert existiert, R = 1 lim k k ak, falls der Grenzwert im Nenner existiert. Dabei sind die Konventionen 1 = 0 und 1 0 = zu treffen. Beweisidee: Quotienten- bzw. Wurzelkriterium für Zahlenreihen. Funktionenreihen TU Bergakademie Freiberg 837
6 Beispiel Der Konvergenzradius von e x = xk k! ist. Tatsächlich ergibt sich mit dem erstgenannten Kriterium R = lim a k k = lim (k + 1)! = lim (k + 1) =. k k! k a k+1 Untersuchen Sie das Konvergenzverhalten der Potenzreihen k k x k, k=1 x k k + 1, x k 2 k. Vergessen Sie nicht, die Randpunkte des Konvergenzintervalls zu untersuchen. Funktionenreihen TU Bergakademie Freiberg 838 Gliedweises Differenzieren und Integrieren Die Ergebnisse von S. 833 gelten natürlich auch für Potenzreihen: Satz Die Potenzreihe a k(x x 0 ) k besitze den Konvergenzradius R > 0. Die Funktion f : (x R, x + R) R, f(x) = a k (x x 0 ) k hat dann folgende Eigenschaften: f ist stetig. f ist auf jedem abgeschlossenen Teilintervall von (x R, x + R) integrierbar, wobei a k f(x) dx = k + 1 (x x 0) k+1 + C. Funktionenreihen TU Bergakademie Freiberg 839 Fortsetzung Satz f ist beliebig oft differenzierbar mit f (x) = ka k (x x 0 ) k 1, f (x) = k=1 k(k 1)a k (x x 0 ) k 2, k=2 usw. Insbesondere ist f (k) (x 0 ) = k! a k. Funktionenreihen TU Bergakademie Freiberg 840
7 Beispiel Aus der Summenformel für die geometrische Reihe erhält man für f : ( 1, 1) R, f(x) = 1 1 x die Potenzreihendarstellung f(x) = 1 1 x = x k = 1 + x + x 2 + x Durch gliedweises Differenzieren (Satz 10.12, Punkt 3) erhält man für die Ableitung die Darstellung f 1 (x) = (1 x) 2 = kx k 1 = (k+1)x k = 1+2x+3x 2 +4x k=1 Wie lautet die Potenzreihendarstellung zu F (x) = ln(1 x) (x 0 = 0, x < 1)? Funktionenreihen TU Bergakademie Freiberg 841 Darstellbarkeit durch Potenzreihen Es stellt sich die Frage, wann z. B. eine unendlich oft differenzierbare Funktion als Potenzreihe geschrieben ( in eine Potenzreihe entwickelt ) werden kann. Aus der Formel in letzten Zeile von Satz ergibt sich, dass für die Koeffizienten immer a k = f (k) (x 0 ) k! gelten muss. Die aus Abschnitt 4.6 bekannte Taylor-Reihe f (k) (x 0 ) (x x 0 ) k k! ist also der einzige Kandidat für eine mögliche Potenzreihendarstellung von f. Funktionenreihen TU Bergakademie Freiberg 842 Warnungen Leider gibt es unendlich oft differenzierbare Funktionen, die man nicht als Potenzreihen schreiben kann. Es kann vorkommen, dass die Taylor-Reihe den Konvergenzradius R = 0 besitzt, d. h. nur für x = x 0 konvergiert. die Taylor-Reihe durchaus konvergiert (R > 0), aber nicht gegen die Funktion f (!!). Ein prominentes Beispiel ist die Funktion { f(x) = e 1 x 2, für x 0; 0, für x = 0, für die f (k) (0) = 0 für alle k N gilt. Die Taylorreihe ist somit die konstante Funktion f = 0 und hat mit f nichts zu tun. Funktionenreihen TU Bergakademie Freiberg 843
8 Wann genau eine unendlich oft differenzierbare Funktion f durch ihre Taylor-Reihe dargestellt wird, ist schwierig zu charakterisieren. Wir begnügen uns mit einer hinreichenden Bedingung: Satz Die Funktion f : I = (x 0 r, x 0 +r) R sei unendlich oft differenzierbar. Gilt r k lim k k! max f (k+1) (x) = 0, x I so besitzt die Taylor-Reihe f (k) (x 0) k! (x x 0 ) k den Konvergenzradius R r, und es gilt f (k) (x 0 ) f(x) = (x x 0 ) k für alle x I. k! Funktionenreihen TU Bergakademie Freiberg 844 Man bestimme die Taylorreihe zu f(x) = sin x (x 0 = 0). Wie verhält es sich mit der Konvergenz? Könnte man diese Potenzreihe auch aus der Formel e ix = cos x + i sin x erhalten? Die Funktion f(x) = sin x und einige ihrer Taylorpolynome T n(x) = n f (k) (0) x k. k! Funktionenreihen TU Bergakademie Freiberg 845 Rechnen mit Potenzreihen Schließlich kann man Potenzreihen gliedweise addieren und in Produkten von Potenzreihen wie bei endlichen Summen ausmultiplizieren: Satz Für Summe und Produkt zweier Potenzreihen a k(x x 0 ) k und b k(x x 0 ) k gilt im gemeinsamen Konvergenzbereich: a k (x x 0 ) k + b k (x x 0 ) k = (a k + b k )(x x 0 ) k bzw. ( ) ( ) a k (x x 0 ) k b k (x x 0 ) k = c k (x x 0 ) k mit c k = a 0 b k + a 1 b k a k b 0. Funktionenreihen TU Bergakademie Freiberg 846
9 Beispiel e x sin(x) = ] ] [1 + x + [x x2 2! + x3 3! + x3 3! + x5 5! + = x + x 2 + x3 3 x5 30 x6 90 x x Bestätigen Sie mindestens die ersten vier Summanden durch detaillierte Rechnung. Funktionenreihen TU Bergakademie Freiberg 847 Division von Potenzreihen Will man die Koeffizienten von c k (x x 0 ) k = a k(x x 0 ) k b k(x x 0 ) k berechnen, formt man zunächst um: ( ) ( ) c k (x x 0 ) k b k (x x 0 ) k = und führt dann einen Koeffizientenvergleich durch. Mit Hilfe von a k (x x 0 ) k sin x = x x3 3! + x5 5! x7 x2 + und cos x = 1 7! 2! + x4 4! x6 6! + berechne man die ersten fünf Koeffizienten der Potenzreihe zu tan x = sin x cos x (x 0 = 0). Funktionenreihen TU Bergakademie Freiberg Fourier-Reihen Im letzten Abschnitt suchen wir nach Reihendarstellungen für periodische Funktionen, speziell für 2π-periodische Funktionen. Als Reihenglieder verwenden wir Funktionen, die selbst 2π-periodisch sind: Definition Eine Reihe der Bauart a (a j cos(jx) + b j sin(jx)) j=1 mit reellen Konstanten a 0, a 1, a 2,... und b 1, b 2, b 3... heißt trigonometrische Reihe. Ist a j = 0 (j N 0 ), spricht man von einer Sinusreihe. Ist b j = 0 (j N), spricht man von einer Kosinusreihe. Joseph Fourier, , französischer Mathematiker und Physiker Zur Erinnerung: Das bedeutet f(x + 2π) = f(x) für alle x R. Funktionenreihen TU Bergakademie Freiberg 849
10 Konvergenz und Eigenschaften der Grenzfunktion Wir gehen zunächst von einer gegebenen trigonometrischen Reihe aus und bemerken: Satz Ist die trigonometrische Reihe a0 2 + j=1 (a j cos(jx) + b j sin(jx)) für alle x R konvergent, so ist f(x) = a (a j cos(jx) + b j sin(jx)) (4) j=1 eine auf R definierte 2π-periodische Funktion. Es macht also umgekehrt nur für 2π-periodische Funktionen Sinn, nach Darstellungen der Form (4) zu suchen. Für Funktionen wie g(x) = x 2 oder h(x) = e x ist dies dagegen zwecklos. Funktionenreihen TU Bergakademie Freiberg 850 Der folgende Satz liefert u. a. den Schlüssel zur Berechnung der gesuchten Reihendarstellungen: Satz Sind die Reihen j=0 a j und j=1 b j absolut konvergent, konvergiert die trigonometrische Reihe a0 2 + j=1 (a j cos(jx) + b j sin(jx)) punktweise auf ganz R. Die Summenfunktion f(x) := a (a j cos(jx) + b j sin(jx)) ist stetig auf R, und es gelten a j = 1 π b j = 1 π π π π π j=1 f(t) cos(jt)dt (j N 0 ), f(t) sin(jt)dt (j N). (5) Funktionenreihen TU Bergakademie Freiberg 851 Hintergrund: Orthogonalitätsrelationen in L 2 ([ π, π]) Um die Darstellungen in (5) zu erhalten, versieht man den Raum L 2 ([ π, π]) aller Funktionen f mit π π f(x) 2 dx < mit dem Skalarprodukt f, g = 1 π π π f(x)g(x) dx. Es lässt sich zeigen, dass die Funktionen sin(nx) und cos(mx) (m N 0, n N) diesbezüglich eine Orthonormalbasis bilden, d. h. 1 π sin(nx) sin(mx)dx = 1 { π 0, falls n m, cos(nx) cos(mx)dx = π π π π 1, falls n = m, 1 π sin(nx) cos(mx)dx = 0 (n N, m N 0). π π Die Darstellung (5) der Koeffizienten ergibt sich damit wie in Satz 6.29 aus a j = f( ), cos(j ) und b j = f( ), sin(j ). Genaugenommen muss man hier den Lebesgueschen Integralbegiff verwenden. Funktionenreihen TU Bergakademie Freiberg 852
11 Darstellbarkeit durch Fourier-Reihen Wir untersuchen nun für eine vorgegebene 2π-periodische Funktion f, ob sie sich in eine trigonometrische Reihe entwickeln lässt. Definition Sei f : R R eine 2π-periodische, auf [ π, π] integrierbare Funktion. Dann heißen die Zahlen a j = 1 π b j = 1 π π π π π f(t) cos(jt)dt (j N 0 ), f(t) sin(jt)dt Fourier-Koeffizienten von f. Die Reihe heißt Fourier-Reihe von f. (j N). ˆf(x) = a (a j cos(jx) + b j sin(jx)) j=1 Funktionenreihen TU Bergakademie Freiberg 853 Anmerkungen Da die Integranden die Periode 2π haben, kann auch jedes andere Intervall der Länge 2π als Integrationsbereich verwendet werden. Das konkrete Rechnen erleichtert häufig: Satz Ist f : R R eine 2π-periodische, in [ π, π] integrierbare, und auf ( π, π) gerade [ungerade] Funktion, dann ist die Fourier-Reihe von f eine Kosinusreihe [eine Sinusreihe]. Man berechne die Fourier-Reihe zum Rechteckpuls { A, für x π/2, f(x) = 0, für π/2 x π. Funktionenreihen TU Bergakademie Freiberg 854 Wie bei den Taylor-Reihen stellen sich nun folgende Fragen: Wann konvergiert die Fourier-Reihe ˆf(x)? Falls sie konvergiert unter welchen Bedingungen gilt dann auch ˆf(x) = f(x)? Zur Beantwortung brauchen wir einen weiteren Begriff: Definition Eine Funktion f : [a, b] R heißt auf [a, b] stückweise glatt, wenn es eine Unterteilung a = x 0 < x 1 < < x n = b von [a, b] gibt, so dass f auf jedem der Teilintervalle [x i 1, x i ] stetig differenzierbar ist. Funktionenreihen TU Bergakademie Freiberg 855
12 Satz Ist die 2π-periodische Funktion f : R R stückweise glatt auf [ π, π], so konvergiert ihre Fourier-Reihe ˆf punktweise auf R. Dabei gilt ˆf(x 0 ) = 1 ( ) lim 2 f(x) + lim f(x) für alle x 0 R. x x 0 x x 0+ Ist f stetig in x 0, so folgt ˆf(x 0 ) = f(x 0 ). Beispiel: A s 1 s 5 A/2 0 s 3 0 pi 2 pi Partialsummen der Fourierentwicklung zum Rechteckpuls, vgl. Bsp. S Funktionenreihen TU Bergakademie Freiberg 856 Weiteres Beispiel Für die Sägezahnfunktion f(x) = x ( x π) ergibt sich a j = 0 (j N 0 ), und b j = 2 ( 1)j+1 j Auch hier stellen wir die ersten Partialsummen dar: (j N). pi s 1 s 3 0 pi s 5 0 pi 2 pi Anmerkung: Tabellen wichtiger Fourierentwicklungen findet man in gängigen Tafelwerken, z. B. Merziger et al., S. 78 ff. Funktionenreihen TU Bergakademie Freiberg 857 Exkurs: Gibbssches Phänomen Wir betrachten die Partialsummen s 29 für Rechteckpuls und Sägezahnfunktion: s 29 pi A s 29 A/2 0 0 pi 0 pi 2 pi 0 pi 2 pi In einer kleinen Umgebung der Sprungstelle überschwingen die Partialsummen s n um etwa 9 % der Sprunghöhe ( overshoot ). Dieses Gibbsche Phänomen verschwindet nicht für n, bewegt sich aber näher an die Sprungstelle. Josiah Willard Gibbs, , US-amerikanischer Physiker Funktionenreihen TU Bergakademie Freiberg 858
13 Ein typisches Problem, welches durch Überschwingen verursacht wird, sind Artefakte im JPG-Bildformat in der Nähe scharfer Kanten. Grund ist u. a. die Verwendung einer Kosinustransformation im Kompressionsalgorithmus, die ganz ähnliche Eigenschaften wie die Fouriertransformation aufweist. Insbesondere für qualitativ hochwertige Balkengrafiken und Diagramme ist JPG daher ein denkbar ungeeignetes Format. Funktionenreihen TU Bergakademie Freiberg 859 Fourier-Entwicklung von Funktionen mit beliebiger Periode Ist f : R R periodisch mit Periode T, bestimmt man die Kreisfrequenz ω 0 = 2π/T und entwickelt wobei a 0 = 2 T sowie f(x) = a [a j cos(jω 0 x) + b j sin(jω 0 x)], s+t s b j = 2 T j=1 f(t) dt und a j = 2 T s+t s f(t) sin(jω 0 t) dt s+t s f(t) cos(jω 0 t) dt, (j N). Man nennt ω 0 die Kreisfrequenz der Grundschwingung und jω 0 (j > 1) die Kreisfrequenzen der harmonischen Oberschwingungen. Die Zahl s R ist beliebig. Funktionenreihen TU Bergakademie Freiberg 860 Ziele erreicht? Sie sollten nun (bzw. nach Abschluss der Übungen/Tutorien): die Begriffe Funktionenfolge und -reihe gut verstanden haben, zwischen punktweiser und gleichmäßiger Konvergenz unterscheiden können und einfache Funktionenfolgen darauf untersuchen können, über die Konvergenzeigenschaften einer Potenzreihe bescheidwissen und Konvergenzradien sicher bestimmen können, Funktionen in Potenzreihen (Taylorreihen) entwickeln und mit Potenzreihen sicher rechnen können, den Begriff der trigonometrischen Reihe verstanden haben, die Fourierreihen zu stückweise glatten, 2π periodischen Funktionen berechnen können und über deren Konvergenz bescheidwissen. Funktionenreihen TU Bergakademie Freiberg 861
14 Das Wort zum Ende... Vielen Dank für Ihre Aufmerksamkeit und Treue und viel Erfolg bei den anstehenden Prüfungen! Und eine erholsame Ferienzeit wo auch immer es Sie hin verschlägt! Funktionenreihen TU Bergakademie Freiberg 862
Mathematik II. (für Informatiker, ET und IK) Oliver Ernst. Sommersemester Professur Numerische Mathematik
 Mathematik II (für Informatiker, ET und IK) Oliver Ernst Professur Numerische Mathematik Sommersemester 2016 Inhalt I 3 Folgen und Reihen 3.1 Folgen 3.2 Grenzwerte und Konvergenz 3.3 Unendliche Reihen
Mathematik II (für Informatiker, ET und IK) Oliver Ernst Professur Numerische Mathematik Sommersemester 2016 Inhalt I 3 Folgen und Reihen 3.1 Folgen 3.2 Grenzwerte und Konvergenz 3.3 Unendliche Reihen
1.1 Vorbemerkung: Konvergenz von Reihen. g = lim. n=0. n=0 a n sei konvergent und schreibt. a n = g. (2) n=0
 1 Taylor-Entwicklung 1.1 Vorbemerkung: Konvergenz von Reihen Gegeben sei eine unendliche Folge a 0,a 1,a,... reeller Zahlen a n R. Hat der Grenzwert g = lim k a n (1) einen endlichen Wert g R, so sagt
1 Taylor-Entwicklung 1.1 Vorbemerkung: Konvergenz von Reihen Gegeben sei eine unendliche Folge a 0,a 1,a,... reeller Zahlen a n R. Hat der Grenzwert g = lim k a n (1) einen endlichen Wert g R, so sagt
INGENIEURMATHEMATIK. 8. Reihen. Sommersemester Prof. Dr. Gunar Matthies
 Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
KAPITEL 9. Funktionenreihen
 KAPITEL 9 Funktionenreihen 9. TaylorReihen............................ 28 9.2 Potenzreihen............................ 223 9.3 Grenzfunktionen von Funktionenfolgen bzw. reihen........ 230 9.4 Anwendungen............................
KAPITEL 9 Funktionenreihen 9. TaylorReihen............................ 28 9.2 Potenzreihen............................ 223 9.3 Grenzfunktionen von Funktionenfolgen bzw. reihen........ 230 9.4 Anwendungen............................
Anleitung zu Blatt 2, Analysis II
 Fachbereich Mathematik der Universität Hamburg Dr. H. P. Kiani Anleitung zu Blatt 2, Analysis II SoSe 202 Funktionenfolgen, Potenzreihen I Die ins Netz gestellten Kopien der Anleitungsfolien sollen nur
Fachbereich Mathematik der Universität Hamburg Dr. H. P. Kiani Anleitung zu Blatt 2, Analysis II SoSe 202 Funktionenfolgen, Potenzreihen I Die ins Netz gestellten Kopien der Anleitungsfolien sollen nur
K. Eppler, Inst. f. Num. Mathematik Übungsaufgaben. 3. Übung WS 17/18: Woche vom
 Übungsaufgaben 3. Übung WS 17/18: Woche vom 3. 10. - 7. 10. 017 Fourierreihen: 16. b,c,e,o), 16.3 a, b), 16.4 a) auch reelle Fourierreihe) Klausureinsicht zu Mathematik II 11.8. 017): 30.10.17, 7.00-8.30
Übungsaufgaben 3. Übung WS 17/18: Woche vom 3. 10. - 7. 10. 017 Fourierreihen: 16. b,c,e,o), 16.3 a, b), 16.4 a) auch reelle Fourierreihe) Klausureinsicht zu Mathematik II 11.8. 017): 30.10.17, 7.00-8.30
Funktionenfolgen, Potenzreihen, Exponentialfunktion
 Kapitel 8 Funktionenfolgen, Potenzreihen, Exponentialfunktion Der in Definition 7. eingeführte Begriff einer Folge ist nicht auf die Betrachtung reeller Zahlen eingeschränkt und das Beispiel {a n } = {x
Kapitel 8 Funktionenfolgen, Potenzreihen, Exponentialfunktion Der in Definition 7. eingeführte Begriff einer Folge ist nicht auf die Betrachtung reeller Zahlen eingeschränkt und das Beispiel {a n } = {x
Übungsklausur Höhere Mathematik I für die Fachrichtung Physik
 Karlsruher Institut für Technologie (KIT) Institut für Analysis Prof. Dr. Tobias Lamm Dr. Patrick Breuning WS /3 6..3 Übungsklausur Höhere Mathematik I für die Fachrichtung Physik Aufgabe ((3++5) Punkte)
Karlsruher Institut für Technologie (KIT) Institut für Analysis Prof. Dr. Tobias Lamm Dr. Patrick Breuning WS /3 6..3 Übungsklausur Höhere Mathematik I für die Fachrichtung Physik Aufgabe ((3++5) Punkte)
Analysis I. Guofang Wang Universität Freiburg
 Universität Freiburg 31.1.2017 Definition 2.2 (uneigentliches Riemann-Integral) Sei I = [a, b) mit a < b. Die Funktion f : I R sei Riemann-integrierbar auf [a, b ] für alle b < b. Falls x lim x b a f(ξ)
Universität Freiburg 31.1.2017 Definition 2.2 (uneigentliches Riemann-Integral) Sei I = [a, b) mit a < b. Die Funktion f : I R sei Riemann-integrierbar auf [a, b ] für alle b < b. Falls x lim x b a f(ξ)
3. Potenzreihen. Definition 7.5. Eine unendliche Reihe der Form. a k x k. Es handelt sich also um eine Funktionenreihe mit f k (x) = a k x k.
 3. Potenzreihen Definition 7.5. Eine unendliche Reihe der Form a x mit x R (veranderlich und a R (onstant heit Potenzreihe, die Zahlen a ( heien Koezienten der Potenzreihe. Es handelt sich also um eine
3. Potenzreihen Definition 7.5. Eine unendliche Reihe der Form a x mit x R (veranderlich und a R (onstant heit Potenzreihe, die Zahlen a ( heien Koezienten der Potenzreihe. Es handelt sich also um eine
Ferienkurs Analysis 1, SoSe Unendliche Reihen. Florian Beye August 15, 2008
 Ferienkurs Analysis 1, SoSe 2008 Unendliche Reihen Florian Beye August 15, 2008 1 Reihen und deren Konvergenz Definition 1.1. Eine reelle bzw. komplexe Reihe ist eine unendliche Summe über die Glieder
Ferienkurs Analysis 1, SoSe 2008 Unendliche Reihen Florian Beye August 15, 2008 1 Reihen und deren Konvergenz Definition 1.1. Eine reelle bzw. komplexe Reihe ist eine unendliche Summe über die Glieder
Folgen und Reihen von Funktionen
 Folgen und Reihen von Funktionen Sehr häufig treten in der Mathematik Folgen bzw. Reihen von Funktionen auf. Ist etwa (f n ) eine Folge von Funktionen, dann können wir uns für ein festes x fragen, ob die
Folgen und Reihen von Funktionen Sehr häufig treten in der Mathematik Folgen bzw. Reihen von Funktionen auf. Ist etwa (f n ) eine Folge von Funktionen, dann können wir uns für ein festes x fragen, ob die
Karteikarten, Analysis 2, Sätze und Definitionen nach der Vorlesung von PD Hanke
 Karteikarten, Analysis 2, Sätze und en nach der Vorlesung von PD Hanke Felix Müller, felix.b.mueller@physik.lmu.de Diese Karteikärtchen sollten alle en und Sätze der Vorlesung Analysis 2 bei Herrn PD Hanke
Karteikarten, Analysis 2, Sätze und en nach der Vorlesung von PD Hanke Felix Müller, felix.b.mueller@physik.lmu.de Diese Karteikärtchen sollten alle en und Sätze der Vorlesung Analysis 2 bei Herrn PD Hanke
Vorlesung Mathematik 2 für Ingenieure (Sommersemester 2016)
 1 Vorlesung Mathematik 2 für Ingenieure (Sommersemester 216) Kapitel 11: Potenzreihen und Fourier-Reihen Prof. Miles Simon Nach Folienvorlage von Prof. Dr. Volker Kaibel Otto-von-Guericke Universität Magdeburg.
1 Vorlesung Mathematik 2 für Ingenieure (Sommersemester 216) Kapitel 11: Potenzreihen und Fourier-Reihen Prof. Miles Simon Nach Folienvorlage von Prof. Dr. Volker Kaibel Otto-von-Guericke Universität Magdeburg.
Approximation von Funktionen
 von Funktionen Fakultät Grundlagen Februar 6 Fakultät Grundlagen von Funktionen Übersicht Problemstellung Taylorpolynom Taylorenreihe Zusammenhang von e-funktion und trigonometrischen Funktionen 3 Fakultät
von Funktionen Fakultät Grundlagen Februar 6 Fakultät Grundlagen von Funktionen Übersicht Problemstellung Taylorpolynom Taylorenreihe Zusammenhang von e-funktion und trigonometrischen Funktionen 3 Fakultät
10 Aus der Analysis. Themen: Konvergenz von Zahlenfolgen Unendliche Reihen Stetigkeit Differenzierbarkeit
 10 Aus der Analysis Themen: Konvergenz von Zahlenfolgen Unendliche Reihen Stetigkeit Differenzierbarkeit Zahlenfolgen Ein unendliche Folge reeller Zahlen heißt Zahlenfolge. Im Beispiel 2, 3, 2, 2 2, 2
10 Aus der Analysis Themen: Konvergenz von Zahlenfolgen Unendliche Reihen Stetigkeit Differenzierbarkeit Zahlenfolgen Ein unendliche Folge reeller Zahlen heißt Zahlenfolge. Im Beispiel 2, 3, 2, 2 2, 2
Folgen. Eine (unendliche) (Zahlen)folge ist eine Abbildung. dann als. notiert, und das wird abgekürzt mit. nennt man die Folgenglieder.
 Folgen Eine (unendliche) (Zahlen)folge ist eine Abbildung Statt dann als schreibt man auch oder ähnlich, die Folge wird notiert, und das wird abgekürzt mit. Die nennt man die Folgenglieder. Mathematik
Folgen Eine (unendliche) (Zahlen)folge ist eine Abbildung Statt dann als schreibt man auch oder ähnlich, die Folge wird notiert, und das wird abgekürzt mit. Die nennt man die Folgenglieder. Mathematik
Einführung in die Fourier-Reihen. 1 Fourier-Reihen: Definitionen
 Vortrag zum Seminar zur Analysis, 05.07.2010 André Stollenwerk, Eva-Maria Seifert Die Fourieranalysis beschäftigt sich mit dem Problem, inwiefern sich Funktionen mittels Sinus und Cosinus, das heißt periodischen
Vortrag zum Seminar zur Analysis, 05.07.2010 André Stollenwerk, Eva-Maria Seifert Die Fourieranalysis beschäftigt sich mit dem Problem, inwiefern sich Funktionen mittels Sinus und Cosinus, das heißt periodischen
Aufgaben zur Analysis I aus dem Wiederholungskurs
 Prof. Dr. H. Garcke, Dr. H. Farshbaf-Shaker, D. Depner WS 8/9 Hilfskräfte: A. Weiß, W. Thumann 6.3.29 NWF I - Mathematik Universität Regensburg Aufgaben zur Analysis I aus dem Wiederholungskurs Die folgenden
Prof. Dr. H. Garcke, Dr. H. Farshbaf-Shaker, D. Depner WS 8/9 Hilfskräfte: A. Weiß, W. Thumann 6.3.29 NWF I - Mathematik Universität Regensburg Aufgaben zur Analysis I aus dem Wiederholungskurs Die folgenden
Fourier-Reihen. Definition. Eine auf R definierte Funktion f heißt periodisch mit der Periode T 0, wenn f(x + T ) = f(x) x R.
 Fourier-Reihen Sehr häufig in der Natur begegnen uns periodische Vorgänge, zb beim Lauf der Gestirne am Nachthimmel In der Physik sind Phänomene wie Schwingungen und Wechselströme periodischer Natur Zumeist
Fourier-Reihen Sehr häufig in der Natur begegnen uns periodische Vorgänge, zb beim Lauf der Gestirne am Nachthimmel In der Physik sind Phänomene wie Schwingungen und Wechselströme periodischer Natur Zumeist
Polynomiale Approximation. und. Taylor-Reihen
 Polynomiale Approximation und Taylor-Reihen Heute gehts um die Approximation von glatten (d.h. beliebig oft differenzierbaren) Funktionen f nicht nur durch Gerade (sprich Polynome vom Grade 1) und Polynome
Polynomiale Approximation und Taylor-Reihen Heute gehts um die Approximation von glatten (d.h. beliebig oft differenzierbaren) Funktionen f nicht nur durch Gerade (sprich Polynome vom Grade 1) und Polynome
Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13)
 1 Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13) Kapitel 5: Konvergenz Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 15. Dezember 2011) Folgen Eine Folge x 0, x 1,
1 Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13) Kapitel 5: Konvergenz Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 15. Dezember 2011) Folgen Eine Folge x 0, x 1,
Tutorium: Analysis und lineare Algebra. Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen
 Tutorium: Analysis und lineare Algebra Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Die Regeln von de l
Tutorium: Analysis und lineare Algebra Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Die Regeln von de l
Häufungspunkte und Satz von Bolzano und Weierstraß.
 Häufungspunkte und Satz von Bolzano und Weierstraß. Definition: Sei (a nk ) k N eine konvergente Teilfolge der Folge (a n ) n N.Dannwirdder Grenzwert der Teilfolge (a nk ) k N als Häufungspunkt der Folge
Häufungspunkte und Satz von Bolzano und Weierstraß. Definition: Sei (a nk ) k N eine konvergente Teilfolge der Folge (a n ) n N.Dannwirdder Grenzwert der Teilfolge (a nk ) k N als Häufungspunkt der Folge
Tutorium: Analysis und lineare Algebra
 Tutorium: Analysis und lineare Algebra Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Die Regeln von de l
Tutorium: Analysis und lineare Algebra Regeln von de l Hospital, Reihen, Funktionen mehrerer Variablen, komplexe Zahlen Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Die Regeln von de l
Brückenkurs Rechentechniken
 Brückenkurs Rechentechniken Dr. Jörg Horst Technische Universität Dortmund Fakultät für Mathematik SS 2014 1 Vollständige Induktion Vollständige Induktion 2 Funktionenfolgen Punktweise Konvergenz Gleichmäßige
Brückenkurs Rechentechniken Dr. Jörg Horst Technische Universität Dortmund Fakultät für Mathematik SS 2014 1 Vollständige Induktion Vollständige Induktion 2 Funktionenfolgen Punktweise Konvergenz Gleichmäßige
10 Differenzierbare Funktionen
 10 Differenzierbare Funktionen 10.1 Definition: Es sei S R, x 0 S Häufungspunkt von S. Eine Funktion f : S R heißt im Punkt x 0 differenzierbar, wenn der Grenzwert f (x 0 ) := f(x 0 + h) f(x 0 ) lim h
10 Differenzierbare Funktionen 10.1 Definition: Es sei S R, x 0 S Häufungspunkt von S. Eine Funktion f : S R heißt im Punkt x 0 differenzierbar, wenn der Grenzwert f (x 0 ) := f(x 0 + h) f(x 0 ) lim h
Orthogonalität von Kosinus und Sinus
 Orthogonalität von Kosinus und Sinus Die Funktionen 1, cos(kx), sin(kx), k >, bilden ein Orthogonalsystem im Raum der quadratintegrierbaren π-periodischen Funktionen: cos(jx) cos(kx) dx = cos(jx) sin(lx)
Orthogonalität von Kosinus und Sinus Die Funktionen 1, cos(kx), sin(kx), k >, bilden ein Orthogonalsystem im Raum der quadratintegrierbaren π-periodischen Funktionen: cos(jx) cos(kx) dx = cos(jx) sin(lx)
Mathematik I Herbstsemester 2018 Kapitel 6: Potenzreihen
 Mathematik I Herbstsemester 208 Kapitel 6: Potenzreihen Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas / 58 6. Potenzreihen Reihen (Zahlenreihen) Konvergenzkriterien für Reihen Notwendiges
Mathematik I Herbstsemester 208 Kapitel 6: Potenzreihen Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas / 58 6. Potenzreihen Reihen (Zahlenreihen) Konvergenzkriterien für Reihen Notwendiges
REIHEN. 1. Definition und Konvergenz. Definition (unendliche) Reihe
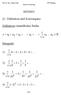 REIHEN 1. Definition und Konvergenz Definition (unendliche) Reihe 1 2 3, s = a + a + a + + a + = a a Beispiele 1) = 1+ 2+ 3+ 4 +... 2) 1 1 1 = 1 + + +... 2 3 3) 1 1 1 1 = 1 + + + +... 10 2 3 10 10 10 4)
REIHEN 1. Definition und Konvergenz Definition (unendliche) Reihe 1 2 3, s = a + a + a + + a + = a a Beispiele 1) = 1+ 2+ 3+ 4 +... 2) 1 1 1 = 1 + + +... 2 3 3) 1 1 1 1 = 1 + + + +... 10 2 3 10 10 10 4)
a 0 +a 1 x+a 2 x n=0 a n x n := lim
 1 Taylor-Entwicklung 1.1 Potenzreihen Def.: Ein Ausdruck der Form a 0 +a 1 +a +... a n n := lim k k a n n, (1) mit einer (unendlichen) Folge reeller Konstanten a 0,a 1,a,... ( Koeffizienten ) und einer
1 Taylor-Entwicklung 1.1 Potenzreihen Def.: Ein Ausdruck der Form a 0 +a 1 +a +... a n n := lim k k a n n, (1) mit einer (unendlichen) Folge reeller Konstanten a 0,a 1,a,... ( Koeffizienten ) und einer
Ferienkurs Analysis 1 - Wintersemester 2014/15. 1 Aussage, Mengen, Induktion, Quantoren
 Ferienkurs Analysis 1 - Wintersemester 2014/15 Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis
Ferienkurs Analysis 1 - Wintersemester 2014/15 Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis
11 Fourier-Analysis Grundlegende Begriffe
 11 Fourier-Analysis 11.1 Grundlegende Begriffe Definition: Eine Funktion f : R R (oder f : R C) heißt periodisch mit der Periode T (oder T-periodisch), falls f(t + T) = f(t) für alle t R. Ziel: Entwicklung
11 Fourier-Analysis 11.1 Grundlegende Begriffe Definition: Eine Funktion f : R R (oder f : R C) heißt periodisch mit der Periode T (oder T-periodisch), falls f(t + T) = f(t) für alle t R. Ziel: Entwicklung
HM I Tutorium 6. Lucas Kunz. 28. November 2018
 HM I Tutorium 6 Lucas Kunz 28. November 208 Inhaltsverzeichnis Theorie 2. Exponentialfunktion.............................. 2.2 Trigonometrische Funktionen......................... 2.3 Potenzreihen...................................
HM I Tutorium 6 Lucas Kunz 28. November 208 Inhaltsverzeichnis Theorie 2. Exponentialfunktion.............................. 2.2 Trigonometrische Funktionen......................... 2.3 Potenzreihen...................................
SPEZIELLE KAPITEL DER MATHEMATIK TEIL 1
 Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik SPEZIELLE KAPITEL DER MATHEMATIK TEIL 1 13. Fourier-Reihen Prof. Dr. Gunar Matthies Wintersemester 216/17
Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik SPEZIELLE KAPITEL DER MATHEMATIK TEIL 1 13. Fourier-Reihen Prof. Dr. Gunar Matthies Wintersemester 216/17
10. Periodische Funktionen, Fourier Reihen
 H.J. Oberle Analysis II SoSe 212 1. Periodische Funktionen, Fourier Reihen Jean Baptiste Joseph Fourier: Joseph Fourier wurde am 21.3.1768 bei Auxerre (Burgund) geboren und starb am 16.5.183 in Paris.
H.J. Oberle Analysis II SoSe 212 1. Periodische Funktionen, Fourier Reihen Jean Baptiste Joseph Fourier: Joseph Fourier wurde am 21.3.1768 bei Auxerre (Burgund) geboren und starb am 16.5.183 in Paris.
20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen
 20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
Aufgabe 1. Multiple Choice (4 Punkte). Kreuzen Sie die richtige(n) Antwort(en) an.
 Analysis I, WiSe 2013/14, 04.02.2014 (Iske), Version A 1 Aufgabe 1. Multiple Choice (4 Punkte). Kreuzen Sie die richtige(n) Antwort(en) an. a) Welche der folgenden Aussagen über Folgen sind sinnvoll und
Analysis I, WiSe 2013/14, 04.02.2014 (Iske), Version A 1 Aufgabe 1. Multiple Choice (4 Punkte). Kreuzen Sie die richtige(n) Antwort(en) an. a) Welche der folgenden Aussagen über Folgen sind sinnvoll und
Analysis I. 6. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 6. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine Relation zwischen den Mengen X und Y.
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 6. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Eine Relation zwischen den Mengen X und Y.
1 Einleitung. 2 Reelle Zahlen. 3 Konvergenz von Folgen
 1 Einleitung Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis 1 aus dem Wintersemester 2008/09
1 Einleitung Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis 1 aus dem Wintersemester 2008/09
Folgen, Reihen, Grenzwerte u. Stetigkeit
 Folgen, Reihen, Grenzwerte u. Stetigkeit Josef F. Bürgler Abt. Informatik HTA Luzern, FH Zentralschweiz HTA.MA+INF Josef F. Bürgler (HTA Luzern) Einf. Infinitesimalrechnung HTA.MA+INF 1 / 33 Inhalt 1 Folgen
Folgen, Reihen, Grenzwerte u. Stetigkeit Josef F. Bürgler Abt. Informatik HTA Luzern, FH Zentralschweiz HTA.MA+INF Josef F. Bürgler (HTA Luzern) Einf. Infinitesimalrechnung HTA.MA+INF 1 / 33 Inhalt 1 Folgen
D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger. Lösung - Serie 13. es kann keine allgemein gültige Aussage getroffen werden.
 D-MAVT/D-MATL Analysis I HS 07 Dr. Andreas Steiger Lösung - Serie 3 MC-Aufgaben (Online-Abgabe). Wenn man zwei beliebig oft differenzierbare Funktionen addiert, dann werden ihre Taylorreihen an einem Punkt
D-MAVT/D-MATL Analysis I HS 07 Dr. Andreas Steiger Lösung - Serie 3 MC-Aufgaben (Online-Abgabe). Wenn man zwei beliebig oft differenzierbare Funktionen addiert, dann werden ihre Taylorreihen an einem Punkt
Periodische Funktionen, Fourier Reihen
 Kapitel 1: Periodische Funktionen, Fourier Reihen 1.1 Grundlegende Begriffe Periodische Funktionen Definition: Eine Funktion f : R R oder f : R C) heißt periodisch mit der Periode T, falls für alle t R
Kapitel 1: Periodische Funktionen, Fourier Reihen 1.1 Grundlegende Begriffe Periodische Funktionen Definition: Eine Funktion f : R R oder f : R C) heißt periodisch mit der Periode T, falls für alle t R
Ferienkurs Analysis 1
 Skript Ferienkurs Analysis 1 Fabian Hafner und Thomas Baldauf TUM Wintersemester 2016/17 04.04.2017 Das Skript wurde teilweise übernommen vom Skript des Ferienkurses WS 2014, verfasst von Andreas Wörfel.
Skript Ferienkurs Analysis 1 Fabian Hafner und Thomas Baldauf TUM Wintersemester 2016/17 04.04.2017 Das Skript wurde teilweise übernommen vom Skript des Ferienkurses WS 2014, verfasst von Andreas Wörfel.
sign: R R, sign(x) := 0 falls x = 0 1 falls x < 0 Diese ist im Punkt x 0 = 0 nicht stetig, denn etwa zu ε = 1 finden wir kein δ > 0
 ANALYSIS FÜR PHYSIK UND VERWANDTE FÄCHER I 81 3. Stetigkeit 3.1. Stetigkeit. Im Folgenden sei D R eine beliebige nichtleere Teilmenge. Typischerweise wird D ein allgemeines Intervall sein, siehe Abschnitt
ANALYSIS FÜR PHYSIK UND VERWANDTE FÄCHER I 81 3. Stetigkeit 3.1. Stetigkeit. Im Folgenden sei D R eine beliebige nichtleere Teilmenge. Typischerweise wird D ein allgemeines Intervall sein, siehe Abschnitt
Kapitel 3. Reihen und ihre Konvergenz
 Kapitel 3 Reihen und ihre Konvergenz Abschnitt 3.1 Der Reihenbegri und erste Beispiele Denitionen zu Reihen, 1 Denition. Sei (a n ) n N0 eine Folge reeller Zahlen. Für n N 0 heiÿt dann die Zahl s n :=
Kapitel 3 Reihen und ihre Konvergenz Abschnitt 3.1 Der Reihenbegri und erste Beispiele Denitionen zu Reihen, 1 Denition. Sei (a n ) n N0 eine Folge reeller Zahlen. Für n N 0 heiÿt dann die Zahl s n :=
Leitfaden a tx t
 Leitfaden -0.7. Potenz-Reihen. Definition: Es sei (a 0, a, a 2,...) eine Folge reeller Zahlen (wir beginnen hier mit dem Index t 0). Ist x R, so kann man die Folge (a 0, a x, a 2 x 2, a 3 x 3,...) und
Leitfaden -0.7. Potenz-Reihen. Definition: Es sei (a 0, a, a 2,...) eine Folge reeller Zahlen (wir beginnen hier mit dem Index t 0). Ist x R, so kann man die Folge (a 0, a x, a 2 x 2, a 3 x 3,...) und
Höhere Mathematik für Physiker II
 Universität Heidelberg Sommersemester 2013 Wiederholungsblatt Übungen zur Vorlesung Höhere Mathematik für Physiker II Prof Dr Anna Marciniak-Czochra Dipl Math Alexandra Köthe Fragen Machen Sie sich bei
Universität Heidelberg Sommersemester 2013 Wiederholungsblatt Übungen zur Vorlesung Höhere Mathematik für Physiker II Prof Dr Anna Marciniak-Czochra Dipl Math Alexandra Köthe Fragen Machen Sie sich bei
6 Fourierreihen und die Fouriertransformation
 Mathematik für Physiker IV, SS 13 Mittwoch 9.5 $Id: fourier.tex,v 1.4 13/5/31 16:8:3 hk Exp hk $ 6 Fourierreihen und die Fouriertransformation 6.1 Die Fourierreihe einer integrierbaren Funktion Am Ende
Mathematik für Physiker IV, SS 13 Mittwoch 9.5 $Id: fourier.tex,v 1.4 13/5/31 16:8:3 hk Exp hk $ 6 Fourierreihen und die Fouriertransformation 6.1 Die Fourierreihe einer integrierbaren Funktion Am Ende
Übungen zu Analysis, SS 2015
 Übungen zu Analysis, SS 215 Ulisse Stefanelli 15. Juni 215 1 Wiederholung 1. Untersuchen Sie das Verhalten der folgenden Folgen a n = n 2 cosh(1/n), b n = ln(ln(n))/n, c n = (2 n n 2 )/n!, 2. Stellen Sie
Übungen zu Analysis, SS 215 Ulisse Stefanelli 15. Juni 215 1 Wiederholung 1. Untersuchen Sie das Verhalten der folgenden Folgen a n = n 2 cosh(1/n), b n = ln(ln(n))/n, c n = (2 n n 2 )/n!, 2. Stellen Sie
3 Folgen, Reihen, Grenzwerte 3.1 Zahlenfolgen Definition: Eine Folge ist eine geordnete Menge von Elementen an (den sogenannten Gliedern ), die
 3 Folgen, Reihen, Grenzwerte 3.1 Zahlenfolgen Definition: Eine Folge ist eine geordnete Menge von Elementen an (den sogenannten Gliedern ), die eindeutig den natürlichen Zahlen zugeordnet sind ( n N, auch
3 Folgen, Reihen, Grenzwerte 3.1 Zahlenfolgen Definition: Eine Folge ist eine geordnete Menge von Elementen an (den sogenannten Gliedern ), die eindeutig den natürlichen Zahlen zugeordnet sind ( n N, auch
Freie Universität Berlin Wintersemester 11/12 Fachbereich Mathematik und Informatik Institut für Mathematik Dr. A. Linke
 Freie Universität Berlin Wintersemester / Fachbereich Mathematik und Informatik Institut für Mathematik Dr. A. Linke Musterlösung zum. Übungsblatt zur Vorlesung Mathematik für Physiker I Differenzierbarkeit,
Freie Universität Berlin Wintersemester / Fachbereich Mathematik und Informatik Institut für Mathematik Dr. A. Linke Musterlösung zum. Übungsblatt zur Vorlesung Mathematik für Physiker I Differenzierbarkeit,
Mathematik für Physiker, Informatiker und Ingenieure
 Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Lösungen der Aufgaben zu Kapitel 9
 Lösungen der Aufgaben zu Kapitel 9 Abschnitt 9. Aufgabe a) Wir bestimmen die ersten Ableitungen von f, die uns dann das Aussehen der k-ten Ableitung erkennen lassen: fx) = x + e x xe x, f x) = e x e x
Lösungen der Aufgaben zu Kapitel 9 Abschnitt 9. Aufgabe a) Wir bestimmen die ersten Ableitungen von f, die uns dann das Aussehen der k-ten Ableitung erkennen lassen: fx) = x + e x xe x, f x) = e x e x
Reihen, Exponentialfunktion Vorlesung
 Reihen, Exponentialfunktion Vorlesung Marcus Jung 5.03.20 Inhaltsverzeichnis Inhaltsverzeichnis Reihen 3. Denition.................................... 3.2 Konvergenzkriterien für Reihen........................
Reihen, Exponentialfunktion Vorlesung Marcus Jung 5.03.20 Inhaltsverzeichnis Inhaltsverzeichnis Reihen 3. Denition.................................... 3.2 Konvergenzkriterien für Reihen........................
hhhhh 8 ( x)/2, <x 0, ( x)/2, 0 <x, , ] hinaus. Diese Funktion ist ungerade, ihre Fourierreihe also eine reine Sinusreihe. Man findet 1 cos nx dx.
![hhhhh 8 ( x)/2, <x 0, ( x)/2, 0 <x, , ] hinaus. Diese Funktion ist ungerade, ihre Fourierreihe also eine reine Sinusreihe. Man findet 1 cos nx dx. hhhhh 8 ( x)/2, <x 0, ( x)/2, 0 <x, , ] hinaus. Diese Funktion ist ungerade, ihre Fourierreihe also eine reine Sinusreihe. Man findet 1 cos nx dx.](/thumbs/68/58579114.jpg) 86 5 Fouriertheorie Für gerades f ist f (x) sin nx ungerade, somit b n = f (x) sin nx dx =. Für ungerades f ist dagegen f cos nx ungerade, also a n = f (x) cos nx dx =..Ò Beispiel Die Sägezahnfunktion
86 5 Fouriertheorie Für gerades f ist f (x) sin nx ungerade, somit b n = f (x) sin nx dx =. Für ungerades f ist dagegen f cos nx ungerade, also a n = f (x) cos nx dx =..Ò Beispiel Die Sägezahnfunktion
Höhere Mathematik für die Fachrichtung Physik
 Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Dipl.-Math. Sebastian Schwarz Höhere Mathematik für die Fachrichtung Physik Lösungsvorschläge zum 6. Übungsblatt Aufgabe
Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Dipl.-Math. Sebastian Schwarz Höhere Mathematik für die Fachrichtung Physik Lösungsvorschläge zum 6. Übungsblatt Aufgabe
Potenzreihen. Potenzreihen sind Funktionenreihen mit einer besonderen Gestalt.
 Potenzreihen Potenzreihen sind Funtionenreihen mit einer besonderen Gestalt Definition Ist (a ) eine Folge reeller (bzw omplexer) Zahlen und x 0 R (bzw z 0 C), dann heißt die Reihe a (x x 0 ) (bzw a (z
Potenzreihen Potenzreihen sind Funtionenreihen mit einer besonderen Gestalt Definition Ist (a ) eine Folge reeller (bzw omplexer) Zahlen und x 0 R (bzw z 0 C), dann heißt die Reihe a (x x 0 ) (bzw a (z
Analysis für Informatiker und Statistiker Nachklausur
 Prof. Dr. Peter Otte Wintersemester 213/14 Tom Bachmann, Sebastian Gottwald 14.3.214 Analysis für Informatiker und Statistiker Nachklausur Lösungsvorschlag Name:.......................................................
Prof. Dr. Peter Otte Wintersemester 213/14 Tom Bachmann, Sebastian Gottwald 14.3.214 Analysis für Informatiker und Statistiker Nachklausur Lösungsvorschlag Name:.......................................................
Folgen, Reihen, Potenzreihen, Exponentialfunktion
 Ferienkurs Seite 1 Technische Universität München Ferienkurs Analysis 1 Hannah Schamoni Wintersemester 2011/12 Folgen, Reihen, Potenzreihen, Exponentialfunktion 20.03.2012 Inhaltsverzeichnis 1 Folgen 2
Ferienkurs Seite 1 Technische Universität München Ferienkurs Analysis 1 Hannah Schamoni Wintersemester 2011/12 Folgen, Reihen, Potenzreihen, Exponentialfunktion 20.03.2012 Inhaltsverzeichnis 1 Folgen 2
Mathematik III. (für Informatiker) Oliver Ernst. Wintersemester 2014/15. Professur Numerische Mathematik
 Mathematik III (für Informatiker) Oliver Ernst Professur Numerische Mathematik Wintersemester 2014/15 Inhalt 10 Differentialgleichungen 11 Potenz- und Fourier-Reihen Oliver Ernst (Numerische Mathematik)
Mathematik III (für Informatiker) Oliver Ernst Professur Numerische Mathematik Wintersemester 2014/15 Inhalt 10 Differentialgleichungen 11 Potenz- und Fourier-Reihen Oliver Ernst (Numerische Mathematik)
Musterlösungen zu Blatt 15, Analysis I
 Musterlösungen zu Blatt 5, Analysis I WS 3/4 Inhaltsverzeichnis Aufgabe 85: Konvergenzradien Aufgabe 86: Approimation von ep() durch Polynome Aufgabe 87: Taylorreihen von cos 3 und sin Aufgabe 88: Differenzenquotienten
Musterlösungen zu Blatt 5, Analysis I WS 3/4 Inhaltsverzeichnis Aufgabe 85: Konvergenzradien Aufgabe 86: Approimation von ep() durch Polynome Aufgabe 87: Taylorreihen von cos 3 und sin Aufgabe 88: Differenzenquotienten
Die Taylorreihe einer Funktion
 Kapitel 6 Die Taylorreihe einer Funktion Dieser Abschnitt beschäftigt sich mit Taylorreihen, Taylorpolynomen und der Restgliedabschätzung für Taylorpolynome. Die Taylorreihe einer reellen Funktion ist
Kapitel 6 Die Taylorreihe einer Funktion Dieser Abschnitt beschäftigt sich mit Taylorreihen, Taylorpolynomen und der Restgliedabschätzung für Taylorpolynome. Die Taylorreihe einer reellen Funktion ist
Ferienkurs der TU München- - Analysis 2 Fourierreihen und Taylorreihen. Marcus Jung, Jonas J. Funke
 Ferienkurs der U München- - Analysis Fourierreihen und aylorreihen Lösung Marcus Jung, Jonas J. Funke 3.8. FOURIERREIHEN Fourierreihen Aufgabe. Sei f : R R stetig und periodisch mit Fourierkoeffizienten
Ferienkurs der U München- - Analysis Fourierreihen und aylorreihen Lösung Marcus Jung, Jonas J. Funke 3.8. FOURIERREIHEN Fourierreihen Aufgabe. Sei f : R R stetig und periodisch mit Fourierkoeffizienten
Der Satz von Taylor. Kapitel 7
 Kapitel 7 Der Satz von Taylor Wir haben bereits die Darstellung verschiedener Funktionen, wie der Exponentialfunktion, der Cosinus- oder Sinus-Funktion, durch unendliche Reihen kennen gelernt. In diesem
Kapitel 7 Der Satz von Taylor Wir haben bereits die Darstellung verschiedener Funktionen, wie der Exponentialfunktion, der Cosinus- oder Sinus-Funktion, durch unendliche Reihen kennen gelernt. In diesem
Lösungsvorschlag zur Übungsklausur zur Analysis I
 Prof. Dr. H. Garcke, Dr. H. Farshbaf-Shaker, D. Depner WS 8/9 NWF I - Mathematik 9..9 Universität Regensburg Lösungsvorschlag zur Übungsklausur zur Analysis I Frage 1 Vervollständigen Sie die folgenden
Prof. Dr. H. Garcke, Dr. H. Farshbaf-Shaker, D. Depner WS 8/9 NWF I - Mathematik 9..9 Universität Regensburg Lösungsvorschlag zur Übungsklausur zur Analysis I Frage 1 Vervollständigen Sie die folgenden
Fourierreihen. Definition. Eine Funktion f(x) heißt periodisch mit der Periode T, wenn f(x + T ) = f(x)
 Fourierreihen Einer auf dem Intervall [, ] definierten Funtion f(x) ann ein (approximierendes) trigonometrisches Polynom (Fourier-Polynom) der Gestalt S n (x) = a + n a cos x + n b sin x zugeordnet werden.
Fourierreihen Einer auf dem Intervall [, ] definierten Funtion f(x) ann ein (approximierendes) trigonometrisches Polynom (Fourier-Polynom) der Gestalt S n (x) = a + n a cos x + n b sin x zugeordnet werden.
Höhere Mathematik II. (Vorlesungskript)
 Fakultät für Luft- und Raumfahrttechnik Institut für Mathematik und Rechneranwendung Universität der Bundeswehr München Höhere Mathematik II (Vorlesungskript) Univ. Prof. Dr. sc. math. Kurt Marti 2 2 L
Fakultät für Luft- und Raumfahrttechnik Institut für Mathematik und Rechneranwendung Universität der Bundeswehr München Höhere Mathematik II (Vorlesungskript) Univ. Prof. Dr. sc. math. Kurt Marti 2 2 L
P n (1) P j (1) + ε 2, j=0. P(1) P j (1) + ε 2 < ε. log(1+x) =
 Zu ε > 0 gibt es ein N N mit P n (1) P j (1) < ε/2 für j,n > N, also gilt Es folgt (1 x) n 1 j=n+1 und schließlich mit n x j P n (1) P j (1) (1 x) ε 2 P n (1) P n (x) (1 x) P(1) P(x) (1 x) für x hinreichend
Zu ε > 0 gibt es ein N N mit P n (1) P j (1) < ε/2 für j,n > N, also gilt Es folgt (1 x) n 1 j=n+1 und schließlich mit n x j P n (1) P j (1) (1 x) ε 2 P n (1) P n (x) (1 x) P(1) P(x) (1 x) für x hinreichend
1 Reihen von Zahlen. Inhalt:
 5 Kapitel 3 Reihen Reihen von Zahlen Inhalt: Konvergenz und Divergenz von Reihen reeller oder komplexer Zahlen, geometrische Reihe, harmonische Reihe, alternierende Reihen. Cauchy-Kriterium, absolute Konvergenz,
5 Kapitel 3 Reihen Reihen von Zahlen Inhalt: Konvergenz und Divergenz von Reihen reeller oder komplexer Zahlen, geometrische Reihe, harmonische Reihe, alternierende Reihen. Cauchy-Kriterium, absolute Konvergenz,
Funktionsgrenzwerte, Stetigkeit
 Funktionsgrenzwerte, Stetigkeit Häufig tauchen in der Mathematik Ausdrücke der Form lim f(x) auf. x x0 Derartigen Ausdrücken wollen wir jetzt eine präzise Bedeutung zuweisen. Definition. b = lim f(x) wenn
Funktionsgrenzwerte, Stetigkeit Häufig tauchen in der Mathematik Ausdrücke der Form lim f(x) auf. x x0 Derartigen Ausdrücken wollen wir jetzt eine präzise Bedeutung zuweisen. Definition. b = lim f(x) wenn
ANALYSIS I FÜR TPH WS 2018/19 3. Übung Übersicht
 ANALYSIS I FÜR TPH WS 208/9 3. Übung Übersicht Aufgaben zu Kapitel 5 und 6 Aufgabe : Konvergenz von Reihen (i) Aufgabe 2: Konvergenz von Reihen (ii) Aufgabe 3: ( ) Konvergenz von Reihen (iii) Aufgabe 4:
ANALYSIS I FÜR TPH WS 208/9 3. Übung Übersicht Aufgaben zu Kapitel 5 und 6 Aufgabe : Konvergenz von Reihen (i) Aufgabe 2: Konvergenz von Reihen (ii) Aufgabe 3: ( ) Konvergenz von Reihen (iii) Aufgabe 4:
n=1 a n mit reellen Zahlen a n einen
 4 Unendliche Reihen 4. Definition und Beispiele Ein altes Problem der Analysis ist es, einer Reihe mit reellen Zahlen einen Wert zuzuordnen. Ein typisches Beispiel ist die unendliche Reihe + +..., die
4 Unendliche Reihen 4. Definition und Beispiele Ein altes Problem der Analysis ist es, einer Reihe mit reellen Zahlen einen Wert zuzuordnen. Ein typisches Beispiel ist die unendliche Reihe + +..., die
Analysis I. 3. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 3. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine Abbildung F von einer Menge L in eine
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 3. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine Abbildung F von einer Menge L in eine
2.3 Konvergenzverhalten von Fourierreihen
 24 2 Fourierreihen 2.3 Konvergenzverhalten von Fourierreihen Wir diskutieren die folgenden Fragen: Unter welchen Umständen konvergiert eine Fourierreihe einer Funktion? Wann kann man eine stückweise stetige
24 2 Fourierreihen 2.3 Konvergenzverhalten von Fourierreihen Wir diskutieren die folgenden Fragen: Unter welchen Umständen konvergiert eine Fourierreihe einer Funktion? Wann kann man eine stückweise stetige
Tangente als Näherung
 Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 1 Tangente als Näherung Weil sich anschaulich die Tangente anschmiegt, ist die Tangentenfunktion p 1 (x) eine Näherung für f(x): f(x) p 1 (x)
Mathematik I für Informatiker Satz von Taylor Taylorreihen p. 1 Tangente als Näherung Weil sich anschaulich die Tangente anschmiegt, ist die Tangentenfunktion p 1 (x) eine Näherung für f(x): f(x) p 1 (x)
ETH Zürich Analysis I Zwischenprüfung Winter 2014 D-BAUG Musterlösungen Dr. Meike Akveld
 ETH Zürich Analysis I Zwischenprüfung Winter 2014 D-BAUG Musterlösungen Dr. Meike Akveld Bitte wenden! 1. Die unten stehende Figur wird beschrieben durch... (a) { (x, y) R 2 x + y 1 }. Richtig! (b) { (x,
ETH Zürich Analysis I Zwischenprüfung Winter 2014 D-BAUG Musterlösungen Dr. Meike Akveld Bitte wenden! 1. Die unten stehende Figur wird beschrieben durch... (a) { (x, y) R 2 x + y 1 }. Richtig! (b) { (x,
Analysis I. Guofang Wang Universität Freiburg
 Universität Freiburg 22.11.2016 3. Mächtigkeit und die komplexe Zahlen Komplexe Zahlen Definition Die komplexe Zahlen sind definiert als C = R 2 = R R, mit (x 1, y 1 ) + (x 2, y 2 ) = (x 1 + x 2, y 1 +
Universität Freiburg 22.11.2016 3. Mächtigkeit und die komplexe Zahlen Komplexe Zahlen Definition Die komplexe Zahlen sind definiert als C = R 2 = R R, mit (x 1, y 1 ) + (x 2, y 2 ) = (x 1 + x 2, y 1 +
Stichpunkte zum Abschnitt Analysis der Höheren Mathematik für Ingenieure I
 Stichpunkte zum Abschnitt Analysis der Höheren Mathematik für Ingenieure I Komplexe Zahlen Definition komplexer Zahlen in der Gaußschen Zahlenebene, algebraische Form, trigonometrische Form, exponentielle
Stichpunkte zum Abschnitt Analysis der Höheren Mathematik für Ingenieure I Komplexe Zahlen Definition komplexer Zahlen in der Gaußschen Zahlenebene, algebraische Form, trigonometrische Form, exponentielle
VIII. Fourier - Reihen
 VIII. Fourier - Reihen Dieses Kapitel enthält eine kurze Einführung in die mathematische Beschreibung von Schwingungen. Übersicht über den Inhalt von Kapitel VIII: 5. Der Satz von Fejér 53. Die Parsevalsche
VIII. Fourier - Reihen Dieses Kapitel enthält eine kurze Einführung in die mathematische Beschreibung von Schwingungen. Übersicht über den Inhalt von Kapitel VIII: 5. Der Satz von Fejér 53. Die Parsevalsche
3 Folgen, Reihen und stetige Funktionen
 Höhere Mathematik 101 3 Folgen, Reihen und stetige Funktionen 3.1 Folgen und Reihen: Definitionen und Beispiele Eine reelle oder komplexe Zahlenfolge ist eine Abbildung, die jeder natürlichen Zahl n eine
Höhere Mathematik 101 3 Folgen, Reihen und stetige Funktionen 3.1 Folgen und Reihen: Definitionen und Beispiele Eine reelle oder komplexe Zahlenfolge ist eine Abbildung, die jeder natürlichen Zahl n eine
Mathematik I für Studierende der Geophysik/Ozeanographie, Meteorologie und Physik Vorlesungsskript
 Mathematik I für Studierende der Geophysik/Ozeanographie, Meteorologie und Physik Vorlesungsskript Janko Latschev Fachbereich Mathematik Universität Hamburg www.math.uni-hamburg.de/home/latschev Hamburg,
Mathematik I für Studierende der Geophysik/Ozeanographie, Meteorologie und Physik Vorlesungsskript Janko Latschev Fachbereich Mathematik Universität Hamburg www.math.uni-hamburg.de/home/latschev Hamburg,
2.12 Potenzreihen. 1. Definitionen. 2. Berechnung 2.12. POTENZREIHEN 207. Der wichtigste Spezialfall von Funktionenreihen sind Potenzreihen.
 2.2. POTENZREIHEN 207 2.2 Potenzreihen. Definitionen Der wichtigste Spezialfall von Funktionenreihen sind Potenzreihen. Eine Potenzreihe mit Entwicklungspunkt x 0 ist eine Reihe a n x x 0 n. Es gilt: es
2.2. POTENZREIHEN 207 2.2 Potenzreihen. Definitionen Der wichtigste Spezialfall von Funktionenreihen sind Potenzreihen. Eine Potenzreihe mit Entwicklungspunkt x 0 ist eine Reihe a n x x 0 n. Es gilt: es
ε δ Definition der Stetigkeit.
 ε δ Definition der Stetigkeit. Beweis a) b): Annahme: ε > 0 : δ > 0 : x δ D : x δ x 0 < δ f (x δ f (x 0 ) ε Die Wahl δ = 1 n (n N) generiert eine Folge (x n) n N, x n D mit x n x 0 < 1 n f (x n ) f (x
ε δ Definition der Stetigkeit. Beweis a) b): Annahme: ε > 0 : δ > 0 : x δ D : x δ x 0 < δ f (x δ f (x 0 ) ε Die Wahl δ = 1 n (n N) generiert eine Folge (x n) n N, x n D mit x n x 0 < 1 n f (x n ) f (x
Fourierreihen. Die erste dieser Aussagen folgt direkt aus der Definition. Für die zweite bemerken
 Fachbereich Mathematik SS 0 J. Latschev Analysis II Fourierreihen In diesem Kapitel der Vorlesung widmen wir uns der Frage, inwieweit man jede periodische Funktion als Reihe in gewissen Standardfunktionen
Fachbereich Mathematik SS 0 J. Latschev Analysis II Fourierreihen In diesem Kapitel der Vorlesung widmen wir uns der Frage, inwieweit man jede periodische Funktion als Reihe in gewissen Standardfunktionen
Nachklausur zur Analysis 1, WiSe 2016/17
 BERGISCHE UNIVERSITÄT WUPPERTAL 04.04.7 Fakultät 4 - Mathematik und Naturwissenschaften Prof. N. V. Shcherbina Dr. T. P. Pawlaschyk www.kana.uni-wuppertal.de Nachklausur zur Analysis, WiSe 06/7 Aufgabe
BERGISCHE UNIVERSITÄT WUPPERTAL 04.04.7 Fakultät 4 - Mathematik und Naturwissenschaften Prof. N. V. Shcherbina Dr. T. P. Pawlaschyk www.kana.uni-wuppertal.de Nachklausur zur Analysis, WiSe 06/7 Aufgabe
Folgen und Reihen. Bernhard Ganter. Institut für Algebra TU Dresden D Dresden
 Folgen und Reihen Bernhard Ganter Institut für Algebra TU Dresden D-0062 Dresden bernhard.ganter@tu-dresden.de Folgen Eine (unendliche) (Zahlen)folge ist eine Abbildung f : N R. Statt f (n) schreibt man
Folgen und Reihen Bernhard Ganter Institut für Algebra TU Dresden D-0062 Dresden bernhard.ganter@tu-dresden.de Folgen Eine (unendliche) (Zahlen)folge ist eine Abbildung f : N R. Statt f (n) schreibt man
Vorlesung: Analysis I für Ingenieure
 Vorlesung: Analysis I für Ingenieure Dozent: Dr. Michael Karow Thema: unendliche Reihen Definition. Eine unendliche Reihe ist der Grenzwert einer Folge von Summen: a k = lim k a k, wobei a k C. Falls der
Vorlesung: Analysis I für Ingenieure Dozent: Dr. Michael Karow Thema: unendliche Reihen Definition. Eine unendliche Reihe ist der Grenzwert einer Folge von Summen: a k = lim k a k, wobei a k C. Falls der
Konvergenz und Stetigkeit
 Mathematik I für Biologen, Geowissenschaftler und Geoökologen 10. Dezember 2012 Konvergenz Definition Fourierreihen Geometrische Reihe Definition: Eine Funktion f : D R d heißt beschränkt, wenn es ein
Mathematik I für Biologen, Geowissenschaftler und Geoökologen 10. Dezember 2012 Konvergenz Definition Fourierreihen Geometrische Reihe Definition: Eine Funktion f : D R d heißt beschränkt, wenn es ein
8. 2A. Integration von Potenzreihen
 8. 2A. Integration von Potenzreihen Wie wir schon mehrfach sahen, sind Potenzreihen ein unentbehrliches Werkzeug für viele Berechnungen in der Ingenieurmathematik. Glücklicherweise darf man Potenzreihen
8. 2A. Integration von Potenzreihen Wie wir schon mehrfach sahen, sind Potenzreihen ein unentbehrliches Werkzeug für viele Berechnungen in der Ingenieurmathematik. Glücklicherweise darf man Potenzreihen
Mathematik III für das MW: WS 15/16 + SS 16. Karsten Eppler Technische Universität Dresden Institut für Numerische Mathematik
 Mathematik III für das MW: WS 15/16 + SS 16 Karsten Eppler Technische Universität Dresden Institut für Numerische Mathematik karsten.eppler@tu-dresden.de http://www.math.tu-dresden.de/ eppler Vorlesungsassistent:
Mathematik III für das MW: WS 15/16 + SS 16 Karsten Eppler Technische Universität Dresden Institut für Numerische Mathematik karsten.eppler@tu-dresden.de http://www.math.tu-dresden.de/ eppler Vorlesungsassistent:
Man schreibt dann lim. = bzw. lim
 Die Funktion f : R R geht für x nach (bzw. ), fallses für allem R + ein t(ε) R + gibt, so dass gilt ist x > t(ε), dann folgt f(x) > M bzw. ist x > t(ε), dann folgt f(x) < M. Man schreibt dann lim x = bzw.
Die Funktion f : R R geht für x nach (bzw. ), fallses für allem R + ein t(ε) R + gibt, so dass gilt ist x > t(ε), dann folgt f(x) > M bzw. ist x > t(ε), dann folgt f(x) < M. Man schreibt dann lim x = bzw.
,...) ist eine Folge, deren Glieder der Null beliebig nahe kommen. (iii) Die Folge a n = ( 1) n + 1 n oder (a n) = (0, 3 2, 2 3, 5 4, 4 5
 3 Folgen 3.1 Definition und Beispiele Eine Abbildung a : Æ Ê heißt (reelle) Zahlenfolge. Statt a(n) schreiben wir kürzer a n und bezeichnen die ganze Folge mit (a n ) n Æ oder einfach (a n ), was aber
3 Folgen 3.1 Definition und Beispiele Eine Abbildung a : Æ Ê heißt (reelle) Zahlenfolge. Statt a(n) schreiben wir kürzer a n und bezeichnen die ganze Folge mit (a n ) n Æ oder einfach (a n ), was aber
April (Voll-) Klausur Analysis I für Ingenieure. Rechenteil
 April (Voll-) Klausur Analysis I für Ingenieure en Rechenteil Aufgabe 7 Punkte (a) Skizzieren Sie die 4-periodische Funktion mit f() = für und f() = für (b) Berechnen Sie für diese Funktion die Fourierkoeffizienten
April (Voll-) Klausur Analysis I für Ingenieure en Rechenteil Aufgabe 7 Punkte (a) Skizzieren Sie die 4-periodische Funktion mit f() = für und f() = für (b) Berechnen Sie für diese Funktion die Fourierkoeffizienten
Ferienkurs Seite 1. Technische Universität München Ferienkurs Analysis 1 Stetigkeit, Konvergenz, Topologie
 Ferienkurs Seite Technische Universität München Ferienkurs Analysis Hannah Schamoni Stetigkeit, Konvergenz, Topologie Lösung 2.03.202. Gleichmäßige Konvergenz Entscheiden Sie, ob die folgenden auf (0,
Ferienkurs Seite Technische Universität München Ferienkurs Analysis Hannah Schamoni Stetigkeit, Konvergenz, Topologie Lösung 2.03.202. Gleichmäßige Konvergenz Entscheiden Sie, ob die folgenden auf (0,
Übungen Analysis I WS 03/04
 Blatt Abgabe: Mittwoch, 29.0.03 Aufgabe : Beweisen Sie, daß für jede natürliche Zahl n gilt: n ( ) n (x + y) n = x i y n i, i (b) n ν 2 = ν= i=0 n(n + )(2n + ), 6 (c) 2 3n ist durch 7 teilbar. Aufgabe
Blatt Abgabe: Mittwoch, 29.0.03 Aufgabe : Beweisen Sie, daß für jede natürliche Zahl n gilt: n ( ) n (x + y) n = x i y n i, i (b) n ν 2 = ν= i=0 n(n + )(2n + ), 6 (c) 2 3n ist durch 7 teilbar. Aufgabe
Konvergenz im quadratischen Mittel - Hilberträume
 CONTENTS CONTENTS Konvergenz im quadratischen Mittel - Hilberträume Contents 1 Ziel 2 1.1 Satz........................................ 2 2 Endlich dimensionale Vektorräume 2 2.1 Defintion: Eigenschaften
CONTENTS CONTENTS Konvergenz im quadratischen Mittel - Hilberträume Contents 1 Ziel 2 1.1 Satz........................................ 2 2 Endlich dimensionale Vektorräume 2 2.1 Defintion: Eigenschaften
Kapitel C. Integrale und Grenzwerte
 Kapitel C Integrale und Grenzwerte Inhalt dieses Kapitels C000 1 Der Satz von Fubini 2 Der Transformationssatz 1 Vertauschen von Integral und eihe 2 Vertauschen von Integral und Limes 3 Vertauschen von
Kapitel C Integrale und Grenzwerte Inhalt dieses Kapitels C000 1 Der Satz von Fubini 2 Der Transformationssatz 1 Vertauschen von Integral und eihe 2 Vertauschen von Integral und Limes 3 Vertauschen von
