Übungen zu Meteorologische Modellierung Teil 'Grundlagen der Numerik'
|
|
|
- Kora Ursler
- vor 7 Jahren
- Abrufe
Transkript
1 Übungen zu Meteorologische Modellierung Teil 'Grundlagen der Numerik' 1. Diskretisierung in der Zeit: Die Evolutionsgleichung Kurzzusammenfassung Zur Erprobung der Verfahren zur zeitlichen Diskretisierung betrachten wir die lineare Differentialgleichung (1) at + F (Evolutionsgleichung, engl. decay equation) Sie stellt die zeitliche Entwicklung einer Größe T bedingt durch einen konstanten Antrieb F und einer linearen Dämpfung mit der Zeitkonstanten τ 1/a dar. Diese Gleichung kann analytisch gelöst werden: T(t) F/a + T exp(-a t). Wobei F/a die Gleichgewichtslösung und T die Abweichung des Anfangswerts T 0 (T(t 0 )) von der stationären Lösung sind. Nun soll die Evolutionsgleichung, also die zeitliche Entwicklung von T, numerisch gelöst werden. Hierzu wird ein Anfangszeitpunkt t 0 und ein Anfangswert von T (T(t 0 ); Anfangswertproblem) festgelegt. Die kontinuierlichen Funktionen t und T, werden durch diskrete Werte ersetzt. Der Lauf der Zeit ergibt sich so, durch das fortwährende hinzufügen von diskreten Zeitschritten, zu einer Folge von Zeitpunkten t n t 0 + n. Die zeitliche Entwicklung von T ergibt sich aus den Werten von T zu den jeweiligen Zeiten (t 0 + n). Nun gilt es noch die Ableitung (/) zu diskretisieren, d.h. durch Werte T n zu den diskreten Zeitpunkten t n darzustellen, um so eine Bestimmungsgleichung für T(t n + n) T n+1 zum nächsten Zeitpunkt t n+1 zu erhalten. Hier gibt es unterschiedliche Möglichkeiten. a) Einschrittverfahren (engl. two level schemes): Einschrittverfahren nutzen nur die Informationen des aktuellen (t) und des nächsten (t+) Zeitpunkts. Die zeitliche Ableitung durch die Werte zu diesen Zeitpunkten ausgedrückt (ein Schritt; oder zwei Zeitebenen). Ausgangspunkt ist eine Taylorentwicklung: T ( t) hieraus ergibt sich direkt die Diskretisierung von / durch T T ( t) T n +1 T und man erhält aus (1) eine Bestimmungsgleichung für T n+1 : T n+1 T n + ( F at) n wobei es für die Berechnung von at unterschiedliche Wahlmöglichkeiten von T gibt: - Euler Verfahren (explizit) at wird zum bekannten Zeitpunkt n ausgewertet: T n+1 T n + ( F - at n )
2 - Implizites Verfahren at wird zum unbekannten Zeitpunkt n+1 ausgewertet: T n+1 T n + ( F - at n+1 ) > T n+1 (T n + F) / (1+ a) - Crank-Nicolson Verfahren at wird zu einem Zeitpunkt zwischen n und n+1 ausgewertet (gewichtetes Mittel): T n+1 T n + ( F - a (g T n + (1-g) T n+1 )) > T n+1 (T n + ( F a g T n ))/ (1+ a(1-g)) mit 0 g 1. Je nach Wahl des Gewichts g wird hier zwischen den Extremen explizit (g1) und implizit (g0) gerechnet. Bemerkenswert ist, dass sich für g0.5 der Verfahrensfehler im Vergleich zum expliziten und impliziten Verfahren um eine Ordnung verbessert, d.h. zu O(2) (O( 2 )) wird (s. unten). - Das Runge-Kutta-Verfahren (4. Ordnung) Zwischen den Zeitpunkten t und t+ werden mehrere ( künstliche ) Stützstellen zur Berechnung der rechten Seite verwendet. Aus einer Taylor Entwicklung höherer (4.) Ordnung der analytischen Lösung (hier für F0!) ergibt sich: T(t+) (1 - a + a 2 2 /2 - a 3 3 /6 + a 4 4 /24) T(t) > T(t+) T(t)+ 1/6 (K 1 + 2K 2 + 2K 3 + K 4 ) mit K 1 -a T(t) K 2 -a (T(t) + K 1 /2) K 3 -a (T(t) + K 2 /2) K 4 -a (T(t) + K 3 ) Oder allgemein für / f(t,t): K 1 f (t 0,T 0 ) K 2 f (t 0 +/2, T 0 + K 1 /2) K 3 f (t 0 +/2, T 0 + K 2 /2) K 4 f (t 0 +, T 0 + K 3 ) und, wie oben, T(t+)T(t)+1/6 (K 1 + 2K 2 + 2K 3 + K 4 ). Es muss also 4 mal die rechte Seite ausgewertet werden (für die jeweiligen T + T). b) Zwei- und Mehrschritt Verfahren Bei den Zweischritt Verfahren (three level schemes) wird zusätzlich die Information des vorhergehenden Zeitpunkts (t-) verwendet (Dies kann auch durch Informationen weiterer Zeitebenen erweitert werden > Mehrschritt Verfahren). Beispiel: Leapfrog Verfahren
3 das Leapfrog Verfahren wird/wurde sehr häufig in numerischen Wetter/Klima Modellen zur Berechnung des adiabatischen Teils verwendet (z.b. PUMA, ECHAM). Wie sich allerdings herausstellt, ist es nur für konservative Prozesse (z.b. Advektion, Schwingungen, etc.) ein geeignetes (stabiles) Verfahren, nicht aber für die dissipative Evolutionsgleichung. Trotzdem soll es hier schon einmal vorgestellt werden. Ausgangspunkt sind die Taylor Entwicklungen: (a) T(t+)T(t)+/ +... (b) T(t-)T(t) - / +... mit (a) - (b) folgt als Diskretisierung von /: T t + ) T ( t ) Tn 2 1 T 2 ( + n 1 für Evolutionsgleichung folgt dann T ( t ) 2 at ( t) + F Wie zu sehen ist, werden hier die zwei Zeitebenen (t-) und (t) zur Berechnung des neuen Wertes T(t+) benötigt. Bei Zweischrittverfahren kommt es typischerweise zum Auftreten einer 'künstlichen' Lösung, dem sog. computational Mode, neben der gewünschten 'Physikalischen'. Beim der Verwendung des Leapfrog Verfahrens für die Evolutionsgleichung, ist dieser Computational Mode immer instabil und macht das Verfahren ungeeignet (s. Vorlesung). Natürlich gibt es noch eine Reihe anderer Ein- und Mehrschrittverfahren. Genannt seinen hier das Lax-Wendroff und das Adams-Bashford Verfahren, die gelegentlich in der Meteorologie Anwendung finden. Das Adams-Bashford Verfahren löst die Gleichung /f(t) durch T(t+)T(t)+ (3f(T(t))-f(T(t-)))/2 Die Zeitebene t- wird hier also zur Berechnung der Steigung verwendet (das Differential jedoch nur mit t und t+. Auch beim Adams-Bashforth Verfahren kommt es zum auftreten eines computational Mode, der jedoch bei der Evolutionsgleichung (bei geeignet kleinem Zeitschritt) mit der Zeit (stark) gedämpft wird. Damit ist das Adams-Bashford auch für dissipative Systeme einsetzbar. Da in Zweischrittverfahren immer zwei bekannte Zeitebenen (t- und t) benötigt werden, muss man sich, wenn nur der Anfangswert (t0) bekannt ist, den Wert bei t auf andere Art beschaffen. Typischerweise geschied dies mit einem Einschrittverfahren. Um diesen Wert möglichst genau zu erhalten wird hierbei häufig das Einschrittverfahren mehrmals hintereinander mit einem kleineren Zeitschritt angewendet. Ein ungenauer Wert begünstigt (verstärkt) den computational Mode. c) Konsistenz, Verfahrensfehler, Konvergenz, Stabilität und Zeitschrittwahl Die Fähigkeit eines numerischen Verfahrens die exakte (analytische) Lösung einer Differentialgleichung zu reproduzieren hängt von mehreren Faktoren ab. Zunächst einmal muss die Diskretisierung konsistent sein, d.h. sie muss gegen das Differential selbst konvergieren (Konsistenz):
4 dt dt lim t 0 T Der Verfahrensfehler ergibt sich aus dem Vergleich zwischen der numerischen und der analytischen Lösung. Setzt man die analytische Lösung in die Differenzengleichung ein, so wird diese i.a. nicht erfüllt. Die Potenz von im Residuum gibt die Ordnung des Fehlers. Beispiel explizites Verfahren (mit F0!): Err T(t) ( exp(-a) a)/ mit T(t) T exp(-at) mit Taylor Entwicklung für exp(-a) > Err T(t) (a 2 /2 +...) Hier ist also der Verfahrensfehler 1. Ordnung (in ). Im Allgemeinen wird ein Verfahren als konvergent bezeichnet, wenn der Fehler (d.h. die Abweichung von exakten Wert T A ) für kleine gegen 0 konvergiert, d.h.: lim T ( t) T ( t) 0 0 A als Norm kommen u.a. der sog. RMS (Root Mean Square) Fehler (Wurzel aus der Summe der quadratischen Abweichungen) und die Maximumsnorm (maximale Abweichung) in Frage. In unserem Beispiel ist Konsistenz gegeben. Die Stabilität eines Verfahrens ist sowohl durch das Verfahren selbst als auch (in vielen Fällen; bei Verwendung expliziter Verfahren) durch die Zeitschrittwahl gegeben. Ein Verfahren ist dann instabil, wenn die numerische und die analytische (richtige) Lösung zeitlich divergieren, d.h. Abweichung zwischen der wirklichen Lösung und dem berechneten Wert mit der Zeit immer größer werden. Zwar sind, bis auf das Leapfrog Schema, die oben angegebenen Verfahren prinzipiell stabil, da der Fehler für -> 0 auch gegen 0 geht, diese Stabilität ist aber nicht unbedingt für alle Zeitschrittlängen gegeben. Im expliziten Schema kann so ein zu großer Zeitschritt zur Instabilität führen: T(t+) T(t) - a T(t) T(t) (1 - a) (F0, T(t) T exp(-at)) Führt man diese Operation nun mehrmals aus (rechnet also in der Zeit voran), ergibt sich T(t+n) T(t) (1 - a) n Das Verfahren divergiert also für a>2. Für 2>a>1 ist das Verfahren zwar stabil (die Lösung konvergiert gegen die analytische), jedoch ergibt sich eine +/- Oszillation. Nur für a<1 ist die numerische Lösung wirklich 'sinnvoll', d.h. eine maximale Zeitschrittlänge von 1/a sollte verwendet werden. Im impliziten Verfahren gibt es diese Beschränkung für den Zeitschritt nicht, da
5 T(t+) T(t) - a T(t+) > T(t+) T(t) / (1 + a) und 1/(1 + a) n für alle gegen 0 (wie verlangt) konvergiert. Es sei jedoch bemerkt, dass die Wahl eines zu langen Zeitschritts in einem an sich stabilen Verfahren zu unsinnigen Ergebnissen führen kann, da die bestimmenden Prozesse auf kleinere Zeiten ablaufen. Generell gilt: je kleiner der Zeitschritt, desto besser (realistischer) die Ergebnisse. Aufgaben: 1. Löse die Evolutionsgleichung numerisch. Erweitere hierzu das Programm zur analytischen Lösung (gleiche Parameter wie bei der analytischen Lösung). Verwende das explizite Euler Verfahren mit dem Zeitschritt 1. Schreibe die numerisch bestimmte Zeitreihe heraus (t0,...200) und plotte sie zusammen mit der analytischen Lösung. 2. Ermittle experimentell (durch Änderung des Zeitschritts und Verwendung des RMS Fehlers und der Maximumsnorm) die Fehlerordnung des expliziten Verfahren 3. Verwende nun auch das implizite, das Crank-Nicolson, das Runge-Kutta und das Adams- Bashforth Verfahren (gleiche Parameter wie 1). Vergleiche die Genauigkeit der verschiedenen Verfahren bei gleichem Zeitschritt durch die Berechnung der Fehler (RMS und Maximum) und ermittle auch hier experimentell die Fehlerordnung. (Beim Zweischrittverfahren kann die numerische Lösung eines der anderen Verfahren oder die analytische Lösung für den benötigten Zeitpunkt t verwendet werden). Zusatzaufgabe (optional): Die Verfahren zur zeitlichen Diskretisierung können natürlich auch für komplexere Gleichungen verwendet werden. Eine sehr bekanntes Gleichungssystem ist das Lorenz Modell, das ja u.a. ein low order Modell der atmosphärischen Konvektion ist (Näheres in der Vorlesung Theoretische Meteorologie). Das Modell ist so bekannt, weil es sog. deterministisches Chaos zeigt. Die Gleichungen sind gegeben durch: X Y Z σx + σy XZ + rx Y XY bz mit den externen Parametern σ (Prandtl Zahl), r (Rayleigh Zahl) und b (Dämpfung). Berechne die numerische Lösung des Lorenz Modells und plotte den berühmten Schmetterling (X(t),Y(t),Z(t)). Klassische Werte der Parameter für das chaotische Verhalten sind dabei σ 10., r28. und b8./3. Als Anfangswert kann z.b. (1,1,1) genommen werden. Als Zeitschritt kann ein Wert von 1/100. genommen werden, es sollten ungefähr Zeitschritte gerechnet werden. Bemerkung: Da, wie aus der Theorie bekannt, das Lorenz Modell sehr sensitiv ist, sollte für wissenschaftliche Studien ein möglichst genaues Schema verwendet werden. Dies ist in vielen Fällen das Runge-Kutta Verfahren. Hier kann zunächst auch einmal das explizite Euler Schema ausprobiert werden. Die Variablen sollten in hoher Genauigkeit (kind8) definiert werden.
2. Numerische Verfahren für AWPe 2.1 Das Euler-Verfahren
 2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
2.1 Das Euler-Verfahren Wir betrachten das AWP y = f (t, y), y(t 0 ) = y 0. (AWP) Unter den Voraussetzungen von Satz 1.1 besitzt es eine eindeutige Lösung, sagen wir über dem Intervall I. Wir wollen diese
Einführung und Beispiele
 Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
Kapitel 7 Gewöhnliche Differentialgleichungen Prof. R. Leithner, E. Zander Einführung in numerische Methoden für Ingenieure 7/2 Einführung und Beispiele Prof. R. Leithner, E. Zander Einführung in numerische
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB)
 Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
Einführung in numerische Methoden für Ingenieure (nach A. Quarteroni, F. Saleri: Wissenschaftliches Rechnen mit MATLAB) Prof. R. Leithner, Dipl. Phys. E. Zander Wintersemester 2010/2011 Kapitel 7 Gewöhnliche
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differenzialgleichungssysteme 5.1-1 1.1 Grundlagen
Simulationstechnik V
 Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Simulationstechnik V
 Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Simulationstechnik V
 Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 2. Teil 2-1 1) Welche Garantie
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung
 Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y(x), welche erfüllt y = f(x,y) y(x 0 ) = y 0 Differentialgleichung Anfangsbedingung Wenn f in x stetig
Differentialgleichungen
 Differentialgleichungen Viele physikalische Probleme können mathematisch als gewöhnliche Differentialgleichungen formuliert werden nur eine unabhängige Variable (meist t), z.b. Bewegungsgleichungen: gleichmäßig
Differentialgleichungen Viele physikalische Probleme können mathematisch als gewöhnliche Differentialgleichungen formuliert werden nur eine unabhängige Variable (meist t), z.b. Bewegungsgleichungen: gleichmäßig
Gewöhnliche Differentialgleichungen
 Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
Gewöhnliche Differentialgleichungen 10. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 22. Mai 2014 Gliederung 1 Aufgabenstellung und Interpretation
Mathematische Grundlagen
 G-CSC Goethe-Center for Scientific Computing der Universität Frankfurt 2 Übung zur Vorlesung Modellierung und Simulation 3 (WS 2013/14) Prof Dr G Queisser Markus Breit, Martin Stepniewski Abgabe: Dienstag,
G-CSC Goethe-Center for Scientific Computing der Universität Frankfurt 2 Übung zur Vorlesung Modellierung und Simulation 3 (WS 2013/14) Prof Dr G Queisser Markus Breit, Martin Stepniewski Abgabe: Dienstag,
Numerische Verfahren
 Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
ODE-Solver. Inhalt. Einleitung. grundlegende Algorithmen. weiterführende Algorithmen
 Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
Martin Reinhardt angewandte Mathematik 8. Semester Matrikel: 50108 ODE-Solver 11. Mai 2011 Inhalt Einleitung grundlegende Algorithmen weiterführende Algorithmen Martin Reinhardt (TUBAF) 1 Orientierung
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel
 - Numerik in der Physik - Simulationen, DGL und Co. Max Menzel 4.1.2011 1 Übersicht Differenzialgleichungen? Was ist das? Wo gibt es das? Lösen von Differenzialgleichungen Analytisch Numerisch Anwendungen
- Numerik in der Physik - Simulationen, DGL und Co. Max Menzel 4.1.2011 1 Übersicht Differenzialgleichungen? Was ist das? Wo gibt es das? Lösen von Differenzialgleichungen Analytisch Numerisch Anwendungen
Numerik I. Gewöhnliche Differentialgleichungen. Prof.Dr.G.Wittum. Teil I:
 Numerik I Prof.Dr.G.Wittum Teil I: Gewönlice Differentialgleicungen Sommersemester 2005 INHALTSVERZEICHNIS 1 Inaltsverzeicnis 1 Numerik gewönlicer Differentialgleicungen 2 1.1 Einleitung....................................
Numerik I Prof.Dr.G.Wittum Teil I: Gewönlice Differentialgleicungen Sommersemester 2005 INHALTSVERZEICHNIS 1 Inaltsverzeicnis 1 Numerik gewönlicer Differentialgleicungen 2 1.1 Einleitung....................................
(d) das zu Grunde liegende Problem gut konditioniert ist.
 Aufgabe 0: (6 Punkte) Bitte kreuzen Sie die richtige Lösung an. Es ist jeweils genau eine Antwort korrekt. Für jede richtige Antwort erhalten Sie einen Punkt, für jede falsche Antwort wird Ihnen ein Punkt
Aufgabe 0: (6 Punkte) Bitte kreuzen Sie die richtige Lösung an. Es ist jeweils genau eine Antwort korrekt. Für jede richtige Antwort erhalten Sie einen Punkt, für jede falsche Antwort wird Ihnen ein Punkt
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe
 Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
Mehrschrittverfahren Ein weiterer, häufig benutzter Verfahrenstyp zur numerischen Lösung der Anfangswertaufgabe y = f(x, y), y(a) =y 0 (1) sind die linearen Mehrschrittverfahren, bei denen man zur Berechnung
Eingebettete Runge Kutta Verfahren DOPRI5(4) Verfahren: FSAL Verfahren
 Eingebettete Runge Kutta Verfahren DOPRI5(4) Verfahren: FSAL Verfahren 0 1 5 3 10 4 5 8 9 1 5 3 9 40 40 44 45 56 15 19372 6561 25360 2187 9017 1 3168 355 33 1 35 348 0 500 1113 35 500 p = 5 348 0 1113
Eingebettete Runge Kutta Verfahren DOPRI5(4) Verfahren: FSAL Verfahren 0 1 5 3 10 4 5 8 9 1 5 3 9 40 40 44 45 56 15 19372 6561 25360 2187 9017 1 3168 355 33 1 35 348 0 500 1113 35 500 p = 5 348 0 1113
Systemanalyse und Modellbildung
 Systemanalyse und Modellbildung Universität Koblenz-Landau Fachbereich 7: Natur- und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) 7. Zeitdiskrete Modelle 7.1
Systemanalyse und Modellbildung Universität Koblenz-Landau Fachbereich 7: Natur- und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) 7. Zeitdiskrete Modelle 7.1
SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle
 Universität Koblenz-Landau Fachbereich 7: Natur-und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle 1. Zeitdiskrete
Universität Koblenz-Landau Fachbereich 7: Natur-und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) SYSTEMANALYSE 2 Kapitel 7: Zeitdiskrete Modelle 1. Zeitdiskrete
Übung zur Vorlesung Numerische Simulationsmethoden in der Geophysik
 Wenke Wilhelms, Julia Weißflog Institut für Geophysik und Geoinformatik Übung zur Vorlesung Numerische Simulationsmethoden in der Geophysik 04. Dezember 2013 Die Diffusionsgleichung 1D-Wärmeleitungsgleichung...
Wenke Wilhelms, Julia Weißflog Institut für Geophysik und Geoinformatik Übung zur Vorlesung Numerische Simulationsmethoden in der Geophysik 04. Dezember 2013 Die Diffusionsgleichung 1D-Wärmeleitungsgleichung...
Mathematische Grundlagen der dynamischen Simulation
 Mathematische Grundlagen der dynamischen Simulation Dynamische Systeme sind Systeme, die sich verändern. Es geht dabei um eine zeitliche Entwicklung und wie immer in der Informatik betrachten wir dabei
Mathematische Grundlagen der dynamischen Simulation Dynamische Systeme sind Systeme, die sich verändern. Es geht dabei um eine zeitliche Entwicklung und wie immer in der Informatik betrachten wir dabei
Systemtheorie. Vorlesung 6: Lösung linearer Differentialgleichungen. Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann
 Systemtheorie Vorlesung 6: Lösung linearer Differentialgleichungen Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann Einführung Viele technischen Anwendungen lassen sich zumindest näherungsweise
Systemtheorie Vorlesung 6: Lösung linearer Differentialgleichungen Fakultät für Elektro- und Informationstechnik, Manfred Strohrmann Einführung Viele technischen Anwendungen lassen sich zumindest näherungsweise
Lösung Semesterendprüfung
 MNUM Mathematik: Numerische Methoden Herbstsemester 17 Dr Christoph Kirsch ZHAW Winterthur Aufgabe 1 : Lösung Semesterendprüfung Wir schreiben zuerst die Gleichungen f(x i ; a, a 1, a y i, i 1,,, 1, als
MNUM Mathematik: Numerische Methoden Herbstsemester 17 Dr Christoph Kirsch ZHAW Winterthur Aufgabe 1 : Lösung Semesterendprüfung Wir schreiben zuerst die Gleichungen f(x i ; a, a 1, a y i, i 1,,, 1, als
Kapitel 1 Gewöhnliche Differentialgleichungen
 Kapitel 1 Gewöhnliche Differentialgleichungen Eines der wichtigsten Einsatzgebiete numerischer Verfahren sind Differentialgleichungen, also Gleichungen, die Funktionen sowie deren Ableitungen in Bezug
Kapitel 1 Gewöhnliche Differentialgleichungen Eines der wichtigsten Einsatzgebiete numerischer Verfahren sind Differentialgleichungen, also Gleichungen, die Funktionen sowie deren Ableitungen in Bezug
Übungsaufgabe Numerische Lösung DGL
 Kallenrode, www.sotere.uos.de Übungsaufgabe Numerische Lösung DGL 1. Bestimmen Sie die Lösung der DGL ẋ = (t 2) 2 + t x mit x(0) = 1 im Bereich von t = 0 bis t = 5 mit Hilfe des Euler schen Streckenzugverfahrens,
Kallenrode, www.sotere.uos.de Übungsaufgabe Numerische Lösung DGL 1. Bestimmen Sie die Lösung der DGL ẋ = (t 2) 2 + t x mit x(0) = 1 im Bereich von t = 0 bis t = 5 mit Hilfe des Euler schen Streckenzugverfahrens,
Übung zur Numerik linearer und nichtlinearer Parameterschätzprobleme A. Franke-Börner, M. Helm
 Übung zur Numerik linearer und nichtlinearer Parameterschätzprobleme A. Franke-Börner, M. Helm Numerik Parameterschätzprobleme INHALT 1. 1D Wärmeleitungsgleichung 1.1 Finite-Differenzen-Diskretisierung
Übung zur Numerik linearer und nichtlinearer Parameterschätzprobleme A. Franke-Börner, M. Helm Numerik Parameterschätzprobleme INHALT 1. 1D Wärmeleitungsgleichung 1.1 Finite-Differenzen-Diskretisierung
Zehnte Vorlesung, 4. Juni 2009, Inhalt. Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen
 Zehnte Vorlesung, 4. Juni 2009, Inhalt Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Wichtige Feststellungen zur Eigenwertaufgabe Ax = λx: Eigenwerte
Zehnte Vorlesung, 4. Juni 2009, Inhalt Eigenwerte und Eigenvektoren (2) Gewöhnliche Differentialgleichungen 1 Eigenwerte und Eigenvektoren Wichtige Feststellungen zur Eigenwertaufgabe Ax = λx: Eigenwerte
PVK Probeprüfung FS 2017
 PVK Probeprüfung FS 07 Lucas Böttcher Numerische Methoden ETH Zürich June 3, 07. Radioaktiver Zerfall Gegeben sind zwei radioaktive Substanzen, welche mit den Raten λ = 0.5 und λ = 0. zerfallen: A λ B
PVK Probeprüfung FS 07 Lucas Böttcher Numerische Methoden ETH Zürich June 3, 07. Radioaktiver Zerfall Gegeben sind zwei radioaktive Substanzen, welche mit den Raten λ = 0.5 und λ = 0. zerfallen: A λ B
5 Randwertprobleme. y = f(t, y, y ) für t J, (5.2a) y(t 0 ) = y 0, y(t) = y T (5.2b) zu gegebener Funktion f und Werten y 0, y T.
 5 Randwertprobleme Bei den bisher betrachteten Problemen handelte es sich um Anfangswertprobleme. In der Praxis treten, insbesondere bei Differentialgleichungen höherer Ordnung, auch Randwertprobleme auf.
5 Randwertprobleme Bei den bisher betrachteten Problemen handelte es sich um Anfangswertprobleme. In der Praxis treten, insbesondere bei Differentialgleichungen höherer Ordnung, auch Randwertprobleme auf.
Zuname: Vorname: KennNr: Matr.Nr: PRÜFUNG AUS MATHEMATIK 3. 1)(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation.
 (8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
(8 P.) Lösen Sie das folgende AWP mit Hilfe der Laplacetransformation. y 7y + 10y = sin(2x), y(0) = 1, y (0) = 3. x ( ) Bemerkung: Für festes a gilt L(e ax ) = 1 und L sin(ax) = arctan a. s a x s Die auftretenden
Numerische Verfahren
 Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München Fakultät
Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München Fakultät
Differenzialgleichungen
 Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
Differenzialgleichungen Fakultät Grundlagen April 2011 Fakultät Grundlagen Differenzialgleichungen Übersicht Grundsätzliches 1 Grundsätzliches Problemstellung Richtungsfeld Beispiel 2 Eulerverfahren Heunverfahren
2.3.1 Explizite Runge-Kutta-Verfahren
 Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
Somit ist y(t + h) = y + hf(t, y ) + h (f t (t, y ) + f y (t, y )f(t, y )) + O(h 3 ) Setzen wir Φ(t, y, h) := f(t, y) + h (f t(t, y) + f y (t, y)f(t, y)), so erhalten wir ein Verfahren mit der Konsistenzordnung
Bildverarbeitung: Diffusion Filters. D. Schlesinger ()Bildverarbeitung: Diffusion Filters 1 / 10
 Bildverarbeitung: Diffusion Filters D. Schlesinger ()Bildverarbeitung: Diffusion Filters 1 / 10 Diffusion Idee Motiviert durch physikalische Prozesse Ausgleich der Konzentration eines Stoffes. Konzentration
Bildverarbeitung: Diffusion Filters D. Schlesinger ()Bildverarbeitung: Diffusion Filters 1 / 10 Diffusion Idee Motiviert durch physikalische Prozesse Ausgleich der Konzentration eines Stoffes. Konzentration
Numerisches Programmieren (IN0019)
 Numerisches Programmieren (IN0019) Frank R. Schmidt Winter Semester 2016/2017 11. Gewöhnliche Differenzialgleichungen................................................................................. 2
Numerisches Programmieren (IN0019) Frank R. Schmidt Winter Semester 2016/2017 11. Gewöhnliche Differenzialgleichungen................................................................................. 2
Iterationsverfahren und Stabilitätsuntersuchung
 1 FÜR INTERESSIERTE! NICHT TESTRELEVANT 1! Iterationsverfahren und Stabilitätsuntersuchung Unter Iterationsverfahren versteht man rekursive numerische Methoden mit welchen auch analytisch nicht lösbare
1 FÜR INTERESSIERTE! NICHT TESTRELEVANT 1! Iterationsverfahren und Stabilitätsuntersuchung Unter Iterationsverfahren versteht man rekursive numerische Methoden mit welchen auch analytisch nicht lösbare
KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.
![KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2. KLAUSUR zur Numerik I mit Lösungen. Aufgabe 1: (10 Punkte) [ wahr falsch ] 1. Die maximale Ordnung einer s-stufigen Quadraturformel ist s 2.](/thumbs/71/65292107.jpg) MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
MATHEMATISCHES INSTITUT PROF. DR. ACHIM SCHÄDLE 9.8.7 KLAUSUR zur Numerik I mit Lösungen Aufgabe : ( Punkte) [ wahr falsch ]. Die maximale Ordnung einer s-stufigen Quadraturformel ist s. [ ]. Der Clenshaw
Optimierung. Optimierung. Vorlesung 4 Newton und Quasi Newton Verfahren (Teil II) 2013 Thomas Brox, Fabian Kuhn
 Optimierung Vorlesung 4 Newton und Quasi Newton Verfahren (Teil II) 1 Newton Verfahren Taylor Approximation 1. Ordnung von Newton Verfahren! 0 Setze 0und berechne Löse lineares Gleichungssystem für : 2
Optimierung Vorlesung 4 Newton und Quasi Newton Verfahren (Teil II) 1 Newton Verfahren Taylor Approximation 1. Ordnung von Newton Verfahren! 0 Setze 0und berechne Löse lineares Gleichungssystem für : 2
Dynamisches Chaos. 1. Einleitung: Determinismus und Chaos
 Dynamisches Chaos 1. Einleitung: Determinismus und Chaos In der üblichen Betrachtungsweise ist der Zufall nur auf dem Mikroniveau erlaubt: - das Boltzmannsche molekulare Chaos; - die quantenmechanischen
Dynamisches Chaos 1. Einleitung: Determinismus und Chaos In der üblichen Betrachtungsweise ist der Zufall nur auf dem Mikroniveau erlaubt: - das Boltzmannsche molekulare Chaos; - die quantenmechanischen
PRÜFUNG AUS MATHEMATIK 3
 (8 P.) Berechnen Sie das Integral tan(ln x) dx. x (8 P.) Bestimmen Sie die allgemeine Lösung der Differentialgleichung y 2y + 2y = x 2 + 5 cos x. (8 P.) Entwickeln Sie f(x) = sin(x) für x [ π/2, π/2] mit
(8 P.) Berechnen Sie das Integral tan(ln x) dx. x (8 P.) Bestimmen Sie die allgemeine Lösung der Differentialgleichung y 2y + 2y = x 2 + 5 cos x. (8 P.) Entwickeln Sie f(x) = sin(x) für x [ π/2, π/2] mit
Computersimulationen in der Astronomie
 Computersimulationen in der Astronomie Fabian Heimann Universität Göttingen, Fabian.Heimann@stud.uni-goettingen.de Astronomisches Sommerlager 2013 Inhaltsverzeichnis 1 Differentialgleichungen 3 1.1 Beispiele.....................................
Computersimulationen in der Astronomie Fabian Heimann Universität Göttingen, Fabian.Heimann@stud.uni-goettingen.de Astronomisches Sommerlager 2013 Inhaltsverzeichnis 1 Differentialgleichungen 3 1.1 Beispiele.....................................
Transport Einführung
 Transport Einführung home/lehre/vl-mhs-1/inhalt/folien/vorlesung/8_transport/deckblatt.tex Seite 1 von 24. p.1/24 1. Einführung 2. Transportgleichung 3. Analytische Lösung Inhaltsverzeichnis 4. Diskretisierung
Transport Einführung home/lehre/vl-mhs-1/inhalt/folien/vorlesung/8_transport/deckblatt.tex Seite 1 von 24. p.1/24 1. Einführung 2. Transportgleichung 3. Analytische Lösung Inhaltsverzeichnis 4. Diskretisierung
h n = (t t 0 )/n Bevor wir diesen Satz beweisen, geben wir noch einen Hilfssatz an, der eine wichtige Abschätzung liefert.
 Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
Kapitel 4 Berechnung von Lösungen 41 Die Euler sche Polygonzugmethode Die Grundlage dieser Methode ist die einfache Beobachtung, dass f(u, t) in der Nähe eines Punktes als nahezu konstant angesehen werden
Begleitmaterial zur Vorlesung Numerik gewöhnlicher Differentialgleichungen
 Begleitmaterial zur Vorlesung Numerik gewöhnlicher Differentialgleichungen Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial
Begleitmaterial zur Vorlesung Numerik gewöhnlicher Differentialgleichungen Andreas Meister Universität Kassel, AG Analysis und Angewandte Mathematik Andreas Meister (Universität Kassel) Begleitmaterial
3. Lineare Mehrschrittverfahren 3.1 Begriffe
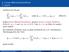 3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
3.1 Begriffe Verfahren der Bauart k α j y n+j = h k β j f n+j, wobei f n+j := f (t n+j, y n+j ), (Mehr-S) heißen lineare Mehrschrittverfahren, genauer lineare k-schritt-verfahren. O.B.d.A. α k = 1 und
Astrophysikalsiches Numerikum: Gewöhnliche Differentialgleichungen am Beispiel Weißer Zwerge
 Astrophysikalsiches Numerikum: Gewöhnliche Differentialgleichungen am Beispiel Weißer Zwerge A. Schweitzer Wintersemester 2005/06 Links, Literatur und weitere Informationen Die Numerical Recepies sind
Astrophysikalsiches Numerikum: Gewöhnliche Differentialgleichungen am Beispiel Weißer Zwerge A. Schweitzer Wintersemester 2005/06 Links, Literatur und weitere Informationen Die Numerical Recepies sind
NUMERIK 1. Sommersemester 2016
 NUMERIK 1 Soerseester 2016 KLAUSUR LÖSUNGSVORSCHLAG Aufgabe 1 (Multiple Choice) (ca. 20 Minuten, 8 Punkte) Kreuzen Sie korrekte Aussagen an. Es können ehrere Antworten richtig sein, indestens eine ist
NUMERIK 1 Soerseester 2016 KLAUSUR LÖSUNGSVORSCHLAG Aufgabe 1 (Multiple Choice) (ca. 20 Minuten, 8 Punkte) Kreuzen Sie korrekte Aussagen an. Es können ehrere Antworten richtig sein, indestens eine ist
Angewandte Mathematik am Rechner 1
 Michael Wand Institut für Informatik. Angewandte Mathematik am Rechner 1 SOMMERSEMESTER 2017 Kapitel 5 Grundlagen Analysis Kontinuierliche Mengen Vollständige Mengen Folgen Iterative Berechnungen Grenzwert:
Michael Wand Institut für Informatik. Angewandte Mathematik am Rechner 1 SOMMERSEMESTER 2017 Kapitel 5 Grundlagen Analysis Kontinuierliche Mengen Vollständige Mengen Folgen Iterative Berechnungen Grenzwert:
7 Das Eulersche Polygonzugverfahren
 35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem
35 7 Das Eulersche Polygonzugverfahren Lösungen von Differentialgleichungen sind nur in speziellen Fällen explizit angebbar; oft können nur Approximationen an Lösungen numerisch berechnet werden. In diesem
Computerphysik. Übungsblatt 6
 Institut für Theoretische Physik der Universität zu Köln Computerphysik Übungsblatt 6 SS 2013 Prof. Dr. Simon Trebst Michael Becker, Peter Bröcker Website: http://www.thp.uni-koeln.de/trebst/lectures/2013-compphys.html
Institut für Theoretische Physik der Universität zu Köln Computerphysik Übungsblatt 6 SS 2013 Prof. Dr. Simon Trebst Michael Becker, Peter Bröcker Website: http://www.thp.uni-koeln.de/trebst/lectures/2013-compphys.html
u(x, 0) = g(x) : 0 x 1 u(0, t) = u(1, t) = 0 : 0 t T
 8.1 Die Methode der Finiten Differenzen Wir beschränken uns auf eindimensionale Probleme und die folgenden Anfangs und Anfangsrandwertprobleme 1) Cauchy Probleme für skalare Erhaltungsgleichungen, also
8.1 Die Methode der Finiten Differenzen Wir beschränken uns auf eindimensionale Probleme und die folgenden Anfangs und Anfangsrandwertprobleme 1) Cauchy Probleme für skalare Erhaltungsgleichungen, also
Entwicklung von Differenzenschemata für geometrische Singularitäten
 Entwicklung von Differenzenschemata für geometrische Singularitäten Graz, Österreich herwig.grogger@fh-joanneum.at DGLR-Fachausschußsitzung T 2.3 Strömungsakustik / Fluglärm DLR Braunschweig 4. Februar
Entwicklung von Differenzenschemata für geometrische Singularitäten Graz, Österreich herwig.grogger@fh-joanneum.at DGLR-Fachausschußsitzung T 2.3 Strömungsakustik / Fluglärm DLR Braunschweig 4. Februar
Für viele technische Anwendungen unverzichtbar!
 Für viele technische Anwendungen unverzichtbar! Page 1 of 26 5.1. Eines der wichtigsten Einsatzgebiete numerischer Verfahren sind, also Gleichungen, die Funktionen sowie deren Ableitungen in Bezug zueinander
Für viele technische Anwendungen unverzichtbar! Page 1 of 26 5.1. Eines der wichtigsten Einsatzgebiete numerischer Verfahren sind, also Gleichungen, die Funktionen sowie deren Ableitungen in Bezug zueinander
( ) Diskretes dynamisches Chaos. 1. Einleitung: Diskrete dynamische Systeme
 Diskretes dynamisches Chaos. Einleitung: Diskrete dynamische Systeme Verschiedene Problemstellungen können zu zeitlich diskreten Systemen (Differenzengleichungen) führen: Zinseszinsrechnung: x(n+) = x(n)
Diskretes dynamisches Chaos. Einleitung: Diskrete dynamische Systeme Verschiedene Problemstellungen können zu zeitlich diskreten Systemen (Differenzengleichungen) führen: Zinseszinsrechnung: x(n+) = x(n)
14 Numerik hyperbolischer Differentialgleichungen
 Numerik II 256 14 Numerik hyperbolischer Differentialgleichungen Während parabolische PDG Diffusionsvorgänge modellieren stellen hyperbolische PDG Modelle für Wellenphänomene dar. Wichtigste Anwendungsgebiete
Numerik II 256 14 Numerik hyperbolischer Differentialgleichungen Während parabolische PDG Diffusionsvorgänge modellieren stellen hyperbolische PDG Modelle für Wellenphänomene dar. Wichtigste Anwendungsgebiete
Extrapolationsverfahren
 Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
Extrapolationsverfahren Vortrag im Rahmen des Seminars Numerik gewöhnlicher Differentialgleichungen unter der Leitung von Prof. Peter Bastian WS 2010/11 Marlene Beczalla 21.12.2010 1. Beschreibung des
Numerik von Anfangswertaufgaben Teil II
 Institut für Numerische Mathematik und Optimierung Numerik von Anfangswertaufgaben Teil II Numerik partieller Differentialgleichungen Oliver Ernst Hörerkreis: 6. Mm, 8. Mm Sommersemester 2012 Inhalt 1.
Institut für Numerische Mathematik und Optimierung Numerik von Anfangswertaufgaben Teil II Numerik partieller Differentialgleichungen Oliver Ernst Hörerkreis: 6. Mm, 8. Mm Sommersemester 2012 Inhalt 1.
D-MATH Numerische Methoden FS 2018 Dr. Vasile Gradinaru Kjetil Olsen Lye. Serie 6
 D-MATH Numerische Methoden FS 08 Dr. Vasile Gradinaru Kjetil Olsen Lye Serie 6 Abgabedatum: Di. 08.0 / Mi. 09.0, in den Übungsgruppen, oder im HG J 68. Koordinatoren: Kjetil Olsen Lye, HG G 6. kjetil.lye@sam.math.ethz.ch
D-MATH Numerische Methoden FS 08 Dr. Vasile Gradinaru Kjetil Olsen Lye Serie 6 Abgabedatum: Di. 08.0 / Mi. 09.0, in den Übungsgruppen, oder im HG J 68. Koordinatoren: Kjetil Olsen Lye, HG G 6. kjetil.lye@sam.math.ethz.ch
Abschnitt 1.7: Schrittweitensteuerung 27
 Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
Abschnitt.7: Schrittweitensteuerung 7 zu oben analoge Schrittweitensteuerung durch Kombination von drei- und vierstufigen Runge- Kutta-Methoden ist nicht möglich, weil die betreffenden Gleichungssysteme
Explizite Runge-Kutta-Verfahren
 Explizite Runge-Kutta-Verfahren Proseminar Numerische Mathematik Leitung: Professor Dr. W. Hofmann Dominik Enseleit 06.07.2005 1 1 Einleitung Nachdem wir schon einige numerische Verfahren zur Lösung gewöhnlicher
Explizite Runge-Kutta-Verfahren Proseminar Numerische Mathematik Leitung: Professor Dr. W. Hofmann Dominik Enseleit 06.07.2005 1 1 Einleitung Nachdem wir schon einige numerische Verfahren zur Lösung gewöhnlicher
Unstetige Galerkin-Verfahren und die lineare Transportgleichung. Tobias G. Pfeiffer Freie Universität Berlin
 Unstetige Galerkin-Verfahren und die lineare Transportgleichung Tobias G. Pfeiffer Freie Universität Berlin Seminar DG-Verfahren, 26. Mai 2009 , Voraussetzungen & Ziele Voraussetzungen Kenntnisse in Numerik
Unstetige Galerkin-Verfahren und die lineare Transportgleichung Tobias G. Pfeiffer Freie Universität Berlin Seminar DG-Verfahren, 26. Mai 2009 , Voraussetzungen & Ziele Voraussetzungen Kenntnisse in Numerik
Nichtlineare Gleichungssysteme
 Kapitel 5 Nichtlineare Gleichungssysteme 51 Einführung Wir betrachten in diesem Kapitel Verfahren zur Lösung von nichtlinearen Gleichungssystemen Nichtlineares Gleichungssystem: Gesucht ist eine Lösung
Kapitel 5 Nichtlineare Gleichungssysteme 51 Einführung Wir betrachten in diesem Kapitel Verfahren zur Lösung von nichtlinearen Gleichungssystemen Nichtlineares Gleichungssystem: Gesucht ist eine Lösung
VF-2: 2. Es seien x = 1 3 und y = π Bei der Berechnung von sin(x) sin(y) in M(10, 12, 99, 99) tritt. Auslöschung auf.
 IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H11 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
IGPM RWTH Aachen Verständnisfragen-Teil NumaMB H11 (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Es müssen mindestens zwei
VF-3: Es seien A R n n beliebig aber regulär, b R n und gesucht sei die Lösung x R n von A x = b.
 NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
NumaMB F14 Verständnisfragen-Teil (24 Punkte) Es gibt zu jeder der 12 Aufgaben vier Teilaufgaben. Diese sind mit wahr bzw. falsch zu kennzeichnen (hinschreiben). Bewertung: Vier Fragen richtig beantwortet
Das Eulerverfahren zum numerischen Lösen von DGLen
 Das Eulerverfahren zum numerischen Lösen von DGLen Thomas Wassong FB17 Mathematik Universität Kassel 06.05.2008 Numerische Verfahren zur Berechnung von Differentialgleichungen Das Eulerverfahren: Programmierung
Das Eulerverfahren zum numerischen Lösen von DGLen Thomas Wassong FB17 Mathematik Universität Kassel 06.05.2008 Numerische Verfahren zur Berechnung von Differentialgleichungen Das Eulerverfahren: Programmierung
Simulationstechnik V
 Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 4. Teil Finite-Volumen-Methode
Simulationstechnik V Vorlesung/Praktikum an der RWTH Aachen Numerische Simulation von Strömungsvorgängen B. Binninger Institut für Technische Verbrennung Templergraben 64 4. Teil Finite-Volumen-Methode
Aufgabenstellung: Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y = y(x).
 I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 2016
 Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden Sommersemester 0 0090 Aufgabe Punkte: Betrachten Sie das lineare Gleichungssystem Ax = b mit A = 0 und b
Angewandte Mathematik und Programmierung
 Angewandte Mathematik und Programmierung Einführung in das Konzept der objektorientierten Anwendungen zu mathematischen Rechnens WS 2012/13 DGL Grundlage Klassifikation Anwendung von lin. Ggln. M. konst.
Angewandte Mathematik und Programmierung Einführung in das Konzept der objektorientierten Anwendungen zu mathematischen Rechnens WS 2012/13 DGL Grundlage Klassifikation Anwendung von lin. Ggln. M. konst.
Einführung 17. Teil I Differentialgleichungen erster Ordnung 21. Kapitel 1 Willkommen in der Welt der Differentialgleichungen! 23
 Inhaltsverzeichnis Einführung 17 Über dieses Buch 17 Konventionen in diesem Buch 17 Was Sie nicht lesen müssen 18 Falsche Voraussetzungen 18 Wie dieses Buch strukturiert ist 18 Teil I: Differentialgleichungen
Inhaltsverzeichnis Einführung 17 Über dieses Buch 17 Konventionen in diesem Buch 17 Was Sie nicht lesen müssen 18 Falsche Voraussetzungen 18 Wie dieses Buch strukturiert ist 18 Teil I: Differentialgleichungen
Ausgleichsproblem. Definition (1.0.3)
 Ausgleichsproblem Definition (1.0.3) Gegeben sind n Wertepaare (x i, y i ), i = 1,..., n mit x i x j für i j. Gesucht ist eine stetige Funktion f, die die Wertepaare bestmöglich annähert, d.h. dass möglichst
Ausgleichsproblem Definition (1.0.3) Gegeben sind n Wertepaare (x i, y i ), i = 1,..., n mit x i x j für i j. Gesucht ist eine stetige Funktion f, die die Wertepaare bestmöglich annähert, d.h. dass möglichst
Euler-Verfahren. exakte Lösung. Euler-Streckenzüge. Folie 1
 exakte Lösung Euler-Verfahren Folie 1 Euler-Streckenzüge Ein paar grundlegende Anmerkungen zur Numerik Die Begriffe Numerik bzw. Numerische Mathematik bezeichnen ein Teilgebiet der Mathematik, welches
exakte Lösung Euler-Verfahren Folie 1 Euler-Streckenzüge Ein paar grundlegende Anmerkungen zur Numerik Die Begriffe Numerik bzw. Numerische Mathematik bezeichnen ein Teilgebiet der Mathematik, welches
Seminar Gewöhnliche Differentialgleichungen
 Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Analysis I. 14. Übungsstunde. Steven Battilana. battilana.uk/teaching
 Analysis I 4. Übungsstunde Steven Battilana stevenb@student.ethz.ch battilana.uk/teaching June 6, 207 Erinnerung Die Reihe a k konvergiert falls, lim S n = lim n n n a k =: a k existiert. Satz (Majoranten/Minorantenkriterium)
Analysis I 4. Übungsstunde Steven Battilana stevenb@student.ethz.ch battilana.uk/teaching June 6, 207 Erinnerung Die Reihe a k konvergiert falls, lim S n = lim n n n a k =: a k existiert. Satz (Majoranten/Minorantenkriterium)
Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 2016/17
 Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 6/7 837 Aufgabe Punkte): Gegeben sei das lineare Gleichungssystem Ax = b mit A = 6 3 und
Institut für Analysis Prof Dr Michael Plum Lösungsvorschlag zur Modulprüfung Numerische Methoden - Wintersemester 6/7 837 Aufgabe Punkte): Gegeben sei das lineare Gleichungssystem Ax = b mit A = 6 3 und
400 Schwingungen. 410 Pendel 420 Untersuchung von oszillierenden Systemen
 4 Schwingungen 41 Pendel 4 Untersuchung von oszillierenden Systemen um was geht es? Schwingungen = Oszillationen Beschreibung von schwingenden Systemen Methoden zur Analyse, Modellierung und Simulation
4 Schwingungen 41 Pendel 4 Untersuchung von oszillierenden Systemen um was geht es? Schwingungen = Oszillationen Beschreibung von schwingenden Systemen Methoden zur Analyse, Modellierung und Simulation
15 Restabschätzung nach Taylor. Potenzreihen
 15 Restabschätzung nach Taylor. Potenzreihen Jörn Loviscach Versionsstand: 21. März 2014, 21:09 Die nummerierten Felder sind absichtlich leer, zum Ausfüllen beim Ansehen der Videos: http://www.j3l7h.de/videos.html
15 Restabschätzung nach Taylor. Potenzreihen Jörn Loviscach Versionsstand: 21. März 2014, 21:09 Die nummerierten Felder sind absichtlich leer, zum Ausfüllen beim Ansehen der Videos: http://www.j3l7h.de/videos.html
Grundlagen der Numerischen Mathematik II
 J Manfred Reimer Grundlagen der Numerischen Mathematik II Studienbuch für Studenten der Mathematik, Informatik, Statistik und aller Naturwissenschaften Mit 29 Abbildungen Akademische Verlagsgesellschaft
J Manfred Reimer Grundlagen der Numerischen Mathematik II Studienbuch für Studenten der Mathematik, Informatik, Statistik und aller Naturwissenschaften Mit 29 Abbildungen Akademische Verlagsgesellschaft
Aufgabenstellung: Explizite gewöhnliche Differentialgleichung 1. Ordnung mit Anfangsbedingung Gesucht ist eine Funktion y = y(x).
 I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
I Neunte Übungseinheit Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen erster Ordnung I. Gewöhnliche Differentialgleichungen erster Ordnung Aufgabenstellung: Explizite gewöhnliche
Euler-Approximation. Leonie van de Sandt. TU Dortmund Prof. Dr. Christine Müller. 5. Juni 2012
 Euler-Approximation Leonie van de Sandt TU Dortmund Prof. Dr. Christine Müller 5. Juni 2012 Leonie van de Sandt (TU Dortmund) Euler-Approximation 5. Juni 2012 1 / 26 Inhaltsverzeichnis 1 Einleitung Leonie
Euler-Approximation Leonie van de Sandt TU Dortmund Prof. Dr. Christine Müller 5. Juni 2012 Leonie van de Sandt (TU Dortmund) Euler-Approximation 5. Juni 2012 1 / 26 Inhaltsverzeichnis 1 Einleitung Leonie
1 Nicht-lineare dynamische Systeme
 1 Nicht-lineare dynamische Systeme 1.1 Charakteristika linerarer Systeme Superpositionsprinzip: Sind x 1 und x Lösungen eines linearen Systems, dann ist auch α 1 x 1 + α x eine Lösung. Berühmte Beispiele:
1 Nicht-lineare dynamische Systeme 1.1 Charakteristika linerarer Systeme Superpositionsprinzip: Sind x 1 und x Lösungen eines linearen Systems, dann ist auch α 1 x 1 + α x eine Lösung. Berühmte Beispiele:
Numerik gewöhnlicher Differentialgleichungen
 Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2016/17 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
Numerik gewöhnlicher Differentialgleichungen Oliver Ernst Professur Numerische Mathematik Wintersemester 2016/17 Inhalt I 1 Einleitung 1.1 Volterras Prinzip 1.2 Begriffe und theoretische Resultate 1.3
Numerische Verfahren für gewöhnliche Differentialgleichungen
 Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Numerische Verfahren für gewöhnliche Differentialgleichungen. Einschrittverfahren I: Einfache Verfahren. Konvergenzordnung. Einschrittverfahren II: Runge Kutta Verfahren 4. Stabilität 5. Schrittweitensteuerung
Numerische Integration von Differential-Gleichungen Das klassische Runge-Kutta-Verfahren
 Numerische Integration von Differential-Gleichungen Das klassische Runge-Kutta-Verfahren Gegeben sei ein Anfangswertproblem erster Ordnung: y = f (x;y y(x 0 = y 0 Wie schon erörtert, beschreibt eine DGl
Numerische Integration von Differential-Gleichungen Das klassische Runge-Kutta-Verfahren Gegeben sei ein Anfangswertproblem erster Ordnung: y = f (x;y y(x 0 = y 0 Wie schon erörtert, beschreibt eine DGl
5 Numerische Mathematik
 6 5 Numerische Mathematik Die Numerische Mathematik setzt sich aus mehreren Einzelmodulen zusammen Für alle Studierenden ist das Modul Numerische Mathematik I: Grundlagen verpflichtend In diesem Modul
6 5 Numerische Mathematik Die Numerische Mathematik setzt sich aus mehreren Einzelmodulen zusammen Für alle Studierenden ist das Modul Numerische Mathematik I: Grundlagen verpflichtend In diesem Modul
Übungen zur Theoretischen Physik 2 Lösungen zu Blatt 1
 Prof.. Greiner, Dr. H. van Hees Sommersemester 214 Übungen zur Theoretischen Physi 2 Lösungen zu Blatt 1 Aufgabe 1: Differentialoperatoren der Vetoranalysis (a) Aus der Definition des Nabla-Operators folgt
Prof.. Greiner, Dr. H. van Hees Sommersemester 214 Übungen zur Theoretischen Physi 2 Lösungen zu Blatt 1 Aufgabe 1: Differentialoperatoren der Vetoranalysis (a) Aus der Definition des Nabla-Operators folgt
System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form:
 C7.5 Differentialgleichungen 1. Ordnung - Allgemeine Aussagen System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form: Kompaktnotation: Anfangsbedingung: Gesuchte Lösung: Gleichungen dieser Art
C7.5 Differentialgleichungen 1. Ordnung - Allgemeine Aussagen System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form: Kompaktnotation: Anfangsbedingung: Gesuchte Lösung: Gleichungen dieser Art
Diplom VP Numerik 28. August 2006
 Diplom VP Numerik 8. August 6 Multiple-Choice-Test Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese Aufgabe
Diplom VP Numerik 8. August 6 Multiple-Choice-Test Punkte) Bei jeder MC-Aufgabe ist mindestens eine Aussage korrekt. Wird dennoch bei einer MC-Aufgabe keine einzige Aussage angekreuzt, gilt diese Aufgabe
D-ITET, D-MATL. Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn
 Name: Wichtige Hinweise D-ITET, D-MATL Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn Prüfungsdauer: 90 Minuten. Nur begründete Resultate werden bewertet. Zugelassene Hilfsmittel: 10 A4-Seiten
Name: Wichtige Hinweise D-ITET, D-MATL Prüfung Numerische Methoden, Sommer 2012 Dr. Lars Kielhorn Prüfungsdauer: 90 Minuten. Nur begründete Resultate werden bewertet. Zugelassene Hilfsmittel: 10 A4-Seiten
Numerische Integration
 A1 Numerische Integration Einführendes Beispiel In einem Raum mit der Umgebungstemperatur T u = 21.7 C befindet sich eine Tasse heissen Kaffees mit der anfänglichen Temperatur T 0 80 C. Wie kühlt sich
A1 Numerische Integration Einführendes Beispiel In einem Raum mit der Umgebungstemperatur T u = 21.7 C befindet sich eine Tasse heissen Kaffees mit der anfänglichen Temperatur T 0 80 C. Wie kühlt sich
Exponentialabbildung für Matrizen und Systeme von Differentialgleichungen
 Proseminar Lineare Algebra SS10 Exponentialabbildung für Matrizen und Systeme von Differentialgleichungen Simon Strahlegger Heinrich-Heine-Universität Betreuung: Prof. Dr. Oleg Bogopolski Inhaltsverzeichnis:
Proseminar Lineare Algebra SS10 Exponentialabbildung für Matrizen und Systeme von Differentialgleichungen Simon Strahlegger Heinrich-Heine-Universität Betreuung: Prof. Dr. Oleg Bogopolski Inhaltsverzeichnis:
Differentialgleichungen
 Kapitel Differentialgleichungen Josef Leydold Mathematik für VW WS 05/6 Differentialgleichungen / Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen: () Erhöhung der
Kapitel Differentialgleichungen Josef Leydold Mathematik für VW WS 05/6 Differentialgleichungen / Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen: () Erhöhung der
Differentialgleichungen
 Kapitel 14 Differentialgleichungen Josef Leydold Mathematik für VW WS 2017/18 14 Differentialgleichungen 1 / 41 Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen:
Kapitel 14 Differentialgleichungen Josef Leydold Mathematik für VW WS 2017/18 14 Differentialgleichungen 1 / 41 Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen:
System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form:
 C7.5 Differentialgleichungen 1. Ordnung - Allgemeine Aussagen System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form: Kompaktnotation: Anfangsbedingung: Gesuchte Lösung: Gleichungen dieser Art
C7.5 Differentialgleichungen 1. Ordnung - Allgemeine Aussagen System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form: Kompaktnotation: Anfangsbedingung: Gesuchte Lösung: Gleichungen dieser Art
3. Berechnen Sie auch die Beschleunigung a als Funktion der Zeit t. 4. Erstellen Sie ein SIMULINK Modell, das x(t) numerisch berechnet.
 unit 1 / Seite 1 Einführung Differenzialgleichungen In physikalischen Anwendungen spielt oft eine Messgrösse in Abhängigkeit von der Zeit die Hauptrolle. Beispiele dafür sind Druck p, Temperatur T, Geschwindigkeit
unit 1 / Seite 1 Einführung Differenzialgleichungen In physikalischen Anwendungen spielt oft eine Messgrösse in Abhängigkeit von der Zeit die Hauptrolle. Beispiele dafür sind Druck p, Temperatur T, Geschwindigkeit
Numerik und Simulation in der Geoökologie
 1/49 Rekapitulation Das Euler-Verfahren für ODE-IVP Eigenschaften von Einschrittverfahren Numerik und Simulation in der Geoökologie Sylvia Moenickes VL 2 WS 2007/2008 2/49 Rekapitulation Das Euler-Verfahren
1/49 Rekapitulation Das Euler-Verfahren für ODE-IVP Eigenschaften von Einschrittverfahren Numerik und Simulation in der Geoökologie Sylvia Moenickes VL 2 WS 2007/2008 2/49 Rekapitulation Das Euler-Verfahren
Diese Fragen sollten Sie auch ohne Skript beantworten können: Was beschreibt der Differenzenquotient? Wie kann man sich die Steigung im vorstellen? Wa
 103 Diese Fragen sollten Sie auch ohne Skript beantworten können: Was beschreibt der Differenzenquotient? Wie kann man sich die Steigung im vorstellen? Was bedeutet das für die Ableitungen? Was ist eine
103 Diese Fragen sollten Sie auch ohne Skript beantworten können: Was beschreibt der Differenzenquotient? Wie kann man sich die Steigung im vorstellen? Was bedeutet das für die Ableitungen? Was ist eine
