GALILEO GALILEI: DIE GOLDWAAGE (IL SAGGIATORE) VON 1623
|
|
|
- Martin Pfeiffer
- vor 7 Jahren
- Abrufe
Transkript
1 MOTTO GALILEO GALILEI: DIE GOLDWAAGE (IL SAGGIATORE) VON 623 La filosofia è scritta in questo grandissimo libro che continuamente ci sta aperto innanzi a gli occhi (io dico l universo), ma non si può intendere se prima non s impara a intender la lingua, e conoscer i caratteri, ne quali è scritto. Egli è scritto in lingua matematica. Die Philosophie steht in jenem großen Buch geschrieben, das uns ständig offen vor Augen liegt (ich spreche vom Universum). Aber dieses Buch ist nicht zu verstehen, ehe man nicht gelernt hat, die Sprache zu verstehen, und die Buchstaben kennt, in denen es geschrieben ist. Es ist in der Sprache der Mathematik geschrieben.
2 Das ADAC-Projekt Gelbe Engel Und was hat das mit Mathematik zu tun? Jörg Rambau Konrad-Zuse-Zentrum für Informationstechnik Berlin Problemstellung Strategie Modellierung Algorithmus Ergebnis
3 PROBLEMSTELLUNG AUS DER SICHT DER PRAKTIKER
4 PROBLEMSTELLUNG AUS DER SICHT DER PRAKTIKER Team:
5 PROBLEMSTELLUNG AUS DER SICHT DER PRAKTIKER Team: S. O. Krumke, L. M. Torres, B. Hiller
6 PROBLEMSTELLUNG AUS DER SICHT DER PRAKTIKER Team: S. O. Krumke, L. M. Torres, B. Hiller System:
7 PROBLEMSTELLUNG AUS DER SICHT DER PRAKTIKER Team: S. O. Krumke, L. M. Torres, B. Hiller System:,500 Hilfefahrzeuge des ADAC
8 PROBLEMSTELLUNG AUS DER SICHT DER PRAKTIKER Team: S. O. Krumke, L. M. Torres, B. Hiller System:,500 Hilfefahrzeuge des ADAC 5,000 Service-Partner
9 PROBLEMSTELLUNG AUS DER SICHT DER PRAKTIKER Team: S. O. Krumke, L. M. Torres, B. Hiller System:,500 Hilfefahrzeuge des ADAC 5,000 Service-Partner 5 Hilfezentralen
10 PROBLEMSTELLUNG AUS DER SICHT DER PRAKTIKER Team: S. O. Krumke, L. M. Torres, B. Hiller System:,500 Hilfefahrzeuge des ADAC 5,000 Service-Partner 5 Hilfezentralen Aufgabe:
11 PROBLEMSTELLUNG AUS DER SICHT DER PRAKTIKER Team: S. O. Krumke, L. M. Torres, B. Hiller System:,500 Hilfefahrzeuge des ADAC 5,000 Service-Partner 5 Hilfezentralen Aufgabe: Auftrag Hilfefahrzeug,
12 PROBLEMSTELLUNG AUS DER SICHT DER PRAKTIKER Team: S. O. Krumke, L. M. Torres, B. Hiller System:,500 Hilfefahrzeuge des ADAC 5,000 Service-Partner 5 Hilfezentralen Aufgabe: Auftrag Hilfefahrzeug, Hilfefahrzeug Tour
13 PROBLEMSTELLUNG AUS DER SICHT DER PRAKTIKER Team: S. O. Krumke, L. M. Torres, B. Hiller System:,500 Hilfefahrzeuge des ADAC 5,000 Service-Partner 5 Hilfezentralen Aufgabe: Auftrag Hilfefahrzeug, Hilfefahrzeug Tour Minimiere Betriebskosten plus Verspätungskosten
14 PROBLEMSTELLUNG AUS DER SICHT DER PRAKTIKER Team: S. O. Krumke, L. M. Torres, B. Hiller System:,500 Hilfefahrzeuge des ADAC 5,000 Service-Partner 5 Hilfezentralen Aufgabe: Auftrag Hilfefahrzeug, Hilfefahrzeug Tour Minimiere Betriebskosten plus Verspätungskosten Online:
15 PROBLEMSTELLUNG AUS DER SICHT DER PRAKTIKER Team: S. O. Krumke, L. M. Torres, B. Hiller System:,500 Hilfefahrzeuge des ADAC 5,000 Service-Partner 5 Hilfezentralen Aufgabe: Auftrag Hilfefahrzeug, Hilfefahrzeug Tour Minimiere Betriebskosten plus Verspätungskosten Online: Zukünftige Aufträge unbekannt
16 PROBLEMSTELLUNG AUS DER SICHT DER PRAKTIKER Team: S. O. Krumke, L. M. Torres, B. Hiller System:,500 Hilfefahrzeuge des ADAC 5,000 Service-Partner 5 Hilfezentralen Aufgabe: Auftrag Hilfefahrzeug, Hilfefahrzeug Tour Minimiere Betriebskosten plus Verspätungskosten Online: Zukünftige Aufträge unbekannt Echtzeit:
17 PROBLEMSTELLUNG AUS DER SICHT DER PRAKTIKER Team: S. O. Krumke, L. M. Torres, B. Hiller System:,500 Hilfefahrzeuge des ADAC 5,000 Service-Partner 5 Hilfezentralen Aufgabe: Auftrag Hilfefahrzeug, Hilfefahrzeug Tour Minimiere Betriebskosten plus Verspätungskosten Online: Zukünftige Aufträge unbekannt Echtzeit: Antwortzeit 5s (Telefonat)
18 PROBLEMSTELLUNG AUS DER SICHT DER PRAKTIKER Team: S. O. Krumke, L. M. Torres, B. Hiller System:,500 Hilfefahrzeuge des ADAC 5,000 Service-Partner 5 Hilfezentralen Aufgabe: Auftrag Hilfefahrzeug, Hilfefahrzeug Tour Minimiere Betriebskosten plus Verspätungskosten Online: Zukünftige Aufträge unbekannt Echtzeit: Antwortzeit 5s (Telefonat) Bislang:
19 PROBLEMSTELLUNG AUS DER SICHT DER PRAKTIKER Team: S. O. Krumke, L. M. Torres, B. Hiller System:,500 Hilfefahrzeuge des ADAC 5,000 Service-Partner 5 Hilfezentralen Aufgabe: Auftrag Hilfefahrzeug, Hilfefahrzeug Tour Minimiere Betriebskosten plus Verspätungskosten Online: Zukünftige Aufträge unbekannt Echtzeit: Antwortzeit 5s (Telefonat) Bislang: Geographische Zerlegung
20 PROBLEMSTELLUNG AUS DER SICHT DER PRAKTIKER Team: S. O. Krumke, L. M. Torres, B. Hiller System:,500 Hilfefahrzeuge des ADAC 5,000 Service-Partner 5 Hilfezentralen Aufgabe: Auftrag Hilfefahrzeug, Hilfefahrzeug Tour Minimiere Betriebskosten plus Verspätungskosten Online: Zukünftige Aufträge unbekannt Echtzeit: Antwortzeit 5s (Telefonat) Bislang: Geographische Zerlegung Manuelles Dispatchen
21 PROBLEMSTELLUNG DIE MATHEMATISCHE SICHT: DAS DVDP
22 PROBLEMSTELLUNG DIE MATHEMATISCHE SICHT: DAS DVDP ADAC ADAC 2 ADAC-Einsatzmittel mit Heimatposition Vertragspartner 2
23 PROBLEMSTELLUNG DIE MATHEMATISCHE SICHT: DAS DVDP ADAC ADAC 2 Eine neue Panne. 2
24 PROBLEMSTELLUNG DIE MATHEMATISCHE SICHT: DAS DVDP ADAC ADAC 2 Zuweisung. 2
25 PROBLEMSTELLUNG DIE MATHEMATISCHE SICHT: DAS DVDP ADAC ADAC 2 Eine weitere Panne. 2
26 PROBLEMSTELLUNG DIE MATHEMATISCHE SICHT: DAS DVDP ADAC ADAC 2 Zuweisung. 2
27 PROBLEMSTELLUNG DIE MATHEMATISCHE SICHT: DAS DVDP ADAC ADAC 2 Noch eine Panne. 2
28 PROBLEMSTELLUNG DIE MATHEMATISCHE SICHT: DAS DVDP ADAC ADAC 2 Ändern der Zuweisung möglich. 2
29 PROBLEMSTELLUNG DIE MATHEMATISCHE SICHT: DAS DVDP ADAC ADAC 2 Und noch eine Panne. 2
30 PROBLEMSTELLUNG DIE MATHEMATISCHE SICHT: DAS DVDP ADAC ADAC 2 Aufträge können zu festen Kosten auch an Vertragspartner vergeben werden. 2
31 PROBLEMSTELLUNG DIE MATHEMATISCHE SICHT: DAS DVDP ADAC Panne behoben. ADAC 2 2
32 PROBLEMSTELLUNG DIE MATHEMATISCHE SICHT: DAS DVDP ADAC ADAC 2 Nächste Panne behoben. Keine Kapazitätsrestriktionen für Partner. 2
33 PROBLEMSTELLUNG DIE MATHEMATISCHE SICHT: DAS DVDP ADAC Zu spät! Aufträge haben ein weiches Zeitfenster. ADAC 2 2
34 PROBLEMSTELLUNG DIE MATHEMATISCHE SICHT: DAS DVDP ADAC Zu spät! Panne behoben. ADAC 2 2
35 PROBLEMSTELLUNG DIE MATHEMATISCHE SICHT: DAS DVDP ADAC Verspätungskosten Verspätungen bedeuten Kosten. ADAC 2 2
36 PROBLEMSTELLUNG DIE MATHEMATISCHE SICHT: DAS DVDP Verspätungskosten Gesamtkosten: ADAC ADAC 2 2
37 PROBLEMSTELLUNG DIE MATHEMATISCHE SICHT: DAS DVDP Verspätungskosten ADAC Gesamtkosten: Fahren, Überstunden, Verspätung, Partner. ADAC 2 2
38 STRATEGIE SCHNAPPSCHUSSOPTIMIERUNG: REPLAN
39 STRATEGIE SCHNAPPSCHUSSOPTIMIERUNG: REPLAN ADAC ADAC 2 Prinzip: Zu jedem Zeitpunkt existiert ein optimaler Plan für die bekannten Aufträge 2
40 STRATEGIE SCHNAPPSCHUSSOPTIMIERUNG: REPLAN ADAC ADAC 2 Bei jedem neuen Auftrag... 2
41 STRATEGIE SCHNAPPSCHUSSOPTIMIERUNG: REPLAN ADAC ADAC 2... wird ein neuer optimaler Plan berechnet. 2
42 STRATEGIE SCHNAPPSCHUSSOPTIMIERUNG: REPLAN ADAC ADAC 2 Durchgezogene Bögen symbolisieren unwiderrufliche Entscheidungen 2
43 STRATEGIE SCHNAPPSCHUSSOPTIMIERUNG: REPLAN ADAC ADAC 2 Ein neuer momentan optimaler Plan. 2
44 STRATEGIE SCHNAPPSCHUSSOPTIMIERUNG: REPLAN ADAC ADAC 2 Die nächste Panne. 2
45 STRATEGIE SCHNAPPSCHUSSOPTIMIERUNG: REPLAN ADAC ADAC 2 Der nächste Plan. 2
46 STRATEGIE SCHNAPPSCHUSSOPTIMIERUNG: REPLAN ADAC ADAC 2 Weitere Pannen... 2
47 STRATEGIE SCHNAPPSCHUSSOPTIMIERUNG: REPLAN ADAC Verspätung ADAC 2... und der momentan beste Plan, etc. 2
48 STRATEGIE SCHNAPPSCHUSSOPTIMIERUNG: REPLAN ADAC Verspätung... und der momentan beste Plan, etc. ADAC 2 Aufgabe: 2
49 STRATEGIE SCHNAPPSCHUSSOPTIMIERUNG: REPLAN ADAC Verspätung ADAC 2... und der momentan beste Plan, etc. Aufgabe: Berechne optimalen Plan in Echtzeit. 2
50 STRATEGIE SCHNAPPSCHUSSOPTIMIERUNG: REPLAN ADAC Verspätung ADAC und der momentan beste Plan, etc. Aufgabe: Berechne optimalen Plan in Echtzeit. Gesucht:
51 STRATEGIE SCHNAPPSCHUSSOPTIMIERUNG: REPLAN ADAC... und der momentan beste Plan, etc. Verspätung ADAC 2 2 Aufgabe: Berechne optimalen Plan in Echtzeit. Gesucht: Schnelles Offline-Optimierungsmodul für das VDP Fahrzeugeinsatzplanung mit weichen Zeitfenstern
52 EXKURS: DAS HANDLUNGSREISENDENPROBLEM (TSP) OHNE ZEITFENSTER
53 EXKURS: DAS HANDLUNGSREISENDENPROBLEM (TSP) OHNE ZEITFENSTER ADAC ADAC 2 Aus dem VDP erzeugen wir... 2
54 EXKURS: DAS HANDLUNGSREISENDENPROBLEM (TSP) OHNE ZEITFENSTER ADAC ADAC 2... durch Weglassen der Partner... 2
55 EXKURS: DAS HANDLUNGSREISENDENPROBLEM (TSP) OHNE ZEITFENSTER ADAC... und Beschränkung auf ein Fahrzeug...
56 EXKURS: DAS HANDLUNGSREISENDENPROBLEM (TSP) OHNE ZEITFENSTER... auf seiner Heimatposition... ADAC
57 EXKURS: DAS HANDLUNGSREISENDENPROBLEM (TSP) OHNE ZEITFENSTER... das berühmte TSP Traveling Saleman Problem Finde kürzeste Rundreise durch alle Städte!
58 EXKURS: DAS HANDLUNGSREISENDENPROBLEM (TSP) OHNE ZEITFENSTER 0km... das berühmte TSP Traveling Saleman Problem Finde kürzeste Rundreise durch alle Städte! Entfernungen symmetrisch
59 EXKURS: DAS HANDLUNGSREISENDENPROBLEM (TSP) OHNE ZEITFENSTER 0km 20km... das berühmte TSP Traveling Saleman Problem Finde kürzeste Rundreise durch alle Städte! Entfernungen symmetrisch durch Pfeile mit Bewertungen symbolisiert
60 EXKURS: DAS HANDLUNGSREISENDENPROBLEM (TSP) OHNE ZEITFENSTER... das berühmte TSP Traveling Saleman Problem Finde kürzeste Rundreise durch alle Städte! Entfernungen symmetrisch durch Pfeile mit Gewichten symbolisiert für jedes Paar von Städten.
61 EXKURS: DAS HANDLUNGSREISENDENPROBLEM (TSP) OHNE ZEITFENSTER Aufträge, Städte, Tische, Stühle egal:
62 EXKURS: DAS HANDLUNGSREISENDENPROBLEM (TSP) OHNE ZEITFENSTER Mathematiker malen Punkte und nennen sie Knoten i V;
63 EXKURS: DAS HANDLUNGSREISENDENPROBLEM (TSP) OHNE ZEITFENSTER Mathematiker malen Punkte 23 und nennen sie Knoten i V; 26 2 die Verbindungen heißen 2 Kanten e = {i, j} E;
64 EXKURS: DAS HANDLUNGSREISENDENPROBLEM (TSP) OHNE ZEITFENSTER 5 4 w(45) w(46) w(4) w(56) w(5) 6 w(34) w(35) w(36) w(3) w(2) w(6) 3 w(23) w(24) w(25) w(26) 2 Mathematiker malen Punkte und nennen sie Knoten i V; die Verbindungen heißen Kanten e = {i, j} E; die Entfernungen werden zu Bewertungen w : E R;
65 EXKURS: DAS HANDLUNGSREISENDENPROBLEM (TSP) OHNE ZEITFENSTER 5 4 w(45) w(46) w(4) w(56) w(5) 6 w(34) w(35) w(36) w(3) w(2) w(6) 3 w(23) w(24) w(25) w(26) 2 Mathematiker malen Punkte und nennen sie Knoten i V; die Verbindungen heißen Kanten e = {i, j} E; die Entfernungen werden zu Bewertungen w : E R; das ganze heißt bewerteter Graph (V, E, w) oder Netzwerk
66 EXKURS: DAS HANDLUNGSREISENDENPROBLEM (TSP) OHNE ZEITFENSTER Eine gültige Tour kann eindeutig durch eine Teilmenge der möglichen Kanten beschrieben werden.
67 EXKURS: DAS HANDLUNGSREISENDENPROBLEM (TSP) OHNE ZEITFENSTER Eine optimale Tour entspricht einer Menge von Kanten mit minimaler Bewertungssumme.
68 EXKURS: WELCHE KANTENMENGEN ENTSPRECHEN TOUREN?
69 EXKURS: WELCHE KANTENMENGEN ENTSPRECHEN TOUREN?
70 EXKURS: WELCHE KANTENMENGEN ENTSPRECHEN TOUREN? F }{{} Kantenteilmenge
71 EXKURS: WELCHE KANTENMENGEN ENTSPRECHEN TOUREN? F }{{} Kantenteilmenge
72 EXKURS: WELCHE KANTENMENGEN ENTSPRECHEN TOUREN? F }{{} Kantenteilmenge x F,2. x F n,n }{{} Inzidenzvektor
73 EXKURS: WELCHE KANTENMENGEN ENTSPRECHEN TOUREN? F }{{} Kantenteilmenge x F,2. x F n,n }{{} Inzidenzvektor mit der Bedeutung x F ij = { 0 wenn {i, j} / F wenn {i, j} F.
74 EXKURS: WELCHE KANTENMENGEN ENTSPRECHEN TOUREN? F }{{} Kantenteilmenge x F,2. x F n,n }{{} Inzidenzvektor mit der Bedeutung x F ij = { 0 wenn {i, j} / F wenn {i, j} F.
75 EXKURS: WELCHE KANTENMENGEN ENTSPRECHEN TOUREN? F }{{} Kantenteilmenge x F,2. x F n,n }{{} Inzidenzvektor mit der Bedeutung x F ij = { 0 wenn {i, j} / F wenn {i, j} F. 0 0 Modellierungsaufgabe: Welche 0--Vektoren entsprechen einer gültigen Tour?
76 EXKURS: WELCHE KANTENMENGEN ENTSPRECHEN TOUREN? Kein Knoten in einer Tour liegt in drei oder mehr Kanten.
77 EXKURS: WELCHE KANTENMENGEN ENTSPRECHEN TOUREN? Kein Knoten in einer Tour liegt in weniger als zwei Kanten.
78 EXKURS: WELCHE KANTENMENGEN ENTSPRECHEN TOUREN? In jedem Knoten enden genau zwei Kanten.
79 EXKURS: WELCHE KANTENMENGEN ENTSPRECHEN TOUREN? In jedem Knoten enden genau zwei Kanten.
80 EXKURS: WELCHE KANTENMENGEN ENTSPRECHEN TOUREN? In jedem Knoten enden genau zwei Kanten.
81 EXKURS: WELCHE KANTENMENGEN ENTSPRECHEN TOUREN? In jedem Knoten enden genau zwei Kanten.
82 EXKURS: WELCHE KANTENMENGEN ENTSPRECHEN TOUREN? In jedem Knoten enden genau zwei Kanten.
83 EXKURS: WELCHE KANTENMENGEN ENTSPRECHEN TOUREN? In jedem Knoten enden genau zwei Kanten.
84 EXKURS: WELCHE KANTENMENGEN ENTSPRECHEN TOUREN? In jedem Knoten enden genau zwei Kanten. Bedingung für Inzidenzvektoren: j:{i,j} E x F i,j = 2 i V
85 EXKURS: WELCHE KANTENMENGEN ENTSPRECHEN TOUREN? Es gibt keine geschlossenen Touren mit weniger als n Knoten.
86 EXKURS: WELCHE KANTENMENGEN ENTSPRECHEN TOUREN? Für jeden Teilgraphen enthält jede Tour mindestens eine Kante, die den Teilgraphen verläßt.
87 EXKURS: WELCHE KANTENMENGEN ENTSPRECHEN TOUREN? 0 Für jeden Teilgraphen enthält jede Tour mindestens eine Kante, die den Teilgraphen verläßt. Bedingung für Inzidenzvektoren: 0 i W j V\W x F i,j W V W V, W
88 EXKURS: WELCHE KANTENMENGEN ENTSPRECHEN TOUREN? ( n2 ) Ein 0--Vektor x {0, } entpricht genau dann einer gültigen Tour, wenn: x i,j = 2 i V j:{i,j} E i W j V\W x i,j W V W V, W Ganzzahliges lineares Programm (ILP)
89 EXKURS: WELTREKORD
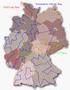
90 EXKURS: WELTREKORD Eine bewiesen optimale Tour durch 5.2 deutsche Städte [Applegate, Bixby, Chvàtal, Cook]
91 EXKURS: WELTREKORD Eine bewiesen optimale Tour durch 5.2 deutsche Städte [Applegate, Bixby, Chvàtal, Cook] Es gibt etwa verschiedene Touren.
92 EXKURS: WELTREKORD Eine bewiesen optimale Tour durch 5.2 deutsche Städte [Applegate, Bixby, Chvàtal, Cook] Es gibt etwa verschiedene Touren. Durch Mathematik: keine kann kürzer sein als die Tour rechts!
93 ZURÜCK ZUM ADAC: EIN BOGENBASIERTES ILP
94 ZURÜCK ZUM ADAC: EIN BOGENBASIERTES ILP j x(,i,j) i t(,j) l x(,o(),i) T(,i) ADAC x(,o(),d()) ADAC 2 x(2,o(2),k) k Modell mit Bogenvariablen und Zeitvariablen x(2,l,m) m y(,k) 2
95 ZURÜCK ZUM ADAC: EIN BOGENBASIERTES ILP j x(,i,j) i t(,j) l x(,o(),i) T(,i) ADAC x(,o(),d()) ADAC 2 x(2,o(2),k) k Fahrzeug bearbeitet Auftrag j direkt nach i. x(2,l,m) m y(,k) 2
96 ZURÜCK ZUM ADAC: EIN BOGENBASIERTES ILP j x(,i,j) i t(,j) l x(,o(),i) T(,i) ADAC x(,o(),d()) ADAC 2 x(2,o(2),k) k Abfahrtzeit von Fahrzeug von Auftrag i. x(2,l,m) m y(,k) 2
97 ZURÜCK ZUM ADAC: EIN BOGENBASIERTES ILP j x(,i,j) i t(,j) l x(,o(),i) T(,i) ADAC x(,o(),d()) ADAC 2 x(2,o(2),k) k Ankunftszeit von Fahrzeug bei Auftrag j. x(2,l,m) m y(,k) 2
98 ZURÜCK ZUM ADAC: EIN BOGENBASIERTES ILP j x(,i,j) i t(,j) l x(,o(),i) T(,i) ADAC x(,o(),d()) ADAC 2 x(2,o(2),k) k Fahrzeug bearbeitet Auftrag i zuerst. x(2,l,m) m y(,k) 2
99 ZURÜCK ZUM ADAC: EIN BOGENBASIERTES ILP j x(,i,j) i t(,j) l x(,o(),i) T(,i) ADAC x(,o(),d()) ADAC 2 x(2,o(2),k) k Fahrzeug fährt direkt nach Hause. x(2,l,m) m y(,k) 2
100 ZURÜCK ZUM ADAC: EIN BOGENBASIERTES ILP j x(,i,j) i t(,j) l x(,o(),i) T(,i) ADAC x(,o(),d()) ADAC 2 x(2,o(2),k) k Vertragspartner bekommt Auftrag k. x(2,l,m) m y(,k) 2
101 ZURÜCK ZUM ADAC: EIN BOGENBASIERTES ILP j x(,i,j)= i x(,j,l)= l x(,l,d())= x(,o(),i)= ADAC ADAC 2 x(2,o(2),k)= x(2,k,d(2))= m y(,m)= 2 k Zulässige Lösung: Gefärbte Bogenmenge, die einer Tourzerlegung entspricht. O. B. d. A.: Bögen Zeiten.
102 ZURÜCK ZUM ADAC: EIN BOGENBASIERTES ILP j x(,j,l)= l x(,l,d())= x(,i,j)= m ADAC i x(,o(),i)= ADAC 2 x(2,o(2),k)= y(,m)= 2 k x(2,k,d(2))= Vereinfachung:. keine Partner a δ (v) ( ) min(c T, w T xy ) x u,a a δ + (o u ) a δ (d u ) a δ + (v) s.t. x u,a = u U (Flußquelle) x u,a = u U (Flußsenke) x u,a = 0 v V(D), u U (Flußerhaltung) T ou 0 u U (Startzeit) T v t v s v v V(D) (Servicezeit) T v e v + s v v V(D) (Freigabe) y v t v l v v V(D) (Verspätung) y v 0 v V(D) (Verspätung) t j T i dist(i, j) + M( x (i,j) ) 0 (i, j) A( D), u U (Zeit-Bogen-Kopplung) x u,a = v V(D) (Partitionierung) u U a δ (v) x u,a {0, } a A(D), u U (Binärvariablen)
103 ZURÜCK ZUM ADAC: EIN BOGENBASIERTES ILP j x(,j,l)= l x(,l,d())= x(,i,j)= m ADAC i x(,o(),i)= ADAC 2 x(2,o(2),k)= y(,m)= 2 k x(2,k,d(2))= Vereinfachung:. keine Partner a δ (v) ( ) min(c T, w T xy ) x u,a a δ + (o u ) a δ (d u ) a δ + (v) s.t. x u,a = u U (Flußquelle) x u,a = u U (Flußsenke) x u,a = 0 v V(D), u U (Flußerhaltung) T ou 0 u U (Startzeit) T v t v s v v V(D) (Servicezeit) T v e v + s v v V(D) (Freigabe) y v t v l v v V(D) (Verspätung) y v 0 v V(D) (Verspätung) t j T i dist(i, j) + M( x (i,j) ) 0 (i, j) A( D), u U (Zeit-Bogen-Kopplung) x u,a = v V(D) (Partitionierung) u U a δ (v) x u,a {0, } a A(D), u U (Binärvariablen)
104 ZURÜCK ZUM ADAC: EIN BOGENBASIERTES ILP j x(,j,l)= l x(,l,d())= x(,i,j)= m ADAC i x(,o(),i)= ADAC 2 x(2,o(2),k)= y(,m)= 2 k x(2,k,d(2))= Vereinfachung:. keine Partner 2. fraktionale x a δ (v) ( ) min(c T, w T xy ) x u,a a δ + (o u ) a δ (d u ) a δ + (v) s.t. x u,a = u U (Flußquelle) x u,a = u U (Flußsenke) x u,a = 0 v V(D), u U (Flußerhaltung) T ou 0 u U (Startzeit) T v t v s v v V(D) (Servicezeit) T v e v + s v v V(D) (Freigabe) y v t v l v v V(D) (Verspätung) y v 0 v V(D) (Verspätung) t j T i dist(i, j) + M( x (i,j) ) 0 (i, j) A( D), u U (Zeit-Bogen-Kopplung) x u,a = v V(D) (Partitionierung) u U a δ (v) x u,a [0, ] a A(D), u U (LP-Relaxierung)
105 ZURÜCK ZUM ADAC: EIN BOGENBASIERTES ILP j x(,j,l)= l x(,l,d())= x(,i,j)= m ADAC i x(,o(),i)= ADAC 2 x(2,o(2),k)= y(,m)= 2 k x(2,k,d(2))= Vereinfachung:. keine Partner 2. fraktionale x a δ (v) ( ) min(c T, w T xy ) x u,a a δ + (o u ) a δ (d u ) a δ + (v) s.t. x u,a = u U (Flußquelle) x u,a = u U (Flußsenke) x u,a = 0 v V(D), u U (Flußerhaltung) T ou 0 u U (Startzeit) T v t v s v v V(D) (Servicezeit) T v e v + s v v V(D) (Freigabe) y v t v l v v V(D) (Verspätung) y v 0 v V(D) (Verspätung) t j T i dist(i, j) + M( x (i,j) ) 0 (i, j) A( D), u U (Zeit-Bogen-Kopplung) x u,a = v V(D) (Partitionierung) u U a δ (v) x u,a [0, ] a A(D), u U (LP-Relaxierung)
106 EIN TOURBASIERTES ILP
107 EIN TOURBASIERTES ILP x(,t) ADAC y(,s) ADAC 2 x(2,t ) 2 Modell mit Tourvariablen für Fahrzeuge und Partner.
108 EIN TOURBASIERTES ILP x(,t) ADAC ADAC 2 Fahrzeug fährt Tour T. y(,s) x(2,t ) 2
109 EIN TOURBASIERTES ILP x(,t) ADAC ADAC 2 Vertragspartner bekommt Aufträge S. y(,s) x(2,t ) 2
110 EIN TOURBASIERTES ILP x(,t) ADAC y(,s) ADAC 2 x(2,t ) 2 Zulässige Lösung: Zerlegung der Aufträge in Touren.
111 EIN TOURBASIERTES ILP x(,t) ADAC y(,s) ADAC 2 x(2,t ) Vereinfachung: keine Partner 2 min c T x s.t. a vt x T = v V(D) (Partitionierung Aufträge) T T T T u x T = u U (Partitionierung Fahrzeuge) x T {0, } T T (Binärvariablen)
112 EIN TOURBASIERTES ILP x(,t) ADAC y(,s) ADAC 2 x(2,t ) Vereinfachung: keine Partner 2 min c T x s.t. a vt x T = v V(D) (Partitionierung Aufträge) T T T T u x T = u U (Partitionierung Fahrzeuge) x T {0, } T T (Binärvariablen) PROBLEM: IN DER PRAXIS VARIABLEN.
113 ALGORITHMUS DYNAMISCHE SPALTENGENERIERUNG
114 ALGORITHMUS DYNAMISCHE SPALTENGENERIERUNG PRICING-PRINZIP: STARTE MIT WENIGEN TOUREN, KONSTRUIERE NACH UND NACH NEUE CHANCENREICHE TOUREN DURCH ZUWEISUNG VON SCHATTENPREISEN ZU AUFTRÄGEN BIS OPTIMALITÄTSKRITERIUM ERFÜLLT
115 ERGEBNIS ECHTZEIT-OPTIMIERUNG MÖGLICH!
116 ERGEBNIS ECHTZEIT-OPTIMIERUNG MÖGLICH! IN DER PRAXIS: EINSATZPLANUNG MIT 200 AUFTRÄGEN UND 00 FAHRZEUGEN I. D. R. BEWIESEN OPTIMAL GELÖST IN s. ILP WIRD DURCH BRANCH&BOUND I. D. R. MIT % OPTIMALITÄTSLÜCKE GELÖST. QUALITÄTSGARANTIE DURCH OPTIMALWERT DER LP-RELAXIERUNG.
117 ERGEBNIS ECHTZEIT-OPTIMIERUNG MÖGLICH! IN DER PRAXIS: EINSATZPLANUNG MIT 200 AUFTRÄGEN UND 00 FAHRZEUGEN I. D. R. BEWIESEN OPTIMAL GELÖST IN s. ILP WIRD DURCH BRANCH&BOUND I. D. R. MIT % OPTIMALITÄTSLÜCKE GELÖST. QUALITÄTSGARANTIE DURCH OPTIMALWERT DER LP-RELAXIERUNG. Kommerzielle Nachimplementierung im Pilotbetrieb beim ADAC
118 ERGEBNIS ECHTZEIT-OPTIMIERUNG MÖGLICH! IN DER PRAXIS: EINSATZPLANUNG MIT 200 AUFTRÄGEN UND 00 FAHRZEUGEN I. D. R. BEWIESEN OPTIMAL GELÖST IN s. ILP WIRD DURCH BRANCH&BOUND I. D. R. MIT % OPTIMALITÄTSLÜCKE GELÖST. QUALITÄTSGARANTIE DURCH OPTIMALWERT DER LP-RELAXIERUNG. Kommerzielle Nachimplementierung im Pilotbetrieb beim ADAC Fortlaufende Modellanpassungen steigern Praxistauglichkeit
119 ERGEBNIS FAZIT
120 ERGEBNIS FAZIT GALILEI HATTE RECHT: ERFOLG UNDENKBAR OHNE MATHEMATISCHE MODELLIERUNG!
121 ERGEBNIS FAZIT GALILEI HATTE RECHT: ERFOLG UNDENKBAR OHNE MATHEMATISCHE MODELLIERUNG! DFG-FORSCHUNGSZENTRUM MATHEMATIK FÜR SCHLÜSSELTECHNOLOGIEN : MODELLIERUNG, SIMULATION UND OPTIMIERUNG REALER PROZESSE
»La filosofia è scritta in questo grandissimo libro che continuamente ci sta aperto innanzi a
MOTTO GALILEO GALILEI: DIE GOLDWAAGE (IL SAGGIATORE) VON 623»La filosofia è scritta in questo grandissimo libro che continuamente ci sta aperto innanzi a gli occhi (io dico l universo), ma non si può intendere
Das Multi Traveling Salesman Problem
Das Multi Traveling Salesman Problem Harald Voit Seminar Ganzzahlige Optimierung 19. bis 21. Januar 2007 Wallenfels Das Multi Traveling Salesman Problem p.1/26 Übersicht Vom TSP zum ATSP Das Multi Traveling
Aufgabe 1: Berechnen Sie für den in Abbildung 1 gegebenen Graphen den. Abbildung 1: Graph für Flussproblem in Übungsaufgabe 1
Lösungen zu den Übungsaufgaben im Kapitel 4 des Lehrbuches Operations Research Deterministische Modelle und Methoden von Stephan Dempe und Heiner Schreier Aufgabe 1: Berechnen Sie für den in Abbildung
3.4 Exakte Verfahren für (Gemischt-) Ganzzahlige Optimierung
32KAPITEL 3. NP-SCHWIERIGE KOMBINATORISCHE OPTIMIERUNGSPROBLEME n Anzahl der Ungleichungen 3 8 4 20 5 40 6 910 7 87.472 8 >488.602.996 Tabelle 3.1: Anzahl der Ungleichungen des LOP-Polytops für n 8 3.4
Kapitel 4. Optimierungsalgorithmen. Technische Universität Wien. Gunnar Klau Technische Universität Wien. Institut für Computergraphik und Algorithmen
Kapitel 4 Optimierungsalgorithmen Gunnar Klau Institut für Computergraphik und Algorithmen 1 Gliederung Kombinatorische vs. Ganzzahlige Optimierung Exakte Verfahren Branch-and-Bound Schnittebenenverfahren
Optimierung für Wirtschaftsinformatiker: Dualität, Ganzzahlige lineare Optimierung
Optimierung für Wirtschaftsinformatiker: Dualität, Ganzzahlige lineare Optimierung Dr. Nico Düvelmeyer Freitag, 24. Juni 2011 1: 1 [1,1] Inhaltsübersicht für heute 1 Dualität Motivation Duales LP Dualitätssätze
Wiederholung zu Flüssen
Universität Konstanz Methoden der Netzwerkanalyse Fachbereich Informatik & Informationswissenschaft SS 2008 Prof. Dr. Ulrik Brandes / Melanie Badent Wiederholung zu Flüssen Wir untersuchen Flüsse in Netzwerken:
Kap. 4: Das Handlungsreisendenproblem (TSP)
Kap. 4: Das Handlungsreisendenproblem (TSP) VO Algorithm Engineering Professor Dr. Petra Mutzel Lehrstuhl für Algorithm Engineering, LS11 7./8. VO 24./26. April 2007 Literatur Mutzel: Skript zu Branch
Kapitel 9: Lineare Programmierung Gliederung
Gliederung 1. Grundlagen 2. Zahlentheoretische Algorithmen 3. Sortierverfahren 4. Ausgewählte Datenstrukturen 5. Dynamisches Programmieren 6. Graphalgorithmen 7. String-Matching 8. Kombinatorische Algorithmen
6. Übung zur Linearen Optimierung SS08
6 Übung zur Linearen Optimierung SS08 1 Sei G = (V, E) ein schlichter ungerichteter Graph mit n Ecken und m Kanten Für eine Ecke v V heißt die Zahl der Kanten (u, v) E Grad der Ecke (a) Ist die Anzahl
Einführung in die Mathematik des Operations Research
Universität zu Köln Mathematisches Institut Prof. Dr. F. Vallentin Einführung in die Mathematik des Operations Research Sommersemester 3 en zur Klausur (7. Oktober 3) Aufgabe ( + 3 + 5 = Punkte). Es sei
Algorithmische Methoden zur Netzwerkanalyse Vorlesung 13, Henning Meyerhenke
Algorithmische Methoden zur Netzwerkanalyse Vorlesung 13, 01.02.2012 Henning Meyerhenke 1 KIT Henning Universität desmeyerhenke: Landes Baden-Württemberg und nationales Algorithmische Forschungszentrum
Optimierung. Optimierung. Vorlesung 9 Lineare Programmierung & Kombinatorische Optimierung Fabian Kuhn
Optimierung Vorlesung 9 Lineare Programmierung & Kombinatorische Optimierung 1 Assignment Problem (Zuordnungsproblem) Gewichtetes Perfektes Bipartites Matching agents Costs tasks Weise jedem Agenten genau
Toleranzbasierte Algorithmen für das Travelling Salesman Problem. Gerold Jäger
Toleranzbasierte Algorithmen für das Travelling Salesman Problem Gerold Jäger (Zusammenarbeit mit Jop Sibeyn, Boris Goldengorin) Institut für Informatik Martin-Luther-Universität Halle-Wittenberg gerold.jaeger@informatik.uni-halle.de
Gibt es in Königsberg einen Spaziergang, bei dem man jede der sieben Pregelbrücken genau einmal überquert?
Graphentheorie Gibt es in Königsberg einen Spaziergang, bei dem man jede der sieben Pregelbrücken genau einmal überquert? Königsberger Brückenproblem Gibt es in Königsberg einen Spaziergang, bei dem man
Theoretische Informatik 1
Theoretische Informatik 1 Approximierbarkeit David Kappel Institut für Grundlagen der Informationsverarbeitung Technische Universität Graz 10.06.2016 Übersicht Das Problem des Handelsreisenden TSP EUCLIDEAN-TSP
3.6 Branch-and-Bound-Verfahren
36 Branch-and-Bound-Verfahren Die Branch-and-Bound -Methode beruht darauf, auf eine intelligente Weise alle zulässigen Lösungen eines kombinatorischen Optimierungsproblems aufzulisten und mit Hilfe von
Optimierungsprobleme auf Graphen
21. April 2009 1 Routenplanung TSP Chinesisches Postbotenproblem 2 Stabile Mengen, Cliquen, Knotenüberdeckungen 3 Färbungsprobleme 4 Schnitt-Probleme 5 Standortprobleme 6 Lineare Anordnungen und azyklische
Überblick Kap. 5: Graph Coloring
Überblick Kap. 5: Graph Coloring Professor Dr. Petra Mutzel Lehrstuhl für Algorithm Engineering, LS11 10./11. VO 18.12.0 / 8.1.07 5.1 Einführung Definition und Motivation Sudoku 5.2 ILP-Formulierungen
Rundreisen Das Travelling-Salesman-Problem
Rundreisen Das Travelling-Salesman-Problem MS Wissenschaft Das Matheschiff Exponatentwicklung: DFG-Forschungszentrum Matheon Konrad-Zuse-Zentrum für Informationstechnik Berlin Im Folgenden werden optimale
Kap. 5: Graph Coloring
Kap. 5: Graph Coloring Professor Dr. Petra Mutzel Lehrstuhl für Algorithm Engineering, LS11 10./11. VO 18.12.06 / 8.1.07 Überblick 5.1 Einführung Definition und Motivation Sudoku 5.2 ILP-Formulierungen
Algorithmische Methoden für schwere Optimierungsprobleme
Algorithmische Methoden für schwere Optimierungsprobleme Prof. Dr. Henning Meyerhenke Institut für Theoretische Informatik 1 KIT Henning Universität desmeyerhenke, Landes Baden-Württemberg Institutund
Lineare Programmierung
Lineare Programmierung WS 2003/04 Rolle der Linearen Programmierung für das TSP 1954: Dantzig, Fulkerson & Johnson lösen das TSP für 49 US-Städte (ca. 6.2 10 60 mögliche Touren) 1998: 13.509 Städte in
Kapitel 7: Flüsse in Netzwerken und Anwendungen Gliederung der Vorlesung
Gliederung der Vorlesung. Fallstudie Bipartite Graphen. Grundbegriffe. Elementare Graphalgorithmen und Anwendungen. Minimal spannende Bäume. Kürzeste Pfade. Traveling Salesman Problem. Flüsse in Netzwerken
Das Linear Ordering Problem Exakte Lösungsverfahren. für NP-schwierige. VO Algorithm Engineering
Das Linear Ordering Problem Exakte Lösungsverfahren VO Algorithm Engineering für NP-schwierige Professor Dr. Petra Mutzel kombinatorische Lehrstuhl für Algorithm Engineering, LS11 Optimierungsprobleme
Optimierung für Nichtmathematiker
Optimierung für Nichtmathematiker Prof. Dr. R. Herzog WS2010/11 1 / 1 Teil IV Konvexe und ganzzahlige Optimierung Vorlesung 11 IV Konvexe und ganzzahlige Optimierung 2 / 34 Inhaltsübersicht 29Lineare Optimierung
Überblick. TSP Vergleich der Lösungen. Das Travelling Salesman Problem. Nearest-Neighbor Heuristik für TSP
Kap..1 Heuristiken Kap.. Approximative Algorithmen und Gütegarantien Professor Dr. Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 3. VO DAP SS 008 14. Juli 009 Überblick
Kap. 7.1 Heuristiken Kap. 7.2 Approximative Algorithmen und Gütegarantien
Kap. 7.1 Heuristiken Kap. 7.2 Approximative Algorithmen und Gütegarantien Professor Dr. Lehrstuhl für Algorithm Engineering, LS11 Fakultät für Informatik, TU Dortmund 23. VO DAP2 SS 2008 14. Juli 2009
Gibt es in Königsberg einen Spaziergang, bei dem man jede der. Pregelbrücken. überquert?
Graphentheorie Gibt es in Königsberg einen Spaziergang, bei dem man jede der sieben Pregelbrücken genau einmal überquert? 1 Königsberger Brückenproblem Im Jahre 1736 Leonhard Euler löste das Problem allgemein
2. Optimierungsprobleme 6
6 2. Beispiele... 7... 8 2.3 Konvexe Mengen und Funktionen... 9 2.4 Konvexe Optimierungsprobleme... 0 2. Beispiele 7- Ein (NP-)Optimierungsproblem P 0 ist wie folgt definiert Jede Instanz I P 0 hat einen
Heuristiken und exakte Algorithmen für das verallgemeinerte Traveling Salesman Problem. Gerold Jäger
Heuristiken und exakte Algorithmen für das verallgemeinerte Traveling Salesman Problem Gerold Jäger Martin-Luther-Universität Halle-Wittenberg (in Zusammenarbeit mit Paul Molitor) DFG-Projekt: Toleranzbasierte
Traveling Salesman Problem (TSP) Präsentation von Burku, Kienzerle, Stollnberger
Traveling Salesman Problem (TSP) Präsentation von Burku, Kienzerle, Stollnberger Inhalt Allgemeine Problembeschreibung Historie Mathematische Beschreibung Algorithmische Komplexität Beispiel Symmetrisches
Überblick. Kap. 1.4: Minimum Weight Perfect Matching. 1.3 Blüten-Schrumpf Algorithmus für Maximum Matching
Kap. 1.4: Minimum Weight Professor Dr. Petra Mutzel Lehrstuhl für Algorithm Engineering, LS11 4. VO 6. November 2006 Überblick kurze Wiederholung: 1.2 Blüten-Schrumpf-Algorithmus für Perfektes Matching
Theoretische Informatik. Exkurs: Komplexität von Optimierungsproblemen. Optimierungsprobleme. Optimierungsprobleme. Exkurs Optimierungsprobleme
Theoretische Informatik Exkurs Rainer Schrader Exkurs: Komplexität von n Institut für Informatik 13. Mai 2009 1 / 34 2 / 34 Gliederung Entscheidungs- und Approximationen und Gütegarantien zwei Greedy-Strategien
Approximationsalgorithmen für NP-harte Optimierungsprobleme
Approximationsalgorithmen für NP-harte Optimierungsprobleme Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 1 / 18 Was tun mit NP-harten Problemen? Viele praxisrelevante
Kapitel 5: Minimale spannende Bäume Gliederung der Vorlesung
Gliederung der Vorlesung 1. Grundbegriffe 2. Elementare Graphalgorithmen und Anwendungen 3. Kürzeste Wege. Minimale spannende Bäume. Färbungen und Cliquen. Traveling Salesman Problem. Flüsse in Netzwerken
Routing A lgorithmen Algorithmen Begriffe, Definitionen Wegewahl Verkehrslenkung
Begriffe, Definitionen Routing (aus der Informatik) Wegewahl oder Verkehrslenkung bezeichnet in der Telekommunikation das Festlegen von Wegen für Nachrichtenströme bei der Nachrichtenübermittlung über
Proseminar Online Algorithmen, Prof. Dr. Rolf Klein
Proseminar Online Algorithmen, Prof. Dr. Rolf Klein Vortrag von Michael Daumen am 13.12.2000 Thema : Minimum Spanning Tree und 2-Approximation der TSP-Tour Inhalt des Vortrags : 1. genaue Vorstellung des
Operations Research. Flüsse in Netzwerken. Flüsse in Netzwerken. Unimodularität. Rainer Schrader. 2. Juli Gliederung.
Operations Research Rainer Schrader Flüsse in Netzwerken Zentrum für Angewandte Informatik Köln 2. Juli 2007 1 / 53 2 / 53 Flüsse in Netzwerken Unimodularität Gliederung Netzwerke und Flüsse bipartite
Optimierung I. Dr. Ulf Lorenz F2.413
Optimierung I Dr. Ulf Lorenz F2.413 flulo@upb.de Organisation Dozent: Dr. Ulf Lorenz F2.413 Fürstenallee 11 email: flulo@upb.de WWW: http://www.upb.de/cs/flulo (hier auch aktuelle Infos + Ü-Zettel) Vorlesungen:
Der Branching-Operator B
Branching 1 / 17 Der Branching-Operator B Unser Ziel: Löse das allgemeine Minimierungsproblem minimiere f (x), so dass Lösung(x). B zerlegt eine Menge von Lösungen in disjunkte Teilmengen. Die wiederholte
Theoretische Grundlagen der Informatik
Theoretische Grundlagen der Informatik Vorlesung am 20. November 2014 INSTITUT FÜR THEORETISCHE 0 KIT 20.11.2014 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Konzentrische U-Bahn-Linienpläne
Bachelor-Kolloquium Konzentrische U-Bahn-Linienpläne Magnus Lechner 19.03.2014 Betreuer: Prof. Dr. Alexander Wolff Dipl.-Inf. Martin Fink Motivation Warum sind U-Bahn-Linienpläne von Interesse? Motivation
Routing Algorithmen. Begriffe, Definitionen
Begriffe, Definitionen Routing (aus der Informatik) Wegewahl oder Verkehrslenkung bezeichnet in der Telekommunikation das Festlegen von Wegen für Nachrichtenströme bei der Nachrichtenübermittlung über
Maximale s t-flüsse in Planaren Graphen
Maximale s t-flüsse in Planaren Graphen Vorlesung Algorithmen für planare Graphen 6. Juni 2017 Guido Brückner INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg
Bäume und Wälder. Definition 1
Bäume und Wälder Definition 1 Ein Baum ist ein zusammenhängender, kreisfreier Graph. Ein Wald ist ein Graph, dessen Zusammenhangskomponenten Bäume sind. Ein Knoten v eines Baums mit Grad deg(v) = 1 heißt
Kapitel 4: Minimal spannende Bäume Gliederung der Vorlesung
Kapitel : Minimal spannende Bäume Gliederung der Vorlesung. Fallstudie Bipartite Graphen 2. Grundbegriffe. Elementare Graphalgorithmen und Anwendungen. Minimal spannende Bäume. Kürzeste Wege. Traveling
Prüfungsklausur Operations Research,
HTWD, FB Informatik/Mathematik Prof. Dr. M. Voigt Prüfungsklausur Operations Research, 10.7.2008 A Name, Vorname Matr. Nr. Aufgabe 1 : In drei Porzellanwerken W 1, W 2 und W 3 werden Speiseservice hergestellt,
Das Prinzip der Suchmaschine Google TM
/9 Das Prinzip der Suchmaschine Google TM Numerische Mathematik WS 20/2 Basieren auf dem Paper The $25,000,000,000 Eigenvector: The Linear Algebra behind Google von Kurt Bryan und Tanya Leise (SIAM Review,
Kapitel 4: Minimale spannende Bäume Gliederung der Vorlesung
Kapitel : Minimale spannende Bäume Gliederung der Vorlesung. Grundbegriffe 2. Elementare Graphalgorithmen und Anwendungen. Kürzeste Wege. Minimale spannende Bäume. Färbungen und Cliquen. Traveling Salesman
Grundlagen der Informatik Kapitel 20. Harald Krottmaier Sven Havemann
Grundlagen der Informatik Kapitel 20 Harald Krottmaier Sven Havemann Agenda Klassen von Problemen Einige Probleme... Approximationsalgorithmen WS2007 2 Klassen P NP NP-vollständig WS2007 3 Klasse P praktisch
Bipartite Graphen. Beispiele
Bipartite Graphen Ein Graph G = (V, E) heiÿt bipartit (oder paar), wenn die Knotenmenge in zwei disjunkte Teilmengen zerfällt (V = S T mit S T = ), sodass jede Kante einen Knoten aus S mit einem Knoten
ADS: Algorithmen und Datenstrukturen 2
ADS: Algorithmen und Datenstrukturen 2 Teil 5 Prof. Peter F. Stadler & Dr. Christian Höner zu Siederdissen Bioinformatik/IZBI Institut für Informatik & Interdisziplinäres Zentrum für Bioinformatik Universität
KAPITEL 4 FLÜSSE IN NETZWERKEN
KAPITEL 4 FLÜSSE IN NETZWERKEN F. VALLENTIN, A. GUNDERT 1. Das Max-Flow-Min-Cut Theorem Es sei D = (V, A) ein gerichteter Graph, s, t V zwei Knoten. Wir nennen s Quelle und t Senke. Definition 1.1. Eine
Sandro Pirkwieser, (Bin Hu, Jakob Puchinger) SS 2010
Lösungsverfahren für Ganzzahlige Optimierung Sandro Pirkwieser, (Bin Hu, Jakob Puchinger) Fortgeschrittene Algorithmen und Datenstrukturen Arbeitsbereich für Algorithmen und Datenstrukturen Institut für
Kürzeste Wege in Graphen. Orte mit Straßenverbindungen. Coma I Rolf Möhring
Kürzeste Wege in Graphen Orte mit Straßenverbindungen Orte als Knoten eines Graphen Straßenverbindungen als Kanten eines Graphen Ungerichteter Graph G = (V,E) Kanten Knoten Knotenmenge V = {,,n} oder {,,n
Probleme aus NP und die polynomielle Reduktion
Probleme aus NP und die polynomielle Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 15. Dezember 2009 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
1 Matroide. 1.1 Definitionen und Beispiele. Seminar zur ganzzahligen Optimierung Thema: Durchschnitt von Matroiden - Satz von Edmonds von Dany Sattler
Seminar zur ganzzahligen Optimierung Thema: Durchschnitt von Matroiden - Satz von Edmonds von Dany Sattler 1 Matroide 1.1 Definitionen und Beispiele 1. Definition (Unabhängigkeitssystem): Ein Mengensystem
Inhalt. 1. Flußprobleme. 2. Matching. 3. Lineares Programmieren. 4. Ganzzahliges Programmieren. 5. NP-Vollständigkeit. 6. Approximationsalgorithmen
Effiziente Algorithmen Einführung 1 Inhalt 1. Flußprobleme 2. Matching. Lineares Programmieren 4. Ganzzahliges Programmieren 5. NP-Vollständigkeit 6. Approximationsalgorithmen 7. Backtracking und Branch-and-Bound
Die Klasse NP und die polynomielle Reduktion
Die Klasse NP und die polynomielle Reduktion Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen Dezember 2011 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit
3 Klassifikation wichtiger Optimierungsprobleme
3 Klassifikation wichtiger Optimierungsprobleme 3.1 Das MIN- -TSP Wir kehren nochmal zurück zum Handlungsreisendenproblem für Inputs (w {i,j} ) 1 i
Die Theorie der Toleranzen und deren Anwendung auf das Traveling Salesman Problem
Die Theorie der Toleranzen und deren Anwendung auf das Traveling Salesman Problem Gerold Jäger 4. Februar 2010 Gerold Jäger Theorie der Toleranzen 4. Februar 2010 1 / 35 Überblick 1 Theorie der Toleranzen
2 Komplement eines Graphen
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum für Mathematik Prof. Dr. Ulrich Bauer, Zi Ye WS2015/2016 Datum: 21. Dezember Übungen zu Fallstudien der Mathematischen Modellbildung (Modellierung mit Graphen) (1
Das Problem des Handlungsreisenden
Seite 1 Das Problem des Handlungsreisenden Abbildung 1: Alle möglichen Rundreisen für 4 Städte Das TSP-Problem tritt in der Praxis in vielen Anwendungen als Teilproblem auf. Hierzu gehören z.b. Optimierungsprobleme
1 Zwei auf einen Streich: Optimierte dynamische Einsatzplanung für Gelbe Engel und Lastenaufzüge
Zwei auf einen Streich: Optimierte dynamische Einsatzplanung für Gelbe Engel und Lastenaufzüge Jörg Rambau und Cornelius Schwarz Lehrstuhl Wirtschaftsmathematik Fakultät für Mathematik, Physik und Informatik
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 6: Matchings und TSP-Problem
Ferienkurs zur algorithmischen diskreten Mathematik Kapitel 6: Matchings und TSP-Problem Dipl-Math. Wolfgang Kinzner 4.4.2012 Kapitel 6: Matchings und TSP-Problem Matching und Matchingproblem Flussalgorithmus
11. Übung zu Algorithmen I 6. Juli 2016
11. Übung zu Algorithmen I 6. Juli 2016 Lisa Kohl lisa.kohl@kit.edu mit Folien von Lukas Barth Roadmap Ausblick: Was sind schwierige Probleme? Travelling Salesman Problem - Reprise ein ILP ein Algorithmus
Drei Vorlesungen über Bäume
Bäume. Einleitung Drei Vorlesungen über Bäume Jens Vygen Nehmen wir einmal an, für einen neuen Zug wollen wir ein komplett neues Schienennetz bauen, das einige Städte miteinander verbindet. Oder ein neues
Bäume und Wälder. Seminar: Graphentheorie Sommersemester 2015 Dozent: Dr. Thomas Timmermann
Bäume und Wälder Seminar: Graphentheorie Sommersemester 2015 Dozent: Dr. Thomas Timmermann Ida Feldmann 2-Fach Bachelor Mathematik und Biologie 6. Fachsemester Inhaltsverzeichnis Einleitung 1 1. Bäume
Fortgeschrittene Netzwerk- und Graph-Algorithmen
Fortgeschrittene Netzwerk- und Graph-Algorithmen Dr. Hanjo Täubig Lehrstuhl für Eziente Algorithmen (Prof. Dr. Ernst W. Mayr) Institut für Informatik Technische Universität München Wintersemester 2007/08
Wir konstruieren eine Wasserrutsche!
Wir konstruieren eine Wasserrutsche! Teilnehmer: Leo Graumann Anh Vu Ho Yiyang Huang Felix Jäger Charlotte Kappler Wilhelm Mebus Alice Wamser Gruppenleiter: René Lamour Caren Tischendorf Heinrich-Hertz-Oberschule,
UNABHÄNGIGER LASTEN. Vorlesung 9 BALANCIERUNG DYNAMISCHER. Graphenalgorithmen und lineare Algebra Hand in Hand
Vorlesung 9 BALANCIERUNG DYNAMISCHER UNABHÄNGIGER LASTEN 266 Lastbalancierung Motivation! Ein paralleles System besteht aus! verschiedenen Recheneinheiten,! die miteinander kommunizieren können! Warum
Zur Zykelschreibweise von Permutationen
Zur Zykelschreibweise von Permutationen Olivier Sète 16. Juni 2010 1 Grundlagen Definition 1.1. Eine Permutation von {1, 2,..., n} ist eine bijektive Abbildung σ : {1, 2,..., n} {1, 2,..., n}, i σ(i).
Kapitel 7: Flüsse in Netzwerken und Anwendungen Gliederung der Vorlesung
Gliederung der Vorlesung 1. Grundbegriffe. Elementare Graphalgorithmen und Anwendungen 3. Kürzeste Wege 4. Minimale spannende Bäume 5. Färbungen und Cliquen 6. Traveling Salesman Problem 7. Flüsse in Netzwerken
Hamiltonsche Graphen
Hamiltonsche Graphen Definition 3.2. Es sei G = (V, E) ein Graph. Ein Weg, der jeden Knoten von G genau einmal enthält, heißt hamiltonscher Weg. Ein Kreis, der jeden Knoten von G genau einmal enthält,
Grundlagen der Graphentheorie. Thomas Kamps 6. Oktober 2008
Grundlagen der Graphentheorie Thomas Kamps 6. Oktober 2008 1 Inhaltsverzeichnis 1 Definition von Graphen 3 2 Unabhängigkeit von Ecken und Kanten 3 3 Teil- und Untergraphen 4 4 Schnitt, Vereinigung und
Methode der kleinsten Quadrate
Versus QR Matrizen mit vollem Rang 27. Mai 2011 Versus QR Inhaltsverzeichnis 1 2 3 Beispiel 4 Beispiel 5 6 Versus QR Kondition Vergleich Beispiel Versus QR Zu finden: Gerade, die den Punkten (0, 6), (1,
Zugeordneter bipartiter Graph
Zugeordneter bipartiter Graph Für ein Transportproblem sei A = {A 1,...,A m } die Menge der Fabriken und B = {B 1,...,B n } sei die Menge der Warenhäuser. Wir ordnen nun einem Transportproblem einen bipartiten
Lagrange-Relaxierung und Subgradientenverfahren
Lagrange-Relaxierung und Subgradientenverfahren Wir wollen nun eine Methode vorstellen, mit der man gegebene Relaxierungen verbessern kann. Wir werden die Idee zunächst an der 1-Baum-Relaxierung des symmetrischen
Mustererkennung: Graphentheorie
Mustererkennung: Graphentheorie D. Schlesinger TUD/INF/KI/IS D. Schlesinger () ME: Graphentheorie 1 / 9 Definitionen Ein Graph ist ein Paar G = (V, E) mit der Menge der Knoten V und der Menge der Kanten:
BERGISCHE UNIVERSITÄT WUPPERTAL FB B: SCHUMPETER SCHOOL OF BUSINESS AND ECONOMICS
Name: Vorname: Matrikel-Nr.: BERGISCHE UNIVERSITÄT WUPPERTAL FB B: SCHUMPETER SCHOOL OF BUSINESS AND ECONOMICS Prüfungsgebiet: MWiWi 1.6 Logistik- und Informationsmanagement Wirtschaftsinformatik Modul
15. Elementare Graphalgorithmen
Graphen sind eine der wichtigste Modellierungskonzepte der Informatik Graphalgorithmen bilden die Grundlage vieler Algorithmen in der Praxis Zunächst kurze Wiederholung von Graphen. Dann Darstellungen
Kombinatorische Optimierung
Kombinatorische Optimierung Zuweisungsprobleme 2 1 3 5 4 Kombinatorische Optimierung Rucksackpackproblem 1 10 2 4 6 3 5 8 6 Aufspannende Bäume Travelling Salesman VLSI Design C. Kanzow, M. Gerdts Kombinatorische
Nachklausur Grundlagen der Algorithmik (Niedermeier/Froese/Chen/Fluschnik, Wintersemester 2015/16)
Berlin, 14. April 2016 Name:... Matr.-Nr.:... Nachklausur Grundlagen der Algorithmik (Niedermeier/Froese/Chen/Fluschnik, Wintersemester 2015/16) 1 / 10 2 / 10 3 / 11 4 / 9 5 / 10 Σ / 50 Einlesezeit: Bearbeitungszeit:
Optimierungsprobleme in der Industrie
Dipl.-Inf. 2006-01-20, TU Darmstadt Gliederung Einleitung Anwendungen, Modelle, Verfahren Einführung, Komplexität, Algorithmen Vorstellung Fazit, Literatur Beteiligte Institutionen www.mrupp.info Diplomarbeit
Grundbegriffe der Informatik
Grundbegriffe der Informatik Einheit 11: Graphen Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/42 Graphische Darstellung von Zusammenhängen schon an vielen Stellen
Hamiltonsche Graphen (2. Teil)
Hamiltonsche Graphen (2. Teil) Themen des Vortrages Für Schachspieler Hamiltons Spiel Sitzordnungen Eine billige Rundreise Ein vielleicht unlösbares Problem Bäcker mit Kenntnissen in Graphentheorie Fazit
Diskrete Strukturen. Hausaufgabe 1 (5 Punkte) Hausaufgabe 2 (5 Punkte) Wintersemester 2007/08 Lösungsblatt Januar 2008
Technische Universität München Fakultät für Informatik Lehrstuhl für Informatik 15 Computergraphik & Visualisierung Prof. Dr. Rüdiger Westermann Dr. Werner Meixner Wintersemester 2007/08 Lösungsblatt 9
Lösungen zu Kapitel 5
Lösungen zu Kapitel 5 Lösung zu Aufgabe : (a) Es gibt derartige Graphen: (b) Offensichtlich besitzen 0 der Graphen einen solchen Teilgraphen. Lösung zu Aufgabe : Es sei G = (V, E) zusammenhängend und V
V. Metriken. Gliederung. I. Motivation. Lesen mathematischer Symbole. Wissenschaftliche Argumentation. Matrizenrechnung. Seite 67
Gliederung I. Motivation II. III. Lesen mathematischer Symbole Wissenschaftliche Argumentation IV. Matrizenrechnung V. Metriken Seite 67 Problemstellung: Gegeben seien 2 Punkte im Raum. Wie groß ist die
f h c 7 a 1 b 1 g 2 2 d
) Man bestimme mit Hilfe des Dijkstra-Algorithmus einen kürzesten Weg von a nach h: c 7 a b f 5 h 3 4 5 i e 6 g 2 2 d Beim Dijkstra-Algorithmus wird in jedem Schritt von den noch unmarkierten Knoten jener
Seminarvortag zum Thema Virtual Private Network Design im Rahmen des Seminars Network Design an der Universität Paderborn
Seminarvortag zum Thema Virtual Private Network Design im Rahmen des Seminars Network Design an der Universität Paderborn Ein 5.55-Approximationsalgorithmus für das VPND-Problem Lars Schäfers Inhalt Einführung:
Ganzzahlige Optimierung (IP)
Thema Ganzzahlige Optimierung (IP) Systematik * Problematik * Pragmatik IP und Branch and Bound 1 Agenda 1. Relevanz der Ganzzahligkeit? 2. Formulierung ganzzahliger Modelle 3. Zur Lösung ganzzahliger
Graphentheorie. Eulersche Graphen. Eulersche Graphen. Eulersche Graphen. Rainer Schrader. 14. November Gliederung.
Graphentheorie Rainer Schrader Zentrum für Angewandte Informatik Köln 14. November 2007 1 / 22 2 / 22 Gliederung eulersche und semi-eulersche Graphen Charakterisierung eulerscher Graphen Berechnung eines
Das Briefträgerproblem
Das Briefträgerproblem Paul Tabatabai 30. Dezember 2011 Inhaltsverzeichnis 1 Problemstellung und Modellierung 2 1.1 Problem................................ 2 1.2 Modellierung.............................
SPEKTRALE GRAPHENTHEORIE
SPEKTRALE GRAPHENTHEORIE 179 Graphen, Matrizen, Spektren! Graph als Matrix:! Adjazenzmatrix! Inzidenzmatrix! Laplacematrix!...! Spektrum: Menge der Eigenwerte! Motivation: Sagt das Spektrum etwas über
4.4 Quadratische Optimierungsprobleme
4.4 Quadratische Optimierungsprobleme 1. Quadratische Programme (QP) 1 2 xt P x + q T x + r s.t. Gx h (4.34) wobei P S n +, G R (m n) und A R (p n) Zielfunktion (ZF) ist (konvex) quadratisch Nebenbedingungen
Relationen und DAGs, starker Zusammenhang
Relationen und DAGs, starker Zusammenhang Anmerkung: Sei D = (V, E). Dann ist A V V eine Relation auf V. Sei andererseits R S S eine Relation auf S. Dann definiert D = (S, R) einen DAG. D.h. DAGs sind
Inhalt. 8.1 Motivation. 8.2 Optimierung ohne Nebenbedingungen. 8.3 Optimierung unter Nebenbedingungen. 8.4 Lineare Programmierung
8. Optimierung Inhalt 8.1 Motivation 8.2 Optimierung ohne Nebenbedingungen 8.3 Optimierung unter Nebenbedingungen 8.4 Lineare Programmierung 8.5 Kombinatorische Optimierung 2 8.1 Motivation Viele Anwendungen
Isomorphie von Bäumen
Isomorphie von Bäumen Alexandra Weinberger 23. Dezember 2011 Inhaltsverzeichnis 1 Einige Grundlagen und Definitionen 2 1.1 Bäume................................. 3 1.2 Isomorphie..............................