Satz von Taylor Taylorreihen
|
|
|
- Dörte Wagner
- vor 7 Jahren
- Abrufe
Transkript
1 Satz von Taylor Taylorreihen Bernhard Ganter Institut für Algebra TU Dresden D Dresden
2 Tangente als Näherung Weil sich anschaulich die Tangente anschmiegt, ist die Tangentenfunktion p 1 (x) eine Näherung für f (x): f (x) p 1 (x) für x a.
3 sin x x für kleine x Beispielsweise ist für f (x) := sin x die Tangente an der Stelle a := 0 die Winkelhalbierende und man hat folglich p 1 (x) = x sin x x für kleine x. Besonders raffiniert sind diese Näherungsformeln nicht. Für die Cosinusfunktion erhält man beispielsweise mit der selben Argumentation cos x 1 für kleine x.
4 Fehlerbetrachtung Eine Näherungsformel ist auch wenig wert, wenn man nichts über den Fehler weiß. Wir leiten deshalb eine Abschätzung her. Dazu betrachten wir eine Stelle b, wobei wir a < b voraussetzen. Die Argumentation für a > b verläuft völlig analog. Wenn a b gilt, ist f (b) p 1 (b). Bezeichnen wir den Fehler ( Rest ), der dabei gemacht wird mit R 1 (b), dann haben wir ausführlicher also f (b) = p 1 (b) + R 1 (b), f (b) = f (a) + f (a)(b a) + R 1 (b).
5 Restgliedabschätzung Um etwas über R 1 (b) herauszubekommen, erweist sich folgender Ansatz als erfolgreich: wir führen eine neue Zahl k ein, die durch R 1 (b) = k (b a) 2 bestimmt ist und definieren dann eine neue Funktion g(x) durch g(x) := f (x) + f (x)(b x) + k(b x) 2. Es ist nicht schwierig, diese Funktion abzuleiten, man muss allerdings voraussetzen, dass die zweite Ableitung von f (x) existiert.
6 g (x) g (x) = f (x) f (x) + f (x)(b x) 2k(b x) = [ f (x) 2k ] (b x). Durch Einsetzen findet man, dass g(a) = g(b) (= f (b)) gilt. Nach dem Mittelwertsatz der Differenzialrechnung existiert deshalb eine Zahl c mit a < c < b und g (c) = g(b) b(a) b a = 0.
7 Ergebnis der Abschätzung Das Ergebnis ist also folgendes: Es gibt eine Zahl c zwischen a und b, für die gilt. R 1 (b) = 1 2 f (c)(b a) 2 Nun wissen wir etwas über R 1 (b), aber es erscheint schwierig, diese Information auszunutzen, denn man hat ja keine Information über die genaue Lage der Stelle c.
8 Oft genügt es jedoch, einfach den schlechtesten aller in Frage kommenden Werte zu nehmen: Kennt man eine Schranke M, so dass f (x) M für alle x zwischen a und b gilt, dann ist sicher R 1 (b) 1 2 M(b a)2. Dies kann man in einen Lehrsatz gießen.
9 Satz über die Approximation Satz: Wenn f (x) in einer Umgebung U von a existiert, dann gilt für jedes x U f (x) = f (a) + f (a)(x a) + R 1 (x), wobei R 1 (x) = 1 2 f (c)(x a) 2 für eine Zahl c zwischen a und x ist. Ist außerdem f (x) M für alle x U, dann gilt auch für alle x U. R 1 (x) 1 M(x a)2 2
10 Satz über die Approximation Satz: Wenn f (x) in einer Umgebung U von a existiert, dann gilt für jedes x U f (x) = f (a) + f (a)(x a) + R 1 (x), wobei R 1 (x) = 1 2 f (c)(x a) 2 für eine Zahl c zwischen a und x ist. Ist außerdem f (x) M für alle x U, dann gilt auch für alle x U. R 1 (x) 1 M(x a)2 2
11 Anwendungsbeispiel (1) Damit können wir nun im Einzelfall eine Abschätzung angeben, was wir am Beispiel der Näherung sin demonstrieren: In diesem Fall ist f (x) = sin x, a = 0, p 1 (x) = x. Wegen f (x) = sin x ist M := 1 eine Schranke, die die Bedingungen des Satzes erfüllt.
12 Anwendungsbeispiel (2) Man hat also R 1 (x) 1 2 x 2, was für x := 0.2 den Wert R 1 (0.2) 0.02 ergibt. Wir erhalten also sin 0.2 = 0.2 ± 0.02, d.h. sin 0.2 [0.18, 0.22]. Der wirkliche Wert ist
13 Anwendungsbeispiel (3) Man kann sich über dieses Beispiel ärgern, denn offenbar gibt es noch Verbesserungsbedarf. Einerseits ist die Näherung sin viel besser als uns die Abschätzung verspricht. Der wirkliche Fehler ist ja mehr als zehnmal kleiner als abgeschätzt. Man wünscht sich also eine wirkungsvollere Fehlerabschätzung. Andererseits zeigt das Beispiel der Cosinusfunktion dafür Grenzen auf. Mit der gleichen Methode erhalten wir die Abschätzung cos 0.2 = 1 ± 0.02, was der Wahrheit ziemlich nahe kommt: der wahre Wert ist cos 0.2 =
14 Von der linearen Approximation... Bei der linearen Approximation wird eine Funktion f (x) an einer Stelle a durch eine lineare Funktion p 1 (x) := a 0 + a 1 x angenähert. Das führt auf f (x) f (a) + f (a)(x a) für x a. Dies ergibt sich aus den Bedingungen f (a) = p 1 (a), f (a) = p 1(a).
15 über die quadratische Approximation... Versucht man allgemeiner, f (x) an der Stelle a durch ein quadratisches Polynom p 2 (x) := a 0 + a 1 x + a 2 x 2 anzunähern, dann fordert man naheliegenderweise f (a) = p 2 (a), f (a) = p 2(a), f (a) = p 2(a), was natürlich nur sinnvoll ist, wenn f (x) existiert. Daraus erhält man p 2 (x) = f (a) + f (a)(x a) + f (a)(x a) 2.
16 ... zum Taylorschen Satz Gegeben sei eine Funktion f (x), die in einer Umgebung der Stelle a n + 1-mal differenzierbar ist. Wir suchen ein Polynom p n (x) vom Grade n mit f (a) = p n (a), f (a) = p n(a), f (a) = p n(a),..., f (n) (a) = p n (n) (a). In Analogie zum Satz über die lineare Approximation erhält man folgendes wichtige Ergebnis:
17 Satz von Taylor Satz: Wenn f (n+1) (x) in einer Umgebung U von a existiert, dann gilt für jedes x U f (x) = f (a) + f (a)(x a) f (a)(x a) ! f (a)(x a) 3 wobei n! f (n) (a)(x a) n + R n (x), R n (x) = für ein c zwischen a und x gilt. 1 (n + 1)! f (n+1) (c)(x a) n+1
18 Zusatz Ist außerdem f (n+1) (x) M n+1 für alle x U, dann gilt auch für alle x U. R n (x) 1 (n + 1)! M n+1 x a n+1
19 Der Satz bedeutet... Als Näherung für die Funktion f (x) an der Stelle a erhält man für vorgegebenen Grad n das Polynom p n (x) = f (a)+f (a)(x a)+ 1 2 f (a)(x a) ! f (a)(x a) n! f (n) (a)(x a) n Der Näherungsfehler wird durch die Funktion R n (x) angegeben; diese kann man mit Hilfe der (n + 1)-ten Ableitung von f (x) abschätzen.
20 Satz von Taylor für a := 0 Wenn f (n+1) (x) in einer Umgebung U von 0 existiert, dann gilt für jedes x U dass f (x) = f (0) + f (0)x f (0)x ! f (0)x n! f (n) (0)x n + R n (x), wobei R n (x) = für ein c zwischen 0 und x gilt. 1 (n + 1)! f (n+1) (c)x n+1 Ist außerdem f (n+1) (x) M n+1 für alle x U, dann gilt auch für alle x U. R n (x) 1 (n + 1)! M n+1 x n+1
21 Anwendungsbeispiel Als erstes Anwendungsbeispiel untersuchen wir den Fall f (x) := cos x, a := 0, n := 2. Als Näherung erhält man cos x x 2 für x 0, im Falle x := 0.2 also cos
22 Fehleabschätzung für das Beispiel Den Fehler schätzen wir mit Hilfe von M 3 := 1 ab zu (gerundet) R 2 (0.2) 1 3! = Diese Näherung ist viel besser als die im vorigen Abschnitt gewonnene (zur Erinnerung: der wirkliche Wert ist cos 0.2 = ).
23 Noch besser (1) Weil die dritte Ableitung der Cosinusfunktion (also sin x) an der Stelle a := 0 verschwindet, erhalten wir für n := 3 das gleiche Näherungspolynom wie oben, nämlich p 3 (x) = x 2 und damit cos x = x 2 + R 3 (x),
24 (2) wobei (mit M 4 := 1) R 3 (x) 1 4! 1 x 4, was für x := 0.2 R 3 (x) 1 4! (0.2)4 = ergibt, eine wirklich gute Abschätzung. Nochmal das Ergebnis cos 0.2 = 0.98 ± und zum Vergleich den wirklichen Wert cos 0.2 =
25 Wiederholung: Potenzreihen Potenzreihen (in x) sind Reihen der Form a 0 + a 1 x + a 2 x a n x n +..., wobei x, a 0, a 1,... Zahlen sind. Eine solche Reihe kann konvergent oder divergent sein, je nach Wahl der a i und von x. Schon die Bezeichnungsweise legt nahe, dass wir eine Potenzreihe nicht nur für ein festes x betrachten, sondern verschiedene Werte von x einsetzen wollen, während die a i festgehalten werden.
26 Polynome unendlichen Grades Man schreibt eine Potenzreihe deshalb als eine Art unendliches Polynom, wie in folgendem Beispiel: x + x x x
27 Konvergenz Man kann dann fragen, für welche x die Reihe konvergiert, und findet folgendes Ergebnis: Satz Eine Potenzreihe konvergiert entweder a 0 + a 1 x + a 2 x a n x n nur für x = 0 und divergiert für alle anderen Werte von x oder 2 für x < r und divergiert für alle x > r, für eine reelle Zahl r, oder 3 konvergiert für alle x.
28 Konvergenzradius Die Menge der x, für die die Reihe konvergiert, ist also in jedem Fall ein Intervall, das Konvergenzintervall der Reihe. Die halbe Länge dieses Intervalls nennt man den Konvergenzradius der Reihe. Eine Potenzreihe hat also den Konvergenzradius Null, den Konvergenzradius r R, oder unendlichen Konvergenzradius ( Konvergenzradius r = ).
29 Beispiel Die geometrische Reihe 1 + x + x 2 + x konvergiert für x < 1 und divergiert für x 1. Ihr Konvergenzradius ist also gleich 1, ihr Konvergenzintervall ist ( 1, +1).
30 Potenzreihen als Funktionen Es liegt nahe, Potenzreihen als Beschreibungen von Funktionen aufzufassen. f (x) := a 0 + a 1 x + a 2 x a n x n +... Der Definitionsbereich einer solchen Funktion ist das Konvergenzintervall, der Funktionswert an der Stelle x ist der jeweilige Grenzwert der Reihe.
31 Ableiten wie Polynome Satz Hat die Potenzreihe f (x) := a 0 + a 1 x + a 2 x a n x n +... den Konvergenzradius r > 0, dann gilt: 1 Die Funktion f (x) ist stetig auf dem Intervall ( r, r). 2 f (x) ist auf dem Intervall ( r, r) differenzierbar, und die Ableitung ist f (x) = a 1 + 2a 2 x + 3a 3 x na n x n 1 +. Der Konvergenzradius dieser Reihe ist ebenfalls r.
32 Eindeutigkeit der Reihe Eine unmittelbare Folgerung aus diesem Satz ist, dass eine Funktion f (x) wenn überhaupt, dann nur durch eine Potenzreihe beschrieben werden kann, denn man hat für ja nach dem Satz, dass f (x) := a 0 + a 1 x + a 2 x a n x n +... a n = 1 n! f (n) (0). Diese Darstellung der Koeffizienten erinnert uns sofort an den Satz von Taylor (für a := 0)!
33 Taylor-Reihen Es wird nun deutlich, was beim Taylorschen Satz geschieht: das Näherungspolynom p n (x) ist jeweils ein Anfangsstück der Potenzreihe! Die Potenzreihe für eine Funktion f (x) nennt man deshalb auch die Taylor-Reihe für f (x) (am Entwicklungspunkt a := 0).
34 Andere Entwicklungspunkte Man kann den Begriff der Potenzreihe verallgemeinern auf Reihen der Form f (x) := a 0 + a 1 (x a) + a 2 (x a) a n (x a) n Dann ist die Beziehung zum Taylorschen Satz besonders deutlich. Wir konzentrieren uns hier auf den Fall a := 0.
35 Beispiel Für f (x) := sin x haben wir f (0) = 0, f (0) = 1, f (0) = 0, f (0) = 1 und f (4) (x) = f (x). Die Folge (f (i) (0) i N 0 ) ist also eine endlose Wiederholung von 0, 1, 0, 1. Die Taylor-Reihe für sin x ist 0 + x + 0 x 3 3! x 5 5! + 0 x 7 7! +.
36 Konvergenz der Sinusreihe Was ist der Konvergenzradius dieser Reihe? Die Sinusfunktion ist für alle x R definiert, aber unser Zugang zur Taylorreihe war der, die Funktion in der Nähe von a := 0 zu approximieren. Wir können also eigentlich nicht erwarten, dass die Taylorreihe weit entfernt von a noch konvergiert.
37 Restglied Konvergenz haben wir offenbar genau dort, wo der Fehler gegen Null geht, also an den Stellen x, an denen lim R n(x) = 0 n gilt. Alle Ableitungen f (n) (x) der Sinusfunktion sind beschränkt und erfüllen f (n) (x) 1 für alle x R. Deshalb können wir im Satz von Taylor alle M n gleich 1 setzen und erhalten R n (x) x n+1 (n + 1)!.
38 Überall konvergent! Folglich gilt für jedes x R lim R x n+1 n(x) = lim n n (n + 1)! = 0. Die Taylor-Reihe für sin x konvergiert also für alle x R, der Konvergenzradius ist unendlich.
39 Taylorreihe für cos x Für alle x gilt also sin x = x x 3 3! + x 5 5! x 7 7! +. Mit Hilfe des Satzes über die Ableitung erhalten wir daraus sogleich eine ebenfalls überall konvergente Potenzreihe für den Cosinus: cos x = 1 x 2 2! + x 4 4! x 6 6! +.
40 Exponentialfunktion Wir haben für f (x) := e x : f (x) := e x f (0) = 1 f (x) := e x f (0) = 1 f (x) := e x f (0) = 1 f (x) := e x f (0) = 1.. f (n) (x) := e x f (n) (0) = 1..
41 Koeffizienten Wegen erhalten wir a n = 1 n! f (n) (0) a n = 1 n!. Wenn es also eine Taylorreihe für die Exponentialfunktion gibt, dann lautet sie 1 + x + x 2 2! + x 3 3! + x 4 4! +...
42 Quotientenkritrium anwenden! r bezeichne den Konvergenzradius der Potenzreihe n=0 a n(x a) n. Dann gilt: Falls lim n a n+1 a n = 0, dann ist r =. Mit a n = xn n! und a n+1 = xn+1 (n+1)! ergibt sich lim a n+1 n a n = lim x n+1 n (n + 1)! n! x n = lim n x n + 1 = 0. Die Potenzreihe der Exponentialfunktion konvergiert überall!
43 Vergleich der Reihen Wir haben gefunden: sin x = x x 3 3! + x 5 5! x 7 cos x = 1 x 2 2! + x 4 4! x 6 7! + 6! + e x = 1 + x + x 2 2! + x 3 3! + x 4 4! +...
44 Kombinationen von sin und cos (1) sin x = x x 3 3! + x 5 5! x 7 cos x = 1 x 2 2! + x 4 4! x 6 7! + 6! + cos x + sin x = 1 + x x 2 2! x 3 3! + x 4 4! + x 5 5!...
45 Kombinationen von sin und cos (2) sin x = x x 3 3! + x 5 5! x 7 cos x = 1 x 2 2! + x 4 4! x 6 7! + 6! + cos x sin x = 1 x x 2 2! + x 3 3! + x 4 4! x 5 5!...
46 Komplexe Argumente Man kann in eine Potenzreihe auch komplexe Zahlen als Argumente einsetzen. Die Konvergenzüberlegungen verallgemeinern sich. Wir gehen darauf hier nicht weiter ein.
47 Komplexe Exponentialfunktion e ix = 1 + ix + (ix)2 2! + (ix)3 3! + (ix)4 4! + (ix)5 5! +... = 1 + ix + i 2 x 2 2! + i 3 x 3 3! + i 4 x 4 4! + i 5 x 5 5! +... = 1 + ix + x 2 2! = 1 x 2 2! + x 4 + ix 3 3! + x 4 4! + ix 5 5! +... (x 4!... + i x 3 3! + x 5 5! +... )
48 Erneuter Vergleich der Reihen sin x = x x 3 3! + x 5 5! x 7 cos x = 1 x 2 2! + x 4 4! x 6 e ix = 1 x 2 2! + x 4 7! + 6! + (x 4!... + i x 3 3! + x 5 5!... ) Daraus folgt: e ix = cos x + i sin x
49 Erneuter Vergleich der Reihen sin x = x x 3 3! + x 5 5! x 7 cos x = 1 x 2 2! + x 4 4! x 6 e ix = 1 x 2 2! + x 4 7! + 6! + (x 4!... + i x 3 3! + x 5 5!... ) Daraus folgt: e ix = cos x + i sin x
50 Eulersche Formel Die schönste Formel der Welt: e iπ + 1 = 0.
51 Eulersche Formel Die schönste Formel der Welt: e iπ + 1 = 0.
52 Exponentialreihe e x = ν=0 x ν ν!. Für x := 3 erhält man z.b. e 3 = ! ! ! ! ! ! ! ! +... =
53 Variationen der Exponentialreihe Man hat Für a > 0 gilt e x = a x = ν=0 x ν ν!. (x ln a) ν ν=0 wegen a = e ln a und folglich a x = (e ln a ) x = e x ln a. ν!
54 e x wächst schneller Wegen gilt e x x n = ν=0 x ν x n ν! = 1 x n + 1 1!x n !x n n! + x (n + 1)! +... x > ( für x > 0) (n + 1)! e x für x. x n Die Exponentialfunktion wächst also schneller als jedes Polynom.
55 Taylorreihe für den Logarithmus ( 1) ν+1 ln(1 + x) = x ν für x ( 1, 1] ν ν=1 Gleichbedeutend: ln(1 x) = ν=1 x ν ν für x [ 1, 1).
56 Auf dem Rand Aus ( 1) ν+1 ln(1 + x) = x ν für x ( 1, 1] ν ν=1 erhält man für x = 1 ( 1) ν+1 ln(1 + 1) =, ν ν=1 also ln 2 =
57 f (x) := (1 + x) α Erster Fall: α eine nicht negative ganze Zahl. Dann gilt der binomische Satz (1 + x) α = α n=0 ( ) α x n für alle x R. n Man ( darf die Summe ruhig bis laufen lassen, denn für n > α ist α ) n = 0.
58 f (x) := (1 + x) α Zweiter Fall: α / N \ {0} Dann gilt die Taylor-Formel (1 + x) α = n=0 ( ) α x n für alle x ( 1, 1). n Dabei ist ( α 0) := 1 und ( ) α α (α 1) (α n + 1) = n n! für n N.
59 Approximation (n 1) ten Grades Satz: Die Potenzreihe f (x) = a ν x ν ν=0 habe den Konvergenzradius R > 0. Es sein n eine feste natürliche Zahl und a n 0. Dann gilt für x 0: n 1 f (x) a ν x ν a n x n. ν=0
60 vor dem Beweis Vorbemerkung: Wie will man eigentlich beweisen, dass etwas ungefähr gleich ist? Das ist doch eine schwammige Formulierung! Antwort: Man kann der Formulierung ihre Schwammigkeit nehmen und ungefähr gleich exakt definieren. Das geht z.b. so: Definition: Zwei Funktionen g(x) und h(x) heißen in der Nähe von x 0 ungefähr gleich, wenn g(x) lim x x 0 h(x) = 1 gilt. Wir schreiben dann g(x) h(x) für x x 0.
61 Beweis des Satzes (1) Wir kürzen ab: Zu zeigen ist dann n 1 g(x) := f (x) a ν x ν. ν=0 g(x) a n x n für x 0, also g(x) lim x 0 a n x n = 1.
62 Beweis des Satzes (2) Also los! g(x) = = n 1 a ν x ν a ν x ν ν=0 a ν x ν ν=n = a n x n + ν=0 a ν x ν ν=n+1 = a n x n + x n+1 a ν x ν (n+1) ν=n+1
63 Beweis des Satzes (3) Aus erhalten wir g(x) = a n x n + x n+1 g(x) a n x n = 1 + x a n ν=n+1 ν=n+1 a ν x ν (n+1) a ν x ν (n+1) Die Potenzreihe ν=n+1 a νx ν (n+1) konvergiert ebenfalls mit Konvergenzradius R (denn sie unterscheidet sich von der ursprünglichen nur um endlich viele Terme).
64 Beweis des Satzes (4) Deshalb gibt es eine Konstante M mit a ν x ν (n+1) < M für x < R 2 ν=n+1 und aus wird g(x) a n x n = 1 + x a n ν=n+1 a ν x ν (n+1) g(x) x 1 M 0 für x 0. a n x n a n Quod erat demonstrandum.
65 Etwas aus der Physik Ein Körper der Masse m 0 wird auf die Geschwindigkeit v gebracht. Die Newtonsche kinetische Energie des Körpers ist dann E kin = m 0v 2 2. Mit zunehmender Geschwindigkeit ändert sich die Masse des Körpers nach der Formel m = m 0. 1 v 2 c 2 Die erhöhte kinetische Energie führt zur Masseerhöhung.
66 Massenzuwachs m = m 0 1 v 2 c 2 = m 0 ( 1 v 2 c 2 ) 1 2 = m 0 (1 + x) α mit x = v 2 = m 0 ν=0 = m 0 ν=0 ( 1 2 ν ( 1 2 ν ) ( v 2 c 2 ) ν ) ( 1) ν v 2ν c 2ν c 2 und α = 1 2
67 Lineare Approximation m = m 0 ν=0 ( 1 2 ν ) ( 1) ν v 2ν c 2ν ( 1 m 0 (1 2 )) v 2 1 c 2 für v 0 = m 0 (1 1 v 2 2 c 2 ) = m 0 m 0v c 2
68 Ergebnis Daher und das ergibt m := m m 0 m 0v c 2 m c 2 E kin für v 0.
Polynomiale Approximation. und. Taylor-Reihen
 Polynomiale Approximation und Taylor-Reihen Heute gehts um die Approximation von glatten (d.h. beliebig oft differenzierbaren) Funktionen f nicht nur durch Gerade (sprich Polynome vom Grade 1) und Polynome
Polynomiale Approximation und Taylor-Reihen Heute gehts um die Approximation von glatten (d.h. beliebig oft differenzierbaren) Funktionen f nicht nur durch Gerade (sprich Polynome vom Grade 1) und Polynome
Brückenkurs Rechentechniken
 Brückenkurs Rechentechniken Dr. Jörg Horst Technische Universität Dortmund Fakultät für Mathematik SS 2014 1 Vollständige Induktion Vollständige Induktion 2 Funktionenfolgen Punktweise Konvergenz Gleichmäßige
Brückenkurs Rechentechniken Dr. Jörg Horst Technische Universität Dortmund Fakultät für Mathematik SS 2014 1 Vollständige Induktion Vollständige Induktion 2 Funktionenfolgen Punktweise Konvergenz Gleichmäßige
Der Satz von Taylor. Kapitel 7
 Kapitel 7 Der Satz von Taylor Wir haben bereits die Darstellung verschiedener Funktionen, wie der Exponentialfunktion, der Cosinus- oder Sinus-Funktion, durch unendliche Reihen kennen gelernt. In diesem
Kapitel 7 Der Satz von Taylor Wir haben bereits die Darstellung verschiedener Funktionen, wie der Exponentialfunktion, der Cosinus- oder Sinus-Funktion, durch unendliche Reihen kennen gelernt. In diesem
( ) Dann gilt f(x) g(x) in der Nähe von x 0, das heisst. Für den Fehler r(h) dieser Näherung erhält man unter Verwendung von ( )
 64 Die Tangente in x 0 eignet sich also als lokale (lineare) Näherung der Funktion in der Nähe des Punktes P. Oder gibt es eine noch besser approximierende Gerade? Satz 4.9 Unter allen Geraden durch den
64 Die Tangente in x 0 eignet sich also als lokale (lineare) Näherung der Funktion in der Nähe des Punktes P. Oder gibt es eine noch besser approximierende Gerade? Satz 4.9 Unter allen Geraden durch den
Die Taylorreihe einer Funktion
 Kapitel 6 Die Taylorreihe einer Funktion Dieser Abschnitt beschäftigt sich mit Taylorreihen, Taylorpolynomen und der Restgliedabschätzung für Taylorpolynome. Die Taylorreihe einer reellen Funktion ist
Kapitel 6 Die Taylorreihe einer Funktion Dieser Abschnitt beschäftigt sich mit Taylorreihen, Taylorpolynomen und der Restgliedabschätzung für Taylorpolynome. Die Taylorreihe einer reellen Funktion ist
18 Höhere Ableitungen und Taylorformel
 8 HÖHERE ABLEITUNGEN UND TAYLORFORMEL 98 8 Höhere Ableitungen und Taylorformel Definition. Sei f : D R eine Funktion, a D. Falls f in einer Umgebung von a (geschnitten mit D) differenzierbar und f in a
8 HÖHERE ABLEITUNGEN UND TAYLORFORMEL 98 8 Höhere Ableitungen und Taylorformel Definition. Sei f : D R eine Funktion, a D. Falls f in einer Umgebung von a (geschnitten mit D) differenzierbar und f in a
INGENIEURMATHEMATIK. 8. Reihen. Sommersemester Prof. Dr. Gunar Matthies
 Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
Mathematik für Bauingenieure
 Mathematik für Bauingenieure von Kerstin Rjasanowa 1. Auflage Mathematik für Bauingenieure Rjasanowa schnell und portofrei erhältlich bei beck-shop.de DIE FACHBUCHHANDLUNG Hanser München 2006 Verlag C.H.
Mathematik für Bauingenieure von Kerstin Rjasanowa 1. Auflage Mathematik für Bauingenieure Rjasanowa schnell und portofrei erhältlich bei beck-shop.de DIE FACHBUCHHANDLUNG Hanser München 2006 Verlag C.H.
Lösungen der Aufgaben zu Kapitel 9
 Lösungen der Aufgaben zu Kapitel 9 Abschnitt 9. Aufgabe a) Wir bestimmen die ersten Ableitungen von f, die uns dann das Aussehen der k-ten Ableitung erkennen lassen: fx) = x + e x xe x, f x) = e x e x
Lösungen der Aufgaben zu Kapitel 9 Abschnitt 9. Aufgabe a) Wir bestimmen die ersten Ableitungen von f, die uns dann das Aussehen der k-ten Ableitung erkennen lassen: fx) = x + e x xe x, f x) = e x e x
konvergent falls Sei eine allgemeine ("gutmütige") Funktion. Frage: kann man sie in der Nähe des Punktes darstellen mittels einer Potenzreihe in
 C5 Funktionen: Reihenentwicklungen C5.1 Taylorreihen Brook Taylor (1685-1731) (Analysis-Vorlesung: Konvergenz von Reihen und Folgen) Grundlegende Frage: Wann / unter welchen Voraussetzungen lässt sich
C5 Funktionen: Reihenentwicklungen C5.1 Taylorreihen Brook Taylor (1685-1731) (Analysis-Vorlesung: Konvergenz von Reihen und Folgen) Grundlegende Frage: Wann / unter welchen Voraussetzungen lässt sich
REIHENENTWICKLUNGEN. [1] Reihen mit konstanten Gliedern. [2] Potenzreihen. [3] Reihenentwicklung von Funktionen. Eine kurze Einführung Herbert Paukert
![REIHENENTWICKLUNGEN. [1] Reihen mit konstanten Gliedern. [2] Potenzreihen. [3] Reihenentwicklung von Funktionen. Eine kurze Einführung Herbert Paukert REIHENENTWICKLUNGEN. [1] Reihen mit konstanten Gliedern. [2] Potenzreihen. [3] Reihenentwicklung von Funktionen. Eine kurze Einführung Herbert Paukert](/thumbs/55/37057337.jpg) Reihenentwicklungen Herbert Paukert 1 REIHENENTWICKLUNGEN Eine kurze Einführung Herbert Paukert [1] Reihen mit konstanten Gliedern [2] Potenzreihen [3] Reihenentwicklung von Funktionen Reihenentwicklungen
Reihenentwicklungen Herbert Paukert 1 REIHENENTWICKLUNGEN Eine kurze Einführung Herbert Paukert [1] Reihen mit konstanten Gliedern [2] Potenzreihen [3] Reihenentwicklung von Funktionen Reihenentwicklungen
1 Reihen von Zahlen. Inhalt:
 5 Kapitel 3 Reihen Reihen von Zahlen Inhalt: Konvergenz und Divergenz von Reihen reeller oder komplexer Zahlen, geometrische Reihe, harmonische Reihe, alternierende Reihen. Cauchy-Kriterium, absolute Konvergenz,
5 Kapitel 3 Reihen Reihen von Zahlen Inhalt: Konvergenz und Divergenz von Reihen reeller oder komplexer Zahlen, geometrische Reihe, harmonische Reihe, alternierende Reihen. Cauchy-Kriterium, absolute Konvergenz,
Karteikarten, Analysis 2, Sätze und Definitionen nach der Vorlesung von PD Hanke
 Karteikarten, Analysis 2, Sätze und en nach der Vorlesung von PD Hanke Felix Müller, felix.b.mueller@physik.lmu.de Diese Karteikärtchen sollten alle en und Sätze der Vorlesung Analysis 2 bei Herrn PD Hanke
Karteikarten, Analysis 2, Sätze und en nach der Vorlesung von PD Hanke Felix Müller, felix.b.mueller@physik.lmu.de Diese Karteikärtchen sollten alle en und Sätze der Vorlesung Analysis 2 bei Herrn PD Hanke
Kapitel 6. Exponentialfunktion
 Kapitel 6. Exponentialfunktion 6.1. Potenzreihen In Kap. 4 haben wir Reihen ν=0 a ν studiert, wo die Glieder feste Zahlen sind. Die Summe solcher Reihen ist wieder eine Zahl, z.b. die Eulersche Zahl e.
Kapitel 6. Exponentialfunktion 6.1. Potenzreihen In Kap. 4 haben wir Reihen ν=0 a ν studiert, wo die Glieder feste Zahlen sind. Die Summe solcher Reihen ist wieder eine Zahl, z.b. die Eulersche Zahl e.
Freie Universität Berlin Wintersemester 11/12 Fachbereich Mathematik und Informatik Institut für Mathematik Dr. A. Linke
 Freie Universität Berlin Wintersemester / Fachbereich Mathematik und Informatik Institut für Mathematik Dr. A. Linke Musterlösung zum. Übungsblatt zur Vorlesung Mathematik für Physiker I Differenzierbarkeit,
Freie Universität Berlin Wintersemester / Fachbereich Mathematik und Informatik Institut für Mathematik Dr. A. Linke Musterlösung zum. Übungsblatt zur Vorlesung Mathematik für Physiker I Differenzierbarkeit,
Funktionenfolgen, Potenzreihen, Exponentialfunktion
 Kapitel 8 Funktionenfolgen, Potenzreihen, Exponentialfunktion Der in Definition 7. eingeführte Begriff einer Folge ist nicht auf die Betrachtung reeller Zahlen eingeschränkt und das Beispiel {a n } = {x
Kapitel 8 Funktionenfolgen, Potenzreihen, Exponentialfunktion Der in Definition 7. eingeführte Begriff einer Folge ist nicht auf die Betrachtung reeller Zahlen eingeschränkt und das Beispiel {a n } = {x
20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen
 20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
Analysis 1 für Informatiker (An1I)
 Hochschule für Technik Rapperswil Analysis 1 für Informatiker (An1I) Stand: 2012-11-13 Inhaltsverzeichnis 1 Funktionen 3 1.1 Gerade, ungerade und periodische Funktionen..................... 3 1.2 Injektive,
Hochschule für Technik Rapperswil Analysis 1 für Informatiker (An1I) Stand: 2012-11-13 Inhaltsverzeichnis 1 Funktionen 3 1.1 Gerade, ungerade und periodische Funktionen..................... 3 1.2 Injektive,
27 Taylor-Formel und Taylor-Entwicklungen
 136 IV. Unendliche Reihen und Taylor-Formel 27 Taylor-Formel und Taylor-Entwicklungen Lernziele: Konzepte: klein o - und groß O -Bedingungen Resultate: Taylor-Formel Kompetenzen: Bestimmung von Taylor-Reihen
136 IV. Unendliche Reihen und Taylor-Formel 27 Taylor-Formel und Taylor-Entwicklungen Lernziele: Konzepte: klein o - und groß O -Bedingungen Resultate: Taylor-Formel Kompetenzen: Bestimmung von Taylor-Reihen
April (Voll-) Klausur Analysis I für Ingenieure. Rechenteil
 April (Voll-) Klausur Analysis I für Ingenieure en Rechenteil Aufgabe 7 Punkte (a) Skizzieren Sie die 4-periodische Funktion mit f() = für und f() = für (b) Berechnen Sie für diese Funktion die Fourierkoeffizienten
April (Voll-) Klausur Analysis I für Ingenieure en Rechenteil Aufgabe 7 Punkte (a) Skizzieren Sie die 4-periodische Funktion mit f() = für und f() = für (b) Berechnen Sie für diese Funktion die Fourierkoeffizienten
Taylorentwicklung von Funktionen einer Veränderlichen
 Taylorentwicklung von Funktionen einer Veränderlichen 17. Januar 2013 KAPITEL 1. MATHEMATISCHE GRUNDLAGEN 1 Kapitel 1 Mathematische Grundlagen 1.1 Stetigkeit, Differenzierbarkeit und C n -Funktionen Der
Taylorentwicklung von Funktionen einer Veränderlichen 17. Januar 2013 KAPITEL 1. MATHEMATISCHE GRUNDLAGEN 1 Kapitel 1 Mathematische Grundlagen 1.1 Stetigkeit, Differenzierbarkeit und C n -Funktionen Der
Leitfaden a tx t
 Leitfaden -0.7. Potenz-Reihen. Definition: Es sei (a 0, a, a 2,...) eine Folge reeller Zahlen (wir beginnen hier mit dem Index t 0). Ist x R, so kann man die Folge (a 0, a x, a 2 x 2, a 3 x 3,...) und
Leitfaden -0.7. Potenz-Reihen. Definition: Es sei (a 0, a, a 2,...) eine Folge reeller Zahlen (wir beginnen hier mit dem Index t 0). Ist x R, so kann man die Folge (a 0, a x, a 2 x 2, a 3 x 3,...) und
Vorlesung: Analysis I für Ingenieure
 Vorlesung: Analysis I für Ingenieure Michael Karow Thema: Satz von Taylor Die Taylor-Entwicklung I Satz von Taylor. Sei f : R D R an der Stelle x n-mal differenzierbar. Dann gilt für x D, n f (k) (x )
Vorlesung: Analysis I für Ingenieure Michael Karow Thema: Satz von Taylor Die Taylor-Entwicklung I Satz von Taylor. Sei f : R D R an der Stelle x n-mal differenzierbar. Dann gilt für x D, n f (k) (x )
Dierentialrechnung mit einer Veränderlichen
 Dierentialrechnung mit einer Veränderlichen Beispiel: Sei s(t) die zum Zeitpunkt t zurückgelegte Wegstrecke. Dann ist die durchschnittliche Geschwindigkeit zwischen zwei Zeitpunkten t 1 und t 2 gegeben
Dierentialrechnung mit einer Veränderlichen Beispiel: Sei s(t) die zum Zeitpunkt t zurückgelegte Wegstrecke. Dann ist die durchschnittliche Geschwindigkeit zwischen zwei Zeitpunkten t 1 und t 2 gegeben
Mathematik für Ökonomen Kompakter Einstieg für Bachelorstudierende Lösungen der Aufgaben aus Kapitel 5 Version 1.0 (11.
 Mathematik für Ökonomen Kompakter Einstieg für Bachelorstudierende Lösungen der Aufgaben aus Kapitel 5 Version.0. September 05) E. Cramer, U. Kamps, M. Kateri, M. Burkschat 05 Cramer, Kamps, Kateri, Burkschat
Mathematik für Ökonomen Kompakter Einstieg für Bachelorstudierende Lösungen der Aufgaben aus Kapitel 5 Version.0. September 05) E. Cramer, U. Kamps, M. Kateri, M. Burkschat 05 Cramer, Kamps, Kateri, Burkschat
Folgen und Reihen. Bernhard Ganter. Institut für Algebra TU Dresden D Dresden
 Folgen und Reihen Bernhard Ganter Institut für Algebra TU Dresden D-0062 Dresden bernhard.ganter@tu-dresden.de Folgen Eine (unendliche) (Zahlen)folge ist eine Abbildung f : N R. Statt f (n) schreibt man
Folgen und Reihen Bernhard Ganter Institut für Algebra TU Dresden D-0062 Dresden bernhard.ganter@tu-dresden.de Folgen Eine (unendliche) (Zahlen)folge ist eine Abbildung f : N R. Statt f (n) schreibt man
4.7 Der Taylorsche Satz
 288 4 Differenziation 4.7 Der Taylorsche Satz Die Differenzierbarkeit, also die Existenz der ersten Ableitung einer Funktion, erlaubt bekanntlich, diese Funktion lokal durch eine affine Funktion näherungsweise
288 4 Differenziation 4.7 Der Taylorsche Satz Die Differenzierbarkeit, also die Existenz der ersten Ableitung einer Funktion, erlaubt bekanntlich, diese Funktion lokal durch eine affine Funktion näherungsweise
Mathematik I - Woche 10
 Mathematik I - Woche 0 Philip Müller Reihen. Was ist eine Reihe Wir hatten bis jetzt Folgen. Eine Folge (a n ) n N ist eine Vorschrift, die von den natürlichen Zahlen, in die reellen Zahlen abbildet. Ein
Mathematik I - Woche 0 Philip Müller Reihen. Was ist eine Reihe Wir hatten bis jetzt Folgen. Eine Folge (a n ) n N ist eine Vorschrift, die von den natürlichen Zahlen, in die reellen Zahlen abbildet. Ein
In der Praxis werden wir häufig mit relativ komplexen Funktionen konfrontiert. y
 Approximationen In der Praxis werden wir häufig mit relativ komplexen Funktionen konfrontiert. y y = f (x) x Um das Arbeiten mit einer komplizierten Funktion zu vermeiden, können wir versuchen, diese Funktion
Approximationen In der Praxis werden wir häufig mit relativ komplexen Funktionen konfrontiert. y y = f (x) x Um das Arbeiten mit einer komplizierten Funktion zu vermeiden, können wir versuchen, diese Funktion
Höhere Mathematik I für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie Lösungsvorschläge zum 7. Übungsblatt
 UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl WS 008/09 Höhere Mathematik I für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie Lösungsvorschläge
UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl WS 008/09 Höhere Mathematik I für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie Lösungsvorschläge
Technische Universität München Zentrum Mathematik. Übungsblatt 7
 Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 7 Hausaufgaben Aufgabe 7. Berechnen Sie die folgenden unbestimmten Integrale.
Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 7 Hausaufgaben Aufgabe 7. Berechnen Sie die folgenden unbestimmten Integrale.
Didaktik der Mathematik der Sekundarstufe II
 Didaktik der Mathematik der Sekundarstufe II Teil 8: Satz von Rolle - Mittelwertsatz - Monotoniekriterium Humboldt-Universität zu Berlin, Institut für Mathematik Sommersemester 2010/11 Internetseite zur
Didaktik der Mathematik der Sekundarstufe II Teil 8: Satz von Rolle - Mittelwertsatz - Monotoniekriterium Humboldt-Universität zu Berlin, Institut für Mathematik Sommersemester 2010/11 Internetseite zur
Animation: Approximation von sin(x) durch Polynome 1-25.Grades
 of 1 19/03/14 09:00 Taylorpolynome zurück Approximation durch Polynome höheren Grades Erklärung Bis jetzt haben wir Funktionen nur durch Polynome 1. und 2.Grades approximiert, nämlich durch die Tangentengerade
of 1 19/03/14 09:00 Taylorpolynome zurück Approximation durch Polynome höheren Grades Erklärung Bis jetzt haben wir Funktionen nur durch Polynome 1. und 2.Grades approximiert, nämlich durch die Tangentengerade
10 Aus der Analysis. Themen: Konvergenz von Zahlenfolgen Unendliche Reihen Stetigkeit Differenzierbarkeit
 10 Aus der Analysis Themen: Konvergenz von Zahlenfolgen Unendliche Reihen Stetigkeit Differenzierbarkeit Zahlenfolgen Ein unendliche Folge reeller Zahlen heißt Zahlenfolge. Im Beispiel 2, 3, 2, 2 2, 2
10 Aus der Analysis Themen: Konvergenz von Zahlenfolgen Unendliche Reihen Stetigkeit Differenzierbarkeit Zahlenfolgen Ein unendliche Folge reeller Zahlen heißt Zahlenfolge. Im Beispiel 2, 3, 2, 2 2, 2
8. 2A. Integration von Potenzreihen
 8. 2A. Integration von Potenzreihen Wie wir schon mehrfach sahen, sind Potenzreihen ein unentbehrliches Werkzeug für viele Berechnungen in der Ingenieurmathematik. Glücklicherweise darf man Potenzreihen
8. 2A. Integration von Potenzreihen Wie wir schon mehrfach sahen, sind Potenzreihen ein unentbehrliches Werkzeug für viele Berechnungen in der Ingenieurmathematik. Glücklicherweise darf man Potenzreihen
Differentialrechnung
 Katharina Brazda 5. März 007 Inhaltsverzeichnis Motivation. Das Tangentenproblem................................... Das Problem der Momentangeschwindigkeit.......................3 Differenzenquotient und
Katharina Brazda 5. März 007 Inhaltsverzeichnis Motivation. Das Tangentenproblem................................... Das Problem der Momentangeschwindigkeit.......................3 Differenzenquotient und
Differential- und Integralrechnung
 Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
Brückenkurs Mathematik TU Dresden 2016 Differential- und Integralrechnung Schwerpunkte: Differentiation Integration Eigenschaften und Anwendungen Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik
SS 2016 Höhere Mathematik für s Studium der Physik 21. Juli Probeklausur. Die Antworten zu den jeweiligen Fragen sind in blauer Farbe notiert.
 SS 6 Höhere Mathematik für s Studium der Physik. Juli 6 Probeklausur Die Antworten zu den jeweiligen Fragen sind in blauer Farbe notiert. Fragen Sei (X, d) ein metrischer Raum. Beantworten Sie die nachfolgenden
SS 6 Höhere Mathematik für s Studium der Physik. Juli 6 Probeklausur Die Antworten zu den jeweiligen Fragen sind in blauer Farbe notiert. Fragen Sei (X, d) ein metrischer Raum. Beantworten Sie die nachfolgenden
Aufgabe 1 Zeigen Sie mittels vollständiger Induktion, dass für alle n N. n(n + 1)(2n + 1) 6. j 2 = gilt.
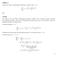 Aufgabe Zeigen Sie mittels vollständiger Induktion, dass für alle n N j 2 j n(n + )(2n + ) gilt. Der Beweis wird mit Hilfe vollständiger Induktion geführt. Wir verifizieren daher zunächst den Induktionsanfang,
Aufgabe Zeigen Sie mittels vollständiger Induktion, dass für alle n N j 2 j n(n + )(2n + ) gilt. Der Beweis wird mit Hilfe vollständiger Induktion geführt. Wir verifizieren daher zunächst den Induktionsanfang,
Übungen Analysis I WS 03/04
 Blatt Abgabe: Mittwoch, 29.0.03 Aufgabe : Beweisen Sie, daß für jede natürliche Zahl n gilt: n ( ) n (x + y) n = x i y n i, i (b) n ν 2 = ν= i=0 n(n + )(2n + ), 6 (c) 2 3n ist durch 7 teilbar. Aufgabe
Blatt Abgabe: Mittwoch, 29.0.03 Aufgabe : Beweisen Sie, daß für jede natürliche Zahl n gilt: n ( ) n (x + y) n = x i y n i, i (b) n ν 2 = ν= i=0 n(n + )(2n + ), 6 (c) 2 3n ist durch 7 teilbar. Aufgabe
10 Differenzierbare Funktionen
 10 Differenzierbare Funktionen 10.1 Definition: Es sei S R, x 0 S Häufungspunkt von S. Eine Funktion f : S R heißt im Punkt x 0 differenzierbar, wenn der Grenzwert f (x 0 ) := f(x 0 + h) f(x 0 ) lim h
10 Differenzierbare Funktionen 10.1 Definition: Es sei S R, x 0 S Häufungspunkt von S. Eine Funktion f : S R heißt im Punkt x 0 differenzierbar, wenn der Grenzwert f (x 0 ) := f(x 0 + h) f(x 0 ) lim h
Stetigkeit von Funktionen
 Stetigkeit von Funktionen Definition. Es sei D ein Intervall oder D = R, x D, und f : D R eine Funktion. Wir sagen f ist stetig wenn für alle Folgen (x n ) n in D mit Grenzwert x auch die Folge der Funktionswerte
Stetigkeit von Funktionen Definition. Es sei D ein Intervall oder D = R, x D, und f : D R eine Funktion. Wir sagen f ist stetig wenn für alle Folgen (x n ) n in D mit Grenzwert x auch die Folge der Funktionswerte
Übungen Ingenieurmathematik
 Übungen Ingenieurmathematik 1. Übungsblatt: Komplexe Zahlen Aufgabe 1 Bestimmen Sie Real- und Imaginärteil der folgenden komplexen Zahlen: a) z =(3+i)+(5 7i), b) z =(3 i)(5 7i), c) z =( 3+i)( 3+ 3 i),
Übungen Ingenieurmathematik 1. Übungsblatt: Komplexe Zahlen Aufgabe 1 Bestimmen Sie Real- und Imaginärteil der folgenden komplexen Zahlen: a) z =(3+i)+(5 7i), b) z =(3 i)(5 7i), c) z =( 3+i)( 3+ 3 i),
a 0, a 1, a 2, a 3,... Dabei stehen die drei Pünktchen für unendlich oft so weiter.
 7 Folgen 30 7 Folgen Wir betrachten nun (unendliche) Folgen von Zahlen a 0, a, a 2, a 3,.... Dabei stehen die drei Pünktchen für unendlich oft so weiter. Bezeichnung Wir bezeichnen mit N die Menge der
7 Folgen 30 7 Folgen Wir betrachten nun (unendliche) Folgen von Zahlen a 0, a, a 2, a 3,.... Dabei stehen die drei Pünktchen für unendlich oft so weiter. Bezeichnung Wir bezeichnen mit N die Menge der
Analysis I. 1. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Das Bild einer Abbildung F: L M. (2) Eine Cauchy-Folge
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Das Bild einer Abbildung F: L M. (2) Eine Cauchy-Folge
P n (1) P j (1) + ε 2, j=0. P(1) P j (1) + ε 2 < ε. log(1+x) =
 Zu ε > 0 gibt es ein N N mit P n (1) P j (1) < ε/2 für j,n > N, also gilt Es folgt (1 x) n 1 j=n+1 und schließlich mit n x j P n (1) P j (1) (1 x) ε 2 P n (1) P n (x) (1 x) P(1) P(x) (1 x) für x hinreichend
Zu ε > 0 gibt es ein N N mit P n (1) P j (1) < ε/2 für j,n > N, also gilt Es folgt (1 x) n 1 j=n+1 und schließlich mit n x j P n (1) P j (1) (1 x) ε 2 P n (1) P n (x) (1 x) P(1) P(x) (1 x) für x hinreichend
Kapitel 6 Folgen und Stetigkeit
 Kapitel 6 Folgen und Stetigkeit Mathematischer Vorkurs TU Dortmund Seite 76 / 226 Definition 6. (Zahlenfolgen) Eine Zahlenfolge (oder kurz: Folge) ist eine Funktion f : 0!. Statt f(n) schreiben wir x n
Kapitel 6 Folgen und Stetigkeit Mathematischer Vorkurs TU Dortmund Seite 76 / 226 Definition 6. (Zahlenfolgen) Eine Zahlenfolge (oder kurz: Folge) ist eine Funktion f : 0!. Statt f(n) schreiben wir x n
Satz von Taylor, Taylor-Reihen
 Satz von Taylor, Taylor-Reihen Die Kenntnis von f liefert gewisse Rücschlüsse auf die Funtion f selbst, zb Monotonie, mögliche loale Extrema Die Kenntnis von f liefert darüberhinaus eine Information, ob
Satz von Taylor, Taylor-Reihen Die Kenntnis von f liefert gewisse Rücschlüsse auf die Funtion f selbst, zb Monotonie, mögliche loale Extrema Die Kenntnis von f liefert darüberhinaus eine Information, ob
3 Folgen, Reihen, Grenzwerte 3.1 Zahlenfolgen Definition: Eine Folge ist eine geordnete Menge von Elementen an (den sogenannten Gliedern ), die
 3 Folgen, Reihen, Grenzwerte 3.1 Zahlenfolgen Definition: Eine Folge ist eine geordnete Menge von Elementen an (den sogenannten Gliedern ), die eindeutig den natürlichen Zahlen zugeordnet sind ( n N, auch
3 Folgen, Reihen, Grenzwerte 3.1 Zahlenfolgen Definition: Eine Folge ist eine geordnete Menge von Elementen an (den sogenannten Gliedern ), die eindeutig den natürlichen Zahlen zugeordnet sind ( n N, auch
Die Tangente als Näherung einer Funktion
 Die Tangente als Näherung einer Funktion Eine Motivation der Ableitung der Wurzelfunktion Marco Johannes Türk 13. Mai 2014 Marco Johannes Türk Die Tangente als Näherung einer Funktion 13. Mai 2014 1 /
Die Tangente als Näherung einer Funktion Eine Motivation der Ableitung der Wurzelfunktion Marco Johannes Türk 13. Mai 2014 Marco Johannes Türk Die Tangente als Näherung einer Funktion 13. Mai 2014 1 /
Folgen, Reihen, Grenzwerte u. Stetigkeit
 Folgen, Reihen, Grenzwerte u. Stetigkeit Josef F. Bürgler Abt. Informatik HTA Luzern, FH Zentralschweiz HTA.MA+INF Josef F. Bürgler (HTA Luzern) Einf. Infinitesimalrechnung HTA.MA+INF 1 / 33 Inhalt 1 Folgen
Folgen, Reihen, Grenzwerte u. Stetigkeit Josef F. Bürgler Abt. Informatik HTA Luzern, FH Zentralschweiz HTA.MA+INF Josef F. Bürgler (HTA Luzern) Einf. Infinitesimalrechnung HTA.MA+INF 1 / 33 Inhalt 1 Folgen
Kapitel 16 : Differentialrechnung
 Kapitel 16 : Differentialrechnung 16.1 Die Ableitung einer Funktion 16.2 Ableitungsregeln 16.3 Mittelwertsätze und Extrema 16.4 Approximation durch Taylor-Polynome 16.5 Zur iterativen Lösung von Gleichungen
Kapitel 16 : Differentialrechnung 16.1 Die Ableitung einer Funktion 16.2 Ableitungsregeln 16.3 Mittelwertsätze und Extrema 16.4 Approximation durch Taylor-Polynome 16.5 Zur iterativen Lösung von Gleichungen
1 Einleitung. 2 Reelle Zahlen. 3 Konvergenz von Folgen
 1 Einleitung Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis 1 aus dem Wintersemester 2008/09
1 Einleitung Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis 1 aus dem Wintersemester 2008/09
Kapitel 7. Exponentialfunktion
 Kapitel 7. Exponentialfunktion 7.1. Potenzreihen In Kap. 5 haben wir Reihen ν=0 a ν studiert, wo die Glieder feste Zahlen sind. Die Summe solcher Reihen ist wieder eine Zahl, z.b. die Eulersche Zahl e.
Kapitel 7. Exponentialfunktion 7.1. Potenzreihen In Kap. 5 haben wir Reihen ν=0 a ν studiert, wo die Glieder feste Zahlen sind. Die Summe solcher Reihen ist wieder eine Zahl, z.b. die Eulersche Zahl e.
Fehlerabschätzung für Taylorpolynome der e-funktion
 Fehlerabschätzung für Talorpolnome der e-funktion f() = e R () = e g() = ++ - -. Wir approimieren die Funktion f() = e durch g() = +! +! und schätzen den Fehler R() auf dem Intervall [,] ab. Sei also e
Fehlerabschätzung für Talorpolnome der e-funktion f() = e R () = e g() = ++ - -. Wir approimieren die Funktion f() = e durch g() = +! +! und schätzen den Fehler R() auf dem Intervall [,] ab. Sei also e
Mathematik für Anwender I
 Prof. Dr. H. Brenner Osnabrück WS 2011/2012 Mathematik für Anwender I Vorlesung 17 Potenzreihen Definition 17.1. Es sei (c n ) n N eine Folge von reellen Zahlen und x eine weitere reelle Zahl. Dann heißt
Prof. Dr. H. Brenner Osnabrück WS 2011/2012 Mathematik für Anwender I Vorlesung 17 Potenzreihen Definition 17.1. Es sei (c n ) n N eine Folge von reellen Zahlen und x eine weitere reelle Zahl. Dann heißt
13 Die trigonometrischen Funktionen
 13 Die trigonometrischen Funktionen Wir schreiben die Werte der komplexen Exponentialfunktion im Folgenden auch als e z = exp(z) (z C). Geometrisch definiert man üblicherweise die Werte der Winkelfunktion
13 Die trigonometrischen Funktionen Wir schreiben die Werte der komplexen Exponentialfunktion im Folgenden auch als e z = exp(z) (z C). Geometrisch definiert man üblicherweise die Werte der Winkelfunktion
Musterlösungen zu Blatt 15, Analysis I
 Musterlösungen zu Blatt 5, Analysis I WS 3/4 Inhaltsverzeichnis Aufgabe 85: Konvergenzradien Aufgabe 86: Approimation von ep() durch Polynome Aufgabe 87: Taylorreihen von cos 3 und sin Aufgabe 88: Differenzenquotienten
Musterlösungen zu Blatt 5, Analysis I WS 3/4 Inhaltsverzeichnis Aufgabe 85: Konvergenzradien Aufgabe 86: Approimation von ep() durch Polynome Aufgabe 87: Taylorreihen von cos 3 und sin Aufgabe 88: Differenzenquotienten
Analysis I. 4. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 4. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine bijektive Abbildung f: M N. () Ein
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 4. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine bijektive Abbildung f: M N. () Ein
Approximation durch Polynome
 durch n Anwendungen: zur Vereinfachung einer gegebenen Funktion durch einen Polynomausdruck. Dann sind übliche Rechenoperation +,,, / möglich. zur Interpolation von Daten einer Tabelle n Beispiel Trotz
durch n Anwendungen: zur Vereinfachung einer gegebenen Funktion durch einen Polynomausdruck. Dann sind übliche Rechenoperation +,,, / möglich. zur Interpolation von Daten einer Tabelle n Beispiel Trotz
,...) ist eine Folge, deren Glieder der Null beliebig nahe kommen. (iii) Die Folge a n = ( 1) n + 1 n oder (a n) = (0, 3 2, 2 3, 5 4, 4 5
 3 Folgen 3.1 Definition und Beispiele Eine Abbildung a : Æ Ê heißt (reelle) Zahlenfolge. Statt a(n) schreiben wir kürzer a n und bezeichnen die ganze Folge mit (a n ) n Æ oder einfach (a n ), was aber
3 Folgen 3.1 Definition und Beispiele Eine Abbildung a : Æ Ê heißt (reelle) Zahlenfolge. Statt a(n) schreiben wir kürzer a n und bezeichnen die ganze Folge mit (a n ) n Æ oder einfach (a n ), was aber
Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13)
 1 Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13) Kapitel 5: Konvergenz Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 15. Dezember 2011) Folgen Eine Folge x 0, x 1,
1 Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13) Kapitel 5: Konvergenz Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 15. Dezember 2011) Folgen Eine Folge x 0, x 1,
6 Weiterer Ausbau der Differentialrechnung
 6 Weiterer Ausbau der Differentialrechnung 6.1 Mittelwertsätze, Extremwerte, Satz von Taylor Motivation: Wie wählt man Höhe und Durchmesser einer Konservendose, so dass bei festem Volumen V möglichst wenig
6 Weiterer Ausbau der Differentialrechnung 6.1 Mittelwertsätze, Extremwerte, Satz von Taylor Motivation: Wie wählt man Höhe und Durchmesser einer Konservendose, so dass bei festem Volumen V möglichst wenig
Misterlösung zur Klausur zur Vorlesung Analysis I, WS08/09, Samstag, (Version C)
 Misterlösung zur Klausur zur Vorlesung Analysis I, WS08/09, Samstag, 14..009 (Version C Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen aus der Vorlesung
Misterlösung zur Klausur zur Vorlesung Analysis I, WS08/09, Samstag, 14..009 (Version C Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen aus der Vorlesung
Es gibt eine Heuristik, mit der sich die Primzahldichte
 Es gibt eine Heuristik, mit der sich die Primzahldichte 1 ln(x) für großes x N plausibel machen lässt. Die Idee besteht darin, das Änderungsverhalten der Primzahldichte bei x zu untersuchen. Den Ansatz
Es gibt eine Heuristik, mit der sich die Primzahldichte 1 ln(x) für großes x N plausibel machen lässt. Die Idee besteht darin, das Änderungsverhalten der Primzahldichte bei x zu untersuchen. Den Ansatz
e x e x x e x + e x (falls die Grenzwerte existieren), e x e x 1 e 2x = lim x 1
 Aufgabe a Hier kann man die Regel von de l Hospital zweimal anwenden (jeweils und die Ableitung des Nenners ist für hinreichend große x ungleich. Dies führt auf e x e x e x + e x e x + e x e x e x e x
Aufgabe a Hier kann man die Regel von de l Hospital zweimal anwenden (jeweils und die Ableitung des Nenners ist für hinreichend große x ungleich. Dies führt auf e x e x e x + e x e x + e x e x e x e x
f(x 0 ) = lim f(b k ) 0 0 ) = 0
 5.10 Zwischenwertsatz. Es sei [a, b] ein Intervall, a < b und f : [a, b] R stetig. Ist f(a) < 0 und f(b) > 0, so existiert ein x 0 ]a, b[ mit f(x 0 ) = 0. Wichtig: Intervall, reellwertig, stetig Beweis.
5.10 Zwischenwertsatz. Es sei [a, b] ein Intervall, a < b und f : [a, b] R stetig. Ist f(a) < 0 und f(b) > 0, so existiert ein x 0 ]a, b[ mit f(x 0 ) = 0. Wichtig: Intervall, reellwertig, stetig Beweis.
Mathematik für Anwender I. Beispielklausur 2 mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Mathematik für Anwender I Beispielklausur 2 mit en Dauer: Zwei volle Stunden + 0 Minuten Orientierung, in denen noch nicht geschrieben werden darf.
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Mathematik für Anwender I Beispielklausur 2 mit en Dauer: Zwei volle Stunden + 0 Minuten Orientierung, in denen noch nicht geschrieben werden darf.
Technische Universität München Zentrum Mathematik. Übungsblatt 2
 Technische Universität München Zentrum Mathematik Mathematik 2 (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 2 Hausaufgaben Aufgabe 2.1 Sei [a, b] R ein Intervall und ( ) n N [a,
Technische Universität München Zentrum Mathematik Mathematik 2 (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 2 Hausaufgaben Aufgabe 2.1 Sei [a, b] R ein Intervall und ( ) n N [a,
3. Potenzreihen. Definition 7.5. Eine unendliche Reihe der Form. a k x k. Es handelt sich also um eine Funktionenreihe mit f k (x) = a k x k.
 3. Potenzreihen Definition 7.5. Eine unendliche Reihe der Form a x mit x R (veranderlich und a R (onstant heit Potenzreihe, die Zahlen a ( heien Koezienten der Potenzreihe. Es handelt sich also um eine
3. Potenzreihen Definition 7.5. Eine unendliche Reihe der Form a x mit x R (veranderlich und a R (onstant heit Potenzreihe, die Zahlen a ( heien Koezienten der Potenzreihe. Es handelt sich also um eine
Reihen/Partialsummenfolgen und vollständige Induktion. Robert Klinzmann
 Reihen/Partialsummenfolgen und vollständige Induktion Robert Klinzmann 3. Mai 00 Reihen / Partialsummen 1 Inhaltsverzeichnis 1 Vorwort Das Prinzip der vollständigen Induktion 3 3 Herleitung der Gauß schen
Reihen/Partialsummenfolgen und vollständige Induktion Robert Klinzmann 3. Mai 00 Reihen / Partialsummen 1 Inhaltsverzeichnis 1 Vorwort Das Prinzip der vollständigen Induktion 3 3 Herleitung der Gauß schen
Ferienkurs Analysis 1 - Wintersemester 2014/15. 1 Aussage, Mengen, Induktion, Quantoren
 Ferienkurs Analysis 1 - Wintersemester 2014/15 Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis
Ferienkurs Analysis 1 - Wintersemester 2014/15 Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis
Kapitel 5 Differential- und Integralrechnung in einer Variablen
 Kapitel 5 Differential- und Integralrechnung in einer Variablen Inhaltsverzeichnis DIE ABLEITUNG... 3 DEFINITIONEN... 3 EIGENSCHAFTEN UND ABLEITUNGSREGELN... 4 TAYLOR SCHE FORMEL UND MITTELWERTSATZ...
Kapitel 5 Differential- und Integralrechnung in einer Variablen Inhaltsverzeichnis DIE ABLEITUNG... 3 DEFINITIONEN... 3 EIGENSCHAFTEN UND ABLEITUNGSREGELN... 4 TAYLOR SCHE FORMEL UND MITTELWERTSATZ...
0.1 Formale Potenzreihen und Konvergenz
 0. Formale Potenzreihen und Konvergenz Erinnerung: Ein Ausdruc der Form a x oder a (x a) mit a R heißt formale Potenzreihe oder unendlich langes Polynom. Seien a = a x und b = b x zwei Potenzreihen. Wir
0. Formale Potenzreihen und Konvergenz Erinnerung: Ein Ausdruc der Form a x oder a (x a) mit a R heißt formale Potenzreihe oder unendlich langes Polynom. Seien a = a x und b = b x zwei Potenzreihen. Wir
Analysis I. 2. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Die Produktmenge aus zwei Mengen L und M.
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Die Produktmenge aus zwei Mengen L und M.
Vorlesung. Funktionen/Abbildungen 1
 Vorlesung Funktionen/Abbildungen 1 1 Grundlagen Hinweis: In dieser Vorlesung werden Funktionen und Abbildungen synonym verwendet. In der Schule wird eine Funktion häufig als eindeutige Zuordnung definiert.
Vorlesung Funktionen/Abbildungen 1 1 Grundlagen Hinweis: In dieser Vorlesung werden Funktionen und Abbildungen synonym verwendet. In der Schule wird eine Funktion häufig als eindeutige Zuordnung definiert.
KAPITEL 9. Funktionenreihen
 KAPITEL 9 Funktionenreihen 9. TaylorReihen............................ 28 9.2 Potenzreihen............................ 223 9.3 Grenzfunktionen von Funktionenfolgen bzw. reihen........ 230 9.4 Anwendungen............................
KAPITEL 9 Funktionenreihen 9. TaylorReihen............................ 28 9.2 Potenzreihen............................ 223 9.3 Grenzfunktionen von Funktionenfolgen bzw. reihen........ 230 9.4 Anwendungen............................
Folgen und Reihen. Thomas Blasi
 Folgen und Reihen Thomas Blasi 02.03.2009 Inhaltsverzeichnis Folgen und Grenzwerte 2. Definitionen und Bemerkungen............................. 2.2 Konvergenz und Beschränktheit.............................
Folgen und Reihen Thomas Blasi 02.03.2009 Inhaltsverzeichnis Folgen und Grenzwerte 2. Definitionen und Bemerkungen............................. 2.2 Konvergenz und Beschränktheit.............................
Angewandte Mathematik und Programmierung
 Angewandte Mathematik und Programmierung Einführung in das Konzept der objektorientierten Anwendungen zu mathematischen Rechnens WS 2013/14 Oft können wir bestimmte mathematische Funktionen nicht genau
Angewandte Mathematik und Programmierung Einführung in das Konzept der objektorientierten Anwendungen zu mathematischen Rechnens WS 2013/14 Oft können wir bestimmte mathematische Funktionen nicht genau
2.12 Potenzreihen. 1. Definitionen. 2. Berechnung 2.12. POTENZREIHEN 207. Der wichtigste Spezialfall von Funktionenreihen sind Potenzreihen.
 2.2. POTENZREIHEN 207 2.2 Potenzreihen. Definitionen Der wichtigste Spezialfall von Funktionenreihen sind Potenzreihen. Eine Potenzreihe mit Entwicklungspunkt x 0 ist eine Reihe a n x x 0 n. Es gilt: es
2.2. POTENZREIHEN 207 2.2 Potenzreihen. Definitionen Der wichtigste Spezialfall von Funktionenreihen sind Potenzreihen. Eine Potenzreihe mit Entwicklungspunkt x 0 ist eine Reihe a n x x 0 n. Es gilt: es
Approximation durch Taylorpolynome
 TU Berlin Fakultät II - Mathematik und Naturwissenschaften Sekretariat MA 4-1 Straße des 17. Juni 10623 Berlin Hochschultag Approximation durch Taylorpolynome Im Rahmen der Schülerinnen- und Schüler-Uni
TU Berlin Fakultät II - Mathematik und Naturwissenschaften Sekretariat MA 4-1 Straße des 17. Juni 10623 Berlin Hochschultag Approximation durch Taylorpolynome Im Rahmen der Schülerinnen- und Schüler-Uni
Aufgaben zur Analysis I aus dem Wiederholungskurs
 Prof. Dr. H. Garcke, Dr. H. Farshbaf-Shaker, D. Depner WS 8/9 Hilfskräfte: A. Weiß, W. Thumann 6.3.29 NWF I - Mathematik Universität Regensburg Aufgaben zur Analysis I aus dem Wiederholungskurs Die folgenden
Prof. Dr. H. Garcke, Dr. H. Farshbaf-Shaker, D. Depner WS 8/9 Hilfskräfte: A. Weiß, W. Thumann 6.3.29 NWF I - Mathematik Universität Regensburg Aufgaben zur Analysis I aus dem Wiederholungskurs Die folgenden
PRÜFUNG AUS ANALYSIS F. INF.
 Zuname: Vorname: Matrikelnummer: PRÜFUNG AUS ANALYSIS F. INF. (GITTENBERGER) Wien, am 2. Juli 2013 (Ab hier freilassen!) Arbeitszeit: 100 Minuten 1) 2) 3) 4) 5) 1)(8 P.) Sei f : R 2 R mit f(x, y) = e x
Zuname: Vorname: Matrikelnummer: PRÜFUNG AUS ANALYSIS F. INF. (GITTENBERGER) Wien, am 2. Juli 2013 (Ab hier freilassen!) Arbeitszeit: 100 Minuten 1) 2) 3) 4) 5) 1)(8 P.) Sei f : R 2 R mit f(x, y) = e x
Beispiel: Bestimmung des Werts 3 2 ( 2 1, 4142) Es gilt 3 1,41 = 3 141/100 = , 707. Es gilt 3 1,42 = 3 142/100 = , 759.
 (4) Exponential- und Logarithmusfunktionen Satz Für jedes b > 1 gibt es eine eindeutig bestimmte Funktion exp b : R R + mit folgenden Eigenschaften. exp b (r) = b r für alle r Q Die Funktion exp b ist
(4) Exponential- und Logarithmusfunktionen Satz Für jedes b > 1 gibt es eine eindeutig bestimmte Funktion exp b : R R + mit folgenden Eigenschaften. exp b (r) = b r für alle r Q Die Funktion exp b ist
Beispielaufgaben rund um Taylor
 Beispielaufgaben rund um Taylor Mirko Getzin Universität Bielefeld Fakultät für Mathematik 19. Februar 014 Keine Gewähr auf vollständige Richtigkeit und perfekter Präzision aller (mathematischen) Aussagen.
Beispielaufgaben rund um Taylor Mirko Getzin Universität Bielefeld Fakultät für Mathematik 19. Februar 014 Keine Gewähr auf vollständige Richtigkeit und perfekter Präzision aller (mathematischen) Aussagen.
differenzierbare Funktionen
 Kapitel IV Differenzierbare Funktionen 18 Differenzierbarkeit und Rechenregeln für differenzierbare Funktionen 19 Mittelwertsätze der Differentialrechnung mit Anwendungen 20 Gleichmäßige Konvergenz von
Kapitel IV Differenzierbare Funktionen 18 Differenzierbarkeit und Rechenregeln für differenzierbare Funktionen 19 Mittelwertsätze der Differentialrechnung mit Anwendungen 20 Gleichmäßige Konvergenz von
Kapitel 5 Reihen 196
 Kapitel 5 Reihen 96 Kapitel 5. Definition und Beispiele 97 Das Material dieses Kapitels können Sie nachlesen in: MICHAEL SPIVAK, Calculus, Kapitel 22 DIRK HACHENBERGER, Mathematik für Informatiker, Kapitel
Kapitel 5 Reihen 96 Kapitel 5. Definition und Beispiele 97 Das Material dieses Kapitels können Sie nachlesen in: MICHAEL SPIVAK, Calculus, Kapitel 22 DIRK HACHENBERGER, Mathematik für Informatiker, Kapitel
Vorlesung Mathematik 2 für Ingenieure (Sommersemester 2016)
 1 Vorlesung Mathematik 2 für Ingenieure (Sommersemester 216) Kapitel 11: Potenzreihen und Fourier-Reihen Prof. Miles Simon Nach Folienvorlage von Prof. Dr. Volker Kaibel Otto-von-Guericke Universität Magdeburg.
1 Vorlesung Mathematik 2 für Ingenieure (Sommersemester 216) Kapitel 11: Potenzreihen und Fourier-Reihen Prof. Miles Simon Nach Folienvorlage von Prof. Dr. Volker Kaibel Otto-von-Guericke Universität Magdeburg.
Mathematik I Herbstsemester 2014
 Mathematik I Herbstsemester 2014 www.math.ethz.ch/education/bachelor/lectures/hs2014/other/mathematik1 BIOL Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas 1 / 32 1 Stetigkeit Grenzwert einer
Mathematik I Herbstsemester 2014 www.math.ethz.ch/education/bachelor/lectures/hs2014/other/mathematik1 BIOL Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/ farkas 1 / 32 1 Stetigkeit Grenzwert einer
Klausur - Analysis I Lösungsskizzen
 Klausur - Analysis I Lösungsskizzen Aufgabe 1.: 5 Punkte Entscheiden Sie, ob folgende Aussagen wahr oder falsch sind. Kennzeichnen Sie wahre Aussagen mit W und falsche Aussagen mit F. Es sind keine Begründungen
Klausur - Analysis I Lösungsskizzen Aufgabe 1.: 5 Punkte Entscheiden Sie, ob folgende Aussagen wahr oder falsch sind. Kennzeichnen Sie wahre Aussagen mit W und falsche Aussagen mit F. Es sind keine Begründungen
EDV für Chemiker: MAPLE - KURS
 EDV für Chemiker: MAPLE - KURS Vorlesung 4 Polynomenschar mit indizierten Koeffizienten > f:=x->a[0]+a[1]*x+a[2]*x^2+a[3]*x^3+a[4]*x^4; f := x a 0 + a 1 x + a 2 x 2 + a 3 x 3 + a 4 x 4 i) An der Stelle
EDV für Chemiker: MAPLE - KURS Vorlesung 4 Polynomenschar mit indizierten Koeffizienten > f:=x->a[0]+a[1]*x+a[2]*x^2+a[3]*x^3+a[4]*x^4; f := x a 0 + a 1 x + a 2 x 2 + a 3 x 3 + a 4 x 4 i) An der Stelle
1 Funktionen und ihre Ableitungen
 1 Funktionen und ihre Ableitungen 1.1 Funktionen Wir nennen eine Grösse y eine Funktion von x, wenn der Wert von y von demjenigen von x abhängt: Zu jedem x wird in eindeutiger Weise ein Wert von y zugeordnet.
1 Funktionen und ihre Ableitungen 1.1 Funktionen Wir nennen eine Grösse y eine Funktion von x, wenn der Wert von y von demjenigen von x abhängt: Zu jedem x wird in eindeutiger Weise ein Wert von y zugeordnet.
TECHNISCHE UNIVERSITÄT MÜNCHEN
 TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Aufgabe 45. Polynome sind stets stetig. Höhere Mathematik für Informatiker II (Sommersemester
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik PROF. DR.DR. JÜRGEN RICHTER-GEBERT, VANESSA KRUMMECK, MICHAEL PRÄHOFER Aufgabe 45. Polynome sind stets stetig. Höhere Mathematik für Informatiker II (Sommersemester
ε δ Definition der Stetigkeit.
 ε δ Definition der Stetigkeit. Beweis a) b): Annahme: ε > 0 : δ > 0 : x δ D : x δ x 0 < δ f (x δ f (x 0 ) ε Die Wahl δ = 1 n (n N) generiert eine Folge (x n) n N, x n D mit x n x 0 < 1 n f (x n ) f (x
ε δ Definition der Stetigkeit. Beweis a) b): Annahme: ε > 0 : δ > 0 : x δ D : x δ x 0 < δ f (x δ f (x 0 ) ε Die Wahl δ = 1 n (n N) generiert eine Folge (x n) n N, x n D mit x n x 0 < 1 n f (x n ) f (x
Die Exponentialfunktion. exp(x)
 Die Exponentialfunktion exp(x) Wir erinnern: Ist f : R R eine glatte Funktion, dann bezeichnet f (x) die Steigung von f im Punkt x. f (x) x x 0 x Wie sehen Funktionen aus mit 3 2 f f (x) = f(x) -3-2 -1
Die Exponentialfunktion exp(x) Wir erinnern: Ist f : R R eine glatte Funktion, dann bezeichnet f (x) die Steigung von f im Punkt x. f (x) x x 0 x Wie sehen Funktionen aus mit 3 2 f f (x) = f(x) -3-2 -1
Konvergenz einer Folge. 1-E1 Ma 1 Lubov Vassilevskaya
 Konvergenz einer Folge 1-E1 Ma 1 Lubov Vassilevskaya Konvergenz einer Folge: Inhalt Drei Verhaltensmuster von Folgen. Beispiele 1 ) = 1 n, = n n +1, 2 ) = ( 1)n n +1 n und ihre graphischen Darstellungen.,
Konvergenz einer Folge 1-E1 Ma 1 Lubov Vassilevskaya Konvergenz einer Folge: Inhalt Drei Verhaltensmuster von Folgen. Beispiele 1 ) = 1 n, = n n +1, 2 ) = ( 1)n n +1 n und ihre graphischen Darstellungen.,
6 Die Bedeutung der Ableitung
 6 Die Bedeutung der Ableitung 24 6 Die Bedeutung der Ableitung Wir wollen in diesem Kapitel diskutieren, inwieweit man aus der Kenntnis der Ableitung Rückschlüsse über die Funktion f ziehen kann Zunächst
6 Die Bedeutung der Ableitung 24 6 Die Bedeutung der Ableitung Wir wollen in diesem Kapitel diskutieren, inwieweit man aus der Kenntnis der Ableitung Rückschlüsse über die Funktion f ziehen kann Zunächst
3.4 Analytische Fortsetzung
 3.4 Analytische Fortsetzung 3.4. Analytische Fortsetzung 49 Es kann vorkommen, dass eine holomorphe Funktion f, definiert durch eine Potenzreihe um den Punkt z 0 mit Konvergenzradius R, über den Rand der
3.4 Analytische Fortsetzung 3.4. Analytische Fortsetzung 49 Es kann vorkommen, dass eine holomorphe Funktion f, definiert durch eine Potenzreihe um den Punkt z 0 mit Konvergenzradius R, über den Rand der
Unendliche Potenzen. Thomas Peters Thomas Mathe-Seiten 7. August 2010
 Unendliche Potenzen Thomas Peters Thomas Mathe-Seiten www.mathe-seiten.de 7. August 00 In diesem Artikel werden wir uns einem zunächst bizarr anmutenden Thema widmen, nämlich den unendlichen Kettenbrüchen,
Unendliche Potenzen Thomas Peters Thomas Mathe-Seiten www.mathe-seiten.de 7. August 00 In diesem Artikel werden wir uns einem zunächst bizarr anmutenden Thema widmen, nämlich den unendlichen Kettenbrüchen,
