Contents. 1 Aussagen Aussagen Verknüpfung von Aussagen Regeln Quantoren Mengen 6
|
|
|
- Hildegard Neumann
- vor 7 Jahren
- Abrufe
Transkript
1 Höhere Mathematik I für die Fachrichtung Elektrotechnik und Informationstechnik Wintersemester 2016/17 Ioannis Anapolitanos Karlsruher Institut für Technologie Institut für Analysis Englerstr. 2, Karlsruhe ioannis.anapolitanos@kit.edu Dies ist eine kurze Vorlesungszusammenfassung, gedacht zur Vorlesungsbegleitung und als Gedächtnisstütze, nicht jedoch als etwas, das für sich selbst stehen könnte (wie etwa ein Lehrbuch). Der Besuch der Vorlesung ist durch die Lektüre in keinem Fall zu ersetzen, es gibt dort noch viel mehr an mündlichen Erklärungen, Beispiele, Erläuterungen und veranschaulichen- den Skizzen, die für Verständnis und Einordnung des präsentierten Stoffes unabdingbar sind. Danksagung: Die Vorlesungszusammenfassung ist eine Änderung der Vorlesungszusammenfassung von Herrn Dr. Kunstmann. Ich danke Herrn Dr. Kunstmann, dass er mir die Möglichkeit gegeben hat seine Zusammenfassung zu verwenden. Contents 1 Aussagen Aussagen Verknüpfung von Aussagen Regeln Quantoren Mengen 6 1
2 2.1 Der Begriff der Menge Beziehungen zwischen Mengen Operationen mit Mengen Die leere Menge Die Potenzmenge Das kartesische Produkt Die Mengen der reellen und komplexen Zahlen Funktionen Zum Begriff der Funktion Komposition Die Umkehrabbildung Gründlichere Einführung der reellen Zahlen Körperaxiome Anordnungsaxiome Supremum und Infimum Das Vollständigkeitsaxiom Natürliche Zahlen Vollständige Induktion Ganze und rationale Zahlen Binomialkoeffizienten Potenzen Wurzeln Mehr über die komplexen Zahlen Polynome Polynomdivision Fundamentalsatz der Algebra Die Gleichung z n = c, c C Folgen und Konvergenz Konvergenz
3 6.2 Grenzwertsätze Monotone Folgen Wichtige Beispiele Teilfolgen Rechnen mit Limes superior und Limes inferior Reihen Definition und Elementare Eigenschaften Absolut konvergente Reihen Majoranten- und Minorantenkriterium Leibnizkriterium für alternierende Reihen Wurzelkriterium Quotientenkriterium Die Exponentialreihe Das Cauchyprodukt Die Exponentialfunktion Sinus und Cosinus Potenzreihen Stetigkeit Limes, Definition der Stetigkeit, Kriterien für Stetigkeit Zwischenwertsatz Einseitige Grenzwerte Monotone Funktionen Logarithmus und trigonometrische Funktionen Differentialrechnung Differentiarbarkeit Ableitungsregeln Mittelwertsatz und Folgerungen Höhere Ableitungen und Taylorsatz
4 10.5 Die Regeln von de l Hospital Ableitung von Potenzreihen Integration Ober- und Untersummen, oberes und unteres Integral Riemann Integrierbarkeit, Riemann Integral Eigenschaften des Riemann Integrals Hauptsatz der Differential- und Integralrechnung, Partielle Integration, Integration durch Substitution
5 1 Aussagen 1.1 Aussagen Eine Aussage ist ein Satz, der entweder wahr (w) oder falsch (f) ist. Im Rahmen der Vorlesung sind wir aber eher an mathematischen Aussagen interessiert. Aussagen bezeichnen wir im folgenden mit A, B, C, Verknüpfung von Aussagen Wir erklären die logische Verknüpfung von Aussagen durch sogenannte Wahrheitstafeln. A B (logisches und (AND)) A w w f f B w f w f A B w f f f A B (logisches oder (OR)) A w w f f B w f w f A B w w w f Achtung: Das logische oder ist nicht exklusiv, dh es ist zugelassen, dass beide Aussagen A und B wahr sind. Negation A ( non A oder nicht A ) A w f A f w Implikation A B wenn A, dann B, A impliziert B, aus A folgt B A w w f f B w f w f A B w f w w Äquivalenz A B A w w f f B w f w f A B w f f w Man sagt: A ist äquivalent zu B, A ist gleichbedeutend mit B, A genau dann, wenn B, A dann und nur dann, wenn B. 5
6 1.3 Regeln bindet stärker als / ; / bindet stärker als /. ( A) A (doppelte Negation) (A B) [(A B) (B A)] (Äquivalenz bedeutet zwei Implikationen) (A B) ( A B) (Negation von und ) (A B) ( A B) (Negation von oder ) (A B) ( A B) (Umformulierung der Implikation) (A B) (A B) (Negation der Implikation) (A B) ( B A) (Kontraposition ). Kommutativität: A B B A und A B B A. Assoziativität: A (B C) (A B) C und A (B C) (A B) C. Deshalb kann man hier die Klammern weglassen. Distributivität: A (B C) (A B) (A C) und A (B C) (A B) (A C). 1.4 Quantoren Eine Aussageform A(x), A(x, y),... ist ein Satz, der eine oder mehrere Variablen x, y,... enthält und der nach dem Ersetzen dieser Variablen durch konkrete Objekte eine Aussage ist. Der Allquantor x : A(x) bedeutet: für alle Objekte x ist die Aussage A(x) wahr. Der Existenzquantor x : A(x) bedeutet: es gibt (mindestens) ein Objekt x, für das die Aussage A(x) wahr ist. Negation: ( x : A(x)) ( x : A(x)) und ( x : A(x)) ( x : A(x)). In den allermeisten Fällen werden Quantoren eingeschränkt und beziehen sich dann nur auf gewisse Objekte, z.b. x mit A(x) : B(x). Die Negation davon ist dann x mit A(x) : B(x). Achtung: Bei All- und Existenzquantor kommt es i.a. auf die Reihenfolge an. Bemerkung: Häufig schreiben wir Quantoren nicht als Zeichen, sondern sprachlich. 2 Mengen 2.1 Der Begriff der Menge Wir verwenden die folgende naive Definition : 6
7 Eine Menge ist die Zusammenfassung wohlbestimmter, wohlunterschiedener Objekte. Diese Objekte heißen Elemente der Menge. x M bedeutet: x ist Element der Menge M, dh x gehört zu M. x M bedeutet: x gehört nicht zu M, dh x M : (x M). Schreibweisen: Ist A(x) eine Aussageform, so kann man schreiben M = {x : A(x)} = Menge aller x, für die A(x) gilt, Häufig schreibt man auch, wenn die Menge M gegeben ist, {x M : A(x)} für {x : (x M) A(x)}. Eine andere Möglichkeit ist die Aufzählung, z.b. M = {1, 2, 3, 9}. 2.2 Beziehungen zwischen Mengen Seien M 1, M 2 Mengen. Definition 2.1. M 1 ist Teilmenge von M 2 : M 1 M 2 : x : (x M 1 x M 2 ) (bzw. x M 1 : x M 2 ). Für M 1 M 2 und M 1 M 2 schreibt man oft der Deutlichkeit halber M 1 M 2. Gleichheit von Mengen: M 1 = M 2 bedeutet, dass M 1 und M 2 dieselben Elemente enthalten, also x : (x M 1 x M 2 ). Da Äquivalenz zwei Implikationen bedeutet (siehe 1.3) bedeutet M 1 = M 2 also M 1 M 2 und M 2 M Operationen mit Mengen Seien M 1, M 2, M 3 und Q Mengen. D (a) Durchschnitt M 1 M 2 := {x : x M 1 x M 2 }. (b) Vereinigung M 1 M 2 := {x : x M 1 x M 2 }. (c) Differenz M 1 \ M 2 := {x M 1 : x M 2 } ( M 1 ohne M 2 ). Regeln für Durchschnitt und Vereinigung: Kommutativität M 1 M 2 = M 2 M 1, M 1 M 2 = M 2 M 1. Assoziativität M 1 (M 2 M 3 ) = (M 1 M 2 ) M 3, M 1 (M 2 M 3 ) = (M 1 M 2 ) M 3. Distributivität: M 1 (M 2 M 3 ) = (M 1 M 2 ) (M 1 M 3 ), M 1 (M 2 M 3 ) = (M 1 M 2 ) (M 1 M 3 ). Außerdem ist M 1 M 1 M 2, M 2 M 1 M 2, M 1 M 2 M 1, M 1 M 2 M 2. de Morgansche Regeln: Wegen 1.3 (Negation von und / oder ) gilt auch Q \ (M 1 M 2 ) = (Q \ M 1 ) (Q \ M 2 ), Q \ (M 1 M 2 ) = (Q \ M 1 ) (Q \ M 2 ). 7
8 2.4 Die leere Menge Die leere Menge enthält keine Elemente, dh x : x. Regeln: M = M, M \ = M, M =, M \ M =, M für jede Menge M. 2.5 Die Potenzmenge Ist M eine Menge, so heißt die Menge aller Teilmengen von M Pot(M) := {N : N M} die Potenzmenge von M (manchmal auch P(M)). 2.6 Das kartesische Produkt Sei n N. Seien M 1, M 2,..., M n Mengen. Die Menge der geordneten n-tupel (x 1, x 2,..., x n ) mit x j M j für alle j {1, 2,..., n} heißt das kartesische Produkt M 1 M 2... M n der Mengen M 1, M 2,..., M n. Also M 1 M 2... M n = {(x 1, x 2,..., x n ) : für alle j {1, 2,..., n} gilt x j M j }. Wir schreiben M n, falls M 1 = M 2 =... = M n = M gilt. 2.7 Die Mengen der reellen und komplexen Zahlen Reelle Zahlen und Betrag Mit R bezeichnen wir die Menge der reellen Zahlen. Für a R heißt a := der Betrag von a. { a, a 0 a, a < 0 Beachte: Es gilt a = a für alle a R, also auch a b = b a für alle a, b R. Anschaulich ist a b der Abstand von a und b auf der Zahlengeraden. Regeln: Seien a, b, c R. Dann gilt: (1) a 0; (2) a = 0 a = 0; (3) ab = a b ; ( ) (4) ±a a und a c (a c und a c) ; (5) a + b a + b Dreiecksungleichung ; (6) a b a b umgekehrte Dreiecksungleichung. Die Menge der komplexen Zahlen 8
9 Wir betrachten eine Zahl i, mit i 2 = 1. Es ist dann C := {x + iy : x, y R} die Menge der komplexen Zahlen. Für z = x + iy C mit x, y R heißt x der Realteil von z (geschrieben Re z) und y heißt der Imaginärteil von z (geschrieben Im z). Komplexe Zahlen z mit Re z = 0 heißen rein imaginär und komplexe Zahlen mit Im z = 0 heißen reell. Also: Man kann mit komplexen Zahlen wie gewohnt rechnen und muss nur i 2 berücksichtigen, etwa (x 1 + iy 1 )(x 2 + iy 2 ) = x 1 x 2 + i(y 1 x 2 + x 1 y 2 ) + i 2 y 1 y 2 = (x 1 x 2 y 1 y 2 ) + i(x 2 y 1 + x 1 y 2 ), = 1 Konjugation und Betrag Zu einer komplexen Zahl z = x + iy heißt z := x iy die konjugierte komplexe Zahl. Es gilt dann z z = x 2 + y 2 0 und z := zz = x 2 + y 2 heißt Betrag der komplexen Zahl z. Rechenregeln: Für alle w, z C gilt: (z) = z, z = z, z + w = z + w, z w = z w, z w = z w, Re z = 1(z + z) und Im z = 1 (z z), 2 2i max{ Re z, Im z } z Re z + Im z z + w z + w (Dreiecksungleichung) und z w z w. Eine komplexe Zahl ist Null genau dann, wenn Real- und Imaginärteil beide Null sind. Ist x + iy 0, so ist das multiplikativ Inverse gegeben durch 3 Funktionen 1 z = 1 x + iy = 3.1 Zum Begriff der Funktion x iy (x + iy)(x iy) = z z. 2 Seien X, Y Mengen. Eine Funktion (oder Abbildung) f : X Y ordnet jedem x X genau ein y Y zu. Für das einem gegebenen x X zugeordnete y Y schreiben wir f(x). Schreibweise f : X Y, x f(x) ( f von X nach Y, x wird abgebildet auf f(x) ). Die Menge {(x, f(x)) : x X} X Y heißt Graph von f. Man kann diesen mit der Funktion f identifizieren. Für eine Funktion f : X Y heißt X Definitionsbereich und Y Wertebereich von f. Für A X heißt f(a) := {f(x) : x A} Bild von A unter f, und für B Y heißt f 1 (B) := {x X : f(x) B} Urbild von B unter f. Insbesondere heißt f(x) = {f(x) : x X} Bild von f (Menge aller y Y, die von f getroffen werden). 9
10 Definition 3.1. Sei f : X Y eine Funktion. (a) f heißt surjektiv, falls f(x) = Y gilt, dh falls jedes y Y von f getroffen wird. (b) f heißt injektiv, falls gilt x 1, x 2 X : x 1 x 2 f(x 1 ) f(x 2 ), dh falls es zu jedem Element im Bild von f genau ein Urbild gibt. (c) f heißt bijektiv, falls f injektiv und surjektiv ist. 3.2 Komposition Sind f : X Y, g : Y Z Funktionen, so definiert g f : X Z, x g(f(x)) eine Funktion g f ( g nach f ), die Hintereinanderausführung oder Komposition von f und g. Satz 3.1. Sind f : X Y, g : Y Z, h : Z W Funktionen, so gilt h (g f) = (h g) f, dh die Hintereinanderausführung von Funktionen ist assoziativ. 3.3 Die Umkehrabbildung Ist f : X Y eine bijektive Funktion, so definiert Y X, y x, falls f(x) = y eine Funktion f 1, die Umkehrabbildung (oder Umkehrfunktion) von f. Beachte: Da f surjektiv ist, gibt es zu jedem y ein solches x. Da f injektiv ist, ist dieses x eindeutig bestimmt. Somit ist f 1 tatsächlich eine Funktion. Bemerkung 3.1. Ist f : X Y bijektiv, so gilt f 1 f = id X und f f 1 = id Y. Satz 3.2. Sind f : X Y und g : Y X Funktionen mit g f = id X und f g = id Y, so ist f bijektiv und es gilt g = f 1. Bemerkung 3.2. Durch Vertauschen der Rollen von f und g folgt auch f = g 1 und insbesondere (f 1 ) 1 = f. Satz 3.3. Sind f : X Y und g : Y Z bijektive Funktionen, so ist g f : X Z bijektiv, und es gilt: (g f) 1 = f 1 g 1 : Z X. 4 Gründlichere Einführung der reellen Zahlen Grundmenge der Analysis ist die Menge R der reellen Zahlen. Wir führen diese Menge durch 15 Axiome ein, dh durch grundlegende Eigenschaften, aus denen sich alle weiteren Rechenregeln herleiten lassen. Wir nehmen dann R als mit diesen Axiomen gegeben an. Eine explizite Konstruktion (die natürlich möglich ist!), führen wir hier nicht durch. 10
11 4.1 Körperaxiome Es gibt Verknüpfungen + : R R R ( plus, wir schreiben a + b) und : R R R ( mal, wir schreiben ab oder a b) mit a, b, c R : (a + b) + c = a + (b + c) (A1) (ab)c = a(bc) (A5) 0 R a R : a + 0 = a (A2) 1 R \ {0} a R : a 1 = a (A6) a R a R : a + ( a) = 0 (A3) a R \ {0} a 1 R : a a 1 = 1 (A7) a, b R : a + b = b + a (A4) ab = ba (A8) a, b, c R : a(b + c) = ab + ac (A9) Dabei sind (A1) und (A5) die Assoziativgesetze, (A4) und (A8) die Kommutativgesetze, und (A9) ist das Distributivgesetz. Schreibweisen: Für a, b R setzen wir a b := a + ( b) und, falls b 0 ist, a b := ab Anordnungsaxiome In R ist eine Ordnung gegeben mit folgenden Eigenschaften: (A10) a, b R : a b oder b a, (A11) a, b, c R : a b und b c a c, (A12) a, b R : a b und b a a = b, (A13) a, b, c R : a b a + c b + c, (A14) a, b, c R : a b und 0 c ac bc. (A11) heißt Transitivität, (A12) heißt Antisymmetrie. Außerdem beinhaltet (A10) auch, dass a a gilt (Reflexivität). (A13) und (A14) bedeuten, dass die Ordnung mit den Verknüpfungen + und verträglich ist. Schreibweisen: b a : a b; a < b : a b und a b; b > a : a < b. Bemerkung 4.1. Aus (A1) (A14) lassen sich alle Rechenregeln für Ungleichungen herleiten. Diese setzen wir von nun an als bekannt voraus. 11
12 Intervalle: Seien a, b R mit a < b. Wir setzen: [a, b] := {x R : a x b} abgeschlossenes Intervall, (a, b) := {x R : a < x < b} offenes Intervall, [a, b) := {x R : a x < b} halboffenes Intervall, (a, b] := {x R : a < x b} halboffenes Intervall, [a, ) := {x R : a x}, (a, ) := {x R : a < x}, (, a] := {x R : x a}, (, a) := {x R : x < a}. Weiter: [a, a] := {a} und (, ) := R. 4.3 Supremum und Infimum Sei M R mit M. M heißt nach oben [unten] beschränkt : γ R x M : x γ [x γ]. In diesem Fall heißt γ eine obere Schranke (OS) [untere Schranke (US)] von M. Eine obere Schranke [untere Schranke] γ von M mit γ M heißt Maximum [Minimum] von M und wird mit max M [min M] bezeichnet. Wegen (A12) sind max M und min M im Falle der Existenz eindeutig bestimmt. Definition 4.1. Ist γ obere Schranke [untere Schranke] von M mit γ γ [γ γ] für jede obere Schranke [untere Schranke] γ von M, so heißt γ Supremum [Infimum] von M (kleinste obere Schranke von M [größte untere Schranke von M]) und wird mit sup M [inf M] bezeichnet. Nach (A12) sind Supremum und Infimum im Falle der Existenz eindeutig bestimmt. Bemerkung 4.2. Ein Maximum ist immer auch Supremum, und es gilt sup M = max M genau dann, wenn sup M M ist (entsprechend für min und inf). 4.4 Das Vollständigkeitsaxiom (A15) Jede nichtleere nach oben beschränkte Teilmenge von R hat ein Supremum. Folgerung 4.1. Jede nichtleere nach unten beschränkte Teilmenge von R hat ein Infimum. Definition 4.2. Eine Menge M R heißt beschränkt, falls M nach oben und nach unten beschränkt ist. 12
13 Bemerkung 4.3. M beschränkt γ 0 x M : x γ. Satz 4.1. Sei B A R. Dann gilt: (1) A beschränkt inf A sup A. (2) A nach oben [nach unten] beschränkt B nach oben [nach unten] beschränkt und sup B sup A [inf B inf A]. (3) Sei A nach oben [nach unten] beschränkt und γ eine obere Schranke [untere Schranke] von A. Dann gilt: γ = sup A für jedes ε > 0 gibt es ein x A mit x > γ ε [γ = inf A für jedes ε > 0 gibt es ein x A mit x < γ + ε]. 4.5 Natürliche Zahlen Satz 4.2. Wir betrachten die Menge N der natürlichen Zahlen. (1) N ist nicht nach oben beschränkt. (2) Für jedes x R gibt es n N mit n > x. (3) Für jedes b R mit b > 0 gibt es n N mit 1 n < b. 4.6 Vollständige Induktion Beweisverfahren durch Induktion Für jedes n N sei A(n) eine Aussage. Es gelte Induktionsanfang (IA) A(1) Induktionsschritt (IS) n N : (A(n) A(n + 1)). Dann ist für jedes n N die Aussage A(n) wahr, dh es gilt n N : A(n). Definition durch Rekursion (bzw. durch Induktion) Es sei G(1) definiert, und für jedes n N sei G(n + 1) definiert unter der Voraussetzung, dass G(1), G(2),..., G(n) schon definiert sind. Dann hat man G(n) für jedes n N definiert. Varianten der Induktion: Man kann die Induktion auch bei z.b. n = 5 beginnen lassen. Zum Beweis von n N mit n 5 : A(n) hat man dann zu zeigen: (IA) A(5) Bei der Abschnittsinduktion zeigt man (IA) (IS) n N mit n 5 : (A(n) A(n + 1)). A(1) (IS) n N : (A(1) A(2)... A(n) A(n + 1)). 13
14 4.7 Ganze und rationale Zahlen Definition 4.3. N 0 := N {0}, Z := N 0 { n : n N} Menge der ganzen Zahlen und Q := { p : p Z, q N} Menge der rationalen Zahlen. q Satz 4.3. Jede nichtleere nach unten beschränkte Teilmenge von Z hat ein Minimum. 4.8 Binomialkoeffizienten Für n, k N 0 mit k n setzt man ( ) n := k n! k!(n k)! ( n über k ). Es gilt ( ( n 0) = 1 = n ) n für alle n N0, ( ) ( n k = n ( n k) für alle n k 0, 4 ) 2 = 4 3 = 6. 2 Lemma 4.1. Für 1 k n gilt ( ) ( n k + n ) ( k 1 = n+1 ) k. 4.9 Potenzen Setze für a R: a 0 := 1, a 1 := a und a n+1 := a n a für jedes n N. Dann gilt a n = a } a {{... a} für jedes n N. Für a 0 und n N setzt man a n := 1. a n n Faktoren Es gelten die bekannten Rechenregeln, also etwa (a m ) n = a m n und a m a n = a m+n. (1) Für alle a, b R und alle n N gilt: a n b n = (a b) n 1 k=0 an 1 k b k. (2) Binomialsatz: Für alle a, b R und n N 0 gilt: (a + b) n = n k=0 ( n k) a k b n k. (3) Bernoullische Ungleichung (BU): Sei x 1. Dann gilt n N: (1 + x) n 1 + nx. (4) Für alle x, y 0 und n N gilt: x y x n y n. Folgerung 4.2. Sei a R. Ist a > 1, so gibt es zu jedem K > 0 ein n N mit a n > K. Ist a (0, 1), so gibt es zu jedem ε > 0 ein n N mit a n < ε Wurzeln Sei n N. Zu jedem a R mit a 0 gibt es genau ein b R mit b 0 und b n = a. Bezeichnung: b = n a, n-te Wurzel aus a. Folgerung 4.3. Für alle a, b 0 gilt wegen 4.9 Rechenregel (4): a b n a n b, und wegen ( n a n b) n = ab gilt n ab = n a n b. 14
15 5 Mehr über die komplexen Zahlen Polarkoordinaten und Eulerformel: Eine komplexe Zahl z = x + iy (wobei x, y R) kann man schreiben mithilfe ihres Betrages r = z und des Winkels ϕ zur positiven x- Achse (dh mithilfe von Polarkoordinaten ). Es ist nämlich x = r cos ϕ und y = r sin ϕ nach Schulmathematik. Verwendet man die Eulerformel e iϕ = cos ϕ + i sin ϕ (ϕ R), so erhält man z = x + iy = r cos ϕ + ir sin ϕ = re iϕ. Multiplikation mit z dreht dann um den Winkel ϕ. Sind sin und cos bekannt, so kann man die Eulerformel als Definition von e iϕ verwenden. 5.1 Polynome Ein Polynom p (oder p(z)) mit komplexen Koeffizienten ist ein formaler Ausdruck p(z) = a n z n + a n 1 z n a 2 z 2 + a 1 z + a 0 mit n N 0 und a j C für alle j {0, 1,..., n}. Das Polynom heißt reell, wenn alle Koeffizienten a j reell sind. Das Polynom heißt vom Grad n, falls a n 0 gilt, und zusätzlich normiert, falls a n = 1 ist. Falls a n = 0 ist, so ist auch p(z) = a n 1 z n a 2 z 2 + a 1 z + a 0, dh führende Nullkoeffizienten kann man weglassen. Es gilt insbesondere p(z) hat den Grad 0 p(z) = a 0 und a 0 0. Das Nullpolynom p(z) = 0 hat keinen Grad. Die Menge aller Polynome mit komplexen Koeffizienten (in der freien Variablen z) bezeichnen wir mit C[z]. Definition 5.1. Ein z 0 C mit p(z 0 ) = 0 heißt Nullstelle des Polynoms p. 5.2 Polynomdivision Seien p, q C[z]\{0} Polynome vom Grad n bzw. k n. Dann gibt es eindeutig bestimmte Polynome m C[z] \ {0} und r C[z] mit Grad m = n k und r = 0 oder Grad r < k und p = mq + r (Division mit Rest). Satz 5.1. Ist p C[z] Polynom vom Grad n 1 und ist z 0 Nullstelle von p, so gibt es ein Polynom q C[z] vom Grad n 1 mit Dabei heißt z z 0 Linearfaktor. p(z) = q(z) (z z 0 ). 15
16 Definition 5.2. Die Vielfachheit (Vfh) einer Nullstelle z 0 von p gibt an, wie oft man p(z) durch den Linearfaktor z z 0 dividieren kann. Folgerung 5.1. Ein Polynom vom Grad n hat höchstens n Nullstellen. 5.3 Fundamentalsatz der Algebra Jedes Polynom vom Grad n 1 hat mindestens eine Nullstelle in C. Folgerung 5.2. Ist p(z) normiertes Polynom vom Grad n 1, so gibt es z 1, z 2,..., z n C mit p(z) = (z z 1 ) (z z 2 )... (z z n ). Eine feste Nullstelle z 0 von p(z) kommt dabei in z 1, z 2,..., z n so oft vor, wie ihre Vielfachheit angibt. 5.4 Die Gleichung z n = c, c C Um die Gleichung zu lösen schreibt man c in Polarkoordinaten (c = re iφ ) und benutzt man den Folgenden Satz Satz 5.2. Die Lösungen von z n = re iφ sind: z j = r 1 n e i (2jπ+φ) n, j = 0, 1,..., n 1. 6 Folgen und Konvergenz Definition 6.1. Eine reelle [komplexe] Zahlenfolge oder Folge ist eine Abbildung N R, n a n [bzw. N C, n a n ]. Wir schreiben (a n ) n N, (a n ) n=1 oder kurz (a n ) oder auch (a 1, a 2, a 3,...). Beispiele: (1) a n = 1 n für alle n N, also (a n) = (1, 1 2, 1 3,...). (2) a n = ( 1) n für alle n N, also (a n ) = ( 1, 1, 1, 1, 1,...). (3) a n = i n für alle n N, also (a n ) = (i, 1, i, 1, i, 1, i, 1,...). Der Begriff der Konvergenz ist für die Analysis von zentraler Bedeutung. 6.1 Konvergenz Sei (a n ) eine Zahlenfolge und a R [bzw. a C]. Wir sagen, dass (a n ) gegen a konvergiert und schreiben lim n a n = a, falls gilt: ε > 0 n }{{} 0 N n n 0 : a n a < ε. = n 0 (ε) 16
17 Das bedeutet: die a n kommen a beliebig nahe oder der Abstand a n a wird beliebig klein, wenn n groß genug ist. Die Zahl a heißt dann Limes oder Grenzwert der Folge (a n ). Eine Folge (a n ) heißt konvergent, falls es ein a R [bzw. a C] so gibt, dass (a n ) gegen a konvergiert. Eine Folge, die nicht konvergiert, heißt divergent. Schreibweisen: Statt lim n a n = a schreibt man auch lim a n = a, a n a (n ) oder a n a. 1 Beispiele: (1) lim n = 0: Sei ε > 0. Nach Satz 4.2 (3) finden wir ein n n 0 N mit 1 n 0 < ε. Für jedes n n 0 gilt dann: 1 n 0 = 1 n 1 < ε. n 0 1 Wir haben lim n = 0 nachgewiesen. n (2) Die Folge (a n ) n N := (( 1) n ) n N ist divergent: Sei a R. Setze { ε := 1/2, falls a {1, 1} 1/2 min{ 1 a, 1 a }, falls a {1, 1}. Dann gilt a n a ε für unendlich viele n N. Folglich konvergiert (a n ) nicht gegen a. Da a beliebig war, ist (a n ) divergent. Bemerkung 6.1. (1) Für jede Zahlenfolge (a n ) und jedes a gilt: lim a n = a lim a n a = 0. Insbesondere ist für a = 0: lim a n = 0 lim a n = 0. (2) Für b C gilt: lim n b n = 0 b < 1. Denn für b 1 gilt b n = b n 1 für alle n N und (b n ) konvergiert nicht gegen Null. Für b < 1 sei ε > 0. Nach Folgerung 4.2 finden wir ein n 0 N mit b n 0 < ε. Für n n 0 gilt dann 0 b n = b n b n 0 < ε. Also ist lim n b n = 0. (3) Der Grenzwert einer Zahlenfolge ist eindeutig bestimmt. (4) Eine konvergente Folge (a n ) ist beschränkt, dh die Menge {a n : n N} ist beschränkt. (5) Ist (z n ) eine komplexe Zahlenfolge, so ist (z n ) genau dann konvergent, wenn die reellen Zahlenfolgen (Re z n ) und (Im z n ) konvergent sind. Genauer gilt für z 0 C: Das liegt an der Abschätzung z n z 0 Re z n Re z 0 und Im z n Im z 0 max{ Re z n Re z 0, Im z n Im z 0 } z n z 0 Re z n Re z 0 + Im z n Im z 0. Konvergiert etwa (z n ) gegen z 0 C, so zeigt die linke Ungleichung, dass Re z n Re z 0 und Im z n Im z 0. Konvergiert hingegen (Re z n ) gegen a R und (Im z n ) gegen b R, so setze z 0 := a + ib, und die rechte Ungleichung zeigt z n z 0. 17
18 Wir beschränken uns deshalb weitgehend auf reelle Zahlenfolgen. (6) Zur Beruhigung: Ist (a n ) eine reelle Zahlenfolge und a C mit a n a, so gilt a R. Wäre nämlich a C \ R, so hätte man für jedes n N: im Widerspruch zu a n a 0. a n a Im a n Im a = Im a =: ε > 0, Wir sagen, dass eine Eigenschaft für fast alle n N gilt, falls es ein n 0 N gibt, so dass die Eigenschaft für alle n n 0 gilt. Beispiel: Für fast alle n N gilt n > Sind eine Folge (a n ) und eine Zahl a gegeben, so gilt: lim a n = a für jedes ε > 0 gilt: a n a < ɛ für fast alle n N. n Bei Konvergenzfragen kommt es also auf endlich viele Folgenglieder nicht an. Für p Z bezeichnet man auch (a n ) n=p als Folge. 6.2 Grenzwertsätze Seien (a n ), (b n ), (α n ) und (c n ) reelle Folgen und a, b R. (1) a n a α n für fast alle n N und α n 0 = a n a. (2) a n a = a n a. (3) a n a und b n b und a n b n für fast alle n = a b. (4) a n a und b n a und a n c n b n für fast alle n c n a. (5) Gilt a n a und b n b, so gilt a n + b n a + b und a n b n a b. Ist b 0, so ist b n 0 für fast alle n und es gilt an b n a b. Beweis. (1) ist leicht. Für (2) verwendet man a n a a n a und (1). Zu (3): Sonst wäre a > b, und mit ε := (a b)/2 ist a n > a ε b + ε > b n für fast alle n, Widerspruch. Zu (4): Ist ε > 0, so gilt für fast alle n: a n a < ɛ, b n a < ɛ, also a ε < a n c n b n < a + ε. Zu (5): Sei ε > 0. Dann a n a < ε/2 und b n b < ε/2 für fast alle n. Also a n + b n (a + b) a n a + b n b < ε/2 + ε/2 = ε für fast alle n. Bei (a n b n ) verwendet man a n b n ab = (a n b n a n b) + (a n b ab) a n b n b + b a n a 18
19 und die Tatsache, dass die konvergente Folge (a n ) beschränkt ist, dh es gibt M > 0 mit a n M für alle n N. Die Behauptung folgt aus (1) und (5) für +. Die Aussage über ( an b n ) muss man nur für a n = 1 zeigen. Sei dazu b 0 und δ := b /2. Dann ist δ > 0 und wir finden n 0 N mit b n b < δ für alle n n 0. Für n n 0 gilt dann auch b n = b (b b n ) b b b n > 2δ δ = δ und 1 1 b n b = b b n b b n woraus die Behauptung folgt. 1 2δ 2 b n b, Beispiele 1) Sei a n = sin(n). Dann a n n 0 = sin(n) 1 und da 1 0 bekommen wir n n n mit Hilfe des Grenzwertsatzes 1), dass a n 0. 2) Sei c n = 2+( 1)n. Dann 1 c n n n 3. Da aber 1 0 und 3 folgt aus dem Grenzwertsatz n n n (4), dass c n Monotone Folgen Eine reelle Folge (a n ) heißt monoton wachsend, falls n N : a n a n+1, monoton fallend, falls n N : a n a n+1, streng monoton wachsend, falls n N : a n < a n+1, streng monoton fallend, falls n N : a n > a n+1. Satz 6.1. Ist eine monoton wachsende [bzw. fallende] reelle Folge (a n ) beschränkt, so konvergiert sie, und zwar gegen sup{a n : n N} [bzw. inf{a n : n N}]. Beweis. Sei (a n ) monoton wachsend und s := sup{a n : n N}. Zu ε > 0 finden wir n 0 N mit a n0 > s ε. Für n n 0 gilt dann s ε < a n0 a n s, also auch a n s < ε. 6.4 Wichtige Beispiele (1) a n 0 für alle n N, a n a und p N p a n p a. Beweis. Wir stellen zunächst fest, dass für alle y > x 0 gilt p y p x p y x. [Es ist nämlich nach dem binomischen Satz ( p y x + p x) p = y x + }{{}... +x y.] 0 Wir erhalten somit p a n p a p a n a für jedes n N. Setzen wir b n := a n a, so gilt b n 0 und es reicht zu zeigen, dass p b n 0. Zu ε > 0 finden wir n 0 mit b n < ε p für alle n n 0. Es gilt dann 0 p b n < ε für alle n n 0. 19
20 (2) n n 1: Setze a n := n n 1. Dann ist a n 0 für alle n, und für n 2 gilt: n ( ) ( ) n n n = (1 + a n ) n = a k n a 2 n(n 1) n = a 2 k 2 2 n, k=0 also 0 a n 2/ n 1. Es folgt a n 0. Für c > 0 gilt n c 1: Für c 1 ist 1 n c n n für fast alle n, und für c (0, 1) ist 1/ n n n c 1 für fast alle n. Wende nun den Grenzwertsatz (4) in 6.2 an. (3) Konvergiert die Folge (a n ) so gilt a n+1 a n 0. Denn es gilt auch a n+1 a, und a n+1 a n 0 folgt aus dem Grenzwertsatz (5) in 6.2. Es gilt aber auch z.b. n + 1 n 0. Für jedes n N ist nämlich n + 1 n = ( n + 1 n)( n n) n n = woraus n + 1 n 0 folgt, obwohl ( n) n N nicht konvergiert. (n + 1) n 1, n n n (4) Sei z C und s n := n k=0 zk für jedes n N. Die Folge (s n ) konvergiert genau dann, wenn z < 1 ist. In diesem Falle gilt lim s n = (1 z) 1. Für z 1 ist nämlich s n+1 s n = z n+1 1, und (s n ) konvergiert nicht (verwende (3) ). Für z < 1 ist s n = 1 zn+1 nach Übungsaufgabe 2) in Blatt 3 und also s 1 z n (1 z) 1 nach Bemerkung 6.1 (2). 6.5 Teilfolgen Ist (a n ) eine Folge und k : N N eine Abbildung mit k(n) < k(n + 1) für alle n N (dh (k(n)) ist eine streng monotone Folge natürlicher Zahlen), so heißt die Folge (a k(n) ) Teilfolge (TF) von (a n ). Beispiel: (a 2, a 4, a 6,...) ist Teilfolge von (a n ), hier ist k(n) = 2n für alle n N. (a 3, a 1, a 7, a 5,...) ist hingegen keine Teilfolge von (a n ). Eine Zahl b heißt Häufungswert (HW) der Folge (a n ), falls es eine Teilfolge von (a n ) gibt, die gegen b konvergiert. Beispiele: (1) Gilt a n a, so konvergiert jede Teilfolge von (a n ) gegen a, dh a ist einziger Häufungswert von (a n ). (2) Die Folge (( 1) n ) hat genau die Häufungswerte 1 und 1: Wegen a 2n 1 und a 2n+1 1 sind 1 und 1 Häufungswerte. Ist b R \ {1, 1} und ε := min{ 1 b, 1 b }/2, so ist ε > 0 und in (b ɛ, b + ɛ) liegen keine Folgenglieder. Somit ist b kein Häufungswert von (a n ). Satz 6.2 ((Bolzano-Weierstraß)). Jede beschränkte Zahlenfolge hat eine konvergente Teilfolge, dh jede beschränkte Zahlenfolge hat einen Häufungswert. Bemerkung 6.2. Der Satz gilt auch für komplexe Zahlenfolgen. 20
21 6.6 Rechnen mit Sei (a n ) eine reelle Folge. a n : K R n 0 N n n 0 : a n > K, a n : K R n 0 N n n 0 : a n < K. Also a n [a n ], falls für jedes K R gilt, dass a n > K [a n < K] für fast alle n N. Achtung: Man redet hier nicht von Konvergenz und auch nicht von Grenzwert, denn ± R, dh und sind keine Zahlen. Man sagt jedoch etwa die Folge a n geht gegen unendlich und schreibt auch lim n a n =. Bemerkung 6.3. (a) Gilt a n ±, so folgt a n und 1/a n 0. Ist a n > 0 für alle n und a n 0, so folgt 1/a n. (b) Ist die reelle Folge (a n ) nicht nach oben [unten] beschränkt, so gibt es eine Teilfolge (a k(n) ) von (a n ) mit a k(n) [bzw. mit a k(n) ]. (c) Für jede monoton wachsende [monoton fallende] Folge (a n ) gibt es a R { } [bzw. a R { }] mit a n a. Konventionen: Für alle a R gilt < a <. Man setzt für a R: a+ =, a =, sowie für a > 0: a =, a ( ) = und für a < 0: a =, a ( ) =. Außerdem setzt man + =, = und =, ( ) =, ( ) ( ) =. Achtung: Die Ausdrücke 0, 0 ( ) und sind nicht definiert! Regeln: Seien (a n ), (b n ) reelle Folgen mit a n a und b n b, wobei a, b R {, }. Dann gilt: a n + b n a + b, falls a + b definiert ist, a n b n a b, falls a b definiert ist. Beachte, dass Bemerkung (a) oben das Verhalten von (1/a n ) beschreibt. Definition 6.2. Sei M R eine Menge. sup M = : M ist nicht nach oben beschränkt, inf M = : M ist nicht nach unten beschränkt. Bemerkung 6.4. Manchmal findet man auch sup := und inf :=. Bemerkung 6.5. Man hat also für M R: sup M = K > 0 x M : x > K, inf M = K > 0 x M : x < K. 21
22 6.7 Limes superior und Limes inferior Sei (a n ) eine reelle Folge. Ist A := {a R {, } : es gibt Teilfolge von a k (n) mit a k(n) a} dann gilt immer A. A hat immer ein Maximum M und ein Minimum m, wobei, wenn z.b. A dann sagen wir max A :=, also der Begriff des Maximums/Minimums hier erweitert den Begriff des Maximums/Minimums einer Teilmenge der reellen Zahlen. Definition 6.3. Wir definieren lim inf a n := m, lim sup a n := M. Ist (a n ) nach beschränkt, dann ist A = {a R {, } : a ist Häufungswert von a n }. Also ist lim inf a n [bzw. lim sup a n ] der kleinste [bzw. größte] Häufungswert von a n. Schreib- und Sprechweisen: Man schreibt auch kurz lim sup n a n oder lim sup a n, sowie lim n a n, lim n a n, lima n und spricht vom Limes superior, entsprechend für lim inf mit lim ( Limes inferior ). Bemerkung 6.6. Ist a n eine Folge und a R {, }. Dann gilt a n a A = a lim inf a n = lim sup a n = a. Zusätzlich gilt: a n a = a k(n) a für alle Teilfolgen a k(n) von a n Beispiel: In der Vorlesung haben wir gezeigt, dass die Folge a n = ( 1) n + 1 die n Häufungswerte {1, 1} hat. Da Sie auch beschränkt ist, folgt, dass lim sup a n = 1 und lim inf a n = 1. 7 Reihen 7.1 Definition und Elementare Eigenschaften Definition 7.1. Sei (a n ) n N eine Folge und s N := N n=1 a n = a 1 + a a N für jedes N N. Die Folge (s N ) N N heißt (unendliche) Reihe und wird mit n=1 a n bezeichnet. Die Zahl s N heißt N-te Partialsumme oder N-te Teilsumme von n=1 a n. Die Reihe n=1 a n heißt konvergent [divergent], falls die Folge (s N ) N N konvergiert [bzw. divergiert]. Ist n=1 a n konvergent, so heißt lim N s N der Reihenwert von n=1 a n und wird ebenfalls mit n=1 a n bezeichnet. 22
23 Bemerkung 7.1. (a) Die Folge (a n ) kann hier reell oder komplex sein. Ist (a n ) komplex, so heißt die Reihe n=1 Re a n Realteil der komplexen Reihe n=1 a n und n=1 Im a n heißt Imaginärteil von n=1 a n. (b) Eine komplexe Reihe konvergiert genau dann, wenn ihr Realteil und ihr Imaginärteil beide konvergieren. In diesem Fall ist n=1 a n = n=1 Re a n + i n=1 Im a n, also Re ( n=1 a n) = n=1 Re a n und Im ( n=1 a n) = n=1 Im a n. Wichtige Beispiele: (1) Die geometrische Reihe n=0 zn, wobei z C, konvergiert genau dann, wenn z < 1. Für z < 1 ist n=0 zn = (1 z) 1. (2) Die harmonische Reihe 1 n=1 ist divergent. n Denn für jedes N N ist s 2N = N }{{} =s N + 1 N + 1 }{{} 1 2N s N + N 1 }{{} 2N 2N = s N N Also ist (s N ) divergent, denn s N s R würde s 2N s N s s = 0 implizieren im Widerspruch zu s 2N s N 1/2 für alle N N. Satz 7.1. Seien (a n ) und (b n ) Folgen und s N := a a N, N N. (1) Monotoniekriterium: Sind alle a n 0 und ist die Folge (s N ) N N beschränkt, so konvergiert n=1 a n. (2) Ist n=1 a n konvergent, p N, so konvergiert n=p+1 a n und n=p+1 a n = n=1 a n p n=1 a n. (3) Ist n=1 a n konvergent und definiert man r N := n=n+1 a n für jedes N N, so gilt r N 0 (N ), dh die Reihenendstücke konvergieren gegen Null. (4) Ist n=1 a n konvergent, so folgt a n 0. (5) Sind n=1 a n und n=1 b n konvergent und α, β R (oder in C), so konvergiert n=1 (αa n + βb n ) und es gilt n=1 (αa n + βb n ) = α n=1 a n + β n=1 b n. Beweis. (1) folgt aus Satz 6.1, angewandt auf die monoton wachsende Folge (s N ) N N. (2) Setzt man σ N := N n=p+1 a n für N p + 1, so ist σ N (N ). (3) Wegen (2) gilt r N = n=1 a n s N n=1 a n n=1 a n = 0. (4) Es ist a n = s n s n 1 0 nach Bemerkung 6.6. (5) folgt aus dem Konvergenzsatz (5) in 6.2. BeispielDie Reihe n=1 ist ( 1)n n ( 1) n n = s N s p n=1 a n s p ist nach (4) divergent denn ( 1)n = n n keine Nullfolge (eine Folge heißt Nullfolge, wenn sie gegen Null konvergiert) also
24 7.2 Absolut konvergente Reihen Die Reihe n=1 a n heißt absolut konvergent, falls n=1 a n konvergiert (dh also, falls die Reihe über die Absolutbeträge der a n konvergiert). Satz 7.2. Ist n=1 a n absolut konvergent, so ist n=1 a n konvergent und es gilt die Dreiecksungleichung für Reihen : a n a n. n=1 n=1 7.3 Majoranten- und Minorantenkriterium Seien (a n ) und (b n ) Folgen. (1) Gilt a n b n für fast alle n N und ist n=1 b n konvergent, so ist n=1 a n absolut konvergent. (2) Gilt a n b n 0 für fast alle n N und ist n=1 b n divergent, so ist auch n=1 a n divergent. Beweis. Für (1) verwende 7.1 (1). (2) folgt aus (1). 7.4 Leibnizkriterium für alternierende Reihen Sei (b n ) eine monoton fallende Folge mit b n 0. Setzt man a n := ( 1) n b n, n N, so konvergiert n=1 a n. Beispiel: Die Reihe ( 1) n n=1 ist konvergent, weil 1 n n Sie ist aber nicht absolut konvergent, weil n=1 ( 1)n n = 1 n n=1 und das ist die harmonische Reihe, die divergent ist. eine monoton fallende Nullfolge ist. Bemerkung: Beachte, dass aus den Voraussetzungen folgt: b n 0 für alle n N. Bemerkung: Monotonie ist hier wichtig! Setzt man nur voraus, dass b n 0 für alle n N und b n 0, so ist die Aussage i.a. falsch (Beispiele in den Übungen). 7.5 Wurzelkriterium Sei (a n ) eine Folge und α := lim sup n n an [0, ]. 24
25 (1) Ist α < 1, so ist n=1 a n absolut konvergent. (2) Ist α > 1, so divergiert n=1 a n. Bemerkung 7.2. Ist α = 1, so liefert das Wurzelkriterium keine Entscheidung.Denn 1 n=1 ist divergent und α = lim sup n 1/n = lim 1/ n n = 1, hingegen ist 1 n n=1 konvergent mit α = lim sup n 1/n 2 = lim 1/( n n) 2 = n 2 1. Beweis. Ist α < 1, so wählen wir β (α, 1). Dann gilt n a n β für fast alle n N, also a n β n für fast alle n N. Wegen β (0, 1) konvergiert n=1 βn, und die Behauptung folgt aus dem Majorantenkriterium. Ist α > 1, so wählen wir γ (1, α). Dann gilt n a n γ 1 für unendlich viele n, also a n 1 für unendlich viele n N. Somit ist a n 0, und nach 7.1 (4) ist n=1 a n divergent. Beispiel: Sei p N. Wir untersuchen Konvergenz von n=1 np x n für x R mit dem Wurzelkriterium. Hier ist a n = n p x n und n an = ( n n) p x x (n ). Also ist n=1 np x n für x < 1 absolut konvergent und für x > 1 divergent. Für x = 1 gilt a n = n p und n=1 np x n ist nach 7.1 (4) divergent. 7.6 Quotientenkriterium Sei (a n ) eine Folge mit a n 0 für fast alle n N und c n := a n+1 a n für n mit a n 0. (1) Ist c n 1 für fast alle n N, so ist n=1 a n divergent. (2) Ist lim sup c n < 1, so ist n=1 a n absolut konvergent. Ist lim inf c n > 1, so divergiert n=1 a n. Bemerkung 7.3. Konvergiert (c n ) gegen α, so ist für α < 1 die Reihe n=1 a n absolut konvergent und für α > 1 ist n=1 a n divergent. Im Falle α = 1 ist keine allgemeine Aussage möglich (man betrachte wieder a n = 1 bzw. a n n = 1 ). n 2 Beweis. (1) Es sei c n 1 für n n 0. Dann ist a n a n 1... a n0 > 0 für alle n n 0, dh a n 0. Nach 7.1 (4) divergiert n=1 a n. (2) Ist α := lim sup c n < 1, so wähle β (α, 1). Es gilt dann c n β für fast alle n N, dh wir finden n 0 mit c n β für alle n n 0. Es folgt a n β a n 1... β n n 0 a n0 = β n ( a n0 β n 0 ) für alle n n 0. Wegen β (0, 1) konvergiert n=1 βn, und nach Majorantenkriterium ist n=1 a n absolut konvergent. Ist lim inf c n > 1, so folgt c n 1 für fast alle n und n=1 a n divergiert nach (1). 25
26 Beispiel Die Reihe n=0 a n mit a n = xn n! ist konvergent für alle x R denn a n+1 a n = x n+1 (n+1)! x n n! = x n Die Exponentialreihe Wir betrachten z n n=0 für z C. Die Reihe konvergiert für jedes z C absolut. n! Definition 7.2. Die Eulersche Zahl ist e := n=0 Satz 7.3. Es gilt e = lim n (1 + 1 n) n. 1. n! 7.8 Das Cauchyprodukt Seien n=0 a n und n=0 b n Reihen. Setze für jedes n N 0 : n c n := a k b n k = a 0 b n + a 1 b n a n 1 b 1 + a n b 0. k=0 Die Reihe n=0 c n heißt das Cauchyprodukt der Reihen n=0 a n und n=0 b n. Satz 7.4. Sind die Reihen n=0 a n und n=0 b n absolut konvergent, so ist auch ihr Cauchyprodukt n=0 c n absolut konvergent und es gilt n=0 c n = ( n=0 a n) ( n=0 b n). Beweis. Es reicht, den Fall a n, b n R und a n 0, b n 0 zu betrachten. Es gilt dann für jedes N N: ( N N ) ( N ) 2N c n a n b n c n, n=0 woraus die Behauptung folgt. n=0 Beispiel: Sei x R mit x < 1. Dann konvergiert n=0 xn absolut. Das Cauchyprodukt von n=0 xn mit sich selber ist ( n ) x k x n k = (n + 1)x n. n=0 Nach dem Satz konvergiert diese Reihe absolut und es gilt ( ) 2 (n + 1)x n = x n 1 = (1 x). 2 n=0 k=0 n=0 26 n=0 n=0 n=0
27 7.9 Die Exponentialfunktion Da die Exponentialreihe nach 7.7 für jedes z C konvergiert, können wir durch E : C C, z E(z) := eine Funktion definieren, E heißt die komplexe Exponentialfunktion. (0) Es gilt E(0) = 1 und E(1) = e (1) Für alle z, w C gilt E(z)E(w) = E(z + w). [Cauchyprodukt für a n = z n /n! und b n = w n /n!; man hat dann n=0 z n n! c n = n a k b n k = k=0 n k=0 z k w n k k! (n k)! = 1 n! n k=0 ( n )z k w n k = k (z + w)n n! nach dem Binomialsatz, und 7.4 gibt die Behauptung.] (2) Für alle z C gilt E(z) 0 und E(z) 1 = E( z), sowie E(z) n = E(nz) für alle n Z. [Es ist 1 = E(0) = E(z + ( z)) = E(z)E( z), woraus E(z) 0 und E(z) 1 = E( z) folgt. Der Rest folgt aus (1).] (3) Für alle x R gilt E(x) R und E(x) > 0; für x > 0 gilt E(x) > 1. [Sei x R. Dann ist E(x) R klar und für x > 0 gilt E(x) = x n 1 + x > 1. }{{} n! 0 n=0 Also ist für x < 0 nach (2): E(x) = E( x) 1 (0, 1).] (4) Für alle x, y R gilt: x < y E(x) < E(y). [Ist x < y, so gilt nach (1) und (3): E(y) = E(y x) E(x) > E(x).] }{{}}{{} >0 >0 (5) Es ist sup{e(x) : x R} = und inf{e(x) : x R} = 0. [Für jedes K > 0 gilt E(K) 1 + K > K (woraus die erste Behauptung folgt) und also auch 0 E( K) = E(K) 1 < 1/K, woraus die zweite Behauptung folgt.] (6) Für alle z C gilt E(z) = E(z). [Dies folgt aus der Definition, sowie der Tatsache, dass w n w für eine komplexe Folge (w n ) impliziert: w n w.] 27
28 (7) Für alle x, y R gilt E(x + iy) = E(x)E(iy) und E(iy) = 1. [Die erste Gleichung folgt aus (1). Mittels (6), (1) und (0) gilt für y R: E(iy) = E(iy)E(iy) = E(iy)E( iy) = E(iy iy) = 1.] (8) Für alle x R gilt n E(x) = E( x n ). [Es gilt nach (2): E( x n )n = E(n x n ) = E(x).] (9) Für alle z C gilt E(z) = E(Re z). [Nach (6), (1) und (8) ist: E(z) = E(z)E(z) = E(z + z) = E(2Re z) = E(Re z).] Bemerkung und Definition: Wegen (2), (8) und 7.7 gilt für alle m Z und alle n N: e m = E(m), Man schreibt deshalb auch e z exp(z) := E(z). ( n 1 e = E, n) Wir zeigen noch die folgenden Abschätzungen: (10) Für alle h C gilt E(h) 1 h E( h ). (11) Für alle h C \ {0} gilt E(h) 1 h ( n m ) em = E = ( n e ) m. n := E(z) für jedes z C. Eine andere Bezeichnung ist 1 h E( h ). Beweis. Es ist E(h) = 1 + h + h2 2! + h3 3! Also E(h) 1 = n=1 h n n! h n=1 womit (10) gezeigt ist. Für h 0 haben wir h n 1 n! h n=1 h n 1 (n 1)! = h E( h ), E(h) 1 h 1 n=1 h n (n + 1)! h n=1 h n 1 n! h E( h ). In der Vorlesung haben wir auch die Abschätzung (12) Für alle h C und N N gilt E(h) N 1 n=0 h n n! h N N! E( h ). 28
29 Diese Abschätzung gibt (10) wenn N = 1 und (12) wenn N = 2. Bemerkung und Definition: Wegen (2), (8) und 7.7 gilt für alle m Z und alle n N: e m = E(m), ( n 1 e = E, n) ( n m ) em = E = ( n e ) m. n Man schreibt deshalb auch e z := E(z) oder exp(z) := E(z) für jedes z C Sinus und Cosinus Wir definieren die Funktionen sin : C C und cos : C C durch sin z := 1 2i (eiz e iz ) und cos z := 1 2 (eiz + e iz ). (0) Es ist sin 0 = 0 und cos 0 = 1. (1) Reihendarstellungen: Für jedes z C gilt: sin z = cos z = n=0 n=0 ( 1) n z 2n+1 (2n + 1)! ( 1) n z 2n (2n)! = z z3 3! + z5 5!..., = 1 z2 2! + z4 4! z6 6! Das folgt aus E(iz) = 1 + iz z2 2 iz3 3! + z4 4! + iz5 5! z6 6! iz7 7! + z8 8! +... E( iz) = 1 iz z2 2 + iz3 3! + z4 4! iz5 5! z6 6! + iz7 7! + z8 8! (2) Eulerformel: Für alle x R gilt sin x R und cos x R, sowie e ix = cos x + i sin x (3) Für alle x R gilt (sin x) 2 + (cos x) 2 = 1, also sin x 1, cos x 1. (4) Additionstheoreme: Für alle z, w C gilt: Abschätzungen: (4) Für alle h C gilt: sin h h E( h ). sin(z + w) = sin z cos w + cos z sin w, cos(z + w) = cos z cos w sin z sin w. 29
30 (5) Für alle h C gilt: cos h 1 h E( h ). (6) Für alle h C \ {0} gilt: sin h 1 h E( h ). (7) Für alle h C \ {0} gilt: h cos h 1 h h E( h ). Man kann die Exponentialfunktion e z so definieren: e z = E(z) Potenzreihen Definition 7.3. Sei z 0 C. Eine Potenzreihe (PR) um z 0 hat die Form n=0 a n(z z 0 ) n, wobei (a n ) n N0 eine Folge in C ist. Die a n heißen Koeffizienten der Potenzreihe und z 0 heißt Entwicklungspunkt. Wir nennen eine Potenzreihe reell, falls z 0 R und alle a n reell sind. Fragen: Für welche z C konvergiert eine gegebene Potenzreihe? Für welche x R konvergiert eine reelle Potenzreihe? Beispiele: Die Potenzreihen für exp, sin und cos konvergieren für jedes z C. Die geometrische Reihe n=0 zn ist für z < 1 absolut konvergent und für z 1 divergent. Alle diese Reihen haben als Entwicklungspunkt z 0 = 0. Bemerkung: Jede Potenzreihe n=0 a n(z z 0 ) n konvergiert für z = z 0, dh im Entwicklungspunkt. Setzt man z = z 0 ein, erhält man nämlich a a a = a 0. Definition 7.4. Sei n=0 a n(z z 0 ) n eine Potenzreihe. Der Konvergenzradius ist definiert durch 1 R := lim sup n (Formel von Cauchy-Hadamard) a n Satz 7.5. z z 0 < R = Potenzreihe absolut konvergent. z z 0 > R = Potenzreihe divergent. Bemerkung: Im Falle R = 0 konvergiert die Potenzreihe also nur für z = z 0 und divergiert für alle z C \ {z 0 }. Im Fall R = ist die Potenzreihe für jedes z C absolut konvergent. Bemerkung: Im Fall R (0, ) lässt sich für z C mit z z 0 = R keine allgemeine Aussage treffen: (a) Die geometrische Reihe n=0 zn hat Konvergenzradius R = 1, sie divergiert für jedes z C mit z = 1. (b) Die Potenzreihe z n n=1 n 2 sie absolut konvergent. hat Konvergenzradius R = 1, für jedes z C mit z = 1 ist Beispiele: (1) Die Potenzreihen für exp, sin, cos haben jeweils Konvergenzradius. 30
31 (2) Die geometrische Reihe n=0 zn hat Konvergenzradius R = 1, ebenso die Potenzreihen n=0 np z n mit p N. Die Potenzreihe n=0 nn z n hat Konvergenzradius R = 0. Beweis des Satzes. Wir haben für z C \ {z 0 }: lim sup n n an (z z 0 ) n = ( lim sup n ) n an z z 0, und die Behauptungen des Satzes folgen aus dem Wurzelkriterium. Satz 7.6. (Konvergenzradius R über Quotienten): Sei n=0 a n(z z 0 ) n eine Potenzreihe. Wenn a n+1 a n α, wobei 0 α, dann R = 1. α Beweis. Das folgt aus dem Quotientenkriterium. Beispiel: Für die Exponentialreihe ist a n = 1/n!, also a n+1 a n = 1 0 und R = 1/0 =. n+1 Auf die Potenzreihen für sin und cos lässt sich der Satz nicht anwenden. Bemerkung: Hier erlauben lim sup a n+1 a n und lim inf a n+1 i.a. keine Entscheidung! Beispiel: a n = ( 2+( 1)n ) n für alle n N 3 0. Dann ist { { 3 n, n ungerade, a n = und a n+1 3 1, n gerade. a n = n, n ungerade, 3 n 1, n gerade. also lim sup a n+1 a n = und lim inf a n+1 a n = 0, aber der Konvergenzradius ist R = 1. a n, 8 Stetigkeit 8.1 Limes, Definition der Stetigkeit, Kriterien für Stetigkeit Definition 8.1 (Limes). Sei f : R R, x 0, y R. Wir sagen wenn ε > 0 δ > 0, so dass lim f(x) = y, x x 0 0 < x x 0 < δ = f(x) y < ε. Bemerkung 8.1. Der Limes kann ähnlich definiert werden, wenn f : D R, mit D Intervall oder endliche Vereinigung von Intervallen 1. In diesem Fall muss 0 < x x 0 < δ durch x D und 0 < x x 0 < δ ersetzt werden. Im Rest der Vorlesung ist mit D eine solche Menge gemeint. Der Limes kann auch für kompliziertere Mengen definiert werden, aber wir führen hier die Definition nicht ein. 1 Hier das Intervall [a, a] = {a} ist nicht zu berücksichtigen 31
32 Definition 8.2. Sei f : D R und x 0 D 2. f heißt stetig in x 0, wenn f heißt stetig, falls sie stetig in y ist y D. lim f(x) = f(x 0 ). x x 0 Beispiel: Die Exponentialfunktion e z ist stetig. In der Tat sei z 0 C. Dann e z e z 0 = e z 0 e z z 0 1 e z 0 e z z 0 z z 0, wobei wir im letzten Schritt die Eigenschaft 10) der Exponentialreihe in 7.9 benutzt haben. Da aber nach der Eigenschaft 9 der Exponentialfunktion, e z z 0 = e Re(z z 0) bekommen wir e z z 0 e z z 0 e, wenn z z 0 1. Also e z e z 0 = e z 0 e z z 0, wenn z z 0 < 1 was zeigt, dass lim z z0 e z = e z 0. Satz 8.1. (i) Alle folgenden Funktionen sind stetig: Polynome, sin, cos, Exponentialfunktion. (ii) f stetig in x 0 und g stetig in f(x 0 ) = g f ist stetig in x 0. (iii) wenn f, g stetig in x 0, dann f + g, f g sind stetig in x 0. Wenn dazu g(x 0 ) 0 dann ist f g stetig in x 0. Beispiel Die Funktion e x2 +x+10 sin( x2 +x+1) ist stetig für alle x 1 als Produkt, Quotient, x 1 Komposition stetiger Funktionen. Satz 8.2. Sei f : D R. Dann lim x x 0 f(x) = y lim f(x n ) = y, für alle Folgen in D/{x 0 } mit x n x 0. Beispiel Sei f : R/{0} R f(x) = cos(1/x). Der Limes lim x 0 f(x) existiert nicht, da a n := 1 0, b 2πn n := 1 0 aber f(a 2πn+π n) = cos(2πn) = 1 1 und f(b n ) = cos(2πn + π) = Zwischenwertsatz Satz 8.3 (Zwischenwertsatz). Seien a < b und f : [a, b] R stetig. Wenn f(a) < f(b) [f(a) > f(b)] und c R mit f(a) < c < f(b) [f(a) > c > f(b)] dann x 0 (a, b) mit f(x 0 ) = c. Folgerung: Sei f : I R stetig, wobei I ein Intervall ist. Dann ist f(i) auch ein Intervall. Beweis der Folgerung. Seien c, d f(i) mit c < d. Sei y 0 [c, d]. Wir finden a, b I mit f(a) = c und f(b) = d. Nach dem Zwischenwertsatz gibt es ein x 0 zwischen a und b mit f(x 0 ) = y 0. Somit ist y 0 f(i), und [c, d] f(i) ist gezeigt. 2 Der Begrief der stetigen Funktion kann für D eine beliebige nicht leere Teilemge von R eingeführt werden (und nicht nur für endliche Verreinigung von Intervallen). Hier führen wir aber diese Definition nicht ein. 32
33 Beispiel: Ist p R[X] ein normiertes Polynom von ungeradem Grad m, so gilt p(r) = R. Beweis. Wegen des Zwischenwertsatzes reicht es zu zeigen, dass p(x) für x und dass p(x) für x. Die Behauptungen sind klar für m = 1. Sei also m 3 und p(x) = x m + a m 1 x m a 1 x + a 0. Für x 1 + a m 1 + a m a 1 + a 0 gilt dann p(x) x m a m 1 x m 1 a m 2 x m 2... a 1 x a 0 x m a m 1 x m 1 a m 2 x m 1... a 1 x m 1 a 0 x m 1 x m 1 (x ( a m 1 + a m a 1 + a 0 )) }{{} 1 x m 1 (x ). Die Aussage für x zeigt man ähnlich. 8.3 Einseitige Grenzwerte Definition 8.3 (Einseitige Grenzwerte). Sei f : R R eine Funktion und x 0, y R. Dann lim f(x) = y [bzw. lim f(x) = y], x x 0 + x x 0 wenn ɛ > 0 δ > 0, so dass x 0 < x < x 0 + δ [bzw. x 0 δ < x < x 0 ] = f(x) y < ɛ. In diesem Fall heißt y rechtsseitiger [bzw. linksseitiger] Limes von f in x 0. Beispiel: Sei D = R und f : R R gegeben durch f(x) := lim x 0+ f(x) = 1 und lim x 0 f(x) = 0. { 1, x (0, 1) 0, x (0, 1). Dann gilt Satz 8.4. Sei f : R R eine Funktion und x 0, y R. Dann ( lim f(x) = y x x 0 lim f(x) = y und lim x x 0 f(x) = y x x 0 + { 1, x (0, 1) Beispiel: Sei D = R und f : R R gegeben durch f(x) :=. Wie im letzten Beispiel. Da lim x 0+ f(x) = 1 und lim x 0 f(x) = 0, existiert der Limes lim x 0 f(x) 0, x (0, 1) nicht. Bemerkung 8.2. Die Definition und der Satz oben sind anwendbar für Funktionen f : D R, wobei D R, wenn es sinnvoll ist, lim x x0 f(x) und lim x x0 + f(x) zu betrachten. Bemerkung 8.3. Man kann lim x x0 f(x) = y mit x 0, y R {, } und lim x x0 ± f(x) = y mit x 0 R, y R {, } betrachten. Die Definitionen sind ähnlich wie im Fall von folgen, und die Intuition ist die gleiche. 33 ).
Ferienkurs Analysis 1 - Wintersemester 2014/15. 1 Aussage, Mengen, Induktion, Quantoren
 Ferienkurs Analysis 1 - Wintersemester 2014/15 Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis
Ferienkurs Analysis 1 - Wintersemester 2014/15 Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis
Folgen, Reihen, Potenzreihen, Exponentialfunktion
 Ferienkurs Seite 1 Technische Universität München Ferienkurs Analysis 1 Hannah Schamoni Wintersemester 2011/12 Folgen, Reihen, Potenzreihen, Exponentialfunktion 20.03.2012 Inhaltsverzeichnis 1 Folgen 2
Ferienkurs Seite 1 Technische Universität München Ferienkurs Analysis 1 Hannah Schamoni Wintersemester 2011/12 Folgen, Reihen, Potenzreihen, Exponentialfunktion 20.03.2012 Inhaltsverzeichnis 1 Folgen 2
MATHEMATIK FÜR NATURWISSENSCHAFTLER I WINTERSEMESTER 2016/ OKTOBER 2016
 MATHEMATIK FÜR NATURWISSENSCHAFTLER I WINTERSEMESTER 2016/17 MARK HAMILTON LMU MÜNCHEN 1.1. Grundbegriffe zu Mengen. 1. 17. OKTOBER 2016 Definition 1.1 (Mengen und Elemente). Eine Menge ist die Zusammenfassung
MATHEMATIK FÜR NATURWISSENSCHAFTLER I WINTERSEMESTER 2016/17 MARK HAMILTON LMU MÜNCHEN 1.1. Grundbegriffe zu Mengen. 1. 17. OKTOBER 2016 Definition 1.1 (Mengen und Elemente). Eine Menge ist die Zusammenfassung
Lösungen Klausur. k k (n + 1) n. für alle n N. Lösung: IA: Für n = 1 ist 1. k k + (n + 1) n+1. k k = k=1. k=1 kk = 1 1 = 1 2 = 2 1.
 Lösungen Klausur Aufgabe (3 Punkte) Zeigen Sie, dass n k k (n + ) n k für alle n N. IA: Für n ist k kk 2 2. IV: Es gilt n k kk (n + ) n für ein n N. IS: Wir haben n+ k k k n k k + (n + ) n+ k IV (n + )
Lösungen Klausur Aufgabe (3 Punkte) Zeigen Sie, dass n k k (n + ) n k für alle n N. IA: Für n ist k kk 2 2. IV: Es gilt n k kk (n + ) n für ein n N. IS: Wir haben n+ k k k n k k + (n + ) n+ k IV (n + )
3 Grenzwert und Stetigkeit 1
 3 Grenzwert und Stetigkeit 3. Grenzwerte bei Funktionen In diesem Abschnitt gilt: I ist immer ein beliebiges Intervall, 0 I oder einer der Endpunkte. 3.. Definition Sei I Intervall, 0 IR und 0 I oder Endpunkt
3 Grenzwert und Stetigkeit 3. Grenzwerte bei Funktionen In diesem Abschnitt gilt: I ist immer ein beliebiges Intervall, 0 I oder einer der Endpunkte. 3.. Definition Sei I Intervall, 0 IR und 0 I oder Endpunkt
Kap. 10: Folgen und Reihen. Eine Funktion a : N Ñ R
 Definition: Zahlenfolge Kap. 10: Folgen und Reihen 10.1 Definition: Zahlenfolge Eine Funktion a : N Ñ R poder Cq heißt reelle (oder komplexe) Zahlenfolge. Man nennt a n apnq das n-te Folgenglied und schreibt
Definition: Zahlenfolge Kap. 10: Folgen und Reihen 10.1 Definition: Zahlenfolge Eine Funktion a : N Ñ R poder Cq heißt reelle (oder komplexe) Zahlenfolge. Man nennt a n apnq das n-te Folgenglied und schreibt
2 Folgen und Reihen. 2.1 Folgen in C Konvergenz von Folgen. := f(n)
 2 Folgen und Reihen 2.1 Folgen in C 2.1.1 Konvergenz von Folgen Eine Folge komplexer Zahlen ist eine Funktion f : N C. Mit a n schreibt man (a n ) n=1, (a n ) oder auch a 1, a 2,.... := f(n) (a n ) heißt
2 Folgen und Reihen 2.1 Folgen in C 2.1.1 Konvergenz von Folgen Eine Folge komplexer Zahlen ist eine Funktion f : N C. Mit a n schreibt man (a n ) n=1, (a n ) oder auch a 1, a 2,.... := f(n) (a n ) heißt
Folgen und Reihen. Thomas Blasi
 Folgen und Reihen Thomas Blasi 02.03.2009 Inhaltsverzeichnis Folgen und Grenzwerte 2. Definitionen und Bemerkungen............................. 2.2 Konvergenz und Beschränktheit.............................
Folgen und Reihen Thomas Blasi 02.03.2009 Inhaltsverzeichnis Folgen und Grenzwerte 2. Definitionen und Bemerkungen............................. 2.2 Konvergenz und Beschränktheit.............................
Lösungen zur Probeklausur zur Vorlesung Analysis I, WS08/09, Samstag, (Version A)
 Lösungen zur Probeklausur zur Vorlesung Analysis I, WS08/09, Samstag, 10.1.009 (Version A) Kennwort: Übungsgruppe: (Sie können ein beliebiges Kennwort wählen, um Ihre Anonymität zu wahren! Da die Probeklausur
Lösungen zur Probeklausur zur Vorlesung Analysis I, WS08/09, Samstag, 10.1.009 (Version A) Kennwort: Übungsgruppe: (Sie können ein beliebiges Kennwort wählen, um Ihre Anonymität zu wahren! Da die Probeklausur
10 Aus der Analysis. Themen: Konvergenz von Zahlenfolgen Unendliche Reihen Stetigkeit Differenzierbarkeit
 10 Aus der Analysis Themen: Konvergenz von Zahlenfolgen Unendliche Reihen Stetigkeit Differenzierbarkeit Zahlenfolgen Ein unendliche Folge reeller Zahlen heißt Zahlenfolge. Im Beispiel 2, 3, 2, 2 2, 2
10 Aus der Analysis Themen: Konvergenz von Zahlenfolgen Unendliche Reihen Stetigkeit Differenzierbarkeit Zahlenfolgen Ein unendliche Folge reeller Zahlen heißt Zahlenfolge. Im Beispiel 2, 3, 2, 2 2, 2
7 KONVERGENTE FOLGEN 35. inf M = Infimum von M. bezeichnet haben. Definition. Sei (a n ) n N eine beschränkte Folge in R. Dann heißt.
 7 KONVERGENTE FOLGEN 35 und die größe untere Schranke mit bezeichnet haben. inf M = Infimum von M Definition. Sei (a n ) n N eine beschränkte Folge in R. Dann heißt der Limes superior der Folge, und lim
7 KONVERGENTE FOLGEN 35 und die größe untere Schranke mit bezeichnet haben. inf M = Infimum von M Definition. Sei (a n ) n N eine beschränkte Folge in R. Dann heißt der Limes superior der Folge, und lim
1 Einleitung. 2 Reelle Zahlen. 3 Konvergenz von Folgen
 1 Einleitung Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis 1 aus dem Wintersemester 2008/09
1 Einleitung Können Sie die folgenden Fragen beantworten? Sie sollten es auf jeden Fall versuchen. Dieser Fragenkatalog orientiert sich an den Themen der Vorlesung Analysis 1 aus dem Wintersemester 2008/09
Misterlösung zur Klausur zur Vorlesung Analysis I, WS08/09, Samstag, (Version C)
 Misterlösung zur Klausur zur Vorlesung Analysis I, WS08/09, Samstag, 14..009 (Version C Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen aus der Vorlesung
Misterlösung zur Klausur zur Vorlesung Analysis I, WS08/09, Samstag, 14..009 (Version C Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen aus der Vorlesung
Vorlesung Mathematik 1 für Ingenieure (Wintersemester 2015/16)
 1 Vorlesung Mathematik 1 für Ingenieure (Wintersemester 2015/16) Kapitel 7: Konvergenz und Reihen Prof. Miles Simon Nach Folienvorlage von Prof. Dr. Volker Kaibel Otto-von-Guericke Universität Magdeburg.
1 Vorlesung Mathematik 1 für Ingenieure (Wintersemester 2015/16) Kapitel 7: Konvergenz und Reihen Prof. Miles Simon Nach Folienvorlage von Prof. Dr. Volker Kaibel Otto-von-Guericke Universität Magdeburg.
Reelle/komplexe Zahlen und Vollständigkeit
 Die folgenden Fragen/Aussagen sind mit ja / wahr oder nein / falsch zu beantworten. Da wir den Stoff der Analysis 1 behandeln, ist im weiteren davon auszugehen dass die Folgen, Reihen, Definitionsbereiche
Die folgenden Fragen/Aussagen sind mit ja / wahr oder nein / falsch zu beantworten. Da wir den Stoff der Analysis 1 behandeln, ist im weiteren davon auszugehen dass die Folgen, Reihen, Definitionsbereiche
Kapitel 5. Die trigonometrischen Funktionen Die komplexen Zahlen Folgen und Reihen in C
 Kapitel 5. Die trigonometrischen Funktionen 5.1. Die komplexen Zahlen 5.. Folgen und Reihen in C 5.10. Definition. Eine Folge (c n n N komplexer Zahlen heißt konvergent gegen c C, falls zu jedem ε > 0
Kapitel 5. Die trigonometrischen Funktionen 5.1. Die komplexen Zahlen 5.. Folgen und Reihen in C 5.10. Definition. Eine Folge (c n n N komplexer Zahlen heißt konvergent gegen c C, falls zu jedem ε > 0
Ferienkurs Analysis 1, SoSe Unendliche Reihen. Florian Beye August 15, 2008
 Ferienkurs Analysis 1, SoSe 2008 Unendliche Reihen Florian Beye August 15, 2008 1 Reihen und deren Konvergenz Definition 1.1. Eine reelle bzw. komplexe Reihe ist eine unendliche Summe über die Glieder
Ferienkurs Analysis 1, SoSe 2008 Unendliche Reihen Florian Beye August 15, 2008 1 Reihen und deren Konvergenz Definition 1.1. Eine reelle bzw. komplexe Reihe ist eine unendliche Summe über die Glieder
Höhere Mathematik I für die Fachrichtung Informatik. Lösungsvorschläge zum 4. Übungsblatt
 KARLSRUHER INSTITUT FÜR TECHNOLOGIE INSTITUT FÜR ANALYSIS Dr. Christoph Schmoeger Heiko Hoffmann WS 0/4 Höhere Mathematik I für die Fachrichtung Informatik Lösungsvorschläge zum 4. Übungsblatt Aufgabe
KARLSRUHER INSTITUT FÜR TECHNOLOGIE INSTITUT FÜR ANALYSIS Dr. Christoph Schmoeger Heiko Hoffmann WS 0/4 Höhere Mathematik I für die Fachrichtung Informatik Lösungsvorschläge zum 4. Übungsblatt Aufgabe
KAPITEL 2. Folgen und Reihen
 KAPITEL 2 Folgen und Reihen 1. Konvergenz und Divergenz Definition 2.1 (Folgen). Eine Abbildung a : N R (bzw. a : N 0 R) nennt man Folge. Statt a : N R schreibt man meist (a n ) n N und a n statt a(n).
KAPITEL 2 Folgen und Reihen 1. Konvergenz und Divergenz Definition 2.1 (Folgen). Eine Abbildung a : N R (bzw. a : N 0 R) nennt man Folge. Statt a : N R schreibt man meist (a n ) n N und a n statt a(n).
1 Reihen von Zahlen. Inhalt:
 5 Kapitel 3 Reihen Reihen von Zahlen Inhalt: Konvergenz und Divergenz von Reihen reeller oder komplexer Zahlen, geometrische Reihe, harmonische Reihe, alternierende Reihen. Cauchy-Kriterium, absolute Konvergenz,
5 Kapitel 3 Reihen Reihen von Zahlen Inhalt: Konvergenz und Divergenz von Reihen reeller oder komplexer Zahlen, geometrische Reihe, harmonische Reihe, alternierende Reihen. Cauchy-Kriterium, absolute Konvergenz,
Lösungsmenge L I = {x R 3x + 5 = 9} = L II = {x R 3x = 4} = L III = { }
 Zur Einleitung: Lineare Gleichungssysteme Wir untersuchen zunächst mit Methoden, die Sie vermutlich aus der Schule kennen, explizit einige kleine lineare Gleichungssysteme. Das Gleichungssystem I wird
Zur Einleitung: Lineare Gleichungssysteme Wir untersuchen zunächst mit Methoden, die Sie vermutlich aus der Schule kennen, explizit einige kleine lineare Gleichungssysteme. Das Gleichungssystem I wird
3. Folgen und Reihen. 3.1 Folgen und Grenzwerte. Denition 3.1 (Folge) Kapitelgliederung
 Kapitelgliederung 3. Folgen und Reihen 3.1 Folgen und Grenzwerte 3.2 Rechenregeln für konvergente Folgen 3.3 Monotone Folgen und Teilfolgen 3.4 Ein Algorithmus zur Wurzelberechnung 3.5 Reihen 3.6 Absolut
Kapitelgliederung 3. Folgen und Reihen 3.1 Folgen und Grenzwerte 3.2 Rechenregeln für konvergente Folgen 3.3 Monotone Folgen und Teilfolgen 3.4 Ein Algorithmus zur Wurzelberechnung 3.5 Reihen 3.6 Absolut
Spickzettel Mathe C1
 Spickzettel Mathe C1 1 Mengenlehre 1.1 Potenzmenge Die Potenzmenge P (Ω) einer Menge Ω ist die Menge aller Teilmengen von Ω. Dabei gilt: P (Ω) := {A A Ω} card P (Ω) = 2 card Ω P (Ω) 1.2 Mengenalgebra Eine
Spickzettel Mathe C1 1 Mengenlehre 1.1 Potenzmenge Die Potenzmenge P (Ω) einer Menge Ω ist die Menge aller Teilmengen von Ω. Dabei gilt: P (Ω) := {A A Ω} card P (Ω) = 2 card Ω P (Ω) 1.2 Mengenalgebra Eine
10 Kriterien für absolute Konvergenz von Reihen
 10 Kriterien für absolute Konvergenz von Reihen 10.1 Majoranten- und Minorantenkriterium 10.3 Wurzelkriterium 10.4 Quotientenkriterium 10.9 Riemannscher Umordnungssatz 10.10 Äquivalenzen zur absoluten
10 Kriterien für absolute Konvergenz von Reihen 10.1 Majoranten- und Minorantenkriterium 10.3 Wurzelkriterium 10.4 Quotientenkriterium 10.9 Riemannscher Umordnungssatz 10.10 Äquivalenzen zur absoluten
Analysis I. 4. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 4. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine bijektive Abbildung f: M N. () Ein
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I 4. Beispielklausur mit en Aufgabe 1. Definiere die folgenden (kursiv gedruckten) Begriffe. (1) Eine bijektive Abbildung f: M N. () Ein
GRUNDLAGEN MATHEMATIK
 Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik GRUNDLAGEN MATHEMATIK 2. Folgen Prof. Dr. Gunar Matthies Wintersemester 2015/16 G. Matthies Grundlagen Mathematik
Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik GRUNDLAGEN MATHEMATIK 2. Folgen Prof. Dr. Gunar Matthies Wintersemester 2015/16 G. Matthies Grundlagen Mathematik
Vorlesungen Analysis von B. Bank
 Vorlesungen Analysis von B. Bank vom 23.4.2002 und 26.4.2002 Zunächst noch zur Stetigkeit von Funktionen f : D(f) C, wobei D(f) C. (Der Text schliesst unmittelbar an die Vorlesung vom 19.4.2002 an.) Auf
Vorlesungen Analysis von B. Bank vom 23.4.2002 und 26.4.2002 Zunächst noch zur Stetigkeit von Funktionen f : D(f) C, wobei D(f) C. (Der Text schliesst unmittelbar an die Vorlesung vom 19.4.2002 an.) Auf
Kapitel 6. Exponentialfunktion
 Kapitel 6. Exponentialfunktion 6.1. Potenzreihen In Kap. 4 haben wir Reihen ν=0 a ν studiert, wo die Glieder feste Zahlen sind. Die Summe solcher Reihen ist wieder eine Zahl, z.b. die Eulersche Zahl e.
Kapitel 6. Exponentialfunktion 6.1. Potenzreihen In Kap. 4 haben wir Reihen ν=0 a ν studiert, wo die Glieder feste Zahlen sind. Die Summe solcher Reihen ist wieder eine Zahl, z.b. die Eulersche Zahl e.
f(x 0 ) = lim f(b k ) 0 0 ) = 0
 5.10 Zwischenwertsatz. Es sei [a, b] ein Intervall, a < b und f : [a, b] R stetig. Ist f(a) < 0 und f(b) > 0, so existiert ein x 0 ]a, b[ mit f(x 0 ) = 0. Wichtig: Intervall, reellwertig, stetig Beweis.
5.10 Zwischenwertsatz. Es sei [a, b] ein Intervall, a < b und f : [a, b] R stetig. Ist f(a) < 0 und f(b) > 0, so existiert ein x 0 ]a, b[ mit f(x 0 ) = 0. Wichtig: Intervall, reellwertig, stetig Beweis.
b liegt zwischen a und c.
 2 DIE ANORDNUNGSAXIOME 5 (2.4) a, b, c R : (a < b 0 < c) ac < bc Monotoniegesetz der Multiplikation Bezeichnungen a > b : b < a (> wird gelesen: größer als ) a b : a < b oder a = b a b : a > b oder a =
2 DIE ANORDNUNGSAXIOME 5 (2.4) a, b, c R : (a < b 0 < c) ac < bc Monotoniegesetz der Multiplikation Bezeichnungen a > b : b < a (> wird gelesen: größer als ) a b : a < b oder a = b a b : a > b oder a =
Kapitel 4 Folgen, Reihen & Funktionen
 Kapitel 4 Folgen, Reihen & Funktionen Inhaltsverzeichnis FOLGEN REELLER ZAHLEN... 3 DEFINITION... 3 GRENZWERT... 3 HÄUFUNGSPUNKT... 4 MONOTONIE... 4 BESCHRÄNKTHEIT... 4 SÄTZE... 4 RECHNEN MIT GRENZWERTEN...
Kapitel 4 Folgen, Reihen & Funktionen Inhaltsverzeichnis FOLGEN REELLER ZAHLEN... 3 DEFINITION... 3 GRENZWERT... 3 HÄUFUNGSPUNKT... 4 MONOTONIE... 4 BESCHRÄNKTHEIT... 4 SÄTZE... 4 RECHNEN MIT GRENZWERTEN...
2.9 Die komplexen Zahlen
 LinAlg II Version 1 3. April 2006 c Rudolf Scharlau 121 2.9 Die komplexen Zahlen Die komplexen Zahlen sind unverzichtbar für nahezu jede Art von höherer Mathematik. Systematisch gehören sie zum einen in
LinAlg II Version 1 3. April 2006 c Rudolf Scharlau 121 2.9 Die komplexen Zahlen Die komplexen Zahlen sind unverzichtbar für nahezu jede Art von höherer Mathematik. Systematisch gehören sie zum einen in
SS 2016 Höhere Mathematik für s Studium der Physik 21. Juli Probeklausur. Die Antworten zu den jeweiligen Fragen sind in blauer Farbe notiert.
 SS 6 Höhere Mathematik für s Studium der Physik. Juli 6 Probeklausur Die Antworten zu den jeweiligen Fragen sind in blauer Farbe notiert. Fragen Sei (X, d) ein metrischer Raum. Beantworten Sie die nachfolgenden
SS 6 Höhere Mathematik für s Studium der Physik. Juli 6 Probeklausur Die Antworten zu den jeweiligen Fragen sind in blauer Farbe notiert. Fragen Sei (X, d) ein metrischer Raum. Beantworten Sie die nachfolgenden
x k = s k=1 y k = y konvergent. Dann folgt (cx k ) = cx für c K. Partialsummenfolge konvergiert
 4 Reihen Im Folgenden sei K R oder K C. 4. Definition. Es sei (x k ) Folge in K. Wir schreiben x k s und sagen, die Reihe x k konvergiere, falls die sogenannte Partialsummen-Folge s n x k n, 2,... in K
4 Reihen Im Folgenden sei K R oder K C. 4. Definition. Es sei (x k ) Folge in K. Wir schreiben x k s und sagen, die Reihe x k konvergiere, falls die sogenannte Partialsummen-Folge s n x k n, 2,... in K
5 Stetigkeit und Differenzierbarkeit
 5 Stetigkeit und Differenzierbarkeit 5.1 Stetigkeit und Grenzwerte von Funktionen f(x 0 ) x 0 Graph einer stetigen Funktion. Analysis I TUHH, Winter 2006/2007 Armin Iske 127 Häufungspunkt und Abschluss.
5 Stetigkeit und Differenzierbarkeit 5.1 Stetigkeit und Grenzwerte von Funktionen f(x 0 ) x 0 Graph einer stetigen Funktion. Analysis I TUHH, Winter 2006/2007 Armin Iske 127 Häufungspunkt und Abschluss.
Analysis I, WS 14/15 Verzeichnis der wichtigsten Definitionen und Sätze
 Analysis I, WS 14/15 Verzeichnis der wichtigsten Definitionen und Sätze Prof. Dr. Lorenz Schwachhöfer Inhaltsverzeichnis 1 Mathematische Grundlagen 2 2 Folgen und Reihen 7 3 Stetigkeit 15 4 Differenzierbarkeit
Analysis I, WS 14/15 Verzeichnis der wichtigsten Definitionen und Sätze Prof. Dr. Lorenz Schwachhöfer Inhaltsverzeichnis 1 Mathematische Grundlagen 2 2 Folgen und Reihen 7 3 Stetigkeit 15 4 Differenzierbarkeit
Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13)
 1 Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13) Kapitel 5: Konvergenz Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 15. Dezember 2011) Folgen Eine Folge x 0, x 1,
1 Vorlesung Mathematik für Ingenieure (WS 11/12, SS 12, WS 12/13) Kapitel 5: Konvergenz Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 15. Dezember 2011) Folgen Eine Folge x 0, x 1,
Klausur - Analysis I Lösungsskizzen
 Klausur - Analysis I Lösungsskizzen Aufgabe 1.: 5 Punkte Entscheiden Sie, ob folgende Aussagen wahr oder falsch sind. Kennzeichnen Sie wahre Aussagen mit W und falsche Aussagen mit F. Es sind keine Begründungen
Klausur - Analysis I Lösungsskizzen Aufgabe 1.: 5 Punkte Entscheiden Sie, ob folgende Aussagen wahr oder falsch sind. Kennzeichnen Sie wahre Aussagen mit W und falsche Aussagen mit F. Es sind keine Begründungen
Übungen Analysis I WS 03/04
 Blatt Abgabe: Mittwoch, 29.0.03 Aufgabe : Beweisen Sie, daß für jede natürliche Zahl n gilt: n ( ) n (x + y) n = x i y n i, i (b) n ν 2 = ν= i=0 n(n + )(2n + ), 6 (c) 2 3n ist durch 7 teilbar. Aufgabe
Blatt Abgabe: Mittwoch, 29.0.03 Aufgabe : Beweisen Sie, daß für jede natürliche Zahl n gilt: n ( ) n (x + y) n = x i y n i, i (b) n ν 2 = ν= i=0 n(n + )(2n + ), 6 (c) 2 3n ist durch 7 teilbar. Aufgabe
INGENIEURMATHEMATIK. 8. Reihen. Sommersemester Prof. Dr. Gunar Matthies
 Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik INGENIEURMATHEMATIK 8. Reihen Prof. Dr. Gunar Matthies Sommersemester 2016 G. Matthies Ingenieurmathematik
3 Folgen, Reihen, Grenzwerte 3.1 Zahlenfolgen Definition: Eine Folge ist eine geordnete Menge von Elementen an (den sogenannten Gliedern ), die
 3 Folgen, Reihen, Grenzwerte 3.1 Zahlenfolgen Definition: Eine Folge ist eine geordnete Menge von Elementen an (den sogenannten Gliedern ), die eindeutig den natürlichen Zahlen zugeordnet sind ( n N, auch
3 Folgen, Reihen, Grenzwerte 3.1 Zahlenfolgen Definition: Eine Folge ist eine geordnete Menge von Elementen an (den sogenannten Gliedern ), die eindeutig den natürlichen Zahlen zugeordnet sind ( n N, auch
5. Reihen. k=1 x k = s. Oft startet man die Folge/Reihe auch bei k =0oder einem anderen Wert. Für Konvergenzfragen macht das keinen Unterschied.
 5 5. Reihen Im Folgenden sei X K n oder ein beliebiger K-Vektorraum mit Norm. 5.. Definition. Es sei (x k ) Folge in X. DieFolge n s n x k n,,... der Partialsummen heißt (unendliche) Reihe und wird mit
5 5. Reihen Im Folgenden sei X K n oder ein beliebiger K-Vektorraum mit Norm. 5.. Definition. Es sei (x k ) Folge in X. DieFolge n s n x k n,,... der Partialsummen heißt (unendliche) Reihe und wird mit
Analysis I - Reelle Zahlen
 November 17, 2008 Algebraische Grundbegriffe und Körper Definition Sei M eine Menge. Jede Funktion f : M M M heißt eine (binäre, innere) Verknüpfung oder eine Operation auf M. Wir schreiben für (a, b)
November 17, 2008 Algebraische Grundbegriffe und Körper Definition Sei M eine Menge. Jede Funktion f : M M M heißt eine (binäre, innere) Verknüpfung oder eine Operation auf M. Wir schreiben für (a, b)
1. Aufgabe [2 Punkte] Seien X, Y zwei nicht-leere Mengen und A(x, y) eine Aussageform. Betrachten Sie die folgenden Aussagen:
![1. Aufgabe [2 Punkte] Seien X, Y zwei nicht-leere Mengen und A(x, y) eine Aussageform. Betrachten Sie die folgenden Aussagen: 1. Aufgabe [2 Punkte] Seien X, Y zwei nicht-leere Mengen und A(x, y) eine Aussageform. Betrachten Sie die folgenden Aussagen:](/thumbs/53/30982501.jpg) Klausur zur Analysis I svorschläge Universität Regensburg, Wintersemester 013/14 Prof. Dr. Bernd Ammann / Dr. Mihaela Pilca 0.0.014, Bearbeitungszeit: 3 Stunden 1. Aufgabe [ Punte] Seien X, Y zwei nicht-leere
Klausur zur Analysis I svorschläge Universität Regensburg, Wintersemester 013/14 Prof. Dr. Bernd Ammann / Dr. Mihaela Pilca 0.0.014, Bearbeitungszeit: 3 Stunden 1. Aufgabe [ Punte] Seien X, Y zwei nicht-leere
10 Differenzierbare Funktionen
 10 Differenzierbare Funktionen 10.1 Definition: Es sei S R, x 0 S Häufungspunkt von S. Eine Funktion f : S R heißt im Punkt x 0 differenzierbar, wenn der Grenzwert f (x 0 ) := f(x 0 + h) f(x 0 ) lim h
10 Differenzierbare Funktionen 10.1 Definition: Es sei S R, x 0 S Häufungspunkt von S. Eine Funktion f : S R heißt im Punkt x 0 differenzierbar, wenn der Grenzwert f (x 0 ) := f(x 0 + h) f(x 0 ) lim h
Brückenkurs Mathematik 2015
 Technische Universität Dresden Fachrichtung Mathematik, Institut für Analysis Dr.rer.nat.habil. Norbert Koksch Brückenkurs Mathematik 2015 1. Vorlesung Logik, Mengen und Funktionen Ich behaupte aber, dass
Technische Universität Dresden Fachrichtung Mathematik, Institut für Analysis Dr.rer.nat.habil. Norbert Koksch Brückenkurs Mathematik 2015 1. Vorlesung Logik, Mengen und Funktionen Ich behaupte aber, dass
Die komplexe Exponentialfunktion und die Winkelfunktionen
 Die komplexe Exponentialfunktion und die Winkelfunktionen In dieser Zusammenfassung werden die für uns wichtigsten Eigenschaften der komplexen und reellen Exponentialfunktion sowie der Winkelfunktionen
Die komplexe Exponentialfunktion und die Winkelfunktionen In dieser Zusammenfassung werden die für uns wichtigsten Eigenschaften der komplexen und reellen Exponentialfunktion sowie der Winkelfunktionen
Mathematik I für Studierende der Physik Vorlesungsskript 1
 Mathematik I für Studierende der Physik Vorlesungsskript 1 Thomas Leistner Department Mathematik Universität Hamburg www.math.uni-hamburg.de/home/leistner Hamburg, Wintersemester 2008/09 1 Version vom
Mathematik I für Studierende der Physik Vorlesungsskript 1 Thomas Leistner Department Mathematik Universität Hamburg www.math.uni-hamburg.de/home/leistner Hamburg, Wintersemester 2008/09 1 Version vom
13 Die trigonometrischen Funktionen
 13 Die trigonometrischen Funktionen Wir schreiben die Werte der komplexen Exponentialfunktion im Folgenden auch als e z = exp(z) (z C). Geometrisch definiert man üblicherweise die Werte der Winkelfunktion
13 Die trigonometrischen Funktionen Wir schreiben die Werte der komplexen Exponentialfunktion im Folgenden auch als e z = exp(z) (z C). Geometrisch definiert man üblicherweise die Werte der Winkelfunktion
Folgen und Reihen. 1 Konvergenz
 Folgen und Reihen Man betrachte viele Zahlen hintereinander geschrieben. Solche Folgen von Zahlen können durch nummeriert werden. Es entsteht eine Zuordnung der natürlichen Zahlen zu den Gliedern der Folge.
Folgen und Reihen Man betrachte viele Zahlen hintereinander geschrieben. Solche Folgen von Zahlen können durch nummeriert werden. Es entsteht eine Zuordnung der natürlichen Zahlen zu den Gliedern der Folge.
6 Reelle und komplexe Zahlenfolgen
 $Id: folgen.tex,v.7 200//29 :58:57 hk Exp hk $ 6 Reelle und komplexe Zahlenfolgen 6. Folgenkonvergenz In der letzten Sitzung hatten wir den Begriff der Konvergenz einer reellen oder komplexen Folge gegen
$Id: folgen.tex,v.7 200//29 :58:57 hk Exp hk $ 6 Reelle und komplexe Zahlenfolgen 6. Folgenkonvergenz In der letzten Sitzung hatten wir den Begriff der Konvergenz einer reellen oder komplexen Folge gegen
Lösungsvorschlag zur Übungsklausur zur Analysis I
 Prof. Dr. H. Garcke, Dr. H. Farshbaf-Shaker, D. Depner WS 8/9 NWF I - Mathematik 9..9 Universität Regensburg Lösungsvorschlag zur Übungsklausur zur Analysis I Frage 1 Vervollständigen Sie die folgenden
Prof. Dr. H. Garcke, Dr. H. Farshbaf-Shaker, D. Depner WS 8/9 NWF I - Mathematik 9..9 Universität Regensburg Lösungsvorschlag zur Übungsklausur zur Analysis I Frage 1 Vervollständigen Sie die folgenden
SBP Mathe Aufbaukurs 3. Imaginäre und komplexe Zahlen. Komplexe Zahlen in der Gaußschen Zahlenebene. Darstellungen komplexer Zahlen.
 SBP Mathe Aufbaukurs 3 # 0 by Clifford Wolf # 0 Antwort Diese Lernkarten sind sorgfältig erstellt worden, erheben aber weder Anspruch auf Richtigkeit noch auf Vollständigkeit. Das Lernen mit Lernkarten
SBP Mathe Aufbaukurs 3 # 0 by Clifford Wolf # 0 Antwort Diese Lernkarten sind sorgfältig erstellt worden, erheben aber weder Anspruch auf Richtigkeit noch auf Vollständigkeit. Das Lernen mit Lernkarten
SBP Mathe Aufbaukurs 3 # 0 by Clifford Wolf. SBP Mathe Aufbaukurs 3
 SBP Mathe Aufbaukurs 3 # 0 by Clifford Wolf SBP Mathe Aufbaukurs 3 # 0 Antwort Diese Lernkarten sind sorgfältig erstellt worden, erheben aber weder Anspruch auf Richtigkeit noch auf Vollständigkeit. Das
SBP Mathe Aufbaukurs 3 # 0 by Clifford Wolf SBP Mathe Aufbaukurs 3 # 0 Antwort Diese Lernkarten sind sorgfältig erstellt worden, erheben aber weder Anspruch auf Richtigkeit noch auf Vollständigkeit. Das
Übungen Ingenieurmathematik
 Übungen Ingenieurmathematik 1. Übungsblatt: Komplexe Zahlen Aufgabe 1 Bestimmen Sie Real- und Imaginärteil der folgenden komplexen Zahlen: a) z =(3+i)+(5 7i), b) z =(3 i)(5 7i), c) z =( 3+i)( 3+ 3 i),
Übungen Ingenieurmathematik 1. Übungsblatt: Komplexe Zahlen Aufgabe 1 Bestimmen Sie Real- und Imaginärteil der folgenden komplexen Zahlen: a) z =(3+i)+(5 7i), b) z =(3 i)(5 7i), c) z =( 3+i)( 3+ 3 i),
Kapitel 1. Grundlagen Mengen
 Kapitel 1. Grundlagen 1.1. Mengen Georg Cantor 1895 Eine Menge ist die Zusammenfassung bestimmter, wohlunterschiedener Objekte unserer Anschauung oder unseres Denkens, wobei von jedem dieser Objekte eindeutig
Kapitel 1. Grundlagen 1.1. Mengen Georg Cantor 1895 Eine Menge ist die Zusammenfassung bestimmter, wohlunterschiedener Objekte unserer Anschauung oder unseres Denkens, wobei von jedem dieser Objekte eindeutig
Folgen, Reihen, Grenzwerte u. Stetigkeit
 Folgen, Reihen, Grenzwerte u. Stetigkeit Josef F. Bürgler Abt. Informatik HTA Luzern, FH Zentralschweiz HTA.MA+INF Josef F. Bürgler (HTA Luzern) Einf. Infinitesimalrechnung HTA.MA+INF 1 / 33 Inhalt 1 Folgen
Folgen, Reihen, Grenzwerte u. Stetigkeit Josef F. Bürgler Abt. Informatik HTA Luzern, FH Zentralschweiz HTA.MA+INF Josef F. Bürgler (HTA Luzern) Einf. Infinitesimalrechnung HTA.MA+INF 1 / 33 Inhalt 1 Folgen
V.1 Konvergenz, Grenzwert und Häufungspunkte
 V.1 Konvergenz, Grenzwert und Häufungspunkte S. 108 110 A. Bereits bekannt: Folge Extrem wichtig: Grenzwert bzw. Konvergenz: a n a oder lim n a n = a : ε R, ε > 0 n 0 N : a n a < ε n n 0 Begriffe: Fast
V.1 Konvergenz, Grenzwert und Häufungspunkte S. 108 110 A. Bereits bekannt: Folge Extrem wichtig: Grenzwert bzw. Konvergenz: a n a oder lim n a n = a : ε R, ε > 0 n 0 N : a n a < ε n n 0 Begriffe: Fast
Zusammenfassung der Vorlesung Einführung in die Analysis
 Zusammenfassung der Vorlesung Einführung in die Analysis Hier werden die wichtigsten Definitionen und Sätze aus der Vorlesung dargestellt, zusammen mit Beweisideen und Querverbindungen. Ziel ist es, die
Zusammenfassung der Vorlesung Einführung in die Analysis Hier werden die wichtigsten Definitionen und Sätze aus der Vorlesung dargestellt, zusammen mit Beweisideen und Querverbindungen. Ziel ist es, die
Vorlesung Mathematik für Ingenieure I (Wintersemester 2007/08)
 1 Vorlesung Mathematik für Ingenieure I (Wintersemester 2007/08) Kapitel 4: Konvergenz und Stetigkeit Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 22. November 2007) Folgen Eine Folge
1 Vorlesung Mathematik für Ingenieure I (Wintersemester 2007/08) Kapitel 4: Konvergenz und Stetigkeit Volker Kaibel Otto-von-Guericke Universität Magdeburg (Version vom 22. November 2007) Folgen Eine Folge
Analysis für Lehramtsstudiengänge
 Analysis für Lehramtsstudiengänge Ein Kompendium zur Vorlesung von L. Recke Inhaltsverzeichnis 1 Grundlagen 3 1.1 Mengen........................................ 3 1.1.1 Untermengen.................................
Analysis für Lehramtsstudiengänge Ein Kompendium zur Vorlesung von L. Recke Inhaltsverzeichnis 1 Grundlagen 3 1.1 Mengen........................................ 3 1.1.1 Untermengen.................................
Konstruktion der reellen Zahlen
 Konstruktion der reellen Zahlen Zur Wiederholung: Eine Menge K (mit mindestens zwei Elementen) heißt Körper, wenn für beliebige Elemente x, y K eindeutig eine Summe x+y K und ein Produkt x y K definiert
Konstruktion der reellen Zahlen Zur Wiederholung: Eine Menge K (mit mindestens zwei Elementen) heißt Körper, wenn für beliebige Elemente x, y K eindeutig eine Summe x+y K und ein Produkt x y K definiert
Modul Grundbildung Analysis WiSe 10/11. A.: Wurde in diesem Kapitel behandelt. C.: Weitere Fragen (Nicht nur für die Klausur interessant)
 Modul Grundbildung Analysis WiSe 10/11 Im Folgenden bedeutet A: Wurde in diesem Kapitel behandelt B: Interessante Aufgaben C: Weitere Fragen (Nicht nur für die Klausur interessant) V1 Konvergenz, Grenzwert
Modul Grundbildung Analysis WiSe 10/11 Im Folgenden bedeutet A: Wurde in diesem Kapitel behandelt B: Interessante Aufgaben C: Weitere Fragen (Nicht nur für die Klausur interessant) V1 Konvergenz, Grenzwert
$Id: stetig.tex,v /06/26 15:40:18 hk Exp $
 $Id: stetig.tex,v 1.11 2012/06/26 15:40:18 hk Exp $ 9 Stetigkeit 9.1 Eigenschaften stetiger Funktionen Am Ende der letzten Sitzung hatten wir eine der Grundeigenschaften stetiger Funktionen nachgewiesen,
$Id: stetig.tex,v 1.11 2012/06/26 15:40:18 hk Exp $ 9 Stetigkeit 9.1 Eigenschaften stetiger Funktionen Am Ende der letzten Sitzung hatten wir eine der Grundeigenschaften stetiger Funktionen nachgewiesen,
Surjektive, injektive und bijektive Funktionen.
 Kapitel 1: Aussagen, Mengen, Funktionen Surjektive, injektive und bijektive Funktionen. Definition. Sei f : M N eine Funktion. Dann heißt f surjektiv, falls die Gleichung f(x) = y für jedes y N mindestens
Kapitel 1: Aussagen, Mengen, Funktionen Surjektive, injektive und bijektive Funktionen. Definition. Sei f : M N eine Funktion. Dann heißt f surjektiv, falls die Gleichung f(x) = y für jedes y N mindestens
Mathematik I für Studierende der Physik Vorlesungsskript
 Mathematik I für Studierende der Physik Vorlesungsskript Vicente Cortés, Ulf Kühn, Thomas Leistner, Ralf Holtkamp Bernd Siebert Department Mathematik Universität Hamburg www.math.uni-hamburg.de/home/siebert
Mathematik I für Studierende der Physik Vorlesungsskript Vicente Cortés, Ulf Kühn, Thomas Leistner, Ralf Holtkamp Bernd Siebert Department Mathematik Universität Hamburg www.math.uni-hamburg.de/home/siebert
Höhere Mathematik I für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie Lösungsvorschläge zum 7. Übungsblatt
 UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl WS 008/09 Höhere Mathematik I für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie Lösungsvorschläge
UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl WS 008/09 Höhere Mathematik I für die Fachrichtungen Elektroingenieurwesen, Physik und Geodäsie Lösungsvorschläge
Kapitel V. Folgen und Konvergenz. V.1 Konvergenz von Zahlenfolgen
 Kapitel V Folgen und Konvergenz V.1 Konvergenz von Zahlenfolgen Wir erinnern an den Begriff der Folge, den wir schon im Kapitel III verwenden. Eine Folge (a n ) n=1 AN in A ist eine Abbildung a ( ) : N
Kapitel V Folgen und Konvergenz V.1 Konvergenz von Zahlenfolgen Wir erinnern an den Begriff der Folge, den wir schon im Kapitel III verwenden. Eine Folge (a n ) n=1 AN in A ist eine Abbildung a ( ) : N
,...) ist eine Folge, deren Glieder der Null beliebig nahe kommen. (iii) Die Folge a n = ( 1) n + 1 n oder (a n) = (0, 3 2, 2 3, 5 4, 4 5
 3 Folgen 3.1 Definition und Beispiele Eine Abbildung a : Æ Ê heißt (reelle) Zahlenfolge. Statt a(n) schreiben wir kürzer a n und bezeichnen die ganze Folge mit (a n ) n Æ oder einfach (a n ), was aber
3 Folgen 3.1 Definition und Beispiele Eine Abbildung a : Æ Ê heißt (reelle) Zahlenfolge. Statt a(n) schreiben wir kürzer a n und bezeichnen die ganze Folge mit (a n ) n Æ oder einfach (a n ), was aber
20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen
 20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
20 Gleichmäßige Konvergenz für Folgen und Reihen von Funktionen 20.1 Folgen und Reihen von Funktionen 20.3 Die Supremumsnorm 20.4 Gleichmäßige Konvergenz von Folgen und Reihen von Funktionen 20.7 Das Cauchy-Kriterium
Funktionenfolgen, Potenzreihen, Exponentialfunktion
 Kapitel 8 Funktionenfolgen, Potenzreihen, Exponentialfunktion Der in Definition 7. eingeführte Begriff einer Folge ist nicht auf die Betrachtung reeller Zahlen eingeschränkt und das Beispiel {a n } = {x
Kapitel 8 Funktionenfolgen, Potenzreihen, Exponentialfunktion Der in Definition 7. eingeführte Begriff einer Folge ist nicht auf die Betrachtung reeller Zahlen eingeschränkt und das Beispiel {a n } = {x
Weitere Eigenschaften
 Weitere Eigenschaften Erklärung der Subtraktion: x y := x + ( y) (5) Die Gleichung a + x = b hat die eindeutig bestimmte Lösung x = b a. Beweis: (a) Zunächst ist x = b a eine Lösung, denn a + x = a + (b
Weitere Eigenschaften Erklärung der Subtraktion: x y := x + ( y) (5) Die Gleichung a + x = b hat die eindeutig bestimmte Lösung x = b a. Beweis: (a) Zunächst ist x = b a eine Lösung, denn a + x = a + (b
Der Fundamentalsatz der Algebra. 1 Motivation
 Vortrag im Rahmen des Proseminars zur Analysis, 24. April 2006 Micha Bittner Motivation Den ersten des Fundamentalsatzes der Algebra erbrachte C.F. Gauss im Jahr 799 im Rahmen seiner Dissertation. Heute
Vortrag im Rahmen des Proseminars zur Analysis, 24. April 2006 Micha Bittner Motivation Den ersten des Fundamentalsatzes der Algebra erbrachte C.F. Gauss im Jahr 799 im Rahmen seiner Dissertation. Heute
n 1, n N \ {1}, 0 falls x = 0,
 IV.1. Stetige Funktionen 77 IV. Stetigkeit IV.1. Stetige Funktionen Stetige Funktionen R R sind vielen sicher schon aus der Schule bekannt. Dort erwirbt man sich die naive Vorstellung, dass eine stetige
IV.1. Stetige Funktionen 77 IV. Stetigkeit IV.1. Stetige Funktionen Stetige Funktionen R R sind vielen sicher schon aus der Schule bekannt. Dort erwirbt man sich die naive Vorstellung, dass eine stetige
eine Folge in R, für die man auch hätte schreiben können, wenn wir alle richtig raten, was auf dem Pünktchen stehen sollte.
 Analysis, Woche 5 Folgen und Konvergenz A 5. Cauchy-Folgen und Konvergenz Eine Folge in R ist eine Abbildung von N nach R und wird meistens dargestellt durch {x n } n=0, {x n} n N oder {x 0, x, x 2,...
Analysis, Woche 5 Folgen und Konvergenz A 5. Cauchy-Folgen und Konvergenz Eine Folge in R ist eine Abbildung von N nach R und wird meistens dargestellt durch {x n } n=0, {x n} n N oder {x 0, x, x 2,...
Folgen und Reihen. Folgen. Inhalt. Mathematik für Chemiker Teil 1: Analysis. Folgen und Reihen. Reelle Funktionen. Vorlesung im Wintersemester 2014
 Inhalt Mathematik für Chemiker Teil 1: Analysis Vorlesung im Wintersemester 2014 Kurt Frischmuth Institut für Mathematik, Universität Rostock Rostock, Oktober 2014... Folgen und Reihen Reelle Funktionen
Inhalt Mathematik für Chemiker Teil 1: Analysis Vorlesung im Wintersemester 2014 Kurt Frischmuth Institut für Mathematik, Universität Rostock Rostock, Oktober 2014... Folgen und Reihen Reelle Funktionen
Dezimalzahlen. Analysis 1
 Dezimalzahlen Definition. Eine endliche Dezimalzahl besteht aus - einem Vorzeichen +,, oder 0 - einer natürlichen Zahl d 0 - einer endlichen Folge von Ziffern d 1,...,d l von 0 bis 9. Die Länge l kann
Dezimalzahlen Definition. Eine endliche Dezimalzahl besteht aus - einem Vorzeichen +,, oder 0 - einer natürlichen Zahl d 0 - einer endlichen Folge von Ziffern d 1,...,d l von 0 bis 9. Die Länge l kann
Mitschrift Mathematik, Vorlesung bei Dan Fulea, 2. Semester
 Mitschrift Mathematik, Vorlesung bei Dan Fulea, 2. Semester Christian Nawroth, Erstellt mit L A TEX 23. Mai 2002 Inhaltsverzeichnis 1 Vollständige Induktion 2 1.1 Das Prinzip der Vollstandigen Induktion................
Mitschrift Mathematik, Vorlesung bei Dan Fulea, 2. Semester Christian Nawroth, Erstellt mit L A TEX 23. Mai 2002 Inhaltsverzeichnis 1 Vollständige Induktion 2 1.1 Das Prinzip der Vollstandigen Induktion................
Häufungspunkte und Satz von Bolzano und Weierstraß.
 Häufungspunkte und Satz von Bolzano und Weierstraß. Definition: Sei (a nk ) k N eine konvergente Teilfolge der Folge (a n ) n N.Dannwirdder Grenzwert der Teilfolge (a nk ) k N als Häufungspunkt der Folge
Häufungspunkte und Satz von Bolzano und Weierstraß. Definition: Sei (a nk ) k N eine konvergente Teilfolge der Folge (a n ) n N.Dannwirdder Grenzwert der Teilfolge (a nk ) k N als Häufungspunkt der Folge
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik
 TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Prof. Dr. Oliver Matte Max Lein Zentralübung Mathematik für Physiker 2 Analysis ) Wintersemester 200/20 Lösungsblatt 5 2..200) 32. Häufungspunkte Sei a
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Prof. Dr. Oliver Matte Max Lein Zentralübung Mathematik für Physiker 2 Analysis ) Wintersemester 200/20 Lösungsblatt 5 2..200) 32. Häufungspunkte Sei a
Kapitel 7. Exponentialfunktion
 Kapitel 7. Exponentialfunktion 7.1. Potenzreihen In Kap. 5 haben wir Reihen ν=0 a ν studiert, wo die Glieder feste Zahlen sind. Die Summe solcher Reihen ist wieder eine Zahl, z.b. die Eulersche Zahl e.
Kapitel 7. Exponentialfunktion 7.1. Potenzreihen In Kap. 5 haben wir Reihen ν=0 a ν studiert, wo die Glieder feste Zahlen sind. Die Summe solcher Reihen ist wieder eine Zahl, z.b. die Eulersche Zahl e.
0 Mengen und Abbildungen, Gruppen und Körper
 0 Mengen und Abbildungen, Gruppen und Körper In diesem Paragrafen behandeln wir einige für die Lineare Algebra und für die Analysis wichtige Grundbegriffe. Wir beginnen mit dem Begriff der Menge. Auf Cantor
0 Mengen und Abbildungen, Gruppen und Körper In diesem Paragrafen behandeln wir einige für die Lineare Algebra und für die Analysis wichtige Grundbegriffe. Wir beginnen mit dem Begriff der Menge. Auf Cantor
Höhere Mathematik I für die Fachrichtung Informatik. Lösungsvorschläge zum 10. Übungsblatt. < 0 für alle t > 1. tan(x) tan(0) x 0
 KARLSRUHER INSTITUT FÜR TECHNOLOGIE INSTITUT FÜR ANALYSIS Dr. Christoph Schmoeger Heiko Hoffmann WS 03/4 Höhere Mathematik I für die Fachrichtung Informatik Lösungsvorschläge zum 0. Übungsblatt Aufgabe
KARLSRUHER INSTITUT FÜR TECHNOLOGIE INSTITUT FÜR ANALYSIS Dr. Christoph Schmoeger Heiko Hoffmann WS 03/4 Höhere Mathematik I für die Fachrichtung Informatik Lösungsvorschläge zum 0. Übungsblatt Aufgabe
Einführung in die Mathematik für Lehramt
 Jürgen Müller Einführung in die Mathematik für Lehramt Skriptum zur Vorlesung Wintersemester 2013/2014 Universität Trier Fachbereich IV Mathematik/Analysis Dank an Elke Gawronski für die Mithilfe bei der
Jürgen Müller Einführung in die Mathematik für Lehramt Skriptum zur Vorlesung Wintersemester 2013/2014 Universität Trier Fachbereich IV Mathematik/Analysis Dank an Elke Gawronski für die Mithilfe bei der
Kapitel V. Folgen und Konvergenz. V.1 Konvergenz von Zahlenfolgen
 Kapitel V Folgen und Konvergenz V.1 Konvergenz von Zahlenfolgen Wir erinnern an den Begriff der Folge, den wir schon im Kapitel III verwenden. Eine Folge (a n ) n=1 AN in A ist eine Abbildung a ( ) : N
Kapitel V Folgen und Konvergenz V.1 Konvergenz von Zahlenfolgen Wir erinnern an den Begriff der Folge, den wir schon im Kapitel III verwenden. Eine Folge (a n ) n=1 AN in A ist eine Abbildung a ( ) : N
Analysis I. 1. Beispielklausur mit Lösungen
 Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Das Bild einer Abbildung F: L M. (2) Eine Cauchy-Folge
Fachbereich Mathematik/Informatik Prof. Dr. H. Brenner Analysis I. Beispielklausur mit en Aufgabe. Definiere die folgenden (kursiv gedruckten) Begriffe. () Das Bild einer Abbildung F: L M. (2) Eine Cauchy-Folge
Vollständigkeit. 1 Konstruktion der reellen Zahlen
 Vortrag im Rahmen des Proseminars zur Analysis, 17.03.2006 Albert Zeyer Ziel des Vortrags ist es, die Vollständigkeit auf Basis der Konstruktion von R über die CAUCHY-Folgen zu beweisen und äquivalente
Vortrag im Rahmen des Proseminars zur Analysis, 17.03.2006 Albert Zeyer Ziel des Vortrags ist es, die Vollständigkeit auf Basis der Konstruktion von R über die CAUCHY-Folgen zu beweisen und äquivalente
Kapitel 1. Grundlagen
 Kapitel 1. Grundlagen 1.1. Mengen Georg Cantor 1895 Eine Menge ist die Zusammenfassung bestimmter, wohlunterschiedener Objekte unserer Anschauung oder unseres Denkens, wobei von jedem dieser Objekte eindeutig
Kapitel 1. Grundlagen 1.1. Mengen Georg Cantor 1895 Eine Menge ist die Zusammenfassung bestimmter, wohlunterschiedener Objekte unserer Anschauung oder unseres Denkens, wobei von jedem dieser Objekte eindeutig
Komplexe Zahlen. Bemerkungen. (i) Man zeigt leicht, dass C mit diesen beiden Operationen
 Komplexe Zahlen Da für jede reelle Zahl x R gilt dass x 0, besitzt die Gleichung x + 1 = 0 keine Lösung in R bzw. das Polynom P (x) = x + 1 besitzt in R (!) keine Nullstelle. Dies führt zur Frage, ob es
Komplexe Zahlen Da für jede reelle Zahl x R gilt dass x 0, besitzt die Gleichung x + 1 = 0 keine Lösung in R bzw. das Polynom P (x) = x + 1 besitzt in R (!) keine Nullstelle. Dies führt zur Frage, ob es
3 Stetigkeit und Grenzwerte von Funktionen
 54 3 STETIGKEIT UND GRENZWERTE VON FUNKTIONEN = q + q+ = q. 3 Stetigkeit und Grenzwerte von Funktionen 3. Stetigkeit Definition 3.. Seien M, N C und sei f : M N eine Funktion. Sei ξ M. Dann heißt f stetig
54 3 STETIGKEIT UND GRENZWERTE VON FUNKTIONEN = q + q+ = q. 3 Stetigkeit und Grenzwerte von Funktionen 3. Stetigkeit Definition 3.. Seien M, N C und sei f : M N eine Funktion. Sei ξ M. Dann heißt f stetig
Kapitel 1. Grundlagen
 Kapitel 1. Grundlagen 1.1. Mengen Georg Cantor 1895 Eine Menge ist die Zusammenfassung bestimmter, wohlunterschiedener Objekte unserer Anschauung oder unseres Denkens, wobei von jedem dieser Objekte eindeutig
Kapitel 1. Grundlagen 1.1. Mengen Georg Cantor 1895 Eine Menge ist die Zusammenfassung bestimmter, wohlunterschiedener Objekte unserer Anschauung oder unseres Denkens, wobei von jedem dieser Objekte eindeutig
f(x nk ) = lim y nk ) = lim Bemerkung 2.14 Der Satz stimmt nicht mehr, wenn D nicht abgeschlossen oder nicht beschränkt ist, wie man z.b.
 Proposition.13 Sei f : D R stetig und D = [a, b] R. Dann ist f(d) beschränkt. Außerdem nimmt f sein Maximum und Minimum auf D an, d.h. es gibt x max D und ein x min D, so dass f(x max ) = sup f(d) und
Proposition.13 Sei f : D R stetig und D = [a, b] R. Dann ist f(d) beschränkt. Außerdem nimmt f sein Maximum und Minimum auf D an, d.h. es gibt x max D und ein x min D, so dass f(x max ) = sup f(d) und
Mathematischer Vorkurs NAT-ING1
 Mathematischer Vorkurs NAT-ING1 (02.09. 20.09.2013) Dr. Robert Strehl WS 2013-2014 Mathematischer Vorkurs TU Dortmund Seite 1 / 40 Kapitel 12 Komplexe Zahlen Kapitel 12 Komplexe Zahlen Mathematischer Vorkurs
Mathematischer Vorkurs NAT-ING1 (02.09. 20.09.2013) Dr. Robert Strehl WS 2013-2014 Mathematischer Vorkurs TU Dortmund Seite 1 / 40 Kapitel 12 Komplexe Zahlen Kapitel 12 Komplexe Zahlen Mathematischer Vorkurs
Aufgabe 1 Zeigen Sie mittels vollständiger Induktion, dass für alle n N. n(n + 1)(2n + 1) 6. j 2 = gilt.
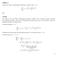 Aufgabe Zeigen Sie mittels vollständiger Induktion, dass für alle n N j 2 j n(n + )(2n + ) gilt. Der Beweis wird mit Hilfe vollständiger Induktion geführt. Wir verifizieren daher zunächst den Induktionsanfang,
Aufgabe Zeigen Sie mittels vollständiger Induktion, dass für alle n N j 2 j n(n + )(2n + ) gilt. Der Beweis wird mit Hilfe vollständiger Induktion geführt. Wir verifizieren daher zunächst den Induktionsanfang,
Die Topologie von R, C und R n
 Die Topologie von R, C und R n Für R haben wir bereits eine Reihe von Strukturen kennengelernt: eine algebraische Struktur (Körper), eine Ordnungsstruktur und eine metrische Struktur (Absolutbetrag, Abstand).
Die Topologie von R, C und R n Für R haben wir bereits eine Reihe von Strukturen kennengelernt: eine algebraische Struktur (Körper), eine Ordnungsstruktur und eine metrische Struktur (Absolutbetrag, Abstand).
Topologische Grundbegriffe I. 1 Offene und Abgeschlossene Mengen
 Topologische Grundbegriffe I Vortrag zum Proseminar Analysis, 26.04.2010 Nina Neidhardt und Simon Langer Im Folgenden soll gezeigt werden, dass topologische Konzepte, die uns schon für die Reellen Zahlen
Topologische Grundbegriffe I Vortrag zum Proseminar Analysis, 26.04.2010 Nina Neidhardt und Simon Langer Im Folgenden soll gezeigt werden, dass topologische Konzepte, die uns schon für die Reellen Zahlen
Skript zur Vorlesung Analysis I
 Skript zur Vorlesung Analysis I Sommersemester 2010 Robert Haller-Dintelmann 30. Juli 2010 Inhaltsverzeichnis I. Zahlen und Mengen 1 1. Grundlegende Begriffe 3 2. Die reellen Zahlen 11 3. Die natürlichen
Skript zur Vorlesung Analysis I Sommersemester 2010 Robert Haller-Dintelmann 30. Juli 2010 Inhaltsverzeichnis I. Zahlen und Mengen 1 1. Grundlegende Begriffe 3 2. Die reellen Zahlen 11 3. Die natürlichen
Höhere Mathematik für Physiker II
 Universität Heidelberg Sommersemester 2013 Wiederholungsblatt Übungen zur Vorlesung Höhere Mathematik für Physiker II Prof Dr Anna Marciniak-Czochra Dipl Math Alexandra Köthe Fragen Machen Sie sich bei
Universität Heidelberg Sommersemester 2013 Wiederholungsblatt Übungen zur Vorlesung Höhere Mathematik für Physiker II Prof Dr Anna Marciniak-Czochra Dipl Math Alexandra Köthe Fragen Machen Sie sich bei
Vollständigkeit; Überabzählbarkeit und dichte Mengen) Als typisches Beispiel für die reellen Zahlen dient die kontinuierlich ablaufende Zeit.
 Kapitel 4 Reelle Zahlen 4.1 Die reellen Zahlen (Schranken von Mengen; Axiomatik; Anordnung; Vollständigkeit; Überabzählbarkeit und dichte Mengen) Als typisches Beispiel für die reellen Zahlen dient die
Kapitel 4 Reelle Zahlen 4.1 Die reellen Zahlen (Schranken von Mengen; Axiomatik; Anordnung; Vollständigkeit; Überabzählbarkeit und dichte Mengen) Als typisches Beispiel für die reellen Zahlen dient die
