Der Satz des Pythagoras
|
|
|
- Lieselotte Weiss
- vor 7 Jahren
- Abrufe
Transkript
1 Der Satz des Pythagoras Das rechtwinklige Dreieck Jedes rechtwinklige Dreieck besitzt eine Hypotenuse (c), das ist die längste Seite des Dreiecks (bzw. diejenige gegenüber dem rechten Winkel). Die anderen beiden Seiten heißen Katheten (a, b). Abb. 1 Jeder Winkel besitzt eine An- und eine Gegenkathete. Die Ankathete ist diejenige Seite, die direkt am Winkel anliegt. Die dem betreffenden Winkel gegenüberliegende Seite heißt Gegenkathete. Die Ankathete vom Winkel α ist b. Sie ist gleichzeitig die Gegenkathete von β. Die Gegenkathete von α ist a. Sie ist gleichzeitig die Ankathete von β. Umgekehrt gilt das ebenso. Der Satz des Pythagoras Das Seitenverhältnis der Seiten eines rechtwinkligen Dreiecks ist im Satz des Pythagoras beschrieben: a 2 + b 2 = c 2 Er lässt sich mithilfe von Umformungen nach den verschiedenen Seiten auflösen, um deren Länge zu berechnen: c = a 2 + b 2 a = c 2 b 2 b = c 2 a 2 Der Satz des Pythagoras gilt unabhängig von den Bezeichnungen der Seiten. Die Hypotenuse eines rechtwinkligen Dreiecks kann auch anders genannt werden, zum Beispiel z oder a. Grundsätzlich gilt: Quadrat der Hypotenuse = Summe aus den Quadraten der Katheten Hierbei sind einfach die Bezeichnungen in den Aufgaben zu beachten und einzusetzen. 1
2 Höhen- und Kathetensatz Hier wird die Hypotenuse c in die Teilstücke p und q unterteilt. Unabhängig von den Bezeichnungen einer Grafik ist p dasjenige Stück, das an die Kathete a angrenzt. Umgekehrt ist q der Teil von der Hypotenuse c, das direkt an b anliegt. Abb. 2 Höhensatz: h 2 =p q Kathetensatz: a 2 =c p bzw. b 2 =c q Die beiden entstandenen Flächen sind jeweils gleich groß. Für b gilt das gleiche. 2
3 Diagonale im Rechteck Auch die Diagonale eines Rechtecks lässt sich über den Satz des Pythagoras bestimmen: l b d b l Das Rechteck lässt sich in zwei deckungsgleiche rechtwinklige Dreiecke mit der Hypotenuse d teilen. Will man nun die Diagonale d berechnen, kann man den Satz des Pythagoras aufstellen und nach d auflösen: d = l 2 + b 2 Soll man in einem Quadrat die Diagonale berechnen, sind l und b gleich. l = b = a Damit sieht die Formel dann so aus: d = a 2 + a 2 = 2 a 2 = a 2 3
4 Beispielaufgaben Satz des Pythagoras Seitenlänge a b c a) 3cm 4cm b) 6m 10m c) 8dm 20dm d) 3 mm 5mm a) a = 3cm; b = 4cm Der Satz des Pythagoras lautet a 2 +b 2 =c 2. a und b sind gegeben, also muss nur nach c aufgelöst werden, indem man die Quadratwurzel zieht: c = a 2 +b 2 = = 25 = 5 => c = 5cm b) a = 6m; c = 10m a und c sind gegeben. Der Satz muss also nach b aufgelöst werden: b = c 2 a 2 = = 64 = 8 => b = 8m c) b = 8dm; c = 20dm b und c sind gegeben. Der Satz muss also nach a aufgelöst werden: a = c 2 b 2 = = ,3 => a 18,3dm d) a = 3 mm ; c = 5mm a und c sind gegeben. Also dieselbe Vorgehensweise wie in b). Dass a als Wurzel angegeben ist, ist unerheblich, da die Wurzel quadriert wird und damit verschwindet. b = c 2 a 2 = 5 2 ( 3) 2 = ,6 => b 4,6mm Seitenlänge a b c a) 3cm 4cm 5cm b) 6m 8m 10m c) 18,3dm 8dm 20dm d) 3 mm 4,6mm 5mm 4
5 Beispielaufgaben Satz des Pythagoras und Flächensätze kombiniert Seitenlänge a b c p q h A a) 4cm 9cm b) 7m 3m a) p = 4cm; q = 9cm Beide Variablen sind in h 2 = p q enthalten => h 2 = p q muss nach h aufgelöst werden: h 2 =p q h = p q = 4 9 = 36 = 6 => h = 6cm In Dreieck ALC gilt: b 2 =h 2 +q 2 In Dreieck LBC gilt: a 2 =h 2 + p 2 => b = h 2 + q 2 = ,8 => b = 10,8cm => a = h 2 + p 2 = ,2 => a = 7,2cm Nach dem Satz des Pythagoras gilt: c = a 2 + b 2 = 18 4,2 Der Flächeninhalt A kann auf zwei Wegen berechnet werden: A = 1 2 h c oder A = 1 2 a b => c = 4,2cm Je nachdem, welche Größen gegeben sind, sollte man die Formel wählen. Grundsätzlich gilt: Flächeninhalt des Dreiecks = 1 Grundlinie Höhe 2 Je nachdem, wie man das Dreieck dreht, sind Höhe und Grundlinie andere Seiten. Sind alle nötigen Größen für beide Formeln gegeben, hat man freie Wahl. A = 0,5 h c = 3 cm 4,2cm = 12,6 cm 2 b) c = 7m; q = 3m Seite c setzt sich aus p und q zusammen: c = p + q p = c q = 7 m 3m = 4 m => p = 4m p und q sind im Höhensatz enthalten: h 2 =p q => h = p q = 4 3 3,5 => h = 3,5m a und b können wie in a) berechnet werden. => a = 5,3m; b = 4,6m A kann wie oben berechnet werden.. => A = 12,25cm 2 Seitenlänge a b c p q h A a) 7,2cm 10,8cm 4,2cm 4cm 9cm 6cm 12,6cm 2 b) 5,3m 4,6m 7m 4m 3m 3,5m 12,25m 2 5
6 Beispielaufgaben aus dem BMT 10 BMT 10, 2009: Aufgabe 7 a) Es gilt 6 2 = ( 11) Verwenden Sie diese Gleichung, um mit Hilfe des Satzes von Pythagoras eine Strecke der La nge 11 cm zu konstruieren. Markieren Sie diese Strecke in der Zeichnung. Der Satz des Pythagoras lautet: c 2 = a 2 +b 2 Hier ist er so formuliert: 6 2 = ( 11) c entspricht also 6cm, a entspricht 11 cm, b entspricht 5cm. Will man ein rechtwinkliges Dreieck konstruieren, benötigt man einen Thaleskreis, der eine Halbkreis um die Mitte der Hypotenuse c mit dem Radius c 2 ist: Jeder Punkt, den man nun auf dem Thaleskreis setzt und mit den Punkten A und B verbindet, erzeugt nun ein rechtwinkliges Dreieck mit der Hypotenuse c = 6cm. c Es wird nach der Seitenlänge 11 cm, also nach a, gesucht. Schlägt man nun einen Kreisbogen um A mit dem Radius b = 5cm, erhält man am Schnittpunkt mit dem Thaleskreis den Punkt C. Die Strecke BC ist dann a = 11 cm. Sie ist in der Zeichnung unten rot markiert. 6
7 b) Vereinfachen Sie den Term (n+1) 2 n 2 und beschreiben Sie, wie sich damit jede Strecke, deren La ngenmaßzahl die Wurzel aus einer ungeraden Zahl gro ßer 1 ist, mit Hilfe des Satzes von Pythagoras konstruieren la sst. Die Vereinfachung des Terms lautet: (n+1) 2 n 2 = (n+1) (n+1) n 2 = n n + 1 n 2 = 2n + 1 (=> der Wert des Terms ist immer eine ungerade Zahl) Der Satz des Pythagoras lautet c 2 = a 2 +b 2. Das passt jedoch nicht zum angegebenen Term (n+1) 2 n 2. Der Satz des Pythagoras lässt sich so umformen, dass es ein Minuszeichen gibt: a= c 2 b 2. Dann entspricht (n+1) der Hypotenuse c und n entspricht der Kathete b. Wenn man die Länge c und die Länge b weiß, kann man die Länge a genau wie in Aufgabe a) konstruieren. Ihre Länge ist (n+1) 2 n 2. BMT 10, 2010: Aufgabe 5 b) Zeigen Sie: Die Ho he eines gleichseitigen Dreiecks mit Seitenla nge a hat die La nge h = 1 3 a 2 a Um die Höhe mithilfe des Satzes von Pythagoras berechnen zu können, braucht man zunächst ein rechtwinkliges Dreieck. In der Abbildung ist die gesuchte Höhe in rot eingetragen. Sie teilt das gleichseitige Dreieck in zwei rechtwinklige Dreiecke. Die Dreiecke ALC und LBC. Sie sind identisch. Die Hypotenuse der Dreiecke ist a, die Katheten sind h und weil h die Mittelsenkrechte von a ist, ist die zweite Kathete a 2. Stellt man hier den Satz des Pythagoras auf, lautet er: a 2 = h 2 + ( a 2 ) 2 a Nach h aufgelöst: h 2 = a 2 ( a 2 ) 2. Zieht man hier die Wurzel, lautet der Term: h = a2 ( a 2 2 ) = a2 1 4 a2 = 3 4 a2 7
8 Man kann hier teilweise radizieren: 3 4 a2 = a2 = a => h = 1 3 a ist korrekt. 2 BMT 10, 2011 Aufgabe 4 Die Abbildung zeigt eine Pyramide der Ho he h. Die quadratische Grundfla che hat die Seitenla nge a, jedes Seitendreieck die Ho he m. a) Erga nzen Sie die Gleichung h = durch einen Term, mit dem h aus a und m berechnet werden kann. h und m schließen mit der Hälfte der Seite a ein rechtwinkliges Dreieck ein. m ist hierbei die Hypotenuse, h und 1 2 a. Der Satz des Pythagoras lautet dann: m 2 = h 2 + ( 1 2 a) 2 Diesen kann man nach h auflösen: h = m2 ( a) 8
Trigonometrie. bekannte Zusammenhänge. 4-Streckensatz: groß/klein = groß/klein. Zusammenhänge im allgemeinen Dreieck:
 Trigonometrie bekannte Zusammenhänge 4-Streckensatz: groß/klein = groß/klein Zusammenhänge im allgemeinen Dreieck: Summe zweier Seiten größer als dritte Seitenlänge: a + b > c Innenwinkelsumme: Summe der
Trigonometrie bekannte Zusammenhänge 4-Streckensatz: groß/klein = groß/klein Zusammenhänge im allgemeinen Dreieck: Summe zweier Seiten größer als dritte Seitenlänge: a + b > c Innenwinkelsumme: Summe der
Zeichnet man nun über die Seiten des Dreiecks die Quadrate der jeweiligen Seiten, dann ergibt sich folgendes Bild:
 9. Lehrsatz von Pythagoras Pythagoras von Samos war ein griechischer Philosoph und Mathematiker, der von ca. 570 v.chr. bis 510 n.chr lebte. Obwohl es über seine gesallschaftliche Stellung verschiedene
9. Lehrsatz von Pythagoras Pythagoras von Samos war ein griechischer Philosoph und Mathematiker, der von ca. 570 v.chr. bis 510 n.chr lebte. Obwohl es über seine gesallschaftliche Stellung verschiedene
Herzlich willkommen zur Demo der mathepower.de Aufgabensammlung
 Herzlich willkommen zur der Um sich schnell innerhalb der ca. 350.000 Mathematikaufgaben zu orientieren, benutzen Sie unbedingt das Lesezeichen Ihres Acrobat Readers: Das Icon finden Sie in der links stehenden
Herzlich willkommen zur der Um sich schnell innerhalb der ca. 350.000 Mathematikaufgaben zu orientieren, benutzen Sie unbedingt das Lesezeichen Ihres Acrobat Readers: Das Icon finden Sie in der links stehenden
1. Algebra 1.1 Terme Man schreibt für einen Term T, der von den Variablen t und m abhängt: m (ausgesprochen: T von t und m)
 Grundwissen Mathematik 7. Klasse 1. Algebra 1.1 Terme Man schreibt für einen Term T, der von den Variablen t und m abhängt: Ttm (, ) = ( t 5+ 6) 20+ m (ausgesprochen: T von t und m) Ein Term besteht aus
Grundwissen Mathematik 7. Klasse 1. Algebra 1.1 Terme Man schreibt für einen Term T, der von den Variablen t und m abhängt: Ttm (, ) = ( t 5+ 6) 20+ m (ausgesprochen: T von t und m) Ein Term besteht aus
Stufen- und Wechselwinkel sind genau dann gleich groß, wenn die Geraden g und h parallel sind.
 1 Sätze über Winkel Geradenkreuzung: Zwei Geraden, die sich in einem Punkt schneiden, nennt man eine Geradenkreuzung. α α Nebeneinander liegende Winkel heißen Nebenwinkel, sie β ergeben zusammen stets
1 Sätze über Winkel Geradenkreuzung: Zwei Geraden, die sich in einem Punkt schneiden, nennt man eine Geradenkreuzung. α α Nebeneinander liegende Winkel heißen Nebenwinkel, sie β ergeben zusammen stets
Sekundarschulabschluss für Erwachsene
 SAE Sekundarschulabschluss für Erwachsene Name: Nummer: Geometrie A 2011 Totalzeit: 60 Minuten Hilfsmittel: Nichtprogrammierbarer Taschenrechner und Geometriewerkzeug Maximal erreichbare Punktzahl: 60
SAE Sekundarschulabschluss für Erwachsene Name: Nummer: Geometrie A 2011 Totalzeit: 60 Minuten Hilfsmittel: Nichtprogrammierbarer Taschenrechner und Geometriewerkzeug Maximal erreichbare Punktzahl: 60
Achsensymmetrie. Konstruktionen. Mathematik-Grundwissen Klassenstufe 7
 Wissen Achsensymmetrie Beispiel Figuren die an einer Achse a gespiegelt werden nennt man achsensymmetrisch bezüglich a. Die Verbindungsstrecke zwischen zwei achsensymmetrischen Punkten wird durch die Achse
Wissen Achsensymmetrie Beispiel Figuren die an einer Achse a gespiegelt werden nennt man achsensymmetrisch bezüglich a. Die Verbindungsstrecke zwischen zwei achsensymmetrischen Punkten wird durch die Achse
Mathematik 36 Ähnlichkeit 01 Name: Vorname: Datum:
 Mathematik 36 Ähnlichkeit 01 Name: Vorname: Datum: Aufgabe 1: Berechne die fehlenden Variablen: a) b) 12 cm 5 cm 8 cm 6 cm 4 cm 6 cm 10 cm 8 cm c) d) u 6 dm 3 dm 9 dm 5 dm 12 m v 6 m 6 m 8 m 15 m Aufgabe
Mathematik 36 Ähnlichkeit 01 Name: Vorname: Datum: Aufgabe 1: Berechne die fehlenden Variablen: a) b) 12 cm 5 cm 8 cm 6 cm 4 cm 6 cm 10 cm 8 cm c) d) u 6 dm 3 dm 9 dm 5 dm 12 m v 6 m 6 m 8 m 15 m Aufgabe
I. Symmetrie. II. Grundkonstruktionen
 I. Symmetrie Achsensymmetrie Zwei Figuren, die bezüglich einer Achse symmetrisch zueinander sind, nennt man achsensymmetrisch. Punktsymmetrie Zwei Figuren, die bei einer Halbdrehung um einen Punkt ineinander
I. Symmetrie Achsensymmetrie Zwei Figuren, die bezüglich einer Achse symmetrisch zueinander sind, nennt man achsensymmetrisch. Punktsymmetrie Zwei Figuren, die bei einer Halbdrehung um einen Punkt ineinander
Kurs 7 Geometrie 2 MSA Vollzeit (1 von 2)
 Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 2815 Bremen Kurs 7 Geometrie 2 MSA Vollzeit (1 von 2) Name: Ich 1. 2. 3. So schätze ich meinen Lernzuwachs ein. kann die
Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 2815 Bremen Kurs 7 Geometrie 2 MSA Vollzeit (1 von 2) Name: Ich 1. 2. 3. So schätze ich meinen Lernzuwachs ein. kann die
2.5. Aufgaben zu Dreieckskonstruktionen
 2.5. Aufgaben zu Dreieckskonstruktionen Aufgabe 1 Zeichne das Dreieck AC mit A( 1 2), (5 0) und C(3 6) und konstruiere seinen Umkreis. Gib den Radius und den Mittelpunkt des Umkreises an. Aufgabe 2 Konstruiere
2.5. Aufgaben zu Dreieckskonstruktionen Aufgabe 1 Zeichne das Dreieck AC mit A( 1 2), (5 0) und C(3 6) und konstruiere seinen Umkreis. Gib den Radius und den Mittelpunkt des Umkreises an. Aufgabe 2 Konstruiere
Elementare Geometrie. Inhaltsverzeichnis. info@mathenachhilfe.ch. Fragen und Antworten. (bitte nur für den Eigengebrauch verwenden)
 fua0306070 Fragen und Antworten Elementare Geometrie (bitte nur für den Eigengebrauch verwenden) Inhaltsverzeichnis 1 Geometrie 1.1 Fragen............................................... 1.1.1 Rechteck.........................................
fua0306070 Fragen und Antworten Elementare Geometrie (bitte nur für den Eigengebrauch verwenden) Inhaltsverzeichnis 1 Geometrie 1.1 Fragen............................................... 1.1.1 Rechteck.........................................
Realschule Abschlussprüfung
 Realschule Abschlussprüfung Annegret Sonntag 4. Januar 2010 Inhaltsverzeichnis 1 Strategie zur Berechnung von ebenen Figuren (Trigonometrie) 3 1.1 Skizze.................................................
Realschule Abschlussprüfung Annegret Sonntag 4. Januar 2010 Inhaltsverzeichnis 1 Strategie zur Berechnung von ebenen Figuren (Trigonometrie) 3 1.1 Skizze.................................................
Formelsammlung Mathematik 9
 I Lineare Funktionen... 9.) Funktionen... 9.) Proportionale Funktionen... 9.) Lineare Funktionen... 9.4) Bestimmung von linearen Funktionen:... II) Systeme linearer Gleichungen... 9.5) Lineare Gleichungen
I Lineare Funktionen... 9.) Funktionen... 9.) Proportionale Funktionen... 9.) Lineare Funktionen... 9.4) Bestimmung von linearen Funktionen:... II) Systeme linearer Gleichungen... 9.5) Lineare Gleichungen
OvTG Gauting, Grundwissen Mathematik 7. Klasse
 1. Symmetrie (vgl. auch Grundwissen 5. Klasse) Achsensymmetrie Zwei Figuren, die bezüglich einer Achse symmetrisch zueinander sind, nennt man achsensymmetrisch. a Punktsymmetrie Zwei Figuren, die bei einer
1. Symmetrie (vgl. auch Grundwissen 5. Klasse) Achsensymmetrie Zwei Figuren, die bezüglich einer Achse symmetrisch zueinander sind, nennt man achsensymmetrisch. a Punktsymmetrie Zwei Figuren, die bei einer
Raumgeometrie - gerade Pyramide
 1.0 Das Quadrat ABCD mit der Seitenlänge 7 cm ist Grundfläche einer geraden Pyramide ABCDS mit der Höhe h = 8 cm. S ist die Pyramidenspitze. 1.1 Fertige ein Schrägbild der Pyramide ABCDS an. 1.2 Berechne
1.0 Das Quadrat ABCD mit der Seitenlänge 7 cm ist Grundfläche einer geraden Pyramide ABCDS mit der Höhe h = 8 cm. S ist die Pyramidenspitze. 1.1 Fertige ein Schrägbild der Pyramide ABCDS an. 1.2 Berechne
Abschlussprüfung Realschule Bayern II / III: 2009 Haupttermin B 1.0 B 1.1
 B 1.0 B 1.1 L: Wir wissen von, dass sie den Scheitel hat und durch den Punkt läuft. Was nichts bringt, ist beide Punkte in die allgemeine Parabelgleichung einzusetzen und das Gleichungssystem zu lösen,
B 1.0 B 1.1 L: Wir wissen von, dass sie den Scheitel hat und durch den Punkt läuft. Was nichts bringt, ist beide Punkte in die allgemeine Parabelgleichung einzusetzen und das Gleichungssystem zu lösen,
INFOMAPPE ZUM EINSTUFUNGSTEST MATHEMATIK AN DER FOS/BOS MEMMINGEN
 INFOMAPPE ZUM EINSTUFUNGSTEST MATHEMATIK AN DER FOS/BOS MEMMINGEN Liebe Schülerinnen und Schüler, wie schnell man einen bereits einmal gekonnten Stoff wieder vergisst, haben Sie sicherlich bereits schon
INFOMAPPE ZUM EINSTUFUNGSTEST MATHEMATIK AN DER FOS/BOS MEMMINGEN Liebe Schülerinnen und Schüler, wie schnell man einen bereits einmal gekonnten Stoff wieder vergisst, haben Sie sicherlich bereits schon
1. Daten und Diagramme Beispiele / Veranschaulichung
 1. Daten und Diagramme / Veranschaulichung Zum Vergleich von Daten sind Säulen- und Balkendiagramme geeignet: Bei dieser Arbeit gab es zweimal die Note 1, siebenmal die Note 2, usw. Die Verteilung innerhalb
1. Daten und Diagramme / Veranschaulichung Zum Vergleich von Daten sind Säulen- und Balkendiagramme geeignet: Bei dieser Arbeit gab es zweimal die Note 1, siebenmal die Note 2, usw. Die Verteilung innerhalb
Minimalziele Mathematik
 Jahrgang 5 o Kopfrechnen, Kleines Einmaleins o Runden und Überschlagrechnen o Schriftliche Grundrechenarten in den Natürlichen Zahlen (ganzzahliger Divisor, ganzzahliger Faktor) o Umwandeln von Größen
Jahrgang 5 o Kopfrechnen, Kleines Einmaleins o Runden und Überschlagrechnen o Schriftliche Grundrechenarten in den Natürlichen Zahlen (ganzzahliger Divisor, ganzzahliger Faktor) o Umwandeln von Größen
Grundwissen. 7. Jahrgangsstufe. Mathematik
 Grundwissen 7. Jahrgangsstufe Mathematik Grundwissen Mathematik 7. Jahrgangsstufe Seite 1 1 Geometrie 1.1 Grundkonstruktionen Lotkonstruktion I: Gegeben ist die Gerade g und der Punkt P, der nicht auf
Grundwissen 7. Jahrgangsstufe Mathematik Grundwissen Mathematik 7. Jahrgangsstufe Seite 1 1 Geometrie 1.1 Grundkonstruktionen Lotkonstruktion I: Gegeben ist die Gerade g und der Punkt P, der nicht auf
Lösungen Kapitel A: Zuordnungen
 Windgeschwindigkeiten Lösungen Kapitel A: Zuordnungen Arbeitsblatt 01: Graphen einer Zuordnung 5 4 3 2 1 0 1 2 3 4 5 6 Tage Strandabschnitte 1 2 3 4 5 6 Muscheln 4,2 2,1 0,7 1,2 7,3 0,5 Arbeitsblatt 02:
Windgeschwindigkeiten Lösungen Kapitel A: Zuordnungen Arbeitsblatt 01: Graphen einer Zuordnung 5 4 3 2 1 0 1 2 3 4 5 6 Tage Strandabschnitte 1 2 3 4 5 6 Muscheln 4,2 2,1 0,7 1,2 7,3 0,5 Arbeitsblatt 02:
Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck
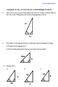 Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck 1) Eine Leiter ist 3m von einer Wand entfernt. Die Leiter ist 5m lang. In welcher Höhe ist die Leiter an die Wand gelehnt und welchen Neigungswinkel
Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck 1) Eine Leiter ist 3m von einer Wand entfernt. Die Leiter ist 5m lang. In welcher Höhe ist die Leiter an die Wand gelehnt und welchen Neigungswinkel
Tag der Mathematik 2007
 Tag der Mathematik 2007 Gruppenwettbewerb Einzelwettbewerb Speed-Wettbewerb Lösungen Allgemeine Hinweise: Als Hilfsmittel dürfen nur Schreibzeug, Geodreieck und Zirkel benutzt werden. Taschenrechner sind
Tag der Mathematik 2007 Gruppenwettbewerb Einzelwettbewerb Speed-Wettbewerb Lösungen Allgemeine Hinweise: Als Hilfsmittel dürfen nur Schreibzeug, Geodreieck und Zirkel benutzt werden. Taschenrechner sind
Grundwissen 9 Bereich 1: Rechnen mit reellen Zahlen
 Bereich 1: Rechnen mit reellen Zahlen Rechenregeln Berechne jeweils: Teilweises Radizieren a) = b) = c) Nenner rational machen a) = b) = c) Bereich 2: Quadratische Funktionen und Gleichungen Scheitelpunktform
Bereich 1: Rechnen mit reellen Zahlen Rechenregeln Berechne jeweils: Teilweises Radizieren a) = b) = c) Nenner rational machen a) = b) = c) Bereich 2: Quadratische Funktionen und Gleichungen Scheitelpunktform
1. Schularbeit R
 1. Schularbeit 23.10.1997... 3R 1a) Stelle die Rechnung 5-3 auf der Zahlengerade durch Pfeile dar! Gibt es mehrere Möglichkeiten der Darstellung? Wenn ja, zeichne alle diese auf! 1b) Ergänze die Tabelle:
1. Schularbeit 23.10.1997... 3R 1a) Stelle die Rechnung 5-3 auf der Zahlengerade durch Pfeile dar! Gibt es mehrere Möglichkeiten der Darstellung? Wenn ja, zeichne alle diese auf! 1b) Ergänze die Tabelle:
Mathematik Geometrie
 Inhalt: Mathematik Geometrie 6.2003 2003 by Reto Da Forno bbildung / bbildungsvorschriften - Ähnlichkeitsabbildungen Seite 1 - Zentrische Streckung Seite 1 - Die Strahlensätze Seite 1 - Kongruenzabbildungen
Inhalt: Mathematik Geometrie 6.2003 2003 by Reto Da Forno bbildung / bbildungsvorschriften - Ähnlichkeitsabbildungen Seite 1 - Zentrische Streckung Seite 1 - Die Strahlensätze Seite 1 - Kongruenzabbildungen
Reelle Zahlen (R)
 Reelle Zahlen (R) Bisher sind bekannt: Natürliche Zahlen (N): N {,,,,,6... } Ganze Zahlen (Z): Z {...,,,0,,,... } Man erkennt: Rationale Zahlen (Q):.) Zwischen den natürlichen Zahlen befinden sich große
Reelle Zahlen (R) Bisher sind bekannt: Natürliche Zahlen (N): N {,,,,,6... } Ganze Zahlen (Z): Z {...,,,0,,,... } Man erkennt: Rationale Zahlen (Q):.) Zwischen den natürlichen Zahlen befinden sich große
Trigonometrische Funktionen
 Trigonometrische Funktionen Rainer Hauser September 013 1 Einleitung 1.1 Der Begriff Funktion Eine Funktion ordnet jedem Element m 1 einer Menge M 1 ein Element m einer Menge M zu. Man schreibt dafür f:
Trigonometrische Funktionen Rainer Hauser September 013 1 Einleitung 1.1 Der Begriff Funktion Eine Funktion ordnet jedem Element m 1 einer Menge M 1 ein Element m einer Menge M zu. Man schreibt dafür f:
Raum- und Flächenmessung bei Körpern
 Raum- und Flächenmessung bei Körpern Prismen Ein Prisma ist ein Körper, dessen Grund- und Deckfläche kongruente Vielecke sind und dessen Seitenflächen Parallelogramme sind. Ist der Winkel zwischen Grund-
Raum- und Flächenmessung bei Körpern Prismen Ein Prisma ist ein Körper, dessen Grund- und Deckfläche kongruente Vielecke sind und dessen Seitenflächen Parallelogramme sind. Ist der Winkel zwischen Grund-
In der Zeichnung unten sind α und β, β und γ, γ und δ, δ und α Nebenwinkel. Scheitelwinkel sind α und γ oder β und δ.
 Entdeckungen an Geraden- und Doppelkreuzungen Schneiden sich zwei Geraden, so entstehen vier Winkel mit Scheitel im Schnittpunkt. Jeweils zwei gleichgroße Winkel liegen sich dabei gegenüber man nennt diese
Entdeckungen an Geraden- und Doppelkreuzungen Schneiden sich zwei Geraden, so entstehen vier Winkel mit Scheitel im Schnittpunkt. Jeweils zwei gleichgroße Winkel liegen sich dabei gegenüber man nennt diese
2. Die Satzgruppe des Pythagoras
 Grundwissen Mathematik 9. Klasse Seite von 17 1.4 Rechnen mit reellen Zahlen a) Multiplizieren und Dividieren von reellen Zahlen + Es gilt: a b = a b mit ab R, 0 Beispiele: 18 = 36 = 6 14 14 7 = = a a
Grundwissen Mathematik 9. Klasse Seite von 17 1.4 Rechnen mit reellen Zahlen a) Multiplizieren und Dividieren von reellen Zahlen + Es gilt: a b = a b mit ab R, 0 Beispiele: 18 = 36 = 6 14 14 7 = = a a
4. Mathematikschulaufgabe
 .0 Berechne folgende Terme:.. x + 4 = x =. (y x) (x + y) =.0 Schreibe ohne Klammern und vereinfache soweit wie möglich:. (x + ) (x 4) =. (0,4x + y) (0,4x y) + (y) =. Ermittle den Extremwert durch Termumformung.
.0 Berechne folgende Terme:.. x + 4 = x =. (y x) (x + y) =.0 Schreibe ohne Klammern und vereinfache soweit wie möglich:. (x + ) (x 4) =. (0,4x + y) (0,4x y) + (y) =. Ermittle den Extremwert durch Termumformung.
Lösungen V.1. Pfeile bedeuten ist auch ein. (Lambacher-Schweizer Geometrie 2, S. 150)
 Lösungen V.1 I: Trapez (zwei parallele Seiten; keine Symmetrie) II: gleichschenkliges Trapez (zwei parallele Seiten, die anderen beiden gleich lang; achsensymmetrisch) III: Drachen(viereck) (jeweils zwei
Lösungen V.1 I: Trapez (zwei parallele Seiten; keine Symmetrie) II: gleichschenkliges Trapez (zwei parallele Seiten, die anderen beiden gleich lang; achsensymmetrisch) III: Drachen(viereck) (jeweils zwei
Kapitel D : Flächen- und Volumenberechnungen
 Kapitel D : Flächen- und Volumenberechnungen Berechnung einfacher Flächen Bei Flächenberechnungen werden die Masse folgendermassen bezeichnet: = Fläche in m 2, dm 2, cm 2, mm 2, etc a, b, c, d = Bezeichnung
Kapitel D : Flächen- und Volumenberechnungen Berechnung einfacher Flächen Bei Flächenberechnungen werden die Masse folgendermassen bezeichnet: = Fläche in m 2, dm 2, cm 2, mm 2, etc a, b, c, d = Bezeichnung
Propädeutikum Mathematik
 Propädeutikum Mathematik Sommersemester 2016 Carsten Krupp BBA Seite 1 Literaturhinweise Cramer, E., Neslehova, J.: Vorkurs Mathematik, Springer, 2004 Piehler, Sippel, Pfeiffer: Mathematik zum Studieneinstieg,
Propädeutikum Mathematik Sommersemester 2016 Carsten Krupp BBA Seite 1 Literaturhinweise Cramer, E., Neslehova, J.: Vorkurs Mathematik, Springer, 2004 Piehler, Sippel, Pfeiffer: Mathematik zum Studieneinstieg,
Geometrie Modul 4b WS 2015/16 Mi HS 1
 Geometrie Modul 4b WS 2015/16 Mi 10-12 HS 1 Benötigte Materialien: Geometrieheft DIN-A-4 blanco weiß, quadratisches Faltpapier/Zettelblock, rundes Faltpapier; Zirkel, Geometriedreieck, Klebstoff, Schere
Geometrie Modul 4b WS 2015/16 Mi 10-12 HS 1 Benötigte Materialien: Geometrieheft DIN-A-4 blanco weiß, quadratisches Faltpapier/Zettelblock, rundes Faltpapier; Zirkel, Geometriedreieck, Klebstoff, Schere
Formeln für Flächen und Körper
 Formeln für Flächen und Körper FLÄCHENBERECHNUNG... QUADRAT... RECHTECK... 3 PARALLELOGRAMM... 3 DREIECK... 4 GLEICHSCHENKLIGES DREIECK... 5 GLEICHSEITIGES DREIECK... 6 TRAPEZ... 7 GLEICHSCHENKLIGES TRAPEZ...
Formeln für Flächen und Körper FLÄCHENBERECHNUNG... QUADRAT... RECHTECK... 3 PARALLELOGRAMM... 3 DREIECK... 4 GLEICHSCHENKLIGES DREIECK... 5 GLEICHSEITIGES DREIECK... 6 TRAPEZ... 7 GLEICHSCHENKLIGES TRAPEZ...
Station A * * 1-4 ca. 16 min
 Station A * * 1-4 ca. 16 min Mit einem 80 m langen Zaun soll an einer Hauswand ein Rechteck eingezäunt werden. Wie lang müssen die Seiten des Rechtecks gewählt werden, damit es einen möglichst großen Flächeninhalt
Station A * * 1-4 ca. 16 min Mit einem 80 m langen Zaun soll an einer Hauswand ein Rechteck eingezäunt werden. Wie lang müssen die Seiten des Rechtecks gewählt werden, damit es einen möglichst großen Flächeninhalt
Trigonometrie und Planimetrie
 Trigonometrie und Planimetrie Hinweis: Die Aufgaben sind in 3 Gruppen gegliedert (G): Grundlagen, Basiswissen einfache Aufgaben (F): Fortgeschritten mittelschwere Aufgaben (E): Experten schwere Aufgaben
Trigonometrie und Planimetrie Hinweis: Die Aufgaben sind in 3 Gruppen gegliedert (G): Grundlagen, Basiswissen einfache Aufgaben (F): Fortgeschritten mittelschwere Aufgaben (E): Experten schwere Aufgaben
F u n k t i o n e n Quadratische Funktionen
 F u n k t i o n e n Quadratische Funktionen Eine Parabolantenne bündelt Radio- und Mikrowellen in einem Brennpunkt. Dort wird die Strahlung detektiert. Die Form einer Parabolantenne entsteht durch die
F u n k t i o n e n Quadratische Funktionen Eine Parabolantenne bündelt Radio- und Mikrowellen in einem Brennpunkt. Dort wird die Strahlung detektiert. Die Form einer Parabolantenne entsteht durch die
- Zeichenutensilien, kein Taschenrechner, keine Formelsammlung
 Bildungsdirektion des Kantons Zürich Mittelschul- und Bildungsamt BMS Aufnahmeprüfung Jahr 2014 Basierend auf Lehrmittel (alt): Arithmetik und Algebra (Hohl) Fach Mathematik Teil 1 Serie D Dauer 45 Minuten
Bildungsdirektion des Kantons Zürich Mittelschul- und Bildungsamt BMS Aufnahmeprüfung Jahr 2014 Basierend auf Lehrmittel (alt): Arithmetik und Algebra (Hohl) Fach Mathematik Teil 1 Serie D Dauer 45 Minuten
Schuljahr 20 / Schule: Lehrkraft: Wochenstundenzahl:
 Schuljahr 20 / Schule: Lehrkraft: Wochenstundenzahl: S E P T E M B E R 9.1 Prozent- und Zinsrechnung 5 Überblick ca. 12 AWT 9.5 9.1 Prozentrechnung Vorbereitende Übungen zum Prozentrechnen (Wiederholung)
Schuljahr 20 / Schule: Lehrkraft: Wochenstundenzahl: S E P T E M B E R 9.1 Prozent- und Zinsrechnung 5 Überblick ca. 12 AWT 9.5 9.1 Prozentrechnung Vorbereitende Übungen zum Prozentrechnen (Wiederholung)
Bezeichnungen am Dreieck
 ezeichnungen am Dreieck Verbindet man drei Punkte, die nicht auf einer Geraden liegen, so entsteht ein Dreieck. llgemeine ezeichnungen: Die Eckpunkte des Dreiecks werden mit den uchstaben, und bezeichnet.
ezeichnungen am Dreieck Verbindet man drei Punkte, die nicht auf einer Geraden liegen, so entsteht ein Dreieck. llgemeine ezeichnungen: Die Eckpunkte des Dreiecks werden mit den uchstaben, und bezeichnet.
Grundwissen-Mathematik-7.Jahrgangsstufe (Algebra) G8
 Grundwissen-Mathematik-7.Jahrgangsstufe (Algebra) G8 Terme Eine Variable ist ein Platzhalter für eine Zahl. Ein Term ist eine sinnvolle Abfolge von Rechenzeichen, Zahlen und Variablen. Beispiel zur Berechnung
Grundwissen-Mathematik-7.Jahrgangsstufe (Algebra) G8 Terme Eine Variable ist ein Platzhalter für eine Zahl. Ein Term ist eine sinnvolle Abfolge von Rechenzeichen, Zahlen und Variablen. Beispiel zur Berechnung
Aufgaben. zu Inhalten der 5. Klasse
 Aufgaben zu Inhalten der 5. Klasse Universität Klagenfurt, Institut für Didaktik der Mathematik (AECC-M) September 2010 Zahlbereiche Es gibt Gleichungen, die (1) in Z, nicht aber in N, (2) in Q, nicht
Aufgaben zu Inhalten der 5. Klasse Universität Klagenfurt, Institut für Didaktik der Mathematik (AECC-M) September 2010 Zahlbereiche Es gibt Gleichungen, die (1) in Z, nicht aber in N, (2) in Q, nicht
Nachhilfe-Kurs Mathematik Klasse 13 Freie Waldorfschule Mitte April 2008
 Nachhilfe-Kurs Mathematik Klasse 13 Freie Waldorfschule Mitte April 8 Zusammenfassung IC Il Corso Advanzato I. Besondere Punkte, Geraden und Ebenen 1. Besondere Ebenen Koordinatenebenen: Wie in dem konkretes
Nachhilfe-Kurs Mathematik Klasse 13 Freie Waldorfschule Mitte April 8 Zusammenfassung IC Il Corso Advanzato I. Besondere Punkte, Geraden und Ebenen 1. Besondere Ebenen Koordinatenebenen: Wie in dem konkretes
II* III* IV* Niveau das kann ich das kann er/sie. Mein Bericht, Kommentar (Einsatz, Schwierigkeiten, Fortschritte, Zusammenarbeit) Name:... Datum:...
 Titel MB 8 LU Nr nhaltliche * * V* Titel MB 8 LU 5 * nhaltliche mein Raumvorstellungsvermögen weiter entwickeln und ebene wie räumliche V Figuren erkennen die Eigenschaften eines regelmässigen Tetraeders
Titel MB 8 LU Nr nhaltliche * * V* Titel MB 8 LU 5 * nhaltliche mein Raumvorstellungsvermögen weiter entwickeln und ebene wie räumliche V Figuren erkennen die Eigenschaften eines regelmässigen Tetraeders
Lernziele Matbu. ch 8
 Lernziele Matbu. ch 8 Beachte auch den Refernzrahmen des Stellwerk8 www. stellwerk- check. ch LU Priorität Grobziel (aus Mathbu.ch 8) Lernziele Begriffe 2 1 Mit gebrochenen Zahlen operieren: Gebrochene
Lernziele Matbu. ch 8 Beachte auch den Refernzrahmen des Stellwerk8 www. stellwerk- check. ch LU Priorität Grobziel (aus Mathbu.ch 8) Lernziele Begriffe 2 1 Mit gebrochenen Zahlen operieren: Gebrochene
Bezeichnung: F F Jede Kongruenzabbildung lässt sich durch Hintereinander Ausführen von höchstens drei Geradenspiegelungen darstellen
 3 6. Ähnlichkeitsabbildungen Bilde eine Figur durch Hintereinander Ausführen von Kongruenzabbildungen (Geradenspiegelungen, Drehungen, Translationen, Punktspiegelungen) und zentrischen Streckungen in eine
3 6. Ähnlichkeitsabbildungen Bilde eine Figur durch Hintereinander Ausführen von Kongruenzabbildungen (Geradenspiegelungen, Drehungen, Translationen, Punktspiegelungen) und zentrischen Streckungen in eine
Themenerläuterung. Die wichtigsten benötigten Formeln
 Themenerläuterung In diesem Kapitel bekommst du Teile von Abmessungen von Spitzkegeln bzw. Kugeln genannt, wie z. B. Radius, Kegelhöhe, Seitenkante, Mantel, Oberfläche und Volumen. Aus diesen Teilangaben
Themenerläuterung In diesem Kapitel bekommst du Teile von Abmessungen von Spitzkegeln bzw. Kugeln genannt, wie z. B. Radius, Kegelhöhe, Seitenkante, Mantel, Oberfläche und Volumen. Aus diesen Teilangaben
Aufgaben zur Übung der Anwendung von GeoGebra
 Aufgabe 1 Aufgaben zur Übung der Anwendung von GeoGebra Konstruieren Sie ein Quadrat ABCD mit der Seitenlänge AB = 6,4 cm. Aufgabe 2 Konstruieren Sie ein Dreieck ABC mit den Seitenlängen AB = c = 6,4 cm,
Aufgabe 1 Aufgaben zur Übung der Anwendung von GeoGebra Konstruieren Sie ein Quadrat ABCD mit der Seitenlänge AB = 6,4 cm. Aufgabe 2 Konstruieren Sie ein Dreieck ABC mit den Seitenlängen AB = c = 6,4 cm,
Lösungen Prüfung Fachmaturität Pädagogik
 Fachmaturität Mathematik 7.0.009 Lösungen Prüfung Lösungen Prüfung Fachmaturität Pädagogik. (7 min,7.5 P.) Brüche Forme so um, dass im Ergebnis maximal ein Bruchstrich vorkommt und nicht mehr weiter gekürzt
Fachmaturität Mathematik 7.0.009 Lösungen Prüfung Lösungen Prüfung Fachmaturität Pädagogik. (7 min,7.5 P.) Brüche Forme so um, dass im Ergebnis maximal ein Bruchstrich vorkommt und nicht mehr weiter gekürzt
Verlauf Material LEK Glossar Lösungen. Passend konstruiert ein Puzzle aus Dreiecken und Vierecken. Wolfgang Göbels, Bergisch Gladbach VORANSICHT
 Reihe 5 S 1 Verlauf Material Passend konstruiert ein Puzzle aus Dreiecken und Vierecken Wolfgang Göbels, Bergisch Gladbach Klasse: 7 9 (G8) Dauer: Inhalt: 3 4 Stunden In ein Puzzle eingekleidete Dreiecks-
Reihe 5 S 1 Verlauf Material Passend konstruiert ein Puzzle aus Dreiecken und Vierecken Wolfgang Göbels, Bergisch Gladbach Klasse: 7 9 (G8) Dauer: Inhalt: 3 4 Stunden In ein Puzzle eingekleidete Dreiecks-
Trage die Ergebnisse in die nachfolgende Tabelle ein. A 3. Größe der Fläche A 1
 Aufgabe: Bestimme die Flächeninhalte A 1, A 2 und A 3. Trage die Ergebnisse in die nachfolgende Tabelle ein. A 1 A 2 A 3 des Winkels Fläche A 1 Fläche A 2 Fläche A 3 1. Dreieck (Ausgangsdreieck) Vergleiche
Aufgabe: Bestimme die Flächeninhalte A 1, A 2 und A 3. Trage die Ergebnisse in die nachfolgende Tabelle ein. A 1 A 2 A 3 des Winkels Fläche A 1 Fläche A 2 Fläche A 3 1. Dreieck (Ausgangsdreieck) Vergleiche
2. Strahlensätze Die Strahlensatzfiguren
 2. Strahlensätze 2.1. Die Strahlensatzfiguren 1) Beispiel Die nebenstehende Figur zeigt eine zentrische Streckung mit Zentrum Z. Man kennt einige Streckenlängen. a) Wie gross ist der Streckungsfaktor k?
2. Strahlensätze 2.1. Die Strahlensatzfiguren 1) Beispiel Die nebenstehende Figur zeigt eine zentrische Streckung mit Zentrum Z. Man kennt einige Streckenlängen. a) Wie gross ist der Streckungsfaktor k?
Berufliches Gymnasium Gelnhausen
 Berufliches Gymnasium Gelnhausen Fachbereich Mathematik Die inhaltlichen Anforderungen für das Fach Mathematik für Schülerinnen und Schüler, die in die Einführungsphase (E) des Beruflichen Gymnasiums eintreten
Berufliches Gymnasium Gelnhausen Fachbereich Mathematik Die inhaltlichen Anforderungen für das Fach Mathematik für Schülerinnen und Schüler, die in die Einführungsphase (E) des Beruflichen Gymnasiums eintreten
Berufliches Schulzentrum Waldkirch Stihl Information zur Aufnahmeprüfung WO. Welche mathematischen Kenntnisse und Fertigkeiten sollten Sie mitbringen?
 Information zur Aufnahmeprüfung WO Mathematik Welche mathematischen Kenntnisse und Fertigkeiten sollten Sie mitbringen? Musterprüfung: Lösen von linearen Gleichungen Aufgabe 1 Lösen von quadratischen Gleichungen
Information zur Aufnahmeprüfung WO Mathematik Welche mathematischen Kenntnisse und Fertigkeiten sollten Sie mitbringen? Musterprüfung: Lösen von linearen Gleichungen Aufgabe 1 Lösen von quadratischen Gleichungen
Lösungen Crashkurs 7. Jahrgangsstufe
 Lösungen Crashkurs 7. Jahrgangsstufe I. Symmetrie und Grundkonstruktionen 1. 2. Jede Raute hat die Eigenschaften: a, b, d, e, g. 3. Der gesuchte Treffpunkt befindet sich dort, wo die Mittelsenkrechte der
Lösungen Crashkurs 7. Jahrgangsstufe I. Symmetrie und Grundkonstruktionen 1. 2. Jede Raute hat die Eigenschaften: a, b, d, e, g. 3. Der gesuchte Treffpunkt befindet sich dort, wo die Mittelsenkrechte der
Geometrie Begriffe und Formeln
 Geometrie Begriffe und Formeln Geometrie setzt sich aus den beiden griechischen Wörtern geo (Erde) und metrein (messen) zusammen, bedeutet ursprünglich Erdvermessen. Alle Gegenstände unseres Universums
Geometrie Begriffe und Formeln Geometrie setzt sich aus den beiden griechischen Wörtern geo (Erde) und metrein (messen) zusammen, bedeutet ursprünglich Erdvermessen. Alle Gegenstände unseres Universums
Mathematik-Dossier Potenzen und Wurzeln Stoffsicherung und repetition.
 Name: Mathematik-Dossier Potenzen und Wurzeln Stoffsicherung und repetition. Inhalt: Potenzen Die zweite Wurzel (Quadratwurzel) Verwendung: Dieses Dossier dient der Repetition und Festigung innerhalb der
Name: Mathematik-Dossier Potenzen und Wurzeln Stoffsicherung und repetition. Inhalt: Potenzen Die zweite Wurzel (Quadratwurzel) Verwendung: Dieses Dossier dient der Repetition und Festigung innerhalb der
Übungsbeispiele- Mathematik 2. Schularbeit, am
 011 Übungsbeispiele- Mathematik. Schularbeit, am 7.1.011 M 3b/I. KL, KV 1.11.011 . Schularbeit: MTHEMTIK KL.: M3b/I. - S. 1) Ergänze die Tabelle! a 1 3 4 5 6 7 8 9 10 a ) Fasse zusammen und schreibe als
011 Übungsbeispiele- Mathematik. Schularbeit, am 7.1.011 M 3b/I. KL, KV 1.11.011 . Schularbeit: MTHEMTIK KL.: M3b/I. - S. 1) Ergänze die Tabelle! a 1 3 4 5 6 7 8 9 10 a ) Fasse zusammen und schreibe als
Nachklausur zur Einführung in die Geometrie im SS 2002 Lösung Aufgabe 1 1.Weg (kurz und einfach):
 Nachklausur zur Einführung in die Geometrie im SS 2002 Lösung ufgabe 1 1.Weg (kurz und einfach): C! **C* Umlaufsinn erhalten Verschiebung oder Drehung Verbindungsgeraden *, *, CC* nicht parallel Drehung
Nachklausur zur Einführung in die Geometrie im SS 2002 Lösung ufgabe 1 1.Weg (kurz und einfach): C! **C* Umlaufsinn erhalten Verschiebung oder Drehung Verbindungsgeraden *, *, CC* nicht parallel Drehung
Jetzt lerne ich Mathematik für die Mittelstufe
 Jetzt lerne ich Mathematik für die Mittelstufe von Dr. rer. nat. Marco Schuchmann, Dipl.-Math. www.alles-mathe.de Seite 2 Seite 3 Vorwort In diesem Buch werden diverse Themen der Mittelstufe bzw. Sekundarstufe
Jetzt lerne ich Mathematik für die Mittelstufe von Dr. rer. nat. Marco Schuchmann, Dipl.-Math. www.alles-mathe.de Seite 2 Seite 3 Vorwort In diesem Buch werden diverse Themen der Mittelstufe bzw. Sekundarstufe
7. Mathematik Olympiade 2. Stufe (Kreisolympiade) Klasse 10 Saison 1967/1968 Aufgaben und Lösungen
 7. Mathematik Olympiade 2. Stufe (Kreisolympiade) Klasse 10 Saison 1967/1968 Aufgaben und Lösungen 1 OJM 7. Mathematik-Olympiade 2. Stufe (Kreisolympiade) Klasse 10 Aufgaben Hinweis: Der Lösungsweg mit
7. Mathematik Olympiade 2. Stufe (Kreisolympiade) Klasse 10 Saison 1967/1968 Aufgaben und Lösungen 1 OJM 7. Mathematik-Olympiade 2. Stufe (Kreisolympiade) Klasse 10 Aufgaben Hinweis: Der Lösungsweg mit
Repetition Mathematik 6. Klasse (Zahlenbuch 6)
 Repetition Mathematik 6. Klasse (Zahlenbuch 6) Grundoperationen / Runden / Primzahlen / ggt / kgv / Klammern 1. Berechne schriftlich: 2'097 + 18 6 16'009 786 481 274 69 d.) 40'092 : 78 2. Die Summe von
Repetition Mathematik 6. Klasse (Zahlenbuch 6) Grundoperationen / Runden / Primzahlen / ggt / kgv / Klammern 1. Berechne schriftlich: 2'097 + 18 6 16'009 786 481 274 69 d.) 40'092 : 78 2. Die Summe von
Brückenkurs Mathematik
 Brückenkurs Mathematik 6.10. - 17.10. Vorlesung 3 Geometrie Doris Bohnet Universität Hamburg - Department Mathematik Mi 8.10.2008 1 Geometrie des Dreiecks 2 Vektoren Länge eines Vektors Skalarprodukt Kreuzprodukt
Brückenkurs Mathematik 6.10. - 17.10. Vorlesung 3 Geometrie Doris Bohnet Universität Hamburg - Department Mathematik Mi 8.10.2008 1 Geometrie des Dreiecks 2 Vektoren Länge eines Vektors Skalarprodukt Kreuzprodukt
Inhaltliche Anforderungen für ein Mathematikstudium an der Pädagogischen Hochschule Karlsruhe
 Inhaltliche Anforderungen für ein Mathematikstudium an der Pädagogischen Hochschule Karlsruhe Liebe Studierende, wenn Sie Mathematik an der Pädagogischen Hochschule Karlsruhe erfolgreich studieren möchten,
Inhaltliche Anforderungen für ein Mathematikstudium an der Pädagogischen Hochschule Karlsruhe Liebe Studierende, wenn Sie Mathematik an der Pädagogischen Hochschule Karlsruhe erfolgreich studieren möchten,
Und so weiter... Annäherung an das Unendliche Lösungshinweise
 Stefanie Anzenhofer, Hans-Georg Weigand, Jan Wörler Numerisch und graphisch. Umfang einer Quadratischen Flocke Abbildung : Quadratische Flocke mit Seitenlänge s = 9. Der Umfang U der Figur beträgt aufgrund
Stefanie Anzenhofer, Hans-Georg Weigand, Jan Wörler Numerisch und graphisch. Umfang einer Quadratischen Flocke Abbildung : Quadratische Flocke mit Seitenlänge s = 9. Der Umfang U der Figur beträgt aufgrund
Aufgabe 1: Der Weidezaun
 Aufgabe 1: Der Weidezaun Eine quadratische Viehweide mit der Fläche 870 m² soll eingezäunt werden. Dabei sollen 3 m für ein Tor freigelassen werden. Wie viel Meter Zaun werden benötigt? Informative Figur:
Aufgabe 1: Der Weidezaun Eine quadratische Viehweide mit der Fläche 870 m² soll eingezäunt werden. Dabei sollen 3 m für ein Tor freigelassen werden. Wie viel Meter Zaun werden benötigt? Informative Figur:
1. Vereinfache wie im Beispiel: 3. Vereinfache wie im Beispiel: 4. Schreibe ohne Wurzel wie im Beispiel:
 1. Zahlenmengen Wissensgrundlage Aufgabenbeispiele Gib die jeweils kleinstmögliche Zahlenmenge an, welche die Zahl enthält? R Q Q oder All diejenigen Zahlen, die sich nicht mehr durch Brüche darstellen
1. Zahlenmengen Wissensgrundlage Aufgabenbeispiele Gib die jeweils kleinstmögliche Zahlenmenge an, welche die Zahl enthält? R Q Q oder All diejenigen Zahlen, die sich nicht mehr durch Brüche darstellen
WF Mathematik: 1. Grundbegriffe der Geometrie
 WF Mathematik: 1. Grundbegriffe der Geometrie Geometrie setzt sich aus den beiden griechischen Wörtern geo (Erde) und metrein (messen) zusammen, bedeutet ursprünglich Erdvermessen. Alle Gegenstände unseres
WF Mathematik: 1. Grundbegriffe der Geometrie Geometrie setzt sich aus den beiden griechischen Wörtern geo (Erde) und metrein (messen) zusammen, bedeutet ursprünglich Erdvermessen. Alle Gegenstände unseres
Analytische Geometrie
 Analytische Geometrie Übungsaufgaben Punkte, Vektoren, Geradengleichungen Gymnasium Klasse 0 Alexander Schwarz www.mathe-aufgaben.com März 04 Aufgabe : Gegeben sind die Punkte O(0/0/0), A(6/6/0), B(/9/0),
Analytische Geometrie Übungsaufgaben Punkte, Vektoren, Geradengleichungen Gymnasium Klasse 0 Alexander Schwarz www.mathe-aufgaben.com März 04 Aufgabe : Gegeben sind die Punkte O(0/0/0), A(6/6/0), B(/9/0),
Korrekturanweisung Mathematik 2015
 Korrekturanweisung Mathematik 2015 Erster allgemeinbildender Schulabschluss Herausgeber Ministerium für Schule und Berufsbildung des Landes Schleswig-Holstein Brunswiker Str. 16-22, 24105 Kiel Aufgabenentwicklung
Korrekturanweisung Mathematik 2015 Erster allgemeinbildender Schulabschluss Herausgeber Ministerium für Schule und Berufsbildung des Landes Schleswig-Holstein Brunswiker Str. 16-22, 24105 Kiel Aufgabenentwicklung
a) Wie lang ist die Kathete a in cm, wenn die Kathete b = 7,8 cm und die Hypotenuse c = 9,8 cm lang sind?
 Besuchen Sie auch die Seite http://www.matheaufgaben-loesen.de/ dort gibt es viele Aufgaben zu weiteren Themen und unter Hinweise den Weg zu den Lösungen. Aufgaben zu Pythagoras, Kathetensatz, Höhensatz
Besuchen Sie auch die Seite http://www.matheaufgaben-loesen.de/ dort gibt es viele Aufgaben zu weiteren Themen und unter Hinweise den Weg zu den Lösungen. Aufgaben zu Pythagoras, Kathetensatz, Höhensatz
Y b 2 - a 2 = p 2 - q 2 (*)
 Um den Flächeninhalt eines Dreieckes zu bestimmen, das keinen rechten Winkel besitzt, muss man bekanntlich die Längen einer Seite mit der dazugehörigen Höhe kennen Wir setzen voraus, dass uns alle 3 Seitenlängen
Um den Flächeninhalt eines Dreieckes zu bestimmen, das keinen rechten Winkel besitzt, muss man bekanntlich die Längen einer Seite mit der dazugehörigen Höhe kennen Wir setzen voraus, dass uns alle 3 Seitenlängen
Umfang des Parallelogramms. Flächeninhalt des Parallelogramms
 Parallelogramm Umfang des Parallelogramms Gegeben ist ein Parallelogramm mit den Seitenlängen a und b. Um den Umfang (u P ) zu berechnen, wird folgende Formel verwendet: u P = 2a + 2b a b a = 6 cm; b =
Parallelogramm Umfang des Parallelogramms Gegeben ist ein Parallelogramm mit den Seitenlängen a und b. Um den Umfang (u P ) zu berechnen, wird folgende Formel verwendet: u P = 2a + 2b a b a = 6 cm; b =
Achsensymmetrie. Konstruktionen M 7.1
 M 7.1 Achsensymmetrie Punkte, die auf der Symmetrieachse liegen und nur diese, sind von zueinander symmetrischen Punkten gleich weit entfernt. Eigenschaften achsensymmetrischer Figuren Die Verbindungsstrecke
M 7.1 Achsensymmetrie Punkte, die auf der Symmetrieachse liegen und nur diese, sind von zueinander symmetrischen Punkten gleich weit entfernt. Eigenschaften achsensymmetrischer Figuren Die Verbindungsstrecke
! "#$% &' (#$ (#$ )* #$ +,' $-. / 01#$#$ '.2
 % Note: mit P.! "#$% &' (#$ (#$ )* #$ +,' $-. / 01#$#$ '. 4+ Körperberechnung: Die Übungsarbeit dient der gezielten Vorbereitung auf die Arbeit. Die Übungsarbeit hat insgesamt 8 Aufgaben mit einigen Teilaufgaben.
% Note: mit P.! "#$% &' (#$ (#$ )* #$ +,' $-. / 01#$#$ '. 4+ Körperberechnung: Die Übungsarbeit dient der gezielten Vorbereitung auf die Arbeit. Die Übungsarbeit hat insgesamt 8 Aufgaben mit einigen Teilaufgaben.
n 0 1 2 3 4 5 6 7 8 9 10 11 12 S n 1250 1244, 085 1214, 075 1220, 136 1226, 167 Nach einem Jahr beträgt der Schuldenstand ca. 1177,09.
 Gymnasium Leichlingen 10a M Lö 2007/08.2 2/2 Aufgaben/Lösungen der Klassenarbeit Nr. 4 von Fr., 2008-04-25 2 45 Aufgabe 1: Die A-Bank bietet Kredite zu einem Zinssatz von 6% pro Jahr an. Ein privater Keditvermittler
Gymnasium Leichlingen 10a M Lö 2007/08.2 2/2 Aufgaben/Lösungen der Klassenarbeit Nr. 4 von Fr., 2008-04-25 2 45 Aufgabe 1: Die A-Bank bietet Kredite zu einem Zinssatz von 6% pro Jahr an. Ein privater Keditvermittler
Vorbereitungskurs Mathematik
 Vorbereitungskurs Mathematik Grundlagen für das Unterrichtsfach Mathematik für die Fachhochschulreifeprüfung Zweijährige Höhere Berufsfachschule Berufsoberschule I Duale Berufsoberschule Inhalt 0. Vorwort...
Vorbereitungskurs Mathematik Grundlagen für das Unterrichtsfach Mathematik für die Fachhochschulreifeprüfung Zweijährige Höhere Berufsfachschule Berufsoberschule I Duale Berufsoberschule Inhalt 0. Vorwort...
Einige grundsätzliche Überlegungen:
 Einige grundsätzliche Überlegungen: 1) Die Wahl der Unbekannten, x, y, z, oder a, b, c oder α, β, γ oder m, n, o. etc. richten sich nach den Beispielen und sind so zu wählen, dass sie am besten zu jenen
Einige grundsätzliche Überlegungen: 1) Die Wahl der Unbekannten, x, y, z, oder a, b, c oder α, β, γ oder m, n, o. etc. richten sich nach den Beispielen und sind so zu wählen, dass sie am besten zu jenen
Zentrale Klassenarbeit 2003
 Zentrale Klassenarbeit 2003 Tipps ab Seite 21, Lösungen ab Seite 31 ZK Mathematik 2003 1. Aufgabe (8 Punkte) [ b 3 a) Vereinfache so weit wie möglich b) Löse die Gleichung 3 2x 3 x = 6. b5 : an 2 c 2n
Zentrale Klassenarbeit 2003 Tipps ab Seite 21, Lösungen ab Seite 31 ZK Mathematik 2003 1. Aufgabe (8 Punkte) [ b 3 a) Vereinfache so weit wie möglich b) Löse die Gleichung 3 2x 3 x = 6. b5 : an 2 c 2n
Mathematik I Prüfung für den Übertritt aus der 8. Klasse
 Aufnahmeprüfung 015 für den Eintritt in das 9. Schuljahr eines Gymnasiums des Kantons Bern Mathematik I Prüfung für den Übertritt aus der 8. Klasse Bitte beachten: - Bearbeitungsdauer: 60 Minuten - Alle
Aufnahmeprüfung 015 für den Eintritt in das 9. Schuljahr eines Gymnasiums des Kantons Bern Mathematik I Prüfung für den Übertritt aus der 8. Klasse Bitte beachten: - Bearbeitungsdauer: 60 Minuten - Alle
WAchhalten und DIagnostizieren
 WAchhalten und DIagnostizieren von Grundkenntnissen und Grundfertigkeiten im Fach Mathematik Klassenstufe 9/10 Teil 1 Annette Kronberger Thomas Weizenegger Stand: 02.04.2016 Einführung 2 Durchgeführte
WAchhalten und DIagnostizieren von Grundkenntnissen und Grundfertigkeiten im Fach Mathematik Klassenstufe 9/10 Teil 1 Annette Kronberger Thomas Weizenegger Stand: 02.04.2016 Einführung 2 Durchgeführte
Grundwissen 7 Bereich 1: Terme
 Grundwissen 7 Bereich 1: Terme Termwerte 1.1 S1 Berechne für den Term T (x) = 3 (x 2) 2 + x 2 die Termwerte T (1), T (2) und T ( 3 2 ). 1.2 S1 Gegeben ist der Term A(m) = 2 2m 5 m Ergänze die folgende
Grundwissen 7 Bereich 1: Terme Termwerte 1.1 S1 Berechne für den Term T (x) = 3 (x 2) 2 + x 2 die Termwerte T (1), T (2) und T ( 3 2 ). 1.2 S1 Gegeben ist der Term A(m) = 2 2m 5 m Ergänze die folgende
Flächenberechnung Flächenberechnung. Mögliche Schritte zur Einführung. Einleitung
 Flächenberechnung Flächenberechnung Einleitung Mögliche Schritte zur Einführung Wie groß ist diese Form? Mit diesem Material kannst du erfahren, wie man bei geometrischen Formen die Fläche berechnen kann.
Flächenberechnung Flächenberechnung Einleitung Mögliche Schritte zur Einführung Wie groß ist diese Form? Mit diesem Material kannst du erfahren, wie man bei geometrischen Formen die Fläche berechnen kann.
Lösungen Kapitel A: Wahrscheinlichkeiten
 Lösungen Kapitel A: Wahrscheinlichkeiten Arbeitsblatt 01: Kombinatorische Zählverfahren (1) Junge, Junge, Mädchen, Mädchen (2) Junge, Mädchen, Junge, Mädchen (3) Junge, Mädchen, Mädchen, Junge (4) Mädchen,
Lösungen Kapitel A: Wahrscheinlichkeiten Arbeitsblatt 01: Kombinatorische Zählverfahren (1) Junge, Junge, Mädchen, Mädchen (2) Junge, Mädchen, Junge, Mädchen (3) Junge, Mädchen, Mädchen, Junge (4) Mädchen,
DSM Das Mathe-Sommer-Ferien-Vergnügen Klasse 9 auf 10 Juni 2016 Aufgaben zur Sicherung eines minimalen einheitlichen Ausgangsniveaus in Klasse 10
 Aufgaben zur Sicherung eines minimalen einheitlichen Ausgangsniveaus in Klasse 10 Die Aufgaben sollen während der Sommerferien gelöst werden, damit notwendige Grundkenntnisse und Grundfertigkeiten nicht
Aufgaben zur Sicherung eines minimalen einheitlichen Ausgangsniveaus in Klasse 10 Die Aufgaben sollen während der Sommerferien gelöst werden, damit notwendige Grundkenntnisse und Grundfertigkeiten nicht
Geometrie Modul 4b WS 2015/16 Mi HS 1
 Geometrie Modul 4b WS 2015/16 Mi 10-12 HS 1 Benötigte Materialien: Geometrieheft DIN-A-4 blanco weiß, quadratisches Faltpapier/Zettelblock, rundes Faltpapier; Zirkel, Geometriedreieck, Klebstoff, Schere
Geometrie Modul 4b WS 2015/16 Mi 10-12 HS 1 Benötigte Materialien: Geometrieheft DIN-A-4 blanco weiß, quadratisches Faltpapier/Zettelblock, rundes Faltpapier; Zirkel, Geometriedreieck, Klebstoff, Schere
GRUNDKURS MATHEMATIK. Zahlenmengen. Natürliche Zahlen. Ganze Zahlen. Gebrochene Zahlen { } Rationale Zahlen { } Irrationale Zahlen { } Reelle Zahlen
 GRUNDKURS MATHEMATIK Zahlenmengen Natürliche Zahlen Ganze Zahlen : 0, 1, 2, 3, Gebrochene Zahlen { } : 0, -1, 1, - Rationale Zahlen { } : 0,,, - Irrationale Zahlen { } : 0, -, Reelle Zahlen Addition und
GRUNDKURS MATHEMATIK Zahlenmengen Natürliche Zahlen Ganze Zahlen : 0, 1, 2, 3, Gebrochene Zahlen { } : 0, -1, 1, - Rationale Zahlen { } : 0,,, - Irrationale Zahlen { } : 0, -, Reelle Zahlen Addition und
42.Trigonometrie - Beziehungen
 4.Trigonometrie - Beziehungen Beziehungen zwischen den Winkelfunktionen tan = cot = sin cos cos sin Aus 3a erhält man durch einfaches Formelumstellen die Hilfssätze 3b und 3c: 3 a tan cot= 3 b tan = cot
4.Trigonometrie - Beziehungen Beziehungen zwischen den Winkelfunktionen tan = cot = sin cos cos sin Aus 3a erhält man durch einfaches Formelumstellen die Hilfssätze 3b und 3c: 3 a tan cot= 3 b tan = cot
Aufgaben zum Basiswissen 7. Klasse
 Aufgaben zum Basiswissen 7. Klasse 1. Achsen- und Punktsymmetrie 1. Aufgabe: Zeichne die Gerade g und alle weiteren Punkte ab und spiegle diese Punkte an der Geraden g und am Zentrum Z. 2. Aufgabe: Zeichne
Aufgaben zum Basiswissen 7. Klasse 1. Achsen- und Punktsymmetrie 1. Aufgabe: Zeichne die Gerade g und alle weiteren Punkte ab und spiegle diese Punkte an der Geraden g und am Zentrum Z. 2. Aufgabe: Zeichne
Berechne schriftlich: a) b) Bilde selbst ähnliche Beispiele.
 Basiswissen Mathematik Klasse 5 / 6 Seite 1 von 12 1 Berechne schriftlich: a) 538 + 28 b) 23 439 Bilde selbst ähnliche Beispiele. 2 Berechne schriftlich: a) 36 23 b) 989: 43 Bilde selbst ähnliche Beispiele.
Basiswissen Mathematik Klasse 5 / 6 Seite 1 von 12 1 Berechne schriftlich: a) 538 + 28 b) 23 439 Bilde selbst ähnliche Beispiele. 2 Berechne schriftlich: a) 36 23 b) 989: 43 Bilde selbst ähnliche Beispiele.
min km/h
 Proportionalität 1. Gegeben sind die folgenden Zuordnungen: 1) x - 3-1 0 0,5 4 y 9 3 0-1,5-6 -1 y : x - 3-3 ) km/h 30 45 60 70 85 100 min 45 30,5 13,5 min km/h 1350 1350 1350 3) s -,5 3,3 7, 8 9,1 4) t
Proportionalität 1. Gegeben sind die folgenden Zuordnungen: 1) x - 3-1 0 0,5 4 y 9 3 0-1,5-6 -1 y : x - 3-3 ) km/h 30 45 60 70 85 100 min 45 30,5 13,5 min km/h 1350 1350 1350 3) s -,5 3,3 7, 8 9,1 4) t
Die in diesem Skriptum behandelten Themen entsprechen etwa dem Niveau der Sekundarstufe I. Kontakt zum Autor:
 Rüdiger Kuhnke Mathematischer Vorkurs zur Physik Die in diesem Skriptum behandelten Themen entsprechen etwa dem Niveau der Sekundarstufe I. Version 0. vom.0.008 Noch nicht vollständig korrigiert Kontakt
Rüdiger Kuhnke Mathematischer Vorkurs zur Physik Die in diesem Skriptum behandelten Themen entsprechen etwa dem Niveau der Sekundarstufe I. Version 0. vom.0.008 Noch nicht vollständig korrigiert Kontakt
7 Ebene Figuren (angepasst an das Lehrmittel Mathematik 1)
 Name: Geometrie-Dossier 7 Ebene Figuren (angepasst an das Lehrmittel Mathematik 1) Inhalt: Fläche und Umfang von Rechteck und Quadrat Dreiecke (Benennung, Konstruktion) Winkelberechnung im Dreieck und
Name: Geometrie-Dossier 7 Ebene Figuren (angepasst an das Lehrmittel Mathematik 1) Inhalt: Fläche und Umfang von Rechteck und Quadrat Dreiecke (Benennung, Konstruktion) Winkelberechnung im Dreieck und
Was bedeutet Trigonometrie und mit was beschäftigt sich die Trigonometrie?
 Einführung Was bedeutet und mit was beschäftigt sich die? Wortkunde: tri bedeutet 'drei' Bsp. Triathlon,... gon bedeutet 'Winkel'/'Eck' Bsp. Pentagon das Fünfeck mit 5 Winkeln metrie bedeutet 'Messung'
Einführung Was bedeutet und mit was beschäftigt sich die? Wortkunde: tri bedeutet 'drei' Bsp. Triathlon,... gon bedeutet 'Winkel'/'Eck' Bsp. Pentagon das Fünfeck mit 5 Winkeln metrie bedeutet 'Messung'
 Abiturprüfung Mathematik 8 Baden-Württemberg (ohne CAS) Wahlteil Aufgaben Analytische Geometrie II, Aufgabe II. Die Punkte A(//), B(//), C(//), F(//), G(//) und H(//) sind die Ecken eines dreiseitigen
Abiturprüfung Mathematik 8 Baden-Württemberg (ohne CAS) Wahlteil Aufgaben Analytische Geometrie II, Aufgabe II. Die Punkte A(//), B(//), C(//), F(//), G(//) und H(//) sind die Ecken eines dreiseitigen
