Bereich Thema Schwierigkeit Geometrie Berechnungen in Rechtwinkligen Dreiecken II ***
|
|
|
- Henriette Beltz
- vor 7 Jahren
- Abrufe
Transkript
1 Ballon Von einem Freiballon aus werden die Orte A und B, die 2700m voneinander entfernt sind, unter den Tiefenwinkeln mit den Winkelweiten α = 66 und β = 24 angepeilt Bestimme, in welcer Höe der Ballon über dem Punkt G scwebt Die Strecke GC abe die Länge, die Strecke GA abe die Länge x x I tan( = x = tan( 24 ; x m II tan(90 24 = ; I eingesetzt in II ergibt tan( m tan( 66 = ; Auflösen dieser Gleicung nac ergibt 2700m = 1500m tan( 66 tan( 24 Der Ballon scwebt in einer Höe von 1500 m über dem Punkt G
2 Geometrie Berecnungen in Rectwinkligen Dreiecken II ** Baum Treffen die Sonnenstralen unter einem Winkel von 30 auf den Boden, so wirft ein Baum einen 45m langen Scatten Bestimme, wie oc der Baum ist Geometrie Berecnungen in Rectwinkligen Dreiecken II ** Die Höe des Baums sei tan( 30 = = 45m tan( 30 ; 26m 45m Der Baum ist ungefär 26m oc
3 Geometrie Berecnungen in Rectwinkligen Dreiecken II * Baustelle 1 Die Handwerkskammer screibt für Leitern einen Anstellwinkel von ca 70 vor Leitern über 7 m Länge müssen zusätzlic abgestützt werden Bestimme, wie oc eine ordnungsgemäß aufgestellte Leiter, die 6 m lang ist, an einer Wand oc reict Geometrie Berecnungen in Rectwinkligen Dreiecken II * Die Höe, die die Leiter an der Wand oc reict, sei sin( 70 = = 6m sin( 70 ; 5,64m 6m Die Leiter reict 5,64m an der Wand oc
4 Geometrie Berecnungen in Rectwinkligen Dreiecken II * Baustelle 2 Die Handwerkskammer screibt für Leitern einen Anstellwinkel von ca 70 vor Leitern über 7 m Länge müssen zusätzlic abgestützt werden Bestimme, wie weit eine ordnungsgemäß aufgestellte Leiter, die 6 m lang ist, von der Wand entfernt auf dem Boden stet Geometrie Berecnungen in Rectwinkligen Dreiecken II * Die Strecke, die die Leiter von der Wand entfernt auf dem Boden stet, sei s s cos( 70 = s = 6m cos(70 ; s 2,05m 6m Die Leiter stet 2,05m von der Wand entfernt auf dem Boden
5 Geometrie Berecnungen in Rectwinkligen Dreiecken II * Baustelle 3 Die Handwerkskammer screibt für Leitern einen Anstellwinkel von ca 70 vor Leitern über 7 m Länge müssen zusätzlic abgestützt werden 15 m an einer Wand oc zu rei- Bestimme, wie lang eine ordnungsgemäß aufgestellte Leiter sein muss, um cen Geometrie Berecnungen in Rectwinkligen Dreiecken II * Die Länge der Leiter sei l 15m 15m sin( 70 = l = ; l 16m l sin( 70 Die Leiter muss 16 m lang sein
6 Geometrie Berecnungen in Rectwinkligen Dreiecken II * Brückenrampe Geplant ist der Bau einer Brücke, die in 50 m Höe über einen Fluss füren soll Die Zufart muss in Uferöe liegen und darf öcstens unter einem Winkel von 3 ansteigen Bestimme, wie lang die Zufart mindestens sein muss Geometrie Berecnungen in Rectwinkligen Dreiecken II * Die Länge der Zufart sei l 50m 50m sin( 3 = l = ; l 955m l sin( 3 Die Zufart muss 955 m lang sein
7 Fabrik Von einer 40 m langen Standlinie AB, die auf einen Fabrikscornstein zuläuft, wird dessen Spitze mit einem Todoliten angepeilt Die Höenwinkel bei A und B aben die Winkelweiten α = 38 und β = 56 Bestimme die Höe des Scornsteins Die Höe des Scornsteins sei, die Strecke vom Punkt B zum Lotfußpunkt der Scornsteinspitze abe die Länge x I tan( 38 = ; 40m + x II tan(56 = x = ; x tan( 56 II eingesetzt in I ergibt tan(38 = ; 40m + tan( 56 Auflösen dieser Gleicung nac ergibt 40m tan( 38 = 66m tan(38 1 tan(56 Der Scornstein ist 66m oc
8 Geometrie Berecnungen in Rectwinkligen Dreiecken II ** Flugrictung 1 Gescwindigkeiten stellt man in der Pysik durc Pfeile dar, Gescwindigkeiten mit versciedenen Rictungen setzt man zusammen, indem man aus den Gescwindigkeitspfeilen Dreiecke bildet Das nebensteende Bild zeigt, wie die Eigengescwindigkeit des Flugzeuges v e und die Windgescwindigkeit v W sic zur Gescwindigkeit v B überlagern, die die Bewegung des Flugzeuges über den Boden angibt α ist der Kompasskurs des Flugzeuges Ein Pilot steuert den Kompasskurs 90, das Flugzeug at die Eigengescwindigkeit 360 km /, die Windgescwindigkeit beträgt 60 km / Bestimme, um welcen Winkel das Flugzeug von seinem Kurs abgelenkt wird Geometrie Berecnungen in Rectwinkligen Dreiecken II ** Die Weite des gesucten Winkels sei ϕ 60 km / 1 tan( ϕ = = ϕ 9,5 360 km / 6 Das Flugzeug wird um einen Winkel der Weite 9,5 von seinem Kurs abgelenkt
9 Flugrictung 2 Gescwindigkeiten stellt man in der Pysik durc Pfeile dar, Gescwindigkeiten mit versciedenen Rictungen setzt man zusammen, indem man aus den Gescwindigkeitspfeilen Dreiecke bildet Das nebensteende Bild zeigt, wie die Eigengescwindigkeit des Flugzeuges r r v e und die Windgescwindigkeit vw sic zur r Gescwindigkeit vb überlagern, die die Bewegung des Flugzeuges über den Boden angibt α ist der Kompasskurs des Flugzeuges Ein Pilot möcte genau Rictung Osten fliegen und steuert den Kompasskurs 80 Die Windgescwindigkeit beträgt 60 km/ Bestimme, mit welcer Eigengescwindigkeit das Flugzeug fliegt, wenn es genau Rictung Osten fliegt Die Eigengescwindigkeit des Flugzeugs sei v e 60km / 60km / sin( = ve = ; ve = 346km / v sin( 10 e Das Flugzeug fliegt mit einer Eigengescwindigkeit von 346 km/
10 Flugrictung 3 Gescwindigkeiten stellt man in der Pysik durc Pfeile dar, Gescwindigkeiten mit versciedenen Rictungen setzt man zusammen, indem man aus den Gescwindigkeitspfeilen Dreiecke bildet Das nebensteende Bild zeigt, wie die Eigengescwindigkeit des Flugzeuges r r v e und die Windgescwindigkeit vw sic zur r Gescwindigkeit vb überlagern, die die Bewegung des Flugzeuges über den Boden angibt α ist der Kompasskurs des Flugzeuges Ein Flugzeug at die Eigengescwindigkeit 420 km/, die Windgescwindigkeit beträgt 40 km/ Bestimme, welcen Kompasskurs der Pilot steuern muss, damit das Flugzeug genau Rictung Osten fliegt Der Kompasskurs des Flugzeuges abe die Weite α 40km / sin( 90 α = 90 α 5,5 α 84, 5 420km / Der Pilot muss den Kompasskurs 84,5 steuern
11 Geometrie Berecnungen in Rectwinkligen Dreiecken II ** Flugzeugstart Ein Flugzeug ebt mit einer Gescwindigkeit von 55m/s (Meter pro Sekunde und einem Winkel von 34 vom Boden ab Bestimme, in welcer Höe sic das Flugzeug nac 6 Sekunden befindet, wenn es weiterin mit der oben angegebenen Gescwindigkeit fliegt und welce Strecke es in dieser Zeit über den Boden überflogen at Geometrie Berecnungen in Rectwinkligen Dreiecken II ** Die Höe des Flugzeugs nac 6 Sekunden sei, die dabei über den Boden zurückgelegte Strecke abe die Lä n- ge s sin( 34 = = 330m sin( 34 ; 185m 6s 55m / s s cos( 34 = s = 330m cos(34 ; s 275m 6s 55m / s Das Flugzeug ist nac 6 s in einer Höe von 185m und at in dieser Zeit über den Boden 275m überflogen
12 Flussbreite Um die Breite eines Flusses zu bestimmen werden von einem Turm aus die beiden Flussufer unter den Tiefenwinkeln mit den Weiten α = 42 und β = 29 angepeilt Bestimme die Breite des Flusses Die Breite des Flusses sei b, die Strecke vom Lotfußpunkt der recten Turmspitze zum linken Flussufer abe die Länge x x + b I tan( = ; 46m x II tan( = x = 46m tan( 48 ; 46m II eingesetzt in I ergibt 46m tan( 48 + b tan( 61 = ; 46m Auflösen dieser Gleicung nac b ergibt b = 46m (tan(61 - tan(48 32m Der Fluss ist 32 m breit
13 Geometrie Berecnungen in Rectwinkligen Dreiecken II ** Flussüberquerung 1 Gescwindigkeiten stellt man in der Pysik durc Pfeile dar, Gescwindigkeiten mit versciedenen Rictungen setzt man zusammen, indem man aus den Gescwindigkeitspfeilen Dreiecke bildet Das nebensteende Bild zeigt, wie die Eigengescwindigkeit des Bootes ve und die Strömungs- r r gescwindigkeit vw sic zur Gescwindigkeit r v B überlagern, die die Bewegung des Bootes über den Boden angibt α ist der Kompasskurs des Bootes Ein Kapitän steuert den Kompasskurs 90, das Boot at die Eigengescwindigkeit 36 km/, die Strömungsgescwindigkeit des Wassers beträgt 12 km/ Bestimme, um welcen Winkel das Boot von seinem Kurs abgelenkt wird Geometrie Berecnungen in Rectwinkligen Dreiecken II ** Die Weite des gesucten Winkels sei ϕ 12km / tan( ϕ = ϕ 18, 4 36km / Das Boot wird um einen Winkel der Weite 18,4 von seinem Kurs abgelenkt
14 Flussüberquerung 2 Gescwindigkeiten stellt man in der Pysik durc Pfeile dar, Gescwindigkeiten mit versciedenen Rictungen setzt man zusammen, indem man aus den Gescwindigkeitspfeilen Dreiecke bildet Das nebensteende Bild zeigt, r wie die Eigengescwindigkeit des Bootes ve und r die Strömungsgescwindigkeit vw sic zur Gescwindigkeit vb überlagern, die die Bewegung r des Bootes über den Boden angibt α ist der Kompasskurs des Bootes Ein Kapitän möcte das gegenüberliegende Ufer im Punkt B erreicen und steuert den Kompasskurs 60 Die Strömungsgescwindigkeit des Wassers beträgt 12 km/ Bestimme, mit welcer Eigengescwindigkeit das Boot faren muss, damit es das gegenüberliegende Ufer im Punkt B erreict Die Eigengescwindigkeit des Bootes sei v e 12km / 12km / sin( = v e = ; ve = 24km / v sin( 30 e Das Boot muss mit einer Eigengescwindigkeit von 24 km/ faren
15 Flussüberquerung 3 Gescwindigkeiten stellt man in der Pysik durc Pfeile dar, Gescwindigkeiten mit versciedenen Rictungen setzt man zusammen, indem man aus den Gescwindigkeitspfeilen Dreiecke bildet Das nebensteende Bild zeigt, wie die Eigengescwindigkeit r des Bootes ve und die Strömungsgescwindigkeit r r v W sic zur Gescwindigkeit vb überlagern, die die Bewegung des Bootes über den Boden angibt α ist der Kompasskurs des Bootes Ein Boot at die Eigengescwindigkeit 14 km/, die Strömungsgescwindigkeit des Wassers beträgt 12 km/ Bestimme, welcen Kompasskurs der Kapitän steuern muss, damit das Boot das gegenüberliegende Ufer im Punkt B erreict Der Kompasskurs des Bootes abe die Weite α 12km / sin( 90 α = 90 α 59 α 31 14km / Das Boot muss mit dem Kompasskurs 31 faren
16 Geometrie Berecnungen in Rectwinkligen Dreiecken II * Gleicscenkliges Dreieck 1 In dem Gleicscenkligen Dreieck ABC ist α = 62 b = 58,6m und Bestimme die Länge der Höe des Dreiecks Geometrie Berecnungen in Rectwinkligen Dreiecken II * sin( 62 = = 58,6m sin( 62 ; 51,7m 58,6m
17 Geometrie Berecnungen in Rectwinkligen Dreiecken II * Gleicscenkliges Dreieck 2 In dem Gleicscenkligen Dreieck ABC ist γ = 98 a = 45,2m und Bestimme die Länge der Höe des Dreiecks Geometrie Berecnungen in Rectwinkligen Dreiecken II * 1 cos( 2 98 = = 45,2m cos(49 ; 29,7m 45,2m
18 Geometrie Berecnungen in Rectwinkligen Dreiecken II * Gleicscenkliges Dreieck 3 In dem Gleicscenkligen Dreieck ABC ist β = 36 c = 124,8m und Bestimme die Länge der Höe des Dreiecks Geometrie Berecnungen in Rectwinkligen Dreiecken II * tan(36 = = 62,4m tan(36 ; 45,3m 1 124,8m 2
19 Geometrie Berecnungen in Rectwinkligen Dreiecken II * Gleicscenkliges Dreieck 4 In dem Gleicscenkligen Dreieck ABC ist γ = 79, 5 c = 9,76m und Bestimme die Länge der Höe des Dreiecks 2011 Tomas Unkelbac Geometrie Berecnungen in Rectwinkligen Dreiecken II * tan( 1 9,76m 2 4,88m 79,5 = = ; 5,87m tan( 39, Tomas Unkelbac
20 Geometrie Berecnungen in Rectwinkligen Dreiecken II * Gleicscenkliges Dreieck 5 In dem Gleicscenkligen Dreieck ABC ist c = 54,7m a = 65,4m und Bestimme die Winkelweite β und die Länge der Höe des Dreiecks Geometrie Berecnungen in Rectwinkligen Dreiecken II * 1 54,7m 2 cos( β = β 65, 3 65,4m sin( 65,3 = = 65,4m sin( 65,3 ; 59,4m 65,4m
21 Geometrie Berecnungen in Rectwinkligen Dreiecken II * Haus Ein Haus ersceint aus der Entfernung 115 m unter dem Höenwinkel 32 Bestimme, wie oc das Haus ist Geometrie Berecnungen in Rectwinkligen Dreiecken II * Die Höe des Hauses sei tan( 32 = = 115m tan(32 ; 72m 115m Das Haus ist 72 m oc
22 Geometrie Berecnungen in Rectwinkligen Dreiecken II ** Höe der Ceopspyramide Die Ceopspyramide in Ägypten at eine Seitenlänge von 230m Wenn ein Betracter 500m von der Pyramide entfernt stet, siet er die Spitze unter einem Winkel von 16 Die Größe des Betracters wird vernaclässigt Bestimme die Höe der Ceopspyramide Geometrie Berecnungen in Rectwinkligen Dreiecken II ** Die Höe der Ceopspyramide sei tan( 16 = = 615m tan(16 ; 176m 500m + 115m Die Ceopspyramide ist 176m oc
23 Kabel zur Insel Vom Ufer aus soll zum Punkt C auf einer Insel in einem See ein Kabel verlegt werden Dazu wurde am Ufer eine Strecke von 100m abgemessen und mit einem Vermessungsgerät der Punkt C auf der Insel jeweils von den Punkten A und B angepeilt Bestimme den Abstand des Punktes C vom Ufer Zu berecnen ist der Abstand des Punktes C zur Strecke AB, d die Höe des Dreiecks auf der Seite AB Seien p und q die beiden Teilstücke der Seite AB bis zum Lotfußpunkt der Höe I tan( 66 = p = ; p tan( 66 II tan( 45 = q = ; q tan( 45 Wegen c = p + q gilt m 100m = + = ( + = ; 69m tan( 66 tan( 45 tan( 66 tan( tan( 66 tan( 45 Der Abstand des Punktes C vom Ufer beträgt 69m
24 Kircturm Der Turmkopf einer Kirce soll als Vermessungspunkt dienen Hierzu muss die Höe bestimmt werden Von den Endpunkten einer auf den Turmkopf zulaufenden Standlinie AB mit AB = 79,94m werden die Winkelweiten α = 25,24 und β = 62,17 gemessen Bestimme die Höe Die Strecke vom Punkt B zum Lotfußpunkt der Kircturmspitze abe die Länge x I tan( 25,24 = ; 79,94m + x II tan( 62,17 = x = ; x tan( 62,17 II eingesetzt in I ergibt tan( 25,24 = ; 79,94m + tan( 62,17 Auflösen dieser Gleicung nac ergibt 79,94m tan( 25,24 = 50,17m tan( 25,24 1 tan( 62,17 Der Kircturm ist 50,17m oc
25 Geometrie Berecnungen in Rectwinkligen Dreiecken II ** Kölner Dom Die Türme des Kölner Doms sind 160m oc An einem scönen Sommertag treffen die Sonnenstralen unter einem Winkel der Weite 35 auf den Vorplatz Bestimme die Länge des Scattens, den die Türme des Doms werfen Geometrie Berecnungen in Rectwinkligen Dreiecken II ** Die Länge des Scattens sei s 160m 160m tan( 35 = s = ; s 229m s tan( 35 Die Türme werfen einen Scatten der Länge 229m
26 Klasse Tema Scwierigkeit 10 Berecnung von rectwinkligen Dreiecken * Leiter Eine 7,10m lange Leiter ist an einer oen Wand so angelent, dass sie am Boden 3,30m von der Wand entfernt ist Bestimme, wie oc die Leiter an der Mauer reict und wie der Winkel zwiscen der Leiter und dem Boden ist 2007 Tomas Unkelbac; Quelle: unbekannt Klasse Tema Scwierigkeit 10 Berecnung von rectwinkligen Dreiecken * Die Höe der Leiter an der Wand sei <P>: 2 2 = (7,10m (3,30m 6,30m 3,30m cos( α = α 62 7, 10m Die Leiter stet 6,30m an der Hausmauer oc Der Winkel zwiscen Leiter und Boden beträgt Tomas Unkelbac; Quelle: unbekannt
27 Geometrie Berecnungen in Rectwinkligen Dreiecken II ** Leitungsmast An einem scönen Sommertag treffen die Sonnenstralen unter einem Winkel der Weite 75º auf den ebenen Boden auf Ein Leitungsmast wirft einen Scatten von 6m Länge Bestimme die Höe des Leitungsmastes Geometrie Berecnungen in Rectwinkligen Dreiecken II ** Die Höe des Leitungsmastes sei tan( 75 = = 6m tan( 75 ; 22,4m 6m Die Höe des Leitungsmastes beträgt 22,4m
28 Leucttürme Von zwei Leucttürmen L 1 und L 2, die 7km voneinander entfernt sind, wird ein Sciff S angepeilt Man misst die Winkelweiten α1 = 42 und α = 55 2 Bestimme die Entfernung des Sciffes von der Küste Zu berecnen ist der Abstand des Punktes S zur Strecke L L 1 2, d die Höe des Dreiecks auf der Seite L L 1 2 Seien p und q die beiden Teilstücke der Seite L L 1 2 bis zum Lotfußpunkt der Höe I tan( 42 = p = ; p tan( 42 II tan(55 = q = ; q tan(55 Wegen c = p + q gilt 1 1 7km 7km = + = ( + = ; 3,87km tan( 42 tan( 55 tan( 42 tan( tan( 42 tan( 55 Das Sciff ist 3,87km von der Küste entfernt
29 Geometrie Berecnungen in Rectwinkligen Dreiecken II ** Liliental Otto LILIENTHAL ( war der erste fliegende Mensc Er flog zum Beispiel mit einem Dracenflieger aus 25 m Höe ca 185 m weit Bestimme, in welcem Gleitwinkel LILIENTHAL geflogen ist Geometrie Berecnungen in Rectwinkligen Dreiecken II ** Der Gleitwinkel abe die Winkelweite α 25m tan( α = α 7, 7 185m Der Gleitwinkel betrug 7,7
30 Loreley Von der Loreley, einem 132 m über dem Rein liegenden Felsen, siet man die beiden Flussufer unter den Tiefenwinkeln mit den Weiten α = 41,4 und β = 65, 6 Bestimme die Breite des Reins an dieser Stelle Die Breite des Reins sei b, die Strecke vom Lotfußpunkt der Loreley am Boden zum recten Flussufer abe die Länge x x + b I tan(90 41,4 = ; 132m x II tan( 90 65,6 = x = 132m tan( 24,4 ; 132m II eingesetzt in I ergibt 132m tan( 24,4 + b tan( 48,6 = ; 132m Auflösen dieser Gleicung nac b ergibt b = 132m (tan(48,6 - tan(24,4 90m Der Rein ist an dieser Stelle 90 m breit
31 Geometrie Berecnungen in Rectwinkligen Dreiecken II * Parallelogramm 1 In dem Parallelogramm ABCD ist a = 8,0cm, d = 10,0cm und α = 60 Bestimme die Länge a der Höe des Parallelogramms und dessen Fläceninalt A Geometrie Berecnungen in Rectwinkligen Dreiecken II * a sin( 60 = 10,0cm a = 10,0cm sin( 60 ; a 8,7cm A = a = 8,0cm 8,7cm = 69,6cm a 2
32 Geometrie Berecnungen in Rectwinkligen Dreiecken II ** Parallelogramm 2 In dem Parallelogramm ABCD ist a = 12,0cm, b = 7,5cm und β = 125 Bestimme die Länge a der Höe des Parallelogramms und dessen Fläceninalt A Geometrie Berecnungen in Rectwinkligen Dreiecken II ** a sin( = 7,5cm a = 7,5cm sin( 55 ; a 6,1cm A = a = 12,0cm 6,1cm = a 73,2cm 2
33 Geometrie Berecnungen in Rectwinkligen Dreiecken II * Prinzessin Um die Prinzessin zu entfüren, at der Ritter die 4,50m lange Leiter unter einem Höenwinkel von 65 an die Burgmauer gelent Bestimme, wie oc die Leiter an der Burgmauer reict Geometrie Berecnungen in Rectwinkligen Dreiecken II * Die Höe der Leiter an der Burgmauer sei sin( 65 = = 4,50m sin( 65 ; 4,08m 4,50m Die Leiter reict 4,08m oc
34 Pultdac In der nebensteenden Abbildung ist ein sogenanntes Pultdac gezeigt Die Bauordnung screibt für die Winkelweiten α und β folgende Wertebereice vor: α 80 und 35 β 45 Bestimme, wie oc das Dac mindestens und öcstens wird Zu berecnen ist der Abstand der Dacspitze zur Strecke AB, d die Höe des Dreiecks auf der Seite AB Seien p und q die beiden Teilstücke der Seite AB bis zum Lotfußpunkt der Höe I tan( 65 = p = ; p tan( 65 II tan(35 = q = ; q tan(35 Wegen c = p + q gilt 1 1 6,50m 6,50m = + = ( + = ; 3,43m tan( 65 tan( 35 tan( 65 tan( tan( 65 tan( 35 Analog ergibt sic mit den beiden anderen Winkeln 5,53m Das Dac wird mindestens 3,43m und öcstens 5,53m oc
35 Rakete Beim Start einer Rakete von Cap Canaveral konnte man von der Zuscauertribüne aus die 10 m oe Spitze der Rakete unter den Höenwinkeln mit den Winkelweiten α = 4, 3 und β = 4, 6 beobacten Bestimme die Höe der Rakete und die Entfernung der Rakete von der Zuscauertribüne Die Höe der Rakete sei, die Strecke von der Zuscauertribüne zum Lotfußpunkt der Spitze der Rakete auf den Boden abe die Länge s 10m I tan( 4,3 = ; s II tan( 4,6 = s = ; s tan( 4,6 II eingesetzt in I ergibt tan( 4,3 = 10m ; tan( 4,6 Auflösen dieser Gleicung nac ergibt 10m = 153m tan( 4,3 1 tan( 4,6 Aus II folgt s = 1900m tan( 4,6 Die Rakete ist 153 m oc und stet von der Zuscauertribüne 1900 m entfernt
36 Ruine Von zwei Peilstäben in der Ebene aus wird die Spitze der Ruine auf dem Berg angepeilt Bestimme den Höenunterscied zwiscen der Ebene und der Spitze der Ruine Die Strecke von der Oberkante des recten Peilstabs zum Lotfußpunkt der Ruine auf die Höe 1,50m abe die Länge x, der Höenunterscied zwiscen der Oberkante der Peilstäbe und der Spitze der Ruine sei ' ' I tan(30 = ; 80m + x ' ' II tan(50 = x = ; x tan( 50 II eingesetzt in I ergibt ' tan(30 = ; ' 80m + tan(50 Auflösen dieser Gleicung nac ' ergibt ' 80m tan( 30 = 89,60m tan( 30 1 tan( 50 Damit liegt die Spitze der Ruine = ' + 1,50m 91,10m öer als die Ebene
37 Geometrie Berecnungen in Rectwinkligen Dreiecken II * Scornstein Ein Scornstein, der 75m oc ist, wirft einen 70m langen Scatten Bestimme die Weite des Winkels, unter dem die Sonnenstralen auf den ebenen Boden treffen Geometrie Berecnungen in Rectwinkligen Dreiecken II * 75m tan( β = β 47 70m Die Sonnenstralen treffen unter einem Winkel der Weite 47 auf den ebenen Boden
38 Geometrie Berecnungen in Rectwinkligen Dreiecken II ** Scüttkegel Beim Aufscütten von Salz, Getreide, Sand usw entstet ein Scüttkegel Der Böscungswinkel (im Bild siest du den Böscungswinkel für Salz ist bei den einzelnen Materialien verscieden Bestimme den Durcmesser eines 3m oen Scüttkegel aus Salz Geometrie Berecnungen in Rectwinkligen Dreiecken II ** Der Durcmesser des Scüttkegels sei d 3m 3m tan( 34 = d = 2 ; d 8,80m d / 2 tan( 34 Der Durcmesser des Scüttkegels beträgt 8,80m
39 Geometrie Berecnungen in Rectwinkligen Dreiecken II * Segelflugzeug 1 Ein Segelflugzeug befindet sic in 1250 m Höe und ist noc 42 km von seinem Ziel entfernt Bestimme, wie groß der Gleitwinkel öcstens sein darf, damit das Segelflugzeug sein Ziel one Unterstützung durc zusätzlicen Aufwind erreict Geometrie Berecnungen in Rectwinkligen Dreiecken II * 1250m tan( α = α 1, m Der Gleitwinkel darf öcstens 1,7 betragen
40 Geometrie Berecnungen in Rectwinkligen Dreiecken II * Segelflugzeug 2 Ein Segelflugzeug befindet sic in Gleitwinkel von 1, m Höe, ist noc 42 km von seinem Ziel entfernt und fliegt mit einem Bestimme, in welcer Höe das Segelflugzeug das Ziel überfliegt, wenn es das Ziel one Unterstützung durc zusätzlicen Aufwind erreict Geometrie Berecnungen in Rectwinkligen Dreiecken II * Die Höe des Segelflugzeugs über dem Zielpunkt sei 1250m tan( 1,5 = ; = 1250m tan( 1, m ; 150m 42000m Das Segelflugzeug überfliegt das Ziel in einer Höe von 150 m
41 Geometrie Berecnungen in Rectwinkligen Dreiecken II ** Tanne Eine Tanne ist 25m oc und wirft einen Scatten von 30m Länge Bestimme die Weite des Winkels, unter dem die Sonnenstralen auf den ebenen Boden treffen Geometrie Berecnungen in Rectwinkligen Dreiecken II ** Die Weite des gesucten Winkels sei α 25m tan( α = α 40 30m Die Sonnenstralen treffen unter einem Winkel der Weite 40 auf den ebenen Boden
42 Geometrie Berecnungen in Rectwinkligen Dreiecken II * Turm Die Höe eines Turmes soll bestimmt werden Dazu at ein Vermessungsingenieur mit Hilfe eines Todoliten den Winkel bestimmt, unter dem ein Betracter den Turm siet Bestimme die Höe des Turmes Geometrie Berecnungen in Rectwinkligen Dreiecken II * Die Höe des Turms sei 1,8m tan( 32 = = 50m tan( ,8m ; 33m 50m Der Turm ist 33m oc
43 Turm am Fluss Von der Spitze eines Turms aus werden zwei Punkte an den beiden Ufern eines Flusses, der 40m breit ist, unter den Tiefenwinkeln mit den Winkelweiten 65 und 28 angepeilt Bestimme, welce Höe der Turm at Der Turm abe die Höe, die Strecke vom Lotfußpunkt der Spitze des Turms zum linken Flussufer abe die Länge x x I tan( = x = tan( 25 ; x + 40m II tan(90 28 = ; I eingesetzt in II ergibt tan( m tan( 62 = ; Auflösen dieser Gleicung nac ergibt 40m = 28m tan( 62 tan( 25 Der Turm ist 28 m oc
44 Turm am See Von der Spitze eines Turms aus werden zwei Punkte an den beiden Ufern eines Sees, der 40m breit ist, unter den Tiefenwinkeln mit den Winkelweiten α = 65 und β = 28 angepeilt Bestimme, welce Höe der Turm at Der Turm abe die Höe, die Strecke vom Lotfußpunkt der Spitze des Turms zum linken Flussufer abe die Länge x x I tan( = x = tan( 25 ; x + 40m II tan(90 28 = ; I eingesetzt in II ergibt tan( m tan( 62 = ; Auflösen dieser Gleicung nac ergibt 40m = 28m tan( 62 tan( 25 Der Turm ist 28 m oc
45 Vermessung am Fluss Um die Breite eines Flusses zu bestimmen, at man an einem Ufer eine Strecke S S von m Länge abgesteckt und am anderen Ufer einen Punkt P durc einen Vermessungsstab markiert Man ermittelt 59 als Weite des Winkels S 2 S 1 P und 71 als Weite des Winkels PS 2 S 1 Bestimme die Breite des Flusses Zu berecnen ist der Abstand des Punktes P zur Strecke S S, d die Höe des Dreiecks auf der Seite S S Seien p und q die beiden Teilstücke der Seite S S 1 2 bis zum Lotfußpunkt der Höe I tan(59 = p = ; p tan(59 II tan( 71 = q = ; q tan( 71 Wegen c = p + q gilt m 400m = + = ( + = ; 423m tan( 59 tan( 71 tan( 59 tan( tan(59 tan( 71 Die Breite des Flusse beträgt 423m
Ballon. Bestimme, in welcher Höhe der Ballon über dem Punkt G schwebt m über dem Punkt G. Der Ballon schwebt in einer Höhe von
 Ballon Von einem Freiballon aus werden die Orte A und B, die 2700m voneinander entfernt sind, unter den Tiefenwinkeln mit den Winkelweiten α = 66 und β = 24 angepeilt. Bestimme, in welcher Höhe der Ballon
Ballon Von einem Freiballon aus werden die Orte A und B, die 2700m voneinander entfernt sind, unter den Tiefenwinkeln mit den Winkelweiten α = 66 und β = 24 angepeilt. Bestimme, in welcher Höhe der Ballon
Baustelle 1. Die Handwerkskammer schreibt für Leitern einen Anstellwinkel von ca. 70 vor. Leitern über 7 m Länge müssen zusätzlich abgestützt werden.
 Baustelle 1 Die Handwerkskammer schreibt für Leitern einen Anstellwinkel von ca. 70 vor. Leitern über 7 m Länge müssen zusätzlich abgestützt werden. Bestimme, wie hoch eine ordnungsgemäß aufgestellte Leiter,
Baustelle 1 Die Handwerkskammer schreibt für Leitern einen Anstellwinkel von ca. 70 vor. Leitern über 7 m Länge müssen zusätzlich abgestützt werden. Bestimme, wie hoch eine ordnungsgemäß aufgestellte Leiter,
Ein Dachfenster ist 1,30m lang. Es ist so aufgeklappt, dass unten ein Spalt von 50cm entsteht.
 * Dachfenster Ein Dachfenster ist 1,30m lang. Es ist so aufgeklappt, dass unten ein Spalt von 50cm entsteht. Bestimme die Weite des Öffnungswinkels des Dachfensters. * Der Winkel hat eine Weite von 22,2.
* Dachfenster Ein Dachfenster ist 1,30m lang. Es ist so aufgeklappt, dass unten ein Spalt von 50cm entsteht. Bestimme die Weite des Öffnungswinkels des Dachfensters. * Der Winkel hat eine Weite von 22,2.
Jgst. 11/I 1.Klausur
 Jgst. /I.Klausur..00 A. Bestimme den Scnittpunkt und den Scnittwinkel der beiden folgenden Geraden: g : x y = 5 : + y = 5x Zunäcst müssen die beiden Geraden auf Normalform gebract werden: x y = 5 y = x
Jgst. /I.Klausur..00 A. Bestimme den Scnittpunkt und den Scnittwinkel der beiden folgenden Geraden: g : x y = 5 : + y = 5x Zunäcst müssen die beiden Geraden auf Normalform gebract werden: x y = 5 y = x
Basisaufgaben - Lösungen
 Arbeitsplan: Trigonometrie am rectwinkligen Dreieck Jargangsstufe 9 Aufgabe 1 Basisaufgaben - Lösungen a) sin δ k m l ; cos δ l m q l ; tan δ k l q, sin ε l m k ; cos ε k m p k ; tan ε l k p b) sin μ 1
Arbeitsplan: Trigonometrie am rectwinkligen Dreieck Jargangsstufe 9 Aufgabe 1 Basisaufgaben - Lösungen a) sin δ k m l ; cos δ l m q l ; tan δ k l q, sin ε l m k ; cos ε k m p k ; tan ε l k p b) sin μ 1
Klasse 9 a/b/c 4. Schulaufgabe aus der Mathematik
 Klasse 9 a/b/c 4. Sculaufgabe aus der Matematik 14. 06. 00 (WWG) Gruppe A 1. Von einem Würfel der Kantenlänge a wird wie unten eingezeicnet eine Pyramide abgescnitten. Berecne das Volumen der Pyramide.
Klasse 9 a/b/c 4. Sculaufgabe aus der Matematik 14. 06. 00 (WWG) Gruppe A 1. Von einem Würfel der Kantenlänge a wird wie unten eingezeicnet eine Pyramide abgescnitten. Berecne das Volumen der Pyramide.
Mathematik GK 11 m3, AB 06 Klausurvorbereitung Differentialq. Lsg x 3 9x 4 2x 2 x 4. 4x 3 9x 4 : 2x 2 x 4 =2x 1 x 3 2x 2 8x
 Aufgabe : Berecne a) 4x 5x 5x 4x b) 4x 9x 4 x x 4 4x 5x 5x : 4x x x 4x x 4x 5x 4x x 4x 4x 4x 9x 4 : x x 4 x x x 8x x x 4 x x 4 c) 4x 4 x 8x 4x 4 x 4x 4 x 4 x 4x x : x x x x 4 4x 4x x x x x Aufgabe : Bestimme
Aufgabe : Berecne a) 4x 5x 5x 4x b) 4x 9x 4 x x 4 4x 5x 5x : 4x x x 4x x 4x 5x 4x x 4x 4x 4x 9x 4 : x x 4 x x x 8x x x 4 x x 4 c) 4x 4 x 8x 4x 4 x 4x 4 x 4 x 4x x : x x x x 4 4x 4x x x x x Aufgabe : Bestimme
Lösung: Variante 1: Sinussatz α = = 119 β = 35 γ = = 26 c = 5,8 sm
 Aufgabe 1: Leuctturm Der Kapitän eine Sciffe mu laut einen Karten beim Paieren einer Landzunge einen betimmten Abtand zum Fetland einalten, um nict auf ein Riff aufzulaufen. Dazu peilt er den Leuctturm
Aufgabe 1: Leuctturm Der Kapitän eine Sciffe mu laut einen Karten beim Paieren einer Landzunge einen betimmten Abtand zum Fetland einalten, um nict auf ein Riff aufzulaufen. Dazu peilt er den Leuctturm
Aufgabenzettel. Löse rechnerisch mit Hilfe geeigneter Funktionsgleichungen. Überprüfe deine Lösung mit einer Zeichnung.
 Matematik Klasse 11 1 Zylinder Zwei Zylinderförmige Gefäße werden mit Wasser gefüllt (siee unten). Jedes Gefäß at einen Grundfläceninalt von 1dm 2 und ist 85cm oc. Erreict der Wasserspiegel des zweiten
Matematik Klasse 11 1 Zylinder Zwei Zylinderförmige Gefäße werden mit Wasser gefüllt (siee unten). Jedes Gefäß at einen Grundfläceninalt von 1dm 2 und ist 85cm oc. Erreict der Wasserspiegel des zweiten
Winkel zeichnen. Hilfe. ACHTUNG! Achte immer genau darauf
 Hilfe Winkel zeichnen 1. Zeichne einen Schenkel (die rote Linie) S 2. Lege das Geodreieck mit der Null am Scheitelpunkt an. (Dort wo der Winkel hinkommen soll) S 3. Möchtest du zum Beispiel einen Winkel
Hilfe Winkel zeichnen 1. Zeichne einen Schenkel (die rote Linie) S 2. Lege das Geodreieck mit der Null am Scheitelpunkt an. (Dort wo der Winkel hinkommen soll) S 3. Möchtest du zum Beispiel einen Winkel
Übungen zum Mathematik-Abitur. Geometrie 1
 Geometrie Übungen zum atematik-abitur -7/8 Übungen zum atematik-abitur Geometrie Gegeben sind die Punkte ( 4 ) und ( 5 6 4) P und die Gerade 7 4 g: x= + r 4 Aufgabe : Die Ebene E entält g und Bestimmen
Geometrie Übungen zum atematik-abitur -7/8 Übungen zum atematik-abitur Geometrie Gegeben sind die Punkte ( 4 ) und ( 5 6 4) P und die Gerade 7 4 g: x= + r 4 Aufgabe : Die Ebene E entält g und Bestimmen
1. Berechne mit dem Taschenrechner Näherungswerte und runde das Ergebnis auf vier Dezimalen a) sin 35,20 b) cos 17,75 c) tan d) cos 3 3
 9 Üben X Trigonometrie 30. Berecne mit dem Tscenrecner Näerungswerte und runde ds Ergebnis uf vier Dezimlen ) sin 35,0 b) cos 7,75 c) tn 44 d) cos 3 3. Berecne die Winkel und gib ds Ergebnis gerundet uf
9 Üben X Trigonometrie 30. Berecne mit dem Tscenrecner Näerungswerte und runde ds Ergebnis uf vier Dezimlen ) sin 35,0 b) cos 7,75 c) tn 44 d) cos 3 3. Berecne die Winkel und gib ds Ergebnis gerundet uf
Bestimmung von Azimut und Abstand: Berechnete Höhe (= Entfernung des gegißten Ortes vom Bildpunkt):
 Bestimmung von Azimut und Abstand: Stundenwinkel: t = Grt + λ + für E-Längen - für W-Längen Berecnete Höe (= Entfernung des gegißten Ortes vom Bildpunkt): sin = sin ϕ sin δ + cos ϕ cosδ cos t Bei der Verwendung
Bestimmung von Azimut und Abstand: Stundenwinkel: t = Grt + λ + für E-Längen - für W-Längen Berecnete Höe (= Entfernung des gegißten Ortes vom Bildpunkt): sin = sin ϕ sin δ + cos ϕ cosδ cos t Bei der Verwendung
Skulptur. 0,25 m. 1,65 m 1,7 m Sockel. 0,6 m 0,6 m 10 m. Aufgabe 1: Die Skulptur
 Aufgabe 1: Die Skulptur Um die Höe einer Skulptur zu bestimmen, die auf einem Sockel stet, stellt sic eine Person (Augenöe 1,70 m) in einer Entfernung von 10 m mit dem Rücken zur Skulptur und ält sic einen
Aufgabe 1: Die Skulptur Um die Höe einer Skulptur zu bestimmen, die auf einem Sockel stet, stellt sic eine Person (Augenöe 1,70 m) in einer Entfernung von 10 m mit dem Rücken zur Skulptur und ält sic einen
Linear. Halbkreis. Parabel
 Vom Parabolspiegel zur Ableitungsfunktion Im Folgenden get es darum erauszufinden, was ein Parabolspiegel ist und wie er funktioniert. Das fürt uns auf wictige Fragen eines Teilgebietes der Matematik,
Vom Parabolspiegel zur Ableitungsfunktion Im Folgenden get es darum erauszufinden, was ein Parabolspiegel ist und wie er funktioniert. Das fürt uns auf wictige Fragen eines Teilgebietes der Matematik,
Orientierungsaufgaben für die BESONDERE LEISTUNGSFESTSTELLUNG ab 2015 MATHEMATIK
 Orientierungsaufgaben für die BESONDERE LEISTUNGSFESTSTELLUNG ab 2015 MATHEMATIK Im Auftrag des TMBWK erarbeitet von den Facberaterinnen und Facberatern Matematik Gymnasium. Hinweise für Prüfungsteilnemerinnen
Orientierungsaufgaben für die BESONDERE LEISTUNGSFESTSTELLUNG ab 2015 MATHEMATIK Im Auftrag des TMBWK erarbeitet von den Facberaterinnen und Facberatern Matematik Gymnasium. Hinweise für Prüfungsteilnemerinnen
3.0 Im folgenden Weg-Zeit-Diagramm ist der Bewegungsablauf eines Mountainbikers dargestellt. s in km 30
 Anwendungsaufgaben - Bewegungen 1 I nebensteenden Gescwindigkeits-Zeit- Diagra sind vier versciedene Bewegungsabläufe dargestellt. Welcer Grap geört zu welcer Bewegung? Begründe. A: Ein Farzeug färt it
Anwendungsaufgaben - Bewegungen 1 I nebensteenden Gescwindigkeits-Zeit- Diagra sind vier versciedene Bewegungsabläufe dargestellt. Welcer Grap geört zu welcer Bewegung? Begründe. A: Ein Farzeug färt it
Diagramm 1 Diagramm 2
 Zweijärige zur Prüfung der Facsculreife fürende Berufsfacscule (BFS) Matematik (9) Hauptprüfung 008 Aufgaben Aufgabe 1 A. 1. Bestimmen Sie die Gleicungen der Geraden g und.. Geben Sie die Koordinaten der
Zweijärige zur Prüfung der Facsculreife fürende Berufsfacscule (BFS) Matematik (9) Hauptprüfung 008 Aufgaben Aufgabe 1 A. 1. Bestimmen Sie die Gleicungen der Geraden g und.. Geben Sie die Koordinaten der
PN1 Einführung in die Physik für Chemiker 1 Prof. J. Lipfert
 PN Einfürung in die Pysik für Cemiker Prof. J. Lipfert en zu Übungsblatt 7 WS 203/4 en zu Übungsblatt 7 Aufgabe Ballscleuder. Zwei Bälle werden übereinander und gleiczeitig fallen gelassen. Die Massen
PN Einfürung in die Pysik für Cemiker Prof. J. Lipfert en zu Übungsblatt 7 WS 203/4 en zu Übungsblatt 7 Aufgabe Ballscleuder. Zwei Bälle werden übereinander und gleiczeitig fallen gelassen. Die Massen
Winkel an sich schneidenden Geraden So wird s gemacht!
 Winkel an sic scneidenden Geraden So wird s gemact! 1. So gest du vor: bedeutet, dass die Geraden g und parallel sind. g α 1 1 1 1 60 Bestimme alle Winkel. α 60 Sceitelwinkel sind gleic groß: α 60 Stufenwinkel
Winkel an sic scneidenden Geraden So wird s gemact! 1. So gest du vor: bedeutet, dass die Geraden g und parallel sind. g α 1 1 1 1 60 Bestimme alle Winkel. α 60 Sceitelwinkel sind gleic groß: α 60 Stufenwinkel
Abschlussprüfung an Fachoberschulen in Bayern NACHTERMIN Mathematik 2015 Geometrie Ausbildungsrichtung Technik
 MK.. B5_T_NB_MK_Loes.xmcd Absclussprüfung an Facobersculen in Bayern NACHTERMIN Matematik 5 Geometrie Ausbildungsrictung Tecnik BE. Ein an den Seiten offener Pavillon aus Holz at die Form eines Quaders,
MK.. B5_T_NB_MK_Loes.xmcd Absclussprüfung an Facobersculen in Bayern NACHTERMIN Matematik 5 Geometrie Ausbildungsrictung Tecnik BE. Ein an den Seiten offener Pavillon aus Holz at die Form eines Quaders,
Realschulabschluss Schuljahr 2004/2005. Mathematik
 Prüfungstag: Mittwoc, 8. Juni 2005 Prüfungsbeginn: 8.00 Ur Realsculabscluss Sculjar 2004/2005 Matematik Hinweise für die Prüfungsteilnemerinnen und -teilnemer Die Arbeitszeit beträgt 150 Minuten. Im Bereic
Prüfungstag: Mittwoc, 8. Juni 2005 Prüfungsbeginn: 8.00 Ur Realsculabscluss Sculjar 2004/2005 Matematik Hinweise für die Prüfungsteilnemerinnen und -teilnemer Die Arbeitszeit beträgt 150 Minuten. Im Bereic
Klasse Thema Schwierigkeit 7 Konstruktion von Dreiecken ***
 Flugichtung 1 Geschwindigkeiten stellt man in de Physik duch Pfeile da, Geschwindigkeiten mit veschiedenen Richtungen setzt man zusammen, indem man aus den Geschwindigkeitspfeilen Deiecke bildet. Das nebenstehende
Flugichtung 1 Geschwindigkeiten stellt man in de Physik duch Pfeile da, Geschwindigkeiten mit veschiedenen Richtungen setzt man zusammen, indem man aus den Geschwindigkeitspfeilen Deiecke bildet. Das nebenstehende
Realschulabschluss/Sekundarabschluss I 2013 Mathematik
 Realsculabscluss/Sekundarabscluss I 0 Matematik Lösung Diese Lösung wurde erstellt von Cornelia Sanzenbacer. Sie ist keine offizielle Lösung des Niedersäcsiscen Kultusministeriums. Hauptteil. a) Zur Berecnung
Realsculabscluss/Sekundarabscluss I 0 Matematik Lösung Diese Lösung wurde erstellt von Cornelia Sanzenbacer. Sie ist keine offizielle Lösung des Niedersäcsiscen Kultusministeriums. Hauptteil. a) Zur Berecnung
Mathematik 7. Jahrgangsstufe
 Probeunterrict 2014 Haupttermin Lösungsinweis M 7 - Zalenrecnen Probeunterrict 2014 an Wirtscaftssculen in Bayern Matematik 7. Jargangsstufe Punkte- und Notensclüssel Zalenrecnen (25 Punkte) und Textrecnen
Probeunterrict 2014 Haupttermin Lösungsinweis M 7 - Zalenrecnen Probeunterrict 2014 an Wirtscaftssculen in Bayern Matematik 7. Jargangsstufe Punkte- und Notensclüssel Zalenrecnen (25 Punkte) und Textrecnen
Klasse Thema Schwierigkeit 7 Konstruktion von Dreiecken ***
 Klasse Thema Schwieigkeit Flugichtung 1 Geschwindigkeiten stellt man in de Physik duch Pfeile da, Geschwindigkeiten mit veschiedenen Richtungen setzt man zusammen, indem man aus den Geschwindigkeitspfeilen
Klasse Thema Schwieigkeit Flugichtung 1 Geschwindigkeiten stellt man in de Physik duch Pfeile da, Geschwindigkeiten mit veschiedenen Richtungen setzt man zusammen, indem man aus den Geschwindigkeitspfeilen
4. Das (symmetrische) - im Querschnitt dreieckige - Dach eines Hauses ist 3,50 Meter
 1. Eine 7 Meter lange Leiter lehnt an einer Hauswand. Sie schließt mit dem Boden eine Winkel von 70 ein. a) In welcher Höhe lehnt die Leiter an der Wand? b) Wie weit ist der Fußpunkt der Leiter von der
1. Eine 7 Meter lange Leiter lehnt an einer Hauswand. Sie schließt mit dem Boden eine Winkel von 70 ein. a) In welcher Höhe lehnt die Leiter an der Wand? b) Wie weit ist der Fußpunkt der Leiter von der
a) Wie hoch ist die Leiter? b) Wie weit stehen die beiden Fußpunkte auseinander? Abbildung 1: Eine Stehleiter
 1. Berechnen Sie die jeweils fehlenden Größen (Winkel α, β und γ, Seiten a, b und c) in den folgenden Dreiecken: a) a = 5 cm, b = 9 cm, γ = 90 b) c = 9 cm, a = 6 cm, γ = 56, 3 (Überlegen Sie zuerst, wo
1. Berechnen Sie die jeweils fehlenden Größen (Winkel α, β und γ, Seiten a, b und c) in den folgenden Dreiecken: a) a = 5 cm, b = 9 cm, γ = 90 b) c = 9 cm, a = 6 cm, γ = 56, 3 (Überlegen Sie zuerst, wo
15 / 16 I GK EF Übung 2 Dez.15
 1 / 16 I GK EF Übung Dez.1 Nr. 1: Ableitungsdefinition - Tangentenberecnung Gegeben ist die ganzrationale Funktion. Grades mit: f(x) = x - x a) Bestimmen Sie die durcscnittlice Änderungsrate (Sekantensteigung)
1 / 16 I GK EF Übung Dez.1 Nr. 1: Ableitungsdefinition - Tangentenberecnung Gegeben ist die ganzrationale Funktion. Grades mit: f(x) = x - x a) Bestimmen Sie die durcscnittlice Änderungsrate (Sekantensteigung)
Trigonometrische Berechnungen
 Trigonometrische Berechnungen Aufgabe 1 Berechnen Sie im rechtwinkligen Dreieck die fehlenden Seiten und Winkel: a) p = 4,93, β = 70,3 b) p = 28, q = 63 c) a = 12,5, p = 4,4 d) h = 9,1, q = 6,0 e) a =
Trigonometrische Berechnungen Aufgabe 1 Berechnen Sie im rechtwinkligen Dreieck die fehlenden Seiten und Winkel: a) p = 4,93, β = 70,3 b) p = 28, q = 63 c) a = 12,5, p = 4,4 d) h = 9,1, q = 6,0 e) a =
Lösungen zu delta 6. Kann ich das noch? Lösungen zu den Seiten 6 und 7
 Kann ic das noc? Lösungen zu den Seiten 6 und 7. a) L = { ; } b) L = {0; } c) L = {} d) ( + )( + ) = 0; L = { ; } e) ( 6)( ) = 0; L = {; 6} f) L = {0}; 0,7 G g) ( 8)( + ) = 0; L = { ; 8} ) ( + )( + ) =
Kann ic das noc? Lösungen zu den Seiten 6 und 7. a) L = { ; } b) L = {0; } c) L = {} d) ( + )( + ) = 0; L = { ; } e) ( 6)( ) = 0; L = {; 6} f) L = {0}; 0,7 G g) ( 8)( + ) = 0; L = { ; 8} ) ( + )( + ) =
Anwendungsaufgaben - Größen und Einheiten 1 Gib jeweils die Messgenauigkeit und die Anzahl der gültigen Ziffern an.
 Anwendungsaufgaben - Größen und Eineiten 1 Gib jeweils die Messgenauigkeit und die Anzal der gültigen Ziffern an. Messgerät Messwert Messgenauigkeit gültige Ziffern Maßband Lineal Messscieber Mikrometer
Anwendungsaufgaben - Größen und Eineiten 1 Gib jeweils die Messgenauigkeit und die Anzal der gültigen Ziffern an. Messgerät Messwert Messgenauigkeit gültige Ziffern Maßband Lineal Messscieber Mikrometer
Lösungen zum Thema Geometrie. Lösungen zur Aufg. 0: a) Gib an, um welche besondere Linie im Dreieck es sich jeweils handelt.
 Lösungen zum Thema Geometrie Lösungen zur Aufg. 0: a) Gib an, um welche besondere Linie im Dreieck es sich jeweils handelt. Höhe h c Winkelhalbierende w α Mittelsenkrechte ms c Seitenhalbierende s c b)
Lösungen zum Thema Geometrie Lösungen zur Aufg. 0: a) Gib an, um welche besondere Linie im Dreieck es sich jeweils handelt. Höhe h c Winkelhalbierende w α Mittelsenkrechte ms c Seitenhalbierende s c b)
Wiederholungsaufgaben Klasse 10
 Wiederholungsaufgaben Klasse 10 (Lineare und quadratische Funktionen / Sinus, Kosinus, Tangens und Anwendungen) 1. In welchem Punkt schneiden sich zwei Geraden, wenn eine Gerade g durch die Punkte A(1
Wiederholungsaufgaben Klasse 10 (Lineare und quadratische Funktionen / Sinus, Kosinus, Tangens und Anwendungen) 1. In welchem Punkt schneiden sich zwei Geraden, wenn eine Gerade g durch die Punkte A(1
= 4. = 2 π. s t. Lösung: Aufgabe 1.a) Der Erdradius beträgt 6.371km. Aufgabe 1.b) Das Meer nimmt 71% der Erdoberfläche ein.
 Aufgabe : Die Die ist der fünftgrößte der neun Planeten unseres Sonnensystems und wiegt 5,98* 0 4 kg. Sie ist zwiscen 4 und 4,5 Millionen Jaren alt und bewegt sic auf einer elliptiscen Ban in einem durcscnittlicen
Aufgabe : Die Die ist der fünftgrößte der neun Planeten unseres Sonnensystems und wiegt 5,98* 0 4 kg. Sie ist zwiscen 4 und 4,5 Millionen Jaren alt und bewegt sic auf einer elliptiscen Ban in einem durcscnittlicen
Vorbereitung für die Arbeit
 Vorbereitung für die Arbeit Trigonometrie: 1. Eine 8 m hohe Fahnenstange wirft einen 13 m langen Schatten. Was ist der Winkel mit dem die Sonne die Fahnenstange trifft? 2. Ein U-Boot wird mit Sonar aufgespürt.
Vorbereitung für die Arbeit Trigonometrie: 1. Eine 8 m hohe Fahnenstange wirft einen 13 m langen Schatten. Was ist der Winkel mit dem die Sonne die Fahnenstange trifft? 2. Ein U-Boot wird mit Sonar aufgespürt.
Realschule Schüttorf November 2006 Mathematik Klasse 10 Wiederholung
 1.) Ein Farradändler verkauft in einer Woce 8 Damen- und 1 Herrenfarräder für 589. Ein Damenfarrad ist 11 günstiger als ein Herrenfarrad. Berecne jeweils den Preis eines Damen- und den Preis eines Herrenfarrades!.)
1.) Ein Farradändler verkauft in einer Woce 8 Damen- und 1 Herrenfarräder für 589. Ein Damenfarrad ist 11 günstiger als ein Herrenfarrad. Berecne jeweils den Preis eines Damen- und den Preis eines Herrenfarrades!.)
Kraft F in N Dehnung s in m
 . Klausur Pysik Leistungskurs Klasse 7. 9. 00 Dauer: 90 in. Wilel T., ein junger, talentierter Bogenscütze darf sic einen neuen Bogen kaufen. Er kann den Bogen it axial 50 N spannen und seine Are reicen
. Klausur Pysik Leistungskurs Klasse 7. 9. 00 Dauer: 90 in. Wilel T., ein junger, talentierter Bogenscütze darf sic einen neuen Bogen kaufen. Er kann den Bogen it axial 50 N spannen und seine Are reicen
Klausur Strömungsmechanik I
 ...... (Name, Matr.-Nr, Unterscrift) Klausur Strömungsmecanik I 09. 03. 2011 1. Aufgabe (11 Punkte) Nac dem Start des Space Suttles fallen die zwei gleic großen, offenen Booster mit jeweils einer Masse
...... (Name, Matr.-Nr, Unterscrift) Klausur Strömungsmecanik I 09. 03. 2011 1. Aufgabe (11 Punkte) Nac dem Start des Space Suttles fallen die zwei gleic großen, offenen Booster mit jeweils einer Masse
Berechnungen am Dreieck
 1 Stern Berechnungen am Dreieck Ein fünfzackiger Stern, wie abgebildet, soll völlig symmetrisch sein (alle fünf Linien sind gleich lang und alle gleichartigen Innenwinkel gleich groß) Die Gesamtlänge der
1 Stern Berechnungen am Dreieck Ein fünfzackiger Stern, wie abgebildet, soll völlig symmetrisch sein (alle fünf Linien sind gleich lang und alle gleichartigen Innenwinkel gleich groß) Die Gesamtlänge der
Zweite Schularbeit Mathematik Klasse 5A am
 Zweite Schularbeit Mathematik Klasse 5A am 10.12.2013 SCHÜLERNAME: Gruppe A Lehrer: Dr. D. B. Westra Grundkompetenzen Grundwissen Grundkompetenzen Grundfertigkeiten Vernetzung und Vertiefung 18 Punkte
Zweite Schularbeit Mathematik Klasse 5A am 10.12.2013 SCHÜLERNAME: Gruppe A Lehrer: Dr. D. B. Westra Grundkompetenzen Grundwissen Grundkompetenzen Grundfertigkeiten Vernetzung und Vertiefung 18 Punkte
2.7. Aufgaben zu Ähnlichkeitsabbildungen
 .7. Aufaben zu Änlickeitsabbildunen Aufabe 1 Strecke das Dreieck AB mit A(3 1), B( 3) und ( ) an Z(1 1) um die Streckfaktoren k 1 =, k = 1, k 3 = 1, k 4 = und k =. Aufabe Strecke das Dreieck AB mit A(
.7. Aufaben zu Änlickeitsabbildunen Aufabe 1 Strecke das Dreieck AB mit A(3 1), B( 3) und ( ) an Z(1 1) um die Streckfaktoren k 1 =, k = 1, k 3 = 1, k 4 = und k =. Aufabe Strecke das Dreieck AB mit A(
Mathematik - Oberstufe
 www.mate-aufgaben.com Matematik - Oberstufe Aufgaben und Musterlösungen zu Ableitungen, Tangenten, Normalen Zielgruppe: Oberstufe Gymnasium Scwerpunkt: Differenzenquotient, Differenzialquotient, Ableitung,
www.mate-aufgaben.com Matematik - Oberstufe Aufgaben und Musterlösungen zu Ableitungen, Tangenten, Normalen Zielgruppe: Oberstufe Gymnasium Scwerpunkt: Differenzenquotient, Differenzialquotient, Ableitung,
7.7. Aufgaben zu Abständen und Winkeln
 7.7. Aufgaben zu Abständen und Winkeln Aufgabe : Schnittwinkel zwischen Geraden Bestimmen Sie die Innenwinkel und ihre Summe für das Viereck ABCD. Berechnen Sie auch die Koordinatengleichung der Trägerebene,
7.7. Aufgaben zu Abständen und Winkeln Aufgabe : Schnittwinkel zwischen Geraden Bestimmen Sie die Innenwinkel und ihre Summe für das Viereck ABCD. Berechnen Sie auch die Koordinatengleichung der Trägerebene,
1 Analytische Geometrie und Grundlagen
 $Id: vektor.tex,v 1.41 2018/05/08 15:50:54 k Exp $ 1 Analytisce Geometrie und Grundlagen 1.5 Abstände und Winkel Am Ende der letzten Sitzung atten wir eine metrisce Form des Stralensatzes ergeleiten, gegeben
$Id: vektor.tex,v 1.41 2018/05/08 15:50:54 k Exp $ 1 Analytisce Geometrie und Grundlagen 1.5 Abstände und Winkel Am Ende der letzten Sitzung atten wir eine metrisce Form des Stralensatzes ergeleiten, gegeben
Tangentensteigung. Gegeben ist die Funktion f(x) = x 2.
 Tangentensteigung Gegeben ist die Funktion () =. Um die Steigung der Tangente im Punkt P( ) zu bestimmen, ermitteln wir zunäcst die Steigung der Sekante durc P( ) und Q( ). Q soll so beweglic sein, dass
Tangentensteigung Gegeben ist die Funktion () =. Um die Steigung der Tangente im Punkt P( ) zu bestimmen, ermitteln wir zunäcst die Steigung der Sekante durc P( ) und Q( ). Q soll so beweglic sein, dass
9 Anhang. 9.1 Verhältnisgleichungen. 9.2 Strahlensätze. Elemente der Geometrie 22
 Elemente der Geometrie 9 Anang 9.1 Verältnisgleicungen Verältnisgleicungen sind spezielle Formen von Gleicungen. Es a werden zwei Quotienten gleic gesetzt. Die Gleicung! b = c d kann man auc screiben als!a:b
Elemente der Geometrie 9 Anang 9.1 Verältnisgleicungen Verältnisgleicungen sind spezielle Formen von Gleicungen. Es a werden zwei Quotienten gleic gesetzt. Die Gleicung! b = c d kann man auc screiben als!a:b
1. Schulaufgabe aus der Physik Lösungshinweise
 . Sculaufgabe 3p Sculjar 2009/200. Sculaufgabe aus der Pysik Lösungsinweise Gruppe A (a) Beim Ruterford-Versuc wird eine ser dünne Goldfolie mit positiv geladenen α-teilcen eines radioaktiven Präparats
. Sculaufgabe 3p Sculjar 2009/200. Sculaufgabe aus der Pysik Lösungsinweise Gruppe A (a) Beim Ruterford-Versuc wird eine ser dünne Goldfolie mit positiv geladenen α-teilcen eines radioaktiven Präparats
Vergleichsarbeit Klasse 9. I. Quadratische Funktionen
 Name: Vergleichsarbeit Klasse 9 I. Quadratische Funktionen 90 Minuten 1. Bestimme den Scheitelpunkt und die Nullstellen des Graphen von f. Gehe dabei möglichst geschickt vor. a) f(x) = 50 5x² b) f(x) =
Name: Vergleichsarbeit Klasse 9 I. Quadratische Funktionen 90 Minuten 1. Bestimme den Scheitelpunkt und die Nullstellen des Graphen von f. Gehe dabei möglichst geschickt vor. a) f(x) = 50 5x² b) f(x) =
Brückenkurs Höhere Mathematik
 Vorkurse der Hochschule Aalen Brückenkurs Höhere Mathematik Aufgabensammlung März 209 Das Grundlagenzentrum (GLZ) wird aus Mitteln des Bundesministeriums für Bildung und Forschung (BMBF) unter dem Förderkennzeichen
Vorkurse der Hochschule Aalen Brückenkurs Höhere Mathematik Aufgabensammlung März 209 Das Grundlagenzentrum (GLZ) wird aus Mitteln des Bundesministeriums für Bildung und Forschung (BMBF) unter dem Förderkennzeichen
14 B Steigung. 1 Miss bei den drei Keilen die Winkel und Strecken und übertrage sie in die Tabelle. Berechne die Steigung.
 Steigung 4 6 Arbeitseft+ Teste dic selbst Miss bei den drei Keilen die Winkel und Strecken und übertrage sie in die Tabelle. Berecne die Steigung. a a a Keil Keil 2 Keil 3 Keil Keil 2 Keil 3 Horizontale
Steigung 4 6 Arbeitseft+ Teste dic selbst Miss bei den drei Keilen die Winkel und Strecken und übertrage sie in die Tabelle. Berecne die Steigung. a a a Keil Keil 2 Keil 3 Keil Keil 2 Keil 3 Horizontale
Tangenten an Funktionsgraphen (Differenzialrechnung) Aufgaben ab Seite 4
 Klasse / Augaben ab Seite 4 rundlagen und Begrie der Dierenzialrecnung Die Zeicnungen und Erklärungen sind etwas ausürlicer als notwendig u versciedene Screibweisen und Darstellungen auzuzeigen. Steigung
Klasse / Augaben ab Seite 4 rundlagen und Begrie der Dierenzialrecnung Die Zeicnungen und Erklärungen sind etwas ausürlicer als notwendig u versciedene Screibweisen und Darstellungen auzuzeigen. Steigung
Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck
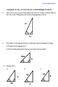 Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck 1) Eine Leiter ist 3m von einer Wand entfernt. Die Leiter ist 5m lang. In welcher Höhe ist die Leiter an die Wand gelehnt und welchen Neigungswinkel
Aufgaben zu sin, cos und tan im rechtwinkligen Dreieck 1) Eine Leiter ist 3m von einer Wand entfernt. Die Leiter ist 5m lang. In welcher Höhe ist die Leiter an die Wand gelehnt und welchen Neigungswinkel
Rudolphs Schlitten. Aufgabe. Autor: Jochen Ricker
 Rudolps Sclitten Autor: Jocen Ricker Aufgabe Endlic ist es wieder soweit: Weinacten stet vor der Tür! Diesmal at der Weinactsmann sic ein ganz besonderes Gescenk für seine Rentiere einfallen lassen. Sie
Rudolps Sclitten Autor: Jocen Ricker Aufgabe Endlic ist es wieder soweit: Weinacten stet vor der Tür! Diesmal at der Weinactsmann sic ein ganz besonderes Gescenk für seine Rentiere einfallen lassen. Sie
Übungsaufgaben zur Kursarbeit
 Übungsaufgaben zur Kursarbeit I) Tema Funktionen. Gib jeweils die maximale Definitionsmenge der Funktion an f(x) = (x ) D f = R (x) = x D = {x R /x } g(x) = (x ) D = {x R /x } g k(x) = x D = {x R /x >
Übungsaufgaben zur Kursarbeit I) Tema Funktionen. Gib jeweils die maximale Definitionsmenge der Funktion an f(x) = (x ) D f = R (x) = x D = {x R /x } g(x) = (x ) D = {x R /x } g k(x) = x D = {x R /x >
Schülerbuchseite 8 11
 Scülerbucseite 8 I Sclüsselkonzept: Ableitung Funktionen Seite 8 Die andere Person muss nict notwendig dieselbe Strecke gefaren sein, nur weil sie denselben Farpreis bezalt at. Es gibt versciedene Verbindungen,
Scülerbucseite 8 I Sclüsselkonzept: Ableitung Funktionen Seite 8 Die andere Person muss nict notwendig dieselbe Strecke gefaren sein, nur weil sie denselben Farpreis bezalt at. Es gibt versciedene Verbindungen,
Weitere Anwendungen von ganzrationalen Funktionen
 Weitere Anwendungen von ganzrationalen Funktionen 1.0 Um Obstkisten aus Pappe erzustellen, werden aus recteckigen Kartonplatten (Länge 16 dm, Breite 1 dm) an den vier Ecken jeweils Quadrate abgescnitten.
Weitere Anwendungen von ganzrationalen Funktionen 1.0 Um Obstkisten aus Pappe erzustellen, werden aus recteckigen Kartonplatten (Länge 16 dm, Breite 1 dm) an den vier Ecken jeweils Quadrate abgescnitten.
Sinus- und Kosinussatz
 Sinus- und Kosinussatz Aufgabe 1 Bestimme für 0 α 360 die zwei Winkel, für die gilt a) sin α = 0,2 b) sin α = -0,74 c) cos α = 0,84 d) cos α = -0,05 e) tan α = 21 f) tan α = -0,51 g) cos α = -0,9 h) tan
Sinus- und Kosinussatz Aufgabe 1 Bestimme für 0 α 360 die zwei Winkel, für die gilt a) sin α = 0,2 b) sin α = -0,74 c) cos α = 0,84 d) cos α = -0,05 e) tan α = 21 f) tan α = -0,51 g) cos α = -0,9 h) tan
Dreieckskonstruktionen Anwendungsaufgaben Lösungen
 Hilfe home Dreieckskonstruktionen nwendungsaufgaben Lösungen ufgabe 1 Konstruiere ein rechtwinklig gleichseitiges Dreieck mit der Hypotenuse c = 8 cm. Zeichne über den Katheten a und b die Quadrate und
Hilfe home Dreieckskonstruktionen nwendungsaufgaben Lösungen ufgabe 1 Konstruiere ein rechtwinklig gleichseitiges Dreieck mit der Hypotenuse c = 8 cm. Zeichne über den Katheten a und b die Quadrate und
Lösungen zu delta 10 H
 Kann ic das noc? Lösungen zu den Seiten 6 und 7. a) T () = ( ) + ( + ) + = = + + 4 + 4 + + = = + + 6 b) T () = ( + a) a(a + ) = = + a + a a a = = c) T () = ( ) ( + ) ( ) = = 4 + 9 6 4 = = d) T 4 () = (
Kann ic das noc? Lösungen zu den Seiten 6 und 7. a) T () = ( ) + ( + ) + = = + + 4 + 4 + + = = + + 6 b) T () = ( + a) a(a + ) = = + a + a a a = = c) T () = ( ) ( + ) ( ) = = 4 + 9 6 4 = = d) T 4 () = (
Themen: Strahlensätze, Trigonometrie, trigonometrische Funktionen
 Mathematik Klasse 10c Vorbereitung Klassenarbeit Nr. 3 am 1.3.019 Themen: Strahlensätze, Trigonometrie, trigonometrische Funktionen Checkliste Was ich alles können soll Ich erkennen die Strahlensatzfiguren
Mathematik Klasse 10c Vorbereitung Klassenarbeit Nr. 3 am 1.3.019 Themen: Strahlensätze, Trigonometrie, trigonometrische Funktionen Checkliste Was ich alles können soll Ich erkennen die Strahlensatzfiguren
Wochenplan Woche vom...
 Wocenplan Woce vom... Temenübersict Arbeitsblatt 1 Holzylinder Inalt, Scwerpunkte des Temas Volumenberecnungen und Masseberecnung für den Holzylinder Kontrolle Arbeitsblatt Netze von, Oberfläcenberecnung,
Wocenplan Woce vom... Temenübersict Arbeitsblatt 1 Holzylinder Inalt, Scwerpunkte des Temas Volumenberecnungen und Masseberecnung für den Holzylinder Kontrolle Arbeitsblatt Netze von, Oberfläcenberecnung,
1.4 Trigonometrie. 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2. 2 Die trigonometrischen Funktionen 3
 1.4 Trigonometrie Inhaltsverzeichnis 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2 2 Die trigonometrischen Funktionen 3 2.1 Was sind trigonometrischen Funktionen?.......................... 3 2.2 Die
1.4 Trigonometrie Inhaltsverzeichnis 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2 2 Die trigonometrischen Funktionen 3 2.1 Was sind trigonometrischen Funktionen?.......................... 3 2.2 Die
Landeswettbewerb Mathematik Baden-Württemberg Musterlösungen 1. Runde 2013/2014
 Landeswettbewerb Matematik aden-württemberg Musterlösungen 1. Runde 01/014 ufgabe 1 Wolfgang will die Zalen 1,,,, 8 an die Ecken eines ctecks screiben und jede Zal einmal verwenden. abei soll die Summe
Landeswettbewerb Matematik aden-württemberg Musterlösungen 1. Runde 01/014 ufgabe 1 Wolfgang will die Zalen 1,,,, 8 an die Ecken eines ctecks screiben und jede Zal einmal verwenden. abei soll die Summe
Bei Windstille bilden die Regentropfen am Fenster eines mit einer Geschwindigkeit v z
 Aufgabe 1 (Verkehrsschild) a) Unter welchem Winkel steigt die Straße an? Schätze zuerst. b) Die Straße überwindet einen Höhenunterschied von 100m. Wie lang ist die Straße? c) Welchen Höhenunterschied überwindet
Aufgabe 1 (Verkehrsschild) a) Unter welchem Winkel steigt die Straße an? Schätze zuerst. b) Die Straße überwindet einen Höhenunterschied von 100m. Wie lang ist die Straße? c) Welchen Höhenunterschied überwindet
Vorbereitungsaufgaben SA1: Symmetrie und Winkelbetrachtungen
 Aufgabe 1 a) Welche Eigenschaft besitzen alle Punkte auf der Mittelsenkrechten zu zwei gegebenen Punkten A und B? b) In einem Dreieck sind zwei Winkel gleich groß und der dritte Winkel doppelt so groß.
Aufgabe 1 a) Welche Eigenschaft besitzen alle Punkte auf der Mittelsenkrechten zu zwei gegebenen Punkten A und B? b) In einem Dreieck sind zwei Winkel gleich groß und der dritte Winkel doppelt so groß.
Übungsaufgaben zur Differential-Rechnung
 Übungsaufgaben zur Differential-Recnung Weitere Übungsaufgaben mit Lösungen gibt es z.b. in Brauc/Dreyer/Haacke, Papula, Stingl, Stöcker, Minorski usw.. Bestimme allgemeines Folgen-Element, Eigenscaften
Übungsaufgaben zur Differential-Recnung Weitere Übungsaufgaben mit Lösungen gibt es z.b. in Brauc/Dreyer/Haacke, Papula, Stingl, Stöcker, Minorski usw.. Bestimme allgemeines Folgen-Element, Eigenscaften
Alle hier gezeigten Aufgaben verwenden Sinussatz und Kosinussatz. Die Sammlung wird weiter ergänzt. Klassenstufe 10. Datei Nr
 Trigonometrie Trainingsaufgaben 2 lle hier gezeigten ufgaben verwenden Sinussatz und Kosinussatz ie Sammlung wird weiter ergänzt Klassenstufe 10 atei Nr. 16032 November 2005 Friedrich uckel INTERNETILITHEK
Trigonometrie Trainingsaufgaben 2 lle hier gezeigten ufgaben verwenden Sinussatz und Kosinussatz ie Sammlung wird weiter ergänzt Klassenstufe 10 atei Nr. 16032 November 2005 Friedrich uckel INTERNETILITHEK
Aufgaben, in denen die Nebenbedingung mithilfe des Strahlensatzes ermittelt wird.
 Differentilrecnung Extremwertufgben Arbeitsbltt Aufgben, in denen die Nebenbedingung mitilfe des Strlenstzes ermittelt wird. Vorwissen 1 Werden zwei Strlen und b mit dem gemeinsmen Anfngspunkt S von zwei
Differentilrecnung Extremwertufgben Arbeitsbltt Aufgben, in denen die Nebenbedingung mitilfe des Strlenstzes ermittelt wird. Vorwissen 1 Werden zwei Strlen und b mit dem gemeinsmen Anfngspunkt S von zwei
Übungsblatt 03. PHYS4100 Grundkurs IV (Physik, Wirtschaftsphysik, Physik Lehramt) Othmar Marti,
 Übungsblatt 03 PHYS4100 Grkurs IV (Pysik, Wirtscaftspysik, Pysik Leramt Otmar Marti, (otmar.marti@pysik.uni-ulm.de 28. 4. 2005 oder 29. 4. 2005 1 Aufgaben 1. Nemen Sie an, dass eine Kugel mit dem Radius
Übungsblatt 03 PHYS4100 Grkurs IV (Pysik, Wirtscaftspysik, Pysik Leramt Otmar Marti, (otmar.marti@pysik.uni-ulm.de 28. 4. 2005 oder 29. 4. 2005 1 Aufgaben 1. Nemen Sie an, dass eine Kugel mit dem Radius
Die Grundfigur der Trigonometrie ist das rechtwinklige Dreieck. Mit ihm fangen wir an.
 TRIGONOMETRIE [ J. Möller, WS Üerlingen] TRIGON = Dreieck Die Trigonometrie ist der Zweig der Mtemtik, der sic mit der Berecnung von Seiten und Winkeln in rectwinkligen und llgemeinen Dreiecken efsst.
TRIGONOMETRIE [ J. Möller, WS Üerlingen] TRIGON = Dreieck Die Trigonometrie ist der Zweig der Mtemtik, der sic mit der Berecnung von Seiten und Winkeln in rectwinkligen und llgemeinen Dreiecken efsst.
14. Landeswettbewerb Mathematik Bayern
 4. Landeswettbewerb Matematik Bayern Lösungsbeispiele für die Aufgaben der. Runde / Aufgabe David wirft einen besnderen Würfel und screibt jeweils die ben liegende Zal auf. Die Abbildung zeigt ein Netz
4. Landeswettbewerb Matematik Bayern Lösungsbeispiele für die Aufgaben der. Runde / Aufgabe David wirft einen besnderen Würfel und screibt jeweils die ben liegende Zal auf. Die Abbildung zeigt ein Netz
Trigonometrie - Sinussatz, Kosinussatz
 Erstelle zu jeder der folgenden Aufgaben zuerst eine maßstäbliche Zeichnung. 1. Berechne die Länge der nicht gegebenen Dreiecksseite im Dreieck ABC: a) b = 6,7 cm c = 5,9 cm α = 63,5 b) b = 2,6 cm c =
Erstelle zu jeder der folgenden Aufgaben zuerst eine maßstäbliche Zeichnung. 1. Berechne die Länge der nicht gegebenen Dreiecksseite im Dreieck ABC: a) b = 6,7 cm c = 5,9 cm α = 63,5 b) b = 2,6 cm c =
Anwendungen 1. b) Berechnen Sie die Hypothenuse c: c) Berechnen Sie die Winkelfunktionen sinα, cosα, und tanα. d) Berechnen Sie die Winkel α und β :
 Für alle Aufgaben gilt: 1. Winkel und Strecken sind auf eine, Winkelfunktionen auf 4 Nachkommastellen zu runden; nehmen Sie für Zwischenresultate mit denen Sie weiterrechnen eine Stelle mehr 2. Erstellen
Für alle Aufgaben gilt: 1. Winkel und Strecken sind auf eine, Winkelfunktionen auf 4 Nachkommastellen zu runden; nehmen Sie für Zwischenresultate mit denen Sie weiterrechnen eine Stelle mehr 2. Erstellen
Fertigungstechnik Technische Kommunikation - Technisches Zeichnen
 Uwe Rat Eckleinjarten 13a. 7580 Bremeraven 0471 3416 rat-u@t-online.de Fertigungstecnik Tecnisce Kommunikation - Tecnisces Zeicnen 11 Projektionszeicnen 11. Körperscnitte und bwicklungen 11..4 Kegelige
Uwe Rat Eckleinjarten 13a. 7580 Bremeraven 0471 3416 rat-u@t-online.de Fertigungstecnik Tecnisce Kommunikation - Tecnisces Zeicnen 11 Projektionszeicnen 11. Körperscnitte und bwicklungen 11..4 Kegelige
Ähnlichkeit, Strahlensatz
 Ähnlichkeit, Strahlensatz Aufgabe 1 Berechne die Strecken x und y. a) links b) rechts Aufgabe 2 Einem Dreieck wurde die Spitze abgeschnitten. Das Reststück in Form eines Trapezes hat Parallelen von 15
Ähnlichkeit, Strahlensatz Aufgabe 1 Berechne die Strecken x und y. a) links b) rechts Aufgabe 2 Einem Dreieck wurde die Spitze abgeschnitten. Das Reststück in Form eines Trapezes hat Parallelen von 15
Übungen zu Frage 62: Nr. 1: Von einer regelmäßigen fünfseitigen Pyramide sind gegeben: Grundkante a = 7,5 cm Mantelfläche M = 190 cm 2
 Üungen tereometrie fünfseitige yrmide Üungen zu Frge 6: Nr : Von einer regelmäßigen fünfseitigen yrmide sind gegeen: Grundknte = 7,5 cm ntelfläce = 90 cm erecnen ie die Höe der eitenfläce und den Winkel
Üungen tereometrie fünfseitige yrmide Üungen zu Frge 6: Nr : Von einer regelmäßigen fünfseitigen yrmide sind gegeen: Grundknte = 7,5 cm ntelfläce = 90 cm erecnen ie die Höe der eitenfläce und den Winkel
1. Schularbeit / Gruppe A
 1. Schularbeit / Gruppe A 3.10.1997 1. Berechnen Sie: 3 3 6 x y 3x b a) : = 1 3ab a y 8 7 b) = 3 a) Formulieren Sie die Rechenregeln für Potenzen mit rationalem Exponenten b) Berechnen und vereinfachen
1. Schularbeit / Gruppe A 3.10.1997 1. Berechnen Sie: 3 3 6 x y 3x b a) : = 1 3ab a y 8 7 b) = 3 a) Formulieren Sie die Rechenregeln für Potenzen mit rationalem Exponenten b) Berechnen und vereinfachen
Analysis: Ableitung, Änderungsrate,Tangente Analysis Klausur zu Ableitung, Änderungsrate, Tangente Gymnasium Klasse 10
 Analysis Klausur zu Ableitung, Änderungsrate, Tangente Gymnasium Klasse 10 Aleander Scwarz www.mate-aufgaben.com Dezember 01 1 Teil 1: one Hilfsmittel Aufgabe 1: Ermittle die Steigung von f() = + 4 an
Analysis Klausur zu Ableitung, Änderungsrate, Tangente Gymnasium Klasse 10 Aleander Scwarz www.mate-aufgaben.com Dezember 01 1 Teil 1: one Hilfsmittel Aufgabe 1: Ermittle die Steigung von f() = + 4 an
Ähnlichkeit: 1.1 Welche der Figuren sind ähnlich zueinander? Kreuze an! Miss benötigte Winkel und Längen in der Zeichnung ab!
 Ähnlichkeit: Ähnliche Figuren: https://www.youtube.com/watch?v=xvpd9cep7qu 1.1 Welche der Figuren sind ähnlich zueinander? Kreuze an! Miss benötigte Winkel und Längen in der Zeichnung ab! 1.2 Welche Vierecke
Ähnlichkeit: Ähnliche Figuren: https://www.youtube.com/watch?v=xvpd9cep7qu 1.1 Welche der Figuren sind ähnlich zueinander? Kreuze an! Miss benötigte Winkel und Längen in der Zeichnung ab! 1.2 Welche Vierecke
Das zweites Gesetz von Newton in einem rotierenden Bezugssystem Geostropische Bewegung Druckkoordinaten
 Näcster Abscnitt => Das zweites Gesetz von Newton in einem rotierenden Bezugssystem Geostropisce Bewegung Druckkoordinaten Matematisce Herleitung der Coriolisbescleunigung Darstellung eines beliebigen
Näcster Abscnitt => Das zweites Gesetz von Newton in einem rotierenden Bezugssystem Geostropisce Bewegung Druckkoordinaten Matematisce Herleitung der Coriolisbescleunigung Darstellung eines beliebigen
Trigonometrie - Sinussatz, Kosinussatz
 Gymnasium / Realschule Trigonometrie - Sinussatz, Kosinussatz Klasse 10 1. Gemäß nebenstehender Zeichnung sind die Stücke AB = c, α und β gegeben. Stelle eine Gleichung für die Strecke AD = x in Abhängigkeit
Gymnasium / Realschule Trigonometrie - Sinussatz, Kosinussatz Klasse 10 1. Gemäß nebenstehender Zeichnung sind die Stücke AB = c, α und β gegeben. Stelle eine Gleichung für die Strecke AD = x in Abhängigkeit
Ferienkurs Theoretische Mechanik SS 2011
 Ferienkurs Teoretisce Mecanik SS Lösungen Freitag Aufgabe : Rotation eines Quaders um die Raumdiagonale Die Hauptacsen verlaufen durc den Scwerpunkt des Quaders parallel zu den Kanten. Die Kante der Länge
Ferienkurs Teoretisce Mecanik SS Lösungen Freitag Aufgabe : Rotation eines Quaders um die Raumdiagonale Die Hauptacsen verlaufen durc den Scwerpunkt des Quaders parallel zu den Kanten. Die Kante der Länge
Berechnungen am rechtwinkligen Dreieck, Satz des Pythagoras
 Berechnungen am rechtwinkligen Dreieck, Satz des Pythagoras Aufgabe 1 Berechne die fehlenden Grössen (a, b, c, h, p, q, A) der rechtwinkligen Dreiecke: a) p = 36, q = 64 b) b = 13, q = 5 c) b = 70, A =
Berechnungen am rechtwinkligen Dreieck, Satz des Pythagoras Aufgabe 1 Berechne die fehlenden Grössen (a, b, c, h, p, q, A) der rechtwinkligen Dreiecke: a) p = 36, q = 64 b) b = 13, q = 5 c) b = 70, A =
Die Ecken werden immer gegen den Uhrzeigersinn beschriftet, sonst falscher Umlaufsinn!
 Berechnungen in Dreiecken Allgemeines zu Dreiecken Innenwinkelsatz α + β + γ = 180 Besondere Dreiecke Gleichschenkliges Dreieck Die Ecken werden immer gegen den Uhrzeigersinn beschriftet, sonst falscher
Berechnungen in Dreiecken Allgemeines zu Dreiecken Innenwinkelsatz α + β + γ = 180 Besondere Dreiecke Gleichschenkliges Dreieck Die Ecken werden immer gegen den Uhrzeigersinn beschriftet, sonst falscher
Teil 1: 2 Gleichungen mit 2 Unbekannten mit Textaufgaben. und 3 Gleichungen mit 2 Unbekannten. Datei Nr Friedrich Buckel. Stand 29.
 Teil 1: Gleicungen mit Unbekannten mit Textaufgaben und 3 Gleicungen mit Unbekannten Datei Nr. 1180 Friedric Buckel Stand 9. Juni 016 Lineare Gleicungssysteme Demo-Text für www.mate-cd.de Dieser Text stet
Teil 1: Gleicungen mit Unbekannten mit Textaufgaben und 3 Gleicungen mit Unbekannten Datei Nr. 1180 Friedric Buckel Stand 9. Juni 016 Lineare Gleicungssysteme Demo-Text für www.mate-cd.de Dieser Text stet
D-MAVT/D-MATL Analysis I HS 2018 Dr. Andreas Steiger. Lösung - Serie 5
 D-MAVT/D-MATL Analysis I HS 08 Dr. Anreas Steiger Lösung - Serie 5 MC-Aufgaben (Online-Abgabe). Es sei f : [a, b] R eine Funktion. Welce er folgenen Aussagen ist rictig? (a) (b) f ist stetig f ist ifferenzierbar.
D-MAVT/D-MATL Analysis I HS 08 Dr. Anreas Steiger Lösung - Serie 5 MC-Aufgaben (Online-Abgabe). Es sei f : [a, b] R eine Funktion. Welce er folgenen Aussagen ist rictig? (a) (b) f ist stetig f ist ifferenzierbar.
2.6. Anwendungs- und Beweisaufgaben zu Kongruenzsätzen
 2.6. Anwendung- und eweiufgben zu Kongruenzätzen Aufgbe ) Ermittle zeicneric die Längen der drei Fläcendigonlen d b, d c und d bc und der Rumdigonlen d de bgebildeten Quder mit den Abmeungen = 4 cm, b
2.6. Anwendung- und eweiufgben zu Kongruenzätzen Aufgbe ) Ermittle zeicneric die Längen der drei Fläcendigonlen d b, d c und d bc und der Rumdigonlen d de bgebildeten Quder mit den Abmeungen = 4 cm, b
Aufgaben Ähnlichkeit:
 Aufgaben Ähnlichkeit: 1. Berechne die gesuchten Zahlwerte, beziehungsweise z. a) 8 21 14 α 18 β α β b) 40 α 16 12 α 22 β β c) d) e) Geometrie-Dossier 3-2 Ähnlichkeit.doc A.Räz Seite 23 2. Berechne die
Aufgaben Ähnlichkeit: 1. Berechne die gesuchten Zahlwerte, beziehungsweise z. a) 8 21 14 α 18 β α β b) 40 α 16 12 α 22 β β c) d) e) Geometrie-Dossier 3-2 Ähnlichkeit.doc A.Räz Seite 23 2. Berechne die
PDF created with pdffactory Pro trial version
 Wiederolungsaufgaben zur Algebra. Berecnen von Termen: a) 8x (7y 6z) (7z 8y) b) ( ) ( ) ( ) xy x y x y c) ( ) ( ) ( ) ab bc ca d) ( x 7ax : 8ax ) a x (, y ) x e) y ( x) ( x) 6 f) (, x)(y x) g) a b : a
Wiederolungsaufgaben zur Algebra. Berecnen von Termen: a) 8x (7y 6z) (7z 8y) b) ( ) ( ) ( ) xy x y x y c) ( ) ( ) ( ) ab bc ca d) ( x 7ax : 8ax ) a x (, y ) x e) y ( x) ( x) 6 f) (, x)(y x) g) a b : a
Mathematik Klasse 5A am
 WIEDERHOLUNG der ZWEITEN SCHULARBEIT Mathematik Klasse 5A am 13.12.2013 SCHÜLERNAME: Gruppe A Lehrer: Dr. D. B. Westra Grundkompetenzen, Grundwissen und Grundfertigkeiten Vernetzung und Vertiefung 32 Punkte
WIEDERHOLUNG der ZWEITEN SCHULARBEIT Mathematik Klasse 5A am 13.12.2013 SCHÜLERNAME: Gruppe A Lehrer: Dr. D. B. Westra Grundkompetenzen, Grundwissen und Grundfertigkeiten Vernetzung und Vertiefung 32 Punkte
Experimentalphysik 1
 Technische Universität München Fakultät für Physik Ferienkurs Experimentalphysik 1 WS 16/17 Lösung 1 Ronja Berg (ronja.berg@tum.de) Katharina Scheidt (katharina.scheidt@tum.de) Aufgabe 1: Superposition
Technische Universität München Fakultät für Physik Ferienkurs Experimentalphysik 1 WS 16/17 Lösung 1 Ronja Berg (ronja.berg@tum.de) Katharina Scheidt (katharina.scheidt@tum.de) Aufgabe 1: Superposition
Übungen. Konstruiere ein Dreieck ABC und dessen Inkreismittelpunkt aus den folgenden. Angaben. Angaben.
 Übungen A1 Konstruiere ein Dreieck ABC und dessen Umkreismittelpunkt aus den folgenden Angaben. a) A( 4 2), B(2 2), C(2 4) b) a = 5cm, b = 4cm und c = 8cm A2 Konstruiere ein Dreieck ABC und dessen Inkreismittelpunkt
Übungen A1 Konstruiere ein Dreieck ABC und dessen Umkreismittelpunkt aus den folgenden Angaben. a) A( 4 2), B(2 2), C(2 4) b) a = 5cm, b = 4cm und c = 8cm A2 Konstruiere ein Dreieck ABC und dessen Inkreismittelpunkt
MATHEMATIK ZUR VORBEREITUNG AUF DEN UNMITTELBAREN EINTRITT IN EINEN REALSCHULREIFELEHRGANG ODER FACHSCHULREIFELEHRGANG DER BUNDESWEHRFACHSCHULE
 ZUR VORBEREITUNG AUF DEN UNMITTELBAREN EINTRITT IN EINEN REALSCHULREIFELEHRGANG ODER FACHSCHULREIFELEHRGANG DER BUNDESWEHRFACHSCHULE MATHEMATIK Lehreinheit 11 Geometrie: Dreiecke und Vierecke II GEOMETRIE:
ZUR VORBEREITUNG AUF DEN UNMITTELBAREN EINTRITT IN EINEN REALSCHULREIFELEHRGANG ODER FACHSCHULREIFELEHRGANG DER BUNDESWEHRFACHSCHULE MATHEMATIK Lehreinheit 11 Geometrie: Dreiecke und Vierecke II GEOMETRIE:
1.4 Trigonometrie I. 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2. 2 Die trigonometrischen Funktionen 4
 1.4 Trigonometrie I Inhaltsverzeichnis 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2 2 Die trigonometrischen Funktionen 4 2.1 Was sind trigonometrischen Funktionen?........................... 4 2.2
1.4 Trigonometrie I Inhaltsverzeichnis 1 Seitenverhältnisse beim rechtwinkligen Dreieck 2 2 Die trigonometrischen Funktionen 4 2.1 Was sind trigonometrischen Funktionen?........................... 4 2.2
Aufgaben aus alten Abschlussarbeiten (2002/ 2003) - R 10 Teil 1
 Aufgaben aus alten Abschlussarbeiten (2002/ 2003) - R 10 Teil 1 (1) 2002-1 Aufgabe 2 (10 Pkt) a) Auf welchen Betrag wachsen 16500 Euro in 12 Jahren bei einer jährlichen Verzinsung von 3,75 % Zinseszins
Aufgaben aus alten Abschlussarbeiten (2002/ 2003) - R 10 Teil 1 (1) 2002-1 Aufgabe 2 (10 Pkt) a) Auf welchen Betrag wachsen 16500 Euro in 12 Jahren bei einer jährlichen Verzinsung von 3,75 % Zinseszins
Übung 11. Fachwerkträger. Aufgabe 01: Aufgabe 02: Aufgabe 03: Aufgabe 04: Aufgabe 05: 170 m. 85 m SEE. E 160 m. x =? 4,4 m.
 Übung 11 Aufgabe 01: C D 170 m 85 m Aufgabe 02: E 160 m B SEE =? A Fachwerkträger 5 m 3 m 3 m 4,4 m Aufgabe 03: 10 40 36 z 15 25 Aufgabe 04: 4 13 18 10 Aufgabe 05: 7 3 Aufgabe 06: 4 m 1 m Aufgabe 07: Ein
Übung 11 Aufgabe 01: C D 170 m 85 m Aufgabe 02: E 160 m B SEE =? A Fachwerkträger 5 m 3 m 3 m 4,4 m Aufgabe 03: 10 40 36 z 15 25 Aufgabe 04: 4 13 18 10 Aufgabe 05: 7 3 Aufgabe 06: 4 m 1 m Aufgabe 07: Ein
Übungen: Trigonometrie
 Übungen: Trigonometrie Polarkoordinaten 1. Berechnen Sie die kartesischen Koordinaten der Punkte A(5; 45 ), B(6; 120 ), C(3,5; 310 ), D(4,8; 235 ); E(2,7; 0 ), F(3,3; 90 ), G(10; 53,13 ), H(3,16; 161,57
Übungen: Trigonometrie Polarkoordinaten 1. Berechnen Sie die kartesischen Koordinaten der Punkte A(5; 45 ), B(6; 120 ), C(3,5; 310 ), D(4,8; 235 ); E(2,7; 0 ), F(3,3; 90 ), G(10; 53,13 ), H(3,16; 161,57
