Natürliche Exponential- und Logarithmusfunktion. Kapitel 5
|
|
|
- Johann Theodor Armbruster
- vor 7 Jahren
- Abrufe
Transkript
1 Natürliche Eponential- und Logarithmusfunktion Kapitel
2 . Die natürliche Eponentialfunktion und ihre Ableitung 48 Arbeitsaufträge. Individuelle Lösungen Jahr in Sekunden in Sekunden in Sekunden Eponentiell (in Sekunden) Jahr 3. n ( + n ) 4 +! +! + 3! n!,0000,0000,00,000 3,3704,6667 4,444,7083,4883,767 6,6,78 7,46,783 8,68,783 9,8,783 0,937,783 00,7048, ,769, ,783,783
3 . Die natürliche Eponentialfunktion und ihre Ableitung L 6. DIN Länge Breite A6 4,87 cm 0, cm,70 A,0 cm 4,87 cm 3,0 A4 9,73 cm,0 cm 3,39 A3 4,04 cm 9,73 cm 3,74 e 4,87; e,0; e 9,73; e 4,04; ln 4,87; ln,0; ln 9,73; ln 4,04;,70 3,0; 3,39 3,74 DIN-A-Maße: Ein Rechteck, dessen Flächeninhalt m beträgt, hat die Länge und die Breite. Die Seiten sollen sich so verhalten, dass beim Halbieren das Seitenverhältnis erhalten bleibt. 0, 0, () = ; () : = : 0,; = 0, ; = 0, ; in () =,9 m; = 0,84 m DIN Länge Breite A0,9 m 0,84 m A 84, cm 9,46 cm A 9,46 cm 4,04 cm A3 4,04 cm 9,73 cm A4 9,73 cm,0 cm A,0 cm 4,87 cm A6 4,87 cm 0, cm 7. a) f(0) = : P (0 ) f() = e : Q ( e ) f () = e ; f (0) = ; f () = e t P : = + t ; P X t P : = t t P : = + t Q : = e + t ; Q X t Q : e = e + t ; t = e t Q : = e e tan ϕ = e + e ; ϕ 37,3 3
4 . Die natürliche Eponentialfunktion und ihre Ableitung 0 Q t P P t Q b) 0 e = ; = 0: P (0 ) f() = e: Q ( e) f () = e ; f (0) = 0; f () = e t Q t P : = 0 t Q : = e + t Q X t Q : e = e + t; t = e t Q : = e e tan ϕ = e; ϕ 79,6 Q P t P 8. G g S a) Schnittpunkt der Graphen und G g : e = e + ; : e + e = ; e, =, = ln 0,, = + ln 0, 4
5 . Die natürliche Eponentialfunktion und ihre Ableitung = (ln e + ln 0,) = 3 3 f ( ln e 3 ) = e ln e 3 = e ln 3 e S ( ln e 3 f () = e 3 e ) ln e 0,0 = 3 e,08 ; S ( 0,0,08); e ln e 3 f ( ln e 3 ) = 0,38 g () = e + g ( ln e 3 ) = e ( ln e 3 ) =,077 tan ϕ = 0,38; ϕ,00 tan ϕ =,007; ϕ 47,9 ϕ = ϕ ϕ 03 b) t A h: e = 0,; e = ; = 0 A (0 ) t B k: e + = ; e + = ; + = 0; = g( ) = B ( ) 9. tp l P P P (0 ) f () = e f (0) = ; m tp = ; m lp = t P : = + ; l P : = + Die Eckpunkte des Dreiecks sind S ( 0), E ( 0) und P ( ). Das Dreieck SEP ist gleichschenklig-rechtwinklig. A SEP = =. Größe der Innenwinkel: 4 ; 4 und V (ln a a) (e = a; = ln a) I ( ln a a) (e = a; = ln a) Zeichnung für a = : E ( ln a a ) (e = a ; = ln a) R (ln a a ) (e = a ; = ln a; = ln a) Das Viereck VIER ist ein Rechteck. G g Gf Länge seiner Seiten: I V ln a bzw. a a. Die Diagonalen schneiden einander auf der -Achse. A = ln a ( a a ) U = ln a + ( a a ) = 4 ln a + ( a a ) p q E R
6 . Die natürliche Eponentialfunktion und ihre Ableitung. P I A G g a P X ; P (a e a ) A X G g ; A (a e a ) Die Graphen und G g schneiden einander im Punkt I (0 ). A PIA = (ea e a ) a = a (ea e a ) a = P ( e ); A ( e) P I = 4 + (e ) 6,69478 IA = 4 + (e ),63676 A P = (e e) = e e 4,67077 U 4,00 Der größte Innenwinkel hat den Scheitel A g () = e ; g () = e; tan ϕ = e; ϕ 3,66 PAI ,66 43,7. s A G g B C 0 a) -Achsenpunkt(e) von : e 0, = 0 keine Lösung von G g : 4 3e 0, = 0 e 0, = 4 3 ; 0, = ln 4 3 ; = ln 4 = ln = ln 9 6 0,7 S (ln 9 6 0) -Achsenpunkt von : T (0 ) = B von G g : T (0 ) = B gemeinsame Punkte von und G g : e 0, = 4 3e 0, ; e 0, (e 0, ) 4e 0, + 3 = 0; (e 0, )(e 0, 3) = 0; e 0, = ; = 0: B (0 ) e 0, = 3; 0, = ln 3; = ln 3 = ln 9 f ( ln 3) = e 0, ln 3 = e ln 3 = 3 A (ln 9 3) 6
7 . Die natürliche Eponentialfunktion und ihre Ableitung b) S (a e 0,a ), T (a 4 e 0,a ) für 0 < a < ln 9 ist 4 3e 0,a > e 0,a ST = d(a) = 4 3e 0,a e 0,a d (a) = 3e 0,a ( 0,) 0, e 0,a =,e 0,a 0,e 0,a d (a) =, e 0,a ( 0,) 0,e 0,a 0, = 0,7 e 0,a 0,e 0,a d (a) = 0:,e 0,a 0,e 0,a = 0 : e 0,a, 0,e a = 0; e a =, 0, = 3; a = ln 3 d (a) ist für jeden zulässigen Wert von a negativ. Die Strecke [ST] ist für a = ln 3 maimal. d ma = 4 3e 0,ln 3 e 0,ln 3 = = 4 3 0,4 3. a) () Da f( ) = ( e ) = ( e ) = ( e e ) f() ist, ist G f nicht smmetrisch zur -Achse. () Da f( ) f() ist, ist nicht punktmmetrisch zum Ursprung [vgl. ()]. (3) -Achsenpunkte: f() = (e ) = 0 e = ; = 0; S (0 0) = (0 0) -Achsenpunkt: f(0) = 0: (0 0) (4) Etrempunkte: f () = (e ) e = (e e ) f () = (e e ) f () = 0; e = ; = 0 f (0) = ( ) = > 0 Der Ursprung ist Tiefpunkt des Graphen. () lim (e ) = lim (e ) = hat die Gerade a: = als waagrechte Asmptote. 3 a b) () Da f( ) = e (e + ) = + e e f() ist, ist G f nicht achsensmmetrisch zur -Achse. () Da f( ) f() ist, ist nicht punktsmmetrisch zum Ursprung. (3) -Achsenpunkte: e (e ) = 0; e > 0 e = ; = ln : S (ln 0) -Achsenpunkt: f(0) = e 0 (e 0 ) = : T (0 ) (4) Etrempunkte: f () = e (e ) + e e = e (e + e ) = e (e ) = e (e ) f () = e (e ) + e e = e (e + e ) = e (e ) f () = 0: e (e ) = 0; e > 0; e = 0: = 0 f (0) = ( ) = > 0. hat den Tiefpunkt T (0 ). 7
8 . Die natürliche Eponentialfunktion und ihre Ableitung () lim e (e ) = ; lim e (e ) = 0 Die -Achse ist (waagrechte) Asmptote von. c) () Da f( ) = e e + = e + e f() ist, ist G f nicht smmetrisch zur -Achse. () Da f( ) f() ist, ist nicht punktsmmetrisch zum Ursprung. (3) -Achsenpunkt(e): e e + = 0; e = 0; e = ; = ln ; S (ln 0) -Achsenpunkt: f(0) = + = ; T (0 ) (4) Etrempunkte: f () = (e + ) e (e ) e (e + ) = e + e e + e (e + ) = 3e (e + ) Für jeden Wert von X D f gilt f () > 0: besitzt keinen Etrempunkt. () lim e e + = lim e e + = ; lim e + = = e besitzt zwei waagrechte Asmptoten: a : = und a : = a a e d) () und () f( ) = + e = e e + = e = f() f() + e ist nicht achsensmmetrisch zur -Achse, jedoch punktsmmetrisch zum Ursprung. (3) -Achsenpunkt(e): e + e = 0; e = ; = 0; S (0 0) -Achsenpunkt: f(0) = 0: S (0 0) (4) Etrempunkte: f () = ( + e )( e ) ( e ) e ( + e ) = e ( e + e ) ( + e ) = 4e ( + e ) < 0 für jeden Wert von X D f : besitzt keinen Etrempunkt. () lim e + e = lim e = ; lim e = e + + e = besitzt zwei waagrechte Asmptoten: a : = und a : =. 8
9 . Die natürliche Eponentialfunktion und ihre Ableitung a a. a) -Achsenpunkt(e): ( 3) 3 = 0; 3 > 0 = 3; = 3 ; = 3 ; S ( 3 0); S ( 3 0) -Achsenpunkt: f(0) = ( 3)3 0 = 3; T (0 3) b) f () = 3 + ( 3) 3 ln 3 = 3 ( ln 3 + ln 3) = 0 f () = 0 ln 3 + ln 3 = 0 = ± 4 + (ln 3) ln 3 = ± + 3(ln 3) ln 3 = ln (ln 3) ),04 = + 3(ln 3) ),87 ln 3 ( steigt im Intervall I = ] ;,87[ sowie im Intervall I 3 = ],04 ; + [; fällt im Intervall I = ],87 ;,04[. hat einen Hochpunkt H (,87 0,) und einen Tiefpunkt T (,04 6,0). < < = < < = < < f () f () > 0 f () = 0 f () < 0 f () = 0 f () > 0 c) 9
10 . Die natürliche Eponentialfunktion und ihre Ableitung 4 8. a) f() = 9e ; f(0) = 9 0 = 0: 0 X lim (9e ) = 0 lim (9e ) = c) f () = 9e + 9e ( ) = 9e ( ); f () = 9e ( )( ) + 9e ( ) = 9e ( + ) = 9e ( ) d) f () = 0; = ; f() = 9e = 9 e 3,3 f () = 9e < 0 besitzt den Hochpunkt H ( 9 e ). T t p I P A S e) f() = 8e = 8 e,44 P ( 8 e ) ; f () = 9 e ( ) = 9 e t P : = 9 e + t; P X t P : 8 e = 8 e + t; t = 36 e t P : = 9 e + 36 e Schnittpunkt von t P mit der -Achse: T ( 0 36 e ) Schnittpunkt von t p mit der -Achse: 9 e + 36 = 0; = 0 = 4 S (4 0) e A ST = 4 36 e = 7 e 9,74 A TIP = 36 e 8 e = 8 e = 4 A ST Das Dreieck TIP nimmt % der Fläche des Dreiecks ST ein. f) A LA = A(s) = s f(s) = s 9se s = 9 s e s A (s) = 9se s + 9 s e s ( ) = 9 (s s )e s = 9 s s( s)e A (s) = 9 ( s)e s + 9 (s s )e s ( ) = 9 ( s s + s )e s = 9 ( 4s + s )e s A (s) = 0: s = 0, s = A (0) = 9 > 0; A () = 9 ( ) e = 9e < 0 Für s = wird der Flächeninhalt dieses Dreiecks maimal. A LA = (9 e ) = 8 e,44 4( ) 9. a) f(0) = = 0; X G f. f() = 4e 4e ; f () = 4e 4 ( )e = 4e + 8e f (0) = = 4; tan ϕ = 4; ϕ 76,0 0
11 . Die natürliche Eponentialfunktion und ihre Ableitung b) f () = 4e + 8e = 8 4e e = 4( e ) e f () = 0; e = 0; = ln ; f(ln ) = 4 4 = < < ln = ln ln < < + f () f () > 0 f () = 0 f () < 0 Vorzeichenwechsel von f () von + nach c) lim 4(e ) e = lim 4 ( e = 0: + + e ) steigt streng Die -Achse ist horizontale Asmptote von. d) hat einen Hochpunkt H (ln ) fällt streng e) f*: f*() = 4(e ) e + = 4e 4 + e e = (e + e ) e ; D f* = Der Graph G g einer Funktion g: g(); D g = D g ma wird in Richtung der -Achse so verschoben, dass er durch den Punkt S (0 t) verläuft. g*: g*() = g() + t 0. a) h(0) = 80 = 3,0; k = 9 + k 80 h() = + 9e = 0,0; + a 9e a = 9,0; e a = 8,0 ; a = 0, ln 8, ,40 80 h() = + 9e 0,40 b) (in Wochen) Höhe h (in cm) 3,0 0,0 86, cm c) h () bedeutet die Wachstumsgeschwindigkeit der Pflanzen (in ), und Woche h () = 0 liefert den Zeitpunkt, zu dem die Wachstumsgeschwindigkeit am größten (oder am kleinsten) ist. 0, ( 0,40)e d) h () = ( + 9e 0,40 ) = 448e 0,40 ( + 9e 0,40 ) 4, e 03 0,40 ( + 9e 0,40 ) ; D h = ]0 ; 30[ h () = ( + 9e 0,40 ) ( 448 0,40e 0,40 0,40) 448e 0,40 ( + 9e 0,40 ) ( 9 0,40e 0,40 ) ( + 9e 0,40 ) = 4 = ( + 9e 0,40 ) ( 448 0,40e 0,40 ) 448e 0,40 ( 9 0,40e 0,40 ) ( + 9e 0,40 ) = 3 = ( 448 0,40e 0,40 ) ( + 9e 0,40 ) ( + 3 9e 0,40 8e 0,40 ) = ( 448 0,40e 0,40 ) ( + 9e 0,40 ) ( 3 9e 0,40 ); D h = ]0 ; 30[ h () = 0: 9e 0,40 = ; e 0,40 0,069; 0,40 ln 0,069; 0 X D h. Nach etwa 0 Wochen ist die Wachstumsgeschwindigkeit am größten, nämlich etwa cm 8 ( Woche ) ; ganz zu Anfang ist sie erst etwa, cm ( Woche ) und gegen Ende nur noch cm etwa 0,03 ( Woche ).
12 . Die Logarithmusfunktion und ihre Ableitung 6 Arbeitsaufträge 3. a) b) g() = e ; g () = e ; g ( 0 ) = e 0 = tan α; f ( 0 ) = tan β = tan (90 α) = tan α = e = 0 e ln 0 also hat f: f() = ln ; D f = = ; 0 +, die Abbleitung f : f () = ; D f = +. 9 L 6. -Achsenpunkt: ( ln ) = 0; ln = ; = e S (e 0) f () = ( ln ) ( ) = ( ln ) 0 < < e = e e < < + f () f () < 0 f () = 0 f () > 0 nimmt streng f ab Vorzeichenwechsel von f fällt streng von nach + Die -Achse ist senkrechte Asmptote: = 0. hat einen Tiefpunkt T (e 0) nimmt streng zu steigt streng
13 . Die Logarithmusfunktion und ihre Ableitung 9. a) f 0, () = ln ( + 0,); f 0, (0) = ln 0,,4 f () = ln ( + ); f (0) = ln = 0 f () = ln ( + 4); f (0) = ln 4,4 0, oberer Graph mittlerer Graph unterer Graph b) Allgmein: f a () = ln ( + a ); a Z {0,; ; } f a ( ) = ( ) ln [( ) + a ] = = ln ( + a ) = f a (): Jeder der drei Graphen 0,, und ist somit smmetrisch zur -Achse. c) f 0, () = + 0, = ( + 0, ) = + 0, = ( 0,7) = ( 3 )( + 3 ) + 0, + 0, f 0, () = 0; = 0; = 3 ; 3 = 3 f 0, (0) = ln 4 = ln 4; E (0 ln 4) f 0, ( ± 3 ) = 3 ln = ; E ( ) ; E 3 ( ) E und E 3 sind die globalen Tiefpunkte von 0, ; 0, besitzt keinen globalen Hochpunkt. f () = + = ( + ) + = 3 + ; f () = 0: = 0; f (0) = 0; E 4 (0 0) besitzt den globalen Tiefpunkt E 4, aber keinen globalen Hochpunkt. f () = + 4 = ( + 4 ) = ( + 3) ; f () = 0: = 0; + 3 0; f(0) = ln 4; E (0 ln 4) besitzt den globalen Tiefpunkt E, aber keinen globalen Hochpunkt. Monotonietabellen: f 0, () = ln ( + 0,) 60 < < 3 = 3 3 < < 0 = 0 0 < < 3 = 3 3 < < f 0, () f 0, () < 0 f 0, () = 0 f 0, () > 0 f 0, () = 0 f 0, () < 0 f 0, () = 0 f 0, () > 0 Vorzeichenwechsel von f 0, () von nach + von + nach von nach + fällt streng hat einen Tiefpunkt T ( 3 3 = E 3 4 ) steigt streng hat einen Hochpunkt H (0 ln 4) = E fällt streng hat einen Tiefpunkt T ( 3 3 = E 4 ) steigt streng f () = ln ( + ) < < 0 = 0 0 < < f () f () < 0 f () = 0 f () > 0 Vorzeichen wechsel von f () von nach + fällt streng hat einen Tiefpunkt T 3 (0 0) = E 4 steigt streng 3
14 . Die Logarithmusfunktion und ihre Ableitung f () = ln ( + 4) < < 0 = 0 0 < < + f () f () < 0 f () = 0 f () > 0 Vorzeichen wechsel von f () von nach + 4 fällt streng hat einen Tiefpunkt steigt streng T 4 (0 ln 4) = E d) f 0, () f () = ln ( + 0,) + ln ( + ) = ln ( + ) ln ( + 0,) > 0, da für jeden Wert von Z stets + > + 0, ist. Also liegt 0, überall oberhalb von. f () f () = ln ( + ) + ln ( + 4) = = ln ( + 4) ln ( + ) > 0, da für jeden Wert von Z stets + 4 > + ist. Also liegt überall oberhalb von. d() = ln ( + ) + ln ( + 4) = ln ( + 4) ln ( + ) = ln ist die Entfernung übereinander liegender Punkte von und. lim d() = lim ( ln ) ( = lim ln = ln = 0: ± ± ± ) Die Graphen nähern sich einander, ohne einander zu berühren. 0. a) -Achsenpunkt(e): ln ( + 4 ) ln = 0; ln ( = ; + 4 = 0; ( ) = 0; = S ( 0) Etrempunkte: 4 ) = ln ; f () = + = 4 4 ( + = 4 4 ) f () = 0; 4 = 0; = Z D f; = z D f Für 0 < < gilt stets f () < 0; für hat den Tiefpunkt S ( 0). b) lim [ ln + 4 ( + 4 ) ; < < + gilt stets f () > 0: ] = + : Dieser Grenzwert eistiert nicht und die -Achse ist 0+ senkrechte Asemptote von. lim [ ln + 4 ] = lim [ ln ( + 4 ) ] = : Dieser Grenzwert eistiert ebenfalls nicht. lim [ ln ( + 4 ) ln ln ] = lim [ ln ( + 4 ) ln ( ) ] = lim [ ln + 4 ] = lim [ ln ( + 4 ) ] = ln = 0: kommt für hinreichend große Werte von dem Graphen G g der + Funktion g: g() = ln ; D g =, beliebig nahe. 4
15 . Die Logarithmusfunktion und ihre Ableitung c) G h G g d) h() = ln () = ln + ln : G h geht aus G g durch Verschieben von G g in Richtung der -Achse um ln nach oben hervor. Schnittpunkt S von G h und : ln ( + 4 ) ln = ln (); ln ( + = ln () + ln ; 4 ) ln ( + 4 ) = ln ( ); + 4 = ; = 4, = ± = Z D f = D h ; = z D f; S ( 0) f ( ) = 0; h () = ; h ( ) = tan ϕ = ; ϕ 63,4 e) Skizze: P A r R Der Rotationskörper ist ein gerader Kreiszlinder, aus dem ein gerader Kreiskegel herausgefräst ist. r Z = ln ; h Z = ; r K = ln ; h K = 0,; s K = (ln ) + 0, V = r Z π h z 3 r K π h K = = (ln ) π 3 (ln ) π 0, = = (ln ) π ( 6 ) = 6 π (ln ),6 A = r Z π h Z + r Z π + r K π s K = = ln π + (ln ) π + (ln ) π (ln ) + 0, = = π ln ( + ln + (ln ) + 0,) ) 7,73
16 Themenseite Wachstumsvorgänge modellieren 6. L Jahre Bestand S = Sättigungsmanko zu Beginn: = 00. Zuwachs nach Jahr: 6 Jahre Sättigungsmanko Zuwachs Bestand Nach Jahren sind 7 4,9% der Sättigungsgrenze erreicht B (t) = k B(t) [S B(t)] as B(t) = a + (S a)e Skt B (t) = 0 [a + (S a)e Skt ] as [(S a)e Skt ( Sk)] [a + (S a)e Skt ] = k as a + (S a)e [ S as Skt a + (S a)e ] Skt 4. S 3; a = 3 h(t) = + 30e = 3 3kt + 6 e 3kt Berechnung von k: t = : 3 h() = 8,8 = + 6 e 3k e 3k = 0,496 k = 0,0 Berechnung der Tabelle: h(t) = 3: ( + 6 e 0,7t 3 ) = + 6e 0,7t Zeit (in Wochen) Höhe (in cm) 4, 0,,6 9,6 3, 33, 34, 34,6 34,8 Das Wachstumsmodell gibt das wirkliche Wachstum gut wieder. 6
17 .3 Üben Festigen Vertiefen L 7. a) f () = e + ( + )e = e ( + 3) f () = 0: =, Monotonietabelle: < <, =,, < < + f () f () < 0 f () = 0 f () > 0 Vorzeichenwechsel von f () fällt streng von nach + hat einen Tiefpunkt T (,, ) steigt steng 64 T N b) f() = ( e ) f () = ( e ) e = e ( e ) f () = 0; e = ; = ln f(ln ) = ( ) = 0 Monotonietabelle: < < ln = ln ln < < + f () f () < 0 f () = 0 f () > 0 Vorzeichenwechsel von f () fällt streng von nach + hat einen Tiefpunkt T (ln e) steigt steng T 7
18 .3 Üben Festigen Vertiefen c) f() = (ln ) f () = (ln ) = (ln ) f () = 0: ln = ; = e f(e) = ( ) = 0 Monotonietabelle: < < e = e e < < + f () f () < 0 f () = 0 f () > 0 Vorzeichenwechsel von f () fällt streng von nach + hat einen Tiefpunkt T (e 0) steigt steng T d) f() = ln + f () = + = + + f () = 0; = 0 f(0) = 0 Monotonietabelle: < < 0 = 0 0 < < f () f () < 0 f () = 0 f () > 0 Vorzeichenwechsel von f () fällt streng von nach + hat einen Tiefpunkt T (0 0) steigt steng 8
19 .3 Üben Festigen Vertiefen 0. a) Nullstelle: f() = 0: = 0 b) f () = e + e ( ) = e e = e ( ) f () = 0: = 0 X D f ; = X D f ; f() = 4 Montonietabelle: 6 < < 0 = 0 0 < < = < < + f () f () < 0 f () = 0 f () > 0 f () = 0 f () < 0 Vorzeichenwechsel von f () fällt streng von nach + hat einen Tiefpunkt T (0 0) steigt steng von + nach hat einen Hochpunkt H ( 4) fällt streng T c) A TP = A(u) = u f(u) = u u e u = u3 e u A (u) = 3 u e u + u3 e u ( ) = u e u (3 u) A (u) = 0; u = 0 keine Lösung: A(0) = 0 u = 3 Für 0 < u < 3 gilt A (u) > 0; für 3 < u < + gilt A (u) < 0. A TP ist für a = 3 maimal. A TP ma = 7e = 3, e = 4,9663,0 lim ( e u3 e ) = lim ( e u 3u e ) = lim ( 3e u u e ) = lim ( 3e u e ) = 0 u u u u u. Für jeden Wert von X gilt stets f( ) = e ( ) = e = f(): Also ist achsensmmetrisch zur -Achse. a) lim e = 0: Also ist die -Achse Asmptote von. ± f () = e ; f () = e ( )e f () = e ( ) f () = 0: = 0; f(0) = e 0 = f (0) = e 0 ( 0) = < 0 hat den Hochpunkt H (0 ). Da außerdem für jeden Wert von X stets f() > 0 ist, gilt W f = ]0 ; ] b) ln 0,8 f( ln ) = F P A L 9
20 .3 Üben Festigen Vertiefen c) [A] [LF] Der Punkt M ( 0 ) halbiert sowohl [A] als auch [LF]; somit ist das Viereck LAF eine Raute. A LAF = A LF = ln = ln 0,83 F A M L. a) Da f(0) = e0 e 0 e 0 + e = 0 0 = 0 ist, verläuft durch den Ursprung. f () = (e + e )(e + e ) (e e )(e e ) (e + e ) = e + + e e + e (e + e ) = 4 (e + e ) f (0) = 4 = ; schneidet die -Achse unter einem 4 -Winkel. b) lim e e = lim e = e + e + e = lim e e = lim e e + e e + = = Gleichungen der beiden waagrechten Asmptoten: a : = und a : = 4 c) f () = ; für jeden Wert von X gilt f () > 0. (e + e ) f ist in ganz streng zunehmend. d) f( ) = e e = e e = f(): e + e e + e Also ist punktsmmetrisch zum Ursprung. e) f) Einer Drehung um 90 gegen den Uhrzeigersinn entspricht eine Spiegelung an der Winkelhalbierenden w des I. und III. Quadranten mit anschließender Spiegelung an der -Achse.. Schritt. an w gespiegelt: * und werden vertauscht: G f = e e e + e 0
21 .3 Üben Festigen Vertiefen. Schritt Diese Gleichung wird nach aufgelöst. e + e = e e e e + = e e ( ) = e = + = ln ( + ) = ln ( + ) f () = ln ( + ) Es muss gelten + > 0 (I) + > 0 > 0 > <, also X ] ; [ (II) + < 0 < 0; < > (Widerspruch) Also: D f = ] ; [ 3. Schritt wird an der -Achse gespiegelt: wird durch ersetzt. f*: f*() = ln ( + ) ; D f* = D f = ] ; [ P*( ) P ( ) ( alt ) ( neu ) durch + ersetzen durch + ersetzen = e e e + e Nach auflösen: e e = e e ; e ( ) = e + e ; e ( + ) = e ( ); : e e ( + ) = ; e = + ; = ln ( + ) ; = ln ( + ) 3. a) vgl. auch. f) + > 0 I. + > 0 > 0; > < also X ] ; [ II. + < 0 < 0 < > (Widerspruch) Also ist D f ma = ] ; [ b) lim ( ln + ) = + lim ln ( + ) = + hat zwei senkrechte Asmptoten: a : = und a : = c) f(0) = ln = ln = 0: verläuft durch den Ursprung.
22 .3 Üben Festigen Vertiefen f() = ln ( + ) ln ( ); f () = + = + + ( + )( ) = f (0) = = ; tan ϕ = ; ϕ 63,4 d) f () = > 0 für jeden Wert von X ] ; [ f ist in D f ma streng zunehmend. e) f( ) = ln + = ln [ ( + ) ] = ln + = f(); also ist punktsmmetrisch zum Ursprung. f) S R 66 g) f( R ) = ; ln + R = ; + R = e; + R R = e e R ; R R + e R = e ; R (e + ) = e ; R = e e + ; e SR = + R = e + ; f*: f*() = f( + SR ) = ln + + e 3e + e + = ln e + + e e ; e + e + D f* = ] SR ; SR [ = ] 3e e + ; e + e + [ P ( ) X * P*( ) X * Gleichung von : = e ; durch + und durch ersetzen: = e = ln ; = ln f*: f*() = ln ; D f* = +
23 .3 Üben Festigen Vertiefen. a) f : f () = e +, D f = b) f : f () = e + ; D f = Gf c) f 3 : f 3 () = e ; D f3 = d) f 4 : f 4 () = e + ; D f4 = 4 3 Hinweis zu d): wird zuerst an der -Achse gespiegelt ( wird durch ersetzt); dann wird der neue Graph um in Richtung der -Achse nach oben verschoben. e) f : f () = e ; D f = f) f 6 : f 6 () = e ; D f6 = 6 3
24 .3 Üben Festigen Vertiefen 6. a) f : f () = ln + ; D f = + b) f : f () = ln ( +); D f = ] ; + [ c) f 3 : f 3 () = ln ; D f3 = + 3 d) f 4 : f 4 () = ln ( ); D f4 = Gf4 4
25 .3 Üben Festigen Vertiefen e) f : f () = ln ( + ); D f = ] ; [ Hinweis: wird zuerst an der -Achse gespiegelt ( wird durch ersetzt); dann wird der neue Graph um nach rechts verschoben. f) f 6 : f 6 () = ln ( ); D f6 = 6 9. a) f(t) = 0 + t e 4 t 67 t f(t) 0 30, 39,6 34, 6 9, 4,9,4, 0, 0, b) f (t) = te 4 t + t ( )e 4 t = e 4 t t( t); f (t) = e 4 t (t t ) + e 4 t ( t) = e 4 t ( t + t + t) = e 4 t (t 4t + ) f (t) = 0; (t = 0) t = f () = e (4 8 + ) = e < 0 Nach Stunden ist der Bestand am größten. c) Im Zeitintervall 0 h < t < h wächst die Population; im Zeitintervall h < t < 0 h nimmt sie ab. f (t) = 0 Da e 4 t 0 ist, gilt t 4t + = 0; t 3,4 = 4 ± 6 8 = 4 ± = ± ; t 3 3,4; t 4 0,9 f (t) = e 4 t (t 4t + ) + e 4 t (t 4) = e 4 t (t 4 t + 4t ) = e 4 t ( t + 6t 6); f ( + ), > 0 f ( ) 80 < 0 Nach etwa 0,6 h ist die Zunahme am größten; nach etwa 3,4 h ist die Abnahme am größten.
26 .3 Üben Festigen Vertiefen 0. a) lim = + 9 e = lim = e hat die beiden waagrechten Asmptoten a : = und a : = 0 b) Beispiele für Eigenschaften der Funktion f : D f = = D f f () > 0 für jeden Wert von X lim f () = 0 ± Maimum von f () für. c) f(4 ln 3) = = + 9 e 4 ln 3 + 9e = ln 3 + 9e = ln ,8 LE f (4 ln 3) 3 LE 0,6 d) t P = =,; P =, P 3 LE,8 LE P = * 4,4 0 * 0 e) () 000 f(0) = = lim f() = 000 = Am Anfang (Zeitpunkt = 0) waren bereits 000 Stück verkauft; insgesamt kann der Hersteller mit einem Absatz von Stück rechnen. () f () = ( 0, ) 9e ( + 9 e 0, ) =, e 0, ( + 9 e 0, ) ; f () = ( + 9 e 0, ) (,e 0, ), e 0, ( + 9e 0, )( 4,e 0, ) ( + 9e 0, ) = 4 =, e 0, ( + 9e 0, 8e 0, ) ( + 9e 0, ) =, e 0, ( 9e 0, ) 3 ( + 9e 0, ) ; 3 f (*) = 0 9e 0,* = 0; e 0,* = 9 ; 0,* = ln 9 ; * = ln 9 = 4 ln 3 4,39 Für 0 < < * nimmt die pro Zeiteinheit abgesetzte Stückzahl streng zu, für * < < + nimmt sie streng ab; somit hat also f () an der Stelle * ein Maimum. 6
27 .3 Üben Festigen Vertiefen (3) f() = 0,9 = 4,; = 4,; 0, + 9e 4,( + 9e 0, ) = ; + 9 0, = 0 9 ; 9e 0, = 9 e 0, = 8 ; e 0, = 8; 0, = ln 8; = ln 8 8,79 Nach etwa 880 Tagen, also nach etwa Jahren, sind etwa 90% des Gesamtabsatzes erreicht. 7
28 Kann ich das? 68. L a) e e + = 0; e = 0; e = 0; e = ; = 0 X G; L = {0} b) ln ( e ) = 0; e = ; e = ; e = ; = 0 X G; L = {0} c) ln + k = 0; + k = ; + k = ; + k = 0; D = 4k ;, = ± 4k Fallunterscheidung: I. D = 4k > 0, 4k < ; k < 4 ; < k < ; da k > 0 ist: 0 < k < Es gibt zwei Lösungen X G, wenn 0 < k < ist: L = { 4k ; + 4k } II. D = 4k = 0; k = : nicht möglich, da k > 0 ist; = X G: k = : Es gibt genau eine Lösung, nämlich L = { } III. D = 4k < 0: Es gibt keine Lösung X G; also ist L = { }. d) e 3 + e = 0; e e 3e + = 0; (e )(e ) = 0; e = ; = ln X G; e = = 0 X G; L = {0 ; ln }. a) ln (e ) + ln (e e ) + e ln = + e + = e + b) ln [ln (e e )] = ln (e ln e) = ln e = c) (e ln + e ln ) : e ln 7 = ( + ) : 7 = 3. a) Der kleinste Wert von f() = ( 3 4 ) sin ist ( 3 4 ) = ( 3 4 ) = 4 3,33; er wird für = π + nπ (n X ) angenommen. b) Der größte Wert von g() = ( ) cos + ist ( ) + = ( ) 3 =,83; er wird für = nπ (n X ) angenommen. 4. a) = ( + ) e + ( + ) e = ( + )( + )e b) = e ln = ; =, falls > 0 ist. c) = (4 + e ) 4e 4e e (4 + e ) = 4e (4 + e e ) (4 + e ) = 6e (4 + e ) e d) = = e + e + e e) = e cos sin f) = ln e = ln e ln = ln ; = g) = (ln ) ( ) ( ln ) (ln ) = ln + ln (ln ) 4 (ln ) = ln 3 (ln ) 3 h) = + = ( + ) 8
29 Kann ich das?. i) = = ( ) = ( ) G g ln (e ) = ln e + ln = + ln : Man erhält G g, indem man um Einheiten in Richtung der -Achse nach oben verschiebt. ln (a) = ln a + ln : Man erhält den Graphen der Funktion G a, indem man um ln a Einheiten in Richtung der -Achse nach oben (für a > ) bzw. um ln a Einheiten nach unten (für 0 < a < ) verschiebt. 6. T(t) T 0 = (T T 0 )e kt Rechnung mit Maßzahlen: 0 4 = (0 4) e k ; 8 = 96e k ; e k = 8 96 ; k = ln 8 96 = 0,6989 ; k 0,7; 40 4 = (0 4) e 0,7t ; 6 = 8 e 0,7t ; e 0,7t = 6 ; 0,7t = ln ; t = ln 6 = 9,40 0 0,7 8 Innerhalb von weiteren rund 0 Minuten kühlt sich die Pfanne von 0 C auf 40 C ab. 7. a) Schnittpunkt mit der -Achse: + = 0; = ; S ( 0) Schnittpunkt mit der -Achse: f(0) = e = = ; T (0 ) 0 b) Ableitung: f () = e ( + )e e = e ( ) e = ; e f (0) = 0 < < 0 = 0 0 < < + f () f () > 0 f () = 0 f () < 0 Vorzeichenwechsel von f () hat von + nach den Hochpunkt H (0 ) = T 9
30 Kann ich das? 3 H = T B A = S 6 lim f() = 0 (Hinweis: vgl.. Aufgabe 7.); für gilt f(). c) f ( ) = e = e; da f ( ) f () = e ( e ) = ist, stehen die Tangenten t A und t B an f () = e ; in den Graphpunkten A bzw. B aufeinander senkrecht. d) F () = e b (a + b) e (e ) = b a b = f(); e b a b = + ; e e Es muss gelten b =, d. h. b =, und b a = ; also a =, d. h. a = : F() = e Probe F () = e ( ) ( )e e = + + = + = f() e e 8. f(0) = 4 = ; der Punkt T (0 ) X liegt nicht auf G III. f () = ( + e ) 4e 4e e ( + e ) = 4e ( + e e ) ( + e ) = 4e ( + e ) ; f (0) = 4 4 = > 0; Die Tangentensteigung im Punkt T ist nur bei G II positiv: G II =. 4e G I : f I () = + e = 4 e + ; 4e G III : f III () = + e = 4e e + e 30
Weitere Ableitungsregeln. Kapitel 4
 Weitere Ableitungsregeln Kapitel . Die Kettenregel L f() = u(v()) g() = v(u()) a) + + b) cos [( + ) ] (cos + ) c) sin ( ) [sin ()] d) e) ( = _ ) _ ( f) cos [π( + )] cos (π) + g) ( ) = h) ( + ) + = + +
Weitere Ableitungsregeln Kapitel . Die Kettenregel L f() = u(v()) g() = v(u()) a) + + b) cos [( + ) ] (cos + ) c) sin ( ) [sin ()] d) e) ( = _ ) _ ( f) cos [π( + )] cos (π) + g) ( ) = h) ( + ) + = + +
Anwendungen der Differentialrechnung Optimieren und Modellieren. Kapitel 7
 Anwendungen der Differentialrechnung ptimieren und Modellieren Kapitel 7 7. Etremwertprobleme 9 Arbeitsaufträge. a) Seitenlängen: cm; cm mit + = 9, also = 9 (und > 0; > 0),5 5 6 7 8 8 7 6 5,5 A (in cm
Anwendungen der Differentialrechnung ptimieren und Modellieren Kapitel 7 7. Etremwertprobleme 9 Arbeitsaufträge. a) Seitenlängen: cm; cm mit + = 9, also = 9 (und > 0; > 0),5 5 6 7 8 8 7 6 5,5 A (in cm
1 Ableitungen. Hinweise und Lösungen:
 Hinweise und Lösungen: http://mathemathemathe.de/analsis/analsis-grundagen Ableitungen Übung.: Einfache Ableitungen - Bestimme die ersten Ableitungen a) f() = 7 + + 8 b) f() = a + a a K(t) = t t + 0 Übung.:
Hinweise und Lösungen: http://mathemathemathe.de/analsis/analsis-grundagen Ableitungen Übung.: Einfache Ableitungen - Bestimme die ersten Ableitungen a) f() = 7 + + 8 b) f() = a + a a K(t) = t t + 0 Übung.:
Analysis: Exponentialfunktionen Analysis
 www.mathe-aufgaben.com Analysis: Eponentialfunktionen Analysis Klausur zu Eponentialfunktionen ohne Wachstum (Ableitung, Stammfunktion, Fläche, Rotationsvolumen, Etremwertaufgabe) Gymnasium ab J Aleander
www.mathe-aufgaben.com Analysis: Eponentialfunktionen Analysis Klausur zu Eponentialfunktionen ohne Wachstum (Ableitung, Stammfunktion, Fläche, Rotationsvolumen, Etremwertaufgabe) Gymnasium ab J Aleander
1 Die natürliche Exponentialfunktion und ihre Ableitung
 Schülerbuchseite 5 5 Lösungen vorläuig VI Natürliche Eponential- und Logarithmusunktion Die natürliche Eponentialunktion und ihre Ableitung S. 5 Durch Ausprobieren erkennt man, dass < a
Schülerbuchseite 5 5 Lösungen vorläuig VI Natürliche Eponential- und Logarithmusunktion Die natürliche Eponentialunktion und ihre Ableitung S. 5 Durch Ausprobieren erkennt man, dass < a
Abitur 2014 Mathematik Infinitesimalrechnung I
 Seite http://www.abiturloesung.de/ Seite 2 Abitur 204 Mathematik Infinitesimalrechnung I Die Abbildung zeigt den Graphen einer Funktion f. Teilaufgabe Teil A (5 BE) Gegeben ist die Funktion f : x x ln
Seite http://www.abiturloesung.de/ Seite 2 Abitur 204 Mathematik Infinitesimalrechnung I Die Abbildung zeigt den Graphen einer Funktion f. Teilaufgabe Teil A (5 BE) Gegeben ist die Funktion f : x x ln
= 4 0 = 4. Hinweis: Dieses Ergebnis folgt auch aus der Punktsymmetrie zum Ursprung des Graphen der Funktion f: x sin x; D f = [ ; ].
![= 4 0 = 4. Hinweis: Dieses Ergebnis folgt auch aus der Punktsymmetrie zum Ursprung des Graphen der Funktion f: x sin x; D f = [ ; ]. = 4 0 = 4. Hinweis: Dieses Ergebnis folgt auch aus der Punktsymmetrie zum Ursprung des Graphen der Funktion f: x sin x; D f = [ ; ].](/thumbs/96/129050460.jpg) 73. a) dx = d x = [x] = = b) sin x dx = [ cos x] = cos + cos ( ) = ( ) + ( ) = Hinweis: Dieses Ergebnis folgt auch aus der Punktsmmetrie zum Ursprung des Graphen der Funktion f: x sin x; D f = [ ; ]. e
73. a) dx = d x = [x] = = b) sin x dx = [ cos x] = cos + cos ( ) = ( ) + ( ) = Hinweis: Dieses Ergebnis folgt auch aus der Punktsmmetrie zum Ursprung des Graphen der Funktion f: x sin x; D f = [ ; ]. e
Zusammenfassung: Differenzialrechnung 2
 LGÖ Ks M 11 Schuljahr 17/18 Zusammenfassung: Differenzialrechnung Inhaltsverzeichnis Etrem- und Wendepunkte... 1 Etremwertprobleme... 8 Etrem- und Wendepunkte Definition: Ist eine reelle Zahl, dann heißt
LGÖ Ks M 11 Schuljahr 17/18 Zusammenfassung: Differenzialrechnung Inhaltsverzeichnis Etrem- und Wendepunkte... 1 Etremwertprobleme... 8 Etrem- und Wendepunkte Definition: Ist eine reelle Zahl, dann heißt
Diskussion einzelner Funktionen
 Diskussion einzelner Funktionen. Wir betrachten die Funktion f mit f() = cos sin (a) Berechne f() für { π, π, π, π, } 5π und zeichne den Grafen von f im - Intervall [ π, ] 5π. Einheiten: cm auf der y-achse,
Diskussion einzelner Funktionen. Wir betrachten die Funktion f mit f() = cos sin (a) Berechne f() für { π, π, π, π, } 5π und zeichne den Grafen von f im - Intervall [ π, ] 5π. Einheiten: cm auf der y-achse,
Lösungen zu ausgewählten Aufgaben der Klasse 11
 Lösungen zu ausgewählten Aufgaben der Klasse 11 S. 9 Nr. a) K() = 0,001 1,9 + 600 + 1000 U() = 00.10 5..10 5 K () U ()..10 5 1.6.10 5 8.10 b) Monotonie : 0 00 00 600 800 1000 K() U() 0 1000 0 00 8800 60000
Lösungen zu ausgewählten Aufgaben der Klasse 11 S. 9 Nr. a) K() = 0,001 1,9 + 600 + 1000 U() = 00.10 5..10 5 K () U ()..10 5 1.6.10 5 8.10 b) Monotonie : 0 00 00 600 800 1000 K() U() 0 1000 0 00 8800 60000
Förderaufgaben EF Arbeitsblatt 1 Abgabe Zeichne die Tangenten bei x=6 und bei x = 4 ein und bestimme die zugehörige Geradengleichung.
 Förderaufgaben EF Arbeitsblatt 1 Abgabe 20.1.15 1. Zeichne die Tangenten bei x=6 und bei x = 4 ein und bestimme die zugehörige Geradengleichung. 2. Bestimme f (x): a) f(x) = x 3 + 4x 2 x + 1 b) f(x) =
Förderaufgaben EF Arbeitsblatt 1 Abgabe 20.1.15 1. Zeichne die Tangenten bei x=6 und bei x = 4 ein und bestimme die zugehörige Geradengleichung. 2. Bestimme f (x): a) f(x) = x 3 + 4x 2 x + 1 b) f(x) =
waagrechte Asymptote: y = ln 2 senkrechte Asymptoten: x = 1 Nullstelle der Tangente in P: x = 3
 Abiturprüfung 006 - - Aufgabe GM.I a) ----- b) 7 x + > 0 für x < oder x > 0 ( x = ist einzige Nullstelle) x lim x ± g(x) = ln ; lim x g(x) = ; lim x 0+ waagrechte Asymptote: y = ln senkrechte Asymptoten:
Abiturprüfung 006 - - Aufgabe GM.I a) ----- b) 7 x + > 0 für x < oder x > 0 ( x = ist einzige Nullstelle) x lim x ± g(x) = ln ; lim x g(x) = ; lim x 0+ waagrechte Asymptote: y = ln senkrechte Asymptoten:
Matur-/Abituraufgaben Analysis
 Matur-/Abituraufgaben Analysis 1. Tropfen Die folgende Skizze zeigt die Kurve k mit der Gleichung y = (1 ) im Intervall 1. Die Kurve k bildet zusammen mit ihrem Spiegelbild k eine zur -Achse symmetrische
Matur-/Abituraufgaben Analysis 1. Tropfen Die folgende Skizze zeigt die Kurve k mit der Gleichung y = (1 ) im Intervall 1. Die Kurve k bildet zusammen mit ihrem Spiegelbild k eine zur -Achse symmetrische
4.4. Aufgaben zu Potenzfunktionen
 .. Aufgaben zu Potenzfunktionen Definition: Eine Funktion der Form f() = c z mit z Z\{;} heißt Potenzfunktion. Aufgabe : Potenzfunktionen mit positiven Eponenten (Parabeln). Ergänze: 9 8 7 6 - - - - -
.. Aufgaben zu Potenzfunktionen Definition: Eine Funktion der Form f() = c z mit z Z\{;} heißt Potenzfunktion. Aufgabe : Potenzfunktionen mit positiven Eponenten (Parabeln). Ergänze: 9 8 7 6 - - - - -
Pflichtteilaufgaben zu Elemente der Kurvendiskussion. Baden-Württemberg
 Pflichtteilaufgaben zu Elemente der Kurvendiskussion Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Aleander Schwarz www.mathe-aufgaben.com September 6 Übungsaufgaben: Ü: Gegeben ist
Pflichtteilaufgaben zu Elemente der Kurvendiskussion Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Aleander Schwarz www.mathe-aufgaben.com September 6 Übungsaufgaben: Ü: Gegeben ist
Trigonometrische Funktionen
 Trigonometrische Funktionen. Gegeben ist die Funktion f() = (sin( π )) Ihr Graph sei K. a) Skizzieren Sie K im Intervall [0,]. Geben Sie die Periode von f an. Geben Sie alle Hoch- und Tiefpunkte von K
Trigonometrische Funktionen. Gegeben ist die Funktion f() = (sin( π )) Ihr Graph sei K. a) Skizzieren Sie K im Intervall [0,]. Geben Sie die Periode von f an. Geben Sie alle Hoch- und Tiefpunkte von K
Abiturprüfung Mathematik 2007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 Abiturprüfung Mathematik 007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (8 Punkte) Das Schaubild einer Polynomfunktion. Grades geht durch den Punkt S(0/) und hat den 3 Wendepunkt
Abiturprüfung Mathematik 007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (8 Punkte) Das Schaubild einer Polynomfunktion. Grades geht durch den Punkt S(0/) und hat den 3 Wendepunkt
Analysis I. Teil 1. Bayern Aufgabe 1. Abitur Mathematik Bayern Abitur Mathematik: Musterlösung. D f =] 3; + [ x = 1
![Analysis I. Teil 1. Bayern Aufgabe 1. Abitur Mathematik Bayern Abitur Mathematik: Musterlösung. D f =] 3; + [ x = 1 Analysis I. Teil 1. Bayern Aufgabe 1. Abitur Mathematik Bayern Abitur Mathematik: Musterlösung. D f =] 3; + [ x = 1](/thumbs/91/105628768.jpg) Abitur Mathematik: Bayern 2012 Teil 1 Aufgabe 1 a) DEFINITIONSMENGE f(x) = ln(x + 3) x + 3 > 0 x > 3 D f =] 3; + [ ABLEITUNG Kettenregel liefert f (x) = 1 x + 3 1 = 1 x + 3 b) DEFINITIONSMENGE 3 g(x) =
Abitur Mathematik: Bayern 2012 Teil 1 Aufgabe 1 a) DEFINITIONSMENGE f(x) = ln(x + 3) x + 3 > 0 x > 3 D f =] 3; + [ ABLEITUNG Kettenregel liefert f (x) = 1 x + 3 1 = 1 x + 3 b) DEFINITIONSMENGE 3 g(x) =
Lösungen zu delta 10. Kann ich das noch? Lösungen zu den Seiten 6 und 7
 Lösungen zu delta 0 Kann ich das noch? Lösungen zu den Seiten 6 und 7. a) L = {} b) L = {0; } c) L = { } d) L = { 6; } e) L = {,; } f) L = { } g) L = {,; } h) L = {7; 0} i) L = { } Summenwert aller Lösungen:.
Lösungen zu delta 0 Kann ich das noch? Lösungen zu den Seiten 6 und 7. a) L = {} b) L = {0; } c) L = { } d) L = { 6; } e) L = {,; } f) L = { } g) L = {,; } h) L = {7; 0} i) L = { } Summenwert aller Lösungen:.
Tutorium Mathematik ITB1(B), WI1(B)
 Tutorium Mathematik ITB(B), WI(B) Aufgabenblatt D Differenzialrechnung Prof Dr Peter Plappert Fachbereich Grundlagen Die Aufgaben dieses Aufgabenblattes sollen ohne die Benutzung von Taschenrechnern bearbeitet
Tutorium Mathematik ITB(B), WI(B) Aufgabenblatt D Differenzialrechnung Prof Dr Peter Plappert Fachbereich Grundlagen Die Aufgaben dieses Aufgabenblattes sollen ohne die Benutzung von Taschenrechnern bearbeitet
Funktionenlehre. Grundwissenskatalog G8-Lehrplanstandard
 GRUNDWISSEN MATHEMATIK Funktionenlehre Grundwissenskatalog G8-Lehrplanstandard Basierend auf den Grundwissenskatalogen des Rhöngmnasiums Bad Neustadt und des Kurt-Huber-Gmnasiums Gräfelfing J O H A N N
GRUNDWISSEN MATHEMATIK Funktionenlehre Grundwissenskatalog G8-Lehrplanstandard Basierend auf den Grundwissenskatalogen des Rhöngmnasiums Bad Neustadt und des Kurt-Huber-Gmnasiums Gräfelfing J O H A N N
Lösungen zu delta 11. Fit für die Oberstufe Lösungen zu den Seiten 6 und 7
 Lösungen zu delta Fit für die Oberstufe Lösungen zu den Seiten 6 und 7. a) 4 = ; 9 = 4; = 6 X G; L = { 6} b) ( 4) + 8 = ( + 4); 8 + 8 = 4; + 0 = ; 4 = ; = =, X G; L = {,} 4 c) + 7 = 0; + 7 = 0; = 7 G;
Lösungen zu delta Fit für die Oberstufe Lösungen zu den Seiten 6 und 7. a) 4 = ; 9 = 4; = 6 X G; L = { 6} b) ( 4) + 8 = ( + 4); 8 + 8 = 4; + 0 = ; 4 = ; = =, X G; L = {,} 4 c) + 7 = 0; + 7 = 0; = 7 G;
Prüfungsteil 1, Aufgabe 3. Analysis. Nordrhein-Westfalen 2012 GK. Aufgabe a (1) Aufgabe a (2) Abitur Mathematik: Musterlösung
 Abitur Mathematik: Prüfungsteil 1, Aufgabe 3 Nordrhein-Westfalen 2012 GK Aufgabe a (1) 1. SCHRITT: BEDINGUNG FÜR PUNKTSYMMETRIE ZUM URSPRUNG PRÜFEN Der Graph der Funktion : ist genau dann punktsymmetrisch
Abitur Mathematik: Prüfungsteil 1, Aufgabe 3 Nordrhein-Westfalen 2012 GK Aufgabe a (1) 1. SCHRITT: BEDINGUNG FÜR PUNKTSYMMETRIE ZUM URSPRUNG PRÜFEN Der Graph der Funktion : ist genau dann punktsymmetrisch
Prüfungsteil B, Aufgabengruppe 2, Analysis. Bayern Aufgabe 1. Bundesabitur Mathematik: Musterlösung. Abitur Mathematik Bayern 2014
 Bundesabitur Mathematik: Prüfungsteil B, Aufgabengruppe, Bayern 014 Aufgabe 1 a) 1. SCHRITT: DEFINITIONSBEREICH BESTIMMEN Bei einem Bruch darf der Nenner nicht null werden, d.h. es muss gelten: x 5 0 x
Bundesabitur Mathematik: Prüfungsteil B, Aufgabengruppe, Bayern 014 Aufgabe 1 a) 1. SCHRITT: DEFINITIONSBEREICH BESTIMMEN Bei einem Bruch darf der Nenner nicht null werden, d.h. es muss gelten: x 5 0 x
Kreis - Kugel Länge des Kreisbogens: Flächeninhalt des Kreissektors: Umrechnung ins Bogenmaß: α. α 360. b: Frequenz c: Phasenverschiebung 1,4 1,4 1,0
 Wirsberg-Gmnasium Grundwissen Mathematik 0. Jahrgangsstufe Lerninhalte Fakten-Regeln-eispiele Kreis - Kugel Länge des Kreisbogens: Flächeninhalt des Kreissektors: Umrechnung ins ogenmaß: α b π r 0 α π
Wirsberg-Gmnasium Grundwissen Mathematik 0. Jahrgangsstufe Lerninhalte Fakten-Regeln-eispiele Kreis - Kugel Länge des Kreisbogens: Flächeninhalt des Kreissektors: Umrechnung ins ogenmaß: α b π r 0 α π
1 Exponentielles Wachstum
 Schülerbuchseite 56 58 Lösungen vorläufig VI Anwendungen der Differential- und Integralrechnung Exponentielles Wachstum S. 56 S. 58 a) H (t) = 4000,0 t b),0 t = e k t,0 = e k k = ln,0 0,0 H (t) = 4000
Schülerbuchseite 56 58 Lösungen vorläufig VI Anwendungen der Differential- und Integralrechnung Exponentielles Wachstum S. 56 S. 58 a) H (t) = 4000,0 t b),0 t = e k t,0 = e k k = ln,0 0,0 H (t) = 4000
Koordinatengeometrie. Aufgabe 4 Untersuchen Sie die Funktion f(x) = x² 9.
 Koordinatengeometrie Aufgabe 1 Gegeben sind der Punkt P (-1; 9) sowie die Geraden g: 3x y + 6 = 0 und h: x + 4y 8 = 0. a) Die Geraden g und h schneiden einander im Punkt S. Berechnen Sie die exakten Koordinaten
Koordinatengeometrie Aufgabe 1 Gegeben sind der Punkt P (-1; 9) sowie die Geraden g: 3x y + 6 = 0 und h: x + 4y 8 = 0. a) Die Geraden g und h schneiden einander im Punkt S. Berechnen Sie die exakten Koordinaten
Mathematik LK13 Kursarbeit Musterlösung Aufgabe I:
 Mathematik LK13 Kursarbeit 1 6.11.14 Musterlösung Aufgabe I: Analysis I 1. Spaß mit natürlichen Eponentialfunktionen Gegeben sind die Funktionen f ()=e ( + ) und g ( )=5 e Untersuchen Sie beide Funktionen
Mathematik LK13 Kursarbeit 1 6.11.14 Musterlösung Aufgabe I: Analysis I 1. Spaß mit natürlichen Eponentialfunktionen Gegeben sind die Funktionen f ()=e ( + ) und g ( )=5 e Untersuchen Sie beide Funktionen
1 Die zweite Ableitung
 Schülerbuchseite 5 Lösungen vorläuig und deren Graphen Die zweite Ableitung S. Um den Graphen der Ableitung zu skizzieren, sucht man zuerst die Punkte mit waagrechten Tangenten. so erhält man die Nullstellen
Schülerbuchseite 5 Lösungen vorläuig und deren Graphen Die zweite Ableitung S. Um den Graphen der Ableitung zu skizzieren, sucht man zuerst die Punkte mit waagrechten Tangenten. so erhält man die Nullstellen
Linearisierung einer Funktion Tangente, Normale
 Linearisierung einer Funktion Tangente, Normale 1 E Linearisierung einer Funktion Abb. 1 1: Die Gerade T ist die Tangente der Funktion y = f (x) im Punkt P Eine im Punkt x = a differenzierbare Funktion
Linearisierung einer Funktion Tangente, Normale 1 E Linearisierung einer Funktion Abb. 1 1: Die Gerade T ist die Tangente der Funktion y = f (x) im Punkt P Eine im Punkt x = a differenzierbare Funktion
Aufgaben e-funktion. Gegeben sind die Funktionen f k (x) = x+k e x. a) Leite g(x) = 1 x k e x. ab.
 Aufgaben e-funktion 7 6 5 4 3-3 - - 3 u 4 - Gegeben sind die Funktionen f k () = +k e. a) Leite g() = k e ab. b) Die Graphen von f und f 3, die -Achse und die Gerade = u (u > 0) begrenzen die Fläche A(u).
Aufgaben e-funktion 7 6 5 4 3-3 - - 3 u 4 - Gegeben sind die Funktionen f k () = +k e. a) Leite g() = k e ab. b) Die Graphen von f und f 3, die -Achse und die Gerade = u (u > 0) begrenzen die Fläche A(u).
Jahrgangsstufe 11. f(x) = 1 12 x4 1 3 x3 3 2 x2 nach allen Regeln der Kunst und zeichnen Sie ihren Graphen.
 Jahrgangsstufe. Diskutieren Sie die Funktion f mit der Gleichung f) = 3 3 3 nach allen Regeln der Kunst und zeichnen Sie ihren Graphen. Lösung: NS: 0 =,69, 0 = 0, 03 = + 6,69 lim f) = + ± f ) = 3 3 3 f
Jahrgangsstufe. Diskutieren Sie die Funktion f mit der Gleichung f) = 3 3 3 nach allen Regeln der Kunst und zeichnen Sie ihren Graphen. Lösung: NS: 0 =,69, 0 = 0, 03 = + 6,69 lim f) = + ± f ) = 3 3 3 f
Abitur 2017 Mathematik Infinitesimalrechnung II
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung II Die Abbildung zeigt den Graphen der in R definierten Funktion g : x p + q sin p, q, r N. ( π r x ) mit Gegeben
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung II Die Abbildung zeigt den Graphen der in R definierten Funktion g : x p + q sin p, q, r N. ( π r x ) mit Gegeben
a) Der Graph von g entsteht durch Verschiebung des Graphen von f um nach. Es gilt also: g(x) = f(x)
 Vertikale Verschiebung a) Der Graph von g entsteht durch Verschiebung des Graphen von f um nach. Es gilt also: g() = f() b) Zeichne den Graphen der Funktion h mit h() = f() ein. Oben oder unten? f() +
Vertikale Verschiebung a) Der Graph von g entsteht durch Verschiebung des Graphen von f um nach. Es gilt also: g() = f() b) Zeichne den Graphen der Funktion h mit h() = f() ein. Oben oder unten? f() +
Abschlussprüfung Berufliche Oberschule 2017 Mathematik 12 Technik - A II - Lösung mit CAS. e 2x mit der maximalen Definitionsmenge D f = IR.
 Abschlussprüfung Berufliche Oberschule 07 Mathematik Technik - A II - Lösung mit Teilaufgabe.0 Gegeben ist die reelle Funktion f mit f( ) e mit der maimalen Definitionsmenge D f IR. Teilaufgabe. ( BE)
Abschlussprüfung Berufliche Oberschule 07 Mathematik Technik - A II - Lösung mit Teilaufgabe.0 Gegeben ist die reelle Funktion f mit f( ) e mit der maimalen Definitionsmenge D f IR. Teilaufgabe. ( BE)
und geben Sie die Gleichungen und Art aller Asymptoten an. an, bestimmen Sie die Koordinaten der Achsenschnittpunkte von G f auflösen x x 2 2 ( 2/ 0)
 Abiturprüfung Berufliche Oberschule Mathematik Nichttechnik - A II - Lösung Teilaufgabe. x Gegeben ist die Funktion f( x) ( x ) in ihrer maximalen Definitionsmenge D f IR. Der zugehörige Graph heißt. Teilaufgabe.
Abiturprüfung Berufliche Oberschule Mathematik Nichttechnik - A II - Lösung Teilaufgabe. x Gegeben ist die Funktion f( x) ( x ) in ihrer maximalen Definitionsmenge D f IR. Der zugehörige Graph heißt. Teilaufgabe.
ist symmetrisch bezüglich der y-achse, da f( x) = f(x) ist. e x + e x = 2 2 (Substitution: a = e x )
 Problemstellung. f() e + e ist symmetrisch bezüglich der y-achse, da f( ) f() ist. Es ist f () e e. Aus f () folgt ; f(). f () e + e vor.
Problemstellung. f() e + e ist symmetrisch bezüglich der y-achse, da f( ) f() ist. Es ist f () e e. Aus f () folgt ; f(). f () e + e vor.
9 Die trigonometrischen Funktionen und ihre Umkehrfunktionen
 Übungsmaterial 9 Die trigonometrischen Funktionen und ihre Umkehrfunktionen Die trigonometrischen Funktionen sind die Sinus-, die Kosinus- und die Tangensfunktion. 9. Eigenschaften der trigonometrischen
Übungsmaterial 9 Die trigonometrischen Funktionen und ihre Umkehrfunktionen Die trigonometrischen Funktionen sind die Sinus-, die Kosinus- und die Tangensfunktion. 9. Eigenschaften der trigonometrischen
Analysis 2. f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt:
 Analysis 2 www.schulmathe.npage.de Aufgaben 1. Gegeben ist die Funktion f durch f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt: f (x) = 6(x
Analysis 2 www.schulmathe.npage.de Aufgaben 1. Gegeben ist die Funktion f durch f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt: f (x) = 6(x
PFLICHTTEIL NT = e x (x+2) = x+2 Oder Umschreiben: f(x) = 1. = (x 2 e x ) 1, und dann Kettenregel
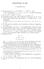 PFLICHTTEIL NT 26 F. LEMMERMEYER (1 Quotientenregel: f (x = x2 e x 2xe x x = e x (x+2 4 x = x+2 3 x 3 e. x Oder Umschreiben: f(x = 1 x 2 e = (x 2 e x 1, und dann Kettenregel x f (x = (x 2 e x 2 (2xe x
PFLICHTTEIL NT 26 F. LEMMERMEYER (1 Quotientenregel: f (x = x2 e x 2xe x x = e x (x+2 4 x = x+2 3 x 3 e. x Oder Umschreiben: f(x = 1 x 2 e = (x 2 e x 1, und dann Kettenregel x f (x = (x 2 e x 2 (2xe x
Graphen zuordnen und Funktionsterme ermitteln
 Aufgaben Analsis Flächenberechnung Ganzrationale Funktion Tangenten ohne Einsatz des GTR Integralfunktion Graphen zuordnen und Funktionsterme ermitteln Wahr oder falsch? Integralfunktion Wahr oder falsch?
Aufgaben Analsis Flächenberechnung Ganzrationale Funktion Tangenten ohne Einsatz des GTR Integralfunktion Graphen zuordnen und Funktionsterme ermitteln Wahr oder falsch? Integralfunktion Wahr oder falsch?
Prüfungsteil B, Aufgabengruppe 1: Analysis. Bayern Aufgabe 1. BundesabiturMathematik: Musterlösung
 Abitur MathematikBayern 04 Prüfungsteil B, Aufgabengruppe BundesabiturMathematik: Prüfungsteil B, Aufgabengruppe : Bayern 04 Aufgabe a). SCHRITT: SCHNITTPUNKTE MIT DEN KOORDINATENACHSEN Die Koordinatenachsen
Abitur MathematikBayern 04 Prüfungsteil B, Aufgabengruppe BundesabiturMathematik: Prüfungsteil B, Aufgabengruppe : Bayern 04 Aufgabe a). SCHRITT: SCHNITTPUNKTE MIT DEN KOORDINATENACHSEN Die Koordinatenachsen
Mathematik Name: Nr.4 K1 Punkte: /30 Note: Schnitt:
 K Punkte: / Note: Schnitt: 9.5.6 Pflichtteil (etwa 4 min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen abgegeben sein, ehe der GTR und die Formalsammlung verwendet werden
K Punkte: / Note: Schnitt: 9.5.6 Pflichtteil (etwa 4 min) Ohne Taschenrechner und ohne Formelsammlung (Dieser Teil muss mit den Lösungen abgegeben sein, ehe der GTR und die Formalsammlung verwendet werden
9 Funktionen und ihre Graphen
 57 9 Funktionen und ihre Graphen Funktionsbegriff Eine Funktion ordnet jedem Element aus einer Menge D f genau ein Element aus einer Menge W f zu. mit = f(), D f Die Menge aller Funktionswerte nennt man
57 9 Funktionen und ihre Graphen Funktionsbegriff Eine Funktion ordnet jedem Element aus einer Menge D f genau ein Element aus einer Menge W f zu. mit = f(), D f Die Menge aller Funktionswerte nennt man
Mathe-Abitur ab 2004: Fundus für den Pflichtbereich Lösungen (1)
 Mathe-Abitur ab 24: Fundus für den Pflichtbereich Lösungen () Die Autoren übernehmen keine Garantie für die Richtigkeit der Lösungen. Auch wurde sicher nicht immer der kürzeste und eleganteste Lösungsweg
Mathe-Abitur ab 24: Fundus für den Pflichtbereich Lösungen () Die Autoren übernehmen keine Garantie für die Richtigkeit der Lösungen. Auch wurde sicher nicht immer der kürzeste und eleganteste Lösungsweg
1 Differenzenquotient und mittlere Änderungsrate
 Schülerbuchseite 8 9 Lösungen vorläufig Differenzenquotient und mittlere Änderungsrate S. 8 a) Da der dargestellte Graph keine Gerade ist, verläuft die Temperaturzunahme nicht gleichmäßig. Temperaturzunahme
Schülerbuchseite 8 9 Lösungen vorläufig Differenzenquotient und mittlere Änderungsrate S. 8 a) Da der dargestellte Graph keine Gerade ist, verläuft die Temperaturzunahme nicht gleichmäßig. Temperaturzunahme
Konvexes Viereck Trapez Drachenviereck Parallelogramm Sehnenviereck Tangentenviereck Überraschung? Haus der Vierecke. Dr.
 Haus der Vierecke Dr. Elke Warmuth Sommersemester 2018 1 / 40 Konvexes Viereck Trapez Drachenviereck Parallelogramm Rhombus Rechteck Sehnenviereck Tangentenviereck Überraschung? 2 / 40 Wir betrachten nur
Haus der Vierecke Dr. Elke Warmuth Sommersemester 2018 1 / 40 Konvexes Viereck Trapez Drachenviereck Parallelogramm Rhombus Rechteck Sehnenviereck Tangentenviereck Überraschung? 2 / 40 Wir betrachten nur
LÖSUNGEN Kurvendiskussion
 M. Sc.Petra Clauÿ Wintersemester 2015/16 Mathematische Grundlagen und Analysis 24. November 2015 LÖSUNGEN Kurvendiskussion Aufgabe 1. Bestimmen Sie die Gleichung der Tangente an den Graphen folgender Funktionen
M. Sc.Petra Clauÿ Wintersemester 2015/16 Mathematische Grundlagen und Analysis 24. November 2015 LÖSUNGEN Kurvendiskussion Aufgabe 1. Bestimmen Sie die Gleichung der Tangente an den Graphen folgender Funktionen
13 3. a) Uhrzeit Wasseranstieg (in cm pro Stunde)
 1 Funktionen als mathematische Modelle Noch it in Dierenzialrechnung? 1 1. a) Höhenänderung zwischen 0 m und 1 00 m (in der Horizontalen): ca. 800 m 600 m = 00 m durchschnittliche Änderungsrate im Intervall
1 Funktionen als mathematische Modelle Noch it in Dierenzialrechnung? 1 1. a) Höhenänderung zwischen 0 m und 1 00 m (in der Horizontalen): ca. 800 m 600 m = 00 m durchschnittliche Änderungsrate im Intervall
4.4. Potenzfunktionen
 .. Potenzfunktionen Definition: Eine Funktion der Form f() = c z mit z \{; } heißt Potenzfunktion.... Potenzfunktionen mit positiven Eponenten (Parabeln) Schaubilder und Wertetabelle: = = - - - - - - -
.. Potenzfunktionen Definition: Eine Funktion der Form f() = c z mit z \{; } heißt Potenzfunktion.... Potenzfunktionen mit positiven Eponenten (Parabeln) Schaubilder und Wertetabelle: = = - - - - - - -
Inhalt der Lösungen zur Prüfung 2015:
 Inhalt der Lösungen zur Prüfung : Pflichtteil... Wahlteil Analysis... 8 Wahlteil Analysis... Wahlteil Analytische Geometrie/Stochastik... Wahlteil Analytische Geometrie/Stochastik... 9 Pflichtteil Lösungen
Inhalt der Lösungen zur Prüfung : Pflichtteil... Wahlteil Analysis... 8 Wahlteil Analysis... Wahlteil Analytische Geometrie/Stochastik... Wahlteil Analytische Geometrie/Stochastik... 9 Pflichtteil Lösungen
Bayern Teil 1. Aufgabe 1. Abitur Mathematik: Musterlösung. Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten:
 Abitur Mathematik: Bayern 2013 Teil 1 Aufgabe 1 a) 1. SCHRITT: DEFINITIONSMENGE BESTIMMEN Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten: 3x + 9 0 x 3 2. SCHRITT: NULLSTELLEN
Abitur Mathematik: Bayern 2013 Teil 1 Aufgabe 1 a) 1. SCHRITT: DEFINITIONSMENGE BESTIMMEN Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten: 3x + 9 0 x 3 2. SCHRITT: NULLSTELLEN
dx nf(x 0). dx f(n 1) (x 0 ) = dn
 4.3. Höhere Ableitungen, Konveität, Newtonverfahren 65 4.3 Höhere Ableitungen, Konveität, Newtonverfahren Ist f:i R differenzierbar auf einem Intervall I, so erhalten wir eine neue Funktion auf I, nämlich
4.3. Höhere Ableitungen, Konveität, Newtonverfahren 65 4.3 Höhere Ableitungen, Konveität, Newtonverfahren Ist f:i R differenzierbar auf einem Intervall I, so erhalten wir eine neue Funktion auf I, nämlich
K2 KLAUSUR 2. Aufgabe Punkte (max) Punkte. (1) Bestimmen Sie die Ableitung von f(x) = 2 x
 K2 KLAUSUR 2 PFLICHTTEIL 202 Aufgabe 2 3 4 5 6 7 8 Punkte (max) 2 2 3 3 5 3 5 3 Punkte () Bestimmen Sie die Ableitung von f(x) = 2 x 2 + 4. (2) Berechnen Sie das Integral 4 ( ) x 2 dx. (3) Lösen Sie die
K2 KLAUSUR 2 PFLICHTTEIL 202 Aufgabe 2 3 4 5 6 7 8 Punkte (max) 2 2 3 3 5 3 5 3 Punkte () Bestimmen Sie die Ableitung von f(x) = 2 x 2 + 4. (2) Berechnen Sie das Integral 4 ( ) x 2 dx. (3) Lösen Sie die
(no title) Ingo Blechschmidt. 12. Juli 2005
 (no title) Ingo Blechschmidt. Juli 5 Inhaltsverzeichnis. Hausaufgaben.......................... Hausaufgabe...................... Hausaufgabe................... 4... Hausaufgabe................... 5..4
(no title) Ingo Blechschmidt. Juli 5 Inhaltsverzeichnis. Hausaufgaben.......................... Hausaufgabe...................... Hausaufgabe................... 4... Hausaufgabe................... 5..4
ANALYTISCHE GEOMETRIE
 matheskript ANALYTISCHE GEOMETRIE und ANALYSIS 5 PFLICHT- und WAHLBEREICH.. Klasse P FHR Q Jens Möller Ausarbeitungen nach dem pdf-skript von Guenter Rau, WS Tübingen Jens Möller WS Überlingen jmoellerowingen@aol.com
matheskript ANALYTISCHE GEOMETRIE und ANALYSIS 5 PFLICHT- und WAHLBEREICH.. Klasse P FHR Q Jens Möller Ausarbeitungen nach dem pdf-skript von Guenter Rau, WS Tübingen Jens Möller WS Überlingen jmoellerowingen@aol.com
. Ihr Schaubild sei &. a) Geben Sie die Asymptoten von & an. b) Bestimmen Sie den Schnittpunkt der Tangente an & im Punkt 1 1 mit der Achse.
 Aufgabe A4/04 Gegeben ist die Funktion mit 2; 0. Das Schaubild von hat im Punkt 1 die Tangente. Ermitteln Sie eine Gleichung von. Die Tangente schneidet die Achse im Punkt. Bestimmen Sie die Koordinaten
Aufgabe A4/04 Gegeben ist die Funktion mit 2; 0. Das Schaubild von hat im Punkt 1 die Tangente. Ermitteln Sie eine Gleichung von. Die Tangente schneidet die Achse im Punkt. Bestimmen Sie die Koordinaten
4 x x kleinste6 Funktionswert für alle x aus einer Umgebung von x 1 ist.
 Differenzialrechnung 51 1.2.2 Etrempunkte Die Funktion f mit f () = 1 12 3 7 4 2 + 10 + 17 3 beschreibt näherungsweise die wöch entlichen Verkaufszahlen von Rasenmähern. Dabei ist die Zeit in Wochen nach
Differenzialrechnung 51 1.2.2 Etrempunkte Die Funktion f mit f () = 1 12 3 7 4 2 + 10 + 17 3 beschreibt näherungsweise die wöch entlichen Verkaufszahlen von Rasenmähern. Dabei ist die Zeit in Wochen nach
Vektoren, Skalarprodukt, Ortslinien
 .0 Gegeben sind die Punkte A(0/-4), C(0/4), sowie die Pfeile mit α [ 90 ; 90 ]. 4cosα AB = 4sinα+ 4. Zeichne die drei Punkte B, B und B 3 mit α { 30;0;30 } in ein KOS.. Zeige: 4cosα CB =. 4sinα 4.3 Zeige,
.0 Gegeben sind die Punkte A(0/-4), C(0/4), sowie die Pfeile mit α [ 90 ; 90 ]. 4cosα AB = 4sinα+ 4. Zeichne die drei Punkte B, B und B 3 mit α { 30;0;30 } in ein KOS.. Zeige: 4cosα CB =. 4sinα 4.3 Zeige,
1 2 x x. 1 2 x 4
 S. Potenzfunktionen mit rationalen Exponenten und ihre Ableitung Zuordung f(x) = x g(x) = x h(x) = x k(x) = x p(x) = x 0, q(x) = x r(x) = x s(x) = x, 6 7 Wurzelfunktionen a) f(x) = x + D = [ ; [ f '(x)
S. Potenzfunktionen mit rationalen Exponenten und ihre Ableitung Zuordung f(x) = x g(x) = x h(x) = x k(x) = x p(x) = x 0, q(x) = x r(x) = x s(x) = x, 6 7 Wurzelfunktionen a) f(x) = x + D = [ ; [ f '(x)
Lösungsblatt zu: Gebrochen rationale, Exponential- und Logarithmus Funktionen
 Lösungsblatt zu: Gebrochen rationale, Exponential- und Logarithmus Funktionen Das hast du schon gelernt: Aufgabe : a) Definitionsbereich TIPP: Definitionsbereich Nenner darf nicht Null werden x 0 x
Lösungsblatt zu: Gebrochen rationale, Exponential- und Logarithmus Funktionen Das hast du schon gelernt: Aufgabe : a) Definitionsbereich TIPP: Definitionsbereich Nenner darf nicht Null werden x 0 x
Klasse11 Übungsblatt1 zu: Geraden, Steigung von Funktionsgraphen,Tangenten,Normalen
 Klasse Übungsblatt zu: Geraden, Steigung von Funktionsgraphen,Tangenten,Normalen Aufgabe: Gegeben sind die Punkte A und B und die Zahl m a) Bestimme die Gleichung der Geraden g durch A und B b) Bestimme
Klasse Übungsblatt zu: Geraden, Steigung von Funktionsgraphen,Tangenten,Normalen Aufgabe: Gegeben sind die Punkte A und B und die Zahl m a) Bestimme die Gleichung der Geraden g durch A und B b) Bestimme
ANALYTISCHE GEOMETRIE
 matheskript ANALYTISCHE GEOMETRIE und ANALYSIS PFLICHTBEREICH Teil A. Klasse ABI 08 Jens Möller Autor: Jens Möller 88 696 Owingen Tel. 0755-6889 jmoellerowingen@aol.com 8. erweiterte Auflage Owingen, Juli
matheskript ANALYTISCHE GEOMETRIE und ANALYSIS PFLICHTBEREICH Teil A. Klasse ABI 08 Jens Möller Autor: Jens Möller 88 696 Owingen Tel. 0755-6889 jmoellerowingen@aol.com 8. erweiterte Auflage Owingen, Juli
Ü b u n g s a r b e i t
 Ü b u n g s a r b e i t Aufgabe. a) Die Querschnittsfläche eines Abwasserkanals ist im unteren Teil von einer Parabel k begrenzt, an die sich nach oben die beiden Geraden g und h anschließen. Bestimmen
Ü b u n g s a r b e i t Aufgabe. a) Die Querschnittsfläche eines Abwasserkanals ist im unteren Teil von einer Parabel k begrenzt, an die sich nach oben die beiden Geraden g und h anschließen. Bestimmen
Korrekturblatt zu 3206 / 6. Auflage 2014
 Korrekturblatt zu 306 / 6. Auflage 014 Lehrbuch Seite 56 3. c) g() = f() + 4 G K 1 1 3 4 Lehrbuch Seite 109 9. Eine Gleichung 3. Grades lasst sich grafisch durch den Graph einer Polnomfunktion 3. Grades
Korrekturblatt zu 306 / 6. Auflage 014 Lehrbuch Seite 56 3. c) g() = f() + 4 G K 1 1 3 4 Lehrbuch Seite 109 9. Eine Gleichung 3. Grades lasst sich grafisch durch den Graph einer Polnomfunktion 3. Grades
5.3. Abstrakte Anwendungsaufgaben
 Aufgabe.. Abstrakte Anwendungsaufgaben In den Raum zwischen der x-achse und dem Graphen von f(x) = x x + soll ein Rechteck möglichst großer Fläche gelegt werden, dessen Ecken auf dem Graphen liegen. Wie
Aufgabe.. Abstrakte Anwendungsaufgaben In den Raum zwischen der x-achse und dem Graphen von f(x) = x x + soll ein Rechteck möglichst großer Fläche gelegt werden, dessen Ecken auf dem Graphen liegen. Wie
1.3 Berechnen Sie die Koordinaten der Wendepunkte des Schaubildes der Funktion f mit f( x) x 6x 13
 Musteraufgaben ab 08 Pflichtteil Aufgabe Seite / BEISPIEL A. Geben Sie Lage und Art der Nullstellen der Funktion f mit f( x) ( x ) ( x ) ; x IR an.. Bestimmen Sie die Gleichung der Tangente in P( f ())
Musteraufgaben ab 08 Pflichtteil Aufgabe Seite / BEISPIEL A. Geben Sie Lage und Art der Nullstellen der Funktion f mit f( x) ( x ) ( x ) ; x IR an.. Bestimmen Sie die Gleichung der Tangente in P( f ())
( 0 ( x) d) Die Funktionsgleichung der Funktion 1 lautet: f( Für x 2 = 0 : Wähle die Werte -1 und 1. Überprüfe x1 = 1,
 Differentialrechnung IV (Wendepunkte) (Kap 7) (Haben Sie Probleme bei der Bearbeitung dieser Aufgaben versuchen Sie diese in Ihrer Kleingruppe mit Hilfe des Arbeitsbuchs Mathematik zu klären Führt dies
Differentialrechnung IV (Wendepunkte) (Kap 7) (Haben Sie Probleme bei der Bearbeitung dieser Aufgaben versuchen Sie diese in Ihrer Kleingruppe mit Hilfe des Arbeitsbuchs Mathematik zu klären Führt dies
8 5 9 : 8 5 ; 0 85<8. 8 : 8 0 > 1 Der Schnittpunkt mit der x-achse ist? 1 0.
 Aufgabe M04A1 Gegeben ist die Funktion mit. Ein Teil des Graphen ist abgebildet. a) Geben Sie die maximale Definitionsmenge von und Gleichungen der Asymptoten von an. besitzt einen Schnittpunkt mit der
Aufgabe M04A1 Gegeben ist die Funktion mit. Ein Teil des Graphen ist abgebildet. a) Geben Sie die maximale Definitionsmenge von und Gleichungen der Asymptoten von an. besitzt einen Schnittpunkt mit der
5.3. Aufgaben zur Kurvenuntersuchung ganzrationaler Funktionen
 .. Aufgaben zur Kurvenuntersuchung ganzrationaler Funktionen Aufgabe : Kurvendiskussion Untersuche die folgenden Funktionen auf Symmetrie, Achsenschnittpunkte, Etrem- und Wendepunkte und zeichne ein Schaubild
.. Aufgaben zur Kurvenuntersuchung ganzrationaler Funktionen Aufgabe : Kurvendiskussion Untersuche die folgenden Funktionen auf Symmetrie, Achsenschnittpunkte, Etrem- und Wendepunkte und zeichne ein Schaubild
Analysis: Klausur Analysis
 Analysis Klausur zu Extrempunkten, Interpretation von Graphen von Ableitungsfunktionen, Tangenten und Normalen, Extremwertaufgaben (Bearbeitungszeit: 90 Minuten) Gymnasium J Alexander Schwarz www.mathe-aufgaben.com
Analysis Klausur zu Extrempunkten, Interpretation von Graphen von Ableitungsfunktionen, Tangenten und Normalen, Extremwertaufgaben (Bearbeitungszeit: 90 Minuten) Gymnasium J Alexander Schwarz www.mathe-aufgaben.com
Stammfunktionen ermitteln
 Stammfunktionen ermitteln Aufgabe ) Ermittle die Stammfunktionen der folgenden Funktionen!. f() = 3. f() = 8³ 3. f() = ² +. f() = 3² + + 5. f() = 6-3 5 + 7³ 6. f() = ²/3 + / 7. f() = / - 3² + /3 8. f()
Stammfunktionen ermitteln Aufgabe ) Ermittle die Stammfunktionen der folgenden Funktionen!. f() = 3. f() = 8³ 3. f() = ² +. f() = 3² + + 5. f() = 6-3 5 + 7³ 6. f() = ²/3 + / 7. f() = / - 3² + /3 8. f()
K A N T O N S S C H U L E I M L E E MATHEMATIK. Grafiktaschenrechner ohne CAS, beliebige Formelsammlung
 K A N T O N S S C H U L E I M L E E W I N T E R T H U R MATURITÄTSPRÜFUNGEN 06 Klasse: 4g Profil: MN Lehrperson: Rolf Kleiner MATHEMATIK Zeit: 3 Stunden Erlaubte Hilfsmittel: Grafiktaschenrechner ohne
K A N T O N S S C H U L E I M L E E W I N T E R T H U R MATURITÄTSPRÜFUNGEN 06 Klasse: 4g Profil: MN Lehrperson: Rolf Kleiner MATHEMATIK Zeit: 3 Stunden Erlaubte Hilfsmittel: Grafiktaschenrechner ohne
1. Fall: 2. Fall: Lösungsblatt zu: Differentialquotient. Tipp: Nullstellen. Tipp: Es reicht, wenn einer der Faktoren Null wird.
 Lösungsblatt zu: Differentialquotient Aufgabe 1: Gegeben: f(x) = 0,5x 3 1,5x² a) Bestimmen Sie die Nullstellen: Nullstellen f(x) = 0 0,5x 3 1,5x 2 = 0 ( 0,5x 2 ausklammern) 0,5x 2 (x + 3) = 0 Es reicht,
Lösungsblatt zu: Differentialquotient Aufgabe 1: Gegeben: f(x) = 0,5x 3 1,5x² a) Bestimmen Sie die Nullstellen: Nullstellen f(x) = 0 0,5x 3 1,5x 2 = 0 ( 0,5x 2 ausklammern) 0,5x 2 (x + 3) = 0 Es reicht,
Wurzelfunktionen Aufgaben
 Wurzelfunktionen Aufgaben. Für jedes k (k > 0) ist die Funktion f k (x) = 8 (x k ) kx, 0 x gegeben. a) Untersuchen Sie die Funktion f k auf Nullstellen und Extrema. Ermitteln Sie lim f k(x) sowie für 0
Wurzelfunktionen Aufgaben. Für jedes k (k > 0) ist die Funktion f k (x) = 8 (x k ) kx, 0 x gegeben. a) Untersuchen Sie die Funktion f k auf Nullstellen und Extrema. Ermitteln Sie lim f k(x) sowie für 0
( ) 6 eine. 1. Führen Sie für die Funktion f mit vollständige Kurvendiskussion durch. eine. 5. Führen Sie für die Funktion f mit f ( x) = 2x
 . Führen Sie für die Funktion f mit vollständige Kurvendiskussion durch. Berücksichtigen Sie dabei die folgenden Punkte: f( ) 0 7 eine -Definitionsmenge; -Symmetrie; -Grenzwertverhalten; -Schnittpunkt
. Führen Sie für die Funktion f mit vollständige Kurvendiskussion durch. Berücksichtigen Sie dabei die folgenden Punkte: f( ) 0 7 eine -Definitionsmenge; -Symmetrie; -Grenzwertverhalten; -Schnittpunkt
Lösung - Serie 2. D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger Welche der folgenden Funktionen ( 1, 1) R sind strikt monoton wachsend?
 D-MAVT/D-MATL Analysis I HS 07 Dr. Andreas Steiger Lösung - Serie.. Welche der folgenden Funktionen (, R sind strikt monoton wachsend? (a (b (c + 3 (d e (e (f arccos Keine. Auf (, 0] ist strikt monoton
D-MAVT/D-MATL Analysis I HS 07 Dr. Andreas Steiger Lösung - Serie.. Welche der folgenden Funktionen (, R sind strikt monoton wachsend? (a (b (c + 3 (d e (e (f arccos Keine. Auf (, 0] ist strikt monoton
11 Üben X Affine Funktionen 1.01
 Üben X Aine Funktionen.0 Zeichne die Graphen zu olgenden Funktionsgleichungen! + + d c b a Augabenkarte von MUED Lösung X Aine Funktionen.0 + + d c b a Üben X Aine Funktionen.0 Bestimme die Funktionsgleichung
Üben X Aine Funktionen.0 Zeichne die Graphen zu olgenden Funktionsgleichungen! + + d c b a Augabenkarte von MUED Lösung X Aine Funktionen.0 + + d c b a Üben X Aine Funktionen.0 Bestimme die Funktionsgleichung
Serie 4: Flächeninhalt und Integration
 D-ERDW, D-HEST, D-USYS Mathematik I HS 5 Dr. Ana Cannas Serie 4: Flächeninhalt und Integration Bemerkung: Die Aufgaben dieser Serie bilden den Fokus der Übungsgruppen vom. und 4. Oktober.. Das Bild zeigt
D-ERDW, D-HEST, D-USYS Mathematik I HS 5 Dr. Ana Cannas Serie 4: Flächeninhalt und Integration Bemerkung: Die Aufgaben dieser Serie bilden den Fokus der Übungsgruppen vom. und 4. Oktober.. Das Bild zeigt
Mittlere-Reife-Prüfung 2007 Mathematik I Aufgabe B2
 Seite http://www.realschulrep.de/ Seite 2 Mittlere-Reife-Prüfung 2007 Mathematik I Aufgabe B2 Aufgabe B2. Der Punkt A 2 2 ist gemeinsamer Eckpunkt von Rauten A B n C n D n. Die Eckpunkte B n 3 liegen auf
Seite http://www.realschulrep.de/ Seite 2 Mittlere-Reife-Prüfung 2007 Mathematik I Aufgabe B2 Aufgabe B2. Der Punkt A 2 2 ist gemeinsamer Eckpunkt von Rauten A B n C n D n. Die Eckpunkte B n 3 liegen auf
5.5. Abituraufgaben zu ganzrationalen Funktionen
 .. Abituraufgaben zu ganzrationalen Funktionen Aufgabe : Kurvendiskussion, Fläche zwischen zwei Schaubildern () Untersuchen Sie f(x) x x und g(x) x auf Symmetrie, Achsenschnittpunkte, Extrempunkts sowie
.. Abituraufgaben zu ganzrationalen Funktionen Aufgabe : Kurvendiskussion, Fläche zwischen zwei Schaubildern () Untersuchen Sie f(x) x x und g(x) x auf Symmetrie, Achsenschnittpunkte, Extrempunkts sowie
Aufgaben zur e-funktion
 Aufgaben zur e-funktion 1.0 Gegeben ist die reelle Funktion f(x) = 2x 2x e 1 x2 mit x R (Abitur 2000 AII). 1.1 Untersuchen Sie das Symmetrieverhalten des Graphen der Funktion f und bestimmen Sie die Nullstellen
Aufgaben zur e-funktion 1.0 Gegeben ist die reelle Funktion f(x) = 2x 2x e 1 x2 mit x R (Abitur 2000 AII). 1.1 Untersuchen Sie das Symmetrieverhalten des Graphen der Funktion f und bestimmen Sie die Nullstellen
= und t ( 2) = f (2) = ergibt sich die Tangentengleichung
 Lösungen Nr. a b c d e f '( = x x f ''( = x 8 6 8 f '( = 0... x = 0 x = 4 Damit ergeben sich wegen ''(0) = < 0 8 f ''(4) = > 0 ein Tiefpunkt T ( 4 0). 8 f ''( = x = 0 x = 6 8 Wegen f '''( = ist f '''()
Lösungen Nr. a b c d e f '( = x x f ''( = x 8 6 8 f '( = 0... x = 0 x = 4 Damit ergeben sich wegen ''(0) = < 0 8 f ''(4) = > 0 ein Tiefpunkt T ( 4 0). 8 f ''( = x = 0 x = 6 8 Wegen f '''( = ist f '''()
Mathematik GK m1/m2/m3, 2. Kl. Funktionenuntersuchung Lösung A
 Aufgabe 1: Kurvendiskussion Führe eine vollständige Funktionsuntersuchung für die Funktion f x = 1 2 x5 1 4 x4 3 2 x3 durch. Dazu gehören alle Teilaufaben, wie sie im Unterricht besprochen wurden und auf
Aufgabe 1: Kurvendiskussion Führe eine vollständige Funktionsuntersuchung für die Funktion f x = 1 2 x5 1 4 x4 3 2 x3 durch. Dazu gehören alle Teilaufaben, wie sie im Unterricht besprochen wurden und auf
Mathematik im Berufskolleg II
 Bohner Ott Deusch Mathematik im Berufskolleg II Ausführliche Lösungen zu im Buch gekennzeichneten Aufgaben ab 6. Auflage 6 ISBN 978--8-- Das Werk und seine Teile sind urheberrechtlich geschützt. Jede Nutzung
Bohner Ott Deusch Mathematik im Berufskolleg II Ausführliche Lösungen zu im Buch gekennzeichneten Aufgaben ab 6. Auflage 6 ISBN 978--8-- Das Werk und seine Teile sind urheberrechtlich geschützt. Jede Nutzung
Vollständige Kurvendiskussion mit Erläuterungen
 Vollständige Kurvendiskussion mit Erläuterungen Aufgabe: Gegeben ist die Funktion =³ 3 +. Führen Sie eine vollständige Kurvendiskussion durch. 1.) Ableitungen: =3 6+1 =6 6 =6 (relevant für die Steigung
Vollständige Kurvendiskussion mit Erläuterungen Aufgabe: Gegeben ist die Funktion =³ 3 +. Führen Sie eine vollständige Kurvendiskussion durch. 1.) Ableitungen: =3 6+1 =6 6 =6 (relevant für die Steigung
Konvexes Viereck Trapez Drachenviereck Parallelogramm Sehnenviereck Tangentenviereck. Haus der Vierecke. Dr. Elke Warmuth. Sommersemester 2018
 Haus der Vierecke Dr. Elke Warmuth Sommersemester 2018 1 / 39 Konvexes Viereck Trapez Drachenviereck Parallelogramm Rhombus Rechteck Sehnenviereck Tangentenviereck 2 / 39 Wir betrachten nur konvexe Vierecke:
Haus der Vierecke Dr. Elke Warmuth Sommersemester 2018 1 / 39 Konvexes Viereck Trapez Drachenviereck Parallelogramm Rhombus Rechteck Sehnenviereck Tangentenviereck 2 / 39 Wir betrachten nur konvexe Vierecke:
Technische Universität Dresden, Fakultät Mathematik Prof. Dr. F. Schuricht, Dr. M. Herrich. der Übungsaufgaben zum Brückenkurs Mathematik 2018
 Technische Universität Dresden, Fakultät Mathematik Prof. Dr. F. Schuricht, Dr. M. Herrich E R G E B N I S S E der Übungsaufgaben zum Brückenkurs Mathematik 08 Ergebnisse zur. Übung am.09.08 Thema: Logik,
Technische Universität Dresden, Fakultät Mathematik Prof. Dr. F. Schuricht, Dr. M. Herrich E R G E B N I S S E der Übungsaufgaben zum Brückenkurs Mathematik 08 Ergebnisse zur. Übung am.09.08 Thema: Logik,
 Haupttermin Pflichtteil - Aufgaben Aufgabe : ( VP) Bilden Sie die Ableitung der Funktion f mit Aufgabe : ( VP) f() 3 e =. Bestimmen Sie eine Stammfunktion der Funktion f mit Aufgabe 3: (3 VP) 5 3 Lösen
Haupttermin Pflichtteil - Aufgaben Aufgabe : ( VP) Bilden Sie die Ableitung der Funktion f mit Aufgabe : ( VP) f() 3 e =. Bestimmen Sie eine Stammfunktion der Funktion f mit Aufgabe 3: (3 VP) 5 3 Lösen
Mathematik I Pflichtteil - Nachtermin Aufgabe P 1. Klasse: Platzziffer: Punkte:
 Prüfungsdauer: Abschlussprüfung 2006 150 Minuten an den Realschulen in Bayern R4/R6 Mathematik I Pflichtteil - Nachtermin Aufgabe P 1 Name: Vorname: Klasse: Platzziffer: Punkte: P 1.0 Gegeben sind der
Prüfungsdauer: Abschlussprüfung 2006 150 Minuten an den Realschulen in Bayern R4/R6 Mathematik I Pflichtteil - Nachtermin Aufgabe P 1 Name: Vorname: Klasse: Platzziffer: Punkte: P 1.0 Gegeben sind der
Abitur 2013 Mathematik Infinitesimalrechnung II
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 213 Mathematik Infinitesimalrechnung II Teilaufgabe Teil 1 1 (5 BE) Geben Sie für die Funktion f mit f(x) = ln(213 x) den maximalen Definitionsbereich
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 213 Mathematik Infinitesimalrechnung II Teilaufgabe Teil 1 1 (5 BE) Geben Sie für die Funktion f mit f(x) = ln(213 x) den maximalen Definitionsbereich
Bayern Musterlösung zu Klausur Analysis, Aufgabengruppe I
 Diese Lösung wurde erstellt von Tanja Reimbold. Sie ist keine offizielle Lösung des Bayerischen Staatsministeriums für Unterricht und Kultus. Teil 1 Aufgabe 1 Definitionsbereich: Bestimmung der Nullstelle
Diese Lösung wurde erstellt von Tanja Reimbold. Sie ist keine offizielle Lösung des Bayerischen Staatsministeriums für Unterricht und Kultus. Teil 1 Aufgabe 1 Definitionsbereich: Bestimmung der Nullstelle
Tutorium Mathematik I M WM Lösungen
 Tutorium Mathematik I M WM Lösungen 3... Durch mehrmaliges Anwenden der Regel von de l Hospital ergibt sich: e e sin() e cos()e sin() sin() cos() e + sin()e sin() cos ()e sin() sin() e + cos()e sin() +
Tutorium Mathematik I M WM Lösungen 3... Durch mehrmaliges Anwenden der Regel von de l Hospital ergibt sich: e e sin() e cos()e sin() sin() cos() e + sin()e sin() cos ()e sin() sin() e + cos()e sin() +
Abitur 2017 Mathematik Infinitesimalrechnung I
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung I Gegeben ist die Funktion g : x 2 4 + x 1 mit maximaler Definitionsmenge D g. Der Graph von g wird mit G g bezeichnet.
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung I Gegeben ist die Funktion g : x 2 4 + x 1 mit maximaler Definitionsmenge D g. Der Graph von g wird mit G g bezeichnet.
Lösungen zu delta 6. Kann ich das noch? Lösungen zu den Seiten 6 und 7
 Kann ic das noc? Lösungen zu den Seiten 6 und 7. a) L = { ; } b) L = {0; } c) L = {} d) ( + )( + ) = 0; L = { ; } e) ( 6)( ) = 0; L = {; 6} f) L = {0}; 0,7 G g) ( 8)( + ) = 0; L = { ; 8} ) ( + )( + ) =
Kann ic das noc? Lösungen zu den Seiten 6 und 7. a) L = { ; } b) L = {0; } c) L = {} d) ( + )( + ) = 0; L = { ; } e) ( 6)( ) = 0; L = {; 6} f) L = {0}; 0,7 G g) ( 8)( + ) = 0; L = { ; 8} ) ( + )( + ) =
Abitur 2010 Mathematik GK Infinitesimalrechnung I
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 2010 Mathematik GK Infinitesimalrechnung I Teilaufgabe 2 (4 BE) Gegeben ist für k R + die Schar von Funktionen f k : x 1 Definitionsbereich D k. Der
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 2010 Mathematik GK Infinitesimalrechnung I Teilaufgabe 2 (4 BE) Gegeben ist für k R + die Schar von Funktionen f k : x 1 Definitionsbereich D k. Der
