Skript zur Vorlesung Baustatik II
|
|
|
- Dirk Gehrig
- vor 7 Jahren
- Abrufe
Transkript
1 BS III Skript zur Vorlesung Baustatik II an der Hochschule Augsburg Hochschule für angewandte Wissenschaften University of Applied Sciences Prof. Dr.-Ing. Gerhard Zirwas
2 BS III Inhalt I. Wiederholungen 3 A. Wiederholung aus TM 1 3 B. Gelenkträger 4 C. Ausnutzung von Symmetrieeigenschaften 5 II. Differentialbeziehungen der Baustatik 7 A. Differentialbeziehungen der Baustatik für Kraftgrößen 7 B. Beispiele C. Differentialbeziehungen der Baustatik für Kraft- und Weggrößen 8 D. Beispiele III. Prinzip virtueller Verschiebungen 11 A. Starre Systeme B. Elsatische Systeme IV. Verformungen und Arbeitssätze 15 A. Arbeiten mit Integraltafeln 16 B. Beispiele Einfeldträger mit Streckenlast Einhüftiger gelenkiger Rahmen mit Streckenlast 21 V. Statisch unbestimmte Rechnung 26 A. Anwendung des Arbeitssatzes bei statisch unbestimmten Systemen 27 B. Beispiele Einfach statisch unbestimmtes System Beispiel: 2-fach statisch unbestimmtes System 32 VI. Stabilität 37 A. Stabilität und TH II 37
3 3/40 BS III I. Wiederholungen A. Wiederholung aus TM Auflagerkräfte Gleichgewichtsbedingungen: Summe der horizontalen Kräfte = 0 Σ H = 0 Summe der vertikalen Kräfte = 0 Σ V = 0 Summe der Momente = 0 Σ M = Schnittgrößen Vorzeichenregel: + N + Q + M + M + N + Q 1.3 Statische Bestimmtheit von Fachwerken: n = s + a - 2k dabei gilt: wenn n = 0, dann ist das System statisch bestimmt. Es bedeuten: n Grad der statischen Unbestimmtheit s Anzahl der Fachwerkstäbe a Anzahl aller Auflagerbedingungen k Anzahl aller Knoten von Stabwerken: n = 3s - a - g dabei gilt: wenn n = 0, dann ist das System statisch bestimmt Es bedeuten: n Grad der statischen Unbestimmtheit s Anzahl der Scheiben a Anzahl aller Auflagerbedingungen g Anzahl der Gelenkkräfte
4 4/40 BS III B. Gelenkträger Ein Gelenkträger ist ein über mehrere Auflager durchlaufender Träger, der an geeigneten Stellen durch Gelenke unterbrochen ist. Die Zerlegung des Systems ermöglicht die Berechnung der Auflagerkräfte an jedem Teilsystem mit Hilfe der Gleichgewichtsbedingungen. Anschließend können mit gewohnter Vorgehensweise die Schnittgrößen ermittelt werden. Dadurch ergeben sich statisch bestimmbare Teilträger. Ausgangssystem: Zerlegung des Systems: Gelenkkräfte: Gelenkkräfte Teilsystem 1 Teilsystem 2 [s. Übungsaufgabe A01 ]
5 5/40 BS III Beispiel: Berechnung von Schnittgrößen q= 5 kn/m q= 7 kn/m 2 m 2 m 1 m 1 m Q M
6 6/40 BS III C. Ausnutzung von Symmetrieeigenschaften Die Berechnung statischer Größen vereinfacht sich, wenn ein zu einer Mittellinie symmetrisches System vorliegt und für ein solches System eine symmetrische oder antimetrische Belastung gegeben ist. Zur Wahrung der Symmetrie wird die Zugfaser zur Definition der Vorzeichen der Schnittgrößen symmetrisch zur Mittellinie gelegt. Wie mit Hilfe von Gleichgewichtsbedingungen für das Gesamtsystem und für entsprechend herausgeschnittene Teilsysteme nachgeprüft werden kann, ergit sich in diesem Falle folgendes: Symmetrisches System symmetrische Belastung A B A v = B v A H = B H N li = N re M li = M re V li = -V re Symmetrisches System antimetrische Belastung A B A v = -B v A H = -B H N li = -N re M li = -M re V li = V re Sonderfälle I.) Bei unterschiedlich ausgebildeten Auflagern A H = 0 A B A H = 0 A B Die unter I.) dargestellten Systeme sind wegen der unterschiedlich ausgebildeten Auflager A und B zwar nicht symmetrisch zur Mittelline. Da jedoch AH gleich null ist (wenn nur vertikale Lasten angreifen oder horizontale Kräfte gleich groß sind) können die Systeme für die dargestellten Lastfälle wie symmetrische Systeme behandelt werden.
7 7/40 BS III II.) Bei Einzellasten die an der Mittellinie vom Stabwerk angreifen A H = 0 A B Eine Einzellast, die in der Mittellinie wirkt, wie es unter II.) dargestellt ist, ist eine symmetrische Bealstung. III.) Bei Einzellasten die senkrecht zur Mittellinie wirkend mittig am Stabwerk angreifen, sowie ein mittig am Stabwerk angreifendes Lastmoment A H = 0 A B A B Bei Einzellasten die senkrecht zur Mittellinie wirkend mittig am Stabwerk angreifen, sowie ein mittig am Stabwerk angreifendes Lastmoment ergeben jeweils eine antimetrische Belastung IV.) In Mittellinie liegender Stab mit symmetrischer Belastung A Eine symmetrische Belastung liefert für einen in der Mittellinie liegenden Stab V=0 und M=0, für ein in der Mittellinie liegendes Auflager sind die senkrecht zur Mittellinie wirkende Auflagerjkraft und das Einspannmoment gleich null.
8 8/40 BS III II. Differentialbeziehungen der Baustatik A. Differentialbeziehungen Schnitt am differentiellen Element dx R = dx
9 9/40 BS III II. Differentialbeziehungen der Baustatik A. Differentialbeziehungen der Baustatik für Kraftgrößen Kraftgrößen: N(x), q(x), σ(x) A σ N σ(x) = N A... Spannung Spannung: - Spannung ist die auf die Fläche A bezogene Normalkraft N - ein Maß für die Materialbeanspruchung GG am Element: q(x) N dx N + dn Σ H = 0: dn = - q(x) dx N = - q(x)
10 10/40 BS III Kraftgrößen: Weggrößen: Verformungen A σ Vorher: dx 1 2 N x 1 x2 B. Differentialbeziehungen der Baustatik für Kraft- und Weggrößen N(x), q(x), σ(x) u(x)... Verschiebung eines Punktes u 1 u 2 σ(x) = N A... Spannung Belastet: dx + du 1 2 Spannung: - Spannung ist die auf die Fläche A bezogene Normalkraft N - ein Maß für die Materialbeanspruchung u 1 u 2 GG am Element: q(x) x 2 = x 1 + dx u 2 = u 1 + du du = u 2 - u 1...Längenänderung des Elements N dx Σ H = 0: dn = - q(x) dx N + dn u (x) = du dx =: ε(x)... Dehnung N = - q(x) Dehnung: - Dehnung ist die auf die Ausgangslänge dx bezogene Längenänderung du
11 11/40 BS III Materialgesetz: Zusammenhang σ ε ε = σ E { + α T T { σ. σ= E ε ε = ε σ + ε T Dehnung infolge: Spannung Temperatur ε E... Elastizitätsmodul α T... Temperaturdehnungskoeffizient Einsetzen: u (x) = ε(x) = N(x) EA + α T T Ableiten für den Fall T = const. führt zur DGL 2. Ordnung des längsbeanspruchten Stabes: EA u (x) = -q(x) Lösung durch Integration und Bestimmung der Integrationskonstanten.
12 12/40 BS III B. Beispiele Gegeben: Statisch bestimmt gelagerter Stab EA = const q(x) = qo x/l qo a x L b Gesucht: - Auflagerreaktionen - Schnittkräfte - Verformungen u(x)
13 13/40 BS III III. Prinzip virtueller Verschiebungen Das aus der Mechanik bekannte Prinzip lautet: Ein Körper oder Körpersystem befindet sich im Gleichgewicht, wenn infolge einer virtuellen, d.h. mit den Bewegungsmöglichkeiten verträglichen (kleinen) Verrückung die Gesamtarbeit aller am System wirkenden Kräfte gleich Null ist. Dabei ist es gleichgültig, wodurch die virtuelle Verrückung hervorgerufen wird. Bei einem statischen System kann man z.b. eine virtuelle Verrückung erzeugen, indem eine innere Fessel / Auflagerfessel "geschnitten" wird und das System dadurch einen zusätzlichen Freiheitsgrad erhält. Dem jetzt labilen System kann an einer Stelle eine mögliche virtuelle Verschiebung eingeprägt werden, ohne die einzelnen Systemteile zu deformieren. Unter Betrachtung der Lagerung und der Gelenkstellen ergeben sich aus rein geometrischen Beziehungen zwangsläufig die Verschiebungen aller anderen Punkte eines Systems. Für den Gleichgewichtszustand muss die Summe der Arbeit aller am System wirkenden Kraftgrößen an der virtuellen Verrückung (virtuelle Arbeit) gleich Null sein. δ W = Kraft * virtuelle Verschiebung bzw. Moment * virtuelle Verdrehung = 0 Auf diese Weise kann man Auflagerreaktionen und Schnittgrößen statisch bestimmter Systeme ermitteln. Es handelt sich beim Prinzip der virtuellen Arbeit um ein unabhängigen Gleichgewichts-Prinzip.
14 14/40 BS III Beispiel: Brücke F1 F2 Lösung: 1. Abzählkriterium 2. s = a = g = n = 3. Virtuelle Verschiebungsfigur F1 F2 4. Virtuelle Arbeit δ W = [s. Übungsaufgaben A02]
15 15/40 BS III IV. Verformungen und Arbeitssätze VORGEHEN: 1. Am Ort und in Richtung der gesuchten Verformungsgröße wird eine virtuelle Hilfskraft mit der Größe 1kN bzw. 1 knm (Einzelkraft, Einzelmoment, Doppelkraft oder Doppelmoment) aufgebracht. Aus dieser Belastung ergeben sich virtuelle Schnittgrößen, die Stabkräfte usw. 2. Die tatsächliche Belastung (F, p, T, ΔT) wird aufgebracht mit realen Verzerrungen usw. ("tatsächlicher Lastzustand") 3. Die Anwendung des Arbeitssatzes liefert die gesuchte Verschiebungsgröße ARBEITSGLEICHUNG: (L) (L) (L) (L) analog ohne Ableitung Torsion (Fachwerkstäbe) (F = Federkraft) (Mφ = Moment in der Drehfeder) Dabei sind: Summe über alle Stäbe; Länge des Einzelstabes Schnittgrößen aus den realen äußeren Belastungen Schnittgrößen aus den virtuellen Kräften 1 Bemerkung: Bei konstanten EA und EI kann die Auswertung der Integrale mit Hilfe einer Integraltafel ausgeführt werden (s. Seite 15). L
16 Integraltafel Hochschule Augsburg - Fakultät A+B - Studiengang: Bauingenieurwesen 16/40 BS III B. Arbeiten mit Integraltafeln
17 17/40 BS III C. Beispiele 1. Einfeldträger mit Streckenlast Gegeben: EI = 733,4 knm 2 Gesucht: Durchbiegung in Feldmitte q = 2,5 kn/m EI 3,6 m Lösungsschritte: 1. Virtueller Zustand 1 EI M 2. Realer Zustand EI M
18 18/40 BS III 3. Berechnen des Arbeitssatzes unter Verwendung z.b. einer Integraltafel l [s. Übungsaufgaben A02-A06 ]
19 19/40 BS III 1.1 Lösung / Beispiel: Einfeldträger mit Streckenlast [Schritt-für-Schritt Anleitung für Bsp 1] Beispiel: Durchbiegung in Feldmitte [EI = 733,4 knm 2 ] q = 2,5 kn/m EI 3,6 m 1.Virtuelle Last 1 wird in Feldmitte in Richtung der Verformungsgröße aufgebracht. 1 EI 2. Schnittgrößen des realen und virtuellen Zustands ermitteln. Realer Zustand: (Einwirkung aller tatsächlicher Belastungen aus dem Ausgangssystem) Virtueller Zusatnd: (Einwirkung der Lastgröße 1) Virtueller Zustand: 1 EI M M [knm] = 0,9 knm Realer Zusatnd: EI M M [knm] = 4,05 knm
20 20/40 BS III 3. Berechnen des Arbeitssatzes unter Verwendung z.b. einer Integraltafel Die Anwendung des Arbeitssatzes/der Arbeitsgleichung liefert die gesuchte Verschiebungsgröße f. l (L) L Ll s. Integraltafel 7 7 Um die Integrale, die sich aus der Arbeitsgleichung ergeben, einfacher lösen zu können, kann man die auf Seite 9 dargestellte Integraltafel benutzen. Dabei ist darauf zu achten, dass die in der Tabelle aufgelisteten Werte noch mit der Länge L zu multiplizieren sind.
21 21/40 BS III 2. Einhüftiger gelenkiger Rahmen mit Streckenlast Gegeben: q= 8 kn/m EA Gesucht: Die Schnittgrößen Lösungsschritte: 1. Realer LF q F M
22 22/40 BS III 2. Virtueller LF 1 M
23 23/40 BS III 3. Berechnen des Arbeitssatzes unter Verwendung z.b. einer Integraltafel l 4. Sonderfall f = 0 5. Ergebnis M
24 24/40 BS III 2.1 Lösung / Beispiel: Einhüftiger gelenkiger Rahmen mit Streckenlast Biegelinie F=1 kn 1 kn Biegelinie F=10 kn 10 kn
25 17,2 knm -15,6 Hochschule Augsburg - Fakultät A+B - Studiengang: Bauingenieurwesen 25/40 BS III 2.1 Lösung / Beispiel: Einhüftiger gelenkiger Rahmen mit Streckenlast Lastbild: q=8 kn/m Momentenlinie: F -15,6 knm M 5,2 kn Biegelinie F=5,2 kn 5,2 kn
26 26/40 BS III V. Statisch unbestimmte Rechnung Das Kraftgrößenverfahren (KGV) ist ein allgemeines Rechenverfahren der Baustatik zur Berechnung statisch unbestimmter Systeme. Ein statisch unbestimmtes System hat mindestens eine Auflagerreaktion (Auflagerkräfte und Schnittgrößen) mehr als Gleichgewichtsbedingungen (Summe Vertikalkräfte, Summe Horizontalkräfte, Summe der Momente um beliebigen Pol), d. h. der Freiheitsgrad des Systems ist kleiner gleich 1. Daher reichen die Gleichgewichtsbedingungen nicht zur Berechnung der Auflagerreaktionen aus. Die zusätzlichen Bedingungen werden aus den Verformungen abgeleitet. VORGEHENSWEISE: 1. Das Tragwerk wird durch Entfernen von Bindungen in ein statisch bestimmtes Hauptsystem überführt. Die inneren Bindungen werden durch Einfügen von gedachten Gelenken (häufig Momentengelenke, aber auch Querkraft- und Normalkraftgelenke) reduziert, die äußeren durch Lösen einzelner oder mehrerer Auflagerbindungen. 2. Hierbei ist darauf zu achten, dass man kein kinematisches (verschiebliches) System erzeugt, denn an diesem kann weder gerechnet werden (das im nächsten Schritt zu bildende Gleichungssystem wird unlösbar infolge Determinante 0), noch ist es sinnvoll zu bauen. Auf die Abzählformeln ist nicht immer Verlass, da sehr wohl auch kinematische Systeme diese Formeln zu Null erfüllen können. Die Unverschieblichkeit muss entweder aus dem Erkennen vom Grundtragwerken (Balken auf zwei Stützen, ggf. mit Auskragung; Schleppträger; Dreigelenkrahmen) und/oder Aufbauprinzipien (1. und 2. Bildungsgesetz für Fachwerke), oder über einen Widerspruch bei der Konstruktion der Verschiebungfigur (Polplan) hergeleitet werden. 3. Vorteilhaft ist auch, wenn das erzeugte Hauptsystem dem Ausgangssystem im Tragverhalten möglichst ähnlich ist (also z. B. nicht aus einem Durchlaufträger mit fünf Feldern durch Wegnahme der innenliegenden vier Lager einen Balken auf zwei Stützen machen, sondern durch Einfügen von Gelenken über den innenliegenden Lagern einen Balken auf zwei Stützen mit anhängenden vier Schleppträgern). 4. Durch die Wegnahme von Bindungen wird die Verträglichkeit verletzt; das bedeutet, im Hauptsystem stellen sich Verformungen ein, die im Ausgangssystem unmöglich sind. Um diesen Widerspruch zu lösen, wird für jede gelöste Bindung eine Kraftgröße eingeführt. Diese muss die am Hauptsystem errechnete Verformung gerade wieder zurückführen, so dass die Verträglichkeit wieder hergestellt wird. Im Prinzip wird also für jede überzählige Bindung eine Verformungsbedingung formuliert, um daraus die Bindungskraft zu gewinnen, d. h. es wird ein lineares Gleichungssystem mit den Kraftgrößen als Unbekannten aufgestellt. 5. Wenn das lineare Gleichungssystem gelöst ist und damit die Kraftgrößen gefunden sind, kann das ganze Tragwerk mittels der Gleichgewichtsbedingungen berechnet werden. ZUSAMMENFASSUNG: Das reale System ist: Es wird ersetzt durch: indem: Last- u. Eigenspannungszustände erfüllen unmittelbar: Das Gleichungssystem besteht aus: Kraftgrößenverfahren n-fach statisch unbestimmt ein statisch bestimmtes Hauptsystem n Bindungen gelöst werden Gleichgewichtsbedingungen Verformungsbedingungen Kraftgrößen xi der Eigenspannungszustände Die Unbekannten sind: Die Lösung ergibt sich aus der Summe von: Lastspannungszustand und n Eigenspannungszuständen
27 27/40 BS III A. Anwendung des Arbeitssatzes bei statisch unbestimmten Systemen 1. Statische Unbestimmtheit prüfen mit dem Abzählkriterium (s.a. Seite...) bei Fachwerken: n = s + a - 2k bei Stabwerken: n = 3s - a - g 2. Wahl eines statisch bestimmten Hauptsystems (n=0). Entfernung von n Lagerungsbedingungen (äußere Unbestimmtheit) oder Einführung von Gelenken (innere Unbestimmtheit), so dass ein statisch bestimmtes Ersatzsystem (Hauptsystem) entsteht. Lagerungsbedingungen oder gelöste Bindungen werden durch ihre zugehörigen statisch unbestimmten Reaktionen = n Kraftgrößen x n (Virtuelle Hilfskraft (mit der Größe 1) an der Stelle x) ersetzt. z.b. 1-fach statisch unbestimmtes Tragwerk, n=1 F mögliche Hauptsysteme F x 1 =1 F x 1 = 1 F x 1 =1 3. Berechnung des Lastspannungszustands (LSZ): Ermittlung der Auflager- und Schnittgrößen am Hauptsystem infolge der tatsächlichen Belastung aus dem Ausgangssystem. 4. Berechnung der n Eigenspannungszustände (ESZ1, ESZ2,...ESZn): Ermittlung der Auflager- und Schnittgrößen am Hauptsystem infolge der Kraftgrößen x i = 1, i = 1, 2,...n [(N 1, Q 1, M 1 ),...(N n, Q n, M n )] 5. Ermittlung der Verformungen/Einflussgrößen δ ik bzw δ i0 Die Berechnung wird mit Hilfe des Prinzips der virtuellen Kräfte durchgeführt, wobei der Zustand i als virtueller und der Zusatnd k bzw. 0 als wirklicher Zustand anzunehmen ist. [Es gilt: δ ik = δ ki ] bei einem ESZ: δ 11, δ 10 [δ11: Überlagerung von ESZ1 + ESZ1, δ10: ESZ1 + LSZ] bei zwei ESZ: δ 11, δ 22, δ 12, δ 10, δ 20 [δ22: ESZ2 + ESZ2, δ12: ESZ1 + ESZ2, δ20: ESZ2 + LSZ] 6. Aufstellen und lösen eines linearen Gleichungssystems (LGS) für die Unbekannten x 1...x n δ 10 + x 1 δ 11 + x 2 δ x n δ 1n = 0 δ 20 + x 1 δ 21 + x 2 δ x n δ 2n = 0 : : : : : δ n0 + x 1 δ n1 + x 2 δ n x n δ nn = 0 Lösen des LGS: - Invertieren der Koeffizientenmatrix 7. Ermittlung der endgültigen Auflager- und Schnittgrößen des statisch unbestimmten Systems mittels Superposition:. N = N 0 + x 1 N 1 + x 2 N x n N n Q = Q 0 + x 1 Q 1 + x 2 Q x n Q n M = M 0 + x 1 M 1 + x 2 M x n M n
28 28/40 BS III B. Beispiele 1. Einfach statisch unbestimmtes System Gegeben: Ein statisch unbestimmt gelagerter Balken der Länge L=10 m unter der Einzellast F= 20 kn Gesucht: Die Schnittgrößen unter der Last F mit dem Arbeitssatz. 1.Statisch bestimmtes Hauptsystem HS F B 2. Schnittgrößen des LSZ und ESZ, sowie des virtuellen Zustands. Realer Zustand: (LF aller tatsächlicher Belastungen am HS) Virtueller Zustand: (Einwirkung der Lastgröße 1 bei w L ) RealeMomene: Virtuelles Moment: F = 20 kn 1 B M M
29 29/40 BS III 3. Berechnen des Arbeitssatzes unter Verwendung z.b. einer Integraltafel l f = w L 4. Sonderfall w L = 0 5. Ergebnis M
30 30/40 BS III 1.1 Lösung / Beispiel: 1-fach statisch unbestimmtes System Biegelinie: B= 5 kn 20 kn 5 kn Biegelinie: B= 8,64 kn 20 kn 8,64 kn Biegelinie: B= 10 kn 20 kn 10 kn
31 31/40 BS III 1.1 Lösung / Beispiel: 1-fach statisch unbestimmtes System Lastbild 20 kn 6 m 4 m Querkraftlinie 11, ,36-8, ,64 V Momentenlinie - 33, ,56 M
32 32/40 BS III 2. Beispiel: 2-fach statisch unbestimmtes System Gegeben: Einhüftiger Rahmen. [q= 8 kn/m, EA ] Gesucht: Die Schnittgrößen ermittelt durch KGV Abzählkriterium: n = 2. Statisch bestimmtes HS (n=0) 3. Lastspannungszustand Mo
33 33/40 BS III 4. Eigenspannungszustand 1, mit x 1 = 1 Eigenspannungszustand 2, mit x 2 = 1 M1 M2 5. δ ik bzw δ i0 δ 11 = δ 12 = δ 22 = δ 10 = δ 20 =
34 34/40 BS III 6. LGS 0 0 δ 10 + x 1 δ 11 + x 2 δ x n δ 1n = 0. x 1 x 2 re. S. δ 11 =... δ 12 =... - δ 10 =... δ 21 =... δ 22 =... - δ 20 =... D N = D 1 = x 1 = D 2 = x 2 = 7. Endgültige Schnittgrößen 0 0 M = M 0 + x 1 M 1 + x 2 M x n M n = M 0 + x 1 M 1 + x 2 M 2 M endg, A = M endg, q = M endg, 1 = M endg, B = Ergebnis: 1
35 35/40 BS III 2.1 Lösung / Beispiel: 2-fach statisch unbestimmtes System LSZ: q = 8 kn/m + 25 knm M o ESZ 1: x 1 - x 1 M 1 ESZ 2: - 3x 2 - M 2 x 2
36 36/40 BS III Lösung / Beispiel: 2-fach statisch unbestimmtes System (Verformungen) Biegelinie LSZ: q = 8 kn/m Biegelinie ESZ 1: x 1 Biegelinie ESZ 2: x 2
37 37/40 BS III VI. Stabilität A. Stabilität und TH II 1. Allgemeines / Knicklast Unter Knicken versteht man in der Technischen Mechanik den Verlust der Stabilität bis hin zum schlagartigen und gewaltsamen Versagen von geraden bzw. leicht gekrümmten Stäben oder Balken unter der Wirkung von Druckkräften, deren Wirkungslinie in der Stabachse liegt, und/oder von Biegemomenten. Knickgefährdet sind besonders technische Konstruktionen wie Säulen und Stützen. Der Verlust der Stabilität äußert sich mit der Belastung rasch wachsenden Formänderungen des Stabes oder des Balkens ab einer bestimmten Belastung (Knicklast), und zwar mit * einem seitlichen Ausweichen der Stabachse oder Balkenachse (Biegeknicken) oder * einem Verdrehen des Stab- bzw. Balkenquerschnitts (Drillknicken) oder * einem seitlichen Ausweichen der Stabachse oder Balkenachse und einem Verdrehen des Stab- bzw. Balkenquerschnitts (Biegedrillknicken, früher auch als Kippen bezeichnet) Die Knicklast ist abhängig von * der Art der Beanspruchung (Verlauf der Druckkräfte und/oder Biegemomente über die Stablänge), * Länge des Stabes oder des Balkens, * Querschnittsform des Stabes oder des Balkens, konstante oder über die Stabachse veränderlicher Flächenträgheitsmomentes, * Materialeigenschaften des Stabes (bei elastischem Material: Elastizitätsmodul und Fließgrenze), * Einspannung bzw. Auflagerung oder Stützung des Stabes oder Balkens Annahmen: * die Stäbe haben konstante Querschnitte und eine konstante Längskraft N (N ist als Druck positiv) * nur Momentenverformungen werden berücksichtigt
38 38/40 BS III Differentialbeziehungen: Biegung A) EI * w = 0...THEORIE I. ORDNUNG (TH I) B) EI * w + No * w = 0...THEORIE II. ORDNUNG (TH II) Beispiel: Kragarm Gegeben: EA Gesucht: Knicklast F Lösung: 1.) Ansatz für w(x) zur DGL nach TH II w(x)= C*(cos(α x)-1)...lösungsansatz L EI w =... x w(x) w =... 2.) einsetzen in DGL:
39 39/40 BS III 3.) Randbedingungen L 4.) Ergebnis:
40 40/40 BS III ZUSAMMENFASSUNG: Mit der Knicklänge s k werden unterschiedliche Randbedingungen berücksichtigt. Insgesamt werden 4 Lagerungsfälle unterschieden Knicklänge s k : 1. Fall 2. Fall 3. Fall 4. Fall N Ki NKi N Ki N Ki Knicklast Nki: Es bedeuten: ANMERKUNG: Eingespannt in einem größeren System (z.b. elastische Einspannung) ergeben sich andere Knicklängen s k
1. EINFLUSSLINIEN FÜR KRAFTGRÖßEN
 Arbeitsblätter 1 Hinweise zur Konstruktion und Berechnung von Einflusslinien Definition: Eine Einflusslinie (EL) liefert den Einfluss einer Wanderlast P = 1 von festgelegter Wirkungsrichtung. längs des
Arbeitsblätter 1 Hinweise zur Konstruktion und Berechnung von Einflusslinien Definition: Eine Einflusslinie (EL) liefert den Einfluss einer Wanderlast P = 1 von festgelegter Wirkungsrichtung. längs des
Eigenspannungszustand: Ermittlung der Schnittgrößen, die durch die Ersatzkräfte hervorgerufen
 www.statik-lernen.de Beispiele (Ein-) Gelenkrahmen Seite Auf den folgenden Seiten wird das 'Kraftgrößenverfahren' (X A -Methode) zur Berechnung der Schnittkräfte statischer Systeme am Beispiel eines 2-fach
www.statik-lernen.de Beispiele (Ein-) Gelenkrahmen Seite Auf den folgenden Seiten wird das 'Kraftgrößenverfahren' (X A -Methode) zur Berechnung der Schnittkräfte statischer Systeme am Beispiel eines 2-fach
ERLÄUTERUNGEN ZUM KRAFTGRÖßENVERFAHREN An einem einfachen Beispiel soll hier das Prinzip des Kraftgrößenverfahrens erläutert werden.
 FACHBEREICH 0 BAUINGENIEURWESEN Arbeitsblätter ERLÄUTERUNGEN ZUM An einem einfachen Beispiel soll hier das Prinzip des Kraftgrößenverfahrens erläutert werden.. SYSTEM UND BELASTUNG q= 20 kn / m C 2 B 4
FACHBEREICH 0 BAUINGENIEURWESEN Arbeitsblätter ERLÄUTERUNGEN ZUM An einem einfachen Beispiel soll hier das Prinzip des Kraftgrößenverfahrens erläutert werden.. SYSTEM UND BELASTUNG q= 20 kn / m C 2 B 4
Statik im Bauwesen. HUSS-MEDIEN GmbH Verlag Bauwesen Berlin. Fritz Bochmann/Werner Kirsch. Band 3: Statisch unbestimmte ebene Systeme
 Fritz Bochmann/Werner Kirsch Statik im Bauwesen Band 3: Statisch unbestimmte ebene Systeme 13. Auflage HUSS-MEDIEN GmbH Verlag Bauwesen 10400 Berlin Inhaltsverzeichnis Einführung 11.1. Allgemeine Grundlagen
Fritz Bochmann/Werner Kirsch Statik im Bauwesen Band 3: Statisch unbestimmte ebene Systeme 13. Auflage HUSS-MEDIEN GmbH Verlag Bauwesen 10400 Berlin Inhaltsverzeichnis Einführung 11.1. Allgemeine Grundlagen
 Statik I Ergänzungen zum Vorlesungsskript Dr.-Ing. Stephan Salber Institut für Statik und Dynamik der Luft- und Raumfahrtkonstruktionen Statik I Vorlesungs- und Übungsmaterial Vorlesung Benutzername: Vorlesungsskript
Statik I Ergänzungen zum Vorlesungsskript Dr.-Ing. Stephan Salber Institut für Statik und Dynamik der Luft- und Raumfahrtkonstruktionen Statik I Vorlesungs- und Übungsmaterial Vorlesung Benutzername: Vorlesungsskript
Modulprüfung Baustatik I am 3. Februar 2016
 HOCHSCHULE WISMAR Fakultät für Ingenieurwissenschaften Bereich Bauingenieurwesen Prof. Dr.-Ing. R. Dallmann Modulprüfung Baustatik I am 3. Februar 016 Name:.................................................................
HOCHSCHULE WISMAR Fakultät für Ingenieurwissenschaften Bereich Bauingenieurwesen Prof. Dr.-Ing. R. Dallmann Modulprüfung Baustatik I am 3. Februar 016 Name:.................................................................
7.1 Grundregeln der Kinematik: Polplan
 7 Einflusslinien 7. Grundregeln der Kinematik: Polplan Trotz der Erfüllung der Bedingungsgleichungen für statisch (un)bestimmte Tragwerke (Abzählkriterien A/B) kann es vorkommen, dass Stabwerksstrukturen
7 Einflusslinien 7. Grundregeln der Kinematik: Polplan Trotz der Erfüllung der Bedingungsgleichungen für statisch (un)bestimmte Tragwerke (Abzählkriterien A/B) kann es vorkommen, dass Stabwerksstrukturen
Baustatik kompakt. Statisch bestimmte und statisch/unbestimmte Systeme
 Prof. Dipl.-Ing. Klaus-Jürgen Schneider Prof. Dipl.-Ing. Erwin Schweda Baustatik kompakt Statisch bestimmte und statisch/unbestimmte Systeme / Neu bearbeitet von: Prof. Dr.-Ing. Christoph Seeßelberg Prof.JDr.-Ing.
Prof. Dipl.-Ing. Klaus-Jürgen Schneider Prof. Dipl.-Ing. Erwin Schweda Baustatik kompakt Statisch bestimmte und statisch/unbestimmte Systeme / Neu bearbeitet von: Prof. Dr.-Ing. Christoph Seeßelberg Prof.JDr.-Ing.
3. Kraftgrößenverfahren
 .Kraftgrößenverfahren von 8. Kraftgrößenverfahren. Prinzip Das Prinzip des Kraftgrößenverfahrens ist es ein statisch unbestimmtes System durch Einschalten von Gelenken und Zerschneiden von Stäben oder
.Kraftgrößenverfahren von 8. Kraftgrößenverfahren. Prinzip Das Prinzip des Kraftgrößenverfahrens ist es ein statisch unbestimmtes System durch Einschalten von Gelenken und Zerschneiden von Stäben oder
Arbeitsunterlagen. Statik 2
 Arbeitsunterlagen Statik 2 WS 2014/15 Stand 07.10.2014 Inhalt 1. Vertiefung KGV 1.1 Eingeprägte Auflagerverformungen 1.2 Vorspannung 1.3 Systeme mit elastischer Lagerung 1.4 Ermittlung von Federsteifigkeiten
Arbeitsunterlagen Statik 2 WS 2014/15 Stand 07.10.2014 Inhalt 1. Vertiefung KGV 1.1 Eingeprägte Auflagerverformungen 1.2 Vorspannung 1.3 Systeme mit elastischer Lagerung 1.4 Ermittlung von Federsteifigkeiten
2. Statisch bestimmte Systeme
 1 von 14 2. Statisch bestimmte Systeme 2.1 Definition Eine Lagerung nennt man statisch bestimmt, wenn die Lagerreaktionen (Kräfte und Momente) allein aus den Gleichgewichtsbedingungen bestimmbar sind.
1 von 14 2. Statisch bestimmte Systeme 2.1 Definition Eine Lagerung nennt man statisch bestimmt, wenn die Lagerreaktionen (Kräfte und Momente) allein aus den Gleichgewichtsbedingungen bestimmbar sind.
Statik. Klausur am Name: Vorname: Matrikelnummer: (bitte deutlich schreiben)
 Diplomprüfung Frühjahr 2009 Prüfungsfach Statik Klausur am 23.02.2009 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig) Aufgabe 1 2 3 4 5 6 7 8 9 Summe mögliche Punkte 20 5 5 25 25 30
Diplomprüfung Frühjahr 2009 Prüfungsfach Statik Klausur am 23.02.2009 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig) Aufgabe 1 2 3 4 5 6 7 8 9 Summe mögliche Punkte 20 5 5 25 25 30
RUHR-UNIVERSITÄT BOCHUM FAKULTÄT FÜR BAUINGENIEURWESEN STATIK UND DYNAMIK. Diplomprüfung Frühjahr Prüfungsfach. Statik. Klausur am
 Diplomprüfung Frühjahr 00 Prüfungsfach Statik Klausur am 0.0.00 Name: Vorname: Matr.-Nr.: (bitte deutlich schreiben!) (9-stellig!) Aufgabe 5 6 7 8 9 Summe mögliche Punkte 7 5 5 6 0 8 0 6 0 erreichte Punkte
Diplomprüfung Frühjahr 00 Prüfungsfach Statik Klausur am 0.0.00 Name: Vorname: Matr.-Nr.: (bitte deutlich schreiben!) (9-stellig!) Aufgabe 5 6 7 8 9 Summe mögliche Punkte 7 5 5 6 0 8 0 6 0 erreichte Punkte
Baumechanik - Repetitorium
 Mechanik und Numerische Methoden Thema 1: Fachwerke Aufgabe 1.1 Ein ebenes Fachwerk wird durch eine Reihe von Einzelkräften unterschiedlicher Größe belastet. a) Weisen Sie nach, dass das Fachwerk statisch
Mechanik und Numerische Methoden Thema 1: Fachwerke Aufgabe 1.1 Ein ebenes Fachwerk wird durch eine Reihe von Einzelkräften unterschiedlicher Größe belastet. a) Weisen Sie nach, dass das Fachwerk statisch
Gelenkträger unter vertikalen und schrägen Einzellasten und einer vertikalen Streckenlast
 www.statik-lernen.de Beispiele Gelenkträger Seite 1 Auf den folgenden Seiten wird das Knotenschnittverfahren zur Berechnung statisch bestimmter Systeme am Beispiel eines Einfeldträgers veranschaulicht.
www.statik-lernen.de Beispiele Gelenkträger Seite 1 Auf den folgenden Seiten wird das Knotenschnittverfahren zur Berechnung statisch bestimmter Systeme am Beispiel eines Einfeldträgers veranschaulicht.
BAUSTATIK I KOLLOQUIUM 10, Lösung
 BAUSTATIK I KOLLOQUIUM 10, Lösung (101-011) Thema: Kraftmethode Aufgabe 1, Lösung Gegeben: Gesucht: Unterspanntes Fachwerk, EA = konstant für alle Stäbe Stabkräfte S i Grad der statischen Unbestimmtheit:
BAUSTATIK I KOLLOQUIUM 10, Lösung (101-011) Thema: Kraftmethode Aufgabe 1, Lösung Gegeben: Gesucht: Unterspanntes Fachwerk, EA = konstant für alle Stäbe Stabkräfte S i Grad der statischen Unbestimmtheit:
Inhaltsverzeichnis. 1 Einführung in die Statik der Tragwerke 1
 1 Einführung in die Statik der Tragwerke 1 1.1 Vorbemerkungen 1 1.1.1 Definition und Aufgabe der Baustatik l 1.1.2 Tragwerksformen irnd deren Idealisierung 2 1.1.2.1 Dreidimensionale Tragelemcnte: Räume
1 Einführung in die Statik der Tragwerke 1 1.1 Vorbemerkungen 1 1.1.1 Definition und Aufgabe der Baustatik l 1.1.2 Tragwerksformen irnd deren Idealisierung 2 1.1.2.1 Dreidimensionale Tragelemcnte: Räume
Modulprüfung Baustatik I am 3. Februar 2016
 HOCHSCHULE WISAR Fakultät für Ingenieurwissenschaften Bereich Bauingenieurwesen Prof. Dr.-Ing. R. Dallmann odulprüfung Baustatik I am. Februar 0 Name:.................................................................
HOCHSCHULE WISAR Fakultät für Ingenieurwissenschaften Bereich Bauingenieurwesen Prof. Dr.-Ing. R. Dallmann odulprüfung Baustatik I am. Februar 0 Name:.................................................................
Baustatik I (WS 2017/2018) 1. Einführung. 1.2 Modellbildung LEHRSTUHL FÜR BAUSTATIK UNIVERSITÄT SIEGEN
 Baustatik I (WS 2017/2018) 1. Einführung 1.2 Modellbildung 1 Statische Berechnungen Für die statischen Berechnungen sind geeignete Tragwerksmodelle mit den maßgebenden Einflussgrößen zu wählen, welche
Baustatik I (WS 2017/2018) 1. Einführung 1.2 Modellbildung 1 Statische Berechnungen Für die statischen Berechnungen sind geeignete Tragwerksmodelle mit den maßgebenden Einflussgrößen zu wählen, welche
Potentielle Energie, P.d.v.K. und P.d.v.V.
 IBSD Institut für Baustatik und Baudynamik Fachbereich Bauingenieurwesen Potentielle Energie, P.d.v.K. und P.d.v.V. Fachgebiet Baustatik 2. Februar 26 Inhaltsverzeichnis 1 Die potentielle Energie 1 1.1
IBSD Institut für Baustatik und Baudynamik Fachbereich Bauingenieurwesen Potentielle Energie, P.d.v.K. und P.d.v.V. Fachgebiet Baustatik 2. Februar 26 Inhaltsverzeichnis 1 Die potentielle Energie 1 1.1
Berechnung von Tragwerken
 Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Wintersemester 2004/2005 Matr.---Nr. :... Fachsemester:... Berechnung von Tragwerken Prüfung am 11.03.2005 (Bearbeitungszeit 90
Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Wintersemester 2004/2005 Matr.---Nr. :... Fachsemester:... Berechnung von Tragwerken Prüfung am 11.03.2005 (Bearbeitungszeit 90
Baustatik II und III (PO 2013)
 Bachelorprüfung Frühjahr 2016 Modul 18 (BI) Baustatik II und III (PO 2013) Klausur am 20.02.2016 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 4 5 6 7 Summe mögliche
Bachelorprüfung Frühjahr 2016 Modul 18 (BI) Baustatik II und III (PO 2013) Klausur am 20.02.2016 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 4 5 6 7 Summe mögliche
5.1 Grundlagen zum Prinzip der virtuellen Kräfte
 5 Prinzip der virtuellen Kräfte 5. Grundlagen zum Prinzip der virtuellen Kräfte Das Prinzip der virtuellen Kräfte (PvK) stellt eine nwendung des Prinzips der virtuellen rbeit dar. Es dient zur Bestimmung
5 Prinzip der virtuellen Kräfte 5. Grundlagen zum Prinzip der virtuellen Kräfte Das Prinzip der virtuellen Kräfte (PvK) stellt eine nwendung des Prinzips der virtuellen rbeit dar. Es dient zur Bestimmung
1. Zug und Druck in Stäben
 1. Zug und Druck in Stäben Stäbe sind Bauteile, deren Querschnittsabmessungen klein gegenüber ihrer änge sind: D Sie werden nur in ihrer ängsrichtung auf Zug oder Druck belastet. D Prof. Dr. Wandinger
1. Zug und Druck in Stäben Stäbe sind Bauteile, deren Querschnittsabmessungen klein gegenüber ihrer änge sind: D Sie werden nur in ihrer ängsrichtung auf Zug oder Druck belastet. D Prof. Dr. Wandinger
6. Arbeitssatz, Prinzip der virtuellen Verschiebungen (PvV) und Prinzip der virtuellen Kräfte (PvK)
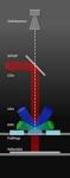 Technische Mechanik 2 (SS 2011) 6. Arbeitssatz, Prinzip der virtuellen Verschiebungen (PvV) und Prinzip der virtuellen Kräfte (PvK) Arbeit: 6.1 Grundbegriffe und Arbeitssatz 6.1 Grundbegriffe und Arbeitssatz
Technische Mechanik 2 (SS 2011) 6. Arbeitssatz, Prinzip der virtuellen Verschiebungen (PvV) und Prinzip der virtuellen Kräfte (PvK) Arbeit: 6.1 Grundbegriffe und Arbeitssatz 6.1 Grundbegriffe und Arbeitssatz
Aufgabensammlung zur Baustatik
 Kai-Uwe Bletzinger Falko Dieringer Rupert Fisch Benedikt Philipp Aufgabensammlung zur Baustatik Übungsaufgaben zur Berechnung ebener Stabtragwerke 5 Carl Hanser Verlag München PDF Bletzinger/Dieringer/Fisch/Philipp,
Kai-Uwe Bletzinger Falko Dieringer Rupert Fisch Benedikt Philipp Aufgabensammlung zur Baustatik Übungsaufgaben zur Berechnung ebener Stabtragwerke 5 Carl Hanser Verlag München PDF Bletzinger/Dieringer/Fisch/Philipp,
Baustatik II. Kapitel IV. Einflusslinien für statisch unbestimmte Systeme. Institute of Structural Engineering Seite 1
 Institute of Structural Engineering Seite Baustatik II Kapitel IV Einflusslinien für statisch unbestimmte Systeme Institute of Structural Engineering Seite 2 Lernziele dieses Kapitels. Sich mit der Form
Institute of Structural Engineering Seite Baustatik II Kapitel IV Einflusslinien für statisch unbestimmte Systeme Institute of Structural Engineering Seite 2 Lernziele dieses Kapitels. Sich mit der Form
Leseprobe. Kai-Uwe Bletzinger, Falko Dieringer, Rupert Fisch, Benedikt Philipp. Aufgabensammlung zur Baustatik
 Leseprobe Kai-Uwe Bletzinger, Falko Dieringer, Rupert Fisch, Benedikt Philipp Aufgabensammlung zur Baustatik Übungsaufgaben zur Berechnung ebener Stabtragwerke ISBN (Buch): 978-3-446-4478-8 Weitere Informationen
Leseprobe Kai-Uwe Bletzinger, Falko Dieringer, Rupert Fisch, Benedikt Philipp Aufgabensammlung zur Baustatik Übungsaufgaben zur Berechnung ebener Stabtragwerke ISBN (Buch): 978-3-446-4478-8 Weitere Informationen
Eigenspannungszustand: Ermittlung der Schnittgrößen, die durch die Ersatzkräfte hervorgerufen
 www.statik-lernen.de Beispiele Zweifeldträger Seite Auf den folgenden Seiten wird das 'Kraftgrößenverfahren' (X A -Methode) zur Berechnung der Schnittkräfte statischer Systeme am Beispiel eines -fach statisch
www.statik-lernen.de Beispiele Zweifeldträger Seite Auf den folgenden Seiten wird das 'Kraftgrößenverfahren' (X A -Methode) zur Berechnung der Schnittkräfte statischer Systeme am Beispiel eines -fach statisch
Einfeldträger. FH Potsdam - FB Bauingenieurwesen Statik der Baukonstruktionen Tragwerksberechnungen mit RuckZuck
 Beginnen Sie mit dem vorgegebenen System Durchlaufträger, 1 Feld. Erzeugen Sie dann alle folgenden Systeme bis inklusive A5) über Systemmanipulation. Einfeldträger A1) Ermitteln Sie und vergleichen Sie
Beginnen Sie mit dem vorgegebenen System Durchlaufträger, 1 Feld. Erzeugen Sie dann alle folgenden Systeme bis inklusive A5) über Systemmanipulation. Einfeldträger A1) Ermitteln Sie und vergleichen Sie
Modulprüfung Baustatik I am 21. November 2018
 HOCHSCHULE WISMAR Fakultät für Ingenieurwissenschaften Bereich Bauingenieurwesen Prof. Dr.-Ing. R. Dallmann Modulprüfung Baustatik I am 1. November 018 Name:.................................................................
HOCHSCHULE WISMAR Fakultät für Ingenieurwissenschaften Bereich Bauingenieurwesen Prof. Dr.-Ing. R. Dallmann Modulprüfung Baustatik I am 1. November 018 Name:.................................................................
Baustatik Theorie I. und II. Ordnung
 Prof. Dr.-Ing. Helmut Rubin Prof. Dipl.-Ing. Klaus-Jürgen Schneider Baustatik Theorie I. und II. Ordnung 4., neu bearbeitete und erweiterte Auflage 2002 Werner Verlag Inhaltsverzeichnis 1 Einführung 11
Prof. Dr.-Ing. Helmut Rubin Prof. Dipl.-Ing. Klaus-Jürgen Schneider Baustatik Theorie I. und II. Ordnung 4., neu bearbeitete und erweiterte Auflage 2002 Werner Verlag Inhaltsverzeichnis 1 Einführung 11
Rahmen. Rahmenwirkung Berechnung einfacher Systeme. Institut für Tragwerksentwurf. Tragwerkslehre 2
 Rahmen Rahmenwirkung Berechnung einfacher Systeme Rahmen Riegel vertikale Lasten horizontale Lasten Stiel biegesteife Ecke Vertikale und horizontale Lagerkräfte Vertikale und horizontale Lagerkräfte Rahmen
Rahmen Rahmenwirkung Berechnung einfacher Systeme Rahmen Riegel vertikale Lasten horizontale Lasten Stiel biegesteife Ecke Vertikale und horizontale Lagerkräfte Vertikale und horizontale Lagerkräfte Rahmen
Grundfachklausur Teil 1 / Statik I
 Technische Universität Darmstadt Institut für Werkstoffe und Mechanik im Bauwesen Fachgebiet Statik Prof. Dr.-Ing. Jens Schneider Grundfachklausur Teil / Statik I im Sommersemester 03, am 09.09.03 Die
Technische Universität Darmstadt Institut für Werkstoffe und Mechanik im Bauwesen Fachgebiet Statik Prof. Dr.-Ing. Jens Schneider Grundfachklausur Teil / Statik I im Sommersemester 03, am 09.09.03 Die
Baustatik I und II. Klausur am Name: Vorname: Matrikelnummer: (bitte deutlich schreiben)
 Bachelorprüfung Herbst 2010 Prüfungsfach Baustatik I und II Klausur am 23.08.2010 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 4 5 6 7 Summe mögliche Punkte 30 29
Bachelorprüfung Herbst 2010 Prüfungsfach Baustatik I und II Klausur am 23.08.2010 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 4 5 6 7 Summe mögliche Punkte 30 29
Technische Mechanik. Fachwerke
 7 Fachwerke Fachwerke Fachwerke Anwendungsbeispiele... Beispiele aus dem Ingenieurwesen (wikipedia.org) Fachwerke 1 Fachwerke Anwendungsbeispiele nanowerk.com (T. Bückmann) wikipedia.org Beispiele aus
7 Fachwerke Fachwerke Fachwerke Anwendungsbeispiele... Beispiele aus dem Ingenieurwesen (wikipedia.org) Fachwerke 1 Fachwerke Anwendungsbeispiele nanowerk.com (T. Bückmann) wikipedia.org Beispiele aus
Baustatik 2. Berechnung statisch unbestimmter Tragwerke. von Raimond Dallmann. 2., aktualisierte Auflage. Hanser München 2009
 Baustatik 2 Berechnung statisch unbestimmter Tragwerke von Raimond Dallmann 2., aktualisierte Auflage Hanser München 2009 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 446 41998 8 Zu Leseprobe schnell
Baustatik 2 Berechnung statisch unbestimmter Tragwerke von Raimond Dallmann 2., aktualisierte Auflage Hanser München 2009 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 446 41998 8 Zu Leseprobe schnell
4. Balken. Brücken Tragflügel KFZ-Karosserie: A-Säule, B-Säule Rahmen: Fahrrad, Motorrad. Prof. Dr. Wandinger 2. Festigkeitslehre TM 2.
 4. Balken Balken sind eindimensionale Idealisierungen für Bauteile, die Längskräfte, Querkräfte und Momente übertragen können. Die Querschnittsabmessungen sind klein gegenüber der Länge. Beispiele: Brücken
4. Balken Balken sind eindimensionale Idealisierungen für Bauteile, die Längskräfte, Querkräfte und Momente übertragen können. Die Querschnittsabmessungen sind klein gegenüber der Länge. Beispiele: Brücken
Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Sommersemester 1999 Matr.---Nr. :... Fachsemester:...
 Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Sommersemester 1999 Matr.---Nr. :... Fachsemester:... Baustatik 1/2 Semestrale am 28.07.1999 (Bearbeitungszeit 45 Minuten) max.
Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Sommersemester 1999 Matr.---Nr. :... Fachsemester:... Baustatik 1/2 Semestrale am 28.07.1999 (Bearbeitungszeit 45 Minuten) max.
Inhaltsverzeichnis. Raimond Dallmann. Baustatik 1. Berechnung statisch bestimmter Tragwerke ISBN:
 Inhaltsverzeichnis Raimond Dallmann Baustatik 1 Berechnung statisch bestimmter Tragwerke ISBN: 978-3-446-42319-0 Weitere Informationen oder Bestellungen unter http://www.hanser.de/978-3-446-42319-0 sowie
Inhaltsverzeichnis Raimond Dallmann Baustatik 1 Berechnung statisch bestimmter Tragwerke ISBN: 978-3-446-42319-0 Weitere Informationen oder Bestellungen unter http://www.hanser.de/978-3-446-42319-0 sowie
Modulprüfung Baustatik II am 16. Februar 2012
 HOCHSCHULE WISMAR Fakultät für Ingenieurwissenschaften Bereich Bauingenieurwesen Prof. Dr.-Ing. R. Dallmann Modulprüfung Baustatik II am. Februar Name:.................................................................
HOCHSCHULE WISMAR Fakultät für Ingenieurwissenschaften Bereich Bauingenieurwesen Prof. Dr.-Ing. R. Dallmann Modulprüfung Baustatik II am. Februar Name:.................................................................
Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Sommersemester 2003 Matr.---Nr. :... Fachsemester:...
 Name :... Vorname :... Sommersemester 2003 Matr.---Nr. :... Fachsemester:... Baustatik 2 Semestrale am 02.07.2003 (Bearbeitungszeit 45 Minuten) max. Punkte 1. / 5 2. / 5 3. / 3 4. / 10 5. / 9 6. / 9 7.
Name :... Vorname :... Sommersemester 2003 Matr.---Nr. :... Fachsemester:... Baustatik 2 Semestrale am 02.07.2003 (Bearbeitungszeit 45 Minuten) max. Punkte 1. / 5 2. / 5 3. / 3 4. / 10 5. / 9 6. / 9 7.
Statik. Klausur am Name: Vorname: Matrikelnummer: (bitte deutlich schreiben)
 Diplomprüfung Herbst 27 Prüfungsfach Statik Klausur am 27.8.27 ame: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 4 5 6 7 8 9 Summe mögliche Punkte 2 5 5 25 25 25 25 25
Diplomprüfung Herbst 27 Prüfungsfach Statik Klausur am 27.8.27 ame: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 4 5 6 7 8 9 Summe mögliche Punkte 2 5 5 25 25 25 25 25
Modulprüfung Baustatik I am 8. Juli 2015
 HOCHSCHULE WISMAR Fakultät für Ingenieurwissenschaften Bereich Bauingenieurwesen Prof. Dr.-Ing. R. Dallmann Modulprüfung Baustatik I am 8. Juli 015 Name:.................................................................
HOCHSCHULE WISMAR Fakultät für Ingenieurwissenschaften Bereich Bauingenieurwesen Prof. Dr.-Ing. R. Dallmann Modulprüfung Baustatik I am 8. Juli 015 Name:.................................................................
Baustatik Theorie I. und II. Ordnung
 Prof. Dr.-Ing. Helmut Rubin Prof. Dipl.-Ing. Klaus-Jürgen Schneider Baustatik Theorie I. und II. Ordnung 3., völlig neu bearbeitete und erweiterte Auflage 1996 Werner-Verlag Inhaltsverzeichnis 1 Einfuhrung
Prof. Dr.-Ing. Helmut Rubin Prof. Dipl.-Ing. Klaus-Jürgen Schneider Baustatik Theorie I. und II. Ordnung 3., völlig neu bearbeitete und erweiterte Auflage 1996 Werner-Verlag Inhaltsverzeichnis 1 Einfuhrung
Lehrveranstaltung Stereostatik
 ehrveranstaltung Stereostatik Thema 7: Berechnung ebener Rahmen Bergische Universität Wuppertal Baumechanik und Numerische Methoden Prof. Dr.-Ing. W. Zahlten Mechanik 1 Ebene Rahmen 7.1 Problemstellung
ehrveranstaltung Stereostatik Thema 7: Berechnung ebener Rahmen Bergische Universität Wuppertal Baumechanik und Numerische Methoden Prof. Dr.-Ing. W. Zahlten Mechanik 1 Ebene Rahmen 7.1 Problemstellung
Biegelinie
 3. Biegelinie Die Biegemomente führen zu einer Verformung der Balkenachse, die als Biegelinie bezeichnet wird. Die Biegelinie wird beschrieben durch die Verschiebung v in y-richtung und die Verschiebung
3. Biegelinie Die Biegemomente führen zu einer Verformung der Balkenachse, die als Biegelinie bezeichnet wird. Die Biegelinie wird beschrieben durch die Verschiebung v in y-richtung und die Verschiebung
Baustatik & Festigkeitslehre Vorlesung & Übung
 Baustatik & Festigkeitslehre Vorlesung & Übung Vortragender: O.Univ.Prof. DI Dr. Dr. Konrad Bergmeister Kraftgrößenverfahren Wenn statisch unbestimmte Systeme berechnet werden sollen, müssen zusätzliche
Baustatik & Festigkeitslehre Vorlesung & Übung Vortragender: O.Univ.Prof. DI Dr. Dr. Konrad Bergmeister Kraftgrößenverfahren Wenn statisch unbestimmte Systeme berechnet werden sollen, müssen zusätzliche
Berechnung von Tragwerken
 Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Sommersemester 2005 Matr.---Nr. :... Fachsemester:... Berechnung von Tragwerken Prüfung am 09.09.2005 (Bearbeitungszeit 90 Minuten)
Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Sommersemester 2005 Matr.---Nr. :... Fachsemester:... Berechnung von Tragwerken Prüfung am 09.09.2005 (Bearbeitungszeit 90 Minuten)
Dankert/Dankert: Technische Mechanik, 5. Auflage Lösungen zu den Aufgaben, Teil 4 (Kapitel 15-17)
 Dankert/Dankert: Technische Mechanik, 5. Auflage Lösungen zu den Aufgaben, Teil 4 (Kapitel 15-17) Lösung 15.1: Element-Steifigkeitsmatrix Jeweils drei 2*2-Untermatrizen einer Element- Steifigkeitsmatrix
Dankert/Dankert: Technische Mechanik, 5. Auflage Lösungen zu den Aufgaben, Teil 4 (Kapitel 15-17) Lösung 15.1: Element-Steifigkeitsmatrix Jeweils drei 2*2-Untermatrizen einer Element- Steifigkeitsmatrix
Diplomprüfung Frühjahr Prüfungsfach. Statik. Klausur am (bitte deutlich schreiben!)
 Diplomprüfung Frühjahr 00 Prüfungsfach Statik Klausur am 04.0.00 Name: Vorname: (bitte deutlich schreiben) Matr.-Nr.: (9-stellig) Aufgabe 4 5 6 7 8 9 Summe mögliche Punkte 7 5 4 6 6 4 4 0 erreichte Punkte
Diplomprüfung Frühjahr 00 Prüfungsfach Statik Klausur am 04.0.00 Name: Vorname: (bitte deutlich schreiben) Matr.-Nr.: (9-stellig) Aufgabe 4 5 6 7 8 9 Summe mögliche Punkte 7 5 4 6 6 4 4 0 erreichte Punkte
Übungsaufgaben Systemmodellierung WT 2015
 Übungsaufgaben Systemmodellierung WT 2015 Robert Friedrich Prof. Dr.-Ing. Rolf Lammering Institut für Mechanik Helmut-Schmidt-Universität / Universität der Bundeswehr Hamburg Holstenhofweg 85, 22043 Hamburg
Übungsaufgaben Systemmodellierung WT 2015 Robert Friedrich Prof. Dr.-Ing. Rolf Lammering Institut für Mechanik Helmut-Schmidt-Universität / Universität der Bundeswehr Hamburg Holstenhofweg 85, 22043 Hamburg
Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Sommersemester 2004 Matr.---Nr. :... Fachsemester:...
 Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Sommersemester 2004 Matr.---Nr. :... Fachsemester:... Baustatik 2 Semestrale am 13.7.2004 (Bearbeitungszeit 45 Minuten) max. Punkte
Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Sommersemester 2004 Matr.---Nr. :... Fachsemester:... Baustatik 2 Semestrale am 13.7.2004 (Bearbeitungszeit 45 Minuten) max. Punkte
In der Technik treten Fachwerke als Brückenträger, Masten, Gerüste, Kräne, Dachbindern usw. auf.
 6. Ebene Fachwerke In der Technik treten Fachwerke als Brückenträger, Masten, Gerüste, Kräne, Dachbindern usw. auf. 6.1 Definition Ein ideales Fachwerk besteht aus geraden, starren Stäben, die miteinander
6. Ebene Fachwerke In der Technik treten Fachwerke als Brückenträger, Masten, Gerüste, Kräne, Dachbindern usw. auf. 6.1 Definition Ein ideales Fachwerk besteht aus geraden, starren Stäben, die miteinander
1. Formänderungsenergie
 1. Formänderungsenergie 1.1 Grundlagen 1. Grundlastfälle 1.3 Beispiele.1-1 1.1 Grundlagen Zugstab: F L F x E, A F W u u An einem am linken Ende eingespannten linear elastischen Stab greift am rechten Ende
1. Formänderungsenergie 1.1 Grundlagen 1. Grundlastfälle 1.3 Beispiele.1-1 1.1 Grundlagen Zugstab: F L F x E, A F W u u An einem am linken Ende eingespannten linear elastischen Stab greift am rechten Ende
Universität für Bodenkultur
 Baustatik Übungen Kolloquiumsvorbereitung Universität für Bodenkultur Department für Bautechnik und Naturgefahren Wien, am 15. Oktober 2004 DI Dr. techn. Roman Geier Theoretischer Teil: Ziele / Allgemeine
Baustatik Übungen Kolloquiumsvorbereitung Universität für Bodenkultur Department für Bautechnik und Naturgefahren Wien, am 15. Oktober 2004 DI Dr. techn. Roman Geier Theoretischer Teil: Ziele / Allgemeine
( ) Winter Montag, 19. Januar 2015, Uhr, HIL E 1. Name, Vorname: Studenten-Nr.:
 Baustatik I+II Sessionsprüfung (101-0113-00) Winter 2015 Montag, 19. Januar 2015, 09.00 12.00 Uhr, HIL E 1 Name, Vorname: Studenten-Nr.: Bemerkungen 1. Die Aufgaben dürfen in beliebiger Reihenfolge bearbeitet
Baustatik I+II Sessionsprüfung (101-0113-00) Winter 2015 Montag, 19. Januar 2015, 09.00 12.00 Uhr, HIL E 1 Name, Vorname: Studenten-Nr.: Bemerkungen 1. Die Aufgaben dürfen in beliebiger Reihenfolge bearbeitet
Biegelinie
 3. Biegelinie Die Biegemomente führen zu einer Verformung der Balkenachse, die als Biegelinie bezeichnet wird. Die Biegelinie wird beschrieben durch die Verschiebung v in y-richtung und die Verschiebung
3. Biegelinie Die Biegemomente führen zu einer Verformung der Balkenachse, die als Biegelinie bezeichnet wird. Die Biegelinie wird beschrieben durch die Verschiebung v in y-richtung und die Verschiebung
TU Dortmund. Vorname: Nachname: Matr.-Nr.: Aufgabe 1 (Seite 1 von 3)
 Aufgabe 1 (Seite 1 von 3) Bei der Messung eines belasteten Blechs wurden drei Dehnungs-Messstreifen (DMS) verwendet und wie rechts dargestellt appliziert. Die Dehnungen der entsprechenden DMS wurden zu
Aufgabe 1 (Seite 1 von 3) Bei der Messung eines belasteten Blechs wurden drei Dehnungs-Messstreifen (DMS) verwendet und wie rechts dargestellt appliziert. Die Dehnungen der entsprechenden DMS wurden zu
www.statik-lernen.de Inhaltsverzeichnis Kräfte und Kraftarten Äußere und innere Kräfte Das zentrale Kräftesystem Momente Auflager Zustandslinien
 www.statik-lernen.de Grundlagen Inhaltsverzeichnis Kräfte und Kraftarten o Bestimmung von Kräften... Seite 1 o Graphische Darstellung... Seite 1 o Einheit der Kraft... Seite 1 o Kräftegleichgewicht...
www.statik-lernen.de Grundlagen Inhaltsverzeichnis Kräfte und Kraftarten o Bestimmung von Kräften... Seite 1 o Graphische Darstellung... Seite 1 o Einheit der Kraft... Seite 1 o Kräftegleichgewicht...
Innere Beanspruchungen - Schnittgrößen
 Innere Beanspruchungen - Schnittgrößen Vorlesung und Übungen 1. Semester BA Architektur Q () M () M () Q () N () N () L - KIT Universität des Landes Baden-Württemberg und nationales orschungszentrum in
Innere Beanspruchungen - Schnittgrößen Vorlesung und Übungen 1. Semester BA Architektur Q () M () M () Q () N () N () L - KIT Universität des Landes Baden-Württemberg und nationales orschungszentrum in
4. Das Verfahren von Galerkin
 4. Das Verfahren von Galerkin 4.1 Grundlagen 4.2 Methode der finiten Elemente 4.3 Beispiel: Stab mit Volumenkraft Prof. Dr. Wandinger 3. Prinzip der virtuellen Arbeit FEM 3.4-1 4.1 Grundlagen Das Verfahren
4. Das Verfahren von Galerkin 4.1 Grundlagen 4.2 Methode der finiten Elemente 4.3 Beispiel: Stab mit Volumenkraft Prof. Dr. Wandinger 3. Prinzip der virtuellen Arbeit FEM 3.4-1 4.1 Grundlagen Das Verfahren
Schnittgrößen und Vorzeichenkonvention
 Schnittgrößen und Vorzeichenkonvention Die äußeren Kräfte (Belastungen) auf einem Tragwerk verursachen innere Kräfte in einem Tragwerk. Da diese inneren Kräfte nur durch ein Freischneiden veranschaulicht
Schnittgrößen und Vorzeichenkonvention Die äußeren Kräfte (Belastungen) auf einem Tragwerk verursachen innere Kräfte in einem Tragwerk. Da diese inneren Kräfte nur durch ein Freischneiden veranschaulicht
Statik. Klausur am Name: Vorname: Matrikelnummer: (bitte deutlich schreiben)
 Diplomprüfung Herbst 2009 Prüfungsfach Statik Klausur am 05.10.2009 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 4 5 6 7 8 9 Summe mögliche Punkte 20 5 5 25 25 30
Diplomprüfung Herbst 2009 Prüfungsfach Statik Klausur am 05.10.2009 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 4 5 6 7 8 9 Summe mögliche Punkte 20 5 5 25 25 30
BAUSTATIK I KOLLOQUIUM 9, Lösung
 BAUSTATIK I KOLLOQUIUM 9, Lösung (101-011) Thema: Kraftmethode Aufgabe 1, Lösung Gegeben: Gesucht: System (EI = konstant) und Einwirkung Q l c f 8EI Schnittkraftlinien n 1 Abzählkriterium für ebene Rahmen:
BAUSTATIK I KOLLOQUIUM 9, Lösung (101-011) Thema: Kraftmethode Aufgabe 1, Lösung Gegeben: Gesucht: System (EI = konstant) und Einwirkung Q l c f 8EI Schnittkraftlinien n 1 Abzählkriterium für ebene Rahmen:
Statik. Klausur am Name: Vorname: Matrikelnummer: (bitte deutlich schreiben)
 Diplomprüfung Frühjahr 2006 Prüfungsfach Statik Klausur am 20.02.2006 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig) Aufgabe 1 2 3 4 5 6 7 8 9 Summe mögliche Punkte 20 4 6 25 20 30
Diplomprüfung Frühjahr 2006 Prüfungsfach Statik Klausur am 20.02.2006 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig) Aufgabe 1 2 3 4 5 6 7 8 9 Summe mögliche Punkte 20 4 6 25 20 30
Baustatik I und II. Klausur am Name: Vorname: Matrikelnummer: (bitte deutlich schreiben)
 Bachelorprüfung Herbst 2009 Prüfungsfach Baustatik I und II Klausur am 05.10.2009 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig) Aufgabe 1 2 3 4 5 6 Summe mögliche Punkte 30 25 25
Bachelorprüfung Herbst 2009 Prüfungsfach Baustatik I und II Klausur am 05.10.2009 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig) Aufgabe 1 2 3 4 5 6 Summe mögliche Punkte 30 25 25
Ruhr-Universität Bochum Bau- und Umweltingenieurwissenschaften Statik und Dynamik. Bachelorprüfung Herbst Klausur am
 Bachelorprüfung Herbst 2012 Modul 13 (BI) / Modul IV 3b (UTRM) Baustatik I und II Klausur am 27.08.2012 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 4 5 6 Summe mögliche
Bachelorprüfung Herbst 2012 Modul 13 (BI) / Modul IV 3b (UTRM) Baustatik I und II Klausur am 27.08.2012 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 4 5 6 Summe mögliche
Sommer Baustatik I+II Sessionsprüfung. Bemerkungen. ( und ) Montag, 08. August 2016, Uhr, HIL G 61 / HIL E 9
 Baustatik I+II Sessionsprüfung (101-0113-00 und 101-0114-00) Sommer 2016 Montag, 08. August 2016, 09.00 12.00 Uhr, HIL G 61 / HIL E 9 Name, Vorname: Studenten-Nr.: Bemerkungen 1. Die Aufgaben dürfen in
Baustatik I+II Sessionsprüfung (101-0113-00 und 101-0114-00) Sommer 2016 Montag, 08. August 2016, 09.00 12.00 Uhr, HIL G 61 / HIL E 9 Name, Vorname: Studenten-Nr.: Bemerkungen 1. Die Aufgaben dürfen in
11 Balkenbiegung Technische Mechanik Balkenbiegung
 11 Balkenbiegung Balkenbiegung 2 Motivation / Einführung Ziele: Berechnung der Balkendurchbiegung (Deformation) Berechnung der Schnittgrößen für statisch unbestimmte Systeme Balken Definition Stabförmig;
11 Balkenbiegung Balkenbiegung 2 Motivation / Einführung Ziele: Berechnung der Balkendurchbiegung (Deformation) Berechnung der Schnittgrößen für statisch unbestimmte Systeme Balken Definition Stabförmig;
Sessionsprüfung Baustatik I+II. Sommer Freitag, 19. August 2011, Uhr, HIL G61
 Sessionsprüfung Baustatik I+II Sommer 011 Freitag, 19. August 011, 09.00 1.00 Uhr, HIL G61 Name, Vorname : Studenten-Nr. : Bemerkungen 1. Die Aufgaben dürfen in beliebiger Reihenfolge bearbeitet werden..
Sessionsprüfung Baustatik I+II Sommer 011 Freitag, 19. August 011, 09.00 1.00 Uhr, HIL G61 Name, Vorname : Studenten-Nr. : Bemerkungen 1. Die Aufgaben dürfen in beliebiger Reihenfolge bearbeitet werden..
Elastizitätslehre Biegebalken
 3. Semester Seite 1/9 Elastizitätslehre Biegebalken 0. Inhalt 0. Inhalt 1 1. Allgemeines 1 2. Begriffe 2 3. Grundlagen 2 4. Biegebalken 2 4.1 Allgemeines 2 4.2 Werkstoff und Randfaserdehnung 3 4.3 Geometrische
3. Semester Seite 1/9 Elastizitätslehre Biegebalken 0. Inhalt 0. Inhalt 1 1. Allgemeines 1 2. Begriffe 2 3. Grundlagen 2 4. Biegebalken 2 4.1 Allgemeines 2 4.2 Werkstoff und Randfaserdehnung 3 4.3 Geometrische
Technische Mechanik. Statik
 Hans Albert Richard Manuela Sander Technische Mechanik. Statik Lehrbuch mit Praxisbeispielen, Klausuraufgaben und Lösungen 4., überarbeitete und erweiterte Auflage Mit 263 Abbildungen ^ Springer Vieweg
Hans Albert Richard Manuela Sander Technische Mechanik. Statik Lehrbuch mit Praxisbeispielen, Klausuraufgaben und Lösungen 4., überarbeitete und erweiterte Auflage Mit 263 Abbildungen ^ Springer Vieweg
Ruhr-Universität Bochum Bau- und Umweltingenieurwissenschaften Statik und Dynamik. Bachelorprüfung Frühjahr Klausur am
 Bachelorprüfung Frühjahr 2013 Modul 13 (BI) / Modul IV 3b (UTRM) Baustatik I und II Klausur am 25.02.2013 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 4 5 Summe mögliche
Bachelorprüfung Frühjahr 2013 Modul 13 (BI) / Modul IV 3b (UTRM) Baustatik I und II Klausur am 25.02.2013 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 4 5 Summe mögliche
Statik II. Lösungsvorschlag zur 3. Hörsaalübung Symmetrie und Antimetrie (KGV)
 Lösungsvorschlag zur Aufgabe 1: Symmetrie und Antimetrie System mit Belastung: Aufteilung der gegebenen Belastung in symmetrische und antimetrische Belastung: symmetrischer Lastfall: antimetrischer Lastfall:
Lösungsvorschlag zur Aufgabe 1: Symmetrie und Antimetrie System mit Belastung: Aufteilung der gegebenen Belastung in symmetrische und antimetrische Belastung: symmetrischer Lastfall: antimetrischer Lastfall:
2. Sätze von Castigliano und Menabrea
 2. Sätze von Castigliano und Menabrea us der Gleichheit von äußerer rbeit und Formänderungsenergie kann die Verschiebung am Lastangriffspunkt berechnet werden, wenn an der Struktur nur eine Last angreift.
2. Sätze von Castigliano und Menabrea us der Gleichheit von äußerer rbeit und Formänderungsenergie kann die Verschiebung am Lastangriffspunkt berechnet werden, wenn an der Struktur nur eine Last angreift.
1.Grundlagen. 1.1 Kräfte. 1.Grundlagen
 .Grundlagen von 7.Grundlagen In diesem Kapitel beschäftigen wir uns kurz mit dem Stoff, welcher später voraus gesetzt wird. Falls es Dir in diesem Kapitel zu schnell geht, empfehle ich folgende Bücher:
.Grundlagen von 7.Grundlagen In diesem Kapitel beschäftigen wir uns kurz mit dem Stoff, welcher später voraus gesetzt wird. Falls es Dir in diesem Kapitel zu schnell geht, empfehle ich folgende Bücher:
Dreigelenkrahmen unter vertikalen und horizontalen Einzellasten sowie horizontaler Streckenlast
 www.statik-lernen.de Beispiele Dreigelenkrahmen Seite 1 Auf den folgenden Seiten wird das Knotenschnittverfahren zur Berechnung statisch bestimmter Systeme am Beispiel eines Dreigelenkrahmens veranschaulicht.
www.statik-lernen.de Beispiele Dreigelenkrahmen Seite 1 Auf den folgenden Seiten wird das Knotenschnittverfahren zur Berechnung statisch bestimmter Systeme am Beispiel eines Dreigelenkrahmens veranschaulicht.
l p h (x) δw(x) dx für alle δw(x).
 1.3 Potentielle Energie 5 In der modernen Statik benutzen wir statt dessen einen schwächeren Gleichheitsbegriff. Wir verlangen nur, dass die beiden Streckenlasten bei jeder virtuellen Verrückung dieselbe
1.3 Potentielle Energie 5 In der modernen Statik benutzen wir statt dessen einen schwächeren Gleichheitsbegriff. Wir verlangen nur, dass die beiden Streckenlasten bei jeder virtuellen Verrückung dieselbe
52 5 Gleichgewicht des ebenen Kraftsystems. Festlager
 52 5 Gleichgewicht des ebenen Kraftsystems Loslager A estlager B BH Einspannung A M A AH A BV AV Abbildung 5.11: Typische Lagerungen eines starren Körpers in der Ebene (oben) und die zugehörigen Schnittskizzen
52 5 Gleichgewicht des ebenen Kraftsystems Loslager A estlager B BH Einspannung A M A AH A BV AV Abbildung 5.11: Typische Lagerungen eines starren Körpers in der Ebene (oben) und die zugehörigen Schnittskizzen
TWL 3 ÜBUNG SCHEIBENKRÄFTE. gegeben: AUFGABE 1.1. W = 39 kn. = 19.5 kn S 1 S 2. gesucht: Ansicht A - A. auf Scheibe S 1
 SCHEIBENKRÄFTE AUFGABE 1.1 Ein Pavillon ist durch eine Flachdach-Deckenscheibe und 3 Wandscheiben S,S und S ausgesteift. 1 2 3 Pendelstützen 1.25 W = 39 kn x 7.50 m A W y = 19.5 kn 45 S 1 S 2 45 S 3 2.50
SCHEIBENKRÄFTE AUFGABE 1.1 Ein Pavillon ist durch eine Flachdach-Deckenscheibe und 3 Wandscheiben S,S und S ausgesteift. 1 2 3 Pendelstützen 1.25 W = 39 kn x 7.50 m A W y = 19.5 kn 45 S 1 S 2 45 S 3 2.50
Der Satz von Betti besagt, dass die reziproken äußeren Arbeiten zweier Systeme, die im Gleichgewicht sind, gleich groß sind A 1,2 = A 2,1.
 Der Satz von Betti oder warum Statik nicht statisch ist. Der Satz von Betti besagt, dass die reziproken äußeren Arbeiten zweier Systeme, die im Gleichgewicht sind, gleich groß sind A 1,2 = A 2,1. (1) Bevor
Der Satz von Betti oder warum Statik nicht statisch ist. Der Satz von Betti besagt, dass die reziproken äußeren Arbeiten zweier Systeme, die im Gleichgewicht sind, gleich groß sind A 1,2 = A 2,1. (1) Bevor
Übung zu Mechanik 1 Seite 34
 Übung zu Mechanik 1 Seite 34 Aufgabe 58 Für das dargestellte System berechne man die Auflagerreaktionen und Schnittgrößen! [m, kn] Aufgabe 59 Bestimmen Sie für das dargestellte System die Auflagerreaktionen
Übung zu Mechanik 1 Seite 34 Aufgabe 58 Für das dargestellte System berechne man die Auflagerreaktionen und Schnittgrößen! [m, kn] Aufgabe 59 Bestimmen Sie für das dargestellte System die Auflagerreaktionen
Baustatik 2. Semestrale am Aufgabe 2 (3 Punkte) (Biegemoment u. Krümmung infolge T) (Normalkraft u. Dehnung infolge T s ) (Senkfeder)
 Baustatik 2 --- Sommersemester 2001 Semestrale Seite 2 Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Sommersemester 2001 Matr.---Nr. :... Fachsemester:... Aufgabe 1 (4 Punkte)
Baustatik 2 --- Sommersemester 2001 Semestrale Seite 2 Technische Universität München Name :... Lehrstuhl für Statik Vorname :... Sommersemester 2001 Matr.---Nr. :... Fachsemester:... Aufgabe 1 (4 Punkte)
Klausur Technische Mechanik
 Institut für Mechanik und Fluiddynamik Prof. Dr.-Ing. Ams Matrikelnummer: Klausur Technische Mechanik 05/02/13 Folgende Angaben sind freiwillig: Name, Vorname: Studiengang: Hinweise: Die Bearbeitungszeit
Institut für Mechanik und Fluiddynamik Prof. Dr.-Ing. Ams Matrikelnummer: Klausur Technische Mechanik 05/02/13 Folgende Angaben sind freiwillig: Name, Vorname: Studiengang: Hinweise: Die Bearbeitungszeit
Grundfachklausur Teil 1 / Statik I
 Technische Universität Darmstadt Institut für Werkstoffe und Mechanik im Bauwesen Fachgebiet Statik Prof. Dr.-Ing. Jens Schneider Grundfachklausur Teil 1 / Statik I im Wintersemester 2013/2014, am 21.03.2014
Technische Universität Darmstadt Institut für Werkstoffe und Mechanik im Bauwesen Fachgebiet Statik Prof. Dr.-Ing. Jens Schneider Grundfachklausur Teil 1 / Statik I im Wintersemester 2013/2014, am 21.03.2014
Grundfachklausur Teil 2 / Statik II
 Technische Universität Darmstadt Institut für Werkstoffe und Mechanik im Bauwesen Fachgebiet Statik Prof. Dr.-Ing. Jens Schneider Grundfachklausur Teil 2 / Statik II im Sommersemester 204, am 08.09.204
Technische Universität Darmstadt Institut für Werkstoffe und Mechanik im Bauwesen Fachgebiet Statik Prof. Dr.-Ing. Jens Schneider Grundfachklausur Teil 2 / Statik II im Sommersemester 204, am 08.09.204
Fragen aus dem Repetitorium II
 Fragen aus dem Repetitorium II Folgend werden die Fragen des Repetitoriums II, welche ihr im Skript ab Seite 182 findet, behandelt. Die Seiten werden ständig aktualisiert und korrigiert, so daß es sich
Fragen aus dem Repetitorium II Folgend werden die Fragen des Repetitoriums II, welche ihr im Skript ab Seite 182 findet, behandelt. Die Seiten werden ständig aktualisiert und korrigiert, so daß es sich
Übung zu Mechanik 2 Seite 62
 Übung zu Mechanik 2 Seite 62 Aufgabe 104 Bestimmen Sie die gegenseitige Verdrehung der Stäbe V 2 und U 1 des skizzierten Fachwerksystems unter der gegebenen Belastung! l l F, l alle Stäbe: EA Übung zu
Übung zu Mechanik 2 Seite 62 Aufgabe 104 Bestimmen Sie die gegenseitige Verdrehung der Stäbe V 2 und U 1 des skizzierten Fachwerksystems unter der gegebenen Belastung! l l F, l alle Stäbe: EA Übung zu
Fachwerkträger. Arten von Bindern und Benennung der Stäbe Nachfolgende Skizze zeigt die möglichen Varianten von Bindern:
 Fachwerkträger Merke: Unter einem Fachwerk versteht man eine Konstruktion, die aus einzelnen geraden Stäben gebildet wird. Diese Stäbe haben die Lasten aufzunehmen. Sie erhalten dadurch Längskräfte. Die
Fachwerkträger Merke: Unter einem Fachwerk versteht man eine Konstruktion, die aus einzelnen geraden Stäben gebildet wird. Diese Stäbe haben die Lasten aufzunehmen. Sie erhalten dadurch Längskräfte. Die
1. Aufgabe: (ca. 12 % der Gesamtpunkte)
 . August 07. Aufgabe: (ca. % der Gesamtunkte) a) Skizzieren Sie an den dargestellten Stäben die Knickformen der vier Euler-Knickfälle inklusive Lagerung und geben Sie zum Eulerfall mit der höchsten Knicklast
. August 07. Aufgabe: (ca. % der Gesamtunkte) a) Skizzieren Sie an den dargestellten Stäben die Knickformen der vier Euler-Knickfälle inklusive Lagerung und geben Sie zum Eulerfall mit der höchsten Knicklast
12) DURCHLAUFTRAEGER und GELENKTRAEGER
 BULEITER HOCHBU S T T I K / F E S T I G K E I T S L E H R E 12) DURCHLUFTREGER und GELENKTREGER 1) Durchlaufträger (Mehrfeldträger) a) llgemeines b) Statisch unbestimmte Systeme c) Methoden zur Durchlaufträgerberechnung
BULEITER HOCHBU S T T I K / F E S T I G K E I T S L E H R E 12) DURCHLUFTREGER und GELENKTREGER 1) Durchlaufträger (Mehrfeldträger) a) llgemeines b) Statisch unbestimmte Systeme c) Methoden zur Durchlaufträgerberechnung
Inhalt 1 Einführung 2 Wirkung der Kräfte 3 Bestimmung von Schwerpunkten
 Inhalt (Abschnitte, die mit * gekennzeichnet sind, enthalten Übungsaufgaben) 1 Einführung... 1 1.1 Begriffe und Aufgaben der Statik... 2 1.1.1 Allgemeine Begriffe 1.1.2 Begriffe für Einwirkungen... 4 1.1.3
Inhalt (Abschnitte, die mit * gekennzeichnet sind, enthalten Übungsaufgaben) 1 Einführung... 1 1.1 Begriffe und Aufgaben der Statik... 2 1.1.1 Allgemeine Begriffe 1.1.2 Begriffe für Einwirkungen... 4 1.1.3
Baustatik II und III (PO 2013)
 Bachelorprüfung Herbst 2015 Modul 18 (BI) Baustatik II und III (PO 2013) Klausur am 28.08.2015 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 4 5 6 7 Summe mögliche
Bachelorprüfung Herbst 2015 Modul 18 (BI) Baustatik II und III (PO 2013) Klausur am 28.08.2015 Name: Vorname: Matrikelnummer: (bitte deutlich schreiben) (9stellig!) Aufgabe 1 2 3 4 5 6 7 Summe mögliche
Statik der Baukonstruktionen: Übungsblätter Lösung Trägerrost kb06 Lö ROST 1. T v [knm]
![Statik der Baukonstruktionen: Übungsblätter Lösung Trägerrost kb06 Lö ROST 1. T v [knm] Statik der Baukonstruktionen: Übungsblätter Lösung Trägerrost kb06 Lö ROST 1. T v [knm]](/thumbs/92/110728515.jpg) Statik der Baukonstruktionen: Übungsblätter Lösung Trägerrost kb0 Lö ROST A. ) M y [knm] V z [kn] Hilfszustand - -.00.00-8.00 -.00.00 -.00.00 8.00-8.00 8.00.00 T [knm]..00 w [mm] 8.00.00 8.00 8.00 8.00.00
Statik der Baukonstruktionen: Übungsblätter Lösung Trägerrost kb0 Lö ROST A. ) M y [knm] V z [kn] Hilfszustand - -.00.00-8.00 -.00.00 -.00.00 8.00-8.00 8.00.00 T [knm]..00 w [mm] 8.00.00 8.00 8.00 8.00.00
Baustatik Formelsammlung
 Baustatik Formelsammlung Jan Höffgen 16. April 2013 Die Formelsammlung wurde auf der Grundlage der Vorlesungen Baustatik I im SS2012 und Baustatik II im WS2012/2013 am KIT erstellt. Es besteht kein Anspruch
Baustatik Formelsammlung Jan Höffgen 16. April 2013 Die Formelsammlung wurde auf der Grundlage der Vorlesungen Baustatik I im SS2012 und Baustatik II im WS2012/2013 am KIT erstellt. Es besteht kein Anspruch
