So nutzen wir diesen wertvollen Rohstoff nachhaltig
|
|
|
- Käthe Heintze
- vor 7 Jahren
- Abrufe
Transkript
1 OS So nutzen wir diesen wertvollen Rohstoff nachhaltig 10 Wissen Wie viel Holz steht in Zürcher Wäldern? / Das Prinzip Nachhaltige Nutzung / Die Menge Nutzholz eines Baumes berechnen / Wie Forstdienste den Holzvorrat eines Waldes bestimmen / Ein hoher Holzvorrat kann Nachteile haben / Gründe für einen tiefen Holzvorrat Unterrichtsideen Eine Baumkluppe herstellen oder improvisieren / Richtig kluppieren und rechnen / Baumhöhen schätzen / Stichprobenflächen anlegen / Den Holzvorrat messen und für ein Waldstück hochrechnen Die Eltern - unter Leitung ihrer Kinder erfahren Wesentliches zu Holzvorrat und Nachhaltigkeit im Wald... messen und berechnen die Nutzholzmenge eines Baumes... bestimmen den Holzvorrat auf Stichprobenflächen... schätzen die Höhe frei stehender Bäume JU W E L E L A N FI
2 Wissen Unterstufe Fächer: Lernziele: Mensch und Umwelt, Mathematik Die Schülerinnen und Schüler können die Nutzholzmenge eines Baumes berechnen können den Holzvorrat auf Stichproben-Flächen systematisch erfassen und die Daten protokollieren können den Holzvorrat eines Waldstückes errechnen Wissen Der Holzvorrat ist die Menge stehenden Holzes pro Waldfläche. Weil wir in der Schweiz höchstens so viel Holz schlagen wie nachwächst, müssen wir wissen, wie viel Holz in unseren Wäldern steht und nachwächst. Holz ist einer der wenigen Rohstoffe der Schweiz. Ein Rohstoff, der ständig nachwächst, CO2-neutral ist, an vielen Orten wächst, einfach zu verarbeiten, vielseitig zu nutzen ist. 1. Der Holzvorrat in unseren Wäldern 2. Die Holzmenge eines Baumes berechnen 3. Den Holzvorrat in einem Wald bestimmen 4. Hoher und tiefer Holzvorrat 1. Der Holzvorrat in unseren Wäldern Im Zürcher Wald stehen durchschnittlich 407 Tariffestmeter (tfm) Holz pro Hektare. Ein Tariffestmeter (tfm) ist das Volumenmass für stehende Bäume und entspricht etwa einem Kubikmeter (m3) nutzbaren Holzes. Bei rund Hektaren Wald stehen im Kanton Zürich also über 20 Millionen Tariffestmeter Holz. Der Holzvorrat der stehenden Bäume wird in Tariffestmetern, das gefällte Holz wird in Kubikmetern gerechnet. Eine Hektare (ha) ist eine Fläche von 100 x 100 Metern. Zum Vergleich: Ein Fussballfeld misst knapp drei Viertel einer Hektare. Im Schweizer Wald stehen durchschnittlich 365 Tariffestmeter Holz pro Hektare. Beeinflusst wird der Holzvorrat durch die Forstdienste unter Berücksichtigung der Nachhaltigkeit. Nachhaltigkeit heisst: Es wird höchstens so viel Holz genutzt, wie nachwächst. Beeinflusst wird der Holzvorrat aber auch durch Naturereignisse wie Stürme, Schneedruck, Lawinen. 2. Der Holzvorrat in unseren Wäldern Um den zu berechnen, beschränkt man sich auf jene Bäume, deren Durchmesser auf Brusthöhe 12 Zentimeter und mehr misst. Der Brusthöhendurchmesser (BHD) wird 130 Zentimeter über dem Boden gemessen. Der Holzvorrat eines Baumes lässt sich mit folgender einfachen Faustregel schätzen: juwel - jugend zeigt wald den eltern 1
3 Wissen Brusthöhendurchmesser (BHD) in Dezimetern 2 / 10 Rechenbeispiel 1: Ein Baum hat einen BHD von 40 cm = 4 dm. Berechnung: 4 x 4 = /10 = 1.6 Tariffestmeter Holzvorrat 3. Den Holzvorrat in einem Wald hochrechnen Für den Förster ist es wichtig zu wissen, wie viel Holz im Wald steht und wie viel nachwächst, damit er diesen nicht übernutzt. Im Zürcher Wald stehen Millionen von Bäumen. Es wäre zu aufwändig, sie einzeln zu messen und zu zählen. Daher misst man den Holzvorrat auf Stichprobenflächen und rechnet die Werte dann auf eine ganze Waldfläche hoch. Im Kanton Zürich misst eine Stichprobenfläche in der Regel 3 Aren (a) = 300 Quadratmeter. Sie ist kreisrund und weist einen Radius von 9.77 m auf. Rechenbeispiel 2 In einer Stichprobenfläche stehen fünf Bäume, die je einen Brusthöhendurchmesser von 40 cm haben (wie oben im Rechenbeispiel 1). Der Holzvorrat auf den 3 a beträgt: 5 x 1.6 tfm = 8 tfm Der Holzvorrat auf 1 ha (= 100 a) beträgt: 8 tfm/ 3a x 100a = etwa 270 tfm 4. Hoher Holzvorrat tiefer Holzvorrat Ein hoher Holzvorrat ist im Wirtschaftswald nicht immer erstrebenswert. Ein hoher Holzvorrat bedeutet meist, dass die Bäume dicht stehen. Bei dicht stehenden Bäumen entwickelt sich ihr Schlankheitsgrad, das ist das Verhältnis von Höhe zum Durchmesser, ungünstig. Bäume mit einem zu hohen Schlankheitsgrad sind instabil. Wenn einzelne Bäume umfallen, zum Beispiel durch Schneedruck, dann kann der Wald grossflächig zusammenbrechen. Ein weiterer Nachteil eines zu hohen Holzvorrates: Wegen der dicht stehenden Bäume scheint nur wenig oder kein Licht in den Wald; der Baumbestand wird sich darum nur schlecht oder gar nicht verjüngen. Ein tiefer kann verschiedene Gründe haben: Übernutzung durch den Menschen, nährstoffarmer Boden, Höhenlage mit tiefen Temperaturen. Bäume, die viel Platz haben, sind in der Regel stabil. Ihr Nachteil ist, dass sie astiger und damit von tieferer Qualität sind. Links und Literatur Waldwerkstatt, Zytglogge Werkbuch, Zytglogge Verlag Bern, 2. Auflage 1995, Martin Ryser, 138 Seiten, ISBN / Seiten (Stockmethode), Seiten (Holzvorrat) Gis-Browser des Kanton Zürichs: juwel - jugend zeigt wald den eltern 2
4 Unterrichtsideen Unterrichtsideen 1. Eine Kluppe herstellen 2. Mit der Kluppe richtig messen und die Holzmenge eines Baumes berechnen 3. Baumhöhe schätzen 4. Stichprobenzentren bestimmen Stichprobenflächen markieren 5. Den Holzvorrat von Stichprobenflächen messen und hochrechnen Tipp zu den Unterrichtsideen Die Unterrichtsideen 2 bis 5 an einem Halbtag im Wald nacheinander durchführen juwel - jugend zeigt wald den eltern 3
5 U 1. nterrichtsideen Eine Kluppe herstellen Fächer: Werken Lernziele: Die Schülerinnen und Schüler kennen das Werkzeug Kluppe stellen das Werkzeug selbst her Zeitbedarf: 150 Minuten Material: Holz gemäss Skizze Vorbereitung: Holz und Skizze bereitstellen Werkunterricht vorbereiten Ablauf Die Kluppe gemäss Foto und Skizze herstellen. Kluppen improvisieren Mit dem angewinkelten Doppelmeter und einem geraden Ast parallel zum abgewinkelten Teil des Doppelmeters messen. Zwei gerade Holzstäbe parallel an den Stamm halten und den Abstand mit einem Doppelmeter messen. juwel - jugend zeigt wald den eltern 4
6 Unterrichtsideen 2. Mit der Kluppe richtig messen und die Holzmenge eines Baumes berechnen Fächer: Lernziele: Zeitbedarf: Mensch und Umwelt, Mathematik Die Schülerinnen und Schüler können das Messinstrument Kluppe korrekt handhaben können die Nutzholzmenge eines Baumes berechnen 60 Minuten Material: Kluppen selbst hergestellt oder improvisiert oder vom Förster zur Verfügung gestellt. 1 Doppelmeter für jedes Zweierteam Wäscheklammern, um an den Kleidern der Schüler 130 cm Höhe anzuzeigen. Vorbereitung: Ein geeignetes Waldstück für die Übung rekognoszieren Ablauf In Zweierteams mehrere Bäume an verschiedenen Orten korrekt messen: o Auf Brusthöhe = 130 Zentimeter über dem Boden o Am Hang bergseits o Bei schräg stehenden Bäumen im rechten Winkel zur Stammachse. Mit der Faustregel Brusthöhendurchmesser (BHD) in Dezimetern 2 / 10 die Nutzholzmenge der Bäume berechnen. juwel - jugend zeigt wald den eltern 5
7 Unterrichtsideen 3. Baumhöhen schätzen Lernziele: Zeitbedarf: Die Schülerinnen und Schüler können mit einer einfachen Methode die Höhe eines stehenden Baumes messen 30 Minuten Material: Holzstock, 70 Zentimeter lang Doppelmeter Messband Vorbereitung: Einen geeigneten, frei stehenden Baum finden Ablauf a) Suche einen Stock, der gleich lang ist wie dein Arm. b) Wenn du keinen findest, dann suche einen längeren Stock. Halte diesen dort, wo die Distanz auch deiner Armlänge entspricht. Den Stock senkrecht in die Faust nehmen und den Arm waagrecht nach vorne ausstrecken. Jetzt mit dem senkrecht gehaltenen Stock in der Faust sich vorwärts oder rückwärts bewegen, bis die Stockspitze und die Baumspitze in einer geraden Linie liegen. Das entspricht der Länge des Baumes ohne die Distanz von deinem Arm zum Boden. Mache 2 Schritte (= x) zurück. Diese 2 Schritte entsprechen der Distanz vom ausgestreckten Arm bis zum Boden = x. Stehen bleiben und den Standort mit einem Stein oder Ast markieren. Die Distanz vom Standort bis zum Stammfuss messen. Das ergibt die Höhe des Baumes = y. juwel - jugend zeigt wald den eltern 6
8 Unterrichtsideen 4. Stichprobenzentren bestimmen Stichprobenflächen markieren Fächer: Lernziele:: Zeitbedarf: Mensch und Umwelt, Mathematik Die Schülerinnen und Schüler verstehen das Prinzip der Stichprobenerhebung können Stichprobenflächen und ihre Zentren selbst bestimmen 90 Minuten Material: Kartenausschnitte der zu untersuchenden Waldabschnitte, aus dem Internet ausgedruckt: Kompass Messband, mindestens 20 Meter Markierband, Holzpflöcke Vorbereitung: Eine Waldfläche rekognoszieren, die folgende Kriterien erfüllt: - ebenes Gelände, mitten im Wald nicht am Waldrand - wenig oder kein Unterwuchs - gleichmässig dicke und hohe Bäume, zum Beispiel gleichaltrige Rottannen oder Buchen Stichprobenflächen für die Gruppenarbeit bestimmen: Kreisförmig, mit einem Radius von 9,77 Metern, mit einem Abstand von etwa 50 Metern voneinander. Ablauf Gruppen von 5 bis 6 Schülerinnen und Schülern bilden Jeder Gruppe eine oder mehrere Stichprobenflächen zuteilen; diese mit dem Kompass möglichst in einer Linie bestimmen Gruppenarbeit: Bei jeder Stichprobenfläche o Das Stichprobenzentrum (Z) festlegen und mit einem Holzpflock markieren o Vom Zentrum aus einen Kreis mit einem Radius von 9,77 Metern abstecken und mit Holzpflöcken markieren o Bestimmen, welche Bäume mit einem Brusthöhendurchmesser 12 Zentimeter zur Stichprobenfläche gehören juwel - jugend zeigt wald den eltern 7
9 Unterrichtsideen 5. Den Holzvorrat von Stichprobenflächen messen und hochrechnen Fächer: Lernziel: Zeitbedarf: Mensch und Umwelt, Mathematik Die Schülerinnen und Schüler können den Holzvorrat auf einer Stichprobenfläche erfassen können den Holzvorrat in einem Waldstück bestimmen haben erste Erfahrungen mit der Beurteilung eines Waldbestandes 90 Minuten Material: 1 Kluppe pro Gruppe Schulkreide, Taschenrechner Arbeitsblatt Holzvorrat-Aufnahmeprotokoll, Schreibzeug und Notizblock Vorbereitung: Je 6er Gruppe eine Stichprobenfläche festgelegt und markiert (Unterrichtsidee 3) Arbeitsanweisungen und Berechnungen durchdacht Ablauf Diskussion mit der Klasse o Wirkt der Waldbestand eher dicht und dunkel oder licht und hell? o Abschätzen: Ist der Holzvorrat hoch oder tief? o Liegt der Holzvorrat über dem Zürcher Durchschnitt von 407 Tariffestmetern pro Hektare? Aufgabenteilung in den Gruppen festlegen: 1 Protokollführerin (Gruppenverantwortliche), 2 Kluppenführer, 1 Markierer, 2 Messbandführerinnen eine im Zentrum, eine am Rand der Stichprobenfläche Arbeitsmethode mit der Klasse absprechen: o Die Nordrichtung bestimmen o Zum Kluppieren im Norden der Stichprobenfläche beginnen o Dann sich in der Stichprobenfläche im Uhrzeigersinn von Baum zu Baum bewegen o Kluppieren eines Baumes vom Stichprobenzentrum her auf der linken Seite und auf Brusthöhe (130 cm). Der lange Teil der Kluppe mit der Masseinheit berührt den Stamm und zeigt gegen das Stichprobenzentrum. o Mit dem Messband entscheiden, ob Bäume am Rand der Stichprobenfläche zu erfassen sind oder nicht. Dazu auf Brusthöhe die Distanz vom Stichprobenzentrum zur Mitte des Baumstammes messen. Distanz 9.76 Meter Baum erfassen; Distanz 9.78 Meter Baum nicht erfassen Gruppenarbeit o Die Bäume mit einem Brusthöhendurchmesser 12 cm messen und im Aufnahmeprotokoll notieren o Erfasste Bäume mit Kreide markieren o Wenn alle Bäume gemessen sind: Den Holzvorrat der Stichprobenfläche zusammenzählen Klassenarbeit o Wenn der Holzvorrat aller Stichprobenflächen der Gruppen berechnet ist: Den Holzvorrat auf das untersuchte Waldstück und auf eine Hektare hochrechnen. o Kontrolle: Wie gut stimmt das Resultat mit den Beurteilungen und Schätzungen zu Beginn der Arbeiten überein? o Was meint der Förster zum Resultat? juwel - jugend zeigt wald den eltern 8
10 F inale JUWEL Finale Die Schülerinnen und Schüler vermitteln ihren Eltern Wissen o zum Holzvorrat im Zürcher Wald o zur nachhaltigen Nutzung des Waldes o zum Thema Hoher und tiefer Holzvorrat... lassen die Eltern den Brusthöhendurchmesser eines Baumes messen und seine Nutzholzmenge berechnen (Unterrichtsidee 2)... messen mit den Eltern den Holzvorrat von Stichprobenflächen und bestimmen den Holzvorrat im ausgewählten Waldstück (Unterrichtsidee 4)... zeigen den Eltern, wie sie die Höhe eines Baumes schätzen können (Unterrichtsidee 5) Schlussrunde unter Eltern, im Beisein der Kinder: Was habe ich gelernt? Was hat mich erstaunt? Zvieri zum Abschluss Zeitbedarf: 1 bis 2½ Stunden Stunden JU W E L juwel - jugend zeigt wald den eltern E L A N FI 9
11 Arbeitsblatt Holzvorrat- Aufnahmeprotokoll Datum Stichprobe Team Gemeinde Lokalname Nr. Fläche Aren Berechnungsformel Holzmenge eines Baumes: Durchmesser in dm x Durchmesser in dm : 10 = Radius m Beispiel: Fichte 5.5 x 5.5 = : 10 = 3.02 Reihenfolge der Baummessung (Beginn Nord, Richtung Ost, Süd, Nord) Baumart Brusthöhen Durchmesser in Dezimeter (ab 12 cm) Ungefähre Holzmenge pro Baum in Tariffestmeter (Tfm) Beispiel Fichte Baum Baum 2 Baum 3 Baum 4 Baum 5 Baum 6 Baum 7 Baum 8 Baum 9 Baum 10 Baum 11 Baum 12 Baum 13 Baum 14 Baum 15 Baum 16 Baum 17 Baum 18 Baum 19 Baum Total Vorrat auf der Stichprobe Nr juwel - jugend zeigt wald den eltern 10
Bäume fällen - gibt Licht und belebt den Wald
 MS / OS Bäume fällen - gibt Licht und belebt den Wald 8 Wissen Wirtschaftswälder sind keine Urwälder / Licht fördert vielfältiges Wachsen im Wald / Wie viel Platz braucht ein Baum? / Jungwuchspflege, Dickungspflege
MS / OS Bäume fällen - gibt Licht und belebt den Wald 8 Wissen Wirtschaftswälder sind keine Urwälder / Licht fördert vielfältiges Wachsen im Wald / Wie viel Platz braucht ein Baum? / Jungwuchspflege, Dickungspflege
Den Wald erkunden und Wesentliches skizzieren
 MS Den Wald erkunden und Wesentliches skizzieren 6 Wissen Was ist ein Kroki? Was ist eine Karte? / Karten in der Forstwirtschaft / Der Waldentwicklungsplan für die strategische Planung / Die Bestandeskarte
MS Den Wald erkunden und Wesentliches skizzieren 6 Wissen Was ist ein Kroki? Was ist eine Karte? / Karten in der Forstwirtschaft / Der Waldentwicklungsplan für die strategische Planung / Die Bestandeskarte
Für diese Arbeiten ein Waldstück wählen, das den Schülern vertraut ist. Sie werden den Wald neu kennen lernen.
 Unterrichtsideen 5. Krokis zeichnen und zu einer Waldkarte zusammenfügen Fächer: Lernziele: Zeitbedarf: Mensch und Umwelt, Bildnerisches Gestalten Die Schülerinnen und Schüler verstehen das Prinzip eines
Unterrichtsideen 5. Krokis zeichnen und zu einer Waldkarte zusammenfügen Fächer: Lernziele: Zeitbedarf: Mensch und Umwelt, Bildnerisches Gestalten Die Schülerinnen und Schüler verstehen das Prinzip eines
UE 6: Exkursion Wald und Klima(wandel)
 UE 6: Exkursion Wald und Klima(wandel) Zeitbedarf: ca. 90 Minuten Inhalt: SuS vermessen Bäume im Wald (Alternative: Schulhof), errechnen deren Kohlenstoffspeicher und suchen nach möglichen Zeichen des
UE 6: Exkursion Wald und Klima(wandel) Zeitbedarf: ca. 90 Minuten Inhalt: SuS vermessen Bäume im Wald (Alternative: Schulhof), errechnen deren Kohlenstoffspeicher und suchen nach möglichen Zeichen des
Bestimmung Was ist der Wald wert? : Arbeitsblatt
 Aufgabe : Ein Waldgebiet aussuchen und beschreiben.) Sucht in eurer Umgebung ein Waldgebiet mit einer Fläche von 0 m x 0 m aus, für dessen Bäume Ihr den Geldwert des Holzes ermitteln wollt..) Markiert
Aufgabe : Ein Waldgebiet aussuchen und beschreiben.) Sucht in eurer Umgebung ein Waldgebiet mit einer Fläche von 0 m x 0 m aus, für dessen Bäume Ihr den Geldwert des Holzes ermitteln wollt..) Markiert
Faustzahlen zu Einzelbaum und Bestandeskenngrößen
 Faustzahlen zu Einzelbaum und Bestandeskenngrößen Siegfried Sperrer Forstliche Ausbildungsstätte Ort / Gmunden Lehrer- und Beraterfortbildungsplan 2009 Gmunden 7. 5. 2009 Volumen Einzelbloch V = d²*π*
Faustzahlen zu Einzelbaum und Bestandeskenngrößen Siegfried Sperrer Forstliche Ausbildungsstätte Ort / Gmunden Lehrer- und Beraterfortbildungsplan 2009 Gmunden 7. 5. 2009 Volumen Einzelbloch V = d²*π*
Kapitel D : Flächen- und Volumenberechnungen
 Kapitel D : Flächen- und Volumenberechnungen Berechnung einfacher Flächen Bei Flächenberechnungen werden die Masse folgendermassen bezeichnet: = Fläche in m 2, dm 2, cm 2, mm 2, etc a, b, c, d = Bezeichnung
Kapitel D : Flächen- und Volumenberechnungen Berechnung einfacher Flächen Bei Flächenberechnungen werden die Masse folgendermassen bezeichnet: = Fläche in m 2, dm 2, cm 2, mm 2, etc a, b, c, d = Bezeichnung
Der WALD, das KLIMA und ICH Ein Forschungsauftrag zu Wald und Klima
 Der WALD, das KLIMA und ICH Ein Forschungsauftrag zu Wald und Klima Zielgruppe: Zeit: Ort: Methode: Basiswissen: Lernziele der Exkursion: Zusatzoption: Material: Schüler: BNE-Bezug: Die Schüler ab 15 Jahre
Der WALD, das KLIMA und ICH Ein Forschungsauftrag zu Wald und Klima Zielgruppe: Zeit: Ort: Methode: Basiswissen: Lernziele der Exkursion: Zusatzoption: Material: Schüler: BNE-Bezug: Die Schüler ab 15 Jahre
MATURITÄTSPRÜFUNGEN 2006
 KANTONSSCHULE ROMANSHORN MATURITÄTSPRÜFUNGEN 2006 MATHEMATIK 3 Std. Klasse 4 Ma hcs Hilfsmittel: Taschenrechner Fundamentum Mathematik und Physik oder Formelsammlung DMK Beachten Sie:Jede Aufgabe ist auf
KANTONSSCHULE ROMANSHORN MATURITÄTSPRÜFUNGEN 2006 MATHEMATIK 3 Std. Klasse 4 Ma hcs Hilfsmittel: Taschenrechner Fundamentum Mathematik und Physik oder Formelsammlung DMK Beachten Sie:Jede Aufgabe ist auf
Waldwirtschaftsplan Forsteinrichtung
 Waldwirtschaftsplan Forsteinrichtung Warum planen? Für einen, der nicht weiß, nach welchem Hafen er steuern will, gibt es keinen günstigen Wind. (Seneca, röm. Philosoph) Nachhaltigkeit "Jede weise Forstdirektion
Waldwirtschaftsplan Forsteinrichtung Warum planen? Für einen, der nicht weiß, nach welchem Hafen er steuern will, gibt es keinen günstigen Wind. (Seneca, röm. Philosoph) Nachhaltigkeit "Jede weise Forstdirektion
Einstiege: Volumen eines Zylinders
 An Abbildungen Höhe und Radius bestimmen und Volumen berechnen (1/3) 1 Schneide die Netze der beiden Zylinder aus und stelle zwei Modelle her. a) Schätze, welcher Zylinder das größere Volumen und die größere
An Abbildungen Höhe und Radius bestimmen und Volumen berechnen (1/3) 1 Schneide die Netze der beiden Zylinder aus und stelle zwei Modelle her. a) Schätze, welcher Zylinder das größere Volumen und die größere
Schriftliche Prüfungsarbeit zum mittleren Schulabschluss 2009 im Fach Mathematik. 27. Mai 2009
 Senatsverwaltung für Bildung, Wissenschaft und Forschung Schriftliche Prüfungsarbeit zum mittleren Schulabschluss 2009 im Fach Mathematik 27. Mai 2009 Arbeitsbeginn: 10.00 Uhr Bearbeitungszeit: 120 Minuten
Senatsverwaltung für Bildung, Wissenschaft und Forschung Schriftliche Prüfungsarbeit zum mittleren Schulabschluss 2009 im Fach Mathematik 27. Mai 2009 Arbeitsbeginn: 10.00 Uhr Bearbeitungszeit: 120 Minuten
c) Der Umfang einer quadratförmigen Rabatte misst 60,4 m. Wie lange ist eine Seitenlänge?
 13.3 Übungen zur Flächenberechnung 13.3.1 Übungen Quadrat Berechnen Sie für diese Quadrate das gesuchte Maß, geben Sie das Resultat in der verlangten Einheit an. a) l 4,8 dm, A? cm 2, U? m A l 2 4,8 2
13.3 Übungen zur Flächenberechnung 13.3.1 Übungen Quadrat Berechnen Sie für diese Quadrate das gesuchte Maß, geben Sie das Resultat in der verlangten Einheit an. a) l 4,8 dm, A? cm 2, U? m A l 2 4,8 2
Mathematik I Prüfung für den Übertritt aus der 9. Klasse
 Aufnahmeprüfung 016 für den Eintritt in das 9. Schuljahr eines Gymnasiums des Kantons Bern Mathematik I Prüfung für den Übertritt aus der 9. Klasse Bitte beachten: - Bearbeitungsdauer: 60 Minuten - Alle
Aufnahmeprüfung 016 für den Eintritt in das 9. Schuljahr eines Gymnasiums des Kantons Bern Mathematik I Prüfung für den Übertritt aus der 9. Klasse Bitte beachten: - Bearbeitungsdauer: 60 Minuten - Alle
ProSilvaSchweiz > Bitterlich-Übung
 ProSilvaSchweiz > Bitterlich-Übung Exkursion vom Donnerstag, 12. November 2015 Forstrevier Bachs ZH > christian.rosset@bfh.ch Berner Fachhochschule Hochschule für Agrar- Forst- und Lebensmittelwissenschaften
ProSilvaSchweiz > Bitterlich-Übung Exkursion vom Donnerstag, 12. November 2015 Forstrevier Bachs ZH > christian.rosset@bfh.ch Berner Fachhochschule Hochschule für Agrar- Forst- und Lebensmittelwissenschaften
Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A Bremen. Die Kursübersicht für das Fach Mathematik
 Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 28195 Bremen Die Kursübersicht für das Fach Mathematik Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe
Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 28195 Bremen Die Kursübersicht für das Fach Mathematik Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe
Betriebswirtschaftslehre
 Betriebswirtschaftslehre 1. Erklären sie an Hand eines Beispiels den Begriff Bonität! Wie wird er ermittelt? Ertragsklasse. Maß für die Ertragsfähigkeit eines Standortes oder Bestandes. Die Summe der jährlichen
Betriebswirtschaftslehre 1. Erklären sie an Hand eines Beispiels den Begriff Bonität! Wie wird er ermittelt? Ertragsklasse. Maß für die Ertragsfähigkeit eines Standortes oder Bestandes. Die Summe der jährlichen
Mathematik I Prüfung für den Übertritt aus der 8. Klasse
 Aufnahmeprüfung 016 für den Eintritt in das 9. Schuljahr eines Gymnasiums des Kantons Bern Mathematik I Prüfung für den Übertritt aus der 8. Klasse Bitte beachten: - Bearbeitungsdauer: 60 Minuten - Alle
Aufnahmeprüfung 016 für den Eintritt in das 9. Schuljahr eines Gymnasiums des Kantons Bern Mathematik I Prüfung für den Übertritt aus der 8. Klasse Bitte beachten: - Bearbeitungsdauer: 60 Minuten - Alle
14 Flächen. Berechnen Sie die Fläche eines trapezförmigen Platzes mit m Höhe und einer Mittellinie von 9.2 m.
 14.3 Aufgaben Rechnen mit der Grundformel (Für alle Aufgaben gilt 3.14) 1 Welchen Umfang hat ein rechteckiges Feld von 51.3 m Länge und 12.6 m Breite? 2 Berechnen Sie die Fläche eines trapezförmigen Platzes
14.3 Aufgaben Rechnen mit der Grundformel (Für alle Aufgaben gilt 3.14) 1 Welchen Umfang hat ein rechteckiges Feld von 51.3 m Länge und 12.6 m Breite? 2 Berechnen Sie die Fläche eines trapezförmigen Platzes
Grundlagen IV der Kathetensatz
 Grundlagen IV der Kathetensatz Der Kathetensatz ergibt sich wie auch der Höhensatz aus dem Ähnlichkeitssatz: b a a c = p a a 2 = p c p q b c = q b b 2 = q c c Löse die folgenden Teilaufgaben mithilfe des
Grundlagen IV der Kathetensatz Der Kathetensatz ergibt sich wie auch der Höhensatz aus dem Ähnlichkeitssatz: b a a c = p a a 2 = p c p q b c = q b b 2 = q c c Löse die folgenden Teilaufgaben mithilfe des
1) Längenmasse. Verwandeln sie in die verlangte Einheit: Aufgaben 2: Ergänzen sie die Matrix, indem sie die Einheiten umrechnen.
 Kapitel B: Masseinheiten 1) Längenmasse Die Länge von Strecken und Distanzen werden mit den Längenmassen angegeben. Die für das Längenmass ist das Meter (m). Weitere gängige en für Längen sind Kilometer
Kapitel B: Masseinheiten 1) Längenmasse Die Länge von Strecken und Distanzen werden mit den Längenmassen angegeben. Die für das Längenmass ist das Meter (m). Weitere gängige en für Längen sind Kilometer
ALGEBRA Der Lösungsweg muss klar ersichtlich sein Schreiben Sie Ihre Lösungswege direkt auf diese Aufgabenblätter
 Berufsmaturitätsschule GIB Bern Aufnahmeprüfung 2005 Mathematik Teil A Zeit: 45 Minuten Name / Vorname:... ALGEBRA Der Lösungsweg muss klar ersichtlich sein Schreiben Sie Ihre Lösungswege direkt auf diese
Berufsmaturitätsschule GIB Bern Aufnahmeprüfung 2005 Mathematik Teil A Zeit: 45 Minuten Name / Vorname:... ALGEBRA Der Lösungsweg muss klar ersichtlich sein Schreiben Sie Ihre Lösungswege direkt auf diese
... Beobachtungspraktikum. 1. Sternbilder
 Beobachtungspraktikum Hinweise Arbeitsmittel Während des Beobachtungspraktikums stehen Sie vor der Aufgabe, einfache Beobachtungen am Sternhimmel selbständig durchzuführen, diese zu protokollieren und
Beobachtungspraktikum Hinweise Arbeitsmittel Während des Beobachtungspraktikums stehen Sie vor der Aufgabe, einfache Beobachtungen am Sternhimmel selbständig durchzuführen, diese zu protokollieren und
Mathematik VOLKSSCHULEN KANTONE SOLOTHURN BASEL-LANDSCHAFT ORIENTIERUNGSARBEIT. Primarschule
 VOLKSSCHULEN KANTONE BASEL-LANDSCHAFT SOLOTHURN Primarschule 5. Klasse Name Vorname Schuljahr 2009/2010 Datum der Durchführung 23. September 2009 ORIENTIERUNGSARBEIT Primarschule Mathematik Hinweise für
VOLKSSCHULEN KANTONE BASEL-LANDSCHAFT SOLOTHURN Primarschule 5. Klasse Name Vorname Schuljahr 2009/2010 Datum der Durchführung 23. September 2009 ORIENTIERUNGSARBEIT Primarschule Mathematik Hinweise für
Mathematik VOLKSSCHULEN KANTONE SOLOTHURN BASEL-LANDSCHAFT ORIENTIERUNGSARBEIT. Primarschule. Lösungen und Korrekturanweisungen
 VOLKSSCHULEN KANTONE BASEL-LANDSCHAFT SOLOTHURN Primarschule 5. Klasse Name Vorname Schuljahr 2009/2010 Datum der Durchführung 23. September 2009 ORIENTIERUNGSARBEIT Primarschule Lösungen und Korrekturanweisungen
VOLKSSCHULEN KANTONE BASEL-LANDSCHAFT SOLOTHURN Primarschule 5. Klasse Name Vorname Schuljahr 2009/2010 Datum der Durchführung 23. September 2009 ORIENTIERUNGSARBEIT Primarschule Lösungen und Korrekturanweisungen
K l a s s e n a r b e i t N r. 2
 K l a s s e n a r b e i t N r. Aufgabe 1 Der Stamm einer Buche hat den Umfang U = 370 cm. a) Berechne den Durchmesser. b) Man kann das Alter eines Baumes an der Anzahl der Jahresringe erkennen. Die durchschnittliche
K l a s s e n a r b e i t N r. Aufgabe 1 Der Stamm einer Buche hat den Umfang U = 370 cm. a) Berechne den Durchmesser. b) Man kann das Alter eines Baumes an der Anzahl der Jahresringe erkennen. Die durchschnittliche
# 1 Hip Crossover. Ausgangslage. Durchführung
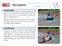 Rumpf # 1 Hip Crossover Lege dich mit dem Rücken auf den Boden und halte dich mit den Armen an einer stabilen Verankerung fest (z.b. Sprossenwand, ). Winkle die Beine und das Becken durch verdrehen des
Rumpf # 1 Hip Crossover Lege dich mit dem Rücken auf den Boden und halte dich mit den Armen an einer stabilen Verankerung fest (z.b. Sprossenwand, ). Winkle die Beine und das Becken durch verdrehen des
Linien auf dem Fussballplatz
 Rechnen Berechnen A10 Linien auf dem Fussballplatz KG US MS OS 20' Wie lange sind alle geraden Linien auf einem Fussballfeld zusammen? Blatt A4 Arbeitsblatt Spielfeldlinien Lösung Taschenrechner 1. Zeichne
Rechnen Berechnen A10 Linien auf dem Fussballplatz KG US MS OS 20' Wie lange sind alle geraden Linien auf einem Fussballfeld zusammen? Blatt A4 Arbeitsblatt Spielfeldlinien Lösung Taschenrechner 1. Zeichne
Arbeitszeit Teil A 45 Minuten Teil B 45 Minuten
 Inhalt/Lernziele Arbeitszeit Teil A 45 Minuten Teil B 45 Minuten Teil A Teiler einer Zahl bestimmen Teilbarkeitsgegeln anwenden Primzahlen kleiner 100 erkennen Quadratzahlen kleiner 300 erkennen Getönte
Inhalt/Lernziele Arbeitszeit Teil A 45 Minuten Teil B 45 Minuten Teil A Teiler einer Zahl bestimmen Teilbarkeitsgegeln anwenden Primzahlen kleiner 100 erkennen Quadratzahlen kleiner 300 erkennen Getönte
Mathematik, 2. Sekundarschule
 Zentrale Aufnahmeprüfung 2009 für die Kurzgymnasien und die Handelsmittelschulen des Kantons Zürich Mathematik, 2. Sekundarschule Von der Kandidatin oder vom Kandidaten auszufüllen: Name:........................
Zentrale Aufnahmeprüfung 2009 für die Kurzgymnasien und die Handelsmittelschulen des Kantons Zürich Mathematik, 2. Sekundarschule Von der Kandidatin oder vom Kandidaten auszufüllen: Name:........................
Illustrierende Aufgaben zum LehrplanPLUS. Windenergie
 Windenergie Stand: 02.0.207 Jahrgangsstufen Fach Übergreifende Bildungs- und Erziehungsziele Zeitrahmen FOS (ABU), BOS 2 (ABU) Physik Technische Bildung eine Unterrichtsstunde Kompetenzerwartung Lehrplan
Windenergie Stand: 02.0.207 Jahrgangsstufen Fach Übergreifende Bildungs- und Erziehungsziele Zeitrahmen FOS (ABU), BOS 2 (ABU) Physik Technische Bildung eine Unterrichtsstunde Kompetenzerwartung Lehrplan
Geometrie-Aufgaben: Ähnlichkeit & Strahlensätze Berechne die fehlenden Strecken: (Skizzen sind nicht masssabgsgetreu)
 Geometrie-Aufgaben: Ähnlichkeit & Strahlensätze 4 1. Berechne die fehlenden Strecken: (Skizzen sind nicht masssabgsgetreu) 1 2 2. Ein Baum und sein Schatten An einem Baum und an seinem Schatten sind die
Geometrie-Aufgaben: Ähnlichkeit & Strahlensätze 4 1. Berechne die fehlenden Strecken: (Skizzen sind nicht masssabgsgetreu) 1 2 2. Ein Baum und sein Schatten An einem Baum und an seinem Schatten sind die
St.Gallische Kantonsschulen Aufnahmeprüfung 2010 Gymnasium. Kandidatennummer: Geburtsdatum: Note: Aufgabe
 St.Gallische Kantonsschulen Aufnahmeprüfung 010 Gymnasium Mathematik 1 ohne Taschenrechner Dauer: 90 Minuten Kandidatennummer: Summe: Geburtsdatum: Note: Aufgabe 1 3 4 5 6 7 8 9 10 11 1 13 Punkte Löse
St.Gallische Kantonsschulen Aufnahmeprüfung 010 Gymnasium Mathematik 1 ohne Taschenrechner Dauer: 90 Minuten Kandidatennummer: Summe: Geburtsdatum: Note: Aufgabe 1 3 4 5 6 7 8 9 10 11 1 13 Punkte Löse
Das weiß ich schon! Das will ich wissen?
 Das weiß ich schon! Das will ich wissen? 1 Schreibe zum Thema Längen : 1. Das weiß ich schon: 2. Das will ich wissen: Bringe Material oder Bücher zum Thema für unseren Thementisch mit! Wer ist der Größte?
Das weiß ich schon! Das will ich wissen? 1 Schreibe zum Thema Längen : 1. Das weiß ich schon: 2. Das will ich wissen: Bringe Material oder Bücher zum Thema für unseren Thementisch mit! Wer ist der Größte?
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Unterrichtsreihe zum Thema "Kreis" Das komplette Material finden Sie hier:
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Unterrichtsreihe zum Thema "Kreis" Das komplette Material finden Sie hier: School-Scout.de Thema: Unterrichtsreihe zum Thema Kreis
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Unterrichtsreihe zum Thema "Kreis" Das komplette Material finden Sie hier: School-Scout.de Thema: Unterrichtsreihe zum Thema Kreis
Obwohl Österreich sehr dicht besiedelt ist, kommt auf jeden Bundesbürger fast ein halber Hektar Wald.
 1. Wald in Österreich Österreich ist mit rund 4 Millionen Hektar Waldfläche - das ist mit 47,6 Prozent nahezu die Hälfte des Bundesgebietes - eines der waldreichsten Länder der EU. Der durchschnittliche
1. Wald in Österreich Österreich ist mit rund 4 Millionen Hektar Waldfläche - das ist mit 47,6 Prozent nahezu die Hälfte des Bundesgebietes - eines der waldreichsten Länder der EU. Der durchschnittliche
Stationstraining. Trage hier ein, wenn du eine Station abgeschlossen hast. Wenn du mit einem Partner gearbeitet hast, trage seinen Vornamen ein.
 Name: Starte an einer Station deiner Wahl. Achtung: es sollten nicht mehr als 4 Schüler gleichzeitig an einer Station arbeiten. Löse die Aufgaben einer Station entsprechend der Anweisung. Bearbeite zuerst
Name: Starte an einer Station deiner Wahl. Achtung: es sollten nicht mehr als 4 Schüler gleichzeitig an einer Station arbeiten. Löse die Aufgaben einer Station entsprechend der Anweisung. Bearbeite zuerst
Mittel- und Oberstufe - MITTEL:
 Praktisches Arbeiten - 3 nrotationsgeschwindigkeit ( 2 ) Mittel- und Oberstufe - MITTEL: Ein Solarscope, Eine genau gehende Uhr, Ein Messschirm, Dieses Experiment kann in einem Raum in Südrichtung oder
Praktisches Arbeiten - 3 nrotationsgeschwindigkeit ( 2 ) Mittel- und Oberstufe - MITTEL: Ein Solarscope, Eine genau gehende Uhr, Ein Messschirm, Dieses Experiment kann in einem Raum in Südrichtung oder
Physik-Prüfung. vom 24. September Lichtausbreitung, Schatten
 Physik-Prüfung vom 24. September 2010 Lichtausbreitung, Schatten Hinweise und Modalitäten: - Beginnen Sie erst mit der Prüfung, wenn das Zeichen dafür gegeben wurde. - Erlaubte Hilfsmittel: Papier, Schreibzeug,
Physik-Prüfung vom 24. September 2010 Lichtausbreitung, Schatten Hinweise und Modalitäten: - Beginnen Sie erst mit der Prüfung, wenn das Zeichen dafür gegeben wurde. - Erlaubte Hilfsmittel: Papier, Schreibzeug,
Mathematik Grundlagen Teil 2
 BBZ Biel-Bienne Eine Institution des Kantons Bern CFP Biel-Bienne Une institution du canton de Berne Berufsmaturität Maturité professionnelle Berufsbildungszentrum Mediamatike r Médiamaticiens Centre de
BBZ Biel-Bienne Eine Institution des Kantons Bern CFP Biel-Bienne Une institution du canton de Berne Berufsmaturität Maturité professionnelle Berufsbildungszentrum Mediamatike r Médiamaticiens Centre de
Mathematik II Prüfung für den Übertritt aus der 9. Klasse
 Aufnahmeprüfung 2014 für den Eintritt in das 9. Schuljahr eines Gymnasiums des Kantons Bern Mathematik II Prüfung für den Übertritt aus der 9. Klasse Bitte beachten: - Bearbeitungsdauer: 60 Minuten - Alle
Aufnahmeprüfung 2014 für den Eintritt in das 9. Schuljahr eines Gymnasiums des Kantons Bern Mathematik II Prüfung für den Übertritt aus der 9. Klasse Bitte beachten: - Bearbeitungsdauer: 60 Minuten - Alle
Übungen aus dem Buch: 65/15; 69/16; 74/8; 97/9a; 101/6c; 101/8; 106/10; 108/Beweise; 116/8a Aufgaben auf S. 151: 1; 2; 3; 4; 5; c Mc.
 AB 25, Seite 1 Satz von Thales 8e 08.03.2012 Aus alten Klassenarbeiten: 1) Trapez: Gegeben ist ein Trapez mit den gegenüber liegenden Seiten a und c und der Höhe h a auf a. Erläutere mit einer Skizze,
AB 25, Seite 1 Satz von Thales 8e 08.03.2012 Aus alten Klassenarbeiten: 1) Trapez: Gegeben ist ein Trapez mit den gegenüber liegenden Seiten a und c und der Höhe h a auf a. Erläutere mit einer Skizze,
Ergebnisse der ersten landesweiten Waldinventur in Brandenburg
 Ergebnisse der ersten landesweiten Waldinventur in Brandenburg 30. Juni 2015 Ergebnisse der ersten landesweiten Waldinventur in Brandenburg 1 Brandenburger Waldinventur (LWI) - wichtige Ergänzung zur Bundeswaldinventur
Ergebnisse der ersten landesweiten Waldinventur in Brandenburg 30. Juni 2015 Ergebnisse der ersten landesweiten Waldinventur in Brandenburg 1 Brandenburger Waldinventur (LWI) - wichtige Ergänzung zur Bundeswaldinventur
A] 40 % + 25 % + 12,5 % B] 30 % + 50 % + 16,6 %
![A] 40 % + 25 % + 12,5 % B] 30 % + 50 % + 16,6 % A] 40 % + 25 % + 12,5 % B] 30 % + 50 % + 16,6 %](/thumbs/55/35914069.jpg) 5 Prozentrechnen Übung 50 Der ganze Streifen entspricht 100 % = 1 000 = 1. Welche Prozent- und Promillesätze stellen die unterschiedlich getönten Flächen dar? Abb. 27 1. 2. 3. Übung 51 Der volle Winkel
5 Prozentrechnen Übung 50 Der ganze Streifen entspricht 100 % = 1 000 = 1. Welche Prozent- und Promillesätze stellen die unterschiedlich getönten Flächen dar? Abb. 27 1. 2. 3. Übung 51 Der volle Winkel
Januar / Februar 2005
 Nr.: Abschlussprüfung im Ausbildungsberuf Vermessungstechniker/Vermessungstechnikerin nach 34 BBiG Januar / Februar 2005 Schriftliche Prüfung Prüfungsfach: Zeit: Hilfsmittel: Anlagen: Technische Mathematik
Nr.: Abschlussprüfung im Ausbildungsberuf Vermessungstechniker/Vermessungstechnikerin nach 34 BBiG Januar / Februar 2005 Schriftliche Prüfung Prüfungsfach: Zeit: Hilfsmittel: Anlagen: Technische Mathematik
Schule. Station Jakobsstab & Co. Teil 1. Klasse. Arbeitsheft. Tischnummer. Teilnehmercode
 Schule Station Jakobsstab & Co. Teil 1 Arbeitsheft Klasse Tischnummer Teilnehmercode Mathematik-Labor Station Jakobsstab & Co. Teil 1 Liebe Schülerinnen und Schüler! Schon immer haben sich die Menschen
Schule Station Jakobsstab & Co. Teil 1 Arbeitsheft Klasse Tischnummer Teilnehmercode Mathematik-Labor Station Jakobsstab & Co. Teil 1 Liebe Schülerinnen und Schüler! Schon immer haben sich die Menschen
Textaufgaben zu Kreisteilen
 1. Miss den Durchmesser eines Eurostücks. Textaufgaben zu Kreisteilen a) Berechne den Flächeninhalt einer Seite und den Umfang. b) Das Eurostück fällt herunter und rollt 6,5 m weit. Gib an, wie oft es
1. Miss den Durchmesser eines Eurostücks. Textaufgaben zu Kreisteilen a) Berechne den Flächeninhalt einer Seite und den Umfang. b) Das Eurostück fällt herunter und rollt 6,5 m weit. Gib an, wie oft es
BESONDERE LEISTUNGSFESTSTELLUNG Schuljahr 2015/2016 MATHEMATIK
 Prüfungstag: 11. Mai 2016 (HAUPTTERMIN) Prüfungsbeginn: 08:00 Uhr BESONDERE LEISTUNGSFESTSTELLUNG Schuljahr 2015/2016 MATHEMATIK Hinweise für die Teilnehmerinnen und Teilnehmer Bearbeitungszeit: 180 Minuten
Prüfungstag: 11. Mai 2016 (HAUPTTERMIN) Prüfungsbeginn: 08:00 Uhr BESONDERE LEISTUNGSFESTSTELLUNG Schuljahr 2015/2016 MATHEMATIK Hinweise für die Teilnehmerinnen und Teilnehmer Bearbeitungszeit: 180 Minuten
Aufgabe 1: Das Stanzblech: Gewicht
 Aufgabe 1: Das Stanzblech: Gewicht Aus einem Blech werden kreisförmige Löcher im abgebildeten hexagonalen Muster ausgestanzt (d.h. die Mittelpunkte benachbarter Kreise bilden gleichseitige Dreiecke). Der
Aufgabe 1: Das Stanzblech: Gewicht Aus einem Blech werden kreisförmige Löcher im abgebildeten hexagonalen Muster ausgestanzt (d.h. die Mittelpunkte benachbarter Kreise bilden gleichseitige Dreiecke). Der
Mathematik Grundlagen Teil 2
 BBZ Biel-Bienne Eine nstitution des Kantons Bern CFP Biel-Bienne Une institution du canton de Berne Berufsmaturität Maturité professionnelle Berufsbildungszentrum Mediamatike r Médiamaticiens Centre de
BBZ Biel-Bienne Eine nstitution des Kantons Bern CFP Biel-Bienne Une institution du canton de Berne Berufsmaturität Maturité professionnelle Berufsbildungszentrum Mediamatike r Médiamaticiens Centre de
Orientierungsmodul Oberstufe OS 1. Zahlen auf dem Zahlenstrahl darstellen und interpretieren. natürliche Zahlen bis 2 Millionen lesen und schreiben
 ernziele Inhalt/ernziele Zahlendarstellung Zahlen auf dem Zahlenstrahl darstellen und interpretieren natürliche Zahlen bis 2 Millionen lesen und schreiben Schwierigkeitsgrad A1 73%, A2 57%, A4 56% A3 68%
ernziele Inhalt/ernziele Zahlendarstellung Zahlen auf dem Zahlenstrahl darstellen und interpretieren natürliche Zahlen bis 2 Millionen lesen und schreiben Schwierigkeitsgrad A1 73%, A2 57%, A4 56% A3 68%
Konstruiere ein Rechteck mit den gegebenen Seitenlängen! Zeichne die beiden Diagonalen ein und miss ihre Länge! a = 84 mm, b = 35 mm.
 1 Rechteck und Quadrat Eigenschaften und Bezeichnungen Die Ecken werden gegen den Uhrzeigersinn beschriftet Gegenüberliegende Seiten sind gleich lang und parallel Benachbarte Seiten stehen normal aufeinander.
1 Rechteck und Quadrat Eigenschaften und Bezeichnungen Die Ecken werden gegen den Uhrzeigersinn beschriftet Gegenüberliegende Seiten sind gleich lang und parallel Benachbarte Seiten stehen normal aufeinander.
Mathematik. Kantonale Fachmittelschulen Aufnahmeprüfung Beachten Sie bitte folgende Rahmenbedingungen:
 Kantonale Fachmittelschulen Aufnahmeprüfung 2016 Mathematik Beachten Sie bitte folgende Rahmenbedingungen: Zum Lösen der Aufgaben stehen Ihnen 120 Minuten zur Verfügung. Schreiben Sie auf jedes Blatt Ihren
Kantonale Fachmittelschulen Aufnahmeprüfung 2016 Mathematik Beachten Sie bitte folgende Rahmenbedingungen: Zum Lösen der Aufgaben stehen Ihnen 120 Minuten zur Verfügung. Schreiben Sie auf jedes Blatt Ihren
Bei den Planetenwegen, die man durchwandern kann, sind die Dinge des Sonnensystems 1 Milliarde mal verkleinert dargestellt.
 Distanzen und Grössen im Planetenweg Arbeitsblatt 1 Bei den Planetenwegen, die man durchwandern kann, sind die Dinge des Sonnensystems 1 Milliarde mal verkleinert dargestellt. Anders gesagt: Der Massstab
Distanzen und Grössen im Planetenweg Arbeitsblatt 1 Bei den Planetenwegen, die man durchwandern kann, sind die Dinge des Sonnensystems 1 Milliarde mal verkleinert dargestellt. Anders gesagt: Der Massstab
Drei Kreise Was ist zu tun?
 1 Drei Kreise Der Radius der Kreise beträgt drei Zentimeter. Zeichnet die Abbildung nach, falls ihr einen Zirkel zur Hand habt. Ansonsten genügt auch eine Skizze. Bestimmt den Flächeninhalt der schraffierten
1 Drei Kreise Der Radius der Kreise beträgt drei Zentimeter. Zeichnet die Abbildung nach, falls ihr einen Zirkel zur Hand habt. Ansonsten genügt auch eine Skizze. Bestimmt den Flächeninhalt der schraffierten
2. Berechnungen mit Pythagoras
 2. Berechnungen mit 2.1. Grundaufgaben 1) Berechnungen an rechtwinkligen Dreiecken a) Wie lang ist die Hypotenuse, wenn die beiden Katheten eines rechtwinkligen Dreiecks 3.6 cm und 4.8 cm lang sind? b)
2. Berechnungen mit 2.1. Grundaufgaben 1) Berechnungen an rechtwinkligen Dreiecken a) Wie lang ist die Hypotenuse, wenn die beiden Katheten eines rechtwinkligen Dreiecks 3.6 cm und 4.8 cm lang sind? b)
Die Waldfunktionen Birgt Leben, liefert Holz, schützt, ist Erholungsraum
 MS Birgt Leben, liefert Holz, schützt, ist Erholungsraum 3 Wissen Wald ist multifunktional: Bietet Lebensraum Nutzen, Schutz, Erholung / Ein Lebensraum für Pflanzen, Tiere und uns Menschen / Zugang offen
MS Birgt Leben, liefert Holz, schützt, ist Erholungsraum 3 Wissen Wald ist multifunktional: Bietet Lebensraum Nutzen, Schutz, Erholung / Ein Lebensraum für Pflanzen, Tiere und uns Menschen / Zugang offen
Sekundarschulabschluss für Erwachsene
 S Lösungen Name: Sekundarschulabschluss für rwachsene Nummer: Geometrie Sek 2017 Totalzeit: 60 Minuten Hilfsmittel: nichtprogrammierbarer Taschenrechner, Geometrie-Werkzeug (Geo-reieck, Zirkel, Massstab)
S Lösungen Name: Sekundarschulabschluss für rwachsene Nummer: Geometrie Sek 2017 Totalzeit: 60 Minuten Hilfsmittel: nichtprogrammierbarer Taschenrechner, Geometrie-Werkzeug (Geo-reieck, Zirkel, Massstab)
Im täglichen Leben und besonders auf Fahrt und Lager werden
 Häuptlingsbuch 29.09.2005 23:51 Uhr Seite 273 Im täglichen Leben und besonders auf Fahrt und Lager werden wir oft vor die Aufgabe gestellt, einen Gegenstand, ein Gebäude oder eine Entfernung zu schätzen
Häuptlingsbuch 29.09.2005 23:51 Uhr Seite 273 Im täglichen Leben und besonders auf Fahrt und Lager werden wir oft vor die Aufgabe gestellt, einen Gegenstand, ein Gebäude oder eine Entfernung zu schätzen
Startklar! Das Gelernte kontrollieren und Schulstoff auffrischen: Hier können Sie sich für Ihre Eignungsabklärung bei Roche vorbereiten.
 Startklar! Das Gelernte kontrollieren und Schulstoff auffrischen: Hier können Sie sich für Ihre Eignungsabklärung bei Roche vorbereiten. Vielen Dank für Ihre Bewerbung um eine Ausbildung bei Roche und
Startklar! Das Gelernte kontrollieren und Schulstoff auffrischen: Hier können Sie sich für Ihre Eignungsabklärung bei Roche vorbereiten. Vielen Dank für Ihre Bewerbung um eine Ausbildung bei Roche und
Aufgabe 1 G: Fläche und Umfang von geradlinig begrenzten Figuren
 Schüler/in Aufgabe 1 G: Fläche und Umfang von geradlinig begrenzten Figuren LERNZIELE: Flächeninhalt mit Rasterzählmethode bestimmen Flächeninhalt und Umfang mit Formeln berechnen Flächeninhalt durch Zerlegen
Schüler/in Aufgabe 1 G: Fläche und Umfang von geradlinig begrenzten Figuren LERNZIELE: Flächeninhalt mit Rasterzählmethode bestimmen Flächeninhalt und Umfang mit Formeln berechnen Flächeninhalt durch Zerlegen
Grundwissen. 5. Jahrgangsstufe. Mathematik
 Grundwissen 5. Jahrgangsstufe Mathematik Grundwissen Mathematik 5. Jahrgangsstufe Seite 1 1 Natürliche Zahlen 1.1 Große Zahlen und Zehnerpotenzen eine Million = 1 000 000 = 10 6 eine Milliarde = 1 000
Grundwissen 5. Jahrgangsstufe Mathematik Grundwissen Mathematik 5. Jahrgangsstufe Seite 1 1 Natürliche Zahlen 1.1 Große Zahlen und Zehnerpotenzen eine Million = 1 000 000 = 10 6 eine Milliarde = 1 000
DOWNLOAD. Lernzirkel Kreis. Albrecht Schiekofer. Downloadauszug aus dem Originaltitel:
 DOWNLOAD Albrecht Schiekofer Lernzirkel Kreis Downloadauszug aus dem Originaltitel: 5 6 7 8 9 0 Lernzirkel A Grundlagen der Geometrie Koordinatensystem (Fachbegriffe) Koordinaten bestimmen Koordinaten
DOWNLOAD Albrecht Schiekofer Lernzirkel Kreis Downloadauszug aus dem Originaltitel: 5 6 7 8 9 0 Lernzirkel A Grundlagen der Geometrie Koordinatensystem (Fachbegriffe) Koordinaten bestimmen Koordinaten
Mathematik für die Ferien Seite 1
 Mathematik für die Ferien Seite. Zähle die natürlichen geraden Zahlen auf, die größer als 0 und kleiner oder gleich 20 sind: 2, 4, 6, 8, 20 2. Schreib als Zahl: Deutschland hat 8 Millionen = 8 000 000
Mathematik für die Ferien Seite. Zähle die natürlichen geraden Zahlen auf, die größer als 0 und kleiner oder gleich 20 sind: 2, 4, 6, 8, 20 2. Schreib als Zahl: Deutschland hat 8 Millionen = 8 000 000
Jogging: Kraft- und Dehnübungen
 MERKBLATT Seite 1/5 Jogging: Kraft- und Dehnübungen Nach einer längeren Pause sollte man sich gut aufs Lauftraining vorbereiten. Dadurch lassen sich Fehlbelastungen und Schäden verhindern. Der Zürcher
MERKBLATT Seite 1/5 Jogging: Kraft- und Dehnübungen Nach einer längeren Pause sollte man sich gut aufs Lauftraining vorbereiten. Dadurch lassen sich Fehlbelastungen und Schäden verhindern. Der Zürcher
Lisa und ihre Freundin haben in den Ferien einen Kochkurs besucht. Nun versuchen sie eine Torte nach einem Rezept im Internet zu backen.
 Muster 1 131. Setze die fehlende Malrechnung so ein, dass die Waage im Gleichgewicht ist. 4 9 3 8 8 5 8 5 151. Für welche Zahl steht das Smily am Schluss? 40 - = 32 + =. 3 = : 6 = Für das Smily steht die
Muster 1 131. Setze die fehlende Malrechnung so ein, dass die Waage im Gleichgewicht ist. 4 9 3 8 8 5 8 5 151. Für welche Zahl steht das Smily am Schluss? 40 - = 32 + =. 3 = : 6 = Für das Smily steht die
Einstieg: Quiz Lehrerinformation
 Lehrerinformation 1/8 Arbeitsauftrag Ziel Die Klasse wird in vier Gruppen aufgeteilt. Jede Gruppe beginnt an einer Arbeit und wechselt nach fünf Minuten. Es liegen Tastkisten bereit, in denen verschiedene
Lehrerinformation 1/8 Arbeitsauftrag Ziel Die Klasse wird in vier Gruppen aufgeteilt. Jede Gruppe beginnt an einer Arbeit und wechselt nach fünf Minuten. Es liegen Tastkisten bereit, in denen verschiedene
DOWNLOAD. Vertretungsstunden Mathematik Klasse: Körperberechnungen. Vertretungsstunden Mathematik 9./10. Klasse. Marco Bettner/Erik Dinges
 DOWNLOAD Marco Bettner/Erik Dinges Vertretungsstunden Mathematik 27 9. Klasse: Marco Bettner/Erik Dinges Bergedorfer Unterrichtsideen Downloadauszug aus dem Originaltitel: Vertretungsstunden Mathematik
DOWNLOAD Marco Bettner/Erik Dinges Vertretungsstunden Mathematik 27 9. Klasse: Marco Bettner/Erik Dinges Bergedorfer Unterrichtsideen Downloadauszug aus dem Originaltitel: Vertretungsstunden Mathematik
Unkorrigiertes Vorabmaterial
 -B-17-01 1 1 Kreis: und Flächeninhalt 1 Bestimme den und den Flächeninhalt des Quadrates. u = A = 2 Schätze die Länge des Kreisumfangs (rote Linie) und des Kreisflächeninhalts (gelbe Fläche). Erkläre,
-B-17-01 1 1 Kreis: und Flächeninhalt 1 Bestimme den und den Flächeninhalt des Quadrates. u = A = 2 Schätze die Länge des Kreisumfangs (rote Linie) und des Kreisflächeninhalts (gelbe Fläche). Erkläre,
Schätzen und Messen. 1. Der eigene Körper als Maß. 2. Entfernungen schätzen. a) mit Hilfe eines Dreiecks
 Schätzen und Messen Seite 1 von 4 Schätzen und Messen 1. Der eigene Körper als Maß Das beste Mittel gegen Sinnestäuschungen ist das Messen, Zählen und Wiegen Plato Messen heißt: aufgrund einer frei gewählten
Schätzen und Messen Seite 1 von 4 Schätzen und Messen 1. Der eigene Körper als Maß Das beste Mittel gegen Sinnestäuschungen ist das Messen, Zählen und Wiegen Plato Messen heißt: aufgrund einer frei gewählten
Prüfungsarbeit Mathematik Gymnasium
 Prüfungsteil 1: Aufgabe 1 a) In welchem Maßstab müsste das abgebildete Modellauto vergrößert werden, damit es ungefähr so groß wäre wie das Original? Kreuze an! 1 : 10 1 : 100 1 : 1 000 1 : 10 000 b) Kann
Prüfungsteil 1: Aufgabe 1 a) In welchem Maßstab müsste das abgebildete Modellauto vergrößert werden, damit es ungefähr so groß wäre wie das Original? Kreuze an! 1 : 10 1 : 100 1 : 1 000 1 : 10 000 b) Kann
Wenn der Wald in Stress gerät
 Wenn der Wald in Stress gerät Heimische Wälder im (Klima-) Wandel Name: 1 MODUL Baumwachstum Holzanatomie Strukturen der Baumscheiben erkunden Arbeitsblatt 1 hier wird Material 1 (Baumscheibenscans) benötigt
Wenn der Wald in Stress gerät Heimische Wälder im (Klima-) Wandel Name: 1 MODUL Baumwachstum Holzanatomie Strukturen der Baumscheiben erkunden Arbeitsblatt 1 hier wird Material 1 (Baumscheibenscans) benötigt
Navigation UMGANG MIT DEM PLANZEIGER
 Navigation UMGANG MIT DEM PLANZEIGER Der Planzeiger Bei den Rangers arbeiten wir unzählig oft mit Karte und Kompass. Wir müssen dabei manchmal äußerst genau sein und schon ein paar Grad können uns irgendwann
Navigation UMGANG MIT DEM PLANZEIGER Der Planzeiger Bei den Rangers arbeiten wir unzählig oft mit Karte und Kompass. Wir müssen dabei manchmal äußerst genau sein und schon ein paar Grad können uns irgendwann
Flächeneinheiten und Flächeninhalt
 Flächeneinheiten und Flächeninhalt Was ist eine Fläche? Aussagen, Zeichnungen, Erklärungen MERKE: Eine Fläche ist ein Gebiet, das von allen Seiten umschlossen wird. Beispiele für Flächen sind: Ein Garten,
Flächeneinheiten und Flächeninhalt Was ist eine Fläche? Aussagen, Zeichnungen, Erklärungen MERKE: Eine Fläche ist ein Gebiet, das von allen Seiten umschlossen wird. Beispiele für Flächen sind: Ein Garten,
Großer Wagen. zum Sternbild. Großer Bär
 B1 Sterne / Sternbilder Termin:....................... 1. Suchen Sie auf einer Sternkarte die Sternbilder Großer Bär, Kleiner Bär und Kassiopeia. 2. Bereiten Sie eine Skizze vor, die den Horizont zeigt
B1 Sterne / Sternbilder Termin:....................... 1. Suchen Sie auf einer Sternkarte die Sternbilder Großer Bär, Kleiner Bär und Kassiopeia. 2. Bereiten Sie eine Skizze vor, die den Horizont zeigt
Damit ich die Prüfungen ständig verbessern kann, bin ich auf deine Rückmeldung angewiesen.
 Lösung Selbsttest Karte / Kompass Damit ich die Prüfungen ständig verbessern kann, bin ich auf deine Rückmeldung angewiesen. Falls bei der einen oder anderen Prüfungsaufgabe Probleme aufgetaucht sind,
Lösung Selbsttest Karte / Kompass Damit ich die Prüfungen ständig verbessern kann, bin ich auf deine Rückmeldung angewiesen. Falls bei der einen oder anderen Prüfungsaufgabe Probleme aufgetaucht sind,
Florian erzählt Sebastian, dass der Durchmesser des Pools dreimal so groß ist, wie er selbst!
 Die Zwillinge Florian und Sebastian haben zu ihrem 12. Geburtstag einen neuen, runden Swimming Pool geschenkt bekommen. Florian ist genau 1,50 m groß. Florian erzählt Sebastian, dass der Durchmesser des
Die Zwillinge Florian und Sebastian haben zu ihrem 12. Geburtstag einen neuen, runden Swimming Pool geschenkt bekommen. Florian ist genau 1,50 m groß. Florian erzählt Sebastian, dass der Durchmesser des
MITTLERER SCHULABSCHLUSS AN DER MITTELSCHULE 2014 MATHEMATIK. 26. Juni :30 Uhr 11:00 Uhr
 MITTLERER SCHULABSCHLUSS AN DER MITTELSCHULE 014 MATHEMATIK 6. Juni 014 8:30 Uhr 11:00 Uhr Platzziffer (ggf. Name/Klasse): Die Benutzung von für den Gebrauch an der Mittelschule zugelassenen Formelsammlungen
MITTLERER SCHULABSCHLUSS AN DER MITTELSCHULE 014 MATHEMATIK 6. Juni 014 8:30 Uhr 11:00 Uhr Platzziffer (ggf. Name/Klasse): Die Benutzung von für den Gebrauch an der Mittelschule zugelassenen Formelsammlungen
Abschlussprüfung Name Klasse MATHEMATIK
 Gym Oberwil FMS Abteilung Abschlussprüfung 2013 Name Klasse_ MATHEMATIK Zeit Hilfsmittel 3 h Taschenrechner (nicht graphikfähig), Formelsammlung Verwenden Sie bitte für jede Aufgabe ein neues Blatt und
Gym Oberwil FMS Abteilung Abschlussprüfung 2013 Name Klasse_ MATHEMATIK Zeit Hilfsmittel 3 h Taschenrechner (nicht graphikfähig), Formelsammlung Verwenden Sie bitte für jede Aufgabe ein neues Blatt und
Die Wälder der Landesforsten in Zahlen
 Die Wälder der Landesforsten in Zahlen Ergebnisse der Bundeswaldinventur 3: 1. Allgemein Die Bundeswaldinventur 3 erfasste zum Stichtag 1. Oktober 12 als Großrauminventur viele Strukturdaten in den Wäldern.
Die Wälder der Landesforsten in Zahlen Ergebnisse der Bundeswaldinventur 3: 1. Allgemein Die Bundeswaldinventur 3 erfasste zum Stichtag 1. Oktober 12 als Großrauminventur viele Strukturdaten in den Wäldern.
Merkblatt 2028 Klimadaten
 Merkblatt 228 Klimadaten Vergleich der Klimadaten im Merkblatt 228 mit den Klimadaten in SIA 381/2 Vergleichsbasis Es gibt 24 Klimastationen, welche in beiden Dokumenten vorkommen. Bei zahlreichen Stationen
Merkblatt 228 Klimadaten Vergleich der Klimadaten im Merkblatt 228 mit den Klimadaten in SIA 381/2 Vergleichsbasis Es gibt 24 Klimastationen, welche in beiden Dokumenten vorkommen. Bei zahlreichen Stationen
Medizinballstossen: Meter. Postenmaterial pro Tn: 1 Tau, 1 (Laternen-) Mast / Baum (4 Tn möglich) Zusatzmaterial pro Tn: -
 Wellen mit Seil Oberkörper: Schultermuskulatur Schulterbreiter Stand, Knie leicht gebeugt, mit den Händen je ein Seilende fassen, Arme abwechslungsweise auf und ab bewegen. Achtung: je schöner das Seil
Wellen mit Seil Oberkörper: Schultermuskulatur Schulterbreiter Stand, Knie leicht gebeugt, mit den Händen je ein Seilende fassen, Arme abwechslungsweise auf und ab bewegen. Achtung: je schöner das Seil
Mathematik, 3. Sekundarschule (Neues Lehrmittel, Erprobungsversion)
 Zentrale Aufnahmeprüfung 2011 für die Kurzgymnasien und die Handelsmittelschulen des Kantons Zürich Mathematik, 3. Sekundarschule (Neues Lehrmittel, Erprobungsversion) Von der Kandidatin oder vom Kandidaten
Zentrale Aufnahmeprüfung 2011 für die Kurzgymnasien und die Handelsmittelschulen des Kantons Zürich Mathematik, 3. Sekundarschule (Neues Lehrmittel, Erprobungsversion) Von der Kandidatin oder vom Kandidaten
Unterrichtsmaterialien
 Unterrichtsmaterialien Fach: Mathematik Jahrgangstufe: 8./9./10. Inhaltsverzeichnis 2 Inhalt Seite 1. Lernziele und curriculare Bezüge 3 2. Die Lernsituation 4 3. Der Unterrichtsverlauf 5 4. Die korrespondierende
Unterrichtsmaterialien Fach: Mathematik Jahrgangstufe: 8./9./10. Inhaltsverzeichnis 2 Inhalt Seite 1. Lernziele und curriculare Bezüge 3 2. Die Lernsituation 4 3. Der Unterrichtsverlauf 5 4. Die korrespondierende
Schriftliche Prüfung Schuljahr: 2008/2009 Schulform: Oberschule B-Kurs/FOR-Klassen Gesamtschule Erweiterungskurs. Mathematik
 Ministerium für Bildung, Jugend und Sport Prüfungen am Ende der Jahrgangsstufe 10 Mathematik Schriftliche Prüfung Schuljahr: 2008/2009 Schulform: Oberschule B-Kurs/FOR-Klassen Gesamtschule Erweiterungskurs
Ministerium für Bildung, Jugend und Sport Prüfungen am Ende der Jahrgangsstufe 10 Mathematik Schriftliche Prüfung Schuljahr: 2008/2009 Schulform: Oberschule B-Kurs/FOR-Klassen Gesamtschule Erweiterungskurs
Geometrie. in 15 Minuten. Geometrie. Klasse
 Klasse Geometrie Geometrie 6. Klasse in 5 Minuten Winkel und Kreis Zeichne und überprüfe in deinem Übungsheft: a) Wo liegen alle Punkte, die von einem Punkt A den Abstand cm haben? b) Färbe den Bereich,
Klasse Geometrie Geometrie 6. Klasse in 5 Minuten Winkel und Kreis Zeichne und überprüfe in deinem Übungsheft: a) Wo liegen alle Punkte, die von einem Punkt A den Abstand cm haben? b) Färbe den Bereich,
SCHRIFTLICHE MATURA 2010
 SCHRIFTLICHE MATURA 2010 Fach: Mathematik Klassen: 7SA Prüfer: Dr. Martin Holzer Name: Diese Arbeit umfasst 4 Aufgaben. Jede der 4 Aufgaben wird mit gleich vielen Punkten bewertet. Für die Darstellung
SCHRIFTLICHE MATURA 2010 Fach: Mathematik Klassen: 7SA Prüfer: Dr. Martin Holzer Name: Diese Arbeit umfasst 4 Aufgaben. Jede der 4 Aufgaben wird mit gleich vielen Punkten bewertet. Für die Darstellung
Mathematik 1: (ohne Taschenrechner) Korrekturanleitung
 Kanton St.Gallen Bildungsdepartement St.Gallische Kantonsschulen Gymnasium Aufnahmeprüfung 013 Mathematik 1: (ohne Taschenrechner) Korrekturanleitung Löse die Aufgaben auf diesen Blättern. Der Lösungsweg
Kanton St.Gallen Bildungsdepartement St.Gallische Kantonsschulen Gymnasium Aufnahmeprüfung 013 Mathematik 1: (ohne Taschenrechner) Korrekturanleitung Löse die Aufgaben auf diesen Blättern. Der Lösungsweg
Haus Kienreich in Hörbranz (Vorarlberg)
 Haus Kienreich in Hörbranz (Vorarlberg) (Haus Kienreich, alpinahaus) Lehrerinformation: Das kleine Grundstück mit freiem Blick auf den nahen Bodensee konnte für die Erweiterung keine Zubau-Flächen bieten.
Haus Kienreich in Hörbranz (Vorarlberg) (Haus Kienreich, alpinahaus) Lehrerinformation: Das kleine Grundstück mit freiem Blick auf den nahen Bodensee konnte für die Erweiterung keine Zubau-Flächen bieten.
Kandidatennummer / Name... Gruppennummer... Aufgabe Total Note
 Mathematik Lösungen Zweiter Teil mit Taschenrechner Kandidatennummer / Name... Gruppennummer... Vorname... Aufgabe 1 2 3 4 5 6 Total Note Punkte total Punkte erreicht 4 5 6 6 6 6 33 Die Prüfung dauert
Mathematik Lösungen Zweiter Teil mit Taschenrechner Kandidatennummer / Name... Gruppennummer... Vorname... Aufgabe 1 2 3 4 5 6 Total Note Punkte total Punkte erreicht 4 5 6 6 6 6 33 Die Prüfung dauert
Download. Klassenarbeiten Mathematik 8. Flächeninhalt und Umfang von Vielecken. Jens Conrad, Hardy Seifert. Downloadauszug aus dem Originaltitel:
 Download Jens Conrad, Hardy Seifert Klassenarbeiten Mathematik 8 Flächeninhalt und Umfang von Vielecken Downloadauszug aus dem Originaltitel: Klassenarbeiten Mathematik 8 Flächeninhalt und Umfang von Vielecken
Download Jens Conrad, Hardy Seifert Klassenarbeiten Mathematik 8 Flächeninhalt und Umfang von Vielecken Downloadauszug aus dem Originaltitel: Klassenarbeiten Mathematik 8 Flächeninhalt und Umfang von Vielecken
Schätzfunktionen der Baumbiomasse und Nährstoffentzug der Hauptbaumarten
 Schätzfunktionen der Baumbiomasse und Nährstoffentzug der Hauptbaumarten Jürgen Nagel Nordwestdeutsche Forstliche Versuchsanstalt Grätzelstr. 2, 37075 Göttingen http://www.nw-fva.de Projekt: Möglichkeiten
Schätzfunktionen der Baumbiomasse und Nährstoffentzug der Hauptbaumarten Jürgen Nagel Nordwestdeutsche Forstliche Versuchsanstalt Grätzelstr. 2, 37075 Göttingen http://www.nw-fva.de Projekt: Möglichkeiten
Berechnungen am rechtwinkligen Dreieck, Satz des Pythagoras
 Berechnungen am rechtwinkligen Dreieck, Satz des Pythagoras Aufgabe 1 Berechne die fehlenden Grössen (a, b, c, h, p, q, A) der rechtwinkligen Dreiecke: a) p = 36, q = 64 b) b = 13, q = 5 c) b = 70, A =
Berechnungen am rechtwinkligen Dreieck, Satz des Pythagoras Aufgabe 1 Berechne die fehlenden Grössen (a, b, c, h, p, q, A) der rechtwinkligen Dreiecke: a) p = 36, q = 64 b) b = 13, q = 5 c) b = 70, A =
Prüfungsarbeit Mathematik Hauptschule (Typ B)
 rüfungsarbeit Mathematik Hauptschule (p B) rüfungsteil : Aufgabe a) In welchem Maßstab müsste das abgebildete Modellauto vergrößert werden, damit es ungefähr so groß wäre wie das Original? Kreuze an! :
rüfungsarbeit Mathematik Hauptschule (p B) rüfungsteil : Aufgabe a) In welchem Maßstab müsste das abgebildete Modellauto vergrößert werden, damit es ungefähr so groß wäre wie das Original? Kreuze an! :
Mathematik II Prüfung für den Übertritt aus der 8. Klasse
 Kantonale Prüfungen 2012 für die Zulassung zum gymnasialen Unterricht im 9. Schuljahr Mathematik II Serie H8 Gymnasien des Kantons Bern Mathematik II Prüfung für den Übertritt aus der 8. Klasse Bitte beachten:
Kantonale Prüfungen 2012 für die Zulassung zum gymnasialen Unterricht im 9. Schuljahr Mathematik II Serie H8 Gymnasien des Kantons Bern Mathematik II Prüfung für den Übertritt aus der 8. Klasse Bitte beachten:
Bewegungshinweise für die Lehrperson
 Bewegungshinweise für die Lehrperson Seillänge: Steht man mit beiden Beinen auf dem Seil, dann reichen die Enden bis unter die Achseln. Starthaltung: Die Beine stehen parallel auf dem Boden und die Arme
Bewegungshinweise für die Lehrperson Seillänge: Steht man mit beiden Beinen auf dem Seil, dann reichen die Enden bis unter die Achseln. Starthaltung: Die Beine stehen parallel auf dem Boden und die Arme
Station Strahlensätze Teil 1. Arbeitsheft. Teilnehmercode
 Station Strahlensätze Teil 1 Arbeitsheft Teilnehmercode Mathematik-Labor Station Strahlensätze Teil 1 Liebe Schülerinnen und Schüler! Schon immer haben sich die Menschen Gedanken gemacht, wie man Strecken
Station Strahlensätze Teil 1 Arbeitsheft Teilnehmercode Mathematik-Labor Station Strahlensätze Teil 1 Liebe Schülerinnen und Schüler! Schon immer haben sich die Menschen Gedanken gemacht, wie man Strecken
Zeichnet man nun über die Seiten des Dreiecks die Quadrate der jeweiligen Seiten, dann ergibt sich folgendes Bild:
 9. Lehrsatz von Pythagoras Pythagoras von Samos war ein griechischer Philosoph und Mathematiker, der von ca. 570 v.chr. bis 510 n.chr lebte. Obwohl es über seine gesallschaftliche Stellung verschiedene
9. Lehrsatz von Pythagoras Pythagoras von Samos war ein griechischer Philosoph und Mathematiker, der von ca. 570 v.chr. bis 510 n.chr lebte. Obwohl es über seine gesallschaftliche Stellung verschiedene
Sicheres Arbeiten. Aufarbeiten von Bäumen
 Sicheres Arbeiten Aufarbeiten von Bäumen Impressum Eigentümer, Herausgeber und Verleger und für die Richtigkeit des Inhaltes: Allgemeine Unfallversicherungsanstalt Abteilung für Unfallverhütung und Berufskrankheitenbekämpfung
Sicheres Arbeiten Aufarbeiten von Bäumen Impressum Eigentümer, Herausgeber und Verleger und für die Richtigkeit des Inhaltes: Allgemeine Unfallversicherungsanstalt Abteilung für Unfallverhütung und Berufskrankheitenbekämpfung
