Prof. Dr. Tatjana Lange. Lehrgebiet: Regelungstechnik Laborübung 04/05:
|
|
|
- Inken Pfeiffer
- vor 7 Jahren
- Abrufe
Transkript
1 Prof. Dr. ajana Lange Lehrgebie: egelungsechnik Laborübung 4/5: hema: Sreckenidenifikaion. Ermilung on egelkennweren aus dem offenen egelkreis. Übungsziele: Veriefung ausgewähler Mehoden der Sreckenidenifikaion aus der Sprunganwor und der Ermilung on egelkennweren aus dem Frequenzgang der offenen Srecke Demonsraion moderner, rechnergesüzer Idenifikaionserfahren Demonsraion des Verhalens geschlossener egelkreise und Vergleich der asächlichen egelkennwere mi den aus dem offenen egelkreis ermielen Weren 2. Grundlagen: 2.. Experimenelle Sysemidenifikaion ennfunkionen des dynamischen Überragungserhalens eines Sysems u() g() G(f) U(f) x() X(f) sind die Gewichsfunkion (Soßanwor) g ( ) die Übergangsfunkion (Sprunganwor) h ( ) der Frequenzgang G bzw. die Überragungsfunkion G () f G( jω ), ω 2πf ( p) ennfunkionen im Zeibereich ennfunkionen im Frequenzbereich Der Zusammenhang zwischen diesen ennfunkionen is wie folg gegeben: g()d Fourier ransformaion } g() G(f )bzw.g( jω) dh() / d p δ + j2πf h() G( p) δ Zur meßechnischen Ermilung dieser ennfunkionen (experimenellen Idenifikaion) benuz man ypischerweise folgende Schalungsanordnungen
2 und Meßsignale: ennfunkion Bereich essignal Gewichsfunkion Zeibereich sehr kurzer Impuls Übergangsfunkion Zeibereich Sprungsignal Frequenzgang / Überragungsfunkion Frequenzbereich harmonisches Signal (punkweise Ermilung) Für einfache Syseme (z.b. -, -, 2 D -Glieder) lassen sich die Parameer der Überragungsfunkion G( p) in der Zeikonsanenform mi einfachen Mieln aus der Sprunganwor (Übergangsfunkion) ermieln: -Glied: ( ) G p + p,63 -Glied: D ( ) G p + p + p D < D D/,63(- / ) D
3 -Glied: G( p) D p + D + p D /,63( / -) D ( D/ -) D > 2-Glied: ( ) Gp ( + p )( + p ) 2 7,2 ( + q) q 2,7 h( /4) 7 3 Ermilung on h( /4) 7 Ermilung on 7 7 /4 7,2( + 2) 2 Ermilung on /4 7 Diagramm zur Ermilung des Zeikonsanenerhälnisses ð siehe Anhang h( /4) 7 Diagramm zur Ermilung des Zeikonsanenerhälnisses:,26,24,22,2,8,6,4,2, 4 Ermilung on q,2,4,6,8 q / 2
4 2.2. Ermilung der eglerkennwere aus dem offenen egelkreis: Wir berachen den in Abb. 2.2.a. gezeigen Sandard-egelkreis, auf den eine sprungförmige Sörung wirk. z () σ() x() + e() egler G (p) u() -u() Srecke G (p) G x () a x() Abb. 2.2.a: Sandard-egelkreis z() (Idealisiere) eglerypen: P-egler G( p) PI-egler: G( p) + p PD-egler G( p) ( + p ) PID-egler G( p) + + p pn Die Überragungsfunkionen der PI-,PD- und PID-egler sind so nich realisierbar, da die für reale Syseme gelende Bedingung "Nennenpolynom Zählerpolynom" nich erfüll is (näherungsweise ealisierung - s. Anlage 2). Für den in Abb. 2.2.a gezeigen egelkreis sind folgende egelkennwere definier: n Saische enngröße: bleibende egelabweichung ( ) B e e z() Dynamische enngrößen: Überschwingweie h Überschwingzei z() m e() e B x() h m
5 Es is nun möglich, aus der Ampliudenkennlinie der offenen ee (s. Abb. 2.2.b) diese drei enngrößen zu ermieln: 2lg G( ω) 2log s I-een -4dB/Dek P-een -2dB/Dek ω s 2 Bereich I saionäres Verhalen ω s Schnifrequenz Bereich II dynamisches Verhalen ω s 2 ω -4dB/Dek Bereich II ohne Bedeuung ω s 2 ω s ω s 2 ω -9 ϕ(ω) -8 γ s > (posiier) Phasenrand Abb. 2.2.b: ypische Ampliuden- und Phasenkennlinien für eine offene ee Uner der Voraussezung, daß eine sprungförmige Sörung z( ) Z σ( ) egelkreis wirk, gil e B auf den Z +, Z - Ampliude der sprungförmigen Sörung m π ω s s h [%] 23. ( 65 ο γ s ) nach Bauer
6 3. Übungsorbereiung: 3.. Ermieln Sie aus der nachfolgend dargesellen Sprunganwor eines unbekannen Sysems dessen Überragungsfunkion und sellen Sie diese als Bodediagramm (nach Berag und Phase) dar. h(),9,8,7,6,5,4,3,2, [s] 3.2. Das on Ihnen idenifiziere Sysem soll nun zusammen mi a) einem P-egler mi dem Parameer b) einem idealen PD-egler mi den Parameern,V 5 in einen egelkreis gemäß Abb. 2.2.a. geschale werden Ermieln Sie nun aus dem Bodediagrammen der offenen ee für beide Fälle die bleibende egelabweichung, die Überschwingzei und die Überschwingweie h. e B m
7 4. Übungsdurchführung: 4.. Ermieln Sie uner Nuzung des blockorienieren Simulaionssysems BOIS die Sprunganworen der mi den Superblöcken SYSEM4.SBL, SYSEM42.SBL, SYSEM43.SBL gegebenen Syseme: Schalungsanordnung: Hinweis: Simulaionszei Zeiablenkung am Oszillographen: 2/aser 4.2. Drucken Sie die Sprunganworen aus und idenifizieren Sie anhand dieser Sprunganworen die Parameer der Überragungsfunkionen der Syseme Überprüfen Sie Ihre Ergebnisse für SYSEM4.SBL, indem Sie dieses Sysem uner Nuzung on BOIS mi erschiedenen essignalen (Sprung, Soß, echeckfolge, Sinusschwingung, auschen) beaufschlagen, die Ein- und Ausgangssignale aufzeichnen und aus diesen Daen mi dem Simulaionsblock IDA das Sysem erneu idenifizieren. Beweren Sie dabei anhand der esquadrasumme auch die Qualiä der Approximaion und diskuieren Sie die Ergebnisse Die on Ihnen unersuche Srecke SYSEM4.SBL soll nun mi einem P-egler zu folgenden egelkreis zusammengeschale werden: x() + e() P-egler G (p) P u() -u() Srecke G (p) G x () a x() z() 4.5. Ermieln Sie uner Nuzung des Simulaionsblocks LISA aus dem Bodediagramm der offenen ee die bleibende egelabweichung e B e ( ) die Überschwingzei m und, falls sinnoll, die Überschwingweie h bei Wirken einer sprungförmigen Sörung z( ) σ( ) Hinweis: In LISA G in Polynomform (p) eingeben: ðdaeiðsysem modifizieren Simulaionszei: am geschlossenen egelkreis für folgende Were des Überragungsfakors P des P-eglers: Simulieren Sie den geschlossenen egelkreis und das Wirken der Sörung mi dem blockorienieren Simulaionssysem BOIS und ergleichen Sie die aus dem
8 Bodediagramm der offenen ee besimmen Güekenngrößen für das egelerhalen mi dem "experimenell" (d.h. mi BOIS) ermielen Weren. Schalungsanordnung: 4.7. Überprüfen Sie durch Simulaion mi BOIS die Ergebnisse der Übungsorbereiung (s. Pk. 3) 4.8. Wiederholen Sie die Schrie 4.5. und 4.6. mi einem PI und einem PID-egler und ergleichen Sie die Ergebnisse. Verwenden Sie dabei folgende eglerparameer: 9 n V Variieren Sie die eglerparameer und beobachen Sie das egelerhalen im geschlossenen egelkreis. 5. Übungsauswerung: Diskuieren Sie die Ergebnisse und beweren Sie die eingesezen eglerypen.
9 Anlage : Diagramm zur Ermilung des Zeikonsanenerhälnisses für,26 -Glieder: 2,24,22 h( /4) 7,2,8,6,4,2,,2,4,6,8 q 2/
10 Anlage 2: ückkopplungsschalungen für die näherungsweise ealisierung on idealen eglern: PI-egler: - PD-egler: - PID-egler - G( p) + p + p mi mi 2 + p 2 p 2 + p + p 2 mi p 2 ( + p)( + p2) ( + p)( + p2) ( )( ) + p + p2 + 2 p G( p) + p ( + p ) ( + p ) ( + ) + p p ( + p ) lim G( p) ) p G( p) + + G p 2 ( + p2 ) ( + p2 ) ( + p ) ( p) lim G( p) + p2 G p { 2 lim G( p) ( ) ( ) ( + p )( + p ) 2 p p bzw. lim G( p) G ( p) p pn mi n + 2 V V p + 2 2
Regelungstechnik 1 - Grundglieder: Analyse im Zeit und Frequenzbereich
 Regelungsechnik - Grundglieder: Analyse im Zei und Frequenzbereich Vorberachungen: Das Überragungsverhalen von linearen Regelkreiselemenen wird vorwiegend durch Sprunganworen bzw. Übergangsfunkionen sowie
Regelungsechnik - Grundglieder: Analyse im Zei und Frequenzbereich Vorberachungen: Das Überragungsverhalen von linearen Regelkreiselemenen wird vorwiegend durch Sprunganworen bzw. Übergangsfunkionen sowie
Regelungstechnik. Steuerung. Regelung. Beim Steuern bewirkt eine Eingangsgröße eine gewünschte Ausgangsgröße (Die nicht auf den Eingang zurückwirkt.
 Regelungsechnik Seuerung Beim Seuern bewirk eine Eingangsgröße eine gewünsche Ausgangsgröße (Die nich auf den Eingang zurückwirk. Seuern is eine Wirkungskee Seuerkee (Eingahnsraße) Bsp. Boiler Regelung
Regelungsechnik Seuerung Beim Seuern bewirk eine Eingangsgröße eine gewünsche Ausgangsgröße (Die nich auf den Eingang zurückwirk. Seuern is eine Wirkungskee Seuerkee (Eingahnsraße) Bsp. Boiler Regelung
Prüfung zum Fach Regelungstechnik für Studierende Lehramt an beruflichen Schulen (Diplom/Bachelor)
 Technische Universiä München Lehrsuhl für Regelungsechnik Prof. Dr.-Ing. B. Lohmann Prüfung zum Fach Regelungsechnik 14.04.2011 für Sudierende Lehram an beruflichen Schulen (Diplom/Bachelor) Name: Vorname:
Technische Universiä München Lehrsuhl für Regelungsechnik Prof. Dr.-Ing. B. Lohmann Prüfung zum Fach Regelungsechnik 14.04.2011 für Sudierende Lehram an beruflichen Schulen (Diplom/Bachelor) Name: Vorname:
Systemtheorie Teil A. - Zeitkontinuierliche Signale und Systeme - Musterlösungen. Manfred Strohrmann Urban Brunner
 Sysemheorie eil A - Zeikoninuierliche Signale und Syseme - Muserlösungen Manfred Srohrmann Urban Brunner Inhal 3 Muserlösungen - Zeikoninuierliche Syseme im Zeibereich 3 3. Nachweis der ineariä... 3 3.
Sysemheorie eil A - Zeikoninuierliche Signale und Syseme - Muserlösungen Manfred Srohrmann Urban Brunner Inhal 3 Muserlösungen - Zeikoninuierliche Syseme im Zeibereich 3 3. Nachweis der ineariä... 3 3.
Prüfung zum Fach Regelungstechnik für Studierende Lehramt an beruflichen Schulen (Diplom/Bachelor)
 Technische Universiä München Lehrsuhl für Regelungsechnik Prof. Dr.-Ing. B. Lohmann Prüfung zum Fach Regelungsechnik 7.9. für Sudierende Lehram an beruflichen Schulen (Diplom/Bachelor) Name: Vorname: Mar.-Nr.
Technische Universiä München Lehrsuhl für Regelungsechnik Prof. Dr.-Ing. B. Lohmann Prüfung zum Fach Regelungsechnik 7.9. für Sudierende Lehram an beruflichen Schulen (Diplom/Bachelor) Name: Vorname: Mar.-Nr.
V 321 Kondensator, Spule und Widerstand Zeit- u. Frequenzverhalten
 V 32 Kondensaor, Spule und Widersand Zei- u. Frequenzverhalen.Aufgaben:. Besimmen Sie das Zei- und Frequenzverhalen der Kombinaionen von Kondensaor und Widersand bzw. Spule und Widersand..2 Ermieln Sie
V 32 Kondensaor, Spule und Widersand Zei- u. Frequenzverhalen.Aufgaben:. Besimmen Sie das Zei- und Frequenzverhalen der Kombinaionen von Kondensaor und Widersand bzw. Spule und Widersand..2 Ermieln Sie
Laplacetransformation in der Technik
 Verallgemeinere Funkionen Laplaceransformaion in der echnik Fakulä Grundlagen Februar 26 Fakulä Grundlagen Laplaceransformaion in der echnik Übersich Verallgemeinere Funkionen Verallgemeinere Funkionen
Verallgemeinere Funkionen Laplaceransformaion in der echnik Fakulä Grundlagen Februar 26 Fakulä Grundlagen Laplaceransformaion in der echnik Übersich Verallgemeinere Funkionen Verallgemeinere Funkionen
HINWEISE zur Identifikation einer Regelstrecke nach Versuchsdaten mit MATLAB
 Die Sprunganwor is der Seckbrief der Regelsrecke. S. Samal, W. Becker: Grundriß der prakischen Regelungsechnik, 0. Auflage, Verlag Oldenbourg, 000, Seie 104 HINWEISE zur Idenifikaion einer Regelsrecke
Die Sprunganwor is der Seckbrief der Regelsrecke. S. Samal, W. Becker: Grundriß der prakischen Regelungsechnik, 0. Auflage, Verlag Oldenbourg, 000, Seie 104 HINWEISE zur Idenifikaion einer Regelsrecke
7 Erzwungene Schwingung bei Impulslasten
 Einmassenschwinger eil I.7 Impulslasen 53 7 Erzwungene Schwingung bei Impulslasen Impulslasen im echnischen Allag sind zum Beispiel Soß- oder Aufprallvorgänge oder Schläge. Die Las seig dabei in kurzer
Einmassenschwinger eil I.7 Impulslasen 53 7 Erzwungene Schwingung bei Impulslasen Impulslasen im echnischen Allag sind zum Beispiel Soß- oder Aufprallvorgänge oder Schläge. Die Las seig dabei in kurzer
Signal- und Systemtheorie for Dummies
 FB Eleroechni Ewas Signal- und Sysemheorie or Dummies Version - Juli Oh No!!!! Pro. Dr.-Ing. ajana Lange Fachhochschule Merseburg FB Eleroechni Pro. Dr.-Ing. ajana Lange Signal- und Sysemheorie or Dummies
FB Eleroechni Ewas Signal- und Sysemheorie or Dummies Version - Juli Oh No!!!! Pro. Dr.-Ing. ajana Lange Fachhochschule Merseburg FB Eleroechni Pro. Dr.-Ing. ajana Lange Signal- und Sysemheorie or Dummies
Reglerdimensionierung nach Ziegler-Nichols
 HTL, Innsbruck Seie von 8 Rober Salvador salvador@hlinn.ac.a Mahemaische / Fachliche Inhale in Sichworen: Regelungsechnik, Laplaceransformaion, Umgang mi komplexen Zahlen, Kurvendiskussion, Differenzialgleichungen
HTL, Innsbruck Seie von 8 Rober Salvador salvador@hlinn.ac.a Mahemaische / Fachliche Inhale in Sichworen: Regelungsechnik, Laplaceransformaion, Umgang mi komplexen Zahlen, Kurvendiskussion, Differenzialgleichungen
Aufgabensammlung. Signale und Systeme 1. Einführung in die Signal- und Systemtheorie. Kontaktinformation: Dr. Mike Wolf, Tel. 2619
 Aufgabensammlung Signale und Syseme 1 für die BA-Sudiengänge EIT, II, BT, MTR, OTR, MT, IN (3. FS) Einführung in die Signal- und Sysemheorie für den BA-Sudiengang WIW-ET (5. FS) Konakinformaion: Dr. Mike
Aufgabensammlung Signale und Syseme 1 für die BA-Sudiengänge EIT, II, BT, MTR, OTR, MT, IN (3. FS) Einführung in die Signal- und Sysemheorie für den BA-Sudiengang WIW-ET (5. FS) Konakinformaion: Dr. Mike
Bildmaterial zur Vorlesung Regelungstechnik Teil I Die Regelstrecke. Wintersemester 2014 Prof. Dr.-Ing. habil. Klaus-Peter Döge
 Bildmaerial zur Vorlesung Regelungsechnik Teil I Die Regelsrecke Winersemeser 214 Prof. Dr.-Ing. habil. Klaus-Peer Döge 2 Regelung des Füllsandes eines Flüssigkeisbehälers mi Abfluss Sollwervorgabe Regler:
Bildmaerial zur Vorlesung Regelungsechnik Teil I Die Regelsrecke Winersemeser 214 Prof. Dr.-Ing. habil. Klaus-Peer Döge 2 Regelung des Füllsandes eines Flüssigkeisbehälers mi Abfluss Sollwervorgabe Regler:
Leseprobe. Ines Rennert, Bernhard Bundschuh. Signale und Systeme. Einführung in die Systemtheorie. ISBN (Buch):
 Leseprobe Ines Renner, Bernhard Bundschuh Signale und Syseme Einführung in die Sysemheorie ISBN (Buch): 978-3-446-43327-4 ISBN (E-Book): 978-3-446-43328- Weiere Informaionen oder Besellungen uner hp://www.hanser-fachbuch.de/978-3-446-43327-4
Leseprobe Ines Renner, Bernhard Bundschuh Signale und Syseme Einführung in die Sysemheorie ISBN (Buch): 978-3-446-43327-4 ISBN (E-Book): 978-3-446-43328- Weiere Informaionen oder Besellungen uner hp://www.hanser-fachbuch.de/978-3-446-43327-4
Kleine Formelsammlung Regelungstechnik
 Kleine Formelsammlung Regelungsechnik von Birgi Seffenhagen. Auflage Kleine Formelsammlung Regelungsechnik Seffenhagen schnell und porofrei erhällich bei beck-shop.de DIE FACHBUCHHANDLUNG Hanser München
Kleine Formelsammlung Regelungsechnik von Birgi Seffenhagen. Auflage Kleine Formelsammlung Regelungsechnik Seffenhagen schnell und porofrei erhällich bei beck-shop.de DIE FACHBUCHHANDLUNG Hanser München
Abb.4.1: Aufbau der Versuchsapparatur
 4. xperimenelle Unersuchungen 4. Aufbau der Versuchsanlage Für die Unersuchungen zum Schwingungs- und Resonanzverhalen sowie Soffausauschprozess wurde eine Versuchsanlage aufgebau. In der Abbildung 4.
4. xperimenelle Unersuchungen 4. Aufbau der Versuchsanlage Für die Unersuchungen zum Schwingungs- und Resonanzverhalen sowie Soffausauschprozess wurde eine Versuchsanlage aufgebau. In der Abbildung 4.
Musterlösung Klausur Regelungstechnik vom
 Musterlösung Klausur egelungstehnik vom 6.03.05 Aufgabe : Mit einem Mikroontroller der für die geforderte egelung einen Ehtzeitbetrieb mit einer Taktzeit von 5 ms gewährleistet, soll ein analoger PI-egler
Musterlösung Klausur egelungstehnik vom 6.03.05 Aufgabe : Mit einem Mikroontroller der für die geforderte egelung einen Ehtzeitbetrieb mit einer Taktzeit von 5 ms gewährleistet, soll ein analoger PI-egler
Kontinuierliche Fourier Transformation
 Koninuierliche Fourier ransformaion f () is eine nichperiodische Funkion. Um die Frequenzen in einem beliebigen Zeisignal zu besimmen, inerpreieren wir die Funkion f () als periodische Funkion mi Periode.
Koninuierliche Fourier ransformaion f () is eine nichperiodische Funkion. Um die Frequenzen in einem beliebigen Zeisignal zu besimmen, inerpreieren wir die Funkion f () als periodische Funkion mi Periode.
Kennzeichnung stochastischer Prozesse
 . Kennzeichnung sochasischer Prozesse...1.0. Der Plaz der sochasischen Prozesse in der Regelungsechnik...1.1. Beschreibung sochasischer Prozesse im Zeibereich...3.1.1. Die Auokorrelaionsfunkion (AKF)...3.1..
. Kennzeichnung sochasischer Prozesse...1.0. Der Plaz der sochasischen Prozesse in der Regelungsechnik...1.1. Beschreibung sochasischer Prozesse im Zeibereich...3.1.1. Die Auokorrelaionsfunkion (AKF)...3.1..
Systemeigenschaften, Nomenklatur und Modellbildung
 Fakulä Informaik Insiu für Angewande Informaik, Professur für Technische Informaionssyseme Sysemeigenschafen, Nomenklaur und Dresden, den 03.08.2011 Gliederung Vorbemerkungen Weiere Sysemeigenschafen Nomenklaur
Fakulä Informaik Insiu für Angewande Informaik, Professur für Technische Informaionssyseme Sysemeigenschafen, Nomenklaur und Dresden, den 03.08.2011 Gliederung Vorbemerkungen Weiere Sysemeigenschafen Nomenklaur
Übungen zur Vorlesung Nachrichtenübertragungstechnik E5iK Blatt 10
 Fachhochschule Augsburg SS 20001 Fachbereich Elekroechnik Modulaion digialer Signale Übungen zur Vorlesung Nachrichenüberragungsechnik E5iK Bla 10 Fragen 1. Welche Voreile biee die digiale Überragung von
Fachhochschule Augsburg SS 20001 Fachbereich Elekroechnik Modulaion digialer Signale Übungen zur Vorlesung Nachrichenüberragungsechnik E5iK Bla 10 Fragen 1. Welche Voreile biee die digiale Überragung von
Prof. Dr. Tatjana Lange
 Prof. Dr. Tatjana Lange Lehrgebiet: Regelungstechnik Laborübung 1: Thema: Einführrung in die digitale Regelung Übungsziele Veranschaulichung der Abtastung von bandbegrenzten Signalen und der Reproduktion
Prof. Dr. Tatjana Lange Lehrgebiet: Regelungstechnik Laborübung 1: Thema: Einführrung in die digitale Regelung Übungsziele Veranschaulichung der Abtastung von bandbegrenzten Signalen und der Reproduktion
Kapitel 2: Fourieranalyse. Analoge, nichtperiodische Signale
 ZHW, NTM, 2005/10, Rur 1 Kapiel 2: Fourieranalyse Analoge, nichperiodische Signale Inhalsverzeichnis 1. FOURIERTRANSFORMATION...1 2. EIGENSCHAFTEN DER FOURIERTRANSFORMATION...2 2.1. LINEARITÄT...2 2.2.
ZHW, NTM, 2005/10, Rur 1 Kapiel 2: Fourieranalyse Analoge, nichperiodische Signale Inhalsverzeichnis 1. FOURIERTRANSFORMATION...1 2. EIGENSCHAFTEN DER FOURIERTRANSFORMATION...2 2.1. LINEARITÄT...2 2.2.
Kapitel 4. Versuch 415 T-Flipflop
 Kapiel 4 Versuch 415 T-Flipflop Flipflops, die mi jeder seigenden oder mi jeder fallenden Takflanke in den engegengesezen Zusand kippen, heissen T Flipflops ( Toggle Flipflops ). T-Flipflops können aus
Kapiel 4 Versuch 415 T-Flipflop Flipflops, die mi jeder seigenden oder mi jeder fallenden Takflanke in den engegengesezen Zusand kippen, heissen T Flipflops ( Toggle Flipflops ). T-Flipflops können aus
Klausur Grundlagen der Elektrotechnik B
 Prof. Dr. Ing. Joacim Böcker Klausur Grundlagen der Elekroecnik B 5.09.009 Name: Marikelnummer: Vorname: Sudiengang: Facprüfung Aufgabe: (Punke) () (8) 3 (30) 4 (3) 5 (8) Leisungsnacweis Noe Noe Noe Klausur
Prof. Dr. Ing. Joacim Böcker Klausur Grundlagen der Elekroecnik B 5.09.009 Name: Marikelnummer: Vorname: Sudiengang: Facprüfung Aufgabe: (Punke) () (8) 3 (30) 4 (3) 5 (8) Leisungsnacweis Noe Noe Noe Klausur
Zeitreihenökonometrie
 Zeireihenökonomerie Kapiel 1 - Grundlagen Einführung in die Verfahren der Zeireihenanalyse (1) Typischerweise beginn man mi einer Beschreibung der jeweils zu unersuchenden Zeireihe (graphisch) Trendverhalen,
Zeireihenökonomerie Kapiel 1 - Grundlagen Einführung in die Verfahren der Zeireihenanalyse (1) Typischerweise beginn man mi einer Beschreibung der jeweils zu unersuchenden Zeireihe (graphisch) Trendverhalen,
Diskrete Integratoren und Ihre Eigenschaften
 Diskree Inegraoren und Ihre Eigenschafen Whie Paper von Dipl.-Ing. Ingo Völlmecke Indusrielle eglersrukuren werden im Allgemeinen mi Hilfe von Inegraoren aufgebau. Aufgrund des analogen Schalungsaufbaus
Diskree Inegraoren und Ihre Eigenschafen Whie Paper von Dipl.-Ing. Ingo Völlmecke Indusrielle eglersrukuren werden im Allgemeinen mi Hilfe von Inegraoren aufgebau. Aufgrund des analogen Schalungsaufbaus
Strömung im Rohr. Versuch: Inhaltsverzeichnis. Fachrichtung Physik. Physikalisches Grundpraktikum. 1 Aufgabenstellung 2
 Fachrichung Physik Physikalisches Grundprakikum Ersell: Bearbeie: Versuch: L. Jahn SR M. Kreller J. Kelling F. Lemke S. Majewsky i. A. Dr. Escher Akualisier: am 29. 03. 2010 Srömung im Rohr Inhalsverzeichnis
Fachrichung Physik Physikalisches Grundprakikum Ersell: Bearbeie: Versuch: L. Jahn SR M. Kreller J. Kelling F. Lemke S. Majewsky i. A. Dr. Escher Akualisier: am 29. 03. 2010 Srömung im Rohr Inhalsverzeichnis
Zeitreihenökonometrie
 Zeireihenökonomerie Kapiel 4 Schäzung univariaer Zeireihenmodelle Y = c+ α Y + + α Y + ε + βε + + β ε p p q q Problem: Direke Schäzung der Parameer α,, αp und β,, βq über OLS nich möglich, da die Residuen
Zeireihenökonomerie Kapiel 4 Schäzung univariaer Zeireihenmodelle Y = c+ α Y + + α Y + ε + βε + + β ε p p q q Problem: Direke Schäzung der Parameer α,, αp und β,, βq über OLS nich möglich, da die Residuen
Gegeben sei folgender Regelkreis mit der Führungsgröße r, dem Regelfehler e und der Ausgangsgröße y: r e R(s) P (s)
 1. Teilklausur SS 16 Gruppe A Name: Matr.-Nr.: Für beide Aufgaben gilt: Gegeben sei folgender Regelkreis mit der Führungsgröße r, dem Regelfehler e und der Ausgangsgröße y: r e R(s) P (s) y Aufgabe 1 (6
1. Teilklausur SS 16 Gruppe A Name: Matr.-Nr.: Für beide Aufgaben gilt: Gegeben sei folgender Regelkreis mit der Führungsgröße r, dem Regelfehler e und der Ausgangsgröße y: r e R(s) P (s) y Aufgabe 1 (6
Viskoelastizität. Kapitel 4.2. Jana Pardeike & Rainer H. Müller, Freie Universität Berlin
 Kapiel 4.2. Viskoelasiziä Jana Pardeike & Rainer H. Müller, Freie Universiä Berlin 1. Gundlegendes Wirken mechanische Kräfe auf einen Körper, so reen in diesem Körper Maerialspannungen auf. Es komm zu
Kapiel 4.2. Viskoelasiziä Jana Pardeike & Rainer H. Müller, Freie Universiä Berlin 1. Gundlegendes Wirken mechanische Kräfe auf einen Körper, so reen in diesem Körper Maerialspannungen auf. Es komm zu
Versuche mit Oszilloskop und Funktionsgenerator
 Fachhochschule für Technik und Wirschaf Berlin EMT- Labor Versuche mi Oszilloskop und Funkionsgeneraor Sephan Schreiber Olaf Drzymalski Messung am 4.4.99 Prookoll vom 7.4.99 EMT-Labor Versuche mi Oszilloskop
Fachhochschule für Technik und Wirschaf Berlin EMT- Labor Versuche mi Oszilloskop und Funkionsgeneraor Sephan Schreiber Olaf Drzymalski Messung am 4.4.99 Prookoll vom 7.4.99 EMT-Labor Versuche mi Oszilloskop
Kommunikationstechnik I
 Kommunikaionsechnik I Prof. Dr. Sefan Weinzierl Muserlösung 5. Aufgabenbla 1. Moden 1.1 Erläuern Sie, was in der Raumakusik uner Raummoden versanden wird. Der Begriff einer sehenden Welle läss sich am
Kommunikaionsechnik I Prof. Dr. Sefan Weinzierl Muserlösung 5. Aufgabenbla 1. Moden 1.1 Erläuern Sie, was in der Raumakusik uner Raummoden versanden wird. Der Begriff einer sehenden Welle läss sich am
Systemtheorie: Übertragungssystem: Beispiele
 Sysemheorie: lieer mahemaische Werkzeuge, um die Umwandlung einer physikalisch kodieren Inormaion in einer andere Darsellung z.b. vom Orsraum in den Fourierraum ohne Inormaionsverlus zu beschreiben. Überragungssysem:
Sysemheorie: lieer mahemaische Werkzeuge, um die Umwandlung einer physikalisch kodieren Inormaion in einer andere Darsellung z.b. vom Orsraum in den Fourierraum ohne Inormaionsverlus zu beschreiben. Überragungssysem:
Analog-Elektronik Protokoll - Transitorgrundschaltungen. Janko Lötzsch Versuch: 07. Januar 2002 Protokoll: 25. Januar 2002
 Analog-Elekronik Prookoll - Transiorgrundschalungen André Grüneberg Janko Lözsch Versuch: 07. Januar 2002 Prookoll: 25. Januar 2002 1 Vorberachungen Bei Verwendung verschiedene Transisor-Grundschalungen
Analog-Elekronik Prookoll - Transiorgrundschalungen André Grüneberg Janko Lözsch Versuch: 07. Januar 2002 Prookoll: 25. Januar 2002 1 Vorberachungen Bei Verwendung verschiedene Transisor-Grundschalungen
1 Experimentelle Entwurfsverfahren für Strecken mit Ausgleich Summenzeitverfahren nach Kuhn... 2
 Inhalsverzeichnis Eperimenelle Enwrfsverfahren für recken mi Asleich.... mmenzeiverfahren nach hn.... erfahren nach Chien, Hrones nd eswick... 4.3 erfahren nach Zieler nd ichols... 6.4 Eperimenelles Einsellverfahren
Inhalsverzeichnis Eperimenelle Enwrfsverfahren für recken mi Asleich.... mmenzeiverfahren nach hn.... erfahren nach Chien, Hrones nd eswick... 4.3 erfahren nach Zieler nd ichols... 6.4 Eperimenelles Einsellverfahren
GRUNDLAGENLABOR CLASSIC RC-GLIED
 GUNDLAGNLABO LASSI -GLID Inhal: 1. inleing nd Zielsezng...2 2. Theoreische Afgaben - Vorbereing...2 3. Prakische Messafgaben...4 Anhang: in- nd Asschalvorgänge...5 Filename: Version: Ahor: _Glied_2_.doc
GUNDLAGNLABO LASSI -GLID Inhal: 1. inleing nd Zielsezng...2 2. Theoreische Afgaben - Vorbereing...2 3. Prakische Messafgaben...4 Anhang: in- nd Asschalvorgänge...5 Filename: Version: Ahor: _Glied_2_.doc
Von der Fourier-Reihe zum Fourier-Integral
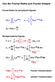 Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
10. Wechselspannung Einleitung
 10.1 Einleiung In Sromnezen benuz man sa Gleichspannung eine sinusförmige Wechselspannung, uner anderem weil diese wesenlich leicher zu erzeugen is. Wie der Name es sag wechsel bei einer Wechselspannung
10.1 Einleiung In Sromnezen benuz man sa Gleichspannung eine sinusförmige Wechselspannung, uner anderem weil diese wesenlich leicher zu erzeugen is. Wie der Name es sag wechsel bei einer Wechselspannung
Kondensator und Spule im Gleichstromkreis
 E2 Kondensaor und Spule im Gleichsromkreis Es sollen experimenelle nersuchungen zu Ein- und Ausschalvorgängen bei Kapaziäen und ndukiviäen im Gleichsromkreis durchgeführ werden. Als Messgerä wird dabei
E2 Kondensaor und Spule im Gleichsromkreis Es sollen experimenelle nersuchungen zu Ein- und Ausschalvorgängen bei Kapaziäen und ndukiviäen im Gleichsromkreis durchgeführ werden. Als Messgerä wird dabei
Prof. Dr. Tatjana Lange
 Prof. Dr. atjaa Lage Lehrgebiet: egelugstechik Laborübug 07: hema: Exerimetelle Bemessug vo egler & Mehrschleifige eglersysteme, hier: askaderegelug. Übugsziele: Awedug des Eistellverfahre ach Ziegler/Nichols
Prof. Dr. atjaa Lage Lehrgebiet: egelugstechik Laborübug 07: hema: Exerimetelle Bemessug vo egler & Mehrschleifige eglersysteme, hier: askaderegelug. Übugsziele: Awedug des Eistellverfahre ach Ziegler/Nichols
I-Strecken (Strecken ohne Ausgleich)
 FELJC 7_I-Srecken.o 1 I-Srecken (Srecken ohne Ausgleich) Woher der Name? Srecken ohne Ausgleich: Bei einem Sprung der Eingangsgrösse (Sellgrösse) nimm die Ausgangsgrösse seig zu, ohne einem fesen Endwer
FELJC 7_I-Srecken.o 1 I-Srecken (Srecken ohne Ausgleich) Woher der Name? Srecken ohne Ausgleich: Bei einem Sprung der Eingangsgrösse (Sellgrösse) nimm die Ausgangsgrösse seig zu, ohne einem fesen Endwer
Leistungselektronik Grundlagen und Standardanwendungen. Übung 3: Kommutierung
 Lehrsuhl für Elekrische Anriebssyseme und Leisungselekronik Technische Universiä München Arcissraße 1 D 8333 München Email: eal@ei.um.de Inerne: hp://www.eal.ei.um.de Prof. Dr.-Ing. Ralph Kennel Tel.:
Lehrsuhl für Elekrische Anriebssyseme und Leisungselekronik Technische Universiä München Arcissraße 1 D 8333 München Email: eal@ei.um.de Inerne: hp://www.eal.ei.um.de Prof. Dr.-Ing. Ralph Kennel Tel.:
Vorlesung 13. Die Frequenzkennlinien / Frequenzgang
 Vorlesung 3 Die Frequenzkennlinien / Frequenzgang Frequenzkennlinien geben das Antwortverhalten eines linearen Systems auf eine harmonische (sinusförmige) Anregung in Verstärkung (Amplitude) und Phasenverschiebung
Vorlesung 3 Die Frequenzkennlinien / Frequenzgang Frequenzkennlinien geben das Antwortverhalten eines linearen Systems auf eine harmonische (sinusförmige) Anregung in Verstärkung (Amplitude) und Phasenverschiebung
1. Signalbeschreibung im Zeitbereich
 . Signalbeschreibung im Zeibereich SiSy, Signal, - Inhalsverzeichnis. Signalklassen * Kapiel 3.4 (Energie und Leisung).2 Symmerie-Eigenschafen von Signalen.3 Verschiebung und Dehnung eines Zeisignals *
. Signalbeschreibung im Zeibereich SiSy, Signal, - Inhalsverzeichnis. Signalklassen * Kapiel 3.4 (Energie und Leisung).2 Symmerie-Eigenschafen von Signalen.3 Verschiebung und Dehnung eines Zeisignals *
Versuch Verweilzeit. Zielstellung: Untersuchung der Verweilzeitcharakteristik mikrofluidischer Bauteile.
 Versuch Verweilzei Zielsellung: Unersuchung er Verweilzeicharakerisik mikrofluiischer Baueile. Grunlagen: In mikrofluiischen Baueilen mi gergem Kanalurchmesser is ie lamare Srömung as vorherrschene Flussregime.
Versuch Verweilzei Zielsellung: Unersuchung er Verweilzeicharakerisik mikrofluiischer Baueile. Grunlagen: In mikrofluiischen Baueilen mi gergem Kanalurchmesser is ie lamare Srömung as vorherrschene Flussregime.
Abiturprüfung Mathematik 2009 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
15 Erzwungene Schwingungen
 11 Unwuchen in elasischen Rooren oder Fahrbahnunebenheien bei Fahrzeugen führen auf erzwungene Schwingungen. Berache werden soll im Folgenden der Fall der Schwingungserregung durch eingepräge Kräfe. Bei
11 Unwuchen in elasischen Rooren oder Fahrbahnunebenheien bei Fahrzeugen führen auf erzwungene Schwingungen. Berache werden soll im Folgenden der Fall der Schwingungserregung durch eingepräge Kräfe. Bei
Musterlösungen zur Klausur. Grundlagen der Regelungstechnik. vom
 Muserlösungen zur Klausur Grundlagen der Regelungsecni vom 4.9. Aufgabe : Linearisierung Pune A. Linearisierung des niclinearen Terms der Modellgleicungen, wobei und die üllsände im Gleicgewic sind. B.
Muserlösungen zur Klausur Grundlagen der Regelungsecni vom 4.9. Aufgabe : Linearisierung Pune A. Linearisierung des niclinearen Terms der Modellgleicungen, wobei und die üllsände im Gleicgewic sind. B.
Wechselspannung. Zeitlich veränderliche Spannung mit periodischer Wiederholung
 Elekrische Schwingungen und Wellen. Wechselsröme i. Wechselsromgrößen ii.wechselsromwidersand iii.verhalen von LC Kombinaionen. Elekrischer Schwingkreis 3. Elekromagneische Wellen Wechselspannung Zeilich
Elekrische Schwingungen und Wellen. Wechselsröme i. Wechselsromgrößen ii.wechselsromwidersand iii.verhalen von LC Kombinaionen. Elekrischer Schwingkreis 3. Elekromagneische Wellen Wechselspannung Zeilich
3.2 Festlegung der relevanten Brandszenarien
 B Anwendungsbeispiel Berechnungen Seie 70.2 Feslegung der relevanen Brandszenarien Eine der wichigsen Aufgaben beim Nachweis miels der Ingenieurmehoden im Brandschuz is die Auswahl und Definiion der relevanen
B Anwendungsbeispiel Berechnungen Seie 70.2 Feslegung der relevanen Brandszenarien Eine der wichigsen Aufgaben beim Nachweis miels der Ingenieurmehoden im Brandschuz is die Auswahl und Definiion der relevanen
Zusammenstellung wichtiger Vorlesungsfolien aus SRT für die weiterführenden RT-Veranstaltungen (Januar 2014)
 Zusammensellung wichiger Vorlesungsfolien aus SRT für die weierführenden RT-Veransalungen (Januar 24) Negaive Feedback Amplifier Harold S. Black (898-983) Aufbau eines ranskoninenalen Telefonnezesmi4 KanälenimJahr923
Zusammensellung wichiger Vorlesungsfolien aus SRT für die weierführenden RT-Veransalungen (Januar 24) Negaive Feedback Amplifier Harold S. Black (898-983) Aufbau eines ranskoninenalen Telefonnezesmi4 KanälenimJahr923
Name: Punkte: Note: Ø:
 Name: Punke: Noe: Ø: Kernfach Physik Abzüge für Darsellung: Rundung: 4. Klausur in K am 5. 5. 0 Ache auf die Darsellung und vergiss nich Geg., Ges., Formeln, Einheien, Rundung...! Angaben: e =,60 0-9 C
Name: Punke: Noe: Ø: Kernfach Physik Abzüge für Darsellung: Rundung: 4. Klausur in K am 5. 5. 0 Ache auf die Darsellung und vergiss nich Geg., Ges., Formeln, Einheien, Rundung...! Angaben: e =,60 0-9 C
Fachgebiet Leistungselektronik und Elektrische Antriebstechnik Prof. Dr.-Ing. Joachim Böcker. Grundlagen der Elektrotechnik B
 Prof. Dr.-Ing. Joachim Böcker Grundlagen der Elekroechnik B 06.10.2016 Name: Marikel-Nr.: Sudiengang: Fachprüfung Leisungsnachweis Aufgabe: 1 2 3 4 5 Tess Σ Noe Punke: 20 20 20 20 20 6 100 Bearbeiungszei:
Prof. Dr.-Ing. Joachim Böcker Grundlagen der Elekroechnik B 06.10.2016 Name: Marikel-Nr.: Sudiengang: Fachprüfung Leisungsnachweis Aufgabe: 1 2 3 4 5 Tess Σ Noe Punke: 20 20 20 20 20 6 100 Bearbeiungszei:
Lösung Klausur. p(t) = (M + dm)v p(t + dt) = M(v + dv) + dm(v + dv u) Wir behalten nur die Terme der ersten Ordnung und erhalten.
 T1 I. Theorieeil a) Zur Zei wird ein Pake der Masse dm mi der Geschwindigkei aus der Rakee ausgesoÿen. Newon's zweies Gesez läss sich schreiben als dp d = F p( + ) p() = F d = Av2 d Der Impuls des Sysems
T1 I. Theorieeil a) Zur Zei wird ein Pake der Masse dm mi der Geschwindigkei aus der Rakee ausgesoÿen. Newon's zweies Gesez läss sich schreiben als dp d = F p( + ) p() = F d = Av2 d Der Impuls des Sysems
Praktikum Grundlagen der Elektrotechnik Versuch 5. Matrikelnummer:... ...
 FH D FB 3 Fachhochschule Düsseldorf Universiy of Applied Sciences Fachbereich Elekroechnik Deparmen of Elecrical Engineering Prakikum Grundlagen der Elekroechnik Versuch 5 Name Marikelnummer:... Anesa
FH D FB 3 Fachhochschule Düsseldorf Universiy of Applied Sciences Fachbereich Elekroechnik Deparmen of Elecrical Engineering Prakikum Grundlagen der Elekroechnik Versuch 5 Name Marikelnummer:... Anesa
Signal und systemtheoretische Analyse elektrophysiologischer Daten (BA INF SA II) Vorlesungsmanuskript. Prof. Dr. Herbert Witte
 Signal und sysemheoreische Analyse elekrophysiologischer Daen BA INF SA II Vorlesungsmanuskrip Prof. Dr. Herber Wie Insiu für Medizinische Saisik, Informaik und Dokumenaion 6 Grundlagen der EEG Regisrierung
Signal und sysemheoreische Analyse elekrophysiologischer Daen BA INF SA II Vorlesungsmanuskrip Prof. Dr. Herber Wie Insiu für Medizinische Saisik, Informaik und Dokumenaion 6 Grundlagen der EEG Regisrierung
14 Kurven in Parameterdarstellung, Tangentenvektor und Bogenlänge
 Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Statistische Analysen am Rechner: Eine Einführung
 Saisische Analysen am Rechner: Eine Einführung Diese Rechnerübung soll einen ersen Einblick in das Programm EViews geben. Dafür werden der Akienmarkindex DAX und der Index des Renenmarkes REX für den Zeiraum
Saisische Analysen am Rechner: Eine Einführung Diese Rechnerübung soll einen ersen Einblick in das Programm EViews geben. Dafür werden der Akienmarkindex DAX und der Index des Renenmarkes REX für den Zeiraum
Vorlesung - Prozessleittechnik 2 (PLT 2)
 Fakulä Elekro- & Informaionsechnik, Insiu für Auomaisierungsechnik, rofessur für rozessleiechnik Vorlesung - rozessleiechnik LT Sicherhei und Zuverlässigkei von rozessanlagen - Sicherheislebenszyklus Teil
Fakulä Elekro- & Informaionsechnik, Insiu für Auomaisierungsechnik, rofessur für rozessleiechnik Vorlesung - rozessleiechnik LT Sicherhei und Zuverlässigkei von rozessanlagen - Sicherheislebenszyklus Teil
Versuch Bauen Sie einen einstufigen Verstärker mit einem n-p-n-transistor nach folgender Schaltung auf!
 1 Versuch 35 Transisorversärker 1. Aufgaben 1.1 Bauen Sie einen einsufigen Versärker mi einem n-p-n-transisor nach folgender Schalung auf! 1.2 Besimmen Sie die größe unverzerr versärke ingangswechselspannung
1 Versuch 35 Transisorversärker 1. Aufgaben 1.1 Bauen Sie einen einsufigen Versärker mi einem n-p-n-transisor nach folgender Schalung auf! 1.2 Besimmen Sie die größe unverzerr versärke ingangswechselspannung
Die Untersuchungen beschränken sich auf harmonische Wechselspannungen und -ströme
 WS 8. Wechselsröme 8.1 Einleiung n Wechselsromkreisen spielen neben Ohmschen Widersänden auch Kondensaoren (Kapaziäen) und Spulen (ndukiviäen) wichige Rolle. n diesem Versuch soll am Beispiel einfacher
WS 8. Wechselsröme 8.1 Einleiung n Wechselsromkreisen spielen neben Ohmschen Widersänden auch Kondensaoren (Kapaziäen) und Spulen (ndukiviäen) wichige Rolle. n diesem Versuch soll am Beispiel einfacher
Fouerierreihen - eine Einführung
 HBL Kapfenberg Fourierreiehen - eine Einführung Seie 1 von 19 Roland Pichler roland.pichler@hl-kapfenberg.ac.a Fouerierreihen - eine Einführung Mahemaische / Fachliche Inhale in Sichworen: Inegralrechnung,
HBL Kapfenberg Fourierreiehen - eine Einführung Seie 1 von 19 Roland Pichler roland.pichler@hl-kapfenberg.ac.a Fouerierreihen - eine Einführung Mahemaische / Fachliche Inhale in Sichworen: Inegralrechnung,
Prof. Dr. W. Zucchini 06 Wiederholung Kap. 1-4 Zeitreihenanalyse Sommer 2003
 Prof. Dr. W. Zucchini 06 Wiederholung Kap. 1-4 Zeireihenanalyse Sommer 2003 I.) Klassische Zeireihenanalyse Komponenen einer Zeireihe: Trend- (u. Zyklus), Saison- und Residualkomponene Addiive und muliplikaive
Prof. Dr. W. Zucchini 06 Wiederholung Kap. 1-4 Zeireihenanalyse Sommer 2003 I.) Klassische Zeireihenanalyse Komponenen einer Zeireihe: Trend- (u. Zyklus), Saison- und Residualkomponene Addiive und muliplikaive
4.1 OLS a) OLS-Schätzung der Koeffizienten der Strukturform
 4. Schäzmehoden 4. 4. OLS a) OLS-Schäzung der Koeffizienen der Srukurform OLS liefer verzerre und nich konsisene Schäzungen der Koeffizienen der Srukurform inerdependener Modelle, weil i.a. Sörvariable
4. Schäzmehoden 4. 4. OLS a) OLS-Schäzung der Koeffizienen der Srukurform OLS liefer verzerre und nich konsisene Schäzungen der Koeffizienen der Srukurform inerdependener Modelle, weil i.a. Sörvariable
5. Übungsblatt zur Linearen Algebra II
 Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
Reglerentwurf nach dem Betragsoptimum
 eglerentwurf nach dem Betragsoptimum. Grundlegende Überlegungen eglerentwurf nach dem Betragsoptimum In diesem Abschnitt beschäftigen wir uns mit einem einfachen Entwurfsverfahren für egler, das ein hervorragendes
eglerentwurf nach dem Betragsoptimum. Grundlegende Überlegungen eglerentwurf nach dem Betragsoptimum In diesem Abschnitt beschäftigen wir uns mit einem einfachen Entwurfsverfahren für egler, das ein hervorragendes
Vom singenden Draht zum DVB-C
 Vom singenden Drah zum DVB-C Is digiale Kommunikaion effiziener? Gerolf Ziegenhain TU Kaiserslauern Übersich Einleiung Begriffsklärung Ziel Analoge Modulaion AM FM Muliplexverfahren Digiale Modulaion QPSK
Vom singenden Drah zum DVB-C Is digiale Kommunikaion effiziener? Gerolf Ziegenhain TU Kaiserslauern Übersich Einleiung Begriffsklärung Ziel Analoge Modulaion AM FM Muliplexverfahren Digiale Modulaion QPSK
26 31 7 60 64 10. 16 6 12 32 33 9
 Lineare Algebra / Analyische Geomerie Grundkurs Zenrale schrifliche Abiurprüfungen im Fach Mahemaik Aufgabe 4 Fruchsäfe in Berieb der Geränkeindusrie produzier in zwei Werken an verschiedenen Sandoren
Lineare Algebra / Analyische Geomerie Grundkurs Zenrale schrifliche Abiurprüfungen im Fach Mahemaik Aufgabe 4 Fruchsäfe in Berieb der Geränkeindusrie produzier in zwei Werken an verschiedenen Sandoren
HAW Hamburg Fakultät Life Sciences - Physiklabor Physikalisches Praktikum
 HAW Hamburg Fakulä Life Sciences - Physiklabor Physikalisches Prakikum Auf- und Enladungen von Kondensaoren in -Gliedern Messung von Kapaziäen Elekrische Schalungen mi -Gliedern finde man z. B. in Funkionsgeneraoren
HAW Hamburg Fakulä Life Sciences - Physiklabor Physikalisches Prakikum Auf- und Enladungen von Kondensaoren in -Gliedern Messung von Kapaziäen Elekrische Schalungen mi -Gliedern finde man z. B. in Funkionsgeneraoren
Grundgebiete der Elektrotechnik II Feedbackaufgabe: Transiente Vorgänge
 heinisch-wesfälische Technische Hochschule Aachen Insiu für Sromricherechni und Elerische Anriebe Universiäsprofessor Dr. ir. i W. De Doncer Grundgebiee der Eleroechni II Feedbacaufgabe: Transiene Vorgänge
heinisch-wesfälische Technische Hochschule Aachen Insiu für Sromricherechni und Elerische Anriebe Universiäsprofessor Dr. ir. i W. De Doncer Grundgebiee der Eleroechni II Feedbacaufgabe: Transiene Vorgänge
MATHEMATIK. Fachabituiprüfung 2013 zum Erwerb der Fachhochschulreife an. Fachoberschulen und Berufsoberschulen. Ausbildungsrichtung Technik
 Fachabiuiprüfung 2013 zum Erwerb der Fachhochschulreife an Fachoberschulen und Berufsoberschulen MATHEMATIK Ausbildungsrichung Technik Diensag, 4. Juni 2013, 9.00-12.00 Uhr Die Schülerinnen und Schüler
Fachabiuiprüfung 2013 zum Erwerb der Fachhochschulreife an Fachoberschulen und Berufsoberschulen MATHEMATIK Ausbildungsrichung Technik Diensag, 4. Juni 2013, 9.00-12.00 Uhr Die Schülerinnen und Schüler
f ( x) = x + x + 1 (quadratische Funktion) f '( x) = x + (Ableitungsfunktion)
 R. Brinkmann hp://brinkmann-du.de Seie.. Tangene und Normale Tangenenseigung Die Seigung eines Funkionsgraphen in einem Punk P ( f ( ) ) is gleichbedeuend mi der Seigung der Tangene in diesem Punk. Nachfolgend
R. Brinkmann hp://brinkmann-du.de Seie.. Tangene und Normale Tangenenseigung Die Seigung eines Funkionsgraphen in einem Punk P ( f ( ) ) is gleichbedeuend mi der Seigung der Tangene in diesem Punk. Nachfolgend
Abiturprüfung Mathematik 2012 (Baden-Württemberg) Berufliche Gymnasien Analysis, Aufgabe 1
 Abiurprüfung Mahemaik 0 (Baden-Würemberg) Berufliche Gymnasien Analysis, Aufgabe. (8 Punke) Die Abbildung zeig das Schaubild einer Funkion h mi der Definiionsmenge [-7 ; 4]. Die Funkion H is eine Sammfunkion
Abiurprüfung Mahemaik 0 (Baden-Würemberg) Berufliche Gymnasien Analysis, Aufgabe. (8 Punke) Die Abbildung zeig das Schaubild einer Funkion h mi der Definiionsmenge [-7 ; 4]. Die Funkion H is eine Sammfunkion
Stochastische Automaten und Quellen
 KAPITEL 2 Sochasische Auomaen und Quellen Sei A ein Sysem allgemeiner Ar (z.b. ein physikalisches Sysem oder eine Nachrichenquelle), das wir zu diskreen Zeipunken = 0, 1,... beobachen. Wir nehmen an: (SA
KAPITEL 2 Sochasische Auomaen und Quellen Sei A ein Sysem allgemeiner Ar (z.b. ein physikalisches Sysem oder eine Nachrichenquelle), das wir zu diskreen Zeipunken = 0, 1,... beobachen. Wir nehmen an: (SA
Grundlagen der Elektrotechnik 3
 Grundlagen der Elekroechnik 3 Kapiel 3. Schalvorgänge - Die aplace Transformaion Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 S. Fachgebie Nachrichenechnische Syseme 3.. Einführung Nuzung einer
Grundlagen der Elekroechnik 3 Kapiel 3. Schalvorgänge - Die aplace Transformaion Prof. Dr.-Ing. I. Willms Grundlagen der Elekroechnik 3 S. Fachgebie Nachrichenechnische Syseme 3.. Einführung Nuzung einer
Universität Ulm Samstag,
 Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
1 Abtastung, Quantisierung und Codierung analoger Signale
 Abasung, Quanisierung und Codierung analoger Signale Analoge Signale werden in den meisen nachrichenechnischen Geräen heuzuage digial verarbeie. Um diese digiale Verarbeiung zu ermöglichen, wird das analoge
Abasung, Quanisierung und Codierung analoger Signale Analoge Signale werden in den meisen nachrichenechnischen Geräen heuzuage digial verarbeie. Um diese digiale Verarbeiung zu ermöglichen, wird das analoge
Modulation. Thema: Modulation
 Übun&Prakikum zu diialen Kommunikaionssysemen Thema: Modulaion Modulaion Ziele Mi diesen rechnerischen und experimenellen Übunen wird die prinzipielle Vorehensweise zur Überraun von binären Daensrömen
Übun&Prakikum zu diialen Kommunikaionssysemen Thema: Modulaion Modulaion Ziele Mi diesen rechnerischen und experimenellen Übunen wird die prinzipielle Vorehensweise zur Überraun von binären Daensrömen
Untersuchung von Gleitentladungen und deren Modellierung durch Funkengesetze im Vergleich zu Gasentladungen
 Unersuchung von Gleienladungen und deren Modellierung durch Funkengeseze im Vergleich zu Gasenladungen Dipl.-Ing. Luz Müller, Prof. Dr.-Ing. Kur Feser Insiu für Energieüberragung und Hochspannungsechnik,
Unersuchung von Gleienladungen und deren Modellierung durch Funkengeseze im Vergleich zu Gasenladungen Dipl.-Ing. Luz Müller, Prof. Dr.-Ing. Kur Feser Insiu für Energieüberragung und Hochspannungsechnik,
1
 FELJC/GOERI@LTAM jean-claude.feles@educaion.lu 1 2. Regelsrecken Nich vergessen: Die Regelsrecke is der wichigse Teil des Regelkreises, denn sie is das Gerä, welches geregel werden soll. Es is also sehr
FELJC/GOERI@LTAM jean-claude.feles@educaion.lu 1 2. Regelsrecken Nich vergessen: Die Regelsrecke is der wichigse Teil des Regelkreises, denn sie is das Gerä, welches geregel werden soll. Es is also sehr
Grenzwertsätze für Zeitreihen
 KAPIEL 6 Grenzwersäze für Zeireihen In diesem Kapiel sellen wir wichige Grenzwersäze für saionäre Zeireihen {X n } in diskreer Zei zusammen. Sei µ = E(X ) und ρ(k) = E(X 1 µ)(x 1+k µ) = Cov (X 1, X 1+k
KAPIEL 6 Grenzwersäze für Zeireihen In diesem Kapiel sellen wir wichige Grenzwersäze für saionäre Zeireihen {X n } in diskreer Zei zusammen. Sei µ = E(X ) und ρ(k) = E(X 1 µ)(x 1+k µ) = Cov (X 1, X 1+k
Stammgruppe trifft sich zum Museumsrundgang Experte erklärt jeweils sein Plakat
 Fachag Mahemaik: Kurvenscharen Ablauf: 1. Sunde Gemeinsame Einsiegsaufgabe. Sunde Sammgruppenaufgaben Sammgruppen (a bis 6 Schüler) Jedes Gruppenmiglied erhäl eine unerschiedliche Aufgabe A, B, C, D in
Fachag Mahemaik: Kurvenscharen Ablauf: 1. Sunde Gemeinsame Einsiegsaufgabe. Sunde Sammgruppenaufgaben Sammgruppen (a bis 6 Schüler) Jedes Gruppenmiglied erhäl eine unerschiedliche Aufgabe A, B, C, D in
Grundlagen der Elektrotechnik B
 Prof. Dr. Ing. Joachim Böcker Grundlagen der Elekroechnik B 24.9.215 Name: Marikelnummer: Vorname: Sudiengang: Fachprüfung Leisungsnachweis Aufgabe: (Punke) 1 (16) 2 (2) 3 (24) 4 (2) 5 (2) Punke Klausur
Prof. Dr. Ing. Joachim Böcker Grundlagen der Elekroechnik B 24.9.215 Name: Marikelnummer: Vorname: Sudiengang: Fachprüfung Leisungsnachweis Aufgabe: (Punke) 1 (16) 2 (2) 3 (24) 4 (2) 5 (2) Punke Klausur
1 Theorie. Versuch 3: Halbleiterbauelemente im Schaltbetrieb. 1.1 Bipolarer Transistor als Schalter in Emitterschaltung
 Labor Elekronische Prof. Dr. P. Suwe Dipl.-ng. B. Ahrend Versuch 3: Halbleierbauelemene im Schalberieb 1 Theorie Bipolare Transisoren und Feldeffekransisoren lassen sich sowohl zum Versärken von Klein-
Labor Elekronische Prof. Dr. P. Suwe Dipl.-ng. B. Ahrend Versuch 3: Halbleierbauelemene im Schalberieb 1 Theorie Bipolare Transisoren und Feldeffekransisoren lassen sich sowohl zum Versärken von Klein-
WORKING PAPERS Arbeitspapiere der Betrieblichen Finanzwirtschaft
 WORKING PAPERS Arbeispapiere der Berieblichen Finanzwirschaf Lehrsuhl für Beriebswirschafslehre, insbes. Beriebliche Finanzwirschaf Bfw29V/03 Zusandsabhängige Bewerung mi dem sochasischen Diskonierungsfakor
WORKING PAPERS Arbeispapiere der Berieblichen Finanzwirschaf Lehrsuhl für Beriebswirschafslehre, insbes. Beriebliche Finanzwirschaf Bfw29V/03 Zusandsabhängige Bewerung mi dem sochasischen Diskonierungsfakor
Flugzeugaerodynamik I Lösungsblatt 2
 Flugzeugaerodynamik I Lösungsbla 2 Lösung Aufgabe Bei der vorliegenden Aufgabe handel es sich um die Nachrechenaufgabe der Skele Theorie. a) Der Koeffizien A 1 is durch die Wölbung des gegebenen Skeles
Flugzeugaerodynamik I Lösungsbla 2 Lösung Aufgabe Bei der vorliegenden Aufgabe handel es sich um die Nachrechenaufgabe der Skele Theorie. a) Der Koeffizien A 1 is durch die Wölbung des gegebenen Skeles
Abiturprüfung 2017 ff Beispielaufgabe Grundkurs Mathematik; Analysis Beispiel Wirkstoff
 Die Bioverfügbarkei is eine Messgröße dafür, wie schnell und in welchem Umfang ein Arzneimiel resorbier wird und am Wirkor zur Verfügung seh. Zur Messung der Bioverfügbarkei wird die Wirksoffkonzenraion
Die Bioverfügbarkei is eine Messgröße dafür, wie schnell und in welchem Umfang ein Arzneimiel resorbier wird und am Wirkor zur Verfügung seh. Zur Messung der Bioverfügbarkei wird die Wirksoffkonzenraion
Nennwert Bemerkung. Bemerkung
 Typ: 4AB10/1105/35 Verwendung Elekronische Auswereeinhei zum Berieb von zwei Doppelschienenschalern () Technische Daen [absolu] Versorgungsspannung U IN 12 V DC -10 % +20 % 10,8 V DC 14,4 V DC Sromaufnahme
Typ: 4AB10/1105/35 Verwendung Elekronische Auswereeinhei zum Berieb von zwei Doppelschienenschalern () Technische Daen [absolu] Versorgungsspannung U IN 12 V DC -10 % +20 % 10,8 V DC 14,4 V DC Sromaufnahme
Abschlussklausur zur Vorlesung Wirtschaftswachstum (4 Kreditpunkte)
 Prof. Dr. Oliver andmann SS 22 Abschlusslausur zur Vorlesung Wirschafswachsum (4 redipune) Hinweise. Die Bearbeiungszei beräg 9 Minuen. 2. Bearbeien Sie alle 3 Aufgaben. 3. Die Aufgaben gehen mi den angegebenen
Prof. Dr. Oliver andmann SS 22 Abschlusslausur zur Vorlesung Wirschafswachsum (4 redipune) Hinweise. Die Bearbeiungszei beräg 9 Minuen. 2. Bearbeien Sie alle 3 Aufgaben. 3. Die Aufgaben gehen mi den angegebenen
Fahrzeugmechatronik Masterstudiengang M 3.2 Sensoren und Aktoren Labor für Automatisierung und Dynamik AuD FB 03MB
 Abb. 6 Dreidimensionale Darstellung des Frequenzgangs G ATP () s, Achsteilungen s 2 π in Hz Prof. Dr. Höcht 1/29 18.06.2006 11:13 Z_ Abb. 7 Einfluß des Pols bei s imaginären Achse, Achsteilungen in Hz
Abb. 6 Dreidimensionale Darstellung des Frequenzgangs G ATP () s, Achsteilungen s 2 π in Hz Prof. Dr. Höcht 1/29 18.06.2006 11:13 Z_ Abb. 7 Einfluß des Pols bei s imaginären Achse, Achsteilungen in Hz
Einführung in gewöhnliche Differentialgleichungen
 Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
Zusammengesetzte Beanspruchungen
 Zusammengeseze Beanspruchungen Lieraur Lesen Sie zu diesem Thema bie das Kapiel D 3 im Handbuch Maschinenbau. Übungsaufgaben finden Sie in der Aufgabensammlung TM (Böge) Nr.97 bis Nr.949 Allgemeines In
Zusammengeseze Beanspruchungen Lieraur Lesen Sie zu diesem Thema bie das Kapiel D 3 im Handbuch Maschinenbau. Übungsaufgaben finden Sie in der Aufgabensammlung TM (Böge) Nr.97 bis Nr.949 Allgemeines In
Übung 3: Fouriertransformation
 ZHAW, SiSy HS202, Rumc, Übung 3: Fouriertransformation Aufgabe Fouriertransformation Dirac-Impuls. a) Bestimmen Sie die Fouriertransformierte S(f) des Dirac-Impulses s(t) = δ(t) und interpretieren Sie
ZHAW, SiSy HS202, Rumc, Übung 3: Fouriertransformation Aufgabe Fouriertransformation Dirac-Impuls. a) Bestimmen Sie die Fouriertransformierte S(f) des Dirac-Impulses s(t) = δ(t) und interpretieren Sie
1 Kinematik der geradlinigen Bewegung eines Punktes 1.1 Freier Fall; Geschwindigkeit, Fallzeit, kinematische Diagramme
 Inhal / Übersich der Aufgaben mi Lösungen XI Aufgabe Erläuerung "Info"-Bild Seie 1 1 Kinemaik der geradlinigen Bewegung eines Punkes 1.1 Freier Fall; Geschwindigkei, Fallzei, kinemaische Diagramme 5 1.2
Inhal / Übersich der Aufgaben mi Lösungen XI Aufgabe Erläuerung "Info"-Bild Seie 1 1 Kinemaik der geradlinigen Bewegung eines Punkes 1.1 Freier Fall; Geschwindigkei, Fallzei, kinemaische Diagramme 5 1.2
Grundlagen der Elektrotechnik B
 Prof. Dr. Ing. Joachim Böcker Grundlagen der Elekroechnik B 29.3.216 Name: Marikelnummer: Vorname: Sudiengang: Fachprüfung Leisungsnachweis Aufgabe: (Punke) 1 (18) 2 (2) 3 (23) 4 (21) 5 (18) Punke Klausur
Prof. Dr. Ing. Joachim Böcker Grundlagen der Elekroechnik B 29.3.216 Name: Marikelnummer: Vorname: Sudiengang: Fachprüfung Leisungsnachweis Aufgabe: (Punke) 1 (18) 2 (2) 3 (23) 4 (21) 5 (18) Punke Klausur
Theoretische Physik I/II
 Theoreische Physik I/II Prof. Dr. M. Bleicher Insiu für Theoreische Physik J.. Goehe-Universiä Frankfur Aufgabenzeel IV 9. Mai hp://h.physik.uni-frankfur.de/ baeuchle/u Lösungen Die Vorlesung wird durch
Theoreische Physik I/II Prof. Dr. M. Bleicher Insiu für Theoreische Physik J.. Goehe-Universiä Frankfur Aufgabenzeel IV 9. Mai hp://h.physik.uni-frankfur.de/ baeuchle/u Lösungen Die Vorlesung wird durch
() 2. K I Aufgabe 5: x(t) W(s) - X(s) G 1 (s) Z 1 (s) Z 2 (s) G 3 (s) G 2 (s) G 4 (s) X(s)
 Seite 1 von 2 Name: Matr. Nr.: Note: Punkte: Aufgabe 1: Ermitteln Sie durch grafische Umwandlung des dargestellten Systems die Übertragungsfunktion X () G s =. Z s 2 () W(s) G 1 (s) G 2 (s) Z 1 (s) G 3
Seite 1 von 2 Name: Matr. Nr.: Note: Punkte: Aufgabe 1: Ermitteln Sie durch grafische Umwandlung des dargestellten Systems die Übertragungsfunktion X () G s =. Z s 2 () W(s) G 1 (s) G 2 (s) Z 1 (s) G 3
Skriptum zur 2. Laborübung. Transiente Vorgänge und Frequenzverhalten
 Elektrotechnische Grundlagen (LU 182.692) Skriptum zur 2. Laborübung Transiente Vorgänge und Frequenzverhalten Martin Delvai Wolfgang Huber Andreas Steininger Thomas Handl Bernhard Huber Christof Pitter
Elektrotechnische Grundlagen (LU 182.692) Skriptum zur 2. Laborübung Transiente Vorgänge und Frequenzverhalten Martin Delvai Wolfgang Huber Andreas Steininger Thomas Handl Bernhard Huber Christof Pitter
Thema 6: Kapitalwert bei nicht-flacher Zinsstruktur:
 Thema 6: Kapialwer bei nich-flacher Zinssrukur: Markzinsmehode Bislang unersell: i i kons. (, K, T) (flache Zinskurve) Verallgemeinerung der KW-Formel auf den Fall beliebiger Zinskurven jedoch ohne weieres
Thema 6: Kapialwer bei nich-flacher Zinssrukur: Markzinsmehode Bislang unersell: i i kons. (, K, T) (flache Zinskurve) Verallgemeinerung der KW-Formel auf den Fall beliebiger Zinskurven jedoch ohne weieres
