Die Chaostheorie a) Geschichtliche Betrachtung Die Chaostheorie Quellenverzeichnis
|
|
|
- Leon Bachmeier
- vor 7 Jahren
- Abrufe
Transkript
1 Die Chaostheorie a) Geschichtliche Betrachtung i. Das mechanistische Naturbild ii. Zweikörperproblem iii. Dreikörperproblem iv. Lagrange-Punkte v. Entdeckung des Chaos b) Die Chaostheorie i. Eigenschaften chaotischer Systeme ii. Beispiel: Doppelpendel iii. Fraktale iv. Bifurkation v. Attraktoren c) Quellenverzeichnis
2 Das mechanistische Naturbild Gründet vor allem auf Newtons Entdeckungen und der Berechnung des Zweikörperproblems Die Zustandsentwicklung eines Systems ist vollständig determiniert und berechenbar Es gibt keinen Unterschied zwischen Vergangenheit und Zukunft keine Historizität Die Unvollkommenheit des menschlichen Geistes erfordert Wahrscheinlichkeit und Zufall
3 Das Zweikörperproblem Betrachtet die Wechselwirkung zweier Körper, ohne äußere Einflüsse Ist Analytisch mit Differentialgleichungen lösbar Bewegung für jeden Zeitpunkt bestimmbar, sofern die Anfangsbedingungen bekannt sind Existiert nur in Sonderfällen z.b. Doppelsterne ohne Planeten, Wasserstoffatom Es wurde nach der Lösung des Dreikörperproblems gesucht
4 Das Dreikörperproblem Galt als eines der schwierigsten mathematischen Probleme Wurde über Jahrhunderte von vielen bekannten Mathematikern untersucht z.b. Leonhard Euler Henri Poincaré bewies, dass eine allgemeine Lösung nicht möglich ist Nur numerische Integrationsverfahren liefern eine näherungsweise Lösung nicht jedes System ist vollständig determiniert
5 Die Lagrange-Punkte
6 Entdeckung des Chaos Beweis, dass ein System mit mindestens drei Körpern nicht Analytisch berechenbar und sehr empfindlich auf Veränderung der Anfangsbedingungen reagiert durch Henri Poincaré Nachweis der Historizität eines Systems durch die Thermodynamik Die Entropie kann unter normalen Bedingungen nur zunehmen Entdeckung des Schmetterlingseffektes
7 Der Schmetterlingseffekt Entdeckt durch Edward Lorenz in 1963 Durch Rundung vollkommen anderes Ergebnis bei Berechnung eines mathematischen Klimamodells "Der Flügelschlag eines Schmetterlings am Amazonas kann einen Wirbelsturm in Florida auslösen" Berechnung des Lorenz-Attraktors Edward Lorenz: Vater der Chaostheorie
8 Die Chaostheorie "Theorie nichtlinearer dynamischer Systeme" Eigenschaften dieser Systeme sind: Sie sind nur über einen bestimmten Zeitraum Näherungsweise vorhersagbar Selbst geringste Abweichungen der Anfangsbedingungen verändern das Gesamte Verhalten des Systems nach einer bestimmten Zeit Der Fehler wächst ins unendliche Trotzdem prinzipiell berechenbar deterministisches Chaos
9 Das Doppelpendel Einfaches Beispiel für die Eigenschaften chaotischer Systeme Reagiert auf Störungen sehr empfindlich Kurze Vorhersagbarkeit Wird durch folgende Bewegungsgleichung beschrieben: 1.Pendel φ1: 2.Pendel φ2:
10 Doppelpendel : Sensitivität auf Anfangsbedingungen Veränderung der Anfangsbedingungen: φ1(t=0)=π/2 φ1(t=0)=1.571 Trotz der geringen Abweichung von 0,0065% stark Verändertes Ergebnis
11 Problem der Messungenauigkeit In keinem Experiment lassen sich die Anfangswerte exakt bestimmen Im Prinzip kann man nur sagen, dass man in einem Bestimmten bereich nicht ist z.b. π = 3,
12 Doppelpendel: Grenzen der Vorhersagbarkeit Zeitschritte: Zeitschritte:
13 Problem der Zeitskala Der Mensch betrachtet nur für ihn interessanten Zeitraum t m Sog. Lyapunov-Zeiten t lyap betrachten Zeitraum des Naturgeschehens 3 Fälle möglich t m << t lyap t m ~ t lyap t m >> t lyap
14 Erkenntnisse der Chaosforschung Chaotische Systeme zeigen bestimmte Verhaltensmuster Rückkopplungen, Iteration, Intermittenzen, Selbstähnlichkeit, Seltsame Attraktoren, Bifurkation Chaotische Systeme aus unterschiedlichen Bereichen laufen unter gleichen Gesetzmäßigkeiten ab
15 Fraktale Wolken sind keine Kugeln, Berge keine Kegel, Küstenlinien keine Kreise. Die Rinde ist nicht glatt - und auch der Blitz bahnt sich seinen Weg nicht gerade." Aus der Einleitung zu Mandelbrots Buch Die fraktale Geometrie der Natur" Von lateinisch frangere (in Stücke zer)brechen Struktur eines natürlichen Fraktals lässt sich entschlüsseln Mit Hilfe von Computermodellen ist ein exater Nachbau möglich
16 Mandelbrot-Menge z z² + C
17 Attraktoren Manche Systeme streben mit verschiedenen Anfangsbedingungen zu demselben Verhalten Sie konvergieren zu einer bestimmten Bahn, dem Attraktor Bei einem Pendel ist das z.b. Ein Fixpunkt Attraktoren können auch chaotisches Verhalten zeigen, diese werden dann als Seltsame Attraktoren bezeichnet
18 Lorenz-Attraktor Beischreibt Turbulenzen bei Luftströmungen Verhalten des Systems lässt sich so auf einen Bereich abgrenzen Berechnung durch 3 gekoppelte Differenztialgleichungen: Dabei gilt: σ=10,r=8/3,b=28
19 Bifurkation
20 Feigenbaumkonstante
21 Quellenverzeichnis
Deterministisches Chaos
 Deterministisches Chaos Um 1900 Henri Poincaré: Bewegung von zwei Planeten um die Sonne kann zu sehr komplizierten Bahnen führen. (chaotische Bahnen) Seit ca. 1970 Entwicklung der Chaostheorie basierend
Deterministisches Chaos Um 1900 Henri Poincaré: Bewegung von zwei Planeten um die Sonne kann zu sehr komplizierten Bahnen führen. (chaotische Bahnen) Seit ca. 1970 Entwicklung der Chaostheorie basierend
8. Deterministisches Chaos
 8. Deterministisches Chaos Widerspruch: deterministisch chaotisch Schmetterlingseffekt: Der Flügelschlag eines Schmetterlings entscheidet über die Entwicklung eines Sturms. Allgemein: kleinste Änderungen
8. Deterministisches Chaos Widerspruch: deterministisch chaotisch Schmetterlingseffekt: Der Flügelschlag eines Schmetterlings entscheidet über die Entwicklung eines Sturms. Allgemein: kleinste Änderungen
Chaos Oder Mandelbrot und Peitsche
 Chaos Oder Mandelbrot und Peitsche Warum kann man das Wetter nicht genau vorhersagen? Du kennst sicher das Problem: du planst mit deiner Familie ein Picknick, dass in letzter Minute abgesagt werden muss,
Chaos Oder Mandelbrot und Peitsche Warum kann man das Wetter nicht genau vorhersagen? Du kennst sicher das Problem: du planst mit deiner Familie ein Picknick, dass in letzter Minute abgesagt werden muss,
7. Systeme mit drei (und mehr) Spezies: chaotische Systeme
 7. Systeme mit drei (und mehr) Spezies: chaotische Systeme Dies kann z.b. Ein System mit mehreren verschiedenen Räubern sein, die die selben Beutetiere jagen. Auch ein nicht autonomes System mit zwei Spezies
7. Systeme mit drei (und mehr) Spezies: chaotische Systeme Dies kann z.b. Ein System mit mehreren verschiedenen Räubern sein, die die selben Beutetiere jagen. Auch ein nicht autonomes System mit zwei Spezies
Chaos im getriebenen nicht-linearen Pendel
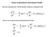 Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
Chaos im getriebenen nicht-linearen Pendel Alle drei Ingredienzen: Nichtlinearität, Reibung, treibende Kraft 2 d θ g dθ = sinθ q + F sin 2 dt L dt ( t) D Ω D Das ist ein so genanntes physikalisches Pendel
Dynamisches Chaos. 1. Einleitung: Determinismus und Chaos
 Dynamisches Chaos 1. Einleitung: Determinismus und Chaos In der üblichen Betrachtungsweise ist der Zufall nur auf dem Mikroniveau erlaubt: - das Boltzmannsche molekulare Chaos; - die quantenmechanischen
Dynamisches Chaos 1. Einleitung: Determinismus und Chaos In der üblichen Betrachtungsweise ist der Zufall nur auf dem Mikroniveau erlaubt: - das Boltzmannsche molekulare Chaos; - die quantenmechanischen
6.1 Beispiele dissipativer Systeme. Der Duffing Ozillator. Bewegungsgleichung: Nichtlinearität
 6.1 Beispiele dissipativer Systeme Der Duffing Ozillator z.b. für (Ueda Oszillator) Potential Bewegungsgleichung: Nichtlinearität nur zwei Parameter Kartierung des Verhaltens in der (f,r)- Ebene äußerst
6.1 Beispiele dissipativer Systeme Der Duffing Ozillator z.b. für (Ueda Oszillator) Potential Bewegungsgleichung: Nichtlinearität nur zwei Parameter Kartierung des Verhaltens in der (f,r)- Ebene äußerst
Die Chaostheorie und Fraktale in der Natur
 Hallertau-Gymnasium Wolnzach Abiturjahrgang 2009/2011 Facharbeit aus dem Leistungskurs Physik Die Chaostheorie und Fraktale in der Natur Eine physikalisch-philosophische Abhandlung über das Wesen der Natur
Hallertau-Gymnasium Wolnzach Abiturjahrgang 2009/2011 Facharbeit aus dem Leistungskurs Physik Die Chaostheorie und Fraktale in der Natur Eine physikalisch-philosophische Abhandlung über das Wesen der Natur
Journalismus als konstruktives Chaos Grundlagen einer chaostheoretischen Journalismustheorie
 Journalismus als konstruktives Chaos Grundlagen einer chaostheoretischen Journalismustheorie Daniela Schimming, Jennifer Richter, Juliana Schmidt Gliederung 1. Grundlagen 2. Nachrichtenjournalismus und
Journalismus als konstruktives Chaos Grundlagen einer chaostheoretischen Journalismustheorie Daniela Schimming, Jennifer Richter, Juliana Schmidt Gliederung 1. Grundlagen 2. Nachrichtenjournalismus und
Nichtlineare Dynamik Einführung
 Nichtlineare Dynamik Einführung Tobias Kerscher gekürzte Internetversion (ohne fremde Bilder) Sommerakademie Ftan 2004, 13. August Gliederung 1. Def: Nichtlineare Physik 2. Typische Beispiele 3. Dynamische
Nichtlineare Dynamik Einführung Tobias Kerscher gekürzte Internetversion (ohne fremde Bilder) Sommerakademie Ftan 2004, 13. August Gliederung 1. Def: Nichtlineare Physik 2. Typische Beispiele 3. Dynamische
Zufall, Determinismus und Chaos Wie viel ist vorhersehbar? Big Data Science in und außerhalb der Physik
 Zufall, Determinismus und Chaos Wie viel ist vorhersehbar? Ausarbeitung zum Vortrag im Rahmen des Hauptseminars Big Data Science in und außerhalb der Physik an der Fakultät für Physik am Karlsruher Institut
Zufall, Determinismus und Chaos Wie viel ist vorhersehbar? Ausarbeitung zum Vortrag im Rahmen des Hauptseminars Big Data Science in und außerhalb der Physik an der Fakultät für Physik am Karlsruher Institut
REFERAT FÜR INNOVATIVE ARCHIKETUREN
 REFERAT FÜR INNOVATIVE ARCHIKETUREN THEMA CHAOSTHEORIE REFERENTEN TIMO BÖLLINGER & DOMINIC ECKART DATUM 9. NOVEMBER 2004 FACHRICHTUNG INFORMATIONSTECHNIK NETZWERK UND SOFTWARETECHNIK AN DER BERUFSAKADEMIE
REFERAT FÜR INNOVATIVE ARCHIKETUREN THEMA CHAOSTHEORIE REFERENTEN TIMO BÖLLINGER & DOMINIC ECKART DATUM 9. NOVEMBER 2004 FACHRICHTUNG INFORMATIONSTECHNIK NETZWERK UND SOFTWARETECHNIK AN DER BERUFSAKADEMIE
Wie lang ist die Küste Großbritanniens?
 Wie lang ist die Küste Großbritanniens? Vortrag am 16.01.2009 Fach: Physik Deterministisches Chaos Ein Vortrag von Tina Rosner und Florian Sachs Werner-von-Siemens-Gymnasium Magdeburg Gliederung 1 Das
Wie lang ist die Küste Großbritanniens? Vortrag am 16.01.2009 Fach: Physik Deterministisches Chaos Ein Vortrag von Tina Rosner und Florian Sachs Werner-von-Siemens-Gymnasium Magdeburg Gliederung 1 Das
Die Entdeckung des Chaos
 Die Entdeckung des Chaos Dieser Artikel beschreibt das sogenannte deterministische Chaos, das in berechenbaren Rückkopplungssystemen zutage tritt. Das per Emailkontakt verfügbare Programm Feigenbaum ermöglicht
Die Entdeckung des Chaos Dieser Artikel beschreibt das sogenannte deterministische Chaos, das in berechenbaren Rückkopplungssystemen zutage tritt. Das per Emailkontakt verfügbare Programm Feigenbaum ermöglicht
Nichtlinearität in der klassischen Physik
 Nichtlinearität in der klassischen Physik Dr. Peter Schlagheck Vorlesung an der Uni Regensburg im Wintersemester 25/26 Inhaltsverzeichnis Klassische Mechanik 2. Lagrange-Formalismus........................................
Nichtlinearität in der klassischen Physik Dr. Peter Schlagheck Vorlesung an der Uni Regensburg im Wintersemester 25/26 Inhaltsverzeichnis Klassische Mechanik 2. Lagrange-Formalismus........................................
Chaos - Nichtlineare Dynamik
 Äg Chaos - Nichtlineare Dynamik Renate Thies Universität Dortmund - Fachbereich Informatik Lehrstuhl für Systemanalyse (LS11) Sommersemester 2004 Chaos - Nichtlineare Dynamik 1/102 Inhaltsverzeichnis Äg
Äg Chaos - Nichtlineare Dynamik Renate Thies Universität Dortmund - Fachbereich Informatik Lehrstuhl für Systemanalyse (LS11) Sommersemester 2004 Chaos - Nichtlineare Dynamik 1/102 Inhaltsverzeichnis Äg
11. Nichtlineare Dynamik und Chaos. Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt.
 11. Nichtlineare Dynamik und Chaos Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt. der Auslenkung Fadenlänge L, Masse m, Auslenkwinkel φ Rücktreibende Kraft: Beschleunigung:
11. Nichtlineare Dynamik und Chaos Bei den meisten bisherigen Phänomenen z. B: Pendelbewegung: Kraft linear als Fkt. der Auslenkung Fadenlänge L, Masse m, Auslenkwinkel φ Rücktreibende Kraft: Beschleunigung:
Die Mathematikerinnen Sonja Kowalewskaja und Amalie Emmy Noether und ihre Beiträge zur Physik
 Die Mathematikerinnen Sonja Kowalewskaja und Amalie Emmy Noether und ihre Beiträge zur Physik Köln, den 26.9.2002 Ute Löw 1. Sonja Kowalewskaja 2. Der starre Körper 3.Die Bewegung von Körpern 4.Chaotische
Die Mathematikerinnen Sonja Kowalewskaja und Amalie Emmy Noether und ihre Beiträge zur Physik Köln, den 26.9.2002 Ute Löw 1. Sonja Kowalewskaja 2. Der starre Körper 3.Die Bewegung von Körpern 4.Chaotische
Durch Simulation dynamische Systeme entdecken Labor 6
 Institut für Automatik D-ITET, 2. Sem. ETH Zürich Dr. F. J. Kraus 28. Mai 2004 Durch Simulation dynamische Systeme entdecken Labor 6 In diesem Labor wollen wir einen kleinen Einblick in die Chaostheorie
Institut für Automatik D-ITET, 2. Sem. ETH Zürich Dr. F. J. Kraus 28. Mai 2004 Durch Simulation dynamische Systeme entdecken Labor 6 In diesem Labor wollen wir einen kleinen Einblick in die Chaostheorie
DAS VORHERGESAGTE CHAOS
 DAS VORHERGESAGTE CHAOS Vorhersagen sind schwierig, besonders wenn sie die Zukunft betreffen, in erster Linie dann, wenn es sich um Wettervorhersagen handelt ein Zitat, das Berühmtheiten wie Nils Bohr
DAS VORHERGESAGTE CHAOS Vorhersagen sind schwierig, besonders wenn sie die Zukunft betreffen, in erster Linie dann, wenn es sich um Wettervorhersagen handelt ein Zitat, das Berühmtheiten wie Nils Bohr
Experimente, Ideen und Entwicklung der Chaostheorie
 Experimente, Ideen und Entwicklung der Chaostheorie Stephan Lück Ursprünge der Chaostheorie Edward Lorenz (1917-2008) Meteorologe einfaches Atmosphärenmodell (ca. 1960) basierend auf Konvektion Modellexperiment
Experimente, Ideen und Entwicklung der Chaostheorie Stephan Lück Ursprünge der Chaostheorie Edward Lorenz (1917-2008) Meteorologe einfaches Atmosphärenmodell (ca. 1960) basierend auf Konvektion Modellexperiment
Von der Schönheit des mathematischen Chaos. Eine Einführung in Seltsame Attraktoren mit jreality
 Von der Schönheit des mathematischen Chaos Eine Einführung in Seltsame Attraktoren mit jreality Inhalt Physikalische Grundlagen Definition Eigenschaften Beispiele Implementierung Demonstration Physikalische
Von der Schönheit des mathematischen Chaos Eine Einführung in Seltsame Attraktoren mit jreality Inhalt Physikalische Grundlagen Definition Eigenschaften Beispiele Implementierung Demonstration Physikalische
Einführendes Beispiel zum lösen einer DGL n-ter Ordnung Dokumentation zum Dreikörperproblem (Sonne, Erde, Mond)
 Projektarbeit zur grafischen Beschreibung des Dreikörperproblems durch numerisches lösen der Bewegungsgleichungen Joachim N. WS 07/08 Einführendes Beispiel zum lösen einer DGL n-ter Ordnung Dokumentation
Projektarbeit zur grafischen Beschreibung des Dreikörperproblems durch numerisches lösen der Bewegungsgleichungen Joachim N. WS 07/08 Einführendes Beispiel zum lösen einer DGL n-ter Ordnung Dokumentation
Seltsame Attraktoren
 1 Seltsame Attraktoren Proseminar: Theoretische Physik Jonas Haferkamp 9. Juli 2014 Abbildung: Poincaré-Schnitt der Duffing-Gleichungen 2 3 Gliederung 1 Motivation 2 Was ist ein (seltsamer) Attraktor?
1 Seltsame Attraktoren Proseminar: Theoretische Physik Jonas Haferkamp 9. Juli 2014 Abbildung: Poincaré-Schnitt der Duffing-Gleichungen 2 3 Gliederung 1 Motivation 2 Was ist ein (seltsamer) Attraktor?
Lernbereich 8: Deterministisches Chaos Experimente, Simulationen und Begriffsbildungen
 Lernbereich 8: Deterministisches Chaos Experimente, Simulationen und Begriffsbildungen Inhaltsangebote Lernbereich Deterministisches Chaos Einführender Überblicksvortag Wir bauen EXPERIMENTIERPHASE 1 Modellierung
Lernbereich 8: Deterministisches Chaos Experimente, Simulationen und Begriffsbildungen Inhaltsangebote Lernbereich Deterministisches Chaos Einführender Überblicksvortag Wir bauen EXPERIMENTIERPHASE 1 Modellierung
Numerische Methoden I Schriftliche Prüfung Gruppe A 23. Jan :00-14:00 (120 min)
 Lehrstuhl für Angewandte Mathematik Montanuniversität Leoben 70 004 Numerische Methoden I Schriftliche Prüfung Gruppe A 23. Jan. 207 2:00-4:00 (20 min) Name Matrikelnummer Mündliche Prüfung: Bitte markieren
Lehrstuhl für Angewandte Mathematik Montanuniversität Leoben 70 004 Numerische Methoden I Schriftliche Prüfung Gruppe A 23. Jan. 207 2:00-4:00 (20 min) Name Matrikelnummer Mündliche Prüfung: Bitte markieren
+ + Personalmanagement Stuff-Turnover. Simulation im Excel. Organizational Headcount. Turnover. Recruitment
 Personalmanagement Stuff-Turnover + Organizational Headcount Recruitment + + Turnover Simulation im Excel Schmetterlingseffekt 1 0,8 x 0,6 0,4 0,2 0 0 5 10 15 2 0 2 5 3 0 n Feigenbaum-Szenario Bifurkationspunkt:
Personalmanagement Stuff-Turnover + Organizational Headcount Recruitment + + Turnover Simulation im Excel Schmetterlingseffekt 1 0,8 x 0,6 0,4 0,2 0 0 5 10 15 2 0 2 5 3 0 n Feigenbaum-Szenario Bifurkationspunkt:
Chaos und Ordnung im Unternehmen
 Frank Deser 2008 AGI-Information Management Consultants May be used for personal purporses only or by libraries associated to dandelon.com network. Chaos und Ordnung im Unternehmen Chaosforschung als ein
Frank Deser 2008 AGI-Information Management Consultants May be used for personal purporses only or by libraries associated to dandelon.com network. Chaos und Ordnung im Unternehmen Chaosforschung als ein
Wir betrachten die zeitliche Entwicklung einer Population N (z.b. die Zahl der Fische in einem Teich). Es gilt dn dt wobei die Symbole bedeuten:
 Kapitel 3 Nichtlineare Systeme 3. Logistische Gleichung Wir betrachten die zeitliche Entwicklung einer Population N (z.b. die Zahl der Fische in einem Teich). Es gilt dn dt wobei die Symbole bedeuten:
Kapitel 3 Nichtlineare Systeme 3. Logistische Gleichung Wir betrachten die zeitliche Entwicklung einer Population N (z.b. die Zahl der Fische in einem Teich). Es gilt dn dt wobei die Symbole bedeuten:
System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form:
 C7.5 Differentialgleichungen 1. Ordnung - Allgemeine Aussagen System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form: Kompaktnotation: Anfangsbedingung: Gesuchte Lösung: Gleichungen dieser Art
C7.5 Differentialgleichungen 1. Ordnung - Allgemeine Aussagen System von n gewöhnlichen DG 1. Ordnung hat die allgemeine Form: Kompaktnotation: Anfangsbedingung: Gesuchte Lösung: Gleichungen dieser Art
Vom Algorithmus zum Chaos: Anwendungen des Computers
 Vom Algorithmus zum Chaos: Anwendungen des Computers (Henner Schneider, Fb Informatik, FH Darmstadt) Die Computer verdanken ihre Entstehung den Schwierigkeiten, die das menschliche Gehirn beim Umgang mit
Vom Algorithmus zum Chaos: Anwendungen des Computers (Henner Schneider, Fb Informatik, FH Darmstadt) Die Computer verdanken ihre Entstehung den Schwierigkeiten, die das menschliche Gehirn beim Umgang mit
Chaos Seminar Wetter und Klima. Dominik Fröschl
 Chaos Seminar Wetter und Klima Dominik Fröschl 05.02.2010 1 Inhaltsverzeichnis 1 Einleitung 3 1.1 Vorbemerkungen......................... 3 1.2 Begriffsklärung.......................... 3 1.3 Entstehung
Chaos Seminar Wetter und Klima Dominik Fröschl 05.02.2010 1 Inhaltsverzeichnis 1 Einleitung 3 1.1 Vorbemerkungen......................... 3 1.2 Begriffsklärung.......................... 3 1.3 Entstehung
3.7 Chaos. Ist N 3, können chaotische Trajektorien auftreten (Zwei-Planeten- Problem, Doppel-Pendel).
 3.7 Chaos Wir untersuchen weiter autonome Systeme der Form dy i dt = f i(y,y 2,..y N ), y i (0) = a i, i =...N () (f i hängt nicht explizit von der Zeit ab). Eindeutigkeit der Lösung: aus y(t) folgt genau
3.7 Chaos Wir untersuchen weiter autonome Systeme der Form dy i dt = f i(y,y 2,..y N ), y i (0) = a i, i =...N () (f i hängt nicht explizit von der Zeit ab). Eindeutigkeit der Lösung: aus y(t) folgt genau
Algorithmen für Chaos und Fraktale
 Dietmar Herrmann Algorithmen für Chaos und Fraktale A... :.., ADDISON-WESLEY PUBLISHING COMPANY Bonn Paris Reading, Massachusetts Menlo Park, California New York. Don Mills, Ontario Wokingham, ; England
Dietmar Herrmann Algorithmen für Chaos und Fraktale A... :.., ADDISON-WESLEY PUBLISHING COMPANY Bonn Paris Reading, Massachusetts Menlo Park, California New York. Don Mills, Ontario Wokingham, ; England
Zeitreihenanalytische Verfahren für die Analyse nichtlinearer Systeme
 Dipl.-Psych. Dr. Dr. Guido Strunk 2010 1 Zeitreihenanalytische Verfahren für die Analyse nichtlinearer Systeme Unterlagen zur Summer School 2010 von Dipl.-Psych. Dr. Dr. Guido Strunk guido.strunk@complexity-research.com
Dipl.-Psych. Dr. Dr. Guido Strunk 2010 1 Zeitreihenanalytische Verfahren für die Analyse nichtlinearer Systeme Unterlagen zur Summer School 2010 von Dipl.-Psych. Dr. Dr. Guido Strunk guido.strunk@complexity-research.com
1. Anfangswertprobleme 1. Ordnung
 1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
1. Anfangswertprobleme 1. Ordnung 1.1 Grundlagen 1.2 Euler-Vorwärts-Verfahren 1.3 Runge-Kutta-Verfahren 1.4 Stabilität 1.5 Euler-Rückwärts-Verfahren 1.6 Differentialgleichungssysteme Prof. Dr. Wandinger
Nichtlineare Phänomene und Selbstorganisation
 Nichtlineare Phänomene und Selbstorganisation Von Dr. rer i.. ibü: Rein*»i M ce Doz. Dr. rer. nat. nabii. Jürn Schmelzer Prof. Dr. rer. nat. habil. Gerd Röpke Universität Rostock Mit zahlreichen Figuren
Nichtlineare Phänomene und Selbstorganisation Von Dr. rer i.. ibü: Rein*»i M ce Doz. Dr. rer. nat. nabii. Jürn Schmelzer Prof. Dr. rer. nat. habil. Gerd Röpke Universität Rostock Mit zahlreichen Figuren
FC3 - Duffing Oszillator
 FC3 - Duffing Oszillator 4. Oktober 2007 Universität Paderborn - Theoretische Physik leer Autor: Stephan Blankenburg, Björn Lange Datum: 4. Oktober 2007 FC3 - Duffing Oszillator 3 1 Theorie komplexer Systeme
FC3 - Duffing Oszillator 4. Oktober 2007 Universität Paderborn - Theoretische Physik leer Autor: Stephan Blankenburg, Björn Lange Datum: 4. Oktober 2007 FC3 - Duffing Oszillator 3 1 Theorie komplexer Systeme
Chaos & Quantenchaos SS 2009
 Chaos & Quantenchaos SS 2009 H. J. Korsch FB Physik Technische Universität Kaiserslautern Einleitung Mathematisches Vorspiel : Hamiltonsche Systeme alternativ Dissipative Systeme Wege ins Chaos Quantenchaos
Chaos & Quantenchaos SS 2009 H. J. Korsch FB Physik Technische Universität Kaiserslautern Einleitung Mathematisches Vorspiel : Hamiltonsche Systeme alternativ Dissipative Systeme Wege ins Chaos Quantenchaos
Gregoire Nicolis/ Ilya Prigogine Die Erforschung des Komplexen
 Gregoire Nicolis/ Ilya Prigogine Die Erforschung des Komplexen Auf dem Weg zu einem neuen Verständnis der Naturwissenschaften Deutsche Ausgabe bearbeitet von Eckhard Rebhan Mit 110 Abbildungen T) Piper
Gregoire Nicolis/ Ilya Prigogine Die Erforschung des Komplexen Auf dem Weg zu einem neuen Verständnis der Naturwissenschaften Deutsche Ausgabe bearbeitet von Eckhard Rebhan Mit 110 Abbildungen T) Piper
Mathematische Grundlagen der dynamischen Simulation
 Mathematische Grundlagen der dynamischen Simulation Dynamische Systeme sind Systeme, die sich verändern. Es geht dabei um eine zeitliche Entwicklung und wie immer in der Informatik betrachten wir dabei
Mathematische Grundlagen der dynamischen Simulation Dynamische Systeme sind Systeme, die sich verändern. Es geht dabei um eine zeitliche Entwicklung und wie immer in der Informatik betrachten wir dabei
Einführung in die Grundlagen der Theoretischen Physik
 Günther Ludwig Einführung in die Grundlagen der Theoretischen Physik Band 1: Raum, Zeit, Mechanik 2., durchgesehene und erweiterte Auflage Vieweg Inhalt Zur Einführung 1 /. Was theoretische Physik nicht
Günther Ludwig Einführung in die Grundlagen der Theoretischen Physik Band 1: Raum, Zeit, Mechanik 2., durchgesehene und erweiterte Auflage Vieweg Inhalt Zur Einführung 1 /. Was theoretische Physik nicht
Praktikumssemesterarbeit für Numerik Aufgabe 1 HU-Berlin, Sommersemester 2005
 Praktikumssemesterarbeit für Numerik Aufgabe HU-Berlin, Sommersemester 2005 Mario Krell Volker Grabsch 24. Juli 2005 Inhaltsverzeichnis Herleitung aus der Physik. Voraussetzungen und Annahmen Allgemein
Praktikumssemesterarbeit für Numerik Aufgabe HU-Berlin, Sommersemester 2005 Mario Krell Volker Grabsch 24. Juli 2005 Inhaltsverzeichnis Herleitung aus der Physik. Voraussetzungen und Annahmen Allgemein
Analyse nichtlinearer dynamischer Systeme der Elektrotechnik
 E. S. Philippow / W. G. Büntig Analyse nichtlinearer dynamischer Systeme der Elektrotechnik Einführung in die numerische Untersuchung einfacher Systeme Mit 198 Bildern und 27 Tabellen Carl Hanser Verlag
E. S. Philippow / W. G. Büntig Analyse nichtlinearer dynamischer Systeme der Elektrotechnik Einführung in die numerische Untersuchung einfacher Systeme Mit 198 Bildern und 27 Tabellen Carl Hanser Verlag
Differentialgleichungen sind überall!
 Differentialgleichungen sind überall! Helmut Abels Fakultät für Mathematik Universität Regensburg Folien und Co.: http://www.uni-r.de/fakultaeten/nat Fak I/abels/Aktuelles.html Tag der Mathematik am Albrecht-Altdorfer-Gymnasium
Differentialgleichungen sind überall! Helmut Abels Fakultät für Mathematik Universität Regensburg Folien und Co.: http://www.uni-r.de/fakultaeten/nat Fak I/abels/Aktuelles.html Tag der Mathematik am Albrecht-Altdorfer-Gymnasium
Darstellende Geometrie - Akad. Dir. Cornelie Leopold - Lehrveranstaltung Architektur und Geometrie: Geometrische Raumstrukturen SS 2005 FRAKTALE
 FRAKTALE Wibke Brandes Fraktale - Wibke Brandes 1 Definition des Begriffs frangere (lat.): zerbrechen, zerteilen fraktal (engl.-frz.-lat.): vielfältig gebrochen, stark gegliedert Fraktal, das; -s, -e:
FRAKTALE Wibke Brandes Fraktale - Wibke Brandes 1 Definition des Begriffs frangere (lat.): zerbrechen, zerteilen fraktal (engl.-frz.-lat.): vielfältig gebrochen, stark gegliedert Fraktal, das; -s, -e:
GRUNDLEGENDE MODELLE. Caroline Herbek
 GRUNDLEGENDE MODELLE Caroline Herbek Lineares Wachstum Charakteristikum: konstante absolute Zunahme d einer Größe N t in einem Zeitschritt Differenzengleichung: N t -N t-1 =d => N t = N t-1 +d (Rekursion)
GRUNDLEGENDE MODELLE Caroline Herbek Lineares Wachstum Charakteristikum: konstante absolute Zunahme d einer Größe N t in einem Zeitschritt Differenzengleichung: N t -N t-1 =d => N t = N t-1 +d (Rekursion)
Differentialgleichungen 2. Differentialgleichungen und Dynamische Systeme. Peter Szmolyan
 Differentialgleichungen 2 Differentialgleichungen und Dynamische Systeme Peter Szmolyan Institut für Analysis und Scientific Computing TU-Wien 1 The theory of dynamical systems is one of the domains of
Differentialgleichungen 2 Differentialgleichungen und Dynamische Systeme Peter Szmolyan Institut für Analysis und Scientific Computing TU-Wien 1 The theory of dynamical systems is one of the domains of
Fraktale und Beispiele aus der Physik
 Fraktale und Beispiele aus der Physik Anschauung Warum beschäftigen Fraktale (auch) Naturwissenschaftler? kurze Wiederholung Konkretes Beispiel: Magnetpendel Das Experiment Mathematische Beschreibung Trajektorien
Fraktale und Beispiele aus der Physik Anschauung Warum beschäftigen Fraktale (auch) Naturwissenschaftler? kurze Wiederholung Konkretes Beispiel: Magnetpendel Das Experiment Mathematische Beschreibung Trajektorien
Anleitung zum Physikpraktikum für Oberstufenlehrpersonen Einführungsversuch (EV) Herbstsemester Physik-Institut der Universität Zürich
 Anleitung zum Physikpraktikum für Oberstufenlehrpersonen Einführungsversuch (EV) Herbstsemester 2017 Physik-Institut der Universität Zürich Inhaltsverzeichnis 1 Einführungsversuch (EV) 11 11 Einleitung
Anleitung zum Physikpraktikum für Oberstufenlehrpersonen Einführungsversuch (EV) Herbstsemester 2017 Physik-Institut der Universität Zürich Inhaltsverzeichnis 1 Einführungsversuch (EV) 11 11 Einleitung
Chaos ist überall - Eine Eigenschaft (nicht nur) amorpher Materialien
 Chaos ist überall - Eine Eigenschaft (nicht nur) amorpher Materialien Doris Ehrt Otto-Schott-Institut für Glaschemie Friedrich-Schiller-Universität Jena Jena, 27.09.2007 Was ist Chaos? Unordnung Wirrwarr
Chaos ist überall - Eine Eigenschaft (nicht nur) amorpher Materialien Doris Ehrt Otto-Schott-Institut für Glaschemie Friedrich-Schiller-Universität Jena Jena, 27.09.2007 Was ist Chaos? Unordnung Wirrwarr
Numerische Integration
 A1 Numerische Integration Einführendes Beispiel In einem Raum mit der Umgebungstemperatur T u = 21.7 C befindet sich eine Tasse heissen Kaffees mit der anfänglichen Temperatur T 0 80 C. Wie kühlt sich
A1 Numerische Integration Einführendes Beispiel In einem Raum mit der Umgebungstemperatur T u = 21.7 C befindet sich eine Tasse heissen Kaffees mit der anfänglichen Temperatur T 0 80 C. Wie kühlt sich
12 COMPUTER SIMULATIONEN, CHAOS, FRAKTALE
 -1-12 COMPUTER SIMULATIONEN, CHAOS, FRAKTALE In diesem Kapitel sollen zwei wichtige Computer-gestützte Methoden behandelt werden, mit denen das Verhalten von vielen Teilchen oder von komplizierten Molekülen
-1-12 COMPUTER SIMULATIONEN, CHAOS, FRAKTALE In diesem Kapitel sollen zwei wichtige Computer-gestützte Methoden behandelt werden, mit denen das Verhalten von vielen Teilchen oder von komplizierten Molekülen
Thema: Visualisierung mit MAPLE
 Ostervortrag zum Linux-Stammtisch am 07.04.2017 Thema: Visualisierung mit MAPLE Sybille Handrock 1 Computeralgebrasysteme Computeralgebra beschäftigt sich mit Methoden zum Lösen mathematischer Probleme
Ostervortrag zum Linux-Stammtisch am 07.04.2017 Thema: Visualisierung mit MAPLE Sybille Handrock 1 Computeralgebrasysteme Computeralgebra beschäftigt sich mit Methoden zum Lösen mathematischer Probleme
Inhomogene lineare Differentialgleichung 1. Ordnung Variation der Konstanten
 http://farm2.static.flickr.com/1126/1106887574_afb6b55b4e.jpg?v=0 Inhomogene lineare Differentialgleichung 1. Ordnung Variation der Konstanten 1-E Joseph Louis Lagrange (1736-1813), ein italienischer Mathematiker
http://farm2.static.flickr.com/1126/1106887574_afb6b55b4e.jpg?v=0 Inhomogene lineare Differentialgleichung 1. Ordnung Variation der Konstanten 1-E Joseph Louis Lagrange (1736-1813), ein italienischer Mathematiker
Gedanken zur Unendlichkeit
 Gedanken zur Unendlichkeit Was erwartet Sie heute abend? Theologie ist eine besondere Wissenschaft Theologie ist mehr als bloße Bibel- Wissenschaft Theologie ist anschlussfähig an andere Wissenschaften
Gedanken zur Unendlichkeit Was erwartet Sie heute abend? Theologie ist eine besondere Wissenschaft Theologie ist mehr als bloße Bibel- Wissenschaft Theologie ist anschlussfähig an andere Wissenschaften
2. Fraktale Geometrie
 2. Fraktale Geometrie Komplexe Systeme ohne charakteristische Längenskala z.b. Risse in festen Materialien, Küstenlinien, Flussläufe und anderes.. Skaleninvariante Systeme Gebrochene Dimensionen Fraktale
2. Fraktale Geometrie Komplexe Systeme ohne charakteristische Längenskala z.b. Risse in festen Materialien, Küstenlinien, Flussläufe und anderes.. Skaleninvariante Systeme Gebrochene Dimensionen Fraktale
Einführung in die Himmelsmechanik und Ephemeridenrechnung
 Einführung in die Himmelsmechanik und Ephemeridenrechnung von Dr. Andreas Guthmann Universität Kaiserslautern Wissenschaftsverlag Mannheim Leipzig Wien Zürich Inhalt Vorrede 1 Inhalt 7 Notation 14 Kapitel
Einführung in die Himmelsmechanik und Ephemeridenrechnung von Dr. Andreas Guthmann Universität Kaiserslautern Wissenschaftsverlag Mannheim Leipzig Wien Zürich Inhalt Vorrede 1 Inhalt 7 Notation 14 Kapitel
Serie 2. D-MATH Numerische Methoden FS 2016 Dr. Vasile Gradinaru Luc Grosheintz
 D-MATH Numerische Methoden FS 206 Dr. Vasile Gradinaru Luc Grosheintz Serie 2 Abgabedatum: Di. 4.3 / Mi. 5.3 oder früher, in den Übungsgruppen Koordinatoren: Luc Grosheintz, HG J 46, luc.grosheintz@sam.math.ethz.ch
D-MATH Numerische Methoden FS 206 Dr. Vasile Gradinaru Luc Grosheintz Serie 2 Abgabedatum: Di. 4.3 / Mi. 5.3 oder früher, in den Übungsgruppen Koordinatoren: Luc Grosheintz, HG J 46, luc.grosheintz@sam.math.ethz.ch
Die Darstellung nichtlinearer Bewegungsabläufe
 Die Darstellung nichtlinearer Bewegungsabläufe Die Darstellung linearer Bewegungsabläufe Manchmal sind die Dinge mehr, als sie auf den ersten Blick zu sein scheinen. Auch chaotische Systeme offenbaren
Die Darstellung nichtlinearer Bewegungsabläufe Die Darstellung linearer Bewegungsabläufe Manchmal sind die Dinge mehr, als sie auf den ersten Blick zu sein scheinen. Auch chaotische Systeme offenbaren
 Vorwort Dynamische Systeme können durch mathematische Gleichungen modelliert werden, die eine eindeutige Vorschrift zur Berechnung der zeitlichen Entwicklung des Systemzustandes darstellen, so daß die
Vorwort Dynamische Systeme können durch mathematische Gleichungen modelliert werden, die eine eindeutige Vorschrift zur Berechnung der zeitlichen Entwicklung des Systemzustandes darstellen, so daß die
Numerische Verfahren
 Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
Numerische Verfahren Numerische Methoden von gewöhnlichen Differentialgleichungen (AWP) Prof. Dr.-Ing. K. Warendorf, Prof. Dr.-Ing. P. Wolfsteiner Hochschule für Angewandte Wissenschaften München (FH)
Simulation zur Periheldrehung
 Simulation zur Periheldrehung Sebastian Hähnel 30.03.2015 Inhaltsverzeichnis 1 Lösung der Einstein-Gleichung 1 2 Lösung der Bewegungsgleichungen 2 3 Dimensionslose Gleichung 4 4 Einige Beispiele 4 1 Lösung
Simulation zur Periheldrehung Sebastian Hähnel 30.03.2015 Inhaltsverzeichnis 1 Lösung der Einstein-Gleichung 1 2 Lösung der Bewegungsgleichungen 2 3 Dimensionslose Gleichung 4 4 Einige Beispiele 4 1 Lösung
nichtlineare dynamische Systeme
 nichtlineare dynamische Systeme dynamische Systeme: - Systeme mit Krafteinwirkung (δυναµιο = Kraft) - zeitabhängige Systemzustände - Zustandsänderung abhängig vom momentanen Zustand deterministisch gleiche
nichtlineare dynamische Systeme dynamische Systeme: - Systeme mit Krafteinwirkung (δυναµιο = Kraft) - zeitabhängige Systemzustände - Zustandsänderung abhängig vom momentanen Zustand deterministisch gleiche
6 chaotische Vorgänge
 6 chaotische Vorgänge Kausalität und Determinismus ( S. 125) sind wesentliche Grundlagen der klassischen Physik: Keine Wirkung tritt ohne Ursache auf, und jede Ursache hat eine Wirkung. Ist der Zustand
6 chaotische Vorgänge Kausalität und Determinismus ( S. 125) sind wesentliche Grundlagen der klassischen Physik: Keine Wirkung tritt ohne Ursache auf, und jede Ursache hat eine Wirkung. Ist der Zustand
J. Neunte Übungseinheit
 J. Neunte Übungseinheit Inhalt der neunten Übungseinheit: Aufgaben dieser Art kommen zum zweiten Kenntnisnachweis. Umformen von Differentialgleichungen 2. und höherer Ordnung auf Systeme 1. Ordnung J.1.
J. Neunte Übungseinheit Inhalt der neunten Übungseinheit: Aufgaben dieser Art kommen zum zweiten Kenntnisnachweis. Umformen von Differentialgleichungen 2. und höherer Ordnung auf Systeme 1. Ordnung J.1.
Diskrete Populationsmodelle für Einzelspezies
 Diskrete Populationsmodelle für Einzelspezies Lisa Zang 30.10.2012 Quelle: J. D. Murray: Mathematical Biology: I. An Introduction, Third Edition, Springer Inhaltsverzeichnis 1. Einführung Einfache Modelle
Diskrete Populationsmodelle für Einzelspezies Lisa Zang 30.10.2012 Quelle: J. D. Murray: Mathematical Biology: I. An Introduction, Third Edition, Springer Inhaltsverzeichnis 1. Einführung Einfache Modelle
Zeitentwicklung von Observablen und Zuständen in der klassischen Mechanik
 Zeitentwicklung von Observablen und Zuständen in der klassischen Mechanik Martin Vojta 05.01.2012 1 Hamiltonsche Mechanik Die Hamiltonsche Mechanik befasst sich mit der Bewegung im Phasenraum. Dabei kann
Zeitentwicklung von Observablen und Zuständen in der klassischen Mechanik Martin Vojta 05.01.2012 1 Hamiltonsche Mechanik Die Hamiltonsche Mechanik befasst sich mit der Bewegung im Phasenraum. Dabei kann
GMA. Grundlagen Mathematik und Analysis. Nullstellen und Fixpunkte Reelle Funktionen 3. Christian Cenker Gabriele Uchida
 GMA Grundlagen Mathematik und Analysis Reelle Funktionen 3 Christian Cenker Gabriele Uchida Data Analytics and Computing Nullstellen cos log : 0, 0,? 1 Fixpunkte Beispiel 1 Beispiel 2 1 0 0 und 1 1sin,?
GMA Grundlagen Mathematik und Analysis Reelle Funktionen 3 Christian Cenker Gabriele Uchida Data Analytics and Computing Nullstellen cos log : 0, 0,? 1 Fixpunkte Beispiel 1 Beispiel 2 1 0 0 und 1 1sin,?
Mathematik 2 für Nichtmathematiker
 Mathematik 2 für Nichtmathematiker Funktionen - Folgen und Reihen - Differential- und Integralrechnung - Differentialgleichungen - Ordnung und Chaos von Professor Dr. Manfred Precht Dipl.-Math. Karl Voit
Mathematik 2 für Nichtmathematiker Funktionen - Folgen und Reihen - Differential- und Integralrechnung - Differentialgleichungen - Ordnung und Chaos von Professor Dr. Manfred Precht Dipl.-Math. Karl Voit
7. Wettervorhersage und Vorhersagbarkeit (aus der Theorie-Vorlesung von K. Fraedrich)
 7. Wettervorhersage und Vorhersagbarkeit (aus der Theorie-Vorlesung von K. Fraedrich) Begriffe Vorhersagbarkeit Vorhersagbarkeit charakterisiert die sensitive Abhängigkeit (Wetter- und Klima) von Anfangs-
7. Wettervorhersage und Vorhersagbarkeit (aus der Theorie-Vorlesung von K. Fraedrich) Begriffe Vorhersagbarkeit Vorhersagbarkeit charakterisiert die sensitive Abhängigkeit (Wetter- und Klima) von Anfangs-
Thermodynamik (Wärmelehre) III kinetische Gastheorie
 Physik A VL6 (07.1.01) Thermodynamik (Wärmelehre) III kinetische Gastheorie Thermische Bewegung Die kinetische Gastheorie Mikroskopische Betrachtung des Druckes Mawell sche Geschwindigkeitserteilung gdes
Physik A VL6 (07.1.01) Thermodynamik (Wärmelehre) III kinetische Gastheorie Thermische Bewegung Die kinetische Gastheorie Mikroskopische Betrachtung des Druckes Mawell sche Geschwindigkeitserteilung gdes
Übungen zu Meteorologische Modellierung Teil 'Grundlagen der Numerik'
 Übungen zu Meteorologische Modellierung Teil 'Grundlagen der Numerik' 1. Diskretisierung in der Zeit: Die Evolutionsgleichung Kurzzusammenfassung Zur Erprobung der Verfahren zur zeitlichen Diskretisierung
Übungen zu Meteorologische Modellierung Teil 'Grundlagen der Numerik' 1. Diskretisierung in der Zeit: Die Evolutionsgleichung Kurzzusammenfassung Zur Erprobung der Verfahren zur zeitlichen Diskretisierung
Klassische Mechanik. WILEY-VCH Verlag GmbH & Co. KGaA. Herbert Goldstein, Charles P. Poole, Jr., und John L Safko
 Herbert Goldstein, Charles P. Poole, Jr., und John L Safko Klassische Mechanik Dritte, vollständig überarbeitete und erweiterte Auflage WILEY- VCH WILEY-VCH Verlag GmbH & Co. KGaA Inhaltsverzeichnis Vorwort
Herbert Goldstein, Charles P. Poole, Jr., und John L Safko Klassische Mechanik Dritte, vollständig überarbeitete und erweiterte Auflage WILEY- VCH WILEY-VCH Verlag GmbH & Co. KGaA Inhaltsverzeichnis Vorwort
Auswertung des Versuches Resonanzverhalten nichtlinearer Oszillatoren
 Auswertung des Versuches Resonanzverhalten nichtlinearer Oszillatoren Andreas Buhr, Matrikelnummer 1229903 23. Juni 2006 Inhaltsverzeichnis 1 Formales 3 2 Überblick über den Versuch 4 3 Grundlagen 4 3.1
Auswertung des Versuches Resonanzverhalten nichtlinearer Oszillatoren Andreas Buhr, Matrikelnummer 1229903 23. Juni 2006 Inhaltsverzeichnis 1 Formales 3 2 Überblick über den Versuch 4 3 Grundlagen 4 3.1
Spezielle Kinetik MC 1.3. Prof. Dr. B. Dietzek. Friedrich-Schiller-Universität Jena, Institut für Physikalische Chemie. Wintersemester 2016/2017
 Spezielle Kinetik MC 1.3 Prof. Dr. B. Dietzek Friedrich-Schiller-Universität Jena, Institut für Physikalische Chemie Wintersemester 2016/2017 B. Dietzek/D. Bender Spezielle Kinetik 1 Physikalische Chemie//Master
Spezielle Kinetik MC 1.3 Prof. Dr. B. Dietzek Friedrich-Schiller-Universität Jena, Institut für Physikalische Chemie Wintersemester 2016/2017 B. Dietzek/D. Bender Spezielle Kinetik 1 Physikalische Chemie//Master
2.3.2 Deterministisches Chaos. - Chaos-Kontexte
 2.3.2 Deterministisches Chaos - Chaos-Kontexte Das Wort Chaos hat in letzter Zeit einen breiten Raum in der öffentlichen Diskussion eingenommen und ist gegenwärtig so populär wie Anfang des Jahrhunderts
2.3.2 Deterministisches Chaos - Chaos-Kontexte Das Wort Chaos hat in letzter Zeit einen breiten Raum in der öffentlichen Diskussion eingenommen und ist gegenwärtig so populär wie Anfang des Jahrhunderts
Juliamengen und Mandelbrotmenge
 Xin Xu Florian Pausinger 18. Januar 2008 Inhaltsverzeichnis 1 Mathematische Grundlagen Komplexe Zahlen Über Iterationen und beschränkte Folgen 2 Quadratische Familie Bildbeispiele 3 Charakterisierung Über
Xin Xu Florian Pausinger 18. Januar 2008 Inhaltsverzeichnis 1 Mathematische Grundlagen Komplexe Zahlen Über Iterationen und beschränkte Folgen 2 Quadratische Familie Bildbeispiele 3 Charakterisierung Über
Elliptische Integrale und das allgemeine geometrische Mittel (agm):
 Elliptische Integrale und das allgemeine geometrische Mittel (agm): Typische Aufgaen der Analysis waren im 8. Jahrhundert nach der Erfindung der Differential- und Integralrechnung durch Leiniz und Newton,
Elliptische Integrale und das allgemeine geometrische Mittel (agm): Typische Aufgaen der Analysis waren im 8. Jahrhundert nach der Erfindung der Differential- und Integralrechnung durch Leiniz und Newton,
Kausalität aus der Sicht eines Physikers
 Siegfried Großmann Kausalität aus der Sicht eines Physikers Für einen Physiker ist das Thema gewissermaßen wissenschaftlicher Alltag. Wir versuchen permanent, aus unseren Beobachtungen zu lernen, wie man
Siegfried Großmann Kausalität aus der Sicht eines Physikers Für einen Physiker ist das Thema gewissermaßen wissenschaftlicher Alltag. Wir versuchen permanent, aus unseren Beobachtungen zu lernen, wie man
Computersimulationen in der Astronomie
 Computersimulationen in der Astronomie Fabian Heimann Universität Göttingen, Fabian.Heimann@stud.uni-goettingen.de Astronomisches Sommerlager 2013 Inhaltsverzeichnis 1 Differentialgleichungen 3 1.1 Beispiele.....................................
Computersimulationen in der Astronomie Fabian Heimann Universität Göttingen, Fabian.Heimann@stud.uni-goettingen.de Astronomisches Sommerlager 2013 Inhaltsverzeichnis 1 Differentialgleichungen 3 1.1 Beispiele.....................................
Kapitel 8: Gewöhnliche Differentialgleichungen 8.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2.
 Kapitel 8: Gewöhnliche Differentialgleichungen 8.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: (enthalten Ableitungen der gesuchten Funktionen) Geschwindigkeit:
Kapitel 8: Gewöhnliche Differentialgleichungen 8.1 Definition, Existenz, Eindeutigkeit von Lösungen Motivation: z.b. Newton 2. Gesetz: (enthalten Ableitungen der gesuchten Funktionen) Geschwindigkeit:
Willkommen. W. Hellenthal, Physik für Mediziner und Tel: 0641/
 Willkommen zur Vorlesung Physik von nach Prof. Dr. Michael Düren W. Hellenthal, Physik für Mediziner und Tel: 0641/9933221 Biologen, Wiss. Verlagsgesellsch. Stuttgart, 23,50 Michael.Dueren@uni-giessen.de
Willkommen zur Vorlesung Physik von nach Prof. Dr. Michael Düren W. Hellenthal, Physik für Mediziner und Tel: 0641/9933221 Biologen, Wiss. Verlagsgesellsch. Stuttgart, 23,50 Michael.Dueren@uni-giessen.de
x=r cos y=r sin } r2 =x 2 y 2
 6. Grenzzyklen Grenzzyklen eistieren in Systemen, die nach einer äußeren Störung wieder ein stabiles periodisches Verhalten annehmen. Sie sind eine weitere Ursache für periodisches Verhalten. 6.1. Modell
6. Grenzzyklen Grenzzyklen eistieren in Systemen, die nach einer äußeren Störung wieder ein stabiles periodisches Verhalten annehmen. Sie sind eine weitere Ursache für periodisches Verhalten. 6.1. Modell
Chaos- und Komplexitätstheorie
 Ich sage euch: Ihr habt Chaos in euch. Friedrich Nietzsche Evolution is chaos with feedback. Joseph Ford Order doesn't come by itself. Benoît Mandelbrot Chaos- und Komplexitätstheorie Dr. Bernhard v. Guretzky
Ich sage euch: Ihr habt Chaos in euch. Friedrich Nietzsche Evolution is chaos with feedback. Joseph Ford Order doesn't come by itself. Benoît Mandelbrot Chaos- und Komplexitätstheorie Dr. Bernhard v. Guretzky
(x x j ) R m [x] (3) x x j x k x j. R m [x]. (4)
![(x x j ) R m [x] (3) x x j x k x j. R m [x]. (4) (x x j ) R m [x] (3) x x j x k x j. R m [x]. (4)](/thumbs/67/57224748.jpg) 33 Interpolation 147 33 Interpolation In vielen praktischen Anwendungen der Mathematik treten Funktionen f auf, deren Werte nur näherungsweise berechnet werden können oder sogar nur auf gewissen endlichen
33 Interpolation 147 33 Interpolation In vielen praktischen Anwendungen der Mathematik treten Funktionen f auf, deren Werte nur näherungsweise berechnet werden können oder sogar nur auf gewissen endlichen
Analysis und Lineare Algebra mit MuPAD
 Analysis und Lineare Algebra mit MuPAD Dehling/Kubach Mögliche Themen für Abschlussprojekte 1 Fourier-Reihen Zu einer integrierbaren Funktion f : [0,2π] R definieren wir die Fourier-Reihe wobei a 0 = 1
Analysis und Lineare Algebra mit MuPAD Dehling/Kubach Mögliche Themen für Abschlussprojekte 1 Fourier-Reihen Zu einer integrierbaren Funktion f : [0,2π] R definieren wir die Fourier-Reihe wobei a 0 = 1
Euler-Verfahren. exakte Lösung. Euler-Streckenzüge. Folie 1
 exakte Lösung Euler-Verfahren Folie 1 Euler-Streckenzüge Ein paar grundlegende Anmerkungen zur Numerik Die Begriffe Numerik bzw. Numerische Mathematik bezeichnen ein Teilgebiet der Mathematik, welches
exakte Lösung Euler-Verfahren Folie 1 Euler-Streckenzüge Ein paar grundlegende Anmerkungen zur Numerik Die Begriffe Numerik bzw. Numerische Mathematik bezeichnen ein Teilgebiet der Mathematik, welches
Dr. Robert Strich Dr. Ysette Weiss Pidstrygach
 Kinder Uni 2008 Geheimnis Mathematik oder wo sich Mathematik verstecken kann Dr. Robert Strich Dr. Ysette Weiss Pidstrygach Mathebrille Wir begeben uns in eine ideale Welt. Unsere Expeditionsausrüstung
Kinder Uni 2008 Geheimnis Mathematik oder wo sich Mathematik verstecken kann Dr. Robert Strich Dr. Ysette Weiss Pidstrygach Mathebrille Wir begeben uns in eine ideale Welt. Unsere Expeditionsausrüstung
Newton-Verfahren und Komplexe Dynamik I
 Johannes Gutenberg-Universität Mainz Institut für Mathematik, FB08 Hauptseminar: Eine Einladung in die Mathematik Newton-Verfahren und Komplexe Dynamik I Paul Klimek betreut von Prof. Dr. Mária Lukácová-Medvidová
Johannes Gutenberg-Universität Mainz Institut für Mathematik, FB08 Hauptseminar: Eine Einladung in die Mathematik Newton-Verfahren und Komplexe Dynamik I Paul Klimek betreut von Prof. Dr. Mária Lukácová-Medvidová
Experimentelle Physik I
 Veranstaltung 4010011 https://campus.studium.kit.edu/event/h7ke2nevdu6ociwvcuiqyw 29. Vorlesung: 6.3 Schwingungen und Wellen (6): Licht und Materie, Nicht-lineare Systeme 9. Februar 2017 Experimentelle
Veranstaltung 4010011 https://campus.studium.kit.edu/event/h7ke2nevdu6ociwvcuiqyw 29. Vorlesung: 6.3 Schwingungen und Wellen (6): Licht und Materie, Nicht-lineare Systeme 9. Februar 2017 Experimentelle
2.7 Nichtlineare Dynamik Determinismus vs. Chaos. 2 Analytische Mechanik
 Die Generatoren M i, i = x,y,z, bilden eine (Lie)- Algebra mit folgenden Eigenschaften Mi,M j M i M j M j M i = εijm k k k Wir können auch zeigen (Übung) dass ebenfalls Li,L j = ε k ij Ł k gilt. Wir überprüfen
Die Generatoren M i, i = x,y,z, bilden eine (Lie)- Algebra mit folgenden Eigenschaften Mi,M j M i M j M j M i = εijm k k k Wir können auch zeigen (Übung) dass ebenfalls Li,L j = ε k ij Ł k gilt. Wir überprüfen
F(x,y,h) = f(x,y), = f(x,y) = f(x + h,y + hf(x,y)).
 170 005 Übungen zu Numerische Methoden I Neunte Übungseinheit 9., 10. und 11. Juni 2008 Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen KNW-Musterbeispiele 9 Gewöhnliche Differentialgleichungen
170 005 Übungen zu Numerische Methoden I Neunte Übungseinheit 9., 10. und 11. Juni 2008 Inhalt der neunten Übungseinheit: Gewöhnliche Differentialgleichungen KNW-Musterbeispiele 9 Gewöhnliche Differentialgleichungen
Das mathematische Pendel
 1 Das mathematische Pendel A. Krumbholz, S. Effendi 25. Juni 2013 2 Inhaltsverzeichnis Inhaltsverzeichnis Inhaltsverzeichnis 1 Einführung 3 1.1 Das mathematische Pendel........................... 3 1.2
1 Das mathematische Pendel A. Krumbholz, S. Effendi 25. Juni 2013 2 Inhaltsverzeichnis Inhaltsverzeichnis Inhaltsverzeichnis 1 Einführung 3 1.1 Das mathematische Pendel........................... 3 1.2
Chaostheorie - Niklas Luhmanns Systemtheorie und Soziale Arbeit
 Geisteswissenschaft Federica Tosi Chaostheorie - Niklas Luhmanns Systemtheorie und Soziale Arbeit Essay Inhaltsverzeichnis 1. Chaostheorie: Begriffklärung und Bedeutung für die Wissenschaft bis heute
Geisteswissenschaft Federica Tosi Chaostheorie - Niklas Luhmanns Systemtheorie und Soziale Arbeit Essay Inhaltsverzeichnis 1. Chaostheorie: Begriffklärung und Bedeutung für die Wissenschaft bis heute
Kunst und Wissenschaft
 Kunst und Wissenschaft HS 8 Visualisierung von Newton-Fraktalen Inhalt 1. Ist Schönheit Harmonie? Mathematik in Musik und Malerei 2. Warum heissen Fraktale Fraktale? oder: was ist hier zerbrochen? 3. Was
Kunst und Wissenschaft HS 8 Visualisierung von Newton-Fraktalen Inhalt 1. Ist Schönheit Harmonie? Mathematik in Musik und Malerei 2. Warum heissen Fraktale Fraktale? oder: was ist hier zerbrochen? 3. Was
Pendel. Versuch: P Vorbereitung - Inhaltsverzeichnis. Physikalisches Anfängerpraktikum 1 Wintersemester 2005/06 Julian Merkert ( )
 Physikalisches Anfängerpraktikum 1 Gruppe Mo-16 Wintersemester 005/06 Julian Merkert (1999) Versuch: P1-0 Pendel - Vorbereitung - Vorbemerkung Das einfachste Modell, um einen Pendelversuch zu beschreiben,
Physikalisches Anfängerpraktikum 1 Gruppe Mo-16 Wintersemester 005/06 Julian Merkert (1999) Versuch: P1-0 Pendel - Vorbereitung - Vorbemerkung Das einfachste Modell, um einen Pendelversuch zu beschreiben,
Würfelt Gott oder würfelt er nicht? p.1/35
 Würfelt Gott oder würfelt er nicht? Die Rolle des Zufalls im Weltbild der Physik Claus Grupen Universität Siegen Dortmund, den 21. Mai 2005 Würfelt Gott oder würfelt er nicht? p.1/35 Eine uralte Frage...
Würfelt Gott oder würfelt er nicht? Die Rolle des Zufalls im Weltbild der Physik Claus Grupen Universität Siegen Dortmund, den 21. Mai 2005 Würfelt Gott oder würfelt er nicht? p.1/35 Eine uralte Frage...
Ferienkurs Theoretische Mechanik 2010 Lagrange Formalismus
 Fakultät für Physik Michael Schrapp Technische Universität München Vorlesung Ferienkurs Theoretische Mechanik 2010 Lagrange Formalismus Inhaltsverzeichnis 1 Motivation 2 2 Generalisierte Koordinaten und
Fakultät für Physik Michael Schrapp Technische Universität München Vorlesung Ferienkurs Theoretische Mechanik 2010 Lagrange Formalismus Inhaltsverzeichnis 1 Motivation 2 2 Generalisierte Koordinaten und
