11.2 Orthogonalität. Wintersemester 2013/2014
|
|
|
- Cornelius Kolbe
- vor 7 Jahren
- Abrufe
Transkript
1 Universität Konstanz Fachbereich Mathematik und Statistik Wintersemester 2013/2014 Markus Scheighofer Lineare Algebra I 11.2 Orthogonalität Definition Seien V ein K-Vektorraum mit Skalarprodukt und v, V. Es heißen v und orthogonal oder senkrecht zueinander (in Zeichen: v ), enn v, = 0. Bemerkung Seien V ein R-Vektorraum mit Skalarprodukt und v, V. Dann v (v, ) = π 2 nach der Definition von Winkeln , denn cos π 2 = 0. Insbesondere stimmt unsere Definition von Senkrechtstehen in R 2 und R 3 nach mit unserer geometrischen Anschauung überein. Satz (Satz von Pythagoras). Sei V ein K-Vektorraum mit Skalarprodukt und seien v, V mit v. Dann v = v + 2 [ ]. Beeis. v+ 2 = v+, v+ = v, v + v, +, v +, = v =0 = v, =0 Bemerkung Die Kürze des Beeises des Satzes von Pythagoras in unserem Rahmen, zeigt in eindrucksvoller Weise, ie einfach man geometrische Sachverhalte mit Hilfe von Skalarprodukten erklären kann. Tatsächlich haben ir aber die Gültigkeit des Satzes von Pythagoras schon mehr oder eniger in den Begriff des Skalarprodukts hineinkodiert (und dies in gerechtfertigt). Man könnte daher sagen, dass der eigentliche Beeis des Satzes von Pythagoras in (a) steht. Es stellt aber (a) nur die Verbindung zur Anschauung her. Da ir innerhalb unseres Formalismus niemals anschaulich argumentieren, sondern die Anschauung nur als Inspiration zum Auffinden formaler Beeise benutzen, ird hier an keiner Stelle gemogelt. Definition [ 6.2.1] Sei V ein Vektorraum mit Skalarprodukt. Seien m N 0 und v 1,..., v m V. Dann heißt (v 1,..., v m ) ein Orthonormalsystem (ONS) (in V ), enn v i v j für alle i, j {1,..., m mit i j und v i = 1 für alle i {1,..., m. Ein ONS, elches V aufspannt, heißt Orthonormalbasis (ONB) von V. Beispiel Die Standardbasis des K n [ 6.2.2] ist eine ONB des K n (versehen mit dem Standardskalarprodukt [ (a)]). Proposition Sei V ein Vektorraum mit Skalarprodukt und (v 1,..., v m ) ein ONS in V. Seien λ 1,..., λ m K und v := m λ iv i. Dann λ i = v i, v für alle i {1,..., m. Beeis. v j, m λ iv i = m λ i v j, v i = λ j v j, v j = λ j für alle j {1,..., m = v j 2 =1 1
2 Korollar Sei V ein Vektorraum mit Skalarprodukt. In V ist jedes ONS linear unabhängig. Insbesondere ist jede ONB von V eine Basis von V. Definition und Proposition Sei V ein Vektorraum mit Skalarprodukt und U ein Unterraum von V. Das orthogonale Komplement von U in V ist definiert durch U := {v V u U : v u und ist selber ieder ein Unterraum von V mit U U = {0 und U (U ). Ist U = span(e) für ein E V, so gilt U = {v V u E : v u. Beeis. Sehr einfache Übung. Definition und Proposition Seien V ein Vektorraum mit Skalarprodukt, U ein Unterraum von V und v, V. Dann gibt es höchstens ein U mit v U. Falls existent, nennt man dieses die orthogonale Projektion von v auf U. Beeis. Seien, U mit v, v U. Dann, =, (v ) (v ) =, v, v = 0. U U U U Beispiel (a) Sei V ein Vektorraum mit Skalarprodukt und U ein Unterraum von V. Ist v U, so ist v selber die orthogonale Projektion von v auf U. Ist v U, so ist sie der Nullvektor. (b) Betrachte den R-Vektorraum R N der reellen Folgen [ 6.1.5, 7.1.5] und darin den Unterraum V := {f f : N R, c R : n N : f(n) c der beschränkten Folgen soie den Unterraum U der Folgen mit endlichem Träger [ 6.2.8(f)]. Dann ist V vermöge f, g := 1 f(i)g(i) (f, g V ) ein Vektorraum mit Skalarprodukt 2 i und U ein Unterraum von V. Das orthogonale Komplement U von U in V besteht offenbar nur aus der Nullfolge. Ist f V, so existiert die orthogonale Projektion von f auf U also genau dann, enn f U (und in diesem Fall ist sie f). Proposition Sei V ein Vektorraum mit Skalarprodukt, (v 1,..., v m ) ein ONS in V, U := span(v 1,..., v m ) und v V. Dann ist m v i, v v i die orthogonale Projektion von v auf U. Insbesondere existiert diese. Beeis. := m v i, v v i U. Um v U zu zeigen, reicht es v j, v = 0 für j {1,..., m zu zeigen. Sei also j {1,..., m. Dann v j, v = v j, v v i, v v i = v j, v v i, v v j, v i {0,1 = v j, v v j, v = 0. 2
3 Korollar Sei V ein Vektorraum mit Skalarprodukt und ONB v = (v 1,..., v n ). Dann gilt v 1, v coord v (v) =. für jedes v V. v n, Beeis. Die orthogonale Projektion eines v V auf V ist v selber [ (a)]. Also gilt nach v = n v i, v v i für alle v V. Proposition (Gram-Schmidtsches Orthogonalisierungsverfahren). Sei V ein Vektorraum mit Skalarprodukt, (v 1,..., v m ) ein ONS in V, U := span(v 1,..., v m ) und v U. Sei dann := m v i, v v i die orthogonale Projektion von v auf U [ ]. v Dann ist (v 1,..., v m, v ) ein ONS und es gilt ( ) v span(v 1,..., v m, v) = span v 1,..., v m,. v Beeis. Sehr einfache Übung. Satz [ ] Jeder endlichdimensionale Vektorraum mit Skalarprodukt besitzt eine ONB. Beeis. Induktion nach der Dimension, obei der Induktionsschritt mit Gram-Schmidt beerkstelligt ird. Korollar Sei V ein Vektorraum mit Skalarprodukt und U ein endlichdimensionaler Unterraum von V. Dann gibt es für jedes v V die orthogonale Projektion P U (v) von v auf U und dadurch ird eine lineare Abbildung P U : V V definiert, deren Kern U und deren Bild U ist. Beeis. Wähle mit eine ONB (v 1,..., v m ) von U. Nach haben ir dann P U (v) = m v i, v v i für alle v U. Mit der Linearität des Skalarprodukts im zeiten Argument (3),(4) rechnet man nun sofort die Linearität von P U nach. Weiter gilt ker P U = { v V v i, v v i = = {v V v 1, v =... = v m, v = = (span(v 1,..., v m )) = U, U im P U nach (a) und selbstverständlich im P U U nach Proposition Sei U ein endlichdimensionaler Unterraum des Vektorraums mit Skalarprodukt V. Dann gilt V = U U [ 8.2.1]. Für endlichdimensionales V gilt insbesondere dim(u) + dim(u ) = dim(v ) [ 8.2.3]. 3
4 Beeis. Für jedes v V gilt v = P U (v) + (v P U (v)), also V = U + U. Weiter ist die U U lineare Abbildung U U U + U, (u, v) u + v injektiv, denn ist (u, v) U U mit u + v = 0, so folgt u = v U U = {0. Korollar Sei U ein Unterraum des endlichdimensionalen K-Vektorraums mit Skalarprodukt V. Dann U = (U ). Beeis. Nach gilt U (U ) und mit angeandt auf U und auf U haben ir dim(u) = dim(v ) dim(u ) = dim((u ) ). Benutze nun Definition Seien V und W Vektorräume mit Skalarprodukt. Dann heißt eine Abbildung f : V W ein Homomorphismus von Vektorräumen mit Skalarprodukt (auch orthogonal oder unitär, ersteres voriegend im Fall K = R und letzteres voriegend im K = C), enn f linear ist und für alle v, V gilt f(v), f() = v,. Ist sie zusätzlich bijektiv, so heißt sie Isomorphismus von Vektorräumen mit Skalarprodukt [beachte, dass die Injektivität automatisch erfüllt ist, da aus f(v) = 0 folgt v, v = f(v), f(v) = 0 und daher v = 0]. Bemerkung Aus der Polarisationsformel folgt, dass man in dieser Definition die Bedingung v, V : f(v), f() = v, ersetzen kann durch v V : f(v) = v. Beispiel Wie in bereits bemerkt ist R ϕ End(R 2 ) für jedes ϕ R ein Automorphismus des R 2 mit Standardskalarprodukt. Satz Seien V und W K-Vektorräume mit Skalarprodukt und sei v = (v 1,..., v n ) eine ONB von V. Sei f : V W linear. Dann ist f genau dann ein Isomorphismus von Vektorräumen mit Skalarprodukt, enn (f(v 1 ),..., f(v n )) eine ONB von W ist. Beeis. Die eine Richtung ist klar. Für die andere sei (f(v 1 ),..., f(v n )) eine ONB von W. Nach ist f ein Isomorphismus von Vektorräumen. Seien nun v, V, eta v = n λ iv i und = n µ iv i mit λ i, µ i K. Zu zeigen ist f(v), f() = v,. Es gilt f(v), f() = λ i f(v i ), µ j f(v j ) = λ i µ j f(v i ), f(v j ) = λ i µ i = j=1 i,j=1 λ i µ j v i, v j = λ i v i, i,j=1 µ j v j = v,. j=1 Korollar Sei n N 0. Je zei n-dimensionale K-Vektorräume mit Skalarprodukt sind als solche isomorph. 4
5 Beeis. Seien V und W n-dimensionale K-Vektorräume mit Skalarprodukt. Wähle ONB (v 1,..., v n ) von V und ( 1,..., n ) von W. Dann ist die lineare Abbildung f : V W mit f(v i ) = i für i {1,..., n [ 6.3.4] ein Isomorphismus von Vektorräumen mit Skalarprodukt. Korollar Sei V ein Vektorraum mit Skalarprodukt und v = (v 1,..., v n ) eine Basis von V. Dann sind äquivalent: (a) v ist ONB von V, (b) vec v : K n V ist ein Isomorphismus von Vektorräumen mit Skalarprodukt. (c) coord v : V K n ist ein Isomorphismus von Vektorräumen mit Skalarprodukt. Definition Eine Matrix A K n n heißt orthogonal (vor allem enn K = C manchmal auch unitär), enn f A ein Isomorphismus des Vektorraums K n mit dem Standardskalarprodukt ist. Satz Seien V und W Vektorräume mit Skalarprodukt und ONB v = (v 1,..., v n ) und = ( 1,..., n ). Sei f : V W linear. Dann gilt: f ist Isomorphismus von Vektorräumen mit Skalarprodukt M(f, v, ) orthogonal. Beeis. Nach gilt f = vec f M(f,v,) coord v und daher f M(f,v,) = coord f vec v. Da vec, coord v, coord und vec v nach Isomorphismen von Vektorräumen mit Skalarprodukt sind, ist f ein solcher genau dann, enn f M(f,v,) einer ist. Satz Sei A K n n. Dann sind äquivalent: (a) A ist orthogonal. (b) Die Spalten von A bilden eine ONB des K n. (c) Die Zeilen von A bilden eine ONB des K n. (d) A A = I n (e) AA = I n (f) A ist invertierbar mit A 1 = A. Beeis. Aus , und folgt (a) (b), da f A (e 1 ),..., f A (e n ) die Spalten von A sind. Direkt aus der Definition der Matrizenmultiplikation folgen (b) (d) und (c) (e). Schließlich gilt (d) (e) (f) egen ( ) cos ϕ sin ϕ Beispiel [ 7.1.4(a)] ist für jedes ϕ R orthogonal. sin ϕ cos ϕ 5
3 Vektorräume abstrakt
 Mathematik I für inf/swt Wintersemester / Seite 7 Vektorräume abstrakt Lineare Unabhängigkeit Definition: Sei V Vektorraum W V Dann heißt W := LH(W := Menge aller Linearkombinationen aus W die lineare
Mathematik I für inf/swt Wintersemester / Seite 7 Vektorräume abstrakt Lineare Unabhängigkeit Definition: Sei V Vektorraum W V Dann heißt W := LH(W := Menge aller Linearkombinationen aus W die lineare
Lineare Algebra I (WS 13/14)
 Lineare Algebra I (WS 13/14) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 15.11.2013 Alexander Lytchak 1 / 12 Erinnerung Eine Abbildung f : V W zwischen reellen Vektorräumen ist linear, wenn
Lineare Algebra I (WS 13/14) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 15.11.2013 Alexander Lytchak 1 / 12 Erinnerung Eine Abbildung f : V W zwischen reellen Vektorräumen ist linear, wenn
Lineare Algebra II 8. Übungsblatt
 Lineare Algebra II 8. Übungsblatt Fachbereich Mathematik SS 11 Prof. Dr. Kollross 1./9. Juni 11 Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G1 (Minitest) Sei V ein euklidischer oder unitärer Vektorraum.
Lineare Algebra II 8. Übungsblatt Fachbereich Mathematik SS 11 Prof. Dr. Kollross 1./9. Juni 11 Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G1 (Minitest) Sei V ein euklidischer oder unitärer Vektorraum.
Lineare Algebra und analytische Geometrie II
 Prof Dr H Brenner Osnabrück SS 26 Lineare Algebra und analytische Geometrie II Vorlesung 2 Orthogonalität Mit dem Skalarprodukt kann man die Eigenschaft zweier Vektoren, aufeinander senkrecht zu stehen,
Prof Dr H Brenner Osnabrück SS 26 Lineare Algebra und analytische Geometrie II Vorlesung 2 Orthogonalität Mit dem Skalarprodukt kann man die Eigenschaft zweier Vektoren, aufeinander senkrecht zu stehen,
Orthonormalisierung. ein euklidischer bzw. unitärer Vektorraum. Wir setzen
 Orthonormalisierung Wie schon im Falle V = R n erwähnt, erhalten wir durch ein Skalarprodukt eine zugehörige Norm (Länge) eines Vektors und in weiterer Folge eine Metrik (Abstand zwischen zwei Vektoren).
Orthonormalisierung Wie schon im Falle V = R n erwähnt, erhalten wir durch ein Skalarprodukt eine zugehörige Norm (Länge) eines Vektors und in weiterer Folge eine Metrik (Abstand zwischen zwei Vektoren).
6.2 Basen. Wintersemester 2013/2014. Definition Seien V ein K-Vektorraum, n N 0 und v 1,..., v n V. (a) Man nennt
 Universität Konstanz Fachbereich Mathematik und Statistik Wintersemester 213/214 Markus Schweighofer Lineare Algebra I 6.2 Basen Definition 6.2.1. Seien V ein K-Vektorraum, n N und v 1,..., v n V. (a)
Universität Konstanz Fachbereich Mathematik und Statistik Wintersemester 213/214 Markus Schweighofer Lineare Algebra I 6.2 Basen Definition 6.2.1. Seien V ein K-Vektorraum, n N und v 1,..., v n V. (a)
1 Euklidische und unitäre Vektorräume
 1 Euklidische und unitäre Vektorräume In diesem Abschnitt betrachten wir reelle und komplexe Vektorräume mit Skalarprodukt. Dieses erlaubt uns die Länge eines Vektors zu definieren und (im Fall eines reellen
1 Euklidische und unitäre Vektorräume In diesem Abschnitt betrachten wir reelle und komplexe Vektorräume mit Skalarprodukt. Dieses erlaubt uns die Länge eines Vektors zu definieren und (im Fall eines reellen
Unter einem reellen inneren Produktraum verstehen wir einen Vektorraum V über
 9 Innere Produkte In diesem Kapitel betrachten wir immer Vektorräume über dem Körper der reellen Zahlen R oder dem Körper der komplexen Zahlen C. Definition 9.1: Sei V ein Vektorraum über R. Ein inneres
9 Innere Produkte In diesem Kapitel betrachten wir immer Vektorräume über dem Körper der reellen Zahlen R oder dem Körper der komplexen Zahlen C. Definition 9.1: Sei V ein Vektorraum über R. Ein inneres
6. Normale Abbildungen
 SKALARPRODUKE 1 6 Normale Abbildungen 61 Erinnerung Sei V ein n-dimensionaler prä-hilbertraum, also ein n-dimensionaler Vektorraum über K (R oder C) versehen auch mit einer Skalarprodukt, ra K Die euklidische
SKALARPRODUKE 1 6 Normale Abbildungen 61 Erinnerung Sei V ein n-dimensionaler prä-hilbertraum, also ein n-dimensionaler Vektorraum über K (R oder C) versehen auch mit einer Skalarprodukt, ra K Die euklidische
42 Orthogonalität Motivation Definition: Orthogonalität Beispiel
 4 Orthogonalität 4. Motivation Im euklidischen Raum ist das euklidische Produkt zweier Vektoren u, v IR n gleich, wenn die Vektoren orthogonal zueinander sind. Für beliebige Vektoren lässt sich sogar der
4 Orthogonalität 4. Motivation Im euklidischen Raum ist das euklidische Produkt zweier Vektoren u, v IR n gleich, wenn die Vektoren orthogonal zueinander sind. Für beliebige Vektoren lässt sich sogar der
Mathematik I. Vorlesung 12. Lineare Abbildungen
 Prof. Dr. H. Brenner Osnabrück WS 2009/2010 Mathematik I Vorlesung 12 Lineare Abbildungen Definition 12.1. Es sei K ein Körper und es seien V und W K-Vektorräume. Eine Abbildung heißt lineare Abbildung,
Prof. Dr. H. Brenner Osnabrück WS 2009/2010 Mathematik I Vorlesung 12 Lineare Abbildungen Definition 12.1. Es sei K ein Körper und es seien V und W K-Vektorräume. Eine Abbildung heißt lineare Abbildung,
= ( n x j x j ) 1 / 2
 15 Skalarprodukte 77 15 Skalarprodukte 15.1 Einführung. a) Ab jetzt sei stets K = R oder K = C, da Wurzeln eine wichtige Rolle spielen werden. b) Nach dem Satz des Pythagoras ist die Länge eines Vektors
15 Skalarprodukte 77 15 Skalarprodukte 15.1 Einführung. a) Ab jetzt sei stets K = R oder K = C, da Wurzeln eine wichtige Rolle spielen werden. b) Nach dem Satz des Pythagoras ist die Länge eines Vektors
Satz 2.8 V sei ein endlichdimensionaler euklidischer Vektorraum. Für jeden Unterraum
 Orthogonalität 123 Dienstag, 27. April 04 Satz 2.8 V sei ein endlichdimensionaler euklidischer Vektorraum. Für jeden Unterraum U von V gilt dann (a) U + U = V, U U = {0}, U, U = 0. (b) (U ) = U. Wir sagen
Orthogonalität 123 Dienstag, 27. April 04 Satz 2.8 V sei ein endlichdimensionaler euklidischer Vektorraum. Für jeden Unterraum U von V gilt dann (a) U + U = V, U U = {0}, U, U = 0. (b) (U ) = U. Wir sagen
7.2 Die adjungierte Abbildung
 7.2 Die adjungierte Abbildung Definition 7.2.1 Eine lineare Abbildung f : V K heißt lineares Funktional oder Linearform. (Diese Definition gilt für beliebige K-Vektorräume, nicht nur für innere Produkträume.)
7.2 Die adjungierte Abbildung Definition 7.2.1 Eine lineare Abbildung f : V K heißt lineares Funktional oder Linearform. (Diese Definition gilt für beliebige K-Vektorräume, nicht nur für innere Produkträume.)
Klausur zur Vorlesung Lineare Algebra II, SoSe 2016,
 Klausur zur Vorlesung Lineare Algebra II, SoSe 6, 6.7.6 Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen und Sätze aus der Vorlesung korrekt zu formulieren
Klausur zur Vorlesung Lineare Algebra II, SoSe 6, 6.7.6 Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen und Sätze aus der Vorlesung korrekt zu formulieren
4 Lineare Abbildungen und Matrizen
 4.1 Lineare Abbildungen Definition 4.1. Es seien V, W K-Vektorräume. Eine Abbildung f : V W heißt linear oder Homomorphismus, wenn für alle u, v V und λ K gilt Beispiel 4.2. L1 f(u + v) = f(u) + f(v),
4.1 Lineare Abbildungen Definition 4.1. Es seien V, W K-Vektorräume. Eine Abbildung f : V W heißt linear oder Homomorphismus, wenn für alle u, v V und λ K gilt Beispiel 4.2. L1 f(u + v) = f(u) + f(v),
Technische Universität München
 Technische Universität München Michael Schreier Ferienkurs Lineare Algebra für Physiker Vorlesung Montag WS 2008/09 1 komplexe Zahlen Viele Probleme in der Mathematik oder Physik lassen sich nicht oder
Technische Universität München Michael Schreier Ferienkurs Lineare Algebra für Physiker Vorlesung Montag WS 2008/09 1 komplexe Zahlen Viele Probleme in der Mathematik oder Physik lassen sich nicht oder
43 Unitäre Vektorräume
 43 Unitäre Vektorräume 43 1 Zusammenfassung In diesem Paragrafen werden die gleichen Themen wie in 41 abgehandelt, jetzt allerdings für den komplexen Fall. Die Aussagen entsprechen sich weitgehend, daher
43 Unitäre Vektorräume 43 1 Zusammenfassung In diesem Paragrafen werden die gleichen Themen wie in 41 abgehandelt, jetzt allerdings für den komplexen Fall. Die Aussagen entsprechen sich weitgehend, daher
Analytische Geometrie
 21 Vorlesungen über Analytische Geometrie für Lehramtstudierende der Schulformen Grund-, Mittel- und Realschule Jens Jordan Universität Würzburg, Wintersemster 2015/16 Hier kommt noch ein schönes Bildchen
21 Vorlesungen über Analytische Geometrie für Lehramtstudierende der Schulformen Grund-, Mittel- und Realschule Jens Jordan Universität Würzburg, Wintersemster 2015/16 Hier kommt noch ein schönes Bildchen
Lösung zu Serie 18. Lineare Algebra D-MATH, HS Prof. Richard Pink
 Lineare Algebra D-MATH, HS 201 Prof. Richard Pink Lösung zu Serie 18 1. Sei V,, ein endlich-dimensionaler unitärer Vektorraum. Zeige, dass zu jeder Sesquilinearform f : V V C eine eindeutige lineare Abbildung
Lineare Algebra D-MATH, HS 201 Prof. Richard Pink Lösung zu Serie 18 1. Sei V,, ein endlich-dimensionaler unitärer Vektorraum. Zeige, dass zu jeder Sesquilinearform f : V V C eine eindeutige lineare Abbildung
Bild, Faser, Kern. Stefan Ruzika. 23. Mai Mathematisches Institut Universität Koblenz-Landau Campus Koblenz
 Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz 23. Mai 2016 Stefan Ruzika 7: Bild, Faser, Kern 23. Mai 2016 1 / 11 Gliederung 1 Schulstoff 2 Körper 3 Vektorräume 4 Basis
Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz 23. Mai 2016 Stefan Ruzika 7: Bild, Faser, Kern 23. Mai 2016 1 / 11 Gliederung 1 Schulstoff 2 Körper 3 Vektorräume 4 Basis
Lösungsskizzen der Klausur zur Linearen Algebra im Herbst 2015
 sskizzen der Klausur zur Linearen Algebra im Herbst 5 Aufgabe I. Es sei (G, ) eine Gruppe mit neutralem Element e und M {x G x x e}. Zeigen Sie: (a) Ist G kommutativ, so ist M eine Untergruppe von G. (b)
sskizzen der Klausur zur Linearen Algebra im Herbst 5 Aufgabe I. Es sei (G, ) eine Gruppe mit neutralem Element e und M {x G x x e}. Zeigen Sie: (a) Ist G kommutativ, so ist M eine Untergruppe von G. (b)
Lineare Algebra I Vorlesung - Prof. Dr. Daniel Roggenkamp & Falko Gauß
 Lineare Algebra I - 26. Vorlesung - Prof. Dr. Daniel Roggenkamp & Falko Gauß Donnerstag 8.12.: 8:30 Uhr - Vorlesung 10:15 Uhr - große Übung / Fragestunde Klausur: Mittwoch, 14.12. 14:15 Uhr, A3 001 Cauchy-Schwarz
Lineare Algebra I - 26. Vorlesung - Prof. Dr. Daniel Roggenkamp & Falko Gauß Donnerstag 8.12.: 8:30 Uhr - Vorlesung 10:15 Uhr - große Übung / Fragestunde Klausur: Mittwoch, 14.12. 14:15 Uhr, A3 001 Cauchy-Schwarz
4 Lineare Abbildungen und Matrizen
 Mathematik I für inf/swt, Wintersemester /, Seite 8 4 Lineare Abbildungen und Matrizen 4 Kern und Injektivität 4 Definition: Sei : V W linear Kern : {v V : v } ist linearer eilraum von V Ü68 und heißt
Mathematik I für inf/swt, Wintersemester /, Seite 8 4 Lineare Abbildungen und Matrizen 4 Kern und Injektivität 4 Definition: Sei : V W linear Kern : {v V : v } ist linearer eilraum von V Ü68 und heißt
Lineare Abbildungen und Darstellungsmatrizen
 KAPITEL 4 Lineare Abbildungen und Darstellungsmatrizen 1. Lineare Abbildungen Definition 4.1 (Lineare Abbildungen). Seien V und W zwei Vektorräume über den selben Körper K. Eine Abbildung f : V W heißt
KAPITEL 4 Lineare Abbildungen und Darstellungsmatrizen 1. Lineare Abbildungen Definition 4.1 (Lineare Abbildungen). Seien V und W zwei Vektorräume über den selben Körper K. Eine Abbildung f : V W heißt
(1) In dieser Aufgabe kreuzen Sie bitte nur die Antworten an, die Sie für richtig halten. Eine Begründung wird nicht verlangt.
 () In dieser Aufgabe kreuzen Sie bitte nur die Antworten an, die Sie für richtig halten. Eine Begründung wird nicht verlangt. a) Es seien A und B beliebige n n-matrizen mit Einträgen in einem Körper K.
() In dieser Aufgabe kreuzen Sie bitte nur die Antworten an, die Sie für richtig halten. Eine Begründung wird nicht verlangt. a) Es seien A und B beliebige n n-matrizen mit Einträgen in einem Körper K.
, v 3 = und v 4 =, v 2 = V 1 = { c v 1 c R }.
 154 e Gegeben sind die Vektoren v 1 = ( 10 1, v = ( 10 1. Sei V 1 = v 1 der von v 1 aufgespannte Vektorraum in R 3. 1 Dann besteht V 1 aus allen Vielfachen von v 1, V 1 = { c v 1 c R }. ( 0 ( 01, v 3 =
154 e Gegeben sind die Vektoren v 1 = ( 10 1, v = ( 10 1. Sei V 1 = v 1 der von v 1 aufgespannte Vektorraum in R 3. 1 Dann besteht V 1 aus allen Vielfachen von v 1, V 1 = { c v 1 c R }. ( 0 ( 01, v 3 =
Lineare Algebra und analytische Geometrie II
 Prof. Dr. H. Brenner Osnabrück SS 206 Lineare Algebra und analytische Geometrie II Vorlesung 33 Das Kreuzprodukt Eine Besonderheit im R 3 ist das sogenannte Kreuzprodukt, das zu zwei gegebenen Vektoren
Prof. Dr. H. Brenner Osnabrück SS 206 Lineare Algebra und analytische Geometrie II Vorlesung 33 Das Kreuzprodukt Eine Besonderheit im R 3 ist das sogenannte Kreuzprodukt, das zu zwei gegebenen Vektoren
Mathematik für Anwender II
 Prof Dr H Brenner Osnabrück SS 22 Mathematik für Anwender II Vorlesung Euklidische Vektorräume Im Anschauungsraum kann man nicht nur Vektoren addieren und skalieren, sondern ein Vektor hat auch eine Länge,
Prof Dr H Brenner Osnabrück SS 22 Mathematik für Anwender II Vorlesung Euklidische Vektorräume Im Anschauungsraum kann man nicht nur Vektoren addieren und skalieren, sondern ein Vektor hat auch eine Länge,
Ferienkurs - Lineare Algebra. Hanna Schäfer. Merkinhalte
 Technische Universität München, Fakultät für Physik Ferienkurs - ineare Algebra Hanna Schäfer 03. März 04 0. inearität. f : M N, x : y = f(x) Merkinhalte. f(x + λy) = f(x) + λf(y), x, y V, λ K 3. ineare
Technische Universität München, Fakultät für Physik Ferienkurs - ineare Algebra Hanna Schäfer 03. März 04 0. inearität. f : M N, x : y = f(x) Merkinhalte. f(x + λy) = f(x) + λf(y), x, y V, λ K 3. ineare
Kapitel 5. Vektorräume mit Skalarprodukt
 Kapitel 5 Vektorräume mit Skalarprodukt 119 120 Kapitel V: Vektorräume mit Skalarprodukt 5.1 Elementare Eigenschaften des Skalarprodukts Dienstag, 20. April 04 Wollen wir in einem Vektorraum wie in der
Kapitel 5 Vektorräume mit Skalarprodukt 119 120 Kapitel V: Vektorräume mit Skalarprodukt 5.1 Elementare Eigenschaften des Skalarprodukts Dienstag, 20. April 04 Wollen wir in einem Vektorraum wie in der
3.3 Skalarprodukte 3.3. SKALARPRODUKTE 153
 3.3. SKALARPRODUKTE 153 Hierzu müssen wir noch die Eindeutigkeit (Unabhängigkeit von der Wahl der Basis bzw. des Koordinatensystems) zeigen. Sei hierzu β eine Bilinearform und q die entsprechende quadratische
3.3. SKALARPRODUKTE 153 Hierzu müssen wir noch die Eindeutigkeit (Unabhängigkeit von der Wahl der Basis bzw. des Koordinatensystems) zeigen. Sei hierzu β eine Bilinearform und q die entsprechende quadratische
2 Euklidische Vektorräume
 Sei V ein R Vektorraum. 2 Euklidische Vektorräume Definition: Ein Skalarprodukt auf V ist eine Abbildung σ : V V R, (v, w) σ(v, w) mit folgenden Eigenschaften ( Axiome des Skalarprodukts) (SP1) σ ist bilinear,
Sei V ein R Vektorraum. 2 Euklidische Vektorräume Definition: Ein Skalarprodukt auf V ist eine Abbildung σ : V V R, (v, w) σ(v, w) mit folgenden Eigenschaften ( Axiome des Skalarprodukts) (SP1) σ ist bilinear,
Lineare Abbildungen und Matrizen
 Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz 31. Mai 2016 Stefan Ruzika 9: Lineare Abbildungen und Matrizen 31. Mai 2016 1 / 16 Gliederung 1 Schulstoff 2 Körper 3 Vektorräume
Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz 31. Mai 2016 Stefan Ruzika 9: Lineare Abbildungen und Matrizen 31. Mai 2016 1 / 16 Gliederung 1 Schulstoff 2 Körper 3 Vektorräume
2. Dezember Lineare Algebra II. Christian Ebert & Fritz Hamm. Skalarprodukt, Norm, Metrik. Matrizen. Lineare Abbildungen
 Algebra und Algebra 2. Dezember 2011 Übersicht Algebra und Algebra I Gruppen & Körper Vektorräume, Basis & Dimension Algebra Norm & Metrik Abbildung & Algebra I Eigenwerte, Eigenwertzerlegung Singulärwertzerlegung
Algebra und Algebra 2. Dezember 2011 Übersicht Algebra und Algebra I Gruppen & Körper Vektorräume, Basis & Dimension Algebra Norm & Metrik Abbildung & Algebra I Eigenwerte, Eigenwertzerlegung Singulärwertzerlegung
2.4 Lineare Abbildungen und Matrizen
 24 Lineare Abbildungen und Matrizen Definition 24 Seien V, W zwei K-Vektorräume Eine Abbildung f : V W heißt lineare Abbildung (lineare Transformation, linearer Homomorphismus, Vektorraumhomomorphismus
24 Lineare Abbildungen und Matrizen Definition 24 Seien V, W zwei K-Vektorräume Eine Abbildung f : V W heißt lineare Abbildung (lineare Transformation, linearer Homomorphismus, Vektorraumhomomorphismus
Kapitel 3 Lineare Algebra
 Kapitel 3 Lineare Algebra Inhaltsverzeichnis VEKTOREN... 3 VEKTORRÄUME... 3 LINEARE UNABHÄNGIGKEIT UND BASEN... 4 MATRIZEN... 6 RECHNEN MIT MATRIZEN... 6 INVERTIERBARE MATRIZEN... 6 RANG EINER MATRIX UND
Kapitel 3 Lineare Algebra Inhaltsverzeichnis VEKTOREN... 3 VEKTORRÄUME... 3 LINEARE UNABHÄNGIGKEIT UND BASEN... 4 MATRIZEN... 6 RECHNEN MIT MATRIZEN... 6 INVERTIERBARE MATRIZEN... 6 RANG EINER MATRIX UND
5 Lineare Abbildungen
 5 Lineare Abbildungen Pink: Lineare Algebra 2014/15 Seite 59 5 Lineare Abbildungen 5.1 Definition Gegeben seien Vektorräume U, V, W über einem Körper K. Definition: Eine Abbildung f : V W heisst K-linear,
5 Lineare Abbildungen Pink: Lineare Algebra 2014/15 Seite 59 5 Lineare Abbildungen 5.1 Definition Gegeben seien Vektorräume U, V, W über einem Körper K. Definition: Eine Abbildung f : V W heisst K-linear,
3.5 Duale Vektorräume und Abbildungen
 3.5. DUALE VEKTORRÄUME UND ABBILDUNGEN 103 3.5 Duale Vektorräume und Abbildungen Wir wollen im Folgenden auch geometrische Zusammenhänge mathematisch beschreiben und beginnen deshalb jetzt mit der Einführung
3.5. DUALE VEKTORRÄUME UND ABBILDUNGEN 103 3.5 Duale Vektorräume und Abbildungen Wir wollen im Folgenden auch geometrische Zusammenhänge mathematisch beschreiben und beginnen deshalb jetzt mit der Einführung
Mathematik für Anwender I
 Prof. Dr. H. Brenner Osnabrück WS 2011/2012 Mathematik für Anwender I Vorlesung 9 Lineare Abbildungen Definition 9.1. Es sei K ein Körper und es seien V und W Vektorräume über K. Eine Abbildung ϕ : V W
Prof. Dr. H. Brenner Osnabrück WS 2011/2012 Mathematik für Anwender I Vorlesung 9 Lineare Abbildungen Definition 9.1. Es sei K ein Körper und es seien V und W Vektorräume über K. Eine Abbildung ϕ : V W
1 Linearkombinationen
 Matthias Tischler Karolina Stoiber Ferienkurs Lineare Algebra für Physiker WS 14/15 A 1 Linearkombinationen Unter einer Linearkombination versteht man in der linearen Algebra einen Vektor, der sich durch
Matthias Tischler Karolina Stoiber Ferienkurs Lineare Algebra für Physiker WS 14/15 A 1 Linearkombinationen Unter einer Linearkombination versteht man in der linearen Algebra einen Vektor, der sich durch
4 Lineare Abbildungen Basisdarstellungen
 4 Lineare Abbildungen Basisdarstellungen (4.1) Seien V,W endlich dimensionale K-Vektorräume, und sei T : V W linear. Sei {v 1,...,v } Basis von V und {w 1,...,w M } Basis von W. Sei T (v j ) = M a kj w
4 Lineare Abbildungen Basisdarstellungen (4.1) Seien V,W endlich dimensionale K-Vektorräume, und sei T : V W linear. Sei {v 1,...,v } Basis von V und {w 1,...,w M } Basis von W. Sei T (v j ) = M a kj w
Ferienkurs Mathematik für Physiker I Skript Teil 2 ( )
 Ferienkurs Mathematik für Physiker I WS 206/7 Ferienkurs Mathematik für Physiker I Skript Teil 2 (28.03.207) Vektorräume Bevor wir zur Definition eines Vektorraumes kommen erinnern wir noch einmal kurz
Ferienkurs Mathematik für Physiker I WS 206/7 Ferienkurs Mathematik für Physiker I Skript Teil 2 (28.03.207) Vektorräume Bevor wir zur Definition eines Vektorraumes kommen erinnern wir noch einmal kurz
Lineare Algebra II 11. Übungsblatt
 Lineare Algebra II Übungsblatt Fachbereich Mathematik SS Prof Dr Kollross 9 / Juni Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G (Minitest (Bearbeitung innerhalb von Minuten und ohne Benutzung des
Lineare Algebra II Übungsblatt Fachbereich Mathematik SS Prof Dr Kollross 9 / Juni Susanne Kürsten Tristan Alex Gruppenübung Aufgabe G (Minitest (Bearbeitung innerhalb von Minuten und ohne Benutzung des
Lineare Algebra I (WS 13/14)
 Lineare Algebra I (WS 13/14) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 29.11.2013 Alexander Lytchak 1 / 13 Wiederholung Der Rang einer linearen Abbildung ist gleich dem Spaltenrang der darstellenden
Lineare Algebra I (WS 13/14) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 29.11.2013 Alexander Lytchak 1 / 13 Wiederholung Der Rang einer linearen Abbildung ist gleich dem Spaltenrang der darstellenden
4.3 Bilinearformen. 312 LinAlg II Version Juni 2006 c Rudolf Scharlau
 312 LinAlg II Version 0 20. Juni 2006 c Rudolf Scharlau 4.3 Bilinearformen Bilinearformen wurden bereits im Abschnitt 2.8 eingeführt; siehe die Definition 2.8.1. Die dort behandelten Skalarprodukte sind
312 LinAlg II Version 0 20. Juni 2006 c Rudolf Scharlau 4.3 Bilinearformen Bilinearformen wurden bereits im Abschnitt 2.8 eingeführt; siehe die Definition 2.8.1. Die dort behandelten Skalarprodukte sind
Euklidische und unitäre Vektorräume
 Kapitel 7 Euklidische und unitäre Vektorräume In diesem Abschnitt ist der Körper K stets R oder C. 7.1 Definitionen, Orthonormalbasen Definition 7.1.1 Sei K = R oder C, und sei V ein K-Vektorraum. Ein
Kapitel 7 Euklidische und unitäre Vektorräume In diesem Abschnitt ist der Körper K stets R oder C. 7.1 Definitionen, Orthonormalbasen Definition 7.1.1 Sei K = R oder C, und sei V ein K-Vektorraum. Ein
5 Analytische Geometrie
 5 Analytische Geometrie Die Grundidee der analytischen Geometrie ist es, geometrische Objekte in Räumen mittels linearer Algebra zu beschreiben 51 Affine Räume Definition 511 Ein affiner Raum (AR) über
5 Analytische Geometrie Die Grundidee der analytischen Geometrie ist es, geometrische Objekte in Räumen mittels linearer Algebra zu beschreiben 51 Affine Räume Definition 511 Ein affiner Raum (AR) über
D-Math/Phys Lineare Algebra II FS 2017 Dr. Meike Akveld. Clicker Fragen
 D-Math/Phys Lineare Algebra II FS 2017 Dr. Meike Akveld Clicker Fragen Frage 1 Wenn eine reelle Matrix einen Eigenvektor hat, so hat es unendlich viele Eigenvektoren Sei u K n einen Eigenvektor von A M
D-Math/Phys Lineare Algebra II FS 2017 Dr. Meike Akveld Clicker Fragen Frage 1 Wenn eine reelle Matrix einen Eigenvektor hat, so hat es unendlich viele Eigenvektoren Sei u K n einen Eigenvektor von A M
3 Definition: 1. Übungsblatt zur Vorlesung Lineare Algebra I. im WS 2003/2004 bei Prof. Dr. S. Goette
 1. Übungsblatt zur Vorlesung Abgabe Donnerstag, den 30.10.03 1 Finden 2 Sei Sie reelle Zahlen a, b, c, so dass a (2, 3, 1) + b (1, 2, 2) + c (2, 5, 3) = (3, 7, 5). (V,, ) ein euklidischer Vektorraum. Zeigen
1. Übungsblatt zur Vorlesung Abgabe Donnerstag, den 30.10.03 1 Finden 2 Sei Sie reelle Zahlen a, b, c, so dass a (2, 3, 1) + b (1, 2, 2) + c (2, 5, 3) = (3, 7, 5). (V,, ) ein euklidischer Vektorraum. Zeigen
Proseminar Lineare Algebra II, SS 11. Blatt
 Blatt 1 1. Berechnen Sie die Determinante der Matrix 0 0 4 1 2 5 1 7 1 2 0 3 1 3 0 α. 2. Stellen Sie folgende Matrix als Produkt von Elementarmatrizen dar: 1 3 1 4 2 5 1 3 0 4 3 1. 3 1 5 2 3. Seien n 2
Blatt 1 1. Berechnen Sie die Determinante der Matrix 0 0 4 1 2 5 1 7 1 2 0 3 1 3 0 α. 2. Stellen Sie folgende Matrix als Produkt von Elementarmatrizen dar: 1 3 1 4 2 5 1 3 0 4 3 1. 3 1 5 2 3. Seien n 2
4.4 Hermitesche Formen
 44 Hermitesche Formen Wie üblich bezeichnen wir das komplex konjugierte Element von ζ = a + bi C (a, b R) mit ζ = a bi Definition 441 Sei V ein C-Vektorraum Eine hermitesche Form (HF) auf V ist eine Abbildung
44 Hermitesche Formen Wie üblich bezeichnen wir das komplex konjugierte Element von ζ = a + bi C (a, b R) mit ζ = a bi Definition 441 Sei V ein C-Vektorraum Eine hermitesche Form (HF) auf V ist eine Abbildung
10 Unitäre Vektorräume
 10 Unitäre Vektorräume Pink: Lineare Algebra 2014/15 Seite 98 10 Unitäre Vektorräume Die Theorie komplexer Vektorräume mit Skalarprodukt folgt denselben Linien wie die Theorie reeller Vektorräume mit Skalarprodukt;
10 Unitäre Vektorräume Pink: Lineare Algebra 2014/15 Seite 98 10 Unitäre Vektorräume Die Theorie komplexer Vektorräume mit Skalarprodukt folgt denselben Linien wie die Theorie reeller Vektorräume mit Skalarprodukt;
5 Lineare Algebra (Teil 3): Skalarprodukt
 5 Lineare Algebra (Teil 3): Skalarprodukt Der Begriff der linearen Abhängigkeit ermöglicht die Definition, wann zwei Vektoren parallel sind und wann drei Vektoren in einer Ebene liegen. Daß aber reale
5 Lineare Algebra (Teil 3): Skalarprodukt Der Begriff der linearen Abhängigkeit ermöglicht die Definition, wann zwei Vektoren parallel sind und wann drei Vektoren in einer Ebene liegen. Daß aber reale
Wiederholung: lineare Abbildungen
 Wiederholung: lineare Abbildungen Def Es seien (V,+, ) und (U, +, ) zwei Vektorräume Eine Abbildung f : V U heißt linear, falls für alle Vektoren v 1, v 2 V und für jedes λ R gilt: (a) f (v 1 + v 2 ) =
Wiederholung: lineare Abbildungen Def Es seien (V,+, ) und (U, +, ) zwei Vektorräume Eine Abbildung f : V U heißt linear, falls für alle Vektoren v 1, v 2 V und für jedes λ R gilt: (a) f (v 1 + v 2 ) =
Musterlösungen zur Linearen Algebra II Weihnachtszettel
 Musterlösungen zur Linearen Algebra II Weihnachtszettel Aufgabe. Welche der folgenden Matrizen 3 0 0 A = 0 4, B = 3, C = 0 0 0 6 0 0 0 sind über R und welche über C diagonalisierbar? Bestimmen Sie dazu
Musterlösungen zur Linearen Algebra II Weihnachtszettel Aufgabe. Welche der folgenden Matrizen 3 0 0 A = 0 4, B = 3, C = 0 0 0 6 0 0 0 sind über R und welche über C diagonalisierbar? Bestimmen Sie dazu
Prüfung Lineare Algebra 2
 1. Überprüfen Sie die folgenden Aussagen: (1) Zwei reelle symmetrische Matrizen sind genau dann ähnlich, wenn sie die gleiche Signatur haben. (2) Jede symmetrische Matrix ist kongruent zu einer Diagonalmatrix,
1. Überprüfen Sie die folgenden Aussagen: (1) Zwei reelle symmetrische Matrizen sind genau dann ähnlich, wenn sie die gleiche Signatur haben. (2) Jede symmetrische Matrix ist kongruent zu einer Diagonalmatrix,
Klausur zu. Lineare Algebra II. Viel Erfolg! Fachbereich Mathematik WS 2012/13 Dr. habil. Matthias Schneider. Bonus Note. Aufgabe
 Klausur zu Lineare Algebra II Fachbereich Mathematik WS 0/3 Dr. habil. Matthias Schneider Aufgabe 3 4 5 6 7 Bonus Note Punktzahl 4 3 3 3 3 0 erreichte Punktzahl Es sind keine Hilfsmittel zugelassen. Die
Klausur zu Lineare Algebra II Fachbereich Mathematik WS 0/3 Dr. habil. Matthias Schneider Aufgabe 3 4 5 6 7 Bonus Note Punktzahl 4 3 3 3 3 0 erreichte Punktzahl Es sind keine Hilfsmittel zugelassen. Die
Lineare Algebra für Physiker 11. Übungsblatt
 Lineare Algebra für Physiker 11. Übungsblatt Fachbereich Mathematik SS 01 Prof. Dr. Matthias Schneider./. Juli 01 Dr. Silke Horn Dipl.-Math. Dominik Kremer Gruppenübung Aufgabe G1 (Minitest) (a) Welche
Lineare Algebra für Physiker 11. Übungsblatt Fachbereich Mathematik SS 01 Prof. Dr. Matthias Schneider./. Juli 01 Dr. Silke Horn Dipl.-Math. Dominik Kremer Gruppenübung Aufgabe G1 (Minitest) (a) Welche
r i w i (siehe (3.7)). r i v, w i = 0.
 Orthogonales Komplement und Orthogonalprojektion Wir betrachten weiterhin einen euklidischen Vektorraum V,,. (6.13) Def.: Ist M V, so heißt das orthogonale Komplement von M. (6.14) Fakt. (i) M ist Untervektorraum
Orthogonales Komplement und Orthogonalprojektion Wir betrachten weiterhin einen euklidischen Vektorraum V,,. (6.13) Def.: Ist M V, so heißt das orthogonale Komplement von M. (6.14) Fakt. (i) M ist Untervektorraum
4 Vektorräume. 4.1 Definition. 4 Vektorräume Pink: Lineare Algebra 2014/15 Seite 48. Sei K ein Körper.
 4 Vektorräume Pink: Lineare Algebra 2014/15 Seite 48 4 Vektorräume 4.1 Definition Sei K ein Körper. Definition: Ein Vektorraum über K, oder kurz ein K-Vektorraum, ist ein Tupel (V,+,, 0 V ) bestehend aus
4 Vektorräume Pink: Lineare Algebra 2014/15 Seite 48 4 Vektorräume 4.1 Definition Sei K ein Körper. Definition: Ein Vektorraum über K, oder kurz ein K-Vektorraum, ist ein Tupel (V,+,, 0 V ) bestehend aus
Mathematik für Physiker, Informatiker und Ingenieure
 Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel V SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel V SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
10.2 Linearkombinationen
 147 Vektorräume in R 3 Die Vektorräume in R 3 sind { } Geraden durch den Ursprung Ebenen durch den Ursprung R 3 Analog zu reellen Vektorräumen kann man komplexe Vektorräume definieren. In der Definition
147 Vektorräume in R 3 Die Vektorräume in R 3 sind { } Geraden durch den Ursprung Ebenen durch den Ursprung R 3 Analog zu reellen Vektorräumen kann man komplexe Vektorräume definieren. In der Definition
Kapitel 7 Lineare Abbildungen und Matrizen II
 Kapitel 7 Lineare Abbildungen und Matrizen II 7.1 Weitere Rechenregeln für Matrizen Aus den bisher gelernten Regeln entnehmen wir den als Übung zu beweisenden Satz 7.1. Es gelten die folgenden Regeln.
Kapitel 7 Lineare Abbildungen und Matrizen II 7.1 Weitere Rechenregeln für Matrizen Aus den bisher gelernten Regeln entnehmen wir den als Übung zu beweisenden Satz 7.1. Es gelten die folgenden Regeln.
Lineare Algebra. 7. Übungsstunde. Steven Battilana. battilana.uk/teaching
 Lineare Algebra 7. Übungsstunde Steven Battilana stevenb@student.ethz.ch battilana.uk/teaching November 9, 27 Erinnerung 2 Vektoräume Sei V ein Vektorraum, U V, U {}. U hiesst Untervektorraum, Unterraum,
Lineare Algebra 7. Übungsstunde Steven Battilana stevenb@student.ethz.ch battilana.uk/teaching November 9, 27 Erinnerung 2 Vektoräume Sei V ein Vektorraum, U V, U {}. U hiesst Untervektorraum, Unterraum,
Tutorium 7. Definition. Sei V ein C-Vektorraum. Eine Abbildung, : V V C heißt komplexes Skalarprodukt : det F k > 0 mit F k := (f i,j ) C k k
 Skalarprodukte Tutorium 7 Bemerkung. Für jeden komplexen Vektorraum V mit dim V und jede komplexe Bilinearform P auf V findet man einen Vektor v mit P (v, v) =. Es gibt also keine positiv definite Bilinearformen
Skalarprodukte Tutorium 7 Bemerkung. Für jeden komplexen Vektorraum V mit dim V und jede komplexe Bilinearform P auf V findet man einen Vektor v mit P (v, v) =. Es gibt also keine positiv definite Bilinearformen
5 Lineare Abbildungen
 5 Lineare Abbildungen Pink: Lineare Algebra HS 2014 Seite 56 5 Lineare Abbildungen 5.1 Definition Gegeben seien Vektorräume U, V, W über einem Körper K. Definition: Eine Abbildung f : V W heisst K-linear,
5 Lineare Abbildungen Pink: Lineare Algebra HS 2014 Seite 56 5 Lineare Abbildungen 5.1 Definition Gegeben seien Vektorräume U, V, W über einem Körper K. Definition: Eine Abbildung f : V W heisst K-linear,
Vektorräume und lineare Abbildungen
 Kapitel 11. Vektorräume und lineare Abbildungen 1 11.1 Vektorräume Sei K ein Körper. Definition. Ein Vektorraum über K (K-Vektorraum) ist eine Menge V zusammen mit einer binären Operation + einem ausgezeichneten
Kapitel 11. Vektorräume und lineare Abbildungen 1 11.1 Vektorräume Sei K ein Körper. Definition. Ein Vektorraum über K (K-Vektorraum) ist eine Menge V zusammen mit einer binären Operation + einem ausgezeichneten
Klausurenkurs zum Staatsexamen (WS 2015/16): Lineare Algebra und analytische Geometrie 5
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 5/6): Lineare Algebra und analytische Geometrie 5 5. (Herbst 9, Thema 3, Aufgabe ) Betrachtet werde die Matrix A := 3 4 5 5 7 7 9 und die lineare Abbildung
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (WS 5/6): Lineare Algebra und analytische Geometrie 5 5. (Herbst 9, Thema 3, Aufgabe ) Betrachtet werde die Matrix A := 3 4 5 5 7 7 9 und die lineare Abbildung
44 Spektralzerlegung normaler Operatoren im endlichdimensionalen Fall
 44 Spektralzerlegung normaler Operatoren im endlichdimensionalen Fall 44 1 Zusammenfassung Dieser Paragraf richtet sich im Aufbau weitgehend nach 42, um den Zerlegungssatz (44.7) analog zum Satz über die
44 Spektralzerlegung normaler Operatoren im endlichdimensionalen Fall 44 1 Zusammenfassung Dieser Paragraf richtet sich im Aufbau weitgehend nach 42, um den Zerlegungssatz (44.7) analog zum Satz über die
7 Lineare Abbildungen und Skalarprodukt
 Mathematik II für inf/swt, Sommersemester 22, Seite 121 7 Lineare Abbildungen und Skalarprodukt 71 Vorbemerkungen Standard Skalarprodukt siehe Kap 21, Skalarprodukt abstrakt siehe Kap 34 Norm u 2 u, u
Mathematik II für inf/swt, Sommersemester 22, Seite 121 7 Lineare Abbildungen und Skalarprodukt 71 Vorbemerkungen Standard Skalarprodukt siehe Kap 21, Skalarprodukt abstrakt siehe Kap 34 Norm u 2 u, u
13 Partielle Ableitung und Richtungsableitung
 3 PARTIELLE ABLEITUNG UND RICHTUNGSABLEITUNG 74 3 Partielle Ableitung und Richtungsableitung 3 Definition und Notiz Sei B R n offen, f : B R m, v R n, so heißt für γ x,v (t) = x + tv d dt f(x + tv) f(x)
3 PARTIELLE ABLEITUNG UND RICHTUNGSABLEITUNG 74 3 Partielle Ableitung und Richtungsableitung 3 Definition und Notiz Sei B R n offen, f : B R m, v R n, so heißt für γ x,v (t) = x + tv d dt f(x + tv) f(x)
Henning Krause Lineare Algebra Julia Sauter SS 2017 Klausur mit Lösungsvorschlag Jan Geuenich
 Henning Krause Lineare Algebra Julia Sauter SS 27 Klausur 2.9.27 mit Lösungsvorschlag Jan Geuenich Aufgabe (4 Punkte: Sei n N und seien A und B zwei (n n-matrizen über einem Körper K. Wahr Falsch (a Es
Henning Krause Lineare Algebra Julia Sauter SS 27 Klausur 2.9.27 mit Lösungsvorschlag Jan Geuenich Aufgabe (4 Punkte: Sei n N und seien A und B zwei (n n-matrizen über einem Körper K. Wahr Falsch (a Es
1 Eigenschaften von Abbildungen
 Technische Universität München Christian Neumann Ferienkurs Lineare Algebra für Physiker Vorlesung Dienstag WS 2008/09 Thema des heutigen Tages sind zuerst Abbildungen, dann spezielle Eigenschaften linearer
Technische Universität München Christian Neumann Ferienkurs Lineare Algebra für Physiker Vorlesung Dienstag WS 2008/09 Thema des heutigen Tages sind zuerst Abbildungen, dann spezielle Eigenschaften linearer
Einführung in die Grundlagen der Numerik
 Einführung in die Grundlagen der Numerik Institut für Numerische Simulation Rheinische Friedrich-Wilhelms-Universität Bonn Wintersemester 2014/2015 Normierter Vektorraum Sei X ein R-Vektorraum. Dann heißt
Einführung in die Grundlagen der Numerik Institut für Numerische Simulation Rheinische Friedrich-Wilhelms-Universität Bonn Wintersemester 2014/2015 Normierter Vektorraum Sei X ein R-Vektorraum. Dann heißt
Klausurenkurs zum Staatsexamen (SS 2015): Lineare Algebra und analytische Geometrie 5
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 5): Lineare Algebra und analytische Geometrie 5 5. (Herbst 9, Thema 3, Aufgabe ) Betrachtet werde die Matrix A := 3 4 5 5 7 7 9 und die lineare Abbildung
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 5): Lineare Algebra und analytische Geometrie 5 5. (Herbst 9, Thema 3, Aufgabe ) Betrachtet werde die Matrix A := 3 4 5 5 7 7 9 und die lineare Abbildung
Übungsklausur Lineare Algebra
 Übungsklausur Lineare Algebra Sommersemester 2010 Johannes Gutenberg-Universität Mainz Diese Übungsklausur ist sehr lang (gut zum Üben). In der richtigen Klausur finden Sie eine Multiple Choice aufgabe
Übungsklausur Lineare Algebra Sommersemester 2010 Johannes Gutenberg-Universität Mainz Diese Übungsklausur ist sehr lang (gut zum Üben). In der richtigen Klausur finden Sie eine Multiple Choice aufgabe
Lineare Algebra I Zusammenfassung
 Prof. Dr. Urs Hartl WiSe 10/11 Lineare Algebra I Zusammenfassung 1 Vektorräume 1.1 Mengen und Abbildungen injektive, surjektive, bijektive Abbildungen 1.2 Gruppen 1.3 Körper 1.4 Vektorräume Definition
Prof. Dr. Urs Hartl WiSe 10/11 Lineare Algebra I Zusammenfassung 1 Vektorräume 1.1 Mengen und Abbildungen injektive, surjektive, bijektive Abbildungen 1.2 Gruppen 1.3 Körper 1.4 Vektorräume Definition
Aufgaben zu Kapitel 20
 Aufgaben zu Kapitel 20 Aufgaben zu Kapitel 20 Verständnisfragen Aufgabe 20 Sind die folgenden Produkte Skalarprodukte? (( R ) 2 ( R 2 )) R : v w,, v v 2 w w 2 (( R ) 2 ( R 2 )) R : v w, 3 v v 2 w w + v
Aufgaben zu Kapitel 20 Aufgaben zu Kapitel 20 Verständnisfragen Aufgabe 20 Sind die folgenden Produkte Skalarprodukte? (( R ) 2 ( R 2 )) R : v w,, v v 2 w w 2 (( R ) 2 ( R 2 )) R : v w, 3 v v 2 w w + v
Skalarprodukt, Norm & Metrik
 Skalarprodukt, Norm & Metrik Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz 11. Mai 2016 Stefan Ruzika 5: Skalarprodukt, Norm & Metrik 11. Mai 2016 1 / 13 Gliederung 1
Skalarprodukt, Norm & Metrik Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz 11. Mai 2016 Stefan Ruzika 5: Skalarprodukt, Norm & Metrik 11. Mai 2016 1 / 13 Gliederung 1
3 Lineare Abbildungen und Matrizen
 3 Lineare Abbildungen und Matrizen Definition 3.1. Es seien V und W zwei Vektorräume über demselben Zahlkörper k. Eine Abbildung heisst linear, falls gilt i) [ λ k ] [ v V ] [ f (λ v) = λ f ( v) ] ii)
3 Lineare Abbildungen und Matrizen Definition 3.1. Es seien V und W zwei Vektorräume über demselben Zahlkörper k. Eine Abbildung heisst linear, falls gilt i) [ λ k ] [ v V ] [ f (λ v) = λ f ( v) ] ii)
Lineare Algebra. 6. Übungsstunde. Steven Battilana. battilana.uk/teaching
 Lineare Algebra 6. Übungsstunde Steven Battilana stevenb@student.ethz.ch battilana.uk/teaching November, 7 Vektoräume Eine Menge E zusammen mit zwei Verknüpfungen + : E E E, x, y x + y Addition : E E E,
Lineare Algebra 6. Übungsstunde Steven Battilana stevenb@student.ethz.ch battilana.uk/teaching November, 7 Vektoräume Eine Menge E zusammen mit zwei Verknüpfungen + : E E E, x, y x + y Addition : E E E,
VII.2. INNERE PRODUKTE 227
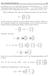 VII.2. INNERE PRODUKTE 227 der Abstand von v zum Teilraum W genannt. Dabei bezeichnet p: V W die Orthogonalprojektion aus Satz VII.2.32 und b 1,...,b k ist eine beliebige Orthonormalbasis von W. Offensichtlich
VII.2. INNERE PRODUKTE 227 der Abstand von v zum Teilraum W genannt. Dabei bezeichnet p: V W die Orthogonalprojektion aus Satz VII.2.32 und b 1,...,b k ist eine beliebige Orthonormalbasis von W. Offensichtlich
Lineare Algebra I (WS 13/14)
 Lineare Algebra I (WS 13/14) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 03.12.2013 Alexander Lytchak 1 / 16 Wiederholung und Beispiele Der Spaltenrang einer Matrix ist gleich ihrem Zeilenrang.
Lineare Algebra I (WS 13/14) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 03.12.2013 Alexander Lytchak 1 / 16 Wiederholung und Beispiele Der Spaltenrang einer Matrix ist gleich ihrem Zeilenrang.
Steilkurs Lineare Algebra 1 einige wichtige Stationen
 Steilkurs Lineare Algebra 1 einige wichtige Stationen Für einen Körper K ist ein K-Vektorraum V eine Menge mit einer kommutativen und assoziativen Verknüpfung + : V V V, für die es ein neutrales Element
Steilkurs Lineare Algebra 1 einige wichtige Stationen Für einen Körper K ist ein K-Vektorraum V eine Menge mit einer kommutativen und assoziativen Verknüpfung + : V V V, für die es ein neutrales Element
4 Elementare Vektorraumtheorie
 4. ELEMENTARE VEKTORRAUMTHEORIE 51 4 Elementare Vektorraumtheorie Im folgenden sei K stets ein Körper. Definition. (i) Eine homogene Gleichung in den Unbekannten ξ 1,..., ξ n ist ein Ausdruck der Gestalt
4. ELEMENTARE VEKTORRAUMTHEORIE 51 4 Elementare Vektorraumtheorie Im folgenden sei K stets ein Körper. Definition. (i) Eine homogene Gleichung in den Unbekannten ξ 1,..., ξ n ist ein Ausdruck der Gestalt
KLAUSUR ZUR LINEAREN ALGEBRA I UND II 2. Oktober 2008 MUSTERLÖSUNG
 KLAUSUR ZUR LINEAREN ALGEBRA I UND II 2. Oktober 2008 MUSTERLÖSUNG Aufgabe 1 Es sei K ein Körper, V ein K-Vektorraum, und seien v 1,..., v n V (n N). (a) Definieren Sie, wann die endliche Familie v 1,...,
KLAUSUR ZUR LINEAREN ALGEBRA I UND II 2. Oktober 2008 MUSTERLÖSUNG Aufgabe 1 Es sei K ein Körper, V ein K-Vektorraum, und seien v 1,..., v n V (n N). (a) Definieren Sie, wann die endliche Familie v 1,...,
Aufgaben und Lösungen zur Klausur Lineare Algebra im Frühjahr 2009
 I. (4 Punkte) Gegeben sei die Menge Aufgaben und Lösungen zur Klausur Lineare Algebra im Frühjahr 9 G := { a c b a, b, c R }. (a) Zeigen Sie, dass G zusammen mit der Matrizenmultiplikation eine Gruppe
I. (4 Punkte) Gegeben sei die Menge Aufgaben und Lösungen zur Klausur Lineare Algebra im Frühjahr 9 G := { a c b a, b, c R }. (a) Zeigen Sie, dass G zusammen mit der Matrizenmultiplikation eine Gruppe
Mathematik II. Vorlesung 46. Der Gradient
 Prof. Dr. H. Brenner Osnabrück SS 2010 Mathematik II Vorlesung 46 Der Gradient Lemma 46.1. Es sei K ein Körper und V ein K-Vektorraum, der mit einer Bilinearform, versehen sei. Dann gelten folgende Aussagen
Prof. Dr. H. Brenner Osnabrück SS 2010 Mathematik II Vorlesung 46 Der Gradient Lemma 46.1. Es sei K ein Körper und V ein K-Vektorraum, der mit einer Bilinearform, versehen sei. Dann gelten folgende Aussagen
Lineare Algebra für D-ITET, D-MATL, RW. Beispiellösung für Serie 10. Aufgabe ETH Zürich D-MATH. Herbstsemester Dr. V. Gradinaru D.
 Dr. V. Gradinaru D. Devaud Herbstsemester 5 Lineare Algebra für D-ITET, D-MATL, RW ETH Zürich D-MATH Beispiellösung für Serie Aufgabe..a Bezüglich des euklidischen Skalarprodukts in R ist die Orthogonalprojektion
Dr. V. Gradinaru D. Devaud Herbstsemester 5 Lineare Algebra für D-ITET, D-MATL, RW ETH Zürich D-MATH Beispiellösung für Serie Aufgabe..a Bezüglich des euklidischen Skalarprodukts in R ist die Orthogonalprojektion
Lineare Algebra II. Prof. Dr. M. Rost. Übungen Blatt 8 (SS 2011) Abgabetermin: Donnerstag, 9. Juni.
 Lineare Algebra II Prof. Dr. M. Rost Übungen Blatt 8 (SS 2011) Abgabetermin: Donnerstag, 9. Juni http://www.math.uni-bielefeld.de/~rost/la2 Erinnerungen, Ergänzungen und Vorgriffe zur Vorlesung: Hermitesche
Lineare Algebra II Prof. Dr. M. Rost Übungen Blatt 8 (SS 2011) Abgabetermin: Donnerstag, 9. Juni http://www.math.uni-bielefeld.de/~rost/la2 Erinnerungen, Ergänzungen und Vorgriffe zur Vorlesung: Hermitesche
1. Hausübung ( )
 Übungen zur Vorlesung»Lineare Algebra B«(SS ). Hausübung (8.4.) Aufgabe Es seien σ (3, 6, 5,, 4, 8,, 7) und τ (3,,, 4, 6, 5, 8, 7). Berechnen Sie σ τ, τ σ, σ, τ, die Anzahl der Inversionen von σ und τ
Übungen zur Vorlesung»Lineare Algebra B«(SS ). Hausübung (8.4.) Aufgabe Es seien σ (3, 6, 5,, 4, 8,, 7) und τ (3,,, 4, 6, 5, 8, 7). Berechnen Sie σ τ, τ σ, σ, τ, die Anzahl der Inversionen von σ und τ
Lineare Algebra I (WS 13/14)
 Lineare Algebra I (WS 13/14) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 05.11.2013 Alexander Lytchak 1 / 14 Linearkombinationen Definition Es sei V ein reeller Vektorraum. Es sei (v i ) i
Lineare Algebra I (WS 13/14) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 05.11.2013 Alexander Lytchak 1 / 14 Linearkombinationen Definition Es sei V ein reeller Vektorraum. Es sei (v i ) i
ABBILDUNGEN ZWISCHEN VEKTORRÄUMEN MIT SKALARPRODUKT
 ABBILDUNGEN ZWISCHEN VEKTORRÄUMEN MIT SKALARPRODUKT G.FELDER, LINEARE ALGEBRA II, FS 2013 27.03.2013 Inhaltsverzeichnis 1. Selbstadjungierte Abbildungen 1 1.1. Adjungierte Abbildungen 1 1.2. Spektralsatz
ABBILDUNGEN ZWISCHEN VEKTORRÄUMEN MIT SKALARPRODUKT G.FELDER, LINEARE ALGEBRA II, FS 2013 27.03.2013 Inhaltsverzeichnis 1. Selbstadjungierte Abbildungen 1 1.1. Adjungierte Abbildungen 1 1.2. Spektralsatz
12. R n als EUKLIDISCHER VEKTORRAUM
 12. R n als EUKLIDISCHER VEKTORRAUM 1 Orthogonalität in der Ebene. Die Vektoren in der Ebene, die (im üblichen Sinne) senkrecht zu einem Vektor x = (x 1, x 2 ) T stehen, lassen sich leicht angeben. Sie
12. R n als EUKLIDISCHER VEKTORRAUM 1 Orthogonalität in der Ebene. Die Vektoren in der Ebene, die (im üblichen Sinne) senkrecht zu einem Vektor x = (x 1, x 2 ) T stehen, lassen sich leicht angeben. Sie
Lineare Algebra. Mathematik II für Chemiker. Daniel Gerth
 Lineare Algebra Mathematik II für Chemiker Daniel Gerth Überblick Lineare Algebra Dieses Kapitel erklärt: Was man unter Vektoren versteht Wie man einfache geometrische Sachverhalte beschreibt Was man unter
Lineare Algebra Mathematik II für Chemiker Daniel Gerth Überblick Lineare Algebra Dieses Kapitel erklärt: Was man unter Vektoren versteht Wie man einfache geometrische Sachverhalte beschreibt Was man unter
Lineare Algebra. 9. Übungsstunde. Steven Battilana.
 Lineare Algebra 9. Übungsstunde Steven Battilana stevenb@student.ethz.ch November 2, 26 Erinnerung Sei x, y 2 E n, 2 E, danngilt: hx, yi = kxkkyk cos( ). Ist m eine beliebige natürliche Zahl, apple i,
Lineare Algebra 9. Übungsstunde Steven Battilana stevenb@student.ethz.ch November 2, 26 Erinnerung Sei x, y 2 E n, 2 E, danngilt: hx, yi = kxkkyk cos( ). Ist m eine beliebige natürliche Zahl, apple i,
Mathematische Grundlagen für die Vorlesung. Differentialgeometrie
 Mathematische Grundlagen für die Vorlesung Differentialgeometrie Dr. Gabriele Link 13.10.2010 In diesem Text sammeln wir die nötigen mathematischen Grundlagen, die wir in der Vorlesung Differentialgeometrie
Mathematische Grundlagen für die Vorlesung Differentialgeometrie Dr. Gabriele Link 13.10.2010 In diesem Text sammeln wir die nötigen mathematischen Grundlagen, die wir in der Vorlesung Differentialgeometrie
Übungen zur Vorlesung Lineare Algebra II, SoSe 2016, Blatt 12
 Übungen zur Vorlesung Lineare Algebra II, SoSe 2016, Blatt 12 Schriftliche Aufgaben Aufgabe 1. Sei A M(n n, C). Zeigen Sie: (1) exp(a) ist invertierbar mit exp(a) 1 = exp( A). (2) Ist A M(n n, C) selbstadjungiert
Übungen zur Vorlesung Lineare Algebra II, SoSe 2016, Blatt 12 Schriftliche Aufgaben Aufgabe 1. Sei A M(n n, C). Zeigen Sie: (1) exp(a) ist invertierbar mit exp(a) 1 = exp( A). (2) Ist A M(n n, C) selbstadjungiert
Lineare Algebra I Lösung der Probeklausur
 David Blottière Patrick Schützdeller WS 6/7 Universität Paderborn Lineare Algebra I Lösung der Probeklausur Aufgabe : M i) M ist linear unabhängig. Seien a,b,c R mit Daraus folgt : Also gilt a = b = c
David Blottière Patrick Schützdeller WS 6/7 Universität Paderborn Lineare Algebra I Lösung der Probeklausur Aufgabe : M i) M ist linear unabhängig. Seien a,b,c R mit Daraus folgt : Also gilt a = b = c
