Versuch 252 Digitale Filter
|
|
|
- Emilia Kranz
- vor 7 Jahren
- Abrufe
Transkript
1 Drittes Physikalisches Institut der Universität Göttingen Bürgerstraße D-3773 Göttingen Oktober 998 Praktikum für Fortgeschrittene Versuch 252 Digitale Filter Analoge Signale werden heute zunehmend durch den Einsatz digitaler Signalverarbeitung gemessen und bearbeitet: sie werden in Zahlenformen (digitale Signale) umgewandelt und auf Digitalrechnern zur Weiterverarbeitung und Auswertung gespeichert. Dieser Versuch führt in die Grundlagen der digitalen Signalverarbeitung ein. Es wird ein schneller Signalprozessor verwendet, um die digitalen Signale so schnell zu verarbeiten, daß die Ergebnisse sofort wieder in analoge Signale zurückgewandelt werden können (Echtzeit-Verarbeitung). Zunächst werden Fehler und Grenzen bei der Umwandlung analoger Signale in digitale Signale untersucht (Samplingtheorem, Quantisierungsrauschen) und anschließend digitale Filter maximal 2. Ordnung realisiert und ausgemessen. Zubehör Signalgenerator (Sinus) für Frequenzen von bis 2 khz Oszilloskop RMS-Röhrenvoltmeter mit db-skala Filter 2. Ordnung mit einstellbaren Koeffizienten (in einem Gehäuse mit AD/DA-Wandlern)
2 Literatur [] A. Lacroix: Digitale Filter. München/Wien: Oldenbourg, 98 [2] H.W. Schüssler: Digitale Systeme zur Signalverarbeitung. Berlin/Heidelberg/New York: Springer, 973 [3] S.D. Stearns: Digitale Verarbeitung analoger Signale. München/Wien: Oldenbourg, 979 [4] S.A. Azizi: Entwurf und Realisierung digitaler Filter. München/Wien: Oldenbourg, 983 [5] A.V. Oppenheim, R.W. Schäfer: Digital Signal Processing. Englewood Cliffs (NJ): Prentice Hall, 978 [6] L.R. Rabiner, B. Gold: Theory and Application of Digital Signal Processing. Englewood Cliffs (NJ): Prentice Hall, 975 2
3 Gang des Versuchs. Quantisierungsrauschen Messen der Leistung des Quantisierungsfehlers bei f s = 25 khz und einem sinusförmigen Eingangssignal von 2 Hz für verschiedene Wortbreiten des AD-Wandlers. 2. Rekursives Filter. Ordnung α = α 2 = β 2 = ; α = β = :5; :9; :98 f s = khz Messung des Frequenzgangs von 2 Hz bis 2 khz. 3. Rekursives Filter. Ordnung α = α 2 = α = rsinγ; β = 2rcosγ; β 2 = ;r 2 r = :9; :95; :99; γ = 3 f s = khz Messung des Frequenzgangs von 2 Hz bis 5 khz. Messung der Impulsantwort. 4. Nichtrekursives Filter β = β 2 = α = α = α 2 = f s = khz Messung des Frequenzgangs von 2 Hz bis 5 khz. Außerdem dasselbe für eine weitere, beliebige Nullstelle im oder auf dem Einheitskreis (die Parameter α i entsprechend selbst wählen). 5. Tiefpaßfilter 2. Ordnung Butterworth: f g = khz [α = 2; α = α 2 = ] =6 β = :43; β 2 = ;:428 f s = khz Tschebyscheff: f g = khz; 3 db Welligkeit [α = 2; α = α 2 = ] =6 β = :532; β 2 = ;:794 f s = khz Messung des Frequenzgangs jeweils von 2 Hz bis 5 khz. 3
4 Auswertung. Auftragung des RMS-Wertes des Quantisierungsrauschens über der Wortbreite des AD-Wandlers. Abschätzung des nutzbaren Dynamikbereichs. 2. Zeichnen des Frequenzgangs und Bestimmung der Grenzfrequenz (3 db - Abfall, full width ). Bestimmung der Abtastfrequenz. Vergleich mit der Theorie. 3. Zeichnen des Frequenzgangs. Bestimmung der Resonanzfrequenz und der Halbwertsbreiten. Bestimmung der Frequenz und des logarithmischen Dekrements aus der Impulsantwort. Vergleich der Meßwerte aus Frequenzgang und Impulsantwort untereinander. Vergleich der Meßwerte mit der Theorie. 4. Zeichnen des Frequenzgangs. Bestimmung der Resonanzfrequenz (=Sperrfrequenz) und Vergleich mit der Theorie. 5. Zeichnen der Frequenzgänge. Bestimmung der Grenzfrequenzen (3 db - Abfall relativ zu H(ω! )). Bestimmen der Welligkeit beim Tschbyscheff-Tiefpaß [H max ; H(ω! )]. Vergleich von Butterworth und Tschebyscheff. Bemerkungen: Es ist darauf zu achten, daß der gemeinsame Faktor für α i so eingestellt wird, daß keine Überläufe auftreten (H(z) muß immer kleiner als 2 sein). Zu 3.: ist Z-Transformierte von H(z) = (r sinγ)z z 2 ; (2rcosγ)z + r 2 h n = r n sin(nγ) : Für den Zusammenhang zwischen logarithmischem Dekrement Λ = ln x(i) max x (i+) max Halbwertsbreite Δ f und Resonanzfrequenz f res gilt näherungsweise Δ f = π Λ f res : 4
5 Theorie. Quantisierungsrauschen Um analoge Signal digital verarbeiten zu können, müssen diese zunächst in binäre Zahlen umgewandelt werden. Dies geschieht mit Hilfe von Digital-Analog-Wandlern. Die Genauigkeit dieser Umwandlung hängt hauptsächlich von der Wortbreite ab, d.h. der Anzahl Bits, mit welcher die Zahlen dargestellt werden können. Ein 2-Bit-Wandler hat z.b. 2 2 = 496 Zahlen zur Darstellung der analogen Werte zur Verfügung. Die Kennlinie dieser Quantisierung entspricht einer Treppenfunktion mit der Stufenhöhe q (Quantisierungsstufe), wobei q = 2 ;W A () mit der Wortbreite W und der Vollaussteuerungsamplitude A. Der beim Quantisieren auftretende Fehler e hängt wie folgt von der Quantisierungsstufe q ab: ; q 2 e q 2 : (2) Im allgemeinen kann dieser Quantisierungsfehler als gleichverteilte Zufallsgröße angenommen werden, deren Verteilung p(e) vom analogen Eingangssignal unabhängig ist: p(e) ==q. Wegen der statischen Eigenschaften des Fehlers spricht man von Quantisierungsrauschen. p(e) /q -q/2 q/2 Abb. : Verteilungsfunktion des Quantisierungsfehlers. Die Varianz des Quantisierungsfehlers ist seiner Leistung proportional und berechnet sich als σ 2 e = Z q=2 ;q=2 p(e)(e; < e >) 2 de = 5 Zq=2 ;q=2 q (e ; )2 de = q2 2 : (3)
6 Um den Einfluß des Quantisierungsrauschens abschätzen zu können, interessiert man sich für das Verhältnis der Varianz des Nutzsignals σ 2 s zur Varianz des Quantisierungsrauschens σ 2 e. Dieses entspricht dem Verhältnis der Leistungen von Signal und Rauschen und wird daher als Signal-Rausch- Abstand (SNR = Signal to Noise Ratio) bezeichnet. Ein voll ausgesteuerter Sinus hat die Varianz σ 2 s = T ZT =2 ;T =2 A 2 sin(2π ft) dt = A2 2 8 = 8 q2 2 2W : (4) Daraus erhalten wir: SNR = σ2 s 2 σ 2 = e 8 22W (5) 2 SNR = log 8 db + 2W log 2dB= W 6dB+ :8dB: (6) Somit erhält man für jedes zusätzliche Bit der Wortbreite eine Verbesserung des SNR von 6 db. Zum Beispiel haben 2-Bit-Wandler einen (maximalen) SNR von 74 db, 6-Bit-Wandler von 96 db. Bei der bisherigen Betrachtung wurde noch kein Einfluß der endlichen Abtastrate (Samplingfrequenz f s ), also kein Rauschen durch Quantisierung der Zeit, berücksichtigt. Man kann sich überlegen, daß eine Erhöhung der Wortbreite bei festem f s dann keine Verbesserung der Qualität mehr bringt, wenn die Änderung des Eingangssignals während einer Abtastperiode T s = = f s bereits größer ist als eine Quantisierungsstufe q. Für einen vollausgesteuerten Sinus der Frequenz f erhält man als Abschätzung der maximalen Wortbreite, bevor dieser Effekt auftritt: d dt A sin(2π ft) 2 T s q = A 2 ;W (7) max: ) π ft s 2 ;W ) W ln( f s=π f ) : (8) ln(2) Oberhalb von W ln( f s =π f )=ln(2) erwartet man daher keine signifikante Verminderung des Rauschens mehr..2 Abtasttheorem Bei der digitalen Signalverarbeitung wird einerseits die Größe des Eingangssignals durch Quantisierung diskret gemacht und andererseits der Zeitverlauf des Signals diskretisiert, indem das Signal in festen Abständen 6
7 t T s o o o o o o o o o o o o o o o o o o o o o o o o t T s t Abb. 2: Beschreibung der Abtastung durch einen Dirac-Kamm. abgetastet wird. Daher stellt sich die Frage, wie ein Zeitsignal durch äquidistante Abtastung verfälscht wird. Um diese Frage zu beantworten, muß man das Spektrum der abgetasteten Funktion betrachten. Formal wird die Abtastung durch die Multiplikation eines analogen Zeitsignals mit einem Dirac-Kamm beschrieben: y n = y(t) comb(t τ) (9) comb(t τ) = δ(t ; kτ): () k=; Das Spektrum der abgetasteten (digitalen) Funktion y n ergibt sich demnach aus der Faltung des Spektrums der ursprünglichen Zeitfunktion y(t) mit dem Spektrum des Dirac-Kamms. Das Spektrum einer Dirac- Kammfunktion ist wiederum ein Dirac-Kamm mit der Periode f s = =τ. Wenn wir mit 7! die Fouriertransformierte bezeichnen, gilt also für das Spektrum des abgetasteten Signals: y(t) 7! Y( f ) comb(t τ) 7! τ comb( f f s) () y n (t) 7! Y n ( f )= τ Y( f ; kf s ): k=; Mit anderen Worten: Das Spektrum des Originalsignals wiederholt sich im Frequenzbereich periodisch mit der Abtastfrequenz f s. Besitzt nun das Spektrum der Zeitfunktion Y(f) Frequenzen oberhalb der halben Abtastfrequenz f s, so kann das digitale Signal in das zugehörige analoge Zeitsignal 7
8 zurückgewandelt werden, indem man es digital-analog wandelt und mit einem Tiefpaß mit einer Abschneidefrequenz von f s =2 die periodischen hochfrequenten Anteile herausfiltert. Bei der digitalen Signalverarbeitung muß also das abzutastende Signal mit f s =2 bandbegrenzt sein. - f g f g Überlappungsbereiche f - f s f g f s f - f s f g f s f Abb. 3: Zum Abtasttheorem. Oben: Spektrum der Zeitfunktion. Mitte: Spektrum der abgetasteten Funktion mit f s < 2 f g. Unten: dasselbe mit f s > 2 f g..3 Digitale Systeme Nachdem wir die Grundlagen der Beziehung zwischen einem analogen und einem digitalen Signal besprochen haben, interessieren uns die Operationen, die mit den digitalen Signalen z.b. in einem Digitalrechner durchgeführt werden können. Die wichtigsten sind hierbei die linearen digitalen Systeme, die sich durch folgende Differenzengleichung beschreiben lassen: y n = M k= α k x n;k + N k= β k y n;k : (2) Der aktuelle Ausgangswert y n berechnet sich also aus N vergangenen Ausgangswerten (y n; ::: y n;n ) und M + vergangenen Eingangswerten (x n ::: x n;m ). 8
9 Ein lineares digitales System kann somit aus den drei Elementen Addierer, Multiplizierer und Verzögerer aufgebaut werden, die sich mit einem Digitalrechner realisieren lassen. x x,n 2,n x + x,n 2,n x n α α x n x n T x n- Abb. 4: Die Elemente Addierer, Multiplizierer und Verzögerer. Eine wichtige Größe zur Beschreibung eines digitalen Systems ist die Einheitsimpulsantwort. Dies ist die Ausgangsfolge des Systems bei Anregung mit einer Eingangsfolge, die aus einer Eins und sonst nur aus Nullen besteht. Aus der Einheitsimpulsantwort h n läßt sich die Ausgangsfolge y n des Systems bei einer beliebigen Eingangsfolge x n berechnen: y n = h k x n;k : (3) k=; Diese spezielle Summe bezeichnet man als Faltungssumme. Als Beispiel betrachte man das folgende System. Ordnung: y n = x n + 2 y n;: (4) Wie man leicht nachrechnet ist die Einheitsimpulsantwort h n h n = 2 4 ::: (5) 8 Im weiteren interessieren wir uns für das Frequenzverhalten dieses Systems, d.h. für Betrag und Phase der Ausgangsfunktion bei einer harmonischen Eingangsfunktion e iωt mit der variablen (Kreis-)Frequenz ω. Die diskrete Eingangsfunktion x n errechnet sich dann zu x n = e iωτn τ = T s : Abtastperiode: (6) Weil es sich um ein lineares System handelt, ist die Ausgangsfunktion ebenfalls eine harmonische Funktion mit der Frequenz ω, so daß gilt: y n; = e iωτ y n 9
10 y n = x n + 2 e;iωτ y n (7) y n = ; x n: 2 e;iωτ Die Übertragungsfunktion H(ω) ist nun der Quotient aus Eingangs- und Ausgangsfunktion bei harmonischer Anregung: y n H(ω) = = x n ; : (8) 2e;iωτ In unserem Beispiel kann nun für beliebige reelle Signale die Übertragungsfunktion H(ω) nach Betrag und Phase ausgewertet werden: Für tiefe Frequenzen (ω ) ist der Betrag maximal, und für ω = π=τ ist der Betrag minimal, so daß sich unterhalb dieser Frequenz eine Tiefpaßcharakteristik ergibt. Im allgemeinen ist die Übertragungsfunktion als das Verhältnis der Fouriertransformierten von Ausgangsfolge (F (y n )) und der Eingangsfolge (F (x n )) definiert: F (y n) H(ω) = F (x n ) = F (h n): (9) Die Berechnung der Übertragungsfunktion nach dieser Formel kann sehr aufwendig sein. Der oben angewandte Trick zur einfachen Berechnung der Übertragungsfunktion durch harmonische Eingangs- und Ausgangsfunktionen kann jedoch auch für ein beliebiges lineares digitales System benutzt werden. Ausgehend von der Differenzengleichung y n = M k= α k x n;k + N k= β k y n;k (2) läßt sich bei harmonischem Eingangssignal x n = e iωτn das Ausgangssignal ausdrücken als y n = M k= α k e ;iωτk x n + N k= β k e ;iωτk y n (2) also y n = M k= α k e ;iωτk x n ; N k= β k e ;iωτk = H(ω τ) =H(eiωτ ): (22) Die Übertragungsfunktion läßt sich also direkt durch die Koeffizienten α k und β k ausdrücken. Für ein digitales System ist es daher sinnvoll, anstelle der Abhängigkeit von ω und τ nur die Abhängigkeit von der zusammengesetzten Größe z = e iωτ zu betrachten: H(z) = Y(z) X(z) = M k= α k z ;k ; N k= β : (23) k z ;k
11 x n α y n T α β T T α 2 β 2 T Abb. 5: Digitales System 2. Ordnung Die Rechenvorschrift, einer zeitvariablen Folge x n eine frequenzabhängige Funktion X(z) zuzuordnen, wird als Z-Transformation bezeichnet. Sie ist mit der Fourier-Transformation (bzw. deren Verallgemeinerung, der Laplace-Transformation) identisch, wenn die richtige Variablenbeziehung z = e iωτ berücksichtigt wird. Für digitale Systeme ist die Z-Transformation jedoch formal einfacher, weil die Koeffizienten der Zeitfolge (Differenzengleichung) mit den Koeffizienten der Z-Transformierten übereinstimmen, die Abhängigkeit von ω und τ in einer Variablen vereinigt ist und die aus der Periodizität der e-funktion resultierende Mehrdeutigkeit eliminiert wird. Allgemein ist die Z-Transformation einer Zahlenfolge fy k g folgendermaßen definiert: Zfy n g = Y(z) = y k z ;k : (24) k= In unserem Beispiel errechnete sich die Übertragungsfunktion nach (8) als H(ω) = ; = 2 e;iωτ ; : (25) 2z; Wir können sie aber auch mit Hilfe von (24) aus der Einheitsimpulsantwort h n berechnen, da H(z) =Zfh n g gilt: H(z) = h n = h n z ;n = n= n n (26) 2 n n= 2 z; = ; : (27) 2z;
12 .4 Pol-Nullstellen-Darstellung der Systemfunktion Man betrachte das folgende System 2. Ordnung: y n = α x n + α x n; + α 2 x n;2 + β y n; + β 2 y n;2 : (28) Dies läßt sich durch eine Schaltung wie in Abbildung 5 realisieren. Die Übertragungsfunktion lautet α + α z ; + α 2 z ;2 α H(z) = ; β z ; ; β 2 z ;2 = z 2 + α z + α 2 z 2 : (29) ; β z ; β 2 Die Polynome der Systemfunktion können auch in Produktform geschrieben werden: H(z) =A (z ; z )(z ; z 2 ) (z ; z )(z ; z : (3) 2 ) Die Nullstellen des Zählerpolynoms (z z 2 ) werden als Nullstellen, die Nullstellen des Nenners (z z 2 ) als Pole des Systems bezeichnet. Aus den Polen und Nullstellen lassen sich mit einfachen geometrischen Methoden Betrag und Phase der Übertragungsfunktion des Systems herleiten. Den Betrag erhalten wir, indem wir auf dem Einheitskreis in der komplexen Ebene (z = e iωτ ) entlangfahren und die Abstände zwischen dem jeweiligen Punkt auf dem Einheitskreis und den Nullstellen multiplizieren. Dieses Produkt muß noch durch die Abstände zwischen dem jeweiligen Punkt und den Polen dividiert werden. Die Phase erhält man entsprechend durch Addition der Winkel zu den Nullstellen und Subtraktion der Winkel zu den Polen. Im i o x x Re o Abb. 6: Beispiel zur geometrischen Abschätzung einer Übertragungsfunktion aus den Nullstellen (o) und Polen (x). 2
13 6.28 Betrag und Phase von H(z) normierte Frequenz Abb. 7: Verlauf von jh(z)j (normiert auf 2π, durchgezogene Linie) und der Phase von H(z) (arg[h(z)], gestrichelte Linie) zu dem Beispiel in Abb Spezielle Filter Üblicherweise werden Filter in der komplexen p-ebene, d.h. im Definitionsbereich der Laplace-Transformation entworfen. Als Beispiel betrachte man den analog realisierten Tiefpaß 2. Ordnung, den Abb. 8 zeigt. L R C Abb. 8: Analoger RCL-Tiefpaß. Dieser Tiefpaß hat die Übertragungsfunktion H(ω) = + RCiω ; LCω 2 (3) oder bei Verallgemeinerung der rein imaginären Variablen iω auf eine komplexe Variable p: H(p) = + RCp + LCp 2 : (32) 3
14 Man erkennt, daß sich die Übertragungsfunktion eines solchen Tiefpasses durch ein Nennerpolynom 2. Ordnung auszeichnet. Durch geeignete Wahl der Koeffizienten lassen sich Tiefpaßfilter mit unterschiedlichen Eigenschaften herstellen. Um ein äquivalentes Filter digital zu realisieren, muß man eine Variablentransformation durchführen, die die p-ebene auf die z-ebene abbildet. Bei dieser Transformation muß die i-achse auf den Einheitskreis abgebildet werden. Dies leistet die sogenannte Bilineartransformation: p! 2 τ Betrachten wir wieder einen Tiefpaß: H(p) = Die Bilineartransformation liefert: H(z) =A ( ; z) ( + z) : (33) + b p + b 2 p 2 : (34) + 2z + z2 + α z + α 2 z 2 : (35) Diese Systemfunktion besitzt zwei Nullstellen bei z = ; und zwei Pole, deren Lage die Abschneidefrequenz, die Flankensteilheit und die maximale Dämpfung des Filters beschreiben. Auf einfache Weise erhalten wir aus einem gegebenen Tiefpaß einen Hochpaß, indem wir z mit ; multiplizieren. Dies entspricht der Transformation ω! π f s ; ω, d.h. einer Spiegelung des Frequenzbereichs an der halben Abtastfrequenz, und liefert in unserem Fall zwei Nullstellen bei z =. Andere Transformationen, z.b. Tiefpaß-Bandpaß-Transformationen, sind möglich. Auf sie wird hier nicht weiter eingegangen, sondern auf die Literatur verwiesen. Der konkrete Entwurf eines digitalen Filters sei am Beispiel eines Butterworth-Tiefpasses 2. Ordnung gezeigt. Bei diesem Filtertyp versucht man, den Frquenzgang im Durchlaßbereich möglichst lange konstant zu halten. Erst ab einer Grenzfrequenz ω g wird gesperrt. Dies erreicht man durch die Übertragungsfunktion jh(p)j 2 = + P 2n (36) mit der normierten Variablen P = ω iω g und der Ordnungszahl n. Für ω = ω g wird das Betragsquadrat jh(p)j 2 = 2.Für ein Filter braucht man jedoch die 4
15 komplexe Übertragungsfunktion. Bei n = 2 ist diese gegeben durch H(P) = + p 2P + P 2 : (37) Die Bilineartransformation (33) verursacht eine tangensförmige Frequenzverzerrung ω 2 τ = τ tan(ω ) (38) 2 wobei ω die analoge Frequenz bezeichnet. Damit die Grenzfrequenz im analogen und im digitalen Fall gleich ist, muß man wie folgt korrigieren: ω = k 2 τ tan(ω τ 2 ) (39) mit τ k = ω g 2 cot(ω τ g ): (4) 2 Dies liefert dann die folgende modifizierte Bilineartransformation: P! cot(ω g τ 2 ) ; z + z : (4) Setzt man etwa f g = khz und f s =/τ = khz, so erhält man das folgende digitale Butterworth-Filter: + 2z + z 2 H(z) =:6743 (42) :428 ; :43z + z2: 5
16 SETTING CTL4 CTL5 CTL CTL2 CTL6 CTL3 M K K K / K K K / / 5 K 5 K 5 K /2 / K 33.3 K 3.3 K /3 /3 25 K 25 K 2.5 K /4 /4 2 K 2 K 2 K /5 /5 66.6K 6.6 K.6 K /6 / K 8.3 K /2 /2 CTL CTL2 CTL3 CTL4 CTL5 CTL6 Einstellung der Abtastfrequenz: z.b. khz Abb. 9: Tabelle der Schalterstellungen für verschiedene Sample- Frequenzen. Nächste zwei Seiten: Schalterstellungen für die Koeffizienten α i, β j. 6
17
18
Prof. Dr. Stefan Weinzierl SNR V = P signal P noise
 Audiotechnik II Digitale Audiotechnik: 5. Tutorium Prof. Dr. Stefan Weinzierl 0.11.01 Musterlösung: 1. November 01, 15:50 1 Dither a) Leiten sie den SNR eines idealen, linearen -bit Wandlers her. Nehmen
Audiotechnik II Digitale Audiotechnik: 5. Tutorium Prof. Dr. Stefan Weinzierl 0.11.01 Musterlösung: 1. November 01, 15:50 1 Dither a) Leiten sie den SNR eines idealen, linearen -bit Wandlers her. Nehmen
ÜBUNG 4: ENTWURFSMETHODEN
 Dr. Emil Matus - Digitale Signalverarbeitungssysteme I/II - Übung ÜBUNG : ENTWURFSMETHODEN 5. AUFGABE: TIEFPASS-BANDPASS-TRANSFORMATION Entwerfen Sie ein nichtrekursives digitales Filter mit Bandpasscharakteristik!
Dr. Emil Matus - Digitale Signalverarbeitungssysteme I/II - Übung ÜBUNG : ENTWURFSMETHODEN 5. AUFGABE: TIEFPASS-BANDPASS-TRANSFORMATION Entwerfen Sie ein nichtrekursives digitales Filter mit Bandpasscharakteristik!
Klausur zur Vorlesung Digitale Signalverarbeitung
 INSTITUT FÜR INFORMATIONSVERARBEITUNG UNIVERSITÄT HANNOVER Appelstraße 9A 067 Hannover Klausur zur Vorlesung Digitale Signalverarbeitung Datum: 0.08.007 Uhrzeit: 09:00 Uhr Zeitdauer: Stunden Hilfsmittel:
INSTITUT FÜR INFORMATIONSVERARBEITUNG UNIVERSITÄT HANNOVER Appelstraße 9A 067 Hannover Klausur zur Vorlesung Digitale Signalverarbeitung Datum: 0.08.007 Uhrzeit: 09:00 Uhr Zeitdauer: Stunden Hilfsmittel:
Vorteile digitaler Filter
 Digitale Filter Vorteile digitaler Filter DF haben Eigenschaften, die mit analogen Filtern nicht realisiert werden können (z.b. lineare Phase). DF sind unabhängig von der Betriebsumgebung (z.b. Temperatur)
Digitale Filter Vorteile digitaler Filter DF haben Eigenschaften, die mit analogen Filtern nicht realisiert werden können (z.b. lineare Phase). DF sind unabhängig von der Betriebsumgebung (z.b. Temperatur)
Klausur zur Vorlesung Digitale Signalverarbeitung
 INSTITUT FÜR THEORETISCHE NACHRICHTENTECHNIK UND INFORMATIONSVERARBEITUNG UNIVERSITÄT HANNOVER Appelstraße 9A 3067 Hannover Klausur zur Vorlesung Digitale Signalverarbeitung Datum: 5.0.005 Uhrzeit: 09:00
INSTITUT FÜR THEORETISCHE NACHRICHTENTECHNIK UND INFORMATIONSVERARBEITUNG UNIVERSITÄT HANNOVER Appelstraße 9A 3067 Hannover Klausur zur Vorlesung Digitale Signalverarbeitung Datum: 5.0.005 Uhrzeit: 09:00
Signale, Transformationen
 Signale, Transformationen Signal: Funktion s(t), t reell (meist t die Zeit, s eine Messgröße) bzw Zahlenfolge s k = s[k], k ganzzahlig s reell oder komplex s[k] aus s(t): Abtastung mit t = kt s, s[k] =
Signale, Transformationen Signal: Funktion s(t), t reell (meist t die Zeit, s eine Messgröße) bzw Zahlenfolge s k = s[k], k ganzzahlig s reell oder komplex s[k] aus s(t): Abtastung mit t = kt s, s[k] =
3. Quantisierte IIR-Filter R
 . Zweierkomplement a) Wie sieht die binäre Darstellung von -5 aus bei den Wortbreiten b = 4, b =, b = 6? b) Berechnen Sie folgende Additionen im Format SINT(4). Geben Sie bei Überlauf auch die Ausgaben
. Zweierkomplement a) Wie sieht die binäre Darstellung von -5 aus bei den Wortbreiten b = 4, b =, b = 6? b) Berechnen Sie folgende Additionen im Format SINT(4). Geben Sie bei Überlauf auch die Ausgaben
9. Vorlesung. Systemtheorie für Informatiker. Dr. Christoph Grimm. Professur Prof. Dr. K. Waldschmidt, Univ. Frankfurt/Main
 9. Vorlesung Systemtheorie für Informatiker Dr. Christoph Grimm Professur Prof. Dr. K. Waldschmidt, Univ. Frankfurt/Main Letzte Woche: Abtastung und Rekonstruktion Abtastung: Wandelt bandbegrenzte kontinuierliche
9. Vorlesung Systemtheorie für Informatiker Dr. Christoph Grimm Professur Prof. Dr. K. Waldschmidt, Univ. Frankfurt/Main Letzte Woche: Abtastung und Rekonstruktion Abtastung: Wandelt bandbegrenzte kontinuierliche
Filterentwurf. Aufgabe
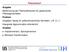 Aufgabe Filterentwurf Bestimmung der Filterkoeffizienten für gewünschte Filtereigenschaften Problem Vorgaben häufig für zeitkontinuierliches Verhalten, z.b. H c (s) Geeignete Approximation erforderlich
Aufgabe Filterentwurf Bestimmung der Filterkoeffizienten für gewünschte Filtereigenschaften Problem Vorgaben häufig für zeitkontinuierliches Verhalten, z.b. H c (s) Geeignete Approximation erforderlich
Übung 6: Analyse LTD-Systeme
 ZHAW, DSV, FS2009, Übung 6: Analyse LTD-Systeme Aufgabe : Pol-Nullstellendarstellung, UTF und Differenzengleichung. Die folgenden Pol-Nullstellen-Darstellungen charakterisieren verschiedene LTD- Systeme,
ZHAW, DSV, FS2009, Übung 6: Analyse LTD-Systeme Aufgabe : Pol-Nullstellendarstellung, UTF und Differenzengleichung. Die folgenden Pol-Nullstellen-Darstellungen charakterisieren verschiedene LTD- Systeme,
Test = 28 Punkte. 1: 2: 3: 4: 5: Punkte: Note:
 ZHAW, DSV1, FS2010, Rumc, 1 Test 1 5 + 5 + 5 + 8 + 5 = 28 Punkte Name: Vorname: 1: 2: : 4: 5: Punkte: Note: Aufgabe 1: AD-DA-System. + 1 + 1 = 5 Punkte Das analoge Signal x a (t) = cos(2πf 0 t), f 0 =750
ZHAW, DSV1, FS2010, Rumc, 1 Test 1 5 + 5 + 5 + 8 + 5 = 28 Punkte Name: Vorname: 1: 2: : 4: 5: Punkte: Note: Aufgabe 1: AD-DA-System. + 1 + 1 = 5 Punkte Das analoge Signal x a (t) = cos(2πf 0 t), f 0 =750
Digitale Signalverarbeitung, Vorlesung 7 - IIR-Filterentwurf
 Digitale Signalverarbeitung, Vorlesung 7 - IIR-Filterentwurf 5. Dezember 2016 Siehe begleitend: Kammeyer / Kroschel, Digitale Signalverarbeitung, 7. Auflage, Kapitel 4.2 1 Filterentwurfsstrategien 2 Diskretisierung
Digitale Signalverarbeitung, Vorlesung 7 - IIR-Filterentwurf 5. Dezember 2016 Siehe begleitend: Kammeyer / Kroschel, Digitale Signalverarbeitung, 7. Auflage, Kapitel 4.2 1 Filterentwurfsstrategien 2 Diskretisierung
MusterModulprüfung. Anteil Transformationen
 MusterModulprüfung Anteil Transformationen Studiengang: Elektrotechnik oder Energiewirtschaft Datum: Prüfer: heute Prof. Dr. Felderhoff Version:.0 (vom 30.1.014) Name: Vorname: Matr.-Nr.: 1 Aufgabe 1 Fourier-Transformation
MusterModulprüfung Anteil Transformationen Studiengang: Elektrotechnik oder Energiewirtschaft Datum: Prüfer: heute Prof. Dr. Felderhoff Version:.0 (vom 30.1.014) Name: Vorname: Matr.-Nr.: 1 Aufgabe 1 Fourier-Transformation
Fouriertransformation, z-transformation, Differenzenglei- chung
 Kommunikationstechnik II 1.Übungstermin 31.10.2007 Fouriertransformation, z-transformation, Differenzenglei- Wiederholung: chung Als Ergänzung dieser sehr knapp gehaltenen Wiederholung wird empfohlen:
Kommunikationstechnik II 1.Übungstermin 31.10.2007 Fouriertransformation, z-transformation, Differenzenglei- Wiederholung: chung Als Ergänzung dieser sehr knapp gehaltenen Wiederholung wird empfohlen:
Filterentwurf. Bernd Edler Laboratorium für Informationstechnologie DigSig - Teil 11
 Filterentwurf IIR-Filter Beispiele für die verschiedenen Filtertypen FIR-Filter Entwurf mit inv. Fouriertransformation und Fensterfunktion Filter mit Tschebyscheff-Verhalten Vorgehensweise bei Matlab /
Filterentwurf IIR-Filter Beispiele für die verschiedenen Filtertypen FIR-Filter Entwurf mit inv. Fouriertransformation und Fensterfunktion Filter mit Tschebyscheff-Verhalten Vorgehensweise bei Matlab /
Datenaquisition. Verstärker Filter. Sensor ADC. Objekt. Rechner
 Datenaquisition Sensor Verstärker Filter ADC Objekt Rechner Datenaquisition Verstärker: - linearer Arbeitsbereich - linearer Frequenzgang - Vorkehrungen gegen Übersteuerung (trends, shot noise) - Verstärkerrauschen
Datenaquisition Sensor Verstärker Filter ADC Objekt Rechner Datenaquisition Verstärker: - linearer Arbeitsbereich - linearer Frequenzgang - Vorkehrungen gegen Übersteuerung (trends, shot noise) - Verstärkerrauschen
Betrachtetes Systemmodell
 Betrachtetes Systemmodell Wir betrachten ein lineares zeitinvariantes System mit der Impulsantwort h(t), an dessen Eingang das Signal x(t) anliegt. Das Ausgangssignal y(t) ergibt sich dann als das Faltungsprodukt
Betrachtetes Systemmodell Wir betrachten ein lineares zeitinvariantes System mit der Impulsantwort h(t), an dessen Eingang das Signal x(t) anliegt. Das Ausgangssignal y(t) ergibt sich dann als das Faltungsprodukt
Digitale Signalverarbeitung Bernd Edler
 Digitale Signalverarbeitung Bernd Edler Wintersemester 2008/2009 Wesentliche Inhalte der Vorlesung Abtastung z-transformation Lineare zeitinvariante Systeme Diskrete Fouriertransformation Systeme bei stochastischer
Digitale Signalverarbeitung Bernd Edler Wintersemester 2008/2009 Wesentliche Inhalte der Vorlesung Abtastung z-transformation Lineare zeitinvariante Systeme Diskrete Fouriertransformation Systeme bei stochastischer
Elektronik Prof. Dr.-Ing. Heinz Schmidt-Walter
 6. Aktive Filter Filterschaltungen sind Schaltungen mit einer frequenzabhängigen Übertragungsfunktion. Man unterscheidet zwischen Tief, Hoch und Bandpässen sowie Sperrfiltern. Diesen Filtern ist gemeinsam,
6. Aktive Filter Filterschaltungen sind Schaltungen mit einer frequenzabhängigen Übertragungsfunktion. Man unterscheidet zwischen Tief, Hoch und Bandpässen sowie Sperrfiltern. Diesen Filtern ist gemeinsam,
Übung 3: Fouriertransformation
 ZHAW, SiSy HS202, Rumc, Übung 3: Fouriertransformation Aufgabe Fouriertransformation Dirac-Impuls. a) Bestimmen Sie die Fouriertransformierte S(f) des Dirac-Impulses s(t) = δ(t) und interpretieren Sie
ZHAW, SiSy HS202, Rumc, Übung 3: Fouriertransformation Aufgabe Fouriertransformation Dirac-Impuls. a) Bestimmen Sie die Fouriertransformierte S(f) des Dirac-Impulses s(t) = δ(t) und interpretieren Sie
1.3 Digitale Audiosignale
 Seite 22 von 86 Abb. 1.2.12 - Wirkung der Schallverzögerung Effekte sind: Delay, Echo, Reverb, Flanger und Chorus Hört man ein akustisches Signal im Raum, dann werden die Signale von Wänden und anderen
Seite 22 von 86 Abb. 1.2.12 - Wirkung der Schallverzögerung Effekte sind: Delay, Echo, Reverb, Flanger und Chorus Hört man ein akustisches Signal im Raum, dann werden die Signale von Wänden und anderen
Lösungsblatt 2 Signalverarbeitung und Klassifikation
 Fakultät für Informatik Übung zu Kognitive Systeme Sommersemester 06 M. Sperber (matthias.sperber@kit.edu) S. Nguyen (thai.nguyen@kit.edu) Lösungsblatt Signalverarbeitung und Klassifikation Aufgabe : Faltung
Fakultät für Informatik Übung zu Kognitive Systeme Sommersemester 06 M. Sperber (matthias.sperber@kit.edu) S. Nguyen (thai.nguyen@kit.edu) Lösungsblatt Signalverarbeitung und Klassifikation Aufgabe : Faltung
Grundlagen der Signalverarbeitung
 Grundlagen der Signalverarbeitung Digitale und analoge Filter Wintersemester 6/7 Wiederholung Übertragung eines sinusförmigen Signals u t = U sin(ω t) y t = Y sin ω t + φ ω G(ω) Amplitude: Y = G ω U Phase:
Grundlagen der Signalverarbeitung Digitale und analoge Filter Wintersemester 6/7 Wiederholung Übertragung eines sinusförmigen Signals u t = U sin(ω t) y t = Y sin ω t + φ ω G(ω) Amplitude: Y = G ω U Phase:
und mit t in Sekunden wird mit einer Frequenz von 8000 Hz abgetastet. Die Abtastung beginnt bei t=0 mit dem Zeitindex n=0.
 Aufgabe 1 Das periodische Signal x t) 0,5 sin(2 f t) 0,5 cos(2 f t) mit f 1000Hz und mit f 2000Hz ( 1 2 1 2 und mit t in Sekunden wird mit einer Frequenz von 8000 Hz abgetastet. Die Abtastung beginnt bei
Aufgabe 1 Das periodische Signal x t) 0,5 sin(2 f t) 0,5 cos(2 f t) mit f 1000Hz und mit f 2000Hz ( 1 2 1 2 und mit t in Sekunden wird mit einer Frequenz von 8000 Hz abgetastet. Die Abtastung beginnt bei
Seminar Digitale Signalverarbeitung Thema: Digitale Filter
 Seminar Digitale Signalverarbeitung Thema: Digitale Filter Autor: Daniel Arnold Universität Koblenz-Landau, August 2005 Inhaltsverzeichnis i 1 Einführung 1.1 Allgemeine Informationen Digitale Filter sind
Seminar Digitale Signalverarbeitung Thema: Digitale Filter Autor: Daniel Arnold Universität Koblenz-Landau, August 2005 Inhaltsverzeichnis i 1 Einführung 1.1 Allgemeine Informationen Digitale Filter sind
Digitale Signalverarbeitung mit MATLAB
 Martin Werner Digitale Signalverarbeitung mit MATLAB Grundkurs mit 16 ausführlichen Versuchen 4., durchgesehene und ergänzte Auflage Mit 180 Abbildungen und 76 Tabellen STUDIUM VIEWEG+ TEUBNER 1 Erste
Martin Werner Digitale Signalverarbeitung mit MATLAB Grundkurs mit 16 ausführlichen Versuchen 4., durchgesehene und ergänzte Auflage Mit 180 Abbildungen und 76 Tabellen STUDIUM VIEWEG+ TEUBNER 1 Erste
Prüfung zur Vorlesung Signalverarbeitung am Name MatrNr. StudKennz.
 442.0 Signalverarbeitung (2VO) Prüfung 8.3.26 Institut für Signalverarbeitung und Sprachkommunikation Prof. G. Kubin Technische Universität Graz Prüfung zur Vorlesung Signalverarbeitung am 8.3.26 Name
442.0 Signalverarbeitung (2VO) Prüfung 8.3.26 Institut für Signalverarbeitung und Sprachkommunikation Prof. G. Kubin Technische Universität Graz Prüfung zur Vorlesung Signalverarbeitung am 8.3.26 Name
Verzerrungsfreies System
 Verzerrungsfreies System x(n) y(n) n n x(n) h(n) y(n) y(n) A 0 x(n a) A 0 x(n) (n a) h(n) A 0 (n a) H(z) A 0 z a Digitale Signalverarbeitung Liedtke 8.1.1 Erzeugung einer linearen Phase bei beliebigem
Verzerrungsfreies System x(n) y(n) n n x(n) h(n) y(n) y(n) A 0 x(n a) A 0 x(n) (n a) h(n) A 0 (n a) H(z) A 0 z a Digitale Signalverarbeitung Liedtke 8.1.1 Erzeugung einer linearen Phase bei beliebigem
Schnelle Fouriertransformation (FFT)
 Schnelle Fouriertransformation (FFT) Inhaltsverzeichnis 1 Schnelle Fouriertransformation (FFT)... 3 1.1 Das Realtime-Konzept der Goldammer-Messkarten... 3 1.2 Das Abtasttheorem oder Regeln für die Abtastung
Schnelle Fouriertransformation (FFT) Inhaltsverzeichnis 1 Schnelle Fouriertransformation (FFT)... 3 1.1 Das Realtime-Konzept der Goldammer-Messkarten... 3 1.2 Das Abtasttheorem oder Regeln für die Abtastung
Signale und Systeme I
 FACULTY OF ENGNEERING CHRISTIAN-ALBRECHTS-UNIVERSITÄT ZU KIEL DIGITAL SIGNAL PROCESSING AND SYSTEM THEORY DSS Signale und Systeme I Musterlösung zur Modulklausur WS 010/011 Prüfer: Prof. Dr.-Ing. Gerhard
FACULTY OF ENGNEERING CHRISTIAN-ALBRECHTS-UNIVERSITÄT ZU KIEL DIGITAL SIGNAL PROCESSING AND SYSTEM THEORY DSS Signale und Systeme I Musterlösung zur Modulklausur WS 010/011 Prüfer: Prof. Dr.-Ing. Gerhard
Tontechnik 2. Digitale Filter. Digitale Filter. Zuordnung diskrete digitale Signale neue diskrete digitale Signale
 Tontechnik 2 Digitale Filter Audiovisuelle Medien HdM Stuttgart Digitale Filter Zuordnung diskrete digitale Signale neue diskrete digitale Signale lineares, zeitinvariantes, diskretes System (LTD-System)
Tontechnik 2 Digitale Filter Audiovisuelle Medien HdM Stuttgart Digitale Filter Zuordnung diskrete digitale Signale neue diskrete digitale Signale lineares, zeitinvariantes, diskretes System (LTD-System)
Erweiterung einer digitalen Übertragungsstrecke mit Einplatinencomputern zur Signalanalyse
 Erweiterung einer digitalen mit Einplatinencomputern Alexander Frömming Mario Becker p.1 Inhalt 1 Ausgangssituation 2 Zielsetzung 3 Theoretische Grundlagen 4 Umsetzung - Hardware 5 Umsetzung - Software
Erweiterung einer digitalen mit Einplatinencomputern Alexander Frömming Mario Becker p.1 Inhalt 1 Ausgangssituation 2 Zielsetzung 3 Theoretische Grundlagen 4 Umsetzung - Hardware 5 Umsetzung - Software
ZHAW, DSV1, FS2010, Rumc, 1. H(z) a) Zeichnen Sie direkt auf das Aufgabenblatt das Betragsspektrum an der Stelle 1.
 ZHAW, DSV, FS200, Rumc, DSV Modulprüfung 7 + 4 + 5 + 8 + 6 = 30 Punkte Name: Vorname: : 2: 3: 4: 5: Punkte: Note: Aufgabe : AD-DA-Umsetzung. + + +.5 +.5 + = 7 Punkte Betrachten Sie das folgende digitale
ZHAW, DSV, FS200, Rumc, DSV Modulprüfung 7 + 4 + 5 + 8 + 6 = 30 Punkte Name: Vorname: : 2: 3: 4: 5: Punkte: Note: Aufgabe : AD-DA-Umsetzung. + + +.5 +.5 + = 7 Punkte Betrachten Sie das folgende digitale
Aufgabe 1 - Pegelrechnung und LTI-Systeme
 KLAUSUR Nachrichtentechnik 06.08.0 Prof. Dr.-Ing. Dr. h.c. G. Fettweis Dauer: 0 min. Aufgabe 3 4 Punkte 5 0 4 50 Aufgabe - Pegelrechnung und LTI-Systeme Hinweis: Die Teilaufgaben (a), (b) und (c) können
KLAUSUR Nachrichtentechnik 06.08.0 Prof. Dr.-Ing. Dr. h.c. G. Fettweis Dauer: 0 min. Aufgabe 3 4 Punkte 5 0 4 50 Aufgabe - Pegelrechnung und LTI-Systeme Hinweis: Die Teilaufgaben (a), (b) und (c) können
Zusammenfassung der 1. Vorlesung
 Zusammenfassung der 1. Vorlesung Einordnung und Motivation Grundlegende Definitionen Kontinuierliches Signal Zeitdiskretes Signal Quantisiertes Signal Digitales Signal Kontinuierliches System Abtastsystem
Zusammenfassung der 1. Vorlesung Einordnung und Motivation Grundlegende Definitionen Kontinuierliches Signal Zeitdiskretes Signal Quantisiertes Signal Digitales Signal Kontinuierliches System Abtastsystem
Digitale Signalverarbeitung
 Daniel Ch. von Grünigen Digitale Signalverarbeitung mit einer Einführung in die kontinuierlichen Signale und Systeme 4. Auflage Mit 222 Bildern, 91 Beispielen, 80 Aufgaben sowie einer CD-ROM mit Lösungen
Daniel Ch. von Grünigen Digitale Signalverarbeitung mit einer Einführung in die kontinuierlichen Signale und Systeme 4. Auflage Mit 222 Bildern, 91 Beispielen, 80 Aufgaben sowie einer CD-ROM mit Lösungen
Einführung in die digitale Signalverarbeitung WS11/12
 Einführung in die digitale Signalverarbeitung WS11/12 Prof. Dr. Stefan Weinzierl Musterlösung 11. Aufgabenblatt 1. IIR-Filter 1.1 Laden Sie in Matlab eine Audiodatei mit Sampling-Frequenz von fs = 44100
Einführung in die digitale Signalverarbeitung WS11/12 Prof. Dr. Stefan Weinzierl Musterlösung 11. Aufgabenblatt 1. IIR-Filter 1.1 Laden Sie in Matlab eine Audiodatei mit Sampling-Frequenz von fs = 44100
Inhaltsverzeichnis. Daniel von Grünigen. Digitale Signalverarbeitung. mit einer Einführung in die kontinuierlichen Signale und Systeme
 Inhaltsverzeichnis Daniel von Grünigen Digitale Signalverarbeitung mit einer Einführung in die kontinuierlichen Signale und Systeme ISBN (Buch): 978-3-446-44079-1 ISBN (E-Book): 978-3-446-43991-7 Weitere
Inhaltsverzeichnis Daniel von Grünigen Digitale Signalverarbeitung mit einer Einführung in die kontinuierlichen Signale und Systeme ISBN (Buch): 978-3-446-44079-1 ISBN (E-Book): 978-3-446-43991-7 Weitere
B Anhang B: Enhanced Resolution
 B Anhang B: Enhanced Resolution Digitales Filtern (Enhanced Resolution) Vorteile Realisierung Die verfügbare Abtastrate der LeCroy-Oszilloskope ist oft höher, als für die Bandbreite des zu analysierenden
B Anhang B: Enhanced Resolution Digitales Filtern (Enhanced Resolution) Vorteile Realisierung Die verfügbare Abtastrate der LeCroy-Oszilloskope ist oft höher, als für die Bandbreite des zu analysierenden
5. Meßfehler. Zufällige Messfehler machen das Ergebnis unsicher - ihre Abschätzung ist nur unter Verwendung statistischer Methoden durchführbar
 5. Meßfehler Man unterscheidet... zufällige Meßfehler systematische Meßfehler Zufällige Messfehler machen das Ergebnis unsicher - ihre Abschätzung ist nur unter Verwendung statistischer Methoden durchführbar
5. Meßfehler Man unterscheidet... zufällige Meßfehler systematische Meßfehler Zufällige Messfehler machen das Ergebnis unsicher - ihre Abschätzung ist nur unter Verwendung statistischer Methoden durchführbar
Versuch 5: Filterentwurf
 Ziele In diesem Versuch lernen Sie den Entwurf digitaler Filter, ausgehend von der Festlegung eines Toleranzschemas für den Verlauf der spektralen Charakteristik des Filters, kennen. Es können Filtercharakteristiken
Ziele In diesem Versuch lernen Sie den Entwurf digitaler Filter, ausgehend von der Festlegung eines Toleranzschemas für den Verlauf der spektralen Charakteristik des Filters, kennen. Es können Filtercharakteristiken
Aufgabe: Summe Punkte (max.): Punkte:
 ZUNAME:.................................... VORNAME:.................................... MAT. NR.:................................... 2. Teilprüfung 389.055 A Signale und Systeme 2 Institute of Telecommunications
ZUNAME:.................................... VORNAME:.................................... MAT. NR.:................................... 2. Teilprüfung 389.055 A Signale und Systeme 2 Institute of Telecommunications
,Faltung. Heavisidefunktion σ (t), Diracimpuls δ (t) Anwendungen. 1) Rechteckimpuls. 2) Sprungfunktionen. 3) Schaltvorgänge
 Heavisidefunktion σ (t), Diracimpuls δ (t),faltung Definition Heavisidefunktion, t > 0 σ ( t) = 0, t < 0 Anwendungen ) Rechteckimpuls, t < T r( t) = = σ ( t + T ) σ ( t T ) 0, t > T 2) Sprungfunktionen,
Heavisidefunktion σ (t), Diracimpuls δ (t),faltung Definition Heavisidefunktion, t > 0 σ ( t) = 0, t < 0 Anwendungen ) Rechteckimpuls, t < T r( t) = = σ ( t + T ) σ ( t T ) 0, t > T 2) Sprungfunktionen,
Skriptum zur 2. Laborübung. Transiente Vorgänge und Frequenzverhalten
 Elektrotechnische Grundlagen (LU 182.692) Skriptum zur 2. Laborübung Transiente Vorgänge und Frequenzverhalten Martin Delvai Wolfgang Huber Andreas Steininger Thomas Handl Bernhard Huber Christof Pitter
Elektrotechnische Grundlagen (LU 182.692) Skriptum zur 2. Laborübung Transiente Vorgänge und Frequenzverhalten Martin Delvai Wolfgang Huber Andreas Steininger Thomas Handl Bernhard Huber Christof Pitter
Digitale Signalverarbeitungssysteme II: Praktikum 1
 Digitale Signalverarbeitungssysteme II: Praktikum 1 Emil Matus 18. November 2010 Technische Universität Dresden Mobile Communications Systems Chair Tel.: +49 351 463 41021 Fax : +49 351 463 41099 Mail:
Digitale Signalverarbeitungssysteme II: Praktikum 1 Emil Matus 18. November 2010 Technische Universität Dresden Mobile Communications Systems Chair Tel.: +49 351 463 41021 Fax : +49 351 463 41099 Mail:
PP Physikalisches Pendel
 PP Physikalisches Pendel Blockpraktikum Frühjahr 2007 (Gruppe 2) 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Ungedämpftes physikalisches Pendel.......... 2 2.2 Dämpfung
PP Physikalisches Pendel Blockpraktikum Frühjahr 2007 (Gruppe 2) 25. April 2007 Inhaltsverzeichnis 1 Einführung 2 2 Theoretische Grundlagen 2 2.1 Ungedämpftes physikalisches Pendel.......... 2 2.2 Dämpfung
Beate Meffert, Olaf Hochmuth: Werkzeuge der Signalverarbeitung, Pearson 2004
 4 Signalverarbeitung 4.1! Grundbegriffe! 4.2! Frequenzspektren, Fourier-Transformation! 4.3! Abtasttheorem: Eine zweite Sicht Weiterführende Literatur (z.b.):!! Beate Meffert, Olaf Hochmuth: Werkzeuge
4 Signalverarbeitung 4.1! Grundbegriffe! 4.2! Frequenzspektren, Fourier-Transformation! 4.3! Abtasttheorem: Eine zweite Sicht Weiterführende Literatur (z.b.):!! Beate Meffert, Olaf Hochmuth: Werkzeuge
Beate Meffert, Olaf Hochmuth: Werkzeuge der Signalverarbeitung, Pearson Ludwig-Maximilians-Universität München Prof. Hußmann Digitale Medien 4-1
 4. Signalverarbeitung 4.1 Grundbegrie 4.2 Frequenzspektren, Fourier-Transormation 4.3 Abtasttheorem: Eine zweite Sicht 4.4 Filter Weiterührende Literatur (z.b.): Beate Meert, Ola Hochmuth: Werkzeuge der
4. Signalverarbeitung 4.1 Grundbegrie 4.2 Frequenzspektren, Fourier-Transormation 4.3 Abtasttheorem: Eine zweite Sicht 4.4 Filter Weiterührende Literatur (z.b.): Beate Meert, Ola Hochmuth: Werkzeuge der
Allpass-Transformation
 Grundidee: Allpass-Transformation Entwurf eines IIR-Filters H p (z) mit bekanntem Verfahren Abbildung des Frequenzgangs durch Transformation der Frequenzvariablen Transformation durch Substitution ζ =
Grundidee: Allpass-Transformation Entwurf eines IIR-Filters H p (z) mit bekanntem Verfahren Abbildung des Frequenzgangs durch Transformation der Frequenzvariablen Transformation durch Substitution ζ =
Zu Beginn der Vorlesung Signale und Systeme ausgegebene Übungsaufgaben V 1.2
 Leibniz Universität Hannover Institut für Kommunikationstechnik Prof. Dr. J. Peissig Zu Beginn der Vorlesung Signale und Systeme ausgegebene Übungsaufgaben V 1.2 Universität Hannover, Institut für Kommunikationstechnik,
Leibniz Universität Hannover Institut für Kommunikationstechnik Prof. Dr. J. Peissig Zu Beginn der Vorlesung Signale und Systeme ausgegebene Übungsaufgaben V 1.2 Universität Hannover, Institut für Kommunikationstechnik,
Versuch 3: Anwendungen der schnellen Fourier-Transformation (FFT)
 Versuch 3: Anwendungen der schnellen Fourier-Transformation (FFT) Ziele In diesem Versuch lernen Sie zwei Anwendungen der Diskreten Fourier-Transformation in der Realisierung als recheneffiziente schnelle
Versuch 3: Anwendungen der schnellen Fourier-Transformation (FFT) Ziele In diesem Versuch lernen Sie zwei Anwendungen der Diskreten Fourier-Transformation in der Realisierung als recheneffiziente schnelle
Systemtheorie Teil B
 d + d z + c d z + c uk d + + yk z d + c d z + c Systemtheorie Teil B - Zeitdiskrete Signale und Systeme Übungsaufgaben Manfred Strohrmann Urban Brunner Inhalt Übungsaufgaben - Signalabtastung und Rekonstruktion...
d + d z + c d z + c uk d + + yk z d + c d z + c Systemtheorie Teil B - Zeitdiskrete Signale und Systeme Übungsaufgaben Manfred Strohrmann Urban Brunner Inhalt Übungsaufgaben - Signalabtastung und Rekonstruktion...
Dynamische Systeme und Zeitreihenanalyse // Komplexe Zahlen 3 p.2/29
 Dynamische Systeme und Zeitreihenanalyse Komplexe Zahlen Kapitel 3 Statistik und Mathematik WU Wien Michael Hauser Dynamische Systeme und Zeitreihenanalyse // Komplexe Zahlen 3 p.0/29 Motivation Für die
Dynamische Systeme und Zeitreihenanalyse Komplexe Zahlen Kapitel 3 Statistik und Mathematik WU Wien Michael Hauser Dynamische Systeme und Zeitreihenanalyse // Komplexe Zahlen 3 p.0/29 Motivation Für die
Prüfungsklausur Digitale Signalverarbeitung Ergebnis der Klausur
 Fakultät für Mathematik und Informatik Elektronische Schaltungen 58084 Hagen 02331 987 1166 Prüfungsklausur Digitale Signalverarbeitung 21411 Datum: 19. März 2011 (Bearbeitungszeit 120 Minuten, 6 Blätter)
Fakultät für Mathematik und Informatik Elektronische Schaltungen 58084 Hagen 02331 987 1166 Prüfungsklausur Digitale Signalverarbeitung 21411 Datum: 19. März 2011 (Bearbeitungszeit 120 Minuten, 6 Blätter)
3. Fourieranalyse und Amplitudenspektren
 3.1 Fourieranalyse 3.1.1 Einleitung Laut dem französischen Mathematiker Fourier (1768-1830) kann jedes periodische Signal in eine Summe von sinusförmigen Signalen mit unterschiedlichen Amplituden, Frequenzen
3.1 Fourieranalyse 3.1.1 Einleitung Laut dem französischen Mathematiker Fourier (1768-1830) kann jedes periodische Signal in eine Summe von sinusförmigen Signalen mit unterschiedlichen Amplituden, Frequenzen
2. Digitale Codierung und Übertragung
 2. Digitale Codierung und Übertragung 2.1 Informationstheoretische Grundlagen 2.2 Speicherbedarf und Kompression 2.3 Digitalisierung Ludwig-Maximilians-Universität München Prof. Hußmann Digitale Medien
2. Digitale Codierung und Übertragung 2.1 Informationstheoretische Grundlagen 2.2 Speicherbedarf und Kompression 2.3 Digitalisierung Ludwig-Maximilians-Universität München Prof. Hußmann Digitale Medien
filter Filter Ziele Parameter Entwurf
 1 Filter Ziele Parameter Entwurf 2.3.2007 2 Beschreibung Pol-Nullstellen- Diagramm Übertragungsfunktion H(z) Differenzengleichung y(n) Impulsantwort h(n): Finite Impulse Response (FIR) Infinite Impulse
1 Filter Ziele Parameter Entwurf 2.3.2007 2 Beschreibung Pol-Nullstellen- Diagramm Übertragungsfunktion H(z) Differenzengleichung y(n) Impulsantwort h(n): Finite Impulse Response (FIR) Infinite Impulse
FH Jena Prüfungsaufgaben - Master Prof. Giesecke FB ET/IT Digitale Signalverarbeitung SS 2012
 FB ET/IT Digitale Signalverarbeitung SS 0 Name, Vorname: Matr.-Nr.: Zugelassene Hilfsmittel: beliebiger Taschenrechner ein mathematisches Formelwerk eine selbsterstellte Formelsammlung Wichtige Hinweise:
FB ET/IT Digitale Signalverarbeitung SS 0 Name, Vorname: Matr.-Nr.: Zugelassene Hilfsmittel: beliebiger Taschenrechner ein mathematisches Formelwerk eine selbsterstellte Formelsammlung Wichtige Hinweise:
Warum z-transformation?
 -Transformation Warum -Transformation? Die -Transformation führt Polynome und rationale Funktionen in die Analyse der linearen eitdiskreten Systeme ein. Die Faltung geht über in die Multiplikation von
-Transformation Warum -Transformation? Die -Transformation führt Polynome und rationale Funktionen in die Analyse der linearen eitdiskreten Systeme ein. Die Faltung geht über in die Multiplikation von
- Sei r(x,y) Eingangsbild, dass nur Rauschen (Quantenrauschen) enthält.
 Eingang System Ausgang - Sei r(x,y) Eingangsbild, dass nur (Quantenrauschen) enthält. - Das Bild enthalte keinerlei Information, d.h. das Spektrum ist weiß und es gibt keine Korrelationen zwischen den
Eingang System Ausgang - Sei r(x,y) Eingangsbild, dass nur (Quantenrauschen) enthält. - Das Bild enthalte keinerlei Information, d.h. das Spektrum ist weiß und es gibt keine Korrelationen zwischen den
Fahrzeugmechatronik Masterstudiengang M 3.2 Sensoren und Aktoren Labor für Automatisierung und Dynamik AuD FB 03MB
 Abb. 6 Dreidimensionale Darstellung des Frequenzgangs G ATP () s, Achsteilungen s 2 π in Hz Prof. Dr. Höcht 1/29 18.06.2006 11:13 Z_ Abb. 7 Einfluß des Pols bei s imaginären Achse, Achsteilungen in Hz
Abb. 6 Dreidimensionale Darstellung des Frequenzgangs G ATP () s, Achsteilungen s 2 π in Hz Prof. Dr. Höcht 1/29 18.06.2006 11:13 Z_ Abb. 7 Einfluß des Pols bei s imaginären Achse, Achsteilungen in Hz
Digitale Signalverarbeitung Übungsaufgaben
 Kapitel : Einleitung -: Analoger Tiefpass Dieser Tiefpass mit den Werten R = Ω, L =.5mH R L und C =.5µF ist wie folgt zu analysieren: U e C R. Es springe U e bei t =.5ms auf 5V und bei t = ms wieder auf.
Kapitel : Einleitung -: Analoger Tiefpass Dieser Tiefpass mit den Werten R = Ω, L =.5mH R L und C =.5µF ist wie folgt zu analysieren: U e C R. Es springe U e bei t =.5ms auf 5V und bei t = ms wieder auf.
Einführung in die Elektronik für Physiker
 Hartmut Gemmeke Forschungszentrum Karlsruhe, IPE gemmeke@ipe.fzk.de Tel.: 0747-8-5635 Einführung in die Elektronik für Physiker 4. Breitbanderstärker und analoge aktie Filter. HF-Verhalten on Operationserstärkern.
Hartmut Gemmeke Forschungszentrum Karlsruhe, IPE gemmeke@ipe.fzk.de Tel.: 0747-8-5635 Einführung in die Elektronik für Physiker 4. Breitbanderstärker und analoge aktie Filter. HF-Verhalten on Operationserstärkern.
x[n-1] x[n] x[n+1] y[n-1] y[n+1]
![x[n-1] x[n] x[n+1] y[n-1] y[n+1] x[n-1] x[n] x[n+1] y[n-1] y[n+1]](/thumbs/72/67333121.jpg) Systeme System Funtion f, die ein Eingangssignal x in ein Ausgangssignal y überführt. zeitdisretes System Ein- und Ausgangssignal sind nur für disrete Zeitpunte definiert y[n] = f (.., x[n-1], x[n], x[n+1],
Systeme System Funtion f, die ein Eingangssignal x in ein Ausgangssignal y überführt. zeitdisretes System Ein- und Ausgangssignal sind nur für disrete Zeitpunte definiert y[n] = f (.., x[n-1], x[n], x[n+1],
1. Klausur Elektrische Netzwerke Veröffentlichte Musterklausur Name:... Vorname:... Matr.-Nr.:... Bewertung. Bearbeitungszeit: 135 Minuten
 1. Klausur Elektrische Netzwerke Veröffentlichte Musterklausur 2013 Name:............................. Vorname:............................. Matr.-Nr.:............................. Bearbeitungszeit: 135
1. Klausur Elektrische Netzwerke Veröffentlichte Musterklausur 2013 Name:............................. Vorname:............................. Matr.-Nr.:............................. Bearbeitungszeit: 135
SYS_A - ANALYSIEREN. Statistik. NTB Druckdatum: SYS A. Histogramm (Praxis) Gaußsche Normalverteilung (Theorie) Gebrauch: bei n > 100
 SYS_A - ANALYSIEREN Statistik Gaußsche Normalverteilung (Theorie) Gebrauch: bei n > 100 Histogramm (Praxis) Realisierung Lage Streuung Zufallsvariable Dichte der Normalverteilung Verteilungsfunktion Fläche
SYS_A - ANALYSIEREN Statistik Gaußsche Normalverteilung (Theorie) Gebrauch: bei n > 100 Histogramm (Praxis) Realisierung Lage Streuung Zufallsvariable Dichte der Normalverteilung Verteilungsfunktion Fläche
d 1 P N G A L S2 d 2
 Abschlussprüfung Nachrichtentechnik 28. Juli 2014 Name:... Vorname:... Matrikelnr.:... Studiengang:... Aufgabe 1 2 3 4 Summe Note Punkte Hinweis: Die Teilaufgaben (a), (b) und (c) können unabhängig voneinander
Abschlussprüfung Nachrichtentechnik 28. Juli 2014 Name:... Vorname:... Matrikelnr.:... Studiengang:... Aufgabe 1 2 3 4 Summe Note Punkte Hinweis: Die Teilaufgaben (a), (b) und (c) können unabhängig voneinander
Digitalisierung. Digitale Übertragung analoger Signale. störsicher (0/1-Codierung, Fehlerkorrektur) präzise (fixe unveränderliche Codeworte)
 Digitale Übertragung analoger Signale Vorteile digitaler Übertragung störsicher (0/1-Codierung, Fehlerkorrektur) präzise (fixe unveränderliche Codeworte) Nachteiler digitaler Übertragung natürliche Signale
Digitale Übertragung analoger Signale Vorteile digitaler Übertragung störsicher (0/1-Codierung, Fehlerkorrektur) präzise (fixe unveränderliche Codeworte) Nachteiler digitaler Übertragung natürliche Signale
Aufgabe: Summe Punkte (max.): Punkte:
 ZUNAME:.................................... VORNAME:.................................... MAT. NR.:................................... 2. Teilprüfung 389.055 B Signale und Systeme 2 Institute of Telecommunications
ZUNAME:.................................... VORNAME:.................................... MAT. NR.:................................... 2. Teilprüfung 389.055 B Signale und Systeme 2 Institute of Telecommunications
Einführung in die Systemtheorie
 Bernd Girod, Rudolf Rabenstein, Alexander Stenger Einführung in die Systemtheorie Signale und Systeme in der Elektrotechnik und Informationstechnik 4., durchgesehene und aktualisierte Auflage Mit 388 Abbildungen
Bernd Girod, Rudolf Rabenstein, Alexander Stenger Einführung in die Systemtheorie Signale und Systeme in der Elektrotechnik und Informationstechnik 4., durchgesehene und aktualisierte Auflage Mit 388 Abbildungen
3.3.1 Digitale Filter
 Leseprobe Digitale Signalverarbeitung Abschnitt aus Algorithmische Bausteine 3.3.1 Digitale Filter In den folgenden Abschnitten sollen die digitalen Filter im Gegensatz zum Abschnitt Grundlagen der DSV
Leseprobe Digitale Signalverarbeitung Abschnitt aus Algorithmische Bausteine 3.3.1 Digitale Filter In den folgenden Abschnitten sollen die digitalen Filter im Gegensatz zum Abschnitt Grundlagen der DSV
Zeitdiskrete, digitale Filter und schnelle Fourier-Transformation (FFT)
 Zeitdiskrete, digitale Filter und schnelle Fourier-Transformation (FFT) Inhaltsverzeichnis 1 Allgemeines Filter... 2 2 Filter auf dem Signalprozessor... 2 3 Zusammenhang Zeitsignal und Frequenzspektrum...
Zeitdiskrete, digitale Filter und schnelle Fourier-Transformation (FFT) Inhaltsverzeichnis 1 Allgemeines Filter... 2 2 Filter auf dem Signalprozessor... 2 3 Zusammenhang Zeitsignal und Frequenzspektrum...
Grundlagen der Elektrotechnik 3. Übungsaufgaben
 Campus Duisburg Grundlagen der Elektrotechnik 3 Nachrichtentechnische Systeme Prof. Dr.-Ing. Ingolf Willms Version Juli 08 Aufgabe 1: Man bestimme die Fourier-Reihenentwicklung für die folgende periodische
Campus Duisburg Grundlagen der Elektrotechnik 3 Nachrichtentechnische Systeme Prof. Dr.-Ing. Ingolf Willms Version Juli 08 Aufgabe 1: Man bestimme die Fourier-Reihenentwicklung für die folgende periodische
Transformationen Übungen 1. 1 Signale und Systeme. 1.1 Gegeben ist die Funktion f(t). Skizzieren Sie folgende Funktionen: a) f(t - 3) b) f(2 t) f(t)
 Transformationen Übungen 1 1 Signale und Systeme 1.1 Gegeben ist die Funktion f(t). Skizzieren Sie folgende Funktionen: a) f(t - 3) b) f(2 t) f(t) 1 c) f(-t) d) f(t + 3) 1 t e) f(t / 4) f) f(t) + 2 g)
Transformationen Übungen 1 1 Signale und Systeme 1.1 Gegeben ist die Funktion f(t). Skizzieren Sie folgende Funktionen: a) f(t - 3) b) f(2 t) f(t) 1 c) f(-t) d) f(t + 3) 1 t e) f(t / 4) f) f(t) + 2 g)
Praktikum I PP Physikalisches Pendel
 Praktikum I PP Physikalisches Pendel Hanno Rein Betreuer: Heiko Eitel 16. November 2003 1 Ziel der Versuchsreihe In der Physik lassen sich viele Vorgänge mit Hilfe von Schwingungen beschreiben. Die klassische
Praktikum I PP Physikalisches Pendel Hanno Rein Betreuer: Heiko Eitel 16. November 2003 1 Ziel der Versuchsreihe In der Physik lassen sich viele Vorgänge mit Hilfe von Schwingungen beschreiben. Die klassische
Signale und Systeme I
 TECHNISCHE FAKULTÄT DER CHRISTIAN-ALBRECHTS-UNIVERSITÄT ZU KIEL DIGITALE SIGNALVERARBEITUNG UND SYSTEMTHEORIE DSS Signale und Systeme I Modulklausur WS 017/018 Prüfer: Prof. Dr.-Ing. Gerhard Schmidt Datum:
TECHNISCHE FAKULTÄT DER CHRISTIAN-ALBRECHTS-UNIVERSITÄT ZU KIEL DIGITALE SIGNALVERARBEITUNG UND SYSTEMTHEORIE DSS Signale und Systeme I Modulklausur WS 017/018 Prüfer: Prof. Dr.-Ing. Gerhard Schmidt Datum:
Systemtheorie abbildender Systeme
 Bandbegrenzung Bild in (b) nicht band-begrenzt: scharfe Kanten = Dirac-Funktionen = weißes Spektrum Erfordert Tapering vor Digitalisierung (Multiplikation mit geeigneter Fensterfunktion; auf Null drücken
Bandbegrenzung Bild in (b) nicht band-begrenzt: scharfe Kanten = Dirac-Funktionen = weißes Spektrum Erfordert Tapering vor Digitalisierung (Multiplikation mit geeigneter Fensterfunktion; auf Null drücken
Kommunikationstechnik II Wintersemester 07/08
 Kommunikationstechnik II Wintersemester 07/08 Prof. Dr. Stefan Weinzierl Musterlösung: 3. Aufgabenblatt. Aufgabe: Up-/Downsampling Die Abtastfolge x[n] wird mit dem Faktor M unter- und dem Faktor L überabgetastet.
Kommunikationstechnik II Wintersemester 07/08 Prof. Dr. Stefan Weinzierl Musterlösung: 3. Aufgabenblatt. Aufgabe: Up-/Downsampling Die Abtastfolge x[n] wird mit dem Faktor M unter- und dem Faktor L überabgetastet.
Musterlösung zur Klausur Digitale Signalverarbeitung
 Musterlösung zur Klausur Digitale Signalverarbeitung Arbeitsgruppe Digitale Signalverarbeitung Ruhr-Universität Bochum 1. Oktober 2007 Aufgabe 1: Transformationen 25 Pkt. Gegeben war das reellwertige kontinuierliche
Musterlösung zur Klausur Digitale Signalverarbeitung Arbeitsgruppe Digitale Signalverarbeitung Ruhr-Universität Bochum 1. Oktober 2007 Aufgabe 1: Transformationen 25 Pkt. Gegeben war das reellwertige kontinuierliche
Elektromagnetische Schwingkreise
 Grundpraktikum der Physik Versuch Nr. 28 Elektromagnetische Schwingkreise Versuchsziel: Bestimmung der Kenngrößen der Elemente im Schwingkreis 1 1. Einführung Ein elektromagnetischer Schwingkreis entsteht
Grundpraktikum der Physik Versuch Nr. 28 Elektromagnetische Schwingkreise Versuchsziel: Bestimmung der Kenngrößen der Elemente im Schwingkreis 1 1. Einführung Ein elektromagnetischer Schwingkreis entsteht
Übung Grundlagen der Elektrotechnik B
 Übung Grundlagen der Elektrotechnik B 1 Übertragungsfunktion, Filter Gegeben sei die folgende Schaltung: R U 2 1. Berechnen Sie die Übertragungsfunktion H( jω)= U 2. 2. Bestimmen Sie die Zeitkonstante.
Übung Grundlagen der Elektrotechnik B 1 Übertragungsfunktion, Filter Gegeben sei die folgende Schaltung: R U 2 1. Berechnen Sie die Übertragungsfunktion H( jω)= U 2. 2. Bestimmen Sie die Zeitkonstante.
SSYLB2 SS06 Daniel Schrenk, Andreas Unterweger Übung 8. Laborprotokoll SSY. Diskrete Systeme II: Stabilitätsbetrachtungen und Systemantwort
 SSYLB SS6 Daniel Schrenk, Andreas Unterweger Übung 8 Laborprotokoll SSY Diskrete Systeme II: Stabilitätsbetrachtungen und Systemantwort Daniel Schrenk, Andreas Unterweger, ITS 4 SSYLB SS6 Daniel Schrenk,
SSYLB SS6 Daniel Schrenk, Andreas Unterweger Übung 8 Laborprotokoll SSY Diskrete Systeme II: Stabilitätsbetrachtungen und Systemantwort Daniel Schrenk, Andreas Unterweger, ITS 4 SSYLB SS6 Daniel Schrenk,
12 3 Komplexe Zahlen. P(x y) z = x + jy
 2 3 Komplexe Zahlen 3 Komplexe Zahlen 3. Grundrechenoperationen Definition Die Menge C = {z = a + jb a, b IR; j 2 = } heißt Menge der komplexen Zahlen; j heißt imaginäre Einheit. (andere Bezeichnung: i)
2 3 Komplexe Zahlen 3 Komplexe Zahlen 3. Grundrechenoperationen Definition Die Menge C = {z = a + jb a, b IR; j 2 = } heißt Menge der komplexen Zahlen; j heißt imaginäre Einheit. (andere Bezeichnung: i)
5. Fourier-Transformation
 Fragestellungen: 5. Fourier-Transformation Bei Anregung mit einer harmonischen Last kann quasistatitisch gerechnet werden, wenn die Erregerfrequenz kleiner als etwa 30% der Resonanzfrequenz ist. Wann darf
Fragestellungen: 5. Fourier-Transformation Bei Anregung mit einer harmonischen Last kann quasistatitisch gerechnet werden, wenn die Erregerfrequenz kleiner als etwa 30% der Resonanzfrequenz ist. Wann darf
Funktion von Delta-Sigma-Wandlern zur Digitaliserung eines analogen Sensorsignals mit einer praktischen Anwendung. Dr.
 Funktion von Delta-Sigma-Wandlern zur Digitaliserung eines analogen Sensorsignals mit einer praktischen Anwendung Dr. Thomas Komarek 1 Übersicht Praktische Anwendung: Super Audio Compact Disc (SACD) Grundlagen
Funktion von Delta-Sigma-Wandlern zur Digitaliserung eines analogen Sensorsignals mit einer praktischen Anwendung Dr. Thomas Komarek 1 Übersicht Praktische Anwendung: Super Audio Compact Disc (SACD) Grundlagen
3. Leistungsdichtespektren
 Stochastische Prozesse: 3. Leistungsdichtespektren Wird das gleiche Geräusch mehrmals gemessen, so ergeben sich in der Regel unterschiedliche zeitliche Verläufe des Schalldrucks. Bei Geräuschen handelt
Stochastische Prozesse: 3. Leistungsdichtespektren Wird das gleiche Geräusch mehrmals gemessen, so ergeben sich in der Regel unterschiedliche zeitliche Verläufe des Schalldrucks. Bei Geräuschen handelt
Runde 9, Beispiel 57
 Runde 9, Beispiel 57 LVA 8.8, Übungsrunde 9,..7 Markus Nemetz, markus.nemetz@tuwien.ac.at, TU Wien, 3..7 Angabe Seien y, z C N und c, d C N ihre Spektralwerte. Außerdem bezeichne (x k ) k die N - periodische
Runde 9, Beispiel 57 LVA 8.8, Übungsrunde 9,..7 Markus Nemetz, markus.nemetz@tuwien.ac.at, TU Wien, 3..7 Angabe Seien y, z C N und c, d C N ihre Spektralwerte. Außerdem bezeichne (x k ) k die N - periodische
5. Beispiele - Filter Seite 15
 5. Beispiele - Filter Seite 15 5.2 Entwurf digitaler Filter Zur Demonstration eines rekursiv implementierten Tiefpasses (FIR Finite Impulse Response bzw. IIR Infinite Impulse Response) soll dieses Beispiel
5. Beispiele - Filter Seite 15 5.2 Entwurf digitaler Filter Zur Demonstration eines rekursiv implementierten Tiefpasses (FIR Finite Impulse Response bzw. IIR Infinite Impulse Response) soll dieses Beispiel
Im Frequenzbereich beschreiben wir das Verhalten von Systemen mit dem Komplexen Frequenzgang: G (jω)
 4 Systeme im Frequenzbereich (jω) 4.1 Allgemeines Im Frequenzbereich beschreiben wir das Verhalten von Systemen mit dem Komplexen Frequenzgang: G (jω) 1 4.2 Berechnung des Frequenzgangs Beispiel: RL-Filter
4 Systeme im Frequenzbereich (jω) 4.1 Allgemeines Im Frequenzbereich beschreiben wir das Verhalten von Systemen mit dem Komplexen Frequenzgang: G (jω) 1 4.2 Berechnung des Frequenzgangs Beispiel: RL-Filter
Kontrollfragen zum Skript Teil 1 beantwortet
 Kontrollfragen zum Skript Teil 1 beantwortet Von J.S. Hussmann Fragen zu SW 1.1 Welche Vorteile hat die DSVB? Programmierbar Parametrierbar Reproduzierbar Wie heisst die Umwandlung eines Zeit-diskreten
Kontrollfragen zum Skript Teil 1 beantwortet Von J.S. Hussmann Fragen zu SW 1.1 Welche Vorteile hat die DSVB? Programmierbar Parametrierbar Reproduzierbar Wie heisst die Umwandlung eines Zeit-diskreten
LTI-Systeme in Frequenzbereich und Zeitbereich
 LTI-Systeme in Frequenzbereich und Zeitbereich LTI-Systeme Frequenzgang, Filter Impulsfunktion und Impulsantwort, Faltung, Fourier-Transformation Spektrum, Zeitdauer-Bandbreite-Produkt Übungen Literatur
LTI-Systeme in Frequenzbereich und Zeitbereich LTI-Systeme Frequenzgang, Filter Impulsfunktion und Impulsantwort, Faltung, Fourier-Transformation Spektrum, Zeitdauer-Bandbreite-Produkt Übungen Literatur
Kapitel 3 Trigonometrische Interpolation
 Kapitel 3 Trigonometrische Interpolation Einführung in die Fourier-Reihen Trigonometrische Interpolation Schnelle Fourier-Transformation (FFT) Zusammenfassung Numerische Mathematik II Herbsttrimester 212
Kapitel 3 Trigonometrische Interpolation Einführung in die Fourier-Reihen Trigonometrische Interpolation Schnelle Fourier-Transformation (FFT) Zusammenfassung Numerische Mathematik II Herbsttrimester 212
SV1: Aktive RC-Filter
 Signal and Information Processing Laboratory Institut für Signal- und Informationsverarbeitung. September 6 Fachpraktikum Signalverarbeitung SV: Aktive RC-Filter Einführung In diesem Versuch wird ein aktives
Signal and Information Processing Laboratory Institut für Signal- und Informationsverarbeitung. September 6 Fachpraktikum Signalverarbeitung SV: Aktive RC-Filter Einführung In diesem Versuch wird ein aktives
4. Dämpfungsmodelle. 4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung. Elastodynamik 3.
 4. Dämpfungsmodelle 4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung 3.4-1 4.1 Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Dabei
4. Dämpfungsmodelle 4.1 Grundlagen 4.2 Viskose Dämpfung 4.3 Modale Dämpfung 4.4 Rayleigh-Dämpfung 4.5 Strukturdämpfung 3.4-1 4.1 Grundlagen Dämpfung ist ein Prozess, bei dem Energie dissipiert wird. Dabei
Mathematik II Frühjahrssemester 2013
 Mathematik II Frühjahrssemester 213 Prof. Dr. Erich Walter Farkas Kapitel 7: Lineare Algebra Kapitel 7.5: Eigenwerte und Eigenvektoren einer quadratischen Matrix Prof. Dr. Erich Walter Farkas Mathematik
Mathematik II Frühjahrssemester 213 Prof. Dr. Erich Walter Farkas Kapitel 7: Lineare Algebra Kapitel 7.5: Eigenwerte und Eigenvektoren einer quadratischen Matrix Prof. Dr. Erich Walter Farkas Mathematik
Fourierreihen periodischer Funktionen
 Fourierreihen periodischer Funktionen periodische Funktion: (3.1) Fourierkoeffizienten und (3.2) (3.3) Fourier-Reihenentwicklungen Cosinus-Reihe: (3.4) (3.5) Exponentialreihe: (3.6) (3.7-3.8) Bestimmung
Fourierreihen periodischer Funktionen periodische Funktion: (3.1) Fourierkoeffizienten und (3.2) (3.3) Fourier-Reihenentwicklungen Cosinus-Reihe: (3.4) (3.5) Exponentialreihe: (3.6) (3.7-3.8) Bestimmung
Filtertypen Filter 1. Ordnung Filter 2. Ordnung Weitere Filter Idee für unser Projekt. Filter. 3. November Mateusz Grzeszkowski
 typen. Ordnung 2. Ordnung Weitere Idee für unser Projekt 3. November 2009 Mateusz Grzeszkowski / 24 Mateusz Grzeszkowski 3. November 2009 typen. Ordnung 2. Ordnung Weitere Idee für unser Projekt Motivation
typen. Ordnung 2. Ordnung Weitere Idee für unser Projekt 3. November 2009 Mateusz Grzeszkowski / 24 Mateusz Grzeszkowski 3. November 2009 typen. Ordnung 2. Ordnung Weitere Idee für unser Projekt Motivation
Elektrische Messtechnik Protokoll - Bestimmung des Frequenzgangs durch eine Messung im Zeitbereich
 Elektrische Messtechnik Protokoll - Bestimmung des Frequenzgangs durch eine Messung im Zeitbereich André Grüneberg Janko Lötzsch Mario Apitz Friedemar Blohm Versuch: 19. Dezember 2001 Protokoll: 6. Januar
Elektrische Messtechnik Protokoll - Bestimmung des Frequenzgangs durch eine Messung im Zeitbereich André Grüneberg Janko Lötzsch Mario Apitz Friedemar Blohm Versuch: 19. Dezember 2001 Protokoll: 6. Januar
