Ein Beitrag zur Perspektive mit gekippter Grundebene
|
|
|
- Käthe Schenck
- vor 7 Jahren
- Abrufe
Transkript
1 Ein Beitrag zur Perspektive mit gekippter Grundebene Von Georg GLAESER, Wien Herrn Prof. Dr. E. Frisch zum 65. Geburtstag gewidmet. Zusammenfassung Die Perspektive mit gekippter Grundebene wird wegen ihres erhäohten Schwierigkeitsgrades im Unterricht aus ZeitgrÄunden meist nur stiefmäutterlich behandelt. Hier soll eine Methode präasentiert werden, die es ermäoglicht, solche Perspektiven mit relativ geringem Aufwand anzufertigen. Dabei wird im wesentlichen die Methode von Hohenberg zum Umzeichnen von Perspektiven herangezogen; diese wird jedoch linienmäa¼ig stark reduziert, was wegen der Äuberlappenden Bilder wichtig erscheint. Die vereinfachte Konstruktion erlaubt eine Interpretation als perspektivisches Einschneideverfahren aus zwei Parallelrissen. Der SchÄuler (Student) kann bereits nach wenigen Unterrichtseinheiten allgemeine Perspektiven erstellen bzw. entzerren. 1 Einleitung F. Hohenberg hat in einem Aufsatz 1 ausfäuhrlich beschrieben, wie zwei Perspektiven mit waagrechter oder gekippter Grundebene 2 mit geringem Aufwand ineinander ÄubergefÄuhrt ( umgezeichnet\) werden käonnen. Insbesondere käonnen normalaxonometrische Bilder und MilitÄaraxonometrien in allgemeine Perspektiven umgezeichnet werden und umgekehrt (Rekonstruktion!). Weil die Konstruktion solcher Axonometrien von SchÄulern und Studenten im allgemeinen ohne Schwierigkeiten erlernt wird, kann man auf vorhandenen Fertigkeiten aufbauen und umso schneller Erfolgserlebnisse erzielen. Deswegen scheint es erstaunlich, da¼ diese Methode in LehrbÄuchern Äuber Darstellende Geometrie kaum beräucksichtigt wird. 2 Umzeichnen von Normalaxonometrien Gegeben sei eine auf der gekippten Grundebene ruhende Szene und deren Normalprojektion auf die Bildebene ¼ (Abb. 1). Der Kippwinkel der Grundebene ist bei einer Stechzirkelaxonometrie\ 3 1 Herstellung von Perspektiven aus axonometrischen oder perspektiven Bildern, Elem. d. Math. X/3, 57{61, BirkhÄauser/Basel, 1955, siehe auch: Hohenberg: Konstruktive Geometrie, 2. oder 3. Au age, Springer/Wien, Auch Perspektive mit lotrechter bzw. geneigter Bildebene. 3 vgl. W. Wunderlich: Darstellende Geometrie II, B.I./Mannheim,
2 vorgegeben, sonst mittels eines Seitenrisses zu ermitteln. Die Normalprojektion soll jetzt in eine Perspektive (Augpunkt O, Bildebene ¼, Distanz d) umgezeichnet werden. Abb. 2a zeigt, wie nach Hohenberg das perspektivische Bild P c des Raumpunkts P (x; y; z) aus dem normalaxonometrischen Bild der z-parallelen Strecke P 0 P (P 0 P = z) ermittelt werden kann: 1. Die Projektionsstrahlen OP und OP 0 aus dem Augpunkt O bilden sich in der Normalprojektion auf die Bildebene ¼ als Kernstrahlen\ O n P n = HP n und O n P 0n = HP 0n durch den Hauptpunkt H ( Kernpunkt\) ab. 2. Das perspektive Bild P 0c des Grundrisses P 0 kann gefunden werden, indem man P 0 läangs einer Fallgeraden f der Grundebene auf die Grundlinie g schiebt (Hilfspunkt P 0f 2 g ½ ¼), was einer Projektion aus dem Fernpunkt F u von f gleichkommt. P 0c liegt dann auf dem perspektiven Bild f c = P 0f Fu c von f. 3. Das perspektive Bild P c von P liegt auf der Verbindung von P 0c mit dem Fluchtpunkt Zu c der z-richtung. Abbildung 1: Die Raumsituation im Seitenri¼ Weil das normalaxonometrische Bild und die entsprechende Perspektive einander am Zeichenblatt Äuberlappen, fäuhrt selbst dieses einfache Verfahren schon nach wenigen Anwendungen zu einer gewissen Verwirrung. Die Konstruktion kann jedoch beträachtlich entlastet werden, wenn man auch den Punkt P aus F u projiziert (Abb. 1). Diese Projektion P f 2 ¼ liegt genau Äuber P 0f und es ist z f = P 0f P f = z=cos. Zusammen mit P 0n P n = z n =cos :z gilt: 2
3 Abbildung 2: a) Umzeichnen nach Hohenberg, b) liniensparendes Umzeichnen z f = c:z n mit c =1= cos 2 = const. Nun lautet die Konstruktionsvorschrift (Abb. 2b): 1. P c liegt (wie vorhin) auf dem Kernstrahl HP n. 2. P c liegt auf P f Fu, c wobei P f auf dem Ordner durch P n liegt, und zwar im Abstand z f = c:z n Äuber der Grundlinie g. Der Abstand z f kann konstruktiv q in einer Hilfs gur (siehe Abb. 2b bzw. Abb. 1) ermittelt werden. Im Fall einer Isometrie (cos = 2 3 ) =35; 264± ) ergibt sich fäur die Konstante c der bequeme Wert 3 2 (vgl. Abb. 3). FÄur die relativ gro¼en Kippwinkel =45 ± bzw. 60 ± stellensichfäur c die ganzzahligen Werte 2 bzw. 4 ein. Besonders einfach ist die Konstruktion natäurlich fäur die Punkte in der Grundebene, weil dann wegen z = z f = 0 die Punkte P 0f und P f zusammenfallen. GegenÄuber der Standard-Konstruktion\ von Hohenberg ergeben sich mehrere Vorteile: Der normalaxonometrische Grundri¼ P 0n mu¼ nicht unbedingt eingezeichnet sein: Die verkäurzte HÄohe z n, die in der Konstruktion vonnäoten ist, kann oft an anderer Stelle abgelesen werden. Der Punkt P c wird direkt konstruiert. Der bei kleinen Kippwinkeln meist schwer erreichbare Fluchtpunkt Zu c wird nicht benäotigt. Die Konstruktion ist vergleichsweise genau (kaum schleifende Schnitte). Punkte, die in unmittelbarer NÄahe von FuH c liegen, sollten allerdings horizontal verschoben werden. Die vereinfachte Konstruktion erlaubt eine Interpretation als Einschneideverfahren im Sinn von Eckhart bzw. Szab o 4 : Der Punkt P f kann ja als Parallelri¼ des Raumpunkts P auf die Bildebene gedeudet 4 Die Erzeugung axonometrischer Risse durch Einschneiden zweier Parallelrisse geht auf Eckhart (1937) zuräuck. Szab o hat das Verfahren verallgemeinert: Unter gewissen Bedindungen käonnen auch Perspektiven aus Parallelrissen bzw. 3
4 werden. Dieser Ri¼ ist a±n zu einem Seitenri¼ und kann anschaulich als ÄuberhÄohter Seitenri¼\ angesprochen werden. Abb. 3 zeigt ein isometrisches Bild, welches in eine Perspektive umgezeichnet wurde. Dabei sind alle Konstruktionslinien eingezeichnet! In der Zeichenpraxis wird man zunäachst die Haupt uchtpunkte X c u und Y c u am Horizont bzw. Z c u auf F c uh aufsuchen 5 und { sofern diese leicht erreichbar sind { in Kombination mit strategisch wichtigen\ Punkten zur Konstruktion der restlichen Punkte heranziehen. Abbildung 3: Umzeichnen einer normalen Axonometrie (Isometrie). Zentralrissen erzeugt werden; siehe dazu: Eine Verallgemeinerung des Eckhardtschen Einschneideverfahrens. Publ. Math. Debrecen 14 (1967), 311{319. Die Bedingungen, die Szab o anfäuhrt, sind im vorliegenden Fall in trivialer Weise erfäullt. 5 Das Fluchtspurdreieck ist bei einer isometrischen Annahme gleichseitig; dies erspart die EinfÄuhrung eines Seitenrisses zur Konstruktion von Zu. c 4
5 3 Umzeichnen von MilitÄarrissen Es sei wieder ein Szene gegeben, die auf einer um den Winkel gekippten Grundebene ruht. Diese Szene wird nun einerseits aus dem Augpunkt O, anderseits aus dem Fernpunkt S u jener Drehsehnenrichtung auf die Bildebene ¼ projiziert, welche gleichsinnig kongruent in ¼ projiziert (Abb. 4). Diese Parallelprojektion ist somit eine MilitÄaraxonometrie, weil sie zur Projektion in kongruent ist. Ein Raumpunkt P geht dabei in einen Bildpunkt P s Äuber, insbesondere entspricht dem Augpunkt O der Kernpunkt S c u = M, also der Me¼punkt von. DasVerkÄurzungsverhÄaltnis v z der z-werte ergibt sich gemäa¼ Abb. 4 aus dem Seitenri¼: v z = tan(45 ± =2). Abbildung 4: Liniensparendes Umzeichnen einer MilitÄaraxonometrie. Die Bildpunkte P c und P s des Raumpunkts P sind mittels der Kernstrahlen durch M gekoppelt, welche die Spuren der Ebene OS u P in ¼ darstellen. Die Projektion der Strecke P 0 P aus dem Fernpunkt F u der Fallinien f von liefert wie vorhin eine lotrechte Strecke P 0f P f auf der Grundlinie g mit der LÄange z f = P 0f P f = z=cos = z s =(v z : cos ). Es gilt somit z f = c:z s mit c = 1 cos : tan(45 ± =2) = const. Eine Konstruktionsvorschrift fäur das perspektive Bild P c lautet daher: 5
6 1. P c liegt auf dem Kernstrahl M P s. 2. P c liegt auf P f F c u, wobei P f auf dem Ordner durch P s liegt, und zwar im Abstand z f = c:z s Äuber der Grundlinie. Die Multiplikation des verkäurzten z-wertes z s mit dem konstanten VergrÄo¼erungsfaktor c kann wieder zeichnerisch (Abb. 4) durchgefäuhrt werden. Bei einem Kippwinkel von =0 ± (Perspektive mit waagrechter Grundebene) ergibt sich bequemerweise v z = c = 1. FÄur = 30 ± stellt sich zwar der ganzzahlige VergrÄo¼erungsfaktor c = 2 ein, das VerzerrungsverhÄaltnis ist mit v z = tan 30 ± = 1= p 3 aber irrational. GÄunstige Werte fäur v z und c stellen sich fäur =36; 870 ± (v z =1=2, c =5=2) und =53; 130 ± (v z =1=3, c =5)ein. Die Konstruktion des Bildpunktes P c aus den beiden Parallelrissen P s und P f erlauben analog zu vorhin eine Interpretation als Einschneideverfahren (vgl. Abb. 5). 4 Entzerrung von Perspektiven Weil das Umzeichnen vom MilitÄarri¼ in die Perspektive umkehrbar ist, kann man die Konstruktion auch verwenden, um eine Perspektive zu entzerren. Dasselbe gilt natäurlich auch beim Umzeichnen einer Perspektive in eine Normalaxonomtrie, allerdings mäussen dort alle drei Koordinatenrichtungen entzerrt werden, wäahrend im Fall der MilitÄaraxonometrie zwei Koordinaten (bei waagrechter Grundebene sogar alle drei) unverzerrt erscheinen. Abb. 5 zeigt eine Rekonstruktion aus einer Perspektive. Man ermittelt zunäachst wie gewohnt das Fluchtspurdreieck XuY c u c Zu c und den Hauptpunkt H als dessen HÄohenschnittpunkt. Fu c liegt auf der HÄohe durch Zu, c der Me¼punkt M am Thaleskreis Äuber XuY c u c. Durch Umkehrung des Einschneideverfahrens erhäalt man dann Äokonomisch einen MilitÄarri¼ und den zugeordneten ÄuberhÄohten Seitenri¼\. Zu beachten ist, da¼ die HÄohen in keinem der Parallelrisse unverzerrt erscheinen. Bemerkenswert ist die planimetrische Rekonstruktion der HÄohe z aus der Strecke z f = c:z s = z=cos : Auf Grund des Strahlensatzes braucht man nur die Strecke z f mittels des Fluchtpunkts Fu c (oder eines beliebigen anderen Fluchtpunkts am Horizont) auf die Hilfsgerade g 0 k g (hg 0 = a) zuräuckzuschieben\ (a ist aus dem Seitenri¼ bekannt). Dies hat einen interessanten Sachverhalt zur Folge: Man erhäalt die HÄohe eines Punktes P, indem man das perspektive Bild P 0c seines Grundrisses aus Fu c auf die Hilfslinie g 0 schiebt\ und die Lotrechte Äuber diesem Hilfspunkt mit der Verbindung P c Fu c schneidet. Dieses Verfahren erspart das Abmessen mittels des Me¼punkts der z-richtung und stimmt au¼erdem im Grenzfall =0 ± (waagrechte Grundebene) mit der dort Äublichen Konstruktion Äuberein. 6
7 Abbildung 5: Entzerrung einer Perspektive durch Umzeichnen in einen MilitÄarri¼. 7
Darstellende Geometrie Übungen. Tutorial. Übungsblatt: Perspektive - Rekonstruktion
 Darstellende Geometrie Übungen Institut für Architektur und Medien Tutorial Übungsblatt: Perspektive - Rekonstruktion Gegeben sind ein Foto von einem quaderförmigen Objekt sowie die Abmessungen des Basisrechteckes.
Darstellende Geometrie Übungen Institut für Architektur und Medien Tutorial Übungsblatt: Perspektive - Rekonstruktion Gegeben sind ein Foto von einem quaderförmigen Objekt sowie die Abmessungen des Basisrechteckes.
Darstellende Geometrie Übungen. Tutorial. Übungsblatt: Perspektive Rekonstruktion - FSI
 Darstellende Geometrie Übungen Institut für 0Irchitektur und IIIedien Tutorial Übungsblatt: Perspektive Rekonstruktion - FSI Gegeben sind ein Foto ( mit lotrechter Bildebene ) von einem quaderförmigen
Darstellende Geometrie Übungen Institut für 0Irchitektur und IIIedien Tutorial Übungsblatt: Perspektive Rekonstruktion - FSI Gegeben sind ein Foto ( mit lotrechter Bildebene ) von einem quaderförmigen
Darstellende Geometrie Übungen Institut für 0Irchitektur und IIIedien. Tutorial 02. Zentralperspektive Rekonstruktion
 Darstellende Geometrie Übungen Institut für 0Irchitektur und IIIedien Tutorial 02 Zentralperspektive Rekonstruktion Um ein perspektives Bild zu rekonstruieren, dh. die realen Abmessungen eines dreidimensionalen
Darstellende Geometrie Übungen Institut für 0Irchitektur und IIIedien Tutorial 02 Zentralperspektive Rekonstruktion Um ein perspektives Bild zu rekonstruieren, dh. die realen Abmessungen eines dreidimensionalen
Parallelprojektion. Das Projektionszentrum liegt im Unendlichen. Projektionsebene. Projektionsrichtung. Quader. Bild des Quaders
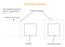 Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
Die Zentralprojektion
 Perspektive Perspektivmodell (S. 1 von 6) / www.kunstbrowser.de Die Zentralprojektion Die Zentralprojektion eines Gegenstandes auf eine ebene Bildfläche ist das Grundprinzip, aus dem sich alle zentralperspektivischen
Perspektive Perspektivmodell (S. 1 von 6) / www.kunstbrowser.de Die Zentralprojektion Die Zentralprojektion eines Gegenstandes auf eine ebene Bildfläche ist das Grundprinzip, aus dem sich alle zentralperspektivischen
Darstellende Geometrie
 Darstellende Geometrie für Architekten und Bauingenieure Skript und Präsenzübungen WS 2010/11 Institut Computational Mathematics Technische Universität Braunschweig Inhaltsverzeichnis 1 Projektionsarten
Darstellende Geometrie für Architekten und Bauingenieure Skript und Präsenzübungen WS 2010/11 Institut Computational Mathematics Technische Universität Braunschweig Inhaltsverzeichnis 1 Projektionsarten
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 29. Februar 2016 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Prüfungsfach: Darstellende Geometrie Termin: 29. Februar 2016 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.30 Uhr 14.30 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Axonometrie. 11 Axonometrien. Grundrissaxonometrie x : y : z = 1 : 1 : 1
 11 n Grundrissaonometrie : : = 1 : 1 : 1 Übersicht "... sstematisch abgewandelt, wird eine Einelfrage in Form möglichst vieler Variationen vorgetragen. Der Betrachter sieht sich in die Position eines Voeurs
11 n Grundrissaonometrie : : = 1 : 1 : 1 Übersicht "... sstematisch abgewandelt, wird eine Einelfrage in Form möglichst vieler Variationen vorgetragen. Der Betrachter sieht sich in die Position eines Voeurs
Projektionen:
 Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
1 Kartesische Normalkoordinatensysteme 5
 Inhaltsverzeichnis 1 Kartesische Normalkoordinatensysteme 5 2 SchrÄagrisse 7 3 Zugeordnete Normalrisse 13 3.1 Hauptrisse....................................... 13 3.2 Grundriss eines Punktes...............................
Inhaltsverzeichnis 1 Kartesische Normalkoordinatensysteme 5 2 SchrÄagrisse 7 3 Zugeordnete Normalrisse 13 3.1 Hauptrisse....................................... 13 3.2 Grundriss eines Punktes...............................
Die Übereckperspektive mit zwei Fluchtpunkten
 Perspektive Perspektive mit zwei Fluchtpunkten (S. 1 von 8) / www.kunstbrowser.de Die Übereckperspektive mit zwei Fluchtpunkten Bei dieser Perspektivart wird der rechtwinklige Körper so auf die Grundebene
Perspektive Perspektive mit zwei Fluchtpunkten (S. 1 von 8) / www.kunstbrowser.de Die Übereckperspektive mit zwei Fluchtpunkten Bei dieser Perspektivart wird der rechtwinklige Körper so auf die Grundebene
Lehrbuch der Konstruktiven Geometrie
 H. Brauner Lehrbuch der Konstruktiven Geometrie Springer-Verlag Wien New York Inhaltsverzeichnis Abbildungsverfahren der Darstellenden Geometrie 1. Elementargeometrische Grundlagen 1.1. Grundbegriffe 12
H. Brauner Lehrbuch der Konstruktiven Geometrie Springer-Verlag Wien New York Inhaltsverzeichnis Abbildungsverfahren der Darstellenden Geometrie 1. Elementargeometrische Grundlagen 1.1. Grundbegriffe 12
Perspektive Vertiefung
 Perspektive Vertiefung Hans-Peter Schröcker Arbeitsbereich Geometrie und CAD, Universität Innsbruck Wintersemester 2007/08 Teil I Einleitung Organisatorisches Perspektive Vertiefung Seminar, 2 Std. Donnerstag,
Perspektive Vertiefung Hans-Peter Schröcker Arbeitsbereich Geometrie und CAD, Universität Innsbruck Wintersemester 2007/08 Teil I Einleitung Organisatorisches Perspektive Vertiefung Seminar, 2 Std. Donnerstag,
6.4.3 Frontalperspektive
 102 KAPITEL 6. ZENTRALPRJEKTIN 6.4.3 Frontalperspektive Wir wollen den Grundriss des in Abb. 6.26 in Frontalperspektive dargestellten U-förmigen Gebäudes bestimmen. Dabei nehmen wir wieder an, dass das
102 KAPITEL 6. ZENTRALPRJEKTIN 6.4.3 Frontalperspektive Wir wollen den Grundriss des in Abb. 6.26 in Frontalperspektive dargestellten U-förmigen Gebäudes bestimmen. Dabei nehmen wir wieder an, dass das
Geometrische Grundlagen der. Architekturdarstellung
 Cornelie Leopold Geometrische Grundlagen der. Architekturdarstellung 4. Auflage Mit 469 Abbildungen unter Mitwirkung von Andreas Matievits STUDIUM 11 VIEWEG+ TEUBNER INHALTSVERZEICHNIS Vorwort 1 EINFÜHRUNG
Cornelie Leopold Geometrische Grundlagen der. Architekturdarstellung 4. Auflage Mit 469 Abbildungen unter Mitwirkung von Andreas Matievits STUDIUM 11 VIEWEG+ TEUBNER INHALTSVERZEICHNIS Vorwort 1 EINFÜHRUNG
14 MATHEMATISCHE GRUNDLAGEN DER COMPUTERGEOMETRIE. x y
 4 MATHEMATISCHE GRUNDLAGEN DER COMPUTERGEOMETRIE 4 Projektionen 4. Parallelprojektion (a) Senkrechte Projektion auf eine Koordinatenebene Wir wählen als Projektionsebene die Ebene, d. h. in den Beeichnungen
4 MATHEMATISCHE GRUNDLAGEN DER COMPUTERGEOMETRIE 4 Projektionen 4. Parallelprojektion (a) Senkrechte Projektion auf eine Koordinatenebene Wir wählen als Projektionsebene die Ebene, d. h. in den Beeichnungen
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 2. September 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 9.00 Uhr 10.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Prüfungsfach: Darstellende Geometrie Termin: 2. September 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 9.00 Uhr 10.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Geometrische Grundlagen der Architekturdarstellung
 Geometrische Grundlagen der Architekturdarstellung von Cornelie Leopold 1. Auflage Springer Vieweg Wiesbaden 2012 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 8348 1838 6 schnell und portofrei
Geometrische Grundlagen der Architekturdarstellung von Cornelie Leopold 1. Auflage Springer Vieweg Wiesbaden 2012 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 8348 1838 6 schnell und portofrei
Zeichnung: Malte Kittelmann AXONOMETRIE
 Zeichnung: Malte Kittelmann 3 AXONOMETRIE Die leichte Überlappung der axonometrischen Grundrisse in der nebenstehenden Abbildung des Reichstagsgebäudes erleichtert das Erkennen, was oben und was unten
Zeichnung: Malte Kittelmann 3 AXONOMETRIE Die leichte Überlappung der axonometrischen Grundrisse in der nebenstehenden Abbildung des Reichstagsgebäudes erleichtert das Erkennen, was oben und was unten
2.2 Projektionen und Kameramodelle
 Graphikprog. GRUNDLEGENDE VERFAHREN UND TECHNIKEN. Projektionen und Kameramodelle Nachdem alle Objekte einer Szenerie mittels der besprochenen Transformationen im D-Weltkoordinatensystem platziert sind,
Graphikprog. GRUNDLEGENDE VERFAHREN UND TECHNIKEN. Projektionen und Kameramodelle Nachdem alle Objekte einer Szenerie mittels der besprochenen Transformationen im D-Weltkoordinatensystem platziert sind,
Darstellende Geometrie Übungen. Tutorial 06. Übungsblatt: Schatten - Perspektive 04. Wohnhaus
 Darstellende Geometrie Übungen Institut für Architektur und Medien Tutorial 06 Übungsblatt: Schatten - Perspektive 04 Wohnhaus Fluchtpunkte und Fluchtspuren (Abb. 01) 1. Zuerst werden die fehlenden Fluchtpunkte
Darstellende Geometrie Übungen Institut für Architektur und Medien Tutorial 06 Übungsblatt: Schatten - Perspektive 04 Wohnhaus Fluchtpunkte und Fluchtspuren (Abb. 01) 1. Zuerst werden die fehlenden Fluchtpunkte
Geometrische Anmerkungen zu den Gedankenstrichen in documenta_landschaft_kunst Hannover
 Geometrische Anmerkungen zu den Gedankenstrichen in documenta_landschaft_kunst Hannover Albert Schmid-Kirsch Die vor kurzem vorgelegte Konzeptstudie zu einer dokumenta-landschaft-kunst in Hannover durch
Geometrische Anmerkungen zu den Gedankenstrichen in documenta_landschaft_kunst Hannover Albert Schmid-Kirsch Die vor kurzem vorgelegte Konzeptstudie zu einer dokumenta-landschaft-kunst in Hannover durch
Jahresplanung Vorschlag 1
 Jahresplanungen zum Lehrplan der AHS-Oberstufe Darstellende Geometrie Jahresplanung Vorschlag 1 7. Klasse Zeitraum Inhalte Hinweise zur Umsetzung 4 Stunden 1. Einführung allgemeine Grundbegriffe Projektionen
Jahresplanungen zum Lehrplan der AHS-Oberstufe Darstellende Geometrie Jahresplanung Vorschlag 1 7. Klasse Zeitraum Inhalte Hinweise zur Umsetzung 4 Stunden 1. Einführung allgemeine Grundbegriffe Projektionen
Normalprojektion. Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion.
 4. Der dreidimensionale Raum 4.5 Hauptrisse Normalprojektion Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion. Zum Beispiel:
4. Der dreidimensionale Raum 4.5 Hauptrisse Normalprojektion Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion. Zum Beispiel:
2.3.1 Rechtshändiges und linkshändiges Koordinatensystem
 2.3. Rechtshändiges und linkshändiges Koordinatensstem Die Koordinatenachsen im dreidimensionalen Raum lassen sich auf wei verschieden Arten anordnen: Linkshändig und Rechtshändig (s. Abbildung 2.9). Um
2.3. Rechtshändiges und linkshändiges Koordinatensstem Die Koordinatenachsen im dreidimensionalen Raum lassen sich auf wei verschieden Arten anordnen: Linkshändig und Rechtshändig (s. Abbildung 2.9). Um
Einerseits: Zentralperspektive
 VOM RAUM IN DIE EBENE UND ZURÜCK Ebene Figuren wie Dreiecke, Vierecke, andere Vielecke, Kreise lassen sich auf einem Zeichenblatt entweder in wahrer Größe oder unter Beibehaltung ihrer Form! maßstäblich
VOM RAUM IN DIE EBENE UND ZURÜCK Ebene Figuren wie Dreiecke, Vierecke, andere Vielecke, Kreise lassen sich auf einem Zeichenblatt entweder in wahrer Größe oder unter Beibehaltung ihrer Form! maßstäblich
Bild 1: Gegeben ist der in der Zentralperspektive zentrale Fluchtpunkt, der Distanzpunkt und der Grundriss des zu zeichnenden Vierecks.
 Bild 1: Gegeben ist der in der Zentralperspektive zentrale, der und der Grundriss des zu zeichnenden Vierecks. Die Breite des Vierecks trägt man auf der ab und verbindet die Schnittpunkte mit dem zentralen
Bild 1: Gegeben ist der in der Zentralperspektive zentrale, der und der Grundriss des zu zeichnenden Vierecks. Die Breite des Vierecks trägt man auf der ab und verbindet die Schnittpunkte mit dem zentralen
8.Perspektive (oder Zentralprojektion)
 8.Perspektive (oder Zentralprojektion) In unseren bisherigen Vorlesungen haben wir uns einfachheitshalber mit Parallelprojektionen beschäftigt. Das menschliche Sehen (damit meinen wir immer das Sehen mit
8.Perspektive (oder Zentralprojektion) In unseren bisherigen Vorlesungen haben wir uns einfachheitshalber mit Parallelprojektionen beschäftigt. Das menschliche Sehen (damit meinen wir immer das Sehen mit
Legt man die vom Betrachter aus gesehen vor den, wird die spätere Konstruktion kleiner als die Risse. Legt man die hinter das Objekt, wird die perspek
 Gegeben ist ein und ein. Der wird auf eine gezeichnet, der unterhalb von dieser in einiger Entfernung und mittig. Parallel zur wird der eingezeichnet. Dieser befindet sich in Augenhöhe. Üblicherweise wird
Gegeben ist ein und ein. Der wird auf eine gezeichnet, der unterhalb von dieser in einiger Entfernung und mittig. Parallel zur wird der eingezeichnet. Dieser befindet sich in Augenhöhe. Üblicherweise wird
Darstellende Geometrie
 Darstellende Geometrie Bei der Darstellenden Geometrie geht es darum, einen räumlichen Gegenstand in einer zweidimensionalen Ebene darzustellen. Dabei wendet man hauptsächlich Projektionen an. Projektionen
Darstellende Geometrie Bei der Darstellenden Geometrie geht es darum, einen räumlichen Gegenstand in einer zweidimensionalen Ebene darzustellen. Dabei wendet man hauptsächlich Projektionen an. Projektionen
Wo viel Licht ist, ist starker Schatten.
 Wo viel Licht ist, ist starker Schatten. (Goethe; Götz von Berlichingen) Perspektive & Schatten Die senkrechte Parallelprojektion (Normalperspektive) Aufriss (Vorderansicht Blick von vorne) Seitenriss
Wo viel Licht ist, ist starker Schatten. (Goethe; Götz von Berlichingen) Perspektive & Schatten Die senkrechte Parallelprojektion (Normalperspektive) Aufriss (Vorderansicht Blick von vorne) Seitenriss
Kapitel 4: Zeichnerische Darstellung von Körpern. Darstellung von Körpern in der Ebene. Ziel bei der Darstellung von räumlichen Figuren (Körpern):
 Kapitel 4: Zeichnerische Darstellung von Körpern Darstellung von Körpern in der Ebene. Quelle im Wesentlichen: Krauter, Elementargeometrie S.1-17 Ziel bei der Darstellung von räumlichen Figuren (Körpern):
Kapitel 4: Zeichnerische Darstellung von Körpern Darstellung von Körpern in der Ebene. Quelle im Wesentlichen: Krauter, Elementargeometrie S.1-17 Ziel bei der Darstellung von räumlichen Figuren (Körpern):
Zentral- und parallelprojektive Darstellungen in Cabri 3D
 Heinz Schumann Zentral- und parallelprojektive Darstellungen in Cabri 3D 1. Einleitung Cabri 3D repräsentiert nicht nur geometrisches Wissen über raumgeometrische Objekte und ihre Generierung, sondern
Heinz Schumann Zentral- und parallelprojektive Darstellungen in Cabri 3D 1. Einleitung Cabri 3D repräsentiert nicht nur geometrisches Wissen über raumgeometrische Objekte und ihre Generierung, sondern
Projektion. Ebene geometrische Projektionen
 Projektion - 1 - Ebene geometrische Projektionen Die ebenen geometrischen Projektionen sind dadurch charakterisiert, daß mit Projektionsstrahlen konstanter Richtung, d.h. entlang von Geraden, auf Ebenen
Projektion - 1 - Ebene geometrische Projektionen Die ebenen geometrischen Projektionen sind dadurch charakterisiert, daß mit Projektionsstrahlen konstanter Richtung, d.h. entlang von Geraden, auf Ebenen
Schriftliche Reifeprüfung aus dem Wahlpflichtfach Darstellende Geometrie am BRG Feldkirchen zum Haupttermin 2015/16. Prüfer: Mag.
 Schriftliche Reifeprüfung aus dem Wahlpflichtfach Darstellende Geometrie am BRG Feldkirchen zum Haupttermin 2015/16 Prüfer: Mag. Iris Steiner Notenschlüssel: Sehr Gut: Gut: Befriedigend: Genügend: Nicht
Schriftliche Reifeprüfung aus dem Wahlpflichtfach Darstellende Geometrie am BRG Feldkirchen zum Haupttermin 2015/16 Prüfer: Mag. Iris Steiner Notenschlüssel: Sehr Gut: Gut: Befriedigend: Genügend: Nicht
Tutorium: Diskrete Mathematik
 Tutorium: Diskrete Mathematik Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Definition I Eine Gerade oder gerade Linie ist ein Element der Geometrie. Anschaulich kann man sich darunter
Tutorium: Diskrete Mathematik Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Definition I Eine Gerade oder gerade Linie ist ein Element der Geometrie. Anschaulich kann man sich darunter
Geometrie 1. 1.)Geometrische Grundkonstruktionen. Halbierung einer Strecke, Mittelsenkrechte. Teilung einer Strecke. Winkelhalbierung.
 Geometrie 1 1.)Geometrische Grundkonstruktionen Halbierung einer Strecke, Mittelsenkrechte Teilung einer Strecke Winkelhalbierung Thaleskreis Konstruktion von Dreiecken Kongruenzsätze: SSS-Satz, SWS-Satz,
Geometrie 1 1.)Geometrische Grundkonstruktionen Halbierung einer Strecke, Mittelsenkrechte Teilung einer Strecke Winkelhalbierung Thaleskreis Konstruktion von Dreiecken Kongruenzsätze: SSS-Satz, SWS-Satz,
iek Institut für Entwerfen und Konstruieren
 Darstellende Geometrie Institut für Entwerfen und Konstruieren Prof. José Luis Moro Matthias Rottner Heiko Stachel 1 Modul Grundlagen der Darstellung und Konstruktion Termine Grundlagen der Darstellung
Darstellende Geometrie Institut für Entwerfen und Konstruieren Prof. José Luis Moro Matthias Rottner Heiko Stachel 1 Modul Grundlagen der Darstellung und Konstruktion Termine Grundlagen der Darstellung
Modul: Ausgewählte Kapitel der Didaktik der Mathematik
 Modul: Ausgewählte Kapitel der Didaktik der Mathematik Raumgeometrie: Körperdarstellungen, Projektionen Pascal Becker, Alexander Simon 11. Dezember 2014 1 / 16 Inhaltsverzeichnis 1 Rahmenlehrpläne 2 Projektionen
Modul: Ausgewählte Kapitel der Didaktik der Mathematik Raumgeometrie: Körperdarstellungen, Projektionen Pascal Becker, Alexander Simon 11. Dezember 2014 1 / 16 Inhaltsverzeichnis 1 Rahmenlehrpläne 2 Projektionen
8.Kreisdarstellung in Perspektive
 8.Kreisdarstellung in Perspektive Kegelschnitte durch fünf Punkte Wie wir bereits wissen, läßt sich ein Kegel grundsätzlich nach 4 verschiedenen Kurven schneiden: Kreis, Ellipse, Parabel oder Hyperbel.
8.Kreisdarstellung in Perspektive Kegelschnitte durch fünf Punkte Wie wir bereits wissen, läßt sich ein Kegel grundsätzlich nach 4 verschiedenen Kurven schneiden: Kreis, Ellipse, Parabel oder Hyperbel.
Das Gleichlauf-Kugelgelenk ein Beispiel zum anwendungsorientierten Unterricht in Darstellender Geometrie
 Proceedings SDG Symposium Darstellende Geometrie, Dresden 15.-17.6.2000 (ISBN 3-86005-258-6), 151 156 Das Gleichlauf-Kugelgelenk ein Beispiel zum anwendungsorientierten Unterricht in Darstellender Geometrie
Proceedings SDG Symposium Darstellende Geometrie, Dresden 15.-17.6.2000 (ISBN 3-86005-258-6), 151 156 Das Gleichlauf-Kugelgelenk ein Beispiel zum anwendungsorientierten Unterricht in Darstellender Geometrie
Grundregeln der Perspektive und ihre elementargeometrische Herleitung
 Vortrag zu Mathematik, Geometrie und Perspektive von Prof. Dr. Bodo Pareigis am 15.10.2007 im Vorlesungszyklus Naturwissenschaften und Mathematische Wissenschaften im Rahmen des Seniorenstudiums der LMU.
Vortrag zu Mathematik, Geometrie und Perspektive von Prof. Dr. Bodo Pareigis am 15.10.2007 im Vorlesungszyklus Naturwissenschaften und Mathematische Wissenschaften im Rahmen des Seniorenstudiums der LMU.
Kreis - Tangente. 2. Vorbemerkung: Satz des Thales Eine Möglichkeit zur Bestimmung der Tangente benutzt den Satz des Thales.
 Kreis - Tangente 1. Allgemeines 2. Satz des Thales 3. Tangente an einem Punkt auf dem Kreis 4. Tangente über Analysis (an einem Punkt eines Ursprungkreises) 5. Tangente von einem Punkt (Pol) an den Kreis
Kreis - Tangente 1. Allgemeines 2. Satz des Thales 3. Tangente an einem Punkt auf dem Kreis 4. Tangente über Analysis (an einem Punkt eines Ursprungkreises) 5. Tangente von einem Punkt (Pol) an den Kreis
DG für Kunstpädagogik
 DG für Kunstpädagogik Kreisdarstellung in Perspektive Kegelschnitte durch fünf Punkte Wie wir bereits wissen, läßt sich ein Kegel grundsätzlich nach 4 verschiedenen Kurven schneiden: Kreis, Ellipse, Parabel
DG für Kunstpädagogik Kreisdarstellung in Perspektive Kegelschnitte durch fünf Punkte Wie wir bereits wissen, läßt sich ein Kegel grundsätzlich nach 4 verschiedenen Kurven schneiden: Kreis, Ellipse, Parabel
9"+#5(00(),(& 7(8.(5+%(
 !"#$%"&'%()*"+, 9"+#5(00(),(& 7(8.(5+%( -%)&'(*+.%/(0&12+&,"#&34(%5"1(06(+1"*+() Inhaltsverzeichnis Vorwort...5 1. Darstellung im Zweitafelverfahren...7 2. Darstellung des Punktes...9 3. Darstellung der
!"#$%"&'%()*"+, 9"+#5(00(),(& 7(8.(5+%( -%)&'(*+.%/(0&12+&,"#&34(%5"1(06(+1"*+() Inhaltsverzeichnis Vorwort...5 1. Darstellung im Zweitafelverfahren...7 2. Darstellung des Punktes...9 3. Darstellung der
KOP1_1_28. Lüftungsschacht
 Titel Relevante(r) Deskriptor(en) Lehrstoff Ausbildungsinhalte Methodisch/Didaktische Hinweise Hilfsmittel Quelle weitere Beispiele Lüftungsschacht Die Schülerinnen und Schüler können normgerechte Zeichnungen
Titel Relevante(r) Deskriptor(en) Lehrstoff Ausbildungsinhalte Methodisch/Didaktische Hinweise Hilfsmittel Quelle weitere Beispiele Lüftungsschacht Die Schülerinnen und Schüler können normgerechte Zeichnungen
Axonometrie. FG Borrego - TU Berlin Architekturdarstellung und Gestaltung Collaborative Design Laboratory
 Axonometrie Rem Koolhaas mit Zoe Zenghelis: Die Stadt des gefangenen Globus, Projekt, New York City, Axonometrische Ansicht von oben, 1972 2 / 35 Parallelprojektion >> Isometrie >> Grundrissaxonometrie
Axonometrie Rem Koolhaas mit Zoe Zenghelis: Die Stadt des gefangenen Globus, Projekt, New York City, Axonometrische Ansicht von oben, 1972 2 / 35 Parallelprojektion >> Isometrie >> Grundrissaxonometrie
AXONOMETRIE. TU Berlin FG Borrego Architekturdarstellung und Gestaltung Collaborative Design Laboratory
 AXONOMETRIE Rem Koolhaas mit Zoe Zenghelis: Die Stadt des gefangenen Globus, Projekt, New York City, Axonometrische Ansicht von oben, 1972 2 / 65 Parallelprojektion >> Isometrie >> Grundrissaxonometrie
AXONOMETRIE Rem Koolhaas mit Zoe Zenghelis: Die Stadt des gefangenen Globus, Projekt, New York City, Axonometrische Ansicht von oben, 1972 2 / 65 Parallelprojektion >> Isometrie >> Grundrissaxonometrie
Darstellende Geometrie Themenbereiche für die mündliche Reifeprüfung
 Darstellende Geometrie, Themenbereiche RP, Seite 1 von 5 Darstellende Geometrie Themenbereiche für die mündliche Reifeprüfung 1. Flächen und Körper, die durch Bewegung erzeugt werden Extrusionskörper und
Darstellende Geometrie, Themenbereiche RP, Seite 1 von 5 Darstellende Geometrie Themenbereiche für die mündliche Reifeprüfung 1. Flächen und Körper, die durch Bewegung erzeugt werden Extrusionskörper und
r a t u Parametergleichung der Geraden durch den Punkt A mit dem Richtungsvektor u t R heisst Parameter
 8 3. Darstellung der Geraden im Raum 3.. Parametergleichung der Geraden Die naheliegende Vermutung, dass eine Gerade des Raumes durch eine Gleichung der Form ax + by + cz +d = 0 beschrieben werden kann
8 3. Darstellung der Geraden im Raum 3.. Parametergleichung der Geraden Die naheliegende Vermutung, dass eine Gerade des Raumes durch eine Gleichung der Form ax + by + cz +d = 0 beschrieben werden kann
SRP DG am BG und BRG Wieselburg 2015/16, Seite 1 von 14, Name: Schriftliche Reifeprüfung Darstellende Geometrie
 SRP DG am BG und BRG Wieselburg 2015/16, Seite 1 von 14, Name: Allgemeines Schriftliche Reifeprüfung Darstellende Geometrie BG und BRG Wieselburg, Haupttermin 2015/16 Klasse 8BD Realgymnasium mit Darstellender
SRP DG am BG und BRG Wieselburg 2015/16, Seite 1 von 14, Name: Allgemeines Schriftliche Reifeprüfung Darstellende Geometrie BG und BRG Wieselburg, Haupttermin 2015/16 Klasse 8BD Realgymnasium mit Darstellender
Analytische Geometrie I
 Analytische Geometrie I Rainer Hauser Januar 202 Einleitung. Geometrie und Algebra Geometrie und Algebra sind historisch zwei unabhängige Teilgebiete der Mathematik und werden bis heute von Laien weitgehend
Analytische Geometrie I Rainer Hauser Januar 202 Einleitung. Geometrie und Algebra Geometrie und Algebra sind historisch zwei unabhängige Teilgebiete der Mathematik und werden bis heute von Laien weitgehend
Geometrische Grundlagen der Architekturdarstellung
 Geometrische Grundlagen der Architekturdarstellung Bearbeitet von Cornelie Leopold 5., überarbeitete und erweiterte Auflage 2015. Buch. x, 298 S. Kartoniert ISBN 978 3 658 07845 4 Format (B x L): 16,7
Geometrische Grundlagen der Architekturdarstellung Bearbeitet von Cornelie Leopold 5., überarbeitete und erweiterte Auflage 2015. Buch. x, 298 S. Kartoniert ISBN 978 3 658 07845 4 Format (B x L): 16,7
Figur in der Bildfläche bzw. Bildebene
 2 ABBILDUNGSMETHODEN 2.1 Projektionsarten Um dreidimensionale Objekte wie Gebäude, Stadträume oder Bauteile darzustellen, werden diese auf eine Bildfläche bzw. eine Bildebene abgebildet. Der hierbei verwendete
2 ABBILDUNGSMETHODEN 2.1 Projektionsarten Um dreidimensionale Objekte wie Gebäude, Stadträume oder Bauteile darzustellen, werden diese auf eine Bildfläche bzw. eine Bildebene abgebildet. Der hierbei verwendete
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 20. März 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 20. März 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Aufgabenstellung zur Wahlfachübung 4
 Darstellende Geometrie für Architekten III Institut für Geometrie und Prakt. Mathematik RWTH Aachen 4.2 Prismen Geometrie der Formen Übung 4 Seite 1 Aufgabenstellung zur Wahlfachübung 4 Hausübung zum Thema
Darstellende Geometrie für Architekten III Institut für Geometrie und Prakt. Mathematik RWTH Aachen 4.2 Prismen Geometrie der Formen Übung 4 Seite 1 Aufgabenstellung zur Wahlfachübung 4 Hausübung zum Thema
 Abiturprüfung Mathematik 0 Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit f() = ( sin() + 7) 5. Aufgabe : ( VP) Berechnen Sie eine Stammfunktion
Abiturprüfung Mathematik 0 Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit f() = ( sin() + 7) 5. Aufgabe : ( VP) Berechnen Sie eine Stammfunktion
Tutorium: Diskrete Mathematik. Vektoren
 Tutorium: Diskrete Mathematik Vektoren Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Definition I Im allgemeinen Sinn versteht man in der linearen Algebra unter einem Vektor ein Element
Tutorium: Diskrete Mathematik Vektoren Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Definition I Im allgemeinen Sinn versteht man in der linearen Algebra unter einem Vektor ein Element
Tutorium: Diskrete Mathematik
 Tutorium: Diskrete Mathematik Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Definition I Im allgemeinen Sinn versteht man in der linearen Algebra unter einem Vektor ein Element eines Vektorraums,
Tutorium: Diskrete Mathematik Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Definition I Im allgemeinen Sinn versteht man in der linearen Algebra unter einem Vektor ein Element eines Vektorraums,
Computational Geometry, MU Leoben
 Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Modul 1 Der Würfel! 1
 Modul 1 Der Würfel! 1 2 3 4 Der 2-1-1-Würfel 5 Der 2-1-1-Würfel 6 Der 5-3-2-Würfel 7 Der 5-3-2-Würfel 8 Der 5-3-2-Würfel 9 Der 5-3-2-Würfel 10 10-2-2-Würfel und 10-3-2-Würfel 11 10-2-2-Würfel und 10-3-2-Würfel
Modul 1 Der Würfel! 1 2 3 4 Der 2-1-1-Würfel 5 Der 2-1-1-Würfel 6 Der 5-3-2-Würfel 7 Der 5-3-2-Würfel 8 Der 5-3-2-Würfel 9 Der 5-3-2-Würfel 10 10-2-2-Würfel und 10-3-2-Würfel 11 10-2-2-Würfel und 10-3-2-Würfel
Drei Flugzeuge unterwegs
 Anwendungsaufgaben: R. 3. 1 Drei Flugzeuge unterwegs Um die Bewegungen dreier Flugzeuge zu analysieren, wird ein räumliches kartesisches Koordinatensystem gewählt, das an die Navigation auf bzw. über der
Anwendungsaufgaben: R. 3. 1 Drei Flugzeuge unterwegs Um die Bewegungen dreier Flugzeuge zu analysieren, wird ein räumliches kartesisches Koordinatensystem gewählt, das an die Navigation auf bzw. über der
Projektion des Torus in isotroper Richtung
 Projektion des Torus in isotroper Richtung Autor(en): Objekttyp: Hohenberg, Fritz Article Zeitschrift: Elemente der Mathematik Band (Jahr): 27 (1972) Heft 4 PDF erstellt am: 30.09.2017 Persistenter Link:
Projektion des Torus in isotroper Richtung Autor(en): Objekttyp: Hohenberg, Fritz Article Zeitschrift: Elemente der Mathematik Band (Jahr): 27 (1972) Heft 4 PDF erstellt am: 30.09.2017 Persistenter Link:
Rekonstruktion eines teilweise entschlüsselten babylonischen Keilschrifttextes aus der Zeit um 2000 v. Chr.
 Rekonstruktion eines teilweise entschlüsselten babylonischen Keilschrifttextes aus der Zeit um 2000 v. Chr. 16 9 25 4 3 5 144 25 169 12 13 49 625 24 7 25 9 25 3 64 100 8 225 64 289 15 144 225 15 1296 225
Rekonstruktion eines teilweise entschlüsselten babylonischen Keilschrifttextes aus der Zeit um 2000 v. Chr. 16 9 25 4 3 5 144 25 169 12 13 49 625 24 7 25 9 25 3 64 100 8 225 64 289 15 144 225 15 1296 225
Zentralperspektive (1 FP) 2-Punkt-Fluchtpunktp. 3-Punkt-Fluchtpunktp.
 Ein Auftrag: Eine Frage der Perspektive... Isometrie Dimetrie Zentralperspektive (1 FP) 2-Punkt-Fluchtpunktp. Sphärische Perspektive curvilinear perspective Kavalliersperspektive, Kabinettperspektive (Eine
Ein Auftrag: Eine Frage der Perspektive... Isometrie Dimetrie Zentralperspektive (1 FP) 2-Punkt-Fluchtpunktp. Sphärische Perspektive curvilinear perspective Kavalliersperspektive, Kabinettperspektive (Eine
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Termin: 14. September 2012 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten vor Beginn der
Prüfungsfach: Termin: 14. September 2012 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten vor Beginn der
Wir gehen aus von euklidischen Anschauungsraum bzw. von der euklidischen Zeichenebene. Parallele Geraden schneiden einander nicht.
 2 Ein wenig projektive Geometrie 2.1 Fernpunkte 2.1.1 Projektive Einführung von Fernpunkten Wir gehen aus von euklidischen Anschauungsraum bzw. von der euklidischen Zeichenebene. Parallele Geraden schneiden
2 Ein wenig projektive Geometrie 2.1 Fernpunkte 2.1.1 Projektive Einführung von Fernpunkten Wir gehen aus von euklidischen Anschauungsraum bzw. von der euklidischen Zeichenebene. Parallele Geraden schneiden
Externistenprüfungen aus Darstellender Geometrie
 Externistenprüfungen aus Darstellender Geometrie Zulassungsprüfung 7.Klasse Zulassungsprüfung 8. Klasse Wahlpflichtfach Reifeprüfung Juni 2008 Seite 1 von 5 Zulassungsprüfung 7. Klasse Die Prüfung teilt
Externistenprüfungen aus Darstellender Geometrie Zulassungsprüfung 7.Klasse Zulassungsprüfung 8. Klasse Wahlpflichtfach Reifeprüfung Juni 2008 Seite 1 von 5 Zulassungsprüfung 7. Klasse Die Prüfung teilt
Parallelprojektive Schattenbilder von Körpern mit Cabri 3D
 Heinz Schumann Parallelprojektive Schattenbilder von Körpern mit Cabri 3D Vorbereitung: die Parallelprojektion Mit Cabri 3D kann man nicht nur räumliche Abbildungen und ihre Eigenschaften im virtuellen
Heinz Schumann Parallelprojektive Schattenbilder von Körpern mit Cabri 3D Vorbereitung: die Parallelprojektion Mit Cabri 3D kann man nicht nur räumliche Abbildungen und ihre Eigenschaften im virtuellen
Abiturprüfung Mathematik 2012 Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen
 Abiturprüfung Mathematik 202 Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen klaus_messner@web.de www.elearning-freiburg.de Pflichtteil 202 2 Aufgabe : Bilden Sie die erste Ableitung
Abiturprüfung Mathematik 202 Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen klaus_messner@web.de www.elearning-freiburg.de Pflichtteil 202 2 Aufgabe : Bilden Sie die erste Ableitung
Projektionen von geometrischen Objekten
 Inhalt: Projektionen von geometrischen Objekten Überblick Hauptrisse Aonometrische Projektionen isometrisch dimetrisch trimetrisch Schiefwinklige Projektionen Kavalierprojektion Kabinettprojektion Perspektivische
Inhalt: Projektionen von geometrischen Objekten Überblick Hauptrisse Aonometrische Projektionen isometrisch dimetrisch trimetrisch Schiefwinklige Projektionen Kavalierprojektion Kabinettprojektion Perspektivische
Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen
 Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen Sebastian Kitz, Wuppertal I Zentralprojektion Eine brennende Kerze kann in guter Näherung als punktförmige Lichtquelle
Von der brennenden Kerze über die Zentralkollineation zur Gruppe der projektiven Abbildungen Sebastian Kitz, Wuppertal I Zentralprojektion Eine brennende Kerze kann in guter Näherung als punktförmige Lichtquelle
Projektionen und Perspektive
 Projektionen und Perspektive 2 Beim räumlichen Zeichnen geht es um das Problem, dreidimensionale Objekte auf einer meist ebenen Zeichenfläche darzustellen. Allgemein wird diese Tätigkeit (bzw. deren Ergebnis)
Projektionen und Perspektive 2 Beim räumlichen Zeichnen geht es um das Problem, dreidimensionale Objekte auf einer meist ebenen Zeichenfläche darzustellen. Allgemein wird diese Tätigkeit (bzw. deren Ergebnis)
Ziel bei der Darstellung von räumlichen Figuren (Körpern): Startseite
 Startseite Zentralprojektion 1 Kapitel 3: Zeichnerische Darstellung von Körpern Darstellung von Körpern in der Ebene. Quelle im Wesentlichen: Krauter, Elementargeometrie S.1-17 Ziel bei der Darstellung
Startseite Zentralprojektion 1 Kapitel 3: Zeichnerische Darstellung von Körpern Darstellung von Körpern in der Ebene. Quelle im Wesentlichen: Krauter, Elementargeometrie S.1-17 Ziel bei der Darstellung
Einige Fragen aus den Elementen der Darstellenden Geometrie,
 Einige Fragen aus den Elementen der Darstellenden Geometrie, Von A. KIEFER (Zürich). (Als Manuskript eingegangen am 4. März 1929.) I. Wenn P', P" in dem System der vereinigten Bildebenen der Grund und
Einige Fragen aus den Elementen der Darstellenden Geometrie, Von A. KIEFER (Zürich). (Als Manuskript eingegangen am 4. März 1929.) I. Wenn P', P" in dem System der vereinigten Bildebenen der Grund und
geschlossene Schachtel mit einem kleinen Loch
 Kameramodellierung Lochkamera Kamerakonstante Kamerazentrum geschlossene Schachtel mit einem kleinen Loch ideale Kamera: Loch hat keine Ausdehnung die Strahlen sind ein Büschel von Geraden Abbildung erfolgt
Kameramodellierung Lochkamera Kamerakonstante Kamerazentrum geschlossene Schachtel mit einem kleinen Loch ideale Kamera: Loch hat keine Ausdehnung die Strahlen sind ein Büschel von Geraden Abbildung erfolgt
Projektion. FG Borrego - TU Berlin Architekturdarstellung und Gestaltung Collaborative Design Laboratory
 Projektion Unterscheidung nach Lage des Projektionszentrums im Unendlichen im Endlichen Parallelprojektion Zentralprojektion Projektionszentrum Z R R Q Q R P R Z' P Q Q Bildebene P Bildebene P Parallelität
Projektion Unterscheidung nach Lage des Projektionszentrums im Unendlichen im Endlichen Parallelprojektion Zentralprojektion Projektionszentrum Z R R Q Q R P R Z' P Q Q Bildebene P Bildebene P Parallelität
Klausur zur Einführung in die Geometrie im SS 2002
 Klausur zur Einführung in die Geometrie im SS 2002 Name, Vorname... Matr.Nr.... Semester-Anzahl im SS 2002:... Studiengang GH/R/S Tutor/in:... Aufg.1 Aufg,2 Aufg.3 Aufg.4 Aufg.5 Aufg.6 Aufg.7 Aufg.8 Gesamt
Klausur zur Einführung in die Geometrie im SS 2002 Name, Vorname... Matr.Nr.... Semester-Anzahl im SS 2002:... Studiengang GH/R/S Tutor/in:... Aufg.1 Aufg,2 Aufg.3 Aufg.4 Aufg.5 Aufg.6 Aufg.7 Aufg.8 Gesamt
 Abiturprüfung Mathematik 200 Baden-Württemberg (ohne CAS) Wahlteil Aufgaben Analytische Geometrie II, 2 Gegeben sind der Punkt A(,/6/,) sowie die Gerade g: x = 0 + t. a) Bestimmen Sie den Schnittpunkt
Abiturprüfung Mathematik 200 Baden-Württemberg (ohne CAS) Wahlteil Aufgaben Analytische Geometrie II, 2 Gegeben sind der Punkt A(,/6/,) sowie die Gerade g: x = 0 + t. a) Bestimmen Sie den Schnittpunkt
4. Mathematik Olympiade 3. Stufe (Bezirksolympiade) Klasse 12 Saison 1964/1965 Aufgaben und Lösungen
 4. Mathematik Olympiade 3. Stufe (Bezirksolympiade) Klasse 1 Saison 1964/1965 Aufgaben und Lösungen 1 OJM 4. Mathematik-Olympiade 3. Stufe (Bezirksolympiade) Klasse 1 Aufgaben Hinweis: Der Lösungsweg mit
4. Mathematik Olympiade 3. Stufe (Bezirksolympiade) Klasse 1 Saison 1964/1965 Aufgaben und Lösungen 1 OJM 4. Mathematik-Olympiade 3. Stufe (Bezirksolympiade) Klasse 1 Aufgaben Hinweis: Der Lösungsweg mit
Aufgabenstellung zur Wahlfachübung 7
 Darstellende Geometrie für Architekten III Institut für Geometrie und Prakt. Mathematik RWTH Aachen Geometrie der Formen Übung 7 Seite 1 Aufgabenstellung zur Wahlfachübung 7 Hausübung zum Thema Rotationshyperboloid
Darstellende Geometrie für Architekten III Institut für Geometrie und Prakt. Mathematik RWTH Aachen Geometrie der Formen Übung 7 Seite 1 Aufgabenstellung zur Wahlfachübung 7 Hausübung zum Thema Rotationshyperboloid
Tutorium: Diskrete Mathematik. Ebenen
 Tutorium: Diskrete Mathematik Ebenen Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Definition Die Ebene ist ein Grundbegri der Geometrie. Allgemein handelt es sich um ein unbegrenzt ausgedehntes,
Tutorium: Diskrete Mathematik Ebenen Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 Definition Die Ebene ist ein Grundbegri der Geometrie. Allgemein handelt es sich um ein unbegrenzt ausgedehntes,
Durchstoßpunkt Gerade Ebene. Vorkurs Darstellende Geometrie. Erstprojizierende Hilfsebene ν durch g. Teil I. Lösung mit erstprojizierender Hilfsebene
 Durchstoßpunkt Gerade Ebene Vorkurs Darstellende Geometrie Durchstoßpunkt Gerade Ebene Bestimmen Sie den Durchstoßpunkt D der Geraden g mit der Ebene ε. Hans-Peter Schröcker Arbeitsbereich Geometrie und
Durchstoßpunkt Gerade Ebene Vorkurs Darstellende Geometrie Durchstoßpunkt Gerade Ebene Bestimmen Sie den Durchstoßpunkt D der Geraden g mit der Ebene ε. Hans-Peter Schröcker Arbeitsbereich Geometrie und
Einführung in die Grundlagen des Technischen Zeichnens: Thema dieser Präsentation: Die Parallelprojektion
 Einführung in die Grundlagen des Technischen Zeichnens: Thema dieser Präsentation: Die Parallelprojektion 1. Was ist eine Projektion? 2. Alles Ansichtssache!? 3. Isometrische Projektion 4. Kabinett-Projektion
Einführung in die Grundlagen des Technischen Zeichnens: Thema dieser Präsentation: Die Parallelprojektion 1. Was ist eine Projektion? 2. Alles Ansichtssache!? 3. Isometrische Projektion 4. Kabinett-Projektion
iek Institut für Entwerfen und Konstruieren
 Grundlaen der Darstellun Institut für Entwerfen und Konstruieren Prof. José Luis Moro Heiko Stacel Mattias Rottner 1 Konstruktion der senkrecten Axonometrie 2 Mertafelprojektion B(A) A B A Aufriss Seitenriss
Grundlaen der Darstellun Institut für Entwerfen und Konstruieren Prof. José Luis Moro Heiko Stacel Mattias Rottner 1 Konstruktion der senkrecten Axonometrie 2 Mertafelprojektion B(A) A B A Aufriss Seitenriss
Sätze über Kreise raumgeometrisch beweisen mit Cabri 3D
 Heinz Schumann Sätze über Kreise raumgeometrisch beweisen mit Cabri 3D Herrn Prof. Dr. Hans Schupp zum 70. Geburtstag gewidmet Das dynamische Raumgeometrie-System Cabri 3D eignet sich nicht nur für die
Heinz Schumann Sätze über Kreise raumgeometrisch beweisen mit Cabri 3D Herrn Prof. Dr. Hans Schupp zum 70. Geburtstag gewidmet Das dynamische Raumgeometrie-System Cabri 3D eignet sich nicht nur für die
Analytische Geometrie II
 Analytische Geometrie II Rainer Hauser März 212 1 Einleitung 1.1 Geradengleichungen in Parameterform Jede Gerade g in der Ebene oder im Raum lässt sich durch einen festen Punkt auf g, dessen Ortsvektor
Analytische Geometrie II Rainer Hauser März 212 1 Einleitung 1.1 Geradengleichungen in Parameterform Jede Gerade g in der Ebene oder im Raum lässt sich durch einen festen Punkt auf g, dessen Ortsvektor
A. N. Danilewsky 31. Fortsetzung von Kapitel 2
 A. N. Danilewsky 31 Fortsetzung von Kapitel 2 2.3 Darstellung von Körpern... 32 2.3.1 Othogonale Parallelprojektion... 32 2.3.2 Stereographische Projektion... 34 2.3.3 Gnomonische Projektion... 42 32 Kristallographie
A. N. Danilewsky 31 Fortsetzung von Kapitel 2 2.3 Darstellung von Körpern... 32 2.3.1 Othogonale Parallelprojektion... 32 2.3.2 Stereographische Projektion... 34 2.3.3 Gnomonische Projektion... 42 32 Kristallographie
Projektive Geometrie
 Projektive Geometrie Einleitung Was ist projektive Geometrie? eine alternative algebraische Repräsentation von geometrischen Objekten (Punkt, Gerade,...) und Transformationen (Translation, Rotation,...)
Projektive Geometrie Einleitung Was ist projektive Geometrie? eine alternative algebraische Repräsentation von geometrischen Objekten (Punkt, Gerade,...) und Transformationen (Translation, Rotation,...)
Darstellende Geometrie (DG) Schule: HTBLuVA St. Pölten Abteilung: Elektronik Lehrperson: Dipl.-Ing. Wolfgang Lenz Jahrgang: 2002 / 03 Klasse: 1AT
 Darstellende Geometrie (DG) Schule: HTBLuVA St. Pölten Abteilung: Elektronik Lehrperson: Dipl.-Ing. Wolfgang Lenz Jahrgang: 2002 / 03 Klasse: 1AT 1 Anmerkung Prof. Lenz ist bereits pensioniert. Im Unterricht
Darstellende Geometrie (DG) Schule: HTBLuVA St. Pölten Abteilung: Elektronik Lehrperson: Dipl.-Ing. Wolfgang Lenz Jahrgang: 2002 / 03 Klasse: 1AT 1 Anmerkung Prof. Lenz ist bereits pensioniert. Im Unterricht
Normalprojektion. Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion.
 4. Der dreidimensionale Raum 4.5 Hauptrisse Normalprojektion Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion. Zum Beispiel:
4. Der dreidimensionale Raum 4.5 Hauptrisse Normalprojektion Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion. Zum Beispiel:
Hans Walser, [ a] Pentagramma mirificum Anregung: [Heinrich 2010]
![Hans Walser, [ a] Pentagramma mirificum Anregung: [Heinrich 2010] Hans Walser, [ a] Pentagramma mirificum Anregung: [Heinrich 2010]](/thumbs/76/73799383.jpg) Hans Walser, [011019a] Pentagramma mirificum Anregung: [Heinrich 010] 1 Worum es geht Ein Pentagramma mirificum ist ein sphärisches Pentagramm mit rechten Winkeln an den Spitzen. Die Abbildung zeigt ein
Hans Walser, [011019a] Pentagramma mirificum Anregung: [Heinrich 010] 1 Worum es geht Ein Pentagramma mirificum ist ein sphärisches Pentagramm mit rechten Winkeln an den Spitzen. Die Abbildung zeigt ein
Computational Geometry, MU Leoben
 Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Nach Lage der Winkel im Achsenkreuz wird unterschieden zwischen:
 Darstellung In der Zeichnung gibt es verschiedene Möglichkeiten einen Körper darzustellen. Die echte perspektivische Darstellung ist gekennzeichnet, durch einen Fluchtpunkt in dem alle Linien, die in der
Darstellung In der Zeichnung gibt es verschiedene Möglichkeiten einen Körper darzustellen. Die echte perspektivische Darstellung ist gekennzeichnet, durch einen Fluchtpunkt in dem alle Linien, die in der
Gegeben sei eine Ebene E und ein Punkt A E mit dem Ortsvektor a und zwei nicht kolli- neare Richtungsvektoren. + λ
 VI. Ebenengleichungen in Parameterform =================================================================6 6.1. Definition ----------------------------------------------------------------------------------------------------------------
VI. Ebenengleichungen in Parameterform =================================================================6 6.1. Definition ----------------------------------------------------------------------------------------------------------------
Stoffverteilung Mathematik Klasse 8 auf Basis der Bildungsstandards 2004
 Seiten und Winkel im Dreieck Abstände einfache Dreieckskonstruktionen, auch Bestimmung wahrer Größen bei Strecken und Flächen im Raum kongruente Figuren Kongruente Figuren 1. Kongruente Figuren 2. Kongruenzsätze
Seiten und Winkel im Dreieck Abstände einfache Dreieckskonstruktionen, auch Bestimmung wahrer Größen bei Strecken und Flächen im Raum kongruente Figuren Kongruente Figuren 1. Kongruente Figuren 2. Kongruenzsätze
6. Die Gruppe der Euklidischen Kongruenztransformationen
 6. Die Gruppe der Euklidischen Kongruenztransformationen Eine Fahne in der euklidischen Ebene besteht aus einem Tripel (P, g, H), wobei P ein Punkt, g eine Halbgerade mit Anfangspunkt P, und H eine Halbebene
6. Die Gruppe der Euklidischen Kongruenztransformationen Eine Fahne in der euklidischen Ebene besteht aus einem Tripel (P, g, H), wobei P ein Punkt, g eine Halbgerade mit Anfangspunkt P, und H eine Halbebene
9. Geometrische Konstruktionen und Geometrische Zahlen.
 9. Geometrische Konstruktionen und Geometrische Zahlen. Die Dreiteilungsgleichnung. Das Problem der Dreiteilung des Winkels wurde von Descartes vollständig gelöst. Dies ist in der Geometrie von Descartes
9. Geometrische Konstruktionen und Geometrische Zahlen. Die Dreiteilungsgleichnung. Das Problem der Dreiteilung des Winkels wurde von Descartes vollständig gelöst. Dies ist in der Geometrie von Descartes
Grundsätzliche Konstruktionshilfen:
 Grundsätzliche Konstruktionshilfen: Konstruktion des Netzes Seite 1 Wahre Größe von Flächen und Geraden Seite 1 Drehen in Hauptlage Seite 2 Wahre Größe durch weiteren Riss Seite 4 Sichtbarkeit Seite 5
Grundsätzliche Konstruktionshilfen: Konstruktion des Netzes Seite 1 Wahre Größe von Flächen und Geraden Seite 1 Drehen in Hauptlage Seite 2 Wahre Größe durch weiteren Riss Seite 4 Sichtbarkeit Seite 5
Lösungen IV ) β = 54,8 ; γ = 70,4 106) a) 65 b) 65 (115?) d) 57,5
 (Stark 7 S. 6ff) Lösungen IV. a) gleichschenklig 0) a) () α = β = 6,7 () β = 7,8 ; γ = 4,4 () α = 4 ; γ = (4) α = β = (80 γ)/ b) 79,6 und 0,8 oder 0, und 0, c) α = β = 64 ; γ = d) gleichschenklig; zwei
(Stark 7 S. 6ff) Lösungen IV. a) gleichschenklig 0) a) () α = β = 6,7 () β = 7,8 ; γ = 4,4 () α = 4 ; γ = (4) α = β = (80 γ)/ b) 79,6 und 0,8 oder 0, und 0, c) α = β = 64 ; γ = d) gleichschenklig; zwei
