7. Materiewellen und Energiequantisierung
|
|
|
- Hedwig Brandt
- vor 7 Jahren
- Abrufe
Transkript
1 Materiewellen und Energiequantisierung 7.1 Energiequantisierung in Atomen Weisses Licht: kontinuierliches Spektrum, d.h. enthält alle Wellenlängen des sichtbaren Bereichs Anregung von Atomen in einem Gas mit niedrigem Druck: Emission von Licht mit bestimmten Wellenlängen E = h = h c Existenz nur bestimmter Wellenlängen bedeutet die Existenz diskreter Energien Energieerhaltung: wenn ein Atom ein Photon bei einer bestimmten Wellenlänge/Energie emittiert oder absorbiert, so muss sich seine Energie um einen bestimmten Betrag ändern Niels Bohr (1913): innere Energie eines Atoms hat nur einen Satz von gewissen erlaubten Energiewerten Franck-Hertz-Experiment (1913) Anregung von Atomen (Ne) durch Stoss mit Elektronen E = E 2 E 1 = h Zunächst elastische Stösse, bis bei der Spannung U r die Anregung von Ne möglich wird durch einen inelastischen Stoss, d.h. die gesamte Energie des Elektrons wird auf das Atom übertragen Bei der doppelten Spannung 2 U r ist die zweifache Anregung möglich 7.2 Bohrsches Modell des Wasserstoffatoms Es war bekannt, dass das Wasserstoffatom aus einem Elektron und einem Proton besteht Aus Spektroskopie- Experimenten war ausserdem bekannt, dass Licht nur bei bestimmten Frequenzen bzw. Energien absorbiert und emittiert wird: Balmer 1885: = n 2 G, wobei G ein empirischer Zahlenwert ist n N=3, 4, 5,, R H = 4 G =109' cm 1, Rydberg-Konstante n 4 RH das gesamte Spektrum des Wasserstoff-Atoms weißt mehrere solche Linien auf: 1 = R 1 H n' 1 mit n'< n 2 n 2
2 7.2 n =1: Lyman-Serie n =2: Balmer Serie n =3: Paschen Serie n =4: Brackett-Serie n =5: Pfund-Serie Experiment: Hg-Dampflampe Klassische Vorstellung: Elektron kreist um Proton, Dynamisches Gleichgewicht: Coulomb-Kraft = Zentripetal-Kraft e r = m r 2 e 2 2 0, bzw. r = 4 0 m 0 2 1/3 Gesamtenergie: E = E kin + E pot, E kin = 1 2 m 0v 2 = 1 2 m 0r 2 2 E pot : Arbeit, die gewonnen wird, wenn man das Elektron aus unendlicher Entfernung zum Abstand r bewegt. E pot = r e r' dr' = e2 < 0 -> Bindungsenergie r Gesamtenergie: E = 1 2 m r e2 4 0 r = 1 e r = 1 e 2 2 m Klassisch: der Radius r ist beliebig, d.h. die möglichen Energien E sind beliebig Ausserdem: ein Elektron bewegt sich auf einer Kreisbahn, d.h. es unterliegt permanent einer Zentripedal-Beschleunigung Beschleunigte Ladung emittiert elektromagnetische Strahlung, d.h. Energieverlust für das Elektron d.h. instabile Atome 1/3 Bohrs Postulate: 1. Es gelten die klassischen Bewegungsgleichungen, jedoch sind nur diskrete Bahnen mit Energien E n erlaubt 2. Die Elektronenbewegung erfolgt strahlungslos. Übergänge zu höheren (tieferen) Energieniveaus erfolgen durch Absorption (Emission) eines Photons mit Frequenz h = E n E n', E n = R Hhc n 2
3 Korrespondenzprinzip: Für grosse Werte von r und n gelten wieder die Gesetze der klassischen Physik Betrachte n n'=1= und n >>1 = R H c 1 n' 1 = R 2 n 2 H c 1 n ( ) 2 1 n 2 = R c 1 1 H n 2 1 n R H c 2 n = 2R Hc 3 n 3 Abstrahlung mit klassischer Umlauf-Frequenz = 2 ( ) 2 1 Gleichsetzen von klassischen Energien und denjenigen, die aus dem Korrespondenzprinzip folgen: E n = R Hhc = 1 e 2 n m 0 ( 4) 2 R 2 H c 2 n 6 d.h. R H = m 0 e4 =109' ± h 3 cm1 c d.h. die Rydbergkonstante wurde auf andere Naturkonstanten zurückgeführt. 1/3 R H hc =13.6 ev ist die Ionisierungsenergie des Wasserstoffatoms im Grundzustand Radius der n-ten (klassischen) Bahn: r n = n e 2 2 m 0 = n 2 a 0 n: Hauptquantenzahl a 0 = 0.53 Angstroem = nm: Bohr scher Radius 7.3 Elektronen und Materiewellen Elektronenstrahlen können durch elektrische und magnetische Felder abgelenkt werden d.h. sie bestehen aus geladenen Teilchen, in diesem Falle aus Elektronen Im Experiment zeigt sich, dass man Elektronenstrahlen ebenso zur Interferenz bringen kann wie Lichtstrahlen aus einem Laser d.h. es muss auch für Materiestrahlen eine Wellenlänge geben De Broglie-Hypothese: = h p Diese Gleichung gilt genauso für massive Teilchen (Elektronen) wie für masselose Teilchen (Photonen)
4 7.4 = E h bzw. h = E gilt nur für masselose Teilchen E = p2 2m gilt für Teilchen mit Masse m Bei makroskopischen Bedingungen sind die Wellenlängen so klein, dass es unter gewöhnlichen Bedingungen nicht möglich ist, Welleneigenschaften wie Interferenz oder Beugung zu beobachten Beispiel: Berechne Wellenlänge eines Staubteilchens mit Masse m =10 6 g, das sich mit einer Geschwindigkeit von v =10 6 m s 1 bewegt Lösung: = h p = h m v = J s (10 19 kg)10 6 m s 1 ( ) = m Diese Länge ist viel kleiner als jegliche Hindernisse oder Öffnungen, so dass die Interferenz dieser Wellen nicht beobachtet werden kann. Bei makroskopischen Teilchen ist die Masse und damit der Impuls noch viel grösser, d.h. die Wellenlänge noch kleiner Deswegen können die Welleneigenschaften von Tennisbällen oder Billardkugel im Experiment nicht beobachtet werden Beispiel: Tennisball mit Masse m=58 g und Geschwindigkeit 100 km/h Lösung: =4.1 x m In der mikroskopischen Welt sieht die Lage anders aus, z.b. Elektronen mit geringer Energie Impuls p -> kinetische Energie E kin = p2 2m Impuls als Funktion der Energie: p = 2mE kin Wellenlänge: = h p = h 2mE kin Interferenz und Beugung von Elektronen Betrachte einen Kristall, der mit einem Elektronenstrahl beschossen wird:
5 7.5 Auf dem Detektorschirm bilden sich konzentrische Kreise Jeder Kreis entspricht einem Beugungsmaximum (siehe Bragg-Beugung mit Röntgenstrahlen) Da Materiestrahlen eine sehr kleine Wellenlänge haben können, können sie benutzt werden, um sehr kleine Objekte abzubilden -> Elektronenmikroskop Stehende Wellen und Energiequantisierung Wenn Elektronen Welleneigenschaften haben, sollte es möglich sein stehende Elektronenwellen zu erzeugen Beispiel Geige: stehende akustische Wellen führen zu wohl definierten (quantisierten) Tönen Stehende Materiewellen: E = h Annahme: quantisierte Energieniveaus in Atomen sind auf stehende Elektronenwellen zurückzuführen Entwicklung der Wellenmechanik bzw. Quantenmechanik Elektron wird mit Hilfe einer Wellenfunktion beschrieben (x,t) Das Verhalten der Wellenfunktion wird durch die Schrödinger-Gleichung beschrieben i (x,t) = 2 2 (x,t) + V (x)(x,t) t 2m x 2 Falls das Potential V(x) bekannt ist, so kann die Wellenfunktion (x,t) berechnet werden 7.4 Interpretation der Wellenfunktion Wellen entlang einer Saite: Wellenfunktion entspricht der Saitenauslenkung in Abhängigkeit von Ort und Zeit Schallwellen: Wellenfunktion entspricht der Auslenkung eines Luftmoleküls, oder der Amplitude des Drucks Elektromagnetische Wellen: Wellenfunktion entspricht der Amplitude des elektrischen oder magnetischen Feldes Elektronenwellen? Quadrat der Wellenfunktion gibt die Wahrscheinlichkeit, ein Elektron an einem bestimmten Ort zu einer bestimmten Zeit zu finden Schrödinger-Gleichung beschreibt zunächst ein einzelnes Teilchen Quadrat der Wellenfunktion: gibt die Wahrscheinlichkeitsdichte an, d.h. die Wahrscheinlichkeit, das Teilchen in einem bestimmten Volumen an einem bestimmten Ort zu finden Wahrscheinlichkeit in einer Dimension, das Teilchen an der Position x im Bereich dx zu finden: 2 (x)dx Allgemein: (x,t) stehende Wellen sind unabhängig von der Zeit: (x)
6 7.6 Die Wahrscheinlichkeit, das Teilchen irgendwo zu finden, muss normiert sein: Um diese Normierungsbedingung erfüllen zu können, muss die Wellenfunktion im Unendlichen verschwinden, d.h. (x =±) = 0 Beispiel: Aufenthaltswahrscheinlichkeit eines klassischen Teilchens + 2 (x) dx =1 klassisches punktförmiges Teilchen befinde sich zwischen zwei Wänden bei x=0 und bei x=8 cm es bewege sich mit konstanter Geschwindigkeit hin und her Wahrscheinlichkeitsdichte P(x): muss überall im Bereich 0<x<8cm gleich gross sein: P(x) = P 0 für 0 < x < 8cm 0 sonst Normierung: a P(x)dx =1= a P(x)dx 8cm 0 = P 0 ( 8cm) P 0 = 1 8cm Wahrscheinlichkeit, das Teilchen bei x=2 cm anzutreffen: da dies einem unendlich dünnen Intervall entspricht, ist die Wahrscheinlichkeit, das Teilchen an genau einem Punkt anzutreffen, =0 Wahrscheinlichkeit, dass Teilchen zwischen x=3.0 cm und x= 3.4 cm anzutreffen: 3.4cm P(x)dx = P 0 ( 3.4cm 3cm)= 1 0.4cm = cm 3cm 7.5 Der Welle-Teilchen Dualismus Photoeffekt oder Hohlraumstrahlung: Licht muss als Teilchen beschrieben werden Interferenz am Spalt: Licht muss durch Welle beschrieben werden Alles, was Impuls und Energie trägt, zeigt sowohl Teilchen- als auch Wellen-Eigenschaften Klassische Physik: die beiden Eigenschaften sind unvereinbar miteinander
7 7.7 Klassisches Teilchen: lässt sich stets lokalisieren, kann als nicht durch eine ausgedehnte Welle beschrieben werden, das Verhalten des Teilchens wird durch Energie- und Impulserhaltung beschrieben Klassische Welle: zeigt Interferenz und Beugung, ihre Energie ist in Raum und Zeit kontinuierlich verteilt Beide Konzepte schliessen sich gegenseitig aus Experimentelle Realität: Elektronen und Photonen können sich sowohl als Teilchen wie als Wellen verhalten Alle Objekte bewegen sich wie Wellen und tauschen Energie aus wie Teilchen Doppelspaltexperiment mit Elektronen: Für ebene Wellen, die auf einen Doppelspalt einfallen, entsteht auf dem dahinter liegenden Schirm eine charakteristische Intensitätsverteilung, die die Interferenzbedingung widerspiegelt. Teilchenbild: Jedes Teilchen hat eine gewisse Wahrscheinlichkeit, irgendwo auf dem Schirm zu landen Die Wahrscheinlichkeitsdichte wird durch 2 (x) beschrieben Wahrscheinlichkeit dort auf dem Schirm aufzutreffen, wo die Interferenzbedingung ein Maximum vorhersagt, ist besonders hoch Dort, wo der Gangunterschied zwischen den beiden Strahlen ist, d.h. destruktive Interferenz, wird die Wahrscheinlichkeit für ein Teilchen, den Schirm zu treffen, nahe bei Null liegen Detektor sieht jeweils ein Teilchen, Gesamtverteilung vieler Ereignisse spiegelt die Wahrscheinlichkeitsverteilung der Welle wider Die Heisenberg sche Unschärferelation Es ist prinzipiell unmöglich, sowohl den Impuls als auch die Position eines Teilchens beliebig genau zu messen. Beispielsweise messe man die Position eines Teilchen mit Licht der Wellenlänge Licht wird am Objekt gestreut, d.h. die Messgenauigkeit für den Ort des Teilchens ist von der Grössenordnung der Wellenlänge x
8 7.8 Um die Genauigkeit der Ortsmessung zu verbessern, kann man Licht mit kürzerer Wellenlänge benutzten, z.b. Röntgenstrahlung Bestimme den Impuls des Teilchens p x durch seine Masse und seine Geschwindigkeit Impuls: messe die Position des Teilchens zu zwei eng benachbarten Zeitpunkten Impuls der Photonen, die zur Messung benutzt werden: p = h Werden diese Photonen am Teilchen gestreut, so ändert sich ihr Impuls auf unkontrollierbare Weise, d.h. die Unschärfe für die Impuls-Messung ist p x h Bei kleiner Wellenlänge (präzise Ortsmessung) ist die Impulsmessung mit einer grossen Unschärfe behaftet Die Herabsetzung der Intensität des Lichts bringt nichts, da damit nur die Zahl der Photonen heruntergesetzt wird, nicht aber der Impulsübertrag zwischen Photonen und Teilchen. Damit das Teilchen zu sehen ist, muss mindestens ein Photon gestreut werden. Produkt von Orts- und Impulsunschärfe: xp x h = h Eine präzisere Formulierung liefert: xp x 1 h mit = 2 2 Diese prinzipielle Untergrenze für die Messgenauigkeit beruht direkt auf dem Welle- Teilchen-Dualismus 7.6 Ein Teilchen im Kasten Zunächst einige quantenmechanische Lösungen ohne direkten Beizug der Schrödingergleichung Betrachte ein Teilchen in einem ein-dimensionalen Kasten der Länge d, d.h. die Wahrscheinlichkeit das Teilchen ausserhalb des Kastens zu finden, ist Null. (x) = 0 für x 0 und für x d Ausserdem sei die Wellenfunktion überall stetig, d.h. (x = 0) = 0 =(x = d) Beispiel: Elektronen befinde sich in der Nähe des Atomkerns und nicht weit davon entfernt Physikalisch sind die Randbedingungen identisch mit denjenigen einer eingespannten Saite, d.h. wir kennen die Lösungen d = n 2, n =1,2,3,... Gesamtenergie des Teilchens ist seine Bewegungsenergie: E = 1 2 mv2 = p2 2m
9 7.9 Mit de Broglie Beziehung: p n = h n ( ) 2 Folgt E n = p 2 n 2m = h / n 2m = h 2 2 2m n Bedingung für stehende Welle: n = 2d n Quantisierte Energiewerte: E n = n 2 h 2 8md 2 = n 2 E 1 Wobei E 1 = h 2 die Grundzustandsenergie ist., d.h. die niedrigste Energie, die ein 2 8md Teilchen in einem ein-dimensionalen Kasten einnehmen kann. Allgemein: Randbedingungen wie (x = 0) = 0 =(x = d) führen in der Quantenmechanik zur Quantisierung der Energie Die niedrigste Energie ist immer von Null verschieden. Dies ist die sogenannte Nullpunktsenergie. Sie ist umso höher, je kleiner der Bereich ist, auf den das Teilchen eingesperrt wird. Atom: Elektron ist in einem gebundenen Zustand Absorption eines Photons -> das Elektron kann in einen höheren Energiezustand übergehen Energie des Photons: h = E n E n' Wellenfunktionen stehender Wellen
10 7.10 Betrachte Amplitude einer schwingenden Saite, die bei x=0 und bei x=d fixiert ist: y n = A n sink n x A n : Konstante k n = 2 : Wellenzahl Wellenfunktionen für Lösungen des Kastenpotentials: n (x) = A n sink n x Mit n = 2d n folgt k n = 2 n = 2 2d n = n d n (x) = A n sin n x d, bzw. für die Wellenfunktionen Normierungsbedingung liefert die Konstante A n : 2 n (x)dx = A 2 n sin(n x d )dx =1 -> d 0 A n = 2, d.h. unabhängig von n! d Normierte Wellenfunktion für Teilchen im Kasten: n (x) = 2 d sin n x d n: Quantenzahl charakterisiert die Wellenfunktion für einen bestimmten Zustand und damit dessen Energie eine Dimension: eine Quantenzahl drei Dimensionen -> Randbedingungen in drei Richtungen -> drei Quantenzahlen Grundzustand: Teilchen befindet sich mit hoher Wahrscheinlichkeit in der Mitte des Kastens 1.angeregter Zustand: Teilchen befindet sich mit hoher Wahrscheinlichkeit links und rechts der Mitte des Kastens, die Wahrscheinlichkeit, das Teilchen genau in der Mitte des Kastens anzutreffen, ist Null
11 7.11 Korrespondenzprinzip: im Limes sehr grosser Quantenzahlen müssen die klassische und die quantenmechanische Berechnung das gleiche Resultat ergeben Sehr hohe Quantenzahlen entsprechen sehr hohen Energien, die relative Differenz der Energien wird jedoch immer kleiner, so dass die Quantisierung der Energie eine immer geringere Rolle spielt. Elektron als klassisches Teilchen: Vorstellung: es fliegt im Kasten hin und her Aber in der Quantenmechanik: Wellenfunktionen charakterisieren stationäre, d.h. zeitunabhängige Zustände Vorstellung: Elektron als Ladungswolke, dessen Ausdehnung und Dichtheitsgrad durch die Wahrscheinlichkeitsverteilung dargestellt wird Grundzustand: Ladungsdichte ist in der Mitte des Kastens hoch 7.7 Erwartungswerte Klassische Mechanik: Position eines Teilchens als Funktion der Zeit Quantenmechanik: man kann nur die Wahrscheinlichkeit angeben, mit der ein bestimmter Wert der Position x gemessen wird Wahrscheinlichkeitsverteilung über die Kastenlänge
12 7.12 Mittelwert von x heisst Erwartungswert: x Erwartungswert=Mittelwert, der bei der Positionsmessung an sehr vielen Teilchen mit der gleichen Wellenfunktion (x) zu erwarten ist 2 (x) gibt die Wahrscheinlichkeit an Definition des Erwartungswerts für die Orstmessung: x = Erwartungswert für eine beliebige Funktion: f (x) = x 2 (x) dx f (x) 2 (x) dx Berechnung von Aufenthaltswahrscheinlichkeiten und Erwartungswerten Betrachte Teilchen im Kasten der Länge d: n (x) = 2 d sin n x d Berechne Wahrscheinlichkeit des Teilchens im Grundzustand (n=1) in einem Intervall der Länge x = 0.01d zentriert um die Position x = 1 2 d (x = d 2 ) = 2 d d sin 2 d = 2 d sin = 2 2 d Aufenthaltswahrscheinlichkeit: 2 (x = d 2 ) = 2 d Wahrscheinlichkeit: P 2 (x = d 2 ) x = d = 0.02 d
7. Das Bohrsche Modell des Wasserstoff-Atoms. 7.1 Stabile Elektronbahnen im Atom
 phys4.08 Page 1 7. Das Bohrsche Modell des Wasserstoff-Atoms 7.1 Stabile Elektronbahnen im Atom Atommodell: positiv geladene Protonen (p + ) und Neutronen (n) im Kern negative geladene Elektronen (e -
phys4.08 Page 1 7. Das Bohrsche Modell des Wasserstoff-Atoms 7.1 Stabile Elektronbahnen im Atom Atommodell: positiv geladene Protonen (p + ) und Neutronen (n) im Kern negative geladene Elektronen (e -
Elemente der Quantenmechanik III 9.1. Schrödingergleichung mit beliebigem Potential 9.2. Harmonischer Oszillator 9.3. Drehimpulsoperator
 VL 8 VL8. VL9. VL10. Das Wasserstoffatom in der klass. Mechanik 8.1. Emissions- und Absorptionsspektren der Atome 8.2. Quantelung der Energie (Frank-Hertz Versuch) 8.3. Bohrsches Atommodell 8.4. Spektren
VL 8 VL8. VL9. VL10. Das Wasserstoffatom in der klass. Mechanik 8.1. Emissions- und Absorptionsspektren der Atome 8.2. Quantelung der Energie (Frank-Hertz Versuch) 8.3. Bohrsches Atommodell 8.4. Spektren
Übungen Quantenphysik
 Ue QP 1 Übungen Quantenphysik Kernphysik Historische Entwicklung der Atommodelle Klassische Wellengleichung 5 Schrödinger Gleichung 6 Kastenpotential (Teilchen in einer Box) 8 Teilchen im Potentialtopf
Ue QP 1 Übungen Quantenphysik Kernphysik Historische Entwicklung der Atommodelle Klassische Wellengleichung 5 Schrödinger Gleichung 6 Kastenpotential (Teilchen in einer Box) 8 Teilchen im Potentialtopf
Bohrsches Atommodell / Linienspektren. Experimentalphysik für Biologen und Chemiker, O. Benson & A. Peters, Humboldt-Universität zu Berlin
 Bohrsches Atommodell / Linienspektren Quantenstruktur der Atome: Atomspektren Emissionslinienspektren von Wasserstoffatomen im sichtbaren Bereich Balmer Serie (1885): 1 / λ = K (1/4-1/n 2 ) 656.28 486.13
Bohrsches Atommodell / Linienspektren Quantenstruktur der Atome: Atomspektren Emissionslinienspektren von Wasserstoffatomen im sichtbaren Bereich Balmer Serie (1885): 1 / λ = K (1/4-1/n 2 ) 656.28 486.13
Periodensystem, elektromagnetische Spektren, Atombau, Orbitale
 Periodensystem, elektromagnetische Spektren, Atombau, Orbitale Als Mendelejew sein Periodensystem aufstellte waren die Edelgase sowie einige andere Elemente noch nicht entdeck (gelb unterlegt). Trotzdem
Periodensystem, elektromagnetische Spektren, Atombau, Orbitale Als Mendelejew sein Periodensystem aufstellte waren die Edelgase sowie einige andere Elemente noch nicht entdeck (gelb unterlegt). Trotzdem
Der Welle-Teilchen-Dualismus
 Quantenphysik Der Welle-Teilchen-Dualismus Welle-Teilchen-Dualismus http://bluesky.blogg.de/2005/05/03/fachbegriffe-der-modernen-physik-ix/ Welle-Teilchen-Dualismus Alles ist gleichzeitig Welle und Teilchen.
Quantenphysik Der Welle-Teilchen-Dualismus Welle-Teilchen-Dualismus http://bluesky.blogg.de/2005/05/03/fachbegriffe-der-modernen-physik-ix/ Welle-Teilchen-Dualismus Alles ist gleichzeitig Welle und Teilchen.
Für Geowissenschaftler. EP WS 2009/10 Dünnweber/Faessler
 Für Geowissenschaftler Termin Nachholklausur Vorschlag Mittwoch 14.4.10 25. Vorlesung EP V. STRAHLUNG, ATOME, KERNE 27. Wärmestrahlung und Quantenmechanik Photometrie Plancksches Strahlungsgesetze, Welle/Teilchen
Für Geowissenschaftler Termin Nachholklausur Vorschlag Mittwoch 14.4.10 25. Vorlesung EP V. STRAHLUNG, ATOME, KERNE 27. Wärmestrahlung und Quantenmechanik Photometrie Plancksches Strahlungsgesetze, Welle/Teilchen
10.7 Moderne Atommodelle
 10.7 Moderne Atommodelle Zu Beginn des 20. Jahrhunderts entwickelte Niels Bohr sein berühmtes Bohrsches Atommodell. Mit diesem Modell konnten die Atomhüllen von einfachen Atomen wie dem Wasserstoffatom
10.7 Moderne Atommodelle Zu Beginn des 20. Jahrhunderts entwickelte Niels Bohr sein berühmtes Bohrsches Atommodell. Mit diesem Modell konnten die Atomhüllen von einfachen Atomen wie dem Wasserstoffatom
ν und λ ausgedrückt in Energie E und Impuls p
 phys4.011 Page 1 8.3 Die Schrödinger-Gleichung die grundlegende Gleichung der Quantenmechanik (in den bis jetzt diskutierten Fällen) eine Wellengleichung für Materiewellen (gilt aber auch allgemeiner)
phys4.011 Page 1 8.3 Die Schrödinger-Gleichung die grundlegende Gleichung der Quantenmechanik (in den bis jetzt diskutierten Fällen) eine Wellengleichung für Materiewellen (gilt aber auch allgemeiner)
10. Das Wasserstoff-Atom Das Spektrum des Wasserstoff-Atoms. im Bohr-Modell:
 phys4.016 Page 1 10. Das Wasserstoff-Atom 10.1.1 Das Spektrum des Wasserstoff-Atoms im Bohr-Modell: Bohr-Modell liefert eine ordentliche erste Beschreibung der grundlegenden Eigenschaften des Spektrums
phys4.016 Page 1 10. Das Wasserstoff-Atom 10.1.1 Das Spektrum des Wasserstoff-Atoms im Bohr-Modell: Bohr-Modell liefert eine ordentliche erste Beschreibung der grundlegenden Eigenschaften des Spektrums
27. Wärmestrahlung, Quantenmechanik (Abschluß: Welle-Teilchen-Dualismus
 26. Vorlesung EP V. STRAHLUNG, ATOME, KERNE 27. Wärmestrahlung, Quantenmechanik (Abschluß: Welle-Teilchen-Dualismus 28. Atomphysik, Röntgenstrahlung, Bohrsches Atommodell Versuche: Elektronenbeugung Linienspektrum
26. Vorlesung EP V. STRAHLUNG, ATOME, KERNE 27. Wärmestrahlung, Quantenmechanik (Abschluß: Welle-Teilchen-Dualismus 28. Atomphysik, Röntgenstrahlung, Bohrsches Atommodell Versuche: Elektronenbeugung Linienspektrum
Abb.15: Experiment zum Rutherford-Modell
 6.Kapitel Atommodelle 6.1 Lernziele Sie kennen die Entwicklung der Atommodelle bis zum linearen Potentialtopf. Sie kennen die Bohrschen Postulate und können sie auch anwenden. Sie wissen, wie man bestimmte
6.Kapitel Atommodelle 6.1 Lernziele Sie kennen die Entwicklung der Atommodelle bis zum linearen Potentialtopf. Sie kennen die Bohrschen Postulate und können sie auch anwenden. Sie wissen, wie man bestimmte
Einführung in die Quantentheorie der Atome und Photonen
 Einführung in die Quantentheorie der Atome und Photonen 23.04.2005 Jörg Evers Max-Planck-Institut für Kernphysik, Heidelberg Quantenmechanik Was ist das eigentlich? Physikalische Theorie Hauptsächlich
Einführung in die Quantentheorie der Atome und Photonen 23.04.2005 Jörg Evers Max-Planck-Institut für Kernphysik, Heidelberg Quantenmechanik Was ist das eigentlich? Physikalische Theorie Hauptsächlich
1.4. Die Wahrscheinlichkeitsinterpretation
 1.4. Die Wahrscheinlichkeitsinterpretation 1.4.1. Die Heisenbergsche Unschärferelation Wie kann der Welle-Teilchen-Dualismus in der Quantenmechanik interpretiert werden? gibt die Wahrscheinlichkeit an,
1.4. Die Wahrscheinlichkeitsinterpretation 1.4.1. Die Heisenbergsche Unschärferelation Wie kann der Welle-Teilchen-Dualismus in der Quantenmechanik interpretiert werden? gibt die Wahrscheinlichkeit an,
SS 2015 Supplement to Experimental Physics 2 (LB-Technik) Prof. E. Resconi
 Quantenmechanik des Wasserstoff-Atoms [Kap. 8-10 Haken-Wolf Atom- und Quantenphysik ] - Der Aufbau der Atome Quantenmechanik ==> Atomphysik Niels Bohr, 1913: kritische Entwicklung, die schließlich Plancks
Quantenmechanik des Wasserstoff-Atoms [Kap. 8-10 Haken-Wolf Atom- und Quantenphysik ] - Der Aufbau der Atome Quantenmechanik ==> Atomphysik Niels Bohr, 1913: kritische Entwicklung, die schließlich Plancks
22. Wärmestrahlung. rmestrahlung, Quantenmechanik
 22. Wärmestrahlung rmestrahlung, Quantenmechanik Plancksches Strahlungsgesetz: Planck (1904): der Austausch von Energie zwischen dem strahlenden System und dem Strahlungsfeld kann nur in Einheiten von
22. Wärmestrahlung rmestrahlung, Quantenmechanik Plancksches Strahlungsgesetz: Planck (1904): der Austausch von Energie zwischen dem strahlenden System und dem Strahlungsfeld kann nur in Einheiten von
8 Das Bohrsche Atommodell. 8. Das Bohrsche Atommodell
 1. Einführung 1.1. Quantenmechanik versus klassische Theorien 1.2. Historischer Rückblick 2. Kann man Atome sehen? Größe des Atoms 3. Weitere Eigenschaften von Atomen: Masse, Isotopie 4. Atomkern und Hülle:
1. Einführung 1.1. Quantenmechanik versus klassische Theorien 1.2. Historischer Rückblick 2. Kann man Atome sehen? Größe des Atoms 3. Weitere Eigenschaften von Atomen: Masse, Isotopie 4. Atomkern und Hülle:
Das Bohrsche Atommodell
 Das Bohrsche Atommodell Auf ein Elektron, welches im elektrischen Feld eines Atomkerns kreist wirkt ein magnetisches Feld. Der Abstand zum Atomkern ist das Ergebnis, der elektrostatischen Coulomb-Anziehung
Das Bohrsche Atommodell Auf ein Elektron, welches im elektrischen Feld eines Atomkerns kreist wirkt ein magnetisches Feld. Der Abstand zum Atomkern ist das Ergebnis, der elektrostatischen Coulomb-Anziehung
Grundbausteine des Mikrokosmos (7) Wellen? Teilchen? Beides?
 Grundbausteine des Mikrokosmos (7) Wellen? Teilchen? Beides? Experimentelle Überprüfung der Energieniveaus im Bohr schen Atommodell Absorbierte und emittierte Photonen hν = E m E n Stationäre Elektronenbahnen
Grundbausteine des Mikrokosmos (7) Wellen? Teilchen? Beides? Experimentelle Überprüfung der Energieniveaus im Bohr schen Atommodell Absorbierte und emittierte Photonen hν = E m E n Stationäre Elektronenbahnen
Das Wasserstoffatom Energiestufen im Atom
 11. 3. Das Wasserstoffatom 11.3.1 Energiestufen im Atom Vorwissen: Hg und Na-Dampflampe liefern ein charakteristisches Spektrum, das entweder mit einem Gitter- oder einem Prismenspektralapparat betrachtet
11. 3. Das Wasserstoffatom 11.3.1 Energiestufen im Atom Vorwissen: Hg und Na-Dampflampe liefern ein charakteristisches Spektrum, das entweder mit einem Gitter- oder einem Prismenspektralapparat betrachtet
9.3.3 Lösungsansatz für die Schrödinger-Gleichung des harmonischen Oszillators. Schrödinger-Gl.:
 phys4.015 Page 1 9.3.3 Lösungsansatz für die Schrödinger-Gleichung des harmonischen Oszillators Schrödinger-Gl.: Normierung: dimensionslose Einheiten x für die Koordinate x und Ε für die Energie E somit
phys4.015 Page 1 9.3.3 Lösungsansatz für die Schrödinger-Gleichung des harmonischen Oszillators Schrödinger-Gl.: Normierung: dimensionslose Einheiten x für die Koordinate x und Ε für die Energie E somit
12.8 Eigenschaften von elektronischen Übergängen. Übergangsfrequenz
 phys4.024 Page 1 12.8 Eigenschaften von elektronischen Übergängen Übergangsfrequenz betrachte die allgemeine Lösung ψ n der zeitabhängigen Schrödinger-Gleichung zum Energieeigenwert E n Erwartungswert
phys4.024 Page 1 12.8 Eigenschaften von elektronischen Übergängen Übergangsfrequenz betrachte die allgemeine Lösung ψ n der zeitabhängigen Schrödinger-Gleichung zum Energieeigenwert E n Erwartungswert
= 6,63 10 J s 8. (die Plancksche Konstante):
 35 Photonen und Materiefelder 35.1 Das Photon: Teilchen des Lichts Die Quantenphysik: viele Größen treten nur in ganzzahligen Vielfachen von bestimmten kleinsten Beträgen (elementaren Einheiten) auf: diese
35 Photonen und Materiefelder 35.1 Das Photon: Teilchen des Lichts Die Quantenphysik: viele Größen treten nur in ganzzahligen Vielfachen von bestimmten kleinsten Beträgen (elementaren Einheiten) auf: diese
Festkörperelektronik 2008 Übungsblatt 1
 Lichttechnisches Institut Universität Karlsruhe (TH) Prof. Dr. rer. nat. Uli Lemmer Dipl.-Phys. Alexander Colsmann Engesserstraße 13 76131 Karlsruhe Festkörperelektronik 1. Übungsblatt 17. April 2008 Dozent:
Lichttechnisches Institut Universität Karlsruhe (TH) Prof. Dr. rer. nat. Uli Lemmer Dipl.-Phys. Alexander Colsmann Engesserstraße 13 76131 Karlsruhe Festkörperelektronik 1. Übungsblatt 17. April 2008 Dozent:
Atome und ihre Eigenschaften
 Atome und ihre Eigenschaften Vom Atomkern zum Atom - von der Kernphysik zur Chemie Die Chemie beginnt dort, wo die Temperaturen soweit gefallen sind, daß die positiv geladenen Atomkerne freie Elektronen
Atome und ihre Eigenschaften Vom Atomkern zum Atom - von der Kernphysik zur Chemie Die Chemie beginnt dort, wo die Temperaturen soweit gefallen sind, daß die positiv geladenen Atomkerne freie Elektronen
10 Teilchen und Wellen. 10.1 Strahlung schwarzer Körper
 10 Teilchen und Wellen Teilchen: m, V, p, r, E, lokalisierbar Wellen: l, f, p, E, unendlich ausgedehnt (harmonische Welle) Unterscheidung: Wellen interferieren 10.1 Strahlung schwarzer Körper JEDER Körper
10 Teilchen und Wellen Teilchen: m, V, p, r, E, lokalisierbar Wellen: l, f, p, E, unendlich ausgedehnt (harmonische Welle) Unterscheidung: Wellen interferieren 10.1 Strahlung schwarzer Körper JEDER Körper
Beschreibe die wesentlichen Unterschiede zwischen den einzelnen Anregungsmöglichkeiten.
 Erkläre den Begriff Anregung eines Atoms Unter Anregung eines Atoms versteht man die Zufuhr von Energie an ein Atom, welche dieses vom Grundzustand in einen höheren Energiezustand, auf ein höheres Energieniveau,
Erkläre den Begriff Anregung eines Atoms Unter Anregung eines Atoms versteht man die Zufuhr von Energie an ein Atom, welche dieses vom Grundzustand in einen höheren Energiezustand, auf ein höheres Energieniveau,
Physik für Mediziner im 1. Fachsemester
 Physik für Mediziner im 1. Fachsemester #25 03/12/2008 Vladimir Dyakonov dyakonov@physik.uni-wuerzburg.de Atomphysik Teil 1 Atommodelle, Atomspektren, Röntgenstrahlung Atomphysik Die Atomphysik ist ein
Physik für Mediziner im 1. Fachsemester #25 03/12/2008 Vladimir Dyakonov dyakonov@physik.uni-wuerzburg.de Atomphysik Teil 1 Atommodelle, Atomspektren, Röntgenstrahlung Atomphysik Die Atomphysik ist ein
Das Rutherfordsche Atommodelle
 Dieses Lernskript soll nochmals die einzelnen Atommodelle zusammenstellen und die Bedeutung der einzelnen Atommdelle veranschaulichen. Das Rutherfordsche Atommodelle Entstehung des Modells Rutherford beschoss
Dieses Lernskript soll nochmals die einzelnen Atommodelle zusammenstellen und die Bedeutung der einzelnen Atommdelle veranschaulichen. Das Rutherfordsche Atommodelle Entstehung des Modells Rutherford beschoss
Durch welchen Schlitz ist das Teilchen geflogen? Beobachtung
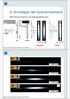 ) Grundlagen der Quantenmechanik Welle-Teilchen-Dualismus: das Doppelspaltexperiment Teilchen Welle Durch welchen Schlitz ist das Teilchen geflogen? Beobachtung Welle-Teilchen-Dualismus: 1) P =... Wahrscheinlichkeitsamplitude
) Grundlagen der Quantenmechanik Welle-Teilchen-Dualismus: das Doppelspaltexperiment Teilchen Welle Durch welchen Schlitz ist das Teilchen geflogen? Beobachtung Welle-Teilchen-Dualismus: 1) P =... Wahrscheinlichkeitsamplitude
14 Teilchen und Wellen
 14 Teilchen und Wellen 14.1 Teilchencharakter von elektromagnetischen Wellen 1411 14.1.1 Strahlung schwarzer Körper 14.1.2 Der Photoeffekt 14.1.3 Technische Anwendungen 14.2 Wellencharakter von Teilchen
14 Teilchen und Wellen 14.1 Teilchencharakter von elektromagnetischen Wellen 1411 14.1.1 Strahlung schwarzer Körper 14.1.2 Der Photoeffekt 14.1.3 Technische Anwendungen 14.2 Wellencharakter von Teilchen
Physik für Maschinenbau. Prof. Dr. Stefan Schael RWTH Aachen
 Physik für Maschinenbau Prof. Dr. Stefan Schael RWTH Aachen Vorlesung 11 Brechung b α a 1 d 1 x α b x β d 2 a 2 β Totalreflexion Glasfaserkabel sin 1 n 2 sin 2 n 1 c arcsin n 2 n 1 1.0 arcsin
Physik für Maschinenbau Prof. Dr. Stefan Schael RWTH Aachen Vorlesung 11 Brechung b α a 1 d 1 x α b x β d 2 a 2 β Totalreflexion Glasfaserkabel sin 1 n 2 sin 2 n 1 c arcsin n 2 n 1 1.0 arcsin
Thema heute: Aufbau der Materie: Das Bohr sche Atommodell
 Wiederholung der letzten Vorlesungsstunde: Erste Atommodelle, Dalton Thomson, Rutherford, Atombau, Coulomb-Gesetz, Proton, Elektron, Neutron, weitere Elementarteilchen, atomare Masseneinheit u, 118 bekannte
Wiederholung der letzten Vorlesungsstunde: Erste Atommodelle, Dalton Thomson, Rutherford, Atombau, Coulomb-Gesetz, Proton, Elektron, Neutron, weitere Elementarteilchen, atomare Masseneinheit u, 118 bekannte
Theoretische Physik mit Maple, WS 2010/ Übungsblatt (Besprechung am ) R( ) ( ( ( ) ( ))) ( ) u ( x)
 Theoretische Physik mit Maple, WS 2010/2011 9. Übungsblatt (Besprechung am 24.1.2011) Quantenmechanische Streuung am Kastenpotential Wir betrachten die zeitunabhängige Schrödinger-Gleichung (ZuSG) und
Theoretische Physik mit Maple, WS 2010/2011 9. Übungsblatt (Besprechung am 24.1.2011) Quantenmechanische Streuung am Kastenpotential Wir betrachten die zeitunabhängige Schrödinger-Gleichung (ZuSG) und
Einleitung Das Rutherford sche Atommodell Das Bohr sche Atommodell. Atommodelle [HERR] Q34 LK Physik. 25. September 2015
![Einleitung Das Rutherford sche Atommodell Das Bohr sche Atommodell. Atommodelle [HERR] Q34 LK Physik. 25. September 2015 Einleitung Das Rutherford sche Atommodell Das Bohr sche Atommodell. Atommodelle [HERR] Q34 LK Physik. 25. September 2015](/thumbs/49/25189684.jpg) Q34 LK Physik 25. September 2015 Geschichte Antike Vorstellung von Leukipp und Demokrit (5. Jahrh. v. Chr.); Begründung des Atomismus (atomos, griech. unteilbar). Anfang des 19. Jahrh. leitet Dalton aus
Q34 LK Physik 25. September 2015 Geschichte Antike Vorstellung von Leukipp und Demokrit (5. Jahrh. v. Chr.); Begründung des Atomismus (atomos, griech. unteilbar). Anfang des 19. Jahrh. leitet Dalton aus
c = Ausbreitungsgeschwindigkeit (2, m/s) λ = Wellenlänge (m) ν = Frequenz (Hz, s -1 )
 2.3 Struktur der Elektronenhülle Elektromagnetische Strahlung c = λ ν c = Ausbreitungsgeschwindigkeit (2,9979 10 8 m/s) λ = Wellenlänge (m) ν = Frequenz (Hz, s -1 ) Quantentheorie (Max Planck, 1900) Die
2.3 Struktur der Elektronenhülle Elektromagnetische Strahlung c = λ ν c = Ausbreitungsgeschwindigkeit (2,9979 10 8 m/s) λ = Wellenlänge (m) ν = Frequenz (Hz, s -1 ) Quantentheorie (Max Planck, 1900) Die
Atommodell führte Rutherford den nach ihm benannten Streuversuch durch. Dabei bestrahlte er eine dünne Goldfolie mit α Teilchen.
 Atommodell nach Rutherford 1911 führte Rutherford den nach ihm benannten Streuversuch durch. Dabei bestrahlte er eine dünne Goldfolie mit α Teilchen. Beobachtung: Fast alle Teilchen fliegen ungestört durch.
Atommodell nach Rutherford 1911 führte Rutherford den nach ihm benannten Streuversuch durch. Dabei bestrahlte er eine dünne Goldfolie mit α Teilchen. Beobachtung: Fast alle Teilchen fliegen ungestört durch.
Aufbau von Atomen. Atommodelle Spektrum des Wasserstoffs Quantenzahlen Orbitalbesetzung Periodensystem
 Aufbau von Atomen Atommodelle Spektrum des Wasserstoffs Quantenzahlen Orbitalbesetzung Periodensystem Wiederholung Im Kern: Protonen + Neutronen In der Hülle: Elektronen Rutherfords Streuversuch (90) Goldatome
Aufbau von Atomen Atommodelle Spektrum des Wasserstoffs Quantenzahlen Orbitalbesetzung Periodensystem Wiederholung Im Kern: Protonen + Neutronen In der Hülle: Elektronen Rutherfords Streuversuch (90) Goldatome
Welleneigenschaften von Elektronen
 Seite 1 von 7 Welleneigenschaften von Elektronen Nachdem Robert Millikan 1911 die Ladung des Elektrons bestimmte, konnte bald auch seine Ruhemasse gemessen werden. Zahlreiche Experimente mit Elektronenstrahlen
Seite 1 von 7 Welleneigenschaften von Elektronen Nachdem Robert Millikan 1911 die Ladung des Elektrons bestimmte, konnte bald auch seine Ruhemasse gemessen werden. Zahlreiche Experimente mit Elektronenstrahlen
Wiederholung der letzten Vorlesungsstunde:
 Wiederholung der letzten Vorlesungsstunde: Das (wellen-) quantenchemische Atommodell Orbitalmodell Beschreibung atomarer Teilchen (Elektronen) durch Wellenfunktionen, Wellen, Wellenlänge, Frequenz, Amplitude,
Wiederholung der letzten Vorlesungsstunde: Das (wellen-) quantenchemische Atommodell Orbitalmodell Beschreibung atomarer Teilchen (Elektronen) durch Wellenfunktionen, Wellen, Wellenlänge, Frequenz, Amplitude,
2. Elementare Stöchiometrie I Definition und Gesetze, Molbegriff, Konzentrationseinheiten
 Inhalt: 1. Regeln und Normen Modul: Allgemeine Chemie 2. Elementare Stöchiometrie I Definition und Gesetze, Molbegriff, Konzentrationseinheiten 3.Bausteine der Materie Atomkern: Elementarteilchen, Kernkräfte,
Inhalt: 1. Regeln und Normen Modul: Allgemeine Chemie 2. Elementare Stöchiometrie I Definition und Gesetze, Molbegriff, Konzentrationseinheiten 3.Bausteine der Materie Atomkern: Elementarteilchen, Kernkräfte,
8.2 Aufbau der Atome. auch bei der Entdeckung der Kathodenstrahlen schienen die Ladungsträger aus den Atomen herauszukommen.
 Dieter Suter - 404 - Physik B3 8.2 Aufbau der Atome 8.2.1 Grundlagen Wenn man Atome als Bausteine der Materie i- dentifiziert hat stellt sich sofort die Frage, woraus denn die Atome bestehen. Dabei besteht
Dieter Suter - 404 - Physik B3 8.2 Aufbau der Atome 8.2.1 Grundlagen Wenn man Atome als Bausteine der Materie i- dentifiziert hat stellt sich sofort die Frage, woraus denn die Atome bestehen. Dabei besteht
9. GV: Atom- und Molekülspektren
 Physik Praktikum I: WS 2005/06 Protokoll zum Praktikum Dienstag, 25.10.05 9. GV: Atom- und Molekülspektren Protokollanten Jörg Mönnich Anton Friesen - Betreuer Andreas Branding - 1 - Theorie Zur Erläuterung
Physik Praktikum I: WS 2005/06 Protokoll zum Praktikum Dienstag, 25.10.05 9. GV: Atom- und Molekülspektren Protokollanten Jörg Mönnich Anton Friesen - Betreuer Andreas Branding - 1 - Theorie Zur Erläuterung
1 Physikalische Hintergrunde: Teilchen oder Welle?
 Skript zur 1. Vorlesung Quantenmechanik, Montag den 11. April, 2011. 1 Physikalische Hintergrunde: Teilchen oder Welle? 1.1 Geschichtliches: Warum Quantenmechanik? Bis 1900: klassische Physik Newtonsche
Skript zur 1. Vorlesung Quantenmechanik, Montag den 11. April, 2011. 1 Physikalische Hintergrunde: Teilchen oder Welle? 1.1 Geschichtliches: Warum Quantenmechanik? Bis 1900: klassische Physik Newtonsche
Von der kosmischen Hintergrundstrahlung zur Heisenbergschen Unbestimmtheitsrelation. eine Einführung in die Quantenmechanik
 Von der kosmischen Hintergrundstrahlung zur Heisenbergschen Unbestimmtheitsrelation eine Einführung in die Quantenmechanik 1) Die Hohlraumstrahlung: Geburt der Quantenmechanik Die kosmische Hintergrundstrahlung
Von der kosmischen Hintergrundstrahlung zur Heisenbergschen Unbestimmtheitsrelation eine Einführung in die Quantenmechanik 1) Die Hohlraumstrahlung: Geburt der Quantenmechanik Die kosmische Hintergrundstrahlung
Entwicklung der Atommodelle
 Entwicklung der Atommodelle Entwicklung der Atommodelle Demokrit 460 v Chr. Nur scheinbar hat ein Ding eine Farbe, nur scheinbar ist es süß oder bitter; in Wirklichkeit gibt es nur Atome im leeren Raum.
Entwicklung der Atommodelle Entwicklung der Atommodelle Demokrit 460 v Chr. Nur scheinbar hat ein Ding eine Farbe, nur scheinbar ist es süß oder bitter; in Wirklichkeit gibt es nur Atome im leeren Raum.
FK Experimentalphysik 3, Lösung 4
 1 Sterne als schwarze Strahler FK Experimentalphysik 3, 4 1 Sterne als schwarze Strahler Betrachten sie folgende Sterne: 1. Einen roten Stern mit einer Oberflächentemperatur von 3000 K 2. einen gelben
1 Sterne als schwarze Strahler FK Experimentalphysik 3, 4 1 Sterne als schwarze Strahler Betrachten sie folgende Sterne: 1. Einen roten Stern mit einer Oberflächentemperatur von 3000 K 2. einen gelben
Atommodell. Atommodell nach Bohr und Sommerfeld Für sein neues Atommodell stellte Bohr folgende Postulate auf:
 Für sein neues Atommodell stellte Bohr folgende Postulate auf: Elektronen umkreisen den Kern auf bestimmten Bahnen, wobei keine Energieabgabe erfolgt. Jede Elektronenbahn entspricht einem bestimmten Energieniveau
Für sein neues Atommodell stellte Bohr folgende Postulate auf: Elektronen umkreisen den Kern auf bestimmten Bahnen, wobei keine Energieabgabe erfolgt. Jede Elektronenbahn entspricht einem bestimmten Energieniveau
Vortragsthema: Die Unschärferelationen Ort/Impuls Energie/Zeit. An einigen Beispielen erläutern
 Vortragsthema: Die Unschärferelationen Ort/Impuls Energie/Zeit An einigen Beispielen erläutern 5. Das Photon: Welle und Teilchen 5.4. Die Plancksche Strahlungsformel Wichtige Punkte: u( ν, T ) = 8πh c
Vortragsthema: Die Unschärferelationen Ort/Impuls Energie/Zeit An einigen Beispielen erläutern 5. Das Photon: Welle und Teilchen 5.4. Die Plancksche Strahlungsformel Wichtige Punkte: u( ν, T ) = 8πh c
VL6. Elemente der Quantenmechanik I 6.1. Schrödingergleichung als Wellengleichung der Materie 6.2. Messungen in der Quantenmechanik
 VL7 VL6. Elemente der Quantenmechanik I 6.1. Schrödingergleichung als Wellengleichung der Materie 6.2. Messungen in der Quantenmechanik VL7. Elemente der Quantenmechanik II 7.1. Wellenpakete als Lösungen
VL7 VL6. Elemente der Quantenmechanik I 6.1. Schrödingergleichung als Wellengleichung der Materie 6.2. Messungen in der Quantenmechanik VL7. Elemente der Quantenmechanik II 7.1. Wellenpakete als Lösungen
VI. Quantenphysik. VI.1 Ursprünge der Quantenphysik, Atomphysik. Physik für Mediziner 1
 VI. Quantenphysik VI.1 Ursprünge der Quantenphysik, Atomphysik Physik für Mediziner 1 Mikroskopische Welt Physik für Mediziner 2 Strahlung des Schwarzen Körpers Schwarzer Körper: eintretendes Licht im
VI. Quantenphysik VI.1 Ursprünge der Quantenphysik, Atomphysik Physik für Mediziner 1 Mikroskopische Welt Physik für Mediziner 2 Strahlung des Schwarzen Körpers Schwarzer Körper: eintretendes Licht im
Quantenmechanik. Eine Kurzvorstellung für Nicht-Physiker
 Quantenmechanik Eine Kurzvorstellung für Nicht-Physiker Die Quantenvorstellung Der Ursprung: Hohlraumstrahlung Das Verhalten eines Von Interesse: idealen Absorbers Energiedichte in Abhängigkeit zur Wellenlänge
Quantenmechanik Eine Kurzvorstellung für Nicht-Physiker Die Quantenvorstellung Der Ursprung: Hohlraumstrahlung Das Verhalten eines Von Interesse: idealen Absorbers Energiedichte in Abhängigkeit zur Wellenlänge
Vorlesung 23: Roter Faden: Die Schrödingergleichung. (Bedeuting in der Quantenmechanik wie F=ma in der klassischen Mechanik)
 Vorlesung 23: Roter Faden: Die Schrödingergleichung (Bedeuting in der Quantenmechanik wie F=ma in der klassischen Mechanik) Juli 12, 2006 Ausgewählte Kapitel der Physik, Prof. W. de Boer 1 Welle Teilchen
Vorlesung 23: Roter Faden: Die Schrödingergleichung (Bedeuting in der Quantenmechanik wie F=ma in der klassischen Mechanik) Juli 12, 2006 Ausgewählte Kapitel der Physik, Prof. W. de Boer 1 Welle Teilchen
5. Kapitel Die De-Broglie-Wellenlänge
 5. Kapitel Die De-Broglie-Wellenlänge 5.1 Lernziele Sie können die De-Broglie-Wellenlänge nachvollziehen und anwenden. Sie kennen den experimentellen Nachweis einer Materiewelle. Sie wissen, dass das Experiment
5. Kapitel Die De-Broglie-Wellenlänge 5.1 Lernziele Sie können die De-Broglie-Wellenlänge nachvollziehen und anwenden. Sie kennen den experimentellen Nachweis einer Materiewelle. Sie wissen, dass das Experiment
Die Welt der Quanten Murmeln oder Wellen? Max Camenzind Senioren Uni WS2013
 Die Welt der Quanten Murmeln oder Wellen? Max Camenzind Senioren Uni Würzburg @ WS2013 Die Krise des mechanischen Weltbildes und die Gründerväter der modernen Physik. Elektromagnetische Strahlung Maxwell,
Die Welt der Quanten Murmeln oder Wellen? Max Camenzind Senioren Uni Würzburg @ WS2013 Die Krise des mechanischen Weltbildes und die Gründerväter der modernen Physik. Elektromagnetische Strahlung Maxwell,
Einführung in die Quantenphysik
 Einführung in die Quantenphysik Klassische Optik Der lichtelektrische Effekt Effekte elektromagnetischer Strahlung Kopenhagen-Interpretation Elektronen Quantenphysik und klassische Physik Atomphysik Klassische
Einführung in die Quantenphysik Klassische Optik Der lichtelektrische Effekt Effekte elektromagnetischer Strahlung Kopenhagen-Interpretation Elektronen Quantenphysik und klassische Physik Atomphysik Klassische
VL6. Elemente der Quantenmechanik I 6.1. Schrödingergleichung als Wellengleichung der Materie 6.2. Messungen in der Quantenmechanik
 VL7 VL6. Elemente der Quantenmechanik I 6.1. Schrödingergleichung als Wellengleichung der Materie 6.2. Messungen in der Quantenmechanik VL7. Elemente der Quantenmechanik II 7.1. Wellenpakete als Lösungen
VL7 VL6. Elemente der Quantenmechanik I 6.1. Schrödingergleichung als Wellengleichung der Materie 6.2. Messungen in der Quantenmechanik VL7. Elemente der Quantenmechanik II 7.1. Wellenpakete als Lösungen
Probeklausur zu Physikalische Chemie II für Lehramt
 Department Chemie Dr. Don C. Lamb http://www.cup.uni-muenchen.de/pc/lamb Probeklausur zu Physikalische Chemie II für Lehramt Zur Bearbeitung der Klausur ist nur der freie Platz dieser vor Ihnen liegenden
Department Chemie Dr. Don C. Lamb http://www.cup.uni-muenchen.de/pc/lamb Probeklausur zu Physikalische Chemie II für Lehramt Zur Bearbeitung der Klausur ist nur der freie Platz dieser vor Ihnen liegenden
Joseph J. Thomson ( ) Nobelpreis 1906
 Joseph J. Thomson (1856 1940) Nobelpreis 1906 Atome Kathoden & Kanalstrahlen Experimenteller Befund von Wiechert, Kaufmann & Thomson 1897: Kathodenstrahlen: Elektrisch negativ geladen. Magnetisch leicht
Joseph J. Thomson (1856 1940) Nobelpreis 1906 Atome Kathoden & Kanalstrahlen Experimenteller Befund von Wiechert, Kaufmann & Thomson 1897: Kathodenstrahlen: Elektrisch negativ geladen. Magnetisch leicht
10.6. Röntgenstrahlung
 10.6. Röntgenstrahlung Am 8. November 1895 entdeckte Wilhelm Conrad Röntgen in Würzburg die Röntgenstrahlung. Seine Entdeckung zählt zu den wohl bedeutendsten Entdeckungen in der Menschheitsgeschichte.
10.6. Röntgenstrahlung Am 8. November 1895 entdeckte Wilhelm Conrad Röntgen in Würzburg die Röntgenstrahlung. Seine Entdeckung zählt zu den wohl bedeutendsten Entdeckungen in der Menschheitsgeschichte.
9. Das Wasserstoff-Atom. 9.1 Das Spektrum des Wasserstoff-Atoms. im Bohr-Modell:
 09. Wasserstoff-Atom Page 1 9. Das Wasserstoff-Atom 9.1 Das Spektrum des Wasserstoff-Atoms im Bohr-Modell: Bohr-Modell liefert eine ordentliche erste Beschreibung der grundlegenden Eigenschaften des Spektrums
09. Wasserstoff-Atom Page 1 9. Das Wasserstoff-Atom 9.1 Das Spektrum des Wasserstoff-Atoms im Bohr-Modell: Bohr-Modell liefert eine ordentliche erste Beschreibung der grundlegenden Eigenschaften des Spektrums
Physik für Mediziner im 1. Fachsemester
 Physik für Mediziner im 1. Fachsemester #26 08/12/2010 Vladimir Dyakonov dyakonov@physik.uni-wuerzburg.de Atomphysik Teil 1 Atommodelle, Atomspektren, Röntgenstrahlung Atomphysik Die Atomphysik ist ein
Physik für Mediziner im 1. Fachsemester #26 08/12/2010 Vladimir Dyakonov dyakonov@physik.uni-wuerzburg.de Atomphysik Teil 1 Atommodelle, Atomspektren, Röntgenstrahlung Atomphysik Die Atomphysik ist ein
Lösungen zu den Aufg. S. 363/4
 Lösungen zu den Aufg. S. 363/4 9/1 Die gemessene Gegenspannung (s. Tab.) entspricht der max. kin. Energie der Photoelektronen; die Energie der Photonen = E kin der Elektronen + Austrittsarbeit ==> h f
Lösungen zu den Aufg. S. 363/4 9/1 Die gemessene Gegenspannung (s. Tab.) entspricht der max. kin. Energie der Photoelektronen; die Energie der Photonen = E kin der Elektronen + Austrittsarbeit ==> h f
Die Wellenfunktion ψ(r,t) ist eine komplexe skalare Größe, da keine Polarisation wie bei elektromagnetischen Wellen beobachtet wurde.
 2. Materiewellen und Wellengleichung für freie Teilchen 2.1 Begriff Wellenfunktion Auf Grund des Wellencharakters der Materie können wir den Zustand eines physikalischen Systemes durch eine Wellenfunktion
2. Materiewellen und Wellengleichung für freie Teilchen 2.1 Begriff Wellenfunktion Auf Grund des Wellencharakters der Materie können wir den Zustand eines physikalischen Systemes durch eine Wellenfunktion
Thema heute: Das Bohr sche Atommodell
 Wiederholung der letzten Vorlesungsstunde: Radioaktive Zerfallsgeschwindigkeit, Altersbestimmungen, Ionisationszähler (Geiger-Müller-Zähler), Szintillationszähler, natürliche radioaktive Zerfallsreihen,
Wiederholung der letzten Vorlesungsstunde: Radioaktive Zerfallsgeschwindigkeit, Altersbestimmungen, Ionisationszähler (Geiger-Müller-Zähler), Szintillationszähler, natürliche radioaktive Zerfallsreihen,
Grundlagen der Quantentheorie
 Grundlagen der Quantentheorie Ein Schwarzer Körper (Schwarzer Strahler, planckscher Strahler, idealer schwarzer Körper) ist eine idealisierte thermische Strahlungsquelle: Alle auftreffende elektromagnetische
Grundlagen der Quantentheorie Ein Schwarzer Körper (Schwarzer Strahler, planckscher Strahler, idealer schwarzer Körper) ist eine idealisierte thermische Strahlungsquelle: Alle auftreffende elektromagnetische
Quantenobjekte Welle? Teilchen?
 1 Quantenobjekte Welle? Teilchen? Bezug zu den Schwerpunkten / RRL Fragestellung(en) Experiment(e) Hintergrund Benutze die Links, um zu den einzelnen Kategorien zu gelangen! Simulationen Übungen / Aufgaben
1 Quantenobjekte Welle? Teilchen? Bezug zu den Schwerpunkten / RRL Fragestellung(en) Experiment(e) Hintergrund Benutze die Links, um zu den einzelnen Kategorien zu gelangen! Simulationen Übungen / Aufgaben
Vorlesung 21: Roter Faden: Das Elektron als Welle Heisenbergsche Unsicherheitsrelation. Versuch: Gasentladung
 Vorlesung 21: Roter Faden: Das Elektron als Welle Heisenbergsche Unsicherheitsrelation Versuch: Gasentladung Juli 7, 2006 Ausgewählte Kapitel der Physik, Prof. W. de Boer 1 Erste Experimente mit Elektronen
Vorlesung 21: Roter Faden: Das Elektron als Welle Heisenbergsche Unsicherheitsrelation Versuch: Gasentladung Juli 7, 2006 Ausgewählte Kapitel der Physik, Prof. W. de Boer 1 Erste Experimente mit Elektronen
Atomphysik und Einführung in die Ideen der Quantentheorie
 Atomphysik und Einführung in die Ideen der Quantentheorie Marc Eyer 8. Januar 01 1 Bohrsches Atommodell Gegen Ende des 19. Jahrhunderts gab es eine Fülle von Experimente und Daten zu Lichtspektren verschiedener
Atomphysik und Einführung in die Ideen der Quantentheorie Marc Eyer 8. Januar 01 1 Bohrsches Atommodell Gegen Ende des 19. Jahrhunderts gab es eine Fülle von Experimente und Daten zu Lichtspektren verschiedener
Der Gesamtbahndrehimpuls ist eine Erhaltungsgrösse (genau wie in der klassischen Mechanik).
 phys4.017 Page 1 10.4.2 Bahndrehimpuls des Elektrons: Einheit des Drehimpuls: Der Bahndrehimpuls des Elektrons ist quantisiert. Der Gesamtbahndrehimpuls ist eine Erhaltungsgrösse (genau wie in der klassischen
phys4.017 Page 1 10.4.2 Bahndrehimpuls des Elektrons: Einheit des Drehimpuls: Der Bahndrehimpuls des Elektrons ist quantisiert. Der Gesamtbahndrehimpuls ist eine Erhaltungsgrösse (genau wie in der klassischen
Hallwachs-Experiment. Bestrahlung einer geladenen Zinkplatte mit dem Licht einer Quecksilberdampflampe
 Hallwachs-Experiment Bestrahlung einer geladenen Zinkplatte mit dem Licht einer Quecksilberdampflampe 20.09.2012 Skizziere das Experiment Notiere und Interpretiere die Beobachtungen Photoeffekt Bestrahlt
Hallwachs-Experiment Bestrahlung einer geladenen Zinkplatte mit dem Licht einer Quecksilberdampflampe 20.09.2012 Skizziere das Experiment Notiere und Interpretiere die Beobachtungen Photoeffekt Bestrahlt
lichen auf sehr engem Raum konzentriert ist und die positive Ladung trägt
 lichen auf sehr engem Raum konzentriert ist und die positive Ladung trägt Kanalstrahlexperimente hatten schwere, positiv geladene Teilchen beim Wasserstoff nachgewiesen Aufgrund von Streuexperimenten postulierte
lichen auf sehr engem Raum konzentriert ist und die positive Ladung trägt Kanalstrahlexperimente hatten schwere, positiv geladene Teilchen beim Wasserstoff nachgewiesen Aufgrund von Streuexperimenten postulierte
1 Die Schrödinger Gleichung
 1 Die Schrödinger Gleichung 1.1 Die Wellenfunktion und ihre Wahrscheinlichkeitsinterpretation Aus den Versuchen der Elektronenbeugung, hat ein Elektron auch Welleneigenschaften. Für freie Elektronen mit
1 Die Schrödinger Gleichung 1.1 Die Wellenfunktion und ihre Wahrscheinlichkeitsinterpretation Aus den Versuchen der Elektronenbeugung, hat ein Elektron auch Welleneigenschaften. Für freie Elektronen mit
Strukturaufklärung (BSc-Chemie): Einführung
 Strukturaufklärung (BSc-Chemie): Einführung Prof. S. Grimme OC [TC] 13.10.2009 Prof. S. Grimme (OC [TC]) Strukturaufklärung (BSc-Chemie): Einführung 13.10.2009 1 / 25 Teil I Einführung Prof. S. Grimme
Strukturaufklärung (BSc-Chemie): Einführung Prof. S. Grimme OC [TC] 13.10.2009 Prof. S. Grimme (OC [TC]) Strukturaufklärung (BSc-Chemie): Einführung 13.10.2009 1 / 25 Teil I Einführung Prof. S. Grimme
Die seltsame Welt der Quanten
 Saturday Morning Physics Die seltsame Welt der Quanten Wie spielt Gott sein Würfelspiel? 12. 11. 2005 Gernot Alber und Gerhard Birkl Institut für Angewandte Physik Technische Universität Darmstadt gernot.alber@physik.tu-darmstadt.de
Saturday Morning Physics Die seltsame Welt der Quanten Wie spielt Gott sein Würfelspiel? 12. 11. 2005 Gernot Alber und Gerhard Birkl Institut für Angewandte Physik Technische Universität Darmstadt gernot.alber@physik.tu-darmstadt.de
9. GV: Atom- und Molekülspektren
 Physik Praktikum I: WS 2005/06 Protokoll zum Praktikum Dienstag, 25.10.05 9. GV: Atom- und Molekülspektren Protokollanten Jörg Mönnich Anton Friesen - Veranstalter Andreas Branding - 1 - Theorie Während
Physik Praktikum I: WS 2005/06 Protokoll zum Praktikum Dienstag, 25.10.05 9. GV: Atom- und Molekülspektren Protokollanten Jörg Mönnich Anton Friesen - Veranstalter Andreas Branding - 1 - Theorie Während
0.1.1 Exzerpt von B. S. 414: Unendlich hoher Potenzialtopf
 1 15.11.006 0.1 119. Hausaufgabe 0.1.1 Exzerpt von B. S. 414: Unendlich hoher Potenzialtopf (Siehe 118. Hausaufgabe.) 0.1. Exzerpt von B. S. 414: Wellenlängen der Wellenfunktion im Fall stehender Wellen
1 15.11.006 0.1 119. Hausaufgabe 0.1.1 Exzerpt von B. S. 414: Unendlich hoher Potenzialtopf (Siehe 118. Hausaufgabe.) 0.1. Exzerpt von B. S. 414: Wellenlängen der Wellenfunktion im Fall stehender Wellen
UNIVERSITÄT BIELEFELD
 UNIVERSITÄT BIELEFELD 6. Atom- und Molekülphysik 6.1 - GV Atom- und Molekülspektren Durchgeführt am 22.11.06 Dozent: Praktikanten (Gruppe 1): Dr. Udo Werner Marcus Boettiger Sarah Dirk Marius Schirmer
UNIVERSITÄT BIELEFELD 6. Atom- und Molekülphysik 6.1 - GV Atom- und Molekülspektren Durchgeführt am 22.11.06 Dozent: Praktikanten (Gruppe 1): Dr. Udo Werner Marcus Boettiger Sarah Dirk Marius Schirmer
Ein Unterrichtsprojekt zur Quantenmechanik am Begabungsstützpunkt
 Ein Unterrichtsprojekt zur Quantenmechanik am Begabungsstützpunkt Andreas Kellerer (BSG Memmingen) Prof. Dr. Reinhold Rückl (Universität Würzburg) Die Rahmenbedingungen: Unterrichtsprojekt für den Kurs
Ein Unterrichtsprojekt zur Quantenmechanik am Begabungsstützpunkt Andreas Kellerer (BSG Memmingen) Prof. Dr. Reinhold Rückl (Universität Würzburg) Die Rahmenbedingungen: Unterrichtsprojekt für den Kurs
Vorlesung 6: Roter Faden: Schrödingergleichung als Wellengleichung der Materie. Messungen in der Quantenmechanik
 Vorlesung 6: Roter Faden: Schrödingergleichung als Wellengleichung der Materie Messungen in der Quantenmechanik Folien auf dem Web: http://www-ekp.physik.uni-karlsruhe.de/~deboer/ Wim de Boer, Karlsruhe
Vorlesung 6: Roter Faden: Schrödingergleichung als Wellengleichung der Materie Messungen in der Quantenmechanik Folien auf dem Web: http://www-ekp.physik.uni-karlsruhe.de/~deboer/ Wim de Boer, Karlsruhe
Atome - Moleküle - Kerne
 Atome - Moleküle - Kerne Band I Atomphysik Von Univ.-Professor Dr. Gerd Otter und Akad.-Direktor Dr. Raimund Honecker III. Physikalisches Institut der Rheinisch-Westfälischen Technischen Hochschule Aachen
Atome - Moleküle - Kerne Band I Atomphysik Von Univ.-Professor Dr. Gerd Otter und Akad.-Direktor Dr. Raimund Honecker III. Physikalisches Institut der Rheinisch-Westfälischen Technischen Hochschule Aachen
1. Auf dem Weg zur Quantentheorie Grundlegende Experimente und Erkenntnisse
 1. Auf dem Weg zur Quantentheorie Grundlegende Experimente und Erkenntnisse 1.1. Theorie der Wärmestrahlung Plancksche Strahlenhypothese Untersuchungen der Hohlraumstrahlung vor 1900 zeigten, dass das
1. Auf dem Weg zur Quantentheorie Grundlegende Experimente und Erkenntnisse 1.1. Theorie der Wärmestrahlung Plancksche Strahlenhypothese Untersuchungen der Hohlraumstrahlung vor 1900 zeigten, dass das
Übungen Atom- und Molekülphysik für Physiklehrer (Teil 2)
 Übungen Atom- und Molekülphysik für Physiklehrer (Teil ) Aufgabe 38) Welche J-Werte sind bei den Termen S, P, 4 P und 5 D möglich? Aufgabe 39) Welche Werte kann der Gesamtdrehimpuls eines f-elektrons im
Übungen Atom- und Molekülphysik für Physiklehrer (Teil ) Aufgabe 38) Welche J-Werte sind bei den Termen S, P, 4 P und 5 D möglich? Aufgabe 39) Welche Werte kann der Gesamtdrehimpuls eines f-elektrons im
A. Mechanik (18 Punkte)
 Prof. Dr. A. Hese Prof. Dr. G. v. Oppen Dipl.-Phys. G. Hoheisel Dipl.-Phys. R. Jung Technische Universität Berlin Name: Vorname: Matr. Nr.: Fachbereich: Platz Nr.: Tutor: A. Mechanik (18 Punkte) 1. Wie
Prof. Dr. A. Hese Prof. Dr. G. v. Oppen Dipl.-Phys. G. Hoheisel Dipl.-Phys. R. Jung Technische Universität Berlin Name: Vorname: Matr. Nr.: Fachbereich: Platz Nr.: Tutor: A. Mechanik (18 Punkte) 1. Wie
1.2 Grenzen der klassischen Physik Michael Buballa 1
 1.2 Grenzen der klassischen Physik 23.04.2013 Michael Buballa 1 1.2 Grenzen der klassischen Physik Die Konzepte klassischer Teilchen und Wellen haben ihren Ursprung in unserer Alltagserfahrung, z.b. Teilchen:
1.2 Grenzen der klassischen Physik 23.04.2013 Michael Buballa 1 1.2 Grenzen der klassischen Physik Die Konzepte klassischer Teilchen und Wellen haben ihren Ursprung in unserer Alltagserfahrung, z.b. Teilchen:
Examensaufgaben QUANTENPHYSIK
 Examensaufgaben QUANTENPHYSIK Aufgabe 1 (Juni 2006) Bei einem Versuch wurden folgende Messwerte ermittelt : Wellenlänge des Lichtes (nm) Gegenspannung (V) 436 0,83 578 0,13 a) Berechne aus diesen Werten
Examensaufgaben QUANTENPHYSIK Aufgabe 1 (Juni 2006) Bei einem Versuch wurden folgende Messwerte ermittelt : Wellenlänge des Lichtes (nm) Gegenspannung (V) 436 0,83 578 0,13 a) Berechne aus diesen Werten
Physikalisches Praktikum A 5 Balmer-Spektrum
 Physikalisches Praktikum A 5 Balmer-Spektrum Versuchsziel Es wird das Balmer-Spektrum des Wasserstoffatoms vermessen und die Rydberg- Konstante bestimmt. Für He und Hg werden die Wellenlängen des sichtbaren
Physikalisches Praktikum A 5 Balmer-Spektrum Versuchsziel Es wird das Balmer-Spektrum des Wasserstoffatoms vermessen und die Rydberg- Konstante bestimmt. Für He und Hg werden die Wellenlängen des sichtbaren
Physik IV Einführung in die Atomistik und die Struktur der Materie
 Physik IV Einführung in die Atomistik und die Struktur der Materie Sommersemester 011 Vorlesung 04 1.04.011 Physik IV - Einführung in die Atomistik Vorlesung 4 Prof. Thorsten Kröll 1.04.011 1 Versuch OH
Physik IV Einführung in die Atomistik und die Struktur der Materie Sommersemester 011 Vorlesung 04 1.04.011 Physik IV - Einführung in die Atomistik Vorlesung 4 Prof. Thorsten Kröll 1.04.011 1 Versuch OH
27. Wärmestrahlung. rmestrahlung, Quantenmechanik
 24. Vorlesung EP 27. Wärmestrahlung rmestrahlung, Quantenmechanik V. STRAHLUNG, ATOME, KERNE 27. Wärmestrahlung, Quantenmechanik Photometrie Plancksches Strahlungsgesetz Welle/Teilchen Dualismus für Strahlung
24. Vorlesung EP 27. Wärmestrahlung rmestrahlung, Quantenmechanik V. STRAHLUNG, ATOME, KERNE 27. Wärmestrahlung, Quantenmechanik Photometrie Plancksches Strahlungsgesetz Welle/Teilchen Dualismus für Strahlung
Radiologie Modul I. Teil 1 Grundlagen Röntgen
 Radiologie Modul I Teil 1 Grundlagen Röntgen Teil 1 Inhalt Physikalische Grundlagen Röntgen Strahlenbiologie Technische Grundlagen Röntgen ROENTGENTECHNIK STRAHLENPHYSIK GRUNDLAGEN RADIOLOGIE STRAHLENBIOLOGIE
Radiologie Modul I Teil 1 Grundlagen Röntgen Teil 1 Inhalt Physikalische Grundlagen Röntgen Strahlenbiologie Technische Grundlagen Röntgen ROENTGENTECHNIK STRAHLENPHYSIK GRUNDLAGEN RADIOLOGIE STRAHLENBIOLOGIE
Leistungskurs Physik (Bayern): Abiturprüfung 2000 Aufgabe III Atomphysik
 Leistungskurs Physik (Bayern): Abiturprüfung 000 Aufgabe III Atomphysik 1. Laserbremsung eines Atomstrahls In einem Atomofen befindet sich Cäsium-Gas der Temperatur T. Die mittlere m Geschwindigkeit der
Leistungskurs Physik (Bayern): Abiturprüfung 000 Aufgabe III Atomphysik 1. Laserbremsung eines Atomstrahls In einem Atomofen befindet sich Cäsium-Gas der Temperatur T. Die mittlere m Geschwindigkeit der
Feynman Vorlesungen über Physik
 Feynman Vorlesungen über Physik Band llhouantenmechanik. Definitive Edition von Richard R Feynman, Robert B. Leighton und Matthew Sands 5., verbesserte Auflage Mit 192 Bildern und 22Tabellen Oldenbourg
Feynman Vorlesungen über Physik Band llhouantenmechanik. Definitive Edition von Richard R Feynman, Robert B. Leighton und Matthew Sands 5., verbesserte Auflage Mit 192 Bildern und 22Tabellen Oldenbourg
Abiturprüfung Physik, Leistungskurs
 Seite 1 von 8 Abiturprüfung 2010 Physik, Leistungskurs Aufgabenstellung: Aufgabe: Energieniveaus im Quecksilberatom Das Bohr sche Atommodell war für die Entwicklung der Vorstellung über Atome von großer
Seite 1 von 8 Abiturprüfung 2010 Physik, Leistungskurs Aufgabenstellung: Aufgabe: Energieniveaus im Quecksilberatom Das Bohr sche Atommodell war für die Entwicklung der Vorstellung über Atome von großer
Klausur -Informationen
 Klausur -Informationen Datum: 4.2.2009 Uhrzeit und Ort : 11 25 im großen Physikhörsaal (Tiermediziner) 12 25 ibidem Empore links (Nachzügler Tiermedizin, bitte bei Aufsichtsperson Ankunft melden) 11 25
Klausur -Informationen Datum: 4.2.2009 Uhrzeit und Ort : 11 25 im großen Physikhörsaal (Tiermediziner) 12 25 ibidem Empore links (Nachzügler Tiermedizin, bitte bei Aufsichtsperson Ankunft melden) 11 25
27. Vorlesung EP V. STRAHLUNG, ATOME, KERNE
 27. Vorlesung EP V. STRAHLUNG, ATOME, KERNE 28. Atomphysik, Röntgenstrahlung (Fortsetzung: Röntgenröhre, Röntgenabsorption) 29. Atomkerne, Radioaktivität (Nuklidkarte, α-, β-, γ-aktivität, Dosimetrie)
27. Vorlesung EP V. STRAHLUNG, ATOME, KERNE 28. Atomphysik, Röntgenstrahlung (Fortsetzung: Röntgenröhre, Röntgenabsorption) 29. Atomkerne, Radioaktivität (Nuklidkarte, α-, β-, γ-aktivität, Dosimetrie)
Sonne. Sonne. Δ t A 1. Δ t. Heliozentrisches Weltbild. Die Keplerschen Gesetze
 Seite 1 von 6 Astronomische Weltbilder und Keplersche Gesetze Heliozentrisches Weltbild Die Sonne steht im Mittelpunkt unseres Sonnensystems, die Planeten umkreisen sie. Viele Planeten werden von Monden
Seite 1 von 6 Astronomische Weltbilder und Keplersche Gesetze Heliozentrisches Weltbild Die Sonne steht im Mittelpunkt unseres Sonnensystems, die Planeten umkreisen sie. Viele Planeten werden von Monden
Die Macht und Ohnmacht der Quantenwelt
 Die Macht und Ohnmacht der Quantenwelt Prof. Dr. Sebastian Eggert Tag der Physik, TU Kaiserslautern, 5. Dezember 2015 Quantenmechanik heute Quanteninformatik Ultrakalte Quantengase Supraleitung und Vielteilchenphysik
Die Macht und Ohnmacht der Quantenwelt Prof. Dr. Sebastian Eggert Tag der Physik, TU Kaiserslautern, 5. Dezember 2015 Quantenmechanik heute Quanteninformatik Ultrakalte Quantengase Supraleitung und Vielteilchenphysik
Klassische Physik - Quantenpysik
 Klassische Physik - Quantenpysik Elektronenfalle aus 40 Eisen- Atomen auf einer Kupfer Oberfläche www.almaden.ibm.com Klassische Physik um 1900 Teilchen und Wellen Rastertunnelmikroskop Wechselwirkungsfreie
Klassische Physik - Quantenpysik Elektronenfalle aus 40 Eisen- Atomen auf einer Kupfer Oberfläche www.almaden.ibm.com Klassische Physik um 1900 Teilchen und Wellen Rastertunnelmikroskop Wechselwirkungsfreie
X. Quantisierung des elektromagnetischen Feldes
 Hamiltonian des freien em. Feldes 1 X. Quantisierung des elektromagnetischen Feldes 1. Hamiltonian des freien elektromagnetischen Feldes Elektromagnetische Feldenergie (klassisch): Modenentwicklung (Moden
Hamiltonian des freien em. Feldes 1 X. Quantisierung des elektromagnetischen Feldes 1. Hamiltonian des freien elektromagnetischen Feldes Elektromagnetische Feldenergie (klassisch): Modenentwicklung (Moden
Übungen zur Physik der Materie 1 Musterlösung Blatt 2 - Quantenmechanik
 Übungen zur Physik der Materie 1 Musterlösung Blatt 2 - Quantenmechanik Sommersemester 2018 Vorlesung: Boris Bergues ausgegeben am 19.04.2018 Übung: Nils Haag (Nils.Haag@lmu.de) besprochen am 24.04.2017
Übungen zur Physik der Materie 1 Musterlösung Blatt 2 - Quantenmechanik Sommersemester 2018 Vorlesung: Boris Bergues ausgegeben am 19.04.2018 Übung: Nils Haag (Nils.Haag@lmu.de) besprochen am 24.04.2017
