I. Pythagoras - der Weise von Samos
|
|
|
- Franka Bretz
- vor 7 Jahren
- Abrufe
Transkript
1 I. Pythagoras - der Weise von Samos Im Allgemeinen ist über das Leben von Pythagoras, dem Weisen von Samos nicht viel bekannt. Pythagoras wurde etwa um 570 v.chr. in Samos geboren und ist wahrscheinlich 496 v.chr. in Metapont gestorben. Er lebte zur gleichen Zeit wie andere bedeutende griechische Mathematiker, wie z.b. Thales und Anaximander, die stets seine Vorbilder waren. Er unternahm viele Reisen und gründete in Kroton (Süditalien) eine Schule, aus der Menschen hoher Sittlichkeit und Geisteskraft hervorgingen. Man unterschied in dieser Schule zwischen den Uneingeweihten, die wissenschaftlichen Elementarunterricht erhielten und den Eingeweihten, die ein akademisches Studium vollzogen. Während dieses Studiums standen sie in persönlichen Verkehr und ständigen Ideenaustausch mit ihrem Meister. Diese Schule wurde aber auch als Geheimbund der Pythagoreer mit philosophisch - ethischen Charakter bezeichnet, da Pythagoras die Seelenwanderung lehrte. In dieser Schule wurden die Gesetze der harmonischen Schwingungen von Saiten untersucht und der heute noch gültige pythagoreische Lehrsatz formuliert. Zum einen galt Pythagoras als Mathematiker, der die Mathematik als die eigentliche Wissenschaft - Mathesis - würdigte und als drittes und höchstes Prinzip hinstellte und übte. Pythagoras selbst galt als mathematisches Genie, der nicht nur die Fähigkeit besaß mathematische Kenntnisse der Ägypter und Babylonier leicht in sich aufzunehmen. Er verstand es auch, das übernommene Material originell zu gestalten, - aus der kaufmännischen Rechenkunst eine Theorie der Zahlen, aus der zünftigen Messkunst eine geometrische Wissenschaft zu konstruieren. Die Mathematik war für ihn nicht nur ein Teil der Philosophie, sondern die Logik selbst und die Mutter aller Spezialwissenschaft. Zum anderen war Pythagoras auch Philosoph, der Zahlen neben der mathematischen Bedeutung noch eine weitere symbolische Bedeutung verlieh. Für ihn sind Zahlen Bilder von Wesen, Hieroglyphen für Götter und deren Eigenschaften. So hat für ihn jede Zahl von eins bis zehn seine spezifische Bedeutung, wie im Folgenden deutlich wird. Bei Pythagoras selbst bedeutet: 1. Monas, der Geist, der Äther, das Einfache aus dem Alles entsteht, die Aktivität. 2. Dhas, der Stoff, die Zweiheit, weil aus der Erde und Wasser bestehend, die Passivität. 3. Trias, die Zeit, männlich gedacht als der Zeitgott, der dreifaltige (Vergangenheit, Gegenwart, Zukunft) Allmächtige. 4. Tetras, der Raum, weiblich gedacht, passiv, die Weltordnung. 5. Pentas, die fünf Elemente der Welt. 6. Heras, die Sechsheit, nämlich die sechs Gattungen beseelter (belebter) Wesen: Götter, Dämonen, Heronen, Menschen, Tiere, Pflanzen. 7. Heptas, die sieben Planeten (die bekannten fünfe mit Einschluß von Sonne und Mond). 8. Oktas, die acht Firmamente oder Sphären, die Oktave nach Intervallen der Tonleiter geordnet, nämlich die sieben durchsichtigen Planeten = Sphären, und die undurchsichtige Fix 1
2 sternsphäre (die Sphärenharmonie ist daher ein mathematisch - kosmischer Begriff, nicht ein akkustischer). 9. Enneas, die neun kosmischen Räume, in welche das All durch die acht Sphären geschieden wird. 10. Dekas, das All. Weiter als zur Zehnheit geht nach Aristoteles ausdrücklicher Angabe die pythagoreische Zahlensymbolik nicht. II. Der Satz des Pythagoras Satz des Pythagoras: Im rechtwinkligen Dreieck ist das Quadrat über der Hypothenuse gleich der Summe der Quadrate über den beiden Katheten. Der Satz des Pythagoras ist einer der bekanntesten Lehrsätze der Elementargeometrie, wenn nicht der bekannteste überhaupt. Wie wäre es sonst zu erklären, dass dieser Satz schon für die verschiedensten Zwecke eingesetzt wurde. 1. Werbezwecke 2
3 2. Briefmarken 3. Logo für ein Schuljubiläum Man muss allerdings erwähnen, dass dieser Lehrsatz lange vor der Zeit von Pythagoras bekannt war. Nun wird sich der ein oder andere fragen, warum er dann ausgerechnet nach Pythagoras benannt ist. Hierzu kann man zwei Dinge sagen: Zum Einen, dass es in der Geschichte der Mathematik wohl so ist, dass die Tatsache, dass ein Lehrsatz nach einer bestimmten Person benannt ist, wohl eher ein sicheres Indiz dafür ist, dass diese Person nichts damit zu tun hatte. Zum anderen kann man sagen, dass diese Aussage wohl hier nur zum Teil zutrifft. Den anfangs erwähnten Pythagoreern (Mitglieder der Schule des Pythagoras) wird nämlich der erste Beweis dieses Lehrsatzes zugeschrieben. Allerdings ist dieser Beweis nicht näher überliefert und somit lassen sich eben nur Spekulationen über seine Art anstellen. III. Pythagorasbeweise 1. Beweis aus den Elementen des Euklid Euklid (um 365 v. Chr. ca. 300 v. Chr.) lehrte Geometrie in Alexandria. 3
4 a) Originalbeweis aus Euklid, Die Elemente, Buch 1 47 aus dem Griechischen übersetzt 4
5 IV. Anwendung Pythagoreische Zahlentripel 1. Definition Unter einem pythagoreischen Zahlentripel versteht man drei natürliche Zahlen, die die Bedingungen des pythagoreischen Lehrsatzes (a² + b² = c², die Summe der Kathetenquadrate ist gleich dem Hypothenusenquadrat) erfüllen. Dies bedeutet, dass die Summe der Quadrate der zwei kleinsten Zahlen des Tripels gleich dem Quadrat der dritten Zahl sein muss. Einfachstes Beispiel hierfür ist das pythagoreische Zahlentripel (3; 4; 5). Beispiel: 3² + 4² = 5² = = 25 Das Beispiel erfüllt also den pythagoreischen Lehrsatz. 2. Verfahren zur Bestimmung pythagoreischer Zahlentripel Wenn man nun alle (natürlich unendlich viele) derartige Tripel bestimmen will, so bemerkt man zunächst, dass mit jedem Tripel a, b und c für jede positive ganze Zahl d auch das Tripel d*a, d*b und d*c pythagoreisch ist. Man kann sich bei der Bestimmung pythagoreischer Zahlentripel auf solche beschränken, deren größter gemeinsamer Teiler 1 ist, die also teilerfremd sind. Man spricht in diesem Fall auch von primitiven pythagoreischen Zahlentripel. Aus der Gleichung a² + b² = c² (1) folgt aber sofort, dass jeder gemeinsame Teiler von a und b schon ein gemeinsamer Teiler von c ist. Ebenso muss wegen a² = c² - b² jeder gemeinsame Teiler von c und b und wegen b² = c² - a² jeder gemeinsame Teiler von c und a auch ein gemeinsamer Teiler aller drei Zahlen sein. Man kann also für die folgenden Überlegungen voraussetzen, dass je zwei dieser drei Zahlen bereits teilerfremd sind. Insbesondere können keine zwei der drei Zahlen gerade sein. Nimmt man nun an, a und b seien beide ungerade, also etwa a = 2 * n + 1 5
6 und b = 2 * m + 1 mit natürlichen Zahlen n und m, und setzt dies in Gleichung (1) ein, so folgt: a² + b² = c² (2 * n + 1)² + (2 * m + 1)² = c² 4 * (n² + m² + n + m) + 2 = c² Bei Division durch 4 lässt also c² den Rest 2. Für eine gerade Zahl c ist aber das Quadrat c² durch 4 ohne Rest teilbar, wohingegen für eine ungerade Zahl c das Quadrat bei Division durch 4 den Rest 1 lässt. Dieser Widerspruch zeigt, dass genau eine der beiden Zahlen gerade ist, z.b. a, und die andere, also dann b, ungerade. Da c und a teilerfremd sind, muss folglich auch c ungerade sein. Damit sind c + b und c b positive ganze Zahlen und man hat die Zerlegung a² = c² - b² = (c + b) * (c b) = 4 * ((c + b)/2) * ((c b)/2) = 4* x * y (2) wobei x = (c + b)/2 und y = (c b)/2 positive ganze Zahlen sind. Diese beiden Zahlen müssen ebenfalls teilerfremd sein, denn ein gemeinsamer Teiler von x und y ist auch ein gemeinsamer Teiler von c = x + y und b = x y. Jeder Primfaktor von a²/4 ist also entweder nur Primfaktor von x oder nur Primfaktor von y. Damit sind aber x und y selbst Quadratzahlen, etwa x = s² und y = t² mit positiven ganzen Zahlen s und t, die wie x und y teilerfremd sein müssen. Insgesamt gilt also für jedes primitive pythagoreische Zahlentripel a = 2 * s * t b = s² - t² c = s² + t² mit teilerfremden positiven ganzen Zahlen s > t, von denen genau eine gerade sein muss, damit b und c ungerade sind. Sind umgekehrt s und t derartige Zahlen und man setzt sie in Gleichung 1 ein, so ergibt sich: a² + b² = c² 4 * s² * t² + (s² - t²)² = c² 4 * s² * t² + s 4 2 * s² * t² + t 4 = c² s * s² * t² + t 4 = c² (s² + t²)² = c² Beispiele für pythagoreische Zahlentripel: (4; 3; 5) (24; 7; 25) (12; 5; 13) (8; 15; 17) 6
7 Zum Abschluss: 7
8 Literatur: Baltzer, Eduard: Pythagoras der Weise von Samos, Heilbronn Baptist, Peter: Pythagoras und kein Ende?, Leipzig Fraedrich, Anna Maria: Die Satzgruppe des Pythagoras, Mannheim
Geschichte von Pythagoras
 Satz von Pythagoras Inhalt Geschichte von Pythagoras Entdeckung des Satzes von Pythagoras Plimpton 322 Lehrsatz Beweise Kathetensatz und Höhensatz Pythagoreische Tripel Kosinussatz Anwendungen des Satzes
Satz von Pythagoras Inhalt Geschichte von Pythagoras Entdeckung des Satzes von Pythagoras Plimpton 322 Lehrsatz Beweise Kathetensatz und Höhensatz Pythagoreische Tripel Kosinussatz Anwendungen des Satzes
Der Satz von Pythagoras
 Der Satz von Pythagoras Diplom Mathematiker Wolfgang Kinzner Technische Universität München 17. Oktober 2013 W. Kinzner (TUM) Der Satz von Pythagoras 17. Oktober 2013 1 / 9 Inhaltsverzeichnis 1 Einleitung
Der Satz von Pythagoras Diplom Mathematiker Wolfgang Kinzner Technische Universität München 17. Oktober 2013 W. Kinzner (TUM) Der Satz von Pythagoras 17. Oktober 2013 1 / 9 Inhaltsverzeichnis 1 Einleitung
Geometrie Satz des Pythagoras
 TG TECHNOLOGISCHE GRUNDLAGEN Kapitel 3 Mathematik Kapitel 3.6 Geometrie Satz des Pythagoras Verfasser: Hans-Rudolf Niederberger Elektroingenieur FH/HTL Vordergut 1, 8772 Nidfurn 055-654 12 87 Ausgabe:
TG TECHNOLOGISCHE GRUNDLAGEN Kapitel 3 Mathematik Kapitel 3.6 Geometrie Satz des Pythagoras Verfasser: Hans-Rudolf Niederberger Elektroingenieur FH/HTL Vordergut 1, 8772 Nidfurn 055-654 12 87 Ausgabe:
Nicht alles ist Zahl
 Nicht alles ist Zahl Pythagoras und seine Lehre 1 Pythagoras Tag der Mathematik 2 Chartres: die septem artes liberales Tag der Mathematik 3 Die septem artes liberales Quadrivium Arithmetik Grammatik Geometrie
Nicht alles ist Zahl Pythagoras und seine Lehre 1 Pythagoras Tag der Mathematik 2 Chartres: die septem artes liberales Tag der Mathematik 3 Die septem artes liberales Quadrivium Arithmetik Grammatik Geometrie
1. Rechensteine und Pythagoräischer Lehrsatz.
 1. Rechensteine und Pythagoräischer Lehrsatz. Der Beginn der wissenschaftlichen Mathematik fällt mit dem Beginn der Philosophie zusammen. Er kann auf die Pythagoräer zurückdatiert werden. Die Pythagoräer
1. Rechensteine und Pythagoräischer Lehrsatz. Der Beginn der wissenschaftlichen Mathematik fällt mit dem Beginn der Philosophie zusammen. Er kann auf die Pythagoräer zurückdatiert werden. Die Pythagoräer
Rekonstruktion eines teilweise entschlüsselten babylonischen Keilschrifttextes aus der Zeit um 2000 v. Chr.
 Rekonstruktion eines teilweise entschlüsselten babylonischen Keilschrifttextes aus der Zeit um 2000 v. Chr. 16 9 25 4 3 5 144 25 169 12 13 49 625 24 7 25 9 25 3 64 100 8 225 64 289 15 144 225 15 1296 225
Rekonstruktion eines teilweise entschlüsselten babylonischen Keilschrifttextes aus der Zeit um 2000 v. Chr. 16 9 25 4 3 5 144 25 169 12 13 49 625 24 7 25 9 25 3 64 100 8 225 64 289 15 144 225 15 1296 225
Der Satz von Pythagoras
 Der Satz von Pythagoras Unterrichtsfach Themenbereich/e Mathematik Der Lehrsatz von Pythagoras einführende Arbeiten Schulstufe (Klasse) 7 / 8 Fachliche Vorkenntnisse Fachliche Kompetenzen Sprachliche Kompetenzen
Der Satz von Pythagoras Unterrichtsfach Themenbereich/e Mathematik Der Lehrsatz von Pythagoras einführende Arbeiten Schulstufe (Klasse) 7 / 8 Fachliche Vorkenntnisse Fachliche Kompetenzen Sprachliche Kompetenzen
Referat über Thales, Pythagoras & Euklid. von Steffen Dremel Klasse 9a
 Referat über Thales, Pythagoras & Euklid von Steffen Dremel Klasse 9a Thales von Milet Geboren: ca. 624 v. Chr. in Milet, Kleinasien Gestorben: ca. 546 v. Chr. War ein griechischer Naturphilosoph, Staatsmann,
Referat über Thales, Pythagoras & Euklid von Steffen Dremel Klasse 9a Thales von Milet Geboren: ca. 624 v. Chr. in Milet, Kleinasien Gestorben: ca. 546 v. Chr. War ein griechischer Naturphilosoph, Staatsmann,
Die Anfänge der Logik
 Die Anfänge der Logik Die Entwicklung des logischen Denkens vor Aristoteles Holger Arnold Universität Potsdam, Institut für Informatik arnold@cs.uni-potsdam.de Grundfragen Was ist Logik? Logik untersucht
Die Anfänge der Logik Die Entwicklung des logischen Denkens vor Aristoteles Holger Arnold Universität Potsdam, Institut für Informatik arnold@cs.uni-potsdam.de Grundfragen Was ist Logik? Logik untersucht
Die Zahl ist das Wesen aller Dinge
 Pythagoras Πυθαγόρας * um 570 v. Chr um 500 v. Chr Mathematiker und Naturphilosoph Ausschnitt aus Die Schule von Athen Raffael 50 -gründete 53v.Chr die religiös-politische Lebensgemeinschaft der Pythagoreer.
Pythagoras Πυθαγόρας * um 570 v. Chr um 500 v. Chr Mathematiker und Naturphilosoph Ausschnitt aus Die Schule von Athen Raffael 50 -gründete 53v.Chr die religiös-politische Lebensgemeinschaft der Pythagoreer.
Brückenkurs. Beweise. Anja Haußen Brückenkurs, Seite 1/23
 Brückenkurs Beweise Anja Haußen 30.09.2016 Brückenkurs, 30.09.2016 Seite 1/23 Inhalt 1 Einführung 2 Sätze 3 Beweise 4 direkter Beweis Brückenkurs, 30.09.2016 Seite 2/23 Einführung Die höchste Form des
Brückenkurs Beweise Anja Haußen 30.09.2016 Brückenkurs, 30.09.2016 Seite 1/23 Inhalt 1 Einführung 2 Sätze 3 Beweise 4 direkter Beweis Brückenkurs, 30.09.2016 Seite 2/23 Einführung Die höchste Form des
Die Menge C der komplexen Zahlen wird im Kapitel Weitere Themen behandelt.
 1 1 Funktionen 1.1 Grundlegende Zahlenmengen Georg Cantor (1845-1918) hat den Begriff der Menge eingeführt. Man versteht darunter die Zusammenfassung einzelner Dinge, welche Elemente genannt werden, zu
1 1 Funktionen 1.1 Grundlegende Zahlenmengen Georg Cantor (1845-1918) hat den Begriff der Menge eingeführt. Man versteht darunter die Zusammenfassung einzelner Dinge, welche Elemente genannt werden, zu
Gittergeometrie und pythagoreische Dreiecke
 Alfred Hoehn und Hans Walser Gittergeometrie und pythagoreische Dreiecke Dieser Artikel wurde von der Praxis der Mathematik zur Publikation angenommen und erscheint demnächst. Kurzfassung Werden in einem
Alfred Hoehn und Hans Walser Gittergeometrie und pythagoreische Dreiecke Dieser Artikel wurde von der Praxis der Mathematik zur Publikation angenommen und erscheint demnächst. Kurzfassung Werden in einem
/ Nur zur privaten Verwendung! Musterausdruck! Skript und Übungsaufgaben Die Satzgruppe des Pythagoras
 Skript und Übungsaufgaben Die Satzgruppe des Pythagoras DER SATZ DES PYTHAGORAS DEFINITION UND BEWEIS AUFGABEN ZUM SATZ DES PYTHAGORAS MIT MUSTERLÖSUNGEN 5 DER KATHETENSATZ DES EUKLID 7 DEFINITION UND
Skript und Übungsaufgaben Die Satzgruppe des Pythagoras DER SATZ DES PYTHAGORAS DEFINITION UND BEWEIS AUFGABEN ZUM SATZ DES PYTHAGORAS MIT MUSTERLÖSUNGEN 5 DER KATHETENSATZ DES EUKLID 7 DEFINITION UND
Fermats Zwei-Quadrate-Satz ein Abriss der Mathematik in Stewarts Artikel Ein Weihnachtslied in Prosa 1 )
 Fermats Zwei-Quadrate-Satz ein Abriss der Mathematik in Stewarts Artikel Ein Weihnachtslied in Prosa 1 ) 1. Primzahlen als Summe von zwei Quadraten Am Weihnachtstag des Jahres 1640 schrieb Pierre de Fermat
Fermats Zwei-Quadrate-Satz ein Abriss der Mathematik in Stewarts Artikel Ein Weihnachtslied in Prosa 1 ) 1. Primzahlen als Summe von zwei Quadraten Am Weihnachtstag des Jahres 1640 schrieb Pierre de Fermat
Seminararbeit zur Zahlentheorie. Die Gaußschen Zahlen
 Universität Paderborn WS 2007/2008 Warburger Str. 100 33098 Paderborn Seminararbeit zur Zahlentheorie Die Gaußschen Zahlen Tatjana Linkin, Svetlana Krez 20. November 2007 INHALTSVERZEICHNIS 1 Inhaltsverzeichnis
Universität Paderborn WS 2007/2008 Warburger Str. 100 33098 Paderborn Seminararbeit zur Zahlentheorie Die Gaußschen Zahlen Tatjana Linkin, Svetlana Krez 20. November 2007 INHALTSVERZEICHNIS 1 Inhaltsverzeichnis
Rechtwinklige Dreiecke, die in einem weiteren Winkel übereinstimmen, sind schon zueinander ähnlich.
 1 9. Ähnlichkeit rechtwinkliger Dreiecke Rechtwinklige Dreiecke, die in einem weiteren Winkel übereinstimmen, sind schon zueinander ähnlich. Die Höhe h zerlegt das Dreieck in zwei ähnliche Teildreiecke
1 9. Ähnlichkeit rechtwinkliger Dreiecke Rechtwinklige Dreiecke, die in einem weiteren Winkel übereinstimmen, sind schon zueinander ähnlich. Die Höhe h zerlegt das Dreieck in zwei ähnliche Teildreiecke
Der Satz des Pythagoras: a 2 + b 2 = c 2
 Der Satz des Pythagoras: a 2 + b 2 = c 2 Beweise: Mathematiker versuchen ihre Behauptungen durch Beweise zu untermauern. Die Suche nach absolut wasserdichten Argumenten ist eine der treibenden Kräfte der
Der Satz des Pythagoras: a 2 + b 2 = c 2 Beweise: Mathematiker versuchen ihre Behauptungen durch Beweise zu untermauern. Die Suche nach absolut wasserdichten Argumenten ist eine der treibenden Kräfte der
Geometrie Modul 4b WS 2015/16 Mi HS 1
 Geometrie Modul 4b WS 2015/16 Mi 10-12 HS 1 Benötigte Materialien: Geometrieheft DIN-A-4 blanco weiß, quadratisches Faltpapier/Zettelblock, rundes Faltpapier; Zirkel, Geometriedreieck, Klebstoff, Schere
Geometrie Modul 4b WS 2015/16 Mi 10-12 HS 1 Benötigte Materialien: Geometrieheft DIN-A-4 blanco weiß, quadratisches Faltpapier/Zettelblock, rundes Faltpapier; Zirkel, Geometriedreieck, Klebstoff, Schere
Lineare Algebra I (WS 13/14)
 Lineare Algebra I (WS 13/14) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 10.01.2014 Alexander Lytchak 1 / 9 Erinnerung: Zwei ganz wichtige Gruppen Für jede Gruppe (G, ) und jedes Element g
Lineare Algebra I (WS 13/14) Alexander Lytchak Nach einer Vorlage von Bernhard Hanke 10.01.2014 Alexander Lytchak 1 / 9 Erinnerung: Zwei ganz wichtige Gruppen Für jede Gruppe (G, ) und jedes Element g
Zahlentheoretische Variationen zum Satz des Pythagoras
 Zahlentheoretische zum Satz des nstitut für Mathematik Humboldt-Universität zu Berlin 17. Januar 2017 Aus Die Pythagoreer von Bartel L. van der Waerden Satz. Ein rechtwinkliges Dreieck mit den Katheten
Zahlentheoretische zum Satz des nstitut für Mathematik Humboldt-Universität zu Berlin 17. Januar 2017 Aus Die Pythagoreer von Bartel L. van der Waerden Satz. Ein rechtwinkliges Dreieck mit den Katheten
Danach arithmetische Fragestellungen wie vollkommene Zahlen und Dreieckszahlen der Griechen.
 Was ist Zahlentheorie? Ursprünglich ist die Zahlentheorie (auch: Arithmetik) ein Teilgebiet der Mathematik, welches sich allgemein mit den Eigenschaften der ganzen Zahlen und insbesondere mit den Lösungen
Was ist Zahlentheorie? Ursprünglich ist die Zahlentheorie (auch: Arithmetik) ein Teilgebiet der Mathematik, welches sich allgemein mit den Eigenschaften der ganzen Zahlen und insbesondere mit den Lösungen
Zahlentheorie I - Tipps & Lösungen. Aktualisiert: 15. Oktober 2016 vers Teilbarkeit
 Schweizer Mathematik-Olympiade smo osm Zahlentheorie I - Tipps & Lösungen Aktualisiert: 15. Oktober 2016 vers. 1.2.0 1 Teilbarkeit Einstieg 1.1 Zeige, dass 900 ein Teiler von 10! ist. Tipp: Schreibe 900
Schweizer Mathematik-Olympiade smo osm Zahlentheorie I - Tipps & Lösungen Aktualisiert: 15. Oktober 2016 vers. 1.2.0 1 Teilbarkeit Einstieg 1.1 Zeige, dass 900 ein Teiler von 10! ist. Tipp: Schreibe 900
Beispiellösungen zu Blatt 77
 µathematischer κorrespondenz- zirkel Mathematisches Institut Georg-August-Universität Göttingen Aufgabe 1 Beispiellösungen zu Blatt 77 Die Zahl 9 ist sowohl als Summe der drei aufeinanderfolgenden Quadratzahlen,
µathematischer κorrespondenz- zirkel Mathematisches Institut Georg-August-Universität Göttingen Aufgabe 1 Beispiellösungen zu Blatt 77 Die Zahl 9 ist sowohl als Summe der drei aufeinanderfolgenden Quadratzahlen,
Vorkurs Mathematik. Vorlesung 2. Primzahlen
 Prof. Dr. H. Brenner Osnabrück WS 2013/2014 Vorkurs Mathematik Vorlesung 2 Primzahlen Das Sieb des Eratosthenes liefert eine einfache Methode, eine Liste von Primzahlen unterhalb einer bestimmten Größe
Prof. Dr. H. Brenner Osnabrück WS 2013/2014 Vorkurs Mathematik Vorlesung 2 Primzahlen Das Sieb des Eratosthenes liefert eine einfache Methode, eine Liste von Primzahlen unterhalb einer bestimmten Größe
Man weiß, dass zwischen zwei aufeinanderfolgenden Quadratzahlen immer mindestens eine Primzahl liegt:
 Primzahlgeheimnis 1 Man weiß, dass zwischen zwei aufeinanderfolgenden Quadratzahlen immer mindestens eine Primzahl liegt: Vervollständige die Quadrate und kringele alle Primzahlen ein: 1 2 5 10 17 26 37
Primzahlgeheimnis 1 Man weiß, dass zwischen zwei aufeinanderfolgenden Quadratzahlen immer mindestens eine Primzahl liegt: Vervollständige die Quadrate und kringele alle Primzahlen ein: 1 2 5 10 17 26 37
ZahlenfolgenZahlenfolgen. Zahlenfolgen. Anna Rodenhausen. Wieviele Dreiecke, wieviele Trapeze?
 Zahlenfolgen Anna Rodenhausen Wieviele Dreiecke, wieviele Trapeze? Wieviele Dreiecke, wieviele Trapeze? # Linien # Dreiecke # Trapeze 0 3 0 3 3 6 5 0 5 6 5 3 Wieviele Dreiecke, wieviele Trapeze? # Linien
Zahlenfolgen Anna Rodenhausen Wieviele Dreiecke, wieviele Trapeze? Wieviele Dreiecke, wieviele Trapeze? # Linien # Dreiecke # Trapeze 0 3 0 3 3 6 5 0 5 6 5 3 Wieviele Dreiecke, wieviele Trapeze? # Linien
Studienmaterial Einführung in das Rechnen mit Resten
 Studienmaterial Einführung in das Rechnen mit Resten H.-G. Gräbe, Institut für Informatik, http://www.informatik.uni-leipzig.de/~graebe 12. April 2000 Die folgenden Ausführungen sind aus Arbeitsmaterialien
Studienmaterial Einführung in das Rechnen mit Resten H.-G. Gräbe, Institut für Informatik, http://www.informatik.uni-leipzig.de/~graebe 12. April 2000 Die folgenden Ausführungen sind aus Arbeitsmaterialien
Literatur zu geometrischen Konstruktionen
 Literatur zu geometrischen Konstruktionen Hadlock, Charles Robert, Field theory and its classical problems. Carus Mathematical Monographs, 19. Mathematical Association of America, Washington, D.C., 1978.
Literatur zu geometrischen Konstruktionen Hadlock, Charles Robert, Field theory and its classical problems. Carus Mathematical Monographs, 19. Mathematical Association of America, Washington, D.C., 1978.
Eine kurze Tabelle soll uns erste Einsichten erleichtern. Der Strich heißt, dass es eine solche Darstellung nicht gibt.
 Summen von Quadraten 1 Physikalische Motivation Eine schwingende Saite hat eine Grundfrequenz F, die von Länge, Dicke, Beschaffenheit der Saite und so fort abhängt Neben dieser Grundfrequenz gibt es auch
Summen von Quadraten 1 Physikalische Motivation Eine schwingende Saite hat eine Grundfrequenz F, die von Länge, Dicke, Beschaffenheit der Saite und so fort abhängt Neben dieser Grundfrequenz gibt es auch
Man weiß, dass zwischen zwei aufeinanderfolgenden Quadratzahlen immer mindestens eine Primzahl liegt:
 Primzahlgeheimnis 1 Man weiß, dass zwischen zwei aufeinanderfolgenden Quadratzahlen immer mindestens eine Primzahl liegt: Vervollständige die Quadrate und kringele alle Primzahlen ein: 1 2 5 10 17 26 37
Primzahlgeheimnis 1 Man weiß, dass zwischen zwei aufeinanderfolgenden Quadratzahlen immer mindestens eine Primzahl liegt: Vervollständige die Quadrate und kringele alle Primzahlen ein: 1 2 5 10 17 26 37
Wie beweise ich etwas? 9. Juli 2012
 Schülerzirkel Mathematik Fakultät für Mathematik. Universität Regensburg Wie beweise ich etwas? 9. Juli 2012 1 Was ist ein Beweis? 1.1 Ein Beispiel Nimm einen Stift und ein Blatt Papier und zeichne fünf
Schülerzirkel Mathematik Fakultät für Mathematik. Universität Regensburg Wie beweise ich etwas? 9. Juli 2012 1 Was ist ein Beweis? 1.1 Ein Beispiel Nimm einen Stift und ein Blatt Papier und zeichne fünf
 Eine löchrige Gerade Eins ist ganz klar: Es gibt unendlich viele rationale Zahlen, und es wird nicht möglich sein, auf der Zahlgeraden irgendein Intervall zu finden, in dem sich keine einzige rationale
Eine löchrige Gerade Eins ist ganz klar: Es gibt unendlich viele rationale Zahlen, und es wird nicht möglich sein, auf der Zahlgeraden irgendein Intervall zu finden, in dem sich keine einzige rationale
Zeichnet man nun über die Seiten des Dreiecks die Quadrate der jeweiligen Seiten, dann ergibt sich folgendes Bild:
 9. Lehrsatz von Pythagoras Pythagoras von Samos war ein griechischer Philosoph und Mathematiker, der von ca. 570 v.chr. bis 510 n.chr lebte. Obwohl es über seine gesallschaftliche Stellung verschiedene
9. Lehrsatz von Pythagoras Pythagoras von Samos war ein griechischer Philosoph und Mathematiker, der von ca. 570 v.chr. bis 510 n.chr lebte. Obwohl es über seine gesallschaftliche Stellung verschiedene
Panorama der Mathematik und Informatik
 Panorama der Mathematik und Informatik 2: Geschichte: Antike Dirk Frettlöh Technische Fakultät 9.4.2015 Bei den alten Griechen: erstmals Beweise (nicht nur Rechenanleitungen = Algorithmen). Themen: Geometrie
Panorama der Mathematik und Informatik 2: Geschichte: Antike Dirk Frettlöh Technische Fakultät 9.4.2015 Bei den alten Griechen: erstmals Beweise (nicht nur Rechenanleitungen = Algorithmen). Themen: Geometrie
4. Griechisch hellenistische Mathematik 4.1 Überblick
 4. Griechisch hellenistische Mathematik 4.1 Überblick Die griechische Mathematik der Antike unterscheidet sich wesentlich von der der Ägypter und Mesopotamier: Es steht nicht mehr die Frage nach dem Wie
4. Griechisch hellenistische Mathematik 4.1 Überblick Die griechische Mathematik der Antike unterscheidet sich wesentlich von der der Ägypter und Mesopotamier: Es steht nicht mehr die Frage nach dem Wie
Was ist Koordinaten-Geometrie?
 Thema Was ist Koordinaten-Geometrie? ist eine Systematische Sammlung von Techniken, um geometrische Probleme Probleme nicht durch Zeichnen, sondern durch Berechnungen zu lösen. Vorgehensweise: 1. Was ist
Thema Was ist Koordinaten-Geometrie? ist eine Systematische Sammlung von Techniken, um geometrische Probleme Probleme nicht durch Zeichnen, sondern durch Berechnungen zu lösen. Vorgehensweise: 1. Was ist
MATHEMATIK BASICS. Rainer Hofer, Marc Peter, Jean-Louis D Alpaos. Trigonometrie
 MATHEMATIK BASICS Rainer Hofer, Marc Peter, Jean-Louis D Alpaos Trigonometrie Vorwort In allen technisch-konstruktiven Berufen sind die Kenntnisse der Dreieckslehre von grosser Bedeutung. Für Lernende,
MATHEMATIK BASICS Rainer Hofer, Marc Peter, Jean-Louis D Alpaos Trigonometrie Vorwort In allen technisch-konstruktiven Berufen sind die Kenntnisse der Dreieckslehre von grosser Bedeutung. Für Lernende,
Die Platonischen Körper
 Die Platonischen Körper Ablauf: 1. Die Studenten erklären den Schülern kurz, wer Platon war, wann und wo er gelebt hat und womit er sich beschäftigt hat. 2. Anschließend wird den Schülern erklärt was Platonische
Die Platonischen Körper Ablauf: 1. Die Studenten erklären den Schülern kurz, wer Platon war, wann und wo er gelebt hat und womit er sich beschäftigt hat. 2. Anschließend wird den Schülern erklärt was Platonische
Der Zwei-Quadrate-Satz von Fermat. Hauptseminar: Eine Einladung in die Mathematik Leitung: Prof. Dr. Lukacova Referent: Julia Breit Datum:
 Der Zwei-Quadrate-Satz von Fermat Hauptseminar: Eine Einladung in die Mathematik Leitung: Prof. Dr. Lukacova Referent: Julia Breit Datum: 09.11.2015 GLIEDERUNG Einleitung Der Zwei-Quadrate-Satz Vorwissen
Der Zwei-Quadrate-Satz von Fermat Hauptseminar: Eine Einladung in die Mathematik Leitung: Prof. Dr. Lukacova Referent: Julia Breit Datum: 09.11.2015 GLIEDERUNG Einleitung Der Zwei-Quadrate-Satz Vorwissen
7. Mathematik Olympiade 3. Stufe (Bezirksolympiade) Klasse 9 Saison 1967/1968 Aufgaben und Lösungen
 7. Mathematik Olympiade. Stufe (Bezirksolympiade) Klasse 9 Saison 967/968 Aufgaben und Lösungen OJM 7. Mathematik-Olympiade. Stufe (Bezirksolympiade) Klasse 9 Aufgaben Hinweis: Der Lösungsweg mit Begründungen
7. Mathematik Olympiade. Stufe (Bezirksolympiade) Klasse 9 Saison 967/968 Aufgaben und Lösungen OJM 7. Mathematik-Olympiade. Stufe (Bezirksolympiade) Klasse 9 Aufgaben Hinweis: Der Lösungsweg mit Begründungen
Spielen mit Zahlen Seminarleiter: Dieter Bauke
 Spielen mit Zahlen Seminarleiter: Dieter Bauke EINLEITUNG Was ist Mathematik? Geometrie und Arithmetik: Untersuchung von Figuren und Zahlen. Wir kombinieren Arithmetik und Geometrie mittels figurierter
Spielen mit Zahlen Seminarleiter: Dieter Bauke EINLEITUNG Was ist Mathematik? Geometrie und Arithmetik: Untersuchung von Figuren und Zahlen. Wir kombinieren Arithmetik und Geometrie mittels figurierter
π geometrisch ermittelt als Gerade im Thaleskreis (mit 99,9%iger Genauigkeit).
 Das geometrische π π geometrisch ermittelt als Gerade im Thaleskreis (mit 99,9%iger Genauigkeit). nach Hans-Werner Meixner und Coautor Christian Meixner Als Basis für die Ausführungen zur geometrischen
Das geometrische π π geometrisch ermittelt als Gerade im Thaleskreis (mit 99,9%iger Genauigkeit). nach Hans-Werner Meixner und Coautor Christian Meixner Als Basis für die Ausführungen zur geometrischen
WS 2009/10. Diskrete Strukturen
 WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
Wieviel Uhr ist es in hundert Stunden? Eine Antwort durch Modulo- Rechnen
 Schülerzirkel Mathematik Fakultät für Mathematik. Universität Regensburg Zahlentheorie I Wieviel Uhr ist es in hundert Stunden? Modulo-Rechnen XI XII I X II IX III VIII IV Zahlentheorie I VII VI V Die
Schülerzirkel Mathematik Fakultät für Mathematik. Universität Regensburg Zahlentheorie I Wieviel Uhr ist es in hundert Stunden? Modulo-Rechnen XI XII I X II IX III VIII IV Zahlentheorie I VII VI V Die
Pythagoreische Rechtecke Vier gleiche rechtwinklige Dreiecke 1.1 Allgemeiner Fall Startdreieck
 Hans Walser, [20040416a] Pythagoreische Rechtecke 1 Vier gleiche rechtwinklige Dreiecke 1.1 Allgemeiner Fall Wir starten mit einem beliebigen rechtwinkligen Dreieck in der üblichen Beschriftung. Startdreieck
Hans Walser, [20040416a] Pythagoreische Rechtecke 1 Vier gleiche rechtwinklige Dreiecke 1.1 Allgemeiner Fall Wir starten mit einem beliebigen rechtwinkligen Dreieck in der üblichen Beschriftung. Startdreieck
3. Die pythagoräische Geometrie.
 II. Geometrie. 3. Die pythagoräische Geometrie. Neben der Zahlenlehre haben sich die Pythagoräer auch mit Geometrie beschäftigt. Schließlich ist ja der bekannte Satz des Pythagoras eng mit ihrem Namen
II. Geometrie. 3. Die pythagoräische Geometrie. Neben der Zahlenlehre haben sich die Pythagoräer auch mit Geometrie beschäftigt. Schließlich ist ja der bekannte Satz des Pythagoras eng mit ihrem Namen
Zerlegung in Quadratzahlen
 Zerlegung in Quadratzahlen Die Zerlegung von natürlichen Zahlen in die Summe von Quadratzahlen ist eine alte, abgeschlossene Theorie, die schon von FERMAT im 17. Jahrhundert und später von EULER, LAGRANGE
Zerlegung in Quadratzahlen Die Zerlegung von natürlichen Zahlen in die Summe von Quadratzahlen ist eine alte, abgeschlossene Theorie, die schon von FERMAT im 17. Jahrhundert und später von EULER, LAGRANGE
Sinus-und Kosinussatz
 Sinus-und Kosinussatz Referentin: Theresia Herrmann a sinα = b sin β = c sinγ = 2r r 1 = r 2 = r a 2 = b 2 +c 2 2 b c cosα b 2 = a 2 +c 2 2 a c cosβ c 2 = a 2 +b 2 2 a b cosγ Gliederung: 1.Sinussatz 2.Beweis
Sinus-und Kosinussatz Referentin: Theresia Herrmann a sinα = b sin β = c sinγ = 2r r 1 = r 2 = r a 2 = b 2 +c 2 2 b c cosα b 2 = a 2 +c 2 2 a c cosβ c 2 = a 2 +b 2 2 a b cosγ Gliederung: 1.Sinussatz 2.Beweis
n: Exponent (= Hochzahl. Zeigt an, wie oft die Basis mit sich selber multipliziert wird.)
 10. Potenzen 10.1 Definition Potenz (Repetition)Begriffe Potenz: n gleiche Faktoren a a n = a a a a a a a a a n n: Exponent (= Hochzahl. Zeigt an, wie oft die Basis mit sich selber multipliziert wird.)
10. Potenzen 10.1 Definition Potenz (Repetition)Begriffe Potenz: n gleiche Faktoren a a n = a a a a a a a a a n n: Exponent (= Hochzahl. Zeigt an, wie oft die Basis mit sich selber multipliziert wird.)
Helmuth Gericke MATHEMATIK IN ANTIKE UND ORIENT. marixveriag
 Helmuth Gericke MATHEMATIK IN ANTIKE UND ORIENT marixveriag Inhaltsverzeichnis 1. Vorgriechische Mathematik 1 1.1 Prähistorische Mathematik 1 1.1.1 Rechensteine 1 1.1.2 Geometrie 2 1.2 Darstellung der
Helmuth Gericke MATHEMATIK IN ANTIKE UND ORIENT marixveriag Inhaltsverzeichnis 1. Vorgriechische Mathematik 1 1.1 Prähistorische Mathematik 1 1.1.1 Rechensteine 1 1.1.2 Geometrie 2 1.2 Darstellung der
Euklid von Alexandria
 Euklid von Alexandria lebte ca. 360 v. Chr. bis ca. 280 v. Chr. systematisierte in 13 Büchern ( Elemente ) das mathematische Wissen der Antike - bis ins 19. Jahrhundert nach Bibel das am meisten verbreitete
Euklid von Alexandria lebte ca. 360 v. Chr. bis ca. 280 v. Chr. systematisierte in 13 Büchern ( Elemente ) das mathematische Wissen der Antike - bis ins 19. Jahrhundert nach Bibel das am meisten verbreitete
Das Schubfachprinzip
 Das Schubfachprinzip Norbert Koksch, Dresden Literatur: Beutelspacher/Zschiegner: Diskrete Mathematik für Einsteiger. Vieweg-Verlag. 1. Was ist das Schubfachprinzip? Die folgenden Aussagen sind offenbar
Das Schubfachprinzip Norbert Koksch, Dresden Literatur: Beutelspacher/Zschiegner: Diskrete Mathematik für Einsteiger. Vieweg-Verlag. 1. Was ist das Schubfachprinzip? Die folgenden Aussagen sind offenbar
2 Der Beweis. Themen: Satz und Beweis Indirekter Beweis Kritik des indirekten Beweises
 2 Der Beweis Themen: Satz und Beweis Indirekter Beweis Kritik des indirekten Beweises Satz und Beweis Ein mathematischer Satz besteht aus einer Voraussetzung und einer Behauptung. Satz und Beweis Ein mathematischer
2 Der Beweis Themen: Satz und Beweis Indirekter Beweis Kritik des indirekten Beweises Satz und Beweis Ein mathematischer Satz besteht aus einer Voraussetzung und einer Behauptung. Satz und Beweis Ein mathematischer
Vorkurs Mathematik. Prof. Udo Hebisch WS 2017/18
 Vorkurs Mathematik Prof. Udo Hebisch WS 2017/18 1 1 Logik 2 1 Logik Unter einer Aussage versteht man in der Mathematik einen in einer natürlichen oder formalen Sprache formulierten Satz, für den eindeutig
Vorkurs Mathematik Prof. Udo Hebisch WS 2017/18 1 1 Logik 2 1 Logik Unter einer Aussage versteht man in der Mathematik einen in einer natürlichen oder formalen Sprache formulierten Satz, für den eindeutig
Der Drei-Quadrate-Satz von Gauß
 Der Drei-Quadrate-Satz von Gauß Bekanntlich ist eine ungerade Primzahl p genau dann Summe zweier Quadratzahlen, wenn p 1 mod 4. Daraus folgt, dass eine positive ganze Zahl n genau dann Summe zweier Quadratzahlen
Der Drei-Quadrate-Satz von Gauß Bekanntlich ist eine ungerade Primzahl p genau dann Summe zweier Quadratzahlen, wenn p 1 mod 4. Daraus folgt, dass eine positive ganze Zahl n genau dann Summe zweier Quadratzahlen
Übungen zum Vorkurs Mathematik für Studienanfänger Ein leeres Produkt ist gleich 1, eine leere Summe 0. ***
 Universität Bonn Mathematisches Institut Dr. Michael Welter Übungen zum Vorkurs Mathematik für Studienanfänger 2013 Einige Zeichen und Konventionen: IN := {1, 2, 3, 4,...} Die Menge der natürlichen Zahlen
Universität Bonn Mathematisches Institut Dr. Michael Welter Übungen zum Vorkurs Mathematik für Studienanfänger 2013 Einige Zeichen und Konventionen: IN := {1, 2, 3, 4,...} Die Menge der natürlichen Zahlen
11. Folgen und Reihen.
 - Funktionen Folgen und Reihen Folgen Eine Folge reeller Zahlen ist eine Abbildung a: N R Statt a(n) für n N schreibt man meist a n ; es handelt sich also bei einer Folge um die Angabe der Zahlen a, a
- Funktionen Folgen und Reihen Folgen Eine Folge reeller Zahlen ist eine Abbildung a: N R Statt a(n) für n N schreibt man meist a n ; es handelt sich also bei einer Folge um die Angabe der Zahlen a, a
Zahlentheorie. Prof. Dr. H. Brenner Osnabrück SS Vorlesung 11 Satz (von Euklid) Es gibt unendlich viele Primzahlen.
 Prof. Dr. H. Brenner Osnabrück SS 2008 Zahlentheorie Vorlesung Satz.. (von Euklid) Es gibt unendlich viele Primzahlen. Beweis. Angenommen, die Menge aller Primzahlen sei endlich, sagen wir {p, p 2,...,
Prof. Dr. H. Brenner Osnabrück SS 2008 Zahlentheorie Vorlesung Satz.. (von Euklid) Es gibt unendlich viele Primzahlen. Beweis. Angenommen, die Menge aller Primzahlen sei endlich, sagen wir {p, p 2,...,
2 Mengen. Menge. Die Summenformel. Die leere Menge. Das kartesische Produkt. Die Produktformel. Die Potenzmenge. Die Binomialzahlen.
 2 Mengen Menge Die Summenformel Die leere Menge Das kartesische Produkt Die Produktformel Die Potenzmenge Die Binomialzahlen Der Binomialsatz Unendliche Mengen Springer Fachmedien Wiesbaden 2016 A. Beutelspacher,
2 Mengen Menge Die Summenformel Die leere Menge Das kartesische Produkt Die Produktformel Die Potenzmenge Die Binomialzahlen Der Binomialsatz Unendliche Mengen Springer Fachmedien Wiesbaden 2016 A. Beutelspacher,
Grundlegendes der Mathematik
 Kapitel 2 Grundlegendes der Mathematik (Prof. Udo Hebisch) 2.1 Logik Unter einer Aussage versteht man in der Mathematik einen in einer natürlichen oder formalen Sprache formulierten Satz, für den eindeutig
Kapitel 2 Grundlegendes der Mathematik (Prof. Udo Hebisch) 2.1 Logik Unter einer Aussage versteht man in der Mathematik einen in einer natürlichen oder formalen Sprache formulierten Satz, für den eindeutig
3. Synthetische Geometrie (synthetein = zusammensetzen)
 3. Synthetische Geometrie (synthetein = zusammensetzen) Wichtig ist in der synthetischen Geometrie das Zusammensetzen von Grundsätzen, Voraussetzungen, Sätzen und Folgerungen. Die SuS lernen die neue Art
3. Synthetische Geometrie (synthetein = zusammensetzen) Wichtig ist in der synthetischen Geometrie das Zusammensetzen von Grundsätzen, Voraussetzungen, Sätzen und Folgerungen. Die SuS lernen die neue Art
Mengenlehre 1-E1. M-1, Lubov Vassilevskaya
 Mengenlehre 1-E1 M-1, Lubov Vassilevskaya Abb.: Schloss (Fragment), Fulda 1-E2 M-1, Lubov Vassilevskaya Abb.: Glöcken, Darstellung einer Menge Ohne es zu wissen begegnet jedes Kleinkind dem Prinzip der
Mengenlehre 1-E1 M-1, Lubov Vassilevskaya Abb.: Schloss (Fragment), Fulda 1-E2 M-1, Lubov Vassilevskaya Abb.: Glöcken, Darstellung einer Menge Ohne es zu wissen begegnet jedes Kleinkind dem Prinzip der
Beispiellösungen zu Blatt 98
 µathematischer κorrespondenz- zirkel Mathematisches Institut Georg-August-Universität Göttingen Aufgabe 1 Beispiellösungen zu Blatt 98 Finde vier paarweise verschiedene positive ganze Zahlen a, b, c, d
µathematischer κorrespondenz- zirkel Mathematisches Institut Georg-August-Universität Göttingen Aufgabe 1 Beispiellösungen zu Blatt 98 Finde vier paarweise verschiedene positive ganze Zahlen a, b, c, d
Der Satz des Pythagoras. Kein Darwinscher Zufall
 Der Satz des Pythagoras. Kein Darwinscher Zufall Detlef Dürr duerr@rz.mathematik.uni-muenchen.de 1. Mai 2012 1 Zahlen-Verhältnisse Die Grunderkenntnis der Gesetzmäßigkeit in der Natur ist Harmonie. Heute
Der Satz des Pythagoras. Kein Darwinscher Zufall Detlef Dürr duerr@rz.mathematik.uni-muenchen.de 1. Mai 2012 1 Zahlen-Verhältnisse Die Grunderkenntnis der Gesetzmäßigkeit in der Natur ist Harmonie. Heute
Vorkurs: Mathematik für Informatiker
 Vorkurs: Mathematik für Informatiker Teil 3 Wintersemester 2016/17 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2016 Steven Köhler Wintersemester 2016/17 Inhaltsverzeichnis Teil 1 Teil
Vorkurs: Mathematik für Informatiker Teil 3 Wintersemester 2016/17 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2016 Steven Köhler Wintersemester 2016/17 Inhaltsverzeichnis Teil 1 Teil
Pythagoras-Box Die komische Seite einer Mathematiktragödie
 Pythagoras-Box Die komische Seite einer Mathematiktragödie Das Gesamtprojekt Vorwort Die Mathematik wird von der Allgemeinheit als eine anspruchsvolle Wissenschaft angesehen. Es liegt auf der Hand, wie
Pythagoras-Box Die komische Seite einer Mathematiktragödie Das Gesamtprojekt Vorwort Die Mathematik wird von der Allgemeinheit als eine anspruchsvolle Wissenschaft angesehen. Es liegt auf der Hand, wie
Tilman Bauer. 4. September 2007
 Universität Münster 4. September 2007 und Sätze nlogik von Organisatorisches Meine Koordinaten: Sprechstunden: Di 13:30-14:30 Do 9:00-10:00 tbauer@uni-muenster.de Zimmer 504, Einsteinstr. 62 (Hochhaus)
Universität Münster 4. September 2007 und Sätze nlogik von Organisatorisches Meine Koordinaten: Sprechstunden: Di 13:30-14:30 Do 9:00-10:00 tbauer@uni-muenster.de Zimmer 504, Einsteinstr. 62 (Hochhaus)
Einige Begriffe und Konzepte aus der Lehre Gurdjieffs.
 Einige Begriffe und Konzepte aus der Lehre Gurdjieffs 1 handelnde Personen Gregor Iwanowitsch Gurdjieff armenischer Philosoph und Tanzlehrer, starb 1949 in Paris, wo er das Institut für die harmonische
Einige Begriffe und Konzepte aus der Lehre Gurdjieffs 1 handelnde Personen Gregor Iwanowitsch Gurdjieff armenischer Philosoph und Tanzlehrer, starb 1949 in Paris, wo er das Institut für die harmonische
Geometrie und Zahlentheorie. Ganzzahlige geometrische Objekte
 1 Geometrie und Zahlentheorie. Ganzzahlige geometrische Objekte Holger Stephan Weierstraß Institut für Angewandte Analysis und Stochastik (WIAS), Berlin 19. Tag der Mathematik 17. Mai 014, TU Berlin Pythagoräische
1 Geometrie und Zahlentheorie. Ganzzahlige geometrische Objekte Holger Stephan Weierstraß Institut für Angewandte Analysis und Stochastik (WIAS), Berlin 19. Tag der Mathematik 17. Mai 014, TU Berlin Pythagoräische
Primzahlen und Pseudoprimzahlen
 1 Primzahlen und Pseudoprimzahlen Holger Stephan Weierstraß Institut für Angewandte Analysis und Stochastik (WIAS), Berlin 20. Tag der Mathematik 9. Mai 2015, Beuth Hochschule für Technik Berlin Primzahlen
1 Primzahlen und Pseudoprimzahlen Holger Stephan Weierstraß Institut für Angewandte Analysis und Stochastik (WIAS), Berlin 20. Tag der Mathematik 9. Mai 2015, Beuth Hochschule für Technik Berlin Primzahlen
GOLDENER SCHNITT UND FIBONACCI-FOLGE
 GOLDENER SCHNITT UND FIBONACCI-FOLGE NORA LOOSE Der Goldene Schnitt - Eine Irrationalität am Ordenssymbol der Pythagoreer Schon im 5 Jahrhundert v Chr entdeckte ein Pythagoreer eine Konsequenz der Unvollständigkeit
GOLDENER SCHNITT UND FIBONACCI-FOLGE NORA LOOSE Der Goldene Schnitt - Eine Irrationalität am Ordenssymbol der Pythagoreer Schon im 5 Jahrhundert v Chr entdeckte ein Pythagoreer eine Konsequenz der Unvollständigkeit
Zahlentheorie für den Gebietswettbewerb für Fortgeschrittene der Österreichischen Mathematik-Olympiade
 Zahlentheorie für den Gebietswettbewerb für Fortgeschrittene der Österreichischen Mathematik-Olympiade Clemens Heuberger 22. September 2014 Inhaltsverzeichnis 1 Zifferndarstellungen in anderen Basen 1
Zahlentheorie für den Gebietswettbewerb für Fortgeschrittene der Österreichischen Mathematik-Olympiade Clemens Heuberger 22. September 2014 Inhaltsverzeichnis 1 Zifferndarstellungen in anderen Basen 1
Perlen der Mathematik
 Claudi Alsina Roger B. Nelsen Perlen der Mathematik 20 geometrische Figuren als Ausgangspunkte für mathematische Erkundungsreisen Aus dem Englischen übersetzt von Thomas Filk ~ Springer Spektrum Inhaltsverzeichnis
Claudi Alsina Roger B. Nelsen Perlen der Mathematik 20 geometrische Figuren als Ausgangspunkte für mathematische Erkundungsreisen Aus dem Englischen übersetzt von Thomas Filk ~ Springer Spektrum Inhaltsverzeichnis
Klassenstufen 7, 8. Aufgabe 1 (6+6+8 Punkte). Magischer Stern:
 Department Mathematik Tag der Mathematik 31. Oktober 2009 Klassenstufen 7, 8 Aufgabe 1 (6+6+8 Punkte). Magischer Stern: e a 11 9 13 12 10 b c d Die Summe S der natürlichen Zahlen entlang jeder der fünf
Department Mathematik Tag der Mathematik 31. Oktober 2009 Klassenstufen 7, 8 Aufgabe 1 (6+6+8 Punkte). Magischer Stern: e a 11 9 13 12 10 b c d Die Summe S der natürlichen Zahlen entlang jeder der fünf
Prof. Dr. Dörte Haftendorn, Leuphana Universität Lüneburg, 2013
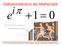 Selbstverständnis der Mathematik i 1 Selbstverständnis der Mathematik Komplexe Zahlen Geometrie i Analysis Nat. Zahlen Null Funktionentheorie Algebra 2 Selbstverständnis der Mathematik : = Menge der Menschen,
Selbstverständnis der Mathematik i 1 Selbstverständnis der Mathematik Komplexe Zahlen Geometrie i Analysis Nat. Zahlen Null Funktionentheorie Algebra 2 Selbstverständnis der Mathematik : = Menge der Menschen,
Logische Grundlagen der Mathematik, WS 2014/15
 Logische Grundlagen der Mathematik, WS 2014/15 Thomas Timmermann 16. Oktober 2014 1 Einleitung Literatur Paul.R. Halmos, Naive Set Theory Ralf Schindler, Logische Grundlagen der Mathematik Peter J. Cameron,
Logische Grundlagen der Mathematik, WS 2014/15 Thomas Timmermann 16. Oktober 2014 1 Einleitung Literatur Paul.R. Halmos, Naive Set Theory Ralf Schindler, Logische Grundlagen der Mathematik Peter J. Cameron,
Zahlenlehre 1. Die Mathematik ist die Königin der Wissenschaften und die Zahlentheorie ist die Königin der Mathematik (Carl Friedrich Gauß)
 Die Mathematik ist die Königin der Wissenschaften und die Zahlentheorie ist die Königin der Mathematik (Carl Friedrich Gauß) 6. Termin, Wien 2014 Mag. a Dagmar Kerschbaumer Letzter Termin g-adische Darstellung
Die Mathematik ist die Königin der Wissenschaften und die Zahlentheorie ist die Königin der Mathematik (Carl Friedrich Gauß) 6. Termin, Wien 2014 Mag. a Dagmar Kerschbaumer Letzter Termin g-adische Darstellung
Kompetenztest. 1 Im rechtwinkligen Dreieck. Satz des Pythagoras. Kompetenztest. Testen und Fördern. Satz des Pythagoras. Name: Klasse: Datum:
 Testen und Fördern Name: Klasse: Datum: 1) Bringe die Satzteile in die richtige Reihenfolge. (Es sind zwei Sätze.) den rechten Winkel einschließen heißen die Seiten, die Katheten, 1 Im rechtwinkligen Dreieck
Testen und Fördern Name: Klasse: Datum: 1) Bringe die Satzteile in die richtige Reihenfolge. (Es sind zwei Sätze.) den rechten Winkel einschließen heißen die Seiten, die Katheten, 1 Im rechtwinkligen Dreieck
Einführung in Algebra und Zahlentheorie Lösungsvorschlag zur Klausur am 16. Februar 2016
 Fakultät für Mathematik Institut für Algebra und Geometrie PD Dr. Stefan Kühnlein Dipl.-Math. oec. Anja Randecker Einführung in Algebra und Zahlentheorie Lösungsvorschlag zur Klausur am 16. Februar 016
Fakultät für Mathematik Institut für Algebra und Geometrie PD Dr. Stefan Kühnlein Dipl.-Math. oec. Anja Randecker Einführung in Algebra und Zahlentheorie Lösungsvorschlag zur Klausur am 16. Februar 016
Mathematisches Institut II Universität Karlsruhe Priv.-Doz. Dr. N. Grinberg
 1 Mathematisches Institut II 06.07.004 Universität Karlsruhe Priv.-Doz. Dr. N. Grinberg SS 05 Schnupperkurs: Ausgewählte Methoden zur Aufgabenlösung Vorlesung 5: Elementare Zahlentheorie: Teilbarkeit Primfaktorzerlegung
1 Mathematisches Institut II 06.07.004 Universität Karlsruhe Priv.-Doz. Dr. N. Grinberg SS 05 Schnupperkurs: Ausgewählte Methoden zur Aufgabenlösung Vorlesung 5: Elementare Zahlentheorie: Teilbarkeit Primfaktorzerlegung
Tag der Mathematik 2016
 Tag der Mathematik 016 Mathematischer Wettbewerb, Klassenstufe 9 10 30. April 016, 9.00 1.00 Uhr Aufgabe 1 Der Mittelwert von 016 (nicht unbedingt verschiedenen) natürlichen Zahlen zwischen 1 und 0 16
Tag der Mathematik 016 Mathematischer Wettbewerb, Klassenstufe 9 10 30. April 016, 9.00 1.00 Uhr Aufgabe 1 Der Mittelwert von 016 (nicht unbedingt verschiedenen) natürlichen Zahlen zwischen 1 und 0 16
Zahlen 25 = = 0.08
 2. Zahlen Uns bisher bekannte Zahlenbereiche: N Z Q R ( C). }{{} später Schreibweisen von rationalen/reellen Zahlen als unendliche Dezimalbrüche = Dezimalentwicklungen. Beispiel (Rationale Zahlen) 1 10
2. Zahlen Uns bisher bekannte Zahlenbereiche: N Z Q R ( C). }{{} später Schreibweisen von rationalen/reellen Zahlen als unendliche Dezimalbrüche = Dezimalentwicklungen. Beispiel (Rationale Zahlen) 1 10
Reihen/Partialsummenfolgen und vollständige Induktion. Robert Klinzmann
 Reihen/Partialsummenfolgen und vollständige Induktion Robert Klinzmann 3. Mai 00 Reihen / Partialsummen 1 Inhaltsverzeichnis 1 Vorwort Das Prinzip der vollständigen Induktion 3 3 Herleitung der Gauß schen
Reihen/Partialsummenfolgen und vollständige Induktion Robert Klinzmann 3. Mai 00 Reihen / Partialsummen 1 Inhaltsverzeichnis 1 Vorwort Das Prinzip der vollständigen Induktion 3 3 Herleitung der Gauß schen
Was haben die folgenden Dinge gemeinsam?
 Was haben die folgenden Dinge gemeinsam? Parthenon zu Athen Mona Lisa von Leonardo da Vinci Nautilus Berliner Fernsehturm CN Tower Obelix Brüder Grimm Ananas Rose Biene Apple Das goldene Zeitalter Der
Was haben die folgenden Dinge gemeinsam? Parthenon zu Athen Mona Lisa von Leonardo da Vinci Nautilus Berliner Fernsehturm CN Tower Obelix Brüder Grimm Ananas Rose Biene Apple Das goldene Zeitalter Der
Brückenkurs Mathematik
 Beweise und Beweisstrategien andreas.kucher@uni-graz.at Institute for Mathematics and Scientific Computing Karl-Franzens-Universität Graz Graz, September 5, 2015 Hinweis zu den Folien Diese Folien sind
Beweise und Beweisstrategien andreas.kucher@uni-graz.at Institute for Mathematics and Scientific Computing Karl-Franzens-Universität Graz Graz, September 5, 2015 Hinweis zu den Folien Diese Folien sind
Irrationale Zahlen. Drei einfache Beweise für die Irrationalität von Zahlen
 Astrophysikalisches Institut Neunhof Mitteilung sd01311, Februar 2010 1 Irrationale Zahlen Drei einfache Beweise für die Irrationalität von Zahlen Übersicht Nach einer kurzen Überlegung im Abschnitt 1
Astrophysikalisches Institut Neunhof Mitteilung sd01311, Februar 2010 1 Irrationale Zahlen Drei einfache Beweise für die Irrationalität von Zahlen Übersicht Nach einer kurzen Überlegung im Abschnitt 1
Übungen zum Vorkurs Mathematik für Studienanfänger 2009 ***
 Universität Bonn Mathematisches Institut Dr. Michael Welter Übungen zum Vorkurs Mathematik für Studienanfänger 2009 Einige Zeichen und Konventionen: IN := {1, 2, 3, 4,...} Die Menge der natürlichen Zahlen
Universität Bonn Mathematisches Institut Dr. Michael Welter Übungen zum Vorkurs Mathematik für Studienanfänger 2009 Einige Zeichen und Konventionen: IN := {1, 2, 3, 4,...} Die Menge der natürlichen Zahlen
6.1.2 Bem.: Für Vierecke ist der Begriff Innenwinkel im allgemeinen nicht sinnvoll. Skizze.
 6 Flächeninhalt 6.1 Vierecke 6.1.1 Def.: Seien A, B, C, D vier verschiedene Punkte in E, keine drei auf einer Geraden, so dass AB, BC, CD, DA einander höchstens in Endpunkten treffen. Dann bilden diese
6 Flächeninhalt 6.1 Vierecke 6.1.1 Def.: Seien A, B, C, D vier verschiedene Punkte in E, keine drei auf einer Geraden, so dass AB, BC, CD, DA einander höchstens in Endpunkten treffen. Dann bilden diese
1 Vorbereitung: Potenzen 2. 2 Einstieg und typische Probleme 3
 Das vorliegende Skript beschäftigt sich mit dem Thema Rechnen mit Kongruenzen. Das Skript entsteht entlang einer Unterrichtsreihe in der Mathematischen Schülergesellschaft (MSG) im Jahr 2013. Die vorliegende
Das vorliegende Skript beschäftigt sich mit dem Thema Rechnen mit Kongruenzen. Das Skript entsteht entlang einer Unterrichtsreihe in der Mathematischen Schülergesellschaft (MSG) im Jahr 2013. Die vorliegende
Zahlentheorie und Geometrie
 1 Zahlentheorie und Geometrie Holger Stephan Weierstraß Institut für Angewandte Analysis und Stochastik (WIAS), Berlin Herbsttagung der Mathematischen Gesellschaft in Hamburg 15. November 2014 Zahlentheorie
1 Zahlentheorie und Geometrie Holger Stephan Weierstraß Institut für Angewandte Analysis und Stochastik (WIAS), Berlin Herbsttagung der Mathematischen Gesellschaft in Hamburg 15. November 2014 Zahlentheorie
Zusammenfassung: Beweisverfahren
 LGÖ Ks VMa 11 Schuljahr 216/217 Zusammenfassung: Beweisverfahren Inhaltsverzeichnis Teilbarkeitslehre... 1 Mathematische Sätze... 1 Bedingungen für innere Extremstellen... 3 Beweisverfahren... 3 Für Experten...
LGÖ Ks VMa 11 Schuljahr 216/217 Zusammenfassung: Beweisverfahren Inhaltsverzeichnis Teilbarkeitslehre... 1 Mathematische Sätze... 1 Bedingungen für innere Extremstellen... 3 Beweisverfahren... 3 Für Experten...
UNSER WELTVERSTÄNDNIS, UNSERE WELTBEZIEHUNG HEUTE
 UNSER WELTVERSTÄNDNIS, UNSERE WELTBEZIEHUNG HEUTE Vortrag auf dem Harmonik-Symposion Nürnberg 06.05.2017 Hans G. Weidinger UNSER WELTBILD Es ist die Sehnsucht des Menschen, das Weltall und seinen eigenen
UNSER WELTVERSTÄNDNIS, UNSERE WELTBEZIEHUNG HEUTE Vortrag auf dem Harmonik-Symposion Nürnberg 06.05.2017 Hans G. Weidinger UNSER WELTBILD Es ist die Sehnsucht des Menschen, das Weltall und seinen eigenen
Lösungsvorschlag zur Nachklausur. Zeigen Sie die folgenden voneinander unabhängigen Aussagen:
 Lösungsvorschlag zur Nachklausur Aufgabe 1 Es seien G eine Gruppe und H, K zwei Untergruppen von G. Weiterhin gelte G = {hk h H, k K}. Zeigen Sie die folgenden voneinander unabhängigen Aussagen: a) Sind
Lösungsvorschlag zur Nachklausur Aufgabe 1 Es seien G eine Gruppe und H, K zwei Untergruppen von G. Weiterhin gelte G = {hk h H, k K}. Zeigen Sie die folgenden voneinander unabhängigen Aussagen: a) Sind
Geometrie 0.1. Homepage zur Veranstaltung: Lehre Geometrie
 Geometrie 0.1 Geometrie Homepage zur Veranstaltung: http://www.juergen-roth.de Lehre Geometrie Geometrie 0.2 Inhaltsverzeichnis Geometrie 0 Geometrie!? 1 Axiome der Elementargeometrie 2 Kongruenzabbildungen
Geometrie 0.1 Geometrie Homepage zur Veranstaltung: http://www.juergen-roth.de Lehre Geometrie Geometrie 0.2 Inhaltsverzeichnis Geometrie 0 Geometrie!? 1 Axiome der Elementargeometrie 2 Kongruenzabbildungen
Zahlentheorie für den Landeswettbewerb für Anfängerinnen und Anfänger der Österreichischen Mathematik-Olympiade
 Zahlentheorie für den Landeswettbewerb für Anfängerinnen und Anfänger der Österreichischen Mathematik-Olympiade Clemens Heuberger 22. September 2014 Inhaltsverzeichnis 1 Dezimaldarstellung 1 2 Teilbarkeit
Zahlentheorie für den Landeswettbewerb für Anfängerinnen und Anfänger der Österreichischen Mathematik-Olympiade Clemens Heuberger 22. September 2014 Inhaltsverzeichnis 1 Dezimaldarstellung 1 2 Teilbarkeit
Datum: Erasmus+ Name: There s something new under the sun. Lösungsblatt. Die Astronomie: Die Wissenschaft der Himmelskörper und des Weltalls.
 Lösungsblatt Weißt du noch was Astronomie bedeutet? Wenn nicht, schlage in deinen Arbeitsblättern zum Thema Weltall nach und erkläre: Die Astronomie: Die Wissenschaft der Himmelskörper und des Weltalls.
Lösungsblatt Weißt du noch was Astronomie bedeutet? Wenn nicht, schlage in deinen Arbeitsblättern zum Thema Weltall nach und erkläre: Die Astronomie: Die Wissenschaft der Himmelskörper und des Weltalls.
Kapitel 1 Die natürlichen und die ganze Zahlen
 Kapitel 1 Die natürlichen und die ganze Zahlen Inhalt 1.1 1.1 Vollständige Induktion z.b. z.b. 1+ 1+ 2 + 3 +...... + n = n(n+1)/2 1.2 1.2 Die Die Peano-Axiome Ein Ein Axiomensystem für für die die natürlichen
Kapitel 1 Die natürlichen und die ganze Zahlen Inhalt 1.1 1.1 Vollständige Induktion z.b. z.b. 1+ 1+ 2 + 3 +...... + n = n(n+1)/2 1.2 1.2 Die Die Peano-Axiome Ein Ein Axiomensystem für für die die natürlichen
