Zinsratentheorie in der Versicherung
|
|
|
- Katja Buchholz
- vor 7 Jahren
- Abrufe
Transkript
1 Zinsratentheorie in der Versicherung Julia Eisenberg
2 Gliederung 1 Bewertung durch Diversifikation Gesetz der großen Zahl Zinssatz, Aufzinsungs- und Diskontierungsfaktoren Verluste und Äquivalenzprinzip Deterministische Bond-Preise Duplikation mit Zerobonds Marktwerte und Zerobonds
3 Gliederung 1 Bewertung durch Diversifikation Gesetz der großen Zahl Zinssatz, Aufzinsungs- und Diskontierungsfaktoren Verluste und Äquivalenzprinzip Deterministische Bond-Preise Duplikation mit Zerobonds Marktwerte und Zerobonds 2 Zerobonds und Zinstheorie Zinsstrukturkurven Beziehung zwischen Terminzins und Kassazins Einfache Zinsen Marktwerte und Terminzinsen
4 Gliederung 1 Bewertung durch Diversifikation Gesetz der großen Zahl Zinssatz, Aufzinsungs- und Diskontierungsfaktoren Verluste und Äquivalenzprinzip Deterministische Bond-Preise Duplikation mit Zerobonds Marktwerte und Zerobonds 2 Zerobonds und Zinstheorie Zinsstrukturkurven Beziehung zwischen Terminzins und Kassazins Einfache Zinsen Marktwerte und Terminzinsen 3 Bonds, Zinsen und Duration
5 1 Bewertung durch Diversifikation Gesetz der großen Zahl Zinssatz, Aufzinsungs- und Diskontierungsfaktoren Verluste und Äquivalenzprinzip Deterministische Bond-Preise Duplikation mit Zerobonds Marktwerte und Zerobonds 2 Zerobonds und Zinstheorie Zinsstrukturkurven Beziehung zwischen Terminzins und Kassazins Einfache Zinsen Marktwerte und Terminzinsen 3 Bonds, Zinsen und Duration
6 Gesetz der großen Zahl Gesetz der großen Zahl Betrachte eine Münze. X i bezeichne das Ergebnis des i-ten Wurfs { X i 1 Kopf =. 0 Zahl D.h. wir haben X i = 1I Ai, wobei 1I die Indikatorfunktion und A i das Ereignis Kopf beim i-ten Wurf bezeichnen.
7 Gesetz der großen Zahl Gesetz der großen Zahl Betrachte eine Münze. X i bezeichne das Ergebnis des i-ten Wurfs { X i 1 Kopf =. 0 Zahl D.h. wir haben X i = 1I Ai, wobei 1I die Indikatorfunktion und A i das Ereignis Kopf beim i-ten Wurf bezeichnen. Das Gesetz der großen Zahl besagt dann wenn n. 1 n n 1I A i E[1I A 1] = P[A 1 ], i=1
8 Gesetz der großen Zahl Portfolio von Versicherungsverträgen Betrachte ein Portfolio von l x identischen n-jährigen Erlebensfallversicherungsverträgen mit Versicherungssumme 1. Für t 0: l x+t = die erwartete Anzahl der Überlebenden im Alter x + t.
9 Gesetz der großen Zahl Portfolio von Versicherungsverträgen Betrachte ein Portfolio von l x identischen n-jährigen Erlebensfallversicherungsverträgen mit Versicherungssumme 1. Für t 0: l x+t = die erwartete Anzahl der Überlebenden im Alter x + t. Annahmen:
10 Gesetz der großen Zahl Portfolio von Versicherungsverträgen Betrachte ein Portfolio von l x identischen n-jährigen Erlebensfallversicherungsverträgen mit Versicherungssumme 1. Für t 0: l x+t = die erwartete Anzahl der Überlebenden im Alter x + t. Annahmen: Alle Versicherten sind zum Zeitpunkt 0 x Jahre alt mit verbleibenden Lebenszeiten T 1,..., T lx und der gleichen Überlebenswahrscheinlichkeit tp x = l x+t l x ( = exp t 0 ) µ(x + u) du
11 Gesetz der großen Zahl Portfolio von Versicherungsverträgen Betrachte ein Portfolio von l x identischen n-jährigen Erlebensfallversicherungsverträgen mit Versicherungssumme 1. Für t 0: l x+t = die erwartete Anzahl der Überlebenden im Alter x + t. Annahmen: Alle Versicherten sind zum Zeitpunkt 0 x Jahre alt mit verbleibenden Lebenszeiten T 1,..., T lx und der gleichen Überlebenswahrscheinlichkeit tp x = l x+t l x ( = exp t 0 ) µ(x + u) du Die Prämie π(0) wird als einmalige Zahlung im Zeitpunkt 0 getätigt.
12 Gesetz der großen Zahl Wir wissen nicht: Wie viele von l x sind nach n Jahren noch am Leben? Ist das Portfolio groß genug die tatsächliche Anzahl der Überlebenden liegt nahe bei der erwarteten Anzahl l x+n. Dies ist die Folge des Gesetzes der großen Zahl: betrachte die Indikatorfunktion 1I [T i >n]. Die Menge [T i > n] beschreibt das Ereignis, dass der i-te Versicherte den Zeitpunkt n überlebt.
13 Gesetz der großen Zahl Wir wissen nicht: Wie viele von l x sind nach n Jahren noch am Leben? Ist das Portfolio groß genug die tatsächliche Anzahl der Überlebenden liegt nahe bei der erwarteten Anzahl l x+n. Dies ist die Folge des Gesetzes der großen Zahl: betrachte die Indikatorfunktion 1I [T i >n]. Die Menge [T i > n] beschreibt das Ereignis, dass der i-te Versicherte den Zeitpunkt n überlebt. Nun ist klar 1 l x l x i=1 1I [T i >n] E[1I [T 1 >n]] = P[T 1 > n] = n p x = l x+n l x
14 Aufzinsungs- und Diskontierungsfaktoren Zinssatz, Aufzinsungs- und Diskontierungsfaktoren Traditionell nimmt man an, dass das Kapital einer V. zu einem jährlichen Zins i investiert wird.
15 Aufzinsungs- und Diskontierungsfaktoren Zinssatz, Aufzinsungs- und Diskontierungsfaktoren Traditionell nimmt man an, dass das Kapital einer V. zu einem jährlichen Zins i investiert wird. 1 i Zinssatz,
16 Aufzinsungs- und Diskontierungsfaktoren Zinssatz, Aufzinsungs- und Diskontierungsfaktoren Traditionell nimmt man an, dass das Kapital einer V. zu einem jährlichen Zins i investiert wird. 1 i Zinssatz, 2 r = log(1 + i) Zinsintensität,
17 Aufzinsungs- und Diskontierungsfaktoren Zinssatz, Aufzinsungs- und Diskontierungsfaktoren Traditionell nimmt man an, dass das Kapital einer V. zu einem jährlichen Zins i investiert wird. 1 i Zinssatz, 2 r = log(1 + i) Zinsintensität, i = e r Aufzinsungsfaktor,
18 Aufzinsungs- und Diskontierungsfaktoren Zinssatz, Aufzinsungs- und Diskontierungsfaktoren Traditionell nimmt man an, dass das Kapital einer V. zu einem jährlichen Zins i investiert wird. 1 i Zinssatz, 2 r = log(1 + i) Zinsintensität, i = e r Aufzinsungsfaktor, 4 v = (1 + i) 1 = e r Diskontierungsfaktor.
19 Aufzinsungs- und Diskontierungsfaktoren Zinssatz, Aufzinsungs- und Diskontierungsfaktoren Traditionell nimmt man an, dass das Kapital einer V. zu einem jährlichen Zins i investiert wird. 1 i Zinssatz, 2 r = log(1 + i) Zinsintensität, i = e r Aufzinsungsfaktor, 4 v = (1 + i) 1 = e r Diskontierungsfaktor. Für die t-jährigen Faktoren setzen wir woraus sich die Differentialgleichung mit S(0) = 1 ergibt. (1 + i) t = e rt = S(t), d S(t) = rs(t) (1) dt
20 Zinssatz, Aufzinsungs- und Diskontierungsfaktoren Wie behandelt man Zinssätze, die während der Laufzeit des Kontraktes nicht konstant bleiben? Eine Möglichkeit ist i(s) zu betrachten, wobei i(s) = jährlicher Zinssatz im Jahre s: S(t) = ( 1 + i(1) ) (1 + i(t) ) ( t ) = exp r(s). s=1
21 Zinssatz, Aufzinsungs- und Diskontierungsfaktoren Wie behandelt man Zinssätze, die während der Laufzeit des Kontraktes nicht konstant bleiben? Eine Möglichkeit ist i(s) zu betrachten, wobei i(s) = jährlicher Zinssatz im Jahre s: S(t) = ( 1 + i(1) ) (1 + i(t) ) ( t ) = exp r(s). Betrachtet man den Fall, wo die Rendite sich mehrmals im Jahr ändert, dann sollte man zum stetigen Zins übegehen. Die Differentialgleichung (1) wird dann zu d S(t) = r(t)s(t). dt Die Lösung für S(0) = 1 ist S(t) = exp s=1 ( t 0 r(u) du ).
22 Verluste und Äquivalenzprinzip Betrachte wieder ein Portfolio von l x Erlebensfallversicherungsverträgen. Die Prämien werden als Einmalprämie π(0) zum Zeitpunkt 0 abbezahlt. Die Anzahl der Überlebenden nach n Jahren ist durch l x+n gegeben. Der Wert der zukünftigen Zahlungen für den Versicherer ist gleich S(n) 1 l x+n ; die Prämieneinnahmen sind gleich l x π(0). Demnach beläuft sich der aktuelle Verlust auf L = l x+n S(n) 1 l x π(0). Wir sagen, dass die Prämie π(0) fair ist, wenn L = 0.
23 Verluste und Äquivalenzprinzip Betrachte wieder ein Portfolio von l x Erlebensfallversicherungsverträgen. Die Prämien werden als Einmalprämie π(0) zum Zeitpunkt 0 abbezahlt. Die Anzahl der Überlebenden nach n Jahren ist durch l x+n gegeben. Der Wert der zukünftigen Zahlungen für den Versicherer ist gleich S(n) 1 l x+n ; die Prämieneinnahmen sind gleich l x π(0). Demnach beläuft sich der aktuelle Verlust auf L = l x+n S(n) 1 l x π(0). Wir sagen, dass die Prämie π(0) fair ist, wenn L = 0. Ist S(n) bekannt, so ist die faire Prämie gegeben durch π(0) = l x+n l x ( exp n 0 ) ( r(u) du = n p x exp n 0 ) r(u) du. Achtung! Dieses Argument funktioniert nur, wenn wir S(n) im Zeitpunkt 0 tatsächlich kennen.
24 Verluste und Äquivalenzprinzip Finanzierungsrisiko eines Versicherungsportfolios Angenommen S(t) ist eine Zufallsvariable. Dann kann S(t) als Finanzierungsrisiko interpretiert werden. Dieses Risiko werden wir auch durch die Portfoliovergrößerung nicht diversifizieren können.
25 Verluste und Äquivalenzprinzip Finanzierungsrisiko eines Versicherungsportfolios Angenommen S(t) ist eine Zufallsvariable. Dann kann S(t) als Finanzierungsrisiko interpretiert werden. Dieses Risiko werden wir auch durch die Portfoliovergrößerung nicht diversifizieren können. Frage: Wie kontrolliere ich das Finanzierungsrisiko?
26 Verluste und Äquivalenzprinzip Finanzierungsrisiko eines Versicherungsportfolios Angenommen S(t) ist eine Zufallsvariable. Dann kann S(t) als Finanzierungsrisiko interpretiert werden. Dieses Risiko werden wir auch durch die Portfoliovergrößerung nicht diversifizieren können. Frage: Wie kontrolliere ich das Finanzierungsrisiko? Antwort in unserer idealen Welt: Durch Handeln mit Zerobonds!
27 Verluste und Äquivalenzprinzip Finanzierungsrisiko eines Versicherungsportfolios Angenommen S(t) ist eine Zufallsvariable. Dann kann S(t) als Finanzierungsrisiko interpretiert werden. Dieses Risiko werden wir auch durch die Portfoliovergrößerung nicht diversifizieren können. Frage: Wie kontrolliere ich das Finanzierungsrisiko? Antwort in unserer idealen Welt: Durch Handeln mit Zerobonds! Definition 1 Ein Zerobond (auch Nullkuponanleihe) ist ein verzinsliches Wertpapier, bei dem es nur eine Auszahlung am Ende der Laufzeit gibt. Ein Zerobond mit Laufzeit n wird auch n-bond genannt. Den Preis eines Zerobonds mit der Laufzeit n bezeichnen wir mit P(t, n).
28 Deterministische Bond-Preise Hier betrachten wir eine völlig deterministische Welt.
29 Deterministische Bond-Preise Hier betrachten wir eine völlig deterministische Welt. Wähle t τ n. Der Preis P(τ, n) zum Zeitpunkt τ eines n-bonds ist dann gegeben durch P(t, n) = P(t, τ)p(τ, n). t τ n P (τ, n)p (t, τ) +P (τ, n) P (τ, n) 1 P (t, n)
30 Deterministische Bond-Preise Hier betrachten wir eine völlig deterministische Welt. Wähle t τ n. Der Preis P(τ, n) zum Zeitpunkt τ eines n-bonds ist dann gegeben durch P(t, n) = P(t, τ)p(τ, n). t τ n P (τ, n)p (t, τ) +P (τ, n) P (τ, n) 1 P (t, n) D.h. insbesondere, dass wir P(t, τ) und P(τ, n) als Diskontierungsfaktoren betrachten können: 1. Kaufe zum Zeitpunkt t P(τ, n) Einheiten eines P(t, τ) Bonds; 2. Kaufe in τ eine Einheit eines P(τ, n)-bonds.
31 Deterministische Bond-Preise Hier betrachten wir eine völlig deterministische Welt. Wähle t τ n. Der Preis P(τ, n) zum Zeitpunkt τ eines n-bonds ist dann gegeben durch P(t, n) = P(t, τ)p(τ, n). t τ n P (τ, n)p (t, τ) +P (τ, n) P (τ, n) 1 P (t, n) D.h. insbesondere, dass wir P(t, τ) und P(τ, n) als Diskontierungsfaktoren betrachten können: 1. Kaufe zum Zeitpunkt t P(τ, n) Einheiten eines P(t, τ) Bonds; 2. Kaufe in τ eine Einheit eines P(τ, n)-bonds. Man kann sogar die Existenz einer Funktion r nachweisen, sodass ( n ) P(t, n) = exp r (u) du. t
32 Duplikation mit Zerobonds Duplikation von Erlebensfallversicherungsportfolien Angenommen der Versicherer investiert zum Zeitpunkt 0 in l x κ Einheiten eines n-bonds.
33 Duplikation mit Zerobonds Duplikation von Erlebensfallversicherungsportfolien Angenommen der Versicherer investiert zum Zeitpunkt 0 in l x κ Einheiten eines n-bonds. Der aktuelle Verlust des Versicherers beläuft sich dann auf L = ( l x+n S(n) 1 l x π(0) ) + l x κ ( P(0, n) S(n) 1) = ( l x+n l x κ ) S(n) 1 + l x ( κp(0, n) π(0) ). Der erste Term ist gleich 0, wenn κ = l x+n /l x ; der zweite Term ist gleich 0, wenn π(0) = n p x P(0, n).
34 Duplikation mit Zerobonds Duplikation von Erlebensfallversicherungsportfolien Angenommen der Versicherer investiert zum Zeitpunkt 0 in l x κ Einheiten eines n-bonds. Der aktuelle Verlust des Versicherers beläuft sich dann auf L = ( l x+n S(n) 1 l x π(0) ) + l x κ ( P(0, n) S(n) 1) = ( l x+n l x κ ) S(n) 1 + l x ( κp(0, n) π(0) ). Der erste Term ist gleich 0, wenn κ = l x+n /l x ; der zweite Term ist gleich 0, wenn π(0) = n p x P(0, n). Die faire Prämie ist dann gegeben durch π(0) = n p x P(0, n). Interpretation: Der Preis eines P(0, n)-bonds multipliziert mit der n-jährigen Überlebenswahrscheinlichkeit.
35 Duplikation mit Zerobonds Duplikation von Erlebensfallversicherungsportfolien Angenommen der Versicherer investiert zum Zeitpunkt 0 in l x κ Einheiten eines n-bonds. Der aktuelle Verlust des Versicherers beläuft sich dann auf L = ( l x+n S(n) 1 l x π(0) ) + l x κ ( P(0, n) S(n) 1) = ( l x+n l x κ ) S(n) 1 + l x ( κp(0, n) π(0) ). Der erste Term ist gleich 0, wenn κ = l x+n /l x ; der zweite Term ist gleich 0, wenn π(0) = n p x P(0, n). Die faire Prämie ist dann gegeben durch π(0) = n p x P(0, n). Interpretation: Der Preis eines P(0, n)-bonds multipliziert mit der n-jährigen Überlebenswahrscheinlichkeit. In einem Portfolio mit l x Verträgen sollte der Versicherer l x np x = l x+n P(0, n)-bonds kaufen.
36 Duplikation mit Zerobonds Duplikation von Todesfallversicherungsportfolien Betrachte ein Portfolio von l x temporären Todesfallversicherungsverträgen.
37 Duplikation mit Zerobonds Duplikation von Todesfallversicherungsportfolien Betrachte ein Portfolio von l x temporären Todesfallversicherungsverträgen. Zum Zeitpunkt 0 beträgt die erwartete Anzahl der Toten im Jahr t d x+t = l x+t l x+t+1. Die Versicherungssumme 1 wird erst am Ende der Periode ausbezahlt. Der Versicherer kauft in 0 l x κ(t) Einheiten eines t-bonds zum Preis P(0, t).
38 Duplikation mit Zerobonds Duplikation von Todesfallversicherungsportfolien Betrachte ein Portfolio von l x temporären Todesfallversicherungsverträgen. Zum Zeitpunkt 0 beträgt die erwartete Anzahl der Toten im Jahr t d x+t = l x+t l x+t+1. Die Versicherungssumme 1 wird erst am Ende der Periode ausbezahlt. Der Versicherer kauft in 0 l x κ(t) Einheiten eines t-bonds zum Preis P(0, t). Der Verlust zum Zeitpunkt 0 beträgt L = = ( n ) n d x+t 1 S(t) 1 l x π(0) + l x k(t) ( P(0, t) S(t) 1) t=1 t=1 t=1 n ( dx+t 1 l x κ(t) ) ( n ) S(t) 1 + l x κ(t)p(0, t) π(0). t=1
39 Duplikation mit Zerobonds Duplikation von Todesfallversicherungsportfolien Der erste Term in der Verlustgleichung ist gleich 0, wenn Der zweite Term ist gleich 0, wenn κ(t) = d x+t 1 l x = t 1 p x 1q x+t 1. π(0) = n t 1p x 1q x+t 1 P(0, t). t=1
40 Duplikation mit Zerobonds Duplikation von Todesfallversicherungsportfolien Der erste Term in der Verlustgleichung ist gleich 0, wenn Der zweite Term ist gleich 0, wenn κ(t) = d x+t 1 l x = t 1 p x 1q x+t 1. π(0) = n t 1p x 1q x+t 1 P(0, t). t=1 Falls die Versicherungssumme direkt nach dem Tod ausgezahlt werden soll, so könnte die Prämie wie folgt aussehen π(0) = n 0 tp x µ(x + t)p(0, t) dt.
41 Marktwerte und Zerobonds Rechnungsgrundlagen erster Ordnung (r, µ ) Aus dem zweiten Kapitel wissen wir π a xn = ba (0) n E x + b ad A 1 xn,
42 Marktwerte und Zerobonds Rechnungsgrundlagen erster Ordnung (r, µ ) Aus dem zweiten Kapitel wissen wir π a xn = ba (0) n E x + b ad A 1 xn, wobei ( n tpx+t = exp n t ) µ (x + τ) dτ,
43 Marktwerte und Zerobonds Rechnungsgrundlagen erster Ordnung (r, µ ) Aus dem zweiten Kapitel wissen wir π a xn = ba (0) n E x + b ad A 1 xn, wobei ( n tpx+t = exp ( n tex+t = exp n t n t ) µ (x + τ) dτ, r (τ) dτ ) n tp x+t,
44 Marktwerte und Zerobonds Rechnungsgrundlagen erster Ordnung (r, µ ) Aus dem zweiten Kapitel wissen wir wobei ( n tpx+t = exp ( n tex+t = exp a x+t n t = π a xn = ba (0) n E x + b ad A 1 xn, n t exp n t n t ( ) µ (x + τ) dτ, ) r (τ) dτ s t n tp x+t, r (τ) dτ ) s tp x+tµ (x + s) ds,
45 Marktwerte und Zerobonds Rechnungsgrundlagen erster Ordnung (r, µ ) Aus dem zweiten Kapitel wissen wir wobei ( n tpx+t = exp ( n tex+t = exp a x+t n t = A 1 x+t n t = π a xn = ba (0) n E x + b ad A 1 xn, n t n t n t n t ( exp ( exp ) µ (x + τ) dτ, ) r (τ) dτ s t s t n tp x+t, ) r (τ) dτ s tpx+tµ (x + s) ds, r (τ) dτ ) s tp x+tµ (x + s) ds.
46 Marktwerte und Zerobonds Rechnungsgrundlagen erster Ordnung und die technische Reserve Die technische Reserve zum Zeitpunkt u der in t garantierten Zahlungen ist V (t, u) = b a (t) n u E x+u + b ad A 1 x+u n u πa x+u n u.
47 Marktwerte und Zerobonds Rechnungsgrundlagen erster Ordnung und die technische Reserve Die technische Reserve zum Zeitpunkt u der in t garantierten Zahlungen ist V (t, u) = b a (t) n u E x+u + b ad A 1 x+u n u πa x+u n u. Für u t haben wir die folgende Differentialgleichung mit u V (t, u) = r (u)v (t, u) + π µ (x + u)r (t, u) V (t, t) = V (t), V (t, n) = b a (t) und R (t, u) = b ad V (t, u).
48 Marktwerte und Zerobonds Marktwert der garantierten Zahlungen Wenden wir das Diversifikations- und Duplikationsargument auf die Zahlungen b a (0) an, so erhalten wir den Marktwert der Überlebenszahlung b a (0)P(t, n) n t p x+t.
49 Marktwerte und Zerobonds Marktwert der garantierten Zahlungen Wenden wir das Diversifikations- und Duplikationsargument auf die Zahlungen b a (0) an, so erhalten wir den Marktwert der Überlebenszahlung b a (0)P(t, n) n t p x+t. Für den Marktwert der Todesfallzahlung erhalten wir n b ad P(t, s) s t p x+t µ(x + s) ds. t
50 Marktwerte und Zerobonds Marktwert der garantierten Zahlungen Wenden wir das Diversifikations- und Duplikationsargument auf die Zahlungen b a (0) an, so erhalten wir den Marktwert der Überlebenszahlung b a (0)P(t, n) n t p x+t. Für den Marktwert der Todesfallzahlung erhalten wir n b ad P(t, s) s t p x+t µ(x + s) ds. t Der Marktwert der zukünftigen Prämien ist gegeben durch π n t P(t, s) s t p x+t ds.
51 Marktwerte und Zerobonds Marktwert der garantierten Zahlungen Wenden wir das Diversifikations- und Duplikationsargument auf die Zahlungen b a (0) an, so erhalten wir den Marktwert der Überlebenszahlung b a (0)P(t, n) n t p x+t. Für den Marktwert der Todesfallzahlung erhalten wir n b ad P(t, s) s t p x+t µ(x + s) ds. t Der Marktwert der zukünftigen Prämien ist gegeben durch π n t P(t, s) s t p x+t ds. Kombinieren wir die drei Faktoren so erhalten wir den Marktwert in t für die in 0 garantierten Zahlungen: V g (0, t) = b a (0)P(t, n) n t p x+t + n t P(t, s) s t p x+t ( µ(x + s)b ad π ) ds.
52 Zerobonds und Zinstheorie 1 Bewertung durch Diversifikation Gesetz der großen Zahl Zinssatz, Aufzinsungs- und Diskontierungsfaktoren Verluste und Äquivalenzprinzip Deterministische Bond-Preise Duplikation mit Zerobonds Marktwerte und Zerobonds 2 Zerobonds und Zinstheorie Zinsstrukturkurven Beziehung zwischen Terminzins und Kassazins Einfache Zinsen Marktwerte und Terminzinsen 3 Bonds, Zinsen und Duration
53 Zinsstrukturkurven Zerobonds und Zinstheorie Zinsstrukturkurven Definition 2 Der konforme Kassazins (continuously compounded spot rate) zum Zeitpunkt t für den Referenzzeitraum [t, T ] ist definiert durch R(t, T ) = 1 T t log ( P(t, T ) ).
54 Zinsstrukturkurven Zerobonds und Zinstheorie Zinsstrukturkurven Definition 2 Der konforme Kassazins (continuously compounded spot rate) zum Zeitpunkt t für den Referenzzeitraum [t, T ] ist definiert durch R(t, T ) = 1 T t log ( P(t, T ) ). Es folgt sofort P(t, T ) = exp ( R(t, T )(T t) ).
55 Zinsstrukturkurven Zerobonds und Zinstheorie Zinsstrukturkurven Definition 2 Der konforme Kassazins (continuously compounded spot rate) zum Zeitpunkt t für den Referenzzeitraum [t, T ] ist definiert durch R(t, T ) = 1 T t log ( P(t, T ) ). Es folgt sofort P(t, T ) = exp ( R(t, T )(T t) ). Definition 3 Die Zinsstrukturkurve zum Zeitpunkt t ist gegeben durch die Abbildung h R(t, t + h).
56 Zerobonds und Zinstheorie Terminzins (Forwardrate) Zinsstrukturkurven Betrachte die Zeiten 0 t T T. Wie findet man den Zins für die Investitionen, die in T beginnen und in T enden?
57 Zerobonds und Zinstheorie Terminzins (Forwardrate) Zinsstrukturkurven Betrachte die Zeiten 0 t T T. Wie findet man den Zins für die Investitionen, die in T beginnen und in T enden? Definition 4 Der effektive Terminzins zum Zeitpunkt t für( den Referenzzeitraum ) ( ) [T, T ] ist definiert durch f (t, T, T ) = log P(t,T ) log P(t,T ) T T.
58 Zerobonds und Zinstheorie Terminzins (Forwardrate) Zinsstrukturkurven Betrachte die Zeiten 0 t T T. Wie findet man den Zins für die Investitionen, die in T beginnen und in T enden? Definition 4 Der effektive Terminzins zum Zeitpunkt t für( den Referenzzeitraum ) ( ) [T, T ] ist definiert durch f (t, T, T ) = log P(t,T ) log P(t,T ) Interpretation: verkaufe in t einen T -Bond und erhalte P(t, T ); in t verwende P(t, T ) um P(t,T ) P(t,T ) in T zahle 1 aus; in T erhalte P(t,T ) P(t,T ) zurück. T T. Einheiten eines T -Bonds zu kaufen;
59 Zerobonds und Zinstheorie Terminzins (Forwardrate) Zinsstrukturkurven Betrachte die Zeiten 0 t T T. Wie findet man den Zins für die Investitionen, die in T beginnen und in T enden? Definition 4 Der effektive Terminzins zum Zeitpunkt t für( den Referenzzeitraum ) ( ) [T, T ] ist definiert durch f (t, T, T ) = log P(t,T ) log P(t,T ) Interpretation: verkaufe in t einen T -Bond und erhalte P(t, T ); T T. in t verwende P(t, T ) um P(t,T ) P(t,T ) Einheiten eines T -Bonds zu kaufen; in T zahle 1 aus; in T erhalte P(t,T ) P(t,T ) zurück. f (t, T, T ) kann also als konstante Verzinsung von T bis T interpretiert werden.
60 Zerobonds und Zinstheorie Zinsstrukturkurven Manchmal ist es besser mit dem sofortigen Terminzins (instantaneous forward rate) zu arbeiten. Definition 5 Ist die Abbildung T P(t, T ) stetig diff.bar, so definieren wir den sofortigen Terminzins durch f (t, T ) = T log ( P(t, T ) ). Die Short Rate (auch Momentanzins) zum Zeitpunkt t ist r(t) = f (t, t).
61 Zerobonds und Zinstheorie Zinsstrukturkurven Manchmal ist es besser mit dem sofortigen Terminzins (instantaneous forward rate) zu arbeiten. Definition 5 Ist die Abbildung T P(t, T ) stetig diff.bar, so definieren wir den sofortigen Terminzins durch f (t, T ) = T log ( P(t, T ) ). Die Short Rate (auch Momentanzins) zum Zeitpunkt t ist r(t) = f (t, t). Aus der obigen Definition folgt sofort T Daraus ergibt sich t f (t, τ) dτ = log ( P(t, T ) ) + log ( ) P(t, t) }{{} =1 P(t, T ) = exp ( T f (t, τ) dτ ). t
62 Zerobonds und Zinstheorie Zinsstrukturkurven Merke: Im Allgemeinen kann man nicht schließen, dass P(t, T ) = exp ( T t f (t, τ) dτ ).
63 Zerobonds und Zinstheorie Zinsstrukturkurven Merke: Im Allgemeinen kann man nicht schließen, dass P(t, T ) = exp ( T t f (t, τ) dτ ). Zurück in unsere ideale Welt!
64 Zerobonds und Zinstheorie Zinsstrukturkurven Merke: Im Allgemeinen kann man nicht schließen, dass P(t, T ) = exp ( T t f (t, τ) dτ ). Zurück in unsere ideale Welt! Es gibt mehrere Möglichkeiten Modelle für einen Bondmarkt zu beschreiben: Bestimme alle P(t, T ) für 0 t T T, wo T den Zeithorizont bezeichnet. Bestimme alle f (t, T ) für 0 t T T und leite daraus alle P(t, T ) und r(t) ab. Bestimme alle r(t) für 0 t T T.
65 Zerobonds und Zinstheorie Beziehung zwischen Terminzins und Kassazins 1 Setze T = t, dann haben wir f (t, t, T ) = R(t, T ), d.h. der Terminzins zum Zeitpunkt t für den Referenzzeitraum [t, T ] stimmt mit dem Kassazins für [t, T ] überein. 2 Wir sehen auch 1 T f (t, τ) dτ = R(t, T ). T t t Der Kassazins in [t, T ] kann also als Mittelwert der sofortigen Terminzinsen interpretiert werden.
66 Zerobonds und Zinstheorie Einfache Zinsen Als Alternative zu den Zinsen von eben kann man auch einfache Zinsen betrachten. Definition 6 Der einfache Kassazins (simple spot rate) für [t, T ] ist gegeben durch L(t, T ) = P(t, T ) 1 (T t)p(t, T ) ; der einfache Terminzins (simple forward rate) für [T, T ] zum Zeitpunkt t ist gegeben durch L(t, T, T ) = P(t, T ) P(t, T ) (T T )P(t, T ).
67 Zerobonds und Zinstheorie Einfache Zinsen Als Alternative zu den Zinsen von eben kann man auch einfache Zinsen betrachten. Definition 6 Der einfache Kassazins (simple spot rate) für [t, T ] ist gegeben durch L(t, T ) = P(t, T ) 1 (T t)p(t, T ) ; der einfache Terminzins (simple forward rate) für [T, T ] zum Zeitpunkt t ist gegeben durch L(t, T, T ) = P(t, T ) P(t, T ) (T T )P(t, T ). Interpretation: 1 P(t, T ) = (T t)l(t, T )P(t, T ) ist der Gewinn im Zeitintervall [t, T ].
68 Zerobonds und Zinstheorie Marktwerte und Terminzinsen Der Marktwert in u der in t garantierten Zahlungen ist gegeben durch V g (t, u) = b a (t) exp ( + n u exp ( s u n u f (u, τ) dτ ) n up x+u f (u, τ) dτ ) s up x+u ( µ(x + s)b ad π ) ds.
69 Zerobonds und Zinstheorie Marktwerte und Terminzinsen Der Marktwert in u der in t garantierten Zahlungen ist gegeben durch V g (t, u) = b a (t) exp ( + n u exp ( s u n u f (u, τ) dτ ) n up x+u f (u, τ) dτ ) s up x+u ( µ(x + s)b ad π ) ds. Dies ist aber eine sehr komplizierte Funktion von u!
70 Zerobonds und Zinstheorie Marktwerte und Terminzinsen Der Marktwert in u der in t garantierten Zahlungen ist gegeben durch V g (t, u) = b a (t) exp ( + n u exp ( s u n u f (u, τ) dτ ) n up x+u f (u, τ) dτ ) s up x+u ( µ(x + s)b ad π ) ds. Dies ist aber eine sehr komplizierte Funktion von u! Deshalb betrachten wir eine einfachere Hilfsfunktion V g,o (t, u) = b a (t) exp ( + n u exp ( s u n u f (t, τ) dτ ) n up x+u f (t, τ) dτ ) s up x+u ( µ(x + s)b ad π ) ds.
71 Die Hilfsfunktion V g,o Zerobonds und Zinstheorie Marktwerte und Terminzinsen Die Funktion V g,o genügt der folgenden DGL u V g,o (t, u) = f (t, u)v g,o (t, u) + π µ(x + u)r g,o (t, u), V g,o (t, t) = V g (t), V g,o (t, n) = b a (t), wobei R g,o (t, u) = b ad V g,o (t, u). Diese Differentialgleichung gibt uns eine alternative Methode V g,o zu bestimmen.
72 Zerobonds und Zinstheorie Das individuelle Bonuspotential Marktwerte und Terminzinsen Die Terminzinsen können auch bei der Berechnung des individuellen Bonuspotentials V ib eingesetzt werden. Die einfachste Situation ist V (t) V (t) V g (t), wobei V (t) die totale Vertragsreserve bezeichnet. Dann ist V ib gegeben durch V ib (t) = V (t) V g (t).
73 Zerobonds und Zinstheorie Das individuelle Bonuspotential Marktwerte und Terminzinsen Die Terminzinsen können auch bei der Berechnung des individuellen Bonuspotentials V ib eingesetzt werden. Die einfachste Situation ist V (t) V (t) V g (t), wobei V (t) die totale Vertragsreserve bezeichnet. Dann ist V ib gegeben durch V ib (t) = V (t) V g (t). Durch Anwendung der Differentialgleichungen für V (t) und V g (t) zusammen mit V (t, n) V g,o (t, n) = b a (t) b a (t) = 0 ergibt sich V ib (t) = n t ( exp s t ( f (t, τ) + µ(x + τ) ) dτ ) c(t, s) ds, c(t, s) = ( f (t, s) r (s) ) V (t, s) + ( µ (x + s) µ(x + s) ) R (t, s).
74 Zerobonds und Zinstheorie Das individuelle Bonuspotential Marktwerte und Terminzinsen Die Terminzinsen können auch bei der Berechnung des individuellen Bonuspotentials V ib eingesetzt werden. Die einfachste Situation ist V (t) V (t) V g (t), wobei V (t) die totale Vertragsreserve bezeichnet. Dann ist V ib gegeben durch V ib (t) = V (t) V g (t). Durch Anwendung der Differentialgleichungen für V (t) und V g (t) zusammen mit V (t, n) V g,o (t, n) = b a (t) b a (t) = 0 ergibt sich V ib (t) = n t ( exp s t ( f (t, τ) + µ(x + τ) ) dτ ) c(t, s) ds, c(t, s) = ( f (t, s) r (s) ) V (t, s) + ( µ (x + s) µ(x + s) ) R (t, s).
75 Zerobonds und Zinstheorie Marktwerte und Terminzinsen Rechnungsgrundlagen erster Ordnung und die technische Reserve Die technische Reserve tum Zeitpunkt u, der in t garantierten Zahlungen ist V (t, u) = b a (t) n u E x+u + b ad A 1 x+u n u πa x+u n u. Für u t haben wir die folgende Differentialgleichung mit u V (t, u) = r (u)v (t, u) + π µ (x + u)r (t, u) V (t, t) = V (t), V (t, n) = b a (t) und R (t, u) = b ad V (t, u).
76 Zerobonds und Zinstheorie Das individuelle Bonuspotential Marktwerte und Terminzinsen Die Terminzinsen können auch bei der Berechnung des individuellen Bonuspotentials V ib eingesetzt werden. Die einfachste Situation ist V (t) V (t) V g (t), wobei V (t) die totale Vertragsreserve bezeichnet. Dann ist V ib gegeben durch V ib (t) = V (t) V g (t). Durch Anwendung der Differentialgleichungen für V (t) und V g (t) zusammen mit V (t, n) V g,o (t, n) = b a (t) b a (t) = 0 ergibt sich V ib (t) = n t ( exp s t ( f (t, τ) + µ(x + τ) ) dτ ) c(t, s) ds, c(t, s) = ( f (t, s) r (s) ) V (t, s) + ( µ (x + s) µ(x + s) ) R (t, s).
77 Zerobonds und Zinstheorie Das individuelle Bonuspotential Marktwerte und Terminzinsen Die Terminzinsen können auch bei der Berechnung des individuellen Bonuspotentials V ib eingesetzt werden. Die einfachste Situation ist V (t) V (t) V g (t), wobei V (t) die totale Vertragsreserve bezeichnet. Dann ist V ib gegeben durch V ib (t) = V (t) V g (t). Durch Anwendung der Differentialgleichungen für V (t) und V g (t) zusammen mit V (t, n) V g,o (t, n) = b a (t) b a (t) = 0 ergibt sich V ib (t) = n t ( exp s t ( f (t, τ) + µ(x + τ) ) dτ ) c(t, s) ds, c(t, s) = ( f (t, s) r (s) ) V (t, s) + ( µ (x + s) µ(x + s) ) R (t, s).
78 Die Hilfsfunktion V g,o Zerobonds und Zinstheorie Marktwerte und Terminzinsen Die Funktion V g,o genügt der folgenden DGL u V g,o (t, u) = f (t, u)v g,o (t, u) + π µ(x + u)r g,o (t, u), V g,o (t, t) = V g (t), V g,o (t, n) = b a (t), wobei R g,o (t, u) = b ad V g,o (t, u). Diese Differentialgleichung gibt uns eine alternative Methode V g,o zu bestimmen.
79 Bonds, Zinsen und Duration 1 Bewertung durch Diversifikation Gesetz der großen Zahl Zinssatz, Aufzinsungs- und Diskontierungsfaktoren Verluste und Äquivalenzprinzip Deterministische Bond-Preise Duplikation mit Zerobonds Marktwerte und Zerobonds 2 Zerobonds und Zinstheorie Zinsstrukturkurven Beziehung zwischen Terminzins und Kassazins Einfache Zinsen Marktwerte und Terminzinsen 3 Bonds, Zinsen und Duration
80 Allgemeine Anleihe Bonds, Zinsen und Duration Die meisten Wertpapiere, die an den Märkten gehandelt werden, haben eine kompliziertere Struktur als die Nullkuponanleihe.
81 Allgemeine Anleihe Bonds, Zinsen und Duration Die meisten Wertpapiere, die an den Märkten gehandelt werden, haben eine kompliziertere Struktur als die Nullkuponanleihe. Betrachte eine Anleihe, die zum Zeitpunkt τ emittiert wurde. Zu den Zeitpunkten τ 1 < < τ n werden die Beträge c 1,..., c n ausgezahlt. Der Wert einer solchen Anleihe zum Zeitpunkt t (nach den möglichen Zahlungen) ist P(t) = P(t, τ i )c i. i, τ i >t Dabei bezeichnet P(t, τ i ) den Preis zum Zeitpunkt t eines Zerobonds mit Laufzeit τ i.
82 Allgemeine Anleihe Bonds, Zinsen und Duration Die meisten Wertpapiere, die an den Märkten gehandelt werden, haben eine kompliziertere Struktur als die Nullkuponanleihe. Betrachte eine Anleihe, die zum Zeitpunkt τ emittiert wurde. Zu den Zeitpunkten τ 1 < < τ n werden die Beträge c 1,..., c n ausgezahlt. Der Wert einer solchen Anleihe zum Zeitpunkt t (nach den möglichen Zahlungen) ist P(t) = P(t, τ i )c i. i, τ i >t Dabei bezeichnet P(t, τ i ) den Preis zum Zeitpunkt t eines Zerobonds mit Laufzeit τ i. Beispiel (Rentenbrief) Betrachte c k = c für k = 1,..., n. Dies liefert den Rentenbrief.
83 References Møller, T and Steffensen, M. (2008). Market-Valuation Methods in Life and Pension Insurance. Cambrige University Press, New York.
Cashflows von Versicherungsverträgen in der Lebensversicherung
 Cashflows von Versicherungsverträgen in der Lebensversicherung 5. Juni 2015 1 / 37 Inhalt Geschäftsmodell der Lebensversicherung Produkte der Lebensversicherung Zahlungsströme unter Unsicherheit Deckungsrückstellung
Cashflows von Versicherungsverträgen in der Lebensversicherung 5. Juni 2015 1 / 37 Inhalt Geschäftsmodell der Lebensversicherung Produkte der Lebensversicherung Zahlungsströme unter Unsicherheit Deckungsrückstellung
Finanzwirtschaft. Teil II: Bewertung. Zinssätze und Renten
 Zinssätze und Renten 1 Finanzwirtschaft Teil II: Bewertung Zinssätze und Renten Agenda Zinssätze und Renten 2 Effektivzinsen Spot-Zinsen Forward-Zinsen Bewertung Kennziffern Zusammenfassung Zinssätze und
Zinssätze und Renten 1 Finanzwirtschaft Teil II: Bewertung Zinssätze und Renten Agenda Zinssätze und Renten 2 Effektivzinsen Spot-Zinsen Forward-Zinsen Bewertung Kennziffern Zusammenfassung Zinssätze und
Übungen zur Versicherungsmathematik
 Übungen zur Versicherungsmathematik I Lebensversicherungsmathematik Vervollständige die folgende Tabelle, wobei jedes der Symbole durch die anderen ausgedrückt werden soll i d i d v r i i d +i v v +i r
Übungen zur Versicherungsmathematik I Lebensversicherungsmathematik Vervollständige die folgende Tabelle, wobei jedes der Symbole durch die anderen ausgedrückt werden soll i d i d v r i i d +i v v +i r
Zinseszins- und Rentenrechnung
 Zinseszins- und Rentenrechnung 1 Berechnen Sie den Zeitpunkt, an dem sich das Einlagekapital K bei a) jährlicher b) monatlicher c) stetiger Verzinsung verdoppelt hat, wobei i der jährliche nominelle Zinssatz
Zinseszins- und Rentenrechnung 1 Berechnen Sie den Zeitpunkt, an dem sich das Einlagekapital K bei a) jährlicher b) monatlicher c) stetiger Verzinsung verdoppelt hat, wobei i der jährliche nominelle Zinssatz
Risk analysis and valuation of life insurance contracts: Combining actuarial and financial approaches
 Risk analysis and valuation of life insurance contracts: Combining actuarial and financial approaches Mario Knoll 5. Dezember 2012 Inhalt Einführung Einführung Produktmerkmal: Zinsgarantien 2 Haupttypen:
Risk analysis and valuation of life insurance contracts: Combining actuarial and financial approaches Mario Knoll 5. Dezember 2012 Inhalt Einführung Einführung Produktmerkmal: Zinsgarantien 2 Haupttypen:
Prüfung Grundprinzipien der Versicherungs- und Finanzmathematik 2015
 Prüfung Grundprinzipien der Versicherungs- und Finanzmathematik 2015 Aufgabe 1: (20 min) a) Gegeben sei ein einperiodiger State Space-Markt mit zwei Zuständen, der aus zwei Wertpapieren bestehe, einer
Prüfung Grundprinzipien der Versicherungs- und Finanzmathematik 2015 Aufgabe 1: (20 min) a) Gegeben sei ein einperiodiger State Space-Markt mit zwei Zuständen, der aus zwei Wertpapieren bestehe, einer
Kapitle 3: Swaps und Forward Swaps
 Kapitle 3: Swaps und Forward Swaps Stefan Ehrenfried Institut für Finanzmathematik Universität Ulm 13.12.2011 Inhaltsverzeichnis 1 Grundlagen 2 Zinsswaps 3 Bewertung 1-jähriger Forward-Swaps Fixed for
Kapitle 3: Swaps und Forward Swaps Stefan Ehrenfried Institut für Finanzmathematik Universität Ulm 13.12.2011 Inhaltsverzeichnis 1 Grundlagen 2 Zinsswaps 3 Bewertung 1-jähriger Forward-Swaps Fixed for
Einführung in die Obligationenmärkte
 Einführung in die Obligationenmärkte Einige wichtige Begriffe Obligationenmarkt (auch Anleihenmarkt) ist der Markt für festverzinsliche Wertpapiere mittlerer bis langfristiger Laufzeit und festem Fälligkeitstermin.
Einführung in die Obligationenmärkte Einige wichtige Begriffe Obligationenmarkt (auch Anleihenmarkt) ist der Markt für festverzinsliche Wertpapiere mittlerer bis langfristiger Laufzeit und festem Fälligkeitstermin.
Zinssätze. Georg Wehowar. 4. Dezember 2007
 4. Dezember 2007 Grundlagen der Zinsrechnung Verschiedene Anleihen Forward Rate Agreement Forward Zinsen Allgemeines Allgemeine Grundlagen K 0... Anfangskapital K t... Kapital nach einer Zeitspanne t Z
4. Dezember 2007 Grundlagen der Zinsrechnung Verschiedene Anleihen Forward Rate Agreement Forward Zinsen Allgemeines Allgemeine Grundlagen K 0... Anfangskapital K t... Kapital nach einer Zeitspanne t Z
Versicherungstechnik
 Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Marius Radermacher, M.Sc. DOOR Aufgabe 9 Versicherungstechnik Übungsblatt 3 Abgabe bis Dienstag, dem 08.11.2016 um 10 Uhr im Kasten 19
Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Marius Radermacher, M.Sc. DOOR Aufgabe 9 Versicherungstechnik Übungsblatt 3 Abgabe bis Dienstag, dem 08.11.2016 um 10 Uhr im Kasten 19
Asset-Liability-Modell einer Lebensversicherung
 Asset-Liability-Modell einer Lebensversicherung Umsetzung eines Bewertungsmodells Seminar Finanzmarktmodelle in der Lebensversicherung betreut von Dr. Zoran Nikolic und Dr. Tamino Meyhöfer Max Gripp, Tanja
Asset-Liability-Modell einer Lebensversicherung Umsetzung eines Bewertungsmodells Seminar Finanzmarktmodelle in der Lebensversicherung betreut von Dr. Zoran Nikolic und Dr. Tamino Meyhöfer Max Gripp, Tanja
Übungsaufgaben zu Kapitel 6: Finanzmärkte und Erwartungen
 Kapitel 6 Übungsaufgaben zu Kapitel 6: Finanzmärkte und Erwartungen Übungsaufgabe 6-1a 6-1a) Welche Typen von Zinsstrukturkurven kennen Sie? Stellen Sie die Typen graphisch dar und erläutern Sie diese.
Kapitel 6 Übungsaufgaben zu Kapitel 6: Finanzmärkte und Erwartungen Übungsaufgabe 6-1a 6-1a) Welche Typen von Zinsstrukturkurven kennen Sie? Stellen Sie die Typen graphisch dar und erläutern Sie diese.
vorschüssige, lebenslängliche Leibrente (whole life annuity-due) Vorschüssige jährliche Zahlungen von 1, solange die versicherte Person am Leben ist.
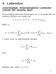 4. Leibrenten vorschüssige, lebenslängliche Leibrente (whole life annuity-due) Vorschüssige jährliche Zahlungen von 1, solange die versicherte Person am Leben ist. NEP ä x : Y = 1 + v + v 2 + + v K = ä
4. Leibrenten vorschüssige, lebenslängliche Leibrente (whole life annuity-due) Vorschüssige jährliche Zahlungen von 1, solange die versicherte Person am Leben ist. NEP ä x : Y = 1 + v + v 2 + + v K = ä
Strukturerhaltende Integrationsverfahren für stochastische Differentialgleichungen in der Modellierung von Zinsderivaten
 Strukturerhaltende Integrationsverfahren für stochastische Differentialgleichungen in der Modellierung von Zinsderivaten Michael Günther, Christian Kahl und Thilo Roßberg Bergische Universität Wuppertal
Strukturerhaltende Integrationsverfahren für stochastische Differentialgleichungen in der Modellierung von Zinsderivaten Michael Günther, Christian Kahl und Thilo Roßberg Bergische Universität Wuppertal
Versicherungstechnik
 Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Marius Radermacher, M.Sc. DOOR Aufgabe 37 Versicherungstechnik Übungsblatt 11 Abgabe bis zum Dienstag, dem 10.01.2017 um 10 Uhr im Kasten
Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Marius Radermacher, M.Sc. DOOR Aufgabe 37 Versicherungstechnik Übungsblatt 11 Abgabe bis zum Dienstag, dem 10.01.2017 um 10 Uhr im Kasten
Definition 2.1 Der Erwartungswert einer diskreten Zufallsvariablen mit Wahrscheinlichkeitsfunktion
 Kapitel 2 Erwartungswert 2.1 Erwartungswert einer Zufallsvariablen Definition 2.1 Der Erwartungswert einer diskreten Zufallsvariablen mit Wahrscheinlichkeitsfunktion È ist definiert als Ü ÜÈ Üµ Für spätere
Kapitel 2 Erwartungswert 2.1 Erwartungswert einer Zufallsvariablen Definition 2.1 Der Erwartungswert einer diskreten Zufallsvariablen mit Wahrscheinlichkeitsfunktion È ist definiert als Ü ÜÈ Üµ Für spätere
Kapitalversicherungen
 Kapitalversicherungen Sanela Omerovic Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 Inhaltsverzeichnis 1 Einführung 1 2 Einfache Versicherungsformen 3 2.1 Todesfallversicherungen (Life Insurance)....................
Kapitalversicherungen Sanela Omerovic Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 Inhaltsverzeichnis 1 Einführung 1 2 Einfache Versicherungsformen 3 2.1 Todesfallversicherungen (Life Insurance)....................
Versicherungstechnik
 Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Marius Radermacher, M.Sc. DOOR Aufgabe 16 Versicherungstechnik Übungsblatt 5 Abgabe bis zum Dienstag, dem 22.11.2016 um 10 Uhr im Kasten
Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Marius Radermacher, M.Sc. DOOR Aufgabe 16 Versicherungstechnik Übungsblatt 5 Abgabe bis zum Dienstag, dem 22.11.2016 um 10 Uhr im Kasten
Grundlagen der Kursrechnung und Renditeermittlung
 Grundlagen der Kursrechnung und Renditeermittlung Eingereicht bei Herrn Dipl.-Math. Norman Markgraf von Marco Halver (MaNr. 277035) marco.halver@gmx.net Bonhoefferstraße 13 47178 Duisburg 1 Gliederung
Grundlagen der Kursrechnung und Renditeermittlung Eingereicht bei Herrn Dipl.-Math. Norman Markgraf von Marco Halver (MaNr. 277035) marco.halver@gmx.net Bonhoefferstraße 13 47178 Duisburg 1 Gliederung
Kurs 00091: Finanzierungs- und entscheidungstheoretische Grundlagen der Betriebswirtschaftslehre. Lösungshinweise zur Einsendearbeit 2 (WS 2010/2011)
 Grundlagen der Betriebswirtschaftslehre, Kurs 00091, KE 4, 5 und 6, WS 010/011 1 Kurs 00091: Finanzierungs- und entscheidungstheoretische Grundlagen der Betriebswirtschaftslehre Lösungshinweise zur Einsendearbeit
Grundlagen der Betriebswirtschaftslehre, Kurs 00091, KE 4, 5 und 6, WS 010/011 1 Kurs 00091: Finanzierungs- und entscheidungstheoretische Grundlagen der Betriebswirtschaftslehre Lösungshinweise zur Einsendearbeit
Optionspreistheorie Seminar Stochastische Unternehmensmodelle
 Seminar Stochastische Unternehmensmodelle Lukasz Galecki Mathematisches Institut Universität zu Köln 1. Juni 2015 1 / 30 Inhaltsverzeichnis 1 Was ist eine Option? Definition einer Option Übersicht über
Seminar Stochastische Unternehmensmodelle Lukasz Galecki Mathematisches Institut Universität zu Köln 1. Juni 2015 1 / 30 Inhaltsverzeichnis 1 Was ist eine Option? Definition einer Option Übersicht über
Finanzierung und Investition
 Kruschwitz/Husmann (2012) Finanzierung und Investition 1/21 Finanzierung und Investition Kruschwitz/Husmann (2012) Oldenbourg Verlag München 7. Auflage, Kapitel 4 Kruschwitz/Husmann (2012) Finanzierung
Kruschwitz/Husmann (2012) Finanzierung und Investition 1/21 Finanzierung und Investition Kruschwitz/Husmann (2012) Oldenbourg Verlag München 7. Auflage, Kapitel 4 Kruschwitz/Husmann (2012) Finanzierung
Mathematik 1 für Wirtschaftsinformatik
 Mathematik 1 für Wirtschaftsinformatik Wintersemester 2012/13 Hochschule Augsburg Unterjährige Raten und jährliche Verzinsung Aufteilung der Zinsperiode in mehrere gleich lange Rentenperioden, d.h.
Mathematik 1 für Wirtschaftsinformatik Wintersemester 2012/13 Hochschule Augsburg Unterjährige Raten und jährliche Verzinsung Aufteilung der Zinsperiode in mehrere gleich lange Rentenperioden, d.h.
2. Mai 2011. Geldtheorie und -politik. Die Risiko- und Terminstruktur von Zinsen (Mishkin, Kapitel 6)
 Geldtheorie und -politik Die Risiko- und Terminstruktur von Zinsen (Mishkin, Kapitel 6) 2. Mai 2011 Überblick Bestimmung des Zinssatzes im Markt für Anleihen Erklärung der Dynamik von Zinssätzen Überblick
Geldtheorie und -politik Die Risiko- und Terminstruktur von Zinsen (Mishkin, Kapitel 6) 2. Mai 2011 Überblick Bestimmung des Zinssatzes im Markt für Anleihen Erklärung der Dynamik von Zinssätzen Überblick
Finanzwirtschaft. Teil II: Bewertung
 Sparpläne und Kreditverträge 1 Finanzwirtschaft Teil II: Bewertung Sparpläne und Kreditverträge Agenda Sparpläne und Kreditverträge 2 Endliche Laufzeit Unendliche Laufzeit Zusammenfassung Sparpläne und
Sparpläne und Kreditverträge 1 Finanzwirtschaft Teil II: Bewertung Sparpläne und Kreditverträge Agenda Sparpläne und Kreditverträge 2 Endliche Laufzeit Unendliche Laufzeit Zusammenfassung Sparpläne und
KAPITEL 5. Erwartungswert
 KAPITEL 5 Erwartungswert Wir betrachten einen diskreten Wahrscheinlichkeitsraum (Ω, P) und eine Zufallsvariable X : Ω R auf diesem Wahrscheinlichkeitsraum. Die Grundmenge Ω hat also nur endlich oder abzählbar
KAPITEL 5 Erwartungswert Wir betrachten einen diskreten Wahrscheinlichkeitsraum (Ω, P) und eine Zufallsvariable X : Ω R auf diesem Wahrscheinlichkeitsraum. Die Grundmenge Ω hat also nur endlich oder abzählbar
Arbitrage Free Pricing
 Beim CAPM wurde gezeigt, dass man Finanztitel basierend auf der Verteilung ihres künftigen Preises bewerten kann. Dabei haben wir [unter der Annahme gewisser Präferenzen des Es] den Preis eines Finanztitels
Beim CAPM wurde gezeigt, dass man Finanztitel basierend auf der Verteilung ihres künftigen Preises bewerten kann. Dabei haben wir [unter der Annahme gewisser Präferenzen des Es] den Preis eines Finanztitels
III. Grundlagen der Lebensversicherungsmathematik III.5. Deckungskapital für Lebensversicherungsprodukte
 III. Grundlagen der Lebensversicherungsmathematik III.5. Deckungskapital für Lebensversicherungsprodukte Universität Basel Herbstsemester 2015 Dr. Ruprecht Witzel ruprecht.witzel@aktuariat-witzel.ch www.aktuariat-witzel.ch
III. Grundlagen der Lebensversicherungsmathematik III.5. Deckungskapital für Lebensversicherungsprodukte Universität Basel Herbstsemester 2015 Dr. Ruprecht Witzel ruprecht.witzel@aktuariat-witzel.ch www.aktuariat-witzel.ch
R e n d i t e n u n t e r U n g e w i ß h e i t
 - 296 - Examenskurs BBL Renditeformen R e n d i t e n u n t e r U n g e w i ß h e i t ex ante vereinbarte Rendite erwartete Rendite - bei Halten bis zur Fälligkeit - bei Halten bis Verkauf vor Fälligkeit
- 296 - Examenskurs BBL Renditeformen R e n d i t e n u n t e r U n g e w i ß h e i t ex ante vereinbarte Rendite erwartete Rendite - bei Halten bis zur Fälligkeit - bei Halten bis Verkauf vor Fälligkeit
Übung zu Forwards, Futures & Optionen
 Übung zu Forwards, Futures & Optionen Vertiefungsstudium Finanzwirtschaft Dr. Eric Nowak SS 2001 Finanzwirtschaft Wahrenburg 15.05.01 1 Aufgabe 1: Forward auf Zerobond Wesentliche Eckpunkte des Forwardgeschäfts:
Übung zu Forwards, Futures & Optionen Vertiefungsstudium Finanzwirtschaft Dr. Eric Nowak SS 2001 Finanzwirtschaft Wahrenburg 15.05.01 1 Aufgabe 1: Forward auf Zerobond Wesentliche Eckpunkte des Forwardgeschäfts:
ifa Institut für Finanz- und Aktuarwissenschaften
 Wechselwirkungen von Asset Allocation, Überschussbeteiligung und Garantien in der Lebensversicherung WIMA 2004 Ulm, 13.11.2004 Alexander Kling, IFA Ulm Helmholtzstraße 22 D-89081 Ulm phone +49 (0) 731/50-31230
Wechselwirkungen von Asset Allocation, Überschussbeteiligung und Garantien in der Lebensversicherung WIMA 2004 Ulm, 13.11.2004 Alexander Kling, IFA Ulm Helmholtzstraße 22 D-89081 Ulm phone +49 (0) 731/50-31230
Das Black-Scholes Modell
 Vathani Arumugathas Das Black-Scholes Modell 1 Das Black-Scholes Modell Vathani Arumugathas Seminar zu Finanzmarktmodellen in der Lebensversicherung, Universität zu Köln 10. Juni 016 Inhaltsverzeichnis
Vathani Arumugathas Das Black-Scholes Modell 1 Das Black-Scholes Modell Vathani Arumugathas Seminar zu Finanzmarktmodellen in der Lebensversicherung, Universität zu Köln 10. Juni 016 Inhaltsverzeichnis
Die Varianz (Streuung) Definition
 Die (Streuung) Definition Diskrete Stetige Ang., die betrachteten e existieren. var(x) = E(X EX) 2 heißt der Zufallsvariable X. σ = Var(X) heißt Standardabweichung der X. Bez.: var(x), Var(X), varx, σ
Die (Streuung) Definition Diskrete Stetige Ang., die betrachteten e existieren. var(x) = E(X EX) 2 heißt der Zufallsvariable X. σ = Var(X) heißt Standardabweichung der X. Bez.: var(x), Var(X), varx, σ
Einleitung. Das Ein-Perioden-Modell ist das einfachste. von derivaten Finanzinstrumenten (hier: Optionen) zu erklären.
 Einleitung Das Ein-Perioden-Modell ist das einfachste Modell, um die Idee der Preisgebung von derivaten Finanzinstrumenten (hier: Optionen) zu erklären. naive Idee der Optionspreisbestimmung: Erwartungswertprinzip
Einleitung Das Ein-Perioden-Modell ist das einfachste Modell, um die Idee der Preisgebung von derivaten Finanzinstrumenten (hier: Optionen) zu erklären. naive Idee der Optionspreisbestimmung: Erwartungswertprinzip
Kapitel 5: Entscheidung unter Unsicherheit
 Kapitel 5: Entscheidung unter Unsicherheit Hauptidee: Die Konsequenzen einer Entscheidung sind oft unsicher. Wenn jeder möglichen Konsequenz eine Wahrscheinlichkeit zugeordnet wird, dann kann eine rationale
Kapitel 5: Entscheidung unter Unsicherheit Hauptidee: Die Konsequenzen einer Entscheidung sind oft unsicher. Wenn jeder möglichen Konsequenz eine Wahrscheinlichkeit zugeordnet wird, dann kann eine rationale
Versicherungstechnik
 Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Marius Radermacher, M.Sc. DOOR Aufgabe 20 Versicherungstechnik Übungsblatt 6 Abgabe bis zum Dienstag, dem 29.11.2016 um 10 Uhr im Kasten
Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Marius Radermacher, M.Sc. DOOR Aufgabe 20 Versicherungstechnik Übungsblatt 6 Abgabe bis zum Dienstag, dem 29.11.2016 um 10 Uhr im Kasten
Inhaltsverzeichnis Grundlegende Formeln und Bezeichnungen Mathematische Grundlagen Lineare Verzinsung
 Inhaltsverzeichnis 1 Grundlegende Formeln und Bezeichnungen... 1 1.1 Wichtige Bezeichnungen... 1 1.2 Grundlegende Formeln... 2 1.3 Umrechnungstabelle der Grundgrößen p, i und q... 3 2 Mathematische Grundlagen...
Inhaltsverzeichnis 1 Grundlegende Formeln und Bezeichnungen... 1 1.1 Wichtige Bezeichnungen... 1 1.2 Grundlegende Formeln... 2 1.3 Umrechnungstabelle der Grundgrößen p, i und q... 3 2 Mathematische Grundlagen...
Kap. 6: Zinsstruktur
 A. Definition B. Zinsstrukturkurven C. Theorien der Zinsstruktur D. Geldpolitische Bedeutung Literatur Gebauer: Kap. VI, Zinsniveau und Zinsstruktur, Abschnitt 6 Mishkin: The Economics of Money, Banking,
A. Definition B. Zinsstrukturkurven C. Theorien der Zinsstruktur D. Geldpolitische Bedeutung Literatur Gebauer: Kap. VI, Zinsniveau und Zinsstruktur, Abschnitt 6 Mishkin: The Economics of Money, Banking,
Risikomanagement: Hintergrund und Ziele
 Risikomanagement: Hintergrund und Ziele Beispiel 1 Anfangskapital V 0 = 100 Spiel: man verliert oder gewinnt 50 mit Wahrsch. jeweils 1/2. Kapital nach dem Spiel V 1 = { 150 mit Wahrsch. 1/2 50 mit Wahrsch.
Risikomanagement: Hintergrund und Ziele Beispiel 1 Anfangskapital V 0 = 100 Spiel: man verliert oder gewinnt 50 mit Wahrsch. jeweils 1/2. Kapital nach dem Spiel V 1 = { 150 mit Wahrsch. 1/2 50 mit Wahrsch.
Inhaltsverzeichnis. Teil I
 Inhaltsverzeichnis Teil I Ein-Perioden-Wertpapiermärkte 3 1.1 Ein-Perioden-Modelle 4 1.2 Portfolios 7 1.3 Optionen und Forward-Kontrakte 9 1.3.1 Optionen 10 1.3.2 Forward-Kontrakte 12 1.4 Die Bewertung
Inhaltsverzeichnis Teil I Ein-Perioden-Wertpapiermärkte 3 1.1 Ein-Perioden-Modelle 4 1.2 Portfolios 7 1.3 Optionen und Forward-Kontrakte 9 1.3.1 Optionen 10 1.3.2 Forward-Kontrakte 12 1.4 Die Bewertung
Kapitalversicherungen
 Kapitalversicherungen Birgit Scharwitzl 10. Dezember 2008 Inhaltsverzeichnis 1 Begriffe und wichtige Definitionen 2 1.1 Prämie................................................... 2 1.2 Gewinnbeteiligung............................................
Kapitalversicherungen Birgit Scharwitzl 10. Dezember 2008 Inhaltsverzeichnis 1 Begriffe und wichtige Definitionen 2 1.1 Prämie................................................... 2 1.2 Gewinnbeteiligung............................................
Zinseszins- und Rentenrechnung
 Zinseszins- und Rentenrechnung 1 Berechnen Sie den Zeitpunkt, an dem sich das Einlagekapital K bei a) jährlicher b) monatlicher c) stetiger Verzinsung verdoppelt hat, wobei i der jährliche nominelle Zinssatz
Zinseszins- und Rentenrechnung 1 Berechnen Sie den Zeitpunkt, an dem sich das Einlagekapital K bei a) jährlicher b) monatlicher c) stetiger Verzinsung verdoppelt hat, wobei i der jährliche nominelle Zinssatz
Bewertung von Forwards, Futures und Optionen
 Bewertung von Forwards, Futures und Optionen Olaf Leidinger 24. Juni 2009 Olaf Leidinger Futures und Optionen 2 24. Juni 2009 1 / 19 Überblick 1 Kurze Wiederholung Anleihen, Terminkontrakte 2 Ein einfaches
Bewertung von Forwards, Futures und Optionen Olaf Leidinger 24. Juni 2009 Olaf Leidinger Futures und Optionen 2 24. Juni 2009 1 / 19 Überblick 1 Kurze Wiederholung Anleihen, Terminkontrakte 2 Ein einfaches
Voraussetzungen 21.05.2012. Finanzmathematik INVESTITIONSRECHNUNG. Kapitel 4 Investitionen Prof. Dr. Harald Löwe
 Finanzmathematik Kapitel 4 Investitionen Prof. Dr. Harald Löwe Sommersemester 2012 1. Abschnitt INVESTITIONSRECHNUNG Voraussetzungen Investition als Zahlungsstrom Vom Investor zur leistende Zahlungen (Anschaffungen,
Finanzmathematik Kapitel 4 Investitionen Prof. Dr. Harald Löwe Sommersemester 2012 1. Abschnitt INVESTITIONSRECHNUNG Voraussetzungen Investition als Zahlungsstrom Vom Investor zur leistende Zahlungen (Anschaffungen,
Portfoliotheorie, Risikomanagenient und die Bewertung von Derivaten
 Jürgen Kremer Portfoliotheorie, Risikomanagenient und die Bewertung von Derivaten Zweite, vollständig überarbeitete und erweiterte Auflage 45J Springer Inhaltsverzeichnis Teill Ein-Perioden- Wertpapiermärkte
Jürgen Kremer Portfoliotheorie, Risikomanagenient und die Bewertung von Derivaten Zweite, vollständig überarbeitete und erweiterte Auflage 45J Springer Inhaltsverzeichnis Teill Ein-Perioden- Wertpapiermärkte
Fernuniversität Hagen Lehrstuhl für Betriebswirtschaftslehre, insbes. Bank- und Finanzwirtschaft PD Dr. Karin Niehoff
 Fernuniversität Hagen Lehrstuhl für Betriebswirtschaftslehre, insbes. Bank- und Finanzwirtschaft PD Dr. Karin Niehoff Kolloquium 08.01.2012 Banken und Börsen Agenda Wertpapierhandel: Insiderhandelsverbot
Fernuniversität Hagen Lehrstuhl für Betriebswirtschaftslehre, insbes. Bank- und Finanzwirtschaft PD Dr. Karin Niehoff Kolloquium 08.01.2012 Banken und Börsen Agenda Wertpapierhandel: Insiderhandelsverbot
Hochschule Rhein-Main. Sommersemester 2015
 Vorlesung Hochschule Rhein-Main Sommersemester 2015 Dr. Roland Stamm 27. April 2015 Diskontfaktoren: Legt man heute (in t) 1 Einheit bis T an, und erhält dafür in T insgesamt x zurück (mit Zinseszins,
Vorlesung Hochschule Rhein-Main Sommersemester 2015 Dr. Roland Stamm 27. April 2015 Diskontfaktoren: Legt man heute (in t) 1 Einheit bis T an, und erhält dafür in T insgesamt x zurück (mit Zinseszins,
Institut für Stochastik Prof. Dr. N. Bäuerle Dipl.-Math. S. Urban
 Institut für Stochastik Prof. Dr. N. Bäuerle Dipl.-Math. S. Urban Lösungsvorschlag studienbegleitende Klausur Finanzmathematik I Aufgabe (7 Punkte) Vorgelegt sei ein Wahrscheinlichkeitsraum (Ω, F, P) und
Institut für Stochastik Prof. Dr. N. Bäuerle Dipl.-Math. S. Urban Lösungsvorschlag studienbegleitende Klausur Finanzmathematik I Aufgabe (7 Punkte) Vorgelegt sei ein Wahrscheinlichkeitsraum (Ω, F, P) und
Mathematik II Frühjahrssemester 2013
 Mathematik II Frühjahrssemester 2013 Prof. Dr. Erich Walter Farkas Kapitel 8. Funktionen von mehreren Variablen 8.2 Partielle Differentiation Prof. Dr. Erich Walter Farkas Mathematik I+II, 8.2 Part. Diff.
Mathematik II Frühjahrssemester 2013 Prof. Dr. Erich Walter Farkas Kapitel 8. Funktionen von mehreren Variablen 8.2 Partielle Differentiation Prof. Dr. Erich Walter Farkas Mathematik I+II, 8.2 Part. Diff.
VERSICHERUNGEN AUF MEHRERE LEBEN. Marta Ja lowiecka. 23 Januar 2009
 VERSICHERUNGEN AUF MEHRERE LEBEN Marta Ja lowiecka 23 Januar 2009 1 1 Einführung Im Folgenden werden betrachtet- basierend auf Modellen und Formeln für einfache Versicherungen auf ein Leben- verschiedene
VERSICHERUNGEN AUF MEHRERE LEBEN Marta Ja lowiecka 23 Januar 2009 1 1 Einführung Im Folgenden werden betrachtet- basierend auf Modellen und Formeln für einfache Versicherungen auf ein Leben- verschiedene
TU Darmstadt FB Mathematik, AG 9 WS 2004/2005 Jakob Creutzig (1 + ρ)
 TU Darmstadt FB Mathematik, AG 9 WS 2004/2005 Jakob Creutzig 9..04 Lösungsvorschläge zum 3. Aufgabenblatt der Vorlesung,,Einführung in die Finanzmathematik Gruppenübungen Aufgabe : Es sei Ω = {, +} n,
TU Darmstadt FB Mathematik, AG 9 WS 2004/2005 Jakob Creutzig 9..04 Lösungsvorschläge zum 3. Aufgabenblatt der Vorlesung,,Einführung in die Finanzmathematik Gruppenübungen Aufgabe : Es sei Ω = {, +} n,
Starthilfe Finanzmathematik
 Bernd Luderer Starthilfe Finanzmathematik Zinsen - Kurse - Renditen 3., überarbeitete und erweiterte Auflage t. \ STUDIUM 11 VI EWEG+ TEUBNER Inhaltsverzeichnis 1 Grundlegende Formeln und Bezeichnungen
Bernd Luderer Starthilfe Finanzmathematik Zinsen - Kurse - Renditen 3., überarbeitete und erweiterte Auflage t. \ STUDIUM 11 VI EWEG+ TEUBNER Inhaltsverzeichnis 1 Grundlegende Formeln und Bezeichnungen
n... Laufzeit der Kapitalanlage = Zeit, während der Zinsen zu zahlen sind (oder gezahlt werden) in Zinsperioden (z.b. Jahre)
 1 2. Zinsrechnung 2.1. Grundbegriffe K... Kapital (caput das Haupt) = Betrag, der der Verzinsung unterworfen ist; Geldbetrag (Währung) z... Zinsen = Vergütung (Preis) für das Überlassen eines Kapitals
1 2. Zinsrechnung 2.1. Grundbegriffe K... Kapital (caput das Haupt) = Betrag, der der Verzinsung unterworfen ist; Geldbetrag (Währung) z... Zinsen = Vergütung (Preis) für das Überlassen eines Kapitals
Lebensversicherungsmathematik. Kurseinheit 4 Prospektive Kalkulation (Aktuarielles Standardverfahren)
 Lebensversicherungsmathematik Kurseinheit 4 (Aktuarielles Standardverfahren) Inhalt Topic Leistungsbarwert und Nettoeinmalprämie Lernziel Grundidee der prospektiven Kalkulation (mit Vor- und Nachteilen)
Lebensversicherungsmathematik Kurseinheit 4 (Aktuarielles Standardverfahren) Inhalt Topic Leistungsbarwert und Nettoeinmalprämie Lernziel Grundidee der prospektiven Kalkulation (mit Vor- und Nachteilen)
HSBC Zertifikate-Akademie
 INHALT WISSEN ZERTIFIKATE-AKADEMIE 1 / 6 HSBC Zertifikate-Akademie Wie der Zins und die Aktie in die Aktienanleihe kommen Liebe Leserinnen und Leser der HSBC Zertifikate-Akademie, in dieser Ausgabe unserer
INHALT WISSEN ZERTIFIKATE-AKADEMIE 1 / 6 HSBC Zertifikate-Akademie Wie der Zins und die Aktie in die Aktienanleihe kommen Liebe Leserinnen und Leser der HSBC Zertifikate-Akademie, in dieser Ausgabe unserer
Tilgungsrechnung. n = ln. K 0 + R / ln(q) (vorschüssig) Eine einfache Formel, um q aus R,n,K n und K 0 auszurechnen, gibt es nicht. q 1. q 1.
 (K + R ) q 1 n = ln K 0 + R / ln(q) (nachschüssig) q 1 n = ln ( K q + R ) q 1 K 0 + R / ln(q) (vorschüssig) q 1 Eine einfache Formel, um q aus R,n,K n und K 0 auszurechnen, gibt es nicht. Tilgungsrechnung
(K + R ) q 1 n = ln K 0 + R / ln(q) (nachschüssig) q 1 n = ln ( K q + R ) q 1 K 0 + R / ln(q) (vorschüssig) q 1 Eine einfache Formel, um q aus R,n,K n und K 0 auszurechnen, gibt es nicht. Tilgungsrechnung
1. Adverse Selektion: Unsicherheit über die Schadenswahrscheinlichkeit 2. Moral Hazard: endogene Schadenshöhe.
 In der bisherigen Analyse haben wir angenommen, dass die Schadenshöhe exogen ist und die Eintrittswahrscheinlichkeit allgemein bekannt ist. Damit schließen wir aber zwei extrem wichtige Charakteristika
In der bisherigen Analyse haben wir angenommen, dass die Schadenshöhe exogen ist und die Eintrittswahrscheinlichkeit allgemein bekannt ist. Damit schließen wir aber zwei extrem wichtige Charakteristika
Derivate und Bewertung
 . Dr. Daniel Sommer Marie-Curie-Str. 3 6439 Frankfurt am Main Klausur Derivate und Bewertung.......... Wintersemester 25/6 Klausur Derivate und Bewertung Wintersemester 25/6 Aufgabe : Statische Optionsstrategien
. Dr. Daniel Sommer Marie-Curie-Str. 3 6439 Frankfurt am Main Klausur Derivate und Bewertung.......... Wintersemester 25/6 Klausur Derivate und Bewertung Wintersemester 25/6 Aufgabe : Statische Optionsstrategien
Diskrete Verteilungen
 KAPITEL 6 Disrete Verteilungen Nun werden wir verschiedene Beispiele von disreten Zufallsvariablen betrachten. 1. Gleichverteilung Definition 6.1. Eine Zufallsvariable X : Ω R heißt gleichverteilt (oder
KAPITEL 6 Disrete Verteilungen Nun werden wir verschiedene Beispiele von disreten Zufallsvariablen betrachten. 1. Gleichverteilung Definition 6.1. Eine Zufallsvariable X : Ω R heißt gleichverteilt (oder
Versicherungstechnik
 Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Dipl.-Math. Rolf Wendt DOOR Aufgabe 5 Versicherungstechnik Übungsblatt 2 Abgabe bis zum Dienstag, dem 27.0.205 um 0 Uhr im Kasten 9 Die
Operations Research und Wirtschaftsinformatik Prof. Dr. P. Recht // Dipl.-Math. Rolf Wendt DOOR Aufgabe 5 Versicherungstechnik Übungsblatt 2 Abgabe bis zum Dienstag, dem 27.0.205 um 0 Uhr im Kasten 9 Die
Problemstellung worum geht es in diesem Kapitel? Kapitel 1 Zinsrechnung. Beispiel Anlage für ein Jahr. Ein einfaches Beispiel
 Kapitel 1 Zinsrechnung Problemstellung worum geht es in diesem Kapitel? 1 Verschiedene Verzinsungsverfahren 2 Häufig auftretende Fragestellung: Wenn man heute einen Betrag X anlegt, wie viel hat man dann
Kapitel 1 Zinsrechnung Problemstellung worum geht es in diesem Kapitel? 1 Verschiedene Verzinsungsverfahren 2 Häufig auftretende Fragestellung: Wenn man heute einen Betrag X anlegt, wie viel hat man dann
Hedging von Zinsrisiken. Vertiefungsstudium Finanzwirtschaft Prof. Dr. Mark Wahrenburg. Bond Yields und Preise von Zerobonds
 Hedging von Zinsrisiken Vertiefungsstudium Finanzwirtschaft Prof. Dr. Mark Wahrenburg Bond Yields und Preise von Zerobonds 3 Zerobonds mit Nominalwert F=100 yield to maturity r=10% (horizontale Zinskurve),
Hedging von Zinsrisiken Vertiefungsstudium Finanzwirtschaft Prof. Dr. Mark Wahrenburg Bond Yields und Preise von Zerobonds 3 Zerobonds mit Nominalwert F=100 yield to maturity r=10% (horizontale Zinskurve),
Mathematik 2 für Wirtschaftsinformatik
 für Wirtschaftsinformatik Sommersemester 2012 Hochschule Augsburg Ewige Renten Eine Rente heißt ewige Rente, wenn Anzahl n der Ratenzahlungen nicht begrenzt, n also beliebig groß wird (n ). Berechnung
für Wirtschaftsinformatik Sommersemester 2012 Hochschule Augsburg Ewige Renten Eine Rente heißt ewige Rente, wenn Anzahl n der Ratenzahlungen nicht begrenzt, n also beliebig groß wird (n ). Berechnung
Wichtige Begriffe in der Finanzmathematik
 Wichtige Begriffe in der Finanzmathematik Forward: Kontrakt, ein Finanzgut zu einem fest vereinbarten Zeitpunkt bzw. innerhalb eines Zeitraums zu einem vereinbarten Erfüllungspreis zu kaufen bzw. verkaufen.
Wichtige Begriffe in der Finanzmathematik Forward: Kontrakt, ein Finanzgut zu einem fest vereinbarten Zeitpunkt bzw. innerhalb eines Zeitraums zu einem vereinbarten Erfüllungspreis zu kaufen bzw. verkaufen.
Kapitel 5: Entscheidung unter Unsicherheit
 Kapitel 5: Entscheidung unter Unsicherheit Hauptidee: Die Konsequenzen einer Entscheidung sind oft unsicher. Wenn jeder möglichen Konsequenz eine Wahrscheinlichkeit zugeordnet wird, dann kann eine rationale
Kapitel 5: Entscheidung unter Unsicherheit Hauptidee: Die Konsequenzen einer Entscheidung sind oft unsicher. Wenn jeder möglichen Konsequenz eine Wahrscheinlichkeit zugeordnet wird, dann kann eine rationale
Risiken für deutsche Lebensversicherer aus einem Zinsanstieg Dr. Till Förstemann, Deutsche Bundesbank
 Risiken für deutsche Lebensversicherer aus einem Zinsanstieg Dr. Till Förstemann, Deutsche Bundesbank Diese Präsentation gibt die Meinung des Autors wieder. Diese entspricht nicht zwangsläufig den Positionen
Risiken für deutsche Lebensversicherer aus einem Zinsanstieg Dr. Till Förstemann, Deutsche Bundesbank Diese Präsentation gibt die Meinung des Autors wieder. Diese entspricht nicht zwangsläufig den Positionen
Biostatistik, Sommer 2017
 1/52 Biostatistik, Sommer 2017 Prof. Dr. Achim Klenke http://www.aklenke.de 7. Vorlesung: 02.06.2017 2/52 Inhalt 1 Wahrscheinlichkeit Bayes sche Formel 2 Diskrete Stetige 3/52 Wahrscheinlichkeit Bayes
1/52 Biostatistik, Sommer 2017 Prof. Dr. Achim Klenke http://www.aklenke.de 7. Vorlesung: 02.06.2017 2/52 Inhalt 1 Wahrscheinlichkeit Bayes sche Formel 2 Diskrete Stetige 3/52 Wahrscheinlichkeit Bayes
Seminar Gewöhnliche Differentialgleichungen
 Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Seminar Gewöhnliche Differentialgleichungen Dynamische Systeme I 1 Einleitung 1.1 Nichtlineare Systeme In den vorigen Vorträgen haben wir uns mit linearen Differentialgleichungen beschäftigt. Nun werden
Test 1 (zu den Kapiteln 1 bis 6)
 Test 1 1 Test 1 (zu den Kapiteln 1 bis 6) Bearbeitungszeit: 90 Minuten Aufgabe T1.1: Bekanntmachung EUR 1.000.000.000,- Anleihe mit variablem Zinssatz der Fix AG von 2003/2013, Serie 111 Zinsperiode: 12.10.2006
Test 1 1 Test 1 (zu den Kapiteln 1 bis 6) Bearbeitungszeit: 90 Minuten Aufgabe T1.1: Bekanntmachung EUR 1.000.000.000,- Anleihe mit variablem Zinssatz der Fix AG von 2003/2013, Serie 111 Zinsperiode: 12.10.2006
Punktweise Konvergenz stückweise glatter Funktionen. 1 Vorbereitungen
 Vortrag zum Seminar zur Fourieranalysis, 3.10.007 Margarete Tenhaak Im letzten Vortrag wurde die Fourier-Reihe einer -periodischen Funktion definiert. Fourier behauptete, dass die Fourier-Reihe einer periodischen
Vortrag zum Seminar zur Fourieranalysis, 3.10.007 Margarete Tenhaak Im letzten Vortrag wurde die Fourier-Reihe einer -periodischen Funktion definiert. Fourier behauptete, dass die Fourier-Reihe einer periodischen
Garantieverzinsung als Funktion der Gesamtverzinsung in der Lebensversicherung. 16. Mai 2014 Philip van Hövell
 Garantieverzinsung als Funktion der Gesamtverzinsung in der Lebensversicherung 16. Mai 2014 Philip van Hövell Agenda Einführung Garantiezins & Überschuss Maximaler Garantiezins Gesamtverzinsung & Anlagerendite
Garantieverzinsung als Funktion der Gesamtverzinsung in der Lebensversicherung 16. Mai 2014 Philip van Hövell Agenda Einführung Garantiezins & Überschuss Maximaler Garantiezins Gesamtverzinsung & Anlagerendite
Mathematik II Frühlingsemester 2015 Kap. 9: Funktionen von mehreren Variablen 9.2 Partielle Differentiation
 Mathematik II Frühlingsemester 2015 Kap. 9: Funktionen von mehreren Variablen 9.2 Partielle Differentiation www.math.ethz.ch/education/bachelor/lectures/fs2015/other/mathematik2 biol Prof. Dr. Erich Walter
Mathematik II Frühlingsemester 2015 Kap. 9: Funktionen von mehreren Variablen 9.2 Partielle Differentiation www.math.ethz.ch/education/bachelor/lectures/fs2015/other/mathematik2 biol Prof. Dr. Erich Walter
34 5. FINANZMATHEMATIK
 34 5. FINANZMATHEMATIK 5. Finanzmathematik 5.1. Ein einführendes Beispiel Betrachten wir eine ganz einfache Situation. Wir haben einen Markt, wo es nur erlaubt ist, heute und in einem Monat zu handeln.
34 5. FINANZMATHEMATIK 5. Finanzmathematik 5.1. Ein einführendes Beispiel Betrachten wir eine ganz einfache Situation. Wir haben einen Markt, wo es nur erlaubt ist, heute und in einem Monat zu handeln.
TrendValor Eine attraktive Anlage. Sie investieren, die Vaudoise sichert ab
 TrendValor Eine attraktive Anlage Sie investieren, die Vaudoise sichert ab Mit Sicherheit gewinnen Eine attraktive Gelegenheit Sie möchten Ihr Kapital für sich arbeiten lassen und etwas für die Altersvorsorge
TrendValor Eine attraktive Anlage Sie investieren, die Vaudoise sichert ab Mit Sicherheit gewinnen Eine attraktive Gelegenheit Sie möchten Ihr Kapital für sich arbeiten lassen und etwas für die Altersvorsorge
Babeş-Bolyai-Universität Cluj-Napoca Fakultät für Wirtschaftswissenschaften und Unternehmensführung Klausur Unternehmensfinanzierung Winter 2011/12
 Babeş-Bolyai-Universität Cluj-Napoca Fakultät für Wirtschaftswissenschaften und Unternehmensführung Klausur Unternehmensfinanzierung Winter 2011/12 Prof. Dr. Alfred Luhmer erster Termin Name: Diese Klausur
Babeş-Bolyai-Universität Cluj-Napoca Fakultät für Wirtschaftswissenschaften und Unternehmensführung Klausur Unternehmensfinanzierung Winter 2011/12 Prof. Dr. Alfred Luhmer erster Termin Name: Diese Klausur
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA)
 Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2014/15 Hochschule Augsburg Rechenregeln für Grenzwerte Gegeben: lim (a n) = a und lim (b n) = b n n kurz:
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2014/15 Hochschule Augsburg Rechenregeln für Grenzwerte Gegeben: lim (a n) = a und lim (b n) = b n n kurz:
Wirtschaftsmathematik Plus für International Management (BA) und Betriebswirtschaft (BA)
 Wirtschaftsmathematik Plus für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2012/13 Hochschule Augsburg Unterjährige einfache Verzinsung In Deutschland Einteilung des Zinsjahres
Wirtschaftsmathematik Plus für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2012/13 Hochschule Augsburg Unterjährige einfache Verzinsung In Deutschland Einteilung des Zinsjahres
Bernd Luderer. Starthilfe Finanzmathematik. Zinsen - Kurse - Renditen. 4., erweiterte Auflage. Springer Spektrum
 Bernd Luderer Starthilfe Finanzmathematik Zinsen - Kurse - Renditen 4., erweiterte Auflage Springer Spektrum Inhaltsverzeichnis 1 Grundlegende Formeln und Bezeichnungen 1 1.1 Wichtige Bezeichnungen 1 1.2
Bernd Luderer Starthilfe Finanzmathematik Zinsen - Kurse - Renditen 4., erweiterte Auflage Springer Spektrum Inhaltsverzeichnis 1 Grundlegende Formeln und Bezeichnungen 1 1.1 Wichtige Bezeichnungen 1 1.2
Klassische Risikomodelle
 Klassische Risikomodelle Kathrin Sachernegg 15. Jänner 2008 1 Inhaltsverzeichnis 1 Einführung 3 1.1 Begriffserklärung.................................. 3 2 Individuelles Risikomodell 3 2.1 Geschlossenes
Klassische Risikomodelle Kathrin Sachernegg 15. Jänner 2008 1 Inhaltsverzeichnis 1 Einführung 3 1.1 Begriffserklärung.................................. 3 2 Individuelles Risikomodell 3 2.1 Geschlossenes
Vorlesung Gesamtbanksteuerung Mathematische Grundlagen I Dr. Klaus Lukas Carsten Neundorf
 Vorlesung Gesamtbanksteuerung Mathematische Grundlagen I Dr. Klaus Lukas Carsten Neundorf 1 Agenda Zinsrechnung Zinseszins Zeitwert des Geldes Strukturkongruente Refinanzierung Rendite Zinskurve 2 Das
Vorlesung Gesamtbanksteuerung Mathematische Grundlagen I Dr. Klaus Lukas Carsten Neundorf 1 Agenda Zinsrechnung Zinseszins Zeitwert des Geldes Strukturkongruente Refinanzierung Rendite Zinskurve 2 Das
3.4 Asymptotische Evaluierung von Sch atzer Konsistenz Konsistenz Definition 3.4.1: konsistente Folge von Sch atzer
 3.4 Asymptotische Evaluierung von Schätzer 3.4.1 Konsistenz Bis jetzt haben wir Kriterien basierend auf endlichen Stichproben betrachtet. Konsistenz ist ein asymptotisches Kriterium (n ) und bezieht sich
3.4 Asymptotische Evaluierung von Schätzer 3.4.1 Konsistenz Bis jetzt haben wir Kriterien basierend auf endlichen Stichproben betrachtet. Konsistenz ist ein asymptotisches Kriterium (n ) und bezieht sich
Finanzmarktökonometrie: Einführung in die Optionsbewertung Sommersemester 2013
 Finanzmarktökonometrie: Einführung in die Optionsbewertung Sommersemester 2013 Walter Sanddorf-Köhle Foliensatz Nr. 3 1 / 46 Ein Einperiodenmodell Beispiel 5 Betrachtet wird nun ein Wertpapiermarkt mit
Finanzmarktökonometrie: Einführung in die Optionsbewertung Sommersemester 2013 Walter Sanddorf-Köhle Foliensatz Nr. 3 1 / 46 Ein Einperiodenmodell Beispiel 5 Betrachtet wird nun ein Wertpapiermarkt mit
3. Prozesse mit kontinuierlicher Zeit
 3. Prozesse mit kontinuierlicher Zeit 3.1 Einführung Wir betrachten nun Markov-Ketten (X(t)) t R +. 0 Wie beim Übergang von der geometrischen zur Exponentialverteilung können wir uns auch hier einen Grenzprozess
3. Prozesse mit kontinuierlicher Zeit 3.1 Einführung Wir betrachten nun Markov-Ketten (X(t)) t R +. 0 Wie beim Übergang von der geometrischen zur Exponentialverteilung können wir uns auch hier einen Grenzprozess
Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Im Bereich der Zinsberechnung wird zwischen der einfachen ( ) Verzinsung und dem Zinseszins
 SS 2017 Torsten Schreiber 287 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Im Bereich der Zinsberechnung wird zwischen der einfachen ( ) Verzinsung und dem Zinseszins ( ) unterschieden. Bei
SS 2017 Torsten Schreiber 287 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Im Bereich der Zinsberechnung wird zwischen der einfachen ( ) Verzinsung und dem Zinseszins ( ) unterschieden. Bei
Ausarbeitung des Seminarvortrags zum Thema
 Ausarbeitung des Seminarvortrags zum Thema Anlagepreisbewegung zum Seminar Finanzmathematische Modelle und Simulationen bei Raphael Kruse und Prof. Dr. Wolf-Jürgen Beyn von Imke Meyer im W9/10 Anlagepreisbewegung
Ausarbeitung des Seminarvortrags zum Thema Anlagepreisbewegung zum Seminar Finanzmathematische Modelle und Simulationen bei Raphael Kruse und Prof. Dr. Wolf-Jürgen Beyn von Imke Meyer im W9/10 Anlagepreisbewegung
Unabhängigkeit KAPITEL 4
 KAPITEL 4 Unabhängigkeit 4.1. Unabhängigkeit von Ereignissen Wir stellen uns vor, dass zwei Personen jeweils eine Münze werfen. In vielen Fällen kann man annehmen, dass die eine Münze die andere nicht
KAPITEL 4 Unabhängigkeit 4.1. Unabhängigkeit von Ereignissen Wir stellen uns vor, dass zwei Personen jeweils eine Münze werfen. In vielen Fällen kann man annehmen, dass die eine Münze die andere nicht
Deckungskapital. Proseminar Versicherungsmathematik. TU Graz. 11. Dezember 2007
 Deckungskapital Gülnur Adanç Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 1 Inhaltsverzeichnis 1 Deckungskapital 2 1.1 Prospektive und Retrospektive Methode.................... 3 1.1.1
Deckungskapital Gülnur Adanç Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 1 Inhaltsverzeichnis 1 Deckungskapital 2 1.1 Prospektive und Retrospektive Methode.................... 3 1.1.1
Hochschule Rhein-Main. Sommersemester 2015
 Vorlesung Hochschule Rhein-Main Sommersemester 2015 Dr. Roland Stamm 29. Juni 2015 Erinnerung Bewertung eines Bonds mit Kupon k, Nominal N, Laufzeit t n: n Π(t) = N k δ(t i 1, t i ) P (t, t i ) + N P (t,
Vorlesung Hochschule Rhein-Main Sommersemester 2015 Dr. Roland Stamm 29. Juni 2015 Erinnerung Bewertung eines Bonds mit Kupon k, Nominal N, Laufzeit t n: n Π(t) = N k δ(t i 1, t i ) P (t, t i ) + N P (t,
Kurs 00091: Finanzierungs- und entscheidungstheoretische Grundlagen der Betriebswirtschaftslehre. Lösungshinweise zur Einsendearbeit 2 (WS 2008/2009)
 Grundlagen der Betriebswirtschaftslehre, Kurs 00091, KE 4, 5 und 6, WS 2008/2009 1 Kurs 00091: Finanzierungs- und entscheidungstheoretische Grundlagen der Betriebswirtschaftslehre Lösungshinweise zur Einsendearbeit
Grundlagen der Betriebswirtschaftslehre, Kurs 00091, KE 4, 5 und 6, WS 2008/2009 1 Kurs 00091: Finanzierungs- und entscheidungstheoretische Grundlagen der Betriebswirtschaftslehre Lösungshinweise zur Einsendearbeit
Risikolebensversicherung Schutz für die Familie
 Risikolebensversicherung Schutz für die Familie Wer befürchten muss, durch den Tod seines Partners in finanzielle Not zu geraten, sollte eine Risiko lebens versicherung abschließen. Wir erklären Ihnen,
Risikolebensversicherung Schutz für die Familie Wer befürchten muss, durch den Tod seines Partners in finanzielle Not zu geraten, sollte eine Risiko lebens versicherung abschließen. Wir erklären Ihnen,
Financial Engineering....eine Einführung
 Financial Engineering...eine Einführung Aufgabe 1: Lösung Überlegen Sie sich, wie man eine Floating Rate Note, die EURIBOR + 37 bp zahlt in einen Bond und einen Standard-Swap (der EURIBOR zahlt) zerlegen
Financial Engineering...eine Einführung Aufgabe 1: Lösung Überlegen Sie sich, wie man eine Floating Rate Note, die EURIBOR + 37 bp zahlt in einen Bond und einen Standard-Swap (der EURIBOR zahlt) zerlegen
Vorlesung Finanzmathematik (TM/SRM/SM/MM) Block : Ausgewählte Aufgaben Investitionsrechnung und festverzinsliche Wertpapiere
 Hochschule Ostfalia Fakultät Verkehr Sport Tourismus Medien apl. Professor Dr. H. Löwe Sommersemester 20 Vorlesung Finanzmathematik (TM/SRM/SM/MM) Block : Ausgewählte Aufgaben Investitionsrechnung und
Hochschule Ostfalia Fakultät Verkehr Sport Tourismus Medien apl. Professor Dr. H. Löwe Sommersemester 20 Vorlesung Finanzmathematik (TM/SRM/SM/MM) Block : Ausgewählte Aufgaben Investitionsrechnung und
Erinnerung an letztes Mal: Erreichbare Kombinationen aus erwarteter Rendite und Risiko (gemessen in Standardabweichung
 Erinnerung an letztes Mal: Erreichbare Kombinationen aus erwarteter Rendite und Risiko (gemessen in Standardabweichung Anteil Aktie 5: 100 % Anteil Aktie 2: 0 % absteigend aufsteigend Anteil Aktie 5: 0
Erinnerung an letztes Mal: Erreichbare Kombinationen aus erwarteter Rendite und Risiko (gemessen in Standardabweichung Anteil Aktie 5: 100 % Anteil Aktie 2: 0 % absteigend aufsteigend Anteil Aktie 5: 0
Mathematische und statistische Methoden II
 Sprechstunde jederzeit nach Vereinbarung und nach der Vorlesung Wallstr. 3, 6. Stock, Raum 06-206 Mathematische und statistische Methoden II Dr. Malte Persike persike@uni-mainz.de lordsofthebortz.de lordsofthebortz.de/g+
Sprechstunde jederzeit nach Vereinbarung und nach der Vorlesung Wallstr. 3, 6. Stock, Raum 06-206 Mathematische und statistische Methoden II Dr. Malte Persike persike@uni-mainz.de lordsofthebortz.de lordsofthebortz.de/g+
R. Brinkmann Seite
 R. Brinkmann http://brinkmann-du.de Seite 7.09.202 Lösungen zur Zinseszinsrechnung Ergebnisse E Auf welchen Betrag wachsen foende Anfangskapitalien an? a) 800 wachsen bei einem Zinssatz von 5% in 0 Jahren
R. Brinkmann http://brinkmann-du.de Seite 7.09.202 Lösungen zur Zinseszinsrechnung Ergebnisse E Auf welchen Betrag wachsen foende Anfangskapitalien an? a) 800 wachsen bei einem Zinssatz von 5% in 0 Jahren
Lösung zu den Testaufgaben zur Mathematik für Chemiker II (Analysis)
 Universität D U I S B U R G E S S E N Campus Essen, Mathematik PD Dr. L. Strüngmann Informationen zur Veranstaltung unter: http://www.uni-due.de/algebra-logic/struengmann.shtml SS 7 Lösung zu den Testaufgaben
Universität D U I S B U R G E S S E N Campus Essen, Mathematik PD Dr. L. Strüngmann Informationen zur Veranstaltung unter: http://www.uni-due.de/algebra-logic/struengmann.shtml SS 7 Lösung zu den Testaufgaben
Aufgaben und Lösungen für die Übung 2 zur Vorlesung Bankmanagement
 UNIVERSITÄT HOHENHEIM INSTITUT FÜR BETRIEBSWIRTSCHAFTSLEHRE LEHRSTUHL FÜR BANKWIRTSCHAFT UND FINANZDIENSTLEISTUNGEN PROF. DR. HANS-PETER BURGHOF Aufgaben und Lösungen für die Übung 2 zur Vorlesung Bankmanagement
UNIVERSITÄT HOHENHEIM INSTITUT FÜR BETRIEBSWIRTSCHAFTSLEHRE LEHRSTUHL FÜR BANKWIRTSCHAFT UND FINANZDIENSTLEISTUNGEN PROF. DR. HANS-PETER BURGHOF Aufgaben und Lösungen für die Übung 2 zur Vorlesung Bankmanagement
LÖSUNG ZUR VORLESUNG MAKROÖKONOMIK I (SoSe 14) Aufgabenblatt 3
 Fakultät Wirtschafts- und Sozialwissenschaften Jun.-Prof. Dr. Philipp Engler, Michael Paetz LÖSUNG ZUR VORLESUNG MAKROÖKONOMIK I (SoSe 14) Aufgabenblatt 3 Aufgabe 1: Geldnachfrage I Die gesamtwirtschaftliche
Fakultät Wirtschafts- und Sozialwissenschaften Jun.-Prof. Dr. Philipp Engler, Michael Paetz LÖSUNG ZUR VORLESUNG MAKROÖKONOMIK I (SoSe 14) Aufgabenblatt 3 Aufgabe 1: Geldnachfrage I Die gesamtwirtschaftliche
ITWM Workshopserie 2012: Mehrfaktor-Zinsmodelle und ihre Implementation
 ITWM Workshopserie 2012: Mehrfaktor-Zinsmodelle und ihre Implementation Aspekte des 2-Faktor-Hull-White-Modells 8. November 2012 Inhalt Weshalb ein Mehrfaktor Modell? 2-Faktor-Modelle Das ursprüngliche
ITWM Workshopserie 2012: Mehrfaktor-Zinsmodelle und ihre Implementation Aspekte des 2-Faktor-Hull-White-Modells 8. November 2012 Inhalt Weshalb ein Mehrfaktor Modell? 2-Faktor-Modelle Das ursprüngliche
Mathematik 1 für Wirtschaftsinformatik
 Mathematik 1 für Wirtschaftsinformatik Wintersemester 2012/13 Hochschule Augsburg Definition der Reihe Gegeben: (a n) unendliche Folge in R Dann heißt (s n) mit Beispiel: eine unendliche Reihe. s n heißt
Mathematik 1 für Wirtschaftsinformatik Wintersemester 2012/13 Hochschule Augsburg Definition der Reihe Gegeben: (a n) unendliche Folge in R Dann heißt (s n) mit Beispiel: eine unendliche Reihe. s n heißt
