Thema: Bildaufbereitung für die Objekterkennung
|
|
|
- Rudolph Meinhardt
- vor 6 Jahren
- Abrufe
Transkript
1 Westfälische Wilhelms-Universität Münster Thema: Bildaufbereitung für die Objekterkennung Ausarbeitung im Rahmen des Seminars Unterstützung von Landminendetektion durch Bildauswertungsverfahren und Robotereinsatz im Fachgebiet Informatik Themensteller: Betreuer: vorgelegt von: Prof. Dr. X. Jiang S. Wachenfeld, Dr. D. Lammers Jana Gliet, Birgit Pieke, Mareike Kritzler und Timo Schreiber Abgabetermin:
2 II Inhaltsverzeichnis Inhaltsverzeichnis...II Abbildungsverzeichnis...III 1 Einleitung Das Bild und seine Wahrnehmung Bildvorverarbeitung Ziele der Bildvorverarbeitung Eigenschaften von Bildern Bildarten Charakteristika von Bildern Bildverbesserung Systematisierung der Verfahren Punktbezogene Operatoren Nachbarschaftsoperatoren Glättungsfilter...16 Mittelwertfilter...16 Medianfilter...16 Zusammenhang zwischen Mittelwert- und Medianfilter Korrektur von uneinheitlichem Hintergrund Geometrische Transformationen Bildverarbeitung im Frequenzraum Einführung in die Fourier Analyse Die Fourier Transformation und ihre Eigenschaften Filtern im Frequenzraum Bildrestaurierung Luftbildauswertung Luftbildauswertung am Beispiel der vorgestellten Methoden Landminenerkennung auf Luftbildern Probleme der Luftbildauswertung...44 Literaturverzeichnis...46 Anhang...47 A Einige Beispiele im Zusammenhang mit Filterung im Frequenzraum...47 A.a Das Spektrum und der Phasenwinkel einer DFT...47
3 III Abbildungsverzeichnis Abb. 1.1: Das elektromagnetische Spektrum...2 Abb. 1.2: Einige bekannte optische Täuschungen...2 Abb. 1.3: Beispiel zur Kontrastsimulation...3 Abb. 2.1: RGB- und HSV-Farbmodelle...6 Abb. 3.1: Kontraststreckung und Binärisierung...10 Abb. 3.2: Grundlegende Grauwerttransformationen...11 Abb. 3.3: Stückweise lineare Transformation...12 Abb. 3.4: Grauwertdehnung...12 Abb. 3.5: Original mit Histogramm...13 Abb. 3.6: Grauwertdehnung mit Histogramm...13 Abb. 3.7: Histogrammausgleich...14 Abb. 3.8: Beispiel einer Nachbarschaftsoperation...15 Abb. 3.9: Beispiel, gefiltert mit Mittelwert- und Medianfilter...18 Abb. 3.10: Beispiel der Korrektur von uneinheitlichem Hintergrund (links: Original).19 Abb. 3.11: Beispiel der Korrektur von eineinheitlichem Farbton (links: Original)...19 Abb. 3.12: Translation...20 Abb. 3.13: Skalierung...20 Abb. 3.14: Tiepoints...21 Abb. 3.15: Nearest Neighbour Interpolation...22 Abb. 3.16: Bilineare Interpolation...22 Abb. 3.17: Zerlegung einer periodischen Funktion als Fourier-Reihe...24 Abb. 3.18: Zentriertes Spektrum eines Bildes...27 Abb. 3.19: Vorgang der Filterung im Frequenzraum...28 Abb. 3.20: Der Notch-Filter...29 Abb. 3.21: Gauß-Hoch- und Tiefpassfilter im Bild- und Frequenzraum...31 Abb. 3.22: Der ideale Tiefpassfilter in der Frequenzdomäne...32 Abb. 3.23: Anwendung des idealen Tiefpassfilters mit Ringeffekten...33 Abb. 3.24: Der Butterworth-Tiefpassfilter...34 Abb. 4.1: Modell der Bildverschlechterung und -restauration...36 Abb. 4.2: Grundlagen des Wiener-Filters und seine Anwendung in der Bildanalyse..37 Abb. 4.3: Restaurierung einer horizontalen Bewegungsunschärfe...39 Abb. 4.4: Restaurierung einer Defokussierung mit dem Wiener Filter...39 Abb. 5.1: Reduzierung von Wolkenschatten durch Unsharp Masking...41 Abb. 5.2: Verzerrung eines Luftbildes bei geneigter Aufnahmerichtung...42 Abb. 5.3: Schematisches Beispiel zur geometrischen Mosaikbildung...42 Abb. 5.4: Schritte der Minenfelderkennung auf Luftbildern: 1. Minenfeldregion, 2. Ergebnis der Minensuche, 3. Abgrenzung des Minenfeldes...44
4 Westfälische Wilhelms-Universität Münster 1 Einleitung Inhalt dieses Referates ist die Darstellung einiger Verfahren der Bildaufbereitung für die Objekterkennung. Diese Verfahren der digitalen Bildverarbeitung werden für die Aufbereitung der von einem Roboter mit Hilfe einer USB - Kamera gewonnenen Bilder benutzt. Es wird das Ziel verfolgt, eine bessere Darstellung der Bilder zu erreichen und es soll möglich werden, bestimmte Eigenschaften oder Strukturen aus den Bildern extrahieren zu können, die für die weitere Verarbeitung von Bedeutung sind. Die Auswahl der hierbei verwendeten Verarbeitungsschritte richtet sich dabei immer nach der vorhandenen Bildqualität. Welches Interesse wir an der digitalen Bildverarbeitung haben, zeigt sich an den zwei Anwendungsbereichen, in die prinzipiell unterschieden wird. Zum einen gibt es die Verbesserung bildlicher Informationen für die menschliche Interpretation, zum anderen die Verarbeitung von Bilddaten für die Speicherung, Übertragung und Repräsentation für autonome Maschinenwahrnehmung. Im Zusammenhang mit der Bildverarbeitung gibt es drei Typen von computerisierten Prozessen, die low-level, mid-level und die high-level Prozesse: Die low-level Prozesse umfassen primitive Operatoren wie Bildvorverarbeitung, z.b. um Rauschen zu reduzieren, Kontrastverbesserung vorzunehmen oder die Bildschärfe zu verstärken. Charakteristisch für diese Prozesse ist, dass sowohl Input als auch Output Bilder sind. Die mid-level Prozesse befassen sich unter anderem mit Segmentierung. Dabei wird das Bild in Regionen oder Objekte eingeteilt und eine Objektbeschreibung vorgenommen. Hier wird als Input ein Bild verwendet und als Output erhält man aus dem Bild extrahierte Attribute. Die high-level Prozesse analysieren ein Bild. Im Folgenden werden einige low-level-verfahren vorgestellt, die ein Bild hervorbringen, mit dem es anschließend möglich ist, Objekte zu erkennen. 1.1 Das Bild und seine Wahrnehmung Ein digitales Bild ist als eine zweidimensionale Funktion f(x,y) definiert und besteht aus einer endlichen Anzahl von Elementen (Pixeln). Jedes von diesen Pixeln (Picture Element) hat eine bestimmte Position und einen Wert. So ist es möglich die verschiedenen Verfahren anzuwenden.
5 2 Bei uns Menschen ist der Sehsinn der ausgeprägteste unserer Sinne. Deshalb ist es nicht überraschend, dass Bilder die wichtigste Rolle in der menschlichen Wahrnehmung spielen, jedoch besitzen wir nur ein eingeschränktes visuelles Band von dem gesamten elektromagnetischen (EM) Spektrum (s. Abb. 1.1) und lassen uns leicht täuschen (s. Abb. 1.2). Abb. 1.1: Quelle: Das elektromagnetische Spektrum Abb. 1.2: Einige bekannte optische Täuschungen Quelle: Gonzales, Woods (2002), S. 42.
6 3 1.2 Bildvorverarbeitung Die digitale Bildvorverarbeitung gliedert sich in die Bereiche Bildverbesserung und Bildrestaurierung. Die Bildverbesserung ist das einfachste und verlockendste Feld der digitalen Bildvorverarbeitung. Hintergrundidee ist, nicht wahrnehmbare Details sichtbar zu machen oder einfach bestimmte Objekte, die in einem Bild interessant sind, deutlicher hervorzuheben. Die Bildverbesserung kann in zwei Kategorien unterteilt werden: Zum einen gibt es die räumliche Domäne. Hier findet die Realisierung auf der E- bene des Bildes statt, dass heißt, die Manipulationen arbeiten direkt auf den Pixeln. Zum anderen existiert die Frequenzdomäne. Dabei wird ein Bild mit Hilfe der Fourier Transformation in Wellen verschiedener Frequenz zerlegt, die globales Filtern ermöglicht. Ein bekanntestes Beispiel für eine Verbesserung ist, den Kontrast eines Bildes zu vergrößern, weil es besser aussieht. Bei der Bildverbesserung handelt es sich dabei um den subjektiven Teil der Bildvorverarbeitung. Quelle: eigene Darstellung Abb. 1.3: Beispiel zur Kontrastsimulation 1 Die Techniken zur Bildrestaurierung haben zum Ziel, ein Bild in einem vorgefertigten Sinn zu verbessern, hier im Gegensatz zur Bildverbesserung als objektiver Prozess. 1.3 Ziele der Bildvorverarbeitung Bildverbesserung und Bildrestaurierung werden also zur Aufbereitung von Bildsignalen benutzt, um wichtige Merkmale hervorzuheben. Folglich werden gering ausgeprägte Strukturen betont, während redundante oder gestörte Bildinformationen unterdrückt werden. 1 Anm.: Die inneren Quadrate haben alle die gleiche Intensität, aber sie wirken dunkler, wenn der Hintergrund heller wird.
7 4 Das Ziel der Bildvorverarbeitung ist, ein Bild zu erstellen, in dem der Bildbereich hervorgehoben ist, der die später zu gewinnenden Daten enthält. Nach der Vorverarbeitung muss sich dieser Datenbereich in der Helligkeit von der Umgebung deutlich unterscheiden. Es soll der subjektiv-visuelle Eindruck verbessert werden. Die Vorverarbeitung ist eine Bildtransformation, bei der als Ergebnis wieder ein Bild entsteht. Dabei wird der Informationsgehalt des Bildes in Anbetracht der späteren Auswertung nicht wesentlich verändert. Weiterhin sollen nachfolgende Verarbeitungsschritte vereinfacht werden.
8 5 2 Eigenschaften von Bildern 2.1 Bildarten Es gibt viele Arten von Bildern, aber allgemein lassen sie sich in die drei Arten Intensitätsbzw. Grauwertbilder, Binärbilder und Farbbilder unterteilen. Diese werden nachfolgend im Detail vorgestellt. Grauwertbilder Bei Grauwertbildern stellt jeder Pixel einen Intensitätswert dar, der bei einer 8-bit Speicherung Werte von 0 bis 255 annehmen kann. Es ergeben sich somit 2 8 = 256 verschiedene Intensitätsstufen, weshalb Grauwertbilder auch als Intensitätsbilder bezeichnet werden. Ein Intensitätswert von 0 entspricht dabei der Farbe schwarz, der Wert 255 der Farbe weiß. Mathematisch gesehen kann ein Grauwertbild als eine Funktion g(r,c) betrachtet werden. Der Funktionswert an der Stelle (r,c) entspricht dem Grauwert, bzw. der Helligkeit des Bildes. Grauwertbilder haben mehrere Vorteile in der Bildverarbeitung. Zum einen haben sie gegenüber Farbbildern einen geringeren Speicherverbrauch und zum anderen lassen sich Bildverarbeitungsoperatoren recht einfach auf ihnen ausführen, da nur ein Kanal mit Werten berücksichtigt werden muss. 2 Binärbilder Aus Grauwertbildern lassen sich durch eine Schwellwertoperation Binärbilder erzeugen, was auch als Binärisierung bezeichnet wird. Dazu wird ein Intensitätswert als Schwellwert festgelegt, so dass jeweils die 0 den Werten unterhalb des Schwellwertes und die 1 denen oberhalb des Wertes zugewiesen wird. Die Visualisierung kann als Zweipegelbild geschehen, bei der den Werten 0 und 1 bestimmte Intensitäts- oder Farbwerte zugeordnet werden. 3 Durch die Schwellwertwahl wird das spätere Bild daher entscheidend beeinflusst. Eine Verwendung in der Bildvorverarbeitung und Objekterkennung finden Binärbilder u. a. bei der Trennung von einem Objekt und dem Hintergrund. 2 3 Viele der folgenden Beispiele beziehen sich daher auf Grauwertbilder. Vgl. Jiang (2002), S. 26.
9 6 Farbbilder Zur Darstellung von Farbbildern gibt es zahlreiche Farbmodelle, von denen hier nur das RGB- und das HSV-Modell kurz vorgestellt werden sollen. Das RGB-Modell beruht auf der additiven Überlagerung der drei Grundfarben rot, grün und blau. Die Farbe Weiß entsteht dabei durch die Überlagerung der drei Farben in voller Intensität. 4 Das HSV-Model hingegen beruht auf der intuitiven Zusammensetzung der Farben, so dass jede Farbe durch ein Tripel hue (Farbton), saturation (Sättigung) und value (Helligkeit) beschrieben wird. Der Vorteil dieses Farbmodells gegenüber dem RGB-Farbmodell besteht darin, dass bei Änderungen der Farbe oder der Helligkeit nur ein Kanal betrachtet werden muss gegenüber allen drei Kanälen im RGB-Modell. Das HSV-Modell ermöglicht daher eine unabhängige Betrachtungsweise von Farb- und Helligkeitsinformationen. 5 Abb. 2.1: RGB- und HSV-Farbmodelle Quelle: Vgl. Preim (2003), S Operationen zur Bildverbesserung lassen sich auf Farbbildern ähnlich durchführen wie auf Grauwertbildern, im RGB-Modell muss dabei in den meisten Fällen die Berechnung auf allen 3 Kanälen durchgeführt werden. Eine Ausnahme bildet u. a. der Medianfilter 6 im RGB-Modell, da es keine sinnvolle lineare Ordnung <= auf Farbvektoren gibt und durch eine unabhängige Betrachtung der Farbkanäle Farben entstehen können, die nicht mehr mit den Ausgangsfarben zusammenhängen. Die Konvertierung eines Farbbildes in ein Grauwertbild ist eindeutig und lässt sich relativ einfach durchführen (im RGB-Modell durch Mittelwertbildung der drei Kanäle). Eine Vgl. Abb Vgl. Pandit (2001), S Vgl. Jiang (2002), S. 25.
10 7 Pseudokolorierung eines Grauwertbildes ist im Gegensatz dazu nicht mehr eindeutig und somit wesentlich aufwendiger. 2.2 Charakteristika von Bildern Charakteristische Eigenschaften von Bildern lassen sich durch Histogramme und statistische Kennwerte wie z. B. Mittelwert oder Varianz beschreiben. Die statistischen Kennwerte ermöglichen eine objektive Beurteilung des Bildes, die nicht durch subjektive Eindrücke beeinflusst wird. In der Bildvorverarbeitung helfen diese Kennwerte zu entscheiden, ob und in welchem Maße bestimmte Verbesserungsverfahren auf ein spezielles Bild angewendet werden können, um bestimmte Merkmale dieses Bildes besser herauszustellen und somit den objektiven Eindruck zu verbessern. Histogramm Unter einem Histogramm eines Grauwertbildes g versteht man die relative oder absolute Häufigkeitsverteilung der im Bild vorkommenden Grauwerte k. Ein absolutes Grauwerthistogramm H(k) ist die Summe aller Pixel mit gleichem Grauwert, ein relatives Histogramm h(k) beschreibt die Wahrscheinlichkeit, mit der ein bestimmter Grauwert im Bild auftritt. { } ( ) (, ) (, ) H k = r c g r c = k absolutes Grauwerthistogramm ( ) h k H( k) = relatives Grauwerthistogramm mit der Größe M M in Ein Histogramm enthält Informationen über die Statistik erster Ordnung eines Bildes. Darunter versteht man Aussagen über das Auftreten von bestimmten Werten, die unabhängig von irgendwelchen anderen benachbarten Werten gemacht werden. Haben zwei Bilder das gleiche Histogramm, so sind sie deswegen nicht notwendigerweise identisch. 7 Auch für Farbbilder lassen sich Histogramme erstellen, doch diese sind entweder vierdimensional (drei Farbdimensionen und eine Häufigkeitsdimension ), was sich schwer darstellen lässt oder beschreiben die drei einzelnen Dimensionen des RGB-Modells, denen der Zusammenhang fehlt. N 7 Vgl. Pandit (2001), S. 50.
11 8 Mittlerer Grauwert Der Mittlere Grauwert f gibt Auskunft über die allgemeine Helligkeit eines Bildes, also darüber, ob bei einer subjektiven Betrachtung dieses Bild als zu hell oder zu dunkel empfunden wird. Je größer der Wert, desto heller erscheint das Bild. Eine Anwendung findet der Mittelwert auch im Frequenzraum im Zusammenhang mit der 2-dim DFT. 8 Berechnet wird der mittlere Grauwert aus den relativen Häufigkeiten wie folgt: 9 N 1 M f = grc (,) = hk NM i r= 0 c= 0 0 ( ) Varianz Die Varianz ist ein Maß für die Abweichungen der Grauwerte aller Pixel vom mittleren Grauwert f. Mit Hilfe der Varianz lässt sich der Kontrast eines Bildes beschreiben. Es wird als kontrastreich bezeichnet, wenn eine weite Streuung der Grauwerte im Histogramm vorliegt, da dann die Grauwertübergänge stärker hervorgehoben werden. Durch den direkten Zusammenhang mit dem mittleren Grauwert errechnet sich die Varianz aus den relativen Häufigkeiten durch folgende Formel: 2 σ ( grc (,) f) hk ( ) ( k f) 1 = = NM i N 1M i r= 0 c= Vgl. Kap Vgl. Jiang (2002), S. 17.
12 9 3 Bildverbesserung 3.1 Systematisierung der Verfahren Um einen besseren Überblick über die große Anzahl von verschiedenen Verfahren zur Bildverbesserung zu bekommen soll hier eine Systematisierung der Verfahren vorgenommen werden. Verschiedene Einteilungskriterien sollen dabei helfen, die unterschiedlichen Verfahren besser in einen globalen Zusammenhang einordnen zu können. Eine Möglichkeit der Gliederung bietet die Unterteilung nach der Anzahl der Pixel, die eine Verarbeitung beeinflussen. Dabei wird zwischen punktbezogenen, lokalen und globalen Operatoren unterschieden. Punktbezogene Operatoren wie z. B. die affine Transformationen beziehen sich bei der Verarbeitung ausschließlich auf einen Punkt, lokale Operatoren wie z. B. Filtermasken auf eine frei wählbare Nachbarschaft und globale Operatoren, wie beispielsweise die Fourier-Transformation, auf das gesamte Bild. 10 Nach einer Einteilung in Bearbeitungsbereiche lassen sich homogene und inhomogene Verfahren unterscheiden. Ein homogenes Verfahren wie z. B. der Mittelwertfilter wird dabei für jede Region eines Bildes gleich benutzt und ist somit unabhängig von der Bildkoordinate. Im Gegensatz dazu steht das inhomogene Verfahren, in dem der Operator von der Bildkoordinate abhängig ist und aus der Umgebung berechnet werden kann. Eine dritte Möglichkeit zur Systematisierung bietet die Einteilung nach der Linearität der Verarbeitung. Lineare Verfahren wie z. B. die Konvertierung in ein Negativbild können rückgängig gemacht werden und sind somit invertierbar. Nichtlineare Verfahren hingegen sind nicht invertierbar. Zu diesen Verfahren zählt auch die Binärisierung, da durch sie die Entropie, d.h. der Informationsgehalt eines Bildes sinkt und nicht wieder rückgängig zu machen ist. 3.2 Punktbezogene Operatoren Alle punktbezogene Grauwerttransformationen basieren auf räumlichen Transformationen, so dass direkt die Pixel eines Bildes manipuliert werden. Die Anwendung dieser Transformationen ist in der Regel spezifisch und problemorientiert. So ist diese Form der Bildverarbeitung ein subjektiver Prozess und beruht auf der visuellen Auswertung der Bildqualität. 10 Vgl. Jiang (2003), S. 20.
13 10 Grauwerttransformationen basieren auf der Gesamtmenge aller Pixel aus denen ein Bild besteht. Die allgemeine Formel lautet: gxy (, ) = T[ f( xy, )] Dabei ist f(x,y) der Grauwert des Eingangsbildes an der Stelle x, y und g(x,y) der Wert des bearbeiteten Bildes. T ist der Operator auf f, der in diesem Fall Grauwerttransformationfunktion ist: s = T(r) Hier sind s und r Variablen bzw. die Grauwerte von f(x,y) und g(x,y) von jedem Punkt x, y. T wird auch Transformationskennlinie genannt. Ein Beispiel in Abb. 3.1 dient zur Verdeutlichung. Abb. 3.1: Kontraststreckung und Binarisierung Quelle: Vgl. Jiang(2003), S In Abb. 3.1 links wird ein höherer Kontrast erzeugt, da die dunklen Pixel im Bild verdunkelt und die hellen Anteile erhellt werden. So eine Transformationsfunktion nennt man auch Kontrastdehnung, oder Kontraststreckung. Bei Abb. 3.1 rechts wird das Eingabebild in ein binäres Bild umgewandelt, da die Werte nur noch zwei Werte annehmen. Hier heißt T auch Schwellwertfunktion. Grundlegende Grauwerttransformationen r und s sind hier wieder die Werte der Pixel vor und nach der Bearbeitung. T ist die Transformation, die s aus r berechnet: s = T(r). Dann können folgende Grundtypen von Transformationen unterschieden werden:
14 11 Abb. 3.2: Grundlegende Grauwerttransformationen Quelle: Gonzales, Woods (2002), S Identität und Negativ. Am einfachsten ist die Identität zu berechnen: s = r. Beim Negativbild wird der Wert r von dem höchst möglichen Grauwert abgezogen. Die Formel lautet: s = 255 r. 2. Logarithmus Transformation (kurz: log Transformation). Die Formel für diese Transformation lautet: s = 255 log( 1 + r ) log 256 mit r >= 0. Diese Formel bewirkt eine Dehnung der Grauwertdynamik im unteren Grauwertbereich und gleichzeitig eine Stauchung im oberen Grauwertbereich. Also werden die dunklen Pixel im Bild expandiert und die hellen komprimiert. Dadurch werden Details im dunklen Bereich besser sichtbar gemacht. Die inverse log Transformation hat genau den gegenteiligen Effekt (als Beispiel das Bild aus dem Skript der Vorlesung Bildverarbeitung auf S. 23). 3. Exponentielle Transformation (power-law Transformation). Sie hat die allgemeine Form: s = 255 * (r/255) γ mit γ als Konstante. Diese Funktion ist vielfältiger anwendbar als die vorherige. Für γ < 1 ist die Funktion ähnlich der Log Transformation. Hier erhöht die exponentielle Transformation die Helligkeit und ermöglicht insbesondere eine bessere Sichtbarkeit
15 12 im dunklen Bereich. Für γ > 1 ist das Verhalten genau umgekehrt. Das bearbeitete Bild wirkt dunkler. Das ermöglicht bei zu hellen Bildern eine bessere Betrachtung. Allgemein werden die exponentiellen Transformationen gebraucht für Kontrastmanipulationen. Die Transformationskennlinien für die ersten drei Grundtypen sind in Abb. 3.2 zu erkennen. 4. Stückweise-lineare Transformation. Bei der Transformation müssen mehr Werte spezifiziert werden als bei den vorherigen. Diese Funktion kann verwendet werden um Bildinhalte aus einem Teilbereich [a,b] hervorzuheben (Abb. 3.3) oder um Grauwerte zu dehnen, z. B. bei kontrastarmen Bildern, bei denen die Grauwerte nur im Intervall [a,b] liegen und dann auf den Bereich [0,255] ausgedehnt werden (Abb. 3.4). Problem hierbei ist, dass man die Intervallgrenzen a und b bestimmen muss. Abb. 3.3: Stückweise lineare Transformation Abb. 3.4: Grauwertdehnung Quelle: Jiang (2003), S. 26.
16 13 Histogrammtransformationen Histogramm: h(r k ) = n k Das Histogramm eines Bildes beschreibt die Häufigkeit des Vorkommens eines Grauwertes. Ein Bild, das ein Histogramm mit großer Ausdehnung der Grauwerte und gleichmäßiger Verteilung hat, wirkt sehr kontrastreich und hat viele Grauwerte. Man kann anhand des Histogramms des Inputbildes eine Transformationsfunktion erstellen. Bei den Histogrammtransformationen gibt es die Histogrammspreizung. Sie nutzt den Wertebereich zur Verbesserung der Darstellung aus. Die Zuordnungsvorschrift ergibt sich aus dem kleinsten und größten im Bild vorkommendem Grauwert. Diese Transformation ist ähnlich der stückweisen linearen Transformation. Mit Hilfe des Histogramms können hierbei die Intervallgrenzen einfach bestimmt werden. In Abb. 3.5 ist das Originalbild dargestellt, das in Abb. 3.6 durch eine Histogrammspreizung transformiert wurde. Abb. 3.5: Original mit Histogramm Quelle: Jiang (2003), S. 27. Abb. 3.6: Grauwertdehnung mit Histogramm Quelle: Jiang (2003), S. 27. Eine weitere Transformation ist der Histogrammausgleich. Es wird das Ziel verfolgt, große Anhäufungen im Histogramm zu strecken oder auch weniger genutzte Grauwertbereiche
17 14 zu stauchen. Insgesamt soll das transformierte Bild damit ein gleichverteiltes Histogramm erhalten. Gesucht ist deshalb eine monotone Abbildung T: [0,255] [0,255], so dass g(x,y) = T(f(x,y)) mit s = T(r) ein gleichverteiltes Histogramm h(r k ) hat. Jedem Grauwert r wird die Summe der bis zu r aufsummierten relativen Häufigkeiten zugeordnet. r s = 255 * hf ( r), mit hf(r) als relative Häufigkeit von r. p= 0 Abb. 3.7: Histogrammausgleich Quelle: Jiang (2003), S. 31. Im Bild ist das Resultat des Histogrammausgleichs deutlich zu erkennen. Es zeigt, dass der Histogrammausgleich ein gutes Verfahren zur Bildverbesserung ist. 3.3 Nachbarschaftsoperatoren Bei den zuvor vorgestellten punktbezogenen Operatoren können die räumlichen Beziehungen der Grauwerte einer kleineren Umgebung nicht erkannt werden. Aus diesem Grund ist eine weitere Gruppe von Operatoren nötig, die die Bildpunkte einer Nachbarschaft in angemessener Weise kombinieren. Sie werden auch Nachbarschaftsoperatoren oder Filter genannt und arbeiten direkt auf den Pixeln des Bildes, wobei f das Eingabebild ist und durch die Operationen zu dem verbesserten Ausgangsbild g wird: g(r,c) = Ω(N(f(r,c)) Eine grundlegende Kombinationsart von Bildpunkten in einer Nachbarschaft ist die lineare Operation mit einer Filtermaske. Eine Maske ist ein kleines (z. B. 3 x 3) zweidimensionales Array, das die Größe der Nachbarschaft abdeckt und stellt sich wie folgt dar: h(u,v), -k u k, -k v k (Annahme bei einer n x n Maske: n= 2k + 1)
18 15 Bei einer Nachbarschaftsoperation wird jeder Bildpunkt, der von der Bildmaske bedeckt wird mit dem entsprechenden Gewicht in der Maske multipliziert. Anschließend werden alle Punkte addiert und die Summe wird an die Position des zentralen Bildpunktes gesetzt, was in der folgenden Formel sichtbar wird: k k g(r,c) = Σ Σ h(u,v) f(r+u, c+v) ( k= (n - 1) / 2) u= - k v= - k Dieser Prozess besteht einfach daraus, dass die Maske sich von Punkt zu Punkt im Bild bewegt und den neuen Punkt durch eine vordefinierte Nachbarschaft berechnet. Abb. 3.8: Beispiel einer Nachbarschaftsoperation Quelle: Gonzales, Woods (2002), S Im Beispiel (s. Abb. 3.8) wird das Bild f mit einer 3x3 Maske h bearbeitet. Als Ergebnis erhält man ein verbessertes, jedoch verkleinertes Bild g: h = f = g =
19 16 Die Nichtberücksichtigung der Randpunkte führt dazu, dass das Bild bei wiederholter Anwendung der Maske immer kleiner wird. Um ein Ergebnisbild derselben Größe zu erhalten, müssen die Randpunkte gesetzt werden. Dazu gibt es mehrere Möglichkeiten, z.b. können die Randpunkte einfach unverändert beibehalten werden Glättungsfilter Durch Glättungsfilter sollen Störungen rückgängig gemacht werden. Störungen in Bildern liegen dann vor, wenn benachbarte Bildpunkte stark unterschiedliche Grauwerte aufweisen, obwohl diese im Normalfall nur wenig schwanken sollten. Dabei wird angenommen, dass Störungen unabhängig von der Position und vom Grauwert des Bildpunktes sind. Das Ergebnis eines solchen Filters ist der Durchschnitt der Pixel, die in der Nachbarschaft der Filtermaske enthalten sind. Der Wert jedes Pixels wird durch den durchschnittlichen Grauwert der Nachbarschaft ersetzt, der durch die Filtermaske definiert wird. Mittelwertfilter Die Idee, die hinter dieser Glättung des Rauschens steht, ist, den arithmetischen Mittelwert der Grauwerte aus der Umgebung eines jeden Bildpunktes durch einen lokalen Filter zu bilden. Bei dem Mittelwertfilter handelt es sich um eine lineare Operation. Die Rechenvorschrift für den Mittelwertfilter sieht wie folgt aus: 1 k k g(r,c) = Σ Σ f (r+u,c+v) (2k+1)² u= - k v= - k Die Maske für ein 3 X 3 großen Ausschnitt stellt sich dann so dar: (k=1) Der Nachteil des Mittelwertfilters besteht darin, dass die Kontraste sich vermindern und so eine Kantenverwischung entsteht. Medianfilter Das Ergebnisbild des Medianfilters ergibt sich als Median der Grauwerte im Bild f innerhalb eines bestimmten Ausschnitts der Größe n x n (wobei n= 2k+1).
20 17 Der Median wird berechnet, indem die (2k+1)² Grauwerte der Größe nach sortiert werden und der (2k²+2k+1)-te Wert der Median wird. Im Beispiel für ein 3 x 3 Fenster in einem Bild wird nach der Formel für die Medianberechnung der 5. Wert der Median: ,1,1,1,2,2,3,4, Median Der Medianfilter ist ein nichtlinearer Operator und gehört zur Klasse der Rangordnungsoperatoren (rank order filtering), d.h. die Eingabedaten werden sortiert, und der mittlere Wert der aufsteigenden Folge wird als Median genommen. Der Vorteil beim Medianfilter liegt darin, dass man als Ergebnis keine verwischten Kanten erhält. Aber Nachteil ist, dass die Ecken abgerundet und kleinere Objekte ausgelöscht werden. Zudem besitzt er eine höhere Rechenkomplexität als andere Operatoren, da die Werte immer der Größe nach sortiert werden müssen. Zusammenhang zwischen Mittelwert- und Medianfilter Der Mittelwert- und der Medianfilter können zusammen hergeleitet werden. Dabei wird für die Nachbarschaft: f(r + u, c + v), -k u, v k ein Grauwert f gesucht, der die (2k+1)² Grauwerte am besten repräsentieren kann. Der Abstand zwischen den Grauwerten f und denen in der Nachbarschaft wird mit einer Abstandsfunktion d() definiert und so ergibt sich die Optimierungsaufgabe. Diese ermittelt den gemeinsamen kleinsten Abstand zwischen dem gesuchten Grauwert f und den Grauwerten aus der Umgebung. Mit verschiedenen Abstandsfunktionen erhält man nun die beiden verschiedenen Filter. Dabei zeigt sich, dass der Medianfilter gegenüber Ausreißern robuster ist als der Mittelwertfilter.
21 18 Abb. 3.9: Beispiel, gefiltert mit Mittelwert- und Medianfilter Quelle: Graber, Folie Korrektur von uneinheitlichem Hintergrund Ein uneinheitlicher Hintergrund kann unterschiedliche Ursachen haben, z.b. Beleuchtung oder Materialeigenschaft. Eine Verbesserungsmöglichkeit besteht in der Modellierung und der Subtraktion des Hintergrundes vom Bild. Dazu wird oft eine polynominale Funktion der Form b(r,c)=a 00 + a 10 r + a 01 c + a 20 r² + a 11 rc + a 02 c² oder eine Funktion höherer Ordnung verwendet. Um die Parameter a ij bestimmen zu können müssen ausreichend Hintergrundpunkte, mindestens aber 6 oder ein Vielfaches davon, manuell oder automatisch bestimmt werden. Eine Möglichkeit ist, das Originalbild in k x k Subbilder aufzuteilen und für jedes Subbild den dunkelsten Punkt zu selektieren. Daraus ergeben sich k² Hintergrundpunkte, für die anschließend die Funktionsapproximation durchgeführt wird.
22 19 Abb. 3.10: Quelle: Jiang (2003), S. 54. Beispiel der Korrektur von uneinheitlichem Hintergrund (links: Original) Abb. 3.11: Quelle: Jiang (2003), S. 54. Beispiel der Korrektur von eineinheitlichem Farbton (links: Original) 3.4 Geometrische Transformationen Bei geometrischen Transformationen nur die Position der Grauwerte verändert. Dabei verändert sich die räumliche Beziehung zwischen den Pixeln. Diese Funktion wird auch rubber-sheet-transformation genannt. Die geometrische Transformation bei der Bildverarbeitung besteht aus 2 Teilen. Erstens wird eine räumliche Transformation durchgeführt, zweitens eine Interpolation. Räumliche Transformation Diese Funktion wird verwendet für die Änderung, Neuordnung oder auch Umgestaltung der Pixel in der Bildebene. Beispiele sind:
23 20 Andere affine Transformationen sind z. B. Rotation, Scherung usw. Ein Bild mit Pixel (x,y) durchlebt geometrische Verzerrungen. Die räumliche Transformation erzeugt ein neues Bild g(x,y ) mit x = r(x,y) und y = s(x,y). Wenn r und s bekannt sind, kann man das frühere Bild wieder herstellen. Da man jedoch r und s meistens nicht kennt, benutzt man sog. tiepoints, Punkte die im Input- und Output- bild exakt bekannte Position haben. Translation Verschiebung um gegebene x- und y-distanzen tx und ty: P = (x, y) P' = (x', y') = (x + tx, y + ty) x = x + tx y = y + ty Abb. 3.12: Translation Skalierung Ziel: Dehnung (bzw. Stauchung) um gegebenen Skalierungsfaktor s mit Zentrum = Ursprung Je nach Skalierungsfaktor s: s<1: Verkleinerung, Stauchung, s>1: Vergrößerung, Dehnung, s=1: keine Änderung x = x * sx und y = y * sy. Abb. 3.13: Skalierung
24 21 Das Bild zeigt zwei korrespondierende Quadrate, das eine aus dem verzerrten Bild und das andere aus dem korrigierten Bild. Die Eckpunkte der Quadrate sind die korrespondierenden tiepoints. Quelle: Gonzales, Woods (2002), S Abb. 3.14: Tiepoints x = c 1 x + c 2 y + c 3 xy + c 4 y = c 5 x + c 6 y + c 7 xy + c 8 Mit acht tiepoints kann man nun die Koeffizienten berechnen. Diese bilden dann das geometrische Verzerrungsmodell und werden gebraucht um alle Pixel innerhalb des Quadrates zu berechnen. Die Auswahl der tiepoints erfolgt durch verschiedene Techniken, abhängig von der Anwendung. Wenn man nun wissen will, welcher Wert im korrigiertem Bild an der Stelle (x 0,y 0 ) ist, muss man nur wissen, wo im verzerrtem Bild f(x 0,y 0 ) ist. Dafür muss man x 0 und y 0 in die Gleichungen einsetzen und bekommt dann die berechneten Werte x 0 und y 0. Der Grauwert im verzerrtem Bild an der Stelle (x 0, y 0 ) ist dann g(x 0, y 0 ). Dann ist f(x 0,y 0 ) = g(x 0, y 0 ). Und so geht man dann Zeile für Zeile und Reihe für Reihe durch das Bild durch. Interpolation Sind nun die Pixel berechnet, kommt es häufig vor, abhängig von den Koeffizienten, dass die Pixelwerte x und y keine Integer sind. Da die Grauwerte aber auf Pixelwerten basieren, die Integer sind, muss eine Grauwertinterpolation durchgeführt werden. Die einfachste Variante ist dabei die Nearest Neighbour Interpolation.
25 22 Abb. 3.15: Nearest Neighbour Interpolation Quelle: Gonzales, Woods (2002), S Hier wird der nächstgelegene Integer Nachbar zum berechneten Pixelwert ausgewählt und der Grauwert dieses Pixels wird dem Pixel zugewiesen. Diese Interpolation ist zwar einfach zu implementieren, aber sie erzeugt unerwünschte Nebeneffekte, z.b. die Verzerrung von glatten Ecken. Eine weitere Interpolation ist die bilineare Interpolation. Hierbei werden die Grauwerte der vier nächsten Nachbarn mit in die Berechnung aufgenommen. Abb. 3.16: Bilineare Interpolation Quelle: Jiang (2003), S. 59. Es gibt auch Interpolationen höherer Ordnung, d. mit Einbezug einer größeren Nachbarschaft, aber im allgemeinem hat die bilineare Interpolation ausreichende Qualität. 3.5 Bildverarbeitung im Frequenzraum Einführung in die Fourier Analyse Neben der punktbasierten Betrachtungsweise existiert ebenfalls die Möglichkeit Bildverarbeitung im Frequenzraum durchzuführen. Dabei liegt die Idee zugrunde, ein Bild als Funk-
26 23 tion zu verstehen, die sich linear in periodische Funktionen separieren lässt in sogenannte Schwingungen verschiedener Frequenzen. Ausgangspunkt ist das Buch La Théorie Analitique de la Chaleur von Jean Baptiste Joseph Fourier. Dort entwarf er 1922 das revolutionäre Konzept, dass jede einigermaßen wohlgeformte periodische Funktion sich als gewichtete Summe von Sinuskurven verschiedener Frequenzen nachbilden lasse. Ursprünglich zur mathematischen Erklärung der Wärmeverbreitung eingesetzt, führte eine Erweiterung der Theorie zur Fourier Transformation, die insbesondere für die Bildverarbeitung von Interesse ist, da sie die Zerlegung finiter Funktionen unterstützt. Zuerst wird jedoch die ursprüngliche Definition Fouriers, die Zerlegung periodischer Funktionen, eingeführt. Sie wird auch als Fourier-Reihe bezeichnet: a 2π kx 2π kx f x a b, mit T als Periode der Funktion f ( x ). ( ) = 0 + [ 2 k = 1 k cos( T ) + k sin( T )] Die Funktion f ( x ) ist dabei definiert als unendliche Summe von Sinus- und Kosinusschwingungen, die jeweils mit eigenen Koeffizienten a und b gewichtet sind. Diese ergeben sich aus Integralen über die eigentliche Funktion und sollen hier nicht weiter vertieft werden. Entscheidend ist, dass sich aus sämtlichen periodischen Schwingungen ohne Informationsverlust die ursprüngliche Funktion herstellen lässt. Es kann dadurch erklärt werden, dass keine Interdependenzen zwischen den einzelnen Schwingungen bestehen, wie z. B. multiplikative Komponenten. Die Menge an Frequenzen (periodische Sinus-/ Kosinusschwingungen), aus denen die Funktion den Frequenzraum von f ( x) k k f ( x ) aufgebaut werden kann, spannen dabei auf. Analog wird jede Schwingung als Frequenzkomponente des Frequenzraumes von f ( x ) bezeichnet. Wird nun ein Bild als zerlegbare Funktion verstanden, so ist es prinzipiell möglich, es aus dem Bildraum oder der Bilddomäne in den Frequenzraum zu konvertieren und nach Bearbeitung wieder in den Bildraum zurückzukonvertieren. Warum verdient aber der Frequenzraum überhaupt Interesse in der Bildverarbeitung? Das Beispiel in Abbildung 3.5 stellt eine einfache Zerlegung einer periodischen Funktion in vier Frequenzkomponenten dar und kann exemplarisch als eindimensionales Bild verstanden werden, wobei von der diskreten Bildbetrachtung zu abstrahieren ist. Interpretiert man die Ordinate als Farbintensitätswert, so ergibt sich eine erstaunliche Beobachtung. Die Schwingungskomponenten hoher Frequenz, d. h. einer häufigen Wiederholung der periodischen Schwingung innerhalb eines festen Abschnittes, tragen zu feinen Details von Farbübergängen bei, während die niedrigen Schwingungskomponenten grobe Farbverläufe skizzieren. Anders ausgedrückt: die hochfrequenten Komponenten beeinflussen kontrastreiche Regionen, während Tieffrequenzanteile Bereiche geringer Intensitätsvariation bestimmen. Jede Frequenzkomponente kann somit als eine globale Eigenschaft des Bildes verstanden werden, unabhängig von der Lokalität der betrachteten Kontrasteigenschaft.
27 24 Der Frequenzraum ermöglicht damit die globale Bearbeitung von Bildeigenschaften im Gegensatz zu den lokalen Nachbarschaftsoperationen in der Bilddomäne. Aus Anschauungsgründen wird nachfolgend mit Graubildern gearbeitet, da der Unterschied zu Farbbildern einzig darin besteht, die Filteroperation auf sämtliche Farbkanäle (z. B. beim RGB- Modell) anzuwenden. Abb. 3.17: Zerlegung einer periodischen Funktion als Fourier-Reihe Quelle: o.a Die Fourier Transformation und ihre Eigenschaften Da in der Bildverarbeitung die Anforderung gestellt wird, mit finit diskreten Funktionen zu arbeiten, beschränken wir uns im weiteren auf die nützlichere Fourier-Transformation, die sich aus der Fourier-Reihe ergibt, wenn ein Grenzübergang für die Periode T durchgeführt wird. Die Fourier-Transformation hebt damit die Beschränkung auf, für Funktionen den Nachweis der Periodizität zu erfüllen und fordert lediglich reelle Funktionen. Für den Fall einer eindimensionalen kontinuierlichen Variablen x besitzt sie die Form:
28 25 Fu ( ) = f( x)exp( j2 πuxdx ), mit j = 1, und der Umkehrung: f ( x) = F( u)exp( j2 πux) du. Anstelle der Sinus- und Kosinuskurven wird die komplexe Schreibweise verwendet, die auf die Euler-Identität exp( jθ ) = cosθ + jsinθ zurückgeht. Die Sinuskomponenten sind dabei den imaginären Zahlanteilen zugeordnet, während die Kosinuskomponenten den Realzahlanteil darstellen. Für die Bildverarbeitung ist aber eine diskrete Summierung statt der Integration notwendig. Ein Bild der Auflösung M N stellt eine diskrete Funktion f ( xy, ) dar, mit x {0,..., M 1} und y {0,..., N 1}. Dies erfordert die diskrete Fourier- Transformation, wobei wir uns zur besseren Anschaulichkeit wieder auf den eindimensionalen Fall beschränken: M 1 1 Fu ( ) = f( x)exp( j2 πux/ M), und der Umkehrung: M M 1 u= 0 x= 0 f ( x) = F( u)exp( j2 πux/ M ), für diskrete u, x von 0 bis ( M 1). Die Berechnung von Fu ( ) erfolgt für jedes u M getrennt. Damit besteht die diskrete Fourier-Transformation (DFT) aus M Termen, die den Frequenzraum aufspannen. Jede dieser Komponenten setzt sich wiederum aus einer Summe von M Sinus-/ Kosinustermen zusammen. Aus den M getrennten Komponenten wird dann bei der Inversion die ursprüngliche Funktion des Bildraumes wiederhergestellt, ohne Informationsverlust. Man sagt auch, dass für sämtliche Fu ( ) den Frequenzraum aufspannt, mit den einzelnen Fu ( ) u M als Frequenzkomponenten. Die Fourier-Transformation kann auch als ein Glasprisma verstanden werden, welches Licht (analog der Bildfunktion) in seine Bestandteile (den Frequenzkomponenten) zerlegt. Wie werden nun die Frequenzkomponenten zur Bildverarbeitung genutzt? Ausgangspunkt ist die Betrachtung der komplexen Frequenzkomponenten Fu ( ) = Ru ( ) + jiu ( ) j = 1, R( u ) als Realteil, I( u ) als Imaginärteil) als Polarvektoren 2 Fu ( ) = Fu ( ) exp( jφ ( u)), mit dem Betrag Fu ( ) = [ R( u) + I 2 ( u)] 0.5 und dem (Phasen-)winkel 1 φ ( u) = tan ( I( u)/ R( u)) (mit. Der Betrag der Polarvektoren wird auch als Spektrum der Fourier-Transformation bezeichnet. Für die folgenden Filter wird ausschließlich das Spektrum genutzt, da z. B. Kontrast durch Helligkeitsunterschiede und nicht durch Farbwerte bestimmt wird (s. Anhang A.a). Vor der Behandlung einiger Filter wird nun die zweidimensionale DFT mit einigen weiteren Eigenschaften vorgestellt, wobei ein Bild der Auflösung M N zugrunde liegt:
29 26 (1) M 1N 1 1 Fuv (, ) = f( xy, )exp[ j2 π ( ux/ M+ vy/ N)], mit der Umkehrung: MN x= 0 y= 0 (2) M 1N 1. f ( xy, ) = Fuv (, )exp[ j2 π ( ux/ M+ vy/ N)] u= 0 v= 0 Dem Bild im Frequenzraum steht ein ebenso großes Bild im Frequenzraum gegenüber, mit uv, als Frequenzraumkoordinaten. Große Werte von uv, bezeichnen hohe Frequenzkomponenten, die ergo kontrastreiche Regionen bestimmen, wie z. B. Ecken und Kanten. Dagegen spezifizieren geringe u,v Werte geringe Intensitätsvariationen, wie beispielsweise einheitliche Zimmerwände. Der Wert am Ursprung entspricht dem mittleren Grauwert des Bildes, da: x= 0 y= (0,0) M 1N 1 1 F(0,0) = f( x, y)exp[ j2 π (0 x/ M 0 / )] MN + y N x= 0 y= 0 M 1N 1 1 F(0,0) = f( x, y ) (siehe mittlerer Grauwert in lokalen Bildoperationen). MN Vor der Bearbeitung eines Bildes in der Frequenzdomäne wird es jedoch so zentriert, dass die Koordinaten abbilden. Dafür wird ( M / 2, N / 2) dem Ursprung entsprechen, d.h. den mittleren Grauwert f ( xy, ) im Bildraum transformiert mit f( x, y) (, )( 1) x y ( + ) f x y. Eine Eigenschaft des Spektrums bei reellem f ( xy, ) ist die Symmetrie am Ursprung ( M /2, N / 2 nach Transformation). Dies ergibt sich wegen der Gültigkeit von Fuv (, ) * = F( u, v) und der Gleichheit des Betrages einer Konjugierten [ F * ( u, v) ] und seines Originals [ Fuv (, ) ]. Die Konjugierte stellt lediglich eine Spiegelung an der reellen Achse dar. Beides, sowohl die Zentriertheit, als auch die Punktsymmetrie, wird in Abb deutlich. Die Bereiche des Frequenzspektrums nahe des Mittelpunktes entsprechen hierbei den kontrastarmen Regionen niedriger Frequenz, mit dem mittleren Grauwert als schwingungsärmstes Zentrum. Radial vom Zentrum nach außen hin nehmen dann die Frequenzkomponenten an Kontrast zu. Diesen Zusammenhang machen sich Frequenzraumfilter zunutze, die kontrastreiche oder arme Bildbereiche herausfiltern möchten.
30 27 Abb. 3.18: Zentriertes Spektrum eines Bildes Filtern im Frequenzraum Der Ablauf des Filterns im Frequenzraum ist in Abb dargestellt. Die bereits erwähnte Zentrierung ist Teil der Vorverarbeitung im Bildraum (s. Schritt 1). Hierzu gehört ebenfalls die Begrenzung von Grauwerten u. ä. Operationen. Anschließend wird das Bild in den Frequenzraum konvertiert (s. Schritt 2). Dabei wird in der Praxis die Fast Fourier Transformation (FFT) angewandt, die mit O( M log M) Multiplikationen/ Additionen statt O( M 2 ) bei der konventionellen Summenbildung (s. Gleichung 1 und 2) auskommt. Dann wird eine Filterfunktion H( x, y) mit Fuv (, ) elementweise multipliziert, d. h. das erste Element von H mit dem ersten Element von F usw. (s. Schritt 3). In diesem Aufsatz werden ausschließlich reelle Funktionen als Filter verwendet, da sie i) zu keiner Phasenverschiebung bei der Filterung führen, und ii) bei der Rückkonvertierung (s. Schritt 4) in den Bildraum ebenfalls zu einer reelle Funktion führen. Etwaige komplexe Zahlanteile werden ignoriert, da sie auf Rundungsfehlern basieren. Die fehlende Phasenverschiebung erklärt sich dadurch, dass der reelle Filter H( x, y) sowohl mit dem reellen, als auch mit dem imaginären Anteil von Fuv (, ) gleichartig multipliziert wird, d. h. das Verhältnis der Real- und Imaginärkomponente nach der Filterung bleibt gleich - ergo gleicher Phasenwinkel. Als letzter Schritt muss die Zentrierung rückgängig gemacht werden. Anschließend kann eine Nachverarbeitung folgen (s. Schritt 5), wie beispielsweise eine Normierung von Grauwerten oder die Zusammenführung der Bildkanäle bei Farbbildern. 2
31 28 Abb. 3.19: Quelle: eigene Darstellung nach Gonzales, Woods (2002), S Vorgang der Filterung im Frequenzraum Die Funktion des ersten zu betrachtenden Filters, dem Notch-Filter, ist, ein begrenztes Intensitätsspektrum des Bildes hindurchzulassen. Im dargestellten Beispiel wird der mittlere Grauwert, d. h. das Zentrum des Frequenzraums, auf Null gesetzt. Der Filter hat dann die folgende Form: 0 if ( u, v) = ( M /2, N /2) Huv (, ) =. 1 otherwise In Abb wird deutlich, wie die Farbintensität des gesamten Bildes herabgesetzt wird, da der mittlere Grauwert, d. h. F(0,0), eine globale Eigenschaft des Bildes in der Bilddomäne darstellt.
32 29 Abb. 3.20: Der Notch-Filter Quelle: Gonzales, Woods (2002), S Da die Veränderung des mittleren Grauwertes ebenfalls als eine lokale Grauwerttransformation bekannt ist, stellt sich die Frage, ob und wie ein Zusammenhang zwischen Filtern im Bild- und Frequenzraum hergestellt werden kann. Eine Antwort liefert folgendes Faltungstheorem: f ( xy, ) hxy (, ) FuvHuv (, ) (, ) M 1N 1 f ( xyhxy, ) (, ) Fuv (, ) Huv (, ), mit 1 f ( xy, ) hxy (, ) = f( mnhx, ) ( my, n) MN und Bildraum Frequenzraum m= 0 n= 0 als Fourier/ inverse Fourier Transformation. Da Nachbarschaftsoperatoren [Bildraumfilter hxy (, ) ] via Faltung [ f ( xy, ) hxy (, ) ] auf die Bildfunktion [ f ( xy], ) angewandt werden, lässt sich aus der ersten Zeile des Theorems folgern, dass zu jedem Bildraumfilter ein entsprechender Frequenzraumfilter existieren muss. Die Ergebnisse der Filterung im Frequenz-, als auch im Bildraum sind dabei über die Fourier-Transformation bzw. ihre Inverse ineinander überführbar. Dadurch wird deutlich, dass die Multiplikation im Frequenzraum der Faltung im Bildraum entspricht und umgekehrt. Es kann darüber hinaus gezeigt werden, dass gilt: hxy (, ) Huv (, ). 11 Damit kann über die Fourier-Transformation aus einem Bildraumfilter der korrespondierende Frequenzraumfilter erzeugt werden und vice versa. Frequenzraumverarbeitung findet damit Verbindung mit der Bildraumverarbeitung, indem man statt getrennter Filter das Fourier- Transformationspaar Domänen erfüllt. hxy (, ); Huv (, ) betrachtet, dass dieselbe Filterfunktion in beiden 11 Anm.: Der Beweis wird mit einer Impulsfunktion geführt, die den Einfluss der Filter auf einen Punkt beschränkt und kann ausführlich in Gonzales, Woods (2002) auf S
33 30 Wofür ist dann die Frequenzraumverarbeitung gut, wenn doch Filter aus dem Bildraum dieselbe Funktion erfüllen? Erstens gibt es über die einfachen Filter hinaus Verfahren zur Bildrestaurierung, die allein im Frequenzraum durchgeführt werden können. Auf den Wiener Filter als ein Beispiel wird dabei im nächsten Abschnitt eingegangen. Zweitens konnte nachgewiesen werden, dass mit der FFT Filterung im Frequenzraum effizienter ist als im Bildraum, wenn die Zahl der Punkte >32 ist. 12 Die meisten Bilder liegen weit über dieser Grenze (z. B Pixel eines normalen Bildes), weshalb die Frequenzraumfilterung meist schneller ist. Nicht zuletzt sind die Filter im Frequenzraum eher der Intuition zugänglich. Dies soll am Beispiel des Gauß-Hochpassfilters deutlich gemacht werden (s. Abb. 3.21, rechte Seite). Hochpassfilter haben die Aufgabe, kontraststarke Regionen (hohe Frequenzen - weit entfernt vom Zentrum F(0,0)) zu verstärken, während sie Regionen mit geringer Intensitätsvariation abschwächen (niedrige Frequenzen - in der Nähe vom Zentrum F(0,0)). Es ist nicht intuitiv, dass der Bildraumfilter von einem positiven Ausschlag im Zentrum erst stark ins Negative verläuft, um sich dann langsam wieder der Abszisse anzunähern (rechts unten). Dagegen ist im Frequenzraum (rechts oben) eindeutig klar, dass die dem Zentrum nahe liegenden niederfrequenten Anteile abgeschwächt werden, während die außen liegenden kontrastreichen Gebiete vollständig durchgelassen werden. Neben dem Gauß-Hochpassfilter existiert ebenfalls der Gauß-Tiefpassfilter. Tiefpassfilter haben die umgekehrte Aufgabe von Hochpassfiltern. Sie lassen niederfrequente Bildanteile durch, während kontrastreiche Bildbereiche abgeschwächt werden (siehe ebenfalls Abb. 3.21). Am Gauß-Tiefpassfilter soll eine fundamentale Beziehung der Reziprozität des Transformationspaares deutlich gemacht werden. Der Gauß-Tiefpassfilter wird definiert als: 2 2 Hu ( ) = Aexp( u / 2 σ ) (im Frequenzraum), hx ( ) = 2πσ Aexp( 2 π σ x) (im Bildraum). 12 Vgl. Gonzales, Woods (2002), S. 166.
34 31 Abb. 3.21: Quelle: Vgl. Gonzales, Woods (2002), S Gauß-Hoch- und Tiefpassfilter im Bild- und Frequenzraum Die Breite der glockenähnlichen Kurvenform wird durch die Variabilität σ spezifiziert (diese kann mit dem später verwendeten Begriff der Cutoff-Frequenz gleichgesetzt werden). Auffällig ist, dass einer schmalen Glocke im Bildraum eine breite Kurve im Frequenzraum entspricht. Dies ist der Fall, da σ einerseits im Zähler liegt, im anderen Fall dagegen im Nenner. Wird der Gauß-Tiefpassfilter im Bildraum verbreitert (σ steigt), so verhält sich der Gauß-Tiefpassfilter im Frequenzraum reziprok und wird schmaler (steigendes σ im Nenner gegenläufiges Verhalten). Dieses reziproke Verhalten ist sämtlichen Filtern inhärent und eine wesentliche Eigenschaft des Fourier-Transformationspaars. Neben dem Gauß-Filter existieren ideale Hoch- und Tiefpassfilter. Statt eines stetigen Ü- bergangs von durchlässigen zu undurchlässigen Frequenzen bestimmt eine Cutoff- Frequenz 3.22). D 0 einen abrupten Übergang der durchzulassenden Frequenzen (siehe Abb.
35 32 Abb. 3.22: Der ideale Tiefpassfilter in der Frequenzdomäne Quelle: Gonzales, Woods (2002), S if ( D( u, v) D0 ) Der ideale Tiefpassfilter hat die Form : Huv (, ) =. 0 if ( D( u, v) > D0 ) Nur die Frequenzen mit der Entfernung Frequenz D 0 Duv (, ) zum Zentrum, die innerhalb der Cutoff- liegen, werden dabei durchgelassen. Allerdings bringt der ideale Tiefpassfilter Probleme mit sich, da bei abnehmender Cutoff-Frequenz, also stärkerem Herausfiltern der hohen Frequenzen, ringförmige Anomalien entstehen (siehe Abb oben). Dies ist leicht zu erklären, da der räumlich transformierte Filter eine glockenförmig abfallende Kurve darstellt, die in negativen und positiven Randschwingungen ausläuft, ähnlich den Wellen bei einem Stein, der ins Wasser geworfen wird. Die Randschwingungen treten dabei umso stärker auf, je schmaler der ideale Tiefpassfilter im Frequenzraum ist (Reziprozität). Dies ist im Funktionsverlauf in Abb rechts unten zu erkennen.
36 33 Abb. 3.23: Quelle: Vgl. Gonzales, Woods (2002), S. 170ff. Anwendung des idealen Tiefpassfilters mit Ringeffekten Neben dem Gauß-Tiefpassfilter (siehe Abb. 3.21, links) gibt es einen weiteren Filter, der diese Nachteile vermeidet, den Butterworth-Tiefpassfilter (s. Abb. 3.24). Er wird definiert als: 1 Huv (, ) =, mit Duv (, ), D wie beim idealen Tiefpassfilter [ Duv (, )/ D0 ] n Die Cutoff-Frequenz D 0 kann im Gegensatz zum idealen Tiefpassfilter nicht als Grenzübergang verstanden werden, sondern wird als Ort definiert, bei dem die Funktion zu einem gewissen Grad abgefallen ist. Dies ist bei der vorigen Formel ein 50 % Abfall, unabhängig davon, welcher Wert für n gewählt wird, da mit Duv (, ) = D0 der Exponentialterm immer 1 ergibt (s. Schnittpunkt im rechten Funktionsverlauf in Abb. 3.24). Der Butterworth-Tiefpassfilter kann durch die Wahl von n verschieden stark abfallen (siehe ebenfalls Abb. 3.24, rechts)., Wie der Funktionsverlauf zeigt, nähert sich der Filter dem idealen Tiefpassfilter an, je größer die Werte für n als Parameter gewählt werden. Wird anderer-
37 34 seits n =1 Filter auf. gesetzt, so weist der Butterworth-Tiefpassfilter Ähnlichkeit mit dem Gauß- Abb. 3.24: Der Butterworth-Tiefpassfilter Quelle: Vgl. Gonzales, Woods (2002), S Sowohl der Gauß, als auch der ideale und der Butterworth-Tiefpassfilter können als Hochpassfilter aus den zugehörigen Tiefpassfiltern auf folgende Weise bestimmt werden: H ( u, v) = 1 H ( u, v). hp hp lp H bezeichnet dabei den Hochpassfilter des zugehörigen Tiefpassfilters. Die Probleme des idealen Tiefpassfilters treten ebenso beim idealen Hochpassfilter auf, lediglich in invertierter Form. Es konnte ebenfalls gezeigt werden, dass der Butterworth-Filter das Bindeglied zwischen dem idealen und dem Gauß-Filter darstellt, indem der Parameter n die Steilheit des Funktionsverlaufs bestimmt und damit beide Filterarten annähern kann. H tp Abschließend werden einige andere Filter im Frequenzraum vorgestellt. Grundsätzliches Problem der Hoch-/ Tiefpassfilter ist, dass sie das Bild verdunkeln. Besonders beim Hochpassfilter wird der mittlere Grauwert nahezu weggefiltert (s. Abb. 3.21, rechts oben im Zentrum). Tiefpassfilter reduzieren zwar lediglich hochfrequente Anteile, der Effekt bleibt aber trotzdem beobachtbar. Lösung ist das Unsharp Masking. Ein hochpassgefiltertes Bild wird z. B. erzeugt, indem vom Original eine tiefpassgefilterte Version subtrahiert wird. Eine Verallgemeinerung ist das High-boost Filtern, bei dem das Original vor Subtraktion gewichtet wird und damit der Beitrag des Originals in seiner Intensität erhöht werden kann. Im folgenden Abschnitt wird im Zusammenhang mit der Bildrestaurierung auf den Wiener Filter eingegangen, der ebenfalls auf der Frequenzraumverarbeitung basiert.
38 35 4 Bildrestaurierung Die Bildrestaurierung hat die Aufgabe ein Bild, bei dem während der Bildaufnahme Störungen aufgetreten sind, zu rekonstruieren oder wiederzugewinnen. Bei den Restaurationstechniken wird die Verschlechterung modelliert und dann der umgekehrte Prozess angewendet, um das Originalbild wiederzugewinnen. Die äußere Erscheinung des Bildes wird verbessert, jedoch objektiv, da die Restaurationstechniken auf mathematischen oder Wahrscheinlichkeitsmodellen basieren. Bei der Bildrestaurierung besitzt man ein a-priori-wissen über die Art der vorliegenden Störung. A-priori-Wissen über die Bildstörung wird entweder vor oder während der Aufnahme gewonnen (z. B. Messung der Richtung und Geschwindigkeit einer Objektbewegung). Je besser diese bekannt ist, desto genauer ist das Ergebnis der Restaurierung. Mögliche Ursachen für Bildstörungen sind: Fehler bei der Bildaufnahme bzw. -übertragung Verschmierung aufgrund von Bewegungen oder Vibrationen der Aufnahmegeräte bzw. Objekte Defokussierung atmosphärische Turbulenzen (bei Luftbildern und in der Astronomie) additive Signale, welche die Helligkeits- und Kontrastwerte verändern Die Störungen werden durch Messen oder Schätzen separat mathematisch modelliert. Um die Verschlechterungsfunktion zu schätzen, gibt es drei Wege: Bildbeobachtung, Schätzen durch Experimente und mathematisches Modellieren. Durch Anwendung der inversen Störfunktion wird versucht, das Originalbild ohne Störungen möglicht gut zu rekonstruieren. Die beste Restaurierung kann erreicht werden, wenn ein stochastisches Modell zu Grunde liegt, wie z.b. beim Wiener Filter. Verschlechterungsprozess Es wird angenommen, dass man die Störung durch ein lineares System beschreiben kann. Der Verschlechterungsprozess wird als Verschlechterungsfunktion h modelliert, die zusammen mit einer additiven Störungsfunktion η(x,y) (die z.b. bei der Bildübertragung oder Bildgewinnung auftritt) auf einem Eingabebild f(x,y) arbeitet, um ein verschlechtertes Bild g(x,y) zu produzieren. Ist nun ein Bild g(x,y), ein wenig Wissen über die Verschlechte-
39 36 rungsfunktion h und über die additive Störungsfunktion η(x,y) gegeben, ist die Aufgabe der Restauration eine Schätzung f (x,y) des Originalbildes zu bekommen. Je mehr über die Störungen η und h bekannt ist, um so näher kommt die Schätzung von f (x,y) an das Original f(x,y) heran. In der räumlichen Domäne sieht das so aus: g(x,y) = h(x,y) * f(x,y) + η(x,y) (η(x,y) kann auch = 0 sein) In der Frequenzdomäne ergibt sich diese Formel: G(u,v) = H(u,v) F(u,v) +N(u,v) In der Frequenzdomäne entspricht der Faltung (*)die Multiplikation. f(x,y) Verschlechterungsfunktion h + g(x,y) Restaurationsfilter f (x,y) Verschlechterung η(x,y) Restauration Abb. 4.1: Quelle: eigene Darstellung nach Gonzales, Woods (2002), S Modell der Bildverschlechterung und -restauration Wiener Filter Dieser Filter gehört zu den stochastischen Bildrestaurierungsverfahren und führt eine optimale Bildverbesserung im statistischen Sinne durch. Unter vielen Ansätzen hat sich der Wiener Filter als universelles Werkzeug für diesen Verfahrensweg herausgestellt.
40 37 Abb. 4.2: Quelle: Lückenhaus, M. (1996). Grundlagen des Wiener-Filters und seine Anwendung in der Bildanalyse Ziel des Wiener Filters ist, unter Ausnutzung des a-priori-wissens über das Bildsignal und die Störung, ein neues Signal so zu berechnen, dass der quadratische Fehler ε², einer Schätzung des Originalbildes f, minimal wird. ε² = E { ( f(i,j) f (i,j) )² } E{} ist der Erwartungswert. Es ist anzunehmen, dass die additive Störungsfunktion und das Bild nicht in Beziehung stehen, dass eins von beiden den Mittelwert null hat und dass die Graustufen in der Schätzung eine lineare Funktion der Stufen in dem verschlechterten Bild sind. Geht man von diesen Bedingungen aus, so erhält man folgende Gleichung: F (u,v ) = H*(u,v)S f (u,v) S f (u,v) H(u,v) ² + S η (u,v) G(u,v) H*(u,v) = G(u,v) H(u,v) ² + S η (u,v)/ S f (u,v)
41 38 1 H(u,v) ² = G(u,v) H(u,v) H(u,v) ² + S η (u,v)/ S f (u,v) Wir benutzen hier die Tatsache, dass das Produkt einer komplexen Größe mit ihrer konjugierten das Gleiche ist, wie die komplexe Größe zum Quadrat, so ist es möglich, die oben gezeigten Umformungsschritte durchzuführen, um eine Formel zu erhalten, die weiter vereinfacht werden kann, wie später gezeigt. H(u,v) = Verschlechterungsfunktion (Fouriertransformation der Bildstörung) H*(u,v) H(u,v) ² = Komplexkonjugierte von H(u,v) = H*(u,v) H(u,v) S η (u,v) = N(u,v) ² S f (u,v) = F(u,v) ² G(u,v) = die spektrale Dichte des Rauschen = die spektrale Dichte des gestörten Bildes = die Transformation des gestörten Bildes Man kann S η (u,v), die spektrale Dichte des Rauschen, also die Stärke der Störung bei bestimmten additiven Störungsfunktionen als konstant betrachten. Dies ist ein Ansatz, der häufig benutzt wird, wenn diese Größe nicht bekannt ist oder nicht geschätzt werden kann, so ergibt sich die folgende Annäherung an unsere ursprüngliche Gleichung: F (u,v ) = 1 H(u,v) ² G(u,v) H(u,v) H(u,v) ² + K wobei K eine spezielle Konstante ist. Das restaurierte Bild in der räumlichen Domäne ist durch die inverse Fouriertransformation von der Frequenzdomänen-Schätzung F (u,v) gegeben. Um den Wiener Filter anwenden zu können müssen daher die Art der Störung H(u,v) und die statistischen Parameter des Rauschens bekannt sein. Wird S η (u,v) gleich null gesetzt, so wird aus dem Wiener Filter der inverse Filter, der hier nicht näher beschrieben wird.
42 39 Abb. 4.3: Restaurierung einer horizontalen Bewegungsunschärfe Quelle: o. A. Abb. 4.4: Restaurierung einer Defokussierung mit dem Wiener Filter Quelle: o. A.
43 40 5 Luftbildauswertung 5.1 Luftbildauswertung am Beispiel der vorgestellten Methoden Der letzte Themenbereich befasst sich im Speziellen mit der Aufbereitung von Luftbildern, die zusammen mit der Bildanalyse als ein Beispiel der Bildvorverarbeitung betrachtet werden sollen. Viele der bisher vorgestellten Verfahren finden auch in der Bearbeitung und Auswertung von Luftbildern Verwendung. Ist es bei der Aufnahme der Bilder zu einer Über- oder Unterbelichtung gekommen, so lassen sich die zu geringen Grauwertunterschiede durch eine Kontrastverbesserung ausgleichen. Diese Verbesserung kann z. B. durch logarithmische oder exponentielle Transformationen, durch Dehnung des Histogramms oder durch einen Histogrammausgleich geschehen. Dabei handelt es sich um punktbezogene Operatoren, die nicht durch Nachbarschaftswerte beeinflusst werden. Zur Reduzierung von gleichmäßigen Störungen, die z. B. durch Verwackelungen des Flugzeugs entstanden sind, eignen sich lokale Operatoren wie Glättungsfilter. Der Medianfilter ist dabei resistent gegenüber Ausreißern, dafür aber im Gegensatz zum Mittelwertfilter auch rechenintensiver. Die Bearbeitung von Bildern im Frequenzraum lässt sich auch auf Luftbilder anwenden. Damit wird eine globale und effiziente Bearbeitung ermöglicht. Mögliche Filter, die im Frequenzraum angewendet werden können, sind z. B. der Hoch- und Tiefpassfilter und das Unsharp Masking. Ein Hochpassfilter dient dabei zur Verschärfung von Kanten und zur Hervorhebung von Details wie z. B. Minenobjekten, da durch ihn geringere Grauwertunterschiede betont werden. Allerdings werden durch diesen Filter auch unerwünschte Rauschanteile oder sonstige Störungen betont, was zu einer Qualitätsminderung im Ergebnisbild führen kann. 13 Tiefpassfilter hingegen haben die entgegengesetzte Wirkung. Sie betonen große Grauwertunterschiede und führen somit zu einer Glättung des Bildes und einer Verwischung von Kanten. Dadurch gehen zwar Details verloren, für eine spätere Kantendetektion ist hingegen eine Glättung meist notwendig, um eine Reduktion auf die wesentlichen Strukturen eines Bildes wie z. B. Kanten vorzunehmen. 13 Vgl. Albertz (2001), S. 108.
44 41 Ein weiteres für die Luftbildauswertung wichtiges Verfahren ist das Unsharp Masking. Dabei können unerwünschte großflächige Grauwertunterschiede, z. B. entstanden durch Wolkenschatten, reduziert werden, so dass ein in der Gesamthelligkeit ausgeglichenes Bild entsteht 14. Abb. 5.1: Quelle: Vgl. Albertz (2001), S Reduzierung von Wolkenschatten durch Unsharp Masking Es zeigt sich also, dass die Auswahl der Bearbeitungsmethoden zur Bildverbesserung stark von der vorliegenden Störung und der Art der Weiterverarbeitung durch die Objekterkennung abhängt. Es findet daher ein Abwägungsprozess zwischen den einzelnen Verfahren zur Bildverbesserung statt, der zu einer Auswahl an Verfahren führen sollte, die das Bild möglichst gut auf eine spätere Objekterkennung vorbereitet. Neben diesen generellen Verfahren für die Bildvorverarbeitung werden bei der Aufbereitung von Luftbildern noch weitere Verfahren benötigt, um Luftbilder z. B. zu entzerren und zu einem zusammenhängenden Bild zusammenzufügen. Eine Entzerrung ist notwendig, da es durch das Aufnahmesystem, das Geländerelief oder eine geneigte Aufnahmerichtung zu Verzerrungen im Bild kommen kann Vgl. Abb Vgl. Abb. 5.2.
45 42 Abb. 5.2: Verzerrung eines Luftbildes bei geneigter Aufnahmerichtung Quelle: Albertz (2001), S. 75. Eine Entzerrung geschieht durch eine geometrische Transformation mit Hilfe von eindeutig bestimmten Passpunkten, aus denen dann die Transformationsfunktion berechnet wird. Diese Passpunkte dienen gleichzeitig auch dazu, das Luftbild zu rektifizieren, d. h. in ein bestimmtes geodätisches Koordinatensystem einzupassen. Dadurch ist es dann möglich, Punkten im Bild einen genauen Ort in der Wirklichkeit zuzuordnen, so dass mögliche Minenobjekte auch am Boden lokalisiert werden können. Um schließlich ein zusammenhängendes Bildmosaik eines Gebiets aus einzelnen Luftbildern erstellen zu können, werden Verknüpfungspunkte benötigt, die in den Überlappungsbereichen benachbarter Bilder liegen. 16 Die praktische Durchführung der Mosaikbildung ist dann im Prinzip wieder eine geometrische Transformation der Bilddaten. 17 Abb. 5.3: Schematisches Beispiel zur geometrischen Mosaikbildung. Quelle: Albertz (2001), S Vgl. Abb Albertz (2001), S. 118.
46 Landminenerkennung auf Luftbildern Eine weitere Möglichkeit die Auswertung von analogen oder digitalen Bildern zur Landminendetektion zu nutzen bietet die Fernerkundung, wenn auch nur in eingeschränktem Maße. Dabei geht es nicht voranging um die Erkennung einzelner Minen, sondern vielmehr um die Eingrenzung größerer Minenfelder. Dieses kann als ein Schritt auf dem Weg zur kompletten Minenräumung aufgefasst werden. In Gebieten, in denen noch keine Mittel zu Minenräumung zur Verfügung stehen, kann es daher schon hilfreich sein zu wissen, welche Gebiete potentiell gefährdet sind, um diese Gebiete speziell kennzeichnen zu können. Mit der Erkennung von Landminen auf Luftbildern beschäftigt sich u. a. das europäische Airborne Minefield Detection Pilot Project. Dabei werden auf Testfeldern in Belgien und Mozambique auch optische Sensoren getestet, die Bilder von 1-32 cm Auflösung aus einer Höhe von ca. 200 m liefern können. Das generelle Modell dieser Erkennung beruht darauf, dass Minen durch eine Strukturveränderung der Vegetation oder des Bodens erkannt werden können. 18 Dazu wurde ein Vorgehensschema entwickelt, das durch vier Verarbeitungsschritte gekennzeichnet ist. Zuerst werden Klassen für Vegetation, Bodenart usw. durch Merkmalsextraktion gebildet u. a. mit Hilfe von statistischen Kennwerten und der Fourier-Transformation. Dann werden die Merkmale ausgewählt, die sich am meisten unterscheiden, um eine Reduzierung der Merkmalsklassen zu erreichen. Der dritte Schritt ist die Aufstellung eines Modells zu jeder der vorher ausgewählten Merkmalsklassen. Jede Klasse kann dann durch einen Merkmalsvektor, eine Kovarianzmatrix und eine a priori Wahrscheinlichkeit beschrieben werden. Der Merkmalsvektor eines Objekts wird schließlich im vierten Schritt mit denen der verschiedenen Klassen verglichen, um Übereinstimmungen zu finden und somit Objekte klassifizieren zu können. Das Ergebnis einer solchen Segmentierung ist ein Binärbild, das mögliche Minenobjekte darstellt. Um falsch klassifizierte Pixel zu entfernen zu können ist allerdings zusätzliches Wissen über die Minenart und -größe nötig. Da mit Hilfe des vorgestellten Verfahrens einzelne Minen nur schwer auszumachen sind, wird versucht nach Minen in regelmäßigen Strukturen zu suchen, um somit Minenfelder besser abgrenzen zu können. Können solche regelmäßigen Strukturen wie z. B. eine Linie gefunden werden, so steigt dann auch gleichzeitig die Wahrscheinlichkeit, dass sich weitere Minen auf dieser Linie befinden, wodurch letztendlich die Suche nach Minen vereinfacht wird. 18 Vgl. Pizurica et. al (1999), S. 2.
47 44 Abb. 5.4: Quelle: Vgl. Pizurica et. al (1999), S. 2. Schritte der Minenfelderkennung auf Luftbildern: 1. Minenfeldregion, 2. Ergebnis der Minensuche, 3. Abgrenzung des Minenfeldes 5.3 Probleme der Luftbildauswertung Die generellen Probleme bei der Luftbildauswertung sind unterschiedlich. Durch eine zu geringe Auflösung und zu kleine Objektgröße wird die Chance geringer, die gesuchten Minen zu entdecken. Je kleiner die Minen und je älter das Minenfeld sind, desto kleiner die Wahrscheinlichkeit auf Erfolg. Das Alter ist insofern entscheidend, da mit zunehmendem Alter des Feldes die Vegetation zunimmt und somit die Minen überwachsen werden. Ein weiteres Problem besteht darin, dass es keine Möglichkeit gibt mit optischen Sensoren in der Form von Luftbildern Minen unter der Erdoberfläche zu orten. Die Erstellung von Luftbildern ist außerdem von den Wetterverhältnissen abhängig, so dass geeignete Wetterbedingungen wie z. B. eine klare Sicht herrschen müssen. Aufgrund diese Probleme war es bisher fast nur möglich Anti-Panzer-Minen zu erkennen, da Anti-Personen-Minen durch ihre geringere Größe keinen ausreichenden Kontrast auf den Bildern darstellten 19. Verbessert werden könnte die vorgestellte Methode durch weiteres a priori Wissen über das Gebiet und die Minen. Es können weiterer Layer hinzugenommen werden, die Informationen über Bodennutzung, z. B. durch Straßen, enthalten. Diese stelle eher sichere Bereiche dar. Dennoch ist die Luftbildauswertung eine Technik mit dessen Hilfe relativ schnell große Gebiete auf Minenfelder überprüft werden können, sofern die äußeren Bedingungen dazu günstig sind. Auch wenn diese Möglichkeit der Minenerkennung bisher hauptsächlich in 19 Vgl. Pizurica, Katartzis, Cornelis, Sahli (1999), S. 6.
48 45 Pilotprojekten eingesetzt und getestet wurde, könnte die Fernerkundung sofern die Auflösungen der Bilder besser und die Suchalgorithmen genauer werden zur Unterstützung der individuellen Minensuche am Boden beitragen.
49 46 Literaturverzeichnis Albertz, J.: Einführung in die Fernerkundung. Grundlagen der Interpretation von Luft- und Satellitenbildern. Wissenschaftliche Buchgesellschaft. 2. Aufl., Darmstadt S Gonzales R.C.; Woods, R.E.: Digital Image Processing. 2. Aufl., New Jersey S Gonzales, R.C.; Woods, E: Digital Image Processing. 2. Aufl., pdf, pter03.pdf. Abrufdatum Graber, G.: BACG Online. Graz. Abrufdatum Jiang, X. : Vorlesung Bildverarbeitung. Universität Münster S Abrufdatum Jiang, X. : Vorlesung Bildanalyse. Universität Münster Abrufdatum Lückenhaus, M.: Grundlagen des Wiener-Filters und seine Anwendung in der Bildanalyse. Diplomarbeit. München O. V.: Das elektromagnetische Spektrum. Abrufdatum Pandit, M.: Methoden der Digitalen Bildverarbeitung für die Anwendung. Fortschritt- Berichte VDI Reihe 10 Band 669. Düsseldorf S Pizurica, V.; Katartzis, A; Cornelis, J; Sahli, H: What can be expected from Computerised Image Analysis for Airborne Minefield Detection? Brussel S Abrufdatum Preim, B.: Vorlesung Computergrafik. Farbe (Wahrnehmung, Farbräume). Madgeburg S Abrufdatum Rehrmann, V.: Foliensammlung Vorlesung digitale Bildverarbeitung Abrufdatum Weitkamp, A.: Untersuchungen zum Einsatz von Laserscanningverfahren beim Monitoring der Deichvorlandentwicklung. Diplomarbeit. Hannover 2001.
50 47 Anhang A Einige Beispiele im Zusammenhang mit Filterung im Frequenzraum A.a Das Spektrum und der Phasenwinkel einer DFT Quelle: Bildausgaben eines Java-Programms
Einführung in die medizinische Bildverarbeitung WS 12/13
 Einführung in die medizinische Bildverarbeitung WS 12/13 Stephan Gimbel Kurze Wiederholung Pipeline Pipelinestufen können sich unterscheiden, beinhalten aber i.d.r. eine Stufe zur Bildvorverarbeitung zur
Einführung in die medizinische Bildverarbeitung WS 12/13 Stephan Gimbel Kurze Wiederholung Pipeline Pipelinestufen können sich unterscheiden, beinhalten aber i.d.r. eine Stufe zur Bildvorverarbeitung zur
1. Filterung im Ortsbereich 1.1 Grundbegriffe 1.2 Lineare Filter 1.3 Nicht-Lineare Filter 1.4 Separabele Filter 1.
 . Filterung im Ortsbereich. Grundbegriffe. Lineare Filter.3 Nicht-Lineare Filter.4 Separabele Filter.5 Implementierung. Filterung im Frequenzbereich. Fouriertransformation. Hoch-, Tief- und Bandpassfilter.3
. Filterung im Ortsbereich. Grundbegriffe. Lineare Filter.3 Nicht-Lineare Filter.4 Separabele Filter.5 Implementierung. Filterung im Frequenzbereich. Fouriertransformation. Hoch-, Tief- und Bandpassfilter.3
Bildverbesserung (Image Enhancement)
 Prof. Dr. Wolfgang Konen, Thomas Zielke Bildverbesserung (Image Enhancement) WS07 7.1 Konen, Zielke Der Prozess der Bildverbesserung (1) Bildverbesserung wird häufig dafür eingesetzt, die für einen menschlichen
Prof. Dr. Wolfgang Konen, Thomas Zielke Bildverbesserung (Image Enhancement) WS07 7.1 Konen, Zielke Der Prozess der Bildverbesserung (1) Bildverbesserung wird häufig dafür eingesetzt, die für einen menschlichen
Computergrafik 2: Filtern im Frequenzraum
 Computergrafik 2: Filtern im Frequenzraum Prof. Dr. Michael Rohs, Dipl.-Inform. Sven Kratz michael.rohs@ifi.lmu.de MHCI Lab, LMU München Folien teilweise von Andreas Butz, sowie von Klaus D. Tönnies (Grundlagen
Computergrafik 2: Filtern im Frequenzraum Prof. Dr. Michael Rohs, Dipl.-Inform. Sven Kratz michael.rohs@ifi.lmu.de MHCI Lab, LMU München Folien teilweise von Andreas Butz, sowie von Klaus D. Tönnies (Grundlagen
Graphische Datenverarbeitung und Bildverarbeitung
 Graphische Datenverarbeitung und Bildverarbeitung Hochschule Niederrhein Bildverbesserung - Filterung Graphische DV und BV, Regina Pohle,. Bildverbesserung - Filterung Einordnung in die Inhalte der Vorlesung
Graphische Datenverarbeitung und Bildverarbeitung Hochschule Niederrhein Bildverbesserung - Filterung Graphische DV und BV, Regina Pohle,. Bildverbesserung - Filterung Einordnung in die Inhalte der Vorlesung
Filter. Industrielle Bildverarbeitung, Vorlesung No M. O. Franz
 Filter Industrielle Bildverarbeitung, Vorlesung No. 5 1 M. O. Franz 07.11.2007 1 falls nicht anders vermerkt, sind die Abbildungen entnommen aus Burger & Burge, 2005. Übersicht 1 Lineare Filter 2 Formale
Filter Industrielle Bildverarbeitung, Vorlesung No. 5 1 M. O. Franz 07.11.2007 1 falls nicht anders vermerkt, sind die Abbildungen entnommen aus Burger & Burge, 2005. Übersicht 1 Lineare Filter 2 Formale
2D Graphik: Bildverbesserung. Vorlesung 2D Graphik Andreas Butz, Otmar Hilliges Freitag, 2. Dezember 2005
 2D Graphik: Bildverbesserung Vorlesung 2D Graphik Andreas Butz, Otmar Hilliges Freitag, 2. Dezember 2005 Themen heute Rauschen, Entropie Bildverbesserung Punktbasiert Flächenbasiert Kantenbasiert Was ist
2D Graphik: Bildverbesserung Vorlesung 2D Graphik Andreas Butz, Otmar Hilliges Freitag, 2. Dezember 2005 Themen heute Rauschen, Entropie Bildverbesserung Punktbasiert Flächenbasiert Kantenbasiert Was ist
Bildverarbeitung: Filterung. D. Schlesinger () Bildverarbeitung: Filterung 1 / 17
 Bildverarbeitung: Filterung D. Schlesinger () Bildverarbeitung: Filterung 1 / 17 Allgemeines Klassische Anwendung: Entrauschung (Fast) jeder Filter basiert auf einem Modell (Annahme): Signal + Rauschen
Bildverarbeitung: Filterung D. Schlesinger () Bildverarbeitung: Filterung 1 / 17 Allgemeines Klassische Anwendung: Entrauschung (Fast) jeder Filter basiert auf einem Modell (Annahme): Signal + Rauschen
Bildverarbeitung Herbstsemester
 Bildverarbeitung Herbstsemester Herbstsemester 2009 2012 Filter Filter 1 Inhalt Lineare und nichtlineare Filter Glättungsfilter (z.b. Gauss-Filter) Differenzfilter (z.b. Laplace-Filter) Lineare Faltung
Bildverarbeitung Herbstsemester Herbstsemester 2009 2012 Filter Filter 1 Inhalt Lineare und nichtlineare Filter Glättungsfilter (z.b. Gauss-Filter) Differenzfilter (z.b. Laplace-Filter) Lineare Faltung
Bildverbesserung. Frequenz-, Punkt- und Maskenoperationen. Backfrieder-Hagenberg
 Bildverbesserung Frequenz-, Punkt- und Maskenoperationen Filtern im Frequenzraum Fouriertransformation f(x)->f( ) Filter-Multiplikation F =FxH Rücktransformation F ( )->f (x) local-domain frequency-domain
Bildverbesserung Frequenz-, Punkt- und Maskenoperationen Filtern im Frequenzraum Fouriertransformation f(x)->f( ) Filter-Multiplikation F =FxH Rücktransformation F ( )->f (x) local-domain frequency-domain
Vorkurs: Mathematik für Informatiker
 Vorkurs: Mathematik für Informatiker Teil 4 Wintersemester 2017/18 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2017 Steven Köhler Wintersemester 2017/18 Inhaltsverzeichnis Teil 1 Teil
Vorkurs: Mathematik für Informatiker Teil 4 Wintersemester 2017/18 Steven Köhler mathe@stevenkoehler.de mathe.stevenkoehler.de 2 c 2017 Steven Köhler Wintersemester 2017/18 Inhaltsverzeichnis Teil 1 Teil
Systemtheorie abbildender Systeme
 Bandbegrenzung Bild in (b) nicht band-begrenzt: scharfe Kanten = Dirac-Funktionen = weißes Spektrum Erfordert Tapering vor Digitalisierung (Multiplikation mit geeigneter Fensterfunktion; auf Null drücken
Bandbegrenzung Bild in (b) nicht band-begrenzt: scharfe Kanten = Dirac-Funktionen = weißes Spektrum Erfordert Tapering vor Digitalisierung (Multiplikation mit geeigneter Fensterfunktion; auf Null drücken
EVC Repetitorium Blender
 EVC Repetitorium Blender Michael Hecher Felix Kreuzer Institute of Computer Graphics and Algorithms Vienna University of Technology INSTITUTE OF COMPUTER GRAPHICS AND ALGORITHMS Filter Transformationen
EVC Repetitorium Blender Michael Hecher Felix Kreuzer Institute of Computer Graphics and Algorithms Vienna University of Technology INSTITUTE OF COMPUTER GRAPHICS AND ALGORITHMS Filter Transformationen
Graphische Datenverarbeitung und Bildverarbeitung
 Graphische Datenverarbeitung und Bildverarbeitung Hochschule Niederrhein Fourier-Transformation Graphische DV und BV, Regina Pohle, 8. Fourier-Transformation 1 Einordnung in die Inhalte der Vorlesung Einführung
Graphische Datenverarbeitung und Bildverarbeitung Hochschule Niederrhein Fourier-Transformation Graphische DV und BV, Regina Pohle, 8. Fourier-Transformation 1 Einordnung in die Inhalte der Vorlesung Einführung
Bildpunkt auf dem Gitter: Pixel (picture element) (manchmal auch Pel)
 4. Digitalisierung und Bildoperationen 4.1 Digitalisierung (Sampling, Abtastung) Rasterung auf 2D-Bildmatrix mathematisch: Abb. einer 2-dim. Bildfunktion mit kontinuierlichem Definitionsbereich auf digitales
4. Digitalisierung und Bildoperationen 4.1 Digitalisierung (Sampling, Abtastung) Rasterung auf 2D-Bildmatrix mathematisch: Abb. einer 2-dim. Bildfunktion mit kontinuierlichem Definitionsbereich auf digitales
Digitale Bildverarbeitung (DBV)
 Digitale Bildverarbeitung (DBV) Prof. Dr. Ing. Heinz Jürgen Przybilla Labor für Photogrammetrie Email: heinz juergen.przybilla@hs bochum.de Tel. 0234 32 10517 Sprechstunde: Montags 13 14 Uhr und nach Vereinbarung
Digitale Bildverarbeitung (DBV) Prof. Dr. Ing. Heinz Jürgen Przybilla Labor für Photogrammetrie Email: heinz juergen.przybilla@hs bochum.de Tel. 0234 32 10517 Sprechstunde: Montags 13 14 Uhr und nach Vereinbarung
Digitale Bildverarbeitung (DBV)
 Digitale Bildverarbeitung (DBV) Prof. Dr. Ing. Heinz Jürgen Przybilla Labor für Photogrammetrie Email: heinz juergen.przybilla@hs bochum.de Tel. 0234 32 10517 Sprechstunde: Montags 13 14 Uhr und nach Vereinbarung
Digitale Bildverarbeitung (DBV) Prof. Dr. Ing. Heinz Jürgen Przybilla Labor für Photogrammetrie Email: heinz juergen.przybilla@hs bochum.de Tel. 0234 32 10517 Sprechstunde: Montags 13 14 Uhr und nach Vereinbarung
Mathematischer Vorkurs für Physiker WS 2012/13: Vorlesung 1
 TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 2012/13: Vorlesung 1 Komplexe Zahlen Das Auffinden aller Nullstellen von algebraischen Gleichungen ist ein Grundproblem, das in der Physik
TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 2012/13: Vorlesung 1 Komplexe Zahlen Das Auffinden aller Nullstellen von algebraischen Gleichungen ist ein Grundproblem, das in der Physik
Digitale Bildverarbeitung (DBV)
 Digitale Bildverarbeitung (DBV) Prof. Dr. Ing. Heinz Jürgen Przybilla Labor für Photogrammetrie Email: heinz juergen.przybilla@hs bochum.de Tel. 0234 32 10517 Sprechstunde: Montags 13 14 Uhr und nach Vereinbarung
Digitale Bildverarbeitung (DBV) Prof. Dr. Ing. Heinz Jürgen Przybilla Labor für Photogrammetrie Email: heinz juergen.przybilla@hs bochum.de Tel. 0234 32 10517 Sprechstunde: Montags 13 14 Uhr und nach Vereinbarung
Struktur des menschlichen Auges. Bildgebende Verfahren in der Medizin und medizinische Bildverarbeitung Bildverbesserung 2 / 99
 Struktur des menschlichen Auges 2 / 99 Detektoren im Auge Ca. 100 150 Mio. Stäbchen Ca. 1 Mio. Zäpfchen 3 / 99 Zapfen Entlang der Sehachse, im Fokus Tagessehen (Photopisches Sehen) Scharfsehen Farbsehen
Struktur des menschlichen Auges 2 / 99 Detektoren im Auge Ca. 100 150 Mio. Stäbchen Ca. 1 Mio. Zäpfchen 3 / 99 Zapfen Entlang der Sehachse, im Fokus Tagessehen (Photopisches Sehen) Scharfsehen Farbsehen
Digitale Bildverarbeitung Einheit 6 Punktoperationen
 Digitale Bildverarbeitung Einheit 6 Punktoperationen Lehrauftrag WS 06/07 Fachbereich M+I der FH-Offenburg Dr. Bernard Haasdonk Albert-Ludwigs-Universität Freiburg Ziele der Einheit Elementare Bildverbesserung
Digitale Bildverarbeitung Einheit 6 Punktoperationen Lehrauftrag WS 06/07 Fachbereich M+I der FH-Offenburg Dr. Bernard Haasdonk Albert-Ludwigs-Universität Freiburg Ziele der Einheit Elementare Bildverbesserung
Funktionen und andere Zuordnungen
 Funktionen und andere Zuordnungen Rainer Hauser November 2011 1 Allgemeine Zuordnungen 1.1 Pfeildarstellung von Zuordnungen Sätze wie Das ist der Schlüssel zu diesem Schloss und Hänsel ist der Bruder von
Funktionen und andere Zuordnungen Rainer Hauser November 2011 1 Allgemeine Zuordnungen 1.1 Pfeildarstellung von Zuordnungen Sätze wie Das ist der Schlüssel zu diesem Schloss und Hänsel ist der Bruder von
FILTER UND FALTUNGEN
 Ausarbeitung zum Vortrag von Daniel Schmitzek im Seminar Verarbeitung und Manipulation digitaler Bilder I n h a l t. Der Begriff des Filters 3 2. Faltungsfilter 4 2. Glättungsfilter 4 2.2 Filter zur Kantendetektion
Ausarbeitung zum Vortrag von Daniel Schmitzek im Seminar Verarbeitung und Manipulation digitaler Bilder I n h a l t. Der Begriff des Filters 3 2. Faltungsfilter 4 2. Glättungsfilter 4 2.2 Filter zur Kantendetektion
Bildverarbeitung: Fourier-Transformation. D. Schlesinger () BV: Fourier-Transformation 1 / 16
 Bildverarbeitung: Fourier-Transformation D. Schlesinger () BV: Fourier-Transformation 1 / 16 Allgemeines Bilder sind keine Vektoren. Bilder sind Funktionen x : D C (Menge der Pixel in die Menge der Farbwerte).
Bildverarbeitung: Fourier-Transformation D. Schlesinger () BV: Fourier-Transformation 1 / 16 Allgemeines Bilder sind keine Vektoren. Bilder sind Funktionen x : D C (Menge der Pixel in die Menge der Farbwerte).
Computergrafik 2: Übung 6. Korrelation im Orts- und Frequenzraum, Filtern im Frequenzraum, Wiener Filter
 Computergrafik : Übung 6 Korrelation im Orts- und Frequenzraum, Filtern im Frequenzraum, Wiener Filter Quiz Warum Filtern im Frequenzraum? Ideales Tiefpassfilter? Parameter? Eigenschaften? Butterworth-Filter?
Computergrafik : Übung 6 Korrelation im Orts- und Frequenzraum, Filtern im Frequenzraum, Wiener Filter Quiz Warum Filtern im Frequenzraum? Ideales Tiefpassfilter? Parameter? Eigenschaften? Butterworth-Filter?
Einführungsbeispiel Kostenfunktion
 Einführungsbeispiel Kostenfunktion Sie bauen eine Fabrik für Luxusautos auf und steigern die Produktion jeden Monat um 1000 Stück. Dabei messen Sie die jeweiligen Kosten und stellen sie grafisch dar. Die
Einführungsbeispiel Kostenfunktion Sie bauen eine Fabrik für Luxusautos auf und steigern die Produktion jeden Monat um 1000 Stück. Dabei messen Sie die jeweiligen Kosten und stellen sie grafisch dar. Die
Objekterkennung durch Vergleich von Farben. Videoanalyse Dr. Stephan Kopf HWS2007 Kapitel 5: Objekterkennung
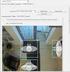 Objekterkennung durch Vergleich von Farben 48 Farbräume (I) Definitionen: Farbe: Sinnesempfindung (keine physikalische Eigenschaft), falls Licht einer bestimmten Wellenlänge auf die Netzhaut des Auges
Objekterkennung durch Vergleich von Farben 48 Farbräume (I) Definitionen: Farbe: Sinnesempfindung (keine physikalische Eigenschaft), falls Licht einer bestimmten Wellenlänge auf die Netzhaut des Auges
Diskrete Signalverarbeitung und diskrete Systeme
 Diskrete Signalverarbeitung und diskrete Systeme Computer- basierte Verarbeitung von Signalen und Realisierung von Systemverhalten erfordern diskrete Signale und diskrete Systembeschreibungen. Wegen der
Diskrete Signalverarbeitung und diskrete Systeme Computer- basierte Verarbeitung von Signalen und Realisierung von Systemverhalten erfordern diskrete Signale und diskrete Systembeschreibungen. Wegen der
Ajdovic/Mühl Farbmodelle FARBMODELLE
 FARBMODELLE Grundlagen: Gegenstände, die von einer Lichtquelle beleuchtet werden, reflektieren und absorbieren jeweils einen Teil des Lichts. Dabei wird das von den Gegenständen reflektierte Licht vom
FARBMODELLE Grundlagen: Gegenstände, die von einer Lichtquelle beleuchtet werden, reflektieren und absorbieren jeweils einen Teil des Lichts. Dabei wird das von den Gegenständen reflektierte Licht vom
Als Summendarstellung der komplexen Zahl bezeichnen wir den bekannten Ausdruck
 A.1 MATHEMATISCHE GRUNDLAGEN In diesem Abschnitt werden die mathematischen Grundlagen zusammengestellt, die für die Behandlung von Übertragungssystemen erforderlich sind. Unter anderem sind dies die komplexen
A.1 MATHEMATISCHE GRUNDLAGEN In diesem Abschnitt werden die mathematischen Grundlagen zusammengestellt, die für die Behandlung von Übertragungssystemen erforderlich sind. Unter anderem sind dies die komplexen
Parallele Algorithmen in der Bildverarbeitung
 Seminar über Algorithmen - SoSe 2009 Parallele Algorithmen in der Bildverarbeitung von Christopher Keiner 1 Allgemeines 1.1 Einleitung Parallele Algorithmen gewinnen immer stärker an Bedeutung. Es existieren
Seminar über Algorithmen - SoSe 2009 Parallele Algorithmen in der Bildverarbeitung von Christopher Keiner 1 Allgemeines 1.1 Einleitung Parallele Algorithmen gewinnen immer stärker an Bedeutung. Es existieren
Segmentierung. Vorlesung FH-Hagenberg SEM
 Segmentierung Vorlesung FH-Hagenberg SEM Segmentierung: Definition Die Pixel eines Bildes A={a i }, i=1:n, mit N der Anzahl der Pixel, werden in Teilmengen S i unterteilt. Die Teilmengen sind disjunkt
Segmentierung Vorlesung FH-Hagenberg SEM Segmentierung: Definition Die Pixel eines Bildes A={a i }, i=1:n, mit N der Anzahl der Pixel, werden in Teilmengen S i unterteilt. Die Teilmengen sind disjunkt
Computergraphik 1 2. Teil: Bildverarbeitung. Fouriertransformation Ende FFT, Bildrestauration mit PSF Transformation, Interpolation
 Computergraphik 1 2. Teil: Bildverarbeitung Fouriertransformation Ende FFT, Bildrestauration mit PSF Transformation, Interpolation LMU München Medieninformatik Butz/Hoppe Computergrafik 1 SS2009 1 2 Repräsentation
Computergraphik 1 2. Teil: Bildverarbeitung Fouriertransformation Ende FFT, Bildrestauration mit PSF Transformation, Interpolation LMU München Medieninformatik Butz/Hoppe Computergrafik 1 SS2009 1 2 Repräsentation
Graphische Datenverarbeitung und Bildverarbeitung
 Graphische Datenverarbeitung und Bildverarbeitung Hochschule Niederrhein Bildverbesserung - Grauwertmodifikation Graphische DV und BV, Regina Pohle, 10. Bildverbesserung - Grauwertmodifikation 1 Einordnung
Graphische Datenverarbeitung und Bildverarbeitung Hochschule Niederrhein Bildverbesserung - Grauwertmodifikation Graphische DV und BV, Regina Pohle, 10. Bildverbesserung - Grauwertmodifikation 1 Einordnung
Erfüllt eine Funktion f für eine feste positive Zahl p und sämtliche Werte t des Definitionsbereichs die Gleichung
 34 Schwingungen Im Zusammenhang mit Polardarstellungen trifft man häufig auf Funktionen, die Schwingungen beschreiben und deshalb für den Ingenieur von besonderer Wichtigkeit sind Fast alle in der Praxis
34 Schwingungen Im Zusammenhang mit Polardarstellungen trifft man häufig auf Funktionen, die Schwingungen beschreiben und deshalb für den Ingenieur von besonderer Wichtigkeit sind Fast alle in der Praxis
Fourier Optik. Zeit. Zeit
 Fourier Optik Beispiel zur Fourier-Zerlegung: diskretes Spektrum von Sinus-Funktionen liefert in einer gewichteten Überlagerung näherungsweise eine Rechteckfunktion Sin t Sin 3t Sin 5t Sin 7t Sin 9t Sin
Fourier Optik Beispiel zur Fourier-Zerlegung: diskretes Spektrum von Sinus-Funktionen liefert in einer gewichteten Überlagerung näherungsweise eine Rechteckfunktion Sin t Sin 3t Sin 5t Sin 7t Sin 9t Sin
Grundlagen der Bildverarbeitung: Übung 3
 Grundlagen der Bildverarbeitung: Übung 3 Michael Korn Raum: BC414, Tel.: 0203-379 - 3583, E-Mail: michael.korn@uni-due.de Michael Korn (michael.korn@uni-due.de) Grundlagen der Bildverarbeitung: Übung 3
Grundlagen der Bildverarbeitung: Übung 3 Michael Korn Raum: BC414, Tel.: 0203-379 - 3583, E-Mail: michael.korn@uni-due.de Michael Korn (michael.korn@uni-due.de) Grundlagen der Bildverarbeitung: Übung 3
Modul Digitale Bildverarbeitung SS16 Bestandteile der Lehrveranstaltung und Prüfung: Vorlesungen Übungsserien Praktika (ImageJ) bis Mai 2016 Projekt
 Modul Digitale Bildverarbeitung SS16 Bestandteile der Lehrveranstaltung und Prüfung: Vorlesungen Übungsserien Praktika (ImageJ) bis Mai 2016 Projekt im Juni 2016 Themen: Digitale Bilder, Eigenschaften
Modul Digitale Bildverarbeitung SS16 Bestandteile der Lehrveranstaltung und Prüfung: Vorlesungen Übungsserien Praktika (ImageJ) bis Mai 2016 Projekt im Juni 2016 Themen: Digitale Bilder, Eigenschaften
Einführung. Ablesen von einander zugeordneten Werten
 Einführung Zusammenhänge zwischen Größen wie Temperatur, Geschwindigkeit, Lautstärke, Fahrstrecke, Preis, Einkommen, Steuer etc. werden mit beschrieben. Eine Zuordnung f, die jedem x A genau ein y B zuweist,
Einführung Zusammenhänge zwischen Größen wie Temperatur, Geschwindigkeit, Lautstärke, Fahrstrecke, Preis, Einkommen, Steuer etc. werden mit beschrieben. Eine Zuordnung f, die jedem x A genau ein y B zuweist,
Addition, Subtraktion und Multiplikation von komplexen Zahlen z 1 = (a 1, b 1 ) und z 2 = (a 2, b 2 ):
 Komplexe Zahlen Definition 1. Eine komplexe Zahl z ist ein geordnetes Paar reeller Zahlen (a, b). Wir nennen a den Realteil von z und b den Imaginärteil von z, geschrieben a = Re z, b = Im z. Komplexe
Komplexe Zahlen Definition 1. Eine komplexe Zahl z ist ein geordnetes Paar reeller Zahlen (a, b). Wir nennen a den Realteil von z und b den Imaginärteil von z, geschrieben a = Re z, b = Im z. Komplexe
Anmerkung: Falls f(x) nicht ganz glatt ist, sondern nur stückweise stetig differenzierbar ist (d.h. Sprünge hat), gilt (Satz v.
 Fourier-Reihen für periodische Funktionen Sei periodisch, mit Periode L: Auch für diesen Fall gilt die Fourier- Reihen-Darstellung (b.3), mit : (b.3) (und stückweise stetig differenzierbar) (c.5) Integral
Fourier-Reihen für periodische Funktionen Sei periodisch, mit Periode L: Auch für diesen Fall gilt die Fourier- Reihen-Darstellung (b.3), mit : (b.3) (und stückweise stetig differenzierbar) (c.5) Integral
Skalare Differenzialgleichungen
 3 Skalare Differenzialgleichungen Differenzialgleichungen stellen eine Beziehung her zwischen einer oder mehreren Funktionen und ihren Ableitungen. Da Ableitungen Veränderungen beschreiben, modellieren
3 Skalare Differenzialgleichungen Differenzialgleichungen stellen eine Beziehung her zwischen einer oder mehreren Funktionen und ihren Ableitungen. Da Ableitungen Veränderungen beschreiben, modellieren
Bildverarbeitung Herbstsemester Punktoperationen
 Bildverarbeitung Herbstsemester 2012 Punktoperationen 1 Inhalt Histogramm und dessen Interpretation Definition von Punktoperationen Änderungen der Bildintensität Linearer Histogrammausgleich Gammakorrektur
Bildverarbeitung Herbstsemester 2012 Punktoperationen 1 Inhalt Histogramm und dessen Interpretation Definition von Punktoperationen Änderungen der Bildintensität Linearer Histogrammausgleich Gammakorrektur
Grundlagen der Computer-Tomographie
 Grundlagen der Computer-Tomographie Quellenangabe Die folgenden Folien sind zum Teil dem Übersichtsvortrag: imbie.meb.uni-bonn.de/epileptologie/staff/lehnertz/ct1.pdf entnommen. Als Quelle für die mathematischen
Grundlagen der Computer-Tomographie Quellenangabe Die folgenden Folien sind zum Teil dem Übersichtsvortrag: imbie.meb.uni-bonn.de/epileptologie/staff/lehnertz/ct1.pdf entnommen. Als Quelle für die mathematischen
Diskrete Cosinustransformation (DCT)
 Fachbereich Medieninformatik Hochschule Harz Diskrete Cosinustransformation (DCT) Referat Björn Wöldecke 10954 Abgabe: 15.01.2007 Inhaltsverzeichnis Einleitung / Vorwort... 1. Methoden zur Datenreduktion...
Fachbereich Medieninformatik Hochschule Harz Diskrete Cosinustransformation (DCT) Referat Björn Wöldecke 10954 Abgabe: 15.01.2007 Inhaltsverzeichnis Einleitung / Vorwort... 1. Methoden zur Datenreduktion...
5. Spezielle stetige Verteilungen
 5. Spezielle stetige Verteilungen 5.1 Stetige Gleichverteilung Eine Zufallsvariable X folgt einer stetigen Gleichverteilung mit den Parametern a und b, wenn für die Dichtefunktion von X gilt: f x = 1 für
5. Spezielle stetige Verteilungen 5.1 Stetige Gleichverteilung Eine Zufallsvariable X folgt einer stetigen Gleichverteilung mit den Parametern a und b, wenn für die Dichtefunktion von X gilt: f x = 1 für
Mathematik II Frühjahrssemester 2013
 Mathematik II Frühjahrssemester 213 Prof. Dr. Erich Walter Farkas Kapitel 7: Lineare Algebra Kapitel 7.5: Eigenwerte und Eigenvektoren einer quadratischen Matrix Prof. Dr. Erich Walter Farkas Mathematik
Mathematik II Frühjahrssemester 213 Prof. Dr. Erich Walter Farkas Kapitel 7: Lineare Algebra Kapitel 7.5: Eigenwerte und Eigenvektoren einer quadratischen Matrix Prof. Dr. Erich Walter Farkas Mathematik
37 Gauß-Algorithmus und lineare Gleichungssysteme
 37 Gauß-Algorithmus und lineare Gleichungssysteme 37 Motivation Lineare Gleichungssysteme treten in einer Vielzahl von Anwendungen auf und müssen gelöst werden In Abschnitt 355 haben wir gesehen, dass
37 Gauß-Algorithmus und lineare Gleichungssysteme 37 Motivation Lineare Gleichungssysteme treten in einer Vielzahl von Anwendungen auf und müssen gelöst werden In Abschnitt 355 haben wir gesehen, dass
Morphologische Filter
 Morphologische Filter Industrielle Bildverarbeitung, Vorlesung No. 8 1 M. O. Franz 28.11.2007 1 falls nicht anders vermerkt, sind die Abbildungen entnommen aus Burger & Burge, 2005. Übersicht 1 Morphologische
Morphologische Filter Industrielle Bildverarbeitung, Vorlesung No. 8 1 M. O. Franz 28.11.2007 1 falls nicht anders vermerkt, sind die Abbildungen entnommen aus Burger & Burge, 2005. Übersicht 1 Morphologische
Wahrscheinlichkeitsverteilungen
 Universität Bielefeld 3. Mai 2005 Wahrscheinlichkeitsrechnung Wahrscheinlichkeitsrechnung Das Ziehen einer Stichprobe ist die Realisierung eines Zufallsexperimentes. Die Wahrscheinlichkeitsrechnung betrachtet
Universität Bielefeld 3. Mai 2005 Wahrscheinlichkeitsrechnung Wahrscheinlichkeitsrechnung Das Ziehen einer Stichprobe ist die Realisierung eines Zufallsexperimentes. Die Wahrscheinlichkeitsrechnung betrachtet
13 Mehrdimensionale Zufallsvariablen Zufallsvektoren
 3 Mehrdimensionale Zufallsvariablen Zufallsvektoren Bisher haben wir uns ausschließlich mit Zufallsexperimenten beschäftigt, bei denen die Beobachtung eines einzigen Merkmals im Vordergrund stand. In diesem
3 Mehrdimensionale Zufallsvariablen Zufallsvektoren Bisher haben wir uns ausschließlich mit Zufallsexperimenten beschäftigt, bei denen die Beobachtung eines einzigen Merkmals im Vordergrund stand. In diesem
Digitale Bildverarbeitung (DBV)
 Digitale Bildverarbeitung (DBV) Prof. Dr. Ing. Heinz Jürgen Przybilla Labor für Photogrammetrie Email: heinz juergen.przybilla@hs bochum.de Tel. 0234 32 10517 Sprechstunde: Montags 13 14 Uhr und nach Vereinbarung
Digitale Bildverarbeitung (DBV) Prof. Dr. Ing. Heinz Jürgen Przybilla Labor für Photogrammetrie Email: heinz juergen.przybilla@hs bochum.de Tel. 0234 32 10517 Sprechstunde: Montags 13 14 Uhr und nach Vereinbarung
Übung zu Einführung in die Informatik # 14
 Übung zu Einführung in die Informatik # 14 Tobias Schill tschill@techfak.uni-bielefeld.de 12. Februar 2016 Aktualisiert am 12. Februar 2016 um 11:13 Erstklausur: Mi, 24.02.2016 von 10-12Uhr Antworten von
Übung zu Einführung in die Informatik # 14 Tobias Schill tschill@techfak.uni-bielefeld.de 12. Februar 2016 Aktualisiert am 12. Februar 2016 um 11:13 Erstklausur: Mi, 24.02.2016 von 10-12Uhr Antworten von
Digitalisierung. Vorlesung FH-Hagenberg DSB
 Digitalisierung Vorlesung FH-Hagenberg DSB Abbildungssysteme Camera obscura einfachstes Abbildungssystem bekannt seit dem Altertum Licht fällt durch eine Lochblende in das Innere einer abgedunkelten Kammer
Digitalisierung Vorlesung FH-Hagenberg DSB Abbildungssysteme Camera obscura einfachstes Abbildungssystem bekannt seit dem Altertum Licht fällt durch eine Lochblende in das Innere einer abgedunkelten Kammer
$Id: linabb.tex,v /01/09 13:27:34 hk Exp hk $
 Mathematik für Ingenieure I, WS 8/9 Freitag 9. $Id: linabb.tex,v.3 9//9 3:7:34 hk Exp hk $ II. Lineare Algebra 9 Lineare Abbildungen 9. Lineare Abbildungen Der folgende Satz gibt uns eine einfachere Möglichkeit
Mathematik für Ingenieure I, WS 8/9 Freitag 9. $Id: linabb.tex,v.3 9//9 3:7:34 hk Exp hk $ II. Lineare Algebra 9 Lineare Abbildungen 9. Lineare Abbildungen Der folgende Satz gibt uns eine einfachere Möglichkeit
Mathematik II Frühlingsemester 2015 Kapitel 8: Lineare Algebra 8.5 Eigenwerte und Eigenvektoren
 Mathematik II Frühlingsemester 215 Kapitel 8: Lineare Algebra 8.5 Eigenwerte und Eigenvektoren www.math.ethz.ch/education/bachelor/lectures/fs215/other/mathematik2 biol Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/
Mathematik II Frühlingsemester 215 Kapitel 8: Lineare Algebra 8.5 Eigenwerte und Eigenvektoren www.math.ethz.ch/education/bachelor/lectures/fs215/other/mathematik2 biol Prof. Dr. Erich Walter Farkas http://www.math.ethz.ch/
Filterprogrammierung in Gimp
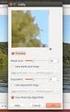 Rüdiger Timpe Alexander Bertschik Filterprogrammierung in Gimp Ein Vortrag im Rahmen des Seminars Manipulation und Verarbeitung digitaler Bilder Inhalt Aufgabenstellung und Motivation...3 Auswahl der Filter...3
Rüdiger Timpe Alexander Bertschik Filterprogrammierung in Gimp Ein Vortrag im Rahmen des Seminars Manipulation und Verarbeitung digitaler Bilder Inhalt Aufgabenstellung und Motivation...3 Auswahl der Filter...3
Lage- und Streuungsparameter
 Lage- und Streuungsparameter Beziehen sich auf die Verteilung der Ausprägungen von intervall- und ratio-skalierten Variablen Versuchen, diese Verteilung durch Zahlen zu beschreiben, statt sie graphisch
Lage- und Streuungsparameter Beziehen sich auf die Verteilung der Ausprägungen von intervall- und ratio-skalierten Variablen Versuchen, diese Verteilung durch Zahlen zu beschreiben, statt sie graphisch
Praktikum-Meßtechnik Verfasser: Dr. H. Bergelt
 TU Bergakademie Freiberg Praktikum-Meßtechnik Verfasser: Dr. H. Bergelt Filter in der Bildverarbeitung. Einleitung Digitale Filter gehören zu den wirkungsvollsten Methoden der Bildverarbeitung. Wir können
TU Bergakademie Freiberg Praktikum-Meßtechnik Verfasser: Dr. H. Bergelt Filter in der Bildverarbeitung. Einleitung Digitale Filter gehören zu den wirkungsvollsten Methoden der Bildverarbeitung. Wir können
Angewandte Mathematik und Programmierung
 Angewandte Mathematik und Programmierung Einführung in das Konzept der objektorientierten Anwendungen zu mathematischen Rechnens SS2013 Inhalt Fourier Reihen Sehen wir in 2 Wochen Lösung der lin. Dgln.
Angewandte Mathematik und Programmierung Einführung in das Konzept der objektorientierten Anwendungen zu mathematischen Rechnens SS2013 Inhalt Fourier Reihen Sehen wir in 2 Wochen Lösung der lin. Dgln.
Übersicht der Vorlesung
 Übersicht der Vorlesung. Einführung. Bildverarbeitung. Morphologische Operationen 4. Bildsegmentierung 5. Merkmale von Objekten 6. Klassifikation 7. Dreidimensionale Bildinterpretation 8. Bewegungsanalyse
Übersicht der Vorlesung. Einführung. Bildverarbeitung. Morphologische Operationen 4. Bildsegmentierung 5. Merkmale von Objekten 6. Klassifikation 7. Dreidimensionale Bildinterpretation 8. Bewegungsanalyse
Digitale Bilder. Ein Referat von Jacqueline Schäfer und Lea Pohl Am
 Digitale Bilder Ein Referat von Jacqueline Schäfer und Lea Pohl Am 06.05.2015 Inhaltsverzeichnis Einheiten Grafiktypen Bildformate Farbtiefe Farbbilder/ Farbräume Quellen Einführung in die Bildverarbeitung
Digitale Bilder Ein Referat von Jacqueline Schäfer und Lea Pohl Am 06.05.2015 Inhaltsverzeichnis Einheiten Grafiktypen Bildformate Farbtiefe Farbbilder/ Farbräume Quellen Einführung in die Bildverarbeitung
3.2. Polarkoordinaten
 3.2. Polarkoordinaten Die geometrische Bedeutung der komplexen Multiplikation versteht man besser durch die Einführung von Polarkoordinaten. Der Betrag einer komplexen Zahl z x + i y ist r: z x 2 + y 2.
3.2. Polarkoordinaten Die geometrische Bedeutung der komplexen Multiplikation versteht man besser durch die Einführung von Polarkoordinaten. Der Betrag einer komplexen Zahl z x + i y ist r: z x 2 + y 2.
Bestimmte Zufallsvariablen sind von Natur aus normalverteilt. - naturwissenschaftliche Variablen: originär z.b. Intelligenz, Körpergröße, Messfehler
 6.6 Normalverteilung Die Normalverteilung kann als das wichtigste Verteilungsmodell der Statistik angesehen werden. Sie wird nach ihrem Entdecker auch Gaußsche Glockenkurve genannt. Die herausragende Stellung
6.6 Normalverteilung Die Normalverteilung kann als das wichtigste Verteilungsmodell der Statistik angesehen werden. Sie wird nach ihrem Entdecker auch Gaußsche Glockenkurve genannt. Die herausragende Stellung
KAPITEL Füllmethoden von Ebenen 493. Zebra.tif
 31 Füllmethoden von Ebenen KAPITEL 31 Bisher haben Sie sich bei der Verwendung von Ebenen ganz auf die richtige Reihenfolge und auf die Ebenenmasken verlassen. Alles, was über einer Ebene liegt, verdeckt
31 Füllmethoden von Ebenen KAPITEL 31 Bisher haben Sie sich bei der Verwendung von Ebenen ganz auf die richtige Reihenfolge und auf die Ebenenmasken verlassen. Alles, was über einer Ebene liegt, verdeckt
Mathematischer Vorkurs Dr. Thomas Zehrt Funktionen 1. 1 Grundlagen 2. 2 Der Graph einer Funktion 4. 3 Umkehrbarkeit 5
 Universität Basel Wirtschaftswissenschaftliches Zentrum Abteilung Quantitative Methoden Mathematischer Vorkurs Dr. Thomas Zehrt Funktionen 1 Inhaltsverzeichnis 1 Grundlagen 2 2 Der Graph einer Funktion
Universität Basel Wirtschaftswissenschaftliches Zentrum Abteilung Quantitative Methoden Mathematischer Vorkurs Dr. Thomas Zehrt Funktionen 1 Inhaltsverzeichnis 1 Grundlagen 2 2 Der Graph einer Funktion
1 Fraktale Eigenschaften der Koch-Kurve
 Anhang Inhaltsverzeichnis Fraktale Eigenschaften der Koch-Kurve iii. Einführung.................................. iii.2 Defintion.................................... iii.3 Gesamtlänge der Koch-Kurve........................
Anhang Inhaltsverzeichnis Fraktale Eigenschaften der Koch-Kurve iii. Einführung.................................. iii.2 Defintion.................................... iii.3 Gesamtlänge der Koch-Kurve........................
Distributed Algorithms. Image and Video Processing
 Chapter 7 High Dynamic Range (HDR) Distributed Algorithms for Quelle: wikipedia.org 2 1 High Dynamic Range bezeichnet ein hohes Kontrastverhältnis in einem Bild Kontrastverhältnis bei digitalem Bild: 1.000:1
Chapter 7 High Dynamic Range (HDR) Distributed Algorithms for Quelle: wikipedia.org 2 1 High Dynamic Range bezeichnet ein hohes Kontrastverhältnis in einem Bild Kontrastverhältnis bei digitalem Bild: 1.000:1
3.3. Drehungen und Spiegelungen
 3.3. Drehungen und Spiegelungen Drehungen und Spiegelungen in der Ebene Die Multiplikation einer komplexen Zahl z = x + i y (aufgefaßt als Punkt oder Ortsvektor der Ebene) mit der Zahl w = e ( ) = i φ
3.3. Drehungen und Spiegelungen Drehungen und Spiegelungen in der Ebene Die Multiplikation einer komplexen Zahl z = x + i y (aufgefaßt als Punkt oder Ortsvektor der Ebene) mit der Zahl w = e ( ) = i φ
INTELLIGENTE DATENANALYSE IN MATLAB
 INTELLIGENTE DATENANALYSE IN MATLAB Bildanalyse Literatur David A. Forsyth: Computer Vision i A Modern Approach. Mark S. Nixon und Alberto S. Aguado: Feature Extraction and Image Processing. Ulrich Schwanecke:
INTELLIGENTE DATENANALYSE IN MATLAB Bildanalyse Literatur David A. Forsyth: Computer Vision i A Modern Approach. Mark S. Nixon und Alberto S. Aguado: Feature Extraction and Image Processing. Ulrich Schwanecke:
1 Umkehrfunktionen und implizite Funktionen
 Mathematik für Physiker III WS 2012/2013 Freitag 211 $Id: implizittexv 18 2012/11/01 20:18:36 hk Exp $ $Id: lagrangetexv 13 2012/11/01 1:24:3 hk Exp hk $ 1 Umkehrfunktionen und implizite Funktionen 13
Mathematik für Physiker III WS 2012/2013 Freitag 211 $Id: implizittexv 18 2012/11/01 20:18:36 hk Exp $ $Id: lagrangetexv 13 2012/11/01 1:24:3 hk Exp hk $ 1 Umkehrfunktionen und implizite Funktionen 13
Kurs über Lineare Gleichungssysteme. PD Dr. Karin Halupczok
 Kurs über Lineare Gleichungssysteme PD Dr. Karin Halupczok Mathematisches Institut Albert-Ludwigs-Universität Freiburg http://home.mathematik.unifreiburg.de/halupczok/diverses.html karin.halupczok@math.uni-freiburg.de
Kurs über Lineare Gleichungssysteme PD Dr. Karin Halupczok Mathematisches Institut Albert-Ludwigs-Universität Freiburg http://home.mathematik.unifreiburg.de/halupczok/diverses.html karin.halupczok@math.uni-freiburg.de
Fixpunkt-Iterationen
 Fixpunkt-Iterationen 2. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 27. Februar 2014 Gliederung Wiederholung: Gleichungstypen, Lösungsverfahren Grundprinzip
Fixpunkt-Iterationen 2. Vorlesung 170 004 Numerische Methoden I Clemens Brand und Erika Hausenblas Montanuniversität Leoben 27. Februar 2014 Gliederung Wiederholung: Gleichungstypen, Lösungsverfahren Grundprinzip
Merkmale von Bildregionen, Einführung in Spektraltechniken
 Merkmale von Bildregionen, Einführung in Spektraltechniken Industrielle Bildverarbeitung, Vorlesung No. 10 1 M. O. Franz 12.12.2007 1 falls nicht anders vermerkt, sind die Abbildungen entnommen aus Burger
Merkmale von Bildregionen, Einführung in Spektraltechniken Industrielle Bildverarbeitung, Vorlesung No. 10 1 M. O. Franz 12.12.2007 1 falls nicht anders vermerkt, sind die Abbildungen entnommen aus Burger
Technische Beschreibung der akustischen Signalkette
 Technische Beschreibung der akustischen Signalkette Wichtige Aufgabe: Vielfältige Medien Gestaltung akustischer Kommunikationsketten (Sprache, Geräusche, Musik, CD, Radio, mp3,...) Unterschiedlichste Information
Technische Beschreibung der akustischen Signalkette Wichtige Aufgabe: Vielfältige Medien Gestaltung akustischer Kommunikationsketten (Sprache, Geräusche, Musik, CD, Radio, mp3,...) Unterschiedlichste Information
Graphische Datenverarbeitung
 Graphische Datenverarbeitung Bildbearbeitung für Rasterbilder Übersicht l Neu Folien:, 28 und ab 56 l Maße zur Beurteilung von Bildern: l Histogramm l Entropie l Punktoperationen: l Lineare Veränderung
Graphische Datenverarbeitung Bildbearbeitung für Rasterbilder Übersicht l Neu Folien:, 28 und ab 56 l Maße zur Beurteilung von Bildern: l Histogramm l Entropie l Punktoperationen: l Lineare Veränderung
Beschränktheit, Monotonie & Symmetrie
 Beschränktheit, Monotonie & Symmetrie ein Referat Dies ist eine Beilage zum Gruppen-SOL - Projekt Potenz- & Exponentialfunktionen Ronald Balestra CH - 8046 Zürich www.ronaldbalestra.ch November 2015 Inhaltsverzeichnis
Beschränktheit, Monotonie & Symmetrie ein Referat Dies ist eine Beilage zum Gruppen-SOL - Projekt Potenz- & Exponentialfunktionen Ronald Balestra CH - 8046 Zürich www.ronaldbalestra.ch November 2015 Inhaltsverzeichnis
Brückenkurs Mathematik. Mittwoch Freitag
 Brückenkurs Mathematik Mittwoch 5.10. - Freitag 14.10.2016 Vorlesung 4 Dreiecke, Vektoren, Matrizen, lineare Gleichungssysteme Kai Rothe Technische Universität Hamburg-Harburg Montag 10.10.2016 0 Brückenkurs
Brückenkurs Mathematik Mittwoch 5.10. - Freitag 14.10.2016 Vorlesung 4 Dreiecke, Vektoren, Matrizen, lineare Gleichungssysteme Kai Rothe Technische Universität Hamburg-Harburg Montag 10.10.2016 0 Brückenkurs
Stefan Ruzika. 24. April 2016
 Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz 24. April 2016 Stefan Ruzika 2: Körper 24. April 2016 1 / 21 Gliederung 1 1 Schulstoff 2 Körper Definition eines Körpers
Stefan Ruzika Mathematisches Institut Universität Koblenz-Landau Campus Koblenz 24. April 2016 Stefan Ruzika 2: Körper 24. April 2016 1 / 21 Gliederung 1 1 Schulstoff 2 Körper Definition eines Körpers
5 Interpolation und Approximation
 5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
5 Interpolation und Approximation Problemstellung: Es soll eine Funktion f(x) approximiert werden, von der die Funktionswerte nur an diskreten Stellen bekannt sind. 5. Das Interpolationspolynom y y = P(x)
Lineare Funktion. Wolfgang Kippels 3. November Inhaltsverzeichnis
 Lineare Funktion Wolfgang Kippels. November 0 Inhaltsverzeichnis Grundlegende Zusammenhänge. Aufbau der Linearen Funktion......................... Nullstellenbestimmung............................. Schnittpunktbestimmung............................
Lineare Funktion Wolfgang Kippels. November 0 Inhaltsverzeichnis Grundlegende Zusammenhänge. Aufbau der Linearen Funktion......................... Nullstellenbestimmung............................. Schnittpunktbestimmung............................
Nichtmonotone Grauwertabbildung
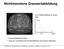 LMU München Medieninformatik Butz/Hilliges 2D Graphics WS2005 02.12.2005 Folie 1 Nichtmonotone Grauwertabbildung Zwei Grauwertfenster in einem Bild. g (g) 0 511 2100 g Erzeugt künstliche Kanten. Grenzen
LMU München Medieninformatik Butz/Hilliges 2D Graphics WS2005 02.12.2005 Folie 1 Nichtmonotone Grauwertabbildung Zwei Grauwertfenster in einem Bild. g (g) 0 511 2100 g Erzeugt künstliche Kanten. Grenzen
Filterung von Bildern (2D-Filter)
 Prof. Dr. Wolfgang Konen, Thomas Zielke Filterung von Bildern (2D-Filter) SS06 6. Konen, Zielke Aktivierung Was, denken Sie, ist ein Filter in der BV? Welche Filter kennen Sie? neuer Pixelwert bilden aus
Prof. Dr. Wolfgang Konen, Thomas Zielke Filterung von Bildern (2D-Filter) SS06 6. Konen, Zielke Aktivierung Was, denken Sie, ist ein Filter in der BV? Welche Filter kennen Sie? neuer Pixelwert bilden aus
Fourier-Reihen und Fourier-Transformation
 Fourier-Reihen und Fourier-Transformation Matthias Dreÿdoppel, Martin Koch, Bernhard Kreft 25. Juli 23 Einleitung Im Folgenden sollen dir und die Fouriertransformation erläutert und mit Beispielen unterlegt
Fourier-Reihen und Fourier-Transformation Matthias Dreÿdoppel, Martin Koch, Bernhard Kreft 25. Juli 23 Einleitung Im Folgenden sollen dir und die Fouriertransformation erläutert und mit Beispielen unterlegt
Eine zweidimensionale Stichprobe
 Eine zweidimensionale Stichprobe liegt vor, wenn zwei qualitative Merkmale gleichzeitig betrachtet werden. Eine Urliste besteht dann aus Wertepaaren (x i, y i ) R 2 und hat die Form (x 1, y 1 ), (x 2,
Eine zweidimensionale Stichprobe liegt vor, wenn zwei qualitative Merkmale gleichzeitig betrachtet werden. Eine Urliste besteht dann aus Wertepaaren (x i, y i ) R 2 und hat die Form (x 1, y 1 ), (x 2,
} Symmetrieachse von A und B.
 5 Symmetrieachsen Seite 1 von 6 5 Symmetrieachsen Gleicher Abstand von zwei Punkten Betrachtet man zwei fest vorgegebene Punkte A und B, drängt sich im Zusammenhang mit dem Abstandsbegriff eine Frage auf,
5 Symmetrieachsen Seite 1 von 6 5 Symmetrieachsen Gleicher Abstand von zwei Punkten Betrachtet man zwei fest vorgegebene Punkte A und B, drängt sich im Zusammenhang mit dem Abstandsbegriff eine Frage auf,
4.1. Vektorräume und lineare Abbildungen
 4.1. Vektorräume und lineare Abbildungen Mengen von Abbildungen Für beliebige Mengen X und Y bezeichnet Y X die Menge aller Abbildungen von X nach Y (Reihenfolge beachten!) Die Bezeichnungsweise erklärt
4.1. Vektorräume und lineare Abbildungen Mengen von Abbildungen Für beliebige Mengen X und Y bezeichnet Y X die Menge aller Abbildungen von X nach Y (Reihenfolge beachten!) Die Bezeichnungsweise erklärt
Analytische Lösung algebraischer Gleichungen dritten und vierten Grades
 Analytische Lösung algebraischer Gleichungen dritten und vierten Grades Inhaltsverzeichnis 1 Einführung 1 2 Gleichungen dritten Grades 3 3 Gleichungen vierten Grades 7 1 Einführung In diesem Skript werden
Analytische Lösung algebraischer Gleichungen dritten und vierten Grades Inhaltsverzeichnis 1 Einführung 1 2 Gleichungen dritten Grades 3 3 Gleichungen vierten Grades 7 1 Einführung In diesem Skript werden
Komplexe Zahlen. Allgemeines. Definition. Darstellungsformen. Umrechnungen
 Komplexe Zahlen Allgemeines Definition Eine komplexe Zahl z x + y i besteht aus einem Realteil Re(z) x und einem Imaginärteil Im(z) y. Der Imaginärteil wird mit der Imaginären-Einheit i multipliziert.
Komplexe Zahlen Allgemeines Definition Eine komplexe Zahl z x + y i besteht aus einem Realteil Re(z) x und einem Imaginärteil Im(z) y. Der Imaginärteil wird mit der Imaginären-Einheit i multipliziert.
Kapitel 7. Bildverarbeitung im Frequenzraum
 Kapitel 7 Bildverarbeitung im Frequenzraum Durchführung von Faltungen im Frequenzraum Filterung im Frequenzraum: Tiefpass- und Hochpass-Filter, etc. Bildrestaurierung Notch-Filter: Entfernung periodischer
Kapitel 7 Bildverarbeitung im Frequenzraum Durchführung von Faltungen im Frequenzraum Filterung im Frequenzraum: Tiefpass- und Hochpass-Filter, etc. Bildrestaurierung Notch-Filter: Entfernung periodischer
Statistik II. Lineare Regressionsrechnung. Wiederholung Skript 2.8 und Ergänzungen (Schira: Kapitel 4) Statistik II
 Statistik II Lineare Regressionsrechnung Wiederholung Skript 2.8 und Ergänzungen (Schira: Kapitel 4) Statistik II - 09.06.2006 1 Mit der Kovarianz und dem Korrelationskoeffizienten können wir den statistischen
Statistik II Lineare Regressionsrechnung Wiederholung Skript 2.8 und Ergänzungen (Schira: Kapitel 4) Statistik II - 09.06.2006 1 Mit der Kovarianz und dem Korrelationskoeffizienten können wir den statistischen
Einführung in die Integralrechnung. Mag. Mone Denninger 13. November 2005
 Einführung in die Integralrechnung Mag. Mone Denninger. November 5 INHALTSVERZEICHNIS 8. Klasse Inhaltsverzeichnis Einleitung Berechnung einfacher Stammfunktionen. Integrationsregeln.........................
Einführung in die Integralrechnung Mag. Mone Denninger. November 5 INHALTSVERZEICHNIS 8. Klasse Inhaltsverzeichnis Einleitung Berechnung einfacher Stammfunktionen. Integrationsregeln.........................
Computergrafik 2: Fourier-Transformation
 Computergrafik 2: Fourier-Transformation Prof. Dr. Michael Rohs, Dipl.-Inform. Sven Kratz michael.rohs@ifi.lmu.de MHCI Lab, LMU München Folien teilweise von Andreas Butz, sowie von Klaus D. Tönnies (Grundlagen
Computergrafik 2: Fourier-Transformation Prof. Dr. Michael Rohs, Dipl.-Inform. Sven Kratz michael.rohs@ifi.lmu.de MHCI Lab, LMU München Folien teilweise von Andreas Butz, sowie von Klaus D. Tönnies (Grundlagen
Debayeringverfahren. 19. Mai Thomas Noack, Nikolai Kosjar. SE Computational Photography - Debayeringverfahren
 Debayeringverfahren Thomas Noack, Nikolai Kosjar 19. Mai 2010 Was bisher geschah... Reduktion der Herstellungskosten durch Einsatz von nur noch einem CCD-Sensor mit Bayer-Filter Problem: Bayer Image Full
Debayeringverfahren Thomas Noack, Nikolai Kosjar 19. Mai 2010 Was bisher geschah... Reduktion der Herstellungskosten durch Einsatz von nur noch einem CCD-Sensor mit Bayer-Filter Problem: Bayer Image Full
Fouriertransformation und Unschärfeprinzip
 Information, Codierung, Komplexität 2 SS 2007 24. April 2007 Das berühmte von Heisenberg in der Quantentheorie beruht, rein mathematisch betrachtet, auf einer grundlegenden Eigenschaft der der Dichtefunktionen
Information, Codierung, Komplexität 2 SS 2007 24. April 2007 Das berühmte von Heisenberg in der Quantentheorie beruht, rein mathematisch betrachtet, auf einer grundlegenden Eigenschaft der der Dichtefunktionen
Technische Universität München Zentrum Mathematik. Übungsblatt 7
 Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 7 Hausaufgaben Aufgabe 7. Für n N ist die Matrix-Exponentialfunktion
Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 7 Hausaufgaben Aufgabe 7. Für n N ist die Matrix-Exponentialfunktion
Digitale Bildverarbeitung Einheit 8 Lineare Filterung
 Digitale Bildverarbeitung Einheit 8 Lineare Filterung Lehrauftrag SS 2008 Fachbereich M+I der FH-Offenburg Dr. Bernard Haasdonk Albert-Ludwigs-Universität Freiburg Ziele der Einheit Verstehen, wie lineare
Digitale Bildverarbeitung Einheit 8 Lineare Filterung Lehrauftrag SS 2008 Fachbereich M+I der FH-Offenburg Dr. Bernard Haasdonk Albert-Ludwigs-Universität Freiburg Ziele der Einheit Verstehen, wie lineare
