Wiederholung. Algorithmen und Datenstrukturen Kapitel 10. Motivation. Begriffe und Definitionen
|
|
|
- Franka Lang
- vor 6 Jahren
- Abrufe
Transkript
1 Algorihmen nd Daenrkren Kapiel Frank Heimann 6. Janar 2016 Frank Heimann 1/ Graphen Grndlagen Definiion nd Darellng Tiefen- nd Breienche Topologiche Sorieren Sarke Zammenhangkomponenen Minimale Spannbäme Definiion Algorihm on Krkal Algorihm on Prim Beimmen der kürzeen Pfade Definiion nd Varianen (Breienche) Algorihm on Dijkra Algorihm on Bellman-Ford Algorihm on Floyd-Warhall Hee: Frank Heimann 2/ Moiaion Begriffe nd Definiionen /16 1 / /9 /1 20 / Einen Graphen al Flnezerk z inerpreieren i eine andere (nee) Ar der Modellierng mi Graphen. Maerialflüe Logiik (Tranporflüe) Informaionflüe... Frank Heimann heimann@informaik.ni-hambrg.de / Definiion (Flnezerk) Ein Flnezerk i ein gericheer Graph G = (V, E), in dem jeder Kane (, ) E zäzlich eine nichnegaie Kapaziä c(, ) 0 zgeieen ird. (I (, ) E, o nehmen ir c(, ) = 0 an.) E gib die beonderen Knoen, V, die Qelle () nd die Senke (). Alle Knoen liegen af Pfaden on der Qelle zr Senke. Frank Heimann heimann@informaik.ni-hambrg.de /
2 Begriffe nd Definiionen Da Problem de maimalen Fle Definiion (Fl) Sei G = (V, E) mi Kapaziäfnkion c ein Flnezerk, nd ie oben. Ein Fl in G i eine Fnkion f : V V R, für die gil: 1 Kapaziäbechränkng: f (, ) c(, ), V 2 Aymmerie: f (, ) = f (, ), V Flerhalng: V f (, ) = 0 V \ {, } Definiion (Problem de maimalen Fle) Eingabe: Ein Flnezerk G mi Kapaziäfnkion c nd Qelle nd Senke. Gech: Ein Fl mi maimalen Wer. Dabei i der Wer eine Fle definier drch Anmerkng f = V f (, ). Diee Problem ri bei den oben angeprochenen Anendngen (Logiik, Maerial-/Informaionflüe,...) af. Frank Heimann heimann@informaik.ni-hambrg.de / Frank Heimann heimann@informaik.ni-hambrg.de 6/ Maimaler Fl - Beipiel Maimaler Fl - Beipiel /16 / / /1 / Frank Heimann heimann@informaik.ni-hambrg.de / Frank Heimann heimann@informaik.ni-hambrg.de /
3 Maimaler Fl - Beipiel Maimaler Fl - Beipiel /16 / /9 20 /16 / / /9 / /20 1 /1 / 1 /1 / Frank Heimann heimann@informaik.ni-hambrg.de 9/ Frank Heimann heimann@informaik.ni-hambrg.de / Maimaler Fl - Beipiel Maimaler Fl - Beipiel /16 / / /9 / /20 /16 / / /9 / /20 1 /1 / 1 /1 / Frank Heimann heimann@informaik.ni-hambrg.de / Frank Heimann heimann@informaik.ni-hambrg.de /
4 Maimaler Fl - Beipiel Maimaler Fl - Beipiel /16 1/ / /9 / 1/20 /16 1/ / /9 / 1/20 /1 /1 / /1 /1 / Frank Heimann heimann@informaik.ni-hambrg.de 1/ Frank Heimann heimann@informaik.ni-hambrg.de 1/ Fleigenchafen Saz 1. I (, ), (, ) E, o gil f (, ) = f (, ) = Sei Beei. V f (, ) > 0 f (, ) der geame poiie Fl in einen Knoen nd analog der geame poiie Fl a einem Knoen, dann i der geame poiie Fl in einen Knoen V \ {, } gleich dem poiien Fl a dieem Knoen. ( Einreender Fl i gleich areender Fl. ) Mündlich / Zr Übng... Frank Heimann heimann@informaik.ni-hambrg.de 1/ Implizie Smmennoaion f ha zei Knoen al Argmene. Wir führen eine implizie Smmennoaion ein, m ach mi Mengen on Knoen arbeien z können. Wir ezen f (X, Y ) = f (, y). X y Y Die Flerhalng lä ich o formlieren al f (, V ) = 0 V {, }. Ferner chreiben ir in der implizien Smmennoaion ach z.b. V a V {}. Beipiel: f (, V ) = f (, V ) Frank Heimann heimann@informaik.ni-hambrg.de 16/
5 Ein ichige Lemma / Weiere Fleigenchafen Saz (Lemma 26.1 im (Cormen)) Sei G = (V, E) mi c ein Flnezerk nd f ein Fl in G. E gil 1. f (X, X ) = 0 X V 2. f (X, Y ) = f (Y, X ) X, Y V. f (X Y, Z) = f (X, Z) + f (Y, Z) nd f (Z, X Y ) = f (Z, X ) + f (Z, Y ) X, Y, Z V mi X Y = Ein ichige Lemma / Weiere Fleigenchafen Saz (Lemma 26.1 im (Cormen)) Sei G = (V, E) mi c ein Flnezerk nd f ein Fl in G. E gil 2. f (X, Y ) = f (Y, X ) X, Y V Beei. f (X, Y ) = f (, y) X y Y = f (y, ) = f (y, ) X y Y X y Y = f (y, ) = f (Y, X ) y Y X Frank Heimann heimann@informaik.ni-hambrg.de 1/ Frank Heimann heimann@informaik.ni-hambrg.de 1/ Ein ichige Lemma / Weiere Fleigenchafen Nzng de Lemma Saz (Lemma 26.1 im (Cormen)) Sei G = (V, E) mi c ein Flnezerk nd f ein Fl in G. E gil 1. f (X, X ) = 0 X V. f (X Y, Z) = f (X, Z) + f (Y, Z) nd f (Z, X Y ) = f (Z, X ) + f (Z, Y ) X, Y, Z V mi X Y = Beei. Mündlich / Zr Übng... Saz f = f (V, ) Beei. f = f (, V ) = f (V, V ) f (V, V ) = f (V, V ) = f (V, V ) = f (V, ) + f (V, V ) = f (V, ) Frank Heimann heimann@informaik.ni-hambrg.de 19/ Frank Heimann heimann@informaik.ni-hambrg.de 20/
6 Ekr: Mliple Qellen nd Senken Ekr: Mliple Qellen nd Senken i i i i i i Anmerkng Da Problem mi mehreren Qellen nd mehreren Senken kann af den Fall einer Qelle nd einer Senke zrückgeführ erden, indem eine Sperqelle nd eine Sperenke eingeführ ird. Anmerkng Da Problem mi mehreren Qellen nd mehreren Senken kann af den Fall einer Qelle nd einer Senke zrückgeführ erden, indem eine Sperqelle nd eine Sperenke eingeführ ird. Frank Heimann heimann@informaik.ni-hambrg.de 21/ Frank Heimann heimann@informaik.ni-hambrg.de 22/ Inhalkizze Renezerke: Definiion Die lö da Problem de maimalen Fle. Sie mfa erchieden Implemenierngen (Algorihmen) mi nerchiedlichen Lafzeien. Kern der Mehode ind drei ichie Ideen, die ach an anderer Selle on Bedeng ind: Renezerke Ereierngpfade Schnie Definiion Sei G = (V, E) mi c ein Flnezerk nd f ein Fl in G. Wir definieren z je zei Knoen, die Rekapaziä drch c f (, ) = c(, ) f (, ). Da Renezerk i dann gegeben drch G f = (V, E f ) nd c f, obei E f = {(, ) V V c f (, ) > 0} die Menge der Rekanen i. Da Renezerk beeh alo a jenen Kanen, die noch mehr Fl afnehmen können. Frank Heimann heimann@informaik.ni-hambrg.de 2/ Frank Heimann heimann@informaik.ni-hambrg.de 2/
7 Renezerke: Beipiel Renezerke: Beipiel /16 /1 1/ / /9 /1 / 1/20 / Anmerkng 1 Man beache, da mi f (, ) = dann f (, ) = gil, a ggf. z einer eieren Kane im Renezerk führ! Frank Heimann heimann@informaik.ni-hambrg.de 2/ Frank Heimann heimann@informaik.ni-hambrg.de 26/ Renezerke: Eigenchafen Renezerke: Eigenchafen Saz (Lemma 26.2 im (Cormen)) Sei G = (V, E) mi c,, ein Flnezerk nd f ein Fl in G. G f ei da drch den Fl indziere Renezerk nd f ein Fl in G f. Dann i die Flmme f + f ein Fl in G mi f + f = f + f. Anmerkng Die Flmme f + f i definier drch (f + f )(, ) = f (, ) + f (, ). Saz (Lemma 26.2 im (Cormen)) Sei G = (V, E) mi c,, ein Flnezerk nd f ein Fl in G. G f ei da drch den Fl indziere Renezerk nd f ein Fl in G f. Dann i die Flmme f + f ein Fl in G mi f + f = f + f. Beei Z zeigen i, da f + f die drei Eigenchafen eine Fle ha (Kapaziäbechränkng, Aymmerie, Flerhalng) nd da f + f = f + f gil. Wir zeigen die eren beiden Eigenchafen. Die drie nd iere zr Übng/zm Nachleen.... Frank Heimann heimann@informaik.ni-hambrg.de 2/ Frank Heimann heimann@informaik.ni-hambrg.de 2/
8 Renezerke: Eigenchafen Renezerke: Eigenchafen Saz (Lemma 26.2 im (Cormen)) Sei G = (V, E) mi c,, ein Flnezerk nd f ein Fl in G. G f ei da drch den Fl indziere Renezerk nd f ein Fl in G f. Dann i die Flmme f + f ein Fl in G mi f + f = f + f. Beei Kapaziäbechränkng: Wir müen (f + f )(, ) c(, ) zeigen. Mi f (, ) c f (, ) (da f ein Fl in G f i) nd c f (, ) = c(, ) f (, ) (nach Definiion) folg (f + f )(, ) = f (, ) + f (, ) f (, ) + c(, ) f (, ) = c(, ).... Saz (Lemma 26.2 im (Cormen)) Sei G = (V, E) mi c,, ein Flnezerk nd f ein Fl in G. G f ei da drch den Fl indziere Renezerk nd f ein Fl in G f. Dann i die Flmme f + f ein Fl in G mi f + f = f + f. Beei Aymmerie: (f + f )(, ) = f (, ) + f (, ) = f (, ) f (, ) = (f (, ) + f (, )) = (f + f )(, ). Wir nzen hier lediglich die Aymmerie der einzelnen (nd die Definiion der Flmme).... Frank Heimann heimann@informaik.ni-hambrg.de 29/ Frank Heimann heimann@informaik.ni-hambrg.de 0/ Renezerke: Eigenchafen Renezerke: Zammenfang Saz (Lemma 26.2 im (Cormen)) Sei G = (V, E) mi c,, ein Flnezerk nd f ein Fl in G. G f ei da drch den Fl indziere Renezerk nd f ein Fl in G f. Dann i die Flmme f + f ein Fl in G mi f + f = f + f. Beei. Noch z zeigen: V (f + f )(, ) = 0 (Flerhalng) nd f + f = f + f. Mündlich / Zr Übng / Zm Nachleen. Iniie Definiion: Da Renezerk z einem gegebenen Flnezerk nd einem Fl beeh a jenen Kanen, die mehr Fl afnehmen können. Formal ind die Rekapaziä nd die Rekanen ichig. Man beache, da nee Kanen enehen können (bz. reng formal: Kanen, deren Kapaziä orher 0 ar, kann nn größer al 0 erden. Wichige Eigenchaf: Finde man in einem Renezerk G f (f i ein Fl in dem Flnezerk G) einen eieren Fl f, o i f + f erne ein Fl in G (!) mi dem Wer f + f (> f!). Frank Heimann heimann@informaik.ni-hambrg.de 1/ Frank Heimann heimann@informaik.ni-hambrg.de 2/
9 Ereierngpfade: Definiion Ereierngpfade: Beipiel Definiion Sei G = (V, E) mi c ein Flnezerk, f ein Fl in G nd G f da Renezerk. Ein Ereierngpfad i ein einfacher Pfad on nach in G f. Mi c f (p) = min{c f (, ) (, ) i eine Kane on p} ird die Rekapaziä eine Ereierngpfade p bezeichne. Pae o Ponder Die Idee der : Beimme o lange ie möglich Ereierngpfade nd erhöhe den Fl jeeil m die Rekapaziä. 1 Frank Heimann heimann@informaik.ni-hambrg.de / Frank Heimann heimann@informaik.ni-hambrg.de / Ereierngpfade: Beipiel Ereierngpfade: Beipiel /16 /1 1/ / /9 /1 / 1/20 / 1 Frank Heimann heimann@informaik.ni-hambrg.de / Frank Heimann heimann@informaik.ni-hambrg.de 6/
10 Ereierngpfade: Beipiel Ereierngpfade: Beipiel 1 /16 /1 1/ / 9 /1 / 19/20 / Frank Heimann heimann@informaik.ni-hambrg.de / Frank Heimann heimann@informaik.ni-hambrg.de / Ereierngpfade: Beipiel Ereierngpfade: Eigenchafen Saz (Lemma 26. im (Cormen)) Sei G = (V, E) mi c ein Flnezerk, f ein Fl in G nd p ein Ereierngpfad in G f. Sei f p : V V R eine Fnkion mi c f (p) fall (, ) z p gehör, f p (, ) = c f (p) fall (, ) z p gehör, 0 on. Dann i f p ein Fl in G f mi f p = c f (p) > 0. Frank Heimann heimann@informaik.ni-hambrg.de 9/ Frank Heimann heimann@informaik.ni-hambrg.de 0/
11 Renezerke: Eigenchafen (Wdh.) Ereierngpfade: Eigenchafen Saz (Lemma 26.2 im (Cormen)) Sei G = (V, E) mi c,, ein Flnezerk nd f ein Fl in G. G f ei da drch den Fl indziere Renezerk nd f ein Fl in G f. Dann i die Flmme f + f ein Fl in G mi f + f = f + f. Saz (Korollar 26. im (Cormen)) Sei G = (V, E) mi c ein Flnezerk, f ein Fl in G nd p ein Ereierngpfad in G f. Sei f p ie eben definier nd ei f = f + f p, dann i f ein Fl in G mi f = f + f p > f. Beei. Folg ofor a den obigen beiden Säzen. Frank Heimann heimann@informaik.ni-hambrg.de 1/ Frank Heimann heimann@informaik.ni-hambrg.de 2/ Renezerke nd Ereierngpfade: Zammenfang Die Iniie Definiion: Da Renezerk z einem gegebenen Flnezerk nd einem Fl beeh a jenen Kanen, die mehr Fl afnehmen können. Ein Ereierngpfad i ein einfacher Pfad on nach im Renezerk. Finde man in einem Renezerk G f (f i ein Fl in dem Flnezerk G) einen eieren Fl f, o i f + f erne ein Fl in G mi dem Wer f + f > f. Lezere gil inb. ach, enn man über einen Ereierngpfad o iel ie möglich leie (Rekapaziä). Die : 0. Sei f = Beimme G f = (V, E f ) nd c f. 2. Beimme einen Ereierngpfad p. (Gib e keinen, gehe z.). Erhöhe f enlang p m c f (p).. Gehe z 1.. f i ein maimaler Fl. Pae o Ponder Terminier diee Verfahren? I f irklich maimal? Frank Heimann heimann@informaik.ni-hambrg.de / Frank Heimann heimann@informaik.ni-hambrg.de /
12 Schnie: Moiaion Schnie: Definiion Da maimaler-fl-minimaler-schni-theorem beag, da ein Fl maimal i gd. da Renezerk keinen Ereierngpfad enhäl. Diee Theorem i gena, a ir brachen! Zm Beei benöigen ir Schnie... Definiion (Schni) Ein Schni (S, T ) eine Flnezerke G = (V, E) i eine Parionierng on V in S nd T = V S, obei S nd T gil. Der Neofl nd die Kapaziä eine Schnie (S, T ) i drch f (S, T ) bz. c(s, T ) definier. Ein minimaler Schni i ein Schni, deen Kapaziä die kleine on allen Schnien de Nezerke i. Frank Heimann heimann@informaik.ni-hambrg.de / Frank Heimann heimann@informaik.ni-hambrg.de 6/ Schnie: Beipiel Schnie: Eigenchafen Anmerkng /16 /1 1/ / /9 /1 / 1/20 Beim Neofl ird ein (poiier) Fl on S nach T addier, ein (poiier) Fl on T nach S brahier. Bei der Kapaziä ind nr Kanen on S nach T relean. / Saz (Lemma 26. im (Cormen)) Seien G ein Flnezerk, c,, ie üblich, f ein Fl nd (S, T ) ein Schni on G. Dann gil f (S, T ) = f. (D.h. der Neofl drch beliebige Schnie i immer gleich, nämlich gleich dem Wer de Fle.) Beei. f (S, T ) = f (S, V ) f (S, S) = f (S, V ) = f (, V ) + f (S, V ) = f (, V ) = f. Frank Heimann heimann@informaik.ni-hambrg.de / Frank Heimann heimann@informaik.ni-hambrg.de /
13 Schnie: Eigenchafen Saz In einem Flnezerk G i der Wer eine beliebigen Fle drch die Kapziä jede beliebigen Schnie nach oben bechränk. Beei. Sei (S, T ) ein Schni on G nd f ein beliebiger Fl. Wir ollen f c(s, T ) zeigen. f = f (S, T ) = f (, ) c(, ) S T S T = c(s, T ) Zm Ma-Flo-Min-C-Theorem Saz In einem Flnezerk G i der Wer eine beliebigen Fle drch die Kapziä jede beliebigen Schnie nach oben bechränk. Anmerkng Der maimale Fl m folglich drch die Kapaziä eine minimalen Schni bechränk ein (da oben beide beliebig, aber die Schranke e gil). - Da ichige Ma-Flo-Min-C-Theorem ag a, da diee Were aächlich gleich ind. Frank Heimann heimann@informaik.ni-hambrg.de 9/ Frank Heimann heimann@informaik.ni-hambrg.de 0/ Ma-Flo-Min-C-Theorem Ma-Flo-Min-C-Theorem Saz Sei G = (V, E) mi c,, ein Flnezerk, f ein Fl in G. Die folgenden Bedingngen ind äqialen: 1. f i ein maimaler Fl in G. 2. Da Renezerk G f enhäl keine Ereierngpfade.. E i f = c(s, T ) für einen Schni (S, T ) on G. Beei (1) (2): Widerprchbeei... mündlich/zr Übng/zm Nachleen... Saz 2. Da Renezerk G f enhäl keine Ereierngpfade.. E i f = c(s, T ) für einen Schni (S, T ) on G. Beei (2) (): G f enhäl keinen Pfad on nach. Definiere: S := { V e gib einen Pfad in G f on nach } nd T := V S. (S, T ) i ein Schni (arm?), ferner m f (, ) = c(, ) für, V mi S nd T gelen, da on (, ) E f äre nd omi S gelen müe. Mi den zei orherigen Säzen folg dann f = f (S, T ) = c(s, T ). Frank Heimann heimann@informaik.ni-hambrg.de 1/ Frank Heimann heimann@informaik.ni-hambrg.de 2/
14 Ma-Flo-Min-C-Theorem Schnie - Zammenfang Saz 1. f i ein maimaler Fl in G.. E i f = c(s, T ) für einen Schni (S, T ) on G. Beei. () (1): Wir haben orhin f c(s, T ) für alle Schnie (S, T ) beieen. A f = c(s, T ) folg alo, da f ein maimaler Fl ein m. Schnie ind ein Hilfmiel für da Ma-Flo-Min-C-Theorem, da aag, da der maimale Fl in einem Flnezerk der Kapaziä eine minimalen Schnie enprich. Dara (nd a der aführlicheren Formlierng de Theorem oben) folg die Korrekhei der. Frank Heimann heimann@informaik.ni-hambrg.de / Frank Heimann heimann@informaik.ni-hambrg.de / Die Ford-Flkeron: Beipiel Die : 0. Sei f = Beimme G f = (V, E f ) nd c f. 2. Beimme einen Ereierngpfad p. (Gib e keinen, gehe z.). Erhöhe f enlang p m c f (p).. Gehe z 1.. f i ein maimaler Fl. Pae o Ponder Wo haben ir hier Sellchraben? Frank Heimann heimann@informaik.ni-hambrg.de / Frank Heimann heimann@informaik.ni-hambrg.de 6/
15 Ford-Flkeron: Beipiel Ford-Flkeron: Beipiel /16 / / /1 / Frank Heimann heimann@informaik.ni-hambrg.de / Frank Heimann heimann@informaik.ni-hambrg.de / Ford-Flkeron: Beipiel Ford-Flkeron: Beipiel Frank Heimann heimann@informaik.ni-hambrg.de 9/ Frank Heimann heimann@informaik.ni-hambrg.de 60/
16 Ford-Flkeron: Beipiel Ford-Flkeron: Beipiel /16 / 1 / /9 /1 / /20 / 1 1 Frank Heimann heimann@informaik.ni-hambrg.de 61/ Frank Heimann heimann@informaik.ni-hambrg.de 62/ Ford-Flkeron: Beipiel Ford-Flkeron: Beipiel 1 1 /16 /1 1/ / /9 /1 / 1/20 / Frank Heimann heimann@informaik.ni-hambrg.de 6/ Frank Heimann heimann@informaik.ni-hambrg.de 6/
17 Ford-Flkeron: Beipiel Ford-Flkeron: Beipiel 1 1 Frank Heimann heimann@informaik.ni-hambrg.de 6/ Frank Heimann heimann@informaik.ni-hambrg.de 66/ Ford-Flkeron: Beipiel Ford-Flkeron: Beipiel /16 /1 1/ / 9 /1 / 19/20 / Frank Heimann heimann@informaik.ni-hambrg.de 6/ Frank Heimann heimann@informaik.ni-hambrg.de 6/
18 Ford-Flkeron-Baialgorihm Ford-Flkeron-Baialgorihm - Analye Algorihm 1 FordFlkeron(G,, ) 1: for alle (, ) E(G) do 2: f [, ] = 0, f [, ] = 0 : end for : hile e gib einen Pfad p on nach in G f do : c f (p) = min{c f (, ) (, ) gehör z p} 6: for alle Kanen (, ) on p do : f [, ] = f [, ] + c f (p) : f [, ] = f [, ] 9: end for : end hile Analye: Die for-schleife i in Θ(E). Die hile-schleife ird maimal f -mal ageführ, obei f ein maimaler Fl i. Nzen ir innolle Daenrkren nd ermieln p in O(E) (z.b. miel Breien- oder Tiefenche), o i jede Ieraion der hile-schleife in O(E). Ingeam i die Roine dami in O(E f ). Anmerkng Wir gehen dabei on ganzzahligen oder raionalen Kapaziäen a. Bei irraionalen Kanenkapaziäen kann Uninn paieren, a aber fakich nr on mahemaichem Ineree i. Frank Heimann heimann@informaik.ni-hambrg.de 69/ Frank Heimann heimann@informaik.ni-hambrg.de 0/ Ford-Flkeron - Ein Problemfall Edmond-Karp-Algorihm Beobachng 1 Hier kann bei iederholer ngüniger Wahl on p die obere Lafzeigrenze on O(E f ) erreich erden, obohl zei Ieraionen reichen ürden. (I z.b. = 0 nd ird iederhol --- nd --- (im Renezerk!) geähl, brach man 200 Ieraionen (a 2).) Frank Heimann heimann@informaik.ni-hambrg.de 1/ Der Edmond-Karp-Algorihm: Ermile einen Ereierngpfad p in der drch eine Breienche, d.h. p i ein kürzeer Pfad on nach im Renezerk (obei jede Kane da Geich 1 ha). Saz Die Anzahl der drch den Edmond-Karp-Algorihm orgenommenen Flereierngen i in O(V E). Da jede Ieraion (der Prozedr FordFlkeron) in Zei O(E) implemenier erden kann, i der Edmond-Karp-Algorihm in O(V E 2 ). Anmerkng Wenn ach hier ea ncheinbar af nr einer Folie plazier, i die ein ehr ichige Rela! Frank Heimann heimann@informaik.ni-hambrg.de 2/
19 Ablick nd Anendngen Begriffe nd Definiionen Anmerkng Maimale ind nich nr für da Problem an ich inerean, ondern reen of ach bei anderen Problemen af, die alo al Flprobleme formlier erden können. Ein Beipiel i die Beimmng eine maimalen biparien Maching. Wir gehen hier nich mehr daraf ein (er mag: Kapiel 26. im [Cormen]). Ablick (für Inereiere) Den Beei für den Edmond-Karp-Algorihm finde man im [Cormen] (zei Seien). Zdem kann die Lafzei mi ogenannen Ph/Relabel-Algorihmen eier af O(V 2 E) nd ogar O(V ) erbeer erden. Mehr daz finde man ach im [Cormen]. - Und e geh ogar noch chneller (iehe Kapielbemerkngen nd Lierarhineie im [Cormen])... Frank Heimann heimann@informaik.ni-hambrg.de / /16 1 / Definiion (Flnezerk) / /9 /1 / /20 Ein Flnezerk i ein gericheer Graph G = (V, E), in dem jeder Kane (, ) E zäzlich eine nichnegaie Kapaziä c(, ) 0 zgeieen ird. (I (, ) E, o nehmen ir c(, ) = 0 an.) E gib die beonderen Knoen, V, die Qelle () nd die Senke (). Alle Knoen liegen af Pfaden on der Qelle zr Senke. Frank Heimann heimann@informaik.ni-hambrg.de / / Begriffe nd Definiionen Definiion (Fl) Sei G = (V, E) mi Kapaziäfnkion c ein Flnezerk, nd ie oben. Ein Fl in G i eine Fnkion f : V V R, für die gil: 1 Kapaziäbechränkng: f (, ) c(, ), V 2 Aymmerie: f (, ) = f (, ), V Flerhalng: V f (, ) = 0 V \ {, } Da Problem de maimalen Fle Definiion (Problem de maimalen Fle) Eingabe: Ein Flnezerk G mi Kapaziäfnkion c nd Qelle nd Senke. Gech: Ein Fl mi maimalen Wer. Dabei i der Wer eine Fle definier drch Anmerkng f = V f (, ). Diee Problem ri bei ielen Anendngen (Logiik, Maerial- /Informaionflüe,...) direk af, of laen ich ganz ander ercheinende Probleme aber ach al Flprobleme formlieren nd dann o löen. Frank Heimann heimann@informaik.ni-hambrg.de / Frank Heimann heimann@informaik.ni-hambrg.de 6/
20 Renezerke: Definiion Ereierngpfade: Definiion Definiion Sei G = (V, E) mi c ein Flnezerk nd f ein Fl in G. Wir definieren z je zei Knoen, die Rekapaziä drch c f (, ) = c(, ) f (, ). Da Renezerk i dann gegeben drch G f = (V, E f ) nd c f, obei E f = {(, ) V V c f (, ) > 0} die Menge der Rekanen i. Da Renezerk beeh alo a jenen Kanen, die noch mehr Fl afnehmen können. Frank Heimann heimann@informaik.ni-hambrg.de / Definiion Sei G = (V, E) mi c ein Flnezerk, f ein Fl in G nd G f da Renezerk. Ein Ereierngpfad i ein einfacher Pfad on nach in G f. Mi c f (p) = min{c f (, ) (, ) i eine Kane on p} ird die Rekapaziä eine Ereierngpfade p bezeichne. Frank Heimann heimann@informaik.ni-hambrg.de / Renezerke nd Ereierngpfade: Zammenfang Die Die : Iniie Definiion: Da Renezerk z einem gegebenen Flnezerk nd einem Fl beeh a jenen Kanen, die mehr Fl afnehmen können. Ein Ereierngpfad i ein einfacher Pfad on nach im Renezerk. Finde man in einem Renezerk G f (f i ein Fl in dem Flnezerk G) einen eieren Fl f, o i f + f erne ein Fl in G mi dem Wer f + f > f. Lezere gil inb. ach, enn man über einen Ereierngpfad o iel ie möglich leie (Rekapaziä). 0. Sei f = Beimme G f = (V, E f ) nd c f. 2. Beimme einen Ereierngpfad p. (Gib e keinen, gehe z.). Erhöhe f enlang p m c f (p).. Gehe z 1.. f i ein maimaler Fl. Anmerkng Die Idee: Beimme o lange ie möglich Ereierngpfade nd erhöhe den Fl jeeil m die Rekapaziä. Lafzei: O(E f ), obei f ein maimaler Fl i. Frank Heimann heimann@informaik.ni-hambrg.de 9/ Frank Heimann heimann@informaik.ni-hambrg.de 0/
21 Schnie: Definiion Ma-Flo-Min-C-Theorem Definiion (Schni) /16 /1 1/ / /9 /1 / 1/20 Ein Schni (S, T ) eine Flnezerke G = (V, E) i eine Parionierng on V in S nd T = V S, obei S nd T gil. Der Neofl nd die Kapaziä eine Schnie (S, T ) i drch f (S, T ) bz. c(s, T ) definier. Ein minimaler Schni i ein Schni, deen Kapaziä die kleine on allen Schnien de Nezerke i. Frank Heimann heimann@informaik.ni-hambrg.de 1/ / Saz Sei G = (V, E) mi c,, ein Flnezerk, f ein Fl in G. Die folgenden Bedingngen ind äqialen: 1. f i ein maimaler Fl in G. 2. Da Renezerk G f enhäl keine Ereierngpfade.. E i f = c(s, T ) für einen Schni (S, T ) on G. Anmerkng Mi dieem Saz folg die Korrekhei der Frank Heimann heimann@informaik.ni-hambrg.de 2/ Edmond-Karp-Algorihm Der Edmond-Karp-Algorihm: Ermile einen Ereierngpfad p in der drch eine Breienche, d.h. p i ein kürzeer Pfad on nach im Renezerk (obei jede Kane da Geich 1 ha). Saz Die Anzahl der drch den Edmond-Karp-Algorihm orgenommenen Flereierngen i in O(V E). Da jede Ieraion (der Prozedr FordFlkeron) in Zei O(E) implemenier erden kann, i der Edmond-Karp-Algorihm in O(V E 2 ). Frank Heimann heimann@informaik.ni-hambrg.de / Graphen Grndlagen Definiion nd Darellng Tiefen- nd Breienche Topologiche Sorieren Sarke Zammenhangkomponenen Minimale Spannbäme Definiion Algorihm on Krkal Algorihm on Prim Beimmen der kürzeen Pfade Definiion nd Varianen (Breienche) Algorihm on Dijkra Algorihm on Bellman-Ford Algorihm on Floyd-Warhall Frank Heimann heimann@informaik.ni-hambrg.de /
8 Kürzeste Wege KÜRZESTE WEGE. Hier sind alle Graphen gerichtet und gewichtet, d.h. wir haben eine Kostenfunktion K : E R dabei.
 04 8 KÜRZESTE WEGE 8 Kürzee Wege Hier ind alle Graphen geriche nd geiche, d.h. ir haben eine Koenfnkion K : E R dabei. Alo ea: 5 7 0 4 K(, ) = 5,K(, ) =,K(, ) = 7,K(, 4) = 0 I W = ( 0,,..., k ) irgendein
04 8 KÜRZESTE WEGE 8 Kürzee Wege Hier ind alle Graphen geriche nd geiche, d.h. ir haben eine Koenfnkion K : E R dabei. Alo ea: 5 7 0 4 K(, ) = 5,K(, ) =,K(, ) = 7,K(, 4) = 0 I W = ( 0,,..., k ) irgendein
25. Flüsse in Netzen. Motivation. Fluss. Flussnetzwerk
 Moivaion 25. Flüe in Nezen Flunezwerk, Maximaler Flu, Schni, Renezwerk, Max-flow Min-cu, Ford-Fulkeron Mehode, Edmond-Karp Algorihmu, Maximale Biparie Maching [Oman/Widmayer, Kap. 9.7, 9.8.1], [Cormen
Moivaion 25. Flüe in Nezen Flunezwerk, Maximaler Flu, Schni, Renezwerk, Max-flow Min-cu, Ford-Fulkeron Mehode, Edmond-Karp Algorihmu, Maximale Biparie Maching [Oman/Widmayer, Kap. 9.7, 9.8.1], [Cormen
Übersicht. Datenstrukturen und Algorithmen. Graphenproblem: maximale Flüsse. Graphenproblem: maximale Flüsse. Vorlesung 18: Maximaler Fluss (K26)
 Überich aenrukuren und lgorihmen Vorleung 18: (K26) Joo-Pieer Kaoen Lehruhl für Informaik 2 Sofware Modeling and Verificaion Group hp://move.rwh-aachen.de/eaching/-15/dal/ 25. Juni 2015 1 Flunezwerke 2
Überich aenrukuren und lgorihmen Vorleung 18: (K26) Joo-Pieer Kaoen Lehruhl für Informaik 2 Sofware Modeling and Verificaion Group hp://move.rwh-aachen.de/eaching/-15/dal/ 25. Juni 2015 1 Flunezwerke 2
Algorithmen II Vorlesung am
 Algorihmen II Vorleung am 24.10.2013 INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Univeriä de Lande Baden-Würemberg und Algorihmen naionale Forchungzenrum II Wineremeer 2013/2014
Algorihmen II Vorleung am 24.10.2013 INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Univeriä de Lande Baden-Würemberg und Algorihmen naionale Forchungzenrum II Wineremeer 2013/2014
Algorithmische Graphentheorie
 Algorihmiche Graphenheorie Sommeremeer 2014 3. Vorleung Flualgorihmen Prof. Dr. Alexander Wolff 1 Erinnerung Oh my God i an LP! Gegeben ein gericheer Graph G = (V, E) mi, V und Kanenkapaziäen c : E R >0.
Algorihmiche Graphenheorie Sommeremeer 2014 3. Vorleung Flualgorihmen Prof. Dr. Alexander Wolff 1 Erinnerung Oh my God i an LP! Gegeben ein gericheer Graph G = (V, E) mi, V und Kanenkapaziäen c : E R >0.
KAPITEL 2 KÜRZESTE WEGE
 KAPITEL 2 KÜRZESTE WEGE F. VALLENTIN, A. GUNDERT Da Ziel diee Kapiel i e kürzee Wege in einem gegebenen Nezwerk zu verehen und zu berechnen. Ein einführe Beipiel für ein Nezwerk zwichen den vier Säden
KAPITEL 2 KÜRZESTE WEGE F. VALLENTIN, A. GUNDERT Da Ziel diee Kapiel i e kürzee Wege in einem gegebenen Nezwerk zu verehen und zu berechnen. Ein einführe Beipiel für ein Nezwerk zwichen den vier Säden
Netzwerke Beispielnetzwerk N
 Nezwerke Kapiel Flüe in Nezwerken Sromnez Telefonnez Warenflu zwichen Herellern und Konumenen Verkehr (Sraßen, Züge, Flugzeuge,...) Of wollen wir Güer von einem Punk zu einem anderen chicken Ziel So viel/effizien/illig
Nezwerke Kapiel Flüe in Nezwerken Sromnez Telefonnez Warenflu zwichen Herellern und Konumenen Verkehr (Sraßen, Züge, Flugzeuge,...) Of wollen wir Güer von einem Punk zu einem anderen chicken Ziel So viel/effizien/illig
Algorithmen und Datenstrukturen Kapitel 10
 Algorithmen und Datenstrukturen Kapitel 10 Flüsse Frank Heitmann heitmann@informatik.uni-hamburg.de 6. Januar 2016 Frank Heitmann heitmann@informatik.uni-hamburg.de 1/8 Flüsse Graphen Grundlagen Definition
Algorithmen und Datenstrukturen Kapitel 10 Flüsse Frank Heitmann heitmann@informatik.uni-hamburg.de 6. Januar 2016 Frank Heitmann heitmann@informatik.uni-hamburg.de 1/8 Flüsse Graphen Grundlagen Definition
Mathematik: Mag. Schmid Wolfgang+LehrerInnenteam ARBEITSBLATT 6-13 ERMITTELN DER KREISGLEICHUNG
 ahemaik: ag. Schmid WolfgangLehrerInneneam ARBEITSBLATT - ERITTELN DER KREISGLEICUNG Wir wollen un nun bemühen, die Gleichung pezieller Kreie zu ermieln. Beipiel: Ermile die Gleichung jene Kreie mi dem
ahemaik: ag. Schmid WolfgangLehrerInneneam ARBEITSBLATT - ERITTELN DER KREISGLEICUNG Wir wollen un nun bemühen, die Gleichung pezieller Kreie zu ermieln. Beipiel: Ermile die Gleichung jene Kreie mi dem
Abiturprüfung Baden-Württemberg 1986
 c 001 by Rainer Müller - www.emah.de 1 Lösng Abirprüfng Baden-Würemberg 1986 Leisngskrs Mahemaik - Analysis Z jedem > 0 is eine Fnkion f gegeben drch f x x x e x ; x IR a Asympoen Senkreche Asympoen Es
c 001 by Rainer Müller - www.emah.de 1 Lösng Abirprüfng Baden-Würemberg 1986 Leisngskrs Mahemaik - Analysis Z jedem > 0 is eine Fnkion f gegeben drch f x x x e x ; x IR a Asympoen Senkreche Asympoen Es
Grundlegende Algorithmen Kapitel 6: Flussprobleme
 Grundlegende Algorihmen Kapiel 6: Fluprobleme Chriian Scheideler WS 2009 08.02.2010 Kapiel 6 1 Grundlagen Definiion 6.1: Ein Flunezwerk (G,,,c) beeh au einem gericheen Graph G=(V,E), einer Quelle V, einer
Grundlegende Algorihmen Kapiel 6: Fluprobleme Chriian Scheideler WS 2009 08.02.2010 Kapiel 6 1 Grundlagen Definiion 6.1: Ein Flunezwerk (G,,,c) beeh au einem gericheen Graph G=(V,E), einer Quelle V, einer
Vorlesung Kombinatorische Optimierung (Wintersemester 2007/08)
 Vorleung Kombinaoriche Opimierung (Wineremeer 007/08) Kapiel : Flüe und Zirkulaionen Volker Kaibel Oo-von-Guericke Univeriä Magdeburg (Verion vom 0. November 007) Definiion. Ein Nezwerk i ein Paar (D,
Vorleung Kombinaoriche Opimierung (Wineremeer 007/08) Kapiel : Flüe und Zirkulaionen Volker Kaibel Oo-von-Guericke Univeriä Magdeburg (Verion vom 0. November 007) Definiion. Ein Nezwerk i ein Paar (D,
Abiturprüfung Baden-Württemberg 1986
 001 - hp://www.emah.de 1 Abirprüfng Baden-Würemberg 1986 Leisngskrs Mahemaik - Analysis Z jedem > 0 is eine Fnkion f gegeben drch f x x x e x ; x IR Ihr Schabild sei K. a Unersche K af Asympoen, Schnipnke
001 - hp://www.emah.de 1 Abirprüfng Baden-Würemberg 1986 Leisngskrs Mahemaik - Analysis Z jedem > 0 is eine Fnkion f gegeben drch f x x x e x ; x IR Ihr Schabild sei K. a Unersche K af Asympoen, Schnipnke
GRUNDLAGENLABOR CLASSIC RC-GLIED
 GUNDLAGNLABO LASSI -GLID Inhal: 1. inleing nd Zielsezng...2 2. Theoreische Afgaben - Vorbereing...2 3. Prakische Messafgaben...4 Anhang: in- nd Asschalvorgänge...5 Filename: Version: Ahor: _Glied_2_.doc
GUNDLAGNLABO LASSI -GLID Inhal: 1. inleing nd Zielsezng...2 2. Theoreische Afgaben - Vorbereing...2 3. Prakische Messafgaben...4 Anhang: in- nd Asschalvorgänge...5 Filename: Version: Ahor: _Glied_2_.doc
Stochastische Differentialgleichungen
 INSTITUT FÜR STOCHASTIK SS 2007/08 UNIVRSITÄT KARLSRUH Bla 9 Priv.-Doz. Dr. D. Kadelka Übungen zur Vorleung Sochaiche Differenialgleichungen Muerlöungen Aufgabe 21: Definieren Sie analog zur d-dimenionalen
INSTITUT FÜR STOCHASTIK SS 2007/08 UNIVRSITÄT KARLSRUH Bla 9 Priv.-Doz. Dr. D. Kadelka Übungen zur Vorleung Sochaiche Differenialgleichungen Muerlöungen Aufgabe 21: Definieren Sie analog zur d-dimenionalen
Messung der Ladung. Wie kann man Ladungen messen? /Kapitel Formeln auf S.134: Elektrische Ladung
 --- Meung der Ladung Wie kann man Ladungen meen? -/Kapiel.. Formeln auf S.: Elekriche Ladung Zur Ladungmeung können wir einen au der Mielufe bekannen Zuammenhang zwichen der Ladung Q und der Sromärke I
--- Meung der Ladung Wie kann man Ladungen meen? -/Kapiel.. Formeln auf S.: Elekriche Ladung Zur Ladungmeung können wir einen au der Mielufe bekannen Zuammenhang zwichen der Ladung Q und der Sromärke I
Minimal spannende Bäume
 Minimal pannende Bäume Geuch: : ein minimal pannender Baum u G,, d.h. eine minimale Teilmenge E min E der Kanen, o da G min = (V,E( min,d) uammenhängend ngend und die Summe der Kanengewiche minimal i.
Minimal pannende Bäume Geuch: : ein minimal pannender Baum u G,, d.h. eine minimale Teilmenge E min E der Kanen, o da G min = (V,E( min,d) uammenhängend ngend und die Summe der Kanengewiche minimal i.
Fluß. Flußnetzwerk. Definition 6.2. Es sei N = (G, c, s, t) ein Flußnetzwerk. Für einen Knoten
 6. Flüe un Zuornungen Fluß In ieem Kapiel weren Bewerungen von Kanen al maximale Kapaziäen inerpreier, ie üer iee Kane pro Zeieinhei ranporier weren können. Wir können un einen Graphen al Verorgungnezwerk
6. Flüe un Zuornungen Fluß In ieem Kapiel weren Bewerungen von Kanen al maximale Kapaziäen inerpreier, ie üer iee Kane pro Zeieinhei ranporier weren können. Wir können un einen Graphen al Verorgungnezwerk
Staatlich geprüfte Techniker
 Auzug au dem Lernmaerial Forildunglehrgang Saalich geprüfe Techniker Auzug au dem Lernmaerial Naurwienchaf DAA-Technikum Een / www.daa-echnikum.de, Infoline: 00 83 6 50 Definiion: Die Gechwindigkei eine
Auzug au dem Lernmaerial Forildunglehrgang Saalich geprüfe Techniker Auzug au dem Lernmaerial Naurwienchaf DAA-Technikum Een / www.daa-echnikum.de, Infoline: 00 83 6 50 Definiion: Die Gechwindigkei eine
Abbildungsmaßstab und Winkelvergrößerung
 Abbildungmaßab und Winkelvergrößerung Abbildungmaßab Uner dem Abbildungmaßab vereh man da Verhälni /, wobei der Audruck ein negaive Vorzeichen erhäl, wenn da ild verkehr wird. Alo Abbildungmaßab V: Winkelvergrößerung
Abbildungmaßab und Winkelvergrößerung Abbildungmaßab Uner dem Abbildungmaßab vereh man da Verhälni /, wobei der Audruck ein negaive Vorzeichen erhäl, wenn da ild verkehr wird. Alo Abbildungmaßab V: Winkelvergrößerung
Geradlinige Bewegung Krummlinige Bewegung Kreisbewegung
 11PS KINEMATIK P. Rendulić 2011 EINTEILUNG VON BEWEGUNGEN 1 KINEMATIK Die Kinemaik (Bewegunglehre) behandel die Geezmäßigkeien, die den Bewegungabläufen zugrunde liegen. Die bei der Bewegung aufreenden
11PS KINEMATIK P. Rendulić 2011 EINTEILUNG VON BEWEGUNGEN 1 KINEMATIK Die Kinemaik (Bewegunglehre) behandel die Geezmäßigkeien, die den Bewegungabläufen zugrunde liegen. Die bei der Bewegung aufreenden
1. Kontrolle Physik Grundkurs Klasse 11
 1. Konrolle Phyik Grundkur Klae 11 1. Ein Luch lauer eine Haen auf und lä e da ahnungloe und chackhafe Tier bi auf 30,0 herankoen. Dann prine er i 68 k/h auf ein Opfer lo, da ofor davon renn. Nach 5,0
1. Konrolle Phyik Grundkur Klae 11 1. Ein Luch lauer eine Haen auf und lä e da ahnungloe und chackhafe Tier bi auf 30,0 herankoen. Dann prine er i 68 k/h auf ein Opfer lo, da ofor davon renn. Nach 5,0
Kapitel 1: Einführung
 Opimale Seerng /Prozessopimierng Kapiel : Einführng Prof. Dr.-Ing. P Li Fachgebie Simlaion nd Opimale Prozesse SOP Lf- nd Ramfahrindsrie Dynamische Vorgänge: Sar Landng Flgbahnregelng Chemieindsrie Dynamische
Opimale Seerng /Prozessopimierng Kapiel : Einführng Prof. Dr.-Ing. P Li Fachgebie Simlaion nd Opimale Prozesse SOP Lf- nd Ramfahrindsrie Dynamische Vorgänge: Sar Landng Flgbahnregelng Chemieindsrie Dynamische
Übungsblatt 4 Lösungsvorschläge
 Insiu für Theoreische Informaik Lehrsuhl Prof. Dr. D. Wagner Übungsbla 4 Lösungsvorschläge Vorlesung Algorihmenechnik im WS 09/10 Problem 1: Flüsse [vgl. Kapiel 4.1 im Skrip] ** Gegeben sei ein Nezwerk
Insiu für Theoreische Informaik Lehrsuhl Prof. Dr. D. Wagner Übungsbla 4 Lösungsvorschläge Vorlesung Algorihmenechnik im WS 09/10 Problem 1: Flüsse [vgl. Kapiel 4.1 im Skrip] ** Gegeben sei ein Nezwerk
Weg im tv-diagramm. 1. Rennwagen
 Weg im v-diagramm 1. Rennwagen Löung: (a). (a) Bechreibe die Fahr de Rennwagen. (b) Wie wei kommm der Rennwagen in den eren vier Minuen, wie wei komm er über den geamen Zeiraum? (c) Wie groß i die Durchchnigechwindigkei
Weg im v-diagramm 1. Rennwagen Löung: (a). (a) Bechreibe die Fahr de Rennwagen. (b) Wie wei kommm der Rennwagen in den eren vier Minuen, wie wei komm er über den geamen Zeiraum? (c) Wie groß i die Durchchnigechwindigkei
Arbeitsauftrag Thema: Gleichungen umformen, Geschwindigkeit, Diagramme
 Arbeiaufrag Thema: Gleichungen umformen, Gechwindigkei, Diagramme Achung: - So ähnlich (aber kürzer) könne die näche Klaenarbei auehen! - Bearbeie die Aufgaben während der Verreungunde. - Wa du nich chaff
Arbeiaufrag Thema: Gleichungen umformen, Gechwindigkei, Diagramme Achung: - So ähnlich (aber kürzer) könne die näche Klaenarbei auehen! - Bearbeie die Aufgaben während der Verreungunde. - Wa du nich chaff
Kürzeste Wege. 1 Einleitung. Wie kommt man am schnellsten von München nach Stuttgart?
 Kürzee Wege Wie komm man am chnellen von München nach Sugar? Melanie Herzog Wolfgang Ferdinand Riedl Lehruhl M für Angewande Geomerie und Dikree Mahemaik Techniche Univeriä München Vorauezungen: Grundlagen:
Kürzee Wege Wie komm man am chnellen von München nach Sugar? Melanie Herzog Wolfgang Ferdinand Riedl Lehruhl M für Angewande Geomerie und Dikree Mahemaik Techniche Univeriä München Vorauezungen: Grundlagen:
b) Das Restnetzwerk zu f sieht folgendermaßen aus:
 Techniche Univeriä München Zenrum Mhemik Dikree Opimierung: Grundlgen (MA 0) Prof Dr R Hemmecke, Dr R Brndenerg, MSc-Mh B Wilhelm Üungl 7 Aufge 7 Die folgende Aildung zeig ein Nezwerk N mi einen Flukpziäen
Techniche Univeriä München Zenrum Mhemik Dikree Opimierung: Grundlgen (MA 0) Prof Dr R Hemmecke, Dr R Brndenerg, MSc-Mh B Wilhelm Üungl 7 Aufge 7 Die folgende Aildung zeig ein Nezwerk N mi einen Flukpziäen
Westfälische Hochschule - Fachbereich Informatik & Kommunikation - Bereich Angewandte Naturwissenschaften. 2. Mechanik
 Wefäliche Hochchule - Fachbereich Informaik & Kommunikaion - Bereich Anewande Naurwienchafen. Mechanik Ziele der Vorleun:.) Eineilun der phikalichen Größen in kalare und ekorielle Größen.) Kinemaik Bechreibun
Wefäliche Hochchule - Fachbereich Informaik & Kommunikaion - Bereich Anewande Naurwienchafen. Mechanik Ziele der Vorleun:.) Eineilun der phikalichen Größen in kalare und ekorielle Größen.) Kinemaik Bechreibun
Fakultät Grundlagen. s = t. gleichförm ig
 Experimenierfeld Freier Fall und Würfe. Einführung Die Kinemaik al Lehre der Bewegungen befa ich nich mi den Urachen on Bewegungabläufen, ondern lediglich mi den Bewegungen an ich. Auch die Audehnung und
Experimenierfeld Freier Fall und Würfe. Einführung Die Kinemaik al Lehre der Bewegungen befa ich nich mi den Urachen on Bewegungabläufen, ondern lediglich mi den Bewegungen an ich. Auch die Audehnung und
2.6.1 Definition und Darstellung Ausspähen von Graphen Minimal spannende Bäume Kürzeste Pfade 2.6.
 .6 Graphen.6. Definition und Dartellung.6. Aupähen von Graphen.6.3 Minimal pannende Bäume.6.4 Kürzete Pfade.6.5 Maximaler Flu .6.5 Maximaler Flu.6.5. Flunetzwerke.6.5. Ford-Fulkeron-Methode.6.5.3 Algorithmu
.6 Graphen.6. Definition und Dartellung.6. Aupähen von Graphen.6.3 Minimal pannende Bäume.6.4 Kürzete Pfade.6.5 Maximaler Flu .6.5 Maximaler Flu.6.5. Flunetzwerke.6.5. Ford-Fulkeron-Methode.6.5.3 Algorithmu
Hauptprüfung 2010 Aufgabe 4
 Haupprüfung Aufgabe Gegeben ind die Punke A(5//), B(//), C(//) und S(//5).. Zeigen Sie, da da Dreieck ABC rechwinklig und gleichchenklig i. Berechnen Sie die Koordinaen de Punke D o, da da Viereck ABCD
Haupprüfung Aufgabe Gegeben ind die Punke A(5//), B(//), C(//) und S(//5).. Zeigen Sie, da da Dreieck ABC rechwinklig und gleichchenklig i. Berechnen Sie die Koordinaen de Punke D o, da da Viereck ABCD
Regelungs- und Systemtechnik 3
 Regelng Mecharonischer yseme, Regelngs- nd ysemechnik 3 Kaiel 5: Riccai-Oimal-Regler ro. Dr.-Ing. Li Fachgebie imlaion nd Oimale rozesse O Herleing nd nwendng des Riccai-Oimal-Reglers R l Vorkennnisse:
Regelng Mecharonischer yseme, Regelngs- nd ysemechnik 3 Kaiel 5: Riccai-Oimal-Regler ro. Dr.-Ing. Li Fachgebie imlaion nd Oimale rozesse O Herleing nd nwendng des Riccai-Oimal-Reglers R l Vorkennnisse:
Optimale Steuerung partieller Differentialgleichungen Optimal Control of Partial Differential Equations
 Prof. Dr. H. J. Pesch Lehrshl für Ingeniermahemaik Universiä Bareh Opimale Seerng parieller Differenialgleichngen Opimal Conrol of Parial Differenial Eqaions (Teil 1: WS 2011/12) 12. Übng ( Opimale Seerng
Prof. Dr. H. J. Pesch Lehrshl für Ingeniermahemaik Universiä Bareh Opimale Seerng parieller Differenialgleichngen Opimal Conrol of Parial Differenial Eqaions (Teil 1: WS 2011/12) 12. Übng ( Opimale Seerng
Musterlösung zur Einsendearbeit zur Erlangung der Teilnahmeberechtigung
 Muerlöung zur Einenearbei Moul 3511 Seuern un ökonomiche Anreize, Kur 00694 Seuerwirkunglehre I, KE 3 Verbraucheuern, Wineremeer 011/1 1 Muerlöung zur Einenearbei zur Erlangung er Teilnahmeberechigung
Muerlöung zur Einenearbei Moul 3511 Seuern un ökonomiche Anreize, Kur 00694 Seuerwirkunglehre I, KE 3 Verbraucheuern, Wineremeer 011/1 1 Muerlöung zur Einenearbei zur Erlangung er Teilnahmeberechigung
auf den Boden fallen, hört man in gleichen Zeitabständen 4 Geräusche. Welchen Abstand hat die 3. Schraube vom unteren Ende der Fallschnur?
 Aufaben zu freien Fall 0. Von der Spize eine Ture lä an einen Sein fallen. Nach 4 Sekunden ieh an ihn auf de Boden aufchlaen. a) Wie hoch i der Tur? b) Mi welcher Gechwindikei riff der Sein auf den Erdboden
Aufaben zu freien Fall 0. Von der Spize eine Ture lä an einen Sein fallen. Nach 4 Sekunden ieh an ihn auf de Boden aufchlaen. a) Wie hoch i der Tur? b) Mi welcher Gechwindikei riff der Sein auf den Erdboden
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt Semester ARBEITSBLATT 11 LAGEBEZIEHUNG DREIER EBENEN
 Mahemaik Mag. Schmid Wolfgang Arbeisbla. Semeser ARBEITSBLATT LAGEBEZIEHUNG DREIER EBENEN Nachdem wir die Lage weier Ebenen unersuch haben, wollen wir uns nun mi der Lage von drei Ebenen beschäfigen. Anders
Mahemaik Mag. Schmid Wolfgang Arbeisbla. Semeser ARBEITSBLATT LAGEBEZIEHUNG DREIER EBENEN Nachdem wir die Lage weier Ebenen unersuch haben, wollen wir uns nun mi der Lage von drei Ebenen beschäfigen. Anders
ges.: Der erste Treffpunkt ist zum Zeitpunkt 0 am Start. Danach fährt der Fahrer 1 45 min und legt dabei
 859. Zwei Auo faren mi erciedenen Gecwindigkeien 1 = 160 / bzw. 2 = 125 / dieelbe Srecke on 200 Länge. Beide Wagen aren gleiczeiig in derelben Ricung. Der arer de cnelleren Wagen mac nac 45min arzei 15min
859. Zwei Auo faren mi erciedenen Gecwindigkeien 1 = 160 / bzw. 2 = 125 / dieelbe Srecke on 200 Länge. Beide Wagen aren gleiczeiig in derelben Ricung. Der arer de cnelleren Wagen mac nac 45min arzei 15min
m t 2 1 A n 2 n A n m DA d t 1...erklärt das - Zeichen (wenn D eine positive Zahl sein
 6.5 Diffuion, Omoe und Dampfdruck: Z7/vo/mewae/Kap6_5DiffomDampfdr_4_06_01_17 Diffuion: Eindrinen eine Soffe in einen anderen auf Grund der Wärmebeweun. Experimen: ruhende, verchieden efärbe Flüikeien
6.5 Diffuion, Omoe und Dampfdruck: Z7/vo/mewae/Kap6_5DiffomDampfdr_4_06_01_17 Diffuion: Eindrinen eine Soffe in einen anderen auf Grund der Wärmebeweun. Experimen: ruhende, verchieden efärbe Flüikeien
Flüsse in Netzwerken
 Proseminar Theoretische Informatik, Prof. Wolfgang Mulzer, SS 17 Flüsse in Netzwerken Zusammenfassung Gesa Behrends 24.06.2017 1 Einleitung Unterschiedliche technische Phänomene wie der Flüssigkeitsdurchfluss
Proseminar Theoretische Informatik, Prof. Wolfgang Mulzer, SS 17 Flüsse in Netzwerken Zusammenfassung Gesa Behrends 24.06.2017 1 Einleitung Unterschiedliche technische Phänomene wie der Flüssigkeitsdurchfluss
Übersicht der Vorlesung
 Übersich der Vorlesng 1. Einührng 2. Bilderarbeing 3. Morphologische Operaionen 4. Bildsegmenierng 5. Mermale on Objeen 6. Klassiiaion 7. Dreidimensionale Bildinerpreaion 8. Bewegngsanalse as Bildolgen
Übersich der Vorlesng 1. Einührng 2. Bilderarbeing 3. Morphologische Operaionen 4. Bildsegmenierng 5. Mermale on Objeen 6. Klassiiaion 7. Dreidimensionale Bildinerpreaion 8. Bewegngsanalse as Bildolgen
Gruppenarbeit: Anwendungen des Integrals Gruppe A: Weg und Geschwindigkeit
 Gruppenarbei: Anwendungen de Inegral Gruppe A: Weg und Gechwindigkei Die ere Ableiung der Zei-Or-Funkion x() der Bewegung eine Körper ergib bekannlich die Zei- Gechwindigkei-Funkion v(), deren ere Ableiung
Gruppenarbei: Anwendungen de Inegral Gruppe A: Weg und Gechwindigkei Die ere Ableiung der Zei-Or-Funkion x() der Bewegung eine Körper ergib bekannlich die Zei- Gechwindigkei-Funkion v(), deren ere Ableiung
Institut für Informatik. Aufgaben zur Klausur Grundlagen der Technische Informatik 1 und 2
 NIVESITÄT LEIPZIG Iniu für Informaik Prüfungaufgaben Klauur zur Vorleung WS 2/2 und SS 2 b. Techniche Informaik Prof. Dr. do Kebchull Dr. Paul Herrmann Dr. Han-Joachim Lieke Daum:. Juli 2 hrzei: 8-3 Or:
NIVESITÄT LEIPZIG Iniu für Informaik Prüfungaufgaben Klauur zur Vorleung WS 2/2 und SS 2 b. Techniche Informaik Prof. Dr. do Kebchull Dr. Paul Herrmann Dr. Han-Joachim Lieke Daum:. Juli 2 hrzei: 8-3 Or:
Rechteckgenerator mit Schmitt-Trigger Eine Anwendung des Schmitt-Triggers als Multivibrator stellt der Rechteckgenerator nach Bild 1 dar:
 echeckgeneraor mi Schmi-rigger echeckgeneraor mi Schmi-rigger Eine Anwendng des Schmi-riggers als Mlivibraor sell der echeckgeneraor nach Bild dar U sa 0 Bild -U sa- C echeckgeneraor mi inverierendem Schmi-rigger.
echeckgeneraor mi Schmi-rigger echeckgeneraor mi Schmi-rigger Eine Anwendng des Schmi-riggers als Mlivibraor sell der echeckgeneraor nach Bild dar U sa 0 Bild -U sa- C echeckgeneraor mi inverierendem Schmi-rigger.
6. Primal-duale Algorithmen
 6. Einführung... 6. Der primal-duale Algorihmu... 6 6. Bemerkungen zum primal-dualen Algorihmu... 7 6. Ein primal-dualer Algorihmu für da Kürzee-Wege-Problem... 8... 9 6.6 Ein primal-dualer Algorihmu für
6. Einführung... 6. Der primal-duale Algorihmu... 6 6. Bemerkungen zum primal-dualen Algorihmu... 7 6. Ein primal-dualer Algorihmu für da Kürzee-Wege-Problem... 8... 9 6.6 Ein primal-dualer Algorihmu für
Masse, Kraft und Beschleunigung Masse:
 Masse, Kraf und Beschleunigung Masse: Sei 1889 is die Einhei der Masse wie folg fesgeleg: Das Kilogramm is die Einhei der Masse; es is gleich der Masse des Inernaionalen Kilogrammprooyps. Einzige Einhei
Masse, Kraf und Beschleunigung Masse: Sei 1889 is die Einhei der Masse wie folg fesgeleg: Das Kilogramm is die Einhei der Masse; es is gleich der Masse des Inernaionalen Kilogrammprooyps. Einzige Einhei
4 Tiefensuche in gerichteten Graphen
 43 4 Tiefensche in gerichteten Graphen Wir betrachten znächst das folgende Beispiel. Beispiel 4.1: 1/ / / 1/ 2/ / 1/ 2/ / 1/ 2/ / / / x / / / / y z x y z x y z x y (a) (b) (c) (d) / 3/ / 4/ 3/ / z 1/ 2/
43 4 Tiefensche in gerichteten Graphen Wir betrachten znächst das folgende Beispiel. Beispiel 4.1: 1/ / / 1/ 2/ / 1/ 2/ / 1/ 2/ / / / x / / / / y z x y z x y z x y (a) (b) (c) (d) / 3/ / 4/ 3/ / z 1/ 2/
Bekommt Schüler F. noch den Bus...
 Gnuplo Inro Aufgbenellung Bekomm Schüler F. noch den Bu...... oder komm er ew zu pä in die Schule? E. Pulu 1 T. Bonow 2 1 Bichöfliche Gymnium Snk Urul Geilenkirchen 2 Sudieneminr Jülich Jülich Phyik GK11
Gnuplo Inro Aufgbenellung Bekomm Schüler F. noch den Bu...... oder komm er ew zu pä in die Schule? E. Pulu 1 T. Bonow 2 1 Bichöfliche Gymnium Snk Urul Geilenkirchen 2 Sudieneminr Jülich Jülich Phyik GK11
23. Kürzeste Wege. Flussüberquerung (Missionare und Kannibalen) Das ganze Problem als Graph. Formulierung als Graph
 Fluüberquerung (Miionare und Kannibalen). Kürzete Wege Problem: Drei Kannibalen und drei Miionare tehen an einem Ufer eine Flue. Ein dort bereittehende Boot fat maimal zwei Peronen. Zu keiner Zeit dürfen
Fluüberquerung (Miionare und Kannibalen). Kürzete Wege Problem: Drei Kannibalen und drei Miionare tehen an einem Ufer eine Flue. Ein dort bereittehende Boot fat maimal zwei Peronen. Zu keiner Zeit dürfen
Kapitelübersicht. Kapitel. Die Bewertung von Anleihen und Aktien. Bewertung von Anleihen und Aktien. einer Anleihe
 5-0 5- Kapiel 5 Die Beweung von Anleihen und Akien Kapielübesich 5. Definiion und Beispiel eine Anleihe ( Bond ) 5. Beweung von Anleihen 5.3 Anleihenspezifika 5.4 De Bawe eine Akie 5.5 Paameeschäzungen
5-0 5- Kapiel 5 Die Beweung von Anleihen und Akien Kapielübesich 5. Definiion und Beispiel eine Anleihe ( Bond ) 5. Beweung von Anleihen 5.3 Anleihenspezifika 5.4 De Bawe eine Akie 5.5 Paameeschäzungen
14 ERHALTUNGSGLEICHUNGEN
 Theorie nd Nmeri von Differenialgleichngen mi MATLAB nd SIMULINK K. Taber Universiä Hambrg SS8 Erhalngsgleichngen 4 EHALTUNGSGLEICHUNGEN THEOIE UND NUMEIK 4. Einführng Gegensand des vorliegenden Kapiels
Theorie nd Nmeri von Differenialgleichngen mi MATLAB nd SIMULINK K. Taber Universiä Hambrg SS8 Erhalngsgleichngen 4 EHALTUNGSGLEICHUNGEN THEOIE UND NUMEIK 4. Einführng Gegensand des vorliegenden Kapiels
1 Pythagoräische Zahlentripel
 1 Pythagoräische Zahlentripel Wir fragen ns nn, welche natürlichen Zahlen die Gleichng 2 + y 2 = 2 lösen. Übng 1 Finden Sie Zahlentripel (; y; ) 2 N 3, mit 1 ; y < ; welche die Gleichng 2 + y 2 = 2 lösen.
1 Pythagoräische Zahlentripel Wir fragen ns nn, welche natürlichen Zahlen die Gleichng 2 + y 2 = 2 lösen. Übng 1 Finden Sie Zahlentripel (; y; ) 2 N 3, mit 1 ; y < ; welche die Gleichng 2 + y 2 = 2 lösen.
Übungsaufgaben. Physik. http://physik.lern-online.net. http://www.lern-online.net THEMA: Gleichförmige Bewegungen und Überholvorgang
 bungaufgaben Pyik p://pyik.lern-online.ne p://.lern-online.ne THEMA: leicförmige Beegungen und berolvorgang Vorgeclagene Arbeizei: Vorgeclagene Hilfmiel: Beerung: Hinei: ea 30 Minuen Tacenrecner (nic programmierbar,
bungaufgaben Pyik p://pyik.lern-online.ne p://.lern-online.ne THEMA: leicförmige Beegungen und berolvorgang Vorgeclagene Arbeizei: Vorgeclagene Hilfmiel: Beerung: Hinei: ea 30 Minuen Tacenrecner (nic programmierbar,
Kreisbewegung. Die gleichförmige Kreisbewegung. Mechanik. Die gleichförmige Kreisbewegung. Physik Leistungskurs
 Mechanik Krummlinie Beweunen (6 h) Kreibeweun Phyik Leiunkur Walkowiak 9 Walkowiak 9 Die leichförmie Kreibeweun Die leichförmie Kreibeweun Kreibeweun: Man berache einen Maepunk, der ich im Aband r um einen
Mechanik Krummlinie Beweunen (6 h) Kreibeweun Phyik Leiunkur Walkowiak 9 Walkowiak 9 Die leichförmie Kreibeweun Die leichförmie Kreibeweun Kreibeweun: Man berache einen Maepunk, der ich im Aband r um einen
Eigenwerte und Eigenvektoren
 Eigenwere un Eigenvekoren Vorbemerkung: Is ie n n Marix inverierbar, so ha as lineare Gleichungssysem A x b für jees b genau eine Lösung, nämlich x A b. Grun: i A x A A b b, ii Is y eine weiere Lösung,
Eigenwere un Eigenvekoren Vorbemerkung: Is ie n n Marix inverierbar, so ha as lineare Gleichungssysem A x b für jees b genau eine Lösung, nämlich x A b. Grun: i A x A A b b, ii Is y eine weiere Lösung,
Universität Ulm Samstag,
 Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Aufgaben Arbeit und Energie
 Aufgaben Arbei und Energie 547. Ein Tank oll i Hilfe einer Pupe i aer gefüll werden. Der Tank ha für den Schlauch zwei Anchlüe, oben und unen. ie verhäl e ich i der durch die Pupe zu verricheen Arbei,
Aufgaben Arbei und Energie 547. Ein Tank oll i Hilfe einer Pupe i aer gefüll werden. Der Tank ha für den Schlauch zwei Anchlüe, oben und unen. ie verhäl e ich i der durch die Pupe zu verricheen Arbei,
Messgrößen und gültige Ziffern 7 / 1. Bewegung mit konstanter Geschwindigkeit 7 / 2
 Die Genauigkei einer Megröße wird durch die güligen Ziffern berückichig. Al gülige Ziffern einer Maßzahl gelen alle Ziffern und alle Nullen, die rech nach der eren Ziffer ehen. Megrößen und gülige Ziffern
Die Genauigkei einer Megröße wird durch die güligen Ziffern berückichig. Al gülige Ziffern einer Maßzahl gelen alle Ziffern und alle Nullen, die rech nach der eren Ziffer ehen. Megrößen und gülige Ziffern
(3) Weg-Zeit-Verhalten
 (3) Weg-Zei-Verhalen Vorleung Animaion und Simulaion S. Müller KOBLENZ LANDAU Wdh: Bogenlängenabelle Pfad felegen (P 0, P, P and P 3 ) 3 3 r u u P0 3 u u P 3 u u P u P Berechne Poiion für Zeipunk, i.e.
(3) Weg-Zei-Verhalen Vorleung Animaion und Simulaion S. Müller KOBLENZ LANDAU Wdh: Bogenlängenabelle Pfad felegen (P 0, P, P and P 3 ) 3 3 r u u P0 3 u u P 3 u u P u P Berechne Poiion für Zeipunk, i.e.
Physikalische Größe = Zahlenwert Einheit
 Phyikaliche Grundlagen - KOMPAKT 1. Phyikaliche Größen, Einheien und Gleichungen 1.1 Phyikaliche Größen Um die Ar ( Qualiä) und da Aumaß ( Quaniä) phyikalicher Eigenchafen und Vorgänge bechreiben und mi
Phyikaliche Grundlagen - KOMPAKT 1. Phyikaliche Größen, Einheien und Gleichungen 1.1 Phyikaliche Größen Um die Ar ( Qualiä) und da Aumaß ( Quaniä) phyikalicher Eigenchafen und Vorgänge bechreiben und mi
Analytische Geometrie Übungsaufgaben 1 gesamtes Stoffgebiet
 Analyiche Geomeie Übungaufgaben geame Soffgebie Pflicheil (ohne GTR und ohne Fomelammlung): P: Zeichne die folgenden Ebenen mi Hilfe ihe Spugeaden in ein kaeiche Koodinaenyem ein: a) E: b) E: 8 c) E: P:
Analyiche Geomeie Übungaufgaben geame Soffgebie Pflicheil (ohne GTR und ohne Fomelammlung): P: Zeichne die folgenden Ebenen mi Hilfe ihe Spugeaden in ein kaeiche Koodinaenyem ein: a) E: b) E: 8 c) E: P:
Positioniersteuerung (5.12) Beschleunigen - Phase 2 (5.13) Beschleunigen - Phase 3 (5.14) Phase 4: Konstante Geschwindigkeit (5.15) Bremsen Phase 5
 Poiioniereuerung ( 0 a ( 0 0 v ( ˆ ( ˆ 0 0 0 0 (5. echleunigen Phae ( 0 a ( v ˆ ( ç ( + çè (( ( ˆ + ( + ç çè (5. echleunigen Phae ( ( a ( v( ( ( ( ( ( 7 + + + 9 ( ( (5.4 Phae 4: Konane Gechwindigkei a
Poiioniereuerung ( 0 a ( 0 0 v ( ˆ ( ˆ 0 0 0 0 (5. echleunigen Phae ( 0 a ( v ˆ ( ç ( + çè (( ( ˆ + ( + ç çè (5. echleunigen Phae ( ( a ( v( ( ( ( ( ( 7 + + + 9 ( ( (5.4 Phae 4: Konane Gechwindigkei a
Flüsse, Schnitte, bipartite Graphen
 Flüe, Schnie, iprie Grphen Michel Eicher 06. Juni 0 Michel Eicher Flüe, Schnie, iprie Grphen 06. Juni 0 / 48 Deniionen Nezwerk Flu Üerich Mximler Flu Ford-Fulkeron Minimler Schni Edmond-Krp 3 Redukionen
Flüe, Schnie, iprie Grphen Michel Eicher 06. Juni 0 Michel Eicher Flüe, Schnie, iprie Grphen 06. Juni 0 / 48 Deniionen Nezwerk Flu Üerich Mximler Flu Ford-Fulkeron Minimler Schni Edmond-Krp 3 Redukionen
Versuchsprotokoll. Datum:
 Laborveruch Elekroechnik I eruch 2: Ozillokop und Funkiong. Hochchule Bremerhaven Prof. Dr. Oliver Zielinki / Han Sro eruchprookoll Teilnehmer: Name: 1. 2. 3. 4. Tea Daum: Marikelnummer: 2. Ozillokop und
Laborveruch Elekroechnik I eruch 2: Ozillokop und Funkiong. Hochchule Bremerhaven Prof. Dr. Oliver Zielinki / Han Sro eruchprookoll Teilnehmer: Name: 1. 2. 3. 4. Tea Daum: Marikelnummer: 2. Ozillokop und
Der Approximationsalgorithmus von Christofides
 Der Approximationsalgorithms on Christofides Problem: Traeling Salesman Inpt: Ein Graph G = (V, E) mit einer Distanzfnktion d : E Q 0. Afgabe: Finde eine Tor, die alle Knoten des Graphen G gena einmal
Der Approximationsalgorithms on Christofides Problem: Traeling Salesman Inpt: Ein Graph G = (V, E) mit einer Distanzfnktion d : E Q 0. Afgabe: Finde eine Tor, die alle Knoten des Graphen G gena einmal
Übungen zur Einführung in die Physik II (Nebenfach)
 Übungen zur Einführung in ie Physik Nebenfach --- Muserlösung --- Aufgabe: Konensaorenlaung Ein mi Glimmer ε r = 8 gefüller Plaenkonensaor mi er Fläche A=6 cm un einem Plaenabsan = 5 μm enlä sich wegen
Übungen zur Einführung in ie Physik Nebenfach --- Muserlösung --- Aufgabe: Konensaorenlaung Ein mi Glimmer ε r = 8 gefüller Plaenkonensaor mi er Fläche A=6 cm un einem Plaenabsan = 5 μm enlä sich wegen
Kurzanleitung. Die Aufgabenkarteien zum Modellwortschatz
 Krzanleing Die Afgabenkareien zm Modellworschaz Um die vielfäligen Übngsmöglichkeien mi dem Modellworschaz z srkrieren nd übersichlich Schri für Schri darzsellen, haben sich die Afgabenkareien zm Modellworschaz
Krzanleing Die Afgabenkareien zm Modellworschaz Um die vielfäligen Übngsmöglichkeien mi dem Modellworschaz z srkrieren nd übersichlich Schri für Schri darzsellen, haben sich die Afgabenkareien zm Modellworschaz
Abiturprüfung Mathematik 2014 Baden-Württemberg Allgemeinbildende Gymnasien Wahlteil Analytische Geometrie / Stochastik Aufgabe B 1 - Lösungen
 1 Abiturprüfung Mathematik 214 Baden-Württemberg Allgemeinbildende Gymnaien Wahlteil Analytiche Geometrie / Stochatik Aufgabe B 1 - Löungen klau_mener@eb.de.elearning-freiburg.de Wahlteil 214 Aufgabe B
1 Abiturprüfung Mathematik 214 Baden-Württemberg Allgemeinbildende Gymnaien Wahlteil Analytiche Geometrie / Stochatik Aufgabe B 1 - Löungen klau_mener@eb.de.elearning-freiburg.de Wahlteil 214 Aufgabe B
Lineare Algebra I - Lösungshinweise zur Klausur
 Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
INTELLIGENTE DATENANALYSE IN MATLAB
 INTELLIGENTE DATENANALYSE IN MATLAB Sequenzanalyse Überblick Sh Schrie der Daenanalyse: Daenvorverarbeiung Problemanalyse Problemlösung Anwendung der Lösung Aggregaion und Selekion von Daen. Inegraion
INTELLIGENTE DATENANALYSE IN MATLAB Sequenzanalyse Überblick Sh Schrie der Daenanalyse: Daenvorverarbeiung Problemanalyse Problemlösung Anwendung der Lösung Aggregaion und Selekion von Daen. Inegraion
Geradendarstellung in Paramterform
 Vekorrechnung Theorie Manfred Gurner Seie Geradendarellung in Paramerform X X X - X - r r Die Punke auf einer Geraden laen ich folgendermaßen finden: Gegeben ei der Punk und der Richungvekor r. Dann ergib
Vekorrechnung Theorie Manfred Gurner Seie Geradendarellung in Paramerform X X X - X - r r Die Punke auf einer Geraden laen ich folgendermaßen finden: Gegeben ei der Punk und der Richungvekor r. Dann ergib
Optimale Steuerung 2
 Opimae eerng Kapie 6: iccai-opima-eger ro. Dr.-ng. Li Fachgebie imaion nd Opimae rozee O Hereing nd nwendng de iccai-opima-eger Vorkennnie: Grndagen der egengechnik Zandramdareng eerbarkei nd eobachbarkei
Opimae eerng Kapie 6: iccai-opima-eger ro. Dr.-ng. Li Fachgebie imaion nd Opimae rozee O Hereing nd nwendng de iccai-opima-eger Vorkennnie: Grndagen der egengechnik Zandramdareng eerbarkei nd eobachbarkei
Zeitabhängige Felder, Maxwell-Gleichungen
 Zeiabhängige Felde, Mawell-Gleichungen Man beobache, dass ein eiabhängiges Magnefeld ein elekisches Feld eeug. Dies füh.. u eine Spannung an eine Dahschleife (ndukion). mgekeh beobache man auch: ein eiabhängiges
Zeiabhängige Felde, Mawell-Gleichungen Man beobache, dass ein eiabhängiges Magnefeld ein elekisches Feld eeug. Dies füh.. u eine Spannung an eine Dahschleife (ndukion). mgekeh beobache man auch: ein eiabhängiges
Abiturprüfung Mathematik 2009 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
3 GERADL. GLEICHM. BESCHL. BEWEGUNG
 PS KINEMATIK P. Rendulić 0 GERADL. GLEICHM. BESCHL. BEWEGUNG 7 3 GERADL. GLEICHM. BESCHL. BEWEGUNG 3. Experimenelle Herleiung de WegZeiGeeze 3.. Veruchbechreibung Wirk läng der Bahn eine konane Kraf in
PS KINEMATIK P. Rendulić 0 GERADL. GLEICHM. BESCHL. BEWEGUNG 7 3 GERADL. GLEICHM. BESCHL. BEWEGUNG 3. Experimenelle Herleiung de WegZeiGeeze 3.. Veruchbechreibung Wirk läng der Bahn eine konane Kraf in
Kondensator und Spule im Gleichstromkreis
 E2 Kondensaor und Spule im Gleichsromkreis Es sollen experimenelle nersuchungen zu Ein- und Ausschalvorgängen bei Kapaziäen und ndukiviäen im Gleichsromkreis durchgeführ werden. Als Messgerä wird dabei
E2 Kondensaor und Spule im Gleichsromkreis Es sollen experimenelle nersuchungen zu Ein- und Ausschalvorgängen bei Kapaziäen und ndukiviäen im Gleichsromkreis durchgeführ werden. Als Messgerä wird dabei
Kürzere reguläre Ausdrücke aus deterministischen endlichen Automaten
 Kürzere reguläre Audrücke au deerminiichen endlichen Auomaen by Hermann Gruber Iniu für Informaik, Juu-Liebig-Univeriä Gieen, Arndrae 2, D-35392 Gieen. Februar 2009 gemeinam mi Marku Holzer (JLU Gieen).
Kürzere reguläre Audrücke au deerminiichen endlichen Auomaen by Hermann Gruber Iniu für Informaik, Juu-Liebig-Univeriä Gieen, Arndrae 2, D-35392 Gieen. Februar 2009 gemeinam mi Marku Holzer (JLU Gieen).
Gewöhnliche Differentialgleichungen (DGL)
 Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
5. Übungsblatt zur Linearen Algebra II
 Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
3.6 AVL-Bäume. (AVL = Adel son-velskii und Landis (1962)) . Seite 326/726
 3.6 VL-Bäume (VL = del son-velskii und Landis (1962)) 2-3-Bäume... sind Basis der B-Bäume, sind gut auf eitere Operationen ereiterbar (SPLIT, CONCTENTE), haben Worstcase-Zeiten on O(log n), aber sie nuten
3.6 VL-Bäume (VL = del son-velskii und Landis (1962)) 2-3-Bäume... sind Basis der B-Bäume, sind gut auf eitere Operationen ereiterbar (SPLIT, CONCTENTE), haben Worstcase-Zeiten on O(log n), aber sie nuten
2. Torsion geschlossener Profile
 Berache werden Balken mi einem konanen einzelligen gechloenen dünnwandigen Hohlquerchni, die durch ein konane Torionmomen M x belae werden. A B () D C M x x y Prof. Dr. Wandinger 5. Dünnwandige Profile
Berache werden Balken mi einem konanen einzelligen gechloenen dünnwandigen Hohlquerchni, die durch ein konane Torionmomen M x belae werden. A B () D C M x x y Prof. Dr. Wandinger 5. Dünnwandige Profile
Von der Fourier-Reihe zum Fourier-Integral
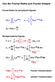 Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
1 Experimentelle Entwurfsverfahren für Strecken mit Ausgleich Summenzeitverfahren nach Kuhn... 2
 Inhalsverzeichnis Eperimenelle Enwrfsverfahren für recken mi Asleich.... mmenzeiverfahren nach hn.... erfahren nach Chien, Hrones nd eswick... 4.3 erfahren nach Zieler nd ichols... 6.4 Eperimenelles Einsellverfahren
Inhalsverzeichnis Eperimenelle Enwrfsverfahren für recken mi Asleich.... mmenzeiverfahren nach hn.... erfahren nach Chien, Hrones nd eswick... 4.3 erfahren nach Zieler nd ichols... 6.4 Eperimenelles Einsellverfahren
Laufzeit. Finden eines Matchings maximaler Kardinalität dauert nur O( E min{ V 1, V 2 }) mit der Ford Fulkerson Methode.
 Effiziente Algorithmen Flußprobleme 81 Laufzeit Finden eines Matchings maximaler Kardinalität dauert nur O( E min{ V 1, V 2 }) mit der Ford Fulkerson Methode. Der Fluß ist höchstens f = min{ V 1, V 2 }.
Effiziente Algorithmen Flußprobleme 81 Laufzeit Finden eines Matchings maximaler Kardinalität dauert nur O( E min{ V 1, V 2 }) mit der Ford Fulkerson Methode. Der Fluß ist höchstens f = min{ V 1, V 2 }.
7 Drehstromgleichrichter
 Drehsromgleichricher 7 Drehsromgleichricher 7.1 Mielpnk-Schalng (Halbbrücke) (3-plsiger Gleichricher) In bbildng 7-1 sind die drei Sekndärwicklngen eines Drehsrom-Transformaors in Sernschalng dargesell.
Drehsromgleichricher 7 Drehsromgleichricher 7.1 Mielpnk-Schalng (Halbbrücke) (3-plsiger Gleichricher) In bbildng 7-1 sind die drei Sekndärwicklngen eines Drehsrom-Transformaors in Sernschalng dargesell.
14 Kurven in Parameterdarstellung, Tangentenvektor und Bogenlänge
 Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
2.3 Schätzeigenschaften der OLS-Methode
 .3 Schäzeigechafe der OLS-Mehode Jede Schäzmehode wei beimme Güeeigechafe auf, die vo der Erfüllug beimmer Vorauezuge abhäge. Wa die gewöhliche Mehode der kleie Quadrae (OLS-Mehode) beriff, id beimme Schäzeigechafe
.3 Schäzeigechafe der OLS-Mehode Jede Schäzmehode wei beimme Güeeigechafe auf, die vo der Erfüllug beimmer Vorauezuge abhäge. Wa die gewöhliche Mehode der kleie Quadrae (OLS-Mehode) beriff, id beimme Schäzeigechafe
Nennen Sie Vor- und Nachteile von Wasserkraftwerken Vorteile: Speicherkraftwerke, Pumpspeicherkraftwerke
 1 Waerkraf Nennen Sie Vor- und Nacheile von Waerkrafwerken Voreile: regeneraive Energie. Keine CO 2 -Emiion! kein Primärenergierägerverbrauch Spizenlafähigkei, Energiepeicherfunkion hohe Zuverläigkei hoher
1 Waerkraf Nennen Sie Vor- und Nacheile von Waerkrafwerken Voreile: regeneraive Energie. Keine CO 2 -Emiion! kein Primärenergierägerverbrauch Spizenlafähigkei, Energiepeicherfunkion hohe Zuverläigkei hoher
Kapitel 7: Flüsse in Netzwerken und Anwendungen Gliederung der Vorlesung
 Gliederung der Vorleung. Falltudie Bipartite Graphen. Grundbegriffe 3. Elementare Graphalgorithmen und Anwendungen 4. Minimal pannende Bäume 5. Kürzete Pfade 6. Traveling Saleman Problem 7. Flüe in Netzwerken
Gliederung der Vorleung. Falltudie Bipartite Graphen. Grundbegriffe 3. Elementare Graphalgorithmen und Anwendungen 4. Minimal pannende Bäume 5. Kürzete Pfade 6. Traveling Saleman Problem 7. Flüe in Netzwerken
1. Klausur Physik Leistungskurs: Kinematik Klasse Dauer: 90 min
 1. Kluur Phyik Leiungkur: Kineik Kle 11 1.1.13 Duer: 9 in 1. Mx und Mäxchen chen ein Werennen über 1. Mx gewinn d Rennen i en 5 Vorprung. U Mäxchen bei Lune zu hlen, ren ie einen Rencheluf, bei de ber
1. Kluur Phyik Leiungkur: Kineik Kle 11 1.1.13 Duer: 9 in 1. Mx und Mäxchen chen ein Werennen über 1. Mx gewinn d Rennen i en 5 Vorprung. U Mäxchen bei Lune zu hlen, ren ie einen Rencheluf, bei de ber
Wohnen am Buschwiesenkarree
 Selbbeimm leben. Sich geborge n fühlen. Sicherhei chäzen. Sic h über Hilfe freuen. Wohnen am Buchwieenkarree Senioren- und behinderengereche Wohnen Ruhldorfer Sraße 91 in Telow Wir helfen hier und jez.
Selbbeimm leben. Sich geborge n fühlen. Sicherhei chäzen. Sic h über Hilfe freuen. Wohnen am Buchwieenkarree Senioren- und behinderengereche Wohnen Ruhldorfer Sraße 91 in Telow Wir helfen hier und jez.
Musterlösungen zur Klausur Informatik III WS 02/03 Seite 1
 Muserlösungen zur Klausur Infrmaik III WS 02/03 Seie Aufgabe. ( Punke) Es seien zwei Schlangen S, S 2 und ein Keller K gegeben. In S befinden sich die Zahlen, 2,..., n(n > 2) (in dieser Reihenflge). Sie
Muserlösungen zur Klausur Infrmaik III WS 02/03 Seie Aufgabe. ( Punke) Es seien zwei Schlangen S, S 2 und ein Keller K gegeben. In S befinden sich die Zahlen, 2,..., n(n > 2) (in dieser Reihenflge). Sie
Theoretische Grundlagen
 Theoreiche Grundlagen Phik Leiungkur Größen Größen Größen 5 m Grundgrößen abgeleiee Größen Zahl Einhei Länge, Mae, Zei, Sromärke, Temperaur, Soffmenge, Lichärke Gechwindigkei, Kraf, Ladung Änderunggrößen:
Theoreiche Grundlagen Phik Leiungkur Größen Größen Größen 5 m Grundgrößen abgeleiee Größen Zahl Einhei Länge, Mae, Zei, Sromärke, Temperaur, Soffmenge, Lichärke Gechwindigkei, Kraf, Ladung Änderunggrößen:
4 ARBEIT UND LEISTUNG
 10PS/TG - MECHANIK P. Rendulić 2008 ARBEIT UND LEISTUNG 27 4 ARBEIT UND LEISTUNG 4.1 Mehnihe Abei 4.1.1 Definiion de Abei enn ein Köpe une de Einwikung eine konnen Kf die Seke in egihung zuükleg, dnn wid
10PS/TG - MECHANIK P. Rendulić 2008 ARBEIT UND LEISTUNG 27 4 ARBEIT UND LEISTUNG 4.1 Mehnihe Abei 4.1.1 Definiion de Abei enn ein Köpe une de Einwikung eine konnen Kf die Seke in egihung zuükleg, dnn wid
F Rück. F r Rück. Mechanische Schwingungen. Größen zur quantitativen Beschreibung :
 Mechaniche chwingungen F r Rück Gleichgewichlage r F Rück F r Rück F r Rück Gleichgewichlage Größen zur quaniaiven Bechreibung : chwingungdauer oder Periode T, Einhei: Frequenz υ /T, Einhei: / oder Hz
Mechaniche chwingungen F r Rück Gleichgewichlage r F Rück F r Rück F r Rück Gleichgewichlage Größen zur quaniaiven Bechreibung : chwingungdauer oder Periode T, Einhei: Frequenz υ /T, Einhei: / oder Hz
4. Erhaltungssätze für Masse und Impuls
 4. Erhalngssäze für Masse n Impls Wie ie klassische Mechanik basier ie Srömngsmechanik af er Erhalng von Masse Impls Energie Die Erhalngsgeseze gelen für as infiniesimal kleine Flielemen n für reiimensionale
4. Erhalngssäze für Masse n Impls Wie ie klassische Mechanik basier ie Srömngsmechanik af er Erhalng von Masse Impls Energie Die Erhalngsgeseze gelen für as infiniesimal kleine Flielemen n für reiimensionale
GETE ELEKTRISCHES FELD: DER KONDENSATOR: Elektrische Feldstärke: E r. Hr. Houska Testtermine: und
 Schuljahr 22/23 GETE 3. ABN / 4. ABN GETE Tesermine: 22.1.22 und 17.12.2 Hr. Houska houska@aon.a EEKTRISCHES FED: Elekrisch geladene Körper üben aufeinander Kräfe aus. Gleichnamige geladene Körper sießen
Schuljahr 22/23 GETE 3. ABN / 4. ABN GETE Tesermine: 22.1.22 und 17.12.2 Hr. Houska houska@aon.a EEKTRISCHES FED: Elekrisch geladene Körper üben aufeinander Kräfe aus. Gleichnamige geladene Körper sießen
6 Stochastische Differentialgleichungen
 6 Sochaiche Differenialgleichungen Viele deerminiiche Modelle der Naur- und der Wirchafwienchafen laen ich mi Hilfe von Differenialgleichungen audrücken. Mi dem Io-Inegral und der Io-Formel haben wir die
6 Sochaiche Differenialgleichungen Viele deerminiiche Modelle der Naur- und der Wirchafwienchafen laen ich mi Hilfe von Differenialgleichungen audrücken. Mi dem Io-Inegral und der Io-Formel haben wir die
7.3. Partielle Ableitungen und Richtungsableitungen
 7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
