|
|
|
- Carsten Hafner
- vor 8 Jahren
- Abrufe
Transkript
1 TechnischeUniversitatMunchen ZentrumMathematik Kreditrisiko ModelleundDerivatebewertung Diplomarbeit AlexanderSzimayer von Abgabetermin:12.Mai1999 Betreuer: Themensteller:Prof.Dr.C.Kluppelberg Dr.M.Borkovec
2 Quellenverwendethabe. Munchen,12.Mai1999 Hiermiterklareich,daichdieDiplomarbeitselbstandigangefertigtundnurdieangegebenen
3 Danksagung Finanzmarkttheoriestetsausgezeichnetbetreuthat. lanborkovec,dermichaufmeinemwegdurchdiestochastischeanalysisunddiestochastische KritikundtatkraftigeUnterstutzungbeiderErstellungdervorliegendenArbeitundbeiDr.Mi- AndieserStellebedankeichmichbeiFrauProf.Dr.ClaudiaKluppelbergfurihrewohlwollende DesweiterengiltmeinDankdenHerrenDr.MichaelHies,Dr.OliverHolznerundStefanMeier. SieregtenmichzudemThemaKreditriskowahrendmeinerZeitalsPraktikantundWerkstudentbeiderBayerischenVereinsbankanundlenktenmichaufdenerstenwesentlichen Schritten. DankgebuhrtzudemHerrnProf.Dr.RalfKornfurseinInteresseunddiekonstruktiveKritik, SchlielichbedankeichmichbeidenMitarbeiterndesLehrstuhlsfurMathematischeStatistik, dieermirentgegengebrachthat. meinefragenzubeantworten,undmeinearbeitinvielerleihinsichtunterstutzthaben. HerrnDipl.{Math.MartinSeverinundFrauAlexandraFranzmann,diesichstetsZeitnahmen, HerrnDr.DirkTasche,FrauDipl.{Math.SusanneEmmer,FrauDipl.{Math.EvelinHofbauer,
4 Inhaltsverzeichnis 2Grundlagen 1Einleitung 2.1KlassischeWahrscheinlichkeitstheorie H2{Semimartingale DieIt^o{FormelunddasDoleans{Dade{Exponential StochastischeIntegrationstheorie ZeitstetigeModellierungdesMarktes 2.5DieBrownscheBewegungalsIntegrator DiestochastischeMarktmodellierung PunktprozesseundstochastischeIntegrationstheorie FolgerungenausdemMarktmodell DasverallgemeinerteBlack&Scholes{Modell Kreditrisikomodelle 4.2DasModellvonJarrow,LandoundTurnbull DeroptionspreistheoretischeAnsatzvonMerton KreditrisikomitstochastischerAusfallsintensitat Derivatebewertung 5.1DiePreisprozesseunterdemaquivalentenMartingalma EinMartingalmodell DerivatebewertungimMartingalmodell Ausblick 119 i
5 Kapitel1 Einleitung DieZielsetzungdervorliegendenDiplomarbeitist,einenUberblickubereinigeausgewahlteKreditrisikomodellezugebenundderenAnwendungsmoglichkeitenaufzuzeigen.Moglichsteinfach stammtderbegri"kreditrisiko"ausdemkreditbereich.amaugenfalligstentretenkreditrisikenbeiderdarlehensvergabeauf.betrachtenwirdiesenfallausdersichtdesglaubigers. dieineinemversprochenenzukunftigenzahlungsstromliegt.wiedernameselbstandeutet, gesprochenistkreditrisikoeinimbankenwesengebrauchlichessynonymfurdieunsicherheit, Schuldzuruckerhalt,undzumanderennachder"Schadenshohe",fallsderKreditnichtzuruckgezahltwerdenkann.DieseProblematiksollenalleKreditrisikomodelleangemessenerfassen. FurihnstelltsichzumeinendieFragenachderWahrscheinlichkeit,mitdererdieausstehende RateverwendetmanauchdieRecoveryRate,die"1 LossRate"betragt. DieAnsatze,denenwirimRahmendieserArbeitBeachtungschenken,behandelndenFallvon Rate,diedenBruchteilderSchuldbeziert,dieimKreditausfallverlorengeht.AnstellederLoss ZentraleBegriesindalsodieAusfallwahrscheinlichkeit,dieDefaultProbability,unddieLoss undturnbull(1997),lando(1998)undschonbucher(1998a)ihrefortsetzungndet. undsingleton(1995)setzteineneueentwicklungein,dieindenarbeitenvonjarrow,lando alsovonfirmenbegebeneanleihen.dieanfangegehenaufmerton(1974)zuruck.mitdue Krediten,dieanBorsengehandeltwerden.EshandeltsichumsogenannteCorporateBonds, WirbehandelndasThemaKreditrisikovomnanzmathemathischenBlickpunktaus.InKapitel2legenwirdiedazunotigenGrundlagenausderWahrscheinlichkeitstheoriedar.WirzitierennutzlicheErgebnisseausBremaud(1981),KaratzasundShreve(1997),ksendahl(1995) It^o{FormelundDoleans{Dade{ExponentialesowieuberH2{SemimartingalenachProtteran. Martingalen.DaranschlieensichAbschnitteuberdiestochastischeIntegrationstheorie,die undprotter(1995).zunachstbefassenwirunsmitstochastischenprozessen,insbesonderemit StochastischeIntegralebezuglichderBrownschenBewegungsindThemadesfolgendenAbschnitts,deraufKaratzasundShreveundksendahlberuht.ZumAbschlustudierenwirnach Kapitel3istderzeitstetigenMarktmodellierunggewidmet.DabeigreifenwiraufdieArbeitenvonHarrisonundPliska(1981)undGrunewald(1998)zuruck.InKapitel3.3untersuchen BremaudPunktprozessealsIntegratoren. dells"voraugengefuhrt. BeispielwerdendieBegrie"aquivalentesMartingalma"und"VollstandigkeiteinesMarktmo- wirdasverallgemeinerteblack&scholes{modell,daseinenaktienmarktmitmehrenaktienbeschreibt,diealskorelliertegeometrischebrownschebewegungenmodelliertsind.andiesem 1
6 KAPITEL1.EINLEITUNG InKapitel4legenwirzuerstdasModellnachMerton(1974)dar,wobeiwiraufdieAusfuhrung 2 BondsundziehendenFirmenwertalserklarendeVariableheran.DieSchuldenderFirmakonnen vonmadan(1998)zuruckgreifen.indiesemmodellbetrachtenwirausschlielichcorporate genaudannnichtmehrzuruckgezahltwerden,wennderfirmenwertbeifalligkeitunterderhohe Scholes,dennderFirmenwertwirdalsgeometrischeBrownscheBewegungmodelliert.ImErgebnislatsicheinCorporateBondalsDerivatdesFirmenwertsdarstellen,undseinWertkann derzahlungsforderungliegt.deransatzbasiertaufdemaktienmarktmodellnachblackund mittelsderblack&scholes{formelberechnetwerden. Anleihewert(t) Firmenwert(t) AnleihewertmiteinerVerschuldungvon0:70undeinerLaufzeitvon10Jahren. Abbildung1.1:SimulierterPfaddesFirmenwertprozemitStartwert1undderentsprechende Zeitt InAbbildung1.1sehenwirdensimuliertenVerlaufeinesaufdenStartwert1normiertenFirmenwertprozesses.ErwirddurcheineGeometrischeBrownscheBewegungohneDriftmitVolatilitat =0:15beschrieben.DiedargestellteAnleihehateineLaufzeitvon10JahrenundeineHohe ditausfalltrittint=10ein.vonderausstehendenschuldinhohevon0:70wirdetwa0:40 WertgegenstandederFirmazurDeckungderSchuldherangezogenwerdenmussen.DerKremenwertdrastischab.VondaansindFirmenwertundAnleihewertfastidentisch,dasamtliche von70%desfirmenwertes,berechnetaufdenstartzeitpunktt=0.imjahr5falltderfir- ImAnsatzvonJarrow,LandoundTurnbull(1997)modellierenwirdasKreditrisiko,indem beglichen,waseinerrecoveryratevon0:57entspricht. wahrendihrerlaufzeitverschiedenenratingklassenzugeordnetwerden.injederratingklasse wirdieratingklassederuntersuchtenanleihebetrachten.ratingssindsubjektiveeinstufungen,dienachderkreditwurdigkeitdesanleiheemittentenvergebenwerden.eineanleihekangenzwischendenratingklassendurcheinezeitstetigehomogenemarkovkettezumodellieren. IndiesemModellkonnenwirdasAusfallereignisprobabilistischbeschreiben.BeimEintrittdes KreditausfallsstelltsichdieFrage,wiehochderWertverlustderAnleiheist,beziehungsweise, welchesummederemittentdenbesitzernseineranleiheauszahlenkann.erfolgtderkreditausfallvordemfalligkeitsterminderanleihe,wirdangenommen,daderemittenteinenfesten BruchteildesAnspruches,dieRecoveryRate,amFalligkeitsterminauszahlt. wirdeineandereausfallwahrscheinlichkeitunterstellt.dieseransatzlegtesnahe,diebewegun- Abbildung1.2zeigtempirischeAusfallwahrscheinlichkeiten,diegegendieZeitaufgetragensind,
7 wobeiwirunsexemplarischaufdreiratingklassenbeschranken.diegrotezahlungsfahigkeit KAPITEL1.EINLEITUNG 3 fallwahrscheinlichkeitdernachsthoherenstufebbbundp3mitderratingklasseb. hatdieratingklasseaa.ihristdiefunktionp1zugeordnet.p2identizierenwirmitderaus- P3(t) P2(t)P1(t) Abbildung1.2:EmpirischeAusfallwahrscheinlichkeitennachRatingklasse.P1entsprichtder bestenratingklasseaa,p2derzweitbestenbbbundp3derdrittbestenb. Zeitt IstdieRecoveryRate,beziehungsweisedieLossRate,vonauenvorgegeben,dannkannmanmit DerKaufereinerDefaultOptionversichertsichgegendenKreditausfalleinerAnleihe.Falltdie aufdieanleihezubewerten.gangigederivatesindbeispielsweisesogenanntedefaultoptions. ihresratingsberechnen.zudembestehtdiemoglichkeit,derivate{alsocontingentclaims{ demansatznachjarrow,landoundturnbulldiepreisevonanleihenmitkreditrisikoanhand Anleiheaus,soerhaltereineEntschadigung.ImanderenFallgehterleeraus.WeitereDerivate sindunteranderemgewohnlicheoptionenaufanleihenmitkreditrisikoundsogenanntespread istgewissermaendasausubungskriteriumeinerspreadoption.inkapitel5.3werdenwirdie Options.DerSpreadbezeichnetdieRenditedierenzzwischendenrisikolosenAnlagenundeinerAnleihemirKreditrisiko.Genauergesagt,sprichtmanhiervonCreditSpread.DerSpread bewerten. hiererwahntenderivategenaueruntersuchenundimmodellnachjarrow,landoundturnbull DasModellvonSchonbucher(1998a)basiertaufUberlegungenvonDueundSingleton(1995). DueundSingletonbetrachtenKreditrisikenineinerWeltmirrisikoneutralenInvestoren. SchonbuchergehteinenSchrittweiter,indemaufBasisdesZinsstrukturmodellsnachHeath, leihenmitkreditrisikogegeben.siesindstochastischegroenundmitdemaktienkursinnerhalb desblack&scholes{modellvergleichbar.eslatsichdanneinebreiteauswahlvonderivaten, densogenanntencreditriskderivatives,bewerten,nichtzuletztdieschonerwahntengewohnlicheoptionenaufanleihenmitkreditrisiko,spreadoptions,defaultoptionsunddefaultswaps. JarrowundMorton(1992)einMarktmodellentwirft.IndiesemModellsinddiePreisederAn- AufdieDerivatebewertunggehenwirinKapitel5ausfuhrlichein
8 Kapitel2 Grundlagen sichinsechsabschnitte.imerstenabschnittbefassenwirunsmitder"klassischenwahrscheinlichkeitstheorie".eswerdengrundlegendebegrieerlautertunddiesatzewiedergegeben,diefur ImdiesemKapitelwerdendienotwendigenGrundlagenderArbeitdargelegt.DasKapitelteilt diearbeitwesentlichsind.daraufbautderzweiteabschnitt"stochastischeintegrationstheorie"auf.dasdoleans{dade{exponentialundh2{semimartingalediskutierenwirindenbeiden AbschlubeschaftigenwirunsmitPunktprozessenundderstochastischenIntegrationstheorie. 2.1 folgendenabschnitten.danachwirddiebrownschebewegungalsintegratorthematisiert.zum DieserAbschnittfatdiewesentlichenDenitionenundSatzevonProtter(1995)undksendahl (1995)zusammen.DermathematischeWeg,zufalligeBewegungenzubeschreiben,fuhrtuns KlassischeWahrscheinlichkeitstheorie zumkonzeptderwahrscheinlichkeitsraume.einwahrscheinlichkeitsraumistdiewelt,inder einstochastischerproze,einezufalligebewegungwiebeispielsweiseeinaktienkurs,eingebettet ist. Denition2.1EsseieineMenge.Dannisteine{AlgebraaufeineFamilieFvon Teilmengenvon,diedieEigenschaftenbesitzt (ii)a2f (i);2f, (iii)a1;a2;:::2f )Ac2F, )A1S Meraum(;F)isteineFunktionP:F![0;1],sodagilt DasPaar(;F)nenntmaneinenMeraum.EinWahrscheinlichkeitsmaPaufeinem i=1ai2f. (ii)diemengena1;a2;:::2fseienpaarweisedisjunkt,danngilt (i)p(;)=0undp()=1, P 1[i=1Ai!= 1Xi=1P(Ai): 4
9 DasTripel(;F;P)heitWahrscheinlichkeitsraum.EinWahrscheinlichkeitsraum(;F;P) KAPITEL2.GRUNDLAGEN 5 JederWahrscheinlichkeitsraum(;F;P)kannvervollstandigtwerden.ManerweitertFumdie istvollstandig,fallsfalleteilmengengvonmitaueremmanullenthalt,d.h. TeilmengenvonmitaueremMaNullundsetztdasMaaufdieerweiterte{Algebrafort. GundinffP(F):F2F;GFg=0)G2F: Denition2.2AufeinerMengebetrachtenwireineFamilieUvonTeilmengenvon.Die dadasereignisfp{fast{sichereintritt. diewahrscheinlichkeit,dadasereignisfeintritt.giltp(f)=1,dannsprechenwirdavon, DieTeilmengenFvonFnenntmanF{mebar.WirinterpretierenFalsEreignisundP(F)als heitdievonuerzeugte{algebra. AufeinemWahrscheinlichkeitsraumkannmaneinStrukturinFormeinerFiltrierungdenieren. HU\fH:Hist{Algebraauf;UHg Denition2.3EineFamilievon{Algebren(Ft)0t1heitFiltrierunginF,wenngilt DieFiltrierungenwerdenspateralsFamilievonInformationsmengeninterpretiert. gen,falls EinltrierterWahrscheinlichkeitssraum;F;P;(Ft)0t1erfulltdieublichenBedingun- 0st1)FsFt und FtF;fur0t1: Wirnehmenimfolgendenan,dadieublichenBedingungenstetserfulltsind. (ii)ft=tu>tfu,furallet0;d.h.diefiltrierung(ft)0t1istrechtsseitigstetig. (i)f0enthaltallep{nullmengenvonf. EineZufallsvariable:7![0;1]isteineStopzeit,fallsdasEreignisftginFtliegt,fur allet2[0;1]. Denition2.4EsseieinltrierterWahrscheinlichkeitsraum;F;P;(Ft)0t1gegeben. Satz2.1DasEreignisf<tgliegtinFt,furallet2[0;1],genaudann,wenneineStopzeit ist. EsgeltendieublichenBedingungen.InsbesondereistdieFiltrierung(Ft)0t1rechtseitigstetig. DaraufgrundetsichderfolgendeSatz. Denition2.5EinstochastischerProzeisteinFamilievonreellwertigenZufallsvariablen gemoglichkeitenwieaktienundanleihen. deniert.stochastischenprozesseinterpretierenwirhierzumeistalspreisprozessevonanla- ImallgemeinensindallestochastischeProzesseaufeinemWahrscheinlichkeitsraum(;F;P) dieaufeinemwahrscheinlichkeitsraum(;f;p)deniertsind.aufeinemltriertenwahrscheinlichkeitssraum;f;p;(ft)0t1heiteinstochastischerprozex=fx(t):t0g XfX(t):t0g; adaptiert,fallsgilt X(t)istFt{mebarfurallet0:
10 Fureinfestest0habenwirauf(;F;P)eineZufallsvariablegegebenmittels KAPITEL2.GRUNDLAGEN 6 Andererseitserhaltenwirfureinfestes!ausdieFunktion!7!X(t;!); fur!2: diewirpfadvonxnennen. t7!x(t;!) furt0; DieGleichheitzweierstochastischerProzessemusorgfaltigdefniertwerden.WirunterscheidenzweiMoglichkeiten. Denition2.6GegebenseieinltrierterWahrscheinlichkeitsraum;F;P;(Ft)0t1und sindgenaudannmodikationen,wenn dieadaptiertenstochastischenprozessex=fx(t):t0gundy=fy(t):t0g.xundy DiebeidenProzessesindgenaudannununterscheidbar,wennP{fast{sichergilt X(t)=Y(t)P{f.s.; furt0: SindXundYModikationen,existierteineP{NullmengeNtfurallet0,sodafuralle!2nNtgiltX(t;!)=Y(t;!).DieMenge[0;1)istuberabzahlbar,alsoistNSt2[0;1)Nt X(t)=Y(t); furt0: nichtunbedingteinep{nullmenge.nmunichteinmalmebarsein.sinddieprozessexund ProzesseModikationen. giltx(t;!)=y(t;!).mitanderenworten,xundybesitzenaufnnidentischepfade.die Yununterscheidbar,gibteseineP{NullmengeN,sodafuralle!2nNundfurallet0 Denition2.7EinstochastischerProzeX=fX(t):t0gaufeinemWahrscheinlichkeitsraum(;F;P)istcadlag,fallserPfadebesitzt,dieP{fast{sicherrechtsseitigstetigsindund NullmengeNliegtinF0{demnachauchinallenFtfurt0.Folglichsindununterscheidbare DerProzeXistcaglad,wennseinePfadeP{fast{sicherlinksseitigstetigsindundderrechtsseitigerLimesanjederStelleexistiert. derenlinksseitigerlimesanjederstelleexistiert. X,wobeiX (t)=lims!t;s<tx(s)deniertistfurt0. Jedercadlag{ProzeX=fX(t):t0gbesitzteinecaglad{Version.Diecaglad{Versionlautet Beispiel1AufeinemltriertenWahrscheinlichkeitsraum;F;P;(Ft)0t1seieinadaptiertercadlag{ProzeX=fX(t):t0ggegeben.ZueinerBorelmengeausdenreellenZahlen Cadlag{ProzessebieteneineelemetaresBeispielfurStopzeiten. denierenwir EinespezielleKlassederstochastischenProzessesindMartingale,Super{undSubmartingale. heitersteintrittszeitvonxin.isteineoenemenge,dannisteinestopzeit. (!)infft>0:x(t;!)2g: einepositivezuwachserwartung;imfalledersupermartingaleverhaltessichumgekehrt. EinMartingalisteinProze,dessenerwarteteZuwachsegleichNullsind.Submartingalehaben
11 Denition2.8AufeinemltriertenWahrscheinlichkeitsraum;F;P;(Ft)0t1seieinad- KAPITEL2.GRUNDLAGEN 7 aptierterprozex=fx(t):t0ggegeben.xheitmartingal(beziehungsweisesupermar- tingalodersubmartingal)bezuglichderfiltrierung(ft)0t1,fallsgilt NachKorollar1vonTheorem9,ChapterI,vonProtter(1995)besitztjedesMartingaleine (ii)furstgiltefx(t)jfsg=x(s)p{f.s.(beziehungsweise""oder""). (i)efjx(t)jg<1; furallet0. WirbereitendasOptionalSamplingTheoremmitdendreifolgendenDenitionenundeinem cadlag{versioneinesmartingals. eindeutigemodikation,dieeincadlag{prozeist.vonnunanbetrachtenwirausschlielichdie Satzvor. Denition2.9X=fX(t):t0gseieincadlag{ProzeundTseieinezufalligeZeit,also einezufallsvariablemitwertenin[0;1].dannheitxt=nxt(t):t0odeniertdurch derintgestoppteproze. Denition2.10EinMartingalX=fX(t):t0gaufeinemltriertenWahrscheinlichkeitsraum;F;P;(Ft)0t1wirddurcheineZufallsvariableYabgeschlossen,wennEfjYjg< 1undX(t)=EfYjFtgfur0t<1gilt. raum(;f;p)istgleichgradigintegrierbar,fallsgilt Denition2.11EineFamilievonZufallsvariablen(U)2AaufeinemWahrscheinlichkeits- XT(t)X(t^T)=X(t)1ft<Tg+X(T)1ftTg HierbeibezeichnetAeinebeliebigeIndexmenge. n!1sup lim2azfjujngjujdp=0: denstochastischenprozealsfamilievonzufallsvariablen,indiziertdurchdie"zeit"t2ir+0. Satz2.2EsseiX=fX(t):t0geinMartingalaufeinemltriertenWahrscheinlichkeitsraum;F;P;(Ft)0t1.Xistgenaudanngleichgradigintegrierbar,wennY=limt!1X(t) ImFalleeinesstochastischenProzessessetzenwirdieIndexmengeAIR+0undinterpretieren EingleichgradigintegrierbaresMartingalkanndurcheineZufallsvariableabgeschlossenwerden. X(1)=Y. P{f.s.existiert,EfjYjg<1undX=fX(t):0t1gisteinMartingal.Hierbeiist kann,istgleichgradigintegrierbar. Satz2.3(DoobsOptionalSamplingTheorem)EsseiX=fX(t):t0geinMartingal DieUmkehrunggiltauch.JedesMartingal,dasdurcheineZufallsvariableabgeschlossenwerden sindx(1)undx(2)integrierbar,undesgilt riablex(1)abgeschlossenwird.1und2seienstopzeitenmit12p{fast{sicher.dann aufeinemltriertenwahrscheinlichkeitsraum;f;p;(ft)0t1,dasdurcheinezufallsva- X(1)=EfX(2)jF1gP{f.s.
12 AufdasOptionalSamplingTheoremstutztsichderBeweisdesfolgendenSatzes. KAPITEL2.GRUNDLAGEN 8 X=fX(t^):0t1gebenfallseingleichgradigintegrierbaresMartingal. tenwahrscheinlichkeitsraum;f;p;(ft)0t1undeinestopzeit.dannist Satz2.4EsseiX=fX(t):t0geingleichgradigintegrierbaresMartingalaufeinemltrier- integrierbarereellwertigezufallsvariablexgegeben.sei'einekonvexefunktionaufdenreellen Satz2.5(JensenscheUngleichung)AufeinemWahrscheinlichkeitsraum(;F;P)seieine EinnutzlicherSatzistdieJensenscheUngleichung. Zahlenund'(X)integrierbar,danngiltfurjede{AlgebraGF Korollar1X=fX(t):t0gseieinMartingalaufdemltriertenWahrscheinlichkeitsraum ;F;P;(Ft)0t1und':IR!IReinekonvexeFunktion.Ist'(X(t))fur0t<1 '(EfXjGg)Ef'(X)jGg: Beweis: MartingalM,jMjisteinSubmartingal. integrierbar,dannist'(x)=f'(x(t)):t0geinsubmartingal.insbesonderegiltfurjedes NachderJensenscheUngleichunggilt DieBetragsfunktionjjistkonvex;demnachistdiezweiteAussageeineKonseqenzderGrundaussagedesKorollars. ='(X(s))P{f.s.; furt0: Ef'(X(t))jFsg'(EfX(t)jFsg) DieDoobscheUngleichungisteinwesentlichesHilfsmittelbeiAbschatzungen. 2 Satz2.6(DoobscheUngleichung)Auf ;F;P;(Ft)0t1seieinpositivesSubmartingalX=fX(t):t0ggegeben.Furallep>1 undqmit1p+1q=1gilt einem ltrierten Wahrscheinlichkeitsraum X(1)2L2(P)unddenierenXsupt0jX(t)j.DannistjXjeinpositivesSubmartingal, Korollar1(DoobschemaximalequadratischeUngleichung)Zusatzlichfordernwir ksup t0jx(t)jklp qsup t0kx(t)klp: undfurp=2gilt WendenwirunsnundenstochastischenProzessenzuundbetrachtenzweielementareBeispiele.ZunachstumschreibenwirZahlprozesseundstudierenspezielldenPoissonproze.Deram Ef(X)2g4EfX(1)2g: haugstenzitierteprozeinderfinanzmathematikistdiebrownschebewegung.sieistein MartingalmitstetigenPfadenundder"gebrauchlicheIntegrator"inderstochastischenIntegrationstheorie.WirbendenunsindennachfolgendenBeispielenimmerineinemltrierten Wahrscheinlichkeitsraum;F;P;(Ft)0t1.
13 Denition2.12(Tn)n0seieineFolgevonstrengwachsendenZufallsvariablenaufF.Essei KAPITEL2.GRUNDLAGEN 9 T0=0.DerProzeN=fN(t):0t1gdeniertdurch mitwerteninin[f1gheitzahlprozebezuglichderfolge(tn)n1 N(t)Xn11ftTng ZahlprozeohneExplosion.SeiT=1,dannistfur0s<t<1 DurchdiebesondereDenitionvonT0istsichergestellt,daN(0)=0P{f.s.gilt.Wirsetzen TsupnTnundnennenTExplosionszeitpunktvonN.IstT=1P{f.s.,dannistNein derzuwachsvonnimintervall(s;t]. N(t) N(s)=Xn11fs<Tntg DerZahlprozeist,sowiewirihndenierthaben,nichtunbedingtadaptiertbezuglichder adaptiertist. Satz2.7EinZahlprozeN=fN(t):0t1gistgenaudannadaptiert,wenndieZufallsvariablen(Tn)n1Stopzeitensind. Filtrierung(Ft)0t1.DernachsteSatzgibtAufschludaruber,inwelchemFalleinZahlproze ZahlprozesseohneExplosionbesitzenrechtsseitigstetigePfademitlinksseitigemGrenzwert, sindalsocadlag{prozesse. Denition2.13EinZahlprozeN=fN(t):0t1gohneExplosionisteinPoissonproze,wenngilt (ii)sinds;t;uundvbeliebigmit0s<t<1,0u<v<1undt s=v u,dann (i)furalle0s<t<1istderzuwachsn(t) N(s)unabhangigvonFs. stationarverteiltezuwachse.uberdieverteilungdesprozessesgibtderfolgendesatzaufschlu. DieEigenschaften(i)und(ii)sindbekanntalsvonderVergangenheitunabhangigeZuwachseund besitzenn(t) N(s)undN(v) N(u)diegleicheVerteilung. Satz2.8N=fN(t):0t1gseieinPoissonproze.Danngilt furn=0;1;2;:::undein0.heitintensitatdespoissonprozesses.n(t)istpoisson{ P(N(t)=n)=e t(t)n verteiltmitparametert.weiterist n! ; var(n(t))=t; EfN(t)g=t; mumandiesteigungkompensieren,damitderaufdieseweisekorrigierteprozeeinmartingal Leichtsiehtman,daderPoissonprozeeinSubmartingalist,daersteigendePfadebesitzt.Wie furt0: ist?dernachstehendesatzbeantwortetdiefrage.
14 Satz2.9N=fN(t):0t1gseieinPoissonprozemitIntensitat.Denierenwirdie KAPITEL2.GRUNDLAGEN 10 ProzesseA=fA(t):0t1gundM=fM(t):0t1gmittels DannistMeinMartingal. M(t)N(t) A(t)=N(t) t; A(t)tund Beweis: furt0: WirnutzendieUnabhangkeitunddieStationaritatderZuwachseaus.Wirmussenzeigen,da M(t)2L1gilt. EfjM(t)jg=EfjN(t) A(t)jg =t+t EfjN(t)j+jA(t)jg =2t<1; =EfN(t)g+EfA(t)g UnterdieserVoraussetzungkonnenwirdenbedingtenErwartungswertvonMberechnen.Fur 0s<tgiltEfM(t)jFsg=EfN(t) tjfsg furallet0: =M(s)+EfN(t) N(s)g (t s) =N(s) s+efn(t) N(s)jFsg (t s) =EfN(t) N(s)+N(s) s (t s)jfsg =M(s)+(t s) (t s) =M(s)+EfN(t s) N(0)g (t s) Damithabenwirgezeigt,daMeinMartingalist. DenProzeAnenntmandenKompensatorvonN.EsgiltN=M A.AbesitztdieEigenschaft dervorhersehbarkeit,daastetigepfadebesitzt.zudemsinddiepfadevonavonbeschranktervariationaufkompaktenintervallen.imfolgendenistdiezerlegungeinesprozessesinein 2 deutung.diebegrie"vorhersehbar"und"vonbeschranktervariation"werdenspatergenau deniert. MartingalundeinenvorhersehbarenProzemitbeschrankterVariationvongrundlegenderBe- WendenwirunsnunderBrownschenBewegungzu. Denition2.14EinreellwertigeradaptierterProzeB=fB(t):0t<1gheit BrownscheBewegung,fallsgilt (ii)furalle0<s<t<1istb(t) B(s)normalverteiltmitErwartungswertNullund (i)furalle0s<t<1istderzuwachsb(t) B(s)unabhangigvonFs. dannnennenwirbeinestandardbrownschebewegung. DieBrownscheBewegungstartetinx,wennP(B(0)=x)=1.Ist=1undstartetBin0, Varianz2(t s)fureinereellekonstante>0.
15 KAPITEL2.GRUNDLAGEN Zeitt BewegungeinMartingalist,besitztsieeinecadlag{Modikation.Wirkonnensogarnochmehr GiltEfjB(0)jg<1,dannistdieBrownscheBewegungeinMartingal.FallsdieBrownsche Abbildung2.1:3simuliertePfadeeinerStandardBrownschenBewegung Satz2.10EsseiB=fB(t):0t<1geineBrownscheBewegung.DannexistierteineModikationvonBmitstetigenPfadenP{fast{sicher. uberdiepfadevonbaussagen. WirbenutzenimweiterenstetseineVersionderBrownschenBewegungmitstetigenPfaden. chastischenintegrationvertrautmachen. Satz2.11EsseiB=fB(t):0t<1geineBrownscheBewegungund(n)n1eineFolge UberdieBrownscheBewegunggibteszweiAussagen,dieunsmitderProblematikdersto- vonngegennullfurn!1,danngiltlimn!1nb=tp{fast{sicher. d.h.:furm>nistmn.denierenwirnbpti2n(b(ti+1) B(ti))2.GehtdieFeinheit vonpartitionendesintervalls[a;a+t],fura0undt>0.diefolge(n)n1seiverfeinernd; DasKonzeptderFolge(n)n1wirdspateraufStopzeitenerweitert.DieAussagedesSatzes fx(t):t0geinebrownschebewegung,wennxeinstetigesmartingalistmit[x;x](t)=t DerProze[;]heitquadratischeVariationoderBracket{Proze.DieBrownscheBewegung kannmithilfederquadratischenvariationcharakterisiertwerden.nachlevyisteinprozex= bleibtjedochindemverallgemeinertenfallerhalten.esgiltdann[b;b](t)=limn!1nb=t. furt0(siehesatz2.45). WirdenierendieVariationeinesProzessesentlangeinesPfades. Denition2.15SeiX=fX(t):0t<1geincadlag{Proze.FureinkompaktesIntervall I[a;b]mit0a<bdenierenwirdieZufallsvariableVI(X)auf(;F;P)durch VI(X)(!)sup 2PXti2jX(ti+1;!) X(ti;!)j; furalle!2;
16 wobeipalleendlichenpartitionenvoniumfat.vi(x)(!)heitdievariationentlangeines KAPITEL2.GRUNDLAGEN 12 riationaufkompaktenintervallen,einfv{proze,wennfurallekompaktenintervalleigilt PfadesdesProzessesXfureingegebenes!2.XisteinProzevonbeschrankterVa- VI(X)<1P{fast{sicher. ImnachstenAbschnittsehenwir,daimFalleeinesFV{ProzessesXmitstetigenPfadendas allevonunbeschranktervariationp{fast{sicher. Satz2.12EsseiB=fB(t):0t<1geineBrownscheBewegung.DiePfadevonBsind WirverallgemeinerndenBegridesMartingals. stochastischeintegralrdxsichpfadweisewiedaslebesgue{stieltjes{integralberechnenlat. Denition2.16EinltrierterWahrscheinlichkeitsraum;F;P;(Ft)0t1seigegeben.Ein fundamentalefolge. wenneinefolgevonwachsendenstopzeiten(n)n1existiertmitlimn!1n=1p{fast{sicher undxn1fn>0geinmartingalfurallen1ist.diefolgevonstopzeiten(n)n1nennenwir adaptiertercadlag{prozex=fx(t):0t<1gheitgenaudanneinlokalesmartingal, EinemoglicheAntwortbietetdernachstehendeSatz. dievoraussetzungenerfullt.unterwelchenbedingungenisteinlokalesmartingaleinmartingal? EinMartingalisteineinfachesBeispielfureinlokalesMartingal.Wirsetzenn=n,dannsind Satz2.13X=fX(t):t0gseieinlokalesMartingalaufdemltriertenWahrscheinlichkeitsraum;F;P;(Ft)0t1. DerProzeX=fX(t):t0gseigegebenmittelsX(t)sup0stjX(s)jfurt0.Ist EfX(t)g<1furallet0,dannistXeinMartingal.GiltzusatzlichEfXg<1,dannist XeingleichgradigintegrierbaresMartingal. Stieltjesgewinnen.SeieinProzeX=fX(t):t0galsIntegratorgegeben,undH=fH(t): DasstochastischeIntegralkonnenwirnichtalsErweiterungderIntegrationnachLebesgueund 2.2 StochastischeIntegrationstheorie t0gderproze,denmanintegrierenmochte.wirversuchendasstochastischeintegral furjedes!2alsdaslebesgue{stieltjes{integralzudenieren.alsvoraussetzungbenotigen IX(H)(!)=Z1 wir,dax(!)aufkompaktavonbeschranktervariationist.diebrownschebewegungerfullt 0H(s;!)dX(s;!) nachsatz2.12diesevoraussetzungnicht.zudemkonntenwirverlangen,dadiepfadevonx dierenzierbarsind;sprichfuralle!2soll dx(t;!) schrankendiemengederintegratorenzustarkein.vieleprozessewiediebrownschebewegung existieren.dannwaredieintegrationstheorienachriemannanwendbar.solcheforderungen dt ; furallet0 kannmanaufdieseweisenichtfassen.einerweiterteskonzeptistnotwendig. DerAufbauderStochastischenIntegrationstheorieimSinnevonIt^oistinProtterausfuhrlich
17 beschrieben.hiergehenwirnichtaufjedesdetailein.wirgebenwesentlicheergebnissean,beschrankenunshierbeizumeistaufintegrandenmitcaglad{pfaden.untergewissentechnischen KAPITEL2.GRUNDLAGEN 13 DasstochastischeIntegralwirdzunachstfureinfachvorhersehbareProzessealsIntegranddeniert.DieProzesse,welcheublicheIntegraleigenschaftenbesitzen,betrachtenwiralszulassigdendenieren.TeilweisegebenwirhierfurErgebnissean. VoraussetzungenkannmandasstochastischeIntegralfurvorhersehbareProzessealsIntegran- IntegratorenundnennensieSemimartingale.DringtmantieferindieTheorieein,siehtman, Stieltjes{Integralszusammen. scheintegralfurfv{prozessealsintegratorenmitderpfadweisenerweiterungdeslebesgue{ sammenhangidentischist.imrahmendes"neuenkonzepts"nachprotterfalltdasstochasti- dadas"klassische"semimartingalnachdoobundmeyermitderdenitionindiesemzu- Denition2.17EinProzeH=fH(t):t0gheiteinfachvorhersehbar,wenner (;F;P;(Ft)t0),derdieublichenBedingungenerfullt. ImweiterenVorgehenbendenwirunsstetsineinemltriertenWahrscheinlichkeitsraum folgendedarstellungbesitzt. wobei0=t1:::tn+1<1eineendlichefolgevonstopzeitenistundhieinefti{mebare Zufallsvariableist,mitjHij<1P{f.s.fur0in.DieMengeallereinfachvorhersehbaren H(t)=H 01f0g(t)+nXi=1Hi1(Ti;Ti+1](t); ProzesseseimitSbezeichnet. DenRaumdereinfachvorhersehbarenProzesseSversehenwirmitderTopologiedergleichmaigenKonvergenzinWahrscheinlichkeit,welchewirTS0nennen.DasIntegraldenierenwirfur endlichewerteannehmen,seil0.denrauml0versehenwirmitdertopologieinwahrscheinlichkeittl0. GegebeneinenProzeX=fX(t):t0gdenierenwirdielineareAbbildungIX:(S;TS0)! (;F;P).DerRaumallerZufallsvariableaufdiesemWahrscheinlichkeitsraum,diefast{sicher einfachvorhersehbareprozesse.esisteinezufallsvariableaufdemwahrscheinlichkeitsraum (L0;TL0)durch HierbeiistH=fH(t):t0geineinfachvorhersehbarerProzederGestalt IX(H)H0X(0)+nXi=1Hi(X(Ti+1) X(Ti)): ObenstehendeDenitionisteinepfadweiseDenitionfurjedes!2. H(t)=H01f0g(t)+nXi=1Hi1(Ti;Ti+1](t): Denition2.18EinProzeX=fX(t):t0gisteintotalesSemimartingal,fallsXein ProzeXteintotalesSemimartingalist. adaptiertercadlag{prozeistunddieabbildungix:(s;ts0)!(l0;tl0)stetigist. DerProzeX=fX(t):t0gheitSemimartingal,fallsfurjedesreellet0dergestoppte unddermengedersemimartingale. DiefolgendenSatzegebenAufschluuberdieStrukturderMengedertotalenSemimartingale
18 Satz2.14DieMengeder(totalen)SemimartingaleisteinVektorraumuberdenreellenZahlen. KAPITEL2.GRUNDLAGEN Satz2.15SeiQeinWahrscheinlichkeitsmaauf(;F),dasabsolutstetigzuPist.Dannist derverkleinertenfiltrierung,bleibtdiesemimartingaleigenschaftbestehen. VerkleinertmandieursprunglicheFiltrierung,sodaeinSemimartingaladaptiertistbezuglich jedes(totale)p-semimartingalein(totales)q{semimartingal. Satz2.16X=fX(t):t0gseieinSemimartingalzurFiltrierung(Ft)t0.Sei(Gt)t0 einefiltrierung,diein(ft)t0enthaltenist;d.h.:gtftfurjedest0.dannistxein Interesseist,welcheIntegratorenzurVerfugungstehen.EsfolgeneinigeBeispiele. G{Semimartingal,fallsXadaptiertistbezuglichderFiltrierung(Gt)t0. SemimartingalebildendieMengederIntegratoreninderstochastischenIntegrationstheorie.Von Satz2.17JedesquadratintegrierbareMartingal(mitcadlag{Pfaden)isteinSemimartingal. DenBegrideslokalenMartingalshabenwirbereitskennengelernt.DasPrinzipderLokalisierunglatsichallgemeinformulieren. Xn1fn>0gdieEigenschaftEfurn1besitzt. Denition2.19SeiX=fX(t):t0geinstochastischerProze.EineEigenschaftEgilt MitdieserDenitionbetrachtenwirdenfolgendenSatz. lokal,fallseinefolgevonwachsendenstopzeiten(n)n1existiertmitlimn!1n=1,soda tingal. Korollar1EinlokalesMartingalmitstetigenPfadenisteinSemimartingal. Satz2.18JedeslokalquadratintegrierbarelokaleMartingalmitcadlag{PfadenisteinSemimar- Korollar2DieBrownscheBewegungisteinSemimartingal. torenwichtig:diefv{prozesse. NebendenlokalquadratintegrierbarenlokalenMartingalenisteineandereKlassevonIntegrarendenProzejAj=fjAj(t):t0gdurch Denition2.20DerstochastischeProzeA=fA(t):t0gseieinFV{Proze.Wirdenie- jajheittotalervariationsproze. jaj(t)sup n12nxk=1ja(tk2n) A(tk 1 2n)j: Satz2.19JederadaptierteFV{Proze(mitendlichertotalerVariationjAj(1))istein(totales) Semimartingal. DertotaleVariationsprozejAjistwachsendundesgiltjAj(t)<1P{fast{sicher,furt0. einsemimartingal.prozesse,diesichindiesedreisummandenaufspaltenlassen,nennenwir zerlegbareprozesse. konstantenproze,einemlokalquadratintegrierbarenmartingalundeinemfv{prozeebenfalls DieMengederSemimartingalebildeneinenVektorraum.DemnachistdieSummeauseinem
19 Denition2.21EinadaptierterProzeX=fX(t):t0gmitcadlag{Pfadenheitzerlegbar,fallserdieDarstellungbesitzt KAPITEL2.GRUNDLAGEN 15 HierbeiistM=fM(t):t0geinlokalquadratintegrierbaresMartingalundA=fA(t):t0g einfv{proze,undesgiltm(0)=a(0)=0. X(t)=X(0)+M(t)+A(t); furt0: zu.wirgehenderfragenach,wiesichdiemengedereinfachvorhersehbarenprozesseals WirhabendieIntegratorenrelativausfuhrlichdiskutiert.NunwendenwirunsdenIntegranden Satz2.20JederzerlegbareProzeisteinSemimartingal. linksseitigstetigsindundderenrechtsseitigergrenzwertexistiert. Denition2.22DieMengedercadlag{ProzessenennenwirD.DieMengederadaptierten Integrandengeeigneterweiternlat.AlsErgebniserhaltenwirdieadaptiertenProzesse,die Prozesse,derenrechtsseitigerGrenzwertexistiertunddielinksseitigstetigsind,diealsocaglad{ Prozessesind,bezeichnenwirmitL. AufdenRaumenSundL0habenwirdieTopologienTS0undTL0kennengelernt.Wirbenotigen eineweitere,einedritteformderkonvergenz. Denition2.23EineFolgevonProzessen(Hn)n1mitHn=fHn(t):t0gkonvergiert gegeneinenprozeh=fh(t):t0ggleichmaigaufkompaktenintervalleninwahrscheinlichkeit,fallsgilt erkennt.wirversehenl,dundsmitdertopologiedergleichmaigenkonvergenzaufkompaktatl,td,beziehungsweisets.dasnachsteergebnisistderschlussel,umdiedenition IX(H)aufLzuerweitern. Satz2.21DerRaumSliegtdichtinLunterderTopologiedergleichmaigenKonvergenzauf DerRaumSliegtinL,wasmandirektausderDenitiondereinfachvorhersehbarenProzesse n!1sup lim0stjhn(s) H(s)j=0P{f.s.; furt0: stochastischenintegraloperator),dereinenprozeaufeinenprozeabbildet. KompaktaTL. IXbildeteinenProzeaufeineZufallsvariableab.NundenierenwireinenOperator(den Denition2.24EsseiH=fH(t):t0g2SundX=fX(t):t0geinstochastischer Prozemitcadlag{Pfaden.Die(lineare)AbbildungJX:S!Distdeniertdurch HierbeiistH=fH(t):t0geineinfachvorhersehbarerProzederGestalt JX(H)H0X(0)+nXi=1HiXTi+1 XTi: JX(H)heitdasstochastischeIntegralvonHbezuglichX. H(t)=H01f0g(t)+nXi=1Hi1(Ti;Ti+1](t):
20 ImweiterenbenutzenwirdiedreigleichwertigenSchreibweisen. KAPITEL2.GRUNDLAGEN 16 DieBeziehungzwischenIXundJXistJX(H)(t)=IXt(H),zudemgiltIX(H)=R10H(s)dX(s). JX(H)=ZH(s)dX(s)=HX: iststetig. Wirhabengesehen,dafureinSemimartingalXderIntegrationsoperatorJXstetigauf(S;TS) Satz2.22EsseiX=fX(t):t0geinSemimartingal.DieAbbildungJX:(S;TS)!(D;TD) ist.zudemliegtsdichtin(l;tl).da(d;td)vollstandigundmetrisierbarist,konnenwirden stochastischenintegrationsoperatorjxvonsauflfortsetzen. Denition2.25EsseiX=fX(t):t0geinSemimartingal.DiestetigeAbbildung schesintegral. ImweiterenVerlaufdesAbschnittsbezeichnetX=fX(t):t0geinSemimartingalund JX:(L;TL)!(D;TD),diemanalsFortsetzungvonJX:S!Derhaltheitstochasti- Stellet0aus. H=fH(t):t0geinenProzeausL.WirwertendasstochastischeIntegralHXander Um0auszuschlieen,schreibenwir (HX)(t)=Zt Zt 0H(s)dX(s)=Z[0;t]H(s)dX(s): MitdiesenBezeichnunggiltRt0H(s)dX(s)=H(0)X(0)+Rt0+H(s)dX(s). 0+H(s)dX(s)=Z(0;t]H(s)dX(s): Denition2.26FurY=fY(t):t0g2DseiderzugehorigeSprunganteil Y=fY(t):t0gdeniertdurchY(t)Y(t) Y(t )furt0.hierbeiist Satz2.23EsseieineStopzeit.Danngilt(HX)=H1[0;]X=H(X). EsfolgteineZusammenstellungvonEigenschaftendesstochastischenIntegrals. Y(0 )0.EsgiltalsoY(0)=Y(0). Satz2.24(Assozitivitat)DerstochastischeIntegralprozeY=HXisteinSemimartingal undfurg=fg(t):t0g2lgilt DiestochastischeIntegrationerhaltdieSemimartingaleigenschaft.IstderIntegratorXeinFV{ Proze,dannwirddieseEigenschaftunterderstochastischenIntegrationebenfallserhalten. GY=G(HX)=(GH)X: H=fH(t):t0g2L,dannistHXununterscheidbarvompfadweiseberechnetenLebesgue{ Satz2.25FallsX=fX(t):t0geinSemimartingalundFV{Prozeistund GleichesgiltfurlokalquadratintegrierbarelokaleMartingale. Satz2.26X=fX(t):t0gseiein(lokalquadratintegrierbares)lokalesMartingalund H=fH(t):t0g2L.DannistdasstochastischeIntegralHXein(lokalquadratintegrierbares)lokalesMartingal. Stieltjes{IntegralundebenfallseinFV{Proze.
21 FurBerechnungenbenotigenwirdienachstehendeDenition. KAPITEL2.GRUNDLAGEN 17 Denition2.27EsseieineendlicheFolgevonendlichenStopzeiten DieFolgeheitzufalligePartition.EineFolgevonzufalligenPartitionen(n)n1 0=01:::k<1: konvergiertzuridentitat,fallsgilt (i)limn!1supknk=1p{fast{sicher. n:n0:::nkn<1 DerquadratischeVariationsprozeeinesSemimartingals,denmanauchals"Bracket{Proze" bezeichnet,spielteinefundamentalerolle. (ii)jjnjjsupkjnk+1 nkjkonvergiertgegen0p{fast{sicher. Denition2.28X=fX(t):t0gundY=fY(t):t0gseienSemimartingale.Der quadratischevariationsprozevon[x;x]=f[x;x](t):t0g,seigegebenmittels DerquadratischeKovariationsprozevonXundYistdeniertdurch [X;X](t)X(t)2 2Zt [X;Y](t)X(t)Y(t) Zt 0X(s )dy(s) Zt 0X(s )dx(s); furt0: AusderDenitionistklar,dadieAbbildung(X;Y)7![X;Y]einesymmetrischeBilinearform ist.deshalbgiltdiepolarisierungsidentitat 0Y(s )dx(s); furt0: DernachsteSatzgibteinigeEigenschaftendesquadratischenVariationsprozewieder. [X;Y]=12([X+Y;X+Y] [X;X] [Y;Y]): wachsenderadaptierterproze,dercadlag{pfadebesitzt.daruberhinausgilt Satz2.27DerquadratischeVariationsprozeeinesSemimartingalsX=fX(t):t0gistein (ii)falls(n)n1einefolgevonzufalligenpartitionenist,diegegendieidentitatstrebt,dann (i)[x;x](0)=x(0)2und[x;x]=(x)2. indertopologiedergleichmaigenkonvergenzaufkompakta. gilt X(0)2+Xi(Xni+1 Xni)2![X;X] Korollar1DerKovariationsproze[X;Y]=f[X;Y](t):t0gzweierSemimartingaleXund YisteinFV{ProzeundebenfallseinSemimartingal. (iii)isteinestopzeit,danngilt[x;x]=[x;x]=[x;x].
22 Korollar2(PartielleIntegration)X=fX(t):t0gundY=fY(t):t0gseien KAPITEL2.GRUNDLAGEN 18 Semimartingale.DannistXY=fX(t)Y(t):t0geinSemimartingalundesgilt (XY)(t)=X(t)Y(t)=Zt 0X(s )dy(s)+zt gebra. Korollar3AlleSemimartingaleaufeinemltriertenWahrscheinlichkeitsraumbildeneineAl- 0Y(s )dx(s)+[x;y](t); furt0: ImfolgendenbetrachtenwireinigeBeispiele,diedasVerstandnisdereingefuhrtenabstrakten Theorieermoglichensollen.Wirzeigen,daderPoissonprozeeinFV{ProzeistunduntersuchendasIntegralRB(s)dB(s). diesprungstellenundmonotonwachsend.insbesondereistdiedierenzn(ti+1;!) N(ti;!) Beispiel2SeiN=fN(t):t0geinPoissonproze.DerPfadN(;!)istkonstantbisauf positiv.furdievariationentlangeinespfadesgilt V[0;t](N)(!)=sup 2PXti2N(ti+1;!) N(ti;!) 2PXti2jN(ti+1;!) N(ti;!)j =sup =N(t;!) N(0;!)=N(t;!); 2PN(t;!) N(0;!) P(N(t)=1)=0furt0.DeshalbistV[0;t](N)<1P{f:s:EinPoissonprozeistfolglicheinFV{Proze. Beispiel3IndiesemBeispielsuchenwirdieLosungdesIntegralsRB(s)dB(s). [B;B](t)=tfurt0.NachdemKorollar2vonSatz2.27gilt B=fB(t):t0gseieineStandardBrownscheBewegung.AusSatz2.11wissenwir Zt DerPoissonprozeisteinPunktprozeohneExplosion.MitanderenWorten furalle!2undt0: 12tverdankenwirderquadratischenVariationderBrownschenBewegung.DasisteinkonkretesBeispiel,dawirdasLebesgue{Stieltjes{IntegralnichtgefahrlosaufstochastischeProzesse ausdehnenkonnen. EinenstochastischerProzemitcadlag{PfadenkannmanalsSummeausseinemstetigenAnteil Denition2.29EsseiX=fX(t):t0geinSemimartingalundX=fX(t):t0gder unddensprungendarstellen. SprunganteilvonX.DerstetigeAnteilvonXistdeniertdurch ImSinnederklassischenIntegrationstheorieerwartenwir12B(t)2.DenzusatzlichenSummanden 0B(s)dB(s)=12B(t)2 t; furt0: Satz2.28EsseiX=fX(t):t0geinadaptierterFV{Prozemitcadlag{Pfaden.Dannist Xc(t)X(t) X derstetigeanteildesquadratischenvariationsprozesses[x;x]c=0.esgiltalso 0stX(s); furt0: [X;X](t)=X(0)2+P0<st(X(s))2.
23 FureinenstetigenFV{ProzeistdiequadratischeVariationeinkonstanterProze.Wirkonnen KAPITEL2.GRUNDLAGEN 19 Kovariationsproze[X;Y]=f[X;Y](t):t0ggilt Satz2.29X=fX(t):t0gundY=fY(t):t0gseienSemimartingale.Furden auchaussagenfurdenquadratischenkovariationprozetreen. (ii)falls(n)n1einefolgevonzufalligenpartitionenist,diegegendieidentitatkonvergiert, (i)[x;y](0)=x(0)y(0)und[x;y]=xy. indertopologiedergleichmaigenkonvergenzaufkompakta. danngilt X(0)Y(0)+Xi(Xni+1 Xni)(Yni+1 Yni)![X;Y] IstXzudemeinadaptierterFV{Proze,erhaltenwir (iii)isteinestopzeit,danngilt[x;y]=[x;y]=[x;y]=[x;y]. BesitztXoderYstetigePfade,dannist[X;Y](t)=X(0)Y(0). [X;Y](t)=X(0)Y(0)+X 0<stX(s)Y(s); furt0: Beispiel4NachBeispiel2giltfureinenPoissonprozeN=fN(t):t0gV[0;t](N)=N(t) einmalzurgleichenzeitspringen. DerquadratischeKovariationsprozeistindiesemFallnichtkonstant,fallsXundYmindestens furallet0.eineweitereaussageist,daneinfv{proze.dervorangegangenesatzlat daneinpunktprozeist. manuberdessenzwischenankunftszeiten,dieunabhangigeexponentialverteiltestopzeitensind. FurdieSprunghohegiltP(fN(s)2:s2[0;t]g)=0furallet0.InsbesondereistNc=0, sichdeswegenaufdiequadratischevariationvonnanwenden.einenpoissonprozekonstruiert [N;N](t)=N(0)2+X =X 0<stN(s) 0<stN(s)2 furallet0hergeleitet. FureinenPoissonprozeNhabenwirdieinteressanteGleichheitV[0;t](N)=[N;N](t)=N(t) =N(t)P{f.s.; furallet0: Satz2.30FallsM=fM(t):t0geinlokalesMartingalistmitEf[M;M](1)g<1,dann ist,beantwortetderfolgendesatz. DieFrage,unterwelchenBedingungeneinlokalesMartingaleinquadratintegrierbaresMartingal istmeinquadratintegrierbaresmartingal.daruberhinausgiltef[m;m](t)g=efm(t)2g,fur It^ostudiertedieBrownscheBewegungalsIntegrator.AusdemnachstenSatzleitetsichdie allet2[0;1]. It^o{IsometriefurIntegrandenausLab.
24 Satz2.31X=fX(t):t0gundY=fY(t):t0gseienSemimartingaleund KAPITEL2.GRUNDLAGEN 20 H=fH(t):t0gundL=fL(t):t0gProzesseausL.Danngilt undinsbesondereerhaltenwir [HX;LY](t)=Zt [HX;HX](t)=Zt 0H(s)L(s)d[X;Y](s); [B;B](t)=t.H=fH(t):t0gseieinProzeausLmitEfR10H(s)2dsg<1.Aus FurdieStandardBrownscheBewegungB=fB(t):t0ggiltnachSatz2.11 0H(s)2d[X;X](s): Satz2.26folgt,daHBeinlokalesMartingalist.[HB;HB](t)=Rt0H(s)2dssieht manausdemletztensatz.wirwendensatz2.30an.hbisteinlokalesmartingalmit Ef[HB;HB](1)g=EfR10H(s)2dsg<1nachVoraussetzung.DamitistHBeinquadratintegrierbaresMartingalundEf[HB;HB](t)g=Ef(HB)(t)2gfurallet0.Wirerhalten dieit^o{isometrie 2.3Ef(Zt DieIt^o{FormelunddasDoleans{Dade{Exponential 0H(s)dB(s))2g=Ef(HB)(t)2g=Ef[HB;HB](t)g=EfZt 0H(s)2dsg: Satz2.32(DieIt^o{Formel)EsseiX=fX(t):t0geinSemimartingalundfeineC2{ Funktionf.UntergewissenBedingungenistf(X)ebenfallseinSemimartingal.DasVerhalten des"dierentials"vonf(x)beschreibtdieit^o{formel. WirbetrachtendasVerhalteneinesSemimartingalsXunterderTransformationdurcheine giltf(x(t)) f(x(0))=zt FunktionaufdenreellenZahlen.Dannistf(X)=ff(X(t)):t0geinSemimartingal,undes +X 0+f0(X(s ))dx(s)+12zt 0<stff(X(s)) f(x(s )) f0(x(s ))X(s)g; 0+f00(X(s ))d[x;x]c(s) DieIt^o{FormelvereinfachtsichineinigenSpezialfallen. furt0: esgilt Korollar1EsseiV=fV(t):t0geinSemimartingalundFV{Proze.FureineC2{Funktion faufdenreellenzahlenistf(v)=ff(v(t)):t0geinsemimartingalundfv{proze,und f(v(t)) f(v(0))=zt +X 0+f0(V(s ))dv(s) FunktionaufdenreellenZahlenausC2.Dannistf(X)=ff(X(t)):t0geinSemimartingal, Korollar2EsseiX=fX(t):t0geinSemimartingalmitstetigenPfadenundfeine 0<stff(V(s)) f(v(s )) f0(v(s ))V(s)g; furt0: undesgilt f(x(t)) f(x(0))=zt 0+f0(X(s))dX(s)+12Zt 0+f00(X(s))d[X;X](s); furt0:
25 DervorangegangeneSatzlatsichaufeinenmehrdimensionalenProzeausdehnen. KAPITEL2.GRUNDLAGEN 21 furk=1;:::;n.fseieinfunktionrn!r,derenpartielleableitungenzweiterordnung Satz2.33EsseiX=(X1;:::;Xn)einn{TupelvonSemimartingalen,Xk=fXk(t):t0g undesgiltfurt0 existierenundstetigsind.dannistf(x)=ff(x1(t);:::;xn(t)):t0geinsemimartingal, f(x(t)) f(x(0))=nxi=1zt ))dxi(s) i;j=1zt +X 0<stff(X(s)) f(x(s )) ))d[xi;xj]c(s) Einelementares,dennochsehrwichtigesBeispielwirdnunbehandelt. ))Xi(s)g: Z(t)=1+Rt0Z(s )dx(s)erfullt.zistfurt0gegebenmittels (eindeutiges)semimartingalz=fz(t):t0g,dasdiestochastischedierentialgleichung Satz2.34EsseiX=fX(t):t0geinSemimartingalmitX(0)=0.Dannexistiertein Denition2.30FureinSemimartingalX=fX(t):t0gmitX(0)=0istdas Z(t)=expX(t) 12[X;X](t)Y 0<st(1+X(s))exp X(s)+12(X(s))2: diestochastischedierentialgleichungz(t)=1+zt stochastischeexponentialvonxdas(eindeutige)semimartingalz=fz(t):t0g,das WiruntersuchendenvorangegangenenSatzfurspezielleKlassenvonProzessen. auche(x)undnenntesdoleans{dade{exponentialvonx. 0Z(s )dx(s),t0,lost.zschreibtman dasdoleans{dade{exponentialvonxdiegestalt Korollar1IstX=fX(t):t0geinSemimartingalundFV{ProzemitX(0)=0,dannhat EineinfachesBeispielerhaltenwir,wennwirXalseinelineareFunktionvonderZeitannehmen. E(X)(t)=exp(X(t))Y 0<st(1+X(s))exp( X(s)); furt0: Beispiel5DerProzeX=fX(t):t0gseideniertdurch HierbeiisteinereelleKonstante.FurdasDoleans{Dade{ExponentialvonXgilt X(t)t; furt0: DennnachDenitionistXeinstetigerFV{Proze. E(X)(t)=exp(t); furt0:
26 Korollar2IstX=fX(t):t0geinstetigesSemimartingalmitX(0)=0,giltfurdas KAPITEL2.GRUNDLAGEN 22 Doleans{Dade{ExponentialvonX EinwichtigesBeispielistdiesogenannte"geometrischeBrownscheBewegung".SieistderProze, durchdenimallgemeinendiepreisprozessevonaktienmodelliertwerden. E(X)(t)=expX(t) 12[X;X](t); furt0: Beispiel6EsseiB=fB(t):t0geineStandardBrownscheBewegung.DerProze X=fX(t):t0gseideniertdurchX(t)t+B(t)furt0.Hierbeisind>0 undreellekonstanten.furt0gilt BrownscheBewegungeinMartingalmitstetigenPfaden,undE(X)(t)=expB(t) 122t. E(X)heitgeometrischeBrownscheBewegung.Ist=0,dannistdiegeometrische E(X)(t)=expB(t)+( 122)t: Abbildung2.2:3simuliertePfadeeinergeoemtrischenBrownschenBewegungmit=0:3und =0:20,sowiederzugehorigeErwartungswert. Zeitt Korollar3IstX=fX(t):t0geinstetigesSemimartingalundFV{ProzemitX(0)=0, dannhatdasdoleans{dade{exponentialvonxdiegestalt Korollar4N=fN(t):0tTgseieinSemimartingal,daszueinerStopzeit,mit>0 P{f.s.,von0auf2IRspringtN(t)1ftg; E(X)(t)=exp(X(t)); furt0: Danngilt E(N)=1+N: fur0tt:
27 Beweis: KAPITEL2.GRUNDLAGEN 23 NisteinSprungproze;esgiltNc=0undN(t)=N(0)+P0<stN(s)furt0.Insbesondere istn(0)=0wegen>0p{f.s. sehenwirmithilfevonsatz2.29[n;n](t)=n(0)2+p0<st(n(s))2furt0.desweiteren E(N)(t)=expN(t) 12[N;N](t)Y 0<st(1+N(s))exp N(s)+12N(s)2 =expn(t) 0<stexp N(s)+12N(s)2Y 0<st N(s)+12N(s)21AY 0<st(1+N(s)) =expn(t) 12[N;N](t)exp N(t)+12[N;N](t)Y 0<st(1+N(s)) 0<st(1+N(s)) =1+N(t) = 0<st(1+N(s)) Y (!)t,danngiltn(;!)=undn(s;!)=0furs2[0;t]nf(!)g.damitsehenwir DieletzteGleichheitergibtsich,daNhochstenseinenSprunginbesitzt.t0seifest.Ist fur0tt: Fur(!)>tgiltN(s;!)=0undN(s;!)=0furs2[0;t],woraus 0<st(1+N(s;!))=1+N(;!)=1+=1+N(t;!): Y folgt.damitistderbeweisabgeschlossen. 0<st(1+N(s;!))=1=1+N(t;!) Y Korollar5X=fX(t):t0gseieinstetigesSemimartingalmitX(0)=0.Danngilt exp(x(t))=ex+12[x;x](t); furt0: 2 Beweis: [[X;X];[X;X]]=0.AufdierechteSeitederBehauptungwendenwirKorollar2an Satz2.27besagt[X;X](t)=(X(t))2furt0.Xistalsstetigvorausgesetzt.Esist hen,da[x;x]einstetigerfv{prozeist.mitsatz2.29schlieenwir[x;[x;x]]=0und [X;X](t)=0furt0.NachKorollardesselbenSatzesist[X;X]einFV{Proze.Wirse- EX+12[X;X](t)=expX(t)+12[X;X](t) 12X+12[X;X];X+12[X;X](t) =exp(x(t)); =expx(t)+12[x;x](t) 12[X;X](t) DamitistdieAussagegezeigt. furt0: DieMengederDoleans{Dade{ExponentialeaufeinemltriertenWahrscheinlichkeitsraumbilden einespezielleprozeklasse. 2
28 Satz2.35EsseienX=fX(t):t0gundY=fY(t):t0gSemimartingalemit KAPITEL2.GRUNDLAGEN 24 X(0)=Y(0)=0.Danngilt InverseE(X) 1.DieInverseE(X) 1hatdieGestalt ImFalleeinesstetigenSemimartingalsXbesitztdesDoleans{Dade{ExponentialE(X)eine E(X)E(Y)=E(X+Y+[X;Y]): DasProduktzweierDoleans{Dade{ExponentialeistwiedereinDoleans{Dade{Exponential. DennochbildendieDoleans{Dade{ExponentialekeineAlgebra,dasieunterderAdditionnicht E(X) 1=E( X+[X;X]): stabilsind.welcheprozesselassensichalsdoleans{dade{exponentialedarstellen?wirnden einsemimartingaly=fy(t):t0g,sodagilt Satz2.36X=fX(t):t0gseieinstriktpositivesSemimartingalemitX(0)=1.Esexistiert eineteilweiseantwortfurstriktpositivesemimartingale. Beweis: InsbesondereistYP{f.s.eindeutig. X=E(Y): istx(t )=lims%tx(s),furt0,undx(0 )=0.AusdiesemGrundexistiert1 Versionvon1X;vergleicheDenition2.7.unddiedarauffolgendeErlauterung.NachDenition DerstochastischeProzeH=fH(t):t0gwerdeerklartdurchH1X.Histdiecaglad{ nicht,wasunszurobenangefuhrtendenitionvonhveranlathat.mittelshdenierenwir Y=fY(t):t0g Y(t)Zt X innull Xisteincadlag{Proze,alsoist1Xebenfallseincadlag{Proze.Zudemistist1Xwohldeniert, 0H(s)dX(s); furt0: daxstriktpositivist.histdiecaglad{versionvon1x,liegtdemnachinl.yistnachsatz 2.24einSemimartingalundesgiltmitderAssoziativitatdesstochastischenIntegrals (X Y)(t)=(X (HX))(t) =((X H)X)(t) =Zt 0X(s )H(s)dX(s) 01fs>0gdX(s) DaX(0)=1undY(0)=0,erhaltenwir =X(t) X(0); 0+dX(s) X(t)=1+Zt furt0: 0X(s )dy(s)=e(y)(t); furt0:
29 EsbleibtdieFragederEindeutigkeitzuklaren.Y=fY(t):t0gseieinweitererProze,der KAPITEL2.GRUNDLAGEN 25 X=E(Y)undY(0)=0erfullt.DerstochstischeProzeZ=fZ(t):t0gseidieDierenz vonyundy,zy Y.NachderebengetroenenAnnahmeistE(Y)=E(Y).Inder Integralschreibweiseistdasgleichbedeutendmit Daraussehenwir 1+Zt 0X(s )dy=1+zt () 0X(s )dz(s)=0 0X(s )dy; furt0: furt0: ProzeHbezuglichdesletztenAusdrucksunderhaltenmitderAssoziativitatnachSatz2.24 Erneutietein,daXalsstriktpositivvorausgestztist.Wirintegrierendenobendenierten (H(X Z))(t)=Zt =Zt 0H(s)d(X Z)(s) 0H(s)X(s )dz(s) =Z(t) Z(0); 01fs>0gdZ(s) henwirz(t)=z(0)furallet0.nachvoraussetzunggilty(0)=y(0)=0.nunist AberX Zistnach()gleichNull,unddeswegengilt(H(X Z))=0.Hierausse- furt0: Z(0)=Y(0) Y(0)=0,wasZ=0P{f.s.impliziert.YundYsindfolglichununterscheidbar. DamitistdieEindeutigkeitgezeigt. MitdenBezeichnungendesBeweisesgeltendiebeidenKorollare. 2 Korollar1XistgenaudanneinFV{Proze,wennYeinFV{Prozeist. Korollar2Xistgenaudannein(lokalquadratintegrierbares)lokalesMartingal,wennYein (lokalquadratintegrierbares)lokalesmartingalist. Beweis: UntergewissenVoraussetzungkonnenwirdieobigenKorollareaufProzesseXausdehnen,die derbeziehungx=e(y). DieBehauptungenfolgendirektausdenSatzen2.26und2.27undderDenitionvonY,sowie nicht{negativsind. 2 Korollar3X=fX(t):t0gseieinpositivesSemimartingalmitX(0)=1undY=fY(t): t0geinsemimartingalmity(0)=0,sodax=e(y)gilt.wirdenierendiestopzeit durch YeinlokalesMartingalist. YbesitzedieZerlegungY=M+eY,wobeiM=fM(t):t0geinlokalesMartingalistund ey=fey(t):t0gdiebeziehungey=eyerfullt.xistgenaudanneinlokalesmartingal,wenn infft0:x(t)=0g:
30 Beweis: KAPITEL2.GRUNDLAGEN 26 WirsetztenXalslokalesMartingalvoraus.DerProzeH=fH(t):t0gseigebenmittels YseialslokalesMartingalvorausgesetzt.AusSatz2.27folgtdirekt,daX=1+X Yein lokalesmartingalist. H(t)(1ftg1 0; X(t );fallst>0 stischenexponentialssehenwir,daxinnicht"stetig"gegennullgeht,sonderndorthin Histwohldeniert,dennX(t )>0aufftg.AusderkonkretenDarstellungdesstocha- fallst=0: springt.insbesondereisthdasproduktzweiercaglad{prozesseundliegtdemnachinl.fur einfestest0undein!2ftgisty(t)aufftgdurch Y(t;!)=Zt vorangegangenensatzes.wegeny=ey+mundey=eyisteydurch P{f.s.eindeutigbestimmt.DieGestaltvonYunddieEindeutigkeitfolgenwieimBeweisdes 0H(s;!)dX(s;!) ey(t)=ey(t)=y(t) M(t)=Zt^ Martingal,schlielichistMalslokalesMartingalvorausgesetzt.AusY=eY+Mfolgtdie P{f.s.eindeutigdarstellbar.eYisteinlokalesMartingal,dennH2LundXisteinlokales 0 H(s)dX(s) M(t^); furt0; Aussage wirdasstochastischeintegralaufvorhersehbareintegrandenausdehnen. RaumallerSemimartingaledieH2{Normein.IneinemaufdieseWeisenormiertenRaumkonnen EinespezielleKlassederSemimartingalesinddieH2{Semimartingale.Hierfuhrenwiraufdem Denition2.31EinadaptierterProzeH=fH(t):t0gheitvorhersehbar,fallsfuralle t0gilt,h(t)istft {mebar.hierbeiistft W0s<tFsdiekleinste{Algebra,diealle {AlgebrenFsmit0s<tenthalt. DieFiltrierungistrechtseitigstetig.EsistW0s<tFs=Ws2[0;t)\QFs,slauftsomitdurcheine tierteprozesse. Denition2.32DasSemimartingalX=fX(t):t0gisteinspeziellesSemimartingal, abzahlbareindexmenge.daseinfachstebeispielfurvorhersehbareprozessesindstetigeadap- fallsxdiezerlegungbesitzt HierbeiistM=fM(t):t0geinlokalesMartingalundA=fA(t):t0geinadaptierter Zerlegung. vorhersehbarerfv{proze,undesgiltm(0)=a(0)=0.diesezerlegungheitkanonische X=X(0)+M+A: barenmartingalsundeinemfv{prozedarstellenlat. "zerlegbar",fallsessichalssummeauseinemkonstantenanteil,einemlokalquadratintegrier- EineandereZerlegunghabenwirinDenition2.21kennengelernt.EineSemimartingalheit
31 Satz2.37IstX=fX(t):t0geinspeziellesSemimartingal,dannistdiekanonischeZerlegungX=X(0)+M+Aeindeutig. KAPITEL2.GRUNDLAGEN 27 adaptierterproze,dereinlokalesmartingalundeinvorhersehbarerfv{prozeist,dannistx DieEindeutigkeitderZerlegunghateinenutzlicheKonsequenz.SeiX=fX(t):t0gein konstant. Denition2.33X=fX(t):t0gseieinspeziellesSemimartingalmitX(0)=0und kanonischerzerlegungx=m+a,wobeim=fm(t):t0geinlokalesmartingalund JetztdenierenwirdieH2{NormfurspezielleSemimartingale. DieH2{NormvonXistgegebendurch A=fA(t):t0geinadaptiertervorhersehbarerFV{Prozeist.ZudemgiltM(0)=A(0)=0. Bemerkung:FormalistdieH2{NormnurfurspezielleSemimartingaleXmitX(0)=0 DerRaumH2bestehtausallenspeziellenSemimartingalen,derenH2{Normendlichist. jjxjjh2(p)jj[m;m](1)1=2jjl2(p)+jjjaj(1)jjl2(p): speziellensemimartingalsx,indemmanx X(0)betrachtet.IstX(0)einefesterelleZahl, dannsagenwir,daxeinh2{semimartingalist,fallsjjx X(0)jjH2<1gilt. deniert.imallgemeinenfallberechnetmannachderobigendenitiondieh2{normeines EinewichtigeAbschatzungfurH2{SemimartingaleliefertderfolgendeSatz,Theorem5,Chapter seiaeinfv{prozeaush2.danngiltfurdietotalevariationvona,efjaj(1)2g<1. EinlokalesMartingalMausH2istnachSatz2.30einquadratintegrierbaresMartingal.Es Satz2.38X=fX(t):t0gseieinH2{SemimartingalmitX(0)=0.Danngilt IV,vonProtter(1995). Korollar1AufeinemltriertenWahrscheinlichkeitsraum;F;P;(Ft)0tTseiY=fY(t): E((sup t0jx(t)j)2)8jjxjj2h2: 0tTgeinH2(P){SemimartingalmitY(0)2IRundQeinzuPaquivalentesMa,wobei T>0einendlicherZeithorizontist.IstYeinlokalesQ{MartingalunddQ dannistyeinq{martingal. Beweis:WirschlieenaufdieMartingaleigenschaftdeslokalenQ{MartingalsYmithilfevon dpquadratintegrierbar, Satz2.13.AlshinreichendeBedingungwirdEQnsup0tTjY(t)jo<1verlangt.L=fL(t): 0tTgseiderProze,derdenMawechselP7!Qbeschreibt.Danngilt L(t)=EPdQ ist.dieerwartungswertoperatorenunterpundqsinddurch AusderGleichungfolgt,daLeinP{Martingalist,dasnachAnnahmesogarquadratintegrierbar dpft; fur0tt: EQfg=EPfL(T)g
 TechnischeUniversitatMunchen ZentrumMathematik Uberlebenszeitanalyse Anwendungender inderpegeversicherung Diplomarbeit FlorianRudolph von Abgabetermin: Betreuerin: Themenstellerin:ProfDrCzado 25Januar2000
TechnischeUniversitatMunchen ZentrumMathematik Uberlebenszeitanalyse Anwendungender inderpegeversicherung Diplomarbeit FlorianRudolph von Abgabetermin: Betreuerin: Themenstellerin:ProfDrCzado 25Januar2000
Bemerkungen. f (x 1,..., x i + x i,..., x n ) f (x 1,..., x n ) lim. f xi (x 1,..., x n ) =
 Bemerkungen Die Erweiterung der Definition von partiellen Ableitungen 1. Ordnung für Funktionen u = f (x 1,..., x n ) mit n > 2 Veränderlichen ist offensichtlich: f xi (x 1,..., x n ) = f (x 1,..., x i
Bemerkungen Die Erweiterung der Definition von partiellen Ableitungen 1. Ordnung für Funktionen u = f (x 1,..., x n ) mit n > 2 Veränderlichen ist offensichtlich: f xi (x 1,..., x n ) = f (x 1,..., x i
Aufgaben für die 14. Übung zur Vorlesung Mathematik 2 für Informatiker: Analysis Sommersemester 2010
 Aufgaben für die 4. Übung zur Vorlesung Mathematik für Informatiker: Analysis Sommersemester 4. Bestimmen Sie den Flächeninhalt der dreiblättrigen Kleeblattkurve γ für ein Kleeblatt. Die Polarkoordinaten-
Aufgaben für die 4. Übung zur Vorlesung Mathematik für Informatiker: Analysis Sommersemester 4. Bestimmen Sie den Flächeninhalt der dreiblättrigen Kleeblattkurve γ für ein Kleeblatt. Die Polarkoordinaten-
Multivariate Kettenregel
 Multivariate Kettenregel Für die Hintereinanderschaltung h = g f : x y = f (x) z = g(y), stetig differenzierbarer Funktionen f : R m R l und g : R l R n gilt h (x) = g (y)f (x), d.h. die Jacobi-Matrix
Multivariate Kettenregel Für die Hintereinanderschaltung h = g f : x y = f (x) z = g(y), stetig differenzierbarer Funktionen f : R m R l und g : R l R n gilt h (x) = g (y)f (x), d.h. die Jacobi-Matrix
Einführung in partielle Differentialgleichungen
 vdf - Lehrbücher und Skripten Einführung in partielle Differentialgleichungen für Ingenieure, Chemiker und Naturwissenschaftler von Norbert Hungerbühler 2., durchgesehene Auflage 2 Einführung in partielle
vdf - Lehrbücher und Skripten Einführung in partielle Differentialgleichungen für Ingenieure, Chemiker und Naturwissenschaftler von Norbert Hungerbühler 2., durchgesehene Auflage 2 Einführung in partielle
D-MAVT/D-MATL Analysis II FS 2017 Dr. Andreas Steiger. Lösung - Serie 15
 D-MAVT/D-MATL Analysis II FS 2017 Dr. Andreas Steiger Lösung - Serie 15 1. Der Wert einer Funktion f : R R fällt am schnellsten in die Richtung (a) (b) (c) der minimalen partiellen Ableitung. entgegengesetzt
D-MAVT/D-MATL Analysis II FS 2017 Dr. Andreas Steiger Lösung - Serie 15 1. Der Wert einer Funktion f : R R fällt am schnellsten in die Richtung (a) (b) (c) der minimalen partiellen Ableitung. entgegengesetzt
Übungen zu Partielle Differentialgleichungen, WS 2016
 Übungen zu Partielle Differentialgleichungen, WS 2016 Ulisse Stefanelli 16. Januar 2017 1 Beispiele 1. Betrachten Sie die Beispiele von nichtlinearen PDG und Systemen, die wir im Kurs diskutiert haben,
Übungen zu Partielle Differentialgleichungen, WS 2016 Ulisse Stefanelli 16. Januar 2017 1 Beispiele 1. Betrachten Sie die Beispiele von nichtlinearen PDG und Systemen, die wir im Kurs diskutiert haben,
2 Mengen bzgl. Knoten r (Wurzel): A = {Knoten v mit ungerader Weglänge (r,v)} B = {Knoten v mit gerader Weglänge (r,v)}
 K. 1.2: t P D. Pt tz Lt ü At E, LS11 3. VO 30. Ot 2006 Ü Ot: Pü / Ü Pt t ü tt G Pt t ü G x t 2 Püt ü Fü: Ü VO 2 Ü 2: 6LP A: Zä Gt Sz Ft t NEU: ( ätt : äß tv tt Ü, t ) ü Pü: St VO Ü, 20 t Püt Ltw: Ü VO
K. 1.2: t P D. Pt tz Lt ü At E, LS11 3. VO 30. Ot 2006 Ü Ot: Pü / Ü Pt t ü tt G Pt t ü G x t 2 Püt ü Fü: Ü VO 2 Ü 2: 6LP A: Zä Gt Sz Ft t NEU: ( ätt : äß tv tt Ü, t ) ü Pü: St VO Ü, 20 t Püt Ltw: Ü VO
Höhere Mathematik für Ingenieure 2
 Höhere Mathematik für Ingenieure 2 Prof. Dr. Swanhild Bernstein Sommersemester 218 Institut für Angewandte Analysis Kurven- und Parameterintegrale Parameterintegrale Typische Beispiele für Parameterintegrale
Höhere Mathematik für Ingenieure 2 Prof. Dr. Swanhild Bernstein Sommersemester 218 Institut für Angewandte Analysis Kurven- und Parameterintegrale Parameterintegrale Typische Beispiele für Parameterintegrale
3 Funktionen in mehreren Variablen
 3 Funktionen in mehreren Variablen Funktionen in mehreren Variablen Wir betrachten nun Abbildungen / Funktionen in mehreren Variablen. Dies sind Funktionen von einer Teilmenge des R d nach R. f : D f R,
3 Funktionen in mehreren Variablen Funktionen in mehreren Variablen Wir betrachten nun Abbildungen / Funktionen in mehreren Variablen. Dies sind Funktionen von einer Teilmenge des R d nach R. f : D f R,
1. Aufgabe 11 Punkte. Musterlösung DGL f. Ing., 10. April Aus
 Musterlösung DGL f. Ing., 0. April 204. Aufgabe Punkte Aus 2 λ 0 λ 0 = 0 2 λ = 0 = (2 λ)( λ) 2 ( λ)( ) = (2 λ)λ 2 λ = λ((2 λ)λ ) = λ(2λ λ 2 ) = λ( 2λ+λ 2 +) = λ(λ ) 2 ergeben sich der der einfache Eigenwert
Musterlösung DGL f. Ing., 0. April 204. Aufgabe Punkte Aus 2 λ 0 λ 0 = 0 2 λ = 0 = (2 λ)( λ) 2 ( λ)( ) = (2 λ)λ 2 λ = λ((2 λ)λ ) = λ(2λ λ 2 ) = λ( 2λ+λ 2 +) = λ(λ ) 2 ergeben sich der der einfache Eigenwert
Exakte Differentialgleichungen
 Kapitel 4 Exakte Differentialgleichungen 4.1 Kurvenscharen Sei D R 2 ein offenes und zusammenhängendes Gebiet. Dann kann man zu jeder D einfach überdeckenden Kurvenschar eine Differentialgleichung erster
Kapitel 4 Exakte Differentialgleichungen 4.1 Kurvenscharen Sei D R 2 ein offenes und zusammenhängendes Gebiet. Dann kann man zu jeder D einfach überdeckenden Kurvenschar eine Differentialgleichung erster
UbungenzurAnalysis2 Prof.Dr.Kohnen WS1996/97 Dr.O.Delzeith
 UbungenzurAnalysis2 Prof.Dr.Kohnen WS1996/97 Dr.O.Delzeith 1.(i)EntscheidenSie,obdieFunktion (ii)berechnensiedieintegrale impunktx0=0dierenzierbarist.bestimmensieggfs.dieableitungf0(x0). (a)1 Z0xf:(R!R
UbungenzurAnalysis2 Prof.Dr.Kohnen WS1996/97 Dr.O.Delzeith 1.(i)EntscheidenSie,obdieFunktion (ii)berechnensiedieintegrale impunktx0=0dierenzierbarist.bestimmensieggfs.dieableitungf0(x0). (a)1 Z0xf:(R!R
Durchschnitts- Grenz- Solidaritäts- Gesamt Durchschn.- Grenz- Einkommen Steuer steuersatz zuschlag KiSt 9% Steuer
 16.000,00-0% 0% - - - 0% 0% 16.100,00 12,00 0% 12% - 1,08 13,08 0% 13% 16.200,00 26,00 0% 14% - 2,34 28,34 0% 15% 16.300,00 40,00 0% 14% - 3,60 43,60 0% 15% 16.400,00 54,00 0% 14% - 4,86 58,86 0% 15% 16.500,00
16.000,00-0% 0% - - - 0% 0% 16.100,00 12,00 0% 12% - 1,08 13,08 0% 13% 16.200,00 26,00 0% 14% - 2,34 28,34 0% 15% 16.300,00 40,00 0% 14% - 3,60 43,60 0% 15% 16.400,00 54,00 0% 14% - 4,86 58,86 0% 15% 16.500,00
Ergebnisse von Kontrollen der amtlichen Lebensmittelüberwachung
 Seite 1 von 18 Seite 2 von 18 Seite 3 von 18 Seite 4 von 18 Seite 5 von 18 Seite 6 von 18 Seite 7 von 18 Seite 8 von 18 Seite 9 von 18 Seite 10 von 18 Seite 11 von 18 Seite 12 von 18 Seite 13 von 18 Seite
Seite 1 von 18 Seite 2 von 18 Seite 3 von 18 Seite 4 von 18 Seite 5 von 18 Seite 6 von 18 Seite 7 von 18 Seite 8 von 18 Seite 9 von 18 Seite 10 von 18 Seite 11 von 18 Seite 12 von 18 Seite 13 von 18 Seite
Klausur zur Vorlesung Stochastik II
 Institut für Mathematische Stochastik WS 24/25 Universität Karlsruhe 7. März 25 Priv-Doz. Dr. D. Kadelka Klausur zur Vorlesung Stochastik II Dauer: 9 Minuten Name: Vorname: Matrikelnummer: Diese Klausur
Institut für Mathematische Stochastik WS 24/25 Universität Karlsruhe 7. März 25 Priv-Doz. Dr. D. Kadelka Klausur zur Vorlesung Stochastik II Dauer: 9 Minuten Name: Vorname: Matrikelnummer: Diese Klausur
Analysis 2 - Übung 1
 Analysis - Übung 1 Felix Knorr 8 März 014 4 Gegeben sei die Polynomfunktion f(x, y xy 10x Man bestimme die Gleichungen ihrer Schnittkurven mit den senkrechten Ebenen x x 0 bzw y y 0 sowie die Höhenlinien
Analysis - Übung 1 Felix Knorr 8 März 014 4 Gegeben sei die Polynomfunktion f(x, y xy 10x Man bestimme die Gleichungen ihrer Schnittkurven mit den senkrechten Ebenen x x 0 bzw y y 0 sowie die Höhenlinien
EntwurfundImplementierungeinerfunktionalenC-Variante mitspeziellerunterstutzungshape-invarianter SingleAssignmentC Array-Operationen
 EntwurfundImplementierungeinerfunktionalenC-Variante mitspeziellerunterstutzungshape-invarianter SingleAssignmentC Array-Operationen derchristian-albrechts-universitat zurerlangungdesdoktorgrades dertechnischenfakultat
EntwurfundImplementierungeinerfunktionalenC-Variante mitspeziellerunterstutzungshape-invarianter SingleAssignmentC Array-Operationen derchristian-albrechts-universitat zurerlangungdesdoktorgrades dertechnischenfakultat
Analysis II (FS 2015): Vektorfelder und Flüsse
 Analysis II (FS 215): Vektorfelder und Flüsse Dietmar A. Salamon ETH-Zürich 7. April 215 1 Der Fluss eines Vektorfeldes Sei U R n eine offene Menge und sei f : U R n eine lokal Lipschitz-stetige Abbildung.
Analysis II (FS 215): Vektorfelder und Flüsse Dietmar A. Salamon ETH-Zürich 7. April 215 1 Der Fluss eines Vektorfeldes Sei U R n eine offene Menge und sei f : U R n eine lokal Lipschitz-stetige Abbildung.
10. Vorlesung Wintersemester
 10. Vorlesung Wintersemester 1 Existenz von Potentialen Für einimensionale Bewegungen unter er Einwirkung einer Kraft, ie nur vom Ort abhängt, existiert immer ein Potential, a man immer eine Stammfunktion
10. Vorlesung Wintersemester 1 Existenz von Potentialen Für einimensionale Bewegungen unter er Einwirkung einer Kraft, ie nur vom Ort abhängt, existiert immer ein Potential, a man immer eine Stammfunktion
Mathematik 3 für Informatik
 Gunter Ochs Wintersemester 5/6 Mathematik 3 für Informatik Lösungen zum Hausaufgabenblatt Lösungshinweise ohne Garnatie auf Fehlerfreiheit c 5. Berechnen Sie die folgenden unbestimmten Integrale: a x 4
Gunter Ochs Wintersemester 5/6 Mathematik 3 für Informatik Lösungen zum Hausaufgabenblatt Lösungshinweise ohne Garnatie auf Fehlerfreiheit c 5. Berechnen Sie die folgenden unbestimmten Integrale: a x 4
Übungen zu Differentialgleichungen (WiSe 12/13)
 Übungen zu Differentialgleichungen WiSe 2/) Blatt 6 22 November 202 Gruppenübung Aufgabe G Sei f t, p) := p 5, t, p) R 2 Gegeben sei das Anfangswertproblem ẋ = f t,x), x0) = ) Bestimmen sie das maximale
Übungen zu Differentialgleichungen WiSe 2/) Blatt 6 22 November 202 Gruppenübung Aufgabe G Sei f t, p) := p 5, t, p) R 2 Gegeben sei das Anfangswertproblem ẋ = f t,x), x0) = ) Bestimmen sie das maximale
Mathematik II Frühjahrssemester 2013
 Mathematik II Frühjahrssemester 2013 Prof. Dr. Erich Walter Farkas Kapitel 8. Funktionen von mehreren Variablen 8.2 Partielle Differentiation Prof. Dr. Erich Walter Farkas Mathematik I+II, 8.2 Part. Diff.
Mathematik II Frühjahrssemester 2013 Prof. Dr. Erich Walter Farkas Kapitel 8. Funktionen von mehreren Variablen 8.2 Partielle Differentiation Prof. Dr. Erich Walter Farkas Mathematik I+II, 8.2 Part. Diff.
Ordnen Sie die Bilder den zugehörigen Funktionen z = f(x, y) zu:
 6. Februar 2012 Lösungshinweise Theorieteil Aufgabe 1: Die folgenden Bilder zeigen drei Niveaumengen N 0 {(x, y) R 2 : f(x, y) 0}: Ordnen Sie die Bilder den zugehörigen Funktionen z f(x, y) zu: (a) z (x
6. Februar 2012 Lösungshinweise Theorieteil Aufgabe 1: Die folgenden Bilder zeigen drei Niveaumengen N 0 {(x, y) R 2 : f(x, y) 0}: Ordnen Sie die Bilder den zugehörigen Funktionen z f(x, y) zu: (a) z (x
Übungen für Partielle Differentialgleichungen Wintersemester 2007/08
 Übungen für Partielle Differentialgleichungen Wintersemester 27/8 1. Leite eine bekannte partielle Differentialgleichung von physikalischen Prinzipien her. 2. Berechne die variationelle Ableitung des folgenden
Übungen für Partielle Differentialgleichungen Wintersemester 27/8 1. Leite eine bekannte partielle Differentialgleichung von physikalischen Prinzipien her. 2. Berechne die variationelle Ableitung des folgenden
Konvergenz gegen einen Prozess mit unabhängigen Zuwächsen - Anwendungen
 Konvergenz gegen einen rozess mit unabhängigen Zuwächsen - Anwendungen Saskia F. Glaffig 20.07.17 "Wiederholung" Definition (vgl. Jacod, Shiryaev, I.3.26: oissonprozess). Ein erweiterter oissonprozess
Konvergenz gegen einen rozess mit unabhängigen Zuwächsen - Anwendungen Saskia F. Glaffig 20.07.17 "Wiederholung" Definition (vgl. Jacod, Shiryaev, I.3.26: oissonprozess). Ein erweiterter oissonprozess
ist reelles lineares Funktional. x(t) ϕ(t) dt ist reelles lineares Funktional für alle ϕ L 2 (0, 1).
 Kapitel 4 Stetige lineare Funktionale 4.1 Der Satz von Hahn - Banach Definition 4.1. Sei X ein linearer normierter Raum über dem Körper K (R oder C). Ein linearer Operator f : X K heißt (reelles oder komplexes)
Kapitel 4 Stetige lineare Funktionale 4.1 Der Satz von Hahn - Banach Definition 4.1. Sei X ein linearer normierter Raum über dem Körper K (R oder C). Ein linearer Operator f : X K heißt (reelles oder komplexes)
Übungen zu Signal- und Systemtheorie
 Fachhochschule Dortmund University of Applied Sciences and Arts Übungen zu Signal- und Systemtheorie (Anteil: Prof. Felderhoff) Version 1.3 für das Wintersemester 016/017 Stand: 05.1.016 von: Prof. Dr.-Ing.
Fachhochschule Dortmund University of Applied Sciences and Arts Übungen zu Signal- und Systemtheorie (Anteil: Prof. Felderhoff) Version 1.3 für das Wintersemester 016/017 Stand: 05.1.016 von: Prof. Dr.-Ing.
Gewöhnliche Dierentialgleichungen
 Gewöhnliche Dierentialgleichungen sind Gleichungen, die eine Funktion mit ihren Ableitungen verknüpfen. Denition Eine explizite Dierentialgleichung (DGL) nter Ordnung für die reelle Funktion t x(t) hat
Gewöhnliche Dierentialgleichungen sind Gleichungen, die eine Funktion mit ihren Ableitungen verknüpfen. Denition Eine explizite Dierentialgleichung (DGL) nter Ordnung für die reelle Funktion t x(t) hat
Martingale. Kapitel 6. 6.1 Martingale in diskreter Zeit. 6.1.1 Definition und Beispiele
 Kapitel 6 Martingale In der Statistik modellieren Martingale z.b. Glücksspiele oder Handelsstrategien in Finanzmärkten und sind ein grundlegendes Hilfsmittel für die statistische Inferenz stochastischer
Kapitel 6 Martingale In der Statistik modellieren Martingale z.b. Glücksspiele oder Handelsstrategien in Finanzmärkten und sind ein grundlegendes Hilfsmittel für die statistische Inferenz stochastischer
Funktionen mehrerer Variabler
 Inhaltsverzeichnis 8 Funktionen mehrerer Variabler 8. Einführende Definitionen und Bemerkungen....................... 8. Graphische Darstellungsmöglichkeiten.......................... 8. Grenzwert und
Inhaltsverzeichnis 8 Funktionen mehrerer Variabler 8. Einführende Definitionen und Bemerkungen....................... 8. Graphische Darstellungsmöglichkeiten.......................... 8. Grenzwert und
Teilnehmer: Herder-Oberschule, Berlin. Gruppenleiter: Humboldt-Universität zu Berlin Humboldt-Universität zu Berlin/Andreas-Oberschule, Berlin
 Berichte der Gruppen Die isoperimetrische Ungleichung und das isoperimetische Problem Teilnehmer: Björn Daase Johanna Ettingshausen Alexander Freyer Tobias Karkuschke Taha-Emre Terzi Herder-Oberschule,
Berichte der Gruppen Die isoperimetrische Ungleichung und das isoperimetische Problem Teilnehmer: Björn Daase Johanna Ettingshausen Alexander Freyer Tobias Karkuschke Taha-Emre Terzi Herder-Oberschule,
15 2,835. 63843 Niedernberg, Nordring/Industriegebiet, Telefon (0 60 28) 9 70 70, Telefax (0 60 28) 97 07 20
 Aluminium-Flachstange kg/mtr 10 x 2 0,054 3 0,081 4 0,108 5 0,135 6 0,162 8 0,216 12 x 3 0,097 5 0,162 6 0,200 8 0,259 15 x 2 0,081 3 0,121 4 0,162 5 0,202 6 0,243 8 0,324 10 0,405 20 x 2 0,108 3 0,162
Aluminium-Flachstange kg/mtr 10 x 2 0,054 3 0,081 4 0,108 5 0,135 6 0,162 8 0,216 12 x 3 0,097 5 0,162 6 0,200 8 0,259 15 x 2 0,081 3 0,121 4 0,162 5 0,202 6 0,243 8 0,324 10 0,405 20 x 2 0,108 3 0,162
ROHRE FUER HOHE TEMPERATUREN ASTM A 106
 ROHRE FUER HOHE TEMPERATUREN ASTM A 106 1/8 10,300 1,240 0,280 10 1/8 10,300 1,450 0,320 30 1/8 10,300 1,730 0,370 STD 40 1/8 10,300 2,410 0,470 XS 80 1/4 13,700 1,650 0,490 10 1/4 13,700 1,850 0,540 30
ROHRE FUER HOHE TEMPERATUREN ASTM A 106 1/8 10,300 1,240 0,280 10 1/8 10,300 1,450 0,320 30 1/8 10,300 1,730 0,370 STD 40 1/8 10,300 2,410 0,470 XS 80 1/4 13,700 1,650 0,490 10 1/4 13,700 1,850 0,540 30
Lösungsvorschläge zur Klausur für mach, umw, fmt, bau, immo, tema, und zugehörige Technikpädagogik
 Prüfung in Höhere Mathematik III. September 8 Lösungsvorschläge zur Klausur für mach, umw, fmt, bau, immo, tema, und zugehörige Technikpädagogik Aufgabe : 8 Punkte Gegeben ist A : v : Bestimmen Sie die
Prüfung in Höhere Mathematik III. September 8 Lösungsvorschläge zur Klausur für mach, umw, fmt, bau, immo, tema, und zugehörige Technikpädagogik Aufgabe : 8 Punkte Gegeben ist A : v : Bestimmen Sie die
Kurven. injektiv, dann heißt K eine Jordan-Kurve.
 Kurven Der Begriff der Kurve, zunächst etwa im R 2 oder R 3, kann auf zwei Arten gebildet werden. Der geometrische Zugang definiert eine Kurve als den geometrischen Ort von Punkten in der Ebene bzw. im
Kurven Der Begriff der Kurve, zunächst etwa im R 2 oder R 3, kann auf zwei Arten gebildet werden. Der geometrische Zugang definiert eine Kurve als den geometrischen Ort von Punkten in der Ebene bzw. im
Seminar Gewöhnliche Dierentialgleichungen
 Seminar Gewöhnliche Dierentialgleichungen Dynamische Systeme II Valentin Jonas 8. 6. 215 1 Einleitung In dem letzten Kapitel "Dynamische Systeme I" ging es vor allem um in t glatte, autonome, dynamische
Seminar Gewöhnliche Dierentialgleichungen Dynamische Systeme II Valentin Jonas 8. 6. 215 1 Einleitung In dem letzten Kapitel "Dynamische Systeme I" ging es vor allem um in t glatte, autonome, dynamische
Mathematik II Frühlingsemester 2015 Kap. 9: Funktionen von mehreren Variablen 9.2 Partielle Differentiation
 Mathematik II Frühlingsemester 2015 Kap. 9: Funktionen von mehreren Variablen 9.2 Partielle Differentiation www.math.ethz.ch/education/bachelor/lectures/fs2015/other/mathematik2 biol Prof. Dr. Erich Walter
Mathematik II Frühlingsemester 2015 Kap. 9: Funktionen von mehreren Variablen 9.2 Partielle Differentiation www.math.ethz.ch/education/bachelor/lectures/fs2015/other/mathematik2 biol Prof. Dr. Erich Walter
HTWD, FB Informatik/Mathematik Prof. Dr. M. Voigt. Mathematik II für Bauingenieure. (f) 4 sin x cos 5 x dx. 3 x e x2 dx (i) e 2x 1 dx.
 HTWD, FB Informatik/Mathematik Prof. Dr. M. Voigt Mathematik II Mathematik II für Bauingenieure Wiederholungsaufgaben zur Prüfungsklausur im Juli 2007 1 Integralrechnung Aufgabe 1 : Berechnen Sie die folgenden
HTWD, FB Informatik/Mathematik Prof. Dr. M. Voigt Mathematik II Mathematik II für Bauingenieure Wiederholungsaufgaben zur Prüfungsklausur im Juli 2007 1 Integralrechnung Aufgabe 1 : Berechnen Sie die folgenden
Doppel- und Dreifachintegrale
 Doppel- und Dreifchintegrle Sei [, b] ein Intervll des R 2 oder R 3 (lso ein Rechteck bzw. ein Quder), i.e. [, b] = [, b ] [ 2, b 2 ] oder [, b] = [, b ] [ 2, b 2 ] [ 3, b 3 ]. Für Intervlle des R 2 bzw.
Doppel- und Dreifchintegrle Sei [, b] ein Intervll des R 2 oder R 3 (lso ein Rechteck bzw. ein Quder), i.e. [, b] = [, b ] [ 2, b 2 ] oder [, b] = [, b ] [ 2, b 2 ] [ 3, b 3 ]. Für Intervlle des R 2 bzw.
BASISPRÜFUNG MATHEMATIK I UND II
 ETH Zürich Sommer 015 Dr. Ana Cannas BASISPRÜFUNG MATHEMATIK I UND II für die Studiengänge Agrar-, Erd-, Lebensmittelund Umweltnaturwissenschaften 1. Sei a) Ist das System lösbar? b) Lösen Sie das System
ETH Zürich Sommer 015 Dr. Ana Cannas BASISPRÜFUNG MATHEMATIK I UND II für die Studiengänge Agrar-, Erd-, Lebensmittelund Umweltnaturwissenschaften 1. Sei a) Ist das System lösbar? b) Lösen Sie das System
Lösung - Serie 7. D-MAVT/D-MATL Analysis I HS 2016 Dr. Andreas Steiger. 1. MC-Aufgaben (Online-Abgabe)
 D-MAVT/D-MATL Analysis I HS 016 Dr. Andreas Steiger Lösung - Serie 7 1. MC-Aufgaben Online-Abgabe 1. Gegeben sind die Kurven K 1 links und K rechts, die beide für wachsenden Parameter t von aussen nach
D-MAVT/D-MATL Analysis I HS 016 Dr. Andreas Steiger Lösung - Serie 7 1. MC-Aufgaben Online-Abgabe 1. Gegeben sind die Kurven K 1 links und K rechts, die beide für wachsenden Parameter t von aussen nach
Wärmeleitungsgleichung,
 Fachbereich Mathematik der Universität Hamburg SoSe 2015 Dr. Hanna Peywand Kiani Wärmeleitungsgleichung, 05.06.2015 Die ins Netz gestellten Kopien der Anleitungsfolien sollen nur die Mitarbeit während
Fachbereich Mathematik der Universität Hamburg SoSe 2015 Dr. Hanna Peywand Kiani Wärmeleitungsgleichung, 05.06.2015 Die ins Netz gestellten Kopien der Anleitungsfolien sollen nur die Mitarbeit während
Risikoneutrale Wahrscheinlichkeit
 Risikoneutrale Wahrscheinlichkeit M. Gruber 11. 6 214 Rev.3 Zusammenfassung Diskontierter Aktienpreisprozess, Risiko-Marktpreis, Risikoneutralität; Verschiebung des Erwartungswerts einer Zufallsvariablen,
Risikoneutrale Wahrscheinlichkeit M. Gruber 11. 6 214 Rev.3 Zusammenfassung Diskontierter Aktienpreisprozess, Risiko-Marktpreis, Risikoneutralität; Verschiebung des Erwartungswerts einer Zufallsvariablen,
DIN (ISO) ABDECKPLATTEN NG
 DIN (ISO) DECKLEN N 6 Systemdruck: luminium bar / Hydraulik Strangguß 5 bar Erklärung SUN estellkode Einschraubventile plus Ventilkörper: Seite iii / Nenndrücke, Werkstoffe: Seite.,9 NOCH 44,5, 57, ZJR
DIN (ISO) DECKLEN N 6 Systemdruck: luminium bar / Hydraulik Strangguß 5 bar Erklärung SUN estellkode Einschraubventile plus Ventilkörper: Seite iii / Nenndrücke, Werkstoffe: Seite.,9 NOCH 44,5, 57, ZJR
10.5 Differentialgeometrie ebener Kurven Tangente, Normale
 1.5 1.5 Differentialgeometrie ebener Kurven 1.5.1 Tangente, Normale Gegeben: Kurve C C := C := { (x { (x y) } y = f(x), a x b y ) x = ϕ(t) y = ψ(t), t 1 t t } oder C heißt glatte Kurve, wenn f stetig differenzierbar
1.5 1.5 Differentialgeometrie ebener Kurven 1.5.1 Tangente, Normale Gegeben: Kurve C C := C := { (x { (x y) } y = f(x), a x b y ) x = ϕ(t) y = ψ(t), t 1 t t } oder C heißt glatte Kurve, wenn f stetig differenzierbar
3 Gewöhnliche Differentialgleichungen 23.4.
 3 Gewöhnliche Differentialgleichungen 23.4. 3.1 Differentialgleichungen erster Ordnung 3.1.1 Fundamentalsätze Definition 3.1. Es sei Ω R d eine offene Menge und V : Ω R d eine Vektorfunktion. Eine Kurve
3 Gewöhnliche Differentialgleichungen 23.4. 3.1 Differentialgleichungen erster Ordnung 3.1.1 Fundamentalsätze Definition 3.1. Es sei Ω R d eine offene Menge und V : Ω R d eine Vektorfunktion. Eine Kurve
DIPLOMARBEIT. BrittaSpeckmann
 WestfälischeWilhelms-UniversitätMünster InstitutfürMathematischeStatistik DIPLOMARBEIT ModellierungundBewertungvonEmbedded OptionsinKreditverträgen BrittaSpeckmann Themaerhaltenvon PDDr.VolkertPaulsen
WestfälischeWilhelms-UniversitätMünster InstitutfürMathematischeStatistik DIPLOMARBEIT ModellierungundBewertungvonEmbedded OptionsinKreditverträgen BrittaSpeckmann Themaerhaltenvon PDDr.VolkertPaulsen
Charakteristikenmethode im Beispiel
 Charakteristikenmethode im Wir betrachten die PDE in drei Variablen xu x + yu y + (x + y )u z = 0. Das charakteristische System lautet dann ẋ = x ẏ = y ż = x + y und besitzt die allgemeine Lösung x(t)
Charakteristikenmethode im Wir betrachten die PDE in drei Variablen xu x + yu y + (x + y )u z = 0. Das charakteristische System lautet dann ẋ = x ẏ = y ż = x + y und besitzt die allgemeine Lösung x(t)
MATHEMATIK 2 FÜR DIE STUDIENGÄNGE CHEMIE UND LEBENSMITTELCHEMIE
 Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik MATHEMATIK 2 FÜR DIE STUDIENGÄNGE CHEMIE UND LEBENSMITTELCHEMIE Integralrechnung für Funktionen mehrerer Variablen
Mathematik und Naturwissenschaften Fachrichtung Mathematik, Institut für Numerische Mathematik MATHEMATIK 2 FÜR DIE STUDIENGÄNGE CHEMIE UND LEBENSMITTELCHEMIE Integralrechnung für Funktionen mehrerer Variablen
8 Die quadratische Variation, und die Integration bzgl. stetiger Semimartingale
 8 Die quadratische Variation, und die Integration bzgl. stetiger Semimartingale 8.1 Der quadratische Variationsprozess eines stetigen, lokalen Martingals 8.3 Die quadratische Variation einer reellen Brownschen
8 Die quadratische Variation, und die Integration bzgl. stetiger Semimartingale 8.1 Der quadratische Variationsprozess eines stetigen, lokalen Martingals 8.3 Die quadratische Variation einer reellen Brownschen
ist ein Eigenvektor der Matrix A = Ist λ der Eigenwert zum Eigenvektor x der Matrix A, so gilt dafür A x = λ x, also
 5. Juli Lösungshinweise Theorieteil Aufgabe : Der Vektor x = ist ein Eigenvektor der Matrix A = Bestimmen Sie den zum Eigenvektor x zugehörigen Eigenwert. 3 3 3 3 (Hinweis: Es ist nicht erforderlich, das
5. Juli Lösungshinweise Theorieteil Aufgabe : Der Vektor x = ist ein Eigenvektor der Matrix A = Bestimmen Sie den zum Eigenvektor x zugehörigen Eigenwert. 3 3 3 3 (Hinweis: Es ist nicht erforderlich, das
x= f(x) p= U (x). (b) Zeigen Sie, dass auf jeder auf einem Intervall existierenden Lösung t x(t) die Energie E(t) := 1 2 p(t)2 + U(x(t)) x 1
 Blatt 1 03042006 H-Ch Grunau Aufgabe 1 Betrachten Sie die Differentialgleichung x= f(x) mit f = U und U C 2 ((α, β), R) und schreiben Sie diese in der Form x= p, p= U (x) (a) Skizzieren Sie die Phasenportraits
Blatt 1 03042006 H-Ch Grunau Aufgabe 1 Betrachten Sie die Differentialgleichung x= f(x) mit f = U und U C 2 ((α, β), R) und schreiben Sie diese in der Form x= p, p= U (x) (a) Skizzieren Sie die Phasenportraits
1. Übungsblatt zur Höheren Mathematik III (P/ET/AI/IT/IKT/MP) WS 2012/13
 Prof. Dr. L. Schwachhöfer Dr. J. Horst Fakultät Mathematik TU Dortmund. Übungsblatt zur Höheren Mathematik III (P/ET/AI/IT/IKT/MP) WS /3 Keine Abgabe. Aufgabe Es seien die folgenden Vektorfelder in R 3
Prof. Dr. L. Schwachhöfer Dr. J. Horst Fakultät Mathematik TU Dortmund. Übungsblatt zur Höheren Mathematik III (P/ET/AI/IT/IKT/MP) WS /3 Keine Abgabe. Aufgabe Es seien die folgenden Vektorfelder in R 3
Hörsaalübung 2 Differentialgleichungen I für Studierende der Ingenieurwissenschaften
 Fachbereich Mathematik der Universität Hamburg WiSe 2018/2019 Dr. Hanna Peywand Kiani Hörsaalübung 2 Differentialgleichungen I für Studierende der Ingenieurwissenschaften Separierbare und lineare Differentialgleichungen
Fachbereich Mathematik der Universität Hamburg WiSe 2018/2019 Dr. Hanna Peywand Kiani Hörsaalübung 2 Differentialgleichungen I für Studierende der Ingenieurwissenschaften Separierbare und lineare Differentialgleichungen
Ferienkurs der TU München- - Analysis 2 Funktionen in mehreren Variablen Vorlesung
 Ferienkurs der TU München- - Analysis 2 Funktionen in mehreren Variablen Vorlesung Jonas J. Funke 30.08.2010-03.09.2010 Inhaltsverzeichnis 1 Funktionen in mehreren Variablen 3 2 Partielle Differentiation
Ferienkurs der TU München- - Analysis 2 Funktionen in mehreren Variablen Vorlesung Jonas J. Funke 30.08.2010-03.09.2010 Inhaltsverzeichnis 1 Funktionen in mehreren Variablen 3 2 Partielle Differentiation
D-MAVT & D-MATL Analysis I & II Sommer 2012 Prof. Dr. Giovanni Felder
 D-MAVT & D-MATL Analysis I & II Sommer 2012 Prof. Dr. Giovanni Felder Prüfung WICHTIG: Die Prüfung dauert 4 Stunden (240 Minuten). Verwenden Sie bitte für jede Aufgabe ein neues Blatt und schreiben Sie
D-MAVT & D-MATL Analysis I & II Sommer 2012 Prof. Dr. Giovanni Felder Prüfung WICHTIG: Die Prüfung dauert 4 Stunden (240 Minuten). Verwenden Sie bitte für jede Aufgabe ein neues Blatt und schreiben Sie
Musterlösung Basisprüfung, Gruppe A Analysis I/II ) = 28π 6
 Winter 8. Single Choice: 6J (a) Der Flächeninhalt einer Kreisscheibe mit Radius R ist gegeben durch πr. Aus Symmetriegründen ist der Flächeninhalt eines Kreisssektors mit 6 gegeben durch πr 6. Folglich
Winter 8. Single Choice: 6J (a) Der Flächeninhalt einer Kreisscheibe mit Radius R ist gegeben durch πr. Aus Symmetriegründen ist der Flächeninhalt eines Kreisssektors mit 6 gegeben durch πr 6. Folglich
Zum Relativgrad zeitvarianter Systeme
 Elgersburg, 16. Februar 2006 Relative degree for linear time-invariant systems Definition n(s) d(s) = c(si n A) 1 b = cb s 1 + cab s 2 +... + ca r 2 b s r 1 + ca r 1 b s r +... : has relative degree r
Elgersburg, 16. Februar 2006 Relative degree for linear time-invariant systems Definition n(s) d(s) = c(si n A) 1 b = cb s 1 + cab s 2 +... + ca r 2 b s r 1 + ca r 1 b s r +... : has relative degree r
n r t d n :40 T http: hdl.h ndl.n t 202.b 0 04
 J hrb h d r Pr f h n l h n L nd n t lt B rl n f ¼r d J hr B nd XL, T l. B rl n V rtr b b d r Pr Ÿ h n l h n L nd n t lt B rl n N. 4, nv l d n tr Ÿ 44 22. n r t d n 20 2 04 2 4: T http: hdl.h ndl.n t 202.b
J hrb h d r Pr f h n l h n L nd n t lt B rl n f ¼r d J hr B nd XL, T l. B rl n V rtr b b d r Pr Ÿ h n l h n L nd n t lt B rl n N. 4, nv l d n tr Ÿ 44 22. n r t d n 20 2 04 2 4: T http: hdl.h ndl.n t 202.b
Brownsche Bewegung. Satz von Donsker. Bernd Barth Universität Ulm
 Brownsche Bewegung Satz von Donsker Bernd Barth Universität Ulm 31.05.2010 Page 2 Brownsche Bewegung 31.05.2010 Inhalt Einführung Straffheit Konvergenz Konstruktion einer zufälligen Funktion Brownsche
Brownsche Bewegung Satz von Donsker Bernd Barth Universität Ulm 31.05.2010 Page 2 Brownsche Bewegung 31.05.2010 Inhalt Einführung Straffheit Konvergenz Konstruktion einer zufälligen Funktion Brownsche
Martingal-Maße. Stochastic Finance: An Introduction in Discrete Time (Hans Föllmer, Alexander Schied) Manuel Müller Mathematisches Institut
 Martingal-Maße Manuel Müller 29.04.2016 Mathematisches Institut Stochastic Finance: An Introduction in Discrete Time (Hans Föllmer, Alexander Schied) Seite 2 Martingal-Maße 29.04.2016 Inhaltsverzeichnis
Martingal-Maße Manuel Müller 29.04.2016 Mathematisches Institut Stochastic Finance: An Introduction in Discrete Time (Hans Föllmer, Alexander Schied) Seite 2 Martingal-Maße 29.04.2016 Inhaltsverzeichnis
Musterlösung Klausur zu Analysis II. Verständnisteil
 Technische Universität Berlin SS 2009 Institut für Mathematik 20.07.2009 Prof. Dr. R. Schneider Fritz Krüger Sebastian Holtz Musterlösung Klausur zu Analysis II Verständnisteil 1. (a) Sei D R n konvex
Technische Universität Berlin SS 2009 Institut für Mathematik 20.07.2009 Prof. Dr. R. Schneider Fritz Krüger Sebastian Holtz Musterlösung Klausur zu Analysis II Verständnisteil 1. (a) Sei D R n konvex
Die Stochastische Integralgleichung X(t) = a + t
 Die Stochastische Integralgleichung X(t) = a + µ(s, X(s))ds + σ(s, X(s))dW (s) Simon Keller 4.12.26 1 Mathematische Grundlagen und Herleitung 1.1 Normalverteilung Eine normalverteilte Zufallsvariable X
Die Stochastische Integralgleichung X(t) = a + µ(s, X(s))ds + σ(s, X(s))dW (s) Simon Keller 4.12.26 1 Mathematische Grundlagen und Herleitung 1.1 Normalverteilung Eine normalverteilte Zufallsvariable X
Übungen zur Vorlesung Mathematik I für Studierende der Chemie (WS 2015/2016) Institut für Chemie und Biochemie, FU Berlin Blatt
 Übungen zur Vorlesung Mathematik I für Studierende der Chemie (WS 05/06) Institut für Chemie und Biochemie, FU Berlin PD Dr. Dirk Andrae Blatt 9 06--6. Bestimmen Sie die Partialbruchzerlegung von (a) x(x
Übungen zur Vorlesung Mathematik I für Studierende der Chemie (WS 05/06) Institut für Chemie und Biochemie, FU Berlin PD Dr. Dirk Andrae Blatt 9 06--6. Bestimmen Sie die Partialbruchzerlegung von (a) x(x
Aufbau von wissenschaftlichen Arbeiten am. Lehrstuhl für Thermische Verfahrenstechnik. Markus Lichti
 1. Jour-fixe am 29.1.2014 Aufbau von wissenschaftlichen Arbeiten am Lehrstuhl für Thermische Verfahrenstechnik Markus Lichti Technische Universität Kaiserslautern Lehrstuhl für Thermische Verfahrenstechnik
1. Jour-fixe am 29.1.2014 Aufbau von wissenschaftlichen Arbeiten am Lehrstuhl für Thermische Verfahrenstechnik Markus Lichti Technische Universität Kaiserslautern Lehrstuhl für Thermische Verfahrenstechnik
13 Mehrdimensionale Zufallsvariablen Zufallsvektoren
 3 Mehrdimensionale Zufallsvariablen Zufallsvektoren Bisher haben wir uns ausschließlich mit Zufallsexperimenten beschäftigt, bei denen die Beobachtung eines einzigen Merkmals im Vordergrund stand. In diesem
3 Mehrdimensionale Zufallsvariablen Zufallsvektoren Bisher haben wir uns ausschließlich mit Zufallsexperimenten beschäftigt, bei denen die Beobachtung eines einzigen Merkmals im Vordergrund stand. In diesem
I. Einführung in die PDGL
 I. Einführung in die PDGL I. Modellierungsbeispiele I.2 Wohlgestelltheit I.3 Klassifizierung I.4 Lösungskonzepte Kapitel I () Vorgehen bei der groben Einteilung von PDGL: ) System von PDGL (ja/nein) 2)
I. Einführung in die PDGL I. Modellierungsbeispiele I.2 Wohlgestelltheit I.3 Klassifizierung I.4 Lösungskonzepte Kapitel I () Vorgehen bei der groben Einteilung von PDGL: ) System von PDGL (ja/nein) 2)
Partielle Differentialgleichungen Prüfung am
 Partielle Differentialgleichungen Prüfung am 27.04.2017 Name, Vorname Matrikelnummer Unterschrift Dauer: 60 Minuten. Keine Unterlagen, kein Handy/PC, kein Taschenrechner, keine Gruppenarbeit. Bitte schreiben
Partielle Differentialgleichungen Prüfung am 27.04.2017 Name, Vorname Matrikelnummer Unterschrift Dauer: 60 Minuten. Keine Unterlagen, kein Handy/PC, kein Taschenrechner, keine Gruppenarbeit. Bitte schreiben
D-MAVT/D-MATL FS 2018 Dr. Andreas Steiger Analysis IILösung - Serie19. sind weder parallel noch stehen sie senkrecht aufeinander.
 -MAVT/-MATL FS 8 r. Andreas Steiger Analysis IILösung - Serie9. ie Fläche S sei einerseits durch die Parameterdarstellung (u, v) r(u, v) und andererseits durch die Gleichung f(x, y, z) = gegeben. Wir betrachten
-MAVT/-MATL FS 8 r. Andreas Steiger Analysis IILösung - Serie9. ie Fläche S sei einerseits durch die Parameterdarstellung (u, v) r(u, v) und andererseits durch die Gleichung f(x, y, z) = gegeben. Wir betrachten
Karl M. Göschka: Merkblatt für den Aufbau wissenschaftlicher Arbeiten. Wien (TU, Institut für Computerlinguistik) 2004.
 Karl M. Göschka: Merkblatt für den Aufbau wissenschaftlicher Arbeiten. Wien (TU, Institut für Computerlinguistik) 2004. [http://www.quarisma.de/thuemmel/merkblatttuwien.pdf] hauptsächlich allg. zu wiss.
Karl M. Göschka: Merkblatt für den Aufbau wissenschaftlicher Arbeiten. Wien (TU, Institut für Computerlinguistik) 2004. [http://www.quarisma.de/thuemmel/merkblatttuwien.pdf] hauptsächlich allg. zu wiss.
6.3 Exakte Differentialgleichungen
 6.3. EXAKTE DIFFERENTIALGLEICHUNGEN 23 6.3 Exakte Differentialgleichungen Andere Bezeichnungen: Pfaffsche Dgl., Dgl. für Kurvenscharen, Nullinien Pfaffscher Formen. 1. Definitionen Pfaffsche Dgl, Dgl.
6.3. EXAKTE DIFFERENTIALGLEICHUNGEN 23 6.3 Exakte Differentialgleichungen Andere Bezeichnungen: Pfaffsche Dgl., Dgl. für Kurvenscharen, Nullinien Pfaffscher Formen. 1. Definitionen Pfaffsche Dgl, Dgl.
Differentialgleichungen. Jochen Merker
 Differentialgleichungen Jochen Merker Sommersemester 2011 2 Inhaltsverzeichnis 1 Elementare Lösungsmethoden und allgemeine Existenzsätze 7 1.1 Lösungen gewöhnlicher Differentialgleichungen..............
Differentialgleichungen Jochen Merker Sommersemester 2011 2 Inhaltsverzeichnis 1 Elementare Lösungsmethoden und allgemeine Existenzsätze 7 1.1 Lösungen gewöhnlicher Differentialgleichungen..............
Analysis I. Guofang Wang , Universität Freiburg
 Universität Freiburg 10.1.2017, 11.1.2017 Definition 1.1 (Ableitung) Die Funktion f : I R n hat in x 0 I die Ableitung a R n (Notation: f (x 0 ) = a), falls gilt: f(x) f(x 0 ) lim = a. (1.1) x x 0 x x
Universität Freiburg 10.1.2017, 11.1.2017 Definition 1.1 (Ableitung) Die Funktion f : I R n hat in x 0 I die Ableitung a R n (Notation: f (x 0 ) = a), falls gilt: f(x) f(x 0 ) lim = a. (1.1) x x 0 x x
K. Eppler, Inst. f. Num. Mathematik Übungsaufgaben. 8. Übung SS 17: Woche vom
 Übungsaufgaben 8. Übung SS 17: Woche vom 22.5. - 26. 5. 2017 Heft Ü 2: 24.15.f; 25.11.b, f; 26.1.a, b, c; + 1 Zusatzaufgabe zur Reduktion bei DGLn Krümmungsvektor, Krümmung im R 3 (R n ) Def. 5.17: Der
Übungsaufgaben 8. Übung SS 17: Woche vom 22.5. - 26. 5. 2017 Heft Ü 2: 24.15.f; 25.11.b, f; 26.1.a, b, c; + 1 Zusatzaufgabe zur Reduktion bei DGLn Krümmungsvektor, Krümmung im R 3 (R n ) Def. 5.17: Der
Topologie metrischer Räume
 Technische Universität München Christoph Niehoff Ferienkurs Analysis für Physiker Vorlesung Montag SS 11 In diesem Teil des Ferienkurses beschäftigen wir uns mit drei Themengebieten. Zuerst wird die Topologie
Technische Universität München Christoph Niehoff Ferienkurs Analysis für Physiker Vorlesung Montag SS 11 In diesem Teil des Ferienkurses beschäftigen wir uns mit drei Themengebieten. Zuerst wird die Topologie
= r ). Beispiele. 1) Kreis. Skizze mit Tangentialvektoren ( x. 2) Zykloide. Skizze für a = r = 1:
 VEKTORANALYSIS Inhalt: 1) Parametrisierte Kurven 2) Vektorfelder 3) Das Linienintegral 4) Potentialfelder 1 Parametrisierte Kurven Definitionen xt () Kurve: x = x() t = y() t, t zt () xt () dxt () Tangentialvektor:
VEKTORANALYSIS Inhalt: 1) Parametrisierte Kurven 2) Vektorfelder 3) Das Linienintegral 4) Potentialfelder 1 Parametrisierte Kurven Definitionen xt () Kurve: x = x() t = y() t, t zt () xt () dxt () Tangentialvektor:
Erzeugendenfunktion. Kapitel Definition und Beispiele. In diesem Kapitel betrachten wir nur Zufallsvariablen mit Werten in N 0.
 Kapitel 4 Erzeugendenfuntion 4.1 Definition und Beispiele In diesem Kapitel betrachten wir nur Zufallsvariablen mit Werten in N. Definition 4.1 (Erzeugendenfuntion) Sei X eine N -wertige Zufallsvariable.
Kapitel 4 Erzeugendenfuntion 4.1 Definition und Beispiele In diesem Kapitel betrachten wir nur Zufallsvariablen mit Werten in N. Definition 4.1 (Erzeugendenfuntion) Sei X eine N -wertige Zufallsvariable.
Gewöhnliche Differentialgleichungen Woche 7. Nicht-lineare und linearisierte Systeme
 Gewöhnliche Differentialgleichungen Woche 7 Nicht-lineare und linearisierte Systeme d 71 Gleichgewichtspunkte Wir werden uns mit Anfangswertproblemen der folgenden Form beschäftigen: { y (t f (t, y(t,
Gewöhnliche Differentialgleichungen Woche 7 Nicht-lineare und linearisierte Systeme d 71 Gleichgewichtspunkte Wir werden uns mit Anfangswertproblemen der folgenden Form beschäftigen: { y (t f (t, y(t,
Klausurenkurs zum Staatsexamen (SS 2012): Differential und Integralrechnung 8
 Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 2012): Differential und Integralrechnung 8 8.1 (Herbst 2002, Thema 1, Aufgabe 6) y = 3y +2x x 8.2 (Frühjahr 2005, Thema 1, Aufgabe 6) (x > 0) y(1)
Dr. Erwin Schörner Klausurenkurs zum Staatsexamen (SS 2012): Differential und Integralrechnung 8 8.1 (Herbst 2002, Thema 1, Aufgabe 6) y = 3y +2x x 8.2 (Frühjahr 2005, Thema 1, Aufgabe 6) (x > 0) y(1)
31. Kurven in Ebene und Raum
 31. Kurven in Ebene und Raum Für ebene Kurven (also Kurven im R gibt es mehrere Darstellungsmöglichkeiten: implizite Darstellung : F (x, y = explizite Darstellung : y = f(x oder x = g(y Parameterdarstellung
31. Kurven in Ebene und Raum Für ebene Kurven (also Kurven im R gibt es mehrere Darstellungsmöglichkeiten: implizite Darstellung : F (x, y = explizite Darstellung : y = f(x oder x = g(y Parameterdarstellung
Stabile periodische Bewegungen (Grenzzyklen)
 Stabile periodische Bewegungen (Grenzzyklen) 1. Nichtlineare Systeme mit zwei Gleichungen Prinzipiell neu: Alle Systeme mit mindestens 2 unabhängigen DGL können als Lösungen geschlossene Kurven im Phasenraum
Stabile periodische Bewegungen (Grenzzyklen) 1. Nichtlineare Systeme mit zwei Gleichungen Prinzipiell neu: Alle Systeme mit mindestens 2 unabhängigen DGL können als Lösungen geschlossene Kurven im Phasenraum
AUFGABENSAMMLUNG ZUM LEHRGEBIET. AUTOMATISIERUNGSTECHNIK bzw. KONTINUIERLICHE SYSTEME
 Dr.-Ing. Tatjana Lange Fachhochschle für Technik nd Wirtschaft Fachbereich Elektrotechnik AUFGABENSAMMLUNG ZUM LEHRGEBIET AUTOMATISIERUNGSTECHNIK bzw. KONTINUIERLICHE SYSTEME. Differentialgleichngen Afgabe.:
Dr.-Ing. Tatjana Lange Fachhochschle für Technik nd Wirtschaft Fachbereich Elektrotechnik AUFGABENSAMMLUNG ZUM LEHRGEBIET AUTOMATISIERUNGSTECHNIK bzw. KONTINUIERLICHE SYSTEME. Differentialgleichngen Afgabe.:
Der Taschenrechner CAS: TI Inspire (Texas Instruments)
 Der Taschenrechner (Texas Instruments) Übersicht: 1. Katalog (wichtige Funktionen un wie man sie aufruft) 2. Funktionen efinieren (einspeichern mit un ohne Parameter) 3. Nullstellen 4. Gleichungen lösen
Der Taschenrechner (Texas Instruments) Übersicht: 1. Katalog (wichtige Funktionen un wie man sie aufruft) 2. Funktionen efinieren (einspeichern mit un ohne Parameter) 3. Nullstellen 4. Gleichungen lösen
6 Der Harmonische Oszillator
 6 Der Harmonische Oszillator Ein Teilchen der Masse m bewege sich auf der x-achse unter dem Einfluß der Rückstellkraft Fx = mω x. 186 Die Kreisfrequenz ω bzw. die Federkonstante k := mω ist neben der Masse
6 Der Harmonische Oszillator Ein Teilchen der Masse m bewege sich auf der x-achse unter dem Einfluß der Rückstellkraft Fx = mω x. 186 Die Kreisfrequenz ω bzw. die Federkonstante k := mω ist neben der Masse
Methoden der computergestützten Produktion und Logistik
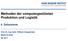 Methoden der computergestützten Produktion und Logistik 6. Zeitsysteme Prof. Dr.-Ing. habil. Wilhelm Dangelmaier Modul W 2336 SS 2017 Allgemeines Zeitsystem Definition: Allgemeines Zeitsystem Wir nehmen
Methoden der computergestützten Produktion und Logistik 6. Zeitsysteme Prof. Dr.-Ing. habil. Wilhelm Dangelmaier Modul W 2336 SS 2017 Allgemeines Zeitsystem Definition: Allgemeines Zeitsystem Wir nehmen
Proseminar zu Dierenzialgleichungen für Lehramtskandidatinnen und -kandidaten
 Proseminar zu Dierenzialgleichungen für Lehramtskandidatinnen und -kandidaten Wintersemester 05/06 Armin Rainer Peter Raith Bezeichnet man die zum Zeitpunkt t vorhandene Stomenge eines radioaktiven Stoes
Proseminar zu Dierenzialgleichungen für Lehramtskandidatinnen und -kandidaten Wintersemester 05/06 Armin Rainer Peter Raith Bezeichnet man die zum Zeitpunkt t vorhandene Stomenge eines radioaktiven Stoes
Lösungen zu Mathematik I/II
 Dr. A. Caspar ETH Zürich, August D BIOL, D CHAB Lösungen zu Mathematik I/II Aufgaben. ( Punkte) a) Wir berechnen lim sin(x ) x 3 + 4x L Hôpital = lim x cos(x ) 3x + 8x = 4. b) Wir benutzen L Hôpital lim
Dr. A. Caspar ETH Zürich, August D BIOL, D CHAB Lösungen zu Mathematik I/II Aufgaben. ( Punkte) a) Wir berechnen lim sin(x ) x 3 + 4x L Hôpital = lim x cos(x ) 3x + 8x = 4. b) Wir benutzen L Hôpital lim
f(x, y) = x 2 4x + y 2 + 2y
 7. Februar Lösungshinweise Theorieteil Aufgabe : Bestimmen Sie die Niveaumengen (Höhenlinien) der Funktion f(x, y) = x 4x + y + y und skizzieren Sie das zugehörige Höhenlinienbild im kartesischen Koordinatensystem
7. Februar Lösungshinweise Theorieteil Aufgabe : Bestimmen Sie die Niveaumengen (Höhenlinien) der Funktion f(x, y) = x 4x + y + y und skizzieren Sie das zugehörige Höhenlinienbild im kartesischen Koordinatensystem
Höhere Mathematik III für Physiker Analysis 2
 Ralitsa Bozhanova Jonas Kindervater Ferienkurs im Anschluss an das Wintersemester 2008 Höhere Mathematik III für Physiker Analysis 2 16. bis 20. Februar 2009 1 Inhaltsverzeichnis Inhaltsverzeichnis 1 Der
Ralitsa Bozhanova Jonas Kindervater Ferienkurs im Anschluss an das Wintersemester 2008 Höhere Mathematik III für Physiker Analysis 2 16. bis 20. Februar 2009 1 Inhaltsverzeichnis Inhaltsverzeichnis 1 Der
Kapitel 7. Differentialrechnung. Josef Leydold Mathematik für VW WS 2017/18 7 Differentialrechnung 1 / 56
 Kapitel 7 Differentialrechnung Josef Leydold Mathematik für VW WS 2017/18 7 Differentialrechnung 1 / 56 Differenzenquotient Sei f : R R eine Funktion. Der Quotient f x = f (x 0 + x) f (x 0 ) x = f (x)
Kapitel 7 Differentialrechnung Josef Leydold Mathematik für VW WS 2017/18 7 Differentialrechnung 1 / 56 Differenzenquotient Sei f : R R eine Funktion. Der Quotient f x = f (x 0 + x) f (x 0 ) x = f (x)
2.5 Aufgabe Aufgabe Aufgabe Aufgabe 8
 4 7 3 / 4 m 5 / 8 x (81) = 4 α f(x) = 3x 2 6x + 9 f(x) = x 2 10x + 9 (x + 2y) 2 =? ( 36m2 ) 9m 5n 2 (5x+y) (2+6) 4 / 7 7 / 7 336 = 4 7 x = 7 7 x 4 7 = 336 : 7 4 Kehrbruch! x = 588 3 / 4 m 5 / 8 x 5 / 8
4 7 3 / 4 m 5 / 8 x (81) = 4 α f(x) = 3x 2 6x + 9 f(x) = x 2 10x + 9 (x + 2y) 2 =? ( 36m2 ) 9m 5n 2 (5x+y) (2+6) 4 / 7 7 / 7 336 = 4 7 x = 7 7 x 4 7 = 336 : 7 4 Kehrbruch! x = 588 3 / 4 m 5 / 8 x 5 / 8
Einführung in Quasi-Monte Carlo Verfahren
 Einführung in Quasi- Markus Zahrnhofer 3. Mai 2007 Markus Zahrnhofer () Einführung in Quasi- 3. Mai 2007 1 / 27 Inhalt der Präsentation 1 Motivierendes Beispiel 2 Einführung 3 quasi- Allgemeines Diskrepanz
Einführung in Quasi- Markus Zahrnhofer 3. Mai 2007 Markus Zahrnhofer () Einführung in Quasi- 3. Mai 2007 1 / 27 Inhalt der Präsentation 1 Motivierendes Beispiel 2 Einführung 3 quasi- Allgemeines Diskrepanz
Serie 4: Gradient und Linearisierung
 D-ERDW, D-HEST, D-USYS Mathematik II FS 5 Dr. Ana Cannas Serie 4: Gradient und Linearisierung Bemerkungen: Die Aufgaben der Serie 4 bilden den Fokus der Übungsgruppen vom 7./9. März.. Wir betrachten die
D-ERDW, D-HEST, D-USYS Mathematik II FS 5 Dr. Ana Cannas Serie 4: Gradient und Linearisierung Bemerkungen: Die Aufgaben der Serie 4 bilden den Fokus der Übungsgruppen vom 7./9. März.. Wir betrachten die
3. Zerlegung von Summen in Faktoren
 Aufgabensammlung Mathematik Faktorzerlegung Kapitel 3 / Seite 1 3. Zerlegung von Summen in Faktoren Zerlege - wenn nichts anderes vermerkt ist - so weit wie möglich in Faktoren! 1. a) 4 + 4y b) 6p 6q c)
Aufgabensammlung Mathematik Faktorzerlegung Kapitel 3 / Seite 1 3. Zerlegung von Summen in Faktoren Zerlege - wenn nichts anderes vermerkt ist - so weit wie möglich in Faktoren! 1. a) 4 + 4y b) 6p 6q c)
Gewöhnliche Differentialgleichungen Woche 6. Existenz nach Picard-Lindelöf
 d Gewöhnliche Differentialgleichungen Woche 6 Existenz nach Picard-Lindelöf 6.1 Vorbereitung für den Existenzsatz 6.1.1 Stetigkeit und Lipschitz-Stetigkeit Definition 6.1 Seien (V 1, 1 und (V 2, 2 zwei
d Gewöhnliche Differentialgleichungen Woche 6 Existenz nach Picard-Lindelöf 6.1 Vorbereitung für den Existenzsatz 6.1.1 Stetigkeit und Lipschitz-Stetigkeit Definition 6.1 Seien (V 1, 1 und (V 2, 2 zwei
Wirtschaftsmathematik: Formelsammlung (V1.40)
 Wirtschaftsmathematik: Formelsammlung (V.40) Grundlagen n! = 2 3... n = 0! = n i für n N, n 0, i= pq-formel Lösung von x 2 + px + q = 0 x /2 = p p 2 ± 2 4 q abc-formel Lösung von ax 2 + bx + c = 0 Binomische
Wirtschaftsmathematik: Formelsammlung (V.40) Grundlagen n! = 2 3... n = 0! = n i für n N, n 0, i= pq-formel Lösung von x 2 + px + q = 0 x /2 = p p 2 ± 2 4 q abc-formel Lösung von ax 2 + bx + c = 0 Binomische
3. Beschreibung dynamischer Systeme im Frequenzbereich
 3. Laplace-Transformation 3. Frequenzgang 3.3 Übertragungsfunktion Quelle: K.-D. Tieste, O.Romberg: Keine Panik vor Regelungstechnik!.Auflage, Vieweg&Teubner, Campus Friedrichshafen --- Regelungstechnik
3. Laplace-Transformation 3. Frequenzgang 3.3 Übertragungsfunktion Quelle: K.-D. Tieste, O.Romberg: Keine Panik vor Regelungstechnik!.Auflage, Vieweg&Teubner, Campus Friedrichshafen --- Regelungstechnik


