Theoretische Grundlagen der Informatik
|
|
|
- Rosa Bachmeier
- vor 6 Jahren
- Abrufe
Transkript
1 Theoretische Grundlagen der Informatik Vorlesung am INSTITUT FÜR THEORETISCHE 0 KIT Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik INSTITUT FÜR THEORETISCHE nationales Forschungszentrum in der Helmholtz-Gemeinschaft
2 Syntaxbäume Syntaxbäume visualisieren die Ableitung eines einzelnen Wortes. An der Wurzel eines Syntaxbaumes steht das Startsymbol. Jeder innere Knoten enthält eine Variable. Die Blätter sind Symbole aus Σ oder ε. Wenn ein innerer Knoten A als Nachfolger von links nach rechts α 1,..., α r V Σ hat, so muss A α 1... α r eine Ableitungsregel der Grammatik sein Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
3 Syntaxbäume - Beispiel Zu den Regeln R = {S 0B 1A, A 0 0S 1AA, B 1 1S 0BB} betrachte die Ableitung S 1A 11AA 11A0 110S0 1100B S 1 A 1 A A 0 S 0 0 B Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
4 Syntaxbäume - Beispiel S 1 A 1 A A 0 S 0 0 B 1 Zu jeder Ableitung gehört genau ein Syntaxbaum. Zu jedem Syntaxbaum gehören jedoch verschiedene Ableitungen des gleichen Wortes Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
5 Syntaxbäume - Beispiel R = {S 0B 1A, A 0 0S 1AA, B 1 1S 0BB} S 1A 11AA 110SA 1100BA 11001A S 1A 11AA 11A0 110S0 1100B S 1 A 1 A A 0 S 0 0 B Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
6 Links/Rechtsableitung, Eindeutigkeit Für Chomsky-2 Grammatiken gilt: Wegen der Kontextfreiheit ist die Reihenfolge, in der abgeleitet wird, für das Ergebnis unerheblich. Eine Linksableitung (Rechtsableitung) ist eine Ableitung, bei der in jedem Schritt die linkeste (rechteste) Variable abgeleitet wird. Eine kontextfreie Grammatik G heißt eindeutig, wenn es für jedes Wort w L(G) genau einen Syntaxbaum gibt. Eine kontextfreie Sprache L heißt eindeutig, wenn es eine eindeutige Grammatik G mit L(G) = L gibt. Ansonsten heißt L inhärent mehrdeutig Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
7 Beispiel Die Sprache erzeugt durch die Grammatik ist eindeutig. L = {0 n 1 n n 1} V = {S} Σ = {0, 1} R = {S 01 0S1} Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
8 Beispiel Die Sprache gegeben durch die Regeln R = {S 0B 1A, A 0 0S 1AA, B 1 1S 0BB} ist nicht eindeutig. (a) S (b) S 1 A 1 A 1 A A 1 A A 0 S S 0 B 1 A Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
9 Chomsky-Normalform Eine kontextfreie Grammatik ist in Chomsky Normalform, wenn alle Regeln von der Form: sind, mit A, B, C V und a Σ. A BC oder A a Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
10 Chomsky-Normalform Eine kontextfreie Grammatik ist in Chomsky Normalform, wenn alle Regeln von der Form: sind, mit A, B, C V und a Σ. A BC oder A a Grammatiken in Chomsky Normalform können also nicht das Wort ε erzeugen. Für kontextfreie Sprachen, die ε enthalten, lässt sich eine Grammatik leicht ergänzen durch die Regeln S ε und S S, wobei S ein neues Startsymbol zur Erzeugung von ε ist Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
11 Chomsky-Normalform Satz: Jede kontextfreie Grammatik, die nicht das leere Wort erzeugt, kann in eine Grammatik in Chomsky Normalform überführt werden. Beweis (konstruktiv): Wir geben eine Schritt für Schritt Überführung der Regeln in Regeln in Normalform an. Großbuchstaben repräsentieren immer Nichtterminale. Kleinbuchstaben repräsentieren immer Terminale Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
12 Chomsky-Normalform Wir veranschaulichen den Beweis an folgendem Beispiel: Grammatik G = (Σ, V, S, R) mit und der folgenden Regelmenge R: Σ = {a, b} V = {A, B, C, D, E, S} S A aaa bbb ε A C a B b C AF CDE ε D A B ab E B F D E Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
13 Schritt 1 Ziel: Alle Regeln enthalten auf der rechten Seite nur Symbole aus V oder nur ein Symbol aus Σ. Vorgehen: Ersetze dazu in allen rechten Seiten von Regeln Symbole aus a Σ durch neue Variablen Y a und füge die Regeln Y a a hinzu Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
14 Schritt 1 Ziel: Alle Regeln enthalten auf der rechten Seite nur Symbole aus V oder nur ein Symbol aus Σ. Vorgehen: Ersetze dazu in allen rechten Seiten von Regeln Symbole aus a Σ durch neue Variablen Y a und füge die Regeln Y a a hinzu. S A aaa bbb ε A C a B b C AF CDE ε D A B ab E B F D E Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE S A Y a AY a Y b BY b ε A C a B b C AF CDE ε D A B Y a Y b E B F D E Y a a Y b b
15 Schritt 2 Ziel: Alle rechten Seiten haben Länge 2. Vorgehen: Sei A B 1... B m Regel mit m > 2. Führe m 2 neue Variablen C 1,..., C m 2 ein, und ersetze die Regel durch neue Regeln A B 1... B m A B 1 C 1 C i B i+1 C i+1 für 1 i m 3 C m 2 B m 1 B m Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
16 Schritt 2 Ziel: Alle rechten Seiten haben Länge 2. S A Y a AY a Y b BY b ε A C a B b C AF CDE ε S A Y a C 1 Y b C 2 ε A C a B b C AF CC 3 ε D A B Y a Y b E B F D E D A B Y a Y b E B F D E C 1 AY a Y a a Y b b C 2 BY b C 3 DE Y a a Y b b Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
17 Schritt 3 Ziel: Es kommen keine Regeln A ε vor. Vorgehen, Phase 1: Finde die Menge V aller Variablen A für die A ε existiert: Es werden erst alle A mit A ε in V aufgenommen. Dann wird geprüft, ob neue Regeln B ε entstehen, wenn man A in allen Regeln auf der rechten Seite A durch ε ersetzt. Ist dies der Fall, so werden die entsprechenden Variablen B in V aufgenommen und genauso behandelt. Das Verfahren hört auf, wenn V sich nicht mehr ändert Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
18 Schritt 3 Ziel: Es kommen keine Regeln A ε vor. Vorgehen, Phase 1: Finde die Menge V aller Variablen A für die A ε existiert: Bemerkung: In Phase 1 werden noch keine Regeln geändert. Die Ersetzung ist also nur testweise. Am Ende enthält V alle Variablen A mit A ε Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
19 Schritt 3 Ziel: Es kommen keine Regeln A ε vor. Vorgehen, Phase 2: Ersetzung. Gegeben V aus Phase 1. Streiche alle Regeln A ε. Für A BC füge die zusätzliche Regel ein. A B falls C V, A C falls B V (Die Regel A BC wird nicht gestrichen) Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
20 Schritt 3 Initialisierung V = {A A ε} = {S, C} Erster Durchlauf liefert: A V = {A, C, S} Zweiter Durchlauf liefert: D V = {A, C, D, S} Dritter Durchlauf liefert: F V = {A, C, D, F, S} Vierter Durchlauf liefert nichts neues S A Y a C 1 Y b C 2 ε A C a B b C AF CC 3 ε D A B Y a Y b E B F D E C 1 AY a C 2 BY b C 3 DE Y a a Y b b Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
21 Schritt 3 Streiche ε-produktionen Simuliere Ableitungen A ε auf den verbleibenden Regeln V = {A, C, D, F, S} S A Y a C 1 Y b C 2 A C a B b C AF F A CC 3 C 3 D A B Y a Y b E B F D E C 1 AY a Y a C 2 BY b C 3 DE E Y a a Y b b Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
22 Schritt 4 Ziel Die Grammatik enthält keine (Ketten-)Regeln der Form A B. Beispiel A B C B C C c Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
23 Schritt 4 Ziel Die Grammatik enthält keine (Ketten-)Regeln der Form A B. Vorgehen Phase 1: Finde alle Kreise A 1 A 2... A n A 1. Phase 1: Ersetze alle A i durch A 1. Phase 2: Betrachte die Regeln der Form A B in umgekehrt Phase 2: topologischer Reihenfolge. Für Regel A B und jede Regel B b füge Regel A b hinzu. Lösche Regel A B Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
24 Schritt 4 Topologische Sortierung der Regelmenge V 1,..., V k Menge von Variablen aus Kettenregeln V 1,..., V k topologisch sortiert, wenn gilt: V i Vj i < j Voraussetzung: Es gibt keine zyklischen Abhängigkeiten Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
25 Abhängigkeitsgraph S A C 1 Y a S A Y a C 1 Y b C 2 A C a B b C F E B C 3 D C AF F A CC 3 C 3 D A B Y a Y b E B F D E C 1 AY a Y a C 2 BY b C 3 DE E Y a a Y b b Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
26 Schritt 4 Phase 1 S C 1 Zyklen A C und A C F D A A C F C 3 Y a A, C, F, D äquivalent Entferne an Zyklen beteiligte Regeln Ersetze Vorkommen von C, F, D in allen Regeln durch A Lösche Regeln der Form A A E D B Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
27 Schritt 4 Phase 1 Zyklus: A C F D A S A Y a C 1 Y b C 2 A C a B b C AF F A CC 3 C 3 D A B Y a Y b E B F D E C 1 AY a Y a C 2 BY b C 3 DE E Y a a Y b b S A Y a C 1 Y b C 2 A a B b A AA AC 3 C 3 A B Y a Y b E B A E C 1 AY a Y a C 2 BY b C 3 AE E Y a a Y b b Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
28 Schritt 4 - Phase 2 S A E B C 3 C 1 Y a S A Y a C 1 Y b C 2 A a AA AC 3 C 3 B Y a Y b E B b E B C 1 AY a Y a C 2 BY b C 3 AE E Y a a Y b b Topologische Sortierung: S, A, C 3, E, B, C 1, Y a Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
29 Schritt 4 - Phase 2 Gehe in umgekehrter topologischer Sortierung vor Ersetze A B durch A β, falls Regel B β existiert Topologische Sortierung: S, A, C 3, E, B, C 1, Y a S A Y a C 1 Y b C 2 A a AA AC 3 C 3 B b E B B Y a Y b E C 1 AY a Y a C 2 BY b C 3 AE E Y a a Y b b S Y a C 1 Y b C 2 a AA AC 3 AE b Y a Y b A a AA AC 3 AE b Y a Y b B b E b C 1 AY a a C 2 BY b C 3 AE b Y a a Y b b Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
30 Sonderbehandlung von ε-produktionen Grammatik ist nun in Chomsky-Normalform, aber G enthält Ableitungsfolge S ε (haben wir entfernt). Erweitere Grammatik um Regeln S S und S ε für neues Startsymbol S Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
31 Der CYK-Algorithmus Satz: Es gibt einen Algorithmus (den Cocke Younger Kasami Algorithmus), der für eine kontextfreie Grammatik G in Chomsky Normalform und ein Wort w Σ in Zeit O( R n 3 ) entscheidet, ob w L(G), wobei n = w und R die Anzahl der Regeln von G ist Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
32 Beweis - Beschreibung des CYK-Algorithmus Sei w = w 1... w n. Sei V ij V so dass A w i... w j impliziert A V ij. Für alle 1 i j n berechne die Menge V ij V. Dann ist w L(G) genau dann, wenn S V 1n ist. Die Tabelle der V ij wird nach wachsendem l := j i aufgebaut, beginnend mit l = 0. Für j i = l > 0 wird die Berechnung von V ij systematisch auf zuvor berechnete V ik, V k+1 j mit i k < j zurückgeführt. Bemerkung Wir benutzen dynamische Programmierung Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
33 CYK-Algorithmus Beispiel w = 1 (01) S SY SC 1 SS Y ( C 2 C 1 Y S C 2 SY ) Y Y Y ( ( Y ) ) e 0 1 V ii+7 V 18 V ii+6 V ii+5 V ii+4 V ii+3 V ii+2 V ii+1 V ii V 17 V 28 V 16 V 27 V 38 V 15 V 26 V 37 V 48 V 14 V 25 V 36 V 47 V 58 V 13 V 24 V 35 V 46 V 57 V 68 V 12 V 23 V 34 V 45 V 56 V 67 V 78 V 11 V 22 V 33 V 44 V 55 V 66 V 77 V 88 1 ( 0 1 ) i Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
34 CYK-Algorithmus Beispiel w = 1 (01) S SY SC 1 SS Y ( C 2 C 1 Y S C 2 SY ) Y Y Y ( ( Y ) ) e 0 1 V ii+7 V 18 V ii+6 V ii+5 V ii+4 V ii+3 V ii+2 V ii+1 V ii V 17 V 28 V 16 V 27 V 38 V 15 V 26 V 37 V 48 V 14 V 25 V 36 V 47 V 58 V 13 V 24 V 35 V 46 V 57 V 68 V 12 V 23 V 34 V 45 V 56 V 67 V 78 V 11 V 22 V 33 V 44 V 55 V 66 V 77 V 88 1 ( 0 1 ) i Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
35 CYK-Algorithmus Vorgehen Fall l = 0: Konstruiere die Mengen V ii, d.h. alle A V mit A w i. Da G in Chomsky Normalform ist, gilt A w i nur, wenn (A w i ) R. Die Berechnung von V ii ist für alle i {1,... n} in O( R ) möglich Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
36 CYK-Algorithmus Beispiel w = 1 (01) S SY SC 1 SS Y ( C 2 C 1 Y S C 2 SY ) Y Y Y ( ( Y ) ) e 0 1 V ii+7 V 18 V ii+6 V ii+5 V ii+4 V ii+3 V ii+2 V ii+1 V ii V 17 V 28 V 16 V 27 V 38 V 15 V 26 V 37 V 48 V 14 V 25 V 36 V 47 V 58 V 13 V 24 V 35 V 46 V 57 V 68 V 12 V 23 V 34 V 45 V 56 V 67 V 78 V 11 V 22 V 33 V 44 V 55 V 66 V 77 V 88 1 ( 0 1 ) i Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
37 CYK-Algorithmus Beispiel w = 1 (01) S SY SC 1 SS Y ( C 2 C 1 Y S C 2 SY ) Y Y Y ( ( Y ) ) e 0 1 V ii+7 V 18 V ii+6 V ii+5 V ii+4 V ii+3 V ii+2 V ii+1 V ii V 17 V 28 V 16 V 27 V 38 V 15 V 26 V 37 V 48 V 14 V 25 V 36 V 47 V 58 V 13 V 24 V 35 V 46 V 57 V 68 V 12 V 23 V 34 V 45 V 56 V 67 V 78 S Y Y Y ( S S Y ) Y 1 ( 0 1 ) i Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
38 CYK-Algorithmus Vorgehen Fall l > 0: Jede Ableitung von w i... w j muss mit einer Regel der Form A BC beginnen, wobei ein k {i,..., j 1} existiert mit B w i... w k und C w k+1... w j Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
39 CYK-Algorithmus Vorgehen Verfahren Speichere alle Mengen V rs als Arrays der Länge V, in denen für jedes A V markiert ist, ob A V rs. Berechnung von V ij : Überprüfe für jede Regel (A BC) R und jedes k, ob B w i... w k durch Ansehen der Stelle B im Array zu V ik und C im Array zu V k+1 j. C w k+1... w j Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
40 CYK-Algorithmus Vorgehen Verfahren Speichere alle Mengen V rs als Arrays der Länge V, in denen für jedes A V markiert ist, ob A V rs. Berechnung von V ij : Überprüfe für jede Regel (A BC) R und jedes k, ob B w i... w k durch Ansehen der Stelle B im Array zu V ik und C im Array zu V k+1 j. C w k+1... w j Bemerkung Dies benötigt Aufwand in O(n R ) Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
41 CYK-Algorithmus Beispiel w = 1 (01) S SY SC 1 SS Y ( C 2 C 1 Y S C 2 SY ) Y Y Y ( ( Y ) ) e 0 1 V ii+7 V 18 V ii+6 V ii+5 V ii+4 V ii+3 V ii+2 V ii+1 V ii V 17 V 28 V 16 V 27 V 38 V 15 V 26 V 37 V 48 V 14 V 25 V 36 V 47 V 58 V 13 V 24 V 35 V 46 V 57 V 68 V 12 V 23 V 34 V 45 V 56 V 67 V 78 S Y Y Y ( S S Y ) Y 1 ( 0 1 ) i Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
42 CYK-Algorithmus Beispiel w = 1 (01) S SY SC 1 SS Y ( C 2 C 1 Y S C 2 SY ) Y Y Y ( ( Y ) ) e 0 1 V ii+7 V 18 V ii+6 V ii+5 V ii+4 V ii+3 V ii+2 V ii+1 V ii V 17 V 28 V 16 V 27 V 38 V 15 V 26 V 37 V 48 V 14 V 25 V 36 V 47 V 58 V 13 V 24 V 35 V 46 V 57 V 68 S S C 2 S Y Y Y ( S S Y ) Y 1 ( 0 1 ) i Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
43 CYK-Algorithmus Beispiel w = 1 (01) S SY SC 1 SS Y ( C 2 C 1 Y S C 2 SY ) Y Y Y ( ( Y ) ) e 0 1 V ii+7 V 18 V ii+6 V ii+5 V ii+4 V ii+3 V ii+2 V ii+1 V ii V 17 V 28 V 16 V 27 V 38 V 15 V 26 V 37 V 48 V 14 V 25 V 36 V 47 V 58 C 2 S S C 2 S Y Y Y ( S S Y ) Y 1 ( 0 1 ) i Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
44 CYK-Algorithmus Beispiel w = 1 (01) S SY SC 1 SS Y ( C 2 C 1 Y S C 2 SY ) Y Y Y ( ( Y ) ) e 0 1 V ii+7 V 18 V ii+6 V ii+5 V ii+4 V ii+3 V ii+2 V ii+1 V ii V 17 V 28 V 16 V 27 V 38 V 15 V 26 V 37 V 48 S C 2 S S C 2 S Y Y Y ( S S Y ) Y 1 ( 0 1 ) i Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
45 CYK-Algorithmus Beispiel w = 1 (01) S SY SC 1 SS Y ( C 2 C 1 Y S C 2 SY ) Y Y Y ( ( Y ) ) e 0 1 V ii+7 V 18 V ii+6 V ii+5 V ii+4 V ii+3 V ii+2 V ii+1 V ii V 17 V 28 V 16 V 27 V 38 C 1 S S C 2 S S C 2 S Y Y Y ( S S Y ) Y 1 ( 0 1 ) i Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
46 CYK-Algorithmus Beispiel w = 1 (01) S SY SC 1 SS Y ( C 2 C 1 Y S C 2 SY ) Y Y Y ( ( Y ) ) e 0 1 V ii+7 V 18 V ii+6 V ii+5 V ii+4 V ii+3 V ii+2 V ii+1 V ii V 17 V 28 C 1 S S C 2 S S C 2 S Y Y Y ( S S Y ) Y 1 ( 0 1 ) i Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
47 CYK-Algorithmus Beispiel w = 1 (01) S SY SC 1 SS Y ( C 2 C 1 Y S C 2 SY ) Y Y Y ( ( Y ) ) e 0 1 V ii+7 V 18 V ii+6 V ii+5 V ii+4 V ii+3 V ii+2 V ii+1 V ii S C 1 S S C 2 S S C 2 S Y Y Y ( S S Y ) Y 1 ( 0 1 ) i Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
48 CYK-Algorithmus Beispiel w = 1 (01) S SY SC 1 SS Y ( C 2 C 1 Y S C 2 SY ) Y Y Y ( ( Y ) ) e 0 1 V ii+7 V ii+6 V ii+5 V ii+4 V ii+3 V ii+2 V ii+1 V ii S S C 1 S S C 2 S S C 2 S Y Y Y ( S S Y ) Y 1 ( 0 1 ) i Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
49 Ergebnisse zum Wortproblem Typ-0 Grammatik. Das Wortproblem ist nicht entscheidbar. Typ-1 Grammatik. Das Wortproblem ist NP-vollständig. Typ-2 Grammatik. Das Wortproblem ist in polynomieller Zeit lösbar. Typ-3 Grammatik. Das Wortproblem ist in linearer Zeit lösbar Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Übungsblatt 7. Vorlesung Theoretische Grundlagen der Informatik im WS 16/17
 Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 7 Vorlesung Theoretische Grundlagen der Informatik im W 16/17 Ausgabe 17. Januar 2017 Abgabe 31. Januar 2017, 11:00 Uhr (im
Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 7 Vorlesung Theoretische Grundlagen der Informatik im W 16/17 Ausgabe 17. Januar 2017 Abgabe 31. Januar 2017, 11:00 Uhr (im
Klammersprache Definiere
 Klammersprache w=w 1...w n {(,)}* heißt korrekt geklammert, falls die Anzahl ( ist gleich der Anzahl ). in jedem Anfangsstück w 1,...,w i (i n) ist die Anzahl ( nicht kleiner als die Anzahl ). Definiere
Klammersprache w=w 1...w n {(,)}* heißt korrekt geklammert, falls die Anzahl ( ist gleich der Anzahl ). in jedem Anfangsstück w 1,...,w i (i n) ist die Anzahl ( nicht kleiner als die Anzahl ). Definiere
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 17. Januar 2012 INSTITUT FÜR THEORETISCHE 0 KIT 18.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Theoretische Grundlagen der Informatik Vorlesung am 17. Januar 2012 INSTITUT FÜR THEORETISCHE 0 KIT 18.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Automatentheorie und formale Sprachen
 Automatentheorie und formale Sprachen VL 8 Chomsky-Grammatiken Kathrin Hoffmann 23. Mai 2012 Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen 23.5. 2012 250 Wortproblem Wortproblem ist das
Automatentheorie und formale Sprachen VL 8 Chomsky-Grammatiken Kathrin Hoffmann 23. Mai 2012 Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen 23.5. 2012 250 Wortproblem Wortproblem ist das
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 18. Januar 2018 INSTITUT FÜR THEORETISCHE 0 18.01.2018 Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE KIT Die Forschungsuniversität
Theoretische Grundlagen der Informatik Vorlesung am 18. Januar 2018 INSTITUT FÜR THEORETISCHE 0 18.01.2018 Dorothea Wagner - Theoretische Grundlagen der Informatik INSTITUT FÜR THEORETISCHE KIT Die Forschungsuniversität
Kontextfreie (Typ-2) Sprachen
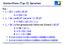 Kontextfreie (Typ-2) prachen Bsp.: L 1 = { n 1 n n>} с {,1}* 1 1 L 2 = {w wє{,1}* und w=w rev } с {,1}* 11 1 ε L 3 = {w w hat genausoviele Nullen wie Einsen} с {,1}* B 1 ε 1 B 1 1 BB 1 11 11 11 11B 111
Kontextfreie (Typ-2) prachen Bsp.: L 1 = { n 1 n n>} с {,1}* 1 1 L 2 = {w wє{,1}* und w=w rev } с {,1}* 11 1 ε L 3 = {w w hat genausoviele Nullen wie Einsen} с {,1}* B 1 ε 1 B 1 1 BB 1 11 11 11 11B 111
Lemma Für jede monotone Grammatik G gibt es eine kontextsensitive
 Lemma Für jede monotone Grammatik G gibt es eine kontextsensitive Grammatik G mit L(G) = L(G ). Beweis im Beispiel (2.): G = (V,Σ, P, S) : P = {S asbc, S abc, CB BC, ab ab, bb bb, bc bc, cc cc}. (i) G
Lemma Für jede monotone Grammatik G gibt es eine kontextsensitive Grammatik G mit L(G) = L(G ). Beweis im Beispiel (2.): G = (V,Σ, P, S) : P = {S asbc, S abc, CB BC, ab ab, bb bb, bc bc, cc cc}. (i) G
Kapitel: Die Chomsky Hierarchie. Die Chomsky Hierarchie 1 / 14
 Kapitel: Die Chomsky Hierarchie Die Chomsky Hierarchie 1 / 14 Allgemeine Grammatiken Definition Eine Grammatik G = (Σ, V, S, P) besteht aus: einem endlichen Alphabet Σ, einer endlichen Menge V von Variablen
Kapitel: Die Chomsky Hierarchie Die Chomsky Hierarchie 1 / 14 Allgemeine Grammatiken Definition Eine Grammatik G = (Σ, V, S, P) besteht aus: einem endlichen Alphabet Σ, einer endlichen Menge V von Variablen
kontextfreie Grammatiken Theoretische Informatik kontextfreie Grammatiken kontextfreie Grammatiken Rainer Schrader 14. Juli 2009 Gliederung
 Theoretische Informatik Rainer Schrader Zentrum für Angewandte Informatik Köln 14. Juli 2009 1 / 40 2 / 40 Beispiele: Aus den bisher gemachten Überlegungen ergibt sich: aus der Chomsky-Hierarchie bleiben
Theoretische Informatik Rainer Schrader Zentrum für Angewandte Informatik Köln 14. Juli 2009 1 / 40 2 / 40 Beispiele: Aus den bisher gemachten Überlegungen ergibt sich: aus der Chomsky-Hierarchie bleiben
Chomsky-Grammatiken 16. Chomsky-Grammatiken
 Chomsky-Grammatiken 16 Chomsky-Grammatiken Ursprünglich von Chomsky in den 1950er Jahren eingeführt zur Beschreibung natürlicher Sprachen. Enge Verwandschaft zu Automaten Grundlage wichtiger Softwarekomponenten
Chomsky-Grammatiken 16 Chomsky-Grammatiken Ursprünglich von Chomsky in den 1950er Jahren eingeführt zur Beschreibung natürlicher Sprachen. Enge Verwandschaft zu Automaten Grundlage wichtiger Softwarekomponenten
Informatik III. Christian Schindelhauer Wintersemester 2006/07 6. Vorlesung
 Informatik III Christian Schindelhauer Wintersemester 2006/07 6. Vorlesung 10.11.2006 schindel@informatik.uni-freiburg.de 1 Kapitel IV Kontextfreie Sprachen Kontextfreie Grammatik Informatik III 6. Vorlesung
Informatik III Christian Schindelhauer Wintersemester 2006/07 6. Vorlesung 10.11.2006 schindel@informatik.uni-freiburg.de 1 Kapitel IV Kontextfreie Sprachen Kontextfreie Grammatik Informatik III 6. Vorlesung
Umformung NTM DTM. Charakterisierung rek. aufz. Spr. Chomsky-3-Grammatiken (T5.3) Chomsky-0-Grammatik Rek. Aufz.
 Chomsky-0-Grammatik Rek. Aufz. Satz T5.2.2: Wenn L durch eine Chomsky-0- Grammatik G beschrieben wird, gibt es eine NTM M, die L akzeptiert. Beweis: Algo von M: Schreibe S auf freie Spur. Iteriere: Führe
Chomsky-0-Grammatik Rek. Aufz. Satz T5.2.2: Wenn L durch eine Chomsky-0- Grammatik G beschrieben wird, gibt es eine NTM M, die L akzeptiert. Beweis: Algo von M: Schreibe S auf freie Spur. Iteriere: Führe
Automaten und formale Sprachen Notizen zu den Folien
 Automaten und formale prachen Notizen zu den Folien 10 Kontextfreie Grammatiken Beispiele für kontextfreien Grammatiken ei Σ = {a, b}. Beispiel 1 (Folie 233, oben) Geben ie eine kontextfreie Grammatik
Automaten und formale prachen Notizen zu den Folien 10 Kontextfreie Grammatiken Beispiele für kontextfreien Grammatiken ei Σ = {a, b}. Beispiel 1 (Folie 233, oben) Geben ie eine kontextfreie Grammatik
Übungsblatt 6. Vorlesung Theoretische Grundlagen der Informatik im WS 17/18
 Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 6 Vorlesung Theoretische Grundlagen der Informatik im WS 17/18 Ausgabe 10. Januar 2018 Abgabe 23. Januar 2018, 11:00 Uhr (im
Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 6 Vorlesung Theoretische Grundlagen der Informatik im WS 17/18 Ausgabe 10. Januar 2018 Abgabe 23. Januar 2018, 11:00 Uhr (im
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie Sprachen (II) 11.06.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie Sprachen (II) 11.06.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Automaten und formale Sprachen Notizen zu den Folien
 Automaten und formale prachen Notizen zu den Folien 10 Kontextfreie Grammatiken Beispiele für kontextfreien Grammatiken ei Σ = {a, b}. Beispiel 1 (Folie 211, oben) Geben ie eine kontextfreie Grammatik
Automaten und formale prachen Notizen zu den Folien 10 Kontextfreie Grammatiken Beispiele für kontextfreien Grammatiken ei Σ = {a, b}. Beispiel 1 (Folie 211, oben) Geben ie eine kontextfreie Grammatik
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Übung am 02.02.2012 INSTITUT FÜR THEORETISCHE 0 KIT 06.02.2012 Universität des Andrea Landes Schumm Baden-Württemberg - Theoretische und Grundlagen der Informatik
Theoretische Grundlagen der Informatik Übung am 02.02.2012 INSTITUT FÜR THEORETISCHE 0 KIT 06.02.2012 Universität des Andrea Landes Schumm Baden-Württemberg - Theoretische und Grundlagen der Informatik
Einführung in Berechenbarkeit, Formale Sprachen und Komplexitätstheorie
 Einführung in Berechenbarkeit, Formale Sprachen und Komplexitätstheorie Wintersemester 2005/2006 07.11.2005 5. Vorlesung 1 Überblick: Kontextfreie Sprachen Formale Grammatik Einführung, Beispiele Formale
Einführung in Berechenbarkeit, Formale Sprachen und Komplexitätstheorie Wintersemester 2005/2006 07.11.2005 5. Vorlesung 1 Überblick: Kontextfreie Sprachen Formale Grammatik Einführung, Beispiele Formale
Was bisher geschah Chomsky-Hierarchie für Sprachen: L 0 Menge aller durch (beliebige) Grammatiken beschriebenen Sprachen L 1 Menge aller monotonen
 Was bisher geschah Chomsky-Hierarchie für Sprachen: L 0 Menge aller durch (beliebige) Grammatiken beschriebenen Sprachen L 1 Menge aller monotonen (Kontextsensitive) Sprachen L 2 Menge aller kontextfreien
Was bisher geschah Chomsky-Hierarchie für Sprachen: L 0 Menge aller durch (beliebige) Grammatiken beschriebenen Sprachen L 1 Menge aller monotonen (Kontextsensitive) Sprachen L 2 Menge aller kontextfreien
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie Sprachen (III) 17.06.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie Sprachen (III) 17.06.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Übersicht 1. Motivation 2. Terminologie
Kontextfreie Sprachen
 Kontextfreie Sprachen Bedeutung: Programmiersprachen (Compilerbau) Syntaxbäume Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung
Kontextfreie Sprachen Bedeutung: Programmiersprachen (Compilerbau) Syntaxbäume Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung
Dank. 1 Ableitungsbäume. 2 Umformung von Grammatiken. 3 Normalformen. 4 Pumping-Lemma für kontextfreie Sprachen. 5 Pushdown-Automaten (PDAs)
 ank Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert iese Vorlesungsmaterialien basieren ganz wesentlich auf den Folien zu den Vorlesungen
ank Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert iese Vorlesungsmaterialien basieren ganz wesentlich auf den Folien zu den Vorlesungen
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie Sprachen (I) 3.06.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Organisatorisches 1. Teilklausur: Mittwoch,
Grundlagen der Theoretischen Informatik 4. Kellerautomaten und kontextfreie Sprachen (I) 3.06.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Organisatorisches 1. Teilklausur: Mittwoch,
2.1 Allgemeines. Was ist eine Sprache? Beispiele:
 Was ist eine Sprache? Beispiele: (a) Deutsch, Japanisch, Latein, Esperanto,...: Natürliche Sprachen (b) Pascal, C, Java, Aussagenlogik,...: Formale Sprachen Wie beschreibt man eine Sprache? (i) Syntax
Was ist eine Sprache? Beispiele: (a) Deutsch, Japanisch, Latein, Esperanto,...: Natürliche Sprachen (b) Pascal, C, Java, Aussagenlogik,...: Formale Sprachen Wie beschreibt man eine Sprache? (i) Syntax
Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I
 Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert Institut für Informatik Sommersemester 2007 B. Beckert Grundlagen d. Theoretischen Informatik:
Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert Institut für Informatik Sommersemester 2007 B. Beckert Grundlagen d. Theoretischen Informatik:
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 10.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Theoretische Grundlagen der Informatik Vorlesung am 10.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Kontextfreie Sprachen
 Kontextfreie Sprachen besitzen große Bedeutung im Compilerbau Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung durch
Kontextfreie Sprachen besitzen große Bedeutung im Compilerbau Chomsky-Normalform effiziente Lösung des Wortproblems (CYK-Algorithmus) Grenzen kontextfreier Sprachen (Pumping Lemma) Charakterisierung durch
Beschreibungskomplexität von Grammatiken Definitionen
 Beschreibungskomplexität von Grammatiken Definitionen Für eine Grammatik G = (N, T, P, S) führen wir die folgenden drei Komplexitätsmaße ein: Var(G) = #(N), Prod(G) = #(P ), Symb(G) = ( α + β + 1). α β
Beschreibungskomplexität von Grammatiken Definitionen Für eine Grammatik G = (N, T, P, S) führen wir die folgenden drei Komplexitätsmaße ein: Var(G) = #(N), Prod(G) = #(P ), Symb(G) = ( α + β + 1). α β
Definition 4 (Operationen auf Sprachen) Beispiel 5. Seien A, B Σ zwei (formale) Sprachen. Konkatenation: AB = {uv ; u A, v B} A + = n 1 An
 Definition 4 (Operationen auf Sprachen) Seien A, B Σ zwei (formale) Sprachen. Konkatenation: AB = {uv ; u A, v B} A 0 = {ɛ}, A n+1 = AA n A = n 0 An A + = n 1 An Beispiel 5 {ab, b}{a, bb} = {aba, abbb,
Definition 4 (Operationen auf Sprachen) Seien A, B Σ zwei (formale) Sprachen. Konkatenation: AB = {uv ; u A, v B} A 0 = {ɛ}, A n+1 = AA n A = n 0 An A + = n 1 An Beispiel 5 {ab, b}{a, bb} = {aba, abbb,
Grammatiken. Grammatiken sind regelbasierte Kalküle zur Konstruktion von Systemen und Sprachen Überprüfung von Systemen und Sprachen
 Grammatiken Grammatiken sind regelbasierte Kalküle zur Konstruktion von Systemen und Sprachen Überprüfung von Systemen und Sprachen Grammatiken eignen sich besonders zur Modellierung beliebig tief geschachtelter,
Grammatiken Grammatiken sind regelbasierte Kalküle zur Konstruktion von Systemen und Sprachen Überprüfung von Systemen und Sprachen Grammatiken eignen sich besonders zur Modellierung beliebig tief geschachtelter,
2. Teilklausur zur Vorlesung Grundlagen der Theoretischen Informatik
 2. Teilklausur zur Vorlesung Grundlagen der Theoretischen Informatik Ulrich Furbach Claudia Schon Christian Schwarz Arbeitsgruppe Künstliche Intelligenz Fachbereich Informatik, Universität Koblenz-Landau
2. Teilklausur zur Vorlesung Grundlagen der Theoretischen Informatik Ulrich Furbach Claudia Schon Christian Schwarz Arbeitsgruppe Künstliche Intelligenz Fachbereich Informatik, Universität Koblenz-Landau
I.5. Kontextfreie Sprachen
 I.5. Kontextfreie prachen Zieht man in Betracht, dass BNF-yteme gerade so beschaffen sind, dass auf der linken eite immer genau ein Nichtterminal steht, so sind das also gerade die Ableitungsregeln einer
I.5. Kontextfreie prachen Zieht man in Betracht, dass BNF-yteme gerade so beschaffen sind, dass auf der linken eite immer genau ein Nichtterminal steht, so sind das also gerade die Ableitungsregeln einer
4.2 Die Chomsky Normalform
 4.2 Die Chomsky Normalform Für algorithmische Problemstellungen (z.b. das Wortproblem) aber auch für den Nachweis von Eigenschaften kontextfreier Sprachen ist es angenehm, von CFG in Normalformen auszugehen.
4.2 Die Chomsky Normalform Für algorithmische Problemstellungen (z.b. das Wortproblem) aber auch für den Nachweis von Eigenschaften kontextfreier Sprachen ist es angenehm, von CFG in Normalformen auszugehen.
Einführung in die Computerlinguistik Chart-Parsing
 Einführung in die Computerlinguistik Chart-Parsing Dozentin: Wiebke sen 21.12.2009 Wiebke sen Einführung CL (Wie 09/10) 1 P = calls calls Wiebke sen Einführung CL (Wie 09/10) 2 P = calls calls Wiebke sen
Einführung in die Computerlinguistik Chart-Parsing Dozentin: Wiebke sen 21.12.2009 Wiebke sen Einführung CL (Wie 09/10) 1 P = calls calls Wiebke sen Einführung CL (Wie 09/10) 2 P = calls calls Wiebke sen
(Prüfungs-)Aufgaben zu formale Sprachen
 (Prüfungs-)Aufgaben zu formale Sprachen (siehe auch bei den Aufgaben zu endlichen Automaten) 1) Eine Grammatik G sei gegeben durch: N = {S, A}, T = {a, b, c, d}, P = { (S, Sa), (S, ba), (A, ba), (A, c),
(Prüfungs-)Aufgaben zu formale Sprachen (siehe auch bei den Aufgaben zu endlichen Automaten) 1) Eine Grammatik G sei gegeben durch: N = {S, A}, T = {a, b, c, d}, P = { (S, Sa), (S, ba), (A, ba), (A, c),
Hallo Welt für Fortgeschrittene
 Hallo Welt für Fortgeschrittene Parsen Thomas Wehr Informatik 2 Programmiersysteme Martensstraße 3 91058 Erlangen Inhalt Theoretische Grundlagen Grammatiken im Allgemeinen Die Chomsky-Hierarchie Die Chomsky-Normalform
Hallo Welt für Fortgeschrittene Parsen Thomas Wehr Informatik 2 Programmiersysteme Martensstraße 3 91058 Erlangen Inhalt Theoretische Grundlagen Grammatiken im Allgemeinen Die Chomsky-Hierarchie Die Chomsky-Normalform
Rekursiv aufzählbare Sprachen
 Kapitel 4 Rekursiv aufzählbare Sprachen 4.1 Grammatiken und die Chomsky-Hierarchie Durch Zulassung komplexer Ableitungsregeln können mit Grammatiken größere Klassen als die kontextfreien Sprachen beschrieben
Kapitel 4 Rekursiv aufzählbare Sprachen 4.1 Grammatiken und die Chomsky-Hierarchie Durch Zulassung komplexer Ableitungsregeln können mit Grammatiken größere Klassen als die kontextfreien Sprachen beschrieben
Theorie der Informatik. Theorie der Informatik. 6.1 Einführung. 6.2 Alphabete und formale Sprachen. 6.3 Grammatiken. 6.4 Chomsky-Hierarchie
 Theorie der Informatik 17. März 2014 6. Formale Sprachen und Grammatiken Theorie der Informatik 6. Formale Sprachen und Grammatiken Malte Helmert Gabriele Röger Universität Basel 17. März 2014 6.1 Einführung
Theorie der Informatik 17. März 2014 6. Formale Sprachen und Grammatiken Theorie der Informatik 6. Formale Sprachen und Grammatiken Malte Helmert Gabriele Röger Universität Basel 17. März 2014 6.1 Einführung
1. Klausur zur Vorlesung Informatik III Wintersemester 2003/2004. Mit Lösung!
 Universität Karlsruhe Theoretische Informatik Fakultät für Informatik WS 23/4 ILKD Prof. Dr. D. Wagner 2. Februar 24. Klausur zur Vorlesung Informatik III Wintersemester 23/24 Mit Lösung! Beachten Sie:
Universität Karlsruhe Theoretische Informatik Fakultät für Informatik WS 23/4 ILKD Prof. Dr. D. Wagner 2. Februar 24. Klausur zur Vorlesung Informatik III Wintersemester 23/24 Mit Lösung! Beachten Sie:
Automaten und formale Sprachen Klausurvorbereitung
 Automaten und formale Sprachen Klausurvorbereitung Rami Swailem Mathematik Naturwissenschaften und Informatik FH-Gießen-Friedberg Inhaltsverzeichnis 1 Definitionen 2 2 Altklausur Jäger 2006 8 1 1 Definitionen
Automaten und formale Sprachen Klausurvorbereitung Rami Swailem Mathematik Naturwissenschaften und Informatik FH-Gießen-Friedberg Inhaltsverzeichnis 1 Definitionen 2 2 Altklausur Jäger 2006 8 1 1 Definitionen
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 17.November 2011 INSTITUT FÜR THEORETISCHE 0 KIT 17.11.2011 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Theoretische Grundlagen der Informatik Vorlesung am 17.November 2011 INSTITUT FÜR THEORETISCHE 0 KIT 17.11.2011 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der
Grundbegriffe. Grammatiken
 Grammatiken Grammatiken in der Informatik sind ähnlich wie Grammatiken für natürliche Sprachen ein Mittel, um alle syntaktisch korrekten Sätze (hier: Wörter) einer Sprache zu erzeugen. Beispiel: Eine vereinfachte
Grammatiken Grammatiken in der Informatik sind ähnlich wie Grammatiken für natürliche Sprachen ein Mittel, um alle syntaktisch korrekten Sätze (hier: Wörter) einer Sprache zu erzeugen. Beispiel: Eine vereinfachte
Tutoraufgabe 1 (ɛ-produktionen):
 Prof aa Dr J Giesl Formale Systeme, Automaten, Prozesse SS 2010 M Brockschmidt, F Emmes, C Fuhs, C Otto, T Ströder Hinweise: Die Hausaufgaben sollen in Gruppen von je 2 Studierenden aus dem gleichen Tutorium
Prof aa Dr J Giesl Formale Systeme, Automaten, Prozesse SS 2010 M Brockschmidt, F Emmes, C Fuhs, C Otto, T Ströder Hinweise: Die Hausaufgaben sollen in Gruppen von je 2 Studierenden aus dem gleichen Tutorium
Grundbegriffe der Informatik Tutorium 12
 Grundbegriffe der Informatik Tutorium 12 Tutorium Nr. 16 Philipp Oppermann 28. Januar 2015 KARLSRUHER INSTITUT FÜR TECHNOLOGIE KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum
Grundbegriffe der Informatik Tutorium 12 Tutorium Nr. 16 Philipp Oppermann 28. Januar 2015 KARLSRUHER INSTITUT FÜR TECHNOLOGIE KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum
Theoretische Informatik Mitschrift
 Theoretische Informatik Mitschrift 2. Grammatiken und die Chomsky-Hierarchie Beispiel: Syntaxdefinition in BNF :=
Theoretische Informatik Mitschrift 2. Grammatiken und die Chomsky-Hierarchie Beispiel: Syntaxdefinition in BNF :=
Grundlagen der Theoretischen Informatik
 1 Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg Wintersemester 2014/15 2 Kontextfreie Grammatiken Definition: Eine Grammatik G
1 Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg Wintersemester 2014/15 2 Kontextfreie Grammatiken Definition: Eine Grammatik G
Übungsblatt Nr. 3. Lösungsvorschlag
 Institut für Kryptographie und Sicherheit Prof. Dr. Jörn Müller-Quade Dirk Achenbach Tobias Nilges Vorlesung Theoretische Grundlagen der Informatik Übungsblatt Nr. 3 Aufgabe 1: Karlsruhe ist nicht genug
Institut für Kryptographie und Sicherheit Prof. Dr. Jörn Müller-Quade Dirk Achenbach Tobias Nilges Vorlesung Theoretische Grundlagen der Informatik Übungsblatt Nr. 3 Aufgabe 1: Karlsruhe ist nicht genug
Einführung in die theoretische Informatik Sommersemester 2017 Übungsblatt Lösungsskizze 7
 Prof. J. Esparza Technische Universität München S. Sickert, J. Krämer KEINE ABGABE Einführung in die theoretische Informatik Sommersemester 2017 Übungsblatt 7 Übungsblatt Wir unterscheiden zwischen Übungs-
Prof. J. Esparza Technische Universität München S. Sickert, J. Krämer KEINE ABGABE Einführung in die theoretische Informatik Sommersemester 2017 Übungsblatt 7 Übungsblatt Wir unterscheiden zwischen Übungs-
Aufgabe Mögliche Punkte Erreichte Punkte a b c d Σ a b c d Σ x1 13
 Universität Karlsruhe Theoretische Informatik Fakultät für Informatik WS 2003/04 ILKD Prof. Dr. D. Wagner 14. April 2004 2. Klausur zur Vorlesung Informatik III Wintersemester 2003/2004 Hier Aufkleber
Universität Karlsruhe Theoretische Informatik Fakultät für Informatik WS 2003/04 ILKD Prof. Dr. D. Wagner 14. April 2004 2. Klausur zur Vorlesung Informatik III Wintersemester 2003/2004 Hier Aufkleber
1 Automatentheorie und Formale Sprachen
 Sanders: TGI October 29, 2015 1 1 Automatentheorie und Formale Sprachen 1.1 Allgemeines Sanders: TGI October 29, 2015 2 Beispiel: Arithmetische Ausdrücke:EXPR Σ={1,a,+,,,(,)} a ist Platzhalter für Konstanten
Sanders: TGI October 29, 2015 1 1 Automatentheorie und Formale Sprachen 1.1 Allgemeines Sanders: TGI October 29, 2015 2 Beispiel: Arithmetische Ausdrücke:EXPR Σ={1,a,+,,,(,)} a ist Platzhalter für Konstanten
Algorithmen und Datenstrukturen (EI)
 Algorithmen und Datenstrukturen (EI) ADS Zentralübung Stefan Schmid 4. Februar 2009 Einturnen... Ein heutiger Computer aus dem Saturn ist im Prinzip eine Turing Maschine? Nein. Zum Beispiel Sprache L =
Algorithmen und Datenstrukturen (EI) ADS Zentralübung Stefan Schmid 4. Februar 2009 Einturnen... Ein heutiger Computer aus dem Saturn ist im Prinzip eine Turing Maschine? Nein. Zum Beispiel Sprache L =
Informatik III. Christian Schindelhauer Wintersemester 2006/07 5. Vorlesung
 Informatik III Christian Schindelhauer Wintersemester 2006/07 5. Vorlesung 09.11.2006 schindel@informatik.uni-freiburg.de 1 Äquivalenzklassen Definition und Beispiel Definition Für eine Sprache L Σ* bezeichnen
Informatik III Christian Schindelhauer Wintersemester 2006/07 5. Vorlesung 09.11.2006 schindel@informatik.uni-freiburg.de 1 Äquivalenzklassen Definition und Beispiel Definition Für eine Sprache L Σ* bezeichnen
Kapitel IV Formale Sprachen und Grammatiken
 Kapitel IV Formale Sprachen und Grammatiken 1. Begriffe und Notationen Sei Σ ein (endliches) Alphabet. Dann Definition 42 1 ist Σ das Monoid über Σ, d.h. die Menge aller endlichen Wörter über Σ; 2 ist
Kapitel IV Formale Sprachen und Grammatiken 1. Begriffe und Notationen Sei Σ ein (endliches) Alphabet. Dann Definition 42 1 ist Σ das Monoid über Σ, d.h. die Menge aller endlichen Wörter über Σ; 2 ist
Formale Sprachen. Script, Kapitel 4. Grammatiken
 Formale Sprachen Grammatiken Script, Kapitel 4 erzeugen Sprachen eingeführt von Chomsky zur Beschreibung natürlicher Sprache bedeutend für die Syntaxdefinition und -analyse von Programmiersprachen Automaten
Formale Sprachen Grammatiken Script, Kapitel 4 erzeugen Sprachen eingeführt von Chomsky zur Beschreibung natürlicher Sprache bedeutend für die Syntaxdefinition und -analyse von Programmiersprachen Automaten
2.1 Grundlagen: Kontextfreie Grammatiken
 2.1 Grundlagen: Kontextfreie Grammatiken Programme einer Programmiersprache können unbeschränkt viele Tokens enthalten, aber nur endlich viele Token-Klassen :-) Als endliches Terminal-Alphabet T wählen
2.1 Grundlagen: Kontextfreie Grammatiken Programme einer Programmiersprache können unbeschränkt viele Tokens enthalten, aber nur endlich viele Token-Klassen :-) Als endliches Terminal-Alphabet T wählen
Informatik 3 Theoretische Informatik WS 2016/17
 Zwischenklausur 2 20. Januar 2017 Informatik 3 Theoretische Informatik WS 2016/17 Prof. Dr. Peter Thiemann Albert-Ludwigs-Universität Freiburg Institut für Informatik Name: Übungsgruppe: Schreiben Sie
Zwischenklausur 2 20. Januar 2017 Informatik 3 Theoretische Informatik WS 2016/17 Prof. Dr. Peter Thiemann Albert-Ludwigs-Universität Freiburg Institut für Informatik Name: Übungsgruppe: Schreiben Sie
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik Sommersemester 2015 23.04.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Bis jetzt 1. Terminologie 2. Endliche Automaten und reguläre Sprachen
Grundlagen der Theoretischen Informatik Sommersemester 2015 23.04.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Bis jetzt 1. Terminologie 2. Endliche Automaten und reguläre Sprachen
Grammatiken. Eine Grammatik G mit Alphabet Σ besteht aus: Variablen V. Startsymbol S V. Kurzschreibweise G = (V, Σ, P, S)
 Grammatiken Eine Grammatik G mit Alphabet Σ besteht aus: Variablen V Startsymbol S V Produktionen P ( (V Σ) \ Σ ) (V Σ) Kurzschreibweise G = (V, Σ, P, S) Schreibweise für Produktion (α, β) P: α β 67 /
Grammatiken Eine Grammatik G mit Alphabet Σ besteht aus: Variablen V Startsymbol S V Produktionen P ( (V Σ) \ Σ ) (V Σ) Kurzschreibweise G = (V, Σ, P, S) Schreibweise für Produktion (α, β) P: α β 67 /
Die Chomsky Hierarchie
 Die Chomsky Hierarchie Slide 1 Die Chomsky Hierarchie Hans U. Simon (RUB) Email: simon@lmi.rub.de Homepage: http://www.ruhr-uni-bochum.de/lmi Die Chomsky Hierarchie Slide 2 Vorgeplänkel: Mathematische
Die Chomsky Hierarchie Slide 1 Die Chomsky Hierarchie Hans U. Simon (RUB) Email: simon@lmi.rub.de Homepage: http://www.ruhr-uni-bochum.de/lmi Die Chomsky Hierarchie Slide 2 Vorgeplänkel: Mathematische
Deterministischer Kellerautomat (DPDA)
 Deterministische Kellerautomaten Deterministischer Kellerautomat (DPDA) Definition Ein Septupel M = (Σ,Γ, Z,δ, z 0,#, F) heißt deterministischer Kellerautomat (kurz DPDA), falls gilt: 1 M = (Σ,Γ, Z,δ,
Deterministische Kellerautomaten Deterministischer Kellerautomat (DPDA) Definition Ein Septupel M = (Σ,Γ, Z,δ, z 0,#, F) heißt deterministischer Kellerautomat (kurz DPDA), falls gilt: 1 M = (Σ,Γ, Z,δ,
Maike Buchin 18. Februar 2016 Stef Sijben. Probeklausur. Theoretische Informatik. Bearbeitungszeit: 3 Stunden
 Maike Buchin 8. Februar 26 Stef Sijben Probeklausur Theoretische Informatik Bearbeitungszeit: 3 Stunden Name: Matrikelnummer: Studiengang: Geburtsdatum: Hinweise: Schreibe die Lösung jeder Aufgabe direkt
Maike Buchin 8. Februar 26 Stef Sijben Probeklausur Theoretische Informatik Bearbeitungszeit: 3 Stunden Name: Matrikelnummer: Studiengang: Geburtsdatum: Hinweise: Schreibe die Lösung jeder Aufgabe direkt
Theoretische Informatik: Berechenbarkeit und Formale Sprachen
 Prof. Dr. F. Otto 24.03.2011 Fachbereich Elektrotechnik/Informatik Universität Kassel Klausur zur Vorlesung Theoretische Informatik: Berechenbarkeit und Formale Sprachen WS 2010/2011 Name:................................
Prof. Dr. F. Otto 24.03.2011 Fachbereich Elektrotechnik/Informatik Universität Kassel Klausur zur Vorlesung Theoretische Informatik: Berechenbarkeit und Formale Sprachen WS 2010/2011 Name:................................
Reguläre Sprachen. R. Stiebe: Theoretische Informatik für ING-IF und Lehrer,
 Reguläre Sprachen Reguläre Sprachen (Typ-3-Sprachen) haben große Bedeutung in Textverarbeitung und Programmierung (z.b. lexikalische Analyse) besitzen für viele Entscheidungsprobleme effiziente Algorithmen
Reguläre Sprachen Reguläre Sprachen (Typ-3-Sprachen) haben große Bedeutung in Textverarbeitung und Programmierung (z.b. lexikalische Analyse) besitzen für viele Entscheidungsprobleme effiziente Algorithmen
Ein Satz der deutschen Sprache besitzt ein Subjekt, ein Prädikat und ein Objekt (SPO).
 1 Grammatiken Autor: Tilman Blumenbach Letzte Änderung: 28. Juni 2012 18:15 Ziel von Grammatiken Wollen die Struktur von Sprachen modellieren und charakterisieren. Beispiel Ein Satz der deutschen Sprache
1 Grammatiken Autor: Tilman Blumenbach Letzte Änderung: 28. Juni 2012 18:15 Ziel von Grammatiken Wollen die Struktur von Sprachen modellieren und charakterisieren. Beispiel Ein Satz der deutschen Sprache
Einführung in die Theoretische Informatik I/ Grundlagen der Theoretischen Informatik. SS 2007 Jun.-Prof. Dr. Bernhard Beckert Ulrich Koch
 Einführung in die Theoretische Informatik I/ Grundlagen der Theoretischen Informatik SS 2007 Jun.-Prof. Dr. Bernhard Beckert Ulrich Koch 3. Teilklausur 25. 07. 2007 Persönliche Daten bitte gut leserlich
Einführung in die Theoretische Informatik I/ Grundlagen der Theoretischen Informatik SS 2007 Jun.-Prof. Dr. Bernhard Beckert Ulrich Koch 3. Teilklausur 25. 07. 2007 Persönliche Daten bitte gut leserlich
Kontextfreie Grammatiken. Kontextfreie Grammatiken 1 / 45
 Kontextfreie Grammatiken Kontextfreie Grammatiken 1 / 45 Was kann man mit kontextfreien Grammatiken anfangen? Kontextfreie Grammatiken, kurz: werden zur Modellierung von KFGs beliebig tief geschachtelten
Kontextfreie Grammatiken Kontextfreie Grammatiken 1 / 45 Was kann man mit kontextfreien Grammatiken anfangen? Kontextfreie Grammatiken, kurz: werden zur Modellierung von KFGs beliebig tief geschachtelten
Deterministische PDAs
 Deterministische PDAs Erinnerung: Ein PDA ist deterministisch, wenn q Q, a Σ, Z Γ: δ(q,a,z) + δ(q,ε,z) 1. Definition: Eine Sprache heißt deterministisch kontextfrei, wenn es für sie einen DPDA gibt. Ziel:
Deterministische PDAs Erinnerung: Ein PDA ist deterministisch, wenn q Q, a Σ, Z Γ: δ(q,a,z) + δ(q,ε,z) 1. Definition: Eine Sprache heißt deterministisch kontextfrei, wenn es für sie einen DPDA gibt. Ziel:
Kapitel 2: Formale Sprachen Gliederung. 0. Grundbegriffe 1. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie
 Gliederung 0. Grundbegriffe 1. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.1. 2.2. Reguläre Sprachen 2.3. Kontextfreie Sprachen 2/1, Folie 1 2015 Prof. Steffen
Gliederung 0. Grundbegriffe 1. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.1. 2.2. Reguläre Sprachen 2.3. Kontextfreie Sprachen 2/1, Folie 1 2015 Prof. Steffen
Mehrdeutige Grammatiken
 Mehrdeutige Grammatiken Wir haben gesehen, dass es auch mehr als eine Linksableitung, d.h. mehr als einen Syntaxbaum geben kann, um das selbe Terminalwort zu erzeugen. Eine Grammatik, die für mindestens
Mehrdeutige Grammatiken Wir haben gesehen, dass es auch mehr als eine Linksableitung, d.h. mehr als einen Syntaxbaum geben kann, um das selbe Terminalwort zu erzeugen. Eine Grammatik, die für mindestens
2. Klausur zur Vorlesung Theoretische Grundlagen der Informatik Wintersemester 2014/2015
 2. Klausur zur Vorlesung Theoretische Grundlagen der Informatik Wintersemester 2014/2015 Hier Aufkleber mit Name und Matrikelnummer anbringen Vorname: Nachname: Matrikelnummer: Beachten Sie: Bringen Sie
2. Klausur zur Vorlesung Theoretische Grundlagen der Informatik Wintersemester 2014/2015 Hier Aufkleber mit Name und Matrikelnummer anbringen Vorname: Nachname: Matrikelnummer: Beachten Sie: Bringen Sie
Normalformen für kontextfreie Grammatiken. Noam CHOMSKY, Sheila GREIBACH. Bäume. Ableitungen in kontextfreien Grammatiken. Grammatik G = (N,T,P,S)
 Noam CHOMSKY, Sheila GREIBACH Normalformen für kontextfreie Grammatiken Noam CHOMSKY (*1928 ) Sheila GREIBACH (*1939) Grammatik G = (N,T,P,S) GREIBACH Normalform: A aw, w N* Erweiterte GREIBACH Normalform:
Noam CHOMSKY, Sheila GREIBACH Normalformen für kontextfreie Grammatiken Noam CHOMSKY (*1928 ) Sheila GREIBACH (*1939) Grammatik G = (N,T,P,S) GREIBACH Normalform: A aw, w N* Erweiterte GREIBACH Normalform:
Formale Sprachen. Grammatiken und die Chomsky-Hierarchie. Rudolf FREUND, Marian KOGLER
 Formale Sprachen Grammatiken und die Chomsky-Hierarchie Rudolf FREUND, Marian KOGLER Grammatiken Das fundamentale Modell zur Beschreibung von formalen Sprachen durch Erzeugungsmechanismen sind Grammatiken.
Formale Sprachen Grammatiken und die Chomsky-Hierarchie Rudolf FREUND, Marian KOGLER Grammatiken Das fundamentale Modell zur Beschreibung von formalen Sprachen durch Erzeugungsmechanismen sind Grammatiken.
Hochschule Bonn-Rhein-Sieg University of Applied Sciences Grantham-Allee Sankt Augustin
 Hochschule Bonn-Rhein-Sieg Uniersity of Applied Sciences Grantham-Allee 20 53757 Sankt Augustin Director b-it Applied Science Institute Fachbereich Informatik Prof. Dr. Kurt-Ulrich Witt Mathematische und
Hochschule Bonn-Rhein-Sieg Uniersity of Applied Sciences Grantham-Allee 20 53757 Sankt Augustin Director b-it Applied Science Institute Fachbereich Informatik Prof. Dr. Kurt-Ulrich Witt Mathematische und
Einführung in die Theoretische Informatik
 Technische Universität München akultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2010 Lösungsblatt 6 11. Juni 2010 Einführung in die Theoretische
Technische Universität München akultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2010 Lösungsblatt 6 11. Juni 2010 Einführung in die Theoretische
1 Die Chomsky-Hirachie
 Hans U. imon Bochum, den 7.10.2008 Annette Ilgen Beispiele zur Vorlesung Theoretische Informatik W 09/10 Vorbemerkung: Hier findet sich eine ammlung von Beispielen und Motivationen zur Vorlesung Theoretische
Hans U. imon Bochum, den 7.10.2008 Annette Ilgen Beispiele zur Vorlesung Theoretische Informatik W 09/10 Vorbemerkung: Hier findet sich eine ammlung von Beispielen und Motivationen zur Vorlesung Theoretische
Nachklausur zur Vorlesung
 Lehrstuhl für Theoretische Informatik Prof. Dr. Markus Lohrey Grundlagen der Theoretischen Informatik Nachklausur Nachklausur zur Vorlesung Grundlagen der Theoretischen Informatik WS 2016/17 / 27. Februar
Lehrstuhl für Theoretische Informatik Prof. Dr. Markus Lohrey Grundlagen der Theoretischen Informatik Nachklausur Nachklausur zur Vorlesung Grundlagen der Theoretischen Informatik WS 2016/17 / 27. Februar
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik Sommersemester 2016 20.04.2016 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Bis jetzt 1. Terminologie 2. Endliche Automaten und reguläre Sprachen
Grundlagen der Theoretischen Informatik Sommersemester 2016 20.04.2016 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Bis jetzt 1. Terminologie 2. Endliche Automaten und reguläre Sprachen
Übungsblatt Nr. 3. Lösungsvorschlag
 Institut für Kryptographie und Sicherheit Prof. Dr. Jörn Müller-Quade Nico Döttling Dirk Achenbach Tobias Nilges Vorlesung Theoretische Grundlagen der Informatik Übungsblatt Nr. 3 svorschlag Aufgabe 1
Institut für Kryptographie und Sicherheit Prof. Dr. Jörn Müller-Quade Nico Döttling Dirk Achenbach Tobias Nilges Vorlesung Theoretische Grundlagen der Informatik Übungsblatt Nr. 3 svorschlag Aufgabe 1
Grundbegriffe der Informatik Tutorium 11
 Grundbegriffe der Informatik Tutorium 11 Tutorium Nr. 32 Philipp Oppermann 29. Januar 2014 KARLSRUHER INSTITUT FÜR TECHNOLOGIE KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum
Grundbegriffe der Informatik Tutorium 11 Tutorium Nr. 32 Philipp Oppermann 29. Januar 2014 KARLSRUHER INSTITUT FÜR TECHNOLOGIE KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum
Theorie der Informatik
 Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen Malte Helmert Gabriele Röger Universität Basel 7. April 2014 Kontextsensitive und allgemeine Grammatiken Wiederholung: (kontextsensitive)
Theorie der Informatik 11. Kontextsensitive und Typ-0-Sprachen Malte Helmert Gabriele Röger Universität Basel 7. April 2014 Kontextsensitive und allgemeine Grammatiken Wiederholung: (kontextsensitive)
Die Vorausschau-Tabelle:
 A 0 i 0 A 1 i 1 β 1 A 2 i 2 β 2 B i β γ Die Vorausschau-Tabelle: Wir setzen M[ [A α Bβ, L], w] = i genau dann wenn (B, i) die Regel B γ ist und: w First k (γ) First k (β) L 440 ([A 0 α 1 A 1 β 1, L 1 ],
A 0 i 0 A 1 i 1 β 1 A 2 i 2 β 2 B i β γ Die Vorausschau-Tabelle: Wir setzen M[ [A α Bβ, L], w] = i genau dann wenn (B, i) die Regel B γ ist und: w First k (γ) First k (β) L 440 ([A 0 α 1 A 1 β 1, L 1 ],
Theoretische Informatik I
 Theoretische nformatik inheit 3 Kontextfreie Sprachen 1. Kontextfreie Grammatiken 2. Pushdown Automaten 3. igenschaften kontextfreier Sprachen Verarbeitung von Programmiersprachen Was ist das einfachste
Theoretische nformatik inheit 3 Kontextfreie Sprachen 1. Kontextfreie Grammatiken 2. Pushdown Automaten 3. igenschaften kontextfreier Sprachen Verarbeitung von Programmiersprachen Was ist das einfachste
2. Klausur zur Vorlesung Theoretische Grundlagen der Informatik Wintersemester 2016/2017
 2. Klausur zur Vorlesung Theoretische Grundlagen der Informatik Wintersemester 2016/2017 Hier Aufkleber mit Name und Matrikelnummer anbringen Vorname: Nachname: Matrikelnummer: Beachten Sie: Bringen Sie
2. Klausur zur Vorlesung Theoretische Grundlagen der Informatik Wintersemester 2016/2017 Hier Aufkleber mit Name und Matrikelnummer anbringen Vorname: Nachname: Matrikelnummer: Beachten Sie: Bringen Sie
VU Software Paradigmen / SS 2012
 VU Software Paradigmen 716.060 / SS 2012 Sandra Fruhmann sandra.fruhmann@student.tugraz.at Inhalt Grammatiken Chomsky Sprachhierarchie Parse Trees Recursive Descent Parser First-, Follow-Mengen 2 Compiler
VU Software Paradigmen 716.060 / SS 2012 Sandra Fruhmann sandra.fruhmann@student.tugraz.at Inhalt Grammatiken Chomsky Sprachhierarchie Parse Trees Recursive Descent Parser First-, Follow-Mengen 2 Compiler
Grundlagen der Informatik II
 Grundlagen der Informatik II Tutorium 2 Professor Dr. Hartmut Schmeck Miniaufgabe * bevor es losgeht * Finden Sie die drei Fehler in der Automaten- Definition. δ: A = E, S, δ, γ, s 0, F, E = 0,1, S = s
Grundlagen der Informatik II Tutorium 2 Professor Dr. Hartmut Schmeck Miniaufgabe * bevor es losgeht * Finden Sie die drei Fehler in der Automaten- Definition. δ: A = E, S, δ, γ, s 0, F, E = 0,1, S = s
Satz 90 Sei A = (Q, Σ, δ, q 0, F ) ein DFA. Der Zeitaufwand des obigen Minimalisierungsalgorithmus ist O( Q 2 Σ ).
 Satz 90 Sei A = (Q, Σ, δ, q 0, F ) ein DFA. Der Zeitaufwand des obigen Minimalisierungsalgorithmus ist O( Q 2 Σ ). Beweis: Für jedes a Σ muss jede Position in der Tabelle nur konstant oft besucht werden.
Satz 90 Sei A = (Q, Σ, δ, q 0, F ) ein DFA. Der Zeitaufwand des obigen Minimalisierungsalgorithmus ist O( Q 2 Σ ). Beweis: Für jedes a Σ muss jede Position in der Tabelle nur konstant oft besucht werden.
Theoretische Grundlagen der Informatik. Vorlesung am 02. November INSTITUT FÜR THEORETISCHE INFORMATIK
 Theoretische Grundlagen der Informatik Vorlesung am 2. November 27 2..27 Dorothea Wagner - Theoretische Grundlagen der Informatik KIT Die Forschungsuniversität in der Vorlesung am 2. November 27 Helmholtz-Gemeinschaft
Theoretische Grundlagen der Informatik Vorlesung am 2. November 27 2..27 Dorothea Wagner - Theoretische Grundlagen der Informatik KIT Die Forschungsuniversität in der Vorlesung am 2. November 27 Helmholtz-Gemeinschaft
Theoretische Informatik I
 Theoretische Informatik I Einheit 3.3 Eigenschaften kontextfreier Sprachen 1. Abschlußeigenschaften 2. Normalformen 3. Prüfen von Eigenschaften / Syntaxanalyse 4. Wann sind Sprachen nicht kontextfrei?
Theoretische Informatik I Einheit 3.3 Eigenschaften kontextfreier Sprachen 1. Abschlußeigenschaften 2. Normalformen 3. Prüfen von Eigenschaften / Syntaxanalyse 4. Wann sind Sprachen nicht kontextfrei?
Hauptklausur zur Vorlesung Theoretische Grundlagen der Informatik Wintersemester 2011/2012
 Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Hauptklausur zur Vorlesung Theoretische Grundlagen der Informatik Wintersemester 2011/2012 Hier Aufkleber mit Name und Matrikelnr. anbringen
Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Hauptklausur zur Vorlesung Theoretische Grundlagen der Informatik Wintersemester 2011/2012 Hier Aufkleber mit Name und Matrikelnr. anbringen
Einführung in Berechenbarkeit, Formale Sprachen und Komplexitätstheorie
 Einführung in Berechenbarkeit, Formale Sprachen und Komplexitätstheorie Wintersemester 2005/2006 07.02.2006 28. und letzte Vorlesung 1 Die Chomsky-Klassifizierung Chomsky-Hierachien 3: Reguläre Grammatiken
Einführung in Berechenbarkeit, Formale Sprachen und Komplexitätstheorie Wintersemester 2005/2006 07.02.2006 28. und letzte Vorlesung 1 Die Chomsky-Klassifizierung Chomsky-Hierachien 3: Reguläre Grammatiken
Theoretische Informatik I (Grundzüge der Informatik I)
 Theoretische Informatik I (Grundzüge der Informatik I) Literatur: Buch zur Vorlesung: Uwe Schöning, Theoretische Informatik - kurzgefasst. Spektrum Akademischer Verlag, Heidelberg/Berlin, 4. Auflage, 2001.
Theoretische Informatik I (Grundzüge der Informatik I) Literatur: Buch zur Vorlesung: Uwe Schöning, Theoretische Informatik - kurzgefasst. Spektrum Akademischer Verlag, Heidelberg/Berlin, 4. Auflage, 2001.
Dank. Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I. Reguläre Ausdrücke als Suchmuster für grep
 Dank Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert Diese Vorlesungsmaterialien basieren ganz wesentlich auf den Folien zu den Vorlesungen
Dank Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert Diese Vorlesungsmaterialien basieren ganz wesentlich auf den Folien zu den Vorlesungen
Wortproblem für kontextfreie Grammatiken
 Wortproblem für kontextfreie Grammatiken G kontextfreie Grammatik. w Σ w L(G)? Wortproblem ist primitiv rekursiv entscheidbar. (schlechte obere Schranke!) Kellerautomat der L(G) akzeptiert Ist dieser effizient?
Wortproblem für kontextfreie Grammatiken G kontextfreie Grammatik. w Σ w L(G)? Wortproblem ist primitiv rekursiv entscheidbar. (schlechte obere Schranke!) Kellerautomat der L(G) akzeptiert Ist dieser effizient?
q 0 q gdw. nicht (q A) (q A) q i+1 q gdw. q i q oder ( a Σ) δ(q, a) i δ(q, a) L = {a n b n : n N} für a, b Σ, a b
 Kap. 2: Endliche Automaten Myhill Nerode 2.4 Minimalautomat für reguläre Sprache Abschnitt 2.4.3 L Σ regulär der Äuivalenzklassen-Automat zu L ist ein DFA mit minimaler Zustandszahl (= index( L )) unter
Kap. 2: Endliche Automaten Myhill Nerode 2.4 Minimalautomat für reguläre Sprache Abschnitt 2.4.3 L Σ regulär der Äuivalenzklassen-Automat zu L ist ein DFA mit minimaler Zustandszahl (= index( L )) unter
...imbeispiel: Die Konkatenation der Blätter des Ableitungsbaums t bezeichnen wir auch mit yield(t). liefert die Konkatenation: name int + int.
 Die Konkatenation der Blätter des Ableitungsbaums t bezeichnen wir auch mit yield(t)....imbeispiel: E 0 E 1 + T 1 T 0 F 2 T 1 F 2 int F 1 int name liefert die Konkatenation: name int + int. 273 Die Grammatik
Die Konkatenation der Blätter des Ableitungsbaums t bezeichnen wir auch mit yield(t)....imbeispiel: E 0 E 1 + T 1 T 0 F 2 T 1 F 2 int F 1 int name liefert die Konkatenation: name int + int. 273 Die Grammatik
Formale Sprachen. Grammatiken. Grammatiken und die Chomsky-Hierarchie. Rudolf FREUND, Marion OSWALD. Grammatiken: Ableitung
 Formale Sprachen rammatiken und die Chomsky-Hierarchie Rudolf FREUND, Marion OSWALD rammatiken Das fundamentale Modell zur Beschreibung von formalen Sprachen durch Erzeugungsmechanismen sind rammatiken.
Formale Sprachen rammatiken und die Chomsky-Hierarchie Rudolf FREUND, Marion OSWALD rammatiken Das fundamentale Modell zur Beschreibung von formalen Sprachen durch Erzeugungsmechanismen sind rammatiken.
Andererseits ist L kontextfrei, wie die einfache kontextfreie Grammatik G = ({a, b},{s}, S, P) mit den Regeln
 REG versus CF Theorem REG ist echt in CF enthalten. Beweis: Wir wissen: L = {a m b m m 1} ist nicht regulär. Andererseits ist L kontextfrei, wie die einfache kontextfreie Grammatik G = ({a, b},{s}, S,
REG versus CF Theorem REG ist echt in CF enthalten. Beweis: Wir wissen: L = {a m b m m 1} ist nicht regulär. Andererseits ist L kontextfrei, wie die einfache kontextfreie Grammatik G = ({a, b},{s}, S,
Formale Grundlagen der Informatik
 Formale Grundlagen der Informatik / 2015 1 Reguläre Ausdrücke Kommen in der Praxis immer dann vor, wenn standardisierte Eingaben erforderlich sind: Telefonnummern: +Land (0) Ort Anschluß Dateinamen: (A-Z,
Formale Grundlagen der Informatik / 2015 1 Reguläre Ausdrücke Kommen in der Praxis immer dann vor, wenn standardisierte Eingaben erforderlich sind: Telefonnummern: +Land (0) Ort Anschluß Dateinamen: (A-Z,
