WS07/08 Automaten und Formale Sprachen 5. Vorlesung
|
|
|
- Reinhardt Hofmann
- vor 6 Jahren
- Abrufe
Transkript
1 WS7/8 Automaten und Formale Sprachen 5. Vorlesung Martin Dietzfelbinger 3. November 27 FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ Stichworte Induktive Definitionen: (i) Basisobjekte, (ii) Regeln, um aus schon konstruierten Objekten neue zu machen. Beispiel : Aussagenlogische Formeln, Auswertung unter einer Belegung. Beispiel 2: Korrekte Klammerausdrücke, nichtrekursive Charakterisierung. Reguläre Ausdrücke r : Induktiv definiert.,, a Σ sind reg.a. Wenn r, r,r 2 reg.a., dann auch (r + r 2 ), (r r 2 ), (r ). Sprache L(r) zu regulärem Ausdruck: Per Induktion über den Aufbau von r definiert. FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ Ziel: DFA s, NFA s, reguläre Ausdrücke sind äquivalent : Mit jedem dieser Formalismen kann man genau die regulären Sprachen beschreiben. Erste Groß-Konstruktion : Von NFA M zu reg.a. r M. Zentrale Idee: Hilfssprachen L(i, j, k), Rekursion über k =,..., Q. Aus Vorlesung vom 6..: Vom regulären Ausdruck zum NFA. Zwei Abschlusseigenschaften Satz (2.3.2) L, L, L 2 regulär L und L L 2 regulär. Die Klasse der regulären Sprachen ist unter den Operationen Konkatenation und Kleene-Abschluss abgeschlossen. FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/
2 Beweis: (a) (Kleene-Abschluss) L sei durch DFA M gegeben. Baue aus M einen äquivalenten reg.a. r = r M. Dann ist L(r )=L,also L regulär. (b) (Konkatenation) L,L 2 seien durch DFA s M,M 2 gegeben. Baue aus M,M 2 äquivalente reg.a.e r bzw. r 2. Dann ist L L 2 = L(r r 2 ),also L L 2 regulär. Interessante Übung: Beweise den Satz direkt mit NFA s (oder -NFA s). Zusammenfassung: (Satz 2.5.) Die Klasse der regulären Sprachen enthält alle endlichen Sprachen und ist abgeschlossen unter: Durchschnitt (DFA-Kreuzproduktkonstruktion) Komplement (Komplement-DFA) Vereinigung (Kreuzpr.-Konstr. oder reg.a.) Konkatenation (reg.a.) Kleene-Abschluss (reg.a.) FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ Das Pumping-Lemma für reguläre Sprachen Eine Methode, um Nicht-Regularität zu beweisen Wie zeigt man, dass eine gegebene Sprache L regulär ist? DFA angeben NFA angeben -NFA angeben Regulären Ausdruck angeben (Reguläre Grammatik angeben später) Zeigen, dass L = L L 2,wobeiL,L 2 regulär. Oder: Durchschnitt, Komplement, Kleene-Abschluss, usw.... NIEMALS ABER: mit dem Pumping-Lemma FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/
3 Beweis des Pumping-Lemmas: L sei reguläre Sprache. Das heißt: L = L M für einen NFA M =(Q, Σ, q, F, δ). Definiere n := Q. Betrachte ein beliebiges x = a a m L, m n. Akzeptierende Berechnung von M für x: Start p a p a 2 p a 3 p a 4... a n p... a m p 2 3 n m (p = q ) entspricht einem Weg P x =(p,...,p m ) von p = q nach p m = q, q F,inG M. Kanten mit a,...,a m markiert. Start p a p a 2 p a 3 2 p a 4 a n 3 p a m... n... p m (p = q ) Schubfachprinzip : Die n +Zustände p,p,...,p n (in Q, mitn = Q ) entlang des Weges können nicht alle verschieden sein es gibt k, l {,...,n} mit k<lund p k = p l. Definiere Teilwörter von x: u := a a k v := a k+ a l w := a l+ a m. Beobachte: (i) x = uvw; (ii) l = uv n; (iii) v = l k. FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ (p ) u = a a k (p k ) v = a k+ a l (p l ) w = a l+ a m (p m ) Weg zerschneiden: Mit u von p nach p k = p l. Mit v von p k nach p l = p k. Mit w von p l = p k nach p m F. Wieder zusammensetzen, aber anders: Mit u von p nach p k. Mit w von p k nach p m F. Mit uw von p nach p m F uw L. Mit u von p nach p k. Mit v von p k nach p k. Mit v von p k nach p k. Mit w von p k nach p m F. Mit uvvw von p nach p m F uv 2 w L. (p ) u = a a k (p k ) v = a k+ a l (p l ) w = a l+ a m (p m ) Weg zerschneiden: Mit u von p nach p k = p l. Mit v von p k nach p l = p k. Mit w von p l = p k nach p m F. Wieder zusammensetzen, aber anders: Mit u von p nach p k. Mit v von p k nach p k. Mit v von p k nach p k. Mit v von p k nach p k. Mit w von p k nach p m F. Mit uvvvw von p nach p m F uv 3 w L. Und so weiter. Man sieht: (iv) Für jedes i ist uv i w L. FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/
4 2.4. Satz (Pumping-Lemma für reguläre Sprachen) Wenn L eine reguläre Sprache ist, dann gibt es ein n derart dass für alle x L mit x n gilt: es gibt Wörter u, v, w Σ mit : (i) x = uvw (ii) uv n (iii) v (iv) uv i w L für alle i ( uv i w = uv v }{{} w ) i mal Eine Struktureigenschaft regulärer Sprachen Kein Bezug zu irgendeiner Darstellungsform! Behauptung (a): L = { m m m N} ist nicht regulär. Beweis: Indirekt. Annahme: L ist regulär. (Ziel: Widerspruch) Nach dem Pumping-Lemma (PL) gibt es ein n, sodass: Für jedes x L, x n, gibt es u, v, w Σ mit (i), (ii), (iii), (iv). Wir wählen nun x := n n. (Es macht nichts, dass wir nicht wissen, wie groß n ist.) Dann ist x L und x =2n n. PL es gibt u, v, w mit (i), (ii), (iii), (iv). FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ L = { m m m N} Haben schon: n, x = n n und u, v, w {, } mit (i) x = uvw, (ii) uv n, (iii) v, (iv) uv i w L für alle i. x = uvw = }{{}}{{} n mal n mal uv n uv besteht nur aus Nullen. v d.h. v uv w = uw = n v n Weil n v <n,istuv w/ L. Widerspruch zu (iv)! Also ist L nicht regulär. Behauptung (b): L 2 = { m2 m N} ist nicht regulär. Beweis: Indirekt. Annahme: L 2 ist regulär. Nach dem Pumping-Lemma (PL) gibt es ein n, sodass: Für jedes x L 2, x n, gibt es u, v, w Σ mit (i), (ii), (iii), (iv) Wir wählen x := n2. Dann ist x = n 2 >n. PL es gibt u, v, w mit (i), (ii), (iii), (iv). FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/
5 L 2 = { m2 m N}. Haben schon: n, x = n n und u, v, w {, } mit (i) x = uvw, (ii) uv n, (iii) v, (iv) uv i w L für alle i. x = uvw = }{{} n 2 mal uv n und v v n. Es ist uv 2 w = u v v w = x + v = n2 + v. Wir wählen i =2. Weil n 2 + v n 2 + n<n 2 +2n +=(n +) 2,istn 2 + v keine Quadratzahl, also uv 2 w/ L 2 Widerspruch zu (iv)! Gegeben: Sprache L. BEWEIS-SCHEMA Behauptung: L ist nicht regulär. [] (Wörtlich) Beweis indirekt. Annahme: L ist regulär. [] (Wörtlich) Dann gibt es ein n mit den im Pumping- Lemma behaupteten Eigenschaften. ( Für jedes x L mit x n gibt es u, v, w mit (i) (iv). ) [2] (Problemspezifisch) Wir wählen ein geeignetes x L, mit x n sodassschritt[4]ausführbar ist. [3] (Wörtlich) Nach dem PL gibt es u, v, w Σ mit (i) (iv). [4] (Problemspezifisch) Wir wählen (zu u, v, w) einpassendes i und zeigen, dass uv i w nicht in L sein kann. [5] (Wörtlich) Widerspruch zu (iv). FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ Äquivalent: SPIEL-SCHEMA Gegeben: Sprache L Behauptung: L ist nicht regulär. Wir (B: diebeweiser, oderdie Braven ) spielen gegen den Gegner G (wie Gemein ) Runde : G gibt uns eine Zahl n. Runde 2: B Wir wählen geschickt ein x L mit x n (sodassrunde4immergutfür uns ausgeht) Runde 3: G gibt uns u, v, w mit (i) x = uvw, (ii) uv n und (iii) v. Wir wissen nicht genau, wieu, v, w in x liegen. Runde 4: B Wir wählen, eventuell abhängig von u, v, w, eini und zeigen, dass uv i w/ L. In einem Durchlauf des Spiels gewinnt B, wennuv i w/ L ist. (Andernfalls gewinnt G.) B hat eine Gewinnstrategie, wennb in Runde 2 immer ein x wählen kann, so dass B in Runde 4 immer ein i wählen kann, das zum Gewinn führt. (Egal was G tut.) Behauptung: Wenn B eine Gewinnstrategie hat, dann ist L nicht regulär. Beweis: Kontraposition des Pumping-Lemmas. FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/
6 Das Pumping-Lemma hat die Form A B wobei A bedeutet L ist regulär und B so aussieht: n x L : x n u, v, w : (i) x = uvw (ii) uv n (iii) v (iv) i : uv i w L. Dazu äquivalent ist die Kontraposition: B A. Dabei ist A: L ist nicht regulär und B ist und B ist n x L : x n ( u, v, w : ((i) x = uvw (ii) uv n (iii) v ) i : uv i w/ L). Wenn B immer gewinnen kann, d.h. eine Gewinnstrategie hat, bedeutet das genau, dass B gilt. Und aus B folgt A. FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ Beh. (c): L 3 = { m l m+l m, l N} ist nicht regulär. (Die Sprache L 3 codiert die unäre Addition.) Beweis: Per SPIEL-SCHEMA... Beweis per SPIEL-SCHEMA: Runde : G gibt uns eine Zahl n Runde 2: B Wir wählen x = n n. Klar: x L 3, x >n. Runde 3: G gibt uns u, v, w mit (i) x = uvw und (ii) uv n und (iii) v. Runde 4: B x beginnt mit genau n Nullen. Wegen (ii) ist uv ein Präfix dieses Teils n, besteht also nur aus Nullen. Also: uv w = uw = n v n, nicht in L 3. Wir wählen i =.Dannistuv i w/ L 3.Fertig. FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/
7 Beh. (d): L 4 = { p p N ist eine Primzahl } ist nicht regulär. Beweis per SPIEL-SCHEMA: Runde : G gibt uns eine Zahl n Runde 2: B Wir wählen x = p für eine Primzahl p n+2. Klar: x L 4 und x >n. Wir wählen: i := uw. Das ist w 2. Nun: uv i w = uw + i v = uw + uw v = uw ( + v ) Dies ist keine Primzahl, weil uw 2 und + v 2. Also: uv i w/ L 4. Wir (B) gewinnen immer. Also ist L 4 nicht regulär. Runde 3: G gibt uns u, v, w mit (i) x = uvw und (ii) uv n und (iii) v. Runde 4: B Wir müssen i so wählen, dass uv i w keine Primzahl ist. Am besten: durch uw teilbar. FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ Beh. (e): L 5 = {w {, } w ist korrekter Klammerausdruck } ist nicht regulär. Beweis per SPIEL-SCHEMA: Runde : G gibt uns eine Zahl n Runde 2: B Wir wählen x = n n. Klar: x L 5, x n. Runde 3: G gibt uns u, v, w mit (i) x = uvw und (ii) uv n und (iii) v. Runde 4: B Wir wählen: i :=. Weil uv n, bestehtuv nur aus Nullen. Also: uv w = n v n / L 5. (Kein korrekter Klammerausdruck, da Anzahl der Nullen und Einsen verschieden.) 2.5 Weitere Abschlusseigenschaften Substitution, Homomorphismus, Inverser Homomorphismus, Spiegelung Substitution Hintergrund: Hierarchische Definition von (regulären) Sprachen. FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/
8 Beispiel : Bezeichner in Pascal-Programmen Pascal: beginnt mit mindestens einem Buchstaben, es folgen Buchstaben und Ziffern in beliebiger Reihenfolge L = L(B(B + Z) ) über dem Alphabet Σ={B, Z} In Wort aus L möchten wir einsetzen: für jedes B einen Buchstaben aus L B = {a, b,...,z, A, B,...,Z} für jedes Z eine Ziffer aus L Z = {,,...,9} Aus BBBBB entsteht April oder IxZwo Aus BZBZZZ entsteht zx23 oder R9R294 Definition (2.5.2) Substitution Seien Σ und Δ Alphabete, L sei Sprache über Σ. Betrachte Funktion f :Σ P(Δ ), d. h. f(a) =L a ist eine Sprache über Δ,für jedes a Σ. Ein Wort w ist in f(l) falls man w = w w 2...w s schreibenkannfür ein Wort a a s L und w L a,...,w s L as. Satz (2.5.3) L, f(a ),...,f(a n ) regulär f(l) regulär. FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ Die Klasse der regulären Sprachen ist unter Substitution abgeschlossen. Wenn wir Sprachen hierarchisch definieren und alle Komponenten reguläre Sprachen sind, ist auch das Ergebnis eine reguläre Sprache. Beweis: SeiM =(Q, Σ,q,F,δ) ein NFA mit L = L M. Für jedes a Σ sei M a ein NFA mit L a = L Ma. In G M, ersetze Kante von M a M a q a q durch eine Kopie q G Ma q wobei eine -Kante von q zum Startzustand von M a führt und -KantenvondenakzeptierendenZuständen von M a zu q Resultat: M. FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/
9 Die -Kanten erzwingen, dass die Unter-NFA s nur in der vorgesehenen Richtung durchlaufen werden können und keine Vermengung passieren kann. Dann: w wird von M akzeptiert es gibt in M einen Weg von q zu einem q F,dessen Kanten mit den Buchstaben von w beschriftet sind es gibt in M einen Weg von q zu einem q F,dessen Kanten mit a,...,a m beschriftet sind und so dass w = w w m mit w i L Mai = L ai w f(l). Also: f(l) =L M,alsof(L) regulär. Homomorphismus: Spezielle Substitution, wo jedes L a genau ein Wort g(a) Δ enthält. Für Buchstaben a Σ setze Wort g(a) Δ ein. Dann: g(a a m ):=g(a ) g(a m ). Beispiel : g() = ara, g() = rat ; L = {, } g(l )={, ara, rat, araara, ararat, ratara, ratrat,...} Satz (2.5.5(a)) L regulär, g :Σ Δ beliebig L = {g(w) w L} regulär. (Folgt aus dem allgemeineren Ergebnis für Substitution.) FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ Diesen Satz benutzt man meistens, um Nichtregularität zu beweisen. Beispiel: DieSpracheL aller vollständig geklammerten arithmetischen Ausdrücke aus ganzen Zahlen, wobei die Zahlen in Dezimaldarstellung gegeben sind... (Beispiel: (((2+7)/(6*8))-(7*(3/(-3)))) ) ist nicht regulär. Beweis: Betrachte folgenden Homomorphismus g: Δ={, }, Σ besteht aus Dezimalziffern, Operatoren, Klammern. g(() =;g()) =;g(a) = für die anderen Zeichen. Dann: g(l) ist die Menge der korrekten Klammerausdrücke. Diese ist nicht regulär, also kann auch L nicht regulär sein. Sprach-Operation Inverser Homomorphismus: Sei g :Σ Δ ein Homomorphismus. Sei L Δ Sprache. Dann: g (L ):={w Σ g(w) L }. Sprache über Σ. Satz (2.5.5(b)) Ist L regulär, dann ist auch g (L ) regulär. FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/
10 Beweis: g (L )= {w = a a m Σ g(w) =g(a ) g(a m ) L }. Sei M =(Q, Δ,q,F,δ ) DFA mit L = L M. Wir bauen neuen DFA M =(Q, Σ,q,F,δ) durch: Damit sofort: w g (L ) g(w) L δ (q,g(w)) F δ(q,w) F w L M. D.h.: g (L )=L M,alsoregulär. Q := Q,q := q,f := F, und δ(q, a) :=δ (q, g(a)), für q Q und a Σ Man zeigt dann (Induktion über m = w ): δ(q, w) =δ(q,a a m )=δ (q, g(a ) g(a m )) = δ (q,g(w)). FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ Spiegelung Beispiele : Spiegelung von Wörtern (a) (b) if fi (c) abracadabra arbadacarba (d) Beispiele : Spiegelung von Sprachen (a) {, } {, } (b) {,,,,...} {,,,,...} (c) L( )={ i j i, j } { j i i, j } = L( ) (d) {a n b n c n n } {c n b n a n n } (e) elle elle ( Palindrom ) FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/
11 . Definition (2.5.6) (a) Für w = a a 2 a n Σ setze w R := a n a 2 a (b) Für L Sprache setze L R := {w R w L} Satz (2.5.7) L regulär L R regulär. 2 Beweise, beide konstruktiv. Einer mit -NFA s, einer mit regulären Ausdrücken. Beweis: WennL = L M für einen -NFA M =(Q, Σ,q,F,δ), dann baue G M so um, dass genau ein akzeptierender Zustand q existiert, d.h. F = {q }. G M : Start, G M : Start Füge neuen Endzustand q hinzu, führe -Kanten von jedem vorherigen Endzustand nach q., FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ Liefert -NFA M für L. G M : Start, G M" :, Drehe in M alle Kanten um; vertausche Start- und Endzustand. Liefert neuen -NFA: M. Klar: Weg in G M von q zu q,mitw beschriftet Weg in G M von q zu q,mitw R beschriftet. Also: L M = L R M. Start Zweiter Beweis, mit regulären Ausdrücken. Beispiel: L = L(((a + b)(b + c)) (ab)), dann L R = L((ba)((b + c)(a + b)) ). Zu jedem reg.a. r gibt es einen reg.a. r mit L(r )=L(r) R. Induktion über den Aufbau von regulären Ausdrücken! (i) r =, r =, r = a: r =, r =, r = a. (ii) r =(r r 2 ): r =(r 2r ). r =(r + r 2 ): r =(r + r 2). r =(r): r =(r ). FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/
12 Stichworte Äquivalenz DFA, NFA, reguläre Ausdrücke. Mehrere wesentliche Konstruktionen. Das Pumping-Lemma: Eine Struktureigenschaft. Mit dem Pumping-Lemma beweist man Nichtregularität von Sprachen. Widerspruchsbeweis-Schema. Alternativ: Spiel-Schema. Abschlusseigenschaften: Vereinigung, Durchschnitt, Komplement, Konkatenation, Kleene-Abschluss, Substitution, Homomorphismus, inverser Homomorphismus, Spiegelung. Bis nächste Woche: Folien aus Netz besorgen. Skript Seiten und 45 5 (letzte Vorlesung) und 5 66 (diese Vorlesung) durcharbeiten. Definitionen lernen, Beispiele ansehen, Fragen vorbereiten. FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/ FG KTuEA, TU Ilmenau Automaten und Formale Sprachen WS7/
Typ-3-Sprachen. Das Pumping-Lemma
 Das Pumping-Lemma Typ-3-Sprachen Um zu zeigen, daß eine Sprache L regulär ist, kannman einen NFA M angeben mit L(M) = L, oder eine rechtslineare Grammatik G angeben mit L(G) =L, oder einen regulären Ausdruck
Das Pumping-Lemma Typ-3-Sprachen Um zu zeigen, daß eine Sprache L regulär ist, kannman einen NFA M angeben mit L(M) = L, oder eine rechtslineare Grammatik G angeben mit L(G) =L, oder einen regulären Ausdruck
Das Pumping-Lemma Formulierung
 Das Pumping-Lemma Formulierung Sei L reguläre Sprache. Dann gibt es ein n N mit: jedes Wort w L mit w n kann zerlegt werden in w = xyz, so dass gilt: 1. xy n 2. y 1 3. für alle k 0 ist xy k z L. 59 / 162
Das Pumping-Lemma Formulierung Sei L reguläre Sprache. Dann gibt es ein n N mit: jedes Wort w L mit w n kann zerlegt werden in w = xyz, so dass gilt: 1. xy n 2. y 1 3. für alle k 0 ist xy k z L. 59 / 162
Die Nerode-Relation und der Index einer Sprache L
 Die Nerode-Relation und der Index einer Sprache L Eine zweite zentrale Idee: Sei A ein vollständiger DFA für die Sprache L. Repäsentiere einen beliebigen Zustand p von A durch die Worte in Σ, die zu p
Die Nerode-Relation und der Index einer Sprache L Eine zweite zentrale Idee: Sei A ein vollständiger DFA für die Sprache L. Repäsentiere einen beliebigen Zustand p von A durch die Worte in Σ, die zu p
Definition (Reguläre Ausdrücke) Sei Σ ein Alphabet, dann gilt: (ii) ε ist ein regulärer Ausdruck über Σ.
 Reguläre Ausdrücke Definition (Reguläre Ausdrücke) Sei Σ ein Alphabet, dann gilt: (i) ist ein regulärer Ausdruck über Σ. (ii) ε ist ein regulärer Ausdruck über Σ. (iii) Für jedes a Σ ist a ein regulärer
Reguläre Ausdrücke Definition (Reguläre Ausdrücke) Sei Σ ein Alphabet, dann gilt: (i) ist ein regulärer Ausdruck über Σ. (ii) ε ist ein regulärer Ausdruck über Σ. (iii) Für jedes a Σ ist a ein regulärer
Sei Σ ein endliches Alphabet. Eine Sprache L Σ ist genau dann regulär, wenn sie von einem regulären Ausdruck beschrieben werden kann.
 Der Satz von Kleene Wir haben somit Folgendes bewiesen: Der Satz von Kleene Sei Σ ein endliches Alphabet. Eine Sprache L Σ ist genau dann regulär, wenn sie von einem regulären Ausdruck beschrieben werden
Der Satz von Kleene Wir haben somit Folgendes bewiesen: Der Satz von Kleene Sei Σ ein endliches Alphabet. Eine Sprache L Σ ist genau dann regulär, wenn sie von einem regulären Ausdruck beschrieben werden
Reguläre Sprachen. R. Stiebe: Theoretische Informatik für ING-IF und Lehrer,
 Reguläre Sprachen Reguläre Sprachen (Typ-3-Sprachen) haben große Bedeutung in Textverarbeitung und Programmierung (z.b. lexikalische Analyse) besitzen für viele Entscheidungsprobleme effiziente Algorithmen
Reguläre Sprachen Reguläre Sprachen (Typ-3-Sprachen) haben große Bedeutung in Textverarbeitung und Programmierung (z.b. lexikalische Analyse) besitzen für viele Entscheidungsprobleme effiziente Algorithmen
Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen
 Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen 18.4. 2012 176 Automatentheorie und formale Sprachen VL 5 Reguläre und nichtreguläre Sprachen Kathrin Hoffmann 18. Aptil 2012 Hoffmann (HAW
Hoffmann (HAW Hamburg) Automatentheorie und formale Sprachen 18.4. 2012 176 Automatentheorie und formale Sprachen VL 5 Reguläre und nichtreguläre Sprachen Kathrin Hoffmann 18. Aptil 2012 Hoffmann (HAW
Grundlagen der theoretischen Informatik
 Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 09.04.2013 Inhalt der Vorlesung Teil I: Automaten und formale Sprachen (Kurt Sieber)
Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 09.04.2013 Inhalt der Vorlesung Teil I: Automaten und formale Sprachen (Kurt Sieber)
Die mathematische Seite
 Kellerautomaten In der ersten Vorlesung haben wir den endlichen Automaten kennengelernt. Mit diesem werden wir uns in der zweiten Vorlesung noch etwas eingängiger beschäftigen und bspw. Ansätze zur Konstruktion
Kellerautomaten In der ersten Vorlesung haben wir den endlichen Automaten kennengelernt. Mit diesem werden wir uns in der zweiten Vorlesung noch etwas eingängiger beschäftigen und bspw. Ansätze zur Konstruktion
Theoretische Informatik für Wirtschaftsinformatik und Lehramt
 Theoretische Informatik für Wirtschaftsinformatik und Lehramt Eigenschaften regulärer Sprachen Priv.-Doz. Dr. Stefan Milius stefan.milius@fau.de Theoretische Informatik Friedrich-Alexander Universität
Theoretische Informatik für Wirtschaftsinformatik und Lehramt Eigenschaften regulärer Sprachen Priv.-Doz. Dr. Stefan Milius stefan.milius@fau.de Theoretische Informatik Friedrich-Alexander Universität
Formale Methoden 1. Gerhard Jäger 23. Januar Uni Bielefeld, WS 2007/2008 1/18
 1/18 Formale Methoden 1 Gerhard Jäger Gerhard.Jaeger@uni-bielefeld.de Uni Bielefeld, WS 2007/2008 23. Januar 2008 2/18 Das Pumping-Lemma Sein L eine unendliche reguläre Sprache über ein endliches Alphabet
1/18 Formale Methoden 1 Gerhard Jäger Gerhard.Jaeger@uni-bielefeld.de Uni Bielefeld, WS 2007/2008 23. Januar 2008 2/18 Das Pumping-Lemma Sein L eine unendliche reguläre Sprache über ein endliches Alphabet
Theoretische Informatik Mitschrift
 5 Eigenschaften regulärer Sprachen 51: Die Nerode-Relation Theoretische Informatik Mitschrift Definition 51: Sei L * L * * mit L :={u, v * * w *:uw L v w L }heißt Nerode-Relation von L Sei ={0,1}, L= *{00}
5 Eigenschaften regulärer Sprachen 51: Die Nerode-Relation Theoretische Informatik Mitschrift Definition 51: Sei L * L * * mit L :={u, v * * w *:uw L v w L }heißt Nerode-Relation von L Sei ={0,1}, L= *{00}
Theorie der Informatik
 Theorie der Informatik 8. Reguläre Sprachen II Malte Helmert Gabriele Röger Universität Basel 24. März 24 Pumping Lemma Pumping Lemma: Motivation Man kann zeigen, dass eine Sprache regulär ist, indem man
Theorie der Informatik 8. Reguläre Sprachen II Malte Helmert Gabriele Röger Universität Basel 24. März 24 Pumping Lemma Pumping Lemma: Motivation Man kann zeigen, dass eine Sprache regulär ist, indem man
Theoretische Informatik Kap 1: Formale Sprachen/Automatentheorie
 Gliederung der Vorlesung. Grundbegriffe. Formale Sprachen/Automatentheorie.. Grammatiken.2..3. Kontext-freie Sprachen 2. Berechnungstheorie 2.. Berechenbarkeitsmodelle 2.2. Die Churchsche These 2.3. Unentscheidbarkeit
Gliederung der Vorlesung. Grundbegriffe. Formale Sprachen/Automatentheorie.. Grammatiken.2..3. Kontext-freie Sprachen 2. Berechnungstheorie 2.. Berechenbarkeitsmodelle 2.2. Die Churchsche These 2.3. Unentscheidbarkeit
liefern eine nicht maschinenbasierte Charakterisierung der regulären
 Reguläre Ausdrücke 1 Ziel: L=L M für NFA M L=L(r) für einen regulären Ausdruck r Reguläre Ausdrücke über einem Alphabet Σ Slide 1 liefern eine nicht maschinenbasierte Charakterisierung der regulären Sprachen
Reguläre Ausdrücke 1 Ziel: L=L M für NFA M L=L(r) für einen regulären Ausdruck r Reguläre Ausdrücke über einem Alphabet Σ Slide 1 liefern eine nicht maschinenbasierte Charakterisierung der regulären Sprachen
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Übung am 3..2 INSTITUT FÜR THEORETISCHE KIT 7..2 Universität des Andrea Landes Schumm Baden-Württemberg - Theoretische und Grundlagen der Informatik INSTITUT FÜR
Theoretische Grundlagen der Informatik Übung am 3..2 INSTITUT FÜR THEORETISCHE KIT 7..2 Universität des Andrea Landes Schumm Baden-Württemberg - Theoretische und Grundlagen der Informatik INSTITUT FÜR
Grenzen der Regularität
 Grenzen der Regularität Um die Mächtigkeit von endlichen Automaten zu verstehen, muss man auch ihre Grenzen kennen. Sei z.b. B = {0 n 1 n n 0} Gibt es einen DEA für B? Es sieht so aus, als müsste sich
Grenzen der Regularität Um die Mächtigkeit von endlichen Automaten zu verstehen, muss man auch ihre Grenzen kennen. Sei z.b. B = {0 n 1 n n 0} Gibt es einen DEA für B? Es sieht so aus, als müsste sich
4. Übung zur Vorlesung Informatik III am
 1 4. Übung zur Vorlesung Informatik III am 16.11.2007 Wiederholung Konkatenation 2 Definition Konkatenation Eine endliche Folge w von Symbolen aus Σ heißt Wort. Die Menge aller Wörter über Σ heißt Σ. Sei
1 4. Übung zur Vorlesung Informatik III am 16.11.2007 Wiederholung Konkatenation 2 Definition Konkatenation Eine endliche Folge w von Symbolen aus Σ heißt Wort. Die Menge aller Wörter über Σ heißt Σ. Sei
FORMALE SYSTEME. 10. Vorlesung: Grenzen regulärer Sprachen / Probleme für Automaten. TU Dresden, 14. November 2016.
 FORMALE SYSTEME 10. Vorlesung: Grenzen regulärer Sprachen / Probleme für Automaten Markus Krötzsch TU Dresden, 14. November 2016 Rückblick Markus Krötzsch, 14. November 2016 Formale Systeme Folie 2 von
FORMALE SYSTEME 10. Vorlesung: Grenzen regulärer Sprachen / Probleme für Automaten Markus Krötzsch TU Dresden, 14. November 2016 Rückblick Markus Krötzsch, 14. November 2016 Formale Systeme Folie 2 von
Satz (Abschluß unter der Stern-Operation)
 Satz (Abschluß unter der Stern-Operation) Wenn L eine reguläre Sprache ist, dann ist auch L regulär. Beweis: Es gibt einen NFA M = (Z, Σ, S, δ, S, E) mit L(M) = L. Wir bauen aus diesem NFA nun wie folgt
Satz (Abschluß unter der Stern-Operation) Wenn L eine reguläre Sprache ist, dann ist auch L regulär. Beweis: Es gibt einen NFA M = (Z, Σ, S, δ, S, E) mit L(M) = L. Wir bauen aus diesem NFA nun wie folgt
Ein deterministischer endlicher Automat (DFA) kann als 5-Touple dargestellt werden:
 Sprachen und Automaten 1 Deterministische endliche Automaten (DFA) Ein deterministischer endlicher Automat (DFA) kann als 5-Touple dargestellt werden: M = (Z,3,*,qo,E) Z = Die Menge der Zustände 3 = Eingabealphabet
Sprachen und Automaten 1 Deterministische endliche Automaten (DFA) Ein deterministischer endlicher Automat (DFA) kann als 5-Touple dargestellt werden: M = (Z,3,*,qo,E) Z = Die Menge der Zustände 3 = Eingabealphabet
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik 3. Endliche Automaten (V) 20.05.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Organisatorisches 1. Teilklausur: Mittwoch, 10.06.2015, D028,
Grundlagen der Theoretischen Informatik 3. Endliche Automaten (V) 20.05.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Organisatorisches 1. Teilklausur: Mittwoch, 10.06.2015, D028,
Suche nach einem solchen Kreis. Endlichkeitstest. Vereinigung und Durchschnitt. Abschlusseigenschaften
 Endlichkeitstest Eingabe: DFA/NFA M. Frage: Ist die von M akzeptierte Sprache endlich? Nahe liegende Beobachtung: In einem DFA/NFA, der eine unendliche Sprache akzeptiert, muss es einen Kreis geben, der
Endlichkeitstest Eingabe: DFA/NFA M. Frage: Ist die von M akzeptierte Sprache endlich? Nahe liegende Beobachtung: In einem DFA/NFA, der eine unendliche Sprache akzeptiert, muss es einen Kreis geben, der
Frank Heitmann 2/47. 1 Ein PDA beginnt im Startzustand z 0 und mit im Keller. 2 Ist der Automat
 Formale Grundlagen der Informatik 1 Kapitel 5 Über reguläre Sprachen hinaus und (Teil 2) Frank Heitmann heitmann@informatik.uni-hamburg.de 21. April 2015 Der Kellerautomat - Formal Definition (Kellerautomat
Formale Grundlagen der Informatik 1 Kapitel 5 Über reguläre Sprachen hinaus und (Teil 2) Frank Heitmann heitmann@informatik.uni-hamburg.de 21. April 2015 Der Kellerautomat - Formal Definition (Kellerautomat
Seien M 1,M 2 NFAs f. die Sprachen L 1 und L 2. Konstruktion eines NFAs für L 1 L 2 : Erzeuge Kopien von M 1 und M 2. p 1
 Beispiel Produktautomat p Vereinfachte Konstruktion f. NFAs Seien M,M 2 NFAs f. die Sprachen L und L 2. Konstruktion eines NFAs für L L 2 : Erzeuge Kopien von M und M 2. p q q p 2 Erzeuge neuen Startzustand
Beispiel Produktautomat p Vereinfachte Konstruktion f. NFAs Seien M,M 2 NFAs f. die Sprachen L und L 2. Konstruktion eines NFAs für L L 2 : Erzeuge Kopien von M und M 2. p q q p 2 Erzeuge neuen Startzustand
Automaten und Formale Sprachen SoSe 2013 in Trier
 Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Automaten und Formale Sprachen SoSe 2013 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 2. Juni 2013 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche
Technische Universität München Sommer 2016 Prof. J. Esparza / Dr. M. Luttenberger, S. Sickert 11. Juli HA-Lösung. TA-Lösung
 Technische Universität München Sommer 26 Prof. J. Esparza / Dr. M. Luttenberger, S. Sickert. Juli 26 HA-Lösung TA-Lösung Einführung in die theoretische Informatik Aufgabenblatt 3 Beachten Sie: Soweit nicht
Technische Universität München Sommer 26 Prof. J. Esparza / Dr. M. Luttenberger, S. Sickert. Juli 26 HA-Lösung TA-Lösung Einführung in die theoretische Informatik Aufgabenblatt 3 Beachten Sie: Soweit nicht
Worterkennung in Texten speziell im Compilerbau 14. April Frank Heitmann 2/65
 Grenzen regulärer Sprachen? Formale Grundlagen der Informatik 1 Kapitel 4 Über reguläre Sprachen hinaus und Frank Heitmann heitmann@informatik.uni-hamburg.de Wir haben mittlerweile einiges kennengelernt,
Grenzen regulärer Sprachen? Formale Grundlagen der Informatik 1 Kapitel 4 Über reguläre Sprachen hinaus und Frank Heitmann heitmann@informatik.uni-hamburg.de Wir haben mittlerweile einiges kennengelernt,
Endliche Automaten. δ : Z Σ Z die Überführungsfunktion, z 0 Z der Startzustand und F Z die Menge der Endzustände (Finalzustände).
 Endliche Automaten Endliche Automaten Definition Ein deterministischer endlicher Automat (kurz DFA für deterministic finite automaton ) ist ein Quintupel M = (Σ, Z, δ, z 0, F), wobei Σ ein Alphabet ist,
Endliche Automaten Endliche Automaten Definition Ein deterministischer endlicher Automat (kurz DFA für deterministic finite automaton ) ist ein Quintupel M = (Σ, Z, δ, z 0, F), wobei Σ ein Alphabet ist,
Lösung zur Klausur. Grundlagen der Theoretischen Informatik im WiSe 2003/2004
 Lösung zur Klausur Grundlagen der Theoretischen Informatik im WiSe 2003/2004 1. Geben Sie einen deterministischen endlichen Automaten an, der die Sprache aller Wörter über dem Alphabet {0, 1} akzeptiert,
Lösung zur Klausur Grundlagen der Theoretischen Informatik im WiSe 2003/2004 1. Geben Sie einen deterministischen endlichen Automaten an, der die Sprache aller Wörter über dem Alphabet {0, 1} akzeptiert,
Formalismen für REG. Formale Grundlagen der Informatik 1 Kapitel 7 Kontextfreie Sprachen. Das Pumping Lemma. Abschlusseigenschaften
 Formalismen für RE Formale rundlagen der Informatik 1 Kapitel 7 Kontextfreie Sprachen Frank Heitmann heitmann@informatik.uni-hamburg.de Satz Zu jeder regulären Sprache L gibt es einen DFA A mit L(A) =
Formalismen für RE Formale rundlagen der Informatik 1 Kapitel 7 Kontextfreie Sprachen Frank Heitmann heitmann@informatik.uni-hamburg.de Satz Zu jeder regulären Sprache L gibt es einen DFA A mit L(A) =
Grundlagen der Theoretischen Informatik, SoSe 2008
 2. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 1 Einelementiges Alphabet (4 Punkte) (a) Geben
2. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 1 Einelementiges Alphabet (4 Punkte) (a) Geben
Automaten und Formale Sprachen SoSe 2007 in Trier. Henning Fernau Universität Trier
 Automaten und Formale Sprachen SoSe 2007 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche Automaten und
Automaten und Formale Sprachen SoSe 2007 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Automaten und Formale Sprachen Gesamtübersicht Organisatorisches Einführung Endliche Automaten und
Endliche Automaten, reguläre Ausdrücke, rechtslineare Grammatiken
 1 / 15 Endliche Automaten, reguläre Ausdrücke, rechtslineare Grammatiken Prof. Dr. Hans Kleine Büning FG Wissensbasierte Systeme WS 08/09 2 / 15 Deterministischer endlicher Automat (DEA) Definition 1:
1 / 15 Endliche Automaten, reguläre Ausdrücke, rechtslineare Grammatiken Prof. Dr. Hans Kleine Büning FG Wissensbasierte Systeme WS 08/09 2 / 15 Deterministischer endlicher Automat (DEA) Definition 1:
Worterkennung in Texten speziell im Compilerbau 20. April Frank Heitmann 2/64
 Grenzen regulärer Sprachen? Formale Grundlagen der Informatik 1 Kapitel 4 Über reguläre Sprachen hinaus und Pumping Lemma Frank Heitmann heitmann@informatik.uni-hamburg.de Wir haben mittlerweile einiges
Grenzen regulärer Sprachen? Formale Grundlagen der Informatik 1 Kapitel 4 Über reguläre Sprachen hinaus und Pumping Lemma Frank Heitmann heitmann@informatik.uni-hamburg.de Wir haben mittlerweile einiges
Einführung in die Theoretische Informatik
 Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2010 Lösungsblatt 3 14. Mai 2010 Einführung in die Theoretische
Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2010 Lösungsblatt 3 14. Mai 2010 Einführung in die Theoretische
FORMALE SYSTEME. 8. Vorlesung: Minimale Automaten. TU Dresden, 6. November Markus Krötzsch Lehrstuhl Wissensbasierte Systeme
 FORMALE SYSTEME 8. Vorlesung: Minimale Automaten Markus Krötzsch Lehrstuhl Wissensbasierte Systeme TU Dresden, 6. November 2017 Rückblick Markus Krötzsch, 6. November 2017 Formale Systeme Folie 2 von 26
FORMALE SYSTEME 8. Vorlesung: Minimale Automaten Markus Krötzsch Lehrstuhl Wissensbasierte Systeme TU Dresden, 6. November 2017 Rückblick Markus Krötzsch, 6. November 2017 Formale Systeme Folie 2 von 26
Theoretische Informatik I
 (702765) Skript zur Vorlesung am 30.6.2000 Aus der vorherigen Vorlesung: Theoretische Informatik I Satz W: Sei X ein Alphabet. Zu jeder regulären Sprache R X * gibt es ein n N, so daß für alle Wörter z
(702765) Skript zur Vorlesung am 30.6.2000 Aus der vorherigen Vorlesung: Theoretische Informatik I Satz W: Sei X ein Alphabet. Zu jeder regulären Sprache R X * gibt es ein n N, so daß für alle Wörter z
Maike Buchin 18. Februar 2016 Stef Sijben. Probeklausur. Theoretische Informatik. Bearbeitungszeit: 3 Stunden
 Maike Buchin 8. Februar 26 Stef Sijben Probeklausur Theoretische Informatik Bearbeitungszeit: 3 Stunden Name: Matrikelnummer: Studiengang: Geburtsdatum: Hinweise: Schreibe die Lösung jeder Aufgabe direkt
Maike Buchin 8. Februar 26 Stef Sijben Probeklausur Theoretische Informatik Bearbeitungszeit: 3 Stunden Name: Matrikelnummer: Studiengang: Geburtsdatum: Hinweise: Schreibe die Lösung jeder Aufgabe direkt
Technische Universität München Sommer 2016 Prof. J. Esparza / Dr. M. Luttenberger, S. Sickert 2. Mai HA-Lösung. TA-Lösung
 Technische Universität München Sommer 2016 Prof. J. Esparza / Dr. M. Luttenberger, S. Sickert 2. Mai 2016 HA-Lösung TA-Lösung Einführung in die theoretische Informatik Aufgabenblatt 2 Beachten Sie: Soweit
Technische Universität München Sommer 2016 Prof. J. Esparza / Dr. M. Luttenberger, S. Sickert 2. Mai 2016 HA-Lösung TA-Lösung Einführung in die theoretische Informatik Aufgabenblatt 2 Beachten Sie: Soweit
Übungsaufgaben zu Formalen Sprachen und Automaten
 Universität Freiburg PD Dr. A. Jakoby Sommer 27 Übungen zum Repetitorium Informatik III Übungsaufgaben zu Formalen Sprachen und Automaten. Untersuchen Sie das folgende Spiel: A B x x 2 x 3 C D Eine Murmel
Universität Freiburg PD Dr. A. Jakoby Sommer 27 Übungen zum Repetitorium Informatik III Übungsaufgaben zu Formalen Sprachen und Automaten. Untersuchen Sie das folgende Spiel: A B x x 2 x 3 C D Eine Murmel
Theoretische Grundlagen der Informatik. Vorlesung am 02. November INSTITUT FÜR THEORETISCHE INFORMATIK
 Theoretische Grundlagen der Informatik Vorlesung am 2. November 27 2..27 Dorothea Wagner - Theoretische Grundlagen der Informatik KIT Die Forschungsuniversität in der Vorlesung am 2. November 27 Helmholtz-Gemeinschaft
Theoretische Grundlagen der Informatik Vorlesung am 2. November 27 2..27 Dorothea Wagner - Theoretische Grundlagen der Informatik KIT Die Forschungsuniversität in der Vorlesung am 2. November 27 Helmholtz-Gemeinschaft
Das Pumping Lemma der regulären Sprachen
 Das Pumping Lemma der regulären Sprachen Frank Heitmann heitmann@informatik.uni-hamburg.de 1 Das Pumping Lemma Das Pumping Lemma der regulären Sprachen macht eine Aussage der Art wenn eine Sprache L regulär
Das Pumping Lemma der regulären Sprachen Frank Heitmann heitmann@informatik.uni-hamburg.de 1 Das Pumping Lemma Das Pumping Lemma der regulären Sprachen macht eine Aussage der Art wenn eine Sprache L regulär
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik Wintersemester 2007 / 2008 Prof. Dr. Heribert Vollmer Institut für Theoretische Informatik 29.10.2007 Reguläre Sprachen Ein (deterministischer) endlicher Automat
Grundlagen der Theoretischen Informatik Wintersemester 2007 / 2008 Prof. Dr. Heribert Vollmer Institut für Theoretische Informatik 29.10.2007 Reguläre Sprachen Ein (deterministischer) endlicher Automat
Algorithmen mit konstantem Platzbedarf: Die Klasse REG
 Algorithmen mit konstantem Platzbedarf: Die Klasse REG Sommerakademie Rot an der Rot AG 1 Wieviel Platz brauchen Algorithmen wirklich? Daniel Alm Institut für Numerische Simulation Universität Bonn August
Algorithmen mit konstantem Platzbedarf: Die Klasse REG Sommerakademie Rot an der Rot AG 1 Wieviel Platz brauchen Algorithmen wirklich? Daniel Alm Institut für Numerische Simulation Universität Bonn August
2.2 Reguläre Sprachen Endliche Automaten
 2.2.1 Endliche Automaten E I N G A B E Lesekopf endliche Kontrolle Signal für Endzustand Ein endlicher Automat liest ein Wort zeichenweise und akzeptiert oder verwirft. endlicher Automat Sprache der akzeptierten
2.2.1 Endliche Automaten E I N G A B E Lesekopf endliche Kontrolle Signal für Endzustand Ein endlicher Automat liest ein Wort zeichenweise und akzeptiert oder verwirft. endlicher Automat Sprache der akzeptierten
Pumping-Lemma. Beispiel. Betrachte die kontextsensitive Grammatik G mit den Produktionen. S asbc abc CB HB HB HC HC BC ab ab bb bb bc bc cc cc.
 Pumping-Lemma Beispiel Betrachte die kontextsensitive Grammatik G mit den Produktionen S asbc abc CB HB HB HC HC BC ab ab bb bb bc bc cc cc. Sie erzeugt z.b. das Wort aabbcc: S asbc aabcbc aabhbc aabhcc
Pumping-Lemma Beispiel Betrachte die kontextsensitive Grammatik G mit den Produktionen S asbc abc CB HB HB HC HC BC ab ab bb bb bc bc cc cc. Sie erzeugt z.b. das Wort aabbcc: S asbc aabcbc aabhbc aabhcc
Einführung in die Theoretische Informatik
 Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2 Lösungsblatt 2. Mai 2 Einführung in die Theoretische Informatik
Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2 Lösungsblatt 2. Mai 2 Einführung in die Theoretische Informatik
Abschluss gegen Substitution. Wiederholung. Beispiel. Abschluss gegen Substitution
 Wiederholung Beschreibungsformen für reguläre Sprachen: DFAs NFAs Reguläre Ausdrücke:, {ε}, {a}, und deren Verknüpfung mit + (Vereinigung), (Konkatenation) und * (kleenescher Abschluss) Abschluss gegen
Wiederholung Beschreibungsformen für reguläre Sprachen: DFAs NFAs Reguläre Ausdrücke:, {ε}, {a}, und deren Verknüpfung mit + (Vereinigung), (Konkatenation) und * (kleenescher Abschluss) Abschluss gegen
Grundlagen der Theoretischen Informatik
 1 Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg Wintersemester 2014/15 2 Kontextfreie Grammatiken Definition: Eine Grammatik G
1 Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg Wintersemester 2014/15 2 Kontextfreie Grammatiken Definition: Eine Grammatik G
Übung Theoretische Grundlagen
 Übung Theoretische Grundlagen Nico Döttling October 25, 22 Automatenminimierung Konstruktion des Äquivalenzklassenautomaten Aus der Vorlesung bekannt Überflüssige Zustände lassen sich effizient erkennen
Übung Theoretische Grundlagen Nico Döttling October 25, 22 Automatenminimierung Konstruktion des Äquivalenzklassenautomaten Aus der Vorlesung bekannt Überflüssige Zustände lassen sich effizient erkennen
Formale Sprachen. Reguläre Sprachen. Rudolf FREUND, Marian KOGLER
 Formale Sprachen Reguläre Sprachen Rudolf FREUND, Marian KOGLER Endliche Automaten - Kleene STEPHEN KLEENE (99-994) 956: Representation of events in nerve nets and finite automata. In: C.E. Shannon und
Formale Sprachen Reguläre Sprachen Rudolf FREUND, Marian KOGLER Endliche Automaten - Kleene STEPHEN KLEENE (99-994) 956: Representation of events in nerve nets and finite automata. In: C.E. Shannon und
Formale Methoden 2 LVA ,
 Formale Methoden 2 LVA 703019, 703020 (http://clinformatik.uibk.ac.at/teaching/ss06/fmii/) Georg Moser (VO) 1 Martin Korp (UE) 2 Friedrich Neurauter (UE) 3 Christian Vogt (UE) 4 1 georg.moser@uibk.ac.at
Formale Methoden 2 LVA 703019, 703020 (http://clinformatik.uibk.ac.at/teaching/ss06/fmii/) Georg Moser (VO) 1 Martin Korp (UE) 2 Friedrich Neurauter (UE) 3 Christian Vogt (UE) 4 1 georg.moser@uibk.ac.at
1 Σ endliches Terminalalphabet, 2 V endliche Menge von Variablen (mit V Σ = ), 3 P (V (Σ ΣV )) {(S, ε)} endliche Menge von Regeln,
 Theorie der Informatik 8. März 25 8. Reguläre Sprachen I Theorie der Informatik 8. Reguläre Sprachen I 8. Reguläre Grammatiken Malte Helmert Gabriele Röger 8.2 DFAs Universität Basel 8. März 25 8.3 NFAs
Theorie der Informatik 8. März 25 8. Reguläre Sprachen I Theorie der Informatik 8. Reguläre Sprachen I 8. Reguläre Grammatiken Malte Helmert Gabriele Röger 8.2 DFAs Universität Basel 8. März 25 8.3 NFAs
1. Klausur zur Vorlesung Informatik III Wintersemester 2003/2004. Mit Lösung!
 Universität Karlsruhe Theoretische Informatik Fakultät für Informatik WS 23/4 ILKD Prof. Dr. D. Wagner 2. Februar 24. Klausur zur Vorlesung Informatik III Wintersemester 23/24 Mit Lösung! Beachten Sie:
Universität Karlsruhe Theoretische Informatik Fakultät für Informatik WS 23/4 ILKD Prof. Dr. D. Wagner 2. Februar 24. Klausur zur Vorlesung Informatik III Wintersemester 23/24 Mit Lösung! Beachten Sie:
äußere Klammern können entfallen, ebenso solche, die wegen Assoziativität von + und Konkatenation nicht notwendig sind:
 3. Reguläre Sprachen Bisher wurden Automaten behandelt und Äquivalenzen zwischen den verschiedenen Automaten gezeigt. DEAs erkennen formale Sprachen. Gibt es formale Sprachen, die nicht erkannt werden?
3. Reguläre Sprachen Bisher wurden Automaten behandelt und Äquivalenzen zwischen den verschiedenen Automaten gezeigt. DEAs erkennen formale Sprachen. Gibt es formale Sprachen, die nicht erkannt werden?
Formale Sprachen und endliche Automaten
 Formale Sprachen und endliche Automaten Formale Sprachen Definition: 1 (Alphabet) Ein Alphabet Σ ist eine endliche, nichtleere Menge von Zeichen oder Symbolen. Ein Wort über dem Alphabet Σ ist eine endliche
Formale Sprachen und endliche Automaten Formale Sprachen Definition: 1 (Alphabet) Ein Alphabet Σ ist eine endliche, nichtleere Menge von Zeichen oder Symbolen. Ein Wort über dem Alphabet Σ ist eine endliche
Grammatiken. Einführung
 Einführung Beispiel: Die arithmetischen Ausdrücke über der Variablen a und den Operationen + und können wie folgt definiert werden: a, a + a und a a sind arithmetische Ausdrücke Wenn A und B arithmetische
Einführung Beispiel: Die arithmetischen Ausdrücke über der Variablen a und den Operationen + und können wie folgt definiert werden: a, a + a und a a sind arithmetische Ausdrücke Wenn A und B arithmetische
1 Σ endliches Terminalalphabet, 2 V endliche Menge von Variablen (mit V Σ = ), 3 P (V (Σ ΣV )) {(S, ε)} endliche Menge von Regeln,
 Theorie der Informatik 9. März 24 7. Reguläre Sprachen I Theorie der Informatik 7. Reguläre Sprachen I Malte Helmert Gabriele Röger Universität Basel 9. März 24 7. Reguläre Grammatiken 7.2 DFAs 7.3 NFAs
Theorie der Informatik 9. März 24 7. Reguläre Sprachen I Theorie der Informatik 7. Reguläre Sprachen I Malte Helmert Gabriele Röger Universität Basel 9. März 24 7. Reguläre Grammatiken 7.2 DFAs 7.3 NFAs
Einführung in die Theoretische Informatik
 Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Sascha Böhme, Lars Noschinski Sommersemester 2 Lösungsblatt 2 3. Mai 2 Einführung in die Theoretische Informatik Hinweis:
Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Sascha Böhme, Lars Noschinski Sommersemester 2 Lösungsblatt 2 3. Mai 2 Einführung in die Theoretische Informatik Hinweis:
Induktive Definition
 Rechenregeln A B = B A A (B C) = (A B) C A (B C) = (A B) C A (B C) = A B A C (B C) A = B A C A {ε} A = A A {ε} = A (A {ε}) = A (A ) = A A A = A + A A = A + A + {ε} = A Beispiel. Real-Zahlen = {0,..., 9}
Rechenregeln A B = B A A (B C) = (A B) C A (B C) = (A B) C A (B C) = A B A C (B C) A = B A C A {ε} A = A A {ε} = A (A {ε}) = A (A ) = A A A = A + A A = A + A + {ε} = A Beispiel. Real-Zahlen = {0,..., 9}
Theoretische Informatik. Alphabete, Worte, Sprachen
 Theoretische Informatik Alphabete, Worte, Sprachen Alphabete, Worte, Sprachen 1. Alphabete und Worte Definitionen, Beispiele Operationen mit Worten Induktionsbeweise 2. Sprachen Definition und Beispiele
Theoretische Informatik Alphabete, Worte, Sprachen Alphabete, Worte, Sprachen 1. Alphabete und Worte Definitionen, Beispiele Operationen mit Worten Induktionsbeweise 2. Sprachen Definition und Beispiele
q 0 q gdw. nicht (q A) (q A) q i+1 q gdw. q i q oder ( a Σ) δ(q, a) i δ(q, a) L = {a n b n : n N} für a, b Σ, a b
 Kap. 2: Endliche Automaten Myhill Nerode 2.4 Minimalautomat für reguläre Sprache Abschnitt 2.4.3 L Σ regulär der Äuivalenzklassen-Automat zu L ist ein DFA mit minimaler Zustandszahl (= index( L )) unter
Kap. 2: Endliche Automaten Myhill Nerode 2.4 Minimalautomat für reguläre Sprache Abschnitt 2.4.3 L Σ regulär der Äuivalenzklassen-Automat zu L ist ein DFA mit minimaler Zustandszahl (= index( L )) unter
Theoretische Grundlagen des Software Engineering
 Theoretische Grundlagen des Software Engineering 2: Eigenschaften von regulären Sprachen schulz@eprover.org Software Systems Engineering Alphabet Definition: Ein Alphabet Σ ist eine nichtleere, endliche
Theoretische Grundlagen des Software Engineering 2: Eigenschaften von regulären Sprachen schulz@eprover.org Software Systems Engineering Alphabet Definition: Ein Alphabet Σ ist eine nichtleere, endliche
2.3 Abschlusseigenschaften
 2.3 Abschlusseigenschaften 2.3 Abschlusseigenschaften In diesem Abschnitt wollen wir uns mit Abschlusseigenschaften der regulären Sprachen, d.h. mit der Frage, ob, gegeben eine Operation und zwei reguläre
2.3 Abschlusseigenschaften 2.3 Abschlusseigenschaften In diesem Abschnitt wollen wir uns mit Abschlusseigenschaften der regulären Sprachen, d.h. mit der Frage, ob, gegeben eine Operation und zwei reguläre
2 2 Reguläre Sprachen. 2.2 Endliche Automaten. Übersicht
 Formale Systeme, Automaten, Prozesse Übersicht 2 2. Reguläre Ausdrücke 2.3 Nichtdeterministische endliche Automaten 2.4 Die Potenzmengenkonstruktion 2.5 NFAs mit ɛ-übergängen 2.6 Minimale DFAs und der
Formale Systeme, Automaten, Prozesse Übersicht 2 2. Reguläre Ausdrücke 2.3 Nichtdeterministische endliche Automaten 2.4 Die Potenzmengenkonstruktion 2.5 NFAs mit ɛ-übergängen 2.6 Minimale DFAs und der
Grundlagen der theoretischen Informatik
 Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 04.06.2013 An den Transitionen sieht man zunächst, dass nur die folgenden Zustandsübergänge
Grundlagen der theoretischen Informatik Kurt Sieber Fakultät IV, Department ETI Universität Siegen SS 2013 Vorlesung vom 04.06.2013 An den Transitionen sieht man zunächst, dass nur die folgenden Zustandsübergänge
Diskrete Mathematik. Arne Dür Kurt Girstmair Simon Legner Georg Moser Harald Zankl
 OLC mputational gic Diskrete Mathematik Arne Dür Kurt Girstmair Simon Legner Georg Moser Harald Zankl Fakultät für Mathematik, Informatik und Physik @ UIBK Sommersemester 2011 GM (MIP) Diskrete Mathematik
OLC mputational gic Diskrete Mathematik Arne Dür Kurt Girstmair Simon Legner Georg Moser Harald Zankl Fakultät für Mathematik, Informatik und Physik @ UIBK Sommersemester 2011 GM (MIP) Diskrete Mathematik
Übungsblatt 6. Vorlesung Theoretische Grundlagen der Informatik im WS 17/18
 Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 6 Vorlesung Theoretische Grundlagen der Informatik im WS 17/18 Ausgabe 10. Januar 2018 Abgabe 23. Januar 2018, 11:00 Uhr (im
Institut für Theoretische Informatik Lehrstuhl Prof. Dr. D. Wagner Übungsblatt 6 Vorlesung Theoretische Grundlagen der Informatik im WS 17/18 Ausgabe 10. Januar 2018 Abgabe 23. Januar 2018, 11:00 Uhr (im
TU Berlin Nachklausur TheGI 2 Automaten und Komplexität (Niedermeier/Hartung/Nichterlein, Sommersemester 2012)
 Berlin, 05. Oktober 2012 Name:... Matr.-Nr.:... TU Berlin Nachklausur TheGI 2 Automaten und Komplexität (Niedermeier/Hartung/Nichterlein, Sommersemester 2012) 1 2 3 4 5 6 7 Σ Bearbeitungszeit: 60 min.
Berlin, 05. Oktober 2012 Name:... Matr.-Nr.:... TU Berlin Nachklausur TheGI 2 Automaten und Komplexität (Niedermeier/Hartung/Nichterlein, Sommersemester 2012) 1 2 3 4 5 6 7 Σ Bearbeitungszeit: 60 min.
Umformung NTM DTM. Charakterisierung rek. aufz. Spr. Chomsky-3-Grammatiken (T5.3) Chomsky-0-Grammatik Rek. Aufz.
 Chomsky-0-Grammatik Rek. Aufz. Satz T5.2.2: Wenn L durch eine Chomsky-0- Grammatik G beschrieben wird, gibt es eine NTM M, die L akzeptiert. Beweis: Algo von M: Schreibe S auf freie Spur. Iteriere: Führe
Chomsky-0-Grammatik Rek. Aufz. Satz T5.2.2: Wenn L durch eine Chomsky-0- Grammatik G beschrieben wird, gibt es eine NTM M, die L akzeptiert. Beweis: Algo von M: Schreibe S auf freie Spur. Iteriere: Führe
Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I. Ulrich Furbach. Sommersemester 2014
 Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Ulrich Furbach Institut für Informatik Sommersemester 2014 Furbach Grundlagen d. Theoretischen Informatik:
Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Ulrich Furbach Institut für Informatik Sommersemester 2014 Furbach Grundlagen d. Theoretischen Informatik:
Automaten und Coinduktion
 Philipps-Univestität Marburg Fachbereich Mathematik und Informatik Seminar: Konzepte von Programmiersprachen Abgabedatum 02.12.03 Betreuer: Prof. Dr. H. P. Gumm Referentin: Olga Andriyenko Automaten und
Philipps-Univestität Marburg Fachbereich Mathematik und Informatik Seminar: Konzepte von Programmiersprachen Abgabedatum 02.12.03 Betreuer: Prof. Dr. H. P. Gumm Referentin: Olga Andriyenko Automaten und
Formale Sprachen und Automaten: Tutorium Nr. 8
 Formale Sprachen und Automaten: Tutorium Nr. 8 15. Juni 2013 Übersicht 1 Nachtrag 2 Besprechung von Übungsblatt 7 Aufgabe 1 Aufgabe 2 Aufgabe 3 3 CFG PDA Definitionen Ein Beispiel! Aufgabe 4 Der PDA als
Formale Sprachen und Automaten: Tutorium Nr. 8 15. Juni 2013 Übersicht 1 Nachtrag 2 Besprechung von Übungsblatt 7 Aufgabe 1 Aufgabe 2 Aufgabe 3 3 CFG PDA Definitionen Ein Beispiel! Aufgabe 4 Der PDA als
Automaten und Formale Sprachen
 Automaten und Formale Sprachen Prof. Dr. Dietrich Kuske FG Theoretische Informatik, TU Ilmenau Wintersemester 2011/12 WS 11/12 1 Organisatorisches zur Vorlesung Informationen, aktuelle Version der Folien
Automaten und Formale Sprachen Prof. Dr. Dietrich Kuske FG Theoretische Informatik, TU Ilmenau Wintersemester 2011/12 WS 11/12 1 Organisatorisches zur Vorlesung Informationen, aktuelle Version der Folien
Grundlagen der Informatik. Prof. Dr. Stefan Enderle NTA Isny
 Grundlagen der Informatik Prof. Dr. Stefan Enderle NTA Isny 1. Automaten und Sprachen 1.1 Endlicher Automat Einen endlichen Automaten stellen wir uns als Black Box vor, die sich aufgrund einer Folge von
Grundlagen der Informatik Prof. Dr. Stefan Enderle NTA Isny 1. Automaten und Sprachen 1.1 Endlicher Automat Einen endlichen Automaten stellen wir uns als Black Box vor, die sich aufgrund einer Folge von
WS07/08 Automaten und Formale Sprachen 8. Vorlesung
 WS07/08 Automaten und Formale Sprachen 8. Vorlesung PD Dr. Niggl (für M.Dietzfelbinger) 4. Dezember 2007 Stichworte (Letzte Vorl.) Konstruktion des Minimalautomaten: 3 Teile Entferne unerreichbare Zustände
WS07/08 Automaten und Formale Sprachen 8. Vorlesung PD Dr. Niggl (für M.Dietzfelbinger) 4. Dezember 2007 Stichworte (Letzte Vorl.) Konstruktion des Minimalautomaten: 3 Teile Entferne unerreichbare Zustände
Eigenschaften regulärer Sprachen
 = {} {0} {0} {} = {0} {} Für L(A) benötigen wir gemäß Gleichung.3 die Mengen R 3 und R3 3. R 3 = R R3 (R33) R3 = {0} {00} {0} {} ({ε} {0, } {0} {}) {0, } {00} = {0} {00} {0} {} ({0, } {0} {}) {0, } {00}
= {} {0} {0} {} = {0} {} Für L(A) benötigen wir gemäß Gleichung.3 die Mengen R 3 und R3 3. R 3 = R R3 (R33) R3 = {0} {00} {0} {} ({ε} {0, } {0} {}) {0, } {00} = {0} {00} {0} {} ({0, } {0} {}) {0, } {00}
Kapitel 2: Formale Sprachen Gliederung. 0. Grundbegriffe 1. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie
 Gliederung. Grundbegriffe. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.. Chomsky-Grammatiken 2.2. Reguläre Sprachen (noch weiter) 2.3. Kontextfreie Sprachen 2/4,
Gliederung. Grundbegriffe. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.. Chomsky-Grammatiken 2.2. Reguläre Sprachen (noch weiter) 2.3. Kontextfreie Sprachen 2/4,
5.2 Endliche Automaten
 114 5.2 Endliche Automaten Endliche Automaten sind Turingmaschinen, die nur endlichen Speicher besitzen. Wie wir bereits im Zusammenhang mit Turingmaschinen gesehen haben, kann endlicher Speicher durch
114 5.2 Endliche Automaten Endliche Automaten sind Turingmaschinen, die nur endlichen Speicher besitzen. Wie wir bereits im Zusammenhang mit Turingmaschinen gesehen haben, kann endlicher Speicher durch
THIA - Übungsblatt 2.
 THIA - Übungsblatt 2. Aufgabe 12 (Eine einfache Sprache). Endliche Ziffernfolgen, die mit einer 0 beginnen, auf die mindestens eine weitere Ziffer folgt, wobei nur die Ziffern 0,..., 7 vorkommen, sollen
THIA - Übungsblatt 2. Aufgabe 12 (Eine einfache Sprache). Endliche Ziffernfolgen, die mit einer 0 beginnen, auf die mindestens eine weitere Ziffer folgt, wobei nur die Ziffern 0,..., 7 vorkommen, sollen
Einführung in die Theoretische Informatik
 Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2 Lösungsblatt 3. April 2 Einführung in die Theoretische Informatik
Technische Universität München Fakultät für Informatik Prof. Tobias Nipkow, Ph.D. Dr. Werner Meixner, Dr. Alexander Krauss Sommersemester 2 Lösungsblatt 3. April 2 Einführung in die Theoretische Informatik
Lösungsvorschläge Blatt 4
 Theoretische Informatik Departement Informatik Prof. Dr. Juraj Hromkovič http://www.ita.inf.ethz.ch/theoinf16 Lösungsvorschläge Blatt 4 Zürich, 21. Oktober 2016 Lösung zu Aufgabe 10 (a) Wir zeigen mit
Theoretische Informatik Departement Informatik Prof. Dr. Juraj Hromkovič http://www.ita.inf.ethz.ch/theoinf16 Lösungsvorschläge Blatt 4 Zürich, 21. Oktober 2016 Lösung zu Aufgabe 10 (a) Wir zeigen mit
kontextfreie Grammatiken Theoretische Informatik kontextfreie Grammatiken kontextfreie Grammatiken Rainer Schrader 14. Juli 2009 Gliederung
 Theoretische Informatik Rainer Schrader Zentrum für Angewandte Informatik Köln 14. Juli 2009 1 / 40 2 / 40 Beispiele: Aus den bisher gemachten Überlegungen ergibt sich: aus der Chomsky-Hierarchie bleiben
Theoretische Informatik Rainer Schrader Zentrum für Angewandte Informatik Köln 14. Juli 2009 1 / 40 2 / 40 Beispiele: Aus den bisher gemachten Überlegungen ergibt sich: aus der Chomsky-Hierarchie bleiben
Einführung in die Computerlinguistik Satz von Kleene
 Einführung in die Computerlinguistik Satz von Kleene Dozentin: Wiebke Petersen 5. Foliensatz Wiebke Petersen Einführung CL 1 Satz von Kleene (Stephen C. Kleene, 1909-1994) Jede Sprache, die von einem deterministischen
Einführung in die Computerlinguistik Satz von Kleene Dozentin: Wiebke Petersen 5. Foliensatz Wiebke Petersen Einführung CL 1 Satz von Kleene (Stephen C. Kleene, 1909-1994) Jede Sprache, die von einem deterministischen
Satz von Kleene. (Stephen C. Kleene, ) Wiebke Petersen Einführung CL 2
 Satz von Kleene (Stephen C. Kleene, 1909-1994) Jede Sprache, die von einem deterministischen endlichen Automaten akzeptiert wird ist regulär und jede reguläre Sprache wird von einem deterministischen endlichen
Satz von Kleene (Stephen C. Kleene, 1909-1994) Jede Sprache, die von einem deterministischen endlichen Automaten akzeptiert wird ist regulär und jede reguläre Sprache wird von einem deterministischen endlichen
Formale Sprachen. Formale Grundlagen (WIN) 2008S, F. Binder. Vorlesung im 2008S
 Formale Grundlagen (WIN) Franz Binder Institut für Algebra Johannes Kepler Universität Linz Vorlesung im 2008S http://www.algebra.uni-linz.ac.at/students/win/fg Inhalt Das Alphabet Σ sei eine endliche
Formale Grundlagen (WIN) Franz Binder Institut für Algebra Johannes Kepler Universität Linz Vorlesung im 2008S http://www.algebra.uni-linz.ac.at/students/win/fg Inhalt Das Alphabet Σ sei eine endliche
FORMALE SYSTEME. 3. Vorlesung: Endliche Automaten. TU Dresden, 17. Oktober Markus Krötzsch
 FORMALE SYSTEME 3. Vorlesung: Endliche Automaten Markus Krötzsch TU Dresden, 17. Oktober 2016 Rückblick Markus Krötzsch, 17. Oktober 2016 Formale Systeme Folie 2 von 31 Wiederholung Mit Grammatiken können
FORMALE SYSTEME 3. Vorlesung: Endliche Automaten Markus Krötzsch TU Dresden, 17. Oktober 2016 Rückblick Markus Krötzsch, 17. Oktober 2016 Formale Systeme Folie 2 von 31 Wiederholung Mit Grammatiken können
Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I
 Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert Institut für Informatik Sommersemester 2007 B. Beckert Grundlagen d. Theoretischen Informatik:
Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Bernhard Beckert Institut für Informatik Sommersemester 2007 B. Beckert Grundlagen d. Theoretischen Informatik:
Theoretische Informatik Mitschrift
 4. Reguläre Ausdrüce Theoretische Informati Mitschrift indutive Beschreibung von Sprachen, die durch endliche Automaten erennbar sind Definition 4.1: Sei Σ ein Alphabet. (a) Die Menge RA(Σ) der regulären
4. Reguläre Ausdrüce Theoretische Informati Mitschrift indutive Beschreibung von Sprachen, die durch endliche Automaten erennbar sind Definition 4.1: Sei Σ ein Alphabet. (a) Die Menge RA(Σ) der regulären
Kapitel 2: Formale Sprachen Gliederung
 Gliederung. Einleitung und Grundbegriffe. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.. Chomsky-Grammatiken 2.2. Reguläre Sprachen Reguläre Grammatiken, ND-Automaten
Gliederung. Einleitung und Grundbegriffe. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.. Chomsky-Grammatiken 2.2. Reguläre Sprachen Reguläre Grammatiken, ND-Automaten
Automatentheorie und formale Sprachen rechtslineare Grammatiken
 Automatentheorie und formale Sprachen rechtslineare Grammatiken Dozentin: Wiebke Petersen 17.6.2009 Wiebke Petersen Automatentheorie und formale Sprachen - SoSe09 1 Pumping lemma for regular languages
Automatentheorie und formale Sprachen rechtslineare Grammatiken Dozentin: Wiebke Petersen 17.6.2009 Wiebke Petersen Automatentheorie und formale Sprachen - SoSe09 1 Pumping lemma for regular languages
Kurz-Skript zur Theoretischen Informatik I
 Kurz-Skript zur Theoretischen Informatik I Inhaltsverzeichnis 1 Grundlagen 2 2 Reguläre Ausdrücke 4 3 Endliche Automaten 5 3.1 Vollständige endliche Automaten................................... 6 3.2 ε
Kurz-Skript zur Theoretischen Informatik I Inhaltsverzeichnis 1 Grundlagen 2 2 Reguläre Ausdrücke 4 3 Endliche Automaten 5 3.1 Vollständige endliche Automaten................................... 6 3.2 ε
Übung zur Vorlesung Theoretische Information. Pumping Lemma
 Übung zur Vorlesung Theoretische Information Pumping Lemma Folie Ein Endlicher Automat q q, q 2, Akzeptierte Sprache? Folie 2 Ein Endlicher Automat q q, q 2, Akzeptierte Sprache? Am Anfang eine, dannach
Übung zur Vorlesung Theoretische Information Pumping Lemma Folie Ein Endlicher Automat q q, q 2, Akzeptierte Sprache? Folie 2 Ein Endlicher Automat q q, q 2, Akzeptierte Sprache? Am Anfang eine, dannach
Reguläre Sprachen und endliche Automaten
 Reguläre Sprachen und endliche Automaten 1 Motivation: Syntaxüberprüfung Definition: Fließkommazahlen in Java A floating-point literal has the following parts: a whole-number part, a decimal point (represented
Reguläre Sprachen und endliche Automaten 1 Motivation: Syntaxüberprüfung Definition: Fließkommazahlen in Java A floating-point literal has the following parts: a whole-number part, a decimal point (represented
Einführung in die Theoretische Informatik Tutorium V
 Einführung in die Theoretische Informatik Tutorium V Michael R. Jung 17. - 19. 11. 2014 EThI - Tutorium V 1 1 Pumping-Lemma 2 Reguläre Grammatiken 3 Beweisansätze für die Aufgaben 20 c,e,f EThI - Tutorium
Einführung in die Theoretische Informatik Tutorium V Michael R. Jung 17. - 19. 11. 2014 EThI - Tutorium V 1 1 Pumping-Lemma 2 Reguläre Grammatiken 3 Beweisansätze für die Aufgaben 20 c,e,f EThI - Tutorium
Zusammenfassung. Endliche Sprachen. Fazit zu endlichen Automaten. Teil 4: Grammatiken und Syntaxanalyse
 Endliche Sprachen Folgerung: Alle endlichen Sprachen sind regulär. Beweis: Sei L={w 1,,w n } Σ*. Dann ist w 1 +L+w n ein regulärer Ausdruck für L. Zusammenfassung Beschreibungsformen für reguläre Sprachen:
Endliche Sprachen Folgerung: Alle endlichen Sprachen sind regulär. Beweis: Sei L={w 1,,w n } Σ*. Dann ist w 1 +L+w n ein regulärer Ausdruck für L. Zusammenfassung Beschreibungsformen für reguläre Sprachen:
Freie Bäume und Wälder
 (Martin Dietzfelbinger, Stand 4.6.2011) Freie Bäume und Wälder In dieser Notiz geht es um eine besondere Sorte von (ungerichteten) Graphen, nämlich Bäume. Im Gegensatz zu gerichteten Bäumen nennt man diese
(Martin Dietzfelbinger, Stand 4.6.2011) Freie Bäume und Wälder In dieser Notiz geht es um eine besondere Sorte von (ungerichteten) Graphen, nämlich Bäume. Im Gegensatz zu gerichteten Bäumen nennt man diese
Minimalautomaten. Minimalautomaten. Frage: Ist der Äquivalenzautomat A der kleinste Automat ( Minimalautomat ) der die Sprache L(A) erkennt?
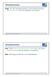 Minimalautomaten Frage: Ist der Äquivalenzautomat A der kleinste Automat ( Minimalautomat ) der die Sprache L(A) erkennt? 1 Minimalautomaten Satz: Falls A keine unerreichbaren Zustände hat, ist A der kleinste
Minimalautomaten Frage: Ist der Äquivalenzautomat A der kleinste Automat ( Minimalautomat ) der die Sprache L(A) erkennt? 1 Minimalautomaten Satz: Falls A keine unerreichbaren Zustände hat, ist A der kleinste
Einführung in die Theoretische Informatik
 Einführung in die Theoretische Informatik Johannes Köbler Institut für Informatik Humboldt-Universität zu Berlin WS 2011/12 Deterministische Kellerautomaten Von besonderem Interesse sind kontextfreie Sprachen,
Einführung in die Theoretische Informatik Johannes Köbler Institut für Informatik Humboldt-Universität zu Berlin WS 2011/12 Deterministische Kellerautomaten Von besonderem Interesse sind kontextfreie Sprachen,
