Technische Universität München. Fakultät für Informatik
|
|
|
- Hella Kaiser
- vor 6 Jahren
- Abrufe
Transkript
1 Technische Universität München Fakultät für Informatik Forschungs- und Lehreinheit Informatik IX Thema: Filterung im Bildraum: Konvolution Proseminar: Grundlagen Bildverstehen/Bildgestaltung Jonas Zaddach Betreuer: Suat Gedikli Abgabetermin: 23. Januar 2007
2 Einleitung Bildtransformationen sind heute alltäglich. Fast jeder Mensch besitzt eine Digitalkamera, mit der er fotografiert. Schon in der Kamera werden die aufgenommenen Bilder verändert, Farben werden angepasst und Hintergrundrauschen des CCD-Sensors aus dem Bild entfernt. Am Computer sind weitere Verbesserungen möglich, wie das Entfernen von Dunst. Wenn das Bild dann gespeichert wird, kommen Bildtransformationen zum Einsatz, um die Daten zuerst in eine effiziente Form zu bringen, in der sie dann gut komprimiert werden können. Durch Entfernung redundanter Bildelemente, wie minimale Farbunterschiede, die für den Betrachter nicht wahrzunehmen sind, kann ebenfalls Speicherplatz eingespart werden. Will man im Urlaub ein Panorama aufnehmen, hat jedoch kein Weitwinkelobjektiv zur Hand, hilft die sogenannte Stich-Funktion des Fotoapparates weiter. Sie entfernt mittels Bildtransformationen die perspektivische Verzerrung der Einzelaufnahmen und erlaubt es so, ein Bild aus mehreren nebeneinander liegenden Bildern zu rekonstruieren. Transformationen sind in vielen Bereichen der Bildverarbeitung wichtig. Im Folgenden sollen die Grundlagen für Bildtransformationen skizziert werden. Abbildung 1: Ungefilterte Bilder Abbildung 2: Bilder nach Bildverbesserung
3 Praktische Anwendung Filterung im Bildraum Betrachtung des Bildes als Signal In vielen Anwendungen des täglichen Lebens wird ein Bild als elektrisches Signal übertragen. Einige der zahllosen Anwendungen sind über Funk gesendete Fernsehsignale, vom Sensor einer Digitalkamera abgegriffene Bilder und Kernspintomograph-Aufnahmen. In der Elektrotechnik arbeitet man schon lange mit Signalen und hat bereits mathematische Formalismen eingeführt, um Signale und Signaltransformationen zu beschreiben. Dieses bereits gewonnene Wissen lässt sich auch für die Verarbeitung von Bildsignalen nutzen. Bild als zweidimensionales Signal Ein Signal ist eine zeitabhängige Größe, es ordnet jedem Zeitpunkt einen Wert zu. Signale in der Analogtechnik sind kontinuierlich, in der Digitaltechnik, wie sie im Computer verwendet wird, sind sie diskret. Dem Signal kann eine Funktion zugeordnet werden, die zu jedem Zeitpunkt den Signalpegel zurück gibt. Ein Bild lässt sich auf viele verschiedene Arten in ein Signal zerlegen. Es liegt nahe, ein zweidimensionales Signal für das Bild zu verwenden, da dies meist in Pixel zerlegt wird, die über ihre x- und y-koordinaten eindeutig gekennzeichnet sind. Jedoch muss die Aufteilung nicht in Pixel erfolgen. Einige mögliche Darstellungen für ein Bild sind: Koordinate x,koordinate y Rotwert r,grünwert g, Blauwert b x, y,r, g,b R Das Signal ist von den Koordinaten abhängig. Jedem Tupel (x,y) wird eindeutig ein RGB- Wert zugeordnet. Im Gegensatz zu einem Signal in der Elektrotechnik ist das Signal nicht anhängig von der Zeit, da ein Bild zu jedem Zeitpunkt gleich ist. In einem Video wäre das Signal auch noch von der Zeit abhängig, dann gäbe es drei Eingabeparameter, denen eindeutig Signalpegel zugeordnet werden. Koordinate x,koordinate y Luminanz Y,Chrominanz Rot U, BlauV x, y,y,u,v R Auch hier ist das Signal von den Koordinaten abhängig. Diesen wird aber nicht eine RGB- Farbe, sondern eine Farbe bestehend aus Luminanz (Helligkeit) und Chrominanz (Farbwert bestehend aus zwei Komponenten: Unterschied von Rot zur Luminanz und Unterschied von Blau zur Luminanz) zugeordnet. Diese Signalform ist dann günstig, wenn man geringe Farbunterschiede filtern will, da der Mensch sehr empfindlich auf Helligkeitsunterschiede reagiert, jedoch nicht so stark auf Farbunterschiede. Daher muss die Auflösung der Chrominanz nicht so hoch sein wie die der Luminanz, wodurch Speicher gespart werden kann. F DCKomponente u, ACKomponente v c u,v R ;c C Im Frequenzraum (Darstellung des Bildes nach der Fouriertransformation) wird jeder Frequenz eine Phase und eine Amplitude zugeordnet. Diese Parameter sind nicht intuitiv verständlich. Trotzdem ist diese Signalrepräsentation sinnvoll, da sich viele Bildtransformationen auf diese Funktion einfacher ausführen lassen als in den oberen beiden Darstellungen. Zum Beispiel Drehungen und Konvolutionen sind im Frequenzraum einfacher zu beschreiben als im Bildraum. Natürlich gibt es noch viel mehr mögliche Repräsentationen für ein Bild. Für jeden Zweck muss man eine angemessene Darstellung des Bildes wählen, damit Transformationen einfach formuliert werden können. Wählt man eine ungünstige Darstellung, kann es unmöglich sein eine Transforma-
4 tion für das Bild zu finden. Signalfilterung Es gibt unterschiedliche Klassen von Filtern. Die Klassen unterscheiden sich in der Komplexität und der Mächtigkeit der Operationen. Punktfilter ändern genau einen Pixel. Damit ist es unter anderem möglich, Helligkeit und Kontrast des Bildes anzupassen. Komplexere Bildverbesserungen wie Rauschentfernung sind mit diesem Filter nicht möglich. Lineare Filter gehen von einem Pixel im Bild aus, ändern aber mehrere Pixel im gefilterten Bild. Das Ergebnis ist nicht abhängig davon wo der Pixel im Bild gewählt wird, sondern nur von der Helligkeit des gewählten Pixels. Daher eignen sich Lineare Filter gut zur Beschreibung von Effekten, die ortsunabhängig sind, wie zum Beispiel Unschärfe. Lokale Einflüsse wie Belichtungsunterschiede können jedoch nicht ausgedrückt werden. Nichtlineare Filter transformieren mehrere Pixel zu mehreren Pixeln im Ergebnisbild. Wie ein Pixel abgebildet wird hängt von den Pixeln ab, die ihn umgeben. Daher können örtliche Veränderungen im Bild mit nichtlinearen Filtern beschreiben werden. Dies ist beispielsweise notwendig, um lokale Helligkeitsunterschiede aus einem Bild zu filtern, wie sie bei kurzen Belichtungszeiten durch den Vorhang im Fotoapparat entstehen. Die dunklen Ränder, die kürzer als die Bildmitte belichtet wurden, müssen dann aufgehellt werden. Man sollte im Kopf behalten, dass die Filterung um so zeitaufwendiger wird, je komplexer der Filter ist. Punktfilter arbeiten wesentlich schneller als Lineare Filter oder Nichtlineare Filter. Deswegen ist es für die Geschwindigkeit der Filterung besser, einen einfachen Filter zu verwenden, wenn das möglich ist. Im Folgenden werden mit der Konvolution die Klasse der linearen Filter erklärt. Was ist Konvolution? Konvolution Eine Konvolution oder Faltung bezeichnet eine lineare Transformation einer Funktion. Durch diese wird eine Funktion auf eine neue Funktion abgebildet: f f '. Mathematisch ist die Konvolution (symbolisiert durch * ) von zwei Funktionen f und g folgendermaßen definiert: g f m,n = g i, j f m i,n j d n d m Im Falle von diskreten Funktionen f und g vereinfacht sich die Konvolution zu: g f m, n = g p,q m p,n q p D q D wobei D=D f D g. D f und D g sind die Definitionsbereiche der diskreten Funktionen f und g. Dadurch können auch Werte, für die kein Funktionswert definiert ist, in eine Funktion eingesetzt werden. Deshalb muss eine Vereinbarung getroffen werden, wie mit solchen Stellen umgegangen werden soll. Dies wird später noch diskutiert. Abbildung der Signalfunktion Die Konvolution lässt sich nun zur Beschreibung von Transformation der Signalfunktion nutzen. Die ursprüngliche Signalfunktion wird durch die Faltung auf eine neue Signalfunktion abgebildet. Damit ist es möglich, Operationen auf ein Bild zu beschreiben. Die diskrete Form der Konvolution erlaubt es, auch auf nicht-kontinuierlichen Daten, wie sie auf
5 dem Computer im Regelfall vorliegen, zu arbeiten. Eigenschaften der Konvolution Die Konvolution erfüllt eine Reihe mathematischer Eigenschaften: Kommutativität: f g m,n = g f m,n Assoziativität: f g h m,n = f g h m,n Durch die Assoziativität ist es möglich, mehrere verkettete Transformationen zu einer zusammenzufassen und diese dann auf mehrere Bilder anzuwenden. So können einige Transformationen eingespart werden. Neutrales Element: f = f Die δ-funktion ist das neutrale Element der Konvolution. Die δ-funktion ist definiert als: x ={ 0 x 0 x=0 }, x dx=1 Eine explizite Definition gibt es nicht. Auf R ist die δ-funktion nicht als Funktion vorhanden, dort wird sie als Distribution bezeichnet. Darstellung als Matrix: Diskrete Funktionen können auch als Vektoren dargestellt werden, indem alle Funktionswerte hintereinander in einen Vektor geschrieben werden. Das ist nützlich, da die Konvolution dann als Matrixmultiplikation auf diesen Vektor ausgedrückt werden kann. Als Ergebnis der Operation erhält man wieder einen Vektor, der die transformierte Signalfunktion darstellt. Umkehrbarkeit: Die Konvolution ist nicht zwangsläufig umkehrbar. Wenn die Determinante der zur Faltung gehörigen Matrix Null ist (also die Matrix nicht invertierbar ist), kann die Konvolution nicht umgekehrt werden. Allerdings ist der Rang der Matrix in der Regel hoch, da die Komponenten stark variieren. Dadurch ist auch die Determinante der Matrix selten Null. Faltungstheorem: F f g = 2 F f F g Nachdem man die Funktionen fouriertransformiert hat, kann die Faltung durch die Multiplikation einfacher ausgeführt werden. Jetzt muss nur noch jede Komponente der Signalfunktion (das entspricht jedem Pixel im Bild) mit jeder Komponente der Abbildungsfunktion multipliziert werden, wodurch sich der Aufwand von O(n²) auf O(n) reduziert (n ist die Anzahl der Pixel im Bild). Die Fouriertransformation selbst hat Laufzeitkosten O n log n, der Gesamtaufwand ist mit O n log n also geringer, als wenn die Faltung direkt ausgerechnet würde. Performanz Die Konvolution ist als Operation teuer gegenüber Operationen auf einzelne Pixel. Wenn man für eine Operation auf einen Pixel die Kosten O(1) annimmt, so sind die Kosten für die Manipulation eines Bildes O(n), wobei n die Anzahl der Pixel im Bild ist. Bei der Konvolution dagegen wird jeder Pixel des Bildes mit jedem Koeffizienten der Abbildungsfunktion multipliziert, die Laufzeit ist also O(n²). Selbst in optimierter Form kann der Aufwand nicht unter O n log n gedrückt werden.
6 Bildränder An den Bildrändern muss eine Vereinbarung getroffen werden, wie die Bildfunktion und die Transformationsfunktion fortgesetzt werden. Das Beispiel (Abbildung 3) wurde mit einer Abbildungsfunktion gefaltet, die Bildunschärfe simuliert. Die Ränder werden je nach Methode unterschiedlich fortgesetzt: Abbildung 3: Ausgangsbild Sowohl Bildfunktion als auch Faltungsfunktion sind außerhalb eines bestimmten Radius um ihren Kern 0 (siehe Abbildung 4). Bei der Faltung wird der Radius des Kerns kleiner. An Stellen, die vorher definiert waren ist der Funktionswert jetzt 0. Dadurch ergibt sich ein schwarzer Trauerrand um das Bild. Deswegen muss man bei dieser Methode das Bild nach der Transformation zuschneiden, um den Rand zu entfernen. Abbildung 4: Mit 0 fortgesetzt An Stellen wo die Faltung nicht definiert ist, setzt man diese mit der Bildfunktion fort (Abbildung 5). Das gibt ein besseres Ergebnis, als wenn diese Werte einfach auf 0 gesetzt werden. Allerdings fällt immer noch ein starker Unterschied zwischen dem gewollt unscharfen Bereich in der Mitte und dem ungewollt scharfen Randbereich auf. Abbildung 6: Periodisch fortgesetzt Abbildung 5: Mit Bildfunktion fortgesetzt Eine weitere Lösung ist es, die Bildfunktion außerhalb ihres Definitionsbereiches periodisch fortzusetzen (Abbildung 6). Dadurch fällt der Unterschied zwischen dem Rand und der Bildmitte kaum noch auf. Das Gute an dieser Lösung ist, dass man die periodische Fortsetzung automatisch erhält, wenn man die Konvolution im Frequenzraum (nach einer Fouriertransformation) ausführt. Man braucht den Bildrand also nicht als Spezialfall zu behandeln, wie es bei den vorherigen beiden Lösungen der Fall war.
7 Punktantwort Experimentelle Ermittlung der Konvolutionsfunktion Die Punktantwort gibt an, wie ein Punkt des ursprünglichen Bildes nach der Transformation aussieht. Es wird davon ausgegangen, dass das Bild nur aus einem infinitesimal kleinen Punkt mit Helligkeit 1 besteht. Im normalen diskreten Fall heißt das, dass der Punkt genau ein Pixel groß ist. Auf diesen Punkt wird nun die Transformation ausgeführt. Das resultierende Bild visualisiert, wie der Punkt nach der Transformation im Bild verteilt ist. Abbildung 8: Ursprüngliches Bild Abbildung 7: Transformiertes Bild Abbildung 9: Punktantwort: x-, y- Achse geben Koordinaten des Punktes an, z-achse ist Intensität Experimentelle Ermittlung Für die experimentelle Ermittlung der Punktantwort gibt es mehrere Möglichkeiten: Aufnahme eines Prüfbildes: Vor oder nach der Aufnahme des Bildes wird unter gleichen Bedingungen ein Prüfbild aufgenommen (Abbildung 10). Das Prüfbild sollte dabei nur einen Punkt enthalten, der bei ruhender Kamera im Idealfall auf genau einen Pixel des Kamerasensors abgebildet wird. In diesem Bild entspricht die Helligkeit des Punktes der Summe aller Punkthelligkeiten, da allen anderen Pixel, die nicht zu dem Punkt gehören, idealerweise schwarz sind und somit den Wert 0 haben.
8 Abbildung 10: Auswirkung der Punktantwort Bild ohne Unschärfe Mit der Kamera aufgenommener Punkt Mit der Kamera aufgenommenes unscharfes Bild Wird nun der Punkt aufgenommen, ist er durch die zu messende Operation (z.b. Unschärfe) verschmiert. Aus diesem verschmierten Bild kann jetzt die Umkehrfunktion der Operation folgendermaßen berechnet werden: f g= f ' f g g= f g g= f ' g= f f Bild g Operation auf Bild f' Bild nach Operation g Umkehroperation δ Delta-Funktion Die Identität der Konvolution; Es gilt f = f Die Umkehrfunktion direkt zu finden ist meistens nahezu unmöglich. Glücklicherweise wird dies durch die Fouriertransformation bedeutend einfacher: F g g =F F g F g =1 F g = 1 F g Der Bruch bedeutet, dass man anstelle der Koeffizienten der Fouriertransformierten von g deren Kehrwerte ( 1/Koeffizient ) nimmt. Wenn es eine Umkehrfunktion g zur Funktion g gibt, ist sie nun einfach zu finden. Allerdings muss es nicht immer eine Umkehrfunktion der Operation geben! Wenn Koeffizienten der Fouriertransformierten von g Null sind, kann die Umkehrfunktion nicht existieren.
9 Abbildung 12: Unscharfes Ausgangsbild F(Bild) F(PSF) Abbildung 11: Punktantwort F -1 ( / )= Ermittlung aus dem Bild: Meist ist es nicht möglich, die Punktantwort durch ein zusätzliches Bild zu messen. Wenn nur ein bereits aufgenommenes Bild vorliegt, muss versucht werden die Punktantwort aus dem Bild zu bestimmen. Dazu sucht man Kanten im Bild. Die Kantensuche an sich ist nicht einfach; es muss erst einmal algorithmisch festgelegt werden, was Kanten sind. Eine brauchbare Definition für Kanten sind abrupte Farbübergänge. Diese können gefunden werden, indem man den Betrag des Gradienten G betrachtet. G f x, y = f x f y f x, y Abbildung 13: scharfes Ergebnis Der Gradient ist im Prinzip die Ableitung der Fläche. Die Länge des Gradientenvektors gibt an, wie stark die größte Steigung ist, während die Richtung die Richtung der stärksten Steigung angibt. Je größer der Betrag, also die Länge des Vektors ist, desto eher liegt an der Stelle im Bild eine Kante vor. Dann nimmt man an, dass an diesen Stellen ideale Kanten vorliegen. Durch den Vergleich der verzerrten Kante im Bild mit einer idealen geraden Linie bekommt man die Verschmierung der Kante. Aus diesem Vergleich kann man dann auf die Punktantwort rückschließen.
10 Abbildung 14: Unscharfes Ausgangsbild Abbildung 15: Vollständig rekonstruiertes Bild Annahme einer Kante im Bild => PSF lässt sich ermitteln Aus PSF lässt sich scharfes Bild rekonstruieren Abbildung 16: Gemessene Punktantwort Fazit Die Darstellung des Bildes als Signal vereinfacht das Filtern, da bereits viel Fachwissen über die Filterung von Signalen bekannt ist. Man kann das bestehende Wissen auf die Bildverarbeitung anwenden, um dort zu filtern. Besonders die Umwandlung des Bildsignals vereinfacht Filteroperationen, zum Beispiel durch die Umwandlung in den Frequenzraum, wo Drehungen einfach beschrieben werden können. Die Signaldarstellung des Bildes lässt sich mit verschiedenen Filteroperationen transformieren. Mit Punkttransformationen lassen sich sehr eingeschränkte Filterungen vornehmen. Die linearen Operationen sind mächtiger, können aber keine lokalen Filterungen im Bild beschreiben; dies ist mit den nichtlinearen Filterungen möglich. Je mächtiger die Klasse ist, desto aufwendiger wird allerdings die Filterung; Punktoperationen sind noch in Echtzeit möglich, lineare Operationen sind in Echtzeit schon sehr schwer zu implementieren. Nichtlineare Filterungen sind aufwendig und benötigen deswegen viel Zeit pro Bild. In diesem Text wurde die Klasse der linearen Operationen erklärt. Für diese Klasse bietet sich die Konvolution als Beschreibung der Operation an. Sie kann als Matrixmultiplikation gesehen werden und bietet damit eine mathematische Formulierung der Filterung. Durch die Transformation der Konvolution in den Frequenzraum kann die Faltung effizient ausgeführt werden, da die Fouriertransformation in Hardware wie in Software bereits implementiert ist. Die Punktantwort ist eine Möglichkeit, die Faltungsfunktion eines Bildes experimentell zu bestimmen. Mit einem Kontrollbild, welches aus genau einem hellen Punkt besteht, lässt sich ausmessen, wie das Bild durch die Filteroperation verändert wird. Selbst ohne Kontrollbild kann man das Bild noch rekonstruieren, indem man Annahmen über den Inhalt macht. Ist zum Beispiel eine Kante im Bild vorhanden, kann man eine verwischte Kante mit einer idealen Kante vergleichen und daraus die Punktantwort ermitteln.
11 In den meisten Fällen ist die Konvolution umkehrbar. Diese Eigenschaft ist sehr nützlich, da man dadurch Störungen aus dem Bild heraus filtern kann, wenn die Störung bekannt ist. Ist zum Beispiel die Punktantwort eines unscharfen Fotos bekannt, kann man daraus die Konvolution bestimmen, diese umkehren und auf das unscharfe Bild anwenden, um ein scharfes Bild zu erhalten. Literatur: Klaus D. Tönnies, Grundlagen der Bildverarbeitung, Pearson Studium, München, 2005, 4. Auflage, Seite Deutsche Wikipedia, Stichwort Konvolution, , Klaus D. Tönnies, Vorlesungsfolien zur Vorlesung Grundlagen der Bildverarbeitung, Sommersemester 2006, Universität Magdeburg, Abbildungsverzeichnis Bilder: Abbildung 1: Ungefilterte Bilder...2 Abbildung 2: Bilder nach Bildverbesserung...2 Abbildung 3: Ausgangsbild...5 Abbildung 4: Mit 0 fortgesetzt...5 Abbildung 5: Mit Bildfunktion fortgesetzt...6 Abbildung 6: Periodisch fortgesetzt...6 Abbildung 7: Transformiertes Bild...7 Abbildung 8: Ursprüngliches Bild...7 Abbildung 9: Point Spread Function: x-, y- Achse geben Koordinaten des Punktes an, z-achse ist Intensität...7 Abbildung 10: Auswirkung der Punktantwort...7 Abbildung 11: Punktantwort...8 Abbildung 12: Unscharfes Ausgangsbild...8 Abbildung 13: scharfes Ergebnis...8 Abbildung 14: Unscharfes Ausgangsbild...9 Abbildung 15: Vollständig rekonstruiertes Bild...9 Abbildung 16: Gemessene Punktantwort...9 Abbildung 1-9, 11-16: Klaus D. Tönnies, Vorlesungsfolien zur Vorlesung Grundlagen der Bildverarbeitung, Sommersemester 2006, Universität Magdeburg, Abbildung 10: Klaus D. Tönnies, Grundlagen der Bildverarbeitung, Pearson Studium, 2005, 4. Auflage, Seite 54
Filter. Industrielle Bildverarbeitung, Vorlesung No M. O. Franz
 Filter Industrielle Bildverarbeitung, Vorlesung No. 5 1 M. O. Franz 07.11.2007 1 falls nicht anders vermerkt, sind die Abbildungen entnommen aus Burger & Burge, 2005. Übersicht 1 Lineare Filter 2 Formale
Filter Industrielle Bildverarbeitung, Vorlesung No. 5 1 M. O. Franz 07.11.2007 1 falls nicht anders vermerkt, sind die Abbildungen entnommen aus Burger & Burge, 2005. Übersicht 1 Lineare Filter 2 Formale
Bildverarbeitung Herbstsemester
 Bildverarbeitung Herbstsemester Herbstsemester 2009 2012 Filter Filter 1 Inhalt Lineare und nichtlineare Filter Glättungsfilter (z.b. Gauss-Filter) Differenzfilter (z.b. Laplace-Filter) Lineare Faltung
Bildverarbeitung Herbstsemester Herbstsemester 2009 2012 Filter Filter 1 Inhalt Lineare und nichtlineare Filter Glättungsfilter (z.b. Gauss-Filter) Differenzfilter (z.b. Laplace-Filter) Lineare Faltung
Computergraphik 1 2. Teil: Bildverarbeitung. Fouriertransformation Ende FFT, Bildrestauration mit PSF Transformation, Interpolation
 Computergraphik 1 2. Teil: Bildverarbeitung Fouriertransformation Ende FFT, Bildrestauration mit PSF Transformation, Interpolation LMU München Medieninformatik Butz/Hoppe Computergrafik 1 SS2009 1 2 Repräsentation
Computergraphik 1 2. Teil: Bildverarbeitung Fouriertransformation Ende FFT, Bildrestauration mit PSF Transformation, Interpolation LMU München Medieninformatik Butz/Hoppe Computergrafik 1 SS2009 1 2 Repräsentation
Graphische Datenverarbeitung und Bildverarbeitung
 Graphische Datenverarbeitung und Bildverarbeitung Hochschule Niederrhein Bildverbesserung - Filterung Graphische DV und BV, Regina Pohle,. Bildverbesserung - Filterung Einordnung in die Inhalte der Vorlesung
Graphische Datenverarbeitung und Bildverarbeitung Hochschule Niederrhein Bildverbesserung - Filterung Graphische DV und BV, Regina Pohle,. Bildverbesserung - Filterung Einordnung in die Inhalte der Vorlesung
FILTER UND FALTUNGEN
 Ausarbeitung zum Vortrag von Daniel Schmitzek im Seminar Verarbeitung und Manipulation digitaler Bilder I n h a l t. Der Begriff des Filters 3 2. Faltungsfilter 4 2. Glättungsfilter 4 2.2 Filter zur Kantendetektion
Ausarbeitung zum Vortrag von Daniel Schmitzek im Seminar Verarbeitung und Manipulation digitaler Bilder I n h a l t. Der Begriff des Filters 3 2. Faltungsfilter 4 2. Glättungsfilter 4 2.2 Filter zur Kantendetektion
Grundlagen der Computer-Tomographie
 Grundlagen der Computer-Tomographie Quellenangabe Die folgenden Folien sind zum Teil dem Übersichtsvortrag: imbie.meb.uni-bonn.de/epileptologie/staff/lehnertz/ct1.pdf entnommen. Als Quelle für die mathematischen
Grundlagen der Computer-Tomographie Quellenangabe Die folgenden Folien sind zum Teil dem Übersichtsvortrag: imbie.meb.uni-bonn.de/epileptologie/staff/lehnertz/ct1.pdf entnommen. Als Quelle für die mathematischen
Bildverbesserung (Image Enhancement)
 Prof. Dr. Wolfgang Konen, Thomas Zielke Bildverbesserung (Image Enhancement) WS07 7.1 Konen, Zielke Der Prozess der Bildverbesserung (1) Bildverbesserung wird häufig dafür eingesetzt, die für einen menschlichen
Prof. Dr. Wolfgang Konen, Thomas Zielke Bildverbesserung (Image Enhancement) WS07 7.1 Konen, Zielke Der Prozess der Bildverbesserung (1) Bildverbesserung wird häufig dafür eingesetzt, die für einen menschlichen
Diskrete Cosinustransformation (DCT)
 Fachbereich Medieninformatik Hochschule Harz Diskrete Cosinustransformation (DCT) Referat Björn Wöldecke 10954 Abgabe: 15.01.2007 Inhaltsverzeichnis Einleitung / Vorwort... 1. Methoden zur Datenreduktion...
Fachbereich Medieninformatik Hochschule Harz Diskrete Cosinustransformation (DCT) Referat Björn Wöldecke 10954 Abgabe: 15.01.2007 Inhaltsverzeichnis Einleitung / Vorwort... 1. Methoden zur Datenreduktion...
Brückenkurs Mathematik. Mittwoch Freitag
 Brückenkurs Mathematik Mittwoch 5.10. - Freitag 14.10.2016 Vorlesung 4 Dreiecke, Vektoren, Matrizen, lineare Gleichungssysteme Kai Rothe Technische Universität Hamburg-Harburg Montag 10.10.2016 0 Brückenkurs
Brückenkurs Mathematik Mittwoch 5.10. - Freitag 14.10.2016 Vorlesung 4 Dreiecke, Vektoren, Matrizen, lineare Gleichungssysteme Kai Rothe Technische Universität Hamburg-Harburg Montag 10.10.2016 0 Brückenkurs
Theoretische Physik 1, Mechanik
 Theoretische Physik 1, Mechanik Harald Friedrich, Technische Universität München Sommersemester 2009 Mathematische Ergänzungen Vektoren und Tensoren Partielle Ableitungen, Nabla-Operator Physikalische
Theoretische Physik 1, Mechanik Harald Friedrich, Technische Universität München Sommersemester 2009 Mathematische Ergänzungen Vektoren und Tensoren Partielle Ableitungen, Nabla-Operator Physikalische
Bildverarbeitung: Filterung. D. Schlesinger () Bildverarbeitung: Filterung 1 / 17
 Bildverarbeitung: Filterung D. Schlesinger () Bildverarbeitung: Filterung 1 / 17 Allgemeines Klassische Anwendung: Entrauschung (Fast) jeder Filter basiert auf einem Modell (Annahme): Signal + Rauschen
Bildverarbeitung: Filterung D. Schlesinger () Bildverarbeitung: Filterung 1 / 17 Allgemeines Klassische Anwendung: Entrauschung (Fast) jeder Filter basiert auf einem Modell (Annahme): Signal + Rauschen
( ) sind. Für einen einzelnen. ( ) berechnet werden: ( )
 23 4 Abbildungen von Funktionsgraphen Der Graph zu einer gegebenen Funktion f ist die Menge aller ( ) sind. Für einen einzelnen Punkte, deren Koordinaten ; f () Punkt des Graphen gibt man einen Wert aus
23 4 Abbildungen von Funktionsgraphen Der Graph zu einer gegebenen Funktion f ist die Menge aller ( ) sind. Für einen einzelnen Punkte, deren Koordinaten ; f () Punkt des Graphen gibt man einen Wert aus
Multimediatechnik / Video
 Multimediatechnik / Video Video-Kompression Zusammenfassung http://www.nanocosmos.de/lietz/mtv 2009 1 Motivation: Video-Kompression Unkomprimierte Datenmengen sind zu groß! TV: 20 MB/s = 72 GB/h (720x576x2x25)
Multimediatechnik / Video Video-Kompression Zusammenfassung http://www.nanocosmos.de/lietz/mtv 2009 1 Motivation: Video-Kompression Unkomprimierte Datenmengen sind zu groß! TV: 20 MB/s = 72 GB/h (720x576x2x25)
Analysis II. Vorlesung 52. Diffeomorphismen
 Prof. Dr. H. Brenner Osnabrück SS 2014 Analysis II Vorlesung 52 Diffeomorphismen Der Satz über die lokale Umkehrbarkeit gibt Anlass zu folgender Definition. Definition 52.1. EsseienV 1 undv 2 endlichdimensionalereellevektorräume
Prof. Dr. H. Brenner Osnabrück SS 2014 Analysis II Vorlesung 52 Diffeomorphismen Der Satz über die lokale Umkehrbarkeit gibt Anlass zu folgender Definition. Definition 52.1. EsseienV 1 undv 2 endlichdimensionalereellevektorräume
Modul Digitale Bildverarbeitung SS16 Bestandteile der Lehrveranstaltung und Prüfung: Vorlesungen Übungsserien Praktika (ImageJ) bis Mai 2016 Projekt
 Modul Digitale Bildverarbeitung SS16 Bestandteile der Lehrveranstaltung und Prüfung: Vorlesungen Übungsserien Praktika (ImageJ) bis Mai 2016 Projekt im Juni 2016 Themen: Digitale Bilder, Eigenschaften
Modul Digitale Bildverarbeitung SS16 Bestandteile der Lehrveranstaltung und Prüfung: Vorlesungen Übungsserien Praktika (ImageJ) bis Mai 2016 Projekt im Juni 2016 Themen: Digitale Bilder, Eigenschaften
++ + = 0 so erhält man eine quadratische Gleichung mit zwei Variablen dx+ey+f = 0 1.1
 Hauptachsentransformation. Einleitung Schneidet man den geraden Kreiskegel mit der Gleichung = + und die Ebene ++ + = 0 so erhält man eine quadratische Gleichung mit zwei Variablen +2 + +dx+ey+f = 0. Die
Hauptachsentransformation. Einleitung Schneidet man den geraden Kreiskegel mit der Gleichung = + und die Ebene ++ + = 0 so erhält man eine quadratische Gleichung mit zwei Variablen +2 + +dx+ey+f = 0. Die
9.2 Invertierbare Matrizen
 34 9.2 Invertierbare Matrizen Die Division ist als Umkehroperation der Multiplikation definiert. Das heisst, für reelle Zahlen a 0 und b gilt b = a genau dann, wenn a b =. Übertragen wir dies von den reellen
34 9.2 Invertierbare Matrizen Die Division ist als Umkehroperation der Multiplikation definiert. Das heisst, für reelle Zahlen a 0 und b gilt b = a genau dann, wenn a b =. Übertragen wir dies von den reellen
Vektoren, Vektorräume
 Vektoren, Vektorräume Roman Wienands Sommersemester 2010 Mathematisches Institut der Universität zu Köln Roman Wienands (Universität zu Köln) Mathematik II für Studierende der Chemie Sommersemester 2010
Vektoren, Vektorräume Roman Wienands Sommersemester 2010 Mathematisches Institut der Universität zu Köln Roman Wienands (Universität zu Köln) Mathematik II für Studierende der Chemie Sommersemester 2010
A2.3 Lineare Gleichungssysteme
 A2.3 Lineare Gleichungssysteme Schnittpunkte von Graphen Bereits weiter oben wurden die Schnittpunkte von Funktionsgraphen mit den Koordinatenachsen besprochen. Wenn sich zwei Geraden schneiden, dann müssen
A2.3 Lineare Gleichungssysteme Schnittpunkte von Graphen Bereits weiter oben wurden die Schnittpunkte von Funktionsgraphen mit den Koordinatenachsen besprochen. Wenn sich zwei Geraden schneiden, dann müssen
1 Eigenschaften von Abbildungen
 Technische Universität München Christian Neumann Ferienkurs Lineare Algebra für Physiker Vorlesung Dienstag WS 2008/09 Thema des heutigen Tages sind zuerst Abbildungen, dann spezielle Eigenschaften linearer
Technische Universität München Christian Neumann Ferienkurs Lineare Algebra für Physiker Vorlesung Dienstag WS 2008/09 Thema des heutigen Tages sind zuerst Abbildungen, dann spezielle Eigenschaften linearer
R.Wagner, Mathematik in der Astronomie
 Mathematik in der Astronomie Roland Wagner Johann Radon Institute for Computational and Applied Mathematics (RICAM) Österreichische Akademie der Wissenschaften (ÖAW) Linz, Austria Linz, 20.Mai 2016 Übersicht
Mathematik in der Astronomie Roland Wagner Johann Radon Institute for Computational and Applied Mathematics (RICAM) Österreichische Akademie der Wissenschaften (ÖAW) Linz, Austria Linz, 20.Mai 2016 Übersicht
Bildverarbeitung: Fourier-Transformation. D. Schlesinger () BV: Fourier-Transformation 1 / 16
 Bildverarbeitung: Fourier-Transformation D. Schlesinger () BV: Fourier-Transformation 1 / 16 Allgemeines Bilder sind keine Vektoren. Bilder sind Funktionen x : D C (Menge der Pixel in die Menge der Farbwerte).
Bildverarbeitung: Fourier-Transformation D. Schlesinger () BV: Fourier-Transformation 1 / 16 Allgemeines Bilder sind keine Vektoren. Bilder sind Funktionen x : D C (Menge der Pixel in die Menge der Farbwerte).
Motivation. Diskretisierung. Überblick. Algorithmik III Algorithmen und Modelle für kontinuierliche Datenstrukturen. Diskretisierung und Quantisierung
 Algorithmik III Algorithmen und Modelle für kontinuierliche Datenstrukturen Motivation Analoge Aufnahme von Sprache, Bildern Digitale Speicherung durch Diskretisierung + Quantisierung Informationsverlust
Algorithmik III Algorithmen und Modelle für kontinuierliche Datenstrukturen Motivation Analoge Aufnahme von Sprache, Bildern Digitale Speicherung durch Diskretisierung + Quantisierung Informationsverlust
44 Orthogonale Matrizen
 44 Orthogonale Matrizen 44.1 Motivation Im euklidischen Raum IR n haben wir gesehen, dass Orthonormalbasen zu besonders einfachen und schönen Beschreibungen führen. Wir wollen das Konzept der Orthonormalität
44 Orthogonale Matrizen 44.1 Motivation Im euklidischen Raum IR n haben wir gesehen, dass Orthonormalbasen zu besonders einfachen und schönen Beschreibungen führen. Wir wollen das Konzept der Orthonormalität
EVC Repetitorium Blender
 EVC Repetitorium Blender Michael Hecher Felix Kreuzer Institute of Computer Graphics and Algorithms Vienna University of Technology INSTITUTE OF COMPUTER GRAPHICS AND ALGORITHMS Filter Transformationen
EVC Repetitorium Blender Michael Hecher Felix Kreuzer Institute of Computer Graphics and Algorithms Vienna University of Technology INSTITUTE OF COMPUTER GRAPHICS AND ALGORITHMS Filter Transformationen
Inhaltsübersicht. Deltafunktion Gammafunktion Fehlerfunktion. Kapitel 13: Spezielle Funktionen
 Inhaltsübersicht Kapitel 13: Spezielle Funktionen Deltafunktion Gammafunktion Fehlerfunktion Notizen zur Vorlesung Mathematik für Materialwissenschaftler 2 1 Die Bezeichnung Delta-Funktion ist streng genommen
Inhaltsübersicht Kapitel 13: Spezielle Funktionen Deltafunktion Gammafunktion Fehlerfunktion Notizen zur Vorlesung Mathematik für Materialwissenschaftler 2 1 Die Bezeichnung Delta-Funktion ist streng genommen
Outline. 1 Vektoren im Raum. 2 Komponenten und Koordinaten. 3 Skalarprodukt. 4 Vektorprodukt. 5 Analytische Geometrie. 6 Lineare Räume, Gruppentheorie
 Outline 1 Vektoren im Raum 2 Komponenten und Koordinaten 3 Skalarprodukt 4 Vektorprodukt 5 Analytische Geometrie 6 Lineare Räume, Gruppentheorie Roman Wienands (Universität zu Köln) Mathematik II für Studierende
Outline 1 Vektoren im Raum 2 Komponenten und Koordinaten 3 Skalarprodukt 4 Vektorprodukt 5 Analytische Geometrie 6 Lineare Räume, Gruppentheorie Roman Wienands (Universität zu Köln) Mathematik II für Studierende
$Id: linabb.tex,v /01/09 13:27:34 hk Exp hk $
 Mathematik für Ingenieure I, WS 8/9 Freitag 9. $Id: linabb.tex,v.3 9//9 3:7:34 hk Exp hk $ II. Lineare Algebra 9 Lineare Abbildungen 9. Lineare Abbildungen Der folgende Satz gibt uns eine einfachere Möglichkeit
Mathematik für Ingenieure I, WS 8/9 Freitag 9. $Id: linabb.tex,v.3 9//9 3:7:34 hk Exp hk $ II. Lineare Algebra 9 Lineare Abbildungen 9. Lineare Abbildungen Der folgende Satz gibt uns eine einfachere Möglichkeit
1 Fraktale Eigenschaften der Koch-Kurve
 Anhang Inhaltsverzeichnis Fraktale Eigenschaften der Koch-Kurve iii. Einführung.................................. iii.2 Defintion.................................... iii.3 Gesamtlänge der Koch-Kurve........................
Anhang Inhaltsverzeichnis Fraktale Eigenschaften der Koch-Kurve iii. Einführung.................................. iii.2 Defintion.................................... iii.3 Gesamtlänge der Koch-Kurve........................
INTELLIGENTE DATENANALYSE IN MATLAB
 INTELLIGENTE DATENANALYSE IN MATLAB Bildanalyse Literatur David A. Forsyth: Computer Vision i A Modern Approach. Mark S. Nixon und Alberto S. Aguado: Feature Extraction and Image Processing. Ulrich Schwanecke:
INTELLIGENTE DATENANALYSE IN MATLAB Bildanalyse Literatur David A. Forsyth: Computer Vision i A Modern Approach. Mark S. Nixon und Alberto S. Aguado: Feature Extraction and Image Processing. Ulrich Schwanecke:
Die Interpretation Optischer Leistungsdaten
 Die Interpretation Optischer Leistungsdaten Einige Fakten über die Carl Zeiss AG Seit 1896 berühmt für Kamera-Objektive Zeiss 1846 von Carl Zeiss gegründet 48 Produktionsstandorte weltweit Die ersten Kamerabilder
Die Interpretation Optischer Leistungsdaten Einige Fakten über die Carl Zeiss AG Seit 1896 berühmt für Kamera-Objektive Zeiss 1846 von Carl Zeiss gegründet 48 Produktionsstandorte weltweit Die ersten Kamerabilder
Filterung von Bildern (2D-Filter)
 Prof. Dr. Wolfgang Konen, Thomas Zielke Filterung von Bildern (2D-Filter) SS06 6. Konen, Zielke Aktivierung Was, denken Sie, ist ein Filter in der BV? Welche Filter kennen Sie? neuer Pixelwert bilden aus
Prof. Dr. Wolfgang Konen, Thomas Zielke Filterung von Bildern (2D-Filter) SS06 6. Konen, Zielke Aktivierung Was, denken Sie, ist ein Filter in der BV? Welche Filter kennen Sie? neuer Pixelwert bilden aus
3.3 Das Abtasttheorem
 17 3.3 Das Abtasttheorem In der Praxis kennt man von einer zeitabhängigen Funktion f einem Signal meist nur diskret abgetastete Werte fn, mit festem > und ganzzahligem n. Unter welchen Bedingungen kann
17 3.3 Das Abtasttheorem In der Praxis kennt man von einer zeitabhängigen Funktion f einem Signal meist nur diskret abgetastete Werte fn, mit festem > und ganzzahligem n. Unter welchen Bedingungen kann
2. Digitale Codierung und Übertragung
 2. Digitale Codierung und Übertragung 2.1 Informationstheoretische Grundlagen 2.2 Speicherbedarf und Kompression 2.3 Digitalisierung Ludwig-Maximilians-Universität München Prof. Hußmann Digitale Medien
2. Digitale Codierung und Übertragung 2.1 Informationstheoretische Grundlagen 2.2 Speicherbedarf und Kompression 2.3 Digitalisierung Ludwig-Maximilians-Universität München Prof. Hußmann Digitale Medien
Übung zu Einführung in die Informatik # 14
 Übung zu Einführung in die Informatik # 14 Tobias Schill tschill@techfak.uni-bielefeld.de 12. Februar 2016 Aktualisiert am 12. Februar 2016 um 11:13 Erstklausur: Mi, 24.02.2016 von 10-12Uhr Antworten von
Übung zu Einführung in die Informatik # 14 Tobias Schill tschill@techfak.uni-bielefeld.de 12. Februar 2016 Aktualisiert am 12. Februar 2016 um 11:13 Erstklausur: Mi, 24.02.2016 von 10-12Uhr Antworten von
Einleitung 2. 1 Koordinatensysteme 2. 2 Lineare Abbildungen 4. 3 Literaturverzeichnis 7
 Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Sonja Hunscha - Koordinatensysteme 1 Inhalt Einleitung 2 1 Koordinatensysteme 2 1.1 Kartesisches Koordinatensystem 2 1.2 Polarkoordinaten 3 1.3 Zusammenhang zwischen kartesischen und Polarkoordinaten 3
Bildbearbeitungstechniken Lehrerinformation
 Lehrerinformation 1/9 Arbeitsauftrag Ziel Zwanzig klassische Elemente der Bildbearbeitung werden vorgestellt. Die Sch arbeiten in Zweierteams und erarbeiten sich das Wissen zu je 1 2. Sie bearbeiten Bildausschnitte,
Lehrerinformation 1/9 Arbeitsauftrag Ziel Zwanzig klassische Elemente der Bildbearbeitung werden vorgestellt. Die Sch arbeiten in Zweierteams und erarbeiten sich das Wissen zu je 1 2. Sie bearbeiten Bildausschnitte,
Kapitel 2: Mathematische Grundlagen
 [ Computeranimation ] Kapitel 2: Mathematische Grundlagen Prof. Dr. Stefan M. Grünvogel stefan.gruenvogel@fh-koeln.de Institut für Medien- und Phototechnik Fachhochschule Köln 2. Mathematische Grundlagen
[ Computeranimation ] Kapitel 2: Mathematische Grundlagen Prof. Dr. Stefan M. Grünvogel stefan.gruenvogel@fh-koeln.de Institut für Medien- und Phototechnik Fachhochschule Köln 2. Mathematische Grundlagen
Systemtheorie abbildender Systeme
 Bandbegrenzung Bild in (b) nicht band-begrenzt: scharfe Kanten = Dirac-Funktionen = weißes Spektrum Erfordert Tapering vor Digitalisierung (Multiplikation mit geeigneter Fensterfunktion; auf Null drücken
Bandbegrenzung Bild in (b) nicht band-begrenzt: scharfe Kanten = Dirac-Funktionen = weißes Spektrum Erfordert Tapering vor Digitalisierung (Multiplikation mit geeigneter Fensterfunktion; auf Null drücken
Mathematischer Vorkurs Lösungen zum Übungsblatt 5
 Mathematischer Vorkurs Lösungen zum Übungsblatt 5 Prof. Dr. Norbert Pietralla/Sommersemester 2012 c.v.meister@skmail.ikp.physik.tu-darmstadt.de Aufgabe 1: Berechnen Sie den Abstand d der Punkte P 1 und
Mathematischer Vorkurs Lösungen zum Übungsblatt 5 Prof. Dr. Norbert Pietralla/Sommersemester 2012 c.v.meister@skmail.ikp.physik.tu-darmstadt.de Aufgabe 1: Berechnen Sie den Abstand d der Punkte P 1 und
Matrizen, Gaußscher Algorithmus 1 Bestimmung der inversen Matrix
 Inhaltsverzeichnis Matrizen, Gaußscher Algorithmus 1 Bestimmung der inversen Matrix Auf dieser Seite werden Matrizen und Vektoren fett gedruckt, um sie von Zahlen zu unterscheiden. Betrachtet wird das
Inhaltsverzeichnis Matrizen, Gaußscher Algorithmus 1 Bestimmung der inversen Matrix Auf dieser Seite werden Matrizen und Vektoren fett gedruckt, um sie von Zahlen zu unterscheiden. Betrachtet wird das
Mathematischer Vorkurs für Physiker WS 2011/12 Vorlesung 3
 TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 2011/12 Vorlesung 3 Differenziation und Integration von Vektorfunktionen Der Ortsvektor: Man kann einen Punkt P im Raum eindeutig durch die
TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 2011/12 Vorlesung 3 Differenziation und Integration von Vektorfunktionen Der Ortsvektor: Man kann einen Punkt P im Raum eindeutig durch die
Versuch C: Auflösungsvermögen Einleitung
 Versuch C: svermögen Einleitung Das AV wird üblicherweise in Linienpaaren pro mm (Lp/mm) angegeben und ist diejenige Anzahl von Linienpaaren, bei der ein normalsichtiges Auge keinen Kontrastunterschied
Versuch C: svermögen Einleitung Das AV wird üblicherweise in Linienpaaren pro mm (Lp/mm) angegeben und ist diejenige Anzahl von Linienpaaren, bei der ein normalsichtiges Auge keinen Kontrastunterschied
Die Lösungen der Gleichung b x = log b (x)
 Die Lösungen der Gleichung b = log b () wgnedin@math.uni-koeln.de 17. Januar 2014 In der ersten Vorlesung des Wintersemesters wurde folgende Frage gestellt: Wieviele Lösungen hat die Gleichung ( ) 1 =
Die Lösungen der Gleichung b = log b () wgnedin@math.uni-koeln.de 17. Januar 2014 In der ersten Vorlesung des Wintersemesters wurde folgende Frage gestellt: Wieviele Lösungen hat die Gleichung ( ) 1 =
Filterprogrammierung in Gimp
 Rüdiger Timpe Alexander Bertschik Filterprogrammierung in Gimp Ein Vortrag im Rahmen des Seminars Manipulation und Verarbeitung digitaler Bilder Inhalt Aufgabenstellung und Motivation...3 Auswahl der Filter...3
Rüdiger Timpe Alexander Bertschik Filterprogrammierung in Gimp Ein Vortrag im Rahmen des Seminars Manipulation und Verarbeitung digitaler Bilder Inhalt Aufgabenstellung und Motivation...3 Auswahl der Filter...3
Graphische Datenverarbeitung und Bildverarbeitung
 Graphische Datenverarbeitung und Bildverarbeitung Hochschule Niederrhein Morphologische Operatoren Graphische DV und BV, Regina Pohle, 5. Morphologische Operatoren Einordnung in die Inhalte der Vorlesung
Graphische Datenverarbeitung und Bildverarbeitung Hochschule Niederrhein Morphologische Operatoren Graphische DV und BV, Regina Pohle, 5. Morphologische Operatoren Einordnung in die Inhalte der Vorlesung
3 Abbildungen von Funktionsgraphen
 32 3 Abbildungen von Funktionsgraphen In Kapitel 1 dieses Workshops haben wir uns mit der Transformation von geometrischen Figuren im Achsenkreuz beschäftigt: mit Verschiebungen, Spiegelungen, Achsenstreckungen
32 3 Abbildungen von Funktionsgraphen In Kapitel 1 dieses Workshops haben wir uns mit der Transformation von geometrischen Figuren im Achsenkreuz beschäftigt: mit Verschiebungen, Spiegelungen, Achsenstreckungen
Theoretische Informatik 1 WS 2007/2008. Prof. Dr. Rainer Lütticke
 Theoretische Informatik 1 WS 2007/2008 Prof. Dr. Rainer Lütticke Inhalt der Vorlesung Grundlagen - Mengen, Relationen, Abbildungen/Funktionen - Datenstrukturen - Aussagenlogik Automatentheorie Formale
Theoretische Informatik 1 WS 2007/2008 Prof. Dr. Rainer Lütticke Inhalt der Vorlesung Grundlagen - Mengen, Relationen, Abbildungen/Funktionen - Datenstrukturen - Aussagenlogik Automatentheorie Formale
Vorkurs Mathematik B
 Vorkurs Mathematik B Dr. Thorsten Camps Fakultät für Mathematik TU Dortmund 8. September 2011 Für die Mathematik zentral sind Abbildungen und Funktionen. Häufig wird zwischen beiden Begriffen nicht unterschieden.
Vorkurs Mathematik B Dr. Thorsten Camps Fakultät für Mathematik TU Dortmund 8. September 2011 Für die Mathematik zentral sind Abbildungen und Funktionen. Häufig wird zwischen beiden Begriffen nicht unterschieden.
Vektorräume und Lineare Abbildungen
 Vektorräume und Lineare Abbildungen Patricia Doll, Selmar Binder, Lukas Bischoff, Claude Denier ETHZ D-MATL SS 07 11.04.2007 1 Vektorräume 1.1 Definition des Vektorraumes (VR) 1.1.1 Grundoperationen Um
Vektorräume und Lineare Abbildungen Patricia Doll, Selmar Binder, Lukas Bischoff, Claude Denier ETHZ D-MATL SS 07 11.04.2007 1 Vektorräume 1.1 Definition des Vektorraumes (VR) 1.1.1 Grundoperationen Um
Problemreduktion durch Transformation am Beispiel des. Erweiterten Euklidschen Algorithmus
 Problemreduktion durch Transformation am Beispiel des Erweiterten Euklidschen Algorithmus Wolfgang Windsteiger JKU Linz, A 4040 Linz, Austria Kurzfassung Transformation beschreibt im Wesentlichen die algorithmische
Problemreduktion durch Transformation am Beispiel des Erweiterten Euklidschen Algorithmus Wolfgang Windsteiger JKU Linz, A 4040 Linz, Austria Kurzfassung Transformation beschreibt im Wesentlichen die algorithmische
ein geeignetes Koordinatensystem zu verwenden.
 1.13 Koordinatensysteme (Anwendungen) Man ist immer bemüht, für die mathematische Beschreibung einer wissenschaftlichen Aufgabe ( Chemie, Biologie,Physik ) ein geeignetes Koordinatensystem zu verwenden.
1.13 Koordinatensysteme (Anwendungen) Man ist immer bemüht, für die mathematische Beschreibung einer wissenschaftlichen Aufgabe ( Chemie, Biologie,Physik ) ein geeignetes Koordinatensystem zu verwenden.
Viele wichtige Operationen können als lineare Abbildungen interpretiert werden. Beispielsweise beschreibt die lineare Abbildung
 Kapitel 3 Lineare Abbildungen Lineare Abbildungen sind eine natürliche Klasse von Abbildungen zwischen zwei Vektorräumen, denn sie vertragen sich per definitionem mit der Struktur linearer Räume Viele
Kapitel 3 Lineare Abbildungen Lineare Abbildungen sind eine natürliche Klasse von Abbildungen zwischen zwei Vektorräumen, denn sie vertragen sich per definitionem mit der Struktur linearer Räume Viele
Vektorräume. 1. v + w = w + v (Kommutativität der Vektoraddition)
 Vektorräume In vielen physikalischen Betrachtungen treten Größen auf, die nicht nur durch ihren Zahlenwert charakterisiert werden, sondern auch durch ihre Richtung Man nennt sie vektorielle Größen im Gegensatz
Vektorräume In vielen physikalischen Betrachtungen treten Größen auf, die nicht nur durch ihren Zahlenwert charakterisiert werden, sondern auch durch ihre Richtung Man nennt sie vektorielle Größen im Gegensatz
Lösungsblatt 2 Signalverarbeitung und Klassifikation
 Fakultät für Informatik Übung zu Kognitive Systeme Sommersemester 06 M. Sperber (matthias.sperber@kit.edu) S. Nguyen (thai.nguyen@kit.edu) Lösungsblatt Signalverarbeitung und Klassifikation Aufgabe : Faltung
Fakultät für Informatik Übung zu Kognitive Systeme Sommersemester 06 M. Sperber (matthias.sperber@kit.edu) S. Nguyen (thai.nguyen@kit.edu) Lösungsblatt Signalverarbeitung und Klassifikation Aufgabe : Faltung
Digitale Bildverarbeitung Einheit 8 Lineare Filterung
 Digitale Bildverarbeitung Einheit 8 Lineare Filterung Lehrauftrag SS 2008 Fachbereich M+I der FH-Offenburg Dr. Bernard Haasdonk Albert-Ludwigs-Universität Freiburg Ziele der Einheit Verstehen, wie lineare
Digitale Bildverarbeitung Einheit 8 Lineare Filterung Lehrauftrag SS 2008 Fachbereich M+I der FH-Offenburg Dr. Bernard Haasdonk Albert-Ludwigs-Universität Freiburg Ziele der Einheit Verstehen, wie lineare
Nichtmonotone Grauwertabbildung
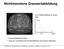 LMU München Medieninformatik Butz/Hilliges 2D Graphics WS2005 02.12.2005 Folie 1 Nichtmonotone Grauwertabbildung Zwei Grauwertfenster in einem Bild. g (g) 0 511 2100 g Erzeugt künstliche Kanten. Grenzen
LMU München Medieninformatik Butz/Hilliges 2D Graphics WS2005 02.12.2005 Folie 1 Nichtmonotone Grauwertabbildung Zwei Grauwertfenster in einem Bild. g (g) 0 511 2100 g Erzeugt künstliche Kanten. Grenzen
2. Vorlesung Wintersemester
 2. Vorlesung Wintersemester 1 Mechanik von Punktteilchen Ein Punktteilchen ist eine Abstraktion. In der Natur gibt es zwar Elementarteilchen (Elektronen, Neutrinos, usw.), von denen bisher keine Ausdehnung
2. Vorlesung Wintersemester 1 Mechanik von Punktteilchen Ein Punktteilchen ist eine Abstraktion. In der Natur gibt es zwar Elementarteilchen (Elektronen, Neutrinos, usw.), von denen bisher keine Ausdehnung
8.2 Invertierbare Matrizen
 38 8.2 Invertierbare Matrizen Die Division ist als Umkehroperation der Multiplikation definiert. Das heisst, für reelle Zahlen a 0 und b gilt b = a genau dann, wenn a b =. Übertragen wir dies von den reellen
38 8.2 Invertierbare Matrizen Die Division ist als Umkehroperation der Multiplikation definiert. Das heisst, für reelle Zahlen a 0 und b gilt b = a genau dann, wenn a b =. Übertragen wir dies von den reellen
Proseminar Datenkomprimierung Dr. U. Tamm. JPEG - Kompression WS 2002/03. Torsten Zichner
 Proseminar Datenkomprimierung Dr. U. Tamm JPEG - Kompression WS 2002/03 Torsten Zichner Inhaltsangabe: 1. Einleitung 2. JPEG Kompression 2.1. Konvertierung des Bildes in ein geeignetes Farbmodell 2.2.
Proseminar Datenkomprimierung Dr. U. Tamm JPEG - Kompression WS 2002/03 Torsten Zichner Inhaltsangabe: 1. Einleitung 2. JPEG Kompression 2.1. Konvertierung des Bildes in ein geeignetes Farbmodell 2.2.
Folgerungen aus dem Auflösungsatz
 Folgerungen aus dem Auflösungsatz Wir haben in der Vorlesung den Satz über implizite Funktionen (Auflösungssatz) kennen gelernt. In unserer Formulierung lauten die Resultate: Seien x 0 R m, y 0 R n und
Folgerungen aus dem Auflösungsatz Wir haben in der Vorlesung den Satz über implizite Funktionen (Auflösungssatz) kennen gelernt. In unserer Formulierung lauten die Resultate: Seien x 0 R m, y 0 R n und
Musterlösung zu den Übungen zur Vorlesung Mathematik für Physiker II. x 2
 Musterlösung zu den Übungen zur Vorlesung Mathematik für Physiker II Wiederholungsblatt: Analysis Sommersemester 2011 W. Werner, F. Springer erstellt von: Max Brinkmann Aufgabe 1: Untersuchen Sie, ob die
Musterlösung zu den Übungen zur Vorlesung Mathematik für Physiker II Wiederholungsblatt: Analysis Sommersemester 2011 W. Werner, F. Springer erstellt von: Max Brinkmann Aufgabe 1: Untersuchen Sie, ob die
Debayeringverfahren. 19. Mai Thomas Noack, Nikolai Kosjar. SE Computational Photography - Debayeringverfahren
 Debayeringverfahren Thomas Noack, Nikolai Kosjar 19. Mai 2010 Was bisher geschah... Reduktion der Herstellungskosten durch Einsatz von nur noch einem CCD-Sensor mit Bayer-Filter Problem: Bayer Image Full
Debayeringverfahren Thomas Noack, Nikolai Kosjar 19. Mai 2010 Was bisher geschah... Reduktion der Herstellungskosten durch Einsatz von nur noch einem CCD-Sensor mit Bayer-Filter Problem: Bayer Image Full
Digitale Bildverarbeitung (DBV)
 Digitale Bildverarbeitung (DBV) Prof. Dr. Ing. Heinz Jürgen Przybilla Labor für Photogrammetrie Email: heinz juergen.przybilla@hs bochum.de Tel. 0234 32 10517 Sprechstunde: Montags 13 14 Uhr und nach Vereinbarung
Digitale Bildverarbeitung (DBV) Prof. Dr. Ing. Heinz Jürgen Przybilla Labor für Photogrammetrie Email: heinz juergen.przybilla@hs bochum.de Tel. 0234 32 10517 Sprechstunde: Montags 13 14 Uhr und nach Vereinbarung
Technische Universität München Zentrum Mathematik. Übungsblatt 12
 Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 1 Hausaufgaben Aufgabe 1.1 Sei f : R R gegeben durch f(x 1, x ) = x 3
Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 1 Hausaufgaben Aufgabe 1.1 Sei f : R R gegeben durch f(x 1, x ) = x 3
1 Linearkombinationen
 Matthias Tischler Karolina Stoiber Ferienkurs Lineare Algebra für Physiker WS 14/15 A 1 Linearkombinationen Unter einer Linearkombination versteht man in der linearen Algebra einen Vektor, der sich durch
Matthias Tischler Karolina Stoiber Ferienkurs Lineare Algebra für Physiker WS 14/15 A 1 Linearkombinationen Unter einer Linearkombination versteht man in der linearen Algebra einen Vektor, der sich durch
Einführung in die Informatik Turing Machines
 Einführung in die Informatik Turing Machines Eine abstrakte Maschine zur Präzisierung des Algorithmenbegriffs Wolfram Burgard Cyrill Stachniss 1/14 Motivation und Einleitung Bisher haben wir verschiedene
Einführung in die Informatik Turing Machines Eine abstrakte Maschine zur Präzisierung des Algorithmenbegriffs Wolfram Burgard Cyrill Stachniss 1/14 Motivation und Einleitung Bisher haben wir verschiedene
In diesem Abschnitt betrachten wir nur quadratische Matrizen mit Komponenten aus einem Körper K, also A K n n für ein n N. Wenn (mit einem n > 1)
 34 Determinanten In diesem Abschnitt betrachten wir nur quadratische Matrizen mit Komponenten aus einem Körper K, also A K n n für ein n N Wenn (mit einem n > 1) a 11 a 12 a 1n a 21 a 22 a 2n A =, (1)
34 Determinanten In diesem Abschnitt betrachten wir nur quadratische Matrizen mit Komponenten aus einem Körper K, also A K n n für ein n N Wenn (mit einem n > 1) a 11 a 12 a 1n a 21 a 22 a 2n A =, (1)
Mathematische und statistische Methoden I
 Prof. Dr. G. Meinhardt 6. Stock, Wallstr. 3 (Raum 06-06) Sprechstunde jederzeit nach Vereinbarung und nach der Vorlesung. Mathematische und statistische Methoden I Dr. Malte Persike persike@uni-mainz.de
Prof. Dr. G. Meinhardt 6. Stock, Wallstr. 3 (Raum 06-06) Sprechstunde jederzeit nach Vereinbarung und nach der Vorlesung. Mathematische und statistische Methoden I Dr. Malte Persike persike@uni-mainz.de
Projektdokumentation
 Thema: Bildschärfung durch inverse Filterung von: Thorsten Küster 11027641 Lutz Kirberg 11023468 Gruppe: Ibv-team-5 Problemstellung: Bei der Übertragung von Kamerabildern über ein Video-Kabel kommt es
Thema: Bildschärfung durch inverse Filterung von: Thorsten Küster 11027641 Lutz Kirberg 11023468 Gruppe: Ibv-team-5 Problemstellung: Bei der Übertragung von Kamerabildern über ein Video-Kabel kommt es
Beate Meffert, Olaf Hochmuth: Werkzeuge der Signalverarbeitung, Pearson 2004
 4 Signalverarbeitung 4.1! Grundbegriffe! 4.2! Frequenzspektren, Fourier-Transformation! 4.3! Abtasttheorem: Eine zweite Sicht Weiterführende Literatur (z.b.):!! Beate Meffert, Olaf Hochmuth: Werkzeuge
4 Signalverarbeitung 4.1! Grundbegriffe! 4.2! Frequenzspektren, Fourier-Transformation! 4.3! Abtasttheorem: Eine zweite Sicht Weiterführende Literatur (z.b.):!! Beate Meffert, Olaf Hochmuth: Werkzeuge
Mathematischer Vorkurs für Physiker WS 2012/13: Vorlesung 1
 TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 2012/13: Vorlesung 1 Komplexe Zahlen Das Auffinden aller Nullstellen von algebraischen Gleichungen ist ein Grundproblem, das in der Physik
TU München Prof. P. Vogl Mathematischer Vorkurs für Physiker WS 2012/13: Vorlesung 1 Komplexe Zahlen Das Auffinden aller Nullstellen von algebraischen Gleichungen ist ein Grundproblem, das in der Physik
Lineare Abbildungen Definitionen von linearer Abbildung, linearer Transformation, affiner Abbildung. Parallentreue und Teilverhältnistreue
 Lineare Abbildungen Vorlesung Lineare Algebra mit integrierten Übungen WS 12 13 Studiengang LBS Unterrichtsfach Mathematik Lineare Algebra, Teil 2 Abbildungen Lineare Abbildungen Lineare Eigenwerte, Eigenvektoren
Lineare Abbildungen Vorlesung Lineare Algebra mit integrierten Übungen WS 12 13 Studiengang LBS Unterrichtsfach Mathematik Lineare Algebra, Teil 2 Abbildungen Lineare Abbildungen Lineare Eigenwerte, Eigenvektoren
2.3.4 Drehungen in drei Dimensionen
 2.3.4 Drehungen in drei Dimensionen Wir verallgemeinern die bisherigen Betrachtungen nun auf den dreidimensionalen Fall. Für Drehungen des Koordinatensystems um die Koordinatenachsen ergibt sich 1 x 1
2.3.4 Drehungen in drei Dimensionen Wir verallgemeinern die bisherigen Betrachtungen nun auf den dreidimensionalen Fall. Für Drehungen des Koordinatensystems um die Koordinatenachsen ergibt sich 1 x 1
Definitionen. Merkblatt lineare Algebra. affiner Teilraum Menge, die durch Addition eines Vektors v 0 zu allen Vektoren eines Vektorraumes V entsteht
 Seite 1 Definitionen affiner Teilraum Menge, die durch Addition eines Vektors v 0 zu allen Vektoren eines Vektorraumes V entsteht ähnliche Matrizen Matrizen, die das gleiche charakteristische Polynom haben
Seite 1 Definitionen affiner Teilraum Menge, die durch Addition eines Vektors v 0 zu allen Vektoren eines Vektorraumes V entsteht ähnliche Matrizen Matrizen, die das gleiche charakteristische Polynom haben
Lineare Gleichungssysteme
 Christian Serpé Universität Münster 14. September 2011 Christian Serpé (Universität Münster) 14. September 2011 1 / 56 Gliederung 1 Motivation Beispiele Allgemeines Vorgehen 2 Der Vektorraum R n 3 Lineare
Christian Serpé Universität Münster 14. September 2011 Christian Serpé (Universität Münster) 14. September 2011 1 / 56 Gliederung 1 Motivation Beispiele Allgemeines Vorgehen 2 Der Vektorraum R n 3 Lineare
Technische Universität München Zentrum Mathematik. Übungsblatt 7
 Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 7 Hausaufgaben Aufgabe 7. Für n N ist die Matrix-Exponentialfunktion
Technische Universität München Zentrum Mathematik Mathematik (Elektrotechnik) Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 7 Hausaufgaben Aufgabe 7. Für n N ist die Matrix-Exponentialfunktion
Mathematische Erfrischungen III - Vektoren und Matrizen
 Signalverarbeitung und Musikalische Akustik - MuWi UHH WS 06/07 Mathematische Erfrischungen III - Vektoren und Matrizen Universität Hamburg Vektoren entstanden aus dem Wunsch, u.a. Bewegungen, Verschiebungen
Signalverarbeitung und Musikalische Akustik - MuWi UHH WS 06/07 Mathematische Erfrischungen III - Vektoren und Matrizen Universität Hamburg Vektoren entstanden aus dem Wunsch, u.a. Bewegungen, Verschiebungen
(Fast) Fourier Transformation und ihre Anwendungen
 (Fast) Fourier Transformation und ihre Anwendungen Johannes Lülff Universität Münster 14.01.2009 Definition Fouriertransformation F (ω) = F [f(t)] (ω) := 1 2π dt f(t)e iωt Fouriersynthese f(t) = F 1 [F
(Fast) Fourier Transformation und ihre Anwendungen Johannes Lülff Universität Münster 14.01.2009 Definition Fouriertransformation F (ω) = F [f(t)] (ω) := 1 2π dt f(t)e iωt Fouriersynthese f(t) = F 1 [F
Hauptseminar Autofokus
 Hauptseminar Autofokus Hans Dichtl 30. Januar 2007 Wann ist ein Bild fokussiert? Wann ist ein Bild fokusiert? Welche mathematischen Modelle stehen uns zur Verfügung? Wie wird das elektronisch und mechanisch
Hauptseminar Autofokus Hans Dichtl 30. Januar 2007 Wann ist ein Bild fokussiert? Wann ist ein Bild fokusiert? Welche mathematischen Modelle stehen uns zur Verfügung? Wie wird das elektronisch und mechanisch
Vorkurs Mathematik B
 Vorkurs Mathematik B Dr. Thorsten Camps Fakultät für Mathematik TU Dortmund 20. September 2011 Definition (R n ) Wir definieren: 1 Der R 2 sei die Menge aller Punkte in der Ebene. Jeder Punkt wird in ein
Vorkurs Mathematik B Dr. Thorsten Camps Fakultät für Mathematik TU Dortmund 20. September 2011 Definition (R n ) Wir definieren: 1 Der R 2 sei die Menge aller Punkte in der Ebene. Jeder Punkt wird in ein
Kurs über Lineare Gleichungssysteme. PD Dr. Karin Halupczok
 Kurs über Lineare Gleichungssysteme PD Dr. Karin Halupczok Mathematisches Institut Albert-Ludwigs-Universität Freiburg http://home.mathematik.unifreiburg.de/halupczok/diverses.html karin.halupczok@math.uni-freiburg.de
Kurs über Lineare Gleichungssysteme PD Dr. Karin Halupczok Mathematisches Institut Albert-Ludwigs-Universität Freiburg http://home.mathematik.unifreiburg.de/halupczok/diverses.html karin.halupczok@math.uni-freiburg.de
Einiges zu den Potenzfunktionen. Exponentialfunktionen
 Einiges zu den Potenzfunktionen Es sind zunächst zwei Arten der Potenzfunktionen zu unterscheiden. Erstens die eigentlichen Potenzfunktionen, bei denen die Variable x als Basis von Potenzen vorkommt. Diese
Einiges zu den Potenzfunktionen Es sind zunächst zwei Arten der Potenzfunktionen zu unterscheiden. Erstens die eigentlichen Potenzfunktionen, bei denen die Variable x als Basis von Potenzen vorkommt. Diese
Rang einer Matrix. 1-E1 Ma 1 Lubov Vassilevskaya
 Rang einer Matrix 1-E1 Ma 1 Lubov Vassilevskaya Unterdeterminante einer nichtquadratischen Matrix M ist eine nichtquadratische 2,3-Matrix: M = 6 2 3 0 5 7 Durch Streichen einer der drei Spalten kann man
Rang einer Matrix 1-E1 Ma 1 Lubov Vassilevskaya Unterdeterminante einer nichtquadratischen Matrix M ist eine nichtquadratische 2,3-Matrix: M = 6 2 3 0 5 7 Durch Streichen einer der drei Spalten kann man
Computergrafik 2: Fourier-Transformation
 Computergrafik 2: Fourier-Transformation Prof. Dr. Michael Rohs, Dipl.-Inform. Sven Kratz michael.rohs@ifi.lmu.de MHCI Lab, LMU München Folien teilweise von Andreas Butz, sowie von Klaus D. Tönnies (Grundlagen
Computergrafik 2: Fourier-Transformation Prof. Dr. Michael Rohs, Dipl.-Inform. Sven Kratz michael.rohs@ifi.lmu.de MHCI Lab, LMU München Folien teilweise von Andreas Butz, sowie von Klaus D. Tönnies (Grundlagen
3 Lineare Abbildungen und Matrizen
 3 Lineare Abbildungen und Matrizen Definition 3.1. Es seien V und W zwei Vektorräume über demselben Zahlkörper k. Eine Abbildung heisst linear, falls gilt i) [ λ k ] [ v V ] [ f (λ v) = λ f ( v) ] ii)
3 Lineare Abbildungen und Matrizen Definition 3.1. Es seien V und W zwei Vektorräume über demselben Zahlkörper k. Eine Abbildung heisst linear, falls gilt i) [ λ k ] [ v V ] [ f (λ v) = λ f ( v) ] ii)
Als Summendarstellung der komplexen Zahl bezeichnen wir den bekannten Ausdruck
 A.1 MATHEMATISCHE GRUNDLAGEN In diesem Abschnitt werden die mathematischen Grundlagen zusammengestellt, die für die Behandlung von Übertragungssystemen erforderlich sind. Unter anderem sind dies die komplexen
A.1 MATHEMATISCHE GRUNDLAGEN In diesem Abschnitt werden die mathematischen Grundlagen zusammengestellt, die für die Behandlung von Übertragungssystemen erforderlich sind. Unter anderem sind dies die komplexen
11. Vorlesung Wintersemester
 11. Vorlesung Wintersemester 1 Ableitungen vektorieller Felder Mit Resultat Skalar: die Divergenz diva = A = A + A y y + A z z (1) Mit Resultat Vektor: die Rotation (engl. curl): ( rota = A Az = y A y
11. Vorlesung Wintersemester 1 Ableitungen vektorieller Felder Mit Resultat Skalar: die Divergenz diva = A = A + A y y + A z z (1) Mit Resultat Vektor: die Rotation (engl. curl): ( rota = A Az = y A y
10.6. Implizite ebene Kurven und Tangenten
 0.6. Implizite ebene Kurven und Tangenten Im Gegensatz zu expliziten Darstellungen sind weder implizite noch Parameterdarstellungen einer Kurve eindeutig. Der Übergang von impliziten zu expliziten Darstellungen
0.6. Implizite ebene Kurven und Tangenten Im Gegensatz zu expliziten Darstellungen sind weder implizite noch Parameterdarstellungen einer Kurve eindeutig. Der Übergang von impliziten zu expliziten Darstellungen
Ausarbeitung zum Modulabschluss. Graphentheorie. spannende Bäume, bewertete Graphen, optimale Bäume, Verbindungsprobleme
 Universität Hamburg Fachbereich Mathematik Seminar: Proseminar Graphentheorie Dozentin: Haibo Ruan Sommersemester 2011 Ausarbeitung zum Modulabschluss Graphentheorie spannende Bäume, bewertete Graphen,
Universität Hamburg Fachbereich Mathematik Seminar: Proseminar Graphentheorie Dozentin: Haibo Ruan Sommersemester 2011 Ausarbeitung zum Modulabschluss Graphentheorie spannende Bäume, bewertete Graphen,
Lineare Algebra, Teil 2 Abbildungen
 Lineare Abbildungen Vorlesung Lineare Algebra mit integrierten Übungen WS 12 13 Studiengang LBS Unterrichtsfach hmth Mathematiktik Lineare Algebra, Teil 2 Abbildungen Lineare Abbildungen Lineare Gleichungssysteme
Lineare Abbildungen Vorlesung Lineare Algebra mit integrierten Übungen WS 12 13 Studiengang LBS Unterrichtsfach hmth Mathematiktik Lineare Algebra, Teil 2 Abbildungen Lineare Abbildungen Lineare Gleichungssysteme
4 Lineare Abbildungen und Matrizen
 4.1 Lineare Abbildungen Definition 4.1. Es seien V, W K-Vektorräume. Eine Abbildung f : V W heißt linear oder Homomorphismus, wenn für alle u, v V und λ K gilt Beispiel 4.2. L1 f(u + v) = f(u) + f(v),
4.1 Lineare Abbildungen Definition 4.1. Es seien V, W K-Vektorräume. Eine Abbildung f : V W heißt linear oder Homomorphismus, wenn für alle u, v V und λ K gilt Beispiel 4.2. L1 f(u + v) = f(u) + f(v),
mit "Skalarprodukt" aus i-tem "Zeilenvektor" und j-tem "Spaltenvektor"
 Zusammenfassung Matrizen Transponierte: Addition: mit Skalare Multiplikation: Matrixmultiplikation: m x p m x n n x p mit ES "Skalarprodukt" aus i-tem "Zeilenvektor" und j-tem "Spaltenvektor" "Determinante"
Zusammenfassung Matrizen Transponierte: Addition: mit Skalare Multiplikation: Matrixmultiplikation: m x p m x n n x p mit ES "Skalarprodukt" aus i-tem "Zeilenvektor" und j-tem "Spaltenvektor" "Determinante"
10.2 Linearkombinationen
 147 Vektorräume in R 3 Die Vektorräume in R 3 sind { } Geraden durch den Ursprung Ebenen durch den Ursprung R 3 Analog zu reellen Vektorräumen kann man komplexe Vektorräume definieren. In der Definition
147 Vektorräume in R 3 Die Vektorräume in R 3 sind { } Geraden durch den Ursprung Ebenen durch den Ursprung R 3 Analog zu reellen Vektorräumen kann man komplexe Vektorräume definieren. In der Definition
JPEG - Kompression. Steffen Grunwald, Christiane Schmidt, Stephan Weck TIT01EGR BA-Mannheim 21. Mai 2002
 JPEG - Kompression Steffen Grunwald, Christiane Schmidt, Stephan Weck TIT01EGR BA-Mannheim 21. Mai 2002 Inhaltsverzeichnis 1 Entwicklung von JPEG 2 1.1 Was heisst und was ist JPEG?................... 2
JPEG - Kompression Steffen Grunwald, Christiane Schmidt, Stephan Weck TIT01EGR BA-Mannheim 21. Mai 2002 Inhaltsverzeichnis 1 Entwicklung von JPEG 2 1.1 Was heisst und was ist JPEG?................... 2
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 25. April 2016 Die Dimensionsformel Definition 3.9 Sei f : V W eine lineare Abbildung zwischen zwei K-Vektorräumen. Der Kern
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 25. April 2016 Die Dimensionsformel Definition 3.9 Sei f : V W eine lineare Abbildung zwischen zwei K-Vektorräumen. Der Kern
II. Lineare Gleichungssysteme. 10 Matrizen und Vektoren. 52 II. Lineare Gleichungssysteme
 52 II Lineare Gleichungssysteme II Lineare Gleichungssysteme 10 Matrizen und Vektoren 52 11 Der Gaußsche Algorithmus 58 12 Basen, Dimension und Rang 62 13 Reguläre Matrizen 66 14 Determinanten 69 15 Skalarprodukte
52 II Lineare Gleichungssysteme II Lineare Gleichungssysteme 10 Matrizen und Vektoren 52 11 Der Gaußsche Algorithmus 58 12 Basen, Dimension und Rang 62 13 Reguläre Matrizen 66 14 Determinanten 69 15 Skalarprodukte
Das Lösen linearer Gleichungssysteme
 Das Lösen linearer Gleichungssysteme Lineare Gleichungen Die Gleichung a 1 x 1 + a 2 x 2 +... + a n x n = b ist eine lineare Gleichung in den n Variablen x 1, x 2,..., x n. Die Zahlen a 1, a 2,..., a n
Das Lösen linearer Gleichungssysteme Lineare Gleichungen Die Gleichung a 1 x 1 + a 2 x 2 +... + a n x n = b ist eine lineare Gleichung in den n Variablen x 1, x 2,..., x n. Die Zahlen a 1, a 2,..., a n
Bildrekonstruktion & Multiresolution
 Bildrekonstruktion & Multiresolution Verkleinern von Bildern? Was ist zu beachten? Es kann aliasing auftreten! Das Abtasttheorem sagt wie man es vermeidet? ===> Page 1 Verkleinern von Bildern (2) Vor dem
Bildrekonstruktion & Multiresolution Verkleinern von Bildern? Was ist zu beachten? Es kann aliasing auftreten! Das Abtasttheorem sagt wie man es vermeidet? ===> Page 1 Verkleinern von Bildern (2) Vor dem
Matrizen. Spezialfälle. Eine m nmatrix ist ein rechteckiges Zahlenschema mit. m Zeilen und n Spalten der Form. A = (a ij ) =
 Matrizen Eine m nmatrix ist ein rechteckiges Zahlenschema mit m Zeilen und n Spalten der Form a 11 a 12 a 1n A = a ij = a 21 a 22 a 2n a m1 a m2 a mn Dabei sind m und n natürliche und die Koezienten a
Matrizen Eine m nmatrix ist ein rechteckiges Zahlenschema mit m Zeilen und n Spalten der Form a 11 a 12 a 1n A = a ij = a 21 a 22 a 2n a m1 a m2 a mn Dabei sind m und n natürliche und die Koezienten a
