Hausarbeit aus. Graphentheorie Formale Grundlagen Professor Franz Binder. zum Thema. Herbert Huber k Seite 1 von 21
|
|
|
- Wolfgang Raske
- vor 6 Jahren
- Abrufe
Transkript
1 Hausarbeit aus Formale Grundlagen Professor Franz Binder zum Thema Graphentheorie Herbert Huber k Seite 1 von 21
2 Inhaltsverzeichnis Graphen Grundlagen und Begriffsdefinitionen...3 Graphenstrukturen...6 Homomorph...6 Isomorph...6 Automorph...6 Ursprünge der Graphentheorie...7 "Das Königsberger Brückenproblem"...7 Der Satz von Euler...8 Offene eulersche Linien...9 Bäume und Wälder...11 Sätze zu Bäumen...11 (Minimaler) Spannbaum...13 Binäre Bäume...13 Planare Graphen...15 Färbungen von Graphen...17 Anwendungen für die Graphentheorie:...19 Abbildungsverzeichnis...20 Literaturverzeichnis...21 Herbert Huber k Seite 2 von 21
3 Graphen Grundlagen und Begriffsdefinitionen Ein Graph besteht aus Ecken (manchmal auch Knoten genannt) und Kanten; dabei verbindet jede Kante genau zwei Ecken. Je zwei Ecken können also durch keine, eine oder mehr als eine Kante verbunden sein. [Diskrete Mathematik für Einsteiger; S 137] Abb.: 1: Zwei Darstellungsformen für denselben Graphen Graphen sind eng verwandt mit Relationen. Abgekürzt werden Graphen mit G, Ecken mit E und Kanten mit K. Aufgabe der Graphentheorie ist es, möglichst allgemeine Verfahren zu enthwickeln, um Probleme in Graphen lösen zu können. Schleifen sind Kanten, die einen Knoten mit sich selbst verbinden. Graphen mit Schleifen und/oder Mehrfachkanten nennt man auch Multigraphen. Zwei Ecken u und v heißen adjazent wenn sie durch eine Kante verbunden sind. Der Grad einer Ecke ist die Anzahl der Kanten die von dieser Ecke ausgehen. Gehen keine Kanten von ihr aus, ist der Grad = 0. Das wäre dann eine isolierte Ecke. Die Anzahl der Ecken in einem Graph, die zusammen einen ungeraden Grad haben, muss gerade sein. In der nachfolgenden Abbildung sind im linken Graphen nur Ecken mit dem Grad drei zu finden, während im rechten Graphen nur Ecken mit dem Grad 4 vorhanden sind. Ein Graph ist vollständig, wenn jede Ecke mit jeder anderen Ecke durch genau eine Kante verbunden ist. Ein solcher vollständiger Graph mit n Ecken hat die Bezeichnung K n. Abb. 2: Vollständige Graphen Herbert Huber k Seite 3 von 21
4 Ein Graph heisst eulersch, wenn man seine Kanten in einem Zug zeichen kann, und am Ende wieder am Ausgangspunkt ankommt. Der rechte Graph in der oberen Abbildung ist so ein eulerscher Graph. Ein Graph enthält einen Hamiltonkreis falls es möglich ist, einen Kreis so zu zeichnen, dass er jeden Knoten des Graphen genau ein mal durchläuft. Eine praktische Anwendung für den Hamiltonkreis ist das Traveling Salesman Problem. Hier soll eine optimale Route für einen Handlungsreisenden gefunden werden. Dieses Problem ist leider sehr schwierig zu lösen, genauer gesagt ist das Problem NP-vollständig. In der unteren Abbildung ist das finden eines Hamiltonkreises für den Würfel links möglich. Rechts jedoch befindet sich ein Petersen-Graph, benannt nach Julius Peterson. In ihm ist kein Hamiltonkreis zu finden. Abb. 3: Links: Ein Würfel mit einem eingezeichneten Hamiltonkreis; Rechts: Ein Peterson-Graph der keinen Hamiltonkreis enthält. Ein Graph ist bipartit, wenn man seine Ecken so schwarz und weiss färben kann, bzw. so in zwei Klassen, meist bezeichnet mit E1 und E2, einteilen kann, dass jede Kante eine schwarze und eine weiße Ecke bzw. eine Klasse mit der anderen Klasse verbindet. Möchte man die beiden Klassen herausheben, spricht man von einer Bipartition{E1, E2}. Vollständig bipartit sind diese Graphen, wenn jede Ecke der einen Klasse mit jeder Ecke der anderen Klasse durch genau eine Kante verbunden ist. Abb. 4: Links: Bipartiter Graph mit schwarzen und weissen Ecken; Rechts: Vollständig bipartiter Graph mit schwarzen und weissen Ecken Ein Kantenzug verbindet die Ecken e 0 bis e s, wobei der Kantenzug wiederum aus den Kanten k 1 bis k s besteht. Sind alle Kanten verschieden, wird ein Kantenzug Weg genannt. Sind alle seine Kanten verschieden und ist der Kantenzug geschlossen, wird er Kreis genannt. Die Länge des Kreises ist dabei die Anzahl seiner Kanten. Zusammenhängend ist ein Graph dann, wenn je zwei Ecken durch einen Kantenzug verbunden werden können. Herbert Huber k Seite 4 von 21
5 Abb. 5: Links: Weg; Rechts: Kreis Ein Weg der kein Kreis ist, heisst eine offene eulersche Linie, wenn jede Kante des Graphen darin genau ein mal vorkommt. Ein Graph kann scheinbar nur dann in einem Zug gezeichnet werden, wenn er einen eulerschen Kreis oder eine offene eulersche Linie besitzt. Ein Graph ist planar, falls er ohne Überschneidungen in der Ebene gezeichnet ist, also so, dass sich zwei Kanten höchstens in einer Ecke schneiden, aber sonst nicht. Ein Graph ist plättbar, wenn er überschneidungsfrei in die Ebene gezeichnet werden kann. Teilgraphen erhält man, indem man aus dem ursprünglichen Graphen beliebig Kanten und/oder Knoten entfernt. Ein Graph heisst zusammenhängend, wenn für jedes Paar von Knoten ein Pfad existiert. Die bisher gezeigten Abbildungen waren alle zusammenhängende Graphen. Graphen die nicht zusammenhängend sind, können zumindest zusammenhängende Teile enthalten. Die grössten zusammenhängenden Teilgraphen heissen dann Komponenten. Herbert Huber k Seite 5 von 21
6 Graphenstrukturen Homomorph Ein Homomorphismus ist eine strukturerhaltende Abbildung, hier die strukturerhaltende Abbildung eines Graphen. Homomorphismen lassen sich allgemeiner als spezielle Morphismen, also strukturverträgliche Abbildungen, definieren. Isomorph Als isomorph bezeichnet man zwei Graphen, die nach Umzeichnung und Umbenennung identisch sind. Zwei isomorphe Graphen liefern, unter Berücksichtigung von Umbenennungen, Datenverarbeitungstechnisch immer das gleiche Ergebnis. In der Mathematik ist ein Isomorphismus eine Abbildung zwischen zwei mathematischen Strukturen, durch die Teile einer Struktur auf bedeutungsgleiche Teile einer anderen Struktur umkehrbar eindeutig (bijektiv) abgebildet werden. Bei der Untersuchung graphentheoretischer Probleme kommt es meist nur auf die Struktur der Graphen, nicht aber auf die Bezeichnung ihrer Knoten an. In den allermeisten Fällen sind die untersuchten Grapheneigenschaften dann invariant bzgl. Isomorphie. Zur Prüfung der Isomorphie zweier Graphen ist kein effizienter Algorithmus bekannt. Mehr noch, die Komplexität des bestmöglichen Algorithmus ist bis heute noch nicht bestimmt. Insbesondere ist die Isomorphie von Graphen eines der wenigen bekannten Probleme in NP, für die weder bekannt ist, ob sie in P enthalten, noch ob sie NP-vollständig ist. Automorph Ein Automorphismus ist ein Isomorphismus eines Objektes auf sich selbst, in diesem Fall von einem Graphen. Herbert Huber k Seite 6 von 21
7 Ursprünge der Graphentheorie "Das Königsberger Brückenproblem" Der Ursprung der Graphentheorie lieg im Jahr 1736, bei dem Mathematiker Leonhard Euler. Im wurde damals folgendes Problem gestellt: Durch die Stadt Königsberg fließt ein Fluss, die Pregel. Diese teilt sich an einer Stelle und umfließt zwei Inseln. Diese sind untereinander und mit den Ufern durch Brücken verbunden. Ist es möglich, einen Spaziergang so zu organisieren, dass man dabei jede Brücke genau einmal überquert? Abb. 6:Königsberg und seine Brücken Euler hat dieses Problem gelöst und damit das Feld der Graphentheorie begründet. Das Königsberger Brückenproblem lässt sich als Graph wie folgt darstellen: Abb. 7: Graph des Königsberger Brückenproblems Herbert Huber k Seite 7 von 21
8 Ist ein Graph in einem Zug so zu zeichnen, dass man am Ende des Zeichenvorganges wieder am Ausgangspunkt angelangt, so ist dieser Graph eulersch. Genauer gesagt, nennt man so einen Graph einen eulerschen Kreis. Sollte der Graph der das Königsberger Brückenproblem darstellt, also ein eulerscher Graph sein, wäre es möglich einen Spaziergang so zu organisieren, dass man dabei jede Brücke genau einmal überquert. Der Satz von Euler Die Frage ob das nun wirklich so ist, lässt sich mit dem Satz von Euler beantworten: Wenn ein Graph G eulersch ist, dann hat jede Ecke von G geraden Grad. Mit anderen Worten: Wenn G eine Ecke ungeraden Grades hat, dann ist G nicht eulersch. Der Graph des Königsberger Brückenproblems hat Ecken vom Grad 3, 3, 3 und 5. Er ist also nicht eulersch. Der geforderte Spaziergang ist folglich nicht möglich. Für den Beweis des Satzes von Euler muss eine beliebige Ecke e des Graphen ausgewählt werden. Für diese Ecke e muss nun bewiesen werden, dass die Anzahl der angrenzenden Ecken gerade ist. (Wenn es mehrere Ecken gibt, muss natürlich für jede Ecke bewiesen werden, dass ihr Grad gerade ist.) Diese Ecke e wird vom eulerschen Kreis durchquert, einige Male, genauer gesagt a Mal. Wobei a für die Anzahl der Durchquerungen von e steht. Bei jedem Durchgang durch e verbraucht der eulersche Kreis zwei Kanten. In a Durchgängen werden also 2a Kanten verbraucht. Da keine Kante zweimal benutzt werden darf, ist der Grad der Ecke e also mindestens gleich 2a. Der Grad kann aber auch nicht größer sein, da jede Kante, also insbesondere jede Kante, die an e angrenzt, in dem eulerschen Kreis mindestens einmal vorkommen muss. Euler hat auch die Umkehrung des obigen Satzes postuliert: Wenn in einem zusammenhängenden Graphen G jede Ecke geraden Grad hat, dann ist G eulersch. Der Beweis dazu lautet: Beweis durch Induktion nach der Anzahl m der Kanten. Induktionsbasis: Wenn G keine Kante hat, ist G eulersch (mit trivialem eulerschen Kreis). Da jede Ecke von G geraden Grad hat und jede Kante zwei verschiedene Ecken verbindet, kann G nicht nur eine Kante besitzen. Wenn G genau zwei Kanten hat, müssen diese, da G zusammenhängend ist, zwei Ecken miteinander verbinden, und auch in diesem Fall sieht man unmittelbar, dass G eulersch ist. Induktionsschritt: Die Anzahl m der Kanten von G sei nun mindestens 2, und die Aussage sei richtig für alle Graphen mit weniger als m Kanten. Da G zusammenhängend ist und jede Ecke geraden Grad hat, hat jede Ecke mindestens den Grad 2. Also gibt es einen Kreis in G. Wir betrachten einen Kreis C maximaler Länge in G und behaupten, dass dies ein eulerscher Kreis ist. Angenommen, C wäre kein eulerscher Kreis. Dann entfernen wir die Kanten von Herbert Huber k Seite 8 von 21
9 C von G. Übrig bleibt ein (eventuell nichtzusammenhängender) Graph G*, in dem jede Ecke geraden Grad hat (eventuell 0). Nach Induktionsannahme gäbe es dann in einer Zusammenhangskomponente einen eulerschen Kreis. Diesen könnten wir mit C vereinigen, wodurch wir einen größeren Kreis erhalten würden. Dieser Widerspruch zur Maximalität von C zeigt, dass C in Wirklichkeit ein eulerscher Kreis ist. Aus obigem Satz folgt zum Beispiel, dass jeder vollständige Graph Kn mit ungeradem n (also K3, K5, K7,...) eulersch ist. Denn jede Ecke von Kn hat den Grad n 1; und wenn n ungerade ist, ist n 1 gerade. [Diskrete Mathematik für Einsteiger; S 142 ff] Offene eulersche Linien Wenn ein Graph eine offene eulersche Linie besitzt, dann hat er genau zwei Ecken ungeraden Grades. Die Umkehrung des Satzes: In jedem zusammenhängenden Graph gilt: Wenn es genau zwei Ecken ungeraden Grades gibt, dann hat der Graph eine offene eulersche Linie. Der Beweis beider Sätze beruht auf demselben Prinzip. Der erste Satz kann auf den Satz von Euler zurückgeführt werden, der zweite Satz kann auf die Umkehrung des Satzes von Euler zurückgeführt werden. Beweis erster Satz: Sei G ein Graph, der eine offene eulersche Linie besitzt. Diese beginnt an einer Ecke e1 und endet an einer anderen Ecke en. Trick: Wir führen künstlich (und nur für kurze Zeit) eine zusätzliche Kante k* ein, die e1 mit en verbindet. Den so erhaltene Graph nennen wir G*; G* hat G nur die Kante k* voraus. Wenn wir an die offene eulersche Linie die Kante k* anhängen, erhalten wir einen eulerschen Kreis von G*. Nun können wir anwenden und erhalten, dass jede Ecke von G* geraden Grad hat. Daraus schließen wir, dass jede Ecke von G, die keine Ecke von k* ist, auch geraden Grad hat. Außerdem folgt, dass die Ecken e1 und en in G ungeraden Grad haben (denn in G* hatten sie geraden Grad, und die Kante k* ist entfernt worden). Also sind e1 und en die einzigen Ecken ungeraden Grades in G. [Diskrete Mathematik für Einsteiger; S 143 ff] Herbert Huber k Seite 9 von 21
10 Beweis zweiter Satz: Sei G ein zusammenhängender Graph, der genau zwei Ecken e1 und en ungeraden Grades hat. Trick: Wir führen künstlich eine zusätzliche Kante k* ein, die e1 mit en verbindet. Sei G* der so erhaltene Graph. Da er nur Ecken geraden Grades hat und zusammenhängend ist, können wir anwenden und erhalten einen eulerschen Kreis von G*. In diesem eulerschen Kreis muss irgendwo die Kante k* vorkommen; sei k1, k2,..., ks, k*, ks+2,..., km der eulersche Kreis. Dann ist ks+2,..., km, k1, k2,..., ks eine offene eulersche Linie von G. Also besitzt G eine offene eulersche Linie. [Diskrete Mathematik für Einsteiger; S 143 ff] Aus den beiden Beweisen lässt sich folgern, dass jede offene eulersche Linie an einer Ecke ungeraden Grades beginnt und an der anderen endet. Das Königsberger Brückenproblem liesse sich also auch dann nicht lösen, wenn man in Kauf nimmt, den Spaziergang an einer anderen Stelle zu beenden als man ihn begonnen hat. Herbert Huber k Seite 10 von 21
11 Bäume und Wälder Ein Baum ist ein Graph der zusammenhängend ist und keinen Kreis enthält. Ein Wald ist ein Graph dessen Komponenten Bäume sind. In einem Baum sind je zwei Ecken durch höchstens eine Kante verbunden. Ausserdem hat jeder Baum mindestens eine Endecke, also eine Ecke mit dem Grad 1. Bäume sind die minimalen, zusammenhängenden Graphen. Wenn man aus einem Baum eine Kante entfernt, entsteht ein nicht zusammenhängender Graph. Von dieser Eigenschaft gilt auch die Umkehrung. Sie charakterisiert Bäume. Bäume sind wichtige Anwendungen von Graphen, zum Beispiel in der Informatik. Bäume eignen sich auch um Sortierungsprozesse darzustellen. Nachfolgend ein graphisches Beispiel für einen Baum: Abb. 8: Baum mit 7 Ecken, 3 davon sind Endecken; Darstellung einer Datenspeicherstruktur als Binärbaum. Sätze zu Bäumen Jeder Baum mit mindestens zwei Ecken hat mindestens eine Endecke. Beweis dazu: Man nehme einen Baum G mit mindestens zwei Ecken an. Wir starten an der Ecke e0 und gehen von ihr aus über eine Kante zur Ecke e1. Ist Ecke e1 eine Endecke haben wir den Beweis erbracht. Ist e1 keine Endecke gehen wir zur nächsten Ecke, und überprüfen wieder ob diese eine Endecke ist. Ist auch diese keine Endecke gehen wir wieder zur nächsten Ecke weiter und überprüfen... usw. Dies wiederholen wir so lange bis wir eine Endecke finden. Das wird zwangsläufig irgendwann der Fall sein, da der Baum nur eine endliche Anzahl von Ecken haben kann und keinen Kreis enthält. Sei G ein Baum mit n Ecken und m Kanten. Dann gilt m = n-1. Herbert Huber k Seite 11 von 21
12 Der Beweis erfolgt durch Induktion nach der Anzahl der Ecken n. Wir nehmen an, dass n = 1 ist. Dann besteht der Baum nur aus einer Ecke. Die Anzahl der Kanten m wäre dann gleich 0. Die Formel m = n -1 würde für diesen Fall also lauten 0 = 1-1. Und das würde eindeutig stimmen. Nun der Induktionsschritt: Sei n >= 1, und sei die Behauptung richtig für alle Bäume mit n Ecken. Wir müssen zeigen, dass sie auch für alle Bäume mit n+1 Ecken gilt, das heißt, dass jeder solche Graph genau n Kanten hat. Sei also G ein Baum mit n+1 Ecken. Wir haben vorhin schon bewiesen das G, wie jeder Baum, mindestens eine Endecke e* hat. Wir entfernen nun diese Endecke e* und die mit e* inzidierende Kante k*. Dadurch erhalten wir wieder einen Baum G*, der nur n Ecken hat. Nach Induktionsannahme hat G* also genau n 1 Kanten. Da G aus G* durch Hinzufügen der Kante k* entsteht, hat G genau eine Kante mehr als G*. Also hat G genau n = n Kanten. Somit gilt die Aussage für n+1. Nach dem Prinzip der vollständigen Induktion gilt die Aussage damit auch allgemein. Sei G ein Graph mit n Ecken und m Kanten. Wenn G zusammenhängend ist, gilt m >= n 1 mit Gleichheit genau dann, wenn G ein Baum ist. Dieser Satz sagt, das Bäume unter allen zusammenhängenden Graphen diejenigen mit der kleinstmöglichen Kantenzahl sind. Der Beweis dieser Aussage lässt sich wieder mittels Induktion antreten, und zwar mit Induktion nach der Anzahl m der Kanten. Wir nehmen zuerst an, m = 0. Dann besteht G nur aus einer Ecke und der Satz gilt. Nun nehmen wir an, m >= 0 und die Aussage sei richtig für alle Graphen mit m Kanten. Sei G ein zusammenhängender Graph mit m+1 Kanten und n Ecken. Wir müssen zeigen, dass m+1 >= n 1 ist mit Gleichheit genau dann, wenn G ein Baum ist. Dazu unterscheiden wir zwei Fälle: 1. Fall: G ist ein Baum. Dann gilt laut dem vorletzten Satz sogar m+1 = n Fall: G ist kein Baum. Wir müssen zeigen, dass m+1 > n 1 gilt. Da G kein Baum ist, besitzt G einen Kreis. Wir entfernen eine Kante k* aus diesem Kreis und erhalten einen Graphen G*, der eine Kante weniger, aber gleich viele Ecken wie G hat. Dieser Graph G* ist zusammenhängend (denn in jedem Weg kann k* - wenn diese Kante überhaupt vorkommt - durch den Rest des Kreises ersetzt werden). Also gilt nach Induktion m = Anzahl der Kanten von G* >= Anzahl der Ecken von G* 1 = n 1. Also gilt m+1 >= n > n 1. Damit gilt die Aussage auch für m+1. Nach dem Prinzip der vollständigen Induktion gilt die Aussage also allgemein. Herbert Huber k Seite 12 von 21
13 (Minimaler) Spannbaum Ein Spannbaum eines Graphen ist ein zusammenhängender Teilgraph, der alle Ecken (Anzahl n) enthält und n-1 Kanten hat. Jeder zusammenhängende Graph besitzt einen Spannbaum. Ein Spannbaum ist ein minimaler Spannbaum, wenn er unter allen Spannbäumen das geringste Gewicht hat. Das Spannbaumproblem tritt in der Praxis beispielsweise bei der kürzesten Verdrahtung von Kommunikationsnetzen auf. Für das Problem des Handlungsreisenden existieren Approximationsalgorithmen, die minimale Spannbäume verwenden. Abb. 9: Spannbaum mit eingezeichnetem minimaler Spannbaum Binäre Bäume Ein Binärbaum ist ein Wurzelbaum, dh er hat eine spezielle Ecke, die Wurzel (root), von der höchstens zwei Kanten (Grad zwei) ausgehen. Alle anderen Ecken haben den Grad drei (Wurzel) oder eins. Binärbäume werden normalerweise so gezeichnet, dass die Wurzel oben ist. Zur Veranschaulichung, Abb. ist ein Binärbaum. Man nennt die Ecken vom Grad eins die Blätter des Baumes. Sie sind Endecken. Die Länge eines längsten Weges, wobei die Wurzel eine Endecke ist, nennt man die Höhe des Baumes. Zur Höhe eines Binärbaumes lässt sich folgendes sagen: (a) Sei G ein binärer Baum der Höhe h. Dann hat G höchstens 2 h Blätter. (b) Ein binärer Baum mit b Blättern hat mindestens die Höhe [ld(b)]. Beweis von (a): Wiederum mittels Induktion, diesmal nach h. Ein binärer Baum der Höhe 0 besteht nur aus der Wurzel, hat also genau 1 (= 20) Blatt. Sei nun h > 0, und sei die Aussage richtig für h 1. Sei G ein binärer Baum der Höhe h. Wir entfernen alle Blätter aus G und erhalten dadurch einen binären Baum G* der Höhe h 1. Nach Induktion hat dieser höchstens 2 h 1 Blätter. Beim Übergang zu G entstehen aus jedem Blatt von G* ein oder zwei Blätter von G. Daher hat G höchstens doppelt so viele Blätter wie G*, also höchstens 2 h 1 *2 = 2 h. Beweis von (b): Nach (a) gilt b <= 2h, das heißt ld(b) <= h. Herbert Huber k Seite 13 von 21
14 Für Binärbäume gibt es auch in der Informatik eine Definition, da sie dort einige Bedeutung haben: Ein Binärbaum ist ein Baum, bei dem jeder Knoten höchstens zwei Nachfolger hat. Seine Datenstruktur besteht aus Knotenobjekten mit zwei Knotenreferenzen. Jeder Knoten hat also zwei Nachfolger Im Binärbaum wird jeder Knoten genau einmal referiert, d.h. ein einem Binärbaum hat jeder Knoten, mit Ausnahme des Wurzelknotens, genau einen Vorgänger. Ein Blatt ist ein Knoten, der keinen Nachfolger hat. Die anderen Knoten heissen auch innere Knoten. [Grundkurs Algorithmen und Datenstrukturen in Java, Eine Einführung in die praktische Informatik; S 125] Herbert Huber k Seite 14 von 21
15 Planare Graphen Ein Graph ist planar, falls er ohne Überschneidungen in der Ebene gezeichnet ist, also so, dass sich zwei Kanten höchstens in einer Ecke schneiden, aber sonst nicht. Abb. Zeigt zum Beispiel planare Graphen. Ein Graph ist plättbar, wenn er überschneidungsfrei in die Ebene gezeichnet werden kann. Abb. 10: Links: Ein plättbarer Graph; Rechts: die planare Version des linken, plättbaren Graphen Jeder planare Graph zerlegt die Ebene in Gebiete. Die Anzahl der Gebiete wird mit g bezeichnet. Es gibt immer mindestens ein Gebiet, das äußere Gebiet. Daraus folgt, es gilt stets: g >= 1. Bäume haben nur ein Aussengebiet. Für sie gilt daher g = 1. In der oberen Abbildung ist g links gleich 6, rechts ist g gleich 5. Die eulersche Polyederformel: Sei G ein zusammenhängender planarer Graph mit n Ecken, m Kanten und g Gebieten. Dann gilt: n m + g = 2. Der Beweis erfolgt durch Induktion nach der Anzahl g der Gebiete. Sei zunächst g = 1. Dann ist G ein Baum. Wie wir bereits früher bewiesen haben, gilt daher n = m+1, das heißt n m + g = (m+1) m + 1 = 2. Sei nun g >= 1, und sei die Aussage richtig für g. Wir zeigen, dass sie auch für g+1 gilt. Sei G ein planarer zusammenhängender Graph mit g+1 Gebieten. Da g+1 > 1 ist, ist G kein Baum. Also gibt es einen Kreis in G. Wir entfernen eine Kante k* dieses Kreises. Da k* an zwei Gebiete von G angrenzt, hat der neue Graph G* ein Gebiet weniger (da zwei vereinigt wurden), also nur noch g* = g Gebiete. Also können wir auf G* die Induktionsvoraussetzung anwenden. Da G* genau m 1 Kanten und n Ecken hat, folgt also 2 = n (m 1) + g = n m + (g+1). Also gilt die Aussage für g+1. Nach dem Prinzip der vollständigen Induktion gilt der Satz damit allgemein. Daraus ergibt sich: Sei G ein zusammenhängender planarer Graph, in dem je zwei Ecken durch Herbert Huber k Seite 15 von 21
16 höchstens eine Kante verbunden sind. Dann gilt: (a) Falls G mindestens drei Ecken hat, dann gilt m <= 3n 6. (Das heißt: Ein planarer Graph hat relativ wenige Kanten.) (b) Es gibt mindestens eine Ecke vom Grad <= 5. Der Beweis kann mittels einer Abzählung erbracht werden. (a) Für ein Gebiet L sei m(l) die Anzahl der Kanten. Da jedes Gebiet mindestens drei Kanten hat, gilt: Nun zählen wir die Paare (k, L), wobei k eine Kante, L ein Gebiet und k ein Teil der Grenze von L ist: Zusammen ergibt sich 2m >= 3g. Schließlich setzen wir das in die Eulersche Polyederformel ein und erhalten: also m <= 3n 6. (b) Die Behauptung gilt natürlich, falls n = 1 oder n = 2 ist. Für n >= 3 wenden wir (a) an und erhalten wobei δ der kleinste Grad von G ist. Also muss δ - n < 6n, also δ < 6 sein. Aus dem obigen lässt sich ausserdem folgern und auch Beweisen, dass die vollständigen Graphen K5 und K3,3 nicht plättbar sind. Deshalb muss jeder nicht plättbare Graph eine Unterteilung von K5 oder K3,3 enthalten. Diese Regel ist auch unter dem Namen "Satz von Kuratowski" bekannt. Abb. 11: Links: K5; Rechts: K3 Herbert Huber k Seite 16 von 21
17 Färbungen von Graphen Der Ursprung dieses Graphen-Problems liegt in der Frage, ob man die Länder auf jeder beliebigen Landkarte mit vier Farben so färben kann, dass je zwei benachbarte Länder verschiedene Farben haben. Und zwar nicht auf einer speziellen Landkarte, sondern auf jeder beliebigen Landkarte. Länder die sich nur an einem Punkt berühren, dürfen allerdings gleich gefärbt sein. Abb. 12: Links: Englands Grafschaften; Rechts Beliebige Karte Die Vierfarbenvermutung sagt nun, dass vier Farben in jedem Fall genug sind. Sie wurde erstmals vom britischen Mathematikstudenten Francis Guthrie in Zusammenhang mit einer Karte von den zahlreichen Grafschaften Englands formuliert. Um dieses Problem mittels Graphen lösen zu können, muss zuerst die Landkarte in einen Graphen, und zwar einen planaren Graphen, übertragen werden. Die Länder sind dabei die Ecken. Haben Länder eine gemeinsame Grenze, werden ihre Ecken-Counterparts mit Kanten verbunden. Da die Kanten nicht gefärbt werden können, werden die Ecken, die die Länder repräsentieren gefärbt. Und zwar so, das je zwei mit einer Kante verbundene Ecken unterschiedliche Farben haben. Es soll nun herausgefunden werden, wie viele Farben dazu mindestens nötig sind. Diese Frage kann man mit folgender Überlegung abstrahieren: Man nehme einen beliebigen Graphen G, egal ob planar oder nicht, egal ob von einer Landkarte oder nicht, an. Die Eckenfärbung von diesem G ist eine Zuordnung von Farben zu den Ecken, so dass keine zwei durch eine Kante verbundenen Ecken die gleiche Farbe haben (Selbe Bedingung wie oben). Als Farben dienen stellvertretend die Zahlen 1, 2,..., n. Die chromatische Zahl von G ist nun definiert als die kleinste natürliche Zahl n, so dass G mit n Farben gefärbt werden kann. Man bezeichnet die chromatische Zahl von G mit χ (chi). Kreise gerader Länge haben zum Beispiel die chromatische Zahl 2, Kreise ungerader Länge die chromatische Zahl 3. Herbert Huber k Seite 17 von 21
18 Jetzt lässt sich die Vierfarbenvermutung als Frage folgendermassen formulieren: Ist die chromatische Zahl eines jeden planaren Graphen höchstens vier? Diese Frage kann wiederum mit Hilfe des Greedy-Algorithmuses gelöst werden. Greedy-Algorithmus: Jeder Graph G kann mit Δ(G) + 1 Farben gefärbt werden. Mit anderen Worten: Es gilt χ(g) <= Δ(G) + 1. Zur Lösung des Vierfarbenproblems wurde 1976 der Vierfarbensatz von Apel und Haken bewiesen. Der Satz lautet: Die chromatische Zahl eines planaren Graphen ist höchstens 4. Das bedeutet: In jeder ebenen Landkarte können die Länder so mit vier Farben gefärbt werden, dass je zwei Länder, die ein Stück gemeinsame Grenze haben, verschieden gefärbt sind. Der Beweis für diesen Satz ist leider überaus kompliziert. Aufbauend auf den Vierfarbensatz gilt allerdings auch der Fünffarbensatz, der mittels Induktion bewiesen werden kann. Der Fünffarbensatz lautet: Die chromatische Zahl eines planaren Graphen ist höchstens 5. Das bedeutet: In jeder ebenen Landkarte können die Länder so mit fünf Farben gefärbt werden, dass je zwei Länder, die ein Stück gemeinsame Grenze haben, verschieden gefärbt sind. Herbert Huber k Seite 18 von 21
19 Anwendungen für die Graphentheorie: Graphen haben mannigfaltige Anwendungen in der realen Welt und sind auch für viele Probleme in der Informatik von essentieller Bedeutung. Hierbei werden die Problemstellungen jeweils so modelliert, dass sie mit der Darstellung als Graph kompatibel sind. Es müssen sich jedenfalls geeignete Ecken und Kanten finden lassen. Einige Anwendungen sind: Die Simulierung von Verkehrsflüssen. Die Strassenkreuzungen sind hierbei die Ecken und die Kanten zwischen diesen sind die Strassen. Routenplaner. Wieder sind Ecken und Kanten stellvertretend für Städte/Orte und Strassen. Das Travelling Salesman Problem stellt hier zb besondere Anforderungen da es eine Rundreise kürzester Länge finden will, eben optimal geeignet für einen Vertreter der alle seine potentiellen Kunden mit möglichst wenig Aufwand besuchen will. Strukturformeln für Moleküle. Elektrische Netzwerke Frequenzzuweisungen im Mobilfunk In der Informatik zum Beispiel zum visualisieren von Speicherstrukturen. Oder auch um Prozesse zu beschreiben. Endliche Automaten sind ebenfalls Graphen. Abb. 13: Ausschnitt Streckennetz der Linzer Linien Herbert Huber k Seite 19 von 21
20 Abbildungsverzeichnis Abb.: 1: Zwei Darstellungsformen für denselben Graphen Abb. 2: Vollständige Graphen Abb. 3: Links: Ein Würfel mit einem eingezeichneten Hamiltonkreis; Rechts: Ein Peterson-Graph der keinen Hamiltonkreis enthält. Abb. 4: Links: Bipartiter Graph mit schwarzen und weissen Ecken; Rechts: Vollständig bipartiter Graph mit schwarzen und weissen Ecken Abb. 5: Links: Weg; Rechts: Kreis Abb. 6:Königsberg und seine Brücken; ( Abb. 7: Graph des Königsberger Brückenproblems Abb. 8: Baum mit 7 Ecken, 3 davon sind Endecken; Darstellung einer Datenspeicherstruktur als Binärbaum. Abb. 9: Spannbaum mit eingezeichnetem minimaler Spannbaum Abb. 10: Links: Ein plättbarer Graph; Rechts: die planare Version des linken, plättbaren Graphen Abb. 11: Links: K5; Rechts: K3; ( Abb. 12: Links: Englands Grafschaften; Rechts Beliebige Karte; ( px-four_colour_map_example.svg.png) Abb. 13: Ausschnitt Streckennetz der Linzer Linien Herbert Huber k Seite 20 von 21
21 Literaturverzeichnis Albrecht Beutelspacher, Marc-Alexander Zschiegner: "Diskrete Mathematik für Einsteiger", Springer Verlag, 3., erweiterte Auflage Gerald Teschl, Susanne Teschl: "Mathematik für Informatiker", Springer Verlag, 3. Auflage Andreas Solymosi, Ulrich Grude: "Grundkurs Algorithmen und Datenstrukturen in Java, Eine Einführung in die praktische Informatik", vieweg Verlag, 3., überarbeitete und erweiterte Auflage Angelika Steger, "Diskrete Strukturen - Band 1: Kombinatorik, Graphentheorie, Algebra", Springer- Verlag Berlin Heidelberg 2002, 2007, 2. Auflage Reinhard Diestel: "Graphentheorie, Elektronische Ausgabe", Springer Verlag Heidelberg 1996, 2000, Zugriff am Zugriff am Zugriff am Zugriff am Zugriff am Herbert Huber k Seite 21 von 21
Der Fünffarbensatz Proseminar: Graphentheorie Sommersemester 2006 Isa Topac, Markus Kunder, Tim Hahn
 Der Fünffarbensatz Proseminar: Graphentheorie Sommersemester 2006 Isa Topac, Markus Kunder, Tim Hahn 1. Geschichte - Frage kommt Mitte des 19 Jahrhunderts auf Wie viele Farben benötigt man um eine Karte
Der Fünffarbensatz Proseminar: Graphentheorie Sommersemester 2006 Isa Topac, Markus Kunder, Tim Hahn 1. Geschichte - Frage kommt Mitte des 19 Jahrhunderts auf Wie viele Farben benötigt man um eine Karte
Diskrete Mathematik. Sebastian Iwanowski FH Wedel. Kap. 6: Graphentheorie
 Referenzen zum Nacharbeiten: Diskrete Mathematik Sebastian Iwanowski FH Wedel Kap. 6: Graphentheorie Lang 6 Beutelspacher 8.1-8.5 Meinel 11 zur Vertiefung: Aigner 6, 7 (7.4: Algorithmus von Dijkstra) Matousek
Referenzen zum Nacharbeiten: Diskrete Mathematik Sebastian Iwanowski FH Wedel Kap. 6: Graphentheorie Lang 6 Beutelspacher 8.1-8.5 Meinel 11 zur Vertiefung: Aigner 6, 7 (7.4: Algorithmus von Dijkstra) Matousek
WS 2009/10. Diskrete Strukturen
 WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
Fünf-Farben-Satz. Seminar aus reiner Mathematik, WS 13/14. Schweighofer Lukas, November Seite 1
 Der Fünf- Farben-Satz Seminar aus reiner Mathematik, WS 13/14 Schweighofer Lukas, November 2013 Seite 1 Inhaltsverzeichnis Vorwort...3 Graphentheoretische Grundlagen...4 Satz 2 (Eulerscher Polyedersatz)...7
Der Fünf- Farben-Satz Seminar aus reiner Mathematik, WS 13/14 Schweighofer Lukas, November 2013 Seite 1 Inhaltsverzeichnis Vorwort...3 Graphentheoretische Grundlagen...4 Satz 2 (Eulerscher Polyedersatz)...7
Isomorphie von Bäumen
 Isomorphie von Bäumen Alexandra Weinberger 23. Dezember 2011 Inhaltsverzeichnis 1 Einige Grundlagen und Definitionen 2 1.1 Bäume................................. 3 1.2 Isomorphie..............................
Isomorphie von Bäumen Alexandra Weinberger 23. Dezember 2011 Inhaltsverzeichnis 1 Einige Grundlagen und Definitionen 2 1.1 Bäume................................. 3 1.2 Isomorphie..............................
Westfählische Wilhelms-Universität. Eulersche Graphen. Autor: Jan-Hendrik Hoffeld
 Westfählische Wilhelms-Universität Eulersche Graphen Autor: 21. Mai 2015 Inhaltsverzeichnis 1 Das Königsberger Brückenproblem 1 2 Eulertouren und Eulersche Graphen 2 3 Auffinden eines eulerschen Zyklus
Westfählische Wilhelms-Universität Eulersche Graphen Autor: 21. Mai 2015 Inhaltsverzeichnis 1 Das Königsberger Brückenproblem 1 2 Eulertouren und Eulersche Graphen 2 3 Auffinden eines eulerschen Zyklus
Vorlesung Diskrete Strukturen Eulersche und Hamiltonsche Graphen
 Vorlesung Diskrete Strukturen Eulersche und Hamiltonsche Graphen Bernhard Ganter WS 2013/14 1 Eulersche Graphen Kantenzug Ein Kantenzug in einem Graphen (V, E) ist eine Folge (a 0, a 1,..., a n ) von Knoten
Vorlesung Diskrete Strukturen Eulersche und Hamiltonsche Graphen Bernhard Ganter WS 2013/14 1 Eulersche Graphen Kantenzug Ein Kantenzug in einem Graphen (V, E) ist eine Folge (a 0, a 1,..., a n ) von Knoten
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 11: Graphen Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2010/2011 1/59 Graphische Darstellung von Zusammenhängen schon
Grundbegriffe der Informatik Einheit 11: Graphen Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2010/2011 1/59 Graphische Darstellung von Zusammenhängen schon
Vorlesung Diskrete Strukturen Eulersche und Hamiltonsche Graphen
 Vorlesung Diskrete Strukturen Eulersche und Hamiltonsche Graphen Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de WS 2009/10 1 Bernhard Ganter, TU Dresden Modul
Vorlesung Diskrete Strukturen Eulersche und Hamiltonsche Graphen Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de WS 2009/10 1 Bernhard Ganter, TU Dresden Modul
Graphentheorie. Eulersche Graphen. Eulersche Graphen. Eulersche Graphen. Rainer Schrader. 14. November Gliederung.
 Graphentheorie Rainer Schrader Zentrum für Angewandte Informatik Köln 14. November 2007 1 / 22 2 / 22 Gliederung eulersche und semi-eulersche Graphen Charakterisierung eulerscher Graphen Berechnung eines
Graphentheorie Rainer Schrader Zentrum für Angewandte Informatik Köln 14. November 2007 1 / 22 2 / 22 Gliederung eulersche und semi-eulersche Graphen Charakterisierung eulerscher Graphen Berechnung eines
1. Einleitung wichtige Begriffe
 1. Einleitung wichtige Begriffe Da sich meine besondere Lernleistung mit dem graziösen Färben (bzw. Nummerieren) von Graphen (speziell von Bäumen), einem Teilgebiet der Graphentheorie, beschäftigt, und
1. Einleitung wichtige Begriffe Da sich meine besondere Lernleistung mit dem graziösen Färben (bzw. Nummerieren) von Graphen (speziell von Bäumen), einem Teilgebiet der Graphentheorie, beschäftigt, und
Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik. Weihnachtsblatt
 Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik Prof. Dr. A. Taraz, Dipl-Math. A. Würfl, Dipl-Math. S. König Weihnachtsblatt Aufgabe W.1 Untersuchen Sie nachstehenden
Technische Universität München Zentrum Mathematik Propädeutikum Diskrete Mathematik Prof. Dr. A. Taraz, Dipl-Math. A. Würfl, Dipl-Math. S. König Weihnachtsblatt Aufgabe W.1 Untersuchen Sie nachstehenden
Ein Turnierplan mit fünf Runden
 Mathematik I für Informatiker Graphen p. 1 Ein Turnierplan mit fünf Runden c b a c b a c b a c b a c b a d e d e d e d e d e Mathematik I für Informatiker Graphen p. 2 Definition: Graph Ein (schlichter)
Mathematik I für Informatiker Graphen p. 1 Ein Turnierplan mit fünf Runden c b a c b a c b a c b a c b a d e d e d e d e d e Mathematik I für Informatiker Graphen p. 2 Definition: Graph Ein (schlichter)
WS 2009/10. Diskrete Strukturen
 WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Kapitel 15: Graphen Thomas Worsch KIT, Institut für Theoretische Informatik Wintersemester 2015/2016 GBI Grundbegriffe der Informatik KIT, Institut für Theoretische Informatik
Grundbegriffe der Informatik Kapitel 15: Graphen Thomas Worsch KIT, Institut für Theoretische Informatik Wintersemester 2015/2016 GBI Grundbegriffe der Informatik KIT, Institut für Theoretische Informatik
Vollständiger Graph. Definition 1.5. Sei G =(V,E) ein Graph. Gilt {v, w} E für alle v, w V,v w, dann heißt G vollständig (complete).
 Vollständiger Graph Definition 1.5. Sei G =(V,E) ein Graph. Gilt {v, w} E für alle v, w V,v w, dann heißt G vollständig (complete). Mit K n wird der vollständige Graph mit n Knoten bezeichnet. Bemerkung
Vollständiger Graph Definition 1.5. Sei G =(V,E) ein Graph. Gilt {v, w} E für alle v, w V,v w, dann heißt G vollständig (complete). Mit K n wird der vollständige Graph mit n Knoten bezeichnet. Bemerkung
Grundlagen der Graphentheorie. Thomas Kamps 6. Oktober 2008
 Grundlagen der Graphentheorie Thomas Kamps 6. Oktober 2008 1 Inhaltsverzeichnis 1 Definition von Graphen 3 2 Unabhängigkeit von Ecken und Kanten 3 3 Teil- und Untergraphen 4 4 Schnitt, Vereinigung und
Grundlagen der Graphentheorie Thomas Kamps 6. Oktober 2008 1 Inhaltsverzeichnis 1 Definition von Graphen 3 2 Unabhängigkeit von Ecken und Kanten 3 3 Teil- und Untergraphen 4 4 Schnitt, Vereinigung und
Eulerweg, Eulerkreis. Das Königsberger Brückenproblem. Definition 3.1. Ein Weg, der jede Kante von G genau einmal
 3. Kreis- und Wegeprobleme Kapitelübersicht 3. Kreis- und Wegeprobleme Eulerweg, Eulerkreis Charakterisierung von eulerschen Graphen Bestimmung von eulerschen Wegen und Kreisen Hamiltonsche Graphen Definition
3. Kreis- und Wegeprobleme Kapitelübersicht 3. Kreis- und Wegeprobleme Eulerweg, Eulerkreis Charakterisierung von eulerschen Graphen Bestimmung von eulerschen Wegen und Kreisen Hamiltonsche Graphen Definition
Daniel Platt Einführung in die Graphentheorie
 Einführung in die Für die Mathematische Schülergesellschaft Leonhard Euler Humboldt Universität zu Berlin, Institut für Mathematik Das vorliegende Skript beschäftigt sich mit dem Thema. Das Skript entsteht
Einführung in die Für die Mathematische Schülergesellschaft Leonhard Euler Humboldt Universität zu Berlin, Institut für Mathematik Das vorliegende Skript beschäftigt sich mit dem Thema. Das Skript entsteht
Bäume und Wälder. Definition 1
 Bäume und Wälder Definition 1 Ein Baum ist ein zusammenhängender, kreisfreier Graph. Ein Wald ist ein Graph, dessen Zusammenhangskomponenten Bäume sind. Ein Knoten v eines Baums mit Grad deg(v) = 1 heißt
Bäume und Wälder Definition 1 Ein Baum ist ein zusammenhängender, kreisfreier Graph. Ein Wald ist ein Graph, dessen Zusammenhangskomponenten Bäume sind. Ein Knoten v eines Baums mit Grad deg(v) = 1 heißt
Elementargeometrie. Prof. Dr. Andreas Meister SS digital von: Frank Lieberknecht
 Prof. Dr. Andreas Meister SS 2004 digital von: Frank Lieberknecht Geplanter Vorlesungsverlauf...1 Graphentheorie...1 Beispiel 1.1: (Königsberger Brückenproblem)... 1 Beispiel 1.2: (GEW - Problem)... 2
Prof. Dr. Andreas Meister SS 2004 digital von: Frank Lieberknecht Geplanter Vorlesungsverlauf...1 Graphentheorie...1 Beispiel 1.1: (Königsberger Brückenproblem)... 1 Beispiel 1.2: (GEW - Problem)... 2
Bäume und Wälder. Seminar: Graphentheorie Sommersemester 2015 Dozent: Dr. Thomas Timmermann
 Bäume und Wälder Seminar: Graphentheorie Sommersemester 2015 Dozent: Dr. Thomas Timmermann Ida Feldmann 2-Fach Bachelor Mathematik und Biologie 6. Fachsemester Inhaltsverzeichnis Einleitung 1 1. Bäume
Bäume und Wälder Seminar: Graphentheorie Sommersemester 2015 Dozent: Dr. Thomas Timmermann Ida Feldmann 2-Fach Bachelor Mathematik und Biologie 6. Fachsemester Inhaltsverzeichnis Einleitung 1 1. Bäume
5 Graphen und Polyeder
 5 Graphen und Polyeder 5.1 Graphen und Eulersche Polyederformel Ein Graph besteht aus einer Knotenmenge V (engl. vertex) und einer Kantenmenge E (engl. edge). Anschaulich verbindet eine Kante zwei Knoten,
5 Graphen und Polyeder 5.1 Graphen und Eulersche Polyederformel Ein Graph besteht aus einer Knotenmenge V (engl. vertex) und einer Kantenmenge E (engl. edge). Anschaulich verbindet eine Kante zwei Knoten,
3 Klassifikation wichtiger Optimierungsprobleme
 3 Klassifikation wichtiger Optimierungsprobleme 3.1 Das MIN- -TSP Wir kehren nochmal zurück zum Handlungsreisendenproblem für Inputs (w {i,j} ) 1 i
3 Klassifikation wichtiger Optimierungsprobleme 3.1 Das MIN- -TSP Wir kehren nochmal zurück zum Handlungsreisendenproblem für Inputs (w {i,j} ) 1 i
Minimal spannender Baum
 Minimal spannender Baum 16 1 2 21 5 11 19 6 6 3 14 33 10 5 4 18 Die Kreise zeigen die vorgesehenen Standorte neu zu errichtender Filialen einer Bank. Entlang der bestehenden Straßen sollen Telefonleitungen
Minimal spannender Baum 16 1 2 21 5 11 19 6 6 3 14 33 10 5 4 18 Die Kreise zeigen die vorgesehenen Standorte neu zu errichtender Filialen einer Bank. Entlang der bestehenden Straßen sollen Telefonleitungen
Aufgabe 4.2 Sei G = (V, E, l) ein ungerichteter, gewichteter und zusammenhängender Graph.
 Aufgabe 4.2 Sei G = (V, E, l) ein ungerichteter, gewichteter und zusammenhängender Graph. a) Es seien W 1 = (V, E 1 ), W 2 = (V, E 2 ) Untergraphen von G, die beide Wälder sind. Weiter gelte E 1 > E 2.
Aufgabe 4.2 Sei G = (V, E, l) ein ungerichteter, gewichteter und zusammenhängender Graph. a) Es seien W 1 = (V, E 1 ), W 2 = (V, E 2 ) Untergraphen von G, die beide Wälder sind. Weiter gelte E 1 > E 2.
Königsberger Brückenproblem
 Philipps-Universität Marburg Fachbereich 12: Mathematik und Informatik PS: Klassische Probleme der Mathematik Leitung: Prof. Dr. Harald Upmeier, Benjamin Schwarz Referentin: Lene Baur WS 2009/2010 Königsberger
Philipps-Universität Marburg Fachbereich 12: Mathematik und Informatik PS: Klassische Probleme der Mathematik Leitung: Prof. Dr. Harald Upmeier, Benjamin Schwarz Referentin: Lene Baur WS 2009/2010 Königsberger
16. Flächenfärbungen
 Chr.Nelius: Graphentheorie (WS 2015/16) 57 16. Flächenfärbungen In der Mitte des 19. Jahrhunderts tauchte eine Vermutung auf, die erst 125 Jahre später bewiesen werden sollte und die eine der bekanntesten
Chr.Nelius: Graphentheorie (WS 2015/16) 57 16. Flächenfärbungen In der Mitte des 19. Jahrhunderts tauchte eine Vermutung auf, die erst 125 Jahre später bewiesen werden sollte und die eine der bekanntesten
Gibt es in Königsberg einen Spaziergang, bei dem man jede der. Pregelbrücken. überquert?
 Graphentheorie Gibt es in Königsberg einen Spaziergang, bei dem man jede der sieben Pregelbrücken genau einmal überquert? 1 Königsberger Brückenproblem Im Jahre 1736 Leonhard Euler löste das Problem allgemein
Graphentheorie Gibt es in Königsberg einen Spaziergang, bei dem man jede der sieben Pregelbrücken genau einmal überquert? 1 Königsberger Brückenproblem Im Jahre 1736 Leonhard Euler löste das Problem allgemein
Graphen und Bäume. A.1 Graphen
 Algorithmen und Datenstrukturen 96 A Graphen und Bäume A.1 Graphen Ein gerichteter Graph (auch Digraph) G ist ein Paar (V, E), wobei V eine endliche Menge und E eine Relation auf V ist, d.h. E V V. V heißt
Algorithmen und Datenstrukturen 96 A Graphen und Bäume A.1 Graphen Ein gerichteter Graph (auch Digraph) G ist ein Paar (V, E), wobei V eine endliche Menge und E eine Relation auf V ist, d.h. E V V. V heißt
Der Fünffarbensatz. Ausarbeitung des Seminarvortrags vom
 Philipps-Universität Marburg Fachbereich 12: Mathematik und Informatik PS Über klassische Probleme der Mathematik Leitung: Prof. Harald Upmeier, Benjamin Schwarz Referentin: Sabrina Klöpfel Wintersemester
Philipps-Universität Marburg Fachbereich 12: Mathematik und Informatik PS Über klassische Probleme der Mathematik Leitung: Prof. Harald Upmeier, Benjamin Schwarz Referentin: Sabrina Klöpfel Wintersemester
Vier-Farben-Vermutung (1)
 Vier-Farben-Vermutung (1) Landkarten möchte man so färben, dass keine benachbarten Länder die gleiche Farbe erhalten. Wie viele Farben braucht man zur Färbung einer Landkarte? Vier-Farben-Vermutung: Jede
Vier-Farben-Vermutung (1) Landkarten möchte man so färben, dass keine benachbarten Länder die gleiche Farbe erhalten. Wie viele Farben braucht man zur Färbung einer Landkarte? Vier-Farben-Vermutung: Jede
William Rowan Hamilton,
 3.2.2 Hamiltonkreise Definition 130. In einem Graph G = (V,E) nennt man einen Kreis, der alle Knoten aus V genau einmal durchläuft, einen Hamiltonkreis. Enthält ein Graph eine Hamiltonkreis, nennt man
3.2.2 Hamiltonkreise Definition 130. In einem Graph G = (V,E) nennt man einen Kreis, der alle Knoten aus V genau einmal durchläuft, einen Hamiltonkreis. Enthält ein Graph eine Hamiltonkreis, nennt man
Lernmodul 2 Graphen. Lernmodul 2: Geoobjekte und ihre Modellierung - Graphen
 Folie 1 von 20 Lernmodul 2 Graphen Folie 2 von 20 Graphen Übersicht Motivation Ungerichteter Graph Gerichteter Graph Inzidenz, Adjazenz, Grad Pfad, Zyklus Zusammenhang, Trennende Kante, Trennender Knoten
Folie 1 von 20 Lernmodul 2 Graphen Folie 2 von 20 Graphen Übersicht Motivation Ungerichteter Graph Gerichteter Graph Inzidenz, Adjazenz, Grad Pfad, Zyklus Zusammenhang, Trennende Kante, Trennender Knoten
II. Wissenschaftliche Argumentation
 Gliederung I. Motivation II. Wissenschaftliche Argumentation i. Direkter Beweis ii. iii. Indirekter Beweis Beweis durch vollständige Induktion Seite 35 II. Wissenschaftliche Argumentation Ein Beweis ist
Gliederung I. Motivation II. Wissenschaftliche Argumentation i. Direkter Beweis ii. iii. Indirekter Beweis Beweis durch vollständige Induktion Seite 35 II. Wissenschaftliche Argumentation Ein Beweis ist
Vorlesung Diskrete Strukturen Graphen: Wieviele Bäume?
 Vorlesung Diskrete Strukturen Graphen: Wieviele Bäume? Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de WS 2013/14 Isomorphie Zwei Graphen (V 1, E 1 ) und (V
Vorlesung Diskrete Strukturen Graphen: Wieviele Bäume? Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de WS 2013/14 Isomorphie Zwei Graphen (V 1, E 1 ) und (V
Der Vier-Farben-Satz
 , Samuel Hetterich, Felicia Raßmann Goethe-Universität Frankfurt, Institut für Mathematik 21.Juni 2013 Wieviele Farben braucht man zum Färben einer Landkarte? Spielregeln Länder mit einer gemeinsamen Grenze
, Samuel Hetterich, Felicia Raßmann Goethe-Universität Frankfurt, Institut für Mathematik 21.Juni 2013 Wieviele Farben braucht man zum Färben einer Landkarte? Spielregeln Länder mit einer gemeinsamen Grenze
Ausarbeitung zum Modulabschluss. Graphentheorie. spannende Bäume, bewertete Graphen, optimale Bäume, Verbindungsprobleme
 Universität Hamburg Fachbereich Mathematik Seminar: Proseminar Graphentheorie Dozentin: Haibo Ruan Sommersemester 2011 Ausarbeitung zum Modulabschluss Graphentheorie spannende Bäume, bewertete Graphen,
Universität Hamburg Fachbereich Mathematik Seminar: Proseminar Graphentheorie Dozentin: Haibo Ruan Sommersemester 2011 Ausarbeitung zum Modulabschluss Graphentheorie spannende Bäume, bewertete Graphen,
Vier-Farbenproblem. (c) Ein etwas schwereres Beispiel...
 Vier-Farbenproblem Kann man jede Landkarte mit vier Farben färben, sodass keine aneindander angrenzenden Länder die gleiche Farbe haben? Versuchen Sie die Karte Deutschlands oder eines der anderen Bilder
Vier-Farbenproblem Kann man jede Landkarte mit vier Farben färben, sodass keine aneindander angrenzenden Länder die gleiche Farbe haben? Versuchen Sie die Karte Deutschlands oder eines der anderen Bilder
Graphentheorie Mathe-Club Klasse 5/6
 Graphentheorie Mathe-Club Klasse 5/6 Thomas Krakow Rostock, den 26. April 2006 Inhaltsverzeichnis 1 Einleitung 3 2 Grundbegriffe und einfache Sätze über Graphen 5 2.1 Der Knotengrad.................................
Graphentheorie Mathe-Club Klasse 5/6 Thomas Krakow Rostock, den 26. April 2006 Inhaltsverzeichnis 1 Einleitung 3 2 Grundbegriffe und einfache Sätze über Graphen 5 2.1 Der Knotengrad.................................
6. Übung zur Linearen Optimierung SS08
 6 Übung zur Linearen Optimierung SS08 1 Sei G = (V, E) ein schlichter ungerichteter Graph mit n Ecken und m Kanten Für eine Ecke v V heißt die Zahl der Kanten (u, v) E Grad der Ecke (a) Ist die Anzahl
6 Übung zur Linearen Optimierung SS08 1 Sei G = (V, E) ein schlichter ungerichteter Graph mit n Ecken und m Kanten Für eine Ecke v V heißt die Zahl der Kanten (u, v) E Grad der Ecke (a) Ist die Anzahl
Algorithmen und Datenstrukturen 2
 Algorithmen und Datenstrukturen 2 Sommersemester 2006 3. Vorlesung Peter F. Stadler Universität Leipzig Institut für Informatik studla@bioinf.uni-leipzig.de Algorithmen für Graphen Fragestellungen: Suche
Algorithmen und Datenstrukturen 2 Sommersemester 2006 3. Vorlesung Peter F. Stadler Universität Leipzig Institut für Informatik studla@bioinf.uni-leipzig.de Algorithmen für Graphen Fragestellungen: Suche
Proseminar Online Algorithmen, Prof. Dr. Rolf Klein
 Proseminar Online Algorithmen, Prof. Dr. Rolf Klein Vortrag von Michael Daumen am 13.12.2000 Thema : Minimum Spanning Tree und 2-Approximation der TSP-Tour Inhalt des Vortrags : 1. genaue Vorstellung des
Proseminar Online Algorithmen, Prof. Dr. Rolf Klein Vortrag von Michael Daumen am 13.12.2000 Thema : Minimum Spanning Tree und 2-Approximation der TSP-Tour Inhalt des Vortrags : 1. genaue Vorstellung des
Algorithmen und Datenstrukturen (WS 2007/08) 63
 Kapitel 6 Graphen Beziehungen zwischen Objekten werden sehr oft durch binäre Relationen modelliert. Wir beschäftigen uns in diesem Kapitel mit speziellen binären Relationen, die nicht nur nur besonders
Kapitel 6 Graphen Beziehungen zwischen Objekten werden sehr oft durch binäre Relationen modelliert. Wir beschäftigen uns in diesem Kapitel mit speziellen binären Relationen, die nicht nur nur besonders
MafI I: Logik & Diskrete Mathematik (F. Hoffmann)
 Lösungen zum 14. und letzten Aufgabenblatt zur Vorlesung MafI I: Logik & Diskrete Mathematik (F. Hoffmann) 1. Ungerichtete Graphen (a) Beschreiben Sie einen Algorithmus, der algorithmisch feststellt, ob
Lösungen zum 14. und letzten Aufgabenblatt zur Vorlesung MafI I: Logik & Diskrete Mathematik (F. Hoffmann) 1. Ungerichtete Graphen (a) Beschreiben Sie einen Algorithmus, der algorithmisch feststellt, ob
Liegt eine Kante k auf einem Zyklus Z, so liegt k auf dem Rand genau zweier
 4 Planare Graphen Bisher wurden Graphen abstrakt durch Mengen E und K und eine Abbildung ψ : K P(E) definiert. In diesem Kapitel beschäftigen wir uns mit einem Abschnitt der sogenannten topologischen Graphentheorie.
4 Planare Graphen Bisher wurden Graphen abstrakt durch Mengen E und K und eine Abbildung ψ : K P(E) definiert. In diesem Kapitel beschäftigen wir uns mit einem Abschnitt der sogenannten topologischen Graphentheorie.
Graphentheorie 1. Diskrete Strukturen. Sommersemester Uta Priss ZeLL, Ostfalia. Hausaufgaben Graph-Äquivalenz SetlX
 Graphentheorie 1 Diskrete Strukturen Uta Priss ZeLL, Ostfalia Sommersemester 2016 Diskrete Strukturen Graphentheorie 1 Slide 1/19 Agenda Hausaufgaben Graph-Äquivalenz SetlX Diskrete Strukturen Graphentheorie
Graphentheorie 1 Diskrete Strukturen Uta Priss ZeLL, Ostfalia Sommersemester 2016 Diskrete Strukturen Graphentheorie 1 Slide 1/19 Agenda Hausaufgaben Graph-Äquivalenz SetlX Diskrete Strukturen Graphentheorie
2 Eulersche Polyederformel und reguläre Polyeder
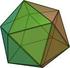 6 2 Eulersche Polyederformel und reguläre Polyeder 2.1 Eulersche Polyederformel Formal besteht ein Graph aus einer Knotenmenge X und einer Kantenmenge U. Jede Kante u U ist eine zweielementige Teilmenge
6 2 Eulersche Polyederformel und reguläre Polyeder 2.1 Eulersche Polyederformel Formal besteht ein Graph aus einer Knotenmenge X und einer Kantenmenge U. Jede Kante u U ist eine zweielementige Teilmenge
\ E) eines Graphen G = (V, E) besitzt die gleiche Knotenmenge V und hat als Kantenmenge alle Kanten des vollständigen Graphen ohne die Kantenmenge E.
 Das Komplement Ḡ = (V, ( V ) \ E) eines Graphen G = (V, E) besitzt die gleiche Knotenmenge V und hat als Kantenmenge alle Kanten des vollständigen Graphen ohne die Kantenmenge E. Ein Graph H = (V, E )
Das Komplement Ḡ = (V, ( V ) \ E) eines Graphen G = (V, E) besitzt die gleiche Knotenmenge V und hat als Kantenmenge alle Kanten des vollständigen Graphen ohne die Kantenmenge E. Ein Graph H = (V, E )
Anmerkungen zur Übergangsprüfung
 DM11 Slide 1 Anmerkungen zur Übergangsprüfung Aufgabeneingrenzung Aufgaben des folgenden Typs werden wegen ihres Schwierigkeitsgrads oder wegen eines ungeeigneten fachlichen Schwerpunkts in der Übergangsprüfung
DM11 Slide 1 Anmerkungen zur Übergangsprüfung Aufgabeneingrenzung Aufgaben des folgenden Typs werden wegen ihres Schwierigkeitsgrads oder wegen eines ungeeigneten fachlichen Schwerpunkts in der Übergangsprüfung
L A TEX Arbeitstechniken. 1. Oktober 2008 Jenny Prasiswa 1
 L A TEX Arbeitstechniken 1. Oktober 2008 Jenny Prasiswa 1 Was ist L A TEX? TEX wissenschaftliches Textsatzprogramm, L A TEX vereinfacht Eingabe durch Makros. + einfaches Setzten mathematischer Formeln
L A TEX Arbeitstechniken 1. Oktober 2008 Jenny Prasiswa 1 Was ist L A TEX? TEX wissenschaftliches Textsatzprogramm, L A TEX vereinfacht Eingabe durch Makros. + einfaches Setzten mathematischer Formeln
Graphen. Leonhard Euler ( )
 Graphen Leonhard Euler (1707-1783) 2 Graph Ein Graph besteht aus Knoten (nodes, vertices) die durch Kanten (edges) miteinander verbunden sind. 3 Nachbarschaftsbeziehungen Zwei Knoten heissen adjazent (adjacent),
Graphen Leonhard Euler (1707-1783) 2 Graph Ein Graph besteht aus Knoten (nodes, vertices) die durch Kanten (edges) miteinander verbunden sind. 3 Nachbarschaftsbeziehungen Zwei Knoten heissen adjazent (adjacent),
Das Briefträgerproblem
 Das Briefträgerproblem Paul Tabatabai 30. Dezember 2011 Inhaltsverzeichnis 1 Problemstellung und Modellierung 2 1.1 Problem................................ 2 1.2 Modellierung.............................
Das Briefträgerproblem Paul Tabatabai 30. Dezember 2011 Inhaltsverzeichnis 1 Problemstellung und Modellierung 2 1.1 Problem................................ 2 1.2 Modellierung.............................
M. Anderegg, E. Müller Graphentheorie
 Graphentheorie In den nächsten zwei Doppellektion lernen Sie ein Gebiet der Mathematik kennen, dass sich komplett von allem bisher Gehörten unterscheidet: Die Graphentheorie. Sie wurde vom Schweizer Mathematiker
Graphentheorie In den nächsten zwei Doppellektion lernen Sie ein Gebiet der Mathematik kennen, dass sich komplett von allem bisher Gehörten unterscheidet: Die Graphentheorie. Sie wurde vom Schweizer Mathematiker
WS 2009/10. Diskrete Strukturen
 WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
Algorithmen & Komplexität
 Algorithmen & Komplexität Angelika Steger Institut für Theoretische Informatik steger@inf.ethz.ch Kürzeste Pfade Problem Gegeben Netzwerk: Graph G = (V, E), Gewichtsfunktion w: E N Zwei Knoten: s, t Kantenzug/Weg
Algorithmen & Komplexität Angelika Steger Institut für Theoretische Informatik steger@inf.ethz.ch Kürzeste Pfade Problem Gegeben Netzwerk: Graph G = (V, E), Gewichtsfunktion w: E N Zwei Knoten: s, t Kantenzug/Weg
Freie Universität Berlin. Diskrete Mathematik. Ralf Borndörfer, Stephan Schwartz. Freie Universität. 08. April 2013
 Diskrete Mathematik Ralf Borndörfer, Stephan Schwartz 08. April 2013 FUB VL Diskrete Mathematik SS 2013 1 Leonhard Euler (1707-1783) e i sin cos f(x) FUB VL Diskrete Mathematik SS 2013 2 Das Königsberger
Diskrete Mathematik Ralf Borndörfer, Stephan Schwartz 08. April 2013 FUB VL Diskrete Mathematik SS 2013 1 Leonhard Euler (1707-1783) e i sin cos f(x) FUB VL Diskrete Mathematik SS 2013 2 Das Königsberger
Vollständige Induktion
 Schweizer Mathematik-Olympiade smo osm Vollständige Induktion Aktualisiert: 1 Dezember 01 vers 100 Eine der wichtigsten Beweistechniken der Mathematik überhaupt ist die (vollständige) Induktion Wir nehmen
Schweizer Mathematik-Olympiade smo osm Vollständige Induktion Aktualisiert: 1 Dezember 01 vers 100 Eine der wichtigsten Beweistechniken der Mathematik überhaupt ist die (vollständige) Induktion Wir nehmen
Graph Paar (V,E) V: nichtleere Menge von Knoten (vertex) E: Menge von Kanten (edges): Relation (Verbindung) zwischen den Knoten
 Graphentheorie Graph Paar (V,E) V: nichtleere Menge von Knoten (vertex) E: Menge von Kanten (edges): Relation (Verbindung) zwischen den Knoten gerichteter Graph (DiGraph (directed graph) E: Teilmenge E
Graphentheorie Graph Paar (V,E) V: nichtleere Menge von Knoten (vertex) E: Menge von Kanten (edges): Relation (Verbindung) zwischen den Knoten gerichteter Graph (DiGraph (directed graph) E: Teilmenge E
9. Übung Algorithmen I
 Timo Bingmann, Christian Schulz INSTITUT FÜR THEORETISCHE INFORMATIK, PROF. SANDERS 1 KIT Timo Universität Bingmann, des LandesChristian Baden-Württemberg Schulz und nationales Forschungszentrum in der
Timo Bingmann, Christian Schulz INSTITUT FÜR THEORETISCHE INFORMATIK, PROF. SANDERS 1 KIT Timo Universität Bingmann, des LandesChristian Baden-Württemberg Schulz und nationales Forschungszentrum in der
Übersicht 2. Mathematik als Beruf? Von logischen Strukturen und spannenden Aufgaben. Martin Oellrich. wer das Problem löste 4
 Mathematik als Beruf? Von logischen Strukturen und spannenden Aufgaben Übersicht 5. April 009 5. April 009 Martin Oellrich 1 vom Problem zur Theorie die Idee weiter denken 3 MathematikerIn werden? Gibt
Mathematik als Beruf? Von logischen Strukturen und spannenden Aufgaben Übersicht 5. April 009 5. April 009 Martin Oellrich 1 vom Problem zur Theorie die Idee weiter denken 3 MathematikerIn werden? Gibt
Diskrete Strukturen Kapitel 1: Einleitung
 WS 2015/16 Diskrete Strukturen Kapitel 1: Einleitung Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_15
WS 2015/16 Diskrete Strukturen Kapitel 1: Einleitung Hans-Joachim Bungartz Lehrstuhl für wissenschaftliches Rechnen Fakultät für Informatik Technische Universität München http://www5.in.tum.de/wiki/index.php/diskrete_strukturen_-_winter_15
Einführung in die Graphentheorie. Modellierung mit Graphen. Aufgabe
 Einführung in die Graphentheorie Modellierung mit Graphen Aufgabe Motivation Ungerichtete Graphen Gerichtete Graphen Credits: D. Jungnickel: Graphen, Netzwerke und Algorithmen, BI 99 G. Goos: Vorlesungen
Einführung in die Graphentheorie Modellierung mit Graphen Aufgabe Motivation Ungerichtete Graphen Gerichtete Graphen Credits: D. Jungnickel: Graphen, Netzwerke und Algorithmen, BI 99 G. Goos: Vorlesungen
Drei Anwendungen der Eulerschen Polyederformel
 Drei Anwendungen der Eulerschen Polyederformel Seminar aus Reiner Mathematik Viktoria Weißensteiner 04. Dezember 2013 Inhaltsverzeichnis 1 Einleitung 2 2 Vorbereitende Theorie 3 2.1 ebene Graphen..........................
Drei Anwendungen der Eulerschen Polyederformel Seminar aus Reiner Mathematik Viktoria Weißensteiner 04. Dezember 2013 Inhaltsverzeichnis 1 Einleitung 2 2 Vorbereitende Theorie 3 2.1 ebene Graphen..........................
2. Symmetrische Gruppen
 14 Andreas Gathmann 2 Symmetrische Gruppen Im letzten Kapitel haben wir Gruppen eingeführt und ihre elementaren Eigenschaften untersucht Wir wollen nun eine neue wichtige Klasse von Beispielen von Gruppen
14 Andreas Gathmann 2 Symmetrische Gruppen Im letzten Kapitel haben wir Gruppen eingeführt und ihre elementaren Eigenschaften untersucht Wir wollen nun eine neue wichtige Klasse von Beispielen von Gruppen
Elemente der Graphentheorie
 Universität Karlsruhe Elemente der Graphentheorie Schnupperkurs SS 2008 verfasst von Prof. Dr. Andreas Kirsch Institut für Algebra und Geometrie Universität Karlsruhe (TH) 1 Literaturliste über Graphentheorie
Universität Karlsruhe Elemente der Graphentheorie Schnupperkurs SS 2008 verfasst von Prof. Dr. Andreas Kirsch Institut für Algebra und Geometrie Universität Karlsruhe (TH) 1 Literaturliste über Graphentheorie
Technische Universität Wien Institut für Computergraphik und Algorithmen Arbeitsbereich für Algorithmen und Datenstrukturen
 Technische Universität Wien Institut für Computergraphik und Algorithmen Arbeitsbereich für Algorithmen und Datenstrukturen 186.172 Algorithmen und Datenstrukturen 1 VL 4.0 Übungsblatt 4 für die Übung
Technische Universität Wien Institut für Computergraphik und Algorithmen Arbeitsbereich für Algorithmen und Datenstrukturen 186.172 Algorithmen und Datenstrukturen 1 VL 4.0 Übungsblatt 4 für die Übung
Dezimaldarstellung ganzer Zahlen (Division mit Rest) 1 Division mit Rest in der Hochschule
 Berufsfeldbezogenes Fachseminar - Zahlentheorie Lisa Laudan Prof. Dr. Jürg Kramer Wintersemester 2014/2015 Dezimaldarstellung ganzer Zahlen (Division mit Rest) 1 Division mit Rest in der Hochschule 1.1
Berufsfeldbezogenes Fachseminar - Zahlentheorie Lisa Laudan Prof. Dr. Jürg Kramer Wintersemester 2014/2015 Dezimaldarstellung ganzer Zahlen (Division mit Rest) 1 Division mit Rest in der Hochschule 1.1
Kapitel 3. Natürliche Zahlen und vollständige Induktion
 Kapitel 3 Natürliche Zahlen und vollständige Induktion In Kapitel 1 haben wir den direkten Beweis, den modus ponens, kennen gelernt, der durch die Tautologie ( A (A = B) ) = B gegeben ist Dabei war B eine
Kapitel 3 Natürliche Zahlen und vollständige Induktion In Kapitel 1 haben wir den direkten Beweis, den modus ponens, kennen gelernt, der durch die Tautologie ( A (A = B) ) = B gegeben ist Dabei war B eine
Hamiltonsche Graphen (2. Teil)
 Hamiltonsche Graphen (2. Teil) Themen des Vortrages Für Schachspieler Hamiltons Spiel Sitzordnungen Eine billige Rundreise Ein vielleicht unlösbares Problem Bäcker mit Kenntnissen in Graphentheorie Fazit
Hamiltonsche Graphen (2. Teil) Themen des Vortrages Für Schachspieler Hamiltons Spiel Sitzordnungen Eine billige Rundreise Ein vielleicht unlösbares Problem Bäcker mit Kenntnissen in Graphentheorie Fazit
Vorlesung. Vollständige Induktion 1
 WS 015/16 Vorlesung Vollständige Induktion 1 1 Einführung Bei der vollständigen Induktion handelt es sich um ein wichtiges mathematisches Beweisverfahren, mit dem man Aussagen, die für alle natürlichen
WS 015/16 Vorlesung Vollständige Induktion 1 1 Einführung Bei der vollständigen Induktion handelt es sich um ein wichtiges mathematisches Beweisverfahren, mit dem man Aussagen, die für alle natürlichen
Vorlesungen vom 5.Januar 2005
 Vorlesungen vom 5.Januar 2005 5 Planare Graphen 5.1 Beispiel: Gas, Wasser, Elektrik Drei eingeschworene Feinde, die im Wald leben, planen Trassen zu den Versorgungswerken für die drei Grundgüter Gas, Wasser
Vorlesungen vom 5.Januar 2005 5 Planare Graphen 5.1 Beispiel: Gas, Wasser, Elektrik Drei eingeschworene Feinde, die im Wald leben, planen Trassen zu den Versorgungswerken für die drei Grundgüter Gas, Wasser
1 Vorbereitung: Potenzen 2. 2 Einstieg und typische Probleme 3
 Das vorliegende Skript beschäftigt sich mit dem Thema Rechnen mit Kongruenzen. Das Skript entsteht entlang einer Unterrichtsreihe in der Mathematischen Schülergesellschaft (MSG) im Jahr 2013. Die vorliegende
Das vorliegende Skript beschäftigt sich mit dem Thema Rechnen mit Kongruenzen. Das Skript entsteht entlang einer Unterrichtsreihe in der Mathematischen Schülergesellschaft (MSG) im Jahr 2013. Die vorliegende
Studientag zur Algorithmischen Mathematik
 Studientag zur Algorithmischen Mathematik Eulertouren, 2-Zusammenhang, Bäume und Baumisomorphismen Winfried Hochstättler Diskrete Mathematik und Optimierung FernUniversität in Hagen 22. Mai 2011 Outline
Studientag zur Algorithmischen Mathematik Eulertouren, 2-Zusammenhang, Bäume und Baumisomorphismen Winfried Hochstättler Diskrete Mathematik und Optimierung FernUniversität in Hagen 22. Mai 2011 Outline
Kapitel 5: Minimale spannende Bäume Gliederung der Vorlesung
 Gliederung der Vorlesung 1. Grundbegriffe 2. Elementare Graphalgorithmen und Anwendungen 3. Kürzeste Wege. Minimale spannende Bäume. Färbungen und Cliquen. Traveling Salesman Problem. Flüsse in Netzwerken
Gliederung der Vorlesung 1. Grundbegriffe 2. Elementare Graphalgorithmen und Anwendungen 3. Kürzeste Wege. Minimale spannende Bäume. Färbungen und Cliquen. Traveling Salesman Problem. Flüsse in Netzwerken
Algorithmen und Datenstrukturen
 Algorithmen und Datenstrukturen Dipl. Inform. Andreas Wilkens aw@awilkens.com Überblick Grundlagen Definitionen Elementare Datenstrukturen Rekursionen Bäume 2 1 Datenstruktur Baum Definition eines Baumes
Algorithmen und Datenstrukturen Dipl. Inform. Andreas Wilkens aw@awilkens.com Überblick Grundlagen Definitionen Elementare Datenstrukturen Rekursionen Bäume 2 1 Datenstruktur Baum Definition eines Baumes
Graphen und Algorithmen
 Graphen und Algorithmen Vorlesung #8: Färbungsprobleme Dr. Armin Fügenschuh Technische Universität Darmstadt WS 2007/2008 Übersicht Knotenfärbung (vs. Kanten- & Kartenfärbung) Satz von Brooks Algorithmen
Graphen und Algorithmen Vorlesung #8: Färbungsprobleme Dr. Armin Fügenschuh Technische Universität Darmstadt WS 2007/2008 Übersicht Knotenfärbung (vs. Kanten- & Kartenfärbung) Satz von Brooks Algorithmen
Quicksort ist ein Divide-and-Conquer-Verfahren.
 . Quicksort Wie bei vielen anderen Sortierverfahren (Bubblesort, Mergesort, usw.) ist auch bei Quicksort die Aufgabe, die Elemente eines Array a[..n] zu sortieren. Quicksort ist ein Divide-and-Conquer-Verfahren.
. Quicksort Wie bei vielen anderen Sortierverfahren (Bubblesort, Mergesort, usw.) ist auch bei Quicksort die Aufgabe, die Elemente eines Array a[..n] zu sortieren. Quicksort ist ein Divide-and-Conquer-Verfahren.
Vorkurs Mathematik und Informatik Mengen, natürliche Zahlen, Induktion
 Vorkurs Mathematik und Informatik Mengen, natürliche Zahlen, Induktion Saskia Klaus 07.10.016 1 Motivation In den ersten beiden Vorträgen des Vorkurses haben wir gesehen, wie man aus schon bekannten Wahrheiten
Vorkurs Mathematik und Informatik Mengen, natürliche Zahlen, Induktion Saskia Klaus 07.10.016 1 Motivation In den ersten beiden Vorträgen des Vorkurses haben wir gesehen, wie man aus schon bekannten Wahrheiten
Definition Gerichteter Pfad. gerichteter Pfad, wenn. Ein gerichteter Pfad heißt einfach, falls alle u i paarweise verschieden sind.
 3.5 Gerichteter Pfad Definition 291 Eine Folge (u 0, u 1,..., u n ) mit u i V für i = 0,..., n heißt gerichteter Pfad, wenn ( i {0,..., n 1} ) [ (u i, u i+1 ) A]. Ein gerichteter Pfad heißt einfach, falls
3.5 Gerichteter Pfad Definition 291 Eine Folge (u 0, u 1,..., u n ) mit u i V für i = 0,..., n heißt gerichteter Pfad, wenn ( i {0,..., n 1} ) [ (u i, u i+1 ) A]. Ein gerichteter Pfad heißt einfach, falls
8 Diskrete Optimierung
 8 Diskrete Optimierung Definition 8.1. Ein Graph G ist ein Paar (V (G), E(G)) besteh aus einer lichen Menge V (G) von Knoten (oder Ecken) und einer Menge E(G) ( ) V (G) 2 von Kanten. Die Ordnung n(g) von
8 Diskrete Optimierung Definition 8.1. Ein Graph G ist ein Paar (V (G), E(G)) besteh aus einer lichen Menge V (G) von Knoten (oder Ecken) und einer Menge E(G) ( ) V (G) 2 von Kanten. Die Ordnung n(g) von
Graphentheorie. Organisatorisches. Organisatorisches. Organisatorisches. Rainer Schrader. 23. Oktober 2007
 Graphentheorie Rainer Schrader Organisatorisches Zentrum für Angewandte Informatik Köln 23. Oktober 2007 1 / 79 2 / 79 Organisatorisches Organisatorisches Dozent: Prof. Dr. Rainer Schrader Weyertal 80
Graphentheorie Rainer Schrader Organisatorisches Zentrum für Angewandte Informatik Köln 23. Oktober 2007 1 / 79 2 / 79 Organisatorisches Organisatorisches Dozent: Prof. Dr. Rainer Schrader Weyertal 80
3. Musterlösung. Problem 1: Boruvka MST
 Universität Karlsruhe Algorithmentechnik Fakultät für Informatik WS 06/07 ITI Wagner. Musterlösung Problem : Boruvka MST pt (a) Beweis durch Widerspruch. Sei T MST von G, e die lokal minimale Kante eines
Universität Karlsruhe Algorithmentechnik Fakultät für Informatik WS 06/07 ITI Wagner. Musterlösung Problem : Boruvka MST pt (a) Beweis durch Widerspruch. Sei T MST von G, e die lokal minimale Kante eines
w a is die Anzahl der Vorkommen von a in w Beispiel: abba a = 2
 1 2 Notation für Wörter Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg w a is die Anzahl der Vorkommen von a in w Beispiel: abba
1 2 Notation für Wörter Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg w a is die Anzahl der Vorkommen von a in w Beispiel: abba
Vervollständigung Lateinischer Quadrate
 Vervollständigung Lateinischer Quadrate Elisabeth Schmidhofer 01.12.2013 Inhaltsverzeichnis 1 Vorwort 3 2 Einleitung 4 2.1 Beispele.............................................. 4 3 Lateinische Quadrate
Vervollständigung Lateinischer Quadrate Elisabeth Schmidhofer 01.12.2013 Inhaltsverzeichnis 1 Vorwort 3 2 Einleitung 4 2.1 Beispele.............................................. 4 3 Lateinische Quadrate
Übung zur Vorlesung Algorithmische Geometrie
 Übung zur Vorlesung Algorithmische Geometrie Dipl.-Math. Bastian Rieck Arbeitsgruppe Computergraphik und Visualisierung Interdisziplinäres Zentrum für Wissenschaftliches Rechnen 8. Mai 2012 B. Rieck (CoVis)
Übung zur Vorlesung Algorithmische Geometrie Dipl.-Math. Bastian Rieck Arbeitsgruppe Computergraphik und Visualisierung Interdisziplinäres Zentrum für Wissenschaftliches Rechnen 8. Mai 2012 B. Rieck (CoVis)
15 G R A P H E N gerichtete graphen
 15 G R A P H E N In den bisherigen Einheiten kamen schon an mehreren Stellen Diagramme und Bilder vor, in denen irgendwelche Gebilde durch Linien oder Pfeile miteinander verbunden waren. Man erinnere sich
15 G R A P H E N In den bisherigen Einheiten kamen schon an mehreren Stellen Diagramme und Bilder vor, in denen irgendwelche Gebilde durch Linien oder Pfeile miteinander verbunden waren. Man erinnere sich
3 Vom Zählen zur Induktion
 7 3 Vom Zählen zur Induktion 3.1 Natürliche Zahlen und Induktions-Prinzip Seit unserer Kindheit kennen wir die Zahlen 1,, 3, 4, usw. Diese Zahlen gebrauchen wir zum Zählen, und sie sind uns so vertraut,
7 3 Vom Zählen zur Induktion 3.1 Natürliche Zahlen und Induktions-Prinzip Seit unserer Kindheit kennen wir die Zahlen 1,, 3, 4, usw. Diese Zahlen gebrauchen wir zum Zählen, und sie sind uns so vertraut,
Einführung in die Graphentheorie. Monika König
 Einführung in die Graphentheorie Monika König 8. 11. 2011 1 Vorwort Diese Seminararbeit basiert auf den Unterkapiteln 1.1-1.3 des Buches Algebraic Graph Theory von Chris Godsil und Gordon Royle (siehe
Einführung in die Graphentheorie Monika König 8. 11. 2011 1 Vorwort Diese Seminararbeit basiert auf den Unterkapiteln 1.1-1.3 des Buches Algebraic Graph Theory von Chris Godsil und Gordon Royle (siehe
Mathematische Probleme, SS 2016 Freitag $Id: convex.tex,v /05/13 14:42:55 hk Exp $
 $Id: convex.tex,v.28 206/05/3 4:42:55 hk Exp $ 3 Konvexgeometrie 3. Konvexe Polyeder In der letzten Sitzung haben wir begonnen uns mit konvexen Polyedern zu befassen, diese sind die Verallgemeinerung der
$Id: convex.tex,v.28 206/05/3 4:42:55 hk Exp $ 3 Konvexgeometrie 3. Konvexe Polyeder In der letzten Sitzung haben wir begonnen uns mit konvexen Polyedern zu befassen, diese sind die Verallgemeinerung der
1. Übung Graphentheorie WS2016/17
 1. Übung Graphentheorie WS2016/17 1. Schreiben Sie für jede Ecke der folgenden 7 Graphen den Grad auf! Welche der Graphen sind regulär? G 1 G 2 G 5 G 3 2. Bestimmen Sie alle paarweise nicht-isomorphen
1. Übung Graphentheorie WS2016/17 1. Schreiben Sie für jede Ecke der folgenden 7 Graphen den Grad auf! Welche der Graphen sind regulär? G 1 G 2 G 5 G 3 2. Bestimmen Sie alle paarweise nicht-isomorphen
Diskrete Mathematik für Informatiker
 Universität Siegen Lehrstuhl Theoretische Informatik Carl Philipp Reh Daniel König Diskrete Mathematik für Informatiker WS 016/017 Übung 7 1. Gegeben sei folgender Graph und das Matching M = {{h, f}, {c,
Universität Siegen Lehrstuhl Theoretische Informatik Carl Philipp Reh Daniel König Diskrete Mathematik für Informatiker WS 016/017 Übung 7 1. Gegeben sei folgender Graph und das Matching M = {{h, f}, {c,
Paper Computer Science Experiment. Computation (NP-Vollständigkeit) Traveling Salesman
 Paper Computer Science Experiment Great Principles of Computing Computation (NP-Vollständigkeit) Thema Traveling Salesman Unterrichtsform Lernen am Modell Voraussetzung Wahrscheinlich kennen viele Schüler/innen
Paper Computer Science Experiment Great Principles of Computing Computation (NP-Vollständigkeit) Thema Traveling Salesman Unterrichtsform Lernen am Modell Voraussetzung Wahrscheinlich kennen viele Schüler/innen
WS 2008/09. Diskrete Strukturen
 WS 2008/09 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0809
WS 2008/09 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0809
Klausur zu Diskrete Strukturen, WS 09/10
 Aufgabenblatt (Gesamtpunktzahl: 50) Klausur zu Diskrete Strukturen, WS 09/10 B.Sc-Modulprüfung / Scheinklausur Dr. Timo Hanke, Lehrstuhl D für Mathematik, RWTH Aachen 06.02.2010 (1. Termin) Name: Matrikelnummer:
Aufgabenblatt (Gesamtpunktzahl: 50) Klausur zu Diskrete Strukturen, WS 09/10 B.Sc-Modulprüfung / Scheinklausur Dr. Timo Hanke, Lehrstuhl D für Mathematik, RWTH Aachen 06.02.2010 (1. Termin) Name: Matrikelnummer:
entheoretische Konzepte und Algorithmen
 Sven Oliver Krumke, Hartmut Noitemeier entheoretische Konzepte und Algorithmen Teubner Inhaltsverzeichnis 1 Einleitung 1 1.1 Routenplanung 1 1.2 Frequenzplanung im Mobilfunk I 1.3 Museumswärter 3 1.4 Das
Sven Oliver Krumke, Hartmut Noitemeier entheoretische Konzepte und Algorithmen Teubner Inhaltsverzeichnis 1 Einleitung 1 1.1 Routenplanung 1 1.2 Frequenzplanung im Mobilfunk I 1.3 Museumswärter 3 1.4 Das
Visualisierung von Graphen
 1 Visualisierung von Graphen Geradlinige Zeichnungen planarer Graphen 6. Vorlesung Sommersemester 2013 (basierend auf Folien von Marcus Krug und Tamara Mchedlidze, KIT) 2 Planare Graphen: Charakterisierung,
1 Visualisierung von Graphen Geradlinige Zeichnungen planarer Graphen 6. Vorlesung Sommersemester 2013 (basierend auf Folien von Marcus Krug und Tamara Mchedlidze, KIT) 2 Planare Graphen: Charakterisierung,
Geraden in der Ebene und Zerlegung von Graphen
 Geraden in der Ebene und Zerlegung von Graphen Proseminar: Beweise aus dem Buch am 17.01.2015 von Ina Seidel 1 Historisches zu Sylvester und Gallai James Joseph Sylvester * 1814, 1897 war britischer Mathematiker.Unter
Geraden in der Ebene und Zerlegung von Graphen Proseminar: Beweise aus dem Buch am 17.01.2015 von Ina Seidel 1 Historisches zu Sylvester und Gallai James Joseph Sylvester * 1814, 1897 war britischer Mathematiker.Unter
Bipartite Graphen. Beispiele
 Bipartite Graphen Ein Graph G = (V, E) heiÿt bipartit (oder paar), wenn die Knotenmenge in zwei disjunkte Teilmengen zerfällt (V = S T mit S T = ), sodass jede Kante einen Knoten aus S mit einem Knoten
Bipartite Graphen Ein Graph G = (V, E) heiÿt bipartit (oder paar), wenn die Knotenmenge in zwei disjunkte Teilmengen zerfällt (V = S T mit S T = ), sodass jede Kante einen Knoten aus S mit einem Knoten
Elementare Beweismethoden
 Elementare Beweismethoden Christian Hensel 404015 Inhaltsverzeichnis Vortrag zum Thema Elementare Beweismethoden im Rahmen des Proseminars Mathematisches Problemlösen 1 Einführung und wichtige Begriffe
Elementare Beweismethoden Christian Hensel 404015 Inhaltsverzeichnis Vortrag zum Thema Elementare Beweismethoden im Rahmen des Proseminars Mathematisches Problemlösen 1 Einführung und wichtige Begriffe
