GPGPU Architectures - Compiler Techniques and Applications SS 2012
|
|
|
- Rosa Müller
- vor 8 Jahren
- Abrufe
Transkript
1 Seminar on GPGPU Architectures - Compiler Techniques and Applications SS 2012 Embedded Systems Group Department of Computer Science University of Kaiserslautern
2 Preface The widespread use of so-called General-Purpose Graphics Processing Units (GPGPUs) in modern computers offers a massively parallel computing power. These processors become more and more flexible, but still their programming requires special programming techniques. Efficient utilization is a non-trivial task and requires (1) explicit parallel programming and (2) new compilation techniques to ease programming of these architectures. Moreover, GPGPUs provide parallelism on different levels, i. e. instruction-level and thread-level parallelism at once, each requiring different implementation techniques. This seminar discusses various approaches to create efficient code for GPGPUs but also considers specific applications of these parallel computers in scientific areas.
3 Contents GPU Architektur und Programmiermöglichkeiten für GPGPU-Anwendungen Marius Gräfe Automatische C-to-CUDA Code Generierung Johannes Kölsch Porting CUDA Code to Multicore CPUs and Other Platforms Frederik Walk OpenACC and the PGI Compiler Dimitri Blatner Dataow Programming on GPUs Maximilian Senftleben An Introduction to the Research on Scratchpad Memory: Denition, Hardware, Known Implementations and WCET Optimisation Julius Roob An Introduction to the Research on Scratchpad Memory with Focus on Performance Improvement - Instruction SPM, SPM on Multicoresystems and SPM on Multitaskingsystems Axel Ratzke Simulation digitaler Schaltungen auf GPUs Yohan Humbert Verikation auf paralleler Hardware Daniel Thielsch
4 Seminararbeit GPU Architektur und Programmiermöglichkeiten für GPGPU-Anwendungen Marius Gräfe University of Kaiserslautern, Embedded Systems Group m graefe10@cs.uni-kl.de 25. Oktober 2012 Alone we can do so little; together we can do so much. Helen Keller 1
5 3 Inhaltsverzeichnis 1 Einleitung 4 2 GPU Architektur Einleitung Allgemeiner Aufbau Konkreter Aufbau (AMD Radeon HD 7970) Stärken und Schwächen CUDA Einleitung Prozessmodell Parallelisierung Speicherhierarchie CUDA C Kompilierung Kerneldefinition und -aufruf Umsetzung der Speicherhierarchie Synchronisation Datentypen PTX Assembler OpenCL Einleitung Prozessmodell Parallelisierung Speicherhierarchie Workflow OpenCL C Kerneldefinition und Speicherhierarchie Synchronisation Datentypen Die OpenCL API (Host-Code) Vergleich zwischen OpenCL und CUDA Grundlegendes Vergleich der Performance Abschließende Bemerkungen 26 2
6 4 1 Einleitung Ursprünglich waren Grafikbeschleuniger genau das, was der Name aussagt: Sie sollten bei grafikintensiven Anwendungen die restlichen Komponenten des Computers entlasten indem sie einen Teil des Berechnungsaufwands übernehmen. Da Grafikberechnungen zum Großteil aus einfachen Gleitkommaadditionen und -Multiplikationen bestehen, wurden diese Berechnungsvorgänge von den Herstellern massiv optimiert und parallelisiert. Jedoch waren diese Fähigkeiten nur im Rahmen der sogenannten Fixed-Function-Pipeline verfügbar. Diese erhielt vom Host-Programm nur Geometriedaten und einige Parameter (wie Lichteinstellungen, Texturen etc.) und erzeugte nach einem unveränderlichen Ablauf das Bild auf dem Monitor. Mit der Zeit wurde die Grafikpipeline immer mehr generalisiert und schließlich komplett programmierbar gestaltet, heute lässt sich ein Grafikprozessor auch für Berechnungen nutzen, welche nichts mit Computergrafik zu tun haben. Mit der Veröffentlichung des CUDA SDK durch NVIDIA Anfang 2007 wurden Grafikbeschleuniger schließlich einfacher für GPGPU Anwendungen nutzbar, allerdings nur mit Grafikkarten von NVIDIA (siehe Kapitel 3, Seite 7) wurde die Spezifikation von OpenCL 1.0 als offener Standard (ähnlich wie OpenGL) veröffentlicht und mittlerweile existieren Implementierungen für eine ganze Reihe unterschiedlicher Geräte (siehe Kapitel 4, Seite 16). 3
7 5 2 GPU Architektur 2.1 Einleitung Eine GPU ist ein massiver Parallelrechner, die aktuellen Spitzenmodelle (Mitte 2012) besitzen 1536 (Nvidia GTX 680) bzw (AMD RADEON HD 7970) Rechenkerne. Da jeder dieser Kerne (im Kontext der Computergrafik auch Shadereinheiten genannt) parallel rechnet, lassen sich beachtliche theoretische Leistungen von ungefähr 3700 GFLOPS 1 erzielen (als Vergleich: ein aktueller Intel Core i7-3930k leistet maximal 307 GFLOPS 2, ein Pentium 4 mit 3,2 GHz lieferte seinerzeit maximal 6,4 GLOPS). Dieses Kapitel beschreibt, wie eine GPU allgemein und, bezogen auf die HD 7970, konkret aufgebaut ist. 2.2 Allgemeiner Aufbau Analog zur CPU spricht man auf der GPU ebenfalls von Threads, wenn man parallel ablaufende Programmteile meint. Das Programm (bzw. der Code) eines Threads nennt man Kernel, der Thread selber ist demnach eine Kernel-Instanz. Eine Kernel-Instanz führt immer den exakt gleichen Programmcode aus, der Programmfluss und die Berechnungsergebnisse hängen somit nur von den eingelesenen Daten ab. Eine GPU ist ein paralleler Streamprozessor, was bedeutet, dass Grafikkarten darauf ausgelegt sind, viele einfache (d.h. skalare) Berechnungen nach einem festen, möglichst verzweigungsfreien und für jeden Datensatz gleichen Schema auszuführen. Sie lässt sich grob in vier Bereiche einteilen: Hauptspeicher, Rechenkerne, Caches und aufgabenspezifische Hardwarebausteine. Der Hauptspeicher, welcher, obwohl der mittlerweile fast identischen Kapazität, nicht mit dem allgemeinen Hauptspeicher des Host-Computers zu verwechseln ist, stellt den Aufbewahrungsort für die zur Berechnung benötigten Daten dar. Zwar ist die Anbindung dieses Speichers an die GPU häufig um ein vielfaches schneller als die Anbindung des RAM s an die CPU des Rechners, trotzdem eignet er sich aufgrund seiner im Vergleich hohen Zugriffszeiten nicht gut für kleine, temporäre Berechnungsergebnisse. Die Rechenkerne sind einfache, skalare Gleitkommaprozessoren welche häufig zu Gruppen zusammengefasst werden. Innerhalb der Gruppe teilen sie sich zum Beispiel Integer-, Branching-, Cache-, Texturund Schedulingeinheiten, auch Register werden häufig geteilt, was bedeutet, dass ein Rechenkern keinesfalls als vollwertiger Prozessor bezeichnet werden kann. Die Caches sind im Vergleich zu denen der CPU extrem klein, sie bewegen sich im Kilobyte-Bereich, wohingegen eine CPU häufig mehrere Megabytes besitzt. Außerdem ist ihre Anzahl, bezogen auf die Menge der Kerne, viel kleiner, es gibt häufig keinen L3, sondern nur einen globalen L2-Cache, und mehrere Kerne teilen sich einen L1-Cache. Aufgabenspezifische Hardwareteile sind nicht programmierbar. Sie übernehmen sowohl allgemeine Managementaufgaben (wie z.b. Cache-Controller, Command-Processor oder Bus-Interfaces), als auch die (wenigen) vorgeschriebenen Schritte der Grafikpipeline, wie die Rasterisierung. 1 AMD Radeon HD 7970, Single Precision 2 Single Precision 4
8 6 2.3 Konkreter Aufbau (AMD Radeon HD 7970) Die Shadereinheiten der HD 7970 sind zu insgesamt 32 Compute Units zusammengefasst. Eine Compute Unit besteht aus vier Vector Units, welche wiederum aus 16 Shadereinheiten bestehen. Jeder Vector Unit steht ein Vector Register von 64 Kilobyte zur Verfügung. Alle Vector Units, bzw. die darin enthaltenden Shadereinheiten, teilen sich einen Scheduler, eine Scalar Unit sowie das zugehörige Scalar-Register (4 Kilobyte), vier Texture Filter Units, 16 Texture Fetch/Store Units, eine Branch & Message Unit, einen Local Data Share sowie einen L1-Cache von 16 Kilobyte. Jeweils vier Compute Units wird ein 16 Kilobyte großer Instruction Cache, ein 32 Kilobyte großer Scalar Data Cache sowie eine komplette Rastereinheit zur Verfügung gestellt. Alle Einheiten teilen sich einen L2-Cache sowie den 3 Gigabyte großen Hauptspeicher. 2.4 Stärken und Schwächen Trotz der großen Rechenleistung ist eine Grafikkarte nicht für alle Aufgaben geeignet. Allem voran muss der auszuführende Algorithmus massiv parallelisierbar sein, sequenzielle Algorithmen sind schlichtweg ungeeignet. Eine GPU kann nicht gut mit Verzweigungen umgehen, zum einen fehlen moderne CPU- Features wie Branch Prediction 3, andererseits kann ein dynamischer Branch eine (langsame) Resynchronisation der Threads zur Folge haben. Wegen der eher spartanischen Cache-Architektur sollte ein einzelner Thread nicht zu viele Daten auf einmal aus dem Hauptspeicher lesen. Threads, welche die gleichen, bzw. ähnliche Speicheradressen ansprechen, sollten gleichzeitig ablaufen um einen Vorteil aus den kleinen Caches zu ziehen und Hauptspeicherzugriffe zu vermeiden. Ein optimaler GPGPU-Algorithmus führt also viele einfache Berechnungen auf wenigen, kleinen Daten parallel aus und ist Branch-frei. Als zusätzliche Schwäche ist das Rechnen mit Gleitkommazahlen bei doppelter Genauigkeit (doubleprecision) zu nennen, vor allem die für Spieler gedachten GPUs sind hier erheblich langsamer als bei einfacher Genauigkeit 4. GPUs für ein professionelles Umfeld (z.b. NVIDIA Tesla oder AMD FireStream ) unterscheiden sich, neben einem oft wesentlich größeren Speicher und/oder Fehlerkorrekturverfahren, durch ihre höhere Geschwindigkeit bei doppelter Genauigkeit von den normalen Modellen, allerdings auch zu einem erheblich höheren Preis. 3 Methode um das Ergebnis einer Branch-Operation mithilfe von Heuristiken vorherzusagen um so Pipeline-Stalls zu verhindern 4 AMD RADEON HD 7970: Faktor 1/4 (DP/SP), NVIDIA GTX 680: Faktor 1/24, NVIDIAs Kepler-Architektur hat allerdings auch bei den professionellen Modellen keinen besseren Faktor, die vorherige Generation Fermi erreichte im professionellen Umfeld 1/2. 5
9 7 3 CUDA 3.1 Einleitung CUDA (Compute Unified Device Architecture) ist eine von NVIDIA entwickelte Architektur zur parallelen Berechnung auf NVIDIA Grafikkarten. Die in der Programmiersprache CUDA C geschriebenen Programme werden mittels eines von NVIDIA bereitgestellten Compilers kompiliert, und können anschließend mithilfe normaler Programmiersprachen (allen vorran C/C++) angesprochen, also ausgeführt werden. Aufgrund seiner hardwarespezifischen und proprietären Herkunft besitzt CUDA ein großes Potenzial für Optimierungen und bietet dem Programmierer viele speziell auf die Hardware abgestimmte Möglichkeiten. Der Nachteil ist allerdings die Beschränkung auf die herstellereigene Hardware, das heißt CUDA Programme können nur auf NVIDIA Hardware ausgeführt werden. Da die Multiplikation großer Matrizen ein häufig herangezogenes Beispiel ist komme ich auch hier häufig darauf zurück. 3.2 Prozessmodell Das einfachste Prozessmodell unter CUDA sieht vier Schritte vor: 1. Die Prozessdaten werden vom Hauptspeicher des Host-Rechners in den Speicher der Grafikkarte kopiert. 2. Die CPU beaufragt die GPU mit der Berechnung. 3. Die GPU führt das Programm parallel in CUDA Threads aus. 4. Das Resultat wird zur Weiterverarbeitung beziehungsweise Auswertung vom Hauptspeicher der Grafikkarte in den Hauptspeicher des Host-Rechners übertragen. 3.3 Parallelisierung Wie bei allen GPGPU Anwendungen muss das Gesamtproblem auch bei CUDA in gleichartige Teilprobleme zerlegt werden, welche dann parallel in sogenannten CUDA Threads ausgeführt werden. Diese Zerlegung kann, basierend auf realen Problemen, in ein, zwei oder drei Dimensionen erfolgen. Zur Berechnung einer eindimensionalen Fouriertransformation (z.b. bei digitaler Audioverarbeitung) bietet sich also eine Dimension an, bei Matrizenmultiplikationen zwei und so weiter. Der Gedanke dahinter ist dass, geometrisch gesprochen, nah beieinanderliegende Threads auf nah beieinanderliegenden (im Sinne der Speicheradressen) Daten operieren sollen, um so die Cache-Architektur besser auszunutzen. Das Programm zur Lösung eines Teilproblems, also, um als Beispiel bei der Matritzenmultiplikation zu bleiben, die Berechnung eines Eintrags der Ergebnismatrix, wird Kernel genannt. Ein Kernel wird von vielen CUDA Threads parallel ausgeführt, man spricht daher auch von Kernel-Instanzen. Außerdem werden mehrere CUDA Threads zu CUDA Thread Blocks gruppiert, die Gesamtheit der Blöcke wird Grid genannt. Die Dimension der Blöcke ist von der Dimension des Grids unabhängig, jedoch besitzen alle Blöcke untereinander die gleiche Dimension (d.h. es können zweidimensionale Blöcke in einem dreidimensionalen Grid ausgeführt werden, aber niemals ein zwei- und ein dreidimensionaler Block gleichzeitig); für eine Beispielhafte Aufteilung siehe Abbildung 1, Seite 8. Innerhalb eines Kernels kann über vordefinierten Variablen (siehe Tabelle 1, Seite 9) unter anderem auf die Position des Threads (welcher die Kernel-Instanz ausführt) bzw. des Blocks innerhalb des Grids zugegriffen werden. Der Multiprozessor (die GPU) erstellt, verwaltet und führt Threads in Gruppen von 32 Stück aus, diese 6
10 8 werden bei CUDA Warp genannt. Wenn die GPU einen oder mehr Blöcke ausführen soll, so partitioniert sie diese in Warps, welche dann von einem Warp Scheduler zur Ausführung eingeteilt werden. Ein Warp führt immer nur eine gemeinsame Instruktion gleichzeitig aus. Falls die Threads innerhalb eines Warps (z.b. aufgrund eines if-statements) unterschiedliche Ausführungspfade nehmen, also divergieren, so werden die unterschiedlichen Pfade sequentiell ausgeführt. Gegeben sei der folgende Pseudocode: if condition then do something else do something different end if Angenommen für die Threads T true gilt condition = wahr und für die Threads T f alse gilt condition = f alsch (T true T f alse = Warp, T true /0, T f alse /0), dann werden zuerst alle Threads in T true parallel ausgeführt und anschließend alle Threads in T f alse (bzw. andersherum). Es können aber innerhalb eines Warps niemals zwei Threads t 1 T true und t 2 T f alse gleichzeitig ausgeführt werden, die volle Leistung wird also nur erreicht wenn alle Threads des Warps den gleichen Pfad nehmen. Block (0,0) Block (1,0) Thr. (0,0) Thr. (1,0) Grid Thr. (0,0) Thr. (1,0) Thr. (0,1) Thr. (1,1) Thr. (0,1) Thr. (1,1) Block (0,1) Block (1,1) Thr. (0,0) Thr. (1,0) Thr. (0,0) Thr. (1,0) Thr. (0,1) Thr. (1,1) Thr. (0,1) Thr. (1,1) Abbildung 1: Beispielhaftes, zweidimensionales Block- und zweidimensionales Threadlayout bei CUDA. In den Klammern stehen jeweils (blockidx.x, blockidx.y) bzw. (threadidx.x, threadidx.y). Dieses Layout währe zum Beispiel für die Multiplikation zweier 8 8 Matrizen geeignet, wobei jeder Thread einen Eintrag der Ergebnismatrix berechnet. 3.4 Speicherhierarchie In CUDA gibt es (wie auch in OpenCL) unterschiedliche Speicherarten. Diese unterscheiden sich wesentlich in ihrer Größe, Geschwindigkeit und den Zugriffsbeschränkungen. Zu allererst ist der Speicher des Host-Programms zu nennen: Dies ist der normale Arbeitsspeicher des Computers, ein Kernel- Programm (bzw. Thread) hat hierauf keinen direkten Zugriff, die Daten müssen erst in den Device Memory übertragen werden. Der Device Memory ist der Hauptspeicher der Grafikkarte und lässt sich von jedem Thread sowohl lesen als auch schreiben. Er ist zwar groß, aber auch vergleichsweise langsam. Als Sonderfall gilt der Constant Memory. Dieser ist ebenfalls von jedem Thread lesbar, kann aber nur 7
11 9 Name Typ Beschreibung griddim dim3 a Größe des Grids, sodass griddim.x griddim.y griddim.z = #BlöckeImGrid ist blockidx uint3 b Block-Index innerhalb des Grids blockdim dim3 Größe eines Blocks, sodass blockdim.x blockdim.y blockdim.z = #T hreadsproblock ist threadidx uint3 Thread-Index innerhalb des Blocks warpsize int Die Größe eines Warps, in Threads Tabelle 1: Vordefinierte Variablen bei CUDA. Diese sind nur in Funktionen welche auf der Grafikkarte ausgeführt werden gültig, d.h. nur innerhalb eines Kernel-Programms. a Vektortyp wie uint3, unspezifizierte Komponenten werden auf 1 initialisiert. b Vektortyp mit 3 Komponenten vom Typ unsigned integer. Zugriff über var.[x y z]. vom Host-Programm geschrieben werden, außerdem ist er meist sehr viel kleiner als der Device Memory. Der Constant Memory ist für die Speicherung von unveränderlichen Konstanten gedacht, der Zugriff auf diese ist stark gecached und daher schnell. Für jeden Thread Block existiert ein Shared Memory. Dieser ist erheblich kleiner als die bisher genannten Speicher aber auch sehr viel schneller. Er lässt sich nur von Threads innerhalb desselben Thread Blocks sowohl lesen als auch schreiben, und stellt somit eine schnelle Möglichkeit der Kommunikation zwischen Threads desselben Blocks dar. Schließlich existiert für jeden Thread ein Register Memory. Dieser ist mit den Registern einer CPU zu vergleichen, extrem schnell, aber auch extrem klein. Außerdem lässt er sich nur vom zugehörigen Thread ansprechen. Für weitere Details bezüglich üblicher Speichergrößen, sowie eine grafische Aufarbeitung, siehe Tabelle 2, Seite 9 und Abbildung 2, Seite 10. Die optimale (Aus-)Nutzung der Speicherhierarchie hat einen maßgeblichen Einfluss auf die Performance des Programms und ist daher immens wichtig. Name Beschreibung Zugriff Typ. Größe host Speicher des Host-Programms, Nur Host-Programm 2-16 GB also RAM des Rechners global Hauptspeicher der Grafikkarte Jeder Thread 1-8 GB constant Kann nur von Host-Programm Jeder Thread 64 kb geschrieben werden, für Threads read-only shared Kleiner, aber schneller Speicher Nur der zugehörige kb Thread-Block registers Noch kleinerer, noch schnellerer Speicher Nur zugehöriger Thread 16 kb Tabelle 2: Speicherhierarchie bei CUDA. 8
12 10 host Host Memory(RAM) CUDA Device PCIe Global Memory Constant Memory CUDA Thread Block CUDA Thread Block Shared CUDA Thread Block Shared CUDA Thread CUDA Thread Block CUDA Thread Shared CUDA CUDA Thread Thread Register CUDA CUDA Thread Thread Shared Register CUDA CUDA Thread Thread Register Register CUDA CUDA Thread Thread Register Register CUDA CUDA Thread Thread Register Register CUDA CUDA Thread Thread Register Register CUDA Thread Register Register CUDA Thread Register Register Register Register Abbildung 2: Speicherhierarchie bei CUDA. 3.5 CUDA C Kompilierung Als Erweiterung der Programmiersprache C ist es in CUDA C möglich Kernel zu definieren, welche nach einem speziellen Aufruf n-mal von n CUDA Threads ausgeführt werden. In CUDA C bestehen die Quelltexte (Dateiendung.cu) aus Host-Code, zur Ausführung auf der CPU des Host-Rechners, und Device-Code (Kernel), zur Ausführung auf der GPU. Die Quelldateien werden mittels des von NVIDIA bereitgestellten Compilers Nvcc kompiliert. Nvcc selbst kann sowohl vollständig kompilierte Objektdateien (Endung.o oder.obj), zur Eingabe in einen normalen Linker, als auch ANSI C Quelltexte (Endung.c), welche mit einem anderen Compiler weiterverarbeitet werden können, ausgeben. Nvcc ist nicht komplett eigenständig, sondern benötigt einen installierten C-Compiler; unter Linux wird standardmäßig von GCC ausgegangen, unter Windows von cl (Teil von Microsoft Visual Studio) Kerneldefinition und -aufruf CUDA C definiert neue Schlüsselwörter, Konstanten und Funktionsaufrufe zum Aufruf der Kernelfunktionen. Zur Definition eines Kernels wird dem Funktionskopf das Schlüsselwort global vorange- 9
13 11 stellt, so währe global void matsq(const float *mat, float *out){... } bereits ein gültiger Kernel; dieser ließe sich aus einer Host-Funktion mittels einer neuen Befehlsform mit dreifachen spitzen Klammern starten: Kernelname<<<dim3 Dg, dim3 Db, size_t Ns, cudastream_ t S>>>( Parameter ); Der Parameter Dg bestimmt hier die Größe des Grids, Db die Größe eines Blocks, Ns die Größe des, zusätzlich zum statisch reservierten, dynamisch für jeden Block zu reservierenden gemeinsamen Speichers (shared-memory), und S ein Stream, auf welchen hier nicht näher eingegangen wird. Nötig sind nur die ersten beiden Parameter, Ns und S sind optional und standardmäßig 0. Innerhalb der Runden Klammern stehen Funktionsparameter anlog zu einem normalen Funktionsaufruf. Um unseren Kernel matsq aufzurufen genügt die Syntax: matsq<<<1, N>>>(A, B). Funkionen, welche innerhalb eines Kernels aufgerufen werden sollen, werden mit dem Schlüsselwort device ausgezeichnet, diese werden dann ebenfalls auf der GPU ausgeführt. Das Schlüsselwort host kennzeichnet Funktionen welche auf dem Host laufen, und nur von anderen Host-Funktionen aufgerufen werden können, allerdings ist es optional, Funktionen ohne device oder global werden immer als normale C/C++ Funktion (und damit als Host-Funktion) interpretiert. Speicherbereiche im Global Memory (wie im Falle des Beispiels die Arrays float *mat und float * out) müssen per cudamalloc() reserviert werden bevor sie per cudamemcpy() mit Daten gefüllt werden können; Kernelprogamme können nicht auf den Speicher des Hosts zugreifen. Nach Aufruf des Kernels lässt sich das Ergebnis schließlich mit cudamemcpy() vom Speicher der Grafikkarte in den Speicher des Hosts transferieren (siehe Kapitel 3.2, Seite 7) Umsetzung der Speicherhierarchie Die Speicherhierarchie in CUDA (siehe Kapitel 3.4, Seite 8) wird mittels der Schlüsselwörter device (global), constant (constant) und shared (shared) realisiert. Lokale Variablen, welche innerhalb einer Kernel-Funktion (bzw. innerhalb einer device Funktion) deklariert werden, und mit keinem dieser Schlüsselwörter ausgezeichnet sind, werden automatisch dem Register-Speicher zugewiesen. Zusätzlich existiert das Schlüsselwort restrict, welches dem Compiler, analog zu dem im C99 Standard eingeführten C-Schlüsselwort restrict, helfen soll die Anzahl an Speicherzugriffen bei Zeigerauflösungen zu reduzieren. Wenn mehrere Zeiger mit restrict ausgezeichnet sind so dürfen diese nicht auf sich überlappende Speicherbereiche zeigen. Man betrachte die folgenden beiden Funktionen in CUDA C: device void foo ( const float *a, const float *b, float * c) { c[0] = a [0] * b [0]; c[1] = a [0] * b [0]; } device void bar ( const float *a, const float *b, float * c) { float atimesb = a [0] * b [0]; c[0] = atimesb ; c[1] = atimesb ; } 10
14 12 Auf den ersten Blick sind diese Funktionen äquivalent. Es ist jedoch möglich dass die Zeiger a und c (bzw. b und c) auf den selben Speicherbereich verweisen, wodurch (in foo) eine Modifikation an c[0] auch den Wert von a[0] (bzw. b[0]) modifiziert. Der Compiler kann also in foo den Wert von a[0] nicht cachen, sondern muss jedes mal eine Operation zum lesen von a[0] einfügen, welche anschließend nur noch von dem ausführenden Prozessor dynamisch zur Laufzeit optimiert werden kann. Das Schlüsselwort restrict (bzw. restrict bei C99) verbietet überlappende Zeiger, und erlaubt dem Compiler so, den Code wie in bar zu optimieren. Die optimierte (und zu bar äquivalente) Funktion währe demnach: device void foobar ( const float * restrict a, const float * restrict b, float * restrict c) { c[0] = a [0] * b [0]; c[1] = a [0] * b [0]; } Da die Speicherbereiche nicht mehr überlappen dürfen, ist es dem Compiler erlaubt, das Ergebnis der Operation a[0] * b[0] innerhalb der Funktion als konstant anzusehen. Damit sind nur noch zwei Lesezugriffe und eine Multiplikation nötig Synchronisation Naturgemäß existieren bei CUDA sehr wenige Synchronisationsmöglichkeiten. Sie beschränken sich im wesentlichen auf Threads des selben Thread Blocks. Die Funktion void synchthreads() wartet bis alle Threads des Thread-Blocks diesen Aufruf erreichet haben und alle Speicherzugriffe auf dem globalen sowie shared-speicher für alle Threads des Blocks sichtbar sind. synchthreads() ist in konditionalem Code (z.b. if-statement) nur erlaubt, wenn die Kondition in allen Threads des Blocks das gleiche Ergebnis liefert. Als Beispiel siehe Listing 1, Seite 13. Bei GPUs welche CUDA 2.x und höher unterstützen existieren noch weitere ähnliche Funktionen: int synchthreads_count(int predicate) ist identisch mit synchthreads(), zusätzlich wird predicate für alle Threads des Blocks ausgewertet und die Anzahl an Threads zurückgegeben, für die predicate ungleich Null ist. int synchthreads_and(int predicate) gibt einen Wert ungleich Null zurück, wenn (und nur wenn) predicate für alle Threads ungleich Null ist, int synchthreads_or(int predicate) gibt analog dazu nur einen Wert ungleich Null zurück, wenn (und nur wenn) predicate für irgendeinen Thread ungleich Null ist. Eine Synchronisation von Threads verschiedener Blöcke ist nur über den Host möglich, also durch den Aufruf einer zweiten Kernelfunktion. Wenn die Threads Daten austauschen sollen, so schreibt die erste Kernelfunktion Daten in den globalen Speicher. Der zweite Kernel liest die Daten im Anschluss aus und verarbeitet sie weiter. Aufgrund des großen Overheads empfiehlt es sich, dies zu vermeiden und möglichst die nativen Synchronisationsmechanismen zu nutzen. Speicherbarrieren (Memory-Fence genannt) werden durch die Funktionen void threadfence_block(), void threadfence() sowie void threadfence_system() realisiert. Sie stellen sicher, dass Zugriffe des aufrufenden Threads auf den global und shared-speicher für, in der selben Reihenfolge, alle Threads des Blocks, alle Threads des Grids, oder alle Threads des Grids inklusive Lesezugriffen des Hosts, sichbar sind. CUDA unterstützt unter Umständen die Ausführung eines Kernels und gleichzeitige Lese/Schreiboperationen durch den Host, siehe hierzu [4, Kapitel Overlap of Data Transfer and 11
15 13 Kernel Execution ]. Da ein Warp immer nur eine gemeinsame Instruktion gleichzeitig ausführt (siehe Kapitel 3.3, Seite 7), sind die Threads innerhalb eines Warps implizit (d.h. auf Befehlsebene) synchronisiert. Dadurch kann eine (langsame) Synchronisation der Threads unter Umständen vermieden werden. 1 // Example for two threads per block 2 global void foo ( const float *a, float * b) 3 { 4 shared float sh [2]; // declare shared memory 5 int id = threadidx. x; // we only use two threads, so id is either 0 or 1 6 sh[id] = a[id] * a[id ]; // calculate " our " result 7 synchthreads (); // synchronize threads 8 int otherid = ( id +1) % 2; // switch ids (0 -> 1, 1 -> 0) 9 b[ id] = sh[ otherid ]; // write the result calculated by the other thread 10 } Listing 1: Beispielhafter CUDA Kernel bei welchem zwei Threads jeweils die Berechnungsergebnisse des anderen benutzen und daher synchronisiert werden müssen Datentypen CUDA C definiert neue Vektordatentypen: [u]charn, [u]shortn, [u]intn, [u]longn, [u]longlongk, floatn und doublek. Der optionale Präfix u steht jeweils für die nicht-vorzeichenbehafteten Varianten, n ist entweder 1, 2, 3 oder 4, und k ist entweder 1 oder 2. Der Zugriff auf einzelne Komponenten geschieht durch die Member x, y, z und w, wobei bei einem Datentyp mit n Komponenten natürlich nur die ersten n der genannten Member gültig sind. Jeder Datentyp hat außerdem einen Konstruktorfunktion der Form make Typname, also zum Beispiel float3 make_float3(float x, float y, float z);. CUDA C definiert eine Menge an neuen Funktionen, welche das Arbeiten mit den Vektordatentypen erleichtern, siehe hierzu [3, Kapitel 5.57] PTX Assembler CUDA benutzt für Kernelprogramme intern PTX (Parallel Thread Execution) Assemblercode. Da eine vollständige Abdeckung der PTX ISA (Instruction Set Architecture) den Rahmen dieses Dokumentes sprengen würde, sei an dieser Stelle auf [5] verwiesen; hier wird lediglich ausgeführt wie der Programmierer PTX Assemblercode direkt in CUDA-C-Programme einfügen kann. Die normale Syntax eines Inline-PTX Befehls lautet wie folgt: asm(" template - string " : " constraint "( output ) : " constraint "( input )); Der Template-String enthält dabei den Befehl an sich sowie die nummerierten Template-Parameter, Output enhält die Ausgabevariablen, Input die Eingabevariablen. Die Constraints beziehen sich auf den Typ der genutzten Register. Es folgt ein einfaches Beispiel: int i; int j = 5; int k = 5; asm(" add. s32 %0, %1, %2;" : "=r"(i) : "r"(j), "r"(k)); //i is now 10 12
16 14 Hier beziehen sich die Platzhalter %0 bis %2 auf die nachfolgenden Variablen i, j und k. "r" bzw. "=r" bezieht sich auf den Registertyp.u32, das Gleichheitszeichen kennzeichnet Variablen in die geschrieben wird. Es existieren die folgenden Registertypen: constraint Typ Beschreibung und CUDA C Typ h.u16.s16 16-Bit Ganzzahl ([unsigned] short int) r.u32.s32 32-Bit Ganzzahl ([unsigned] int) l.u64.s64 64-Bit Ganzzahl ([unsigned] long long) f.f32 32-Bit Fließkommazahl (float) d.f64 64-Bit Fließkommazahl (double) Zu beachten ist, dass beispielsweise der Registertyp.u32 sowohl für vorzeichenbehaftete als auch vorzeichenlose Ganzzahlen verwendet werden kann, da u-register mit s-registern kompatibel sind sofern sie die selbe Größe bestitzen. Als was der Registerinhalt schließlich interpretiert wird bestimmt die Operation, so wurde im Beispiel oben add.s32 verwendet, was einer vorzeichenbehafteten Ganzzahladdition entspricht. Aus diesen Gründen wird bei den Constraints nicht zwischen vorzeichenbehaftet und vorzeichenlos unterschieden, sie dienen in erster Linie nur der Bestimmung der Größe eines Parameters. Das asm-statement aus dem Beispiel erzeugt den Code: ld.s32 r1, [j]; ld.s32 r2, [k]; add.s32 r3, r1, r2; st.s32 [i], r3; Zwar mag die Syntax des asm-statements etwas verwirrend wirken, es lassen sich jedoch mehrere Instruktionen nacheinander angeben, wobei die Template-Parameter mehrfach genutzt werden können. Als Beispiel die Funktion cube, welche die dritte Potenz einer Ganzzahl berechnet: device int cube ( int x) { return x* x* x; } Diese Funktion lässt sich mittels PTX Assembler in folgende umschreiben: device int cube ( int x) { int y; asm(". reg. u32 t1;" // temporal register t1 " mul.lo.u32 t1, %1, %1;" // t1 = x * x " mul.lo.u32 %0, t1, %1;" // y = t1 * x : "=r"(y) : "r"(x) ); // output : y, input : x return y; } Die drei Anweisungszeilen werden hier mittels der normalen C/C++ String-Syntax aneinandergereiht. Falls die Funktion cube vom Compiler inlined 5 wird, so kann es zu Namenskonflikten kommen, da das Register t1 mehrfach deklariert wird. Um dies zu vermeiden können die PTX Anweisungen (analog zum Scope bei C/C++) mit geschweiften Klammern eingefasst werden. Da das asm()-statement nicht überprüft in welchem Speicherbereich ein Register liegt, obliegt es dem Nutzer die korrekten Befehle zu benutzen. 5 Inlining einer Funktion: Der Compiler fügt an die Stelle des Aufrufs den Inhalt der Funktion ein, anstatt einen Sprungbefehl zu setzen. 13
17 15 1 // Device code 2 global void mmult ( const float *A, const float *B, float *C, 3 int wa, int wb) 4 { 5 int i = blockidx. x * blockdim. x + threadidx. x; 6 int j = blockidx. y * blockdim. y + threadidx. y; 7 8 float val = 0; 9 for( int k = 0; k < wa; k ++ ) 10 val += A[wA*j+k] * B[wB*k+i]; 11 C[wA*j+i] = val ; 12 } // Host code 15 void RandomInit ( float * data, int size ) { 16 for ( int i = 0; i < size ; ++ i) 17 data [i] = rand () / ( float ) RAND_MAX ; 18 } int main ( int argc, char ** argv ) 21 { 22 // Define sizes of matrices, A (1024 x512 ), B (512 x2048 ) => C (512 x512 ) 23 int wa = 1024; int ha = 512; 24 int wb = ha; int hb = 2048; 25 int wc = ha; int hc = wb; 26 size_t sizea = wa * ha * sizeof ( float ); 27 size_t sizeb = wb * hb * sizeof ( float ); 28 size_t sizec = wc * hc * sizeof ( float ); // Allocate matrices in host memory 31 float * h_a = ( float *) malloc ( sizea ); 32 float * h_b = ( float *) malloc ( sizeb ); 33 float * h_c = ( float *) malloc ( sizec ); // Initialize input vectors 36 RandomInit (h_a, wa*ha); 37 RandomInit (h_b, wb*hb); // Allocate vectors in device memory 40 float * d_a, d_b, d_c; 41 cudamalloc (( void **) &d_a, sizea ); 42 cudamalloc (( void **) &d_b, sizeb ); 43 cudamalloc (( void **) &d_c, sizec ); // Copy vectors from host memory to device memory 46 cudamemcpy ( d_a, h_a, sizea, cudamemcpyhosttodevice ); 47 cudamemcpy ( d_b, h_b, sizeb, cudamemcpyhosttodevice ); // Invoke kernel 50 dim3 threads (16, 16) ; 51 dim3 grid ( wc / threads.x, hc / threads. y ); 52 mmult<<<grid, threads>>>( d_a, d_b, d_c, wa, wb); // Copy result from device memory ( d_c ) to host memory ( h_c ) 55 cudamemcpy ( h_c, d_c, sizec, cudamemcpydevicetohost ); 56 } Listing 2: CUDA Kernel und Host-Programm zur Multiplikation zweier Matrizen. Kernel und Host- Code stehen in der selben Datei. Fehlerbehandlung und Speicherfreigabe sind zwecks Übersichtlichkeit entfernt worden. 14
18 16 4 OpenCL 4.1 Einleitung OpenCL (Open Computing Language) ist ein ursprünglich von Apple entwickelter, offener Standard für parallele Berechnungen auf uneinheitlichen Parallelrechnern. Im Gegensatz zu CUDA ist OpenCL also mit allen Geräten kompatibel für die eine konforme Implementierung existiert. NVIDIA bietet eine Implementierung an, welche auf CUDA basiert, AMD eine, welche auf ihrer GPGPU-Schnittstelle ATI-Stream basiert. Außerdem existieren Implementierungen für x86 CPUs, DSPs und Cell Prozessoren, was OpenCL zu einer sehr flexiblen Technologie macht. In direkter Konkurrenz zu CUDA ist festzustellen, dass es OpenCL aufgrund seiner platformunabhängigen Natur an Low-Level Zugriffen auf die Hardware fehlt 6, allerdings ist OpenCL im Moment auch die einzige bequeme Möglichkeit sowohl Platform- als auch Geräteunabhängige GPGPU-Anwendungen zu entwickeln. 4.2 Prozessmodell Das Prozessmodell in OpenCL ist, bis auf die Umbenennung von CUDA Thread in Work-Item identisch zu dem in CUDA (siehe Kapitel 3.2, Seite 7). 4.3 Parallelisierung Die Parallelisierung unter OpenCL unterscheidet sich nicht wesentlich von der in CUDA (siehe Kapitel 3.3, Seite 7), auch in OpenCL wird das Gesamtproblem in mehreren Dimensionen in Teilprobleme zerlegt. Mehrere Work Items werden hierbei zu Work Groups zusammengefasst, dies entspricht der Zusammenfassung von CUDA Threads zu CUDA Thread Blocks, ein Work-Item führt einen Kernel also genau einmal aus. Innerhalb der Kernelfunktionen gibt es in OpenCL Funktionen zum Abfragen der Position innerhalb einer Work Group, der Position bezüglich aller Work Items usw. Die große Anzahl dieser Funktionen kann dem Programmierer etwas Arbeit abnehmen, so kann man die in CUDA häufig anzutreffende Berechnung blockidx.x * blockdim.x + threadidx.x durch den Funktionsaufruf get_global_id(0) abkürzen. 4.4 Speicherhierarchie OpenCL kennt fünf unterschiedliche Arten Speicher: Host, Global, Constant, Local und Private. Der Host-Speicher ist hierbei der normale Arbeitsspeicher des Host-Rechners, Global der Hauptspeicher der Grafikkarte (bzw. des Devices da OpenCL nicht auf GPUs beschränkt ist), Constant ein Konstantenspeicher, Local der lokale Speicher der Work Group und Private der private Speicher eines Work Items. Die typischen Größen sind, zumindest auf Grafikkarten, dieselben wie bei CUDA, und auch die Zugriffsbeschränkungen sind identisch, einzig die Benennung ist etwas anders: Der Local-Memory heißt bei CUDA Shared und der Private-Memory heißt Register; daher siehe auch Tabelle 2, Seite 9. Für eine angepasste Grafik der Speicherhierarchie siehe Abbildung 3, Seite wenn man von herstellereigenen Erweiterungen des Standards absieht 15
19 17 host Host Memory(RAM) Device PCIe Global Memory Constant Memory Work-Group Work-Group Local Work-Group Local Work-Item Work-Group Work-Item Local Work-Item Private Work-Item Local Private Work-Item Private Private Work-Item Private Private Work-Item Private Private Work-Item Private Private Work-Item Private Private Work-Item Private Private Private Private Abbildung 3: Speicherhierarchie bei OpenCL. 4.5 Workflow Die API und der Workflow von OpenCL unterscheidet sich wesentlich von dem von CUDA. Zur Einbindung in ein in C/C++ geschriebenes Programm werden sowohl die C-Headerdateien als auch eine vom Hersteller der Implementierung bereitgestellte, statisch gelinkte Bibliothek (.lib) benötigt. Im Kontext von GPU-Anwendungen ist die Bibliothek lediglich eine Brücke zwischen dem Programm und der eigentlichen Implementierung im Grafikkartentreiber, so ist die von AMD bereitgestellte Bibliothek OpenCL.lib mit Grafikkarten (bzw. deren Treibern) von NVIDIA kompatibel. Da die OpenCL API als normale Programmbibliothek eingebunden wird, ist kein besonderer Compiler (wie bei CUDA) nötig. Kernelfunktionen werden der Implementierung zur Laufzeit als Quellcode (Stringbasiert) übergeben und Just-In-Time für genau das Gerät, für welches die OpenCL-Implementierung geschrieben wurde, kompiliert. Dies hat den Vorteil, dass der Programmierer zur Entwicklungszeit nicht zwingend wissen muss, auf welchen Geräten sein Code später ausgeführt wird. Solange er standardkonformen Code schreibt, kann er davon ausgehen, dass sein Programm korrekt läuft. Häufig wird der Grafikkartentreiber beim Programmstart mit der Kompilierung der Kernel beauftragt, was zwangsläufig eine (gegenüber dem vorkompilierten Code von CUDA) längere Startphase der Applikation zur Folge hat. Es besteht die Möglichkeit die Kernel beim ersten Programmstart kompilieren zu lassen und den vom Grafikkartentreiber produzier- 16
20 18 ten Binärcode in einer Datei abzuspeichern, sodass bei folgenden Starts nur diese Datei geladen werden muss (falls sich an der Systemkonfiguration nichts geändert hat). Ob sich dieser Aufwand lohnt ist von Fall zu Fall unterschiedlich, die Kompilierung einfacher Kernelfunktionen benötigt häufig weniger als eine Sekunde Zeit. Die OpenCL API ist in ihrer Syntax an die OpenGL API angelehnt, der Kompilierungsworkflow ähnelt der Kompilierung von GLSL 7 -Shadern. 4.6 OpenCL C Analog zu CUDA ist die zum Entwickeln von Kernelfunktionen genutzte Sprache OpenCL C eine Abwandlung der Programmiersprache C, genauer eine Abwandlung des C99 Standards, und definiert im Wesentlichen neue Schlüsselwörter, Datentypen und Funktionen. Anders als bei CUDA wird OpenCL C nur für die Kernelfunktionen ( Device-Code ), und nicht für Host-Code benutzt. Dies hat einen etwas komplexer anmutenden Host-Code zur Folge; ein gesondert einzurichtender und -stellender Compiler entfällt aber. OpenCL C ist keine Obermenge von C99, da es einige Einschränkungen definiert: Unter anderem werden Zeiger auf Funktionen, Bit-Felder, Arrays mit variabler Länge sowie Rekursion nicht unterstützt. Für Details sei der Leser auf [6, Kapitel 6.8 Restrictions ] verwiesen Kerneldefinition und Speicherhierarchie Ein Kernel wird durch das vorangestellte Schlüsselwort kernel definiert. Falls die Funktionsparameter Zeiger enthalten, so müssen diese mit einem Speicherbereichsqualifizierer ausgezeichnet werden: kernel void matsq ( global const float *A, global float *B) {... } In OpenCL C existieren die folgenden Speicherbereichsqualifizierer: global, constant, local und private, diese beziehen sich auf die in Kapitel 4.4 genannte Speicherhierarchie. Lokale Variablen innerhalb des Funktionsrumpfes einer Kernelfunktion werden automatisch zu private. Da die Kernelfunktionen bei OpenCL gesondert kompiliert werden, und nicht zusammen mit dem Host-Code wie bei CUDA, existiert kein Schlüsselwort um Funktionen zu kennzeichnen, welche aus einer Kernelfunktion aufgerufen werden sollen (wie device bei CUDA). Eine zur Ausführung auf dem Device bestimmte Funktion erhält kein besonderes Schlüsselwort, kernel kommt lediglich zur Anwendung wenn die Funktion vom Host aus als Kernel gestartet werden soll. Eine Auflistung der Work-Item Funtionen in OpenCL C ist der Tabelle 3, Seite 21 zu entnehmen. Für ein Beispiel einer Kernelfunktion in OpenCL sei auf Listing 3, Seite 19 verwiesen Synchronisation Die Synchronisation von Work-Items innerhalb einer Work-Group wird über die Funktion void barrier ( cl_ mem_ fence_ flags flags ) realisiert. Alle Work-Items einer Work-Group müssen den Aufruf an barrier() getätigt haben bevor einem von ihnen erlaubt ist weiterzuarbeiten. Zusätzlich zur Synchronisation wird auch sichergestellt, dass Speicherzugriffe für andere Work-Items der selben Work-Group sichtbar sind, ob dies nur auf dem Local-Memory oder auch auf dem Global-Memory geschieht kann gesteuert werden, indem flags auf die Konstante CLK_LOCAL_MEM_FENCE oder CLK_GLOBAL_MEM_FENCE gesetzt wird. Das Pendant zu CUDA s 7 OpenGL Shading Language 17
21 19 synchthreads() währe somit barrier(clk_global_mem_fence). Speicherbarrieren werden über die Funktion void mem_ fence ( cl_ mem_ fence_ flags flags ) gesetzt, für flags lassen sich die gleichen Konstanten wie bei barrier einsetzen. mem_fence stellt sicher, dass alle Speicherzugriffe, die vor dem Aufruf von mem_fence angeordnet wurden, vor Speicherzugriffen, welche nach dem Aufruf angeordnet werden, abgeschlossen sind, ordnet also die Speicherzugriffe. Zusätzlich imlementieren die Funktionen void read_ mem_ fence ( cl_ mem_ fence_ flags flags ) und void write_ mem_ fence ( cl_ mem_ fence_ flags flags ) eine Anordnung der Speicherzugriffe exklusiv bei Lese- bzw. Schreibzugriffen. Wie auch bei CUDA ist eine Synchronisation von Work-Items verschiedener Work-Groups nur über den Host möglich, also über den Aufruf einer anderen Kernelfunktion Datentypen OpenCL C definiert eine Reihe an neuen Datentypen, die Wichtigsten sind hierbei die Vektordatentypen charn, ucharn, shortn, ushortn, intn, uintn, longn, ulongn und floatn, n gibt jeweils die Anzahl an Elementen an und kann 2, 3, 4, 8 oder 16 betragen. Die Datentypen sind bis auf floatn alle Ganzzahltypen, deren Größen betragen aufsteigend 8, 16, 32 und 64 Bit pro Element, der Präfix u steht für unsigned und kennzeichnet vorzeichenlose Ganzzahlen. Als Ausnahme ist floatn ein 32-bit Gleitkommatyp. Bei Operationen auf den Vektordatentypen setzt der Compiler automatisch die für seine Architektur passenden Instruktionen ein, falls möglich sollten sie gegenüber skalarer Rechnung bevorzugt werden. Für eine komplette Auflistung der Datentypen sowie den Zugriffsmethoden und -beschränkungen siehe [6, Kapitel 6.1 Supported Data Types ]. Zusätzlich zu den Datentypen führt OpenCL C eine Reihe an Funktionen ein, die es erleichtern mit den Typen zu arbeiten, wie zum Beispiel eine Kreuz- und Skalarproduktfunktion. Für eine vollständige Liste sei auf [6, Kapitel 6.11 Built-in Functions ] verwiesen. 1 kernel void mmult ( global const float *A, 2 global const float *B, 3 global float *C, 4 int wa, int wb) 5 { 6 int i = get_global_id (0) ; 7 int j = get_global_id (1) ; 8 9 float val = 0; 10 for( int k = 0; k < wa; k ++ ) 11 val += A[wA*j+k] * B[wB*k+i]; 12 C[wA*j+i] = val ; 13 } Listing 3: OpenCL C Kernel zur Anwendung bei einer Matrizenmultiplikation. 18
22 Die OpenCL API (Host-Code) Da OpenCL im Kern lediglich eine API ist, und keinen gesonderten Compiler mit sich bringt, ergeben sich einige Unterschiede zu CUDA. In OpenCL werden alle Elemente des Programms, also Kernel, Speicherpuffer und so weiter, als Objekte gehandhabt. Da die OpenCL API auf C basiert liefert sie, analog zu OpenGL, sogenannte Handles, also Referenzen auf die Objekte zurück. Da OpenCL Funktionen meist sehr viele Parameter besitzen, gebe ich hier nur die Funktionsnamen an, für Details siehe [6]. Über clgetdeviceids() können die im System vorhandenen (bzw. von der Implementierung unterstützten) Devices abgefragt werden, ein Parameter device_type spezifiziert hierbei die gewünsche Art des Devices, so z.b. CL_DEVICE_TYPE_CPU oder CL_DEVICE_TYPE_GPU. Als nächstes kann über clcreatecontext() ein für das Device gültiger OpenCL-Kontext erstellt werden, nur innerhalb diesem ist die nachfolgende Erstellung von Objekten gültig. Anschließend kann z.b. über clcreateprogramwithsource() ein Programmobjekt aus OpenCL C Quelltext erstellt werden, dies wird dann mittels clbuildprogram() kompiliert. Ein Programmobjekt kann mehrere Kernelfunktionen enthalten, ein auf eine einzige Kernelfunktion bezogenes Kernelobjekt erhält man aus dem Programmobjekt über clcreatekernel(). Speicherpuffer auf dem Device werden mittels clcreatebuffer() beantragt. Um auf den erstellten Objekten Operationen auszuführen, also z.b. das Füllen eines Speicherpuffers oder die Ausführung eines Kernels, ist eine Command Queue nötig; diese führt die beantragten Operationen (auch Commands genannt) dann, meist asynchron, aus. Eine Applikation kann mehrere Command-Queues erstellen und so mehrere Aufgaben asynchron ausführen lassen, ohne dass die Applikation selbst (Betriebssystem-)Threads auf dem Host erstellen müsste 8. Eine Command-Queue lässt sich über clcreatecommandqueue() erstellen. Über Funktionen mit dem Präfix clenqueue*() lassen sich Aufträge in die Queue einreihen, so kann z.b. über clenqueuewritebuffer() und clenqueuereadbuffer() das Befüllen bzw. Auslesen eines Speicherpuffers beantragt werden. Da die Queue asynchron arbeitet, sollte vor der Weiterverarbeitung von Berechnungsergebnissen clfinish() auf der Queue aufgerufen werden. Dieser Aufruf blockiert, bis alle in der Queue befindlichen Aufträge fertiggestellt wurden. Da es bei OpenCL keine spezielle Befehlsform zum Aufruf von Kerneln (wie die dreifachen spitzen Klammern bei CUDA) gibt, müssen die Funktionsparameter vor dem Aufruf über clsetkernelarg() gesetzt werden, anschließend kann die parallele Ausführung des Kernels mittels der Funktion clenqueuendrangekernel() beantragt werden. Die Funktion nimmt hierbei unter anderem die gewünschte Anzahl an Dimensionen, die Gesamtanzahl der Work-Items und die Anzahl der Work-Items in einer Work-Group (jeweils in den gewünschten Dimensionen) entgegen. Ein Programm in Pseudo-C++ könnte also wie folgt ablaufen: device = clgetdeviceids ( CL_ DEVICE_ TYPE_ GPU ); context = clcreatecontext ( device ); queue = clcreatecommandqueue ( context ); program = clcreateprogramwithsource ( context, " kernel foo ( global float *a) { a[ get_global_id (0) ] = 1.0 f; }" ); clbuildprogram ( program ); kernel = clcreatekernel ( program, " foo "); a_ device = clcreatebuffer ( context, sizeof ( float ) * 4096) ; float a_host [4096]; clsetkernelarg ( kernel, 0, & a_device ); clenqueuendrangekernel ( queue, kernel, 4096, 128) ; 8 Dies gilt nur falls sich die Queues keine Objekte Teilen, also jede Queue auf ihrem eigenen Satz an Objekten operiert. 19
23 21 Funktion Beschreibung CUDA Pendant uint get work dim() size t get global size(uint dimid) size t get global id(uint dimid) size t get local size(uint dimid) size t get local id(uint dimid) size t get num groups(uint dimid) size t get group id(uint dimid) size t get global offset(uint dimid) Anzahl der momentan genutzten Dimensionen Gesamtanzahl der Work- Items. Eindeutige globale ID des Work-Items Anzahl der Work-Items in einer Work-Group Eindeutige lokale ID des Work-Items innerhalb der Work-Group Gesamtanzahl der Work- Groups Globale, eindeutige ID der Work-Group Ein optionaler Offset- Parameter welcher beim starten des Kernels angegeben werden kann griddim.α * blockdim.α blockidx.α * blockdim.α + threadidx.α blockdim.α threadidx.α griddim.α blockidx.α Tabelle 3: Vordefinierte Work-Item Funktionen bei OpenCL C. dimid indiziert jeweils die Dimension die abgefragt werden soll, also 0 für die x-achse, 1 für die y-achse und 2 für die z-achse. Anders als bei CUDA wird nicht.x/.y/.z verwendet da OpenCL auch für mehr als drei Dimensionen spezifiziert ist (auch wenn nicht jedes Gerät dies unterstützen muss). Der Selektor α steht für x, y oder z, je nachdem welchen Wert dimid hat. clenqueuereadbuffer ( queue, a_device, a_host, sizeof ( float ) * 4096) ; Dieser Pseudocode soll lediglich den prinzipiellen Ablauf einer Anwendung andeuten. Es wurden zwecks Verständnis viele Funktionsparameter weggelassen oder umgeordnet. Ein vollständiges und korrektes Beispielprogramm in C++ ist in Listing 4, Seite 22 abgebildet. Um mit den in genannten Datentypen im Host-Code zu arbeiten, definiert die OpenCL API für fast jeden Datentyp aus dem Device-Code ein Pendant im Host-Code. Gegenüber dem Device-Code erhalten die Datentypen den Präfix cl, also z.b. cl float4 anstatt float4. 20
24 22 1 const char kernel_src [] = 2 " kernel void mmult ( global const float *A, " 3 " global const float *B, " 4 " global float *C, " 5 " int wa, int wb) " 6 "{ " 7 " int i = get_global_id (0) ; " 8 " int j = get_global_id (1) ; " 9 " " 10 " float val = 0; " 11 " for ( int k = 0; k < wa; k ++ ) " 12 " val += A[wA*j+k] * B[wB*k+i]; " 13 " C[wA*j+i] = val; " 14 "} "; void RandomInit ( float * data, int size ) { 17 for ( int i = 0; i < size ; ++ i ) 18 data [ i] = rand () / ( float ) RAND_MAX ; 19 } int main ( int argc, const char * argv []) 22 { 23 // define sizes of matrices, A (1024 x512 ), B (512 x2048 ) => C (512 x512 ) 24 int sa [] = {1024, 512}; 25 int sb [] = {sa [1], 2048}; 26 int sc [] = {sa [1], sb [0]}; 27 size_t sizea = sa [0] * sa [1] * sizeof ( float ); 28 size_t sizeb = sb [0] * sb [1] * sizeof ( float ); 29 size_t sizec = sc [0] * sc [1] * sizeof ( float ); // get platform 32 cl_uint num_platforms ; cl_platform_id platform ; 33 cl_int err = clgetplatformids (1, & platform, & num_platforms ); // get device 36 cl_device_id device ; 37 clgetdeviceids ( platform, CL_DEVICE_TYPE_GPU, 1, & device, 0); // create context, command queue, program and kernel 40 cl_context context = clcreatecontext (0, 1, & device, 0, 0, & err ); 41 cl_command_queue cmd_queue = clcreatecommandqueue ( context, device, 0, 0); 42 cl_program program = clcreateprogramwithsource ( context, 1, & kernel_src,0,& err ); 43 clbuildprogram ( program, 0, 0, 0, 0, 0); 44 cl_kernel kernel = clcreatekernel ( program, " mmult ", & err ); // create memory objects 47 float * hosta = new float [ sizea ]; 48 float * hostb = new float [ sizeb ]; 49 float * hostc = new float [ sizec ]; 50 RandomInit (hosta, sa [0]* sa [1]) ; 51 RandomInit (hostb, sb [0]* sb [1]) ; 52 cl_mem deva = clcreatebuffer ( context, CL_MEM_READ_ONLY, sizea, 0, 0); 53 cl_mem devb = clcreatebuffer ( context, CL_MEM_READ_ONLY, sizeb, 0, 0); 54 cl_mem devc = clcreatebuffer ( context, CL_MEM_WRITE_ONLY, sizec, 0, 0); 55 21
25 23 56 // set memory objects as kernel arguments 57 clsetkernelarg ( kernel, 0, sizeof ( cl_mem ), & deva ); 58 clsetkernelarg ( kernel, 1, sizeof ( cl_mem ), & devb ); 59 clsetkernelarg ( kernel, 2, sizeof ( cl_mem ), & devc ); // calculate work sizes 62 size_t ws_global [] = { sc [0], sc [1]}; 63 size_t ws_local [] = {16, 8}; // 128 items per group // transfer input matrices from host to device, 66 // calculate result and transfer result from device to host 67 clenqueuewritebuffer ( cmd_queue, deva, CL_FALSE, 0, sizea, hosta, 0, 0, 0); 68 clenqueuewritebuffer ( cmd_queue, devb, CL_FALSE, 0, sizeb, hostb, 0, 0, 0); 69 clenqueuendrangekernel ( cmd_queue, kernel, 2, 0, ws_global, ws_local, 0, 0, 0); 70 clenqueuereadbuffer ( cmd_queue, devc, CL_FALSE, 0, sizec, hostc, 0, 0, 0); 71 clfinish ( cmd_queue ); // The Result is now in hostc and ready for further processing. 74 return 0; 75 } Listing 4: Matrizenmultiplikation mittels OpenCL. Speicherfreigabe und Fehlerbehandlung sind entfernt worden. Man beachte dass dieser Quellcode mit einem normalen C++ Compiler kompiliert werden würde. 22
26 24 5 Vergleich zwischen OpenCL und CUDA 5.1 Grundlegendes Eine direkte Konkurrenz beider Technologien ist aufgrund der stark unterschiedlichen Ansätze nur bedingt vorhanden, schließlich lässt sich OpenCL, aufgrund seines breiteren Ansatzes, viel universeller einsetzen als CUDA. Da sich jedoch OpenCL, ebenso wie CUDA, für GPGPU Anwendungen nutzen lässt, fällt ein Vergleich beider Technologien, bezogen auf dieses Einsatzgebiet, nahe. Die grundlegenden Vorteile von CUDA sind die Hardwarenähe, sowie die daraus resultierenden Programmier- und Optimierungsmöglichkeiten, eine sehr ausführliche Dokumentation und viele gute Tools. Da das gesamte Ökosystem CUDA s aus einer Hand stammt, sind kurze Versionsintervalle seitens NVIDIA einfach umzusetzen, neue Möglichkeiten der Hardware sind meist zeitnah zur Verwendung in CUDA verfügbar. Der Große Nachteil ist die Bindung an Soft- und Hardware von NVIDIA. Für OpenCL spricht vor allem die Universalität, OpenCL ist unabhängig von Hard- und Software da es einen freien Standard darstellt. 5.2 Vergleich der Performance Ein Vergleich der Performance ist nur auf Hardware von NVIDIA möglich. Die OpenCL-Implementierung stammt damit (gezwungenermaßen) ebenfalls von NVIDIA, wodurch die Ergebnisse zumindest kritisch zu beäugen sind. Da es allerdings für beide Technologien keine andere Möglichkeit zur direkten Konkurrenz gibt, ist ein solcher Vergleich trotzdem sinnvoll. So könnte ein/e Entwickler/in zum Beispiel wissen wollen, wie groß der Performanceverlust ist, wenn er/sie, aufgrund der Plattformunabhängigkeit, eine in CUDA realisierte Applikation nach OpenCL portiert. Die Ausarbeitung [8, A Performance Comparison of CUDA and OpenCL] präsentiert sehr ausführliche Ergebnisse, an welchen ich mich im Folgenden orientiere. Die Autoren nutzen zur Messung der Performance die wissenschaftliche Applikation AQUA, welche ein Quanten-Spin-System simuliert. Als Problemlänge wird die Anzahl der Quantenbits (Qubits) verwendet; ein genaues Verständnis der Funktionsweise AQUAs ist für die Interpretation der Ergebnisse nicht nötig. Da sich die entsprechenden Kernel der OpenCL bzw. CUDA-Implementierung kaum unterscheiden, der Host-Code aber sehr wohl, sind Unterschiede in der Laufzeit im wesentlichen auf das zugrundeliegende Framework zurückzuführen. Als Hardware wurde eine (mittlerweile nicht mehr aktuelle) NVIDIA GeForce GTX-260, sowie CUDA 2.3 genutzt. Um Detailbetrachtungen zu ermöglichen, wurden vier verschiedene Messungen durchgeführt: Die reine Laufzeit der Kernel, die zum Datentransfer benötigte Zeit, die Laufzeit der GPU-Anwendung (Laufzeit der Kernel, plus Zeit für den Datentransfer) und die Gesamtlaufzeit (inkl. Erkennung der GPU, Compilierung der Kernel für OpenCL, Datentransfer, Berechnung usw.). Da sich die OpenCL-Implementierung durchgängig als etwas langsamer als die in CUDA geschriebene erwies, und reine Zahlenwerte wenig Aussagekraft haben (sofern man nicht detaillierte Kenntnisse über das konkrete Problem hat), stelle ich in Tabelle 4, Seite 25 die von OpenCL zusätzlich benötigte Zeit in Prozent dar. Es ist festzustellen, dass die OpenCL-Implementierung mindestens 12,7% und maximal 67,4% langsamer ist als ihr CUDA-Pendant. Der interessanteste Wert ist der Mittelwert der GPU-Laufzeit, dieser ist bei OpenCL um 27,4% höher. Die Ergebnisse repräsentieren natürlich nur die Unterschiede bei einem einzigen konkreten Problem und sind daher nicht universell anwendbar, dennoch ist ein eindeutiger Trend zu erkennen. Da die genutzte CUDA Version 2.3 bereits im Juli 2009 veröffentlicht wurde, könnte der heutige Unterschied anders aussehen, jedoch wird CUDA vermutlich, aufgrund seiner Verbundenheit 23
27 25 Qubits (Problemgröße) Kernellaufzeit Datentransfer GPU-Laufzeit Gesamtlaufzeit 8 13,8 22,2 13,7 45, ,9 53,3 22,7 38, ,8 56,0 17,4 26, ,7 41,0 44,7 50, ,6 37,7 62,5 67, ,8 36,7 17,9 21, ,7 36,3 12,7 15,7 27,5 40,5 27,4 37,9 Tabelle 4: Messergebnisse aus [8]. Dargestellt ist die von der OpenCL-Implementierung zusätzlich benötigte Zeit in Prozent (Zeit OpenCL /Zeit CUDA 1). mit der Hardware, immer etwas schneller sein als OpenCL. Die Frage ob CUDA oder OpenCL die bessere Technologie ist stellt sich nicht, sondern lediglich welche Technologie für einen bestimmten Anwendungszweck besser geeignet ist. Bei GPGPU- Anwendungen die in erster Linie möglichst performant sein sollen, ist, die entsprechende Hardware vorrausgesetzt, CUDA die bessere Wahl. Wenn Plattform- sowie Herstellerunabhängigkeit gefordert ist, dann OpenCL. Unabhängig davon spielen in der Praxis noch andere Faktoren eine Rolle, wie zum Beispiel Vorkenntnisse der Entwickler oder bereits existierender Programmcode. Es bleibt also die Aufgabe des/der Entwicklers/in, seine Bedürfnisse und Vorraussetzungen zu erkennen und im Hinblick darauf die Vor- und Nachteile abzuwägen, um schließlich eine Entscheidung zu treffen. 24
28 26 6 Abschließende Bemerkungen In dieser Ausarbeitung wurde sowohl die besondere Architektur einer GPU, als auch die Möglichkeiten der Programmierung mittels CUDA und OpenCL, beschrieben. CUDA und OpenCL stellen momentan sicher zwei der wichtigsten Werkzeuge zur GPGPU-Programmierung dar, es gibt jedoch noch eine ganze Reihe anderer Technologien (z.b. Microsoft DirectCompute) auf die ich hier nicht näher eingegangen bin und welche unter Umständen eine Alternative darstellen können. Die vollständige und lückenlose Abdeckung dieser Themenbereiche ist aufgrund des Umfangs nahezu unmöglich, trotzdem hoffe ich dem Leser einen Einblick in die heutigen Technologien gegeben zu haben. 25
29 27 Abbildungsverzeichnis 1 Beispiel: Threadlayout bei CUDA Speicherhierarchie bei CUDA Speicherhierarchie bei OpenCL Tabellenverzeichnis 1 Vordefinierte Variablen bei CUDA Speicherhierarchie bei CUDA Vordefinierte Work-Item Funktionen bei OpenCL C Messergebnisse der Performanceunterschiede zwischen OpenCL und CUDA Listings 1 CUDA Kernel mit Synchronisation CUDA Kernel und Host-Programm zur Multiplikation zweier Matrizen OpenCL C Kernel zur Anwendung bei einer Matrizenmultiplikation Vollständige Matrizenmultiplikation mittels OpenCL Literatur [1] NVIDIA Corporation (2011): The CUDA Compiler Driver NVCC. Available at download.nvidia.com/compute/devzone/docs/html/c/doc/nvcc.pdf. [Online; zugegriffen am ]. [2] NVIDIA Corporation (2011): Using inline PTX Assembly in CUDA. Available at download.nvidia.com/compute/devzone/docs/html/c/doc/using Inline PTX Assembly In CUDA. pdf. [Online; zugregriffen am ]. [3] NVIDIA Corporation (2012): CUDA API Reference Manual, Version 4.2. Available at download.nvidia.com/compute/devzone/docs/html/c/doc/cuda Toolkit Reference Manual.pdf. [Online; zugregriffen am ]. [4] NVIDIA Corporation (2012): NVIDIA CUDA C Programming Guide, Version 4.2. Available at developer.download.nvidia.com/compute/devzone/docs/html/c/doc/cuda C Programming Guide. pdf. [Online; zugegriffen am ]. [5] NVIDIA Corporation (2012): PARALLEL THREAD EXECUTION ISA VERSION 3.0. Available at http: //developer.download.nvidia.com/compute/devzone/docs/html/c/doc/ptx isa 3.0.pdf. [Online; zugregriffen am ]. [6] Khronos OpenCL Working Group (2011): The OpenCL Specification, Version 1.1. Available at khronos.org/registry/cl/specs/opencl-1.1.pdf. [Online; zugregriffen am ]. [7] Advanced Micro Devices Inc. (2012): AMD Accelerated Parallel Processing (APP) SDK OpenCL Programming Guide. Available at Accelerated Parallel Processing OpenCL Programming Guide.pdf. [Online; zugregriffen am ]. [8] Kamran Karimi, Neil G. Dickson & Firas Hamze (2011): A Performance Comparison of CUDA and OpenCL. Available at [9] Wikipedia (2012): CUDA Wikipedia, The Free Encyclopedia. Available at w/index.php?title=cuda&oldid= [Online; accessed 1-August-2012]. 26
30 28 [10] Wikipedia (2012): OpenCL Wikipedia, The Free Encyclopedia. Available at w/index.php?title=opencl&oldid= [Online; accessed 1-August-2012]. 27
31 Automatische C-to-CUDA Code Generierung Johannes Kölsch University of Kaiserslautern Contents 1 Abstract 2 2 Einführung 2 3 C# und CUDA C# GPU-Architektur und das CUDA Programmier-Modell GPU Architektur Das CUDA-Programmier-Modell Das CUDA-Ausführungs-Modell Der C-to-CUDA Code-Generator Step 1: Pluto Scanner/Parser Affine Transformation Network Multilevel Tiling und Parallelism Extraction On-chip Memory Management und Data Movement CLooG Syntaktisches Post-processing Performanz des generierten Codes Coulomb Potential Fazit 15 28
32 2 1 Abstract In der heutigen Zeit werden Grafikprozessoren (GPUs) nichtmehr nur in ihrem ursprünglichen Sinne eingesetzt, sondern auch, um aufwändige Rechenoperationen durchzuführen, die sich sehr gut parallelisieren lassen (z.b. Matrixmultiplikationen). NVIDIA hat in diesem Zusammenhang das Programmier-Modell CUDA (Compute Unified Device Architecture) entwickelt, das performante Implementierungen für diese Operationen bereitstellt. Für den Programmierer ist es allerdings sehr kompliziert, CUDA-Code direkt zu implementieren, da die Sprache durch explizit anzugebende Speicher-Hierarchien und vielschichtige Parallelität ein hohes Ma an Schwierigkeitsgrad erreicht. Deshalb ist es von groem Interesse, Prozedurale Programme (z.b. C#-Code) direkt in effiziente CUDA-Programme umzuwandeln. Im Folgenden wird ein Compiler-Framework dargestellt, das automatisch parallelen und effizienten CUDA-Code aus einem sequentiellen C#-Programm erstellt. Durch die Nutzung verschiedener öffentlich zugänglicher Compiler und Tools wird ein C-to-CUDA Compiler entwickelt, der zweifach parallelen CUDA-Code mit optimiertem Datenzugriff, erzeugt. Die Performanz des automatisch erzeugten Codes wird durch verschiedene Benchmarks festgestellt, und so bestätigt, dass eine weitaus geringere Laufzeit des gleichen Programms zu erwarten ist, als wenn es auf einer Multi-Core CPU ausgeführt werden würde. 2 Einführung Grafik-Prozessoren stellen momentan die stärksten Multi-Core-Systeme dar, die genutzt werden. Mit inzwischen mehreren Tera-FLOPS an Peak-Performance stellen sie normale CPUs weit in den Schatten. Dadurch werden sie nun immer häufiger genutzt, um algorithmisch lösbare Probleme zu lösen. Dieser Vorgang wird als general-purpose computation on GPUs (kurz GPGPUs) bezeichnet. Durch die Einführung von NVIDIAs CUDA gibt es nun ein Prorammier-Modell, das dem Programmierer Methoden bereitstellt, um effizient allgemeine Rechenvorgänge auf die GPU auszulagern. Im Vergleich zu anderen GPGPU- APIs ist CUDA einfacher zu bedienen, aber es reicht noch nicht an parallele Programmier- Modelle für Multi-Core CPUs (z.b. OpenMP) heran. Daher ist es von groem Interesse, einen Compiler zu entwickeln, der direkt aus sequentiellem Code parallelen CUDA-Code erzeugen kann. Es wurde bereits eine Vielzahl von Optimierungen entwickelt, die zur Kompilierzeit von regulären Programmen arbeiten. Diese basieren auf polyhedrischen Abstraktionen von Programmen und Daten-Abhängigkeiten. Das in dieser Seminararbeit beschriebene Compiler-Framework nutzt zwei solcher Optimierungen, um schnellen und effizienten CUDA-Code zu erzeugen. 1. CLooG 29
33 3 CLooG (siehe Abschnitt 4.4) ist ein Programm, das die polyhedrische Abstraktion eines Programmes in Code mit konkreten Schleifen umwandelt. 2. Pluto Pluto (siehe Abschnitt 4.1) ist ein source-to-source Optimierer, der automatisch Parallelisierung und Lokalitätsoptimierungen von Programmen für Multi-Core Systeme bereitstellt. 3 C# und CUDA 3.1 C# C# ist eine sehr weit verbreitete, imperativ-prozedurale Programmiersprache. Die Anwendungsbereiche reichen von Anwendungen für PCs bis hin zu eingebetteten Systemen und Kerneln für Betriebssysteme. Viele heute verwendete objektorientierte Programmiersprachen orientieren sich syntaktisch an C#. C# wurde mehrfach standardisiert, da sehr viele Dialekte entstanden sind. Da auf sehr vielen Systemen die Standard C Library zur Verfügung steht, können Programme in C gut portiert werden. C bietet zwar wenig Sicherheit aber erreicht dadurch eine einfache Kompilierbarkeit. 3.2 GPU-Architektur und das CUDA Programmier-Modell In folgendem Abschnitt wird ein kurzer Überblick über die GPU Architektur und das CUDA- Interface gegeben GPU Architektur Die GPU-Architektur der neueren Grafikkarten-Generationen von NVIDIA ist wie folgt aufgebaut: Auf einer GPU gibt es mehrere Streaming-Multiprozessoren, die jeweils wieder eine bestimmte Anzahl Streaming-Prozessoren beherbergen. Die NVIDIA GeForce 680 verfügt als Beispiel über 8 Streaming Multiprozessoren, die jeweils 192 Streaming-Prozessoren enthalten. Jeder Streaming-Prozessor verfügt über einen eigenen lokalen Speicher (local memory). Dieser ist privat für den Thread, der gerade auf dem Streaming-Prozessor läuft. Daher ist dieser Speicher nur für temporäre Daten gut geeignet. Die Streaming-Prozessoren innerhalb eines Streaming-Multiprozessors teilen sich einen lokalen Speicher (shared memory), über den sie sehr schnell kommunizieren können. Dieser ist in sogenannten textitbanks organisiert. 30
34 4 Die Streaming-Multiprozessoren kommunizieren währenddessen über einen deutlich langsameren DRAM (globaler Speicher). Dieser globale Speicher hat sehr hohe Zugriffszeiten. Daher ist es für eine effiziente Code-Ausführung essentiell, die Zugriffe auf diesen Speicher zu reduzieren. Der Constant Cache und der Texture Cache in Abbildung 1 sind read-only Regionen des globalen Speichers. Der Constant Cache lsst sich schnell auslesen, hat aber den Nachteil, dass er nur einen einzigen Port hat. Daher ist es vorteilhaft, wenn verschiedene Streaming- Prozessoren den gleichen Wert daraus zur selben Zeit bentigen. Weiterhin hat jeder Streaming-Multiprozessor eine eigene feste Anzahl von Registern. Es ist von extremer Wichtigkeit, die Zugriffe auf den DRAM Bereich auerhalb des Chips zu reduzieren und die On-Chip Speicherbereiche effizient zu nutzen. Figure 1: CUDA-Architektur [2] 31
35 Das CUDA-Programmier-Modell Das CUDA-Programmier-Modell stellt dem Programmierer eine kleine Bibliothek zur verfgung, wodurch dieser auf primitive Synchronisierungen sowie auf Thread- und Speicherhierarchien zugreifen kann. Ein CUDA-Programm besteht aus einem Host-Programm, das auf der CPU ausgefhrt wird. Dieses Host-Programm startet dann mehrere CUDA-Kernels, die alle auf der GPU ausgefhrt werden. Diese Kernels wiederum sind parallel und werden daher von mehreren Threads ausgeführt. Diese Threads sind in Gruppen (den sogenannten Thread-Blocks) organisiert. Die Synchronisierung innerhalb der Threads ist als Barrieren- Synchronisation implementiert. Sie kommunizieren miteinander ber den schon unter Punkt besprochenen shared memory- Bereich. Die Thread-Blocks innerhalb eines Kernels sind in grids organisiert. Jeder Thread eines Thread-Blocks hat eine einzigartige ID und kann somit identifiziert werden. Genauso verhlt es sich auch mit den Thread-Blocks selbst. Sie werden durch die einzigartige Block-ID identifiziert. Der Programmierer kann bevor der Kernel gestartet wird festlegen, welche Dimensionen die Thread-Blocks und die Threads haben sollen. Jeder dieser Threads innerhalb eines Kernels hat Zugang zu den einzelnen Speicherbereichen. Sie haben alle einen privaten lokalen Speicherbereich und Registerbereich, knnen aber auch auf den externen DRAM des Chips zugreifen Das CUDA-Ausführungs-Modell Das Programmier-Modell von NVIDIA basiert, nicht wie andere Ausfhrungsmodelle auf SIMD (Single Instruction Stream, Multiple Data Stream), sondern auf SIMT (Single Instruction Stream, Multiple Threads). Das heit genauer, dass der Kernel gleichzeitig auf allen Streaming-Multiprozessoren ausgefhrt wird. Dadurch agiert jeder ausgeführte Thread, der auf einem eigenen Streaming-Prozessor läuft, in seiner eigenen Umgebung (Registerinhalte und Instruktions-Adresse). Dennoch fhren alle Threads zur gleichen Zeit den gleichen Befehl aus. Die Thread-Gruppen, die diesen Befehl ausfhren heissen warps. Die Threads eines einzelnen warps werden alle auf eigenen Streaming-Prozessoren ausgeführt. Durch den CUDA runtime scheduler wird auf einem Streaming-Multiprozessor kein overhead produziert, um die warps zu planen. Ein warp, dessen operanden im nächsten Befehl bereit sind, kann ausgeführt werden. Unter diesen bereiten warps wird dann einer nach einer prioritätsorientierten Scheduling-Strategie für die Ausführung ausgewhlt. Dieser Prozess ist für den Programmierer komplett transparent. Die Ressourcen innerhalb eines Streaming- Multiprozessors werden von dem aktuell ausgeführten Thread-Block geteilt. Also knnen je nach Speicherkomplexität der einzelnen Thread Blocks unterschiedlich viele Thread-Blocks gleichzeitig auf einem Streaming-Multiprozessor ausgeführt werden. Ist ein Thread-Block mit der Ausführung fertig, so kann dieser durch einen anderen wartenden Thread-Block ersetzt werden. 32
36 6 4 Der C-to-CUDA Code-Generator Im folgenden Kapitel wird der Code-Generator ausführlich beschrieben. Zuerst ein kurzer berblick ber die einzelnen Schritte, die das Compiler-Framework ausführt, um effizienten CUDA-Code zu erhalten: 1. Zuerst muss das C-Programm von einem Scanner und Parser in einen abstrakten Syntax-Baum umgewandelt werden. Aus diesem abstrakten Syntax-Baum werden dann direkt die Array-Zugriffs-Funktionen und Iterationsraum-Polytope extrahiert. 2. Aus den in Schritt 1 extrahierten Array-Zugriffs-Funktionen und Iterationsraum-Polytope werden nun Daten-Abhngigkeiten analysiert und Abhngigkeits-Polytope erstellt. 3. Aus diesen Abhngigkeiten werden dann ausdrucksweise Transformationen erstellt. Diese stellen die neue lexikographische Ordnung des Programms dar. 4. Nun muss das Programm in die einzelnen Threads aufgeteilt werden und entsprechend parallelisiert werden. Die in Schritt 3 erzeugten affine ausdrucksweise Transformationen werden nun als teilende Hyperplanes verwendet. Daraus können Breiche von Ausdrcken höherer Dimensionen generiert werden. 5. Zuletzt kommt ein Polyhedraler Code-Generator (hier CLooG) zum einsatz. der aus den transformierten statement Polytopen und den affinen Transformationen den fertigen CUDA-Code generiert. Figure 2: Das C-to-CUDA Compiler-Framework [2] Um die Effizienz des so erstellten CUDA-Codes sicherzustellen, ist es von groer Wichtigkeit, dass die Speicherzugriffe auf On- und Off-Chip-Speicher berprft werden und gegebenen- 33
37 7 falls optimiert werden. Zugriffe auf Off-Chip-Speicher sollte dabei soweit wie mglich vermieden werden, da dieser Zugriff sehr lange dauert. Um Diese Zugriffe zu optimieren werden im vorgestellten Compiler-Framework zwei ffentlich verfgbare frameworks und tools verwendet. Zum einen Pluto (nheres unter Punkt 4.1) und zum anderen CLooG (nheres unter Punkt 4.4). Der in den folgenden Abschnitten beschriebene Ablauf des Compiler-Frameworks ist in 4 schematisch dargestellt. 4.1 Step 1: Pluto Pluto ist ein automatisches Parallelisierungs-Tool, das auf dem polyhedrischen Modell basiert. Es findet automatisch affine Transformationen, die kommunikations- und lokalittsoptimiert sind. Pluto muss affine Transformationen finden, die folgende Eigenschaften erfllen: Eine Menge von affinen Transformations-Funktionen ist genau dann eine teilende Hyperebene, wenn jedes paar von abhängigen statements in ihr nur eine Abhängigkeit in Vorärtsrichtung auf dieser Ebene besitzt. Wird diese Bedingung erfüllt, so ist die Transformation g ltig im transformierten Programm. Die Menge aller affinen Transformations-Funktionen, die für jedes Paar von abhängigen statements dieser Menge die Eigenschaft, dass das vorhergehende Ereignis nicht von dem späteren abhängig ist, erfüllt, ist legitim und kann somit als teilende Hyperplane eingesetzt werden. Diese Transformationen werden dann als teilende Hyperplanes eingesetzt, die die Schleifen im transformierten Programm darstellen Scanner/Parser Der Parser des Pluto-Frameworks weit keine Besonderheiten gegenüber anderen Parsern auf. Der erstellt zunächst aus dem eingegebenen C-Programm einen abstrakten Syntax- Baum, den er dann auf richtigkeit hin überprüft. Aus diesem abstrakten Syntax-Baum können nun schon die Affinen Transformationen abgeleitet werden Affine Transformation Network CUDA erlangt, dass ein Programm in mehrere Thrad-Blocks aufgeteilt ist, die wiederum in einzelne Threads aufgeteilt sind. Um die äussere Teilung durchzuführen, können die affinen Transformationen, die von Pluto erzeugt wurden, verwendet werden. Um die Teilung innerhalb der Thread-Blocks (also auf Thread-Level durchzuführen muss Pluto modifiziert werden. Dies wird dadurch erreicht, dass Pluto beim finden von affinen Transformationen folgende erweiterte Bedingungen auferlegt werden: 34
38 8 1. Wenn zwei statements das gleiche Element eines Arrays adressieren, so werden diese beiden statements genau zur gleichen Zeit von zwei verschiedenen Threads ausgeführt 2. Weiterhin werden die beiden statements die das gleiche Element addressieren auf adjazenten Prozessoren ausgeführt 4.2 Multilevel Tiling und Parallelism Extraction CLooG teilt den Code nun auf einzelne Threads und Thread-Blcke auf. Dies geschieht nach folgendem Algorithmus. Algorithmus 1: Generierung des Mehrebenen parallelen Codes 1 for jedes level do 2 for jedes statement s do 3 for jede Transformation do 4 Erhöhe die Dimension der statement domain um 1, damit sie die Iteratoren des Mutterknotens enthlt. ; 5 Füge Einschränkungen für den Superknoten-Iterator und die Teil-Grösse hinzu Füge die Scattering-Functions der Mutterknoten hinzu.; 6 if level soll parallelisiert werden then 7 if es existieren doall-schleifen then 8 Markiere diese als parallel 9 end 10 else 11 Transformiere den ersten nicht-sequentiellen Schleifen-Durchlauf. Markiere ihn als sequentiell und die weiteren Durchläufe als parallel 12 end 13 end 14 end 15 end 16 end 35
39 9 4.3 On-chip Memory Management und Data Movement Wie bereits angesprochen ist es sehr wichtig Daten effizient in und aus dem On-Chip memory zu verschieben und somit die Zugriffe auf das Off-Chip Memory zu reduzieren. Um Daten zu identifizieren, die Kandidaten für den On-Chip Memory sind, werden die Zugriffe auf eine Array-Referenz gezählt. Die Daten, auf die oft zugegriffen wird werden im On- Chip Memory gespeichert. Die ist der Fall, da nicht zusammenhängende Zugriffe sehr hohe Zugriffskosten erzeugen. Es gibt zwei Arten von Data-Movement-Code. 1. Code, der Daten in den shared memory Breich verschiebt (copy-in statements) 2. Code, der Daten aus dem shared memory in den globla memory Bereich verschiebt (copy-out statements) Auf Thread-Block Ebene müssen die Data-movement statements nach folgendem Schema platziert werden: 1. copy-in 2. computation 3. copy-out So kann eine korrekte parallele Ausführung des Codes garantiert werden. Für eine gegebene Menge von statements, die aufeinander folgen, werden die Speicherbereiche, auf die die statements zugreifen, bestimmt, indem für jedes der statements der Iterationsraum bestimmt und dann für jede Referenz innerhalb dieses Raumes die Array- Access-Function gefunden. Die so gefundenen Speicherbereiche, auf die durch lese- und schreibbefehle zugegriffen wird, werden nun als einzelne Polytope interpretiert. AUs dieser Interpretation kann direkt die Grösse des zu reservierenden Speicher-Buffers bestimmt werden. Der Code, der die Daten in den Speicher und aus dem Speicher wieder heraus bewegt muss nun noch im CUDA-Code platziert werden. Die Befehle werden nach Algorithmus 2 platziert. Die Zugriffe auf den globalen Speicher können weiterhin dadurch reduziert werden, dass bestimmte Daten in den konstanten Speicher oder auch Texturbereich des Grafikchips geladen werden. Dieser Speicherbereich ist bei der CUDA-Architektur durch Cache realisiert und bietet daher sehr kurze Zugriffszeiten. Es werden für diessen Speicherbereich solche Daten ausgesucht, die von vielen Threads innerhalb eines warps simultan gelesen werden. Wenn verschiedene Threads innerhalb eines warps verschiedene Werte im konstanten Speicher lesen müssen, so werden diese Zugriffe serialisiert. Es werden Arrays gesucht, auf die nur Lese- und keine Schreibzugriffe erfolgen. Diese Arrays sind gute Kandidaten für den konstanten Speicherbereich. 36
40 10 Algorithmus 2: Generierung und Platzierung von Daten-Bewegungs-Code 1 for jedes Array A do 2 for Alle Referenzen des Arrays do 3 Finde den Speicherbereich, der durch die Referenzen adressiert wird. 4 end 5 Teile die gefundenen Speicherbereiche in maximale und disjunkte Mengen, sodass jedes dieser Teile eine Untermenge von Datenbereichen hat, die sich nicht mit Speicherbereichen von anderen Teilen berlappen.; 6 Für jedes dieser Teile finde die convexe Hülle seiner Speicherbereiche. Die Bounding box um diese Convexen Hüllen ergibt den Speicherbuffer, den der Teil braucht. ; 7 for jedes statement s do 8 for alle lesenden Referenzen auf das Array do 9 Finde den Speicherbereich, in dem gelesen wird, und nutze ihn für copy-in statements. ; 10 Benutze dabei identity-scattering-functions 11 end 12 for alle schreibenden Referenzen auf das Array do 13 Finde den Speicherbereich, in den geschrieben wird, und nutze ihn für copy-out statements. ; 14 Benutze dabei identity-scattering-functions 15 end 16 end 17 end 18 Sei die Anzahl von copy-in statements c und die Anzahl von copy-out statements d.; 19 Füge eine neue Dimension in die scattering.functions ein.; 20 Diese Diemnsion hat einen konstanten Wert.; 21 Dieser Wert ist ist 0 bis c-1 für copy-in statements, c für die eigentliche Berechnung und c+1 bis d für copy-out statements. 4.4 CLooG CLooG steht für Chunky Loop Generator. Es ist freie Software um Code für das Scannen von Z-Polyedern zu generieren. CLooG wurde ursprünglich dafür geschrieben, das Code- Generierungs-Problem für Kompiler-Optimierungen zu lösen. Heutzutage wird CLooG in einem sehr breiten Aufgabenfeld verwendet. Zum Beispiel kann er eingesetzt werden, um Kontrollautomaten für High-level Synthese zu erstellen oder um die beste Polynomiale Approximation einer Funktion zu finden. CLooG überlässt dabei allerdings dem Benutzer volle Kontrolle über die Qualität des generierten Codes. Es wurde 37
41 11 geschrieben, um Overhead zu vermeiden und sehr effektiven Code zu generieren. Figure 3: Die Arbeitsweise von CLooG 4.5 Syntaktisches Post-processing Der nun generierte Code ist noch nicht direkt vom CUDA-Compiler in Maschinencode übersetzbar. Der von CLooG erstellte Code muss noch durch Post-processing nachbearbeitet werden. Genauer müssen hier nun noch zwei Eigenschaften des Codes hergestellt werden: 1. Generierung von Thread-zentrischem Code 2. Synchronisierungs-Aufrufe in den Code einfügen Die Generierung von Thread-zentrischem Code ist ein wichtiger Aspekt von CUDA. Zum Beispiel muss solcher Code generiert werden, wenn die Berechnung über viele Threads verteilt wird. 38
42 12 Ein Thread innerhalb des Systems kann eindeutig über seine Thread-ID und seinen Thread-Block, dem er zugehört identifiziert werden. Algorithmus 3: Parallele CUDA-Code Generierung 1 Übergib den computation-code, den Daten-Bewegungs-Code und die generierten scatteringg-functions an CLooG, sodass dieser CLAST generiert. ; 2 Parse CLAST, um Untergrenzen und Schleifenerh hungen von parallelen Schleifen thread-zentrisch zu machen.; 3 Parse CLAST, um Untergrenzen und Schleifenerh hungen von Daten-Bewegungs-Schleifen thread-zentrisch zu machen; 4 Platziere Barrieren-Synchronisation an jeder Iteration von als sequentiell markierten Schleifen und jeweils an das Ende von Daten-Bewegungs-Code.; 5 Gib den modifizierten CLAST-Code aus, um daraus CUDA-Code zu erzeugen. 5 Performanz des generierten Codes In diesem Abschnitt wird noch auf die Performanz des mit dem vorgestellten Framework generierten Codes betrachtet. Es werden verschieden Benchmarks betrachtet, und die darin erzielten Ergebnisse mit Code der auf einer Vier-Kern CPU ausgeführt wird verglichen. Weiterhin wird der generierte Code nocheinmal Hand-optimiert, um eine noch höhere Leistung zu erzielen. 5.1 Coulomb Potential Bei diesem Benchmark wird das elektrische Potential für jeden Punkt eines Volumens berechnet, in dem Punktladungen verteilt sind. Dies geschieht nach dem Algorithmus 4. 39
43 13 Algorithmus 4: Berechnung des Coulomb Potentials 1 for t1=0, t1 < VOLY, t1++ do 2 for t2=0, t2 < VOLX, t2++ do 3 for t3=0, t3 < NATOMS, t3++ do 4 energy[f(t1,t2)]=f(t3) 5 end 6 end 7 end Figure 4: Performance des Frameworks beim CP-Benchmark In Figure 4 ist leicht zu erkennen, dass der vom C-to-CUDA-Framework generiert Code eine sehr gute Performanz besitzt im Gegensatz zum Code, der auf der 4-Kern-CPU ausgeführt wird. Er erreicht sogar fast die Geschwindigkeit des Hand-optimierten Codes. Weiterhin erkennt man den starken Performanzanstieg, wenn statt dem geteilten Speicherbereich der konstante Speicher auf der GPU verwendet wird. Dies ist leicht dadurch zu erklären, dass bei Verwendung des constant memory sehr viele Zugriffe auf den global memory Bereich und somit auf langsamen Speicher, gespart werden können. 40
44 14 Algorithmus 5 zeigt den Code, den das Framework aus dem Code in Algorithmus 34 generiert hat. Dieser Code ist auf zwie levels parallel ausführbar und Thread-zentrisch. Das äussere Level kann auf Thread-Blocks abgebildet werden, während das innere Level auf einzelne CUDA-Threads abgebildet wird. Weiterhin kann in Algorithmus 5 der eingefügte Daten-Bewegungs-Code und die eigentliche Berechnung gefunden werden. Algorithmus 5: Parallele Code-Struktur und Datenbewegungs-Code 1 int by = BlockIdx.y; 2 int bx = BlockIdx.x; 3 int ty = threadidx.x; 4 int tx = threadidx.y; 5 int t1,t2,t3,t4,t5,t6; 6 for (t1=by, t1 <= floord(voly-1,16), t1+=nblksy) do 7 for (t2=bx, t2 <= floord(volx-1,16), t2+=nblksx) do 8 for (t3=0, t3 <= NATOMS-1, t3+=256) do 9 //Data movement Code; 10 shared float atomss[1024]; 11 for (t6=4*t3+thready*nthreadsx+threadx, t6 <= min(4*natoms-1, 4*t3+1023), t6+=nthreadsx*nthreadsy) do 12 atomss[t6-4*t3] = atoms[t6]; 13 end 14 syncthreads(); 15 //Parallele Schleifen über die Threads verteilt; 16 //Schleifen syntaktisch modifiziert für die Thread-Identifier; 17 for (t4=max(0,16*t1)+ty, t4 <= min(voly-1, 16*t1+15), t4+=nthrdsy) do 18 for (t5=max(0,16*t2)+tx, t5 <= min(volx-1, 16*t2+15), t5+=nthrdsx) do 19 //Berechnung des Coulomb Potentials ; 20 for (t6=t3, t6 <= min(natoms-1, t3+255), t6++) do 21 //Berechnung der Energy aus CP-Algorithmus; 22 end 23 end 24 end 25 end 26 end 27 end 41
45 15 6 Fazit In dieser Seminararbeit wurde dargestellt, wie ein C-to-CUDA Compiler Framework funktioniert. Das Framework nimmt dabei reinen C-Code als Eingabe und generiert daraus schnellen und effizienten CUDA-Code. Die Performanz des generierten Codes wurde anhand eines Benchmarks, nmlich des Berechnung des Coulomb-Potentials, nachgewiesen. Dieses Compiler-Framework erlaubt es dem Programmierer schnellen parallel ausführbaren Code zu erzeugen, ohne dabei Mehraufwand betreiben zu müssen. Der generierte Code ist weiterhin noch lesbar und kann somit noch weiter optimiert werden, was nocheinmal einen klaren Geschwindigkeitsanstieg bei der Ausführung bedeuten kann. 42
46 16 References [1] Muthu Manikandan Baskaran, Uday Bondhugula, Sriram Krishnamoorthy, J. Ramanujam, Atanas Rountev & P. Sadayappan (2008): A compiler framework for optimization of affine loop nests for gpgpus. In: Proceedings of the 22nd annual international conference on Supercomputing, ICS 08, ACM, New York, NY, USA, pp , doi: / Available at [2] Muthu Manikandan Baskaran, J. Ramanujam & P. Sadayappan (2010): Automatic C-to-CUDA code generation for affine programs. In: Proceedings of the 19th joint European conference on Theory and Practice of Software, international conference on Compiler Construction, CC 10/ETAPS 10, Springer-Verlag, Berlin, Heidelberg, pp , doi: / Available at [3] H. Blume, J. von Livonius, L. Rotenberg, T. G. Noll, H. Bothe & J. Brakensiek (2008): OpenMP-based parallelization on an MPCore multiprocessor platform - A performance and power analysis. J. Syst. Archit. 54(11), pp , doi: /j.sysarc Available at [4] Uday Bondhugula, Albert Hartono, J. Ramanujam & P. Sadayappan (2008): A practical automatic polyhedral parallelizer and locality optimizer. In: Proceedings of the 2008 ACM SIGPLAN conference on Programming language design and implementation, PLDI 08, ACM, New York, NY, USA, pp , doi: / Available at [5] NVIDIA CUDA (2012): Available at html. [6] Paul Feautrier (1996): Automatic Parallelization in the Polytope Model. In: The Data Parallel Programming Model: Foundations, HPF Realization, and Scientific Applications, Springer- Verlag, London, UK, UK, pp Available at id= [7] CLooG: The Chunky Loop Generator (2012): Available at [8] Naga Govindaraju, Scott Larsen, Jim Gray & Dinesh Manocha (2006): A Memory Model for Scientific Algorithms on Graphics Processors. In: Supercomputing, SC 06. Proceedings of the ACM/IEEE SC 2006 Conference, p. 6, doi: /sc Available at http: //dx.doi.org/ /sc [9] Martin Griebl (2004): Automatic Parallelization of Loop Programs for Distributed Memory Architectures. [10] Martin Griebl, Paul Feautrier & Christian Lengauer (2000): Index Set Splitting. Int. J. Parallel Program. 28(6), pp , doi: /a: Available at org/ /a: [11] General-Purpose Computation Using Graphics Hardware (2012): Available at gpgpu.org/. 43
47 17 [12] S. Lee, S.J. Min & R. Eigenmann (2009): OpenMP to GPGPU: a compiler framework for automatic translation and optimization. In: Proceedings of the 14th ACM SIGPLAN symposium on Principles and practice of parallel programming, ACM, p [13] Seyong Lee, Seung-Jai Min & Rudolf Eigenmann (2009): OpenMP to GPGPU: a compiler framework for automatic translation and optimization. In: Proceedings of the 14th ACM SIGPLAN symposium on Principles and practice of parallel programming, PPoPP 09, ACM, New York, NY, USA, pp , doi: / Available at acm.org/ / [14] Amy Wingmui Lim (2001): Improving parallelism and data locality with affine partitioning. Ph.D. thesis. AAI [15] David B. Loveman (1977): Program Improvement by Source-to-Source Transformation. J. ACM 24(1), pp , doi: / Available at / [16] Pluto: A polyhedral automatic parallelizer & locality optimizer for multicores (2012): Available at [17] Shane Ryoo, Christopher I. Rodrigues, Sara S. Baghsorkhi, Sam S. Stone, David B. Kirk & Wen-mei W. Hwu (2008): Optimization principles and application performance evaluation of a multithreaded GPU using CUDA. In: Proceedings of the 13th ACM SIGPLAN Symposium on Principles and practice of parallel programming, PPoPP 08, ACM, New York, NY, USA, pp , doi: / Available at [18] Nicolas Vasilache, Cedric Bastoul, Albert Cohen & Sylvain Girbal (2006): Violated dependence analysis. In: Proceedings of the 20th annual international conference on Supercomputing, ICS 06, ACM, New York, NY, USA, pp , doi: / Available at [19] M. Wolfe (2008): Compilers and More: A GPU and Accelerator Programming Model. Available at a_gpu_and_accelerator_programming_model.html. 44
48 Porting CUDA code to multicore CPUs and other platforms Frederik Walk University of Kaiserslautern, Embedded Systems Group f walk09@cs.uni-kl.de Contents 1 Introduction 2 2 CUDA Architecture Language extensions CUDA on Multicore Processors MCUDA Code Portation Execution Performance Optimizations Limitations OpenCL Architecture Language extensions CUDA to OpenCL Code Portation Swan CU2CL Performance Portability Performance of CUDA and OpenCL on the same platform Performance of ported OpenCL code on other platforms Optimizations Future 16 7 Conclusion 17 45
49 2 1 Introduction When NVIDIA introduced CUDA in 2006 and thereby finally made general purpose computing on GPUs simpler and more understandable, a lot of highly data parallel algorithm implementations, which now could be run at a reasonable performance even on standard consumer hardware, began to appear. Very soon other vendors, like AMD, began to open up their parallel computing platforms too and a vast field of different hardware and programming interfaces was the result. The next logical step was to unify all those interfaces to a single framework. This was done when Apple proposed OpenCL to the Khronos Group in 2008, which now maintains it as an open standard that a lot of vendors have implemented by now. But still, CUDA is a few years older then OpenCL and there has been put a lot of work into the plenty of CUDA programs already written. Therefore it is desirable to port over these already written programs to other platforms by using OpenCL, instead of reimplementing them. CPUs are also getting more and more cores and additional instructions to do SIMD like calculations, making them also suitable for parallel computing. It is not to expect that CPUs will reach the same performance as those highly data parallel algorithms on GPUs today, but it is still interesting if the characteristics of CUDA code can be used to improve the execution efficiency on CPUs. The following text will start with a quick overview of CUDA and its code and architecture. Then there will be a description how CUDA code can be ported to CPUs using the MCUDA framework. Afterwards it will continue with an overview of OpenCL and how code can be ported from CUDA to OpenCL. Then there will be a performance analysis of the ported code and it will conclude with an outlook to the future of portation of CUDA code. 2 CUDA In 2006 NVIDIA introduced CUDA, which allowed general purpose computing to be done on NVIDIA GPUs [9]. Its architecture closely resembles the actual hardware architecture of NVIDIA graphics cards. CUDA also came with a language extension for C called CUDA C and an API to hide most of the device management to make the GPU easily programmable. 2.1 Architecture A CUDA program consists of host code, which is run on the CPU, and device code, which is run on the GPU and consists of so called kernel functions. The host code is compiled and run like normal a C program, the kernels however are executed multiple times in parallel as CUDA threads, each having its own thread local memory. Threads are again organized in blocks, which are assigned to one of the GPU s multiprocessors. All blocks are organized in the grid. Each thread and block has its own index which is available from within the kernel code as threadidx and blockidx. All threads in a block can access the block local shared memory. Variables declared as shared are copied in each blocks shared memory and allow efficient cooperation between the thread in a block. Threads in a block are further grouped into warps, which are executed by the multiprocessor like a SIMD instruction. [9] Another type of memory on CUDA devices is the constant memory. Variables in constant memory cannot change during the program execution, but are broadcast to certain number of threads and cached more aggressively, therefore saving a lot of memory bandwidth. Finally there is the texture memory. It is also read-only, but has its caching optimized for two-dimensional access. [11] 46
50 3 Figure 1: The CUDA device model. [7] 2.2 Language extensions CUDA C is basically standard C with a few keywords added. The keywords device, global and host help the CUDA compiler to distinguish between code written to be run on the host and the device. Host code and device code are then fed into the appropriate compilers, which is, in the case of the host code, the default C compiler. The CUDA compiler then generates an intermediate, assembly like language called PTX, from the device code, which is fed to the graphics card driver and then translated to target hardware instruction set on runtime [10]. Another type of keywords enable the programmer to declare in which part of the device memory a variable should reside, to efficiently use the different types of memory described above [11]. NVIDIA also gives you a handful of prebuilt datatypes and functions that make GPU programming a lot easier, but are not necessary to use the GPU [11] [9]. Important to mention here is the syncthreads() function that allows a barrier synchronization across all threads of the same block, meaning all threads have to enter and leave the function at the same time. Also, a special syntax for kernel invocation (<<< >>>) was added. This very small extensions to the C language makes CUDA not only quite easy to learn, but also simplifys the source-to-source translation into other languages, as we will see in the later sections. 3 CUDA on Multicore Processors The CUDA toolset already comes with an emulator for GPUs on CPUs, but it is meant for debugging purposes rather than efficiently running CUDA code on GPUs. It runs one OS thread for every CUDA 47
51 4 thread and uses native mutexes for synchronization. Therefore a massive amount of overhead is generated for the number of threads a typical CUDA program creates [1]. So an other approach to efficiently map the CUDA architecture to the CPU architecture has to be found. 3.1 MCUDA The MCUDA framework [12] provides a source-to-source translator, based on the Cetus framework, to map CUDA kernels to standard C and a runtime framework to run these kernels on a common CPU. Both these tools are designed to port over as much as possible of the performance coming from the special characteristics of CUDA code and the features of CUDA devices. CUDA programs gain a lot of performance from kernel functions with very similar control flow and as well lose much performance from accesses to the global memory, which has very high latency compared to the local memory spaces. This encourages programmers to write code with very regular control flow and high data locality. Further all threads in a block can be executed independently, so the basic idea is to run each block, not each thread, per CPU core. The regular control flow in the thread blocks make it likely that the SIMD instructions, which available on current CPUs, can be used. Thread-local and shared memory spaces also roughly fit into the CPUs L1 cache, therefore maintaining the data locality on the CPU Code Portation Since the host code is already running on the CPU and no device specific initializations have to be made, most of the translation process focuses on the kernel functions. The first step is to translate the control flow, therefore transforming the thread-level kernel functions into block-level functions. This is done be serializing the kernel functions in each block using a so called thread loop, and explicitly introducing the threadidx variable (cf. Figure 2). void add(float a*, float b*, float c*) { int i = threadidx.x; if(i < VECTOR_SIZE) c[i] = a[i] + b[i]; } void add(float a*, float b*, float c*, dim3 blockdim, dim3 blockidx, dim3 griddim) { dim3 threadidx; } //Thread Loop start for(threadidx.y = 0; threadidx.y < blockdim.y; threadidx.y++) { for(threadidx.x = 0; threadidx.x < blockdim.y; threadidx.y++) { //Kernel Code int i = threadidx.x; if(i < VECTOR_SIZE) c[i] = a[i] + b[i]; } } //Thread Loop end Figure 2: The add function of a simple vector addition without and with a thread loop 48
52 5 Thread-local variables are now effectively reused in each iteration of the thread loop and the shared variables stay visible for all iterations since they are declared outside the loop. If the kernel contains synchronization statement, meaning a statement which all threads have to enter and leave at the same time, further transformations have to be done. This transformation is called loop fission when applied directly to the thread loop and deep fission when applied to a scope within the thread loop. If the synchronization statement is directly within the scope of a thread loop, the thread loop is simply split around it (See Figure 3). void kernel (...) {... thread_loop { //Code before barrier syncthreads(); //Code after barrier } } void kernel (...) {... thread_loop { //Code before barrier } } thread_loop { //Code after barrier } Figure 3: Loop fission applied directly to the thread loop If not, the scope around the synchronization statement is split in two thread loops, side effects in the control structures are removed and the scope itself is declared as a new synchronization statement, as demonstrated in Figure 4. This is called deep fission and can be safely done, because the CUDA model requires the control flow affecting synchronization to be thread-independent within a block. All early-exit and irregular control statements are also marked as synchronization points. This not always needed, but it secures the program s consistency. These steps are repeated until all synchronization statements are converted. For the serialized threads, this loop fissions have the same effect as a barrier synchronization, since the second thread loop is entered only after all threads have completed the first one. After the control flow is transformed, all variables used in more than one thread loop are buffered by creating an array containing the values for different threads. Variables used only in a single loop can safely be reused. References to variables outside thread loops are represented by buffer element 0 since they stay the same across all threads, and therefore using any of the elements is sufficient. Shared variables simply have the shared keyword removed as they are visible to all logical threads anyway. (cf. Figure 5) In the host code, the kernel launch statements and some of the basic API functions (e. g. memcpys) can stay untouched, since they are reimplemented by the MCUDA framework, the remaining API and library calls have to be ported manually Execution When the kernel launch function is invoked, the host thread stores the launch parameters to global variables and enters a barrier synchronization point. The worker threads, which represent the device, also enter this barrier, when they become idle. On exit, the host thread advances to a second barrier, all worker threads begin executing the block functions, using the launch parameters, and enter the second barrier 49
53 6 void kernel (...) {... thread_loop {... for(int i=1; i<10; i++) { //Code before barrier syncthreads(); //Code after barrier }... } } (a) Kernel function with synchronization void kernel (...) {... thread_loop {... //Remove side effects //by transforming the //for into a while loop int i=1 } } //Begin new sync statement while(i<10) { thread_loop { //Code before barrier } thread_loop { //Code after barrier i++; } } //End new sync statement... void kernel (...) {... thread_loop{... //Remove side effects //by transforming the //for into a while loop int i=1 } (b) Applying deep fission } while(i<10) { thread_loop { //Code before barrier } thread_loop { //Code after barrier i++; } } thread_loop {... } (c) Applying loop fission Figure 4: Applying deep fission on a for-loop 50
54 7 void kernel (...) {... int k; int a,b,c; shared float data[16]; } thread_loop { b = data[threadidx.x]/2; a = 0; } while(a < 16) { thread_loop { for(k=0,k<64,k++) { c += k*b; } } thread_loop { a++; } } thread_loop { data[threadidx.x] = c; } void kernel (...) {... //Variables only used in //a single thread loop int k; //Variables used in //multiple thread loops int a[],b[],c[]; //Shared variables float data[16]; } thread_loop { b[tid] = data[threadidx.x]/2; a[tid] = 0; } //Variable outside of thread loop while(a[0] < 16) { thread_loop { for(k=0,k<64,k++) { c[tid] += k*b[tid]; } } thread_loop { a[tid]++; } } thread_loop { data[threadidx.x] = c[tid]; } Figure 5: Code before and after replicating variables. when there a no blocks left to execute. When leaving the second barrier, the host thread returns to the host code, and the worker threads enter the first barrier again. The blocks can be assigned either statically or dynamically to the worker threads. When scheduled statically, each worker thread gets a set of blocks, at most one block larger than the set of any other block, and executes it. On dynamic scheduling each worker thread acquires the next block to executed after it has finished executing one block until there are no blocks left Performance To test the performance of MCUDA, implementations of algorithms which have proven to be very efficient on GPUs (Matrix multiplication, Coulombic Potential, Magnetic Resonance Imaging) were compared to their highly optimized CPU counterparts. The results (cf. Figure 6) show, that the ported code is at least half as fast, therefore giving a reasonable performance for not specially tuned code. The MCUDA implementations also scale very well, nearly linear, with the number of CPU cores, at least for a small number of cores. This should be beneficial for future CPUs with more cores. Dynamic block scheduling is marginal faster than the static method and is expected to give more distinct 51
55 8 Figure 6: Performance of MCUDA with different numbers of worker threads and scheduling techniques. [12] improvements for a considerably larger number of threads Optimizations The same way CUDA kernels are typically fine-tuned to perform better on specific GPU hardware, the kernels can be optimized for the CPU architecture (e. g. varying the number of kernels per block, loop unrolling etc.). Experiments showed, that the optimal optimization points for GPU and CPU are very different. For example loop unrolling boosts CUDA implementations, since branches cost o lot of time on GPUs, on CPUs however loop unrolling prevents the compiler from using SSE or MMX instructions. Therefore tuning the CUDA code for CPUs before portation can improve the performance. Also a liveness analysis on the variables before replicating them, could help to improve the amount of memory used, by only buffering those variables which have a live value a the end of the thread loop Limitations The MCUDA framework can only translate the kernel functions automatically, the host code has to be ported manually. For kernel invocation however, MCUDA uses the CUDA syntax and the basic CUDA memory management functions are also reimplemented. If the host code only uses these, no further portation has to be done. Also, with the introduction of OpenCL, MCUDA itself became obsolete, since there exist OpenCL implementations for CPUs. Still, it should be possible to use the techniques used by MCUDA for the OpenCL CPU implementations. 52
56 9 4 OpenCL OpenCL is a framework, whose specification was released in 2008 by the Khronos Group, to write programs that can execute on many different platforms, like GPUs,CPUs or even DSPs, and is not restricted to NVIDIA hardware like CUDA. However many aspects of OpenCLs code and architecture are quite similar to CUDA. 4.1 Architecture The OpenCL model (cf. Figure 7) specifies that there is one processor to coordinate the execution, the host, and one or more processors to execute the kernels, the devices. Like CUDA, kernels are executed multiple times in parallel as work-items. These are grouped in work-groups, the whole of all work groups is called NDRange. Figure 7: The OpenCL device model. [7] The OpenCL memory model consists of global memory and read-only constant memory, accessible by all work-groups, local memory restricted to its work-group, and work-item local private memory. In contrast to CUDA there is no texture memory specified, since OpenCL is designed not only to run on GPUs. [3] The host code is compiled by the corresponding compiler for the host, but since the implementation of the OpenCL API is platform specific, the kernel code is compiled during runtime. [2] One can easily see, that, apart from a few device specific features, the basic architecture of CUDA and OpenCL is very alike. 53
57 10 CUDA OpenCL thread work-item thread-block work-group grid NDRange local memory private memory shared memory local memory global memory global memory constant memory constant memory texture memory - Table 1: Comparison between CUDA and OpenCL terminology 4.2 Language extensions OpenCL is also an extension to standard C. It add qualifiers to define in which memory region a variable does reside in ( global, local, private and constant) and to mark kernel functions ( kernel). OpenCL also provides a API for memory management and kernel invocation, but since OpenCL supports a variety of different platforms the API has to offer functions that are more low-level than those in the CUDA API too. All of the device and kernel management the CUDA does implicitly, like managing the command cues to control the devices or compiling or managing kernels, which are objects in OpenCL and can not be used the same function-like way as in CUDA, has to be done explicitly in OpenCL, making the code a lot more verbose. This is also the reason kernel code should be put to separate file, since they are compiled from strings, making the code rather unreadable when directly embedded in the host code. [5] 5 CUDA to OpenCL 5.1 Code Portation As we can see, OpenCLs architecture and code is relatively similar to CUDA. Thus, porting the code is mainly replacing keywords and API functions [7][2]. Furthermore the additional setup procedures needed by OpenCL have to be added and kernel and host code have to be split into different files. However manually porting the code is a very tedious and time consuming work, so projects to automate the process were created Swan A first step into simplifying the portation of existing CUDA code to OpenCL is the Swan tool [5]. Code ported with Swan can be built for CUDA and OpenCL targets, making it easy to support and maintain multiple platforms. It consists of the two components swan and libswan. swan is a source-code processing tool for CUDA kernel sources. It takes the sources, which have to be in their own source files, does a source-to-source translation for OpenCL targets and then passes the code to the appropriate compiler. Because of the close similarities between CUDA C and OpenCL C, the source-to-source translation is done with a set of regular expressions and does not need a complex C parser. The result is a C header file containing the compiled source and a entry-point function to invoke the kernel, taking the kernel launch parameters as additional parameters. 54
58 11 libswan provides functions similar to those of the CUDA API (e. g. for memory management), and is implemented for both CUDA and OpenCL. The correct implementation is chosen at compile time. To port existing CUDA programs (cf. Figure 8), each kernel is put into a separate source file and the corresponding header files are included in the host code. Then the kernel calls are replaced be entry-point functions from the header files. Lastly the CUDA API calls are replaced by the appropriate swan API calls. global void kernel(int *param) {... } void host() { int *param; int hparam = 42; //CUDA accepts int launch parameters int grid, block; //Allocate memory on the GPU cudamalloc((void**)¶m,sizeof(int)); cudamemcpy(param,&hparam,sizeof(int), cudamemcpyhosttodevice); #include "kernel.kh" void host() { int *param; int hparam = 42; //Swan needs vectors which are filled //using swandecompose dim3 grid, block; //Allocate memory on the GPU param = (int*) swanmalloc(sizeof(int)); swanmemcpyhtod(&hparam,param,sizeof(int)); //Launch the kernel swandecompose(&grid,&block,4,16); //Launch the kernel grid=4; block=16; kernel(grid,block,0,param);... } kernel<<<grid,block>>>(param);... //Clean up cudafree(param); } //Clean up swanfree(param); Figure 8: Porting CUDA to Swan [5] The resulting code can now be used on both CUDA and OpenCL platforms, but since it s neither CUDA nor OpenCL code, Swan is more an additional abstraction layer than a source-to-source translator. Close resemblance to CUDA C and hiding of the OpenCL setup procedures make Swan quite easy to use for CUDA programmers, but even if the translation of the kernels is done automatically, porting most of the host code by hand and missing equivalents of some CUDA API functions mean a lot of work, especially for larger programs. The performance of the OpenCL version is about 50% compared to the CUDA version on the same hardware. Examination of the PTX code produced by the different compilers showed, that the OpenCL compiler produced a lot less efficient code CU2CL A project which aims to fully automate the code translation process is the CU2CL framework [8]. It is a plugin for the Clang compiler framework and already provides automatic translation for the most commonly used parts of the CUDA API. Clang was chosen since it already provides all the tools needed for code analysis and rewriting, therefore requiring few additional code and reducing the possibility of 55
59 12 errors. CU2CL recursively walks and analyzes the Abstract Syntax Tree generated from the original source by Clang and then does a string-based rewrite directly on the source file, not the AST, using Clangs rewriting mechanism. Since most of the code of a CUDA program is normal C code, and both CUDA and OpenCL are C based, this approach only touches the CUDA specific parts of the code. This leaves the original structure, especially comments, intact and simplifies maintainability and further development on the generated OpenCL code. Rewriting itself is based on common patterns. Reoccurring types of rewrites (e. g. CUDA API calls, see Figure 9) are generalized, making the framework more modular and easy to expand. // CUDA float *newdevptr;... cudamalloc((void **) &newdevptr, size); // OpenCL cl_mem newdevptr;... newdevptr = clcreatebuffer(clcontext, CL_MEM_READ_WRITE, size, NULL, NULL); Figure 9: Rewriting a common CUDA API call [8]. To completely translate the CUDA program some #include directives must also be rewritten. Because #inlcudes are not present in the AST, CU2CL registers a callback with the Clang preprocessor which then provides all necessary information for rewriting them. CUDA specific headers are removed entirely, system headers, like stdio.h are removed from the OpenCL kernel files, since they cannot be used there. Included CUDA sources are split into two new files for host and device code and the #includes are rewritten to point to the host code files, device code is not included since it is only used during runtime. CU2CL already supports the most commonly used CUDA API calls, therefore only very few to no lines have to be ported manually after the translation process. These manual changes are quite simple and can easily be added in the future through CU2CLs modular architecture. On the performance side, the automatically translated code performs just as well as its manually ported counterpart. In comparison to the original CUDA code it again performs noticeably worse, which again is explained by the NVIDIA OpenCL compiler, doing not as many optimizations as the CUDA compiler. 5.2 Performance Portability After a CUDA program is ported over to OpenCL, the next question one may ask is: How does the OpenCL implementation perform in comparison to the CUDA implementation? Thus, performance comparisons between those implementations were made on the same platform, to keep the comparison fair, as well as on platforms from different vendors, which is one of the main reasons for porting programs over in the first place. Since the code ported by methods described above perform almost the same [8][5], analyzing the manually ported versions should be enough to draw reasonable conclusions. 56
60 Performance of CUDA and OpenCL on the same platform In [7] several algorithms were ported and compared. From the NVIDIA GPU Computing SDK the bandwidthtest, which just uses API call and does no additional computation, and the matrixmul benchmarks were chosen. Also selected were the Coulombic Potential (CP) and the Magnetic Resonance Imaging Q and FHD (MRH-Q and MRI-FHD) benchmarks from the Parboil benchmark suite [4], because their memory access pattern are very well-suited for GPUs, so their kernels should be able to run without having to wait for memory accesses. Figure 10: Performance comparison between CUDA and OpenCL [7]. As Figure 10 shows, the OpenCL versions are a lot slower than the CUDA versions. Only the bandwidthtests execution time is about the same, which shows that the additional execution time does not come from the different API calls but from the execution of the kernels. Further this narrows the problem down to the different compilers used to build the kernels. Analyzing the PTX code generated by both compilers showed, that the CUDA compiler applies several optimizations to the code while the OpenCL compiler by default does not. The most important optimizations the CUDA compiler uses are loop unrolling, to reduce the number of branches and index calculations, common subexpression elimination, where reoccurring expressions are replaced by a variable holding the computed value, and loop invariant code motion, which moves calculations outside loops if they are unchanged by the loop. Additionally the OpenCL compiler tends to group similar instructions, whereas the CUDA compiler interleaves memory access and calculation instructions, allowing to overlap I/O and computation through pipelining [2]. The CUDA compiler also makes use of NVIDIA device specific instructions, such as mad and rsqrt. Manually applying these to the PTX code puts the performance of the OpenCL programs within close range of the CUDA ones (cf. Figure 11). Nevertheless, the OpenCL compiler supports optimizations for floating point calculations, invoked by the -cl-fast-relaxed-math option. The performance of the programs compiled with this 57
61 14 option can also be seen in Figure 11. With optimizations turned on, some of the OpenCL variants also come within range of CUDA, but the OpenCL compilers optimizations are still not as mature and complete, which explains the small differences in performance. The performance of the CP algorithm comes from the OpenCL compiler not using NVIDIAs native rsqrt instruction, which saves a lot of time consuming division operations in this case. OpenCL does, in fact, support these native instructions by using the native prefix before certain functions, but then the implementation and therefore the accuracy of the calculation becomes platform specific [6]. This leads to another drawback of the -cl-fast-relaxed-math option: When used, the precision of floating point calculations are not IEEE 754 compliant anymore.[6] Figure 11: Performance of optimized OpenCL code. [7] Performance of ported OpenCL code on other platforms. In [7] the ported CUDA code was also tested in different platforms. It was run on an Intel Core i7 with 4 cores, a NVIDIA Tesla C1060 and a Radeon HD 5870, which, in theory, has much higher peak performance (2720 Gflop/s on Radeon to 933 Gflop/s on Tesla). NVIDIA s OpenCL compiler was used for Tesla and AMD s OpenCL implementations was used for both Radeon and CPU. On all platforms both the automatically optimized and unoptimized versions were tested, the results can be seen in Figure 12 Because the Benchmarks make extensive use of data parallelism and regular memory access patterns, which GPUs are optimized for, the CPU performs a lot worse than the GPUs. Also the -cl-fast-relaxed-math parameter doesn t affect the performance on the Intel and AMD platform, which suggests that the optimizations do not work with the AMD compiler yet. Comparing the unoptimized benchmarks shows, that it depends on the application whether the Tesla or the Radeon GPU perform better. 58
62 15 Figure 12: Performance of OpenCL on different platforms. [7] To analyze the sustained performance, the benchmarks were run with different workgroup sizes. The result for the MRI-FHD is shown in Figure 13. The normalized execution time is the kernel execution time by the best kernel execution time for the corresponding hardware. This shows that the optimal parameters for each algorithm still depend on the platform. The work-group sizes have to be large enough to hide I/O, but not too large since hardware resources are limited. Additionally, in case of GPUs the work-group sizes should be a multiple of the warp sizes (wavefront sizes for AMD) supported by the hardware, because that is the number of thread that are executed in parallel on the hardware and therefore the only way to fully utilize the GPU Optimizations As we can see, even if OpenCL is designed with code portability in mind, OpenCL can perform just as well as CUDA. The major problem are the current implementations of the OpenCL compiler, which do few to no optimizations. But since OpenCL is quite young in comparison to CUDA, it is to be expected that the implementations will get better in the next few years. Still, as the comparison of the sustained performance shows, the code has to be tuned to reach to optimal performance an each hardware platform. One approach to automatically do this hardware dependent optimizations is called auto-tuning. The idea of auto-tuning is to have a large number of code variants for the ported program and the empirically select the one that performs best on the given hardware. The auto-tuning infrastructure typically consists of code generator, which produces the different code variants based on templates by applying different parameters and optimization techniques, and a heuristic search engine, which tries to find the best variant out of the previously generated ones. The search engine itself limits its search space, if possible, by using knowledge of the target hardware and previously evaluated results. [2] The major problem with auto- 59
63 16 Figure 13: Normalized performance for different work-group sizes. [7] tuning is, that generating the templates automatically is hard, since the parameters and parameter spaces are dependent on the algorithm that is to be tuned, and have to be selected carefully to not affect the algorithms correctness. Another possibility is to reduce the additional setup time needed by OpenCL. This can be done by compiling the kernels only once on deployment instead of every time when the program is executed, using OpenCLs clgetprograminfo to get the intermediate code and saving it to disk. This especially saves time when there are a lot of different kernels or when applied to a library. [2] 6 Future As we can see, the greatest performance losses are induced by the OpenCL compilers. Since OpenCL is relatively young and it is being actively developed at the moment, it is to be expected, that OpenCL compilers will mature further. Modern optimization techniques and tuning for the target hardware are likely to be implemented. Additionally some improvements on the translation frameworks can be done. For CU2CL optimizing the generated code for the target platform is planned [8] and first experiments with auto-tuning have already be conducted [2]. On the mere portation side, most of the work is done as CU2CL showed. There is still a bit of the CUDA API left to be supported, but the groundwork to easily add additional transformations has been done and implementing them is planned for the near future. Another interesting project, but not in the scope of this work, is Ocelot [1]. It does not translate or even touch the original source code, it rather implements an alternative CUDA driver API which can 60
64 17 execute the PTX code generated by the NVIDIA compiler. Thus it can even by used on programs where the original source code is not available. The project is already implemented for quite a few backends and is still in active development. 7 Conclusion As we can see, porting CUDA code to other platforms is no big problem anymore. Especially porting to OpenCL is rather simple, since its principles and architecture are very alike to CUDA. Porting the code manually is possible, but very time consuming. Frameworks for automatic code portation have been implemented and are working, but still need a certain amount of manual work in the most cases. However the step to a fully automatic translation is mainly supporting the remaining parts of the CUDA API. The portation however only works on the functional side as of now. The ported code performs very poor on other platforms. It can be tuned to perform as well a CUDA, but currently not automatically. Until this is the case, it is unlikely that code portation from CUDA will play a big role in real world applications. A lot of work is to be done in both improving the compilers and adding optimizations to the portation frameworks. 61
65 18 References [1] Gregory Diamos, Andrew Kerr & Mukil Kesavan (2009): Translating GPU Binaries to Tiered SIMD Architectures with Ocelot. Technical Report. Available at translating-gpu-binaries-to-tiered-many-core-architectures-with-ocelot. [2] Peng Du, Rick Weber, Piotr Luszczek, Stanimire Tomov, Gregory Peterson & Jack Dongarra (2010): From CUDA to OpenCL: Towards a Performance-portable Solution for Multi-platform GPU Programming. Technical Report, Department of Computer Science, UTK, Knoxville Tennessee. Available at library/2010.html. [3] Benedict Gaster, Lee Howes, David R. Kaeli, Perhaad Mistry & Dana Schaa (2011): Heterogeneous Computing with OpenCL. Elsevier Science. [4] The IMPACT Research Group: Parboil Benchmark suite. Available at illinois.edu/parboil.aspx. [5] Matt J. Harvey & Gianni De Fabritiis (2011): Swan: A tool for porting CUDA programs to OpenCL. Computer Physics Communications 182(4), pp Available at db/journals/cphysics/cphysics182.html#harveyf11. [6] The Khronos Group Inc.: OpenCL 1.0 Reference Pages. Available at registry/cl/sdk/1.0/docs/man/xhtml/. [7] Kazuhiko Komatsu, Katsuto Sato, Yusuke Arai, Kentaro Koyama, Hiroyuki Takizawa & Hiroaki Kobayashi (2010): Evaluating Performance and Portability of OpenCL Programs. In: The Fifth International Workshop on Automatic Performance Tuning. Available at workshops-iwapt/komatsu-sato-arai-koyama-takizawa-kobayashi.pdf. [8] Gabriel Martinez, Mark Gardner & Wu-chun Feng (2011): CU2CL: A CUDA-to-OpenCL Translator for Multi- and Many-Core Architectures. In: Proceedings of the 2011 IEEE 17th International Conference on Parallel and Distributed Systems, ICPADS 11, IEEE Computer Society, Washington, DC, USA, pp , doi: /icpads Available at [9] NVIDIA (2012): CUDA C Programming Guide 4.2. Available at nvidia.com/compute/devzone/docs/html/c/doc/cuda_c_programming_guide.pdf. [10] NVIDIA (2012): Parallel Thread Execution ISA 3.1. Available at ptx_isa_3.1.pdf. [11] Jason Sanders & Edward Kandrot (2010): CUDA by Example: An Introduction to General-Purpose GPU Programming, 1 edition. Addison-Wesley Professional. [12] John Stratton, Sam Stone & Wen mei Hwu (2008): MCUDA: An Efficient Implementation of CUDA Kernels on Multi-cores. Technical Report IMPACT-08-01, University of Illinois at Urbana-Champaign. Available at 62
66 OpenACC and the PGI Compiler Dimitri Blatner University of Kaiserslautern, Embedded Systems Group d blatne@cs.uni-kl.de Abstract In the field of High Performance Computing (HPC) there is a big movement towards hybrid systems, consisting of accelerators such as GPGPUs (General Purpose Graphic Processor Units) that share computations with CPUs. In fact, future systems become more and more integrated for efficiency reasons. Applications for these systems need to be programmed in an effective and easy way, that means understandable and fast and abstracting from technical conditions. Therefore the following pages present the OpenACC API (Application Program Interface) targeting the acceleration of programs via compiler directives and providing easy mechanisms for both accelerators and many/multi-core processors. Also the PGI compiler for OpenACC are presented, which is one of the first OpenACC compilers and widely used in the HPC (High Performance Computing) world. 1 Introduction Since the beginning of General Purpose GPUs (Graphic Processor Units) the market for these hybrid systems has increased very fast. Now they play an important role in the world of HPC, not only for workstation or desktop PCs. The reasons are simple. They can process more parallel computations with 500 and more cores in modern GPUs compared to up to 8 physical cores in todays CPUs, they have a fast GPU memory and they also have a better performance per watt ratio. In fact, power consumption is one of the biggest problems today when maintaining HPC clusters and computer centers. The first GPGPU cards came from Nvidia in mid 2007, which currently is also the market leader. These cards are based on GPU technology, but are dedicated for acceleration of massively parallel computations. Today, more and more of the worlds fastest supercomputers in the Top500 list 1 contain GPGPUs to speed up computations, mainly from Nvidia 2. The upcoming Nvidia GPGPU 3 has almost 2500 small ALUs 4 with about 1.17 TFLOPS 5 peak performance in double precision. Hybrid systems usually are not limited to GPGPUs as coprocessors or accelerator cards for certain or special arithmetic operations or other complex instructions. Now, programmers have the quite complex task of producing code that can exploit the additional speed of different accelerator cards. Accelerator cards usually can not access the application memory directly, data copying to the accelerators memory via the CPU is very time consuming and the main challenge for high performance applications. Since different accelerators may have different instruction sets or computation possibilities, a deep knowledge 1 Top500 list, June 2012: (see Rank 5, 6, 10, 14, etc.) 2 More information on Tesla GPGPUs at 3 Specification of the Tesla K20 GPGPU, see 4 Arithmetic Logic Unit, see 5 Tera (10 12 ) Floating Point Operations Per Second 63
67 2 of those instructions and used hardware is often required in order to develop applications for them. In case of GPGPUs the instructions set is often limited to quite fundamental arithmetic operations on scalars and vectors. Therefore a CPU is still needed for the main application logic. Recently, Intel has announced a new coprocessor 6 based on their Xeon server CPUs with about 62 cores and 1 TFLOPS peak performance in double precision understanding the x86 instruction set. The HPC and multimedia electronic markets (mobile phones, tablets, etc.) shows that there is a trend towards more and more integrated logic circuits and acceleration units in the future for power and performance reasons. This trend can be seen in the newer AMD APUs 7 and Intel CPUs 8 and most of todays smart phones. With Nvidias GPGPUs also the Compute Unified Device Architecture 9 (CUDA) [24] were introduced providing a toolkit containing libraries, development tools, language extensions and compiler directives. Although CUDA delivers good performance and is widely used in HPC based and even consumer systems, the effort writing CUDA applications is very high and the applications run only cards from Nvidia. This is one big reason while a year later the open standard Open Compute Language (OpenCL) [12] was published by the Khronos Group 10 providing a cross-platform development framework supporting heterogeneous hardware. OpenCL is cross-platform compatible and has a rich feature set with many in-built functions, but a slower performance than CUDA due to a higher abstraction of specific hardware. It turns out that programming with OpenCL is also quite challenging, since the abstraction level needed for easier programming is not very high. This leads to the idea of OpenACC which this paper will present. The rest of the paper is structured as follows: Section 2 Related Work presents the references used in this work and additional approaches related to OpenACC. Section 3 Hybrid Architectures gives an overview about hybrid architectures and their limits as a foundation to understand current research efforts establishing new standards for future systems. Section 4 OpenACC presents the OpenACC standard in detail with examples, compiler techniques and a performance comparison. Section 5 PGI Accelerator OpenACC Compiler presents the PGI Accelerator compiler for OpenACC as well as some compiler techniques and a performance analysis. Section 6 HSA shows a recently introduced formation for developing standards for heterogeneous architectures. Section 7 Conclusions summarizes the information from this paper and gives a concluding evaluation. 2 Related Work Although this paper presents only OpenACC standard and PGI Accelerator Compiler, other works have to be considered to give a good overview about the current state of the art. This section presents some common or alternative approaches for multicore and accelerator programming, namely OpenMP, Open- MPC, hicuda and some high -level aspects of OpenCL. Afterwards the papers used in this work for 6 Intel Xeon Phi, see 7 Accelerated processing unit, see 8 Intel Quick Sync Video, see 9 Article What is CUDA at 10 Consortium for open IT standards with leading industry members, see 64
68 3 OpenACC and the PGI compiler are presented. 2.1 OpenMP OpenMP [8, 1, 7] is currently the de facto standard programming model for multicore and SMP systems in industry. It was developed by a group of hardware and software manufacturers with Oracle, Intel, Hewlett-Packard and IBM. The programming model extends the languages C/C++ and Fortran by compiler directives, #pragma omp... for C/C++ and!$omp... for Fortran. The main focus of OpenMP is to produce highly portable code, that keeps both parallel programming and parallelization of existing sequential code as simple as possible for the programmer. This makes it a cross-platform solution, since it does not depend on a specific compiler or hardware. OpenMP implements a fork-join based concept of threads, forking the main application thread into as much as needed sub-threads that work in parallel whenever the corresponding compiler directive is given. At the end of a parallel region the subthreads are joined together. OpenMP also supports the concept of tasks explicitly by compiler directives, meaning that it can define code blocks which are called frequently and can be executed independently from the rest of the code with the use of a dynamic dispatcher and a task queue. The basic OpenMP programming model neither supports heterogeneous multicore systems nor the usage of accelerators. This is where OpenACC wants to score. 2.2 OpenCL OpenCL [18, 12] defines itself as a programming framework for heterogeneous compute resources, see Figure 1. As mentioned in the introduction it was published by the Khronos Group with Nvidia as the chair and Apple as specification editor. The first implementation of OpenCL was within the MacOS 10.6 operating system.,!-&'./)0*1)%'$#"%&'2"*3*45' 1%"6#"+(4$%'*4$"%(&%&' A+%"5*45' 840%"&%$0*#4' 7!-&' 84$"%(&*45)9'5%4%"()' 1/"1#&%'2(0(:1("())%)' $#+1/0*45'./)0*: 1"#$%&&#"' 1"#5"(++*45' '%?5?'@1%4.!' B%0%"#5%4%#/&',#+1/0*45' 7"(1;*$&' <!8&'(42' =;(2*45' Figure 1: The application field of OpenCL. [12] OpenCL mainly is an huge API which makes it very portable. The memory architecture is hierarchical and very similar to the one of CUDA except for some differences in terminology. It was build around existing GPU architectures today. The memory management is explicit, accelerator functions are also called kernels. OpenCL applications are compiled in two phases, first into an Intermediate Representation (IR) at compile time and second into binary code during runtime, which results in a higher 65
69 4 initialization time. Nevertheless OpenCL is more abstract (or in a sense high -level), because it allows to generate code for completely different accelerator architectures, unlike CUDA at the moment. With version 1.2 of OpenCL it is possible to treat embedded kernels, e. g. implemented on FPGAs, as normal OpenCL kernels 11 without requiring knowledge of how to invoke the embedded kernels. This demonstrates the power or the possibility of abstract programming models with OpenCL as an example. 2.3 OpenMPC OpenMPC (OpenMP Extended for CUDA) [21] 12 shows an approach to use the OpenMP programming model along with CUDA accelerators, but differs slightly in the execution model [6]. Therefore additional compiler directives and environment variables help the compiler to split the application code into host and accelerator code. It provides a compilation system and an API that highly abstracts from the CUDA programming model. The steps of the compilation flow are showed in Figure 2. Figure 2: OpenMPC compilation flow. The (A) marks additional compile passes for automatic code tuning. [21] Additionally, OpenMPC provides several optimization tools, e. g. for memory management, and provides a so called search space pruner tool that analyzes the given OpenMP application and suggests possible optimization settings for CUDA related parameters. Figure 3 shows the main compiler directives of OpenMPC. With clauses the programmer can finetune and optimize the code, they are described in detail in [21]. #pragma cuda gpurun [clause [,] clause ]...] #pragma cuda cpurun [clause [,] clause ]...] #pragma cuda nogpurun #pragma cuda ainfo procname(pname) kernelid(kid) Figure 3: OpenMPC compiler directives. [21] The evaluation shows that OpenMPC applications have over 80 percent of the performance of handwritten CUDA applications, tested with different common algorithms. This is a very good performance result with regards to the high abstraction level of this programming model Also available as an online version, see 66
70 5 2.4 hicuda hicuda [14] is another approach similar to OpenMPCs for a high-level abstraction of the CUDA programming model. It provides compiler directives together with a so called directive handler and a sourceto-source compiler for CUDA code generation. The directives allow many customization options via clauses like in OpenMPC or OpenMP for data partitioning, memory management and the definition of kernel/host parts and loops. These clauses are abbreviations for CUDA related language constructs and preferences. The compilation flow is showed in Figure 4. Figure 4: hicuda compilation toolchain. [14] First, the C/C++ code, annotated with compiler directives, is preprocessed by the directive handler, so accelerator functions and host functions are split and CUDA related preferences are set. Afterwards the source-to-source compiler translates the intermediate code to valid CUDA source code, that is later compiled by the native CUDA C compiler tool chain. During these steps no special analyzation or optimization process is run. In other terms, hicuda simply provides abbreviations to CUDA language constructs via C/C++ compiler directives, so that the programmer does not write CUDA code directly. It does not free the programmer from the CUDA programming model, but reduces many lines of code. Programmers still have to know how data should be moved between the host and the accelerator, which code has to form the kernel and so on. The evaluation of hicuda was done on an old GeForce 8800GT graphics card with CUDA version 1.1 compatibility with different standard parallelization algorithms. This, of course, is not representative for the whole potential of hicuda, but it shows that a speed up similar to hand-written CUDA code is possible. At the end, it also is a very flexible approach that can benefit from further improvements of the native CUDA compiler and additionally gives the freedom to implement own compiler optimizations. 2.5 OpenMP for Accelerators OpenMP for Accelerators [6] extends the OpenMP programming model by new compiler directives. The programming model and the directives are very similar to the ones of OpenACC providing clauses for memory management and other customizations. It targets the ease of programming accelerating applications without altering existing code. Applications may still run without an accelerator. The additional compiler directives identify regions that can be offloaded to the accelerator without being restricted to specific accelerators. This implies a very portable code as well as an easy and flexible mechanism to accelerate existing code. The main work has to be done by the compiler, since OpenMP for Accelerators does not say how exactly to implement the directives. The evaluation of the accelerator supported code was done with a none specified compiler and shows a speed up comparable to a pure OpenMP implementation, when no additional accelerator is used. It 67
71 6 states that PGI s CUDA compiler (see Section 5) achieves 5 times the speed with hand-written CUDA code, which is of course not the target of this approach. 2.6 Papers used in this work A Comparative Study of OpenACC Implementations [25] accull: An OpenACC Implementation with CUDA and OpenCL Support [27] Directive-based Programming for GPUs: A Comparative Study [26] Experiences with High-Level Programming Directives for Porting Applications to GPUs [16] Moving Heterogeneous GPU Computing into the Mainstream with Directive-Based, High-Level Programming Models (Position Paper) [22] OpenACC First Experiences with Real-World Applications [28] OpenACC Implementations Comparison [23] The OpenACC Application Programming Interface [4] Using Compiler Directives for Accelerating CFD Applications on GPUs [17] Generalized parallelization methodology for heterogeneous HPC platforms [20] Performance of FORTRAN and C GPU Extensions for a Benchmark Suite of Fourier Pseudospectral Algorithms [9] Towards high performance and usability programming model for heterogeneous HPC platforms [19] PGI Accelerator Compilers OpenACC Getting Started Guide [13] PGI Accelerator Programming Model for Fortran & C [3] Porting and scaling OpenACC applications on massively-parallel, GPU-accelerated supercomputers [15] 3 Hybrid Architectures Most computer systems, whether personal or high performance, underlay a hybrid architecture consisting of one or more CPUs and a coprocessor with own dedicated memory. It can be compared to hybrid fuel/electro motors in newer cars. The opposite is an architecture consisting of a single type of processors in a single or clustered system, e. g. homogeneous SMP clusters. Figure 5 shows an overview of a single computer system based on a hybrid architeture. In fact, almost all systems are based on this architecture, from personal computers using a CUDA/OpenCL compatible graphic card to high performance clusters like the Cray XK7 13 using AMD Opteron processors along with Nvidia Tesla GPGPUs as coprocessors. In this context people also talk about heterogeneous computing, because the computation of an application is done by different architectures in collaboration. Figure 5 also shows the great bottle neck of the architecture, the connection between CPU and accelerator. Not only data is transferred via the PCIe-2 connection, but also all control information. Therefore, one has to focus on minimizing data transfers to the accelerator, using asynchronous communication and keeping as much data as long as possible resident in the accelerator s memory. The asynchronous communication is very important, so that the CPU and the accelerator may continue their computation while in parallel data is transferred between them. The communication is typically implemented via the DMA controller used also for writing to external storage devices without having the CPU to interfere. The main reason causing this bottleneck is the existence of two separate memories for the CPU and the accelerator, because a complete shared memory is very cost expensive. 13 Specification of the Cray XK7 system, see 68
72 7 Main Memory 32 GB ECC DDR3 Acc. Memory 5GB ECC GDDR5 ~ 42 GB/s ~ 200 GB/s CPU ~ 150 GFLOPS PCIe-2 8 GB/s Accelerator ~ 1.17 TFLOPS Figure 5: Overview of a single hybrid computer architecture found in most systems today with example performance values. It can easily be observed that hybrid architectures are a short-lived solution as long as the communication between the CPU and the accelerator is so limited. Nevertheless, we can already see a great change in future architectures that is accompanied by a change in programming paradigms. Hence, there is a need for a flexible and adaptable way of programming highly parallel applications for various system architectures [19]. As mentioned in the introduction, a more integrated architecture is also the trend in electronics for tablet PCs and mobile phones making the traditional hybrid architecture obsolete. 4 OpenACC At the end of 2011, the OpenACC group was founded by CAPS Enterprise, Cray Inc., The Portland Group Inc. and Nvidia 14. They developed the standard in cooperation, where all companies but Nvidia provide compilers for OpenACC (more in Section 5.2 Alternative Compiler). Then, in november 2011, the OpenACC API specification version 1.0 [4] was released, based on the popular OpenMP programming model for multicore and SMP architectures. OpenACC is developed for acceleration of existing applications by offloading parts of the code to an accelerator device, e. g. a GPGPU, being portable and platform independent. The future idea is to merge OpenMP into OpenACC having one standard for heterogeneous architectures utilizing both CPUs and accelerators. This approach also reduces the very cost intensive development time for heavy parallel applications, see Figure 6. The paper [20] gives an overview over todays technology and programming methodology for hybrid or heterogeneous architectures, including OpenACC. Although OpenACC is very abstract, the paper states that OpenACC orientates on the current technology without having a generalized sight on hybrid or heterogeneous architectures and shows its limitations among other programming models. In their opinion, the division of the code into host code and offloaded accelerator is similar to CUDA that does not allow the host to support the accelerator by doing some of the accelerators computations, but instead 14 About OpenACC, see 69
73 8 just let the host manage the control flow. Therefore, the paper tries to find a more generalized view respectively methodology for programming different architectures exploiting both the multicore and accelerator performance. It suggests extensions to the OpenMP and OpenACC programming models for a better generalization/abstraction for future systems. Unfortunately, no concrete approaches for the implementation are proposed. The problem is that current hardware architectures already work in a specific way, so the offloading principle is the first step in the right direction. Since OpenMP and OpenACC are meant to be merged in the future, the standard develops in the idea of the paper. a) Serial (CPU) code 1 real(8)::a(m,n),b(n,m) 2 do i = 1,m 3 do j = 1,n 4 b(j,i) = a(i,j) 5 end do 6 end do b) ACC directive code 1 real(8)::a(m,n),b(n,m) 2!$acc region 3!$acc do 4 do i = 1,m 5!$acc do 6 do j = 1,n 7 b(j,i) = a(i,j) 8 end do 9 end do 10!$acc end region c) CUDA kernel 1 attributes(global) subroutine & mt_kernel(m,n,a,b) 2 real(8) :: a(m,n),b(n,m) 3 integer,parameter :: bsize = 16 4 j = (blockidx%x-1)*bsize + threadidx%x 5 i = (blockidx%y-1)*bsize + threadidx%y 6 b(j,i) = a(i,j) 7 end subroutine mt_kernel d) CUDA host code 1 real(8),device,allocatable,dimension(:,:) & :: a_dv,b_dv 2 integer,parameter :: bsize = 16 3 type(dim3) :: dgrid,dblock 4 allocate(a_dv(m,n),b_dv(n,m)) 5 a_dv = a!copy data to device 6 dblock = dim3(bsize,bsize,1) 7 dgrid = dim3(m/bsize,n/bsize,1) 8 call mt_kernel<<<dgrid,dblock>>> & (m,n,a_dv,b_dv) 9 b = b_dv!copy data back to host 10 deallocate(a_dv, b_dv) Figure 6: Comparison between OpenACC annotated and CUDA code. a) shows a matrix transposition example and b) the same with OpenACC directives. The CUDA code therefore is in c) and d). [17] Usually a programmer, writing CUDA [14, 24] or OpenCL [12], has to know and consider the underlying hardware used by his application and how it behaves, even though OpenCL offers a higher abstraction than CUDA. He also determines the parts of the code he needs to be accelerated, starts up and shuts down the accelerator, writes a CUDA/OpenCL kernel by hand considering memory allocation, memory copying, arranging input and output data the right way for fast computations and coalescing memory accesses and so on. Now, if just the problem size changes, sometimes the kernel code must also be changed to be compatible with the hardware. The programmer has to focus more on device-specific code instead of implementing algorithmic enhancements [27]. It is easy to see that this is not an optimal approach. Now, the question is how to effectively program applications for these systems. There typically exist three concepts as illustrated in Figure 7: (1) using libraries that are optimized for certain tasks, (2) using compiler directives that guide the compilers, and (3) using new language constructs that often produce the best performance, but need more time to be written. The first two concepts are more handy for the programmer. Programming libraries are often tailored to a problem, using optimized data structures and even considering architecture dependent hardware characteristics (for cross-platform compatibility). 70
74 9 Application Programming Libraries Compiler Directives Language Constructs easier to use faster Figure 7: Typical ways to improve the performance of an application. From the developers point of view, the focus can stay on the algorithm. Language constructs are widely used by CUDA and OpenCL, providing the possibilty to write more performant architecture specific code. Usually, this results in faster code, approximately 20 to 40 percent are common. Sometimes the speed up of hand-written code compared to compiler generated code is even zero or negative, because todays compilers become more and more powerful. CUDA and OpenCL both provide language constructs and programming libraries, where CUDA is technology specific and runs on Nvidia GPGPUs only. Both languages are quite hard to program, the code must be structured in special accelerator functions (usually called kernels) invoked by the main (or host) application. Although OpenCL has a high -level API, it does not add much comfort for programming. After writing some kernel functions, the code has to be tuned and optimized to gain a performance benefit. Now, if the underlying system changes due to an upgrade or if the application shall run on a different system, the code must usually be adapted, which is not always an easy task due to different CUDA compute capabilities on different hardware. Furthermore, debugging is one of the most challenging task for CUDA and OpenCL applications. Some alternative approaches to manage this difficulties are OpenMPC [21], hicuda [14] and OpenMP for Accelerators [6] as mentioned in Section 2. OpenACC provides compiler directives and library functions for the programming languages C/C++ and Fortran, very similar to the well known and widely used OpenMP API [1, 7] for Shared Memory Processor (SMP) systems. This approach is cross-platform compatible and may also result in a complete framework for heterogeneous systems in the future. The API is also portable, so called runtime routines can run in different environments in the presence as well as the absence of an accelerator [4]. OpenACC moves the acceleration and parallelization problems to library functions and the compiler, still giving programmers the ability to guide the compiler via directives. The compiler itself has to manage cache coherency, data movement and so on, as OpenACC requires them to be done implicitly. In real world scenarios, explicit guidance of the compiler via directives is necessary to achieve the best performance. The programmer uses OpenACC directives to mark compute intensive code regions, which are then offloaded to the accelerator, i. e. the the enclosed code is only run by one or more available accelerators. Only marked regions are accelerated. OpenACC distinguishes between several different regions, the most important ones are the parallel regions and kernels regions. Typically, parallel regions contain work-sharing loops, where each iteration of the loop computes a fixed piece of work and is (at most) 71
75 10 independent from the other iterations. Kernels regions execute the code region as a kernel, i. e. typically one or more nested loops that are divided into domains and are executed by N threads in any order in parallel. In CUDA or OpenCL a single, but specific, function is called a kernel. OpenACC does not specify how the compiler has to partition the loops, so at the end the compiler is the responsible factor for the overall performance. In fact, it is still important that the programmer know the capabilities of the accelerator since current compilers do not automatically produce performant code. If the the host and the accelerator do not share the same memory address space, which is the case most of the time, the programmer has to make more precise compiler directives in order to reduce data transfers between the host and the accelerator. Compilers can not easily reduce the amount of data transfers by itself. Additionally, limited accelerator memory can prevent the compiler from offloading regions to the accelerator [4]. 4.1 Directives The following definitions are taken from the OpenACC API v1.0 specification [4]. Compiler directives are specified using the preprocessor keyword #pragma in C and C++ and the comment keyword!$, followed by acc and the directive name in Fortran, so the compiler knows it is an OpenACC directive. The syntax for C and C++ is defined as: #pragma acc directive-name [clause [[,] clause]...] new-line The squared brackets [ ] intend that the argument is optional. For Fortran the syntax is:!$acc directive-name [clause [[,] clause]...] There are 7 sorts of directives sorted by their functionality, namely (1) parallel, (2) kernels, (3) data / host_data, (4) loop, (5) cache, (6) declare and (7) update / wait. Every directive has a validity domain that is called a region and is usually indicated by a structured code block, e. g. a for-loop construct. (1) The most important construct is the parallel directive. The syntax therefore is: #pragma acc parallel [clause [[,] clause]...] new-line C/C++ structure block or!$acc parallel [clause [[,] clause]...] new-line Fortran structure block!$acc end parallel Whenever a parallel region is reached, groups of workers (also called gangs) are created. Then, each worker (that is a thread or a group of threads) starts the execution of the structured block. During the execution of the parallel region, the amount of gangs and workers are fixed. No other parallel region or kernels region can be executed inside a parallel region. The optional clause can be one of 72
76 11 if ( condition ) async [( scalar-integer-expression )] num gangs( scalar-integer-expression ) num workers( scalar-integer-expression ) vector length ( scalar-integer-expression ) reduction( operator:list ) copy( list ) copyin( list ) copyout( list ) create( list ) present( list ) present or copy( list ) present or copyin( list ) present or copyout( list ) present or create ( list ) deviceptr( list ) private( list ) firstprivate ( list ) Each parallel region has an implicit barrier at its end. After the parallel region, the execution continues after all gangs completed their computation. The async clause prevents this barrier, so that the host does not have to wait for the gangs to finish their evaluations (like the nowait clause in OpenMP) and can continue the execution asynchronously to the accelerators execution. This is useful if the host prepares new data to be processed on the accelerator. The if clause causes the compiler to create two copies of the parallel region, one on the host and one the accelerator. If the condition within the clause evaluates to true, the copy on the accelerator will be executed, otherwise the parallel region is executed on the host side. The num_gangs clause and analogously the num_workers clause define the amount of gangs and workers per gang in the parallel region, which can be an advantage for the exploration of all available accelerator compute cores. The clause vector_length simply defines the vector length for SIMD 15 instructions or automatically vectorized loops for each worker in a gang. The clause reduction is again the OpenACC counterpart for the OpenMP reduction clause. It is mostly used when at the end of a parallel computiation all part evaluations have to be processed into one result variable, e. g. summarizing partial sums or finding the maximum/minimum over all partial evaluations. The variables listed in the deviceptr clause indicate that the variables point to the devices memory, so that no data has to be copied from the host to the accelerator. This is useful when several functions are applied several times to the same data that is already is on the device. As for reduction, the private clause causes each gang to have an own copy of the specified variable like in OpenMP. This is typically used for index variables or others that do not have to be shared between different loop iterations or gangs, so that no overhead synchronization happens due to cache/memory coherency. 15 Single Instruction Multiple Data 73
77 12 The firstprivate clause is similar to the private clause except that each copy of the private variable in each gang is initialized with its last value on the host before reaching the parallel region. For the right behaviour of data movement between the host and the accelerator, several clauses give hints to the compiler. These clauses are very important to prevent unnecessary memory transfers as they are very time consuming and inhibit the execution on the accelerator. E. g. in the simple case of a matrix multiplication of a NxM with a MxN matrix with M >> N, the resulting matrix has the small size NxN, so just a small part of the accelerators memory has to be copied back to the host. The following clauses can be applied to variables, complete arrays or subarrays. The variable list inside the copy clause shows the compiler which data has to be copied from host to the accelerator memory (in case they do not share the same address space) before the execution of the parallel region begins. After completing the execution all the data is then copied back to the host. The clause variant copyin tells the compiler which data to copy only from the host to the accelerator memory before executing the parallel region and copyout tells analogously which data has only to be copied back to the host after the execution. Subarrays can be defined with the syntax: arr [ lower index : length ], where the lower array index has to be constant. The subarray arr [ 5 : n ] means the elements a[5], a[6],... a[n 1]. The usage of the create clause results in memory allocation for the specified variable list on the accelerator, but with the difference that no data will be copied from the host to the accelerator or vice versa. This can be used for storing intermediate results on the accelerator which the host do not need to know. The present clause indicates the variables or arrays, that are already available in the accelerators memory avoiding data movement, e. g. if the application defines some variables which point to or are part of larger dataset that has already been copied. The four clauses present_or_copy, present_or_copyin, present_or_copyout and present_or_create are used to first test whether the variables or arrays are already available in the accelerator memory and copy(in/out) or create them if they are not available. (2) The next important construct ist the kernels directive. Kernels regions are typically used for multiple nested loops. In the following only the C/C++ syntax will be used for clarity, the Fortran syntax is analogue to our first construct. #pragma acc kernels [clause [[,] clause]...] new-line structure block Whenever a kernels region is reached, the structure block is compiled and divided into a sequence of kernels that are executed in order. One kernel is simply a function that runs on OpenACC compatible accelerators just like kernels in OpenCL and CUDA, but with the property of being highly parallelizable. Usually, one nested loop is mapped to one kernel where the body of the loop maps to the body of the kernel function. Kernel regions allow the same clauses as parallel regions except for num_gangs, num_workers, vector_length, reduction and (first)private. The semantics of the clauses also remain the same. The number of gangs and workers may differ for each kernel. (3) The data construct can define variables, arrays or subarrays to be allocated on the device s memory. For this data region one can specify how the data is transferred (if it is desired), just like the data clauses for the parallel and kernels directives. The allocation is valid for the duration of the region 74
78 13 where the data directive is specified, not for the surrounding region. The directive may appear inside of other directives, commonly inside parallel or kernels regions, but can also enclose other directives. #pragma acc data/host data [clause [[,] clause]...] new-line structure block The host_data construct makes the address of the device s data available to the host and has only one possible clause use_device(list), where the variables used in list must be present on the accelerator. The host data construct may only appear within other regions. (4) The loop construct only applies to a for-loop (do-loop in Fortran) that must immediately follow the directive. It can precisely describe the way the loop shall be parallelized by its clauses. #pragma acc loop [clause [[,] clause]...] new-line for loop Supported clauses are collapse, gang, worker, vector, seq, independent, private and reduction. The collapse clause is used when the loop contains other loops and takes a natural number as an argument defining the number of nested loops to be associated with the loop region. The seq clause forces the loop to be processed sequentially, while the independent clause indicates that each iteration is independent. The clauses gang, worker and vector indicate whether the loop shall be parallelized among gangs, workers or vector operations. Some of the clauses may only appear in the context of a parallel or kernels regions, see [4] for more details. The loop construct can be combined with the parallel or kernels construct, #pragma acc parallel loop... respectively #pragma acc kernels loop.... (5) The cache construct may appear right before or within a loop. #pragma acc cache( list ) new-line Array elements or subarrays can specified to be kept in the highest cache level possible for processing the loop. (6) The declare construct is used at the declaration of variables or arrays (but not subarrays) allocating them on the devices memory for the duration of the region in which the declare directive appears in. #pragma acc declare declclause [[,] declclause]... new-line All data clauses are valid for this construct and the new device_resident clause that indicates variables only to be allocated in the device memory and not the host. So the host may not be able to access the variable. (7) There are two execution directives, namely the update and the wait constructs. The update construct may appear within an explicit or implicit data region causing to update variables or arrays on the host with the values from the device or vice versa. #pragma acc update clause [[,] clause]... new-line 75
79 14 The available clauses are host (specifying the variables/arrays to be updated on the host), device (specifying the variables/arrays to be updated on the device), if (updating only for a true condition) and async (updating the data asynchronously). The wait construct may appear anywhere in the application causing to wait for an asynchronous task to be finished until the next operations are executed. #pragma acc wait [( scalar-integer-expression )] new-line If an argument is specified with the wait directive, the application waits for an asynchronous operation with the same number specified. If no argument is specified, the wait directive causes the application to wait for all asynchronous activities to finish. 4.2 Library Routines and Environment Variables Beside compiler directives OpenACC provides the programmer with lots of library routines that are not mandatory. Programmers shall include openacc.h for C/C++ or openacc_lib.h respectively the openacc module for Fortran. When used, the application may be less portable in case systems do not support the OpenACC API. This can be bypassed with the use of the _OPENACC preprocessor statement at compile time. In the following the library functions are listed with a short description. The data type acc_device_ t defines a type for accelerator devices. For convenience only the C/C++ functions are considered: int acc get num devices ( acc device t ) ; - returns the number of attached devices of given accelerator type void acc set device type ( acc device t ) ; - sets the accelerator type to be used for parallel or kernels regions acc device t acc get device type ( void ) ; - returns the accelerator type used for next regions void acc set device num ( int, acc device t ) ; - sets which device to use for next regions int acc get device num ( acc device t ) ; - returns the number of the used device of given device type int acc async test ( int ) ; - tests if all asynchronous operations associated with the given number have finished execution int acc async test all ( ) ; - tests for completion of all asynchronous operations void acc async wait ( int ) ; - waits for completion of all asynchronous operations associated with the given number void acc async wait all ( ) ; - waits for completion of all asynchronous operations void acc init ( acc device t ) ; - initializes runtime for given accelerator type void acc shutdown ( acc device t ) ; - shuts down the connection to the given accelerator type int acc on device ( acc device t ) ; - tells whether it is running on a particular device for given type 76
80 15 void* acc malloc ( size t ) ; - allocates memory on the accelerator void acc free ( void* ) ; - frees memory on the accelerator Right now, there exist only two environment variables for OpenACC as follows: export ACC DEVICE TYPE=NVIDIA - defines the default accelerator type used when executing parallel or kernels regions, if the application is compiled to use multiple accelerator types export ACC DEVICE NUM=1 - defines the default device number to use when executing parallel or kernels regions 4.3 Limitations The papers [22] and [28] state that all the directive based approaches have more or less limitations as they where developed for hybrid host+accelerator architectures and not for clusters or distributed systems. For OpenACC these limitations are valid: (1) Only scalar reductions there is no way to define and express complex or complete custom reductions, e. g. for finding the maximum over all computation results and storing the index together with this maximum. (2) Critical sections or atomic operations (like for example in OpenMP) that must not be parallelized due to side effects and therefore have to be handled sequentially. OpenMPC implements this for a special case, when also a reduction pattern is defined. (3) No fine-grained synchronizations the programmer can define updates on variables or waits for asynchronous operations, but there is no way to control fine-grained synchronizations, e. g. within accelerated loops. It is not the best practice to have this kind of synchronization, but for certain problems it may sometimes not be possible to avoid it. (4) No function calls within accelerator regions since current accelerators do not support function calls within highly parallel computations, OpenACC (or at least OpenACC compilers) do not allow function calls inside parallelized regions if they can not be inlined. (5) Limited pointer operation support most instructions operate on array-based variables, but an extensive pointer arithmetic is not supported, e. g. calculating addresses for future computations. (6) Scalability only for host+accelerator architectures current research and industry computer systems are large scale distributed systems. To increase the scalability some sort of a MPI 16 capability is needed to integrate data distribution, synchronization and parallelization for these systems. (7) Untransparent debugging the abstraction of OpenACC implies hiding of information, so the developer do not have to see how his code is accelerated. When it comes to unwanted side effects, wrong results during computation or incorrectly translated directives, it is desired to get the right overview on how the directives are translated (if they are translated) and how the code is then executed. The compiler has to face this problem and generate appropriate information for the programmer, even for high dimensional problems. (8) No asynchronous data transfers data transfers between host and accelerator can not be asynchronous relative to each other, they just can be asynchronous to the computation of the host or accelerator. Some- 16 For more details, see 77
81 16 times it is wanted to have more than one transfer to or from the accelerator while it already processes data. (9) No automatic exploration of multiple accelerator cards OpenACC only allows to offload regions to a specific accelerator card. If more than one accelerator are attached, the programmer can not dynamically offload code to one of them, but instead have to define the accelerator he wants the next region to be offloaded to. Not a theoretical, but a practical limit is the dependency of OpenACC to good compilers. OpenACC hides the technical details and trusts the compiler to produce optimal code. Today, one may think that compilers are so powerful that they can optimize code in almost every case. This is maybe true for sequential applications, where compilers have been developed over 20 years, but for highly parallel applications this is not the case as the performance analysis in Section 5 shows. For parallel code the compilers have to be much more complex to achieve parallelism of non-trivial nested loops. Probably the biggest problem of almost all OpenACC compilers today are non-coalesced memory accesses, memory alignments and reduction of memory transfers. 5 PGI Accelerator OpenACC Compiler Before OpenACC was published, PGI had already a directive based programming model, namely PGI Accelerator [2, 13, 3] with an own compiler supporting both C and Fortran. With version 12 of the compiler the OpenACC directives were integrated and the programming model (version 1.3) was slightly changed to obtain full compatibility. Many OpenACC directives were already part of the PGI compiler with other names, e. g. the PGI region directive matches the OpenACC kernels directive [3]. In the following, some aspects of the PGI compiler are mentioned from [3]. Currently, not all available directives of OpenACC are implemented by PGI, i. e. the host data directive and three clauses for other directives [13]. Targeting other accelerator devices than used after acc shutdown ( acc device t ) ; is also not supported right now. On the other side, the PGI compiler supports two clauses mirror and reflected that are similar to the OpenACC present data clause, but offer more information to the compiler for automatic checking for data availability. It further extends OpenACC by the support for non-linear arrays in the accelerators memory. The binaries for invoking the compiler are pgcc and pgfortran for C respectively Fortran programs. OpenACC directives are enabled by adding the flags -acc or -ta=nvidia to the PGI compiler. The compiler can give additional feedback with the -Minfo flag and can also generate multiple versions of an application with the -fast flag for CUDA devices, one version for CUDA version 1.0 capability (and higher) and one for version 2.0 capability (and higher). In many benchmarks the PGI compilers show a very good performance compared to other compilers, see Section Compiler Techniques One speciality of the PGI Accelerator programming model is the implicit and automatic reduction detection by the compiler and implicit cache management. With the introduction of explicit OpenACC directives the PGI compiler now supports implicit and explicit reductions and cache behaviors [13]. The compiler supports offloading to an accelerator only for explicitly marked regions, no automatic 78
82 17 offloading is supported. On absence of accelerator directives the application code can be parallelized with the -mp option among CPU threads utilizing multicore architectures. As it is a standard in todays compilers and required by OpenACC, the PGI compiler supports implicit and explicit loop unrolling, parallelization and vectorization. Loops are also parallelized using loop tiling respectively strip-mining, i. e. loops are segmented into smaller chunks so that the loop chunks can be directly mapped to the accelerator hardware [25]. Concurrency is increased by using data-level (according to data dependencies) and task-level parallelism, generating tasks out of frequently called independent code blocks and executing as many of them concurrently as possible. Coalesced accesses Non-coalesced accesses Figure 8: Problem of non-coalesced memory accesses of most accelerator compilers. The PGI OpenACC compiler analyses the code in different stages and processes all the gained control data by a planner module [25]. How exactly the analysis and compile techniques are applied to the code is of course the business secret of PGI, but Section 5.3 shows that the PGI compiler has a lots improvement potential as other compilers can achieve much better results in special cases. The paper [17] states that one of the biggest problems of todays compilers are non-coalesced memory accesses. Figure 8 demonstrates the meaning of the problem. It requires to manipulate the code to achieve a beneficial aligning and if so, the applications performance usually increases dramatically. The compiler also does not support function calls within parallelized regions that can not be inlined. 79
83 Alternative Compiler CAPS HMPP 17 [11, 10, 25] provides a rich toolkit consisting of an own set of compiler directives like the PGI accelerator model, a runtime environment and compiler tools for C and Fortran. In HMPP-only applications, the programmer has to define so called codelets that are functions to be run on an accelerator, either generated by a tool or hand-written. This programming model of course requires more effort in development than pure directive based approaches like OpenACC or the PGI Accelerator model. CAPS HMPP is also part of the OpenACC standard and the new version supports now OpenACC directives. The Cray Compiling Environment 18 is a set of compilers for C/C++ and Fortran, libraries and additional tools for code analysis and profiling. The compilers are mainly used in Cray supercomputer systems, but are not limited to them. The compilers support OpenACC and OpenMP directives. Not all OpenACC directives and clauses are supported and the implementation is at a non-fixed stadium, i. e. it may change in the behavior in the future. The accull [25, 27] OpenACC compiler was developed by the HPC group at the university of La Laguna in Spain and is the first open OpenACC compiler with both CUDA and also OpenCL support, unlike other OpenACC compilers. It is a two-layer approach consisting of a source-to-source compiler and a runtime library called Frangollo. The compiler is based on their own YaCF compiler framework 19. It generates a hierarchical project structure with compile instructions ready for compilation instead of generating a binary file. This enables the possibility for further optimizations by skilled programmers. The OpenACC annotations are translated into calls to the runtime library, which itself generates OpenCL and CUDA structures based on analysis of the code. Currently, not all OpenACC directives and clauses are supported, but the most common ones (see [27]). The evaluation of the compiler was done with different server, workstation and desktop environments with Tesla GPGPUs, onboard GPUs and non-accelerated multicore CPUs. A molecular dynamic simulation and a mandelbrot computation set were benchmarked among other benchmarks [27]. AccULL surprises with a performance comparable to OpenMP on systems with no GPU or onboard graphics. Although it is not a commercial compiler, other performance comparisons between accull and the PGI and CAPS compilers show that accull do not need to hide behind the commercial compilers, see Section 5.3 for details. The compiler framework supports the integration of other commercial compilers for taking advantage of pre-existing features like vectorization and memory allocation techniques. 5.3 Benefits and Performance Analysis This section presents some performance comparisons between the PGI Accelerator compiler and others. The paper [25] (in their point of view) tried to create real world implementation scenarios that an average scientist or engineer would produce. The evaluation covers a simple matrix multiplication, the HotSport thermal simulation, non-linear DNA sequence alignment optimization and LU decomposition. Evaluated compiler environments were OpenMP, PGI Accelerator, hicuda and accull. The PGI compiler shows the best performance for simple matrix multiplication and DNA sequence alignment, but 17 See product website, 18 Cray Compiling Environment Release Overview and Installation Guide at 19 For more information see 80
84 19 scales badly for the HotSpot problem. No compiler were able to produce a faster code than natively compiled hand-written CUDA code. The papers [23] respectively [26] by the accull developers show a direct performance comparison between the CAPS, the PGI and the accull compiler for the LU decomposition, HotSpot, Path Finder and Matrix Multiplication problems. After the first release of the accull compiler, the evaluation shows a great increase in performance of accull, so that PGI is slower in the average. The CAPS compiler is the slowest one of all three and is about half as fast as the accull compiler in the tested benchmarks. Figure 9 shows the implementation and Figure 10 the result of the performance measurement. 1 #pragma acc data copyin( power [0: row col ], 2 _resultado [ 0: row col ]) copy ( _temp [ 0: row col ]) 3 { 4 for ( i = 0; i < num_iterations ; i++) { 5 #pragma acc kernels loop private ( r ) independent 6 for ( r = 0; r < row ; r++) { 7 #pragma acc loop private ( c ) independent 8 for ( c = 0; c < col ; c++) { 9 double delta ; // Start computation Figure 9: Annotated loops in the HotSpot problem using OpenACC directives. [23] Figure 10: Average performance of all tested benchmarks. [23] The paper [17] compares different directives for optimizing code with the PGI compiler version 11 and native CUDA code. It shows that the best directive based approach is about 30-40% slower than 81
85 20 native CUDA code for two different computing environments. It states that the achieved performance with GPUs are far away from being satisfactorily, but is acceptable due to fact that the development effort is very small compared to CUDA. The key to performance are directive adjustments minimizing the data transfers and memory accesses, but this often requires also a change in the code. Figure 11 shows one performance analysis of the directive based approach, which OpenACC in version 12 of the PGI compiler should also fulfill, compared to CUDA accelerated code a) Pleiades-GPU b) hyperwall-gpu Gflop/s Problem Size cuda, simple cuda, cached Problem Size acc directive host, simple host, blocked Figure 11: Performance comparison of a double precision matrix multiplication on both GPUs and CPUs. [17] The paper [16] took two existing CUDA applications and annotated them with OpenMP, CAPS HMPP and PGI Accelerator directives and measured the performance. Then, they tried to adjust the directives, so the translated code more or less matches the hand-written CUDA code. Since OpenACC is related to the PGI or the HMPP programming model, the results should be valid for OpenACC as well. The evaluation confirms the conclusions of the other papers that directive based programming leaves much room for improvement and gains about 30-40% of the CUDA performance in average. Figure 12 and 13 show the results of the performance comparison after all adjustments were made to optimize the produced code by OpenMP, CAPS HMPP and PGI. The paper [28] presents another performance analysis of OpenACC with two real world applications, namely a Bevel Gear Cutting Simulation used in engineering and a computation of the Neuromagnetic Inverse Problem from the field of medicine. The evaluation was done on a 12-core AMD processor with a Tesla C2050 GPGPU and a 4-core Intel Westmere processor. They compared an OpenCL implementation with an OpenACC and a PGI Accelerator annotated version and also showed the performance gap between PGI Accelerator and OpenACC directives. The results can be seen in Figure 14 and 15. They also measured the programmability/productivity by changed lines of code for each programming model. In the engineering application, OpenACC reaches about 80% of the performance of the best effort OpenCL version, which is quite high compared to the programmability. The medicine application is more complex, so OpenACC looses much performance and achieves about 40% of the OpenCL implementation. The paper states that this distressing result may be enhanced with compiler optimizations and still are encouraging, because the OpenACC implementation 82
86 21 S3D Thermodynamics Timings (Seconds) SERIAL HMPP HMPP Kernel HMPP Data Transfer PGI PGI Kernel PGI Data Transfer CUDA 0.29 CUDA Kernel CUDA Data Transfer OpenMP 12 Threads (best) (a) S3D Thermodynamics Timing Table (b) S3D Thermodynamics Speedup Figure 12: S3D thermodynamics kernel experiment. [16] HOMME/SE Timings (Miliseconds) SERIAL HMPP Kernel PGI Kernel CUDA OpenMP 4 Threads (best) (a)homme/se Timing Table (b)homme/se Divergence Sphere Speedup Figure 13: HOMME/SE kernel experiment. [16] needed only 46 lines of code (loc) to change whereas the OpenCL needed about 630 loc for optimization. The last paper [15] ported the Himeno benchmark 20 to the Cray XK6 supercomputer with OpenACC as a case study towards exa-scale 21 systems in the future. The Himeno benchmark is used with Fortran 2008 features, in particular co-arrays (CAF). They measured the scalability of the system using strong scaling 22 with up to 128 nodes, each consisting of a 16-core AMD Opteron 6200-series and a NVIDIA 20 The Himeno Benchmark by R. Himeno, see 21 Computers that can execute one exa (10 18 ) FLOPS and more 22 Strong scaling uses a fixed problem size for benchmarking, for every benchmark run the size of processing nodes is increased 83
87 22 %! $" '#!" '!!" 1234,, !"#$%&'()*+( $! #" #! &!" %!" $!" " #!"! &'()*+,-.+/'&'0( 1023*+,-.+/'&'0(!" ()*+, -.*/-0,/ Figure 14: Simulation of the Bevel Gear Cutting in engineering. [28]!"#$%"&$'(%)*+,-$(.-/0( &!! %!! $!! #!! "!!! '()*+, -./011 '()*0++ #!!" +!" *!" )!" (!" '!" &!" %!" $!" #!"!" 89:;00 <64=;>>,-./0, $6-7 Figure 15: Neuromagnetic Inverse Problem in medicine. [28] Tesla X2090 GPGPU connected via a high-speed interconnect by Cray utilized by MPI/OpenMP. The Himeno benchmark was annotated and optimized with OpenACC directives enabling asynchronous data transfers and compiled with a pre-release Cray compiler. The results show a nice scalability curve for the benchmark, with the most optimized OpenACC version with asynchronous data transfers as the fastest version. With an increasing number of nodes, the time needed for data transfers becomes almost as high as the actual kernel execution time on the accelerators, which is less efficient. Nevertheless, the performance is in the range of 0.5 to 4.5 tera FLOPS for the whole system, which is far away from the peak performance of the Cray XK6. The problem may of course be the used benchmark application. It would be nice to see the scalability for several thousands of nodes, as exa-scale computing expects multiple magnitudes of the benchmarked performance, and if OpenACC can really maintain the same scalability as for up to 128 nodes. A very interesting point is that the whole benchmark (consisting of about 670 loc) was entirely ported to the GPU using only 26 additional directives for the blocking respectively 29 directives for the asynchronous version. The asynchronous clause automatically increased the overall performance by 5 to 84
88 23 10%. 6 HSA This chapter covers an effort of AMD to develop a highly integrated heterogeneous computing architecture and therefore both the hardware and the software. The Heterogeneous System Architecture (HSA) came out of the AMD Fusion architecture, which integrates CPU and GPU on one single chip. HSA is another name and targets the generalization of the fusion approach developing new methods under an open industry standard to create and efficiently exploit parallelism of future heterogeneous architectures. Therefore, the HSA foundation 23 was initiated in mid 2012 by AMD together with ARM, Samsung, Texas Instruments among others and forming working groups for different application domains. Right now, this initiative gains more and more interest by the industry and developers since the market leader in embedded systems ARM has become a member of HSA. Figure 16: Desired HSA position in software development. [5] One interesting aspect of HSA is the combined address space for the CPU and the GPU using clever address mapping mechanisms 24. The shared address space enables a great performance boost of GPGPU accelerated applications since the memory transfer time, the largest limiting performance factor, is drastically reduced. Developing applications for these systems will be much easier than for current hybrid architectures. For the upcoming 3rd generation of AMD s APUs and the future, much effort goes into increasing the performance for HPC application domains. For exploiting future heterogeneous architectures, HSA realized the importance of having a big developer community and supports them with applications, compilers, profiling and optimizer tools, runtime 23 See for more information 24 AMD I/O Virtualization Technology (IOMMU) Specification, see TechDocs/48882.pdf 85
89 24 libraries and lots of learning resources. As many developers have experiences in many different programming languages, HSA wants to support a wide range of programming languages (currently C/C++, C#, Java and some functional languages are supported). On the software side, HSA wants to be as easy to program as possible and therefore adapts even its hardware architectures (as seen in current AMD APUs and Opteron Server CPUs). It enables automatic work sharing between CPU and GPU and provides extensions to OpenCL, which are already used by Adobe products like Photoshop. Currently, a Visual Studio plugin C++ AMP is available, where programmers can offload code regions to the accelerator by two additional language keywords. Programmers also do not have to worry about cache coherency anymore. HSA provides context switching of threads on accelerators, so accelerators can be programmed a lot like CPUs. Also a new intermediate language (IL) called HSAIL was developed. HSA should not be mixed up with OpenCL, as it provides lots of own extensions to OpenCL and has its own development and runtime environment. All in all, it is a trend-setting approach and the support from the industry is definitely very promising. 7 Conclusions This paper presented the OpenACC programming model in detail with remarks on its application field, benefits, limits and tradeoffs and showed the potential that lies in this approach. Additionally, the PGI compiler was presented among alternative compilers and performance measurements. Without exceptions, all used papers have a positive opinion about OpenACC. Although the performance is in average 30-40% less than hand-written CUDA or OpenCL code, it is very good with respect to higher productivity and low knowledge requirements for the programmer. As the market is changing continuously it is open whether OpenACC gets the state of the art or not, but its foundations are solid and enjoy a big developer base. This also depends on the improvement of available OpenACC compilers. The approach is very promising and in fact demonstrates many improvements and possibilities over existing approaches. 86
90 25 References [1] The OpenMP API specification for parallel programming. Available at http: // [2] PGI Resources PGI Accelerator. Available at [3] (2010): PGI Accelerator Programming Model for Fortran & C, 1.3 edition. The Portland Group. [4] (2011): The OpenACC Application Programming Interface, 1.0 edition. [5] (2012): Available at testberichte html. [6] James C. Beyer, Eric J. Stotzer, Alistair Hart & Bronis R. de Supinski (2011): OpenMP for Accelerators. In: IWOMP, pp Available at [7] Barbara Chapman, Gabriele Jost & Ruud van der Pas (2007): Using OpenMP: Portable Shared Memory Parallel Programming (Scientific and Engineering Computation). The MIT Press. [8] Liang T. Chen & Deepankar Bairagi (2010): Developing Parallel Programs - A Discussion of Popular Models. Technical Report, Oracle Corporation. [9] B. Cloutier, B. K. Muite & P. Rigge (2012): Performance of FORTRAN and C GPU Extensions for a Benchmark Suite of Fourier Pseudospectral Algorithms. ArXiv e-prints. [10] CAPS Entreprise: http: // www. caps-entreprise. com/ wp-content/ uploads/ 2012/ 07/ CAPS_ PROD_ EN_ openacc_ pdf. [11] CAPS Entreprise (2012): HMPP Directives. [12] Khronos Group (2011): OpenCL Overview. Available at developers/library/overview/opencl-overview.pdf. [13] The Portland Group (2012): PGI Accelerator Compilers OpenACC Getting Started Guide, 12.6 edition. [14] Tianyi David Han & Tarek S. Abdelrahman (2009): hicuda: a high-level directive-based language for GPU programming. In: Proceedings of 2nd Workshop on General Purpose Processing on Graphics Processing Units, GPGPU-2, ACM, New York, NY, USA, pp , doi: / Available at http: //doi.acm.org/ / [15] A. Hart, R. Ansaloni & A. Gray (2012): Porting and scaling OpenACC applications on massivelyparallel, GPU-accelerated supercomputers. The European Physical Journal Special Topics 210, pp. 5 16, doi: /epjst/e y. Available at [16] Oscar Hernandez, Wei Ding, Barbara Chapman, Christos Kartsaklis, Ramanan Sankaran & Richard Graham (2012): Experiences with High-Level Programming Directives for Porting Applications to GPUs. In Rainer Keller, David Kramer & Jan-Philipp Weiss, editors: Facing the Multicore - Challenge II, Lecture Notes in Computer Science 7174, Springer Berlin / Heidelberg, pp Available at / _ / [17] Haoqiang Jin, Mark Kellogg & Piyush Mehrotra (2012): Using Compiler Directives for Accelerating CFD Applications on GPUs. In BarbaraM. Chapman, Federico Massaioli, MatthiasS. Müller & Marco Rorro, editors: OpenMP in a Heterogeneous World, Lecture Notes in Computer Science 7312, Springer Berlin Heidelberg, pp , doi: / Available at _12. [18] Khronos Group (2011): The OpenCL Specification. [19] Myungho Lee, Heeseung Jo & Dong Hoon Choi (2012): Towards high performance and usability programming model for heterogeneous HPC platforms. In: Computing Technology and Information Management (ICCM), th International Conference on, 1, pp [20] Myungho Lee, Heeseung Jo, Dong Hoon Choi & Sung Wook Baik (2012): Generalized parallelization methodology for heterogeneous HPC platforms. In: Cloud Computing and Social Networking (ICCCSN), 2012 International Conference on, pp. 1 6, doi: /icccsn
91 26 [21] Seyong Lee & Rudolf Eigenmann (2010): OpenMPC: Extended OpenMP Programming and Tuning for GPUs. In: Proceedings of the 2010 ACM/IEEE International Conference for High Performance Computing, Networking, Storage and Analysis, SC 10, IEEE Computer Society, Washington, DC, USA, pp. 1 11, doi: /sc Available at [22] Seyong Lee & Jeffrey S. Vetter (2012): Moving Heterogeneous GPU Computing into the Mainstream with Directive-Based, High-Level Programming Models (Position Paper). In: DOE Exascale Research Conference. [23] I. L opez-rodriguez (2012): OpenACC Implementations Comparison. [24] NVIDIA Corp. (2007): NVIDIA CUDA: Compute Unified Device Architecture. [25] R. Reyes, I. L opez, J.J. Fumero & F. de Sande (2012): A Comparative Study of OpenACC Implementations. [26] R. Reyes, I. López-Rodríguez, JJ. Fumero & F. de Sande (2012): Directive-based Programming for GPUs: A Comparative Study. In: Proc. of the 14th IEEE International Conference on High Performance Computing and Communications (HPCC-2012), IEEE. [27] Ruymán Reyes, Iván López-Rodríguez, Juan Fumero & Francisco de Sande (2012): accull: An OpenACC Implementation with CUDA and OpenCL Support. In Christos Kaklamanis, Theodore Papatheodorou & Paul Spirakis, editors: Euro-Par 2012 Parallel Processing, Lecture Notes in Computer Science 7484, Springer Berlin / Heidelberg, pp Available at / [28] Sandra Wienke, Paul Springer, Christian Terboven & Dieter an Mey (2012): OpenACC First Experiences with Real-World Applications. In Christos Kaklamanis, Theodore Papatheodorou & Paul Spirakis, editors: Euro-Par 2012 Parallel Processing, Lecture Notes in Computer Science 7484, Springer Berlin / Heidelberg, pp Available at /
92 Dataflow Programming on GPUs Maximilian Senftleben University of Kaiserslautern, Embedded Systems Group m senftl@cs.uni-kl.de 1 Introduction The ongoing paradigm shift towards parallel programming and computation offers much potential to improve computation performance but likewise requires more advanced knowledge of parallel programming. Heterogeneous systems with multi-core CPUs, GPUs, and FPGAs offer the access to different forms of parallelism (data, task parallelism), but there are few high-level parallel programming models available which do not require extensive knowledge of the devices. The programming of hybrid systems is very complex, often to difficult to achieve for mainstream programmers. The massive parallelism introduced by GPUs can be better exploited by using dataflow programming. In this document an overview of different possible dataflow programming models which abstract from the most complex programming aspects is given. Each model s key characteristics are described and its results concerning performance are presented. The document closes with a brief comparison of the presented models and their benefits. 1.1 Dataflow programming Dataflow programming models a program as a directed graph consisting of nodes, which represent computations, and edges, which represent data connections. Dataflow focuses on the connection structure of a program, the way the data takes through it. Dataflow programming reduces the need of global state information of a program as the data flowing between nodes and their internal state characterize the systems state. This paradigm is inherently parallel as each node can operate as soon as it has its input data, not requiring any state information from the rest of the system. To run of a dataflow program only a method to coordinate and buffer the messages passed around is needed to maintain the system s state, which is handled by the language s runtime. 89
93 2 2 General This chapter gives a brief overview of the matter to be discussed or the foundations it is based on. 2.1 SystemC SystemC is a high level system design language and is based on C++. It extends C++ by constructs to model properties of hardware systems: parallelism scheduling and synchronization via modules, processes and channels. SystemC also provides its own event-driven real-time simulation kernel. The language, being open-source and very similar to C++, is widely used at universities to model hardware systems. 2.2 CUDA [9] CUDA (Compute Unified Device Architecture) is an architecture developed by NVIDA, which allows to write programs, which can be executed on GPUs. Most often C FOR CUDA is used to program code for a GPU. C FOR CUDA is based on Standard C and extended/restricted with NVIDIA modifications. Figure 1: CUDA processing flow Figure 1 shows the processing flow of CUDA applications: first, all required data is copied into the GPU memory, then the CPU instructs the GPU to start the processing, then the GPU executes the program in parallel in each core and finally the results are copied back to the main memory. 2.3 Message Passing Interface (MPI) [11] The Message Passing Interface (MPI) is a standard for message exchange in parallel computations among (potentially) distributed systems first published in It aims to provide high performance, scalability and portability. MPI does not define a concrete implementation but defines a set of operations and their semantic (Interface). Implementations are available on a wide range of machines and bindings for different programming languages exists (e.g. C, Fortran, Python, OCaml). MPI supports point-to-point and collective communication. 90
94 3 A MPI program consists of multiple processes, each executing its own code, which communicate via calls to MPI communication primitives. MPI calls can be local, non-local, blocking, nonblocking, or collective. 2.4 Polyhedral Process Network [13] Polyhedral Process Networks are a subclass of Kahn Process Networks. Kahn Process Networks consist of processes, channels (unbounded FIFOs) and synchronization happens via blocking reads. PPNs on the other hand have only bounded FIFOs/memories and use blocking writes to cover this restriction. Figure 2: PPN Example (a), example process P2 (b) [6, Fig. 3] Figure 2 shows an example PPN and an example for what a process may look like Definition [13] A polyhedral process network is a directed graph with a set of processes P as vertices and communication channels C as edges. Each process P i P has the following characteristics a statement identifier s i, a dimension d i, an iteration domain D i Z d i. Each channel C i C has the following characteristics a source process S i P, a target process T i P, a source access identifier corresponding to one of the accesses in the statement s Si, a target access identifier corresponding to one of the accesses in the statement s Ti, a polyhedral relation M i D Si D Ti mapping iterations from the source domain to the target domain, a type (e.g., FIFO), a piecewise quasi-polynomial buffer size. 91
95 Static Affine Nested-Loop Programs (SANLP) [14] SANLP is a subset of the C language. An SANLP consists of a set of statements, each possibly enclosed in loops and/or guarded by conditions (nested). Its control flow is known at compile time (static) and it only consists of expressions of the form ax+b (affine). The integer set called iteration domain is the set of iterator vectors for which a statement is executed. Its linear inequalities express the lower and upper bounds of the enclosing loops PPN Extraction from SANLP [13] [14] [12] Figure 3: Derivation of a PN [12, Fig. 2] As shown in Figure 3 the extraction of a PPN from a SANLP is achieved in four steps. 1. Preprocessing: The SANLP is converted to a network representation. A single process representing all executions of one assignment statement. 2. Consumption Restructuring: The data consumption is restructured such that each array written to by different processes is replaced by separated memory arrays for each producer process. 3. Production Restructuring: The data production is restructured such that each array read by different processes is replaced by separated memory arrays for each consumer process. 4. Communication Model Selection: Depending on the producer/consumer pair different types of communication and synchronization mechanism are used to derive a valid PPN. 2.5 Concurrent Collections (CnC) [5] Concurrent Collections (CnC) is a parallel programming model developed by Intel. It is influenced by stream processing, dynamic dataflow, and tuple spaces. CnC defines three main constructs step collections, data item collections, and control tag collections. Each collection represents a set of dynamic instances. A step collection corresponds to a computation and its instances correspond to an invocation of the computation. A data collection consists of a set of data items indexed by item tags. Data items are accessed via get/put operations on the collection. They are required to be immutable and can only be put once. Control tag instances are used for control. A 92
96 5 put operation on a control collection prescribes (creates) step instances of some step collections with the control tag as input. A CnC program is defined statically as a CnC (specification) graph which defines the collections and their relationships. In a CnC graph a node represents a collection while a directed edge represents a put, get or prescribe operation. Figure 4: CnC graph example [5, Fig. 1] Figure 4 shows an example of a CnC graph. Rectangles represent data item collections, ellipses step collections, and hexagons control tag collections. Dotted edges represent prescription operations, and arrows represent get/put operations of data items (production/consumption). Environment communication is represented by squiggly edges. A whole CnC program consists of the specification, code for each step, implementing the computation for each node, and the environment, the user code which interacts with the CnC graph. Data instances can be produced and consumed by the environment, control instances can be produced by the environment and used to prescribe conditional execution. The collection tag usage is defined as follows: Putting a tag into a control collection will cause the corresponding steps to eventually execute, when their input is ready. The execution of a step takes the tag indexing the step instance as input argument which contains the information to compute the tags of all its input and output data. Data collection tags are used as indices in an associative container, in which an element indexed by one tag can only be written once. This immutability provides determinism. 93
97 6 3 SysCellC [8] 3.1 Overview In this publication a compile flow is presented, which constructs an implementation on a multi-gpu cluster system for a given SystemC program. Therefore, the program is mapped to the GPU-API while SystemC channels abstract the communication between GPUs. 3.2 Approach The aforementioned compile flow is described in seven steps which can be seen in the overfiew in Figure 5 Figure 5: SysCellC design flow [8, Fig. 1] Step 1 Starting with application code in SystemC (with sc module for modeling computation processes and SystemC primitive channels sc signal and sc fifo modeling streams) we divide the processes in two types: computation intensive ones and others which are dedicated to application monitoring, environment communication and (CPU) memory management. The computation intensive ones are mapped on the GPUs, while the other ones are mapped to the CPUs. Due to the (usually) great amount of data to be processed in comparison with the smaller GPU video memory the data has to be sized and tiled to optimize overlapping between communication and computation. Sometimes applications require data to be prefetched from CPU memory, the SystemC application has to take care of all these prefetching processes. The processes mapped on GPUs are subject to some restrictions to express the synchronization between concurrent components: They are not allowed to have wait() primitives and they should only be sensitive to their sensitivity list. The processes are only sensible to a signal that can be viewed as a clock. Therefore, a process may only block when it is finished. 94
98 7 Step 2 The next step is the manual partitioning of the SystemC code in a computation data parallel part, which is mapped to the GPUs and the other part which is mapped to the CPUs guided by profiling information. Step 3 This step consists of the transformation of the SystemC code in an XML intermediate representation by the SCXML parser provided. Each XML file represents a SystemC component and contains its most important characteristics: in/out ports (name, type and size), declared processes (name and type), sensitivity list structural information: name and type of components in a hierarchical tree, names of subcomponent connections and component port bindings SystemC s sc signal and sc fifo in intra and inter cluster node communication are overloaded and implemented with the MPI version 2 (MPI-2) standard. Step 4 The SystemC components are allocated to the different GPUs and CPUs using the SYNDEX tool which in turn uses the XML files and profiling reports. SYNDEX inputs: a hierarchical conditioned data-flow graph of computing and communication operations with their data type and size and their components execution time. a graph representing the architecture specification composed of processors and communication medias. The processor is characterized by supported tasks, execution time (obtained during profiling) and worst case transfer time for each type of data on the interconnect (obtained by data size estimations). SYNDEX uses a heuristic for mapping and scheduling of asynchronous tasks (i.e. communication through sc fifo). Step 5 Using the previous gathered information the C code for CPUs and GPUs is generated. It embeds a lightweight SystemC scheduler on the CPUs to preserve the SystemC model s operational semantics. The code is architecture independent due to GPU library overloading and the implementation of the MPI based SystemC channel interface library. The GPU kernel launcher function (on SystemC level) can call a GPU kernel or launch a CPU multithreaded version for code verification in a CPU environment. Step 6 A single binary multithreaded code for the CPUs and GPUs is compiled from the C code using the tool SYSCELLC. The MPI standard is used to implement the SystemC channel interfaces. Step 7 In this step the implemented system is used to generate profiling information for reuse and optimization in the 4th step. 95
99 8 3.3 Results The described approach was applied on three test cases (a producer/consumer case, a CDMA radiocommunication system and a visual attention model) and the resulting code was compared with the native SystemC execution on 1 CPU. The sizes of the generated C source code and the original SystemC code are similar, which means the described technique does not introduce bloated code. The execution time of the resulting code was between 10 and 35 times faster ( 10 for the CDMA test case, 35 for the other test cases) than the native implementation on 1 CPU. 96
100 9 4 Efficient Stream Buffer Mechanism for Dataflow Execution on Heterogeneous Platforms with GPUs [2] 4.1 Overview The publication describes the approach to map streaming applications using a Process Network (PN) model of computation onto heterogeneous architectures. As Figure 6a shows, the PN model provides coarse-grained task and pipeline parallelism while optimization of individual nodes may provide finegrained data parallelism. Figure 6: Data-Driven Execution: Asynchronous Processing + Stream Buffer Communication [2, Fig. 3] 4.2 Approach There exist compiler techniques that derive Polyhedral Process Networks (PPN) from a class of sequential nested loop programs, e.g. the pn compiler [14] which works on Static Affine Nested-Loop Programs (SANLP, subset of C language). A prototype framework for mapping the PPN onto a hybrid system was build using the pthread library for the multi-core CPU workload and CUDA 4.0 API for access to the GPU. The framework is based on the asynchronous execution of dataflow independent computations and coarse-grain pipeline parallelism in a PN model. Furthermore, a Stream Buffer (SB) mechanism is introduced which provides the functionality to enable pipelined CPU-GPU communication/execution. For each nested loop body statement a process is generated in a PPN. The node domain of a process is constructed by its iteration space. Channels are used for passing the input and output of processes as data tokens between processes, which are blocked until input data becomes available. The processes are mapped to threads on either GPU or CPU and execute asynchronously and pass the following 97
101 10 execution phases for each token (single frame): stream data in - blocking read, computation - function execution, stream data out - blocking write. The computation corresponds to the execution of the nested loop body. It can optionally be optimized by polyhedral techniques (e.g. locality or special GPU support) [4, 1, 3] The iteration domain of GPU nodes can be mapped to the N-dimensional range of the CUDA-kernel, s.t. the computation function is executed by a large number of lightweight CUDA threads in parallel. Different kernels are executed in different and parallel CUDA streams if the target device supports concurrent kernel execution. The SB mechanism uses dataflow to exploit pipeline parallelism on a hybrid platform. It allows data transfer between host and GPU device to happen concurrent to computations. As all communication of the PPN model is point-to-point each channel is implemented by a Stream Buffer. The implementation itself is based on a Circular Buffer and pointers to reduce data movement in FIFO usage. Semaphores emptycount and fullcount realize blocking write to and blocking read from the channel. The Stream Buffers are implemented using a distributed memory approach using double buffering and its communication by asynchronous memory transfers. Additional threads monitor the transfers and signal data availability to the blocked (waiting) processes. Figure 6b-e illustrates the implementation of the Stream Buffer mechanism. 4.3 Results Using the asynchronous execution model and stream support an I/O transfer and computation pipeline is realized. The results obtained from a synthetic producer-transformer-consumer streaming application predict that synchronization overheads are rather low and good overlap of memory transfers and computations can be achieved. 98
102 11 5 CnC-CUDA [7] 5.1 Overview In this publication Intel s Concurrent Collections (CnC) programming model is extended to a model called CnC-CUDA to address hybrid system as well. The paper includes a definition for multithreaded steps for GPU execution and the automatic data and control flow generation between CPU and GPU steps. Furthermore a CnC implementation based on Java is presented and used as foundation for the CnC-CUDA implementation. 5.2 Approach CnC was implemented in Habanero-Java (HJ), a programming language developed at the Rice university, because it includes useful constructs to implement CnC primitves as shown in Table 1. CnC construct Tag Prescription Item Collection put() on Item Collection get() on Item Collection Translation to HJ Java String object / point object async or delayed async java.util.concurrent.concurrenthashmap Nonblocking put() on CurrentHashMap Blocking or nonblocking get() on CurrentHashMap Table 1: Summary of mapping CnC primitives to HJ primitives [7, Tbl. 1] The mentioned CnC programming model was extended in order to support CUDA steps efficiently. First the graph syntax was extended to support GPU steps in addition to CPU steps and to specify constants in the graph file, which later can be used in CPU (HJ) and GPU (CUDA) code. These constants are used to declare correct sized item collections for exchange between CPU and GPU. The CnC Parser generates Access functions for each item collection. The item collections maintain the standard Put and Get access methods for each individual data item which are put into a ConcurrentHashMap. As soon as enough tags have been put, the corresponding items in the ConcurrentHashMap are collected, converted to a C friendly format (e.g. replace Java primitive datatype wrapper classes by their primitive type) and passed to CUDA. Because those single Put and Get operations yield a significant performance overhead, the primitives PutRegion and GetRegion are introduced as a much more efficient alternative. PutRegion/GetRegion allow the programmer to put/get a (potentially multidimensional) region of integers associated with a similarly dimensioned array of items. This array can be directly passed to the CUDA kernel and eliminates the get/put operations for each individual item. Tag collections are automatically generated using the type definitions in the graph file. Tag collections control execution and synchronization of computation steps. Depending on the functionality of the device a mutex indicating the usage and therefore accessibility to new computations is used. The number of CUDA computation steps that can be prescribed by another CUDA computation step is limited to 1. Therefore, if one CUDA step prescribes another one, the second one is invoked immediately after the first one on the GPU without returning to the CPU. Synchronization between host and device computation steps is achieved by calling a CUDA tag collections Wait() method, which blocks 99
103 12 until all launched kernels returned and their result was transfered to the main memory. The PutRegion operation places a region of integer tags into the tag collection and immediately launches a CUDA kernel for all tags in the range once all required data items are available. The item collection property One-For-All passes the same data to each thread on a device and can result in better memory usage and performance. Only the actual CUDA kernel must be written, the translator generates stub codes that allocate memory and copy the data structures to the device before a step is executed and free the device memory after the kernel finishes. For now CUDA kernels can only put a single item on each item collection of its outputs. 5.3 Results Four different benchmarks were used to compare the runtime on different programming models: Fourier coefficient analysis (Series, Java Grande Forum (JGF) benchmark suite), successive overrelaaxation (SOR, JGF), IDEA encryption (Crypt, JGF), Heart Wall Tracking program (Rodinia benchmark suite). Each was run on varying data sizes using CnC-CUDA, CnC-HJ, Serial C, hand-coded CUDA, and the original single-threaded Java benchmark. The measured runtime included the memory transfer overhead. The execution of the GPU CnC-CUDA code compared to the CPU CnC-HJ code led to a speedup in almost every benchmark run between from factor 2 up to 400. In most benchmarks the speedup grows with the data size, except for the JGF Crypt benchmark, where the speedup for varying data sizes stays between 2 and 3. The JGF Series benchmarks profit most from CnC-CUDA in greater data sizes: the speedup grows from to when the data size is increased by a factor of 100. The benchmark results show that the performance speedup of excessive parallelism on GPUs can be used by non-device-expert programmers as well. 100
104 13 6 PTask: operating system abstractions to manage GPUs as compute devices [10] 6.1 Overview A set of OS abstractions called PTask API is introduced. Its supported dataflow programming model uses a directed acyclic graph to assemble individual tasks. Vertices are called ptasks and represent the executable code and edges represent the data flow between the vertices. PTasks main goals are usage of a single resource manger to provide guarantees for fairness and isolation, providing of a data flow programming model which abstracts from device management and provide a programming environment that allows code to be modular and fast. 6.2 Approach The PTask API is built on different OS-level abstractions: PTask, Port, Channel, Graph, Datablock and Template. A ptask is similar to the well known OS process abstraction while mainly executed on a GPU (or similar devices), is managed by the OS and provides some input and output resources which can be bound to ports. A port is a kernel namespace object which can be bound to ptask input and output resources and represents a data source or sink. A channel connects a port to another port, or to other data sources and sinks in the system. The collection of ptasks connected via their ports by channels represent a graph. A datablock represents a data flow unit in a graph. A template provides meta-data describing datablocks to assist mapping datablocks to threads on a GPU. New system calls address these new abstractions, e.g. sys push inserts data in a channel, blocking if its capacity is reached and sys pull retrieves data from a channel, blocking if its empty. The stand-alone user-mode library implementation supports ptasks coded in HLSL (DirectX), CUDA, and OpenCL. The PTask runtime can schedule multiple independent graphs in parallel and takes care of fairness and efficiency. A ptask can be in one of four states: Waiting, Queued, Executing, or Completed. The prototype implementation supports four different scheduling modes: first-available, fifo, priority, and data-aware. In first-available mode every ptask is assigned a manager thread, these threads compete for available accelerators. The fifo mode enhances the first-available mode with queuing. Priority mode enhances ptasks with a static priority and proxy priority (OS manger thread priority). Dataaware mode works similar to priority mode, but takes data memory spaces into account, such that it preferes accelerators where most of the data is already up-to-date. 6.3 Results The PTask implementation was evaluated with a gestural interface on Windows 7, an encrypted file system on Linux, and microbenchmarks. Five different implementations of the gestural interface are compared: a host-based CPU only version, a handcoded GPU optimized version, a piped version (four different processes connected by pipes), a modular version which combines all processes of the piped version, and the version implemented using the PTask API. The evaluation uses a Core2-Quad CPU and a NVIDIA GTX 580 GPU. The 101
105 14 PTask version achieves higher maximum throughput (275.3 MB/s) than even the hand-coded version (248.2 MB/s) and supports real-time data rates with low CPU utilization. EncFS (FUSE-based encrypted file system for Linux) was modified to use a GPU for AES encryption. A sequential read and write of a 200MB file are 17% and 28% faster than the version using the SSL software library implementation. The evaluation uses a NVIDIA FTX470 GPU, Intel Core i5 3.20Ghz CPU, 12GB RAM, 2 SATA SSD 80GB in a striped RAID. Multiple GPU tasks can render the GPU scheduler useless (e.g. a 30 slowdown), therefore the GPU scheduling mechanism in the kernel (PTSched) is used to eliminate this problem. The micro-benchmarks include bitonic sort, matrix multiplication, matrix addition, and matrix copy kernels with input matrix and image sizes ranging from 64x64 to 1024x1024. The mean speedup for the different benchmarks over a single-threaded, modular GPU-based implementation is 93% and over a handcoded version 10%. 102
106 15 7 HyperFlow: A Heterogeneous Dataflow Architecture [15] 7.1 Overview HyperFlow is a dataflow architecture which provides different abstraction layers over computation resources. It supports heterogeneous computation resources and can provide optimized implementations for each task depending on which resource it is executed. This enables a high degree of portability as a taks does not have to be assigned to a resource statically but could be executed efficiently on different resources. 7.2 Approach The following abstractions layers are provided by HyperFlow: Interconnected Task-Oriented Modules (TOMs) represent pipelines, and are executed as flows in a token-based way. A TOM consists of several parameters such as the number of input and output ports. A TOM does not contain an implementation of the task it represents, but refers to a list of of task implementation objects, which perform the actual computation. The execution of a TOM at runtime requires the presence of a task implementation that matches he system resources. Pipelines are executed by sending instruction tokens to processing units and retrieving data tokens as results. In HyperFlow these tokens are modeled as flow between connected TOMs. Flows might by generated on the completion of module executions and are classified as waiting, live, or dead. HyperFlow maintains a flow cache to store incoming flows until all required input data is available, and then executes the corresponding module. The actual computing resources are encapsulated by Virtual Processing Elements (VPEs). A VPE manages the execution on a specific computing resource and provides the required context. A VPE waits for tasks to be executed as soon as its managed resource becomes available. Then it assures that the required input data resides in its current context. HyperFlow provides a datatransfer path between each VPE by assuming that each VPE has access to main CPU memory. Figure 7 gives an overview of the HyperFlow architecture, which consists of the former mentioned TOMs and VPEs and furthermore the Execution Engine and VPE Scheduler. 103
107 16 Figure 7: HyperFlow Architecture. [15, Fig. 1] The Execution Engine (EE) is the main controlling component of HyperFlow. It is responsible for VPE initialization and assignment to a corresponding resource as well as for management of the flows. The EE dispatchs newly generated waiting flows to the VPE Scheduler as well as the state of VPE resources. The VPE Scheduler manages waiting flows and schedules them for execution on available VPEs. It uses two queues, one for waiting flows and one for the ones currently executing. Flows are assigned a identification number which are used to determine the execution order and to support global scheduling strategies. The VPE Scheduler also takes care of multiple data instances for the same module not to be mixed up. HyperFlow s Memory Management requires each data object to inherit from the predefined DATA class, which implements reference-counted objects with a copy-on-write approach. This enables using references instead of copies on the one hand, and eliminates read-after-write or write-after-write hazards on the other side. Alternatively different approaches could be implemented by overriding the DATA class, e.g. if the default implementation performs badly with a given data-copy intensive application. 104
108 Results One of the main differences to similar approaches is the separation of task specification and its implementation. The pipelines described in HyperFlow are allowed to have feedback communication (cyclic graphs). The first real-case application evaluated is a image-based edge detection pipeline. Compared to the visualization API VTK, Hyperflow runs between 4 (using 1 CPU) to 6 (using 8 CPUs) faster than VTK and 2 (using 8 CPUs) to 4 (using 1 CPU) faster than a hand-tuned VTK version. The next evaluation treats the application of Streaming Multigrid Gradient-Domain Processing, which revealed a speedup towards the original implementation between 1.26 and Another real-case application was the Parallel isosurface extraction which was compared to the approach of Isenburg et al s. The performance comparison using between 1 and 64 CPUs showed HyperFlow consistently outperforms Isenburg et al s approach. 105
109 18 8 Conclusion 8.1 Remarks All of the presented models yield a significant speedup of parallel applications towards their sequential implementation, but it should be noticed that the results show potential speedups for selected applications as most of the models only apply to a specific class of problems and do not perform well with others. 8.2 Comparison of results The SysCellC approach describes a compile flow that uses the SystemC constructs channel, fifo, and module to describe a dataflow program. The SystemC channels are implemented with the MPI standard. The approach of Balevic on the other side is based on PPNs which can be obtained directly from SANLP programs. The dataflow is implemented by a StreamBuffer mechanism which enables piplined execution between CPU and GPU. CnC-CUDA uses programs in form of a CnC graph which can be compared to PPNs, but the execution of a step depends on control tags. PTask is an API which works on dataflow graphs and executes them under one resource manager which enables it to give fairness and performance guarantees. Hyperflow also works on a dataflow network of connected TOMs, which may have different implementations for different devices. Hyperflow supports programs with data feedback. From the author s point of view the PPN approach seems to be one of the more interesting approachs in terms of academic research as it is a more formal underlying model and it still can be used to represent a wide set of problems. 106
110 19 References [1] Ana Balevic and Bart Kienhuis. A data parallel view on polyhedral process networks. In Proceedings of the 14th International Workshop on Software and Compilers for Embedded Systems, SCOPES 11, pages 38 47, New York, NY, USA, ACM. [2] Ana Balevic and Bart Kienhuis. An efficient stream buffer mechanism for dataflow execution on heterogeneous platforms with gpus. In Proceedings of the 2011 First Workshop on Data-Flow Execution Models for Extreme Scale Computing, DFM 11, pages 53 57, Washington, DC, USA, IEEE Computer Society. [3] Muthu Manikandan Baskaran, J. Ramanujam, and P. Sadayappan. Automatic c-to-cuda code generation for affine programs. In Proceedings of the 19th joint European conference on Theory and Practice of Software, international conference on Compiler Construction, CC 10/ETAPS 10, pages , Berlin, Heidelberg, Springer-Verlag. [4] Uday Bondhugula, Albert Hartono, J. Ramanujam, and P. Sadayappan. A practical automatic polyhedral parallelizer and locality optimizer. In Proceedings of the 2008 ACM SIGPLAN conference on Programming language design and implementation, PLDI 08, pages , New York, NY, USA, ACM. [5] Michael G. Burke, Kathleen Knobe, Ryan Newton, and Vivek Sarkar. The concurrent collections programming model. Technical Report TR 10-12, Department of Computer Science, Rice University, [6] Emanuele Cannella, Onur Derin, Paolo Meloni, Giuseppe Tuveri, and Todor Stefanov. Adaptivity support for mpsocs based on process migration in polyhedral process networks. VLSI Des., 2012:2:2 2:2, January [7] Max Grossman, Alina Simion Sbîrlea, Zoran Budimlić, and Vivek Sarkar. Cnc-cuda: declarative programming for gpus. In Proceedings of the 23rd international conference on Languages and compilers for parallel computing, LCPC 10, pages , Berlin, Heidelberg, Springer-Verlag. [8] Dominique Houzet, Sylvain Huet, and Anis Rahman. Syscellc: a data-flow programming model on multigpu. Procedia Computer Science, 1(1): , [9] NVIDIA Corporation. NVIDIA CUDA C Programming Guide, 4.2 rev 15 edition, [10] Christopher J. Rossbach, Jon Currey, Mark Silberstein, Baishakhi Ray, and Emmett Witchel. Ptask: operating system abstractions to manage gpus as compute devices. In Proceedings of the Twenty-Third ACM Symposium on Operating Systems Principles, SOSP 11, pages , New York, NY, USA, ACM. [11] Marc Snir, Steve W. Otto, David W. Walker, Jack Dongarra, and Steven Huss-Lederman. MPI: The Complete Reference. MIT Press, Cambridge, MA, USA, [12] Alexandru Turjan, Bart Kienhuis, and Ed Deprettere. Translating affine nested-loop programs to process networks. In Proceedings of the 2004 international conference on Compilers, architecture, and synthesis for embedded systems, CASES 04, pages , New York, NY, USA, ACM. [13] Sven Verdoolaege. Polyhedral process networks. Springer, [14] Sven Verdoolaege, Hristo Nikolov, and Todor Stefanov. pn: a tool for improved derivation of process networks. EURASIP J. Embedded Syst., 2007(1):19 19, January [15] Huy T. Vo, Daniel K. Osmari, João Comba, Peter Lindstrom, and Cláudio T. Silva. Hyperflow: A heterogeneous dataflow architecture. In Hank Childs, Torsten Kuhlen, and Fabio Marton, editors, EGPGV, pages Eurographics Association,
111 An Introduction to the Research on Scratchpad Memory: Definition, Hardware, Known Implementations and WCET Optimisation Julius Roob University of Kaiserslautern, Embedded Systems Group Contents 1 Introduction Definition: Scratchpad Memory Contents of This Paper Motivation Energy Efficiency 3 3 Known Applications / Implementations of Scratchpad Memory Systems Microcontrollers Cuda and OpenCL Emotion Engine[10] Cell Architecture Code Overlay Cache Locking Architectures Cache Locking vs. Scratchpad Scratchpad in real-time systems Caches WCET Centric Data Allocation to Scratchpad Memory[15] ILP Knapsack Branch and Bound Greedy Heuristic Optimal Static WCET-aware Scratchpad Allocation of Program Code [5] ILP Compiler Evaluation WCET-Centric Software-controlled Instruction Caches for Hard Real-Time Systems[11] Definition of Problem Choice of Reload Points
112 Choice of Content to Load&Lock Example Implementation Details Genetic Algorithm Evaluation Conclusion 18 7 Bibliography 18 Abstract Together with [13], this papers aims to be an introduction to the concept and a summary of the current research on the topic of Scratchpad Memory(SPM). The topics I focus on are the hardware aspects, energy efficiency, both the general concept of SPM and known implementations and applications, as well as the issue of worst-case execution time in hard real-time systems. 1 Introduction 1.1 Definition: Scratchpad Memory Scratchpad Memory(SPM) is the term chosen for cache-like software-managed memory. It is significantly smaller than the main memory, ranging from below 1-KB to several KB in research applications and being at 256-KB in the SPEs of the Cell (Section 3.4) multiprocessor. Being located on the same chip as - and close to - the CPU core, its access latencies are negligible compared to those of the main memory. Unlike caches, SPM is not transparent to software. It is mapped into an address range different from the external RAM, which is outlined in Figure 1. Figure 1: Cache and SPM memory model[6] Some implementations make it possible for the CPU to continue its calculations while data is transferred from RAM to SPM or vice versa by employing an asynchronous DMA controller. Even without it being asynchronous, transfers from or to RAM are often handled by a special controller that moves data in blocks rather than having the CPU using load and store instructions. There are approaches that use both a SPM and a regular cache. 109
113 3 In multicore processors, there may be a separate SPM per core, which can, depending on the implementation, be used as private buffer memory, ease communication between cores or both. (see Section 3.4 for an example). 1.2 Contents of This Paper After the definition and motivation of SPM, in Section 2 I will discuss the hardware details and impact on energy efficiency. Section 3 will name examples for known applications, with a focus on the Cell multiprocessor. A short explanation of cache locking, as well as some implemented examples are given in Section 4 together with a comparison of the concepts Finally, Section 5 gives an introduction to SPM in WCET optimisations, summarising three papers on both static allocation of data and code, as well as dynamic cache locking. 1.3 Motivation Modern computer applications require more RAM to perform tasks than can be embedded into the processor core. Apart from some low-power embedded systems, most processors utilise cache hierarchies to lessen the speed penalty caused by access to external memory. Cache is a small temporary buffer managed by hardware, employing usually hard-wired displacement strategies like least-recently-used(lru), first-in-first-out(fifo) or randomised approaches. Since these displacement strategies are written to perform good for a wide spectrum of use cases, they are less optimal than a strategy that is tailored to a specific application by a compiler that knows about the whole program structure and may even employ profiling data. Furthermore, because of its lack of most of the management logic cache requires, SPM is less demanding both in chip area and complexity. This will be further explained in Section 2. WCET calculation in hard real-time systems is easier and provides tighter estimates when employing SPM, since it is more predictable and gives developers or compilers more possibilities to optimise. 2 Energy Efficiency The main advantage of cache over SPM is that it is transparent to software. To achieve this, it needs to know which memory addresses lie within blocks that are currently stored in the cache. Tags are the parts of memory addresses that are required to map a block of cache memory to the address in the RAM it belongs to. They are stored next to the cache blocks they belong too in so-called tag lines, see Figure 2. Next to the tag lines and the necessary logic to determine whether a memory access is already cached, a controller that fetches previously uncached memory blocks and takes care of block displacement is required. Depending on the implementation, there may be different mechanisms like write-back and write-through as well as several displacement strategies available that applications or the operating system can choose from. Since the on-chip cache is a major part in the energy consumption of a modern processor, requiring from 25% to 45%, increasing its efficiency or replacing it with SPM has a significant impact on the energy consumption of the whole processor. To compare the energy and area efficiency of SPM and cache, [16] modifies an existing processor, the ARM7TDMI, to use an SPM instead of the previously built-in cache. They employ the energy-away encc compiler with the post pass option of assigning code and data blocks with the knapsack algorithm. After optimised compilation, the resulting executable is emulated using ARMulator which emits a trace 110
114 4 Figure 2: Cache memory organisation [16] of all memory access operations. Those can can be used to determine both the energy consumption of the SPM and the cache. The observed average reduction in time and area are 34% and 18% for constant cycle times and SPM is about 3 times more efficient than a 4-way set associative cache when energy is concerned. Utilising profiling and graph partitioning to optimise SPM allocation as well as a custom management unit with an instruction to load code into the SPM, [6] achieved a 50.7% energy reduction and an 53.2% improve in performance. 3 Known Applications / Implementations of Scratchpad Memory Systems This section is dedicated to widespread architectures whose memory model fits the definition of scratchpad memory. 3.1 Microcontrollers Both the Atmel megaavr[1] and the STMicroelectronics STM32 ARM Cortex based microcontroller have interfaces to connect external memory. These extend the internal ram and are mapped at own address ranges in the address space available to the processor. Because the on-chip memory for those is an order of magnitude faster and smaller than the external RAM, it can be considered a scratchpad memory. 3.2 Cuda and OpenCL Cuda is a framework for general purpose GPU programming (GPGPU) developed by NVIDIA and is restricted to their GPU architectures. OpenCL is an open standard designed to be portable to more architectures, including even multicore CPUs and Cell (Section 3.4). Both can benefit from Scratchpad Memory Optimisation as well. The GPU architectures are outlined in Figure 3 and Figure 4. Software written for both Cuda or OpenCL has to explicitly manage the allocation of contents and transfers of those between different memory levels. Before being used for calculations, data has to be 111
115 5 Figure 3: GPU Architecture in CUDA[8] Figure 4: GPU Architecture in OpenCL[8] transferred between the RAM of the host system and the memory built onto the graphics adaptor or other accelerator device. A main problem of GPGPU calculations is the latency and bandwidth of those transfers, since, especially with GPUs, they are an order of magnitude slower than on-device operations. 3.3 Emotion Engine[10] The Emotion Engine powering the PlayStation 2 featured a 16-KB scratchpad memory, used mainly to improve communication between the CPU and both the floating-point SIMD-VLIW processors. 3.4 Cell Architecture The Cell multiprocessor employed in the PlayStation 3 as well as high-performance clusters features two approaches for software-managed memory hierarchy. It was developed by Sony, IBM and Toshiba with the purpose of establishing a platform that provides high performance, energy efficiency and support for real-time applications. One Cell processor consists of one PowerPC Element and 8 Synergistic Processing Elements(SPE), the structure of which is outlined in Figure 5. A single SPE consists of 256-KB local storage, a SIMD Synergistic Processing Unit(SPU) and a DMA controller. The local storage fits the definition of Scratchpad Memory since both the content of the local storage and the DMA transfers from and to RAM are software-controlled. Those DMA transfers are asynchronous, which means there can be up to 16 queued DMA transfers without forcing the SPU to wait for their completion. Being unable to access memory outside of their local storage without DMA 112
116 6 Figure 5: Schema Cell Architecture, [7] transfers, the code running on the SPU may be required to be split into overlays, the details of which will be discussed in Section The local storage of each SPE is mapped into the global address space to allow both the other SPEs and the PPE to transfer data from and to it. This allows programmers to choose the data flow model that best fits the application, for example they can organise their SPEs into a chain, in which data is efficiently streamed from one element to the next, being processed at every station. The PowerPC Element embedded in the Cell multiprocessor is a general purpose CPU that allows a Operating System to manage the other processors. It posses 32-KB first-level instruction and data caches as well as a 512-KB second-level cache, the latter of which employs replacement management tables that allow the operating system to lock contents to cache Code Overlay Without transferring data through the DMA controller of its SPE, each SPU can only access and execute the contents of the local storage associated with it.[7] Code Overlay[3] is a mapping technique to execute programs that are larger than the available memory (local storage) by splitting that memory into regions, and the program code into corresponding segments. Multiple segments can be linked to the address of one region, meaning they can be swapped at run-time by means of transferring another segment with its functions into a region. This leads to a behaviour known from caches: When a called function is not mapped to its region, there is an overlay miss and it has to loaded before execution can continue. There is a toolchain available integrated into the GNU Compiler Collection that can automatically generate overlays for SPU applications[2]. [3] introduces a Code Overlay Generator(COG) that aims at producing a more optimal overlay mapping than the default IBM Cell SPU compiler. Their approach is based on a heuristic that works without constructing or solving an ILP, instead relying on a heuristic. A more detailed report on optimisations for instruction SPM for average-case execution time optimisation is given in [13]. 113
117 7 4 Cache Locking Cache locking is a technique available in some systems that allow the operating system or application to control cache behaviour. Locking data in the cache, i. e. keeping it from being evicted, can be used to make memory access more predictable or even optimise the average execution time. Since the approaches and algorithms targeted at optimising by cache locking are similar to those for Scratchpad Memory, I included this section. 4.1 Architectures [12] lists Coldfire MCF5249, PowerPC 440, MPC5554, ARM 940 and ARM 946E-S as architectures that support cache locking. Cell: The PowerPC element of the Cell multiprocessor allows software to lock cache contents in place, which allows it to optimise memory access, among others, for fast predictable response times in hard real-time systems. x86: Cache locking is not a supported feature of the x86 architecture, but still possible through processor-specific cache control mechanisms. While the use of those is discouraged in performancecritical scenarios, there are some applications that make use of this feature: CAR: Cache as RAM is a technique employed by the coreboot open-source bios to increase the amount of memory available to the CPU before the initialisation of the RAM controller. CARMA: Carma is a framework to establish a trusted computing base requiring only the CPU of a computer to be trusted. It is motivated by the fact that PCI allows hardware to access the RAM and memory mapped regions in other peripherals. This provided an entry point for malware nested in PCI devices (e. g. NIC firmware flash) as well as cold-boot attacks where sensitive information is gained by freezing RAM chips and thus being able to read their contents after removing them from the system. The technique employed by CARMA is based on the approach of CAR. But, instead of using L1 cache, they are mapping and locking a portion of RAM into the L2 cache, which gives it a piece of general-purpose memory instead of splitting instruction and data memory. 4.2 Cache Locking vs. Scratchpad For example, in [12], Isabelle Puaut and Christophe Pais compare the effects of the instruction cache locking optimisation from [11] for both SPM and locked cache. The differences between the two mechanisms is hidden by a function Load that takes care of the following: Cache Locking: When relying on cache locking, Load scans all the program lines of the basic block to load and checks if there are free cache lines in each set a line is mapped to. If there is available cache lines, it then locks the scanned content in cache. This approach requires little or no modification of the original memory layout. Scratchpad: For SPM, Load uses a first-fit strategy to allocate an entire basic block. This has to be done at compile-time to determine the memory address the block will be executed at. This is an example for the portability of algorithms between SPM an cache locking optimisation. The detailed results are given in Figure 6, while scratchpad memory is not generally better than cache in the given scenario, the WCET is not significantly higher. Furthermore, the authors voice the following concerns: 114
118 8 Figure 6: On-chip/Off-chip/reload ratios for locked caches & scratchpad memories, [12] Figure 7: Impact of Basic block size, [12] Cache pollution: The granularity of caching, meaning cache lines of fixed size, may lead to cache pollution, the consequence of which is that data is unintentionally locked into the cache because it s located in the same line as data that is intentionally locked. SPM fragmentation: As with any memory management, scratchpad memory may become fragmented when exposed to continuous allocations and deallocations. Cache pollution directly affects the WCET because the time needed to load and lock a cache block is longer than necessary when including data that is not needed. Cache is able to handle large basic blocks without performance loss because it is working with the independent granularity of its own block size. SPM, on the other hand, is very susceptible to basic blocks that are to large for the available memory, which may be worsened by aforementioned fragmentation. An example is given in Figure 7, where the j f dctint benchmark shows the explained behaviour. 5 Scratchpad in real-time systems When developing software for hard real-time it is crucial to prove that it can meet specified reaction times. These are proven by calculating the worst-case execution time, short WCET. Naturally - it is in the interest of developers, and those who evaluate hard real-time systems, to give as tight an upper bound as possible. Optimising for WCET differs from average-case execution time (ACET) optimisation because it has to rely on the formal calculation and guarantee of the execution time along the worst-case execution path(wcep). Because of this, most of the algorithms geared towards reducing the ACET are not suitable for WCET reduction, especially those relying on profiling. 115
119 9 5.1 Caches There are several aspects of cache behaviour that make it difficult to guarantee tight WCET boundaries. Having a processor with cache leads to unpredictable timing, since its internal state at a specific point of time is unknown to compiler and developer. This leads to WCET estimates being pessimistic, assuming cache misses wherever it s not clear if a page is cached, or even having to ignore the cache entirely[9]. A further aspect of those uncertainties, timing anomalies, may lead to cache misses being better for the whole WCET than a cache hit, which further complicates giving tight boundaries[14]. Using Scratchpad Memory alleviates those problems - as well as providing a method to specifically optimise execution time of the worst case execution path. 5.2 WCET Centric Data Allocation to Scratchpad Memory[15] In [15], the authors analyse different approaches to lower the WCET of an application by statically allocating data to SPM. First, they formulate an ILP which, when solved, produces an optimal allocation of variables to the scratchpad. After that, there is an analysis of both knapsack and branch-and-bound approaches to solving the problem faster, as well as a greedy heuristic to be able to allocate larger amounts of data within reasonable time. While the approaches given in this paper can be used to allocate variables on the stack, it is only possible for non-recursive ones that can be treated as global variables ILP The basis of the ILP to optimise the WCET is a set of decisions S v {0,1} that determines for each variable v allvars whether it is allocated to SPM(S v = 1) or conventional memory(s v = 0). To ensure that all the allocated variables actually fit in the SPM, there is the constraint S v area v scratchpad size v allvars that ensures that the sum of the area needed for each allocated variable area v is lower than the size of the SPM scratchpad size. Calculation of the WCET of a loop is done through analysis of the directed acyclic graph(dag) representing its control flow. It is assumed that the DAG of each loop has exactly one source and one sink node, the latter may be a virtual sink node when none is given. The WCET of the DAG rooted in each basic block i is called W i. It is calculated from the sink node in the DAG to the source node, the first being W sink = cost sink v allvars S v gain v n v,sink where cost i is the execution time of the basic block i and the reduction of which is calculated by multiplying the gain in access time of each variable gain v through it s allocation to scratchpad with the number of occurrences n v,i. Similarly for every edge in the DAG i j: W i W j + (cost i v allvars S v gain v n v,i ) Which gives us the WCET of the loop body as W source. The WCET of the whole program can be determined by multiplying the WCET of each loop with the a known constant lb, which is the known 116
120 10 maximum number of iterations. This gives us the maximum execution time cost of the innermost loops, which can now be used to construct the same constraints for the next level of loop nesting until the WCET for W entry, the unique entry node of the program, is known. Thus, the objective function of the ILP is the WCET of the entire program: W entry Knapsack While formulating memory allocation as a knapsack problem may be an intuitive choice, it is not appropriate for WCET-optimising SPM allocation. The problem is that the reduction achieved through the allocation of variables to scratchpad is not additive. This is because, whenever one path is optimised, it might become faster than another path, leading to that being the new worst-case execution path, which lessens the achieved reduction in worstcase execution time. A graphical example of changing WCEPs is given in Figure 15 in Section 5.5. Since the WCET reduction achieved through the allocation of each variable is heavily dependent on the allocation of other variables, knapsack can not be used to solve the allocation problem in this instance Branch and Bound Branch and bound is the improved approach chosen to find a perfect solution to the ILP given in Section To not be forced to try all the possible combinations of variable allocations, branch and bound is an approach that utilises a heuristic to discard large amounts of possible solutions without calculating the result of all of them. This is achieved by representing the decision of the allocation of each variable as a layer in a tree structure. While traversing the tree, after each WCET that is lower than the WCETs found before, all those subtrees not yet traversed are discarded for which a heuristic shows that their lowest possible WCET is above the minimum already found. See Figure 8 for a graphical example. Figure 8: Pruning the branch-and-bound search tree [15] A good heuristic for the upper bound of a subtree, referred to as UB() from now on, is essential for the branch-and-bound approach to be able to cut away large portions of the decision tree. This is essential to lessen the computational effort required for finding an optimal solution. 117
121 11 While it is not reliable to optimise the worst-case execution time, knapsack optimisation provides a definite upper bound for the possible WCET reduction through variable allocation. It is solved through dynamic programming, and requires the following parameters: 1. Variables v i to allocate. 2. Size of each variable area vi to allocate. 3. Limit given through the size of the SPM: scratchpad s ize 4. Maximum possible execution time reduction through allocation of variables given by the maximum reduction achieved on any execution path: bound v The effort necessary is still exponential, which is why even branch-and-bound is not feasible for larger programs and large SPM Greedy Heuristic To provide a feasible solution to the problem of static data allocation to SPM, there is a greedy heuristic given in [15] that has a significantly lower complexity. The results of a comparison given in Figure 10 Figure 9: Greedy heuristic given in [15] indicate that the given greedy heuristic is close to the optimal case when considering the achieved WCET reduction. [15] incorporate unfeasible path detection to further reduce their WCET. They detect unfeasible paths by searching for conflicting assignments that are of the form variable := constant and conditional branches of the form variablerelational operatorconstant. For further information, the reader is referred to [4]. 5.3 Optimal Static WCET-aware Scratchpad Allocation of Program Code [5] While the previous paper focused on data allocation to SPM, [5], as the title indicates, focuses on the allocation of program code. 118
122 12 Figure 10: WCET reduction through optimisation with original ILP, branch-and-bound and greedy heuristic for various applications[15] ILP The ILP defined is very similar to the one given in [15], which is why I will narrow the explanation down to the differences between the two. First, program code is usually worked with on the granularity of basic blocks, but defining decision variables for those makes no difference in the general ILP layout. A more important consideration done in [15] is the size and speed penalty of jump and branch instructions. Encoding limits the address distance an instruction can jump or branch over, which, together with SPM being mapped to a different address space than the RAM leads to more instructions being 119
123 13 required when there is a transfer from basic block to basic block across the two types of memory. Figure 11: Possible jump scenarios[15] x i, x j and x k are the decision variables for the basic blocks b i, b j and b k. There are three scenarios to transfer control between basic blocks on typical embedded processors, depicted in Figure 11. Implicit jumps transfer control between consecutive blocks without a jump or branch instruction, when the end of one basic block is reached and the next one begins. The execution time penalty for placing basic blocks connected by implicit jumps in different memory spaces can be modelled by: jp i impl = (x i x j ) P high represents the logical XOR, P high is the jump penalty for jumping across memory spaces. Unconditional jumps are penalised when the basic blocks lie in different memory spaces. When they share the same, there is the much smaller penalty P low. The basic blocks may even be consecutive in the memory they are allocated to, which happens when all in-between blocks are allocated differently, and causes a penalty of 0. The general penalty caused by unconditional jumps from block b i to b j is defined as: jp i uncond = (x i x j ) P high + (x i x j ) (1 (x i x k )) P low b k Figure11b A conditional jump is regarded as a combination of both implicit and unconditional jump, it s penalty being: jp i cond = (x i x j ) P high + (x i x j ) P high + (x i x j ) (1 (x i x k )) P low b k Figure11c Those three are then integrated into the ILP, being added to the WCET at every edge in the directed acyclic graph that represents the given code. Aside from those performance impacts, the memory consumption of additional jump instructions has to be considered when allocating code to SPM. [15] gives the following size penalty for the different jump conditions: Compiler (x i x j ) S impl if JS ofb i isimplicit (x i x j ) S uncond if JS ofb i isuncond. s i = (x i x k ) S impl + (x i x j ) S uncond if JS ofb i iscond. 0 else To use the given ILP, [15] used the architecture of their WCET-aware C compiler WCC. ILP-based WCET-aware SPM code allocation is done after all other optimisations. The entire architecture is outlined in Figure
124 14 Figure 12: WCET-aware compiler WCC[15] Evaluation For evaluation, [15] uses 73 different real-life benchmarks, the result for some of which is given in Figure 13: WCET reduction estimates for different benchmarks[15] Figure 13. The size of the scratchpad is 48kb, 47 of which are usable after reserving 1b for system code. Program code size of all benchmarks are between 52 bytes and 18kB, so all of them fit into the SPM. Each of the five benchmarks was run with the scratchpad size being restricted to 10%, 20% etc. up to 100% of the program size. 5.4 WCET-Centric Software-controlled Instruction Caches for Hard Real-Time Systems[11] Definition of Problem [11] provides WCET optimisation through dynamic cache locking. Puaut first gives a greedy algorithm to find near-optimal solutions that are then used as an initial population for a genetic algorithm which further optimises the result. Unlike the previously discussed static SPM allocations, dynamic SPM or cache locking changes the allocation of variables or basic blocks during program execution. The dynamic allocation of can be split into two problems: First, the choice of reload points at which new content gets locked in the cache and old content may be evicted. Second, the data to load at these reload points has to be determined. 121
125 Choice of Reload Points While reload points(rp) could be placed at every instruction in the program, the vast number of possibilities would cause an enormous complexity. In [11], the author chooses to limit the placement of reload points to natural locations, which are the headers of functions and loops. To limit the amount of reload points, the user may specify max reload points. To decide whether a RP is worth choosing, an estimate of the possible WCET reduction is calculated. For those calculations it is necessary to give an overview of the cache model used: The instruction cache is W-way set associative. It contains B blocks of S B byte each, with the total size being S C = B S B. Because the instruction size of the CPU is fixed, each cache block can hold exactly ipcl instructions. There are several constants to describe timing behaviour of the cache: 1. t hit and t miss are the latencies caused by cache hits and misses. 2. t i and t l are caused by loading and locking the cache respectively. The number of cache misses required for load and lock of pl instruction lines is t i +t l pl To evaluate whether a reload point is worth being placed before the loop L, the greedy algorithm uses the Cost function CF(L) given below. Furthermore, it relies on a function f (bb) or f (pl) that gives the number of executions of a basic block bb or instruction line pl on the WCEP of the loop L. While pl(l) returns all instruction lines of the loop, m f pl(l) returns all the most executed instructions that fit into the cache. WCET cache(l) = f (pl i ) (t miss + (ipcl 1) t hit ) pl i pl(l) WCET locked(l) = f (pl i ) ipcl t hit pl i m f pl(l) + f (pl i ) ipcl t miss pl i pl(l) m f pl(l) + ph pre head(l) f (ph) (t i +t l m f pl(l) ) CF(L) = WCET cache(l) WCET locked(l) CF(L) indicates the benefit of placing a reload point in the pre-header of loop L. If CF(L) is positive, the WCET of the loop L is expected to be lower when cache content is locked in the reload point preceding it. The greedy algorithm sorts the reload points and selects the max reload points first Choice of Content to Load&Lock For each RP that is decided to be worth using, the benefit of the load&lock of each basic block(bb) following that RP is considered. Similarly to the benefit of RP, this is done through a formula that weighs the estimated WCET using cache in regular LRU mode against that achieved while locking the BB to said cache. The actual algorithm defined in [11] for this step is given in Figure 14. It chooses the N most beneficial basic blocks, iterates the reload points and loads all program lines of each basic block at all the reload points that precede it. This is done iteratively until there are no more beneficial basic blocks or the WCET after an iteration is worse than that of the iteration before. A lower value for N means that the WCEP and WCET are reevaluated more often, which increases the effect of the optimisation. 122
126 16 Figure 14: Selection of cache contents[11] The choice of beneficial basic blocks(selectmostbene f icialbb) is, like the choice of reload points, done through evaluation of a cost function: Example WCET cache(bb, L) = WCET nocache(bb, L) = WCET locked(bb, L) = pl i PL(bb) pl i PL(bb) pl i PL(bb) f (pl i ) (t miss + (ipcl 1) t hit ) f (pl i ) ipcl t miss f (pl i ) ipcl t hit + f (ph) (t i B bb +t l bb ) ph pre head(l) CF(bb, L) =(WCET locked(bb, L) WCET cache(bb, L)) + (WCET locked(bb, L) WCET nocache(bb, L)) An example for two iterations of the greedy algorithm is given in Figure 15. It shows the behaviour Figure 15: Example for the greedy algorithm given in [11] 123
127 17 previously discussed in Section 5.2.2: Allocation of contents on the WCEP to either SPM or locked cache may change the WCEP, leading to less reduction in WCET than on the original path, which is not additive Implementation Details Instead of restructuring the code or executable of the given application, one approach for inserting reload points given in [11] relies on the debug function of the processor platform being used. A breakpoint is used at every reload point, the exception caused by which is captured by the processor and handled by an external manager that takes care of the cache locking Genetic Algorithm A genetic algorithm uses Darwin s theory of evolution to find solutions to a problem. It does so by evaluating the fitness of individuals in a pool of specimens and applying evolutionary mechanisms, e. g. crossover and mutation. There is no guarantee that a evolutionary algorithm finds a good solution, and the time it takes for a random initial population to become reasonably fit is too long. Because of this, the genetic algorithm is used to increase the fitness of the results of the greedy heuristic given before. The formal definition of the parameters for said algorithm is as follows: 1. Codification: (Representation of an individual) Individuals are represented by chromosomes, which are arrays of tuples of the form (rp,contents) rp identifies a reload point and contents the cache contents to be locked at that point. 2. Fitness: The fitness of an individual is the WCET it achieves. 3. Selection: The probability of the selection of one individual is linearly dependent on its WCET. 4. Crossover and mutation: Crossover is done by randomly selecting a point in the chromosome, everything before which comes from one parent, everything after from the other. There are three mutation mechanisms implemented: M rem removes one randomly selected reload point, M add adds a random reload point and M chg randomly changes the content of one reload point. 5.5 Evaluation To evaluate the performance of both the greedy heuristic and the genetic algorithm, Puaut compares the Figure 16: Performance results given in [11], miss ratio of LRU, PPR, the heuristic and genetic algorithm hit to miss ratio the Heptane open source cache-aware WCET estimation tool yields for compiled MIPS R2000/R3000 binary code. They are compared to regular cache using the cache replacement strategies LRU and pseudo round-robin(prr), the latter of which is chosen because it is a hard to predict strategy. Figure 16 shows that neither the results of the greedy algorithm nor their genetically optimised versions yield a better miss ratio than LRU. There are, however, cases in which the hard to predict PRR strategy 124
128 18 performs worse, which indicates that hard to predict cache replacement strategies could be an application for the algorithms proposed in [11]. 6 Conclusion The basic message every paper on SPM that I read carries is: SPM is able to compete with regular cache, not seldom overcoming the efficiency cache can offer. Development on optimising compilers continues making advancements, so it should be only a matter of time before optimisations for explicitly managed memory hierarchies are implemented outside of research compilers. While general-purpose systems require more work to make existing applications work with SPM, embedded systems have the benefit of having software that is often tailored to, or at least specifically compiled for the specific architecture. Together with increased energy efficiency and, compared to cache, decreased complexity, this makes SPM a perfect mechanism to optimise embedded systems. Even tho most of the interesting optimisations for general-purpose and high-performance multicore systems are explained in the paper of my colleague Axel Ratzke[13], there are conclusions I can draw from my research on the known applications of scratchpad memory and explicitly managed memory hierarchies: The success of GPGPU programming for high-performance and especially high-efficiency calculations and the success of the Cell architecture indicate that the concept of Scratchpad memory is a worthwhile and important topic for research on optimisation of those applications. Mobile devices, specifically Android smartphones with their java-based portable applications, would require a JIT to be able to optimise software for SPM, which is something I would like to see being researched. In conclusion: Being able to automatically compile and optimise code to properly use explicitly managed memory hierarchies appears to be an important step to increase the efficiency of computing applications. 7 Bibliography References [1] ATmega640/1280/1281/2560/2561 Datasheet, revision P, updated: 10/2012. Available at atmel.com/devices/atmega1280.aspx?tab=documents. [2] Software Development Kit for Multicore Acceleration, Version 3.1, Programmer s Guide. Available at http: // [3] Michael A. Baker, Amrit Panda, Nikhil Ghadge, Aniruddha Kadne & Karam S. Chatha (2010): A performance model and code overlay generator for scratchpad enhanced embedded processors. In: Proceedings of the eighth IEEE/ACM/IFIP international conference on Hardware/software codesign and system synthesis, CODES/ISSS 10, ACM, New York, NY, USA, pp , doi: / Available at [4] Ting Chen, Tulika Mitra, Abhik Roychoudhury & Vivy Suhendra (2005): Exploiting branch constraints without exhaustive path enumeration. In: In 5th International Workshop on Worst-Case Execution Time Analysis (WCET. [5] H. Falk & J.C. Kleinsorge (2009): Optimal static WCET-aware scratchpad allocation of program code. In: Design Automation Conference, DAC th ACM/IEEE, pp
129 19 [6] Andhi Janapsatya, Sri Parameswaran & A. Ignjatovic (2004): Hardware/software managed scratchpad memory for embedded system. In: Proceedings of the 2004 IEEE/ACM International conference on Computer-aided design, ICCAD 04, IEEE Computer Society, Washington, DC, USA, pp , doi: /iccad Available at [7] J. A. Kahle, M. N. Day, H. P. Hofstee, C. R. Johns, T. R. Maeurer & D. Shippy (2005): Introduction to the cell multiprocessor. IBM J. Res. Dev. 49(4/5), pp Available at cfm?id= [8] Katsuto Sato Kazuhiko Komatsu, Hiroyuki Takizawa Yusuke Arai, Kentaro Koyama & Hiroaki Kobayashi1: Evaluating Performance and Portability of OpenCL Programs. [9] Stefan Metzlaff, Irakli Guliashvili, Sascha Uhrig & Theo Ungerer (2011): A dynamic instruction scratchpad memory for embedded processors managed by hardware. In: Proceedings of the 24th international conference on Architecture of computing systems, ARCS 11, Springer-Verlag, Berlin, Heidelberg, pp Available at [10] Masaaki Oka & Masakazu Suzuoki (1999): Designing and Programming the Emotion Engine. IEEE Micro 19(6), pp , doi: / Available at [11] Isabelle Puaut (2006): WCET-Centric Software-controlled Instruction Caches for Hard Real-Time Systems. In: Proceedings of the 18th Euromicro Conference on Real-Time Systems, ECRTS 06, IEEE Computer Society, Washington, DC, USA, pp , doi: /ecrts Available at org/ /ecrts [12] Isabelle Puaut & Christophe Pais (2007): Scratchpad memories vs locked caches in hard real-time systems: a quantitative comparison. In: Proceedings of the conference on Design, automation and test in Europe, DATE 07, EDA Consortium, San Jose, CA, USA, pp Available at cfm?id= [13] Axel Ratzke (2012): An introduction to the research on Scratchpad memory with focus on performance improvement - Instruction SPM, SPM on Multicoresystems and SPM on Multitaskingsystems. [14] Jan Reineke, Björn Wachter, Stephan Thesing, Reinhard Wilhelm, Ilia Polian, Jochen Eisinger & Bernd Becker (2006): A Definition and Classification of Timing Anomalies. In: 6th Intl Workshop on Worst-Case Execution Time (WCET) Analysis. [15] V. Suhendra, T. Mitra, A. Roychoudhury & Ting Chen (2005): WCET centric data allocation to scratchpad memory. In: Real-Time Systems Symposium, RTSS th IEEE International, pp. 10 pp. 232, doi: /rtss [16] Lehrstuhl Informatik Xii, Rajeshwari Banakar, Rajeshwari Banakar, Stefan Steinke, Stefan Steinke, Bo sik Lee, Bo sik Lee, M. Balakrishnan, M. Balakrishnan, Peter Marwedel & Peter Marwedel (2001): Comparison of Cache- and Scratch-Pad based Memory Systems with respect to Performance, Area and Energy Consumption. 126
130 An Introduction to the Research on Scratchpad Memory with Focus on Performance Improvement - Instruction SPM, SPM on Multicoresystems and SPM on Multitaskingsystems Axel Ratzke University of Kaiserslautern, Embedded Systems Group a ratzke09@cs.uni-kl.de Abstract In this paper a short introduction of the broad field of scratchpad memories will be given. The main focus is on the improvement of performance by the proper use of scratchpad memories. Several techniques for the automatically optimal usage of available on-chip memory space will be presented. 1 Introduction In modern embedded systems the number of processing elements increases steadily. Therefore modern architectures have to deal with the problem of the bottleneck of limited memory. As the systems continuously get faster, the memory remains the weak point. Common solutions to this problem are hierarchical cache memory structures. Since caches are hardware controlled, it is quite difficult to use them efficiently in a system with only limited resources. Furthermore, it can remain unpredictable which information will be stored in the caches and which will be displaced again. To avoid these kinds of problems the use of scratchpad memories became more and more popular in embedded systems. Scratchpad memories basically are small, fast and explicitly software-managed local on-chip memories. Since they are controlled by software, they offer a bunch of advantages for special purpose systems. The abandonment of additional hardware saves space on the chip, which is mostly limited. Second software-managed memories offer the advantage of considerably faster access, since it is assumed that a request hits. Additionally, software solutions are simpler to implement and design errors can be addressed efficiently. This paper will put its main focus on the performance improvement of scratchpad memories (SPM). To consider the broad spectrum of their use appropriately in this work it is divided into the aspects of storing instructions into the SPM, the extension of the problem of optimal usage of the SPM to multicore systems with various separated SPMs and the usage of SPMs in systems dedicated to several distinct processes. In each of these aspects some approaches to solve one or several problems this aspect reveals, are presented. The rest of this work is structured as follows: Section 2 presents the problem of optimal usage of SPM considering only instruction storage. Two approaches to this problem are presented. Section 3 extends the problem to the proper usage in multicore environments. Three approaches to performance improvement are presented. Section 4 presents one possibility to adapt an SPM-based memory architecture to support several distinct processes. Finally it concludes in Section
131 2 2 Instruction SPM As stated above the main focus of this paper is on the performance improvement of systems using scratchpad memories. By the use of a scratchpad memory, the performance of a system can be increased by two options. The first one is data allocation, but this paper will focus on the second option, i. e. instruction allocation. The reason for this is that embedded systems are often designed particularly for special purposes and therefore there are often only a few applications working on them. That is why it is possible to exploit this by saving the often executed instruction blocks in the scratchpad memory in order to obtain a performance gain. Usually there are again two options for doing so. The first is the static approach - here the SPM is filled with instructions before the execution of an application and these instructions are not removed until the execution is finished. It is obvious that this approach wastes a lot of available memory space and therefore does not achieve the best results. The second approach is dynamic - here instructions are not transported into the SPM until they are needed for execution. On one hand this enables a better usage of the available memory space, But then on the other hand it seems much more difficult for the programmer to manage the SPM. That is the reason why solutions are searched to hand this problem over to the compilers, which should be able to handle this problem much more efficiently than humans. For this reason in the following two different approaches to dynamic instruction allocation are introduced. In this first approach presented here, propose [29] in "Dynamic Overlay of Scratchpad Memory for Energy Minimization" a profile-based approach which places instructions as well as data into the SPM by regarding their span of life. The technique is to find the points where code to store in respectively load from the SPM needs to be inserted. These points have to be placed optimally to generate as few overhead as possible. Also the technique has to generate the addresses of variables and code in the SPM in order to place as many variables and code segments in the SPM as possible. The actual problem is to store memory objects into the SPM when they are needed and to write them back when they are not needed anymore. The authors state this problem to be proven to be NP-complete. To solve this problem efficiently it is divided into two smaller subproblems by the authors. The first subproblem is to decide whether a memory object should be assigned to the SPM or the main memory and to find the optimal position for the placement of the corresponding code. The second subproblem is to compute optimal addresses in the SPM for these memory objects. Both subproblems have been proven to be NP-complete. An algorithm consisting of four steps is used to solve that problem. At first variables and code segments of the application are spotted as memory objects. In the second step a liveness analysis is executed to find the live range of the memory objects. The third step is to decide whether these objects are stored into the SPM or the main memory. In the final step for all objects that are stored in to the SPM, the addresses are computed. In doing so the following types of variables and code segments are regarded as potential candidates (called memory objects): global variables (scalar and non-scalar), since they need space in the data memory in both types, non-scalar local variables, since the authors assume that frequently accessed scalar variables at execution time are stored in the registers and so do not need to be stored in the SPM, and frequently executed code segments, called traces which are identified with the trace generation technique. A trace is a frequently executed straight path of basic blocks which improves the processor s performance through its spatial locality. In addition the authors state that traces lead to an unconditional jump every time so that they form atomic units of instructions that are free to move. Afterwards the liveness analysis is executed on the control flow graph of every function. Here the set of 128
132 3 basic blocks of a function builds the set of nodes and the edges are built by the flow of control while the functions execution. The authors extend the principle of DEF-USE-chains from [21] to determine the liveness of the memory objects. A reference to a memory object is can be classified as DEF, MOD or USE. If a reference assigns a new value to every element of a memory object, it is DEF. If it does so to only some of the elements of a memory object, it is MOD and a reading reference is USE. These attributes are assigned to the nodes in the control flow graph. After that a combination of static and profiling based analysis methods is applied in order to find the basic blocks which contain references to variables. Static methods are used to find the blocks which contain references and profiling is used to seperate DEF references from MOD references (and vice versa). Traces are regarded like variables, but USE is assigned to their corresponding blocks. Finally, a fixed point algorithm is used to find the span of life of every object. Now the memory assignment problem is formulated as integer linear programming problem. In this process memory objects are mapped to the SPM on the edges of the control flow graph. According to the authors this allows an efficient determination of the optimal points for the insertion of the transport code. To every object on every edge of the control flow graph an element of the set of static attributes Attrib STAT IC = {DEF, MOD, USE, CONT} is assigned. DEF is assigned to every edge emerging from a node with DEF attribute. In contrast MOD respectively USE are assigned to every edge leading to a node with MOD respectively USE attribute. If a memory object is live on an edge, CONT is assigned to the edge. Also spill attributes Attrib SPILL = {LOAD, STORE} are assigned to the edges to model the transport of memory objects. The LOAD attribute is assigned to the edges where the corresponding object can be loaded from the main memory to the SPM. Accordingly the STORE attribute is assigned to edges where the object can be stored back from the SPM to the main memory. The LOAD attribute is assigned to the edges which are marked with MOD, USE or CONT, or emerge from a diverge-node (i. e. a node with out-degree greater than one). Accordingly the STORE attribute is assigned to edges marked with DEF or leading to a merge-node (i. e. a node with in-degree greater than one). So spill attributes only can be assigned to edges which are already defined as DEF, MOD, USE or CONT. To enforce this, the binay decision variable Xjk i is defined, which models the assignment from memory object mo k to the SPM on edge e i. Xjk i = 1 if and only if mo k is present on the SPM at edge e i and an operation corresponding at j is performed and 0 otherwise. Here e i E,at j Attrib STAT IC Attrib SPILL and mo k MO. The objective function is represented by the energy savings that are possible through this technique. The savings have to be maximized. i {E pro f it (i, j,mo k ) Xjk i E load cost(i,mo k ) XLOADk i E store cost(i,mo k ) XSTOREk i } (1) k Here E pro f it (i, j,mo k ) are the savings by assigning the mo k to the SPM at e i and E load cost (i,mo k ), E store cost (i,mo k ) are the energy costs for transporting memory object mo k to respectively from SPM at edge e i. The authors take the savings from [26]. Now the constraints for the linear programming problem are built. First the constraints which enforce a correct flow of the liveness of the memory objects. X i DEFk X j CONT k X i STOREk = 0 mo k MO (2) X i USEk X j CONT k X i LOADk = 0 mo k MO (3) 129
133 4 X i MODk X j CONT k X i LOADk = 0 mo k MO (4) X i CONT k X j CONT k X i LOADk = 0 mo k MO (5) The constraints (6) to (9) are added to ensure this also on merge-nodes. X i LOADk X i jk 0 e i {e i1...e in }at j {at j1...at jn } (6) Here e i1 to e in are the edges leading into a merge-node. Xj1k i1 in =... = Xjnk s.t.at j1...at jn Attrib STAT IC (7) X i STOREk X i jk 0 e i {e i1...e in }at j {at j1...at jn } (8) Xj1k i1 in =... = Xjnk s.t.at j1...at jn Attrib STAT IC (9) Here e i1 to e in are the edges coming from a diverge-node. Finally the total space of the available SPM is added to the constraints so that the memory objects which are assigned to the SPM are not able to exceed it. Xjk i Size(mo k) ScratchpadSize e i E (10) k The problem posed above is solved with a commercial ILP solver [4]. The number of all variables in the formulation lies in O( MO E ) according to the authors. Finally the address assignment problem is solved. In the step above during the ILP formulation it was implicitly assumed by the authors that the size of all memory objects togehter does not exceed the size of the SPM, when the size on every edge is smaller than the SPM - and so the addresses can be computed. When a bad assignment strategy is used, this assumption can be false due to SPM fragmentation. As a consequence it can happen that that addresses can not be assigned to objects although there would be enough space for them. If all objects have got the same size, this problem can be trivial - in other cases this problem becomes NP-complete. Now the problem is formulated as mixed integer linear programming problem. To compute the address of a memory object, the authors first compute the offset of its start address to the base address of the SPM. The integer variable O i j models the offset of memory object mo j at edge e i and 0 O i j ScratchpadSize Size(mo j ) (11) holds. Next the constraints for the problem formulation are formulated. The offset of two memory objects which are defined on the same edge, must not overlap. This will be enforced with O i j O i k + L ui jk Size(mo k) e i E (12) O i k Oi j + L u i jk Size(mo j) L e i E (13) where u i jk = 1 if and only if Oi k - Oi j Size(mo j) is satisfied and 0 if and only if O i j - Oi k Size(mo k) is satisfied. These constraints have to be repeated for every two memory objects which are assigned to the SPM at the same edge. 130
134 5 Thus constraints are added to ensure that for a given memory object mo k the offset for every edge on which it is assigned to the SPM does not change. O i k O j k L vi j k = 0 e i,e j E (14) with v i j k = 1 if and only if Oi k O j k and 0 otherwise. This constraint is reformulated for every valid two edges, too. A valid solution can be recognized by the offsets of memory objects which remain the same on pairs of edges. So the objective function is the sum of the binary variable v i j k for every valid pair of edges for every memory object. This function has to be minimized. i j v i j k (15) k Also this problem is solved with the help of the ILP solver [4], but with its branch and bound procedure. According to the authors this can take long time for some instances of the problem. The technique was tested with a system consisting of an ARM7T processor core, an on-chip SPM and an offchip main memory. The here presented algorithm to solve the overlay problem was compared to the static allocation technique from [25]. At first the benchmarks were compiled using an energy optimizing C compiler and next the trace generation [28] was applied, before the presented allocation technique was used. The so generated maschine code was executed by ARMulator [1]. The tests were executed with benchmarks of MediaBenchII [2], UTDSP benchmark suite and a benchmark consisting of sorting routines from [25]. As a result an application needs on average 21% less CPU-cycles if the technique presented above was used. This technique seems quite conservative, as it seems that profiling data and formulating the problem of optimal SPM use as an linear programming problem is a common approach. Moreover the problem is identified as NP-complete. But then this paper describes a way to use existing SPM space for both instructions and data, which is quite an advantage on systems with only limited die-area. Figure 1: Edge Detection: Comparison with a static allocation approach In the paper presented next, a quite different approach is shown where the content of the SPM is not determined before execution but rather at runtime. In "Scratchpad Memory Management for Portable Systems with a Memory Management Unit" [15] a dynamic strategy for horizontally partitioned memory subsystems for contemporary embedded processors was developed. The memory subsystem is fitted with a memory management unit and a SPM that is physically addressed and mapped to the virtual address area. Furthermore, to spare energy costs and further increase 131
135 6 Figure 2: Performance and Code Size: Comparison with a static allocation approach the system s speed, a small minicache is implemented. The procedure is based on using the page fault exceptions of the memory management unit to track page accesses and copy often used code into the SPM, before it is executed. Because the smallest unit to copy code into the SPM is a memory page, the authors state that good code placement is of the utmost importance in this procedure. A postpass-optimizer is used to divide the application s binaries by the use of its profile data into the three categories: pageable, cacheable and uncacheable. Pageable code is aggregated to pages with the same size as an physical memory management unit page and copied into the SPM as needed, while the other two categories are stored at fixed positions at the external memory. They describe their memory system as follows. To avoid the difficulties of todays standard architectures (e. g. architectures where a the MMU first translates the virtual address to a physical address which is compared to the SPM base register und SPM accesses occur only if this address belongs to its address area or architectures where the SPM and the cache are accessed at the same time) the authors provide the following architecture. A horizontally partitioned on-chip memory subsystem for the instruction side of a harvard architecture and additionally a micro-tlb, a SPM and a direct-mapped minicache. The micro- TLB s task is to translate the virtuall addresses from the core s instruction fetch. The resulting physical address is checked against the register of the SPM area to decide if the request should be forewarded to the SPM or if it should be forewarded to the minicache. This means if the address is located beyond the SPM, the minicache will be addressed. The minicache has the purpose to reduce the costs for requests beyond the SPM. As disadvantage it is to mention that the the assignment from virtual-to-physical-translation with the SPM/Cache access increases the latency of the instruction fetch with the time of an micro-tlb access. For cores up to 500 Mhz relief can be procedured by an additional cycle. For cores beyond 500 Mhz it is possible to intersect the instruction fetch pipeline to help according to the authors The Scratchpad Memory Manager which manages the SPM as a global resource is neither dependent on the size of the SPM nor a certain amount of running applications and is fully integrated into the runtime environment. Pageable code is aggregated to pages whose size equates to the size of a virtual memory page. As soon as an application s binary is loaded, the runtime environment creates the virtuall-to-physical-assignment by building the MMU tables which assign the physical addresses to virtual addresses. At first all assignments to physical code are rendered unusable by invalidating the check bits. Now the application starts by setting the PC to the corresponding entry point and as soon as the PC reaches pageable code, the MMU throws a prefetch abort execution because the assignment in the page table is missing. Once this exception is forewarded to the SPMM by the runtime environment, the SPMM loads the necessary page into the SPM and creates an appropriate assignment to the virtual page in the page table and then the aborted instruction fetch phase is restarted. Pages already residing in the SPM are 132
136 7 not affected by this procedure. If there s more code to be stored in the SPM as free pages are available, already loaded pages have to be replaced. Since these pages always have to be read but not written, they do not need to be written back into the external memory. To override a page only its assignment in the page table has to be invalidated. The SPMM monitors which pages are free and which are occupied and decides which page should be used next by a simple round robin strategy. The Postpass-Optimizer used in this paper belongs to the Seoul National University Advanced Compiler tool kit, which is itroduced in [22]. It is simply called SNACK-pop and works with the ARM/Thumb instructionset including the DSP expansions, while ARM floatingpoint instructions are not supported. According to the authors, using a postpass-optimizer offers three advantages. Every binary can be optimized for the SPM-allocation technique without access to the source code and the need of recompiling the whole application. Also the optimizer allows optimizing the whole program complete with libraries which would not be possible on the source level. Last but not least postpass optimization is perfect suitable for low level code layout arrangement optimizations. As input for the optimizer serve the application s binaries and libraries in the ARM ELF format, which will be deassembled to the code sections and data sections. All unidentified symbols are resolved and in the next step the code blocks are further partitioned into functions consisting of basic blocks, and branches with hard coded offset are resolved and replaced by relocation information, so that the optimizer is free to move code as needed. As soon as SNACK-pop encounters a pointer pointing on constant data in its pool, it removes it und moves the data to a global data area which is not marked as pageable, before adjusting the pointer. This is necessary since thrashing can occur if big constants can override each other in the SPM due to their size. In order to gather profile data of the application, instrumentation code is added to every function and the image is simulated on an instruction set simulator to compare it with an unaltered reference image. In this way a bunch of profiles and instruction traces are created with different training data sets. In the next step the new created profile data is fed to the optimizer again to define the average number of accesses of a code block and for each block in function level it is defined if it falls to one of the categories pageable, cacheable or uncacheable as follows. Code which is read on average less then once is classified as uncacheable since it would only produce cache misses. Possibly occuring hits based on local closeness are negligible due to the small access number. For every other block the energy which would be necessary to execute the code from the cache is calculated and compared to the energy which would be needed to execute the block from the SPM added to the amount of energy needed to copy the code from main memory to the SPM. If the first value is the smaller one, the code will be assigned to the cache, in the other case it will be assigned to the SPM. Thereafter function splitting similar to the one in [23] is used. At first the code blocks are resorted according to their intended position in the memory and new branch instructions are added as needed to keep the control flow graph valid. The text step is to split the functions into partial functions for the partial blocks in order to locate them in the SPM, the cache or the external memory. The code for the according partial functions is then located there respectively. Now the code has to be placed into the pages optimally. Since this problem is NP-hard, the authors act by the following heuristic. At first all loops in the dynamic call graph are found. Here the authors do not only mean loops in the traditional way, but rather functions where the number of accesses by a father function divided by the number of accesses of the father function exceeds a certain threshold. On the source level the effect is just the same according to the authors. For every of these loop headers the loop members are identified by computing the loop s closure, which means the loop contains all functions in its body that are called at least as often as the loop header itself. Now the loop call graph is built (i. e. a 133
137 8 simply directed graph with loops as its nodes and edges between them if one loop is a subloop of the other) and went through from the innermost loop to the outermost. For every pageable function, that is not already bined in a bin, a bin is created in which it is bined. After every node in the loop call graph is processed, the size of the bins is calculated (i. e. bordered) so that they cannot grow to infinity. Up next all loops which contain inner loops (i. e. non leaf-nodes) are looked at. Every function from the outer loops is moved to the bins of the inner loops, as long as they fit, by using the bestfit algorithm from Introduction to algorithms [14]. Here the principle is to aggregate functions with strong temporal vicinity to obtain a better usage of the bins and avoid internal fragmentation. Once there is no function left to be moved, the size of the bins is recalculated. Functions which are marked as pageable but do not belong to any of the loops are processed at last. The loop call graph is processed towards its root and for every access to such a type of function, a fictive loop with a threshold of one is calculated. If a loop contains both an inner loop and such a function, it will be tried to bin the function into the bin of the inner loop. All functions that are left over are bined into an extra bin. Once SNACK-pop is done with the code arrangement, it builds the new ELF binaries and adds six new symbols which describe size and location of every of the three code regions (paged, cached and uncached). As soon as an ELF binary is loaded, the SPMM searches for these symbols and if it finds them, the memory assignments are established according to them - if not, only the minicache is used for this unoptimized image. In order to test the approach SNACK-armism [22] was used. As a reference system serves a fully cached system with 4-way associative virtually-indexed, physically-tagged instruction and data caches. As performance metric the total execution time was used. Tested was with benchmarks fom MiBench [17], MediaBench [19], the official ISO MP3 decoder [6], MPEG-4 XviD encoding/decoding [7] and a combined benchmark consisting of Quicksort, Dijkstra, SHA, ADPCM-enc, ADPCMdec, and Bitcount. The tests showed that on average 85% of the pages space was used, while 15% of a page remained unallocated. On average the use of the SPMM with a small minicache increased the performance by 12% against a convential instruction cache with similar die-area. On the negative side one page fault costs 190 instructions, 270 loads from, and 29 stores to SDRAM on average. This paper seems quite promising since it is the starting point for several researches to this subject of the authors. One advantage of the approach is obviously its flexibility. It does not need to be known what program will be running on the system. This might be usefull for systems that are created for more than one single purpose. But then one can clearly see that there are still some disadvantages. First of all is the waste of SPM space through not fully packed pages (15% of a page remain unused on average!). Next is the latency incuring if the SPMM needs to react, when new pages need to be loaded into the SPM, and to actually load them from main memory to the SPM. 3 SPM on Multicore Systems After two ways to exploit available on-chip memory optimally und improving performance for singlecore systems the problem has to be expanded to multicore systems. On multicore systems it has to be dealt with several new problems. Since one has more cores to execute processes together, communication between them has to be considered. Also often to every core its own private SPM is assigned, so that the data needed for the execution has to be divided between these SPMs optimally or has to be copied to each of them. In this section three approaches for using the available scratchpad memory space to gain additional per- 134
138 9 formance are considered. The first one uses linear programming to determine optimal storage of data on an multicore system. A technique based on Integer Linear Programming for integrated task mapping and or scheduling, SPM partitioning and data mapping for MPSoC is introduced in "Integrated Scratchpad Memory Optimization and Task Scheduling for MPSoC Architectures" [27]. Here the authors act on the assumption of working with data only, but the problem formulation can be generalized to data or code blocks in general. In the supposed architecture every processor has got its own private SPM, but also got access to the other processors private SPM with a higher latency. It is assumed to start with an application and a kind of a budget for the total SPM with the target to find a data mapping and a configuration for the processors private SPM suited for maximizing the application s performance. Since the best configuration for an processor s SPM depends on the tasks mapped to it, task mapping and scheduling and the SPM configuration depend on each other. As said above the architecture consists of several cores which can communicate with each other by using a shared off-chip memory via bus. A virtually shared scratchpad is used, which means every processor has its own private SPM but can access the other SPMs too with a higher latency (so called remote SPM). For reasons of simplification the latency of every off-chip memory access is assumed as a constant and conflicts eventually occuring on the bus are absorbed this way and furthermore it is assumed that every memory area can be mapped to at least one SPM. The author s goal is to find the optimal SPM configuration, which minimizes the initation intervall, for a given task graph, architectural model and limit of the available SPM space. A task graph is a directed acyclic graph which describes the single tasks of an application as nodes and the communication between them as edges. Every task can be mapped to every processor, so that every execution time for every processor is associated with every node. This execution time for a task executed by a processor depends on the position of the data in the SPM, so that the execution time is calculated with all data variables placed in the off-chip memory. An edge from one task to another in the graph models a data transfer between them, so the amount of data transported is associated with every edge and in addition every task is associated with the size of and access frequency to the data variables, received by profiling. It is assumed that an application is given in such a graph. The pipelined implemention benefits from different processors executing different iterations of the task graph at the same time. In sequential execution of an application the aim is to minimize the execution time of a single iteration of the task graph, whereas in pipelined implementation however the aim is to minimize the afore-mentioned initation interval, the time between the start of two following iterations of the task graph. So the problem of the beginning is divided into three smaller problems: first the mapping/scheduling of the tasks to processors respectively communication between the tasks. Second the allocation of the optimal size of each private SPM. And third the allocation of the data varibales of each task to every single SPM. All these problems can be formulated as integer linear programming problems. For reasons of simplification, in the following description the authors assume that the present MPSoC architecture consists of four heterogenous processors, so that the execution time of a task is the same on every processor. But they also mention that this is no requirement for the problem formulation. The first small problem is now described as ILP formulation to optimize the performance by task mapping/scheduling. This is the initial situation: if an application got N tasks, they are denoted as T 1...T N. T N is without loss of generality the last task (i. e. it has no successors in the task graph) - if there are several such tasks, a dummy task is added as the last one. Further on there are M available homogenous 135
139 10 or heterogenous processors, described as P 1...P M and with every task T i related is its execution time on every processor P j, time i, j. As mentioned before, it is assumed that every variable is placed in the off-chip memory. One task can be mapped to exactly one processor, which is expressed by X i, j. X i, j = 1, if task T i is mapped to processor P j and 0 otherwise. So M j=1 holds. The execution time for every task T i is expressed by Time i = X i, j = 1 (16) M j=1 X i, j time i, j (17) StartTask i and EndTask i respectively describe the point of the beginning or the end of the task, so that EndTask i = StartTask i + Time i 1 (18) holds. The optimization s objection function is the smallest value for EndTask N for the last task T N of the application (i. e. to minimize the critical path through the task graph). This function has now to be optimized in respect of the already mentioned constraints (16) - (18) plus the following constraints. Every predecessor of a task T i has to be already processed before it can be started with its execution. If a predecessor T h additionally was mapped to another processor, the task has to wait for the end of the communication between it and its predecessor and a latency of comm h,i occurs. This inter-task communication is modeled as task C h,i (where T h is the predecessor and T i is the task which is now to be executed) on the shared bus. The points of time StartComm h,i and EndComm h,i are described analogous to their equivalent of tasks. Now and StartComm h,i EndTask h + 1 (19) StartTask i EndComm h,i + 1 (20) have to hold to ensure that predecessor tasks and communication with them are completed before the execution of a task. Costs arise only, if T h and T i are mapped to different processors, so this is avoided by the following constraint EndComm h,i = StartComm h,i + L h,i comm h,i 1 (21) where L h,i = 1 if and only if T h and T i are mapped to different processors. Next it has to be ensured that two independent tasks which are assigned to the same processor have different lifetimes. So for two independent tasks T i and T i, L i,i is defined as above and additionally B i,i = 0, if T i and T i are assigned to the same processor and T i is executed after T i. B i,i is defined analoguos. So this condition can be formulated with the next three constraints: B i,i + B i,i L i,i = 1 (22) StartTask i EndTask i B i,i + 1 (23) 136
140 11 StartTask i EndTask i B i,i + 1 (24) Of course communication between single tasks must not overlap and so for different communication tasks C h,i and C f,g it is defined: V h,i, f,g +V f,g,h,i = 1 (25) StartComm h,i EndComm f,g V h,i, f,g + 1 (26) StartComm f,g EndComm h,i V f,g,h,i + 1 (27) where V h,i, f,g = 1if and only if C f,g happens after C h,i (and 0 otherwise). V f,g,h,i respectively analoguos. Now the formulation of the task scheduling is extended to consider pipelined scheduling - tasks are distributed among pipeline stages of the same size, in a synchronous pipelined execution. The initation interval which describes the length of a pipeline stage is equal to the maximal time needed to handle every task on a stage. It is the objective to distribute the tasks in regard of their dependencies and needed resources among the pipeline stages so that the initation interval will be minimized. It is important that every processor can be used in only one pipeline stage, because all stages are executed in parallel in different instances of tasks in the steady state. Then again every stage can use more then one processor so that there is a maximum of M stages of the pipeline. In consequence of this observation the formulation of task mapping and scheduling is adapted so that it works as before and then in the next step the different processors are assigned to the different pipeline stages. To model the assignment of a processor to a pipeline stage, the varibale W is introduced: W j,s = 1 if and only if processor P j is assigned to the s th pipeline stage. So M s=1 W j,s = 1 (28) holds. With this condition it is possible that no processor is assigned to some stages, which is a result of the fact that some stages have got more then one processor. Such invalid stages are ignored. The function which has to be optimized is the minimum of the initation interval. To describe the maximum amount of time needed to execute all tasks of a stage, the values StartStage s and EndStage s are introduced in order to mark the points of time where a Stage s starts respectively ends. So II EndStage s StartStage s + 1 (29) holds for every s: 1... M. Obviously a pipeline stage must not overlap with another, so that similar to the tasks it is defined: B s,t + B t,s = 1 (30) StartStage s EndStage t B s,t + 1 (31) StartStage t EndStage s B t,s + 1 (32) where B s,t = 1 if and only if Stage t is executed after Stage s and B t,s = 1 if and only if Stage s is executed after Stage t. A pipeline stage has to cover the whole execution time of the processes assigned to it and this is modeled for every stage s: 1... M and every processor j: 1... M by StartStage s StartProc j + (1 W j,s ) (33) 137
141 12 and EndStage s EndProc j + (1 W j,s ) (34) StartProc j and EndProc j mark the points of time where processor P j starts respectively ends its execution. They are calculated from the earliest startpoint respectively the latest endpoint for all tasks assigned to the processor. For every processor j: 1... M and every task i: 1... N and StartProc j StartTask i + (1X i, j ) (35) EndProc j EndTask i (1X i, j ) (36) have to hold. The communication tasks which are executed on a shared bus which is used throughout all pipeline stages must not be forgotten. Communications between different stages are executed at the same time in one II. The constraints (25) to (27) are in charge of preventing the communications in one pipeline stage from overlaping. But it has to be enforced that the communications between different pipeline stages do not overlap. In order to achieve that, the authors normalize the communication tasks execution intervals by setting the starting time (respectively ending time) relatively to the starting time (respectively ending time) of the pipeline stage to which they are assigned. Now the variable F is defined: F h,i,s = 1 if and only if C h,i is assigned to stage s, and 0 otherwise. Now it can be expressed: M s=1 F h,i,s = 1 (37) So every communication task is included in the interval of the stage to which it is assigned. StartStage s StartComm h,i + (1 F h,i,s ) (38) and EndStage s EndComm h,i (1 F h,i,s ) (39) Finally the mutually exclusion of all pairs of independent communication tasks C h,i and C f,g is demanded: and (StartComm h,i StartStage s ) (EndComm f,g StartStage t ) V h,i,s, f,g,t + 1 (40) (StartComm f,g StartStage t ) (EndComm h,i StartStage s ) V f,g,t,h,i,s + 1 (41) In this formulation V h,i,s, f,g,t = 1 if and only if C h,i is scheduled in Stage s, C f,g in Stage t and the normalized interval of C h,i is scheduled after the normalized interval of C f,g (V f,g,t,h,i,s analogous respectively). Now to the heart of the problem: The SPM partitioning and data allocation. The number of all variables is specified as R and some of them may be used by several tasks. The number of accesses of a variable is determined by profiling. A variable is associated with this number and its size in bytes, called area v. The first value is dependent on the processor on which the task is executed, it is expressed through the value f req v,i, j which tells how often a variable v is accessed if task T i is mapped to processor P j. Each of these accesses causes a different latency, dependent on where v is located - the latency of zero, if v is located on processor P j s private SPM, a constant latency of cross penalty, if it is located on a remote 138
142 13 SPM, and a constant latency of penalty (which will generally be more than cross penalty), if it is located in the off-chip memory. Whether a variable v is located in the SPM of a processor P j is expressed through S v, j. In the described architecture a variable can be allocated to one SPM at maximum: M j=1 S v, j 1 (42) One constraint of the problem is the SPM area available in total, which is used as input to the problem: R M v=1 j=1 S v, j area v total area (43) The objective function is one of the two already mentioned, depending on whether a pipelined setting is used or not. The last thing to consider now is the execution time which can only be reduced due to data allocation to on-chip memory. To consider this, equation (17) has to be replaced by the last two constraints: Time i = M j=1 (X i, j time i, j R v=1 f req v,i, j gain v,i, j ) (44) gain v,i, j = Y v,i, j penalty + Z v,i, j (penalty cross penalty) (45) where Y v,i, j = 1 if and only if variable v and task T i have been mapped to processor P j and Z v,i, j = 1 if and only if task T i has ben assigned to processor P j and v has been assigned to another processors SPM. In order to test the here presented technique, three strategies are used. The equal partitioning strategy (EQ) ignores data allocation to the SPM while task scheduling. The available SPM is divided equally between all tasks. This is a simple Knapsack problem, for which optimal solutions are known according to the authors. The partially flexible strategy (PF) also ignores data allocation to the SPM while task scheduling. Here SPM partitioning and data allocation are computed simultaneously by a simplified version of the ILP where some variables already are known. The completely flexible strategy (CF) works the same way as described above for the simultaneous task scheduling, SPM partitioning and data allocation. For the actual tests five benchmarks were used. Four of them were taken from MiBench [17] and MediaBench [19]. The fifth benchmark, called enhance, was an altered version of the image enhancement application from [24]. The applications were profiled to find the important execution blocks and every application then was divided in a certain number of tasks, where every task corresponded to such a block. This information was used to find the dependencies between tasks and to compute the communication costs. So the task graph for every application was built. For the tests the SimpleScalar cycle-accurate architectural simulation platform [11] was used. An instrumented version of the SimpleScalar profiler was used to determine the size of the variables, the access frequency and the execution time in processor cycles for every single task. As mentioned before it was assumed that off-chip accesses are constant and do not lead to conflicts on the bus. Both scalar variables and array variables were regarded. For the solution of the ILP the already mentioned solver CPLEX [4] was used. At first EQ and PF were compared to each other - the flexibility of PF compared to EQ leads to a significant performance increase for the benchmakrs excuted with the first strategy in most of the cases. While comparing PF 139
143 14 and CF it was observed that further performance increases depend heavily on the characteristics of the applications. The worst-case occured when the SPM was neither to small nor to big and according to the authors, this was expected because this is the most difficult case for scheduling. Altogether it was shown that flexible SPM partitioning can increase the performance by 60% compared to equal partitioning and integration of memory optimization in task scheduling can increase performance up to 80%. This paper shows quite extensive the interaction between task scheduling and memory optimization and it shows also that the expensive CF strategy is not always necessary for optimal solutions and better performance, depending on the desired application. One a bit unusal approach of gainig performance on multicore systems is delivered in "Exploiting Shared Scratch Pad Memory in Embedded Multiprocessor Systems" [18]. The authors propose an optimizing algorithm targeting eliminating extra off-chip memory accesses caused by interprocessor communication. This approach is especially suited for image processing embedded systems. They focus on an SoC with an off-chip DRAM which can hold data as well as instructions. The SoC consists of multiple processors and their private SPMs and also there are inter-processor-communication / synchronization machnisms, clock circuity and some ASIC. The SPMs build a virtually shared SPM, in which every processor can access its own private SPM as well as the remote SPMs of the other processors fast and only access to DRAM is much more expensive and slower than an access to one of the SPMs. The system uses a loop-level parallelized application as input and in the model described, every loop-nest is as parallelized as possible. All processors work together on the computation of one parallel loop and every processor executes a subset of the loop iteration. Once the computation of a loop is completed, the processors synchronize on a construct called barrier before they start the computation of the next loop. For this (and any other) communication they use fast on-chip links. Because of this strategy every processor works on his own part of the array in the code and since the local SPM is generally way smaller than the part of the array on which is worked, the processor divides these parts further in data tiles for execution. If work on such a tile is finished either it will be droped or written back to off-chip memory, if it was modified. To improve reusability of the data in the VS-SPM, intra-processor-reusability or inter-processor-reusability can be used. Here intra-processor-reusability targets optimizing the access pattern of a single processor and according to the authors the strategy does not make much sense on a multicore system, since it totally disregards inter-processor data sharing effects. These effects are very important in environments where the memories of several processors may partially overlap. On the contrary inter-processorreusability concentrates more on the application i. e. the access pattern of every processor is regarded. The problem of compiling array-dominated applications for VS-SPM based systems is divided into two smaller problems by the authors: Data tile shape/size selection and access pattern selection. The first one is described as the first step in compiling - it is the determination of the form and size of the data tiles. Important in this process are the available SPM space and the data access pattern of the application and the authors state this problem as important but do not pursue it any further since the paper s focus is on the second problem. During the paper all tiles are assumed as rectangular and all the processors are assumed to possess the same size of SPM and work on identical tiles. The access pattern selection is the scheduling step - here for a known tile shape/size an access pattern is determined which minimizes additional off-chip accesses by reducing the inter-processor communication. Now a compile technique is presented to address this problem. The degree of freedom of a given tile describes the tile s options to move on the given data space and an access pattern matrix H is defined which describes in which sequence the data tiles are accessed. 140
144 15 This matrix dimensions are dictated by the degree of freedom. The authors limit themselves to twodimensional arrays, but state that their technique can be adapted to higher dimensions as well. Every column of such a matrix corresponds to an axis and the value of the vector of this axis determines the direction in which the axis along the array will be accessed. Direction vectors for every processor are defined with respect to his neighbours - here the goal is to ensure that whenever a processor needs non-local elements of an array, another processor can deliver from his SPM. To achieve this goal the here presented scheduling strategy makes use of the following mathematical law. Scheduling equality: H T i v i, j = H T j v j,i (46) For two processors i and j, schedules through the matrices H i respectively H j reduce additional off-chip memory accesses. The algorithm based on this law consits of three steps: A symbolic scheduling matrix is assigned to every processor, where its rank is equal to the degree of freedom of the data tile. Now the scheduling equalities are built by using direction vectors and the scheduling matrices. Altogether these equalities build the constraint for eliminating additional DRAM-access by inter-processor communication. In the end the scheduling matrix of an arbitrary processor is initialized with an arbitrary value and now the scheduling matrices of the remaining processors can be computed using the scheduling equalities. For nested loops which may include flow-dependencies, the algorithm is nearly the same as for loops without dependencies so that only the scheduling matrix has to consider these dependencies. The approach for this problem consists of two steps: At first the first two steps of the aforementioned algorithem are applied, but now the algorithm differs in the initialization of the scheduling matrix. Not an arbitrary matrix will be computed, but all acceptable matrices for a processor and then all options for the corresponding matrices of every other processor are regarded. From all these solutions now the matrix which does not violate any data dependencies is chosen. If there is no such matrix, a default scheduling scheme that does not violate any data dependency will be used. But this does not necessarily avoid extra DRAM-accesses. The test environment for this approach consisted of a compiler environment and an in-house simulator. The algorithm was implemented with the SUIF (Stanford University Intermediate Format) experimental compiler infrastructure [10]. The simulator takes parallel C-code as input and simulates a multicore environment. A local SPM for every processor with an access latency of two cycles was assumed and also inter-process communication was simulated. For every necessary synchronization a latency of one cycle was assumed. In order to parallelize the applications an aggressive strategy was used. Every but the innermost loop of a nest was parallelized if legal. Four array-dominated applications of the image processing realm were used: 3D, dfe, splat and wave. But the authors failed to deliver the results for the performance in their work, despite the fact that they stated an increase of performance in their abstract. Also the reported energy savings are to be regarded with caution since the authors only compare the energy consumption of a system using their algorithm. So this might be an interessting approach to the problem of the use of SPMs on multicore systems, but the results do not show much information. Also the bruteforcing in the case of dependencies in the loop nests is rather disappointing. After two different techniques for simple multicore systems, it is time to expand the problem to several levels of parallelism. With multiple levels of parallelism the problem of best usage of the available SPM space gets more complicated. 141
145 16 Figure 3: Energy savings in %: Non-Local SPM optimizations compared to local SPM optimizations (sensitivity to the number of processors) Figure 4: Energy savings in %: Non-Local SPM optimizations compared to local SPM optimizations (sensitivity to the shape of the tile and size of the available SPM space) In "Automatic Data Movement and Computation Mapping for Multi-level Parallel Architectures with Explicitly Managed Memories" [12] the problem of scratchpad management for parallel architectures with more than one level is addressed. The authors developed a framework based on the polyhedron model for loop nest optimization which allocates automatically storage space in SPM, determins the access functions of references to arrays in SPMs and generates the code for moving local scratchpad memory data to global off-chip memory (and vice versa) automatically. The access functions of all array references and the iteration spaces of all statements in a program block are used as input by the framework, which divides the set of all data spaces accessed by all references of the array which is to store in the SPM. The partitioning is achieved through transformation into an equivalent graph problem. The storage allocation is accomplished through an algorithm in four steps by the framework: at first it generates one local memory array for each partition. For these partitions of data spaces the framework determines if it has adequate reuse in a program block, which is the case if there is one or morereference that accesses data space unregularly or if there is other in some form remarkable reuse of data space. These partitions are marked as beneficial to be copied to the SPM. The next step is to find the local memory storage for the partition. For every partition of data spaces the framework determines the upper and lower bounds of every dimension of its convex hull in form of an affine function of parameters of the program block by using parametric integer programming software. These induce the size of the local memory array to be created for the partition. Next the access functions of local memory array references have to be determined by the framework. The 142
146 17 aim is to find the corresponding access function for the local memory array reference for each reference to the original array in the given program block, therefore it is searched for the bound expressions of each dimension of the aforementioned convex hull. Some dimensions of the original data space do not appear in the convex hull and are represented as affine functions that appear in the polytope. With the help of CLooG [3] an array access function matrix is built, in which every row represents the array subscript of a dimension in the original data space. From this matrix the rows that belong to the dimensions in the original array that do not appear in the local memory array are removed. Now it is possible to calculate the corresponding local memory access from the original global memory access. For every partition of data spaces for which a local memory array is created the following procedure is used: with CLooG the data spaces that are accessed by read (respectively write) references are scanned and the loop structure of the code that moves data from global memory to local memory (respectively vice versa) is generated. Now the loop body is built by creating a matrix out of an identity matrix and an additional row representing each one of the corresponding dimensions that do not appear in the convex hull as an affine function of the dimension that appear in the convex hull and program parameters. The upper bounds of the data moved in to (respectively out of) the local memory array are estimated using - among others - techniques already used for the storage allocation. For further calculations over the polyhedrons the authors use polylib [8]. In future versions of their framework the authors plan to implement further optimizations of the movement code depending on data dependency information to spare space on the SPM. Now the authors use this framework for their multi-level tiling approach on multiple levels of parallelism. They use a framework [13] to find the available parallelism in a program by discovering groups of permutable loops as well as time loops and space loops. The available parallelism is distributed all over the various levels of parallel units of the system by tiling the space loops. Generally there are as many levels of tiling as the number of levels of parallel units but there can be levels of tiling added when necessary by tiling the permutable loops. The authors consider a two-level parallel architecture for example. The number of parallel processes at outer and inner levels is fixed to be a multiple of the number of physical parallel processors at the level. Then the space loops of the outer levels are tiled to equal tiles across the outer-level parallel processors. If one of those tiles requires more local memory than available an additional level of tiling is introduced which means that the tile is split into sub-tiles which are processed sequentially within the outer-level tile. With an optimization problem formulated by the authors now an optimal set of tile sizes as atomic unit of computation in an outer-level tile is found by an algorithm, designed to to minimize data movement cost between local memory and global memory, under the constraint that active local memory used by the process does not exceed a given upper limit. After the outer-level tiling is completed it is time for the inner-level tiling of the space loops. The approach was tested on a GPU. The architecture of a GPU offers several levels of parallelism, namely between the processor-cores and between the multiple SIMD-units of the processors. The processors communicate with each other with an off-chip DRAM, the SIMD-units communicate with each other through a fast local scratchpad. The tests were conducted on a NVIDIA GeForce 8800 GTX GPU device. The CUDA kernels were compiled with NCC to generate code which was started from the host system. The host system was an Intel Core2 Duo processor at 2.13 GHz with 2 MB L2 cache. For the test two kernels were used, namely Mpeg4 Motion Estimation (ME) kernel and 1-D Jacobi kernel. The first needs no synchronization while the second needs synchronization between the thread blocks. In comparision to an execution without SPM and only with GPU DRAM, Mpeg4Motion und 1-D Jacobi can be executed 8 respectively 10 times faster. In comparision with the CPU these values increase to 100 and 15. Generally it was to observe 143
147 18 that the performance increased with the number of thread blocks untill the point was reached where the synchronization costs took over. So the authors of the paper show an approach to optimally use scratchpad memories in systems with multiple levels of parallelism. They based their technique upon the polyhedron model and used linear programming to solve some smaller subproblems, but they also state that there is a limit to their technique when the number of thread blocks reached a point with to expensive synchronization costs. Figure 5: Execution Time: 1-D Jacobi for several problem sizes Figure 6: Execution Time: 1-D Jacobi for smaller problem sizes for varying thread blocks 4 SPM on Multitasking Systems The last aspect of the use of scratchpad memories for performance improvement is the situation on multitasking systems. In the context of explicitly different applications competing for available memory resources, an extension of an already introduced approach will be shown. In "Scratchpad Memory Management in a Multitasking Environment" [16] a SPM manager capable of code allocation supporting dynamically created processes is presented as an extension of the work from section 2. The authors designed a SPM manager for loading code of running processes into the SPM at runtime what differs their approach from the usually designs which work before execution. For this purpose a new dynamic SPM code allocation technique for systems running an operating system 144
148 19 Figure 7: Execution Time: 1-D Jacobi for larger problem sizes for varying tile sizes with virtual memory and preemptive multitasking was developed. In short the code is profiled and a postpass optimizer sorts the code of an application based on the access frequency. Temporally local code is then packed into pages with the size of an MMU page whereas local data is separated from the code into data pages. Every page s binary contains information of the access frequency and if it belongs to a loop, added by the postpass optimizer. These binaries are created independet of the available SPM size so the decision which page is loaded into the SPM is made at runtime - whenever a new process changes its status (i. e. is created, terminated or otherwise changed) the SPM manager is notified by the OS and then loads the code page into the SPM by intercepting the MMU s page fault exceptions and allocates the SPM to the current running processes. Hereby the SPM manager works as follows: The SPMM awaits a traditional cache as well as a softwaremanged SPM working on the system. It then decides which code pages should be loaded into its SPM and which should be loaded into the traditional cache. This decision depends highly on the utilized sharing strategy of the SPM, but also only SPM optimized pages will be loaded into the SPM whereas unoptimized pages will be loaded into the cache by default. So the SPMM needs to be informed whenever a new process is created, termianted, scheduled, changes its ready-to-run status or an MMU page fault occurs. When a new process is created its binary contains a map listing all code block access frequencies and loop affiliations, if its SPM-optimized. If it is informed, the SPMM redistributes the SPM between all processes which have access to the SPM and the SPM is also able to modify a process virtual memory mapping depending on the active sharing strategy, the information in the aforementioned map and the number of available pages. To load the pages in the SPM there is a little trick: if the page needs to be loaded into SPM before execution its memory mappings are marked as invalid so that whenever they are reached in the control flow the MMU triggers a page fault exception - this alerts the SPMM which starts to load the pages into SPM and fixes their memory mapping before restarting the last instruction. The same procedure is used, if there is no free page in the SPM: the SPMM chooses a target page by its sharing strategy and marks its memory mapping as invalid so that it will trigger a page fault when accessed the next time. The SPMM uses a round robin strategy to decide which page has to be replaced so there is no need of additional hardware and the computation costs can be kept low. The decision which page will be loaded into the cache and which page will be loaded into the SPM before execution of a process is based upon the number of the pages available for the process. If the number of needed pages surpasses the number of pages available thrashing occurs - in this case the SPMM will transfer the at least used page to the cache. 145
149 20 To warrant easy integration into already existing OS the SPMM is built as a module. So it has to be notified in cases of creation, scheduling or termination of a process, changing of the ready-to-run status of a process or a page fault, in order to be able to react. Basically the SPM can be seen as an additional layer in the hierarchy of virtual memory with paging and so it does not interfere with paging to external memory media and there are only minor changes to the page fault exception handler necessary to forward page faults, caused by the SPM, to the SPMM. The authors suggest three different SPM sharing strategies, where a page will be put into and which page will be replaced if a page fault exception occurs depends on the sharing strategy. As soon as a process joins or leaves, the available space will be redistributed among the active processes. The shared strategy is simple. Basically the SPM can be understood as a fully-associtive softwaremanaged cache with round robin replacement strategy - all processes share the SPM and a single pointer points which page will be replaced next. As soon as a page fault occurs the aforementioned pointer will be placed on the next free page and if there is no free page in the SPM left, the pointer will be placed on the page which should be replaced if a new page has to be loaded. This strategy is simple to implement and has no need of complex computation, but obviously is not fair. In the dedicated strategy the SPM is distributed by the active processes, where each process has got its own area which can only be accessed by it. In these areas there is also a pointer pointing at the pages next to be replaced and if there is no free page left, again the next page to be replaced is decided by a round robin strategy. The size of these areas is determined by one of the two divison policies. In the maximum-workingset policy, at runtime the size of the maximum-workingset of each process is calculated by the postpass-optimizer. The size of the area allocated to a process is determined proportionally to the size of the process maximum-workingset. This policy is static, which means, as long as there is no change in the number of the active processes, there is no change in the size of each process allocated area. The on-demand policy divides the SPM through the current working-set of the running processes by using the average number of page faults over a certain time for each process. The average number of page faults is determined by the connection of the number of all pages reserved for a process and the current workingset. So in this strategy the number of page faults is steadyly gauged and the average case adapted. Once a process is scheduled, short time before, the current average number of page faults is compared to the last average number of page faults and if there are not only minor or none differences, the divison of the areas will be adjusted again. Last one is the dedicated with pool strategy. This strategy can be seen as a mix of both of the previous strategies: one part of the SPM is shared among all the processes. This part is always assigned to the currently active process while the rest of the SPM is divided as in the dedicated strategy. This strategy is the standard case since with a shared area in the size of zero blocks the SPM is divided like in the dedicated strategy and with a shared area in the size of the whole SPM, it is divided like in the shared strategy. The information needed by the SPMM is delivered by the postpass-optimizer. To obtain best results and save energy, multiple times used code has to be loaded from the SPM, whereas instructions, which are rarely used, have to be executed from the cache or even external memory. Necessary to that end is the postpass-optimizer, which builds the profile data used bei the SPMM. The postpass-optimizer used in this paper is based on the one in [15] which has already been presented. The postpass-optimizer first deassembles thr ARM ELF binaries and then analyzes the traces from training runs and sorts the code of an application by access frequency. In doing so temporally local code will be aggregated to pages in the size of a MMU memory page and furthermore it builds the control flow graph of the whole application and thereby discovers loops. Once the whole code is aggregated to 146
150 21 pages, the loop hierarchy is used to decide the maximum working set of the application. Furthermore to increase the code density within a page the following optimizations are used: on the function level unregularly used blocks are separated from regularly used ones and assigned to distinct pages, while on the loop level functions are arranged according to the access frequency. First functions of the innermost loop are handled, they are assigned to pages first. The outermost loop s functions are handled last, their code is only placed in those pages to avoid internal fragementation. Further on the optimizer exfiltrates constant pools, which are small data sections in the ARM code, so called data pools, that contain constants which are to big to be encoded as immediate operand or global data address, because if they are placed in the SPM, they bring about further delays. These constant pools are aggregated to pages like normal code and due to narrow scope of the immediate operands placed nearby the corresponding code. After the optimization of the application it does not contain separated text areas and data areas but single pages for code and for data. Next to building the final data and code layout the postpass-optimizer adds a code block map. This map contains every block s access freqency and the belongig of every loop. Last but not least the new ELF binaries, which will behave the same on systems without a SPM, are built. The tests were carried out on a cycle-accurate ARM architecture simulator [20]. A small RTE was built, which consisted of a loader, a preempting round robin scheduler and a SPMM. All applications had the same priority. The loader loads processes from the RAM and assigns stack areas and heap areas to newly created processes. As soons as a process tried to access an unmapped instruction, a latency of 69 instructions occured during the loading of the page. 15 benchmarks were used for the tests to ensure representative selection. Nine of them were taken fom MiBench [17] and MediaBench [19], a H.264 video decoder [5], the official ISO MP3 decoder [6], MPEG-4 XviD encoding/decoding [7], and a public key encryption tool, Pretty Good Privacy (PGP) [9]. Additionally some applications were combined to a benchmark called combine again. As a reference system, an RTE was created on an ARM926EJ-S core with virtually-indexed, virtuallytagged caches. In doing so its cache was set to the smallest size which allowed a miss ratio of approximately 1%. For the reference case the benchmarks were arranged of the original single process applications. With the dedicated strategy the approach was dissappointing. Completly separated private SPMs for every application led to multiple page faults. On the average performance was increased by 19%. With rising size of the shared pool the dedicated with pool strategy outperformed the reference system. With increasing size of 1 4, 2 4 and 3 4 also the performance increased by 32%, 39% and 43%. Due to the overall smallest number of page faults, the shared strategy reached the highest performance. Its disadvantage of liability to applications with a big working-set (what could lead to displacement of pages of smaller applications) carried no weight, as expected by the authors. It led up to 47% performance increase. This work shows a quite useful application of the dynamic allocation technique developed by the authors earlier. It indicates that dividing the availbale SPM space into private SPMs for every application doesn t work effectively and comes up with two better solutions to the problem. Additionally it is a way of allocating SPM space to several applications without the need to know which applications will be running (and when) before execution. This makes the approach quite flexible. However some of the flaws remain. With the allocation of data and instructions to pages, memory space is still wasted. Also there still remains a certain latency for the SPMM to load pages into the SPM if needed. 147
151 22 5 Conclusion In this paper first two different ways for storing instructions into a SPM im order to achieve a performance gain were introduced. The first work addressed the overlay problem to store both instructions and variables optimally. It used linear programming. The second went a new way to use the SPM dynamically by using mechanisms of virtuall memory management. As shown it suffers from some problems like not entirely used SPM space but it set the stage for the approach to use scratchpad memories in multitasking environments, shown later in this paper. In the second part of this paper, the problem was extended to the use of multiple processors. The first paper in this part explored the interaction between task scheduling and memory optimization. It showed that the computation epensive approach introduced is not always necessary in order to achieve optimal SPM allocation. Next was an quite original approach to gain performance by reducing inter-processor communication with optimal access patterns to the scratchpad memories. But it failed to deliver its results in meaningful data. The last paper in this section extended the problem of using scratchpad memories in systems with several processors to increase performance to multiple levels of parallelism. The technique proposed in this paper reaches its limits when the number of thread blocks pass a point where the synchronization costs overwhelm the performance gain. The last part again picks up the second approach from the first part and considers the aspects of multitasking systems. It shows two better solutions than to divide the availbale SPM into private SPMs for every application. But it still delivers some flaws like wasted memory space and a certain latency caused by the scratchpad memory manager used. 6 Bibliography References [1] ARM. Available at [2] Benchmark Suite for Multimedia and Communication Systems. Available at edu/mediabenchii/. [3] CLooG: The Chunky Loop Generator. Available at [4] CPLEX. Available at [5] H.264 Video Codec. Available at [6] MP3 Reference Decoder. Available at [7] MPEG-4 Video Codec. Available at [8] PolyLib - A library of polyhedral functions. Available at [9] Pretty Good Privacy (PGPi). Available at [10] S.P. Amarasinghe, J.M. Anderson, M.S. Lam & C.W. Tseng (1995): An overview of the SUIF compiler for scalable parallel machines. Proceedings of the Seventh SIAM Conference on Parallel Processing for Scientific Compiler. [11] Todd Austin, Eric Larson & Dan Ernst (2002): SimpleScalar: An Infrastructure for Computer System Modeling. Computer 35(2), pp , doi: / Available at
152 23 [12] Muthu Manikandan Baskaran, Uday Bondhugula, Sriram Krishnamoorthy, J. Ramanujam, Atanas Rountev & P. Sadayappan (2008): Automatic data movement and computation mapping for multi-level parallel architectures with explicitly managed memories. In: Proceedings of the 13th ACM SIGPLAN Symposium on Principles and practice of parallel programming, PPoPP 08, ACM, New York, NY, USA, pp. 1 10, doi: / Available at [13] Uday Bondhugula, Muthu Baskaran, Sriram Krishnamoorthy, J. Ramanujam, A. Rountev & P. Sadayappan (2007): Affine transformations for communication minimal parallelization and locality optimization of arbitrarily-nested loop sequences. Technical Report OSU-CISRC-5/07-TR43, The Ohio State University. [14] Thomas T. Cormen, Charles E. Leiserson & Ronald L. Rivest (1990): Introduction to algorithms. MIT Press, Cambridge, MA, USA. [15] Bernhard Egger, Jaejin Lee & Heonshik Shin (2006): Scratchpad memory management for portable systems with a memory management unit. In: Proceedings of the 6th ACM & IEEE International conference on Embedded software, EMSOFT 06, ACM, New York, NY, USA, pp , doi: / Available at [16] Bernhard Egger, Jaejin Lee & Heonshik Shin (2008): Scratchpad memory management in a multitasking environment. In: Proceedings of the 8th ACM international conference on Embedded software, EMSOFT 08, ACM, New York, NY, USA, pp , doi: / Available at acm.org/ / [17] M. R. Guthaus, J. S. Ringenberg, D. Ernst, T. M. Austin, T. Mudge & R. B. Brown (2001): MiBench: A free, commercially representative embedded benchmark suite. In: Proceedings of the Workload Characterization, WWC IEEE International Workshop, WWC 01, IEEE Computer Society, Washington, DC, USA, pp. 3 14, doi: /wwc Available at [18] Mahmut Kandemir, J. Ramanujam & A. Choudhary (2002): Exploiting shared scratch pad memory space in embedded multiprocessor systems. In: Proceedings of the 39th annual Design Automation Conference, DAC 02, ACM, New York, NY, USA, pp , doi: / Available at org/ / [19] Chunho Lee, Miodrag Potkonjak & William H. Mangione-Smith (1997): MediaBench: a tool for evaluating and synthesizing multimedia and communicatons systems. In: Proceedings of the 30th annual ACM/IEEE international symposium on Microarchitecture, MICRO 30, IEEE Computer Society, Washington, DC, USA, pp Available at [20] Jaejin Lee, Junghyun Kim, Choonki Jang, Seungkyun Kim, Bernhard Egger, Kwangsub Kim & SangYong Han (2008): FaCSim: a fast and cycle-accurate architecture simulator for embedded systems. SIGPLAN Not. 43(7), pp , doi: / Available at [21] Steven S. Muchnick (1997): Advanced compiler design and implementation. Morgan Kaufmann Publishers Inc., San Francisco, CA, USA. [22] Chanik Park, Junghee Lim, Kiwon Kwon, Jaejin Lee & Sang Lyul Min (2004): Compiler-assisted demand paging for embedded systems with flash memory. In: Proceedings of the 4th ACM international conference on Embedded software, EMSOFT 04, ACM, New York, NY, USA, pp , doi: / Available at [23] Karl Pettis & Robert C. Hansen (1990): Profile guided code positioning. In: Proceedings of the ACM SIG- PLAN 1990 conference on Programming language design and implementation, PLDI 90, ACM, New York, NY, USA, pp , doi: / Available at [24] Jan Sjödin & Carl von Platen (2001): Storage allocation for embedded processors. In: Proceedings of the 2001 international conference on Compilers, architecture, and synthesis for embedded systems, CASES 01, ACM, New York, NY, USA, pp , doi: / Available at /
153 24 [25] S. Steinke, L. Wehmeyer, B. Lee & P. Marwedel (2002): Assigning Program and Data Objects to Scratchpad for Energy Reduction. In: Proceedings of the conference on Design, automation and test in Europe, DATE 02, IEEE Computer Society, Washington, DC, USA, pp Available at citation.cfm?id= [26] Stefan Steinke, Markus Knauer, Lars Wehmeyer & Peter Marwedel (2001): An accurate and fine grain instruction-level energy model supporting software optimizations. In: in Proc. Int. Wkshp Power & Timing Modeling, Optimization & Simulation (PATMOS). [27] Vivy Suhendra, Chandrashekar Raghavan & Tulika Mitra (2006): Integrated scratchpad memory optimization and task scheduling for MPSoC architectures. In: Proceedings of the 2006 international conference on Compilers, architecture and synthesis for embedded systems, CASES 06, ACM, New York, NY, USA, pp , doi: / Available at [28] Hiroyuki Tomiyama & Hiroto Yasuura (1996): Optimal Code Placement of Embedded Software for Instruction Caches. In: In Proc. of European Design and Test Conference, IEEE, pp [29] Manish Verma, Lars Wehmeyer & Peter Marwedel (2004): Dynamic Overlay of Scratchpad Memory for Energy Minimization. In: Proceedings of the international conference on Hardware/Software Codesign and System Synthesis: 2004, CODES+ISSS 04, IEEE Computer Society, Washington, DC, USA, pp , doi: /codes+isss Available at 150
154 Simulation digitaler Schaltungen auf GPUs Yohan Humbert Technische Universität Kaiserslautern, Embedded Systems Group Zusammenfassung Grafikprozessoren sind aufgrund ihrer Architektur Spezialisten, was die Ausführung paralleler Prozesse betrifft. Seit Einführung der Programmierschnittstelle CUDA gestaltet sich die nicht-grafische Programmierung von Grafikprozessoren weitaus flexibler und einfacher, als mit Programmierschnittstellen wie OpenGL oder DirextX, welche vor allem zur grafischen Programmierung ausgelegt sind. Aufgrund dessen werden Grafikprozessoren seit einigen Jahren immer mehr zur Beschleunigung paralleler Prozesse aus den verschiedensten Anwendungsgebieten verwendet. Diese Arbeit befasst sich mit der Recherche und Untersuchung von Verfahren zur Simulation digitaler Schaltungen auf Grafikprozessoren. Es werden zwei Verfahren vorgestellt, die mit verschiedenen Ansätzen eine geeignete Umsetzung demonstrieren. Hierbei liegt der Fokus vor allem auf den grundlegenden Konzepten und Ideen, die in den Verfahren zum Einsatz kommen. 1 Einleitung Ursprünglich sollten Grafikprozessoren (englisch: Graphics Processing Unit - kurz: GPU) ausschließlich zur grafischen Berechnung verwendet werden. In den letzten Jahren hat sich jedoch der Trend entwickelt, handelsübliche GPUs, neben ihrer Hauptaufgabe, auch für andere mathematische Berechnungen zu verwenden. Diese Zweckentfremdung von GPUs wird General Purpose Computation on Graphics Processing Unit (kurz: GPGPU) genannt. Zwar existiert diese Idee schon seit dem Erscheinen der ersten programmierbaren Grafikkarten, allerdings waren diese noch nicht für solche Aufgaben ausgelegt und dementsprechend war der Entwicklungsaufwand sehr hoch. Erst mit der Einführung der Compute Unified Device Architecture (kurz: CUDA) von NVIDIA wurde die Umsetzung von GPGPU für Programmierer derartig vereinfacht, dass der GPGPU-Ansatz seitdem in vielen Bereichen eingesetzt wird [1]. Mit CUDA bietet NVIDIA erstmals eine leicht zugängliche Programmierschnittstelle (englisch: Application Programming Interface - kurz: API) zur Entwicklung paralleler Applikationen für GPUs. Der große Vorteil von GPUs besteht in der hohen potentiellen Parallelität. Im Gegensatz zu gewöhnlichen Hauptprozessoren (englisch: Central Processing Unit - kurz: CPU) sind GPUs nicht für die schnelle Abarbeitung von sequentiellen Operationen auf einzelne Datenelemente (Single Instruction Single Data - kurz: SISD) optimiert. Stattdessen ist die GPU-Architektur darauf ausgelegt, eine bestimmte Operation auf mehreren Datenelementen bzw. einem Datensatz parallel auszuführen (Single Instruction Multiple Data - kurz: SIMD). Das hat den Vorteil, dass Probleme, die sich gut parallelisieren lassen, viel schneller abgearbeitet werden können, als dies mit einer CPU möglich wäre. Es sind aber nicht alle Probleme für die GPGPU-Anwendung geeignet. Beispielsweise sind Algorithmen, die auf iterativen Berechnungen basieren, bei denen eine Iteration das Ergebnis der vorherigen Iteration verwendet, nicht zur parallelen Bearbeitung geeignet. Damit ein Algorithmus auf der GPU eine signifikante Beschleunigung erfährt, muss die Berechnung eines einzelnen Elementes weitestgehend unabhängig von anderen Elementen und 151
155 2 Zwischenergebnissen sein. Ein gutes Beispiel hierfür ist die Matrixaddition. Es ist offensichtlich, dass hierbei alle Elemente der Ergebnismatrix unabhängig voneinander sind und parallel berechnet werden können. Eine weitere mögliche Anwendung stellt die Simulation von digitalen Schaltungen dar. Diese wird primär zur Verifikation von digitalen Entwürfen verwendet und bildet somit einen wichtigen Prozess während der Hardwareentwicklung. In Folge immer komplexer werdenden Schaltungen, bildet die Verifikation mittlerweile die ressourcen- und kostenintensivste Aufgabe im Hardwareentwicklungsprozess [10] [4]. Obwohl Entwicklungsunternehmen enorme Ressourcen in den Simulationsprozess investieren, können die nötigen Leistungsanforderungen zur Simulation hochkomplexer Entwürfe nicht mehr erfüllt werden. Dies führt in vielen Fällen dazu, dass große Teile des Entwurfs ungeprüft ausgeliefert werden müssen. Die Folge sind unvorhergesehene Fehler, die dann meist kostenintensive Rückrufaktionen nach sich ziehen. Entsprechend herrscht seit längerer Zeit das Bedürfnis der Leistungssteigerung in diesem Bereich. Aktuelle kommerzielle Logiksimulatoren sind vorwiegend sequentieller Natur und nutzen demzufolge die Parallelisierbarkeit, die eine digitale Schaltung mit sich führt, nicht aus. Deshalb bildet dieser Bereich ein aktuelles Forschungsgebiet, das immer mehr Beachtung findet. In den letzten Jahren haben sich Forschungsgruppen verschiedener Fakultäten mit diesem Thema auseinandergesetzt und teils unabhängig voneinander unterschiedliche Verfahren zur parallelen Ausführung von Logiksimulationen auf GPUs entwickelt. Ziel dieser Arbeit ist es, den aktuellen Forschungsstand zusammenzuführen und ausgewählte Verfahren vorzustellen. 2 Aufbau der Arbeit Die Arbeit ist folgendermaßen aufgebaut: Das Kapitel 3 soll dem Leser zuerst das notwendige Hintergrundwissen vermitteln, um die späteren Verfahren besser nachvollziehen zu können. Hier wird zum einen die CUDA-Architektur 3.1 vorgestellt und zum anderen erfolgt in Kapitel 3.2 eine kurze Exkursion in die Thematik der Simulation. In Kapitel 4 wird der Stand der Forschung zusammengeführt. Darauf aufbauend werden die in dieser Arbeit behandelten Verfahren grob eingeordnet. Die Kapitel 5 und 6 behandeln zwei ausgewählte Verfahren zur parallelen Simulation von digitalen Schaltungen. Da sich beide Verfahren von der Funktionsweise her stark unterscheiden, werden sie in getrennten Kapiteln vorgestellt. Nachdem die unterschiedlichen Ansätze ausführlich erklärt wurden, werden sie im letzten Kapitel 7 gegenübergestellt und auf geeignete Einsatzgebiete untersucht. 3 Hintergrundwissen 3.1 CUDA Bevor detailliert auf die API CUDA eingegangen wird, soll zuerst der Unterschied zwischen der Funktionsweise und dem Einsatzgebiet einer CPU und einer GPU veranschaulicht werden. Beide Verarbeitungseinheiten besitzen nämlich vollkommen unterschiedliche Entwurfsphilisophien (siehe Abb. 1). Die CPU besteht aus wenigen sehr leistungsstarken algorithmisch-logischen-einheiten (englisch: Arithmetic Logic Unit - kurz: ALU) und ausgeprägten Kontrollfluss- und Cachetechniken. Handelsübliche Prozessoren besitzen heutzutage bis zu acht Recheneinheiten, im Serverbereich sind es sogar bis zu 16. Dieses sogenannte Multicore-Prinzip unterscheidet sich jedoch immer noch stark vom Manycore-Prinzip der GPUs. Das Multicore-Prinzip von CPUs ist auf die sequentielle Abarbeitung ausgelegt. Da ein Großteil der heute eingesetzten Software nicht vollständig von mehreren Recheneinheiten profitieren kann, 152
156 3 Abbildung 1: Entwurfsphilosophien von CPU und GPU [18] besitzt die CPU eine ausprägte Kontrolllogik, um die sequentiellen Anwendungen effizienter ausführen zu können. Es wird also sozusagen auf bestimmte Art und Weise versucht, Probleme sequentieller Natur mit Hilfe von Parallelität zu beschleunigen. Die GPU besitzt im Gegensatz zur CPU nicht wenige leistungsstarke Recheneinheiten, sondern sehr viele, aber leistungsschwächere ALUs. So ist es möglich, einfache Operationen auf große Datensätze parallel anzuwenden. Deshalb müssen die auszuführenden Probleme von Haus aus zur massiv-parallelen Ausführung geeignet sein. Dies sind Problemstellungen, bei denen häufig gleiche Berechnungen auf unabhängige Datenelemente ausgeführt werden. Wird diese Charakteristik nicht erfüllt, kann, verglichen mit der CPU, in den meisten Fällen keine Leistungssteigerung erzielt werden. Insgesamt kommt der Kontrolllogik und den Caches somit keine höchste Priorität zu und die verfügbare Chipfläche wird mit möglichst vielen Recheneinheiten belegt. Da GPUs für die Grafikberechnung entwickelt wurden, besitzen sie eine sehr hohe Speicherbrandweite, um beispielsweise Grafiktexturen schnell laden zu können. Die aktuell schnellste 1 im Handel erhältliche GPU, die für CUDA-Anwendungen eingesetzt werden kann, ist die NVIDIA GeForce GTX 690 mit 3072 Recheneinheiten und einer Speicherbandbreite von 384 GB/s [19]. Bevor CUDA im Jahr 2007 von Nvidia eingeführt wurde, war es notwendig, die Programmierung von GPUs über die Grafikprogrammierschnittstellen OpenGL oder DirectX vorzunehmen. Der Programmierer musste deshalb große Kenntnisse in der Grafikprogrammierung aufweisen, um GPGPU- Applikationen zu entwickeln. Zudem waren die verfügbaren Operationen auf Grafikberechnungen ausgelegt. Eine nicht-grafische Anwendung musste also zuerst auf die spezifischen Operationen adaptiert werden, was meist mit einem erhöhten Entwicklungsaufwand verbunden war. CUDA hingegen ist eine auf der weit verbreiteten Hochsprache C basierende Programmierschnittstelle mit deren Hilfe die GPU als Ausführungsmedium für den Quellcode angesprochen werden kann. Es werden Funktionen bereitgestellt, mit denen der Zugriff auf den Speicher und die Konfiguration der Grafikkarte ermöglicht wird. Die grundlegende Architektur wird von Nvidia als SIMT (Single Instruction Multiple Threads) bezeichnet und ist dem SIMD-Prinzip sehr ähnlich [18]. Eine Methode wird demnach gleichzeitig auf mehrere Datenelemente angewendet. Die grundlegenden Methoden, die auf der GPU ausgeführt werden, tragen die Bezeichnung Kernel. Beim Aufruf wird diese von N verschiedenen Threads parallel ausgeführt. Zur Strukturierung der Threads stehen zwei verschiedene Gruppierungen zur Verfügung, Blöcke und Grids. In der linken Grafik von Abbildung 2 ist dies veranschaulicht. Einem Kernel wird genau ein Grid zugewiesen. Ein Grid besteht aus mehreren Blöcken, die in einem 1 Stand:
157 4 Abbildung 2: Architektur von CUDA [18] ein- oder zweidimensionalem Array geordnet sind. Die Blöcke bestehen wiederum aus den eigentlichen Threads, welche in einem zwei- oder dreidimensionalem Array angeordnet sind. Die maximale Anzahl an Threads pro Block beträgt ab CUDA 2.x Jeder Thread besitzt eine eindeutige ID, die zur Adressierung des vom Thread zu bearbeitenden Datenelements verwendet wird. Jeder Thread besitzt eigene Register und einen kleinen lokalen Speicher (Local Memory). Die Threads eines Blockes werden auf einem Streaming Multiprocessor (kurz: SM) ausgeführt und besitzen einen gemeinsamen Speicher, den Shared Memory. Es ist den Threads eines Blockes also möglich miteinander zu kommunizieren und gemeinsam Synchronisationstechniken zu verwenden (siehe Abb. 2 mittlere Grafik). Wichtig hierbei ist, dass Threads verschiedener Blöcke ohne weiteres nicht miteinander kommunizieren können. Dies wird an der Zuweisung der Blöcke in Abhängigkeit von der vorhandenen Anzahl an SMs deutlich (siehe Abb. 2 rechte Grafik). Die CUDA-Anwendung besteht hier beispielsweise aus acht Blöcken. Es ist zu erkennen, dass die Blöcke unabhängig voneinander den verfügbaren SMs zur Ausführung zugeteilt werden. Dieses Prinzip, transparent scalabilty genannt, ermöglicht eine von der Grafikkarte unabhängige Programmierung. Demzufolge ergibt sich bei Grafikkarten mit unterschiedlicher Anzahl an Multiprozessoren eine andere Ausführungsreihenfolge der einzelnen Blöcke und eine Synchronisation bzw. Kommunikation ist deshalb unpraktikabel. Zur Ausführung werden die Blöcke in Gruppen von je 32 Threads (ein warp) gegliedert und den Recheneinheiten der SMs zugeteilt. Die Threads eines Warps starten gleichzeitig, können allerdings bei ihrer Ausführung beliebig verzweigen. Dabei führen alle Threads eines Warps pro Berechnungsschritt eine gemeinsame Instruktion aus, weshalb es zur bestmöglichen Performance wichtig ist, dass alle Threads möglichst den gleichen Ausführungspfad verfolgen. Solch eine ideale Situation ist für reale Anwendungszwecke jedoch schwer einzuhalten. Für den Fall, dass die Threads verschiedene Ausführungspfade verfolgen, werden diese unterschiedlichen Pfade seriell ausgeführt. Es wird also ein Pfad nach dem anderen ausgeführt, bis sie wieder zusammenlaufen. Demzufolge sollten komplexe Verzweigungen innerhalb eines Warps möglichst vermieden werden. Für den Datenaustausch zwischen der CPU und der GPU steht ein großer globaler Speicher zur Verfügung (Global Memory). Hier können die relevanten Daten, die von den Threads bearbeitet werden sollen, von der CPU abgelegt werden. Im Gegenzug werden die Ergebnisse ebenfalls hier abgespeichert und können nach Beendigung des Kernels von der CPU ausgelesen werden. Außerdem kann der globale Speicher zum Kommunikationsaustausch zwischen den Blöcken verwendet werden. Zu erwähnen 154
158 5 ist, dass der Speicherzugriff für einen Thread beim globalen Speicher bis zu 400 Ausführungsschritte benötigt, wobei der Speicherzugriff auf den lokalen bzw. gemeinsamen Speicher nur lediglich einen Berechnungsschritt in Anspruch nimmt. Für eine effiziente Programmausführung gilt es also den Speicherzugriff dementsprechend sinnvoll zu wählen. Die beiden weiteren Speicher, Constant Memory und Texture Memory, verhalten sich dem globalen Speicher ähnlich, mit der Ausnahme, dass es sich hierbei um read-only Speicher handelt. Da sie aber in den Verfahren, die in dieser Arbeit vorgestellt werden, keine besondere Rolle spielen, soll hier nicht weiter auf ihre Funktionalität eingegangen werden. Der Programmablauf einer CUDA-Anwendung auf CPU (Host) und GPU (Device) kann wie folgt dargestellt werden (siehe Abb. 3): Ein mit CUDA geschriebenes Programm besteht aus zwei unterschiedlichen Arten von Programmcode. Einem sequentiellen Teil, der einer gewöhnlichen sequentiellen C-Anwendung gleicht und auf der CPU ausgeführt wird und einem parallelen Teil, der von der GPU durchgeführt wird. Soll nun ein berechnungsintensiver Abschnitt von der GPU beschleunigt werden, kann dies durch eine Kernelmethode realisiert werden, die in dem sequentiellen Quellcode aufgerufen wird. Ab diesem Zeitpunkt übernimmt die GPU die Ausführung. Die Grafikkarte dient somit nicht als unabhängige Komponente, sondern als sogenannter Coprozessor 2. Da jedoch kein automatischer Datenaustausch zwischen Host und Device stattfindet, müssen die für die Berechnung relevanten Daten vor dem Aufruf der Kernelmethode manuell in den globalen Speicher der GPU geschrieben werden. Ist die GPU mit der Berechnung fertig, können die Ergebnisse aus dem globalen Speicher entnommen werden. Momentan ist es nicht möglich mehrere Kernel parallel auszuführen. Zur Durchführung mehrerer Methoden auf der GPU müssen diese demnach nacheinander von der CPU aufgerufen werden. Zu erwähnen bleibt, dass der Aufruf der Kernelmethode asynchron ist. Die CPU kann also weiter mit der Berechnung fortfahren, während Abbildung 3: Programmablauf von CUDA [18] die GPU die aufgerufene Methode bearbeitet [18]. 2 Der Coprozessor ist ein spezieller Prozessor, der den Hauptprozessor um bestimmte Funktionen erweitert und ihn entlastet. 155
159 6 3.2 Simulation Die Simulation einer Schaltung bedeutet ein (Software-)Modell der Schaltung zu verwenden, um ihr Verhalten zu analysieren und zu verifizieren. Hierzu werden den Eingängen des Modells Signalwerte zugewiesen, sogenannte Stimuli, und die entsprechenden Ausgänge mit Hilfe des Modells berechnet und beobachtet. Somit kann überprüft werden, ob die Berechnung des Schaltungsmodells mit dem erwarteten Ergebnis übereinstimmt. Dieser Prozess wird Verifizierung genannt und spielt, wie bereits in der Einleitung erwähnt, eine herausragende Rolle im Hardwareentwicklungsprozess. Damit annähernd alle Eventualitäten abgedeckt werden umfasst eine Simulation vieler solcher Testfälle (Testszenario). Bei komplexen Systemen können jedoch nicht alle möglichen Testfälle behandelt werden, da beispielsweise bereits ein 16-Bit-Addierer über 2 32 (ca. 4,3 Mrd.) unterschiedliche Stimuli verfügt. Für komplexe Schaltungen können Simulatoren demnach Fehler finden, aber nicht aussagen, ob die Schaltung fehlerfrei ist. Aufgrund der stetig steigenden Komplexität von elektrischen Systemen ist es notwendig während des Hardwareentwicklungsprozesses mit abstrakten Modellen zu arbeiten. Beginnend mit einem sehr abstrakten Modell wird dieses im Zuge des Entwicklungsprozesses nach und nach mit weiteren Details ergänzt und somit verfeinert. Die hieraus resultierenden Abstraktionsebenen wurden 1983 von Daniel D. Gajski und Robert Kuhn im Y-Diagramm (Gajski-Diagramm) zusammengefasst (siehe Abb. 4) [3]. Abbildung 4: Y-Diagramm [3] Das Diagramm sieht einen Entwicklungsprozess von außen (abstrakt) nach innen (detailliert) vor. Für jede Ebene werden drei grundsätzliche Sichten unterschieden. Zum einen die Struktur, die angibt, aus welchen Bauelementen (Subsystemen) die Schaltung (System) in der entsprechenden Entwurfsebene dargestellt wird. Mit dem Verhalten werden die mathematischen Methoden festgehalten, welche zur Beschreibung bzw. Berechnung des Systemverhaltens notwendig sind. Die Geometrie betrachtet die geometrischen Eigenschaften des Systems und seiner Subsysteme. Für den Simulationsprozess ist die Entwurfsebene der zu simulierenden Schaltung von herausragender Bedeutung. Je nachdem in welcher Abstraktionsebene die Schaltung dargestellt wird, muss die Implementierung des Simulators entsprechend gewählt werden. In dieser Arbeit werden nur diejenigen Verfahren vorgestellt, die von einem Schaltungsentwurf in Logikebene ausgehen. Die digitalen Schaltungen werden demnach anhand von Gattern, Flipflops und Leitungen dargestellt und das Systemverhalten mit Hilfe von Booleschen Gleichungen modelliert. Der Einfachheit halber wird diese Art der Simulation nachfolgend Logiksimulation genannt. Es existieren viele verschiedene Techniken zur Logiksimulation. Die verschiedenen Ansätze lassen sich mittels drei Klassifizierungen einordnen (siehe Abb. 5). 156
160 7 Abbildung 5: Klassifizierungen der (diskreten) Logiksimulation Da bei der Logiksimulation die Schaltungen digitaler Natur sind, handelt es sich hier immer um zeitund wertdiskrete Abläufe. Dies bedeutet, dass die Auswertung nur zu bestimmten Taktzeitpunkten erfolgt (Zeitdiskretisierung) und die Werte festgelegte Abstufungen einnehmen (Wertdiskretisierung). Im Gegensatz zu analogen Schaltungen, wo Verzögerungen und Zwischenwerte eine wichtige Rolle spielen, werden die Zustände zwischen den Taktflanken bei digitalen Schaltungen übersprungen. Dies vereinfacht den Simulationsprozess ungemein, sodass auch komplexere Schaltungen simuliert werden können. Bezüglich des Simulationsverfahrens werden zwei grundlegende Ansätze unterschieden: kompilierende und interpretierende Verfahren [13] [17]. Bei dem kompilierenden Verfahren (englisch: compiled code) wird der Schaltungsentwurf direkt in ein ausführbares Programm übersetzt. Die übersetzte Schaltung bildet somit den eigentlichen Simulator, welcher sofort ausgeführt werden kann. Um die kausalen Abhängigkeiten der einzelnen Gatter zu erfüllen, werden die Gatter entsprechend ihrem Abstand zu den primären Eingängen eingestuft (englisch: levelizing). Kompilierende Simulatoren zeichnen sich durch eine hohe Ausführungsgeschwindigkeit aus. Ein großer Nachteil ist aber die Inflexibilität, da jede kleinste Änderung an der Schaltung ein erneutes Kompilieren erfordert. Das interpretierende Verfahren hingegen wandelt den Schaltungsentwurf in eine spezielle Datenstruktur um. Der Simulator bildet eine separate Einheit, welche Operationen auf die konstruierte Datenstruktur anwendet. Der eigentliche Simulator ist somit unabhängig von der Schaltung und kann für verschiedene Schaltmodelle verwendet werden. Es entsteht keine Kompilierungszeit, wie es bei kompilierenden Verfahren der Fall ist. Insgesamt sind interpretierende Simulatoren flexibler als kompilierende Verfahren, weisen aber meist eine langsamere Ausführungsgeschwindigkeit auf. Abgesehen von diesen beiden Simulationsverfahren wird in der Fachliteratur die tabellengesteuerte Simulation erwähnt [13]. Hierbei handelt es sich weniger um ein eigenes Verfahren, sondern mehr um eine Technik, die im Zuge der anderen Verfahren verwendet werden kann. Diese Technik sieht vor, das Verhalten der einzelnen Gatter in Tabellenform abzuspeichern. Somit können die einzelnen Gattertypen anhand einer Wahrheitstabelle definiert und dementsprechend ausgewertet werden. So lassen sich neben der zweiwertigen Logik auch Mehrstufige implementieren. Zusätzlich kann auch die Netzliste der Schaltung in einer geeigneten Tabelle abgespeichert werden. Weiter lassen sich Simulatoren anhand des verwendeten Algorithmus zur Auswertung der Gatter unterscheiden, dem äquitemporalen bzw. vergesslichen (englisch: oblivious) und dem ereignisgesteuerten (englisch: event-driven) Ansatz [14]. Bei ersterem werden immer alle Gatter in jedem Simulationszyklus ausgewertet, unabhängig davon, ob eine Änderung an den Eingängen erfolgte. Es werden somit keine Informationen aus vorherigen Zyklen verwendet. Dies hat den Nachteil, dass viele Gatter neu ausgewertet werden, auch wenn dies eigentlich nicht notwendig wäre. Der Ansatz benötigt jedoch nur ein simples 157
161 8 Schedulingverfahren und kommt mit statischen Datenstrukturen aus, was insgesamt die Implementierung enorm vereinfacht. Äquitemporale Algorithmen werden vorwiegend bei kompilierenden Verfahren verwendet. Anders verläuft die Auswertung im ereignisgesteuerten Algorithmus. Hier werden in jedem Zyklus nur diejenigen Gatter ausgewertet, an deren Eingänge seit dem letzten Zyklus tatsächlich eine Änderung wahrgenommen wurde. Nur in diesem Fall ist es notwendig, das Gatter neu auszuwerten. Da vor allem in großen Schaltungen die Aktivitätsrate sehr gering ausfällt [2], ist dieser Algorithmus potentiell effizienter, als der zuvor beschriebene äquitemporale Ansatz. Ein Nachteil liegt jedoch in dem zusätzlichen Kommunikationsoverhead, der für das Schedulingverfahren vonnöten ist. Es muss eine dynamische Analyse der einzelnen Gatter erfolgen, um die im nächsten Schritt aktiven Elemente zu bestimmen. Dies hat auch eine aufwändigere Implementierung zur Folge. Ereignisgesteuerte Algorithmen wurden anfänglich vorwiegend in interpretierenden Verfahren eingesetzt. Ein Einsatz im Zuge eines kompilierenden Verfahrens ist aber ebenso praktikabel und wird mittlerweile oft umgesetzt. Soll die Simulation parallel erfolgen, so muss ein weiterer Punkt beachtet werden. Angenommen es werden unterschiedliche Gatter auf verschiedenen Recheneinheiten ausgewertet, dann muss sichergestellt werden, dass die kausalen Abhängigkeiten zwischen den einzelnen Gattern unverletzt bleiben. In der Literatur werden hierzu zwei grundverschiedene Techniken vorgestellt, die synchrone und die asynchrone Parallelisierungstechnik [15]. Bei ersterer arbeiten alle Recheneinheiten in gleichen Taktschritten und haben eine gemeinsame Sicht der Zeit (englisch: global-clock). Die Ereignisse werden in derselben Reihenfolge wie bei einem sequentiellen Simulator bearbeitet. Diejenigen Ereignisse, die zur selben Zeit (Takt) aufgetreten sind, werden parallel ausgeführt und mittels einer Barriere synchronisiert (englisch: barrier synchronization), bevor die nächsten Ereignisse bearbeitet werden. Auf diese Weise wird sichergestellt, dass die kausalen Abhängigkeiten der Gatter nicht verletzt werden. Das asynchrone Verfahren unterscheidet sich in der Sicht der Zeit der einzelnen Recheneinheiten. Jede Recheneinheit hat ihre eigene lokale Sicht. Demzufolge müssen sie bestimmte Regeln einhalten, damit die Ausführung global korrekt erfolgt und so die kausalen Abhängigkeiten in der Schaltung eingehalten werden. Wie dies genau funktioniert, wird in Kapitel 6 genauer erläutert. Dort wird ein asynchrones Verfahren zur Logiksimulation vorgestellt. 4 Stand der Forschung Bereits seit den 1980er Jahren wird eine intensive Forschung im Bereich der Logiksimulation betrieben. Zu dieser Zeit wurden schon die grundlegenden Konzepte entwickelt, die heutzutage in modernen Simulatoren verwendet werden. Beispielsweise stellte im Jahr 1987 die Forschungsgruppe um B. Bryant einen kompilierenden Simulator für MOS-Schaltungen vor [22]. Zeitgleich wurde unter der Bezeichnung HSS (High-Speed-Simulator) ein weiteres Verfahren zur Logiksimulation auf Gatterebene entwickelt [25]. Ende der 80er und Anfang der 90er Jahre richteten sich die Forschungsbemühungen vor allem auf die Weiterentwicklung ereignisgesteuerter Simulatoren. So wurden in mehreren Forschungsgruppen kompilierende ereignisgesteuerte Verfahren entworfen, die verglichen mit bisherigen Simulatoren, Beschleunigungen im teils zweistelligen Bereich erzielten [26] [14]. Einige Jahre später begann die Untersuchung paralleler Algorithmen zur Logiksimulation [16] [23] [15]. Hierbei wurden jedoch noch keine massivparallelen Architekturen, wie bei Grafikkarten, verwendet, sondern verteilte Systeme und Multiprozessoren. Eine der ersten Versuche parallele Logiksimulationen auf einem Grafikprozessor auszuführen, wurde 2007 von Perinkulam im Zuge einer Dissertation durchgeführt [20]. Jedoch konnte hier, verglichen mit der Ausführung auf einer normalen CPU, keine Beschleunigung erzielt werden. Als Hauptgründe 158
162 9 nennt Perinkulam zum einen das Fehlen wichtiger mathematischer Funktionen zur Berechnung nichtgrafischer Probleme und zum anderen den hohen Kommunikationsoverhead zwischen CPU und GPU. Erst mit der Einführung von CUDA war es möglich effiziente Verfahren für die Ausführung auf Grafikkarten zu entwickeln. Es folgten eine Reihe verschiedener Ansätze, die alle von der Flexibilität der neuen Programmierschnittstelle Gebrauch machen. In diesem Bereich besonders aktiv, ist eine Forschungsgruppe der Universität Michigan, bestehend aus D. Chatterjee, A. DeOrio und V. Bertacco veröffentlichten sie mit der Bezeichnung GCS ein kompilierendes äquitemporales synchrones Verfahren zur parallelen Logiksimulation auf GPUs [8]. Noch im selben Jahr wurde von ihnen ein ereignisgesteuerter Ansatz vorgestellt [7]. Die Vorteile beider Verfahren wurden zwei Jahre später zusammengeführt und so ein hybrider (äquitemporal und ereignisgesteuert) Logiksimulator entworfen [9]. Dessen Aufbau und Funktionsweise wird in Kapitel 5 detailliert behandelt. Zeitgleich (2011) befasste sich eine andere Forschungsgruppe, bestehend aus Y. Zhu (Universität Beihang), B. Wang und Y. Deng (beide Universität Tsinghua), mit der Entwicklung eines interpretierenden, ereignisgesteuerten, asynchronen Logiksimulator [24]. Da dieser Ansatz aufgrund der Asynchronität und des interpretierenden Verfahrens, eine vollkommen andere Funktionsweise aufweist, wird er gesondert in Kapitel 6 vorgestellt. Es existieren noch weitere Projekte, welche die Simulation digitaler Schaltungen auf GPUs mittels CUDA demonstrieren [12] [21]. Diese werden jedoch in dieser Arbeit nicht vorgestellt, da sie entweder einen anderen Anwendungsbereich adressieren (Fehlersimulation in [12]) oder mit Schaltungsentwürfen höherer Abstraktionsebene (Register-Transfer-Ebene in [21]) arbeiten, was eine gemeinsame Erklärung und Gegenüberstellung schwierig macht. 5 Synchrones Verfahren In diesem Kapitel wird ein kompilierendes, hybrides, synchrones Verfahren zur parallelen Logiksimulation auf CUDA-GPUs vorgestellt. Der Simulator wurde im Juli 2011 unter der Bezeichnung Gate-Level Concurrent Simulator (GCS) von einer Forschungsgruppe, bestehend aus D. Chatterjee, A. DeOrio und V. Bertacco, der Universität Michigan in einer Publikation vorgestellt [9]. Vor diesem Verfahren wurde von derselben Forschungsgruppe bereits ein rein äquitemporaler und ein rein ereignisgesteuerter Ansatz präsentiert [8] [7]. Darauf aufbauend entstand das nachfolgende Verfahren, welches die Vorteile der beiden Ansätze vereint. Bevor detailliert auf den GCS eingegangen wird, soll das grundlegende Konzept zunächst dargestellt werden. 5.1 Grundkonzept Bekanntlich kann ein Problem erst dann auf einer GPU effizient ausgeführt werden, wenn eine Zerlegung des Problems in unabhängige parallele Berechnungen möglich ist. Auf den ersten Blick erweist sich eine digitale Schaltung aufgrund der starken kausalen Abhängigkeiten zwischen den einzelnen Gattern als eher ungeeignet. Ist eine Schaltung frei von Rückkoppelungen, lässt sich jedoch eine Technik anwenden, die vor allem für sehr große Schaltungen ein enormes Potential zur Parallelisierung offenbart. Werden nämlich die Gatter einer digitalen Schaltung nach ihrer Entfernung von den primären Eingängen (englisch: Primary Inputs) eingestuft (englisch: levelization), sind die Gatter einer Stufe voneinander unabhängig. Genauer gesagt bedeutet dies, dass die Gatter einer Stufe nur von den Werten der vorherigen Stufe abhängig sind und somit parallel berechnet werden können. Die einfachste Lösung besteht offensichtlich darin, alle Gatter einer Stufe parallel von einzelnen Threads berechnen zu lassen. Wird die 159
163 10 Beendigung dieser Berechnungen zudem synchronisiert, kann die komplette Schaltung Stufe für Stufe nacheinander parallel berechnet werden (siehe Abb. 6). Nach diesem Prinzip verfährt der Simulator, der in der ersten Publikation vorgestellt wurde [8]. Abbildung 6: Äquitemporale und synchrone Simulation Mit diesem Ansatz konnte, verglichen mit einem modernen ereignisgesteuerten sequentiellen Simulator, bereits eine signifikante Verbesserung (durchschnittlicher Beschleunigungsfaktor von ca. 14x) erzielt werden. Jedoch sorgt die äquitemporale Berechnung dafür, dass in jedem Zyklus viele Gatter ausgewertet werden, obwohl dies nicht notwendig ist. Genauer gesagt liegt die Aktivitätsrate in Schaltungen weit unter 40 Prozent. Anfang der 90er Jahre wurde bereits belegt, dass die Größe der Schaltung enormen Einfluss auf die Aktivitätsrate hat. Je größer die Schaltung, desto geringer fällt im Durchschnitt die Aktivitätsrate aus [2]. So sind Raten im Bereich von 5 bis 15 Prozent keine Seltenheit. Daher liegt es nahe stattdessen einen ereignisgesteuerten Algorithmus zu verwenden. Hierzu wird eine zentrale Verwaltung von Ereignislisten benötigt, in denen die im nächsten Berechnungsschritt aktiven Gatter festgehalten werden. Zudem müssen die Gatter einer Stufe hier ebenfalls synchronisiert werden, was, bezogen auf komplexe Schaltungen, zu einem Problem führt. Sobald die Anzahl von Gattern in einer Stufe die maximale Anzahl an Threads in einem Block überschreitet, ist eine blockübergreifende Synchronisation notwendig. CUDA stellt hierzu keine Funktionen bereit und eine Synchronisation ist somit nur mit Hilfe einer Abbildung 7: Konzept der hybriden Auswertung des GCS [9] Kommunikation über den globalen Speicher möglich. Aufgrund der hohen Zugriffszeiten auf den globalen Speicher, würde sich diese Vorgehensweise als Flaschenhals der parallelen Ausführung bewahrheiten. Deshalb ist es für eine effiziente Anwendung notwendig, die Gatter in Gruppen (Makro- Gatter) einzuteilen (Partitionierung), die dann jeweils einem Threadblock zugewiesen werden können. Das Konzept des GCS sieht es vor, auf Ebene der Makro-Gatter eine ereignisgesteuerte Auswertung zu implementieren, während innerhalb eines Makro-Gatters weiterhin eine äquitemporale Auswertung erfolgt (siehe Abb. 7). In der Abbildung ist ein mögliches Szenario dargestellt, bei dem nur die dunkel gefärbten Makro- Gatter aktiv sind. Ein Makro-Gatter wird nur dann berechnet, 160
164 11 wenn sich mindestens einer der Werte der Eingänge seit dem letzten Simulationszyklus verändert hat. Auf diese Weise kann der Overhead, welcher aufgrund der Verwaltung der Ereignislisten entsteht, minimal gehalten werden. Außerdem wird durch den homogenen Daten- und Kontrollfluss der Threads innerhalb eines Blockes eine effiziente Ausführung ermöglicht. Die globale Verwaltung einer Ereignisliste würde hier die Ausführung stark beeinträchtigen. 5.2 Aufbau und Ablauf Kompilierende Simulatoren können grundsätzlich in zwei Phasen unterteilt werden. Zum einen in die Kompilierungsphase und zum anderen in die Simulationsphase. Bevor die eigentliche Simulation beginnt, wird der Schaltungsentwurf in der Kompilierungsphase analysiert und dementsprechend bearbeitet. In dieser Phase gilt es, die digitale Schaltung in eine für die CUDA-Speicherhierarchie geeignete Datenstruktur zu überführen und diese dann in dem Speicher der GPU zu Simulationszwecken abzulegen. Zudem wird der CUDA-Code erstellt, der den Datenfluss innerhalb der Datenstruktur implementiert. Danach kann die Simulationsphase beginnen. Der erzeugte Simulator wird mit Testfällen (Stimuli) gefüttert und berechnet die Ergebnisse des Modells. Offensichtlich ist die Ausführungsgeschwindigkeit größtenteils von der Kompilierungsphase abhängig. Der Aufbau der Datenstruktur und der Ablauf der Berechnungsvorgänge haben gehörigen Einfluss auf die Effizienz des kompilierenden Simulators. In Abbildung 8 ist der Aufbau und Ablauf des GCS veranschaulicht. Abbildung 8: Aufbau und Ablauf des GCS Als Eingabe erhält der Simulator eine digitale Schaltung in Gatterebene, die im ersten Bearbeitungsschritt in eine geeignete Datenstruktur überführt wird. Danach erfolgt eine Partitionierung der Gatter in eine Menge gestufter Makro-Gatter. Anschließend werden die Makro-Gatter an die GPU-Architektur angepasst, bevor schließlich das Gesamtsystem in die Simulationsphase übergeht. 5.3 Kompilierungsphase Erzeugung der Datenstruktur Die erste grundlegende Aufgabe beim Entwurf eines kompilierenden Verfahrens liegt in der Wahl einer geeigneten Datenstruktur zur Abspeicherung aller simulationsrelevanter Daten. Der GCS verwendet hierfür das tabellengesteuerte Prinzip, welches bereits in Kapitel 3.2 erläutert wurde. Für die Simulationsphase wird eine Datenstruktur bestehend aus den folgenden Informationen bereitgestellt: Schaltnetzto- 161
165 12 pologie, Werte der primären Eingänge/Ausgänge, Zwischenwerte innerhalb der Schaltung und für jeden Gattertyp eine Wahrheitstabelle zur Auswertung in Form einer mehrstufigen (0,1,X,Y) Lookup-Tabelle. Da jeder Thread während der Simulation denselben CUDA-Code ausführt, müssen Letztere eine homogene Form aufweisen. Die Wahrheitstabellen bilden zudem zusammen mit den Zwischenwerten die meist frequentierten Daten, weshalb sie in dem zugriffsnahen lokalen/gemeinsamen Speicher bereitgestellt werden. Da die Threads eines Blockes die berechneten Werte untereinander austauschen müssen, hat dies für die Zwischenwerte nicht nur Geschwindigkeitsgründe. Auch wenn die Netzwerktopologie genauso oft benötigt wird, kann sie aufgrund der geringen Größe des Speichers dort nicht ebenfalls Platz finden. Stattdessen wird die Netzwerktopologie zusammen mit den Werten der primären Ein- und Ausgänge im globalen Speicher abgelegt. Aus der Sicht des Simulators kann das Schaltnetz als gerichteter azyklischer Graph aufgefasst werden. Dabei entsprechen die Knoten den logischen Gattern und die Kanten deren Verbindungen untereinander Partitionierung Im nächsten Schritt erfolgt die Partitionierung der Schaltung. Die Gatter werden zuerst nach ihrer Entfernung zu den primären Eingängen eingestuft, sodass die Eingänge aller Gatter einer Stufe nur von Gattern vorheriger Stufen abhängig sind. So können die Gatter Stufe für Stufe, von den primären Eingängen bis zu den primären Ausgängen, parallel berechnet werden. Im nächsten Schritt wird die gestufte Schaltung in Makro-Gatter aufgeteilt. Dieser Prozess ist essentiell für die spätere Effizienz des Simulators und muss deshalb bestimmte Eigenschaften erfüllen. Beispielsweise soll die Simulationszeit eines Makro-Gatters weit über der Zeit, die zur Berechnung der momentan aktiven Makro-Gatter benötigt wird, liegen. Genauer gesagt bedeutet dies, dass die reine Simulationszeit höher sein sollte, als die für die Ereignissteuerung zusätzlich benötigte Berechnungszeit. Ein weiterer Punkt betrifft die Unabhängigkeit der einzelnen Makro-Gatter. Da diese jeweils einem Block zugewiesen werden, kann eine Kommunikation zwischen Makro-Gattern nur mittels des langsamen globalen Speichers erfolgen. Somit ist es wichtig, dass kein Datenaustausch zwischen den Makro-Gattern erfolgt und diese unabhängig voneinander simuliert werden können. Hierbei kann es aufgrund der Überlappung von Makro-Gattern zur Replikation von Gattern kommen (d.h., ein Gatter ist in mehreren Makro-Gattern enthalten). Die letzte Bedingung an den Partitionierungsprozess betrifft die Synchronisation auf Makro-Gatter-Ebene. Um zyklische Abhängigkeiten zu verhindern, muss, wie schon zuvor auf Gatter-Ebene, auch auf Makro-Gatter-Ebene eine Einstufung erfolgen. So ist sichergestellt, dass alle Eingangswerte eines Makro-Gatters bereits vorliegen und sich während des Simulationsschrittes nicht verändern. In Abbildung 9 ist die Unterteilung in Makro-Gatter veranschaulicht. Zur Partitionierung werden die Variablen gap und lid verwendet. Die Erstere gibt an wie viele Stufen ein Makro-Gatter umfassen soll. Die bereits gestufte Schaltung wird demnach in Ebenen (englisch: layers) unterteilt. Für jede Ebene werden die Makro-Gatter dann folgendermaßen gebildet: An der oberen Grenze der Ebene wird eine bestimmte Anzahl (lid) von Verbindungen ausgewählt. Es wird dann ausgehend von diesen Verbindungen (Ausgänge der Ebene) bis zu den Eingängen der Ebene jeweils der Einflusskegel aufgespannt. Alle Gatter, die in dem Ein- Abbildung 9: Partitionierung in Makro-Gatter [9] flussbereich einer Verbindung liegen, werden dem 162
166 13 Makro-Gatter zugeordnet. Daraus resultiert eine bezüglich der Ebene unabhängige Menge von Gattern, welche stufenweise parallel simuliert werden kann. Um die Anzahl an Makro-Gattern pro Ebene gering zu halten, werden mehrere Makro-Gatter anschließend noch geeignet zusammengefügt. Damit möglichst wenige Gatterreplikationen auftreten, wird hierbei darauf geachtet, dass jeweils diejenigen Makro-Gatter vereint werden, welche die meisten gemeinsamen Gatter enthalten. Ist dieser Prozess beendet, werden für die spätere Simulation noch die Verbindungen, welche an der Grenze zwischen zwei Ebenen (und somit auch Makro-Gattern) liegen, in einer Liste zu überwachender Verbindungen abgespeichert. Zur Bestimmung der im nächsten Simulationsschritt aktiven Makro-Gatter reicht es dann aus, die in dieser Liste enthaltenen Verbindungen zu beobachten. Wie bereits erwähnt, ist die Partitionierung der Schaltung in Makro-Gatter essentiell für die spätere Performance der Simulation. Die Herangehensweise bei der Partitionierung ist nämlich ausschlaggebend für die spätere Effizienz der ereignisgesteuerten Simulation. Das Ziel ist es, die Aktivitätsrate der Makro-Gatter zu senken, sodass ein Großteil der Schaltung in einem Simulationszyklus nicht neu berechnet werden muss. Für die Konfiguration der Partitionierung stehen die beiden Variablen lid und gap zur Verfügung. Um die Aktivitätsrate gering zu halten, müssen diese Werte entsprechend der Schaltung gewählt werden. Der GCS verwendet zur Bestimmung des idealen Wertepaares < lid, gap > folgende Heuristik: Es werden für ein definiertes Intervall von Wertepaaren die Partitionierungen testweise erstellt. Diese werden dann unter Berücksichtigung der nachfolgenden Messwerte ausgewertet: Anzahl, Größe und durchschnittliche Aktivitätsraten der Makro-Gatter und die Anzahl zu überwachender Verbindungen. Die Aktivitätsraten ergeben sich aus kurzen Simulationen repräsentativer Testfälle. Innerhalb der genannten Testdaten wird nun das lokale Optimum ausgewählt und mit dem zugehörigen Wertepaar die Kompilierungsphase fortgeführt. Eine zusätzliche Optimierung zur Reduktion der Aktivitätsrate betrifft das Kriterium nach dem die Makro-Gatter zusammengefügt werden. Die Idee besteht darin, die Makro-Gatter nicht wie bisher beschrieben anhand der Anzahl gemeinsamer Gatter zusammenzufügen, sondern ausgehend von ihrer Aktivitätsrate. In diesem Fall werden diejenigen Makro-Gatter vereint, welche annähernd gleiche Aktivitätsraten aufweisen (siehe Abb. 10). Abbildung 10: Vergleich der verschiedenen Ansätze zur Zusammenfügung von Makro-Gattern Die dunkel gefärbten Makro-Gatter weisen eine höhere Aktivitätsrate auf, als die hell gefärbten Makro- Gatter. Mit Hilfe der Abbildung wird die Motivation klar veranschaulicht. Indem die Makro-Gatter ähnlicher Aktivitätsrate zusammengefügt werden, kann verhindert werden, dass die Vereinigung von zwei Makro-Gattern hoher und niedriger Aktivitätsrate in einem Makro-Gatter hoher Aktivitätsrate resultiert. Mit dem neuen Verfahren ergeben sich neue Makro-Gatter annähernd gleicher Aktivitätsrate, was insgesamt zu einer verbesserten Performance führt. Die zusätzlichen Gatterreplikationen können hierbei vernachlässigt werden, da der Mehrnutzen aufgrund der geringeren Aktivitätsrate überwiegt. 163
167 Anpassung der Makro-Gatter Nachdem die Partitionierung abgeschlossen ist, kann jedes Makro-Gatter als Menge von Gattern angesehen werden, die einem Threadblock zur Simulation zugewiesen ist. Innerhalb eines Makro-Gatters erfolgt dann die Simulation auf äquitemporale Weise, d.h. die Gatter werden Stufe für Stufe von den Threads des Blockes bearbeitet. Die Vorgehensweise bei der Erzeugung der Makro-Gattern führt offensichtlich zu kegelförmigen Teilschaltungen. Während die Spitze eines Makro-Gatters nur wenige, durch die Variable lid bestimmte, Gatter enthält, weist die Basis weitaus mehr Gatter auf (Breite des Makro- Gatters). Da jede Stufe parallel abgearbeitet werden soll, werden zu Beginn so viele Threads benötigt, wie Gatter an der Basis (niedrigste Stufe) vorhanden sind. Dies führt dazu, dass zum Schluss der Simulation des jeweiligen Makro-Gatters viele Threads nicht mehr ausgelastet werden (siehe Abb. 11). Zudem kann es sein, dass die Breite eines Makro-Gatters die maximale Anzahl an Threads in einem Block überschreitet. In diesem Fall wäre es nicht möglich alle Gatter einer Stufe parallel zu bearbeiten. Abbildung 11: Macro-gate balancing [9] Deshalb werden die Makro-Gatter von der Kegelförmigen in eine möglichst rechteckige Form überführt, die höchstens so breit ist, wie Threads pro Block zur Verfügung stehen (macro-gate balancing). So wird sichergestellt, dass genügend Threads zur stufenweisen parallelen Abarbeitung vorhanden sind und diese zudem optimal ausgelastet werden. Dieser Prozess stellt den letzten Schritt der Kompilierungsphase dar. Das Ergebnis sind ausgewogene Makro-Gatter, die in jeder Stufe annähernd dieselbe Anzahl an Gattern aufweisen. Somit werden weniger Threads benötigt und die Lastverteilung auf die einzelnen Threads wird optimiert. Bei der Zuweisung der Gatter zu den neuen Stufen muss darauf geachtet werden, dass die Abhängigkeiten der Gatter untereinander nicht verletzt werden. In einer neuen Stufe dürfen sich demnach nur Gatter befinden, die auch vorher in der gleichen Stufe waren. Für den GCS wird eine Breite von 128 Threads für jeden Block festgelegt. Das heißt, dass jedes Makro-Gatter höchstens 128 Gatter pro Stufe aufweist, welche von nebenläufigen Threads bearbeitet werden. Für die Wahl dieser Anzahl an Threads werden verschiedene Gründe genannt. Für eine effizienten Ausführung ist es beispielsweise wichtig, dass die Anzahl an Threads ein Vielfaches der Warpgröße (32 Threads) darstellt. Für den genannten Wert konnten die Berechnungen zudem am besten auf die Threads verteilt werden. Für kleinere Werte wurden die Makro-Gatter zu hoch, was insgesamt zu einer höheren Ausführungszeit führte. Bei größeren Werten wurden Threads im oberen Bereich der Makro- Gatter nicht mehr effizient ausgelastet. Offensichtlich ist die Wahl einer geeigneten Anzahl aber stark von der Art und Größe der simulierten Schaltung abhängig. 5.4 Simulationsphase Sobald die Kompilierungsphase beendet ist, werden alle simulationsrelevanten Daten von der CPU auf die GPU übertragen. Der eigentliche Simulationsprozess wird dann von der GPU ausgeführt. Dabei werden die Makro-Gatter mittels des ereignisgesteuerten Ansatzes zur Ausführung ausgewählt und bearbeitet, indem zwei Kernel abwechselnd agieren. Ein Kernel ist für die Simulation der Makro-Gatter der aktuellen Ebene zuständig und der zweite Kernel wertet mittels der Listen (der zu überwachenden Verbindungen zwischen zwei Ebenen), die in der nächsten Ebene aktiven Makro-Gatter aus. Jedes Makro-Gatter wird von einem Threadblock bearbeitet und innerhalb der Makro-Gatter erfolgt die Simu- 164
168 15 lation auf äquitemporale Weise. Somit ergeben sich zwei Stufen der Parallelität. Zum einen werden die aktiven Makro-Gatter einer Ebene von jeweils einem Threadblock (eventuell) parallel auf verschiedenen Multiprozessoren bearbeitet und zum anderen werden Gatter einer Stufe innerhalb eines Makro-Gatters von verschiedenen Threads nebenläufig simuliert. Alle primären Eingänge und Ausgänge der Makro-Gatter, Listen der zu überwachenden Verbindungen und die Netztopologie werden im globalen Speicher abgelegt. Die Zwischenwerte der Verbindungen innerhalb eines Makro-Gatters sowie die Wahrheitstabellen zur Auswertung der Gattertypen befinden sich im zugriffsnahen lokalen/gemeinsamen Speicher. Zur Auswertung eines Gatters muss ein Thread demnach immer auf den globalen Speicher zugreifen (Netztopologie). Aus Platzgründen ist dies anders nicht möglich. Die Netztopologie besteht aus einer zweidimensionalen Matrix, die alle Informationen zu den einzelnen Gattern enthält. Das Indextupel entspricht dabei der Position der ausgehenden Verbindung des Gatters im ausgewogenen Makro-Gatter und der Inhalt der Matrixzelle enthält den Typ und die Matrixindizes der Eingänge des Gatters. Aufgrund der klaren Struktur der einzelnen Makro-Gatter können die Zugriffe auf den globalen Speicher gebündelt abgearbeitet werden. Genauer gesagt wird pro Stufe im Makro-Gatter nur ein Zugriff auf den globalen Speicher benötigt, da alle relevanten Gatter in der Matrix direkt benachbart sind. Die Werte der Eingänge werden dann direkt aus dem lokalen Speicher gelesen und mittels der Wahrheitstabelle der Wert des Ausgangs bestimmt, der ebenfalls im lokalen Speicher abgelegt wird. Sobald ein Makro-Gatter komplett simuliert ist, werden die ermittelten primären Ausgänge im globalen Speicher gespeichert. Diese dienen als primäre Eingänge für die Makro-Gatter der nächsten Ebene. 5.5 Auswertung und Probleme Zu Testzwecken wurden der GCS sowie ein moderner ereignisgesteuerter sequentieller Simulator mit geeigneten Szenarien bzw. Stimuli gefüttert. Hierbei wurde eine Reihe von repräsentativen Schaltungen verwendet, die von mehreren Tausend bis zu über einer Million Gatter enthalten. Auf eine genauere Beschreibung des sequentiellen Simulators wird leider verzichtet. Als Grafikkarte wurde die NVIDIA 8800 GT verwendet, welche 14 Multiprozessoren mit jeweils 600 MHz und 512 MB globalen Speicher besitzt. Der sequentielle Simulator wurde auf einem Linux-System mit einem 2.4 GHz Intel Core 2 Quad Multiprozessor (4 Kerne) ausgeführt. Das gleiche System verwendete auch der GPU Simulator. Verglichen mit dem sequentiellen Simulator konnten mit dem GCS Beschleunigungen bis zu einem Faktor von ca. 50x erreicht werden, wobei der durchschnittliche Wert bei ca. 13x lag. Dabei wird jedoch nur die reine Simulationszeit betrachtet. Die Kompilierungszeit, die beim GCS zwei bis drei Mal so lange benötigt, wie bei dem sequentiellen Simulator, wird nicht beachtet. Zudem liegt der Median bei 7,34x, und zeigt, dass die Testergebnisse stark abweichen, d.h. die Simulationszeit maßgeblich von der Schaltung abhängt. Während des Testverfahrens wurden auch verschiedene Aspekte ausgewertet, die nur den GCS betreffen. Beispielsweise konnte festgestellt werden, dass die Vereinigung der Makro-Gatter nach ähnlicher Aktivitätsrate bezüglich der Simulationszeit durchweg bessere Ergebnisse erzielte, als die Vereinigung nach den meisten gemeinsamen Gattern. Die mittlere Aktivitätsrate der Makro-Gatter und die durchschnittliche Anzahl an zu überwachenden Verbindungen belief sich jeweils bei 30 Prozent. Auffällig war zudem die hohe Anzahl an Gatterreplikationen. Diese beträgt bei Verwendung der Vereinigung nach Aktivitätsrate ca. 50 Prozent und bei der Vereinigung nach gemeinsamen Gattern ca. 35 Prozent. Es muss demnach ein großer Anteil der Gatter mehrfach berechnet werden. Insgesamt bietet der GCS, verglichen mit einem aktuellen sequentiellen Simulator, also eine deutliche Steigerung der Berechnungszeit. Es existieren jedoch noch einige limitierende Faktoren. Beispielsweise ist die Gatterreplikation sehr hoch, was von der Tatsache abhängt, dass die Makro-Gatter aufgrund 165
169 16 des langsamen globalen Speichers nicht miteinander kommunizieren sollen. Weiterhin kommt der Aspekt der notwendigen Synchronisation hinzu. Damit keine kausalen Abhängigkeiten in der Schaltung verletzt werden, muss sowohl auf der Ebene der Makro-Gatter, als auch auf der Ebene der Gatter nach jeder Stufe eine Synchronisation erfolgen. Hier wird eindeutig Rechenleistung liegen gelassen. Aufgrund der relativ langen Kompilierungsphase ist der GCS vor allem dann geeignet, wenn nach einmaliger Kompilierung eine hohe Anzahl verschiedener Stimuli bearbeitet werden soll. Wenn die Simulationphase mehrere Stunden oder gar Tage dauert, ist die notwendige Kompilierungszeit dann vernachlässigbar. Zusammenfassend verfolgt der GCS einen interessanten Ansatz zur Simulation digitaler Schaltungen auf GPUs, bei dem das vorhandene Parallelisierungspotential digitaler Schaltungen gut umgesetzt wird. 166
170 17 6 Asynchrones Verfahren Dieses Kapitel behandelt ein interpretierendes, ereignisgesteuertes, asynchrones Verfahren zur parallelen Logiksimulation mittels CUDA auf GPUs. Das Verfahren wurde 2011 von einer Forschungsgruppe, bestehend aus Y. Zhu (Universität Beihang), B. Wang und Y. Deng (beide Universität Tsinghua) in einer Publikation vorgestellt [24]. Wie bereits im vorherigen Kapitel, soll vorerst das Grundkonzept des Simulators veranschaulicht werden, bevor genauer auf die Details eingegangen wird. 6.1 Grundkonzept Das Verfahren verwendet das Konzept der parallelen, diskreten, ereignisgesteuerten Simulation (kurz: PDES) [11]. Hierbei wird das physikalische System, welches simuliert werden soll, zuerst in Teilsysteme zerlegt (englisch: model decomposition). Diese Teilprozesse des Gesamtsystems werden physikalische Prozesse (PP) genannt. Das Verhalten jedes einzelnen PPs wird von einem logischen Prozess (LP) modelliert. Jeder LP stellt somit ein Teilverhalten des Gesamtsystems dar und die einzelnen LPs können nebenläufig auf verschiedenen Recheneinheiten ausgeführt werden, sodass jeder LP seinen Teil vom Ganzen simuliert. Die einzelnen PPs des Gesamtsystems sind offensichtlich nicht voneinander unabhängig, d.h. eine Änderung des Zustandes eines PPs kann eine Änderung des Zustandes eines anderen PPs beeinflussen. Zur Berücksichtigung dieser kausalen Abhängigkeiten, werden zum Nachrichtenaustausch gerichtete Verbindungen zwischen den LPs eingefügt. Bezüglich des ursprünglichen Systems existiert genau dann eine Verbindung zwischen LPx und LPy, wenn auch im physikalischen System eine Verbindung (d.h. eine Abhängigkeit) zwischen den korrespondierenden PPx und PPy vorhanden ist. Die Kommunikation erfolgt dann über zeitgestempelte Ereignisse. Hierzu besitzt jeder LP eine lokale Sicht auf die Zeit, die im physikalischen System verstreicht (nicht zu verwechseln mit der Simulationszeit). Ein Ereignis enthält also den veränderten Zustand des LP und die physikalische Zeit, an der die Änderung erfolgte. Sowohl die eingegangenen als auch die ausgehenden Ereignisse werden innerhalb jedes LPs in Warteschlangen abgelegt, in der die Ereignisse chronologisch geordnet werden. Das nächste Ereignis, das in der Warteschlange gelesen wird, ist somit immer dasjenige, das als erstes in die Schlange eingefügt wurde (First-In-First-Out). Um das Gesamtkonzept begreifbar zu machen, ist in Abbildung 12 ein einfaches Beispiel für eine Schaltung mit drei Gattern veranschaulicht. Abbildung 12: Modell der PDES für Schaltung mit 3 Gattern 167
171 18 Zur Vereinfachung wird davon ausgegangen, dass nur Gatter mit jeweils zwei Eingängen und einem Ausgang Verwendung finden (jede Schaltung kann mit solchen Gattern realisiert werden). Das physikalische System stellt die Gesamtschaltung dar, während ein PP ein Gatter repräsentiert. Jedem Gatter wird somit ein LP zugewiesen, der für die Simulation dieses Gatters zuständig ist und sonst unabhängig von dem Gesamtsystem agiert. Zwei LPs kommunizieren genau dann miteinander, wenn in der Ausgangsschaltung die Schnittstellen der zugehörigen Gatter miteinander verbunden sind. Zu klären bleibt die Frage nach einem geeigneten Algorithmus zur Ausführung der einzelnen LPs. Während der Simulation dürfen die kausalen Abhängigkeiten der einzelnen Ereignisse nicht verletzt werden. Um globale Korrektheit der Simulation sicherstellen zu können, müssen die LPs bei der Verarbeitung der Ereignisse die folgenden Regel erfüllen (bekannt als local causality constraint): Jeder logische Prozess muss die eingehenden Ereignisse in nicht-absteigender Reihenfolge bearbeiten. Wenn ein LP ein Ereignis bearbeitet, muss also sichergestellt sein, dass zu keinem späteren Zeitpunkt ein Ereignis mit kleinerem Zeitstempel eintritt. Hierzu werden in der Literatur zwei Paradigmen unterschieden: konservative und optimistische Algorithmen. Bei letzterem erlaubt der Simulator fehlerhafte Situationen, erkennt diese und mittels Backtracking wird zur letzten fehlerfreien Situation zurückgekehrt und ein anderer Berechnungsweg gewählt. Das in diesem Kapitel vorgestellte Verfahren zur Logiksimulation verwendet aber ersteres, den konservativen Ansatz, bei dem keinerlei fehlerhafte Situationen akzeptiert werden. Das heißt ein LP wird kein Ereignis bearbeiten, bevor er sich komplett sicher ist, dass zu keinem späteren Zeitpunkt ein Ereignis mit kleinerem Zeitstempel eintreffen kann. Offensichtlich kann es hierbei zu Verklemmungen kommen. Ein asynchroner konservativer Algorithmus, der dieses Problem behebt und im Zuge des Logiksimulators eingesetzt wird, ist unter dem Namen CMB-Algorithmus bekannt. Er wurde bereits in den 80er Jahren von R. Bryant [5] und K. M. Chandy und Y. Misra [6] unabhängig voneinander entworfen. Zur Vermeidung von Verklemmungen verwendet der Algorithmus sogenannte Null-Nachrichten (englisch: null-messages). Wenn ein LPx während der Verarbeitung eines Ereignisses eigentlich kein neues Ereignis erzeugen würde, da sich der innere Zustand nicht verändert, wird trotzdem ein Ereignis erstellt, das nur den aktuellen Zeitstempel T null enthält. Wird dieses Ereignis an einen Nachfolger von LPx gesendet, weiß dieser, dass an dem Eingang bis zu dem angegebenen Zeitstempel T null keine Änderung erfolgt und kann dementsprechend mit der Simulation fortfahren. Der Zeitpunkt, bis zu dem ein LP die Simulation fortsetzen kann, ohne kausale Abhängigkeiten zu verletzen, wird T min bezeichnet (sicherer Auswertungszeitpunkt). Bezüglich eines Gatters mit den zwei Eingängen e0 und e1 kann der sichere Auswertungszeitpunkt T min folgendermaßen berechnet werden: T min = min t (max t (e0),max t (e1)). Intuitiv kann T min als derjenige Zeitpunkt angesehen werden, bis zu dem alle Vorgängerprozesse des betrachteten Prozesses bereits simuliert wurden. 6.2 Umsetzung Nachdem das grundlegende Konzept des parallelen asynchronen Logiksimulators beschrieben wurde, soll nun die Umsetzung zur Ausführung auf einer GPU betrachtet werden. Die Adaptierung an die GPU- Architektur lässt sich in drei Entscheidungsprozesse unterteilen: Programmablauf: Aufteilung des Gesamtproblems auf parallel ausgeführte Threads Datenstruktur: Erzeugung einer geeigneten Datenstruktur für die Ereignisse und Warteschlangen Speicherverwaltung: Effiziente Verwaltung der Datenstruktur 168
172 Programmablauf Zur parallelen Simulation wird die digitale Schaltung zunächst in eine interne Darstellung transformiert, in welcher jedes Gatter einem LP zugeordnet wird. Dabei werden die primären Eingänge wie (virtuelle) Gatter behandelt. Während der Simulation führt dann jeder LP drei Berechnungsschritte abwechselnd nacheinander aus. Der LP empfängt Ereignisse an den Eingängen, wertet das Gatter dementsprechend aus und sendet das resultierende Ereignis an den Ausgang. Dieser Berechnungsprozess wird von jedem LP kontinuierlich wiederholt, sodass während der Simulation eine wellenförmige Fortschreitung innerhalb der Schaltung entsteht. Den Simulationsprozess bilden drei Kernel, die nacheinander wiederholt ausgeführt werden: extract, fetch und evaluate. Als erstes wird das extract-kernel ausgeführt, welches nur die primären Eingänge betrifft (virtuelle Gatter). Die anliegenden Stimuli werden zusammen mit dem aktuellen Zeitstempel in die Warteschlange des Ausgangspins eingefügt. Danach werden alle Ereignisse der Ausgangspins (aller LPs) in die Warteschlangen der nachfolgenden Eingangspins eingetragen. Dieser Prozess kann aus Sicht der Eingangspins als Abholung der Ereignisse angesehen werden und wird entsprechend als fetch bezeichnet. Tatsächlich ist dieser Vorgang auch aus der Perspektive der Eingänge implementiert. Da in Schaltungen die Anzahl von Pins weitaus höher ist als die Anzahl an Gattern, wird hierdurch eine höhere Parallelität erzielt. Zum Schluss eines Simulationszyklus werden die realen Gatter im Zuge des evaluate-kernels ausgewertet. Für jedes Gatter wird entsprechend der anliegenden Ereignisse ein neues Ereignis mit aktuellem Zeitstempel erzeugt, das in der Warteschlange des Ausgangspins eingefügt wird. Die Auswertung der Gatter erfolgt, wie auch beim Verfahren in Kapitel 5, mit Hilfe von Wahrheitstabellen. Das Verfahren verwendet demnach ebenfalls den tabellengesteuerten Ansatz. In Abbildung 13 ist die Zuweisung der Threads in jedem Kernel veranschaulicht. Abbildung 13: Threadzuweisung im jeweiligen Kernel [24] Die Schaltung besteht aus den drei Gattern g0, g1 und g2 mit den jeweiligen Eingangspins gi0 und gi1 für i = [0,1,2]. Die primären Eingänge sind mit a, b, c und d gekennzeichnet und die zugewiesenen Threads mit ti für i = [0,1,2,3,4,5]. In dem extract-kernel behandelt jeder Thread jeweils einen primären Eingang, während innerhalb des fetch-kernels jedem Thread ein Eingangspin zugewiesen ist. Schließlich wird im Zuge des evaluate-kernels jedes reale Gatter von einem Thread bearbeitet. 169
173 Datenstruktur Für den Nachrichtenaustausch der Ereignisse zwischen den LPs und zur Abspeicherung des aktuellen Zustands der einzelnen LPs werden drei Arrays bereitgestellt und manipuliert. Diese tragen folgende Bezeichnungen: output pin, input pin FIFOS und gate status. In dem Array output pin wird für jedes Gatter die Warteschlange der Ereignisse am Ausgangspin bereitgestellt. Das Array input pin FIFOS enthält für jeden einzelnen Eingangspin der Gatter die geordnete Warteschlange der anliegenden Ereignisse. Der aktuelle Zustand jedes einzelnen Gatters - anliegende Werte an den Eingängen und sichere Auswertungszeit T min - wird in gate status abgespeichert. In Abbildung 14 ist eine Beispielschaltung mit zugehöriger Datenstruktur veranschaulicht. Abbildung 14: Beispielschaltung und zugehörige Datenstruktur [24] Der Nachrichtenaustausch während eines Simulationsschrittes wird realisiert, indem im Zuge des fetch-kernels alle Ereignisse aus dem Array output pin in die entsprechenden Warteschlangen im Array input pin FIFOS geschrieben werden. Zur Auswertung wird dann aus den beiden Warteschlangen der Eingangspins das Ereignis mit dem kleinsten Zeitstempel bestimmt und an das Array gate status übermittelt Speicherverwaltung In der Praxis werden meist sehr komplexe Schaltungen simuliert. Für solche umfangreichen Schaltentwürfe stellt sich die limitierte Speichergröße von GPUs als Hindernis dar, weil alle während der Simulation erzeugten Ereignisse im Speicher festgehalten werden müssen. Aktuelle GPUs stellen leider keine dynamische Speicherverwaltung zur Verfügung, um dieses Problem zu bewältigen. Demnach müsste vor Ausführung der eigentlichen Simulation den Warteschlangen jedes Eingangspins (input pin FIFOS) eine feste Größe zugewiesen werden. Dies ist jedoch schwer umsetzbar, da der Nachrichtenaustausch 170
174 21 während der Simulation sehr stark von der Art und Größe der digitalen Schaltung abhängt. Eine vorherige Festlegung der Größe der Warteschlangen würde deshalb entweder zu permanentem Überlauf oder zu ineffizienter Auslastung der Warteschlangen führen. Zudem ist die Anzahl an zu behandelnden Ereignissen stark vom Gatter (bzgl. Position in Schaltung) und der Zeit abhängig, d.h. die Anzahl eintreffender Ereignisse variiert von Eingangspin zu Eingangspin und für jeden Eingangspin von Zeit zu Zeit. Aus genannten Gründen verwendet der Logiksimulator für das Array input pin FIFOS eine dynamische Speicherverwaltung, die es erlaubt während der Simulation Speicherplatz zuzuweisen und bei Bedarf wieder freizugeben. Hierzu wird ein Großteil des verfügbaren Speichers in sogenannte Seiten (englisch: page) gleicher Größe aufgeteilt, welche fortlaufend indiziert sind. Jede Seite kann hierbei eine konstante Anzahl an Ereignissen festhalten. Somit stellt eine Seite innerhalb der Speicherverwaltung die kleinste Einheit an Speicherplatz dar. Zu Beginn wird jedem Eingangspin eine fixe Größe an Seiten zugeteilt. Die Indizes der restlichen (verfügbaren) Seiten werden in einer globalen Warteschlange eingetragen. Während der Simulation können dann bei Bedarf für einen spezifischen Eingangspin zusätzliche Seiten zugeteilt werden. Ebenso ist es möglich, bereits zugeteilte, nicht verwendete Seiten freizugeben. Die Zuteilung zusätzlicher Seiten erfolgt nach jeder Ausführung des fetch-kernels und die Freigabe nicht verwendeter Seiten wird nach der Ausführung des evaluate-kernels bearbeitet. Eine detaillierte Beschreibung der dynamischen Speicherverwaltung ist in [24] zu finden Optimierungen Das bisher beschriebene Verfahren wurde zur Leistungssteigerung noch mit einigen Optimierungen versehen. Beispielsweise soll den unterschiedlichen Verzweigungspfaden innerhalb eines Warps entgegengewirkt werden. Zur effizienten Ausführung eines Warps ist es bekanntlich von Bedeutung, dass die Threads ähnliche Berechnungspfade verfolgen. Bei einer realen Schaltung sind Gatter unterschiedlicher Merkmale aber willkürlich verteilt. Erfolgt die Zuteilung der Gatter an die Threads basierend auf dieser Anordnung, so ist es sehr wahrscheinlich, dass viele Threads innerhalb eines Warps verschiedene Ausführungspfade durchlaufen. Für die spätere Zuweisung der Gatter an die einzelnen Threads spielt die Anordnung in der Schaltung jedoch keine Rolle. Demzufolge werden die Gatter bezüglich Gattertyp und Anzahl der Eingänge sortiert und abgespeichert. Werden die Gatter nun fortlaufend den Threads zugeteilt, ist eine homogene Ausführung innerhalb der Warps höchstwahrscheinlich. Weiterhin umfasst das Verfahren Optimierungen zur Verbesserung der dynamischen Speicherverwaltung, die bei Interesse in der Publikation nachgelesen werden können [24]. 6.3 Auswertung und Probleme Zur Auswertung wurde der parallele Logiksimulator mit einem eigens programmierten sequentiellen, ereignisgesteuerten Simulator verglichen. Hierzu wurden, wie bereits bei dem synchronen Verfahren, eine Reihe von repräsentativen Schaltungen verwendet und mit geeigneten Stimuli gefüttert. Es wurden zum einen zufällige Stimuli und zum anderen offizielle, mit der jeweiligen Testschaltung veröffentlichte, Stimuli verwendet. Beide Simulatoren wurden auf einem Computer mit einem 2.66 GHz Intel Core 2 Duo Multiprozessor (2 Kerne) ausgeführt. Als Grafikkarte kam die NVIDIA GTX 280 zum Einsatz, welche über 30 Multiprozessoren mit jeweils 602 MHz und 1 GB globalen Speicher verfügt. Verglichen mit dem sequentiellen Simulator konnte für zufällige Stimuli eine Beschleunigung bis zu einem Faktor von ca. 270x erreicht werden, wobei der durchschnittliche Wert bei ca. 48x lag. Der Median liegt bei ca. 12x, und zeigt, dass die Testergebnisse enorm abweichen. Bei Verwendung der offiziellen Stimuli erreicht der 171
175 22 parallele Simulator eine Beschleunigung bis zu einem Faktor von ca. 59x, wobei der durchschnittliche Wert bei ca. 14x lag. Hier liegt der Median bei ca. 4x. Die Effizienz des Verfahrens scheint demnach sehr stark von der Schaltung abzuhängen. Für die offiziellen Stimuli war der parallele Simulator sogar zum Teil (bei zwei Schaltmodellen) langsamer als der sequentielle Simulator. Dies wird wie folgt begründet: Bei einem der beiden betroffenen Schaltmodellen erhalten die primären Eingänge, unter Verwendung der offiziellen Stimuli, beispielsweise nur alle 500 Zyklen neue Werte. Werden dagegen zufällige Stimuli verwendet, so beträgt dieser Wert nur fünf Zyklen. Das heißt, dass der Simulator in diesem Fall viel stärker beschäftigt wird. Zudem werden bei den offiziellen Stimuli alle primären Eingänge während der genannten 500 Zyklen sozusagen immer wieder mit denselben Werten gefüttert. Bekanntlich werden dann nur Null-Nachrichten versendet, da sich der interne Zustand nicht verändert hat. Insgesamt führen diese Beobachtungen zu der Feststellung, dass der parallele Simulator nur aufgrund mangelnder Aktivität (innerhalb der offiziellen Stimuli) schlechter abschneidet als der sequentielle Simulator. 7 Fazit In dieser Arbeit wurden zwei aktuelle Verfahren zur Simulation digitaler Schaltungen auf GPUs vorgestellt. Beide Verfahren konnten, im Vergleich zu einem sequentiellen Simulator, für zufällige Stimuli durchschnittliche Beschleunigungen um den Faktor 13x (synchrones Verfahren) bzw. 48x (asynchrones Verfahren) erzielen. Eine Gegenüberstellung der Verfahren ist jedoch aufgrund der verschiedenen Rahmenbedingungen nicht möglich. Die verwendeten sequentiellen Simulatoren werden nur spärlich beschrieben und die zur Auswertung eingesetzten Rechensysteme unterscheiden sich in vielen Punkten. Zudem wurden beide Verfahren anhand verschiedener Schaltmodelle bewertet, welche wiederum mit unterschiedlichen Stimuli gefüttert wurden. Bezüglich des Einsatzgebietes ist das synchrone Verfahren aufgrund der Kompilierungszeit nur dann geeignet, wenn für ein Schaltmodell viele aufeinanderfolgende Testfälle angewendet werden sollen. Das asynchrone Verfahren hat diesbezüglich keine Einschränkung, ist aber bekanntlich vor allem für Testszenarien mit hoher Aktivität geeignet. Insgesamt bieten beide Verfahren interessante Konzepte zur massiv-parallelen Simulation digitaler Schaltungen. Anhand der vollkommen unterschiedlichen Ansätze wird deutlich, dass es viele sinnvolle Wege geben kann die Logiksimulation auf die Architektur von Grafikprozessoren zu adaptieren. In beiden Verfahren wurden in der Auswertung durchweg gute Ergebnisse erzielt. Es bleibt nur offen, inwiefern die Auswertungsszenarien den Gegebenheiten in der Praxis entsprechen. Es wurden nämlich vorrangig zufällig generierte Stimuli erzeugt, welche sich von realen in der Praxis auftretenden Szenarien stark unterscheiden. Nur bei dem asynchronen Verfahren wurde der Simulator auch mit offiziellen Testszenarien ausgeführt. Doch gerade dann konnte der parallele Logiksimulator keine guten Ergebnisse mehr erzielen und hatte verglichen mit dem sequentiellen Simulator sogar das Nachsehen. Zudem werden in der Praxis meist Gatterverzögerungen bei der Simulation mit eingerechnet (standard-delay-format). Das heißt, dass die Verzögerungszeiten der einzelnen Gatter berücksichtigt werden. Im synchronen Verfahren werden diese Verzögerungszeiten nicht berücksichtigt (zero-delay format). Eine Erweiterung des Verfahrens um diese Komponente würde die Effizienz mehr oder weniger stark beeinträchtigen. Das zweite Verfahren bietet die Möglichkeit, die Gatterverzögerungen für die einzelnen Gatter in einer Tabelle bereitzustellen. In jedem Auswertungsschritt können diese dann abgelesen und berücksichtigt werden. Es bleibt abzuwarten inwiefern die vorhandenen Verfahren weiter optimiert werden oder eventuell neue Techniken Verwendung finden, die die bisherigen Probleme umgehen. Für den asynchronen Simulator wurde bereits eine Erweiterung um die Register-Transfer-Ebene angekündigt. Zudem ist eine Applikation an andere Anwendungsbereiche, wie beispielsweise der Netzwerksimulation, geplant. 172
176 23 Literatur [1] A. Nischwitz, M. Fischer, P. Haberäcker, G. Socher (2011): Computergrafik und Bildverarbeitung: Band I: Computergrafik. Vieweg+Teubner Verlag, 3. Auflage. Kapitel 17. [2] M. L. Bailey (2006): How circuit size affects parallelism. Trans. Comp.-Aided Des. Integ. Cir. Sys. 11(2), pp [3] T. Beierlein & O. Hagenbruch (2004): Taschenbuch Mikroprozessortechnik. Fachbuchverl. Leipzig im Carl- Hanser-Verlag. [4] J. Bergeron (2000): Writing testbenches: functional verification of HDL models. Kluwer Academic Publishers, Norwell, MA, USA. [5] R. E. Bryant (1977): Simulation of Packet Communication Architecture Computer Systems. Technical Report, Cambridge, MA, USA. [6] K. M. Chandy & J. Misra (1979): Distributed Simulation: A Case Study in Design and Verification of Distributed Programs. IEEE Transactions on Software Engineering 5, pp [7] D. Chatterjee, A. DeOrio, V. Bertacco (2009): Event-Driven Gate-Level Simulation with GP-GPUs. University of Michigan. [8] D. Chatterjee, A. DeOrio, V. Bertacco (2009): GCS: High-performance gate-level simulation with GPGPUs. University of Michigan. [9] D. Chatterjee, A. DeOrio, V. Bertacco (2011): Gate-Level Simulation with GPU Computing. University of Michigan. [10] D. Edenfeld, A. B. Kahng, M. Rodgers, Y. Zorian (2004): 2003 Technology Roadmap for Semiconductors. Computer 37, pp [11] R. M. Fujimoto (1989): Parallel discrete event simulation. In: Proceedings of the 21st conference on Winter simulation, WSC 89, ACM, New York, NY, USA, pp [12] K. Gulati & S. Khatri (2008): Towards acceleration of fault simulation using graphics processing units. In: Proceedings of the 45th annual Design Automation Conference, DAC 08, ACM, New York, NY, USA, pp [13] G. Herrmann & D. Müller (2004): ASIC - Entwurf und Test. Fachbuchverl. Leipzig im Carl-Hanser-Verlag. [14] D. Lewis (1991): A hierarchical compiled code event-driven logic simulator. IEEE Trans. on CAD of Integrated Circuits and Systems 10(6), pp [15] M. L. Bailey, J. V. Briner Jr., R. D. Chamberlain (1994): Parallel logic simulation of VLSI systems. ACM Comput. Surv. 26(3), pp [16] G. Meister (1993): A Survey on Parallel Logic Simulation. University of Saarland, Department of Computer Science. [17] S. A. Misera (2007): Simulation von Fehlern in digitalen Schaltungen mit SystemC. Dissertation, Technische Universität Cottbus. [18] Nvidia: NVIDIA CUDA C Programming Guide Version compute/devzone/docs/html/c/doc/cuda_c_programming_guide.pdf. Aufgerufen am: [19] Nvidia: Technische Daten: GeForce GTX html. Aufgerufen am: [20] A. Perinkulam (2007): Logic Simulation using Graphics Processors. Dissertation, University of Massachusetts Amherst. [21] H. Qian & Y. Deng (2011): Accelerating RTL simulation with GPUs. In: Proceedings of the International Conference on Computer-Aided Design, ICCAD 11, IEEE Press, Piscataway, NJ, USA, pp [22] R. Bryant, D. Beatty, K. Brace, K. Cho, T. Sheffler (1987): COSMOS: A compiled simulator for MOS circuits. In: Proceedings of the 24th Design Automation Conference, pp
177 24 [23] W. Baker, A. Mahmood, B. Carlson (1996): Parallel event-driven logic simulation algorithms: tutorial and comparative evaluation. IEE Proceedings - Circuits, Devices and Systems 143(4), pp [24] Y. Zhu, B. Wang, Y. Deng (2011): Massively Parallel Logic Simulation with GPUs. ACM Trans. Des. Autom. Electron. Syst. 16(3), pp. 29:1 29:20. [25] Z. Barzilai, J. Carter, B. Rosen, J. Rutledge (1987): HSS A High-Speed Simulator. IEEE Trans. on CAD of Integrated Circuits and Systems 6(4), pp [26] Z. Wang, P. Maurer (1990): LECSIM: A Levelized Event Driven Compiled Logic Simulation. In: DAC 90, pp
178 Verifikation auf paralleler Hardware Daniel Thielsch University of Kaiserslautern Zusammenfassung Die Verifikation sicherheitskritischer Systeme ist heutzutage gängige Praxis. Insbesondere das Model- Checking hat sich als unverzichtbar erwiesen, wenn es darum geht die Eigenschaften eines Systems zu überprüfen. Doch die tendenziell wachsende Komplexität dieser Systeme überfordert die Model-Checker zunehmend und macht eine Lösung des Problems unpraktikabel. Die vorliegende Arbeit beschäftigt sich daher mit der Suche nach performanteren Algorithmen, die in den einzelnen Arbeitsschritte des Model- Checking eingesetzt werden können. Vorrangiges Ziel ist dabei die Bereitstellung paralleler Algorithmen, die mit der jeweiligen Problemgröße skalieren. Es werden im Zuge dieser Arbeit daher sowohl parallele Algorithmen zur Zustandsgenerierung, als auch Algorithmen zur Graphzerlegung vorgestellt. Für das eigentliche Model-Checking liegt der Fokus auf den beiden Algorithmen MAP sowie OWCTY, die spezfisch für die Ausführung auf GPU-Architekturen optimiert wurden. Ein nachfolgender Vergleich zwischen den parallelen Model-Checking Algorithmen mit ihren sequentiellen Ausführungen rundet die Arbeit ab und zeigt die deutliche Überlegenheit der parallelen Implementierungen. 1 Einführung 1.1 Motivation Der Alltag der meisten Menschen ist heutzutage vorzugsweise durch die Handhabe und Nutzung von elektronischen Gerätschaften geprägt. In nicht allzu ferner Zukunft, werden selbst einfache Kleidungsstücke elektronische Komponenten besitzen, sodass der Nutzer stets in regem Kontakt zu aller Art von elektronischen Geräten stehen wird. Abseits von dieser Zukunftsvision stellt sich jedoch die Frage, wie die Funktionalität dieser Komponenten und immer komplexeren Geräte gewährleistet werden kann. Die gängige Praxis vom Testen der entsprechenden Anwendungsfälle und Fehlerszenarien, stößt bisweilen schon heute an ihre Grenzen[15]. Kaum noch jemand ist in der Lage komplexe Systeme in ihrer Vollständigkeit zu überschauen, geschweige denn alle Arten von möglichen Fehlern im Vorfeld zu partizipieren. An diesem Punkt setzt die formale Verifikation an. Sie erlaubt endgültige Aussagen über das betreffende System, sodass jede Art von Testen entfallen kann. Die Grundlagen der formalen Verifikation sind hierbei eine formale Spezifikation des implementierten Systems und formale Anforderungen an das gewünschte System. Diese Anforderungen werden nun in Relation zur Spezifikation des implementierten Systems betrachtet, wobei verschiedenste mathematische Verfahren letzten Endes einen eindeutigen Beweis erbringen ob die Implementierung die gestellten Anforderungen erfüllt oder verletzt. Eine dieser mathematischen Techniken zur formalen Verifikation nennt sich Model Checking. Hierbei wird auf algorithmische Weise versucht herauszufinden ob das Verhalten des betrachteten Systems während der Ausführung bestimmten Anforderungen gehorcht. 175
179 2 Zur Formulierung dieser Anforderungen verwendet man sogenannte temporale Logiken, die Aussagen über zeitliche Verläufe treffen können, ohne diese explizit zu benennen. Die Idee des Model Checking funktioniert ganz hervorragend, wenn es sich um kleinere Systeme handelt, die nur eine sehr begrenzte Anzahl von Funktionszuständen kennen. Sie führt allerdings zu Problemen, wenn Systeme betrachtet werden, die sich aus vielen Komponenten zusammensetzten, die unabhängig voneinander in den verschiedensten Zuständen verharren können. Denn der Funktionsweise nach untersucht Model Checking den gesamten Zustandsraum eines Systems, sodass jede zusätzlich parallel arbeitende Komponente zu einer exponentiellen Vermehrung der Zustandsmenge führt. Dieses Problem ist auch bekannt unter dem Namen state space explosion problem. Zur Vermeidung und Bekämpfung dieses Problems wurden vielfältige Techniken vorgeschlagen und verwirklicht, unter ihnen am erfolgreichsten die partial order reduction[19] und die symbolic representation[14] von Zustandsmengen. Bei wahrlich großen Systemen stoßen jedoch auch diese Techniken an ihre Grenzen, sodass als einziger Ausweg die gebündelte Rechenkraft mehrerer Computer genutzt werden muss, um die Verifikation durchführen zu können. Hinzu kommt, dass der technische Fortschritt im Bereich der Computer sich nicht mehr aus einer Erhöhung der Taktfrequenz des jeweiligen Prozessors speist, sondern vielmehr auf eine Bündelung vieler Prozessoren setzt, deren Anzahl die Performance des Systems bestimmt. Den jeweiligen Rechnernetzwerken oder auch Multi-Core-Architekturen ist jedoch gemein, dass sie herkömmliche, sequentielle Aufgabenstellungen zwar ohne Probleme ausführen können, aber keinesfalls wesentlich schnellere Resultate liefern als Rechner mit nur einem gleich getakteten Prozessor. Erst die Abarbeitung einer Aufgabenstellung, dem Algorithmus, in paralleler Art, erlaubt es aus der Vielzahl von Recheneinheiten einen Vorteil zu ziehen. Zu diesem Zweck muss das jeweilige Problem allerdings in geeigneter Formulierung vorliegen. Da die menschliche Denkart jedoch primär sequentiell ist, erfordert die Lösung eines Problems zur parallelen Verarbeitung erheblichen Anstrengung und Kreativität. Ziel dieser Arbeit ist es daher für jeden der Schritte innerhalb des Model-Checking geeignete parallelle Algorithmen vorzustellen, die das jeweilige Problem nicht nur lösen, sondern auch mit steigender Parallelität skalieren. 1.2 Gliederung Der Rest der Arbeit ist daher wie folgt gegliedert: Abschnitt 2 gibt eine kurze Einführung in die Transitions- Systeme, temporale Logik und graphentheoretische Notationen. Diese werden anschließend in Abschnitt 3 benötigt, wenn es um die parallele Generierung von Zuständen sowie dem Erkennen von strongly connected components, den SCC s geht. In der Folge befasst sich Abschnitt 4 dann hauptsächlich mit dem Model Checking auf GPU s und den verwendeten Algorithmen, zur Lösung dieses Problems. Eine abschließende Evaluierung der Performance der diversen Algorithmen als auch ein Schlusswort sind in Abschnitt 5 zu finden. Es sei im folgenden außerdem darauf hingewiesen, dass in der vorliegenden Arbeit die meisten englischsprachigen Fachbegriffe nicht ins deutsche überführt wurden. Dies ist weniger auf mangelnden Arbeitsethos des Verfassers oder auf Zeitgründe zurückzuführen, als viel mehr eine Konsequenz der Tatsache, dass viele dieser Begriffe nur unzureichende Übersetzungen im Deutschen haben. Sind diese dennoch vorhanden, so ist der ursprüngliche Sinn selbst für Eingeweihte nur schwer wieder zu erkennen, sodass auf eine Übersetzung der Fachbegriffe überwiegend verzichtet wurde. 176
180 3 2 Related Work 2.1 LTL und ω-automaten Man unterscheidet zwei Arten des Model-Checking[22]: Das lokale Model Checking und das Globale. Beide unterscheiden sich hinsichtlich der Berücksichtigung von Systemzuständen. Lokales Model- Checking zeichnet sich dadurch aus, dass es stets nur einen Teil des gesamten Zustandsraums auf die Anforderung hin überprüft, wohingegen globales Model-Checking alle Zustände von Beginn an in die Überprüfung einbezieht. Weiterhin unterscheidet man die Algorithmen des Model-Checking da hingehend, ob die Transitionsrelation, die innerhalb von Transitionssystemen Nachfolgezustände charakterisiert, eine explizite Form oder eine symbolische Form besitzt. Bei einer expliziten Form, werden alle Transitionen eines Systems explizit angegeben, sodass die Nachfolgezustände eines Zustandes direkt bestimmbar sind. Die symbolische Form hingegen arbeitet mit Gruppen von Zuständen. Man erhält sie, indem man alle Systemzustände als Belegungen boolescher Variablen codiert und anschließend sowohl für die Zustandsmenge als auch für die Transitionsrelation eine charakteristische Funktion bestimmt, die genau dann erfüllt ist, wenn die implizierte Belegung durch die Zustände die boolesche Funktion erfüllt. Obwohl jedes explizite Modell in ein symbolisches überführt werden kann und die Codierung der Zustände eine wesentlich kompaktere Beschreibung erlaubt, benötigen die hier vorgestellten Algorithmen eine explizite Modell-Beschreibung. Es liegt in der Natur der verwendeten temporalen Logik LTL, dass Algorithmen für symbolische Beschreibungen nur unwesentliche Vorteile bieten und zudem mehr Forschungsaufwand benötigen[14]. Zum Verständnis des LTL-Model-Checkings, d.h. dem Model Checking Problem bezogen auf Anforderungen, die mittels einer LTL-Formel formuliert werden, ist es unabdingbar zunächst das altbekannte Modell des endlichen Automaten zu erweitern, sodass statt endlicher Eingabefolgen, auch unendliche Folgen akzeptiert werden können. Automaten, die solche unendlichen Eingabefolgen akzeptieren, bezeichnet man als ω-automaten. Ein beliebiger, endlicher ω- Automat A muss folgende Definition[11] erfüllen: wobei sich A zusammensetzt aus: Q := {q 0,...,q n }, der Zustandsmenge Σ := {a 1,...,a m }, dem Alphabet q 0, dem Initialzustand A := (Q, Σ, q 0,, Acc), (Q A) Q, einer Transitionsrelation und Acc Q, der Menge akzeptierender Zustände Ein ω-automat verhält sich ganz analog zu einem herkömmlichen endlichen Automaten. Er startet in seinem Initialzustand q 0 und nutzt die Transitionsrelation, um durch Lesen eines Symbols des Alphabets Σ in einen Nachfolgezustand zu gelangen. Durch wiederholtes Einlesen und Anwenden der Transitionsrelation, bewegt sich der Automat dabei von Zustand zu Zustand. Die eingelesenen Symbolfolgen der Länge n eines Alphabets Σ werden auch als Wörter s := a 1.a 2...a n bezeichnet. Sollte die Transitionsrelation für einen Zustand q und ein Symbol a mehrere Nachfolgezustände ermöglichen, so ist der Automat nicht-deterministisch. Der Unterschied zwischen einem endlichen Automaten und einem endlichen ω-automaten liegt nun in der Akzeptanz dieser Worte. Während ein endlicher Automat nur endliche Worte akzeptiert, nämlich jene die ihn in einen Zustand der Menge Acc führen, akzeptiert ein 177
181 4 ω-automat unendliche Worte. Die Frage, wann ein beliebiger Automat ein unendliches Wort nun akzeptiert oder nicht akzeptiert lässt sich verschieden beantworten. Je nach Akzeptanzbedingung, kann man daher verschiedene Klassen von ω-automaten unterscheiden. Die hier verwendete Akzeptanzbedingung beschreibt die Klasse der Büchi-Automaten. Diese akzeptieren all jene Wörter, die bei ihrer Eingabe dazu führen, dass mindestens ein Zustand aus der Menge Acc unendlich oft durchlaufen wird. Diese sehr umgangssprachliche Erläuterung wird nun formalisiert. Ein unendliches Wort ω := a 1.a 2... wird aufgefasst als eine nach links endliche, nach rechts unendliche Symbolfolge, sodass i N : a i Σ. Die Menge aller unendlicher Worte über Σ wird mit Σ ω bezeichnet. Ein ω-automat akzeptiert nun ω :=a 0.a 1... Σ ω, falls eine Zustandsfolge r := q 0.q 1.q 2... (run) exisitiert, sodass i N: (q i,a i,q i+1 ) gilt und weiterhin In f (r) Acc = /0, wobei Inf(r) := {q Q count r (q) = } count r (q) = {i N r i = q} Der Zweck dieser Büchi-Automaten erschließt sich bei der Betrachtung nicht-terminierende Systeme, insbesondere reaktiver Systeme. Endliche Automaten können solche Systeme zwar ebenfalls modellieren, machen aber keine Aussage über die Ausführungssemantik, da sie ausschließlich endlich viele Zustandsübergänge betrachten können. Ein Büchi-Automat hingegen spezifiziert exakt, welche Wörter, respektive Zustandsfolgen, zulässige Verhaltensweisen eines Automaten darstellen. Während Büchi-Automaten ein adäquates Mittel darstellen um Systeme zu beschreiben, eignen sich temporalen Logiken hervorragend zur Beschreibung von Systemeigenschaften. Die temporale Logik LTL (linear time logic) ist dabei nur eine von vielen Logiken, die es erlaubt Aussagen über die Zeit zu treffen, ohne gleichzeitig konkrete Zeitpunkte zu definieren. Anschaulich betrachtet spezifiziert eine LTL-Formel unendliche Läufe, d.h. Zustandsfolgen, innerhalb eines Transitions-Systems. Die Eigenschaften werden dabei mittels der einzulesenden Symbole und entsprechender Pfadoperatoren spezifiziert. Einige dieser Pfadoperatoren sind beispielsweise ϕ, ϕ oder ϕ 1 Uϕ 2, mit ϕ i eine LTL-Formel. Die einstelligen Operatoren und besagen dabei, dass in der Zukunft (Future) ein Zeitpunkt existiert, sodass ϕ gelten muss oder aber, dass alle (Globally) Zeitpunkte ϕ erfüllen. Im Gegensatz dazu besagt der Operator U, dass ϕ 1 bis zu dem Zeitpunkt gilt, an dem ϕ 2 gilt. All diese Operatoren können beliebig geschachtelt werden, sodass sich mittels der elementaren Symbole des Alphabets und der Pfadoperatoren korrekte LTL-Formeln konstruieren lassen. Als Beispiel sei die LTL-Formel (ϕ 1 ϕ 2 ) angeführt, die besagt, dass immer gilt, sobald ϕ 1 zu einem Zeitpunkt erfüllt ist, existiert ein späterer Zeitpunkt, an dem ϕ 2 erfüllt ist. Man kann diese Formel so interpretieren, dass sie eine gewisse Art von Fairness erzwingt, da für jedes erfüllte ϕ 1 immer auch ϕ 2 eventuell erfüllt werden muss. Eigenschaften dieser Form werden tatsächlich Fairness constraints genannt und sind neben den Safety constraints, eine der häufigsten LTL-Formeln. Die weiteren Details der LTL-Logik, einschließlich genauer Definition von Syntax und Semantik seien hier ausgespart. Die Grundidee der LTL-Logik reicht bereits aus, um LTL-Model-Checking ausreichend nachvollziehen zu können. Für eine vollständige Definition und Erläuterung der LTL-Logik sei daher auf [11] verwiesen. Das Problem des LTL-Model-Checking stellt sich nun wie folgt dar: Überprüfe für einen Büchi Automaten A und eine LTL-Formel φ, ob A = φ gilt, d.h. dass alle möglichen Läufe ausgehend vom Initialzustand die Eigenschaft, definiert von f, erfüllen. Die Idee des LTL-Model-Checking ist es, diese Überprüfung ausschließlich mittels eines Büchi-Automaten zu realisieren. Hilfreich ist dabei das theoretische Resultat, dass zu jeder LTL-Formel ein äquivalenter Büchi-Automat konstruiert werden kann [11]. Die Frage ob A ein Modell von φ ist kann daher auf das folgendes Problem reduziert werden: 178
182 5 A = f gdw. L(A) L(A φ ) gdw. L(A) L(A φ ) = /0 gdw. L(A) L(A φ ) = /0 d.h. dass A genau dann ein Modell für f ist, falls der Schnitt der beiden Sprachen L(A) und L(A φ ) ist. Zu genau diesem Resultat gelangt man mit den folgenden Überlegungen. Statt der zu prüfenden Eigenschaft f, wird zunächst die Negation von f betrachtet. Da f eine LTL-Formel ist, ist natürlich auch f eine LTL-Formel, sodass ein korrespondierender Büchi-Automat zu f konstruiert werden kann. Das besondere ist nun, dass dieser Automat, der Einfachheit halber hier mit N 1 bezeichnet, alle jene Läufe repräsentieren, die f verletzten. Bildet man nun das synchrone Produkt 2 des zu überprüfenden Automaten A und dem so eben konstruierten Automaten N, ergibt sich ein neuer Büchi-Automat, der Produktautomat. Für diesen gilt, dass seine Sprache genau dann leer ist, d.h. kein Wort akzeptiert wird, wenn der Büchi-Automat A keinen Lauf erlaubt, der die Eigenschaft f verletzt. Wie schon gesehen wird ein Wort bzw. eine Zustandsfolge nur dann akzeptiert, wenn mindestens ein akzeptierender Zustand unendlich oft in diesem Lauf durchlaufen wird. Nun besitzt ein Büchi-Automat aber per Definition nur eine endliche Zustandsmenge, woraus sich die Schlussfolgerung ergibt, dass mindestens ein akzeptierender Zustand innerhalb einer Schleife liegen muss, sodass diese Schleife unendlich oft durchlaufen werden kann. Angewandt auf den Produktautomaten bedeutet das, dass der Automat genau die leere Sprache akzeptiert, wenn in dem Automaten kein akzeptierender Zustand innerhalb einer Schleife liegt. Dass sich das Problem sogar gänzlich getrennt von jedem Automaten betrachten lässt, wird deutlich wenn man sich einen Büchi-Automaten durch einen gerichteten Graphen repräsentiert denkt 3. Während das Leerheitsproblem eines Büchi-Automaten keine triviale Lösung kennt, zeigt sich,dass das Finden von Schleifen innerhalb eines Graphen ein vertrautes Problem der Graphentheorie ist. Eventuelle Lösungsansätze des Model- Checking Problems haben ihren Ursprung daher meist in der Graphentheorie. Es kann daher im weiteren Verlauf stets die Annahme getroffen werden, dass der Produktautomat in Form eines gerichteten Graphen vorliegt. 2.2 Notationen Die Reduktion des Model-Checkings in den Bereich der Graphentheorie lässt es sinnvoll erscheinen, sich mit den grundlegenden Begrifflichkeiten und Definitionen der Graphentheorie zu befassen. Viele davon sind zum Verständnis der Algorithmen zwingend notwendig und sollen daher an dieser Stelle kurz erläutert[1] werden. Ein gerichteter Graph G ist definiert als ein Paar (V,E), bestehend aus V, der Menge von Knoten, und E V xv der Menge gerichteter Kanten. Für eine Kante (u,v) E gilt daher, dass die Kante von u nach v gerichtet ist. Hat man ein Knotenpaar (u,v) E gegeben, so kann man v auch als den direkten Nachfolger von u und u als den direkten Vorgänger von v bezeichnen. Ist die Rede vom Eingangsgrad (in degree) oder dem Ausgangsgrad (out degree) eines Knoten v, so ist damit die Anzahl unmittelbarer Vorgänger bzw. unmittelbarer Nachfolger gemeint. Weiterhin gilt, dass ein Knoten v genau dann von einem Knoten u erreichbar ist, wenn es eine Sequenz gerichteter Kanten (u,x 1 ),(x 1,x 2 ),...,(x k,v) gibt, die von u zu v führen. Falls alle Knoten betrachtet werden sollen, die von u erreichbar sind, spricht man auch von 1 Eine gängige Bezeichnung ist never-claim-automaton 2 Der Produktautomat wird gebildet durch das synchrone Einlesen eines Wortes über beiden Automaten 3 Die Kontenmenge des Graphen entspricht der Zustandsmenge Q des Automaten, wogegen die Kanten durch die Transitionsrelation gebildet werden 179
183 6 der forward closure bezüglich u. Dabei kann angenommen werden, dass u sich selbst immer erreichen kann. Genau so gut, kann es jedoch vorkommen, dass statt der erreichbaren Nachfolger, alle Vorgänger des Knoten u von Interesse sind. Dazu nutzt man statt des Graphen G, den transponierten Graphen G T := (V,E T ), dessen Kanten im Vergleich zu G alle invertiert 4 wurden. Der forward closure von u in G T liefert dann alle unmittelbaren und mittelbaren Vorgänger von u in G, auch genannt backward closure. Ist eine Menge von Knoten C V gegeben, so nennt man die Menge stark zusammenhängend (strongly connected), falls für beliebige u, v C gilt, dass v von u erreichbar ist. Eine starke Komponente (strongly connected component - SCC) bezeichnet eine maximal stark zusammenhängende Menge C V, für die kein C existiert, sodass C C V und C ebenfalls stark zusammenhängend ist. Sollte die Menge C nur aus einem Knoten u bestehen, für den gilt (u,u) E, dann nennt man C auch trivial, anderweitig liegt eine nicht-triviale SCC vor. Unterteilt man einen Graphen G in die Menge seiner SCC s und kontrahiert anschließend alle jene Knoten, die zu derselben SCC gehören, zu einem einzigen Knoten, so stellt man fest, dass dieser neue Graph Q, ein azyklischer (schleifenfreier) Graph ist. Wie sich noch zeigen wird, hat die Zerlegung in diesen Quotientengraphen Q die angenehme Konsequenz, dass jede SCC unabhängig von den jeweils anderen auf bestimmte Eigenschaften hin untersucht werden kann. Denn Schleifen können allenfalls in einer SCC auftreten, nie jedoch innerhalb des Quotientengraphen Q. 3 Parallele Berechnungen auf der CPU Nach einer kurzen Einführung in die Thematik des Model-Checking, gilt es zu der zentralen Fragestellung der Motivation zurückzukehren. Wie kann das LTL-Model-Checking Problem für reale Systeme mittels Parallelität möglichst performant gelöst werden? Die Beantwortung dieser Frage zielt zunächst darauf für jedes Teilproblem des Model-Checking parallele Lösungsansätze zu finden. Die nun folgenden Abschnitte sind dabei eine Art Vorverarbeitung, vor der eigentlichen Suche nach akzeptierenden Schleifen. 3.1 Parallele Zustandsgenerierung Den Anfang macht dabei die Zustandsgenerierung des Produktautomaten. Das Bedarf zunächst näherer Erläuterung. Wie bereits erwähnt, leiden reale System unter dem Problem der state space explosion. Der Zustandsraum ist dermaßen groß, dass der Arbeitsspeicher eines einzelnen Rechners das Problem nicht mehr fassen kann. Bildet man für ein reale System und eine LTL-Formels daher den Produktautomaten so leidet auch dieser unter derselben Problematik. Um das Ganze abzuschwächen wird der dem Produktautomaten entsprechende Graph daher meist in symbolischer Repräsentation angegeben. Ein kurzer Vergleich mit den Lösungsalgorithmen zeigt jedoch schnell, dass diese eine explizite Aufzählung aller Zustände und Zustandspaare erwarten. Es bleibt daher nichts anderes übrig, als die symbolische Repräsentation in eine explizite Form zu überführen. Glücklicherweise lässt sich eben jene Überführung parallelisieren. Man denke sich ein Netzwerk von N Rechnern, die den Zustandsraum generieren sollen. Jedem dieser Rechner wird durch eine Partitionsfunktion h : S [0,N 1] eine Menge von Zuständen S i zugeordnet. Die Partitionsfunktions h : S {0,...,N 1} ist derweil so gewählt, dass es keine Überschneidungen zwischen den Zuständigkeiten für die einzelnen Zustände gibt, d.h. S i S j = /0. Der Grundgedanke ist nun, dass alle Rechner eine Instanz des parallelen Algorithmus Distributor abarbeiten und in dessen Verlauf schrittweise den Zustandsraum S sowie die Transitionen T des symbolischen 4 Invertierung bedeutet in diesem Zusammenhang, jede Kante der Form e = (u,v) wird ersetzt durch e = (v,u) 180
184 7 Graphen generieren. Die Vorgehensweise ist die folgende: Für einer der Zustände s i der noch nicht bearbeitet wurde, wird geschaut welches seine Nachfolgezustände suc(s i )sind. Gehört ein Nachfolgezustand s zu dem arbeitenden Rechner und wurde noch nie bearbeitet, so wird der Knoten in seine Liste V i der noch nicht bearbeitenden Zustände abgelegt. Anderweitig prüft der Rechner, welchem anderem Rechner der generierte Nachfolgezustand s zugeordnet ist und schickt eine Nachricht Arc(n i (s),a,s )mit der generierten Transition an den zugehörigen Rechner h(s ). Diese Nachricht wird dann in einer rechnerspezifischen Queue (Warteschlange) abgelegt, bis der jeweilige Rechner auf sie reagiert. Wichtig ist, dass alle Zustände eine Identifizierung n i (s) (ID) zugewiesen bekommen, die innerhalb des Netzwerkes eindeutig ist. Für die Zuweisung dieser ID ist immer der Rechner zuständig, dem der Zustand logisch gehört. Hat ein Rechner die Liste der zu bearbeitenden Zustände abgearbeitet, prüft er seine Queue auf eingegangene Nachrichten. Es wird angenommen dass das Senden und Empfangen keine blockierenden Operationen sind. Die Terminierung der Zustandsgenerierung tritt dann ein, wenn alle Rechner keinerlei Aktivitäten mehr ausführen und auch ihre Queues vollständig abgearbeitet wurden. Auf weitere Details bezüglich der Terminierung sei an dieser Stelle verzichtet, da es keinerlei Erkenntnisgewinn mit sich bringt. Der so eben beschriebene Algorithmus Distributor kann Abbildung 3.1 entnommen werden und stimmt bis auf die Anweisungen zur Terminierung mit dem Algorithmus aus [16] überein. 3.2 Partitionsfunktion Bei näherer Betrachtung des so eben vorgestellten Algorithmus fällt auf, das die Partitionsfunktion eine bedeutende Rolle einnimmt. Sie bestimmt einerseits die Anzahl an Rechnern, die parallel innerhalb eines Netzwerkes arbeiten und bestimmt andererseits die Lasten, d.h. die Menge an Zuständen, die ein bestimmter Rechner zu verwalten hat. Natürlich sucht man eine Funktion die den idealen Kompromiss zwischen möglichst hoher Auslastung eines Rechners bei gleichzeitig hoher Parallelität innerhalb des Netzwerkes bietet. Keine allzu leichte Aufgabe, allerdings lösbar, wenn man sich an einem Konzept der Graphentheorie orientiert, den stark zusammenhängenden Komponenten (SCC s). Diese stellen perse Zustandsmengen dar, die stark voneinander abhängen. Es gibt nun zwei Varianten[18] zum Finden der Partitionsfunktion, die beide auf dem Konzept der SCC beruhen. Während die erste Varinate den Büchi-Automaten nutzt, der aus der negierten LTL-Formel hervorgegangen, konzentriert sich die zweite Variante auf den Produktautomaten. Beide funktionieren indes analog, sodass hier nur die erste Variante erklärt werden soll. Grundlage der ersten Variante ist der schon angesprochene never-claim Automat. Seine Untersuchung ist insofern hilfreich, als dass er bei der Konstruktion des Produktautomaten genutzt wird und Erkenntnisse im Zusammenhang des never-claim Automaten auf den letztendlichen Produktautomaten übertragbar sind. Es ergibt sich daher, dass eine Zerlegung des never-claim Automaten in seine Bestandteile, die SCC s, gleichzeitig immer auch eine Zerlegung des Produktautomaten darstellt. Auf welche Art und Weise die SCC s eines Automaten gefunden werden können, sei Thema des nächsen Abschnitts. Praktikabel wird das Ganze jedoch erst durch die Tatsache, dass der never-claim Automat eine im Vergleich zum Systemautomaten nahezu verschwindend geringe Größe besitzt. Ausgehend vom never-claim Automat und von der Annahme, dass der Automat in k SCC s unterteilbar ist, kann daher eine Partitionsfunktion π folgendermaßen definiert werden: Sei der Produktautomat M N gegeben mit der Zustandsmenge Q, dann bildet π : Q {0,...,k} zwei Zustände genau dann auf dieselbe SCC ab, wenn sie bereits im never-claim Automaten in derselben SCC lagen. Genauer heißt dass, wenn s = (s m,s n ) Q und i = scc(s n ), dann gilt π((s m,s n )) = i. Die Partitionsfunktion unterteilt den Produktautomaten daher in SCC s P i, für die gilt P i = {s Q π(s) = i}, i {0,...,k}. Wichtig ist zudem die Erkenntnis, dass Schleifen ebenfalls nur innerhalb der SCC s auftreten können, da der Quotientengraph bestehend aus den 181
185 8 Methode Distributor function DISTRIBUTOR(in i, s 0,, h, N; out S i, A i, T i ) initiator i := (h(s 0 ) == i); L i := /0; E i := /0; A i := /0; T i := /0; c i := i; if initiator i then n i (s 0 ) := c i ; V i := {s 0 }; S i := {n i (s 0 )}; else V i := /0; S i := /0; end if terminated i := false; while terminted i do if V i /0 then choose s V i ; V i := V i \{s}; E i := E i {s} for all (s,a,s ) succ(s) do if h(s ) == i then L i := L i {(n i (s),a,s )} elsesend(h(s ), Arc(n i (s),a,s )); end if end for else if L i /0 then choose (n,a,s) L i ; L i := L i \{(n,a,s)} if s E i V i then c i := c i + N; n i (s) := c i ; V i := V i {s}; S i := S i {n i (s)}; end if A i := A i {a}; T i := T i {(n,a,n i (s))}; else if RECEIVE(m) && m == Arc(n,a,s) then L i := L i {(n,a,s)}; end if... termination routine end if end while end function verdichteten SCC s ausschließlich azyklisch ist. Die geringe Größe des never-claim Automaten, macht diesen Ansatz äußert schnell und praktikabel, begründet aber auch seinen entscheidenden Nachteil, dass die Partitionsfunktion schlicht auf zu wenige Rechner abbildet. Das liegt daran, dass LTL-Spezifikationen in der Regel eher schlicht gehalten sind und der so entstehende never-claim Automaten über relativ wenige SCC s verfügt, die sich die Partitionsfunktion zu Nutze machen kann. Im schlechtesten Fall ist es sogar möglich, dass statt einer Vielzahl von SCC s schlicht eine einzige gefunden wird, die überhaupt keine Parallelität ermöglicht. In der Praxis ist daher kein eindeutiger Ansatz erkennbar, der garantieren könnte, dass eine parallele Berechnung des Zustandsraums auf möglichst vielen Rechnern durchgeführt werden kann. 182
186 9 3.3 Identifikation stark zusammenhängender Komponenten (SCCs) Nachdem sich gezeigt hat, dass SCC s ein hilfreiches Konstrukt innerhalb der Graphentheorie sind, ist es nun angebracht, darzulegen wie die SCC s eines Graphen gefunden werden können. Normalerweise nutzt man für diesen Unterfangen den sequentiellen Algorithmus von Tarjan, der bewiesenermaßen[4] in optimaler Zeit 5, die Berechnung der SCC s für einen Graphen durchführt. Allerdings hat der Algorithmus das Problem, dass er sich nicht parallelisieren lässt, begründet durch die Tiefensuche (depth-firstsearch), die innerhalb des Algorithmus zum Einsatz kommt. Für die parallele Zerlegung eines Graphen ist es daher entscheidend einen anderen Ansatz zu wählen. Ein Ansatz, der heutzutage oftmals Verwendung findet, versucht eine Zerlegung des Graphen, abhängig von einem sogenannten Pivot Element. Das ist ein Knoten, der zu Beginn des Algorithmus rein zufällig gewählt wird. Ausgehend von diesem Pivot Element, wird einerseits die forward-closure, als auch die backward-closure bezüglich diesem Element 6 berechnet. All jene Knoten, die nun innerhalb des Schnittes der beiden closures vorkommen, bilden dann ein SCC. Das wird insofern deutlich, als dass man sich die Definition einer SCC ins Gedächtnis ruft, die eben genau die Forderung stellt, dass jeder Knoten einer SCC jeden anderen Knoten innerhalb derselben SCC erreichen kann. Die restlichen Knoten des Graphen, die nicht innerhalb des Schnittes liegen, lassen sich anschließend aufteilen in die Mengen i. Knoten, die in der forward-closure vorkommen, aber nicht in der backward-closure ii. Knoten, die in der backward-closure vorkommen, aber nicht in der forward-closure iii. Knoten, die in keiner der beiden closures vorkommen Diese drei Knotenmengen bilden drei unabhängige Instanzen desselben Problems. Da keine von ihnen das Pivot Element enthält und es keinerlei Überschneidungen zwischen den Knotenmengen gibt, kann die Suche nach SCC s in jeder der drei Mengen unabhängig von den jeweils anderen Kontenmengen durchgeführt werden. Der Algorithmus, der diese Berechnungsvorschrift umsetzt, nennt sich Foward- Backward (FB)-Algorithmus[1] und ist in Abbildung 3.3 zu sehen. Aus der Abbildung wird ersichtlich, dass der Algorithmus durch die Aufteilung der Knotenmenge in drei unabhängige Teilprobleme, sehr schnell große Teile der gesamten Knotenmenge erfassen kann und bei einer ausreichend großen Anzahl an Rechnern, mit der Problemgröße skaliert. Sollte die Performance allerdings noch nicht ausreichen, so kann der Algorithmus um eine Prozedur namens Trimming ergänzt werden. Diese Erweiterung sorgt dafür, dass eine Reihe von trivialen SCC s von Beginn an, nicht in den Algorithmus einbezogen werden. Dazu wird überprüft ob es Knoten gibt deren Eingangsgrad null ist. Solche Knoten können stets nur eine triviale SCC bilden. Enthält der um diese Knoten bereinige Graph, erneut Knoten mit Eingangsgrad null, so werden auch diese entfernt, bis schließlich keine Veränderung mehr auftritt und der gewohnte FB-Algorithmus seine Arbeit auf der bereinigten Knotenmenge verrichten kann. Sind letzten Endes alle SCC s eines Graphen gefunden, können die SCC s zur Bestimmung einer Partitionsfunktion genutzt werden. Problematisch ist nur, dass auch der FB-Algorithmus eine explizite Darstellung eines Automaten, respektive des gerichteten Graphen als Eingabe erwartet. Da die Bestimmung der SCC s aber gerade dem Zweck dient, die Generierung des Zustandsraumes so performant wie möglich zu gestalten, bleibt hier ein Widerspruch übrig. Der Produktautomat ist im Falle des Model- Checking daher gänzlich ungeeignet zur Bestimmung einer passenden Partitionsfunktion, da die Suche nach SCC, gerade jene explizite Darstellung voraussetzt, die wir bestimmen möchten. Geeigneter ist daher der never-claim Automat, für dessen geringe Größe, mit unwesentlichem Aufwand eine explizite Darstellung generierbar oder aber möglicherweise sogar schon gegeben ist. Weiterhin sollte angemerkt 5 Komplexität O( V + E ), mit V = #Knoten und E = #Kanten 6 Es sei darauf hingewiesen, dass das Pivot Element stets Teil beider closures ist 183
187 10 Forward-Backward Algorithmus function FB(V) if V /0 then pivot := PIVOT(V ); F := FWD(pivot,V ); B := BWD(pivot,V ); F B is SCC in parallel do FB(F\B) FB(B\F) FB(V \(F B)) end in parallel end if end function werden, dass die bislang vorgestellten parallelen Algorithmen, auf jeder möglichen Hardwareplattform ausgeführt werden können. Immer unter der Voraussetzung, das eine Implementierung des jeweiligen Algorithmus in einer realen Programmiersprache vorliegt. Das mag zunächst verwundern, wird sich aber mit dem kommenden Abschnitt ändern. Denn die dort vorgestellten Algorithmen sind zuallererst Algorithmen, die auf GPU s der Firma NVIDIA laufen und mittels des Frameworks CUDA für die Plattformen optimiert wurden. Nichtsdestotrotz ist die Grundidee der Algorithmen auch ohne spezifisches Expertenwissen verständlich und ihre Wirkungsweise anhand von Beispielen anschaulich erläutert. 4 Paralleles GPU Computing 4.1 Einführung zu CUDA Um den Begrifflichkeiten um CUDA trotzdem einen Bezug zu geben, soll hier eine kurze Einführung gegeben werden. Die Abkürzung CUDA meint Compute Unfied Device Architectures und versteht sich als Softwareumgebung inklusive parallelem Programmiermodell, die es Programmierern ermöglicht jede Art von Code auf einer neueren GPU der Marke NVIDIA laufen zu lassen. Alleine diese Vorstellung, dass GPU s eines Tages neben der Beschleunigung von Pixelberechnungen mehr zu bieten haben könnten, war vor etlichen Jahren noch undenkbar. Tatsächlich aber haben sich NVIDIA s aktuelle GPU s im Laufe der Jahre so rasant weiterentwickelt, dass ihre Architektur heutzutage größtenteils aus einer Vielzahl frei programmierbaren, parallel arbeitenden Prozessoren besteht. Diese Vielzahl kann bei aktuellen GPU s gerne einmal bis zu 128 Kerne betragen und übertrifft die gängige 4-8 Kerne moderner CPU s bei weitem. Zur Verwaltung dieser großen Anzahl von Kernen, wird auf der Hardware Ebene daher auch das Konzept der Multi-Prozessoren verwendet. Diese bestehen aus einer gleichen Anzahl von skalaren Kernen, denen jeweils eine eigene Instruction Unit, sowie Shared Memory und bestimmter 7 Cache zugeordnet ist. Jeder dieser Kerne hat zudem Zugriff auf eine Menge von 32bit Registern, verfügt aber 7 Der Kern verfügt über Texturen, wie auch Konstanten-Cache, nicht jedoch über L 1,L 2 oder L 3 Cache 184
188 11 des Weiteren über keine Art von Cache, die dem der CPU s vergleichbar wäre. Die Multiprozessoren arbeiten entsprechend dem SIMD-Konzept und arbeiten eine Programmanweisung auf unterschiedlichen Daten simultan ab. Kommunikation findet zwischen den Multiprozessoren nur über den gemeinsamen Speicher der GPU statt, der von allen bearbeitet werden kann. Viel interessanter als die technische Seite ist für den Programmierer aber die Programmierung einer solchen GPU. Zu diesem Zweck hat NVIDIA die Programmiersprache C/C++ um etliche Konstrukte zur parallelen Programmierung, wie der Threadverwaltung, dem Speicherzugriff und den Threadhierarchien erweitert. Ein CUDA Programm besteht dabei stets aus einem sogenannten sequentiellen Host Programm und einem oder mehrerer paralleler Kernels. Der Host Code wird zumeist auf der CPU ausgeführt, wohingegen die Kernels auf der GPU abgearbeitet werden. Ein Kernel kann man sich so vorstellen, dass er ein sequentielles Programm in mehreren Threads, die sich alle nur in den zu bearbeitenden Daten unterscheiden. Zur Organisation dieser Threads und besseren Handhabung können die Threads in Blöcken organisiert werden. Ein Kernel wird daher meist von einer Reihe von Blöcken ausgeführt, die ihrerseits ein gewisse Anzahl von Threads logisch trennen. Identifizieren kann man die einzelnen Blöcke oder auch Threads mittels automatisch zugewiesener ID s, die eine eindeutige Wiedererkennung ermöglichen. Für weitere Details zu CUDA sei der Leser auf die Referenzen [17] und [20] verwiesen, die umfassendere Einblicke in die Fähigkeiten und Funktionsweise des Frameworks ermöglichen. Es ist daher für das Verständnis der nachfolgenden Algorithmus völlig ausreichend, eine Unterscheidung zwischen Host und Kernel Code vorzunehmen, mit dem Wissen dass ein Kernel stets auf der GPU, mittels parallel arbeitender Threads, ausgeführt wird. Diese letztlich kurze Einführung beschließt dann auch die Grundlagen und vorbereitenden Schritte, sodass es nun an der Zeit ist, ein Blick auf die eigentlichen Model-Checking Algorithmen zu wagen. 4.2 Maximal Accepting Predecessor Algorithmus Einer dieser Algorithmen zum Finden akzeptierender Schleifen ist der Maximal Acceptiong Predecessor (MAP) Algorithmus[13]. Er wird hier in seiner successor Variante[7] vorgestellt, doch dazu gleich mehr. Als Eingabe erwartet der Algorithmus einen gerichteten Graphen, der im Falle des Model-Checking der symbolischen Repräsentation des Produktautomaten entspricht. Dieser wurde im Schritt Zustandsgenerierung in eine explizite Darstellung gebracht und kann nun in der äquivalenten Form als Graph verwendet werden. Die Eingabe ist daher ein Graph G := (V,E,v 0,A), mit der Knotenmenge V, Kantenmenge E und den Startknoten v 0. Zusätzlich enthält der Graph allerdings ein Prädikat A, dass angibt, ob ein Knoten akzeptierend ist, oder nicht. Für die Arbeitsweise des Algorithmus ist es entscheidend eine Ordnungsrelation < auf der Menge der Knoten einzuführen. Der einfachste Fall ist es die Knoten schlicht durch zu nummerieren, sodass als Ordnungsrelation beispielsweise < auf den natürlichen Zahlen gewählt werden kann. Anschließend wird die Ordnungsrelation auf die Menge V { }( V ) erweitert, wobei für alle v V gilt < v. Mit Hilfe dieser Ordnungsrelation ist nun möglich die namensgebende Funktion map : V V { } zu definieren, die für jeden Knoten den größten akzeptierenden Nachfolger bestimmt, d.h. den akzeptierenden Knoten, der im Vergleich zu den restlichen Nachfolgern mittels Ordnungsrelation größer gewertet wird. Existiert kein solcher Nachfolger, wird dem Knoten der Wert zugeordnet. Alles in allem definiert sich map für einen Knoten u dann zu map(u) := max{,v (u,v) E + A(v)}. Die Menge E + beschreibt in diesem Zusammenhang nicht mehr als die transitive forward-closure bezüglich dem Knoten u. Kernidee des Algorithmus ist es nun mehr, einen Knoten v zu finden, der sein eigener größter Nachfolger ist, sodass gilt map(v) = v. In diesem Fall ist garantiert, dass der Knoten v innerhalb einer Schleife liegen muss. Das Problem an dieser Vorgehensweise ist, dass innerhalb des Graphen mit großer Wahrscheinlichkeit mehrere akzeptierende Knoten existieren, die außerhalb von Schleifen liegen. 185
189 12 Algorithmus MAP Input: gerichteter Graph G := (V,E,v 0,A) lineare Ordnungsrelation < Output: { true G enthält akzeptierende Schleife false function MAP((G,<)) while v V : A(v) do map := ComputeAllMaps(G,<); for all u V do if u = map(u) then return true; else A(map(u)) := false; end if end for end while return false; end function otherwise Sind diese Knoten überdies vom Knoten v erreichbar und entsprechend der Ordnungsrelation größer, so gilt map(v)! = v, obwohl v akzeptierend ist und innerhalb einer Schleife liegt. Umgehen lässt sich das Problem, wenn nach jeder abschließenden Berechnung der map Werte, all jene akzeptierenden Knoten als nicht akzeptierend markiert werden, die in irgendeinem Wert der Funktion map vorkommen. Danach wiederholt sich die Berechnung aller map-werte, bis zu guter Letzt entweder eine akzeptierende Schleife gefunden wurde oder aber keine akzeptierenden Knoten mehr übrig sind. Der MAP Algorithmus ist in Abbildung 4.1 dargestellt und benötigt für die Berechnung der Werte der Funktion map eine Methode namens ComputeAllMaps() 4.2. Diese Methode trägt die Hauptlast der Berechnung, denn sie muss für alle Knoten, die vom Startknoten aus erreichbar sind, die Werte der Funktion map berechnen. Zu Beginn der Berechnung wird allen Knoten zunächst der Wert zugewiesen. Danach beginnt die eigentliche Berechnung der Werte. Für jede Kante (u,v) wird dazu überprüft ob v ein akzeptierender Knoten ist, ist dies der Fall, so wird dem aktualisierten Wert map(u), das Maximum der Werte map(u),map(v) bzw. v zugewiesen. Andernfalls bezieht die Aktualisierung nur die Werte map(u) und map(v) für die Maximumbildung ein. Wurde der Wert map(u) abgeändert, so ist es wahrscheinlich, dass auch dem Vorgängerknoten von u ein aktualisierter Wert zugewiesen werden muss. Die Aktualisierungen und Überprüfungen können daher ein Weile andauern und enden erst zu dem Zeitpunkt an dem festgestellt wird, dass die Werte der map Funktion innerhalb einer Iteration der while-schleife keine Änderung erfahren haben. Im schlechtesten Falle liegt die Gesamtlaufzeit des MAP Algorithmus im Bereich von O(V 2 ( V + E ). Diese Komplexität kommt insbesondere dann zustande, wenn der Graph fast ausschließlich aus akzeptierenden Knoten besteht, was jedoch nicht als Normalfall betrachtet werden sollte. Unglücklicherweise hängt die Laufzeit des Algorithmus stark von der zu Beginn definierten Ordnungsrelation ab. Je 186
190 13 ComputeAllMaps(G,<) Input: gerichteter Graph G := (V,E,v 0,A) lineare Ordnungsrelation < Output: map Funktion function COMPUTEALLMAPS((G,<)) for all u V do map(u) = end for while map prevmap do prevmap := map; for all (u,v) E do if A(v) then map(u) := max{map(u),map(v),v}; else map(u) := max{map(u),map(v)}; end if end for end while return map end function nachdem wie diese Relation gewählt ist, kann eine akzeptierende Schleife innerhalb eines Graphen bereits in der ersten Iteration oder aber auch erst in der V -ten Iteration gefunden werden. Das Finden einer optimalen Ordnungsrelation ist jedoch selbst wieder im Bereich der Komplexität des MAP-Algorithmus angesiedelt, sodass ausschließlich simple Heuristiken für diese Aufgabe verwendet werden. 4.3 One Way Catch Them Young Algorithmus Der zweite Algorithmus zum Lösen des Model-Checking Problems ist der One Way Catch Them Young (OWCTY) Algorithmus[22, 7]. Im Vergleich zu dem eben besprochenen MAP Algorithmus verwendet OWCTY einen gänzlich anderen Ansatz. Der Grundgedanke des OWCTY Algorithmus ist es eine Menge von Knoten vorzuhalten, die auf einer akzeptierenden Schleife liegen könnten. Mit Hilfe festgelegter Regeln entfernt der Algorithmus dann Schritt für Schritt Knoten aus dieser sogenannten Approximationsmenge, bis die Menge leer ist oder aber keinerlei Regel mehr angewandt werden kann. In letzterem Falle ist garantiert, dass der Graph eine akzeptierende Schleife besitzt. Der Algorithmus prüft zunächst nach, welche Knoten vom Startknoten erreichbar sind. Jene Knoten, die erreicht werden können, bilden schließlich die 0-te Approximationsmenge. Ausgehend von dieser Menge beginnt der Algorithmus Knoten zu entfernen. Ihm stehen hierzu zwei Regeln zur Verfügung. Regel Nr.1 besagt, dass ein Knoten aus der Approximationsmenge entfernt werden darf, falls er von keinem akzeptierenden Knoten innerhalb derselben Menge erreichbar ist. Regel Nr. 2 wiederum spezifiziert, dass all jene Knoten aus der Approximationsmenge entfernt werden können, die einen Eingangsgrad 0 besitzen, d.h. die keinen Vorgänger innerhalb der Approximationsmenge habe. Der Ausgangspunkt dieser Regeln ist dabei die Idee, nur sol- 187
191 14 Algorithmus OWCTY Input: gerichteter Graph G := (V,E,v 0,A) Output: { true G enthält akzeptierende Schleife false function OWCTY(G) S := Reachability(v 0 ); old := /0; while S old do old := S; S := Reachability({s s S A(s)) S := Elimination(S); end while return S /0; end function otherwise che Knoten aus der Approximationsmenge zu entfernen, die außerhalb einer akzeptierenden Schleife liegen müssen. Wurden alle Knoten aus der Approximationsmenge entfernt so kann der Graph auch über keine akzeptierende Schleife verfügen. Abbildung 4.3 zeigt den Algorithmus als Berechnungsvorschrift. Die Regeln 1 und 2 sind in der while-schleife durch die Aufrufe der Methoden Reachability bzw. Elimination umgesetzt. Die Approximationsmenge ist mit S bezeichnet und wird solange entsprechend den Regeln bearbeitet, bis die Berechnung der while-schleife einen Fixpunkt erreicht. Ein großer Vorteil des OWCTY Algorithmus ist seine im Vergleich zum MAP Algorithmus doch deutlich günstigere Komplexität von O( V ( V + E ). Diese Komplexität ist jedoch noch sehr großzügig bemessen, denn die while-schleife wird in der Praxis weitaus weniger als V -mal durchlaufen. Wie oft die while-schleife letzten Endes durchlaufen wird, lässt sich mit Hilfe des Quotientengraphen sogar eindeutig festlegen. Gilt für den längsten Weg innerhalb des Quotientengraphen, dass insgesamt h SCC s durchlaufen werden so vereinfacht sich die Komplexität des Algorithmus zu O(h ( V + E ). Insgesamt ein deutlich genauere Abschätzung als zuvor. 4.4 CUDA Algorithmen Um beide Algorithmen nun eine CUDA konforme Form zu überführen, Bedarf es allerdings noch etwas Vorarbeit. Problem ist hierbei, dass Datenstrukturen, die innerhalb eines Kernels eingesetzt werden, für den parallelen Zugriff multipler Threads ausgelegt sein müssen. Weiterhin sollte die Datenstruktur in einer möglichst kompakten Form vorliegen, um die Zahl der Speicherzugriffe so wie gering wie möglich zu halten. Es liegt daher nahe, für die Arbeit mit Kerneln vorwiegend auf Vektorstrukturen zurückzugreifen Compressed Sparse Row Representation - CSR Im Falle des Model-Checking soll daher der gerichtete Graph des Produktautomaten in eine Vektornotation überführt werden. Der Graph des Produktautomaten wird von einer Matrix, der sogenannten Adjazenzmatrix, repräsentiert. Man nummeriert hierzu alle Knoten des Graphen durch und erhält eine 188
192 15 Methode Reachability Input: gerichteter Graph G := (V,E) und Menge von Knoten S Output: Menge von Knoten R := {v V s S : (s,v) E + } function REACHABILITY(G,S) R := /0; while S /0 do choose s from S; S := S\{s}; for all v such that (s,v) E do if v R then S := S {v}; R := R {v}; end if end for end while return R; end function Matrix der Größe V * V, deren Eintrag a ik genau dann 1 ist, wenn die Kante (i,k) E innerhalb des Graphen vorhanden ist. Sollte die Kante nicht vorhanden sein, so wird dies durch den Wert 0 repräsentiert. Die Betrachtung mehrerer Adjazenzmatrizen unterschiedlicher Graphen führt schnell zu der Erkenntnis, dass die Matrizen in der Regel überwiegend aus Nullen bestehen. Nur hier und da, werden sie an den Stellen, die Kanten darstellen, von einer Eins unterbrochen. Diese spärlich besetzten Matrizen (sparse matrices) bieten daher die Möglichkeit eine wesentlich kompaktere Darstellung zu finden, die denselben Informationsgehalt wie die entsprechende Adjazenzmatrix enthält. Das hier gewählt Format zur Darstellung der Adjazenzmatrizen, nennt sich Compressed Sparse Row (CSR) Representation und wurde in [17] eingeführt. Es überführt die Adjazenzmatrix in insgesamt drei Vektoren A v, A e und A i. Der Vektor A v repräsentiert für jede Zeile der Matrix, die Einträge, die von Null verschieden sind und besteht bei einer Adjazenzmatrix ausschließlich aus Einsen. Die Auflistung beginnt wie bei Matrizen üblich mit der obersten Zeile. Der Vektor A e hingegen, gibt für jeden Eintrag in A v, den Spaltenindex an, während der Vektor A i für jede Zeile diejenigen Einträge aufaddiert die bislang von Null verschieden waren. Verdeutlichen lässt sich diese Transformation relativ gut mittels der Abbildung 4.4.1, in der eine allgemeine Matrix in einer CSR Form überführt wird. Relativ klar erkennbar ist, dass der Vektor A v alle von Null verschiedenen Einträge der Matrix der Reihe nach auflistet. Für den Vektor A e lässt sich zudem schnell überprüfen, dass der Spaltenindex des Wertes A v [2] = 5, dem Werte an der Stelle A e [2] = 1 entspricht. Interessanter wird es jedoch mit dem Vektor A i. Möchte man wissen, wieviele Einträge in Zeile k 8 vorhanden sind, so muss lediglich der Wert A i [k + 1] A i [k] berechnet werden. Für die Zeile 1, ergibt sich daraus ein Wert 3 2 = 1. Vereinfachen lässt sich diese Repräsentation noch durch die Tatsache, dass die Einträge in Adjazenzmatrizen stets nur den Wert 1 oder 0 besitzen. Der Vektor A v ist daher vernachlässigbar, da die Menge der von Null verschiedenen Einträge bereits durch die Größe des Vektors A e impliziert wird. 8 Die Indizierung beginnt im vorliegenden Fall bei 0 189
193 16 Methode Elimination Input: gerichteter Graph G := (V,E) und Menge von Knoten S Output: Menge von Knoten R := {r S c 0,...,c n 1 S : 0 i<n i : (c i,c i+1modn ) E 0 i<n j : (c j = r (c j,r) E + )} function ELIMINATION(G,S) R := S; old := /0; elim := {e R r R : (r,e) E}; while old elim do old := elim; R := R\elim; elim := {e R r R : (r,e) E}; end while return R; end function CUDA MAP Der Host Code des Algorithmus CUDA MAP[9], dargestellt in Abbildung 4.4.2, unterscheidet sich nicht allzu stark von dem ursprünglichen MAP Algorithmus. Auffällig ist zunächst nur die Verwendung zweier verschachtelter while-schleifen.das mag zunächst verwundern, wird aber verständlich angesichts der Tatsache, dass die ursprünglich eigenständige Methode ComputeAllMaps() in den Host- Code integriert wurde. Die äußere while-schleife gleicht daher auch der while-schleife des sequentiellen MAP Algorithmus, während die innere while-schleife, die Funktion der while-schleife der Methode ComputeAllMaps() übernimmt. Nach dem Start des Algorithmus beginnt zuerst eine kurze Phase der Initialisierung, in dessen Verlauf CreateRepresentation() die CSR Form des Graphen generiert, sowie die Daten anschließend durch den Aufruf CopyToGPU in den GPU-Speicher schreibt. Die Variable Maps speichert derweil für jeden Knoten des Graphen den Wert der Funktion map, den Wert der Funktion map der vorangegangenen äußeren Iteration, sozusagen oldmap und weiterhin das Prädikat A(v), um zu bestimmen ob ein Knoten akzeptierend ist oder nicht. Den Wert der vorangegangenen Iteration erlaubt es Teilgraphen innerhalb des Graphen zu identifizieren. Denn besitzen zwei Knoten, nach einer äußeren Iteration unterschiedliche Werte für die map Funktion, so müssen sie auf getrennten akzeptierenden Schleifen liegen. Abgrenzen lassen sich Teilgraphen in einer laufenden Iteration durch den Vergleich der alten map Funktion. Man vermeidet somit, dass Werte der map Funktion in Teilgraphen propagiert werden, die logisch getrennt sein müssten A v := [ ] A e := [ ] A i := [ ] Abbildung 1: Beispiel zur Transformation einer Matrix in das CSR-Format 190
194 17 CUDA MAP Algorithmus - Host Code [7] Input: gerichteter Graph G := (V,E,v 0,A) lineare Ordnungsrelation < Output: { true G enthält akzeptierende Schleife false otherwise function CUDAMAP((G,<)) CreateRepresentation(G,A e,a i,maps); acccyclefound,fixpointfound,unmarked := false,false,false; CopyToGPU((A e,a i,maps) (ga e,ga i,gmaps)); while unmarked acccyclefound do while fixpointfound acccyclefound do fixpointfound := true; MapKernel(gA e, ga i, gmaps, acccyclefound, fixpointfound); end while unmarked := false; UnmarkAccKernel(gMaps, unmarked); end while return acccyclefound; end function Die eigentliche Berechnung der Werte der map Funktion wird schließlich durch den Kernel Map- Kernel umgesetzt. Für jeden Knoten wird hierzu ein Thread gestartet, der eine Instanz des Kernels abarbeitet und den aktuellen Wert für den Knoten berechnet. Hierzu überprüft jeder Knoten, die Werte seiner direkten Nachfolgeknoten und aktualisiert seinen eigenen Wert, falls diese einen höheren Wert in der Funktion map besitzen. Die ursprüngliche If-Then-Else Abfrage in der Methode ComputeAllMaps(), die eine Unterscheidung vornahm, wenn ein Nachfolgeknoten akzeptierend war, wird nun anhand der Funktion maxacc(v, u) vorgenommen. Wurde innerhalb einer äußeren Funktion keine Änderung im Bezug auf die Funktion map festgestellt, so wird die innere while-schleife beendet und es wird der zweite Kernel UnmarkAccKernel aufgerufen. Der Übersicht halber sei der Kernel in dieser Arbeit nicht aufgeführt, kann jedoch in?? gefunden werden. Er nimmt sich im Vergleich zu den restlichen Berechnungen sehr einfach aus und überprüft schlicht für jeden einzelnen Knoten, ob dieser Knoten akzeptierend ist und wenn ja, ob der Knoten für die nächste Iteration akzeptierend bleibt. Sollte der Wert der Funktion map für diesen Knoten nämlich kleiner sein, als die Zahl, mit der der Knoten bezeichnet wird, so kann daraus geschlossen werden, dass sich der Wert des Knotens durch den Graphen propagiert hat und der Knoten selbst auf keiner akzeptierenden Schleife liegen kann. Denn anderweitig hätte er einen höheren Wert in der Funktion map als seine eigene Bezeichnung oder aber der Wert wäre gleich, womit eine akzeptierende Schleife gefunden wäre. Nach dieser Überprüfung für sämtliche Knoten, wurde entweder eine akzeptierende Schleife gefunden, sodass der Algorithmus terminieren kann oder aber es wird die nächste Iteration der äußeren while-schleife gestartet, um die Berechnungen, mit der nun geringeren Anzahl akzeptierender Knoten, zu wiederholen. 191
195 18 MapKernel - GPU Code (wird für v V parallel ausgeführt) [7] Input: ga e,ga i,gmaps, acccyclefound, fixpointfound function KERNEL MAPKERNEL(gA e,ga i,gmaps, acccyclefound, fixpointfound) myvertex,candidate := gmaps[v], ; for all u succ(v) do succ(v) = {ga e [ga i [v]],...,ga e [ga i [v + 1]} mysucc := gmaps[u]; if myvertex.oldmap == mysucc.oldmap then candidate := max{candidate, maxacc(v,u)}; end if end for if candidate == v then acccyclefound := true; end if if candidate > myvertex.map then myvertex.map, fixpointfound := candidate, false; end if gmaps[v] := myvertex; end function Obgleich CUDA Map seine Arbeit deutlich schneller verrichtet als die sequentielle Variante des Algorithmus, bleibt ein Problem bestehen. Die Laufzeit des Algorithmus steht und fällt mit der gewählten Ordnungsrelation. Ähnlich dem sequentiellen MAP Algorithmus, ist es daher entscheidend die Gesamtlaufzeit immer im Kontext der gewählten Ordnungsrelationen zu interpretieren und gegebenenfalls Heuristiken einzusetzen, um die Laufzeit zu verbessern CUDA OWCTY Ähnlich dem CUDA MAP Algorithmus orientiert sich der Host Code von CUDA OWCTY[10] stark an der sequentiellen Variante des Algorithmus. Auffällig ist jedoch die große Anzahl an Kernel Funktionen, die es dem Algorithmus ermöglichen einen Großteil der Berechnungen zu parallelisieren. Dies beginnt bereits mit dem Aufruf des VisAcceptingKernel(), der bei allen akzeptierenden Knoten das Flag setzt, dass sie bereits besucht (visited) wurden. Dies ergibt erst dann Sinn, wenn man einen Blick auf die Methode Reachability() wirft. Im Gegensatz zu dem Gros der Aufrufe ist Reachability keine reine Kernel Funktion. Stattdessen führt die Methode weiteren Host Code aus, hat aber auch Aufrufe auf einen Kernel namens ForwardReachabilityKernel(), der überprüft ob der jeweilige Knoten während der Vorwärtssuche bereits erreicht wurde. Ist dies der Fall, werden alle Nachfolgeknoten ebenfalls als visited markiert. Falls nicht, wird der Knoten eventuell in einer der folgenden Iterationen erreicht. Wichtig ist zudem, dass die Vorwärtssuche stets von den akzeptierenden Knoten gestartet wird, die innerhalb der Approximationsmenge sind. Diese Approximationsmenge definiert sich in CUDA OWCTY durch die Menge aller Knoten, die bislang nicht gelöscht wurden, gekennzeichnet mit dem Flag elim = f alse. All diejenigen Knoten, die nach Beenden der Methode Reachability(), nicht als visited markiert wurden, werden im Anschluss durch den TestSetKernel aus der Approximationsmenge gelöscht (elim = true). Der Aufruf 192
196 19 CUDA OWCTY Algorithmus - Host Code [7] Input: gerichteter Graph G := (V,E,v 0,A) Output: { true G enthält akzeptierende Schleife false otherwise function CUDAOWCTY(G) CreateRepresentation(G,A e,a i,flags); CopyToGPU((A e,a i,flags) (ga e,ga i,gflags)); VisAcceptingKernel(gA e,ga i,flags); fixpointnotfound, acccyclefound := true, false; while fixpointnotfound do Reachability(gA e,ga i,flags); TestSetKernel(gFlags); fixpointnotfound := false; Elimination(gA e, ga i, Flags, acccyclefound, fixpointnotfound); end while return acccyclefound; end function der Methode Reachability und TestSetKernel ist daher äquivalent zur ersten Regel des OWCTY Algorithmus, alle jene Knoten zu entfernen, die von keinem akzeptierenden Knoten aus erreichbar sind. Indes gestaltet sich die Umsetzung der zweiten Regel, dem entfernen von Konten mit Eingangsgrad 0, etwas schwieriger. Denn das Überprüfen der Anzahl der Vorgängerknoten eines jeden Knoten, setzt eine Funktion voraus, die die Vorgänger des Knoten aufzählen kann. Für den Gebrauch des OWCTY Algorithmus steht jedoch nur eine Nachfolgefunktion zur Verfügung, die einfach anhand der CSR Repräsentation gewonnen werden kann. Für eine Vorgängerfunktion müsste dazu eine zweite CSR Repräsentation des transponierten Graphen erstellt werden, die einerseits zusätzlichen Speicher als auch in der Berechnung zu kostspielig wäre. Um die Berechnung dieser Vorgängerfunktion daher vollständig zu vermeiden greift die Methode Elimination() zu einem Trick. Mit Hilfe des Flags elimprep = true werden zunächst alle Knoten der Approximationsmenge als demnächst zu löschen gekennzeichnet. Der anschließende Aufruf des Kernels ProgressKernel() überprüft danach, ob ein Knoten Nachfolgeknoten in der Approximationsmenge besitzt. Bei all den Knoten, für die das zutrifft wird daraufhin das Flag elimprep = f alse zurückgesetzt. Ein zweiter Kernel CheckKernel löscht im Anschluss alle jene Knoten, deren Flag elimprep noch gesetzt ist, denn sie können über keinerlei Vorgängerknoten innerhalb der Approximationsmenge verfügen. All diese Berechnungen werden letzten Endes, analog dem sequentiellen OWCTY Algorithmus, solange durchgeführt, bis die Approximationsmenge nicht mehr verändert oder aber keine Elemente mehr übrig geblieben sind. 193
197 20 Elimination Prozedur - GPU Code (wird für v V parallel ausgeführt) [7] Input: ga e, ga i, gflags, acccyclefound, fixpointnotfound; function KERNEL ELIMINIATION(gA e, ga i, gflags, acccyclefound, fixpointnotfound) changefound := true; while changefound do ProgressKernel(gA e, ga i, gflags); changefound, acccyclefound := false, false; CheckKernel(gFlags, changefound, acccyclefound); fixpointnotfound := changefound? true : fixpointnotfound; end while end function function KERNEL PROGRESSKERNEL(gA e, ga i, gflags) if gflags[v].elim then for all u succ(v) do if gflags[u].elim gflags[u].elimprep then gflags[u].elimprep := false; end if end for end if end function function KERNEL CHECKKERNEL(gFlags, changefound, acccylcefound) if gflags[v].elim then if gflags[v].elimprep then gflags[v].elim, changefound := true, true; else gflags[v].elimprep, acccyclefound := true, true; end if end if end function 194
198 21 5 Konklusion 5.1 Evaluation Nachdem die Model Checking Algorithmen in ihrer sequentiellen Form als auch als CUDA Implementierung ausführlich abgehandelt wurden, wird es Zeit der Frage nachzugehen wie sich die Laufzeiten der einzelnen Implementierungen zueinander verhalten. Der Fokus liegt dabei ausnahmslos auf den Algorithmen MAP und OWCTY, sowie ihren CUDA Varianten. Ausgespart seien daher die Zustandsgenerierung, sowie die Zerlegung eines Graphen anhand seiner SCC s, deren Details in [16] bzw. [6] zu finden sind. Die Testreihen wurden auf einer Linux Workstation mit einem Vierkern Prozessor AMD Phenom(tm) II X4 3Ghz, 8 GB 1066 MHz RAM und zwei Nvidia Geforce GTX 280 Grafikkarten je 1GB Speicher, durchgeführt. In Tabelle 5.1 sind die Ergebnisse dieser Testreihen zusammengefasst. Als Testszenarien wurde unter anderem bekannte Problem wie das Philosophenproblem (phils) oder die Steuerung eines Aufzugs (elevator) mit den entsprechenden LTL-Anforderungen gewählt. Die genauen Details der Testszenarien, sowie ihre jeweilige Problemgröße, kann [7] entnommen werden. Insgesamt werden in der Tabelle fünf Algorithmen präsentiert. Neben den bereits bekannten, findet sich noch ein Algorithmus namens CUDA OWCTY Reverse wieder. Der Algorithmus ist, wie bereits der Name andeutet, eine abgewandelte Form des CUDA OWCTY, mit dem Unterschied, dass er statt einer Vorwärtssuche eine Rückwärtssuche durchführt und statt Knoten mit Eingangsgrad 0 zu entfernen, nur Knoten mit Ausgangsgrad 0 entfernt. Inbesondere diese letzte Änderung macht es möglich die eingesetzte Methode Elimination deutlich einfacher anhand der Nachfolgefunktion zu implementieren. Wie man sehen kann wird jeder mit Bezeichnung des Testszenaries noch ein Tupel von Zahlen mitgeführt. Diese beiden Zahlen stellen die Gesamtlaufzeiten der sequentiellen Varianten des MAP bzw. des OWCTY Algorithmus dar. Die Laufzeiten der CUDA Implementierungen werden hingegen unterteil in die Zeit zur Konvertierung in das CSR Format (CSR time), sowie die eigentliche Berechnungszeit (CUDA time) auf der GPU. Es zeigt sich, dass die CUDA Implementierung die sequentiellen Algorithmen im Schnitt um den Faktor 3-5 unterbieten. Während diese Erkenntnis noch zu erwarten ist, erstaunt es umso mehr zu sehen, dass die Gesamtlaufzeit der CUDA Implementierung im wesentlichen durch die Konvertierungszeit in das CSR Format bestimmt wird. Die eigentliche Berechnungszeit auf der GPU liegt nach der anfänglichen Initialisierung des Algorithmus weit unter den sequentiellen Algorithmen und macht deutlich über welche Rechenkraft heutige GPU s verfügen. Aber es gibt auch Unterschiede zwischen den CUDA Implementierungen. So wird anhand der Tabelle deutlich, dass in den gewählten Testszenarien CUDA MAP zumeist eine leicht schlechtere Laufzeit liefert als die OWCTY Implementierungen. Das ist insofern erklärbar, als dass bereits gezeigt wurde, dass die Wahl der Ordnungsrelation die Laufzeit der MAP Algorithmen erheblich bestimmt. OWC- TY Implementierung hingegen sind weitestgehend unabhängig von der Ordnung der Knoten und leiden dementsprechend nicht unter diesem Effekt. 5.2 Letzte Anmerkungen Die Aussage, dass Model Checking vom seinem Ansatz her für heutige Systeme nicht mehr praktikabel sei, hat sich mit der vorliegenden Arbeit nicht bestätigt. Viel mehr hat sich gezeigt, dass nahezu jeder Schritt des Model Checking durch die Anwendung alternativer Algorithmen beschleunigt werden kann. Erfolgsgeheimnis dieser Beschleunigung ist indes die Parallelität der eingesetzten Algorithmen, die es erlaubt selbst komplexeste Probleme mit einer Vielzahl von Rechnern zu lösen. So wie die Zustandsgenerierung, an ein Netzwerk von von Rechnern verteilt werden kann, erlauben parallele Model Checking 195
199 22 Abbildung 2: Laufzeiten der verschiedenen Algorithmen in Sekunden 196
CUDA. Moritz Wild, Jan-Hugo Lupp. Seminar Multi-Core Architectures and Programming. Friedrich-Alexander-Universität Erlangen-Nürnberg
 CUDA Seminar Multi-Core Architectures and Programming 1 Übersicht Einleitung Architektur Programmierung 2 Einleitung Computations on GPU 2003 Probleme Hohe Kenntnisse der Grafikprogrammierung nötig Unterschiedliche
CUDA Seminar Multi-Core Architectures and Programming 1 Übersicht Einleitung Architektur Programmierung 2 Einleitung Computations on GPU 2003 Probleme Hohe Kenntnisse der Grafikprogrammierung nötig Unterschiedliche
Proseminar. GPU-Computing Cuda vs. OpenCL. SS 2013 Alexander Stepanov
 Proseminar GPU-Computing Cuda vs. OpenCL SS 2013 Alexander Stepanov Inhaltsverzeichnis 1. Einführung: Warum GPU Computing? CPU vs. GPU GPU Architektur 2. CUDA Architektur Beispiel Matrix Multiplikation
Proseminar GPU-Computing Cuda vs. OpenCL SS 2013 Alexander Stepanov Inhaltsverzeichnis 1. Einführung: Warum GPU Computing? CPU vs. GPU GPU Architektur 2. CUDA Architektur Beispiel Matrix Multiplikation
4D Server v12 64-bit Version BETA VERSION
 4D Server v12 64-bit Version BETA VERSION 4D Server v12 unterstützt jetzt das Windows 64-bit Betriebssystem. Hauptvorteil der 64-bit Technologie ist die rundum verbesserte Performance der Anwendungen und
4D Server v12 64-bit Version BETA VERSION 4D Server v12 unterstützt jetzt das Windows 64-bit Betriebssystem. Hauptvorteil der 64-bit Technologie ist die rundum verbesserte Performance der Anwendungen und
C++ Grundlagen. ++ bedeutet Erweiterung zum Ansi C Standard. Hier wird eine Funktion eingeleitet
 C++ Grundlagen ++ bedeutet Erweiterung zum Ansi C Standard Hier wird eine Funktion eingeleitet Aufbau: In dieser Datei stehen die Befehle, die gestartet werden, wenn das Programm gestartet wird Int main()
C++ Grundlagen ++ bedeutet Erweiterung zum Ansi C Standard Hier wird eine Funktion eingeleitet Aufbau: In dieser Datei stehen die Befehle, die gestartet werden, wenn das Programm gestartet wird Int main()
Binäre Bäume. 1. Allgemeines. 2. Funktionsweise. 2.1 Eintragen
 Binäre Bäume 1. Allgemeines Binäre Bäume werden grundsätzlich verwendet, um Zahlen der Größe nach, oder Wörter dem Alphabet nach zu sortieren. Dem einfacheren Verständnis zu Liebe werde ich mich hier besonders
Binäre Bäume 1. Allgemeines Binäre Bäume werden grundsätzlich verwendet, um Zahlen der Größe nach, oder Wörter dem Alphabet nach zu sortieren. Dem einfacheren Verständnis zu Liebe werde ich mich hier besonders
Softwaretests in Visual Studio 2010 Ultimate Vergleich mit Java-Testwerkzeugen. Alexander Schunk Marcel Teuber Henry Trobisch
 Softwaretests in Visual Studio 2010 Ultimate Vergleich mit Java-Testwerkzeugen Alexander Schunk Henry Trobisch Inhalt 1. Vergleich der Unit-Tests... 2 2. Vergleich der Codeabdeckungs-Tests... 2 3. Vergleich
Softwaretests in Visual Studio 2010 Ultimate Vergleich mit Java-Testwerkzeugen Alexander Schunk Henry Trobisch Inhalt 1. Vergleich der Unit-Tests... 2 2. Vergleich der Codeabdeckungs-Tests... 2 3. Vergleich
Seminararbeit GPU Architektur und Programmiermöglichkeiten für GPGPU-Anwendungen
 Seminararbeit GPU Architektur und Programmiermöglichkeiten für GPGPU-Anwendungen Marius Gräfe University of Kaiserslautern, Embedded Systems Group m graefe10@cs.uni-kl.de 25. Oktober 2012 Alone we can
Seminararbeit GPU Architektur und Programmiermöglichkeiten für GPGPU-Anwendungen Marius Gräfe University of Kaiserslautern, Embedded Systems Group m graefe10@cs.uni-kl.de 25. Oktober 2012 Alone we can
Parallele Algorithmen mit OpenCL. Universität Osnabrück, Henning Wenke, 2013-05-08
 Parallele Algorithmen mit OpenCL Universität Osnabrück, Henning Wenke, 2013-05-08 Aufräumen Ressourcen in umgekehrter Abhängigkeitsreihenfolge freigeben Objekte haben Reference-Count (RC), initial 1 clrelease
Parallele Algorithmen mit OpenCL Universität Osnabrück, Henning Wenke, 2013-05-08 Aufräumen Ressourcen in umgekehrter Abhängigkeitsreihenfolge freigeben Objekte haben Reference-Count (RC), initial 1 clrelease
OpenGL. (Open Graphic Library)
 OpenGL (Open Graphic Library) Agenda Was ist OpenGL eigentlich? Geschichte Vor- und Nachteile Arbeitsweise glscene OpenGL per Hand Debugging Trend Was ist OpenGL eigentlich? OpenGL ist eine Spezifikation
OpenGL (Open Graphic Library) Agenda Was ist OpenGL eigentlich? Geschichte Vor- und Nachteile Arbeitsweise glscene OpenGL per Hand Debugging Trend Was ist OpenGL eigentlich? OpenGL ist eine Spezifikation
Grundlagen verteilter Systeme
 Universität Augsburg Insitut für Informatik Prof. Dr. Bernhard Bauer Wolf Fischer Christian Saad Wintersemester 08/09 Übungsblatt 3 12.11.08 Grundlagen verteilter Systeme Lösungsvorschlag Aufgabe 1: a)
Universität Augsburg Insitut für Informatik Prof. Dr. Bernhard Bauer Wolf Fischer Christian Saad Wintersemester 08/09 Übungsblatt 3 12.11.08 Grundlagen verteilter Systeme Lösungsvorschlag Aufgabe 1: a)
Objektorientierte Programmierung
 Objektorientierte Programmierung 1 Geschichte Dahl, Nygaard: Simula 67 (Algol 60 + Objektorientierung) Kay et al.: Smalltalk (erste rein-objektorientierte Sprache) Object Pascal, Objective C, C++ (wiederum
Objektorientierte Programmierung 1 Geschichte Dahl, Nygaard: Simula 67 (Algol 60 + Objektorientierung) Kay et al.: Smalltalk (erste rein-objektorientierte Sprache) Object Pascal, Objective C, C++ (wiederum
OpenCL. Programmiersprachen im Multicore-Zeitalter. Tim Wiersdörfer
 OpenCL Programmiersprachen im Multicore-Zeitalter Tim Wiersdörfer Inhaltsverzeichnis 1. Was ist OpenCL 2. Entwicklung von OpenCL 3. OpenCL Modelle 1. Plattform-Modell 2. Ausführungs-Modell 3. Speicher-Modell
OpenCL Programmiersprachen im Multicore-Zeitalter Tim Wiersdörfer Inhaltsverzeichnis 1. Was ist OpenCL 2. Entwicklung von OpenCL 3. OpenCL Modelle 1. Plattform-Modell 2. Ausführungs-Modell 3. Speicher-Modell
1 Vom Problem zum Programm
 Hintergrundinformationen zur Vorlesung GRUNDLAGEN DER INFORMATIK I Studiengang Elektrotechnik WS 02/03 AG Betriebssysteme FB3 Kirsten Berkenkötter 1 Vom Problem zum Programm Aufgabenstellung analysieren
Hintergrundinformationen zur Vorlesung GRUNDLAGEN DER INFORMATIK I Studiengang Elektrotechnik WS 02/03 AG Betriebssysteme FB3 Kirsten Berkenkötter 1 Vom Problem zum Programm Aufgabenstellung analysieren
.NET Code schützen. Projekt.NET. Version 1.0
 .NET Code schützen Projekt.NET Informationsmaterial zum Schützen des.net Codes Version 1.0 Autor: Status: Ablage: Empfänger: Seiten: D. Hoyer 1 / 6 Verteiler : Dokument1 Seite 1 von 1 Änderungsprotokoll
.NET Code schützen Projekt.NET Informationsmaterial zum Schützen des.net Codes Version 1.0 Autor: Status: Ablage: Empfänger: Seiten: D. Hoyer 1 / 6 Verteiler : Dokument1 Seite 1 von 1 Änderungsprotokoll
Programmierbeispiele und Implementierung. Name: Michel Steuwer E-Mail: michel.steuwer@wwu.de
 > Programmierbeispiele und Implementierung Name: Michel Steuwer E-Mail: michel.steuwer@wwu.de 2 > Übersicht > Matrix Vektor Multiplikation > Mandelbrotmenge / Apfelmännchen berechnen > Kantendetektion
> Programmierbeispiele und Implementierung Name: Michel Steuwer E-Mail: michel.steuwer@wwu.de 2 > Übersicht > Matrix Vektor Multiplikation > Mandelbrotmenge / Apfelmännchen berechnen > Kantendetektion
Einführung in die C-Programmierung
 Einführung in die C-Programmierung Warum C? Sehr stark verbreitet (Praxisnähe) Höhere Programmiersprache Objektorientierte Erweiterung: C++ Aber auch hardwarenahe Programmierung möglich (z.b. Mikrokontroller).
Einführung in die C-Programmierung Warum C? Sehr stark verbreitet (Praxisnähe) Höhere Programmiersprache Objektorientierte Erweiterung: C++ Aber auch hardwarenahe Programmierung möglich (z.b. Mikrokontroller).
Einführung in PHP. (mit Aufgaben)
 Einführung in PHP (mit Aufgaben) Dynamische Inhalte mit PHP? 2 Aus der Wikipedia (verkürzt): PHP wird auf etwa 244 Millionen Websites eingesetzt (Stand: Januar 2013) und wird auf etwa 80 % aller Websites
Einführung in PHP (mit Aufgaben) Dynamische Inhalte mit PHP? 2 Aus der Wikipedia (verkürzt): PHP wird auf etwa 244 Millionen Websites eingesetzt (Stand: Januar 2013) und wird auf etwa 80 % aller Websites
Einführung in die C++ Programmierung für Ingenieure
 Einführung in die C++ Programmierung für Ingenieure MATTHIAS WALTER / JENS KLUNKER Universität Rostock, Lehrstuhl für Modellierung und Simulation 14. November 2012 c 2012 UNIVERSITÄT ROSTOCK FACULTY OF
Einführung in die C++ Programmierung für Ingenieure MATTHIAS WALTER / JENS KLUNKER Universität Rostock, Lehrstuhl für Modellierung und Simulation 14. November 2012 c 2012 UNIVERSITÄT ROSTOCK FACULTY OF
The ToolChain.com. Grafisches Debugging mit der QtCreator Entwicklungsumgebung
 The ToolChain Grafisches Debugging mit der QtCreator Entwicklungsumgebung geschrieben von Gregor Rebel 2014-2015 Hintergrund Neben dem textuellen Debuggen in der Textkonsole bieten moderene Entwicklungsumgebungen
The ToolChain Grafisches Debugging mit der QtCreator Entwicklungsumgebung geschrieben von Gregor Rebel 2014-2015 Hintergrund Neben dem textuellen Debuggen in der Textkonsole bieten moderene Entwicklungsumgebungen
Systeme 1. Kapitel 6. Nebenläufigkeit und wechselseitiger Ausschluss
 Systeme 1 Kapitel 6 Nebenläufigkeit und wechselseitiger Ausschluss Threads Die Adressräume verschiedener Prozesse sind getrennt und geschützt gegen den Zugriff anderer Prozesse. Threads sind leichtgewichtige
Systeme 1 Kapitel 6 Nebenläufigkeit und wechselseitiger Ausschluss Threads Die Adressräume verschiedener Prozesse sind getrennt und geschützt gegen den Zugriff anderer Prozesse. Threads sind leichtgewichtige
Tutorium Informatik 1. Aufgabe 2: Formatierte Ein- und Ausgabe
 Tutorium Informatik 1 Aufgabe 2: Formatierte Ein- und Ausgabe Fachbereich: Elektrotechnik Inhaltsverzeichnis 1 Aufgabe 1 2 Benötigte Funktionen und Schlüsselwörter 2 Robert Halas / FH Regensburg - 2003
Tutorium Informatik 1 Aufgabe 2: Formatierte Ein- und Ausgabe Fachbereich: Elektrotechnik Inhaltsverzeichnis 1 Aufgabe 1 2 Benötigte Funktionen und Schlüsselwörter 2 Robert Halas / FH Regensburg - 2003
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
schnell und portofrei erhältlich bei beck-shop.de DIE FACHBUCHHANDLUNG mitp/bhv
 Roboter programmieren mit NXC für Lego Mindstorms NXT 1. Auflage Roboter programmieren mit NXC für Lego Mindstorms NXT schnell und portofrei erhältlich bei beck-shop.de DIE FACHBUCHHANDLUNG mitp/bhv Verlag
Roboter programmieren mit NXC für Lego Mindstorms NXT 1. Auflage Roboter programmieren mit NXC für Lego Mindstorms NXT schnell und portofrei erhältlich bei beck-shop.de DIE FACHBUCHHANDLUNG mitp/bhv Verlag
Objektorientierte Programmierung für Anfänger am Beispiel PHP
 Objektorientierte Programmierung für Anfänger am Beispiel PHP Johannes Mittendorfer http://jmittendorfer.hostingsociety.com 19. August 2012 Abstract Dieses Dokument soll die Vorteile der objektorientierten
Objektorientierte Programmierung für Anfänger am Beispiel PHP Johannes Mittendorfer http://jmittendorfer.hostingsociety.com 19. August 2012 Abstract Dieses Dokument soll die Vorteile der objektorientierten
5 DATEN. 5.1. Variablen. Variablen können beliebige Werte zugewiesen und im Gegensatz zu
 Daten Makro + VBA effektiv 5 DATEN 5.1. Variablen Variablen können beliebige Werte zugewiesen und im Gegensatz zu Konstanten jederzeit im Programm verändert werden. Als Variablen können beliebige Zeichenketten
Daten Makro + VBA effektiv 5 DATEN 5.1. Variablen Variablen können beliebige Werte zugewiesen und im Gegensatz zu Konstanten jederzeit im Programm verändert werden. Als Variablen können beliebige Zeichenketten
Deklarationen in C. Prof. Dr. Margarita Esponda
 Deklarationen in C 1 Deklarationen Deklarationen spielen eine zentrale Rolle in der C-Programmiersprache. Deklarationen Variablen Funktionen Die Deklarationen von Variablen und Funktionen haben viele Gemeinsamkeiten.
Deklarationen in C 1 Deklarationen Deklarationen spielen eine zentrale Rolle in der C-Programmiersprache. Deklarationen Variablen Funktionen Die Deklarationen von Variablen und Funktionen haben viele Gemeinsamkeiten.
etutor Benutzerhandbuch XQuery Benutzerhandbuch Georg Nitsche
 etutor Benutzerhandbuch Benutzerhandbuch XQuery Georg Nitsche Version 1.0 Stand März 2006 Versionsverlauf: Version Autor Datum Änderungen 1.0 gn 06.03.2006 Fertigstellung der ersten Version Inhaltsverzeichnis:
etutor Benutzerhandbuch Benutzerhandbuch XQuery Georg Nitsche Version 1.0 Stand März 2006 Versionsverlauf: Version Autor Datum Änderungen 1.0 gn 06.03.2006 Fertigstellung der ersten Version Inhaltsverzeichnis:
VB.net Programmierung und Beispielprogramm für GSV
 VB.net Programmierung und Beispielprogramm für GSV Dokumentation Stand vom 26.05.2011 Tel +49 (0)3302 78620 60, Fax +49 (0)3302 78620 69, info@me-systeme.de, www.me-systeme.de 1 Inhaltsverzeichnis Vorwort...2
VB.net Programmierung und Beispielprogramm für GSV Dokumentation Stand vom 26.05.2011 Tel +49 (0)3302 78620 60, Fax +49 (0)3302 78620 69, info@me-systeme.de, www.me-systeme.de 1 Inhaltsverzeichnis Vorwort...2
Virtueller Seminarordner Anleitung für die Dozentinnen und Dozenten
 Virtueller Seminarordner Anleitung für die Dozentinnen und Dozenten In dem Virtuellen Seminarordner werden für die Teilnehmerinnen und Teilnehmer des Seminars alle für das Seminar wichtigen Informationen,
Virtueller Seminarordner Anleitung für die Dozentinnen und Dozenten In dem Virtuellen Seminarordner werden für die Teilnehmerinnen und Teilnehmer des Seminars alle für das Seminar wichtigen Informationen,
Der Aufruf von DM_in_Euro 1.40 sollte die Ausgabe 1.40 DM = 0.51129 Euro ergeben.
 Aufgabe 1.30 : Schreibe ein Programm DM_in_Euro.java zur Umrechnung eines DM-Betrags in Euro unter Verwendung einer Konstanten für den Umrechnungsfaktor. Das Programm soll den DM-Betrag als Parameter verarbeiten.
Aufgabe 1.30 : Schreibe ein Programm DM_in_Euro.java zur Umrechnung eines DM-Betrags in Euro unter Verwendung einer Konstanten für den Umrechnungsfaktor. Das Programm soll den DM-Betrag als Parameter verarbeiten.
Tutorium Rechnerorganisation
 Woche 2 Tutorien 3 und 4 zur Vorlesung Rechnerorganisation 1 Christian A. Mandery: KIT Universität des Landes Baden-Württemberg und nationales Grossforschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu
Woche 2 Tutorien 3 und 4 zur Vorlesung Rechnerorganisation 1 Christian A. Mandery: KIT Universität des Landes Baden-Württemberg und nationales Grossforschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Es sollte die MS-DOS Eingabeaufforderung starten. Geben Sie nun den Befehl javac ein.
 Schritt 1: Installation des Javacompilers JDK. Der erste Start mit Eclipse Bevor Sie den Java-Compiler installieren sollten Sie sich vergewissern, ob er eventuell schon installiert ist. Gehen sie wie folgt
Schritt 1: Installation des Javacompilers JDK. Der erste Start mit Eclipse Bevor Sie den Java-Compiler installieren sollten Sie sich vergewissern, ob er eventuell schon installiert ist. Gehen sie wie folgt
Grundlagen von Python
 Einführung in Python Grundlagen von Python Felix Döring, Felix Wittwer November 17, 2015 Scriptcharakter Programmierparadigmen Imperatives Programmieren Das Scoping Problem Objektorientiertes Programmieren
Einführung in Python Grundlagen von Python Felix Döring, Felix Wittwer November 17, 2015 Scriptcharakter Programmierparadigmen Imperatives Programmieren Das Scoping Problem Objektorientiertes Programmieren
GPGPU-Programmierung
 12 GPGPU-Programmierung 2013/04/25 Diese Folien enthalten Graphiken mit Nutzungseinschränkungen. Das Kopieren der Graphiken ist im Allgemeinen nicht erlaubt. Motivation (1) General Purpose Computing on
12 GPGPU-Programmierung 2013/04/25 Diese Folien enthalten Graphiken mit Nutzungseinschränkungen. Das Kopieren der Graphiken ist im Allgemeinen nicht erlaubt. Motivation (1) General Purpose Computing on
Fachbericht zum Thema: Anforderungen an ein Datenbanksystem
 Fachbericht zum Thema: Anforderungen an ein Datenbanksystem von André Franken 1 Inhaltsverzeichnis 1 Inhaltsverzeichnis 1 2 Einführung 2 2.1 Gründe für den Einsatz von DB-Systemen 2 2.2 Definition: Datenbank
Fachbericht zum Thema: Anforderungen an ein Datenbanksystem von André Franken 1 Inhaltsverzeichnis 1 Inhaltsverzeichnis 1 2 Einführung 2 2.1 Gründe für den Einsatz von DB-Systemen 2 2.2 Definition: Datenbank
Praxiseinheit: Realisierung einer hardwarebeschleunigten Disparitätenberechnung zur automatischen Auswertung von Stereobildern
 Praxiseinheit: Realisierung einer hardwarebeschleunigten Disparitätenberechnung zur automatischen Auswertung von Stereobildern Institut für Betriebssysteme und Rechnerverbund TU Braunschweig 25.10., 26.10.
Praxiseinheit: Realisierung einer hardwarebeschleunigten Disparitätenberechnung zur automatischen Auswertung von Stereobildern Institut für Betriebssysteme und Rechnerverbund TU Braunschweig 25.10., 26.10.
Computerarithmetik ( )
 Anhang A Computerarithmetik ( ) A.1 Zahlendarstellung im Rechner und Computerarithmetik Prinzipiell ist die Menge der im Computer darstellbaren Zahlen endlich. Wie groß diese Menge ist, hängt von der Rechnerarchitektur
Anhang A Computerarithmetik ( ) A.1 Zahlendarstellung im Rechner und Computerarithmetik Prinzipiell ist die Menge der im Computer darstellbaren Zahlen endlich. Wie groß diese Menge ist, hängt von der Rechnerarchitektur
Stellen Sie bitte den Cursor in die Spalte B2 und rufen die Funktion Sverweis auf. Es öffnet sich folgendes Dialogfenster
 Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
Es gibt in Excel unter anderem die so genannten Suchfunktionen / Matrixfunktionen Damit können Sie Werte innerhalb eines bestimmten Bereichs suchen. Als Beispiel möchte ich die Funktion Sverweis zeigen.
GPU Architektur CUDA - OpenCL
 GPU Architektur und Programmiermöglichkeiten für GPGPU-Anwendungen kernel void matsq( global const float *mat, global float *out ) { int dim = get_global_size(0); //Matrix dimension int i = get_global_id(0);
GPU Architektur und Programmiermöglichkeiten für GPGPU-Anwendungen kernel void matsq( global const float *mat, global float *out ) { int dim = get_global_size(0); //Matrix dimension int i = get_global_id(0);
Suche schlecht beschriftete Bilder mit Eigenen Abfragen
 Suche schlecht beschriftete Bilder mit Eigenen Abfragen Ist die Bilderdatenbank über einen längeren Zeitraum in Benutzung, so steigt die Wahrscheinlichkeit für schlecht beschriftete Bilder 1. Insbesondere
Suche schlecht beschriftete Bilder mit Eigenen Abfragen Ist die Bilderdatenbank über einen längeren Zeitraum in Benutzung, so steigt die Wahrscheinlichkeit für schlecht beschriftete Bilder 1. Insbesondere
Anwenderdokumentation PersoSim
 Anwenderdokumentation PersoSim Die nachfolgende Anwenderdokumentation soll dem Anwender bei der Installation und den ersten Schritten im Umgang mit PersoSim helfen. Installation Grundvoraussetzung für
Anwenderdokumentation PersoSim Die nachfolgende Anwenderdokumentation soll dem Anwender bei der Installation und den ersten Schritten im Umgang mit PersoSim helfen. Installation Grundvoraussetzung für
Erweiterung der Aufgabe. Die Notenberechnung soll nicht nur für einen Schüler, sondern für bis zu 35 Schüler gehen:
 VBA Programmierung mit Excel Schleifen 1/6 Erweiterung der Aufgabe Die Notenberechnung soll nicht nur für einen Schüler, sondern für bis zu 35 Schüler gehen: Es müssen also 11 (B L) x 35 = 385 Zellen berücksichtigt
VBA Programmierung mit Excel Schleifen 1/6 Erweiterung der Aufgabe Die Notenberechnung soll nicht nur für einen Schüler, sondern für bis zu 35 Schüler gehen: Es müssen also 11 (B L) x 35 = 385 Zellen berücksichtigt
Folgende Einstellungen sind notwendig, damit die Kommunikation zwischen Server und Client funktioniert:
 Firewall für Lexware professional konfigurieren Inhaltsverzeichnis: 1. Allgemein... 1 2. Einstellungen... 1 3. Windows XP SP2 und Windows 2003 Server SP1 Firewall...1 4. Bitdefender 9... 5 5. Norton Personal
Firewall für Lexware professional konfigurieren Inhaltsverzeichnis: 1. Allgemein... 1 2. Einstellungen... 1 3. Windows XP SP2 und Windows 2003 Server SP1 Firewall...1 4. Bitdefender 9... 5 5. Norton Personal
Konzepte der Informatik
 Konzepte der Informatik Vorkurs Informatik zum WS 2011/2012 26.09. - 30.09.2011 17.10. - 21.10.2011 Dr. Werner Struckmann / Christoph Peltz Stark angelehnt an Kapitel 1 aus "Abenteuer Informatik" von Jens
Konzepte der Informatik Vorkurs Informatik zum WS 2011/2012 26.09. - 30.09.2011 17.10. - 21.10.2011 Dr. Werner Struckmann / Christoph Peltz Stark angelehnt an Kapitel 1 aus "Abenteuer Informatik" von Jens
.htaccess HOWTO. zum Schutz von Dateien und Verzeichnissen mittels Passwortabfrage
 .htaccess HOWTO zum Schutz von Dateien und Verzeichnissen mittels Passwortabfrage Stand: 21.06.2015 Inhaltsverzeichnis 1. Vorwort...3 2. Verwendung...4 2.1 Allgemeines...4 2.1 Das Aussehen der.htaccess
.htaccess HOWTO zum Schutz von Dateien und Verzeichnissen mittels Passwortabfrage Stand: 21.06.2015 Inhaltsverzeichnis 1. Vorwort...3 2. Verwendung...4 2.1 Allgemeines...4 2.1 Das Aussehen der.htaccess
Wintersemester Maschinenbau und Kunststofftechnik. Informatik. Tobias Wolf http://informatik.swoke.de. Seite 1 von 18
 Kapitel 3 Datentypen und Variablen Seite 1 von 18 Datentypen - Einführung - Für jede Variable muss ein Datentyp festgelegt werden. - Hierdurch werden die Wertemenge und die verwendbaren Operatoren festgelegt.
Kapitel 3 Datentypen und Variablen Seite 1 von 18 Datentypen - Einführung - Für jede Variable muss ein Datentyp festgelegt werden. - Hierdurch werden die Wertemenge und die verwendbaren Operatoren festgelegt.
OpenMP am Beispiel der Matrizenmultiplikation
 OpenMP am Beispiel der Matrizenmultiplikation David J. Meder, Dr. Victor Pankratius IPD Tichy Lehrstuhl für Programmiersysteme KIT die Kooperation von Forschungszentrum Karlsruhe GmbH und Universität Karlsruhe
OpenMP am Beispiel der Matrizenmultiplikation David J. Meder, Dr. Victor Pankratius IPD Tichy Lehrstuhl für Programmiersysteme KIT die Kooperation von Forschungszentrum Karlsruhe GmbH und Universität Karlsruhe
Übung: Verwendung von Java-Threads
 Übung: Verwendung von Java-Threads Ziel der Übung: Diese Übung dient dazu, den Umgang mit Threads in der Programmiersprache Java kennenzulernen. Ein einfaches Java-Programm, das Threads nutzt, soll zum
Übung: Verwendung von Java-Threads Ziel der Übung: Diese Übung dient dazu, den Umgang mit Threads in der Programmiersprache Java kennenzulernen. Ein einfaches Java-Programm, das Threads nutzt, soll zum
Unterprogramme. Funktionen. Bedeutung von Funktionen in C++ Definition einer Funktion. Definition einer Prozedur
 Unterprogramme Unterprogramme sind abgekapselte Programmfragmente, welche es erlauben, bestimmte Aufgaben in wiederverwendbarer Art umzusetzen. Man unterscheidet zwischen Unterprogrammen mit Rückgabewert
Unterprogramme Unterprogramme sind abgekapselte Programmfragmente, welche es erlauben, bestimmte Aufgaben in wiederverwendbarer Art umzusetzen. Man unterscheidet zwischen Unterprogrammen mit Rückgabewert
Qt-Projekte mit Visual Studio 2005
 Qt-Projekte mit Visual Studio 2005 Benötigte Programme: Visual Studio 2005 Vollversion, Microsoft Qt 4 Open Source s. Qt 4-Installationsanleitung Tabelle 1: Benötigte Programme für die Qt-Programmierung
Qt-Projekte mit Visual Studio 2005 Benötigte Programme: Visual Studio 2005 Vollversion, Microsoft Qt 4 Open Source s. Qt 4-Installationsanleitung Tabelle 1: Benötigte Programme für die Qt-Programmierung
Java Kurs für Anfänger Einheit 5 Methoden
 Java Kurs für Anfänger Einheit 5 Methoden Ludwig-Maximilians-Universität München (Institut für Informatik: Programmierung und Softwaretechnik von Prof.Wirsing) 22. Juni 2009 Inhaltsverzeichnis Methoden
Java Kurs für Anfänger Einheit 5 Methoden Ludwig-Maximilians-Universität München (Institut für Informatik: Programmierung und Softwaretechnik von Prof.Wirsing) 22. Juni 2009 Inhaltsverzeichnis Methoden
Einführung. GPU-Versuch. Andreas Schäfer Friedrich-Alexander-Universität Erlangen-Nürnberg
 GPU-Versuch andreas.schaefer@cs.fau.de Friedrich-Alexander-Universität Erlangen-Nürnberg Praktikum Parallele Rechnerarchitekturen SS2014 Outline 1 Einführung 2 Outlook 1 Einführung 2 Eine kurze Geschichte
GPU-Versuch andreas.schaefer@cs.fau.de Friedrich-Alexander-Universität Erlangen-Nürnberg Praktikum Parallele Rechnerarchitekturen SS2014 Outline 1 Einführung 2 Outlook 1 Einführung 2 Eine kurze Geschichte
Inhalt. 1 Einleitung AUTOMATISCHE DATENSICHERUNG AUF EINEN CLOUDSPEICHER
 AUTOMATISCHE DATENSICHERUNG AUF EINEN CLOUDSPEICHER Inhalt 1 Einleitung... 1 2 Einrichtung der Aufgabe für die automatische Sicherung... 2 2.1 Die Aufgabenplanung... 2 2.2 Der erste Testlauf... 9 3 Problembehebung...
AUTOMATISCHE DATENSICHERUNG AUF EINEN CLOUDSPEICHER Inhalt 1 Einleitung... 1 2 Einrichtung der Aufgabe für die automatische Sicherung... 2 2.1 Die Aufgabenplanung... 2 2.2 Der erste Testlauf... 9 3 Problembehebung...
Mikrocontroller Grundlagen. Markus Koch April 2011
 Mikrocontroller Grundlagen Markus Koch April 2011 Übersicht Was ist ein Mikrocontroller Aufbau (CPU/RAM/ROM/Takt/Peripherie) Unterschied zum Mikroprozessor Unterschiede der Controllerarten Unterschiede
Mikrocontroller Grundlagen Markus Koch April 2011 Übersicht Was ist ein Mikrocontroller Aufbau (CPU/RAM/ROM/Takt/Peripherie) Unterschied zum Mikroprozessor Unterschiede der Controllerarten Unterschiede
Binärdarstellung von Fliesskommazahlen
 Binärdarstellung von Fliesskommazahlen 1. IEEE 754 Gleitkommazahl im Single-Format So sind in Gleitkommazahlen im IEEE 754-Standard aufgebaut: 31 30 24 23 0 S E E E E E E E E M M M M M M M M M M M M M
Binärdarstellung von Fliesskommazahlen 1. IEEE 754 Gleitkommazahl im Single-Format So sind in Gleitkommazahlen im IEEE 754-Standard aufgebaut: 31 30 24 23 0 S E E E E E E E E M M M M M M M M M M M M M
VBA-Programmierung: Zusammenfassung
 VBA-Programmierung: Zusammenfassung Programmiersprachen (Definition, Einordnung VBA) Softwareentwicklung-Phasen: 1. Spezifikation 2. Entwurf 3. Implementierung Datentypen (einfach, zusammengesetzt) Programmablaufsteuerung
VBA-Programmierung: Zusammenfassung Programmiersprachen (Definition, Einordnung VBA) Softwareentwicklung-Phasen: 1. Spezifikation 2. Entwurf 3. Implementierung Datentypen (einfach, zusammengesetzt) Programmablaufsteuerung
GPGPU-Programmierung
 12 GPGPU-Programmierung 2014/04/29 Diese Folien enthalten Graphiken mit Nutzungseinschränkungen. Das Kopieren der Graphiken ist im Allgemeinen nicht erlaubt. Motivation (1) General Purpose Computing on
12 GPGPU-Programmierung 2014/04/29 Diese Folien enthalten Graphiken mit Nutzungseinschränkungen. Das Kopieren der Graphiken ist im Allgemeinen nicht erlaubt. Motivation (1) General Purpose Computing on
Monitore. Klicken bearbeiten
 Sascha Kretzschmann Institut für Informatik Monitore Formatvorlage und deren Umsetzung des Untertitelmasters durch Klicken bearbeiten Inhalt 1. Monitore und Concurrent Pascal 1.1 Warum Monitore? 1.2 Monitordefinition
Sascha Kretzschmann Institut für Informatik Monitore Formatvorlage und deren Umsetzung des Untertitelmasters durch Klicken bearbeiten Inhalt 1. Monitore und Concurrent Pascal 1.1 Warum Monitore? 1.2 Monitordefinition
Compute Unified Device Architecture CUDA
 Compute Unified Device Architecture 06. Februar 2012 1 / 13 Gliederung 2 / 13 : Compute Unified Device Architecture entwickelt von Nvidia Corporation spezifiziert Software- und Hardwareeigenschaften Ziel:
Compute Unified Device Architecture 06. Februar 2012 1 / 13 Gliederung 2 / 13 : Compute Unified Device Architecture entwickelt von Nvidia Corporation spezifiziert Software- und Hardwareeigenschaften Ziel:
Klausurteilnehmer. Wichtige Hinweise. Note: Klausur Informatik Programmierung, 17.09.2012 Seite 1 von 8 HS OWL, FB 7, Malte Wattenberg.
 Klausur Informatik Programmierung, 17.09.2012 Seite 1 von 8 Klausurteilnehmer Name: Matrikelnummer: Wichtige Hinweise Es sind keinerlei Hilfsmittel zugelassen auch keine Taschenrechner! Die Klausur dauert
Klausur Informatik Programmierung, 17.09.2012 Seite 1 von 8 Klausurteilnehmer Name: Matrikelnummer: Wichtige Hinweise Es sind keinerlei Hilfsmittel zugelassen auch keine Taschenrechner! Die Klausur dauert
Zahlensysteme: Oktal- und Hexadezimalsystem
 20 Brückenkurs Die gebräuchlichste Bitfolge umfasst 8 Bits, sie deckt also 2 8 =256 Möglichkeiten ab, und wird ein Byte genannt. Zwei Bytes, also 16 Bits, bilden ein Wort, und 4 Bytes, also 32 Bits, formen
20 Brückenkurs Die gebräuchlichste Bitfolge umfasst 8 Bits, sie deckt also 2 8 =256 Möglichkeiten ab, und wird ein Byte genannt. Zwei Bytes, also 16 Bits, bilden ein Wort, und 4 Bytes, also 32 Bits, formen
M. Graefenhan 2000-12-07. Übungen zu C. Blatt 3. Musterlösung
 M. Graefenhan 2000-12-07 Aufgabe Lösungsweg Übungen zu C Blatt 3 Musterlösung Schreiben Sie ein Programm, das die Häufigkeit von Zeichen in einem eingelesenen String feststellt. Benutzen Sie dazu ein zweidimensionales
M. Graefenhan 2000-12-07 Aufgabe Lösungsweg Übungen zu C Blatt 3 Musterlösung Schreiben Sie ein Programm, das die Häufigkeit von Zeichen in einem eingelesenen String feststellt. Benutzen Sie dazu ein zweidimensionales
Vorkurs C++ Programmierung
 Vorkurs C++ Programmierung Klassen Letzte Stunde Speicherverwaltung automatische Speicherverwaltung auf dem Stack dynamische Speicherverwaltung auf dem Heap new/new[] und delete/delete[] Speicherklassen:
Vorkurs C++ Programmierung Klassen Letzte Stunde Speicherverwaltung automatische Speicherverwaltung auf dem Stack dynamische Speicherverwaltung auf dem Heap new/new[] und delete/delete[] Speicherklassen:
Übungen 19.01.2012 Programmieren 1 Felix Rohrer. Übungen
 Übungen if / else / else if... 2... 2 Aufgabe 2:... 2 Aufgabe 3:... 2 Aufgabe 4:... 2 Aufgabe 5:... 2 Aufgabe 6:... 2 Aufgabe 7:... 3 Aufgabe 8:... 3 Aufgabe 9:... 3 Aufgabe 10:... 3 switch... 4... 4 Aufgabe
Übungen if / else / else if... 2... 2 Aufgabe 2:... 2 Aufgabe 3:... 2 Aufgabe 4:... 2 Aufgabe 5:... 2 Aufgabe 6:... 2 Aufgabe 7:... 3 Aufgabe 8:... 3 Aufgabe 9:... 3 Aufgabe 10:... 3 switch... 4... 4 Aufgabe
Zählen von Objekten einer bestimmten Klasse
 Zählen von Objekten einer bestimmten Klasse Ziel, Inhalt Zur Übung versuchen wir eine Klasse zu schreiben, mit der es möglich ist Objekte einer bestimmten Klasse zu zählen. Wir werden den ++ und den --
Zählen von Objekten einer bestimmten Klasse Ziel, Inhalt Zur Übung versuchen wir eine Klasse zu schreiben, mit der es möglich ist Objekte einer bestimmten Klasse zu zählen. Wir werden den ++ und den --
1 Mathematische Grundlagen
 Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Architektur Verteilter Systeme Teil 2: Prozesse und Threads
 Architektur Verteilter Systeme Teil 2: Prozesse und Threads 21.10.15 1 Übersicht Prozess Thread Scheduler Time Sharing 2 Begriff Prozess und Thread I Prozess = Sequentiell ablaufendes Programm Thread =
Architektur Verteilter Systeme Teil 2: Prozesse und Threads 21.10.15 1 Übersicht Prozess Thread Scheduler Time Sharing 2 Begriff Prozess und Thread I Prozess = Sequentiell ablaufendes Programm Thread =
Führen Sie zum Einstieg in die Materie einige Systemdiagnosen durch. Benutzen Sie dabei winmsd.exe.
 Aufgabe 1.1: Systeminformationen Führen Sie zum Einstieg in die Materie einige Systemdiagnosen durch. Benutzen Sie dabei winmsd.exe. a) Wie lautet der Name des von Ihnen verwendeten Rechners? Der Systemname
Aufgabe 1.1: Systeminformationen Führen Sie zum Einstieg in die Materie einige Systemdiagnosen durch. Benutzen Sie dabei winmsd.exe. a) Wie lautet der Name des von Ihnen verwendeten Rechners? Der Systemname
Kundenspezifische Preise im Shop WyRu Online-Shop
 Kundenspezifische Preise im Shop WyRu Online-Shop Team WyRu Christian Wyk / Günter Rubik SCS Bürocenter B1, A-2334 Vösendorf Internet http://www.wyru.at Kundenspezifische Preise sind ein Feature des WyRu
Kundenspezifische Preise im Shop WyRu Online-Shop Team WyRu Christian Wyk / Günter Rubik SCS Bürocenter B1, A-2334 Vösendorf Internet http://www.wyru.at Kundenspezifische Preise sind ein Feature des WyRu
Verhindert, dass eine Methode überschrieben wird. public final int holekontostand() {...} public final class Girokonto extends Konto {...
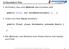 PIWIN I Kap. 8 Objektorientierte Programmierung - Vererbung 31 Schlüsselwort: final Verhindert, dass eine Methode überschrieben wird public final int holekontostand() {... Erben von einer Klasse verbieten:
PIWIN I Kap. 8 Objektorientierte Programmierung - Vererbung 31 Schlüsselwort: final Verhindert, dass eine Methode überschrieben wird public final int holekontostand() {... Erben von einer Klasse verbieten:
In 12 Schritten zum mobilen PC mit Paragon Drive Copy 11 und Microsoft Windows Virtual PC
 PARAGON Technologie GmbH, Systemprogrammierung Heinrich-von-Stephan-Str. 5c 79100 Freiburg, Germany Tel. +49 (0) 761 59018201 Fax +49 (0) 761 59018130 Internet www.paragon-software.com Email sales@paragon-software.com
PARAGON Technologie GmbH, Systemprogrammierung Heinrich-von-Stephan-Str. 5c 79100 Freiburg, Germany Tel. +49 (0) 761 59018201 Fax +49 (0) 761 59018130 Internet www.paragon-software.com Email sales@paragon-software.com
Programmierung für Mathematik (HS13)
 software evolution & architecture lab Programmierung für Mathematik (HS13) Übung 5 1 Aufgabe: Eclipse IDE 1.1 Lernziele 1. Die Entwicklungsumgebung Eclipse einrichten. 2. Eclipse kennen lernen und mit
software evolution & architecture lab Programmierung für Mathematik (HS13) Übung 5 1 Aufgabe: Eclipse IDE 1.1 Lernziele 1. Die Entwicklungsumgebung Eclipse einrichten. 2. Eclipse kennen lernen und mit
Das große ElterngeldPlus 1x1. Alles über das ElterngeldPlus. Wer kann ElterngeldPlus beantragen? ElterngeldPlus verstehen ein paar einleitende Fakten
 Das große x -4 Alles über das Wer kann beantragen? Generell kann jeder beantragen! Eltern (Mütter UND Väter), die schon während ihrer Elternzeit wieder in Teilzeit arbeiten möchten. Eltern, die während
Das große x -4 Alles über das Wer kann beantragen? Generell kann jeder beantragen! Eltern (Mütter UND Väter), die schon während ihrer Elternzeit wieder in Teilzeit arbeiten möchten. Eltern, die während
Kurzeinführung LABTALK
 Kurzeinführung LABTALK Mit der Interpreter-Sprache LabTalk, die von ORIGIN zur Verfügung gestellt wird, können bequem Datenmanipulationen sowie Zugriffe direkt auf das Programm (Veränderungen der Oberfläche,
Kurzeinführung LABTALK Mit der Interpreter-Sprache LabTalk, die von ORIGIN zur Verfügung gestellt wird, können bequem Datenmanipulationen sowie Zugriffe direkt auf das Programm (Veränderungen der Oberfläche,
Stift-Karussell in M-Plot einrichten
 Einsteiger Fortgeschrittene Profis markus.meinl@m-quest.ch Version 1.0 Voraussetzungen für diesen Workshop Die M-Quest Suite 2005 oder höher ist auf einem Rechner installiert Das Produkt M-Plot Suite ist
Einsteiger Fortgeschrittene Profis markus.meinl@m-quest.ch Version 1.0 Voraussetzungen für diesen Workshop Die M-Quest Suite 2005 oder höher ist auf einem Rechner installiert Das Produkt M-Plot Suite ist
Einführung in die Java- Programmierung
 Einführung in die Java- Programmierung Dr. Volker Riediger Tassilo Horn riediger horn@uni-koblenz.de WiSe 2012/13 1 Wichtig... Mittags keine Pommes... Praktikum A 230 C 207 (Madeleine + Esma) F 112 F 113
Einführung in die Java- Programmierung Dr. Volker Riediger Tassilo Horn riediger horn@uni-koblenz.de WiSe 2012/13 1 Wichtig... Mittags keine Pommes... Praktikum A 230 C 207 (Madeleine + Esma) F 112 F 113
Speicher in der Cloud
 Speicher in der Cloud Kostenbremse, Sicherheitsrisiko oder Basis für die unternehmensweite Kollaboration? von Cornelius Höchel-Winter 2013 ComConsult Research GmbH, Aachen 3 SYNCHRONISATION TEUFELSZEUG
Speicher in der Cloud Kostenbremse, Sicherheitsrisiko oder Basis für die unternehmensweite Kollaboration? von Cornelius Höchel-Winter 2013 ComConsult Research GmbH, Aachen 3 SYNCHRONISATION TEUFELSZEUG
Diplomarbeit. Konzeption und Implementierung einer automatisierten Testumgebung. Thomas Wehrspann. 10. Dezember 2008
 Konzeption und Implementierung einer automatisierten Testumgebung, 10. Dezember 2008 1 Gliederung Einleitung Softwaretests Beispiel Konzeption Zusammenfassung 2 Einleitung Komplexität von Softwaresystemen
Konzeption und Implementierung einer automatisierten Testumgebung, 10. Dezember 2008 1 Gliederung Einleitung Softwaretests Beispiel Konzeption Zusammenfassung 2 Einleitung Komplexität von Softwaresystemen
Robot Karol für Delphi
 Robot Karol für Delphi Reinhard Nitzsche, OSZ Handel I Version 0.1 vom 24. Januar 2003 Zusammenfassung Nach der Einführung in die (variablenfreie) Programmierung mit Robot Karol von Freiberger und Krško
Robot Karol für Delphi Reinhard Nitzsche, OSZ Handel I Version 0.1 vom 24. Januar 2003 Zusammenfassung Nach der Einführung in die (variablenfreie) Programmierung mit Robot Karol von Freiberger und Krško
C++ Tutorial: Timer 1
 C++ Tutorial: Timer 1 Timer v1.0 Einleitung Raum und Zeit sind spätestens seit der kopernikanischen Wende wichtige Gegenstände des Denkens geworden. In einem Programm bestimmt die Zeit die Abläufe und
C++ Tutorial: Timer 1 Timer v1.0 Einleitung Raum und Zeit sind spätestens seit der kopernikanischen Wende wichtige Gegenstände des Denkens geworden. In einem Programm bestimmt die Zeit die Abläufe und
OpenCL. Seminar Programmiersprachen im Multicore-Zeitalter Universität Siegen Tim Wiersdörfer tim.wiersdoerfer@student.uni-siegen.
 OpenCL Seminar Programmiersprachen im Multicore-Zeitalter Universität Siegen Tim Wiersdörfer tim.wiersdoerfer@student.uni-siegen.de Abstract: In diesem Dokument wird ein grundlegender Einblick in das relativ
OpenCL Seminar Programmiersprachen im Multicore-Zeitalter Universität Siegen Tim Wiersdörfer tim.wiersdoerfer@student.uni-siegen.de Abstract: In diesem Dokument wird ein grundlegender Einblick in das relativ
Die Programmiersprache C
 Die Programmiersprache C höhere Programmiersprache (mit einigen Assembler-ähnlichen Konstrukten) gut verständliche Kommandos muss von Compiler in maschinenlesbaren Code (Binärdatei) übersetzt werden universell,
Die Programmiersprache C höhere Programmiersprache (mit einigen Assembler-ähnlichen Konstrukten) gut verständliche Kommandos muss von Compiler in maschinenlesbaren Code (Binärdatei) übersetzt werden universell,
5.2 Neue Projekte erstellen
 5.2 Neue Projekte erstellen Das Bearbeiten von bestehenden Projekten und Objekten ist ja nicht schlecht wie aber können Sie neue Objekte hinzufügen oder gar völlig neue Projekte erstellen? Die Antwort
5.2 Neue Projekte erstellen Das Bearbeiten von bestehenden Projekten und Objekten ist ja nicht schlecht wie aber können Sie neue Objekte hinzufügen oder gar völlig neue Projekte erstellen? Die Antwort
Informationen zur Verwendung von Visual Studio und cmake
 Inhaltsverzeichnis Informationen zur Verwendung von Visual Studio und cmake... 2 Erste Schritte mit Visual Studio... 2 Einstellungen für Visual Studio 2013... 2 Nutzung von cmake... 6 Installation von
Inhaltsverzeichnis Informationen zur Verwendung von Visual Studio und cmake... 2 Erste Schritte mit Visual Studio... 2 Einstellungen für Visual Studio 2013... 2 Nutzung von cmake... 6 Installation von
4 Aufzählungen und Listen erstellen
 4 4 Aufzählungen und Listen erstellen Beim Strukturieren von Dokumenten und Inhalten stellen Listen und Aufzählungen wichtige Werkzeuge dar. Mit ihnen lässt sich so ziemlich alles sortieren, was auf einer
4 4 Aufzählungen und Listen erstellen Beim Strukturieren von Dokumenten und Inhalten stellen Listen und Aufzählungen wichtige Werkzeuge dar. Mit ihnen lässt sich so ziemlich alles sortieren, was auf einer
Albert HAYR Linux, IT and Open Source Expert and Solution Architect. Open Source professionell einsetzen
 Open Source professionell einsetzen 1 Mein Background Ich bin überzeugt von Open Source. Ich verwende fast nur Open Source privat und beruflich. Ich arbeite seit mehr als 10 Jahren mit Linux und Open Source.
Open Source professionell einsetzen 1 Mein Background Ich bin überzeugt von Open Source. Ich verwende fast nur Open Source privat und beruflich. Ich arbeite seit mehr als 10 Jahren mit Linux und Open Source.
Propädeutikum. Dipl.-Inf. Frank Güttler
 Propädeutikum 2015 Vorbereitungskurs Informatikstudium Erfolgreich Studieren Programmieren (C-Kurs) guettler@informatik.uni-leipzig.de Universität Leipzig Institut für Informatik Technische Informatik
Propädeutikum 2015 Vorbereitungskurs Informatikstudium Erfolgreich Studieren Programmieren (C-Kurs) guettler@informatik.uni-leipzig.de Universität Leipzig Institut für Informatik Technische Informatik
Grundlagen von CUDA, Sprachtypische Elemente
 Grundlagen von CUDA, Sprachtypische Elemente Stefan Maskanitz 03.07.2009 CUDA Grundlagen 1 Übersicht 1. Einleitung 2. Spracheigenschaften a. s, Blocks und Grids b. Speicherorganistion c. Fehlerbehandlung
Grundlagen von CUDA, Sprachtypische Elemente Stefan Maskanitz 03.07.2009 CUDA Grundlagen 1 Übersicht 1. Einleitung 2. Spracheigenschaften a. s, Blocks und Grids b. Speicherorganistion c. Fehlerbehandlung
Dokumentation von Ük Modul 302
 Dokumentation von Ük Modul 302 Von Nicolas Kull Seite 1/ Inhaltsverzeichnis Dokumentation von Ük Modul 302... 1 Inhaltsverzeichnis... 2 Abbildungsverzeichnis... 3 Typographie (Layout)... 4 Schrift... 4
Dokumentation von Ük Modul 302 Von Nicolas Kull Seite 1/ Inhaltsverzeichnis Dokumentation von Ük Modul 302... 1 Inhaltsverzeichnis... 2 Abbildungsverzeichnis... 3 Typographie (Layout)... 4 Schrift... 4
Automatisierung ( Fernsteuerung ) von Excel unter Microsoft Windows Tilman Küpper (tilman.kuepper@hm.edu)
 HMExcel Automatisierung ( Fernsteuerung ) von Excel unter Microsoft Windows Tilman Küpper (tilman.kuepper@hm.edu) Inhalt 1. Einleitung...1 2. Beispiele...2 2.1. Daten in ein Tabellenblatt schreiben...2
HMExcel Automatisierung ( Fernsteuerung ) von Excel unter Microsoft Windows Tilman Küpper (tilman.kuepper@hm.edu) Inhalt 1. Einleitung...1 2. Beispiele...2 2.1. Daten in ein Tabellenblatt schreiben...2
Dokumentation IBIS Monitor
 Dokumentation IBIS Monitor Seite 1 von 16 11.01.06 Inhaltsverzeichnis 1. Allgemein 2. Installation und Programm starten 3. Programmkonfiguration 4. Aufzeichnung 4.1 Aufzeichnung mitschneiden 4.1.1 Inhalt
Dokumentation IBIS Monitor Seite 1 von 16 11.01.06 Inhaltsverzeichnis 1. Allgemein 2. Installation und Programm starten 3. Programmkonfiguration 4. Aufzeichnung 4.1 Aufzeichnung mitschneiden 4.1.1 Inhalt
Nach der Anmeldung im Backend Bereich landen Sie im Kontrollzentrum, welches so aussieht:
 Beiträge erstellen in Joomla Nach der Anmeldung im Backend Bereich landen Sie im Kontrollzentrum, welches so aussieht: Abbildung 1 - Kontrollzentrum Von hier aus kann man zu verschiedene Einstellungen
Beiträge erstellen in Joomla Nach der Anmeldung im Backend Bereich landen Sie im Kontrollzentrum, welches so aussieht: Abbildung 1 - Kontrollzentrum Von hier aus kann man zu verschiedene Einstellungen
Zeichen bei Zahlen entschlüsseln
 Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Parallele Algorithmen mit OpenCL. Universität Osnabrück, Henning Wenke,
 Parallele Algorithmen mit OpenCL Universität Osnabrück, Henning Wenke, 203-04-24 Was bisher geschah Host Device Platform Führt aus Führt aus Device Context Applikation Java, C++, Kernel (OpenCL C) Memory
Parallele Algorithmen mit OpenCL Universität Osnabrück, Henning Wenke, 203-04-24 Was bisher geschah Host Device Platform Führt aus Führt aus Device Context Applikation Java, C++, Kernel (OpenCL C) Memory
2 Darstellung von Zahlen und Zeichen
 2.1 Analoge und digitale Darstellung von Werten 79 2 Darstellung von Zahlen und Zeichen Computer- bzw. Prozessorsysteme führen Transformationen durch, die Eingaben X auf Ausgaben Y abbilden, d.h. Y = f
2.1 Analoge und digitale Darstellung von Werten 79 2 Darstellung von Zahlen und Zeichen Computer- bzw. Prozessorsysteme führen Transformationen durch, die Eingaben X auf Ausgaben Y abbilden, d.h. Y = f
Lexware professional und premium setzen bis einschließlich Version 2012 den Sybase SQL-Datenbankserver
 Eine Firewall für Lexware professional oder premium konfigurieren Inhaltsverzeichnis: 1. Allgemein... 1 2. Einstellungen... 1 3. Die Firewall von Windows 7 und Windows 2008 Server... 2 4. Die Firewall
Eine Firewall für Lexware professional oder premium konfigurieren Inhaltsverzeichnis: 1. Allgemein... 1 2. Einstellungen... 1 3. Die Firewall von Windows 7 und Windows 2008 Server... 2 4. Die Firewall
Installation SQL- Server 2012 Single Node
 Installation SQL- Server 2012 Single Node Dies ist eine Installationsanleitung für den neuen SQL Server 2012. Es beschreibt eine Single Node Installation auf einem virtuellen Windows Server 2008 R2 mit
Installation SQL- Server 2012 Single Node Dies ist eine Installationsanleitung für den neuen SQL Server 2012. Es beschreibt eine Single Node Installation auf einem virtuellen Windows Server 2008 R2 mit
INHALT 1. INSTALLATION DES V-MODELL XT UNTER WINDOWS 7 2. INSTALLATION DES V-MODELL XT UNTER WINDOWS VISTA
 INHALT 1. INSTALLATION DES V-MODELL XT UNTER WINDOWS 7 2. INSTALLATION DES V-MODELL XT UNTER WINDOWS VISTA 1. INSTALLATION DES V-MODELL XT UNTER WINDOWS 7 VORBEDINGUNGEN Als Vorbedingungen sollte bereits
INHALT 1. INSTALLATION DES V-MODELL XT UNTER WINDOWS 7 2. INSTALLATION DES V-MODELL XT UNTER WINDOWS VISTA 1. INSTALLATION DES V-MODELL XT UNTER WINDOWS 7 VORBEDINGUNGEN Als Vorbedingungen sollte bereits
GPGPU-Architekturen CUDA Programmiermodell Beispielprogramm. Einführung CUDA. Ralf Seidler. Friedrich-Alexander-Universität Erlangen-Nürnberg
 Einführung CUDA Friedrich-Alexander-Universität Erlangen-Nürnberg PrakParRA, 18.11.2010 Outline 1 GPGPU-Architekturen 2 CUDA Programmiermodell 3 Beispielprogramm Outlook 1 GPGPU-Architekturen 2 CUDA Programmiermodell
Einführung CUDA Friedrich-Alexander-Universität Erlangen-Nürnberg PrakParRA, 18.11.2010 Outline 1 GPGPU-Architekturen 2 CUDA Programmiermodell 3 Beispielprogramm Outlook 1 GPGPU-Architekturen 2 CUDA Programmiermodell
