Das Verhalten realer Gase Modellbildung, Grenzen und Kurvendiskussion
|
|
|
- Henriette Kurzmann
- vor 6 Jahren
- Abrufe
Transkript
1 erfasser : Jan Keuer JKeuer@addcom.de Roswitha-Gymnasium Bad Gandersheim Mathematiurs MaL11 Schuljahr 1998/99 Das erhalten realer Gase Modellbildung, Grenzen und Kurvendisussion Facharbeit erfasser : Jan Keuer Betreuer : StR Jörg Wimmel Ausgabetermin : Abgabetermin : Bewertung :
2 Unterschrift Schüler Unterschrift Fachlehrer 1. Einleitung Für die Behandlung des erhaltens realer Gase ist es hilfreich, sich zunächst mit den Grundlagen der heorie der sogenannten idealen Gase vertraut zu machen. Dadurch, daß ein Gas exat den Gesetzen der idealen Gase folgt, ergibt sich erst die Notwendigeit, sich mit realen Gasen genauer zu beschäftigen und eigene Gesetzmäßigeiten für sie zu entwiceln. Bei der Betrachtung eines idealen Gases wird außer Acht gelassen, daß die Gasmoleüle ein Eigenvolumen besitzen, welches das Gesamtvolumen des Gases, wenn zunächst auch nur geringfügig, beeinflußt. Ebenso wird z.b. nicht berücsichtigt, daß im Gas intermoleulare Wechselwirungen ( Anziehungsräfte ) herrschen, die das erhalten des Gases im geschlossenen Raum beeinflussen. Da Meßergebnisse durch diese Fatoren unter normalen Bedingungen nicht sehr star beeinflußt werden, genügt es häufig, das erhalten realer Gase über die Gleichungen der idealen Gase zu bestimmen und die entstehenden Fehler nicht zu berücsichtigen. Die Fehler, die hierbei auftreten, werden zudem mit leiner werdendem Druc und steigender emeratur, also mit zunehmender erdünnung des Gases, zunehmend leiner. Für genauere Ergebnisse, die reale Gase betreffen, bedarf es aber einiger verbesserter Zustandsgleichungen, die die oben genannten Fatoren ( Eigenvolumen etc. ) berücsichtigen. Im nächsten Kaitel soll zunächst aber nur das erhalten der idealen Gase ( eigentl. das ideale Gas, da es nur das eine, theoretische Modell gibt )beschrieben werden. Im dritten Kaitel werden dann die realen Gase mit ihren Zustandsgleichungen beschrieben. Sollte hier nichts anderes erwähnt sein, gelten alle Gleichungen und Aussagen für jeweils ein mol des Gases, da dies die zur Berechnung am häufigsten benutzte Gasmenge ist.
3 Ideale Gase Geht man, laut dem Gesetz von GAY-LUSSAC, von einer bestimmten Gasmenge aus, die bei einem bestimmten Druc und einer emeratur das olumen hat und erwärmt diese Gasmenge bei gleichbleibendem Druc auf eine beliebige emeratur, so gilt für das neue olumen 1 des Gases die Gleichung : 1 (a) Nun ann man nach dem BOYLE-MARIOEschen Gesetz die olumenänderung von 1 auf bei onstant gehaltener emeratur durch Änderung des Druces von auf den Druc berechnen. Hier gilt für das neue olumen : 1 oder : 1 (b) Nun setzt man in Gleichung (b) 1 aus Gleichung (a) ein und erhält so folgende Gleichung : (c) Eine Division durch ergibt dann : Diese Gleichung (d) sagt aus, daß der erm (d) für ein ideales Gas immer onstant ist, sich also auch berechnen läßt, da der Wert bei den Ausgangsbedingungen der gleiche ist wie bei beliebigen Endwerten. Diese Konstante hat, je nachdem, welche Einheiten man für Druc, emeratur und olumen verwendet, verschiedene Werte.
4 Diese Konstante wächst, bei gleichem Druc, olumen und emeratur, roortional mit der eilchenzahl. - - Bei 1 atm Druc, C und dem daraus resultierenden Molvolumen von,414 l ergibt sich dann als universelle Gasonstante R folgender Wert : mol l 1atm,414 R mol 7,14 K atm l,86 K mol (siehe auch : BRDIČKA : Grundlagen der hysial. Chemie, S.196) Also ergibt sich aus der Gleichung, daß R sein muß. Aus dieser Gleichung ergibt sich dann die absolut zentrale ideale Zustandsgleichung (für ein mol Gas ) : R Für n mole Gas wäre entsrechend : nr In den allermeisten Fällen gehen alle anderen Gleichung von dieser atsache, daß der Druc multiliziert mit dem olumen gleich der emeratur multiliziert mit einer Konstanten ( und gegebenenfalls mal die Anzahl der mole ) ist, aus, oder werden von ihr abgeleitet auch die meisten Gleichungen der realen Gase, wie wir noch sehen werden.
5 Das erhalten idealer Gase Die Gleichung R, nach aufgelöst, ergibt nun die Funtion f ( ), 85, (e) die bei jeweils onstanter emeratur und für ein mol ideales Gas, ein -- Diagramm mit folgenden Grahen ergibt : --Diagram m für 1 mol ideales Gas 16 Druc ( atm ) K K 5 K 7 K olumen ( l ) Die Grahen dieser Funtion haben alle einen zweiten Arm, der genau symmetrisch zur y-achse verläuft. Dieser läßt sich hier jedoch vernachlässigen, da diese Funtionswerte ein negatives olumen voraussetzen würden, was hysialisch unmöglich ist. Deutlich zu sehen ist hier, daß sämtliche Grahen streng monoton fallend sind, was auch die Ableitung zeigt. Sie lautet : R f ( ) (f)
6 Sie ist im gesamten Bereich negativ, da der Zähler hier immer negativ und der Nenner immer ositiv ist. Diese Grahen sind auch anschaulich logisch zu erlären, da sich mit steigendem Druc von außen das olumen stetig verleinern muß Diese Grahen zeigen auch, daß sich ein ideales Gas nicht verflüssigen läßt, bei einem beliebig hohen Druc und einer beliebig niedrigen emeratur! Eine erflüssigung würde nämlich bedeuten, daß der Grah bei einem bestimmten Druc waagerecht zur x-achse laufen müßte, das olumen also bei gleichbleibendem Druc star verringert würde, was in der Realität Meßergebnisse zeigen würden. Wenn die Ableitung (f) jedoch eine Nullstelle hat, ist die Ausgangsfuntion streng monoton fallend :,85 (g) Gleichung (g) hat nur eine Lösung für, hier wäre der Druc aber für alle Ableitungen der --Kurven K K 5 K 7 K olumina, was hysialisch unmöglich ist. Für alle emeraturen über K ergibt sich jedoch eine Lösung für diese Gleichung (g). Sie zeigt für emeraturen über K obige Kurvenschar, deren Kurven eine Nullstelle haben, was heißt, daß die Ausgangsurven tatsächlich streng monoton fallend sind, da hier für alle emeraturen (ausgenommen K) der Monotoniesatz gilt, der besagt, daß eine Funtion f(x) streng monoton fallend ist, wenn für alle x gilt : f (x) <, was hier zutrifft.
7 - 5 - Eine erflüssigung ommt durch die Anziehungsräfte der Moleüle untereinander zustande.da diese, wie schon in der Einleitung erwähnt, bei idealen Gasen jedoch nicht berücsichtigt werden, ließe sich ein ideales Gas also nicht verflüssigen - es wäre, da die Moleüle eines idealen Gases ein Eigenvolumen besitzen, unendlich weit omressibel, bis zu einem olumen von. Da sich aber jedes Gas, nötigenfalls bei sehr hohen Drücen und / oder sehr tiefen emeraturen, verflüssigen läßt, und auch ein Gas das olumen einnehmen ann, tritt bei den Gleichungen der idealen Gase zur Beschreibung der realen Gase offensichtlich ein Fehler auf, der besonders schwerwiegend ist, wenn man nun den organg des erflüssigens von Gasen berechnen möchte. Um das Eigenvolumen, die Wechselwirungen u.s.w. zu berücsichtigen, bedürfen die Zustandsgleichungen der idealen Gase anscheinend einiger Korreturen.
8 Reale Gase Im 19. Jahrhundert haben sich viele Wissenschaftler mit dem erhalten von Gasen und besonders mit dem organg des erflüssigens beschäftigt. Hierbei haben sie festgestellt, daß die exerimentell ermittelten Kurven nicht ganz den Kurven der idealen Gase folgen, sondern von ihnen abweichen. Dies ist besonders star in dem Bereich der Kurve zu sehen, in dem sich das Gas verflüssigt. Da die Zustandsgleichungen der idealen Gase eine erflüssigung vorsehen, mußten sie orrigiert werden. In den Gleichungen mußten das Eigenvolumen der Gasmoleüle sowie die intermoleularen Wechselwirungen berücsichtigt werden, um reale Gase besser zu beschreiben. J. van der Waals hat die wohl beannteste Gleichung, die wohl auch am häufigsten benutzt wird, aufgestellt. Er hat die ideale Zustandsgleichung R ( für 1 mol Gas ) folgendermaßen orrigiert : Er subtrahierte vom olumen einen eil b, der inomressibel ist, also das Eigenvolumen der Gasmoleüle darstellt. Zusätzlich addierte er zum Druc den sogenannten Binnendruc, der im Gas herrscht. Dieser eil stellt die Anziehungsräfte zwischen den Moleülen dar. Prallen Moleüle an eine Wand, so überwiegen die Anziehungsräfte der Moleüle, die nach innen wiren. Diese Kraft ist roortional der Anzahl der Moleüle in der olumeneinheit des Gases bzw. seiner Dichte. Die Anzahl der Moleüle in der Grenzfläche ist ihrerseits jedoch auch der Dichte des Gases roortional, so daß der resultierende innere Druc roortional dem Quadrat der Dichte oder umgeehrt roortional dem Quadrat des Molvolumens ist ( 1). So ergibt
9 sich die zentrale Zustandsgleichung der realen Gase, die van-der-waalssche Gleichung ( hier für 1 mol ) : a + ( b) R (h) Der Proortionalitätsfator a, der für die Anziehungsräfte steht, und der Wert b sind für jedes Gas unterschiedliche Werte, wobei b nach van der Waals gleich dem vierfachen des Eigenvolumens der Moleüle ist Das erhalten realer Gase Diese Zustandsgleichung (h) nach aufgelöst ergibt die Gleichung R a ( b), (i) ( b) die als Funtion R a ( b) f ( ) folgende Kurven ergibt, bei denen ( b) die emeratur jeweils onstant gehalten wurde und für a und b die idealen Werte für Wasser, nämlich a5,58 und b,1 und R,86 eingesetzt wurden, die in entsrechenden Einheiten angegeben werden müssen, damit sie in der Gleichung angewandt werden önnen. --Diagramm für 1 mol Wasser Druc (atm) ,,4,6,8 1 olumen (l) 7 K 47 K 57 K 647 K 77 K In folgender abelle sind die Parameter für einige Stoffe angegeben :
10 atm l Stoff a ( mol l ) b ( mol H,19, H O 5,58,1 ) N 1,7,9 O 1,8, CO,67,4 ( aus : Greiner,Neise,Stöcer : hermodyn. und Statist. Mathem. ; S. ) Deutlich zu sehen ist bei Kurven unter 647 K, daß sie ein loales Minimum sowie ein loales Maximum und zwei Wendeunte haben. Hier erhält man für einen Druc drei Werte für das Molvolumen. Oberhalb dieser emeratur erhält man nur einen reellen Wert ( hyerbelartiger erlauf ). Unterhalb von 647 K sind es jedoch Kurven. Ordnung. Hier lassen sich auch, sofern vorhanden, die Nullstellen der Funtion berechnen. Der Bereich zwischen den Nullstellen ist hysialisch gesehen völlig irreal, da hier der Druc negativ wäre. Das bedeutet, hier wäre der Binnendruc a zu groß. Das gilt z.b. für Wasser bei der emeratur 47 K im Intervall ],45;,9855[, da die Nullstellen der Funtion hier liegen : a + ( b) R nach aufgelöst mit a5,58, b,1, R,85 und 47 K und gleich null gesetzt : 8,89 (,14 +,45) (,1) (j) Nullstellen :, n1 45, n 9855 Außerdem haben die Kurven unterhalb von 647 K einen Abschnitt zwischen den loalen Extrema, in dem der Grah steigt. Das bedeutet, daß hier mit abnehmendem Druc auch das olumen leiner wird, das Gas verdichtet
11 sich selbständig, was zunächst unmöglich erscheint. In diesem Bereich findet jedoch die erflüssigung des Gases statt, die Anziehungsräfte der Moleüle ziehen das Gas sozusagen zusammen. Oberhalb der 647 K gibt es diese Extrema nicht mehr, das heißt, das Gas ann nicht verflüssigt werden, auch nicht bei dem größten Druc oder dem leinsten olumen. Die emeratur, oberhalb der es nicht mehr möglich ist, ein Gas zu verflüssigen, nennt man Boyle emeratur oder auch, seltener, ritische emeratur. Sie beträgt z.b. bei Wasser 647 K oder 74 C Um nun den Bereich auf dem Grahen zu bestimmen, in dem die erflüssigung stattfindet, muß durch einen Punt auf dem Grahen, der zwischen dem Minimum und dem Maximum liegt, eine Gerade, die arallel zur x-achse läuft, gezogen werden. Die beiden Flächen zwischen der Geraden und dem Grahen, die über dem Minimum bzw. unter dem Zur erflüssigung eines Gases Druc (atm) 5 4 1,,4,6 --Kurve eines realen Gases erlauf der Kurve bei exerimenteller Ermittlung olumen (l) Maximum liegen, müssen zusätzlich exat gleich groß sein. Diese Gerade schneidet den Grahen dreimal, nämlich einmal lins des Minimums, zwischen den Extrema und rechts des Maximums. Die Schnittunte der Geraden mit dem Grahen lins und rechts der loalen Extrema zeigen nun die Grenzen des Phasenüberganges an. Erhöht man den
12 Druc, beginnt das Gas beim Schnittunt rechts des Maximums, sich zu verflüssigen und ist beim Schnittunt lins des Minimums vollständig verflüssigt. Ab hier ist die Steigung der Kurve viel stärer negativ, was bedeutet, daß auch große Drucerhöhungen nur leine olumenverleinerungen bewiren, was auch anschaulich logisch ist, da sich eine Flüssigeit schwieriger omrimieren läßt als ein Gas. Die Gerade zeigt auch den erlauf der Kurve an, die exerimentell ermittelt werden würde, da hier das olumen bei einem bestimmten Druc lötzlich leiner wird ohne, daß der Druc weiter erhöht wird. Im Exeriment ann es auch den Bereich, in dem mit steigendem Druc das olumen größer wird ( zwischen den Extrema ), nicht geben Berechnung der Konstanten Der Druc, der bei der ritischen emeratur ( Boyle-emeratur ) aufgewendet werden muß, um das Gas zu verflüssigen, wird der ritische Druc genannt. Das olumen des Gases bei der ritischen emeratur und dem ritischen Druc ist das ritische olumen ( ). Sie önnen exerimentell bestimmt werden oder auch rechnerisch, wie im folgenden gezeigt wird. Die ritischen Werte eines Gases hängen nämlich mit den Konstanten a und b der van-der-waals Gleichung zusammen. Um sie zu berechnen, benötigt man die van-der-waalssche Gleichung für den ritischen Zustand eines Gases, die lautet : R a a b b + + () Aus der atsache, daß im ritischen Punt alle drei Wurzeln der ubischen Gleichung für gleich dem ritischen olumen sind, folgt : ( ) Diese Gleichung (l) ausmultiliziert ergibt nun : ( ) (l)
13 + (m) Jetzt önnen die Koeffizienten der Gleichungen () und (m) miteinander verglichen werden, und man erhält : b R + ; a ; a b (n) Hieraus ergibt sich : b (o) Jetzt ann man in (n) einsetzen : ab ab 7 b () Multiliziert mit und dann dividiert durch 7b : b ab 7 ab 7b Geürzt ergibt sich dann für : a 7b (q) Jetzt setzt man die Gleichungen (o) und (r) in b R + ein und ann so folgendermaßen bestimmen : Division durch : R 7b 9b b + (r) a 9b R 7b a b + (s) Division durch 9b : 1 7b R 9a + a (t)
14 Durch Kürzen erhalten wir jetzt : 1 7b R oder 8a 8a 7 b R (u) Also erhalten wir zusammengefaßt folgende Definitionen der ritischen Werte eines realen Gases mit Hilfe der van-der-waalsschen Konstanten a und b : a 8a b ; ; 7b 7 b R Man ann umgeehrt auch die van-der-waalsschen Konstanten über die ritischen Konstanten bestimmen, die exerimentell bestimmt werden önnen. Folglich önnen die Konstanten a und b, sowie die universelle Gasonstante R auch auf exerimentellem Wege bestimmt werden : Durch Umformung von ab ergibt sich : a Ebenso durch Umformung ergibt sich aus b : b Die Gasonstante R ergibt sich wie folgt : 8a In setzen wir für a und b die oben ermittelten Werte ein : 7 b R ( ) 8 7 R Die Klammern aufgelöst ergibt und mit R multiliziert ergibt : (v) 4 R 9 (w) Durch geteilt und geürzt ergibt schließlich : 8 R (x) (siehe auch zu.. : BRDIÇKA ; Grundlagen der hysial. Chemie, S.5 f.)
15 .. Weitere Zustandsgleichungen Eine weitere häufig benutzte Zustandsgleichung zur Beschreibung des erhaltens realer Gase ist die CLAUSIUSsche irialgleichung. Sie ist im Prinzi ebenfalls eine erweiterte Zustandsgleichung der idealen Gase. Sie lautet : + R + B( ) + C( ) D( )... Die Koeffizienten B,C,D... nennt man irialoeffizienten, die für jedes Gas unterschiedlich sind. Sie sind von der emeratur abhängig. Zur ereinfachung wird häufig beim linearen erm abgebrochen : R + B( ) Wird die Zustandsgleichung nicht nach dem Druc, sondern nach der Dichte entwicelt, sieht die irialentwiclung folgendermaßen aus : N N R + B ( ) + C ( )... (aus : Greiner, Neise, Stöcer : hermodynami und statistische Mechani, S.18) Natürlich önnen alle Gleichungen auch für eine beliebige eilchenzahl und nicht unbedingt für ein mol Gas aufgestellt werden, am häufigsten wird jedoch diese Menge betrachtet. Die ideale Zustandsgleichung lautet dann z.b. für N eilchen : N (y) Die Konstante ist die BOLZMANNsche Proortionalitätsonstante, deren J Wert 1,866 ±,1 1 beträgt ( 4 ). Bei N 6 1 eilchen, also gerade K einem mol eilchen, ergibt sich für N die Gasonstante R, womit die Gleichung wieder R lautet. Ebenso läßt sich auch die van-der- Waalssche Gleichung für N mol anwenden :
16 + N a ( Nb) N (z) (siehe hierzu auch : Greiner,Neise,Stöcer:hermodyn. Und statist. Mechani,S.8,18,19) Es gibt auch eine vereinfachte Form der van-der-waals-gleichung, bei der ab nach Auflösen der Klammern das Glied vernachlässigt wird, da es in R vielen Fällen, wenn man für setzt, um den Wert 1 liegt, und bei a R ebenfalls für nach der idealen Zustandsgleichung eingesetzt wird. Dann erhält man : a R + b (A) R (siehe : BRDIČKA : Grundlagen der hysial. Chemie, S. 47 ) ergleicht man diese Gleichung mit der CLAUSIUSschen irialentwiclung, die beim linearen erm abgebrochen wurde, so sieht man, daß a B b sein muß. Diese Gleichung (A) zeigt auch, wie star der erm R bei realen Gasen vom Wert R bei idealen Gasen abweicht. Bei niedrigen emeraturen ist der erm R a >b, so daß mit steigendem a Druc abnimmt, bei hohen emeraturen ist b>, vergrößert sich also R mit steigendem Druc. Die emeratur, bei der emeratur, oder auch Boyle-emeratur. a b ist, ist die ritische R (vgl. hierzu : BRDIÇKA, Grundlagen der hysial. Chemie, S.47)
17 Abschließend hier noch einmal alle wichtigen Gleichungen und Beziehungen : Die ideale Zustandsgleichung für ein mol : R und für n mol : nr wobei R, je nach verwendeten Einheiten, z.b. atm l,86 ist. K mol Die van-der-waalssche Zustandsgleichung der realen Gase lautet für ein mol : oder für N eilchen : a + ( b) R N + a ( Nb) N Die van-der-waals-gleichung nach aufgelöst, ergibt die Funtion R a ( b) f ( ), ( b) deren Grahen das --Diagramm der realen Gase zeigen. Die Konstanten a, b und R stehen folgendermaßen mit den ritischen Werten, und in Zusammenhang : und a ; b ; a b ; ; 7b 8 R 8 a 7 b R
18 Die Clausiussche irialgleichung lautet, wenn sie nach Drücen entwicelt wird : + R + B( ) + C( ) D( )... Sie wird der Einfachheit halber jedoch häufig beim linearen Glied abgebrochen. Im ergleich mit der vereinfachten van-der-waalsschen Gleichung a R + b sieht man, daß der Koeffizient B gleich R a b sein muß. R Literaturverzeichnis 1.) BRDIČKA : Grundlagen der hysialischen Chemie Berlin 1977.) Greiner, Neise, Stöcer : hermodynami und statistische Mechani Franfurt a.m. 1987
19 .) Schülerduden : Die Chemie Kurzverweise : () 1 : BRDIČKA : Grundlagen der hysialischen Chemie S. 46 ( ): BRDIČKA : Grundlagen der hysialischen Chemie S. 5 ( ) : BRDIČKA : Grundlagen der hysialischen Chemie S. 5 ( ) 4 : Greiner, Neise, Stöcer : hermodynami und statistische Mechani, S.9
2.1 Bestimmung einiger Isothermen von Schwefelhexafluorid SF 6
 Atom- und Kernphysi-Versuch 31 AKP-31-1 Zustandsgrößen realer Gase 1 Vorbereitung Koexistenz von Flüssigeiten und Dampf, Dampfdruc, Verdampfungswärme, Koexistenz von Festörper und Flüssigeit, Koexistenz
Atom- und Kernphysi-Versuch 31 AKP-31-1 Zustandsgrößen realer Gase 1 Vorbereitung Koexistenz von Flüssigeiten und Dampf, Dampfdruc, Verdampfungswärme, Koexistenz von Festörper und Flüssigeit, Koexistenz
1. Thermodynamische Potentiale, Maxwellgleichungen
 69 KAPIEL G hermodynamische Potentiale 1. hermodynamische Potentiale, Maxwellgleichungen hermodynamische Potentiale sind Funktionen von den Zustandsvariablen. Wir haben schon die innere Energie kennengelernt,
69 KAPIEL G hermodynamische Potentiale 1. hermodynamische Potentiale, Maxwellgleichungen hermodynamische Potentiale sind Funktionen von den Zustandsvariablen. Wir haben schon die innere Energie kennengelernt,
T p = T = RT. V b. ( ) 2 V p. V b. 2a(V b)2 V 3 RT. 2a(V b) V 3 (p+ a V 2 )
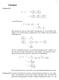 3 Lösung zu 83. Lösungen ( C C = T ( = T ( ( ( 2 van-der-waals Gas: ( ( b + a 2 = T = T b a 2 Man beachte das dies nur eine andere Formulierung der van-der-waals Gleichung ist als auf dem letzten Aufgabenzettel.
3 Lösung zu 83. Lösungen ( C C = T ( = T ( ( ( 2 van-der-waals Gas: ( ( b + a 2 = T = T b a 2 Man beachte das dies nur eine andere Formulierung der van-der-waals Gleichung ist als auf dem letzten Aufgabenzettel.
Polynome. Ein Term der Form. mit n und a 0 heißt Polynom. Die Zahlen a, a, a,... heißen Koeffizienten des Polynoms.
 Polynome Ein Term der Form a x + a x + a x + a x +... + a x + a x + a n n 1 n 2 n 3 2 1 2 3 4 n 2 n 1 n mit n und a 0 heißt Polynom. 1 Die Zahlen a, a, a,... heißen Koeffizienten des Polynoms. 1 2 3 Als
Polynome Ein Term der Form a x + a x + a x + a x +... + a x + a x + a n n 1 n 2 n 3 2 1 2 3 4 n 2 n 1 n mit n und a 0 heißt Polynom. 1 Die Zahlen a, a, a,... heißen Koeffizienten des Polynoms. 1 2 3 Als
Quadratische Funktion
 Quadratische Funktion 1. Übliche Formen 1) Allgemeine Form: y = f(x) = a x 2 + b x + c a, b, c Konstanten Grundlegender Fall a = 1, b = 0, c = 0, also y = x 2 : "Normalparabel" Vorteil: Keine Brüche für
Quadratische Funktion 1. Übliche Formen 1) Allgemeine Form: y = f(x) = a x 2 + b x + c a, b, c Konstanten Grundlegender Fall a = 1, b = 0, c = 0, also y = x 2 : "Normalparabel" Vorteil: Keine Brüche für
Theorie 3: Graphische Veranschaulichung der Fallunterscheidung
 Die Formel von Cardano - mit grahischer Lösung Theorie : Grahische Veranschaulichung der Fallunterscheidung Gegeben ist eine kubische Gleichung in reduzierter Form: x x = 0 mit 0 IR. Definieren Sie einen
Die Formel von Cardano - mit grahischer Lösung Theorie : Grahische Veranschaulichung der Fallunterscheidung Gegeben ist eine kubische Gleichung in reduzierter Form: x x = 0 mit 0 IR. Definieren Sie einen
Lineare Funktionen. Die lineare Funktion
 1 Die lineare Funktion Für alle m, t, aus der Zahlenmenge Q heißt die Funktion f: x m x + t lineare Funktion. Die Definitionsmenge ist Q (oder je nach Zusammenhang ein Teil davon). Der Graph der linearen
1 Die lineare Funktion Für alle m, t, aus der Zahlenmenge Q heißt die Funktion f: x m x + t lineare Funktion. Die Definitionsmenge ist Q (oder je nach Zusammenhang ein Teil davon). Der Graph der linearen
Analysis I Mathematik für InformatikerInnen II SoSe 12 Musterlösungen zur Prüfungsklausur vom 18. Juli 2012
 Humboldt-Universität zu Berlin Mathematisch-Naturwissenschaftliche Faultät II Institut für Mathemati Unter den Linden 6, D-0099 Berlin Prof. Andreas Griewan Ph.D. Dr. Thomas M. Surowiec Dr. Fares Maalouf
Humboldt-Universität zu Berlin Mathematisch-Naturwissenschaftliche Faultät II Institut für Mathemati Unter den Linden 6, D-0099 Berlin Prof. Andreas Griewan Ph.D. Dr. Thomas M. Surowiec Dr. Fares Maalouf
Einführung. Ablesen von einander zugeordneten Werten
 Einführung Zusammenhänge zwischen Größen wie Temperatur, Geschwindigkeit, Lautstärke, Fahrstrecke, Preis, Einkommen, Steuer etc. werden mit beschrieben. Eine Zuordnung f, die jedem x A genau ein y B zuweist,
Einführung Zusammenhänge zwischen Größen wie Temperatur, Geschwindigkeit, Lautstärke, Fahrstrecke, Preis, Einkommen, Steuer etc. werden mit beschrieben. Eine Zuordnung f, die jedem x A genau ein y B zuweist,
Übungsaufgaben zu linearen Gleichungen und Funktionen117
 Übungsaufgaben zu linearen Gleichungen und Funktionen117 Anmerkung: Die Funktionsgraphen sollen den Zusammenhang nur noch einmal veranschaulichen. Sie sind zur Lösung der Aufgabe nicht erforderlich. Die
Übungsaufgaben zu linearen Gleichungen und Funktionen117 Anmerkung: Die Funktionsgraphen sollen den Zusammenhang nur noch einmal veranschaulichen. Sie sind zur Lösung der Aufgabe nicht erforderlich. Die
Aufgabe zum Thema: Gebrochen - rationale Funktionen
 Aufgabe zum Thema: Gebrochen - rationale Funktionen Eine gebrochen-rationale Funktion Z (x) hat als Zähler- N (x) funktion Z (x) eine lineare Funktion und als Nennerfunktion N (x) eine ganz-rationale Funktion
Aufgabe zum Thema: Gebrochen - rationale Funktionen Eine gebrochen-rationale Funktion Z (x) hat als Zähler- N (x) funktion Z (x) eine lineare Funktion und als Nennerfunktion N (x) eine ganz-rationale Funktion
Institut für Physikalische Chemie Albert-Ludwigs-Universität Freiburg
 Institut für Physikalische Chemie Albert-Ludigs-Universität Freiburg Lösungen zum 4. Übungsblatt zur orlesung Physikalische Chemie I SS 00 Prof. Dr. Bartsch 4. (6 Punkte) In einem Behälter mit der Grundfläche
Institut für Physikalische Chemie Albert-Ludigs-Universität Freiburg Lösungen zum 4. Übungsblatt zur orlesung Physikalische Chemie I SS 00 Prof. Dr. Bartsch 4. (6 Punkte) In einem Behälter mit der Grundfläche
Wirtschaftsmathematik
 Wirtschatsmathematik ür die Betriebswirtschatslehre (B.Sc.) Sommersemester 017 Dr. rer. nat. habil. E-mail: adam-georg.balogh@h-da.de 1 Kurvendiskussion / Analyse von Funktionen Anwendung der Dierentialrechnung
Wirtschatsmathematik ür die Betriebswirtschatslehre (B.Sc.) Sommersemester 017 Dr. rer. nat. habil. E-mail: adam-georg.balogh@h-da.de 1 Kurvendiskussion / Analyse von Funktionen Anwendung der Dierentialrechnung
Musterlösung zur Klausur Analysis I für Lehramt Gymnasium Wintersemester 2017/18, am
 Musterlösung zur Klausur Analysis I für Lehramt Gymnasium Wintersemester 07/8, am 9.3.08 Aufgabe : Zeigen Sie, dass für alle n N gilt: n n+ n ( ) (8 Punte) Beweis mittels vollständiger Indution n : ( )
Musterlösung zur Klausur Analysis I für Lehramt Gymnasium Wintersemester 07/8, am 9.3.08 Aufgabe : Zeigen Sie, dass für alle n N gilt: n n+ n ( ) (8 Punte) Beweis mittels vollständiger Indution n : ( )
Höhere Mathematik I für Ingenieurinnen und Ingenieure Lösungen zur 11. und 12. Übung
 TU Bergakademie Freiberg Vorl. Frau Prof. Dr. Swanhild Bernstein Übung Dipl.-Math. Daniel Lorenz Freiberg, WS 017/18 Höhere Mathematik I für Ingenieurinnen und Ingenieure Lösungen zur 11. und 1. Übung
TU Bergakademie Freiberg Vorl. Frau Prof. Dr. Swanhild Bernstein Übung Dipl.-Math. Daniel Lorenz Freiberg, WS 017/18 Höhere Mathematik I für Ingenieurinnen und Ingenieure Lösungen zur 11. und 1. Übung
Bayern Teil 1. Aufgabe 1. Abitur Mathematik: Musterlösung. Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten:
 Abitur Mathematik: Bayern 2013 Teil 1 Aufgabe 1 a) 1. SCHRITT: DEFINITIONSMENGE BESTIMMEN Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten: 3x + 9 0 x 3 2. SCHRITT: NULLSTELLEN
Abitur Mathematik: Bayern 2013 Teil 1 Aufgabe 1 a) 1. SCHRITT: DEFINITIONSMENGE BESTIMMEN Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten: 3x + 9 0 x 3 2. SCHRITT: NULLSTELLEN
Mathematik Semester 3 / Arbeitsblatt f (x) = x x 3 4 x. 5 x 3 20 x. x 2 1
 9.2 Aufgaben Aufgabe 16.39 aus dem Buch. 1. f (x) = x4 + 1 x 3 + x 4. f (x) = x4 1 2 x 3 8 x 2. f (x) = x3 + 1 x 3 4 x 5. f (x) = x5 + 1 5 x 3 20 x 3. f (x) = 4 x2 x 2 + 1 6. f (x) = x2 2 x 2 7. f (x)
9.2 Aufgaben Aufgabe 16.39 aus dem Buch. 1. f (x) = x4 + 1 x 3 + x 4. f (x) = x4 1 2 x 3 8 x 2. f (x) = x3 + 1 x 3 4 x 5. f (x) = x5 + 1 5 x 3 20 x 3. f (x) = 4 x2 x 2 + 1 6. f (x) = x2 2 x 2 7. f (x)
Damit läßt sich die Aufgabe durch einfaches Rechnen zeigen: k=1
 Aufgabe (4 Punte) Sei A eine n m-matrix Die Matrix A T ist die m n-matrix, die durch Vertauschen der Zeilen und Spalten aus A hervorgeht (dh: aus Zeilen werden Spalten, und umgeehrt) Die Matrix A T heißt
Aufgabe (4 Punte) Sei A eine n m-matrix Die Matrix A T ist die m n-matrix, die durch Vertauschen der Zeilen und Spalten aus A hervorgeht (dh: aus Zeilen werden Spalten, und umgeehrt) Die Matrix A T heißt
Vorlesung Mathematik WS 08/09. Friedel Bolle. Vorbemerkung
 Vorlesung Mathemati WS 08/09 Vorbemerung Weshalb Mathemati für Öonomen? Das werden Sie selbst sehen im Grundstudium in - Miroöonomie - Statisti - Maroöonomie - BWL: Prodution und dazu in einer Reihe von
Vorlesung Mathemati WS 08/09 Vorbemerung Weshalb Mathemati für Öonomen? Das werden Sie selbst sehen im Grundstudium in - Miroöonomie - Statisti - Maroöonomie - BWL: Prodution und dazu in einer Reihe von
Physik 4 Praktikum Auswertung Zustandsdiagramm Ethan
 Physik 4 Praktikum Auswertung Zustandsdiagramm Ethan Von J.W., I.G. 2014 Seite 1. Kurzfassung......... 2 2. Theorie.......... 2 2.1. Zustandsgleichung....... 2 2.2. Koexistenzgebiet........ 3 2.3. Kritischer
Physik 4 Praktikum Auswertung Zustandsdiagramm Ethan Von J.W., I.G. 2014 Seite 1. Kurzfassung......... 2 2. Theorie.......... 2 2.1. Zustandsgleichung....... 2 2.2. Koexistenzgebiet........ 3 2.3. Kritischer
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
Differentialrechnung. Mathematik W14. Christina Sickinger. Berufsreifeprüfung. v 1 Christina Sickinger Mathematik W14 1 / 79
 Mathematik W14 Christina Sickinger Berufsreifeprüfung v 1 Christina Sickinger Mathematik W14 1 / 79 Die Steigung einer Funktion Wir haben bereits die Steigung einer linearen Funktion kennen gelernt! Eine
Mathematik W14 Christina Sickinger Berufsreifeprüfung v 1 Christina Sickinger Mathematik W14 1 / 79 Die Steigung einer Funktion Wir haben bereits die Steigung einer linearen Funktion kennen gelernt! Eine
Mathe - Lernzettel: Nullstellen, Monotonie und Ableitungen
 Mathe - Lernzettel: Nullstellen, Monotonie und Ableitungen Leun4m 29. April 2015 Version: 0 Ich kann nicht für Richtigkeit garantieren! Inhaltsverzeichnis 1 Themenübersicht 1 2 Funktionen und Graphen 2
Mathe - Lernzettel: Nullstellen, Monotonie und Ableitungen Leun4m 29. April 2015 Version: 0 Ich kann nicht für Richtigkeit garantieren! Inhaltsverzeichnis 1 Themenübersicht 1 2 Funktionen und Graphen 2
Kurvendiskussion von Polynomfunktionen
 Kurvendiskussion von Polynomfunktionen Theorie: Für die weiteren Berechnungen benötigen wie die 1. f (x) und 2. f (x) Ableitung der zu untersuchenden Funktion f (x). Wir werden viele Gleichungen lösen
Kurvendiskussion von Polynomfunktionen Theorie: Für die weiteren Berechnungen benötigen wie die 1. f (x) und 2. f (x) Ableitung der zu untersuchenden Funktion f (x). Wir werden viele Gleichungen lösen
Basistext Kurvendiskussion
 Basistext Kurvendiskussion In einer Kurvendiskussion sollen zu einer vorgegebenen Funktion (bzw. Funktionsschar) Aussagen über ihrem Verlauf gemacht werden. Im Nachfolgenden werden die einzelnen Untersuchungspunkte
Basistext Kurvendiskussion In einer Kurvendiskussion sollen zu einer vorgegebenen Funktion (bzw. Funktionsschar) Aussagen über ihrem Verlauf gemacht werden. Im Nachfolgenden werden die einzelnen Untersuchungspunkte
4. Anwendung der Differentialrechnung: Kurvendiskussion 4.1. Maxima und Minima einer Funktion.
 4. Anwendung der Differentialrechnung: Kurvendiskussion 4.1. Maxima und Minima einer Funktion. Definition 4.3. Es sei f : R D R eine auf D erklarte Funktion. Die Funktion f hat in a D eine globales oder
4. Anwendung der Differentialrechnung: Kurvendiskussion 4.1. Maxima und Minima einer Funktion. Definition 4.3. Es sei f : R D R eine auf D erklarte Funktion. Die Funktion f hat in a D eine globales oder
Kapitel 8 Einführung der Integralrechnung über Flächenmaße
 8. Flächenmaße 8.1 Flächenmaßfunktionen zu nicht negativen Randfunktionen Wir wenden uns einem auf den ersten Blick neuen Thema zu, der Ermittlung des Flächenmaßes A von Flächen A, die vom nicht unterhalb
8. Flächenmaße 8.1 Flächenmaßfunktionen zu nicht negativen Randfunktionen Wir wenden uns einem auf den ersten Blick neuen Thema zu, der Ermittlung des Flächenmaßes A von Flächen A, die vom nicht unterhalb
1 Polynome III: Analysis
 1 Polynome III: Analysis Definition: Eine Eigenschaft A(x) gilt nahe bei a R, falls es ein δ > 0 gibt mit A(x) gilt für alle x (a δ, a + δ)\{a} =: U δ (a) Beispiele: x 2 5 nahe bei 0 (richtig). Allgemeiner:
1 Polynome III: Analysis Definition: Eine Eigenschaft A(x) gilt nahe bei a R, falls es ein δ > 0 gibt mit A(x) gilt für alle x (a δ, a + δ)\{a} =: U δ (a) Beispiele: x 2 5 nahe bei 0 (richtig). Allgemeiner:
Dieses Kapitel vermittelt:
 2 Funktionen Lernziele Dieses Kapitel vermittelt: wie die Abhängigkeit quantitativer Größen mit Funktionen beschrieben wird die erforderlichen Grundkenntnisse elementarer Funktionen grundlegende Eigenschaften
2 Funktionen Lernziele Dieses Kapitel vermittelt: wie die Abhängigkeit quantitativer Größen mit Funktionen beschrieben wird die erforderlichen Grundkenntnisse elementarer Funktionen grundlegende Eigenschaften
Skript Analysis. sehr einfach. Erstellt: Von:
 Skript Analysis sehr einfach Erstellt: 2017 Von: www.mathe-in-smarties.de Inhaltsverzeichnis Vorwort... 2 1. Funktionen... 3 2. Geraden... 6 3. Parabeln... 9 4. Quadratische Gleichungen... 11 5. Ableitungen...
Skript Analysis sehr einfach Erstellt: 2017 Von: www.mathe-in-smarties.de Inhaltsverzeichnis Vorwort... 2 1. Funktionen... 3 2. Geraden... 6 3. Parabeln... 9 4. Quadratische Gleichungen... 11 5. Ableitungen...
Wärmelehre/Thermodynamik. Wintersemester 2007
 Einführung in die Physik I Wärmelehre/hermodynamik Wintersemester 7 ladimir Dyakonov #3 am..7 Folien unter: htt://www.hysik.uni-wuerzburg.de/ep6/teaching.html.3 Ideales Gas Exerimentelle Bestimmung der
Einführung in die Physik I Wärmelehre/hermodynamik Wintersemester 7 ladimir Dyakonov #3 am..7 Folien unter: htt://www.hysik.uni-wuerzburg.de/ep6/teaching.html.3 Ideales Gas Exerimentelle Bestimmung der
Lineare Funktion. Wolfgang Kippels 21. März 2011
 Lineare Funktion Wolfgang Kippels. März 0 Inhaltsverzeichnis Grundlegende Zusammenhänge. Aufbau der Linearen Funktion......................... Nullstellenbestimmung............................. Schnittpunktbestimmung............................
Lineare Funktion Wolfgang Kippels. März 0 Inhaltsverzeichnis Grundlegende Zusammenhänge. Aufbau der Linearen Funktion......................... Nullstellenbestimmung............................. Schnittpunktbestimmung............................
6 Die Bedeutung der Ableitung
 6 Die Bedeutung der Ableitung 24 6 Die Bedeutung der Ableitung Wir wollen in diesem Kapitel diskutieren, inwieweit man aus der Kenntnis der Ableitung Rückschlüsse über die Funktion f ziehen kann Zunächst
6 Die Bedeutung der Ableitung 24 6 Die Bedeutung der Ableitung Wir wollen in diesem Kapitel diskutieren, inwieweit man aus der Kenntnis der Ableitung Rückschlüsse über die Funktion f ziehen kann Zunächst
Quadratische Funktionen
 Quadratische Funktionen Mag. DI Rainer Sickinger HTL v 2 Mag. DI Rainer Sickinger Quadratische Funktionen 1 / 33 Definition Quadratische Funktion Definition (Quadratische Funktion) Sei D R und f : D R
Quadratische Funktionen Mag. DI Rainer Sickinger HTL v 2 Mag. DI Rainer Sickinger Quadratische Funktionen 1 / 33 Definition Quadratische Funktion Definition (Quadratische Funktion) Sei D R und f : D R
Eigenschaften von Funktionen
 Eigenschaften von Funktionen Mag. Christina Sickinger HTL v 1 Mag. Christina Sickinger Eigenschaften von Funktionen 1 / 48 Gegeben sei die Funktion f (x) = 1 4 x 2 1. Berechnen Sie die Steigung der Funktion
Eigenschaften von Funktionen Mag. Christina Sickinger HTL v 1 Mag. Christina Sickinger Eigenschaften von Funktionen 1 / 48 Gegeben sei die Funktion f (x) = 1 4 x 2 1. Berechnen Sie die Steigung der Funktion
G S. p = = 1 T. =5 K R,db K R
 TFH Berlin Regelungstechnik Seite von 0 Aufgabe 2: Gegeben: G R p =5 p 32ms p 32 ms G S p = p 250 ms p 8 ms. Gesucht ist das Bodediagramm von G S, G R und des offenen Regelkreises. 2. Bestimmen Sie Durchtrittsfrequenz
TFH Berlin Regelungstechnik Seite von 0 Aufgabe 2: Gegeben: G R p =5 p 32ms p 32 ms G S p = p 250 ms p 8 ms. Gesucht ist das Bodediagramm von G S, G R und des offenen Regelkreises. 2. Bestimmen Sie Durchtrittsfrequenz
2n n + 2. n + (1 + j) 1. 2n + 2 = 1. 2n + 2. (n + 1) + j + 2 1
 Aufgabe Die strenge Monotonie zeigen wir mittels vollständiger Indution. Indutionsanfang: Trivialerweise ist f streng monoton wachsend. Indutionsschritt: Wir nehmen an, es sei gezeigt, dass für ein gewisses
Aufgabe Die strenge Monotonie zeigen wir mittels vollständiger Indution. Indutionsanfang: Trivialerweise ist f streng monoton wachsend. Indutionsschritt: Wir nehmen an, es sei gezeigt, dass für ein gewisses
Die Steigung m ist ein Quotient zweier Differenzen und heißt daher Differenzenquotient.
 Seite Definition lineare Funktion Eine Funktion f mit dem Funktionsterm f(x) = m x + b, also der Funktionsgleichung y = m x + b, heißt lineare Funktion. Ihr Graph G f ist eine Gerade mit der Steigung m
Seite Definition lineare Funktion Eine Funktion f mit dem Funktionsterm f(x) = m x + b, also der Funktionsgleichung y = m x + b, heißt lineare Funktion. Ihr Graph G f ist eine Gerade mit der Steigung m
Kurvendiskussion. Mag. Mone Denninger 10. Oktober Extremwerte (=Lokale Extrema) 2. 5 Monotonieverhalten 3. 6 Krümmungsverhalten 4
 Mag. Mone Denninger 10. Oktober 2004 Inhaltsverzeichnis 1 Definitionsmenge 2 1.1 Verhalten am Rand und an den Lücken des Definitionsbereichs............................ 2 2 Nullstellen 2 3 Extremwerte
Mag. Mone Denninger 10. Oktober 2004 Inhaltsverzeichnis 1 Definitionsmenge 2 1.1 Verhalten am Rand und an den Lücken des Definitionsbereichs............................ 2 2 Nullstellen 2 3 Extremwerte
Abitur 2011 G8 Musterabitur Mathematik Infinitesimalrechnung
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 211 G8 Musterabitur Mathematik Infinitesimalrechnung I Teilaufgabe 1 (3 BE) Bestimmen Sie die Nullstellen der Funktion f : x (e x 2) (x 3 2x ) mit Definitionsbereich
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 211 G8 Musterabitur Mathematik Infinitesimalrechnung I Teilaufgabe 1 (3 BE) Bestimmen Sie die Nullstellen der Funktion f : x (e x 2) (x 3 2x ) mit Definitionsbereich
Flächenberechnung mit Integralen
 Flächenberechnung mit Integralen Wolfgang Kippels 28. April 208 Inhaltsverzeichnis Vorwort 2 2 Einleitung 2 3 Übungsaufgaben 3 3. Aufgabe................................... 3 3.2 Aufgabe 2...................................
Flächenberechnung mit Integralen Wolfgang Kippels 28. April 208 Inhaltsverzeichnis Vorwort 2 2 Einleitung 2 3 Übungsaufgaben 3 3. Aufgabe................................... 3 3.2 Aufgabe 2...................................
Mathematik I - Woche 4
 Mathematik I - Woche 4 Philip Müller 1 Ableitung 1.1 Bedeutung der Ableitung Die Bedeutung 1 der ersten Ableitung ist, dass sie ein Mass für die Änderung einer Funktion ist. Wenn der Wert der Ableitung
Mathematik I - Woche 4 Philip Müller 1 Ableitung 1.1 Bedeutung der Ableitung Die Bedeutung 1 der ersten Ableitung ist, dass sie ein Mass für die Änderung einer Funktion ist. Wenn der Wert der Ableitung
Skripten für die Oberstufe. Kurvendiskussion. f (x) f (x)dx = e x.
 Skripten für die Oberstufe Kurvendiskussion x 3 f (x) x f (x)dx = e x H. Drothler 0 www.drothler.net Kurvendiskussion Zusammenfassung Seite Um Funktionsgraphen möglichst genau zeichnen zu können, werden
Skripten für die Oberstufe Kurvendiskussion x 3 f (x) x f (x)dx = e x H. Drothler 0 www.drothler.net Kurvendiskussion Zusammenfassung Seite Um Funktionsgraphen möglichst genau zeichnen zu können, werden
Die Funktion ist gegeben durch ; 0. a) Die Tangente an den Graphen von im Punkt verläuft durch 0 0,5. Bestimmen Sie die Koordinaten von.
 Aufgabe A1.1 Die Anzahl der Käufer einer neu eingeführen Smartphone-App soll modelliert werden. Dabei wird die momentane Änderungsrate beschrieben durch die Funktion 6000, ; 0 ( in Monaten nach Einführung,
Aufgabe A1.1 Die Anzahl der Käufer einer neu eingeführen Smartphone-App soll modelliert werden. Dabei wird die momentane Änderungsrate beschrieben durch die Funktion 6000, ; 0 ( in Monaten nach Einführung,
1. Aufgabe (6 Punkte) Zeigen Sie mit Hilfe der vollständigen Induktion, dass folgende Gleichheit gilt für alle n N, n 2. k (k + 1)! = 1 1 n!.
 . Aufgabe (6 Punte) Zeigen Sie mit Hilfe der vollständigen Indution, dass folgende Gleichheit gilt für alle n N, n 2 n ( + )! n!. [6P] Ind. Anfang: n 2 oder l.s. ( + )! 2 r.s. 2! 2. ( + )! 2! 2! 2 2 2
. Aufgabe (6 Punte) Zeigen Sie mit Hilfe der vollständigen Indution, dass folgende Gleichheit gilt für alle n N, n 2 n ( + )! n!. [6P] Ind. Anfang: n 2 oder l.s. ( + )! 2 r.s. 2! 2. ( + )! 2! 2! 2 2 2
Grundlagen der Physik II
 Grundlagen der Physik II Othmar Marti 09. 07. 2007 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Wärmelehre Grundlagen der Physik II 09. 07. 2007 Klausur Die Klausur
Grundlagen der Physik II Othmar Marti 09. 07. 2007 Institut für Experimentelle Physik Physik, Wirtschaftsphysik und Lehramt Physik Seite 2 Wärmelehre Grundlagen der Physik II 09. 07. 2007 Klausur Die Klausur
Gruppennummer: lfd. Nummer: Datum:
 Ernst-Moritz-Arndt Universität Greifswald Institut für Physi Versuch W5 - p(v )-Diagramm eines realen Gases Name: Mitarbeiter: Gruppennummer: lfd. Nummer: Datum: 1. Aufgabenstellung 1.1. Versuchsziel Nehmen
Ernst-Moritz-Arndt Universität Greifswald Institut für Physi Versuch W5 - p(v )-Diagramm eines realen Gases Name: Mitarbeiter: Gruppennummer: lfd. Nummer: Datum: 1. Aufgabenstellung 1.1. Versuchsziel Nehmen
Wiederholung von Äquivalenzumformungen (Lösen linearer Gleichungen): Wiederholung von Äquivalenzumformungen (Lösen von Ungleichungen):
 Prof. U. Stephan WiIng 1. Wiederholung von Äquivalenzumformungen (Lösen linearer Gleichungen): Bitte lösen Sie die folgenden Aufgaben und prüfen Sie, ob Sie Lücken dabei haben. Bestimmen Sie jeweils die
Prof. U. Stephan WiIng 1. Wiederholung von Äquivalenzumformungen (Lösen linearer Gleichungen): Bitte lösen Sie die folgenden Aufgaben und prüfen Sie, ob Sie Lücken dabei haben. Bestimmen Sie jeweils die
Die Binomialreihe. Sebastian Schulz. Ausarbeitung zum Vortrag im Proseminar Analysis (Wintersemester 2008/09, Leitung Prof. Dr.
 Die Binomialreihe Sebastian Schulz Ausarbeitung zum Vortrag im Proseminar Analysis (Wintersemester 008/09, Leitung Prof. Dr. Eberhard Freitag Zusammenfassung: Diese Ausarbeitung beschäftigt sich mit der
Die Binomialreihe Sebastian Schulz Ausarbeitung zum Vortrag im Proseminar Analysis (Wintersemester 008/09, Leitung Prof. Dr. Eberhard Freitag Zusammenfassung: Diese Ausarbeitung beschäftigt sich mit der
Quadratische Gleichungen
 Quadratische Gleichungen TEIL 1: Die Quadratische Funktion und die Quadratische Gleichung Bei linearen Funktionen kommt nur in der 1. Potenz vor. Bei quadratischen Funktion kommt in der. Potenz vor. Daneben
Quadratische Gleichungen TEIL 1: Die Quadratische Funktion und die Quadratische Gleichung Bei linearen Funktionen kommt nur in der 1. Potenz vor. Bei quadratischen Funktion kommt in der. Potenz vor. Daneben
Versuchsprotokoll von Thomas Bauer und Patrick Fritzsch. Münster, den
 M Geoppelte Pendel Versuchsprotooll von Thomas Bauer und Patric Fritzsch Münster, den.1.1 INHALTSVERZEICHNIS 1. Einleitung. Theoretische Grundlagen.1 Die Pendelbewegung. Dder Kopplungsgrad 3. Versuchsbeschreibung
M Geoppelte Pendel Versuchsprotooll von Thomas Bauer und Patric Fritzsch Münster, den.1.1 INHALTSVERZEICHNIS 1. Einleitung. Theoretische Grundlagen.1 Die Pendelbewegung. Dder Kopplungsgrad 3. Versuchsbeschreibung
Anwendungen der Differentialrechnung
 KAPITEL 5 Anwendungen der Differentialrechnung 5.1 Maxima und Minima einer Funktion......................... 80 5.2 Mittelwertsatz.................................... 82 5.3 Kurvendiskussion..................................
KAPITEL 5 Anwendungen der Differentialrechnung 5.1 Maxima und Minima einer Funktion......................... 80 5.2 Mittelwertsatz.................................... 82 5.3 Kurvendiskussion..................................
Aufgaben zum Stirlingschen Kreisprozess Ein Stirling-Motor arbeite mit 50 g Luft ( M= 30g mol 1 )zwischen den Temperaturen = 350 C und T3
 Aufgaben zum Stirlingschen Kreisrozess. Ein Stirling-Motor arbeite mit 50 g Luft ( M 0g mol )zwischen den emeraturen 50 C und 50 C sowie den olumina 000cm und 5000 cm. a) Skizzieren Sie das --Diagramm
Aufgaben zum Stirlingschen Kreisrozess. Ein Stirling-Motor arbeite mit 50 g Luft ( M 0g mol )zwischen den emeraturen 50 C und 50 C sowie den olumina 000cm und 5000 cm. a) Skizzieren Sie das --Diagramm
Flächenberechnung mit Integralen
 Flächenberechnung mit Integralen W. Kippels 30. April 204 Inhaltsverzeichnis Übungsaufgaben 2. Aufgabe................................... 2.2 Aufgabe 2................................... 2.3 Aufgabe 3...................................
Flächenberechnung mit Integralen W. Kippels 30. April 204 Inhaltsverzeichnis Übungsaufgaben 2. Aufgabe................................... 2.2 Aufgabe 2................................... 2.3 Aufgabe 3...................................
Lineare Funktion. Wolfgang Kippels 3. November Inhaltsverzeichnis
 Lineare Funktion Wolfgang Kippels. November 0 Inhaltsverzeichnis Grundlegende Zusammenhänge. Aufbau der Linearen Funktion......................... Nullstellenbestimmung............................. Schnittpunktbestimmung............................
Lineare Funktion Wolfgang Kippels. November 0 Inhaltsverzeichnis Grundlegende Zusammenhänge. Aufbau der Linearen Funktion......................... Nullstellenbestimmung............................. Schnittpunktbestimmung............................
Höhere Mathematik für die Fachrichtung Physik
 Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Dipl.-Math. Sebastian Schwarz WS 018/019 5.10.018 Höhere Mathemati für die Fachrichtung Physi Lösungsvorschläge zum. Übungsblatt
Karlsruher Institut für Technologie Institut für Analysis Dr. Christoph Schmoeger Dipl.-Math. Sebastian Schwarz WS 018/019 5.10.018 Höhere Mathemati für die Fachrichtung Physi Lösungsvorschläge zum. Übungsblatt
Analysis: Klausur Analysis
 Analysis Klausur zu Ableitung, Extrem- und Wendepunkten, Interpretation von Graphen von Ableitungsfunktionen, Tangenten und Normalen (Bearbeitungszeit: 90 Minuten) Gymnasium J Alexander Schwarz www.mathe-aufgaben.com
Analysis Klausur zu Ableitung, Extrem- und Wendepunkten, Interpretation von Graphen von Ableitungsfunktionen, Tangenten und Normalen (Bearbeitungszeit: 90 Minuten) Gymnasium J Alexander Schwarz www.mathe-aufgaben.com
Analysis 2. f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt:
 Analysis 2 www.schulmathe.npage.de Aufgaben 1. Gegeben ist die Funktion f durch f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt: f (x) = 6(x
Analysis 2 www.schulmathe.npage.de Aufgaben 1. Gegeben ist die Funktion f durch f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt: f (x) = 6(x
D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger. Lösung - Serie 6. (n+1)!. Daraus folgt, dass e 1/x < (n+
 D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger Lösung - Serie 6 1. MC-Aufgaben (Online-Abgabe) 1. Für alle ganzen Zahlen n 1 gilt... (a) e 1/x = o(x n ) für x 0 + (b) e 1/x = o(x n ) für x 0 + (c)
D-MAVT/D-MATL Analysis I HS 2017 Dr. Andreas Steiger Lösung - Serie 6 1. MC-Aufgaben (Online-Abgabe) 1. Für alle ganzen Zahlen n 1 gilt... (a) e 1/x = o(x n ) für x 0 + (b) e 1/x = o(x n ) für x 0 + (c)
(Unvollständige) Zusammenfassung Analysis Grundkurs
 (Unvollständige) Zusammenfassung Analysis Grundkurs. Ableitungs und Integrationsregeln (Folgende 0 Funktionen sind alles Funktionen aus dem Zentralabitur Grundkurs.) a) f(t) = 0,0t e 0,t b) f(t) = t 3
(Unvollständige) Zusammenfassung Analysis Grundkurs. Ableitungs und Integrationsregeln (Folgende 0 Funktionen sind alles Funktionen aus dem Zentralabitur Grundkurs.) a) f(t) = 0,0t e 0,t b) f(t) = t 3
Abitur 2010 Mathematik GK Infinitesimalrechnung I
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 2010 Mathematik GK Infinitesimalrechnung I Teilaufgabe 2 (4 BE) Gegeben ist für k R + die Schar von Funktionen f k : x 1 Definitionsbereich D k. Der
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 2010 Mathematik GK Infinitesimalrechnung I Teilaufgabe 2 (4 BE) Gegeben ist für k R + die Schar von Funktionen f k : x 1 Definitionsbereich D k. Der
Situationsgrafik: a) Maximale momentane Änderungsrate: Bestimmung des Hochpunktes von mit dem GTR.
 Lösung A1.1 Lösungslogik GTR-Einstellungen: Y1=6000, Y2= 1 Y3=4000 Y4= 1 Y5=5000 Situationsgrafik: a) Maximale momentane Änderungsrate: Bestimmung des Hochpunktes von mit dem GTR. Zeitraum Änderungsrate
Lösung A1.1 Lösungslogik GTR-Einstellungen: Y1=6000, Y2= 1 Y3=4000 Y4= 1 Y5=5000 Situationsgrafik: a) Maximale momentane Änderungsrate: Bestimmung des Hochpunktes von mit dem GTR. Zeitraum Änderungsrate
ETH Zürich Repetitionsprüfung D-MAVT, D-MATL Analysis I/II Prof. Dr. Urs Lang
 EH Zürich Repetitionsprüfung..7 D-MA, D-MAL Analysis I/II Prof. Dr. Urs Lang. [6 Punkte] Gegeben sei die attelfläche = {(x, y, z) R : z = x y } sowie der Punkt Q = (,, 5). Bestimmen ie die kleinste Zahl
EH Zürich Repetitionsprüfung..7 D-MA, D-MAL Analysis I/II Prof. Dr. Urs Lang. [6 Punkte] Gegeben sei die attelfläche = {(x, y, z) R : z = x y } sowie der Punkt Q = (,, 5). Bestimmen ie die kleinste Zahl
Quadratische Funktion
 Quadratische Funktion Wolfgang Kippels 6. Oktober 018 Inhaltsverzeichnis 1 Vorwort Zusammenstellung der Grundlagen 3.1 Nullstellen................................... 3. Scheitelpunkt.................................
Quadratische Funktion Wolfgang Kippels 6. Oktober 018 Inhaltsverzeichnis 1 Vorwort Zusammenstellung der Grundlagen 3.1 Nullstellen................................... 3. Scheitelpunkt.................................
Quadratische Funktion - Übungen
 Quadratische Funktion - Übungen 1a) "Verständnisfragen" zu "Scheitel und Allgemeine Form" - mit Tipps. Teilweise: Trotz der Tipps nicht immer einfach! Wir haben die Formeln: Allgemeine Form: y = a x 2
Quadratische Funktion - Übungen 1a) "Verständnisfragen" zu "Scheitel und Allgemeine Form" - mit Tipps. Teilweise: Trotz der Tipps nicht immer einfach! Wir haben die Formeln: Allgemeine Form: y = a x 2
Differentialrechnung im R n
 Kapitel 9 Differentialrechnung im R n Bisher haben wir uns mit Funtionen beschäftigt, deren Verhalten durch eine einzelne Variable beschrieben wird. In der Praxis reichen solche Funtionen in der Regel
Kapitel 9 Differentialrechnung im R n Bisher haben wir uns mit Funtionen beschäftigt, deren Verhalten durch eine einzelne Variable beschrieben wird. In der Praxis reichen solche Funtionen in der Regel
Abkürzungen & Begriffe
 A Bedeutungen Abkürzungen & Begriffe Abzisse ist ein normaler x-wert [ Ordinate] arcsin, arccos, arctan sind die korrekten Bezeichnungen für: sin -, cos -, tan -. [Die üblichen Bezeichnungen sin -, cos
A Bedeutungen Abkürzungen & Begriffe Abzisse ist ein normaler x-wert [ Ordinate] arcsin, arccos, arctan sind die korrekten Bezeichnungen für: sin -, cos -, tan -. [Die üblichen Bezeichnungen sin -, cos
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil Wahlteil Analysis 8 Wahlteil Analysis Wahlteil Analysis 9 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 9 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
Pflichtteil Wahlteil Analysis 8 Wahlteil Analysis Wahlteil Analysis 9 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 9 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
Unter Kurvendiskussion versteht man die Untersuchung einer gegebenen Funktion auf bestimmte Merkmale und Eigenschaften:
 1 KURVENDISKUSSION Unter Kurvendiskussion versteht man die Untersuchung einer gegebenen Funktion auf bestimmte Merkmale und Eigenschaften: 1.1 Definitionsbereich Zuerst bestimmt man den maximalen Definitionsbereich
1 KURVENDISKUSSION Unter Kurvendiskussion versteht man die Untersuchung einer gegebenen Funktion auf bestimmte Merkmale und Eigenschaften: 1.1 Definitionsbereich Zuerst bestimmt man den maximalen Definitionsbereich
TU Dresden Fachrichtung Mathematik Institut für Numerische Mathematik 1. Dr. M. Herrich SS 2017
 TU Dresden Fachrichtung Mathematik Institut für Numerische Mathematik 1 Prof. Dr. K. Eppler Institut für Numerische Mathematik Dr. M. Herrich SS 2017 Aufgabe 1 Übungen zur Vorlesung Mathematik II 4. Übung,
TU Dresden Fachrichtung Mathematik Institut für Numerische Mathematik 1 Prof. Dr. K. Eppler Institut für Numerische Mathematik Dr. M. Herrich SS 2017 Aufgabe 1 Übungen zur Vorlesung Mathematik II 4. Übung,
Arbeitsblätter zur Vergleichsklausur EF. Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf.
 Arbeitsblätter zur Vergleichsklausur EF Arbeitsblatt I.1 Nullstellen Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf. Beachte den Satz: Ein Produkt wird null, wenn einer der
Arbeitsblätter zur Vergleichsklausur EF Arbeitsblatt I.1 Nullstellen Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf. Beachte den Satz: Ein Produkt wird null, wenn einer der
Reales Gas und kritischer Punkt Seite 1
 1. Aufgabenstellung Reales Gas und ritischer Punt Seite 1 1.1. Die Isothermen des Gases Schwefelhexafluorid ( SF 6 ) sind verschiedene Temperaturen aufzunehmen und gemeinsam in einem p ( )-Diagramm darzustellen.
1. Aufgabenstellung Reales Gas und ritischer Punt Seite 1 1.1. Die Isothermen des Gases Schwefelhexafluorid ( SF 6 ) sind verschiedene Temperaturen aufzunehmen und gemeinsam in einem p ( )-Diagramm darzustellen.
Die Transzendenz von e
 Die Transzendenz von e Stephan Wojtowytsch 2. Juni 29 Wir wollen zeigen, dass die eulersche Zahl e transzendent ist. Transzendente Zahlen sind Zahlen, die nicht als Nullstellen von Polynomen mit ganzen
Die Transzendenz von e Stephan Wojtowytsch 2. Juni 29 Wir wollen zeigen, dass die eulersche Zahl e transzendent ist. Transzendente Zahlen sind Zahlen, die nicht als Nullstellen von Polynomen mit ganzen
5.5. Prüfungsaufgaben zur graphischen Integration und Differentiation
 5.5. Prüfungsaufgaben zur graphischen Integration und Differentiation Aufgabe : Verschiebung und Streckung trigonometrischer Funktionen (5) a) Bestimmen Sie die Periode p sowie die Nullstellen der Funktion
5.5. Prüfungsaufgaben zur graphischen Integration und Differentiation Aufgabe : Verschiebung und Streckung trigonometrischer Funktionen (5) a) Bestimmen Sie die Periode p sowie die Nullstellen der Funktion
Aufgaben zum Aufstellen von Funktionen aus gegebenen Bedingungen
 Augaben zum Austellen von Funktionen aus gegebenen Bedingungen 1. Die Parabel Gp ist der Graph der quadratischen Funktion p(. Diese Parabel schneidet die x-achse im Punkt N(6/0). Ihr Scheitelpunkt S(/yS)
Augaben zum Austellen von Funktionen aus gegebenen Bedingungen 1. Die Parabel Gp ist der Graph der quadratischen Funktion p(. Diese Parabel schneidet die x-achse im Punkt N(6/0). Ihr Scheitelpunkt S(/yS)
Prüfungsteil B, Aufgabengruppe 1: Analysis. Bayern Aufgabe 1. BundesabiturMathematik: Musterlösung
 Abitur MathematikBayern 04 Prüfungsteil B, Aufgabengruppe BundesabiturMathematik: Prüfungsteil B, Aufgabengruppe : Bayern 04 Aufgabe a). SCHRITT: SCHNITTPUNKTE MIT DEN KOORDINATENACHSEN Die Koordinatenachsen
Abitur MathematikBayern 04 Prüfungsteil B, Aufgabengruppe BundesabiturMathematik: Prüfungsteil B, Aufgabengruppe : Bayern 04 Aufgabe a). SCHRITT: SCHNITTPUNKTE MIT DEN KOORDINATENACHSEN Die Koordinatenachsen
Zur Thermodynamik des idealen Gases (GK Physik 1)
 Zur hermodynamik des idealen Gases (GK Physik 1 Zusammenfassung im Hinblick auf Prozesse. Reinhard Honegger, im Januar 2012. 1 Grundbegriffe 1.1 Zustandsgleichung = Ideale Gasgleichung Druck, olumen, emeratur
Zur hermodynamik des idealen Gases (GK Physik 1 Zusammenfassung im Hinblick auf Prozesse. Reinhard Honegger, im Januar 2012. 1 Grundbegriffe 1.1 Zustandsgleichung = Ideale Gasgleichung Druck, olumen, emeratur
5. Die Thermodynamischen Potentiale
 5. Die hermodynamischen Potentiale 5.1. Einführung der Potentiale Gibbs'sche Fundamentalgleichung. d = du + d, du + d δ Q d = = Ist die Entroie als Funktion von U und bekannt, = ( U, ) dann lassen sich
5. Die hermodynamischen Potentiale 5.1. Einführung der Potentiale Gibbs'sche Fundamentalgleichung. d = du + d, du + d δ Q d = = Ist die Entroie als Funktion von U und bekannt, = ( U, ) dann lassen sich
Die Lösungen der Gleichung b x = log b (x)
 Die Lösungen der Gleichung b = log b () wgnedin@math.uni-koeln.de 17. Januar 2014 In der ersten Vorlesung des Wintersemesters wurde folgende Frage gestellt: Wieviele Lösungen hat die Gleichung ( ) 1 =
Die Lösungen der Gleichung b = log b () wgnedin@math.uni-koeln.de 17. Januar 2014 In der ersten Vorlesung des Wintersemesters wurde folgende Frage gestellt: Wieviele Lösungen hat die Gleichung ( ) 1 =
Analysis I Lösung von Serie 9
 FS 07 9.. MC Fragen: Ableitungen (a) Die Figur zeigt den Graphen einer zweimal differenzierbaren Funktion f. Was lässt sich über f, f und f sagen? Nichts Die Funktion f ist positiv. Die Funktion f ist
FS 07 9.. MC Fragen: Ableitungen (a) Die Figur zeigt den Graphen einer zweimal differenzierbaren Funktion f. Was lässt sich über f, f und f sagen? Nichts Die Funktion f ist positiv. Die Funktion f ist
mathphys-online POTENZFUNKTIONEN
 POTENZFUNKTIONEN Potenzfuntionen Inhaltsverzeichnis Kapitel Inhalt Seite Definition Parabeln Hyperbeln Wurzelfuntionen 6 Graphien erstellt mit Mathcad 5 Januar 0 Potenzfuntionen Potenzfuntionen. Definition
POTENZFUNKTIONEN Potenzfuntionen Inhaltsverzeichnis Kapitel Inhalt Seite Definition Parabeln Hyperbeln Wurzelfuntionen 6 Graphien erstellt mit Mathcad 5 Januar 0 Potenzfuntionen Potenzfuntionen. Definition
Mathematik für Naturwissenschaftler II SS 2010
 Mathematik für Naturwissenschaftler II SS 2010 Lektion 19 8. Juli 2010 Kapitel 14. Gewöhnliche Differentialgleichungen zweiter Ordnung 14.1 Systeme gewöhnlicher linearer Differentialgleichungen erster
Mathematik für Naturwissenschaftler II SS 2010 Lektion 19 8. Juli 2010 Kapitel 14. Gewöhnliche Differentialgleichungen zweiter Ordnung 14.1 Systeme gewöhnlicher linearer Differentialgleichungen erster
13. Funktionen in einer Variablen
 13. Funktionen in einer Variablen Definition. Seien X, Y Mengen. Eine Funktion f : X Y ist eine Vorschrift, wo jedem Element der Menge X eindeutig ein Element von Y zugeordnet wird. Wir betrachten hier
13. Funktionen in einer Variablen Definition. Seien X, Y Mengen. Eine Funktion f : X Y ist eine Vorschrift, wo jedem Element der Menge X eindeutig ein Element von Y zugeordnet wird. Wir betrachten hier
Arbeitsblätter Förderplan EF
 Arbeitsblätter Förderplan EF I.1 Nullstellen bestimmen Lösungen I.2 Parabeln: Nullstellen, Scheitelpunkte,Transformationen Lösungen I.3 Graphen und Funktionsterme zuordnen Lösungen II.1 Transformationen
Arbeitsblätter Förderplan EF I.1 Nullstellen bestimmen Lösungen I.2 Parabeln: Nullstellen, Scheitelpunkte,Transformationen Lösungen I.3 Graphen und Funktionsterme zuordnen Lösungen II.1 Transformationen
QUADRATISCHE FUNKTIONEN
 QUADRATISCHE FUNKTION DARSTELLUNG MIT DER FUNKTIONSGLEICHUNG Allgemeine Form - Vorzeichen von a gibt an, ob die Funktion nach oben (+) oder unten (-) geöffnet ist. Der Wert (Betrag) von gibt an, ob die
QUADRATISCHE FUNKTION DARSTELLUNG MIT DER FUNKTIONSGLEICHUNG Allgemeine Form - Vorzeichen von a gibt an, ob die Funktion nach oben (+) oder unten (-) geöffnet ist. Der Wert (Betrag) von gibt an, ob die
Aufgaben Kreisprozesse. 1. Ein ideales Gas durchläuft den im V(T)- Diagramm dargestellten Kreisprozess. Es ist bekannt:
 Aufgaben Kreisrozesse. Ein ideales Gas durchläuft den im ()- Diagramm dargestellten Kreisrozess. Es ist bekannt: 8 cm 6 cm 00 K 8MPa MPa a) Geben Sie die fehlenden Zustandsgrößen, und für die Zustände
Aufgaben Kreisrozesse. Ein ideales Gas durchläuft den im ()- Diagramm dargestellten Kreisrozess. Es ist bekannt: 8 cm 6 cm 00 K 8MPa MPa a) Geben Sie die fehlenden Zustandsgrößen, und für die Zustände
1 Q12: Lösungen bsv 2.2
 Q: Lösungen bsv... 3. 4. Graphisches Bestimmen einer Integralfunktion a) Nullstellen (laut Graph): x = 0; x = VZT x < 0 x = 0 0 < x < x > f(x) - 0 + 0 - G Io TIP HOP b) Aus der Abbildung ergibt sich: VZT
Q: Lösungen bsv... 3. 4. Graphisches Bestimmen einer Integralfunktion a) Nullstellen (laut Graph): x = 0; x = VZT x < 0 x = 0 0 < x < x > f(x) - 0 + 0 - G Io TIP HOP b) Aus der Abbildung ergibt sich: VZT
Kurvendiskussion. Gesetzmäßigkeiten. Lineare Funktionen. Funktionsgleichung
 Kurvendiskussion Gesetzmäßigkeiten Lineare Funktionen Funktionsgleichung y = mx + c m: Steigung c: y-achsenabschnitt (Funktionswert für y, bei dem der Graph die y-achse schneidet Beispiel : y = x 3 mit
Kurvendiskussion Gesetzmäßigkeiten Lineare Funktionen Funktionsgleichung y = mx + c m: Steigung c: y-achsenabschnitt (Funktionswert für y, bei dem der Graph die y-achse schneidet Beispiel : y = x 3 mit
Viele Statistiken werden durch endliche Folgen beschrieben. (z.b. Anzahl der Studierenden an der TU München in den Jahren 1962 bis 1976)
 Kapitel 9 Folgen und Reihen 9.1 Folgen 9.1.1 Was ist eine Folge? Abbildungen, die auf N definiert sind (mit Werten z.b. in R), heißen (unendliche) Folgen. Abb., die auf einer endlichen Menge aufeinander
Kapitel 9 Folgen und Reihen 9.1 Folgen 9.1.1 Was ist eine Folge? Abbildungen, die auf N definiert sind (mit Werten z.b. in R), heißen (unendliche) Folgen. Abb., die auf einer endlichen Menge aufeinander
1.2 Weisen Sie rechnerisch nach, dass das Schaubild der Funktion mit 4P! bei 1 einen Sattelpunkt aufweist.
 Aufgabe A1 1.1 Erläutere anhand einer Skizze, ob das Integral 3P größer, kleiner oder gleich Null ist. 1.2 Für eine Funktion gilt: (1) 0 für 2 und 1 (2) 23 (3) 13 (4) 2 (5) 1 6 Welche Aussagen lassen sich
Aufgabe A1 1.1 Erläutere anhand einer Skizze, ob das Integral 3P größer, kleiner oder gleich Null ist. 1.2 Für eine Funktion gilt: (1) 0 für 2 und 1 (2) 23 (3) 13 (4) 2 (5) 1 6 Welche Aussagen lassen sich
PC-Übung Nr.3 vom
 PC-Übung Nr.3 vom 31.10.08 Sebastian Meiss 25. November 2008 1. Die Säulen der Thermodynamik Beantworten Sie folgende Fragen a) Welche Größen legen den Zustand eines Gases eindeutig fest? b) Welche physikalischen
PC-Übung Nr.3 vom 31.10.08 Sebastian Meiss 25. November 2008 1. Die Säulen der Thermodynamik Beantworten Sie folgende Fragen a) Welche Größen legen den Zustand eines Gases eindeutig fest? b) Welche physikalischen
Teil 1 Gleichungen und Ungleichungen
 Teil 1 Gleichungen und Ungleichungen Gleichungen Eine mathematische Gleichung ist eine logische Aussage über die Gleichheit von Termen. Das, was links vom Gleichheitszeichen (=) steht, hat den gleichen
Teil 1 Gleichungen und Ungleichungen Gleichungen Eine mathematische Gleichung ist eine logische Aussage über die Gleichheit von Termen. Das, was links vom Gleichheitszeichen (=) steht, hat den gleichen
AMPELABFRAGE LINEAREN FUNKTIONEN. Lineare Funktionen. Autor: Volker Altrichter
 AMPELABFRAGE ZU LINEAREN FUNKTIONEN Autor: Volker Altrichter Aufgabe 1: 2 Gegeben ist die Gleichung einer Geraden: 3 4 y = x 2, x IR. Welche der folgenden Aussagen ist richtig? Die Gerade hat die Steigung
AMPELABFRAGE ZU LINEAREN FUNKTIONEN Autor: Volker Altrichter Aufgabe 1: 2 Gegeben ist die Gleichung einer Geraden: 3 4 y = x 2, x IR. Welche der folgenden Aussagen ist richtig? Die Gerade hat die Steigung
f : x y = mx + t Der Graph einer linearen Funktion ist eine Gerade, welche die y-achse im Punkt S schneidet. = m 2 x 2 m x 1
 III. Funktionen und Gleichungen ================================================================== 3.1. Lineare Funktionen Eine Funktion mit der Zuordnungvorschrift f : x y = mx + t und m, t R heißt lineare
III. Funktionen und Gleichungen ================================================================== 3.1. Lineare Funktionen Eine Funktion mit der Zuordnungvorschrift f : x y = mx + t und m, t R heißt lineare
ANALYSIS. 3. Extremwertaufgaben (folgt)
 ANALYSIS 1. Untersuchung ganzrationaler Funktionen 1.1 Symmetrie 2 1.2 Ableitung 2 1.3 Berechnung der Nullstellen 3 1.4 Funktionsuntersuchung I 4 1.5 Funktionsuntersuchung II 6 2. Bestimmung ganzrationaler
ANALYSIS 1. Untersuchung ganzrationaler Funktionen 1.1 Symmetrie 2 1.2 Ableitung 2 1.3 Berechnung der Nullstellen 3 1.4 Funktionsuntersuchung I 4 1.5 Funktionsuntersuchung II 6 2. Bestimmung ganzrationaler
Übungsaufgaben Folgen und Reihen
 Kallenrode, www.sotere.uos.de Übungsaufgaben Folgen und Reihen. Untersuchen Sie die folgenden Folgen auf Monotonie, Beschränktheit und Konvergenz (geben Sie gegebenenfalls den Grenzwert an): inverse Fakultäten:,,
Kallenrode, www.sotere.uos.de Übungsaufgaben Folgen und Reihen. Untersuchen Sie die folgenden Folgen auf Monotonie, Beschränktheit und Konvergenz (geben Sie gegebenenfalls den Grenzwert an): inverse Fakultäten:,,
Parabeln - quadratische Funktionen
 Parabeln - quadratische Funktionen Roland Heynkes 9.11.005, Aachen Das Gleichsetzungsverfahren und die davon abgeleiteten Einsetzungs- und Additionsverfahren kennen wir als Methoden zur Lösung linearer
Parabeln - quadratische Funktionen Roland Heynkes 9.11.005, Aachen Das Gleichsetzungsverfahren und die davon abgeleiteten Einsetzungs- und Additionsverfahren kennen wir als Methoden zur Lösung linearer
