Klassische Lebensversicherungsmathematik (Repetition)
|
|
|
- Christian Leon Frank
- vor 8 Jahren
- Abrufe
Transkript
1 Klassische Lebensversicherungsmathematik (Repetition) Hansörg Furrer (Swiss Life) Michael Koller (Swiss Life) Das Ziel dieses Dokumentes ist es, die wesentlichen Merkmale der klassischen Lebensversicherungsmathematik zu repetieren. Grundlage dazu sind die Vorlesungsnotizen von Prof. Michael Koller. Das vorliegende Dokument unterscheidet sich insofern von den eben genannten Notizen, als hier für die Bewertung einer Geldeinheit Begriffe aus der modernen Finanzmathematik verwendet werden. Die Gründe dazu sind einerseits in einem sich verändernden regulatorischen Umfeld und seinen neuen Bewertungsmethoden zu finden (Beispiel Solvency II ), andererseits soll auch die Grundlage geschaffen werden für die noch zu behandelnden Themen wie Embedded Value oder Fair Value. Wir sind der Meinung, dass die Lebensversicherungsmathematik nicht als eigenständige Disziplin betrachtet werden sollte, sondern vielmehr als ein in Wechselwirkung zu anderen Bereichen der Versicherungs- und Finanzmathematik stehendes Gebilde. Insbesondere muss der Aktuar der dritten Generation (Zitat Prof. Hans Bühlmann) also auch in der modernen Finanzmathematik sattelfest sein. Schematisch lässt sich die Situation im Lehrbereich der Universität und ETH Zürich wie folgt darstellen: Risk based supervision Term structure and Credit Risk Models Lebens versicherungs Mathematik 1&2 Corporate Finance Risk Management 1 Finanzmathematik 1.1 Barwert eines Kapitals Ein Lebensversicherungsvertrag ist im wesentlichen gekennzeichnet durch zwei Arten von Faktoren: biometrische finanzielle 1
2 Vernachlässigen wir für den Moment die biometrischen Faktoren, so stellen wir fest, dass die Bewertung eines solchen Vertrages auf die Bewertung einer Geldeinheit bei Vertragsbeginn hinausläuft. Es ist bekannt, dass der Wert einer Geldeinheit heute verschieden vom Wert morgen ist (time value of money). Für die Bewertung sind folgende Begriffe und Notationen nötig: Definition 1 (T -maturity zero-bond) Ein T -maturity zero-bond (Anleihe der Dauer T ohne zwischenzeitliche Zahlungen) ist ein Vertrag, der dem Halter die Zahlung einer Geldeinheit zum Zeitpunkt T garantiert, ohne zwischenzeitliche Zahlungen. Notation: P (t, T ): Wert des Vertrages zur Zeit t, 0 t T (zero-coupon bond price). Offensichtlich gilt P (T, T ) 1. In der Folge geht es darum, den Wert P (t, T ) für t T zu bestimmen. Dazu führen wir zusätzlich folgenden stochastischen Prozess ein: Definition 2 (Bank account numeraire) Der Bank account numeraire B stellt eine risikofreie Investition dar, bei der die Profite kontinuierlich gutgeschrieben werden anhand der aktuellen risikofreien Zinskurve. Die Dynamik von B ist gegeben durch db(t) B(t)r t dt B(0) 1. Die stochastische Differentialgleichung (1) hat die Lösung { t B(t) exp 0 (1) } r s ds, (2) wobei r t die instantane Zinsrate für risikoloses Borgen oder Leihen von Geld über das infinitesimale Zeitintervall [t, t + t bezeichnet. Der stochastische Prozess r {r(t) : t 0} heisst short rate Prozess. Gleichung (2) finden wir übrigens in den Vorlesungsnotizen auf Seite 8 wieder. Sie lautet dort K n exp{ n 0 δ(s) ds}k 0. Definition 3 (Stochastischer Diskontfaktor) Der stochastische Diskontfaktor D(t, T ) zwischen den beiden Zeitpunkten t und T ist derenige Geldbetrag zur Zeit t, der äquivalent zu einer Geldeinheit zahlbar zum Zeitpunkt T ist. Er ist gegeben durch D(t, T ) : B(t) B(T ) T e t r s ds. Es stellt sich nun die Frage, was der Zusammenhang zwischen D(t, T ) und P (t, T ) ist. ➀ r deterministisch. Falls r deterministisch ist, so ist auch D(t, T ) deterministisch und es gilt für alle Paare (t, T ), dass D(t, T ) P (t, T ). ➁ r stochastisch. Falls r t stochastisch ist, so ist auch der Diskontfaktor D(t, T ) eine zufällige Grösse, die durch die zukünftige Entwicklung von r zwischen t und T bestimmt wird. Der Bond Preis P (t, T ) ergibt sich aus der Forderung, dass alle diskontierten handelbaren Finanzinstrumente Martingale unter dem risikoneutralen Wahrscheinlichkeitsmass Q sind. 2
3 Insbesondere ist also der Prozess Z {Z (t) : 0 t T } mit Z (t) P (t, T )/B(t) ein Q-Martingal. Die Martingalbedingung lautet E Q [Z (t) F s Z (s) für 0 s t T oder [ P (t, T ) E Q Fs P (s, T ) B(t) B(s) Setze nun t T und beachte dass P (T, T ) 1. Somit [ 1 E Q F s B(T ) P (s, T ) B(s) Multipliziere beide Seiten mit B(s). Da B(s) F s -messbar ist, gilt zudem Mit s t folgern wir schliesslich [ B(s) E Q Fs P (s, T ) B(T ) [ B(t) E Q F t P (t, T ) (3) B(T ) oder E Q [ D(t, T ) F t P (t, T ), womit der allgemeine Zusammenhang hergestellt ist zwischen dem Diskontfaktor D(t, T ) und dem Bond Preis P (t, T ). Im Spezialfall wo r deterministisch ist, gilt E Q [ B(t)/B(T ) F t B(t)/B(T ) und somit sind wir zurück im Fall 1. Definition 4 (yield-to-maturity) Der yield-to-maturity y ist gegeben durch folgende Beziehung: P (t, T )e y 1 woraus wir schliessen können log P (t, T ) y y(t, T ). T t Aus den Gleichungen (2) und (3) ist ersichtlich, dass die Bond Preise durch die Spezifikation des short rate Prozesses bestimmt sind. Es gelten die folgenden Zusammenhänge: log P (t, T ) y(t, T ) T t (yield-to-maturity) [ B(t) Festlegung von r t P (t, T ) E Q F t B(T ) (zero-coupon bond price) f(t, T ) T log P (t, T ) (instantaneous forward rates) 3
4 Es stellt sich nun die Frage, wie der short rate Prozess r modelliert werden soll. Typischerweise wird die Dynamik von r als Diffusionsprozess beschrieben, d.h. in der Form dr t µ(t, r t ) dt + σ(t, r t ) dw (t), wobei der Prozess W {W (t) : t 0} eine Brownsche Bewegung (bezüglich Q) bezeichnet. Die einschlägige Literatur umfasst eine Vielzahl von Zinsmodellen. Im folgenden beschreiben wir kurz die drei bekanntesten Abbildung 1: Simulation eines short rate Prozesses r, dessen Dynamik der stochastischen Differentialgleichung (4) genügt mit κ m σ 1. Beispiel 1: Vasicek Modell. Im Vasicek Modell wird die Dynamik von r durch einen sogennannten mean-reverting Ornstein- Uhlenbeck -Prozess beschrieben. d.h. dr t κ(m r t ) dt + σ dw (t), t 0, (4) mit Konstanten κ, m und σ. Die stochastische Differentialgleichung (4) hat die Lösung r t e κ(t s) r s + m ( 1 e κ(t s)) + σ t s e κ(t u) dw (u), woraus folgt, dass die Zufallsvariable r t (bedingt) normalverteilt ist. Denn für eine lokal beschränkte Borel messbare Funktion ξ auf R + ist der stochastische Prozess Z(t) : t 0 ξ(s) dw (s) ein Gauss scher Prozess mit Erwartungswertfunktion E[Z(t) 0 und Kovarianzfunktion R(s, t) : Cov ( Z(s), Z(t) ) s t 0 ξ(u) 2 du, wobei a b : min{a, b}, siehe zum Beispiel Revuz and Yor [9, Seite 135. Insbesondere schliessen wir daraus, dass der Wert r t negativ sein kann mit positiver Wahrscheinlichkeit. Beispiel 2: Cox-Ingersoll-Ross Modell (CIR). Im CIR-Modell wird die Dynamik von r durch einen sogenannten square-root -Prozess beschrieben, d.h. dr t κ(m r t ) dt + σ r t dw (t), t 0. (5) Die Lösung von (5) lässt sich beschreiben mit Hilfe des Quadrates eines (in der Zeit translatierten) δ-dimensionalen Bessel-Prozesses, d.h. r t e κt Z δ M t, 4
5 wobei δ 4κm/σ 2 und M(t) σ/2 t 0 exp{κu/2} dw (u). Mit Zd {Z d (t) : t 0} bezeichnen wir das Quadrat eines d-dimensionalen Bessel Prozesses, siehe Revuz und Yor [9, Seite 420. Das heisst, Z d erfüllt die stochastische Differentialgleichung dz d (t) d dt + 2 Z d (t) dw (t), Z d (0) x. Es folgt, dass r t > 0 fast sicher falls 2κm > σ 2. Beispiel 3: Hull-White Modell. Das Hull-White Modell basiert ebenfalls auf dem Vasicek Modell, edoch mit zeitabhängigen Koeffizienten. Hull-White (1994) betrachten dr t ( ϑ(t) + ar t ) dt + σ dw (t), t 0, (6) wobei a, σ positive Konstanten sind. Die Lösung der Differentialgleichung (6) lautet r t e a(t s) r s + t s e a(t u) ϑ(u) du + σ t s e a(t u) dw (u). Der Vorteil des Hull-White Modells liegt darin, dass eine exakte Angleichung an die momentan im Markt beobachtete yield-kurve möglich ist. Mit anderen Worten, die Funktion ϑ(t ) lässt sich eindeutig darstellen in Abhängigkeit von f (M) (0, T ) / T log P (M) (0, T ), wobei P (M) (0, T ) die zur Zeit t 0 im Markt beobachteten Bond Preise bezeichnen. 1.2 Barwert einer Rente Definition 5 (Barwert einer Rente). Der Barwert einer Rente ist gleich dem Wert der zukünftigen Rentenzahlungen zu einem bestimmten Zeitpunkt. Notation für Rentenbarwerte: a : nachschüssig ä : vorschüssig Beispiel: Ganzährig vorschüssig zahlbare ewige Rente. t t Wir gehen von einer diskreten, konstanten Verzinsung aus. Die Rentenzahlungen zu den Zeitpunkten t 0, 1, 2, 3,... betragen eweils eine Geldeinheit. Mit der klassischen Schreibweise lässt sich der Rentenbarwert zum Zeitpunkt t 0 darstellen als ( 1 ä ) ( 1 ) i 1 + i v k (7) k0 mit v (1+i) 1. Nun wollen wir ä ausdrücken mit Hilfe der Sprache der modernen Finanzmathematik. Wir stellen zuerst fest, dass der (diskrete) bank account numeraire B gegeben ist 5
6 durch B(t) (1 + i) t. Wir erinneren daran, dass allgemein gilt P (t, T ) E Q [ B(t)/B(T ) F t, siehe (3). Mit B(t) (1 + i) t schliessen wir, da i konstant ist, Insbesondere für t 0: P (t, T ) P (0, T ) ( 1 ) T t. 1 + i ( 1 ) T v T. 1 + i Also gilt für den Rentenbarwert zum Zeitpunkt t 0 ä P (0, k). (8) k0 Bemerkung 6 Vergleichen wir die Darstellungen (7) und (8) für den Rentenbarwert zum Zeitpunkt t 0, so stellen wir fest, dass letztere viel allgemeiner ist. Insbesondere erlaubt Darstellung (8), den Rentenbarwert für einen positiven Bewertungszeitpunkt t zu bestimmen. Der Barwert wäre dann k t P (t, k). Ebenso schliesst die Notation (8) stochastische Zinsen mitein. 2 Technischer Zinssatz Wie erwähnt, wird die Preisbildung eines Lebensversicherungsproduktes bestimmt durch biometrische finanzielle Faktoren. Definition 7 (Technischer Zinssatz). Der technische Zinssatz ist ein garantierter Zinssatz, mit dem eine Versicherungsgesellschaft Gelder zu verzinsen hat. Der technische Zinssatz entspricht somit einem Minimalzins, mit dem Gelder zu verzinsen sind. Man beachte, dass der technische Zinssatz in der Regel als konstant angenommen wird, was einer Unabhängigkeit des technischen Zinssatzes von den realen Finanzmarktdaten gleichkommt. Im Rahmen einer sich ändernden regulatorischen Aufsicht (für Europa: Solvency II, siehe [7; für die Schweiz: Swiss Solvency Test SST, [1) wird edoch verlangt, dass marktnahe Bewertungsmethoden verwendet werden. Den Unterschied zwischen einem traditionellen Bewertungsansatz und einem marktnahen (marked-to-market) wollen wir anhand eines einfachen Beispiels illustrieren. Beispiel: Reine Erlebensfallversicherung gegen Einmalprämie. Wir betrachten eine reine Erlebensfallversicherung gegen Einmalprämie. Ein solcher Vertrag ist gekennzeichnet durch einen Anfangszeitpunkt t 0 (policy inception date) und einen Endzeitpunkt t T (policy end date). Die Versicherungsnehmerin erhält eine Geldeinheit, falls sie beim Ablauf der Versicherung zum Zeitpunkt T am Leben ist. Notation: L(t): Verpflichtungen der Versicherungs-Gesellschaft zur Zeit t, 0 t T. a) Traditioneller Bewertungsansatz Der traditionelle Bewertungsansatz ist dadurch charakterisiert, dass hier mit dem technischen Zinssatz δ diskontiert wird. Zusätzlich gehen wir von einer kontinuierlichen Verzinsung aus. 6
7 Dann gilt für 0 t T L(t) 1 e δ(t t) T p x. (9) Man beachte, dass die zum Zeitpunkt t 0 geleistete Einmalprämie Π 0 keinen Einfluss auf (9) hat. Die Grösse t p x stellt die Wahrscheinlichkeit dar, dass eine x-ährige Person t Jahre überlebt. b) Marktnaher Bewertungsansatz (marked-to-market) Der marktnahe Ansatz unterscheidet sich vom traditionellen Ansatz durch die Bewertung der Geldeinheit bei Vertragsbeginn. Im Rahmen des Swiss Solvency Tests SST wird der marktnahe Wert einer Versicherungsverpflichtung definiert als der Erwartungswert (unter dem risikoneutralen Wahrscheinlichkeitsmass) der zukünftigen diskontierten 1, vertraglich zugesicherten cash flows, siehe [1, Seite 17. Für das Beispiel der reinen Erlebensfallversicherung bedeutet dies [ 1 L(t) B(t) E Q B(T ) 1 {T x>t } F t, (10) wobei B(t) exp{ t 0 r s ds} den bank account numeraire (kontinuierliche Verzinsung) und T x die Rest-Lebenszeit einer x-ährigen Person bezeichnet. Unter der Annahme, dass das Mortalitätsrisiko unabhängig vom finanziellen Risiko ist, gilt [ B(t) [ L(t) E Q Ft E Q 1{Tx>T } B(T ) [ P (t, T ) E P ζ 1{Tx>T } [ P (t, T ) E P [ζ E P 1{Tx>T } P (t, T ) T p x, (11) wobei ζ dq/dp die Radon-Nikodym Dichte der Masstransformation vom physischen Wahrscheinlichkeitsmass P zum risiko-neutralen Mass Q darstellt. Insbesondere gilt E P [ζ 1. Ein Vergleich von (9) mit (11) zeigt, dass beim traditionellen Bewertungsansatz mit dem technischen Zinssatz diskontiert wird, während bei marktnaher Betrachtungsweise zero-bonds die Diskontfunktion übernehmen. Kontinuierliche Verzinsung: Bank account numeraire: Einfache Verzinsung: B(t) e t 0 rs ds B(t) (1 + i) t r konstant: B(t) e rt Bond Preis (r konstant): P (0, k) e rk P (0, k) ( 1 ) k v k 1 + i 1 Die Diskontierung wird auf der Basis der zum Berechnungszeitpunkt gültigen risikolosen Zinskurve ermittelt 7
8 3 Arten von Lebensversicherungen Die gängigsten Arten von Lebensversicherungen lassen sich grob unterteilen einerseits in Kapital- und andererseits in Rentenversicherungen: Kapitalversicherungen: a) Todesfallversicherungen (lebenslänglich (whole life insurance) oder temporär (term insurance)) b) Reine Erlebensfallversicherung (pure endowment) c) Gemischte Versicherung (endowment) d) Fondsgebundene Versicherungen Rentenversicherungen: a) Leibrente b) Temporäre Rente Ausgehend von diesen Grundbausteinen lassen sich weitere Arten von Lebensversicherungen ableiten wie zum Beispiel Versicherungen auf mehrere Leben etc. 3.1 Der Wert einer Lebensversicherung Die in der Lebensversicherungsindustrie gängigen Bewertungsmethoden wie Embedded Value und Fair Value finden wir im Prinzip auch im Bereich Corporate Finance wieder (Stichwort NPV-Regel (Net present value)). Sie gründen also auf den zukünftigen diskontierten Zahlungsströmen (cash flows). Wir treffen nun die Annahme, dass alle Zahlungsströme eines Versicherungsproduktes immer zu Jahresbeginn erfolgen. Das legt folgende Zeiteichung nahe: Der Zeitpunkt t 0 entspreche dem , der Zeitpunkt t 1 dem und so weiter. Es bezeichne T 0 den Anfangszeitpunkt (policy inception date) und T E den Endpunkt eines Versicherungsvertrages (policy end date), wobei T E T 0. Wir gehen also davon aus, dass die Zahlungsströme zu den Zeitpunkten T 0 n n k T E erfolgten oder erfolgen werden. Die cash flows können unterteilt werden in cash-inflows respektive cash-outflows Cash-inflows: Prämien Cash-outflows: + Todesfall-Leistungen + Erlebensfall-Leistungen + Renten-Leistungen + Rückkaufs-Leistungen + Andere Leistungen (cash) + Kommissionen + Verwaltungskosten (inklusive Kosten zur Verwaltung von Kapitalanlagen) 8
9 Notation: Z(m): Die zum Zeitpunkt m anfallenden cash flows. Mit L(t) bezeichnen wir wiederum die Verpflichtungen der Versicherungs-Gesellschaft zum Zeitpunkt t. Wir postulierten Unabhängigkeit zwischen den finanziellen und den biometrischen Risiken und schliessen daraus für t [ 1, ). Speziell für t 0, 1 haben wir [ k L(t) E Q Z(m)D(t, m) F t m m k [ E Q Z(m) B(t) F t B(m) k [ [ E Q Z(m) B(t) F t EQ F t B(m) m k [ E Q Z(m) F t P (t, m). m L(0) L(1) k [ E Q Z(m) P (0, m), (12) m1 k [ E Q Z(m) F 1 P (1, m). (13) m2 Bei reinen Kapitalversicherungen beispielsweise sind es die Ereignisse Tod, Überleben und Rückkauf, welche Zahlungsströme auslösen. Demzufolge können wir schreiben Z() Z (T ) () + Z (R) () + Z (U) (). (14) Wir nehmen an, dass die Zahlungsströme beim Eintritt des entsprechenden Ereignisses deterministisch sind und bezeichnen diese mit z ( ). Wir können daher schreiben Z (T ) () z (T ) Z (R) () z (R) Z (U) () z (U) 1 (T ) {T x ( 1,, T x (R) >} 1 (T ) {T x >, T x (R) ( 1,} 1 (T ) {T x >, T x (R) >}, wobei die Zufallsvariable T x (T ) die zukünftige Lebensdauer einer x-ährigen Person bezeichne. Analog werde für eine x-ährige Person mit T x (R) die Dauer bis zum Rückkauf der Police beschrieben. Es gilt T x (R) T x (T ) oder T x (R) wenn kein Rückkauf erfolgt. Aufgrund der Linearität des Erwartungswertes gilt E[Z() E [ Z (T ) () + E [ Z (R) () + E [ Z (U) () mit E [ Z (T ) () z (T ) P [ T x (T ) ( 1,, T x (R) > E [ Z (R) () z (R) P [ T x (T ) >, T x (R) ( 1, E [ Z (U) () z (U) P [ T x (T ) >, T x (R) >. 9
10 Es seien q x, p x die einährigen Sterbe- bzw. Überlebenswahrscheinlichkeiten 2. Ordnung einer x-ährigen Person. Wir schreiben p x p x λ x + p x (1 λ x ) und nennen λ x die (bedingte) Stornorate, 0 λ x 1. Mit obiger Notation finden wir P [ T (T ) x P [ T (T ) x ( 1,, T x (R) > 2 k0 >, T x (R) ( 1, 2 P [ T (T ) x k0 >, T x (R) > 1 k0 p x+k (1 λ x+k ) q x+ 1, p x+k (1 λ x+k ) p x+ 1 λ x+ 1 p x+k (1 λ x+k ). Die bedingten Erwartungswerte E[Z() F 1 (notwendig für die Bestimmung von (13)) berechnen sich analog. Beispiel: Reine Erlebensfallversicherung Als konkrete Anwendung betrachten wir das uns bekannte Beispiel der reinen Erlebensfallversicherung und wollen ihren (marktnahen) Wert berechnen. Aus obigen Ausführungen folgt, dass wir dazu die Grössen z (T ), z (R), z (U) bestimmen müssen. Wir haben einerseits z (T ) 0,. denn das Ereignis Tod löst zu keinem Zeitpunkt eine Zahlung aus. Die Zahlungen bei Rückkauf fassen wir zusammen im Vektor z (R) (z 1,..., z k ), wobei z z (R). Die Zahlungsströme zum Zeitpunkt, k 1, für das Ereignis Überleben im Intervall ( 1, setzen sich zusammen aus Prämien, garantierten Überschüssen b (Boni) und Kosten κ. Für k kommt zusätzlich noch die Erlebensfall-Leistung hinzu. Somit gilt z (U) { π + b + κ, {1,..., k 1}, b + κ + z (U), k. Um die Analogie zu Abschnitt in den Vorlesungsnotizen herzustellen, gehen wir von einer Einmalprämieneinlage aus und setzen λ x 0, was E [ Z (R) () 0 impliziert. Vernachlässigen wir darüberhinaus die Kosten und die garantierten Überschüsse und nehmen zusätzlich an, dass die Überlebensfall-Leistung eine Geldeinheit betrage, so reduziert sich (15) zu z (U) Zusammenfassend finden wir für (12) { 0, {1,..., k 1}, 1, k. A 1 x:n : L(0) P (0, k) k p x Dies ist zu vergleichen mit dem entsprechenden Ausdruck auf Seite 30 in den Vorlesungsnotizen. 10 (15)
11 Literatur [1 BPV. Schweizer Solvenztest (2003). Bundesamt für Privatversicherungen BPV, Bern, Version 12. Dezember [2 BPV. Sensitivitätsanalyse und Szenarien in der Lebensversicherung (2004). Bundesamt für Privatversicherungen BPV, Bern. [3 BPV. Vorschläge für die Bewertung der Liabilities im Geschäft der Beruflichen Vorsorge (2004). Arbeitspapier im Rahmen des SST. Bundesamt für Privatversicherungen BPV, Bern. [4 Brigo, D. and Mercurio, F. (2001). Interest Rate Models: Theory and Practice. Springer, Berlin. [5 Ekern, S. and Persson, S. (1996). Exotic unit-linked life insurance contracts. The Geneva Papers on Risk and Insurance Theory, Vol. 21, [6 Musiela, M. and Rutkowski, M. (1998). Martingale Methods in Financial Modeling. Springer, Berlin. [7 Solvency II-Reflections on the general outline of a framework directive and mandates for further technical work. market/insurance/docs/markt /markt en.pdf [8 Tanskanen, A. J. and Lukkarinen, J. (2003). Fair valuation of path-dependent participating life insurance contracts. Insurance: Mathematics and Economics, Vol. 33, [9 Revuz, D. and Yor, M. (1994). Continuous Martingales and Brownian Motion. Springer, Berlin. 11
Zinseszins- und Rentenrechnung
 Zinseszins- und Rentenrechnung 1 Berechnen Sie den Zeitpunkt, an dem sich das Einlagekapital K bei a) jährlicher b) monatlicher c) stetiger Verzinsung verdoppelt hat, wobei i der jährliche nominelle Zinssatz
Zinseszins- und Rentenrechnung 1 Berechnen Sie den Zeitpunkt, an dem sich das Einlagekapital K bei a) jährlicher b) monatlicher c) stetiger Verzinsung verdoppelt hat, wobei i der jährliche nominelle Zinssatz
Ausarbeitung des Seminarvortrags zum Thema
 Ausarbeitung des Seminarvortrags zum Thema Anlagepreisbewegung zum Seminar Finanzmathematische Modelle und Simulationen bei Raphael Kruse und Prof. Dr. Wolf-Jürgen Beyn von Imke Meyer im W9/10 Anlagepreisbewegung
Ausarbeitung des Seminarvortrags zum Thema Anlagepreisbewegung zum Seminar Finanzmathematische Modelle und Simulationen bei Raphael Kruse und Prof. Dr. Wolf-Jürgen Beyn von Imke Meyer im W9/10 Anlagepreisbewegung
Im Jahr t = 0 hat eine Stadt 10.000 Einwohner. Nach 15 Jahren hat sich die Einwohnerzahl verdoppelt. z(t) = at + b
 Aufgabe 1: Im Jahr t = 0 hat eine Stadt 10.000 Einwohner. Nach 15 Jahren hat sich die Einwohnerzahl verdoppelt. (a) Nehmen Sie lineares Wachstum gemäß z(t) = at + b an, wobei z die Einwohnerzahl ist und
Aufgabe 1: Im Jahr t = 0 hat eine Stadt 10.000 Einwohner. Nach 15 Jahren hat sich die Einwohnerzahl verdoppelt. (a) Nehmen Sie lineares Wachstum gemäß z(t) = at + b an, wobei z die Einwohnerzahl ist und
Finanzwirtschaft. Teil II: Bewertung. Zinssätze und Renten
 Zinssätze und Renten 1 Finanzwirtschaft Teil II: Bewertung Zinssätze und Renten Agenda Zinssätze und Renten 2 Effektivzinsen Spot-Zinsen Forward-Zinsen Bewertung Kennziffern Zusammenfassung Zinssätze und
Zinssätze und Renten 1 Finanzwirtschaft Teil II: Bewertung Zinssätze und Renten Agenda Zinssätze und Renten 2 Effektivzinsen Spot-Zinsen Forward-Zinsen Bewertung Kennziffern Zusammenfassung Zinssätze und
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Rente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren Rentenperiode = Zeitabstand zwischen zwei Rentenzahlungen
 1 3.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind
1 3.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind
Finanzmathematik. Wirtschaftswissenschaftliches Zentrum Universität Basel. Mathematik für Ökonomen 1 Dr. Thomas Zehrt
 Wirtschaftswissenschaftliches Zentrum Universität Basel Mathematik für Ökonomen 1 Dr. Thomas Zehrt Finanzmathematik Literatur Gauglhofer, M. und Müller, H.: Mathematik für Ökonomen, Band 1, 17. Auflage,
Wirtschaftswissenschaftliches Zentrum Universität Basel Mathematik für Ökonomen 1 Dr. Thomas Zehrt Finanzmathematik Literatur Gauglhofer, M. und Müller, H.: Mathematik für Ökonomen, Band 1, 17. Auflage,
Beispiel 48. 4.3.2 Zusammengesetzte Zufallsvariablen
 4.3.2 Zusammengesetzte Zufallsvariablen Beispiel 48 Ein Würfel werde zweimal geworfen. X bzw. Y bezeichne die Augenzahl im ersten bzw. zweiten Wurf. Sei Z := X + Y die Summe der gewürfelten Augenzahlen.
4.3.2 Zusammengesetzte Zufallsvariablen Beispiel 48 Ein Würfel werde zweimal geworfen. X bzw. Y bezeichne die Augenzahl im ersten bzw. zweiten Wurf. Sei Z := X + Y die Summe der gewürfelten Augenzahlen.
Rekursionen. Georg Anegg 25. November 2009. Methoden und Techniken an Beispielen erklärt
 Methoden und Techniken an Beispielen erklärt Georg Anegg 5. November 009 Beispiel. Die Folge {a n } sei wie folgt definiert (a, d, q R, q ): a 0 a, a n+ a n q + d (n 0) Man bestimme eine explizite Darstellung
Methoden und Techniken an Beispielen erklärt Georg Anegg 5. November 009 Beispiel. Die Folge {a n } sei wie folgt definiert (a, d, q R, q ): a 0 a, a n+ a n q + d (n 0) Man bestimme eine explizite Darstellung
Im weiteren werden die folgenden Bezeichnungen benutzt: Zinsrechnung
 4.2 Grundbegriffe der Finanzmathematik Im weiteren werden die folgenden Bezeichnungen benutzt: K 0 Anfangskapital p Zinsfuß pro Zeiteinheit (in %) d = p Zinssatz pro Zeiteinheit 100 q = 1+d Aufzinsungsfaktor
4.2 Grundbegriffe der Finanzmathematik Im weiteren werden die folgenden Bezeichnungen benutzt: K 0 Anfangskapital p Zinsfuß pro Zeiteinheit (in %) d = p Zinssatz pro Zeiteinheit 100 q = 1+d Aufzinsungsfaktor
4. Versicherungsangebot
 4. Versicherungsangebot Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie (FS 11) Versicherungsangebot 1 / 13 1. Einleitung 1.1 Hintergrund In einem grossen Teil
4. Versicherungsangebot Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie (FS 11) Versicherungsangebot 1 / 13 1. Einleitung 1.1 Hintergrund In einem grossen Teil
SS 2014 Torsten Schreiber
 SS 2014 Torsten Schreiber 221 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Wird im Bereich der Rentenrechnung die zugehörige zu Beginn eines Jahres / einer Zeitperiode eingezahlt, so spricht
SS 2014 Torsten Schreiber 221 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Wird im Bereich der Rentenrechnung die zugehörige zu Beginn eines Jahres / einer Zeitperiode eingezahlt, so spricht
Aufgabenset 1 (abzugeben 16.03.2012 an LK@wacc.de)
 Aufgabenset 1 (abzugeben 16.03.2012 an LK@wacc.de) Aufgabe 1 Betrachten Sie die Cashflows der Abbildung 1 (Auf- und Abwärtsbewegungen finden mit gleicher Wahrscheinlichkeit statt). 1 Nehmen Sie an, dass
Aufgabenset 1 (abzugeben 16.03.2012 an LK@wacc.de) Aufgabe 1 Betrachten Sie die Cashflows der Abbildung 1 (Auf- und Abwärtsbewegungen finden mit gleicher Wahrscheinlichkeit statt). 1 Nehmen Sie an, dass
Kapitalversicherungen
 Kapitalversicherungen Sanela Omerovic Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 Inhaltsverzeichnis 1 Einführung 1 2 Einfache Versicherungsformen 3 2.1 Todesfallversicherungen (Life Insurance)....................
Kapitalversicherungen Sanela Omerovic Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 Inhaltsverzeichnis 1 Einführung 1 2 Einfache Versicherungsformen 3 2.1 Todesfallversicherungen (Life Insurance)....................
Korrigenda Handbuch der Bewertung
 Korrigenda Handbuch der Bewertung Kapitel 3 Abschnitt 3.5 Seite(n) 104-109 Titel Der Terminvertrag: Ein Beispiel für den Einsatz von Future Values Änderungen In den Beispielen 21 und 22 ist der Halbjahressatz
Korrigenda Handbuch der Bewertung Kapitel 3 Abschnitt 3.5 Seite(n) 104-109 Titel Der Terminvertrag: Ein Beispiel für den Einsatz von Future Values Änderungen In den Beispielen 21 und 22 ist der Halbjahressatz
Einleitung. Das Ein-Perioden-Modell ist das einfachste. von derivaten Finanzinstrumenten (hier: Optionen) zu erklären.
 Einleitung Das Ein-Perioden-Modell ist das einfachste Modell, um die Idee der Preisgebung von derivaten Finanzinstrumenten (hier: Optionen) zu erklären. naive Idee der Optionspreisbestimmung: Erwartungswertprinzip
Einleitung Das Ein-Perioden-Modell ist das einfachste Modell, um die Idee der Preisgebung von derivaten Finanzinstrumenten (hier: Optionen) zu erklären. naive Idee der Optionspreisbestimmung: Erwartungswertprinzip
SS 2014 Torsten Schreiber
 SS 2014 Torsten Schreiber 204 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Bei der Rentenrechnung geht es um aus einem angesparten Kapital bzw. um um das Kapital aufzubauen, die innerhalb
SS 2014 Torsten Schreiber 204 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Bei der Rentenrechnung geht es um aus einem angesparten Kapital bzw. um um das Kapital aufzubauen, die innerhalb
9.2. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83
 9.. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83 Die Grundfrage bei der Anwendung des Satzes über implizite Funktionen betrifft immer die folgende Situation: Wir haben eine Funktion f : V W und eine Stelle x
9.. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83 Die Grundfrage bei der Anwendung des Satzes über implizite Funktionen betrifft immer die folgende Situation: Wir haben eine Funktion f : V W und eine Stelle x
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren
 Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Lineargleichungssysteme: Additions-/ Subtraktionsverfahren W. Kippels 22. Februar 2014 Inhaltsverzeichnis 1 Einleitung 2 2 Lineargleichungssysteme zweiten Grades 2 3 Lineargleichungssysteme höheren als
Güte von Tests. die Wahrscheinlichkeit für den Fehler 2. Art bei der Testentscheidung, nämlich. falsch ist. Darauf haben wir bereits im Kapitel über
 Güte von s Grundlegendes zum Konzept der Güte Ableitung der Gütefunktion des Gauss im Einstichprobenproblem Grafische Darstellung der Gütefunktionen des Gauss im Einstichprobenproblem Ableitung der Gütefunktion
Güte von s Grundlegendes zum Konzept der Güte Ableitung der Gütefunktion des Gauss im Einstichprobenproblem Grafische Darstellung der Gütefunktionen des Gauss im Einstichprobenproblem Ableitung der Gütefunktion
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Gehen wir einmal davon aus, dass die von uns angenommenen
 geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
SS 2014 Torsten Schreiber
 SS 2014 Torsten Schreiber 239 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Durch die wird ein Zahlungsstrom beschrieben, der zur Rückführung eines geliehenen Geldbetrags dient. Der zu zahlende
SS 2014 Torsten Schreiber 239 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Durch die wird ein Zahlungsstrom beschrieben, der zur Rückführung eines geliehenen Geldbetrags dient. Der zu zahlende
50. Mathematik-Olympiade 2. Stufe (Regionalrunde) Klasse 11 13. 501322 Lösung 10 Punkte
 50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
Würfelt man dabei je genau 10 - mal eine 1, 2, 3, 4, 5 und 6, so beträgt die Anzahl. der verschiedenen Reihenfolgen, in denen man dies tun kann, 60!.
 040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
Zeichen bei Zahlen entschlüsseln
 Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Finanzwirtschaft. Teil II: Bewertung
 Zeitwert des Geldes 1 Finanzwirtschaft Teil II: Bewertung Zeitwert des Geldes Zeitwert des Geldes 2 Bewertung & Zeitwert des Geldes Finanzwirtschaft behandelt die Bewertung von Real- und Finanzwerten.
Zeitwert des Geldes 1 Finanzwirtschaft Teil II: Bewertung Zeitwert des Geldes Zeitwert des Geldes 2 Bewertung & Zeitwert des Geldes Finanzwirtschaft behandelt die Bewertung von Real- und Finanzwerten.
Anhand des bereits hergeleiteten Models erstellen wir nun mit der Formel
 Ausarbeitung zum Proseminar Finanzmathematische Modelle und Simulationen bei Raphael Kruse und Prof. Dr. Wolf-Jürgen Beyn zum Thema Simulation des Anlagenpreismodels von Simon Uphus im WS 09/10 Zusammenfassung
Ausarbeitung zum Proseminar Finanzmathematische Modelle und Simulationen bei Raphael Kruse und Prof. Dr. Wolf-Jürgen Beyn zum Thema Simulation des Anlagenpreismodels von Simon Uphus im WS 09/10 Zusammenfassung
vorschüssige, lebenslängliche Leibrente (whole life annuity-due) Vorschüssige jährliche Zahlungen von 1, solange die versicherte Person am Leben ist.
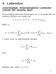 4. Leibrenten vorschüssige, lebenslängliche Leibrente (whole life annuity-due) Vorschüssige jährliche Zahlungen von 1, solange die versicherte Person am Leben ist. NEP ä x : Y = 1 + v + v 2 + + v K = ä
4. Leibrenten vorschüssige, lebenslängliche Leibrente (whole life annuity-due) Vorschüssige jährliche Zahlungen von 1, solange die versicherte Person am Leben ist. NEP ä x : Y = 1 + v + v 2 + + v K = ä
Zinsen, Zinseszins, Rentenrechnung und Tilgung
 Zinsen, Zinseszins, Rentenrechnung und Tilgung 1. Zinsen, Zinseszins 2. Rentenrechnung 3. Tilgung Nevzat Ates, Birgit Jacobs Zinsrechnen mit dem Dreisatz 1 Zinsen Zinsrechnen mit den Formeln Zinseszins
Zinsen, Zinseszins, Rentenrechnung und Tilgung 1. Zinsen, Zinseszins 2. Rentenrechnung 3. Tilgung Nevzat Ates, Birgit Jacobs Zinsrechnen mit dem Dreisatz 1 Zinsen Zinsrechnen mit den Formeln Zinseszins
Senkung des technischen Zinssatzes und des Umwandlungssatzes
 Senkung des technischen Zinssatzes und des Umwandlungssatzes Was ist ein Umwandlungssatz? Die PKE führt für jede versicherte Person ein individuelles Konto. Diesem werden die Beiträge, allfällige Einlagen
Senkung des technischen Zinssatzes und des Umwandlungssatzes Was ist ein Umwandlungssatz? Die PKE führt für jede versicherte Person ein individuelles Konto. Diesem werden die Beiträge, allfällige Einlagen
7 Rechnen mit Polynomen
 7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
2. Gesundheitsfinanzierung
 2. Gesundheitsfinanzierung Inhalte dieses Abschnitts 2.1 Grundmodell der Versicherung Versicherungsmotiv Optimale Versicherungsnachfrage Aktuarisch faire und unfaire Prämien 145 2.1 Grundmodell der Versicherung
2. Gesundheitsfinanzierung Inhalte dieses Abschnitts 2.1 Grundmodell der Versicherung Versicherungsmotiv Optimale Versicherungsnachfrage Aktuarisch faire und unfaire Prämien 145 2.1 Grundmodell der Versicherung
1 Mathematische Grundlagen
 Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
SS 2014 Torsten Schreiber
 SS 2014 Torsten Schreiber 193 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Bei einer Abschreibung werden eines Gutes während der Nutzungsdauer festgehalten. Diese Beträge stellen dar und dadurch
SS 2014 Torsten Schreiber 193 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Bei einer Abschreibung werden eines Gutes während der Nutzungsdauer festgehalten. Diese Beträge stellen dar und dadurch
Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR)
 Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR) Eine Firma stellt USB-Sticks her. Sie werden in der Fabrik ungeprüft in Packungen zu je 20 Stück verpackt und an Händler ausgeliefert. 1 Ein Händler
Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR) Eine Firma stellt USB-Sticks her. Sie werden in der Fabrik ungeprüft in Packungen zu je 20 Stück verpackt und an Händler ausgeliefert. 1 Ein Händler
n... Laufzeit der Kapitalanlage = Zeit, während der Zinsen zu zahlen sind (oder gezahlt werden) in Zinsperioden (z.b. Jahre)
 3. Finanzmathematik 3.1. Zinsrechnung 3.1.1. Grundbegriffe K... Kapital (caput - das Haupt) = Betrag, der der Verzinsung unterworfen ist; Geldbetrag (Währung) z... Zinsen = Vergütung (Preis) für das Überlassen
3. Finanzmathematik 3.1. Zinsrechnung 3.1.1. Grundbegriffe K... Kapital (caput - das Haupt) = Betrag, der der Verzinsung unterworfen ist; Geldbetrag (Währung) z... Zinsen = Vergütung (Preis) für das Überlassen
Das Black-Scholes Marktmodell
 Das Black-Scholes Marktmodell Andreas Eichler Institut für Finanzmathematik Johannes Kepler Universität Linz 8. April 2011 1 / 14 Gliederung 1 Einleitung Fortgeschrittene Finanzmathematik einfach erklärt
Das Black-Scholes Marktmodell Andreas Eichler Institut für Finanzmathematik Johannes Kepler Universität Linz 8. April 2011 1 / 14 Gliederung 1 Einleitung Fortgeschrittene Finanzmathematik einfach erklärt
Rente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren Rentenperiode = Zeitabstand zwischen zwei Rentenzahlungen
 5.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind zwei
5.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind zwei
Statistische Thermodynamik I Lösungen zur Serie 1
 Statistische Thermodynamik I Lösungen zur Serie Zufallsvariablen, Wahrscheinlichkeitsverteilungen 4. März 2. Zwei Lektoren lesen ein Buch. Lektor A findet 2 Druckfehler, Lektor B nur 5. Von den gefundenen
Statistische Thermodynamik I Lösungen zur Serie Zufallsvariablen, Wahrscheinlichkeitsverteilungen 4. März 2. Zwei Lektoren lesen ein Buch. Lektor A findet 2 Druckfehler, Lektor B nur 5. Von den gefundenen
Vorlesung Finanzmathematik (TM/SRM/SM/MM) Block : Ausgewählte Aufgaben Investitionsrechnung und festverzinsliche Wertpapiere
 Hochschule Ostfalia Fakultät Verkehr Sport Tourismus Medien apl. Professor Dr. H. Löwe Sommersemester 20 Vorlesung Finanzmathematik (TM/SRM/SM/MM) Block : Ausgewählte Aufgaben Investitionsrechnung und
Hochschule Ostfalia Fakultät Verkehr Sport Tourismus Medien apl. Professor Dr. H. Löwe Sommersemester 20 Vorlesung Finanzmathematik (TM/SRM/SM/MM) Block : Ausgewählte Aufgaben Investitionsrechnung und
Basis und Dimension. Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren.
 Basis und Dimension Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren. Definition. Sei V ein K-Vektorraum und (v i ) i I eine Familie von Vektoren
Basis und Dimension Als nächstes wollen wir die wichtigen Begriffe Erzeugendensystem und Basis eines Vektorraums definieren. Definition. Sei V ein K-Vektorraum und (v i ) i I eine Familie von Vektoren
Mathematik 1 für Wirtschaftsinformatik
 Mathematik 1 für Wirtschaftsinformatik Wintersemester 2012/13 Hochschule Augsburg Äquivalenzprinzip der Finanzmathematik Das Äquivalenzprinzip der Finanzmathematik für Vergleich von Zahlungen, welche
Mathematik 1 für Wirtschaftsinformatik Wintersemester 2012/13 Hochschule Augsburg Äquivalenzprinzip der Finanzmathematik Das Äquivalenzprinzip der Finanzmathematik für Vergleich von Zahlungen, welche
Charakteristikenmethode im Beispiel
 Charakteristikenmethode im Wir betrachten die PDE in drei Variablen xu x + yu y + (x + y )u z = 0. Das charakteristische System lautet dann ẋ = x ẏ = y ż = x + y und besitzt die allgemeine Lösung x(t)
Charakteristikenmethode im Wir betrachten die PDE in drei Variablen xu x + yu y + (x + y )u z = 0. Das charakteristische System lautet dann ẋ = x ẏ = y ż = x + y und besitzt die allgemeine Lösung x(t)
Quantilsschätzung als Werkzeug zur VaR-Berechnung
 Quantilsschätzung als Werkzeug zur VaR-Berechnung Ralf Lister, Aktuar, lister@actuarial-files.com Zusammenfassung: Zwei Fälle werden betrachtet und die jeweiligen VaR-Werte errechnet. Im ersten Fall wird
Quantilsschätzung als Werkzeug zur VaR-Berechnung Ralf Lister, Aktuar, lister@actuarial-files.com Zusammenfassung: Zwei Fälle werden betrachtet und die jeweiligen VaR-Werte errechnet. Im ersten Fall wird
Deckungskapital. Proseminar Versicherungsmathematik. TU Graz. 11. Dezember 2007
 Deckungskapital Gülnur Adanç Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 1 Inhaltsverzeichnis 1 Deckungskapital 2 1.1 Prospektive und Retrospektive Methode.................... 3 1.1.1
Deckungskapital Gülnur Adanç Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 1 Inhaltsverzeichnis 1 Deckungskapital 2 1.1 Prospektive und Retrospektive Methode.................... 3 1.1.1
 Name:... Matrikel-Nr.:... 3 Aufgabe Handyklingeln in der Vorlesung (9 Punkte) Angenommen, ein Student führt ein Handy mit sich, das mit einer Wahrscheinlichkeit von p während einer Vorlesung zumindest
Name:... Matrikel-Nr.:... 3 Aufgabe Handyklingeln in der Vorlesung (9 Punkte) Angenommen, ein Student führt ein Handy mit sich, das mit einer Wahrscheinlichkeit von p während einer Vorlesung zumindest
Kapitalversicherungen
 Kapitalversicherungen Birgit Scharwitzl 10. Dezember 2008 Inhaltsverzeichnis 1 Begriffe und wichtige Definitionen 2 1.1 Prämie................................................... 2 1.2 Gewinnbeteiligung............................................
Kapitalversicherungen Birgit Scharwitzl 10. Dezember 2008 Inhaltsverzeichnis 1 Begriffe und wichtige Definitionen 2 1.1 Prämie................................................... 2 1.2 Gewinnbeteiligung............................................
Professionelle Seminare im Bereich MS-Office
 Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis Das komplette Material finden Sie hier: Download bei School-Scout.de
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis Das komplette Material finden Sie hier: Download bei School-Scout.de
Prof. Dr. Arnd Wiedemann Methodische Grundlagen des Controlling und Risikomanagements
 Prof. Dr. Arnd Wiedemann Methodische Grundlagen des Controlling und Risikomanagements Prof. Dr. Arnd Wiedemann Methoden CRM / WS 12-13 1 Agenda Teil A: Teil B: Teil C: Finanzmathematisches Basiswissen
Prof. Dr. Arnd Wiedemann Methodische Grundlagen des Controlling und Risikomanagements Prof. Dr. Arnd Wiedemann Methoden CRM / WS 12-13 1 Agenda Teil A: Teil B: Teil C: Finanzmathematisches Basiswissen
Bericht zur Prüfung im Oktober 2003 über Mathematik der Lebensversicherung (Grundwissen)
 Bericht zur Prüfung im Oktober 2003 über Mathematik der Lebensversicherung Grundwissen) Jürgen Strobel Köln) und Hans-Jochen Bartels Mannheim) Am 04.10.2003 wurde in Köln die zehnte Prüfung über Mathematik
Bericht zur Prüfung im Oktober 2003 über Mathematik der Lebensversicherung Grundwissen) Jürgen Strobel Köln) und Hans-Jochen Bartels Mannheim) Am 04.10.2003 wurde in Köln die zehnte Prüfung über Mathematik
Universität Bonn 28. Juli 2010 Fachbereich Rechts- und Wirtschaftswissenschaften Statistische Abteilung Prof. Dr. A. Kneip. KLAUSUR Statistik B
 Universität Bonn 28. Juli 2010 Fachbereich Rechts- und Wirtschaftswissenschaften Statistische Abteilung Prof. Dr. A. Kneip Sommersemester 2010 KLAUSUR Statistik B Hinweise zur Bearbeitung: Bei allen Teilaufgaben
Universität Bonn 28. Juli 2010 Fachbereich Rechts- und Wirtschaftswissenschaften Statistische Abteilung Prof. Dr. A. Kneip Sommersemester 2010 KLAUSUR Statistik B Hinweise zur Bearbeitung: Bei allen Teilaufgaben
Was ist Sozial-Raum-Orientierung?
 Was ist Sozial-Raum-Orientierung? Dr. Wolfgang Hinte Universität Duisburg-Essen Institut für Stadt-Entwicklung und Sozial-Raum-Orientierte Arbeit Das ist eine Zusammen-Fassung des Vortrages: Sozialräume
Was ist Sozial-Raum-Orientierung? Dr. Wolfgang Hinte Universität Duisburg-Essen Institut für Stadt-Entwicklung und Sozial-Raum-Orientierte Arbeit Das ist eine Zusammen-Fassung des Vortrages: Sozialräume
11. April 2011. Geldtheorie und -politik. Definition und Bestimmung von Zinssätzen (Mishkin, Kapitel 4)
 Geldtheorie und -politik Definition und Bestimmung von Zinssätzen (Mishkin, Kapitel 4) 11. April 2011 Überblick Barwertkonzept Kreditmarktinstrumente: Einfaches Darlehen, Darlehen mit konstanten Raten,
Geldtheorie und -politik Definition und Bestimmung von Zinssätzen (Mishkin, Kapitel 4) 11. April 2011 Überblick Barwertkonzept Kreditmarktinstrumente: Einfaches Darlehen, Darlehen mit konstanten Raten,
Tutorium zur Mathematik (WS 2004/2005) - Finanzmathematik Seite 1
 Tutorium zur Mathematik WS 2004/2005) - Finanzmathematik Seite 1 Finanzmathematik 1.1 Prozentrechnung K Grundwert Basis, Bezugsgröße) p Prozentfuß i Prozentsatz i = p 100 ) Z Prozentwert Z = K i bzw. Z
Tutorium zur Mathematik WS 2004/2005) - Finanzmathematik Seite 1 Finanzmathematik 1.1 Prozentrechnung K Grundwert Basis, Bezugsgröße) p Prozentfuß i Prozentsatz i = p 100 ) Z Prozentwert Z = K i bzw. Z
einfache Rendite 0 145 85 1 160 90 2 135 100 3 165 105 4 190 95 5 210 110
 Übungsbeispiele 1/6 1) Vervollständigen Sie folgende Tabelle: Nr. Aktie A Aktie B Schlusskurs in Schlusskurs in 0 145 85 1 160 90 2 135 100 3 165 105 4 190 95 5 210 110 Arithmetisches Mittel Standardabweichung
Übungsbeispiele 1/6 1) Vervollständigen Sie folgende Tabelle: Nr. Aktie A Aktie B Schlusskurs in Schlusskurs in 0 145 85 1 160 90 2 135 100 3 165 105 4 190 95 5 210 110 Arithmetisches Mittel Standardabweichung
1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage:
 Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Übungsaufgaben Tilgungsrechnung
 1 Zusatzmaterialien zu Finanz- und Wirtschaftsmathematik im Unterricht, Band 1 Übungsaufgaben Tilgungsrechnung Überarbeitungsstand: 1.März 2016 Die grundlegenden Ideen der folgenden Aufgaben beruhen auf
1 Zusatzmaterialien zu Finanz- und Wirtschaftsmathematik im Unterricht, Band 1 Übungsaufgaben Tilgungsrechnung Überarbeitungsstand: 1.März 2016 Die grundlegenden Ideen der folgenden Aufgaben beruhen auf
Lebensversicherung. http://www.konsument.at/cs/satellite?pagename=konsument/magazinartikel/printma... OBJEKTIV UNBESTECHLICH KEINE WERBUNG
 Seite 1 von 6 OBJEKTIV UNBESTECHLICH KEINE WERBUNG Lebensversicherung Verschenken Sie kein Geld! veröffentlicht am 11.03.2011, aktualisiert am 14.03.2011 "Verschenken Sie kein Geld" ist der aktuelle Rat
Seite 1 von 6 OBJEKTIV UNBESTECHLICH KEINE WERBUNG Lebensversicherung Verschenken Sie kein Geld! veröffentlicht am 11.03.2011, aktualisiert am 14.03.2011 "Verschenken Sie kein Geld" ist der aktuelle Rat
Rekursionen (Teschl/Teschl 8.1-8.2)
 Rekursionen (Teschl/Teschl 8.1-8.2) Eine Rekursion kter Ordnung für k N ist eine Folge x 1, x 2, x 3,... deniert durch eine Rekursionsvorschrift x n = f n (x n 1,..., x n k ) für n > k, d. h. jedes Folgenglied
Rekursionen (Teschl/Teschl 8.1-8.2) Eine Rekursion kter Ordnung für k N ist eine Folge x 1, x 2, x 3,... deniert durch eine Rekursionsvorschrift x n = f n (x n 1,..., x n k ) für n > k, d. h. jedes Folgenglied
XONTRO Newsletter. Makler. Nr. 16
 XONTRO Newsletter Makler Nr. 16 Seite 1 In XONTRO werden zum 24. Januar 2005 folgende Änderungen eingeführt: Inflationsindexierte Anleihen Stückzinsberechnung für französische und italienische Staatsanleihen
XONTRO Newsletter Makler Nr. 16 Seite 1 In XONTRO werden zum 24. Januar 2005 folgende Änderungen eingeführt: Inflationsindexierte Anleihen Stückzinsberechnung für französische und italienische Staatsanleihen
ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN
 ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN CHRISTIAN HARTFELDT. Zweiter Mittelwertsatz Der Mittelwertsatz Satz VI.3.4) lässt sich verallgemeinern zu Satz.. Seien f, g : [a, b] R auf [a,
ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN CHRISTIAN HARTFELDT. Zweiter Mittelwertsatz Der Mittelwertsatz Satz VI.3.4) lässt sich verallgemeinern zu Satz.. Seien f, g : [a, b] R auf [a,
Skript und Aufgabensammlung Terme und Gleichungen Mathefritz Verlag Jörg Christmann Nur zum Privaten Gebrauch! Alle Rechte vorbehalten!
 Mathefritz 5 Terme und Gleichungen Meine Mathe-Seite im Internet kostenlose Matheaufgaben, Skripte, Mathebücher Lernspiele, Lerntipps, Quiz und noch viel mehr http:// www.mathefritz.de Seite 1 Copyright
Mathefritz 5 Terme und Gleichungen Meine Mathe-Seite im Internet kostenlose Matheaufgaben, Skripte, Mathebücher Lernspiele, Lerntipps, Quiz und noch viel mehr http:// www.mathefritz.de Seite 1 Copyright
Dynamische Methoden der Investitionsrechnung
 4 Dynamische Methoden der Investitionsrechnung Lernziele Das Konzept des Gegenwartswertes erklären Den Überschuss oder Fehlbetrag einer Investition mit Hilfe der Gegenwartswertmethode berechnen Die Begriffe
4 Dynamische Methoden der Investitionsrechnung Lernziele Das Konzept des Gegenwartswertes erklären Den Überschuss oder Fehlbetrag einer Investition mit Hilfe der Gegenwartswertmethode berechnen Die Begriffe
Informationsblatt Induktionsbeweis
 Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Finanzwirtschaft Teil III: Budgetierung des Kapitals
 Finanzmärkte 1 Finanzwirtschaft Teil III: Budgetierung des Kapitals Kapitalwertmethode Agenda Finanzmärkte 2 Kapitalwertmethode Anwendungen Revolvierende Investitionsprojekte Zusammenfassung Kapitalwertmethode
Finanzmärkte 1 Finanzwirtschaft Teil III: Budgetierung des Kapitals Kapitalwertmethode Agenda Finanzmärkte 2 Kapitalwertmethode Anwendungen Revolvierende Investitionsprojekte Zusammenfassung Kapitalwertmethode
Ihre Joker für eine entspannte Vorsorge
 Ihre oker für eine entspannte Vorsorge GarantiePlus Pflegeption GarantiePlus Ihr Vorsorge-oker in oker ist immer etwas Besonderes, denn damit haben Sie einen Trumpf in der Hand. So wie unsere neue Leistung
Ihre oker für eine entspannte Vorsorge GarantiePlus Pflegeption GarantiePlus Ihr Vorsorge-oker in oker ist immer etwas Besonderes, denn damit haben Sie einen Trumpf in der Hand. So wie unsere neue Leistung
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen
 Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen 1. Quadratische Gleichungen Quadratische Gleichungen lassen sich immer auf die sog. normierte Form x 2 + px + = 0 bringen, in
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen 1. Quadratische Gleichungen Quadratische Gleichungen lassen sich immer auf die sog. normierte Form x 2 + px + = 0 bringen, in
Austausch- bzw. Übergangsprozesse und Gleichgewichtsverteilungen
 Austausch- bzw. Übergangsrozesse und Gleichgewichtsverteilungen Wir betrachten ein System mit verschiedenen Zuständen, zwischen denen ein Austausch stattfinden kann. Etwa soziale Schichten in einer Gesellschaft:
Austausch- bzw. Übergangsrozesse und Gleichgewichtsverteilungen Wir betrachten ein System mit verschiedenen Zuständen, zwischen denen ein Austausch stattfinden kann. Etwa soziale Schichten in einer Gesellschaft:
Derivate und Bewertung
 . Dr. Daniel Sommer Marie-Curie-Str. 30 60439 Franfurt am Main Klausur Derivate und Bewertung.......... Wintersemester 2008/09 Klausur Derivate und Bewertung Wintersemester 2008/09 Aufgabe 1: Zinsurven,
. Dr. Daniel Sommer Marie-Curie-Str. 30 60439 Franfurt am Main Klausur Derivate und Bewertung.......... Wintersemester 2008/09 Klausur Derivate und Bewertung Wintersemester 2008/09 Aufgabe 1: Zinsurven,
Wirtschaftsmathematik für International Management (BA)
 Wirtschaftsmathematik für International Management (BA) Wintersemester 2012/13 Hochschule Augsburg : Gliederung 1 Grundlegende 2 Grundlegende 3 Lineare Algebra 4 Lineare Programme 5 Folgen und Reihen 6
Wirtschaftsmathematik für International Management (BA) Wintersemester 2012/13 Hochschule Augsburg : Gliederung 1 Grundlegende 2 Grundlegende 3 Lineare Algebra 4 Lineare Programme 5 Folgen und Reihen 6
Prozentrechnung. Wir können nun eine Formel für die Berechnung des Prozentwertes aufstellen:
 Prozentrechnung Wir beginnen mit einem Beisiel: Nehmen wir mal an, ein Handy kostet 200 und es gibt 5% Rabatt (Preisnachlass), wie groß ist dann der Rabatt in Euro und wie viel kostet dann das Handy? Wenn
Prozentrechnung Wir beginnen mit einem Beisiel: Nehmen wir mal an, ein Handy kostet 200 und es gibt 5% Rabatt (Preisnachlass), wie groß ist dann der Rabatt in Euro und wie viel kostet dann das Handy? Wenn
Themenschwerpunkt Sofortrente
 Themenschwerpunkt Sofortrente Inhalt: Sofortrente, Ansparrente Gemeinsamkeiten und Unterschiede. Sofortrente nach Maß Verschiedene Gestaltungsmöglichkeiten. Sofortrente und Steuern Über die Besteuerung
Themenschwerpunkt Sofortrente Inhalt: Sofortrente, Ansparrente Gemeinsamkeiten und Unterschiede. Sofortrente nach Maß Verschiedene Gestaltungsmöglichkeiten. Sofortrente und Steuern Über die Besteuerung
Mathematik 1. Inhaltsverzeichnis. Prof. Dr. K. Melzer. karin.melzer@hs-esslingen.de http://www.hs-esslingen.de/de/mitarbeiter/karin-melzer.
 Mathematik 1 Prof Dr K Melzer karinmelzer@hs-esslingende http://wwwhs-esslingende/de/mitarbeiter/karin-melzerhtml Inhaltsverzeichnis 1 Finanzmathematik 1 11 Folgen und Reihen 1 111 Folgen allgemein 1 112
Mathematik 1 Prof Dr K Melzer karinmelzer@hs-esslingende http://wwwhs-esslingende/de/mitarbeiter/karin-melzerhtml Inhaltsverzeichnis 1 Finanzmathematik 1 11 Folgen und Reihen 1 111 Folgen allgemein 1 112
Wichtige Begriffe in der Finanzmathematik
 Wichtige Begriffe in der Finanzmathematik Forward: Kontrakt, ein Finanzgut zu einem fest vereinbarten Zeitpunkt bzw. innerhalb eines Zeitraums zu einem vereinbarten Erfüllungspreis zu kaufen bzw. verkaufen.
Wichtige Begriffe in der Finanzmathematik Forward: Kontrakt, ein Finanzgut zu einem fest vereinbarten Zeitpunkt bzw. innerhalb eines Zeitraums zu einem vereinbarten Erfüllungspreis zu kaufen bzw. verkaufen.
Data Mining: Einige Grundlagen aus der Stochastik
 Data Mining: Einige Grundlagen aus der Stochastik Hagen Knaf Studiengang Angewandte Mathematik Hochschule RheinMain 21. Oktober 2015 Vorwort Das vorliegende Skript enthält eine Zusammenfassung verschiedener
Data Mining: Einige Grundlagen aus der Stochastik Hagen Knaf Studiengang Angewandte Mathematik Hochschule RheinMain 21. Oktober 2015 Vorwort Das vorliegende Skript enthält eine Zusammenfassung verschiedener
Lineare Differentialgleichungen erster Ordnung erkennen
 Lineare Differentialgleichungen erster Ordnung In diesem Kapitel... Erkennen, wie Differentialgleichungen erster Ordnung aussehen en für Differentialgleichungen erster Ordnung und ohne -Terme finden Die
Lineare Differentialgleichungen erster Ordnung In diesem Kapitel... Erkennen, wie Differentialgleichungen erster Ordnung aussehen en für Differentialgleichungen erster Ordnung und ohne -Terme finden Die
Modellbildungssysteme: Pädagogische und didaktische Ziele
 Modellbildungssysteme: Pädagogische und didaktische Ziele Was hat Modellbildung mit der Schule zu tun? Der Bildungsplan 1994 formuliert: "Die schnelle Zunahme des Wissens, die hohe Differenzierung und
Modellbildungssysteme: Pädagogische und didaktische Ziele Was hat Modellbildung mit der Schule zu tun? Der Bildungsplan 1994 formuliert: "Die schnelle Zunahme des Wissens, die hohe Differenzierung und
Gründe für fehlende Vorsorgemaßnahmen gegen Krankheit
 Gründe für fehlende Vorsorgemaßnahmen gegen Krankheit politische Lage verlassen sich auf Familie persönliche, finanzielle Lage meinen, sich Vorsorge leisten zu können meinen, sie seien zu alt nicht mit
Gründe für fehlende Vorsorgemaßnahmen gegen Krankheit politische Lage verlassen sich auf Familie persönliche, finanzielle Lage meinen, sich Vorsorge leisten zu können meinen, sie seien zu alt nicht mit
Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema
 Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema 2x 4 + x 3 + x + 3 div x 2 + x 1 = 2x 2 x + 3 (2x 4 + 2x 3 2x 2 ) x 3 + 2x 2 + x + 3 ( x
Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema 2x 4 + x 3 + x + 3 div x 2 + x 1 = 2x 2 x + 3 (2x 4 + 2x 3 2x 2 ) x 3 + 2x 2 + x + 3 ( x
Lineare Funktionen. 1 Proportionale Funktionen 3 1.1 Definition... 3 1.2 Eigenschaften... 3. 2 Steigungsdreieck 3
 Lineare Funktionen Inhaltsverzeichnis 1 Proportionale Funktionen 3 1.1 Definition............................... 3 1.2 Eigenschaften............................. 3 2 Steigungsdreieck 3 3 Lineare Funktionen
Lineare Funktionen Inhaltsverzeichnis 1 Proportionale Funktionen 3 1.1 Definition............................... 3 1.2 Eigenschaften............................. 3 2 Steigungsdreieck 3 3 Lineare Funktionen
Institut für Stochastik Prof. Dr. N. Bäuerle Dipl.-Math. S. Urban
 Institut für Stochastik Prof. Dr. N. Bäuerle Dipl.-Math. S. Urban Lösungsvorschlag 8. Übungsblatt zur Vorlesung Finanzmathematik I Aufgabe Hedging Amerikanischer Optionen Wir sind in einem arbitragefreien
Institut für Stochastik Prof. Dr. N. Bäuerle Dipl.-Math. S. Urban Lösungsvorschlag 8. Übungsblatt zur Vorlesung Finanzmathematik I Aufgabe Hedging Amerikanischer Optionen Wir sind in einem arbitragefreien
Numerische Mathematik I 4. Nichtlineare Gleichungen und Gleichungssysteme 4.1 Wo treten nichtlineare Gleichungen auf?
 Numerische Mathematik I 4. Nichtlineare Gleichungen und Gleichungssysteme 4.1 Wo treten nichtlineare Gleichungen auf? Andreas Rieder UNIVERSITÄT KARLSRUHE (TH) Institut für Wissenschaftliches Rechnen und
Numerische Mathematik I 4. Nichtlineare Gleichungen und Gleichungssysteme 4.1 Wo treten nichtlineare Gleichungen auf? Andreas Rieder UNIVERSITÄT KARLSRUHE (TH) Institut für Wissenschaftliches Rechnen und
Charakteristikum des Gutachtenstils: Es wird mit einer Frage begonnen, sodann werden die Voraussetzungen Schritt für Schritt aufgezeigt und erörtert.
 Der Gutachtenstil: Charakteristikum des Gutachtenstils: Es wird mit einer Frage begonnen, sodann werden die Voraussetzungen Schritt für Schritt aufgezeigt und erörtert. Das Ergebnis steht am Schluß. Charakteristikum
Der Gutachtenstil: Charakteristikum des Gutachtenstils: Es wird mit einer Frage begonnen, sodann werden die Voraussetzungen Schritt für Schritt aufgezeigt und erörtert. Das Ergebnis steht am Schluß. Charakteristikum
XONTRO Newsletter. Kreditinstitute. Nr. 18
 XONTRO Newsletter Kreditinstitute Nr. 18 Seite 1 In XONTRO werden zum 24. Januar 2005 folgende Änderungen eingeführt: Inflationsindexierte Anleihen Stückzinsberechnung für französische und italienische
XONTRO Newsletter Kreditinstitute Nr. 18 Seite 1 In XONTRO werden zum 24. Januar 2005 folgende Änderungen eingeführt: Inflationsindexierte Anleihen Stückzinsberechnung für französische und italienische
Swiss Life Vorsorge-Know-how
 Swiss Life Vorsorge-Know-how Thema des Monats: Sofortrente Inhalt: Sofortrente, Ansparrente Gemeinsamkeiten und Unterschiede. Sofortrente nach Maß Verschiedene Gestaltungsmöglichkeiten. Sofortrente und
Swiss Life Vorsorge-Know-how Thema des Monats: Sofortrente Inhalt: Sofortrente, Ansparrente Gemeinsamkeiten und Unterschiede. Sofortrente nach Maß Verschiedene Gestaltungsmöglichkeiten. Sofortrente und
SST: - In Kraft - Ab 2011 verbindlich - Modellabhängig
 Standardmodell oder internes Modell in der Lebensversicherung? Prüfungskolloquium zum Aktuar SAV 2010 Caroline Jaeger, Allianz Suisse Ursprung der Fragestellung Solvency I: - Risikounabhängig - Formelbasiert
Standardmodell oder internes Modell in der Lebensversicherung? Prüfungskolloquium zum Aktuar SAV 2010 Caroline Jaeger, Allianz Suisse Ursprung der Fragestellung Solvency I: - Risikounabhängig - Formelbasiert
Aufgaben zur Flächenberechnung mit der Integralrechung
 ufgaben zur Flächenberechnung mit der Integralrechung ) Geben ist die Funktion f(x) = -x + x. a) Wie groß ist die Fläche, die die Kurve von f mit der x-chse einschließt? b) Welche Fläche schließt der Graph
ufgaben zur Flächenberechnung mit der Integralrechung ) Geben ist die Funktion f(x) = -x + x. a) Wie groß ist die Fläche, die die Kurve von f mit der x-chse einschließt? b) Welche Fläche schließt der Graph
Mathematischer Vorbereitungskurs für Ökonomen
 Mathematischer Vorbereitungskurs für Ökonomen Dr. Thomas Zehrt Wirtschaftswissenschaftliches Zentrum Universität Basel Gleichungen Inhalt: 1. Grundlegendes 2. Lineare Gleichungen 3. Gleichungen mit Brüchen
Mathematischer Vorbereitungskurs für Ökonomen Dr. Thomas Zehrt Wirtschaftswissenschaftliches Zentrum Universität Basel Gleichungen Inhalt: 1. Grundlegendes 2. Lineare Gleichungen 3. Gleichungen mit Brüchen
Prüfung Grundprinzipien der Versicherungs- und Finanzmathematik 2015
 Prüfung Grundprinzipien der Versicherungs- und Finanzmathematik 2015 Aufgabe 1: (20 min) a) Gegeben sei ein einperiodiger State Space-Markt mit zwei Zuständen, der aus zwei Wertpapieren bestehe, einer
Prüfung Grundprinzipien der Versicherungs- und Finanzmathematik 2015 Aufgabe 1: (20 min) a) Gegeben sei ein einperiodiger State Space-Markt mit zwei Zuständen, der aus zwei Wertpapieren bestehe, einer
Kommutationszahlen und Versicherungsbarwerte für Leibrenten 2001/2003
 Kommutationszahlen und Versicherungsbarwerte für Leibrenten 2001/2003 Tabellen zur jährlich und monatlich vorschüssigen Zahlungsweise Statistisches Bundesamt Impressum Herausgeber: Statistisches Bundesamt
Kommutationszahlen und Versicherungsbarwerte für Leibrenten 2001/2003 Tabellen zur jährlich und monatlich vorschüssigen Zahlungsweise Statistisches Bundesamt Impressum Herausgeber: Statistisches Bundesamt
Finanzwirtschaft. Teil II: Bewertung
 Sparpläne und Kreditverträge 1 Finanzwirtschaft Teil II: Bewertung Sparpläne und Kreditverträge Agenda Sparpläne und Kreditverträge 2 Endliche Laufzeit Unendliche Laufzeit Zusammenfassung Sparpläne und
Sparpläne und Kreditverträge 1 Finanzwirtschaft Teil II: Bewertung Sparpläne und Kreditverträge Agenda Sparpläne und Kreditverträge 2 Endliche Laufzeit Unendliche Laufzeit Zusammenfassung Sparpläne und
15.3 Bedingte Wahrscheinlichkeit und Unabhängigkeit
 5.3 Bedingte Wahrscheinlichkeit und Unabhängigkeit Einführendes Beispiel ( Erhöhung der Sicherheit bei Flugreisen ) Die statistische Wahrscheinlichkeit, dass während eines Fluges ein Sprengsatz an Bord
5.3 Bedingte Wahrscheinlichkeit und Unabhängigkeit Einführendes Beispiel ( Erhöhung der Sicherheit bei Flugreisen ) Die statistische Wahrscheinlichkeit, dass während eines Fluges ein Sprengsatz an Bord
Hochschule Rhein-Main. Sommersemester 2015
 Vorlesung Hochschule Rhein-Main Sommersemester 2015 Dr. Roland Stamm 29. Juni 2015 Erinnerung Bewertung eines Bonds mit Kupon k, Nominal N, Laufzeit t n: n Π(t) = N k δ(t i 1, t i ) P (t, t i ) + N P (t,
Vorlesung Hochschule Rhein-Main Sommersemester 2015 Dr. Roland Stamm 29. Juni 2015 Erinnerung Bewertung eines Bonds mit Kupon k, Nominal N, Laufzeit t n: n Π(t) = N k δ(t i 1, t i ) P (t, t i ) + N P (t,
16 Risiko und Versicherungsmärkte
 16 Risiko und Versicherungsmärkte Entscheidungen bei Unsicherheit sind Entscheidungen, die mehrere mögliche Auswirkungen haben. Kauf eines Lotterieloses Kauf einer Aktie Mitnahme eines Regenschirms Abschluss
16 Risiko und Versicherungsmärkte Entscheidungen bei Unsicherheit sind Entscheidungen, die mehrere mögliche Auswirkungen haben. Kauf eines Lotterieloses Kauf einer Aktie Mitnahme eines Regenschirms Abschluss
4. Jeder Knoten hat höchstens zwei Kinder, ein linkes und ein rechtes.
 Binäre Bäume Definition: Ein binärer Baum T besteht aus einer Menge von Knoten, die durch eine Vater-Kind-Beziehung wie folgt strukturiert ist: 1. Es gibt genau einen hervorgehobenen Knoten r T, die Wurzel
Binäre Bäume Definition: Ein binärer Baum T besteht aus einer Menge von Knoten, die durch eine Vater-Kind-Beziehung wie folgt strukturiert ist: 1. Es gibt genau einen hervorgehobenen Knoten r T, die Wurzel
Was ist clevere Altersvorsorge?
 Was ist clevere Altersvorsorge? Um eine gute Altersvorsorge zu erreichen, ist es clever einen unabhängigen Berater auszuwählen Angestellte bzw. Berater von Banken, Versicherungen, Fondsgesellschaften und
Was ist clevere Altersvorsorge? Um eine gute Altersvorsorge zu erreichen, ist es clever einen unabhängigen Berater auszuwählen Angestellte bzw. Berater von Banken, Versicherungen, Fondsgesellschaften und
Tarifarten im Rahmen der Tarifoptimierung
 Tarifarten im Rahmen der Tarifoptimierung BA510_201601 txt 2 3 Wir unterscheiden im Rahmen der Tarifoptimierung folgende Tarifarten Konventionell Konzeptversicherungen Dax-Rente Fondsgebunden OptimumGarant
Tarifarten im Rahmen der Tarifoptimierung BA510_201601 txt 2 3 Wir unterscheiden im Rahmen der Tarifoptimierung folgende Tarifarten Konventionell Konzeptversicherungen Dax-Rente Fondsgebunden OptimumGarant
Repetitionsaufgaben Wurzelgleichungen
 Repetitionsaufgaben Wurzelgleichungen Inhaltsverzeichnis A) Vorbemerkungen B) Lernziele C) Theorie mit Aufgaben D) Aufgaben mit Musterlösungen 4 A) Vorbemerkungen Bitte beachten Sie: Bei Wurzelgleichungen
Repetitionsaufgaben Wurzelgleichungen Inhaltsverzeichnis A) Vorbemerkungen B) Lernziele C) Theorie mit Aufgaben D) Aufgaben mit Musterlösungen 4 A) Vorbemerkungen Bitte beachten Sie: Bei Wurzelgleichungen
