Vorlesung PC I Thermodynamik Teil B: Thermodynamische Funktionen, Berechnungen und mathematische Methoden
|
|
|
- Minna Junge
- vor 6 Jahren
- Abrufe
Transkript
1 Vorlesung PC I hermodynamik eil B: hermodynamische Funktionen, Berechnungen und mathematische Methoden Martin Quack, Jürgen Stohner Sommer 2006
2 2 PC I, hermodynamik, Martin Quack, Jürgen Stohner, SS 2006 Inhaltsverzeichnis Seite Vorbemerkung 3 B.1. hermodynamik und Funktionen von mehreren 4 Variablen B.2. Funktion von zwei Variablen, artielle Ableitungen und 5 totale Differentiale B.3. Grundgleichungen für extensive Zustandsfunktionen 7 der hermodynamik B.4. Allgemeine Gleichgewichtsbedingungen 11 B.5. Das Chemische Potential 12 B.6. Phasengleichgewicht 14 B.7. Chemisches Gleichgewicht und Reaktionsgrössen 16 B.8. Reale Gase 22 B.9. Mischungen und Lösungen 33
3 eil B: hermodynamische Funktionen, Berechnungen und mathematische Methoden Vorbemerkung In eil A (Ka. 1 bis 10) wurden die emirischen, hysikalisch-chemischen Grundlagen und Grundgesetze erlernt und mit einfachsten mathematischen Methoden bearbeitet. Dies genügt für viele einfache, wichtige Anwendungen der hermodynamik. Zur Herleitung exakter mathematischer Beziehungen zwischen den verschiedenen thermodynamischen Grössen benötigt man weitergehende Methoden. Hiermit kann man dann auch komlexere thermodynamische Probleme behandeln. Das ist das Ziel des folgenden eils B der Vorlesung. Die raktische Bedeutung solcher weitergehender Rechnungen besteht darin, dass man oft aus bekannten gemessenen Grössen thermodynamischer Systeme neue, benötigte Grössen berechnen kann, ohne neue Exerimente durchzuführen, oder dass man Exerimente so lanen kann, dass sehr einfache Messungen für die Ermittlung von komlexen Grössen genügen, deren direkte Messung sehr schwierig oder raktisch unmöglich wäre. Die folgenden Stichworte sollen als komakte Sammlung wesentlicher Beziehungen und Formeln dienen. Sie sind kein Skrit und kein Lehrbuch. Für ausführliche Darstellungen sei auf die im Verzeichnis zitierte Lehrbuchliteratur hingewiesen (z.b. Margenau Murhy Bd. 1 und Perrin für die Mathematik, Denbigh für die hermodynamik). 3
4 4 PC I, hermodynamik, Martin Quack, Jürgen Stohner, SS 2006 B.1. hermodynamik und Funktionen von mehreren Variablen Die Zustände von thermodynamischen Systemen können in einem Zustandsraum betrachtet werden, der durch eine abhängige Variable (Funktion) als Funktion von F unabhängigen Variablen dargestellt wird, wobei F die Zahl der Freiheitsgrade ist. Die frei wählbaren Punkte im Raum der Dimension F legen den Zustand fest. Alle anderen Eigenschaften ergeben sich dann aus der Natur des thermodynamischen Systems. Als einfachstes Beisiel können wir die Darstellung des Volumens V = f(, ) eines reinen Gases mit den unabhängigen Variablen, wählen. Die Festlegung von und legt unter den betrachteten Bedingungen auch V fest. Man kann aber auch (V,) oder (, V ) oderu(v,), H(, ), G(, ) oders(, ) darstellen. Weiterhin könnte man auch U(S, V ), oder S(U, V ) oder S(V, ) betrachten. Die Verwendung diverser mathematischer Beziehungen in der hermodynamik (auch wesentlich komlexerer Systeme mit mehr Freiheitsgraden) läuft im Wesentlichen auf die Umrechnung zwischen diesen Darstellungen hinaus. Was man berechnet, hängt dann von der hysikalisch-chemischen Problemstellung ab. Es sei hier bemerkt, dass rinziiell Zustände in einem grösseren Raum mit mehr als F Variablen betrachtet werden könnten, wenn mehrere Phasen ohne Gleichgewicht vorliegen. Wenn Gleichgewicht zwischen mehreren Phasen vorliegen soll, beschränkt die Gibbssche Phasenregel jedoch die möglichen Gleichgewichtszustände auf den erwähnten Unterraum. Die anderen Zustände sind nicht möglich (oder keine Gleichgewichtszustände). Eine wichtige Eigenschaft von Gleichgewichtszuständen besteht darin, dass sie nur durch Angabe der Werte der unabhängigen Variablen festgelegt sind, die Vorgeschichte oder der Weg dahin ist unwesentlich. Es geht also zunächst um die mathematischen Eigenschaften von solchen Funktionen mehrerer Variablen.
5 B.2. Funktion von zwei Variablen, artielle Ableitungen und totale Differentiale Wir betrachten eine Funktion z = F (x, y) Gemäss der Grahik ist das eine Fläche in einem dreidimensionalen Raum. 5 Bild B1: Eine Funktion von 2 Variablen. Das betrifft zum Beisiel reine Phasen eines Stoffes. Wir definieren die artiellen Ableitungen nach x bei konstantem y ( ) ( ) F(x, y) z = (1) x x und nach y bei konstantem x ( ) F(x, y) y y x = y ( ) z y x In der Grahik ist ( z/ x)y beisielhaft als Steigung der Funktion F (x, y 0 ) an der Stelle x 0,y 0 dargestellt. Nicht immer ist die Reihenfolge der Differentiationen unwesentlich (es gilt also mathematisch nicht immer) ( x ( )) F(x, y) = y ( y ( )) F(x, y) x (2) (3) Wenn jedoch die Funktionen und ihre Ableitungen stetig sind, gilt 2 z x y = ( ) z = ( ) z = 2 z x y y x y x (4)
6 6 PC I, hermodynamik, Martin Quack, Jürgen Stohner, SS 2006 Das gilt raktisch stets für die Funktionen der hermodynamik und wird auch als Satz von Schwarz bezeichnet. Betrachtet man eine differentielle Änderung dz, solässt diese sich nach der aylorschen Entwicklung aus den unabhängigen Beiträgen der Änderungen dx und dy zusammensetzen, man nennt dies ein totales Differential. dz = ( z x ) ( ) z dx + dy y y x (5a) = A(x, y)dx + B(x, y)dy (5b) mit den Funktionen Gemäss Gl. (4) gilt A(x, y) def. = B(x, y) def. = ( ) A(x, y) y x ( ) z x ( ) z y y x ( ) B(x, y) = x y (6a) (6b) (7) Diese allgemeine Beziehung findet in der hermodynamik vielfältige Anwendung. Man sricht hier auch von einer Pfaffschen Form oder einem exakten Differential (mit Bezug zur Pfaffschen Differentialgleichung und dem Prinzi von Carathéodory, welches wir hier nicht weiter behandeln, siehe Literatur, z.b. Münster). Die Gültigkeit von Gl. (7) ist im übrigen eine notwendige und hinreichende Bedingung, dass Gl. (5) ein exaktes Differential ist. Wir werden weitere Beziehungen säter angeben. Die Beziehungen lassen sich in offensichtlicher Weise auf Funktionen mehrerer Variablen verallgemeinern.
7 B.3. Grundgleichungen für extensive Zustandsfunktionen der hermodynamik Enthalie: H = U + V (8) Helmholtzenergie (auch freie Energie): A = U S (9) Gibbsenergie (auch freie Enthalie, oder auch freie Energie, nach Gibbs) G = U + V S (10a) = H S (10b) = A + V (10c) otale Differentiale: d U = d S d V (11) Anmerkung: Nach dem ersten Hautsatz ist auch d U = δq rev + δw, woraus sich (11) ergibt, unter den entsrechenden Voraussetzungen. Aus Gl. (8) erhält man mit der Produktregel: dh =du + dv + V d (12a) = ds + V d (12b) ((12b) ergibt sich mit Gl. (11)). Analog erhält man aus Gl. (9) da =du ds Sd (13a) = ds dv ds Sd (13b) Also:dA = Sd dv (13c) (für (13b) verwendet man Gl. (11)). Ebenfalls erhält man aus Gl. (10) dg =da + dv + V d (14a) = Sd + V d (14b) Aus Gl. (11) kann man eine Gleichung für d S erhalten 7 ds = 1 du + dv (15a) = 1 dh V d (15b)
8 8 PC I, hermodynamik, Martin Quack, Jürgen Stohner, SS 2006 Betrachtet man die allgemeine Schreibweise der Differentiale, z.b. ( ) ( ) U U du = ds + dv (16) S V V S so ergibt sich durch Koeffizientenvergleich ( ) U = (17) S V ( ) U = (18) V Analog ergibt sich aus den Gleichungen für dh, da, dg, ds: ( ) H = (19) S ( ) H = V (20) S ( ) A = S (21) V ( ) A = (22) V ( ) G = S (23) ( ) G = V (24) ( ) S = 1 (25) U V ( ) S = (26) V U ( ) S = 1 (27) H ( ) S = V (28) H Man kann diese Gleichungen allgemein benutzen, um die Zustandsfunktionen durch Integration exlizit zu erhalten (auch aus entsrechenden exerimentellen Daten). Ein Beisiel, das wir schon im Kaitel 1 behandelt haben, ist S
9 die Entroie S(U) =S(U 0 )+ U U 0 1 du bei V = const. (29) Bei Kenntnis der Funktion U( )oder 1 (U) ergibtsichauchs( ), soweit eindeutig definiert (ohne Phasenumwandlung). Anwendung des Schwarzschen Satzes (Gl. (4) und (7)) auf Gl. (13) und (14) ergibt ( ) ( ) S = (30) V ) ( S = ( V V ) 9 (31) Die raktische Bedeutung von Gl. (31) liegt darin, dass man die Druckabhängigkeit der Entroie bei konstanter emeratur durch Messung des thermischen Ausdehnungskoeffizienten ( ( V/) ) eines Stoffes bei konstantem Druck erhalten kann. Das ist eine einfache thermomechanische Grösse. Überzeugen Sie sich, dass Sie durch Integration bei = const. aus Gl. (30) mit Hilfe der Idealgasgleichung die schon aus eil A bekannte Volumenabhängigkeit der Entroie erhalten, sowie analog aus Gl. (31) die Druckabhängigkeit. Wärmekaazitäten sind weitere einfach messbare Grössen ( ) H C = (32) C V = ) ( U V (33) Setzt man in Gl. (15b) = const., (d =0), so ergibt sich durch Einsetzen ( ) S C = (34) ebenso mit (15a) und V = const C V = ( ) S V (35) Diese 35 Gleichungen bilden die Grundlage vieler nützlicher Rechnungen, wobei man sich Gl. (1-15) und (32-35) besonders einrägen sollte. Alle anderen und zahlreiche weitere lassen sich in sehr einfacher Weise hieraus erzeugen. Die hier angegebenen Grundgleichungen genügen, um raktisch alle
10 10 PC I, hermodynamik, Martin Quack, Jürgen Stohner, SS 2006 thermodynamischen Funktionen reiner Stoffe auf die Messung sehr einfacher Grössen zurückzuführen. Weitere Überlegungen sind bei der Betrachtung von Mischungen und chemischen Reaktionen notwendig, wie im folgenden Abschnitt zu zeigen ist. Als Ergänzung zu Gleichung (30-35) hätte man noch gerne die Volumen- und Druckabhängigkeit der inneren Energie und der Enthalie. Hierzu gehen wir wie folgt vor. Wir schreiben zunächst das totale Differential ds als Funktion von dv und d. ( ) S ds = V ( ) = dv + ( S ) V d (36a) dv + C V V d (36b) wobei wir Gl. (30) und (35) verwendet haben, um (36b) zu erhalten. Nun setzen wir ds in Gl. (11) ein [( ) du = [ ( ) = V V dv + C ] V d dv ] dv + C V d (37a) (37b) Also ist ( ) ( ) U = (38a) V V ( ) S = (38b) V Gl (38a) gibt die Volumenabhängigkeit von U in Form einfach messbarer Grössen. Analog gehen wir für dh vor, mit ( ) S ds = d + ( ) V = ( S ) d + C d d (39a) (39b) Wir setzen ds in Gl. (12) ein [ ( ) ] C V dh = d d + V d (40a) [ ( ) ] V = V d + C d (40b)
11 11 Also ist ( ) H ( ) V = V ( ) S = V + (41a) (41b) Gl. (41a) gibt uns die Druckabhängigkeit der Enthalie in Form einfach messbarer Grössen. Durch Einsetzen der Idealgasgleichung kann man sich davon überzeugen, dass für ideale Gase U nicht von V, und H nicht von abhängt. Allgemein erhalten wir aus den Gleichungen (30) - (41) die emeratur-, Volumen- und Druckabhängigkeit der Grundfunktionen U, H, S in Form leicht exerimentell bestimmbarer Grössen für reine Stoffe und Einhasensysteme, woraus man dann die Funktionen A und G erzeugen kann. Die Gleichungen werden gelegentlich auch als Zusammenfassung der thermodynamischen Zustandsgleichung reiner Stoffe bezeichnet. B.4. Allgemeine Gleichgewichtsbedingungen Aus den Gleichungen für die Differentiale und dem 2. Hautsatz ergeben sich nach dem in eil A (Ka. 1 bis 10) für G ausführlich diskutierten Verfahren die Gleichgewichtsbedingungen thermodynamischer Systeme, mit den Randbedingungen verschiedener festgehaltener unabhängiger Variablen als Maximal- oder Minimalrinzi, sowie analog die Klassifizierung reversibler, irreversibler natürlicher, und unnatürlicher (unmöglicher) Prozesse. Die Ergebnisse sind in der folgenden abelle aufgeführt.
12 12 PC I, hermodynamik, Martin Quack, Jürgen Stohner, SS 2006 B.5. Das Chemische Potential Wir betrachten eine homogene Phase mit k verschiedenen Substanzen. Die innere Energie U wird nun zusätzlich zu S und V noch von den Stoffmengen n i der Stoffe B i abhängen. Wir können schreiben ( ) ( ) U U i=k ( ) U du = ds + dv + dn i (42) S V,n i V S,n i n i S,V,n j i i=1 wobei in dieser Gleichung n i kollektiv für alle Stoffe B i konstant genommen wird, wenn an der artiellen Ableitung n i steht, ausser wo exlizit ein n i durch n j i ausgeschlossen wird. Für konstante Werte n i gelten offenbar die
13 13 früheren Gleichungen, also ( ) U = (43) S V,n ( ) i U = (44) V S,n i Wir definieren das chemische Potential μ i nach Gl. (45) ( ) def. U μ i = n i womit aus Gl. (44) Gl. (46) erhalten wird S,V,n j i (45) du = ds dv + μ i dn i (46) Diese Gleichung wird auch als Gibbssche Fundamentalgleichung bezeichnet. Wir addieren auf beiden Seiten d(v S), um einen analogen Ausdruck für dg zu erhalten, da wir normalerweise als Randbedingungen in der chemischen hermodynamik (, )= const bevorzugen, da G = U + V S (Gl.(10)) wird gemäss der Produktregel der Differentialrechnung dg =du +d(v S)=dU + dv + V d ds Sd (47a) = ds dv + k i=1 μ idn i + dv + V d ds Sd (47b) = Sd + V d + k i=1 μ idn i (47c) Allgemein gilt natürlich: dg = ( ) G d +,n i ( ) G d +,n i k ( ) G i=1 n i,,n j i dn i (47d) Durch Koeffizientenvergleich in Gl. (41c) und Gl. (41d) folgt also insbesondere ( ) ( ) G U μ i = n i n i,,n j i = S,V,n j i (48) neben den schon in Gl. (23) und (24) gegebenen Ableitungen. Deshalb wird das chemische Potential μ i auch häufig als artielle molare Gibbsenergie
14 14 PC I, hermodynamik, Martin Quack, Jürgen Stohner, SS 2006 bezeichnet. μ i ist eine intensive Grösse wie und und ebenso wie eine emeraturdifferenz Δ als Potential für einen Wärmefluss zum emeraturausgleich betrachtet werden kann, wirkt das chemische Potential als Grundlage für einen Substanztransfer zum Konzentrationsausgleich bei Diffusion oder zur Gleichgewichtseinstellung bei einer chemischen Reaktion. Hierin liegt die grosse Bedeutung des chemischen Potentials für die Chemie. Völlig analog zur obigen Herleitung für dg lässt sich zeigen (Aufgabe!) mit dh = ds + V d + k i=1 μ idn i (49) da = Sd dv + k i=1 μ idn i (50) ds = 1 du + dv k i=1 ( ) H μ i = n i S,,n j i = ( ) A n i μ i dn i (51),V,n j i (52) und ( ) μ i S = (53) n i U,V,n j i Gl. (51) wird als Entroiedarstellung der Gibbsschen Fundamentalgleichung bezeichnet. B.6. Phasengleichgewicht Wir betrachten ein System mit einer Komonente aus zwei Phasen α und β bei der Randbedingung = const, = const. Die Gleichgewichtsbedingung ist, dass G ein Minimum hat, also dg =0=dG (α) +dg (β) (54) wobei G = G (α) + G (β) (55) Das Gesamtsystem sei geschlossen (ohne Stofftransfer nach aussen), aber jede Phase für sich sei ein offenes System, es ist also Stofftransfer zwischen den Phasen zur Gleichgewichtseinstellung möglich. Wegen d = 0, d = 0 gilt offenbar dg = μ (α) dn (α) + μ (β) dn (β) = 0 (56) mit dn (α) = dn (β) (57)
15 15 da dn (α) +dn (β) = 0 nach unserer Voraussetzung. Also ist μ (α) dn (α) μ (β) dn (α) = 0 (58) μ (α) = μ (β) (59) Die Gleichgewichtsbedingung ist also, dass das chemische Potential des StoffesinbeidenPhasengleichist.Dieslässt sich offenbar auf k Stoffe erweitern, wobei für jeden Stoff B i gilt μ (α) i = μ (β) i (60) Wenn mehr als zwei Phasen im Gleichgewicht vorliegen, muss offenbar ebenfalls gelten μ (α) i = μ (β) i = μ (γ) i =... (61) Die Gleichgewichtsbedingung Gl. (61) erlaubt uns ein einfaches Verständnis der Phasenregel. Die Zahl unabhängiger intensiver Variablen ohne irgendwelche zusätzlichen Bedingungen wäre für K Komonenten (unabhängige Stoffe oder Molekülarten) durch 2 = (, ) lus die Anzahl von Molenbrüchen x i (Konzentrationen) der Stoffe in jeder Phase gegeben, also P (K 1) für Phasen, da nur K 1Molenbrüche x i frei wählbar sind und ein Molenbruch durch die Bedingung x i = 1 festgelegt wird. Die otalzahl Z der Variablen wäre also Z = P (K 1) + 2 (62) Diese sind jedoch nicht alle unabhängig, frei wählbar, da esinsgesamt K(P 1) algebraische Gleichungen vom y der Gl.(60) gibt, die es uns erlauben, einen eil der Variablen aus den anderen zu berechnen. Die verbleibende Zahl der frei wählbaren Variablen ist dann F = Z K(P 1) (63a) = P (K 1) + 2 K(P 1) (63b) = K +2 P (63c) oder F + P = K + 2 (63d) Sofern alle Stoffmengen unabhängig variabel sind, sind die hier einzusetzenden Zahlen der Komonenten K gerade die Zahlen der Molekülarten. Sofern jedoch Gleichgewichte zwischen diesen Stoffen die relativen Konzentrationen festlegen, würde für jede linear unabhängige Gleichgewichtsreaktion die Gleichung für die Gleichgewichtskonstante die Zahl der Freiheitsgrade um 1
16 16 PC I, hermodynamik, Martin Quack, Jürgen Stohner, SS 2006 erniedrigen. Man müsste also die Zahl R solcher Gleichgewichte auf der rechten Seite abziehen. Es hat sich aber eingebürgert, die Zahl der Komonenten K so zu definieren, dass diese Bedingung berücksichtigt wird, also K = N R (64) wobei N die Gesamtzahl der Stoffe oder Molekülarten ist. Hierbei kommt es allerdings darauf an, dass sich ein Gleichgewicht zwischen mehreren Stoffen wirklich einstellt. Wenn man also das System H 2 /O 2 /H 2 O betrachtet, so besteht dies aus drei Komonenten, wenn sich in der Gasmischung das Gleichgewicht zwischen H 2,O 2 und H 2 O nicht einstellt, aber nur aus zwei Komonenten, wenn man mit einem Katalysator (z.b. Pt) für Gleichgewichtseinstellung gemäss 2H 2 +O 2 =2H 2 O (65) sorgt. Umgekehrt ist für reines flüssiges Wasser die Zahl der Komonenten stets eins, unabhängig davon, wie viele verschiedene eilchen man hier annimmt (z.b. H +, H 3 O +, OH,H 5 O + 2, (H 2 O) 2,...), sofern nur alle diese eilchen im Gleichgewicht stehen, da man für jedes zusätzlich eingeführte eilchen (Molekül, Ion,...) eine zusätzliche Reaktionsgleichung erhält. Anwendungsbeisiele für die Herleitung thermodynamischer Beziehungen bei Phasengleichgewichten reiner Stoffe: Clausius-Claeyron-Gleichung, Plancksche Gleichung (Denbigh Ka ) B.7. Chemisches Gleichgewicht und Reaktionsgrössen Wir betrachten gemäss Ka. 0 eine chemische Reaktion der allgemeinen Form 0= ν i B i (66a) oder ν 1 B 1 ν 2 B 2 ν 3 B 3...= ν n B n + ν n+1 B n+1... (66b) oder ν 1 B 1 + ν 2 B 2 + ν 3 B 3...= ν n B n + ν n+1 B n (66c) Hierbei werden die Reaktanden auf die linke, die Produkte auf die rechte Gleichungsseite geschrieben. Die ν i sind ositiv für Produkte, negativ für Reaktanden. Die Reaktionslaufzahl ξ nach de Donder erlaubt es uns, den
17 Reaktionsfortschritt unabhängig vom betrachteten Stoff zu formulieren (siehe Ka. 0): ξ = n i n i0 (67) ν i mit n i als Stoffmenge für B i und n i0 als Stoffmenge von B i zu Beginn der Reaktion (mit ξ = 0). Es gilt offenbar dξ = dn i (68) ν i wobei ξ und dξ nicht mehr vom betrachteten Stoff B i abhängen. Hiermit erhalten wir aus Gl. (47): dg = Sd + V d + k i=1 μ iν i dξ (69a) ( ) ( ) ( ) G G G = d + d + dξ (69b) ξ,ξ Koeffizientenvergleich in Gl. (69) ergibt ( ) G = i=k i=1 ξ ν iμ i (70), Diese Grösse hat noch eine naheliegende Interretation: Es ist die Differenz der chemischen Potentiale μ i oder der artiellen molaren Gibbsenergien der Produkte minus der entsrechenden Grössen der Reaktanden für einen Formelumsatz. Man schreibt auch Δ r G = i=k i=1 ν iμ i (71) Dabei ist zu beachten, dass es sich hierbei um eine intensive Grösse handelt (die μ i sind ebenfalls intensive Grössen). Anschaulich entsricht Δ r G der Änderung der Gibbsenergie des Systems, wenn die Reaktion bei hyothetisch konstant gehaltener Zusammensetzung um einen Formelumsatz fortschreitet (Δξ =1mol).MankannΔ r als Abkürzung der Schreibweise eines Differentialoerators auffassen ( ) Δ r (72) ξ, Nach de Donder nennt man das negative ( Δ r G)auchAffinität der Reaktion. Gemäss den allgemeinen Gleichgewichtsbedingungen läuft bei (, ) = const. eine Reaktion sontan für negatives Δ r G<0,ξ, 17
18 18 PC I, hermodynamik, Martin Quack, Jürgen Stohner, SS 2006 (ositive Affinität) ab und Gleichgewicht herrscht, wenn Δ r G =0 (Δ r G>0 entsricht einem unnatürlichen Prozess). Aus den gemischten Ableitungen in Gl. (69) erhalten wir folgende Beziehungen für die artielle molare Reaktionsentroie Δ r S und das artielle molare Reaktionsvolumen Δ r V 2 G ξ = 2 G ξ (73) also ebenso ( ) Δr G,ξ ( ) Δr G,ξ = = ( ) S ξ, ( ) V ξ, Δ r S (74) =Δ r V (75) Allgemein definiert man beliebige Reaktionsgrössen Δ r X (X = U, H, A etc.) ( ) X =Δ r X (76) ξ, Weitere nützliche Beziehungen ergeben sich für Δ r H und Δ r U aus den Grundgleichungen. Wir schreiben zunächst ( ) A A = U S = U + (77) V,n i und analog ( ) G G = H S = H +,n i (78) A = U ( ) A + V,n i (79) (A/ ) = 1 = 1 ( ) A + A 1 ( ) A A V,n i 2 (80a) (80b)
19 Dividiert man Gl. (79) durch und setzt A/ 2 in Gl. (80b) ein, so erhält man (A/ ) = 1 ( ) A U V,n i 1 ( ) (A) (81a) 2 V,n i 19 = U 2 (81b) Völlig analog erhält man aus Gl. (78) ( ) (G/ ) = H (82),n i 2 Gl. (81) und (82) werden auch als Gibbs-Helmholtz-Gleichungen bezeichnet. Differenziert man artiell nach ξ, so erhält man nach Vertauschen der Reihenfolge der Differentiation ( ) (Δr G/ ),ξ = Δ rh 2 (83) Verwendet man weiterhin d 1 d = 1 (84) 2 so findet man ( ) (Δr G/ ) =Δ r H (85) (1/ ),ξ Alle Gleichungen können völlig analog auch für die chemischen Potentiale der betreffenden Stoffe im Standardzustand eingesetzt werden, wobei dies dann den molaren Gibbsenergien der betreffenden Stoffe in ihrem jeweiligen Standardzustand entsricht. Schreibt man K K a K K f unter den jeweils zutreffenden Randbedingungen für die Gleichgewichtskonstanten K (Ka. 6), so findet man Δ r G = ν i μ i wobei z.b. für ideale Gase gilt μ i = μ i + R ln( i / ) (86) mit den Partialdrücken i und dem Standarddruck oder allgemeiner μ i = μ i + R ln a i (87)
20 20 PC I, hermodynamik, Martin Quack, Jürgen Stohner, SS 2006 mit den Aktivitäten a i, oder schliesslich für reale Gase mit den Fugazitäten f i μ i = μ i + R ln f i (88) Es gilt also wiederum Δ r G = R ln K (89) mit der Gleichgewichtskonstanten K = i a i ν i (90) Aus Gl. (85) folgt hiermit die van t Hoff-Gleichung ln K( ) (1/ ) = Δ rh ( ) R (91) wobei wir exlizit zum Ausdruck gebracht haben, dass diese Gleichung thermodynamisch exakt mit temeraturabhängigem Δ r H ( ) gilt. Man kann die van t Hoff-Gleichung auch durch exlizite Ableitung des Ausdruckes für ln K herleiten ln K = Δ r G /R = Δ rh R + Δ rs R (92) ( ) ln K = Δ r H R + ( ) Δr S (93a) R = 1 Δ r H + Δ rh + 1 Δ r S (93b) R R 2 R Schreibt man nun Δ r = / ξ und vertauscht die Reihenfolge der artiellen Ableitungen, so ergibt sich ln K = 1 ( ) H + Δ rh + 1 ( ) S R ξ R 2 R ξ = 1 R Δ rc + Δ rh + 1 R 2 R Δ rc = Δ rh R 2 (94) Substitution von d durch d(1/ ) ergibt Gl. (91). Man sieht in Gl. (94), dass sich die Beiträge der emeraturabhängigkeiten der Reaktionsenthalie und der Reaktionsentroie gerade komensieren, so das es den Anschein hat, als
21 könnte man Gl. (92) mit konstantem Δ r H und Δ r S nach differenzieren und das richtige Ergebnis erhalten, was aber nur durch die Komensation zustande kommt. Die emeraturabhängigkeit der Reaktionsenthalie wird auch als Kirchhoffsche Gleichung bezeichnet (Gl. (95)) ( ) ( Δr H C ) = =Δ r C,ξ ξ = ν i C,i (95), i mit den Molwärmen C,i der Stoffe in ihrem Standardzustand. Ebenso hat man für die emeraturabhängigkeit der Reaktionsentroie exlizit ( ) Δr S = ( ) ( ( S C )) =,ξ ξ ξ, ( C ) 21 = 1 = 1 = 1 ξ Δ rc ( ) r ΔH,ξ (96) wobei wir diese Beziehung schon in Gl. (94) verwendet haben. Eine völlig analoge Vorgehensweise kann man verwenden, um die Druckabhängigkeit der Gleichgewichtskonstanten bei konstanter emeratur zu ermitteln, sowie die Druckabhängigkeit weiterer Reaktionsgrössen (man gehe von der allgemeinen Gleichung (69) aus und führe dies als Übung durch).
22 22 PC I, hermodynamik, Martin Quack, Jürgen Stohner, SS 2006 B.8. Reale Gase Ein ideales Gas ist dadurch gekennzeichnet, dass es keine Wechselwirkung zwischen den Molekülen gibt. Es gilt die Zustandsgleichung für ein ideales Gas V = nr V m = R (97a) (97b) die den Druck, das Molvolumen V m = V/n und die emeratur miteinander verknüft. Für reale Gase ist dagegen die Näherung, dass keine Wechselwirkungen zwischen Molekülen wirksam sind, oft nicht sehr brauchbar. Wenn die Moleküle nahe beisammen sind, werden anziehende und abstossende Kräfte wirksam. Wechselwirkungen zwischen den Molekülen sind daher besonders bedeutsam bei hohen Drücken bzw. kleinen Molvolumina, denn dann sind ja die Moleküle besonders nahe beisammen. Ein Mass für das Abweichen vom Idealgasverhalten ist der Komressibilitätsfaktor Z Z = V m R der für ein ideales Gas genau 1 beträgt. (98) 8.1. Zustandsgleichungen Es gibt verschiedene Möglichkeiten, ausgehend von der Zustandsgleichung eines idealen Gases ein reales Gas durch Korrekturterme zu beschreiben. Eine besonders einfache Formel ist (V m B) =R (99) wobei das B im Allgemeinen noch von der emeratur abhängt. Die Vander-Waals-Gleichung, dieschonfrüher behandelt wurde, benutzt 2 Korrekturkonstanten a und b: ( + a ) (V Vm 2 m b) =R (100) Die Virialgleichungen stellen die Korrektur zum Idealgasverhalten als eine Reihenentwicklung in oder V m dar: V m = R (1 + B + C ) oder (101a) ( V m = R 1+ B + C ) +... (101b) V m Vm 2
23 Dabei ist der erste Summand in der Klammer 1 der sogenannte 1. Virialkoeffizient, B der 2. Virialkoeffizient, C der 3. Virialkoeffizient usw. B, C, und die höheren Virialkoeffizienten hängen von der emeratur ab. Sie sind für verschiedene Gase in abellenwerken aufgeführt (z.b. Handbook of Chemistry and Physics, siehe Literaturverzeichnis) Der Joule-homson-Effekt Im Joule-homson-Exeriment wird ein Gas in einem Reservoir unter hohem Druck 1 und emeratur 1 über ein Druckreduzierventil oder einfach durch eine orösen Stofen adiabatisch in ein zweites Reservoir mit reduziertem Druck 2 und emeratur 2 exandiert. Das Exeriment ist in folgender Skizze angedeutet Ä Ä Kolben P 1 P Kolben Reduzier-, Drosselventil oder oröser Stofen Die Exansion im Joule-homson-Exeriment erfolgt isenthalisch, also unter der Bedingung konstanter Enthalie, wie folgende Überlegung zeigt: Während eines Kolbenhubs Δ (siehe Skizze) verringert sich in der linken Abteilung das Volumen von V 1 auf 0. Dabei wird die Arbeit W =+ 1 V 1 am System verrichtet (Druck-Volumenarbeit). In der rechten Abteilung nimmt das Volumen von 0 auf V 2 zu, wobei die Arbeit W = 2 V 2 frei wird. Insgesamt ist also die verrichtete Arbeit W = 1 V 1 2 V 2. Da die Exansion adiabatisch sein soll, ist Q = 0 und die Änderung der inneren Energie ist nach dem 1. Hautsatz durch ΔU = W gegeben. Es gilt also U 2 U 1 = 1 V 1 2 V 2 (102a) U V 1 = U V 2 (102b) H 1 = H 2 (denn H = U + V ) (102c)
24 24 PC I, hermodynamik, Martin Quack, Jürgen Stohner, SS 2006 Diese adiabatische Exansion ist also isenthalisch. Für reale Gase findet man oft, dass 2 1 ist, oft, aber nicht immer ist 2 < 1. Wie sehr sich die emeratur bei der Druckänderung unter isenthalen Bedingungen ändert, wird durch den Joule-homson-Koeffizient μ J beschrieben (zur Unterscheidung vom chemischen Potential mit dem dem Index J versehen): ( ) μ J = (103) H Wenn μ J > 0ist,hatmaneineAbkühlung bei der isenthalen, adiabatischen Exansion. yische Isenthalen (Kurven im, Zustandsdiagramm gleicher Enthalie) sind in folgender Skizze angedeutet. Links im i P gestrichelten Bereich ist die Steigung μ J der Isenthalen ositiv, hier findet also eine Abkühlung statt. Man kann die Exansion als Kühlvorrichtung nutzen. Ausserhalb des gestrichelten Bereiches ist keine Abkühlung möglich, anstelle eines Kühlaggregates hätte man nur eine (teure) Heizung vorliegen! Oberhalb i, der oberen Inversionstemeratur, ist rinziiell in keinem Druckbereich eine Kühlung möglich. ( Für Stickstoff ) ist i z.b. 350 ( C, ) und für H Wasserstoff H 2 78 C. Statt μ J = ist in der Regel einfacher und genauer messbar. Im Exeriment baut man dazu eine Heizung in H die
25 rechte Seite des Aufbaus ein (siehe Skizze), so dass konstant bleibt, 2 = 1. ΔH ist dabei die dazu nötige elektrische Heizleistung, und Δ ist der ebenfalls leicht ( messbare ) Druckunterschied zwischen der linken und der rechten H Seite. ΔH/Δ nennt man den isothermen Joule-homson- Koeffizient. Aus einer Anwendung der mathematischen Zyklenregel (siehe unten) findet man den Zusammenhang μ J = 1 ( ) H (104) C ( ) H Für ein ideales Gas ist 0, da H = U + V m = U + R gilt und die innere Energie U eines idealen Gases nicht vom Druck abhängt. Für ein ideales Gas beobachtet man daher keine emeraturveränderung bei dem Joule-homson-Exeriment. Achtung: Der Joule-homson-Effekt ist nicht mit der gewöhnlichen, einfachen adiabatischen Exansion zu verwechseln! Bei einer solchen Exansion kühlen sich auch ideale Gase ab, denn das System verrichtet dann Volumenarbeit an der Umgebung, wobei die innere Energie U verringert wird. Selbstverständlich kann man auch eine solche Anordnung als Kühlvorrichtung benutzen. Eine weitverbreitete Anwendung des Joule-homson-Effektes ist die Gasverflüssigung in einem Linde- Kühlaggregat. Durch schrittweise Abkühlung mit Hilfe des Joule-homson- Effektes wird das Gas schliesslich zum auunkt abgekühlt und verflüssigt. Der Aufbau ist in der folgenden Skizze angedeutet: 25 Luft oder Stickstoff kann man auf diese Weise ausgehend von Zimmertemeratur abkühlen und schliesslich verflüssigen. Will man dagegen Wasserstoff verflüssigen, so muss man bei Anwendung dieses Verfahrens zuerst unter die Inversionstemeratur i = 78 Cabkühlen, was mit flüssigem Stickstoff
26 26 PC I, hermodynamik, Martin Quack, Jürgen Stohner, SS 2006 geschehen kann. Sodann kann man H 2 alleine mit Hilfe des Joule-homson- Effektes kühlen. Alternativ kann man ein System bauen, bei welchem die Exansion unter Verrichtung von Arbeit erfolgt Einige Rechenrezete zum Variablenwechsel Oft ist eine gewünschte Variable nicht oder nur schlecht zugänglich und man möchte deshalb eine thermodynamische Grösse mit einer leichter messbaren Variablen ausdrücken. Dafür sind folgende 2 Regeln zum Variablenwechsel nützlich: Regel 1 Regel 1 soll gleich an einem Beisiel erläutert werden. Gegeben sei z.b. die innere Energie als Funktion von emeratur und Volumen, U = U(,V ). Das totale Differential ist dann du = ( ) ( ) U U d + dv (105) V V ( ) ( ) ( ) U U U Nun sind und leicht messbar, gesucht sei aber.den V V Zusammenhang zwischen ( ) den beiden Ableitungen findet man, indem man Gl. 1 (105) formal mit auf beiden Seiten multiliziert. Aus Gl. (105) wird somit ( ) ( ) ( ) ( ) U U U V = + (106) V V womit der gesuchte Zusammenhang hergeleitet wurde. Regel 2 Zyklenregel : Gegeben sei z(x, y). Das totale Differential dieser Funktion ist dann dz = Wird diese Gleichung mit ( ) 1, erhält man x z 0= ( ) z dx + x y 1 x ( ) z dy (107) y x bei konstantem z formal multiliziert, also ( ) z + x y ( ) z y x ( ) y x z (108a)
27 Die 0 rührt daher, dass ja z konstant sein soll (d z = 0). Dieses Ergebnis kann man noch umformen zu ( ) ( ) ( ) z z y = (108b) x y y x x z ( ) ( ) ( ) z y x = 1 (108c) y x x z z y Man beachte die zyklische Anordnung der Variablen x, y und z, woher dann auch der Name Zyklenregel rührt. Eine Anwendung der ( Zyklenregel ) hatten wir beim Joule-homson-Effekt kennengelernt: μ = ist gesucht, ( ) H H aber ist besser messbar. Die Zyklenregel gibt den Zusammenhang zwischen den beiden Ableitungen: ( ) ( ) ( ) H = (109) H H bzw. μ J = 1 ( ) H (110) C ( ) H mit C = Chemisches Potential und Fugazität realer Gase Ein tyischer Verlauf des chemischen Potentials μ eines idealen Gases (gestrichelte Gerade) und eines realen Gases (durchgezogene Linie) ist im folgenden Bild skizziert: ì 27 ideal real ì 0 x P ln P i 0
28 28 PC I, hermodynamik, Martin Quack, Jürgen Stohner, SS 2006 Für ein ideales Gas gilt: ( ) μ i (, )=μ i ( )+R ln i (111a) Dabei bezeichnet das hochgestellte Zeichen den Standarddruck, gewöhnlich 1 bar. Bei konstanter emeratur ist das chemische Potential μ eines idealen Gases also roortional zum Logarithmus des dimensionslosen Druckes i / (siehe gestrichelte Gerade in der Skizze). Man kann Gl. (111a) als Definition für die thermodynamische Zustandsgleichung eines reinen, idealen Gases i nehmen und dann zeigen, dass die gewöhnliche Zustandsgleichung des idealen Gases folgt. Es gilt nämlich ( μi ),n i = G n i = G n i = V = v i n i (111b) wobei v i das Molvolumen des reinen Gases ist, was hier identisch mit dem artiellen Molvolumen ist. Weiterhin gilt nach Gl. (111a) μ i (, ) i = R ln i i = R/ i (111c) Also ist v i = R/ i oder nach Multilikation mit der Stoffmenge n i des Gases i V = n i v i = nr/ i (111d) (111e) was der gewöhnlichen Zustandsgleichung des idealen Gases entsricht. Bei realen Gasen findet man dagegen Abweichungen von dieser idealen Geraden: Bei tiefen Drücken i hat man nahezu ideales Verhalten, bei höheren Drücken machen sich aber molekulare Wechselwirkungen bemerkbar, die zu Abweichungen führen (siehe durchgezogene Linie in der Skizze). Das chemische Potential eines realen Gases wird durch Gl. (112) beschrieben, μ i (, )=μ i ( )+R ln γ i i (112) wobei γ i der Fugazitätskoeffizient ist, er ist abhängig von der emeratur, vom Druck und der Zusammensetzung, also γ i (, 1, 2,...). Man führt nun die Grösse f i = γ i i (113)
29 ein. f i ist die Fugazität, sie ist gewissermassen der effektive, reduzierte, wirksame Druck des realen Gases. Wenn f i wie hier in Gl. (113) gegeben ist, hat die Fugazität keine Einheit. Oft wird sie aber über f i = γ i i definiert, wobei sie dann eine Einheit mit der Dimension des Druckes hat. Damit ist also: μ i (, )=μ i ( )+R ln f i (114a) lim γ i = 1 bzw. lim f i = i (114b) i 0 i 0 Die Gleichung (114a) kann man auch als Definition der Fugazität auf der Grundlage des chemischen Potentials auffassen. Wenn man μ i gegen ln f i aufträgt, erhält man nach Gl. (114a) eine Gerade für ein reales Gas, ähnlich wie bei der Auftragung von μ i gegen ln i für ein ideales Gas. Anders ausgedrückt ist der Standardzustand eines Gases zu μ i ein hyothetischer Zu- stand, wo = und γ = 1 gilt, also der hyothetische Zustand, wo das Gas bei 1 bar Druck vorliegt und gleichzeitig ideales Verhalten zeigt (mit γ = 1). Achtung: μ i in Gl. (114a) ist das Standardotential für den wirksamen Druck entsrechend der Fugazität f =1(oderf = 1 bar): Das ist nicht der tatsächliche Druck = 1 bar, sondern in der Regel etwas höher (Punkt x in der Skizze). Beisiel für die Fugazität eines realen Gases: Stickstoff N 2,bei 273 K ( =1bar) / f γ Man erkennt, dass für kleine Drücke ( 1 bar) die Fugazität raktisch mit dem Druck übereinstimmt. Bei mittleren Drücken ist / >f, denn der effektiv wirksame Druck ist kleiner als beim idealen Gas, da hier anziehende intermolekulare Kräfte überwiegen. Bei sehr hohen Drücken ist schliesslich / <f,denn da hier abstossende intermolekulare Kräfte überwiegen, ist der wirksame Druck grösser. Die Erfahrung zeigt, dass die Fugazitäten reiner Gase (nicht Mischungen) als Funktion der reduzierten emeratur und des reduzierten Druckes red = red = kritisch kritisch 29
30 30 PC I, hermodynamik, Martin Quack, Jürgen Stohner, SS 2006 für die meisten realen Gase näherungsweise gleich sind. Wenn man in der hermodynamik eine Beziehung für ein ideales Gas hergeleitet hat, kann man in der Regel diese Beziehung auch für reale Gase verwenden, wenn man die entsrechenden Partialdrücke i in dieser Beziehung durch die Fugazitäten f i ersetzt. Die Gleichgewichtskonstante K ist z.b. für ideale Gase ( i ) νi (115a) K = i und entsrechend für reale Gase K = i f ν i i (115b) wobei die ν i die stöchiometrischen Koeffizienten sind Zusammenhang zwischen f i und i Die Fugazitäten f i kann man gut exerimentell oder theoretisch mit Hilfe der Messung des Molvolumens V m als Funktion des Druckes bestimmen, was hier hergeleitet werden soll: Für ein reines Gas (keine Mischung) gilt, ( ) μ = V m denn und ( ) G μ = G m = = V ( ) G n, Diese Beziehungen wurden schon früher hergeleitet; der Index m bezeichnet molare Grössen. Also gilt für eine konstante emeratur Es gilt aber auch (siehe oben, Gl. (114a)) dμ = V m d ( =const.) (116a) dμ = R dlnf ( =const.) (116b) Gleichsetzen gibt V m d = R dlnf (116c)
31 R dln(/ ) auf beiden Seiten abgezogen gibt dann V m d R dln ( ( ) / ) f = R dln (116d) / ( ) f unter Berücksichtigung von ln =lnf ln (/ ). Mit d ln (/ )= / d erhalten wir ( Vm R 1 ) d =dln f (/ ) 31 (116e) Gl. (116e) von 0 bis integriert, gibt uns nun schliesslich die gewünschte Fugazität f und den Fugazitätskoeffizienten γ bei dem Druck ( ) f ln γ =ln = / 0 ( Vm R 1 ) d = 0 Z 1 d (117) mit dem Komressibilitätsfaktor Z aus Gl. (98). Hierbei wird verwendet, dass γ i 1, wenn 0 geht, so dass die untere Grenze des Integrals auf der linken Seite von Gl. (117) mit lim 0 [f/ ( / ) ]=1zuln(1)=0 wird und verschwindet. Man muss also exerimentell das Molvolumen V m als Funktion des Druckes von = 0 bis = bestimmen, das Integral in Gl. (117) ermitteln und erhält somit f bei. Alternativ kann man für V m auch einen theoretischen Ausdruck einsetzen wie er sich z.b. aus der Van-der-Waals-Gleichung für reale Gase ergibt. Diese Herleitung war für ein reines Gas. Für eine Mischung realer Gase kann man eine analoge Herleitung durchführen, die aber viel umfangreicher ist, denn γ = γ(, 1, 2...) hängt ja noch von der Zusammensetzung ab (siehe Denbigh, Literaturverzeichnis). Führen Sie als Übung die Integration in Gl. (117) für ein van-der-waals-gas aus (z.b. mit van-der-waals-konstanten für Stickstoff, die Sie aus V K und K in abelle 4.1, eil A, berechnen). Berechnen Sie f und γ für diverse Drucke und vergleichen Sie mit den Werten der abelle in Ka. B.8.5. ragen Sie auch den Integranden grahisch auf und diskutieren Sie den Funktionsverlauf. Führen sie dieselben Rechnungen auch für die Gleichung nach Clausius mit den Konstanten a, b, c, die Sie für Stickstoff aus K, K,V K berechnen können (siehe Aufgabe 4 am Ende von Ka. 4, eil A). Wir haben in eil A auch schon eine weitere Möglichkeit kennen gelernt, die Fugazitäten exerimentell zu bestimmen, nämlich durch Messung der Sannung einer geeigneten elektrochemischen Zelle.
32 32 PC I, hermodynamik, Martin Quack, Jürgen Stohner, SS emeratur- und Druckabhängigkeit der Fugazität und des chemischen Standardotentials Bei einem sehr hohen Druck, bei dem das reale Gas durch die Fugazität f i beschrieben wird, gilt, wenn man die Definitionsgleichung für μ i etwas anders aufschreibt μ i Dieser Ausdruck auf beiden Seiten nach ergibt ( μ d i d ) = μ i R ln f i (118) mit =const. artiell abgeleitet ( = μi ) ( ) ln fi R (119),n i,ni Aus der Gibbs-Helmholtz-Gleichung folgt, dass der erste erm auf der rechten Seite H i,m entsricht, wobei H 2 i,m die artielle molare Enthalie der Substanz i in einer Gasmischung ist, die durch f i beschrieben wird. Man erhält schliesslich ( μ ) i d = H ( ) i,m ln fi R (120) d 2,n i Eine entsrechende Überlegung stellt man für einen tiefen Druck i an, wo Idealgasverhalten vorliege ( i / = f i ). Aus der Definitionsgleichung für μ i hat man jetzt μ i = μ i R ln( i / ) (121) Dieser Ausdruck auf beiden Seiten artiell nach abgeleitet ergibt ( μ ) i ( d = μi ) ( ) ln i R (122) d,n i,ni Aus der Gibbs-Helmholtz-Gleichung und dem Satz von Schwarz folgt, dass der erste erm auf der rechten Seite H i,m entsricht, wobei H 2 i,m die artielle molare Enthalie der Substanz i in einer Gasmischung ist, die durch Idealgasverhalten beschrieben wird; für ein ideales Gas ist H i,m nicht vom
33 Druck abhängig (siehe Diskussion des Joule-homson-Effektes). Der zweite erm auf der rechten Seite ist 0 für ein ideales Gas, denn bei konstantem Druck und konstanter Zusammensetzung n i ist der Partialdruck i ja nicht abhängig von der emeratur. Man erhält schliesslich ( μ i ),n i = H i,m 2 33 = H i,m 2 (123) wobei H i allgemein die Enthalie des idealen Gases bei der emeratur ist, was H i entsricht. Gl. (120) und (123) haben die selbe linke Seite und können somit gleichgesetzt werden. Wenn man dann noch nach ln f i auflöst, erhält man die gesuchte emeraturabhängigkeit der Fugazität ( ) ln fi = H i,m H i,m (124),n i R 2 Die Bestimmung der emeraturabhängigkeit der Fugazität ist also auf eine Enthaliemessung zurückgeführt. Ganz ähnlich kann man auch die Druckabhängigkeit der Fugazität herleiten (Details siehe Denbigh, Literaturverzeichnis), wobei man ( ) ln fi = V i,m (125),n i R erhält. V i,m ist hier das artielle Molvolumen der Substanz i bei der emeratur.
34 34 PC I, hermodynamik, Martin Quack, Jürgen Stohner, SS 2006 B.9. Mischungen und Lösungen 9.1 Integration der Grundgleichungen Ausgehend von einer der thermodynamischen Grundgleichungen kann man durch Integration auf eine neue Darstellung für thermodynamische Grössen gelangen. Die Grundgleichung für U lautet z.b. du = ds dv k μ i dn i (126) i=1 Daraus folgt offensichtlich durch Integration, dass U = S V i μ i n i (127) Veranschaulichung: Man habe ein System mit U, S, V, n i,und. Jetzt verdole man das System Gemäss der Gl. (126) ist dabei die Änderung der inneren Energie ΔU = ΔS ΔV μ i Δn i (128), und die μ i sind intensive Grössen, die sich bei der Verdoelung nicht ändern. U, S und n i dagegen sind extensive Grössen, die sich genau verdoeln. Also ist ΔU = U, ΔS = S, Δn i = n i die Änderung bei der Verdoelung. Dieses Ergebnis in Gl. (128) eingesetzt ergibt ΔU = U = S V μ i n i (129)
35 Dies ist identisch mit Gl. (127). Analoge Herleitungen lassen sich auch auf die anderen thermodynamischen Grundgleichungen anwenden. Aus folgt mit einer ähnlichen Herleitung und aus folgt und aus folgt schliesslich 35 dg = Sd + V d + μ i dn i (130) G = μ i n i (131) dh = ds + V d + μ i dn i (132) H = S + μ i n i (133) da = Sd dv + μ i dn i (134) A = V + μ i n i (135) Durch Einsetzen sieht man leicht, dass diese integrierten Grundgleichungen mit den schon früher gegebenen Beziehungen oder G = U + V S H = G + S etc. komatibel sind. Damit kann man jetzt die Gibbs-Duhem-Gleichung herleiten Gibbs-Duhem-Gleichung Aus Gl. (131) folgt unter Anwendung der Produktregel dg = n i dμ i + μ i dn i (136) Wenn man diese Gleichung mit der thermodynamischen Grundgleichung (130) vergleicht, folgt direkt k n i dμ i = Sd + V d (137) i=1
36 36 PC I, hermodynamik, Martin Quack, Jürgen Stohner, SS 2006 Dies ist die Gibbs-Duhem-Gleichung. Bei k Komonenten einer Mischung gibt es k + 2 intensive Variablen, aber wegen der Gibbs-Duhem-Gleichung, die die Variablen miteinander verknüft, nur k + 1 unabhängige intensive Variablen bei einer Änderung; die letzte Variable ergibt sich dann notwendigerweise aus der Gibbs-Duhem-Gleichung. Anwendungsbeisiel: Gegeben sei eine Mischung zweier Komonenten, A und B. und seien konstant. Dann folgt aus der Gibbs-Duhem-Gleichung n A dμ A + n B dμ B = 0 (138) d.h. wenn sich μ A ändert, muss sich μ B entsrechend in die andere Richtung ändern. 9.3 Partialdruck binärer Mischungen Wir betrachten im Folgenden binäre flüssige Mischungen im Gleichgewicht mit der Gashase und wollen die Partialdrücke i der Gashase in Abhängigkeit von der Zusammensetzung x i der flüssigen Phase bei konstanter emeratur untersuchen. Dabei beschränken wir uns auf 2 Stoffe, die sich nur mischen und keine chemischen Reaktionen eingehen; die Stoffe sind also z.b. keine Elektrolyte. Manchmal findet man einen sehr einfachen Zusammenhang zwischen i, dem Partialdruck einer Komonente i in der Gashase, mit x i dem Molenbruch in der Flüssigkeit: i = x i i (139) Für x i = 1 liegt ein reiner Stoff vor, und entsrechend ist i der Gleichgewichts- Damfdruck des reinen Stoffes. Im Folgenden deutet ein hochgestellter Stern immer die entsrechende Eigenschaft des reinen Stoffes an. Dieses Verhalten (Gl. (139)) nennt man das Raoultsche Gesetz für eine sogenannte ideale Mischung. Es ist oft besonders gut erfüllt, wenn sich zwei chemisch ähnliche Flüssigkeiten mischen, wie Benzol und oluol oder Benzol (C 6 H 6 ) und Perdeuterobenzol (C 6 D 6 ). In Wirklichkeit (reale Mischungen) findet man dagegen oft Abweichungen von der Raoultschen Geraden:
37 37 P i Henry-Gerade real Raoult-Gerade * P i 0 1 x i Meist nähert sich die exerimentelle Kurve für den Partialdruck i nur für x i 1 der Raoultschen Gerade an, also i = x i i. Für den andern Grenzfall x i 0, also bei hoher Verdünnung, hat man oft näherungsweise auch ein lineares Verhalten, aber mit einer anderen Steigung: i = x i K i (140) Dies ist das Henry-Gesetz für eine sogenannte ideale, verdünnte Mischung. K i ist die Henry-Konstante der Komonente i in der gegebenen Mischung. Sie hat die Einheit eines Druckes. Die hysikalische Grundlage für das Verhalten nach Raoult oder Henry wird im Folgenden beschrieben: Im Gleichgewicht zwischen Gashase und Flüssigkeit hat man gleiche Geschwindigkeiten für die Kondensation des Damfes (roortional zum Partialdruck i ) und Verdamfung der Flüssigkeit (roortional zum Molenbruch x i in der Flüssigkeit). Also gilt k i = k x i (141a) oder i = k k x i (141b) Da für x i = 1 der Damfdruck i vorliegt, ist k = k i und Gl. (141b) geht somit in das Raoultsche Gesetz für eine ideale Lösung (Gl. (142)) über i = i x i (142) Dieses Verhalten gilt exakt im Grenzfall x i 1. Für x i 0 dagegen sind die Moleküle des Stoffs i so hochverdünnt, dass diese nur von Lösungsmittelmolekülen umgeben sind. Der Stoff i verhält dann wie eine andere, modifizierte Flüssigkeit
38 38 PC I, hermodynamik, Martin Quack, Jürgen Stohner, SS 2006 mit einem hyothetischen reinen Damfdruck i,mod.wennman i,mod mit der Henry-Konstante K i identifiziert, erhält man statt Gl. (142) i = K i x i (143) das Henry-Gesetz für eine ideale, verdünnte Lösung. Für eine binäre Mischung aus den Stoffen A und B kann man die entsrechenden Partialdrücke ( A und B ) und den otaldruck bei einer gegebenen emeratur in einem Diagramm darstellen, wie hier für CS 2 und Azeton gezeigt: total CS 2 P i Azeton x CS2 0 1 x Azeton 1 0 Dabei sind die durchgezogenen Kurven die realen Drücke. Die gestrichelten Geraden entsrechen dem Raoultschen Gesetz; sie sind die Asymtoten für x i 1. Die geunkteten Geraden entsrechen dem Henryschen Gesetz; sie sind die Asymtoten für x i 0. B.9.4 Chemisches Potential μ i von idealen und realen Mischungen Für ein ideales Gas ist das chemische Potential in der Gashase als Funktion des Druckes ( ) μ Gas i = μ,gas i i + R ln (144) Wenn der Stoff i rein vorliegt, gilt somit im Gleichgewicht zwischen Gas und flüssiger Phase ( ) μ,fl i = μ,gas i + R ln i (145)
39 Der Stern als Index kennzeichnet hier wie üblich den reinen Stoff. Falls der Stoff i in einer Mischung vorliegt, gilt entsrechend für den Stoff i in der flüssigen Phase μ fl i = μ,gas i ( ) i + R ln Beide Gleichungen kombiniert, wobei das μ,gas i schliesslich μ fl i = μ,fl i + R ln ( i i 39 (146) eliminiert wird, ergibt dann ) (147) Das chemische Potential eines Stoffes i in der flüssigen Mischung, μ fl i, lässt sich also durch Messungen des Damfdruckes, i, bestimmen! Für ideale Mischungen lässt sich somit μ i auf folgende Arten berechnen: a) Ideale Mischung nach Raoult: Es gilt i = x i i. Dies in Gl. (147) eingesetzt ergibt μ fl i = μ,fl i + R ln x i (148) Hierbei ist μ,fl i = μ,fl i das chemische Potential des reinen Stoffes, d.h. für x i 1. Dieser Standardzustand muss nicht real existieren. In einer Zucker- /Wasserlösung z.b. kann x i 1für Zucker rinziiell nicht erreicht werden, da reiner Zucker ja ein Festkörer ist, in der Flüssigkeit aber gelöst vorliegt. b) Ideal verdünnte Mischung nach Henry: Aus i = x i K i folgt mit Gl. (147) μ fl i = μ,fl i + R ln ( i i ) = μ,fl i + R ln K i i } {{ } μ,fl i + R ln x i (149)
40 40 PC I, hermodynamik, Martin Quack, Jürgen Stohner, SS 2006 Hier werden die zwei ersten erme auf der rechten Seite zu μ,fl i zusammengefasst. μ i ist hier ein etwas seltsamer Standardzustand: Er beschreibt den Fall x i 1, aber dennoch soll der Stoff i dabei nach Henry ideal verdünnt bleiben (also x i 0); μ,fl i ist also ein hyothetischer Zustand, der real nicht eintritt. Im folgenden ext wird der Index fl für das chemische Potential weggelassen. Für eine ideale Mischung nach Raoult oder Henry ist also μ i gegen ln x i aufgetragen eine Gerade. Das kann man auch direkt als eine Definition für eine ideale Mischung auffassen. Für eine reale Mischung dagegen wird es Abweichungen von einer Geradenform geben. Wie bei einem realen Gas, bei dem man dasrealgasverhalten mit der Fugazität beschreibt, führt man daher für eine reale Mischung einen Korrekturfaktor ein μ i = μ i + R ln(γ i x i ) (150) μ i = μ i + R ln a i wobei γ i = γ i (,, x i...) deraktivitätskoeffizient des Stoffes i ist und a i = γ i x i (151) die Aktivität (die effektive oder wirksame Konzentration) des Stoffes i. μ i gegen die ln(a i ) aufgetragen gibt also nach Gl. (150) ebenfalls eine Gerade. Es gibt jetzt rinziiell zwei 2 Möglichkeiten, a i zu definieren: Man korrigiert das reale x i auf die Raoult-Gerade hin (I) oder auf die Henry-Gerade hin (II). Die entsrechenden a i sind unterschiedlich. Für Konvention (I) soll lim γ i = 1 sein, das reale μ i nähert sich asymtotisch dem Verhalten gemäss x i 1 der Raoult-Geraden für x i 1. Konvention (II) wird meist für einen gelösten Stoff i in grosser Verdünnung gewählt. Hier ist lim γ i = 1, d.h. das reale xi 0 μ i nähert sich asymtotisch dem Verhalten gemäss der Henry-Geraden für x i 0. Wie oben diskutiert, ist μ i in Konvention (II) ein hyothetischer Standardzustand für x i =1.
41 41 * Lösung A+ B, * A B flüssig Lösung + festes A Lösung + festes B M festes A+ festes B x B Gleichgewicht zwischen einer idealen Mischung (A + B) und einem reinen Festkörer (A oder B, keine Mischkristalle AB): Löslichkeit, Gefrierunktserniedrigung Wir betrachten die Mischung von zwei Stoffen im Fest-/Flüssig-Gleichgewicht. Nach der Gibbsschen Phasenregel haben wir dann zwei Freiheitsgrade, nämlich den Druck und die emeratur. Für einen gegebenen Druck kann man also die Gleichgewichtskurve zwischen fester und flüssiger Phase als Funktion der Zusammensetzung und der emeratur in einem 2-dimensionalen Diagramm darstellen. Ein solches Phasendiagramm ist oben skizziert. Dabei sei A das Lösungsmittel (z.b. H 2 O), und B der gelöste Stoff (z.b. Kochsalz NaCl). A ist dann die Schmelztemeratur (Gefrierunkt) des reinen A (H 2 O) und B die Schmelztemeratur des reinen B (NaCl). Die Kurve von A bis M zeigt eine Gefrierunktserniedrigung der Lösung bei Zugabe von B (im Beisiel H 2 OmitNaClbeiAtmoshärendruck bis ca. 22 C). Die Kurve von M bis B ist die Löslichkeitskurve von B in dem Lösungsmittel A: bei einer gegebenen emeratur kann maximal x B gelöst sein, wenn man x B grösser machen will, kommt man in den Bereich Lösung + festes B, d.h. nicht alles B kann mehr gelöst werden. Diese Gleichgewichtskurve im Phasendiagramm soll nun thermodynamisch genauer beschrieben werden. Im Folgenden bezeichne ein * einen reinen Stoff, der Index s den Festkörer, fl die Flüssigkeit und i den Stoff A oder B. Das chemische Potential des reinen Festkörers ist μ s i, das der als ideal angenommenen flüssigen Mischhase ist μ fl i = μ fl i + R ln x i
42 42 PC I, hermodynamik, Martin Quack, Jürgen Stohner, SS 2006 Im Gleichgewicht sind beide Potentiale gleich μ fl i μ s i = μ fl i eingesetzt, nach ln x i auflöst und nach bei konstantem Druck abgeleitet, gibt ( ) [ ( ) ln xi = 1 μ fl i ( ) ] μ s i (152) R [ ] = 1 H fl i,m R H s i,m (153) 2 2 = Δ SchmHi (154) R 2 wobei in Gl. (152) die Gibbs-Helmholtz-Beziehungen eingesetzt werden. H fl i,m ist die molare Enthalie des reinen, flüssigen Stoffes i bei der emeratur, und entsrechend ist Hi,m s die molare Enthalie des reinen, festen Stoffes i. Die Differenz Δ Schm Hi ist dann die molare Schmelzenthalie bei der emeratur und dem Druck. Gl. (154) beschreibt die Gleichgewichtskurve des Phasendiagramms (ideale Lösung A + B im Gleichgewicht mit einem reinen Festkörer A oder B, bei einem gegebenen Druck). Wenn man i = B setzt und den rechten eil des Diagramms betrachtet, gibt Gl. (154) die emeraturabhängigkeit der Löslichkeit von B. Wennmani = A setzt und den linken eil des Diagramms betrachtet, gibt Gl. (154) nach einer Integration die Gefrierunktserniedrigung von A wieder. 9.6 Gefrierunktserniedrigung der Lösung A + B relativ zum reinen Lösungsmittel A Mit der Näherung, dass Δ Schm HA in einem kleinen emeraturbereich von A, dem Gefrierunkt des reinen Lösungsmittel A, bis, dem erniedrigten Gefrierunkt der Mischung, nicht von der emeratur abhängt, lässt sich Gl. (154) einfach integrieren: Integration von x A, bis x A =1bzw.A gibt ln 1 x A = 1 R A = Δ SchmH A R Δ Schm HA d 2 (155) ( 1 1 ) A (156) Δ SchmHA Δ (157) RA 2
14 Massenwirkungsgesetz
 14 Massenwirkungsgesetz Im vorherigen Abschnitt haben wir uns mit der Mischungsentroie beschäftigt, die aber nur einen Asekt der Mischung von idealen Gasen berücksichtigt, nämlich des Mischens und rennens
14 Massenwirkungsgesetz Im vorherigen Abschnitt haben wir uns mit der Mischungsentroie beschäftigt, die aber nur einen Asekt der Mischung von idealen Gasen berücksichtigt, nämlich des Mischens und rennens
4. Freie Energie/Enthalpie & Gibbs Gleichungen
 4. Freie Energie/Enthalie & Gibbs Gleichungen 4.3. Gibbs sche Gleichungen Fundamentalgleichungen der D weitere Fundamentalgleichungen basierend auf: einsetzen von (): d d d Ausdifferenzierung der Definition
4. Freie Energie/Enthalie & Gibbs Gleichungen 4.3. Gibbs sche Gleichungen Fundamentalgleichungen der D weitere Fundamentalgleichungen basierend auf: einsetzen von (): d d d Ausdifferenzierung der Definition
Skizze zur Veranschaulichung der Legendretransformation
 9 Die thermodynamischen Funktionen G und H Ehe das Schema des vorherigen Abschnittes zur Konstruktion weiterer thermodynamischer Potentiale zu Ende gebracht wird, kurz einige Erläuterungen zur Legendretransformation.
9 Die thermodynamischen Funktionen G und H Ehe das Schema des vorherigen Abschnittes zur Konstruktion weiterer thermodynamischer Potentiale zu Ende gebracht wird, kurz einige Erläuterungen zur Legendretransformation.
Temperaturabhängigkeit von Enthalpie H und Entropie S
 Prof. Dr. Norbert Ham 1/5 8. emeraturabhängigkeit von Enthalie und Entroie emeraturabhängigkeit von Enthalie H und Entroie S In abellenwerken sind Enthalien und Entroien in der Regel bezogen auf Standardbedingungen,
Prof. Dr. Norbert Ham 1/5 8. emeraturabhängigkeit von Enthalie und Entroie emeraturabhängigkeit von Enthalie H und Entroie S In abellenwerken sind Enthalien und Entroien in der Regel bezogen auf Standardbedingungen,
Physikalische Chemie Physikalsiche Chemie I SoSe 2009 Prof. Dr. Norbert Hampp 1/10 5. Zustandsfunktionen Idealer und Realer Gase. ZustandsÄnderungen
 Prof. Dr. Norbert Ham 1/10 5. Zustandsfunktionen Idealer und Realer Gase ZustandsÄnderungen Die rennung zwischen unserem System und der ÅUmweltÇ wird durch eine Wand realisiert. WÄnde kånnen unterschiedliche
Prof. Dr. Norbert Ham 1/10 5. Zustandsfunktionen Idealer und Realer Gase ZustandsÄnderungen Die rennung zwischen unserem System und der ÅUmweltÇ wird durch eine Wand realisiert. WÄnde kånnen unterschiedliche
Musterlösung Übung 10
 Musterlösung Übung 10 Aufgabe 1: Phasendiagramme Abbildung 1-1: Skizzen der Phasendiagramme von Wasser (links) und Ethanol (rechts). Die Steigung der Schmelzkurven sind zur besseren Anschaulichkeit überzogen
Musterlösung Übung 10 Aufgabe 1: Phasendiagramme Abbildung 1-1: Skizzen der Phasendiagramme von Wasser (links) und Ethanol (rechts). Die Steigung der Schmelzkurven sind zur besseren Anschaulichkeit überzogen
Inhalt 1 Grundlagen der Thermodynamik
 Inhalt 1 Grundlagen der Thermodynamik..................... 1 1.1 Grundbegriffe.............................. 2 1.1.1 Das System........................... 2 1.1.2 Zustandsgrößen........................
Inhalt 1 Grundlagen der Thermodynamik..................... 1 1.1 Grundbegriffe.............................. 2 1.1.1 Das System........................... 2 1.1.2 Zustandsgrößen........................
Thermische Energie kann nicht mehr beliebig in andere Energieformen umgewandelt werden.
 Wärmemenge: hermische Energie kann nicht mehr beliebig in andere Energieformen umgewandelt werden. Sie kann aber unter gewissen oraussetzungen von einem Körer auf einen nderen übertragen werden. Dabei
Wärmemenge: hermische Energie kann nicht mehr beliebig in andere Energieformen umgewandelt werden. Sie kann aber unter gewissen oraussetzungen von einem Körer auf einen nderen übertragen werden. Dabei
Prof. Dr. Peter Vogl, Thomas Eissfeller, Peter Greck. Übung in Thermodynamik und Statistik 4B Blatt 8 (Abgabe Di 3. Juli 2012)
 U München Physik Department, 33 http://www.wsi.tum.de/33 eaching) Prof. Dr. Peter Vogl, homas Eissfeller, Peter Greck Übung in hermodynamik und Statistik 4B Blatt 8 Abgabe Di 3. Juli 202). Extremalprinzip
U München Physik Department, 33 http://www.wsi.tum.de/33 eaching) Prof. Dr. Peter Vogl, homas Eissfeller, Peter Greck Übung in hermodynamik und Statistik 4B Blatt 8 Abgabe Di 3. Juli 202). Extremalprinzip
Physikalisch-chemische Grundlagen der thermischen Verfahrenstechnik
 Lüdecke Lüdecke Thermodynamik Physikalisch-chemische Grundlagen der thermischen Verfahrenstechnik Grundlagen der Thermodynamik Grundbegriffe Nullter und erster Hauptsatz der Thermodynamik Das ideale Gas
Lüdecke Lüdecke Thermodynamik Physikalisch-chemische Grundlagen der thermischen Verfahrenstechnik Grundlagen der Thermodynamik Grundbegriffe Nullter und erster Hauptsatz der Thermodynamik Das ideale Gas
Mathematik II Frühlingsemester 2015 Kap. 9: Funktionen von mehreren Variablen 9.2 Partielle Differentiation
 Mathematik II Frühlingsemester 2015 Kap. 9: Funktionen von mehreren Variablen 9.2 Partielle Differentiation www.math.ethz.ch/education/bachelor/lectures/fs2015/other/mathematik2 biol Prof. Dr. Erich Walter
Mathematik II Frühlingsemester 2015 Kap. 9: Funktionen von mehreren Variablen 9.2 Partielle Differentiation www.math.ethz.ch/education/bachelor/lectures/fs2015/other/mathematik2 biol Prof. Dr. Erich Walter
Für die Abhängigkeit der Freiheitsgrade von der Zahl der Komponenten und der Phasen eines Systems existiert die Gibbs sche Phasenregel: F = K P + 2
 hasengleichgewichte Definitionen: hase: Homogener Raumbereich, innerhalb dessen sich keine physikalische Größe (z.b. Dichte, Zusammensetzung, emperatur...) sprunghaft ändert. Das Berührungsgebiet zweier
hasengleichgewichte Definitionen: hase: Homogener Raumbereich, innerhalb dessen sich keine physikalische Größe (z.b. Dichte, Zusammensetzung, emperatur...) sprunghaft ändert. Das Berührungsgebiet zweier
Lehrbuch der Thermodynamik
 Ulrich Nickel Lehrbuch der Thermodynamik Eine verständliche Einführung Ж HANSER Carl Hanser Verlag München Wien VII Inhaltsverzeichnis 1 GRUNDBEGRIFFE DER THERMODYNAMIK 1 Einführung 1 Systeme 3 offene
Ulrich Nickel Lehrbuch der Thermodynamik Eine verständliche Einführung Ж HANSER Carl Hanser Verlag München Wien VII Inhaltsverzeichnis 1 GRUNDBEGRIFFE DER THERMODYNAMIK 1 Einführung 1 Systeme 3 offene
8.2 Thermodynamische Gleichgewichte, insbesondere Gleichgewichte in Mehrkomponentensystemen Mechanisches und thermisches Gleichgewicht
 8.2 Thermodynamische Gleichgewichte, insbesondere Gleichgewichte in Mehrkomponentensystemen Mechanisches und thermisches Gleichgewicht 8.2-1 Stoffliches Gleichgewicht Beispiel Stickstoff Sauerstoff: Desweiteren
8.2 Thermodynamische Gleichgewichte, insbesondere Gleichgewichte in Mehrkomponentensystemen Mechanisches und thermisches Gleichgewicht 8.2-1 Stoffliches Gleichgewicht Beispiel Stickstoff Sauerstoff: Desweiteren
8. Mehrkomponentensysteme. 8.1 Partielle molare Größen. Experiment 1 unter Umgebungsdruck p:
 8. Mehrkomponentensysteme 8.1 Partielle molare Größen Experiment 1 unter Umgebungsdruck p: Fügen wir einer Menge Wasser n mit Volumen V (molares Volumen v m =V/n) bei einer bestimmten Temperatur T eine
8. Mehrkomponentensysteme 8.1 Partielle molare Größen Experiment 1 unter Umgebungsdruck p: Fügen wir einer Menge Wasser n mit Volumen V (molares Volumen v m =V/n) bei einer bestimmten Temperatur T eine
Wärmelehre/Thermodynamik. Wintersemester 2007
 Einführung in die Physik I Wärmelehre/Thermodynamik Wintersemester 2007 ladimir Dyakonov #13 am 30.01.2007 Folien im PDF Format unter: htt://www.hysik.uni-wuerzburg.de/ep6/teaching.html Raum E143, Tel.
Einführung in die Physik I Wärmelehre/Thermodynamik Wintersemester 2007 ladimir Dyakonov #13 am 30.01.2007 Folien im PDF Format unter: htt://www.hysik.uni-wuerzburg.de/ep6/teaching.html Raum E143, Tel.
8.2 Thermodynamische Gleichgewichte, insbesondere Gleichgewichte in Mehrkomponentensystemen Mechanisches und thermisches Gleichgewicht
 8.2 Thermodynamische Gleichgewichte, insbesondere Gleichgewichte in Mehrkomponentensystemen Mechanisches und thermisches Gleichgewicht 8.2-1 Stoffliches Gleichgewicht Beispiel Stickstoff Sauerstoff: Desweiteren
8.2 Thermodynamische Gleichgewichte, insbesondere Gleichgewichte in Mehrkomponentensystemen Mechanisches und thermisches Gleichgewicht 8.2-1 Stoffliches Gleichgewicht Beispiel Stickstoff Sauerstoff: Desweiteren
Kapitel 4. Thermodynamisches Gleichgewicht zwischen zwei Systemen. 4.1 Systeme im thermischen Kontakt 1; E 1 =? 2; E 2 =?
 Kapitel 4 hermodynamisches Gleichgewicht zwischen zwei Systemen Im letzten Abschnitt haben wir am Beispiel des idealen Gases die Entropie (S(E)) bestimmt, und zwar im Rahmen des mikrokanonischen Ensembles
Kapitel 4 hermodynamisches Gleichgewicht zwischen zwei Systemen Im letzten Abschnitt haben wir am Beispiel des idealen Gases die Entropie (S(E)) bestimmt, und zwar im Rahmen des mikrokanonischen Ensembles
Phasengleichgewicht und Phasenübergänge. Gasförmig
 Phasengleichgewicht und Phasenübergänge Siedetemperatur Flüssig Gasförmig Sublimationstemperatur Schmelztemperatur Fest Aus unserer Erfahrung mit Wasser wissen wir, dass Substanzen ihre Eigenschaften bei
Phasengleichgewicht und Phasenübergänge Siedetemperatur Flüssig Gasförmig Sublimationstemperatur Schmelztemperatur Fest Aus unserer Erfahrung mit Wasser wissen wir, dass Substanzen ihre Eigenschaften bei
Einführung in die Physikalische Chemie Teil 2: Makroskopische Phänomene und Thermodynamik
 Einführung in die Phsikalische Chemie Teil 2: Makroskopische Phänomene und Thermodnamik Kapitel 7: Boltzmann-Verteilung Kapitel 8: Statistische Beschreibung makroskopischer Grössen Kapitel 9: Thermodnamik:
Einführung in die Phsikalische Chemie Teil 2: Makroskopische Phänomene und Thermodnamik Kapitel 7: Boltzmann-Verteilung Kapitel 8: Statistische Beschreibung makroskopischer Grössen Kapitel 9: Thermodnamik:
Übung 3. Ziel: Bedeutung/Umgang innere Energie U und Enthalpie H verstehen (Teil 2) Verständnis des thermodynamischen Gleichgewichts
 Ziel: Bedeutung/Umgang innere Energie U und Enthalpie H verstehen (Teil 2) adiabatische Flammentemperatur Verständnis des thermodynamischen Gleichgewichts Definition von K X, K c, K p Berechnung von K
Ziel: Bedeutung/Umgang innere Energie U und Enthalpie H verstehen (Teil 2) adiabatische Flammentemperatur Verständnis des thermodynamischen Gleichgewichts Definition von K X, K c, K p Berechnung von K
Thomas Eissfeller, Peter Greck, Tillmann Kubis, Christoph Schindler
 U München Reinhard Scholz Physik Department, 33 homas Eissfeller, Peter Greck, illmann Kubis, Christoph Schindler http://www.wsi.tum.de/33/eaching/teaching.htm Übung in heoretischer Physik 5B (hermodynamik)
U München Reinhard Scholz Physik Department, 33 homas Eissfeller, Peter Greck, illmann Kubis, Christoph Schindler http://www.wsi.tum.de/33/eaching/teaching.htm Übung in heoretischer Physik 5B (hermodynamik)
4. Freie Energie/Enthalpie & Gibbs Gleichungen
 4. Freie Energie/Enthalpie & Gibbs Gleichungen 1. Eigenschaften der Materie in der Gasphase 2. Erster Hauptsatz: Arbeit und Wärme 3. Entropie und Zweiter Hauptsatz der hermodynamik 4. Freie Enthalpie G,
4. Freie Energie/Enthalpie & Gibbs Gleichungen 1. Eigenschaften der Materie in der Gasphase 2. Erster Hauptsatz: Arbeit und Wärme 3. Entropie und Zweiter Hauptsatz der hermodynamik 4. Freie Enthalpie G,
11. Der Phasenübergang
 11. Der Phasenübergang - Phasendiagramme, Kritischer Punkt und ripelpunkt - Gibbssche Phasenregel - Phasenübergänge 1. und 2. Ordnung - Das Phasengleichgewicht - Clausius-Clapeyron-Gleichung - Pictet-routon-Regel,
11. Der Phasenübergang - Phasendiagramme, Kritischer Punkt und ripelpunkt - Gibbssche Phasenregel - Phasenübergänge 1. und 2. Ordnung - Das Phasengleichgewicht - Clausius-Clapeyron-Gleichung - Pictet-routon-Regel,
DAMPFDRUCK EINER REINEN FLÜSSIGKEIT. 1. Versuchsplatz. 2. Allgemeines zum Versuch
 DAMPFDRUCK EINER REINEN FLÜSSIGKEI 1. ersuchslatz Komonenten: - hermostat - Woulffsche Flasche - Dreihalskolben mit ersuchssubstanz - hermometer - Druckmesser - Druckanzeige 2. Allgemeines zum ersuch Befindet
DAMPFDRUCK EINER REINEN FLÜSSIGKEI 1. ersuchslatz Komonenten: - hermostat - Woulffsche Flasche - Dreihalskolben mit ersuchssubstanz - hermometer - Druckmesser - Druckanzeige 2. Allgemeines zum ersuch Befindet
Multiple-Choice Test. Alle Fragen können mit Hilfe der Versuchsanleitung richtig gelöst werden.
 PCG-Grundpraktikum Versuch 1- Dampfdruckdiagramm Multiple-Choice Test Zu jedem Versuch im PCG wird ein Vorgespräch durchgeführt. Für den Versuch Dampfdruckdiagramm wird dieses Vorgespräch durch einen Multiple-Choice
PCG-Grundpraktikum Versuch 1- Dampfdruckdiagramm Multiple-Choice Test Zu jedem Versuch im PCG wird ein Vorgespräch durchgeführt. Für den Versuch Dampfdruckdiagramm wird dieses Vorgespräch durch einen Multiple-Choice
Aufgaben zum Stirlingschen Kreisprozess Ein Stirling-Motor arbeite mit 50 g Luft ( M= 30g mol 1 )zwischen den Temperaturen = 350 C und T3
 Aufgaben zum Stirlingschen Kreisrozess. Ein Stirling-Motor arbeite mit 50 g Luft ( M 0g mol )zwischen den emeraturen 50 C und 50 C sowie den olumina 000cm und 5000 cm. a) Skizzieren Sie das --Diagramm
Aufgaben zum Stirlingschen Kreisrozess. Ein Stirling-Motor arbeite mit 50 g Luft ( M 0g mol )zwischen den emeraturen 50 C und 50 C sowie den olumina 000cm und 5000 cm. a) Skizzieren Sie das --Diagramm
Statistische Thermodynamik I Lösungen zur Serie 11
 Statistische Thermodynamik I Lösungen zur Serie Verschiedenes 20 Mai 206 Barometrische Höhenformel: Betrachte die rdatmosphäre im homogenen Gravitationspotential M gz der rde Unter der Annahme, dass sich
Statistische Thermodynamik I Lösungen zur Serie Verschiedenes 20 Mai 206 Barometrische Höhenformel: Betrachte die rdatmosphäre im homogenen Gravitationspotential M gz der rde Unter der Annahme, dass sich
Zur Erinnerung. p isotherm. Stichworte aus der 20. Vorlesung: Poisson sche leichungen/adiabaten- Gleichungen: Kreisprozesse:
 Zur Erinnerung Stichworte aus der 20. Vorlesung: Poisson sche leichungen/adiabaten- Gleichungen: T V V 1 const. const. adiabatisch ( V ) 0 V V 0 R T0 isotherm ( V ) V Kreisrozesse: Ein thermodynamisches
Zur Erinnerung Stichworte aus der 20. Vorlesung: Poisson sche leichungen/adiabaten- Gleichungen: T V V 1 const. const. adiabatisch ( V ) 0 V V 0 R T0 isotherm ( V ) V Kreisrozesse: Ein thermodynamisches
Thermodynamik für Werkstoffingenieure und Metallurgen
 Thermodynamik für Werkstoffingenieure und Metallurgen Eine Einführung 2., stark überarbeitete Auflage Von Prof. Dr.-Ing. Martin G. Frohberg Technische Universität Berlin Mit 99 Abbildungen und 14 Tabellen
Thermodynamik für Werkstoffingenieure und Metallurgen Eine Einführung 2., stark überarbeitete Auflage Von Prof. Dr.-Ing. Martin G. Frohberg Technische Universität Berlin Mit 99 Abbildungen und 14 Tabellen
Lösung zu den Testaufgaben zur Mathematik für Chemiker II (Analysis)
 Universität D U I S B U R G E S S E N Campus Essen, Mathematik PD Dr. L. Strüngmann Informationen zur Veranstaltung unter: http://www.uni-due.de/algebra-logic/struengmann.shtml SS 7 Lösung zu den Testaufgaben
Universität D U I S B U R G E S S E N Campus Essen, Mathematik PD Dr. L. Strüngmann Informationen zur Veranstaltung unter: http://www.uni-due.de/algebra-logic/struengmann.shtml SS 7 Lösung zu den Testaufgaben
Karl Stephan Franz Mayinger. Thermodynamik. Grundlagen und technische Anwendungen. Zwölfte, neubearbeitete und erweiterte Auflage
 Karl Stephan Franz Mayinger Thermodynamik Grundlagen und technische Anwendungen Zwölfte, neubearbeitete und erweiterte Auflage Band 2 Mehrstoffsysteme und chemische Reaktionen Mit 135 Abbildungen Springer-Verlag
Karl Stephan Franz Mayinger Thermodynamik Grundlagen und technische Anwendungen Zwölfte, neubearbeitete und erweiterte Auflage Band 2 Mehrstoffsysteme und chemische Reaktionen Mit 135 Abbildungen Springer-Verlag
Differentialgleichungen
 Kapitel Differentialgleichungen Josef Leydold Mathematik für VW WS 05/6 Differentialgleichungen / Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen: () Erhöhung der
Kapitel Differentialgleichungen Josef Leydold Mathematik für VW WS 05/6 Differentialgleichungen / Ein einfaches Modell (Domar) Im Domar Wachstumsmodell treffen wir die folgenden Annahmen: () Erhöhung der
Multiple-Choice Test. Alle Fragen können mit Hilfe der Versuchsanleitung richtig gelöst werden.
 PCG-Grundpraktikum Versuch 8- Reale Gas Multiple-Choice Test Zu jedem Versuch im PCG wird ein Vorgespräch durchgeführt. Für den Versuch Reale Gas wird dieses Vorgespräch durch einen Multiple-Choice Test
PCG-Grundpraktikum Versuch 8- Reale Gas Multiple-Choice Test Zu jedem Versuch im PCG wird ein Vorgespräch durchgeführt. Für den Versuch Reale Gas wird dieses Vorgespräch durch einen Multiple-Choice Test
Inhaltsverzeichnis. 1 Grundlagen der Thermodynamik l VII
 VII Inhaltsverzeichnis 1 Grundlagen der Thermodynamik l 1.1 Einfahrung 1 1.2 Materie 2 1.3 Energie 2 1.3.1 Vorbemerkungen 2 1.3.2 Kinetische und potentielle Energie 3 1.3.3 Äußere und Innere Energie 4
VII Inhaltsverzeichnis 1 Grundlagen der Thermodynamik l 1.1 Einfahrung 1 1.2 Materie 2 1.3 Energie 2 1.3.1 Vorbemerkungen 2 1.3.2 Kinetische und potentielle Energie 3 1.3.3 Äußere und Innere Energie 4
Die 4 Phasen des Carnot-Prozesses
 Die 4 Phasen des Carnot-Prozesses isotherme Expansion: A B V V T k N Q ln 1 1 isotherme Kompression: adiabatische Kompression: adiabatische Expansion: 0 Q Q 0 C D V V T k N Q ln 2 2 S Q 1 1 /T1 T 1 T 2
Die 4 Phasen des Carnot-Prozesses isotherme Expansion: A B V V T k N Q ln 1 1 isotherme Kompression: adiabatische Kompression: adiabatische Expansion: 0 Q Q 0 C D V V T k N Q ln 2 2 S Q 1 1 /T1 T 1 T 2
a) Welche der folgenden Aussagen treffen nicht zu? (Dies bezieht sind nur auf Aufgabenteil a)
 Aufgabe 1: Multiple Choice (10P) Geben Sie an, welche der Aussagen richtig sind. Unabhängig von der Form der Fragestellung (Singular oder Plural) können eine oder mehrere Antworten richtig sein. a) Welche
Aufgabe 1: Multiple Choice (10P) Geben Sie an, welche der Aussagen richtig sind. Unabhängig von der Form der Fragestellung (Singular oder Plural) können eine oder mehrere Antworten richtig sein. a) Welche
Zur Erinnerung. Wärmetransport durch: -Wärmekonvektion -Wärmestrahlung -Wärmeleitung. Planck sches Strahlungsgesetz. Stefan-Boltzman-Gesetz
 Zur Erinnerung Stichworte aus der 9. orlesung: Wärmetransort durch: -Wärmekonvektion -Wärmestrahlung -Wärmeleitung Planck sches Strahlungsgesetz Stefan-Boltzman-Gesetz Wiensches erschiebungsgesetz Hautsätze
Zur Erinnerung Stichworte aus der 9. orlesung: Wärmetransort durch: -Wärmekonvektion -Wärmestrahlung -Wärmeleitung Planck sches Strahlungsgesetz Stefan-Boltzman-Gesetz Wiensches erschiebungsgesetz Hautsätze
Dampfdruck, molare Verdampfungsenthalpie und Raoultsches Gesetz
 Damfdruck, molare Verdamfungsenthalie und Raoultsches Gesetz 1 Ziel des Versuches Bestimmung der molaren Verdamfungsenthalie von Wasser aus der emeraturabhängigkeit des Damfdrucks (Clausius-Claeyron-Gleichung).
Damfdruck, molare Verdamfungsenthalie und Raoultsches Gesetz 1 Ziel des Versuches Bestimmung der molaren Verdamfungsenthalie von Wasser aus der emeraturabhängigkeit des Damfdrucks (Clausius-Claeyron-Gleichung).
Wärmelehre/Thermodynamik. Wintersemester 2007
 Einführung in die Physik I Wärmelehre/hermodynamik Wintersemester 7 ladimir Dyakonov #3 am..7 Folien unter: htt://www.hysik.uni-wuerzburg.de/ep6/teaching.html.3 Ideales Gas Exerimentelle Bestimmung der
Einführung in die Physik I Wärmelehre/hermodynamik Wintersemester 7 ladimir Dyakonov #3 am..7 Folien unter: htt://www.hysik.uni-wuerzburg.de/ep6/teaching.html.3 Ideales Gas Exerimentelle Bestimmung der
Liste der Formelzeichen. A. Thermodynamik der Gemische 1
 Inhaltsverzeichnis Liste der Formelzeichen XV A. Thermodynamik der Gemische 1 1. Grundbegriffe 3 1.1 Anmerkungen zur Nomenklatur von Mischphasen.... 4 1.2 Maße für die Zusammensetzung von Mischphasen....
Inhaltsverzeichnis Liste der Formelzeichen XV A. Thermodynamik der Gemische 1 1. Grundbegriffe 3 1.1 Anmerkungen zur Nomenklatur von Mischphasen.... 4 1.2 Maße für die Zusammensetzung von Mischphasen....
16 Vektorfelder und 1-Formen
 45 16 Vektorfelder und 1-Formen 16.1 Vektorfelder Ein Vektorfeld v auf D R n ist eine Abbildung v : D R n, x v(x). Beispiele. Elektrisches und Magnetisches Feld E(x), B(x), Geschwindigkeitsfeld einer Strömung
45 16 Vektorfelder und 1-Formen 16.1 Vektorfelder Ein Vektorfeld v auf D R n ist eine Abbildung v : D R n, x v(x). Beispiele. Elektrisches und Magnetisches Feld E(x), B(x), Geschwindigkeitsfeld einer Strömung
Einführung in die Physikalische Chemie: Inhalt
 Einführung in die Physikalische Chemie: Inhalt Kapitel 11: Das chemische Gleichgewicht Inhalt: Literatur: 11.1 Motivation 11.2 Mischungen und reale Systeme 11.3 Beschreibung des Reaktionsgleichgewichts
Einführung in die Physikalische Chemie: Inhalt Kapitel 11: Das chemische Gleichgewicht Inhalt: Literatur: 11.1 Motivation 11.2 Mischungen und reale Systeme 11.3 Beschreibung des Reaktionsgleichgewichts
5 Potenzreihenansatz und spezielle Funktionen
 5 Potenzreihenansatz und spezielle Funktionen In diesem Kapitel betrachten wir eine Methode zur Lösung linearer Differentialgleichungen höherer Ordnung, die sich anwenden läßt, wenn sich alle Koeffizienten
5 Potenzreihenansatz und spezielle Funktionen In diesem Kapitel betrachten wir eine Methode zur Lösung linearer Differentialgleichungen höherer Ordnung, die sich anwenden läßt, wenn sich alle Koeffizienten
FAQ Entropie. S = k B ln W. 1.) Ist die Entropie für einen Zustand eindeutig definiert?
 FAQ Entroie S = k B ln W 1.) Ist die Entroie für einen Zustand eindeutig definiert? Antwort: Nein, zumindest nicht in der klassischen Physik. Es sei an die Betrachtung der Ortsraum-Entroie des idealen
FAQ Entroie S = k B ln W 1.) Ist die Entroie für einen Zustand eindeutig definiert? Antwort: Nein, zumindest nicht in der klassischen Physik. Es sei an die Betrachtung der Ortsraum-Entroie des idealen
Phasengleichgewicht. 1. Experimentelle Bestimmung des Dampfdrucks von Methanol als Funktion der Temperatur. A fl. A g
 Physikalisch-Chemische Praktika Phasengleichgewicht Versuch T-2 Aufgaben 1. Experimentelle Bestimmung des Dampfdrucks von Methanol als Funktion der Temperatur. 2. Ermittlung der Phasenumwandlungsenthalpie
Physikalisch-Chemische Praktika Phasengleichgewicht Versuch T-2 Aufgaben 1. Experimentelle Bestimmung des Dampfdrucks von Methanol als Funktion der Temperatur. 2. Ermittlung der Phasenumwandlungsenthalpie
10. und 11. Vorlesung Sommersemester
 10. und 11. Vorlesung Sommersemester 1 Die Legendre-Transformation 1.1 Noch einmal mit mehr Details Diese Ableitung wirkt einfach, ist aber in dieser Form sicher nicht so leicht verständlich. Deswegen
10. und 11. Vorlesung Sommersemester 1 Die Legendre-Transformation 1.1 Noch einmal mit mehr Details Diese Ableitung wirkt einfach, ist aber in dieser Form sicher nicht so leicht verständlich. Deswegen
Die freie Energie wird also bei konstantem Volumen und konstanter Temperatur minimal
 Die freie Energie wird also bei konstantem Volumen und konstanter Temperatur minimal 7.2 Die Enthalpie Die Enthalpie H ist definiert als H = U + pv, womit wir für die Änderung erhalten dh = pdv + TdS +
Die freie Energie wird also bei konstantem Volumen und konstanter Temperatur minimal 7.2 Die Enthalpie Die Enthalpie H ist definiert als H = U + pv, womit wir für die Änderung erhalten dh = pdv + TdS +
Physikalische Chemie 0 Klausur, 22. Oktober 2011
 Physikalische Chemie 0 Klausur, 22. Oktober 2011 Bitte beantworten Sie die Fragen direkt auf dem Blatt. Auf jedem Blatt bitte Name, Matrikelnummer und Platznummer angeben. Zu jeder der 25 Fragen werden
Physikalische Chemie 0 Klausur, 22. Oktober 2011 Bitte beantworten Sie die Fragen direkt auf dem Blatt. Auf jedem Blatt bitte Name, Matrikelnummer und Platznummer angeben. Zu jeder der 25 Fragen werden
Mathematik II für Studierende der Informatik. Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016
 und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
und Wirtschaftsinformatik (Analysis und lineare Algebra) im Sommersemester 2016 5. Juni 2016 Definition 5.21 Ist a R, a > 0 und a 1, so bezeichnet man die Umkehrfunktion der Exponentialfunktion x a x als
18 Höhere Ableitungen und Taylorformel
 8 HÖHERE ABLEITUNGEN UND TAYLORFORMEL 98 8 Höhere Ableitungen und Taylorformel Definition. Sei f : D R eine Funktion, a D. Falls f in einer Umgebung von a (geschnitten mit D) differenzierbar und f in a
8 HÖHERE ABLEITUNGEN UND TAYLORFORMEL 98 8 Höhere Ableitungen und Taylorformel Definition. Sei f : D R eine Funktion, a D. Falls f in einer Umgebung von a (geschnitten mit D) differenzierbar und f in a
7 Die Hamilton-Jacobi-Theorie
 7 Die Hamilton-Jacobi-Theorie Ausgearbeitet von Rolf Horn und Bernhard Schmitz 7.1 Einleitung Um die Hamilton schen Bewegungsgleichungen q k = H(q, p) p k ṗ k = H(p, q) q k zu vereinfachen, führten wir
7 Die Hamilton-Jacobi-Theorie Ausgearbeitet von Rolf Horn und Bernhard Schmitz 7.1 Einleitung Um die Hamilton schen Bewegungsgleichungen q k = H(q, p) p k ṗ k = H(p, q) q k zu vereinfachen, führten wir
Prof. Dr. Rolf Linn
 Prof. Dr. Rolf Linn 6.4.5 Übungsaufgaben zu Mathematik Analysis. Einführung. Gegeben seien die Punkte P=(;) und Q=(5;5). a) Berechnen Sie den Anstieg m der Verbindungsgeraden von P und Q. b) Berechnen
Prof. Dr. Rolf Linn 6.4.5 Übungsaufgaben zu Mathematik Analysis. Einführung. Gegeben seien die Punkte P=(;) und Q=(5;5). a) Berechnen Sie den Anstieg m der Verbindungsgeraden von P und Q. b) Berechnen
A 1.1 a Wie groß ist das Molvolumen von Helium, flüssigem Wasser, Kupfer, Stickstoff und Sauerstoff bei 1 bar und 25 C?
 A 1.1 a Wie groß ist das Molvolumen von Helium, flüssigem Wasser, Kupfer, Stickstoff und Sauerstoff bei 1 bar und 25 C? (-> Tabelle p) A 1.1 b Wie groß ist der Auftrieb eines Helium (Wasserstoff) gefüllten
A 1.1 a Wie groß ist das Molvolumen von Helium, flüssigem Wasser, Kupfer, Stickstoff und Sauerstoff bei 1 bar und 25 C? (-> Tabelle p) A 1.1 b Wie groß ist der Auftrieb eines Helium (Wasserstoff) gefüllten
Mathematik für Biologen mathematische Ergänzungen und Beispiele Teil I
 Mathematik für Biologen mathematische Ergänzungen und Beispiele Teil I 1. Mengen und Abbildungen In der Mathematik beschäftigt man sich immer -direkt oder indirekt- mit Mengen. Wir benötigen den Mengenbegriff
Mathematik für Biologen mathematische Ergänzungen und Beispiele Teil I 1. Mengen und Abbildungen In der Mathematik beschäftigt man sich immer -direkt oder indirekt- mit Mengen. Wir benötigen den Mengenbegriff
Gewöhnliche Dierentialgleichungen
 Gewöhnliche Dierentialgleichungen sind Gleichungen, die eine Funktion mit ihren Ableitungen verknüpfen. Denition Eine explizite Dierentialgleichung (DGL) nter Ordnung für die reelle Funktion t x(t) hat
Gewöhnliche Dierentialgleichungen sind Gleichungen, die eine Funktion mit ihren Ableitungen verknüpfen. Denition Eine explizite Dierentialgleichung (DGL) nter Ordnung für die reelle Funktion t x(t) hat
Verflüssigung von Gasen / Joule-Thomson-Effekt
 Sieden und Kondensation: T p T p S S 0 1 RTSp0 1 ln p p0 Dampfdrucktopf, Autoklave zur Sterilisation absolute Luftfeuchtigkeit relative Luftfeuchtigkeit a ( g/m 3 ) a pw rel S ps rel 1 Taupunkt erflüssigung
Sieden und Kondensation: T p T p S S 0 1 RTSp0 1 ln p p0 Dampfdrucktopf, Autoklave zur Sterilisation absolute Luftfeuchtigkeit relative Luftfeuchtigkeit a ( g/m 3 ) a pw rel S ps rel 1 Taupunkt erflüssigung
Physikalische Chemie I
 Ideale Gase 0. Hautsatz der hermodynamik: Wenn A im thermischen Gleichgewicht mit b ist und desgleichen B mit C, so sind auch A und c miteinander im thermischen Gleichgewicht. Gesetz von Boyle: V = Konstante
Ideale Gase 0. Hautsatz der hermodynamik: Wenn A im thermischen Gleichgewicht mit b ist und desgleichen B mit C, so sind auch A und c miteinander im thermischen Gleichgewicht. Gesetz von Boyle: V = Konstante
Einführung in die Integralrechnung. Mag. Mone Denninger 13. November 2005
 Einführung in die Integralrechnung Mag. Mone Denninger. November 5 INHALTSVERZEICHNIS 8. Klasse Inhaltsverzeichnis Einleitung Berechnung einfacher Stammfunktionen. Integrationsregeln.........................
Einführung in die Integralrechnung Mag. Mone Denninger. November 5 INHALTSVERZEICHNIS 8. Klasse Inhaltsverzeichnis Einleitung Berechnung einfacher Stammfunktionen. Integrationsregeln.........................
PC - Prüfungsfragen - Prof. Breuer
 Inhalt: Seite 1. Zustandsfunktionen und Beisiele. Entroie am absoluten Nullunkt 3. Definition Entroie ( absolut bestimmbare Größen ) 4. C, C V (Definition, Messung, Grah, Berechnung, Debye / Dulong-Petit
Inhalt: Seite 1. Zustandsfunktionen und Beisiele. Entroie am absoluten Nullunkt 3. Definition Entroie ( absolut bestimmbare Größen ) 4. C, C V (Definition, Messung, Grah, Berechnung, Debye / Dulong-Petit
Grundpraktikum Physikalische Chemie V 18/19. Molekulargewichtsbestimmung. nach Rast, Dumas und durch. Gefrierpunktserniedrigung nach Beckmann
 Grundpraktikum Physikalische Chemie V 8/9 Molekulargewichtsbestimmung nach Rast, Dumas und durch Gefrierpunktserniedrigung nach Beckmann Kurzbeschreibung: Wird eine Substanz in einem bestimmten flüssigen
Grundpraktikum Physikalische Chemie V 8/9 Molekulargewichtsbestimmung nach Rast, Dumas und durch Gefrierpunktserniedrigung nach Beckmann Kurzbeschreibung: Wird eine Substanz in einem bestimmten flüssigen
Bekannter Stoff aus dem 1. Semester:
 Bekannter Stoff aus dem 1. Semester: Atombau! Arten der Teilchen! Elemente/Isotope! Kernchemie! Elektronenhülle/Quantenzahlen Chemische Bindung! Zustände der Materie! Ionenbindung! Atombindung! Metallbindung
Bekannter Stoff aus dem 1. Semester: Atombau! Arten der Teilchen! Elemente/Isotope! Kernchemie! Elektronenhülle/Quantenzahlen Chemische Bindung! Zustände der Materie! Ionenbindung! Atombindung! Metallbindung
Quadratische Gleichungen
 Quadratische Gleichungen TEIL 1: Die Quadratische Funktion und die Quadratische Gleichung Bei linearen Funktionen kommt nur in der 1. Potenz vor. Bei quadratischen Funktion kommt in der. Potenz vor. Daneben
Quadratische Gleichungen TEIL 1: Die Quadratische Funktion und die Quadratische Gleichung Bei linearen Funktionen kommt nur in der 1. Potenz vor. Bei quadratischen Funktion kommt in der. Potenz vor. Daneben
Lösung zur Übung 19 SS 2012
 Lösung zur Übung 19 SS 01 69) Beim radioaktiven Zerfall ist die Anzahl der pro Zeiteinheit zerfallenden Kerne dn/dt direkt proportional zur momentanen Anzahl der Kerne N(t). a) Formulieren Sie dazu die
Lösung zur Übung 19 SS 01 69) Beim radioaktiven Zerfall ist die Anzahl der pro Zeiteinheit zerfallenden Kerne dn/dt direkt proportional zur momentanen Anzahl der Kerne N(t). a) Formulieren Sie dazu die
Systemanalyse und Modellbildung
 und Modellbildung Universität Koblenz-Landau Fachbereich 7: Natur- und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) 8. Thermodynamik und Informationstheorie
und Modellbildung Universität Koblenz-Landau Fachbereich 7: Natur- und Umweltwissenschaften Institut für Umweltwissenschaften Dr. Horst Niemes(Lehrbeauftragter) 8. Thermodynamik und Informationstheorie
Einführung in die Physikalische Chemie: Inhalt. Einführung in die Physikalische Chemie:
 Einführung in die Physikalische Chemie: Inhalt Einführung in die Physikalische Chemie: Inhalt Kapitel 9: Prinzipien der Thermodynamik Inhalt: 9.1 Einführung und Definitionen 9.2 Der 0. Hauptsatz und seine
Einführung in die Physikalische Chemie: Inhalt Einführung in die Physikalische Chemie: Inhalt Kapitel 9: Prinzipien der Thermodynamik Inhalt: 9.1 Einführung und Definitionen 9.2 Der 0. Hauptsatz und seine
Vorlesung Physikalische Chemie IV Statistische Thermodynamik realer chemischer Systeme"
 Vorlesung Physikalische Chemie IV Statistische hermodynamik realer chemischer Systeme" Dietmar Paschek SS 6 Flory-Huggins heorie (III) Polymer-Lösungen: Osmotischer Druck Statistische hermodynamik realer
Vorlesung Physikalische Chemie IV Statistische hermodynamik realer chemischer Systeme" Dietmar Paschek SS 6 Flory-Huggins heorie (III) Polymer-Lösungen: Osmotischer Druck Statistische hermodynamik realer
Thermodynamik I. Sommersemester 2012 Kapitel 2, Teil 2. Prof. Dr. Ing. Heinz Pitsch
 Thermodynamik I Sommersemester 2012 Kapitel 2, Teil 2 Prof. Dr. Ing. Heinz Pitsch Kapitel 2, Teil 2: Übersicht 2 Zustandsgrößen 2.3 Bestimmung von Zustandsgrößen 2.3.1 Bestimmung der Phase 2.3.2 Der Sättigungszustand
Thermodynamik I Sommersemester 2012 Kapitel 2, Teil 2 Prof. Dr. Ing. Heinz Pitsch Kapitel 2, Teil 2: Übersicht 2 Zustandsgrößen 2.3 Bestimmung von Zustandsgrößen 2.3.1 Bestimmung der Phase 2.3.2 Der Sättigungszustand
Bei der Wärmeübertragung handelt es sich um die Veränderung des thermischen Anteils der inneren Energie. Thermische Energie ist definiert als
 Prof. r.-ing. Matthias ind Institut für hermische Verfahrenstechnik r.-ing. homas etzel ärmeübertragung I Lösung r 1. Übung (inleitung: Bilanz, inetik ie innere nergie U ist eine extensive Zustandsgröße,
Prof. r.-ing. Matthias ind Institut für hermische Verfahrenstechnik r.-ing. homas etzel ärmeübertragung I Lösung r 1. Übung (inleitung: Bilanz, inetik ie innere nergie U ist eine extensive Zustandsgröße,
Allgemeine Chemie. SS 2014 Thomas Loerting. Thomas Loerting Allgemeine Chemie
 Allgemeine Chemie SS 2014 Thomas Loerting 1 Inhalt 1 Der Aufbau der Materie (Teil 1) 2 Die chemische Bindung (Teil 2) 3 Die chemische Reaktion (Teil 3) 2 Definitionen von den an einer chemischen Reaktion
Allgemeine Chemie SS 2014 Thomas Loerting 1 Inhalt 1 Der Aufbau der Materie (Teil 1) 2 Die chemische Bindung (Teil 2) 3 Die chemische Reaktion (Teil 3) 2 Definitionen von den an einer chemischen Reaktion
W2 Gasthermometer. 1. Grundlagen: 1.1 Gasthermometer und Temperaturmessung
 W2 Gasthermometer Stoffgebiet: Versuchsziel: Literatur: emperaturmessung, Gasthermometer, Gasgesetze Mit Hilfe eines Gasthermometers ist der Ausdehnungs- und Druckkoeffizient von Luft zu bestimmen. Beschäftigung
W2 Gasthermometer Stoffgebiet: Versuchsziel: Literatur: emperaturmessung, Gasthermometer, Gasgesetze Mit Hilfe eines Gasthermometers ist der Ausdehnungs- und Druckkoeffizient von Luft zu bestimmen. Beschäftigung
1) Ein offenes System zeichnet sich immer durch eine konstante Temperatur aus. zeichnet sich immer durch eine konstante Masse aus.
 1) Ein offenes System zeichnet sich immer durch eine konstante Temperatur aus. zeichnet sich immer durch eine konstante Masse aus. kann mit der Umgebung Energie austauschen. kann mit der Umgebung Entropie
1) Ein offenes System zeichnet sich immer durch eine konstante Temperatur aus. zeichnet sich immer durch eine konstante Masse aus. kann mit der Umgebung Energie austauschen. kann mit der Umgebung Entropie
Physik 2 (B.Sc. EIT) 2. Übungsblatt
 Institut für Physik Werner-Heisenberg-Weg 9 Fakultät für Elektrotechnik 85577 München / Neubiberg Universität der Bundeswehr München / Neubiberg Prof Dr H Baumgärtner Übungen: Dr-Ing Tanja Stimpel-Lindner,
Institut für Physik Werner-Heisenberg-Weg 9 Fakultät für Elektrotechnik 85577 München / Neubiberg Universität der Bundeswehr München / Neubiberg Prof Dr H Baumgärtner Übungen: Dr-Ing Tanja Stimpel-Lindner,
Nachklausur zum Modul Physikalische Chemie 1
 Nachklausur zum Modul Physikalische Chemie 1 Sommersemester 2007 Wintersemester 2007 / 08 29. Januar 2008 Angaben zur Person (BITTE LESERLICH UND IN DRUCKBUCHSTABEN) Name, Vorname... Geburtsdatum und -ort...
Nachklausur zum Modul Physikalische Chemie 1 Sommersemester 2007 Wintersemester 2007 / 08 29. Januar 2008 Angaben zur Person (BITTE LESERLICH UND IN DRUCKBUCHSTABEN) Name, Vorname... Geburtsdatum und -ort...
25. Adiabatische Expansion eines idealen Gases 1
 25. Adiabatische Exansion eines idealen Gases 1 25. ADABASHE EXPANSON ENES DEALEN GASES 1. Aufgabe Für Luft als annähernd ideales Gas sollen sowohl die Molwäre bei konstante Druck, d.h.,, als auch das
25. Adiabatische Exansion eines idealen Gases 1 25. ADABASHE EXPANSON ENES DEALEN GASES 1. Aufgabe Für Luft als annähernd ideales Gas sollen sowohl die Molwäre bei konstante Druck, d.h.,, als auch das
Versuchsprotokoll Kapitel 6
 Versuchsprotokoll Kapitel 6 Felix, Sebastian, Tobias, Raphael, Joel 1. Semester 21 Inhaltsverzeichnis Einleitung...3 Versuch 6.1...3 Einwaagen und Herstellung der Verdünnungen...3 Photospektrometrisches
Versuchsprotokoll Kapitel 6 Felix, Sebastian, Tobias, Raphael, Joel 1. Semester 21 Inhaltsverzeichnis Einleitung...3 Versuch 6.1...3 Einwaagen und Herstellung der Verdünnungen...3 Photospektrometrisches
Klausur Physikalische Chemie für TUHH (Chemie III)
 07.03.2012 14.00 Uhr 17.00 Uhr Moritz / Pauer Klausur Physikalische Chemie für TUHH (Chemie III) Die folgende Tabelle dient Korrekturzwecken und darf vom Studenten nicht ausgefüllt werden. 1 2 3 4 5 6
07.03.2012 14.00 Uhr 17.00 Uhr Moritz / Pauer Klausur Physikalische Chemie für TUHH (Chemie III) Die folgende Tabelle dient Korrekturzwecken und darf vom Studenten nicht ausgefüllt werden. 1 2 3 4 5 6
Physikalische Chemie Physikalische Chemie I SoSe 2009 Prof. Dr. Norbert Hampp 1/9 1. Das Ideale Gas. Thermodynamik
 Prof. Dr. Norbert Hampp 1/9 1. Das Ideale Gas Thermodynamik Teilgebiet der klassischen Physik. Wir betrachten statistisch viele Teilchen. Informationen über einzelne Teilchen werden nicht gewonnen bzw.
Prof. Dr. Norbert Hampp 1/9 1. Das Ideale Gas Thermodynamik Teilgebiet der klassischen Physik. Wir betrachten statistisch viele Teilchen. Informationen über einzelne Teilchen werden nicht gewonnen bzw.
Grundlagen der statistischen Physik und Thermodynamik
 Grundlagen der statistischen Physik und Thermodynamik "Feuer und Eis" von Guy Respaud 6/14/2013 S.Alexandrova FDIBA 1 Grundlagen der statistischen Physik und Thermodynamik Die statistische Physik und die
Grundlagen der statistischen Physik und Thermodynamik "Feuer und Eis" von Guy Respaud 6/14/2013 S.Alexandrova FDIBA 1 Grundlagen der statistischen Physik und Thermodynamik Die statistische Physik und die
6 Differentialgleichungen
 88 6 Differentialgleichungen Eine Differentialgleichung ist eine Gleichung, in der eine unbekannte Funktion y = y(x) und Ableitungen (die erste oder auch höhere) von y vorkommen. Lösungen einer Differentialgleichung
88 6 Differentialgleichungen Eine Differentialgleichung ist eine Gleichung, in der eine unbekannte Funktion y = y(x) und Ableitungen (die erste oder auch höhere) von y vorkommen. Lösungen einer Differentialgleichung
Physikdepartment. Ferienkurs zur Experimentalphysik 4. Daniel Jost 10/09/15
 Physikdepartment Ferienkurs zur Experimentalphysik 4 Daniel Jost 10/09/15 Inhaltsverzeichnis Technische Universität München 1 Kurze Einführung in die Thermodynamik 1 1.1 Hauptsätze der Thermodynamik.......................
Physikdepartment Ferienkurs zur Experimentalphysik 4 Daniel Jost 10/09/15 Inhaltsverzeichnis Technische Universität München 1 Kurze Einführung in die Thermodynamik 1 1.1 Hauptsätze der Thermodynamik.......................
Dampfdruck von Flüssigkeiten (Clausius-Clapeyron' sche Gleichung)
 Versuch Nr. 57 Dampfdruck von Flüssigkeiten (Clausius-Clapeyron' sche Gleichung) Stichworte: Dampf, Dampfdruck von Flüssigkeiten, dynamisches Gleichgewicht, gesättigter Dampf, Verdampfungsenthalpie, Dampfdruckkurve,
Versuch Nr. 57 Dampfdruck von Flüssigkeiten (Clausius-Clapeyron' sche Gleichung) Stichworte: Dampf, Dampfdruck von Flüssigkeiten, dynamisches Gleichgewicht, gesättigter Dampf, Verdampfungsenthalpie, Dampfdruckkurve,
Formelsammlung zur Vorlesung Physikalische Chemie I (Thermodynamik)
 Formelsammlung zur Vorlesung Physikalische Chemie I (hermodynamik) Ulrich K. Deiters Institut für Physikalische Chemie, Universität zu Köln 1 Symbole M N N A n p R V Molmasse eilchenzahl Avogadro-Konstante,
Formelsammlung zur Vorlesung Physikalische Chemie I (hermodynamik) Ulrich K. Deiters Institut für Physikalische Chemie, Universität zu Köln 1 Symbole M N N A n p R V Molmasse eilchenzahl Avogadro-Konstante,
Aufgabe: Es sind die kryoskopischen Konstante von Wasser und die Molmassen von darin löslichen Substanzen zu bestimmen.
 Versuchsanleitungen zum Praktikum Physikalische Chemie für nfänger 1 4 Kryoskopie ufgabe: Es sind die kryoskopischen Konstante von Wasser und die Molmassen von darin löslichen Substanzen zu bestimmen.
Versuchsanleitungen zum Praktikum Physikalische Chemie für nfänger 1 4 Kryoskopie ufgabe: Es sind die kryoskopischen Konstante von Wasser und die Molmassen von darin löslichen Substanzen zu bestimmen.
Kapitel VI. Euklidische Geometrie
 Kapitel VI. Euklidische Geometrie 1 Abstände und Lote Wiederholung aus Kapitel IV. Wir versehen R n mit dem Standard Skalarprodukt x 1 y 1.,. := x 1 y 1 +... + x n y n x n y n Es gilt für u, v, w R n und
Kapitel VI. Euklidische Geometrie 1 Abstände und Lote Wiederholung aus Kapitel IV. Wir versehen R n mit dem Standard Skalarprodukt x 1 y 1.,. := x 1 y 1 +... + x n y n x n y n Es gilt für u, v, w R n und
R C 1s =0, C T 1
 Aufgaben zum Themengebiet Aufladen und Entladen eines Kondensators Theorie und nummerierte Formeln auf den Seiten 5 bis 8 Ein Kondensator mit der Kapazität = 00μF wurde mit der Spannung U = 60V aufgeladen
Aufgaben zum Themengebiet Aufladen und Entladen eines Kondensators Theorie und nummerierte Formeln auf den Seiten 5 bis 8 Ein Kondensator mit der Kapazität = 00μF wurde mit der Spannung U = 60V aufgeladen
wegen adiabater Kompression, d.h. kein Wärmeaustausch mit der Umgebung, gilt:
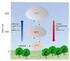 Ü 7. Adiabate Komression on Luft Luft wird in einem adiabaten Zylinder on. bar, T 5 C solange erdichtet bis eine Endtemeratur on T 00 C erreicht wird. Gesucht sind die zur Verdichtung erforderliche Arbeit
Ü 7. Adiabate Komression on Luft Luft wird in einem adiabaten Zylinder on. bar, T 5 C solange erdichtet bis eine Endtemeratur on T 00 C erreicht wird. Gesucht sind die zur Verdichtung erforderliche Arbeit
Fehlerfortpflanzung & Extremwertbestimmung. Folie 1
 Fehlerfortpflanzung & Etremwertbestimmung Folie 1 Fehlerfortpflanzung Einführung In vielen technischen Zusammenhängen sind die Werte bestimmter Größen nicht genau bekannt sondern mit einer Unsicherheit
Fehlerfortpflanzung & Etremwertbestimmung Folie 1 Fehlerfortpflanzung Einführung In vielen technischen Zusammenhängen sind die Werte bestimmter Größen nicht genau bekannt sondern mit einer Unsicherheit
Teil 1. Differenzial Unbestimmtes Integral Stammfunktionen (unbestimmte und bestimmte)
 ANALYSIS Einführung in die Integralrechnung Teil Differenzial Unbestimmtes Integral Stammfunktionen (unbestimmte und bestimmte) Einfache Theorie wie im Unterricht Mit vielen Beispielen und Übungsaufgaben
ANALYSIS Einführung in die Integralrechnung Teil Differenzial Unbestimmtes Integral Stammfunktionen (unbestimmte und bestimmte) Einfache Theorie wie im Unterricht Mit vielen Beispielen und Übungsaufgaben
Praktikumsprotokoll Physikalisch-Chemisches Anfängerpraktikum
 Praktikumsrotokoll Physikalisch-Chemisches Anfängerraktikum Tobias Schabel Datum des Praktikumstags: 14.11.25 Matthias Ernst Protokoll-Datum: 8.12.25 Grue A-11 Assistent: N. Kaernaum 6. Versuch: HG - Homogenes
Praktikumsrotokoll Physikalisch-Chemisches Anfängerraktikum Tobias Schabel Datum des Praktikumstags: 14.11.25 Matthias Ernst Protokoll-Datum: 8.12.25 Grue A-11 Assistent: N. Kaernaum 6. Versuch: HG - Homogenes
Thermodynamik. Christian Britz
 Hauptsätze der Klassische nanoskaliger Systeme 04.02.2013 Inhalt Einleitung Hauptsätze der Klassische nanoskaliger Systeme 1 Einleitung 2 Hauptsätze der 3 4 Klassische 5 6 7 nanoskaliger Systeme 8 Hauptsätze
Hauptsätze der Klassische nanoskaliger Systeme 04.02.2013 Inhalt Einleitung Hauptsätze der Klassische nanoskaliger Systeme 1 Einleitung 2 Hauptsätze der 3 4 Klassische 5 6 7 nanoskaliger Systeme 8 Hauptsätze
8. Reale Gase D1-1. Bereiten Sie folgende Themengebiete vor
 D1-1 8. Reale Gase Bereiten Sie folgende Themengebiete vor Modell des idealen Gases, ideales Gasgesetz reales Gas, van der Waals-Gleichung, Virialgleichungen pv- und pt-diagramme, kritische Isotherme kinetische
D1-1 8. Reale Gase Bereiten Sie folgende Themengebiete vor Modell des idealen Gases, ideales Gasgesetz reales Gas, van der Waals-Gleichung, Virialgleichungen pv- und pt-diagramme, kritische Isotherme kinetische
Kapitel 10 - Gase. Kapitel 10 - Gase. Gase bestehen aus räumlich weit voneinander getrennten Atome/Moleküle in schneller Bewegung
 Kapitel 0 - Gase Gase bestehen aus räumlich weit voneinander getrennten Atome/Moleküle in schneller ewegung Druck Kraft pro Fläche in Pa(scal) oder bar Normdruck = 760mm = 0,35 KPa =,035 bar = atm Messung
Kapitel 0 - Gase Gase bestehen aus räumlich weit voneinander getrennten Atome/Moleküle in schneller ewegung Druck Kraft pro Fläche in Pa(scal) oder bar Normdruck = 760mm = 0,35 KPa =,035 bar = atm Messung
9. Vorlesung Wintersemester
 9. Vorlesung Wintersemester 1 Die Phase der angeregten Schwingung Wertebereich: bei der oben abgeleiteten Formel tan φ = β ω ω ω0. (1) ist noch zu sehen, in welchem Bereich der Winkel liegt. Aus der ursprünglichen
9. Vorlesung Wintersemester 1 Die Phase der angeregten Schwingung Wertebereich: bei der oben abgeleiteten Formel tan φ = β ω ω ω0. (1) ist noch zu sehen, in welchem Bereich der Winkel liegt. Aus der ursprünglichen
Chemisches Potential und Nernstgleichung Carsten Stick
 Chemisches Potential und Nernstgleichung Carsten Stick Definition der mechanischen Arbeit: Kraft mal Weg W = F! ds W = Arbeit oder Energie; F = Kraft; s = Weg Diese Definition lässt sich auch auf die Kompression
Chemisches Potential und Nernstgleichung Carsten Stick Definition der mechanischen Arbeit: Kraft mal Weg W = F! ds W = Arbeit oder Energie; F = Kraft; s = Weg Diese Definition lässt sich auch auf die Kompression
1. Ziel des Versuchs. 2. Theorie. Dennis Fischer Gruppe 9 Magdalena Boeddinghaus
 Versuch Nr. 12: Gasthermometer 1. Ziel des Versuchs In diesem Versuch soll die Temperaturmessung durch Druckmessung erlernt werden. ußerdem soll der absolute Nullpunkt des Thermometers bestimmt werden.
Versuch Nr. 12: Gasthermometer 1. Ziel des Versuchs In diesem Versuch soll die Temperaturmessung durch Druckmessung erlernt werden. ußerdem soll der absolute Nullpunkt des Thermometers bestimmt werden.
VERSUCH 16 CHEMISCHES GLEICHGEWICHT IN DER GASPHASE
 GRUNDPRAKTIKUM PHYSIKALISCHE CHEMIE VERSUCH 16 CHEMISCHES GLEICHGEWICHT IN DER GASPHASE Kurzbeschreibung: Die Temperaturabhängigkeit des chemischen Gasphasen-Gleichgewichts wird unter isobaren Bedingungen
GRUNDPRAKTIKUM PHYSIKALISCHE CHEMIE VERSUCH 16 CHEMISCHES GLEICHGEWICHT IN DER GASPHASE Kurzbeschreibung: Die Temperaturabhängigkeit des chemischen Gasphasen-Gleichgewichts wird unter isobaren Bedingungen
Praktikum I PP Physikalisches Pendel
 Praktikum I PP Physikalisches Pendel Hanno Rein Betreuer: Heiko Eitel 16. November 2003 1 Ziel der Versuchsreihe In der Physik lassen sich viele Vorgänge mit Hilfe von Schwingungen beschreiben. Die klassische
Praktikum I PP Physikalisches Pendel Hanno Rein Betreuer: Heiko Eitel 16. November 2003 1 Ziel der Versuchsreihe In der Physik lassen sich viele Vorgänge mit Hilfe von Schwingungen beschreiben. Die klassische
1 Lambert-Beersches Gesetz
 Physikalische Chemie II Lösung 6 23. Oktober 205 Lambert-Beersches Gesetz Anhand des idealen Gasgesetzes lässt sich die Teilchenkonzentration C wie folgt ausrechnen: C = N V = n N A V pv =nrt = N A p R
Physikalische Chemie II Lösung 6 23. Oktober 205 Lambert-Beersches Gesetz Anhand des idealen Gasgesetzes lässt sich die Teilchenkonzentration C wie folgt ausrechnen: C = N V = n N A V pv =nrt = N A p R
Übung 4. SS 2013 Übung - Einführung in die Verbrennung - Methling, Özuylasi 1
 Ziel: Grundlagen der chemischen Reaktionskinetik verstehen Verstehen qualitativer Reaktionsverläufe Aufstellung des Zeitgesetzes Umgang mit nicht reagierenden Stoßpartner (M) Berechnung Geschwindigkeitskoeffizient
Ziel: Grundlagen der chemischen Reaktionskinetik verstehen Verstehen qualitativer Reaktionsverläufe Aufstellung des Zeitgesetzes Umgang mit nicht reagierenden Stoßpartner (M) Berechnung Geschwindigkeitskoeffizient
