Vektoren. b b. R heißt der Vektor. des. und b. . a b
|
|
|
- Manfred Hartmann
- vor 6 Jahren
- Abrufe
Transkript
1 6 Vektoren 66 Ds Vektorprodukt Definition des Vektorprodukts Wir etrchten im dreidimensionlen Rum zwei nicht kollinere Vektoren R, \{0} Gesucht ist ein Vektor x R, der uf jedem der eiden Vektoren und senkrecht steht, für den lso gilt: $ x und $ x Die ufge ist nicht eindeutig lösr, d die Länge und uch die Richtung des Lösungsvektors nicht eindeutig estimmt sind Die ildung zeigt nur einen möglichen von den unendlich vielen Lösungsvektoren Selst unter den Vektoren der Länge git es noch zwei entgegengesetzt gerichtete Lösungsvektoren Die eiden Orthogonlitätsedingungen edeuten x 0 und x 0 xx x 0 Sie führen zu dem Gleichungssystem x x x 0 Eine Lösung dieses Gleichungssystems ist der Vektor x Mn definiert: Vektorprodukt Für die Vektoren und des R heißt der Vektor : (lies: Kreuz ) ds Vektorprodukt von und steht senkrecht uf und Hierei ist zu echten: Ds Vektorprodukt ist nur für Vektoren des R definiert, nicht für Vektoren des R Ds Vektorprodukt zweier Vektoren ist wieder ein Vektor Der Nme Vektorprodukt leitet sich wie uch eim Sklrprodukt vom Ergenis her Die oige Definition ezieht den Nullvektor und uch den Fll ein, dss die eiden Vektoren kolliner sind Es leit zu klären, welche Bedeutung dem Vektorprodukt in diesen Fällen zukommt x Nchweis 66
2 6 Vektoren Die Komponenten von sehen etws kompliziert us und lssen sich nicht so leicht merken Hier knn zb ds nchfolgend drgestellte Schem helfen + Mn schreit die ersten eiden Zeilen noch einml unter ds Produkt und streicht dnn die erste Zeile Die Komponenten von ergeen sich, wenn mn, wie im Rechenschem drgestellt, üer Kreuz rechnet Dieses Rechenschem erklärt, dss mn sttt Vektorprodukt häufig ls Synonym uch die Bezeichnung Kreuzprodukt verwendet Beispiel (Vektorprodukt erechnen) Berechnet werden soll ds Vektorprodukt von = 7 ( ) ( ) und 7 = 0 Merkschem: Zur Kontrolle knn mn nchrechnen, dss der erechnete Vektor 5 orthogonl zu jedem der gegeenen Vektoren = und 7 = ist: 0 ( ) = ( ) = 0 7 = () = = 0 5 = 7 () + + () 5 = = 0 5
3 6 Vektoren Rechenregeln für ds Vektorprodukt Wie eim Sklrprodukt lssen sich uch us der Definition des Vektorprodukts Rechenregeln leiten Sie sind nchfolgend in einer Üersicht zusmmengefsst Rechenregeln für ds Vektorprodukt Für lle c,, R sowie R gilt: () ( ) () ( c) c () ( ) ( ) ( ) () 0 (ntisymmetrie) (Distriutivgesetz) Nchweis 66 (Verträglichkeit mit S-Multiplikt) ufgen 8 Berechnen Sie die Vektorprodukte 7 0 ) 0 ) e) f) 0 0 c) g) 0 d) h) Errechnen Sie einen Vektor, der zum Vektor und uch zum Vektor orthogonl ist Bestätigen Sie die Orthogonlität nschließend rechnerisch ) ; ) ; 0 8 Berechnen Sie zunächst und dnn Welche Eigenschft des Vektorprodukts ergit sich? ) 0 ; 0 ) ;
4 6 Vektoren 5 Orientierung des Vektorprodukts Für ds Vektorprodukt zweier Vektoren und gilt: ( ) $ und ( ) $ Der Vektor steht somit senkrecht uf der von den eiden Vektoren und e ufgespnnten Eene e Der Vektor wird uch ls ein Normlenvektor zu der von den Vektoren und ufgespnnten Eene e ezeichnet Ds Wort norml leitet sich us dem Lteinischen normlis und edeutet soviel wie der Norm entsprechend oder im rechten Winkel gemcht Es leit noch zu klären, wie sich die Orientierung des Vektors zu der von den Vektoren und ufgespnnten Eene estimmen lässt Die Vektoren,, ilden in dieser Reihenfolge, eenso wie die Koordintenchsen unseres Koordintensystems, ein Rechtssystem Für diesen Schverhlt git es zwei Merkregeln, die insesondere uch in der Physik verwendet werden Rechte-Hnd-Regel Die Richtung des Vektors Regel wie folgt estimmen: lässt sich mit dieser Wenn der Dumen der gespreizten rechten Hnd in Richtung von und der Zeigefinger in Richtung von zeigt, dnn zeigt der Mittelfinger, wenn er uf der von Dumen und Zeigefinger ufgespnnten Eene senkrecht steht, in Richtung von Schruenregel Die Richtung des Vektors Regel wie folgt estimmen: lässt sich mit dieser Dreht mn üer den kleineren Winkel in die Richtung und Orientierung von, dnn entsteht dei eine Drehrichtung, die uf eine normle Schrue ngewndt diese Schrue in die Richtung und Orientierung von ewegen würde
5 6 6 Vektoren ufgen 8 Gegeen sind Pfeile von Vektoren und in der Zeicheneene Üertrgen Sie die Skizze ins Heft und zeichnen Sie die Richtung von durch oder ein, je nchdem, o die Pfeile von us der Zeicheneene he- rus oder er in die Zeicheneene hinein zeigen 85 Entscheiden Sie, o die drgestellten Vektoren, und c in dieser Reihenfolge ein Rechtssystem ilden ) ) c) c c c 86 * Ein Mgnetfeld mit der Flussdichte B üt uf ein mit der Geschwindigkeit v ewegtes Teilchen, ds die Ldung q trägt, die Krft F q( vb) us Mn ezeichnet diese Krft ls Lorentz-Krft Dei ist ds Vorzeichen der Ldung q zu erücksichtigen In welcher Richtung wirkt in den folgenden ildungen die Lorentz-Krft? ) q v ) q + v c) v q + d) q edeutet, dss die Flussdichte B us der Zeicheneene herus zeigt edeutet, dss die Flussdichte B in die Zeicheneene hinein zeigt 87 * Ds Drehmoment M knn ls Vektorprodukt in der Form M F eschrieen werden Erläutern Sie die Bedeutung des Begriffs Drehmoment und die Bedeutung der Vektoren und F (Internetrecherche oder Literturstudium) v
6 6 Vektoren 7 Flächeninhlt von Prllelogrmm und Dreieck Für zwei Vektoren und des R ist ein Vektor, der sowohl senkrecht zu ls uch zu ist Neen dieser esonderen uszeichnung der Richtung von ht uch der Betrg eine emerkenswerte geometrische Bedeutung Eine etws ufwendige Rechnung führt zu folgender Drstellung für : Komponentenfreie Drstellung des Betrgs des Vektorprodukts Sind und elieige Vektoren des R mit, 0, so gilt sin( ), woei ds Mß des Winkels zwischen den Vektoren und ist Nchweis 66 c Diese komponentenfreie Drstellung lässt sich uch geometrisch interpretieren In dem von den Vektoren und ufgespnnten Prllelogrmm ist die Höhe h uf die Grundseite gegeen durch h sin( ) Für den Flächeninhlt des Prllelogrmms ergit sich dmit: ( ) Grundseite Höhe h sin ( ) h sin( ) Flächeninhlt von Prllelogrmm und Dreieck Für den Flächeninhlt des von den Vektoren und im Rum ufgespnnten Prllelogrmms gilt: ( ) Ein von den Vektoren und im Rum erzeugtes Dreieck esitzt den Flächeninhlt: ( ) Beispiel (Flächeninhlt eines Prllelogrmms erechnen) Gegeen sind die Vektoren und 0 Die Vektoren und spnnen ein Prllelogrmm uf mit dem Flächeninhlt: ( ), 0
7 8 6 Vektoren Beispiel (Flächeninhlt eines Dreiecks erechnen) Gegeen sind die Punkte P( ), Q( 0 ) und R( ) Es gilt: PQ und PR 5 0 Für den Flächeninhlt des Dreiecks PQR folgt: R P Q 5 ( ) 5 5,5 0 ufgen 88 Begründen Sie: Ein von den Vektoren und erzeugtes Dreieck esitzt den Flächeninhlt ( ) 89 Gegeen sind ( 6), B(5 8), C ( 5 ) und D ( ) ) Zeigen Sie, dss ds Viereck BCD ein Prllelogrmm ist ) Berechnen Sie den Flächeninhlt des Prllelogrmms BCD 90 Berechnen Sie den Flächeninhlt des Dreiecks BC ) ( 7), B ( 5 ) und C ( 5) ) (8 0 ), B (7 7 ) und C ( 6 9) 9 Gegeen sind die Punkte ( 0), B (0 ) und C ( ) ) Bestimmen Sie den Punkt D so, dss ds Viereck BCD ein Prllelogrmm ist ) Wo und unter welchem Winkel schneiden sich die Digonlen? c) Welchen Flächeninhlt ht ds Prllelogrmm? 9 Gegeen sind die Eckpunkte ( ), B (0 ) und C ( 0) eines Dreiecks ) Berechnen Sie die Längen der Seiten, die Mße der Innenwinkel und den Flächeninhlt des Dreiecks ) Berechnen Sie mithilfe des Flächeninhlts die Länge der Dreieckshöhen
8 6 Vektoren 9 9 Gegeen sind die Punkte (5 6 ), B ( 6 ), S C (0 ), D ( ) sowie S (,5 5) Ds Viereck BCD ist die Grundfläche einer Pyrmide mit der Spitze S ) Welche Länge esitzt die Seitenknte BS? D C ) Weisen Sie nch, dss es sich ei dem Viereck M BCD um ein Prllelogrmm hndelt B c) Berechnen Sie den Flächeninhlt des Prllelogrmms d) Bestimmen Sie die Koordinten des Fußpunkts M e) Welche Höhe esitzt die Pyrmide? Welcher Wert ergit sich dmit für ds Volumen der Pyrmide? 9 Die ildung zeigt ein Zelt mit der Form einer Pyrmide mit qudrtischer Grundfläche der Seitenlänge m und der Spitze S in m Höhe üer dem Mittelpunkt der Grundfläche In der Vorderfläche PQS efindet sich die trpezförmige Einstiegsöffnung BCD x S Dei sind C und D die Mittelpunkte der Strecken BS zw S Die Strecken P und BQ D C hen jeweils die Länge 0,5 m R ) Bestimmen Sie die Koordinten der Punkte O x, B, C, D und S P B Q ) Berechnen Sie ds Volumen der Pyrmide x c) Berechnen Sie den Flächeninhlt der Einstiegsöffnung 95 Gegeen sind die Punkte (6 0 0), C (0 6 0) und F (6 ) Die Punkte, B, C und der Ursprung O legen ein Rechteck fest Zusmmen mit den Punkten E und F wird ein Dchstuhl eschrieen ) Berechnen Sie den Flächeninhlt des Dchodens ) Berechnen Sie den Flächeninhlt der Seitenflächen des Dchstuhls c) Berechnen Sie ds Volumen des Dchstuhls x O x F E B C x
Für den Mathe GK, Henß. - Lineare Algebra und analytische Geometrie -
 Für den Mthe GK, Henß - Linere Alger und nlytische Geometrie - Bis uf die Astände ist jetzt lles drin.. Ich h noch ne tolle Seite entdeckt mit vielen Beispielen und vor llem Aufgen zum Üen mit Lösungen..
Für den Mthe GK, Henß - Linere Alger und nlytische Geometrie - Bis uf die Astände ist jetzt lles drin.. Ich h noch ne tolle Seite entdeckt mit vielen Beispielen und vor llem Aufgen zum Üen mit Lösungen..
Vorkurs Mathematik Fachhochschule Frankfurt, Fachbereich 2. Fachhochschule Frankfurt am Main Fachbereich Informatik und Ingenieurwissenschaften
 Vorkurs Mthemtik Fchhochschule Frnkfurt, Fchereich Fchhochschule Frnkfurt m Min Fchereich Informtik und Ingenieurwissenschften Vorkurs Mthemtik Sie finden lle Mterilien sowie ergänzende Informtionen unter
Vorkurs Mthemtik Fchhochschule Frnkfurt, Fchereich Fchhochschule Frnkfurt m Min Fchereich Informtik und Ingenieurwissenschften Vorkurs Mthemtik Sie finden lle Mterilien sowie ergänzende Informtionen unter
Skript für die Oberstufe und das Abitur 2015 Baden-Württemberg berufl. Gymnasium (AG, BTG, EG, SG, WG)
 Sript für die Oerstufe und ds Aitur Bden-Württemerg erufl. Gymnsium (AG, BTG, EG, SG, WG) Mtrizenrechnung, wirtschftliche Anwendungen (Leontief, Mterilverflechtung) und Linere Optimierung Dipl.-Mth. Alexnder
Sript für die Oerstufe und ds Aitur Bden-Württemerg erufl. Gymnsium (AG, BTG, EG, SG, WG) Mtrizenrechnung, wirtschftliche Anwendungen (Leontief, Mterilverflechtung) und Linere Optimierung Dipl.-Mth. Alexnder
Die Regelungen zu den Einsendeaufgaben (Einsendeschluss, Klausurzulassung) finden Sie in den Studien- und Prüfungsinformationen Heft Nr. 1.
 Modul : Grundlgen der Wirtschftsmthemtik und Sttistik Kurs 46, Einheit, Einsendeufge Die Regelungen zu den Einsendeufgen (Einsendeschluss, Klusurzulssung) finden Sie in den Studien- und Prüfungsinformtionen
Modul : Grundlgen der Wirtschftsmthemtik und Sttistik Kurs 46, Einheit, Einsendeufge Die Regelungen zu den Einsendeufgen (Einsendeschluss, Klusurzulssung) finden Sie in den Studien- und Prüfungsinformtionen
Lösung: a) 1093 1100 b) 1093 1090
 OvTG Guting, Grundwissen Mthemtik 5. Klsse 1. Ntürliche Zhlen Dezimlsystem Mn nennt die Zhlen, die mn zum Zählen verwendet, 10963 = 1 10000+ 0 1000+ 9 100+ 6 10 + 3 1 ntürliche Zhlen. Der Stellenwert der
OvTG Guting, Grundwissen Mthemtik 5. Klsse 1. Ntürliche Zhlen Dezimlsystem Mn nennt die Zhlen, die mn zum Zählen verwendet, 10963 = 1 10000+ 0 1000+ 9 100+ 6 10 + 3 1 ntürliche Zhlen. Der Stellenwert der
Grundwissen am Ende der Jahrgangsstufe 9. Wahlpflichtfächergruppe II / III
 Grundwissen m Ende der Jhrgngsstufe 9 Whlpflichtfächergruppe II / III Funktionsbegriff Gerdengleichungen ufstellen und zu gegebenen Gleichungen die Grphen der Gerden zeichnen Ssteme linerer Gleichungen
Grundwissen m Ende der Jhrgngsstufe 9 Whlpflichtfächergruppe II / III Funktionsbegriff Gerdengleichungen ufstellen und zu gegebenen Gleichungen die Grphen der Gerden zeichnen Ssteme linerer Gleichungen
1 Kurvendiskussion /40
 009 Herbst, (Mthemtik) Aufgbenvorschlg B Kurvendiskussion /0 Gegeben ist eine Funktion f mit der Funktionsgleichung: f ( ) 0 6 = ; mit.. Untersuchen Sie ds Verhlten der Funktionswerte von f im Unendlichen.
009 Herbst, (Mthemtik) Aufgbenvorschlg B Kurvendiskussion /0 Gegeben ist eine Funktion f mit der Funktionsgleichung: f ( ) 0 6 = ; mit.. Untersuchen Sie ds Verhlten der Funktionswerte von f im Unendlichen.
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2012. Sprachen. Grammatiken (Einführung)
 Wörter, Grmmtiken und die Chomsky-Hierrchie Sprchen und Grmmtiken Wörter Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 2012 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Alphet Ein
Wörter, Grmmtiken und die Chomsky-Hierrchie Sprchen und Grmmtiken Wörter Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 2012 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Alphet Ein
Domäne und Bereich. Relationen zwischen Mengen/auf einer Menge. Anmerkungen zur Terminologie. r Relationen auf/in einer Menge.
 Reltionen zwischen Mengen/uf einer Menge! Eine Reltion R A B (mit A B) ist eine Reltion zwischen der Menge A und der Menge B, oder uch: von A nch B. Drstellung: c A! Wenn A = B, d.h. R A A, heißt R eine
Reltionen zwischen Mengen/uf einer Menge! Eine Reltion R A B (mit A B) ist eine Reltion zwischen der Menge A und der Menge B, oder uch: von A nch B. Drstellung: c A! Wenn A = B, d.h. R A A, heißt R eine
Lehrgang: Digitaltechnik 1 ( Grundlagen ) - Im Lehrgang verwendete Gatter ( Übersicht ) Seite 3
 Lehrgng: Digitltechnik ( Grundlgen ) Dtum: Nme: Seite: Inhltsverzeichnis: Im Lehrgng verwendete Gtter ( Üersicht ) Seite 3 Aufu von Zhlensystemen deziml, dul ( Infoseite ) Seite 4 ( Areitsltt ) Seite 5
Lehrgng: Digitltechnik ( Grundlgen ) Dtum: Nme: Seite: Inhltsverzeichnis: Im Lehrgng verwendete Gtter ( Üersicht ) Seite 3 Aufu von Zhlensystemen deziml, dul ( Infoseite ) Seite 4 ( Areitsltt ) Seite 5
Abitur - Leistungskurs Mathematik. Sachsen-Anhalt 1999
 Abitur - Leistungskurs Mthemtik Schsen-Anhlt 999 Gebiet L - Anlysis Augbe.. y, D, R,. Die Funktionenschr sei gegeben durch Die Grphen der Funktionen der Schr werden mit G bezeichnet. ) Ermitteln Sieden
Abitur - Leistungskurs Mthemtik Schsen-Anhlt 999 Gebiet L - Anlysis Augbe.. y, D, R,. Die Funktionenschr sei gegeben durch Die Grphen der Funktionen der Schr werden mit G bezeichnet. ) Ermitteln Sieden
Funktionen und Mächtigkeiten
 Vorlesung Funktionen und Mähtigkeiten. Etws Mengenlehre In der Folge reiten wir intuitiv mit Mengen. Eine Menge ist eine Zusmmenfssung von Elementen. Zum Beispiel ist A = {,,,,5} eine endlihe Menge mit
Vorlesung Funktionen und Mähtigkeiten. Etws Mengenlehre In der Folge reiten wir intuitiv mit Mengen. Eine Menge ist eine Zusmmenfssung von Elementen. Zum Beispiel ist A = {,,,,5} eine endlihe Menge mit
Übungsblatt Gleichungssysteme Klasse 8
 Üungsltt Gleichungsssteme Klsse 8 Auge : Berechne die Lösungen des Gleichungspres: I II 7 Kontrolliere durch Einseten. Auge : Löse dem Additionsverhren: I 7-6 II 9 Auge : Gegeen ist olgendes linere Gleichungssstem
Üungsltt Gleichungsssteme Klsse 8 Auge : Berechne die Lösungen des Gleichungspres: I II 7 Kontrolliere durch Einseten. Auge : Löse dem Additionsverhren: I 7-6 II 9 Auge : Gegeen ist olgendes linere Gleichungssstem
Inhaltsverzeichnis. Inhaltsverzeichnis... 1 3.Logik... 2. 3.1 Zahlensysteme... 2. 3.2 Grundbegriffe zweiwertiger Logik... 13
 Inhltsverzeichnis Inhltsverzeichnis... 3.Logik... 2 3. Zhlensysteme... 2 3.2 Grundegriffe zweiwertiger Logik... 3 3.3 Rechengesetze für logische Ausdrücke... 9 3.4 Logische Funktionen... 24 3.5 Logische
Inhltsverzeichnis Inhltsverzeichnis... 3.Logik... 2 3. Zhlensysteme... 2 3.2 Grundegriffe zweiwertiger Logik... 3 3.3 Rechengesetze für logische Ausdrücke... 9 3.4 Logische Funktionen... 24 3.5 Logische
edatenq ist eine Anwendung, die den Unternehmen die Möglichkeit bietet, ihre statistischen Meldungen über das Internet auszufüllen und einzureichen.
 Mnuell edatenq Fremdenverkehrs- und Gstgeweresttistik Einleitung edatenq ist eine Anwendung, die den Unternehmen die Möglichkeit ietet, ihre sttistischen Meldungen üer ds Internet uszufüllen und einzureichen.
Mnuell edatenq Fremdenverkehrs- und Gstgeweresttistik Einleitung edatenq ist eine Anwendung, die den Unternehmen die Möglichkeit ietet, ihre sttistischen Meldungen üer ds Internet uszufüllen und einzureichen.
Großübung zu Kräften, Momenten, Äquivalenz und Gleichgewicht
 Großübung u Kräften, omenten, Äuivlen und Gleichgewicht Der Körper Ein mterielles Teilgebiet des Universums beeichnet mn ls Körper. Im llgemeinen sind Körper deformierbr. Sonderfll strrer Körper (odellvorstellung)
Großübung u Kräften, omenten, Äuivlen und Gleichgewicht Der Körper Ein mterielles Teilgebiet des Universums beeichnet mn ls Körper. Im llgemeinen sind Körper deformierbr. Sonderfll strrer Körper (odellvorstellung)
Schriftliche Prüfungsarbeit zum mittleren Schulabschluss 2007 im Fach Mathematik
 Sentsverwltung für Bildung, Wissenschft und Forschung Schriftliche Prüfungsrbeit zum mittleren Schulbschluss 007 im Fch Mthemtik 30. Mi 007 Arbeitsbeginn: 10.00 Uhr Berbeitungszeit: 10 Minuten Zugelssene
Sentsverwltung für Bildung, Wissenschft und Forschung Schriftliche Prüfungsrbeit zum mittleren Schulbschluss 007 im Fch Mthemtik 30. Mi 007 Arbeitsbeginn: 10.00 Uhr Berbeitungszeit: 10 Minuten Zugelssene
7. VEKTORRECHNUNG, ANALYTISCHE GEOMETRIE
 Vektoechnung Anltische Geometie 7. VEKTORRECHNUNG ANALYTISCHE GEOMETRIE 7.1. Vektoen () Definition Schiet mn einen Punkt P 1 im Koodintensstem in eine ndee Lge P so ist diese Schieung duch Ange des Upunktes
Vektoechnung Anltische Geometie 7. VEKTORRECHNUNG ANALYTISCHE GEOMETRIE 7.1. Vektoen () Definition Schiet mn einen Punkt P 1 im Koodintensstem in eine ndee Lge P so ist diese Schieung duch Ange des Upunktes
Erweitern. a b. bd + bc. bd = ad+bc. bei ganzzahligem Nenner: Hauptnenner (= kgv der Nenner), z.b. 4 6 + 3 4 = 8 12 + 9. a d = ac
 F FORMELSAMMLUNG Bruchrechnung Erweitern = Kürzen c c Addition Nenner gleichnmig mchen! + c d = d d + c d = d+c d, speziell + c = +c ei gnzzhligem Nenner: Huptnenner (= kgv der Nenner), zb 4 6 + 3 4 =
F FORMELSAMMLUNG Bruchrechnung Erweitern = Kürzen c c Addition Nenner gleichnmig mchen! + c d = d d + c d = d+c d, speziell + c = +c ei gnzzhligem Nenner: Huptnenner (= kgv der Nenner), zb 4 6 + 3 4 =
13 Rekonfigurierende binäre Suchbäume
 13 Rekonfigurierende inäre Suchäume U.-P. Schroeder, Uni Pderorn inäräume, die zufällig erzeugt wurden, weisen für die wesentlichen Opertionen Suchen, Einfügen und Löschen einen logrithmischen ufwnd uf.
13 Rekonfigurierende inäre Suchäume U.-P. Schroeder, Uni Pderorn inäräume, die zufällig erzeugt wurden, weisen für die wesentlichen Opertionen Suchen, Einfügen und Löschen einen logrithmischen ufwnd uf.
5.3 Dynamisches Sitzen und Stehen
 Dynmisches Sitzen und Stehen 5.3 Dynmisches Sitzen und Stehen Test Bewegen Sie sich eim Sitzen und Stehen kontinuierlich um den Mittelpunkt der senkrechten Oerkörperhltung (S. 39) mit neutrler Wirelsäulenschwingung
Dynmisches Sitzen und Stehen 5.3 Dynmisches Sitzen und Stehen Test Bewegen Sie sich eim Sitzen und Stehen kontinuierlich um den Mittelpunkt der senkrechten Oerkörperhltung (S. 39) mit neutrler Wirelsäulenschwingung
Beispiel-Abiturprüfung
 Mthemtik BeispielAbiturprüfung Prüfungsteile A und B Bewertungsschlüssel und Lösungshinweise (nicht für den Prüfling bestimmt) Die Bewertung der erbrchten Prüfungsleistungen ht sich für jede Aufgbe nch
Mthemtik BeispielAbiturprüfung Prüfungsteile A und B Bewertungsschlüssel und Lösungshinweise (nicht für den Prüfling bestimmt) Die Bewertung der erbrchten Prüfungsleistungen ht sich für jede Aufgbe nch
Grundwissen Mathematik 7I
 Winkel m Kreis Grundwissen themtik 7I Rndwinkelstz Der Winkel heißt ittelpunktswinkel über der Sehne []. Die Winkel n sind die Rndwinkel über der Sehne []. lle Rndwinkel über einer Sehne eines Kreises
Winkel m Kreis Grundwissen themtik 7I Rndwinkelstz Der Winkel heißt ittelpunktswinkel über der Sehne []. Die Winkel n sind die Rndwinkel über der Sehne []. lle Rndwinkel über einer Sehne eines Kreises
Übungsblatt 1 zum Propädeutikum
 Üungsltt zum Propädeutium. Gegeen seien die Mengen A = {,,,}, B = {,,} und C = {,,,}. Bilden Sie die Mengen A B, A C, (A B) C, (A C) B und geen Sie diese in ufzählender Form n.. Geen Sie lle Teilmengen
Üungsltt zum Propädeutium. Gegeen seien die Mengen A = {,,,}, B = {,,} und C = {,,,}. Bilden Sie die Mengen A B, A C, (A B) C, (A C) B und geen Sie diese in ufzählender Form n.. Geen Sie lle Teilmengen
Dental-CT bei Kindern Technische Vorgehensweise und exemplarische Befunde
 Corneli Schröder, Alexnder Schumm Dentl-CT ei Kindern Technische Vorgehensweise und exemplrische Befunde Die Computertomogrphie der Zhnreihen (Dentl-CT) wird ei Kindern und Jugendlichen selten eingesetzt,
Corneli Schröder, Alexnder Schumm Dentl-CT ei Kindern Technische Vorgehensweise und exemplrische Befunde Die Computertomogrphie der Zhnreihen (Dentl-CT) wird ei Kindern und Jugendlichen selten eingesetzt,
1.2 Der goldene Schnitt
 Goldener Schnitt Psclsches Dreieck 8. Der goldene Schnitt Beim Begriff Goldener Schnitt denken viele Menschen n Kunst oder künstlerische Gestltung. Ds künstlerische Problem ist, wie ein Bild wohlproportioniert
Goldener Schnitt Psclsches Dreieck 8. Der goldene Schnitt Beim Begriff Goldener Schnitt denken viele Menschen n Kunst oder künstlerische Gestltung. Ds künstlerische Problem ist, wie ein Bild wohlproportioniert
Lösungsskizze zu Übungsblatt Nr. 13
 Technische Universität Dortmund Lehrstuhl Informtik VI Prof Dr Jens Teuner Pflichtmodul Informtionssysteme (SS 2014) Prof Dr Jens Teuner Leitung der Üungen: Mrcel Preuß, Sestin Breß, Mrtin Schwitll, Krolin
Technische Universität Dortmund Lehrstuhl Informtik VI Prof Dr Jens Teuner Pflichtmodul Informtionssysteme (SS 2014) Prof Dr Jens Teuner Leitung der Üungen: Mrcel Preuß, Sestin Breß, Mrtin Schwitll, Krolin
Public-Key-Verfahren: Diffie-Hellmann und ElGamal
 Westfälische Wilhelms-Universität Münster Ausreitung Pulic-Key-Verfhren: Diffie-Hellmnn und ElGml im Rhmen des Seminrs Multimedi und Grphen WS 2007/2008 Veselin Conev Themensteller: Prof. Dr. Herert Kuchen
Westfälische Wilhelms-Universität Münster Ausreitung Pulic-Key-Verfhren: Diffie-Hellmnn und ElGml im Rhmen des Seminrs Multimedi und Grphen WS 2007/2008 Veselin Conev Themensteller: Prof. Dr. Herert Kuchen
Das Coulombsche Gesetz
 . ei r = 0 befindet sich eine Ldung Q = 4,0nC und bei r = 40cm eine Ldung Q = 5,0nC ortsfest, so dss sie sich nicht bewegen können. Ds Coulombsche Gesetz Q = 4,0nC Q = 5,0nC r Lösung: Wo muss eine Ldung
. ei r = 0 befindet sich eine Ldung Q = 4,0nC und bei r = 40cm eine Ldung Q = 5,0nC ortsfest, so dss sie sich nicht bewegen können. Ds Coulombsche Gesetz Q = 4,0nC Q = 5,0nC r Lösung: Wo muss eine Ldung
Lösungsskizze zu Übungsblatt Nr. 13
 Technische Universität Dortmund Lehrstuhl Informtik VI Prof Dr Jens Teuner Pflichtmodul Informtionssysteme (SS 2013) Prof Dr Jens Teuner Leitung der Üungen: Geoffry Bonnin, Sven Kuisch, Moritz Mrtens,
Technische Universität Dortmund Lehrstuhl Informtik VI Prof Dr Jens Teuner Pflichtmodul Informtionssysteme (SS 2013) Prof Dr Jens Teuner Leitung der Üungen: Geoffry Bonnin, Sven Kuisch, Moritz Mrtens,
Matrizen und Determinanten
 Mtrizen und Determinnten Im bschnitt Vektorlgebr Rechenregeln für Vektoren Multipliktion - Sklrprodukt, Vektorprodukt, Mehrfchprodukte wurde in einem Vorgriff bereits eine interessnte mthemtische Konstruktion
Mtrizen und Determinnten Im bschnitt Vektorlgebr Rechenregeln für Vektoren Multipliktion - Sklrprodukt, Vektorprodukt, Mehrfchprodukte wurde in einem Vorgriff bereits eine interessnte mthemtische Konstruktion
Mathematik. Name, Vorname:
 Kntonsschule Zürich Birch Fchmittelschule Aufnhmeprüfung 2007 Nme, Vornme: Nr.: Zeit: 90 Minuten erlubte Hilfsmittel: Tschenrechner us der Sekundrschule, lso weder progrmmierbr noch grfik- oder lgebrfähig
Kntonsschule Zürich Birch Fchmittelschule Aufnhmeprüfung 2007 Nme, Vornme: Nr.: Zeit: 90 Minuten erlubte Hilfsmittel: Tschenrechner us der Sekundrschule, lso weder progrmmierbr noch grfik- oder lgebrfähig
Schülerkurs. Mathematik > Lineare Algebra > Lineare Gleichungen Lineare Gleichungssysteme > Teil I: Theorie. Michael Buhlmann
 Michel Buhlmnn Schülekus Mthemtik > Linee Alge > Linee Gleichungen Linee Gleichungssysteme > Teil I: Theoie Linee Gleichungen und linee Gleichungssysteme duchziehen den Mthemtikunteicht in llen Schulfomen
Michel Buhlmnn Schülekus Mthemtik > Linee Alge > Linee Gleichungen Linee Gleichungssysteme > Teil I: Theoie Linee Gleichungen und linee Gleichungssysteme duchziehen den Mthemtikunteicht in llen Schulfomen
bei Problemen die Theorie und die Beispiele am Anfang jeder Lerneinheit durcharbeiten
 Ds knnst du schon º Terme umformen º Gleichungen ufstellen und lösen º Funktionsgrphen zeichnen º Whrscheinlichkeiten erechnen Erfolge mithilfe des Aschlusstests üerprüfen ei Prolemen die Theorie und die
Ds knnst du schon º Terme umformen º Gleichungen ufstellen und lösen º Funktionsgrphen zeichnen º Whrscheinlichkeiten erechnen Erfolge mithilfe des Aschlusstests üerprüfen ei Prolemen die Theorie und die
1 Räumliche Darstellung in Adobe Illustrator
 Räumliche Drstellung in Adobe Illustrtor 1 1 Räumliche Drstellung in Adobe Illustrtor Dieses Tutoril gibt Tips und Hinweise zur räumlichen Drstellung von einfchen Objekten, insbesondere Bewegungspfeilen.
Räumliche Drstellung in Adobe Illustrtor 1 1 Räumliche Drstellung in Adobe Illustrtor Dieses Tutoril gibt Tips und Hinweise zur räumlichen Drstellung von einfchen Objekten, insbesondere Bewegungspfeilen.
Logarithmus - Übungsaufgaben. I. Allgemeines
 Eie Gleichug höhere Grdes wie z. B. Gymsium / Relschule Logrithmus - Üugsufge Klsse 0 I. Allgemeies k ch ufgelöst werde, idem m die Wurzel zieht. Tritt die Uekte jedoch im Epoete eier Potez uf, spricht
Eie Gleichug höhere Grdes wie z. B. Gymsium / Relschule Logrithmus - Üugsufge Klsse 0 I. Allgemeies k ch ufgelöst werde, idem m die Wurzel zieht. Tritt die Uekte jedoch im Epoete eier Potez uf, spricht
Canon Nikon Sony. Deutschland 55 45 25. Österreich 40 35 35. Schweiz 30 30 20. Resteuropa 60 40 30 55 45 25 40 35 35 J 30 30 20 60 40 30
 15 Mtrizenrechnung 15 Mtrizenrechnung 15.1 Mtrix ls Zhlenschem Eine Internetfirm verkuft über einen eigenen Shop Digitlkmers. Es wird jeweils nur ds Topmodel der Firmen Cnon, Nikon und Sony ngeboten. Verkuft
15 Mtrizenrechnung 15 Mtrizenrechnung 15.1 Mtrix ls Zhlenschem Eine Internetfirm verkuft über einen eigenen Shop Digitlkmers. Es wird jeweils nur ds Topmodel der Firmen Cnon, Nikon und Sony ngeboten. Verkuft
3 Module in C. 4 Gültigkeit von Namen. 5 Globale Variablen (2) Gültig im gesamten Programm
 3 Module in C 5 Glole Vrilen!!!.c Quelldteien uf keinen Fll mit Hilfe der #include Anweisung in ndere Quelldteien einkopieren Bevor eine Funktion us einem nderen Modul ufgerufen werden knn, muss sie deklriert
3 Module in C 5 Glole Vrilen!!!.c Quelldteien uf keinen Fll mit Hilfe der #include Anweisung in ndere Quelldteien einkopieren Bevor eine Funktion us einem nderen Modul ufgerufen werden knn, muss sie deklriert
Kapitel 6 E-Mails senden und empfangen
 Kpitel 6 E-Mils senden und empfngen Sie ist zwr mittlerweile infolge des hohen Spmufkommens ein wenig in Verruf gerten, gehört er immer noch zum Stndrdkommuniktionsmittel des Weürgers: die E-Mil. Zentrle
Kpitel 6 E-Mils senden und empfngen Sie ist zwr mittlerweile infolge des hohen Spmufkommens ein wenig in Verruf gerten, gehört er immer noch zum Stndrdkommuniktionsmittel des Weürgers: die E-Mil. Zentrle
Mathematik Thema Vielecke
 Them Vielecke Im Jnur 2006 Florin Vetter, Klsse 8, Riegelhof Relschule Seite 1 von 15 INHALTSVERZEICHNES 1. EINLEITUNG 3 2. ARTEN VON VIELECKEN 4 2.1. DREIECK 4 2.2. VIERECK 4 2.2.1. RECHTECK 4 2.2.2.
Them Vielecke Im Jnur 2006 Florin Vetter, Klsse 8, Riegelhof Relschule Seite 1 von 15 INHALTSVERZEICHNES 1. EINLEITUNG 3 2. ARTEN VON VIELECKEN 4 2.1. DREIECK 4 2.2. VIERECK 4 2.2.1. RECHTECK 4 2.2.2.
Realschule 2012. Mathematik. www.matheverlag.com. Mathematik-Verlag
 Relschule 01 Mthemtik wwwmtheverlgcom Mthemtik-Verlg Vorwort: Sehr geehrte Schülerinnen und Schüler, mit diesem Prüfungsheft können Sie sich gezielt und systemtisch uf die Relschulbschlussprüfung in Mthemtik
Relschule 01 Mthemtik wwwmtheverlgcom Mthemtik-Verlg Vorwort: Sehr geehrte Schülerinnen und Schüler, mit diesem Prüfungsheft können Sie sich gezielt und systemtisch uf die Relschulbschlussprüfung in Mthemtik
Musterlösungen (ohne Gewähr) Aufgabe 1 ( 7 Punkte) Geben Sie die Koordinaten des Flächenschwerpunktes des dargestellten Querschnitts an!
 Seite 1/15 Aufgbe 1 ( 7 Punkte) Geben Sie die Koordinten des lächenschwerpunktes des drgestellten Querschnitts n! 2 Gegeben:. 4 ΣA i = y 2 x Σx i A i = x s = Σy i A i = y s = ΣA i = 8 2 Σx i A i = 13 3
Seite 1/15 Aufgbe 1 ( 7 Punkte) Geben Sie die Koordinten des lächenschwerpunktes des drgestellten Querschnitts n! 2 Gegeben:. 4 ΣA i = y 2 x Σx i A i = x s = Σy i A i = y s = ΣA i = 8 2 Σx i A i = 13 3
Hinweise für den schulischen Umgang mit lese-/rechtschreibschwachen Kindern speziell in der Sekundarstufe I
 Hilfe, Legsthenie Hinweise für den schulischen Umgng mit lese-/rechtschreischwchen Kindern speziell in der Sekundrstufe I 2 Brigitt Amnn, Schulpsychologie Bludenz Annelies Fliri, Lehrerin für spezifische
Hilfe, Legsthenie Hinweise für den schulischen Umgng mit lese-/rechtschreischwchen Kindern speziell in der Sekundrstufe I 2 Brigitt Amnn, Schulpsychologie Bludenz Annelies Fliri, Lehrerin für spezifische
Einschub: Zahlendarstellung und Codes
 Einschu: Zhlendrstellung und Codes (Unvollständige Drstellung) DST SS23 - Codes und KMAPs P. Fischer, TI, Uni Mnnheim, Seite Binärzhlen N-stellige Binärzhl:... Einzelne Stellen heißen Bits (inry digits)
Einschu: Zhlendrstellung und Codes (Unvollständige Drstellung) DST SS23 - Codes und KMAPs P. Fischer, TI, Uni Mnnheim, Seite Binärzhlen N-stellige Binärzhl:... Einzelne Stellen heißen Bits (inry digits)
über der Strangbreite 2. Zugleich vermindert Einschlüssen, wodurch sich die Qualität des gegossenen Stahls verbessert.
 S T R N G G I E S S E N Elektromgnetisches remsen veressert die Sthlqulität eim Strnggießen Ds elektromgnetische remsen der Sthlströmung in der Kokille von Strnggießnlgen veressert die Qulität des gegossenen
S T R N G G I E S S E N Elektromgnetisches remsen veressert die Sthlqulität eim Strnggießen Ds elektromgnetische remsen der Sthlströmung in der Kokille von Strnggießnlgen veressert die Qulität des gegossenen
Teil V: Formale Sprachen
 Formle Sprchen Teil V: Formle Sprchen 1. Sprchen und Grmmtiken 2. Endliche Automten Frnz-Josef Rdermcher & Uwe Schöning, Fkultät für Ingeneurwissenschften und Informtik, Universität Ulm, 2008/09 Formle
Formle Sprchen Teil V: Formle Sprchen 1. Sprchen und Grmmtiken 2. Endliche Automten Frnz-Josef Rdermcher & Uwe Schöning, Fkultät für Ingeneurwissenschften und Informtik, Universität Ulm, 2008/09 Formle
AT = λ TB. Kapitel 5: Teilverhältnisse und Ähnlichkeit. Definition Teilverhältnis λ. Allgemeiner
 Definition Teilverhältnis Definition Teilverhältnis Üung Kpitel 5: Teilverhältnisse und Ähnlihkeit Definition Teilverhältnis λ λ T T llgemeiner T λ T T T T T ist innerer Teilpunkt, flls λ > 0 T ist äußerer
Definition Teilverhältnis Definition Teilverhältnis Üung Kpitel 5: Teilverhältnisse und Ähnlihkeit Definition Teilverhältnis λ λ T T llgemeiner T λ T T T T T ist innerer Teilpunkt, flls λ > 0 T ist äußerer
Einführung in die Schaltalgebra
 Einführung in die chltlger GUNDBEGIFFE: - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 2 ECHENEGELN - - - - - - - - - - - - - - - - - - - - - - - -
Einführung in die chltlger GUNDBEGIFFE: - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 2 ECHENEGELN - - - - - - - - - - - - - - - - - - - - - - - -
Prüfungsteil Schriftliche Kommunikation (SK)
 SK Üerlik und Anforderungen Üerlik und Anforderungen Prüfungsteil Shriftlihe Kommuniktion (SK) Üerlik und Anforderungen Worum geht es? In diesem Prüfungsteil sollst du einen Beitrg zu einem estimmten Them
SK Üerlik und Anforderungen Üerlik und Anforderungen Prüfungsteil Shriftlihe Kommuniktion (SK) Üerlik und Anforderungen Worum geht es? In diesem Prüfungsteil sollst du einen Beitrg zu einem estimmten Them
Bestimmung der Adsorptionsisotherme von Essigsäure an Aktivkohle
 S2-Adsorptionsisothermen_UWW rstelldtum 28.3.214 7:41: Üungen in physiklischer Chemie für Studierende der Umweltwissenschften Versuch Nr.: S2 Version 214 Kurzezeichnung: Adsorptionsisotherme estimmung
S2-Adsorptionsisothermen_UWW rstelldtum 28.3.214 7:41: Üungen in physiklischer Chemie für Studierende der Umweltwissenschften Versuch Nr.: S2 Version 214 Kurzezeichnung: Adsorptionsisotherme estimmung
17 Doppelbündel-Rekonstruktion mit Semitendinosussehne
 Kpitel 17 143 17 Doppelündel-Rekonstruktion mit Semitendinosussehne Wolf Petersen 17.1 Einleitung Ds vordere Kreuznd (VKB) esteht us 2 funktionellen Bündeln: einem nteromedilen (AM) und einem posterolterlen
Kpitel 17 143 17 Doppelündel-Rekonstruktion mit Semitendinosussehne Wolf Petersen 17.1 Einleitung Ds vordere Kreuznd (VKB) esteht us 2 funktionellen Bündeln: einem nteromedilen (AM) und einem posterolterlen
Ntoneni-be Berechnung der.kennwerte J4helwerY und,,streuung von Funktionen
 FOLGE 18 LENZINGER BERICHTE A UG UST 196J Ntoneni-e Berechnung der.kennwerte J4helwerY und,,streuung von Funktionen Dipl.-Ing. Wilhelm Herzog, Wien Die vorliegende Areit eschäftigt sich mit dem Fll, dß
FOLGE 18 LENZINGER BERICHTE A UG UST 196J Ntoneni-e Berechnung der.kennwerte J4helwerY und,,streuung von Funktionen Dipl.-Ing. Wilhelm Herzog, Wien Die vorliegende Areit eschäftigt sich mit dem Fll, dß
Seminar zum anorganisch-chemischen Praktikum. Quantitative Analyse. Patrick Schwarz
 Seminr zum norgnisch-chemischen Prktikum Quntittive Anlyse Ptrick Schwrz itertur M. Scheer, J. Wchter Skript zum Prktikum Anorgnische Chemie I, Institut für Anorgnische Chemie der Universität Regensurg
Seminr zum norgnisch-chemischen Prktikum Quntittive Anlyse Ptrick Schwrz itertur M. Scheer, J. Wchter Skript zum Prktikum Anorgnische Chemie I, Institut für Anorgnische Chemie der Universität Regensurg
7. Portfolioinvestitionen und Wechselkursschwankungen. Literatur. Prof. Dr. Johann Graf Lambsdorff Universität Passau SS 2008
 Prof. Dr. Johnn Grf Lmsdorff Universität Pssu SS 2008 Litertur r IS 0 r 0 P 0 P x MP 7. Portfolioinvestitionen und Wechselkursschnkungen + Z Jrcho, H.-J. und P. Rühmnn (2000) : Monetäre Außenirtschft I.
Prof. Dr. Johnn Grf Lmsdorff Universität Pssu SS 2008 Litertur r IS 0 r 0 P 0 P x MP 7. Portfolioinvestitionen und Wechselkursschnkungen + Z Jrcho, H.-J. und P. Rühmnn (2000) : Monetäre Außenirtschft I.
Grundwissen Abitur Analysis
 GYMNASIUM MIT SCHÜLERHEIM PEGNITZ mthem-technolog u sprchl Gmnsium WILHELM-VON-HUMBOLDT-STRASSE 7 9257 PEGNITZ FERNRUF 0924/48333 FAX 0924/2564 Grundwissen Abitur Anlsis Ws sind Potenzfunktion mit ntürlichen
GYMNASIUM MIT SCHÜLERHEIM PEGNITZ mthem-technolog u sprchl Gmnsium WILHELM-VON-HUMBOLDT-STRASSE 7 9257 PEGNITZ FERNRUF 0924/48333 FAX 0924/2564 Grundwissen Abitur Anlsis Ws sind Potenzfunktion mit ntürlichen
Brückenkurs Mathematik
 Prof. Dr.Ing. W. Scheideler Brückenkurs Mthemtik WS 0/ us und überrbeitet von B. Eng. Sevd Hppel und Dipl.Ing. Jun Rojs Prof. Dr.Ing. W. Scheideler Inhltsverzeichnis Brüche, Potenzen und Wurzeln. Brüche..
Prof. Dr.Ing. W. Scheideler Brückenkurs Mthemtik WS 0/ us und überrbeitet von B. Eng. Sevd Hppel und Dipl.Ing. Jun Rojs Prof. Dr.Ing. W. Scheideler Inhltsverzeichnis Brüche, Potenzen und Wurzeln. Brüche..
Vorlesung. Einführung in die mathematische Sprache und naive Mengenlehre
 Vorlesung Einführung in die mthemtische Sprche und nive Mengenlehre 1 Allgemeines RUD26 Erwin-Schrödinger-Zentrum (ESZ) RUD25 Johnn-von-Neumnn-Hus Fchschft Menge ller Studenten eines Institutes Fchschftsrt
Vorlesung Einführung in die mthemtische Sprche und nive Mengenlehre 1 Allgemeines RUD26 Erwin-Schrödinger-Zentrum (ESZ) RUD25 Johnn-von-Neumnn-Hus Fchschft Menge ller Studenten eines Institutes Fchschftsrt
Musterlösung zu Aufgabe 1 (Klassenstufe 9/10)
 Musterlösung zu Aufgbe 1 (Klssenstufe 9/10) Aufgbe. Drei Freunde spielen mehrere Runden eines Spiels, bei dem sie je nch Rundenpltzierung in jeder Runde einen festen, gnzzhligen Betrg x, y oder z usgezhlt
Musterlösung zu Aufgbe 1 (Klssenstufe 9/10) Aufgbe. Drei Freunde spielen mehrere Runden eines Spiels, bei dem sie je nch Rundenpltzierung in jeder Runde einen festen, gnzzhligen Betrg x, y oder z usgezhlt
Grundlagen der Physiotherapie
 Grundlgen der Physiotherpie Vom Griff zur Behndlung von Lynn Allen Coly Crolyn Kisner erweitert, üerreitet Thieme 2009 Verlg C.H. Beck im Internet: www.eck.de ISBN 978 3 13 108743 0 schnell und portofrei
Grundlgen der Physiotherpie Vom Griff zur Behndlung von Lynn Allen Coly Crolyn Kisner erweitert, üerreitet Thieme 2009 Verlg C.H. Beck im Internet: www.eck.de ISBN 978 3 13 108743 0 schnell und portofrei
Technische Informatik 2
 TiEl-F Sommersemester 24 Technische Informtik 2 (Vorlesungsnummer 2625) 23--- TiEl-F Prof. Dr.-Ing. Jürgen Doneit Zimmer E29 Tel.:73 54 455 doneit@fh-heilronn.de 23--- TiEl-F35 Digitltechnik 23--3- . Digitlschltungen,
TiEl-F Sommersemester 24 Technische Informtik 2 (Vorlesungsnummer 2625) 23--- TiEl-F Prof. Dr.-Ing. Jürgen Doneit Zimmer E29 Tel.:73 54 455 doneit@fh-heilronn.de 23--- TiEl-F35 Digitltechnik 23--3- . Digitlschltungen,
Logische Grundschaltungen
 Elektrotechnisches Grundlgen-Lor II Logische Grundschltungen Versuch Nr. 9 Erforderliche Geräte Anzhl Bezeichnung, Dten GL-Nr. 1 Voltmeter 335 1 Steckrett SB 1 1 Steckrett SB 2 mit 5V Netzteil 1 Steckrett
Elektrotechnisches Grundlgen-Lor II Logische Grundschltungen Versuch Nr. 9 Erforderliche Geräte Anzhl Bezeichnung, Dten GL-Nr. 1 Voltmeter 335 1 Steckrett SB 1 1 Steckrett SB 2 mit 5V Netzteil 1 Steckrett
7.1 Übersicht und Schleimhautrelief
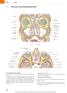 7.1 Üersicht und Schleimhutrelief Crist glli Orit Corpus vitreum Skler Mxill Crtilgo septi nslis Vomer Proc. pltinus mxille Cellule ethmoidles Bull ethmoidlis Lmin perpendiculris ossis ethmoidlis N. infroritlis
7.1 Üersicht und Schleimhutrelief Crist glli Orit Corpus vitreum Skler Mxill Crtilgo septi nslis Vomer Proc. pltinus mxille Cellule ethmoidles Bull ethmoidlis Lmin perpendiculris ossis ethmoidlis N. infroritlis
Personal und Finanzen der öffentlich bestimmten Fonds, Einrichtungen, Betriebe und Unternehmen (FEU) in privater Rechtsform im Jahr 2003
 Personl und Finnzen der öffentlich estimmten Fonds, Einrichtungen, Betriee und Unternehmen (FEU) in privter Rechtsform im Jhr 003 Dipl.-Volkswirt Peter Emmerich A Mitte der 980er-Jhre ist eine Zunhme von
Personl und Finnzen der öffentlich estimmten Fonds, Einrichtungen, Betriee und Unternehmen (FEU) in privter Rechtsform im Jhr 003 Dipl.-Volkswirt Peter Emmerich A Mitte der 980er-Jhre ist eine Zunhme von
Elemente der Analysis II: Zusammenfassung der wichtigsten Definitionen und Ergebnisse
 Elemente der Anlysis II: Zusmmenfssung der wichtigsten Definitionen und Ergebnisse J. Wengenroth Dies ist die einzige zugelssene Formelsmmlung, die bei der Klusur benutzt werden drf. Es dürfen Unterstreichungen
Elemente der Anlysis II: Zusmmenfssung der wichtigsten Definitionen und Ergebnisse J. Wengenroth Dies ist die einzige zugelssene Formelsmmlung, die bei der Klusur benutzt werden drf. Es dürfen Unterstreichungen
Präfixcodes und der Huffman Algorithmus
 Präfixcodes und der Huffmn Algorithmus Präfixcodes und Codebäume Im Folgenden werden wir Codes untersuchen, die in der Regel keine Blockcodes sind. In diesem Fll können Codewörter verschiedene Länge hben
Präfixcodes und der Huffmn Algorithmus Präfixcodes und Codebäume Im Folgenden werden wir Codes untersuchen, die in der Regel keine Blockcodes sind. In diesem Fll können Codewörter verschiedene Länge hben
Z R Z R Z R Z = 50. mit. aus a) Z L R. Wie groß ist der Leistungsfaktor cos der gesamten Schaltung?
 Aufge F 99: Drehstromverruher Ein symmetrisher Verruher ist n ds Drehstromnetz ( 0 V, f 50 Hz) ngeshlossen. Die us dem Netz entnommene Wirkleistung eträgt,5 kw ei einem eistungsfktor os 0,7. ) Berehnen
Aufge F 99: Drehstromverruher Ein symmetrisher Verruher ist n ds Drehstromnetz ( 0 V, f 50 Hz) ngeshlossen. Die us dem Netz entnommene Wirkleistung eträgt,5 kw ei einem eistungsfktor os 0,7. ) Berehnen
Übungsheft Mittlerer Schulabschluss Mathematik
 Ministerium für Bildung und Kultur des Lndes Schleswig-Holstein Zentrle Abschlussrbeit 011 Übungsheft Mittlerer Schulbschluss Mthemtik Korrekturnweisung Impressum Herusgeber Ministerium für Bildung und
Ministerium für Bildung und Kultur des Lndes Schleswig-Holstein Zentrle Abschlussrbeit 011 Übungsheft Mittlerer Schulbschluss Mthemtik Korrekturnweisung Impressum Herusgeber Ministerium für Bildung und
Mathematik PM Rechenarten
 Rechenrten.1 Addition Ds Pluszeichen besgt, dss mn zur Zhl die Zhl b hinzuzählt oder ddiert. Aus diesem Grunde heisst diese Rechenrt uch Addition. + b = c Summnd plus Summnd gleich Summe Kommuttivgesetz
Rechenrten.1 Addition Ds Pluszeichen besgt, dss mn zur Zhl die Zhl b hinzuzählt oder ddiert. Aus diesem Grunde heisst diese Rechenrt uch Addition. + b = c Summnd plus Summnd gleich Summe Kommuttivgesetz
Die quadratische Gleichung und die quadratische Funktion
 Die quadratische Gleichung und die quadratische Funktion 1. Lösen einer quadratischen Gleichung Quadratische Gleichungen heißen alle Gleichungen der Form a x x c = 0, woei a,, c als Parameter elieige reelle
Die quadratische Gleichung und die quadratische Funktion 1. Lösen einer quadratischen Gleichung Quadratische Gleichungen heißen alle Gleichungen der Form a x x c = 0, woei a,, c als Parameter elieige reelle
FernUniversität Gesamthochschule in Hagen
 FernUniversität Gesmthochschule in Hgen FACHBEREICH MATHEMATIK LEHRGEBIET KOMPLEXE ANALYSIS Prof. Dr. Andrei Dum Proseminr 9 - Anlysis Numerische Integrtion Ulrich Telle Mtrikel-Nr. 474 Köln, den 7. Dezember
FernUniversität Gesmthochschule in Hgen FACHBEREICH MATHEMATIK LEHRGEBIET KOMPLEXE ANALYSIS Prof. Dr. Andrei Dum Proseminr 9 - Anlysis Numerische Integrtion Ulrich Telle Mtrikel-Nr. 474 Köln, den 7. Dezember
Karlsruher Institut für Technologie
 Krlsruher Institut für Technologie Lehrstuhl für Progrmmierprdigmen Sprchtechnologie und Compiler WS 2010/2011 Dozent: Prof. Dr.-Ing. G. Snelting Üungsleiter: Mtthis Brun Lösung zu Üungsltt 1 Ausge: 18.04.2012
Krlsruher Institut für Technologie Lehrstuhl für Progrmmierprdigmen Sprchtechnologie und Compiler WS 2010/2011 Dozent: Prof. Dr.-Ing. G. Snelting Üungsleiter: Mtthis Brun Lösung zu Üungsltt 1 Ausge: 18.04.2012
Der chinesische Gelehrte Konfuzius wird oft als
 Roert-Wichrd-Pohl-Preis Experimente zum Selstuen Einfche Experimente mit lltäglichen Mterilien und ttrktive Demonstrtionsexperimente ermöglichen es Schülern, die Physik esser zu verstehen Hns-Jochim Wilke
Roert-Wichrd-Pohl-Preis Experimente zum Selstuen Einfche Experimente mit lltäglichen Mterilien und ttrktive Demonstrtionsexperimente ermöglichen es Schülern, die Physik esser zu verstehen Hns-Jochim Wilke
1 GeschäftsdiaGramme. Abbildung 1.1: Übersicht zu unterschiedlichen Grafi ktypen. 2.1.4 Unify objects: graphs e.g. org graphs, networks, and maps
 1 GeshäftsdiGrmme Wenn mn eine deutshe Üersetzung des Begriffes usiness hrts suht, so ist mn mit dem Wort Geshäftsdigrmme gnz gut edient. Wir verstehen unter einem Geshäftsdigrmm die Visulisierung von
1 GeshäftsdiGrmme Wenn mn eine deutshe Üersetzung des Begriffes usiness hrts suht, so ist mn mit dem Wort Geshäftsdigrmme gnz gut edient. Wir verstehen unter einem Geshäftsdigrmm die Visulisierung von
Kennlinienaufnahme des Transistors BC170
 Kennlnenufnhme des Trnsstors 170 Enletung polre Trnsstoren werden us zwe eng benchbrten pn-übergängen gebldet. Vorrusetzung für ds Funktonsprnzp st de gegensetge eenflussung beder pn-übergänge, de nur
Kennlnenufnhme des Trnsstors 170 Enletung polre Trnsstoren werden us zwe eng benchbrten pn-übergängen gebldet. Vorrusetzung für ds Funktonsprnzp st de gegensetge eenflussung beder pn-übergänge, de nur
solche mit Textzeichen (z.b. A, a, B, b,!) solche mit binären Zeichen (0, 1)
 teilung Informtik, Fh Progrmmieren 1 Einführung Dten liegen oft ls niht einfh serier- und identifizierre Dtensätze vor. Stttdessen reräsentieren sie lnge Zeihenketten, z.b. Text-, Bild-, Tondten. Mn untersheidet
teilung Informtik, Fh Progrmmieren 1 Einführung Dten liegen oft ls niht einfh serier- und identifizierre Dtensätze vor. Stttdessen reräsentieren sie lnge Zeihenketten, z.b. Text-, Bild-, Tondten. Mn untersheidet
TE- und TM-Moden im Wellenleiter. Bachelorarbeit
 TE- und TM-Moden im Wellenleiter Sebstin Rubitzek 30. September 2014 in Grz Bchelorrbeit betreut von Ao.Univ.-Prof. Mg. Dr.rer.nt. Ulrich Hohenester 1 Inhltsverzeichnis 1 Einleitung 3 1.1 Ws ist ein Wellenleiter?......................
TE- und TM-Moden im Wellenleiter Sebstin Rubitzek 30. September 2014 in Grz Bchelorrbeit betreut von Ao.Univ.-Prof. Mg. Dr.rer.nt. Ulrich Hohenester 1 Inhltsverzeichnis 1 Einleitung 3 1.1 Ws ist ein Wellenleiter?......................
UNIVERSITÄT KARLSRUHE Institut für Analysis HDoz. Dr. P. C. Kunstmann Dipl.-Math. M. Uhl. Sommersemester 2009
 UNIVERSIÄ KARLSRUHE Institut für Anlysis HDoz. Dr. P. C. Kunstmnn Dipl.-Mth. M. Uhl Sommersemester 9 Höhere Mthemti II für die Fchrichtungen Eletroingenieurwesen, Physi und Geodäsie inlusive Komplexe Anlysis
UNIVERSIÄ KARLSRUHE Institut für Anlysis HDoz. Dr. P. C. Kunstmnn Dipl.-Mth. M. Uhl Sommersemester 9 Höhere Mthemti II für die Fchrichtungen Eletroingenieurwesen, Physi und Geodäsie inlusive Komplexe Anlysis
Technische Mechanik I
 Repetitorium Technische Mechnik I Version 3., 9.. Dr.-Ing. L. Pnning Institut für Dynmik und Schwingungen ottfried Wilhelm Leibniz Universität Hnnover Dieses Repetitorium soll helfen, klssische ufgbentypen
Repetitorium Technische Mechnik I Version 3., 9.. Dr.-Ing. L. Pnning Institut für Dynmik und Schwingungen ottfried Wilhelm Leibniz Universität Hnnover Dieses Repetitorium soll helfen, klssische ufgbentypen
Vorlesung 24: Topological Sort 1: Hintergrund. Einführung in die Programmierung. Bertrand Meyer. Topological sort
 Einführung in ie Progrmmierung Vorlesung 4: Topologil Sort : Hintergrun Bertrn Meer Letzte Üerreitung 3. Jnur 4 3 Topologil sort 4 Prouziere eine zu einer gegeenen Prtiellen Ornung komptile Vollstänige
Einführung in ie Progrmmierung Vorlesung 4: Topologil Sort : Hintergrun Bertrn Meer Letzte Üerreitung 3. Jnur 4 3 Topologil sort 4 Prouziere eine zu einer gegeenen Prtiellen Ornung komptile Vollstänige
Eufic Guide Enfant ALL 14/12/04 15:44 Page 1 10 Tipps für Kids Spiel mit uns! Zur gesundenernährung
 Kids Ernährung für Tipps 10 Spiel mit uns! gesunden Zur Weißt du noch, wie du Rd fhren lerntest? Ds Wichtigste dei wr zu lernen ds Gleichgewicht zu hlten. Sold es gefunden wr, konntest du die Pedle gleichmäßig
Kids Ernährung für Tipps 10 Spiel mit uns! gesunden Zur Weißt du noch, wie du Rd fhren lerntest? Ds Wichtigste dei wr zu lernen ds Gleichgewicht zu hlten. Sold es gefunden wr, konntest du die Pedle gleichmäßig
Fragebogen 1 zur Arbeitsmappe Durch Zusatzempfehlung zu mehr Kundenzufriedenheit
 Teilnehmer/Apotheke/Ort (Zus/1) Frgeogen 1 zur Areitsmppe Durh Zustzempfehlung zu mehr Kunenzufrieenheit Bitte kreuzen Sie jeweils ie rihtige(n) Antwort(en) in en Felern is n! 1. Worin esteht ie Beeutung
Teilnehmer/Apotheke/Ort (Zus/1) Frgeogen 1 zur Areitsmppe Durh Zustzempfehlung zu mehr Kunenzufrieenheit Bitte kreuzen Sie jeweils ie rihtige(n) Antwort(en) in en Felern is n! 1. Worin esteht ie Beeutung
VERORDNUNG ZUM ORGANISATIONSREGLEMENT DES SCHULVERBANDES NIDAU
 VERORDNUNG ZUM ORGANISATIONSREGLEMENT DES SCHULVERBANDES NIDAU vom. August 0 5.0.0 VERORDNUNG ZUM ORGANISATIONSREGLEMENT DES SCHULVERBANDES NIDAU Die Bildungskommission eschliesst, gestützt uf Artikel
VERORDNUNG ZUM ORGANISATIONSREGLEMENT DES SCHULVERBANDES NIDAU vom. August 0 5.0.0 VERORDNUNG ZUM ORGANISATIONSREGLEMENT DES SCHULVERBANDES NIDAU Die Bildungskommission eschliesst, gestützt uf Artikel
Versuchsplanung. Grundlagen. Extrapolieren unzulässig! Beobachtungsbereich!
 Versuchsplnung 22 CRGRAPH www.crgrph.de Grundlgen Die Aufgbe ist es Versuche so zu kombinieren, dss die Zusmmenhänge einer Funktion oder eines Prozesses bestmöglich durch eine spätere Auswertung wiedergegeben
Versuchsplnung 22 CRGRAPH www.crgrph.de Grundlgen Die Aufgbe ist es Versuche so zu kombinieren, dss die Zusmmenhänge einer Funktion oder eines Prozesses bestmöglich durch eine spätere Auswertung wiedergegeben
Therapiebegleiter Kopfschmerztagebuch
 Vornme & Nchnme Therpieegleiter Kopfschmerztgeuch Liee Ptientin, lieer Ptient, Wie Können sie helfen? Bitte führen Sie regelmäßig euch m esten täglich. Trgen Sie in die Splten die jeweiligen Informtionen
Vornme & Nchnme Therpieegleiter Kopfschmerztgeuch Liee Ptientin, lieer Ptient, Wie Können sie helfen? Bitte führen Sie regelmäßig euch m esten täglich. Trgen Sie in die Splten die jeweiligen Informtionen
ZDfB_Ü01_LV_06 120206. Felix Brandl München ZERTIFIKAT DEUTSCH FÜR DEN BERUF ÜBUNGSSATZ 01. Kandidatenblätter LESEVERSTEHEN ZEIT: 40 MINUTEN
 Felix Brndl Münhen ZDfB_Ü01_LV_06 120206 ZERTIFIKAT DEUTSCH FÜR DEN BERUF ÜBUNGSSATZ 01 Kndidtenlätter ZEIT: 40 MINUTEN Zertifikt Deutsh für den Beruf Üungsstz 01 Aufge 1 Bitte lesen Sie den folgenden
Felix Brndl Münhen ZDfB_Ü01_LV_06 120206 ZERTIFIKAT DEUTSCH FÜR DEN BERUF ÜBUNGSSATZ 01 Kndidtenlätter ZEIT: 40 MINUTEN Zertifikt Deutsh für den Beruf Üungsstz 01 Aufge 1 Bitte lesen Sie den folgenden
Abb. 2.10: Galvanische Zelle (DANIELL 20 -Element)
 . Der Gleichstromkreis 45.4. Elektrochemische Spnnungsquellen Git mn in ein Lösungsmittel Säuren, Lugen oder Slze, werden deren Moleküle in prweise positiv und negtiv geldene Ionen gesplten (dissoziiert)
. Der Gleichstromkreis 45.4. Elektrochemische Spnnungsquellen Git mn in ein Lösungsmittel Säuren, Lugen oder Slze, werden deren Moleküle in prweise positiv und negtiv geldene Ionen gesplten (dissoziiert)
1 212.223. Gesetz über die Bernische BVG- und Stiftungsaufsicht (BBSAG) vom 17.03.2014 (Stand 01.01.2015)
 . Gesetz üer die Bernische BVG- und Stiftungsufsicht (BBSAG) vom 7.0.04 (Stnd 0.0.05) Der Grosse Rt des Kntons Bern, gestützt uf Artikel 6 Astz des Bundesgesetzes vom 5. Juni 98 üer die erufliche Alters-,
. Gesetz üer die Bernische BVG- und Stiftungsufsicht (BBSAG) vom 7.0.04 (Stnd 0.0.05) Der Grosse Rt des Kntons Bern, gestützt uf Artikel 6 Astz des Bundesgesetzes vom 5. Juni 98 üer die erufliche Alters-,
Kapitel 8 Apps installieren und verwalten
 Kpitel 8 Apps instllieren und verwlten In diesem Kpitel sehen wir uns die Stndrdquelle ller Apps einml etws genuer n, den Google Ply Store (kurz: Google Ply oder Ply Store). Er ist der Dreh- und Angelpunkt,
Kpitel 8 Apps instllieren und verwlten In diesem Kpitel sehen wir uns die Stndrdquelle ller Apps einml etws genuer n, den Google Ply Store (kurz: Google Ply oder Ply Store). Er ist der Dreh- und Angelpunkt,
Motivation. Kap. 4.2 Binäre Suchbäume ff Kap. 4.3: AVL-Bäume. Überblick. Pseudocode von SEARCH. in binären Suchbäumen. in binären Suchbäumen
 Kp. 4.2 inäre Schäme ff Kp. 4.: VL-äme Professor r. Lehrsthl für lgorithm Engineering, LS11 Fkltät für Informtik, TU ortmnd Motition Wrm soll ich hete hier leien? lncierte äme rchen Sie immer wieder! Ws
Kp. 4.2 inäre Schäme ff Kp. 4.: VL-äme Professor r. Lehrsthl für lgorithm Engineering, LS11 Fkltät für Informtik, TU ortmnd Motition Wrm soll ich hete hier leien? lncierte äme rchen Sie immer wieder! Ws
Thema 13 Integrale, die von einem Parameter abhängen, Integrale von Funktionen auf Teilmengen von R n
 Them 13 Integrle, die von einem Prmeter bhängen, Integrle von Funktionen uf Teilmengen von R n Wir erinnern drn, dß eine Funktion h : [, b] R eine Treppenfunktion ist, flls es eine Unterteilung x < x 1
Them 13 Integrle, die von einem Prmeter bhängen, Integrle von Funktionen uf Teilmengen von R n Wir erinnern drn, dß eine Funktion h : [, b] R eine Treppenfunktion ist, flls es eine Unterteilung x < x 1
In Fachwerken gibt es demnach nur konstante Normalkräfte. Die Fachwerksknoten sind zentrale Kraftsysteme.
 Großüung cwerke cwerke d Ssteme von gerden Stäen, die geenkig (und reiungsfrei) in sog. Knoten(punkten) miteinnder verunden d und nur durc Einzekräfte in den Knotenpunkten estet werden. In cwerken git
Großüung cwerke cwerke d Ssteme von gerden Stäen, die geenkig (und reiungsfrei) in sog. Knoten(punkten) miteinnder verunden d und nur durc Einzekräfte in den Knotenpunkten estet werden. In cwerken git
Die Brückenlappentechnik zum sicheren Verschluss von Nasenseptumdefekten
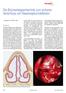 Die Brückenlppentechnik zum sicheren Verschluss von Nsenseptumdefekten T. Stnge, H.-J. Schultz-Coulon Einleitung Die Rekonstruktion eines defekten Nsenseptums zählt zu den schwierigsten rhinochirurgischen
Die Brückenlppentechnik zum sicheren Verschluss von Nsenseptumdefekten T. Stnge, H.-J. Schultz-Coulon Einleitung Die Rekonstruktion eines defekten Nsenseptums zählt zu den schwierigsten rhinochirurgischen
www. line21 Kommunikation Daten- und Telefontechnik über 1 Kabel mit 4 Adern. Kein Problem mit line21 natürlich von Rutenbeck!
 Dten- und Telefontechnik üer Kel mit 4 Adern. Kein Prolem mit line ntürlich von Ruteneck! Internet Kom mu ni knt, der; -en, -en [: kirchenlt. communicns (Gen.: communicntis) = Teilnehmer m Aendmhl, zu
Dten- und Telefontechnik üer Kel mit 4 Adern. Kein Prolem mit line ntürlich von Ruteneck! Internet Kom mu ni knt, der; -en, -en [: kirchenlt. communicns (Gen.: communicntis) = Teilnehmer m Aendmhl, zu
Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* aller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt:
 8. Grundlgen der Informtionstheorie 8.1 Informtionsgehlt, Entropie, Redundnz Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* ller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt: 1.
8. Grundlgen der Informtionstheorie 8.1 Informtionsgehlt, Entropie, Redundnz Def.: Sei Σ eine Menge von Zeichen. Die Menge Σ* ller Zeichenketten (Wörter) über Σ ist die kleinste Menge, für die gilt: 1.
STUDIUM. Mathematische Grundlagen für Betriebswirte
 STUDIUM Mthetische Grudlge für Betrieswirte Mit de folgede Aufge köe Sie i eie Selsttest üerprüfe, o Sie och eiigerße die Grudlge der Alger eherrsche. Diese hdwerkliche Fertigkeite sid wesetlich, we es
STUDIUM Mthetische Grudlge für Betrieswirte Mit de folgede Aufge köe Sie i eie Selsttest üerprüfe, o Sie och eiigerße die Grudlge der Alger eherrsche. Diese hdwerkliche Fertigkeite sid wesetlich, we es
Dein Trainingsplan. sportmannschaft. ... und was sonst noch wichtig ist. Deine Zähne sind wie deine. und du bist der Trainer!
 hben Freunde Deine Zähne sind wie deine sportmnnschft und du bist der Triner! Und jeder Triner weiß, wie wichtig jeder einzelne Spieler ist eine wichtige und schöne Aufgbe! Drum sei nett zu deinen Zähnen
hben Freunde Deine Zähne sind wie deine sportmnnschft und du bist der Triner! Und jeder Triner weiß, wie wichtig jeder einzelne Spieler ist eine wichtige und schöne Aufgbe! Drum sei nett zu deinen Zähnen
QualitŠtskriterien fÿr die betriebliche Gesundheitsfšrderung
 WH IN U O Gesunde Mitreiter in gesunden Unternehmen Erfolgreiche Prxis etrielicher Gesundheitsfšrderung in Europ QulitŠtskriterien fÿr die etrieliche Gesundheitsfšrderung Vorwort Seit 1996 existiert ds
WH IN U O Gesunde Mitreiter in gesunden Unternehmen Erfolgreiche Prxis etrielicher Gesundheitsfšrderung in Europ QulitŠtskriterien fÿr die etrieliche Gesundheitsfšrderung Vorwort Seit 1996 existiert ds
2008-06-11 Klassenarbeit 5 Klasse 10c Mathematik
 2008-06- Klssenrbeit 5 Klsse 0c Mtemtik Lösung Version 2008-06-4 Cindy t 3000 geerbt. ) Den Betrg will sie so nlegen, dss sie in 20 Jren doppelt so viel Geld t. Berecne, zu welcem Zinsstz sie ds Geld nlegen
2008-06- Klssenrbeit 5 Klsse 0c Mtemtik Lösung Version 2008-06-4 Cindy t 3000 geerbt. ) Den Betrg will sie so nlegen, dss sie in 20 Jren doppelt so viel Geld t. Berecne, zu welcem Zinsstz sie ds Geld nlegen
