Aufgabensammlung Theo Inf I 1
|
|
|
- Lena Armbruster
- vor 6 Jahren
- Abrufe
Transkript
1 Aufgabensammlung Theo Inf I 1 1 Grundlagen Aufgabe 1.1 Bestimmen Sie w und w b für w = abacbba. Aufgabe 1.2 Bestimmen Sie alle a) Teilworte der Länge 3 b) Präfixe c) Suffixe des Wortes w = abacbba. Aufgabe 1.3 Bilden Sie für die Sprachen a) L = {a} b) L = {aa, b} c) L = die Mengen L 0, L 2 und L 0 L 1 L 2. Aufgabe 1.4 Geben Sie für die informell beschriebenen Sprachen je eine formale Beschreibung an. Zugrundeliegendes Alphabet sei jeweils Σ = {a, b, c}. a) Die Sprache aller Wörter, die mit mindestens zwei a beginnen. b) Die Sprache aller Wörter, die eine gerade Anzahl von b enthalten. c) Die Sprache aller Wörter, in denen nach einem c immer mindestens ein b folgt (nicht zwingend unmittelbar). Aufgabe 1.5 Tragen Sie in die Tabelle ein, ob die angegebenen Wörter in der Sprache enthalten sind oder nicht. Mit L a, L b, L c sind die Sprachen aus Aufgabe 1.4 gemeint. ε ab aac bba cbbaabbc aaacbcab aabbacaacb L a L b L c Konstruieren Sie ein (möglichst kurzes) Wort, das in keiner der drei Sprachen enthalten ist, und ein (möglichst kurzes), das in L a \ (L b L c ) enthalten ist. Aufgabe 1.6 Betrachten Sie die Sprachen L 1 = {a n n 0}, L 2 = {a n b n n 0}, L 3 = {a n b m n m, n, m 0}. Welche Teilmengenbeziehungen gelten zwischen diesen?
2 Aufgabensammlung Theo Inf I 2 2 Reguläre Ausdrücke Aufgabe 2.1 Beweisen Sie folgende Rechenregeln für reguläre Ausdrücke ( bedeutet: erzeugt dieselbe Sprache): a) α β β α b) α α c) α ε ε α α d) α α e) α α α f) ε g) ε α α (ε α) h) α α α Aufgabe 2.2 Es seien α und β zwei reguläre Ausdrücke. a) Gilt allgemein (α β) α β? b) Falls nein, gibt es spezielle Ausdrücke, für die die Aussage doch stimmt? Aufgabe 2.3 Es seien α und β zwei reguläre Ausdrücke. a) Gilt allgemein (α β) α β? b) Falls nein, gibt es spezielle Ausdrücke, für die die Aussage doch stimmt? Aufgabe 2.4 Es seien α und β zwei reguläre Ausdrücke. a) Gilt allgemein α β β α? b) Falls nein, gibt es spezielle Ausdrücke, für die die Aussage doch stimmt? Aufgabe 2.5 Es seien α = (a ε)b und β = b (ab ) zwei reguläre Ausdrücke. Ist α β? Aufgabe 2.6 Auf REXP Σ sei die Relation definiert durch α β genau dann, wenn L(α) L(β) a) Beweisen Sie: α β genau dann, wenn L(α) L(β) = L(α). b) Beweisen Sie: α β genau dann, wenn L(α) L(β) = L(β). c) Beweisen Sie: α β genau dann, wenn (α β) β. Aufgabe 2.7 Auf REXP Σ sei die Relation definiert durch α β genau dann, wenn (α β) β Beweisen Sie, dass die Relation eine Ordnungsrelation auf REXP Σ bildet. Aufgabe 2.8 Geben Sie für die in Aufgabe 1.4 genannten Sprachen je einen regulären Ausdruck an.
3 Aufgabensammlung Theo Inf I 3 3 Endliche Automaten Aufgabe 3.1 Gegeben sei der endliche Automat A = ({a, b}, {s 0, s 1 }, δ, s 0, {s 1 }), wobei δ durch die folgende Tabelle gegeben sei: δ s 0 s 1 a s 0 s 0 b s 1 s 1 b) Beschreiben Sie L(A) informell. c) Beschreiben Sie L(A) formal. d) Geben Sie einen regulären Ausdruck an, der L(A) erzeugt. Aufgabe 3.2 Gegeben sei der endliche Automat A = ({a}, {0, 1, 2, 3, 4, 5}, δ, 0, {2, 5}), wobei δ durch die folgende Tabelle gegeben sei: δ a {1, 3} {2} {1} {4} {5} {3} b) Beschreiben Sie L(A) informell. c) Beschreiben Sie L(A) formal. d) Geben Sie einen regulären Ausdruck an, der L(A) erzeugt. Aufgabe 3.3 Gegeben sei der endliche Automat A = ({a}, {0, 1, 2, 3, 4}, δ, 0, {2, 4}), wobei δ durch die folgende Tabelle gegeben sei: δ a {1} {2, 3} {1} {4} {1} b) Geben Sie einen regulären Ausdruck an, der L(A) erzeugt. Begründen Sie, warum Ihr Ausdruck korrekt ist. Aufgabe 3.4 Gegeben sei der endliche Automat A = ({a, b, c}, {0, 1, 2, 3}, δ, 0, {3}), wobei δ durch die folgende Tabelle gegeben sei: δ a b c b) Beschreiben Sie L(A) informell. c) Beschreiben Sie L(A) formal. d) Geben Sie einen regulären Ausdruck an, der L(A) erzeugt.
4 Aufgabensammlung Theo Inf I 4 Aufgabe 3.5 Gegeben sei der endliche Automat A = ({a, b}, {A, B}, δ, {A}, {B}), wobei δ durch die folgende Tabelle gegeben sei: δ A B a {A} b {A, B} b) Beschreiben Sie L(A) informell. c) Beschreiben Sie L(A) formal. d) Vervollständigen Sie den Automaten. Aufgabe 3.6 Gegeben sei der endliche Automat A = ({a, b}, {S, A, B, F }, δ, {S}, {S, F }) mit δ gegeben durch δ S A B F a {A, F } {A, F } {B} b {B, F } {A} {B, F } b) Beschreiben Sie L(A) informell. c) Beschreiben Sie L(A) formal. d) Geben Sie einen regulären Ausdruck an, der L(A) erzeugt. Aufgabe 3.7 Gegeben sei der endliche Automat A = ({a}, {s 0, s 1, s 2, s 3, s 4, s 5 }, δ, s 0, {s 1, s 4 }), mit δ(s i, a) = { si+1 falls 0 i < 5 s 0 falls i = 5 b) Beschreiben Sie L(A) informell. c) Beschreiben Sie L(A) formal. d) Geben Sie einen regulären Ausdruck an, der L(A) erzeugt. Aufgabe 3.8 Gegeben sei der endliche Automat A = ({a}, {0, 1, 2, 3, 4, 5}, δ, 0, {0, 2, 3, 4, 5}), wobei δ durch die folgende Tabelle gegeben sei: δ a b) Beschreiben Sie L(A) informell. c) Beschreiben Sie L(A) formal. d) Geben Sie einen regulären Ausdruck an, der L(A) erzeugt. Aufgabe 3.9 Geben Sie für die in Aufgabe 1.4 genannten Sprachen je einen endlichen Automaten an. Zeichnen Sie ein Zustandsdiagramm und geben Sie die Zustandstransformation zusätzlich als Tabelle an. Aufgabe 3.10 Für c N sei L c = {w {a, b} a c ist Infix von w}. Geben Sie eine formale Definition für eine Familie von vollständigen Automaten A c an mit L c = L(A c ).
5 Aufgabensammlung Theo Inf I 5 Aufgabe 3.11 Konstruieren Sie einen vollständigen endlichen Automaten A 23, der die Sprache L 23 = {w {a, b} w a = 2m w b = 3n, m, n N} akzeptiert. Tipp: Sie können die Sprache geeignet in zwei Sprachen zerlegen, für diese jeweils einen endlichen Automaten angeben und aus diesen beiden Automaten dann den Produktautomaten bilden. Aufgabe 3.12 Konstruieren Sie einen vollständigen endlichen Automaten, der die Sprache L = {w {a, b} w a = o mod 5 w b = 1 mod 2} akzeptiert. Tipp: Sie können die Sprache geeignet in zwei Sprachen zerlegen, für diese jeweils einen endlichen Automaten angeben und aus diesen beiden Automaten dann den Produktautomaten bilden. Aufgabe 3.13 Betrachten Sie den endlichen Automaten aus Aufgabe 5.11 A = ({a, b}, {0, 1, 2, 3, 4, 5}, δ, 0, {3, 4,5}) mit δ a b a) Geben Sie eine informelle Beschreibung für die Sprache an, die von A akzeptiert wird. b) Geben Sie eine formale Beschreibung für die Sprache an, die von A akzeptiert wird. c) Geben Sie einen regulären Ausdruck an, der die Sprache beschreibt, die von A akzeptiert wird.
6 Aufgabensammlung Theo Inf I 6 4 Deterministische und nichtdeterministische EA Aufgabe 4.1 Gegeben sei der nichtdeterministische endliche Automat A = ({a}, {0, 1, 2, 3, 4, 5}, δ, {0}, {0, 2, 5}), mit δ a {1, 3} {2} {1, 3} {4} {5} {1, 3} b) Konstruieren Sie mit dem in der Vorlesung vorgestellten Verfahren einen zu A äquivalenten deterministischen Automaten A d. c) Zeichnen Sie das Zustandsdiagramm von A d. d) Beschreiben Sie L(A) informell. e) Beschreiben Sie L(A) formal. f) Geben Sie einen regulären Ausdruck an, der L(A) erzeugt. Aufgabe 4.2 Konstruieren Sie mit dem in der Vorlesung vorgestellten Verfahren einen äquivalenten deterministischen EA zu dem Automaten A aus Aufgabe 3.5. A = ({a, b}, {A, B}, δ, {A}, {B}), mit δ A B a {A} b {A, B} Aufgabe 4.3 Gegeben sei der nichtdeterministische endliche Automat A = ({0, 1}, {s 0, s 1, s 2, s 3 }, δ, s 0, {s 3 }) mit δ s 0 s 1 s 2 s 3 0 {s 1, s 2, s 3 } 1 {s 2, s 3 } {s 1, s 3 } b) Konstruieren Sie mit dem in der Vorlesung vorgestellten Verfahren einen zu A äquivalenten deterministischen Automaten A d. c) Zeichnen Sie das Zustandsdiagramm von A d. d) Beschreiben Sie L(A) informell. e) Beschreiben Sie L(A) formal. f) Geben Sie einen regulären Ausdruck an, der L(A) erzeugt. Aufgabe 4.4 Konstruieren Sie zu dem nichtdeterministischen Automaten aus Aufgabe 3.6 A = ({a, b}, {S, A, B, F }, δ, {S}, {S, F }) mit δ gegeben durch δ S A B F a {A, F } {A, F } {B} b {B, F } {A} {B, F } einen äquivalenten deterministischen Automaten A d. Geben Sie zu A d auch das Zustandsdiagramm an!
7 Aufgabensammlung Theo Inf I 7 Aufgabe 4.5 Konstruieren Sie zu dem nichtdeterministischen Automaten A = ({a, b}, {s 0, s a, s b, s aa, s ab, s ba, s bb }, δ, s 0, {s a, s b, s aa, s bb }), mit δ s 0 s a s b s aa s ab s ba s bb a {s a, s ab } {s aa, s ab } {s ba } b {s b, s ba } {s ab } {s ba, s bb } einen äquivalenten deterministischen Automaten A d. Aufgabe 4.6 Konstruieren Sie zu dem nichtdeterministischen Automaten A = ({a, b}, {s 0, s 1, s 2, s 3 }, δ, s 0, {s 3 }), mit δ s 0 s 1 s 2 s 3 a {s 1, s 2 } {s 1 } {s 2, s 3 } b {s 1, s 3 } {s 3 } einen äquivalenten deterministischen Automaten A d. Geben Sie zu A d auch das Zustandsdiagramm an! Aufgabe 4.7 Gegeben sei der nichtdeterministische Automaten aus Aufgabe 3.3 A = ({a}, {0, 1, 2, 3, 4}, δ, 0, {2, 4}), mit: δ a {1} {2, 3} {1} {4} {1} Konstruieren Sie mit dem in der Vorlesung vorgestellten Verfahren einen zu A äquivalenten deterministischen Automaten A d. Geben Sie zu A d auch das Zustandsdiagramm an! Aufgabe 4.8 Konstruieren Sie zu dem nichtdeterministischen Automaten A = ({a, b}, {1, 2, 3}, δ, 1, {1}), wobei δ durch die folgende Tabelle gegeben sei: δ a {2, 3} {1} b {2, 3} {3} einen äquivalenten deterministischen Automaten A d. Geben Sie zu A d auch das Zustandsdiagramm an! Aufgabe 4.9 Sei A = ({a}, {0, 1, 2, 3}, δ, 0, {2, 3}), mit δ a {1, 2} {1, 2} {3} {0, 1, 2} ein nichtdeterministischer Automat. b) Konstruieren Sie mit dem in der Vorlesung vorgestellten Verfahren einen zu A äquivalenten deterministischen Automaten A d. c) Zeichnen Sie das Zustandsdiagramm von A d. d) Beschreiben Sie L(A) informell. e) Beschreiben Sie L(A) formal. f) Geben Sie einen regulären Ausdruck an, der L(A) erzeugt. Aufgabe 4.10 Gegeben sei der nichtdeterministische endliche Automat A = ({0, 1}, {s 0, s 1, s 2, s 3, sa 4 }, δ, s 0, {s 4 }) mit δ s 0 s 1 s 2 s 3 s 4 0 {s 0, s 1 } {s 4 } {s 4 } 1 {s 0 } {s 2, s 3 } {s 4 } {s 4 } Konstruieren Sie zu A schrittweise mit dem in der Vorlesung vorgestellten Verfahren einen äquivalenten deterministischen endlichen Automaten A d.
8 Aufgabensammlung Theo Inf I 8 5 Minimale EA Aufgabe 5.1 Konstruieren Sie schrittweise zu dem deterministischen EA A = ({a, b}, {0, 1, 2, 3, 4}, δ, 0, {2, 4}), mit δ a b einen äquivalenten minimalen Automaten A min. Geben Sie δ min als Zustandsdiagramm an! Aufgabe 5.2 Minimieren Sie mit dem in der Vorlesung vorgestellten Verfahren den Automaten A aus Aufgabe 3.8. A = ({a}, {0, 1, 2, 3, 4, 5}, δ, 0, {0, 2, 3,4, 5}), mit δ a Aufgabe 5.3 Minimieren Sie mit dem in der Vorlesung vorgestellten Verfahren den Automaten A aus Aufgabe 3.7. A = ({a}, {s 0, s 1, s 2, s 3, s 4, s 5 }, δ, s 0, {s 1, s 4 }), mit { si+1 falls 0 i < 5 δ(s i, a) = sonst s 0 Aufgabe 5.4 Konstruieren Sie schrittweise zu dem deterministischen EA A = ({a, b}, {0, 1, 2, 3, 4, 5, 6}, δ, 0, {1, 2, 3, 4}) mit δ a b einen äquivalenten minimalen Automaten A min. Geben Sie δ min als Zustandsdiagramm an! Aufgabe 5.5 Konstruieren Sie schrittweise zu dem deterministischen EA A = ({a, b}, {0, 1, 2, 3}, δ, 0, {2, 3}) mit δ a b einen äquivalenten minimalen Automaten A min. Interpretieren Sie das Ergebnis! Aufgabe 5.6 Konstruieren Sie schrittweise zu dem deterministischen EA A = ({a, b}, {0, 1, 2, 3, 4, 5}, δ, 0, {3, 4, 5}) mit δ a b einen äquivalenten minimalen Automaten A min. Aufgabe 5.7 Konstruieren Sie schrittweise zu dem deterministischen EA A = ({a, b}, {0, 1, 2, 3, 4, 5}, δ, 0, {1, 2, 5}) mit δ a b einen äquivalenten minimalen Automaten A min.
9 Aufgabensammlung Theo Inf I 9 Aufgabe 5.8 Konstruieren Sie schrittweise zu dem deterministischen EA A = ({a, b}, {0, 1, 2, 3}, δ, 0, {1, 2, 3}) mit δ a b einen äquivalenten minimalen Automaten A min. Aufgabe 5.9 Konstruieren Sie schrittweise zu dem deterministischen EA A = ({a, b}, {0, 1, 2, 3}, δ, 3, {3}) mit δ a b einen äquivalenten minimalen Automaten A min. Aufgabe 5.10 Konstruieren Sie schrittweise zu dem deterministischen EA A = ({a, b}, {0, 1, 2, 3}, δ, 0, {0}) mit δ a b einen äquivalenten minimalen Automaten A min. Aufgabe 5.11 Konstruieren Sie schrittweise zu dem deterministischen EA A = ({a, b}, {0, 1, 2, 3, 4, 5}, δ, 0, {3, 4, 5}) mit δ a b einen äquivalenten minimalen Automaten A min.
10 Aufgabensammlung Theo Inf I 10 6 Rechtslineare Grammatiken Aufgabe 6.1 Gegeben sei die rechtslineare Grammatik G = ({a, b}, {S, A, B, C, D}, P, S) mit P = { S aa bb, A aa bc ε, B bb ad ε, C aa bc, D ad bb } a) Beschreiben Sie L(G) informell. b) Beschreiben Sie L(G) formal. c) Geben Sie einen regulären Ausdruck an, der L(G) erzeugt. d) Geben Sie einen endlichen Automaten an, der L(G) akzeptiert. Aufgabe 6.2 Gegeben sei die rechtslineare Grammatik G = ({a, b}, {S, A}, P, S) mit P = { S as ba A as ba ε } a) Beschreiben Sie L(G) informell. b) Beschreiben Sie L(G) formal. c) Geben Sie einen regulären Ausdruck an, der L(G) erzeugt. d) Geben Sie einen endlichen Automaten an, der L(G) akzeptiert. Aufgabe 6.3 Gegeben sei die rechtslineare Grammatik G = ({a, b, c}, {S, A}, P, S) mit P = { S aa a, A aa ba ca a } a) Beschreiben Sie L(G) informell. b) Beschreiben Sie L(G) formal. c) Geben Sie einen regulären Ausdruck an, der L(G) erzeugt. d) Geben Sie einen endlichen Automaten an, der L(G) akzeptiert. Aufgabe 6.4 Gegeben sei die rechtslineare Grammatik G = ({a, b}, {S, A, B}, P, S) mit P = { S aa bb a b ε, A aa ba a, B ab bb b } a) Beschreiben Sie L(G) informell. b) Beschreiben Sie L(G) formal. c) Geben Sie einen regulären Ausdruck an, der L(G) erzeugt. d) Geben Sie einen endlichen Automaten an, der L(G) akzeptiert. e) Geben Sie einen vollständigen, deterministischen, minimalen endlichen Automaten an, der L(G) akzeptiert. Aufgabe 6.5 Für k N sei L k = {w {a, b} a k ist ein Teilwort von w} Geben Sie die formale Definition an für eine Familie von rechtslinearen Grammatiken G k mit L k = L(G k ), k N.
11 Aufgabensammlung Theo Inf I 11 Aufgabe 6.6 Geben Sie für die in Aufgabe 1.4 genannten Sprachen je eine rechtslineare Grammatik an. Aufgabe 6.7 Gegeben sei die Grammatik G = ({a, b}, {S, A, B, C, D, E}, P, S) mit P = { S a ε aa bb, A as bc, B ac bd, C ab be, D ae bs, E ad ba } a) Leiten Sie drei Wörter mit jeweils mindestens fünf Buchstaben ab. b) Beschreiben Sie L(G) informal. c) Geben Sie eine formale Beschreibung für L(G) an. d) Geben Sie mithilfe des in der Vorlesung vorgestellten Verahrens einen zu G äquivalenten endlichen Automaten an. *) Geben Sie mithilfe des in der Vorlesung vorgestellten Verfahrens eine zu G äquivalente linkslineare Grammatik an. Aufgabe 6.8 Es sei α = ((a b) (c (a b)) ) REXP {a,b,c}. Geben SIe eine Grammatik G an mit L(G) = L(α). Aufgabe 6.9 Ein Polynom über Z stellen wir allgemein in der Art ±a 1 x i1 ± a 2 x i2 ±... ± a k x i k dar. Dabei sind a j N, 1 j k, die Koeffizienten, sowie x die Variable mit den Exponenten i j N 0, 1 j k. Ein Beispiel für ein Polynom ist +3x 1 + 5x 4 2x 2 1x 1 + 6x 0 + 3x 4 7x 3 Wir wollen nun die Koeffizienten und die Exponenten in Strichnotation darstellen: a durch a bzw. i j durch ij. Das Beispiel sieht so kodiert wie folgt aus: + x + x x x + x + x x Um Verwechslungen mit dem -Zeichen der rechtslinearen Grammatiken zu vermeiden, benutzen wir die Zeichen a und b: Das Beispiel sieht dann so kodiert aus: +aaaxb + aaaaaxbbbb aaxbb axb + aaaaaax + aaaxbbbb aaaaaaaxbbb Diese Kodierung kann als Wort über dem Alphabet Σ = {x, a, b,+, } aufgefasst werden. Es sei nun P(Z) die Menge aller Wörter über Σ, die korrekte Kodierungen von Polynomen über Z darstellen. Geben Sie eine rechtslineare Grammatik G an mit L(G) = P(Z).
12 Aufgabensammlung Theo Inf I 12 7 Abschlußeigenschaften regulärer Sprachen und das Pumping-Lemma Aufgabe 7.1 Sind folgende Sprachen regulär? Beweisen Sie Ihre Antworten. a) L n = {a i b i 0 i n} für jedes n N b) L = n 0 L n c) L = {a 2n n 0} Aufgabe 7.2 Es sei Σ = {a, b} und L 1, L 2 Σ. Treffen folgende Aussagen zu? Begründen Sie Ihre Antworten. a) Wenn L 1 regulär und L 1 L 2, dann ist auch L 2 regulär. b) Wenn L 2 regulär und L 1 L 2, dann ist auch L 1 regulär. c) Wenn L 1 nicht regulär und L 1 L 2, dann ist auch L 2 nicht regulär. d) Wenn L 2 nicht regulär und L 1 L 2, dann ist auch L 1 nicht regulär. Aufgabe 7.3 Für k N 0 sei L k = {a km b m m N 0 }. a) Für welche k N 0 ist L k regulär? b) Für welche k N 0 ist L k nicht regulär? Beweisen Sie Ihre Antworten. Aufgabe 7.4 Sind folgende Sprachen regulär? Begründen Sie Ihre Antworten. a) L 1 = {a m b n m, n 0} b) L 2 = {a m b n m, n 0, m n} c) L 3 = {a m a n m, n 0, m = n} d) L 4 = {a 2m b m m 0} Aufgabe 7.5 Für welche c N 0 sind die Sprachen L c = {a nc n 0} regulär, für welche nicht? Beweisen Sie Ihre Antwort. Aufgabe 7.6 Ist die Sprache L = {a m b n c m+n m, n 0} regulär? Beweisen Sie Ihre Antwort. Aufgabe 7.7 Sind folgende Sprachen für jedes c N 0 regulär? Beweisen Sie Ihre Antwort. a) L c = {a cm a m m 0} b) L c = {a cm b m m 0} Aufgabe 7.8 Sind folgende Sprachen regulär für jedes k N 0? Beweisen Sie Ihre Antwort. a) L k = {a m a n m, n 0, m = kn} b) L = {a 2m b m m 0} Aufgabe 7.9 Ist die Sprache L = {a m ba n m, n 0, m = n} regulär? Beweisen Sie Ihre Antwort. Aufgabe 7.10 Sind folgende Sprachen regulär? Beweisen Sie Ihre Antwort.
13 Aufgabensammlung Theo Inf I 13 a) L 1 = {a m b n m, n 0, m + n 1000} b) L 2 = {a m b n m, n 0, m n 1000} Aufgabe 7.11 Ist die Sprache L = {a m ba n m, n 0, m = n} regulär? Beweisen Sie Ihre Antwort. Aufgabe 7.12 Ist die Sprache L = {a m ba n m, n 0, m n} regulär? Beweisen Sie Ihre Antwort. Aufgabe 7.13 b N ist ein Teiler von a N 0 genau dann, wenn ein q N 0 existiert, so dass a = b q gilt. Wir schreiben dafür b a. a) Ist die Sprache L = {a p a q p N, q N 0, p q} regulär? Beweisen Sie Ihre Antwort. b) Ist die Sprache L = {a p b q p N, q N 0, p q} regulär? Beweisen Sie Ihre Antwort. Aufgabe 7.14 Es seien L 1 = {a 2m b 3n m, n N 0 } und L 2 = {a 2k b 3k k N 0 } a) Ist L 1 regulär? Beweisen Sie Ihre Aussage! b) Ist L 2 regulär? Beweisen Sie Ihre Aussage! c) Betrachten Sei folgenden Beweis für Aufgabe a): Offensichtlich ist L 1 {a m b n m, n N 0 } =: L L ist offensichtlich regulär (wird z.b. durch den regulären Ausdruck a b beschrieben). Also muss L 1 als Teilmenge von L auch regulär sein. Ist dies ein korrekter Beweis? Begründen Sie Ihre Antwort! Aufgabe 7.15 Beweisen Sie mithilfe des Pumping-Lemmas, dass die Sprache L = {a p p P} nicht regulär ist. Tipp: Wählen Sie i = geeignete Primzahl +1.
14 Aufgabensammlung Theo Inf I 14 8 Anwendungen Aufgabe 8.1 Ein Polynom über Z stellen wir allgemein in der Art ±a 1 x i1 ± a 2 x i2 ±... ± a k x i k dar. Dabei sind a j N, 1 j k, die Koeffizienten, sowie x die Variable mit den Exponenten i j N 0, 1 j k. Ein Beispiel für ein Polynom ist +3x 1 + 5x 4 2x 2 1x 1 + 6x 0 + 3x 4 7x 3 Wir wollen nun die Koeffizienten und die Exponenten in Strichnotation darstellen: a durch a bzw. i j durch ij. Das Beispiel sieht so kodiert wie folgt aus: + x + x x x + x + x x Diese Kodierung kann als Wort über dem Alphabet Σ = {x,, +, } aufgefasst werden. Es sei nun P(Z) die Menge aller Wörter über Σ, die korrekte Kodierungen von Polynomen über Z darstellen. Geben Sie einen regulären Ausdruck α an mit L(α) = P(Z). Geben Sie einen endlichen Automaten A an mit L(A) = P(Z). Aufgabe 8.2 Eine lineare Gleichung über Z stellen wir allgemein in der Art ±a i1 x i1 ± a i2 x i2 ±... ± a ik x ik = ±b dar. Dabei sind i j N, 1 j k, die Indizes, x ij, 1 j k die Variablen, und für die Koeffizienten a ij, 1 j k, k N gilt a ij N und für die Konstante b gilt b N 0. Ein Beipsiel für eine lineare Gleichung über Z ist: +3x 1 + 5x 4 2x 2 1x 1 + 3x 4 = +1 Wir wollen nun die Indizes, die Exponenten und die Koeffizienten in Strichnotation darstellen: a durch a bzw. i durch i sowie b durch b. Das Beispiel sieht so kodiert wie folgt aus: + x + x x x + x = + Dabei werden in dieser Kodierung die Blanks weggelassen. Zu beachten ist, dass, wenn b = 0 ist, rechts vom Gleichheitszeichen nur + oder steht. Ein lineares Gleichungssystem besteht nun aus einer nichtleeren Folge durch Kommata getrennter Kodierungen von linearen Gleichungen, die mit einem Semikolon endet. Ein mögliches Beispiel mit drei Gleichungen ist: + x + x x x + x = +, x + x + x x = +, + x + x x = ; Diese Kodierung kann als Wort über dem Alphabet Σ = {x,, +,, =,,, ; } aufgefasst werden. Es sei nun LG die Menge aller Wörter über Σ, die korrekte Kodierungen von linearen Gleichungssystemen darstellen. Geben Sie einen endlichen Automaten A an mit L(A) = LG. Aufgabe 8.3 Eine F-Nummer ist eine Ziffernfolge a = a 0 a 1... a 12 mit 13 Ziffern. Eine F-Nummer ist korrekt genau dann, wenn 12 w i a i = 0 mod 10 gilt. Dabei ist w i = { 3, falls i gerade 7, falls i ungerade i=0 Konstruieren Sie einen endlichen Automaten, der genau die korrekten F-Nummern akzeptiert.
15 Aufgabensammlung Theo Inf I 15 Aufgabe 8.4 Eine X-Nummer ist eine Ziffernfolge a = a 1... a 9 mit 9 Ziffern a i mit 1 a i i für 1 i 9. Eine X-Nummer ist korrekt genau dann, wenn 9 i a i = 0 mod 10 i=1 gilt. Konstruieren Sie einen endlichen Automaten, der genau die korrekten X-Nummern akzeptiert. Aufgabe 8.5 Eine D-Nummer ist eine Ziffernfolge a = a 1... a 12 mit 13 Ziffern a i {0, 1, 2,..., 9, X} für 1 i 12. X steht für eine Ziffer mit der Wertigkeit 10. Eine D-Nummer ist korrekt genau dann, wenn a i {0, 1, 2,..., 9} für 1 i 11, a i {0, 1, 2,..., 9, X} für i = 12, sowie 12 i=1 w ia i = 0 mod 11 gilt. Dabei ist { 1, falls i gerade w i = 3, falls i ungerade Konstruieren Sie einen endlichen Automaten, der genau die korrekten D-Nummern akzeptiert. Aufgabe 8.6 Eine EAN-Nummer (Europäische Artikelnummer) ist eine Ziffernfolge a = a 0... a 12 mit 13 Ziffern. Eine EAN- Nummer ist korrekt genau dann, wenn 12 i=0 w ia i = 0 mod 10 gilt. Dabei ist w i = { 1, falls i gerade 3, falls i ungerade Konstruieren Sie einen endlichen Automaten, der genau die korrekten EAN-Nummern akzeptiert. Aufgabe 8.7 Eine C-Nummer ist eine zehnstellige Ziffernfolge a = a 1... a 10 mit a i {0, 1, 2,..., 9} für 1 i 9 und a 10 {0, 1, 2,..., 9, X}, wobei X für den Wert 10 steht. Eine C-Nummer ist korrekt genau dann, wenn 10 i=1 a i = 0 mod 11 und 10 i=1 i a i = 0 mod 11 gilt. Konstruieren Sie einen endlichen Automaten, der genau die korrekten C-Nummern akzeptiert. Aufgabe 8.8 Eine ISBN-Nummer ist eine zehnstellige Ziffernfolge a = a 1...a 10 mit a i {0, 1, 2,..., 9} für 1 i 9 und a 10 {0, 1, 2,..., 9, X}, wobei X für den Wert 10 steht. Eine ISBN-Nummer ist korrekt genau dann, wenn 10 i=1 i a i = 0 mod 11 gilt. Konstruieren Sie einen endlichen Automaten, der genau die korrekten ISBN-Nummern akzeptiert. Aufgabe 8.9 In Java gelten folgende Syntaxregeln für die Darstellung von Gleitkommazahlen: Gleitkommazahlen bestehen aus einem optionalen Vorzeichen (+ oder -), einer Ziffernfolge (ohne führende Nullen oder = 0) für den Vorkommaanteil und einem Nachkommaanteil oder einer Exponentangabe (oder beidem). Der Nachkommaanteil besteht aus einem Punkt und einer nichtleeren Ziffernfolge, die Exponentangabe besteht aus einem e oder E, gefolgt von einem optionalen Vorzeichen und mindestens einer, maximal zwei Ziffern. Beispiel: e E3 sind gültige Darstellungen, e sind keine gültigen Darstellungen. a) Geben Sie einen regulären Ausdruck für Gleitkommazahlen an. b) Konstruieren Sie einen endlichen Automaten, der genau die korrekten Gleitkommadarstellungen akzeptiert.
16 Aufgabensammlung Theo Inf I 16 9 Mealy- und Moore-Maschinen Aufgabe 9.1 Konstruieren Sie eine Mealy-Maschine, die die Funktion f : {0, 1, 2} + {0, 1, 2} + definiert durch k f(x 1 x 2...x n ) = y 1 y 2...y n mit y k = x i mod 3 i=1 für 1 k n berechnet. Berechnen Sie schrittweise f M (2122). Aufgabe 9.2 Konstruieren Sie eine Mealy-Maschine, die die Funktion f : {0, 1, 2...9} {0} {0, 1, 2...9} + definiert durch f(x) = x 2 berechnet, wobei x = x 1x 2... x n 0 eine Zahl im Dezimalsystem mit Einerziffer = 0 beschreibt. Berechnen Sie schrittweise f M (99180). Aufgabe 9.3 Es sei f die Funktion f : {0, 1, 2...9} + {0, 1, 2...9} + definiert durch f(x) = 2x. Konstruieren Sie eine Mealy-Maschine und geben Sie eine geeignete Eingabecodierung α : {0, 1, 2...9} + Σ sowie eine geeignete Ausgabecodierung β : {0, 1, 2...9} + an, sodass f(x) = β(f M (α(x))). Berechnen Sie schrittweise f M (991872). Aufgabe 9.4 Die Funktion f : {0, 1,...9} {a} {0, 1,...9} + sei für n 0 definiert durch f(x 1 x 2...x n a) = x 1 x 2... x n p mit p = n x i mod 10 Die Funktion reproduziert also von der Eingabefolge x 1 x 2... x n a, n 0 die ersten n Ziffern und ersetzt den Platzhalter a durch die Prüfziffer p. Dabei ist p der Rest, der bleibt, wenn die Summe der n Ziffern x 1, x 2,...x n durch 10 geteilt wird. Es gilt also z.b. f(987a) = 9874 Konstruieren Sie einen Mealy-Automaten M, der die Funktion f berechnet. Berechnen Sie schrittweise f M (987a). Aufgabe 9.5 In der Signal- und Bildverarbeitung benötigt man Rauschfilter, um z.b. Schmutz zu beseitigen. In unserem Fall sei ein Schwarz-Weiß-Bild durch eine Folge von Nullen und Einsen codiert. In der Regel sind größere zusammenhängende Regionen schwarz oder weiß, sehr selten nur einzelne Pixel. Durch Flecken oder Staub können aber einzelne Pixel verfälscht sein. Es ist sinnvoll, derartige Sequenzen zu glätten und die Anzahl farblich unterschiedlicher Regionen im Bild zu veringern, um tatsächliche Farbregionen zu rekonstruieren. Konstruieren Sie eine Mealy-Maschine M, die ein 0-1-Eingabefolge auf diese Art gättet: Ein Farbwechsel findet nur statt, wenn mindestens zwei aufeinander folgende Bits gleich sind. Es soll also z.b. gelten: f M (01) = 00, f M (10) = 11, f M (001) = 000, f M (010) = 000, f M (011) = 001, f M ( ) = Berechnen Sie für Ihre Maschine schrittweise f M (011). Aufgabe 9.6 Geben Sie eine Mealy-Maschine M an, die die Funktion f : {0, 1} {0, 1, 2} definiert durch f(x 1 x 2 x 3... x n ) = x 1 y 2... y n mit y i = x i 1 + x i, 2 i n berechnet. Es gilt also z.b. f( ) = Berechnen Sie für Ihre Maschine schrittweise f M (1101). i=1
17 Aufgabensammlung Theo Inf I 17 Aufgabe 9.7 Die Funktion f : {0, 1} {0, 1, 2} sei definiert durch f(x 1 x 2... x n ) = y 1 y 2... y n mit y k = k i=1 x i(3) 1 k n Dabei ist a(3) der kleinste positive Rest, der bleibt, wenn a durch 3 geteilt wird. Es gilt also z.b. f( ) = a) Konstruieren Sie eine Mealy-Maschine M, die f berechnet. b) Berechnen Sie f m (1101) schrittweise. Aufgabe 9.8 Geben Sie die formale Definition und das Zustandsdiagramm einer Mealy-Maschine M an, die die Funktion f : {0, 1} {0, 1, 2} definiert durch f(x 1 x 2 x 3... x n ) = x 1 y 2... y n mit y i = x i 1 x i, 2 i n berechnet. Es gilt also z.b. f( ) = Berechnen Sie für Ihre Maschine schrittweise f M (1101). Aufgabe 9.9 Konstruieren Sie eine endliche Moore-Maschine, die einen Ringzähler modulo p realisiert (p N)! Die Eingaben sind Wörter über dem Alphabet {0, +, }. Dabei bedeutet das Zeichen 0 Zurücksetzen des Zählers auf 0 (reset), + bedeutet Erhöhen des Zählers um 1 (increment) und bedeutet Erniedrigen des Zählers um 1 (decrement). Hat der Zähler den Wert p 1, liefert increment den Wert 0. Hat der Zähler den Wert 0, liefert decrement den Wert p 1. Die Maschine soll nach jeder Eingabe den korrekten Zählerstand ausgeben. Beispiel: f M (+ + +) = 3 f M ( ) = p 2 f M ( ) = p 1 Dabei sei f M (w) = λ(δ (s 0, w)). Berechnen Sie schrittweise f M (+ + 0 ) für Ihre Maschine M.
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Tutorium 4 26..25 INSTITUT FÜR THEORETISCHE INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu
Grundbegriffe der Informatik Tutorium 4 26..25 INSTITUT FÜR THEORETISCHE INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Tutorium 27 29..24 FAKULTÄT FÜR INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Definition
Grundbegriffe der Informatik Tutorium 27 29..24 FAKULTÄT FÜR INFORMATIK KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Definition
2: Zahlentheorie / Restklassen 2.1: Modulare Arithmetik
 Stefan Lucks Diskrete Strukturen (WS 2009/10) 57 2: Zahlentheorie / Restklassen 2.1: Modulare Arithmetik Uhr: Stunden mod 24, Minuten mod 60, Sekunden mod 60,... Rechnerarithmetik: mod 2 w, w {8, 16, 32,
Stefan Lucks Diskrete Strukturen (WS 2009/10) 57 2: Zahlentheorie / Restklassen 2.1: Modulare Arithmetik Uhr: Stunden mod 24, Minuten mod 60, Sekunden mod 60,... Rechnerarithmetik: mod 2 w, w {8, 16, 32,
Wortproblem für kontextfreie Grammatiken
 Wortproblem für kontextfreie Grammatiken G kontextfreie Grammatik. w Σ w L(G)? Wortproblem ist primitiv rekursiv entscheidbar. (schlechte obere Schranke!) Kellerautomat der L(G) akzeptiert Ist dieser effizient?
Wortproblem für kontextfreie Grammatiken G kontextfreie Grammatik. w Σ w L(G)? Wortproblem ist primitiv rekursiv entscheidbar. (schlechte obere Schranke!) Kellerautomat der L(G) akzeptiert Ist dieser effizient?
Grammatiken. Einführung
 Einführung Beispiel: Die arithmetischen Ausdrücke über der Variablen a und den Operationen + und können wie folgt definiert werden: a, a + a und a a sind arithmetische Ausdrücke Wenn A und B arithmetische
Einführung Beispiel: Die arithmetischen Ausdrücke über der Variablen a und den Operationen + und können wie folgt definiert werden: a, a + a und a a sind arithmetische Ausdrücke Wenn A und B arithmetische
Theorie der Informatik
 Theorie der Informatik 6. Formale Sprachen und Grammatiken Malte Helmert Gabriele Röger Universität Basel 17. März 2014 Einführung Beispiel: Aussagenlogische Formeln Aus dem Logikteil: Definition (Syntax
Theorie der Informatik 6. Formale Sprachen und Grammatiken Malte Helmert Gabriele Röger Universität Basel 17. März 2014 Einführung Beispiel: Aussagenlogische Formeln Aus dem Logikteil: Definition (Syntax
Motivation. Formale Grundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen. Informales Beispiel. Informales Beispiel.
 Kontextfreie Kontextfreie Motivation Formale rundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen Bisher hatten wir Automaten, die Wörter akzeptieren Frank Heitmann heitmann@informatik.uni-hamburg.de
Kontextfreie Kontextfreie Motivation Formale rundlagen der Informatik 1 Kapitel 5 Kontextfreie Sprachen Bisher hatten wir Automaten, die Wörter akzeptieren Frank Heitmann heitmann@informatik.uni-hamburg.de
Grundlagen der Theoretischen Informatik
 Grundlagen der Theoretischen Informatik 3. Endliche Automaten (V) 21.05.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Bis jetzt Determinierte endliche Automaten (DEAs) Indeterminierte
Grundlagen der Theoretischen Informatik 3. Endliche Automaten (V) 21.05.2015 Viorica Sofronie-Stokkermans e-mail: sofronie@uni-koblenz.de 1 Bis jetzt Determinierte endliche Automaten (DEAs) Indeterminierte
Formale Sprachen, reguläre und kontextfreie Grammatiken
 Formale Sprachen, reguläre und kontextfreie Grammatiken Alphabet A: endliche Menge von Zeichen Wort über A: endliche Folge von Zeichen aus A A : volle Sprache über A: Menge der A-Worte formale Sprache
Formale Sprachen, reguläre und kontextfreie Grammatiken Alphabet A: endliche Menge von Zeichen Wort über A: endliche Folge von Zeichen aus A A : volle Sprache über A: Menge der A-Worte formale Sprache
11. Primfaktorzerlegungen
 78 Andreas Gathmann 11 Primfaktorzerlegungen Euch ist sicher aus der Schule bekannt, dass sich jede positive ganze Zahl a als Produkt a = p 1 p n von Primzahlen schreiben lässt, und dass diese Darstellung
78 Andreas Gathmann 11 Primfaktorzerlegungen Euch ist sicher aus der Schule bekannt, dass sich jede positive ganze Zahl a als Produkt a = p 1 p n von Primzahlen schreiben lässt, und dass diese Darstellung
Prüfziffern. Man versucht, solche Fehler zu erkennen, indem man der Zahl eine weitere Ziffern, die sog. Prüfziffern, hinzufügt.
 Prüfziffern Bei der Erfassung von langen Zahlen können Fehler auftreten: Ziffern werden weggelassen oder hinzugefügt, zwei benachbarte Ziffern werden vertauscht, eine Ziffer wird falsch übernommen, usw..
Prüfziffern Bei der Erfassung von langen Zahlen können Fehler auftreten: Ziffern werden weggelassen oder hinzugefügt, zwei benachbarte Ziffern werden vertauscht, eine Ziffer wird falsch übernommen, usw..
Theoretische Informatik I
 Theoretische Informatik I Einheit 2.4 Grammatiken 1. Arbeitsweise 2. Klassifizierung 3. Beziehung zu Automaten Beschreibungsformen für Sprachen Mathematische Mengennotation Prädikate beschreiben Eigenschaften
Theoretische Informatik I Einheit 2.4 Grammatiken 1. Arbeitsweise 2. Klassifizierung 3. Beziehung zu Automaten Beschreibungsformen für Sprachen Mathematische Mengennotation Prädikate beschreiben Eigenschaften
1. Der Begriff Informatik 2. Syntax und Semantik von Programmiersprachen. I.2. I.2. Grundlagen von von Programmiersprachen.
 1. Der Begriff Informatik 2. Syntax und Semantik von Programmiersprachen I.2. I.2. Grundlagen von von Programmiersprachen. - 1 - 1. Der Begriff Informatik "Informatik" = Kunstwort aus Information und Mathematik
1. Der Begriff Informatik 2. Syntax und Semantik von Programmiersprachen I.2. I.2. Grundlagen von von Programmiersprachen. - 1 - 1. Der Begriff Informatik "Informatik" = Kunstwort aus Information und Mathematik
Informatik I WS 07/08 Tutorium 24
 Info I Tutorium 24 Informatik I WS 07/08 Tutorium 24 20.12.07 Bastian Molkenthin E-Mail: infotut@sunshine2k.de Web: http://infotut.sunshine2k.de Rückblick Semi-Thue-Systeme Ein Semi-Thue-System besteht
Info I Tutorium 24 Informatik I WS 07/08 Tutorium 24 20.12.07 Bastian Molkenthin E-Mail: infotut@sunshine2k.de Web: http://infotut.sunshine2k.de Rückblick Semi-Thue-Systeme Ein Semi-Thue-System besteht
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Grundbegriffe der Informatik Einheit 15: Reguläre Ausdrücke und rechtslineare Grammatiken Thomas Worsch Universität Karlsruhe, Fakultät für Informatik Wintersemester 2008/2009 1/25 Was kann man mit endlichen
Der Zwei-Quadrate-Satz von Fermat
 Der Zwei-Quadrate-Satz von Fermat Proseminar: Das BUCH der Beweise Fridtjof Schulte Steinberg Institut für Informatik Humboldt-Universität zu Berlin 29.November 2012 1 / 20 Allgemeines Pierre de Fermat
Der Zwei-Quadrate-Satz von Fermat Proseminar: Das BUCH der Beweise Fridtjof Schulte Steinberg Institut für Informatik Humboldt-Universität zu Berlin 29.November 2012 1 / 20 Allgemeines Pierre de Fermat
Grundlagen der Informatik II. Teil I: Formale Modelle der Informatik
 Grundlagen der Informatik II Teil I: Formale Modelle der Informatik 1 Einführung GdInfoII 1-2 Ziele/Fragestellungen der Theoretischen Informatik 1. Einführung abstrakter Modelle für informationsverarbeitende
Grundlagen der Informatik II Teil I: Formale Modelle der Informatik 1 Einführung GdInfoII 1-2 Ziele/Fragestellungen der Theoretischen Informatik 1. Einführung abstrakter Modelle für informationsverarbeitende
Zusammenfassung. 1 Wir betrachten die folgende Signatur F = {+,,, 0, 1} sodass. 3 Wir betrachten die Gleichungen E. 4 Dann gilt E 1 + x 1
 Zusammenfassung Zusammenfassung der letzten LV Einführung in die Theoretische Informatik Woche 7 Harald Zankl Institut für Informatik @ UIBK Wintersemester 2014/2015 1 Wir betrachten die folgende Signatur
Zusammenfassung Zusammenfassung der letzten LV Einführung in die Theoretische Informatik Woche 7 Harald Zankl Institut für Informatik @ UIBK Wintersemester 2014/2015 1 Wir betrachten die folgende Signatur
Grundlagen Theoretischer Informatik I SoSe 2011 in Trier. Henning Fernau Universität Trier fernau@uni-trier.de
 Grundlagen Theoretischer Informatik I SoSe 2011 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik I Gesamtübersicht Organisatorisches; Einführung Logik
Grundlagen Theoretischer Informatik I SoSe 2011 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Grundlagen Theoretischer Informatik I Gesamtübersicht Organisatorisches; Einführung Logik
Vorlesung. 1 Zahlentheorie in Z. Leitfaden. 1.1 Teilbarkeit. Angela Holtmann. Algebra und Zahlentheorie. (natürliche Zahlen ohne die Null)
 Algebra und Zahlentheorie Vorlesung Algebra und Zahlentheorie Leitfaden 1 Zahlentheorie in Z Bezeichnungen: Z := {..., 3, 2, 1, 0, 1, 2, 3,...} (ganze Zahlen) und N := {1, 2, 3,...} (natürliche Zahlen
Algebra und Zahlentheorie Vorlesung Algebra und Zahlentheorie Leitfaden 1 Zahlentheorie in Z Bezeichnungen: Z := {..., 3, 2, 1, 0, 1, 2, 3,...} (ganze Zahlen) und N := {1, 2, 3,...} (natürliche Zahlen
Formale Sprachen und deren Grammatiken. Zusammenhang mit der Automatentheorie.
 Formale Sprachen Formale Sprachen und deren Grammatiken. Zusammenhang mit der Automatentheorie. Inhaltsübersicht und Literatur Formale Sprachen: Definition und Darstellungen Grammatiken für formale Sprachen
Formale Sprachen Formale Sprachen und deren Grammatiken. Zusammenhang mit der Automatentheorie. Inhaltsübersicht und Literatur Formale Sprachen: Definition und Darstellungen Grammatiken für formale Sprachen
Theoretische Informatik 2 (WS 2006/07) Automatentheorie und Formale Sprachen / Kontextfreie Sprachen und Kellerautomaten
 Inhalt 1 Einführung 2 Automatentheorie und Formale Sprachen Grammatiken Reguläre Sprachen und endliche Automaten Kontextfreie Sprachen und Kellerautomaten Kontextsensitive und Typ 0-Sprachen 3 Berechenbarkeitstheorie
Inhalt 1 Einführung 2 Automatentheorie und Formale Sprachen Grammatiken Reguläre Sprachen und endliche Automaten Kontextfreie Sprachen und Kellerautomaten Kontextsensitive und Typ 0-Sprachen 3 Berechenbarkeitstheorie
Grundbegriffe der Informatik
 Grundbegriffe der Informatik Einheit 8: kontextfreie Grammatiken Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2009/2010 1/37 Überblick Kontextfreie Grammatiken
Grundbegriffe der Informatik Einheit 8: kontextfreie Grammatiken Thomas Worsch Karlsruher Institut für Technologie, Fakultät für Informatik Wintersemester 2009/2010 1/37 Überblick Kontextfreie Grammatiken
Mathematische Grundlagen der Informatik 2
 Zusammenfassung Math2I Mathematische Grundlagen der Informatik 2 Emanuel Duss emanuel.duss@gmail.com 12. April 2013 1 Zusammenfassung Math2I Mathematische Grundlagen der Informatik 2 Dieses Dokument basiert
Zusammenfassung Math2I Mathematische Grundlagen der Informatik 2 Emanuel Duss emanuel.duss@gmail.com 12. April 2013 1 Zusammenfassung Math2I Mathematische Grundlagen der Informatik 2 Dieses Dokument basiert
Formale Sprachen. Script, Kapitel 4. Grammatiken
 Formale Sprachen Grammatiken Script, Kapitel 4 erzeugen Sprachen eingeführt von Chomsky zur Beschreibung natürlicher Sprachen bedeutend für die Syntaxdefinition von Programmiersprachen (Compilerbau) Automaten
Formale Sprachen Grammatiken Script, Kapitel 4 erzeugen Sprachen eingeführt von Chomsky zur Beschreibung natürlicher Sprachen bedeutend für die Syntaxdefinition von Programmiersprachen (Compilerbau) Automaten
Programmiersprachen und Übersetzer
 Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Theoretische Informatik
 Theoretische Informatik - das Quiz zur Vorlesung Teil I - Grundzüge der Logik In der Logik geht es um... (A) die Formen korrekten Folgerns (B) die Unterscheidung von wahr und falsch (C) das Finden von
Theoretische Informatik - das Quiz zur Vorlesung Teil I - Grundzüge der Logik In der Logik geht es um... (A) die Formen korrekten Folgerns (B) die Unterscheidung von wahr und falsch (C) das Finden von
Kapitel 2: Formale Sprachen Gliederung
 Gliederung 0. Einleitung und Grundbegriffe 1. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.1. Chomsky-Grammatiken 2.2. Reguläre Sprachen 2.3. Kontextfreie Sprachen
Gliederung 0. Einleitung und Grundbegriffe 1. Endliche Automaten 2. Formale Sprachen 3. Berechnungstheorie 4. Komplexitätstheorie 2.1. Chomsky-Grammatiken 2.2. Reguläre Sprachen 2.3. Kontextfreie Sprachen
Gleitkommaarithmetik und Pivotsuche bei Gauß-Elimination. Lehrstuhl für Angewandte Mathematik Wintersemester 2009/10. 14.
 Gleitkommaarithmetik und Pivotsuche bei Gauß-Elimination Vorlesung Computergestützte Mathematik zur Linearen Algebra Lehrstuhl für Angewandte Mathematik Wintersemester 2009/0 4. Januar 200 Instabilitäten
Gleitkommaarithmetik und Pivotsuche bei Gauß-Elimination Vorlesung Computergestützte Mathematik zur Linearen Algebra Lehrstuhl für Angewandte Mathematik Wintersemester 2009/0 4. Januar 200 Instabilitäten
Programmieren I. Formale Sprachen. www.kit.edu. Institut für Angewandte Informatik
 Programmieren I Formale Sprachen KIT Universität des Landes Baden-Württemberg und nationales Großforschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Formale Sprachen: Allgemeines Sprachen werden
Programmieren I Formale Sprachen KIT Universität des Landes Baden-Württemberg und nationales Großforschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Formale Sprachen: Allgemeines Sprachen werden
Technische Informatik - Eine Einführung
 Martin-Luther-Universität Halle-Wittenberg Fachbereich Mathematik und Informatik Lehrstuhl für Technische Informatik Prof. P. Molitor Ausgabe: 2005-02-21 Abgabe: 2005-02-21 Technische Informatik - Eine
Martin-Luther-Universität Halle-Wittenberg Fachbereich Mathematik und Informatik Lehrstuhl für Technische Informatik Prof. P. Molitor Ausgabe: 2005-02-21 Abgabe: 2005-02-21 Technische Informatik - Eine
Teil II. Schaltfunktionen
 Teil II Schaltfunktionen 1 Teil II.1 Zahlendarstellung 2 b-adische Systeme Sei b IN mit b > 1 und E b = {0, 1,..., b 1} (Alphabet). Dann ist jede Fixpunktzahl z (mit n Vorkomma und k Nachkommastellen)
Teil II Schaltfunktionen 1 Teil II.1 Zahlendarstellung 2 b-adische Systeme Sei b IN mit b > 1 und E b = {0, 1,..., b 1} (Alphabet). Dann ist jede Fixpunktzahl z (mit n Vorkomma und k Nachkommastellen)
Übungsaufgaben und Lösungen. zur Vorlesung. Theoretische Grundlagen der Informatik
 UNIVERSITÄT KONSTANZ Theoretische Grundlagen der Informatik SS 3 Fachbereich Informatik & Informationswissenschaft www.inf.uni-konstanz.de/algo/lehre/ss3/theo Dr. Bernd Gärtner, Carola Haid, Jasper Möller,
UNIVERSITÄT KONSTANZ Theoretische Grundlagen der Informatik SS 3 Fachbereich Informatik & Informationswissenschaft www.inf.uni-konstanz.de/algo/lehre/ss3/theo Dr. Bernd Gärtner, Carola Haid, Jasper Möller,
Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit
 Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit Sommersemester 2011 Dozent: Prof. Dr. J. Rothe, Prof. Dr. M. Leuschel J. Rothe (HHU Düsseldorf)
Informatik IV Theoretische Informatik: Formale Sprachen und Automaten, Berechenbarkeit und NP-Vollständigkeit Sommersemester 2011 Dozent: Prof. Dr. J. Rothe, Prof. Dr. M. Leuschel J. Rothe (HHU Düsseldorf)
Bestimmung einer ersten
 Kapitel 6 Bestimmung einer ersten zulässigen Basislösung Ein Problem, was man für die Durchführung der Simplexmethode lösen muss, ist die Bestimmung einer ersten zulässigen Basislösung. Wie gut das geht,
Kapitel 6 Bestimmung einer ersten zulässigen Basislösung Ein Problem, was man für die Durchführung der Simplexmethode lösen muss, ist die Bestimmung einer ersten zulässigen Basislösung. Wie gut das geht,
Ergänzungen zur Analysis I
 537. Ergänzungsstunde Logik, Mengen Ergänzungen zur Analysis I Die Behauptungen in Satz 0.2 über die Verknüpfung von Mengen werden auf die entsprechenden Regelnfür die Verknüpfung von Aussagen zurückgeführt.
537. Ergänzungsstunde Logik, Mengen Ergänzungen zur Analysis I Die Behauptungen in Satz 0.2 über die Verknüpfung von Mengen werden auf die entsprechenden Regelnfür die Verknüpfung von Aussagen zurückgeführt.
Einführung in die Theoretische Informatik
 Einführung in die Theoretische Informatik Woche 10 Harald Zankl Institut für Informatik @ UIBK Wintersemester 2014/2015 Zusammenfassung Zusammenfassung der letzten LV Satz Sei G = (V, Σ, R, S) eine kontextfreie
Einführung in die Theoretische Informatik Woche 10 Harald Zankl Institut für Informatik @ UIBK Wintersemester 2014/2015 Zusammenfassung Zusammenfassung der letzten LV Satz Sei G = (V, Σ, R, S) eine kontextfreie
Mathematik 1. Inhaltsverzeichnis. Prof. Dr. K. Melzer. karin.melzer@hs-esslingen.de http://www.hs-esslingen.de/de/mitarbeiter/karin-melzer.
 Mathematik 1 Prof Dr K Melzer karinmelzer@hs-esslingende http://wwwhs-esslingende/de/mitarbeiter/karin-melzerhtml Inhaltsverzeichnis 1 Matrizenrechnung 2 11 Matrixbegri 2 12 Spezielle Matrizen 3 13 Rechnen
Mathematik 1 Prof Dr K Melzer karinmelzer@hs-esslingende http://wwwhs-esslingende/de/mitarbeiter/karin-melzerhtml Inhaltsverzeichnis 1 Matrizenrechnung 2 11 Matrixbegri 2 12 Spezielle Matrizen 3 13 Rechnen
Einführung in die Informatik Grammars & Parsers
 Einführung in die Informatik Grammars & Parsers Grammatiken, Parsen von Texten Wolfram Burgard Cyrill Stachniss 12.1 Einleitung Wir haben in den vorangehenden Kapiteln meistens vollständige Java- Programme
Einführung in die Informatik Grammars & Parsers Grammatiken, Parsen von Texten Wolfram Burgard Cyrill Stachniss 12.1 Einleitung Wir haben in den vorangehenden Kapiteln meistens vollständige Java- Programme
Advanced Encryption Standard. Copyright Stefan Dahler 20. Februar 2010 Version 2.0
 Advanced Encryption Standard Copyright Stefan Dahler 20. Februar 2010 Version 2.0 Vorwort Diese Präsentation erläutert den Algorithmus AES auf einfachste Art. Mit Hilfe des Wissenschaftlichen Rechners
Advanced Encryption Standard Copyright Stefan Dahler 20. Februar 2010 Version 2.0 Vorwort Diese Präsentation erläutert den Algorithmus AES auf einfachste Art. Mit Hilfe des Wissenschaftlichen Rechners
Sprachen/Grammatiken eine Wiederholung
 Sprachen/Grammatiken eine Wiederholung Was sind reguläre Sprachen? Eigenschaften regulärer Sprachen Sprachen Begriffe Symbol: unzerlegbare Grundzeichen Alphabet: endliche Menge von Symbolen Zeichenreihe:
Sprachen/Grammatiken eine Wiederholung Was sind reguläre Sprachen? Eigenschaften regulärer Sprachen Sprachen Begriffe Symbol: unzerlegbare Grundzeichen Alphabet: endliche Menge von Symbolen Zeichenreihe:
Kapitel 2. Methoden zur Beschreibung von Syntax
 1 Kapitel 2 Methoden zur Beschreibung von Syntax Grammatik, die sogar Könige zu kontrollieren weiß... aus Molière, Les Femmes Savantes (1672), 2. Akt 2 Ziele Zwei Standards zur Definition der Syntax von
1 Kapitel 2 Methoden zur Beschreibung von Syntax Grammatik, die sogar Könige zu kontrollieren weiß... aus Molière, Les Femmes Savantes (1672), 2. Akt 2 Ziele Zwei Standards zur Definition der Syntax von
Einführung in die Informatik I
 Einführung in die Informatik I Das Rechnen in Zahlensystemen zur Basis b=2, 8, 10 und 16 Prof. Dr. Nikolaus Wulff Zahlensysteme Neben dem üblichen dezimalen Zahlensystem zur Basis 10 sind in der Informatik
Einführung in die Informatik I Das Rechnen in Zahlensystemen zur Basis b=2, 8, 10 und 16 Prof. Dr. Nikolaus Wulff Zahlensysteme Neben dem üblichen dezimalen Zahlensystem zur Basis 10 sind in der Informatik
Ermittlung von IBAN und BIC anhand von Kontonummer und Bankleitzahl in der Sparkassen-Finanzgruppe
 Ermittlung von IBAN und BIC anhand von Kontonummer und Bankleitzahl Vorwort: Die Ermittlung einer IBAN anhand der im Inlandszahlungsverkehr gebräuchlichen Kontound Bankidentifikationen - in Deutschland
Ermittlung von IBAN und BIC anhand von Kontonummer und Bankleitzahl Vorwort: Die Ermittlung einer IBAN anhand der im Inlandszahlungsverkehr gebräuchlichen Kontound Bankidentifikationen - in Deutschland
Theoretische Informatik
 Theoretische Informatik Einheit 1 Mathematische Methodik 1. Problemlösen 2. Beweistechniken 3. Wichtige Grundbegriffe Methodik des Problemlösens Klärung der Voraussetzungen Welche Begriffe sind zum Verständnis
Theoretische Informatik Einheit 1 Mathematische Methodik 1. Problemlösen 2. Beweistechniken 3. Wichtige Grundbegriffe Methodik des Problemlösens Klärung der Voraussetzungen Welche Begriffe sind zum Verständnis
Planungsblatt Mathematik für die 4E
 Planungsblatt Mathematik für die 4E Woche 26 (von 09.03 bis 13.03) Hausaufgaben 1 Bis Mittwoch 11.03: Auf dem Planungsblatt stehen einige Aufgaben als Übung für die SA. Bereite diese Aufgaben vor! Vor
Planungsblatt Mathematik für die 4E Woche 26 (von 09.03 bis 13.03) Hausaufgaben 1 Bis Mittwoch 11.03: Auf dem Planungsblatt stehen einige Aufgaben als Übung für die SA. Bereite diese Aufgaben vor! Vor
Kapitel 4. Euklidische Ringe und die Jordansche Normalform. 4.1 Euklidische Ringe
 Kapitel 4 Euklidische Ringe und die Jordansche Normalform 4.1 Euklidische Ringe Die Ringe der ganzen Zahlen, Z, sowie Polynomringe über Körpern, K[X], wobei K ein Körper ist, haben die folgenden Gemeinsamheiten:
Kapitel 4 Euklidische Ringe und die Jordansche Normalform 4.1 Euklidische Ringe Die Ringe der ganzen Zahlen, Z, sowie Polynomringe über Körpern, K[X], wobei K ein Körper ist, haben die folgenden Gemeinsamheiten:
1 Syntax von Programmiersprachen
 1 Syntax von Programmiersprachen Syntax ( Lehre vom Satzbau ): formale Beschreibung des Aufbaus der Worte und Sätze, die zu einer Sprache gehören; im Falle einer Programmier-Sprache Festlegung, wie Programme
1 Syntax von Programmiersprachen Syntax ( Lehre vom Satzbau ): formale Beschreibung des Aufbaus der Worte und Sätze, die zu einer Sprache gehören; im Falle einer Programmier-Sprache Festlegung, wie Programme
3.3 Eigenwerte und Eigenräume, Diagonalisierung
 3.3 Eigenwerte und Eigenräume, Diagonalisierung Definition und Lemma 3.3.1. Sei V ein K-Vektorraum, φ End K (V ), λ K. Wir defnieren den zu λ gehörigen Eigenraum von φ als Dies ist ein Unterraum von V.
3.3 Eigenwerte und Eigenräume, Diagonalisierung Definition und Lemma 3.3.1. Sei V ein K-Vektorraum, φ End K (V ), λ K. Wir defnieren den zu λ gehörigen Eigenraum von φ als Dies ist ein Unterraum von V.
Anhang I zur Vorlesung Kryptologie: Elementare Zahlentheorie
 Anhang I zur Vorlesung Kryptologie: Elementare Zahlentheorie von Peter Hellekalek Fakultät für Mathematik, Universität Wien, und Fachbereich Mathematik, Universität Salzburg Tel: +43-(0)662-8044-5310 Fax:
Anhang I zur Vorlesung Kryptologie: Elementare Zahlentheorie von Peter Hellekalek Fakultät für Mathematik, Universität Wien, und Fachbereich Mathematik, Universität Salzburg Tel: +43-(0)662-8044-5310 Fax:
TheGI 1: Grundlagen und algebraische Strukturen Prof. Dr.-Ing. Uwe Nestmann - 09. Februar 2010. 2. Schriftliche Leistungskontrolle (EK)
 TheGI 1: Grundlagen und algebraische Strukturen Prof. Dr.-Ing. Uwe Nestmann - 09. Februar 2010 2. Schriftliche Leistungskontrolle (EK) Punktzahl In dieser schriftlichen Leistungskontrolle sind 100 Punkte
TheGI 1: Grundlagen und algebraische Strukturen Prof. Dr.-Ing. Uwe Nestmann - 09. Februar 2010 2. Schriftliche Leistungskontrolle (EK) Punktzahl In dieser schriftlichen Leistungskontrolle sind 100 Punkte
Endlicher Automat (EA)
 Endlicher Automat (EA) siehe auch Formale Grundlagen 3 1 Motivation: Automaten für die Modellierung, Spezifikation und Verifikation verwenden! Definition Ein Endlicher Automat A = (S,I,Σ,T,F) besteht aus
Endlicher Automat (EA) siehe auch Formale Grundlagen 3 1 Motivation: Automaten für die Modellierung, Spezifikation und Verifikation verwenden! Definition Ein Endlicher Automat A = (S,I,Σ,T,F) besteht aus
Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema
 Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema 2x 4 + x 3 + x + 3 div x 2 + x 1 = 2x 2 x + 3 (2x 4 + 2x 3 2x 2 ) x 3 + 2x 2 + x + 3 ( x
Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema 2x 4 + x 3 + x + 3 div x 2 + x 1 = 2x 2 x + 3 (2x 4 + 2x 3 2x 2 ) x 3 + 2x 2 + x + 3 ( x
Binärdarstellung von Fliesskommazahlen
 Binärdarstellung von Fliesskommazahlen 1. IEEE 754 Gleitkommazahl im Single-Format So sind in Gleitkommazahlen im IEEE 754-Standard aufgebaut: 31 30 24 23 0 S E E E E E E E E M M M M M M M M M M M M M
Binärdarstellung von Fliesskommazahlen 1. IEEE 754 Gleitkommazahl im Single-Format So sind in Gleitkommazahlen im IEEE 754-Standard aufgebaut: 31 30 24 23 0 S E E E E E E E E M M M M M M M M M M M M M
Ein polyadisches Zahlensystem mit der Basis B ist ein Zahlensystem, in dem eine Zahl x nach Potenzen von B zerlegt wird.
 Zahlensysteme Definition: Ein polyadisches Zahlensystem mit der Basis B ist ein Zahlensystem, in dem eine Zahl x nach Potenzen von B zerlegt wird. In der Informatik spricht man auch von Stellenwertsystem,
Zahlensysteme Definition: Ein polyadisches Zahlensystem mit der Basis B ist ein Zahlensystem, in dem eine Zahl x nach Potenzen von B zerlegt wird. In der Informatik spricht man auch von Stellenwertsystem,
Kleiner Satz von Fermat
 Kleiner Satz von Fermat Satz Kleiner Satz von Fermat Sei p P. Dann gilt a p a mo p für alle a Z. Wir führen zunächst eine Inuktion für a 0 urch. IA a = 0: 0 p 0 mo p. IS a a+1: Nach vorigem Lemma gilt
Kleiner Satz von Fermat Satz Kleiner Satz von Fermat Sei p P. Dann gilt a p a mo p für alle a Z. Wir führen zunächst eine Inuktion für a 0 urch. IA a = 0: 0 p 0 mo p. IS a a+1: Nach vorigem Lemma gilt
Optimalitätskriterien
 Kapitel 4 Optimalitätskriterien Als Optimalitätskriterien bezeichnet man notwendige oder hinreichende Bedingungen dafür, dass ein x 0 Ω R n Lösung eines Optimierungsproblems ist. Diese Kriterien besitzen
Kapitel 4 Optimalitätskriterien Als Optimalitätskriterien bezeichnet man notwendige oder hinreichende Bedingungen dafür, dass ein x 0 Ω R n Lösung eines Optimierungsproblems ist. Diese Kriterien besitzen
Aufgabentypen die in der Klausur vorkommen
 Aufgabentypen die in der Klausur vorkommen können 1. Nennen Sie fünf wichtige Anwendungsgebiete der Computerlinguistik. 2. Für welches der drei Anwendungsgebiete Maschinelle Übersetzung, Rechtschreibkorrektur
Aufgabentypen die in der Klausur vorkommen können 1. Nennen Sie fünf wichtige Anwendungsgebiete der Computerlinguistik. 2. Für welches der drei Anwendungsgebiete Maschinelle Übersetzung, Rechtschreibkorrektur
Gleichungen Lösen. Ein graphischer Blick auf Gleichungen
 Gleichungen Lösen Was bedeutet es, eine Gleichung zu lösen? Was ist überhaupt eine Gleichung? Eine Gleichung ist, grundsätzlich eine Aussage über zwei mathematische Terme, dass sie gleich sind. Ein Term
Gleichungen Lösen Was bedeutet es, eine Gleichung zu lösen? Was ist überhaupt eine Gleichung? Eine Gleichung ist, grundsätzlich eine Aussage über zwei mathematische Terme, dass sie gleich sind. Ein Term
Musterlösungen zur Linearen Algebra II Blatt 5
 Musterlösungen zur Linearen Algebra II Blatt 5 Aufgabe. Man betrachte die Matrix A := über dem Körper R und über dem Körper F und bestimme jeweils die Jordan- Normalform. Beweis. Das charakteristische
Musterlösungen zur Linearen Algebra II Blatt 5 Aufgabe. Man betrachte die Matrix A := über dem Körper R und über dem Körper F und bestimme jeweils die Jordan- Normalform. Beweis. Das charakteristische
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I. Ulrich Furbach. Sommersemester 2014
 Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Ulrich Furbach Institut für Informatik Sommersemester 2014 Furbach Grundlagen d. Theoretischen Informatik:
Vorlesung Grundlagen der Theoretischen Informatik / Einführung in die Theoretische Informatik I Ulrich Furbach Institut für Informatik Sommersemester 2014 Furbach Grundlagen d. Theoretischen Informatik:
Mengensysteme, Wahrscheinlichkeitsmaße
 Kapitel 1 Mengensysteme, Wahrscheinlichkeitsmaße Der Großteil der folgenden fundamentalen Begriffe sind schon aus der Vorlesung Stochastische Modellbildung bekannt: Definition 1.1 Eine Familie A von Teilmengen
Kapitel 1 Mengensysteme, Wahrscheinlichkeitsmaße Der Großteil der folgenden fundamentalen Begriffe sind schon aus der Vorlesung Stochastische Modellbildung bekannt: Definition 1.1 Eine Familie A von Teilmengen
Frank Weinhold Professur VSR Fakultät für Informatik TU Chemnitz Mai 2011
 Rechnernetze Übung 5 Frank Weinhold Professur VSR Fakultät für Informatik TU Chemnitz Mai 2011 Ziel: Nachrichten fehlerfrei übertragen und ökonomisch (wenig Redundanz) übertragen Was ist der Hamming-Abstand?
Rechnernetze Übung 5 Frank Weinhold Professur VSR Fakultät für Informatik TU Chemnitz Mai 2011 Ziel: Nachrichten fehlerfrei übertragen und ökonomisch (wenig Redundanz) übertragen Was ist der Hamming-Abstand?
Q(n) = n 0 +n 1 +n 2 +...+n k.
 25 2 Kongruenzen Mit Hilfe der hier definierten Kongruenz können Aussagen über Teilbarkeit einfacher formuliert und bewiesen werden, und man erhält eine Differenzierung der Zahlen, die bezüglich einer
25 2 Kongruenzen Mit Hilfe der hier definierten Kongruenz können Aussagen über Teilbarkeit einfacher formuliert und bewiesen werden, und man erhält eine Differenzierung der Zahlen, die bezüglich einer
Lösungen zur Vorrundenprüfung 2006
 Lösungen zur Vorrundenprüfung 2006 Zuerst einige Bemerkungen zum Punkteschema. Eine vollständige und korrekte Lösung einer Aufgabe ist jeweils 7 Punkte wert. Für komplette Lösungen mit kleineren Fehlern
Lösungen zur Vorrundenprüfung 2006 Zuerst einige Bemerkungen zum Punkteschema. Eine vollständige und korrekte Lösung einer Aufgabe ist jeweils 7 Punkte wert. Für komplette Lösungen mit kleineren Fehlern
4.2.4 Reguläre Grammatiken
 4.2.4 Reguläre Grammatiken Eine reguläre Grammatik ist eine kontextfreie Grammatik, deren Produktionsregeln weiter eingeschränkt sind Linksreguläre Grammatik: A w P gilt: w = ε oder w = Ba mit a T und
4.2.4 Reguläre Grammatiken Eine reguläre Grammatik ist eine kontextfreie Grammatik, deren Produktionsregeln weiter eingeschränkt sind Linksreguläre Grammatik: A w P gilt: w = ε oder w = Ba mit a T und
Formale Sprachen und Grammatiken
 Formale Sprachen und Grammatiken Jede Sprache besitzt die Aspekte Semantik (Bedeutung) und Syntax (formaler Aufbau). Die zulässige und korrekte Form der Wörter und Sätze einer Sprache wird durch die Syntax
Formale Sprachen und Grammatiken Jede Sprache besitzt die Aspekte Semantik (Bedeutung) und Syntax (formaler Aufbau). Die zulässige und korrekte Form der Wörter und Sätze einer Sprache wird durch die Syntax
Seminararbeit für das SE Reine Mathematik- Graphentheorie
 Seminararbeit für das SE Reine Mathematik- Graphentheorie Der binäre Rang, der symplektische Graph, die Spektralzerlegung und rationale Funktionen Vortrag am 24.01.2012 Heike Farkas 0410052 Inhaltsverzeichnis
Seminararbeit für das SE Reine Mathematik- Graphentheorie Der binäre Rang, der symplektische Graph, die Spektralzerlegung und rationale Funktionen Vortrag am 24.01.2012 Heike Farkas 0410052 Inhaltsverzeichnis
Kongruenzrechnung. 2 Kongruenzrechnung 7 2.1 Rechnenregeln Addition und Multiplikation... 7 2.2 Rechenregeln bzgl. verschiedener Moduln...
 Kongruenzrechnung Inhaltsverzeichnis 1 Einführung und Definitionen 2 1.1 Einige Beispiele aus dem Alltag..................... 2 1.2 Kongruenzrechnung im Alltag und Rechenproben........... 3 1.3 Kongruenzen
Kongruenzrechnung Inhaltsverzeichnis 1 Einführung und Definitionen 2 1.1 Einige Beispiele aus dem Alltag..................... 2 1.2 Kongruenzrechnung im Alltag und Rechenproben........... 3 1.3 Kongruenzen
Einführung in die Kodierungstheorie
 Einführung in die Kodierungstheorie Einführung Vorgehen Beispiele Definitionen (Code, Codewort, Alphabet, Länge) Hamming-Distanz Definitionen (Äquivalenz, Coderate, ) Singleton-Schranke Lineare Codes Hamming-Gewicht
Einführung in die Kodierungstheorie Einführung Vorgehen Beispiele Definitionen (Code, Codewort, Alphabet, Länge) Hamming-Distanz Definitionen (Äquivalenz, Coderate, ) Singleton-Schranke Lineare Codes Hamming-Gewicht
Zusammenfassung Grundzüge der Informatik 4
 Zusammenfassung Grundzüge der Informatik 4 Sommersemester 04 Thorsten Wink 21. September 2004 Version 1.2 Dieses Dokument wurde in L A TEX 2εgeschrieben. Stand: 21. September 2004 Inhaltsverzeichnis 1
Zusammenfassung Grundzüge der Informatik 4 Sommersemester 04 Thorsten Wink 21. September 2004 Version 1.2 Dieses Dokument wurde in L A TEX 2εgeschrieben. Stand: 21. September 2004 Inhaltsverzeichnis 1
5.1 Drei wichtige Beweistechniken... 55 5.2 Erklärungen zu den Beweistechniken... 56
 5 Beweistechniken Übersicht 5.1 Drei wichtige Beweistechniken................................. 55 5. Erklärungen zu den Beweistechniken............................ 56 Dieses Kapitel ist den drei wichtigsten
5 Beweistechniken Übersicht 5.1 Drei wichtige Beweistechniken................................. 55 5. Erklärungen zu den Beweistechniken............................ 56 Dieses Kapitel ist den drei wichtigsten
4. Übungsblatt zu Mathematik für Informatiker I, WS 2003/04
 4. Übungsblatt zu Mathematik für Informatiker I, WS 2003/04 JOACHIM VON ZUR GATHEN, OLAF MÜLLER, MICHAEL NÜSKEN Abgabe bis Freitag, 14. November 2003, 11 11 in den jeweils richtigen grünen oder roten Kasten
4. Übungsblatt zu Mathematik für Informatiker I, WS 2003/04 JOACHIM VON ZUR GATHEN, OLAF MÜLLER, MICHAEL NÜSKEN Abgabe bis Freitag, 14. November 2003, 11 11 in den jeweils richtigen grünen oder roten Kasten
X = {x 1,x 2,...} sei ein Symbolalphabet eines Kodes. In diesem Kode sind card(x) = X Sachverhalte darstellbar
 3. Kodierung Wir wollen Kodierung nicht als Verschlüsselung zum Zwecke der Geheimhaltung auffassen, sondern als Mittel zur Darstellung von Sachverhalten so, daß eine Rechner mit diesen Sachverhalten umgehen
3. Kodierung Wir wollen Kodierung nicht als Verschlüsselung zum Zwecke der Geheimhaltung auffassen, sondern als Mittel zur Darstellung von Sachverhalten so, daß eine Rechner mit diesen Sachverhalten umgehen
Mathematikaufgaben zur Vorbereitung auf das Studium
 Hochschule für Technik und Wirtschaft Dresden (FH) Fachbereich Informatik/Mathematik Mathematikaufgaben zur Vorbereitung auf das Studium Studiengänge Informatik Medieninformatik Wirtschaftsinformatik Wirtschaftsingenieurwesen
Hochschule für Technik und Wirtschaft Dresden (FH) Fachbereich Informatik/Mathematik Mathematikaufgaben zur Vorbereitung auf das Studium Studiengänge Informatik Medieninformatik Wirtschaftsinformatik Wirtschaftsingenieurwesen
Mathematische Grundlagen 2. Termrechnen
 Inhaltsverzeichnis: 2. Termrechnen... 2 2.1. Bedeutung von Termen... 2 2.2. Terme mit Variablen... 4 2.3. Vereinfachen von Termen... 5 2.3.1. Zusammenfassen von gleichartigen Termen... 5 2.3.2. Vereinfachen
Inhaltsverzeichnis: 2. Termrechnen... 2 2.1. Bedeutung von Termen... 2 2.2. Terme mit Variablen... 4 2.3. Vereinfachen von Termen... 5 2.3.1. Zusammenfassen von gleichartigen Termen... 5 2.3.2. Vereinfachen
Codes und Codegitter. Katharina Distler. 27. April 2015
 Codes und Codegitter Katharina Distler 7. April 015 Inhaltsverzeichnis 1 Codes 4 Codegitter 14 Einleitung Die folgende Seminararbeit behandelt das Konzept von Codes und Codegittern. Da sie bei der Informationsübertragung
Codes und Codegitter Katharina Distler 7. April 015 Inhaltsverzeichnis 1 Codes 4 Codegitter 14 Einleitung Die folgende Seminararbeit behandelt das Konzept von Codes und Codegittern. Da sie bei der Informationsübertragung
REG versus CF. Theorem REG ist echt in CF enthalten.
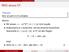 REG versus CF Theorem REG ist echt in CF enthalten. Beweis: Wir wissen: L = {a m b m m 1} ist nicht regulär. Andererseits ist L kontextfrei, wie die einfache kontextfreie Grammatik G = ({a, b}, {S}, S,
REG versus CF Theorem REG ist echt in CF enthalten. Beweis: Wir wissen: L = {a m b m m 1} ist nicht regulär. Andererseits ist L kontextfrei, wie die einfache kontextfreie Grammatik G = ({a, b}, {S}, S,
7. Formale Sprachen und Grammatiken
 7. Formale Sprachen und Grammatiken Computer verwenden zur Verarbeitung von Daten und Informationen künstliche, formale Sprachen (Maschinenspr., Assemblerspachen, Programmierspr., Datenbankspr., Wissensrepräsentationsspr.,...)
7. Formale Sprachen und Grammatiken Computer verwenden zur Verarbeitung von Daten und Informationen künstliche, formale Sprachen (Maschinenspr., Assemblerspachen, Programmierspr., Datenbankspr., Wissensrepräsentationsspr.,...)
Grundlagen der Theoretischen Informatik, SoSe 2008
 1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
1. Aufgabenblatt zur Vorlesung Grundlagen der Theoretischen Informatik, SoSe 2008 (Dr. Frank Hoffmann) Lösung von Manuel Jain und Benjamin Bortfeldt Aufgabe 2 Zustandsdiagramme (6 Punkte, wird korrigiert)
KAPITEL 0. Einführung
 Lineare Algebra KAPITEL 0 Einführung Dieses Skript zur Vorlesung Lineare Algebra an der Goethe Universität Frankfurt im Sommersemester 2011 befindet sich noch in der Entstehung und wird fortlaufend aktualisiert
Lineare Algebra KAPITEL 0 Einführung Dieses Skript zur Vorlesung Lineare Algebra an der Goethe Universität Frankfurt im Sommersemester 2011 befindet sich noch in der Entstehung und wird fortlaufend aktualisiert
Übungen zum Ferienkurs Lineare Algebra WS 14/15
 Übungen zum Ferienkurs Lineare Algebra WS 14/15 Linearkombinationen, Basen, Lineare Abbildungen 2.1 Lineare Unabhängigkeit Sind die folgenden Vektoren linear unabhängig? (a) 1, 2, 3 im Q Vektorraum R (b)
Übungen zum Ferienkurs Lineare Algebra WS 14/15 Linearkombinationen, Basen, Lineare Abbildungen 2.1 Lineare Unabhängigkeit Sind die folgenden Vektoren linear unabhängig? (a) 1, 2, 3 im Q Vektorraum R (b)
Das Briefträgerproblem
 Das Briefträgerproblem Paul Tabatabai 30. Dezember 2011 Inhaltsverzeichnis 1 Problemstellung und Modellierung 2 1.1 Problem................................ 2 1.2 Modellierung.............................
Das Briefträgerproblem Paul Tabatabai 30. Dezember 2011 Inhaltsverzeichnis 1 Problemstellung und Modellierung 2 1.1 Problem................................ 2 1.2 Modellierung.............................
V 2 B, C, D Drinks. Möglicher Lösungsweg a) Gleichungssystem: 300x + 400 y = 520 300x + 500y = 597,5 2x3 Matrix: Energydrink 0,7 Mineralwasser 0,775,
 Aufgabenpool für angewandte Mathematik / 1. Jahrgang V B, C, D Drinks Ein gastronomischer Betrieb kauft 300 Dosen Energydrinks (0,3 l) und 400 Liter Flaschen Mineralwasser und zahlt dafür 50, Euro. Einen
Aufgabenpool für angewandte Mathematik / 1. Jahrgang V B, C, D Drinks Ein gastronomischer Betrieb kauft 300 Dosen Energydrinks (0,3 l) und 400 Liter Flaschen Mineralwasser und zahlt dafür 50, Euro. Einen
DLP. Adolphe Kankeu Tamghe papibobo@informatik.uni-bremen.de ALZAGK SEMINAR. Bremen, den 18. Januar 2011. Fachbereich Mathematik und Informatik 1 / 27
 DLP Adolphe Kankeu Tamghe papibobo@informatik.uni-bremen.de Fachbereich Mathematik und Informatik ALZAGK SEMINAR Bremen, den 18. Januar 2011 1 / 27 Inhaltsverzeichnis 1 Der diskrete Logarithmus Definition
DLP Adolphe Kankeu Tamghe papibobo@informatik.uni-bremen.de Fachbereich Mathematik und Informatik ALZAGK SEMINAR Bremen, den 18. Januar 2011 1 / 27 Inhaltsverzeichnis 1 Der diskrete Logarithmus Definition
Algorithmen II Vorlesung am 15.11.2012
 Algorithmen II Vorlesung am 15.11.2012 Kreisbasen, Matroide & Algorithmen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales
Algorithmen II Vorlesung am 15.11.2012 Kreisbasen, Matroide & Algorithmen INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Landes Baden-Württemberg und Algorithmen nationales
Grammatiken und die Chomsky-Hierarchie
 Grammatiken und die Chomsky-Hierarchie Def.: Eine Grammatik G=(Σ,V,S,R) besteht aus endlichem Alphabet Σ endlicher Variablenmenge V mit V Σ= Startsymbol SєV endlicher Menge R с (V Σ) + x(v Σ)* von Ableitungsregeln
Grammatiken und die Chomsky-Hierarchie Def.: Eine Grammatik G=(Σ,V,S,R) besteht aus endlichem Alphabet Σ endlicher Variablenmenge V mit V Σ= Startsymbol SєV endlicher Menge R с (V Σ) + x(v Σ)* von Ableitungsregeln
Erinnerung/Zusammenfassung zu Abbildungsmatrizen
 Erinnerung/Zusammenfassung zu Abbildungsmatrizen Thomas Coutandin (cthomas@student.ethz.ch) 7. November 2 Abbildungsmatrizen Im Folgenden betrachten wir stets endlich dimensionale K-Vektorräume (K irgend
Erinnerung/Zusammenfassung zu Abbildungsmatrizen Thomas Coutandin (cthomas@student.ethz.ch) 7. November 2 Abbildungsmatrizen Im Folgenden betrachten wir stets endlich dimensionale K-Vektorräume (K irgend
Aufgaben des MSG-Zirkels 10b Schuljahr 2007/2008
 Aufgaben des MSG-Zirkels 10b Schuljahr 2007/2008 Alexander Bobenko und Ivan Izmestiev Technische Universität Berlin 1 Hausaufgaben vom 12.09.2007 Zahlentheorie 1 Aufgabe 1.1 Berechne die (quadratischen)
Aufgaben des MSG-Zirkels 10b Schuljahr 2007/2008 Alexander Bobenko und Ivan Izmestiev Technische Universität Berlin 1 Hausaufgaben vom 12.09.2007 Zahlentheorie 1 Aufgabe 1.1 Berechne die (quadratischen)
Formale Grundlagen der Informatik 1 Kapitel 12 Zusammenfassung
 Formale Grundlagen der Informatik 1 Kapitel 12 Zusammenfassung Frank Heitmann heitmann@informatik.uni-hamburg.de 13. Mai 2014 Frank Heitmann heitmann@informatik.uni-hamburg.de 1/17 Überblick Wir hatten
Formale Grundlagen der Informatik 1 Kapitel 12 Zusammenfassung Frank Heitmann heitmann@informatik.uni-hamburg.de 13. Mai 2014 Frank Heitmann heitmann@informatik.uni-hamburg.de 1/17 Überblick Wir hatten
Single Parity check Codes (1)
 Single Parity check Codes (1) Der Single Parity check Code (SPC) fügt zu dem Informationsblock u = (u 1, u 2,..., u k ) ein Prüfbit (englisch: Parity) p hinzu: Die Grafik zeigt drei Beispiele solcher Codes
Single Parity check Codes (1) Der Single Parity check Code (SPC) fügt zu dem Informationsblock u = (u 1, u 2,..., u k ) ein Prüfbit (englisch: Parity) p hinzu: Die Grafik zeigt drei Beispiele solcher Codes
1. Formale Sprachen 1.2 Grammatiken formaler Sprachen
 1. Formale Sprachen 1.2 Grammatiken formaler Sprachen Die Regeln zur Bildung korrekter Wörter einer Sprache kann man in einer natürlichen Sprache formulieren. Da dies jedoch wieder Mehrdeutigkeiten mit
1. Formale Sprachen 1.2 Grammatiken formaler Sprachen Die Regeln zur Bildung korrekter Wörter einer Sprache kann man in einer natürlichen Sprache formulieren. Da dies jedoch wieder Mehrdeutigkeiten mit
Mathematik für Informatiker II. Beispiellösungen zur Probeklausur. Aufgabe 1. Aufgabe 2 (5+5 Punkte) Christoph Eisinger Sommersemester 2011
 Mathematik für Informatiker II Christoph Eisinger Sommersemester 211 Beispiellösungen zur Probeklausur Aufgabe 1 Gegeben sind die Polynome f, g, h K[x]. Zu zeigen: Es gibt genau dann Polynome h 1 und h
Mathematik für Informatiker II Christoph Eisinger Sommersemester 211 Beispiellösungen zur Probeklausur Aufgabe 1 Gegeben sind die Polynome f, g, h K[x]. Zu zeigen: Es gibt genau dann Polynome h 1 und h
Was ist Mathematik? Eine Strukturwissenschaft, eine Geisteswissenschaft, aber keine Naturwissenschaft.
 Vorlesung 1 Einführung 1.1 Praktisches Zeiten: 10:00-12:00 Uhr Vorlesung 12:00-13:00 Uhr Mittagspause 13:00-14:30 Uhr Präsenzübung 14:30-16:00 Uhr Übungsgruppen Material: Papier und Stift wacher Verstand
Vorlesung 1 Einführung 1.1 Praktisches Zeiten: 10:00-12:00 Uhr Vorlesung 12:00-13:00 Uhr Mittagspause 13:00-14:30 Uhr Präsenzübung 14:30-16:00 Uhr Übungsgruppen Material: Papier und Stift wacher Verstand
Diskrete Mathematik für Informatiker
 Diskrete Mathematik für Informatiker Markus Lohrey Universität Siegen Wintersemester 2014/2015 Lohrey (Universität Siegen) Diskrete Mathematik Wintersem. 2014/2015 1 / 344 Organisatorisches zur Vorlesung
Diskrete Mathematik für Informatiker Markus Lohrey Universität Siegen Wintersemester 2014/2015 Lohrey (Universität Siegen) Diskrete Mathematik Wintersem. 2014/2015 1 / 344 Organisatorisches zur Vorlesung
Primzahlen im Schulunterricht wozu?
 Primzahlen im Schulunterricht wozu? FRANZ PAUER, FLORIAN STAMPFER (UNIVERSITÄT INNSBRUCK) 1. Einleitung Eine natürliche Zahl heißt Primzahl, wenn sie genau zwei Teiler hat. Im Lehrplan der Seundarstufe
Primzahlen im Schulunterricht wozu? FRANZ PAUER, FLORIAN STAMPFER (UNIVERSITÄT INNSBRUCK) 1. Einleitung Eine natürliche Zahl heißt Primzahl, wenn sie genau zwei Teiler hat. Im Lehrplan der Seundarstufe
Mathematische Grundlagen der Kryptographie. 1. Ganze Zahlen 2. Kongruenzen und Restklassenringe. Stefan Brandstädter Jennifer Karstens
 Mathematische Grundlagen der Kryptographie 1. Ganze Zahlen 2. Kongruenzen und Restklassenringe Stefan Brandstädter Jennifer Karstens 18. Januar 2005 Inhaltsverzeichnis 1 Ganze Zahlen 1 1.1 Grundlagen............................
Mathematische Grundlagen der Kryptographie 1. Ganze Zahlen 2. Kongruenzen und Restklassenringe Stefan Brandstädter Jennifer Karstens 18. Januar 2005 Inhaltsverzeichnis 1 Ganze Zahlen 1 1.1 Grundlagen............................
Lineare Algebra - alles was man wissen muß
 Statistik für Bioinformatiker SoSe 3 Rainer Spang Lineare Algebra - alles was man wissen muß Der Titel ist natürlich gelogen, aber was wir hier zusammengetragen haben ist zumindest ein Anfang. Weniger
Statistik für Bioinformatiker SoSe 3 Rainer Spang Lineare Algebra - alles was man wissen muß Der Titel ist natürlich gelogen, aber was wir hier zusammengetragen haben ist zumindest ein Anfang. Weniger
