Erklären Sie, mit welcher Grundidee die Ableitung einer Funktion f an der Stelle x 0 definiert ist? Man bildet den Differenzenquotienten y
|
|
|
- Nelly Beutel
- vor 6 Jahren
- Abrufe
Transkript
1 I. Methode y x ; f (x 0 ) I. Methode y x ; f (x 0 ) Erklären Sie, mit welcher Grundidee die Ableitung einer Funktion f an der Stelle x 0 definiert ist? Man bildet den Differenzenquotienten y x und dann den Grenzwert für x 0. Wenn dieser Grenzwert existiert, nennt man dies f (x 0 ). I. Beispiel y x ; f (x 0 ) I. Beispiel - Lösung y x ; f (x 0 ) Zusatz: Bestimmen Sie ohne Anwendung der Ableitungsregeln die Ableitung f (2) der Funktion f(x) = x 2 + an der Stelle x 0 = 2. y = f(2+h) f(2) =... = h2 +4h = h + 4 x h h lim(h + 4) = 4 h 0 - Lösung I.2 Methode grafische Ableitung I.2 Methode grafische Ableitung Wie geht man vor, wenn man, ausgehend vom Schaubild der Funktion, grafisch das Schaubild der Ableitung zeichnen soll?. Man untersucht die Stellen mit f (x i ) = 0 und markiert diese Stellen auf der x-achse. 2. Man berücksichtigt den entsprechenden VZW an diesen Stellen und zeichnet die Ableitungsfunktion ein Lösung I.2 Beispiel grafische Ableitung I.2 Beispiel grafische Ableitung Gegeben ist G f. Skizzieren Sie das Schaubild der Ableitungsfunktion G f Lösung
2 I.3 Methode grafische Aufleitung Wie geht man vor, wenn man, ausgehend vom Schaubild der Ableitungsfunktion, grafisch das Schaubild einer Aufleitungsfunktion erstellen soll? I.3 Methode grafische Aufleitung. Spätere Hop/Tip als Senkrechte markieren = Stellen mit f (x) = 0 und VZW 2. Extremstellen von f (spätere Wep) als Senkrechte markieren 3. Eine Randbedingung als Punkt markieren 4. Alle Infos sinnvoll verbinden / verarbeiten Lösung I.3 Beispiel grafische Aufleitung I.3 Beispiel grafische Aufleitung Gegeben ist das Schaubild einer Ableitungsfunktion f. Skizzieren Sie das Schaubild der Funktion f mit f( ) = Lösung I 2. Beispiel Ableitungsregeln I 2. Beispiel Ableitungsregeln Bilden Sie die erste Ableitung (ohne Quotientenoder gar Produktregel!!!): f(x) = 6x3 + 2x 2 + 4x. (9/2f) 2x f(x) = 3x 2 + x + 2 f (x) = 6x Lösung I 2.2 Beispiel Ableitungsregeln I 2.2 Beispiel Ableitungsregeln Bilden Sie die erste Ableitung: f t (x) = tx 3 + 3tx 2 7x + t. (9/5b) f t(x) = 3tx 2 + 6tx Lösung
3 I 2.3 Methode Berührung... Die Schaubilder der Funktionen f und g (a) berühren sich (b) schneiden sich orthogonal in einem Punkt P. Beschreiben Sie, welche Bedingungen erfüllt sein müssen. I 2.3 Methode Berührung... Für die Berührung:. f(u) = g(u), d.h. Schnittbedingung, und 2. f (u) = g (u), d.h. gleiche Steigung für den orthogonalen Schnitt:. f(u) = g(u), d.h. Schnittpunkt und 2. f (u) g (u) =, d.h. orthogonale Steigung Bemerkung: Falls eine der Funktionen eine Funktionenschar f t ist, ergibt sich damit ein Gleichungssysteme (2 Gl mit 2 Var u und t); Lösung: späteren Berührstellen u und Scharparameter t Lösung I 2.3 Beispiel Berührung... I 2.3 Beispiel Berührung... (a) Gegeben sind die Funktionen f mit f(x) = x 3 x und g mit g(x) = x 2 + 4x 3. Zeigen Sie, dass sich ihre Graphen berühren. (b) Gegeben sind die Funktionen f mit f(x) = x 3 und g mit g(x) = ax Bestimmen Sie den Parameter a so, dass sich die Schaubilder von g und f orthogonal schneiden. (GTR) a) f = g x = ; x 2 = 5 mögl. Bstellen; 3 da f() = g() = 0 ist diese Stelle eine Berührstelle, während x 2 = 5 mit f( 5) g( 5) keine Berührstelle ist. b) f = führt zu a = (.Gl); g 6x 3 f = g und (.Gl) eingesetzt: x 4 2x + = 0, 6 mit GTR gelöst: x = 0, 0833; a = 287, 75 und x 2 =, 286; a 2 = 0, Lösung I 3 Methode Krümmung I 3 Methode Krümmung Wie ist die Rechts- bzw. Linkskurve eines Graphen festgelegt? Eine (math. negative) Rechtskrümmung (im Uhrzeigersinn) liegt vor, wenn. die Tangentensteigung kleiner wird oder 2. f monoton fallend ist oder 3. f negativ ist. Beispiel: y = x 2 Analog gilt für die Linkskrümmung: f monoton steigend oder f > 0 Beispiel: y = x Lösung I 3 Beispiel Krümmung I 3 Beispiel Krümmung Es ist f(x) = 3 x3 x 2 x + 5. Überprüfen Sie 3 rechnerisch auf Links- bzw. Rechtskurve. (23/8b) f (x) = 2x 2 > 0 x >, d.h. für x > Linkskurve, für x < Rechtskurve Lösung
4 I 4 Methode Extrema Wie geht man vor, wenn man eine Funktion auf Extremstellen untersuchen muss? I 4 Methode Extrema. notwendige Bedingung: f (x) = 0 mögliche Extremstellen x i 2. hinreichende Bdg: (2.a) VZW von f an der Stelle x i ; falls : HOP, falls : TIP oder (2.b) f (x i ) < 0: HOP; f (x i ) > 0: TIP falls f (x i ) = 0 muss man (2.a) durchführen! Lösung I 4 Beispiel Extrema I 4 Beispiel Extrema Bestimmen Sie die Extremstellen der Funktion f mit f(x) = 2x 3 3x 2 +. (27/7a) x = 0 HOP-Stelle; x = TIP-Stelle Lösung I 5. Methode Wendepunkte I 5. Methode Wendepunkte Wie geht man vor, wenn man eine Funktion auf Wendepunkte untersuchen muss?. notwendige Bedingung: f (x) = 0 mögliche Wendetellen x i 2. hinreichende Bdg: (2.a) VZW von f an der Stelle x i oder (2.b) f (x i ) 0: WEP falls f (x i ) = 0 muss man (2.a) durchführen!) Lösung I 5. Beispiel Wendepunkte I 5. Beispiel Wendepunkte Bestimmen Sie die Wendepunkte der Funktion f mit f(x) = 0, 5x 4 + 2x 2. (30/6b) notw: f (x) = 6x = 0 x /2 = ± 2/3 mögl. Wep hinr: f (x) = 2x; ) f (x i ) 0 W /2 (± Lösung
5 I 5.2 Methode Wendetangente I 5.2 Methode Wendetangente Wie geht man vor, wenn man die Wendetangente eines Schaubilds bestimmen soll? (mit/ohne GTR). Wep bestimmen W (x W y W ) 2. mit dem GTR die Tangente bestimmen oder von Hand: (PSF) m = f (x W ); y = m(x x W ) + y W Lösung I 5.2 Beispiel Wendetangente I 5.2 Beispiel Wendetangente Bestimmen Sie die Gleichung der Tangente im Wendepunkte des Graphen von f mit f(x) = 6 x3 0, 75x (3/a) W (, ); m = f (, 5) = 9 8 PSF y = 9 8 x Lösung I 6. Methode ATG I 6. Methode ATG Es gibt drei Problemtypen im Umkreis der Tangente. Welche? Wie werden sie jeweils gelöst? (mit GTR). Tangente in B(u f(u)) des Schaubilds: im GTR direkt oder PSF: y = f (u)(x u) + y B 2. Tangente mit gegebener Steigung m: Gleichung: f (x) = m lösen x i. Dann wie. 3. Tangente von außen durch P (a b) oft GTR: ATG so(!) notieren: y = f (u)(x u) + f(u) P einsetzen: b = f (u)(a u) + f(u) b f (u)(a u) = f(u) Bemerkung: im GTR sieht dies so aus: Y = f(x); y 2 = nderive(y, X, X); y 3 = b Y 2 (a X) Gleichung in u lösen (d.h. Schnitt Y Y 3 ). Dann wie Lösung I 6. Beispiel ATG I 6. Beispiel ATG Gegeben ist die Funktion f mit f(x) = 0, 5x 3 2x 2 +. Bestimmen Sie (mit GTR) jeweils die Gleichung der Tangente im Punkt B(4 f(4)) mit der Steigung,5.. y = 8x 3 2. u = 3 ; u 2 = 3 t : y =, 5x +, 259; t 2 : y =, 5x 8 3. B(, 5); y = 5, 5x die durch den Punkt P (0 4) geht. - Lösung
6 I 6.2 Methode Normale I 6.2 Methode Normale Gegeben ist der Graph einer Funktion f. Was versteht man unter einer Normalen und wie kann man sie bestimmen? Eine Normale steht orthogonal zu einer Tangente, sie schneidet das Schaubild senkrecht im Berührpunkt B(u f(u)) der zugehörigen Tangente mit dem Schaubild. m = PSF y = m(x u) + y f (u) B Lösung I 6.2 Beispiel Normale I 6.2 Beispiel Normale Bestimmen Sie die Gleichung der Normalen des Graphen von f mit f(x) = im Punkt x B(4 3).(33/5b) n: y = 4(x 4) + 3 = 4x 3 Tangente t: y = 0, 25x Lösung I 8.. Beispiel Mini-Max (GTR) I 8.. Beispiel Mini-Max (GTR) Gegeben sind die Funktionen f und g durch f(x) = x 2 + und g(x) = (x 2) Für welche Werte x [0; 2] wird die Differenz der Funktionswerte minimal? (40/) d(x) = f(x) g(x) mit GTR (Skizze!!!) im GTR: Y = f(x); Y 2 = g(x); Y 3 = abs(y Y 2 ) T ( ); Lösung: für x = Lösung I 8..2 Beispiel Mini-Max (GTR) I 8..2 Beispiel Mini-Max (GTR) Gegeben ist die Funktion f(x) = 2x(3 x) 2. Für welche Stelle x [0; 3] wird der Abstand zum Ursprung extremal? d(x) = x 2 + f(x) 2 mit GTR (Skizze!!!) H(, 0 8, 06); T (2, 629 2, 727) Max bei x =, 0; Min bei x = 2, 629 im GTR: Y = f(x); Y 2 = (X 2 + Y 2 ) Lösung
7 I 8.2. Beispiel Flächen (GTR) I 8.2. Beispiel Flächen (GTR) Gegeben ist die Funktion f mit f(x) = x Die Koordinatenachsen und ihre Parallelen durch den Punkt P (u f(u)) legen ein Rechteck fest. Für welches u [0; 2] ist der Flächeninhalt des Rechtecks am größten? A(u) = u f(u) mit GTR (Skizze!!!) H(, 5 3, 08); Lösung: für u =, Lösung I Beispiel Flächen (GTR) I Beispiel Flächen (GTR) Gegeben ist die Funktion f mit f(x) = x 3 + 6x 2 + 9x. Die Punkte A(u f(u)), B(0 0) und C(u 0) legen ein Dreieck fest. Für welches u [ 3; 0] wird der Flächeninhalt des Dreiecks am größten? A(u) = 0, 5u f(u) mit GTR (Skizze!!!) H(, 5 2, 5); Lösung: u =, 5 Hinweis: da u < 0 und f(u) < 0 ist obiger Ansatz sinnvoll. Eigentlich müsste stehen: A(u) = 0, 5 ( u) ( f(u)) = 0, 5u f(u) Lösung
8 II Methode Verkettung Beschreiben Sie, was man unter einer Verkettung von Funktionen versteht. Was unterscheidet f g und g f? Geben Sie ein Beispiel. II Methode Verkettung Die Hintereinanderausführung bei einer Funktionstermberechnung. Etwa bei f(x) = (2x 3) 4 wird, wenn man f() berechnen will, zuerst g() = 2 3 = und dann f(g()) = f( ) = ( ) 4 = berechnet. Man muss also f(g) = g 4 nach g(x) = 2x 3 berechnen: f g: f nach g g nach f wäre: zuerst hoch 4 und dann mal 2-3 also g(f(x)) = 2x Lösung II Beispiel Verkettung II Beispiel Verkettung Die Funktion f kann als Verkettung u v aufgefasst werden. Nennen Sie die Funktionen u und v. Wie lautet die Funktion g = v u? (a) f(x) = x + 2 und (b) f(x) = sin(x 2 ) (a) v(x) = x + 2; u(x) = x f(x) = u(v(x)) = u(x + 2) = x + 2 g(x) = v(u(x)) = v( x) = x + 2 (b) v(x) = x 2 ; u(x) = sin x f(x) = u(v(x)) = u(x 2 ) = sin(x 2 ) g(x) = v(u(x)) = v(sin x) = (sin x) 2 - Lösung II 2 Methode Kettenregel II 2 Methode Kettenregel Wie lautet die Kettenregel für Ableitungen? innere Ableitung mal äußere Ableitung f(g(x)) = f (g(x)) g (x) Lösung II 2 Beispiel Kettenregel II 2 Beispiel Kettenregel Leiten Sie ab: (60/4ah) (a) f(x) = 0, 25 sin(2x + π) (b) g(x) = 7x 2 5. (a) f (x) = 0, 25 cos(2x + π) 2 = 0, 5 cos(2x + π) (b) f 7x (x) = 7x2 5 Regel: f(x) = g(x)) f (x) = g (x) 2 g(x) Lösung
9 II 3 Methode Produktregel II 3 Methode Produktregel Wie lautet die Produktregel für Ableitungen? f(x) = u(x) v(x) f (x) = u (x)v(x) + u(x)v (x) Lösung II 3 Beispiel Produktregel II 3 Beispiel Produktregel Leiten Sie ab: (63/2ge) (a) f(x) = 3x sin 2 (x) (b) f(x) = (5 4x) 3 x 2. (a) f (x) = 3 sin x(sin x + 2x cos x) (b) f (5 4x)2 (x) = (4x + 0) x Lösung II 4. Methode Quotientenregel II 4. Methode Quotientenregel Wie lautet die Quotientenregel für Ableitungen? f(x) = u(x) v(x) f (x) = u (x)v(x) u(x)v (x) (v(x)) Lösung II 4. Beispiel Quotientenregel II 4. Beispiel Quotientenregel Leiten Sie ab: (65/3ad) (a) f(x) = x2 (x + 4) 2 (b) f(x) = 2x 3. 2x (a) f (x) = 2x2 + 6x 8 (x + 4) 3 (b) f 7 4x (x) = 4x 2 2x Lösung
10 II 4.2. Beispiel keine QuotRegel!! II 4.2. Beispiel keine QuotRegel!! Leiten Sie ab: (65/4ab) (a) f(x) = 3 5 2x (b) f(x) = (x 2 ) 3 (a) f(x) = 3(5 2x) f (x) = 3(5 2x) 2 ( 2) = 6 (5 2x) 2 (b) f(x) = (x 2 ) 3 f (x) = 3(x 2 ) 4 2x = 6x (x 2 ) Lösung II Beispiel keine QuotRegel!! II Beispiel keine QuotRegel!! Leiten Sie ab: (65/4cd) (a) f(x) = x 3x2 x 3 (b) f(x) = 6x2 + x 3 3x (a) f(x) = x 2 3 x = x 2 3x f (x) = 2x 3 + 3x 2 = 2 x x 2 = 3x 2 x 3 (b) f(x) = 2x + 3 x = 2x + 3 x f (x) = 2 + x 2 = 2 + x Lösung II 5. Beispiel Exponentialfunktion II 5. Beispiel Exponentialfunktion Bilden Sie die erste Ableitung: (67/j, 3f) (a) f(x) = 0, 4e 5x (b) f(x) = ex + x. (a) f (x) = 2e 5x (b) f (x) = xex e x x Lösung II 5.2 Beispiel Exponentialfunktion II 5.2 Beispiel Exponentialfunktion Bestimmen Sie die Extrem- und Wendepunkte des Graphen von f(x) = x 2 e 0,5x. (68/9d) T (0 0); H( 4 6 e 2 ) W (, 7...); W 2 ( 6, 83...) Lösung
11 II 6 Methode Logarithmus Erkläre die Funktion f(x) = ln x. (Definition von ln x; Besonderheiten des Schaubilds) II 6 Methode Logarithmus y = ln x entsteht aus y = e x durch eine Spiegelung an der. Winkelhalbierenden y = x (Umkehrfunktion: Die Blickrichtung hat sich geändert. Normalerweise schaut man bei Funktionen vom x-wert zum y-wert; bei einer Umkehrfunktion aber vom y-wert zum x-wert. Wenn man aber die übliche Blickrichtung beibehalten will, muss man eine Variablenumbenennung vornehmen: y = e x x = ln y; führt zu: y = ln x.) Lösung II 6 Beispiel Logarithmus II 6 Beispiel Logarithmus Löse die Gleichungen: (70/2g, 8gh) (a) 2e 3x+4 = 2 e (b) e 2x 6 (5 e 3x ) = 0 (c) 2e x + 5 = 8e x. (a) x = 5 3 (b) x = 3 ln 5 (c) Subst: u = e x 2u 2 + 5u 8 = 0 u = 0, 5; u 2 = 6 x = ln(0, 5); x 2 : k.l Lösung II 7. Beispiel Funktionenschar II 7. Beispiel Funktionenschar Welchen Einfluss haben die Parameter (a) in f t (x) = x 2 + tx und (b) in f(x) = sin(tx). (73/ci) (a) f t (x) = x(x + t). Alle Schaubilder sind nach oben geöffnete Normalparabeln und gehen durch den Ursprung und haben als weitere Nullstelle N 2 ( t 0). (b) t bewirkt eine Streckung/Stauchung in x-richtung: Periode p = 2π t Lösung II 7.2 Beispiel Funktionenschar II 7.2 Beispiel Funktionenschar Gegeben ist die Funktionenschar f t mit f t (x) = e tx 4. (a) Welche Steigung hat f t an der Stelle 0? (b) Für welchen Wert von t ist diese Steigung? (73/3b) (a) f t(0) = t (b) f t(x) = t = - Lösung
12 III Methode Größe aus f Erkläre, wie man von (dem Schaubild) der Änderungsrate einer Größe auf den Bestand der Größe schließen kann. Gib ein Beispiel dazu. III Methode Größe aus f. Man muss den Flächeninhalt zwischen Schaubild und x-achse abschätzen. 2. Die FE beträgt das Produkt aus x-achsen-einheit und y-achseneinheit. 3. Zum Abschätzen kann man Rechtecke (Ober-/Untersumme) oder Trapeze verwenden. 4. am besten: Trapezformel: für jedes Trapez neu berechnen: r = rechter Rand; l = linker Rand f(r) + f(l) A i = m h = TrapezBreite 2 - Lösung III Beispiel Größe aus f III Beispiel Größe aus f Bei einem Auto werden folgende Geschwindigkeiten gemessen. t [s] v [m/s] 2 2,5 3, Bestimmen Sie einen Schätzwert für die in diesem Zeitraum zurückgelegte Strecke. s = 494, 75 m (Trapezmethode) - Lösung III 2 Methode Integral III 2 Methode Integral Was ist die Grundidee beim Integral? Wie kann ein Integral positiv bzw. negativ werden? Grundidee: Summe von unendlich vielen Rechtecken (Ober- / Untersumme). Der Grenzwert dieses Rechteckflächen muss für die Ober- und Untersumme gleich sein. Ein Integral b a f(x) dx wird dann positiv, wenn. f(x) > 0 im Intervall und 2. a < b (übliche Integrationsrichtung) oder beides umgekehrt, also f(x) < 0 und a > b Lösung III 2 Beispiel Integral III 2 Beispiel Integral Entscheiden Sie ohne Rechnung, ob das Integral positiv, negativ oder null ist: (94/7abd*e) (a) (c*) x 2 dx e x dx (b) (d) 0 4π 0 x 4 dx sin(x) dx (a), da f(x) > 0 (übliche Integrationsrichtung) (b), da f(x) < 0 (übliche Integrationsrichtung) (c*), da f(x) > 0 (neg. Integrationsrichtung) (d) 0, da sich die beiden Flächen gegenseitig aufheben (Integrationsrichtung egal) Lösung
13 III 3 Methode Hauptsatz Erläutere den Hauptsatz der Differential- und Integralrechnung. III 3 Methode Hauptsatz Der Kern besteht darin, dass die Ableitung einer Flächeninhaltsfunktion A a (x) die Randfunktion x f(x) ergibt, kurz: mit A a (x) = f(t) dt Hauptsatz: A a(x) = f(x), d.h. A a ist eine Stammfunktion von f! Eine Folge davon ist, dass b a f(x) dx = [F (x)] b a = F (b) F (a). a Lösung III 3 Beispiel Hauptsatz III 3 Beispiel Hauptsatz Berechne (ohne GTR) das Integral: (97/4b; 6d) 4 (a) x 2 dx 2 2 (b) 0, 5x dx 4 2 (c) 4x 3 3x 2 dx t (a) (b) 3 (c) t 3 t Lösung III 4. Beispiel Stammfunktionen III 4. Beispiel Stammfunktionen Bestimmen Sie eine Stammfunktion: (0/h; 2d; 02/2c) (a) f(x) = cos(4x π) (b) f(x) = 3 4x (c) f(x) = (2x 3) 2 (a) F (x) = sin(4x π) 0, 25 (b) f(x) = (3 4x) F (x) = ln( 3 4x ) 4 = 0, 25 ln( 3 4x ) (c) f(x) = (2x 3) 3 F (x) = 2 (2x 3) 2 2 = 4(2x 3) 2 (d) f(x) = + x + x3 3x 3 (d) f(x) = 3 x x F (x) = 6x 2 3x + 3 x Lösung III 4.2 Beispiel Stammfunktionen III 4.2 Beispiel Stammfunktionen Welche Stammfunktion von f mit f(t) = 2e 0,5t hat an der Stelle 0 den Funktionswert? (02/3c) F (t) = 4e 0,5t + c F (0) = 4 + c = x = Lösung
14 III 5. Methode Integralfunktion Was ist eine Integralfunktion I a von einer Funktion f zu einer unteren Schranke a? Wie geht man vor, wenn man eine Integralfunktion I a zu einem gegebenen Schaubild G f zu einer unteren Schranke a zeichnen soll? III 5. Methode Integralfunktion Anschaulich: die Fläche zwischen dem Schaubild x und der x-achse ab der Stelle a: I a (x) = f(t) dt. Spätere Hop/Tip als Senkrechte markieren = Nullstellen von f 2. Spätere Wep als Senkrechte markieren = Extrempunkte von f 3. (a 0) als ein Punkt von I a einzeichnen da I a (a) = a f(t) dt = 0 a 4. Die Infos sinnvoll verbinden. a Lösung III 5. Beispiel Integralfunktion III 5. Beispiel Integralfunktion Die Funktion v mit v(t) = 30(e 0,3t ) beschreibt die Geschwindigkeit eines Autos (t in s, v(t) in m/s). (GTR) (a) Wie weit fährt das Auto in 0 t 4? Wie lange benötigt das Auto für die Strecke von 60 m... (b)... aus dem Stand; (c)... ab dem Zeitpunkt t = 4? (a) s = 4 0 (b) s(t) = (c) s(t) = v(t) dt = 50, 9 m t 0 t 4 v(x) dx = 60 t = 4, 458 s (GTR) v(x) dx = 60 t = 6, 534 s (GTR) Lösung III 5.2. Beispiel grafische Aufleitung III 5.2. Beispiel grafische Aufleitung Skizzieren Sie die Integralfunktion zum Schaubild von f zur unteren Schranke a = Lösung III Beispiel grafische Aufleitung III Beispiel grafische Aufleitung Gegeben sind f, f und F. Ordnen Sie jeweils einen Graphen zu (mit Begründung). (06/) Hop von F = Nst von f mit VZW ; Tip von f = Nst von f mit VZW Lösung
15 III 6. Beispiel Flächen Gegeben ist die Funktion f mit f(x) = x 2. Berechnen Sie die markierte Fläche: (09/a) III 6. Beispiel Flächen A = [ ] [ ] 0 3 x3 x 2 3 x3 x = Lösung III 6.2 Beispiel Flächen III 6.2 Beispiel Flächen Gegeben ist die Funktion f mit f(x) = x 2 + und g mit g(x) = + 2. Berechnen Sie die markierte x Fläche: f(x) g(x) = x 2 + x [ ] 3 A = 3 x3 + ln x x = ln 3 7, Lösung III 7 Methode Unbegrenzte Flächen III 7 Methode Unbegrenzte Flächen Gib ein Beispiel für eine unbegrenzte Fläche. Wie kann man vorgehen, um diesen Flächeninhalt zu berechnen? z.b.: f(x) = e x ; die Fläche ab der Stelle x = 0 bis + u. A(u) = f(x) dx berechnen lim u A(u) untersuchen, ob der Grenzwert existiert Lösung III 7 Beispiel Unbegrenzte Flächen III 7 Beispiel Unbegrenzte Flächen Der Graph der Funktion f mit f(x) = 2e x schließt mit den Koordinatenachsen eine nach links nicht begrenzte Fläche ein. Zeigen Sie, dass diese Fläche einen endlichen Inhalt A hat. (2/3). A(u) = 0 u 2. lim u (2 2eu ) = 2 2e x dx = [2e x ] 0 u = 2 2e u - Lösung
16 III 8 Methode Mittelwert Was ist der Mittelwert einer Funktion und wie kann man ihn berechnen? III 8 Methode Mittelwert Wenn eine Funktion f nicht konstant ist, dann schwankt sie in einem bestimmten Intervall [a, b] um einen mittleren Funktionswert f f = b f(x) dx b a a Beispiel: f(x) = sin x + 50 schwankt bei der Betrachtung großer Intervalle um 50. Wenn man bei f nur ein kleines Intervall um 0, 5π betrachtet, ist der mittlere Funktionswert ungefähr 50+=5, weil sin(0, 5π) = Lösung III 8 Beispiel Mittelwert III 8 Beispiel Mittelwert Die Tageslänge beträgt in Madrid ungefähr H(t) = 2 + 2, 4 sin[0, 072(t 80)], (t in Tagen nach Jahresbeginn, H(t) in Stunden). Bestimmen sie die durchschnittliche Tagesdauer im Juni? (4/9; GTR) Hinweis: In der Mathematik hat jeder Monat 30 Tage, der 6. Monat Juni besteht dann aus den Tagen 50 bis 80. Im Buch steht das anders; aber der. Monat bezieht sich doch auf das Intervall [0; 30] Tage...?!? H = 4, 36 h Lösung III 9. Methode Volumenintegral III 9. Methode Volumenintegral Bei Rotation eines Schaubilds im Intervall [a, b] um die x-achse gilt: Wie kann man das Volumen eines Rotationskörpers berechnen? V = π b (f(x)) 2 dx Vergleiche das Volumen eines winzig kleinen Zylinders... : V = G h = πr 2 h = π(f(x)) 2 x Lösung III 9. Beispiel Volumenintegral III 9. Beispiel Volumenintegral Die gefärbte Fläche rotiert um die x-achse. Bestimmen Sie das Volumen des Drehkörpers. V = 2, 5π a Lösung
17 III 9.2. Beispiel Volumenintegral Die gefärbte Fläche rotiert um die x-achse. Bestimmen Sie das Volumen des Drehkörpers. (GTR) III 9.2. Beispiel Volumenintegral V = π 4 0 (3 + x) 2 (2 x + ) 2 dx = 48π Lösung III Beispiel Volumenintegral III Beispiel Volumenintegral Die Fläche unter dem Graphen von f mit f(x) = über [; z] rotiert um die x-achse. x Untersuchen Sie, ob der dabei entstehende Drehkörper für z + ein endliches Volumen hat. (7/) u V (u) = π lim V (u) = π u + ( x dx = π ) 2 u Lösung
18 IV. Methode Achsensymmetrie Wie kann man eine Achsensymmetrie eines Graphen nachweisen? (zur y-ache oder zu x = a) IV. Methode Achsensymmetrie y-achse: es muss für alle x gelten: f( x) = f(x) d.h. man setzt x in den Funktionsterm ein und muss solange umformen, bis man erkennt, dass f(x) (nicht) herauskommt. zu x = a: es muss für alle x gelten: f(a u) = f(a + u) d.h. man setzt einmal a u und einmal a + u in den Funktionsterm ein und stellt fest, ob beide Terme (un-)gleich sind. - Lösung IV. Beispiel Achsensymmetrie IV. Beispiel Achsensymmetrie Überprüfen Sie das Schaubild der Funktion auf Symmetrie: (a) f(x) = x 2 + x 6 ; (33/a) (b) f(x) = e x + e x (Vermutung mit dem GTR) (a) achsensym. zu y-achse, da eine gerade Funktion (= Polynom mit nur geradzahlige Hochzahlen) (b) Vermutung x = ist Symmetrieachse: f( + u) = f( u) e (+u) + e (+u) = e ( u) + e ( u) e u + e u = e u + e u und dies stimmt für alle u - Lösung IV.2 Methode Punktsymmetrie IV.2 Methode Punktsymmetrie Wie kann man eine Punktsymmetrie eines Graphen nachweisen (zum Ursprung oder zu Z(a b))? zum Ursprung: es muss für alle x gelten: f( x) = f(x) oder f ist eine ungerade Funktion, d.h. sie ist ein Polynom und enthält nur ungeradzahlige Hochzahlen. zu Z(a b): Der Mittelwert von den Funktionswerten um x = a ist b f(a + u) + f(a u) 2 = b Lösung IV.2 Beispiel Punktsymmetrie IV.2 Beispiel Punktsymmetrie Überprüfen Sie das Schaubild der Funktion auf Symmetrie: (a) f(x) = 3x 3 + 2x (b) f(x) = x 3 3x 2. (Vermutung mit dem GTR; 59/2b) (a) ungerade Funktion, deshalb punktsymmetrisch zum Ursprung (b) Vermutung Z( 2): Es muss gelten: f( + u) + f( u) = 2 2 f( + u) + f( u) = 4 Wenn man die x-werte ( ± u) einsetzt und die Terme korrekt vereinfacht, kommt 4 = 4 heraus, also ist Z der Symmetriepunkt Lösung
19 IV 2 Methode Polstellen Welche Arten von Polstellen gibt es und wie erkennt man sie im Funktionsterm? IV 2 Methode Polstellen. es gibt Pole mit / ohne VZW 2. entscheidend ist die Hochzahl bei der NennerNst 3. doppelte / vierfache /... Pol ohne VZW (z.b. x 2 ; (x 3) 4... ) 4. einfache / dreifache /... Pol mit VZW (z.b. x, (x 2), (x + 3) 3... ) Hinweis: x 3 hat keine dreifache NennerNst, sondern ± nur eine einfache! Lösung IV 2 Beispiel Polstellen IV 2 Beispiel Polstellen Bestimme die Null- und Polstellen von: (a) f(x) = x x 2 4 (b) f(x) = x2 9 x 2 (x ) 2 (c) f(x) = x2 4x 5 x(x + 2) 2 (a) N( 0); Pole: x = 2; x = 2 je mit VZW (b) N (3 0); N 2 ( 3 0); Pole: x = 0; x = je ohne VZW (c) N (5 0); N 2 ( 0); Pole: x = 0 mit VZW; x = 2 ohne VZW Lösung IV 3 Methode Verhalten x ± IV 3 Methode Verhalten x ± Welche Fälle kann man bei gebrochenrationalen Funktionen bezüglich des Verhaltens für x ± unterscheiden? (Stichwort: Zählergrad, Nennergrad; gibt jeweils Beispiele von Funktionen.). Z=N der Grenzwert existiert, z.b. 6x 3 +4 = 2 mit waager. Asymp. y = 2 3x 3 2x lim x 2. Z = N+ kein Grenzwert, schräge Asymptote z.b. f(x) = 4x3 +3x 2 + 4x 2 2x ± ; As: y = x +, Z > N+ der Grenzwert existiert nicht, z.b. f(x) = 2x4 +4 ± 3x 2 2x 4. Z<N der Grenzwert ist 0, z.b. lim x 2x 2 +4 = 0 mit waager. Asymp. y = 2 3x 3 2x Lösung IV 3 Beispiel Verhalten x ± IV 3 Beispiel Verhalten x ± Untersuchen Sie die Funktionen auf Null- und Polstellen, sowie das Verhalten für große x. Skizzieren Sie mit diesen Informationen die Schaubilder. (a) f(x) = 3x 4 5x + (b) f(x) = x2 6x + 8 2x(x ) Lösung
20 IV 4. Beispiel Besondere Punkte IV 4. Beispiel Besondere Punkte Bestimmen Sie die Extremstellen von f(x) = e 2x 2e x 2x. (42/3d) notw. Bdg.: Lösen von f (x) = 0 führt - nach einer Substitution - einmal zu x = ln 3 als möglicher Extremstelle und zu k.l. für die zweite u-lösung die hinr. Bedingung bestätigt die Tip-Stelle x Lösung IV 4.2 Beispiel Besondere Punkte IV 4.2 Beispiel Besondere Punkte Bestimmen Sie die Wendestellen von f(x) = (x 2 2) e x. (42/4a) notw. Bdg.: Lösen von f (x) = e x (x 2 + 4x) = 0 führt zu den beiden möglichen Wep-Stellen x = 0 und x 2 = 4 die hinr. Bedingung f (x /2 ) 0 bestätigt beide Wep-Stellen Lösung IV 5. Beispiel Funktionsanalyse IV 5. Beispiel Funktionsanalyse Welche Eigenschaften der Funktion lassen sich ohne GTR erkennen (46/3a): f(x) = 4x2 x 2 4x und g(x) = 0x e x2 f: x zunächst herauskürzen: f(x) = 4x x 4 (spätestens bei gleicher Null- und Polstelle muss man dies bemerken!!!) dann: N(0 0) einfach; Pol: x = 4; waagerechte Asymptote y = 4; D : x 0; x 4 wegen D nur: fast punktsym. zu (4 4); g: Asymptote y = 0; N(0 0) einfach; punktsym. zum Ursprung Lösung IV 5.2 Beispiel Funktionsanalyse IV 5.2 Beispiel Funktionsanalyse Untersuchen Sie die Funktion f(x) = (x 2) e x auf Monotonie und Extremstellen. (ohne GTR; 46/5b) f (x) = e x (x ); man kann x = als Tipstelle bestimmen Monotonie: für x > ist f monoton wachsend, da f (x) > 0 für x < ist f monoton fallend, da f (x) < Lösung
21 IV 6 Methode Funktionsschar Was versteht man unter der Ortslinie einer Punkteschar und wie kann man sie bestimmen? IV 6 Methode Funktionsschar Besondere Punkte P t (x(t) y(t)) einer Funktionsschar (z.b. Extrema oder Wendepunkte) können auf einer besonderen Linie im Koordinatensystem liegen. Diese Linie wird als Ortslinie der Punkte bezeichnet. Beispiel: P t (t 2 + 2t 4) (mit GeoGebra zeigen). die t-gleichung x P = x(t) nach t auflösen: x = t 2 + t = ± x 2. diese(n) t-wert in die t-gleichung y P = y(t) einsetzen: y = 2t 4 y = ±2 x 4 (in diesem Beispiel entstehen zwei Ortslinie) Lösung IV 6 Beispiel Funktionsschar IV 6 Beispiel Funktionsschar Bestimmen Sie die Ortslinie der Extrempunkte der Funktionenschar f k (x) = x k e x ; k R +. (50/0c). f (x) = k e x = 0 x H = ln ( k) = ln k 2. y H = ln ( k) k e ln( ( k) = ln ) k k ; k H( ln k ln ( k) ) 3. x H = ln k x = ln k k = e x = e x 4. y H = ln ( ) e = ln(e x ) = x x 5. y = x Ortslinie Lösung IV 7 Methode Trigonometrie IV 7 Methode Trigonometrie Erläutern Sie den Einfluss der Parameter bei f(x) = a sin(b(x c)) + d.. a = Amplitude 2. b: legt die Periode fest: p = 2π b 3. c = x- Verschiebung 4. d = y- Verschiebung Lösung IV 7 Beispiel Trigonometrie IV 7 Beispiel Trigonometrie Skizzieren Sie - ohne GTR - das Schaubild von f(x) = 2 sin(π(x 4)) 3 Kontrolle: GTR Lösung
22 IV 8 Methode Funktionsanpassung Wie geht man vor, wenn man aus einer Punkt-Liste (Wertetabelle) mit dem GTR eine Näherungskurve bestimmen will? IV 8 Methode Funktionsanpassung. Eingabe Wertetabelle in zwei GTR Listen. 2. die Punkteschar im Grafikbildschirm anschauen: im GTR: StatPlot Art der Näherungskurve bestimmen (linear, quadratisch, kubisch, trigonometrisch etc.) 4. entsprechende Regression auswählen und Ergebnis als Funktion speichern / notieren. 5. Kontrolle von Punkteschar und Näherungskurve im Bildschirm Lösung IV 8 Beispiel Funktionsanpassung IV 8 Beispiel Funktionsanpassung Bestimmen sie aus den Punkten eine passende Näherungskurve. mit CubicReg ergibt sich: f(x) = 0, 4x 3 2, 58x 2 + 3, 2x +, 6 - Lösung IV WT Methode Schiefe Asymptote IV WT Methode Schiefe Asymptote Eine schiefe Asymptote ist eine lineare Näherungsfunktion mit einer Steigung m 0. Was versteht man unter einer schiefen Asymptote? (Beispiel) Sie kann bei gebrochenrationalen Funktionen entstehen, falls der Zählergrad = Nennergrad +, z.b: f(x) = 3x2 +5x+ x = 3x x. y = 3x + 5 ist die schräge Asymptote. oder z.b. durch eine Addition einer linearen Funktion zu einer Exponentialfunktion: Beispiel: f(x) = e x + 0, 5x 3 y = 0, 5x 3 ist die schräge Asymptote Lösung IV WT Beispiel Schiefe Asymptote IV WT Beispiel Schiefe Asymptote Geben Sie eine gebrochenrationale Funktion an, deren Graph die Asymptoten y = x + 4 und x = 6 hat. (6/4f) z.b. das einfachste Beispiel: y = x x Lösung
23 V Methode Folgen Was ist eine explizite bzw. rekursive Beschreibung einer Folge? Gib ein Beispiel. V Methode Folgen explizit: Man kann den Funktions-/ Folgenwert direkt berechnen, ohne Vorgängerwerte zu kennen, z.b. a n = a(n) = 2n + 5 rekursiv: Man berechnet Folgewerte mit Hilfe von Vorgängerfolgewerte, z.b. Startwert: a 0 = 5 Rekursionsvorschrift: a n = a n + 2 gilt für n. Folge (a n ) : 5, 7, 9,, 3,... - Lösung V Beispiel Folgen V Beispiel Folgen Bestimmen Sie eine rekursive und eine explizite Darstellung der Folge: -, 0, 3, 8, 5, 24, 36,... (74/4d). die erste Differenzenfolge lautet: (a n ) :, 3, 5, 7,... also nicht konstant, also keine lineare Folge. 2. die zweite Differenzenfolge lautet: 2 (a n ) : 2, 2, 2, 2..., also konstant, also ist die Folge eine quadratische Folge 3. Ein scharfer Blick kann zeigen: a = a n = a n + (2n 3) n 2 - Lösung V 2 Methode Folgen-Eigenschaften V 2 Methode Folgen-Eigenschaften Wie kann man die Monotonie einer Folge nachweisen? für monoton wachsend zu zeigen: f(n + ) f(n) 0 oder f(n + ) f(n) oder (falls alle f(n) > 0) : f(n+) f(n). Bemerkung: bei Funktionen mit D = R bildet man natürlich die Ableitung und löst eine entsprechende Ungleichung. Diese kann man aber bei Folgen mit D = N nicht bilden! Lösung V 2 Beispiel Folgen-Eigenschaften V 2 Beispiel Folgen-Eigenschaften Untersuchen Sie die Folge a n = Monotonie. (76/2b) 2n 2n 3 auf Behauptung: (a n ) monoton fallend; z.z. a n+ < a n 2(n + ) 2(n + ) 3 < 2n 2n 3 2(n + 2)(2n 3) < 2n(2n ) 6 < 0 (wahr) für alle n (a n ) monoton fallend Lösung
24 V 3 Methode Grenzwert von Folgen Was ist die Idee bei der Definition eines Grenzwertes einer Folge? (Skizze! Stichwort: Schlauch...) V 3 Methode Grenzwert von Folgen anschaulich: eine Folge (a n ) hat den Grenzwert g, wenn für jede beliebige Dünne eines Schlauches um den Grenzwert alle Folgeglieder sich ab einer bestimmten Stelle n 0 im Schlauch befinden. in der mathematischen Formelsprache: (a n ) hat den Grenzwert g für jede beliebig kleine Zahl ɛ gibt es eine Zahl n 0 (die natürlich von ɛ abhängt), so dass für alle n > n 0 gilt: a n g < ɛ Lösung V 3 Beispiel Grenzwert von Folgen V 3 Beispiel Grenzwert von Folgen Bestimmen Sie den Grenzwert der Folge a n = 2n + mit Hilfe der Grenzwertsätze. n (80/2b) 2n + lim n ± n = lim n ± n = lim n ( 2 + n) = 2 ( ) 2 + n n = Lösung V 4 Methode expo. Wachstum V 4 Methode expo. Wachstum Wie kann man eine (Zahlen-)Folge auf exponentielles Wachstum untersuchen? Man muss die Quotienten aufeinanderfolgender y-werte bilden. Wenn diese ungefähr gleich sind, handelt es sich um exponentielles Wachstum. Bemerkungen:. dies setzt voraus, dass die Abstände der x-werte gleich sind 2. bei linearem Wachstum bildet man Differenzen; bei quadratischem Differenzen von Differenzen etc Lösung V 4 Beispiel expo. Wachstum V 4 Beispiel expo. Wachstum Untersuchen Sie die Folge auf exponentielles Wachstum: (83/-III) n B(n) Die Folge der Quotienten lautet: 66 5 = 0, 776; = 0, 773; 0, 784; 0, 75; 0, 8; 0, d.h. sie sind ungefähr gleich groß d.h. für den Wachstumsfaktor b gilt: b 0, 78 und die Bestandsfunktion lautet: B(n) = 85 0, 78 x Lösung
25 V 5 Methode beschränktes Wachstum Durch welche geometrische Veränderungen erhält man das Schaubild des beschränkten Wachstums aus einem exponentiellen Wachstum? Was bedeutet dies algebraisch für den Funktionsterm? V 5 Methode beschränktes Wachstum Beispiel: Erwärmung eines Objekts auf Zimmertemperatur. Die monoton fallende Exponentialfunktion f(x) = e kx (k > 0) wird.... mit einem Faktor a > 0 in y-richtung gestreckt: f(x) = a e kx 2. an der x-achse nach unten gespiegelt: f(x) = a e kx 3. und zum Schluss in y-richtung verschoben f(x) = S a e kx Lösung V 5 Beispiel beschränktes Wachstum V 5 Beispiel beschränktes Wachstum Zeichnen Sie für verschiedene k > 0 jeweils den Graphen der Funktion f mit f k (x) = 0 6e kx. Beschreiben Sie die Abhängigkeit von dem Parameter k. (88/9) GTR! je größer k, desto steiler ist das Schaubild. Gut erkennbar im Punkt A(0 4) mit der Steigung m = f (0) = 6k e k 0 = 6k Lösung V 6. Methode DGL expo. V 6. Methode DGL expo. (a) Wie lautet die DGL des exponentiellen Wachstums? (b) Was bedeutet diese anschaulich (für ein Schaubild; prozentuale Änderung)? (c) Wie lautet der Zusammenhang DGL & Funktionsterm? (a) y = k y, d.h. die Änderungsrate f (x) ist proportional zum Bestand f(x) (b) Es handelt sich um eine Exponentialfunktion (steigend oder fallend). Die Änderungsrate ist 00k%, z.b. für k = 0, 07 ist dies eine Abnahme um 7%. (c) f (x) = k f(x) f(x) = a e kx mit einer frei wählbaren Randbedingung, etwa a = f(0) Lösung V 6. Beispiel DGL expo. V 6. Beispiel DGL expo. (a) Geben Sie zu der Funktion f eine DGL an: f(x) = 500e 0,x. (9/3b) (b) Geben Sie die Lösung der DGL an für: y = 0, 2y und f(0) = 0. (9/4b) (a) f (x) = 0, f(x) und f(0) = 500; Abnahme um 0% je Zeiteinheit. (b) f(x) = a e 0,2x f(0) = a = 0 a = 0 f(x) = 0e 0,2x Lösung
26 V 6.2 Methode DGL beschr. (a) Wie lautet die DGL des beschränkten Wachstums? (b) Was bedeutet diese anschaulich für ein Schaubild? (c) Wie lautet der Zusammenhang DGL & Funktionsterm? V 6.2 Methode DGL beschr. (a) y = k (S y), d.h. die Änderungsrate f (x) ist proportional zum Sättigungsmanko S f(x) mit einer oberen Schranke S. (b) Es handelt sich um eine verschobene Exponentialfunktion (steigend oder fallend). (c) f (x) = k (S f(x)) f(x) = S + a e kx mit einer frei wählbaren Randbedingung, etwa f(0) = S + a a = f(0) S Lösung V 6.2 Beispiel DGL beschr. V 6.2 Beispiel DGL beschr. (a) Geben Sie zu der Funktion f eine DGL an: f(x) = 00 30e 0,x. (9/3d) (b) Geben Sie die Lösung der DGL an für: y = 0, (5 y) und f(0) = 0. (9/4d) (a) f (x) = 0, (00 f(x)) und f(0) = 70 (b) f(x) = 5 + a e 0,x f(0) = 5 + a = 0 a = 5 f(x) = 5 + 5e 0,x Lösung V 7 Methode DGL logist. V 7 Methode DGL logist. (a) Wie lautet die DGL des logistischen Wachstums? (b) Wie lautet der Zusammenhang DGL & Funktionsterm? (a) y = k y (S y), d.h. die Änderungsrate f (x) ist proportional zum Produkt aus dem aktuellen Bestand f(x) und dem Sättigungsmanko (S f(x)). (b) f (x) = c f(x) (S f(x)) S f(x) = und k = cs + a e kx mit einer frei wählbaren Randbedingung, etwa f(0) = S + a a = S f(0) Lösung V 7 Beispiel DGL logist. V 7 Beispiel DGL logist. (a) Geben Sie zu der Funktion f eine DGL an: 0 f(x) = + 4e. 0,5x (b) Geben Sie die Lösung der DGL an für: y = 0, 05y(5 y) und f(0) = 0. (a) f (x) = c f(x) (0 f(x)) mit c = 0, 5 0 f (x) = 0, 05 f(x) (0 f(x)) (b) k = 0, 05 5 = 0, 075 f(x) = mit a = 5 = 0, f(x) = 0, 5e. 0,075x 5 + ae 0,075x Lösung
27 VI Methode Gauss-Verfahren Mit welchen Verfahren kann man ein Gleichungssystem lösen? Wie funktioniert das Gauss-Verfahren zur Lösung eines LGS? VI Methode Gauss-Verfahren allgemein: Einsetzungsverfahren d.h. eine Gleichung wird nach einer Variablen aufgelöst und in die anderen Gleichungen eingesetzt. Dadurch erhält man ein GS das Gleichung weniger, aber auch Variable weniger enthält. Dieses reduzierte GS löst man weiter nach dem Einsetzungsverfahren... Das Gauss-Verfahren für LGS verwendet nur die Addition von 2 Gleichungen und Multiplikation von Gleichung um ein reduziertes LGS zu erhalten. Im GTR: Befehl rref([a]) mit der Matrix [A]. - Lösung VI Beispiel Gauss-Verfahren VI Beispiel Gauss-Verfahren Lösen Sie das LGS (24/3b; mit/ohne GTR): 2x 3x 2 x 3 = 2x 2 + 3x 3 = 4x + 2x 2 + 3x 3 = 6 Interpretieren Sie das LGS und die Lösung geometrisch. x =, 25; x 2 = 0, 5; x 3 = 0 Geometrisch bedeutet das LGS den Schnitt dreier Ebenen im dreidimensionalen Raum. Als Schnittgebilde ergibt sich ein Punkt. - Lösung VI 2 Methode LGS Lösungsvielfalt VI 2 Methode LGS Lösungsvielfalt (a) Was versteht man unter einem über- / unterbestimmten LGS? (b) Was kann man i.d.r. über die Lösungsmengen solcher LGS aussagen? (c) Ist die Einschränkung i.d.r. (in b) nötig?!? (a,b) Wenn ein GS mehr Gleichungen als Variablen hat, nennt man dies ein überbestimmtes GS. Da für eine eindeutige Lösung die Anzahl der Variablen mit der der Gleichungen übereinstimmen muss, ist es i.d.r. unwahrscheinlich, dass sich die überzähligen Gleichungen durch Einsetzen der Lösungen erfüllen werden. Ein unterbestimmtes GS ergibt i.d.r. unendlich viele Lösungen oder k.l. (vgl. c) (c) Man kann stets zwei Gleichungen erstellen, die sich widersprechen, etwa x = und x = 2. Egal wie viele Gleichungen mit irgendwelchen Variablen man zu diesen beiden Gleichungen dazu gesellt: das System der Gleichungen wird stets unlösbar bleiben! Lösung VI 2 Beispiel LGS Lösungsvielfalt VI 2 Beispiel LGS Lösungsvielfalt Geben Sie die konkrete Lösungen des zur der GTR-Anzeige gehörenden rref-ergebnisses eines LGS an: (27/2) Anschaulich handelt es sich um den Schnitt dreier Ebenen, der mit einem LGS gelöst wird: (a) x = 4; x 2 = 2; x 3 = 2; Punkt P (4 2 2) (b) k.l (c) x = 2x 3 ; x 2 = + x 3 ; x 3 = bel. 2 Gerade: x = + t Welche anschaulichen Bedeutungen haben jeweils 0 die Lösungsmengen? Lösung
28 VI 3. Methode Funktionsbestimmung Wie muss man vorgehen, wenn man aus Angaben über Extrem-, Wendepunkte, Nullstellen und weiteren Punkten eine Funktionsgleichung bestimmen soll? VI 3. Methode Funktionsbestimmung Beispiel: Polynom dritten Grades. Funktionsansatz festlegen: z.b. allgemeiner Ansatz: f(x) = ax 3 + bx 2 + cx + d oder Nullstellenform f(x) = a(x b)(x c)(x d) oder Mischform f(x) = (x c) 2 (ax + b); H/T(c 0). 2. Anzahl der Parameter = Anzahl der Gleichungen sonst erhält man eine Funktionsschar. 3. Aufstellen der Gleichungen: Nullstellen/einfache Punkte = Gleichung; Extrema / Wendepunkte = 2 Gleichungen. 4. Lösen des GS (meist LGS) Lösung VI 3. Beispiel Funktionsbestimmung VI 3. Beispiel Funktionsbestimmung (a) Bestimmen Sie eine ganzrationale Funktion, deren Graph den Wendepunkt W (0 0) mit der x-achse als Wendetangente und den Tiefpunkt T ( 2) hat. (22/a) (b) Bestimmen Sie alle ganzrationalen Funktionen zweiten Grades, deren Graphen durch die Punkte A( 4 0) und B(0 4) gehen. (220/3c) (a) Ansatz f(x) = x 3 (ax + b) mit dem TIP führt zu a = 6; b = 8 (b) Ansatz f(x) = ax 2 + bx 4 und dem Punkt A führt zu b = 4a also der Funktionsschar f a (x) = ax 2 + (4a )x Lösung VI 3.2 Methode Funktionsbestimmung VI 3.2 Methode Funktionsbestimmung Zusatz: Um einen passenden Funktionsterm zu finden eignet sich z.b.: (a) f(x) = ax 3 + bx 2 + cx + d mit T (u 0); H(0 v) = (a) ein Polynom 3. [oder 4.] Grades 4 Gleichungen f(x) = a(x u) 2 (x + u) 2 mit f(0) = v = Gleichung (b) eine trigonometrische Funktion f(x) = (ax + b)(x u) 2 mit H(0 v) = 2 Gleichungen oder (c) eine gebrochenrationale oder eine (b) f(x) = v 2 logistische Funktion (mit Einschränkungen) cos(bx) + v 2 und p = 2π b = 2u (c) Näherungslösungen: gebrochenrationaler Ansatz: Erläutere die verschiedenen Ansätze. f(x) = b x 4 mit f(u) = 0, 00 und f(0) = v bzw. + c v logistische Ansatz f(x) = mit f(0) = v 0, 00 + aekx und f(u) = 0, 00 oder andere Funktionstypen Lösung VI 3.2 Beispiel Funktionsbestimmung VI 3.2 Beispiel Funktionsbestimmung Folgendes Schaubild kann mit verschiedenen Funktionstypen angenähert werden. Gib eine Lösung an. Kennst du noch eine weitere Möglichkeit? (Zusatz) (a) f(x) = 0, 5 cos(πx) + 0, 5 (b) f(x) = a(x 2) 2 x 2 mit f() = a = (c) Näherungslösung: f(x) = = e 3(x )2 e 3(x ) Lösung
29 VII Methode Wdh. Vektoren VII Methode Wdh. Vektoren Veranschaulichen Sie die Addition und Multiplikation von Vektoren mit einer Skizze. - Lösung VII Beispiel Wdh. Vektoren VII Beispiel Wdh. Vektoren Veranschauliche mit zwei Vektoren a und b folgenden Vektor (239/ac) (a) c = 4 a + b und (b) d = 5 a 2 b - Lösung VII 2 Methode Geraden VII 2 Methode Geraden Was bedeuten in der Geradengleichung x = p + t r die einzelnen Bestandteile? Lösung VII 2 Beispiel Geraden VII 2 Beispiel Geraden Untersuchen Sie die beiden Geraden auf einen Schnittpunkt: (24/c) 3 2 g: x = + t h: x = 3 + t Das zugehörige LGS führt zu einem Widerspruch, also gibt es keinen Schnittpunkt: also ein Widerspruch in der letzten Zeile Lösung
30 VII 3 Methode Längen von Vektoren VII 3 Methode Längen von Vektoren Was ist ein Einheitsvektor? Wie kann man einen Vektor auf eine bestimmte Länge verkürzen/verlängern? Ein Einheitsvektor v 0 ist ein Vektor mit der Länge. Man muss seine Länge bestimmen l = x 2 + x x 2 3 und anschließend durch diese Länge l teilen Lösung VII 3 Beispiel Längen von Vektoren VII 3 Beispiel Längen von Vektoren 3 Bestimmen Sie für 2 die Länge und den zugehörigen Einheitsvektor. (244/b) Wie lautet der zugehörige Vektor mit der Länge 0? l = = 4 v 0 = v = Lösung VII 5. Methode Skalarprodukt VII 5. Methode Skalarprodukt Wie kann man unter Verwendung des Skalarprodukts nachweisen, dass ein Parallelogramm ABCD sogar ein Rechteck [eine Raute] ist? Für ein Parallelogramm ABCD muss gelten: AB = DC oder AD = BC. Falls zusätzlich noch gilt: AB AD AB AD = 0, ist das Parallelogramm sogar ein Rechteck. Falls zusätzlich noch gilt: BD AC BD AC = 0, ist das Parallelogramm sogar eine Raute Lösung VII 5. Beispiel Skalarprodukt VII 5. Beispiel Skalarprodukt Geben Sie die Gleichung einer Geraden h an, die die Gerade g orthogonal schneidet. g: x = + t (252/3b) Der Stützpunkt wird übernommen. Gesucht ist also nur ein Vektor, der zu r g orthogonal ist, z.b.: oder 3 oder 0 oder also h: x = + t Lösung
31 VII 5.2. Beispiel Skalarprodukt VII 5.2. Beispiel Skalarprodukt Zeichnen Sie eine Figur, so dass gilt: P Q QR = 0. (252/6a) Lösung VII Beispiel Skalarprodukt VII Beispiel Skalarprodukt Bestimmen Sie alle(!) Vektoren, die zu a = und b = 5 2 orthogonal sind. (252/8b) 2 3 Mit dem Kreuzprodukt berechnetman den orthogonalen Vektor n = a 7 b = 7 alle Vektoren sind dann alle Vielfache von n, also 7 nt = t Lösung VII 6 Methode Ebenen VII 6 Methode Ebenen Eine Ebene kann man in der Parameter-, der Normalen- oder der Koordinatenform angeben. Wie lauten diese und wenn möglich welche anschauliche Bedeutung haben die einzelnen Bestandteile? Lösung VII 6 Beispiel Ebenen VII 6 Beispiel Ebenen 3 Eine Ebene geht durch den Punkt P ( 2 ) und NF: x 2 2 = hat den Normalenvektor 2. Bestimmen Sie KF: 3x 2x 2 + 7x 3 = = 0 7 eine Ebenengleichung in PF, NF und KF. 7 0 (255/a) PF: x = 2 + t 0 + s Die Spannvektoren müssen orthogonal zum Normalenvektor sein Lösung
32 VII 7. Beispiel Ebenengleichungen VII 7. Beispiel Ebenengleichungen Eine Ebene geht durch die Punkte A(0 2 ), B(6 5 0) und C( 0 ). Bestimmen Sie die KF. (258/a) AB AC = 2 5 2x + x 2 + 5x 3 = Lösung VII 7.2 Beispiel Ebenengleichungen VII 7.2 Beispiel Ebenengleichungen Bestimmen Sie die Ebenengleichung in KF von: 2 2 x = + t 3 + s. (259/4a) = x 3x 2 + 7x 3 = Lösung VII 8 Methode Ebenen zeichnen VII 8 Methode Ebenen zeichnen Was ist die Spurpunkteform der Ebene? Wozu wird sie benötigt? Wenn man die Koordinatenform durch d teilt, entsteht die Spurpunkteform: E: x s + x 2 s 2 + x 3 s 3 =. Die Zahlen im Nenner geben die Koordinaten der Spurpunkte an: S (s 0 0), S 2 (0 s 2 0) und S 3 (0 0 s 3 ). Mit Hilfe der Spurpunkte kann man gut die Ebene ins Koordi einzeichnen. Falls es nur zwei Spurpunkte gibt, ist die Ebene parallel zu einer Koordinatenachse. Falls es nur einen Spurpunkt gibt, ist die Ebene parallel zu einer Koordinatenebene Lösung VII 8 Beispiel Ebenen zeichnen VII 8 Beispiel Ebenen zeichnen (a)zeichne folgende Ebenen in ein Koordi: E: 2x + 2x 2 + 3x 3 = 6 und F: 3x 4, 5x 3 = 9 ((26/bf) (b) Bestimmen Sie die Ebenengleichungen: (a) (b) G: x 3 = 2; E: x + x 2 = 4; F: 2x + 3x 2 + 6x 3 = Lösung
33 VII 9 Methode Schnitt E & g Wie geht man vor, wenn man eine Ebene mit einer Gerade schneidet? VII 9 Methode Schnitt E & g. Gerade als laufenden Punkt P t denken / schreiben. 2. Die Koordinaten von P t in die Ebenengleichung (in KF!) einsetzen. Die entstehende Gleichung in t muss man lösen t Die Zahl t 0 in die Gerade / den laufenden Punkt einsetzen, dann erhält man den Schnittpunkt S = P t Lösung VII 9 Beispiel Schnitt E & g VII 9 Beispiel Schnitt E & g Bestimmen sie die gemeinsamen Punkte der Geraden g undder Ebene E. 4 g: x = 6 + t 2 und 2 3 E: 5x 2 7x 3 = 3. (263/b) 5(6 + 2t) 7(2 + 3t) = 3 t = 3 S ( ) 9 - Lösung VII 0 Methode Schnitt E & F VII 0 Methode Schnitt E & F Wie geht man vor, wenn man eine Ebene E mit einer Ebene F schneidet?. Beide Ebenen müssen in der KF vorliegen. 2. Beide Gleichungen stellen ein LGS dar: 2 Gleichungen, 3 Variablen. Man muss also eine Variable eliminieren. Dann hat man eine Gleichung in zwei Variablen. Eine der beiden Variable kann man als t umbenennen und muss nun die beiden anderen Variablen in Abhängigkeit von t schreiben. 3. Es entsteht eine Schnittgerade. Bemerkung: Falls E F, muss n E = k n F sein. Dann gibt es keine Schnittgerade Lösung VII 0 Beispiel Schnitt E & F VII 0 Beispiel Schnitt E & F Bestimmen Sie den Schnitt von: (a) E: : x x 2 + 2x 3 = 7 und F: 6x + x 2 x 3 = 7. (267/d) (b) E: : 4x 2 = 5 und F: 6x + 5x 3 = 0 (267/g) (a) s: x = (b) s: x = t 0 0, 25 + t Lösung
34 VIII Methode d(p,e) VIII Methode d(p,e). Man erstellt die Lotgerade h: x = p + t n E Beschreiben Sie, wie man den Abstand eines Punktes P von einer Ebene E ohne HNF bestimmt. 2. Man bildet den Schnittpunkt h E = {F } genauer, man benötigt nur t 0 = Man bestimmt die Länge des Vektors: d(p, E) = P F = t 0 n E = t 0 n E. Hinweis: Man muss F ist nicht unbedingt aufschreiben! - Lösung VIII Beispiel d(p,e) VIII Beispiel d(p,e) Berechnen Sie den Abstand von A zu E (ohne HNF). (28/a) E: 3x 2 + 4x 3 = 0 und A(3 7) F (3 4 3); der Abstand beträgt 5 - Lösung VIII 2 Methode d(p,e) VIII 2 Methode d(p,e) Wie bestimmt man den Abstand eines Punktes P von einer Ebene E mit HNF? Für die Ebene E in KF mit: x n E = d gilt: Formel: d(p, E) = p n E d n E Lösung VIII 2 Beispiel d(p,e) VIII 2 Beispiel d(p,e) Berechnen Sie den Abstand von A zu E (mit HNF). (284/c) 5 4 E: x 4 = 0 und A(2 2) 0 2 d = 0, d.h. der Punkt A liegt in der Ebene E Lösung
35 VIII 3 Methode d(p,g) Beschreiben Sie zwei Methoden, wie man den Abstand eines Punktes P von einer Geraden g bestimmen kann. VIII 3 Methode d(p,g). Hilfsebene.. Hilfsebene H g durch P: ( x p) r g = 0.2. H g = {F } Fußpunkt.3. d(g, P ) = d(f, P ) = P F 2. laufender Verbindungsvektor v t (orthogonal) 2.. v t = Q t P 2.2. Q t P r g, also: Q t P r g = 0. Gl. in t lösen Lösung t 0 führt zum Fußpunkt F und es gilt: d(g, P ) = d(f, P ) = P F. 3. laufender Verbindungsvektor v t (Minimax) d(t) = Q t P GTR: Minimum bestimmen Lösung VIII 3 Beispiel d(p,g) VIII 3 Beispiel d(p,g) Berechnen Sie den Abstand des Punktes R von der Geraden g auf zwei Arten. (287/2b) R(9 4 9) und g: x = t d = 289 = Lösung VIII 4. Methode d(g,h) VIII 4. Methode d(g,h) Beschreibe, wie man (nur) den Abstand von zwei windschiefen Geraden g und h bestimmt. Wichtiger Hinweis: Die Fußpunkte müssen nicht bestimmt werden!!!. Hilfsebene H, die die Gerade g enhält und den Richtungsvektor von h. n H = r g r h ( x p g ) n H = 0 in KF schreiben. 2. d(g, h) = d(p h, H) (Formel mit HNF) Lösung VIII 4. Beispiel d(g,h) VIII 4. Beispiel d(g,h) Bestimme den Abstand der beiden windschiefen Geraden. (290/c) g: x = 3 + t 4 0 und h: x = t 8 0 H: x x 2 x 3 = 8; d(g, h) = 6 3 = Lösung
36 VIII 4.2 Methode d(g,h) VIII 4.2 Methode d(g,h) Beschreibe, wie man die beiden Punkte bestimmt, in denen zwei windschiefe Geraden g und h einen kürzesten Abstand haben.. Doppelt laufender Verbindungsvektor zwischen dem laufenden Punkt P t von g und Q s von h aufstellen: v t,s. 2. Orthogonalitätsbedingungen: v t,s r g und v t,s r h führen zu einem LGS (2 Gl, 2 Var: s, t). 3. LGS lösen; Ergebnisse s 0 und t 0 in die Geraden einsetzen = Fußpunkte F g, F h Lösung VIII 4.2 Beispiel d(g,h) VIII 4.2 Beispiel d(g,h) Bestimme die beiden Punkte, in denen die zwei windschiefe Geraden einen kürzesten Abstand haben. (290/c) g: x = 3 + t 4 0 und h: x = t 8 0 F g (7 5 4), F h (5 7 6); Abstand der Geraden: Lösung VIII 5 Methode α( a, b) VIII 5 Methode α( a, b) Wie kann man den Winkel zwischen zwei Vektoren a und b bestimmen? Formel: cos α = α = arccos(...) a b a b 0 α < Lösung VIII 5 Beispiel α( a, b) VIII 5 Beispiel α( a, b) Bestimmen Sie den Winkel zwischen den beiden Vektoren a und b. (294/c) a = 3 und b = cos α = α = 57, = = 0, Lösung
37 VIII 6. Methode α(g, h) VIII 6. Methode α(g, h) Wie bestimmt man den Schnittwinkel zwischen zwei Geraden g und h? Formel: cos α = r g r h r g r h α = arccos(...) 0 α < Lösung VIII 6. Beispiel α(g, h) VIII 6. Beispiel α(g, h) Bestimmen Sie die Größe des Schnittwinkels der beiden sich schneidenden Geraden. (296/b) g: x = t 7 ; h: x = t α = 30, Lösung VIII 6.2 Methode α(e, F ) VIII 6.2 Methode α(e, F ) Wie bestimmt man den Schnittwinkel zwischen zwei Ebenen E und F? Formel: cos α = n E n F n E n F α = arccos(...) 0 α < Lösung VIII 6.2 Beispiel α(e, F ) VIII 6.2 Beispiel α(e, F ) Bestimmen Sie die Größe des Schnittwinkels zwischen E und E 2. (296/2c) E : 3x + 5x 2 = 0 und E 2 : 2x 3x 2 3x 3 = 3 α = 70, Lösung
38 VIII 6.3 Methode α(g, E) VIII 6.3 Methode α(g, E) Wie bestimmt man den Schnittwinkel zwischen einer Geraden g und einer Ebenen E? Formel: sin α = r g n E r g n E α = arccos(...) 0 α < Lösung VIII 6.3 Beispiel α(g, E) VIII 6.3 Beispiel α(g, E) Bestimmen Sie die Größe des Schnittwinkels der Geraden g: x = 4 + t 2 mit der Ebenen E: 9 6x 3x 2 = 8. (297/3c) α = 0, d.h. g und E sind parallel. Da P g nicht in E liegt gibt es also gar keinen Schnittwinkel! Lösung VIII 7. Methode A g A VIII 7. Methode A g A Beschreiben Sie, wie man einen Punkt A an einer Geraden g spiegelt.. Hilfsebene H: ( x a) r g = 0 2. H g = {F g } 3. a = f g + AF g Lösung VIII 7. Beispiel A g A VIII 7. Beispiel A g A Gegeben ist der Punkt A(4 3 7). Berechnen Sie die Koordinaten des Bildpunktes A bei der Spiegelung an der Geraden durch P (4 2 ) und Q(0 45 3). (30/c) 4 2 Gerade (P Q) : x = 2 + t 4 Hilfeebene H: 2x + x 2 + 4x 3 = 3 (A eingesetzt) H (P Q) t 0 = F g (2 3) 2 AF = 4 a = f g + AF A (0 5 3) Lösung
39 VIII 7.2 Methode A E A VIII 7.2 Methode A E A Beschreiben Sie, wie man einen Punkt A an einer Ebene E spiegelt.. Lotgerade l: x = a + t n E 2. l E t 0 3. a = a + 2t 0 n E - Lösung VIII 7.2 Beispiel A E A VIII 7.2 Beispiel A E A Gegeben ist der Punkt A(4 3 7). Berechnen Sie die Koordinaten des Bildpunktes A bei der Spiegelung an der Ebenen E: x + x 2 x = 0. (30/b) t 0 = 2 ( 3 ; A 2 2 ) Lösung VIII Zusatz Methode a b VIII Zusatz Methode a b Was beschreiben anschaulich die Formeln (a) a b bzw. (b) ( a b) c und (c) 6 ( a b) c? Erkläre mit einer Skizze! (a) a b ist der Flächeninhalt des von a und b aufgespannten Parallelogramms (b) ( a b) c = Volumen des von a, b und c aufgespannten Parallelotops (Spats) (c) 6 ( a b) c = Volumen der von a, b und c aufgespannten dreiseitigen Pyramide Lösung VIII Zusatz Beispiel a b VIII Zusatz Beispiel a b Berechnen Sie den Flächeninhalt des Dreiecks ABC mit A(4 7 5), B(0 5 9) und C(8 7 3). (304/4a) Berechnen Sie das Volumen der dreiseitigen Pyramide ABCD mit A( 7 5 2), B( 9 6), C(5 2 ) und D( 2 0 9). (288/6) A = 0, 5 AB AC = 6 V = 6 ( AB AC) AD = = = Lösung
Zusammenfassung Abitursstoff Mathematik
 Zusammenfassung Abitursstoff Mathematik T. Schneider, J. Wirtz, M. Blessing 2015 Inhaltsverzeichnis 1 Analysis 2 1.1 Monotonie............................................ 2 1.2 Globaler Verlauf........................................
Zusammenfassung Abitursstoff Mathematik T. Schneider, J. Wirtz, M. Blessing 2015 Inhaltsverzeichnis 1 Analysis 2 1.1 Monotonie............................................ 2 1.2 Globaler Verlauf........................................
Abitur 2011 G8 Musterabitur Mathematik Infinitesimalrechnung
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 211 G8 Musterabitur Mathematik Infinitesimalrechnung I Teilaufgabe 1 (3 BE) Bestimmen Sie die Nullstellen der Funktion f : x (e x 2) (x 3 2x ) mit Definitionsbereich
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 211 G8 Musterabitur Mathematik Infinitesimalrechnung I Teilaufgabe 1 (3 BE) Bestimmen Sie die Nullstellen der Funktion f : x (e x 2) (x 3 2x ) mit Definitionsbereich
f(x) = 3x 2 + x + 2 f (x) = 6x + 1
 I. Beispiel y x ; f (x ) I. Beispiel y x ; f (x ) Zusatz: Bestimmen Sie ohne Anwendung der Ableitungsregeln die Ableitung f (2) der Funktion f(x) = x 2 + an der Stelle x = 2. y = f(2+h) f(2) =... = h2
I. Beispiel y x ; f (x ) I. Beispiel y x ; f (x ) Zusatz: Bestimmen Sie ohne Anwendung der Ableitungsregeln die Ableitung f (2) der Funktion f(x) = x 2 + an der Stelle x = 2. y = f(2+h) f(2) =... = h2
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil... Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analysis 3... 5 Wahlteil Analytische Geometrie... Wahlteil Analytische Geometrie... Lösungen: 00 Pflichtteil Lösungen zur Prüfung 00: Pflichtteil
Pflichtteil... Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analysis 3... 5 Wahlteil Analytische Geometrie... Wahlteil Analytische Geometrie... Lösungen: 00 Pflichtteil Lösungen zur Prüfung 00: Pflichtteil
Crashkurs sin 2 x + 5 cos 2 x = sin 2 x 2 sin x = 3
 Crashkurs. Funktion mit Parameter/Ortskurve - Wahlteil Analysis.. Gegeben sei für t > die Funktion f t durch f t (x) = 4 x 4t x 2 ; x R\{}. a) Welche Scharkurve geht durch den Punkt Q( 4)? b) Bestimme
Crashkurs. Funktion mit Parameter/Ortskurve - Wahlteil Analysis.. Gegeben sei für t > die Funktion f t durch f t (x) = 4 x 4t x 2 ; x R\{}. a) Welche Scharkurve geht durch den Punkt Q( 4)? b) Bestimme
Abitur 2014 Mathematik Infinitesimalrechnung I
 Seite http://www.abiturloesung.de/ Seite 2 Abitur 204 Mathematik Infinitesimalrechnung I Die Abbildung zeigt den Graphen einer Funktion f. Teilaufgabe Teil A (5 BE) Gegeben ist die Funktion f : x x ln
Seite http://www.abiturloesung.de/ Seite 2 Abitur 204 Mathematik Infinitesimalrechnung I Die Abbildung zeigt den Graphen einer Funktion f. Teilaufgabe Teil A (5 BE) Gegeben ist die Funktion f : x x ln
1.3 Berechnen Sie die Koordinaten der Wendepunkte des Schaubildes der Funktion f mit f( x) x 6x 13
 Musteraufgaben ab 08 Pflichtteil Aufgabe Seite / BEISPIEL A. Geben Sie Lage und Art der Nullstellen der Funktion f mit f( x) ( x ) ( x ) ; x IR an.. Bestimmen Sie die Gleichung der Tangente in P( f ())
Musteraufgaben ab 08 Pflichtteil Aufgabe Seite / BEISPIEL A. Geben Sie Lage und Art der Nullstellen der Funktion f mit f( x) ( x ) ( x ) ; x IR an.. Bestimmen Sie die Gleichung der Tangente in P( f ())
Abitur 2017 Mathematik Infinitesimalrechnung II
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung II Die Abbildung zeigt den Graphen der in R definierten Funktion g : x p + q sin p, q, r N. ( π r x ) mit Gegeben
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung II Die Abbildung zeigt den Graphen der in R definierten Funktion g : x p + q sin p, q, r N. ( π r x ) mit Gegeben
Abitur 2010 Mathematik GK Infinitesimalrechnung I
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 2010 Mathematik GK Infinitesimalrechnung I Teilaufgabe 2 (4 BE) Gegeben ist für k R + die Schar von Funktionen f k : x 1 Definitionsbereich D k. Der
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 2010 Mathematik GK Infinitesimalrechnung I Teilaufgabe 2 (4 BE) Gegeben ist für k R + die Schar von Funktionen f k : x 1 Definitionsbereich D k. Der
Bestimmen Sie jeweils die Lösungsmenge der Gleichung: 1. Bestimmen Sie jeweils die Lösungsmenge der Gleichung:
 Baden-Württemberg Übungsaufgaben für den Pflichtteil Gleichungslehre Stichworte: lineare Gleichungen; quadratische Gleichungen; Gleichungen höherer Ordnung; Substitution; Exponentialgleichungen; trigonometrische
Baden-Württemberg Übungsaufgaben für den Pflichtteil Gleichungslehre Stichworte: lineare Gleichungen; quadratische Gleichungen; Gleichungen höherer Ordnung; Substitution; Exponentialgleichungen; trigonometrische
Kern- und Schulcurriculum Mathematik Klasse 11/12. Stand Schuljahr 2012/13
 Kern- und Schulcurriculum Mathematik Klasse 11/12 Stand Schuljahr 2012/13 UE 1 Wiederholung Funktionen Änderungsrate Ableitung Ableitung berechnen Ableitungsfunktion Ableitungsregeln für Potenz, Summe
Kern- und Schulcurriculum Mathematik Klasse 11/12 Stand Schuljahr 2012/13 UE 1 Wiederholung Funktionen Änderungsrate Ableitung Ableitung berechnen Ableitungsfunktion Ableitungsregeln für Potenz, Summe
3 Differenzialrechnung
 Differenzialrechnung 3 Differenzialrechnung 3.1 Ableitungsregeln Übersicht Beispiel Vorgehen Potenzfunktionen f(x) = x 4 f (x) = 4 x 3 f(x) = x f (x) = 1 x 0 = 1 f(x) = x Hochzahl f (x) = Hochzahl x Hochzahl
Differenzialrechnung 3 Differenzialrechnung 3.1 Ableitungsregeln Übersicht Beispiel Vorgehen Potenzfunktionen f(x) = x 4 f (x) = 4 x 3 f(x) = x f (x) = 1 x 0 = 1 f(x) = x Hochzahl f (x) = Hochzahl x Hochzahl
Abitur 2013 Mathematik Infinitesimalrechnung II
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 213 Mathematik Infinitesimalrechnung II Teilaufgabe Teil 1 1 (5 BE) Geben Sie für die Funktion f mit f(x) = ln(213 x) den maximalen Definitionsbereich
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 213 Mathematik Infinitesimalrechnung II Teilaufgabe Teil 1 1 (5 BE) Geben Sie für die Funktion f mit f(x) = ln(213 x) den maximalen Definitionsbereich
Probleme lösen mit Hilfe von Ableitungen, Extrem- und Wendepunkten
 Kompetenzen und Inhalte des Bildungsplans Unterrichtsinhalte Die Schülerinnen und Schüler können - besondere Eigenschaften von Funktionen rechnerisch und mithilfe des GTR bestimmen; Bestimmung von Extrem-
Kompetenzen und Inhalte des Bildungsplans Unterrichtsinhalte Die Schülerinnen und Schüler können - besondere Eigenschaften von Funktionen rechnerisch und mithilfe des GTR bestimmen; Bestimmung von Extrem-
Abiturprüfung Mathematik 2007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 Abiturprüfung Mathematik 007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (8 Punkte) Das Schaubild einer Polynomfunktion. Grades geht durch den Punkt S(0/) und hat den 3 Wendepunkt
Abiturprüfung Mathematik 007 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (8 Punkte) Das Schaubild einer Polynomfunktion. Grades geht durch den Punkt S(0/) und hat den 3 Wendepunkt
PFLICHTTEIL NT = e x (x+2) = x+2 Oder Umschreiben: f(x) = 1. = (x 2 e x ) 1, und dann Kettenregel
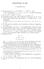 PFLICHTTEIL NT 26 F. LEMMERMEYER (1 Quotientenregel: f (x = x2 e x 2xe x x = e x (x+2 4 x = x+2 3 x 3 e. x Oder Umschreiben: f(x = 1 x 2 e = (x 2 e x 1, und dann Kettenregel x f (x = (x 2 e x 2 (2xe x
PFLICHTTEIL NT 26 F. LEMMERMEYER (1 Quotientenregel: f (x = x2 e x 2xe x x = e x (x+2 4 x = x+2 3 x 3 e. x Oder Umschreiben: f(x = 1 x 2 e = (x 2 e x 1, und dann Kettenregel x f (x = (x 2 e x 2 (2xe x
Schulcurriculum Mathematik Kursstufe November 2011
 Schulcurriculum Mathematik Kursstufe November 2011 Inhalte Leitidee / Kompetenzen Bemerkungen Die Schülerinnen und Schüler können Analysis Bestimmung von Extrem- und Wendepunkten: Höhere Ableitungen Bedeutung
Schulcurriculum Mathematik Kursstufe November 2011 Inhalte Leitidee / Kompetenzen Bemerkungen Die Schülerinnen und Schüler können Analysis Bestimmung von Extrem- und Wendepunkten: Höhere Ableitungen Bedeutung
a) Begründen Sie, dass der Graph von f symmetrisch zum Punkt S 0 2 f) Ermitteln Sie eine Gleichung der Tangente im Punkt B
 I. Wendepunkte 1. Bestimmen Sie Art und Lage der Extrempunkte sowie die Wendepunkte des Graphen der Funktion f mit der angegebenen Funktionsgleichung. a) f(x) 1 b) 12 (x + 1) (x 2) (x + 6) f(x) 1 4 x4
I. Wendepunkte 1. Bestimmen Sie Art und Lage der Extrempunkte sowie die Wendepunkte des Graphen der Funktion f mit der angegebenen Funktionsgleichung. a) f(x) 1 b) 12 (x + 1) (x 2) (x + 6) f(x) 1 4 x4
Analysis 2. f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt:
 Analysis 2 www.schulmathe.npage.de Aufgaben 1. Gegeben ist die Funktion f durch f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt: f (x) = 6(x
Analysis 2 www.schulmathe.npage.de Aufgaben 1. Gegeben ist die Funktion f durch f(x) = x2 6x + 8 x 2 6x + 5 a) Ermitteln Sie den Definitionsbereich der Funktion f. Weisen Sie nach, dass gilt: f (x) = 6(x
Arbeitsblätter Förderplan EF
 Arbeitsblätter Förderplan EF I.1 Nullstellen bestimmen Lösungen I.2 Parabeln: Nullstellen, Scheitelpunkte,Transformationen Lösungen I.3 Graphen und Funktionsterme zuordnen Lösungen II.1 Transformationen
Arbeitsblätter Förderplan EF I.1 Nullstellen bestimmen Lösungen I.2 Parabeln: Nullstellen, Scheitelpunkte,Transformationen Lösungen I.3 Graphen und Funktionsterme zuordnen Lösungen II.1 Transformationen
Differenzialrechnung
 Mathe Differenzialrechnung Differenzialrechnung 1. Grenzwerte von Funktionen Idee: Gegeben eine Funktion: Gesucht: y = f(x) lim f(x) = g s = Wert gegen den die Funktion streben soll (meist 0 oder ) g =
Mathe Differenzialrechnung Differenzialrechnung 1. Grenzwerte von Funktionen Idee: Gegeben eine Funktion: Gesucht: y = f(x) lim f(x) = g s = Wert gegen den die Funktion streben soll (meist 0 oder ) g =
B Anwendungen der Differenzialrechnung
 B Anwendungen der Differenzialrechnung Kurvendiskussionen Um den Verlauf eines Funktionsgraphen zu bestimmen, kann eine Wertetabelle aufgestellt werden. Dies kann jedoch sehr mühselig sein und es ist nicht
B Anwendungen der Differenzialrechnung Kurvendiskussionen Um den Verlauf eines Funktionsgraphen zu bestimmen, kann eine Wertetabelle aufgestellt werden. Dies kann jedoch sehr mühselig sein und es ist nicht
1.3 Berechnen Sie die Koordinaten der Wendepunkte des Schaubildes der Funktion f mit f( x) x 6x 13
 Pflichtteil Aufgabe BEISPIEL A. Geben Sie Lage und Art der Nullstellen der Funktion f mit 4 f( x) ( x ) ( x ) ; x IR an.. Bestimmen Sie die Gleichung der Tangente in P( f ()) an das Schaubild der Funktion
Pflichtteil Aufgabe BEISPIEL A. Geben Sie Lage und Art der Nullstellen der Funktion f mit 4 f( x) ( x ) ( x ) ; x IR an.. Bestimmen Sie die Gleichung der Tangente in P( f ()) an das Schaubild der Funktion
Abitur 2017 Mathematik Infinitesimalrechnung I
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung I Gegeben ist die Funktion g : x 2 4 + x 1 mit maximaler Definitionsmenge D g. Der Graph von g wird mit G g bezeichnet.
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 217 Mathematik Infinitesimalrechnung I Gegeben ist die Funktion g : x 2 4 + x 1 mit maximaler Definitionsmenge D g. Der Graph von g wird mit G g bezeichnet.
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil Wahlteil Analysis 8 Wahlteil Analysis Wahlteil Analysis 9 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 9 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
Pflichtteil Wahlteil Analysis 8 Wahlteil Analysis Wahlteil Analysis 9 Wahlteil Analytische Geometrie Wahlteil Analytische Geometrie 9 Lösungen: Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte
Bayern Teil 1. Aufgabe 1. Abitur Mathematik: Musterlösung. Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten:
 Abitur Mathematik: Bayern 2013 Teil 1 Aufgabe 1 a) 1. SCHRITT: DEFINITIONSMENGE BESTIMMEN Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten: 3x + 9 0 x 3 2. SCHRITT: NULLSTELLEN
Abitur Mathematik: Bayern 2013 Teil 1 Aufgabe 1 a) 1. SCHRITT: DEFINITIONSMENGE BESTIMMEN Der Term unter der Wurzel darf nicht negativ werden. Es muss also gelten: 3x + 9 0 x 3 2. SCHRITT: NULLSTELLEN
Mathematik Curriculum Kursstufe
 Mathematik Curriculum Kursstufe Kompetenzen und Inhalte des Bildungsplans Leitidee Funktionaler können besondere Eigenschaften von Funktionen rechnerisch und mithilfe des GTR bestimmen. Unterrichtsinhalte
Mathematik Curriculum Kursstufe Kompetenzen und Inhalte des Bildungsplans Leitidee Funktionaler können besondere Eigenschaften von Funktionen rechnerisch und mithilfe des GTR bestimmen. Unterrichtsinhalte
Skripten für die Oberstufe. Kurvendiskussion. f (x) f (x)dx = e x.
 Skripten für die Oberstufe Kurvendiskussion x 3 f (x) x f (x)dx = e x H. Drothler 0 www.drothler.net Kurvendiskussion Zusammenfassung Seite Um Funktionsgraphen möglichst genau zeichnen zu können, werden
Skripten für die Oberstufe Kurvendiskussion x 3 f (x) x f (x)dx = e x H. Drothler 0 www.drothler.net Kurvendiskussion Zusammenfassung Seite Um Funktionsgraphen möglichst genau zeichnen zu können, werden
Kursarbeit Nr.1 LK Mathematik NAME :
 Kursarbeit Nr.1 LK Mathematik 7. 10. 2004 1. Bestimmen Sie eine Stammfunktion F zur angegebenen Funktion f! a) f :R R, f x =1 1 x 100 b) f :R R, f x =sin 2 x 5 x c) f :R R, f x = x 5 x 3 2 2 x 2 2. Berechnen
Kursarbeit Nr.1 LK Mathematik 7. 10. 2004 1. Bestimmen Sie eine Stammfunktion F zur angegebenen Funktion f! a) f :R R, f x =1 1 x 100 b) f :R R, f x =sin 2 x 5 x c) f :R R, f x = x 5 x 3 2 2 x 2 2. Berechnen
a) Prüfen Sie, ob die Graphen der Funktionen f und g orthogonal sind: f(x) = 1,5x 1; g(x) =
 50 Kapitel 2: Rationale Funktionen und ihre Anwendungen 2.2.5 Orthogonale Geraden Geraden, die senkrecht aufeinander stehen, werden als zueinander orthogonale Geraden bezeichnet. Der Graph von g entsteht
50 Kapitel 2: Rationale Funktionen und ihre Anwendungen 2.2.5 Orthogonale Geraden Geraden, die senkrecht aufeinander stehen, werden als zueinander orthogonale Geraden bezeichnet. Der Graph von g entsteht
Inhalt der Lösungen zur Prüfung 2015:
 Inhalt der Lösungen zur Prüfung : Pflichtteil... Wahlteil Analysis... 8 Wahlteil Analysis... Wahlteil Analytische Geometrie/Stochastik... Wahlteil Analytische Geometrie/Stochastik... 9 Pflichtteil Lösungen
Inhalt der Lösungen zur Prüfung : Pflichtteil... Wahlteil Analysis... 8 Wahlteil Analysis... Wahlteil Analytische Geometrie/Stochastik... Wahlteil Analytische Geometrie/Stochastik... 9 Pflichtteil Lösungen
Abitur 2012 Mathematik Infinitesimalrechnung I
 Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 212 Mathematik Infinitesimalrechnung I Geben Sie zu den Funktionstermen jeweils den maximalen Definitionsbereich sowie einen Term der Ableitungsfunktion
Seite 1 http://www.abiturloesung.de/ Seite 2 Abitur 212 Mathematik Infinitesimalrechnung I Geben Sie zu den Funktionstermen jeweils den maximalen Definitionsbereich sowie einen Term der Ableitungsfunktion
Zusammenfassung Mathematik 2012 Claudia Fabricius
 Zusammenfassung Mathematik Claudia Fabricius Funktion: Eine Funktion f ordnet jedem Element x einer Definitionsmenge D genau ein Element y eines Wertebereiches W zu. Polynom: f(x = a n x n + a n- x n-
Zusammenfassung Mathematik Claudia Fabricius Funktion: Eine Funktion f ordnet jedem Element x einer Definitionsmenge D genau ein Element y eines Wertebereiches W zu. Polynom: f(x = a n x n + a n- x n-
Pflichtteil Wahlteil Analysis Wahlteil Analysis Wahlteil Analysis Wahlteil Analytische Geometrie 1...
 Pflichtteil... Wahlteil Analysis... 7 Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analytische Geometrie... 9 Wahlteil Analytische Geometrie... 008 Pflichtteil Lösungen zur Prüfung 008: Pflichtteil
Pflichtteil... Wahlteil Analysis... 7 Wahlteil Analysis... Wahlteil Analysis... Wahlteil Analytische Geometrie... 9 Wahlteil Analytische Geometrie... 008 Pflichtteil Lösungen zur Prüfung 008: Pflichtteil
Abiturprüfung Mathematik 2005 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis Gruppe I, Aufgabe A
 Abiturprüfung Mathematik (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis Gruppe I, Aufgabe A Für jedes a > ist eine Funktion f a definiert durch fa (x) = x (x a) mit x R a Das Schaubild von f
Abiturprüfung Mathematik (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis Gruppe I, Aufgabe A Für jedes a > ist eine Funktion f a definiert durch fa (x) = x (x a) mit x R a Das Schaubild von f
Arbeitsblätter zur Vergleichsklausur EF. Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf.
 Arbeitsblätter zur Vergleichsklausur EF Arbeitsblatt I.1 Nullstellen Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf. Beachte den Satz: Ein Produkt wird null, wenn einer der
Arbeitsblätter zur Vergleichsklausur EF Arbeitsblatt I.1 Nullstellen Aufgabe 1 Bestimme die Lösungen der folgenden Gleichungen möglichst im Kopf. Beachte den Satz: Ein Produkt wird null, wenn einer der
Fassung Herzog-Christoph-Gymnasium Beilstein. Funktionaler Zusammenhang. Modellieren. Algorithmus -zusammengesetzte Funktionen ableiten.
 Inhalte Leitideen Kompetenzen Analysis Die Schülerinnen und Schüler können Bestimmung von Extrem- und Wendepunkten Höhere Ableitungen Die Bedeutung der zweiten Ableitung Kriterien für Extremstellen Kriterien
Inhalte Leitideen Kompetenzen Analysis Die Schülerinnen und Schüler können Bestimmung von Extrem- und Wendepunkten Höhere Ableitungen Die Bedeutung der zweiten Ableitung Kriterien für Extremstellen Kriterien
www.mathe-aufgaben.com
 Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit f(x) = x sin( x + ) Aufgabe : ( VP) Berechnen Sie das Integral
Abiturprüfung Mathematik Baden-Württemberg (ohne CAS) Pflichtteil Aufgaben Aufgabe : ( VP) Bilden Sie die erste Ableitung der Funktion f mit f(x) = x sin( x + ) Aufgabe : ( VP) Berechnen Sie das Integral
Wurzelfunktionen Aufgaben
 Wurzelfunktionen Aufgaben. Für jedes k (k > 0) ist die Funktion f k (x) = 8 (x k ) kx, 0 x gegeben. a) Untersuchen Sie die Funktion f k auf Nullstellen und Extrema. Ermitteln Sie lim f k(x) sowie für 0
Wurzelfunktionen Aufgaben. Für jedes k (k > 0) ist die Funktion f k (x) = 8 (x k ) kx, 0 x gegeben. a) Untersuchen Sie die Funktion f k auf Nullstellen und Extrema. Ermitteln Sie lim f k(x) sowie für 0
Hauptprüfung Abiturprüfung 2015 (ohne CAS) Baden-Württemberg
 Baden-Württemberg: Abitur 01 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 01 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Baden-Württemberg: Abitur 01 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 01 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Lösungsblatt zu: Gebrochen rationale, Exponential- und Logarithmus Funktionen
 Lösungsblatt zu: Gebrochen rationale, Exponential- und Logarithmus Funktionen Das hast du schon gelernt: Aufgabe : a) Definitionsbereich TIPP: Definitionsbereich Nenner darf nicht Null werden x 0 x
Lösungsblatt zu: Gebrochen rationale, Exponential- und Logarithmus Funktionen Das hast du schon gelernt: Aufgabe : a) Definitionsbereich TIPP: Definitionsbereich Nenner darf nicht Null werden x 0 x
Analysis. A1 Funktionen/Funktionsklassen. 1 Grundbegriffe. 2 Grundfunktionen
 A1 Funktionen/Funktionsklassen 1 Grundbegriffe Analysis A 1.1 Gegeben sei die Funktion f mit f(x) = 2 x 2 + x. a) Bestimme, wenn möglich, die Funktionswerte an den Stellen 0, 4 und 2. b) Gib die maximale
A1 Funktionen/Funktionsklassen 1 Grundbegriffe Analysis A 1.1 Gegeben sei die Funktion f mit f(x) = 2 x 2 + x. a) Bestimme, wenn möglich, die Funktionswerte an den Stellen 0, 4 und 2. b) Gib die maximale
Analysis 8.
 Analysis 8 www.schulmathe.npage.de Aufgaben Gegeben sind die Funktionen f a durch f a (x) = a x x + (x R x ; a R a ) a) Geben Sie die Koordinaten der Schnittpunkte der Graphen der Funktionen f a mit den
Analysis 8 www.schulmathe.npage.de Aufgaben Gegeben sind die Funktionen f a durch f a (x) = a x x + (x R x ; a R a ) a) Geben Sie die Koordinaten der Schnittpunkte der Graphen der Funktionen f a mit den
(x 1. Vektoren. g: x = p + r u. p r (u1. x 2. u 2. p 2
 Vektoren Mit der Vektorrechnung werden oft geometrische Probleme gelöst. Wenn irgendwelche Aufgabenstellungen geometrisch darstellbar sind, z.b. Flugbahnen oder Abstandsberechnungen, dann können sie mit
Vektoren Mit der Vektorrechnung werden oft geometrische Probleme gelöst. Wenn irgendwelche Aufgabenstellungen geometrisch darstellbar sind, z.b. Flugbahnen oder Abstandsberechnungen, dann können sie mit
ToDo-Liste für s Mathe-Abi 2009
 ToDo-Liste für s Mathe-Abi 2009 7. Februar 2009 1 Grenzwerte und Folgen 1. Unterschied arithmetische Folge zu geometrische Folge 2. Rekursive Darstellung von Zerfalls- und Wachstumsvorgängen (a) lineares
ToDo-Liste für s Mathe-Abi 2009 7. Februar 2009 1 Grenzwerte und Folgen 1. Unterschied arithmetische Folge zu geometrische Folge 2. Rekursive Darstellung von Zerfalls- und Wachstumsvorgängen (a) lineares
± 1 +2= 1 2 ± =1 2 ± 2,25= 1 2 ±1,5 x 2= 1 2 1,5= 1 ; x 3= ,5=2
 Aufgabe 1: Gegeben ist die Funktion f (x)= 2x2 x 3 +x 4 Bestimme jeweils... 1.1...alle Nullstellen von f. x 5 +x 4 Nullstellen von f: Nullstellen des Zählers, die nicht Nullstellen des Nenners sind. Nullstellen
Aufgabe 1: Gegeben ist die Funktion f (x)= 2x2 x 3 +x 4 Bestimme jeweils... 1.1...alle Nullstellen von f. x 5 +x 4 Nullstellen von f: Nullstellen des Zählers, die nicht Nullstellen des Nenners sind. Nullstellen
1. Teil Repetitionen zum Thema (bisherige) Funktionen
 Analysis-Aufgaben: Rationale Funktionen 2 1. Teil Repetitionen zum Thema (bisherige) Funktionen 1. Die folgenden Funktionen sind gegeben: f(x) = x 3 x 2, g(x) = x 4 + 4 (a) Bestimme die folgenden Funktionswerte/-
Analysis-Aufgaben: Rationale Funktionen 2 1. Teil Repetitionen zum Thema (bisherige) Funktionen 1. Die folgenden Funktionen sind gegeben: f(x) = x 3 x 2, g(x) = x 4 + 4 (a) Bestimme die folgenden Funktionswerte/-
Aufgaben zum Grundwissen Mathematik 11. Jahrgangstufe Teil 1
 Aufgaben zum Grundwissen Mathematik 11. Jahrgangstufe Teil 1 Lehrplan: M 11.1.1 Graphen gebrochen-rationaler Funktionen M 11.1.2 Lokales Differenzieren Passende Kapitel im Schulbuch Fokus Mathematik 11:
Aufgaben zum Grundwissen Mathematik 11. Jahrgangstufe Teil 1 Lehrplan: M 11.1.1 Graphen gebrochen-rationaler Funktionen M 11.1.2 Lokales Differenzieren Passende Kapitel im Schulbuch Fokus Mathematik 11:
Zusammenfassung der Kurvendiskussion
 Zusammenfassung der Kurvendiskussion Diskussionspunkte 1 Größtmögliche Definitionsmenge D f 2 Symmetrieeigenschaften des Graphen G f 3 Nullstellen, Polstellen, Schnittpunkte mit der y-achse, Vielfachheit
Zusammenfassung der Kurvendiskussion Diskussionspunkte 1 Größtmögliche Definitionsmenge D f 2 Symmetrieeigenschaften des Graphen G f 3 Nullstellen, Polstellen, Schnittpunkte mit der y-achse, Vielfachheit
Aufgaben für Analysis in der Oberstufe. Robert Rothhardt
 Aufgaben für Analysis in der Oberstufe Robert Rothhardt 14. Juni 2011 2 Inhaltsverzeichnis 1 Modellierungsaufgaben 5 1.1 Musterabitur S60................................ 5 1.2 Musterabitur 3.1.4 B / S61..........................
Aufgaben für Analysis in der Oberstufe Robert Rothhardt 14. Juni 2011 2 Inhaltsverzeichnis 1 Modellierungsaufgaben 5 1.1 Musterabitur S60................................ 5 1.2 Musterabitur 3.1.4 B / S61..........................
Förderaufgaben EF Arbeitsblatt 1 Abgabe Zeichne die Tangenten bei x=6 und bei x = 4 ein und bestimme die zugehörige Geradengleichung.
 Förderaufgaben EF Arbeitsblatt 1 Abgabe 20.1.15 1. Zeichne die Tangenten bei x=6 und bei x = 4 ein und bestimme die zugehörige Geradengleichung. 2. Bestimme f (x): a) f(x) = x 3 + 4x 2 x + 1 b) f(x) =
Förderaufgaben EF Arbeitsblatt 1 Abgabe 20.1.15 1. Zeichne die Tangenten bei x=6 und bei x = 4 ein und bestimme die zugehörige Geradengleichung. 2. Bestimme f (x): a) f(x) = x 3 + 4x 2 x + 1 b) f(x) =
Pflichtteilaufgaben zu Funktionenkompetenz. Baden-Württemberg
 Pflichtteilaufgaben zu Funktionenkompetenz Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com September 016 1 Übungsaufgaben: Ü1: Die Abbildung zeigt
Pflichtteilaufgaben zu Funktionenkompetenz Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com September 016 1 Übungsaufgaben: Ü1: Die Abbildung zeigt
Lösungen zur Prüfung 2014: Pflichtteil
 Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte Kenntnisse: Analysis: Ableiten mit Produktregel, Integral mit Stammfunktion berechnen, Gleichung lösen, Kosinusfunktion, Nullstellen, Funktionswerte
Pflichtteil Lösungen zur Prüfung : Pflichtteil Benötigte Kenntnisse: Analysis: Ableiten mit Produktregel, Integral mit Stammfunktion berechnen, Gleichung lösen, Kosinusfunktion, Nullstellen, Funktionswerte
Selbsteinschätzungstest Auswertung und Lösung
 Selbsteinschätzungstest Auswertung und Lösung Abgaben: 46 / 587 Maximal erreichte Punktzahl: 8 Minimal erreichte Punktzahl: Durchschnitt: 7 Frage (Diese Frage haben ca. 0% nicht beantwortet.) Welcher Vektor
Selbsteinschätzungstest Auswertung und Lösung Abgaben: 46 / 587 Maximal erreichte Punktzahl: 8 Minimal erreichte Punktzahl: Durchschnitt: 7 Frage (Diese Frage haben ca. 0% nicht beantwortet.) Welcher Vektor
1.2 Berechne den Inhalt der Fläche, die das Schaubild von mit 5P der -Achse einschließt.
 Diese Aufgaben sind zu bearbeiten. Sie können nicht abgewählt werden. Aufgabe A1 1. Gegeben ist die Funktion mit 2 3; 1.1 Eine der folgenden Abbildung zeigt das Schaubild. 6P Untersuche für jede der Abbildungen,
Diese Aufgaben sind zu bearbeiten. Sie können nicht abgewählt werden. Aufgabe A1 1. Gegeben ist die Funktion mit 2 3; 1.1 Eine der folgenden Abbildung zeigt das Schaubild. 6P Untersuche für jede der Abbildungen,
5.5. Prüfungsaufgaben zur graphischen Integration und Differentiation
 5.5. Prüfungsaufgaben zur graphischen Integration und Differentiation Aufgabe : Verschiebung und Streckung trigonometrischer Funktionen (5) a) Bestimmen Sie die Periode p sowie die Nullstellen der Funktion
5.5. Prüfungsaufgaben zur graphischen Integration und Differentiation Aufgabe : Verschiebung und Streckung trigonometrischer Funktionen (5) a) Bestimmen Sie die Periode p sowie die Nullstellen der Funktion
Kreissektoren und Bogenmaß
 M 10.1 Kreissektoren und Bogenmaß In einem Kreis mit Radius r gilt für einen Kreissektor mit Mittelpunktswinkel α: Länge des Kreisbogens Fläche des Kreissektors b = α α 2rπ A = 360 360 πr2 Das Bogenmaß
M 10.1 Kreissektoren und Bogenmaß In einem Kreis mit Radius r gilt für einen Kreissektor mit Mittelpunktswinkel α: Länge des Kreisbogens Fläche des Kreissektors b = α α 2rπ A = 360 360 πr2 Das Bogenmaß
Abkürzungen & Begriffe
 A Bedeutungen Abkürzungen & Begriffe Abzisse ist ein normaler x-wert [ Ordinate] arcsin, arccos, arctan sind die korrekten Bezeichnungen für: sin -, cos -, tan -. [Die üblichen Bezeichnungen sin -, cos
A Bedeutungen Abkürzungen & Begriffe Abzisse ist ein normaler x-wert [ Ordinate] arcsin, arccos, arctan sind die korrekten Bezeichnungen für: sin -, cos -, tan -. [Die üblichen Bezeichnungen sin -, cos
Abitur Mathematik Baden-Württemberg 2012
 Abitur Mathematik: Baden-Württemberg 2012 Im sind keine Hilfsmittel zugelassen. Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist die Verkettung der Potenzfunktion g(x)
Abitur Mathematik: Baden-Württemberg 2012 Im sind keine Hilfsmittel zugelassen. Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist die Verkettung der Potenzfunktion g(x)
Pflichtteil. Baden-Württemberg Aufgabe 1. Aufgabe 2. Musterlösung. Abitur Mathematik Baden-Württemberg Abitur Mathematik: Musterlösung
 Abitur Mathematik: Baden-Württemberg 2013 Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist das Produkt einer ganzrationalen Funktion u(x) = 2x 2 + 5x und einer Verkettung
Abitur Mathematik: Baden-Württemberg 2013 Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist das Produkt einer ganzrationalen Funktion u(x) = 2x 2 + 5x und einer Verkettung
Mathemathik-Prüfungen
 M. Arend Stand Juni 2005 Seite 1 1980: Mathemathik-Prüfungen 1980-2005 1. Eine zur y-achse symmetrische Parabel 4.Ordnung geht durch P 1 (0 4) und hat in P 2 (-1 1) einen Wendepunkt. 2. Diskutieren Sie
M. Arend Stand Juni 2005 Seite 1 1980: Mathemathik-Prüfungen 1980-2005 1. Eine zur y-achse symmetrische Parabel 4.Ordnung geht durch P 1 (0 4) und hat in P 2 (-1 1) einen Wendepunkt. 2. Diskutieren Sie
Sollten sich (Flüchtigkeits )Fehler eingeschlichen haben, bitte ich um eine kurze Nachricht an hans
 Sollten sich (Flüchtigkeits )Fehler eingeschlichen haben, bitte ich um eine kurze Nachricht an hans josef.coenen@web.de Abitour Analytische Geometrie Leistungskurs Aufgaben 1. Welche Lagebeziehungen zwischen
Sollten sich (Flüchtigkeits )Fehler eingeschlichen haben, bitte ich um eine kurze Nachricht an hans josef.coenen@web.de Abitour Analytische Geometrie Leistungskurs Aufgaben 1. Welche Lagebeziehungen zwischen
Unterrichtsinhalte. Der Aufbau zusammengesetzter Funktionen aus elementaren Funktionen (ca. 3 5 Std.) Produkt, Quotient und Verkettung von Funktionen
 Kompetenzen und Inhalte des Bildungsplans Unterrichtsinhalte Hinweise/Vorschläge zur Erweiterung und Vertiefung des Kompetenzerwerbs - besondere Eigenschaften von Funktionen rechnerisch und mithilfe des
Kompetenzen und Inhalte des Bildungsplans Unterrichtsinhalte Hinweise/Vorschläge zur Erweiterung und Vertiefung des Kompetenzerwerbs - besondere Eigenschaften von Funktionen rechnerisch und mithilfe des
1.2 Weisen Sie rechnerisch nach, dass das Schaubild der Funktion mit 4P! bei 1 einen Sattelpunkt aufweist.
 Aufgabe A1 1.1 Erläutere anhand einer Skizze, ob das Integral 3P größer, kleiner oder gleich Null ist. 1.2 Für eine Funktion gilt: (1) 0 für 2 und 1 (2) 23 (3) 13 (4) 2 (5) 1 6 Welche Aussagen lassen sich
Aufgabe A1 1.1 Erläutere anhand einer Skizze, ob das Integral 3P größer, kleiner oder gleich Null ist. 1.2 Für eine Funktion gilt: (1) 0 für 2 und 1 (2) 23 (3) 13 (4) 2 (5) 1 6 Welche Aussagen lassen sich
5.5. Abituraufgaben zu ganzrationalen Funktionen
 .. Abituraufgaben zu ganzrationalen Funktionen Aufgabe : Kurvendiskussion, Fläche zwischen zwei Schaubildern () Untersuchen Sie f(x) x x und g(x) x auf Symmetrie, Achsenschnittpunkte, Extrempunkts sowie
.. Abituraufgaben zu ganzrationalen Funktionen Aufgabe : Kurvendiskussion, Fläche zwischen zwei Schaubildern () Untersuchen Sie f(x) x x und g(x) x auf Symmetrie, Achsenschnittpunkte, Extrempunkts sowie
Analysis I. Teil 1. Bayern Aufgabe 1. Abitur Mathematik Bayern Abitur Mathematik: Musterlösung. D f =] 3; + [ x = 1
![Analysis I. Teil 1. Bayern Aufgabe 1. Abitur Mathematik Bayern Abitur Mathematik: Musterlösung. D f =] 3; + [ x = 1 Analysis I. Teil 1. Bayern Aufgabe 1. Abitur Mathematik Bayern Abitur Mathematik: Musterlösung. D f =] 3; + [ x = 1](/thumbs/91/105628768.jpg) Abitur Mathematik: Bayern 2012 Teil 1 Aufgabe 1 a) DEFINITIONSMENGE f(x) = ln(x + 3) x + 3 > 0 x > 3 D f =] 3; + [ ABLEITUNG Kettenregel liefert f (x) = 1 x + 3 1 = 1 x + 3 b) DEFINITIONSMENGE 3 g(x) =
Abitur Mathematik: Bayern 2012 Teil 1 Aufgabe 1 a) DEFINITIONSMENGE f(x) = ln(x + 3) x + 3 > 0 x > 3 D f =] 3; + [ ABLEITUNG Kettenregel liefert f (x) = 1 x + 3 1 = 1 x + 3 b) DEFINITIONSMENGE 3 g(x) =
Abschlussprüfung Fachoberschule 2016 Mathematik
 Abschlussprüfung Fachoberschule 06 Aufgabenvorschlag A Funktionsuntersuchung /6 Gegeben ist die Funktion f mit der Funktionsgleichung f ( x) = x + x; x IR. Berechnen Sie die Funktionswerte f( x ) für folgende
Abschlussprüfung Fachoberschule 06 Aufgabenvorschlag A Funktionsuntersuchung /6 Gegeben ist die Funktion f mit der Funktionsgleichung f ( x) = x + x; x IR. Berechnen Sie die Funktionswerte f( x ) für folgende
Pflichtteil. Baden-Württemberg Aufgabe 1. Aufgabe 2. Musterlösung. Abitur Mathematik Baden-Württemberg Abitur Mathematik: Musterlösung
 Abitur Mathematik: Baden-Württemberg 14 Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist das Produkt einer einfachen Funktion u(x) = x und einer Verkettung v(x) = e x
Abitur Mathematik: Baden-Württemberg 14 Aufgabe 1 1. SCHRITT: STRUKTUR DER FUNKTION BESCHREIBEN Der Funktionsterm von f ist das Produkt einer einfachen Funktion u(x) = x und einer Verkettung v(x) = e x
K2 KLAUSUR 2. Aufgabe Punkte (max) Punkte. (1) Bestimmen Sie die Ableitung von f(x) = 2 x
 K2 KLAUSUR 2 PFLICHTTEIL 202 Aufgabe 2 3 4 5 6 7 8 Punkte (max) 2 2 3 3 5 3 5 3 Punkte () Bestimmen Sie die Ableitung von f(x) = 2 x 2 + 4. (2) Berechnen Sie das Integral 4 ( ) x 2 dx. (3) Lösen Sie die
K2 KLAUSUR 2 PFLICHTTEIL 202 Aufgabe 2 3 4 5 6 7 8 Punkte (max) 2 2 3 3 5 3 5 3 Punkte () Bestimmen Sie die Ableitung von f(x) = 2 x 2 + 4. (2) Berechnen Sie das Integral 4 ( ) x 2 dx. (3) Lösen Sie die
Mathematik-Verlag, 1
 Mathematik-Verlag, www.matheverlag.com 1 005 Pflichtteil Lösungen zur Prüfung 005: Pflichtteil Benötigte Kenntnisse: Analysis: Ableiten, Stammfunktion, ganzrationale Gleichungen, Asymptoten, Normalengleichung,
Mathematik-Verlag, www.matheverlag.com 1 005 Pflichtteil Lösungen zur Prüfung 005: Pflichtteil Benötigte Kenntnisse: Analysis: Ableiten, Stammfunktion, ganzrationale Gleichungen, Asymptoten, Normalengleichung,
Kurvendiskussion. Gesetzmäßigkeiten. Lineare Funktionen. Funktionsgleichung
 Kurvendiskussion Gesetzmäßigkeiten Lineare Funktionen Funktionsgleichung y = mx + c m: Steigung c: y-achsenabschnitt (Funktionswert für y, bei dem der Graph die y-achse schneidet Beispiel : y = x 3 mit
Kurvendiskussion Gesetzmäßigkeiten Lineare Funktionen Funktionsgleichung y = mx + c m: Steigung c: y-achsenabschnitt (Funktionswert für y, bei dem der Graph die y-achse schneidet Beispiel : y = x 3 mit
K2 MATHEMATIK KLAUSUR 4. Aufgabe PT Ana Geo Sto Gesamtpunktzahl Punkte (max) Punkte Notenpunkte
 K MATHEMATIK KLAUSUR 4 17.03.017 Aufgabe PT Ana Geo Sto Gesamtpunktzahl Punkte (max 0 0 10 10 60 Punkte Notenpunkte PT 1 3 4 5 6 7 * Summe P. (max 3 3 4 4 0 Punkte WT Ana A.1a b c A 1. Summe P. (max 6
K MATHEMATIK KLAUSUR 4 17.03.017 Aufgabe PT Ana Geo Sto Gesamtpunktzahl Punkte (max 0 0 10 10 60 Punkte Notenpunkte PT 1 3 4 5 6 7 * Summe P. (max 3 3 4 4 0 Punkte WT Ana A.1a b c A 1. Summe P. (max 6
Analysis II. Abitur Mathematik Bayern 2012 Musterlösung. Bayern Teil 1. Aufgabe 1. Aufgabe 2. Abitur Mathematik: Musterlösung.
 Abitur Mathematik: Musterlösung Bayern 2012 Teil 1 Aufgabe 1 2x + 3 f(x) = x² + 4x + 3 DEFINITIONSMGE Nullstellen des Nenners:! x² + 4x + 3=0 Lösungen x 1,2 = 4 ± 16 12 2 = 2 ± 1, d.h. x 1 = 3 und x 2
Abitur Mathematik: Musterlösung Bayern 2012 Teil 1 Aufgabe 1 2x + 3 f(x) = x² + 4x + 3 DEFINITIONSMGE Nullstellen des Nenners:! x² + 4x + 3=0 Lösungen x 1,2 = 4 ± 16 12 2 = 2 ± 1, d.h. x 1 = 3 und x 2
Grundwissen Abitur Geometrie 15. Juli 2012
 Grundwissen Abitur Geometrie 5. Juli 202. Erkläre die Begriffe (a) parallelgleiche Pfeile (b) Vektor (c) Repräsentant eines Vektors (d) Gegenvektor eines Vektors (e) Welcher geometrische Zusammenhang besteht
Grundwissen Abitur Geometrie 5. Juli 202. Erkläre die Begriffe (a) parallelgleiche Pfeile (b) Vektor (c) Repräsentant eines Vektors (d) Gegenvektor eines Vektors (e) Welcher geometrische Zusammenhang besteht
H. Gruber, R. Neumann. Erfolg im Mathe-Abi. Basiswissen Rheinland-Pfalz. Übungsbuch für den Grund- und Leistungskurs mit Tipps und Lösungen
 H. Gruber, R. Neumann Erfolg im Mathe-Abi Basiswissen Rheinland-Pfalz Übungsbuch für den Grund- und Leistungskurs mit Tipps und Lösungen Inhaltsverzeichnis Inhaltsverzeichnis Analysis 1 Von der Gleichung
H. Gruber, R. Neumann Erfolg im Mathe-Abi Basiswissen Rheinland-Pfalz Übungsbuch für den Grund- und Leistungskurs mit Tipps und Lösungen Inhaltsverzeichnis Inhaltsverzeichnis Analysis 1 Von der Gleichung
Lernkarten. Analytische Geometrie. 6 Seiten
 Lernkarten Analytische Geometrie 6 Seiten Zum Ausdrucken muss man jeweils eine Vorderseite drucken, dann das Blatt wenden, nochmals einlegen und die Rückseite drucken. Am besten druckt man die Karten auf
Lernkarten Analytische Geometrie 6 Seiten Zum Ausdrucken muss man jeweils eine Vorderseite drucken, dann das Blatt wenden, nochmals einlegen und die Rückseite drucken. Am besten druckt man die Karten auf
 Abiturprüfung Mathematik 006 Baden-Württemberg (ohne CAS) Haupttermin Pflichtteil - Aufgaben Aufgabe : ( VP) Bilden Sie die Ableitung der Funktion f mit f(x) sin(4x ). Aufgabe : ( VP) Geben Sie eine Stammfunktion
Abiturprüfung Mathematik 006 Baden-Württemberg (ohne CAS) Haupttermin Pflichtteil - Aufgaben Aufgabe : ( VP) Bilden Sie die Ableitung der Funktion f mit f(x) sin(4x ). Aufgabe : ( VP) Geben Sie eine Stammfunktion
Abitur 2010 Mathematik LK Geometrie V
 Seite http://www.abiturloesung.de/ Seite Abitur Mathematik LK Geometrie V Gegeben sind in einem kartesischen Koordinatensystem des R der Punkt A( ) und die Menge der Punkte B k ( k) mit k R. Die Punkte
Seite http://www.abiturloesung.de/ Seite Abitur Mathematik LK Geometrie V Gegeben sind in einem kartesischen Koordinatensystem des R der Punkt A( ) und die Menge der Punkte B k ( k) mit k R. Die Punkte
ISBN
 1 Zeitraum Ziele / Inhalte (Sach- und Methodenkompetenz) Klassenarbeit Analysis Grenzwerte 1. Die explizite und rekursive Beschreibung von Zahlenfolgen verstehen und Eigenschaften von Zahlenfolgen kennen
1 Zeitraum Ziele / Inhalte (Sach- und Methodenkompetenz) Klassenarbeit Analysis Grenzwerte 1. Die explizite und rekursive Beschreibung von Zahlenfolgen verstehen und Eigenschaften von Zahlenfolgen kennen
Hauptprüfung 2007 Aufgabe 3
 Hauptprüfung 7 Aufgabe. Gegeben sind die Funktionen f, g und h mit f (x) = sin x g (x) = sin(x) +, x h(x) = sin x Ihre Schaubilder sind Beschreiben Sie, wie hervorgehen.. Skizzieren Sie K g. K f, K f,
Hauptprüfung 7 Aufgabe. Gegeben sind die Funktionen f, g und h mit f (x) = sin x g (x) = sin(x) +, x h(x) = sin x Ihre Schaubilder sind Beschreiben Sie, wie hervorgehen.. Skizzieren Sie K g. K f, K f,
(Quelle Abitur BW 2004) Gegeben sind die Schaubilder der Funktion mit, ihrer Ableitungsfunktion, einer Stammfunktion von und der Funktion mit.
 Aufgabe A5/04 Die Abbildung zeigt das Schaubild der Ableitungsfunktion einer Funktion. Welche der folgenden Aussagen über die Funktion sind wahr, falsch oder unentscheidbar? (1) ist streng monoton wachsend
Aufgabe A5/04 Die Abbildung zeigt das Schaubild der Ableitungsfunktion einer Funktion. Welche der folgenden Aussagen über die Funktion sind wahr, falsch oder unentscheidbar? (1) ist streng monoton wachsend
K2 KLAUSUR Pflichtteil
 K2 KLAUSUR 10.02.2012 MATHEMATIK Pflichtteil: Aufgabe 1 2 3 4 5 6 7 8 Punkte (max) 2 2 3 4 5 3 4 3 Punkte Wahlteil Analysis Aufgabe a b c Punkte (max) 9 5 4 Punkte Wahlteil Geometrie Aufgabe a b c Punkte
K2 KLAUSUR 10.02.2012 MATHEMATIK Pflichtteil: Aufgabe 1 2 3 4 5 6 7 8 Punkte (max) 2 2 3 4 5 3 4 3 Punkte Wahlteil Analysis Aufgabe a b c Punkte (max) 9 5 4 Punkte Wahlteil Geometrie Aufgabe a b c Punkte
Analysis f(x) = x 2 1. (x D f )
 Analysis 15 www.schulmathe.npage.de Aufgaben 1. Gegeben ist die Funktion f mit f(x) = x3 x 1 (x D f ) a) Geben Sie den maximalen Definitionsbereich der Funktion f an. Zeigen Sie, dass der Graph der Funktion
Analysis 15 www.schulmathe.npage.de Aufgaben 1. Gegeben ist die Funktion f mit f(x) = x3 x 1 (x D f ) a) Geben Sie den maximalen Definitionsbereich der Funktion f an. Zeigen Sie, dass der Graph der Funktion
Pflichtteilaufgaben zu Elemente der Kurvendiskussion. Baden-Württemberg
 Pflichtteilaufgaben zu Elemente der Kurvendiskussion Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Aleander Schwarz www.mathe-aufgaben.com September 6 Übungsaufgaben: Ü: Gegeben ist
Pflichtteilaufgaben zu Elemente der Kurvendiskussion Baden-Württemberg Hilfsmittel: keine allgemeinbildende Gymnasien Aleander Schwarz www.mathe-aufgaben.com September 6 Übungsaufgaben: Ü: Gegeben ist
Analysis: Klausur Analysis
 Analysis Klausur zu Ableitung, Extrem- und Wendepunkten, Interpretation von Graphen von Ableitungsfunktionen, Tangenten und Normalen (Bearbeitungszeit: 90 Minuten) Gymnasium J Alexander Schwarz www.mathe-aufgaben.com
Analysis Klausur zu Ableitung, Extrem- und Wendepunkten, Interpretation von Graphen von Ableitungsfunktionen, Tangenten und Normalen (Bearbeitungszeit: 90 Minuten) Gymnasium J Alexander Schwarz www.mathe-aufgaben.com
Gebrochen rationale Funktion f(x) = x2 +1
 Gebrochen rationale Funktion f() = +. Der Graph der Funktion f ist punktsmmetrisch, es gilt: f( ) = ( ) + f() = f( ) = + = + = f(). An der Stelle = 0 ist f nicht definiert, an dieser Stelle liegt ein Pol
Gebrochen rationale Funktion f() = +. Der Graph der Funktion f ist punktsmmetrisch, es gilt: f( ) = ( ) + f() = f( ) = + = + = f(). An der Stelle = 0 ist f nicht definiert, an dieser Stelle liegt ein Pol
R. Brinkmann Seite
 R. Brinkmann http://brinkmann-du.de Seite 1 1.08.016 Kurvendiskussion Vorbetrachtungen Um den Graphen einer Funktion zeichnen und interpretieren zu können, ist es erforderlich einiges über markante Punkte
R. Brinkmann http://brinkmann-du.de Seite 1 1.08.016 Kurvendiskussion Vorbetrachtungen Um den Graphen einer Funktion zeichnen und interpretieren zu können, ist es erforderlich einiges über markante Punkte
Der folgende Katalog soll Beispiele dafür aufzeigen, was konkret verlangt werden kann, ohne dabei den Anspruch auf Vollständigkeit zu erheben.
 Fundus für den Pflichtbereich / Mathematik-Abitur ab 4 Themenbereiche Der Pflichtteil soll aus kleineren Aufgaben bestehen, die ohne Hilfsmittel zu bearbeiten sind. Er soll die Grundkompetenzen abprüfen.
Fundus für den Pflichtbereich / Mathematik-Abitur ab 4 Themenbereiche Der Pflichtteil soll aus kleineren Aufgaben bestehen, die ohne Hilfsmittel zu bearbeiten sind. Er soll die Grundkompetenzen abprüfen.
Die gebrochenrationale Funktion
 Die gebrochenrationale Funktion Definition: Unter einer gebrochenrationalen Funktion versteht man den Quotienten zweier ganzrationaler Funktionen, d.h. Funktionen der Form f :x! a n xn + a n 1 x n 1 +...+
Die gebrochenrationale Funktion Definition: Unter einer gebrochenrationalen Funktion versteht man den Quotienten zweier ganzrationaler Funktionen, d.h. Funktionen der Form f :x! a n xn + a n 1 x n 1 +...+
G13 KLAUSUR 1. (1) (2 VP) Bilden Sie die erste Ableitung der Funktion f mit. f(x) = e 2x+1 x
 G3 KLAUSUR PFLICHTTEIL Aufgabe 2 3 4 5 6 7 8 Punkte (max) 2 2 3 3 5 3 5 3 Punkte () (2 VP) Bilden Sie die erste Ableitung der Funktion f mit f(x) = e 2x+. x (2) (2 VP) Gegeben ist die Funktion f mit f(x)
G3 KLAUSUR PFLICHTTEIL Aufgabe 2 3 4 5 6 7 8 Punkte (max) 2 2 3 3 5 3 5 3 Punkte () (2 VP) Bilden Sie die erste Ableitung der Funktion f mit f(x) = e 2x+. x (2) (2 VP) Gegeben ist die Funktion f mit f(x)
Fachcurriculum Mathematik Kursstufe Kepler-Gymnasium Pforzheim
 Kompetenzen und Inhalte des Bildungsplans - besondere Eigenschaften von Funktionen rechnerisch und mithilfe des CAS bestimmen; Unterrichtsinhalte Analysis Bestimmung von Extrem- und Wendepunkten (ca. 8-11
Kompetenzen und Inhalte des Bildungsplans - besondere Eigenschaften von Funktionen rechnerisch und mithilfe des CAS bestimmen; Unterrichtsinhalte Analysis Bestimmung von Extrem- und Wendepunkten (ca. 8-11
Schwerpunktaufgaben zur Vorbereitung auf die Leistungsfeststellung
 Schwerpunktaufgaben zur Vorbereitung auf die Leistungsfeststellung 1. Lösen Sie folgendes Gleichungssystem mit Hilfe des Gauß-Verfahrens. Überprüfen Sie Ihr Ergebnis mit dem Taschenrechner. ganzzahlig
Schwerpunktaufgaben zur Vorbereitung auf die Leistungsfeststellung 1. Lösen Sie folgendes Gleichungssystem mit Hilfe des Gauß-Verfahrens. Überprüfen Sie Ihr Ergebnis mit dem Taschenrechner. ganzzahlig
5. Geraden und Ebenen im Raum 5.1. Lineare Abhängigkeit und Unabhängigkeit von Vektoren
 5 Geraden und Ebenen im Raum 5 Lineare Abhängigkeit und Unabhängigkeit von Vektoren Definition: Die Vektoren a,a,,a n heißen linear abhängig, wenn mindestens einer dieser Vektoren als Linearkombination
5 Geraden und Ebenen im Raum 5 Lineare Abhängigkeit und Unabhängigkeit von Vektoren Definition: Die Vektoren a,a,,a n heißen linear abhängig, wenn mindestens einer dieser Vektoren als Linearkombination
B Differenzialrechnung
 A Funktionen Seite 1 Abhängigkeiten entstehen... 4 2 Der Funktionsbegriff... 6 3 Lineare Funktionen... 8 4 Lineare Regression... 1 5 Funktionsscharen... 12 6 Betragsfunktionen... 13 7 Potenzfunktionen...
A Funktionen Seite 1 Abhängigkeiten entstehen... 4 2 Der Funktionsbegriff... 6 3 Lineare Funktionen... 8 4 Lineare Regression... 1 5 Funktionsscharen... 12 6 Betragsfunktionen... 13 7 Potenzfunktionen...
Diese Funktion ist mein Typ!
 Diese Funktion ist mein Typ! Überblick über die wichtigsten Funktionstypen der 10.Jgst.: Lineare Funktionen Quadratische Funktionen Ganzrationale Funktionen Gebrochen-rationale Funktionen Trigonometrische
Diese Funktion ist mein Typ! Überblick über die wichtigsten Funktionstypen der 10.Jgst.: Lineare Funktionen Quadratische Funktionen Ganzrationale Funktionen Gebrochen-rationale Funktionen Trigonometrische
Abiturprüfung Mathematik 2012 Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen
 Abiturprüfung Mathematik 202 Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen klaus_messner@web.de www.elearning-freiburg.de Pflichtteil 202 2 Aufgabe : Bilden Sie die erste Ableitung
Abiturprüfung Mathematik 202 Baden-Württemberg Allgemeinbildende Gymnasien Pflichtteil Lösungen klaus_messner@web.de www.elearning-freiburg.de Pflichtteil 202 2 Aufgabe : Bilden Sie die erste Ableitung
MATHEMATIK K1 EINSTIEGSARBEIT (OHNE GTR)
 MATHEMATIK K EINSTIEGSARBEIT (OHNE GTR Einige Stichworte: Bruchrechnen: bei Addition und Subtraktion beide Brüche auf den Hauptnenner bringen Man teilt durch einen Bruch, indem man mit dessen Kehrwert
MATHEMATIK K EINSTIEGSARBEIT (OHNE GTR Einige Stichworte: Bruchrechnen: bei Addition und Subtraktion beide Brüche auf den Hauptnenner bringen Man teilt durch einen Bruch, indem man mit dessen Kehrwert
