Mengen. (Nicht-) Elemente einer Menge { 3, 4 } { 1, { 2 }, { 3, 4 }, { 5 } } 3 { 1, { 2 }, { 3, 4 }, { 5 } }

Transkript

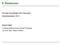
1 Mengen Definition (Intuitive Mengenlehre) Eine Menge ist die Zusammenfassung von Elementen unserer Anschauung zu einem wohldefinierten Ganzen. (Georg Cantor) Notation 1. Aufzählung aller Elemente: { 1, { 2 }, { 3, 4 }, { 5 } } 1. Beschreibung der Eigenschaften der Elemente: { x x mod 2 = 0 } Informell wird auch geschrieben: { 2, 4, 6, 8, } (Nicht-) Elemente einer Menge { 3, 4 } { 1, { 2 }, { 3, 4 }, { 5 } } 3 { 1, { 2 }, { 3, 4 }, { 5 } } Grundprinzipien Axiom der Extensionalität: Zwei Mengen A und B sind genau dann gleich, wenn sie die gleichen Elemente enthalten. A = B ( x : x A x B ) Beispiel: { 1, 2, 3 } = { n n n < 4 } Axiom der Komprehension: Für jede Eigenschaft können wir eine Menge bilden, die genau die Elemente enthält, die diese Eigenschaft haben. Mengen, Relationen, Funktionen 1

2 Eigenschaften Mengenzugehörigkeit Teilmengen x : ( x { a 1, a n } x = a 1 x = a n ) x : ( x { y P(y) } P(x) ) Die Menge T heisst eine (unechte) Teilmenge der Menge A, wenn jedes Element, das in der Teilmenge T liegt, auch in der Menge A liegt: T A ( x : x T x A ) Beispiele: { 2 } { 1, 2 } { 1, 2 } { 1, 2 } Die Menge T heisst eine echte Teilmenge der Menge A, wenn T eine Teilmenge von A, aber nicht gleich A ist: T A ( x : x T x A ) T A Beispiel: { 2 } { 1, 2 } Mengen, Relationen, Funktionen 2

3 Prominente Mengen = Menge der natürlichen Zahlen ohne 0 = { 1, 2, 3, } 0 = Menge der natürlichen Zahlen mit 0 0 = { 0, 1, 2, 3, } = Menge der ganzen Zahlen = { 0, 1, -1, 2, -2, 3, -3, } = Menge der rationalen Zahlen = { a / b a b } = Menge der reellen Zahlen = Menge der komplexen Zahlen Mengen, Relationen, Funktionen 3

4 Spezielle Mengen (1) Durchschnittsmenge Der Durchschnitt zweier Mengen A und B ist die Menge aller Elemente, die sowohl in A als auch in B enthalten sind. Vereinigungsmenge A B = { x x A x B } Die Vereinigung zweier Mengen A und B ist die Menge aller Elemente, die in A oder in B enthalten sind. Leere Menge A B = { x x A x B } Die leere Menge ist die Menge, die kein Element enthält. Sie wird oder {} geschrieben: Komplementärmenge = { x x x } oder x : x Ist eine Grundmenge G und eine Menge A mit A G gegeben, so ist die Komplementärmenge A c definiert durch: A c = { x x A x G } Mengen, Relationen, Funktionen 4

5 Spezielle Mengen (2) Potenzmenge Sei A eine Menge. Die Potenzmenge einer beliebigen Menge A ist die Menge P(A) aller Teilmengen von A. P(A) = { U U A } Beispiel: P( { 1, 2 } ) = {, { 1 }, { 2 }, { 1, 2 } } Differenzmenge Seien A und B beliebige Mengen. Die Differenz A B, gesprochen A minus B, ist die Menge aller Elemente, die in A aber nicht in B liegen. A - B = { x x A x B } Beispiel: { 1, 2, 3 } - { 3, 4 } = { 1, 2 } Symmetrische Differenzmenge Die symmetrische Differenz zweier Mengen A und B ist die Menge A B aller Elemente, die genau in einer der beiden Mengen liegen. A B = ( A B ) ( A B ) Beispiel: { 1, 2, 3 } { 3, 4 } = { 1, 2, 4 } Mengen, Relationen, Funktionen 5

6 Weitere Eigenschaften Kardinalität einer Menge Sei A eine Menge mit endlich vielen Elementen. Die Anzahl A nennt man die Mächtigkeit oder Kardinalität der Menge. Zwei endliche Mengen haben dieselbe Kardinalität, wenn die Anzahl Elemente in beiden Mengen gleich ist. Die Kardinalität von unendlichen Mengen wird später definiert. Disjunktheit Zwei Mengen A und B heissen disjunkt, wenn ihr Durchschnitt leer ist. Paarweise Disjunktheit A B = Eine Menge X von Mengen heisst paarweise disjunkt, wenn der Durchschnitt von jedem Paar von Mengen leer ist. A, B X : A B A B = Mengen, Relationen, Funktionen 6

7 Familien von Mengen Familie von Mengen Menge M von Mengen A i, die durch eine Indexmenge I indiziert sind: i : i I A i M Vereinigung M = i I A i = { x i I : x A i } Durchschnitt M = i I A i = { x i I : x A i } Mengen, Relationen, Funktionen 7

8 Mengengesetze Idempotenz A A = A A A = A Kommutativität A B = B A A B = B A Assoziativität (A B) C = A (B C) (A B) C = A (B C) Distributivität A (B C) = (A B) (A C) A (B C) = (A B) (A C) Absorption A (A B) = A A (A B) = A Reflexivität A A A A Kontraktion (A B) A (A B) A Monotonie A B A C B C A B A C B C Existiert eine Grundmenge G mit A,B G, so gelten ferner: Neutrale Elemente A G = A A = A Invariable Elemente A = A G = G Extremalität A G A De Morgansche (A B) c = A c B c (A B) c = A c B c Regeln Komplement A c A = G A c A = Mengen, Relationen, Funktionen 8

9 Beweise in der Mengenlehre Venn Diagramme: graphische Veranschaulichung; allenfalls mit Fallunterscheidungen Direkter Beweis durch Anwendung von Definitionen, Axiomen und Gesetzen. Indirekter Beweis durch Negation der Aussage und Angabe eines Gegenbeispiels. Um A = B zu beweisen, beweise man A B und B A. Transfer Methode: Eine mengentheoretische Formel wird in eine äquivalente aussagenlogische Formel umgewandelt, die dann bewiesen wird. Diese Methode beruht auf der Verwandtschaft zwischen Aussagenlogik und Mengenlehre, die damit zu tun hat, dass beide Systeme Boole sche Algebren sind. Mengenlehre Aussagenlogik Mengen, Relationen, Funktionen 9

10 Direkter Beweis: ist Teilmenge jeder Menge Gegeben: 1. T A x : x T x A 2. x : x Zu beweisen: A Beweis: A x : x x A (1) A x : x A (2) A ( ist die immer falsche Aussage, die immer wahre) (1) Definition von, (2) Axiom für, x ist für jedes x falsch, (3) Q ist für jede Aussage Q wahr (3) Mengen, Relationen, Funktionen 10

11 Indirekter Beweis: ist nicht echte Teilmenge jeder Menge Gegeben: 1. T A ( x : x T x A ) T A 2. x : x Zu beweisen: ( A ) Beweis: Annahme des Gegenteils: A Gegenbeispiel: A = Einsetzen in der Definition: ( x : x x ) ( x : x x ) ist ein Widerspruch. Mengen, Relationen, Funktionen 11

12 Direkter Beweis: ( A B ) ( A B ) = ( A B ) ( B A ) Gegeben: Die Definitionen von,,,, Beweis: ( A B ) ( B A ) = { x x A x B } { x x A x B } = (1) { x ( x A x B ) ( x A x B ) } = (2) { x ( x A x B ) ( x A x B ) } = (3) { x ( x A x A ) ( x A x B ) ( x B x A ) ( x B x B ) } = (4) { x ( x A x B ) ( x B x A ) } = (5) ( A B ) ( B A ) (1) Definitionen,, (2) Definition, (3) Definition und, de Morgan, (4) Distributivität, (5) Vereinfachung, Definitionen,. Mengen, Relationen, Funktionen 12

13 Geordnete Paare und n-tupel Geordnete Paare ( a, b ) heisst das geordnete Paar der Elemente a und b. Gleichheit von Paaren Die Paare (a 1, b 1 ) und (a 2, b 2 ) sind genau dann gleich, wenn a 1 = a 2 b 1 = b 2 n-tupel (a 1,, a n ) heisst das geordnete n-tupel der Elemente a 1 bis a n. Gleichheit von n-tupeln Die n-tupel ( a 1,, a n ) und ( b 1,, b n ) sind genau dann gleich, wenn a 1 = b 1 a n = b n. Mengen, Relationen, Funktionen 13

14 Relationen Kartesisches Produkt Das kartesische Produkt der beiden Mengen A und B ist die Menge A B aller geordneten Paare (a, b) mit a A, b B. A B = { ( a, b ) a A b B } Man schreibt A 2 = A A, A 3 = A A A, usw. Binäre Relationen Sei A eine Menge. Eine binäre Relation R auf A ist eine Teilmenge des kartesischen Produkts der Menge A mit sich selbst. R A A Seien A 1 und A 2 Mengen. Eine binäre Relation R auf A 1 und A 2 ist eine Teilmenge des kartesischen Produkts A 1 A 2. R A 1 A 2 Infixnotation: Für (a, b) R schreibt man auch arb. n-stellige Relationen Seien A 1, A 2,, A n Mengen. Eine n-stellige Relation R auf A 1, A 2,, A n ist eine Teilmenge des kartesischen Produkts der Mengen A 1, A 2,, A n. R A 1 A 2 A n Mengen, Relationen, Funktionen 14

15 Die 16 binären Relationen auf A = {1,2} R i {1,2} {1,2} R 1 R 9 {(1,2),(2,1)} R 2 {(1,1)} R 10 {(1,2),(2,2)} R 3 {(1,2)} R 11 {(2,1),(2,2)} R 4 {(2,1)} R 12 {(1,1),(1,2),(2,1)} R 5 {(2,2)} R 13 {(1,1),(1,2),(2,2)} R 6 {(1,1),(1,2)} R 14 {(1,1),(2,1),(2,2)} R 7 {(1,1),(2,1)} R 15 {(1,2),(2,1),(2,2)} R 8 {(1,1),(2,2)} R 16 {(1,1),(1,2),(2,1),(2,2)} Mengen, Relationen, Funktionen 15

16 Spezielle Relationen Umkehrrelation Sei R A B eine Relation. Die Umkehrrelation zur Relation R ist die Relation R -1 B A mit Komposition von Relationen R -1 = { ( b, a ) ( a, b ) R } Seien R 1 A B und R 2 B C Relationen. Die Komposition R 1 R 2 A C von R 1 und R 2 wird definiert durch a A, c C : ( a, c ) R 1 R 2 b B : ( a, b ) R 1 ( b, c ) R 2 Beispiel für Komposition von Relationen Programme können als Relationen ihrer Eingabe- und Ausgabewerte verstanden werden. Die Hintereinanderausführung von zwei Programmen entspricht dann der Komposition der entsprechenden Relationen. Mengen, Relationen, Funktionen 16

17 Eigenschaften von Relationen Eine Relation R A B ist Linkstotal: Jedes Element a A tritt in mindestens einem Paar ( a, b ) R links auf. a A : b B : ( a, b ) R Rechtstotal: Jedes Element b B tritt in mindestens einem Paar ( a, b ) R rechts auf. b B : a A : ( a, b ) R Linkseindeutig: Für ein b B zu dem es ein a A gibt mit ( a, b ) R ist dieses linke a eindeutig. a 1, a 2 A : ( b B : ( a 1, b ) R ( a 2, b ) R ) a 1 = a 2 Rechtseindeutig: Für ein a A zu dem es ein b B gibt mit ( a, b ) R ist dieses rechte b eindeutig. b 1, b 2 B : ( a A : ( a, b 1 ) R ( a, b 2 ) R ) b 1 = b 2 Mengen, Relationen, Funktionen 17

18 Beispiel: Ein/Ausgabe Relation von Programmen INTEGER A READ (A) WHILE (A <> 0) DO { A := A - 2 } WRITE (A) Datentyp INTEGER: beliebig grosse ganze Zahlen Ein/Ausgabe Relation: R mit ( x, y ) R genau dann, wenn das Programm auf die Eingabe von x mit der Ausgabe von y reagiert. Ist das Programm linkstotal, rechtstotal, linkseindeutig, rechtseindeutig? Mengen, Relationen, Funktionen 18

19 Eigenschaften von binären Relationen Eine binäre Relation R X X heisst Reflexiv: Jedes Element x steht zu sich selber in Relation. x X : ( x, x ) R Irreflexiv: Kein Element steht zu sich selber in Relation. x X : ( x, x ) R Symmetrisch: Zu jedem Paar in der Relation ist auch das gespiegelte Paar in der Relation. x, y X : ( x, y ) R ( y, x ) R Antisymmetrisch (identitiv): Zu jedem Paar in der Relation ist das gespiegelte Paar nur dann in der Relation, wenn die Elemente gleich sind. x, y X : ( x, y ) R ( y, x ) R x = y Asymmetrisch: Zu jedem Paar in der Relation ist das gespiegelte Paar nicht in der Relation. Transitiv: x, y X : ( x, y ) R ( y, x ) R x, y, z X : ( x, y ) R ( y, z ) R ( x, z ) R Mengen, Relationen, Funktionen 19

20 Äquivalenzrelationen Eine Äquivalenzrelation auf einer Menge M ist eine binäre Relation M M die reflexiv, symmetrisch und transitiv ist. Gleichheit ("=") ist die prototypische Äquivalenzrelation. Partition: Sei M eine Menge. Eine Partition von M ist eine Menge P von Teilmengen von M, also P P (M), für die die folgenden Eigenschaften gelten: 1. Keine Teilmenge der Partition ist leer. 2. Die Teilmengen der Partition sind paarweise disjunkt. 3. Die Vereinigung aller Teilmengen der Partition ist die Menge M. Äquivalenzklassen: Sei M M eine Äquivalenzrelation. Zu jedem Element m M heisst die Menge (m) = { x M x m } die von m erzeugte Äquivalenzklasse. Für jede Äquivalenzrelation auf einer Menge X bildet die Menge der Äquivalenzklassen von eine Partition P von X. Mengen, Relationen, Funktionen 20

21 Beispiel einer Äquivalenzrelation a b modulo n d.h. a und b geben bei der Division durch n den gleichen Rest r 0 definiert eine Äquivalenzrelation m auf der Menge a = k 1 * n + r b = k 2 * n + r (k i, r = 0,..., n-1) a m b a b = k * n Reflexivität a : a m a (a a = 0 * n) Symmetrie a, b : a m b b m a (a b = k * n, b a = - k * n) Transitivität a, b, c : a m b b m c a m c (a b = k 1 * n, b c = k 2 * n, a - c = (k 1 + k 2 )* n) Mengen, Relationen, Funktionen 21

22 Beispiel einer Äquivalenzrelation Die Menge aller Zahlen a, die bei der Division durch n den gleichen Rest r 0 ergeben, bilden eine Äquivalenzklasse (r). Da r = 0,..., n-1, gibt es n m Äquivalenzklassen. Für n = 5 erhalten wir (0) m = { a a m 0} = {..., -10, -5, 0, 5, 10,...} (1) m = { a a m 1} = {..., -9, -4, 1, 6, 11,...} (2) m = { a a m 2} = {..., -8, -3, 2, 7, 12,...} (3) m = { a a m 3} = {..., -7, -2, 3, 8, 13,...} (4) m = { a a m 4} = {..., -6, -1, 4, 9, 14,...} Die Menge der Äquivalenzklassen von m bildet eine Partition von, denn keine Äquivalenzklasse ist leer die Äquivalenzklassen sind paarweise disjunkt (0) m (1) m (2) (3) m (4) m = Mengen, Relationen, Funktionen 22

23 Weitere Beispiele von Äquivalenzrelationen Gegeben sei die Menge aller Menschen. Welche der folgenden Relationen sind Äquivalenzrelationen? x steht zu y in Relation, falls x und y die gleiche Sprache sprechen. x steht zu y in Relation, falls x älter oder genauso alt wie y ist. x steht zu y in Relation, falls x und y sich gegenseitig kennen. Mengen, Relationen, Funktionen 23

24 Hüllen Sei M eine Menge und R M M eine Relation. Wir suchen nun nach der kleinsten Anzahl von geordneten Paaren aus M M, die wir zu R hinzufügen müssen, damit die so erweiterte Relation Hülle genannt bestimmte Eigenschaften besitzt. 1. Die transitive Hülle von R ist die Relation <R> t M M definiert durch: ( x, y ) <R> t ( x, y ) R n : t 1, t 2,, t n : (x, t 1 ), ( t 1, t 2 ),, ( t n-1, t n ), ( t n, y ) <R> t 2. Die symmetrische Hülle von R ist die Relation <R> s M M definiert durch: ( x, y ) <R> s (( x, y ) R ( y, x ) R) <R> s = R R -1 Mengen, Relationen, Funktionen 24

25 Hüllen 3. Die reflexiv-transitive Hülle von R ist die Relation <R> rt M M definiert durch: ( x, y ) <R> rt (( x, y ) <R> t x = y) 4. Die reflexiv-symmetrisch-transitive Hülle von R ist die Relation <R> rst M M definiert durch: <R> rst = <<R> s > rt <R> rst ist die kleinste Erweiterung von R zu einer Äquivalenzrelation. Mengen, Relationen, Funktionen 25

26 Funktionen Eine Funktion f ist eine binäre Relation f A B, die linkstotal und rechtseindeutig ist: Zu jedem a A gibt es genau ein b B mit (a, b) f. Bei Funktionen schreibt man f : A B anstatt f A B und f(a) = b anstatt (a, b) f. Terminologie 1. A heisst der Definitionsbereich von f. 2. B heisst der Wertebereich von f. 3. Die Menge f(a) = { f(a) a A } heisst das Bild von f. Eigenschaften von Funktionen 1. Eine Funktion ist surjektiv, wenn sie rechtstotal ist. 2. Eine Funktion ist injektiv, wenn sie linkseindeutig ist. 3. Eine Funktionen ist bijektiv, wenn sie surjektiv und injektiv ist. Sind f : A B und g : B C Funktionen, so bezeichnet g f : A C die Komposition von f und g, die durch (g f)(a) = g(f(a)) definiert ist. Mengen, Relationen, Funktionen 26

27 Spezielle Funktionen Identität Die Funktion id A : A A, die durch id A (a) = a definiert ist, heisst die Identität. Konstante Funktion Eine Funktion c : A B, die für alle Werte des Arguments denselben Wert hat, heisst konstant. Umkehrfunktion Eine Funktion g : B A heisst eine Umkehrfunktion einer Funktion f : A B, wenn g f : A A gleich id A ist, und f g : B B gleich id B ist. Eine Funktion hat genau dann eine Umkehrfunktion, wenn sie bijektiv ist. Diese Umkehrfunktion ist eindeutig. Charakteristische Funktion Gegen sei eine Menge A und ein Element a A. Die Funktion x a : A {0,1} ist definiert als x a (a) = 1 und x a (b) = 0 für b a und heisst die charakterische Funktion von a.. Mengen, Relationen, Funktionen 27

28 Kardinalität von Mengen Anzahl von Elementen (informell) Sei A eine Menge mit endlich vielen Elementen. Die Anzahl A nennt man die Mächtigkeit oder Kardinalität der Menge. Zwei endliche Mengen haben dieselbe Kardinalität, wenn die Anzahl Elemente in beiden Mengen gleich ist. Nimmt man je ein Element aus beiden Mengen heraus, bleiben am Ende zwei leere Mengen. Cantor hat diese Idee für unendliche Mengen weiterentwickelt: Zwei unendliche Mengen haben dieselbe Kardinalität, wenn sich die Elemente beider Mengen paaren lassen: Mengen, Relationen, Funktionen 28

29 Kardinalität von Mengen (2) Formaler: X = Y es gibt eine Bijektion zwischen X und Y X Y es gibt eine injektive Funktion von X nach Y Die Relation definiert durch X Y es gibt eine Bijektion zwischen X und Y ist eine Äquivalenzrelation. Wir definieren nun X als die Äquivalenzklasse (X) Die Kardinalität von ist 0 (Aleph null). 0 ist die kleinste unendliche Kardinalzahl. Mengen mit der Kardinalzahl 0 werden abzählbar unendlich genannt. Eine weitere Kardinalzahl ist c. Dies ist die Kardinalität von P( ) und. Mengen mit der Kardinalzahl c werden überabzählbar genannt. Cantors Diagonalisierungsargument beweist c <> 0. Mengen, Relationen, Funktionen 29

30 Cantors Diagonalisierungsargument für P( ) > Beweis durch Widerspruch. Wir nehmen an, dass P( ). D.h., man kann jeder Teilmenge von eine Zahl aus so zuordnen, dass jede Zahl aus höchstens einmal benutzt wird. Uns interessieren die Paare, bei denen die Teilmenge von die Zahl aus nicht enthält, mit der sie gepaart wird. Beim Paar (1, {2}) z.b. enthält die Teilmenge die Zahl nicht, jedoch beim Paar (2, {2, 3}) enthält sie sie. Wir definieren eine Teilmenge M so, dass M die Zahlen enthält, die entweder nicht gepaart sind oder mit einer Teilmenge von gepaart sind, die die Zahl nicht enthalten. M ist eine Teilmenge von. Also muss es ein Paar (z, M) geben. Ist z ein Element von M? Ja: Dann ist z gepaart mit einer Menge, die z enthält. Das ist ein Widerspruch zur Definition von M. Nein: Dann ist z gepaart mit einer Menge aus P( ) (nämlich M), die z nicht enthält. Nach der Definition von M muss z dann aber ein Element von M sein. Widerspruch. Also muss P( ) > gelten. Mengen, Relationen, Funktionen 30

31 Russelsches Paradox in der naiven Mengenlehre Axiom der Komprehension: Für jede Eigenschaft können wir eine Menge bilden, die genau die Elemente enthält, die diese Eigenschaft haben. Der Begriff der Eigenschaft muss eingeschränkt werden, sonst entsteht ein Widerspruch. Beispiel: Man definiere M als die Mengen aller Mengen, die sich selbst nicht enthalten: Frage: Enthält M sich selber? M = { X X X } Ja. Wenn M sich selbst enthält, dann darf M sich selbst nicht enthalten Nein. Wenn M sich selbst nicht enthält, dann muss M sich selbst enthalten Wir wissen aber aus der Logik, dass aus einem Widerspruch alles abgeleitet werden kann. Mengen, Relationen, Funktionen 31

32 Rechnen mit Kardinalitäten Für endliche Mengen gilt: A B = A + B A B A B C = A + B + C A B A C B C + A B C A - B = A - B, falls B A A B = A B Für abzählbar unendliche Mengen gilt: = = 0 Was ist mit 0-0? Mengen, Relationen, Funktionen 32