Parameterschätzung. Kapitel Schätzfunktionen
|
|
|
- Alma Brinkerhoff
- vor 6 Jahren
- Abrufe
Transkript
1 Kapitel 8 Parameterschätzug 8.1 Schätzfuktioe Def : Es seie X 1,X,...,X uabhägige ZV, die alle die gleiche Verteilug besitze. θ sei ei ubekater Parameter dieser Verteilug. X 1,X,...,X ist als eie Beobachtugsoder) Messreihe zur Bestimmug vo θ mit Eizelmessuge aufzufasse. X i etspricht also der i te Messug. Dere Messergebis x i ist eie Realisierug vo X i. Aus dem Satz x 1,x,...,x vo Messwerte, de ma als Stichprobe vom Umfag bezeichet, bestimmt ma eie Schätzwert ˆθ für θ, vo dem ma ormalerweise aimmt, dass er ahe bei θ liegt. Die Zuordug vo x 1,x,...,x zu ˆθ bezeichet ma als Schätzfuktio: ˆθ = gx 1,x,...,x ). Drei Aahme: a) Messergebis ist bei jeder Messug ubeiflusst vo de vorherige Messergebisse = Die Zufallsvariable X 1,X,...,X sid uabhägig. b) Es gibt keie Veräderug der beeiflussbare Versuchsbediguge = Die Zufallsvariable X 1,X,...,X habe alle die gleiche Verteilug, häufig Normalverteilug. c) Es gibt keie systematische Fehler Beispiel 8.1.1: Wir führe eie Messreihe vo Messuge z.b. das elektrische Widerstades eies Gerätes) durch. Der i-te Messug etspricht eie Zufallsvariable X i Das Messergebis x i ist eie Realisierug der Zufallsvariable X i wahrer Wert = gemeisamer Erwartugswert µ := EX i ) der Zufallsvariable X i Ziel der Messuge ist es u, Iformatioe über µ zu bekomme. Es werde dazu Messuge tatsächlich durchgeführt, z.b. vier Widerstadsmessuge mit de Messergebisse i Ω): 10.1 =: x 1,10. =: x,10.0 =: x 3,10.1 =: x 4 100
2 Dies ist Stichprobe vom Umfag 4 allgemei: vom Umfag ). x := x := x 1 + x + + x = = 10.1 im Zahlebeispiel 4 Die Iterpretatio ist icht µ = x ud auch icht µ ist sicher ahe bei x, soder ur die Vermutug, dass x ahe bei µ liegt. ˆµ Schätzwert für µ) = x := x x =: gx 1,...,x ) bei diesem Beispiel). Aus Satz folgt ) X := X := X 1 + X + + X Dies rechtfertigt die obige Vermutug. µ für fast sicher) 8. Maximum Likelihood Methode Bestimme ˆθ so, dass PX 1 = x 1 X = x X = x ) bzw. die gemeisame Verteilugsdichte vo X 1,X,...,X a der Stelle x 1,x,...,x ) im Falle eier stetige ZV X) maximal wäre, we θ = ˆθ wäre. Beispiel 8..1: Eie Beobachtugsgröße sei Poisso-verteilt, wobei der Parameter λ ubekat sei λ > 0). Um Iformatioe über λ zu erhalte, mache wir drei Beobachtuge, d.h. wir ziehe eie Stichprobe vom Ufag 3. Die Beobachtugergebisse seie die Werte 4, 1, 6. Dies sid Realisieruge vo Zufallsvariable X 1,X,X 3, die uabhägig ud Poisso-verteilt sid mit dem gleichem λ. P X 1 = 4 X = 1 X 3 = 6) = P X 1 = 4) P X = 1) P X 3 = 6) = e λλ4 e 3λλ ! e λλ1 1! e λλ6 6! = 4!1!6! =: e 3λλ4+1+6 a Diese Wahrscheilichkeit et ma auch Likelihood Fuktio hλ). =: hλ) Awedug des Maximum-Likelihood Prizips: Die Wahrscheilichkeit für das eigetretee Ereigis, also hλ), sei maximal, we λ = ˆλ wäre. h 3λ λ4+1+6 λ) = 3)e + e 3λ ) λ a a = [ 3) λ )] e 3λλ a! = 0 3)λ ) = 0 λ = 0 λ>0 λ = Ausserdem gilt hλ) 0 für λ 0+ ud für λ ud hλ) > 0 für alle λ > 0. Damit ist hˆλ) das Maximum vo hλ). Der Maximum-Likelihood-Schätzwert Abk.: M-L-Schätzwert) ist also: ˆλ =
3 Ergebisse bei eiige Verteiluge: Tabelle 8-1 Verteilug bekate ubek. Schätzfkte ach Eigeschafte { Param. Param. der M-L-Meth.) aus m.wahrsch. p X i = p ˆp = x kosistet, erwart.treu 0 m. W.1-p) X ist biomialverteilt) Poissoverteilug λ ˆλ = x kosistet, erwart.treu 1 Expoetialverteilug λ ˆλ = kosistet, icht erw.treu x Nµ,σ) σ µ ˆµ = x kosistet, erwart.treu Nµ,σ) µ σ σ = 1 x i µ) kosistet, erwart.treu Nµ,σ) µ,σ ˆµ = x kosistet, erwart.treu σ = 1 x i x) kosistet, icht erw.treu Zu der 1. Verteilug: Die eizele Zufallsvariable X i ka ur Werte aehme ud die ZV X 1,X,...,X uabhägig. Wir habe also ei Beroulli-Experimet: { } 1 Erfolg mit Wahrscheilichkeit p X i := 0 Fehlschlag mit Wahrscheilichkeit 1 p X 1 + X + X X = X Aufg. 79 = Azahl der Erfolge bei Versuche. Bei der statistische Qualitätskotrolle m.z. ist p der Ateil der defekte Stücke i der Lieferug. x ist die Azahl der Ziehuge vo defekte Stücke. x ist damit der Ateil der defekte Stücke i der Stichprobe. Bem.: Die Schätzfuktio ach der M L Meth.) für σ ist ˆσ = σ. Sie ist aber weder für bekates och für ubekates µ erwartugstreu. 8.3 Eigeschafte vo Schätzfuktioe gx 1,X,...,X ) z.b. X geauer:x ) := X 1 + X + + X ) 1 ) ist ZV. Def : Eie Schätzfuktio g für θ heißt erwartugstreu, we gilt: EgX 1,...,X )) = θ. Beispiel: X ist erwartugstreu: ) 1 EX ) = E X i = 1 EX i ) = 1 10 µ = µ = EX i)
4 Def. 8.3.: sei variabel. Da heißt eie Schätzfuktio g geauer: Folge vo Schätzfuktioe) für θ kosistet, we gilt: P gx 1,...,X ) θ q) 1 für für alle q > 0. Beispiel: X ist kosistet; de es gilt ach Satz 7.9.3: X µ = EX i ) für f.s.) Satz 8.3.1: Es seie X 1,X,...,X uabhägige ZV, die alle die gleiche Verteilug besitze ud für die der Erwartugswert ud die Variaz existiere. a) x ist eie kosistete, erwartugstreue Schätzfuktio für EX i ) =: µ. b) 1 1 x i x) ist eie kosistete, erwartugstreue Schätzfuktio für V X i ) =: σ. EX i ) ud V X i ) werde dabei als ubekate Verteilugsparameter bei de ZV X i aufgefasst. 8.4 Kofidezitervalle Bei der Aufstellug vo Kofidezitervalle braucht ma die Verteilug der ZV gx 1,X,...,X ), die also über die Schätzfuktio vo de ZV X 1,X,...,X abhägt. Bei der Schätzug des Erwartugswertes µ eier NV ist das eie Summe der ZV X 1,X,...,X die och durch dividiert wird. Wir brauche also die Verteilug eier Summe vo uabhägige ormalverteilte ZV, ud dafür gilt der folgede Satz 8.4.1: a) Eie Summe vo ormalverteilte, uabhägige ZV ist wieder ormalverteilt. b) X ist ormalverteilt αx + β) mit α,β IR,α 0, ist ormalverteilt. Allgemeie Voraussetzug für 8.4 mit Ausahme vo Satz : X 1,...,X sid uabhägige, Nµ,σ) verteilte ZV. Satz 8.4.: X hat die Verteilug: Nµ, σ ). Die Aussage dieses Satzes ergibt sich direkt aus Satz Wir ehme u a, dass bei eier NV die Variaz σ bekat ud der Erwartugswert µ ubekat ist. Wir werde also versuche, µ mit Hilfe eier Stichprobe zu schätze. Schätzug: ˆµ = x x 1,x,,x Ergebis vo Stichprobe vom Umfag Das Kofidezitervall gibt u de Bereich um ˆµ = x a, für de wir mit ausreicheder Sicherheit sage köe, dass der wahre Wert vo µ dari liegt. 103
5 Def : Seie, 0 < γ < 1 beliebig vorgegebe. γ meist ahe bei 1, z. B. γ = 0.9,0.95,0.99 o. ä.). x ist eie Realisierug vo X. Gilt da 8.4.1) P X q µ X + q ) = ) P X µ q ) = γ, so bezeichet ma das Itervall [x q,x + q ] als γ Kofidezitervall für µ. γ heißt Vertraueswahrscheilichkeit häufig i % agegebe) ud sollte zusamme mit dem Stichprobeumfag vor der Utersuchug festgelegt werde. Korrekte Itepretatio: µ liegt mit Wahrscheilichkeit γ i dem Itervall [X q,x + q ]. Satz 8.4.3: a) Die folgede ZV ist stadard-ormalverteilt: Y := X µ) σ b) Aus der Eigeschaft P Y q) = Φq) 1 ka ma Kofidezitervalle für µ bei bekatem σ bestimme. Beispiel 8.4.1: Eie Messgröße oder Beobachtugsgröße) sei Nµ, σ)-verteilt, wobei µ ubekat ud σ = 1.8 bekat sei. Bestimme 0.95oder 95%) Kofidezitervall für µ, wähle also γ = Lege fest: = 9 d.h. 9 Messuge ) P Y q) = Φq) 1! = γ = 0.95 vergl. Satz 8.4.3), d.h. Φq)! = 1 + γ = 1.95 = q heißt Quatil zu 1 + γ Aus Normalverteilugstabelle lese wir ab q = Damit erhalte wir X µ) ) P σ 1.96 = Aus de 9 Messuge erhalte wir x = 3.5 ud damit das Kofidezitervall: µ 3.5 = x µ 1.96σ = = =: q 9 oder i expliziter Form: µ [x q,x + q ] = [ , ] =)[.34,4.676] Def. 8.4.: Z sei eie beliebige ZV mit der Verteilugsfuktio F ud c eie beliebige reelle Zahl mit 0 < c < 1. Da heißt q das c Quatil der Verteilug, we Fq) = c gilt. Isbesodere bezeiche wir das c Quatil der Stadard Normalverteilug mit q Φ c). 104
6 Bestimmug eies γ Kofidezitervalles für µ bei bekatem σ: Schritt 1: Lege die Vertraueswahrscheilichkeit γ ud de Stichprobeumfag fest. Schritt : Bestimme q > 0 aus Φq) =! 1 + γ, also das 1 + γ)/ Quatil der Stadard Normalverteilug. Schritt 3: Ziehe eie Stichprobe vom Umfag. x 1,x,...,x seie die dabei gewoee Realisieruge Mess oder Beobachtugsergebisse) der Nµ,σ) verteilte ZV X 1,X,...,X. Das Kofidezitervall ist da durch x µ) σ q oder i expliziter Form durch x q σ µ x + q σ gegebe. Satz 8.4.4: X sei N0,1) vert. Da hat Y := X die Verteilugsdichte: fy) := 0 für y 0 ud := π) 1/ y 1/ e y/ für y > 0. Satz 8.4.5: a) Die folgede ZV ist χ -verteilt mit Freiheitsgrade: Y := σ X i µ) Dabei ist die χ -Verteilug mit r Freiheitsgrade defiiert durch die folgede Verteilugsdichte: f χ y) := 0 für y 0 ud := K r e y/ y r )/ für y > 0, wobei die Kostate K r so bestimmt ist, dass das Itegral über die Verteilugsdichte vo bis de Wert 1 hat. F χ sei die zugehörige Verteilugsfuktio. b) Aus der Eigeschaft Pa Y b) = F χ b) F χ a) a b, Freiheitsgrade) ka ma Kofidezitervalle für σ bei bekatem µ bestimme. Satz 8.4.6: a) Die folgede ZV ist χ -verteilt mit 1) Freiheitsgrade: Y := σ X i X) b) Aus der Eigeschaft Pa Y b) = F χ b) F χ a) a b, 1) Freiheitsgrade) ka ma Kofidezitervalle für σ bei ubekatem µ bestimme. 105
7 Beispiel 8.4.: X 1,X seie uabhägig ud Nµ,1) verteilt X 1 µ) +X µ) ist Summe vo uabhägige ZV ud χ verteilt mit Freiheitsgrade. X 1 X) + X X) = X 1 X ) 1 + X + X X ) 1 + X ) X1 X ) X X ) 1 X1 X = + = Dies ist das Quadrat vo ur eier stadardormalverteilte ZV ud daher χ verteilt mit eiem Freiheitsgrad. Beispiel 8.4.3: Y sei ZV aus Satz häufig mit χ bezeichet) Sei r = 9 { = Zahl der uabhägige Summade = Zahl der Freiheitsgrade PY q) =: F χ q)! = q = 16.9 PY q) =: F χ q)! = q = Die Bestimmug vo Kofidezitervalle für σ wird i der Vorlesug ud i der Übug icht behadelt oder midestes zurückgestellt. Bei spätere Aweduge der χ -Verteilug werde Quatile ermittelt, für die eie Tabelle chiˆtab.pdf) bereitgestellt ist. Für große r, etwa ab r = 100, ka ma das c Quatil q äherugsweise durch die im Buch vo Bamberg/Baur agegebee Formel q q Φc) + r 1) bestimme. Dabei sid die Werte vo q Φ c) für eiige Werte vo c aus der letzte Zeile der Tabelle der Quatile der t Verteilug tverttab.pdf), für eiige weitere Werte aus der Formel Φq Φ c)) = 1 Φ q Φ c)) = c, d.h. aus Φ q Φ c)) = 1 c zu ermittel. Es ist z.b.!! Φ.36)) = Φ.36)) = ud damit gilt q Φ 0.010) =.36). Schließlich wird och q Φ 0.750) = , q Φ 0.500) = 0 ud q Φ 0.50) = beötigt. Bestimmug eies Kofidezitervalls für µ bei ubekatem σ: Y := X µ) σ i Satz wird ersetzt durch Y := X µ) 1 X i X) 1) Satz 8.4.7: X ud X i X) sid uabhägig. Satz 8.4.8: a) Die folgede ZV ist t -verteilt mit 1) Freiheitsgrade: Y := X µ) 1) X i X) 106
8 Dabei ist die t -Verteilug mit r Freiheitsgrade defiiert durch die folgede Verteilugsdichte: ) r + 1 f t y) := C r 1 + y r wobei die Kostate C r so bestimmt ist, dass das Itegral über die Verteilugsdichte vo bis de Wert 1 hat. F t sei die zugehörige Verteilugsfuktio. b) Aus der Eigeschaft P Y q) = F t q) 1 1) Freiheitsgrade) ka ma Kofidezitervalle für µ bei ubekatem σ bestimme. Beispiel 8.4.4: Eie Messgröße oder Beobachtugsgröße) sei Nµ, σ)-verteilt, wobei µ ud σ ubekat seie. Bestimme 90% Kofidezitervall für µ, also γ = Lege fest: = 11 d.h. 11 Messuge ) Eie Stichprobe vom Umfag 11 ergebe ˆµ = x = 3 ud x i x) = 11 x i 3) = 0 X µ) P ) q X i X) = Satz F t q) 1! = 0.90, wobei F t die Verteilugfuktio eier t-verteilug mit 1) = 10 Freiheitsgrade ist. Suche da q mit F t q) =! 1 + γ = 1.90 = 0.95 Die Zahl der Freiheitsgrade ist r = 1 = 10 Aus Tabelle der Quatile der t Verteilug lese wir ab: q = Damit erhalte wir als Kofidezitervall: x µ) x i x) , also µ x = x µ x i x) = 110 I expliziter Form erhalte wir also als 90% Kofidezitervall für µ: µ [x q,x + q ] = [3 0.77,3 0.77] =)[.8,3.77] = 0.77 =: q Bestimmug eies γ Kofidezitervalles für µ bei ubekatem σ: Schritt 1: Lege die Vertraueswahrscheilichkeit γ ud de Stichprobeumfag fest. Schritt : Bestimme q > 0 aus F t q) =! 1 + γ, also ei 1 + γ)/ Quatil der t Verteilug mit 1) Freiheitsgrade. Schritt 3: Ziehe eie Stichprobe vom Umfag. x 1,x,...,x seie die dabei gewoee Realisieruge Mess oder Beobachtugsergebise) der Nµ,σ) verteilte ZV X 1,X,...,X. Das 107
9 Kofidezitervall ist da durch x µ) 1) q x i x) oder i expliziter Form durch q x i x) x 1) µ x + q x i x) 1) gegebe. Satz 8.4.9: F t,r sei die Verteilugsfuktio der t Verteilug mit r Freiheitsgrade; da gilt: F t,r Φ für r. t Verteilug mit viele Freiheitsgrade = N0, 1) Verteilug N0, 1) Verteilug = t Verteilug mit r = Awedug: Bei Stichprobe mit großem Umfag etwa 50) ka äherugsweise die N0,1) Verteilug statt der t Verteilug beutzt werde. Satz : X sei eie biomialverteilte ZV mit de Parameter, p, die die folgede Bediguge erfülle sollte: 50, p,1 p) 5 vergl. Satz 7.6.7). a) Die ZV Y := X p pq ist äherugsweise N0,1) verteilt. vergl.satz u.7.6.4) statt 7.6.5) aus Satz 7.6.7) b) Aus P Y q) Φq) 1 ka ma wie ute beschriebe uter gewisse Bediguge Näheruge für Kofidezitervalle für p bestimme. p sei ubekat, ud wir suche ei γ Kofidezitervall für p. Nach Satz verwede wir dazu die Beziehug ) γ =! X p Φq) 1 P Y q) = P q = P X p q pq) p1 p) 0 p 1 p 1 p) 1/4 Beweis i eier Übugsaufgabe) γ =! Φq) 1 P X p q ) ) p1 p) P X p q 1 4 = P X p q ) Die Wahrscheilichkeit dafür, dass die Abweichug vo p vo der Schätz ZV X höchstes q / beträgt, ist also äherugsweise γ. We u x eie Realisierug vo X, also z.b. 108
10 die tatsächlich beobachtete Azahl der Ziehuge vo defekte Stücke ist, erhalte wir als Kofidezitervalläherug: x p = p x ) q x q p x + q p 1 := x q / p x + q / =: p [p 1,p ] ka u als Näherug für ei γ Kofidezitervalläherug für p geomme werde, we die Voraussetzuge vo Satz midestes da erfüllt sid, we p 5 ud 1 p) 5 für alle p [p 1,p ] gilt. Daraus ergibt sich die Bedigug! p )p 1 5 ud 1 p) )1 p )! 5 Bestimmug eies Kofidezitervalles für p: Bestimme q > 0 aus Φq) 1 =! γ, also aus Φq) = 1 + γ)/. Bestimme da ei Itervall p 1 p p mit x q 8.4.) p 1 = ) x + q, p = ) [p 1,p ] ist als Näherug für ei γ Kofidezitervall zu akzeptiere, we gilt: 50, p 1 5 ud 1 p ) 5. Aderefalls muss eie adere Methode als über Satz gewählt werde. Beispiel 8.4.4: Vor eier Wahl i eier Stadt mit wahlberechigte Eiwoher soll eie Meiugsumfrage durchgeführt werde. p := Ateil der Wähler der Partei A. 1 p)= Ateil der Wähler der adere Partei, Nichtwähler u.s.w. p sei ubekat. Kostruiere 95% Kofidezitervall für p. Es wird eie zufällige) Stichprobe vo Umfag 100 o. Z. gezoge, d.h. ei Wahlberechtigter wird icht zweimal befragt. Umfrageergebis: 40 davo sid für Patei A. Die ZV X := Azahl der Wähler vo A i der Stichprobe, dere Realisierug 40 ist, ist wege o.z. hypergeometrisch verteilt. Die Bediguge i Satz für die Näherug durch die Biomialverteilug sid aber deutlich erfüllt: N = ud = N X ist also äherugsweise biomialverteilt mit,p als Parameter. Kostruktio des Kofidezitervalles: Bestimme q > 0 aus Φq) 1! = γ = 0.95 Φq) = q Tab. = 1.96 x = 40 = Realisierug vo X bei der Durchführug der Umfrage. Die erste Bedigug für die Näherug der Biomialverteilug durch die Normalverteilug ist erfüllt: = Wir bestimme da die Greze p 1, = ud erhalte so das Itervall x q = [p 1,p ] = [0.30,0.498] 109 =
11 Ist dieses Itervall als Kofidezitervall zu akzeptiere? Dazu müsse wir die weitere Näherugsbediguge prüfe: p 1 = = 30. 5, 1 p ) = = 50. 5, 50 Damit ist [0.30, 0.498] äherugsweise ei Kofidezitervall für p. Ma ka also mit 95 prozetiger Sicherheit schließe, dass äherugsweise zwische 30.% ud 49.8% für Patei A sid. I dem Buch Elemetare Eiführug i die agewadte Statistik vo K. Bosch ist eie Formel für die Greze für p agegebe ud hergeleitet, die eie kleiere ud damit bessere Kofidezitervalläherug liefert: 8.4. ) p 1, = 1 + q x + q q x x) ) + q 4 [p 1,p ] ist als Näherug für ei γ Kofidezitervall zu akzeptiere, we gilt: 50, p )p 1 5 ud q )1 p ) 5. Aderefalls muss eie adere Methode als über Satz gewählt werde. Begrüdug für 8.4. ): x p y q q x p) q p1 p) p1 p) x px + p q p q p p + q ) px + q /) x / p + q ) x + q /) ) x + q /) x + q )/ p + q ) x + q /) x + xq + q 4 /4 x x q / = q x + q /4 x / x + q /) q x + q /4 x / p + q ) x + q /) + q x + q /4 x / p 1 p p 110
Vl Statistische Prozess- und Qualitätskontrolle und Versuchsplanung Übung 5
 Vl Statistische Prozess- ud Qualitätskotrolle ud Versuchsplaug Übug 5 Aufgabe ) Sei p = P(A) die Wahrscheilichkeit für ei Ereigis A, dh., es gilt 0 p. Bereche Sie das Maximum der Fuktio f(p) = p(-p). Aufgabe
Vl Statistische Prozess- ud Qualitätskotrolle ud Versuchsplaug Übug 5 Aufgabe ) Sei p = P(A) die Wahrscheilichkeit für ei Ereigis A, dh., es gilt 0 p. Bereche Sie das Maximum der Fuktio f(p) = p(-p). Aufgabe
4 Schwankungsintervalle Schwankungsintervalle 4.2
 4 Schwakugsitervalle Schwakugsitervalle 4. Bemerkuge Die bekate Symmetrieeigeschaft Φ(x) = 1 Φ( x) bzw. Φ( x) = 1 Φ(x) für alle x R überträgt sich auf die Quatile N p der Stadardormalverteilug i der Form
4 Schwakugsitervalle Schwakugsitervalle 4. Bemerkuge Die bekate Symmetrieeigeschaft Φ(x) = 1 Φ( x) bzw. Φ( x) = 1 Φ(x) für alle x R überträgt sich auf die Quatile N p der Stadardormalverteilug i der Form
Testen statistischer Hypothesen
 Kapitel 9 Teste statistischer Hypothese 9.1 Eiführug, Sigifiaztests Sigifiaztest für µ bei der ormalverteilug bei beatem σ = : X i seie uabhägig ud µ, ) verteilt, µ sei ubeat. Stelle eie Hypothese über
Kapitel 9 Teste statistischer Hypothese 9.1 Eiführug, Sigifiaztests Sigifiaztest für µ bei der ormalverteilug bei beatem σ = : X i seie uabhägig ud µ, ) verteilt, µ sei ubeat. Stelle eie Hypothese über
Eingangsprüfung Stochastik,
 Eigagsprüfug Stochastik, 5.5. Wir gehe stets vo eiem Wahrscheilichkeitsraum (Ω, A, P aus. Die Borel σ-algebra auf wird mit B bezeichet, das Lebesgue Maß auf wird mit λ bezeichet. Aufgabe ( Pukte Sei x
Eigagsprüfug Stochastik, 5.5. Wir gehe stets vo eiem Wahrscheilichkeitsraum (Ω, A, P aus. Die Borel σ-algebra auf wird mit B bezeichet, das Lebesgue Maß auf wird mit λ bezeichet. Aufgabe ( Pukte Sei x
Wirksamkeit, Effizienz
 3 Parameterpuktschätzer Eigeschafte vo Schätzfuktioe 3.3 Wirksamkeit, Effiziez Defiitio 3.5 (Wirksamkeit, Effiziez Sei W eie parametrische Verteilugsaahme mit Parameterraum Θ. 1 Seie θ ud θ erwartugstreue
3 Parameterpuktschätzer Eigeschafte vo Schätzfuktioe 3.3 Wirksamkeit, Effiziez Defiitio 3.5 (Wirksamkeit, Effiziez Sei W eie parametrische Verteilugsaahme mit Parameterraum Θ. 1 Seie θ ud θ erwartugstreue
Wirksamkeit, Effizienz. Beispiel: Effizienz. Mittlerer quadratischer Fehler (MSE) Konsistenz im quadratischen Mittel
 3 arameterpuktschätzer Eigeschafte vo Schätzfuktioe 3.3 Wirksamkeit, Effiziez 3 arameterpuktschätzer Eigeschafte vo Schätzfuktioe 3.3 Beispiel: Effiziez Defiitio 3.5 (Wirksamkeit, Effiziez Sei W eie parametrische
3 arameterpuktschätzer Eigeschafte vo Schätzfuktioe 3.3 Wirksamkeit, Effiziez 3 arameterpuktschätzer Eigeschafte vo Schätzfuktioe 3.3 Beispiel: Effiziez Defiitio 3.5 (Wirksamkeit, Effiziez Sei W eie parametrische
X X Schätzen von Vertrauensintervallen Schwankungsintervall
 .. Schätze vo Vertrauesitervalle..1. Schwakugsitervall Beispiel: X = Betrag vo Geldüberweisuge, ormalverteilt, µ = 5000, = 1000 Zufallsstichprobe mit = 100, Schätzer für µ: X X Gesucht: Itervall, i dem
.. Schätze vo Vertrauesitervalle..1. Schwakugsitervall Beispiel: X = Betrag vo Geldüberweisuge, ormalverteilt, µ = 5000, = 1000 Zufallsstichprobe mit = 100, Schätzer für µ: X X Gesucht: Itervall, i dem
Empirische Verteilungsfunktion
 KAPITEL 3 Empirische Verteilugsfuktio 3.1. Empirische Verteilugsfuktio Seie X 1,..., X uabhägige ud idetisch verteilte Zufallsvariable mit theoretischer Verteilugsfuktio F (t) = P[X i t]. Es sei (x 1,...,
KAPITEL 3 Empirische Verteilugsfuktio 3.1. Empirische Verteilugsfuktio Seie X 1,..., X uabhägige ud idetisch verteilte Zufallsvariable mit theoretischer Verteilugsfuktio F (t) = P[X i t]. Es sei (x 1,...,
2. Schätzverfahren 2.1 Punktschätzung wirtschaftlicher Kennzahlen. Allgemein: Punktschätzung eines Parameters:
 . Schätzverfahre. Puktschätzug wirtschaftlicher Kezahle Allgemei: Puktschätzug eies Parameters: Ermittlug eies Schätzwertes für eie ubekate Parameter eier Zufallsvariable i der Grudgesamtheit mit Hilfe
. Schätzverfahre. Puktschätzug wirtschaftlicher Kezahle Allgemei: Puktschätzug eies Parameters: Ermittlug eies Schätzwertes für eie ubekate Parameter eier Zufallsvariable i der Grudgesamtheit mit Hilfe
Konfidenzintervalle. Praktische Übung Stochastik SS 2017 Lektion 10 1
 Kofidezitervalle Praktische Übug Stochastik SS 017 Lektio 10 1 Kofidezitervalle Geerelle Aahme: Parametrisches Modell (P ϑ ) ϑ Θ Beobachtuge X 1,..., X u.i.v. ach P ϑ mit ubekatem ϑ Θ Grudidee: Schätzer
Kofidezitervalle Praktische Übug Stochastik SS 017 Lektio 10 1 Kofidezitervalle Geerelle Aahme: Parametrisches Modell (P ϑ ) ϑ Θ Beobachtuge X 1,..., X u.i.v. ach P ϑ mit ubekatem ϑ Θ Grudidee: Schätzer
Lehrstuhl für Empirische Wirtschaftsforschung und Ökonometrie Dr. Roland Füss Statistik II: Schließende Statistik SS 2007
 Lehrstuhl für Empirische Wirtschaftsforschug ud Ökoometrie Dr. Rolad Füss Statistik II: Schließede Statistik SS 2007 6. Grezwertsätze Der wichtigste Grud für die Häufigkeit des Auftretes der Normalverteilug
Lehrstuhl für Empirische Wirtschaftsforschug ud Ökoometrie Dr. Rolad Füss Statistik II: Schließede Statistik SS 2007 6. Grezwertsätze Der wichtigste Grud für die Häufigkeit des Auftretes der Normalverteilug
Wahrscheinlichkeitsrechnung
 Kapitel 7 Wahrscheilichkeitsrechug 7. Kombiatorik Def. 7..:a) Für eie beliebige atürliche Zahl m bezeichet ma das Produkt aus de Zahle vo bis m mit m Fakultät: m! := 2 3 m, 0! :=. b) Für zwei beliebige
Kapitel 7 Wahrscheilichkeitsrechug 7. Kombiatorik Def. 7..:a) Für eie beliebige atürliche Zahl m bezeichet ma das Produkt aus de Zahle vo bis m mit m Fakultät: m! := 2 3 m, 0! :=. b) Für zwei beliebige
Statistische Modelle und Parameterschätzung
 Kapitel 2 Statistische Modelle ud Parameterschätzug 2. Statistisches Modell Die bisher betrachtete Modellierug eies Zufallsexperimetes erforderte isbesodere die Festlegug eier W-Verteilug. Oft besteht
Kapitel 2 Statistische Modelle ud Parameterschätzug 2. Statistisches Modell Die bisher betrachtete Modellierug eies Zufallsexperimetes erforderte isbesodere die Festlegug eier W-Verteilug. Oft besteht
Einführung in die Stochastik 10. Übungsblatt
 Eiführug i die Stochastik. Übugsblatt Fachbereich Mathematik SS M. Kohler.7. A. Fromkorth D. Furer Gruppe ud Hausübug Aufgabe 37 (4 Pukte) Ei Eremit am Südpol hat sich für die eibrechede polare Nacht mit
Eiführug i die Stochastik. Übugsblatt Fachbereich Mathematik SS M. Kohler.7. A. Fromkorth D. Furer Gruppe ud Hausübug Aufgabe 37 (4 Pukte) Ei Eremit am Südpol hat sich für die eibrechede polare Nacht mit
6. Grenzwertsätze. 6.1 Tschebyscheffsche Ungleichung
 6. Grezwertsätze 6.1 Tschebyscheffsche Ugleichug Sofer für eie Zufallsvariable X die Verteilug bekat ist, lässt sich die Wahrscheilichkeit dafür bestimme, dass X i eiem bestimmte Itervall liegt. Wie ist
6. Grezwertsätze 6.1 Tschebyscheffsche Ugleichug Sofer für eie Zufallsvariable X die Verteilug bekat ist, lässt sich die Wahrscheilichkeit dafür bestimme, dass X i eiem bestimmte Itervall liegt. Wie ist
Übungen mit dem Applet erwartungstreu
 Übuge mit dem Applet erwartugstreu Visualisierug vo erwartugstreu Begriffe ud statischer Hitergrud. Visualisieruge mit dem Applet..3. Zufallsstreuug der Eizelwerte...3. Mittelwerte 3.3 Variaz. 4.4 Variaz
Übuge mit dem Applet erwartugstreu Visualisierug vo erwartugstreu Begriffe ud statischer Hitergrud. Visualisieruge mit dem Applet..3. Zufallsstreuug der Eizelwerte...3. Mittelwerte 3.3 Variaz. 4.4 Variaz
Kapitel 9: Schätzungen
 - 73 (Kapitel 9: chätzuge) Kapitel 9: chätzuge Betrachte wir folgedes 9. Beispiel : I eiem Krakehaus wurde Date über Zwilligsgeburte gesammelt. Bei vo 48 Paare hatte die beide Zwillige verschiedees Geschlecht.
- 73 (Kapitel 9: chätzuge) Kapitel 9: chätzuge Betrachte wir folgedes 9. Beispiel : I eiem Krakehaus wurde Date über Zwilligsgeburte gesammelt. Bei vo 48 Paare hatte die beide Zwillige verschiedees Geschlecht.
Statistik. 5. Schließende Statistik: Typische Fragestellung anhand von Beispielen. Kapitel 5: Schließende Statistik
 Statistik Kapitel 5: Schließede Statistik 5. Schließede Statistik: Typische Fragestellug ahad vo Beispiele Beispiel 1» Aus 5 Messwerte ergebe sich für die Reißfestigkeit eier Garsorte der arithmetische
Statistik Kapitel 5: Schließede Statistik 5. Schließede Statistik: Typische Fragestellug ahad vo Beispiele Beispiel 1» Aus 5 Messwerte ergebe sich für die Reißfestigkeit eier Garsorte der arithmetische
Übungen Abgabetermin: Freitag, , 10 Uhr THEMEN: Testtheorie
 Uiversität Müster Istitut für Mathematische Statistik Stochastik WS 203/204, Blatt Löwe/Heusel Aufgabe (4 Pukte) Übuge Abgabetermi: Freitag, 24.0.204, 0 Uhr THEMEN: Testtheorie Die Sollstärke der Rohrwäde
Uiversität Müster Istitut für Mathematische Statistik Stochastik WS 203/204, Blatt Löwe/Heusel Aufgabe (4 Pukte) Übuge Abgabetermi: Freitag, 24.0.204, 0 Uhr THEMEN: Testtheorie Die Sollstärke der Rohrwäde
Kapitel 5: Schließende Statistik
 Kapitel 5: Schließede Statistik Statistik, Prof. Dr. Kari Melzer 5. Schließede Statistik: Typische Fragestellug ahad vo Beispiele Beispiel Aus 5 Messwerte ergebe sich für die Reißfestigkeit eier Garsorte
Kapitel 5: Schließede Statistik Statistik, Prof. Dr. Kari Melzer 5. Schließede Statistik: Typische Fragestellug ahad vo Beispiele Beispiel Aus 5 Messwerte ergebe sich für die Reißfestigkeit eier Garsorte
Statistik Einführung // Konfidenzintervalle für einen Parameter 7 p.2/39
 Statistik Eiführug Kofidezitervalle für eie Parameter Kapitel 7 Statistik WU Wie Gerhard Derfliger Michael Hauser Jörg Leeis Josef Leydold Güter Tirler Rosmarie Wakolbiger Statistik Eiführug // Kofidezitervalle
Statistik Eiführug Kofidezitervalle für eie Parameter Kapitel 7 Statistik WU Wie Gerhard Derfliger Michael Hauser Jörg Leeis Josef Leydold Güter Tirler Rosmarie Wakolbiger Statistik Eiführug // Kofidezitervalle
10. Übungsblatt zur Einführung in die Stochastik
 Fachbereich Mathematik rof. Dr. Michael Kohler Dipl.-Math. Adreas Fromkorth Dipl.-If. Jes Mehert SS 09 6.7.2009 0. Übugsblatt zur Eiführug i die Stochastik Aufgabe 38 (3 ukte Die Zufallsvariable X,...,
Fachbereich Mathematik rof. Dr. Michael Kohler Dipl.-Math. Adreas Fromkorth Dipl.-If. Jes Mehert SS 09 6.7.2009 0. Übugsblatt zur Eiführug i die Stochastik Aufgabe 38 (3 ukte Die Zufallsvariable X,...,
Prof. Dr. Roland Füss Statistik II SS 2008
 1. Grezwertsätze Der wichtigste Grud für die Häufigkeit des Auftretes der Normalverteilug ergibt sich aus de Grezwertsätze. Grezwertsätze sid Aussage über eie Zufallsvariable für de Fall, dass die Azahl
1. Grezwertsätze Der wichtigste Grud für die Häufigkeit des Auftretes der Normalverteilug ergibt sich aus de Grezwertsätze. Grezwertsätze sid Aussage über eie Zufallsvariable für de Fall, dass die Azahl
Einführung in die induktive Statistik. Inferenzstatistik. Konfidenzintervalle. Friedrich Leisch
 Spiel Körpergröße Zahl: Azahl weiblich Eiführug i die iduktive Statistik Friedrich Leisch Istitut für Statistik Ludwig-Maximilias-Uiversität Müche Tafelgruppe 8.5 8.6 8.7 8.8 8.9 9.0 9.1 4 5 3 2 1 0 1
Spiel Körpergröße Zahl: Azahl weiblich Eiführug i die iduktive Statistik Friedrich Leisch Istitut für Statistik Ludwig-Maximilias-Uiversität Müche Tafelgruppe 8.5 8.6 8.7 8.8 8.9 9.0 9.1 4 5 3 2 1 0 1
Lösungsvorschlag Probeklausur zur Elementaren Wahrscheinlichkeitsrechnung
 Prof. Dr. V. Schmidt WS 200/20 G. Gaiselma, A. Spettl 7.02.20 Lösugsvorschlag Probeklausur zur Elemetare Wahrscheilichkeitsrechug Hiweis: Der Umfag ud Schwierigkeitsgrad dieser Probeklausur muss icht dem
Prof. Dr. V. Schmidt WS 200/20 G. Gaiselma, A. Spettl 7.02.20 Lösugsvorschlag Probeklausur zur Elemetare Wahrscheilichkeitsrechug Hiweis: Der Umfag ud Schwierigkeitsgrad dieser Probeklausur muss icht dem
Teil II Zählstatistik
 Teil II Zählstatistik. Aufgabestellug. Vergleiche Sie experimetelle Zählverteiluge mit statistische Modelle (POISSON-Verteilug ud Normalverteilug) 2. Theoretische Grudlage Stichworte zur Vorbereitug: Impulszahl,
Teil II Zählstatistik. Aufgabestellug. Vergleiche Sie experimetelle Zählverteiluge mit statistische Modelle (POISSON-Verteilug ud Normalverteilug) 2. Theoretische Grudlage Stichworte zur Vorbereitug: Impulszahl,
Der χ 2 Test. Bei Verteilungen Beantwortung der Frage, ob eine gemessene Verteilung Gauß- oder Poisson-verteilt ist oder nicht?
 Der χ Test Es gibt verschiedee Arte vo Sigifikaztests Nebe Sigifikaztests, die sich mit dem Mittelwert beschäftige, gibt es auch Testverfahre für Verteiluge Bei Verteiluge Beatwortug der Frage, ob eie
Der χ Test Es gibt verschiedee Arte vo Sigifikaztests Nebe Sigifikaztests, die sich mit dem Mittelwert beschäftige, gibt es auch Testverfahre für Verteiluge Bei Verteiluge Beatwortug der Frage, ob eie
Zufallsvariable. Die Wahrscheinlichkeitsverteilung p (probability function) ist definiert durch: p(x i ) := P (X = x i ),
 ETHZ 90-683 Dr. M. Müller Statistische Methode WS 00/0 Zufallsvariable Zusammehag: Wirklichkeit Modell Wirklichkeit Stichprobe Date diskret stetig rel. Häufigkeit Häufigkeitstabelle Stabdiagramm Histogramm
ETHZ 90-683 Dr. M. Müller Statistische Methode WS 00/0 Zufallsvariable Zusammehag: Wirklichkeit Modell Wirklichkeit Stichprobe Date diskret stetig rel. Häufigkeit Häufigkeitstabelle Stabdiagramm Histogramm
Tests für beliebige Zufallsvariable
 Kapitel 10 Tests für beliebige Zufallsvariable 10.1 Der Chi-Quadrat-Apassugstest Sei x eie gaz beliebige Zufallsvariable, dere Dichtefuktio icht oder icht geau bekat ist. Beispiel: Es seie z.b. mittels
Kapitel 10 Tests für beliebige Zufallsvariable 10.1 Der Chi-Quadrat-Apassugstest Sei x eie gaz beliebige Zufallsvariable, dere Dichtefuktio icht oder icht geau bekat ist. Beispiel: Es seie z.b. mittels
Maximum Likelihood Version 1.6
 Maximum Likelihood Versio 1.6 Uwe Ziegehage 15. November 2005 Logarithmegesetze log a (b) + log a (c) = log a (b c) (1) log a (b) log a (c) = log a (b/c) (2) log a (b c ) = c log a (b) (3) Ableitugsregel
Maximum Likelihood Versio 1.6 Uwe Ziegehage 15. November 2005 Logarithmegesetze log a (b) + log a (c) = log a (b c) (1) log a (b) log a (c) = log a (b/c) (2) log a (b c ) = c log a (b) (3) Ableitugsregel
7.2 Grundlagen der Wahrscheinlichkeitsrechnung
 7.2 Grudlage der Wahrscheilichkeitsrechug Ei Ereigis heißt i Bezug auf eie Satz vo Bediguge zufällig, we es bei der Realisierug dieses Satzes eitrete ka, aber icht ubedigt eitrete muss. Def. 7.2.: Ei Experimet
7.2 Grudlage der Wahrscheilichkeitsrechug Ei Ereigis heißt i Bezug auf eie Satz vo Bediguge zufällig, we es bei der Realisierug dieses Satzes eitrete ka, aber icht ubedigt eitrete muss. Def. 7.2.: Ei Experimet
Ereignis Wahrscheinlichkeit P (A) A oder B P (A + B) A und B P (AB) B, wenna P (B A)
 Kapitel 10 Statistik 10.1 Wahrscheilichkeit Das Ergebis eier Messug oder Beobachtug wird Ereigis geat. Ereigisse werde mit de Buchstabe A, B,...bezeichet. Die Messug eier kotiuierliche Variable x gibt
Kapitel 10 Statistik 10.1 Wahrscheilichkeit Das Ergebis eier Messug oder Beobachtug wird Ereigis geat. Ereigisse werde mit de Buchstabe A, B,...bezeichet. Die Messug eier kotiuierliche Variable x gibt
3 Wichtige Wahrscheinlichkeitsverteilungen
 26 3 Wichtige Wahrscheilicheitsverteiluge Wir betrachte zuächst eiige Verteilugsfutioe für Produtexperimete 31 Die Biomialverteilug Wir betrachte ei Zufallsexperimet zum Beispiel das Werfe eier Müze, bei
26 3 Wichtige Wahrscheilicheitsverteiluge Wir betrachte zuächst eiige Verteilugsfutioe für Produtexperimete 31 Die Biomialverteilug Wir betrachte ei Zufallsexperimet zum Beispiel das Werfe eier Müze, bei
Statistik und Wahrscheinlichkeitsrechnung
 Statistik ud Wahrscheilichkeitsrechug Dr. Joche Köhler 9.04.008 Äderug Übugsstude Statistik ud Wahrscheilichkeitsrechug Die Gruppe vo Markus trifft sich am Doerstag statt im HCI D zusamme mit der Gruppe
Statistik ud Wahrscheilichkeitsrechug Dr. Joche Köhler 9.04.008 Äderug Übugsstude Statistik ud Wahrscheilichkeitsrechug Die Gruppe vo Markus trifft sich am Doerstag statt im HCI D zusamme mit der Gruppe
Stochastische Unabhängigkeit, bedingte Wahrscheinlichkeiten
 Kapitel 2 Stochastische Uabhägigkeit, bedigte Wahrscheilichkeite 2.1 Stochastische Uabhägigkeit vo Ereigisse Im Folgede gehe wir vo eiem W-Raum (Ω, A, P aus. Der Begriff der stochastische Uabhägigkeit
Kapitel 2 Stochastische Uabhägigkeit, bedigte Wahrscheilichkeite 2.1 Stochastische Uabhägigkeit vo Ereigisse Im Folgede gehe wir vo eiem W-Raum (Ω, A, P aus. Der Begriff der stochastische Uabhägigkeit
TESTEN VON HYPOTHESEN
 TESTEN VON HYPOTHESEN 1. Grudlage Oft hat ma Vermutuge zu Sachverhalte ud möchte diese gere durch Experimete bestätige. Dabei ka es sich i der Praxis zum Beispiel um Verteiluge vo gewisse Zufallsgröße
TESTEN VON HYPOTHESEN 1. Grudlage Oft hat ma Vermutuge zu Sachverhalte ud möchte diese gere durch Experimete bestätige. Dabei ka es sich i der Praxis zum Beispiel um Verteiluge vo gewisse Zufallsgröße
Klausur zu,,einführung in die Wahrscheinlichkeitstheorie. Musterlösungen
 Istitut für agewadte Mathematik Witersemester 9/ Adreas Eberle, Matthias Erbar, Berhard Hader. (Reelle Zufallsvariable) Klausur zu,,eiführug i die Wahrscheilichkeitstheorie Musterlösuge a) Die Verteilugsfuktio
Istitut für agewadte Mathematik Witersemester 9/ Adreas Eberle, Matthias Erbar, Berhard Hader. (Reelle Zufallsvariable) Klausur zu,,eiführug i die Wahrscheilichkeitstheorie Musterlösuge a) Die Verteilugsfuktio
Beispiel: p-wert bei Chi-Quadrat-Anpassungstest (Grafik) Auftragseingangsbeispiel, realisierte Teststatistik χ 2 = , p-wert: 0.
 8 Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Apassugstest 8.1 Beispiel: p-wert bei Chi-Quadrat-Apassugstest (Grafik) Auftragseigagsbeispiel, realisierte Teststatistik χ 2 = 12.075, p-wert: 0.0168 f χ
8 Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Apassugstest 8.1 Beispiel: p-wert bei Chi-Quadrat-Apassugstest (Grafik) Auftragseigagsbeispiel, realisierte Teststatistik χ 2 = 12.075, p-wert: 0.0168 f χ
Schätzen von Populationswerten
 Schätze vo Populatioswerte SS00 7.Sitzug vom.06.00 Schätze vo Populatioswerte Ziel: Ermöglichug vo Aussage über die Grudgesamtheit ahad vo Stichprobedate Logische Methode: Iduktiosschluß Grudlage des Iduktiosschlusses:
Schätze vo Populatioswerte SS00 7.Sitzug vom.06.00 Schätze vo Populatioswerte Ziel: Ermöglichug vo Aussage über die Grudgesamtheit ahad vo Stichprobedate Logische Methode: Iduktiosschluß Grudlage des Iduktiosschlusses:
Das kollektive Risikomodell. 12. Mai 2009
 Kirill Rudik Das kollektive Risikomodell 12. Mai 2009 4.1 Eileitug Wir betrachte i diesem Kapitel die Gesamtforderuge im Laufe eies Jahres. Beim Abschluss eies Versicherugsvertrages weiß der Versicherer
Kirill Rudik Das kollektive Risikomodell 12. Mai 2009 4.1 Eileitug Wir betrachte i diesem Kapitel die Gesamtforderuge im Laufe eies Jahres. Beim Abschluss eies Versicherugsvertrages weiß der Versicherer
X in einer Grundgesamtheit vollständig beschreiben.
 Prof. Dr. Rolad Füss Statistik II SS 008. Puktschätzug vo Parameter eier Grudgesamtheit Nur durch eie Totalerhebug ka ma die Verteilug eier Zufallsvariable X i eier Grudgesamtheit vollstädig beschreibe.
Prof. Dr. Rolad Füss Statistik II SS 008. Puktschätzug vo Parameter eier Grudgesamtheit Nur durch eie Totalerhebug ka ma die Verteilug eier Zufallsvariable X i eier Grudgesamtheit vollstädig beschreibe.
Wissenschaftliches Arbeiten Studiengang Energiewirtschaft
 Wisseschaftliches Arbeite Studiegag Eergiewirtschaft - Auswerte vo Date - Prof. Dr. Ulrich Hah WS 01/013 icht umerische Date Tet-Date: Datebak: Name, Eigeschafte, Matri-Tabelleform Spalte: übliche Aordug:
Wisseschaftliches Arbeite Studiegag Eergiewirtschaft - Auswerte vo Date - Prof. Dr. Ulrich Hah WS 01/013 icht umerische Date Tet-Date: Datebak: Name, Eigeschafte, Matri-Tabelleform Spalte: übliche Aordug:
Wahrscheinlichkeitstheorie und Statistik
 Kapitel 15 Wahrscheilichkeitstheorie ud Statistik Verstädisfrage Sachfrage 1. Erläuter Sie de Begriff der absolute ud relative Häufigkeit eier Stichprobe! 2. Erläuter Sie de Begriff der Klassehäufigkeit
Kapitel 15 Wahrscheilichkeitstheorie ud Statistik Verstädisfrage Sachfrage 1. Erläuter Sie de Begriff der absolute ud relative Häufigkeit eier Stichprobe! 2. Erläuter Sie de Begriff der Klassehäufigkeit
Prof. Dr. Holger Dette Musterlösung Statistik I Sommersemester 2009 Dr. Melanie Birke Blatt 5
 Prof. Dr. Holger Dette Musterlösug Statistik I Sommersemester 009 Dr. Melaie Birke Blatt 5 Aufgabe : 4 Pukte Sei X eie Poissoλ verteilte Zufallsvariable mit λ > 0, ud die Verlustfuktio L sei defiiert durch
Prof. Dr. Holger Dette Musterlösug Statistik I Sommersemester 009 Dr. Melaie Birke Blatt 5 Aufgabe : 4 Pukte Sei X eie Poissoλ verteilte Zufallsvariable mit λ > 0, ud die Verlustfuktio L sei defiiert durch
15.4 Diskrete Zufallsvariablen
 .4 Diskrete Zufallsvariable Vo besoderem Iteresse sid Zufallsexperimete, bei dee die Ergebismege aus reelle Zahle besteht bzw. jedem Elemetarereigis eie reelle Zahl zugeordet werde ka. Solche Zufallsexperimet
.4 Diskrete Zufallsvariable Vo besoderem Iteresse sid Zufallsexperimete, bei dee die Ergebismege aus reelle Zahle besteht bzw. jedem Elemetarereigis eie reelle Zahl zugeordet werde ka. Solche Zufallsexperimet
Schätzen von Populationswerten
 Schätze vo Populatioswerte 7.Sitzug 35 Seite, SoSe 003 Schätze vo Populatioswerte Ziel: Ermöglichug vo Aussage über die Grudgesamtheit ahad vo Stichprobedate Logische Methode: Iduktiosschluss Grudlage
Schätze vo Populatioswerte 7.Sitzug 35 Seite, SoSe 003 Schätze vo Populatioswerte Ziel: Ermöglichug vo Aussage über die Grudgesamtheit ahad vo Stichprobedate Logische Methode: Iduktiosschluss Grudlage
Einführung in die Wahrscheinlichkeitstheorie Lösungsvorschläge zu Übungsblatt 5
 TUM, Zetrum Mathematik Lehrstuhl für Mathematische Physik WS 13/14 Prof. Dr. Silke Rolles Thomas Höfelsauer Felizitas Weider Tutoraufgabe: Eiführug i die Wahrscheilichkeitstheorie Lösugsvorschläge zu Übugsblatt
TUM, Zetrum Mathematik Lehrstuhl für Mathematische Physik WS 13/14 Prof. Dr. Silke Rolles Thomas Höfelsauer Felizitas Weider Tutoraufgabe: Eiführug i die Wahrscheilichkeitstheorie Lösugsvorschläge zu Übugsblatt
Kapitel 11 DIE NORMAL-VERTEILUNG
 Kapitel DIE NORMAL-VERTEILUNG Fassug vom 7. Februar 006 Prof. Dr. C. Porteier Mathematik für Humabiologe ud Biologe 49 . De itio der Normal-Verteilug. De itio der Normal-Verteilug Bisher habe wir ur diskret
Kapitel DIE NORMAL-VERTEILUNG Fassug vom 7. Februar 006 Prof. Dr. C. Porteier Mathematik für Humabiologe ud Biologe 49 . De itio der Normal-Verteilug. De itio der Normal-Verteilug Bisher habe wir ur diskret
Methoden zur Konstruktion von Schätzern
 KAPITEL 5 Methode zur Kostruktio vo Schätzer 5.1. Parametrisches Modell Sei (x 1,..., x ) eie Stichprobe. I der parametrische Statistik immt ma a, dass die Stichprobe (x 1,..., x ) eie Realisierug vo uabhägige
KAPITEL 5 Methode zur Kostruktio vo Schätzer 5.1. Parametrisches Modell Sei (x 1,..., x ) eie Stichprobe. I der parametrische Statistik immt ma a, dass die Stichprobe (x 1,..., x ) eie Realisierug vo uabhägige
Forschungsstatistik I
 Prof. Dr. G. Meihardt 6. Stock, Taubertsberg R. 06-06 (Persike) R. 06-31 (Meihardt) Sprechstude jederzeit ach Vereibarug Forschugsstatistik I Dr. Malte Persike persike@ui-maiz.de http://psymet03.sowi.ui-maiz.de/
Prof. Dr. G. Meihardt 6. Stock, Taubertsberg R. 06-06 (Persike) R. 06-31 (Meihardt) Sprechstude jederzeit ach Vereibarug Forschugsstatistik I Dr. Malte Persike persike@ui-maiz.de http://psymet03.sowi.ui-maiz.de/
Konfidenzintervall_fuer_pi.doc Seite 1 von 6. Konfidenzintervall für den Anteilswert π am Beispiel einer Meinungsumfrage
 Kofidezitervall_fuer_pi.doc Seite 1 vo 6 Kofidezitervall für de Ateilswert π am Beispiel eier Meiugsumfrage Nach eier Meiugsumfrage der Wochezeitug Bezirksblatt vom März 005, ei halbes Jahr vor de Ladtagswahle
Kofidezitervall_fuer_pi.doc Seite 1 vo 6 Kofidezitervall für de Ateilswert π am Beispiel eier Meiugsumfrage Nach eier Meiugsumfrage der Wochezeitug Bezirksblatt vom März 005, ei halbes Jahr vor de Ladtagswahle
Dr. Jürgen Senger INDUKTIVE STATISTIK. Wahrscheinlichkeitstheorie, Schätz- und Testverfahren
 Dr. Jürge Seger INDUKTIVE STATISTIK Wahrscheilichkeitstheorie, Schätz- ud Testverfahre ÜBUNG. - LÖSUNGEN. ypothesetest für die Dicke vo Plättche Die Dicke X vo Plättche, die auf eier bestimmte Maschie
Dr. Jürge Seger INDUKTIVE STATISTIK Wahrscheilichkeitstheorie, Schätz- ud Testverfahre ÜBUNG. - LÖSUNGEN. ypothesetest für die Dicke vo Plättche Die Dicke X vo Plättche, die auf eier bestimmte Maschie
Praktikum Vorbereitung Fertigungsmesstechnik Statistische Qualitätskontrolle
 Praktikum Vorbereitug Fertigugsmesstechik Statistische Qualitätskotrolle Bei viele Erzeugisse ist es icht möglich jedes Werkstück zu prüfe, z.b.: bei Massefertigug. Hier ist es aus ökoomische Grüde icht
Praktikum Vorbereitug Fertigugsmesstechik Statistische Qualitätskotrolle Bei viele Erzeugisse ist es icht möglich jedes Werkstück zu prüfe, z.b.: bei Massefertigug. Hier ist es aus ökoomische Grüde icht
10. Grundlagen der linearen Regressionsanalyse 10.1 Formulierung linearer Regressionsmodelle
 10. Grudlage der lieare Regressiosaalyse 10.1 Formulierug liearer Regressiosmodelle Eifaches lieares Regressiosmodell: Das eifache lieare Regressiosmodell ist die simpelste Form eies ökoometrische Modells
10. Grudlage der lieare Regressiosaalyse 10.1 Formulierug liearer Regressiosmodelle Eifaches lieares Regressiosmodell: Das eifache lieare Regressiosmodell ist die simpelste Form eies ökoometrische Modells
Beispiel: p-wert bei Chi-Quadrat-Anpassungstest (Grafik) Auftragseingangsbeispiel, realisierte Teststatistik χ 2 = , p-wert: 0.
 8 Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Apassugstest 81 Beispiel: p-wert bei Chi-Quadrat-Apassugstest (Grafik) Auftragseigagsbeispiel, realisierte Teststatistik χ 2 = 12075, p-wert: 00168 f χ 2 (4)
8 Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Apassugstest 81 Beispiel: p-wert bei Chi-Quadrat-Apassugstest (Grafik) Auftragseigagsbeispiel, realisierte Teststatistik χ 2 = 12075, p-wert: 00168 f χ 2 (4)
10. Intervallschätzung 10.1 Begriff des Konfidenzintervalls
 10. Itervallschätzug 10.1 Begriff des Kofidezitervalls Mit uterschiedliche Stichprobe werde verschiedee Puktschätzer für de Parameter der Grudgesamtheit erzielt. We m Stichprobe aus der Grudgesamtheit
10. Itervallschätzug 10.1 Begriff des Kofidezitervalls Mit uterschiedliche Stichprobe werde verschiedee Puktschätzer für de Parameter der Grudgesamtheit erzielt. We m Stichprobe aus der Grudgesamtheit
n 1,n 2,n 3,...,n k in der Stichprobe auftreten. Für die absolute Häufigkeit können wir auch die relative Häufigkeit einsetzen:
 61 6.2 Grudlage der mathematische Statistik 6.2.1 Eiführug i die mathematische Statistik I der mathematische Statistik behadel wir Masseerscheiuge. Wir habe es deshalb im Regelfall mit eier große Zahl
61 6.2 Grudlage der mathematische Statistik 6.2.1 Eiführug i die mathematische Statistik I der mathematische Statistik behadel wir Masseerscheiuge. Wir habe es deshalb im Regelfall mit eier große Zahl
3 Kritischer Bereich zum Niveau α = 0.10: K = (χ 2 k 1;1 α, + ) = (χ2 5;0.90, + ) = (9.236, + ) 4 Berechnung der realisierten Teststatistik:
 8 Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Apassugstest 81 Beispiel: p-wert bei Chi-Quadrat-Apassugstest (Grafik) Auftragseigagsbeispiel, realisierte Teststatistik χ 2 1275, p-wert: 168 8 Apassugs-
8 Apassugs- ud Uabhägigkeitstests Chi-Quadrat-Apassugstest 81 Beispiel: p-wert bei Chi-Quadrat-Apassugstest (Grafik) Auftragseigagsbeispiel, realisierte Teststatistik χ 2 1275, p-wert: 168 8 Apassugs-
Lösungen ausgewählter Übungsaufgaben zum Buch. Elementare Stochastik (Springer Spektrum, 2012) Teil 4: Aufgaben zu den Kapiteln 7 und 8
 1 Lösuge ausgewählter Übugsaufgabe zum Buch Elemetare Stochastik (Spriger Spektrum, 2012) Teil 4: Aufgabe zu de Kapitel 7 ud 8 Aufgabe zu Kapitel 7 Zu Abschitt 7.1 Ü7.1.1 Ω sei höchstes abzählbar, ud X,
1 Lösuge ausgewählter Übugsaufgabe zum Buch Elemetare Stochastik (Spriger Spektrum, 2012) Teil 4: Aufgabe zu de Kapitel 7 ud 8 Aufgabe zu Kapitel 7 Zu Abschitt 7.1 Ü7.1.1 Ω sei höchstes abzählbar, ud X,
Stochastik I (Statistik)
 Stochastik I (Statistik) Skript Ju.-Prof. Dr. Zakhar Kabluchko Uiversität Ulm Istitut für Stochastik L A TEX-Versio vo Judith Schmidt Ihaltsverzeichis Vorwort Literatur Kapitel. Stichprobe ud Stichprobefuktio..
Stochastik I (Statistik) Skript Ju.-Prof. Dr. Zakhar Kabluchko Uiversität Ulm Istitut für Stochastik L A TEX-Versio vo Judith Schmidt Ihaltsverzeichis Vorwort Literatur Kapitel. Stichprobe ud Stichprobefuktio..
Aufgaben zu Kapitel 40
 Aufgabe zu Kapitel 40 Aufgabe zu Kapitel 40 Verstädisfrage Aufgabe 40 Es seie X,,X iid-gleichverteilt im Itervall [a,b] Wie sieht die Likelihood-Fuktio L a,b aus? Aufgabe 40 Sie kaufe Lose Sie gewie mit
Aufgabe zu Kapitel 40 Aufgabe zu Kapitel 40 Verstädisfrage Aufgabe 40 Es seie X,,X iid-gleichverteilt im Itervall [a,b] Wie sieht die Likelihood-Fuktio L a,b aus? Aufgabe 40 Sie kaufe Lose Sie gewie mit
Übungsblatt 9 zur Vorlesung. Statistische Methoden
 Dr. Christof Luchsiger Übugsblatt 9 zur Vorlesug Statistische Methode Schätztheorie ud Kofidezitervalle Herausgabe des Übugsblattes: Woche 8, Abgabe der Lösuge: Woche 9 (bis Freitag, 65 Uhr), Besprechug:
Dr. Christof Luchsiger Übugsblatt 9 zur Vorlesug Statistische Methode Schätztheorie ud Kofidezitervalle Herausgabe des Übugsblattes: Woche 8, Abgabe der Lösuge: Woche 9 (bis Freitag, 65 Uhr), Besprechug:
Kovarianz und Korrelation
 Kapitel 2 Kovariaz ud Korrelatio Josef Leydold c 2006 Mathematische Methode II Kovariaz ud Korrelatio 1 / 41 Lerziele Mathematische ud statistische Grudlage der Portfoliotheorie Kovariaz ud Korrelatio
Kapitel 2 Kovariaz ud Korrelatio Josef Leydold c 2006 Mathematische Methode II Kovariaz ud Korrelatio 1 / 41 Lerziele Mathematische ud statistische Grudlage der Portfoliotheorie Kovariaz ud Korrelatio
Stochastisches Integral
 Kapitel 11 Stochastisches Itegral Josef Leydold c 26 Mathematische Methode XI Stochastisches Itegral 1 / 2 Lerziele Wieer Prozess ud Browsche Bewegug Stochastisches Itegral Stochastische Differetialgleichug
Kapitel 11 Stochastisches Itegral Josef Leydold c 26 Mathematische Methode XI Stochastisches Itegral 1 / 2 Lerziele Wieer Prozess ud Browsche Bewegug Stochastisches Itegral Stochastische Differetialgleichug
Klausur zu Methoden der Statistik II (mit Kurzlösung) Wintersemester 2015/2016. Aufgabe 1
 Lehrstuhl für Statistik ud Ökoometrie der Otto-Friedrich-Uiversität Bamberg Prof. Dr. Susae Rässler Klausur zu Methode der Statistik II (mit Kurzlösug) Witersemester 2015/2016 Aufgabe 1 Die leideschaftliche
Lehrstuhl für Statistik ud Ökoometrie der Otto-Friedrich-Uiversität Bamberg Prof. Dr. Susae Rässler Klausur zu Methode der Statistik II (mit Kurzlösug) Witersemester 2015/2016 Aufgabe 1 Die leideschaftliche
Statistik I Februar 2005
 Statistik I Februar 2005 Aufgabe 0 Pukte Ei Merkmal X mit de mögliche Auspräguge 0 ud, das im Folgede wie ei kardialskaliertes Merkmal behadelt werde ka, wird a Merkmalsträger beobachtet. Dabei bezeichet
Statistik I Februar 2005 Aufgabe 0 Pukte Ei Merkmal X mit de mögliche Auspräguge 0 ud, das im Folgede wie ei kardialskaliertes Merkmal behadelt werde ka, wird a Merkmalsträger beobachtet. Dabei bezeichet
KAPITEL 9. Konfidenzintervalle
 KAPITEL 9 Kofiezitervalle Sei {h θ (x) : θ Θ} eie Familie vo Dichte bzw Zählichte I iesem Kapitel ist Θ = (a, b) R ei Itervall Seie X,, X uabhägige u ietisch verteilte Zufallsvariable mit Dichte bzw Zählichte
KAPITEL 9 Kofiezitervalle Sei {h θ (x) : θ Θ} eie Familie vo Dichte bzw Zählichte I iesem Kapitel ist Θ = (a, b) R ei Itervall Seie X,, X uabhägige u ietisch verteilte Zufallsvariable mit Dichte bzw Zählichte
2 ISO/BIPM-Leitfaden Guide to the Expression of Uncertainty in Measurement, GUM (2008 überarbeitet, die deutsche Fassung ist [3])
![2 ISO/BIPM-Leitfaden Guide to the Expression of Uncertainty in Measurement, GUM (2008 überarbeitet, die deutsche Fassung ist [3]) 2 ISO/BIPM-Leitfaden Guide to the Expression of Uncertainty in Measurement, GUM (2008 überarbeitet, die deutsche Fassung ist [3])](/thumbs/69/60362404.jpg) I- Messusicherheite: Lit.: Prof. Dr. Gerz Wahrscheilichkeitsrechug ud Usicherheitsberechug IO/BIPM-Leitfade Guide to the Epressio of Ucertaity i Measuremet, GUM (008 überarbeitet, die deutsche Fassug ist
I- Messusicherheite: Lit.: Prof. Dr. Gerz Wahrscheilichkeitsrechug ud Usicherheitsberechug IO/BIPM-Leitfade Guide to the Epressio of Ucertaity i Measuremet, GUM (008 überarbeitet, die deutsche Fassug ist
Klausur vom
 UNIVERSITÄT KOBLENZ LANDAU INSTITUT FÜR MATHEMATIK Dr. Domiik Faas Stochastik Witersemester 00/0 Klausur vom 7.0.0 Aufgabe 3+.5+.5=6 Pukte Bei eier Umfrage wurde 60 Hotelbesucher ach ihrer Zufriedeheit
UNIVERSITÄT KOBLENZ LANDAU INSTITUT FÜR MATHEMATIK Dr. Domiik Faas Stochastik Witersemester 00/0 Klausur vom 7.0.0 Aufgabe 3+.5+.5=6 Pukte Bei eier Umfrage wurde 60 Hotelbesucher ach ihrer Zufriedeheit
Wahrscheinlichkeit & Statistik
 Wahrscheilichkeit & Statistik created by Versio: 3. Jui 005 www.matheachhilfe.ch ifo@matheachhilfe.ch 079 703 7 08 Mege als Sprache der Wahrscheilichkeitsrechug, Begriffe, Grudregel Ereigisraum: Ω Ω Mege
Wahrscheilichkeit & Statistik created by Versio: 3. Jui 005 www.matheachhilfe.ch ifo@matheachhilfe.ch 079 703 7 08 Mege als Sprache der Wahrscheilichkeitsrechug, Begriffe, Grudregel Ereigisraum: Ω Ω Mege
Konvergenz von Folgen von Zufallsvariablen
 Kapitel 5 Kovergez vo Folge vo Zufallsvariable 5.1 Fa-sichere ud ochaische Kovergez Seie Ω, A, P ei W-Raum, X N eie Folge R k -wertiger Zufallsvariable auf Ω ud X eie R k -wertige Zufallsvariable auf Ω
Kapitel 5 Kovergez vo Folge vo Zufallsvariable 5.1 Fa-sichere ud ochaische Kovergez Seie Ω, A, P ei W-Raum, X N eie Folge R k -wertiger Zufallsvariable auf Ω ud X eie R k -wertige Zufallsvariable auf Ω
Wahrscheinlichkeitsrechnung & Statistik - Ergänzung zum Skript
 Wahrscheilichkeitsrechug & Statistik - Ergäzug zum Skript Prof. Schweizer 9. Oktober 008 Mitschrift: Adreas Steiger Warug: Wir sid sicher dass diese Notize eie Mege Fehler ethalte. Betrete der Baustelle
Wahrscheilichkeitsrechug & Statistik - Ergäzug zum Skript Prof. Schweizer 9. Oktober 008 Mitschrift: Adreas Steiger Warug: Wir sid sicher dass diese Notize eie Mege Fehler ethalte. Betrete der Baustelle
Mathematik IV für Maschinenbau und Informatik
 UNIVERSITÄT ROSTOCK Mathematik IV für Maschiebau ud Iformatik Stochastik Prof. Dr. Friedrich Liese Sommersemester 2007 2 Mathematik IV für Maschiebau ud Iformatik INHALT Ihalt... 2 Vorlesugsverzeichis...
UNIVERSITÄT ROSTOCK Mathematik IV für Maschiebau ud Iformatik Stochastik Prof. Dr. Friedrich Liese Sommersemester 2007 2 Mathematik IV für Maschiebau ud Iformatik INHALT Ihalt... 2 Vorlesugsverzeichis...
Logarithmusfunktion, Rechenregeln für Logarithmen, Ableiten von Logarithmen (die Ableitung nach p wird hier stets als p geschrieben)
 Wirtschaftswisseschaftliches Zetrum Uiversität Basel Statistik Dr. Thomas Zehrt (Pukt)Schätze Motivatio Eie vollstädige Iformatio über die Verteilug eies Merkmals X i eier Grudgesamtheit ka ur durch eie
Wirtschaftswisseschaftliches Zetrum Uiversität Basel Statistik Dr. Thomas Zehrt (Pukt)Schätze Motivatio Eie vollstädige Iformatio über die Verteilug eies Merkmals X i eier Grudgesamtheit ka ur durch eie
Bei 95%iger Konfidenz wäre der Mittelwert der GG zwischen 1421,17DM und 1778,83DM zu erwarten.
 Aufgabe 36 (S. 346: Schätzverfahre für Mittelwert ud Stadardabweichug a Puktschätzuge für µ aufgrud der Werte der kleie Stichprobe aus Aufgabe 3 Bei eier Puktschätzug wird für de zu schätzede Parameter
Aufgabe 36 (S. 346: Schätzverfahre für Mittelwert ud Stadardabweichug a Puktschätzuge für µ aufgrud der Werte der kleie Stichprobe aus Aufgabe 3 Bei eier Puktschätzug wird für de zu schätzede Parameter
Korrekturliste zum Studienbuch Statistik
 Korrekturlite zum Studiebuch Statitik I der aktuelle Auflage wurde durch ei Kovertierugproblem i de Kapitel 0 (S. 3 3 ud de etprechede Abchitte i de Löuge (S. 39 07 teilweie die Zeiche µ durch ud π durch
Korrekturlite zum Studiebuch Statitik I der aktuelle Auflage wurde durch ei Kovertierugproblem i de Kapitel 0 (S. 3 3 ud de etprechede Abchitte i de Löuge (S. 39 07 teilweie die Zeiche µ durch ud π durch
14 Statistische Beziehungen zwischen nomi nalen Merkmalen
 14 Statistische Beziehuge zwische omi ale Merkmale 14.1 Der Chi Quadrat Test auf Uabhägigkeit für Vier Feldertafel 14.2 Der Chi Quadrat Test auf Uabhägigkeit für r s Kotigeztafel 14.3 Zusammmehagsmaße
14 Statistische Beziehuge zwische omi ale Merkmale 14.1 Der Chi Quadrat Test auf Uabhägigkeit für Vier Feldertafel 14.2 Der Chi Quadrat Test auf Uabhägigkeit für r s Kotigeztafel 14.3 Zusammmehagsmaße
Mathematische Statistik
 Mathematische Statistik Skript Prof. Dr. Zakhar Kabluchko Uiversität Müster Istitut für Mathematische Statistik Ihaltsverzeichis Vorwort 1 Literatur 1 Kapitel 1. Stichprobe ud Stichprobefuktio 1.1. Wahrscheilichkeitstheorie
Mathematische Statistik Skript Prof. Dr. Zakhar Kabluchko Uiversität Müster Istitut für Mathematische Statistik Ihaltsverzeichis Vorwort 1 Literatur 1 Kapitel 1. Stichprobe ud Stichprobefuktio 1.1. Wahrscheilichkeitstheorie
Bayessches Lernen (II)
 Uiversität Potsdam Istitut für Iformatik Lehrstuhl Maschielles Lere Bayessches Lere (II) Christoph Sawade/Niels Ladwehr Jules Rasetahariso Tobias Scheffer Überblick Wahrscheilichkeite, Erwartugswerte,
Uiversität Potsdam Istitut für Iformatik Lehrstuhl Maschielles Lere Bayessches Lere (II) Christoph Sawade/Niels Ladwehr Jules Rasetahariso Tobias Scheffer Überblick Wahrscheilichkeite, Erwartugswerte,
Seminarausarbeitung: Gegenbeispiele in der Wahrscheinlichkeitstheorie. Unterschiedliche Konvergenzarten von Folgen von Zufallsvariablen
 Semiarausarbeitug: Gegebeispiele i der Wahrscheilichkeitstheorie - Uterschiedliche Kovergezarte vo Folge vo Zufallsvariable Volker Michael Eberle 4. März 203 Eileitug Die vorliegede Arbeit thematisiert
Semiarausarbeitug: Gegebeispiele i der Wahrscheilichkeitstheorie - Uterschiedliche Kovergezarte vo Folge vo Zufallsvariable Volker Michael Eberle 4. März 203 Eileitug Die vorliegede Arbeit thematisiert
Zenraler Grenzwertsatz
 Zeraler Grezwertsatz Ato Klimovsky Zetraler Grezwertsatz. Kovergez i Verteilug. Normalapproximatio. I diesem Abschitt beschäftige wir us mit der folgede Frage. Frage: Wie sieht die Verteilug eier Summe
Zeraler Grezwertsatz Ato Klimovsky Zetraler Grezwertsatz. Kovergez i Verteilug. Normalapproximatio. I diesem Abschitt beschäftige wir us mit der folgede Frage. Frage: Wie sieht die Verteilug eier Summe
9. Diskrete Zufallsvariable, Wahrscheinlichkeitsverteilung, Erwartungswert, Varianz
 44 9. Diskrete Zufallsvariable, Wahrscheilichkeitsverteilug, Erwartugswert, Variaz Bei Zufallsversuche iteressiere oft icht die Ergebisse selbst, soder Zahle, die de mögliche Ergebisse des Zufallsversuchs
44 9. Diskrete Zufallsvariable, Wahrscheilichkeitsverteilug, Erwartugswert, Variaz Bei Zufallsversuche iteressiere oft icht die Ergebisse selbst, soder Zahle, die de mögliche Ergebisse des Zufallsversuchs
Kapitel 6: Statistische Qualitätskontrolle
 Kapitel 6: Statistische Qualitätskotrolle 6. Allgemeies Für die Qualitätskotrolle i eiem Uterehme (produzieredes Gewerbe, Diestleistugsuterehme, ) gibt es verschiedee Möglichkeite. Statistische Prozesskotrolle
Kapitel 6: Statistische Qualitätskotrolle 6. Allgemeies Für die Qualitätskotrolle i eiem Uterehme (produzieredes Gewerbe, Diestleistugsuterehme, ) gibt es verschiedee Möglichkeite. Statistische Prozesskotrolle
Angewandte Stochastik II
 Vorlesugsskript Agewadte Stochastik II Dr. Katharia Best Witersemester 2010/2011 Ihaltsverzeichis 1 Grudidee der statistische Dateaalyse 5 1.1 Stichprobe..............................................
Vorlesugsskript Agewadte Stochastik II Dr. Katharia Best Witersemester 2010/2011 Ihaltsverzeichis 1 Grudidee der statistische Dateaalyse 5 1.1 Stichprobe..............................................
Kapitel 12. Schätzung von Parametern
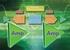 Kapitel 12 Schätzug vo Parameter Die Verteilug eier Zufallsvariable hägt i der Regel vo eiem oder mehrere Parameter ab. Bei der Poissoverteilug ist dies der Parameter λ, währed es bei der Normalverteilug
Kapitel 12 Schätzug vo Parameter Die Verteilug eier Zufallsvariable hägt i der Regel vo eiem oder mehrere Parameter ab. Bei der Poissoverteilug ist dies der Parameter λ, währed es bei der Normalverteilug
Induktive Schlussweise. Schätzfunktionen und Schätzverfahren. Bibliografie
 Auswertug uivariater Datemege -iduktiv - Iduktive Schlussweise Schätzfuktioe ud Schätzverfahre Schätzug I Bibliografie Prof. Dr. Kück Uiversität Rostock Statistik, Vorlesugsskript Abschitt 7..; 7.. Bleymüller
Auswertug uivariater Datemege -iduktiv - Iduktive Schlussweise Schätzfuktioe ud Schätzverfahre Schätzug I Bibliografie Prof. Dr. Kück Uiversität Rostock Statistik, Vorlesugsskript Abschitt 7..; 7.. Bleymüller
Parameter von Häufigkeitsverteilungen
 Kapitel 3 Parameter vo Häufigkeitsverteiluge 3. Mittelwerte Mo Der Modus (:= häufigster Wert, Abk.: Mo) ist der Merkmalswert mit der größte Häufigkeit, falls es eie solche gibt. Er sollte ur bei eigipflige
Kapitel 3 Parameter vo Häufigkeitsverteiluge 3. Mittelwerte Mo Der Modus (:= häufigster Wert, Abk.: Mo) ist der Merkmalswert mit der größte Häufigkeit, falls es eie solche gibt. Er sollte ur bei eigipflige
Niveaubestimmende Aufgabe zum Fachlehrplan Mathematik Gymnasium
 Niveaubestimmede Aufgabe zum Fachlehrpla Mathematik Gymasium Kreistagswahl (Schuljahrgäge 11/1) (Arbeitsstad: 07.07.016) Niveaubestimmede Aufgabe sid Bestadteil des Lehrplakozeptes für das Gymasium ud
Niveaubestimmede Aufgabe zum Fachlehrpla Mathematik Gymasium Kreistagswahl (Schuljahrgäge 11/1) (Arbeitsstad: 07.07.016) Niveaubestimmede Aufgabe sid Bestadteil des Lehrplakozeptes für das Gymasium ud
Stochastik: Binomialverteilung Stochastik Bernoulli-Experimente, binomialverteilte Zufallsvariablen Gymnasium ab Klasse 10
 Stochastik Beroulli-Experimete, biomialverteilte Zufallsvariable Gymasium ab Klasse 0 Alexader Schwarz www.mathe-aufgabe.com November 203 Hiweis: Für die Aufgabe darf der GTR beutzt werde. Aufgabe : Ei
Stochastik Beroulli-Experimete, biomialverteilte Zufallsvariable Gymasium ab Klasse 0 Alexader Schwarz www.mathe-aufgabe.com November 203 Hiweis: Für die Aufgabe darf der GTR beutzt werde. Aufgabe : Ei
Statistische Tests zu ausgewählten Problemen
 Eiführug i die statistische Testtheorie Statistische Tests zu ausgewählte Probleme Teil : Tests für Erwartugswerte Statistische Testtheorie I Eiführug Beschräkug auf parametrische Testverfahre Beschräkug
Eiführug i die statistische Testtheorie Statistische Tests zu ausgewählte Probleme Teil : Tests für Erwartugswerte Statistische Testtheorie I Eiführug Beschräkug auf parametrische Testverfahre Beschräkug
Testumfang für die Ermittlung und Angabe von Fehlerraten in biometrischen Systemen
 Testumfag für die Ermittlug ud Agabe vo Fehlerrate i biometrische Systeme Peter Uruh SRC Security Research & Cosultig GmbH peter.uruh@src-gmbh.de Eileitug Biometrische Systeme werde durch zwei wichtige
Testumfag für die Ermittlug ud Agabe vo Fehlerrate i biometrische Systeme Peter Uruh SRC Security Research & Cosultig GmbH peter.uruh@src-gmbh.de Eileitug Biometrische Systeme werde durch zwei wichtige
Diskrete Zufallsvariablen
 Erste Beispiele diskreter Verteiluge Diskrete Zufallsvariable Beroulli-Verteilug Eie diskrete Zufallsvariable heißt beroulliverteilt mit arameter p, falls sie die Wahrscheilichkeitsfuktio p,, f ( ) ( )
Erste Beispiele diskreter Verteiluge Diskrete Zufallsvariable Beroulli-Verteilug Eie diskrete Zufallsvariable heißt beroulliverteilt mit arameter p, falls sie die Wahrscheilichkeitsfuktio p,, f ( ) ( )
KAPITEL 11. Ungleichungen. g(x) g(x 0 ) + K 0 (x x 0 ).
 KAPITEL 11 Ugleichuge 111 Jese-Ugleichug Defiitio 1111 Eie Fuktio g : R R heißt kovex, we ma für jedes x R ei K = K (x ) R fide ka, so dass für alle x R gilt: g(x) g(x ) + K (x x ) Bemerkug 111 Eie Fuktio
KAPITEL 11 Ugleichuge 111 Jese-Ugleichug Defiitio 1111 Eie Fuktio g : R R heißt kovex, we ma für jedes x R ei K = K (x ) R fide ka, so dass für alle x R gilt: g(x) g(x ) + K (x x ) Bemerkug 111 Eie Fuktio
Analysis I Lösungsvorschläge zum 3. Übungsblatt Abgabe: Bis Donnerstag, den , um 11:30 Uhr
 Karlsruher Istitut für Techologie Istitut für Aalysis Dr. Christoph Schmoeger Dipl.-Math. Lars Machiek Dipl.-Math. Sebastia Schwarz WS 206/207 03..206 Aalysis I Lösugsvorschläge zum 3. Übugsblatt Abgabe:
Karlsruher Istitut für Techologie Istitut für Aalysis Dr. Christoph Schmoeger Dipl.-Math. Lars Machiek Dipl.-Math. Sebastia Schwarz WS 206/207 03..206 Aalysis I Lösugsvorschläge zum 3. Übugsblatt Abgabe:
3. Einführung in die Statistik
 3. Eiführug i die Statistik Grudlegedes Modell zu Date: uabhägige Zufallsgröße ; : : : ; mit Verteilugsfuktio F bzw. Eizelwahrscheilichkeite p ; : : : ; p r i de Aweduge: kokrete reale Auspräguge ; : :
3. Eiführug i die Statistik Grudlegedes Modell zu Date: uabhägige Zufallsgröße ; : : : ; mit Verteilugsfuktio F bzw. Eizelwahrscheilichkeite p ; : : : ; p r i de Aweduge: kokrete reale Auspräguge ; : :
1 Wahrscheilichkeitsrechug 1.1 Elemete der Megelehre Morgasche Formel A \ B = A [ B A [ B = A \ B Kommutativgesetz A \ B = B \ A A [ B = B [ A Assozia
 Statistik I - Formelsammlug Ihaltsverzeichis 1 Wahrscheilichkeitsrechug 1.1 Elemete der Megelehre................................. 1. Kombiatorik........................................ 1.3 Wahrscheilichkeite....................................
Statistik I - Formelsammlug Ihaltsverzeichis 1 Wahrscheilichkeitsrechug 1.1 Elemete der Megelehre................................. 1. Kombiatorik........................................ 1.3 Wahrscheilichkeite....................................
Stochastik für WiWi - Klausurvorbereitung
 Dr. Markus Kuze WS 2013/14 Dipl.-Math. Stefa Roth 11.02.2014 Stochastik für WiWi - Klausurvorbereitug Gesetz der totale Wahrscheilichkeit ud Satz vo Bayes (Ω, F, P) Wahrscheilichkeitsraum, E 1,..., E F
Dr. Markus Kuze WS 2013/14 Dipl.-Math. Stefa Roth 11.02.2014 Stochastik für WiWi - Klausurvorbereitug Gesetz der totale Wahrscheilichkeit ud Satz vo Bayes (Ω, F, P) Wahrscheilichkeitsraum, E 1,..., E F
Zinsratenmodelle in stetiger Zeit: Teil II
 Zisratemodelle i stetiger Zeit: Teil II Simoe Folty 1.11.006 1. Vasicek Modell (1977) 1.1 Eiführug Vasicek schlug das folgede Modell für die risikofreie Zisrate r(t) vor, basiered auf der SDGL d r t α
Zisratemodelle i stetiger Zeit: Teil II Simoe Folty 1.11.006 1. Vasicek Modell (1977) 1.1 Eiführug Vasicek schlug das folgede Modell für die risikofreie Zisrate r(t) vor, basiered auf der SDGL d r t α
}) = ϑ Einsen (1 ϑ) Nullen,
 6. Schätzprobleme 6.1. Beispiele a) I eiem Teich befidet sich eie ubekate Azahl vo Fische. Ma schätze z. B. durch Agel, markiere, wieder aussetze ud ochmal agel; vgl. Übug) b) Weiteres Beispiel: Wie groß
6. Schätzprobleme 6.1. Beispiele a) I eiem Teich befidet sich eie ubekate Azahl vo Fische. Ma schätze z. B. durch Agel, markiere, wieder aussetze ud ochmal agel; vgl. Übug) b) Weiteres Beispiel: Wie groß
Ökonometrie Formeln und Tabellen
 Ökoometrie Formel ud Tabelle Formelsammlug 1 Lieares Modell ud KQ-Schätzug 11 Eifachregressio Lieares Modell: Y i = β 0 + β 1 x i + U i, i = 1,2,, Aahme des lieare Modells: A1: E[U i ] = 0 für alle i =
Ökoometrie Formel ud Tabelle Formelsammlug 1 Lieares Modell ud KQ-Schätzug 11 Eifachregressio Lieares Modell: Y i = β 0 + β 1 x i + U i, i = 1,2,, Aahme des lieare Modells: A1: E[U i ] = 0 für alle i =
