Definition Eine Metrik d auf der Menge X ist eine Abbildung d : X X IR
|
|
|
- Sabine Albrecht
- vor 6 Jahren
- Abrufe
Transkript
1 0 Inhaltsverzeichnis 1 Metrik Definition einer Metrik Abstand eines Punktes von einer Menge Einbettung eines metrischen Raumes in einen Banachraum Vervollständigung eines metrischen Raumes Kompakte metrische Räume Häufungspunkte für Folgen Verallgemeierter Heine Borelscher Satz Lemma von Lebesgue
2 1 Metrische Räume 1 1 Metrik 1.1 Definition einer Metrik Definition Eine Metrik d auf der Menge X ist eine Abbildung d : X X IR 1. d(x, y) = d(y, x) 2. d(x, y) d(x, z) + d(z, y) 3. d(x, y) = 0 x = y Definition Ein metrischer Raum ist ein Paar (X, d) bestehend aus einer Menge und einer Metrik d auf X. Proposition d(x, a) d(x, b) d(a, b). Beweis. Dreiecksungleichung und die Symmetrie d(b, a) = d(a, b) ergeben. d(x, a) d(x, b) + d(b, a) d(x, b) d(x, a) + d(a, b) d(x, a) d(x, b) d(a, b) d(x, b) d(x, a) d(b, a) d(x, a) d(x, b) ist gleich ±(d(x, a) d(x, b)) je nach Vorzeichen. In beiden Fällen ergibt sich d(a, b). 1.2 Abstand eines Punktes von einer Menge Definition Sei A X, A. Der Abstand des Punktes von der Teilmenge A ist d(x, A) := inf{d(x, a) a A}. Proposition d(x, A) d(y, A) d(x, y) Beweis. Für alle a A d(y, A) d(y, a) = d(y, a) d(x, a) + d(x, a) d(x, y) + d(x, a) Zu ɛ > 0 findet man ein a A mit d(x, a) d(x, A) + ɛ. d(y, A) d(y, a) = d(y, a) d(x, a) + d(x, a) d(x, y) + d(x, a) d(x, y) + d(x, A) + ɛ. 1 L0203-VA2-A.tex
3 2 Wir sehen, daß für jedes ɛ > 0 gilt d(y, A) d(x, A) d(x, y) + ɛ. Also folgt d(y, A) d(x, A) d(x, y). Analog sieht man d(x, A) d(y, A) d(y, x) = d(x, y). Beides zusammen ergibt d(x, A) d(y, A) d(x, y). Definition Der Durchmesser δ(a) der Teilmenge A X ist das Supremum in [0, ] aller möglichen Abstände d(x, y) von Punkten x, y A. δ(a) := sup{d(x, y) x A und y A} [0, ] Es gilt: Für a A und r > δ(a) gilt A B(a; r), denn, wenn x A, dann sind x, a A und somit folgt d(x, a) δ(a) < r, also x B(a, r). 1.3 Einbettung eines metrischen Raumes in einen Banachraum Sei (X, d) metrischer Raum. x 0 X. B(X):=Banachraum der beschränkten Funktionen X IR mit der Supremumsnorm. Proposition Es gibt eine isometrische Abbildung Φ : X B(X), a Φ a von X in den Banchraum B(X). Es gilt damit d(a, b) := Φ a Φ b für alle a, b X. Insbesondere kommt die Metrik d auf der Menge X aus der Norm des Banachraumes B(X). Beweis. Zu a X definiere Φ a : X IR durch Φ a (x) := d(x, a) d(x, x 0 ). Φ a (x) = d(x, a) d(x, x 0 ) d(a, x 0 ) und Φ a (a) = Φ a (x 0 ) = d(a, x 0 ). Es ist also Φ a eine beschränkte Funnktion und somit Φ a B(X). Ferner ist Φ a = sup{ Φ a (x) : x X} = d(a, x 0 ) = max{ Φ a (x) : x X}. Φ a (x) Φ b (x) = d(x, a) d(x, b) d(a, b) Φ a Φ b = sup{ Φ a (x) Φ b (x) : x X} = sup{ d(x, a) d(x, b) : x X} = d(a, b). Diese Formel zeigt, daß Φ eine Isometrie ist. Man hat das wie folgt zu sehen: Φ a Φ b ist der Abstand zwischen Φ a und Φ b im Banachraum B(X) und dieser ist gleich d(a, b) dem Abstand von a zu b im Raum X. Für a = x 0 ist Φ a = 0 die Nullfunktion, also das Nullelement von B(X). Korollar. Φ : X B(X) ist injektiv. Beweis. Aus Φ a = Φ b folgt d(a, b) = Φ a Φ b = 0 und hieraus a = b.
4 3 1.4 Vervollständigung eines metrischen Raumes Proposition Jeder metrische Raum läßt sich vervollständigen. Beweis. Es ist X i.w. gleich Φ(X) B(X), wenn man a X mit Φ a identifiziert. So kann man X B(X) als Teilmenge von B(X) ansehen. Die Metrik auf (X, d) kommt dann von einer Norm, d.h., man hat d(a, b) = a b. Nimmt man den Abschluß von X B(X), so ist X X. Der Raum X ist vollständig, weil abgeschlossene Teilmengen von Banachräumen vollständig sind. 2 Kompakte metrische Räume 2.1 Häufungspunkte für Folgen Definition Man nennt a IR Häufungspunkt (HP) der Folge (x n ) n IN, wenn zu jedem ɛ > 0, die Menge der n IN mit d(x n, a) < ɛ unendlich ist. a ist HP von (x n ) n IN : ɛ>0 Λ ɛ := {n IN d(x n, a) < ɛ} ist unendlich. Das ist i.a. der Begriff von Häufungspunkt einer Folge für topologischen Räume. Proposition In metrischen Räumen (X, d) sind die Häufungspunkte einer Folge die Grenzwerte ihrer konvergenten Teilfolgen. Beweis: Wir zeigen: a HP von x n Es gibt eine Teilfolge x nk mit a = lim k x nk. : Sei a ein Häufungspunkt von x n. Wir konstruieren induktiv über k eine Zahlenfolge n 1 < n 2 <... < n k <... in IN, so daß d(x nk, a) < 1. k Wir beginnen mit einem n 1, was wir aus Λ ɛ := {n IN d(x n, a) < ɛ} für ɛ = 1 wählen. Seien jetzt n 1 <... < n k konstruiert. Nach Definition von HP ist Λ 1/(k+1) := {n IN; d(x n, a) < 1 } IN unendlich. und k+1 man findet hierin ein n k+1, was größer ist als das bereits vorliegende n k. Konvergiert diese Folge gegen a? Klar, denn d(x nk, a) < 1 k. In topologischen Räumen ist diese Konvergenz keineswegs klar (und i.a. sogar falsch). Dort hat man zu zeigen, daß in jeder Umgebung U von a alle Folgenglieder von (x nk ) k IN ab einem gewissen k 0 = k 0 (U) liegen. In metrischen Räumen sind Umgebungen von a X per Definition solche Teilmengen, die eine offenen Kugel B(a, 1 k 0 ) enthalten. Ab diesem k 0, also für k k 0, gilt x nk B(a, 1 k ) B(a, 1 k 0 ) U. : Ist a = lim k x nk, dann findet man zu jedem ɛ > 0 ein k 0, so daß für alle k k 0 folgt d(x nk, a) < ɛ. Dann gilt n k0, n k0 +1,... Λ ɛ und Λ ɛ ist unendlich.
5 4 Anmerkung. Die Aussage gilt ganz allgemein auch für topologische Räume. Die Beweisrichtung funktioniert allgemein nicht. Es gibt dazu ein (spitzfindiges) Gegenbeispiel, das man in Boto von Querenburg: Mengentheoretische Topologie, Springer Verlag, 1970, S. 93, A 8.3 findet. Dennoch gilt allgemeiner, als nur für metrische Räume, z.b. dann, wenn jeder Punkt a X eine abzählbare Umgebungsbasis (B k (a)) k IN hat. Abzählbare Umgebungsbasis bedeutet, daß es zu jedem Punkt a in X abzählbar viele Umgebungen (B k (a)) k IN gibt, so daß in jeder beliebigen Umgebung U von a eine Umgebung der Form B k0 (a) liegt. VA2: HeinBor Definition Sei E ein metrischer Raum E heißt folgenkompakt, wenn jede Folge einen Häufungspunkt besitzt. Dazu äquivalent, wenn jede Folge eine konvergente Teilfolge besitzt. Definition Ein weiterer Begriff ist präkompakt oder totalbeschränkt. Der metrische Raum E heißt präkompakt oder totalbeschränkt, wenn es zu jedem ɛ > 0 eine endliche Teilmenge F ɛ gibt. so daß für jedes x X der Abstand zu F ɛ kleiner als ɛ E ist präkompakt (totalbeschränkt) bedeutet also: Zu jedem ɛ > 0 gibt es endlich viele Punkte x 1,..., x n E, so daß (a) jedes x E von einem geeigneten x i einen Abstand d(x, x i ) < ɛ hat, oder (b) für jedes x E gilt x B(x i, ɛ) für ein geeignetes i = 1,.., n, oder (c) E = B(x 1, ɛ)... B(x n, ɛ) (a), (b), (c) sind gleichbedeutend. Definition Eine Überdeckung (U λ ) λ J der Menge E besteht aus Teilmengen U λ E, wobei λ J eine Menge J durchläuft, so daß jeder Punkt von x in (wenigstens) einem U λ liegt. Eine Überdeckung von E ist also nichts anderes als eine Abbildung einer Menge J in die Potenzmenge P(E) J P(E), λ U λ E, so daß E = λ J U λ. Dabei ist die Vereinigung λ J U λ aller U λ definiert als λ J U λ := {x E λ J x U λ }. Die Menge J nennt man Indexmenge der Überdeckung. Definition Eine Teilüberdeckung von (U λ ) λ J ist eine Überdeckung der Form (U λ ) λ J, wobei J eine Teilmenge von J ist; J J. Bei einer endlichen Teilüberdeckung verlangt man, daß J eine endlich Teilmenge von J ist.
6 5 Definition Sei E ein metrischer Raum mit der Metrik d : E E IR. Eine offene Überdeckung von E besteht aus offenen Teilmengen U λ. Der metrische Raum E heißt kompakt, wenn jede offene Überdeckung von X eine endliche Teilüberdeckung besitzt. E kompakt bedeutet: Wenn immer E = λ J U λ, mit in E offenen U λ, gibt es endlich viele Indizes λ 1,..., λ n J, so daß E = U λ1... U λn. Der Begriff kompakt ist allein mit Hilfe von offenen Mengen formuliert und hängt somit nur von diesen ab. Man beachte daß unterschiedliche Metriken, die gleiche Topologie, also die gleichen offenen Mengen liefern können. Insofern hängt kompakt nicht von solchen Metriken ab. Der Begriff totalbeschränkt hängt aber stark von den Metriken auf E ab. 2.2 Verallgemeierter Heine Borelscher Satz Hierzu gilt der Satz 2.1 Für einen metrischen Raum E sind äquivalent. (a) E ist kompakt. (b) Jede Folge in E besitzt einen HP. (E ist folgenkompakt.) (c) E ist präkompakt und vollständig. (Vollständig bedeutet, daß jede Cauchyfolge in E konvergiert.) Beweis. (a) (b):(indirekt) Angenommen es gäbe eine Folge (x n ) n IN von E ohne HP. Dann ist jeder Punkt p E kein HP. Zu jedem p E findet man eine offene Kugel U p um p, so daß Λ p := {n x n U p } IN endlich ist. Weil E kompakt ist, folgt E = U p1 U pk. Einerseits ist Λ p1 Λ pk endlich und andererseits = IN, also unendlich. Das ist ein Widerspruch. (b) (c): (i) Wir zeigen zunächst: E ist vollständig. Sei x n eine CF. Nach (b) besitzt x n einen HP a Cauchyfolgen x n konvergieren gegen den HP a einer Teilefolge. (ii) Zeige E ist präkompakt. Beweis indirekt. Angenommen E nicht präkompakt. Dann gibt es α > 0 und keine endliche Überdeckung mit Kugeln vom Radius α von E. So findet man induktiv x n E, so daß x n+1 B(x 1, α) B(x n, α).
7 6 Hier gilt d(x i, x j ) α für alle i j. Die Folge der x i hat einen HP a. Es gibt eine Teilfolge x nk, die gegen a konvergiert. d(x nk, x nk+1 ) α. Für k folgt d(a, a) α > 0. (c) (a): (indirekt) Wir nehmen an, daß E nicht kompakt sei. Dann findet man eine offene Überdeckung (U λ ) λ Λ von E, die keine endliche Teilüberseckung enthält. Zu 2 n gibt es eine endliche Menge F n E, so daß E = x F n B(x, 2 n ). Durch Induktion über n findet man ein B n = B(x n, 2 n ) mit x n F n, so daß B n nicht von endlich vielen U λ überdeckt wird. Unter den B(x, 2 n 1 ) mit x F n+1 findet man eine Kugel B n+1 mit B n B n+1 und B n+1 wird nicht von endlich vielen U λ überdeckt. Die Mittelpunkte x n der Kugeln bilden eine Cauchyfolge. Weil B n B n+1, folgt d(x n, x n+1 ) 2 n + 2 n 1 < 2 n+1 d(x n, x n+k ) d(x n, x n+1 ) + + d(x n+k 1, x n+k ) 2 n n k+2 = 2 n+1 ( k+1 ) 2 n+1 2 Die Cauchyfolge konvergiert gegen einen Punkt a E. a liegt in einem U λ0. U λ0 ist offen und somit gibt es eine Kugel B(a, α) U λ0. Für hinreichend großes n gilt d(a, x n ) < α/2 und 2 n < α/2. Hierfür ist B n B(a, α) U λ0, denn x B n d(x, a) d(x, x n ) + d(x n, a) < 2 n + α/2 < α/2 + α/2 = α. Nun wird dieses B n durch das U λ0 überdeckt. Das ist ein Widerspruch. Bemerkungen. Das offene Intervall ]0, 1[ ist totalbeschränkt (präkompakt). Totalbeschränkt impliziert stets beschränkt. Die Umkehrung ist falsch. x y Auf IR ist d (x, y) := eine Metrik. Diese liefert die gleichen offenen Mengen, 1+ x y die gleichen Cauchyfolgen, ja sogar die gleichen offenen Kugeln, wie die Standardmetrik d(x, y) := x y. Der metrische Raum (IR, d ), also IR mit dieser neuen Metrik d, ist beschränkt, denn d (x, y) < 1 für alle x, y IR. Er ist auch vollständig, weil die Cauchyfolgen von d und d übereinstimmen. Wäre nun (IR, d ) totalbeschränkt, dann würde nach dem Satz folgen, daß IR kompakt wäre. Das ist ein Widerspruch.
8 7 Gleiche offenen Kugeln für d und d im vorigen Beispiel bedeutet B(x, r) = B (x, ρ), wobei ρ = ρ(r) = r. 1+r Daß mit den einen die Präkompaktheitsbedingung (totale Beschränktheit) vorliegt und bei den anderen Kugeln nicht, liegt an den unterschiedlichen Radien r und ρ, obwohl ja die Kugeln B(x, r) und B (x, ρ) als Mengen gleich sind. Für Teilmengen E IR n gilt: Beschränkt ist gleichbedeutend mit totalbeschränkt. 2.3 Lemma von Lebesgue. Das folgende Lemma wird nach Henri Lebesgue ( ) benannt: Lemma Sei U eine offene Überdeckung des kompakten metrischen Raumes Raumes X. Dann gibt es eine Zahl ɛ > 0, so daß jede (offene) Kugel B(x, ɛ) von X in einem geeigneten U U liegt. Definition Man nennt ɛ eine Lebesguezahl der offenen Überdeckung U. Beweis. Der Beweis geht indirekt. Angenommen die offene Überdeckung U besäße keine Lebesguezahl ɛ. Dann ist auch jede Zahl 1/n (n IN) keine. Also findet man zu jedem n eine Kugel B(a n, 1/n), die in keinem U von U liegt. In dem kompakten Raum X besitzt a n eine konvergente Teilfolge b j := a nj. Bei Teilfolgen ist n 1 < n 2 <... und somit ist auch n j j. Weil B(a nj, 1/n j ) B(b j, 1/j) liegt auch B(b j, 1/j) in keinem U U, für alle j IN. Andererseits: Sei b = lim j b j. Dieses b liegt in einem U U. Weil U offen ist, gibt es eine offene Kugel B(b, 2r) U. Nun wählt man j IN, so groß, daß d(b j, b) und 1/j beide < r sind. Dann folgt B(b j, 1/j) B(b, 2r) U. Das liefert einen Widerspruch. Nun noch zu der Begründung der Inklusion: Aus x B(b j, 1/j) folgt d(b j, x) < 1/j und somit: d(b, x) d(b, b j ) + d(b j, x) < r + 1/j < r + r < 2r, also x B(b, 2r).
Induktive Limiten. Arpad Pinter, Tobias Wöhrer. 30. Jänner 2010
 Induktive Limiten Arpad Pinter, Tobias Wöhrer 30. Jänner 2010 1 Inhaltsverzeichnis 1 Induktiver Limes von Mengen 2 2 Induktiver Limes von Vektorräumen 4 3 Lokalkonvexe topologische Vektorräumen 7 4 Induktiver
Induktive Limiten Arpad Pinter, Tobias Wöhrer 30. Jänner 2010 1 Inhaltsverzeichnis 1 Induktiver Limes von Mengen 2 2 Induktiver Limes von Vektorräumen 4 3 Lokalkonvexe topologische Vektorräumen 7 4 Induktiver
Einführung in die Funktionalanalysis
 Einführung in die Funktionalanalysis Bernhard Gsell Skriptum zur Vorlesung gelesen von Prof. Wolfgang Woess 21. August 2014 Dies ist die Umsetzung meiner Vorlesungsmitschrift zu Einführung in die Funktionalanalysis,
Einführung in die Funktionalanalysis Bernhard Gsell Skriptum zur Vorlesung gelesen von Prof. Wolfgang Woess 21. August 2014 Dies ist die Umsetzung meiner Vorlesungsmitschrift zu Einführung in die Funktionalanalysis,
Beispiel 11.2. Wenn p ein Polynom vom Grad größer gleich 1 ist, ist q : C Ĉ definiert durch q (z) =
 Funktionentheorie, Woche Funktionen und Polstellen. Meromorphe Funktionen Definition.. Sei U C offen und sei f : U gilt, nennt man f meromorph auf U: Ĉ eine Funktion. Wenn folgendes. P := f hat keine Häufungspunkte;.
Funktionentheorie, Woche Funktionen und Polstellen. Meromorphe Funktionen Definition.. Sei U C offen und sei f : U gilt, nennt man f meromorph auf U: Ĉ eine Funktion. Wenn folgendes. P := f hat keine Häufungspunkte;.
Matrizennorm. Definition 1. Sei A M r,s (R). Dann heißt A := sup die Matrixnorm. Wir wissen zunächst nicht, ob A eine reelle Zahl ist.
 Matrizennorm Es seien r,s N Mit M r,s (R bezeichnen wir die Menge der reellen r s- Matrizen (also der linearen Abbildungen R s R r, und setze M s (R := M s,s (R (also die Menge der linearen Abbildungen
Matrizennorm Es seien r,s N Mit M r,s (R bezeichnen wir die Menge der reellen r s- Matrizen (also der linearen Abbildungen R s R r, und setze M s (R := M s,s (R (also die Menge der linearen Abbildungen
Absolute Stetigkeit von Maßen
 Absolute Stetigkeit von Maßen Definition. Seien µ und ν Maße auf (X, Ω). Dann heißt ν absolut stetig bezüglich µ (kurz ν µ ), wenn für alle A Ω mit µ(a) = 0 auch gilt dass ν(a) = 0. Lemma. Sei ν ein endliches
Absolute Stetigkeit von Maßen Definition. Seien µ und ν Maße auf (X, Ω). Dann heißt ν absolut stetig bezüglich µ (kurz ν µ ), wenn für alle A Ω mit µ(a) = 0 auch gilt dass ν(a) = 0. Lemma. Sei ν ein endliches
Ergänzungen zur Analysis I
 537. Ergänzungsstunde Logik, Mengen Ergänzungen zur Analysis I Die Behauptungen in Satz 0.2 über die Verknüpfung von Mengen werden auf die entsprechenden Regelnfür die Verknüpfung von Aussagen zurückgeführt.
537. Ergänzungsstunde Logik, Mengen Ergänzungen zur Analysis I Die Behauptungen in Satz 0.2 über die Verknüpfung von Mengen werden auf die entsprechenden Regelnfür die Verknüpfung von Aussagen zurückgeführt.
Mengensysteme, Wahrscheinlichkeitsmaße
 Kapitel 1 Mengensysteme, Wahrscheinlichkeitsmaße Der Großteil der folgenden fundamentalen Begriffe sind schon aus der Vorlesung Stochastische Modellbildung bekannt: Definition 1.1 Eine Familie A von Teilmengen
Kapitel 1 Mengensysteme, Wahrscheinlichkeitsmaße Der Großteil der folgenden fundamentalen Begriffe sind schon aus der Vorlesung Stochastische Modellbildung bekannt: Definition 1.1 Eine Familie A von Teilmengen
Analysis I III. Vorlesungsskriptum WS 2005/06 WS 2006/07. Fakultät für Mathematik, Ruhr-Universität Bochum
 Analysis I III Vorlesungsskriptum WS 2005/06 WS 2006/07 R. Verfürth Fakultät für Mathematik, Ruhr-Universität Bochum Inhaltsverzeichnis Kapitel I. Aufbau des Zahlsystems 5 I.1. Die natürlichen Zahlen
Analysis I III Vorlesungsskriptum WS 2005/06 WS 2006/07 R. Verfürth Fakultät für Mathematik, Ruhr-Universität Bochum Inhaltsverzeichnis Kapitel I. Aufbau des Zahlsystems 5 I.1. Die natürlichen Zahlen
Reelle Analysis. Vorlesungsskript. Enno Lenzmann, Universität Basel. 7. November 2013
 Reelle Analysis Vorlesungsskript Enno Lenzmann, Universität Basel 7. November 2013 6 L p -Räume Mit Hilfe der Masstheorie können wir nun die sog. L p -Räume einführen. Diese Räume sind wichtig in vielen
Reelle Analysis Vorlesungsskript Enno Lenzmann, Universität Basel 7. November 2013 6 L p -Räume Mit Hilfe der Masstheorie können wir nun die sog. L p -Räume einführen. Diese Räume sind wichtig in vielen
2 3 x3 17. x k dx = x k x k+1 k +1. Mit jeder weiteren partiellen Integration reduziert sich der Grad des Faktors x n, induktiv erhalten wir also
 Universität Konstanz Fachbereich Mathematik und Statistik Repetitorium Analysis 0 Dr DK Huynh Blatt 8 Aufgabe 6 Bestimmen Sie (a) (x + x 7x+)dx (c) (f) x n exp(x)dx (n N fest) sin (x)dx (g) (b) (d) ln(x)dx
Universität Konstanz Fachbereich Mathematik und Statistik Repetitorium Analysis 0 Dr DK Huynh Blatt 8 Aufgabe 6 Bestimmen Sie (a) (x + x 7x+)dx (c) (f) x n exp(x)dx (n N fest) sin (x)dx (g) (b) (d) ln(x)dx
Vorlesung. Funktionen/Abbildungen 1
 Vorlesung Funktionen/Abbildungen 1 1 Grundlagen Hinweis: In dieser Vorlesung werden Funktionen und Abbildungen synonym verwendet. In der Schule wird eine Funktion häufig als eindeutige Zuordnung definiert.
Vorlesung Funktionen/Abbildungen 1 1 Grundlagen Hinweis: In dieser Vorlesung werden Funktionen und Abbildungen synonym verwendet. In der Schule wird eine Funktion häufig als eindeutige Zuordnung definiert.
Topologie. Prof. Dr. Dirk Ferus. Wintersemester 2004/5
 Topologie Prof. Dr. Dirk Ferus Wintersemester 2004/5 Version vom 04.02.2005 Inhaltsverzeichnis 1 Topologische Räume und stetige Abbildungen 7 1.1 Metrische und topologische Räume.................................
Topologie Prof. Dr. Dirk Ferus Wintersemester 2004/5 Version vom 04.02.2005 Inhaltsverzeichnis 1 Topologische Räume und stetige Abbildungen 7 1.1 Metrische und topologische Räume.................................
9.2. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83
 9.. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83 Die Grundfrage bei der Anwendung des Satzes über implizite Funktionen betrifft immer die folgende Situation: Wir haben eine Funktion f : V W und eine Stelle x
9.. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83 Die Grundfrage bei der Anwendung des Satzes über implizite Funktionen betrifft immer die folgende Situation: Wir haben eine Funktion f : V W und eine Stelle x
Folgen. Kapitel 3. 3.1 Zinsrechnung
 Kapitel 3 Folgen Eine Folge reeller Zahlen ordnet natürlichen Zahlen jeweils eine reelle Zahl zu. Liegen beispielsweise volkswirtschaftliche Daten quartalsweise vor, so kann man diese als Folge interpretieren.
Kapitel 3 Folgen Eine Folge reeller Zahlen ordnet natürlichen Zahlen jeweils eine reelle Zahl zu. Liegen beispielsweise volkswirtschaftliche Daten quartalsweise vor, so kann man diese als Folge interpretieren.
4. Woche Decodierung; Maximale, Perfekte und Optimale Codes. 4. Woche: Decodierung; Maximale, Perfekte und Optimale Codes 69/ 140
 4 Woche Decodierung; Maximale, Perfekte und Optimale Codes 4 Woche: Decodierung; Maximale, Perfekte und Optimale Codes 69/ 140 Szenario für fehlerkorrigierende Codes Definition (n, M)-Code Sei C {0, 1}
4 Woche Decodierung; Maximale, Perfekte und Optimale Codes 4 Woche: Decodierung; Maximale, Perfekte und Optimale Codes 69/ 140 Szenario für fehlerkorrigierende Codes Definition (n, M)-Code Sei C {0, 1}
Grundlagen der Variationsrechnung
 Universität des Saarlandes Fachrichtung 6.1 Mathematik /home/lehrstuhl/ag-fuchs/olli/work/texstyles/eule-eps-conv Grundlagen der Variationsrechnung Eine anwendungsorientierte Einführung in die lineare
Universität des Saarlandes Fachrichtung 6.1 Mathematik /home/lehrstuhl/ag-fuchs/olli/work/texstyles/eule-eps-conv Grundlagen der Variationsrechnung Eine anwendungsorientierte Einführung in die lineare
Inoffizielles Skriptum zur Vorlesung Höhere Mathematik für Informatiker basierend auf Vorlesungen an der Universität Karlsruhe (TH) 2000 2004
 Höhere Mathεmatik für Informatiker Inoffizielles Skriptum zur Vorlesung Höhere Mathematik für Informatiker basierend auf Vorlesungen an der Universität Karlsruhe (TH) 2 24 ii Inhaltsverzeichnis I Eindimensionale
Höhere Mathεmatik für Informatiker Inoffizielles Skriptum zur Vorlesung Höhere Mathematik für Informatiker basierend auf Vorlesungen an der Universität Karlsruhe (TH) 2 24 ii Inhaltsverzeichnis I Eindimensionale
50. Mathematik-Olympiade 2. Stufe (Regionalrunde) Klasse 11 13. 501322 Lösung 10 Punkte
 50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
Optimalitätskriterien
 Kapitel 4 Optimalitätskriterien Als Optimalitätskriterien bezeichnet man notwendige oder hinreichende Bedingungen dafür, dass ein x 0 Ω R n Lösung eines Optimierungsproblems ist. Diese Kriterien besitzen
Kapitel 4 Optimalitätskriterien Als Optimalitätskriterien bezeichnet man notwendige oder hinreichende Bedingungen dafür, dass ein x 0 Ω R n Lösung eines Optimierungsproblems ist. Diese Kriterien besitzen
a n + 2 1 auf Konvergenz. Berechnen der ersten paar Folgenglieder liefert:
 Beispiel: Wir untersuchen die rekursiv definierte Folge a 0 + auf Konvergenz. Berechnen der ersten paar Folgenglieder liefert: ( ) (,, 7, 5,...) Wir können also vermuten, dass die Folge monoton fallend
Beispiel: Wir untersuchen die rekursiv definierte Folge a 0 + auf Konvergenz. Berechnen der ersten paar Folgenglieder liefert: ( ) (,, 7, 5,...) Wir können also vermuten, dass die Folge monoton fallend
1 Stochastische Prozesse in stetiger Zeit
 1 Stochastische Prozesse in stetiger Zeit 1.1 Grundlagen Wir betrachten zufällige Prozesse, definiert auf einem Wahrscheinlichkeitsraum (Ω, F, P), welche Werte in einen fest gewählten Zustandsraum annehmen.
1 Stochastische Prozesse in stetiger Zeit 1.1 Grundlagen Wir betrachten zufällige Prozesse, definiert auf einem Wahrscheinlichkeitsraum (Ω, F, P), welche Werte in einen fest gewählten Zustandsraum annehmen.
Geometrische Mannigfaltigkeiten
 Geometrische Mannigfaltigkeiten Thilo Kuessner Abstract Kurzfassung der Vorlesung: Definitionen, Beispiele und Sätze, keine Beweise. Definition 1. Ein topologischer Raum ist eine Menge X mit einer Familie
Geometrische Mannigfaltigkeiten Thilo Kuessner Abstract Kurzfassung der Vorlesung: Definitionen, Beispiele und Sätze, keine Beweise. Definition 1. Ein topologischer Raum ist eine Menge X mit einer Familie
1 Die reellen Zahlen. 1. Ziele des Mathematikstudiums: Die Studierenden sollen lernen,
 1 Die reellen Zahlen 1. Ziele des Mathematikstudiums: Die Studierenden sollen lernen, präzise und logisch zu denken, komplexe Strukturen schnell und gründlich zu erfassen, Dinge kritisch zu hinterfragen
1 Die reellen Zahlen 1. Ziele des Mathematikstudiums: Die Studierenden sollen lernen, präzise und logisch zu denken, komplexe Strukturen schnell und gründlich zu erfassen, Dinge kritisch zu hinterfragen
Nicht-archimedische Zahlen
 Skript zur Vorlesung Nicht-archimedische Zahlen Wintersemester 2012/13 Frankfurt am Main Prof. Dr. Annette Werner Inhaltsverzeichnis 1 Einleitung 1 2 Nicht-archimedische Absolutbeträge 2 3 Bälle und Topologie
Skript zur Vorlesung Nicht-archimedische Zahlen Wintersemester 2012/13 Frankfurt am Main Prof. Dr. Annette Werner Inhaltsverzeichnis 1 Einleitung 1 2 Nicht-archimedische Absolutbeträge 2 3 Bälle und Topologie
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Mathematische Methoden der Physik: Funktionalanalytische Methoden. Technische Universität Clausthal WS 1998/99
 Mathematische Methoden der Physik: Funktionalanalytische Methoden Technische Universität Clausthal WS 1998/99 W. Lücke 3 Vorwort Als Funktionalanalysis bezeichnet man die Analysis von Funktionen, deren
Mathematische Methoden der Physik: Funktionalanalytische Methoden Technische Universität Clausthal WS 1998/99 W. Lücke 3 Vorwort Als Funktionalanalysis bezeichnet man die Analysis von Funktionen, deren
GNS-Konstruktion und normale Zustände. 1 Rückblick. 2 Beispiel für einen Typ-II 1 -Faktor
 GNS-Konstruktion und normale Zustände 1 Rückblick Wir betrachten von-neumann-algebren M B(H), d.h. Unteralgebren mit 1 H M, die in der schwachen Operatortopologie (und damit in jeder der anderen) abgeschlossen
GNS-Konstruktion und normale Zustände 1 Rückblick Wir betrachten von-neumann-algebren M B(H), d.h. Unteralgebren mit 1 H M, die in der schwachen Operatortopologie (und damit in jeder der anderen) abgeschlossen
Theoretische Informatik
 Theoretische Informatik für die Studiengänge Ingenieur-Informatik berufsbegleitendes Studium Lehramt Informatik (Sekundar- und Berufsschule) http://theo.cs.uni-magdeburg.de/lehre04s/ Lehrbeauftragter:
Theoretische Informatik für die Studiengänge Ingenieur-Informatik berufsbegleitendes Studium Lehramt Informatik (Sekundar- und Berufsschule) http://theo.cs.uni-magdeburg.de/lehre04s/ Lehrbeauftragter:
Modern Methods in Nonlinear Optimization
 Modern Methods in Nonlinear Optimization Regularisierung Inverser Probleme Prof. Dr. Bastian von Harrach Technische Universität München, Fakultät für Mathematik - M1 Wintersemester 2010/2011 http://www-m1.ma.tum.de/bin/view/lehrstuhl/harrach_ws1011_modernmethods
Modern Methods in Nonlinear Optimization Regularisierung Inverser Probleme Prof. Dr. Bastian von Harrach Technische Universität München, Fakultät für Mathematik - M1 Wintersemester 2010/2011 http://www-m1.ma.tum.de/bin/view/lehrstuhl/harrach_ws1011_modernmethods
11. Primfaktorzerlegungen
 78 Andreas Gathmann 11 Primfaktorzerlegungen Euch ist sicher aus der Schule bekannt, dass sich jede positive ganze Zahl a als Produkt a = p 1 p n von Primzahlen schreiben lässt, und dass diese Darstellung
78 Andreas Gathmann 11 Primfaktorzerlegungen Euch ist sicher aus der Schule bekannt, dass sich jede positive ganze Zahl a als Produkt a = p 1 p n von Primzahlen schreiben lässt, und dass diese Darstellung
TECHNISCHE UNIVERSITÄT MÜNCHEN. Abzählbarkeit, Injektivität, Sürjektivität und Bijektivität
 TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Prof. Dr. Friedrich Roesler Ralf Franken, PhD Max Lein Lineare Algebra 1 WS 26/7 en Blatt 4 13.11.26 Abzählbarkeit, Injektivität, Sürjektivität und Bijektivität
TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Prof. Dr. Friedrich Roesler Ralf Franken, PhD Max Lein Lineare Algebra 1 WS 26/7 en Blatt 4 13.11.26 Abzählbarkeit, Injektivität, Sürjektivität und Bijektivität
Aufgaben zur Vorlesung Analysis II Prof. Dr. Holger Dette SS 2012 Lösungen zu Blatt 6
 Aufgben zur Vorlesung Anlysis II Prof. Dr. Holger Dette SS 0 Lösungen zu Bltt 6 Aufgbe. Die Funktion f : [, ) R sei in jedem endlichen Teilintervll von [, ) Riemnnintegrierbr. Für n N sei I n := f() d.
Aufgben zur Vorlesung Anlysis II Prof. Dr. Holger Dette SS 0 Lösungen zu Bltt 6 Aufgbe. Die Funktion f : [, ) R sei in jedem endlichen Teilintervll von [, ) Riemnnintegrierbr. Für n N sei I n := f() d.
Handreichung. zur Mathematikvorlesung für. Wirtschaftswissenschaftler)
 1 Handreichung zur Mathematikvorlesung für Wirtschaftswissenschaftler) Dr.Dr. Christina Schneider 2 Hinweis Das vorliegende Manuskript versteht sich als kurze und kompakte Handreichung zu meiner Vorlesung
1 Handreichung zur Mathematikvorlesung für Wirtschaftswissenschaftler) Dr.Dr. Christina Schneider 2 Hinweis Das vorliegende Manuskript versteht sich als kurze und kompakte Handreichung zu meiner Vorlesung
Mathematik 1. Lösungsvorschläge zum 2. Übungsblatt
 Hochschule Regensburg Fakultät Informatik/Mathematik Christoph Böhm Wintersemester 0/0 Wirtschaftsinformatik Bachelor IW Informatik Bachelor IN Vorlesung Mathematik Mathematik Lösungsvorschläge zum Übungsblatt
Hochschule Regensburg Fakultät Informatik/Mathematik Christoph Böhm Wintersemester 0/0 Wirtschaftsinformatik Bachelor IW Informatik Bachelor IN Vorlesung Mathematik Mathematik Lösungsvorschläge zum Übungsblatt
Grundlagen der Stochastischen Analysis. Egbert Dettweiler
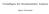 Grundlagen der Stochastischen Analysis Egbert Dettweiler Vorwort Der erste Teil des vorliegenden Manuskripts ist im wesentlichen eine Vorlesungsausarbeitung einer im Sommersemester 23 an der Universität
Grundlagen der Stochastischen Analysis Egbert Dettweiler Vorwort Der erste Teil des vorliegenden Manuskripts ist im wesentlichen eine Vorlesungsausarbeitung einer im Sommersemester 23 an der Universität
Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler
 Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler Wintersemester 3/4 (.3.4). (a) Für z = + i und z = 3 4i berechne man z z und z z. Die Ergebnisse sind in kartesischer Form anzugeben.
Kommentierte Musterlösung zur Klausur HM I für Naturwissenschaftler Wintersemester 3/4 (.3.4). (a) Für z = + i und z = 3 4i berechne man z z und z z. Die Ergebnisse sind in kartesischer Form anzugeben.
w a is die Anzahl der Vorkommen von a in w Beispiel: abba a = 2
 1 2 Notation für Wörter Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg w a is die Anzahl der Vorkommen von a in w Beispiel: abba
1 2 Notation für Wörter Grundlagen der Theoretischen Informatik Till Mossakowski Fakultät für Informatik Otto-von-Guericke Universität Magdeburg w a is die Anzahl der Vorkommen von a in w Beispiel: abba
Vorlesung Analysis und Numerische Mathematik (für Informatiker) gehalten von Werner Römisch Winter-Semester 1992/93 bis Sommer-Semester 1994
 Vorlesung Analysis und Numerische Mathematik (für Informatiker) gehalten von Werner Römisch Winter-Semester 1992/93 bis Sommer-Semester 1994 1 Inhaltsverzeichnis 0 Einleitung 4 1 Mengen, Abbildungen, Zahlen
Vorlesung Analysis und Numerische Mathematik (für Informatiker) gehalten von Werner Römisch Winter-Semester 1992/93 bis Sommer-Semester 1994 1 Inhaltsverzeichnis 0 Einleitung 4 1 Mengen, Abbildungen, Zahlen
2.12 Potenzreihen. 1. Definitionen. 2. Berechnung 2.12. POTENZREIHEN 207. Der wichtigste Spezialfall von Funktionenreihen sind Potenzreihen.
 2.2. POTENZREIHEN 207 2.2 Potenzreihen. Definitionen Der wichtigste Spezialfall von Funktionenreihen sind Potenzreihen. Eine Potenzreihe mit Entwicklungspunkt x 0 ist eine Reihe a n x x 0 n. Es gilt: es
2.2. POTENZREIHEN 207 2.2 Potenzreihen. Definitionen Der wichtigste Spezialfall von Funktionenreihen sind Potenzreihen. Eine Potenzreihe mit Entwicklungspunkt x 0 ist eine Reihe a n x x 0 n. Es gilt: es
Modulabschlussklausur Analysis II
 Modulabschlussklausur Analysis II. Juli 015 Bearbeitungszeit: 150 min Aufgabe 1 [5/10 Punkte] Es sei a R und f a : R 3 R mit f a (x, y, z) = x cos(y) + z 3 sin(y) + a 3 + (z + ay a y) cos(x) a) Bestimmen
Modulabschlussklausur Analysis II. Juli 015 Bearbeitungszeit: 150 min Aufgabe 1 [5/10 Punkte] Es sei a R und f a : R 3 R mit f a (x, y, z) = x cos(y) + z 3 sin(y) + a 3 + (z + ay a y) cos(x) a) Bestimmen
3. Die Eigenschaften der reellen Zahlen II: Geordnete Körper
 32 Andreas Gathmann 3. Die Eigenschaften der reellen Zahlen II: Geordnete Körper Wir haben bisher von den reellen Zahlen nur die Körpereigenschaften, also die Eigenschaften der vier Grundrechenarten ausgenutzt
32 Andreas Gathmann 3. Die Eigenschaften der reellen Zahlen II: Geordnete Körper Wir haben bisher von den reellen Zahlen nur die Körpereigenschaften, also die Eigenschaften der vier Grundrechenarten ausgenutzt
Mathematik für Physiker, Informatiker und Ingenieure I Skriptum des WS 2007/08
 Mathematik für Physiker, Informatiker und Ingenieure I Skriptum des WS 2007/08 Prof. Dr. M. v. Golitschek Institut für Mathematik Universität Würzburg Literatur: Suchen Sie doch hin und wieder die Bibliotheken
Mathematik für Physiker, Informatiker und Ingenieure I Skriptum des WS 2007/08 Prof. Dr. M. v. Golitschek Institut für Mathematik Universität Würzburg Literatur: Suchen Sie doch hin und wieder die Bibliotheken
Frohe Weihnachten und ein gutes neues Jahr!
 Frohe Weihnachten und ein gutes neues Jahr! Die mit dem Stern * gekennzeichneten Übungen sind nicht verpflichtend, aber sie liefern zusätzliche Punkte. Unten wird immer mit I das reelle Intervall [0, 1]
Frohe Weihnachten und ein gutes neues Jahr! Die mit dem Stern * gekennzeichneten Übungen sind nicht verpflichtend, aber sie liefern zusätzliche Punkte. Unten wird immer mit I das reelle Intervall [0, 1]
17. Penalty- und Barriere-Methoden
 H.J. Oberle Optimierung SoSe 01 17. Penalty- und Barriere-Methoden Penalty- und Barriere Methoden gehören zu den ältesten Ansätzen zur Lösung allgemeiner restringierter Optimierungsaufgaben. Die grundlegende
H.J. Oberle Optimierung SoSe 01 17. Penalty- und Barriere-Methoden Penalty- und Barriere Methoden gehören zu den ältesten Ansätzen zur Lösung allgemeiner restringierter Optimierungsaufgaben. Die grundlegende
5.1 Drei wichtige Beweistechniken... 55 5.2 Erklärungen zu den Beweistechniken... 56
 5 Beweistechniken Übersicht 5.1 Drei wichtige Beweistechniken................................. 55 5. Erklärungen zu den Beweistechniken............................ 56 Dieses Kapitel ist den drei wichtigsten
5 Beweistechniken Übersicht 5.1 Drei wichtige Beweistechniken................................. 55 5. Erklärungen zu den Beweistechniken............................ 56 Dieses Kapitel ist den drei wichtigsten
Nichtlineare hyperbolische Gleichungen.
 Nichtlineare hyperbolische Gleichungen. 1 Hyperbolische Gleichungen 1.1 Einleitung In dieser Vorlesung geht es um hyperbolische Gleichungen. Es sind Evolutionsgleichungen. Das heißt, wir haben ein System
Nichtlineare hyperbolische Gleichungen. 1 Hyperbolische Gleichungen 1.1 Einleitung In dieser Vorlesung geht es um hyperbolische Gleichungen. Es sind Evolutionsgleichungen. Das heißt, wir haben ein System
Die Cantor-Funktion. Stephan Welz
 Die Cantor-Funktion Stephan Welz Ausarbeitung zum Vortrag im Proseminar Überraschungen und Gegenbeispiele in der Analysis (Sommersemester 2009, Leitung PD Dr. Gudrun Thäter) Zusammenfassung: In dieser
Die Cantor-Funktion Stephan Welz Ausarbeitung zum Vortrag im Proseminar Überraschungen und Gegenbeispiele in der Analysis (Sommersemester 2009, Leitung PD Dr. Gudrun Thäter) Zusammenfassung: In dieser
Diskrete Mathematik für Informatiker
 Diskrete Mathematik für Informatiker Markus Lohrey Universität Siegen Wintersemester 2014/2015 Lohrey (Universität Siegen) Diskrete Mathematik Wintersem. 2014/2015 1 / 344 Organisatorisches zur Vorlesung
Diskrete Mathematik für Informatiker Markus Lohrey Universität Siegen Wintersemester 2014/2015 Lohrey (Universität Siegen) Diskrete Mathematik Wintersem. 2014/2015 1 / 344 Organisatorisches zur Vorlesung
1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage:
 Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Data Mining: Einige Grundlagen aus der Stochastik
 Data Mining: Einige Grundlagen aus der Stochastik Hagen Knaf Studiengang Angewandte Mathematik Hochschule RheinMain 21. Oktober 2015 Vorwort Das vorliegende Skript enthält eine Zusammenfassung verschiedener
Data Mining: Einige Grundlagen aus der Stochastik Hagen Knaf Studiengang Angewandte Mathematik Hochschule RheinMain 21. Oktober 2015 Vorwort Das vorliegende Skript enthält eine Zusammenfassung verschiedener
11.3 Komplexe Potenzreihen und weitere komplexe Funktionen
 .3 Komplexe Potenzreihen und weitere komplexe Funktionen Definition.) komplexe Folgen: z n = x n + j. y n mit zwei reellen Folgen x n und y n.) Konvergenz: Eine komplexe Folge z n = x n + j. y n heißt
.3 Komplexe Potenzreihen und weitere komplexe Funktionen Definition.) komplexe Folgen: z n = x n + j. y n mit zwei reellen Folgen x n und y n.) Konvergenz: Eine komplexe Folge z n = x n + j. y n heißt
Fraktale Geometrie: Julia Mengen
 Fraktale Geometrie: Julia Mengen Gunnar Völkel 1. Februar 007 Zusammenfassung Diese Ausarbeitung ist als Stoffsammlung für das Seminar Fraktale Geometrie im Wintersemester 006/007 an der Universität Ulm
Fraktale Geometrie: Julia Mengen Gunnar Völkel 1. Februar 007 Zusammenfassung Diese Ausarbeitung ist als Stoffsammlung für das Seminar Fraktale Geometrie im Wintersemester 006/007 an der Universität Ulm
Stochastische Prozesse Gliederung zur Vorlesung im Sommersemester 2006
 Stochastische Prozesse Gliederung zur Vorlesung im Sommersemester 26 Markus Reiß Universität Heidelberg reiss@statlab.uni-heidelberg.de VORLÄUFIGE FASSUNG: 28. Juli 26 Inhaltsverzeichnis 1 Der Poissonprozess
Stochastische Prozesse Gliederung zur Vorlesung im Sommersemester 26 Markus Reiß Universität Heidelberg reiss@statlab.uni-heidelberg.de VORLÄUFIGE FASSUNG: 28. Juli 26 Inhaltsverzeichnis 1 Der Poissonprozess
Jurgen Muller Analysis I-IV
 Jurgen Muller Analysis I-IV Skriptum zur Vorlesung Wintersemester 5/6 bis Sommersemester 7 Universitat Trier Fachbereich IV Mathematik/Analysis Dank an Elke Gawronski und Judith Wahlen fur die Mithilfe
Jurgen Muller Analysis I-IV Skriptum zur Vorlesung Wintersemester 5/6 bis Sommersemester 7 Universitat Trier Fachbereich IV Mathematik/Analysis Dank an Elke Gawronski und Judith Wahlen fur die Mithilfe
Galerkin-Diskretisierung von Eigenwertproblemen für partielle Differentialgleichungen
 Galerkin-Diskretisierung von Eigenwertproblemen für partielle Differentialgleichungen Bachelorarbeit zur Erlangung des akademischen Grades Bachelor of Science an der Technischen Universität Berlin Verfasser:
Galerkin-Diskretisierung von Eigenwertproblemen für partielle Differentialgleichungen Bachelorarbeit zur Erlangung des akademischen Grades Bachelor of Science an der Technischen Universität Berlin Verfasser:
Vom goldenen Schnitt zum Alexanderplatz in Berlin
 Vom goldenen Schnitt zum Alexanderplatz in Berlin Mathematik von 1200 bis 2004 Stefan Kühling, Fachbereich Mathematik skuehling @ fsmath.mathematik.uni-dortmund.de Schnupper Uni 26. August 2004 1 1 Goldener
Vom goldenen Schnitt zum Alexanderplatz in Berlin Mathematik von 1200 bis 2004 Stefan Kühling, Fachbereich Mathematik skuehling @ fsmath.mathematik.uni-dortmund.de Schnupper Uni 26. August 2004 1 1 Goldener
Folgen und endliche Summen
 Kapitel 2 Folgen und endliche Summen Folgen und ihre Eigenschaften Endliche arithmetische und geometrische Folgen und Reihen Vollständige Induktion Anwendungen Folgen/endliche Summen Eigenschaften Folgen
Kapitel 2 Folgen und endliche Summen Folgen und ihre Eigenschaften Endliche arithmetische und geometrische Folgen und Reihen Vollständige Induktion Anwendungen Folgen/endliche Summen Eigenschaften Folgen
Diskrete Strukturen und Logik WiSe 2007/08 in Trier. Henning Fernau Universität Trier fernau@uni-trier.de
 Diskrete Strukturen und Logik WiSe 2007/08 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Diskrete Strukturen und Logik Gesamtübersicht Organisatorisches Einführung Logik & Mengenlehre
Diskrete Strukturen und Logik WiSe 2007/08 in Trier Henning Fernau Universität Trier fernau@uni-trier.de 1 Diskrete Strukturen und Logik Gesamtübersicht Organisatorisches Einführung Logik & Mengenlehre
Theoretische Informatik
 Theoretische Informatik Einheit 1 Mathematische Methodik 1. Problemlösen 2. Beweistechniken 3. Wichtige Grundbegriffe Methodik des Problemlösens Klärung der Voraussetzungen Welche Begriffe sind zum Verständnis
Theoretische Informatik Einheit 1 Mathematische Methodik 1. Problemlösen 2. Beweistechniken 3. Wichtige Grundbegriffe Methodik des Problemlösens Klärung der Voraussetzungen Welche Begriffe sind zum Verständnis
1 Ordnung muß sein. 1.1 Angeordnete Körper. 1.2 Folgerungen aus den Anordnungsaxiomen. ( c) (b a) > 0. Somit a c b c > 0.
 1 Ordnung uß sein 1.1 Angeordnete Körper Wir nehen einal an, daß es in eine Körper Eleente gibt, die wir positiv nennen. Welche Eigenschaften sollen diese haben? O1) Wenn x und y positiv sind, dann auch
1 Ordnung uß sein 1.1 Angeordnete Körper Wir nehen einal an, daß es in eine Körper Eleente gibt, die wir positiv nennen. Welche Eigenschaften sollen diese haben? O1) Wenn x und y positiv sind, dann auch
Die Weierstraßsche Funktion
 Die Weierstraßsche Funktion Nicolas Weisskopf 7. September 0 Zusammenfassung In dieser Arbeit führen wir die Weierstraßsche Funktion ein und untersuchen einige ihrer Eigenschaften. Wir zeigen, dass jede
Die Weierstraßsche Funktion Nicolas Weisskopf 7. September 0 Zusammenfassung In dieser Arbeit führen wir die Weierstraßsche Funktion ein und untersuchen einige ihrer Eigenschaften. Wir zeigen, dass jede
3. Zusammenhang. 22 Andreas Gathmann
 22 Andreas Gathmann 3. Zusammenhang Eine der anschaulichsten Eigenschaften eines topologischen Raumes ist wahrscheinlich, ob er zusammenhängend ist oder aus mehreren Teilen besteht. Wir wollen dieses Konzept
22 Andreas Gathmann 3. Zusammenhang Eine der anschaulichsten Eigenschaften eines topologischen Raumes ist wahrscheinlich, ob er zusammenhängend ist oder aus mehreren Teilen besteht. Wir wollen dieses Konzept
Aufgaben und Lösungen zu Mathematik für Studierende der Ingenieurwissenschaften II. Heinrich Voß
 Aufgaben und Lösungen zu Mathematik für Studierende der Ingenieurwissenschaften II Heinrich Voß Institut für Angewandte Mathematik der Universität Hamburg 99 Inhaltsverzeichnis Folgen und Reihen 2. Einführende
Aufgaben und Lösungen zu Mathematik für Studierende der Ingenieurwissenschaften II Heinrich Voß Institut für Angewandte Mathematik der Universität Hamburg 99 Inhaltsverzeichnis Folgen und Reihen 2. Einführende
1.5 Folgerungen aus dem Kolmogoroff- Axiomensystem P( ) = 0.
 1.5 Folgerungen aus dem Kolmogoroff- Axiomensystem Folg. 2 Sei (Ω, E, P) W.-raum. Seien A, B,A 1,...,A n Ereignisse. Es gelten die folgenden Aussagen: 1. P(A) = 1 P(A). 2. Für das unmögliche Ereignis gilt:
1.5 Folgerungen aus dem Kolmogoroff- Axiomensystem Folg. 2 Sei (Ω, E, P) W.-raum. Seien A, B,A 1,...,A n Ereignisse. Es gelten die folgenden Aussagen: 1. P(A) = 1 P(A). 2. Für das unmögliche Ereignis gilt:
Schwach ergodische Prozesse
 Schwach ergodische Prozesse Von der Fakultät für Naturwissenschaften der Universität Duisburg-Essen (Standort Duisburg) zur Erlangung des akademischen Grades eines Doktors der Naturwissenschaften genehmigte
Schwach ergodische Prozesse Von der Fakultät für Naturwissenschaften der Universität Duisburg-Essen (Standort Duisburg) zur Erlangung des akademischen Grades eines Doktors der Naturwissenschaften genehmigte
3.3 Eigenwerte und Eigenräume, Diagonalisierung
 3.3 Eigenwerte und Eigenräume, Diagonalisierung Definition und Lemma 3.3.1. Sei V ein K-Vektorraum, φ End K (V ), λ K. Wir defnieren den zu λ gehörigen Eigenraum von φ als Dies ist ein Unterraum von V.
3.3 Eigenwerte und Eigenräume, Diagonalisierung Definition und Lemma 3.3.1. Sei V ein K-Vektorraum, φ End K (V ), λ K. Wir defnieren den zu λ gehörigen Eigenraum von φ als Dies ist ein Unterraum von V.
Seminar Analysis Konvexe Funktionen und einige wichtige Ungleichungen
 Seminar Analysis Konvexe Funktionen und einige wichtige Ungleichungen Michael Schaeer 3.04.03 Abstract This seminar is about convex functions and several imortant ineualities. At the beginning the term
Seminar Analysis Konvexe Funktionen und einige wichtige Ungleichungen Michael Schaeer 3.04.03 Abstract This seminar is about convex functions and several imortant ineualities. At the beginning the term
klar. Um die zweite Bedingung zu zeigen, betrachte u i U i mit u i = 0. Das mittlere -Zeichen liefert s
 Nachtrag zur allgemeinen Vektorraum-Theorie. 1.5.15. Direkte Summen. Sei V ein Vektorraum, seien U 1,..., U t Unterräume, wir schreiben V = U 1 U 2 U t = t i=1 U i falls die folgenden beiden Bedingungen
Nachtrag zur allgemeinen Vektorraum-Theorie. 1.5.15. Direkte Summen. Sei V ein Vektorraum, seien U 1,..., U t Unterräume, wir schreiben V = U 1 U 2 U t = t i=1 U i falls die folgenden beiden Bedingungen
Stochastische Eingangsprüfung, 17.05.2008
 Stochastische Eingangsprüfung, 17.5.8 Wir gehen stets von einem Wahrscheinlichkeitsraum (Ω, A, P) aus. Aufgabe 1 ( Punkte) Sei X : Ω [, ) eine integrierbare Zufallsvariable mit XdP = 1. Sei Q : A R, Q(A)
Stochastische Eingangsprüfung, 17.5.8 Wir gehen stets von einem Wahrscheinlichkeitsraum (Ω, A, P) aus. Aufgabe 1 ( Punkte) Sei X : Ω [, ) eine integrierbare Zufallsvariable mit XdP = 1. Sei Q : A R, Q(A)
Modul Diskrete Mathematik WiSe 2011/12
 1 Modul Diskrete Mathematik WiSe 2011/12 Ergänzungsskript zum Kapitel 4.2. Hinweis: Dieses Manuskript ist nur verständlich und von Nutzen für Personen, die regelmäßig und aktiv die zugehörige Vorlesung
1 Modul Diskrete Mathematik WiSe 2011/12 Ergänzungsskript zum Kapitel 4.2. Hinweis: Dieses Manuskript ist nur verständlich und von Nutzen für Personen, die regelmäßig und aktiv die zugehörige Vorlesung
Vorlesung. 1 Zahlentheorie in Z. Leitfaden. 1.1 Teilbarkeit. Angela Holtmann. Algebra und Zahlentheorie. (natürliche Zahlen ohne die Null)
 Algebra und Zahlentheorie Vorlesung Algebra und Zahlentheorie Leitfaden 1 Zahlentheorie in Z Bezeichnungen: Z := {..., 3, 2, 1, 0, 1, 2, 3,...} (ganze Zahlen) und N := {1, 2, 3,...} (natürliche Zahlen
Algebra und Zahlentheorie Vorlesung Algebra und Zahlentheorie Leitfaden 1 Zahlentheorie in Z Bezeichnungen: Z := {..., 3, 2, 1, 0, 1, 2, 3,...} (ganze Zahlen) und N := {1, 2, 3,...} (natürliche Zahlen
Mathematik für Studierende der Biologie und des Lehramtes Chemie Wintersemester 2013/14. Auswahl vorausgesetzter Vorkenntnisse
 UNIVERSITÄT DES SAARLANDES FACHRICHTUNG 6.1 MATHEMATIK Dipl.-Math. Kevin Everard Mathematik für Studierende der Biologie und des Lehramtes Chemie Wintersemester 2013/14 Auswahl vorausgesetzter Vorkenntnisse
UNIVERSITÄT DES SAARLANDES FACHRICHTUNG 6.1 MATHEMATIK Dipl.-Math. Kevin Everard Mathematik für Studierende der Biologie und des Lehramtes Chemie Wintersemester 2013/14 Auswahl vorausgesetzter Vorkenntnisse
5. Verschiedene Repräsentanten
 5. Verschiedene Repräsentanten 5.1. Die Sätze Hall und König Sei I := {1,...,n}, und sei A(I) = (A 1,...,A n ) eine Familie von Teilmengen einer endlichen Menge E. Zu K I seien A(K) := (A i : i K) und
5. Verschiedene Repräsentanten 5.1. Die Sätze Hall und König Sei I := {1,...,n}, und sei A(I) = (A 1,...,A n ) eine Familie von Teilmengen einer endlichen Menge E. Zu K I seien A(K) := (A i : i K) und
Kapitel 4. Euklidische Ringe und die Jordansche Normalform. 4.1 Euklidische Ringe
 Kapitel 4 Euklidische Ringe und die Jordansche Normalform 4.1 Euklidische Ringe Die Ringe der ganzen Zahlen, Z, sowie Polynomringe über Körpern, K[X], wobei K ein Körper ist, haben die folgenden Gemeinsamheiten:
Kapitel 4 Euklidische Ringe und die Jordansche Normalform 4.1 Euklidische Ringe Die Ringe der ganzen Zahlen, Z, sowie Polynomringe über Körpern, K[X], wobei K ein Körper ist, haben die folgenden Gemeinsamheiten:
Erfüllbarkeit und Allgemeingültigkeit
 Theoretische Informatik: Logik, M. Lange, FB16, Uni Kassel: 3.3 Aussagenlogik Erfüllbarkeit 44 Erfüllbarkeit und Allgemeingültigkeit Def.: eine Formel ϕ heißt erfüllbar, wennesein I gibt, so dass I = ϕ
Theoretische Informatik: Logik, M. Lange, FB16, Uni Kassel: 3.3 Aussagenlogik Erfüllbarkeit 44 Erfüllbarkeit und Allgemeingültigkeit Def.: eine Formel ϕ heißt erfüllbar, wennesein I gibt, so dass I = ϕ
2.1 Codes: einige Grundbegriffe
 Gitter und Codes c Rudolf Scharlau 2. Mai 2009 51 2.1 Codes: einige Grundbegriffe Wir stellen die wichtigsten Grundbegriffe für Codes über dem Alphabet F q, also über einem endlichen Körper mit q Elementen
Gitter und Codes c Rudolf Scharlau 2. Mai 2009 51 2.1 Codes: einige Grundbegriffe Wir stellen die wichtigsten Grundbegriffe für Codes über dem Alphabet F q, also über einem endlichen Körper mit q Elementen
Übungen zur Experimentalphysik 3
 Übungen zur Experimentalphysik 3 Prof. Dr. L. Oberauer Wintersemester 2010/2011 7. Übungsblatt - 6.Dezember 2010 Musterlösung Franziska Konitzer (franziska.konitzer@tum.de) Aufgabe 1 ( ) (8 Punkte) Optische
Übungen zur Experimentalphysik 3 Prof. Dr. L. Oberauer Wintersemester 2010/2011 7. Übungsblatt - 6.Dezember 2010 Musterlösung Franziska Konitzer (franziska.konitzer@tum.de) Aufgabe 1 ( ) (8 Punkte) Optische
Stochastische Analysis. Zufallsmatrizen. Roland Speicher Queen s University Kingston, Kanada
 Stochastische Analysis für Zufallsmatrizen Roland Speicher Queen s University Kingston, Kanada Was ist eine Zufallsmatrix? Zufallsmatrix = Matrix mit zufälligen Einträgen A : Ω M N (C) Was ist eine Zufallsmatrix?
Stochastische Analysis für Zufallsmatrizen Roland Speicher Queen s University Kingston, Kanada Was ist eine Zufallsmatrix? Zufallsmatrix = Matrix mit zufälligen Einträgen A : Ω M N (C) Was ist eine Zufallsmatrix?
TEILWEISE ASYNCHRONE ALGORITHMEN
 TEILWEISE ASYNCHRONE ALGORITHMEN FRANK LANGBEIN Literatur: D. Berseas, J. Tsitsilis: Parallel and distributed computatoin, pp. 48 489 URI: http://www.langbein.org/research/parallel/ Modell teilweiser asynchroner
TEILWEISE ASYNCHRONE ALGORITHMEN FRANK LANGBEIN Literatur: D. Berseas, J. Tsitsilis: Parallel and distributed computatoin, pp. 48 489 URI: http://www.langbein.org/research/parallel/ Modell teilweiser asynchroner
Prof. Dr. Thilo Meyer-Brandis. Finanzmathematik 1 WS 2012/13
 Prof. Dr. Thilo Meyer-Brandis Finanzmathematik 1 WS 2012/13 Dieses Skript gibt den Inhalt der Vorlesung Finanzmathematik I: Eine Einführung in diskreter Zeit wieder und basiert auf dem Buch Stochastic
Prof. Dr. Thilo Meyer-Brandis Finanzmathematik 1 WS 2012/13 Dieses Skript gibt den Inhalt der Vorlesung Finanzmathematik I: Eine Einführung in diskreter Zeit wieder und basiert auf dem Buch Stochastic
Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema
 Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema 2x 4 + x 3 + x + 3 div x 2 + x 1 = 2x 2 x + 3 (2x 4 + 2x 3 2x 2 ) x 3 + 2x 2 + x + 3 ( x
Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema 2x 4 + x 3 + x + 3 div x 2 + x 1 = 2x 2 x + 3 (2x 4 + 2x 3 2x 2 ) x 3 + 2x 2 + x + 3 ( x
Quantitative Risk Management
 Quantitative Risk Management Copulas und Abhängigkeit Johannes Paschetag Mathematisches Institut der Universität zu Köln Wintersemester 2009/10 Betreuung: Prof. Schmidli, J. Eisenberg i Inhaltsverzeichnis
Quantitative Risk Management Copulas und Abhängigkeit Johannes Paschetag Mathematisches Institut der Universität zu Köln Wintersemester 2009/10 Betreuung: Prof. Schmidli, J. Eisenberg i Inhaltsverzeichnis
Lösungen und Lösungshinweise zum Grundkurs Analysis 2
 Lösungen und Lösungshinweise zum Grundkurs Analysis 2 Vorbemerkung: Bei einem Buchprojekt dauert meist alles etwas länger als geplant. So ging es mir mit dem Erscheinungdatum des zweiten Bandes, der sich
Lösungen und Lösungshinweise zum Grundkurs Analysis 2 Vorbemerkung: Bei einem Buchprojekt dauert meist alles etwas länger als geplant. So ging es mir mit dem Erscheinungdatum des zweiten Bandes, der sich
Seminararbeit für das SE Reine Mathematik- Graphentheorie
 Seminararbeit für das SE Reine Mathematik- Graphentheorie Der binäre Rang, der symplektische Graph, die Spektralzerlegung und rationale Funktionen Vortrag am 24.01.2012 Heike Farkas 0410052 Inhaltsverzeichnis
Seminararbeit für das SE Reine Mathematik- Graphentheorie Der binäre Rang, der symplektische Graph, die Spektralzerlegung und rationale Funktionen Vortrag am 24.01.2012 Heike Farkas 0410052 Inhaltsverzeichnis
Hauptprüfung Abiturprüfung 2014 (ohne CAS) Baden-Württemberg
 Baden-Württemberg: Abitur 04 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 04 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Baden-Württemberg: Abitur 04 Pflichtteil www.mathe-aufgaben.com Hauptprüfung Abiturprüfung 04 (ohne CAS) Baden-Württemberg Pflichtteil Hilfsmittel: keine allgemeinbildende Gymnasien Alexander Schwarz www.mathe-aufgaben.com
Bestimmung einer ersten
 Kapitel 6 Bestimmung einer ersten zulässigen Basislösung Ein Problem, was man für die Durchführung der Simplexmethode lösen muss, ist die Bestimmung einer ersten zulässigen Basislösung. Wie gut das geht,
Kapitel 6 Bestimmung einer ersten zulässigen Basislösung Ein Problem, was man für die Durchführung der Simplexmethode lösen muss, ist die Bestimmung einer ersten zulässigen Basislösung. Wie gut das geht,
S=[n] Menge von Veranstaltungen J S kompatibel mit maximaler Größe J
![S=[n] Menge von Veranstaltungen J S kompatibel mit maximaler Größe J S=[n] Menge von Veranstaltungen J S kompatibel mit maximaler Größe J](/thumbs/26/8373971.jpg) Greedy-Strategie Definition Paradigma Greedy Der Greedy-Ansatz verwendet die Strategie 1 Top-down Auswahl: Bestimme in jedem Schritt eine lokal optimale Lösung, so dass man eine global optimale Lösung
Greedy-Strategie Definition Paradigma Greedy Der Greedy-Ansatz verwendet die Strategie 1 Top-down Auswahl: Bestimme in jedem Schritt eine lokal optimale Lösung, so dass man eine global optimale Lösung
Vorlesung Analysis I für Informatiker & Statistiker. Universität München, WS 11/12. Prof. Dr. Max v. Renesse mrenesse@math.tu-berlin.
 Vorlesung Analysis I für Informatiker & Statistiker Universität München, WS 11/12 Prof. Dr. Max v. Renesse mrenesse@math.tu-berlin.de Kapitel 1: Grundlagen 1.1 Aussagenlogik Elementare Aussagenlogik Definition
Vorlesung Analysis I für Informatiker & Statistiker Universität München, WS 11/12 Prof. Dr. Max v. Renesse mrenesse@math.tu-berlin.de Kapitel 1: Grundlagen 1.1 Aussagenlogik Elementare Aussagenlogik Definition
Apfelmännchen Theorie und Programmierung
 Apfelmännchen Theorie und Programmierung Das Thema "Apfelmännchen" gehört zum Oberthema "Chaos und Ordnung in dynamischen Systemen". Es ist ein relativ neues Forschungsgebiete der Mathematik ( ab ca. 1980
Apfelmännchen Theorie und Programmierung Das Thema "Apfelmännchen" gehört zum Oberthema "Chaos und Ordnung in dynamischen Systemen". Es ist ein relativ neues Forschungsgebiete der Mathematik ( ab ca. 1980
Codierung. Auszug aus dem Skript von Maciej Liśkiewicz und Henning Fernau
 Codierung Auszug aus dem Skript von Maciej Liśkiewicz und Henning Fernau Ein bisschen Informationstheorie Betrachten wir das folgende Problem: Wie lautet eine sinnvolle Definition für das quantitative
Codierung Auszug aus dem Skript von Maciej Liśkiewicz und Henning Fernau Ein bisschen Informationstheorie Betrachten wir das folgende Problem: Wie lautet eine sinnvolle Definition für das quantitative
Vorlesung Analysis I / Lehramt
 Vorlesung Analysis I / Lehramt TU Dortmund, Wintersemester 2012/ 13 Winfried Kaballo Die Vorlesung Analysis I für Lehramtsstudiengänge im Wintersemester 2012/13 an der TU Dortmund basiert auf meinem Buch
Vorlesung Analysis I / Lehramt TU Dortmund, Wintersemester 2012/ 13 Winfried Kaballo Die Vorlesung Analysis I für Lehramtsstudiengänge im Wintersemester 2012/13 an der TU Dortmund basiert auf meinem Buch
Codierungstheorie Rudolf Scharlau, SoSe 2006 9
 Codierungstheorie Rudolf Scharlau, SoSe 2006 9 2 Optimale Codes Optimalität bezieht sich auf eine gegebene Quelle, d.h. eine Wahrscheinlichkeitsverteilung auf den Symbolen s 1,..., s q des Quellalphabets
Codierungstheorie Rudolf Scharlau, SoSe 2006 9 2 Optimale Codes Optimalität bezieht sich auf eine gegebene Quelle, d.h. eine Wahrscheinlichkeitsverteilung auf den Symbolen s 1,..., s q des Quellalphabets
13.5 Der zentrale Grenzwertsatz
 13.5 Der zentrale Grenzwertsatz Satz 56 (Der Zentrale Grenzwertsatz Es seien X 1,...,X n (n N unabhängige, identisch verteilte zufällige Variablen mit µ := EX i ; σ 2 := VarX i. Wir definieren für alle
13.5 Der zentrale Grenzwertsatz Satz 56 (Der Zentrale Grenzwertsatz Es seien X 1,...,X n (n N unabhängige, identisch verteilte zufällige Variablen mit µ := EX i ; σ 2 := VarX i. Wir definieren für alle
t r Lineare Codierung von Binärbbäumen (Wörter über dem Alphabet {, }) Beispiel code( ) = code(, t l, t r ) = code(t l ) code(t r )
 Definition B : Menge der binären Bäume, rekursiv definiert durch die Regeln: ist ein binärer Baum sind t l, t r binäre Bäume, so ist auch t =, t l, t r ein binärer Baum nur das, was durch die beiden vorigen
Definition B : Menge der binären Bäume, rekursiv definiert durch die Regeln: ist ein binärer Baum sind t l, t r binäre Bäume, so ist auch t =, t l, t r ein binärer Baum nur das, was durch die beiden vorigen
Hilbertraum-Methoden
 Skript zur Vorlesung Hilbertraum-Methoden SS 2013 Peter Junghanns Hinweis: Das vorliegende Skript stellt nur ein Gerüst zu den Inhalten der Vorlesung dar. Die Vorlesung selbst bietet weiterführende Erläuterungen,
Skript zur Vorlesung Hilbertraum-Methoden SS 2013 Peter Junghanns Hinweis: Das vorliegende Skript stellt nur ein Gerüst zu den Inhalten der Vorlesung dar. Die Vorlesung selbst bietet weiterführende Erläuterungen,
Das Briefträgerproblem
 Das Briefträgerproblem Paul Tabatabai 30. Dezember 2011 Inhaltsverzeichnis 1 Problemstellung und Modellierung 2 1.1 Problem................................ 2 1.2 Modellierung.............................
Das Briefträgerproblem Paul Tabatabai 30. Dezember 2011 Inhaltsverzeichnis 1 Problemstellung und Modellierung 2 1.1 Problem................................ 2 1.2 Modellierung.............................
Eine mathematische Reise ins Unendliche. Peter Koepke Universität Bonn
 Eine mathematische Reise ins Unendliche Peter Koepke Universität Bonn Treffen sich die Schienen im Unendlichen? Gibt es unendlich ferne Punkte? Gibt es unendliche Zahlen? 1 Antwort: Nein! , so prostestire
Eine mathematische Reise ins Unendliche Peter Koepke Universität Bonn Treffen sich die Schienen im Unendlichen? Gibt es unendlich ferne Punkte? Gibt es unendliche Zahlen? 1 Antwort: Nein! , so prostestire
Seminar Analysis und Geometrie Professor Dr. Martin Schmidt - Markus Knopf - Jörg Zentgraf. - Fixpunktsatz von Schauder -
 Unverstät Mannhem Fakultät für Mathematk und Informatk Lehrstuhl für Mathematk III Semnar Analyss und Geometre Professor Dr. Martn Schmdt - Markus Knopf - Jörg Zentgraf - Fxpunktsatz von Schauder - Ncole
Unverstät Mannhem Fakultät für Mathematk und Informatk Lehrstuhl für Mathematk III Semnar Analyss und Geometre Professor Dr. Martn Schmdt - Markus Knopf - Jörg Zentgraf - Fxpunktsatz von Schauder - Ncole
Projektive Moduln. Lemma/Definition 1.1. Folgende Aussagen für einen R-Modul P sind äquivalent: (i) P erfüllt folgende Liftungseigenschaft:
 Seminar Summen von Quadraten und K-Theorie Projektive Moduln Im Folgenden sei R ein assoziativer Ring mit Eins, nicht notwendigerweise kommutativ. R-Modul ist im Folgenden stets ein Rechts-R-Modul. Ein
Seminar Summen von Quadraten und K-Theorie Projektive Moduln Im Folgenden sei R ein assoziativer Ring mit Eins, nicht notwendigerweise kommutativ. R-Modul ist im Folgenden stets ein Rechts-R-Modul. Ein
Höhere Mathematik 3. Apl. Prof. Dr. Norbert Knarr. Wintersemester 2015/16. FB Mathematik
 Höhere Mathematik 3 Apl. Prof. Dr. Norbert Knarr FB Mathematik Wintersemester 2015/16 4. Homogene lineare Dierentialgleichungen 4.1. Grundbegrie 4.1.1. Denition. Es sei J R ein Intervall und a 0 ; : :
Höhere Mathematik 3 Apl. Prof. Dr. Norbert Knarr FB Mathematik Wintersemester 2015/16 4. Homogene lineare Dierentialgleichungen 4.1. Grundbegrie 4.1.1. Denition. Es sei J R ein Intervall und a 0 ; : :
