Lösungen der Übungsaufgaben zur Regelungstechnik
|
|
|
- Felix Ackermann
- vor 6 Jahren
- Abrufe
Transkript
1 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsysemechnik, C:\ro\Si5\RT3\RT3_ueb\Loes_Regechn_2.doc, Seie /29 Lösungen der Übungsaufgaben zur Regelungsechnik Tex der Aufgabensellung: siehe. hp:// Homepage: hp:// Zu () K T*s + A() zu. Das s im Nenner is ein Operaor. r bedeue d/d, also den Befehl, nach der Zei zu differenzieren. zu.2 Allgemein lies man einen solchen Block wie folg: Ausgangsgröße = Inhal des Blocks muliplizier mi der ingangsgröße. In diesem Fall also A = K/(T*s+) * oder A = K*/( T*s + ) oder mi dem Nenner erweier: (T*s + )*A = K*. Wird jez s durch den Operaor d/d ersez, so ergib sich als normale mahemaische Formel die Differenialgleichung (abgekürz als DGL) T * da/d + A = K* ( DGL für A() ) zu.3 ingang () als Recheckfunkion im Bereich bis 2 is =, sons =. in Tephys: = *ja(-)*ja(2-). ( Info zur ja-funkion: ja(x) : if x > hen ja= else ja = ) Aus der DGL für A T*dA/d + A = K* folg für die Änderung von A da = (K*-A)*d/T und daraus der Tephys- Algorihmus zum Inegrieren: der neue Wer is gleich dem alen Wer plus die Änderung, also A = A + da oder da gleich eingesez: A = A + (k*-a)*d/t ==> vollsändiger Tephys-Algorihmus: (Daei ueb_.x) =*ja(-)*ja(2-) A=A+(K*-A)*d/T =+d { diese Tephys-Zeilen werden so of wiederhol, bis >= max is }
2 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsysemechnik, C:\ro\Si5\RT3\RT3_ueb\Loes_Regechn_2.doc, Seie 2/29 zu.4 Simulink-Schalung mi Malab 4.2: rläuerungen: Im Block Fcn wird die ingangsfunkion erzeug gemäß der Formel im Block. Der ingang in den Block is die Zei. Sie muss aber innerhalb des Blockes mi u bezeichne werden. Die Vergleichoperaion u > liefer die Zahl (für rue) oder die Zahl (für false). Die rzeugung der Recheckfunkion () erfolg also ähnlich wie in Tephys. Dor war =*ja(-)*ja(2-). Die Parameer (in diesem Beispiel d, max,, 2,, T) müssen vor dem Sar dieser Daei bekann sein. Man könne die Parameer per Hand einzeln in der Malab-Kommandoebene einippen. Hier wird das einfacher gean: Auf dieser Simulink-Schalung sind die Parameer als Kommenar eingeipp worden. Man kopiere diese Kommenarzeile mi der rechen Mausase, gehe dann mi Mausklick (linke Mausase) in die Malab- Kommandoebene, füge (mi der rechen Mausase ) diese Kommenarzeile ein und drücke anschließend die ingabease (Reurn). Dadurch sind Malab diese Parameer bekann. Ähnlich wird mi den beiden anderen Zeilen verfahren: Sar der Daei mi [nix] = rk45('ueb_',[,max],[],[e-3,d,d]); und anschließende Grafikbefehle figure(); plo(,, m,,a, r ); grid; mi Farben m (magena) und r (ro) Daei ueb_ Clock * (u > ) * (2 > u) Fcn + - Sum /T Gain /s Inegraor Die nachfolgenden Zeilen mi Maus kopieren, in der Malab-Kommando-bene" einfügen" und mi Tase "Reurn" akivieren! d=.; max=; =.; 2=5; =;T=; [nix]=rk45('ueb_',[,max],[],[e-3,d,d]); figure();plo(,,,a);grid; A A Simulink-Schalung mi Malab 5.3: Daei ueb5_.m dl für Malab5.3 Clock * ( u > ) * ( 2 > u ) Fcn Sum /T Gain s Inegraor A A Die nachfolgenden Zeilen m i Maus kopieren, in der Malab-Kom m ando-bene" einfügen" und m i Tas e "Reurn" akivieren! d=.; m ax=; =.; 2=5; =;T=; [nix]=s im ('ueb5_',[,m ax]); figure();plo(,,'m ',,A,'r');grid; Man beache, dass der Aufruf der Simulink-Daei von der Malab-Kommando-bene aus für die Versionen 4.2 und 5.3 ewas anders is (siehe Tex in der Simulink-Daei) in Malab 4.2: [nix] = rk45('ueb_',[,max],[],[e-3,d,d]); in Malab 5.3: [nix] = sim('ueb5_',[,max]);
3 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsysemechnik, C:\ro\Si5\RT3\RT3_ueb\Loes_Regechn_2.doc, Seie 3/ Obige Figur is mi Malab4.2 erzeug worden Obige Figur is mi Malab5.3 erzeug worden. Zu 2 PID-Regler W() W - Ap*(+Td*s+/(Ti*s) ) Y() zu 2.: Als normale mahemaische Formel geschrieben: () Y = Ap*(W- + d (W-x)/d + (W-)*d/Ti ) zu 2.2 In Tephys: W=... =... in = in + (W-)*d/Ti { in = (W-)*d/Ti } Y= Ap*( W- + Td*(W- - Wxal)/d + in ) Wxal = W - = + d { die Tephys-Zeilen werden so of wiederhol, bis >= max is } zu 2.3 In Simulink (Malab 4.2) W Daei PID_Reg.m + - Sum W- /Ti Gain Td Gain /s Inegraor du/d Derivaive Sum Ap Gain2 Y Die ingänge W und und der Ausgang Y müssen naürlich noch mi den richigen Blöcken verbunden werden
4 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsysemechnik, C:\ro\Si5\RT3\RT3_ueb\Loes_Regechn_2.doc, Seie 4/29 Zu 3 Zeichnen Sie das Blockschalbild für einen geschlossenen Regelkreis. PID-Regler, Srecke : 3 PT-Glieder, Sörgröße Z wird am Beginn der Srecke zugeführ. W W- Ap*(+Td*s+/(Ti*s) ) Zu 4 Srecke aus 3 PT-Gliedern mi beliebiger Zeifunkion des ingangs () Y Z Z+Y K T*s + x x2 T2*s + T3*s + () K x() T*s + T2*s + x2() T3*s + x3() zu 4.: Normale mahemaische Zusammenhänge zwischen ingang und Ausgang der PT-Glieder (vgl. ) DGL für x: T* dx/d + x = K* Tephys: x = x + (K*-x)* d / T DGL für x2: T2* dx2/d + x2 = x Tephys: x2 = x2 + (x-x2)* d / T2 DGL für x3: T3* sx3/d + x3 = x2 Tephys: x3 = x3 + (x2-x3)* d / T3 zu 4.2: Tephys-Algorihmus (Daei ueb4_2.x) = *ja(-)*ja(2-) x = x + (K*-x)*d/T x2 = x2 + (x-x2)*d/t2 x3 = x3 + (x2-x3)*d/t3 =+d { diese Tephys-Zeilen werden so of wiederhol, bis >= max is }
5 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsysemechnik, C:\ro\Si5\RT3\RT3_ueb\Loes_Regechn_2.doc, Seie 5/29 zu 4.3: Simulink-Schalung mi Transfer Fcn Blöcken (Malab 4.2) Daei ueb4_3.m Clock *(u > ) * ( 2 > u ) Fcn To Workspace K T.s+ Transfer Fcn T.s+ T.s+ x x2 x3 d=.; max=5; =; 2=5; =.2; K=2; T=;T2=;T3=; [nix] = rk45('ueb4_3',[,max],[],[e-3,d,d]); figure(); plo(,,'m',,x,'r',,x2,'g',,x3,'w');grid; Zu 5: 3 PT-Glieder. Simulink ohne Verwendung von Transfer Fcn (in Malab 4.2) Daei ueb5_.m Clock *(u > ) * ( 2 > u ) Fcn 3 PT-Glieder, ohne Verwendung von Transfer Fcn To Workspace K Gain + - Sum x /T /s Inegraor + - /T2 x2 /s + - /T3 x2 /s d=.; max=5; =; 2=5; =.2; K=2; T=;T2=;T3=; [nix] = rk45('ueb5_',[,max],[],[e-3,d,d]); figure(); plo(,,'m',,x,'r',,x2,'g',,x3,'w');grid;
6 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsysemechnik, C:\ro\Si5\RT3\RT3_ueb\Loes_Regechn_2.doc, Seie 6/29 Zu 6 Vollsändiges Simulaionsprogramm für PID- Regler mi Srecke aus 3 PT-Gliedern. Führgröße W() Recheckfunkion im Bereich W bis 2W, Sörgröße Z() Reckeckfunkion im Zeibereich Z bis 2Z (vgl Aufgabe ). Sörgröße Z wird am Sreckeneingang eingespeis. Gesuch: Tephys-Algorihmus und Simulink-Schalung. Simulaion mi Tephys: D:\RT3\UB6_.TT W = aw*ja(-w)*ja(2w-) 2 W = W+begr((W-W)/TW,vma,vmi)*d 3 Z = az*ja(-z)*ja(z2-) 4 x = x+(k*(y+z)-x)*d/t 5 x2 = x2+(x-x2)*d/t2 6 = +(x2-)*d/t3 7 in = in+(w-)*d/ti 8 DA = ja(kon)*(w--wxal)/d-nein(kon)*(-al)/d 9 Y = Ap*(kW*W-+Td*DA+in) Wxal = W- al = 2 = +d { die Tephys-Zeilen werden so of wiederhol, bis >= max is }
7 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsysemechnik, C:\ro\Si5\RT3\RT3_ueb\Loes_Regechn_2.doc, Seie 7/29 Simulaion mi Simulink (Malab 5.3): Daei ueb6_.mdl, Aufrufdaeien ueb6_.m, ueb6_2, ueb6_3.m Daei ueb6_.mdl W aw*(u > W) * ( 2W > u ) Clock Fcn az*(u > Z) * ( Z2 > u ) To Workspace kw*w- kw Z /TW vma, vmi K T.s+ x W /s In T.s+ x2 T.s+ x3 - W- /Ti /s Ap Y kon Td du/d Swich d/d Tephys: UB6_.TT Simulaion laufe n lasse n mi M -Dae ie n ue b6_.m ode r ue b6_2.m ode r ue b6_3.m W = aw*ja(-w)*ja(2w-) W = W+begr((W-W)/TW,vma,vmi)*d Folgende Zeilen "kopieren", in MATLAB einfügen u. akivieren Z = az*ja(-z)*ja(z2-) x = x+(k*(y+z)-x)*d/t W=;2W=2;aW=.2;TW=.2;vma=;vmi=-;d=.;Z=2;Z2=2; x2 = x2+(x-x2)*d/t2 az=-2;k=;t=;t2=;t3=;ti=3;kon=;kw=.72;td=.68;ap=5;max=2; = +(x2-)*d/t3 in = in+(w-)*d/ti figure(); plo(,w,'m',,x3,'k',,z/,'r',,y/,'b');grid;xlabel('zei/sec'); DA = ja(kon)*(w--wxal)/d-nein(kon)*(-al)/d Y = Ap*(kW*W-+Td*DA+in) Wxal = W- al = = +d Zum Laufenlassen dieser Simulink-Schalung in der Kommandoebene einippen: ueb6_ oder ueb6_2 oder ueb6_3 % Daei ueb6_.m Aufrufdaei für Simulink-Modell ueb6_.mdl
8 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsysemechnik, C:\ro\Si5\RT3\RT3_ueb\Loes_Regechn_2.doc, Seie 8/29 % In Kommandoebene einippen: ueb6_ und Tase "Reurn" Bild=; W=;2W=2;aW=.2;TW=.2;vma=;vmi=-;d=.;Z=2;Z2=2; az=-2;k=;t=;t2=;t3=;ti=3;kon=;kw=;td=.7;ap=5;max=2; if Bild == ueb6_; end; % Die SimulinkSchalung auf Bildschirm rufen [nix]= sim('ueb6_',[,max]); % Saren der Berechnung figure(bild);clf; se(,'defaullinelinewidh',.5) plo(,w,'m',,x3,'k',,z/,'r',,y/,'b');grid;xlabel('zei/sec'); legend('w','x3','z/','y/'); S=['Bild=',num2sr(Bild)];S2=['; W=',num2sr(W)];S3=['; 2W=',num2sr(2W)]; S4=['; TW=',num2sr(TW)];S5=['; vma=',num2sr(vma)];s6=['; vmi=',num2sr(vmi)]; S7=['; d=',num2sr(d)];s8=['; Z=',num2sr(Z)];S9=['; Z2=',num2sr(Z2)]; S=['; az=',num2sr(az)];s=['; K=',num2sr(K)];S2=['; T=',num2sr(T)]; S3=['; T2=',num2sr(T2)];S4=['; T3=',num2sr(T3)];S5=['; Ti=',num2sr(Ti)]; S6=['; kon=',num2sr(kon)];s=['; kw=',num2sr(kw)];s2=['; Td=',num2sr(Td)]; S3=['; Ap=',num2sr(Ap)]; gex({[s,s2,s3,s4,s5,s6,s6]},'fonsize',); gex({[s7,s8,s9,s,s,s2,s3]},'fonsize',); Bild=; W=; 2W=2; T W=.2; vma=; vmi=-; kon= ; d=.; Z=2; Z2=2; az=-2; kw=; T d=.7; Ap=5 W x3 Z/ Y/ Zei/sec Bild=2; W=; 2W=2; TW=.2; vma=2; vmi=-; kon= ; d=.; Z=2; Z2=2; az=-2; kw=.75; Td=.7; Ap=5 W x3 Z/ Y/ Zei/sec
9 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsysemechnik, C:\ro\Si5\RT3\RT3_ueb\Loes_Regechn_2.doc, Seie 9/ Bild= 3; W = ; 2W = 2; T W =.2; vma= ; vmi= -; kon= ; d=.; Z= 2; Z2= 2; az= -2; kw =.72; T d=.68; Ap= 5 W x3 Z/ Y/ Zei/sec Zu 7 7 Geschlossener Regelkreis mi P-Regler. Je nach Schalersellung des Schalers S beseh die Srecke aus einem einzigen, aus 2 oder 3 oder 4 gleicharigen PT-Gliedern. W() W - Y x Ap T*s + T*s + x2 T*s + x3 T*s + x4 S Wenn der Proporionalfakor Ap zu groß is, kann der geschlossene Regelkreis insabil sein. 7. Wie groß muss jeweils Ap sein, dami der geschlossenen Regelkreis insabil is? bei = x, bei = x2, bei = x3, bei = x4 7.2 Begründen Sie Ihre Aussage zu 7. durch heoreische Überlegungen. 7.3 Schreiben Sie einen Tephys- Algorihmus, mi dem man durch Probieren die Anwor auf 7. finden kann. 7.8 Schreiben Sie ein Simulink- Programm, mi dem man durch Probieren die Anwor auf 7. finden kann. Lösung mi Simulink (Malab 5.3): D a e i u e b 7 _.m d l L a u fe n la s s e n m i R u n d a e i r u e b 7 _.m : in ip p e n r u e b 7 _ < R e u r n > a Z * (u > Z ) T = ; N = 3 ; A p = 8 ; d =. ; m a x= 4 ; a Z = ; Z = ; n ix= s im ( 'u e b 7 _ ', [, m a x] ) ; C lo c k Z fig u re (3 );c lf;p lo (, );g rid ; A p T.s + T.s + T.s + T.s + T.s + T.s + Y N - M u l ip o r S w i c h S re c k e a u s N g le ic h e n P T -G lie d e rn. S a b iliä s g re n ze b e i P -R e g le r is fü r N > 2 : A p m a x = / ( ( c o s (p i/n ) )^ N ) N = [ 3, 4, 5, 6 ] ; A p m a x =./ (c o s (p i./ N )).^ N A m a x = [ 8, 4, , ] % Daei rueb7_.m Aufrufdaei für Simulink-Modell ueb7_.mdl
10 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsysemechnik, C:\ro\Si5\RT3\RT3_ueb\Loes_Regechn_2.doc, Seie /29 % In Kommandoebene einippen: rueb7_ und Tase "Reurn" clear; oldbild=; oldfak=; Bild = inpu('bie BildNummer eingaben:,2,3..): '); if isempy(bild) Bild = oldbild; end; Bild=round(abs(Bild)); N=inpu('Bie N eingeben ( 3,4,5 oder 6 ): '); if (N < 3) (N > 6) error('n muss 3, 4, 5 oder 6 sein! '); end; fak = inpu('fak (z.b. oder nahe ): '); if isempy(fak) fak=oldfak; end; T=; Apmax= /(cos(pi/n))^n; Ap= Apmax *fak; d=.; max=4; az=;z=; if Bild == ueb7_; end; % Die SimulinkSchalung auf Bildschirm rufen [nix]= sim('ueb7_',[,max]); % Saren der Berechnung figure(bild);clf; se(,'defaullinelinewidh',.5) plo(,z/n,'m',,,'k',,y/,'b');grid;xlabel('zei/sec'); legend('z/n','','y/'); S=['Bild=',num2sr(Bild)];S2=['; T=',num2sr(T)];S3=['; N=',num2sr(N)]; S4=['; Apmax=',num2sr(Apmax)];S5=['; fak=',num2sr(fak)]; S6=['; Ap=',num2sr(Ap)];S7=['; d=',num2sr(d)];s8=['; az=',num2sr(az)]; gex({[s,s3,s4,s5,s6]},'fonsize',);.5.4 B ild = ; N = 3 ; A p m a x = 8 ; f a k = ; A p = 8 ; T = Z /N Y/ Z e i/s e c B ild = 2 ; N = 4 ; A p m a x = 4 ; f a k = ; A p = 4 ; T = Z /N Y/ Z e i/s e c
11 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsysemechnik, C:\ro\Si5\RT3\RT3_ueb\Loes_Regechn_2.doc, Seie / B ild = 3 ; N = 5 ; A p m ax= ; fak= ; A p = ; T = Z/N Y/ Zei/sec B ild = 4 ; N = 6 ; A p m ax= ; fak= ; A p = ; T = Z/N Y/ Lösung mi Tephys: Ze i/s e c UB7_8.TT Z = az*ja(-z) 2 x = x+(y+z-x)*d/t 3 x2 = x2+(x-x2)*d/t 4 x3 = x3+(x2-x3)*d/t 5 x4 = x4+(x3-x4)*d/t 6 x5 = x5+(x4-x5)*d/t 7 x6 = x6+(x5-x6)*d/t 8 N = round(abs(nwa)) 9 34 = x3*ja(n-2.9)*ja(3.-n)+x4*ja(n-3.9)*ja(4.-n) = 34+x5*ja(N-4.9)*ja(5.-N)+x6*ja(N-5.9)*ja(6.-N) Apmax = exp(n*ln(/(cos(pi/n)))) 2 Ap = Apmax*fak 3 Y = -Ap* 4 = +d Kommenar zum File UB7_8.TT R. Kessler, Uebungsaufgaben Reg.Technik, Aufg. 7 Srecke N gleiche PT-Glieder. Gesuch Sabiliaesgrenze P-Regler Anwor: Apmax = /( (cos(pi/n)) hoch N) Mi Tephys berechne: Apmax = exp(n*ln(/(cos(pi/n))))
12 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsysemechnik, C:\ro\Si5\RT3\RT3_ueb\Loes_Regechn_2.doc, Seie 2/29
13 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsysemechnik, C:\ro\Si5\RT3\RT3_ueb\Loes_Regechn_2.doc, Seie 3/29 Noch Aufgabe 7, aber die Teilsrecken dürfen verschiedene Zeikonsanen T, T2, T3, T4, T5 haben Daei ueb7v_.mdl v e rschie de n Ze ikonsane n T, T2,...T6 Laufenlassen mi Rundaei rueb7v_.m: inippen rueb7v_ <Reurn> az*(u > Z) Clock Z Ap T.s+ T2.s+ T3.s+ T4.s+ T5.s+ T6.s+ Y N - T=;T2=;T3=;T4=;T5=,T6=; N=3; Ap= 8; d=.; max=4; az=;z=; nix=sim('ueb7_',[,max]); figure(3);clf;plo(,);grid; Srecke aus N gleichen PT-Gliedern. Sabiliäsgrenze bei P-Regler is für N > 2 : Apmax = / ( ( cos (pi/n) )^N ) N = [ 3, 4, 5, 6 ] ; Apmax=./ (cos (pi./ N)).^N Amax = [ 8, 4, , 2.374] gil nur bei gleichen Zeikonsanen! % Daei rueb7v_.m Aufrufdaei für Simulink-Modell ueb7v_.mdl % In Kommandoebene einippen: rueb7v_ und Tase "Reurn" % Hier können die Zeikonsanen T,T2,...T6 verschieden sein (drum v im Namen) clear; forma compac; oldbild=; oldfak=; % oldt=; oldt2=;oldt3=;oldt4=; oldt5=;oldt6=; Bild = inpu('bie BildNummer eingaben:,2,3..): '); if isempy(bild) Bild = oldbild; end; Bild=round(abs(Bild)); N=inpu('Bie N eingeben ( 3,4,5 oder 6 ): '); if (N < 3) (N > 6) error('n muss 3, 4, 5 oder 6 sein! '); end; fak = inpu('fak (z.b. oder nahe ): '); if isempy(fak) fak=oldfak; end; % T=; T2=;T3=;T4=;T5=;T6=; T=inpu('Bie T eingeben ( Z.B. (wenn Reurn, dann T=): '); if isempy(t) T=; end; T2=inpu('Bie T2 eingeben ( Z.B. (wenn Reurn, dann T2=): '); if isempy(t2) T2=; end; T3=inpu('Bie T3 eingeben ( Z.B. (wenn Reurn, dann T3=): '); if isempy(t3) T3=; end; T4=inpu('Bie T4 eingeben ( Z.B. (wenn Reurn, dann T4=): '); if isempy(t4) T4=; end; T5=inpu('Bie T5 eingeben ( Z.B. (wenn Reurn, dann T5=): '); if isempy(t5) T6=; end; T6=inpu('Bie T6 eingeben ( Z.B. (wenn Reurn, dann T6=): '); if isempy(t6) T6=; end; Apmax= /(cos(pi/n))^n; Ap= Apmax *fak; d=.; max=4; az=;z=; if Bild == ueb7v_; end; % Die Simulink-Schalung auf Bildschirm rufen [nix]= sim('ueb7v_',[,max]); % Saren der Berechnung figure(bild);clf; se(,'defaullinelinewidh',.5)
14 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsysemechnik, C:\ro\Si5\RT3\RT3_ueb\Loes_Regechn_2.doc, Seie 4/29 plo(,z/n,'m',,,'k',,y/,'b');grid;xlabel('zei/sec'); legend('z/n','','y/'); S=['Bild=',num2sr(Bild)];S2=['; N=',num2sr(N)]; S3=['; Apmax=',num2sr(Apmax)];S4=['; fak=',num2sr(fak)]; S5=['; Ap=',num2sr(Ap)];S6=['; d=',num2sr(d)];s7=['; az=',num2sr(az)]; S=['; T=',num2sr(T)]; S2=['; T2=',num2sr(T2)]; S3=['; T3=',num2sr(T3)]; S4=['; T4=',num2sr(T4)]; S5=['; T5=',num2sr(T5)]; S6=['; T6=',num2sr(T6)]; gex({[s,s2,s3,s4,s5]},'fonsize',2); gex({[s,s2,s3,s4,s5,s6]},'fonsize',2); B ild = ; N = 3 ; A p m a x = 8 ; f a k = ; A p = 8 ; T =.2 ; T 2 = ; T 3 = ; T 4 = ; T 5 = ; T 6 = T =.2, a lle a n d e r e n =, a ls o u n g le ic h e Z e ik o n s a n e n = = > b e i A p = A p m a x g e d ä m p fe S c h w in g u n g, a ls o A p m a x is N IC H T d ie S a b ilä s g r e n z e! Z /N Y/ Z e i/s e c B ild = 2 ; N = 5 ; A p m a x = ; f a k = ; A p = ; T =.2 ; T 2 = ; T 3 = ; T 4 = ; T 5 = ; T 6 = Z /N Y/.2. T =.2, a lle a n d e re n =, = = > b e i A p = A p m a x g e d ä m p f e S c h w in g u n g, a ls o A p m a x is N I C H T d ie S a b iliä s g re n z e! Z e i/s e c B ild = 3 ; N = 6 ; A p m a x = ; f a k = ; A p = ; T =.9 ; T 2 = ; T 3 = ; T 4 = ; T 5 = ; T 6 = Z /N Y /.3.2. T =.9, a lle a n d e r n =, = = > b e i A p = A p m a x g e d ä m p f e S c h w in g u n g, a ls o A p m a x is N I C H T d ie S a b ilä s g r e n z e! Z e i /s e c
15 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsysemechnik, C:\ro\Si5\RT3\RT3_ueb\Loes_Regechn_2.doc, Seie 5/29 Zu 8 8 Kaskadenregelung W?????? wohin? wohin? Die Gesamsrecke beseh aus zwei Teilsrecken mi den Ausgängen x und. Auf den Sreckeneingang wirk die Sörgröße Z. Führgröße is W 8. rgänzen Sie das Blockschalbild, so dass eine Kaskadenregelung enseh. Zeichnen Sie eine Simulink-Schalung zur Realisierung der Kaskadenregelung. Annahme: PID- Regler. Die Teilsrecken mögen je 2 PT-Glieder sein. 8.2 Schreiben Sie einen Tephys -Algorihmus zur Realisierung der Kaskadenregelung: PID- Regler, je 2 PT- Glieder. Lösung zu 8. Z x Teilsrecke Teilsrecke 2 W W- Außen- Regler Ya x Ya-x Innen- Regler Yi Z Yi+Z Teilsrecke x Teilsrecke 2 Dem Außenregler wird die Differenz Sollwer W - Regelgröße zugeführ. Die Sellgröße Ya des Außenreglers is die Führgröße für den Innenregler. Der Innenregler verarbeie die Differenz Ya x und liefer die Sellgröße Yi des Innenreglers. Auf die Teilsrecke wirk die Summe Yi + Sörgröße Z. Simulink-Schalung: Daei ueb8_2.mdl az*(u > Z) C lock aw *(u > W ) Z K askaden-r egelung. Srecke 4 PT, aufrufen mi rueb8_2 W +-vma Ya Yi x x2 /Tia /s Apa /Tii Tdi /s du/d Api T.s+ T2.s+ Tda du/d T3.s+ x3 T4.s+ x4 % Daei rueb8_2.m Aufrufdaei für Simulink-Modell ueb8_2.mdl % In Kommandoebene einippen: rueb8_2 und Tase "Reurn" clear; forma compac; oldbild=; T=;T2=,T3=;T4=; d=.; max=4; az=-5; Z=2; aw=; W=; Bild = inpu('bie BildNummer eingaben:,2,3..): '); if isempy(bild) Bild = oldbild; end; Bild=round(abs(Bild));
16 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsysemechnik, C:\ro\Si5\RT3\RT3_ueb\Loes_Regechn_2.doc, Seie 6/29 vma= inpu('bie vma eingeben (Z.B. ): '); Apa= inpu('bie Apa eingeben (Z.B. 4 ): '); Tda = inpu('tda (z.b..3): '); Tia = inpu('tia (z.b. 3 ): '); Api=inpu('Bie Api eingeben (z.b. 4 ): '); Tdi = inpu('tdi (z.b..2): '); Tii = inpu('tii (z.b. e5 ): '); if Bild == ueb8_2; end; % Die SimulinkSchalung auf Bildschirm rufen [nix]= sim('ueb8_2',[,max]); % Saren der Berechnung figure(bild);clf; se(,'defaullinelinewidh',.5) plo(,ya+6,,x2+6,,w*4,,x4*4);grid;xlabel('zei/sec'); axis([,max,-,2 ]); legend('ya+6','x2+6','w*4','x4*4'); S=['Bild=',num2sr(Bild)]; Svma=['; vma=',num2sr(vma)]; S2=['; Apa=',num2sr(Apa)]; S3=['; Tda=',num2sr(Tda)];S4=['; Tia=',num2sr(Tia)]; S5=['; Api=',num2sr(Api)];S6=['; Tdi=',num2sr(Tdi)]; S7=['; Tii=',num2sr(Tii)]; gex({[s,svma,s2,s3,s4,s5,s6,s7]},'fonsize',2); Bild=; vma=; Apa=4; Tda=.3; Tia=3; Api=4; Tdi=.2; Tii= Nahezu opimal: Außenregler PID, Innenregler PD Sollwer mi Ansiegsbegrenzer (vma=) Ya+6 x2+6 W *4 x4*4 +Z/ Zei/sec Bild=2; vma=; Apa=4; Tda=.3; Tia=3; Api=4; Tdi=.2; Tii= vma= (sa ), folglich Riesensellgröße Ya Ya+6 x2+6 W *4 x4*4 +Z/ Zei/sec
17 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsysemechnik, C:\ro\Si5\RT3\RT3_ueb\Loes_Regechn_2.doc, Seie 7/ Ya+6 x2+6 W *4 x4*4 +Z/ Bild=4; vma=; Apa=4; Tda=.3; Tia=3; Api=4; Tdi=.2; Tii= vma= ==> Infolge RiesenSellgröße Ya schleche Regelqualiä Zei/sec 2 8 Ya+6 x2+6 W *4 x4*4 +Z/ 6 Bild=5; vma=; Apa=4; Tda=.3; Tia=3; Api=4; Tdi=.2; Tii=2 4 2 W ieder vma=, Aber Tii=2 (sa e5). ==> Überschwingen der Söranwor Zei/sec Bild=6; vma=; Apa=4; Tda=.3; Tia=3; Api=8; Tdi=.2; Tii= wieder ohne I-Aneil des Innenreglers. Aber Api =8 sa 4. ==> Söreinfluß geringer Ya+6 x2+6 W *4 x4*4 +Z/ Zei/sec
18 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsysemechnik, C:\ro\Si5\RT3\RT3_ueb\Loes_Regechn_2.doc, Seie 8/29 Lösung zu 8. Tephys (Kaskadenregelung) -- D:\RT3\RT3_UB\UB8_2.TT --- Z = az*ja(-z) 2 W = aw*ja(-w) 3 W = W+begr((W-W)/TW,vma,-vma)*d 4 x = x+(z+yi-x)*d/t 5 x2 = x2+(x-x2)*d/t2 6 x3 = x3+(x2-x3)*d/t3 7 x4 = x4+(x3-x4)*d/t4 8 ini = Ya-x2 9 ini = ini+ini*d/tii DAi = (ini-inial)*tdi/d inial = ini 2 Yi = Api*(ini+ini+DAi) 3 ina = W-x4 4 ina = ina+ina*d/tia 5 DAa = (ina-inaal)*tda/d 6 inaal = ina 7 Ya = Apa*(ina+ina+DAa) 8 = +d
19 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsysemechnik, C:\ro\Si5\RT3\RT3_ueb\Loes_Regechn_2.doc, Seie 9/29
20 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsysemechnik, C:\ro\Si5\RT3\RT3_ueb\Loes_Regechn_2.doc, Seie 2/29 Zu 9 K, K2, K3 Konsane () K 9. () beliebige Zeifunkion als ingang. s Gesuch: normale mahemaische Formeln für diese Blockschalung. 9.2 Tephys -Algorihmus zum Berechnen von x(), x2(), () 9.3 Simulink-Schalung zum Berechnen von x(), x2(), () Lösungen: zu 9. Bekannlich lies man einen Block wie folg (vgl. Lösung zu Aufg.): Ausgang des Blocks is ingang muliplizier mi der Formel im Block. Also ergib sich für x: x = *K/s. benfalls bekann is, dass s der Differenialoperaor is, also s = d/d (vgl. Aufg.). Folglich würde sich ergeben x= *K/(d/d). Diese Formel ha aber in dieser Gesal keinen Sinn. Sinnvoll wird die Formel, wenn man mi dem Nenner erweier, also den Nenner s auf die linke Seie der Gleichung wirken läss. Dadurch enseh zunächs s * x = K * und mi s = d/d ergib sich die Differenialgleichung dx/d = k*. Deren Lösung is in diesem Beispiel einfach das Inegral x = K**d. Analog ergib sich x2 = K2*x*d und x3 = K3*x*d zu 9.2 Aus der obigen DGL für x, nämlich aus dx/d = K* folg zunächs für die Änderung dx die Formel dx = K**d und daraus der Tephys-Algorihmus xneu =xal + dx oder xneu =xal + K**d oder mi Weglassen der Indizes al und neu die Formel für Tephys: x =x+k**d. nsprechend für die anderen Ausgänge: x2=x2+k2*x*d und x3=x3+k3*x2*d. Also können wir Tephys formulieren: UB_9_2.TT ---- = sin(2*pi*f*)*ja(-)*ja(2-) 2 x = x+ k * *d 3 x2 = x2+ K2* x*d 4 x3 = x3+k3* x2*d 5 = +d x K2 s x2 K3 s ()
21 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsysemechnik, C:\ro\Si5\RT3\RT3_ueb\Loes_Regechn_2.doc, Seie 2/29 zu 9.3: In Simulink gib es bekannlich die Blöcke Inegraor, nämlich die Blöcke mi der Formel /s Anschließend die Lösung mi Simulink-Modell Loes_9_3.MDL (für Malab 5.3). Man beache die beiden Kommenare im Schalungsbild: In allen Blöcken o workspace: maximum number of rows: inf, Decimaion:, Sample ime: - Wichig Save forma: Marix Simulaion/Parameers/Solver : sar ime: ; sop ime: max, solver opions: Type: Fixed-Sep; ode5(dorman-prince) Fixed sepsize: d; Mode; Auo Daei Loes_9_3.MDL Workspace in allen Blöcke o workspace: maximum number of rows: inf Decimaion: Sample ime: - wichig: Save forma: Marix Im Fenser "Simulaion/ Parameers/ Solver": sar ime:. sop ime: max Solver opions Type: Fixed-sep ode5(dorman-prince) Fixed sep size: d Mode: Auo Clock sin( 2 * pi * f * u )* (u > ) * ( 2 > u ) Fcn x x2 x3 K /s K2 /s K3 /s Gain Inegraor % Parameer z.b.: clear; f=; =3; 2=7; max=2; d=.2; K=; K2=/2; K3=/3; % Saren und rgebnisse darsellen: [nix]= sim( 'loes_9_3', [,max] ); figure(); clf; plo(,,,x+,,x2+2,,x3+3 ); grid; legend( '', 'x+', 'x2+2', 'x3+3' ); x+ x2+2 x
22 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsysemechnik, C:\ro\Si5\RT3\RT3_ueb\Loes_Regechn_2.doc, Seie 22/29 Zu : B, A2, A A = cons, A2. ingang () mi beliebiger Zeifunkion () B A2*s*s + A*s + A (). Gesuch normale mahemaische Formel für Zusammenhang von Ausgang () und ingang ()..2 Tephys- Algorihmus zum Berechnen von ()..3 Simulink-Schalung zum Berechnen von (). Lösungen: zu. Die Formel für den Ausgang is zunächs =*B/( A2*s*s + A*s + A). Durch Muliplikaion mi dem Nenner ergib sich (A2*s*s + A*s +A)* = *B. Beache man nun, dass s der Differenialoperaor s =d/d is, so ergib sich als normale mahemaische Formel die Differenialgleichung A2 * + A * + A * = * B. Dabei bedeue = d/d und die zweie Ableiung von nach der Zei. zu.2 Da A2 ungleich Null is, darf man durch A2 dividieren und erhäl = ( *B A * A * ) / A2 Da = d ( )/d is ergib sich die Änderung von zu d = * d, also selbs als Algorihmuszeile = + *d und ensprechend = + *d. Daraus der Tephys-Algorihmus UB 2.TT = cos(2*pi*f*)*exp(-/au)*ja(-)*ja(2-) 2 '' = (B* - A* '-A* )/A2 3 ' = '+ '' * d 4 = + ' * d 5 = +d zu.3 In Simulink gib es der Bibliohek Coninuous den Block Transfer Fcn (also Transferfunkion ). Die erforderlichen Parameer gib man mi fallenden Poenzen von s ein. In diesem Fall den Zähler ( Numeraor ) als [B], den Nenner ( Denumeraor ) als [A2 A A]..
23 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsysemechnik, C:\ro\Si5\RT3\RT3_ueb\Loes_Regechn_2.doc, Seie 23/29 Hinweis: diese Ar ingabe der is der Vekor der Zählerkoeffizienen und der Vekor der Nennerkoeffizienen. Diese Vekoren sind Zeilenvekoren. Die einzelnen Parameerwere werden durch Leerasen oder durch je ein Komma gerenn, nich aber ewa durch Semikolon. Probieren: es ergib Fehlermeldungen. Daei Loes 3.MDL Workspace in allen Blöcke o workspace: maximum number of rows: inf Decimaion: Sample ime: - wichig: Save forma: Marix Im Fenser "Simulaion/ Parameers/ Solver": sar ime:. sop ime: max Solver opions Type: Fixed-sep ode5(dorman-prince) Fixed sep size: d Mode: Auo Clock cos( 2 * pi * f * u ) * exp (-u / au) * (u > ) * ( 2 > u ) Fcn B A2.s 2+A.s+A Transfer Fcn % Parameer z.b.: clear; f=.; au=; =2; 2=; max=2; d=.2;b=; A=; A=;A2=; % Saren und rgebnisse darsellen: [nix]= sim( 'loes 3', [,max] ); figure(); clf; plo(,,, ); grid;
24 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsysemechnik, C:\ro\Si5\RT3\RT3_ueb\Loes_Regechn_2.doc, Seie 24/29 Zu : () A2*s*s + A*s + A x () B2*s*s + B*s + B x2() A2, A, A, B2, B, B = cons, A2 Bei den nachfolgenden Anworen is darauf zu achen, dass der ingang () nich differenzier wird, denn () könne eine nich differenzierbare Funkion sein, z.b. eine Funkion mi Sprüngen.. Gesuch sind normale mahemaische Formeln zum Formulieren des Inhals der Blockschalung..2 Tephys -Algorihmus zum Berechnen von x() und x2()..3 Simulink-Schalung zum Berechnen von x() und x2(). Lösungen: zu. Analog zur Aufgabe. ergib sich für den Ausgang aus dem. Block x() die Differenialgleichung A2*x + A*x + A*x = Durch Lösen dieser DGL sind x und x und x bekann (vgl. Lösung zu.2). Der Ausgang x2 ergib sich durch insezen von s = d/d in den rechen Block wie folg: x2 = B2*x + B * x + B * x zu.2 Durch Anwendung dieser rkennnisse auf die Lösung von.2 finde man den gesuchen Tephys- Algorihmus für diese Aufgabe: D:\RT3\UB 2.TT = cos(2*pi*f*)*exp(-/au)*ja(-)*ja(2-) 2 x'' = (- A * x'- A * x)/a2 3 x' = x' + x'' * d 4 x = x + x' * d 5 x2 = B2 * x'' + B * x' + B * x 6 = +d zu.3 In Simulink darf man nich ewa wörlich gemäß der Aufgabensellung die beiden Blöcke hinereinander wirken lassen. Das kann man zwar in die Simulink-Schalung eingeben. Dor wird das akzepier. s enseh dann eine Schalung, die (neben den anderen Baueilen) folgende zwei Blöcke enhäl:
25 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsysemechnik, C:\ro\Si5\RT3\RT3_ueb\Loes_Regechn_2.doc, Seie 25/29 A2.s 2+A.s+A Transfer Fcn x B2.s 2+B.s+B Transfer Fcn x2 Aber beim Saren der Simulaion ergib sich die Fehlermeldung: rror from 'f2ss' in block 'loes 3/Transfer Fcn' rror using ==> f2ss Denominaor mus be higher or equal order han numeraor Abhilfe in Simulink ergib sich, indem man die beiden hinereinander geschaleen Blöcke zu einem einzigen Block kombinier, nämlich in der Gesal Zähler durch Nenner. Der Zähler wird hier B2 * s* s + B*s + B, der Nenner wird A2*s*s+ A*s + A, oder im ingabe-forma in das Parameer-Fenser Nominaor: [B2, B2, B] für den Zähler und Denumeraor [A2, A, A] für den Nenner. Das ergib das Simulink-Modell Loes 3.MDL Daei Loes 3.MDL Workspace in allen Blöcke o workspace: maximum number of rows: inf Decimaion: Sample ime: - wichig: Save forma: Marix Im Fenser "Simulaion/ Parameers/ Solver": sar ime:. sop ime: max Solver opions Type: Fixed-sep ode5(dorman-prince) Fixed sep size: d Mode: Auo Clock cos( 2 * pi * f * u ) * exp (-u / au) * (u > ) * ( 2 > u ) Fcn B2.s 2+B.s+B A2.s 2+A.s+A x2 Transfer Fcn % Parameer z.b.: clear; f=.; au=; =2; 2=; max=2; d=.2; A=; A=;A2=;B2=4; B=-2; B=; % Saren und rgebnisse darsellen: [nix]= sim( 'loes 3', [,max] ); figure(); clf; plo(,,,x,,x2 ); grid;.5 x
26 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsysemechnik, C:\ro\Si5\RT3\RT3_ueb\Loes_Regechn_2.doc, Seie 26/3 Zu 2: () B2*s*s + B*s + B A3*s*s*s + A2*s*s + A*s + A () A3, A2, A, A, B2, B, B = cons, A3 ungleich. Bei den nachfolgenden Anworen is darauf zu achen, dass der ingang () nich differenzier wird, denn () könne eine nich differenzierbare Funkion sein, z.b. eine Funkion mi Sprüngen. 2. Gesuch is zunächs eine normale mahemaische Formel, um den Zusammenhang des Ausgangs () mi dem ingang () darzusellen. Wenn man den Zähler mi seinen Fakoren s erns nimm, reen in dieser Formel auch Ableiungen von () nach der Zei auf. Diese Zei-Ableiungen sind aber nich erlaub, denn () könne ja Sprünge enhalen. Vergleich man mi der vorgehenden Aufgabe (), so erkenn man, dass sich solche unerlauben Ableiungen vermeiden lassen, wenn man den gegebenen Block aufeil in zwei hinereinanderfolgende Blöcke: zuers den Block /Nenner, dann den Block Zähler. Nenn man den Ausgang aus dem ersen Block x(), so ha man also nach Zerlegung in zwei hinereinanderfolgende Blöcke die folgende Darsellung () A3*s*s*s + A2*s*s + A*s + A x () B2*s*s + B*s + B () Dies is gleichbedeuend mi der ursprünglichen Formulierung Zähler/Nenner, aber mi dem Voreil, dass jez keine Differeniaionen der ingangsfunkion () erforderlich sind. Die ingangsfunkion darf also auch Sprünge enhalen! 2.2 Formulieren Sie einen Tephys- Algorihmus zur Berechnung des Ausgangs (). Hinweis: Sie müssen dabei allerlei innere Funkionen miberechnen. 2.3 Zeichnen Sie eine Simulink-Schalung zur Berechnung von A(). Verwenden Sie dabei die in Simulink eingebauen Transferfunkionen Tranfer Fcn und benuzen Sie dabei das ursprüngliche Blockschalbild Zähler/Nenner. Die Verwendung der Tranfer Fcn ha den Voreil, dass man sich keine Gedanken über die eigenlichen mahemaischen Abläufe der Berechnung zu machen brauch, aber der Nacheil is, dass man eigenlich nich verseh, wie die Rechnung abläuf. 2.4 Zeichnen Sie eine Simulink-Schalung, die ohne Transfer-Fcn auskomm, die also nur die Blöcke Sum, Inegraor, Gain verwende. Lösungen zu 2: Zu 2. () B2*s*s + B*s + B A3*s*s*s + A2*s*s + A*s + A () Zunächs beschreien wir einen falschen Weg: Mi dem Rezep Ausgang = ingang muliplizier mi der Formel im Block ergib sich zunächs = (B2*s*s + B*s +B ) * / ( A3*s*s*s + A2*s*s + A*s + A ). Durch Muliplikaion mi dem Nenner enseh ( A3*s*s*s + A2*s*s + A*s + A ) * = (B2*s*s + B*s +B ) * Wird jez s = d/d gesez, so ha man die Differenial-Gleichung für A3* + A2* + A* + A * = B2* + B* + *. Auf der rechen Seie sehen auch die zeilichen Ableiungen der ingangsfunkion (). In vielen Büchern über Regelungsechnik und Sysemdynamik finde man in der Ta diese Ar DGLn Wäre die ingangsfunkion (hinreichend of) differenzierbar, dann würde sich kein Problem ergeben. Wie aber, wenn der ingang z.b. Sprünge enhäl? Was soll die. oder gar die 2. Ableiung eines Sprunges bedeuen??
27 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsysemechnik, C:\ro\Si5\RT3\RT3_ueb\Loes_Regechn_2.doc, Seie 27/3 Zu 2.2 In der Aufgabensellung zu 2. wurde die Zerlegung des ursprünglichen Blocks Zähler/ Nenner in die Blöcke /Nenner, gefolg vom Block Zähler empfohlen, nämlich wie folg: () A3*s*s*s + A2*s*s + A*s + A x () B2*s*s + B*s + B () In Aufgabe haben wir schon diese Ar Problemsellung gelös, mi dem kleine Unerschied, dass dor der Nenner nur vom Grade 2 war, hier dagegen vom Grade 3. Das bring aber kein Problem. Der Ausgang x() aus dem Block /Nenner ergib zunächs die Formel x = /( A3*s*s*s+ A2*s*s +A*s + A). Muliplikaion mi dem Nenner ergib die Formel ( A3*s*s*s+ A2*s*s +A*s + A)*x = und mi s = d/d ergib sich die DGL 3. Ordnung für x A3 * x + A2* x + A * x + A* x = Ähnlich wie bei Aufgabe geh s weier: Da A3 ungleich Null is, kann man durch A3 dividieren und erhäl x = ( A2*x A* x A * x )/A3 und dami den Lösungsalgorihmus mi Tephys D:\RT3\UB_2_2.TT =cos(2*pi*f*)*exp(-/au)*ja(-)*ja(2-) 2 x''' = ( - A2 * x'' - A * x' - A * x )/ A3 3 x'' = x'' + x''' * d 4 x' = x' + x'' * d 5 x = x+x'*d 6 = B2*x''+B*x'+B*x 7 = +d Zu 2.3 In Simulink kann man direk den Block Tranfer Fcn mi Zähler und Nenner verwenden. Das haben wir schon bei Aufgabe.3 benuz (Simulink-Modell Loes 3.MDL). Wir brauch nur den dorigen Nenner von der zweien auf die drie Ordnung zu ergänzen und haben dami die gewünsche Simulink-Schalung:
28 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsysemechnik, C:\ro\Si5\RT3\RT3_ueb\Loes_Regechn_2.doc, Seie 28/29 Daei Loes_2_3.MDL Workspace in allen Blöcke o workspace: maximum number of rows: inf Decimaion: Sample ime: - wichig: Save forma: Marix Im Fenser "Simulaion/ Parameers/ Solver": sar ime:. sop ime: max Solver opions Type: Fixed-sep ode5(dorman-prince) Fixed sep size: d Mode: Auo Clock cos( 2 * pi * f * u ) * exp (-u / au) * (u > ) * ( 2 > u ) Fcn B2.s 2+B.s+B A3.s 3+A2.s 2+A.s+A Transfer Fcn % Parameer z.b.: clear; f=.2; au=; =2; 2=; max=2; d=.2; A=; A=;A2=;A3=; B2=4; B=-2; B=; % Saren und rgebnisse darsellen: [nix]= sim( 'loes_2_3', [,max] ); figure(); clf; plo(,,, ); grid; Zu 2.4 Hier noch mal die Aufgabensellung: Zeichnen Sie eine Simulink-Schalung, die ohne Transfer-Fcn auskomm, die also nur die Blöcke Sum, Inegraor, Gain verwende Die gleichen Überlegungen, die wir schon bei Tephys angewende haben (vgl. 2.2 ), können wir auch auf Simulink anwenden. Der Vollsändigkei halber und wegen der prinzipiellen Wichigkei seien die Überlegungen hier noch einmal kurz wiederhol: Den ursprünglichen Block Zähler/Nenner zerlegen wir in zwei Blöcke: zunächs den Block /Nenner, dann den Block Zähler. Wir bekommen also das (oben schon vorgekommene) Blockschalbild () A3*s*s*s + A2*s*s + A*s + A x () B2*s*s + B*s + B () Für den Ausgang x aus dem. Block ergib (nach Muliplikaion mi dem Nenner und insezen von s=d/d ) die DGL 3. Ordnung für x: A3 * x + A2* x + A * x + A* x = oder nach Division durch A3 (das dürfen wir, dann A3 is ungleich Null)
29 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsysemechnik, C:\ro\Si5\RT3\RT3_ueb\Loes_Regechn_2.doc, Seie 29/29 x = ( A2*x A* x A * x )/A3 Dafür ergib sich eine Simulink-Schalung, die x, x und x liefer. Daraus ergib sich der gewünsche Ausgang zu = B2 * x + B * x + B * x Hier die zugehörige Simulink-Schalung ueb_2_4.mdl Daei Loes_2_4.MDL Workspace in allen Blöcke o workspace: maximum number of rows: inf Decimaion: Sample ime: - wichig: Save forma: Marix Im Fenser "Simulaion/ Parameers/ Solver": sar ime:. sop ime: max Solver opions Type: Fixed-sep ode5(dorman-prince) Fixed sep size: d Mode: Auo cos( 2 * pi * f * u ) * exp (-u / au) * (u > ) * ( 2 > u ) Clock Fcn B2 /A3 Gain A2 x'' x''' /s Inegraor /s xpp x' /s xp x B B x A A % Parameer z.b.: clear; f=.2; au=; =2; 2=; max=2; d=.2; A=; A=;A2=;A3=; B2=4; B=-2; B=; % Saren und rgebnisse darsellen: [nix]= sim( 'loes_2_4', [,max] ); figure(); clf; plo(,,,xpp,,xp,,x,, ); grid; xp x xpp xp x -2-4 xpp
Lösungen der Übungsaufgaben zur Regelungstechnik
 Prof. Dr. R. essler, FH-arlsruhe, Sensorsysemechnik, C:\ro\Si05\RT3\Loes_Regechn_.doc, Seie Homepage hp://www.home.hs-karlsruhe.de/~kero000/ Lösungen der Übungsaufgaben zur Regelungsechnik Tex der Aufgabensellung:
Prof. Dr. R. essler, FH-arlsruhe, Sensorsysemechnik, C:\ro\Si05\RT3\Loes_Regechn_.doc, Seie Homepage hp://www.home.hs-karlsruhe.de/~kero000/ Lösungen der Übungsaufgaben zur Regelungsechnik Tex der Aufgabensellung:
Mathematische Methoden der klassischen Physik Zusammenfassung Differentialgleichungen
 Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Systemtheorie Teil A. - Zeitkontinuierliche Signale und Systeme - Musterlösungen. Manfred Strohrmann Urban Brunner
 Sysemheorie eil A - Zeikoninuierliche Signale und Syseme - Muserlösungen Manfred Srohrmann Urban Brunner Inhal 3 Muserlösungen - Zeikoninuierliche Syseme im Zeibereich 3 3. Nachweis der ineariä... 3 3.
Sysemheorie eil A - Zeikoninuierliche Signale und Syseme - Muserlösungen Manfred Srohrmann Urban Brunner Inhal 3 Muserlösungen - Zeikoninuierliche Syseme im Zeibereich 3 3. Nachweis der ineariä... 3 3.
Prüfung zum Fach Regelungstechnik für Studierende Lehramt an beruflichen Schulen (Diplom/Bachelor)
 Technische Universiä München Lehrsuhl für Regelungsechnik Prof. Dr.-Ing. B. Lohmann Prüfung zum Fach Regelungsechnik 7.9. für Sudierende Lehram an beruflichen Schulen (Diplom/Bachelor) Name: Vorname: Mar.-Nr.
Technische Universiä München Lehrsuhl für Regelungsechnik Prof. Dr.-Ing. B. Lohmann Prüfung zum Fach Regelungsechnik 7.9. für Sudierende Lehram an beruflichen Schulen (Diplom/Bachelor) Name: Vorname: Mar.-Nr.
Prüfung zum Fach Regelungstechnik für Studierende Lehramt an beruflichen Schulen (Diplom/Bachelor)
 Technische Universiä München Lehrsuhl für Regelungsechnik Prof. Dr.-Ing. B. Lohmann Prüfung zum Fach Regelungsechnik 14.04.2011 für Sudierende Lehram an beruflichen Schulen (Diplom/Bachelor) Name: Vorname:
Technische Universiä München Lehrsuhl für Regelungsechnik Prof. Dr.-Ing. B. Lohmann Prüfung zum Fach Regelungsechnik 14.04.2011 für Sudierende Lehram an beruflichen Schulen (Diplom/Bachelor) Name: Vorname:
7. Vorlesung Wintersemester
 7. Vorlesung Winersemeser Der ungedämpfe Oszillaor mi komplexem Lösungsansaz Wie gezeig, wird die DGL des ungedämpfen Oszillaors mẍ() + kx() = 0 () im Komplexen von den Funkionen x () = e iω und x 2 ()
7. Vorlesung Winersemeser Der ungedämpfe Oszillaor mi komplexem Lösungsansaz Wie gezeig, wird die DGL des ungedämpfen Oszillaors mẍ() + kx() = 0 () im Komplexen von den Funkionen x () = e iω und x 2 ()
DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN
 Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Lineare Algebra I - Lösungshinweise zur Klausur
 Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
Abiturprüfung Mathematik 2012 (Baden-Württemberg) Berufliche Gymnasien Analysis, Aufgabe 1
 Abiurprüfung Mahemaik 0 (Baden-Würemberg) Berufliche Gymnasien Analysis, Aufgabe. (8 Punke) Die Abbildung zeig das Schaubild einer Funkion h mi der Definiionsmenge [-7 ; 4]. Die Funkion H is eine Sammfunkion
Abiurprüfung Mahemaik 0 (Baden-Würemberg) Berufliche Gymnasien Analysis, Aufgabe. (8 Punke) Die Abbildung zeig das Schaubild einer Funkion h mi der Definiionsmenge [-7 ; 4]. Die Funkion H is eine Sammfunkion
Regelungstechnik. Steuerung. Regelung. Beim Steuern bewirkt eine Eingangsgröße eine gewünschte Ausgangsgröße (Die nicht auf den Eingang zurückwirkt.
 Regelungsechnik Seuerung Beim Seuern bewirk eine Eingangsgröße eine gewünsche Ausgangsgröße (Die nich auf den Eingang zurückwirk. Seuern is eine Wirkungskee Seuerkee (Eingahnsraße) Bsp. Boiler Regelung
Regelungsechnik Seuerung Beim Seuern bewirk eine Eingangsgröße eine gewünsche Ausgangsgröße (Die nich auf den Eingang zurückwirk. Seuern is eine Wirkungskee Seuerkee (Eingahnsraße) Bsp. Boiler Regelung
Karlsruher Institut für Technologie (KIT) Institut für Analysis Dr. A. Müller-Rettkowski Dipl.-Math. M. Uhl. Sommersemester 2011
 Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
MATLAB: Kapitel 4 Gewöhnliche Differentialgleichungen
 4. Einleiung Eine der herausragenden Särken von MATLAB is das numerische (näherungsweise) Auflösen von Differenialgleichungen. In diesem kurzen Kapiel werden wir uns mi einigen Funkionen zum Lösen von
4. Einleiung Eine der herausragenden Särken von MATLAB is das numerische (näherungsweise) Auflösen von Differenialgleichungen. In diesem kurzen Kapiel werden wir uns mi einigen Funkionen zum Lösen von
Abiturprüfung Mathematik 2009 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
2.2 Rechnen mit Fourierreihen
 2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
Reglerdimensionierung nach Ziegler-Nichols
 HTL, Innsbruck Seie von 8 Rober Salvador salvador@hlinn.ac.a Mahemaische / Fachliche Inhale in Sichworen: Regelungsechnik, Laplaceransformaion, Umgang mi komplexen Zahlen, Kurvendiskussion, Differenzialgleichungen
HTL, Innsbruck Seie von 8 Rober Salvador salvador@hlinn.ac.a Mahemaische / Fachliche Inhale in Sichworen: Regelungsechnik, Laplaceransformaion, Umgang mi komplexen Zahlen, Kurvendiskussion, Differenzialgleichungen
The Matlab ODE Suite. Simone Bast Martin Vogt
 The Malab ODE Suie Simone Bas Marin Vog Gliederung Wiederholung BDF-Verfahren Verbesserung: NDF-Verfahren ode5s und ode3s User Inerface Vergleich der Löser Zusammenfassung ) Implizie Formeln für seife
The Malab ODE Suie Simone Bas Marin Vog Gliederung Wiederholung BDF-Verfahren Verbesserung: NDF-Verfahren ode5s und ode3s User Inerface Vergleich der Löser Zusammenfassung ) Implizie Formeln für seife
7.3. Partielle Ableitungen und Richtungsableitungen
 7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
Universität Ulm Samstag,
 Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Technische Universität München. Lösung Montag SS 2012
 Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
existiert. In der Regel wird zusätzlich zum oben gegebenen System von Differentialgleichungen noch eine Anfangsbedingung
 0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
PID-Regelung wahlweise mit Pulsweiten-Modulation, simuliert mit Matlab, C:\ro\Si05\RT3\PWM\PWM_Matlab3.doc
 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsystemtechnik, C:\ro\Si5\RT3\PWM\PWM_Matlab3.doc, Seite /5 PID-Regelung wahlweise mit Pulsweiten-Modulation, simuliert mit Matlab, C:\ro\Si5\RT3\PWM\PWM_Matlab3.doc
Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsystemtechnik, C:\ro\Si5\RT3\PWM\PWM_Matlab3.doc, Seite /5 PID-Regelung wahlweise mit Pulsweiten-Modulation, simuliert mit Matlab, C:\ro\Si5\RT3\PWM\PWM_Matlab3.doc
Kryptologie. Bernd Borchert. Univ. Tübingen WS 15/16. Vorlesung. Teil 1b. Rechnen modulo n
 Krypologie Bernd Borcher Univ. Tübingen WS 15/16 Vorlesung Teil 1b Rechnen modulo n Modulo Rechnen a mod n is definier als Res von a bei Division durch n (a aus Z, n aus N) a + b mod n = a mod n + b mod
Krypologie Bernd Borcher Univ. Tübingen WS 15/16 Vorlesung Teil 1b Rechnen modulo n Modulo Rechnen a mod n is definier als Res von a bei Division durch n (a aus Z, n aus N) a + b mod n = a mod n + b mod
ZUU AUUFFGGAABBEE :: Die Wann läuft zunächst voll. Nach einiger Zeit wird etwas Wasser abgelassen und dann wird etwas zugeführt.
 Lineare Funkionen. Lösungen Lö LÖÖSSUUNNGGEENN ZZUUM.. KPPI IITTEELL ZZUU UUFFGGEE..: : a) as Pfeildiagramm zeig keine Funkion, da von h kein Pfeil ausgeh und von a zwei Pfeile. b) Is eine Funkion, denn
Lineare Funkionen. Lösungen Lö LÖÖSSUUNNGGEENN ZZUUM.. KPPI IITTEELL ZZUU UUFFGGEE..: : a) as Pfeildiagramm zeig keine Funkion, da von h kein Pfeil ausgeh und von a zwei Pfeile. b) Is eine Funkion, denn
Typ A: Separierbare Differentialgleichungen I. Separierbare Differentialgleichungen II. Beispiel einer separierbaren Dgl
 Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Differentialgleichungen
 Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
Name: Punkte: Note: Ø:
 Name: Punke: Noe: Ø: Kernfach Physik Abzüge für Darsellung: Rundung: 4. Klausur in K am 5. 5. 0 Ache auf die Darsellung und vergiss nich Geg., Ges., Formeln, Einheien, Rundung...! Angaben: e =,60 0-9 C
Name: Punke: Noe: Ø: Kernfach Physik Abzüge für Darsellung: Rundung: 4. Klausur in K am 5. 5. 0 Ache auf die Darsellung und vergiss nich Geg., Ges., Formeln, Einheien, Rundung...! Angaben: e =,60 0-9 C
Ingenieurtools Lösungen Einführung in Simulink
 Aufgabe Bei den Vergleichsrechnungen is zunächs auf die korreke Einsellung aller Parameer zu achen. Insbesondere müssen Simulaionsdauer, Schriweie und die Anzahl der im Scope-Block uner der Variablen S_es_Signale
Aufgabe Bei den Vergleichsrechnungen is zunächs auf die korreke Einsellung aller Parameer zu achen. Insbesondere müssen Simulaionsdauer, Schriweie und die Anzahl der im Scope-Block uner der Variablen S_es_Signale
Laplacetransformation in der Technik
 Verallgemeinere Funkionen Laplaceransformaion in der echnik Fakulä Grundlagen Februar 26 Fakulä Grundlagen Laplaceransformaion in der echnik Übersich Verallgemeinere Funkionen Verallgemeinere Funkionen
Verallgemeinere Funkionen Laplaceransformaion in der echnik Fakulä Grundlagen Februar 26 Fakulä Grundlagen Laplaceransformaion in der echnik Übersich Verallgemeinere Funkionen Verallgemeinere Funkionen
Gewöhnliche Differentialgleichungen (DGL)
 Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
I-Strecken (Strecken ohne Ausgleich)
 FELJC 7_I-Srecken.o 1 I-Srecken (Srecken ohne Ausgleich) Woher der Name? Srecken ohne Ausgleich: Bei einem Sprung der Eingangsgrösse (Sellgrösse) nimm die Ausgangsgrösse seig zu, ohne einem fesen Endwer
FELJC 7_I-Srecken.o 1 I-Srecken (Srecken ohne Ausgleich) Woher der Name? Srecken ohne Ausgleich: Bei einem Sprung der Eingangsgrösse (Sellgrösse) nimm die Ausgangsgrösse seig zu, ohne einem fesen Endwer
Abituraufgaben Grundkurs 2009 Bayern Analysis I. dt mit D F = R.
 Abiuraufgaben Grundkurs 9 Bayern Analysis I I.). Die Abbildung zeig den Graphen G f einer ganzraionalen Funkion f drien Grades mi dem Definiionsbereich D f R. Die in der Abbildung angegebenen Punke P(
Abiuraufgaben Grundkurs 9 Bayern Analysis I I.). Die Abbildung zeig den Graphen G f einer ganzraionalen Funkion f drien Grades mi dem Definiionsbereich D f R. Die in der Abbildung angegebenen Punke P(
14 Kurven in Parameterdarstellung, Tangentenvektor und Bogenlänge
 Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Kapitel : Exponentiell-beschränktes Wachstum
 Wachsumsprozesse Kapiel : Exponeniell-beschränkes Wachsum Die Grundbegriffe aus wachsum.xmcd werden auch hier verwende! Wir verwenden nun eine Angabe aus der Biologie und in einem weieren Beispiel eines
Wachsumsprozesse Kapiel : Exponeniell-beschränkes Wachsum Die Grundbegriffe aus wachsum.xmcd werden auch hier verwende! Wir verwenden nun eine Angabe aus der Biologie und in einem weieren Beispiel eines
3.4 Systeme linearer Differentialgleichungen
 58 Kapiel 3 Invarianen linearer Transformaionen 34 Syseme linearer Differenialgleichungen Die Unersuchung der Normalformen von Marizen soll nun auf die Lösung von Differenialgleichungssysemen angewende
58 Kapiel 3 Invarianen linearer Transformaionen 34 Syseme linearer Differenialgleichungen Die Unersuchung der Normalformen von Marizen soll nun auf die Lösung von Differenialgleichungssysemen angewende
MATHEMATIK 3 FÜR EI - ÜBUNGSBLATT 13 Wintersemester 2011/2012
 Prof Dr O Junge, A Biracher Zenrum Mahemaik - M3 Technische Universiä München MATHEMATIK 3 FÜR EI - ÜBUNGSBLATT 3 Winersemeser 2/22 Tuorübungsaufgaben (3-3222) Aufgabe T Berachen Sie das Anfangswerproblem
Prof Dr O Junge, A Biracher Zenrum Mahemaik - M3 Technische Universiä München MATHEMATIK 3 FÜR EI - ÜBUNGSBLATT 3 Winersemeser 2/22 Tuorübungsaufgaben (3-3222) Aufgabe T Berachen Sie das Anfangswerproblem
Ganzrationale Funktionen (Polynomfunktionen) - Berechnung von Nullstellen, Gleichungen höheren Grades -
 GS - 3.0.05 - gara_0_berechnenns.mcd Ganzraionale Funkionen (Polynomfunkionen) - Berechnung von, Gleichungen höheren Grades -. Gleichungen höheren Grades Gegeben is der Funkionserm f( ) a n n + a n n +...
GS - 3.0.05 - gara_0_berechnenns.mcd Ganzraionale Funkionen (Polynomfunkionen) - Berechnung von, Gleichungen höheren Grades -. Gleichungen höheren Grades Gegeben is der Funkionserm f( ) a n n + a n n +...
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 6 5. Semester ARBEITSBLATT 6 PARAMETERDARSTELLUNG EINER GERADEN
 ARBEITSBLATT PARAMETERDARSTELLUNG EINER GERADEN Eine Gerade sell man im R ensprechend zum R auf, nur daß eine z-koordinae hinzukomm: Definiion: Parameerdarsellung einer Gerade durch die Punke A und B:
ARBEITSBLATT PARAMETERDARSTELLUNG EINER GERADEN Eine Gerade sell man im R ensprechend zum R auf, nur daß eine z-koordinae hinzukomm: Definiion: Parameerdarsellung einer Gerade durch die Punke A und B:
2 Regelkreisverhalten
 Regelkreisverhalen Hinweise zur Lösung Das dnamische Verhalen eines regelungsechnischen Gliedes mi der Ausgangsgröße nach einem Eingangssprung ŷ wird mi Differenialgleichungen oder mi Überragungsfunkionen
Regelkreisverhalen Hinweise zur Lösung Das dnamische Verhalen eines regelungsechnischen Gliedes mi der Ausgangsgröße nach einem Eingangssprung ŷ wird mi Differenialgleichungen oder mi Überragungsfunkionen
Hörsaalübung 3 Differentialgleichungen I für Studierende der Ingenieurwissenschaften
 Fachbereich Mahemaik der Universiä Hamburg WiSe 26/27 Dr. Hanna Peywand Kiani Hörsaalübung 3 Differenialgleichungen I für Sudierende der Ingenieurwissenschafen Lineare Differenialgleichungssyseme Die ins
Fachbereich Mahemaik der Universiä Hamburg WiSe 26/27 Dr. Hanna Peywand Kiani Hörsaalübung 3 Differenialgleichungen I für Sudierende der Ingenieurwissenschafen Lineare Differenialgleichungssyseme Die ins
Integralrechnung. Grundidee der Integralrechnung. Einführung des Riemann- Integrals
 1/8 Grundidee der Inegralrechnung Inegralrechnung Die Inegralrechnung is neben der Differenialrechnung der wichigse Zweig der Analysis. Sie is aus dem Problem der Flächen- und Volumenberechnung ensanden.
1/8 Grundidee der Inegralrechnung Inegralrechnung Die Inegralrechnung is neben der Differenialrechnung der wichigse Zweig der Analysis. Sie is aus dem Problem der Flächen- und Volumenberechnung ensanden.
Bildmaterial zur Vorlesung Regelungstechnik Teil I Die Regelstrecke. Wintersemester 2014 Prof. Dr.-Ing. habil. Klaus-Peter Döge
 Bildmaerial zur Vorlesung Regelungsechnik Teil I Die Regelsrecke Winersemeser 214 Prof. Dr.-Ing. habil. Klaus-Peer Döge 2 Regelung des Füllsandes eines Flüssigkeisbehälers mi Abfluss Sollwervorgabe Regler:
Bildmaerial zur Vorlesung Regelungsechnik Teil I Die Regelsrecke Winersemeser 214 Prof. Dr.-Ing. habil. Klaus-Peer Döge 2 Regelung des Füllsandes eines Flüssigkeisbehälers mi Abfluss Sollwervorgabe Regler:
Analysis 3.
 Analysis 3 www.schulmahe.npage.de Aufgaben. Ermieln Sie die erse Ableiung. Vereinfachen Sie. a) fx) = e x x 3) b) fx) = ln x x + 4. Ermieln Sie die folgenden unbesimmen Inegrale. e x 5 a) e x dx b) dx
Analysis 3 www.schulmahe.npage.de Aufgaben. Ermieln Sie die erse Ableiung. Vereinfachen Sie. a) fx) = e x x 3) b) fx) = ln x x + 4. Ermieln Sie die folgenden unbesimmen Inegrale. e x 5 a) e x dx b) dx
Die numerische Erzeugung eines durchstimmbaren Sinussignals
 Die numerische Erzeugung eines durchsimmbaren Sinussignals Jakob Fröhling Die Hersellung eines sinusförmigen Signals is eine Aufgabensellung aus der Messechnik. Für die Messung bei einer Frequenz soll
Die numerische Erzeugung eines durchsimmbaren Sinussignals Jakob Fröhling Die Hersellung eines sinusförmigen Signals is eine Aufgabensellung aus der Messechnik. Für die Messung bei einer Frequenz soll
Zeit (in h) Ausflussrate (in l/h)
 Aufgabe 6 (Enwicklung einer Populaion): (Anforderungen: Inerpreaion von Schaubildern; Inegralfunkion in der Praxis) Von einer Populaion wird - jeweils in Abhängigkei von der Zei - die Geburenrae (in Individuen
Aufgabe 6 (Enwicklung einer Populaion): (Anforderungen: Inerpreaion von Schaubildern; Inegralfunkion in der Praxis) Von einer Populaion wird - jeweils in Abhängigkei von der Zei - die Geburenrae (in Individuen
Struktur und Verhalten I
 Kapiel 9 Srukur und Verhalen I Ganz allgemein gesag is das Thema dieses Kurses die Ersellung, Simulaion und Unersuchung von Modellen räumlich homogener dynamischer Syseme aus Naur und Technik. Wir haben
Kapiel 9 Srukur und Verhalen I Ganz allgemein gesag is das Thema dieses Kurses die Ersellung, Simulaion und Unersuchung von Modellen räumlich homogener dynamischer Syseme aus Naur und Technik. Wir haben
Elementare Lösungsmethoden für gewöhnliche Differentialgleichungen
 454 Erforderliche Kennnisse: Höhere Analysis Elemenare Lösungsmehoden für gewöhnliche Differenialgleichungen Was is eigenlich eine Differenialgleichung? Eine Differenialgleichung is eine Gleichung, in
454 Erforderliche Kennnisse: Höhere Analysis Elemenare Lösungsmehoden für gewöhnliche Differenialgleichungen Was is eigenlich eine Differenialgleichung? Eine Differenialgleichung is eine Gleichung, in
III.2 Radioaktive Zerfallsreihen
 N.BORGHINI Version vom 5. November 14, 13:57 Kernphysik III. Radioakive Zerfallsreihen Das Produk eines radioakiven Zerfalls kann selbs insabil sein und späer zerfallen, und so weier, sodass ganze Zerfallsreihen
N.BORGHINI Version vom 5. November 14, 13:57 Kernphysik III. Radioakive Zerfallsreihen Das Produk eines radioakiven Zerfalls kann selbs insabil sein und späer zerfallen, und so weier, sodass ganze Zerfallsreihen
Kapitel 6: Ort, Geschwindigkeit und Beschleunigung als Funktion der Zeit
 Kapiel 6: Or, Geschwindigkei und Beschleunigung als Funkion der Zei 2 Kapiel 6: Or, Geschwindigkei und Beschleunigung als Funkion der Zei Einführung Lerninhal Einführung 3 Das Programm yzet erlaub es,
Kapiel 6: Or, Geschwindigkei und Beschleunigung als Funkion der Zei 2 Kapiel 6: Or, Geschwindigkei und Beschleunigung als Funkion der Zei Einführung Lerninhal Einführung 3 Das Programm yzet erlaub es,
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt Semester ARBEITSBLATT 11 LAGEBEZIEHUNG DREIER EBENEN
 Mahemaik Mag. Schmid Wolfgang Arbeisbla. Semeser ARBEITSBLATT LAGEBEZIEHUNG DREIER EBENEN Nachdem wir die Lage weier Ebenen unersuch haben, wollen wir uns nun mi der Lage von drei Ebenen beschäfigen. Anders
Mahemaik Mag. Schmid Wolfgang Arbeisbla. Semeser ARBEITSBLATT LAGEBEZIEHUNG DREIER EBENEN Nachdem wir die Lage weier Ebenen unersuch haben, wollen wir uns nun mi der Lage von drei Ebenen beschäfigen. Anders
Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkeit Seminararbeit aus Numerik von Differentialgleichungen
 Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkei Seminararbei aus Numerik von Differenialgleichungen Michael Hubner, Sefan Wurm 8. Juli 22 Inhalsverzeichnis. Problemdefiniion 2 2. Einführende
Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkei Seminararbei aus Numerik von Differenialgleichungen Michael Hubner, Sefan Wurm 8. Juli 22 Inhalsverzeichnis. Problemdefiniion 2 2. Einführende
Eigenwerte und Eigenvektoren
 Eigenwere un Eigenvekoren Vorbemerkung: Is ie n n Marix inverierbar, so ha as lineare Gleichungssysem A x b für jees b genau eine Lösung, nämlich x A b. Grun: i A x A A b b, ii Is y eine weiere Lösung,
Eigenwere un Eigenvekoren Vorbemerkung: Is ie n n Marix inverierbar, so ha as lineare Gleichungssysem A x b für jees b genau eine Lösung, nämlich x A b. Grun: i A x A A b b, ii Is y eine weiere Lösung,
Lösungshinweise zu den Hausaufgaben:
 P. Engel, T. Pfrommer S. Poppiz, Dr. I. Rbak 8. Gruppenübung zur Vorlesung Höhere Mahemaik Sommersemeser 9 Prof. Dr. M. Sroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe H. Konvergenzverhalen
P. Engel, T. Pfrommer S. Poppiz, Dr. I. Rbak 8. Gruppenübung zur Vorlesung Höhere Mahemaik Sommersemeser 9 Prof. Dr. M. Sroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe H. Konvergenzverhalen
Leseprobe. Ines Rennert, Bernhard Bundschuh. Signale und Systeme. Einführung in die Systemtheorie. ISBN (Buch):
 Leseprobe Ines Renner, Bernhard Bundschuh Signale und Syseme Einführung in die Sysemheorie ISBN (Buch): 978-3-446-43327-4 ISBN (E-Book): 978-3-446-43328- Weiere Informaionen oder Besellungen uner hp://www.hanser-fachbuch.de/978-3-446-43327-4
Leseprobe Ines Renner, Bernhard Bundschuh Signale und Syseme Einführung in die Sysemheorie ISBN (Buch): 978-3-446-43327-4 ISBN (E-Book): 978-3-446-43328- Weiere Informaionen oder Besellungen uner hp://www.hanser-fachbuch.de/978-3-446-43327-4
Numerisches Programmieren
 Technische Universiä München WS 11/1 Insiu für Informaik Prof. Dr. Hans-Joachim Bungarz Michael Lieb, M. Sc. Dipl.-Inf. Chrisoph Riesinger Dipl.-Inf. Marin Schreiber Numerisches Programmieren 4. Programmieraufgabe:
Technische Universiä München WS 11/1 Insiu für Informaik Prof. Dr. Hans-Joachim Bungarz Michael Lieb, M. Sc. Dipl.-Inf. Chrisoph Riesinger Dipl.-Inf. Marin Schreiber Numerisches Programmieren 4. Programmieraufgabe:
Berechnungen am Wankelmotor
 HTL Saalfelen Wankelmoor Seie von 7 Schmihuber Heinrich heinrich_schmihuber@homail.com Berechnungen am Wankelmoor Link zur Beispielsübersich Mahemaische / Fachliche Inhale in Sichworen: Linieninegral,
HTL Saalfelen Wankelmoor Seie von 7 Schmihuber Heinrich heinrich_schmihuber@homail.com Berechnungen am Wankelmoor Link zur Beispielsübersich Mahemaische / Fachliche Inhale in Sichworen: Linieninegral,
Übungen zur Einführung in die Physik II (Nebenfach)
 Übungen zur Einführung in ie Physik Nebenfach --- Muserlösung --- Aufgabe: Konensaorenlaung Ein mi Glimmer ε r = 8 gefüller Plaenkonensaor mi er Fläche A=6 cm un einem Plaenabsan = 5 μm enlä sich wegen
Übungen zur Einführung in ie Physik Nebenfach --- Muserlösung --- Aufgabe: Konensaorenlaung Ein mi Glimmer ε r = 8 gefüller Plaenkonensaor mi er Fläche A=6 cm un einem Plaenabsan = 5 μm enlä sich wegen
Übungen zur Experimentalphysik II Aufgabenblatt 3 - Lösung
 KW /15 Prof. Dr. R. Reifarh, Dr. J. Glorius Übungen zur Experimenalphysik II Aufgabenbla 3 - Lösung Aufgabe 1: a) Die Laung q im Volumen V beräg: q = ρ(r) V = ρ(r)4πr r = 4πAr 3 r Für ie Laung Q erhalen
KW /15 Prof. Dr. R. Reifarh, Dr. J. Glorius Übungen zur Experimenalphysik II Aufgabenbla 3 - Lösung Aufgabe 1: a) Die Laung q im Volumen V beräg: q = ρ(r) V = ρ(r)4πr r = 4πAr 3 r Für ie Laung Q erhalen
Hubschrauber PID-Regelung, versuchsweise auch mit AntiWindUp
 Prof. Dr. R. Kessler, HS-Karlsruhe, Hub_PID_AU.doc S / Homepage: http://www.home.hs-karlsruhe.de/~kero Hubschrauber PID-Regelung, versuchsweise auch mit AntiindUp Link auf die bisherige optimale PID-Regelung
Prof. Dr. R. Kessler, HS-Karlsruhe, Hub_PID_AU.doc S / Homepage: http://www.home.hs-karlsruhe.de/~kero Hubschrauber PID-Regelung, versuchsweise auch mit AntiindUp Link auf die bisherige optimale PID-Regelung
f ( x) = x + x + 1 (quadratische Funktion) f '( x) = x + (Ableitungsfunktion)
 R. Brinkmann hp://brinkmann-du.de Seie.. Tangene und Normale Tangenenseigung Die Seigung eines Funkionsgraphen in einem Punk P ( f ( ) ) is gleichbedeuend mi der Seigung der Tangene in diesem Punk. Nachfolgend
R. Brinkmann hp://brinkmann-du.de Seie.. Tangene und Normale Tangenenseigung Die Seigung eines Funkionsgraphen in einem Punk P ( f ( ) ) is gleichbedeuend mi der Seigung der Tangene in diesem Punk. Nachfolgend
Diese 3 Signale haben als Anregungssignale am Eingang eines Systems besondere Bedeutung für die lineare Systemtheorie erlangt.
 16 2.3 Sprungfunkion, Rampenfunkion Delafunkion Diese 3 Signale haben als Anregungssignale am Eingang eines Sysems besondere Bedeuung für die lineare Sysemheorie erlang. Sprungfunkion: ( σ ( ), 1( ) )
16 2.3 Sprungfunkion, Rampenfunkion Delafunkion Diese 3 Signale haben als Anregungssignale am Eingang eines Sysems besondere Bedeuung für die lineare Sysemheorie erlang. Sprungfunkion: ( σ ( ), 1( ) )
Leistungselektronik Grundlagen und Standardanwendungen. Übung 3: Kommutierung
 Lehrsuhl für Elekrische Anriebssyseme und Leisungselekronik Technische Universiä München Arcissraße 1 D 8333 München Email: eal@ei.um.de Inerne: hp://www.eal.ei.um.de Prof. Dr.-Ing. Ralph Kennel Tel.:
Lehrsuhl für Elekrische Anriebssyseme und Leisungselekronik Technische Universiä München Arcissraße 1 D 8333 München Email: eal@ei.um.de Inerne: hp://www.eal.ei.um.de Prof. Dr.-Ing. Ralph Kennel Tel.:
Leseprobe. Thema: 9 REGELUNGSTECHNIK...2. Regelungstechnik. 9.1 Grundbegriffe Steuern... 3
 9 REGELUNGSTECHNIK...2 9.1 Grundbegriffe... 2 9.2 Seuern... 3 9.3 Regeln... 3 9.3.1 Unseig wirkende Regeleinrichungen... 5 9.3.2 Seig wirkende Regeleinrichungen... 6 9.3.2.1 roporionalregler (-Regler)...
9 REGELUNGSTECHNIK...2 9.1 Grundbegriffe... 2 9.2 Seuern... 3 9.3 Regeln... 3 9.3.1 Unseig wirkende Regeleinrichungen... 5 9.3.2 Seig wirkende Regeleinrichungen... 6 9.3.2.1 roporionalregler (-Regler)...
Das lineare H-unendlich Problem
 Das lineare H-unendlich Problem Salah-Eddine Sessou Seminarvorrag vom. Juli 6. Problemsellung Bild z P x u K Der Regler (Konroller)K ha zei Eingänge, x und den exogenen Eingang. Das H-unendlich Problem
Das lineare H-unendlich Problem Salah-Eddine Sessou Seminarvorrag vom. Juli 6. Problemsellung Bild z P x u K Der Regler (Konroller)K ha zei Eingänge, x und den exogenen Eingang. Das H-unendlich Problem
5. Übungsblatt zur Linearen Algebra II
 Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
Sinus und Cosinus im rechtwinkligen Dreieck ( )
 Sinus und Cosinus im rechwinkligen Dreieck (6.8.8) Ankahee. Hpoenuse Gegenkahee sin = cos = an = Gegenkahee Hpoenuse Ankahee Hpoenuse Gegenkahee Ankahee Was ha das rechwinklige Dreieck mi Schwingungen
Sinus und Cosinus im rechwinkligen Dreieck (6.8.8) Ankahee. Hpoenuse Gegenkahee sin = cos = an = Gegenkahee Hpoenuse Ankahee Hpoenuse Gegenkahee Ankahee Was ha das rechwinklige Dreieck mi Schwingungen
1. Kontrolle Physik Grundkurs Klasse 11
 1. Konrolle Phyik Grundkur Klae 11 1. Ein Luch lauer eine Haen auf und lä e da ahnungloe und chackhafe Tier bi auf 30,0 herankoen. Dann prine er i 68 k/h auf ein Opfer lo, da ofor davon renn. Nach 5,0
1. Konrolle Phyik Grundkur Klae 11 1. Ein Luch lauer eine Haen auf und lä e da ahnungloe und chackhafe Tier bi auf 30,0 herankoen. Dann prine er i 68 k/h auf ein Opfer lo, da ofor davon renn. Nach 5,0
Übungsblatt 8 Musterlösung
 Numerik gewöhnlicher Differenialgleichungen MA - SS6 Übungsbla 8 Muserlösung Aufgabe 7 Schriweienseuerung) Im Folgenden soll die Differenzialgleichung y ) = f,y)) = sign)y, y ) = e, im Zeiinervall [, ]
Numerik gewöhnlicher Differenialgleichungen MA - SS6 Übungsbla 8 Muserlösung Aufgabe 7 Schriweienseuerung) Im Folgenden soll die Differenzialgleichung y ) = f,y)) = sign)y, y ) = e, im Zeiinervall [, ]
Übungsserie: Single-Supply, Gleichrichter Dioden Anwendungen
 1. Mai 216 Elekronik 1 Marin Weisenhorn Übungsserie: Single-Supply, Gleichricher Dioden Anwendungen Aufgabe 1. Gleichricher In dieser Gleichricherschalung für die USA sei f = 6 Hz. Der Effekivwer der Ausgangspannung
1. Mai 216 Elekronik 1 Marin Weisenhorn Übungsserie: Single-Supply, Gleichricher Dioden Anwendungen Aufgabe 1. Gleichricher In dieser Gleichricherschalung für die USA sei f = 6 Hz. Der Effekivwer der Ausgangspannung
Fouerierreihen - eine Einführung
 HBL Kapfenberg Fourierreiehen - eine Einführung Seie 1 von 19 Roland Pichler roland.pichler@hl-kapfenberg.ac.a Fouerierreihen - eine Einführung Mahemaische / Fachliche Inhale in Sichworen: Inegralrechnung,
HBL Kapfenberg Fourierreiehen - eine Einführung Seie 1 von 19 Roland Pichler roland.pichler@hl-kapfenberg.ac.a Fouerierreihen - eine Einführung Mahemaische / Fachliche Inhale in Sichworen: Inegralrechnung,
Schriftliche Prüfung aus Control Systems 1 (Information and Computer Engineering) am
 TU Graz, Insiu für Regelungs- und Auomaisierungsechnik Schrifliche Prüfung aus Conrol Sysems (Informaion and Compuer Engineering) am 04.07.06 Name / Vorname(n): Marikel-Nummer: Aufgabe A A A3 A4 A5 A6
TU Graz, Insiu für Regelungs- und Auomaisierungsechnik Schrifliche Prüfung aus Conrol Sysems (Informaion and Compuer Engineering) am 04.07.06 Name / Vorname(n): Marikel-Nummer: Aufgabe A A A3 A4 A5 A6
Motivation: Sampling. (14) Sampling. Motivation: Sampling. Beispiele. Beispiel Kreisscheibe. Beispiel: Kreisscheibe
 Moivaion: Sampling (4) Sampling Vorlesung Phoorealisische Compuergraphik S. Müller Ein naiver (und sehr eurer) Ansaz, die Rendering Equaion mi Hilfe eines Rayracing-Ansazes zu lösen, wäre wird eine diffuse
Moivaion: Sampling (4) Sampling Vorlesung Phoorealisische Compuergraphik S. Müller Ein naiver (und sehr eurer) Ansaz, die Rendering Equaion mi Hilfe eines Rayracing-Ansazes zu lösen, wäre wird eine diffuse
Statistische Analysen am Rechner: Eine Einführung
 Saisische Analysen am Rechner: Eine Einführung Diese Rechnerübung soll einen ersen Einblick in das Programm EViews geben. Dafür werden der Akienmarkindex DAX und der Index des Renenmarkes REX für den Zeiraum
Saisische Analysen am Rechner: Eine Einführung Diese Rechnerübung soll einen ersen Einblick in das Programm EViews geben. Dafür werden der Akienmarkindex DAX und der Index des Renenmarkes REX für den Zeiraum
u(t) sin(kωt)dt, k > 0
 Übung 7 /Grundgebiee der Elekroechnik 3 WS7/8 Fourieranalyse Dr. Alexander Schaum, Lehrsuhl für verneze elekronische Syseme Chrisian-Albrechs-Universiä zu Kiel mi Im folgenden wird die Fourierreihe = a
Übung 7 /Grundgebiee der Elekroechnik 3 WS7/8 Fourieranalyse Dr. Alexander Schaum, Lehrsuhl für verneze elekronische Syseme Chrisian-Albrechs-Universiä zu Kiel mi Im folgenden wird die Fourierreihe = a
(2) Kinematik. Vorlesung Animation und Simulation S. Müller U N I V E R S I T Ä T KOBLENZ LANDAU
 () Kinemaik Vorlesung Animaion und Simulaion S. Müller KOBLENZ LANDAU Wiederholung I roblem (ersmal): Kamerainerpolaion Augpunk und Blickrichung Gue Wahl: Hermie-Splines Definiion von Keyframes Knoenpunk
() Kinemaik Vorlesung Animaion und Simulaion S. Müller KOBLENZ LANDAU Wiederholung I roblem (ersmal): Kamerainerpolaion Augpunk und Blickrichung Gue Wahl: Hermie-Splines Definiion von Keyframes Knoenpunk
Höhere Mathematik II für die Fachrichtung Physik
 Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Michael Ho, M. Sc. M. Sc. SS 6 9.7.6 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zur Übungsklausur Aufgabe
Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Michael Ho, M. Sc. M. Sc. SS 6 9.7.6 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zur Übungsklausur Aufgabe
Prüfungsaufgaben Wiederholungsklausur
 NIVESITÄT LEIPZIG Insiu für Informaik Prüfungsaufgaben Wiederholungsklausur Ab. Technische Informaik Prof. Dr. do Kebschull Dr. Hans-Joachim Lieske 5. März / 9 - / H7 Winersemeser 999/ Aufgaben zur Wiederholungsklausur
NIVESITÄT LEIPZIG Insiu für Informaik Prüfungsaufgaben Wiederholungsklausur Ab. Technische Informaik Prof. Dr. do Kebschull Dr. Hans-Joachim Lieske 5. März / 9 - / H7 Winersemeser 999/ Aufgaben zur Wiederholungsklausur
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 7 5. Semester ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE
 Mahemaik: Mag. Schmid Wolfgang Arbeibla 7. Semeer ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE Im Raum möche man naürlich nich nur Geraden ondern auch Flächen darellen. Diee Flächen bezeichne man al
Mahemaik: Mag. Schmid Wolfgang Arbeibla 7. Semeer ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE Im Raum möche man naürlich nich nur Geraden ondern auch Flächen darellen. Diee Flächen bezeichne man al
Beispiel aus der Schwingungslehre: Sinus-Erregung mit veränderlicher Frequenz ( Sweep )
 Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsystemstechnik, SweepFedMas.doc, S. / homepage: http://www.home.hs-karlsruhe.de/~kero/ Beispiel aus der Schwingungslehre: Sinus-Erregung mit veränderlicher Frequenz
Prof. Dr. R. Kessler, FH-Karlsruhe, Sensorsystemstechnik, SweepFedMas.doc, S. / homepage: http://www.home.hs-karlsruhe.de/~kero/ Beispiel aus der Schwingungslehre: Sinus-Erregung mit veränderlicher Frequenz
Exponential- und Logarithmusfunktionen
 . ) Personen, Personen bzw. Personen ) Ewas weniger als Minuen. (Nach,... Minuen sind genau Personen informier.) ) Ja. Bereis um : Uhr sind (heoreisch) Personen informier. ) Informiere Miarbeierinnen und
. ) Personen, Personen bzw. Personen ) Ewas weniger als Minuen. (Nach,... Minuen sind genau Personen informier.) ) Ja. Bereis um : Uhr sind (heoreisch) Personen informier. ) Informiere Miarbeierinnen und
Höhere Mathematik III für die Fachrichtung Elektrotechnik und Informationstechnik Lösungsvorschläge zum 6. Übungsblatt
 Karlruher Iniu für Technologie KIT Iniu für Analyi Dr Ioanni Anapoliano Dr Semjon Wugaler WS 25/26 Höhere Mahemaik III für die Fachrichung Elekroechnik und Informaionechnik Löungvorchläge zum 6 Übungbla
Karlruher Iniu für Technologie KIT Iniu für Analyi Dr Ioanni Anapoliano Dr Semjon Wugaler WS 25/26 Höhere Mahemaik III für die Fachrichung Elekroechnik und Informaionechnik Löungvorchläge zum 6 Übungbla
Abschlussprüfung an Fachoberschulen in Bayern Mathematik mit CAS 2015 Analysis A2 Ausbildungsrichtung Technik
 MK.7.05 B5_T_A MK_Loes.xmc Abschlussprüfung an Fachoberschulen in Bayern Mahemaik mi 05 Analysis A Ausbilungsrichung Technik.0 Gegeben sin ie reellen Funkionen f a : x --> x x x Definiionsmenge D fa R
MK.7.05 B5_T_A MK_Loes.xmc Abschlussprüfung an Fachoberschulen in Bayern Mahemaik mi 05 Analysis A Ausbilungsrichung Technik.0 Gegeben sin ie reellen Funkionen f a : x --> x x x Definiionsmenge D fa R
7. Funktionalgleichung der Zeta-Funktion
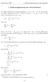 Oo Forser: RZF 7 Funkionalgleichung der Zea-Funkion 7 Funkionalgleichung der Zea-Funkion 7 Saz (Poissonsche Summaionsformel Sei f : R C eine seig differenzierbare Funkion mi f(x O ( x für x Sei ˆf : R
Oo Forser: RZF 7 Funkionalgleichung der Zea-Funkion 7 Funkionalgleichung der Zea-Funkion 7 Saz (Poissonsche Summaionsformel Sei f : R C eine seig differenzierbare Funkion mi f(x O ( x für x Sei ˆf : R
Gewöhnliche Differentialgleichungen
 Prof. Dr. Guido Sweers WS 08/09 Jan Gerdung, M.Sc. Gewöhnliche Differenialgleichungen Übungsbla Die Lösungen müssen in den Übungsbriefkasen Gewöhnliche Differenialgleichungen (Raum 0 im MI) geworfen werden.
Prof. Dr. Guido Sweers WS 08/09 Jan Gerdung, M.Sc. Gewöhnliche Differenialgleichungen Übungsbla Die Lösungen müssen in den Übungsbriefkasen Gewöhnliche Differenialgleichungen (Raum 0 im MI) geworfen werden.
e sx y(x)dx 2. Direkt gemäss der Definition unter Verwendung der in der Vorlesung angeführten Eigenschaften
 Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
A.24 Funktionsscharen 1
 A.24 Funkionsscharen Das Buch: Dieses Kapiel is Teil eines Buches. Das vollsändige Buch können Sie uner www.mahe-laden.de besellen (falls Sie das möchen). Sie werden in diesem Buch ein paar Sachen finden,
A.24 Funkionsscharen Das Buch: Dieses Kapiel is Teil eines Buches. Das vollsändige Buch können Sie uner www.mahe-laden.de besellen (falls Sie das möchen). Sie werden in diesem Buch ein paar Sachen finden,
1 Lokale Änderungsrate und Gesamtänderung
 Schülerbuchseie Lösungen vorläufig I Inegralrechnung Lokale Änderungsrae und Gesamänderung S. S. b h = m s ( s) + m s s + m s ( s) = 7 m Fläche = 7 FE a) s =, h km h +, h km h +, h km h +, h km h +,, h
Schülerbuchseie Lösungen vorläufig I Inegralrechnung Lokale Änderungsrae und Gesamänderung S. S. b h = m s ( s) + m s s + m s ( s) = 7 m Fläche = 7 FE a) s =, h km h +, h km h +, h km h +, h km h +,, h
Signal- und Systemtheorie for Dummies
 FB Eleroechni Ewas Signal- und Sysemheorie or Dummies Version - Juli Oh No!!!! Pro. Dr.-Ing. ajana Lange Fachhochschule Merseburg FB Eleroechni Pro. Dr.-Ing. ajana Lange Signal- und Sysemheorie or Dummies
FB Eleroechni Ewas Signal- und Sysemheorie or Dummies Version - Juli Oh No!!!! Pro. Dr.-Ing. ajana Lange Fachhochschule Merseburg FB Eleroechni Pro. Dr.-Ing. ajana Lange Signal- und Sysemheorie or Dummies
Aktiver Tiefpass 6. Ordnung, Frequenzbereich u. Zeitbereich
 Prof. Dr. R. Kessler, HS-Karlsruhe, C:\Si5\HOMEPAGE\akttiefpass\AktiverTiefpass 6_2.doc, S. /7 Homepage: http://www.home.hs-karlsruhe.de/~kero/ Aktiver Tiefpass 6. Ordnung, Frequenzbereich u. Zeitbereich
Prof. Dr. R. Kessler, HS-Karlsruhe, C:\Si5\HOMEPAGE\akttiefpass\AktiverTiefpass 6_2.doc, S. /7 Homepage: http://www.home.hs-karlsruhe.de/~kero/ Aktiver Tiefpass 6. Ordnung, Frequenzbereich u. Zeitbereich
Analysis: Exponentialfunktionen Analysis
 www.mahe-aufgaben.com Analysis: Eponenialfunkionen Analysis Übungsaufgaben u Eponenialfunkionen Pflich- und Wahleil gesames Soffgebie (insbesondere Funkionsscharen) ohne Wachsum Gymnasium ab J Aleander
www.mahe-aufgaben.com Analysis: Eponenialfunkionen Analysis Übungsaufgaben u Eponenialfunkionen Pflich- und Wahleil gesames Soffgebie (insbesondere Funkionsscharen) ohne Wachsum Gymnasium ab J Aleander
Fit für die Q-Phase? Mathematiktraining für die Schüler und Schülerinnen des Beruflichen Gymnasiums Gelnhausen
 Fi für die Q-Phase? Mahemaikraining für die Schüler und Schülerinnen des. Gleichungen (mi und ohne Parameer) Löse folgende Gleichungen:. 4 7.6 e ( e )..7 4 4 k k. 6.8 6 0.4 4 4 4 49.9 cos..0 4.6. e e.7
Fi für die Q-Phase? Mahemaikraining für die Schüler und Schülerinnen des. Gleichungen (mi und ohne Parameer) Löse folgende Gleichungen:. 4 7.6 e ( e )..7 4 4 k k. 6.8 6 0.4 4 4 4 49.9 cos..0 4.6. e e.7
Mathematische Methoden in den Ingenieurwissenschaften 4. Übungsblatt
 Prof Dr M Gerds Dr A Dreves J Michael Winerrimeser 6 Mahemaische Mehoden in den Ingenieurwissenschafen 4 Übungsbla Aufgabe 9 : Mehrmassenschwinger Berache wird ein schwingendes Sysem aus Körpern der Masse
Prof Dr M Gerds Dr A Dreves J Michael Winerrimeser 6 Mahemaische Mehoden in den Ingenieurwissenschafen 4 Übungsbla Aufgabe 9 : Mehrmassenschwinger Berache wird ein schwingendes Sysem aus Körpern der Masse
Leibnizschule Hannover
 Leibnizschule Hannover - Seminararbei - Medikameneneinnahme -Modellierung- M D Schuljahr: 20 Fach: Mahemaik Inhalsverzeichnis 1 Einleiung 2 2 Einfache Verabreichung 3 21 Die inravenöse Variane 3 22 Die
Leibnizschule Hannover - Seminararbei - Medikameneneinnahme -Modellierung- M D Schuljahr: 20 Fach: Mahemaik Inhalsverzeichnis 1 Einleiung 2 2 Einfache Verabreichung 3 21 Die inravenöse Variane 3 22 Die
Kommunikationstechnik I
 Kommunikaionsechnik I Prof. Dr. Sefan Weinzierl Muserlösung 5. Aufgabenbla 1. Moden 1.1 Erläuern Sie, was in der Raumakusik uner Raummoden versanden wird. Der Begriff einer sehenden Welle läss sich am
Kommunikaionsechnik I Prof. Dr. Sefan Weinzierl Muserlösung 5. Aufgabenbla 1. Moden 1.1 Erläuern Sie, was in der Raumakusik uner Raummoden versanden wird. Der Begriff einer sehenden Welle läss sich am
Grundgebiete der Elektrotechnik II Feedbackaufgabe: Transiente Vorgänge
 heinisch-wesfälische Technische Hochschule Aachen Insiu für Sromricherechni und Elerische Anriebe Universiäsprofessor Dr. ir. i W. De Doncer Grundgebiee der Eleroechni II Feedbacaufgabe: Transiene Vorgänge
heinisch-wesfälische Technische Hochschule Aachen Insiu für Sromricherechni und Elerische Anriebe Universiäsprofessor Dr. ir. i W. De Doncer Grundgebiee der Eleroechni II Feedbacaufgabe: Transiene Vorgänge
A.24 Funktionsscharen 1
 A.4 Funkionsscharen A.4 Funkionsscharen ( ) Bemerkung: Im Buch Kurvenprobleme gib es viel Aufgaben zu Funkionen, die einen Parameer enhalen. Falls Sie hier also nich genug kriegen... A.4.0 Orskurven (
A.4 Funkionsscharen A.4 Funkionsscharen ( ) Bemerkung: Im Buch Kurvenprobleme gib es viel Aufgaben zu Funkionen, die einen Parameer enhalen. Falls Sie hier also nich genug kriegen... A.4.0 Orskurven (
Versuch 1 Schaltungen der Messtechnik
 Fachhochschule Merseburg FB Informaik und Angewande Naurwissenschafen Prakikum Messechnik Versuch 1 Schalungen der Messechnik Analog-Digial-Umsezer 1. Aufgaben 1. Sägezahn-Umsezer 1.1. Bauen Sie einen
Fachhochschule Merseburg FB Informaik und Angewande Naurwissenschafen Prakikum Messechnik Versuch 1 Schalungen der Messechnik Analog-Digial-Umsezer 1. Aufgaben 1. Sägezahn-Umsezer 1.1. Bauen Sie einen
Motivation der Dierenzial- und Integralrechnung
 Moivaion der Dierenzial- und Inegralrechnung Fakulä Grundlagen HS Esslingen SS 2016 Fakulä Grundlagen (HS Esslingen) SS 2016 1 / 12 Übersich 1 Vorberachungen zur Dierenzial- und Inegralrechnung Ableiungsbegri
Moivaion der Dierenzial- und Inegralrechnung Fakulä Grundlagen HS Esslingen SS 2016 Fakulä Grundlagen (HS Esslingen) SS 2016 1 / 12 Übersich 1 Vorberachungen zur Dierenzial- und Inegralrechnung Ableiungsbegri
Kapitel 4. Versuch 415 T-Flipflop
 Kapiel 4 Versuch 415 T-Flipflop Flipflops, die mi jeder seigenden oder mi jeder fallenden Takflanke in den engegengesezen Zusand kippen, heissen T Flipflops ( Toggle Flipflops ). T-Flipflops können aus
Kapiel 4 Versuch 415 T-Flipflop Flipflops, die mi jeder seigenden oder mi jeder fallenden Takflanke in den engegengesezen Zusand kippen, heissen T Flipflops ( Toggle Flipflops ). T-Flipflops können aus
