Kapitel 8: Zeitdiskrete Zufallssignale

Transkript

1 ZHAW, DSV2, 2007, Rumc, 8-1 Kapitel 8: Zeitdiskrete Zufallssignale Inhaltsverzeichnis 1. STOCHASTISCHER PROZESS STATISTISCHE EIGENSCHAFTEN EINER ZUFALLSVARIABLEN STATISTISCHE EIGENSCHAFTEN VON 2 ZUFALLSVARIABLEN STATISTISCHE EIGENSCHAFTEN VON ZUFALLSSIGNALEN BESCHREIBUNG VON ZUFALLSSIGNALEN IM FREQUENZBEREICH DISKRETE FILTERUNG VON ZUFALLSSIGNALEN...11 Literatur [1] S.J. Mitra, Digital Signal Processing, 3rd Edition, Mc Graw Hill, 2006, ISBN Stochastischer Prozess Das zeitdiskrete Zufallssignal Z[.] =..., Z[-1], Z[0], Z[1],... ist ein stochastischer Prozess und besteht typischerweise aus einer unendlich langen Folge bzw. einem Ensemble von Zufallsvariablen Z[n], n = -,...,. Der Verlauf eines Zufallssignals Z[.] lässt sich nicht mit einer mathematischen Formel beschreiben. Man kann aber die statistischen Eigenschaften wie z.b. den Mittelwert der Amplitude der Zufallsvariablen Z[n] zum Zeitpunkt nt s beschreiben. Weiter kann man auch den statistischen Zusammenhang zwischen den Zufallsvariablen Z[m] und Z[n] zu den Zeitpunkten mt s und nt s beschreiben. In Abbildung 8-1 sind zwei verschiedene Musterverläufe eines zeitdiskreten Zufallssignals Z[.] dargestellt.

2 ZHAW, DSV2, 2007, Rumc, 8-2 Abbildung 8-1: Zwei verschiedene Musterverläufe eines zeitdiskreten Zufallssignals. Die Amplitude der Zufallsvariablen Z[n] ist in diesem Beispiel mittelwertfrei und normalbzw. gaussverteilt, unabhängig vom Zeitpunkt nt s. Kleine Werte sind also wahrscheinlicher als grosse Werte. Es ist kein statistischer Zusammenhang zwischen zwei aufeinander folgenden Zufallsvariablen Z[n] und Z[n+1] zu erkennen. Das Signal ändert manchmal beliebig schnell. 2. Statistische Eigenschaften von 1 Zufallsvariablen Die statistischen Eigenschaften einer Zufallsvariablen Z hängen von ihrer Wahrscheinlichkeitsdichtefunktion p Z (z) ab. Für jede Wahrscheinlichkeitsdichtefunktion p Z (z) gilt: p z(z) dz=1 - (8.1) P(z<α) α = p z(z) dz (8.2) Der Mittelwert E{Z} und der quadratische Mittelwert E{Z 2 } einer reellwertigen Zufallsvariablen Z sind wie folgt definiert: E{Z} = z p z(z) dz, (8.3) 2 E{Z } = z 2 p z(z) dz. (8.4)

3 ZHAW, DSV2, 2007, Rumc, 8-3 Der Erwartungswert E{.} ist ein linearer Operator, d.h. für zwei Zufallsvariablen Z 1 und Z 2 und zwei Konstanten k 1 und k 2 gilt: E{k 1 Z 1 +k 2 Z 2 } = k 1 E{Z 1 } + k 2 E{Z 2 }. (8.5) Die Varianz ist die mittlere quadratische Abweichung vom Mittelwert E{Z}, d.h. Var(Z) = E{ (Z-E{Z}) 2 } (8.6) Durch Ausmultiplizieren und Verwenden der Linearitätseigenschaft (8.5) erhält man die nützliche Identität Var(Z) = E{Z 2 } (E{Z}) 2. (8.7) Die Standardabweichung ist wie folgt definiert: σ Z = (Var(Z)). Betrachten Sie die uniforme Wahrscheinlichkeitsdichtefunktion p Z (z) der Zufallsvariablen Z in Abbildung p Z (z) 1 Abbildung 8-2: Uniforme Wahrscheinlichkeitsdichtefunktion. Diese Wahrscheinlichkeitsdichtefunktion p Z (z) erfüllt die Bedingung (8.1). Die Wahrscheinlichkeit P(z<0.75), dass der Wert z der Zufallsvariablen Z kleiner als 0.75 ist, ist 75%. Für den Mittelwert und den quadratischen Mittelwert gelten: E{Z} = 1/2 und E[Z 2 ] = 1/3. Für die Varianz gilt mit (8.7): Var(Z) = 1/3 (1/2) 2 = 1/12. In Abbildung 8-3 ist die Gauss sche Wahrscheinlichkeitsdichtefunktion Z 2 (z-e[z]) - 2 2σ Z 1 p Z(z)= e σ 2π (8.8) mit Mittelwert E{Z} = 0 und Standardabweichung σ Z = (Var(Z) = 1 dargestellt.

4 ZHAW, DSV2, 2007, Rumc, 8-4 Abbildung 8-3: Wahrscheinlichkeitsdichtefuntkion einer Gauss schen Zufallsvariablen mit Mittelwert Null und Standardabweichung 1. Bekanntlich liegen fast 70% der Werte z der Zufallsvariablen Z im Intervall [-σ Z, σ Z ] und ca. 95% im Intervall [-2σ Z, 2σ Z ]. Diese Tatsache folgt aus Gleichung (8.2) und den Tabellenwerten P(z 1) = bzw. P(z 2) = sowie der Symmetrieeigenschaft P(z -α) = 1 - P(z α). Es gibt auch Zufallsvariablen, die nur diskrete Amplitudenwerte z k annehmen können. Für solche Zufallsvariablen sind die Gleichungen (8.1) bis (8.4) entsprechend zu modifizieren (Summen statt Integrale). Betrachten Sie die Augenzahl Z eines fairen Würfels. Die Wahrscheinlichkeit P Z (1) =... = P Z (6) = 1/6. Die Summe der Wahrscheinlichkeiten gibt 1. Für den Erwartungswert gilt: 1 1 k Z k = = 3.5. k = E{Z} = z P (z ) 3. Statistische Eigenschaften von 2 Zufallsvariablen Bei zwei Zufallsvariablen X und Y interessieren neben den individuellen, statistischen Eigenschaften auch die sogenannten Verbundeigenschaften. Für die Verbund-Wahrscheinlichkeitsdichtefunktion p XY (x,y) von X und Y gilt: p xy(x,y) dx dy = 1 (8.9) - α β P(x α,y β)= (8.10) p (x,y) dx dy xy Die Verbundeigenschaften der Zufallsvariablen X und Y werden durch die (Kreuz-) Korrelation und die (Kreuz-) Covarianz beschrieben. Sie sind wie folgt definiert:

5 ZHAW, DSV2, 2007, Rumc, 8-5 Korrelation: E{X Y} = x y p (x,y) dx dy (8.11) xy - Covarianz: E{(X-E[X]) (Y-E[Y])} = E{X Y} - E{X} E{Y} (8.12) Zwei Zufallsvariablen sind unkorreliert, wenn gilt und statistisch unabhängig, wenn gilt E{X Y} = E{X} E{Y}, (8.13) p XY (x,y) = p X (x) p Y (y). (8.14) Statistisch unabhängige Zufallsvariablen X und Y sind unkorreliert, weil E{X Y} = x y p (x,y) dx dy xy xp - (x) dx yp (y) dy = E{X} E{Y} X - - Y gilt. Das Umgekehrte trifft nicht immer zu, d.h. zwei unkorrelierte Zufallsvariablen X und Y sind nicht notwendigerweise statistisch unabhängig. Durch Einsetzen von (8.13) in (8.12) folgt, dass die Covarianz von zwei unkorrelierten Zufallsvariablen X und Y Null ist. 4. Statistische Eigenschaften von Zufallssignalen Der Mittelwert des diskreten Zufallssignals Z[.] zum Zeitpunkt nt s ist gegeben durch den Mittelwert E{Z[n]} der Zufallsvariablen Z[n] zum Zeitpunkt nt s, d.h. E{Z[n]} = z p (z) dz. (8.15) Z[n] Der mittlere, quadratische Wert bzw. der mean-square-wert des diskreten Zufallssignals Z[.] zum Zeitpunkt nt s ist gegeben durch Z[n]. (8.16) 2 2 E{(Z[n]) } = z p (z) dz Oft interessiert der statistische Zusammenhang zwischen zwei Zufallsvariablen Z[m] und Z[n] eines diskreten Zufallssignals Z[.] zu zwei verschiedenen Zeitpunkten m und n. So einen Zusammenhang stellt die Autokorrelationsfunktion (AKF) R ZZ [m,n] = E{Z[m] Z[n]} (8.17) her. Sie ist ein Mass für die Ähnlichkeit benachbarter Sample im Zufallssignal Z[.].

6 ZHAW, DSV2, 2007, Rumc, 8-6 Ein weiterer Zusammenhang liefert die Auto-Covarianz-Funktion E{ (Z[m]-E{Z[m]}) (Z[n]-E{Z[n]) } = R ZZ [m,n] - E{Z[m]} E{Z[n]}. (8.18) Die Korrelation zwischen zwei diskreten Zufallssignalen X[.] und Y[.] wird durch die Kreuzkorrelationsfunktion (KKF) und die Kreuz-Covarianz-Funktion R XY [m,n] = E{X[m] Y[n]} (8.19) E{ (X[m]-E{ X[m]}) (Y[n]-E{Y[n]}) } = R XY [m,n] - E{X[m]} E{Y[n]} (8.20) beschrieben. Die KKF ist ein Mass für die Ähnlichkeit der Zufallssignale X[.] und Y[.]. Sowohl Autokorrelations- und Auto-Covarianz-Funktionen wie auch Kreuzkorrelations- und Kreuz-Covarianz-Funktionen sind Funktionen von zwei Zeitindizes m und n. Es gibt aber eine grosse Klasse von Zufallssignalen, die sogenannten wide-sense oder schwach stationären Zufallssignale, bei denen die statistischen Eigenschaften unabhängig vom Zeitindex n sind, d.h. für alle m und n. E{Z[n]} = m Z R ZZ [m,n] = R ZZ [m-n] = R ZZ [n-m] (8.21) R XY [m,n] = R XY [m-n] = R YX [n-m] In der Praxis ist oft nur eine beschränkte Anzahl Signalwerte z[n] eines Musters eines diskreten Zufallssignals Z[.] verfügbar. Aus diesen Werten können die statistischen Eigenschaften geschätzt werden, wenn das Zufallssignal stationär und ergodisch ist und die Anzahl bekannter Werte genügend gross ist. Bei einem ergodischen Signal stimmen Zeit- und Ensemble-Mittelwert im Grenzfall überein, d.h. 1 N mz = E{Z[n]} = lim z[n] N 2N+1, (8.22) n = N 1 N R ZZ[m] = E{Z[n] Z[n+m]} = lim z[n] z[n+m] N 2N+1. (8.23) n = N In der Praxis approximiert man natürlich die unendlichen Summen mit endlichen Summen.

7 ZHAW, DSV2, 2007, Rumc, 8-7 In Abbildung 8-4 sind 1000 Werte von 2 verschiedenen Zufallssignalen Z1[.] und Z2[.] sowie ihre AKF R Z1Z1 [.] und R Z2Z2 [.] dargestellt. Abbildung 8-4: Zwei verschiedene Zufallssignale und resultierende AKF. Benachbarte Werte von Z1[.] sind wenig korreliert bzw. sind sich fast nicht ähnlich. Das Zufallssignal Z1[.] ändert sich schnell. Benachbarte Werte von Z2[.] sind stark korreliert bzw. sind sich ähnlich. Das Zufallssignal Z2[.] ändert sich nur langsam.

8 ZHAW, DSV2, 2007, Rumc, 8-8 Die folgenden 30 Signalwerte x[n] =..., ,... stammen von einem stationären, ergodischen Zufallssignal X[.] mit unabhängigen Zufallsvariablen X[n], für die P X (-1) = P X (1) = 0.5 gilt, siehe auch Abbildung 8-5. Abbildung 8-5: Zwei bipolare, stationäre, ergodische Zufallssignale. Aus diesen 30 Werten lassen sich die statistischen Eigenschaften von X[.] tatsächlich ziemlich genau schätzen, wie die folgenden Vergleiche zeigen: Mittelwert (Ensemble): m X = E{X[n]} = 0.5 (-1) = 0 Mittelwert (Zeit): ( (-1)) / 30 = -2/30 = -1/15 Autokorrelation (Ensemble): R XX [0] = E{(X[n]) 2 } = 1 Autokorrelation (Zeit): (30 1)/30 = 1 Autokorrelation (Ensemble): R XX [1] = E{X[n] X[n+1]} = E{X[n]} E{X[n+1]} = 0 Autokorrelation (Zeit): ( (-1))/29 = 1/29 Zwei aufeinander folgende Signalwerte sind unkorreliert. Das Signal weist schnelle Änderungen auf, siehe Abbildung 8-5.

9 ZHAW, DSV2, 2007, Rumc, 8-9 Filtert man die 30 Signalwerte aus dem letzten Beispiel mit dem Filter H(z) = z -1, so resultieren die folgenden (zufälligen) Ausgangswerte (Anfangswert = -1) y[n] =..., ,... siehe Abbildung 8-5. Für die Autokorrelationsfunktion an den Stellen n=0 und n=1 findet man: Autokorrelation (Ensemble): R YY [0] = E{(Y[n]) 2 } = E{ (0.5 X[n]+0.5 X[n-1]) 2 } = 0.5 Autokorrelation (Zeit): 16/30 Autokorrelation (Ensemble): R YY [1] = E{Y[n] Y[n+1]} = E{(0.5 X[n]+0.5 X[n-1]) (0.5 X[n+1]+0.5 X[n])} = 0.25 E{(X[n]) 2 } = 0.25 Autokorrelation (Zeit): 7/30 Zwei aufeinander folgende Werte sind wegen der Filterung korreliert. Das Zufallssignal Y[.] am Ausgang des TP-Filters ändert weniger schnell als das Zufallssignal X[.] am Filtereingang, siehe Abbildung 8-5. Der Autokorrelationswert kann wieder gut mit dem Zeitmittelwert geschätzt werden. Beispiel Der mean-square-wert E{z 2 [n]} stellt eigentlich die Leistung von z[n] dar. Das deterministische Sinus-Signal z[n] = sin(2πn/n) hat die Leistung: 1 N-1 E{z 2 [n]} = sin 2 (2πn/N) = 0.5 N n = 0

10 ZHAW, DSV2, 2007, Rumc, Beschreibung von Zufallssignalen im Frequenzbereich Zufallssignale können nicht nur im Zeitbereich, sondern auch im Frequenzbereich charakterisiert werden. Im Folgenden betrachten wir ausschliesslich schwach-stationäre, mittelwertfreie, reellwertige Zufallssignale Z[.]. Zufallssignale Z[.] haben kein eigentliches Spektrum wie es die deterministischen Signale haben. Zufallssignale Z[.] haben aber ein Leistungsdichtespektrum P ZZ (f) [W/Hz]. Wiener und Khintchine haben gezeigt, dass das Leistungsdichtespektrum P ZZ (f) eines Zufallssignals Z[.] und die Autokorrelationsfunktion AKF R ZZ [m] ein Fourierpaar bilden, d.h. ZZ ZZ -jm2πft s = R ZZ (z=e j2πfts ) (8.24) m= P (f)= R [m] e f s /2 1 jm2πfts R ZZ[m] = P ZZ(f) e df fs f s /2 (8.25) Das Leistungsdichtespektrum P ZZ (f) ist eine reellwertige und gerade Funktion. Aus (8.25) folgt für die mittlere Leistung des Zufallssignals Z[.]: 2 1 E{ Z [n]} =R ZZ[0] = P (f) df f s f s /2 ZZ. (8.26) f s /2 Beispiel Wir betrachten ein schwach-stationäres, (mittelwertfreies), reellwertiges Zufallssignal Z[.] mit unkorrelierten Signalwerten, d.h. E{Z[n] Z[n+m]} = E{Z[n]} E{Z[n+m]} = 0 wenn m 0. Das Zufallssignal Z[.] hat eine impulsartige Autokorrelationsfunktion (AKF), d.h. R ZZ [m] = E{Z 2 [n]} δ[m], wobei δ[.] die Dirac-Delta-Folge darstellt, siehe Abbildung 8-6. Aus dem Wiener-Khintchine-Theorem (8.24) folgt, dass das betrachtete Zufallssignal Z[.] ein konstantes Leistungsdichtespektrum besitzt, d.h. P ZZ (f) = R ZZ [0], siehe Abbildung 8-6. Das Zufallssignal Z[.] wird deshalb auch weisses Rauschen genannt. R ZZ [m] P ZZ (f) E[Z 2 [n]] m -f s /2 f s /2 f Abbildung 8-6: AKF und Leistungsdichtespektrum von weissem Rauschen.

11 ZHAW, DSV2, 2007, Rumc, 8-11 Beispiel Das Zufallssignal Z 1 [.] in Abbildung 8-4 besitzt wegen der impulsartigen AKF ein weisses bzw. flaches Spektrum. Der Signalverlauf weist schnelle Änderungen auf. Es ist keine Korrelation bzw. Ähnlichkeit zwischen den Signalwerten erkennbar. Das Zufallssignal Z 2 [.] in Abbildung 8-4 besitzt ein TP-artiges Spektrum. Der Signalverlauf ändert nur langsam. Benachbarte Signalwerte sind stark korreliert bzw. ähnlich. Analog zum Leistungsdichtespektrum ist das Kreuz-Leistungsdichtespektrum für die Zufallssignale X[.] und Y[.] definiert: XY XY -jm2πft s. (8.27) m= P (f)= R [m] e 6. Diskrete Filterung von Zufallssignalen Wenn am Eingang eines linearen, zeitdiskreten, zeitinvarianten bzw. digitalen Filters H(z) ein schwach-stationäres, mittelwertfreies, reellwertiges Zufallssignal X[.] anliegt, ist das Ausgangssignal Y[.] auch wieder ein schwach-stationäres, mittelwertfreies, reellwertiges Zufallssignal, siehe auch Abbildung 8-7. X[.] H(z) Y[.] Abbildung 8-7: Filterung eines Zufallssignals mit einem digitalen Filter H(z). Zwischen den Leistungsdichtespektren des Ein- und des Ausgangssignals gilt der folgende Zusammenhang (ohne Beweis) P YY (f) = IH(f)I 2 P XX (f), (8.28) wobei H(f) den Frequenzgang des digitalen Filters H(z) darstellt, d.h. H(f) = H(z=e j2πfts ). Weiter gilt der folgende Zusammenhang zwischen dem Leistungsdichtespektrum des Eingangssignals und dem Kreuz-Leistungsdichtespektrum zwischen dem Ein- und dem Ausgangssignal (ohne Beweis) P YX (f) = H(f) P XX (f). (8.29) Beide Gleichungen (8.28) und (8.29) werden in der Praxis für die Systemidentifikation [von H(z)] verwendet. Meistens wird am Filtereingang weisses Rauschen verwendet. Die Leistungsdichtespektren können z.b. mit Hilfe der DFT/FFT aus den entsprechenden Korrelationsfunktionen gewonnen werden.

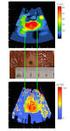
12 ZHAW, DSV2, 2007, Rumc, 8-12 Beispiel Beim Zufallssignal Z 2 [.] in Abbildung 8-4 handelt es sich um TP-gefiltertes, weisses Rauschen. Das Betragsspektrum des TP-Filters in db kann mit Gleichung (8.28) wie folgt bestimmt werden: IH(f)I [db] = 10 log 10 [P YY (f)/konst]. In Abbildung 8-8 ist das geglättete Betragsspektrum des gesuchten TP-Filters dargestellt. Es handelt sich um ein Butterworth-TP 4. Ordnung (4 mal 6 db pro Oktave) mit einer Grenzfrequenz von 100 Hz. Abbildung 8-8: Via Leistungsdichtespektren identifiziertes TP-Filter.