Inhaltsverzeichnis. Finanzmathe Formelsammlung v.2.3 1
|
|
|
- Michael Schreiber
- vor 8 Jahren
- Abrufe
Transkript
1 Finanzmathe Formelsammlung v Inhaltsverzeichnis I Zinsrechnung 1 I.1 Jährliche Verzinsung I.1.1 Einfache Verzinsung I.1.2 Zinseszinsen I.2 Unterjährliche Verzinsung I.2.1 Einfache Verzinsung I.2.2 Unterjährliche Zinseszinsen I.2.3 Effektivverzinsung I.2.4 Konformer (unterjähriger Perio den-) Zinssatz k I.3 Beso ndere Laufzeiten I.3.1 Gemischte Zinsen I.3.2 Stetige Verzinsung II Rentenrechnung 2 II.1 Jährliche Rentenzahlungen bei jährlich nachschüssigen Zinseszinsen II.1.1 Nachschüssige Rentenzahlungen II.1.2 Vorschüssige Rentenzahlungen II.2 Unterjährliche Rentenzahlungen II.2.1 Nachschüssige unterjährliche Rentenzahlung bei nachschüssigen jährlichen Zinsen 3 II.2.2 Vorschüssige unterjährliche Rentenzahlung bei nachschüssigen jährlichen Zinsen 3 II.2.3 Unterjährliche Renten mit indentischer Zins- und Rentenperiode II.2.4 Unterjährliche Renten mit unterjährlicher längererzinsperiode II.3 Ewige Rente II.4 Annuitätenmetho de II.5 Dynamische Rente III Tilgungsrechnung 4 III.1 Ratentilgung III.1.1 jährliche Ratentilgung III.1.2 unterjährliche Ratentilgung III.2 Annuitäten III.2.1 jährliche Annuitätentilgung III.2.2 unterjährliche Annuitätentilgung III.2.3 Prozentannuitätentilgung IV Abschreibungen 6 IV.1 lineare AfA IV.2 Degressive AfA o V Kurs und Effektivverzinsung 7 V.1 Berwertung vo n Zinsschulden V.1.1 Jährliche Zinsschuld hne Agio /Jahresco upo n V.1.2 Jährliche Zinsschuld mit Aufgeld (Agio ) V.1.3 Unterjährliche Zinsschuld V.2 Bewertung vo n Ratenschulden V.2.1 Jährliche Ratenschuld V.2.2 Jährlich aufgescho bene Ratenschuld V.2.3 Unterjährliche Ratenschuld V.3 Bewertung von Annuitätenschulden V.3.1 jährliche Annuitätenschuld V.3.2 Jährliche Prozentannuitätenschuld V.4 Effektivverzinsung vo n Teilzahlungskrediten
2 Finanzmathe Formelsammlung v VI Versicherungsmathematik 9 VI.1 Sterbetafeln VI.2 Lebensversicherung VI.2.1 Todesfallversicherung auf Lebenszeit gegen Sofortbetrag VI.2.2 Todesfallversicherung - Beitragszahlung auf Lebenszeit VI.2.3 To desfallversicherung - befristet, gegen So fo rtbetrag VI.2.4 Todesfallversicherung auf Lebenszeit, Beitragszahlungen befristet VI.2.5 Todesfallversicherung - Beitragszahlungen und Versicherungsleistung befristet. 11 VI.2.6 Erlebensfallversicherung gegen So fo rtbetrag VI.2.7 Erlebensfallversicherung - Beitragszahlung bis zum Tode, spätestens zum Versicherungsende VI.2.8 Gemischte Versicherung - gegen So fo rtbetrag VI.2.9 Gemischte Versicherung - Beitragszahlungen bis zum Todesfall, spätestens zum Versicherungsende VI.2.10Gemischte Versicherung - befristete Zahlungen VI.2.11Versicherung mit Bo nus VI.3 Rentenversicherungen (Leibrenten) VI.3.1 Leibrente auf Lebenszeit VI.3.2 Befristete Leibrente VI.3.3 Aufgescho bene Leibrente auf Lebenszeit VI.3.4 Aufgescho bene Leibrente auf n Jahre befristet VIINullstellen bestimmen 13 VII.1Schätzen VII.2Interpo latio n VII.3Newtonsches Näherungsverfahren
3 Finanzmathe Formelsammlung v I Zinsrechnung Zinssatz i = K1 K0 K 0 I.1 Jährliche Verzinsung Zinsperiode 1 Jahr (nachschüssig). Laufzeit n Jahre. I.1.1 Einfache Verzinsung K 1 = K 0 + Z K n = K 0 (1 + n i) BarwertK 0 = K n 1+n i i = 1 n (K n 1) K 0 n = 1 i (K n K 0 1) I.1.2 Zinseszinsen K n = K 0 (1 + i) n = K 0 q n Kn i = n 1 K 0 n = log K n log K 0 log q I.2 Unterjährliche Verzinsung Zinsperiode < 1Jahr I.2.1 Einfache Verzinsung Wir auf ein Jahr hochgerechnet. I.2.2 Unterjährliche Zinseszinsen Zinsperioden pro Jahr m Laufzeit in Jahren n i = i m q =1+i K n = K 0 q m n
4 Finanzmathe Formelsammlung v I.2.3 Effektivverzinsung Effektiver Zinssatz j j =(1+i ) m 1 K n = K 0 (1 + j) n I.2.4 Konformer (unterjähriger Perioden-) Zinssatz k k = m 1+i 1 K n = K 0 (1 + k) m n I.3 Besondere Laufzeiten I.3.1 Gemischte Zinsen K n = K 0 (1 + i) n1 (1 + n 2 i) I.3.2 Stetige Verzinsung K n = K 0 e i n II II.1 II.1.1 Rentenrechnung Jährliche Rentenzahlungen bei jährlich nachschüssigen Zinseszinsen Nachschüssige Rentenzahlungen n = R n = r qn 1 R 0 = R n q n = r 1 q n qn 1 q n = R n r () + 1 = r [ ] log 1+ Rn r () log q [ log = R 0 () r ] 1 R0 r () log q II.1.2 Vorschüssige Rentenzahlungen R 0 q n = R n = r q qn 1 ( ) log 1 R0 (q 1) r q n = log q q n 1 = 1 R0 (q 1) r q
5 Finanzmathe Formelsammlung v II.2 II.2.1 Unterjährliche Rentenzahlungen Nachschüssige unterjährliche Rentenzahlung bei nachschüssigen jährlichen Zinsen Ersatzrentenrate r e = r [m + i2 ] (m 1) R n = r e qn 1 II.2.2 Vorschüssige unterjährliche Rentenzahlung bei nachschüssigen jährlichen Zinsen r e = r [m + i2 ] (m +1) R n = r e qn 1 II.2.3 Unterjährliche Renten mit indentischer Zins- und Rentenperiode q =1+i =1+ i n q n m 1 Nachschüssig:R n = r q 1 R 0 = R n q n m Vorschüssig: R n = r q q n m 1 q 1 R n R 0 = r q n m = r 1 q n m q n m 1 1 q 1 II.2.4 Unterjährliche Renten mit unterjährlicher längerer Zinsperiode m Zinsperioden pro Jahr c Rentenperioden pro Zinsperiode m c Rentenperioden pro Jahr Zinsperiodenkonforme Ersatzrentenrate: [ ] re = r c + i 2 (c 1) Nachschüssig re = r [c + i 2 ] (c +1) Vorschüssig R n = re q n m 1 q 1 R 0 = R n q n m
6 Finanzmathe Formelsammlung v II.3 Ewige Rente R 0 = r = r i II.4 G E A Annuitätenmethode Kapitalwert Einnahme Ausgabe Rentenformel: r = R 0 q n () Einnnahmeannuität: e = E qn () Ausgabeannuität: a = A qn () Überschußannuitätp = G qn () II.5 Dynamische Rente s = 1 ( q n ) 1 n III Tilgungsrechnung Agio- Aufgeld in Prozent der Tilgung auf die Annuität! III.1 Ratentilgung Tilgungsrate (T) ist konstant. III.1.1 jährliche Ratentilgung S 0 - Schuldsumme T = S 0 n Restschuld nach r Jahren: S r = T (n r) Zinsbetrag nach r Jahren: z r = T (n r +1) i Annuität nach r Jahren: A r = T (1 + (n r +1) i)
7 Finanzmathe Formelsammlung v III.1.2 unterjährliche Ratentilgung m Tilgungsperioden pro Jahr A v/r S v/r z v/r Annuitäten nach v Perioden des r. Jahres: Restschuld nach v Perioden des r. Jahres: Zinsbelastung nach v Perioden des r. Jahres: T = S 0 n m i = i m S v/r = T (m (n r +1) v) z v/r = T (m (n r +1) v +1) i A v/r = T (1 + (m (n r +1) v +1) i ) III.2 Annuitäten A = T + Z = Konstant III.2.1 jährliche Annuitätentilgung Rentenformel: R n = r qn 1 A := r Schuldsumme: S 0 = R 0 A = S 0 q n Restschuld nach r Jahren: S r = S 0 qn q r q r 1 Tilgung nach r Jahren: (Ende des Jahres)T r = S 0 i Zinsbelastung nach r Jahren: Z r = S 0 i qn q r 1 III.2.2 unterjährliche Annuitätentilgung Monatsannuität a, monatlich Nachschüssig. Die ersten 12 Monatsannuitäten werden auf die erste Jahresannuität (A) bezogen. a = r; A = r e c Tilgungsperioden / Zinsperiode z j S j z j s j Zinsbelastung am Jahresende: Restschuld zu Beginn des Jahres: Zinsbelastung am Ende der j. Zinsperiode (Unterjährlich) Schuldsumme am Ende der j. Zinsperiode
8 Finanzmathe Formelsammlung v A a = m + i keine Zinsen 2 (m 1)enthält A = S 0 q n q n enthält Zinsen 1 z j = i (S j a m 1 ) 2 S j = S j 1 m a + z j 1 z j = i m (s j 1 a c 1 2 ) s j = s j 1 c a + z j III.2.3 Prozentannuitätentilgung Laufzeit: n = log A log T 1 log q n = n 1 + n 2 ; n 1 istganzzahlig Abschlußzahlung: A s = s 0 q n1 A qn1 1 Schulden JA + A = q Schulden JE IV Abschreibungen Nennwert : K 0 Anschaffungswert, Neuwert Nutzungsdauer : n in Jahren Buchwert: K m nach m Jahren(m n) Abschreibungsbetrag: Q m auch Quote Restwert: K n Altwert, Schrottwert IV.1 lineare AfA Jährliche AfA ist konstant Q 1 = Q 2 = Q 3 = = Q Q = K 0 K n n Abschreibungsprozentsatz:i = Q K 0 Buchwert nach m AfAs: K m = K 0 (n m)+m K n n IV.2 Degressive AfA K m = K 0 (1 i) m Q m = K 0 (1 i) m 1 i = f(m) Übergang lin nach degr AfA:m n 1 i m ist letztes Jahr f. degr AfA
9 Finanzmathe Formelsammlung v V Kurs und Effektivverzinsung Realkapital ist Barwert aller Leistungen bei Effektivverzinsung K 0 Nennwert (N) ist Barwert der Einnnahmen bei Nominalverzinsung K 0 Kurs C 0 C 0 = K 0 K V.1 Berwertung von Zinsschulden Tilgung am Ende der Laufzeit (n Jahre) Zinsen nachschüssig, jährlich V.1.1 Jährliche Zinsschuld ohne Agio/Jahrescoupon i : Effektivverzinsung (Marktzins) i : Nominalverzinsung (Anleihenverzinsung) 1 C 0 = p q n q n 1 q q n Abkürzung: f n = 1 q n q n 1 q 1 Rentenbarwertfaktor V.1.2 Jährliche Zinsschuld mit Aufgeld (Agio) α : Aufgeld in Prozent vom Nennwert V.1.3 C 0 = p f n α q n Unterjährliche Zinsschuld m Zinsperioden pro Jahr Periodenzinssatz p = p m (Nominal) p = p m (Effektiv) C 0 = ( p + p ) m i (m 1) f n α q n f n = 1 q n q n 1 q 1 V.2 Bewertung von Ratenschulden Tilgungsraten, Nachschüssige Zinsberechnung
10 Finanzmathe Formelsammlung v V.2.1 Jährliche Ratenschuld Tilgungsraten Jährlich, Zinsabrechnung jährlich T B Z B C 0 Barwert der Tilgungsrate Barwert der Zinsen Barwert bei jährlicher Ratenschuld V.2.2 T B = 100 n f n Z B = 100 n p p (n f n ) C 0 = T B + Z B = 100 ( )] pp [f n n + (n f n ) Jährlich aufgeschobene Ratenschuld k Jahre sind Tilgungsfrei, jährlich p DM Zinsen (N=100) danach n Jahre Tilgung V.2.3 C 0 = p f k [f n n + pp ] (n f n ) 1 q k Unterjährliche Ratenschuld m Tilgungsperioden pro Jahr t r e T B Z J Z B C 0 Unterjährliche Tilgungsrate Konforme Ersatzrentenrate (Nachschüssig) Barwert der Tilgungsrate Zinsersparnis projahr Barwert aller Zinszahlungen Kurs r e = 100 m n t = Nennwert m n i [n + (m 1)] 2 T B = 100 i [n + n m 2 (m 1)] f n Z j = 100 m n i (m 1) 2 (Jährliche Ratenschuld) Z B = 100 p n p (n f n) Z B = 100 p n p (n f n) 100 i m n 2 (m 1) f n C 0 = T B + Z B
11 Finanzmathe Formelsammlung v V.3 Bewertung von Annuitätenschulden V.3.1 A:Annuität jährliche Annuitätenschuld A = S 0 q n C 0 = S 0 q n f n = A f n aufgeschobene Annuitätenschuld (jährl.) k Jahre Tilgungsfrei, n Jahre Tilgung C 0 = p f k + A f n 1 q k V.3.2 Jährliche Prozentannuitätenschuld A = p + t = konst n = n 1 + n 2 n 1 ist Ganzzahlig n = log A log T 1 log q A s = S 0 q n1 A qn1 C 0 =(p + t) f n A s q n 1 aufgeschobene Annuitätenschuld (jährlich) k Jahre Tilgungsfrei, n Jahre Tilgung C 0 = p f k +[(p + t) f n 1 + A s 1 1 q n 1 ] q k V.4 Effektivverzinsung von Teilzahlungskrediten k m i Z j S j Tilgungsperioden insgesamt Tilgungsperioden / Jahr Jahreseffektivverzinsung Zinsen der Periode j Restschuld zu Beginn der Periode j i k m = j=1 Z j k J=1 S j VI Versicherungsmathematik nur Lebensversicherung!
12 Finanzmathe Formelsammlung v VI.1 B x r x S x S x B x G x G x B x E x A x Sterbetafeln Bevölkerungsgröße zu Beginn des Jahres x = Bx+1 Bx B x jährliche Wachstumsrate Sterbefälle im Jahr x Sterberate Geburtenanzahl Geburtenrate Einwandereranzahl Auswandereranzahl B x+1 B x = G x S x + E x A x VI.2 q = 1, 04 W (25 75) = l 75 l 25 Lebensversicherung VI.2.1 Todesfallversicherung auf Lebenszeit gegen Sofortbetrag s Versicherungssumme x Alter (zu Beginn des Jahres) A x Sofortbetrag l x A x Leistung aller Versicherungsnehmer w Höchstalter (100 Jahre) D x / l x ν x ν = 1 q w l x A x = d k ν k x+1 k=x l x A x ν x = w d k ν k+1 k=x VI.2.2 A x = M x D x Todesfallversicherung - Beitragszahlung auf Lebenszeit B x jährlicher Beitrag B x = M x N x Monatlicher Beitrag
13 Finanzmathe Formelsammlung v r = B x m + i 2 (m 1) VI.2.3 Todesfallversicherung - befristet, gegen Sofortbetrag befristet auf n Jahre na x = M x M x+n D x VI.2.4 Todesfallversicherung auf Lebenszeit, Beitragszahlungen befristet M x nb x = N x N x+n Monatsbeitrag: VI.2.5 r = B x m + i 2 (m 1) Todesfallversicherung - Beitragszahlungen und Versicherungsleistung befristet nnb x = M x M x+n N x N x+n VI.2.6 Erlebensfallversicherung gegen Sofortbetrag E x = D x+n D x VI.2.7 Erlebensfallversicherung - Beitragszahlung bis zum Tode, spätestens zum Versicherungsende F x = D x+n N x N x+n VI.2.8 Gemischte Versicherung - gegen Sofortbetrag A x:n = M x M x+n + D x+n D x VI.2.9 Gemischte Versicherung - Beitragszahlungen bis zum Todesfall, spätestens zum Versicherungsende VI.2.10 B x:n = M x M x+n + D x+n N x N x+n Gemischte Versicherung - befristete Zahlungen n - Versicherungsdauer t - Zahlungsdauer ta x:n = M x M x+n + D x+n N x N x+t
14 Finanzmathe Formelsammlung v VI.2.11 Bonus in % von s Versicherung mit Bonus VI.3 VI.3.1 s x R G x = M x + s 100 D x+n N x N x+n Rentenversicherungen (Leibrenten) Leibrente auf Lebenszeit Durchschnitt eines vorschüssigen Rentenbarwertes Rentenrate (jährlich) s x = R Nx R x vorschüssig s x = s x Rnachschüssig VI.3.2 Befristete Leibrente s x = R Nx N x+n vorschüssig D x s x = s x Rnachschüssig VI.3.3 Aufgeschobene Leibrente auf Lebenszeit s x = R Nx+t vorschüssig D x s x = s x Rnachschüssig VI.3.4 Aufgeschobene Leibrente auf n Jahre befristet s x = R Nx+t N x+t+n vorschüssig D x s x = s x Rnachschüssig
15 Finanzmathe Formelsammlung v VII VII.1 VII.2 Nullstellen bestimmen Schätzen Interpolation VII.3 q 0 = q 1 +(q 1 q 2 ) G(q 1 ) G(q 2 ) G(q 1 ) Newtonsches Näherungsverfahren q 0 = q 1 G(q 1) G (q 1 )
Finanzmathematik - Grundlagen
 Finanzmathematik - Grundlagen Formelsammlung Zugelassene Formelsammlung zur Klausur im Sommersemester 2005 Marco Paatrifon Institut für Statistik und Mathematische Wirtschaftstheorie Zinsrechnung Symbole
Finanzmathematik - Grundlagen Formelsammlung Zugelassene Formelsammlung zur Klausur im Sommersemester 2005 Marco Paatrifon Institut für Statistik und Mathematische Wirtschaftstheorie Zinsrechnung Symbole
Einführung in einige Teilbereiche der Wirtschaftsmathematik für Studierende des Wirtschaftsingenieurwesens
 in einige Teilbereiche der für Studierende des Wirtschaftsingenieurwesens Sommersemester 2013 Hochschule Augsburg Unterjährige Raten und jährliche Verzinsung Aufteilung der Zinsperiode in mehrere gleich
in einige Teilbereiche der für Studierende des Wirtschaftsingenieurwesens Sommersemester 2013 Hochschule Augsburg Unterjährige Raten und jährliche Verzinsung Aufteilung der Zinsperiode in mehrere gleich
SS 2014 Torsten Schreiber
 SS 2014 Torsten Schreiber 221 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Wird im Bereich der Rentenrechnung die zugehörige zu Beginn eines Jahres / einer Zeitperiode eingezahlt, so spricht
SS 2014 Torsten Schreiber 221 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Wird im Bereich der Rentenrechnung die zugehörige zu Beginn eines Jahres / einer Zeitperiode eingezahlt, so spricht
Mathematik 1 für Wirtschaftsinformatik
 Mathematik 1 für Wirtschaftsinformatik Wintersemester 2012/13 Hochschule Augsburg Äquivalenzprinzip der Finanzmathematik Das Äquivalenzprinzip der Finanzmathematik für Vergleich von Zahlungen, welche
Mathematik 1 für Wirtschaftsinformatik Wintersemester 2012/13 Hochschule Augsburg Äquivalenzprinzip der Finanzmathematik Das Äquivalenzprinzip der Finanzmathematik für Vergleich von Zahlungen, welche
SS 2014 Torsten Schreiber
 SS 2014 Torsten Schreiber 239 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Durch die wird ein Zahlungsstrom beschrieben, der zur Rückführung eines geliehenen Geldbetrags dient. Der zu zahlende
SS 2014 Torsten Schreiber 239 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Durch die wird ein Zahlungsstrom beschrieben, der zur Rückführung eines geliehenen Geldbetrags dient. Der zu zahlende
Zinsen, Zinseszins, Rentenrechnung und Tilgung
 Zinsen, Zinseszins, Rentenrechnung und Tilgung 1. Zinsen, Zinseszins 2. Rentenrechnung 3. Tilgung Nevzat Ates, Birgit Jacobs Zinsrechnen mit dem Dreisatz 1 Zinsen Zinsrechnen mit den Formeln Zinseszins
Zinsen, Zinseszins, Rentenrechnung und Tilgung 1. Zinsen, Zinseszins 2. Rentenrechnung 3. Tilgung Nevzat Ates, Birgit Jacobs Zinsrechnen mit dem Dreisatz 1 Zinsen Zinsrechnen mit den Formeln Zinseszins
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA)
 Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2015/16 Hochschule Augsburg Rentenrechnung Definition Rente: Zahlungsstrom mit Zahlungen in gleichen
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2015/16 Hochschule Augsburg Rentenrechnung Definition Rente: Zahlungsstrom mit Zahlungen in gleichen
Mathematik 1. Inhaltsverzeichnis. Prof. Dr. K. Melzer. karin.melzer@hs-esslingen.de http://www.hs-esslingen.de/de/mitarbeiter/karin-melzer.
 Mathematik 1 Prof Dr K Melzer karinmelzer@hs-esslingende http://wwwhs-esslingende/de/mitarbeiter/karin-melzerhtml Inhaltsverzeichnis 1 Finanzmathematik 1 11 Folgen und Reihen 1 111 Folgen allgemein 1 112
Mathematik 1 Prof Dr K Melzer karinmelzer@hs-esslingende http://wwwhs-esslingende/de/mitarbeiter/karin-melzerhtml Inhaltsverzeichnis 1 Finanzmathematik 1 11 Folgen und Reihen 1 111 Folgen allgemein 1 112
SS 2014 Torsten Schreiber
 SS 2014 Torsten Schreiber 193 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Bei einer Abschreibung werden eines Gutes während der Nutzungsdauer festgehalten. Diese Beträge stellen dar und dadurch
SS 2014 Torsten Schreiber 193 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Bei einer Abschreibung werden eines Gutes während der Nutzungsdauer festgehalten. Diese Beträge stellen dar und dadurch
Bernd Luderer. Starthilfe Finanzmathematik. Zinsen - Kurse - Renditen. 4., erweiterte Auflage. Springer Spektrum
 Bernd Luderer Starthilfe Finanzmathematik Zinsen - Kurse - Renditen 4., erweiterte Auflage Springer Spektrum Inhaltsverzeichnis 1 Grundlegende Formeln und Bezeichnungen 1 1.1 Wichtige Bezeichnungen 1 1.2
Bernd Luderer Starthilfe Finanzmathematik Zinsen - Kurse - Renditen 4., erweiterte Auflage Springer Spektrum Inhaltsverzeichnis 1 Grundlegende Formeln und Bezeichnungen 1 1.1 Wichtige Bezeichnungen 1 1.2
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA)
 Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2014/15 Hochschule Augsburg Grundlagentest Ungleichungen! Testfrage: Ungleichungen 1 Die Lösungsmenge
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2014/15 Hochschule Augsburg Grundlagentest Ungleichungen! Testfrage: Ungleichungen 1 Die Lösungsmenge
Finanzmathematik. Lehrbuch der Zins-, Renten-,Tilgungs-, Kurs- und Renditerechnung. von. Dr. Dr. h.c. Lutz Kruschwitz
 Finanzmathematik Lehrbuch der Zins-, Renten-,Tilgungs-, Kurs- und Renditerechnung von Dr. Dr. h.c. Lutz Kruschwitz Professor für Betriebswirtschaftslehre an der Freien Universität Berlin 5., überarbeitete
Finanzmathematik Lehrbuch der Zins-, Renten-,Tilgungs-, Kurs- und Renditerechnung von Dr. Dr. h.c. Lutz Kruschwitz Professor für Betriebswirtschaftslehre an der Freien Universität Berlin 5., überarbeitete
Finanzmathematik. Dr. Bommhardt. Das Vervielfältigen dieses Arbeitsmaterials zu nicht kommerziellen Zwecken ist gestattet. www.bommi2000.
 Finanzmathematik Dr. Bommhardt. Das Vervielfältigen dieses Arbeitsmaterials zu nicht kommerziellen Zwecken ist gestattet. www.bommi2000.de Das Tilgungsrechnen Für Kredite gibt es drei unterschiedliche
Finanzmathematik Dr. Bommhardt. Das Vervielfältigen dieses Arbeitsmaterials zu nicht kommerziellen Zwecken ist gestattet. www.bommi2000.de Das Tilgungsrechnen Für Kredite gibt es drei unterschiedliche
Grundbegriffe Gegenstand der Tilgungsrechnung ist ein von einem Gläubiger (z. B. Bank) an einen Schuldner ausgeliehener Geldbetrag S;
 1 5.3. Tilgungsrechnung Grundbegriffe Gegenstand der Tilgungsrechnung ist ein von einem Gläubiger (z. B. Bank) an einen Schuldner ausgeliehener Geldbetrag S; Bezeichnung: S... Schuld, Darlehen, Kredit
1 5.3. Tilgungsrechnung Grundbegriffe Gegenstand der Tilgungsrechnung ist ein von einem Gläubiger (z. B. Bank) an einen Schuldner ausgeliehener Geldbetrag S; Bezeichnung: S... Schuld, Darlehen, Kredit
3.3. Tilgungsrechnung
 3.3. Tilgungsrechnung Grundbegriffe Gegenstand der Tilgungsrechnung ist ein von einem Gläubiger (z. B. Bank) an einen Schuldner ausgeliehener Geldbetrag S; Bezeichnung: S... Schuld, Darlehen, Kredit Es
3.3. Tilgungsrechnung Grundbegriffe Gegenstand der Tilgungsrechnung ist ein von einem Gläubiger (z. B. Bank) an einen Schuldner ausgeliehener Geldbetrag S; Bezeichnung: S... Schuld, Darlehen, Kredit Es
Kirsten Wüst. Finanzmathematik. Vom klassischen Sparbuch zum modernen Zinsderivat GABLER
 Kirsten Wüst Finanzmathematik Vom klassischen Sparbuch zum modernen Zinsderivat GABLER I Inhaltsverzeichnis VORWORT V INHALTSVERZEICHNIS VII ABBILDUNGSVERZEICHNIS XV TABELLENVERZEICHNIS XVII 1 ZINSFINANZINSTRUMENTE
Kirsten Wüst Finanzmathematik Vom klassischen Sparbuch zum modernen Zinsderivat GABLER I Inhaltsverzeichnis VORWORT V INHALTSVERZEICHNIS VII ABBILDUNGSVERZEICHNIS XV TABELLENVERZEICHNIS XVII 1 ZINSFINANZINSTRUMENTE
Im weiteren werden die folgenden Bezeichnungen benutzt: Zinsrechnung
 4.2 Grundbegriffe der Finanzmathematik Im weiteren werden die folgenden Bezeichnungen benutzt: K 0 Anfangskapital p Zinsfuß pro Zeiteinheit (in %) d = p Zinssatz pro Zeiteinheit 100 q = 1+d Aufzinsungsfaktor
4.2 Grundbegriffe der Finanzmathematik Im weiteren werden die folgenden Bezeichnungen benutzt: K 0 Anfangskapital p Zinsfuß pro Zeiteinheit (in %) d = p Zinssatz pro Zeiteinheit 100 q = 1+d Aufzinsungsfaktor
Finanzwirtschaft. Teil II: Bewertung
 Sparpläne und Kreditverträge 1 Finanzwirtschaft Teil II: Bewertung Sparpläne und Kreditverträge Agenda Sparpläne und Kreditverträge 2 Endliche Laufzeit Unendliche Laufzeit Zusammenfassung Sparpläne und
Sparpläne und Kreditverträge 1 Finanzwirtschaft Teil II: Bewertung Sparpläne und Kreditverträge Agenda Sparpläne und Kreditverträge 2 Endliche Laufzeit Unendliche Laufzeit Zusammenfassung Sparpläne und
Grundlagen und Anwendungsmoglichkeiten in der Investitions- und Bankwirtschaft. von. Prof. Dr. Konrad Wimmer. begrundet von.
 Finanzmathematik Grundlagen und Anwendungsmoglichkeiten in der Investitions- und Bankwirtschaft von Prof. Dr. Konrad Wimmer begrundet von Eugen Caprano t 7., vollstandig tiberarbeitete Auflage Verlag Franz
Finanzmathematik Grundlagen und Anwendungsmoglichkeiten in der Investitions- und Bankwirtschaft von Prof. Dr. Konrad Wimmer begrundet von Eugen Caprano t 7., vollstandig tiberarbeitete Auflage Verlag Franz
Finanzmathematik mit Excel
 Finanzmathematik mit Excel Seminar zur Finanzwirtschaft im Wintersemester 2014/15 Dipl.-Math. Timo Greggers B.Sc. VWL Janina Mews M.Sc. BWL Dienstag 14.15-15.45 (Beginn: 28.10.2014) PC-Labor (Walter-Seelig-Platz
Finanzmathematik mit Excel Seminar zur Finanzwirtschaft im Wintersemester 2014/15 Dipl.-Math. Timo Greggers B.Sc. VWL Janina Mews M.Sc. BWL Dienstag 14.15-15.45 (Beginn: 28.10.2014) PC-Labor (Walter-Seelig-Platz
Finanzmathematik. Grundlagen und Anwendungsmöglichkeiten in der Investitions- und Bankwirtschaft. begründet von Eugen Caprano f
 Finanzmathematik Grundlagen und Anwendungsmöglichkeiten in der Investitions- und Bankwirtschaft 2008 AGI-Information Management Consultants May be used for personal purporses only or by libraries associated
Finanzmathematik Grundlagen und Anwendungsmöglichkeiten in der Investitions- und Bankwirtschaft 2008 AGI-Information Management Consultants May be used for personal purporses only or by libraries associated
Wirtschaftsmathematik für International Management (BA)
 Wirtschaftsmathematik für International Management (BA) Wintersemester 2012/13 Hochschule Augsburg : Gliederung 1 Grundlegende 2 Grundlegende 3 Lineare Algebra 4 Lineare Programme 5 Folgen und Reihen 6
Wirtschaftsmathematik für International Management (BA) Wintersemester 2012/13 Hochschule Augsburg : Gliederung 1 Grundlegende 2 Grundlegende 3 Lineare Algebra 4 Lineare Programme 5 Folgen und Reihen 6
Kreditmanagement. EK Finanzwirtschaft
 EK Finanzwirtschaft a.o.univ.-prof. Mag. Dr. Christian KEBER Fakultät für Wirtschaftswissenschaften www.univie.ac.at/wirtschaftswissenschaften christian.keber@univie.ac.at Kreditmanagement 1 Kreditmanagement
EK Finanzwirtschaft a.o.univ.-prof. Mag. Dr. Christian KEBER Fakultät für Wirtschaftswissenschaften www.univie.ac.at/wirtschaftswissenschaften christian.keber@univie.ac.at Kreditmanagement 1 Kreditmanagement
SS 2014 Torsten Schreiber
 SS 2014 Torsten Schreiber 204 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Bei der Rentenrechnung geht es um aus einem angesparten Kapital bzw. um um das Kapital aufzubauen, die innerhalb
SS 2014 Torsten Schreiber 204 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Bei der Rentenrechnung geht es um aus einem angesparten Kapital bzw. um um das Kapital aufzubauen, die innerhalb
Rente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren Rentenperiode = Zeitabstand zwischen zwei Rentenzahlungen
 1 3.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind
1 3.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind
Finanzmathematik. Zinsrechnung I 1.)
 Finanzmathematik Zinsrechnung I 1.) Ein Vater leiht seinem Sohn am 1.1. eines Jahres 1.000.- DM. Es wird vereinbart, dass der Sohn bei einfacher Verzinsung von 8% das Kapital einschließlich der Zinsen
Finanzmathematik Zinsrechnung I 1.) Ein Vater leiht seinem Sohn am 1.1. eines Jahres 1.000.- DM. Es wird vereinbart, dass der Sohn bei einfacher Verzinsung von 8% das Kapital einschließlich der Zinsen
Starthilfe Finanzmathematik
 Bernd Luderer Starthilfe Finanzmathematik Zinsen - Kurse - Renditen 3., überarbeitete und erweiterte Auflage t. \ STUDIUM 11 VI EWEG+ TEUBNER Inhaltsverzeichnis 1 Grundlegende Formeln und Bezeichnungen
Bernd Luderer Starthilfe Finanzmathematik Zinsen - Kurse - Renditen 3., überarbeitete und erweiterte Auflage t. \ STUDIUM 11 VI EWEG+ TEUBNER Inhaltsverzeichnis 1 Grundlegende Formeln und Bezeichnungen
5. Finanzwirtschaft 5.1 Inhalt und Aufgaben
 5. Finanzwirtschaft 5.1 Inhalt und Aufgaben Die Funktionalbereiche der Unternehung und die Eingliederung der Finanzwirtschaft: Finanzwirtschaft Beschaffung Produktion Absatz Märkte für Produktionsfaktoren
5. Finanzwirtschaft 5.1 Inhalt und Aufgaben Die Funktionalbereiche der Unternehung und die Eingliederung der Finanzwirtschaft: Finanzwirtschaft Beschaffung Produktion Absatz Märkte für Produktionsfaktoren
Praktische Lebensversicheru ngsmathematik
 Karl MichaelOrtmann Praktische Lebensversicheru ngsmathematik Mit zahlreichen Beispielen, Abbildungen und Anwendungen STUDIUM 11 VIEWEG+ TEUBNER Inhaltsverzeichnis 1 Einleitung 1 1.1 Wesen der Versicherung
Karl MichaelOrtmann Praktische Lebensversicheru ngsmathematik Mit zahlreichen Beispielen, Abbildungen und Anwendungen STUDIUM 11 VIEWEG+ TEUBNER Inhaltsverzeichnis 1 Einleitung 1 1.1 Wesen der Versicherung
Rentenrechnung 5. unterjhrige Verzinsung mit Zinseszins K n. q m n =K 0. N=m n N= m=anzahl der Zinsperioden n=laufzeit. aa) K 10
 Rentenrechnung 5 Kai Schiemenz Finanzmathematik Ihrig/Pflaumer Oldenburg Verlag 50.Am 0.0.990 wurde ein Sparkonto von 000 eröffnet. Das Guthaben wird vierteljährlich mit % verzinst. a.wie hoch ist das
Rentenrechnung 5 Kai Schiemenz Finanzmathematik Ihrig/Pflaumer Oldenburg Verlag 50.Am 0.0.990 wurde ein Sparkonto von 000 eröffnet. Das Guthaben wird vierteljährlich mit % verzinst. a.wie hoch ist das
Rente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren Rentenperiode = Zeitabstand zwischen zwei Rentenzahlungen
 5.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind zwei
5.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind zwei
Zinseszins- und Rentenrechnung
 Zinseszins- und Rentenrechnung 1 Berechnen Sie den Zeitpunkt, an dem sich das Einlagekapital K bei a) jährlicher b) monatlicher c) stetiger Verzinsung verdoppelt hat, wobei i der jährliche nominelle Zinssatz
Zinseszins- und Rentenrechnung 1 Berechnen Sie den Zeitpunkt, an dem sich das Einlagekapital K bei a) jährlicher b) monatlicher c) stetiger Verzinsung verdoppelt hat, wobei i der jährliche nominelle Zinssatz
n... Laufzeit der Kapitalanlage = Zeit, während der Zinsen zu zahlen sind (oder gezahlt werden) in Zinsperioden (z.b. Jahre)
 3. Finanzmathematik 3.1. Zinsrechnung 3.1.1. Grundbegriffe K... Kapital (caput - das Haupt) = Betrag, der der Verzinsung unterworfen ist; Geldbetrag (Währung) z... Zinsen = Vergütung (Preis) für das Überlassen
3. Finanzmathematik 3.1. Zinsrechnung 3.1.1. Grundbegriffe K... Kapital (caput - das Haupt) = Betrag, der der Verzinsung unterworfen ist; Geldbetrag (Währung) z... Zinsen = Vergütung (Preis) für das Überlassen
Grundlagen: Folgen u. endliche Reihen Zinsrechnung Renten-/Investitionsrechnung Tilgungsrechnung Abschreibungen. Finanzmathematik. Fakultät Grundlagen
 Finanzmathematik Fakultät Grundlagen September 2011 Fakultät Grundlagen Finanzmathematik Grundlagen: Folgen und endliche Reihen Rentenrechnung Fakultät Grundlagen Finanzmathematik Folie: 2 Folgen Reihen
Finanzmathematik Fakultät Grundlagen September 2011 Fakultät Grundlagen Finanzmathematik Grundlagen: Folgen und endliche Reihen Rentenrechnung Fakultät Grundlagen Finanzmathematik Folie: 2 Folgen Reihen
Aufgaben zur Finanzmathematik, Nr. 1
 Aufgaben zur Finanzmathematik, Nr. 1 1.) Ein Unternehmen soll einen Kredit in Höhe von 800.000 in fünf gleich großen Tilgungsraten zurückzahlen. Der Zinssatz beträgt 6,5 % p. a. Erstellen Sie einen Tilgungsplan!
Aufgaben zur Finanzmathematik, Nr. 1 1.) Ein Unternehmen soll einen Kredit in Höhe von 800.000 in fünf gleich großen Tilgungsraten zurückzahlen. Der Zinssatz beträgt 6,5 % p. a. Erstellen Sie einen Tilgungsplan!
b) Wie hoch ist der Betrag nach Abschluss eines Studiums von sechs Jahren?
 Fachhochschule Köln Fakultät für Wirtschaftswissenschaften Prof. Dr. Arrenberg Raum 221, Tel. 39 14 jutta.arrenberg@fh-koeln.de Übungen zur Mathematik für Prüfungskandidaten und Prüfungskandidatinnen Unterjährliche
Fachhochschule Köln Fakultät für Wirtschaftswissenschaften Prof. Dr. Arrenberg Raum 221, Tel. 39 14 jutta.arrenberg@fh-koeln.de Übungen zur Mathematik für Prüfungskandidaten und Prüfungskandidatinnen Unterjährliche
lebensbegleitenden Finanzmathematik
 Martin Hödlmoser Das lxl der lebensbegleitenden Finanzmathematik Kredit-, Darlehens-, Leasingraten Rendite von Veranlagungen (Sparbücher, Wertpapiere,...) Zinsverrechnungsmodalitäten Tilgungspläne Grundzüge
Martin Hödlmoser Das lxl der lebensbegleitenden Finanzmathematik Kredit-, Darlehens-, Leasingraten Rendite von Veranlagungen (Sparbücher, Wertpapiere,...) Zinsverrechnungsmodalitäten Tilgungspläne Grundzüge
Tilgungsrechnung. (K n + R n = ln. / ln(q) (nachschüssig) + R. / ln(q) (vorschüssig)
 (K n + R n = ln n = ln q 1 K 0 + R q 1 (K n q + R q 1 K 0 q + R q 1 ) / ln(q) (nachschüssig) ) / ln(q) (vorschüssig) Eine einfache Formel, um q aus R,n,K n und K 0 auszurechnen, gibt es nicht. Tilgungsrechnung
(K n + R n = ln n = ln q 1 K 0 + R q 1 (K n q + R q 1 K 0 q + R q 1 ) / ln(q) (nachschüssig) ) / ln(q) (vorschüssig) Eine einfache Formel, um q aus R,n,K n und K 0 auszurechnen, gibt es nicht. Tilgungsrechnung
Finanzwirtschaft. Teil II: Bewertung. Zinssätze und Renten
 Zinssätze und Renten 1 Finanzwirtschaft Teil II: Bewertung Zinssätze und Renten Agenda Zinssätze und Renten 2 Effektivzinsen Spot-Zinsen Forward-Zinsen Bewertung Kennziffern Zusammenfassung Zinssätze und
Zinssätze und Renten 1 Finanzwirtschaft Teil II: Bewertung Zinssätze und Renten Agenda Zinssätze und Renten 2 Effektivzinsen Spot-Zinsen Forward-Zinsen Bewertung Kennziffern Zusammenfassung Zinssätze und
Übungsblatt 1 Finanzmathematik
 Übungsblatt 1 Finanzmathematik 1. Können bei einfacher Verzinsung von 6% und einer Anlagedauer von einem halben Jahr aus 1.000 e mehr als 1.030 e werden? 2. Ein fester Anlagebetrag wird bei der Privatbank
Übungsblatt 1 Finanzmathematik 1. Können bei einfacher Verzinsung von 6% und einer Anlagedauer von einem halben Jahr aus 1.000 e mehr als 1.030 e werden? 2. Ein fester Anlagebetrag wird bei der Privatbank
Finanzmathematik, Investition und Finanzierung
 Finanzmathematik, Investition und Finanzierung Aufgaben und Fälle / von Prof. Dr. Christa Drees-Behrens Prof. Dr. Matthias Kirspel Prof. Dr. Andreas Schmidt Prof. Helmut Schwanke 2., überarbeitete Auflage
Finanzmathematik, Investition und Finanzierung Aufgaben und Fälle / von Prof. Dr. Christa Drees-Behrens Prof. Dr. Matthias Kirspel Prof. Dr. Andreas Schmidt Prof. Helmut Schwanke 2., überarbeitete Auflage
Übungsaufgaben zur Einführung in die Finanzmathematik. Dr. Sikandar Siddiqui
 Übungsaufgaben zur Einführung in die Finanzmathematik Übungsaufgaben Aufgabe 1: A hat B am 1.1.1995 einen Betrag von EUR 65,- geliehen. B verpflichtet sich, den geliehenen Betrag mit 7% einfach zu verzinsen
Übungsaufgaben zur Einführung in die Finanzmathematik Übungsaufgaben Aufgabe 1: A hat B am 1.1.1995 einen Betrag von EUR 65,- geliehen. B verpflichtet sich, den geliehenen Betrag mit 7% einfach zu verzinsen
Übungsaufgaben Tilgungsrechnung
 1 Zusatzmaterialien zu Finanz- und Wirtschaftsmathematik im Unterricht, Band 1 Übungsaufgaben Tilgungsrechnung Überarbeitungsstand: 1.März 2016 Die grundlegenden Ideen der folgenden Aufgaben beruhen auf
1 Zusatzmaterialien zu Finanz- und Wirtschaftsmathematik im Unterricht, Band 1 Übungsaufgaben Tilgungsrechnung Überarbeitungsstand: 1.März 2016 Die grundlegenden Ideen der folgenden Aufgaben beruhen auf
vorschüssige, lebenslängliche Leibrente (whole life annuity-due) Vorschüssige jährliche Zahlungen von 1, solange die versicherte Person am Leben ist.
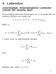 4. Leibrenten vorschüssige, lebenslängliche Leibrente (whole life annuity-due) Vorschüssige jährliche Zahlungen von 1, solange die versicherte Person am Leben ist. NEP ä x : Y = 1 + v + v 2 + + v K = ä
4. Leibrenten vorschüssige, lebenslängliche Leibrente (whole life annuity-due) Vorschüssige jährliche Zahlungen von 1, solange die versicherte Person am Leben ist. NEP ä x : Y = 1 + v + v 2 + + v K = ä
Inhaltsverzeichnis VII. Symbol- und Ab kürzungs Verzeichnis. 1. Finanzmathematik. 1.1. Zins- und Zinseszinsrechnung
 VII Inhaltsverzeichnis Symbol- und Ab kürzungs Verzeichnis XIV 1. Finanzmathematik 1.1. Zins- und Zinseszinsrechnung 1-1 Zins- und Endwertberechnung 1-2 Anfangskapital 1-3 Unterjährige Verzinsung 1-4 Grundbegriffe
VII Inhaltsverzeichnis Symbol- und Ab kürzungs Verzeichnis XIV 1. Finanzmathematik 1.1. Zins- und Zinseszinsrechnung 1-1 Zins- und Endwertberechnung 1-2 Anfangskapital 1-3 Unterjährige Verzinsung 1-4 Grundbegriffe
Mathematik-Klausur vom 4.2.2004
 Mathematik-Klausur vom 4.2.2004 Aufgabe 1 Ein Klein-Sparer verfügt über 2 000, die er möglichst hoch verzinst anlegen möchte. a) Eine Anlage-Alternative besteht im Kauf von Bundesschatzbriefen vom Typ
Mathematik-Klausur vom 4.2.2004 Aufgabe 1 Ein Klein-Sparer verfügt über 2 000, die er möglichst hoch verzinst anlegen möchte. a) Eine Anlage-Alternative besteht im Kauf von Bundesschatzbriefen vom Typ
6 Berechnung der Kapitalentwicklung auf der Basis der Zinseszinsrechnung
 6 Berechnung der Kaitalentwicklung auf der Basis der Zinseszinsrechnung 61 Wertentwicklung ohne Gut- oder Lastschrift von Zinsen Beisiele: 1 Konstante Produktionszunahme Produktion im 1 Jahr: P 1 Produktion
6 Berechnung der Kaitalentwicklung auf der Basis der Zinseszinsrechnung 61 Wertentwicklung ohne Gut- oder Lastschrift von Zinsen Beisiele: 1 Konstante Produktionszunahme Produktion im 1 Jahr: P 1 Produktion
Tutorium zur Mathematik (WS 2004/2005) - Finanzmathematik Seite 1
 Tutorium zur Mathematik WS 2004/2005) - Finanzmathematik Seite 1 Finanzmathematik 1.1 Prozentrechnung K Grundwert Basis, Bezugsgröße) p Prozentfuß i Prozentsatz i = p 100 ) Z Prozentwert Z = K i bzw. Z
Tutorium zur Mathematik WS 2004/2005) - Finanzmathematik Seite 1 Finanzmathematik 1.1 Prozentrechnung K Grundwert Basis, Bezugsgröße) p Prozentfuß i Prozentsatz i = p 100 ) Z Prozentwert Z = K i bzw. Z
Investition und Finanzierung. Aufgaben und Fälle
 Finanzmathematik, Investition und Finanzierung Aufgaben und Fälle von Prof. Dr. Christa Drees-Behrens Prof. Dr. Matthias Kirspel Prof. Dr. Andreas Schmidt Prof. Helmut Schwanke 2., überarbeitete Auflage
Finanzmathematik, Investition und Finanzierung Aufgaben und Fälle von Prof. Dr. Christa Drees-Behrens Prof. Dr. Matthias Kirspel Prof. Dr. Andreas Schmidt Prof. Helmut Schwanke 2., überarbeitete Auflage
Aufgabenskript für Finanzierung
 Aufgabenskript für Finanzierung Komplex 1: Außenfinanzierung Ü 1-1 In der Hauptversammlung der Maschinen AG wurde beschlossen, das gezeichnete Kapital um 60 Mio. auf 300 Mio. aufzustocken. Der Kurs der
Aufgabenskript für Finanzierung Komplex 1: Außenfinanzierung Ü 1-1 In der Hauptversammlung der Maschinen AG wurde beschlossen, das gezeichnete Kapital um 60 Mio. auf 300 Mio. aufzustocken. Der Kurs der
Formelsammlung Grundlagen der Wirtschaftsmathematik
 Ausgabe 2007-09 Formelsammlung Grundlagen der Wirtschaftsmathematik 1 Stichwortverzeichnis (mit Seitenzahlen) Abschreibungen 14 Formelzeichen 2 Grenzerlös, Grenzumsatz 6 Grenzfunktionen, weitere 7 Grenzgewinn
Ausgabe 2007-09 Formelsammlung Grundlagen der Wirtschaftsmathematik 1 Stichwortverzeichnis (mit Seitenzahlen) Abschreibungen 14 Formelzeichen 2 Grenzerlös, Grenzumsatz 6 Grenzfunktionen, weitere 7 Grenzgewinn
Investition und Finanzierung
 Investition und Finanzierung - Vorlesung 6 - Prof. Dr. Rainer Elschen Prof. Dr. Rainer Elschen -92 - Die Interne Zinsfußmethode (1) Entscheidungsgröße: Interner Zinsfuß r Entscheidungsregel: r Max u.d.b.
Investition und Finanzierung - Vorlesung 6 - Prof. Dr. Rainer Elschen Prof. Dr. Rainer Elschen -92 - Die Interne Zinsfußmethode (1) Entscheidungsgröße: Interner Zinsfuß r Entscheidungsregel: r Max u.d.b.
Anlage zur Satzung. der Sterbe-Unterstützungs-Vereinigung der Beschäftigten der Stadt München. Regelung der Beitrags- und Leistungstarife
 Anlage zur Satzung der Sterbe-Unterstützungs-Vereinigung der Beschäftigten der Stadt München Regelung der Beitrags- und Leistungstarife (in der ab 2015 geltenden Fassung) Anlage zur Satzung STUV Seite
Anlage zur Satzung der Sterbe-Unterstützungs-Vereinigung der Beschäftigten der Stadt München Regelung der Beitrags- und Leistungstarife (in der ab 2015 geltenden Fassung) Anlage zur Satzung STUV Seite
UNIVERSITÄT HOHENHEIM
 UNIVERSITÄT HOHENHEIM INSTITUT FÜR LANDWIRTSCHAFTLICHE BETRIEBSLEHRE FACHGEBIET: PRODUKTIONSTHEORIE UND RESSOURCENÖKONOMIK Prof. Dr. Stephan Dabbert Planung und Entscheidung (B 00202) Lösung Aufgabe 7
UNIVERSITÄT HOHENHEIM INSTITUT FÜR LANDWIRTSCHAFTLICHE BETRIEBSLEHRE FACHGEBIET: PRODUKTIONSTHEORIE UND RESSOURCENÖKONOMIK Prof. Dr. Stephan Dabbert Planung und Entscheidung (B 00202) Lösung Aufgabe 7
Prüfung Grundprinzipien der Versicherungs- und Finanzmathematik 2015
 Prüfung Grundprinzipien der Versicherungs- und Finanzmathematik 2015 Aufgabe 1: (20 min) a) Gegeben sei ein einperiodiger State Space-Markt mit zwei Zuständen, der aus zwei Wertpapieren bestehe, einer
Prüfung Grundprinzipien der Versicherungs- und Finanzmathematik 2015 Aufgabe 1: (20 min) a) Gegeben sei ein einperiodiger State Space-Markt mit zwei Zuständen, der aus zwei Wertpapieren bestehe, einer
Hageböke & Webel 24.09.2012
 1. Was ist günstiger? oder? Die Prüfung des Finanzierungsvergleichs für das Wirtschaftsgut zum Preis von 39.900,00 EUR kommt unter wirtschaftlichen Gesichtspunkten zum Ergebnis, dass die Alternative finanzierung
1. Was ist günstiger? oder? Die Prüfung des Finanzierungsvergleichs für das Wirtschaftsgut zum Preis von 39.900,00 EUR kommt unter wirtschaftlichen Gesichtspunkten zum Ergebnis, dass die Alternative finanzierung
Klassische Finanzmathematik (Abschnitt KF.1 )
 Die Finanzatheatik ist eine Disziplin der angewandten Matheatik, die sich insbesondere it der Analyse und de Vergleich von Zahlungsströen und die theoretisch Erittlung des Geldwertes von Finanzprodukten.
Die Finanzatheatik ist eine Disziplin der angewandten Matheatik, die sich insbesondere it der Analyse und de Vergleich von Zahlungsströen und die theoretisch Erittlung des Geldwertes von Finanzprodukten.
Gewinnbeteiligung der Versicherungsnehmer
 80 Gewinnbeteiligung der Versicherungsnehmer In den folgenden Abschnitten wird für die einzelnen Tarifgruppen beschrieben, wie sie an den laufenden Gewinnanteilen und den Schluss-Gewinnanteilen beteiligt
80 Gewinnbeteiligung der Versicherungsnehmer In den folgenden Abschnitten wird für die einzelnen Tarifgruppen beschrieben, wie sie an den laufenden Gewinnanteilen und den Schluss-Gewinnanteilen beteiligt
Die Laufzeit muss nun ebenfalls in Monaten gerechnet werden und beträgt 25 12 = 300 Monate. Damit liefert die Sparkassenformel (zweiter Teil):
 Lösungen zur Mathematikklausur WS 2004/2005 (Versuch 1) 1.1. Hier ist die Rentenformel für gemischte Verzinsung (nachschüssig) zu verwenden: K n = r(12 + 5, 5i p ) qn 1 q 1 = 100(12 + 5, 5 0, 03)1, 0325
Lösungen zur Mathematikklausur WS 2004/2005 (Versuch 1) 1.1. Hier ist die Rentenformel für gemischte Verzinsung (nachschüssig) zu verwenden: K n = r(12 + 5, 5i p ) qn 1 q 1 = 100(12 + 5, 5 0, 03)1, 0325
Unter einer Rente versteht man eine regelmässige und konstante Zahlung.
 Anwendungen aus der Finanzmathematik a) Periodische Zahlungen: Renten und Leasing Unter einer Rente versteht man eine regelmässige und konstante Zahlung Beispiele: monatliche Krankenkassenprämie, monatliche
Anwendungen aus der Finanzmathematik a) Periodische Zahlungen: Renten und Leasing Unter einer Rente versteht man eine regelmässige und konstante Zahlung Beispiele: monatliche Krankenkassenprämie, monatliche
Im Jahr t = 0 hat eine Stadt 10.000 Einwohner. Nach 15 Jahren hat sich die Einwohnerzahl verdoppelt. z(t) = at + b
 Aufgabe 1: Im Jahr t = 0 hat eine Stadt 10.000 Einwohner. Nach 15 Jahren hat sich die Einwohnerzahl verdoppelt. (a) Nehmen Sie lineares Wachstum gemäß z(t) = at + b an, wobei z die Einwohnerzahl ist und
Aufgabe 1: Im Jahr t = 0 hat eine Stadt 10.000 Einwohner. Nach 15 Jahren hat sich die Einwohnerzahl verdoppelt. (a) Nehmen Sie lineares Wachstum gemäß z(t) = at + b an, wobei z die Einwohnerzahl ist und
Kapitalversicherungen
 Kapitalversicherungen Sanela Omerovic Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 Inhaltsverzeichnis 1 Einführung 1 2 Einfache Versicherungsformen 3 2.1 Todesfallversicherungen (Life Insurance)....................
Kapitalversicherungen Sanela Omerovic Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 Inhaltsverzeichnis 1 Einführung 1 2 Einfache Versicherungsformen 3 2.1 Todesfallversicherungen (Life Insurance)....................
Besondere Versicherungsbedingungen. Teilungsordnung
 Besondere Versicherungsbedingungen Teilungsordnung Besondere Versicherungsbedingungen für die interne Teilung aufgrund des Gesetzes über den Versorgungsausgleich (Teilungsordnung) 1. Anwendungsbereich
Besondere Versicherungsbedingungen Teilungsordnung Besondere Versicherungsbedingungen für die interne Teilung aufgrund des Gesetzes über den Versorgungsausgleich (Teilungsordnung) 1. Anwendungsbereich
Übungsaufgaben. zur Vorlesung ( B A C H E L O R ) Teil E Betriebliche Finanzwirtschaft. Dr. Horst Kunhenn. Vertretungsprofessor
 Übungsaufgaben zur Vorlesung FINANZIERUNG UND CONTROLLING ( B A C H E L O R ) Teil E Betriebliche Finanzwirtschaft Dr. Horst Kunhenn Vertretungsprofessor Institut für Technische Betriebswirtschaft (ITB)
Übungsaufgaben zur Vorlesung FINANZIERUNG UND CONTROLLING ( B A C H E L O R ) Teil E Betriebliche Finanzwirtschaft Dr. Horst Kunhenn Vertretungsprofessor Institut für Technische Betriebswirtschaft (ITB)
Gewinnbeteiligung der Versicherungsnehmer
 ERGO Direkt Lebensversicherung AG 79 Gewinnbeteiligung der Versicherungsnehmer In den folgenden Abschnitten wird für die einzelnen Tarifgruppen beschrieben, wie sie an den laufenden Gewinnanteilen und
ERGO Direkt Lebensversicherung AG 79 Gewinnbeteiligung der Versicherungsnehmer In den folgenden Abschnitten wird für die einzelnen Tarifgruppen beschrieben, wie sie an den laufenden Gewinnanteilen und
Barwertbestimmung und Effektivzins bei Anleihen. von Fanny Dieckmann
 Barwertbestimmung und Effektivzins bei Anleihen von Fanny Dieckmann Inhalt Definitionen Anleihenstruktur Anleihenbewertung Barwertbestimmung Renditebestimmung Bewertung von Sonderformen Literaturverzeichnis
Barwertbestimmung und Effektivzins bei Anleihen von Fanny Dieckmann Inhalt Definitionen Anleihenstruktur Anleihenbewertung Barwertbestimmung Renditebestimmung Bewertung von Sonderformen Literaturverzeichnis
Überlegungen zur transparenten Gestaltung einer Lebensversicherung
 Überlegungen zur transparenten Gestaltung einer Lebensversicherung 1 Transparenz ist zielorientiert ist kein Selbstzweck hat Grenzen 2 Produkttransparenz Markttransparenz Klarheit über die Leistung Vertragsmacht
Überlegungen zur transparenten Gestaltung einer Lebensversicherung 1 Transparenz ist zielorientiert ist kein Selbstzweck hat Grenzen 2 Produkttransparenz Markttransparenz Klarheit über die Leistung Vertragsmacht
Anwendungen in der elementaren Zinsrechnung. Kapitalwert zum Zeitpunkt j (nach j Zinsperioden) Bsp. 1. 0 1 2 3 4 Zeitpunkte
 Anwendungen in der elementaren Zinsrechnung Zinssatz (Rendite) je Zinsperiode i = p% p= Prozentpunkte Zinsfaktor (Aufzinsungsfaktor) q =1+i Diskontfaktor (Abzinsungsfaktor) v =1/(1 + i) =q 1 Laufzeit n
Anwendungen in der elementaren Zinsrechnung Zinssatz (Rendite) je Zinsperiode i = p% p= Prozentpunkte Zinsfaktor (Aufzinsungsfaktor) q =1+i Diskontfaktor (Abzinsungsfaktor) v =1/(1 + i) =q 1 Laufzeit n
Investition und Finanzierung. Investition Teil 1
 Fernstudium Guide Online Vorlesung Wirtschaftswissenschaft Investition und Finanzierung Investition Teil 1 Dieses Werk ist urheberrechtlich geschützt. Jegliche unzulässige Form der Entnahme, des Nachdrucks,
Fernstudium Guide Online Vorlesung Wirtschaftswissenschaft Investition und Finanzierung Investition Teil 1 Dieses Werk ist urheberrechtlich geschützt. Jegliche unzulässige Form der Entnahme, des Nachdrucks,
Mathematik-Klausur vom 28.01.2008
 Mathematik-Klausur vom 28.01.2008 Studiengang BWL PO 1997: Aufgaben 1,2,3,4 Dauer der Klausur: 90 Min Studiengang B&FI PO 2001: Aufgaben 1,2,3,4 Dauer der Klausur: 90 Min Studiengang BWL PO 2003: Aufgaben
Mathematik-Klausur vom 28.01.2008 Studiengang BWL PO 1997: Aufgaben 1,2,3,4 Dauer der Klausur: 90 Min Studiengang B&FI PO 2001: Aufgaben 1,2,3,4 Dauer der Klausur: 90 Min Studiengang BWL PO 2003: Aufgaben
Übungen zur Vorlesung QM II Unterjährliche Renten Aufgabe 8.1 Ein Auto wird auf Leasingbasis zu folgenden Bedingungen erworben:
 Technische Hochschule Köln Fakultät für Wirtschafts- und Rechtswissenschaften Prof. Dr. Arrenberg Raum 22, Tel. 394 jutta.arrenberg@th-koeln.de Übungen zur Vorlesung QM II Unterjährliche Renten Aufgabe
Technische Hochschule Köln Fakultät für Wirtschafts- und Rechtswissenschaften Prof. Dr. Arrenberg Raum 22, Tel. 394 jutta.arrenberg@th-koeln.de Übungen zur Vorlesung QM II Unterjährliche Renten Aufgabe
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA)
 Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2014/15 Hochschule Augsburg Unterjährige Verzinsung Zahlung von Zinsen nicht jährlich, sondern in kürzeren
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2014/15 Hochschule Augsburg Unterjährige Verzinsung Zahlung von Zinsen nicht jährlich, sondern in kürzeren
5. Kurs- und Renditerechnung mit Excel
 188 Kurs- und Renditerechnung mit Excel 5. Kurs- und Renditerechnung mit Excel 5.1 Einführung Für die Kursrechnung sollen neben bereits definierten Größen und Symbolen folgende verwendet werden: K 0 Nominalkapital
188 Kurs- und Renditerechnung mit Excel 5. Kurs- und Renditerechnung mit Excel 5.1 Einführung Für die Kursrechnung sollen neben bereits definierten Größen und Symbolen folgende verwendet werden: K 0 Nominalkapital
Wichtiges Thema: Ihre private Rente und der viel zu wenig beachtete - Rentenfaktor
 Wichtiges Thema: Ihre private Rente und der viel zu wenig beachtete - Rentenfaktor Ihre private Gesamtrente setzt sich zusammen aus der garantierten Rente und der Rente, die sich aus den über die Garantieverzinsung
Wichtiges Thema: Ihre private Rente und der viel zu wenig beachtete - Rentenfaktor Ihre private Gesamtrente setzt sich zusammen aus der garantierten Rente und der Rente, die sich aus den über die Garantieverzinsung
Kapitalversicherungen
 Kapitalversicherungen Birgit Scharwitzl 10. Dezember 2008 Inhaltsverzeichnis 1 Begriffe und wichtige Definitionen 2 1.1 Prämie................................................... 2 1.2 Gewinnbeteiligung............................................
Kapitalversicherungen Birgit Scharwitzl 10. Dezember 2008 Inhaltsverzeichnis 1 Begriffe und wichtige Definitionen 2 1.1 Prämie................................................... 2 1.2 Gewinnbeteiligung............................................
Berechnungen Modelle Investitionsrechnung V1
 Berechnungen Modelle Investitionsrechnung V1 Statische Modelle zur Vorteilhaftigkeitsbeurteilung 2.1 Kostenvergleichsrechnung Abkürzungen A 0 DGK i L T U Z Anschaffungsauszahlung Durchschnittlich gebundenes
Berechnungen Modelle Investitionsrechnung V1 Statische Modelle zur Vorteilhaftigkeitsbeurteilung 2.1 Kostenvergleichsrechnung Abkürzungen A 0 DGK i L T U Z Anschaffungsauszahlung Durchschnittlich gebundenes
Besteuerung der 1., 2. und 3. Säule Luzern
 Prämienabzüge 1. Säule Beiträge der 1. Säule können vollumfänglich vom Einkommen abgezogen werden. 2. Säule Beiträge der 2. Säule können vollumfänglich vom Einkommen abgezogen werden. Von den Einkünften
Prämienabzüge 1. Säule Beiträge der 1. Säule können vollumfänglich vom Einkommen abgezogen werden. 2. Säule Beiträge der 2. Säule können vollumfänglich vom Einkommen abgezogen werden. Von den Einkünften
Mathematik-Klausur vom 16.4.2004
 Mathematik-Klausur vom 16..200 Aufgabe 1 Die Wucher-Kredit GmbH verleiht Kapital zu einem nominellen Jahreszinsfuß von 20%, wobei sie die anfallenden Kreditzinsen am Ende eines jeden Vierteljahres der
Mathematik-Klausur vom 16..200 Aufgabe 1 Die Wucher-Kredit GmbH verleiht Kapital zu einem nominellen Jahreszinsfuß von 20%, wobei sie die anfallenden Kreditzinsen am Ende eines jeden Vierteljahres der
Wirtschaftsmathematik
 Einführung in einige Teilbereiche der Wintersemester 2016 Prof. Dr. Stefan Etschberger HSA m+1 re = r m + i 2 Äquivalenzprinzip der Finanzmathematik Das Äquivalenzprinzip der Finanzmathematik für Vergleich
Einführung in einige Teilbereiche der Wintersemester 2016 Prof. Dr. Stefan Etschberger HSA m+1 re = r m + i 2 Äquivalenzprinzip der Finanzmathematik Das Äquivalenzprinzip der Finanzmathematik für Vergleich
Besteuerung der 1., 2. und 3. Säule Zürich
 0BPrämienabzüge 1. Säule Beiträge der 1. Säule können vollumfänglich vom Einkommen abgezogen werden. 2. Säule Beiträge der 2. Säule können vollumfänglich vom Einkommen abgezogen werden. 6BSäule 3b Von
0BPrämienabzüge 1. Säule Beiträge der 1. Säule können vollumfänglich vom Einkommen abgezogen werden. 2. Säule Beiträge der 2. Säule können vollumfänglich vom Einkommen abgezogen werden. 6BSäule 3b Von
 Definition Gegenwartswert (Barwert) Der Wert des Geldes ist, über den man in der Gegenwart verfügen kann, ist grösser als der Wert des Geldes, den man in der Zukunft erhalten/zahlen wird. Diskontierung
Definition Gegenwartswert (Barwert) Der Wert des Geldes ist, über den man in der Gegenwart verfügen kann, ist grösser als der Wert des Geldes, den man in der Zukunft erhalten/zahlen wird. Diskontierung
Mathematik-Klausur vom 05.10.2011 Finanzmathematik-Klausur vom 26.09.2011
 Mathematik-Klausur vom 05.10.2011 Finanzmathematik-Klausur vom 26.09.2011 Studiengang BWL DPO 2003: Aufgaben 2,3,4 Dauer der Klausur: 60 Min Studiengang B&FI DPO 2003: Aufgaben 2,3,4 Dauer der Klausur:
Mathematik-Klausur vom 05.10.2011 Finanzmathematik-Klausur vom 26.09.2011 Studiengang BWL DPO 2003: Aufgaben 2,3,4 Dauer der Klausur: 60 Min Studiengang B&FI DPO 2003: Aufgaben 2,3,4 Dauer der Klausur:
Deckungskapital. Proseminar Versicherungsmathematik. TU Graz. 11. Dezember 2007
 Deckungskapital Gülnur Adanç Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 1 Inhaltsverzeichnis 1 Deckungskapital 2 1.1 Prospektive und Retrospektive Methode.................... 3 1.1.1
Deckungskapital Gülnur Adanç Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 1 Inhaltsverzeichnis 1 Deckungskapital 2 1.1 Prospektive und Retrospektive Methode.................... 3 1.1.1
.nzinn. :mni. Dldenbourg Verlag München Wien. 7, unveränderte Auflage. von Prof. Dr. Karl Bosch
 .nzinn :mni von Prof. Dr. Karl Bosch 7, unveränderte Auflage Dldenbourg Verlag München Wien Inhaltsverzeichnis Vorwort IX Kapitel 1: Mathematische Grundlagen 1 1.1. Die arithmetische Zahlenfolge 2 1.2.
.nzinn :mni von Prof. Dr. Karl Bosch 7, unveränderte Auflage Dldenbourg Verlag München Wien Inhaltsverzeichnis Vorwort IX Kapitel 1: Mathematische Grundlagen 1 1.1. Die arithmetische Zahlenfolge 2 1.2.
Gleich lautende Erlasse der obersten Finanzbehörden der Länder v. 10.10.2010 - BStBl 2010 I S. 810
 von 30 18.02.2013 14:14 Gleich lautende Erlasse der obersten Finanzbehörden der Länder v. 10.10.2010 - BStBl 2010 I S. 810 Bezug: FinMin Baden-Württemberg, Erlass vom 7. Dezember 2001, Az. S 3103/4,Oberste_FinBeh_der_Laender
von 30 18.02.2013 14:14 Gleich lautende Erlasse der obersten Finanzbehörden der Länder v. 10.10.2010 - BStBl 2010 I S. 810 Bezug: FinMin Baden-Württemberg, Erlass vom 7. Dezember 2001, Az. S 3103/4,Oberste_FinBeh_der_Laender
Aufgabe 5 Excel 2013 (Fortgeschrittene)
 - 1 - Aufgabe 5 Excel 2013 (Fortgeschrittene) 1. Starten Sie Excel und geben die Tabelle Hypothekenanalyse ein. Achten Sie bitte darauf, dass in den Zellen B10 und C11:G21 noch keine Angaben erfolgen.
- 1 - Aufgabe 5 Excel 2013 (Fortgeschrittene) 1. Starten Sie Excel und geben die Tabelle Hypothekenanalyse ein. Achten Sie bitte darauf, dass in den Zellen B10 und C11:G21 noch keine Angaben erfolgen.
Das Diskontrechnen Dr. Bommhardt. Das Vervielfältigen dieses Arbeitsmaterials zu nicht kommerziellen Zwecken ist gestattet. www.bommi2000.
 Das Diskontrechnen Dr. Bommhardt. Das Vervielfältigen dieses Arbeitsmaterials zu nicht kommerziellen Zwecken ist gestattet. www.bommi2000.de 1 Begriffe zum Diskontrechnen Das Diskontrechnen: -... ermittelt
Das Diskontrechnen Dr. Bommhardt. Das Vervielfältigen dieses Arbeitsmaterials zu nicht kommerziellen Zwecken ist gestattet. www.bommi2000.de 1 Begriffe zum Diskontrechnen Das Diskontrechnen: -... ermittelt
5. Fallstudie zum Operativen Konzern- Controlling
 5. Fallstudie zum Operativen Konzern- Controlling Bilanzierung von Leasingverhältnissen und Controlling Prof. Dr. Hans Dirrigl Gliederung der heutigen Fallstudie Thema der Fallstudie: IAS 17 Gliederung
5. Fallstudie zum Operativen Konzern- Controlling Bilanzierung von Leasingverhältnissen und Controlling Prof. Dr. Hans Dirrigl Gliederung der heutigen Fallstudie Thema der Fallstudie: IAS 17 Gliederung
für Besteuerungszeitpunkte nach dem 31. Dezember 2009 für Zwecke der Erbschaft- und Schenkungsteuer.
 Bewertung von Kapitalforderungen und Kapitalschulden sowie von Ansprüchen/Lasten bei wiederkehrenden Nutzungen und Leistungen nach dem 31. Dezember 2009 für Zwecke der Erbschaft- und Schenkungsteuer Bezug:
Bewertung von Kapitalforderungen und Kapitalschulden sowie von Ansprüchen/Lasten bei wiederkehrenden Nutzungen und Leistungen nach dem 31. Dezember 2009 für Zwecke der Erbschaft- und Schenkungsteuer Bezug:
Kommutationszahlen und Versicherungsbarwerte für Leibrenten 2001/2003
 Kommutationszahlen und Versicherungsbarwerte für Leibrenten 2001/2003 Tabellen zur jährlich und monatlich vorschüssigen Zahlungsweise Statistisches Bundesamt Impressum Herausgeber: Statistisches Bundesamt
Kommutationszahlen und Versicherungsbarwerte für Leibrenten 2001/2003 Tabellen zur jährlich und monatlich vorschüssigen Zahlungsweise Statistisches Bundesamt Impressum Herausgeber: Statistisches Bundesamt
Bernd Kuppinger. Finanzmathematik. WlLEY
 Bernd Kuppinger Finanzmathematik WlLEY 5 Inhalt Einleitung 13 1 Es geht ums Geld 17 1.1 Zeit und Geld 17 1.2 Inflation und Deflation 18 1.3 Barwert und Endwert 21 1.3.1 Nominalwert und Äquivalenzprinzip
Bernd Kuppinger Finanzmathematik WlLEY 5 Inhalt Einleitung 13 1 Es geht ums Geld 17 1.1 Zeit und Geld 17 1.2 Inflation und Deflation 18 1.3 Barwert und Endwert 21 1.3.1 Nominalwert und Äquivalenzprinzip
Altersarmut Assekuranz, der ungeliebte Retter?
 Altersarmut Assekuranz, der ungeliebte Retter? Dr. Johannes Lörper Öffentliche Veranstaltung des Vereins zur Förderung der Versicherungswissenschaft in Berlin 14.11.2013 1 Agenda Der Sparprozess in der
Altersarmut Assekuranz, der ungeliebte Retter? Dr. Johannes Lörper Öffentliche Veranstaltung des Vereins zur Förderung der Versicherungswissenschaft in Berlin 14.11.2013 1 Agenda Der Sparprozess in der
Test 1 (zu den Kapiteln 1 bis 6)
 Test 1 1 Test 1 (zu den Kapiteln 1 bis 6) Bearbeitungszeit: 90 Minuten Aufgabe T1.1: Bekanntmachung EUR 1.000.000.000,- Anleihe mit variablem Zinssatz der Fix AG von 2003/2013, Serie 111 Zinsperiode: 12.10.2006
Test 1 1 Test 1 (zu den Kapiteln 1 bis 6) Bearbeitungszeit: 90 Minuten Aufgabe T1.1: Bekanntmachung EUR 1.000.000.000,- Anleihe mit variablem Zinssatz der Fix AG von 2003/2013, Serie 111 Zinsperiode: 12.10.2006
Inhaltsverzeichnis Einleitung Elementare Finanzmathematik Biometrische Rechnungsgrundlagen
 Inhaltsverzeichnis 1 Einleitung... 1 1.1 Wesen der Versicherung... 2 1.2 Versicherungssparten... 3 1.3 Formen der Lebensversicherung... 4 1.4 Geschäftsverbindung... 6 1.5 Bedeutung der Lebensversicherung...
Inhaltsverzeichnis 1 Einleitung... 1 1.1 Wesen der Versicherung... 2 1.2 Versicherungssparten... 3 1.3 Formen der Lebensversicherung... 4 1.4 Geschäftsverbindung... 6 1.5 Bedeutung der Lebensversicherung...
Darlehen - als Möglichkeit der... -Finanzierung
 Darlehen - als Möglichkeit der.... -Finanzierung Situation: Bestattungsinstitut Thomas Bayer e. K. benötigt für ein Investitionsprojekt 0.000 Euro. Die Hausbank bietet dieses Darlehen mit folgenden Konditionen
Darlehen - als Möglichkeit der.... -Finanzierung Situation: Bestattungsinstitut Thomas Bayer e. K. benötigt für ein Investitionsprojekt 0.000 Euro. Die Hausbank bietet dieses Darlehen mit folgenden Konditionen
Inhaltsverzeichnis. Bibliografische Informationen digitalisiert durch
 1 Zinsrechnung 1 1.1 Grundbegriffe der Zinsrechnung 1 1.2 Die vier Fragestellungen der Zinsrechnung 3 1.3 Jährliche Verzinsung 5 1.3.1 Einfache Zinsen 5 1.3.1.1 Berechnung des Endkapitals 5 1.3.1.2 Berechnung
1 Zinsrechnung 1 1.1 Grundbegriffe der Zinsrechnung 1 1.2 Die vier Fragestellungen der Zinsrechnung 3 1.3 Jährliche Verzinsung 5 1.3.1 Einfache Zinsen 5 1.3.1.1 Berechnung des Endkapitals 5 1.3.1.2 Berechnung
Versicherungsüberblick
 Versicherungsüberblick I. Versicherungsüberblick Tarifbeschreibung: PLUS.invest private (Tarif 62) Fondsgebundene Rentenversicherung mit Absicherung bei Tod durch Beitragsrückgewähr/ und einer flexiblen
Versicherungsüberblick I. Versicherungsüberblick Tarifbeschreibung: PLUS.invest private (Tarif 62) Fondsgebundene Rentenversicherung mit Absicherung bei Tod durch Beitragsrückgewähr/ und einer flexiblen
Zur Vorlesung - Lebensversicherungsmathematik - Rundschreiben 64/41 des Reichsaufsichtsamts für Privatversicherung
 Zur Vorlesung - Lebensversicherungsmathematik - Rundschreiben 64/41 des Reichsaufsichtsamts für Privatversicherung Dr. J. Bartels für das Wintersemester 2015/16 Reichsaufsichtsamt Berlin W 15, den 17.
Zur Vorlesung - Lebensversicherungsmathematik - Rundschreiben 64/41 des Reichsaufsichtsamts für Privatversicherung Dr. J. Bartels für das Wintersemester 2015/16 Reichsaufsichtsamt Berlin W 15, den 17.
Exponentialfunktionen
 Exponentialfunktionen Teil 6 Höhere Finanzmathematik Sehr ausführliches Themenheft (d. h. mit Theorie) Aber auch mit vielen Trainingsaufgaben Es handelt sich um eine Anwendung von Exponentialfunktionen
Exponentialfunktionen Teil 6 Höhere Finanzmathematik Sehr ausführliches Themenheft (d. h. mit Theorie) Aber auch mit vielen Trainingsaufgaben Es handelt sich um eine Anwendung von Exponentialfunktionen
Mathematik-Klausur vom 2. Februar 2006
 Mathematik-Klausur vom 2. Februar 26 Studiengang BWL DPO 1997: Aufgaben 1,2,3,5,6 Dauer der Klausur: 12 Min Studiengang B&FI DPO 21: Aufgaben 1,2,3,5,6 Dauer der Klausur: 12 Min Studiengang BWL DPO 23:
Mathematik-Klausur vom 2. Februar 26 Studiengang BWL DPO 1997: Aufgaben 1,2,3,5,6 Dauer der Klausur: 12 Min Studiengang B&FI DPO 21: Aufgaben 1,2,3,5,6 Dauer der Klausur: 12 Min Studiengang BWL DPO 23:
