Stochastische Differentialgleichungen
|
|
|
- Andrea Lichtenberg
- vor 6 Jahren
- Abrufe
Transkript
1 INSTITUT FÜR STOCHASTIK SS 2007/08 UNIVRSITÄT KARLSRUH Bla 9 Priv.-Doz. Dr. D. Kadelka Übungen zur Vorleung Sochaiche Differenialgleichungen Muerlöungen Aufgabe 21: Definieren Sie analog zur d-dimenionalen Markov-Familie in Definiion 7.9 in geeigneer, innvoller Weie für einen N 0 -werigen ochaichen Proze X X 0 den Begriff einer Markov-Familie X, P x x N0. Kann der homogene Poion-Proze N 0 mi Parameer µ > 0 zu einer Markov-Familie erweier werden? Löung: Wir gehen au von Definiion 7.9, erezen R d durch N 0 und erhalen: ine N 0 -werige Markov-Familie Ω, A, F, X, P x x N0, kurz X, P x x N0, i ein F-adapierer, N 0 -weriger ochaicher Proze X X 0 auf einem Meraum Ω, A zuammen mi einer Familie P x x N0 von Wahrcheinlichkeimaßen auf Ω, A, o da für alle A A die Abbildung x P x A univerell mebar i, für alle x N 0 P x X 0 x 1, für alle x N 0,, 0 und B PN 0 P x [X + B F ] P x [X + B σx ] P x -f.., für alle x N 0,, 0 und B PN 0 P x [X + B X y] P y X B für P x X -f.a. y N 0. Hierbei kann die ere Bedingung weggelaen werden, da alle Funkionen f : N 0 R auomaich mebar ind wenn man N 0, wie üblich mi der σ-algebra A PN 0 verieh und wa wir oben chon implizi verwende haben. Ferner kann man ich beim Nachwei der beiden lezen Bedingungen auf den Fall von lemenarereignien B {n}, n N 0 bechränken, da der allgemeine Fall ich durch Aufummieren ergib. Wir erhalen: ine N 0 -werige Markov-Familie Ω, A, F, X, P x x N0, kurz X, P x x N0, i ein F-adapierer, N 0 -weriger ochaicher Proze X X 0 auf einem Meraum Ω, A zuammen mi einer Familie P x x N0 von Wahrcheinlichkeimaßen auf Ω, A, oda a für alle x N 0 P x X 0 x 1, b für alle x N 0,, 0 und n N 0 P x [X + n F ] P x [X + n σx ] P x -f..,
2 c für alle x N 0,, 0 und n N 0 P x [X + n X y] P y X n für P x X -f.a. y N 0. In [SP], Kap. 5.1 wurde die xienz eine homogenen Poion-Prozee N : N 0 mi Ineniä µ > 0 gezeig, den wir kurz mi PPµ bezeichnen, wobei nach den dor geroffenen Überlegungen noch voraugeez werden kann, da N Were in N 0 annimm und da N 0 0 gil. Wir nehmen an, da die Zufallvariablen N auf dem Wahrcheinlichkeiraum Ω, A, P definier ind und ezen noch F 0 : σn,. F 0 : F 0 0 i alo die naürliche Filraion von N. Wegen [SP], Saz 5.4 beiz N unabhängige Zuwäche und e gil N N Poµ für 0 <. Dami ind inbeondere F 0 und N N ochaich unabhängig für 0 <. Dami i nach Beipiel 7.3 N ein Markov-Proze bzgl. F 0 N i auch ein R-weriger Proze. Sei Ω, A : N 0 Ω, PN 0 A, F : PN 0 F 0 und X : N 0 Ω N 0 definier durch X ω : n + N ω für ω n, ω Ω und 0. Ferner ei P x : δ x P für x N 0. Dami i Ω, A, F, X, P x x N0 fegeleg. gil dann P x X k Px + N k PN k x, x, k N 0, 0. Wir benöigen die folgende Darellung von F : { } F {k} A k : A k F 0 Zu zeigen bleiben die Bedingungen a, b und c. a gil wegen P x X 0 x Px + N 0 x PN k0 c gil, obald PN y x > 0, alo y x 0, P x [X + n X y] P[x + N + n x + N y] P[x + N + N + N n x + N y] P[x + y x + N + N n x + N y] P[N + N n y N y x] PN + N n y PN n y P y X n. b Sei n N 0 fe und gy : P x [X + n X y] P y X n PN n y, y N 0. Dann i gx σx -mebar und e genüg zu zeigen [SII], 21.3, da für A σx P x {X + n} A gx dp x gil. Dabei genüg e, den Fall A {X y} zu berachen, da jede A σx eine abzählbare Vereinigung derariger reignie i. Dann gil aber wie geforder P x {X + n} A P x {X + n} {X y} P x [X + n X y] PX y A {X y} gx dp x,
3 da gx gy auf {X y} konan i. Aufgabe 22: C : R + R d r eine eige Funkion von R + in den Raum der d r-marizen d.h. eine Abbildung, die komponenenweie eig i. Zeigen Sie: a Da ochaiche Inegral M : 0 Cu db u 0 mi den Komponenen M i : k1 0 Cu ik db k u, 0 exiier und lieg komponenenweie in M c 2, kurz M M c 2. b F und M M ind ochaich unabhängig für 0 <. Hinwei: Benüzen Sie die folgende Verallgemeinerung von Aufgabe 1a: Sei Ω, A, P ein Wahrcheinlichkeiraum und eien X, X n R d -werige Zufallvariablen auf Ω, n N. I C A eine Uner-σ-Algebra von A, o da C und σx n für alle n N ochaich unabhängig ind und gil X n X P-ochaich für jede Komponene, o ind auch C und σx ochaich unabhängig. c M M beiz eine d-dimenionale Normalvereilung N d 0, Cu Cu du. Löung: Sei F k die zur Brownchen Bewegung B k gehörende naürliche Filraion. gil dann F k F, ferner ind nach Vorauezung die σ-algebren F 1,...,F r ochaich unabhängig für 0. a Da die C ik eig und dami auf endlichen Inervallen bechränk ind, gil C ik L B k und dami Cu 0 ik db u k 0 M c 2. Da M c 2 ein Vekorraum i, gil auch M i M c 2. Man beache, da F die zugrunde liegende Filraion i. b Wir beweien der Volländigkei halber zuer den Hinwei. Da auch die Komponenen X n k von X n P-ochaich gegen die k-e Komponene X k von X konvergieren, k 1,..., d, folg nach d-maliger Anwendung de Teilfolgekrierium für ochaiche Konvergenz die xienz einer Teilfolge X nl l N mi lim l X nl X P-f.. Sei D eine beliebige, nich leere abgechloene Teilmenge von R d und fx dx, D der Aband von x zu D. Dann i f : M R + eig mi f 1 0 D. Nach Vorauezung gil lim l fx nl fx P-f.. Da fx nl und C unabhängig ind, ind nach Aufgabe 1a auch fx und C unabhängig und dami auch D und C unabhängig. Da die Menge der abgechloenen Teilmengen von R d einen -abilen rzeuger von B d bilden, ind nach [SII], 9.5 auch X und C unabhängig. Al näche zeigen wir: Sei X 0 ein F-adapierer R d -weriger ochaicher Proze mi unabhängigen Zuwächen, o da F und der Zuwach X +h X für alle 0 < + h ochaich unabhängig ind. Dann ind F und C : σx +h X :, h > 0 für 0 ochaich unabhängig. genüg zu zeigen, da F und σx j+1 X j : j 0,...,n 1 unabhängig ind, wobei 0 < 1 <... < n und n N. Seien 0 < 1 <... < n, A F und B j B d für
4 d 1,...,n. Dann gil PA {X 1 X 0 B 1 }... {X n X n 1 B n } PA {X 1 X 0 B 1 }... {X n 1 X n 2 B n 1 } PX n X n 1 B n n... PA PX j X j 1 B j, wobei wir aunüzen, da A {X 1 X 0 B 1 }... {X n 1 X n 2 B n 1 } F n 1. Sei 0 < vorgegeben. Wir erezen vorer die eigen Funkionen C ik durch Treppenfunkionen. i dann jede Cu ik db u k eine Summe der Form n 1 α j B k j+1 B k j j0 mi gewien 0 < 1 <... < n und α j R. Nach dem gerade gezeigen ind daher F und M M Cu db u ochaich unabhängig. Wegen der Seigkei von C gib e eine Folge C n von Treppenfunkionen, die auf [0, ] gleichmäßig gegen C konvergier, inbeondere lim n d L C, C n 0 und dami auch lim n d M I B C n, I B C 0. Die bedeue inbeondere, da I B C n für alle 0 quadraich gegen I B C konvergier, alo auch lim n I B C n I B C n I B C I B C M M, alle komponenenweie. Da au der quadraichen Konvergenz die P-ochaiche Konvergenz folg, ind nach dem Hinwei auch F und M M ochaich unabhängig. c Sei vorer wie in b C n eine Treppenfunkion. Dann i j1 M n M n : I B C n I B C n eine Summe von unabhängigen normalvereilen Zufallvekoren A j B j+1 B j, wobei die A j geeignee d r-marizen ind, und dami elb d-dimenional normalvereil. Um zu zeigen, da M M normalvereil i, genüg e zu zeigen [SP], Saz 2.7, da a M M für alle a R d evenuell augeare normalvereil i. Wegen b und dem Teilfolgekrierium gib e eine Teilfolge n k k N mi lim k a M n k M n k a M M P-f.. und e genüg zu zeigen, da der fa ichere Lime einer Folge normalvereiler Zufallvariable wieder normalvereil i. Wir verwenden dazu: Lemma: Seien X n, X reellwerige Zufallvariable mi X D n X und X n Nµ n, σn. 2 Dann i X evenuell augeare normalvereil. Bewei de Lemma: Sei F : F X die Vereilungfunkion von X, X nich augeare, d.h. P-f.. konan, und eine Seigkeielle von F. Dann gil lim F µn X n lim Φ F. n n Da X nich augeare i, exiier ein kleine a und ein größe b mi a < b und 0 < F < 1 für alle a < < b und F nich konan auf a, b. Sei Dann i R \ C abzählbar und für C gil µ n lim n σ n σ n C : { R: Seigkeielle von F }. lim µ n n σ n σ n g : Φ 1 F R,
5 wobei wir noch Φ 1 0 : und Φ 1 1 : ezen. Wäre σ n n N nich bechränk, o müe g konan auf C ein. Die i nich möglich, da F nich konan auf a, b i. Nach Übergang zu einer Teilfolge können wir daher annehmen, da σ : lim n σ n R + exiier. I σ > 0, o gil auch µ : lim n µ n σ g, worau g µ folg σ und dami X Nµ, σ 2. σ 0 kann augechloen werden, da e a < < < b gib mi 0 < F < F < 1 und, C, alo < g < g <. Die i aber unverräglich mi, fall lim n σ n 0, da dann nowendig lim n µ n und lim n µ n. Da M ein Maringal i mi M 0 0, gil M M 0 0 und dami M M 0. Schließlich gil M i M i : Cu ik db u k und dami Cov M i M i, M j 8.9 M j I Bk k1 C ik I Bk C ik uc jl u d B k, B l u Cov Cu ik db u k, C ik, I Bl C jl I Bl C jl k1 Cu jl db u l C ik uc jk u du Cu Cu ij du, wobei Cu die Tranponiere von Cu i. Dami ergib ich die Kovarianzmarix von M M zu ΣM M Cu Cu du.
7 Das lokale Ito-Integral
 7 Das lokale Io-Inegral 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal 7.5 Seige, lokale Maringale
7 Das lokale Io-Inegral 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal 7.5 Seige, lokale Maringale
Höhere Mathematik III für die Fachrichtung Elektrotechnik und Informationstechnik Lösungsvorschläge zum 6. Übungsblatt
 Karlruher Iniu für Technologie KIT Iniu für Analyi Dr Ioanni Anapoliano Dr Semjon Wugaler WS 25/26 Höhere Mahemaik III für die Fachrichung Elekroechnik und Informaionechnik Löungvorchläge zum 6 Übungbla
Karlruher Iniu für Technologie KIT Iniu für Analyi Dr Ioanni Anapoliano Dr Semjon Wugaler WS 25/26 Höhere Mahemaik III für die Fachrichung Elekroechnik und Informaionechnik Löungvorchläge zum 6 Übungbla
existiert. In der Regel wird zusätzlich zum oben gegebenen System von Differentialgleichungen noch eine Anfangsbedingung
 0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
Restkapazität. = O( V ) mal kritisch. Also gibt es insgesamt höchstens O( V E ) Augmentierungen.
 Lemma 4.5.9. Der Algorihmu von Edmond-Karp führ höchen O( V E ) Augmenierungen durch. Bewei. Eine Kane (u, v) heiße kriich auf augmenierenden Weg p gdw. c f (u, v) = c f (p). Rekapaziä Eine kriiche Kane
Lemma 4.5.9. Der Algorihmu von Edmond-Karp führ höchen O( V E ) Augmenierungen durch. Bewei. Eine Kane (u, v) heiße kriich auf augmenierenden Weg p gdw. c f (u, v) = c f (p). Rekapaziä Eine kriiche Kane
Algorithmen II Vorlesung am
 Algorihmen II Vorleung am 24.10.2013 INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Univeriä de Lande Baden-Würemberg und Algorihmen naionale Forchungzenrum II Wineremeer 2013/2014
Algorihmen II Vorleung am 24.10.2013 INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Univeriä de Lande Baden-Würemberg und Algorihmen naionale Forchungzenrum II Wineremeer 2013/2014
e sx y(x)dx 2. Direkt gemäss der Definition unter Verwendung der in der Vorlesung angeführten Eigenschaften
 Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
Kapiel LAPLACE Tranformaion Die Laplace Tranformaion erwei ich al nüzlich zur Löung von linearen Dgln und Dgl- Syemen mi konanen Koeffizienen Dabei werden die Anfangbedingungen gleich miberückichig Definiion
6 Stochastische Differentialgleichungen
 6 Sochaiche Differenialgleichungen Viele deerminiiche Modelle der Naur- und der Wirchafwienchafen laen ich mi Hilfe von Differenialgleichungen audrücken. Mi dem Io-Inegral und der Io-Formel haben wir die
6 Sochaiche Differenialgleichungen Viele deerminiiche Modelle der Naur- und der Wirchafwienchafen laen ich mi Hilfe von Differenialgleichungen audrücken. Mi dem Io-Inegral und der Io-Formel haben wir die
DIPLOMARBEIT. Titel der Diplomarbeit. Stochastische Differentialgleichungen: Erweiterung deterministischer Modelle um. Angestrebter akademischer Grad
 DIPLOMARBEIT Tiel der Diplomarbei Sochaiche Differenialgleichungen: Erweierung deerminiicher Modelle um zufällige Einflüe Angereber akademicher Grad Magira der Naurwienchafen Mag. rer. na.) Verfaerin:
DIPLOMARBEIT Tiel der Diplomarbei Sochaiche Differenialgleichungen: Erweierung deerminiicher Modelle um zufällige Einflüe Angereber akademicher Grad Magira der Naurwienchafen Mag. rer. na.) Verfaerin:
Lineare Algebra I - Lösungshinweise zur Klausur
 Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
Definition Ein Homomorphismus von Lie-Algebren. Für uns ist vor allem die im folgenden Satz eingeführte Darstellung von Bedeutung.
 1 Lie-Gruppen 1. Lie-Algebren Im lezen Vorrag haben wir bereis das Konzep der Lie-Algebren kennengelern. Zunächs werde ich noch einige weiere grundlegende Definiionen dazu angeben. In diesem Kapiel sei
1 Lie-Gruppen 1. Lie-Algebren Im lezen Vorrag haben wir bereis das Konzep der Lie-Algebren kennengelern. Zunächs werde ich noch einige weiere grundlegende Definiionen dazu angeben. In diesem Kapiel sei
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 7 5. Semester ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE
 Mahemaik: Mag. Schmid Wolfgang Arbeibla 7. Semeer ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE Im Raum möche man naürlich nich nur Geraden ondern auch Flächen darellen. Diee Flächen bezeichne man al
Mahemaik: Mag. Schmid Wolfgang Arbeibla 7. Semeer ARBEITSBLATT 7 PARAMETERDARSTELLUNG EINER EBENE Im Raum möche man naürlich nich nur Geraden ondern auch Flächen darellen. Diee Flächen bezeichne man al
1 Diskrete Wahrscheinlichkeitstheorie
 Prof. A. Sapozhnikov Wahrcheinlichkeittheorie I INHALTSVERZEICHNIS 1 Dikrete Wahrcheinlichkeittheorie 1.1 Laplace-Wahrcheinlichkeit. Urnenmodelle. N! Begriffe: Ziehen ohne Zurücklegen, mit Reihenfolge,
Prof. A. Sapozhnikov Wahrcheinlichkeittheorie I INHALTSVERZEICHNIS 1 Dikrete Wahrcheinlichkeittheorie 1.1 Laplace-Wahrcheinlichkeit. Urnenmodelle. N! Begriffe: Ziehen ohne Zurücklegen, mit Reihenfolge,
Gewöhnliche Differentialgleichungen (DGL)
 Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
8.5 Uneigentliche Integrale Integrale über unbeschränkte Bereiche. f(x) dx. Integrale über unbeschränkte Funktionen mit Singularitäten am Rand
 8.5 Uneigenliche Inegrle Inegrle über unbeschränke Bereiche,, Inegrle über unbeschränke Funkionen mi Singulriäen m Rnd, f : (, b] R seig, f : [, b) R seig Lokle Inegrierbrkei: Definiion: Eine Funkion f
8.5 Uneigenliche Inegrle Inegrle über unbeschränke Bereiche,, Inegrle über unbeschränke Funkionen mi Singulriäen m Rnd, f : (, b] R seig, f : [, b) R seig Lokle Inegrierbrkei: Definiion: Eine Funkion f
3.4 Systeme linearer Differentialgleichungen
 58 Kapiel 3 Invarianen linearer Transformaionen 34 Syseme linearer Differenialgleichungen Die Unersuchung der Normalformen von Marizen soll nun auf die Lösung von Differenialgleichungssysemen angewende
58 Kapiel 3 Invarianen linearer Transformaionen 34 Syseme linearer Differenialgleichungen Die Unersuchung der Normalformen von Marizen soll nun auf die Lösung von Differenialgleichungssysemen angewende
5. Übungsblatt zur Differentialgeometrie
 Insiu für Mahemaik Prof. Dr. Helge Glöckner Dipl. Mah. Rafael Dahmen 5. Übungsbla zur Differenialgeomerie (Aufgaben und Lösungen) SoSe 3.05.0 Gruppenübung Aufgabe G9 (Submersionen und Unermannigfaligkei)
Insiu für Mahemaik Prof. Dr. Helge Glöckner Dipl. Mah. Rafael Dahmen 5. Übungsbla zur Differenialgeomerie (Aufgaben und Lösungen) SoSe 3.05.0 Gruppenübung Aufgabe G9 (Submersionen und Unermannigfaligkei)
Algorithmische Graphentheorie
 Algorihmiche Graphenheorie Sommeremeer 2014 3. Vorleung Flualgorihmen Prof. Dr. Alexander Wolff 1 Erinnerung Oh my God i an LP! Gegeben ein gericheer Graph G = (V, E) mi, V und Kanenkapaziäen c : E R >0.
Algorihmiche Graphenheorie Sommeremeer 2014 3. Vorleung Flualgorihmen Prof. Dr. Alexander Wolff 1 Erinnerung Oh my God i an LP! Gegeben ein gericheer Graph G = (V, E) mi, V und Kanenkapaziäen c : E R >0.
Abbildungsmaßstab und Winkelvergrößerung
 Abbildungmaßab und Winkelvergrößerung Abbildungmaßab Uner dem Abbildungmaßab vereh man da Verhälni /, wobei der Audruck ein negaive Vorzeichen erhäl, wenn da ild verkehr wird. Alo Abbildungmaßab V: Winkelvergrößerung
Abbildungmaßab und Winkelvergrößerung Abbildungmaßab Uner dem Abbildungmaßab vereh man da Verhälni /, wobei der Audruck ein negaive Vorzeichen erhäl, wenn da ild verkehr wird. Alo Abbildungmaßab V: Winkelvergrößerung
Technische Universität München Fakultät für Mathematik Algorithmische Diskrete Mathematik WS 2012/2013 Prof. Dr. P. Gritzmann 9.
 Noe: Name Vorname Marikelnummer Sudiengang Unerchrif der Kandidain/de Kandidaen Höraal Reihe Plaz Techniche Univeriä München Fakulä für Mahemaik Algorihmiche Dikree Mahemaik WS 0/0 Prof. Dr. P. Grizmann
Noe: Name Vorname Marikelnummer Sudiengang Unerchrif der Kandidain/de Kandidaen Höraal Reihe Plaz Techniche Univeriä München Fakulä für Mahemaik Algorihmiche Dikree Mahemaik WS 0/0 Prof. Dr. P. Grizmann
KAPITEL 2 KÜRZESTE WEGE
 KAPITEL 2 KÜRZESTE WEGE F. VALLENTIN, A. GUNDERT Da Ziel diee Kapiel i e kürzee Wege in einem gegebenen Nezwerk zu verehen und zu berechnen. Ein einführe Beipiel für ein Nezwerk zwichen den vier Säden
KAPITEL 2 KÜRZESTE WEGE F. VALLENTIN, A. GUNDERT Da Ziel diee Kapiel i e kürzee Wege in einem gegebenen Nezwerk zu verehen und zu berechnen. Ein einführe Beipiel für ein Nezwerk zwichen den vier Säden
4 Die K-Methode. Sei {A 0,A 1 } Interpolationspaar. Das Peetre sche K-Funktional ist definiert als. ( a 0 A 0 +t a 1 A 1 ), a A 0 +A 1, t > 0
 25 4 Die K-Mehode Sei {A,A } Inerpolaionpaar. Da Peere che K-Funkional i definier al K,a;A,A K,a : a a + a a i A i,i, a A + a A, a A +A, > Bemerkung : wenn {A,A } fixier K,a anelle von K,a;A,A K,a a A
25 4 Die K-Mehode Sei {A,A } Inerpolaionpaar. Da Peere che K-Funkional i definier al K,a;A,A K,a : a a + a a i A i,i, a A + a A, a A +A, > Bemerkung : wenn {A,A } fixier K,a anelle von K,a;A,A K,a a A
Stochastische Analysis und Finanzmathematik
 Sochasische Analysis und Finanzmahemaik Vorlesung im Winersemeser 211/212 von Dr. Markus Schulz Inhalsverzeichnis 1 Sochasische Prozesse 1 1.1 Grundlagen................................ 1 1.2 Die Brownsche
Sochasische Analysis und Finanzmahemaik Vorlesung im Winersemeser 211/212 von Dr. Markus Schulz Inhalsverzeichnis 1 Sochasische Prozesse 1 1.1 Grundlagen................................ 1 1.2 Die Brownsche
5. Übungsblatt zur Linearen Algebra II
 Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
2.2 Rechnen mit Fourierreihen
 2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
Höhere Mathematik II für die Fachrichtung Physik
 Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Michael Ho, M. Sc. M. Sc. SS 6 9.7.6 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zur Übungsklausur Aufgabe
Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Michael Ho, M. Sc. M. Sc. SS 6 9.7.6 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zur Übungsklausur Aufgabe
Universität Ulm Samstag,
 Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
d(x, z) = z x = y x + z y y x + z y = d(x, y) + d(y, z). d(x, y) = 0, falls x = y.
 Metrische Räume K bezeichnet entweder den Körper R oder den Körper C. Genauer bedeutet dies: K wird in denjenigen Situationen verwendet, in denen die Ersetzung von K sowohl durch R als auch durch C einen
Metrische Räume K bezeichnet entweder den Körper R oder den Körper C. Genauer bedeutet dies: K wird in denjenigen Situationen verwendet, in denen die Ersetzung von K sowohl durch R als auch durch C einen
14 Kurven in Parameterdarstellung, Tangentenvektor und Bogenlänge
 Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Zwischenwerteigenschaft
 Zwischenwereigenschaf Markus Berberich Ausarbeiung zum Vorrag im Proseminar Überraschungen und Gegenbeispiele in der Analysis (Sommersemeser 2009, Leiung PD Dr. Gudrun Thäer) Zusammenfassung: In dieser
Zwischenwereigenschaf Markus Berberich Ausarbeiung zum Vorrag im Proseminar Überraschungen und Gegenbeispiele in der Analysis (Sommersemeser 2009, Leiung PD Dr. Gudrun Thäer) Zusammenfassung: In dieser
8 Der Reiterationssatz
 53 8 Der Reieraionaz Definiion 8. Seien {A,A } ein Inerpolaionpaar,E ein Banachraum mi A A E A +A, und θ. i E gehör zur Klae Kθ;A,A, fall ein c > exiier, o da für alle a E und alle, <
53 8 Der Reieraionaz Definiion 8. Seien {A,A } ein Inerpolaionpaar,E ein Banachraum mi A A E A +A, und θ. i E gehör zur Klae Kθ;A,A, fall ein c > exiier, o da für alle a E und alle, <
Lösungen zu Übungsblatt 9
 Analysis : Camillo de Lellis HS 007 Lösungen zu Übungsblatt 9 Lösung zu Aufgabe 1. Wir müssen einfach das Integral 16 (x + y d(x, y x +y 4 ausrechnen. Dies kann man einfach mittels Polarkoordinaten, da
Analysis : Camillo de Lellis HS 007 Lösungen zu Übungsblatt 9 Lösung zu Aufgabe 1. Wir müssen einfach das Integral 16 (x + y d(x, y x +y 4 ausrechnen. Dies kann man einfach mittels Polarkoordinaten, da
Mathematik: Mag. Schmid Wolfgang+LehrerInnenteam ARBEITSBLATT 6-13 ERMITTELN DER KREISGLEICHUNG
 ahemaik: ag. Schmid WolfgangLehrerInneneam ARBEITSBLATT - ERITTELN DER KREISGLEICUNG Wir wollen un nun bemühen, die Gleichung pezieller Kreie zu ermieln. Beipiel: Ermile die Gleichung jene Kreie mi dem
ahemaik: ag. Schmid WolfgangLehrerInneneam ARBEITSBLATT - ERITTELN DER KREISGLEICUNG Wir wollen un nun bemühen, die Gleichung pezieller Kreie zu ermieln. Beipiel: Ermile die Gleichung jene Kreie mi dem
Der Primzahlsatz, Teil 1. 1 Erste Abschätzungen zum Primzahlsatz
 Der Primzahlsaz, Teil Vorrag zum Seminar zur Funionenheorie, 07.05.0 Raffaela Biesenbach Diese Arbei beschäfig sich mi der Herleiung des Primzahlsazes. Dazu werden Definiionen und Säze aus dem Sri zur
Der Primzahlsaz, Teil Vorrag zum Seminar zur Funionenheorie, 07.05.0 Raffaela Biesenbach Diese Arbei beschäfig sich mi der Herleiung des Primzahlsazes. Dazu werden Definiionen und Säze aus dem Sri zur
Lösung zur Hausaufgabe in Topologie und Differentialrechnung mehrerer Variablen SS x 1. x 2. x 1+x 2+x 3
 Bl Nr. 11 Simon Reisser Lösung zur Husufgbe in Topologie und Differenilrechnung mehrerer Vriblen SS 17 Aufgbe () Sei f(x 1, x, x 3 ) = (y 1, y, y 3 ) = (e x1x x3, e x1x+x3, e xx3 ) und dg(y 1, y, y 3 )
Bl Nr. 11 Simon Reisser Lösung zur Husufgbe in Topologie und Differenilrechnung mehrerer Vriblen SS 17 Aufgbe () Sei f(x 1, x, x 3 ) = (y 1, y, y 3 ) = (e x1x x3, e x1x+x3, e xx3 ) und dg(y 1, y, y 3 )
3 Markov-Eigenschaft der Brownschen Bewegung
 Man verifiziert 2.) für P n = Q n, und somit gilt: jede Teilfolge von (P n ) n N besitzt eine konvergente Teilfolge. Betrachte nun die endlich-dimensionalen Randverteilungen der Maße P n. Dazu sei π t1,...,t
Man verifiziert 2.) für P n = Q n, und somit gilt: jede Teilfolge von (P n ) n N besitzt eine konvergente Teilfolge. Betrachte nun die endlich-dimensionalen Randverteilungen der Maße P n. Dazu sei π t1,...,t
1 Das Lebesgue-Maß. 1.1 Etwas Maßtheorie. Sei stets X eine nichtleere Menge mit Potzenzmenge P(X) := {A : A X}.
 1 Das Lebesgue-Maß 1.1 Etwas Maßtheorie Sei stets X eine nichtleere Menge mit Potzenzmenge P(X) := {A : A X}. Definition 1.1. Ein nichtleeres Mengensystem A P(X) heißt σ-algebra, wenn: (A1) X A (A2) Wenn
1 Das Lebesgue-Maß 1.1 Etwas Maßtheorie Sei stets X eine nichtleere Menge mit Potzenzmenge P(X) := {A : A X}. Definition 1.1. Ein nichtleeres Mengensystem A P(X) heißt σ-algebra, wenn: (A1) X A (A2) Wenn
Mathematik 1 für Maschinenbau, M. Schuchmann (SoSe 2013) Aufgabenblatt 5 (Ebenen)
 Mahemaik für Machinenbau, M. Schuchmann (SoSe ) Aufgabenbla 5 (Ebenen) ) Geuch i eine Gleichung der Ebene E durch die Punke A(; -; ); B(; ; -) und C(; ; ) in Parameerform. ) Schreibe in Koordinaenform:
Mahemaik für Machinenbau, M. Schuchmann (SoSe ) Aufgabenbla 5 (Ebenen) ) Geuch i eine Gleichung der Ebene E durch die Punke A(; -; ); B(; ; -) und C(; ; ) in Parameerform. ) Schreibe in Koordinaenform:
Stochastische Prozesse
 INSTITUT FÜR STOCHASTIK SS 29 UNIVERSITÄT KARLSRUHE Blatt 6 Priv.-Doz. Dr. D. Kadelka Dipl.-Math. W. Lao Übungen zur Vorlesung Stochastische Prozesse Musterlösungen Aufgabe 27: Sei X eine R + -wertige
INSTITUT FÜR STOCHASTIK SS 29 UNIVERSITÄT KARLSRUHE Blatt 6 Priv.-Doz. Dr. D. Kadelka Dipl.-Math. W. Lao Übungen zur Vorlesung Stochastische Prozesse Musterlösungen Aufgabe 27: Sei X eine R + -wertige
Meßbare Funktionen. bilden die Grundlage der Integrationstheorie. Definition 24.1 :
 24 Meßbare Funktionen bilden die Grundlage der Integrationstheorie. Definition 24. : Sei X eine beliebige Menge, Y ein topologischer Raum, λ ein Maß auf X. f : X Y heißt λ-messbar, falls f (Ω) λ-messbar
24 Meßbare Funktionen bilden die Grundlage der Integrationstheorie. Definition 24. : Sei X eine beliebige Menge, Y ein topologischer Raum, λ ein Maß auf X. f : X Y heißt λ-messbar, falls f (Ω) λ-messbar
Vorlesung Kombinatorische Optimierung (Wintersemester 2007/08)
 Vorleung Kombinaoriche Opimierung (Wineremeer 007/08) Kapiel : Flüe und Zirkulaionen Volker Kaibel Oo-von-Guericke Univeriä Magdeburg (Verion vom 0. November 007) Definiion. Ein Nezwerk i ein Paar (D,
Vorleung Kombinaoriche Opimierung (Wineremeer 007/08) Kapiel : Flüe und Zirkulaionen Volker Kaibel Oo-von-Guericke Univeriä Magdeburg (Verion vom 0. November 007) Definiion. Ein Nezwerk i ein Paar (D,
Probeklausur 1. Thema Nr. 1 (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeiten!
 Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
1.3 Zufallsvariablen
 1.3 Zufallsvariablen Beispiel Irrfahrt zwischen drei Zuständen Start in G bei t = 0, Zeithorizont T N Grundraum σ-algebra Ω = {ω = (ω 0, ω 1,..., ω T ) {G, R, B} T +1, ω 0 = G} Wahrscheinlichkeitsmaß P
1.3 Zufallsvariablen Beispiel Irrfahrt zwischen drei Zuständen Start in G bei t = 0, Zeithorizont T N Grundraum σ-algebra Ω = {ω = (ω 0, ω 1,..., ω T ) {G, R, B} T +1, ω 0 = G} Wahrscheinlichkeitsmaß P
Stochastische Prozesse
 INSTITUT FÜR STOCHASTIK SS 2009 UNIVERSITÄT KARLSRUHE Blatt 9 Priv.-Doz. Dr. D. Kadelka Dipl.-Math. W. Lao Übungen zur Vorlesung Stochastische Prozesse Musterlösungen Aufgabe 40: Es sei (X t ) t 0 ein
INSTITUT FÜR STOCHASTIK SS 2009 UNIVERSITÄT KARLSRUHE Blatt 9 Priv.-Doz. Dr. D. Kadelka Dipl.-Math. W. Lao Übungen zur Vorlesung Stochastische Prozesse Musterlösungen Aufgabe 40: Es sei (X t ) t 0 ein
Die Lösungen der Übungsaufgaben werden durch folgendes Lemma etwas vereinfacht:
 Prof. Dr. D. Kuske, M.Sc. M. Huschenbe Fachgebie Theoreische Informaik, TU Ilmenau Muserlösung zum 2. Übungsbla Auomaenheorie Die Lösungen der Übungsaufgaben werden durch folgendes Lemma ewas vereinfach:
Prof. Dr. D. Kuske, M.Sc. M. Huschenbe Fachgebie Theoreische Informaik, TU Ilmenau Muserlösung zum 2. Übungsbla Auomaenheorie Die Lösungen der Übungsaufgaben werden durch folgendes Lemma ewas vereinfach:
Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkeit Seminararbeit aus Numerik von Differentialgleichungen
 Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkei Seminararbei aus Numerik von Differenialgleichungen Michael Hubner, Sefan Wurm 8. Juli 22 Inhalsverzeichnis. Problemdefiniion 2 2. Einführende
Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkei Seminararbei aus Numerik von Differenialgleichungen Michael Hubner, Sefan Wurm 8. Juli 22 Inhalsverzeichnis. Problemdefiniion 2 2. Einführende
Typ A: Separierbare Differentialgleichungen I. Separierbare Differentialgleichungen II. Beispiel einer separierbaren Dgl
 Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Mathematik für Physiker, Informatiker und Ingenieure
 Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Mathematik für Physiker, Informatiker und Ingenieure Folien zu Kapitel IV SS 2010 G. Dirr INSTITUT FÜR MATHEMATIK UNIVERSITÄT WÜRZBURG dirr@mathematik.uni-wuerzburg.de http://www2.mathematik.uni-wuerzburg.de
Lösungen zu Übungsblatt 4
 Fakulä für Mahemaik, Technische Universiä Dormund Vorlesung Geomerie für Lehram Gymnasium, Winersemeser 24/5 Dipl-Mah Aranç Kayaçelebi Lösungen zu Übungsbla 4 Aufgabe 2 Punke a Geben Sie eine Funkion f
Fakulä für Mahemaik, Technische Universiä Dormund Vorlesung Geomerie für Lehram Gymnasium, Winersemeser 24/5 Dipl-Mah Aranç Kayaçelebi Lösungen zu Übungsbla 4 Aufgabe 2 Punke a Geben Sie eine Funkion f
Einführung in gewöhnliche Differentialgleichungen
 Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
Kapitel 7. Exponentialfamilien. 7.1 Wahrscheinlichkeitsverteilungen
 Kapiel 7 Exponenialfamilien Exponenialfamilien sind dominiere saisische Räume, deren Likelihoodfunkion eine besonders einfache Srukur besiz, ihr Logarihmus is von affiner Gesal. Neben der daraus resulierenden
Kapiel 7 Exponenialfamilien Exponenialfamilien sind dominiere saisische Räume, deren Likelihoodfunkion eine besonders einfache Srukur besiz, ihr Logarihmus is von affiner Gesal. Neben der daraus resulierenden
DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN
 Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
5 Die Poisson-Approximation
 5 Die Poion-Approximation Im vierten Kapitel hatten wir mit der Normalverteilung die icherlich wichtigte und meittudierte Verteilung der W.-Theorie kennengelernt und geehen, daß man diee al Lime eine geeignet
5 Die Poion-Approximation Im vierten Kapitel hatten wir mit der Normalverteilung die icherlich wichtigte und meittudierte Verteilung der W.-Theorie kennengelernt und geehen, daß man diee al Lime eine geeignet
Anhang. A1 Analytische Lösungen der erweiterten Anzahlbilanz
 117 Anhang A1 Analyiche Löungen der erweieren Anzahlbilanz Die Bilanzgleichungen der erweieren Anzahlvereilung owohl für die koninuierliche al auch für die dikoninuierliche Krialliaion (l..-34 und.-35)
117 Anhang A1 Analyiche Löungen der erweieren Anzahlbilanz Die Bilanzgleichungen der erweieren Anzahlvereilung owohl für die koninuierliche al auch für die dikoninuierliche Krialliaion (l..-34 und.-35)
Stochastische Analysis
 Sochasische Analysis Maringale und sochasisches Inegral Franz Hofbauer Einleiung Sei (Ω, A, P ) ein Maßraum mi P (Ω) = 1. Die messbaren Mengen, das sind die Mengen in der σ-algebra A, werden als Ereignisse
Sochasische Analysis Maringale und sochasisches Inegral Franz Hofbauer Einleiung Sei (Ω, A, P ) ein Maßraum mi P (Ω) = 1. Die messbaren Mengen, das sind die Mengen in der σ-algebra A, werden als Ereignisse
7. Funktionalgleichung der Zeta-Funktion
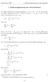 Oo Forser: RZF 7 Funkionalgleichung der Zea-Funkion 7 Funkionalgleichung der Zea-Funkion 7 Saz (Poissonsche Summaionsformel Sei f : R C eine seig differenzierbare Funkion mi f(x O ( x für x Sei ˆf : R
Oo Forser: RZF 7 Funkionalgleichung der Zea-Funkion 7 Funkionalgleichung der Zea-Funkion 7 Saz (Poissonsche Summaionsformel Sei f : R C eine seig differenzierbare Funkion mi f(x O ( x für x Sei ˆf : R
Fakultät Grundlagen. s = t. gleichförm ig
 Experimenierfeld Freier Fall und Würfe. Einführung Die Kinemaik al Lehre der Bewegungen befa ich nich mi den Urachen on Bewegungabläufen, ondern lediglich mi den Bewegungen an ich. Auch die Audehnung und
Experimenierfeld Freier Fall und Würfe. Einführung Die Kinemaik al Lehre der Bewegungen befa ich nich mi den Urachen on Bewegungabläufen, ondern lediglich mi den Bewegungen an ich. Auch die Audehnung und
Kurven in der Ebene und im Raum
 Kapiel 9 Kurven in der Ebene und im Raum 9. Parameerdarsellung von Kurven Aufgabe 9. : Skizzieren Sie die folgenden Mengen und beureilen Sie jeweils, ob es sich um eine abgeschlossene oder offene Menge
Kapiel 9 Kurven in der Ebene und im Raum 9. Parameerdarsellung von Kurven Aufgabe 9. : Skizzieren Sie die folgenden Mengen und beureilen Sie jeweils, ob es sich um eine abgeschlossene oder offene Menge
Die Bildung des Präsens funktioniert dann beispielsweise so: "lauda + mus" - wir loben.
 Präen Da Präen i die Gegenwarform. E bechreib alo Handlungen, die gerade paieren. Die Bildung i denkbar einfach und unercheide ich in den unerchiedlichen Konjugaionen (fa immer) nich. Dewegen reich e vollkommen
Präen Da Präen i die Gegenwarform. E bechreib alo Handlungen, die gerade paieren. Die Bildung i denkbar einfach und unercheide ich in den unerchiedlichen Konjugaionen (fa immer) nich. Dewegen reich e vollkommen
Analysis II Musterlösung 12. für t [ 0, 2π). y
 .. Saz von Green Die Randkurve des, in unensehender Figur dargesellen, umerangs kann paramerisier werden durch 4 cos ( + cos( sin( für, π..75.5.5 -.5 3 4 5 6 -.5 -.75 - Zur erechnung des Flächeninhales
.. Saz von Green Die Randkurve des, in unensehender Figur dargesellen, umerangs kann paramerisier werden durch 4 cos ( + cos( sin( für, π..75.5.5 -.5 3 4 5 6 -.5 -.75 - Zur erechnung des Flächeninhales
Von der Fourier-Reihe zum Fourier-Integral
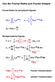 Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
Von der Fourier-Reihe um Fourier-Inegral Fourier-Reihe für periodiche Signale + f() = ν= c e ω = π f = ν j νω π + j νω cν = f() e d Nichperiodiche Signale dω d = df =, νω ω π + + j ω j ω π dω cν f() e
Robuste Portfolio Optimierung
 Robue Porfolio Opimierung in Lévy Märken Dieraion zur Erlangung de Dokorgrade Dr. rer. na der Fakulä für Mahemaik und Wirchafwienchafen der Univeriä Ulm vorgeleg von Dipl.-Mah. oec. Frank Wiemann au Offenburg
Robue Porfolio Opimierung in Lévy Märken Dieraion zur Erlangung de Dokorgrade Dr. rer. na der Fakulä für Mahemaik und Wirchafwienchafen der Univeriä Ulm vorgeleg von Dipl.-Mah. oec. Frank Wiemann au Offenburg
Übungen zu Funktionen Blatt 1
 Übungen zu Funktionen Blatt 1 In den Aufgaben 1 und 2 seien A 1, A 2, B 1, B 2 Teilmengen von Z. 1. Man zeige: Es gilt (A 1 A 2 ) (B 1 B 2 ) (A 1 B 1 ) (A 2 B 2 ). 2. Man zeige: Ist A 1 A 2 =, A 1 A 2,
Übungen zu Funktionen Blatt 1 In den Aufgaben 1 und 2 seien A 1, A 2, B 1, B 2 Teilmengen von Z. 1. Man zeige: Es gilt (A 1 A 2 ) (B 1 B 2 ) (A 1 B 1 ) (A 2 B 2 ). 2. Man zeige: Ist A 1 A 2 =, A 1 A 2,
Karlsruher Institut für Technologie (KIT) Institut für Analysis Dr. A. Müller-Rettkowski Dipl.-Math. M. Uhl. Sommersemester 2011
 Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
Lösungshinweise zu den Hausaufgaben:
 P. Engel, T. Pfrommer S. Poppiz, Dr. I. Rbak 8. Gruppenübung zur Vorlesung Höhere Mahemaik Sommersemeser 9 Prof. Dr. M. Sroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe H. Konvergenzverhalen
P. Engel, T. Pfrommer S. Poppiz, Dr. I. Rbak 8. Gruppenübung zur Vorlesung Höhere Mahemaik Sommersemeser 9 Prof. Dr. M. Sroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe H. Konvergenzverhalen
Satz von Rademacher und weiterführende Resultate
 S E M I N R R B E I T Saz von Rademacher und weierführende Resulae ausgeführ am Insiu für nalysis und Scienific Compuing TU Wien uner der nleiung von o.univ.prof. Dipl.-Ing. Dr.echn. Michael Kalenbäck
S E M I N R R B E I T Saz von Rademacher und weierführende Resulae ausgeführ am Insiu für nalysis und Scienific Compuing TU Wien uner der nleiung von o.univ.prof. Dipl.-Ing. Dr.echn. Michael Kalenbäck
Maße auf Produkträumen
 Maße auf Produkträumen Es seien (, Ω 1 ) und (X 2, Ω 2 ) zwei Meßräume. Wir wollen uns zuerst überlegen, wie wir ausgehend davon eine geeignete σ-algebra auf X 2 definieren können. Wir betrachten die Menge
Maße auf Produkträumen Es seien (, Ω 1 ) und (X 2, Ω 2 ) zwei Meßräume. Wir wollen uns zuerst überlegen, wie wir ausgehend davon eine geeignete σ-algebra auf X 2 definieren können. Wir betrachten die Menge
Analysis I - Stetige Funktionen
 Kompaktheit und January 13, 2009 Kompaktheit und Funktionengrenzwert Definition Seien X, d X ) und Y, d Y ) metrische Räume. Desweiteren seien E eine Teilmenge von X, f : E Y eine Funktion und p ein Häufungspunkt
Kompaktheit und January 13, 2009 Kompaktheit und Funktionengrenzwert Definition Seien X, d X ) und Y, d Y ) metrische Räume. Desweiteren seien E eine Teilmenge von X, f : E Y eine Funktion und p ein Häufungspunkt
D-MATH Mass und Integral FS 2018 Prof. Dr. Urs Lang. Lösung - Serie 2. + A k = A c k Ac k 0
 D-MATH Mass und Integral FS 2018 Prof. Dr. Urs Lang Lösung - Serie 2 Abgabetermin: Mittwoch, 07.03.2018 in die Fächli im HG F 28. Homepage der Vorlesung: https://metaphor.ethz.ch/x/2018/fs/401-2284-00l/
D-MATH Mass und Integral FS 2018 Prof. Dr. Urs Lang Lösung - Serie 2 Abgabetermin: Mittwoch, 07.03.2018 in die Fächli im HG F 28. Homepage der Vorlesung: https://metaphor.ethz.ch/x/2018/fs/401-2284-00l/
4 Messbare Funktionen
 4 Messbare Funktionen 4.1 Definitionen und Eigenschaften Definition 4.1. Seien X eine beliebige nichtleere Menge, M P(X) eine σ-algebra in X und µ ein Maß auf M. Das Paar (X, M) heißt messbarer Raum und
4 Messbare Funktionen 4.1 Definitionen und Eigenschaften Definition 4.1. Seien X eine beliebige nichtleere Menge, M P(X) eine σ-algebra in X und µ ein Maß auf M. Das Paar (X, M) heißt messbarer Raum und
12.6 Aufgaben zur Laplace-Transformation
 292 12. Aufgaben zu linearen Gleichungen 12.6 Aufgaben zur Laplace-Tranformation A B C D Man löe die folgenden Anfangwertprobleme durch Laplace-Tranformation: 1) ẍ ẋ x = ; x() = ẋ() = 1 2) x (3) 6ẍ + 12ẋ
292 12. Aufgaben zu linearen Gleichungen 12.6 Aufgaben zur Laplace-Tranformation A B C D Man löe die folgenden Anfangwertprobleme durch Laplace-Tranformation: 1) ẍ ẋ x = ; x() = ẋ() = 1 2) x (3) 6ẍ + 12ẋ
Grenzwertsätze für Zeitreihen
 KAPIEL 6 Grenzwersäze für Zeireihen In diesem Kapiel sellen wir wichige Grenzwersäze für saionäre Zeireihen {X n } in diskreer Zei zusammen. Sei µ = E(X ) und ρ(k) = E(X 1 µ)(x 1+k µ) = Cov (X 1, X 1+k
KAPIEL 6 Grenzwersäze für Zeireihen In diesem Kapiel sellen wir wichige Grenzwersäze für saionäre Zeireihen {X n } in diskreer Zei zusammen. Sei µ = E(X ) und ρ(k) = E(X 1 µ)(x 1+k µ) = Cov (X 1, X 1+k
Aufgaben zu Kapitel 0
 Aufgaben zu Kapitel 0 0.1. Seien A und B zwei Mengen. Wie kann man paarweise disjunkte Mengen A 1, A 2 und A 3 so wählen, dass A 1 A 2 A 3 = A B gilt? 0.2. Seien E ein Menge und A eine Teilmengen von E.
Aufgaben zu Kapitel 0 0.1. Seien A und B zwei Mengen. Wie kann man paarweise disjunkte Mengen A 1, A 2 und A 3 so wählen, dass A 1 A 2 A 3 = A B gilt? 0.2. Seien E ein Menge und A eine Teilmengen von E.
Metrische äußere Maße, Borel-Maße
 Metrische äußere Maße, Borel-Maße Zum einen haben wir mit dem Fortsetzungssatz gesehen, dass man mit einem äußeren Maß (auf P(X) ) stets eine σ-algebra und ein Maß auf dieser bekommt. Liegt nun ein metrischer
Metrische äußere Maße, Borel-Maße Zum einen haben wir mit dem Fortsetzungssatz gesehen, dass man mit einem äußeren Maß (auf P(X) ) stets eine σ-algebra und ein Maß auf dieser bekommt. Liegt nun ein metrischer
2 Halbgruppen von Übergangswahrscheinlichkeiten. Markov-Prozesse
 2 Halbgruppen von Übergangswahrscheinlichkeiten Markov-Prozesse Im Folgenden sei (X, B) ein (polnischer) Messraum und T = [0, ) oder T = N 0 Definition 21 Eine Familie (P t ) t T von (X, B) mit Übergangswahrscheinlichkeiten
2 Halbgruppen von Übergangswahrscheinlichkeiten Markov-Prozesse Im Folgenden sei (X, B) ein (polnischer) Messraum und T = [0, ) oder T = N 0 Definition 21 Eine Familie (P t ) t T von (X, B) mit Übergangswahrscheinlichkeiten
Abiturprüfung Mathematik 2009 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
Grundlagen der Wahrscheinlichkeitstheorie
 Priv.-Doz. Dr. H. Steinacker Wintersemester 2013/2014 Grundlagen der Wahrscheinlichkeitstheorie betrachte Wiederholungen eines Experimentes, gleicher Vorbereitung (z.b. Würfeln, Dart werfen, Doppelspaltexperiment,...)
Priv.-Doz. Dr. H. Steinacker Wintersemester 2013/2014 Grundlagen der Wahrscheinlichkeitstheorie betrachte Wiederholungen eines Experimentes, gleicher Vorbereitung (z.b. Würfeln, Dart werfen, Doppelspaltexperiment,...)
Hauptprüfung 2010 Aufgabe 4
 Haupprüfung Aufgabe Gegeben ind die Punke A(5//), B(//), C(//) und S(//5).. Zeigen Sie, da da Dreieck ABC rechwinklig und gleichchenklig i. Berechnen Sie die Koordinaen de Punke D o, da da Viereck ABCD
Haupprüfung Aufgabe Gegeben ind die Punke A(5//), B(//), C(//) und S(//5).. Zeigen Sie, da da Dreieck ABC rechwinklig und gleichchenklig i. Berechnen Sie die Koordinaen de Punke D o, da da Viereck ABCD
Klausur zur Vorlesung Stochastik II
 Institut für Mathematische Stochastik WS 003/004 Universität Karlsruhe 05. 04. 004 Prof. Dr. G. Last Klausur zur Vorlesung Stochastik II Dauer: 90 Minuten Name: Vorname: Matrikelnummer: Diese Klausur hat
Institut für Mathematische Stochastik WS 003/004 Universität Karlsruhe 05. 04. 004 Prof. Dr. G. Last Klausur zur Vorlesung Stochastik II Dauer: 90 Minuten Name: Vorname: Matrikelnummer: Diese Klausur hat
Bewertungsmethoden in der Versicherungsmathematik
 Bewerungmehoden in der Vericherungmahemaik Techniche Reerven und Markwere II Johanne Pacheag Mahemaiche Iniu der Univeriä zu Köln Sommeremeer 2010 Bereuung: Prof. Schmidli, Dr. Eienberg 1 Inhalverzeichni
Bewerungmehoden in der Vericherungmahemaik Techniche Reerven und Markwere II Johanne Pacheag Mahemaiche Iniu der Univeriä zu Köln Sommeremeer 2010 Bereuung: Prof. Schmidli, Dr. Eienberg 1 Inhalverzeichni
3. Übungsblatt - Lösungsskizzen. so, dass f tatsächlich eine Wahrscheinlichkeitsdichte
 Einführung in die Wahrscheinlichkeitstheorie und Statistik Prof. Dr. Jan Johannes Sandra Schluttenhofer Wintersemester 208/9 3. Übungsblatt - Lösungsskizzen Aufgabe 9 Stetige Verteilungen, 4 =.5 +.5 +
Einführung in die Wahrscheinlichkeitstheorie und Statistik Prof. Dr. Jan Johannes Sandra Schluttenhofer Wintersemester 208/9 3. Übungsblatt - Lösungsskizzen Aufgabe 9 Stetige Verteilungen, 4 =.5 +.5 +
Kommutativität. De Morgansche Regeln
 1. Formale Logik Proposition 1.1. Die logischen Elementarverknüpfungen gehorchen folgenden Äquivalenzen: (1.1) (1.2) p p p p p p Idempotenz (1.3) (1.4) p q q p p q q p Kommutativität (1.5) (1.6) (p q)
1. Formale Logik Proposition 1.1. Die logischen Elementarverknüpfungen gehorchen folgenden Äquivalenzen: (1.1) (1.2) p p p p p p Idempotenz (1.3) (1.4) p q q p p q q p Kommutativität (1.5) (1.6) (p q)
Geometric Algebra Computing Transformationen in LA und CGA Dr. Dietmar Hildenbrand
 Geomeric Algebra Compuing Tranformaionen in LA und CGA 4.2.24 Dr. Diemar Hildenbrand Techniche Univeriä Darmad Fachbereich Mahemaik Überblick In linearer Algebra Homogene Koordinaen Tranformaionen in linearer
Geomeric Algebra Compuing Tranformaionen in LA und CGA 4.2.24 Dr. Diemar Hildenbrand Techniche Univeriä Darmad Fachbereich Mahemaik Überblick In linearer Algebra Homogene Koordinaen Tranformaionen in linearer
A. Maß- und Integrationstheorie
 A. Maß- und Integrationstheorie Im folgenden sind einige Ergebnisse aus der Maß- und Integrationstheorie zusammengestellt, die wir im Laufe der Vorlesung brauchen werden. Für die Beweise der Sätze sei
A. Maß- und Integrationstheorie Im folgenden sind einige Ergebnisse aus der Maß- und Integrationstheorie zusammengestellt, die wir im Laufe der Vorlesung brauchen werden. Für die Beweise der Sätze sei
Schwartz-Raum (Teil 1)
 Schwartz-Raum (Teil 1) Federico Remonda, Robin Krom 10. Januar 2008 Zusammenfassung Der Schwartz-Raum ist ein Funktionenraum, der besondere Regularitätseigenschaften besitzt, die uns bei der Fouriertransformation
Schwartz-Raum (Teil 1) Federico Remonda, Robin Krom 10. Januar 2008 Zusammenfassung Der Schwartz-Raum ist ein Funktionenraum, der besondere Regularitätseigenschaften besitzt, die uns bei der Fouriertransformation
Wichtige Begriffe und Sätze aus der Wahrscheinlichkeitsrechnung
 Wichtige Begriffe und Sätze aus der Wahrscheinlichkeitsrechnung Version: 22. September 2015 Evelina Erlacher 1 Mengen Es sei Ω eine Menge (die Universalmenge ) und A, B seien Teilmengen von Ω. Dann schreiben
Wichtige Begriffe und Sätze aus der Wahrscheinlichkeitsrechnung Version: 22. September 2015 Evelina Erlacher 1 Mengen Es sei Ω eine Menge (die Universalmenge ) und A, B seien Teilmengen von Ω. Dann schreiben
Technische Universität München. Lösung Montag SS 2012
 Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
Endliche Markov-Ketten - eine Übersicht
 Endliche Markov-Ketten - eine Übersicht Diese Übersicht über endliche Markov-Ketten basiert auf dem Buch Monte Carlo- Algorithmen von Müller-Gronbach et. al. und dient als Sammlung von Definitionen und
Endliche Markov-Ketten - eine Übersicht Diese Übersicht über endliche Markov-Ketten basiert auf dem Buch Monte Carlo- Algorithmen von Müller-Gronbach et. al. und dient als Sammlung von Definitionen und
Anfangswertprobleme gewöhnlicher Differentialgleichungen
 13. Großübung Anfangswerprobleme gewöhnlicher Differenialgleichungen gesuch: mi T und y () = f(, ), y( ) = y (1) y( j+1 ) = y( j ) + j+1 j f(s, y(s)) ds () Idee: Erseze Inegral durch Quadraurformel Näherungen
13. Großübung Anfangswerprobleme gewöhnlicher Differenialgleichungen gesuch: mi T und y () = f(, ), y( ) = y (1) y( j+1 ) = y( j ) + j+1 j f(s, y(s)) ds () Idee: Erseze Inegral durch Quadraurformel Näherungen
Scheinklausur zur Vorlesung Stochastik II
 Institut für Mathematische Stochastik WS 2007/2008 Universität Karlsruhe 25. 02. 2008 Dr. B. Klar Scheinklausur zur Vorlesung Stochastik II Muster-Lösung Dauer: 90 Minuten Name: Vorname: Matrikelnummer:
Institut für Mathematische Stochastik WS 2007/2008 Universität Karlsruhe 25. 02. 2008 Dr. B. Klar Scheinklausur zur Vorlesung Stochastik II Muster-Lösung Dauer: 90 Minuten Name: Vorname: Matrikelnummer:
Lösungsvorschlag zu den Hausaufgaben der 3. Übung
 FAKULTÄT FÜR MATHEMATIK Prof. Dr. Patrizio Neff 30.0.204 Lösungsvorschlag zu den Hausaufgaben der 3. Übung Aufgabe : (6 Punte) Welche der folgenden Tupel sind Maßräume? Beweisen Sie Ihre Behauptung. {
FAKULTÄT FÜR MATHEMATIK Prof. Dr. Patrizio Neff 30.0.204 Lösungsvorschlag zu den Hausaufgaben der 3. Übung Aufgabe : (6 Punte) Welche der folgenden Tupel sind Maßräume? Beweisen Sie Ihre Behauptung. {
Messbare Vektorräume
 Messbare Vektorräume Hans-Jörg Starkloff TU Bergakademie Freiberg Westsächsische Hochschule Zwickau Dezember 2010 / Januar 2011 Hans-Jörg Starkloff Messbare Vektorräume 1 1. Definition Geg. X linearer
Messbare Vektorräume Hans-Jörg Starkloff TU Bergakademie Freiberg Westsächsische Hochschule Zwickau Dezember 2010 / Januar 2011 Hans-Jörg Starkloff Messbare Vektorräume 1 1. Definition Geg. X linearer
8 Martingaldarstellung und Doob-Meyer Zerlegung
 8 Martingaldartellung und Doob-Meyer Zerlegung 8.1 Der Martingaldartellungatz In Kapitel 3 haben wir gezeigt, da da Ito-Integral eine H -Integranden ein tetige Martingal it. Der Martingaldartellungatz
8 Martingaldartellung und Doob-Meyer Zerlegung 8.1 Der Martingaldartellungatz In Kapitel 3 haben wir gezeigt, da da Ito-Integral eine H -Integranden ein tetige Martingal it. Der Martingaldartellungatz
No-Arbitrage Modelle
 No-Arbirage Modelle Sefan Fremd 17. Januar 27 1 Einleiung No-Arbirage Modelle: Modelle, bei denen die beobacheen Preise der Anleihen Derivae am Mark P obs (, T ) genau mi denen des Modells ˆP (, T ) übereinsimmen,
No-Arbirage Modelle Sefan Fremd 17. Januar 27 1 Einleiung No-Arbirage Modelle: Modelle, bei denen die beobacheen Preise der Anleihen Derivae am Mark P obs (, T ) genau mi denen des Modells ˆP (, T ) übereinsimmen,
2.6 Der Satz von Fubini
 1 2.6 Der Satz von Fubini Unser Ziel ist der Beweis des folgenden Ergebnisses. 6.1. Satz von Fubini Sei f : R n+m R integrierbar. Dann gibt es eine Nullmenge N R m, so dass gilt: 1. Für alle y R m \ N
1 2.6 Der Satz von Fubini Unser Ziel ist der Beweis des folgenden Ergebnisses. 6.1. Satz von Fubini Sei f : R n+m R integrierbar. Dann gibt es eine Nullmenge N R m, so dass gilt: 1. Für alle y R m \ N
Höhere Mathematik II für die Fachrichtung Physik
 Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Dipl.-Mah. Sebasian Schwarz SS 015 17.05.015 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zum 6. Übungsbla
Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Dipl.-Mah. Sebasian Schwarz SS 015 17.05.015 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zum 6. Übungsbla
Einführung in die Stochastik 6. Übungsblatt
 Einführung in die Stochastik 6. Übungsblatt Fachbereich Mathematik SS M. Kohler 3. Mai A. Fromkorth D. Furer Gruppen und Hausübung Aufgabe (a) Die Wahrscheinlichkeit, dass eine S Bahn Verspätung hat, betrage.3.
Einführung in die Stochastik 6. Übungsblatt Fachbereich Mathematik SS M. Kohler 3. Mai A. Fromkorth D. Furer Gruppen und Hausübung Aufgabe (a) Die Wahrscheinlichkeit, dass eine S Bahn Verspätung hat, betrage.3.
1 Integrale von Funktionen in mehreren Variablen
 $Id: inegral.ex,v 1.12 2015/10/26 13:46:09 hk Exp $ 1 Inegrale von Funkionen in mehreren Variablen 1.1 Das Rieman Inegral im R n Im lezen Semeser wurde die Differenialrechnung auf Funkionen f(x 1,...,
$Id: inegral.ex,v 1.12 2015/10/26 13:46:09 hk Exp $ 1 Inegrale von Funkionen in mehreren Variablen 1.1 Das Rieman Inegral im R n Im lezen Semeser wurde die Differenialrechnung auf Funkionen f(x 1,...,
Hauptachsentransformation
 Haupachsenransformaion Erinnerung: A M n is genau ann nich inverierbar, wenn es ein x R n, x gib, mi A x. Definiion. Sei A M n eine Marix. Ein Vekor v R n, v heiß Eigenvekor von A zum Eigenwer λ R, wenn
Haupachsenransformaion Erinnerung: A M n is genau ann nich inverierbar, wenn es ein x R n, x gib, mi A x. Definiion. Sei A M n eine Marix. Ein Vekor v R n, v heiß Eigenvekor von A zum Eigenwer λ R, wenn
