Wiederholung Quadratische Funktionen (Parabeln)
|
|
|
- Stephanie Hofmann
- vor 6 Jahren
- Abrufe
Transkript
1 SEITE 1 VON 7 Wiederholung Quadratische Funktionen (Parabeln) VON HEINZ BÖER 1. Regeln a) Funktionsvorschriften Normalform f(x) = a x² + b x + c Normalparabel: f(x) = x 2 Graf der Normalparabel Die einfachste Form liegt vor, wenn a = 1 und b = c = 0 gilt. Der Graf geht durch (0/0). Vier weitere Punkte erhält man, indem man von (0/0) eine Einheit nach rechts geht und eine nach oben; eine nach links und eine nach oben, zwei nach rechts und 4 nach oben, zwei nach links und 4 nach oben. Die 5 Punkte müssen noch elegant (nicht durch Strecken!) durch eine Kurve verbunden werden. Andere Formen: Die Formvariable a bestimmt die Form der Parabel. a > 0 nach oben geöffnet a < 0 nach unten geöffnet a > 1 schlanker als die Normalparabel a < 1 breiter als die Normalparabel Die Formvariable c gibt den Schnittpunkt mit der y-achse an: S y (0 c). Scheitelpunktform f(x) = a(x - x S )² + y S Scheitelpunkt ist S(x S y S ) Achtung: Es gibt einen Vorzeichenwechsel von x S ist in der Funktionsvorschrift zum Scheitelpunktwert! a hat dieselbe Bedeutung wie bei der Normalform oben. Umrechnung von der Scheitelpunktform in die Normalform: ausmultiplizieren. b) Vom Grafen zur Funktionsvorschrift Ablesen des Scheitelpunktes S(x S y S ); Eintragen der beiden Werte in die Scheitelpunktform. Vom Scheitelpunkt eine Einheit nach rechts gehen und ablesen, wie weit man von dort nach oben oder unten (negatives Vorzeichen) gehen muss, bis man wieder auf den Grafen trifft. Den Wert (mit Vorzeichen) für a in die Scheitelpunktform eintragen. Ergibt sich a = 1, so liegt eine verschobene Normalparabel vor. Ist der Wert für a in der Grafik schlecht ablesbar, dann liest man irgendeinen gut ablesbaren Punkt auf dem Grafen ab (nicht S, da der Punkt oben schon ausgewertet wurde) und setzt den x-wert in die Scheitelpunktform für x ein, den y-wert für f(x). Da x S und y S schon eingetragen waren, erhält man eine Gleichung, in der nur noch a unbekannt ist. Die Gleichung ist zu lösen. Soll die Normalform der Funktionsvorschrift bestimmt werden, so wird ausmultipliziert (s.o. a7).
2 SEITE 2 VON 7 c) Von gegebenen Daten zur Funktionsvorschrift Sind S(x S y S ) und a gegeben, so setzt man die drei Daten in die Scheitelpunktform ein und ist fertig. Falls gewünscht, erhält man die Normalform durch Ausmultiplizieren. Ist S und ein weiterer Punkt gegeben, so setzt man x S und y S ein und geht vor wie in b2. Sind drei Punkte gegeben, so wählt man die Normalform und setzt man den x-wert des ersten Punktes für x ein, den y-wert für f(x). Macht man das für alle drei Punkte, so erhält man drei Gleichungen, die nur noch a, b und c als Variablen enthalten. Das Gleichungssystem muss dann gelöst werden. d) Von der Funktionsvorschrift in Scheitelpunktform zum Grafen Zeichnen Sie den Scheitelpunkt in das Koordinatensystem. Ist a = 1, dann liegt eine verschobene Normalparabel vor. Gehen Sie von S eine Einheit nach rechts und eine nach oben, eine nach links und eine nach oben, zwei nach rechts und vier nach oben, zwei nach links und vier nach oben; genauso wie beim Zeichnen der Normalparabel (s.o. a3), hier starten Sie lediglich bei dem gegebenen Scheitelpunkt S. Ist a = -1, so verfahren Sie ebenso, gehen nur jeweils eine bzw. vier Einheiten nach unten statt oben. Ist a nicht 1 oder -1, so gehen Sie vom Scheitelpunkt S eine Einheit nach rechts und den Wert von a je nach Vorzeichen nach oben oder unten, ebenso eine Einheit nach links; zwei nach rechts und 4a nach oben bzw. unten, ebenso zwei nach links. Verbinden Sie die fünf Punkte elegant durch eine Kurve (keine Strecken zeichnen!). e) Von der Funktionsvorschrift in Normalform zum Grafen Dazu gibt es zwei verschiedene Wege: 1. Erstellen einer kompletten Wertetabelle, Punkte einzeichnen und elegant verbinden (umständlich, anfällig für Rechenfehler und in der Regel nicht zu empfehlen). Zudem wird der Scheitelpunkt evtl. nicht getroffen. 2. Bestimmen charakteristischer Punkte der Parabel, Einzeichnen und elegante Verbindung dieser Punkte zu einer Parabelkurve. Sinnvolle Punkte sind die Nullstellen: durch p-q-formel oder quadratische Ergänzung bestimmen siehe Kapitel Quadratische Gleichungen. der Scheitelpunkt: der x-wert liegt mitten zwischen den beiden Nullstellen (falls vorhanden) bzw. noch leichter: der x-wert des Scheitelpunktes ergibt sich direkt p als xs = aus der p-q-formel bei der Nullstellen-Bestimmung oben (auch 2
3 SEITE 3 VON 7 wenn keine Nullstellen existieren). Den Funktionswert y S des Scheitelpunktes gewinnt man durch Einsetzen y S = f(x S ). der Schnittpunkt mit der y-achse: Ablesen von c in der Funktionsvorschrift. Die vier Punkte müssen dann noch elegant zu einer Kurve verbunden werden. Falls es keine Nullstellen gibt, hat man nur 2 Punkte. Dann sollte man zwei weitere Punkte (wie in einer Wertetabelle) zusätzlich bestimmen, damit man die Kurve elegant hinbekommt. 2. Beispiele a) Funktionsvorschriften f(x) = -2 x² + 4 x + 1: Funktionsvorschrift in Normalform mit a = -2; b = +4; c = +1; Die Parabel ist nach unten geöffnet, da a < 0. Sie ist schlanker als die Normalparabel, da a < -1 bzw. im Betrag a > 1. Sie schneidet bei S y (0 1) die y-achse, da c = 1. f(x) = -2 (x - 1)² + 3; Scheitelpunktform mit S(1 3) Vorzeichenwechsel beim x-wert! Multipliziert man den Funktionsterm rechts aus (binomische Formel II beachten), so ergibt sich die Normalform der Funktionsvorschrift -2 (x - 1)² + 3 = - 2 (x 2 2 x + 1) + 3 = -2 x² + 4 x ; also f(x) = -2 x² + 4 x + 1. b) Vom Grafen zur Funktionsvorschrift Lesen Sie S(3-4) ab und setzen Sie den Punkt in die Scheitelpunktform ein: f(x) = a (x - 3)² - 4. Zeichnen Sie von S eine Einheit nach rechts, gehen Sie von dort 1,5 Einheiten nach oben, dann treffen Sie wieder auf die Parabel, also a = 1,5. Insgesamt f(x) = 1,5 (x - 3)² - 4. Ist Ihnen die Ablesung von a zu unsicher, so notieren Sie einen gut ablesbaren Punkt, etwa (5 2), setzen Sie den x- und y-wert in die Scheitelpunktform von oben ein (5 für x, 2 für f(x)) und berechnen Sie a: 2 = a (5-3)² = = 4 a a = 1,5 Die Normalform erhält man durch Ausmultiplizieren: 1,5 (x² - 6 x + 9) - 4 = 1,5 x² - 9 x + 13,5-4; also f(x) = 1,5 x² - 9 x + 9,5. Zur Kontrolle: Im Grafen ist zu erkennen, dass die Parabel bei c = 9,5 die y-achse schneidet.
4 SEITE 4 VON 7 c) Von gegebenen Daten zur Funktionsvorschrift In dem Brückengrafen soll die Breite w = 80 m betragen und die Höhe h = 20 m. Bei dem eingezeichneten Koordinatensystem liegt der Scheitelpunkt im Ursprung S(0 0). Also gilt: f(x) = a (x - 0)² + 0 = a x². a ist in der Zeichnung nicht ablesbar, indem man eine Einheit nach rechts geht. Aber aus den Daten kann man die Koordinaten des Punktes I (rechts) bestimmen: er liegt den halben w-wert rechts von E, also x = 40, und um die Höhe h tiefer, also y = -20. Die Koordinaten setzt man in die Funktionsgleichung ein: -20 = a 40² -20 = 1600 a a = -0,0125. Insgesamt: f(x) = -0,0125 x². Eine Parabel verläuft durch die Punkte A(0-5), B(2 11), C(-1-7). Setzen Sie die Punktkoordinaten in die Normalform f(x) = a x² + b x + c ein. Sie erhalten 3 Gleichungen A: f(0) = a 0² + b 0+ c = -5; hieraus ergibt sich c = -5. Der nun bekannte c-wert kann in die folgenden 2 Gleichungen eingesetzt werden. B: f(2) = a 2² + b 2-5 = a + 2 b = 16 Das ist Gleichung I. C: f(-1) = a (-1)² + b (-1) - 5 = a - b = -2 Das ist Gleichung II. Aus B und C erhalten Sie zwei Gleichungen mit zwei Variablen. Diese können Sie mit den bekannten Methoden lösen. Hier bietet sich das Additionsverfahren an. I: 4 a + 2 b = 16 + a in I einsetzen: b = 16-8 II 2: 2 a - 2 b = b = 8 : 2 6 a = 12 : 6 b = 4 a = 2 Die berechneten a-, b- und c-werte werden eingesetzt: f(x) = 2 x ² + 4 x - 5.
5 SEITE 5 VON 7 d) Von der Funktionsvorschrift in Scheitelpunktform zum Grafen Soll der Graf zu f(x) = -(x + 2)² + 5 gezeichnet werden, so bestimmen Sie den Scheitelpunkt S(-2 5) aus dem Funktionsterm und zeichnen ihn ein. Da a = -1, gehen Sie von S eine Einheit nach rechts und eine nach unten und machen ein Kreuzchen bei (-1 4), ebenso nach rechts bei (-3 4). Gehen Sie von S zwei nach rechts und vier nach unten, so erhalten Sie (0 1) bzw. links (-4 1). Elegant als Kurve verbunden ergibt sich der linke Graf eine nach unten geöffnete verschobene Normalparabel. Zu f(x) = 0,5 (x - 3)² + 1, ist der Scheitelpunkt S(3 1) einzuzeichnen. Von dort geht man wie bei der Normalparabel eins nach rechts und links, ebenso zwei nach rechts und links. Nur die Werte, die senkrecht zu laufen sind, müssen mit 0,5 multipliziert werden: Also geht man eins nach rechts und 0,5 nach oben, ebenso nach links. Das ergibt die Punkte (4 1,5) und (2 1,5). Geht man zwei nach rechts, muss 0,5 4 = 2 nach oben gegangen werden, entsprechend links. So erhält man (5 3) und (1 3). Die elegante Kurve sollte dann aussehen wie der rechte Graf. e) Von der Funktionsvorschrift in Normalform zum Grafen Zu f(x) = - 0,57 x² + 3 x + 4 ergibt sich die Wertetabelle x f(x) -10,13-4,28 0,43 4 6,43 7,72 7,87 6,88 4,75 1,48-2,93 und der zugehörige Graf rechts. Skizzieren Sie den Grafen zu f(x) = 0,25 x² - 0,75 x ) Berechnung des Schnittpunktes P mit der y-achse f(0) = 0,25 0² - 0, = -1; also P(0/-1) 2) Berechnung der Nullstellen 0,25 x² - 0,75 x - 1 = 0 : 0,25 x² - 3 x - 4 = 0 x 1 = 1,5 + 2, ; x 2 = 1,5-2, x 1 = 4; x 2 = -1 N 1 (4 0) und N 2 (-1 0) Die Nullstellen können auch mit quadratischer Ergänzung bestimmt werden.
6 SEITE 6 VON 7 3) Berechnung des Scheitelpunktes S Wegen der Symmetrie der Parabel liegt der x-wert des Scheitelpunktes x s genau zwischen den Nullstellen. Das ist in der p-q-formel immer der Wert x s = -p/2. Hier ist also x s = 1,5. y s = f(1,5) = 0,25 1,5² - 0,75 1,5-1 = -1,5625-1,6; also S(1,5-1,6). 4) Graf skizzieren Der Graf geht durch die Punkte P(0-1), N 1 (4 0), N 2 (-1 0) und S(1,5-1,6) (siehe oben).
7 SEITE 7 VON 7 3. Übungen Zu a) 1. Beschreiben Sie Scheitelpunkt, Öffnung und Form der Parabel: f 1 (x) = (x - 4)² + 2; f 2 (x) = -2(x + 3)² - 12; f 3 (x) = 0,5 (x + 3,5)² Notieren Sie die drei Funktionsvorschriften aus 1 in der Normalform und geben Sie zusätzlich den Schnittpunkt mit der y-achse an. 3. Zeichnen Sie die Normalparabel und notieren Sie typische Punkte. Zu b) Bestimmen Sie die Funktionsvorschriften für die beiden Parabeln. Ermitteln Sie auch die Normalform der Funktionsvorschrift und prüfen Sie die Schnittpunkte mit der y-achse. Zu c) Bestimmen Sie eine Funktionsvorschrift. 1. Eine Parabel geht durch S(-2/3) und den Punkt P(1/21). 2. Auf einer Parabel liegen die Punkte A(2/-1), B(0/1), C(3/-5). Zu d) Skizzieren Sie die Grafen zu 1. f(x) = (x - 5)² f(x) = - 2,5 (x + 1)² + 5 Zu e) f(x) = 2 x 2-2 x - 4 Bestimmen Sie Nullstellen, Scheitelpunkt und Schnittpunkt mit der y-achse und skizzieren Sie den Grafen.
Mathematik 9. Quadratische Funktionen
 Mathematik 9 Funktionen Eine Zuordnung f, die jedem x einer Menge D (Definitionsmenge) genau ein Element y = f(x) einer Menge Z (Zielmenge) zuordnet, heißt Funktion. Dabei heißt y = f(x) Funktionswert
Mathematik 9 Funktionen Eine Zuordnung f, die jedem x einer Menge D (Definitionsmenge) genau ein Element y = f(x) einer Menge Z (Zielmenge) zuordnet, heißt Funktion. Dabei heißt y = f(x) Funktionswert
Vorbereitung auf die erste Klassenarbeit
 01 QUADRATISCHE FUNKTIONEN Wiederholungen Alles um Quadratische Funktionen Vorbereitung auf die erste Klassenarbeit Aufgabe 1: Schuljahr 2017/18 Seite 1/12 Aufgabe 2: Schuljahr 2017/18 Seite 2/12 Aufgabe
01 QUADRATISCHE FUNKTIONEN Wiederholungen Alles um Quadratische Funktionen Vorbereitung auf die erste Klassenarbeit Aufgabe 1: Schuljahr 2017/18 Seite 1/12 Aufgabe 2: Schuljahr 2017/18 Seite 2/12 Aufgabe
y x oder y 3x. Nenne eine Gleichung einer Parabel, die den Scheitelpunkt im Ursprung hat und nach oben geöffnet ist.
 Parabeln Magische Wand Parabeln Magische Wand 10.1 10. 10.3 10.4 10.5 0.1 0. 0.3 0.4 0.5 30.1 30. 30.3 30.4 30.5 50.1 50. 50.3 50.4 50.5 70.1 70. 70.3 70.4 70.5 100.1 100. 100.3 100.4 100.5 10.1 10.1 10.1
Parabeln Magische Wand Parabeln Magische Wand 10.1 10. 10.3 10.4 10.5 0.1 0. 0.3 0.4 0.5 30.1 30. 30.3 30.4 30.5 50.1 50. 50.3 50.4 50.5 70.1 70. 70.3 70.4 70.5 100.1 100. 100.3 100.4 100.5 10.1 10.1 10.1
Quadratische Funktion
 Quadratische Funktion sind Funktionen die nur eine Variable enthalten, deren Exponent 2 ist und keine Variable die einen Exponenten enthält, der größer ist als 2. Zum Beispiel die quadratische Funktion
Quadratische Funktion sind Funktionen die nur eine Variable enthalten, deren Exponent 2 ist und keine Variable die einen Exponenten enthält, der größer ist als 2. Zum Beispiel die quadratische Funktion
Verschiedene Varianten von Aufgaben zu Parabeln
 Verschiedene Varianten von Aufgaben zu Parabeln 1) Gesucht werden die Nullstellen der Parabel mit der Gleichung: a) f(x) = 2x² 4x 16 b) f(x) = 5/3 (x 1) (x + 3) c) f(x) = - 1/2 (x + 4)² + 8 d) f(x) = 2x²
Verschiedene Varianten von Aufgaben zu Parabeln 1) Gesucht werden die Nullstellen der Parabel mit der Gleichung: a) f(x) = 2x² 4x 16 b) f(x) = 5/3 (x 1) (x + 3) c) f(x) = - 1/2 (x + 4)² + 8 d) f(x) = 2x²
Quadratische Funktionen Arbeitsblatt 1
 Quadratische Funktionen Arbeitsblatt 1 Spezielle quadratische Funktion Die Funktionsgleichung einer speziellen quadratischen Funktion hat die Form y = 3 x 2. Der dazugehörige Graph heißt Parabel. Bei einer
Quadratische Funktionen Arbeitsblatt 1 Spezielle quadratische Funktion Die Funktionsgleichung einer speziellen quadratischen Funktion hat die Form y = 3 x 2. Der dazugehörige Graph heißt Parabel. Bei einer
Themenerläuterung. Die wichtigsten benötigten Formeln 1. Der Umgang mit der Mitternachtsformel
 Themenerläuterung In diesem Kapitel wirst du mit linearen Funktionen (=Gerade) und quadratischen Funktionen (=Parabel) konfrontiert. Du musst wissen, wie man eine Geradengleichung durch zwei vorgegebene
Themenerläuterung In diesem Kapitel wirst du mit linearen Funktionen (=Gerade) und quadratischen Funktionen (=Parabel) konfrontiert. Du musst wissen, wie man eine Geradengleichung durch zwei vorgegebene
Beide Geraden haben die Steigung 2, also sind sie parallel zueinander.
 Themenerläuterung In diesem Kapitel wirst du mit linearen Funktionen (=Gerade) und quadratischen Funktionen (=Parabel) konfrontiert. Du musst wissen, wie man eine Geradengleichung durch zwei vorgegebene
Themenerläuterung In diesem Kapitel wirst du mit linearen Funktionen (=Gerade) und quadratischen Funktionen (=Parabel) konfrontiert. Du musst wissen, wie man eine Geradengleichung durch zwei vorgegebene
7 Aufgaben im Dokument. Aufgabe P5/2010
 Aufgabe P5/2010 7 Aufgaben im Dokument Die nach unten geöffnete Parabel hat die Gleichung 5. Zeichnen Sie die Parabel in ein Koordinatensystem. Die Gerade hat die Steigung und schneidet die -Achse im Punkt
Aufgabe P5/2010 7 Aufgaben im Dokument Die nach unten geöffnete Parabel hat die Gleichung 5. Zeichnen Sie die Parabel in ein Koordinatensystem. Die Gerade hat die Steigung und schneidet die -Achse im Punkt
und schneidet die -Achse im Punkt 0 3. Berechnen Sie die Koordinaten der Schnittpunkte von und. Lösung: 4 1;2 4
 7 Aufgaben im Dokument Aufgabe P5/2010 Die nach unten geöffnete Parabel hat die Gleichung 5. Zeichnen Sie die Parabel in ein Koordinatensystem. Die Gerade hat die Steigung und schneidet die -Achse im Punkt
7 Aufgaben im Dokument Aufgabe P5/2010 Die nach unten geöffnete Parabel hat die Gleichung 5. Zeichnen Sie die Parabel in ein Koordinatensystem. Die Gerade hat die Steigung und schneidet die -Achse im Punkt
Ich kenne den Nullproduktsatz und kann ihn anwenden, um Gleichungen in faktorisierter Form (wie (2x+5) (7 5x)=0 ) zu lösen.
 Klasse 9c Mathematik Vorbereitung zur Klassenarbeit Nr. am 1..018 Themen: Quadratische Funktionen und Gleichungen Checkliste Was ich alles können soll Ich kenne die allgemeine Form f(x) = ax²+bx+c und
Klasse 9c Mathematik Vorbereitung zur Klassenarbeit Nr. am 1..018 Themen: Quadratische Funktionen und Gleichungen Checkliste Was ich alles können soll Ich kenne die allgemeine Form f(x) = ax²+bx+c und
QUADRATISCHE FUNKTIONEN (Funktionen des 2 e Grades)
 QUADRATISCHE FUNKTIONEN (Funktionen des 2 e Grades) I. Einführung: Allgemeine Funktionsgleichung: y = ax 2 + px + q Aufgabe 2 1 (Westermann EK, S.14) II. Terminologie: a.) Abhängige Variable (erklärte
QUADRATISCHE FUNKTIONEN (Funktionen des 2 e Grades) I. Einführung: Allgemeine Funktionsgleichung: y = ax 2 + px + q Aufgabe 2 1 (Westermann EK, S.14) II. Terminologie: a.) Abhängige Variable (erklärte
QUADRATISCHE FUNKTIONEN
 QUADRATISCHE FUNKTION DARSTELLUNG MIT DER FUNKTIONSGLEICHUNG Allgemeine Form - Vorzeichen von a gibt an, ob die Funktion nach oben (+) oder unten (-) geöffnet ist. Der Wert (Betrag) von gibt an, ob die
QUADRATISCHE FUNKTION DARSTELLUNG MIT DER FUNKTIONSGLEICHUNG Allgemeine Form - Vorzeichen von a gibt an, ob die Funktion nach oben (+) oder unten (-) geöffnet ist. Der Wert (Betrag) von gibt an, ob die
Themenerläuterung. Die wichtigsten benötigten Formeln
 Themenerläuterung In diesem Kapitel wirst du mit linearen Funktionen (=Gerade) und quadratischen Funktionen (=Parabel) konfrontiert. Du musst wissen, wie man eine Geradengleichung durch zwei vorgegebene
Themenerläuterung In diesem Kapitel wirst du mit linearen Funktionen (=Gerade) und quadratischen Funktionen (=Parabel) konfrontiert. Du musst wissen, wie man eine Geradengleichung durch zwei vorgegebene
f. y = 0,2x g. y = 1,5x + 5 h. y = 4 6x i. y = 4 + 5,5x j. y = 0,5x + 3,5
 11. Lineare Funktionen Übungsaufgaben: 11.1 Zeichne jeweils den Graphen der zugehörigen Geraden a. y = 0,5x 0,25 b. y = 0,1x + 2 c. y = 2x 2 d. 2x + 4y 5 = 0 e. y = x f. y = 0,2x g. y = 1,5x + 5 h. y =
11. Lineare Funktionen Übungsaufgaben: 11.1 Zeichne jeweils den Graphen der zugehörigen Geraden a. y = 0,5x 0,25 b. y = 0,1x + 2 c. y = 2x 2 d. 2x + 4y 5 = 0 e. y = x f. y = 0,2x g. y = 1,5x + 5 h. y =
Einfache quadratische Funktionen und Gleichungen. x y Wertetabelle. y-achse
 Einfache quadratische Funktionen und Gleichungen Eine quadratische Funktion hat allgemein die Funktion: y = ax 2 + bx + c Dabei gilt: a, b und c R und a 0 Der Graph, der hierbei entsteht ist eine Parabel.
Einfache quadratische Funktionen und Gleichungen Eine quadratische Funktion hat allgemein die Funktion: y = ax 2 + bx + c Dabei gilt: a, b und c R und a 0 Der Graph, der hierbei entsteht ist eine Parabel.
Quadratische Funktion
 Quadratische Funktion Wolfgang Kippels 6. Oktober 018 Inhaltsverzeichnis 1 Vorwort Zusammenstellung der Grundlagen 3.1 Nullstellen................................... 3. Scheitelpunkt.................................
Quadratische Funktion Wolfgang Kippels 6. Oktober 018 Inhaltsverzeichnis 1 Vorwort Zusammenstellung der Grundlagen 3.1 Nullstellen................................... 3. Scheitelpunkt.................................
m und schneidet die y-achse im Punkt P(0/3).
 Aufgabe (Pflichtbereich 999) Eine Parabel hat die Gleichung y x 6x, 75. Bestimme rechnerisch die Koordinaten ihres Scheitelpunktes. Berechne die Entfernung des Scheitelpunktes vom Ursprung des Koordinatensystems.
Aufgabe (Pflichtbereich 999) Eine Parabel hat die Gleichung y x 6x, 75. Bestimme rechnerisch die Koordinaten ihres Scheitelpunktes. Berechne die Entfernung des Scheitelpunktes vom Ursprung des Koordinatensystems.
Lösungen zum Arbeitsblatt: y = mx + b Alles klar???
 I. Zeichnen von Funktionen a) Wertetabelle x -4-3 - -1 0 1 3 4 y =,5x -10-7,5-5 -,5 0,5 5 7,5 10 y = - x,7 1,3 0,7 0-0,7-1,3 - -,7 3 y = x 1,5-9,5-7,5-5,5-3,5-1,5 0,5,5 4,5 6,5 y = - 1 x + 4 3,5 3,5 1,5
I. Zeichnen von Funktionen a) Wertetabelle x -4-3 - -1 0 1 3 4 y =,5x -10-7,5-5 -,5 0,5 5 7,5 10 y = - x,7 1,3 0,7 0-0,7-1,3 - -,7 3 y = x 1,5-9,5-7,5-5,5-3,5-1,5 0,5,5 4,5 6,5 y = - 1 x + 4 3,5 3,5 1,5
Realschulabschluss Funktionen (Pflichtteil) ab 2010 Lösung P5/2010 Lösungslogik Erstellung der Graphik. Die Parabel ist nach unten geöffnet, breiter u
 Lösung P5/2010 Erstellung der Graphik. Die Parabel ist nach unten geöffnet, breiter und in Richtung nicht verschoben, der Scheitel liegt somit bei 0 5. Aufstellung der Geradengleichung. Berechnung der
Lösung P5/2010 Erstellung der Graphik. Die Parabel ist nach unten geöffnet, breiter und in Richtung nicht verschoben, der Scheitel liegt somit bei 0 5. Aufstellung der Geradengleichung. Berechnung der
Übungsaufgabe z. Th. lineare Funktionen und Parabeln
 Übungsaufgabe z. Th. lineare Funktionen und Parabeln Gegeben sind die Parabeln: h(x) = 8 x + 3 x - 1 9 und k(x) = - 8 x - 1 1 8 x + 11 a) Bestimmen Sie die Koordinaten der Schnittpunkte A und C der Graphen
Übungsaufgabe z. Th. lineare Funktionen und Parabeln Gegeben sind die Parabeln: h(x) = 8 x + 3 x - 1 9 und k(x) = - 8 x - 1 1 8 x + 11 a) Bestimmen Sie die Koordinaten der Schnittpunkte A und C der Graphen
Klassenarbeit Mathematik Bearbeitungszeit 90 min. Di SB22 Z Gruppe A NAME:
 R. Brinkmann http://brinkmann-du.de Seite 0..0 Klassenarbeit Mathematik Bearbeitungszeit 90 min. Di.0.0 SB Z Gruppe A NAME: Hilfsmittel: Taschenrechner Alle se sind soweit möglich durch Rechnung zu begründen..
R. Brinkmann http://brinkmann-du.de Seite 0..0 Klassenarbeit Mathematik Bearbeitungszeit 90 min. Di.0.0 SB Z Gruppe A NAME: Hilfsmittel: Taschenrechner Alle se sind soweit möglich durch Rechnung zu begründen..
Quadratische Funktionen Die Normalparabel
 Quadratische Funktionen Die Normalparabel Kreuze die Punkte an, die auf der Normalparabel liegen. A ( 9) B ( ) C ( 9) D ( ) E (9 ) F (0 0) Die Punkte A bis J sollen auf der Normalparabel liegen. Gib, falls
Quadratische Funktionen Die Normalparabel Kreuze die Punkte an, die auf der Normalparabel liegen. A ( 9) B ( ) C ( 9) D ( ) E (9 ) F (0 0) Die Punkte A bis J sollen auf der Normalparabel liegen. Gib, falls
d) Die Parabel verläuft symmetrisch zur Achse durch die Punkte ( 1 0,5) und (2 5,5).
 Dokument mit 26 Aufgaben Aufgabe A Der Wasserstrahl eines Springbrunnens hat eine Höhe von 6 und eine Weite von 6. Martin hat Lust unter dem Wasserstrahl durchzulaufen. a) Wähle ein geeigneters Koordinatensystem
Dokument mit 26 Aufgaben Aufgabe A Der Wasserstrahl eines Springbrunnens hat eine Höhe von 6 und eine Weite von 6. Martin hat Lust unter dem Wasserstrahl durchzulaufen. a) Wähle ein geeigneters Koordinatensystem
Einführung in die Quadratischen Funktionen
 Einführung in die Quadratischen Funktionen Problemstellung: In einer Fabrikhalle soll ein Pausenraum neu eingerichtet werden. Die dazu bestellten flexiblen Trennwände sind zusammen 15 m lang. Das Aufstellen
Einführung in die Quadratischen Funktionen Problemstellung: In einer Fabrikhalle soll ein Pausenraum neu eingerichtet werden. Die dazu bestellten flexiblen Trennwände sind zusammen 15 m lang. Das Aufstellen
Nullstellen. Somit ergibt sich x = 4 oder x = -4, da das Quadrat beider Zahlen 16 ergibt. Man schreibt
 Nullstellen Aufgabe 1 Gegeben ist die folgende quadratische Funktion: Bestimme die Nullstellen. f( x) x² 3 x² 3 : x² 16 16 x² 16 Somit ergibt sich x = 4 oder x = -4, da das Quadrat beider Zahlen 16 ergibt.
Nullstellen Aufgabe 1 Gegeben ist die folgende quadratische Funktion: Bestimme die Nullstellen. f( x) x² 3 x² 3 : x² 16 16 x² 16 Somit ergibt sich x = 4 oder x = -4, da das Quadrat beider Zahlen 16 ergibt.
Übungsaufgaben zu quadratischen Gleichungen und Parabeln
 Übungsaufgaben zu quadratischen Gleichungen und Parabeln Binomische Formeln:. binomische Formel: ( a + b) = a + ab + b. binomische Formel:. binomische Formel: ( a b) = a ab + b ( a + b)(a b) = a b Lösungsformel
Übungsaufgaben zu quadratischen Gleichungen und Parabeln Binomische Formeln:. binomische Formel: ( a + b) = a + ab + b. binomische Formel:. binomische Formel: ( a b) = a ab + b ( a + b)(a b) = a b Lösungsformel
1 Benenne Gemeinsamkeiten und Unterschiede der beiden Graphen und gib die zugehörigen Funktionsgleichungen an.
 Teste dich! - (/6) Benenne Gemeinsamkeiten und Unterschiede der beiden Graphen und gib die zugehörigen Funktionsgleichungen an. 0 Cornelsen Verlag, Berlin. Alle Rechte vorbehalten. Gemeinsamkeiten: Beide
Teste dich! - (/6) Benenne Gemeinsamkeiten und Unterschiede der beiden Graphen und gib die zugehörigen Funktionsgleichungen an. 0 Cornelsen Verlag, Berlin. Alle Rechte vorbehalten. Gemeinsamkeiten: Beide
A3.2 Quadratische Funktionen
 A. Quadratische Funktionen Die Quadratfunktion Definition: Eine reelle Funktion f: = a + b + c, D = R (a, b, c R a 0) heißt quadratische Funktion. Beispiele:. f: =. f: = 0,5 - + Die Quadratfunktion f:
A. Quadratische Funktionen Die Quadratfunktion Definition: Eine reelle Funktion f: = a + b + c, D = R (a, b, c R a 0) heißt quadratische Funktion. Beispiele:. f: =. f: = 0,5 - + Die Quadratfunktion f:
g 2 g 1 15/16 I Übungen 2 EF Be Sept. 15 p 1 p 2
 15/16 I Übungen EF Be Sept. 15 Nr. 1: a) Funktion oder Relation? Welcher Graph gehört zu einer Funktion, welcher nicht? Begründe Deine Antwort kurz. a) und d) sind keine Funktionen, da die Zuordnungen
15/16 I Übungen EF Be Sept. 15 Nr. 1: a) Funktion oder Relation? Welcher Graph gehört zu einer Funktion, welcher nicht? Begründe Deine Antwort kurz. a) und d) sind keine Funktionen, da die Zuordnungen
Bestimme dazu die Nullstellen, Scheitelpunkt und Schnittpunkt mit der y-achse und ergänze evtl. einige Punkte durch eine Wertetabelle.
 Klasse Art Schwierigkeit Mathematisches Schema Nr. 9 Üben xx Quadratische Funktion 1 Skizziere den Graphen der durch y = 0,5 x 2 + x - 4 gegebenen quadratischen Funktion. Bestimme dazu die Nullstellen,
Klasse Art Schwierigkeit Mathematisches Schema Nr. 9 Üben xx Quadratische Funktion 1 Skizziere den Graphen der durch y = 0,5 x 2 + x - 4 gegebenen quadratischen Funktion. Bestimme dazu die Nullstellen,
Graphen quadratischer Funktionen und deren Nullstellen
 Binomische Formeln Mithilfe der drei binomischen Formeln kann man Funktionen bzw. Gleichungen vereinfachen. 1. Binomische Formel ( Plusformel ) a 2 + 2 a b+ b 2 = (a+ b) 2 Herleitung: (a+ b) 2 = (a+ b)
Binomische Formeln Mithilfe der drei binomischen Formeln kann man Funktionen bzw. Gleichungen vereinfachen. 1. Binomische Formel ( Plusformel ) a 2 + 2 a b+ b 2 = (a+ b) 2 Herleitung: (a+ b) 2 = (a+ b)
Schritt 1: Skizze anfertigen. Schritt 2: Volumenformel für das Prisma anwenden. M GYM K09 BY 3.KA ML Var1. Aufgabe 1
 Aufgabe 1 Schritt 1: Skizze anfertigen Um dir besser vorstellen zu können, wie der Getränkekarton aussehen soll und wie die Abmessungen zusammenhängen, solltest du dir als allererstes eine saubere Skizze
Aufgabe 1 Schritt 1: Skizze anfertigen Um dir besser vorstellen zu können, wie der Getränkekarton aussehen soll und wie die Abmessungen zusammenhängen, solltest du dir als allererstes eine saubere Skizze
Schritt 1: Koordinaten in die allgemeine Funktionsgleichung einsetzen
 Aufgabe 1a) Schritt 1: S in die Scheitelpunktform einsetzen 0,5 2 Schritt 2: Koordinaten von P einsetzen und a berechnen 2,25 1,5 0,5 2 0,25 Schritt 3: Funktionsterm aufstellen 0,25 0,5 2 als Scheitelpunktform,
Aufgabe 1a) Schritt 1: S in die Scheitelpunktform einsetzen 0,5 2 Schritt 2: Koordinaten von P einsetzen und a berechnen 2,25 1,5 0,5 2 0,25 Schritt 3: Funktionsterm aufstellen 0,25 0,5 2 als Scheitelpunktform,
Gleichsetzungsverfahren
 Funktion Eine Funktion ist eine Zuordnung, bei der zu jeder Größe eines ersten Bereichs (Ein gabegröße) genau eine Größe eines zweiten Bereichs (Ausgabegröße) gehört. Eine Funktion wird durch eine Funktionsvorschrift
Funktion Eine Funktion ist eine Zuordnung, bei der zu jeder Größe eines ersten Bereichs (Ein gabegröße) genau eine Größe eines zweiten Bereichs (Ausgabegröße) gehört. Eine Funktion wird durch eine Funktionsvorschrift
Mathematik Übungsaufgaben zur Vorbereitung auf die 3. Klausur Lösung. 1. Formen Sie die Scheitel(punkt)form der quadratischen Funktion
 Datum:.0.0 Thema: Quadratische Funktionen. Formen Sie die Scheitel(punkt)form der quadratischen Funktion f mit f(x) = ( x ) + in die Polynomdarstellung um und bestimmen Sie die Nullstellen und den Schnittpunkt
Datum:.0.0 Thema: Quadratische Funktionen. Formen Sie die Scheitel(punkt)form der quadratischen Funktion f mit f(x) = ( x ) + in die Polynomdarstellung um und bestimmen Sie die Nullstellen und den Schnittpunkt
Parabeln - quadratische Funktionen
 Parabeln - quadratische Funktionen Roland Heynkes 9.11.005, Aachen Das Gleichsetzungsverfahren und die davon abgeleiteten Einsetzungs- und Additionsverfahren kennen wir als Methoden zur Lösung linearer
Parabeln - quadratische Funktionen Roland Heynkes 9.11.005, Aachen Das Gleichsetzungsverfahren und die davon abgeleiteten Einsetzungs- und Additionsverfahren kennen wir als Methoden zur Lösung linearer
Eine Gerade hat die Gleichung 22. Eine zweite Gerade hat die Steigung und schneidet die -Achse im Punkt
 7 Aufgaben im Dokument Aufgabe P6/2003 Eine nach oben geöffnete Normalparabel hat den Scheitelpunkt 2 3. Die Gerade hat die Steigung 1 und schneidet die Parabel in 4 1. Berechnen Sie die Koordinaten des
7 Aufgaben im Dokument Aufgabe P6/2003 Eine nach oben geöffnete Normalparabel hat den Scheitelpunkt 2 3. Die Gerade hat die Steigung 1 und schneidet die Parabel in 4 1. Berechnen Sie die Koordinaten des
Schwerpunktaufgaben zur Vorbereitung auf die Leistungsfeststellung
 Schwerpunktaufgaben zur Vorbereitung auf die Leistungsfeststellung 1. Lösen Sie folgendes Gleichungssystem mit Hilfe des Gauß-Verfahrens. Überprüfen Sie Ihr Ergebnis mit dem Taschenrechner. ganzzahlig
Schwerpunktaufgaben zur Vorbereitung auf die Leistungsfeststellung 1. Lösen Sie folgendes Gleichungssystem mit Hilfe des Gauß-Verfahrens. Überprüfen Sie Ihr Ergebnis mit dem Taschenrechner. ganzzahlig
Quadratische Funktion
 Quadratische Funktion Wolfgang Kippels. September 017 Inhaltsverzeichnis 1 Vorwort Zusammenstellung der Grundlagen 3 3 Aufgaben 3.1 Aufgabe 1:................................... 3. Aufgabe :...................................
Quadratische Funktion Wolfgang Kippels. September 017 Inhaltsverzeichnis 1 Vorwort Zusammenstellung der Grundlagen 3 3 Aufgaben 3.1 Aufgabe 1:................................... 3. Aufgabe :...................................
Aufstellen der Funktionsgleichung aus gegebenen Bedingungen
 R. Brinkmann http://brinkmann-du.de Seite.0.0 Aufstellen der Funktionsgleichung aus gegebenen Bedingungen Drei unterschiedliche Punkte, die alle auf einer Parabel liegen sollen sind gegeben. Daraus soll
R. Brinkmann http://brinkmann-du.de Seite.0.0 Aufstellen der Funktionsgleichung aus gegebenen Bedingungen Drei unterschiedliche Punkte, die alle auf einer Parabel liegen sollen sind gegeben. Daraus soll
Themenerläuterung. Die wichtigsten benötigten Formeln 1. Der Umgang mit der Mitternachtsformel
 Themenerläuterung In diesem Kapitel wirst du mit linearen Funktionen (=Gerade) und quadratischen Funktionen (=Parabel) konfrontiert. Du musst wissen, wie man eine Geradengleichung durch zwei vorgegebene
Themenerläuterung In diesem Kapitel wirst du mit linearen Funktionen (=Gerade) und quadratischen Funktionen (=Parabel) konfrontiert. Du musst wissen, wie man eine Geradengleichung durch zwei vorgegebene
Quadratische Funktion
 Quadratische Funktion 1. Übliche Formen 1) Allgemeine Form: y = f(x) = a x 2 + b x + c a, b, c Konstanten Grundlegender Fall a = 1, b = 0, c = 0, also y = x 2 : "Normalparabel" Vorteil: Keine Brüche für
Quadratische Funktion 1. Übliche Formen 1) Allgemeine Form: y = f(x) = a x 2 + b x + c a, b, c Konstanten Grundlegender Fall a = 1, b = 0, c = 0, also y = x 2 : "Normalparabel" Vorteil: Keine Brüche für
1. Selbsttest Heron-Verfahren Gleichungen
 1. Selbsttest 1.1. Heron-Verfahren Mit dem Heron-Verfahren soll ein Näherungswert für 15 gefunden werden. Führe die ersten drei Schritte des Heron- Verfahrens durch. Gib dann unter Verwendung der Werte
1. Selbsttest 1.1. Heron-Verfahren Mit dem Heron-Verfahren soll ein Näherungswert für 15 gefunden werden. Führe die ersten drei Schritte des Heron- Verfahrens durch. Gib dann unter Verwendung der Werte
Ü b u n g s a r b e i t
 Ü b u n g s a r b e i t Aufgabe. a) Die Querschnittsfläche eines Abwasserkanals ist im unteren Teil von einer Parabel k begrenzt, an die sich nach oben die beiden Geraden g und h anschließen. Bestimmen
Ü b u n g s a r b e i t Aufgabe. a) Die Querschnittsfläche eines Abwasserkanals ist im unteren Teil von einer Parabel k begrenzt, an die sich nach oben die beiden Geraden g und h anschließen. Bestimmen
Die nach oben geöffnete Normalparabel verläuft durch die Punkte 1 5 und Die Parabel hat die Gleichung 2. Besitzen die beiden Parabeln
 Dokument mit 11 Aufgaben Aufgabe W3a/2010 Im Schaubild sind die Geraden und dargestellt. Entnehmen Sie zur Bestimmung ihrer Gleichungen geeignete Werte. Berechnen Sie die Koordinaten des Schnittpunkts
Dokument mit 11 Aufgaben Aufgabe W3a/2010 Im Schaubild sind die Geraden und dargestellt. Entnehmen Sie zur Bestimmung ihrer Gleichungen geeignete Werte. Berechnen Sie die Koordinaten des Schnittpunkts
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Geraden & Parabeln - Was mache ich, wenn?
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: - Was mache ich, wenn? Das komplette Material finden Sie hier: School-Scout.de Inhalt Seite Vorwort 5 Spickzettel 6-7 MindMap Geraden
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: - Was mache ich, wenn? Das komplette Material finden Sie hier: School-Scout.de Inhalt Seite Vorwort 5 Spickzettel 6-7 MindMap Geraden
1. Gegeben sind die Scheitelpunkte von Parabeln. Gib die Funktionsgleichungen an. a) S(-3/5) b) S(-1/-8) c) S(1/-0,5) d) S(0,5/0,2)
 Vermischte Übungen (1) Verschiebung der Normalparabel 1. Gegeben sind die Scheitelpunkte von Parabeln. Gib die Funktionsgleichungen an. a) S(-3/5) b) S(-1/-8) c) S(1/-0,5) d) S(0,5/0,). In der Abbildung
Vermischte Übungen (1) Verschiebung der Normalparabel 1. Gegeben sind die Scheitelpunkte von Parabeln. Gib die Funktionsgleichungen an. a) S(-3/5) b) S(-1/-8) c) S(1/-0,5) d) S(0,5/0,). In der Abbildung
Berechnung der Schnittpunkte durch Gleichsetzung. Bestimmung der Scheitelpunkte von und. Verdeutlichung der Situation durch ein Schaubild.
 Lösung W3a/2010 Aufstellung der Geradengleichungen und. Schnittpunktberechnung von durch Gleichsetzung. Aufstellung der Parabelgleichung durch die Punkte und. Umstellung der allgemeinen Parabelgleichung
Lösung W3a/2010 Aufstellung der Geradengleichungen und. Schnittpunktberechnung von durch Gleichsetzung. Aufstellung der Parabelgleichung durch die Punkte und. Umstellung der allgemeinen Parabelgleichung
PARABELN. 10. Klasse
 PARABELN 0. Klasse Jens Möller Owingen Tel. 0755-9 HUjmoellerowingen@aol.comU INHALTSVERZEICHNIS NORMALPARABEL PARABELN MIT FORMFAKTOR VERSCHIEBUNG IN Y-RICHTUNG VERSCHIEBUNG IN X-RICHTUNG 5 ALLGEMEINE
PARABELN 0. Klasse Jens Möller Owingen Tel. 0755-9 HUjmoellerowingen@aol.comU INHALTSVERZEICHNIS NORMALPARABEL PARABELN MIT FORMFAKTOR VERSCHIEBUNG IN Y-RICHTUNG VERSCHIEBUNG IN X-RICHTUNG 5 ALLGEMEINE
Mathematik Klasse 9d, AB 14 Übungszettel Parabel Lösung
 Aufgabe : Gegeben sind die folgenden Parabeln: a) f x =2x 2 8x 2 b) f 2 x = 0 x2 x c) f 3 x = 4 x2 2 x 2 Beschreibe die Parabel, in dem du den Scheitelpunkt angibst, ob sie enger oder weiter als die ist,
Aufgabe : Gegeben sind die folgenden Parabeln: a) f x =2x 2 8x 2 b) f 2 x = 0 x2 x c) f 3 x = 4 x2 2 x 2 Beschreibe die Parabel, in dem du den Scheitelpunkt angibst, ob sie enger oder weiter als die ist,
, 1,52,251,75, 1,5 4, 1,52
 Lösung A1 Detaillierte Lösung: Lösungsschritte: 1. An der Parabelgleichung ist ersichtlich, dass es sich um eine nach oben geöffnete Normalparabel handelt, die in positiver -Richtung verschoben ist und
Lösung A1 Detaillierte Lösung: Lösungsschritte: 1. An der Parabelgleichung ist ersichtlich, dass es sich um eine nach oben geöffnete Normalparabel handelt, die in positiver -Richtung verschoben ist und
4.2. Aufgaben zu quadratischen Funktionen
 .. Aufgaben zu quadratischen Funktionen Aufgabe : Stauchung und Streckung der Normalparabel a) Zeichne die Schaubilder der folgenden Funktionen in das Koordinatensstem. b) Vervollständige die darunter
.. Aufgaben zu quadratischen Funktionen Aufgabe : Stauchung und Streckung der Normalparabel a) Zeichne die Schaubilder der folgenden Funktionen in das Koordinatensstem. b) Vervollständige die darunter
Realschule Schüttorf Arbeitsblatt Mathematik Klasse 10d Dezember 2006 Quadratische Funktionen
 Arbeitsblatt Mathematik Klasse 0d Dezember 006. Bestimme zu den vier Parabeln die zugehörigen Funktionsgleichungen.. Beschreibe den Verlauf der folgenden Funktionen. Benutze dabei folgende Begriffe: gestreckt
Arbeitsblatt Mathematik Klasse 0d Dezember 006. Bestimme zu den vier Parabeln die zugehörigen Funktionsgleichungen.. Beschreibe den Verlauf der folgenden Funktionen. Benutze dabei folgende Begriffe: gestreckt
Die Steigung m ist ein Quotient zweier Differenzen und heißt daher Differenzenquotient.
 Seite Definition lineare Funktion Eine Funktion f mit dem Funktionsterm f(x) = m x + b, also der Funktionsgleichung y = m x + b, heißt lineare Funktion. Ihr Graph G f ist eine Gerade mit der Steigung m
Seite Definition lineare Funktion Eine Funktion f mit dem Funktionsterm f(x) = m x + b, also der Funktionsgleichung y = m x + b, heißt lineare Funktion. Ihr Graph G f ist eine Gerade mit der Steigung m
Mathematisches Thema Quadratische Funktionen 1. Art Anwenden. Klasse 10. Schwierigkeit x. Klasse 10. Mathematisches Thema
 Quadratische Funktionen 1 1.) Zeige, dass die Funktion in der Form f() = a 2 + b +c geschrieben werden kann und gebe a, b und c an. a) f() = ( -5) ( +7) b) f() = ( -1) ( +1) c) f() = 3 ( - 4) 2.) Wie heißen
Quadratische Funktionen 1 1.) Zeige, dass die Funktion in der Form f() = a 2 + b +c geschrieben werden kann und gebe a, b und c an. a) f() = ( -5) ( +7) b) f() = ( -1) ( +1) c) f() = 3 ( - 4) 2.) Wie heißen
Als Untersuchungsbeispiel diene die Funktion: f(x) = x 6x + 5
 R. Brinkmann http://brinkmann-du.de Seite 07..009 Achsenschnittpunkte quadratischer Funktionen y P y ( 0 y ) s P ( 0) S y s f() P ( 0) s Bei der Betrachtung des Graphen in nebenstehender Abbildung fallen
R. Brinkmann http://brinkmann-du.de Seite 07..009 Achsenschnittpunkte quadratischer Funktionen y P y ( 0 y ) s P ( 0) S y s f() P ( 0) s Bei der Betrachtung des Graphen in nebenstehender Abbildung fallen
Quadratische Funktion - Übungen
 Quadratische Funktion - Übungen 1a) "Verständnisfragen" zu "Scheitel und Allgemeine Form" - mit Tipps. Teilweise: Trotz der Tipps nicht immer einfach! Wir haben die Formeln: Allgemeine Form: y = a x 2
Quadratische Funktion - Übungen 1a) "Verständnisfragen" zu "Scheitel und Allgemeine Form" - mit Tipps. Teilweise: Trotz der Tipps nicht immer einfach! Wir haben die Formeln: Allgemeine Form: y = a x 2
Die y Koordinate des Scheitelpunktes ist 0, der Scheitelpunkt liegt auf der x Achse, es gibt also genau eine Nullstelle.
 Aufgabe 1 Schritt 1: Auswertung der Funktionsgleichung Die Parabel ist in der Scheitelpunktform angegeben. Öffnung a ist negativ, das heißt, die Parabel ist nach unten geöffnet. Scheitelpunkt Die Koordinaten
Aufgabe 1 Schritt 1: Auswertung der Funktionsgleichung Die Parabel ist in der Scheitelpunktform angegeben. Öffnung a ist negativ, das heißt, die Parabel ist nach unten geöffnet. Scheitelpunkt Die Koordinaten
1. Klassenarbeit Lösungsvorschlag
 EI 10c M 2009-10 MATHEMATIK 1 1. Klassenarbeit Lösungsvorschlag Vergleiche deine Lösungen mit diesem Lösungsvorschlag. Helft euch gegenseitig bei Fragen oder fragt mich direkt! AUFGABE 1 Die Gerade g geht
EI 10c M 2009-10 MATHEMATIK 1 1. Klassenarbeit Lösungsvorschlag Vergleiche deine Lösungen mit diesem Lösungsvorschlag. Helft euch gegenseitig bei Fragen oder fragt mich direkt! AUFGABE 1 Die Gerade g geht
Einführungsphase Mathematik. Thema: Quadratische Funktionen. quadratische Gleichungen
 Thema: Quadratische Funktionen quadratische Gleichungen Normalform einer linearen Funktion Normalform einer quadratischen Funktion Handelt es sich um quadratische Funktionen??? Ja, denn a = 3, b = 0, c
Thema: Quadratische Funktionen quadratische Gleichungen Normalform einer linearen Funktion Normalform einer quadratischen Funktion Handelt es sich um quadratische Funktionen??? Ja, denn a = 3, b = 0, c
Leitprogramm Funktionen
 3. Quadratische Funktionen (Zeit 10 Lektionen) Lernziel: Grundform y = ax + bx + c und Scheitelform y = a(x + m) + n der Funktionsgleichungen quadratischer Funktionen kennen. Bedeutung der Parameter a,
3. Quadratische Funktionen (Zeit 10 Lektionen) Lernziel: Grundform y = ax + bx + c und Scheitelform y = a(x + m) + n der Funktionsgleichungen quadratischer Funktionen kennen. Bedeutung der Parameter a,
Aufgabe W2a/2005 Eine Parabel hat die Gleichung 4 1. Durch den Scheitelpunkt der Parabel und durch den Punkt %6 5 geht die Gerade. Berechnen Sie die G
 Dokument mit 10 Aufgaben Aufgabe W3a/2003 Die Normalparabel hat die Gleichung 4 6. Die Normalparabel ist nach unten geöffnet und hat den Scheitel 0 6. Durch die Schnittpunkte beider Parabeln verläuft die
Dokument mit 10 Aufgaben Aufgabe W3a/2003 Die Normalparabel hat die Gleichung 4 6. Die Normalparabel ist nach unten geöffnet und hat den Scheitel 0 6. Durch die Schnittpunkte beider Parabeln verläuft die
Einführung der quadratischen Funktionen
 R. Brinkmann http://brinkmann-du.de Seite 08.0.008 Einführung der quadratischen Funktionen Jeder, der sich auf die Führerscheinprüfung vorbereitet sollte wissen, dass sich der Anhalteweg eines bremsenden
R. Brinkmann http://brinkmann-du.de Seite 08.0.008 Einführung der quadratischen Funktionen Jeder, der sich auf die Führerscheinprüfung vorbereitet sollte wissen, dass sich der Anhalteweg eines bremsenden
Thomas Wilkens Seite
 Thomas Wilkens Seite 08..007 Einführung der quadratischen Funktionen Sarah bereitet sich auf die Führerscheinprüfung vor. Sie hat gelernt, dass sich der Anhalteweg eines bremsenden Autos auf trockener
Thomas Wilkens Seite 08..007 Einführung der quadratischen Funktionen Sarah bereitet sich auf die Führerscheinprüfung vor. Sie hat gelernt, dass sich der Anhalteweg eines bremsenden Autos auf trockener
Was ist eine Funktion?
 Lerndomino zum Thema Funktionsbegriff Kopiereen Sie die Seite (damit Sie einen Kontrollbogen haben), schneiden Sie aus der Kopie die "Dominosteine" zeilenweise aus, mischen Sie die "Dominosteine" und verteilen
Lerndomino zum Thema Funktionsbegriff Kopiereen Sie die Seite (damit Sie einen Kontrollbogen haben), schneiden Sie aus der Kopie die "Dominosteine" zeilenweise aus, mischen Sie die "Dominosteine" und verteilen
Realschule Schüttorf Arbeitsblatt Mathematik Klasse 10d Dezember 2006 Quadratische Funktionen
 1.) Entscheide, ohne zu zeichnen, ob die Parabeln - eng/weit, - nach oben/nach unten geöffnet, - nach oben/nach unten verschoben sind. Als Vergleich soll die Normalparabel dienen. a) y = 3 x² - 3 b) y=
1.) Entscheide, ohne zu zeichnen, ob die Parabeln - eng/weit, - nach oben/nach unten geöffnet, - nach oben/nach unten verschoben sind. Als Vergleich soll die Normalparabel dienen. a) y = 3 x² - 3 b) y=
Download VORSCHAU. Hausaufgaben: Quadratische Funktionen. Üben in drei Diferenzierungsstufen. Otto Mayr. zur Vollversion
 Download Otto Mar Hausaufgaben: Quadratische Funktionen Üben in drei Diferenzierungsstufen Downloadauszug aus dem Originaltitel: Hausaufgaben: Quadratische Funktionen Üben in drei Differenzierungsstufen
Download Otto Mar Hausaufgaben: Quadratische Funktionen Üben in drei Diferenzierungsstufen Downloadauszug aus dem Originaltitel: Hausaufgaben: Quadratische Funktionen Üben in drei Differenzierungsstufen
Inhalt. Vorwort 4. Quadratische Funktionen Einführung in das Thema 5-6. Ergänzung von Werten in Wertetabellen 9-10
 Inhalt Seite Vorwort 4 1 Quadratische Funktionen Einführung in das Thema 5-6 2 Die Funktionsgleichung = 2 7-8 Ergänzung von Werten in Wertetabellen 9-10 4 Erstellen von Wertetabellen und Zeichnen von Graphen
Inhalt Seite Vorwort 4 1 Quadratische Funktionen Einführung in das Thema 5-6 2 Die Funktionsgleichung = 2 7-8 Ergänzung von Werten in Wertetabellen 9-10 4 Erstellen von Wertetabellen und Zeichnen von Graphen
Funktionsgraphen (Aufgaben)
 Gymnasium Pegnitz JS 9 August 2007 Funktionsgraphen (Aufgaben) 1. Betrachte die beiden linearen Funktionen f(x) = x + 2 und g(x) = x 3 und die quadratische Funktion p(x) = f(x) g(x) (a) Zeichne die Graphen
Gymnasium Pegnitz JS 9 August 2007 Funktionsgraphen (Aufgaben) 1. Betrachte die beiden linearen Funktionen f(x) = x + 2 und g(x) = x 3 und die quadratische Funktion p(x) = f(x) g(x) (a) Zeichne die Graphen
Kurs 9 Quadratische und exponentielle Funktionen MSA Vollzeit (1 von 2)
 Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 28195 Bremen Kurs 9 Quadratische und exponentielle Funktionen MSA Vollzeit (1 von 2) Name: Ich So schätze ich meinen Lernzuwachs
Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 28195 Bremen Kurs 9 Quadratische und exponentielle Funktionen MSA Vollzeit (1 von 2) Name: Ich So schätze ich meinen Lernzuwachs
Check-1. (1/8) erstellt: (WUL); zuletzt geändert: (WUL)
 Check-1 (1/8) erstellt: 01.06.2017 (WUL); zuletzt geändert: 06.06.2017 (WUL) Nullstellen Nullstellen Die Punkte einer Funktion die die x-achse durchstoßen oder berühren nennt man Nullstellen. Sie haben
Check-1 (1/8) erstellt: 01.06.2017 (WUL); zuletzt geändert: 06.06.2017 (WUL) Nullstellen Nullstellen Die Punkte einer Funktion die die x-achse durchstoßen oder berühren nennt man Nullstellen. Sie haben
Download. Hausaufgaben: Quadratische Funktionen. Üben in drei Differenzierungsstufen. Otto Mayr. Downloadauszug aus dem Originaltitel:
 Download Otto Mar Hausaufgaben: Quadratische Funktionen Üben in drei Differenzierungsstufen Downloadauszug aus dem Originaltitel: Hausaufgaben: Quadratische Funktionen Üben in drei Differenzierungsstufen
Download Otto Mar Hausaufgaben: Quadratische Funktionen Üben in drei Differenzierungsstufen Downloadauszug aus dem Originaltitel: Hausaufgaben: Quadratische Funktionen Üben in drei Differenzierungsstufen
Parabeln Magische Wand
 Parabeln Magische Wand Hinweise für die Lehrkraft Die Ziele dieses Spiels sind Zusammenarbeit, Festigung der Kenntnisse über Parabeln, Schnelligkeit und Absprache. Das Spiel lässt sich je nach Intension
Parabeln Magische Wand Hinweise für die Lehrkraft Die Ziele dieses Spiels sind Zusammenarbeit, Festigung der Kenntnisse über Parabeln, Schnelligkeit und Absprache. Das Spiel lässt sich je nach Intension
1. Vereinfache wie im Beispiel: 3. Vereinfache wie im Beispiel: 4. Schreibe ohne Wurzel wie im Beispiel:
 1. Zahlenmengen Wissensgrundlage Aufgabenbeispiele Gib die jeweils kleinstmögliche Zahlenmenge an, welche die Zahl enthält? R Q Q oder All diejenigen Zahlen, die sich nicht mehr durch Brüche darstellen
1. Zahlenmengen Wissensgrundlage Aufgabenbeispiele Gib die jeweils kleinstmögliche Zahlenmenge an, welche die Zahl enthält? R Q Q oder All diejenigen Zahlen, die sich nicht mehr durch Brüche darstellen
Theorie: Quadratische Funktionen
 1 Theorie: Quadratische Funktionen Ben Hambrecht Inhaltsverzeichnis 1 Zahlenfolgen und ihre Differenzen 2 2 Parabeln 3 3 Einfache quadratische Funktionen 4 4 Allgemeine quadratische Funktionen 5 5 Quadratische
1 Theorie: Quadratische Funktionen Ben Hambrecht Inhaltsverzeichnis 1 Zahlenfolgen und ihre Differenzen 2 2 Parabeln 3 3 Einfache quadratische Funktionen 4 4 Allgemeine quadratische Funktionen 5 5 Quadratische
Klassenarbeit Quadratische Funktionen
 Klassenarbeit Quadratische Funktionen Schreibe die Rechnungen sorgfältig mit Ansatz, Lösungsweg und Kommentaren auf. Skizzen sind sorgfältig und mit Lineal zu erstellen, Ergebnisse zu unterstreichen. Runde
Klassenarbeit Quadratische Funktionen Schreibe die Rechnungen sorgfältig mit Ansatz, Lösungsweg und Kommentaren auf. Skizzen sind sorgfältig und mit Lineal zu erstellen, Ergebnisse zu unterstreichen. Runde
Aufgabe Welche Bedingungen müssen für die Koeffizienten der Funktion f(x) = x 2 + a 1 x + a 0 erfüllt sein, damit f(x) keine Nullstellen besitzt?
 R. Brinkmann http://brinkmann-du.de Seite 0.0.0 Lösungen Parabeln aus gegebenen Bedingungen I en: A A A A Welche Bedingungen müssen für die Koeffizienten der Funktion f() = + a + a 0 erfüllt sein, damit
R. Brinkmann http://brinkmann-du.de Seite 0.0.0 Lösungen Parabeln aus gegebenen Bedingungen I en: A A A A Welche Bedingungen müssen für die Koeffizienten der Funktion f() = + a + a 0 erfüllt sein, damit
y = y = 2'500 Darstellung in Grafik: P 2 (800 2'500) x (Stk) 1'000
 . Kostenfunktion a) Vorgaben und Fragestellung Über die Herstellungskosten eines Produkts ist folgendes bekannt: Die variablen Material- und Lohnkosten betragen CHF. pro Stück. Die Fikosten belaufen sich
. Kostenfunktion a) Vorgaben und Fragestellung Über die Herstellungskosten eines Produkts ist folgendes bekannt: Die variablen Material- und Lohnkosten betragen CHF. pro Stück. Die Fikosten belaufen sich
Potenzen Potenzfunktionen und ihre Eigenschaften Abbilden von Funktionsgraphen
 Wie können Gleichungen der Form x n = a; a 0 n N gelöst werden? Wir benötigen die n-te Wurzel: n x = a Was ist, wenn n Q statt n N? (Q: rationale Zahlen; alle Brüche, auch negative N: natürliche Zahlen;
Wie können Gleichungen der Form x n = a; a 0 n N gelöst werden? Wir benötigen die n-te Wurzel: n x = a Was ist, wenn n Q statt n N? (Q: rationale Zahlen; alle Brüche, auch negative N: natürliche Zahlen;
Musterprüfung Mathematik an Wirtschaftsschulen Aufgabe B2 Funktionale Zusammenhänge
 Seite 1 Musterprüfung Mathematik an Wirtschaftsschulen Aufgabe B2 Funktionale Zusammenhänge Modul B2 Im Sportunterricht der 10. Klasse werden Wurfspiele durchgeführt. Um die Note 1 zu erhalten, muss der
Seite 1 Musterprüfung Mathematik an Wirtschaftsschulen Aufgabe B2 Funktionale Zusammenhänge Modul B2 Im Sportunterricht der 10. Klasse werden Wurfspiele durchgeführt. Um die Note 1 zu erhalten, muss der
Klassenarbeit Mathematik Bearbeitungszeit 90 min. Mi SG26 D Gruppe A NAME: c) Überprüfen Sie das Ergebnis von a) mit dem Wurzelsatz von Vieta.
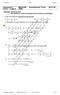 R. Brinkmann Seite 8..03 Klassenarbeit Mathematik Bearbeitungszeit 90 min. Mi 6..06 SG6 D Gruppe A NAME: Hilfsmittel: Taschenrechner. Alle Ergebnisse sind soweit möglich durch Rechnung zu begründen.. Lösen
R. Brinkmann Seite 8..03 Klassenarbeit Mathematik Bearbeitungszeit 90 min. Mi 6..06 SG6 D Gruppe A NAME: Hilfsmittel: Taschenrechner. Alle Ergebnisse sind soweit möglich durch Rechnung zu begründen.. Lösen
Der Graph einer quadratischen Funktion geht durch die gegebenen Punkte. Bestimme der Funktionsterm. a) 1 2 ; 2 1 und 4 13 b) 1 5,5 ; 2 5 und 3 5,5 c)
 Dokument mit 26 Aufgaben Aufgabe A1 Bestimme die Gleichung der Parabel, wenn folgendes bekannt ist: a) Die Parabel verläuft durch die Punkte 1 2,5, 2 1 und 0 3. b) Für die Funktion der Parabel gilt 2 1,
Dokument mit 26 Aufgaben Aufgabe A1 Bestimme die Gleichung der Parabel, wenn folgendes bekannt ist: a) Die Parabel verläuft durch die Punkte 1 2,5, 2 1 und 0 3. b) Für die Funktion der Parabel gilt 2 1,
1 Lineare Funktionen. 1 Antiproportionale Funktionen
 Funktion Eine Funktion ist eine Zuordnung, bei der zu jeder Größe eines ersten Bereichs (Ein gabegröße) genau eine Größe eines zweiten Bereichs (Ausgabegröße) gehört. Eine Funktion wird durch eine Funktionsvorschrift
Funktion Eine Funktion ist eine Zuordnung, bei der zu jeder Größe eines ersten Bereichs (Ein gabegröße) genau eine Größe eines zweiten Bereichs (Ausgabegröße) gehört. Eine Funktion wird durch eine Funktionsvorschrift
Hausaufgaben und Lösungen
 Hausaufgaben und Lösungen Die folgenden Seiten sind nicht thematisch, sondern chronologisch geordnet. Die Lösungen der Hausaufgaben werden hier erst nach der Besprechung der Hausaufgaben veröffentlicht.
Hausaufgaben und Lösungen Die folgenden Seiten sind nicht thematisch, sondern chronologisch geordnet. Die Lösungen der Hausaufgaben werden hier erst nach der Besprechung der Hausaufgaben veröffentlicht.
Klassenarbeit Mathematik Bearbeitungszeit 90 min. Di SG10 D Gruppe A NAME:
 R. Brinkmann http://brinkmann-du.de Seite 8.. Klassenarbeit Mathematik Bearbeitungszeit 9 min. Di 8.. SG D Gruppe A NAME: Hilfsmittel: Taschenrechner Alle Ergebnisse sind soweit möglich durch Rechnung
R. Brinkmann http://brinkmann-du.de Seite 8.. Klassenarbeit Mathematik Bearbeitungszeit 9 min. Di 8.. SG D Gruppe A NAME: Hilfsmittel: Taschenrechner Alle Ergebnisse sind soweit möglich durch Rechnung
R. Brinkmann Seite Klassenarbeit für Nachschreiber Mathematik Bearbeitungszeit 90 min.
 R. Brinkmann http://brinkmann-du.de Seite 8..0 Klassenarbeit für Nachschreiber Mathematik Bearbeitungszeit 90 min. SG9 D NAME: Hilfsmittel: Taschenrechner Alle Ergebnisse sind soweit möglich durch Rechnung
R. Brinkmann http://brinkmann-du.de Seite 8..0 Klassenarbeit für Nachschreiber Mathematik Bearbeitungszeit 90 min. SG9 D NAME: Hilfsmittel: Taschenrechner Alle Ergebnisse sind soweit möglich durch Rechnung
QUADRATISCHE UND KUBISCHE FUNKTION
 QUADRATISCHE UND KUBISCHE FUNKTION Quadratische Funktion 1. Bedeutung der Parameter Als quadratische Funktionen werde alle Funktionen bezeichnet, die die Form y = a*x² + b*x + c aufweisen, also alle, bei
QUADRATISCHE UND KUBISCHE FUNKTION Quadratische Funktion 1. Bedeutung der Parameter Als quadratische Funktionen werde alle Funktionen bezeichnet, die die Form y = a*x² + b*x + c aufweisen, also alle, bei
Übungen zu Kurvenscharen
 Übungen zu Kurvenscharen. Gegeben ist die Geradenschar g t : = (t ) ( t) + 9 (t 9) mit D(g t ) = R, t R. a) Zeichnen Sie die Graphen der Funktionen g und g in ein Koordinatensstem. b) Geben Sie die Schnittpunkte
Übungen zu Kurvenscharen. Gegeben ist die Geradenschar g t : = (t ) ( t) + 9 (t 9) mit D(g t ) = R, t R. a) Zeichnen Sie die Graphen der Funktionen g und g in ein Koordinatensstem. b) Geben Sie die Schnittpunkte
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Quadratische Funktionen & Gleichungen... Kinderleicht
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Quadratische Funktionen & Gleichungen... Kinderleicht Das komplette Material finden Sie hier: School-Scout.de Inhalt Seite Vorwort
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Quadratische Funktionen & Gleichungen... Kinderleicht Das komplette Material finden Sie hier: School-Scout.de Inhalt Seite Vorwort
Übungen zur Linearen und zur Quadratischen Funktion
 Übungen zur Linearen und zur Quadratischen Funktion W. Kippels 24. November 2013 Inhaltsverzeichnis 1 Die Aufgabenstellungen 2 1.1 Aufgabe 1:................................... 2 1.2 Aufgabe 2:...................................
Übungen zur Linearen und zur Quadratischen Funktion W. Kippels 24. November 2013 Inhaltsverzeichnis 1 Die Aufgabenstellungen 2 1.1 Aufgabe 1:................................... 2 1.2 Aufgabe 2:...................................
Vorbereitungsmappe. Grundlagen vor dem Eintritt in die 11. Klasse FOS / 12. Klasse BOS
 Vorbereitungsmappe Grundlagen vor dem Eintritt in die 11. Klasse FOS / 12. Klasse BOS Liebe Schülerinnen und Schüler, vor dem Eintritt in die 11. Klasse FOS / 12. Klasse BOS stellt sich vor allem im Fach
Vorbereitungsmappe Grundlagen vor dem Eintritt in die 11. Klasse FOS / 12. Klasse BOS Liebe Schülerinnen und Schüler, vor dem Eintritt in die 11. Klasse FOS / 12. Klasse BOS stellt sich vor allem im Fach
Expertenpuzzle Quadratische Funktionen
 Phase 1 Lösung für die Expertengruppe I Im Folgenden sollen die in IR definierten Funktionen a : x x, b : x x 0,5, c : x x und d: x x 3 untersucht werden. Die Abbildung zeigt den Graphen G a von a, also
Phase 1 Lösung für die Expertengruppe I Im Folgenden sollen die in IR definierten Funktionen a : x x, b : x x 0,5, c : x x und d: x x 3 untersucht werden. Die Abbildung zeigt den Graphen G a von a, also
Quadratische Funktionen in Anwendung und Erweiterung des Potenzbegriffs
 und Erweiterung des Potenzbegriffs Schnittpunkte von Graphen 1. Die Funktionsterme werden gleichgesetzt zur rechnerischen Bestimmung der Koordinaten gemeinsamer Punkte.. Von der entstehenden Gleichung
und Erweiterung des Potenzbegriffs Schnittpunkte von Graphen 1. Die Funktionsterme werden gleichgesetzt zur rechnerischen Bestimmung der Koordinaten gemeinsamer Punkte.. Von der entstehenden Gleichung
Grundwissen 9. Sabine Woellert
 Grundwissen 9 1. Quadratische Funktion... 2 1.1 Definition... 2 1.2 Eigenschaften der Normalparabel ( ):... 2 1.3 Veränderung der Normalparabel... 2 1.4 Normalform, Scheitelform... 4 1.5 Berechnung der
Grundwissen 9 1. Quadratische Funktion... 2 1.1 Definition... 2 1.2 Eigenschaften der Normalparabel ( ):... 2 1.3 Veränderung der Normalparabel... 2 1.4 Normalform, Scheitelform... 4 1.5 Berechnung der
c) Die Parabel ist nach oben geöffnet, der Scheitelpunkt liegt auf der x Achse und ist somit auch die einzige Nullstelle.
 Aufgabe 1 Schritt 1: Koordinaten der Scheitelpunkte Die Funktionsgleichungen sind schon in der Scheitelform angegeben. Du musst die Scheitelpunkte eigentlich nur noch ablesen. a) 0,75; 3 b) 3; 1,5 c) ;
Aufgabe 1 Schritt 1: Koordinaten der Scheitelpunkte Die Funktionsgleichungen sind schon in der Scheitelform angegeben. Du musst die Scheitelpunkte eigentlich nur noch ablesen. a) 0,75; 3 b) 3; 1,5 c) ;
Quadratische Funktionen
 Lernlandkarte Quadratische Funktionen Achsenschnittpunkte y-achsenabschnitt: = Allgemeine Parabelgleichung = + + Nullstellen: = p-q-formel + + = 0 / = ± Öffnung, Dehnung, Stauchung Aufstellen der Funktionsgleichung
Lernlandkarte Quadratische Funktionen Achsenschnittpunkte y-achsenabschnitt: = Allgemeine Parabelgleichung = + + Nullstellen: = p-q-formel + + = 0 / = ± Öffnung, Dehnung, Stauchung Aufstellen der Funktionsgleichung
Einführung. Ablesen von einander zugeordneten Werten
 Einführung Zusammenhänge zwischen Größen wie Temperatur, Geschwindigkeit, Lautstärke, Fahrstrecke, Preis, Einkommen, Steuer etc. werden mit beschrieben. Eine Zuordnung f, die jedem x A genau ein y B zuweist,
Einführung Zusammenhänge zwischen Größen wie Temperatur, Geschwindigkeit, Lautstärke, Fahrstrecke, Preis, Einkommen, Steuer etc. werden mit beschrieben. Eine Zuordnung f, die jedem x A genau ein y B zuweist,
