Musterlösung Analysis 3 - Maßtherorie
|
|
|
- Evagret Lichtenberg
- vor 6 Jahren
- Abrufe
Transkript
1 Musterlösung Analysis 3 - Maßtherorie 10. März 2011 Aufgabe 1: Zum Aufwärmen (i) Zeige, dass die Mengensysteme {, X} und P(X) σ-algebren sind. Es sind jeweils nur die Charakteristika nachzuweisen. (1) Zunächst {, X} X {, X} X c = (A {, X} A c {, X}) X = X {, X} (2) und nun P(X) X {, X} A P(X) A c X A c P(X) A n P(X), n N A n X A n P(X) (ii) Konstruiere die kleinste σ-algebra über der Menge X, die {A} mit A X enthält. Antwort: Wir behaupten A := {, A, A c, X} ist die gesuchte σ-algebra. Zunächst zeigen wir, dass A eine σ-algebra ist. X A X c = und A, A c A (B A B c A) X = X, A A c = X, A = A, usw. A Kurz kann man dies auch folgendermaßen ausdrücken: A ist nach Konstruktion eine σ-algebra. Nun noch der Beweis, dass dies die kleinste σ-algebra ist. X, müssen in jeder σ-algebra enthalten sein, können also nicht entfernt werden, außerdem kann keine Menge, welche A enthält entfernt werden, da A dieses Element enthalten soll. Des weiteren kann dann aber nicht mehr A c entfernt werden, da sonst Punkt 2 unserer Charakterisierung nicht mehr erfüllt wäre. Daher kann durch kein Entfernen von Elementen aus A eine kleinere σ-algebra konstruiert werden. (iii) Mache Dir klar, dass jedes Maß auch ein Inhalt ist. Da eine σ-algebra auch ein Ring ist, sowie die σ-additivität die endliche Additivität impliziert, ist dies der Fall. (iv) Beweise die Monotonie-Eigenschaft von Inhalten aus der Vorlesung. Sei A B, dann gilt µ(b) = µ(a (B \ A)) = µ(a) + µ(b \ A) µ(a) 1
2 (v) Was ist der Unterschied zwischen einer Borel-messbaren und Lebesgue-messbaren Mengen? Antwort: Eine Lebesgue-messbare Menge besteht aus der Vereinigung einer Borel-messbaren Menge B und einer Nullmenge N des Lebesgue-Borel Maßes. (vi) Wie ist das Bildmaß eines Maßes µ : A R unter einer Abbildung f : (X, A) (Y, B) definiert und welche Bedingung muss an die Abbildung gestellt werden, damit das Bildmaß sauber definiert ist. Antwort: (X, A), (Y, B) müssen Messräume sein und f selbst muss A-B-messbar sein. Dann definiert man das Bildmaß für B B durch f(µ)(b) := µ(f 1 (B)). Aufgabe 2: Mengentheorie (i) Zeige die folgenden Eigenschaften mengentheoretischer Operationen: (a) A B = B A A B = (A \ B) (B \ A) = (B \ A) (A \ B) = B A (b) C c B \ A = B \ (A C) C c B \ A = C c (B A c ) = B (C A) c = B \ (A C) (c) n=1 B \ A n = B \ ( n=1 B \ A n = n=1 (B Ac n) = B ( c = B \ ( (d) n=1 B \ A n = B \ ( n=1 B \ A n = n=1 (B Ac n) = B ( c = B \ ( (ii) Zeige folgende Aussagen (1) lim A n = A n, falls (A n ) wachsend ist n=1 lim inf A n = A k = n=1 A n lim sup A n lim inf A n (2) lim A n = A n, falls (A n ) fallend ist n=1 lim inf A n = A k = A k = A k = lim sup A n Das heißt, dass jede monotone Folge von Mengen konvergiert. Hinweis: Verwende die Definition der Konvergenz von Mengenfolgen aus der Vorlesung, welche den lim sup und lim inf verwendet. (iii) Zeige, dass (lim sup A n ) c = lim inf Ac n für eine Folge von Teilmengen aus X gilt. Die folgt einfach aus dem Dualitätsprinzip (lim sup A n ) c = A n ) c = ( ( A n ) c = A c n = lim inf Ac n 2
3 (iv) Es seien (A n ), (B n ) konvergente Folgen von Teilmengen von X. Zeige, dass die Folgen (A c n), (A n B n ), (A n B n ), (A n \B n ), (A n B N ) ebenfalls konvergieren und bestimme deren Limites. Die Konvergenzbedingung lautet lim inf A n = lim sup A n und wegen (lim sup A n ) c = lim inf Ac n folgt schon die erste Behauptung. Deren Limes lautet lim Ac n = lim inf Ac n = (lim sup A n ) c = A c mit A := lim A n. Genauso lässt sich lim (A n B n ) = (lim sup A n ) (lim sup B n ) = A B und lim (A n B n ) = (lim sup A n ) (lim sup B n ) = A B zeigen. Die letzten beiden lassen sich aus einer Kombination dieser Regeln und der jeweiligen Definition zeigen. (v) Sei (A n ) eine fallende Folge von Teilmengen von X, B X und es gelte A n A, dann gilt B \ A n B \ A. Zunächst zeigen wir das (B \ A n ) eine wachsende Folge ist, dass also (B \ A n ) (B \ A n+1 ) gilt. Das folgt aber aus der Voraussetzung, dass (A n ) fallend ist, denn dies bedeutet A n A n+1 A c n A c n+1. Und damit folgt (B \ A n ) = (B A c n) (B A n+1 ) = (B \ A n+1 ) Da jede monotone Folge von Mengen konvergiert, folgt die Behauptung. Aufgabe 3: Ringe und Algebren (i) Es seien R ein Ring über X und A := R {A c : A R}. Dann ist A die kleinste Algebra über X, die R umfasst. Ist R ein σ-ring, so ist A die kleinste σ-algebra, welche R umfasst. Sei R zunächst ein Ring. Dann gilt R X A A A A c A Die zweite Aussage folgt aus der Definition von A. Für den Beweis der letzten Eigenschaft unterscheiden wir drei verschiedene Fälle. Seien A, B A, dann unterscheidet man: (1) A, B R A B R A B A (2) A, B c R A \ B c = A B R A B A (3) A c, B c R A c B c R (A c B c ) c = A B A Sei R nun ein σ-ring, dann bleibt nur noch die σ-additivität zu zeigen. Seien A n A, n N, dann unterscheiden eir wieder drei Fälle: (1) A n R, n N A n R A n A (2) A c ñ, A n R, n ñ n ñ A n \ A c ñ R n ñ A n Añ R A n A (3) A c n R, n N Ac n R ( Ac n) c = A n A Hierbei werden die Fälle, dass mehrere aber nicht alle A c n in R liegen auf den Fall (2) zurückgeführt. (ii) Es seien f : X Y eine Abbildung und A P(X). Ist A eine σ-algebra, so gilt dies auch für B := {B Y : f 1 (B) A}. Aus der Eigenschaft von Abbildungen x X y Y : f(x) = y folgt, dass f 1 ( ) =. Es wird in jedem Schritt implizit von der Tatsache gebrauch gemacht, dass A eine σ-algebra ist. Mache Dir klar, wann dies der Fall ist. (1) X A = c = (f 1 ( )) c = f 1 ( c ) = f 1 (Y ) Y B (2) Sei B B, dann gilt A A : f 1 (B) = A, und daraus folgt A A c = f 1 (B c ) B c B 3
4 (3) Sei B n B, n N, dann gilt n N A n A : f 1 (B n ) = A n und es folgt A A n = f 1 (B n ) = f 1 ( B n ) B n B (iii) Sei B eine σ-algebra über Y und f : X Y eine Abbildung. Zeige, dass A := f 1 (B) eine σ-algebra über X ist. Aus der Eigenschaft der Abbildung x X y Y : f(x) = y folgt, dass f 1 (Y ) = X. Mit f 1 (B) = {f 1 (B) : B B} folgt (1) Y B A f 1 (Y ) = X (2) A A B B : f 1 (B) = A A c = f 1 (B c ) und mit B c B folgt A c A. (3) A n A, n N n N B n B : f 1 (B n ) = A n A n = f 1 ( B n) und da B n B gilt, folgt A n A. (iv) Zeige, ob A := {A P(X) : A ist endlich oder A c ist endlich } eine σ-algebra ist. Hinweis: Unterscheide nach der Mächtigkeit X. (1) X < X < A A A X A n A X A A < X \ A = A c A A n X n A n X n A n < n A n A oder die Kurzfassung A = P(X). (2) X = Ist keine σ-algebra, denn: Es existiert eine Folge paarweiser verschiedener Elemente (x k ) k N aus X und setzte A k := x 2k, dann gilt A k A, aber sowohl k N A k = {x 2, x 4,... }, als auch X \ k N A k {x 1, x 3,... } sind nicht endlich. Daher gilt k N A k / A und A ist somit keine σ-algebra. (v) Zeige, dass A := {A P(X) : A ist abzählbar oder A c ist abzählbar } eine σ-algebra ist. A ist eine σ-algebra, denn: (1) X \ X = ist endlich, und damit abzählbar. (2) Sei A A, dann ist entweder A = X \ (X \ A) = X \ A c, oder X \ A = A c abzählbar und damit A c A (3) Seien A k A, k N. Erster Fall, alle A k sind abzählbar, dann folgt auch, dass k N A k abzählbar ist. Zweiter Fall, es existiert ein k N, so dass A k überabzählbar ist (hier nimmt man o.b.d.a. an, dass die restlichen A k abzählbar sind). Da aber A k A gilt, muss A c k abzählbar sein. Damit und mit X \ A k = (X \ A k) (X \ A k ) X \ A k k N folgt nun, dass k N A k A. k N,k k (vi) Sei X und (G i ) i I (I eine beliebige Indexmenge) eine Familie von σ-algebren über X. Zeige, ob die folgenden Aussagen richtig oder falsch sind: 4
5 (1) i G i ist eine σ-algebra. Die Aussage stimmt, denn: (2) i G i ist eine σ-algebra. X G i, i X i G i A G i, i A c G i, i A c I G i A n G i, n, i n A n G i, i n A n I G i Ist keine σ-algebra, denn es existiert ein Gegenbeispiel: Seien G 1 = {, A, A c, X} und G 2 = {, B, B c, X}, dann sind G 1 und G 2 σ-algebren. Dies gilt aber nicht für die Menge G 1 G 2, da diese z.b. nicht das Element A B enthält. (vii) Seien f : X Y eine Abbildung, X, Y und E P(Y ) beliebig. Zeige, dass gilt f 1 (σ(e)) = σ(f 1 (E)) Hinweis: Verwende, dass B = {B Y : f 1 (B) σ(f 1 (E))} und f 1 (σ(e)) σ-algebren sind. : Wie schon weiter oben gezeigt wurde ist B = {B Y : f 1 (B) σ(f 1 (E))} eine σ-algebra mit E B und daraus folgt σ(e) B f 1 (σ(e)) f 1 (B) σ(f 1 (E)) : Wir verwenden, dass f 1 (σ(e)) eine σ-algebra ist: E f 1 (E) σ(f 1 (E)) σ(e) f 1 (σ(e)) σ(f 1 (σ(e))) = f 1 (σ(e)) (viii) Es sei E := {{x} : x R}. Bestimme σ(e). Nach der Definition der σ-algebra muss σ(e) mindestens alle endlichen und abzählbaren Mengen R und deren Komplemente enthalten. Daher gilt σ(e) A := {A R : A ist abzählbar oder A c ist abzählbar oder} Es wurde weiter oben gezeigt, dass A eine σ-algebra ist, dass also A = σa gilt. Da außerdem E A gilt, folgt σ(e) A. Es gilt also σ(e) = A Aufgabe 4: Inhalte und Maße (i) Seien µ : R R ein Inhalt auf dem Ring R, A 1, A 2, R µ-nullmengen und A R beliebig. Ist A n A k, so ist A eine µ-nullmenge. 0 µ(a) µ( n µ(a) = 0 A k ) n A k = 0 (ii) Seien X und µ : P(X) R ein Inhalt mit µ(x) = 1 und µ(a) {0, 1}, A X, sowie A := {A X : µ(a) = 1}. Zeige, dass folgende Aussagen wahr sind: 5
6 (1) / A µ(x) = µ(x ) = µ(x) + µ( ) µ( ) = 0 (2) A A, A B X B A 1 = µ(a) µ(b) µ(x) 1 µ(b) = 1 (3) A, B A A B A Zunächst gilt µ(a B) µ(x) = 1 und daher 1 = µ(a) µ(a B) µ(a) + µ(b) µ(a B) = 1 µ(a B) = 1 (4) A X A A oder A c A Angenommen es gelte A / A und A c / A, dann gilt µ(a) = 0µ(A c ) und somit µ(x) = µ(a A c ) = µ(a) + µ(a c ) = 0 was ein Widerspruch zur Definition von µ darstellt. (iii) Sei wiederum A = {A X : A abzählbar oder A c abzählbar } und X überabzählbar. Dann ist { 0, falls B abzählbar ist µ(b) = 1, falls B c abzählbar ist ein Maß auf A. Weiter oben wurde schon gezeigt, dass A eine σ-algebra ist. Zunächst gilt µ( ) = 0 und µ 0 Sei (A n ) nun eine Folge disjunkter Mengen aus A. Zunächst nehmen wir an, dass alle A n abzählbar sind, dann folgt, dass auch A n abzählbar ist. Daher gilt ( ) µ A n = 0 = µ(a n ) Nun gebe es ein ñ N, so dass Añ überabzählbar ist. Dann muss A c ñ abzählbar sein, da Añ A. Da alle A n paarweise disjunkt sind, folgt A n A c ñ, n ñ und somit sind alle A n, n ñ abzählbar. Daher gilt nun (beachte µ(a n ) = 0, n ñ und (Añ A n ) c A c ñ ist abzählbar) womit µ ein Maß über A ist. ( ) µ A n = 1 = µ(a n ) (iv) Sei µ : R R ein Inhalt auf dem Ring R. Zeige µ ist σ-additiv Für jede Folge (A n ) von Mengen aus R mit A n A R gilt µ(a n ) µ(a) Dies bezeichnet man auch als die Stetigkeit von unten. Hinweis: Betrachte die Zerlegung R A = A 1 k=2 A k \ A k 1. : Zunächst einmal gilt (A k+1 \ A k ) (A k \ A k 1 ) = A k+1 A c k A k A c k 1 = n ñ 6
7 die einzelnen Summanden sind also paarweise disjunkt und zusammen mit dem Hinweis gilt: µ(a) = µ(a 1 ) + µ (A k \ A k 1 ) ( k=2 ) = lim µ(a 1 ) + n µ(a k \ A k 1 ) ( k=2 ) = lim µ A 1 n A k \ A k 1 k=2 = lim µ(a n) : Gezeigt werden soll die σ-additivität von µ. Sei dazu (B n ) eine Folge disjunkter Mengen in B mit B := B n R und sei A n := n k N B k, so gilt A n B. Dann folgt mit Hilfe der Vorraussetzung µ(b) = lim µ(a n) = lim n µ(b k ) = µ(b k ) (v) Seien a 1, a 2, > 0 und E := {x R n : x x2 a 2 n 1 a < 1} der dazugehörige offene Ellipsoid. 2 n Zeige, dass E Borel-meßbar ist und λ n (E) = a 1 a n λ n (K 1 (0)) gilt. Als offene Menge des R n ist E Borel-messbar (E ist Element eines der möglichen Erzeuger der Borelschen Mengen, welche eben die Borel-messbaren Mengen sind). E ist offen, da es eine stetige Abbildung f : R n R n (siehe weiter unten) gibt, so dass E das Urbild der Einheitskugel unter f ist. Sei A := diag(a 1,..., a n ) und f(x) = A 1 x. Mit Hilfe der Gleichung f(λ n ) = det(f) 1 λ n aus der Vorlesung mit dem Bildmaß f(λ)(b) = λ(f 1 (B)), B R n ergibt sich nun λ n (f 1 (K 1 (0))) = a 1 a n λ n (K 1 (0)) und es bleibt noch zu zeigen, dass f 1 (K 1 (0)) = E gilt. Dazu beachte man, dass die Definition des Urbildes f 1 (A) = {x R n : f(x) A} lautet. Nun gilt a i < x i < a i für alle i = 1,..., n und x E. Daraus folgt, dass 1 < [f(x)] i < 1 für alle i = 1,..., n und damit f 1 (K 1 (0)) = E. 7
TECHNISCHE UNIVERSITÄT MÜNCHEN
 Prof. Dr. D. Castrigiano Dr. M. Prähofer Zentralübung 38. Einschränkung eines Maßes TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Mathematik für Physiker 4 (Analysis 3) http://www.ma.tum.de/hm/ma9204
Prof. Dr. D. Castrigiano Dr. M. Prähofer Zentralübung 38. Einschränkung eines Maßes TECHNISCHE UNIVERSITÄT MÜNCHEN Zentrum Mathematik Mathematik für Physiker 4 (Analysis 3) http://www.ma.tum.de/hm/ma9204
Grundlagen Mengenlehre, Maßtheorie
 Grundlagen Mengenlehre, Maßtheorie 12. März 2011 1 Grundlagen der Mengenlehre - Rechnen mit Mengen Im folgenden bezeichnen wir mit P(X) die Menge aller Teilmengen von X, die sogenannte Potenzmenge von
Grundlagen Mengenlehre, Maßtheorie 12. März 2011 1 Grundlagen der Mengenlehre - Rechnen mit Mengen Im folgenden bezeichnen wir mit P(X) die Menge aller Teilmengen von X, die sogenannte Potenzmenge von
D-MATH Mass und Integral FS 2018 Prof. Dr. Urs Lang. Lösung - Serie 2. + A k = A c k Ac k 0
 D-MATH Mass und Integral FS 2018 Prof. Dr. Urs Lang Lösung - Serie 2 Abgabetermin: Mittwoch, 07.03.2018 in die Fächli im HG F 28. Homepage der Vorlesung: https://metaphor.ethz.ch/x/2018/fs/401-2284-00l/
D-MATH Mass und Integral FS 2018 Prof. Dr. Urs Lang Lösung - Serie 2 Abgabetermin: Mittwoch, 07.03.2018 in die Fächli im HG F 28. Homepage der Vorlesung: https://metaphor.ethz.ch/x/2018/fs/401-2284-00l/
Aufgaben zu Kapitel 0
 Aufgaben zu Kapitel 0 0.1. Seien A und B zwei Mengen. Wie kann man paarweise disjunkte Mengen A 1, A 2 und A 3 so wählen, dass A 1 A 2 A 3 = A B gilt? 0.2. Seien E ein Menge und A eine Teilmengen von E.
Aufgaben zu Kapitel 0 0.1. Seien A und B zwei Mengen. Wie kann man paarweise disjunkte Mengen A 1, A 2 und A 3 so wählen, dass A 1 A 2 A 3 = A B gilt? 0.2. Seien E ein Menge und A eine Teilmengen von E.
4 Messbare Funktionen
 4 Messbare Funktionen 4.1 Definitionen und Eigenschaften Definition 4.1. Seien X eine beliebige nichtleere Menge, M P(X) eine σ-algebra in X und µ ein Maß auf M. Das Paar (X, M) heißt messbarer Raum und
4 Messbare Funktionen 4.1 Definitionen und Eigenschaften Definition 4.1. Seien X eine beliebige nichtleere Menge, M P(X) eine σ-algebra in X und µ ein Maß auf M. Das Paar (X, M) heißt messbarer Raum und
Übungsblatt 5 zur Vorlesung Wahrscheinlichkeitstheorie
 Dr. Christoph Luchsinger Übungsblatt 5 zur Vorlesung Wahrscheinlichkeitstheorie Allgemeine Masse Herausgabe des Übungsblattes: Woche 13, Abgabe der Lösungen: Woche 14 (bis Freitag, 16.15 Uhr), Besprechung:
Dr. Christoph Luchsinger Übungsblatt 5 zur Vorlesung Wahrscheinlichkeitstheorie Allgemeine Masse Herausgabe des Übungsblattes: Woche 13, Abgabe der Lösungen: Woche 14 (bis Freitag, 16.15 Uhr), Besprechung:
Serie 2 Lösungsvorschläge
 D-Math Mass und Integral FS 214 Prof. Dr. D. A. Salamon Serie 2 Lösungsvorschläge 1. Seien folgende Mengen gegeben: und für a, b R R := [, ] := R {, }, (a, ] := (a, ) { }, [, b) := (, b) { }. Wir nennen
D-Math Mass und Integral FS 214 Prof. Dr. D. A. Salamon Serie 2 Lösungsvorschläge 1. Seien folgende Mengen gegeben: und für a, b R R := [, ] := R {, }, (a, ] := (a, ) { }, [, b) := (, b) { }. Wir nennen
Metrische äußere Maße, Borel-Maße
 Metrische äußere Maße, Borel-Maße Zum einen haben wir mit dem Fortsetzungssatz gesehen, dass man mit einem äußeren Maß (auf P(X) ) stets eine σ-algebra und ein Maß auf dieser bekommt. Liegt nun ein metrischer
Metrische äußere Maße, Borel-Maße Zum einen haben wir mit dem Fortsetzungssatz gesehen, dass man mit einem äußeren Maß (auf P(X) ) stets eine σ-algebra und ein Maß auf dieser bekommt. Liegt nun ein metrischer
Reelle Analysis. Vorlesungsskript. Enno Lenzmann, Universität Basel. 11. Oktober 2013
 Reelle Analysis Vorlesungsskript Enno Lenzmann, Universität Basel 11. Oktober 2013 3 Fortsetzung von Prämassen zu Massen Der Begriff des Prämasses ist nicht ausreichend, um eine geschmeidige Integrationstheorie
Reelle Analysis Vorlesungsskript Enno Lenzmann, Universität Basel 11. Oktober 2013 3 Fortsetzung von Prämassen zu Massen Der Begriff des Prämasses ist nicht ausreichend, um eine geschmeidige Integrationstheorie
Ferienkurs in Maß- und Integrationstheorie
 Zentrum Mathematik Technische Universität München Dipl. Math. Wolfgang Erb WS 9/ Übungsblatt Ferienkurs in Maß- und Integrationstheorie Aufgabe. (σ-algebren Sei eine Menge und A eine σ-algebra in. Seien
Zentrum Mathematik Technische Universität München Dipl. Math. Wolfgang Erb WS 9/ Übungsblatt Ferienkurs in Maß- und Integrationstheorie Aufgabe. (σ-algebren Sei eine Menge und A eine σ-algebra in. Seien
Maße auf Produkträumen
 Maße auf Produkträumen Es seien (, Ω 1 ) und (X 2, Ω 2 ) zwei Meßräume. Wir wollen uns zuerst überlegen, wie wir ausgehend davon eine geeignete σ-algebra auf X 2 definieren können. Wir betrachten die Menge
Maße auf Produkträumen Es seien (, Ω 1 ) und (X 2, Ω 2 ) zwei Meßräume. Wir wollen uns zuerst überlegen, wie wir ausgehend davon eine geeignete σ-algebra auf X 2 definieren können. Wir betrachten die Menge
Meßbare Funktionen. bilden die Grundlage der Integrationstheorie. Definition 24.1 :
 24 Meßbare Funktionen bilden die Grundlage der Integrationstheorie. Definition 24. : Sei X eine beliebige Menge, Y ein topologischer Raum, λ ein Maß auf X. f : X Y heißt λ-messbar, falls f (Ω) λ-messbar
24 Meßbare Funktionen bilden die Grundlage der Integrationstheorie. Definition 24. : Sei X eine beliebige Menge, Y ein topologischer Raum, λ ein Maß auf X. f : X Y heißt λ-messbar, falls f (Ω) λ-messbar
KONSTRUKTION VON MASSEN
 KONSTRUKTION VON MASSEN MARCUS HEITEL 1. Einleitung Wir wollen im Folgenden das Lebesguemaß konstruieren. Dieses soll die Eigenschaft λ ( [a, b = b a für a, b R besitzen. Nun ist ein Maß aber auf einer
KONSTRUKTION VON MASSEN MARCUS HEITEL 1. Einleitung Wir wollen im Folgenden das Lebesguemaß konstruieren. Dieses soll die Eigenschaft λ ( [a, b = b a für a, b R besitzen. Nun ist ein Maß aber auf einer
Zufallsvariable, Verteilung, Verteilungsfunktion
 Kapitel 5 Zufallsvariable, Verteilung, Verteilungsfunktion 5.1 Zufallsvariable Sei (Ω, A, P ) ein beliebiger Wahrscheinlichkeitsraum. Häufig interessiert nicht ω selbst, sondern eine Kennzahl X(ω), d.h.
Kapitel 5 Zufallsvariable, Verteilung, Verteilungsfunktion 5.1 Zufallsvariable Sei (Ω, A, P ) ein beliebiger Wahrscheinlichkeitsraum. Häufig interessiert nicht ω selbst, sondern eine Kennzahl X(ω), d.h.
Kapitel 19. Das Lebesgue Maß σ Algebren und Maße
 Kapitel 19 Das Lebesgue Maß 19.1 σ Algebren und Maße 19.2 Das äußere Lebesgue Maß 19.3 Das Lebesgue Maß 19.4 Charakterisierungen des Lebesgue Maßes 19.5 Messbare Funktionen 19.1 σ Algebren und Maße Wir
Kapitel 19 Das Lebesgue Maß 19.1 σ Algebren und Maße 19.2 Das äußere Lebesgue Maß 19.3 Das Lebesgue Maß 19.4 Charakterisierungen des Lebesgue Maßes 19.5 Messbare Funktionen 19.1 σ Algebren und Maße Wir
Wahrscheinlichkeitstheorie und Maßtheorie
 KAPITEL 7 Wahrscheinlichkeitstheorie und Maßtheorie 7.1. Vorüberlegungen Die folgenden drei Beispiele sind Spezialfälle des Oberbegriffs Maß. Beispiel 7.1.1 (Verteilung der Ladung oder der Masse). Man
KAPITEL 7 Wahrscheinlichkeitstheorie und Maßtheorie 7.1. Vorüberlegungen Die folgenden drei Beispiele sind Spezialfälle des Oberbegriffs Maß. Beispiel 7.1.1 (Verteilung der Ladung oder der Masse). Man
σ-algebren, Definition des Maßraums
 σ-algebren, Definition des Maßraums Ziel der Maßtheorie ist es, Teilmengen einer Grundmenge X auf sinnvolle Weise einen Inhalt zuzuordnen. Diese Zuordnung soll so beschaffen sein, dass dabei die intuitiven
σ-algebren, Definition des Maßraums Ziel der Maßtheorie ist es, Teilmengen einer Grundmenge X auf sinnvolle Weise einen Inhalt zuzuordnen. Diese Zuordnung soll so beschaffen sein, dass dabei die intuitiven
Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie. Tobias Ried
 Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie Tobias Ried. März 2 2 Aufgabe (Messbarkeit der Komposition zweier Abbildungen). Seien (X, A), (Y, B) und (Z, C) Messräume und f : (X,
Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie Tobias Ried. März 2 2 Aufgabe (Messbarkeit der Komposition zweier Abbildungen). Seien (X, A), (Y, B) und (Z, C) Messräume und f : (X,
Skriptbausteine zur Vorlesung Maßtheorie
 Skriptbausteine zur Vorlesung Maßtheorie Vorlesender: Prof. Dr. Bernd Hofmann Der folgende Text soll die Nacharbeit der Vorlesung erleichtern und dabei an Definitionen, Sätze und Beispiele erinnern. Das
Skriptbausteine zur Vorlesung Maßtheorie Vorlesender: Prof. Dr. Bernd Hofmann Der folgende Text soll die Nacharbeit der Vorlesung erleichtern und dabei an Definitionen, Sätze und Beispiele erinnern. Das
Meßbare Funktionen. Die angemessenen Abbildungen zwischen Meßräumen sind die meßbaren Funktionen.
 Meßbare Funktionen Die angemessenen Abbildungen zwischen Meßräumen sind die meßbaren Funktionen. Definition. Seien (X, Ω 1 ) und (Y, Ω 2 ) Meßräume. Eine Abbildung f : X Y heißt Ω 1 -Ω 2 -meßbar oder kurz
Meßbare Funktionen Die angemessenen Abbildungen zwischen Meßräumen sind die meßbaren Funktionen. Definition. Seien (X, Ω 1 ) und (Y, Ω 2 ) Meßräume. Eine Abbildung f : X Y heißt Ω 1 -Ω 2 -meßbar oder kurz
Stochastik I. Vorlesungsmitschrift
 Stochastik I Vorlesungsmitschrift Ulrich Horst Institut für Mathematik Humboldt-Universität zu Berlin Inhaltsverzeichnis 1 Grundbegriffe 1 1.1 Wahrscheinlichkeitsräume..................................
Stochastik I Vorlesungsmitschrift Ulrich Horst Institut für Mathematik Humboldt-Universität zu Berlin Inhaltsverzeichnis 1 Grundbegriffe 1 1.1 Wahrscheinlichkeitsräume..................................
Lösungen zu Übungsblatt 9
 Analysis : Camillo de Lellis HS 007 Lösungen zu Übungsblatt 9 Lösung zu Aufgabe 1. Wir müssen einfach das Integral 16 (x + y d(x, y x +y 4 ausrechnen. Dies kann man einfach mittels Polarkoordinaten, da
Analysis : Camillo de Lellis HS 007 Lösungen zu Übungsblatt 9 Lösung zu Aufgabe 1. Wir müssen einfach das Integral 16 (x + y d(x, y x +y 4 ausrechnen. Dies kann man einfach mittels Polarkoordinaten, da
Lehrstuhl IV Stochastik & Analysis. Stochastik II. Wahrscheinlichkeitstheorie I. Skriptum nach einer Vorlesung von Hans-Peter Scheffler
 Fachschaft Mathematik Uni Dortmund Lehrstuhl IV Stochastik & Analysis Stochastik II Wahrscheinlichkeitstheorie I Skriptum nach einer Vorlesung von Hans-Peter Scheffler Letzte Änderung: 26. November 2002
Fachschaft Mathematik Uni Dortmund Lehrstuhl IV Stochastik & Analysis Stochastik II Wahrscheinlichkeitstheorie I Skriptum nach einer Vorlesung von Hans-Peter Scheffler Letzte Änderung: 26. November 2002
Maße und Integrale. begleitend zur Vorlesung Stochastik I Humboldt-Universität zu Berlin SS 2008 P. Imkeller. Berlin, den 26.
 Maße und Integrale begleitend zur Vorlesung Stochastik I Humboldt-Universität zu Berlin SS 2008 P. Imkeller Berlin, den 26. April 2008 Inhaltsverzeichnis 1 Konstruktion von Maßen 3 2 Konstruktion von Integralen
Maße und Integrale begleitend zur Vorlesung Stochastik I Humboldt-Universität zu Berlin SS 2008 P. Imkeller Berlin, den 26. April 2008 Inhaltsverzeichnis 1 Konstruktion von Maßen 3 2 Konstruktion von Integralen
Maßtheorie. Skript zur Vorlesung von Prof. Dr. Michael Kohler. Sommersemester 2005 und Wintersemester 2005/2006
 Maßtheorie Skript zur Vorlesung von Prof. Dr. Michael Kohler Sommersemester 2005 und Wintersemester 2005/2006 1 1 Grundbegriffe der Maßtheorie Ziel: Konstruktion von Maßzahlen (wie z. B. Länge / Fläche
Maßtheorie Skript zur Vorlesung von Prof. Dr. Michael Kohler Sommersemester 2005 und Wintersemester 2005/2006 1 1 Grundbegriffe der Maßtheorie Ziel: Konstruktion von Maßzahlen (wie z. B. Länge / Fläche
Existenz des Lebesgue-Borel-Maßes
 A Existenz des Lebesgue-Borel-Maßes In diesem (nicht prüfungsrelevanten) Anhang tragen wir u.a. die Existenz des Lebesgue- Borel-Maßes nach. 52 Es empfiehlt sich, diesen Anhang erst nach Kapitel 5 zu lesen
A Existenz des Lebesgue-Borel-Maßes In diesem (nicht prüfungsrelevanten) Anhang tragen wir u.a. die Existenz des Lebesgue- Borel-Maßes nach. 52 Es empfiehlt sich, diesen Anhang erst nach Kapitel 5 zu lesen
Lösungsvorschläge für das 5. Übungsblatt
 Lösungsvorschläge für das 5. Übungsblatt Aufgabe 6 a) Sei = [0, ], f(x) := [e x ] für x. Hierbei ist [y] := maxk Z k y} für y. Behauptung: f ist messbar und es ist f(x) dx = 2 log 2. falls x [0, log 2),
Lösungsvorschläge für das 5. Übungsblatt Aufgabe 6 a) Sei = [0, ], f(x) := [e x ] für x. Hierbei ist [y] := maxk Z k y} für y. Behauptung: f ist messbar und es ist f(x) dx = 2 log 2. falls x [0, log 2),
1 Grundlagen der Maßtheorie
 1 Grundlagen der Maßtheorie In diesem Kapitel führen wir die Mengensysteme ein, die eine systematische Betrachtung von Ereignissen und zufälligen Beobachtungen in der Wahrscheinlichkeitstheorie erlauben.
1 Grundlagen der Maßtheorie In diesem Kapitel führen wir die Mengensysteme ein, die eine systematische Betrachtung von Ereignissen und zufälligen Beobachtungen in der Wahrscheinlichkeitstheorie erlauben.
1 Endlich additive Volumen auf R n
 Endlich additive Volumen auf R n In Satz. im Skript haben wir gezeigt, dass kein σ-additives Volumen auf der Potenzmenge P (R n ) definiert werden kann. Man könnte sich vorstellen, das Problem ist aus
Endlich additive Volumen auf R n In Satz. im Skript haben wir gezeigt, dass kein σ-additives Volumen auf der Potenzmenge P (R n ) definiert werden kann. Man könnte sich vorstellen, das Problem ist aus
Serie 1 Lösungsvorschläge
 D-Math Mass und Integral FS 2014 Prof. Dr. D. A. Salamon Serie 1 Lösungsvorschläge 1. a) Seien A, B X zwei Mengen, so dass keine der Mengen A \ B, B \ A, A B und X \ (A B) leer ist. Bestimmen Sie die Kardinalität
D-Math Mass und Integral FS 2014 Prof. Dr. D. A. Salamon Serie 1 Lösungsvorschläge 1. a) Seien A, B X zwei Mengen, so dass keine der Mengen A \ B, B \ A, A B und X \ (A B) leer ist. Bestimmen Sie die Kardinalität
Hausdorff-Maß und Hausdorff-Dimension. Jens Krüger
 Hausdorff-Maß und Hausdorff-Dimension Jens Krüger Inhaltsverzeichnis 1 Einleitung 2 2 Grundlagen aus der Maßtheorie 3 3 Die Konstruktion des Hausdorff-Maßes 4 4 Eigenschaften des Hausdorff-Maßes und Hausdorff-Dimension
Hausdorff-Maß und Hausdorff-Dimension Jens Krüger Inhaltsverzeichnis 1 Einleitung 2 2 Grundlagen aus der Maßtheorie 3 3 Die Konstruktion des Hausdorff-Maßes 4 4 Eigenschaften des Hausdorff-Maßes und Hausdorff-Dimension
Lösungen der Übungsaufgaben von Kapitel 3
 Analysis I Ein Lernbuch für den sanften Wechsel von der Schule zur Uni 1 Lösungen der Übungsaufgaben von Kapitel 3 zu 3.1 3.1.1 Bestimmen Sie den Abschluss, den offenen Kern und den Rand folgender Teilmengen
Analysis I Ein Lernbuch für den sanften Wechsel von der Schule zur Uni 1 Lösungen der Übungsaufgaben von Kapitel 3 zu 3.1 3.1.1 Bestimmen Sie den Abschluss, den offenen Kern und den Rand folgender Teilmengen
Multiplikationsoperatoren
 Multiplikationsoperatoren Dennis Dyck 07.04.2014 1 Einleitung In dem ersten Vortrag des eminars soll es um die Untersuchung von Multiplikationsoperatoren gehen. Es werden grundlegende Eigenschaften hergeleitet
Multiplikationsoperatoren Dennis Dyck 07.04.2014 1 Einleitung In dem ersten Vortrag des eminars soll es um die Untersuchung von Multiplikationsoperatoren gehen. Es werden grundlegende Eigenschaften hergeleitet
Der Satz von Lusin. Markus Schuster Juni 2012 Universita t Ulm
 Der Satz von Lusin Markus Schuster 29-30 Juni 2012 Universita t Ulm Maßtheorie Seminar 2012 Seite 2 Der Satz von Lusin Markus Schuster 29-30 Juni 2012 Inhaltsverzeichnis Motivation Definitionen Der Satz
Der Satz von Lusin Markus Schuster 29-30 Juni 2012 Universita t Ulm Maßtheorie Seminar 2012 Seite 2 Der Satz von Lusin Markus Schuster 29-30 Juni 2012 Inhaltsverzeichnis Motivation Definitionen Der Satz
A. Maß- und Integrationstheorie
 A. Maß- und Integrationstheorie Im folgenden sind einige Ergebnisse aus der Maß- und Integrationstheorie zusammengestellt, die wir im Laufe der Vorlesung brauchen werden. Für die Beweise der Sätze sei
A. Maß- und Integrationstheorie Im folgenden sind einige Ergebnisse aus der Maß- und Integrationstheorie zusammengestellt, die wir im Laufe der Vorlesung brauchen werden. Für die Beweise der Sätze sei
Stochastik. Skript zur Vorlesung von Prof. Dr. Michael Kohler Sommersemester 2007
 Stochastik Skript zur Vorlesung von Prof. Dr. Michael Kohler Sommersemester 2007 1 1. Grundbegriffe der Maßtheorie Ziel: Konstruktion von Maßzahlen (wie z. B. Wahrscheinlichkeit / Länge / Fläche / Volumen
Stochastik Skript zur Vorlesung von Prof. Dr. Michael Kohler Sommersemester 2007 1 1. Grundbegriffe der Maßtheorie Ziel: Konstruktion von Maßzahlen (wie z. B. Wahrscheinlichkeit / Länge / Fläche / Volumen
Erwartungswert als Integral
 Erwartungswert als Integral Anton Klimovsky Gemischte ZVen, allgemeine ZVen, Erwartungswert für allgemeine ZVen, Lebesgue-Integral bzgl. WMaß, Eigenschaften des Integrals, Lebesgue-Maß, Lebesgue-Integral
Erwartungswert als Integral Anton Klimovsky Gemischte ZVen, allgemeine ZVen, Erwartungswert für allgemeine ZVen, Lebesgue-Integral bzgl. WMaß, Eigenschaften des Integrals, Lebesgue-Maß, Lebesgue-Integral
2 Allgemeine Integrationstheorie
 2 Allgemeine Integrationstheorie In diesem Abschnitt ist (,S,µ) ein Maßraum, und wir betrachten R immer mit der σ Algebra B(R). Ziel ist es, messbare Funktionen f : R zu integrieren. Das Maß µ wird uns
2 Allgemeine Integrationstheorie In diesem Abschnitt ist (,S,µ) ein Maßraum, und wir betrachten R immer mit der σ Algebra B(R). Ziel ist es, messbare Funktionen f : R zu integrieren. Das Maß µ wird uns
Zusammenfassung der Vorlesung. Analysis 3. Stefan Müller Universität Bonn Wintersemester
 Zusammenfassung der Vorlesung Analysis 3 Stefan Müller Universität Bonn Wintersemester 2016-2017 Dies ist eine gekürzte Zusammenfassung und kein vollständiges Skript der Vorlesung. Deshalb kann diese Zusammenfassung
Zusammenfassung der Vorlesung Analysis 3 Stefan Müller Universität Bonn Wintersemester 2016-2017 Dies ist eine gekürzte Zusammenfassung und kein vollständiges Skript der Vorlesung. Deshalb kann diese Zusammenfassung
Musterlösung Serie 8
 D-MATH Lineare Algebra I HS 018 Prof. Richard Pink Musterlösung Serie 8 Dimension, Direkte Summe & Komplemente 1. Zeige: Für jedes Erzeugendensystem E eines Vektorraums V und jede linear unabhängige Teilmenge
D-MATH Lineare Algebra I HS 018 Prof. Richard Pink Musterlösung Serie 8 Dimension, Direkte Summe & Komplemente 1. Zeige: Für jedes Erzeugendensystem E eines Vektorraums V und jede linear unabhängige Teilmenge
Analysis III - Bachelorversion
 Analysis III - Bachelorversion Die Mitarbeiter von http://mitschriebwiki.nomeata.de/ 28. September 217 Inhaltsverzeichnis Inhaltsverzeichnis 2 I. Vorwort 5 I.1. Über dieses Skriptum..................................
Analysis III - Bachelorversion Die Mitarbeiter von http://mitschriebwiki.nomeata.de/ 28. September 217 Inhaltsverzeichnis Inhaltsverzeichnis 2 I. Vorwort 5 I.1. Über dieses Skriptum..................................
Maß- und Integrationstheorie
 Prof. H.C. Grunau E. Sassone 1 15.10.2002 1.1 Aufgabe Maß- und Integrationstheorie WS 2002/03 Gegeben seien diese 4 Operationen über Mengen:,, \ und (symmetrische ifferenz) [A B = (A \ B) (B \ A)] 1 Wenn
Prof. H.C. Grunau E. Sassone 1 15.10.2002 1.1 Aufgabe Maß- und Integrationstheorie WS 2002/03 Gegeben seien diese 4 Operationen über Mengen:,, \ und (symmetrische ifferenz) [A B = (A \ B) (B \ A)] 1 Wenn
Kompaktheit in topologischen Räumen
 Kompaktheit in topologischen Räumen Joel Gotsch 21. Januar 2011 Inhaltsverzeichnis 1 Notation und Allgemeines 2 2 Definitionen 2 2.1 Allgemeine Definitionen..................... 2 2.2 Globale Kompaktheitseigenschaften...............
Kompaktheit in topologischen Räumen Joel Gotsch 21. Januar 2011 Inhaltsverzeichnis 1 Notation und Allgemeines 2 2 Definitionen 2 2.1 Allgemeine Definitionen..................... 2 2.2 Globale Kompaktheitseigenschaften...............
Maßtheorie und Integralrechnung mehrerer Variablen
 Maßtheorie und Integralrechnung mehrerer Variablen Jan Swoboda 29. März 2014 Inhaltsverzeichnis Einleitung 1 1 Maßtheorie 3 1.1 Messbare Räume und messbare Abbildungen.................. 3 1.2 Maße und
Maßtheorie und Integralrechnung mehrerer Variablen Jan Swoboda 29. März 2014 Inhaltsverzeichnis Einleitung 1 1 Maßtheorie 3 1.1 Messbare Räume und messbare Abbildungen.................. 3 1.2 Maße und
Maß & Integral de Gruyter Lehrbuch, Berlin 2015 ISBN:
 Maß & Integral de Gruyter Lehrbuch, Berlin 205 ISBN: 978 3 03484 9 Lösungshandbuch René L. Schilling & Franziska Kühn Dresden, Januar 205 Diese Version: Februar 206 R.L. Schilling: Maß & Integral Dank.
Maß & Integral de Gruyter Lehrbuch, Berlin 205 ISBN: 978 3 03484 9 Lösungshandbuch René L. Schilling & Franziska Kühn Dresden, Januar 205 Diese Version: Februar 206 R.L. Schilling: Maß & Integral Dank.
Aufgaben und Lösungen Ausarbeitung der Übungsstunde zur Vorlesung Analysis I
 Aufgaben und en Ausarbeitung der Übungsstunde zur Vorlesung Analysis I Wintersemester 2008/2009 Übung 6 Einleitung Eventuell auftretende Fragen zum Übungsblatt sollen beantwortet werden. Dazu ist es erforderlich,
Aufgaben und en Ausarbeitung der Übungsstunde zur Vorlesung Analysis I Wintersemester 2008/2009 Übung 6 Einleitung Eventuell auftretende Fragen zum Übungsblatt sollen beantwortet werden. Dazu ist es erforderlich,
Topologische Grundbegriffe I. 1 Offene und Abgeschlossene Mengen
 Topologische Grundbegriffe I Vortrag zum Proseminar Analysis, 26.04.2010 Nina Neidhardt und Simon Langer Im Folgenden soll gezeigt werden, dass topologische Konzepte, die uns schon für die Reellen Zahlen
Topologische Grundbegriffe I Vortrag zum Proseminar Analysis, 26.04.2010 Nina Neidhardt und Simon Langer Im Folgenden soll gezeigt werden, dass topologische Konzepte, die uns schon für die Reellen Zahlen
Im gesamten Kapitel sei Ω eine nichtleere Menge. Wir bezeichnen die Potenzmenge
 1 Mengensysteme Ein Mengensystem ist eine Familie von Teilmengen einer Grundmenge und damit eine Teilmenge der Potenzmenge der Grundmenge. In diesem Kapitel untersuchen wir Mengensysteme, die unter bestimmten
1 Mengensysteme Ein Mengensystem ist eine Familie von Teilmengen einer Grundmenge und damit eine Teilmenge der Potenzmenge der Grundmenge. In diesem Kapitel untersuchen wir Mengensysteme, die unter bestimmten
Scheinklausur zur Vorlesung Stochastik II
 Institut für Mathematische Stochastik WS 2007/2008 Universität Karlsruhe 25. 02. 2008 Dr. B. Klar Scheinklausur zur Vorlesung Stochastik II Muster-Lösung Dauer: 90 Minuten Name: Vorname: Matrikelnummer:
Institut für Mathematische Stochastik WS 2007/2008 Universität Karlsruhe 25. 02. 2008 Dr. B. Klar Scheinklausur zur Vorlesung Stochastik II Muster-Lösung Dauer: 90 Minuten Name: Vorname: Matrikelnummer:
ARBEITSUNTERLAGEN ZUR VORLESUNG UND ÜBUNG AN DER UNIVERSITÄT DES SAARLANDES MAß-, INTEGRATIONS-
 ARBEITSUNTERLAGEN ZUR VORLESUNG UND ÜBUNG AN DER UNIVERSITÄT DES SAARLANDES MAß-, INTEGRATIONS- und WAHRSCHEINLICHKEITSTHEORIE im SS 2014 Übung Maß- und Integrationstheorie (SS 2014) 1 Aufgabe 1 (σ-algebra)
ARBEITSUNTERLAGEN ZUR VORLESUNG UND ÜBUNG AN DER UNIVERSITÄT DES SAARLANDES MAß-, INTEGRATIONS- und WAHRSCHEINLICHKEITSTHEORIE im SS 2014 Übung Maß- und Integrationstheorie (SS 2014) 1 Aufgabe 1 (σ-algebra)
Analysis 2. Vorlesungsausarbeitung zum SS von Prof. Dr. Klaus Fritzsche. Inhaltsverzeichnis
 Bergische Universität Gesamthochschule Wuppertal Fachbereich Mathematik Analysis 2 Kapitel 3 Integrationstheorie Vorlesungsausarbeitung zum SS 2001 von Prof Dr Klaus Fritzsche Inhaltsverzeichnis 1 Maßtheorie
Bergische Universität Gesamthochschule Wuppertal Fachbereich Mathematik Analysis 2 Kapitel 3 Integrationstheorie Vorlesungsausarbeitung zum SS 2001 von Prof Dr Klaus Fritzsche Inhaltsverzeichnis 1 Maßtheorie
Zusammenfassung der Lebesgue-Integrationstheorie
 Zusammenfassung der Lebesgue-Integrationstheorie Das Lebesguesche Integral verallgemeinert das Riemannsche Integral. Seine Vorteile liegen für unsere Anwendungen vor allem bei den wichtigen Konvergenzsätzen,
Zusammenfassung der Lebesgue-Integrationstheorie Das Lebesguesche Integral verallgemeinert das Riemannsche Integral. Seine Vorteile liegen für unsere Anwendungen vor allem bei den wichtigen Konvergenzsätzen,
2. Integration. {x : f(x) <a+ 1 n }
 9 2.1. Definition. 2. Integration in Maß ist eine nichtnegative, abzählbar additive Mengenfunktion. in Maßraum ist ein Tripel (X,,µ) bestehend aus einem messbaren Raum X mit der -lgebra und einem auf definierten
9 2.1. Definition. 2. Integration in Maß ist eine nichtnegative, abzählbar additive Mengenfunktion. in Maßraum ist ein Tripel (X,,µ) bestehend aus einem messbaren Raum X mit der -lgebra und einem auf definierten
Höhere Analysis. dω = Reiner Lauterbach. Vorlesung. Universität Hamburg, WS 2015/2016
 Höhere Analysis Vorlesung Reiner Lauterbach M dω = M ω Universität Hamburg, WS 2015/2016 ii Inhaltsverzeichnis 12 Integration im R n 5 12.1 Mengenalgebren............................ 6 12.2 Inhalt und
Höhere Analysis Vorlesung Reiner Lauterbach M dω = M ω Universität Hamburg, WS 2015/2016 ii Inhaltsverzeichnis 12 Integration im R n 5 12.1 Mengenalgebren............................ 6 12.2 Inhalt und
10 Der Umordnungssatz und das Cauchy-Produkt
 10 Der Umordnungssatz und das Cauchy-Produkt Wir wollen, unter anderem, zeigen, dass man absolut konvergente Reihen beliebig umirdnen kann, ohne das sich der Wert der Reihe verändert. Achtung: Die Aussage
10 Der Umordnungssatz und das Cauchy-Produkt Wir wollen, unter anderem, zeigen, dass man absolut konvergente Reihen beliebig umirdnen kann, ohne das sich der Wert der Reihe verändert. Achtung: Die Aussage
Thema 3 Folgen, Grenzwerte
 Thema 3 Folgen, Grenzwerte Definition Eine Folge von reellen Zahlen ist eine Abbildung von N in R d.h. jedem n N ist eine Zahl a n zugeordnet. Wir schreiben für eine solche Folge. Beispiele. (a n ) n N
Thema 3 Folgen, Grenzwerte Definition Eine Folge von reellen Zahlen ist eine Abbildung von N in R d.h. jedem n N ist eine Zahl a n zugeordnet. Wir schreiben für eine solche Folge. Beispiele. (a n ) n N
Kurzskript zur Maßtheorie (Teil der Vorlesung Analysis III, Wintersemester 2010/11, gehalten von D. Grieser)
 Kurzskript zur Maßtheorie (Teil der Vorlesung Analysis III, Wintersemester 2010/11, gehalten von D. Grieser) 13. Januar 2011 Inhaltsverzeichnis Vorwort..................................................
Kurzskript zur Maßtheorie (Teil der Vorlesung Analysis III, Wintersemester 2010/11, gehalten von D. Grieser) 13. Januar 2011 Inhaltsverzeichnis Vorwort..................................................
Absolute Stetigkeit von Maßen
 Absolute Stetigkeit von Maßen Definition. Seien µ und ν Maße auf (X, Ω). Dann heißt ν absolut stetig bezüglich µ (kurz ν µ ), wenn für alle A Ω mit µ(a) = 0 auch gilt dass ν(a) = 0. Lemma. Sei ν ein endliches
Absolute Stetigkeit von Maßen Definition. Seien µ und ν Maße auf (X, Ω). Dann heißt ν absolut stetig bezüglich µ (kurz ν µ ), wenn für alle A Ω mit µ(a) = 0 auch gilt dass ν(a) = 0. Lemma. Sei ν ein endliches
Kommutativität. De Morgansche Regeln
 1. Formale Logik Proposition 1.1. Die logischen Elementarverknüpfungen gehorchen folgenden Äquivalenzen: (1.1) (1.2) p p p p p p Idempotenz (1.3) (1.4) p q q p p q q p Kommutativität (1.5) (1.6) (p q)
1. Formale Logik Proposition 1.1. Die logischen Elementarverknüpfungen gehorchen folgenden Äquivalenzen: (1.1) (1.2) p p p p p p Idempotenz (1.3) (1.4) p q q p p q q p Kommutativität (1.5) (1.6) (p q)
3 Markov-Eigenschaft der Brownschen Bewegung
 Man verifiziert 2.) für P n = Q n, und somit gilt: jede Teilfolge von (P n ) n N besitzt eine konvergente Teilfolge. Betrachte nun die endlich-dimensionalen Randverteilungen der Maße P n. Dazu sei π t1,...,t
Man verifiziert 2.) für P n = Q n, und somit gilt: jede Teilfolge von (P n ) n N besitzt eine konvergente Teilfolge. Betrachte nun die endlich-dimensionalen Randverteilungen der Maße P n. Dazu sei π t1,...,t
1.3 Zufallsvariablen
 1.3 Zufallsvariablen Beispiel Irrfahrt zwischen drei Zuständen Start in G bei t = 0, Zeithorizont T N Grundraum σ-algebra Ω = {ω = (ω 0, ω 1,..., ω T ) {G, R, B} T +1, ω 0 = G} Wahrscheinlichkeitsmaß P
1.3 Zufallsvariablen Beispiel Irrfahrt zwischen drei Zuständen Start in G bei t = 0, Zeithorizont T N Grundraum σ-algebra Ω = {ω = (ω 0, ω 1,..., ω T ) {G, R, B} T +1, ω 0 = G} Wahrscheinlichkeitsmaß P
Aktuelle Themen aus der Stochastik Wintersemester 2017/2018 Abschnitt 5: Endliche Maße und schwache Konvergenz von Maßen in metrischen Räumen
 Aktuelle Themen aus der Stochastik Wintersemester 2017/2018 Abschnitt 5: Endliche Maße und schwache Konvergenz von Maßen in metrischen Räumen Prof. Dr. Hans-Jörg Starkloff TU Bergakademie Freiberg Institut
Aktuelle Themen aus der Stochastik Wintersemester 2017/2018 Abschnitt 5: Endliche Maße und schwache Konvergenz von Maßen in metrischen Räumen Prof. Dr. Hans-Jörg Starkloff TU Bergakademie Freiberg Institut
Klausur zur Vorlesung Stochastik II
 Institut für Mathematische Stochastik WS 24/25 Universität Karlsruhe 7. März 25 Priv-Doz. Dr. D. Kadelka Klausur zur Vorlesung Stochastik II Dauer: 9 Minuten Name: Vorname: Matrikelnummer: Diese Klausur
Institut für Mathematische Stochastik WS 24/25 Universität Karlsruhe 7. März 25 Priv-Doz. Dr. D. Kadelka Klausur zur Vorlesung Stochastik II Dauer: 9 Minuten Name: Vorname: Matrikelnummer: Diese Klausur
Kapitel V. Folgen und Konvergenz. V.1 Konvergenz von Zahlenfolgen
 Kapitel V Folgen und Konvergenz V.1 Konvergenz von Zahlenfolgen Wir erinnern an den Begriff der Folge, den wir schon im Kapitel III verwenden. Eine Folge (a n ) n=1 AN in A ist eine Abbildung a ( ) : N
Kapitel V Folgen und Konvergenz V.1 Konvergenz von Zahlenfolgen Wir erinnern an den Begriff der Folge, den wir schon im Kapitel III verwenden. Eine Folge (a n ) n=1 AN in A ist eine Abbildung a ( ) : N
{ Anzahl Elemente in A wenn endlich, sonst,
 Analysis 3, Woche 3 Maße II 3.1 Äußeres Maß Man könnte hoffen, nachdem man durch die Erweiterung von X, A, µ zu X, A, µ einen vollständigen Maßraum konstruiert hat, dass auch alle Mengen messbar sein sollten.
Analysis 3, Woche 3 Maße II 3.1 Äußeres Maß Man könnte hoffen, nachdem man durch die Erweiterung von X, A, µ zu X, A, µ einen vollständigen Maßraum konstruiert hat, dass auch alle Mengen messbar sein sollten.
Kapitel II - Wahrscheinlichkeitsraum
 Institut für Volkswirtschaftslehre (ECON) Lehrstuhl für Ökonometrie und Statistik Kapitel II - Wahrscheinlichkeitsraum Wahrscheinlichkeitstheorie Prof. Dr. W.-D. Heller Hartwig Senska Carlo Siebenschuh
Institut für Volkswirtschaftslehre (ECON) Lehrstuhl für Ökonometrie und Statistik Kapitel II - Wahrscheinlichkeitsraum Wahrscheinlichkeitstheorie Prof. Dr. W.-D. Heller Hartwig Senska Carlo Siebenschuh
Maß- und Integrationstheorie
 Maß- und Integrationstheorie Klaus Ritter Kaiserslautern, SS 2014 Literatur Insbesondere J. Elstrodt, Maß- und Integrationstheorie, Springer, Berlin, 1. Auflage 1996, 7. Auflage 2011. Vorkenntnisse Grundlagen
Maß- und Integrationstheorie Klaus Ritter Kaiserslautern, SS 2014 Literatur Insbesondere J. Elstrodt, Maß- und Integrationstheorie, Springer, Berlin, 1. Auflage 1996, 7. Auflage 2011. Vorkenntnisse Grundlagen
Analysis III, WS 2011/2012 Montag $Id: masse.tex,v /10/31 15:48:07 hk Exp $
 $Id: masse.tex,v 1.8 2011/10/31 15:48:07 hk Exp $ 2 Maßräume 2.2 Meßbare Abbildungen Der nächste Grundbegriff sind die meßbaren Abbildungen. Erinnern Sie sich daran das wir eigentlich einen Integralbegriff
$Id: masse.tex,v 1.8 2011/10/31 15:48:07 hk Exp $ 2 Maßräume 2.2 Meßbare Abbildungen Der nächste Grundbegriff sind die meßbaren Abbildungen. Erinnern Sie sich daran das wir eigentlich einen Integralbegriff
Übungsaufgaben zu Analysis 1 Lösungen von Blatt VI vom
 Prof. Dr. Moritz Kaßmann Fakultät für Mathematik Wintersemester 04/05 Universität Bielefeld Übungsaufgaben zu Analysis Lösungen von Blatt VI vom 0..4 Aufgabe VI. (6 Punkte) Gegeben sind die Folgen (a n)
Prof. Dr. Moritz Kaßmann Fakultät für Mathematik Wintersemester 04/05 Universität Bielefeld Übungsaufgaben zu Analysis Lösungen von Blatt VI vom 0..4 Aufgabe VI. (6 Punkte) Gegeben sind die Folgen (a n)
Große Mengen und Ultrafilter. 1 Große Mengen
 Vortrag zum Seminar zur Analysis, 31.10.2012 Marcel Marnitz In diesem Vortrag wird das Konzept mathematischer Filter eingeführt. Sie werden in späteren Vorträgen zur Konstruktion der hyperreellen Zahlen
Vortrag zum Seminar zur Analysis, 31.10.2012 Marcel Marnitz In diesem Vortrag wird das Konzept mathematischer Filter eingeführt. Sie werden in späteren Vorträgen zur Konstruktion der hyperreellen Zahlen
1 Elemente der Wahrscheinlichkeitstheorie
 H.-J. Starkloff Unendlichdimensionale Stochastik Kap. 01 11. Oktober 2010 1 1 Elemente der Wahrscheinlichkeitstheorie 1.1 Messbare Räume Gegeben seien eine nichtleere Menge Ω und eine Menge A von Teilmengen
H.-J. Starkloff Unendlichdimensionale Stochastik Kap. 01 11. Oktober 2010 1 1 Elemente der Wahrscheinlichkeitstheorie 1.1 Messbare Räume Gegeben seien eine nichtleere Menge Ω und eine Menge A von Teilmengen
x, y 2 f(x)g(x) dµ(x). Es ist leicht nachzuprüfen, dass die x 2 setzen. Dann liefert (5.1) n=1 x ny n bzw. f, g = Ω
 5. Hilberträume Definition 5.1. Sei H ein komplexer Vektorraum. Eine Abbildung, : H H C heißt Skalarprodukt (oder inneres Produkt) auf H, wenn für alle x, y, z H, α C 1) x, x 0 und x, x = 0 x = 0; ) x,
5. Hilberträume Definition 5.1. Sei H ein komplexer Vektorraum. Eine Abbildung, : H H C heißt Skalarprodukt (oder inneres Produkt) auf H, wenn für alle x, y, z H, α C 1) x, x 0 und x, x = 0 x = 0; ) x,
Klausur - Analysis I Lösungsskizzen
 Klausur - Analysis I Lösungsskizzen Aufgabe 1.: 5 Punkte Entscheiden Sie, ob folgende Aussagen wahr oder falsch sind. Kennzeichnen Sie wahre Aussagen mit W und falsche Aussagen mit F. Es sind keine Begründungen
Klausur - Analysis I Lösungsskizzen Aufgabe 1.: 5 Punkte Entscheiden Sie, ob folgende Aussagen wahr oder falsch sind. Kennzeichnen Sie wahre Aussagen mit W und falsche Aussagen mit F. Es sind keine Begründungen
I Grundbegriffe 1 1 Wahrscheinlichkeitsräume Bedingte Wahrscheinlichkeiten und Unabhängigkeit Reellwertige Zufallsvariablen...
 Inhaltsverzeichnis I Grundbegriffe 1 1 Wahrscheinlichkeitsräume......................... 1 2 Bedingte Wahrscheinlichkeiten und Unabhängigkeit........... 7 3 Reellwertige Zufallsvariablen........................
Inhaltsverzeichnis I Grundbegriffe 1 1 Wahrscheinlichkeitsräume......................... 1 2 Bedingte Wahrscheinlichkeiten und Unabhängigkeit........... 7 3 Reellwertige Zufallsvariablen........................
1 falls x 2. falls x = 1 und. 0 falls x > 1. eine Lebesgue-integrierbare Majorante. Somit können wir den Satz von Lebesgue anwenden:
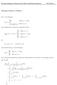 Lösungsvorschläge zur Klausur 045 Maß- und Integrationstheorie WS 205/6 Lösungsvorschlag zu Aufgabe Sei f n der Integrant 0 falls x > 2 und f n x) falls x 2. 3+sin 2n)+x x 4n Sein punktweiser Grenzwert
Lösungsvorschläge zur Klausur 045 Maß- und Integrationstheorie WS 205/6 Lösungsvorschlag zu Aufgabe Sei f n der Integrant 0 falls x > 2 und f n x) falls x 2. 3+sin 2n)+x x 4n Sein punktweiser Grenzwert
Reelle Analysis: Mehrfachintegration
 Reelle Analysis: Mehrfachintegration Universität Paderborn, WS 2008/09 Prof. Dr. Helge Glöckner Inhaltsverzeichnis: Vorwort....................................................................i Literatur..................................................................
Reelle Analysis: Mehrfachintegration Universität Paderborn, WS 2008/09 Prof. Dr. Helge Glöckner Inhaltsverzeichnis: Vorwort....................................................................i Literatur..................................................................
Einführung und Grundlagen
 Kapitel 1 Einführung und Grundlagen Generelle Notation: Ω, A, P sei ein W-Raum im Hintergrund nie weiter spezifiziert Die betrachteten Zufallsvariablen seien auf Ω definiert, zb X : Ω, A M, A, wobei M,
Kapitel 1 Einführung und Grundlagen Generelle Notation: Ω, A, P sei ein W-Raum im Hintergrund nie weiter spezifiziert Die betrachteten Zufallsvariablen seien auf Ω definiert, zb X : Ω, A M, A, wobei M,
Vorlesungsskript,,Integrationstheorie
 Vorlesungsskript,,Integrationstheorie Christoph Kühn aktuelle Version: 15. Februar 2013 Das Skript wird parallel zur Vorlesung im Wintersemester 2012/13 aufgebaut, Hinweise auf Fehler sind sehr willkommen.
Vorlesungsskript,,Integrationstheorie Christoph Kühn aktuelle Version: 15. Februar 2013 Das Skript wird parallel zur Vorlesung im Wintersemester 2012/13 aufgebaut, Hinweise auf Fehler sind sehr willkommen.
Kapitel III: Lebesgue-Zerlegung von Massen
 Reinhard Höpfner Vorlesung Stochastik Kapitel III: Lebesgue-Zerlegung von Massen SoSe 16 WS 16/17 Institut für Mathematik, Johannes Gutenberg Universität Mainz October 31, 2016 1 Übersicht zu Kapitel III
Reinhard Höpfner Vorlesung Stochastik Kapitel III: Lebesgue-Zerlegung von Massen SoSe 16 WS 16/17 Institut für Mathematik, Johannes Gutenberg Universität Mainz October 31, 2016 1 Übersicht zu Kapitel III
Übungsblatt 2 - Analysis 2, Prof. G. Hemion
 Tutor: Martin Friesen, martin.friesen@gmx.de Übungsblatt 2 - Analysis 2, Prof. G. Hemion Um die hier gestellten Aufgaben zu lösen brauchen wir ein wenig Kentnisse über das Infimum bzw. Supremum einer Menge.
Tutor: Martin Friesen, martin.friesen@gmx.de Übungsblatt 2 - Analysis 2, Prof. G. Hemion Um die hier gestellten Aufgaben zu lösen brauchen wir ein wenig Kentnisse über das Infimum bzw. Supremum einer Menge.
Aufgabensammlung zur Analysis 1
 Analysis 1 18.12.2017 Prof. Dr. H. Koch Dr. F. Gmeineder Abgabe: Keine Abgabe. Aufgabensammlung zur Analysis 1 Anmerkungen: Das vorliegende Blatt enthält eine Auswahl von Aufgaben, die auf Klausuren zur
Analysis 1 18.12.2017 Prof. Dr. H. Koch Dr. F. Gmeineder Abgabe: Keine Abgabe. Aufgabensammlung zur Analysis 1 Anmerkungen: Das vorliegende Blatt enthält eine Auswahl von Aufgaben, die auf Klausuren zur
Zusammenfassung der Vorlesung. Analysis 3. Stefan Müller Universität Bonn Wintersemester
 Zusammenfassung der Vorlesung Analysis 3 Stefan Müller Universität Bonn Wintersemester 2016-2017 Dies ist eine gekürzte Zusammenfassung und kein vollständiges Skript der Vorlesung. Deshalb kann diese Zusammenfassung
Zusammenfassung der Vorlesung Analysis 3 Stefan Müller Universität Bonn Wintersemester 2016-2017 Dies ist eine gekürzte Zusammenfassung und kein vollständiges Skript der Vorlesung. Deshalb kann diese Zusammenfassung
Höhere Mathematik I für die Fachrichtung Informatik. Lösungsvorschläge zum 4. Übungsblatt
 KARLSRUHER INSTITUT FÜR TECHNOLOGIE INSTITUT FÜR ANALYSIS Dr. Christoph Schmoeger Heiko Hoffmann WS 0/4 Höhere Mathematik I für die Fachrichtung Informatik Lösungsvorschläge zum 4. Übungsblatt Aufgabe
KARLSRUHER INSTITUT FÜR TECHNOLOGIE INSTITUT FÜR ANALYSIS Dr. Christoph Schmoeger Heiko Hoffmann WS 0/4 Höhere Mathematik I für die Fachrichtung Informatik Lösungsvorschläge zum 4. Übungsblatt Aufgabe
Das Lebesgue-Maß im R p
 Das Lebesgue-Maß im R p Wir werden nun im R p ein metrisches äußeres Maß definieren, welches schließlich zum Lebesgue-Maß führen wird. Als erstes definieren wir das Volumen von Intervallen des R p. Seien
Das Lebesgue-Maß im R p Wir werden nun im R p ein metrisches äußeres Maß definieren, welches schließlich zum Lebesgue-Maß führen wird. Als erstes definieren wir das Volumen von Intervallen des R p. Seien
Vollständigkeit. 1 Konstruktion der reellen Zahlen
 Vortrag im Rahmen des Proseminars zur Analysis, 17.03.2006 Albert Zeyer Ziel des Vortrags ist es, die Vollständigkeit auf Basis der Konstruktion von R über die CAUCHY-Folgen zu beweisen und äquivalente
Vortrag im Rahmen des Proseminars zur Analysis, 17.03.2006 Albert Zeyer Ziel des Vortrags ist es, die Vollständigkeit auf Basis der Konstruktion von R über die CAUCHY-Folgen zu beweisen und äquivalente
Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist:
![Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist: Musterlösung. Aufgabe 1 a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [0, 1] R, die folgendermaßen definiert ist:](/thumbs/63/49291408.jpg) Musterlösung Aufgabe a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [, ] R, die folgendermaßen definiert ist: f(x) := { für x R \ Q für x Q f ist offensichtlich beschränkt. Wir zeigen,
Musterlösung Aufgabe a) Die Aussage ist falsch. Ein Gegenbeispiel ist die Funktion f : [, ] R, die folgendermaßen definiert ist: f(x) := { für x R \ Q für x Q f ist offensichtlich beschränkt. Wir zeigen,
3 Das n-dimensionale Integral
 3 Das n-dimensionale Integral Ziel: Wir wollen die Integrationstheorie für f : D R n R entwickeln. Wir wollen den Inhalt (beziehungsweise das Maß ) M einer Punktmenge des R n definieren für eine möglichst
3 Das n-dimensionale Integral Ziel: Wir wollen die Integrationstheorie für f : D R n R entwickeln. Wir wollen den Inhalt (beziehungsweise das Maß ) M einer Punktmenge des R n definieren für eine möglichst
Maßtheorie. Wie interpretiert man Volumenmessung? Ziel :
 23 Maßtheorie Ziel : Entwicklung allgemeiner Konzepte, die es gestatten, z.b. Volumina und Oberflächen von Körpern R 3 sinnvoll zu definieren und zu berechnen; sinnvoll soll heißen : für den Einheitswürfel
23 Maßtheorie Ziel : Entwicklung allgemeiner Konzepte, die es gestatten, z.b. Volumina und Oberflächen von Körpern R 3 sinnvoll zu definieren und zu berechnen; sinnvoll soll heißen : für den Einheitswürfel
Kapitel II Kontinuierliche Wahrscheinlichkeitsräume
 Kapitel II Kontinuierliche Wahrscheinlichkeitsräume 1. Einführung 1.1 Motivation Interpretation der Poisson-Verteilung als Grenzwert der Binomialverteilung. DWT 1.1 Motivation 211/476 Beispiel 85 Wir betrachten
Kapitel II Kontinuierliche Wahrscheinlichkeitsräume 1. Einführung 1.1 Motivation Interpretation der Poisson-Verteilung als Grenzwert der Binomialverteilung. DWT 1.1 Motivation 211/476 Beispiel 85 Wir betrachten
Definition 3.1. Sei A X. Unter einer offenen Überdeckung von A versteht man eine Familie (U i ) i I offener Mengen U i X mit U i
 3 Kompaktheit In der Analysis I zeigt man, dass stetige Funktionen f : [a, b] R auf abgeschlossenen, beschränkten Intervallen [a, b] gleichmäßig stetig und beschränkt sind und dass sie ihr Supremum und
3 Kompaktheit In der Analysis I zeigt man, dass stetige Funktionen f : [a, b] R auf abgeschlossenen, beschränkten Intervallen [a, b] gleichmäßig stetig und beschränkt sind und dass sie ihr Supremum und
Bálint Farkas. Analysis 3. Skript zur Vorlesung in WS2014/ Mai c by B. Farkas. compiled: 21-May-2015/11:13
 Bálint Farkas Analysis 3 Skript zur Vorlesung in WS2014/2015 21. Mai 2015 c by B. Farkas V O R B E M E R K U N G E N Dieses Skript beinhaltet das Material der Vorlesung Analysis 3 gehalten an der Bergischen
Bálint Farkas Analysis 3 Skript zur Vorlesung in WS2014/2015 21. Mai 2015 c by B. Farkas V O R B E M E R K U N G E N Dieses Skript beinhaltet das Material der Vorlesung Analysis 3 gehalten an der Bergischen
Misterlösung zur Klausur zur Vorlesung Analysis I, WS08/09, Samstag, (Version C)
 Misterlösung zur Klausur zur Vorlesung Analysis I, WS08/09, Samstag, 14..009 (Version C Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen aus der Vorlesung
Misterlösung zur Klausur zur Vorlesung Analysis I, WS08/09, Samstag, 14..009 (Version C Vokabelbuch In diesem Teil soll getestet werden, inwieweit Sie in der Lage sind, wichtige Definitionen aus der Vorlesung
Differential- und Integralrechnung 3 (Lebesgue-Integral und die Integralsätze von Stokes und Gauss)
 Kurz-Skript zu Differential- und Integralrechnung 3 (Lebesgue-Integral und die Integralsätze von Stokes und Gauss) Thomas Schick Last compiled 31. Dezember 2003; last edited 31.12. 2003 or later Hinweis:
Kurz-Skript zu Differential- und Integralrechnung 3 (Lebesgue-Integral und die Integralsätze von Stokes und Gauss) Thomas Schick Last compiled 31. Dezember 2003; last edited 31.12. 2003 or later Hinweis:
Analysis III. Vorlesung 61
 Prof. Dr. H. Brenner Osnabrück WS 2014/2015 Analysis III Vorlesung 61 In diesem Kurs beschäftigen wir uns mit dem Flächeninhalt von ebenen Gebilden und den Volumina von räumlichen Gebilden. Für ein Rechteck
Prof. Dr. H. Brenner Osnabrück WS 2014/2015 Analysis III Vorlesung 61 In diesem Kurs beschäftigen wir uns mit dem Flächeninhalt von ebenen Gebilden und den Volumina von räumlichen Gebilden. Für ein Rechteck
Kapitel I: Grundbegriffe
 Reinhard Höpfner Vorlesung Stochastik I Kapitel I: Grundbegriffe Sommersemester 2016 Institut für Mathematik, Johannes Gutenberg Universität Mainz May 11, 2016 1 Übersicht zu Kapitel I : A. Einführung
Reinhard Höpfner Vorlesung Stochastik I Kapitel I: Grundbegriffe Sommersemester 2016 Institut für Mathematik, Johannes Gutenberg Universität Mainz May 11, 2016 1 Übersicht zu Kapitel I : A. Einführung
Grundlagen der Maßtheorie
 Kapitel 4 Grundlagen der Maßtheorie 4.1 Das Maßproblem Das vielleicht ursprünglichste Problem der Geometrie ist das sogenannten Maßproblem. Dessen Behandlung steht im Zentrum dieses vierten Kapitels. Unsere
Kapitel 4 Grundlagen der Maßtheorie 4.1 Das Maßproblem Das vielleicht ursprünglichste Problem der Geometrie ist das sogenannten Maßproblem. Dessen Behandlung steht im Zentrum dieses vierten Kapitels. Unsere
die gewünschte Schranke gefunden, denn es gilt (trivialerweise) für n N
 .5. VOLLSTÄNDIGKEIT VON R 37 Lemma.5. (Beschränktheit konvergenter Folgen) Konvergente Folgen in R sind beschränkt. Beweis. Angenommen die Folge a n n N konvergiert gegen A R. Zu ε > 0 existiert ein N
.5. VOLLSTÄNDIGKEIT VON R 37 Lemma.5. (Beschränktheit konvergenter Folgen) Konvergente Folgen in R sind beschränkt. Beweis. Angenommen die Folge a n n N konvergiert gegen A R. Zu ε > 0 existiert ein N
Darstellungssatz von Riesz in vollständig regulären Räumen. Carina Pöll Wintersemester 2012
 Darstellungssatz von Riesz in vollständig regulären Räumen Carina Pöll 0726726 Wintersemester 2012 Inhaltsverzeichnis 1 Einleitung 1 2 Definitionen und Resultate aus der Topologie 1 3 Der Darstellungssatz
Darstellungssatz von Riesz in vollständig regulären Räumen Carina Pöll 0726726 Wintersemester 2012 Inhaltsverzeichnis 1 Einleitung 1 2 Definitionen und Resultate aus der Topologie 1 3 Der Darstellungssatz
12 Biholomorphe Abbildungen
 12 Biholomorphe Abbildungen 2 Funktionenräume Wir erinnern zunächst an den Weierstraßschen Konvergenzsatz : 2.1 Satz. Sei G C ein Gebiet, (f n ) eine Folge holomorpher Funktionen auf G, die auf G kompakt
12 Biholomorphe Abbildungen 2 Funktionenräume Wir erinnern zunächst an den Weierstraßschen Konvergenzsatz : 2.1 Satz. Sei G C ein Gebiet, (f n ) eine Folge holomorpher Funktionen auf G, die auf G kompakt
