Normalprojektion. Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion.
|
|
|
- Hans Berger
- vor 6 Jahren
- Abrufe
Transkript
1 4. Der dreidimensionale Raum 4.5 Hauptrisse Normalprojektion Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion. Zum Beispiel: Der Normalriss einer Kugel ist ein Kreis. Durch ein räumliches kartesisches Koordinatensystem sind drei wichtige Normalprojektionen bestimmt. Sie liefern die drei Hauptrisse: Abbildung Sehstrahl Bildebene Bezeichnung Grundrissprojektion s 1 entgegen z-pfeil π 1 P Aufrissprojektion s 2 entgegen x-pfeil π 2 P Kreuzrissprojektion s 3 entgegen y-pfeil π 3 P Der Parallelriss einer Kugel ist eine Ellipse (Sehstrahl s nicht normal zur Bildebene). Hinweis: In der ÖNORM existiert auch der Kreuzriss von links ; dabei verläuft der Sehstrahl s 3 in Richtung von y. Die ÖNORM ist ein offizielles Dokument, welches u. a. das Aussehen von technischen Zeichnungen festlegt. Ordner Der Grundriss P (x y 0) (Ansicht von oben) liegt in der Grundrissebene π 1. Der Aufriss P (0 y z) (Ansicht von vorne) liegt in der Aufrissebene π 2. Der Kreuzriss P (x 0 z) (Ansicht von rechts) liegt in der Kreuzrissebene π 3. Aus einem Hauptriss kann man nur zwei der drei Raumkoordinaten ablesen. Wir benötigen daher zur Festlegung eines Objekts mindestens zwei Hauptrisse (z. B. Grund- und Aufriss). Es kommt dann jeweils eine Koordinate doppelt vor. Wir legen daher geschickterweise unsere Risse so in die Zeichenebene, dass die gemeinsamen Koordinatenachsen parallel liegen. Dann liegen z. B. Grund- und Aufriss eines Punktes auf einem Ordner. 18
2 4. Der dreidimensionale Raum Hauptrisse zeichnen A4.4: Zeichne auf dem Arbeitsblatt Ü51 die Hauptrisse eines Tschupikwürfels (siehe Fußnote S. 20) ein. a) Konstruiere auf dem Arbeitsblatt die Projektion des Objekts auf die Bildebenen π 1, π 2 und π 3. b) Übertrage die Raumsituation in Grund-, Auf- und Kreuzriss. c) Bemale das Objekt in allen Rissen so, dass Flächen in parallelen Ebenen in derselben Farbe erscheinen. 1) Wir beschriften die Eckpunkte des Objekts und erkennen, dass im Grundriss (Ansicht von oben) das Rechteck 9, 10, 11, 12 und das Quadrat 5, 6, 7, 8 sichtbar sind. Wir zeichnen daher in der Bildebene π 1 das Rechteck 9, 10, 11, 12 und das Quadrat 5, 6, 7, 8 ein. 2) Die Kante 3, 4 liegt unterhalb des Rechtecks 9, 10, 11, 12. Bei der Grundrissprojektion verdeckt daher das Rechteck diese Kante. Wir zeichnen die Kante 3, 4 strichliert ein. Alle weiteren Kanten des Tschupikwürfels werden von sichtbaren Kanten verdeckt und brauchen daher nicht eingetragen werden. Tipp: Im Internet gibt es einen Bastelbogen und ein virtuelles Modell dieses Tschupikwürfels ( Verwende diese begleitend zur Aufgabe A4.4. Im Aufriss sind nur das Quadrat 1, 2, 6, 5 und das Polygon 3,10, 9, 8, 7 sichtbar. 3) Die Projektionen des Tschupikwürfels in die Bildebenen π 2 und π 3 (Auf- und Kreuzrissprojektion) können wir auf die gleiche Art und Weise erstellen. 4) Bisher zeigt unsere Zeichnung nur die Entstehung der drei Hauptrisse. Wir sehen Grund-, Auf- und Kreuzriss in unserer räumlichen Skizze verzerrt. Daher übertragen wir die Figuren in die auf dem Arbeitsblatt vorbereiteten Hauptrisse. Die Kante 5, 8 liegt tiefer als das Rechteck 9, 10, 11, 12. Im Grundriss kann man dies durch eine Aussparung 1) kennzeichnen. Im Kreuzriss sind nur das Quadrat 2, 3, 7, 6 und das Rechteck 3, 4, 11, 10 sichtbar. 1) Hinweis: In der Geometrie kennzeichnet man das Dahinterliegen oft durch Unterbrechen einer Linie. g liegt hinter h 19
3 4. Der dreidimensionale Raum Hauptrisse Ü51b: Hauptrisse in geordneter Lage a) Konstruiere in der Modellfigur die Projektion des Objekts auf die Bildebenen π 1, π 2 und π 3. b) Übertrage die Raumsituation in Grund-, Auf- und Kreuzriss. c) Bemale das Objekt in allen Rissen so, dass Flächen in parallelen Ebenen in derselben Farbe erscheinen. Zusatzaufgabe: Versuche auch den Kreuzriss von links einzutragen. 69
4 4. Der dreidimensionale Raum Sichtbarkeitsbestimmungen Ü68: Schachfigur in zwei Ansichten Führe den Läufer eines Designschachs in der jeweils richtigen Sichtbarkeit aus und bemale dazu Flächen in parallelen Ebenen in derselben Farbe. Ü69: Mulde in vier verschiedenen Ansichten Stelle die Schuttmulde in der jeweils richtigen Sichtbarkeit dar und bemale dazu Flächen in parallelen Ebenen in derselben Farbe. 82
5 7. Perspektive Zeichnen in der Perspektive Ü125: Schachbrettmuster durch Halbieren Gegeben ist der Zentralriss eines Quadrates. Zerteile in der Perspektive das Quadrat in 8 8 Teilquadrate und färbe das Ergebnis wie ein Schachbrett. Ü126: Einlagefächer eines Kastens Gegeben ist der Zentralriss eines quaderförmigen Kastens. Konstruiere 16 gleich große Kastenfächer, wie sie auf dem Foto zu sehen sind. 111
Normalprojektion. Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion.
 4. Der dreidimensionale Raum 4.5 Hauptrisse Normalprojektion Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion. Zum Beispiel:
4. Der dreidimensionale Raum 4.5 Hauptrisse Normalprojektion Verlaufen die Projektionsstrahlen s einer Parallelprojektion normal zur Bildebene π, so spricht man von einer Normalprojektion. Zum Beispiel:
Projektionen:
 Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
Projektionen: Die darstellende Geometrie beschäftigt sich damit, räumliche Objekte in die Ebene abzubilden. Dies geschieht mit Hilfe von Projektionen. Eine Projektion, die uns die Natur vormacht, und die
Raumecke mit Modellen
 Raumecke mit Modellen Reinhold Felzmann Manfred Blümel Raumecke mit Modellen Reinhold Felzmann Manfred Blümel 1. Lehrplanbezug und Ziele Die Arbeit mit der Raumecke und den Körpermodellen kann einen effizienten
Raumecke mit Modellen Reinhold Felzmann Manfred Blümel Raumecke mit Modellen Reinhold Felzmann Manfred Blümel 1. Lehrplanbezug und Ziele Die Arbeit mit der Raumecke und den Körpermodellen kann einen effizienten
Technische Darstellung
 Fakultät Maschinenwesen Institut für Festkörpermechanik Professur für Getriebelehre Prof. Dr. rer. nat. habil. Dr. h. c. Karl-Heinz Modler Bearbeiter: Dr.-Ing. Kerstin Becker Telefon: +49 351 463-32732
Fakultät Maschinenwesen Institut für Festkörpermechanik Professur für Getriebelehre Prof. Dr. rer. nat. habil. Dr. h. c. Karl-Heinz Modler Bearbeiter: Dr.-Ing. Kerstin Becker Telefon: +49 351 463-32732
Geometrische Grundlagen der Architekturdarstellung
 Geometrische Grundlagen der Architekturdarstellung Bearbeitet von Cornelie Leopold 5., überarbeitete und erweiterte Auflage 2015. Buch. x, 298 S. Kartoniert ISBN 978 3 658 07845 4 Format (B x L): 16,7
Geometrische Grundlagen der Architekturdarstellung Bearbeitet von Cornelie Leopold 5., überarbeitete und erweiterte Auflage 2015. Buch. x, 298 S. Kartoniert ISBN 978 3 658 07845 4 Format (B x L): 16,7
Projektion. FG Borrego - TU Berlin Architekturdarstellung und Gestaltung Collaborative Design Laboratory
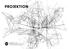 Projektion Unterscheidung nach Lage des Projektionszentrums im Unendlichen im Endlichen Parallelprojektion Zentralprojektion Projektionszentrum Z R R Q Q R P R Z' P Q Q Bildebene P Bildebene P Parallelität
Projektion Unterscheidung nach Lage des Projektionszentrums im Unendlichen im Endlichen Parallelprojektion Zentralprojektion Projektionszentrum Z R R Q Q R P R Z' P Q Q Bildebene P Bildebene P Parallelität
Darstellende Geometrie
 Darstellende Geometrie für Architekten und Bauingenieure Skript und Präsenzübungen WS 2010/11 Institut Computational Mathematics Technische Universität Braunschweig Inhaltsverzeichnis 1 Projektionsarten
Darstellende Geometrie für Architekten und Bauingenieure Skript und Präsenzübungen WS 2010/11 Institut Computational Mathematics Technische Universität Braunschweig Inhaltsverzeichnis 1 Projektionsarten
Kanten ergänzen. Lisa hat Schrägrisse von Pyramiden gezeichnet. Dabei sind ihr Fehler passiert. Ergänze die fehlenden Kanten. Möglicher Lösungsweg
 Kanten ergänzen Lisa hat Schrägrisse von Pyramiden gezeichnet. Dabei sind ihr Fehler passiert. Ergänze die fehlenden Kanten. Möglicher Lösungsweg Einrichtungshaus 1. Hier siehst du zwei Bilder eines Einrichtungshauses:
Kanten ergänzen Lisa hat Schrägrisse von Pyramiden gezeichnet. Dabei sind ihr Fehler passiert. Ergänze die fehlenden Kanten. Möglicher Lösungsweg Einrichtungshaus 1. Hier siehst du zwei Bilder eines Einrichtungshauses:
Parallelprojektion. Das Projektionszentrum liegt im Unendlichen. Projektionsebene. Projektionsrichtung. Quader. Bild des Quaders
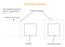 Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
Parallelprojektion Das Projektionszentrum liegt im Unendlichen. Projektionsebene Projektionsrichtung Quader Bild des Quaders Zentralprojektion Auge und Kamera Sowohl das Sehen mit dem Auge als auch das
Darstellende Geometrie
 Darstellende Geometrie Bei der Darstellenden Geometrie geht es darum, einen räumlichen Gegenstand in einer zweidimensionalen Ebene darzustellen. Dabei wendet man hauptsächlich Projektionen an. Projektionen
Darstellende Geometrie Bei der Darstellenden Geometrie geht es darum, einen räumlichen Gegenstand in einer zweidimensionalen Ebene darzustellen. Dabei wendet man hauptsächlich Projektionen an. Projektionen
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 2. September 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 9.00 Uhr 10.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
Prüfungsfach: Darstellende Geometrie Termin: 2. September 2015 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 9.00 Uhr 10.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir
SRP DG am BG und BRG Wieselburg 2015/16, Seite 1 von 14, Name: Schriftliche Reifeprüfung Darstellende Geometrie
 SRP DG am BG und BRG Wieselburg 2015/16, Seite 1 von 14, Name: Allgemeines Schriftliche Reifeprüfung Darstellende Geometrie BG und BRG Wieselburg, Haupttermin 2015/16 Klasse 8BD Realgymnasium mit Darstellender
SRP DG am BG und BRG Wieselburg 2015/16, Seite 1 von 14, Name: Allgemeines Schriftliche Reifeprüfung Darstellende Geometrie BG und BRG Wieselburg, Haupttermin 2015/16 Klasse 8BD Realgymnasium mit Darstellender
Geometrie 1. 1.)Geometrische Grundkonstruktionen. Halbierung einer Strecke, Mittelsenkrechte. Teilung einer Strecke. Winkelhalbierung.
 Geometrie 1 1.)Geometrische Grundkonstruktionen Halbierung einer Strecke, Mittelsenkrechte Teilung einer Strecke Winkelhalbierung Thaleskreis Konstruktion von Dreiecken Kongruenzsätze: SSS-Satz, SWS-Satz,
Geometrie 1 1.)Geometrische Grundkonstruktionen Halbierung einer Strecke, Mittelsenkrechte Teilung einer Strecke Winkelhalbierung Thaleskreis Konstruktion von Dreiecken Kongruenzsätze: SSS-Satz, SWS-Satz,
Wo viel Licht ist, ist starker Schatten.
 Wo viel Licht ist, ist starker Schatten. (Goethe; Götz von Berlichingen) Perspektive & Schatten Die senkrechte Parallelprojektion (Normalperspektive) Aufriss (Vorderansicht Blick von vorne) Seitenriss
Wo viel Licht ist, ist starker Schatten. (Goethe; Götz von Berlichingen) Perspektive & Schatten Die senkrechte Parallelprojektion (Normalperspektive) Aufriss (Vorderansicht Blick von vorne) Seitenriss
Figur in der Bildfläche bzw. Bildebene
 2 ABBILDUNGSMETHODEN 2.1 Projektionsarten Um dreidimensionale Objekte wie Gebäude, Stadträume oder Bauteile darzustellen, werden diese auf eine Bildfläche bzw. eine Bildebene abgebildet. Der hierbei verwendete
2 ABBILDUNGSMETHODEN 2.1 Projektionsarten Um dreidimensionale Objekte wie Gebäude, Stadträume oder Bauteile darzustellen, werden diese auf eine Bildfläche bzw. eine Bildebene abgebildet. Der hierbei verwendete
KOP1_1_28. Lüftungsschacht
 Titel Relevante(r) Deskriptor(en) Lehrstoff Ausbildungsinhalte Methodisch/Didaktische Hinweise Hilfsmittel Quelle weitere Beispiele Lüftungsschacht Die Schülerinnen und Schüler können normgerechte Zeichnungen
Titel Relevante(r) Deskriptor(en) Lehrstoff Ausbildungsinhalte Methodisch/Didaktische Hinweise Hilfsmittel Quelle weitere Beispiele Lüftungsschacht Die Schülerinnen und Schüler können normgerechte Zeichnungen
Grundsätzliche Konstruktionshilfen:
 Grundsätzliche Konstruktionshilfen: Konstruktion des Netzes Seite 1 Wahre Größe von Flächen und Geraden Seite 1 Drehen in Hauptlage Seite 2 Wahre Größe durch weiteren Riss Seite 4 Sichtbarkeit Seite 5
Grundsätzliche Konstruktionshilfen: Konstruktion des Netzes Seite 1 Wahre Größe von Flächen und Geraden Seite 1 Drehen in Hauptlage Seite 2 Wahre Größe durch weiteren Riss Seite 4 Sichtbarkeit Seite 5
Kompetenzmodell. Geometrisches Zeichnen. Arbeitsblätter
 Kompetenzmodell Geometrisches Zeichnen Arbeitsblätter 4.10.2012 Inhaltsdimension Arbeitsblätter Risse Lesen und Skizzieren Bausteine Länge von Strecken Flächenmodelle Bedienung eines CAD-Programms 3D-CAD-Software:
Kompetenzmodell Geometrisches Zeichnen Arbeitsblätter 4.10.2012 Inhaltsdimension Arbeitsblätter Risse Lesen und Skizzieren Bausteine Länge von Strecken Flächenmodelle Bedienung eines CAD-Programms 3D-CAD-Software:
Quader und Würfel. 1. Kreuze jene Wörter oder Bilder an, die Körper bezeichnen. Mathematische Bildung von der Schulstufe
 Geometrische Körper Diagnoseblatt 5. Schulstufe Quader und Würfel 1. Kreuze jene Wörter oder Bilder an, die Körper bezeichnen Kreis Schuhschachtel Eistüte Fahrkarte Kugel Seite 1 2. Kannst du Quader und
Geometrische Körper Diagnoseblatt 5. Schulstufe Quader und Würfel 1. Kreuze jene Wörter oder Bilder an, die Körper bezeichnen Kreis Schuhschachtel Eistüte Fahrkarte Kugel Seite 1 2. Kannst du Quader und
Zeichnung: Malte Kittelmann AXONOMETRIE
 Zeichnung: Malte Kittelmann 3 AXONOMETRIE Die leichte Überlappung der axonometrischen Grundrisse in der nebenstehenden Abbildung des Reichstagsgebäudes erleichtert das Erkennen, was oben und was unten
Zeichnung: Malte Kittelmann 3 AXONOMETRIE Die leichte Überlappung der axonometrischen Grundrisse in der nebenstehenden Abbildung des Reichstagsgebäudes erleichtert das Erkennen, was oben und was unten
8.Perspektive (oder Zentralprojektion)
 8.Perspektive (oder Zentralprojektion) In unseren bisherigen Vorlesungen haben wir uns einfachheitshalber mit Parallelprojektionen beschäftigt. Das menschliche Sehen (damit meinen wir immer das Sehen mit
8.Perspektive (oder Zentralprojektion) In unseren bisherigen Vorlesungen haben wir uns einfachheitshalber mit Parallelprojektionen beschäftigt. Das menschliche Sehen (damit meinen wir immer das Sehen mit
Perspektive Vertiefung
 Perspektive Vertiefung Hans-Peter Schröcker Arbeitsbereich Geometrie und CAD, Universität Innsbruck Wintersemester 2007/08 Teil I Einleitung Organisatorisches Perspektive Vertiefung Seminar, 2 Std. Donnerstag,
Perspektive Vertiefung Hans-Peter Schröcker Arbeitsbereich Geometrie und CAD, Universität Innsbruck Wintersemester 2007/08 Teil I Einleitung Organisatorisches Perspektive Vertiefung Seminar, 2 Std. Donnerstag,
9"+#5(00(),(& 7(8.(5+%(
 !"#$%"&'%()*"+, 9"+#5(00(),(& 7(8.(5+%( -%)&'(*+.%/(0&12+&,"#&34(%5"1(06(+1"*+() Inhaltsverzeichnis Vorwort...5 1. Darstellung im Zweitafelverfahren...7 2. Darstellung des Punktes...9 3. Darstellung der
!"#$%"&'%()*"+, 9"+#5(00(),(& 7(8.(5+%( -%)&'(*+.%/(0&12+&,"#&34(%5"1(06(+1"*+() Inhaltsverzeichnis Vorwort...5 1. Darstellung im Zweitafelverfahren...7 2. Darstellung des Punktes...9 3. Darstellung der
Praktikum Schau Geometrie
 Praktikum Schau Geometrie Intuition, Erklärung, Konstruktion Teil 1 Sehen auf intuitive Weise Teil 2 Formale Perspektive mit Aufriss und Grundriss Teil 3 Ein niederländischer Maler zeigt ein unmögliches
Praktikum Schau Geometrie Intuition, Erklärung, Konstruktion Teil 1 Sehen auf intuitive Weise Teil 2 Formale Perspektive mit Aufriss und Grundriss Teil 3 Ein niederländischer Maler zeigt ein unmögliches
1) ie Linien der abgebildeten Bauteile entsprechen den Linienarten nach DIN EN ISO
 1) ie Linien der abgebildeten Bauteile entsprechen den Linienarten nach DIN EN ISO 128-24. Ordnen Sie den gekennzeichneten Linien die korrekten Linienarten zu! A B C D F G J K Verwenden Sie dazu die in
1) ie Linien der abgebildeten Bauteile entsprechen den Linienarten nach DIN EN ISO 128-24. Ordnen Sie den gekennzeichneten Linien die korrekten Linienarten zu! A B C D F G J K Verwenden Sie dazu die in
1 Kartesische Normalkoordinatensysteme 5
 Inhaltsverzeichnis 1 Kartesische Normalkoordinatensysteme 5 2 SchrÄagrisse 7 3 Zugeordnete Normalrisse 13 3.1 Hauptrisse....................................... 13 3.2 Grundriss eines Punktes...............................
Inhaltsverzeichnis 1 Kartesische Normalkoordinatensysteme 5 2 SchrÄagrisse 7 3 Zugeordnete Normalrisse 13 3.1 Hauptrisse....................................... 13 3.2 Grundriss eines Punktes...............................
Geometrische Grundlagen der. Architekturdarstellung
 Cornelie Leopold Geometrische Grundlagen der. Architekturdarstellung 4. Auflage Mit 469 Abbildungen unter Mitwirkung von Andreas Matievits STUDIUM 11 VIEWEG+ TEUBNER INHALTSVERZEICHNIS Vorwort 1 EINFÜHRUNG
Cornelie Leopold Geometrische Grundlagen der. Architekturdarstellung 4. Auflage Mit 469 Abbildungen unter Mitwirkung von Andreas Matievits STUDIUM 11 VIEWEG+ TEUBNER INHALTSVERZEICHNIS Vorwort 1 EINFÜHRUNG
Axonometrie. 11 Axonometrien. Grundrissaxonometrie x : y : z = 1 : 1 : 1
 11 n Grundrissaonometrie : : = 1 : 1 : 1 Übersicht "... sstematisch abgewandelt, wird eine Einelfrage in Form möglichst vieler Variationen vorgetragen. Der Betrachter sieht sich in die Position eines Voeurs
11 n Grundrissaonometrie : : = 1 : 1 : 1 Übersicht "... sstematisch abgewandelt, wird eine Einelfrage in Form möglichst vieler Variationen vorgetragen. Der Betrachter sieht sich in die Position eines Voeurs
2.3.1 Rechtshändiges und linkshändiges Koordinatensystem
 2.3. Rechtshändiges und linkshändiges Koordinatensstem Die Koordinatenachsen im dreidimensionalen Raum lassen sich auf wei verschieden Arten anordnen: Linkshändig und Rechtshändig (s. Abbildung 2.9). Um
2.3. Rechtshändiges und linkshändiges Koordinatensstem Die Koordinatenachsen im dreidimensionalen Raum lassen sich auf wei verschieden Arten anordnen: Linkshändig und Rechtshändig (s. Abbildung 2.9). Um
iek Institut für Entwerfen und Konstruieren
 Darstellende Geometrie Institut für Entwerfen und Konstruieren Prof. José Luis Moro Matthias Rottner Heiko Stachel 1 Modul Grundlagen der Darstellung und Konstruktion Termine Grundlagen der Darstellung
Darstellende Geometrie Institut für Entwerfen und Konstruieren Prof. José Luis Moro Matthias Rottner Heiko Stachel 1 Modul Grundlagen der Darstellung und Konstruktion Termine Grundlagen der Darstellung
Geometrische Grundlagen der Architekturdarstellung
 Geometrische Grundlagen der Architekturdarstellung von Cornelie Leopold 1. Auflage Springer Vieweg Wiesbaden 2012 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 8348 1838 6 schnell und portofrei
Geometrische Grundlagen der Architekturdarstellung von Cornelie Leopold 1. Auflage Springer Vieweg Wiesbaden 2012 Verlag C.H. Beck im Internet: www.beck.de ISBN 978 3 8348 1838 6 schnell und portofrei
Externistenprüfungen aus Darstellender Geometrie
 Externistenprüfungen aus Darstellender Geometrie Zulassungsprüfung 7.Klasse Zulassungsprüfung 8. Klasse Wahlpflichtfach Reifeprüfung Juni 2008 Seite 1 von 5 Zulassungsprüfung 7. Klasse Die Prüfung teilt
Externistenprüfungen aus Darstellender Geometrie Zulassungsprüfung 7.Klasse Zulassungsprüfung 8. Klasse Wahlpflichtfach Reifeprüfung Juni 2008 Seite 1 von 5 Zulassungsprüfung 7. Klasse Die Prüfung teilt
Legt man die vom Betrachter aus gesehen vor den, wird die spätere Konstruktion kleiner als die Risse. Legt man die hinter das Objekt, wird die perspek
 Gegeben ist ein und ein. Der wird auf eine gezeichnet, der unterhalb von dieser in einiger Entfernung und mittig. Parallel zur wird der eingezeichnet. Dieser befindet sich in Augenhöhe. Üblicherweise wird
Gegeben ist ein und ein. Der wird auf eine gezeichnet, der unterhalb von dieser in einiger Entfernung und mittig. Parallel zur wird der eingezeichnet. Dieser befindet sich in Augenhöhe. Üblicherweise wird
Darstellung dreidimensionaler Figuren in der Ebene. Schrägbild
 Mathematik Bl Darstellung dreidimensionaler Figuren in der Ebene Schrägbild Das Bild bei einer schrägen Parallelprojektion heisst Schrägbild und wird durch folgende Merkmale bestimmt: - Zur Zeichenebene
Mathematik Bl Darstellung dreidimensionaler Figuren in der Ebene Schrägbild Das Bild bei einer schrägen Parallelprojektion heisst Schrägbild und wird durch folgende Merkmale bestimmt: - Zur Zeichenebene
Darstellende Geometrie (DG) Schule: HTBLuVA St. Pölten Abteilung: Elektronik Lehrperson: Dipl.-Ing. Wolfgang Lenz Jahrgang: 2002 / 03 Klasse: 1AT
 Darstellende Geometrie (DG) Schule: HTBLuVA St. Pölten Abteilung: Elektronik Lehrperson: Dipl.-Ing. Wolfgang Lenz Jahrgang: 2002 / 03 Klasse: 1AT 1 Anmerkung Prof. Lenz ist bereits pensioniert. Im Unterricht
Darstellende Geometrie (DG) Schule: HTBLuVA St. Pölten Abteilung: Elektronik Lehrperson: Dipl.-Ing. Wolfgang Lenz Jahrgang: 2002 / 03 Klasse: 1AT 1 Anmerkung Prof. Lenz ist bereits pensioniert. Im Unterricht
Hans Walser. Raumgeometrie. Modul 4 Die Ebene
 Hans Walser Raumgeometrie Modul 4 Die Ebene Hans Walser: Modul 4, Die Ebene ii Modul 4 für die Lehrveranstaltung Raumgeometrie Sommer 2000 Erstausgabe Sommer 2002 Überarbeitung Sommer 2003 Fehlerkorrekturen,
Hans Walser Raumgeometrie Modul 4 Die Ebene Hans Walser: Modul 4, Die Ebene ii Modul 4 für die Lehrveranstaltung Raumgeometrie Sommer 2000 Erstausgabe Sommer 2002 Überarbeitung Sommer 2003 Fehlerkorrekturen,
Computational Geometry, MU Leoben
 Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Kapitel 4: Zeichnerische Darstellung von Körpern. Darstellung von Körpern in der Ebene. Ziel bei der Darstellung von räumlichen Figuren (Körpern):
 Kapitel 4: Zeichnerische Darstellung von Körpern Darstellung von Körpern in der Ebene. Quelle im Wesentlichen: Krauter, Elementargeometrie S.1-17 Ziel bei der Darstellung von räumlichen Figuren (Körpern):
Kapitel 4: Zeichnerische Darstellung von Körpern Darstellung von Körpern in der Ebene. Quelle im Wesentlichen: Krauter, Elementargeometrie S.1-17 Ziel bei der Darstellung von räumlichen Figuren (Körpern):
Körper erkennen und beschreiben
 Vertiefen 1 Körper erkennen und beschreiben zu Aufgabe 6 Schulbuch, Seite 47 6 Passt, passt nicht Nenne zu jeder Aussage alle Formen, auf die die Aussage zutrifft. a) Die Form hat keine Ecken. b) Die Form
Vertiefen 1 Körper erkennen und beschreiben zu Aufgabe 6 Schulbuch, Seite 47 6 Passt, passt nicht Nenne zu jeder Aussage alle Formen, auf die die Aussage zutrifft. a) Die Form hat keine Ecken. b) Die Form
Die Übereckperspektive mit zwei Fluchtpunkten
 Perspektive Perspektive mit zwei Fluchtpunkten (S. 1 von 8) / www.kunstbrowser.de Die Übereckperspektive mit zwei Fluchtpunkten Bei dieser Perspektivart wird der rechtwinklige Körper so auf die Grundebene
Perspektive Perspektive mit zwei Fluchtpunkten (S. 1 von 8) / www.kunstbrowser.de Die Übereckperspektive mit zwei Fluchtpunkten Bei dieser Perspektivart wird der rechtwinklige Körper so auf die Grundebene
Was kann ich? 1 Geometrie. Vierecke (Teil 1)
 Was kann ich? 1 Geometrie. Vierecke (Teil 1) 1 Markiere Strecken rot und Geraden blau. 2 Welche Strecken und Geraden sind senkrecht zueinander, welche parallel? Schreibe mit den Zeichen und. 3 Zeichne
Was kann ich? 1 Geometrie. Vierecke (Teil 1) 1 Markiere Strecken rot und Geraden blau. 2 Welche Strecken und Geraden sind senkrecht zueinander, welche parallel? Schreibe mit den Zeichen und. 3 Zeichne
Jahresplanung Vorschlag 1
 Jahresplanungen zum Lehrplan der AHS-Oberstufe Darstellende Geometrie Jahresplanung Vorschlag 1 7. Klasse Zeitraum Inhalte Hinweise zur Umsetzung 4 Stunden 1. Einführung allgemeine Grundbegriffe Projektionen
Jahresplanungen zum Lehrplan der AHS-Oberstufe Darstellende Geometrie Jahresplanung Vorschlag 1 7. Klasse Zeitraum Inhalte Hinweise zur Umsetzung 4 Stunden 1. Einführung allgemeine Grundbegriffe Projektionen
Darstellende Geometrie Themenbereiche für die mündliche Reifeprüfung
 Darstellende Geometrie, Themenbereiche RP, Seite 1 von 5 Darstellende Geometrie Themenbereiche für die mündliche Reifeprüfung 1. Flächen und Körper, die durch Bewegung erzeugt werden Extrusionskörper und
Darstellende Geometrie, Themenbereiche RP, Seite 1 von 5 Darstellende Geometrie Themenbereiche für die mündliche Reifeprüfung 1. Flächen und Körper, die durch Bewegung erzeugt werden Extrusionskörper und
Mitschriebe, Skripten, Bücher, einfacher Taschenrechner
 Prüfungsfach: Darstellende Geometrie Termin: 20. März 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
Prüfungsfach: Darstellende Geometrie Termin: 20. März 2014 Prüfungsbeginn: Prüfungsende: zugel. Hilfsmittel: Hinweis: 13.00 Uhr 14.00 Uhr Mitschriebe, Skripten, Bücher, einfacher Taschenrechner Wir bitten
DARSTELLENDE GEOMETRIE I
 DARSTELLENDE GEOMETRIE I VON DR. RUDOLF BEREIS Professor und Direktor des Instituts für Geometrie an der Technischen Universität Dresden Mit 361 Abbildungen AKADEMIE-VERLAG BERLIN 1964 h. INHALT Hinweise
DARSTELLENDE GEOMETRIE I VON DR. RUDOLF BEREIS Professor und Direktor des Instituts für Geometrie an der Technischen Universität Dresden Mit 361 Abbildungen AKADEMIE-VERLAG BERLIN 1964 h. INHALT Hinweise
Riss lesen mit Solid Edge
 Riss lesen mit Solid Edge Konstruktion eines Würfels mit Ausschnitt Wähle die Datei Tschupik2a.dft In Solid Edge Zeichnung (Draft) ist es möglich aus den gegebenen Hauptrissen den Schrägriss abzuleiten.
Riss lesen mit Solid Edge Konstruktion eines Würfels mit Ausschnitt Wähle die Datei Tschupik2a.dft In Solid Edge Zeichnung (Draft) ist es möglich aus den gegebenen Hauptrissen den Schrägriss abzuleiten.
14 MATHEMATISCHE GRUNDLAGEN DER COMPUTERGEOMETRIE. x y
 4 MATHEMATISCHE GRUNDLAGEN DER COMPUTERGEOMETRIE 4 Projektionen 4. Parallelprojektion (a) Senkrechte Projektion auf eine Koordinatenebene Wir wählen als Projektionsebene die Ebene, d. h. in den Beeichnungen
4 MATHEMATISCHE GRUNDLAGEN DER COMPUTERGEOMETRIE 4 Projektionen 4. Parallelprojektion (a) Senkrechte Projektion auf eine Koordinatenebene Wir wählen als Projektionsebene die Ebene, d. h. in den Beeichnungen
Einerseits: Zentralperspektive
 VOM RAUM IN DIE EBENE UND ZURÜCK Ebene Figuren wie Dreiecke, Vierecke, andere Vielecke, Kreise lassen sich auf einem Zeichenblatt entweder in wahrer Größe oder unter Beibehaltung ihrer Form! maßstäblich
VOM RAUM IN DIE EBENE UND ZURÜCK Ebene Figuren wie Dreiecke, Vierecke, andere Vielecke, Kreise lassen sich auf einem Zeichenblatt entweder in wahrer Größe oder unter Beibehaltung ihrer Form! maßstäblich
2 log. Aufgabe 1) a) Fassen Sie zu einem Logarithmus zusammen. (ohne Taschenrechner; Lösungsweg sichtbar) 0.5P
 Aufgabe 1) a) Fassen Sie zu einem Logarithmus zusammen. (ohne Taschenrechner; Lösungsweg sichtbar) 2 log 7 a 5 log 7 b b) Zerlegen Sie den Logarithmus in maximal viele Summanden. (ohne Taschenrechner;
Aufgabe 1) a) Fassen Sie zu einem Logarithmus zusammen. (ohne Taschenrechner; Lösungsweg sichtbar) 2 log 7 a 5 log 7 b b) Zerlegen Sie den Logarithmus in maximal viele Summanden. (ohne Taschenrechner;
Darstellende Geometrie Übungen. Tutorial. Übungsblatt: Perspektive Rekonstruktion - FSI
 Darstellende Geometrie Übungen Institut für 0Irchitektur und IIIedien Tutorial Übungsblatt: Perspektive Rekonstruktion - FSI Gegeben sind ein Foto ( mit lotrechter Bildebene ) von einem quaderförmigen
Darstellende Geometrie Übungen Institut für 0Irchitektur und IIIedien Tutorial Übungsblatt: Perspektive Rekonstruktion - FSI Gegeben sind ein Foto ( mit lotrechter Bildebene ) von einem quaderförmigen
Geometrie. in 15 Minuten. Geometrie. Klasse
 Klasse Geometrie Geometrie 6. Klasse in 5 Minuten Winkel und Kreis Zeichne und überprüfe in deinem Übungsheft: a) Wo liegen alle Punkte, die von einem Punkt A den Abstand cm haben? b) Färbe den Bereich,
Klasse Geometrie Geometrie 6. Klasse in 5 Minuten Winkel und Kreis Zeichne und überprüfe in deinem Übungsheft: a) Wo liegen alle Punkte, die von einem Punkt A den Abstand cm haben? b) Färbe den Bereich,
1. Das Koordinatensystem
 Liebe Schülerin! Lieber Schüler! In den folgenden Unterrichtseinheiten wirst du die Unterrichtssoftware GeoGebra kennen lernen. Mit ihrer Hilfe kannst du verschiedenste mathematische Objekte zeichnen und
Liebe Schülerin! Lieber Schüler! In den folgenden Unterrichtseinheiten wirst du die Unterrichtssoftware GeoGebra kennen lernen. Mit ihrer Hilfe kannst du verschiedenste mathematische Objekte zeichnen und
6.4.3 Frontalperspektive
 102 KAPITEL 6. ZENTRALPRJEKTIN 6.4.3 Frontalperspektive Wir wollen den Grundriss des in Abb. 6.26 in Frontalperspektive dargestellten U-förmigen Gebäudes bestimmen. Dabei nehmen wir wieder an, dass das
102 KAPITEL 6. ZENTRALPRJEKTIN 6.4.3 Frontalperspektive Wir wollen den Grundriss des in Abb. 6.26 in Frontalperspektive dargestellten U-förmigen Gebäudes bestimmen. Dabei nehmen wir wieder an, dass das
Philipp-Melanchthon-Gymnasium Bautzen Lk Mathematik Kl. 11. Schwerpunkt: Aufgaben ohne HM Abitur Sachsen
 Übungen zur Analytischen Abitur 00 Die Punkte A( 0), B( 0) und C(5 0) sind Eckpunkte eines Rechtecks ABCD. Der Punkt S ist die Spitze einer geraden Pyramide mit dem Rechteck ABCD als Grundfläche und der
Übungen zur Analytischen Abitur 00 Die Punkte A( 0), B( 0) und C(5 0) sind Eckpunkte eines Rechtecks ABCD. Der Punkt S ist die Spitze einer geraden Pyramide mit dem Rechteck ABCD als Grundfläche und der
Konstruieren mit Word
 Konstruieren mit Word Aktiviere als erstes die Symbolleiste zum Zeichnen: Positioniere sie nach deinem Geschmack! Tipp: Hat man vor, eine oder mehrere Grafiken in ein Dokument einzufügen, so ist es ratsam,
Konstruieren mit Word Aktiviere als erstes die Symbolleiste zum Zeichnen: Positioniere sie nach deinem Geschmack! Tipp: Hat man vor, eine oder mehrere Grafiken in ein Dokument einzufügen, so ist es ratsam,
Die Zentralprojektion
 Perspektive Perspektivmodell (S. 1 von 6) / www.kunstbrowser.de Die Zentralprojektion Die Zentralprojektion eines Gegenstandes auf eine ebene Bildfläche ist das Grundprinzip, aus dem sich alle zentralperspektivischen
Perspektive Perspektivmodell (S. 1 von 6) / www.kunstbrowser.de Die Zentralprojektion Die Zentralprojektion eines Gegenstandes auf eine ebene Bildfläche ist das Grundprinzip, aus dem sich alle zentralperspektivischen
Geometrische Objekte im 3-dimensionalen affinen Raum oder,... wie nützlich ist ein zugehöriger Vektorraum der Verschiebungen
 Geometrische Objekte im -dimensionalen affinen Raum Bekanntlich versteht man unter geometrischen Objekten Punktmengen, auf die man die üblichen Mengenoperationen wie z.b.: Schnittmenge bilden: - aussagenlogisch:
Geometrische Objekte im -dimensionalen affinen Raum Bekanntlich versteht man unter geometrischen Objekten Punktmengen, auf die man die üblichen Mengenoperationen wie z.b.: Schnittmenge bilden: - aussagenlogisch:
Lineare Funktionen. Klasse 8 Aufgabenblatt für Lineare Funktionen Datum: Donnerstag,
 Lineare Funktionen Aufgabe 1: Welche der folgenden Abbildungen stellen eine Funktion dar? Welche Abbildungen stellen eine lineare Funktion dar? Ermittle für die linearen Funktionen eine Funktionsgleichung.
Lineare Funktionen Aufgabe 1: Welche der folgenden Abbildungen stellen eine Funktion dar? Welche Abbildungen stellen eine lineare Funktion dar? Ermittle für die linearen Funktionen eine Funktionsgleichung.
Gegeben ist die Funktion f durch. Ihr Schaubild sei K.
 Aufgabe I 1 Gegeben ist die Funktion f durch. Ihr Schaubild sei K. a) Geben Sie die maximale Definitionsmenge D f an. Untersuchen Sie K auf gemeinsame Punkte mit der x-achse. Bestimmen Sie die Intervalle,
Aufgabe I 1 Gegeben ist die Funktion f durch. Ihr Schaubild sei K. a) Geben Sie die maximale Definitionsmenge D f an. Untersuchen Sie K auf gemeinsame Punkte mit der x-achse. Bestimmen Sie die Intervalle,
Arbeitsunterlagen zu einem kompetenzorientierten Unterricht aus Geometrischem Zeichnen
 Arbeitsunterlagen zu einem kompetenzorientierten Unterricht aus Geometrischem Zeichnen Autor/innen -Team: Sybille Mick (Koordination) Siegfried Eibl Josef Gabl Dagmar Hochhauser Sigrid Ranger Johann Schmied
Arbeitsunterlagen zu einem kompetenzorientierten Unterricht aus Geometrischem Zeichnen Autor/innen -Team: Sybille Mick (Koordination) Siegfried Eibl Josef Gabl Dagmar Hochhauser Sigrid Ranger Johann Schmied
Computational Geometry, MU Leoben
 Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Download. Mathe an Stationen. Mathe an Stationen. Das 5x5-Geobrett in der Sekundarstufe I. Marco Bettner, Erik Dinges
 Download Marco Bettner, Erik Dinges Mathe an Stationen Das 5x5-Geobrett in der Sekundarstufe I Downloadauszug aus dem Originaltitel: Sekundarstufe I Marco Bettner Erik Dinges Mathe an Stationen Umgang
Download Marco Bettner, Erik Dinges Mathe an Stationen Das 5x5-Geobrett in der Sekundarstufe I Downloadauszug aus dem Originaltitel: Sekundarstufe I Marco Bettner Erik Dinges Mathe an Stationen Umgang
Basteln und Zeichnen
 Titel des Arbeitsblatts Seite Inhalt 1 Falte eine Hexentreppe 2 Falte eine Ziehharmonika 3 Die Schatzinsel 4 Das Quadrat und seine Winkel 5 Senkrechte und parallele Linien 6 Ein Scherenschnitt 7 Bastle
Titel des Arbeitsblatts Seite Inhalt 1 Falte eine Hexentreppe 2 Falte eine Ziehharmonika 3 Die Schatzinsel 4 Das Quadrat und seine Winkel 5 Senkrechte und parallele Linien 6 Ein Scherenschnitt 7 Bastle
Einführung GAM. Beispiel 1: Quader
 Einführung GAM GAM gliedert sich in eine Menüleiste (oben) in der man die Befehle zur Konstruktion und zur Bearbeitung der Körper findet. Rechts findet man unter anderem die Rissleiste, in der man die
Einführung GAM GAM gliedert sich in eine Menüleiste (oben) in der man die Befehle zur Konstruktion und zur Bearbeitung der Körper findet. Rechts findet man unter anderem die Rissleiste, in der man die
Name: Bearbeitungszeitraum:
 Meine Geomappe Name: Bearbeitungszeitraum: vom bis zum Aufgabe 1 Zeichne einen Kreis mit a) Radius 2 cm. b) Radius 3,5 cm. c) Radius 1,7 cm. Aufgabe 2 Zeichne einen Kreis mit einem Durchmesser von 5 cm
Meine Geomappe Name: Bearbeitungszeitraum: vom bis zum Aufgabe 1 Zeichne einen Kreis mit a) Radius 2 cm. b) Radius 3,5 cm. c) Radius 1,7 cm. Aufgabe 2 Zeichne einen Kreis mit einem Durchmesser von 5 cm
Modul: Ausgewählte Kapitel der Didaktik der Mathematik
 Modul: Ausgewählte Kapitel der Didaktik der Mathematik Raumgeometrie: Körperdarstellungen, Projektionen Pascal Becker, Alexander Simon 11. Dezember 2014 1 / 16 Inhaltsverzeichnis 1 Rahmenlehrpläne 2 Projektionen
Modul: Ausgewählte Kapitel der Didaktik der Mathematik Raumgeometrie: Körperdarstellungen, Projektionen Pascal Becker, Alexander Simon 11. Dezember 2014 1 / 16 Inhaltsverzeichnis 1 Rahmenlehrpläne 2 Projektionen
Thema Geometrie Räumliche Vorstellung
 Seite 1 1. Drei-Tafel-Projektion Eine wunderbar einfache Visualisierungsmöglichkeit der 3-Tafel-Projektion besteht im entsprechenden Falten eines DIN-A 4 Blattes. Hier besteht einerseits die Möglichkeit
Seite 1 1. Drei-Tafel-Projektion Eine wunderbar einfache Visualisierungsmöglichkeit der 3-Tafel-Projektion besteht im entsprechenden Falten eines DIN-A 4 Blattes. Hier besteht einerseits die Möglichkeit
Geometrische Anmerkungen zu den Gedankenstrichen in documenta_landschaft_kunst Hannover
 Geometrische Anmerkungen zu den Gedankenstrichen in documenta_landschaft_kunst Hannover Albert Schmid-Kirsch Die vor kurzem vorgelegte Konzeptstudie zu einer dokumenta-landschaft-kunst in Hannover durch
Geometrische Anmerkungen zu den Gedankenstrichen in documenta_landschaft_kunst Hannover Albert Schmid-Kirsch Die vor kurzem vorgelegte Konzeptstudie zu einer dokumenta-landschaft-kunst in Hannover durch
SCHRIFTLICHE ABITURPRÜFUNG 2006 Mathematik (Grundkursniveau) Arbeitszeit: 210 Minuten
 Mathematik (Grundkursniveau) Arbeitszeit: 210 Minuten Es sind die drei Pflichtaufgaben und eine Wahlpflichtaufgabe zu lösen. Der Prüfling entscheidet sich für eine Wahlpflichtaufgabe. Die zur Bewertung
Mathematik (Grundkursniveau) Arbeitszeit: 210 Minuten Es sind die drei Pflichtaufgaben und eine Wahlpflichtaufgabe zu lösen. Der Prüfling entscheidet sich für eine Wahlpflichtaufgabe. Die zur Bewertung
Lernrückblick. 1 a) Ich weiß, wie ich ein Schrägbild in der Kabinettprojektion zeichne: 2 a) Ich kann einen Körper aus folgenden Ansichten zeichnen:
 1 a) Ich weiß, wie ich ein Schrägbild in der Kabinettprojektion zeichne: b) Beispiel 2 a) Ich kann einen Körper aus folgenden Ansichten zeichnen: b) Beispiel 3 Entscheide dich. Ich fühle mich fit im Bereich
1 a) Ich weiß, wie ich ein Schrägbild in der Kabinettprojektion zeichne: b) Beispiel 2 a) Ich kann einen Körper aus folgenden Ansichten zeichnen: b) Beispiel 3 Entscheide dich. Ich fühle mich fit im Bereich
Technische Universität München Zentrum Mathematik. Übungsblatt 11
 Technische Universität München Zentrum Mathematik Mathematik Elektrotechnik Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 11 Hausaufgaben Aufgabe 11.1 Berechnen Sie jeweils die Jacobi-Matrix folgender
Technische Universität München Zentrum Mathematik Mathematik Elektrotechnik Prof. Dr. Anusch Taraz Dr. Michael Ritter Übungsblatt 11 Hausaufgaben Aufgabe 11.1 Berechnen Sie jeweils die Jacobi-Matrix folgender
Computational Geometry, MU Leoben
 Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Computational Geometry, MU Leoben www.unileoben.ac.at Computational Geometry Lehrveranstaltung: Darstellende Geometrie I, Übungen SS 2011 http://institute.unileoben.ac.at/anggeom/dg1 Übungsleiterin: S.
Inhaltsverzeichnis. geometrischer Objekte auszufüllen. Die Liste der Lösungen kann auch eine ABC Liste zu diesen Themen sein.
 Lückentexte 1 zu den Themen: I. Der Kreis als Figur in der Ebene II. Der Kreis als Figur im Raum III. Die Kugel Multiple Choice Aufgabe zum Thema IV. Ebene Schnitte einer Kugel Kreuzworträtsel zu den Themen:
Lückentexte 1 zu den Themen: I. Der Kreis als Figur in der Ebene II. Der Kreis als Figur im Raum III. Die Kugel Multiple Choice Aufgabe zum Thema IV. Ebene Schnitte einer Kugel Kreuzworträtsel zu den Themen:
Ziel bei der Darstellung von räumlichen Figuren (Körpern): Startseite
 Startseite Zentralprojektion 1 Kapitel 3: Zeichnerische Darstellung von Körpern Darstellung von Körpern in der Ebene. Quelle im Wesentlichen: Krauter, Elementargeometrie S.1-17 Ziel bei der Darstellung
Startseite Zentralprojektion 1 Kapitel 3: Zeichnerische Darstellung von Körpern Darstellung von Körpern in der Ebene. Quelle im Wesentlichen: Krauter, Elementargeometrie S.1-17 Ziel bei der Darstellung
Schuleigener Arbeitsplan Fach: Mathematik Jahrgang: 5
 Stand:.0.206 Sommerferien Zahlen und Operationen» Zahlen sachangemessen runden» große Zahlen lesen und schreiben» konkrete Repräsentanten großer Zahlen nennen» Zahlen auf der Zahlengeraden und in der Stellenwerttafel
Stand:.0.206 Sommerferien Zahlen und Operationen» Zahlen sachangemessen runden» große Zahlen lesen und schreiben» konkrete Repräsentanten großer Zahlen nennen» Zahlen auf der Zahlengeraden und in der Stellenwerttafel
(0, 3, 4) (3, 3, 4) (3, 3, 0)
 Übungsmaterial 1 2 Vektoren im Raum 2.1 Das räumliche Koordinatensystem Abbildung 1 zeigt das Koordinatensystem im R 3, dem dreidimensionalen Raum, mit eingefügtem Quader. Die Koordinaten einiger Eckpunkte
Übungsmaterial 1 2 Vektoren im Raum 2.1 Das räumliche Koordinatensystem Abbildung 1 zeigt das Koordinatensystem im R 3, dem dreidimensionalen Raum, mit eingefügtem Quader. Die Koordinaten einiger Eckpunkte
Baue mit dem Material so, dass andere dein Bauwerk nach einem Foto nachbauen können.
 Aufgabe 2.3 Idee und Aufgabenentwurf Rainer Meiers, Nicolaus-Voltz-Grundschule, Losheim am See, Klassenstufe 2 (Januar 2013) Baue mit dem Material so, dass andere dein Bauwerk nach einem Foto nachbauen
Aufgabe 2.3 Idee und Aufgabenentwurf Rainer Meiers, Nicolaus-Voltz-Grundschule, Losheim am See, Klassenstufe 2 (Januar 2013) Baue mit dem Material so, dass andere dein Bauwerk nach einem Foto nachbauen
Vorlesung Algorithmen für hochkomplexe Virtuelle Szenen
 Vorlesung Algorithmen für hochkomplexe Virtuelle Szenen Sommersemester 2012 Matthias Fischer mafi@upb.de Vorlesung 12 26.6.2012 Matthias Fischer 374 Übersicht Motivation Modell der Sichtbarkeit Eigenschaft
Vorlesung Algorithmen für hochkomplexe Virtuelle Szenen Sommersemester 2012 Matthias Fischer mafi@upb.de Vorlesung 12 26.6.2012 Matthias Fischer 374 Übersicht Motivation Modell der Sichtbarkeit Eigenschaft
Aufgabe 1 Erstelle mit Hilfe von GEOGEBRA ein dynamisches Geometrie-Programm, das die Mittelsenkrechte
 AB Mathematik Experimentieren mit GeoGebra Merke Alle folgenden Aufgaben sind mit dem Programm GEOGEBRA auszuführen! Eine ausführliche Einführung in die Bedienung des Programmes erfolgt im Unterricht.
AB Mathematik Experimentieren mit GeoGebra Merke Alle folgenden Aufgaben sind mit dem Programm GEOGEBRA auszuführen! Eine ausführliche Einführung in die Bedienung des Programmes erfolgt im Unterricht.
1 Strg. Strg. Attribute übernehmen: Aktivieren (X) Zeiger über dem Objekt) T-Taste zeigt Hilfskreis und Parallelen
 Aktivieren (X) Zeiger über dem Objekt) T-Taste zeigt Hilfskreis und Parallelen Attribute übernehmen: KLICK Objekt vorher sichtbar durch Mouse Over Zoomen Kurztastenbefehle Lupenfunktion (y) Zoom + Zoom
Aktivieren (X) Zeiger über dem Objekt) T-Taste zeigt Hilfskreis und Parallelen Attribute übernehmen: KLICK Objekt vorher sichtbar durch Mouse Over Zoomen Kurztastenbefehle Lupenfunktion (y) Zoom + Zoom
Abiturprüfung 2000 LK Mathematik Baden-Württemberg
 Abiturprüfung 000 LK Mathematik Baden-Württemberg Aufgabe I 1 Analysis ( )² Gegeben ist die Funktion f durch f ( ) = ; D f. Ihr Schaubild sei K. ( 4) a) Geben Sie die maimale Definitionsmenge D f an. Untersuchen
Abiturprüfung 000 LK Mathematik Baden-Württemberg Aufgabe I 1 Analysis ( )² Gegeben ist die Funktion f durch f ( ) = ; D f. Ihr Schaubild sei K. ( 4) a) Geben Sie die maimale Definitionsmenge D f an. Untersuchen
Schrägbilder zeichnen
 Was sind Schrägbilder und welchen Zweck haben sie? Durch ein Schrägbild wird auf einer ebenen Fläche (z.b. Blatt Papier) ein Körper räumlich dargestellt (räumliche Perspektive des Körpers). Es gibt sehr
Was sind Schrägbilder und welchen Zweck haben sie? Durch ein Schrägbild wird auf einer ebenen Fläche (z.b. Blatt Papier) ein Körper räumlich dargestellt (räumliche Perspektive des Körpers). Es gibt sehr
Probleme und Möglichkeiten zur Entwicklung des räumlichen Vorstellungsvermögens (RVV)
 Probleme und Möglichkeiten zur Entwicklung des räumlichen Vorstellungsvermögens (RVV) 1. Schülerleistungen 2. Darstellenden Geometrie und RVV im MU 3. Fachliche und begriffliche Probleme 4. Ergebnisse
Probleme und Möglichkeiten zur Entwicklung des räumlichen Vorstellungsvermögens (RVV) 1. Schülerleistungen 2. Darstellenden Geometrie und RVV im MU 3. Fachliche und begriffliche Probleme 4. Ergebnisse
Geometrie Winkel und Vierecke PRÜFUNG 02. Ohne Formelsammlung! Name: Klasse: Datum: Punkte: Note: Klassenschnitt/ Maximalnote : Ausgabe: 2.
 GEOMETRIE PRÜFUNGSVORBEREITUNG Seite 1 Geometrie Winkel und Vierecke PRÜFUNG 02 Name: Klasse: Datum: : Note: Ausgabe: 2. Mai 2011 Klassenschnitt/ Maximalnote : Selbsteinschätzung: / (freiwillig) Für alle
GEOMETRIE PRÜFUNGSVORBEREITUNG Seite 1 Geometrie Winkel und Vierecke PRÜFUNG 02 Name: Klasse: Datum: : Note: Ausgabe: 2. Mai 2011 Klassenschnitt/ Maximalnote : Selbsteinschätzung: / (freiwillig) Für alle
:= Modellabbildung. Bildsynthese (Rendering) Bildsynthese
 Geometrisches Modell bestehend aus Datenstrukturen zur Verknüpfung geometrischer Primitive, welche eine Gesamtszene beschreiben Bildsynthese := Modellabbildung Pixelbasiertes Modell zur Darstellung eines
Geometrisches Modell bestehend aus Datenstrukturen zur Verknüpfung geometrischer Primitive, welche eine Gesamtszene beschreiben Bildsynthese := Modellabbildung Pixelbasiertes Modell zur Darstellung eines
Schriftliche Reifeprüfung aus dem Wahlpflichtfach Darstellende Geometrie am BRG Feldkirchen zum Haupttermin 2015/16. Prüfer: Mag.
 Schriftliche Reifeprüfung aus dem Wahlpflichtfach Darstellende Geometrie am BRG Feldkirchen zum Haupttermin 2015/16 Prüfer: Mag. Iris Steiner Notenschlüssel: Sehr Gut: Gut: Befriedigend: Genügend: Nicht
Schriftliche Reifeprüfung aus dem Wahlpflichtfach Darstellende Geometrie am BRG Feldkirchen zum Haupttermin 2015/16 Prüfer: Mag. Iris Steiner Notenschlüssel: Sehr Gut: Gut: Befriedigend: Genügend: Nicht
KULTUSMINISTERIUM DES LANDES SACHSEN-ANHALT
 KULTUSMINISTERIUM DES LANDES SACHSEN-ANHALT Abitur 2001 Mathematik (Leistungskurs) Arbeitszeit: 00 Minuten Der Prüfling wählt nach Empfehlung durch die Lehrkraft je eine Aufgabe aus den Gebieten L 1, L
KULTUSMINISTERIUM DES LANDES SACHSEN-ANHALT Abitur 2001 Mathematik (Leistungskurs) Arbeitszeit: 00 Minuten Der Prüfling wählt nach Empfehlung durch die Lehrkraft je eine Aufgabe aus den Gebieten L 1, L
Zentralperspektive (1 FP) 2-Punkt-Fluchtpunktp. 3-Punkt-Fluchtpunktp.
 Ein Auftrag: Eine Frage der Perspektive... Isometrie Dimetrie Zentralperspektive (1 FP) 2-Punkt-Fluchtpunktp. Sphärische Perspektive curvilinear perspective Kavalliersperspektive, Kabinettperspektive (Eine
Ein Auftrag: Eine Frage der Perspektive... Isometrie Dimetrie Zentralperspektive (1 FP) 2-Punkt-Fluchtpunktp. Sphärische Perspektive curvilinear perspective Kavalliersperspektive, Kabinettperspektive (Eine
Bild 1: Gegeben ist der in der Zentralperspektive zentrale Fluchtpunkt, der Distanzpunkt und der Grundriss des zu zeichnenden Vierecks.
 Bild 1: Gegeben ist der in der Zentralperspektive zentrale, der und der Grundriss des zu zeichnenden Vierecks. Die Breite des Vierecks trägt man auf der ab und verbindet die Schnittpunkte mit dem zentralen
Bild 1: Gegeben ist der in der Zentralperspektive zentrale, der und der Grundriss des zu zeichnenden Vierecks. Die Breite des Vierecks trägt man auf der ab und verbindet die Schnittpunkte mit dem zentralen
DER EULER SCHE POLYEDERSATZ
 ngabe nwendungsbereich Querverbindungen RUMVORSTLLUNG R ULR SH POLRST in in ein Würfelraster (Hilfslinienraster im bstand von 1 inheit) eingebettetes Modell ist in einem axonometrischen Riss gegeben. ie
ngabe nwendungsbereich Querverbindungen RUMVORSTLLUNG R ULR SH POLRST in in ein Würfelraster (Hilfslinienraster im bstand von 1 inheit) eingebettetes Modell ist in einem axonometrischen Riss gegeben. ie
Die 3D-Parameter des Adjust-Fensters im Programm Apophysis 2.08 Beta 3D Hack
 Die 3D-Parameter des Adjust-Fensters im Programm Apophysis 2.08 Beta 3D Hack Perspective und Pitch Das Bild wurde mit 4 TF s, jede mit der Variation Sinusoidalxy, erstellt. Wenn Sinusoidalxy_height = 0
Die 3D-Parameter des Adjust-Fensters im Programm Apophysis 2.08 Beta 3D Hack Perspective und Pitch Das Bild wurde mit 4 TF s, jede mit der Variation Sinusoidalxy, erstellt. Wenn Sinusoidalxy_height = 0
G Z A K T U E L L. Klagenfurt 28. bis 30. September Werner Gems HTL Saalfelden PA/PH Salzburg.
 Klagenfurt 28. bis 30. September 2006 Werner Gems HTL Saalfelden PA/PH Salzburg wgems@sbg.at `kein der Geometrie Unkundiger trete unter mein Dach Platon 428 348 v.chr. GEMS, 2006 G E O M E T R I E ein
Klagenfurt 28. bis 30. September 2006 Werner Gems HTL Saalfelden PA/PH Salzburg wgems@sbg.at `kein der Geometrie Unkundiger trete unter mein Dach Platon 428 348 v.chr. GEMS, 2006 G E O M E T R I E ein
2.3 Linienarten und Linienbreiten nach DIN 15 T1
 Angebots- Zeichnung Fundament- Zeichnung Zeichnung zur Erläuterung einer Ausschreibung oder zur Abgabe eines Angebotes Enthält Angaben über die Fertigung des Fundamentes für die Aufstellung der Maschine
Angebots- Zeichnung Fundament- Zeichnung Zeichnung zur Erläuterung einer Ausschreibung oder zur Abgabe eines Angebotes Enthält Angaben über die Fertigung des Fundamentes für die Aufstellung der Maschine
Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A Bremen. Die Kursübersicht für das Fach Mathematik
 Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 28195 Bremen Die Kursübersicht für das Fach Mathematik Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe
Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe 172 A 28195 Bremen Die Kursübersicht für das Fach Mathematik Erwachsenenschule Bremen Abteilung I: Sekundarstufe Doventorscontrescarpe
M 3.1. Seite 1. Modul 3.1 Geometrie: Umgang mit dem Geodreieck. Thema. 1. Umgang mit dem Geodreieck. Datum
 Seite. Wie zeichnet man zueinander senkrechte Geraden?. Zeichne zunächst mit deinem Geodreieck eine Gerade von 2 cm. 2. Nun drehst du dein Geodreieck wie rechts abgebildet. Achte darauf, dass die Gerade
Seite. Wie zeichnet man zueinander senkrechte Geraden?. Zeichne zunächst mit deinem Geodreieck eine Gerade von 2 cm. 2. Nun drehst du dein Geodreieck wie rechts abgebildet. Achte darauf, dass die Gerade
Grundlagen der Vektorrechnung
 Grundlagen der Vektorrechnung Ein Vektor a ist eine geordnete Liste von n Zahlen Die Anzahl n dieser Zahlen wird als Dimension des Vektors bezeichnet Schreibweise: a a a R n Normale Reelle Zahlen nennt
Grundlagen der Vektorrechnung Ein Vektor a ist eine geordnete Liste von n Zahlen Die Anzahl n dieser Zahlen wird als Dimension des Vektors bezeichnet Schreibweise: a a a R n Normale Reelle Zahlen nennt
18.7 Übungen Übungen 341
 18.7 Übungen 341 18.7 Übungen 18.1 Skizzieren Sie die dargestellten Körper (freihand) in Vorder-, Seiten- und Draufsicht. Wenn Sie Schwierigkeiten mit der räumlichen Vorstellung haben, bauen Sie die Körper
18.7 Übungen 341 18.7 Übungen 18.1 Skizzieren Sie die dargestellten Körper (freihand) in Vorder-, Seiten- und Draufsicht. Wenn Sie Schwierigkeiten mit der räumlichen Vorstellung haben, bauen Sie die Körper
VektorWorks - Einführungskurs
 - Einführungskurs Ablauf: Step1 - die Arbeitsoberfläche Step2 - ein neues Dokument anlegen Step3 - Grundformen anlegen Step4-2D-Formen bearbeiten Step5 - Ebenen und Klassen Start Step6 - Vermaßen Step7
- Einführungskurs Ablauf: Step1 - die Arbeitsoberfläche Step2 - ein neues Dokument anlegen Step3 - Grundformen anlegen Step4-2D-Formen bearbeiten Step5 - Ebenen und Klassen Start Step6 - Vermaßen Step7
Freies und konstruktives Zeichnen
 Lehrplan Freies und konstruktives Zeichnen Fachoberschule Fachbereich Design Ministerium für Bildung, Kultur und Wissenschaft Hohenzollernstraße 60, 66117 Saarbrücken Postfach 10 24 52, 66024 Saarbrücken
Lehrplan Freies und konstruktives Zeichnen Fachoberschule Fachbereich Design Ministerium für Bildung, Kultur und Wissenschaft Hohenzollernstraße 60, 66117 Saarbrücken Postfach 10 24 52, 66024 Saarbrücken
Realschule. 1. Schulaufgabe aus der Mathematik. Klasse 8 / I ; B 1, 1,5(
 1. Schulaufgabe aus der Mathematik 1. Gegeben sind die Punkte A,, ( ; B, 0,5( und C 0,5 ( 1.1 Konstruiere den Umkreis k des Dreiecks mit Mittelpunkt M. 1. Kennzeichne die Lösungsmenge mit grüner Farbe:
1. Schulaufgabe aus der Mathematik 1. Gegeben sind die Punkte A,, ( ; B, 0,5( und C 0,5 ( 1.1 Konstruiere den Umkreis k des Dreiecks mit Mittelpunkt M. 1. Kennzeichne die Lösungsmenge mit grüner Farbe:
