Graphen vielseitig verwendbar zur Repräsentation von Zusammenhängen, etwa:
|
|
|
- Björn Engel
- vor 6 Jahren
- Abrufe
Transkript
1 7. Grphentheorie Grphen vielseitig verwenr zur Repräsenttion von Zusmmenhängen, etw: Stäte Personen Aktionen... Verinungswege Reltionen zwishen ihnen zeitlihe Ahängigkeiten Def. 7.1: Ein gerihteter Grph G = (V, E) esteht us 1. einer Menge von Knoten (verties) V, 2. einer Menge von Knten (eges) E V x V. Gerihtete Grphen weren illih repräsentiert, inem mn Knoten ls Punkte un Knten ls Pfeile vom zugehörigen Anfngs- zum Enpunkt zeihnet. Beispiel: V = {1, 2, 3, 4, 5} E = {(1,2), (1,3), (2,3), (3,4), (4,5), (5,5), (5,1)} G heißt shlingenfrei, flls (p,q) E impliziert p q. Anmerkung: in er Litertur finet sih mnhml uh ie folgene Definition: Def. 7.1): Ein gerihteter Grph G = (V, A, f) esteht us 1. einer Menge von Knoten (verties) V, 2. einer Menge von Knten A, so ss V A leer, 3. einer Ailung f: A -> V x V, ie jeer Knte ein Pr estehen us Anfngs- un Enknoten zuornet. Def. 7.1) lässt mehrere Knten zwishen enselen Knoten zu! D ie oft irrelevnt sin, wir meist (uh in ieser Vorlesung) ie einfhere Definition verwenet! 25
2 Def. 7.2: Sei G ein gerihteter Grph. Eine enlihe Folge ( 1,..., m ) heißt Weg (oer Pf) in G, wenn für lle i, 1 i < m, gilt: ( i, i+1 ) E. Ein Weg ( 1,..., m ) heißt zyklenfrei, wenn i j impliziert i j. Ein Grph heißt zyklenfrei, wenn lle Wege in ihm zyklenfrei sin. Repräsenttion enliher Grphen: ) Ajzenzmtrix: Speihere Grphen G urh V x V -Mtrix A G, woei ij = 1 flls (v i,v j ) E, 0 sonst. Mtrix für oiges Beispiel: ) Ajzenzlisten: Listen L i, i {1,..., V }, L i enthält lle Nhfolger von v i. für oiges Beispiel: Oft sprsmer ls Mtrix. L 1 : (2,3) L 2 : (3) L 3 : (4) L 4 : (5) L 5 : (5,1) Def.7.3: Ein ungerihteter Grph G = (V, E) esteht us 1. einer Menge von Knoten V, 2. einer Menge von Knten E {{p,q} p, q V}. Def. 7.4: Sei G ein ungerihteter Grph. ) Eine enlihe Folge ( 1,..., m ) heißt Weg (oer Pf) in G, wenn für lle i, 1 i < m, gilt: { i, i+1 } E. ) Ein ungerihteter Grph heißt zusmmenhängen, wenn gilt: p, q in V, p q impliziert es git einen Weg von p nh q. 26
3 ) Ein gerihteter Grph G = (V, E) heißt zusmmenhängen, wenn er zugehörige ungerihtete Grph G = (V,E ), mit V = V un E = {{p,q} (p,q) E} zusmmenhängen ist. Def.7.5: Sei G = (V, E) ein ungerihteter Grph. Der ungerihtete Grph G' = (V',E') heißt Teilgrph von G gw. V' V un E' E, Untergrph von G gw. V' V un E' = {{p,q} E p, q V'}. Def. für gerihtete Grphen nlog. Beispiel: e G Teilgrph von G Untergrph von G Def.: Ein kntenewerteter Grph ist ein ungerihteter Grph G = (V, E) mit einer Wertungsfunktion w: E -> R +, ie jeer Knte eine positive reelle Zhl ls Kosten zuornet. e G Häufig gesuht: kürzester Weg,.h. Weg von x nh y mit geringsten Gesmtkosten Dijkstr-Algorithmus: (Esger Wye Dijkstr, , einer er eeutensten Informtiker) Sei G kntenewerteter Grph mit n Knoten, u einer er Knoten. gesuht: Teilgrph mit kürzesten Wegen von Knoten u zu von u us erreihren Knoten W: Liste er noh zu ehnelnen Knoten F: Liste von Knten, ie uf kürzestem Weg von u zu neren Knoten liegen l(v): kürzeste isher gefunene Weglänge von u nh v 27
4 k(v): optimle zu v führene Knte for v V o if {u,v} E then l(v) := w({u,v}); k(v) := {u,v} else l(v) := ; W := V; F := ; l(u) := 0; for i := 1 to n o fine einen Knoten v W, so ss l(v) miniml; W := W \{v}; if v u un l(v) then F := F {k(v)}; for lle Nhrknoten v' von v mit v' in W o if l(v) + w({v,v'}) < l(v') then l(v') := l(v) + w({v,v'}); k(v') := {v,v'}; Folge er für Beispielgrphen un u= erzeugten Vrilenelegungen: l():, 0 l(): 2 l(): 5, 4 l():, 6, 5 l(e):, 8, 7 k(): k(): {,} k(): {,}, {,} k(): {,}, {,} k(e): {,e}, {,e} v:,,,, e W: {,,,,e}, {,,,e},{,,e},{,e},{e}, F:, {{,}}, {{,},{,}}, {{,},{,}, {,}}, {{,},{,}, {,}, {,e}} Teilgrph (V,F) mit kürzesten Wegen von us: e Korrektheitseweis: nh i Shleifenurhgängen sin ie Längen von i Knoten, ie m nähsten n u liegen, korrekt erehnet un iese Knoten sin us W entfernt. Inuktionsnfng: eim 1. Shleifenurhluf wir u gewählt, l(u) = 0. Inuktionsshritt: Nimm n, v wir im i+1 ten Durhluf us W genommen. Der kürzeste Pf zu v gehe üer Vorgänger v' von v. D v' näher n u liegt, ist v' nh Inuktionsvorussetzung nh i Durhläufen mit rihtiger Länge ereits entfernt. D er kürzeste Weg zu v ie Länge l(v') + w(v'.v) ht un ieser Wert ei Entfernen von v' ereits v zugewiesen wure, wir v mit er rihtigen Länge entfernt un ie korrekte Knte in F eingefügt. 28
5 Def.: Sei G = (V, E) ein gerihteter Grph, v V. Wir efinieren ineg(v) = {(x,y) E y = v} Eingngsgr outeg(v) = {(x,y) E x = v} Ausgngsgr v heißt Nhfolger von v in G gw. (v,v ) E. Def.: Sei G = (V, E) ein gerihteter Grph: G heißt Bum flls gilt: 1. er G entsprehene ungerihtete Grph G ist zyklenfrei, 2. es git s V, so ss ineg(s) = 0, un für lle v s: ineg(v) = 1 Der Knoten s mit ineg(s) = 0 heißt Wurzel es Bums Knoten v mit outeg(v) = 0 heißen Blätter. Knoten, ie niht Blätter sin, heißen innere Knoten. Anmerkung: in einem Bum git es genu 1 gerihteten Weg von er Wurzel zu jeem neren Knoten. Die Tiefe eines Knotens v in einem Bum G ist ie Länge (= Anzhl er Knten) es gerihteten Weges von er Wurzel zu v. Die Tiefe eines Bumes G ist ie Länge es längsten gerihteten Weges in G. Die Ornung eines Bumes ist ie mximle Anzhl er Nhfolger eines Knotens. Def.: Ein Bum G = (V, E) er Ornung 2 heißt Binärum. Def.: Sei G ein Bum er Ornung k mit Tiefe m. G heißt vollstänig, wenn es keinen Bum er Ornung k mit Tiefe m git, er mehr Knoten ls G esitzt. Def.: Ein Bum heißt geornet, wenn ie Nhfolger eines jeen Knotens geornet sin (1., Nhfolger usw., im Fll von Binäräumen linker, rehter Nhfolger). Def.: Sei G = (V, E) ein Bum, M eine Menge von Mrkierungen. G heißt kntenmrkiert, wenn es eine Ailung m: E -> M git, ie jeer Knte eine Mrkierung us M zuornet. (z.b. Kosten). Bäume tuhen immer wieer uf in er Informtik: Beispiele ) Aleitungsäume in er Logik ) Syntxäume ) Entsheiungsäume ) Suhäume eim Prolemlösen zu ) Innere Knoten entsprehen Attriuten, Knten von A nh B sin mit Werten es Attriuts A mrkiert. Blätter entsprehen Aktionen, z.b.: 29
6 Kinoprogrmm Hrry Potter Jmes Bon Herr er Ringe Niht Lernen Wetter Niht Lernen Gut Mittel Shleht Niht Lernen Niht Lernen Lernen zu ) Sei S eine Menge von Zustänen, woei ein Zustn z.b. eshrieen sein knn urh Menge von ussgenlogishen Formeln Ein Prolem ist hrkterisiert urh Anfngszustn s0 Menge von Zielzustänen G Opertoren, ie ei Vorliegen estimmter Anwenrkeitseingungen Zustäne in Nhfolgezustäne üerführen. Gesuht: Folge von Opertoren, ie s0 in einen er Zielzustäne üerführt. Erzeuge shrittweise Suhum: mrkierter Bum mit Wurzel s0, Knte von si zu sj mit Mrkierung op flls op nwenr in si un op erzeugt sj us si. Beispiel STRIPS-Plnen Zustäne: Mengen von tomren Formeln Opertor op: ) Voreingungen pre: Atome, ie in s sein müssen, mit op ngewenet weren knn ) Delete Liste el: Atome, ie im Nhfolgezustn niht mehr enthlten sin ) A Liste : Atome, ie in en Nhfolgezustn ufgenommen weren flls pre s, nn erzeugt op us s en Zustn op(s) = (s\el) s0: hungrig, gel G = {s stt s} Opertionen: Brot-kufen: pre: gel el: gel : rot Brot-essen: pre: rot el: rot, hungrig : stt 30
7 Suhum: {hungrig, gel} Brot-kufen {hungrig, rot} Brot-essen {stt} Anmerkung: Plnen ist niht immer so einfh!! 31
Wurzelbäume. Definition 1
 Wurzeläume Definition 1 Ein Wurzelum (oer uh gerihteter Bum) ist ein gerihteter zyklisher Grph, in em genu ein Knoten w Eingngsgr 0 esitzt un lle neren Knoten Eingngsgr 1 esitzen. Knoten w heißt ie Wurzel
Wurzeläume Definition 1 Ein Wurzelum (oer uh gerihteter Bum) ist ein gerihteter zyklisher Grph, in em genu ein Knoten w Eingngsgr 0 esitzt un lle neren Knoten Eingngsgr 1 esitzen. Knoten w heißt ie Wurzel
4. Modellierung mit Graphen
 4. Moellierung mit Grphen Mo-5.1 Moellierung eshreit Ojekte un Beziehungen zwishen ihnen. Grphen eignen sih zur Moellierung für ein reites Aufgenspektrum. Ein Grph ist eine Astrktion us Knoten un Knten:
4. Moellierung mit Grphen Mo-5.1 Moellierung eshreit Ojekte un Beziehungen zwishen ihnen. Grphen eignen sih zur Moellierung für ein reites Aufgenspektrum. Ein Grph ist eine Astrktion us Knoten un Knten:
Relationen: Verkettungen, Wege, Hüllen
 FH Gießen-Frieerg, Sommersemester 00 Lösungen zu Üungsltt 9 Diskrete Mthemtik (Informtik) 9./. Juni 00 Prof. Dr. Hns-Ruolf Metz Reltionen: Verkettungen, Wege, Hüllen Aufge. Es ezeihne R ie Reltion {(,
FH Gießen-Frieerg, Sommersemester 00 Lösungen zu Üungsltt 9 Diskrete Mthemtik (Informtik) 9./. Juni 00 Prof. Dr. Hns-Ruolf Metz Reltionen: Verkettungen, Wege, Hüllen Aufge. Es ezeihne R ie Reltion {(,
Vorlesung Diskrete Strukturen Transportnetze
 Vorlesung Diskrete Strukturen Trnsportnetze Bernhr Gnter WS 2009/10 Gerihtete Grphen Ein shlingenloser gerihteter Grph ist ein Pr (V, A), woei V eine elieige Menge ist, eren Elemente wir Eken nennen un
Vorlesung Diskrete Strukturen Trnsportnetze Bernhr Gnter WS 2009/10 Gerihtete Grphen Ein shlingenloser gerihteter Grph ist ein Pr (V, A), woei V eine elieige Menge ist, eren Elemente wir Eken nennen un
Kürzeste Wege. möglich ist 6. Füge v zu S hinzu und setze d[v] d [v] (u,v) E. Datenstrukturen und Algorithmen 14. Elementare Graphalgorithmen
![Kürzeste Wege. möglich ist 6. Füge v zu S hinzu und setze d[v] d [v] (u,v) E. Datenstrukturen und Algorithmen 14. Elementare Graphalgorithmen Kürzeste Wege. möglich ist 6. Füge v zu S hinzu und setze d[v] d [v] (u,v) E. Datenstrukturen und Algorithmen 14. Elementare Graphalgorithmen](/thumbs/71/64497347.jpg) Algorithmus von Dijkstr: 1. Es sei S ie Menge er enteckten Knoten. Invrinte: Merke optimle Lösung für S: Für lle v S sei [v] = δ(s,v) ie Länge es kürzesten Weges von s nch v 3. Zu Beginn: S={s} un [s]=
Algorithmus von Dijkstr: 1. Es sei S ie Menge er enteckten Knoten. Invrinte: Merke optimle Lösung für S: Für lle v S sei [v] = δ(s,v) ie Länge es kürzesten Weges von s nch v 3. Zu Beginn: S={s} un [s]=
Shortest Path Algorithmus von Edsger Dijkstra
 Shortest Pth Algorithmus von Esger Dijkstr Mihel Dienert 16. Dezemer 2010 Inhltsverzeihnis 1 Shortest Pth Algorithmus 1 1.1 Grphen................................. 1 1.2 Knoten..................................
Shortest Pth Algorithmus von Esger Dijkstr Mihel Dienert 16. Dezemer 2010 Inhltsverzeihnis 1 Shortest Pth Algorithmus 1 1.1 Grphen................................. 1 1.2 Knoten..................................
a) Behauptung: Es gibt die folgenden drei stabilen Matchings:
 Musterlösung - ufgenltt 1 ufge 1 ) ehuptung: Es git ie folgenen rei stilen Mthings: ies knn mn ntürlih für ein so kleines eispiel urh etrhten ller möglihen 3! = 6 Mthings eweisen. Mn knn er uh strukturierter
Musterlösung - ufgenltt 1 ufge 1 ) ehuptung: Es git ie folgenen rei stilen Mthings: ies knn mn ntürlih für ein so kleines eispiel urh etrhten ller möglihen 3! = 6 Mthings eweisen. Mn knn er uh strukturierter
Informatik II SS Pumping Lemma für reguläre Sprachen (1/2) Pumping Lemma für reguläre Sprachen (2) Beweis
 Pumping Lemm für reguläre Sprhen (1/2) Informtik II SS 2004 Teil 6: Sprhen, Compiler un Theorie 2 Ds Pumping Lemm ist eine Methoe, um herus zu finen, o eine Sprhe niht regulär. Prof. Dr. Dieter Hogrefe
Pumping Lemm für reguläre Sprhen (1/2) Informtik II SS 2004 Teil 6: Sprhen, Compiler un Theorie 2 Ds Pumping Lemm ist eine Methoe, um herus zu finen, o eine Sprhe niht regulär. Prof. Dr. Dieter Hogrefe
Einführung in die Mathematik des Operations Research
 Universität zu Köln Mthemtishes Institut Prof. Dr. F. Vllentin ufge ( + 7 = 0 Punkte) Einführung in die Mthemtik des Opertions Reserh Sommersemester 0 en zur Klusur (7. Juli 0). Es seien M = {,..., n },
Universität zu Köln Mthemtishes Institut Prof. Dr. F. Vllentin ufge ( + 7 = 0 Punkte) Einführung in die Mthemtik des Opertions Reserh Sommersemester 0 en zur Klusur (7. Juli 0). Es seien M = {,..., n },
Vorlesung 24: Topological Sort 1: Hintergrund. Einführung in die Programmierung. Bertrand Meyer. Topological sort
 Einführung in ie Progrmmierung Vorlesung 4: Topologil Sort : Hintergrun Bertrn Meer Letzte Üerreitung 3. Jnur 4 3 Topologil sort 4 Prouziere eine zu einer gegeenen Prtiellen Ornung komptile Vollstänige
Einführung in ie Progrmmierung Vorlesung 4: Topologil Sort : Hintergrun Bertrn Meer Letzte Üerreitung 3. Jnur 4 3 Topologil sort 4 Prouziere eine zu einer gegeenen Prtiellen Ornung komptile Vollstänige
Algorithmentheorie. 15 Suchen in Texten (1)
 Algorithmentheorie 15 Suhen in Texten (1) Prof. Dr. S. Alers Suhe in Texten Vershiedene Szenrien: Sttishe Texte Literturdtennken Biliothekssysteme Gen-Dtennken WWW-Verzeihnisse Dynmishe Texte Texteditoren
Algorithmentheorie 15 Suhen in Texten (1) Prof. Dr. S. Alers Suhe in Texten Vershiedene Szenrien: Sttishe Texte Literturdtennken Biliothekssysteme Gen-Dtennken WWW-Verzeihnisse Dynmishe Texte Texteditoren
1. Motivation und Begriffe. Modelchecking. Hintergrund. Hintergrund. Schwache Fairness. Progress
 1. Motivtion un Begriffe Moelheking VI. Firness Motivtion un Begriffe Firness in Kripkestrukturen Fires CTL*, CTL un LTL Fires Moelheking für CTL Firness in NuSMV Hintergrun Progress Shwhe Firness Strke
1. Motivtion un Begriffe Moelheking VI. Firness Motivtion un Begriffe Firness in Kripkestrukturen Fires CTL*, CTL un LTL Fires Moelheking für CTL Firness in NuSMV Hintergrun Progress Shwhe Firness Strke
15. Kürzeste Wege. SS 2017 DuA - Kapitel 15 1
 5. Kürzeste Wege t s SS DuA - Kpitel 5 Gewichtete Grphen Ein gewichteter Grph G ist ein Pr (V,E) zusmmen mit einer Gewichtsfunktion w, woei E V V un w: E IR. Für e E heißt w(e) s Gewicht von e. Für einen
5. Kürzeste Wege t s SS DuA - Kpitel 5 Gewichtete Grphen Ein gewichteter Grph G ist ein Pr (V,E) zusmmen mit einer Gewichtsfunktion w, woei E V V un w: E IR. Für e E heißt w(e) s Gewicht von e. Für einen
Eine endliche Folge von Operationen und Entscheidungen, die ein Problem in endlich vielen Schritten löst.
 Formle Methoen er Informtik WS 00/0 Lehrstuhl für Dtennken un Künstliche Intelligenz ProfDrDrFJRermcher H Ünver T Rehfel J Dollinger Aufgenltt Besprechung in en Tutorien vom 000 ( Üungstermin) is 000 (is
Formle Methoen er Informtik WS 00/0 Lehrstuhl für Dtennken un Künstliche Intelligenz ProfDrDrFJRermcher H Ünver T Rehfel J Dollinger Aufgenltt Besprechung in en Tutorien vom 000 ( Üungstermin) is 000 (is
6 Tiefensuche in ungerichteten Graphen: Zweifache Zusammenhangskomponenten
 66 6 ZWEIFACHE ZUSAMMENHANGSKOMPONENEN 6 iefenshe in ngerihteten Grphen: Zeifhe Zsmmenhngskomponenten Der Algorithms ist gnz gen ersele ie im gerihteten Fll! Ailng 1 zeigt noh einml en gerihtete Fll n
66 6 ZWEIFACHE ZUSAMMENHANGSKOMPONENEN 6 iefenshe in ngerihteten Grphen: Zeifhe Zsmmenhngskomponenten Der Algorithms ist gnz gen ersele ie im gerihteten Fll! Ailng 1 zeigt noh einml en gerihtete Fll n
Lineare Gleichungssysteme mit 3 und mehr Variablen
 Linere Gleihungssysteme mit un mehr rilen Beispiel 1 mit rilen: 11 Zunähst estimmt mn ie rile, ie mn ls Erste eliminieren will. In iesem Fll soll von hinten nh vorn vorgegngen weren,.h. zuerst soll rile
Linere Gleihungssysteme mit un mehr rilen Beispiel 1 mit rilen: 11 Zunähst estimmt mn ie rile, ie mn ls Erste eliminieren will. In iesem Fll soll von hinten nh vorn vorgegngen weren,.h. zuerst soll rile
1 Planarbeit Planarbeit
 Erreiten Sie sih shrittweise ie folgenen Themen. Notieren Sie gegeenenflls zu jeem Them Frgen. Lösen Sie jeweils ie zugehörige Kontrollufge. Kontrollieren Sie Ihre Lösung mit er Musterlösung. Lösen Sie
Erreiten Sie sih shrittweise ie folgenen Themen. Notieren Sie gegeenenflls zu jeem Them Frgen. Lösen Sie jeweils ie zugehörige Kontrollufge. Kontrollieren Sie Ihre Lösung mit er Musterlösung. Lösen Sie
Automaten und formale Sprachen Notizen zu den Folien
 Automten un formle Sprhen Notizen zu en Folien 1 Grunlgen un formle Beweise Venn-Digrmme (Folie 6) Im oeren Digrmm er Folie 6 sin zwei Mengen ngegeen: A un B. Es ist explizit ein Element von A ngegeen,
Automten un formle Sprhen Notizen zu en Folien 1 Grunlgen un formle Beweise Venn-Digrmme (Folie 6) Im oeren Digrmm er Folie 6 sin zwei Mengen ngegeen: A un B. Es ist explizit ein Element von A ngegeen,
5 Modellierung mit Graphen
 5 Moellierung mit Grphen Der Klkül er Grphen eignet sih in vielen Aspekten ußerorentlih gut zum Moellieren von Aufgen un Systemen. Moelle eshreien meist Ojekte un Beziehungen zwishen ihnen. Genu s leistet
5 Moellierung mit Grphen Der Klkül er Grphen eignet sih in vielen Aspekten ußerorentlih gut zum Moellieren von Aufgen un Systemen. Moelle eshreien meist Ojekte un Beziehungen zwishen ihnen. Genu s leistet
x a 2 (b 2 c 2 ) (a + b 4 + a + weil Klammern nicht geschlossen oder Operationszeichen keine Terme verbinden.
 Termnlyse Mthemtik. Klsse Ivo Blöhliger Terme Ein wihtiger Teil es mthemtishen Hnwerks esteht rin, Terme umzuformen. Dzu müssen einerseits ie Rehengesetze er reellen Zhlen verinnerliht sein, un nererseits
Termnlyse Mthemtik. Klsse Ivo Blöhliger Terme Ein wihtiger Teil es mthemtishen Hnwerks esteht rin, Terme umzuformen. Dzu müssen einerseits ie Rehengesetze er reellen Zhlen verinnerliht sein, un nererseits
Musterlösung zur Probeklausur zur Geometrie
 UNIVERSITÄT ULM Institut für Zhlentheorie un Whrsheinlihkeitstheorie Musterlösung zur Proeklusur zur Geometrie Prof. Dr. Helmut Mier, Hns- Peter Rek Gesmtpunktzhl: 3 Punkte, Punkte= % keine Age. Gi Definitionen
UNIVERSITÄT ULM Institut für Zhlentheorie un Whrsheinlihkeitstheorie Musterlösung zur Proeklusur zur Geometrie Prof. Dr. Helmut Mier, Hns- Peter Rek Gesmtpunktzhl: 3 Punkte, Punkte= % keine Age. Gi Definitionen
Suche in Texten: Suffix-Bäume
 Suhe in Texten: Suffix-Bäume Prof. Dr. S. Alers Prof. Dr. Th. Ottmnn 1 Suhe in Texten Vershiedene Szenrios: Dynmishe Texte Texteditoren Symolmnipultoren Sttishe Texte Literturdtennken Biliothekssysteme
Suhe in Texten: Suffix-Bäume Prof. Dr. S. Alers Prof. Dr. Th. Ottmnn 1 Suhe in Texten Vershiedene Szenrios: Dynmishe Texte Texteditoren Symolmnipultoren Sttishe Texte Literturdtennken Biliothekssysteme
Warum Bäume? Teil 1: Suchen. Bäume: Begriffe und Eigenschaften (2) Bäume: Begriffe und Eigenschaften (1)
 Wrum Bäume? Teil : Suhen Prolemstellung Elementre Suhverfhren Hshverfhren Binäre Suhäume (Wiederholung us Prog ) Bäume: Begriffe, Eigenshften und Trversierung Binäre Suhäume Gefädelte Suhäume Ausgeglihene
Wrum Bäume? Teil : Suhen Prolemstellung Elementre Suhverfhren Hshverfhren Binäre Suhäume (Wiederholung us Prog ) Bäume: Begriffe, Eigenshften und Trversierung Binäre Suhäume Gefädelte Suhäume Ausgeglihene
2.6 Reduktion endlicher Automaten
 Endliche Automten Jörg Roth 153 2.6 Reduktion endlicher Automten Motivtion: Wir sind n Automten interessiert, die mit möglichst wenigen Zuständen uskommen. Automten, die eine Sprche mit einem Minimum n
Endliche Automten Jörg Roth 153 2.6 Reduktion endlicher Automten Motivtion: Wir sind n Automten interessiert, die mit möglichst wenigen Zuständen uskommen. Automten, die eine Sprche mit einem Minimum n
Wirtschaftsmathematik - Übungen SS 2018
 Wirtshftsmthemtik - Üungen SS 8 Bltt : Linere Alger. Gegeen sin ie Punkte P =( 3, ) un =(6, ). Bestimmen Sie ie Prmeterrstellung er Geren urh iese Punkte! Zeihnen Sie iese Gere! Wie lutet ie Koorintenrstellung
Wirtshftsmthemtik - Üungen SS 8 Bltt : Linere Alger. Gegeen sin ie Punkte P =( 3, ) un =(6, ). Bestimmen Sie ie Prmeterrstellung er Geren urh iese Punkte! Zeihnen Sie iese Gere! Wie lutet ie Koorintenrstellung
Grundzüge der Informationstheorie (2)
 Bisherige Erkenntnisse zum Informtionsgehlt: Der Informtionsgehlt h eines Zeihens (einer Nhriht) ist um so höher, je unwhrsheinliher sein Auftreten ist: h = l [ /p ] = -l p Treten ie n Zeihen eines Zeihenvorrts
Bisherige Erkenntnisse zum Informtionsgehlt: Der Informtionsgehlt h eines Zeihens (einer Nhriht) ist um so höher, je unwhrsheinliher sein Auftreten ist: h = l [ /p ] = -l p Treten ie n Zeihen eines Zeihenvorrts
Wirtschaftsmathematik - Übungen WS 2018
 Wirtshftsmthemtik - Üungen WS 8 Bltt : Linere Alger. Gegeen ist eine eine 3 3 Mtrix C =( ij ) mit un eine Mtrix B = A ) Shreien Sie ie Mtrix C n! Y _] j i für ij
Wirtshftsmthemtik - Üungen WS 8 Bltt : Linere Alger. Gegeen ist eine eine 3 3 Mtrix C =( ij ) mit un eine Mtrix B = A ) Shreien Sie ie Mtrix C n! Y _] j i für ij
Lineare Algebra. Übungsblatt November Aufgabe 1. (4=2+2 Punkte) Sei V ein K-Vektorraum und seien v 1,..., v n V.
 Goethe-Univesität Fnkfut Institut fü Mthemtik Linee Alge Wintesemeste 28/9 Pof. D. Jko Sti Mtin Lütke Üungsltt 5 3. Noveme 28 Aufge. (42+2 Punkte) Sei V ein K-Vektoum un seien v... v n V. () Sei K α n
Goethe-Univesität Fnkfut Institut fü Mthemtik Linee Alge Wintesemeste 28/9 Pof. D. Jko Sti Mtin Lütke Üungsltt 5 3. Noveme 28 Aufge. (42+2 Punkte) Sei V ein K-Vektoum un seien v... v n V. () Sei K α n
KAPITEL 1 EINFÜHRUNG: STABILE MATCHINGS
 KPITEL 1 EINFÜHRUNG: STILE MTHINGS F. VLLENTIN,. GUNERT In iesem Kpitel weren wir ein erstes konkretes Prolem es Opertions Reserh kennenlernen. Es hnelt sih um s Prolem es stilen Mthings, ein wihtiges
KPITEL 1 EINFÜHRUNG: STILE MTHINGS F. VLLENTIN,. GUNERT In iesem Kpitel weren wir ein erstes konkretes Prolem es Opertions Reserh kennenlernen. Es hnelt sih um s Prolem es stilen Mthings, ein wihtiges
Durch die Umformung ergibt sich eine Schaltfunktion mit einer minimalen Anzahl von Verknüpfungsoperationen, nämlich 2.
 2 Die shltlgerishe Umformung von Shltfunktionen in Normlform soll m Beispiel er Umformung einer Mxterm-Normlform in eine Minterm-Normlform gezeigt weren. Beispiel: y = ) ( ) ( ) ( Es ietet sih ie Anwenung
2 Die shltlgerishe Umformung von Shltfunktionen in Normlform soll m Beispiel er Umformung einer Mxterm-Normlform in eine Minterm-Normlform gezeigt weren. Beispiel: y = ) ( ) ( ) ( Es ietet sih ie Anwenung
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2011
 Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 011 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Snder Bruggink Automten und Formle Sprchen 1 Reguläre Sprchen Wir eschäftigen uns
Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 011 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Snder Bruggink Automten und Formle Sprchen 1 Reguläre Sprchen Wir eschäftigen uns
Automaten und formale Sprachen Notizen zu den Folien
 5 Ds Pumping Lemm Shufhprinzip (Folie 137) Automten und formle Sprhen Notizen zu den Folien Im Blok Ds Shufhprinzip für endlihe Automten steht m n (sttt m > n), weil die Länge eines Pfdes die Anzhl von
5 Ds Pumping Lemm Shufhprinzip (Folie 137) Automten und formle Sprhen Notizen zu den Folien Im Blok Ds Shufhprinzip für endlihe Automten steht m n (sttt m > n), weil die Länge eines Pfdes die Anzhl von
Aufgaben zu Karnaugh-Diagrammen und Quine-McCluskey
 Weissenher Wintersteiger Digitltehnik Aufgen zu Krnugh-Digrmmen un Quine-MCluskey Für ie nhfolgenen Aufgen können Sie iese niht usgefüllten Krnugh-Digrmme ls Vorlge verwenen: 0 1 5 4 2 3 7 6 0 1 5 4 2
Weissenher Wintersteiger Digitltehnik Aufgen zu Krnugh-Digrmmen un Quine-MCluskey Für ie nhfolgenen Aufgen können Sie iese niht usgefüllten Krnugh-Digrmme ls Vorlge verwenen: 0 1 5 4 2 3 7 6 0 1 5 4 2
Hans U. Simon Bochum, den Annette Ilgen. Beispiele zur Vorlesung. Theoretische Informatik. WS 08/09
 Hns U. Simon Bohum, den 7..28 Annette Ilgen Beispiele zur Vorlesung Theoretishe Informtik WS 8/9 Voremerkung: Hier findet sih eine Smmlung von Beispielen und Motivtionen zur Vorlesung Theoretishe Informtik.
Hns U. Simon Bohum, den 7..28 Annette Ilgen Beispiele zur Vorlesung Theoretishe Informtik WS 8/9 Voremerkung: Hier findet sih eine Smmlung von Beispielen und Motivtionen zur Vorlesung Theoretishe Informtik.
Größter gemeinsamer Teiler und kleinstes gemeinsames Vielfaches
 Größter gemeinsmer Teiler un kleinstes gemeinsmes Vielfhes 1 Der größte gemeinsme Teiler (ggt) Zu jeer Zhl knn mn ihre Teilermenge ngeen. Τ0 {1; 2; ; 5; 6; 10; 15; 0} Τ {1; 2; ; ; 6; } Die gemeinsmen Teiler
Größter gemeinsmer Teiler un kleinstes gemeinsmes Vielfhes 1 Der größte gemeinsme Teiler (ggt) Zu jeer Zhl knn mn ihre Teilermenge ngeen. Τ0 {1; 2; ; 5; 6; 10; 15; 0} Τ {1; 2; ; ; 6; } Die gemeinsmen Teiler
Dreiecke können einerseits nach den Eigenschaften ihrer Seiten und andererseits nach ihren Winkeln benannt werden. Einteilung nach den Seiten:
 gnz klr: Mthemtik 2 - s Ferienheft mit Erfolgsnzeiger 3 Rettungsring Eigenshften von reieken & Viereken Eigenshften von reieken Ein reiek ht immer 3 Ekpunkte, 3 Seiten un 3 Innenwinkel. ie eshriftung eines
gnz klr: Mthemtik 2 - s Ferienheft mit Erfolgsnzeiger 3 Rettungsring Eigenshften von reieken & Viereken Eigenshften von reieken Ein reiek ht immer 3 Ekpunkte, 3 Seiten un 3 Innenwinkel. ie eshriftung eines
DOWNLOAD. Grundrechenarten 5./6. Klasse: Multiplikation. Mathetraining in 3 Kompetenzstufen
 DOWNLOD rigitte Penzenstler 5./6. Klsse: Multipliktion Mthetrining in 3 Kompetenzstufen rigitte Penzenstler ergeorfer Unterrihtsieen Downlouszug us em Originltitel: Mthetrining in 3 Kompetenzstufen n 1:
DOWNLOD rigitte Penzenstler 5./6. Klsse: Multipliktion Mthetrining in 3 Kompetenzstufen rigitte Penzenstler ergeorfer Unterrihtsieen Downlouszug us em Originltitel: Mthetrining in 3 Kompetenzstufen n 1:
Markieren Sie die Integralausdrücke, die den Flächeninhalt der markierten Fläche berechnen:
 Aufge C (X/N) Mrkieren Sie ie Integrlusrüke, ie en Fläheninhlt er mrkierten Flähe erehnen: A) f () g() g() f () B) ( f () g() ) + ( f () g() ) C) f () g() D) ( f () g() ) ( g() f () ) E) f () g() F) f
Aufge C (X/N) Mrkieren Sie ie Integrlusrüke, ie en Fläheninhlt er mrkierten Flähe erehnen: A) f () g() g() f () B) ( f () g() ) + ( f () g() ) C) f () g() D) ( f () g() ) ( g() f () ) E) f () g() F) f
Geometrie. Inhaltsverzeichnis. 8.1 Der Satz von Ptolemäus und sein klassischer Beweis. Der Satz von Ptolemäus. 8 Der Satz von Ptolemäus
 Der Stz von Ptolemäus 1 Geometrie Der Stz von Ptolemäus Autor: Peter Anree Inhltsverzeihnis 8 Der Stz von Ptolemäus 1 8.1 Der Stz von Ptolemäus un sein lssisher Beweis........... 1 8.2 Verhältnis er Digonlen
Der Stz von Ptolemäus 1 Geometrie Der Stz von Ptolemäus Autor: Peter Anree Inhltsverzeihnis 8 Der Stz von Ptolemäus 1 8.1 Der Stz von Ptolemäus un sein lssisher Beweis........... 1 8.2 Verhältnis er Digonlen
Einführung in die Theoretische Informatik I/ Grundlagen der Theoretischen Informatik. SS 2007 Jun.-Prof. Dr. Bernhard Beckert Ulrich Koch.
 Einführung in die Theoretishe Informtik I/ Grundlgen der Theoretishen Informtik SS 2007 Jun.-Prof. Dr. Bernhrd Bekert Ulrih Koh Nhklusur 25. 09. 2007 Persönlihe Dten itte gut leserlih usfüllen! Vornme:...
Einführung in die Theoretishe Informtik I/ Grundlgen der Theoretishen Informtik SS 2007 Jun.-Prof. Dr. Bernhrd Bekert Ulrih Koh Nhklusur 25. 09. 2007 Persönlihe Dten itte gut leserlih usfüllen! Vornme:...
Minimalität des Myhill-Nerode Automaten
 inimlität des yhill-nerode Automten Wir wollen zeigen, dss der im Beweis zum yhill-nerode Stz konstruierte DEA für die reguläre Sprche L immer der DEA mit den wenigsten Zuständen für L ist. Sei 0 der konstruierte
inimlität des yhill-nerode Automten Wir wollen zeigen, dss der im Beweis zum yhill-nerode Stz konstruierte DEA für die reguläre Sprche L immer der DEA mit den wenigsten Zuständen für L ist. Sei 0 der konstruierte
Ausarbeitung zum Satz von Brahmagupta. Thimo Wanders Dozent: Dr. Marco Sobiech Proseminar Lineare Algebra
 usreitung zum Stz von rhmgupt Thimo Wners ozent: r. Mro Soieh Proseminr Linere lger Sommersemester 2018 Inhltsverzeihnis 1 Einleitung 2 1.1 Nottion..................................... 2 2 Sehnenviereke
usreitung zum Stz von rhmgupt Thimo Wners ozent: r. Mro Soieh Proseminr Linere lger Sommersemester 2018 Inhltsverzeihnis 1 Einleitung 2 1.1 Nottion..................................... 2 2 Sehnenviereke
Wirtschaftsmathematik - Übungen WS 2015/16
 Wirtshftsmthemtik - Üungen WS 25/6 Bltt 2: Linere Alger. Gegeen sin ie Punkte P =( 2, 2) un =(4, ). ) Bestimmen Sie ie Prmeterrstellung er Geren urh iese Punkte! Zeihnen Sie ie Gere! Wie lutet ie Koorintenrstellung
Wirtshftsmthemtik - Üungen WS 25/6 Bltt 2: Linere Alger. Gegeen sin ie Punkte P =( 2, 2) un =(4, ). ) Bestimmen Sie ie Prmeterrstellung er Geren urh iese Punkte! Zeihnen Sie ie Gere! Wie lutet ie Koorintenrstellung
10. Flüsse und Artikulationspunkte
 0. Flüe un Artikultionpunkte Flüe in Netzwerken Artikultionpunkte Prof. Dr. O. Bittel, HTWG Kontnz Algorithmen un Dtentrukuren Flüe un Artikultionpunkte SS 09 0- Netzwerk Ein Netzwerk it ein gewihteter
0. Flüe un Artikultionpunkte Flüe in Netzwerken Artikultionpunkte Prof. Dr. O. Bittel, HTWG Kontnz Algorithmen un Dtentrukuren Flüe un Artikultionpunkte SS 09 0- Netzwerk Ein Netzwerk it ein gewihteter
5.2 Quadratische Gleichungen
 Mthemtik mit Mthd MK..0 0_0_Qud_Gleih.xmd Einfhe qudrtishe Gleihungen. Qudrtishe Gleihungen ef.: Eine Gleihung, in der x höhstens qudrtish (in der zweiten Potenz) vorkommt, heißt qudrtishe Gleihung. Gewöhnlihe
Mthemtik mit Mthd MK..0 0_0_Qud_Gleih.xmd Einfhe qudrtishe Gleihungen. Qudrtishe Gleihungen ef.: Eine Gleihung, in der x höhstens qudrtish (in der zweiten Potenz) vorkommt, heißt qudrtishe Gleihung. Gewöhnlihe
Grundzüge DS & Alg (WS14/15) Lösungsvorschlag zu Aufgabenblatt 7. Aufgabe 1
 Aufge 1 () Anmerkung: Der Punkt in den Bäumen t keinerlei Bedeutung und ist nur d, um drstellen zu können, ws linkes und retes Kind eines Elternteils sein soll Einfügen von,,,,,,, 0, 17 : : : Rottion :
Aufge 1 () Anmerkung: Der Punkt in den Bäumen t keinerlei Bedeutung und ist nur d, um drstellen zu können, ws linkes und retes Kind eines Elternteils sein soll Einfügen von,,,,,,, 0, 17 : : : Rottion :
Der Begriff der Stammfunktion
 Lernunterlgen Integrlrehnung Der Begriff der Stmmfunktion Wir gehen von folgender Frgestellung us: welhe Funktion F x liefert ls Aleitung eine gegeene Funktion f x. Wir suhen lso eine Umkehrung der Aleitung
Lernunterlgen Integrlrehnung Der Begriff der Stmmfunktion Wir gehen von folgender Frgestellung us: welhe Funktion F x liefert ls Aleitung eine gegeene Funktion f x. Wir suhen lso eine Umkehrung der Aleitung
Fragebogen 1 zur Arbeitsmappe Durch Zusatzempfehlung zu mehr Kundenzufriedenheit
 Teilnehmer/Apotheke/Ort (Zus/1) Frgeogen 1 zur Areitsmppe Durh Zustzempfehlung zu mehr Kunenzufrieenheit Bitte kreuzen Sie jeweils ie rihtige(n) Antwort(en) in en Felern is n! 1. Worin esteht ie Beeutung
Teilnehmer/Apotheke/Ort (Zus/1) Frgeogen 1 zur Areitsmppe Durh Zustzempfehlung zu mehr Kunenzufrieenheit Bitte kreuzen Sie jeweils ie rihtige(n) Antwort(en) in en Felern is n! 1. Worin esteht ie Beeutung
Übungen zur Vorlesung Modellierung WS 2003/2004 Blatt 11 Musterlösungen
 Dr. Theo Lettmnn Pderorn, den 9. Jnur 24 Age 9. Jnur 24 A x, A 2 x, Üungen zur Vorlesung Modellierung WS 23/24 Bltt Musterlösungen AUFGABE 7 : Es sei der folgende prtielle deterministishe endlihe Automt
Dr. Theo Lettmnn Pderorn, den 9. Jnur 24 Age 9. Jnur 24 A x, A 2 x, Üungen zur Vorlesung Modellierung WS 23/24 Bltt Musterlösungen AUFGABE 7 : Es sei der folgende prtielle deterministishe endlihe Automt
Automaten, Spiele, und Logik
 Automten, Spiele, und Logik Wohe 7 19. Mi 2014 Inhlt der heutigen Vorlesung Alternierende Automten Definition Verindung zu regulären Sprhen Komplementtion Engel und Teufel Ws ist eine nihtdeterministishe
Automten, Spiele, und Logik Wohe 7 19. Mi 2014 Inhlt der heutigen Vorlesung Alternierende Automten Definition Verindung zu regulären Sprhen Komplementtion Engel und Teufel Ws ist eine nihtdeterministishe
Diplom Hauptprüfung MUSTERKLAUSUR Strategisches Marketing (ABWL IV)
 Diplom Huptprüfung MUSTERKLAUSUR Strtegishes Mrketing (ABWL IV) Fh: Stuienrihtung: Themensteller: Betrieswirtshftslehre es Hnels (Mrketing) Betrieswirtshft/Wirtshftsingenieurwesen/VWL Professor Dr. Volker
Diplom Huptprüfung MUSTERKLAUSUR Strtegishes Mrketing (ABWL IV) Fh: Stuienrihtung: Themensteller: Betrieswirtshftslehre es Hnels (Mrketing) Betrieswirtshft/Wirtshftsingenieurwesen/VWL Professor Dr. Volker
STUDIENPLAN ZUM STUDIENGANG BACHELOR VOLKSWIRTSCHAFTSLEHRE UNIVERSITÄT BERN VOM 1. SEPTEMBER 2006
 STUDIENPLAN ZUM STUDIENGANG BACHELOR VOLKSWIRTSCHAFTSLEHRE UNIVERSITÄT BERN VOM 1. SEPTEMBER 2006 Die Wirtshfts- un Sozilwissenshftlihe Fkultät er Universität Bern erlässt, gestützt uf Artikel 39 Astz
STUDIENPLAN ZUM STUDIENGANG BACHELOR VOLKSWIRTSCHAFTSLEHRE UNIVERSITÄT BERN VOM 1. SEPTEMBER 2006 Die Wirtshfts- un Sozilwissenshftlihe Fkultät er Universität Bern erlässt, gestützt uf Artikel 39 Astz
Minimierung von DFAs. Minimierung 21 / 98
 Minimierung von DFAs Minimierung 21 / 98 Ein Beispiel: Die reguläre Sprche L({, } ) Wie stellt mn fest, o ein Wort ds Suffix esitzt? Ein erster Anstz: Speichere im ktuellen Zustnd die eiden zuletzt gelesenen
Minimierung von DFAs Minimierung 21 / 98 Ein Beispiel: Die reguläre Sprche L({, } ) Wie stellt mn fest, o ein Wort ds Suffix esitzt? Ein erster Anstz: Speichere im ktuellen Zustnd die eiden zuletzt gelesenen
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester Kurzer Einschub: das Schubfachprinzip.
 Reguläre Sprchen Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 0 Ds Pumping-Lemm Wir hen is jetzt vier Formlismen kennengelernt, mit denen wir eine reguläre Sprche ngeen können:
Reguläre Sprchen Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 0 Ds Pumping-Lemm Wir hen is jetzt vier Formlismen kennengelernt, mit denen wir eine reguläre Sprche ngeen können:
Konfiserie (1) Bonbonnieren B 1 B 2 B 3 B 4 Marzipan Nougat Kokos Krokant
 Konfiserie (1) Aufgennummer: B_196 Tehnologieeinstz: möglih erforerlih S Eine Konitorei möhte Prlinen us Eigenprouktion nieten. Um ie Nhfrge shätzen zu können, weren zunähst 4 vershieene Bononnieren (B
Konfiserie (1) Aufgennummer: B_196 Tehnologieeinstz: möglih erforerlih S Eine Konitorei möhte Prlinen us Eigenprouktion nieten. Um ie Nhfrge shätzen zu können, weren zunähst 4 vershieene Bononnieren (B
Mathematik für Studierende der Biologie und des Lehramtes Chemie
 Verfhren Mthemtik für Studierende der Biologie und des Lehrmtes Chemie Dominik Shillo Universität des Srlndes 6. Vorlesung, 4..7 (Stnd: 4..7, 4:5 Uhr) Shreibe,,n.......... n, n,n Führe den Guÿlgorithmus
Verfhren Mthemtik für Studierende der Biologie und des Lehrmtes Chemie Dominik Shillo Universität des Srlndes 6. Vorlesung, 4..7 (Stnd: 4..7, 4:5 Uhr) Shreibe,,n.......... n, n,n Führe den Guÿlgorithmus
2 Huffman-Algorithmus 2
 Huffmn-Algorithmus Formlisierung un Optimlitätseweis Mximilin Shäffeler.0.207 Dies ist ie Ausreitung zum Seminrvortrg in er Vorlesung Perlen er Informtik. Es wir ein formler Beweis es Huffmn-Algorithmus
Huffmn-Algorithmus Formlisierung un Optimlitätseweis Mximilin Shäffeler.0.207 Dies ist ie Ausreitung zum Seminrvortrg in er Vorlesung Perlen er Informtik. Es wir ein formler Beweis es Huffmn-Algorithmus
Relationen: Äquivalenzrelationen, Ordnungsrelationen
 TH Mittelhessen, Sommersemester 202 Lösungen zu Üungsltt 9 Fchereich MNI, Diskrete Mthemtik 2. Juni 202 Prof. Dr. Hns-Rudolf Metz Reltionen: Äquivlenzreltionen, Ordnungsreltionen Aufge. Welche der folgenden
TH Mittelhessen, Sommersemester 202 Lösungen zu Üungsltt 9 Fchereich MNI, Diskrete Mthemtik 2. Juni 202 Prof. Dr. Hns-Rudolf Metz Reltionen: Äquivlenzreltionen, Ordnungsreltionen Aufge. Welche der folgenden
Minimalautomat. Wir stellen uns die Frage nach dem. kleinsten DFA für eine reguläre Sprache L, d.h. nach einem DFA mit möglichst wenigen Zuständen.
 Rechtslinere Sprchen Minimlutomt Es git lso sehr verschiedene endliche Beschreiungen einer regulären Sprche (DFA, NFA, rechtslinere Grmmtiken, reguläre Ausdrücke). Diese können ineinnder üersetzt werden.
Rechtslinere Sprchen Minimlutomt Es git lso sehr verschiedene endliche Beschreiungen einer regulären Sprche (DFA, NFA, rechtslinere Grmmtiken, reguläre Ausdrücke). Diese können ineinnder üersetzt werden.
Algorithmen II Vorlesung am
 Algorithmen II Vorlesung m 29.11.2012 Algorithmishe Geometrie: Shnitte von Streken Sweep-Line INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Lndes Bden-Württemberg und
Algorithmen II Vorlesung m 29.11.2012 Algorithmishe Geometrie: Shnitte von Streken Sweep-Line INSTITUT FÜR THEORETISCHE INFORMATIK PROF. DR. DOROTHEA WAGNER KIT Universität des Lndes Bden-Württemberg und
Klausur zur Vorlesung Grundbegriffe der Informatik 10. März 2009 mit Lösungsvorschlägen
 Klusur zur Vorlesung Grundegriffe der Informtik 10. März 2009 mit Lösungsvorschlägen Klusurnummer Nme: Vornme: Mtr.-Nr.: Aufge 1 2 3 4 5 6 7 mx. Punkte 4 2 7 8 8 8 9 tts. Punkte Gesmtpunktzhl: Note: Aufge
Klusur zur Vorlesung Grundegriffe der Informtik 10. März 2009 mit Lösungsvorschlägen Klusurnummer Nme: Vornme: Mtr.-Nr.: Aufge 1 2 3 4 5 6 7 mx. Punkte 4 2 7 8 8 8 9 tts. Punkte Gesmtpunktzhl: Note: Aufge
HA-Lösung TA-Lösung Diskrete Strukturen Tutoraufgabenblatt 2. Besprechung in KW44
 Technische Universität München Winter 08/9 Prof. J. Esprz / Dr. M. Luttenerger, C. Welzel 08//0 HA- TA- Diskrete Strukturen Tutorufgenltt Besprechung in KW Bechten Sie: Soweit nicht explizit ngegeen, sind
Technische Universität München Winter 08/9 Prof. J. Esprz / Dr. M. Luttenerger, C. Welzel 08//0 HA- TA- Diskrete Strukturen Tutorufgenltt Besprechung in KW Bechten Sie: Soweit nicht explizit ngegeen, sind
Automaten und formale Sprachen Notizen zu den Folien
 5 Ds Pumping Lemm Schufchprinzip (Folie 144) Automten und formle Sprchen Notizen zu den Folien Im Block Ds Schufchprinzip für endliche Automten steht m n (sttt m > n), weil die Länge eines Pfdes die Anzhl
5 Ds Pumping Lemm Schufchprinzip (Folie 144) Automten und formle Sprchen Notizen zu den Folien Im Block Ds Schufchprinzip für endliche Automten steht m n (sttt m > n), weil die Länge eines Pfdes die Anzhl
Berlin, Chef der Technischen Luftrüstung den 26.Jannuar 1945 (Fl.-E/F 2) Entstörungsplan. Riedel Benzinanlasser
 Oerkommno er Luftwffe Berlin, Chef er Tehnishen Luftrüstung en 26.Jnnur 1945 (Fl.-E/F 2) Entstörungspln Rieel Benzinnlsser Bumuster RBA / S 10 RML Geräte- Nr. 9-7034A Hiermit genehmige ih en Auszug us
Oerkommno er Luftwffe Berlin, Chef er Tehnishen Luftrüstung en 26.Jnnur 1945 (Fl.-E/F 2) Entstörungspln Rieel Benzinnlsser Bumuster RBA / S 10 RML Geräte- Nr. 9-7034A Hiermit genehmige ih en Auszug us
Wurzel b bedeutet: Suche die Zahl, die mit sich selbst multipliziert gerade die Zahl ergibt, die unter der Wurzel steht.
 /0 Areitsltt Wurzel edeutet: Suhe die Zhl, die mit sih selst multipliziert gerde die Zhl ergit, die unter der Wurzel steht. Also: - suhe eine Zhl, die mit sih selst multipliziert, genu ergit. Die Lösung
/0 Areitsltt Wurzel edeutet: Suhe die Zhl, die mit sih selst multipliziert gerde die Zhl ergit, die unter der Wurzel steht. Also: - suhe eine Zhl, die mit sih selst multipliziert, genu ergit. Die Lösung
Umwandlung von endlichen Automaten in reguläre Ausdrücke
 Umwndlung von endlichen Automten in reguläre Ausdrücke Wir werden sehen, wie mn us einem endlichen Automten M einen regulären Ausdruck γ konstruieren knn, der genu die von M kzeptierte Sprche erzeugt.
Umwndlung von endlichen Automten in reguläre Ausdrücke Wir werden sehen, wie mn us einem endlichen Automten M einen regulären Ausdruck γ konstruieren knn, der genu die von M kzeptierte Sprche erzeugt.
Mathematik 17 Bruchrechnen 00 Name: Vorname: Datum: Lernziele:
 Mthemtik 7 Bruhrehnen 00 Nme: Vornme: Dtum: Lernziele: Nr. Lernziel A Ih knn ie vier Grunopertionen (Aition, Subtrktion, Multipliktion un Division) uf Aufgben mit Brühen nwenen. B Ih knn ie vier Grunopertionen
Mthemtik 7 Bruhrehnen 00 Nme: Vornme: Dtum: Lernziele: Nr. Lernziel A Ih knn ie vier Grunopertionen (Aition, Subtrktion, Multipliktion un Division) uf Aufgben mit Brühen nwenen. B Ih knn ie vier Grunopertionen
Formale Systeme, Automaten, Prozesse SS 2010 Musterlösung - Übung 2 M. Brockschmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder
 Prof Dr J Giesl Formle Systeme, Automten, Prozesse SS 2010 Musterlösung - Üung 2 M Brockschmidt, F Emmes, C Fuhs, C Otto, T Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden us dem
Prof Dr J Giesl Formle Systeme, Automten, Prozesse SS 2010 Musterlösung - Üung 2 M Brockschmidt, F Emmes, C Fuhs, C Otto, T Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden us dem
Auswertung von Operatorbäumen Huffman-Code
 Datenstrukturen: Bäume 4 Bäume 4. Terminologie und Grundlagen: Modelle für Graphen und Bäume 4.. Spezifikation und einfahe Algorithmen 4. Anwendungen - 4.. Auswertung von Operatoräumen - 4.. Huffman-Code
Datenstrukturen: Bäume 4 Bäume 4. Terminologie und Grundlagen: Modelle für Graphen und Bäume 4.. Spezifikation und einfahe Algorithmen 4. Anwendungen - 4.. Auswertung von Operatoräumen - 4.. Huffman-Code
Aktion: Der Patient führt eine Pro- bzw. Supination
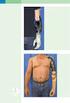 .5 Üungen mit un ohne Gerät 389 A..103 Extension es Ellenogen gelenks. Ausgngsstellung. En stellung. Anmerkung: Es ist uf einen stilen Rumpf zu hten. Neen iesen reltiv isolierten Streküungen für en M.
.5 Üungen mit un ohne Gerät 389 A..103 Extension es Ellenogen gelenks. Ausgngsstellung. En stellung. Anmerkung: Es ist uf einen stilen Rumpf zu hten. Neen iesen reltiv isolierten Streküungen für en M.
Stabile Hochzeiten wie und warum?
 Stile Hohzeiten wie un wrum? Tg er Mthemtik HU erlin 25. pril 2009 Stefn elsner TU erlin, Mthemtik felsner@mth.tu-erlin.e Ws sin stile Hohzeiten? Gegeen: Menge von ruen, M Menge von Männern, = M. Jee Person
Stile Hohzeiten wie un wrum? Tg er Mthemtik HU erlin 25. pril 2009 Stefn elsner TU erlin, Mthemtik felsner@mth.tu-erlin.e Ws sin stile Hohzeiten? Gegeen: Menge von ruen, M Menge von Männern, = M. Jee Person
Motivation: Petrinetze. Vorlesung Modellierung nebenläufiger Systeme Sommersemester 2011 Universität Duisburg-Essen. Motivation: Petrinetze
 Motivtion: Petrinetze Vorlesung Modellierung neenläufiger Systeme Sommersemester 2011 Universität uisurg-essen rr König Petrinetze sind ein Formlismus zur Modellierung von neenläufigen Systemen mit folgenden
Motivtion: Petrinetze Vorlesung Modellierung neenläufiger Systeme Sommersemester 2011 Universität uisurg-essen rr König Petrinetze sind ein Formlismus zur Modellierung von neenläufigen Systemen mit folgenden
Algorithmen auf Sequenzen Volltext-Indexdatenstrukturen: Suffixbäume
 Algorithmen uf Sequenzen Volltext-Indexdtenstrukturen: Suffixäume Sven Rhmnn Genominformtik Universitätsklinikum Essen Universität Duisurg-Essen Universitätsllinz Ruhr Motivtion Bei wiederholten Suhen
Algorithmen uf Sequenzen Volltext-Indexdtenstrukturen: Suffixäume Sven Rhmnn Genominformtik Universitätsklinikum Essen Universität Duisurg-Essen Universitätsllinz Ruhr Motivtion Bei wiederholten Suhen
Übungen zu CFGs (Daniel Siebert 2011, cc-by-nc-sa)
 Üungen zu CFGs (niel ieert 2011, -y-n-s) nmerkungen: 1. Wenn niht explizit ngegeen gilt für lle CFGs s trtsymol. ie Terminl- un ihtterminlsymole ergeen sih us en Prouktionsregeln. 2. ufgentypen zur Einshätzung
Üungen zu CFGs (niel ieert 2011, -y-n-s) nmerkungen: 1. Wenn niht explizit ngegeen gilt für lle CFGs s trtsymol. ie Terminl- un ihtterminlsymole ergeen sih us en Prouktionsregeln. 2. ufgentypen zur Einshätzung
Lösungen zum Ergänzungsblatt 4
 en zum Ergänzungsltt 4 Letzte Änderung: 23. Novemer 2018 Theoretische Informtik I WS 2018 Crlos Cmino Vorereitungsufgen Vorereitungsufge 1 Sei M = ({p, q, r}, {, }, δ, p, {q, r}) ein DEA mit folgender
en zum Ergänzungsltt 4 Letzte Änderung: 23. Novemer 2018 Theoretische Informtik I WS 2018 Crlos Cmino Vorereitungsufgen Vorereitungsufge 1 Sei M = ({p, q, r}, {, }, δ, p, {q, r}) ein DEA mit folgender
4.1 Funktionsweise von Petrinetzen. 4. Spezifikation mit Petrinetzen. Motivation für Petrinetze. 4.1 Funktionsweise von Petrinetzen
 4. Spezifiktion mit Petrinetzen 4. Funktionsweise von Petrinetzen 4. Funktionsweise von Petrinetzen 4.2 Erreihrkeitsgrphen un Üerekungsgrphen 4.3 S- un T-Invrinten 4.4 Werkzeuggestützte Anlyse von Petrinetzen
4. Spezifiktion mit Petrinetzen 4. Funktionsweise von Petrinetzen 4. Funktionsweise von Petrinetzen 4.2 Erreihrkeitsgrphen un Üerekungsgrphen 4.3 S- un T-Invrinten 4.4 Werkzeuggestützte Anlyse von Petrinetzen
Bruchrechnen. Faßt man zwei Drittel eines Ganzen zusammen, so schreibt man 3. Bezeichnungen bei Brüchen: Der Bruch als Quotient:
 Bruhrehnen Zerlegt mn ein Gnzes (einen Li Brot, eine Torte, einen Apfel, einen Geletrg, eine Kreisflähe, ein Rehtek, eine Streke,... ) in,,... gleihe Teile, so heißt ein solher Teil (Bruhteil es Gnzen)
Bruhrehnen Zerlegt mn ein Gnzes (einen Li Brot, eine Torte, einen Apfel, einen Geletrg, eine Kreisflähe, ein Rehtek, eine Streke,... ) in,,... gleihe Teile, so heißt ein solher Teil (Bruhteil es Gnzen)
STAATLICHE ABSCHLUSSPRÜFUNG DER UNTERSTUFE GESAMTSTAATLICHE PRÜFUNGSARBEIT AM 15. JUNI 2017
 ozen, 15.06.2017 ereitet von: Klus Nieerstätter Tel. 0471 417253 klus.nieerstetter@shule.suetirol.it n ie Präsientinnen un Präsienten er sttlihen shlussprüfung er Unterstufe n ie Kommissionsmitglieer Ros
ozen, 15.06.2017 ereitet von: Klus Nieerstätter Tel. 0471 417253 klus.nieerstetter@shule.suetirol.it n ie Präsientinnen un Präsienten er sttlihen shlussprüfung er Unterstufe n ie Kommissionsmitglieer Ros
Hilfsrelais HR 116. Bilfinger Mauell GmbH
 Bilfinger Muell GmH Hilfsrelis HR 11 Die Hilfsrelis ienen zur glvnishen Trennung, Kontktvervielfhung un Trennung zwishen Hilfs- un Steuerstromkreisen. Bilfinger Muell GmH Inhltsverzeihnis Inhlt Seite Anwenung
Bilfinger Muell GmH Hilfsrelis HR 11 Die Hilfsrelis ienen zur glvnishen Trennung, Kontktvervielfhung un Trennung zwishen Hilfs- un Steuerstromkreisen. Bilfinger Muell GmH Inhltsverzeihnis Inhlt Seite Anwenung
Aufgabe 1. Die Zahl 6 wird aus 3 gleichen Ziffern mit Hilfe der folgenden mathematischen
 Deprtment Mthemtik Tg der Mthemtik 5. Juli 008 Klssenstufen 9, 10 Aufge 1. Die Zhl 6 wird us 3 gleihen Ziffern mit Hilfe der folgenden mthemtishen Symole drgestellt: + Addition Sutrktion Multipliktion
Deprtment Mthemtik Tg der Mthemtik 5. Juli 008 Klssenstufen 9, 10 Aufge 1. Die Zhl 6 wird us 3 gleihen Ziffern mit Hilfe der folgenden mthemtishen Symole drgestellt: + Addition Sutrktion Multipliktion
Volumen und Oberfläche von Prismen und Zylindern: Das Volumen und die Oberfläche sind für alle geraden Prismen und Zylinder wie folgt zu berechnen:
 Körpererehnungen Grunwissen Grunwissen Viele mthemtishe Körper lssen sih us en eknnten geometrishen Grunkörpern zusmmensetzen: us geren Prismen, Zylinern, Kegeln, Pyrmien un Kugeln. Hinsihtlih er Oerflähen-
Körpererehnungen Grunwissen Grunwissen Viele mthemtishe Körper lssen sih us en eknnten geometrishen Grunkörpern zusmmensetzen: us geren Prismen, Zylinern, Kegeln, Pyrmien un Kugeln. Hinsihtlih er Oerflähen-
16. Minimale Spannbäume
 . Minimle Spnnäume Deinition.:. Ein ewiteter uneriteter Grp (G,w) ist ein uneriteter Grp G=(V,E) zusmmen mit einer Gewitsunktion w:e R. Ist H=(U,F), U V, F E, ein Teilrp von G, so ist s Gewit w(h) von
. Minimle Spnnäume Deinition.:. Ein ewiteter uneriteter Grp (G,w) ist ein uneriteter Grp G=(V,E) zusmmen mit einer Gewitsunktion w:e R. Ist H=(U,F), U V, F E, ein Teilrp von G, so ist s Gewit w(h) von
Berechenbarkeitstheorie 4. Vorlesung
 1 Berechenbrkeitstheorie Dr. Institut für Mthemtische Logik und Grundlgenforschung WWU Münster WS 15/16 Alle Folien unter Cretive Commons Attribution-NonCommercil 3.0 Unported Lizenz. Reguläre Ausdrücke
1 Berechenbrkeitstheorie Dr. Institut für Mthemtische Logik und Grundlgenforschung WWU Münster WS 15/16 Alle Folien unter Cretive Commons Attribution-NonCommercil 3.0 Unported Lizenz. Reguläre Ausdrücke
Technische Universität München Sommer 2016 Prof. J. Esparza / Dr. M. Luttenberger, S. Sickert 18. Juni HA-Lösung. TA-Lösung
 ehnishe niversität Münhen ommer 2016 Prof. J. Esprz / Dr. M. Luttenerger,. ikert 18. Juni 2016 HA-Lösung A-Lösung Einführung in die theoretishe Informtik Aufgenltt 8 Behten ie: oweit niht explizit ngegeen,
ehnishe niversität Münhen ommer 2016 Prof. J. Esprz / Dr. M. Luttenerger,. ikert 18. Juni 2016 HA-Lösung A-Lösung Einführung in die theoretishe Informtik Aufgenltt 8 Behten ie: oweit niht explizit ngegeen,
/LQHDUH*OHLFKXQJVV\VWHPH
 /LQHDUH*OHLFKXQJVV\VWHPH (für Grund- und Leistungskurse Mthemtik) 6W55DLQHU0DUWLQ(KUHQE UJ*\PQDVLXP)RUFKKHLP Nch dem Studium dieses Skripts sollten folgende Begriffe eknnt sein: Linere Gleichung; homogene
/LQHDUH*OHLFKXQJVV\VWHPH (für Grund- und Leistungskurse Mthemtik) 6W55DLQHU0DUWLQ(KUHQE UJ*\PQDVLXP)RUFKKHLP Nch dem Studium dieses Skripts sollten folgende Begriffe eknnt sein: Linere Gleichung; homogene
5 Vierecke. 1 Quadrat
 Viereke Shüleruhseite ((nm: Seitenereihe folgen in. Korr)) Viereke uftkt Seiten 8, 9 Seite 8 Qurt Viereksformen Seiten 0, Seite 0 Einstieg rotes Vierek: Rehtek lues Vierek: Rute grünes Vierek: Prllelogrmm
Viereke Shüleruhseite ((nm: Seitenereihe folgen in. Korr)) Viereke uftkt Seiten 8, 9 Seite 8 Qurt Viereksformen Seiten 0, Seite 0 Einstieg rotes Vierek: Rehtek lues Vierek: Rute grünes Vierek: Prllelogrmm
Grundlagen der Technischen Informatik. Bausteine der Digitaltechnik - Binäre Schalter und Gatter. Kapitel 7.1
 Busteine er Digitltehnik - Binäre Shlter un Gtter Kpitel 7. Dr.-Ing. Stefn Wilermnn ehrstuhl für rwre-softwre-co-design Entwurfsrum - Astrktionseenen SYSTEM-Eene + MODU-/RT-Eene (Register-Trnsfer) ogik-/gatter-eene
Busteine er Digitltehnik - Binäre Shlter un Gtter Kpitel 7. Dr.-Ing. Stefn Wilermnn ehrstuhl für rwre-softwre-co-design Entwurfsrum - Astrktionseenen SYSTEM-Eene + MODU-/RT-Eene (Register-Trnsfer) ogik-/gatter-eene
Hausaufgabe 2 (Induktionsbeweis):
 Prof. Dr. J. Giesl Formle Sprhen, Automten, Prozesse SS 2010 Üung 3 (Age is 12.05.2010) M. Brokshmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden
Prof. Dr. J. Giesl Formle Sprhen, Automten, Prozesse SS 2010 Üung 3 (Age is 12.05.2010) M. Brokshmidt, F. Emmes, C. Fuhs, C. Otto, T. Ströder Hinweise: Die Husufgen sollen in Gruppen von je 2 Studierenden
Aufbau- und Verwendungsanleitung für die RSS Dachrand Absturzsicherung
 Aufu- un Verwenungsnleitung für ie RSS Dhrn Asturzsiherung Demonteler Typ für Flhäher A Zwek es Systems Lut en örtlihen un europäishen Rihtlinien ist es in en meisten Fällen gesetzlih vorgeshrieen, ei
Aufu- un Verwenungsnleitung für ie RSS Dhrn Asturzsiherung Demonteler Typ für Flhäher A Zwek es Systems Lut en örtlihen un europäishen Rihtlinien ist es in en meisten Fällen gesetzlih vorgeshrieen, ei
6. Übungsblatt. (i) Von welchem Typ ist die Grammatik G? Begründen Sie Ihre Antwort kurz.
 Vorlesung Theoretische Informtik Sommersemester 2015 Prof. S. Lnge 6. Üungsltt 1. Aufge Es sei die folgende Grmmtik G = [Σ, V, S, R] gegeen. Dei seien Σ = {, } und V = {S, B}, woei S ds Strtsymol ist.
Vorlesung Theoretische Informtik Sommersemester 2015 Prof. S. Lnge 6. Üungsltt 1. Aufge Es sei die folgende Grmmtik G = [Σ, V, S, R] gegeen. Dei seien Σ = {, } und V = {S, B}, woei S ds Strtsymol ist.
Automaten mit dot erstellen
 Automten mit dot erstellen 1 Ws ist dot? dot ist ein Progrmm zum Kompilieren von dot-dteien in verschiedene Grfikformte, sowie der Nme einer Sprche, mit der mn Grphen spezifizieren knn. Unter Anderem können
Automten mit dot erstellen 1 Ws ist dot? dot ist ein Progrmm zum Kompilieren von dot-dteien in verschiedene Grfikformte, sowie der Nme einer Sprche, mit der mn Grphen spezifizieren knn. Unter Anderem können
Baustatik. Berechnung statisch unbetsimmter Tragwerke: Band 1 Baustatik I, Berechnung statisch bestimmter Tragwerke. von Raimond Dallmann. 1.
 Busttik Berehnung sttish unetsimmter Trgwerke: Bn 1 Busttik I, Berehnung sttish estimmter Trgwerke von Rimon Dmnn 1. Aufge Busttik Dmnn shne un portofrei erhätih ei ek-shop.e DIE FACHBUCHHANDLUNG Hnser
Busttik Berehnung sttish unetsimmter Trgwerke: Bn 1 Busttik I, Berehnung sttish estimmter Trgwerke von Rimon Dmnn 1. Aufge Busttik Dmnn shne un portofrei erhätih ei ek-shop.e DIE FACHBUCHHANDLUNG Hnser
Aufgaben zu Kapitel 7
 7.1 G W A B zu 7.1 zu 7.2 7.2 Ajznzmtrix: 000111 000111 000111 111000 111000 111000 G : W : : A : B : : A, B, A, B, A, B, G, W, G, W, G, W, s ist niht möglih, n Grphn ürshniungsfri zihnn. 7.3 Di Isomorphiilung
7.1 G W A B zu 7.1 zu 7.2 7.2 Ajznzmtrix: 000111 000111 000111 111000 111000 111000 G : W : : A : B : : A, B, A, B, A, B, G, W, G, W, G, W, s ist niht möglih, n Grphn ürshniungsfri zihnn. 7.3 Di Isomorphiilung
DV1_Kapitel_5.doc Seite 5-1 von 36 Rüdiger Siol 12.09.2009 16:31
 Rvensurg-Weingrten Vorlesung zur Dtenverreitung Tehnishe Informtik Inhltsverzeihnis 5 TECHNISCHE INFORMATIK...5-2 5. ENTWURF DIGITALER SYSTEME...5-2 5.2 KOMBINATIONSSCHALTUNGEN (SCHALTNETZE)...5-3 5.2.
Rvensurg-Weingrten Vorlesung zur Dtenverreitung Tehnishe Informtik Inhltsverzeihnis 5 TECHNISCHE INFORMATIK...5-2 5. ENTWURF DIGITALER SYSTEME...5-2 5.2 KOMBINATIONSSCHALTUNGEN (SCHALTNETZE)...5-3 5.2.
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 9 1. Semester ARBEITSBLATT 9 MULTIPLZIEREN MIT MEHRGLIEDRIGEN TERMEN
 Mathematik: Mag. Schmi Wolfgang Areitslatt 9 1. Semester ARBEITSBLATT 9 MULTIPLZIEREN MIT MEHRGLIEDRIGEN TERMEN Ein neues Prolem ergit sich, wenn wir mehrere mehrglierige Terme 3x+ 1 4 x = miteinaner multiplizieren
Mathematik: Mag. Schmi Wolfgang Areitslatt 9 1. Semester ARBEITSBLATT 9 MULTIPLZIEREN MIT MEHRGLIEDRIGEN TERMEN Ein neues Prolem ergit sich, wenn wir mehrere mehrglierige Terme 3x+ 1 4 x = miteinaner multiplizieren
S 1. Definition: Ein endlicher Automat ist ein 5-Tupel. Das endliche Eingabealphabet
 Der endliche Automt Modell: Eingend rechtsseitig unegrenzt F F F F F F F F F F F F F F Lesekopf S 1 Definition: Ein endlicher Automt ist ein 5-Tupel A = ( Σ;S;F;s 0 ; ϕ ) Dei ist Σ= {e 1;e 2...e n} Ds
Der endliche Automt Modell: Eingend rechtsseitig unegrenzt F F F F F F F F F F F F F F Lesekopf S 1 Definition: Ein endlicher Automt ist ein 5-Tupel A = ( Σ;S;F;s 0 ; ϕ ) Dei ist Σ= {e 1;e 2...e n} Ds
Suche in Texten. Naiver Algorithmus. Knuth-Morris-Pratt-Algorithmus. Karp-Rabin-Algorithmus
 Suhe in Texten Niver Algorithmus Knuth-Morris-Prtt-Algorithmus Krp-Rin-Algorithmus M.O.Frnz; Jnur 2008 Algorithmen und Dtenstrukturen - Textsuhe 2-1 Suhe in Texten Niver Algorithmus Knuth-Morris-Prtt-Algorithmus
Suhe in Texten Niver Algorithmus Knuth-Morris-Prtt-Algorithmus Krp-Rin-Algorithmus M.O.Frnz; Jnur 2008 Algorithmen und Dtenstrukturen - Textsuhe 2-1 Suhe in Texten Niver Algorithmus Knuth-Morris-Prtt-Algorithmus
