Formelsammlung Schließende Statistik
|
|
|
- Caroline Boer
- vor 6 Jahren
- Abrufe
Transkript
1 Prof. Dr. Philipp Sibbertsen Wirtschaftswissenschaftliche Fakultät Leibniz Universität Hannover Formelsammlung Schließende Statistik Inhaltsverzeichnis 1 Spezielle theoretische Verteilungen und Grenzwertsätze 1.1 Normalverteilung Allgemeine Normalverteilung Standardnormalverteilung Eigenschaften normalverteilter Zufallsvariablen Quantile und Schwankungsintervalle Bernoulli- und Binomialverteilung Bernoulli-Verteilung Binomialverteilung Grenzwertsätze Der Zentrale Grenzwertsatz (ZGWS Spezialfall des Zentralen Grenzwertsatzes für die Binomialverteilung 5 Grundlagen der induktiven Statistik 6.1 Tschebyschevsche Ungleichung Eigenschaften des arithmetischen Mittels Eigenschaften von Anteilswerten Erwartungswert von empirischer Varianz und Stichprobenvarianz Eigenschaften der Stichprobenfunktion = X Ȳ Punktschätzung Eigenschaften von Schätzern Maximum Likelihood-Schätzung Intervallschätzung Konfidenzintervall für den unbekannten Erwartungswert einer Grundgesamtheit Konfidenzintervall für den unbekannten Anteilswert einer Grundgesamtheit 10 5 Statistische Signifikanztests Fehler 1. und. Art Einstichprobentests Test auf einen Erwartungswert Test auf einen Anteilswert Test auf einen Median Test auf Anpassung an ein Verteilungsmodell Zweistichprobentests
2 5.3.1 Test auf Erwartungswerte bei unverbundenen Stichproben Test auf Erwartungswerte bei verbundenen Stichproben Test bei zweidimensionalen Verteilungen Test auf einen Korrelationskoeffizienten Test auf monotone Unabhängigkeit Test auf Unabhängigkeit Regressionsanalyse Das lineare Modell Bestimmtheitsmaß im einfachen linearen Modell Konfidenzintervalle Hypothesentests
3 1 Spezielle theoretische Verteilungen und Grenzwertsätze 1.1 Normalverteilung Allgemeine Normalverteilung Notation X N(µ;σ Dichtefunktion f(x = 1 σ π exp ( 1 ( x µ σ mit σ > 0 und µ R Verteilungsfunktion F(x o = x o ( 1 σ π exp 1 Erwartungswert E(X = µ Varianz V(X = σ ( x µ dx mit σ > 0 und µ R σ 1.1. Standardnormalverteilung Notation Z N(µ = 0;σ = 1 Dichtefunktion f(z = φ(z = 1 π exp ( z Verteilungsfunktion F(z = Φ(z = z ( 1 exp t dt π Standardisierungsverfahren Ist X N(µ;σ, so gilt Z := X µ N(0;1 und somit σ ( x µ F(x = P(X x = Φ = Φ(z. σ 3
4 1.1.3 Eigenschaften normalverteilter Zufallsvariablen Lineartransformation normalverteilter Zufallsvariablen Ist X N(µ;σ und Y = a+bx mit a,b R gilt: Y N(a+bµ;b σ. Linearkombination normalverteilter Zufallsvariablen Sind X i N(µ i ;σi und unabhängig, gilt: Y = ( a i X i N a i µ i ; a iσi. Symmetrie Die Normalverteilung ist symmetrisch. Damit gilt: E(X = µ = x 0,5 = x h F(µ x = 1 F(µ+x für jedes x Φ( z = 1 Φ(z Quantile und Schwankungsintervalle Quantile x 1 = µ+z 1 σ Zentrales Schwankungsintervall für normalverteilte Zufallsvariablen P(x X x 1 = P(µ+σ z X µ+σ z 1 = 1 k-faches zentrales Schwankungsintervall P(µ k σ X µ+k σ = P(X µ+k σ P(X µ k σ = Φ(k Φ( k = Φ(k 1 für k > 0 1. Bernoulli- und Binomialverteilung 1..1 Bernoulli-Verteilung Notation X BE(p 4
5 Wahrscheinlichkeitsfunktion P(X = x = Erwartungswert E(X = p Varianz V(X = p(1 p { 1 p für x = 0 p für x = Binomialverteilung Notation X B(n;p Wahrscheinlichkeitsfunktion ( n p x (1 p (n x für x = 0,1,...,n f(x = P(X = x = x 0 sonst Verteilungsfunktion F(x = P(X x = x i=0 ( n p i (1 p (n i i für x = 0,1,...,n Ableseregeln für die Verteilungstabellen für p > 0, 5 f(x;n,p = f(n x;n,1 p F(x;n,p = 1 F(n x 1;n,1 p Erwartungswert E(X = np Varianz V(X = np(1 p Quantile Zentrales Schwankungsintervall x 1 = min(x F(x 1, P(x u X x o 1 gilt mit: ( x u = max x F(x ( ; x o = min x F(x 1. Additivität der Binomialverteilung (Reproduktionseigenschaft SinddieZufallsvariablenX 1 undx voneinanderunabhängigbinomialverteiltgemäß X 1 B(n 1 ;p, X B(n ;p, gilt für die Summe der Zufallsvariablen X = X 1 +X : X B((n 1 +n ;p. 5
6 1.3 Grenzwertsätze Der Zentrale Grenzwertsatz (ZGWS Gegeben sind X 1,...,X n unabhängig, identisch verteilte Zufallsvariablen mit E(X i = µ und V(X i = σ > 0 und deren standardisierte Summe Z n = X i nµ nσ = 1 n X i µ. σ Dann konvergiert die Verteilung von Z n für n gegen die Standardnormalverteilung, also Schreibe Z n appr N(0;1. lim P(Z n z = Φ(z. n Faustregel: Der ZGWS gilt als erfüllt, wenn n Spezialfall des Zentralen Grenzwertsatzes für die Binomialverteilung Auch die Binomialverteilung konvergiert nach dem ZGWS für n gegen die Normalverteilung. Die Approximation gilt als hinreichend gut, wenn die Faustregeln: erfüllt sind. n 30, np 10 und n(1 p 10 Es ergibt sich: ( x np P(X x = F(x Φ np(1 p ( ( b np a np P(a X b Φ Φ np(1 p np(1 p Quantile x 1 = np+z 1 np(1 p, Zentrales Schwankungsintervall P(x u X x o 1 gilt mit: x u = np z 1 / np(1 p; xo = np+z 1 / np(1 p. 6
7 Grundlagen der induktiven Statistik.1 Tschebyschevsche Ungleichung Sei X eine Zufallsvariable mit E(X = µ < und V(X = σ <. Dann gilt P(µ kσ X µ+kσ 1 1 k, bzw. mit kσ = ε: P(µ ε X µ+ε 1 σ ε.. Eigenschaften des arithmetischen Mittels Es seien X 1,X,...,X n iid Stichprobenvariablen mit E(X i = µ und V(X i = σ. Dann gilt für die Stichprobenfunktion X = 1 X n i E( X = µ und V( X = σ n. Verteilung, Schwankungsintervalle (SI und Mindeststichprobenumfänge (n Situationen 1. X ist normalverteilt oder. X ist nicht normalverteilt, aber der ZGWS ist erfüllt Verteilung von X ( X N µ, σ SI n P ( µ z 1 σ n X µ+z 1 σ n = 1 ( z1 σ ( z1 σ n = L n ε Situation SI n X ist nicht normalverteilt und der ZGWS ist nicht erfüllt Mit der Tschebyschevschen Ungleichung gilt für symmetrische Intervalle um µ: P ( µ ε X µ+ε 1 σ P (µ k n σ X µ+k n σ P nε 1 1 k bzw. mit ε = k σ n : ( µ σ n X µ+ σ n 1 n σ ε = 4σ L Schwaches Gesetz der großen Zahl lim P( µ X ε = 1 bzw. plim n n 7 X = µ.
8 .3 Eigenschaften von Anteilswerten Sei i {1,...,n} : X i BE(p und damit X = n X i B(n;p. Dann gilt für die Stichprobenfunktion ˆp = X (relative Häufigkeit als Schätzer für den unbekannten n Anteilswert p einer Grundgesamtheit E(ˆp = p und V (ˆp = 1 n p(1 p. Verteilung, Schwankungsintervalle (SI und Mindeststichprobenumfänge (n Situation Verteilung von ˆp = X n ˆp appr ZGWS ist erfüllt N ( p; 1 p(1 p, somit gilt für Wahrscheinlichkeiten: n P ( ( X x x n n Φ n. n p p(1 p SI ( P p z 1 n n 4z 1 p(1 p L bzw. n z 1 L p(1 p X p+z n n 1 = z 1 p(1 p ε = z 1 4ε p(1 p = 1 n (falls p unbekannt.4 Erwartungswert von empirischer Varianz und Stichprobenvarianz Seien s (Empirische Varianz bzw. ˆσ (Stichprobenvarianz Schätzfunktionen für die unbekannte Varianz σ. Dann gilt E(s = n 1 n σ sowie E(ˆσ = σ mit ˆσ = n n 1 s = 1 n 1 (X i X..5 Eigenschaften der Stichprobenfunktion = X Ȳ Es seien X und Ȳ die arithmetischen Mittel zweier unabhängiger Stichproben mit E( X = µ X, V( X = σ X n X, E(Ȳ = µ Y, V(Ȳ = σ Y n Y. Verteilung der Stichprobenfunktion = X Ȳ ( 1. X und Y normalverteilt: N µ X µ Y ; σ X nx + σ Y n Y,.X undy nichtnormalverteilt,aberzgwserfüllt: appr N ( µ X µ Y ; σ X nx + σ Y n Y. 8
9 3 Punktschätzung 3.1 Eigenschaften von Schätzern Sei ˆθ ein Schätzer für den unbekannten Parameter(-vektor θ einer Verteilung. Unverzerrtheit (Erwartungstreue E(ˆθ = θ Verzerrung (Bias Bias(θ, ˆθ = E(ˆθ θ Asymptotische Unverzerrtheit lim E(ˆθ = θ n Mittlerer quadratischer Fehler (Mean Squared Error MSE(θ, ˆθ = E[(ˆθ θ ] = Bias(θ, ˆθ +V(ˆθ Starke Konsistenz lim MSE(θ, ˆθ = 0 n (Schwache Konsistenz lim P( ˆθ θ > ε = 0 n 3. Maximum Likelihood-Schätzung Es seien X 1,...,X n iid Zufallsvariablen mit (gegebenen Realisationen x 1,...,x n, unbekanntem Parameter(-vektor θ und der gemeinsamen Wahrscheinlichkeits- bzw. Dichtefunktion f(x 1,...,x n θ. Likelihood- und Log-Likelihoodfunktion L(θ = f(x 1,...,x n θ = lnl(θ = lnf(x i θ n f(x i θ Maximum Likelihood-Prinzip: Wähle θ gemäß L(ˆθ = max θ L(θ bzw. f(x 1,...,x n ˆθ = maxf(x 1,...,x n θ. θ Aus ln L(θ θ! = 0 ergibt sich der Maximum Likelihood-Schätzer ˆθ := ˆθ(x 1,...,x n. 9
10 4 Intervallschätzung Es sei 1 das Konfidenzniveau, z w das w-quantil der N(0;1-Verteilung, σ die Varianz der Grundgesamtheit und ˆσ ein geeigneter (erwartungstreuer Schätzer für die unbekannte Varianz der Grundgesamtheit. Weiterhin bezeichnen X bzw. ˆp erwartungstreue Schätzer für den gesuchten unbekannten Parameter der Grundgesamtheit. L = ε bezeichnet die Länge des KIs. 4.1 Konfidenzintervall für den unbekannten Erwartungswert einer Grundgesamtheit Situation 1: σ ist bekannt Situationen Konfidenzintervall Mindeststichprobenumfang 1. X ist normalverteilt oder. X ist nicht normalverteilt, aber n 30 [ ] X σ ±z1 n ( z1 σ ( z1 σ n = L ε Situation X ist nicht normalverteilt, n < 30 [ ] Konfidenzintervall X ± σ n ( Mindeststichprobenumfang n = σ σ L ε Situation : σ ist unbekannt und muss mit ˆσ geschätzt werden Situation X ist normalverteilt, n < 30 [ ] Konfidenzintervall X ˆσ ±tn 1,1 n Mindeststichprobenumfang nicht bestimmbar Situation X ist beliebig verteilt und n 30 [ ] Konfidenzintervall X ˆσ ±z1 n Mindeststichprobenumfang nicht bestimmbar Situation X ist nicht normalverteilt, ZGWS nicht erfüllt kein Konfidenzintervall bestimmbar 10
11 4. Konfidenzintervall für den unbekannten Anteilswert einer Grundgesamtheit Situation Konfidenzintervall ZGWS für Binomialverteilung nicht erfüllt [ ] ˆp± 1 4n Mindeststichprobenumfang n 1 L = 1 4ε Situation ZGWS für Binomialverteilung erfüllt: Konfidenzintervall Mindeststichprobenumfang n ( z1 L n 30, nˆp 10, n(1 ˆp 10 [ ] ˆp(1 ˆp ˆp±z 1 n = ( z1 ε 5 Statistische Signifikanztests Es bezeichnet H 0 die Nullhypothese und H 1 die Alternativhypothese. Weiterhin bezeichnet das Signifikanzniveau des Tests. 5.1 Fehler 1. und. Art Realität \ Testentscheidung H 0 ablehnen H 0 nicht ablehnen H 0 wahr Fehler 1. Art richtige Entscheidung H 1 wahr richtige Entscheidung Fehler. Art p-wert: Das Signifikanzniveau, bei dem die Nullhypothese gerade noch abgelehnt werden kann. Ist das Signifikanzniveau kleiner als der p-wert, kann die Nullhypothese somit nicht mehr verworfen werden. 11
12 5. Einstichprobentests 5..1 Test auf einen Erwartungswert Weiterhin bezeichnet σ die Varianz der Grundgesamtheit. Ist diese unbekannt, muss sie durch eine geeignete Schätzfunktion ˆσ für die unbekannte Varianz geschätzt werden. µ 0 ist der vorzugebende Wert, auf den der unbekannte Erwartungswert µ der Grundgesamtheit getestet werden soll. X ist dabei ein erwartungstreuer Schätzer für den unbekannten Parameter µ. Hypothesenpaar: H 0 : µ = µ 0 H 1 : µ µ 0 H 0 : µ µ 0 H 1 : µ > µ 0 H 0 : µ µ 0 H 1 : µ < µ 0 Situationen: 1. X ist normalverteilt, σ ist bekannt oder. X ist nicht normalverteilt, aber n 30, σ ist bekannt. Prüfgröße: Z = X µ 0 σ n Situation: X ist beliebig verteilt, σ ist unbekannt, n 30 Prüfgröße: Z = X µ 0 ˆσ n Z > z 1 Lehne H 0 ab, falls Z > z 1 Z < z 1 Situation: X ist normalverteilt, aber n < 30, σ ist unbekannt Prüfgröße: T = X µ 0 ˆσ n T > t n 1,1 Lehne H 0 ab, falls T > t n 1,1 T < t n 1,1 1
13 5.. Test auf einen Anteilswert Es ist p 0 der vorzugebende Wert, auf den der unbekannte Anteilswert p der Grundgesamtheit getestet werden soll. ˆp ist dabei ein erwartungstreuer Schätzer für den unbekannten Parameter p. Situation: ZGWS für Binomialverteilung erfüllt: n 30, np 0 10, n(1 p 0 10 Hypothesenpaar: H 0 : p = p 0 H 1 : p p 0 H 0 : p p 0 H 1 : p > p 0 H 0 : p p 0 H 1 : p < p 0 Prüfgröße: Z = ˆp p 0 n p0 (1 p 0 Z > z 1 Lehne H 0 ab, falls Z > z 1 Z < z 1 Situation: ZGWS für Binomialverteilung nicht erfüllt (Binomialtest Hypothesenpaar: H 0 : p = p 0 H 1 : p p 0 H 0 : p p 0 H 1 : p > p 0 H 0 : p p 0 H 1 : p < p 0 Prüfgröße: X:= Anzahl der Erfolge, d.h. die Anzahl des Auftretens des Ereignisses, das unter H 0 mit Wahrscheinlichkeit p 0 eintritt Lehne H 0 ab, falls X < c u oder X > c o X > c o X < c u Die kritischen Werte des Binomialtests können der Verteilungstabelle einer mit n und p 0 binomialverteilten Zufallsvariablen X entnommen werden: Zweiseitiger Binomialtest: c u = x (x F(x;n,p = min 0 c o = x 1 (x F(x;n,p = min 0 1 Einseitiger Binomialtest: c u = x = min(x F(x;n,p 0 c o = x 1 = min(x F(x;n,p
14 5..3 Test auf einen Median Situation: Der Median x 0,5 wird auf einen vorgegebenen Wert x 0 getestet. Hypothesenpaar: H 0 : x 0,5 = x 0 H 0 : x 0,5 x 0 H 0 : x 0,5 x 0 H 1 : x 0,5 x 0 H 1 : x 0,5 > x 0 H 1 : x 0,5 < x 0 Prüfgröße ZGWS nicht erfüllt: n + = n(x i x 0 ZGWS erfüllt: Z = ˆp p n 0 p0 (1 p 0 mit ˆp = n+ n und p 0 = 0,5 Entscheidungsregeln und kritische Werte können Abschnitt 5.. entnommen werden Test auf Anpassung an ein Verteilungsmodell Situation: Es wird die Nullypothese getestet, ob das Merkmal X in der Grundgesamtheit dem Verteilungsmodell F 0 folgt. Hierzu werden die bei GültigkeitdesModellserwartetenHäufigkeitenñ i denempirischen Häufigkeiten gegenübergestellt. Hypothesenpaar: H 0 : X F 0 H 1 : X F 0 Prüfgröße: X = k (n i ñ i ñ i Lehne H 0 ab, falls X > χ ν,1 Anmerkung 1: Die Anzahl der Freiheitsgrade ν ist gleich der um 1 verringerten Anzahl der Klassen, abzüglich der Anzahl der geschätzten Parameter m: ν = k m 1. Anmerkung : Der Test ist nur anwendbar, falls alle erwarteten Häufigkeiten größer oder gleich 5 sind: i : ñ i 5. Falls diese Bedingung nicht erfüllt ist, müssen benachbarte Klassen zusammengefasst werden. 14
15 5.3 Zweistichprobentests Es ist k 0 der vorzugebende Wert, auf den die unbekannte Differenz der Erwartungswerte von X und Y in der Grundgesamtheit getestet werden soll. X und Y sind dabei erwartungstreue Schätzer für die unbekannten Parameter µ X und µ Y Test auf Erwartungswerte bei unverbundenen Stichproben Situation: Es liegt ein unverbundenes Zweistichprobenproblem vor. 1. X und Y normalverteilt, Varianzen bekannt oder. X und Y beliebig verteilt, aber n X,n Y 30, Varianz(en unbekannt Hypothesenpaar: H 0 : µ X µ Y = k 0 H 0 : µ X µ Y k 0 H 0 : µ X µ Y k 0 H 1 : µ X µ Y k 0 H 1 : µ X µ Y > k 0 H 1 : µ X µ Y < k 0 Prüfgröße: Z = X Y k 0 σ Y n Y + σ X nx Im Falle unbekannter Varianzen müssen σx, σ Y durch die Schätzungen ˆσ X, ˆσ Y ersetzt werden. Z > z 1 Lehne H 0 ab, falls Z > z 1 Z < z 1 Anmerkung: Sind X und Y normalverteilt, n X,n Y < 30 und die Varianzen unbekannt, so ist die obige Prüfgröße t ν -verteilt mit ν = ν ist auf eine ganze Zahl abzurunden. (ˆσ X + ˆσ Y n X n Y 1 n X 1 ˆσ X n X + 1 n Y 1 ˆσ Y n Y. 15
16 5.3. Test auf Erwartungswerte bei verbundenen Stichproben Situation: Es liegt ein verbundenes Zweistichprobenproblem vor. X und Y seien normalverteilt mit unbekannten Varianzen. Die Entscheidung erfolgt auf Basis der Differenz D = X Y. Hypothesenpaar: H 0 : µ D = k 0 H 0 : µ D k 0 H 0 : µ D k 0 H 1 : µ D k 0 H 1 : µ D > k 0 H 1 : µ D < k 0 Prüfgröße: T = D k 0 n ˆσ D mit ˆσ D = 1 n 1 (D i D = n n 1 (D D sowie D = 1 n D i = X Y T > t n 1,1 Lehne H 0 ab, falls T > t n 1,1 T < t n 1,1 Anmerkung: Dieser Test kann in großen Stichproben mit n X, n Y 30, wie die vorangegangenen Tests, auch ohne weitere Verteilungsannahmen für X und Y als Z-Test mit kritischen Werten der Normalverteilung durchgeführt werden. 16
17 5.4 Test bei zweidimensionalen Verteilungen Test auf einen Korrelationskoeffizienten Situation: X und Y sind normalverteilt. Hypothesenpaar: H 0 : ρ = 0 H 0 : ρ 0 H 0 : ρ 0 H 1 : ρ 0 H 1 : ρ > 0 H 1 : ρ < 0 Prüfgröße: T = r n 1 r Dabei bezeichnet r den empirischen Korrelationskoeffizienten. T > t n,1 Lehne H 0 ab, falls T > t n,1 T < t n,1 Situation: X und Y sind normalverteilt, n 30. Hypothesenpaar: H 0 : ρ = ρ 0 H 0 : ρ ρ 0 H 0 : ρ ρ 0 H 1 : ρ ρ 0 H 1 : ρ > ρ 0 H 1 : ρ < ρ 0 Prüfgröße: Z = 1 ( ( ( 1+r 1+ρ0 n 3 ln ln 1 r 1 ρ 0 Dabei bezeichnet r den empirischen Korrelationskoeffizienten. Z > z 1 Lehne H 0 ab, falls Z > z 1 Z < z 1 17
18 5.4. Test auf monotone Unabhängigkeit Situation: X und Y sind mindestens ordinal-skalierte Einzelwerte, n 30. Hypothesenpaar: H 0 : X und Y sind monoton unabhängig H 1 : X und Y sind monoton abhängig Prüfgröße: Z = r s n 1 Dabei bezeichnet r s den Rangkorrelationskoeffizienten von Spearman. Lehne H 0 ab, falls Z > z Test auf Unabhängigkeit Situation: Es liegt eine Kontingenztabelle vor. Das Skalenniveau ist beliebig, es wird kein Verteilungsmodell unterstellt. Hypothesenpaar: H 0 : X und Y sind unabhängig H 1 : X und Y sind abhängig Prüfgröße: Prüfgröße ist der χ -Koeffizient zu X und Y χ = J L (n jl ñ jl ñ j=1 jl l=1 Lehne H 0 ab, falls χ > χ (L 1(J 1,1 Anmerkung: Der Test ist nur anwendbar, falls alle erwarteten Häufigkeiten größer oder gleich 5 sind: ñ jl 5 für alle j,l. Falls diese Bedingung nicht erfüllt ist, müssen benachbarte Klassen zusammengefasst werden. 18
19 6 Regressionsanalyse Die in den folgenden Formeln enthaltenen Summen werden wie folgt abgekürzt: - aus Einzeldaten: Σ x := n x i, Σ xx := n x i, Σ y := n y i, Σ yy := n yi - aus Korrelationstabelle: Σ x := J x j n j, Σ xx := J x j n j, Σ y := L y l n l, Σ yy := L j=1 Σ xy := J j=1l=1 L x j y l n jl j=1 l=1 Σ xy := n x i y i yl n l, l=1 6.1 Das lineare Modell Kleinste Quadrate-Ausgleichsgerade ŷ i = â+ˆbx i KQ-Schätzer für den Steigungskoeffizienten ˆb = (xi x(y i ȳ (xi x KQ-Schätzer für die Konstante Residuen geschätzte Störgrößenvarianz ˆσ = 1 n û i = 1 n = s xy s x â = ȳ ˆb x û i = y i ŷ i geschätzte Varianz der geschätzten Konstanten x ˆσ â = i ˆσ n ( x i n x = nσ xy Σ x Σ y xy x ȳ = nσ xx (Σ x x x (y i â ˆb x i = n ( s y n 1 s xy s x geschätzte Varianz des geschätzten Steigungskoeffizienten ˆσ ˆb = ˆσ x i n x = ˆσ n s x 19
20 6. Bestimmtheitsmaß im einfachen linearen Modell R = r = = (ŷ i ȳ = (y i ȳ s ŷ s y = ˆb s x s y = [ (x i x(y i ȳ ] = 1 (x i x (y i ȳ (nσ xy Σ x Σ y [ nσxx (Σ x ][ nσ yy (Σ y ] û i (y i ȳ 6.3 Konfidenzintervalle Unter der Annahme u i N(0;σ für alle i gilt: für den Modellparameter a: für den Modellparameter b: [â±tn, 1 ˆσ ] â ] [ˆb±tn, 1 ˆσˆb Anmerkung: Wenn n 30 ist, wird t n, 1 durch z 1 ersetzt. 6.4 Hypothesentests Es sind a 0 bzw. b 0 die vorzugebenden Werte, auf die die Modellparameter getestet werden sollen. Unter der Annahme u i N(0,σ für alle i gilt: Hypothesen: H 0 : a = a 0 H 1 : a a 0 H 0 : a a 0 H 1 : a > a 0 H 0 : a a 0 H 1 : a < a 0 Prüfgröße: T = â a 0 ˆσâ Entscheidung Lehne H 0 ab, falls T > t n,1 T > t n,1 T < t n,1 Anmerkung: Wenn n 30, werden die Normalverteilungsquantile als kritische Werte benutzt. 0
21 Hypothesen: H 0 : b = b 0 H 1 : b b 0 H 0 : b b 0 H 1 : b > b 0 H 0 : b b 0 H 1 : b < b 0 Prüfgröße: T = ˆb b 0 ˆσˆb Lehne H 0 ab, falls T > t n,1 T > t n,1 T < t n,1 Anmerkung 1: Wenn n 30, werden die Normalverteilungsquantile als kritische Werte benutzt. Anmerkung :Esgilt: ˆb 0 = r n ˆσˆb 1 r, sodass fürdietests aufh 0 : b = 0bzw. H 0 : b 0, H 0 : b 0 die Prüfgröße auch aus T = r n 1 r berechnet werden kann. 1
Philipp Sibbertsen Hartmut Lehne. Statistik. Einführung für Wirtschafts- und. Sozialwissenschaftler. 2., überarbeitete Auflage. 4^ Springer Gabler
 Philipp Sibbertsen Hartmut Lehne Statistik Einführung für Wirtschafts- und Sozialwissenschaftler 2., überarbeitete Auflage 4^ Springer Gabler Inhaltsverzeichnis Teil I Deskriptive Statistik 1 Einführung
Philipp Sibbertsen Hartmut Lehne Statistik Einführung für Wirtschafts- und Sozialwissenschaftler 2., überarbeitete Auflage 4^ Springer Gabler Inhaltsverzeichnis Teil I Deskriptive Statistik 1 Einführung
Wichtige Definitionen und Aussagen
 Wichtige Definitionen und Aussagen Zufallsexperiment, Ergebnis, Ereignis: Unter einem Zufallsexperiment verstehen wir einen Vorgang, dessen Ausgänge sich nicht vorhersagen lassen Die möglichen Ausgänge
Wichtige Definitionen und Aussagen Zufallsexperiment, Ergebnis, Ereignis: Unter einem Zufallsexperiment verstehen wir einen Vorgang, dessen Ausgänge sich nicht vorhersagen lassen Die möglichen Ausgänge
Einführung in die Induktive Statistik: Testen von Hypothesen
 Einführung in die Induktive Statistik: Testen von Hypothesen Jan Gertheiss LMU München Sommersemester 2011 Vielen Dank an Christian Heumann für das Überlassen von TEX-Code! Testen: Einführung und Konzepte
Einführung in die Induktive Statistik: Testen von Hypothesen Jan Gertheiss LMU München Sommersemester 2011 Vielen Dank an Christian Heumann für das Überlassen von TEX-Code! Testen: Einführung und Konzepte
Statistik I für Betriebswirte Vorlesung 14
 Statistik I für Betriebswirte Vorlesung 14 Dr. Andreas Wünsche TU Bergakademie Freiberg Institut für Stochastik 13. Juli 017 Dr. Andreas Wünsche Statistik I für Betriebswirte Vorlesung 14 Version: 8. Juli
Statistik I für Betriebswirte Vorlesung 14 Dr. Andreas Wünsche TU Bergakademie Freiberg Institut für Stochastik 13. Juli 017 Dr. Andreas Wünsche Statistik I für Betriebswirte Vorlesung 14 Version: 8. Juli
0 sonst. a) Wie lautet die Randwahrscheinlichkeitsfunktion von Y? 0.5 y = 1
 Aufgabe 1 (2 + 2 + 2 + 1 Punkte) Gegeben sei folgende gemeinsame Wahrscheinlichkeitsfunktion f(x, y) = P (X = x, Y = y) der Zufallsvariablen X und Y : 0.2 x = 1, y = 1 0.3 x = 2, y = 1 f(x, y) = 0.45 x
Aufgabe 1 (2 + 2 + 2 + 1 Punkte) Gegeben sei folgende gemeinsame Wahrscheinlichkeitsfunktion f(x, y) = P (X = x, Y = y) der Zufallsvariablen X und Y : 0.2 x = 1, y = 1 0.3 x = 2, y = 1 f(x, y) = 0.45 x
3 Grundlagen statistischer Tests (Kap. 8 IS)
 3 Grundlagen statistischer Tests (Kap. 8 IS) 3.1 Beispiel zum Hypothesentest Beispiel: Betrachtet wird eine Abfüllanlage für Mineralwasser mit dem Sollgewicht µ 0 = 1000g und bekannter Standardabweichung
3 Grundlagen statistischer Tests (Kap. 8 IS) 3.1 Beispiel zum Hypothesentest Beispiel: Betrachtet wird eine Abfüllanlage für Mineralwasser mit dem Sollgewicht µ 0 = 1000g und bekannter Standardabweichung
6. Schätzverfahren für Parameter
 6. Schätzverfahren für Parameter Ausgangssituation: Ein interessierender Zufallsvorgang werde durch die ZV X repräsentiert X habe eine unbekannte Verteilungsfunktion F X (x) Wir interessieren uns für einen
6. Schätzverfahren für Parameter Ausgangssituation: Ein interessierender Zufallsvorgang werde durch die ZV X repräsentiert X habe eine unbekannte Verteilungsfunktion F X (x) Wir interessieren uns für einen
Fit for Abi & Study Stochastik
 Fit for Abi & Study Stochastik Prof. Dr. Tilla Schade Hochschule Harz 15. und 16. April 2014 No. 1 Stochastik besteht aus: Wahrscheinlichkeitsrechnung Statistik No. 2 Gliederung Grundlagen Zufallsgrößen
Fit for Abi & Study Stochastik Prof. Dr. Tilla Schade Hochschule Harz 15. und 16. April 2014 No. 1 Stochastik besteht aus: Wahrscheinlichkeitsrechnung Statistik No. 2 Gliederung Grundlagen Zufallsgrößen
FORMELSAMMLUNG STATISTIK B
 Somersemester 2012 FORMELSAMMLUNG STATISTIK B Prof. Kneip / Dr. Scheer / Dr. Arns Version vom April 2012 Inhaltsverzeichnis 1 Wahrscheinlichkeitsrechnung 2 2 Diskrete Zufallsvariablen 5 3 Stetige Zufallsvariablen
Somersemester 2012 FORMELSAMMLUNG STATISTIK B Prof. Kneip / Dr. Scheer / Dr. Arns Version vom April 2012 Inhaltsverzeichnis 1 Wahrscheinlichkeitsrechnung 2 2 Diskrete Zufallsvariablen 5 3 Stetige Zufallsvariablen
Theorie Parameterschätzung Ausblick. Schätzung. Raimar Sandner. Studentenseminar "Statistische Methoden in der Physik"
 Studentenseminar "Statistische Methoden in der Physik" Gliederung 1 2 3 Worum geht es hier? Gliederung 1 2 3 Stichproben Gegeben eine Beobachtungsreihe x = (x 1, x 2,..., x n ): Realisierung der n-dimensionalen
Studentenseminar "Statistische Methoden in der Physik" Gliederung 1 2 3 Worum geht es hier? Gliederung 1 2 3 Stichproben Gegeben eine Beobachtungsreihe x = (x 1, x 2,..., x n ): Realisierung der n-dimensionalen
Statistik II. Statistische Tests. Statistik II
 Statistik II Statistische Tests Statistik II - 12.5.2006 1 Test auf Anteilswert: Binomialtest Sei eine Stichprobe unabhängig, identisch verteilter ZV (i.i.d.). Teile diese Stichprobe in zwei Teilmengen
Statistik II Statistische Tests Statistik II - 12.5.2006 1 Test auf Anteilswert: Binomialtest Sei eine Stichprobe unabhängig, identisch verteilter ZV (i.i.d.). Teile diese Stichprobe in zwei Teilmengen
Wahrscheinlichkeit und Statistik: Zusammenfassung
 HSR Hochschule für Technik Rapperswil Wahrscheinlichkeit und Statistik: Zusammenfassung beinhaltet Teile des Skripts von Herrn Hardy von Lukas Wilhelm lwilhelm.net 12. Januar 2007 Inhaltsverzeichnis 1
HSR Hochschule für Technik Rapperswil Wahrscheinlichkeit und Statistik: Zusammenfassung beinhaltet Teile des Skripts von Herrn Hardy von Lukas Wilhelm lwilhelm.net 12. Januar 2007 Inhaltsverzeichnis 1
Statistik. Sommersemester Prof. Dr. Stefan Etschberger HSA. für Betriebswirtschaft und International Management
 Statistik für Betriebswirtschaft und International Management Sommersemester 2014 Prof. Dr. Stefan Etschberger HSA Streuungsparameter Varianz Var(X) bzw. σ 2 : [x i E(X)] 2 f(x i ), wenn X diskret Var(X)
Statistik für Betriebswirtschaft und International Management Sommersemester 2014 Prof. Dr. Stefan Etschberger HSA Streuungsparameter Varianz Var(X) bzw. σ 2 : [x i E(X)] 2 f(x i ), wenn X diskret Var(X)
Dynamische Systeme und Zeitreihenanalyse // Multivariate Normalverteilung und ML Schätzung 11 p.2/38
 Dynamische Systeme und Zeitreihenanalyse Multivariate Normalverteilung und ML Schätzung Kapitel 11 Statistik und Mathematik WU Wien Michael Hauser Dynamische Systeme und Zeitreihenanalyse // Multivariate
Dynamische Systeme und Zeitreihenanalyse Multivariate Normalverteilung und ML Schätzung Kapitel 11 Statistik und Mathematik WU Wien Michael Hauser Dynamische Systeme und Zeitreihenanalyse // Multivariate
Einführung in die Statistik
 Einführung in die Statistik Analyse und Modellierung von Daten Von Prof. Dr. Rainer Schlittgen 4., überarbeitete und erweiterte Auflage Fachbereich Materialwissenschaft! der Techn. Hochschule Darmstadt
Einführung in die Statistik Analyse und Modellierung von Daten Von Prof. Dr. Rainer Schlittgen 4., überarbeitete und erweiterte Auflage Fachbereich Materialwissenschaft! der Techn. Hochschule Darmstadt
Zufallsvariablen. Diskret. Stetig. Verteilung der Stichprobenkennzahlen. Binomial Hypergeometrisch Poisson. Normal Lognormal Exponential
 Zufallsvariablen Diskret Binomial Hypergeometrisch Poisson Stetig Normal Lognormal Exponential Verteilung der Stichprobenkennzahlen Stetige Zufallsvariable Verteilungsfunktion: Dichtefunktion: Integralrechnung:
Zufallsvariablen Diskret Binomial Hypergeometrisch Poisson Stetig Normal Lognormal Exponential Verteilung der Stichprobenkennzahlen Stetige Zufallsvariable Verteilungsfunktion: Dichtefunktion: Integralrechnung:
1.1.1 Ergebnismengen Wahrscheinlichkeiten Formale Definition der Wahrscheinlichkeit Laplace-Experimente...
 Inhaltsverzeichnis 0 Einführung 1 1 Zufallsvorgänge und Wahrscheinlichkeiten 5 1.1 Zufallsvorgänge.......................... 5 1.1.1 Ergebnismengen..................... 6 1.1.2 Ereignisse und ihre Verknüpfung............
Inhaltsverzeichnis 0 Einführung 1 1 Zufallsvorgänge und Wahrscheinlichkeiten 5 1.1 Zufallsvorgänge.......................... 5 1.1.1 Ergebnismengen..................... 6 1.1.2 Ereignisse und ihre Verknüpfung............
Institut für Stochastik Prof. Dr. N. Henze Dipl.-Math. V. Riess
 Institut für Stochastik Prof. Dr. N. Henze Dipl.-Math. V. Riess Name: Vorname: Matrikelnummer: Lösungsvorschlag zur Klausur zur Vorlesung Wahrscheinlichkeitstheorie und Statistik (Stochastik) Datum: 07.
Institut für Stochastik Prof. Dr. N. Henze Dipl.-Math. V. Riess Name: Vorname: Matrikelnummer: Lösungsvorschlag zur Klausur zur Vorlesung Wahrscheinlichkeitstheorie und Statistik (Stochastik) Datum: 07.
5. Spezielle stetige Verteilungen
 5. Spezielle stetige Verteilungen 5.1 Stetige Gleichverteilung Eine Zufallsvariable X folgt einer stetigen Gleichverteilung mit den Parametern a und b, wenn für die Dichtefunktion von X gilt: f x = 1 für
5. Spezielle stetige Verteilungen 5.1 Stetige Gleichverteilung Eine Zufallsvariable X folgt einer stetigen Gleichverteilung mit den Parametern a und b, wenn für die Dichtefunktion von X gilt: f x = 1 für
Klassifikation von Signifikanztests
 Klassifikation von Signifikanztests Nach Verteilungsannahmen: verteilungsabhängig: parametrischer [parametric] Test verteilungsunabhängig: nichtparametrischer [non-parametric] Test Bei parametrischen Tests
Klassifikation von Signifikanztests Nach Verteilungsannahmen: verteilungsabhängig: parametrischer [parametric] Test verteilungsunabhängig: nichtparametrischer [non-parametric] Test Bei parametrischen Tests
Kapitel 3 Schließende Statistik
 Motivation Grundgesamtheit mit unbekannter Verteilung F Stichprobe X 1,...,X n mit Verteilung F Realisation x 1,...,x n der Stichprobe Rückschluss auf F Dr. Karsten Webel 160 Motivation (Fortsetzung) Kapitel
Motivation Grundgesamtheit mit unbekannter Verteilung F Stichprobe X 1,...,X n mit Verteilung F Realisation x 1,...,x n der Stichprobe Rückschluss auf F Dr. Karsten Webel 160 Motivation (Fortsetzung) Kapitel
Klausur zu Statistik II
 GOETHE-UNIVERSITÄT FRANKFURT FB Wirtschaftswissenschaften Statistik und Methoden der Ökonometrie Prof. Dr. Uwe Hassler Wintersemester 03/04 Klausur zu Statistik II Matrikelnummer: Hinweise Hilfsmittel
GOETHE-UNIVERSITÄT FRANKFURT FB Wirtschaftswissenschaften Statistik und Methoden der Ökonometrie Prof. Dr. Uwe Hassler Wintersemester 03/04 Klausur zu Statistik II Matrikelnummer: Hinweise Hilfsmittel
3 Statistische Schätzungen
 3 Statistische Schätzungen In der Wahrscheinlichkeitstheorie geht es darum, über Modelle Ereignisse zu bewerten bzw. Voraussagen über ihr Eintreten zu treffen. Sind nun umgekehrt Daten bekannt, und wollen
3 Statistische Schätzungen In der Wahrscheinlichkeitstheorie geht es darum, über Modelle Ereignisse zu bewerten bzw. Voraussagen über ihr Eintreten zu treffen. Sind nun umgekehrt Daten bekannt, und wollen
Statistik I für Betriebswirte Vorlesung 13
 Statistik I für Betriebswirte Vorlesung 13 Dr. Andreas Wünsche TU Bergakademie Freiberg Institut für Stochastik 6. Juli 2017 Dr. Andreas Wünsche Statistik I für Betriebswirte Vorlesung 13 Version: 7. Juli
Statistik I für Betriebswirte Vorlesung 13 Dr. Andreas Wünsche TU Bergakademie Freiberg Institut für Stochastik 6. Juli 2017 Dr. Andreas Wünsche Statistik I für Betriebswirte Vorlesung 13 Version: 7. Juli
Klassifikation von Signifikanztests
 Klassifikation von Signifikanztests nach Verteilungsannahmen: verteilungsabhängige = parametrische Tests verteilungsunabhängige = nichtparametrische Tests Bei parametrischen Tests werden im Modell Voraussetzungen
Klassifikation von Signifikanztests nach Verteilungsannahmen: verteilungsabhängige = parametrische Tests verteilungsunabhängige = nichtparametrische Tests Bei parametrischen Tests werden im Modell Voraussetzungen
Bestimmte Zufallsvariablen sind von Natur aus normalverteilt. - naturwissenschaftliche Variablen: originär z.b. Intelligenz, Körpergröße, Messfehler
 6.6 Normalverteilung Die Normalverteilung kann als das wichtigste Verteilungsmodell der Statistik angesehen werden. Sie wird nach ihrem Entdecker auch Gaußsche Glockenkurve genannt. Die herausragende Stellung
6.6 Normalverteilung Die Normalverteilung kann als das wichtigste Verteilungsmodell der Statistik angesehen werden. Sie wird nach ihrem Entdecker auch Gaußsche Glockenkurve genannt. Die herausragende Stellung
Verteilung von Summen
 Verteilung von Summen Beispiel: Würfelwurf Frage: Wie verhält sich die Verteilung der Augensumme von -Würfeln bei wachsendem? Zur Beantwortung führen wir ein Simulationseperiment durch. 6 Würfe mit 1 Würfel
Verteilung von Summen Beispiel: Würfelwurf Frage: Wie verhält sich die Verteilung der Augensumme von -Würfeln bei wachsendem? Zur Beantwortung führen wir ein Simulationseperiment durch. 6 Würfe mit 1 Würfel
Kapitel 3 Schließende Statistik
 Beispiel 3.4: (Fortsetzung Bsp. 3.) bekannt: 65 i=1 X i = 6, also ˆp = X = 6 65 = 0, 4 Überprüfen der Voraussetzungen: (1) n = 65 30 () n ˆp = 6 10 (3) n (1 ˆp) = 39 10 Dr. Karsten Webel 194 Beispiel 3.4:
Beispiel 3.4: (Fortsetzung Bsp. 3.) bekannt: 65 i=1 X i = 6, also ˆp = X = 6 65 = 0, 4 Überprüfen der Voraussetzungen: (1) n = 65 30 () n ˆp = 6 10 (3) n (1 ˆp) = 39 10 Dr. Karsten Webel 194 Beispiel 3.4:
5. Schließende Statistik (Inferenzstatistik, konfirmatorische Verfahren)
 5. Schließende Statistik (Inferenzstatistik, konfirmatorische Verfahren) 5.1. Einführung Schätzen unbekannter Parameter im Modell, z.b. Wahrscheinlichkeiten p i (Anteile in der Gesamtmenge), Erwartungswerte
5. Schließende Statistik (Inferenzstatistik, konfirmatorische Verfahren) 5.1. Einführung Schätzen unbekannter Parameter im Modell, z.b. Wahrscheinlichkeiten p i (Anteile in der Gesamtmenge), Erwartungswerte
DWT 2.1 Maximum-Likelihood-Prinzip zur Konstruktion von Schätzvariablen 330/467 Ernst W. Mayr
 2.1 Maximum-Likelihood-Prinzip zur Konstruktion von Schätzvariablen Wir betrachten nun ein Verfahren zur Konstruktion von Schätzvariablen für Parameter von Verteilungen. Sei X = (X 1,..., X n ). Bei X
2.1 Maximum-Likelihood-Prinzip zur Konstruktion von Schätzvariablen Wir betrachten nun ein Verfahren zur Konstruktion von Schätzvariablen für Parameter von Verteilungen. Sei X = (X 1,..., X n ). Bei X
Stichwortverzeichnis. Robert Galata, Sandro Scheid. Deskriptive und Induktive Statistik für Studierende der BWL. Methoden - Beispiele - Anwendungen
 Stichwortverzeichnis Robert Galata, Sandro Scheid Deskriptive und Induktive Statistik für Studierende der BWL Methoden - Beispiele - Anwendungen Herausgegeben von Robert Galata, Markus Wessler ISBN (Buch):
Stichwortverzeichnis Robert Galata, Sandro Scheid Deskriptive und Induktive Statistik für Studierende der BWL Methoden - Beispiele - Anwendungen Herausgegeben von Robert Galata, Markus Wessler ISBN (Buch):
Grundidee. χ 2 Tests. Ausgangspunkt: Klasseneinteilung der Beobachtungen in k Klassen. Grundidee. Annahme: Einfache Zufallsstichprobe (X 1,..., X n ).
 Grundidee χ 2 -Anpassungstest χ 2 -Unabhängigkeitstest χ 2 -Homogenitätstest χ 2 Tests Grundidee Ausgangspunkt: Klasseneinteilung der Beobachtungen in k Klassen Annahme: Einfache Zufallsstichprobe (X 1,,
Grundidee χ 2 -Anpassungstest χ 2 -Unabhängigkeitstest χ 2 -Homogenitätstest χ 2 Tests Grundidee Ausgangspunkt: Klasseneinteilung der Beobachtungen in k Klassen Annahme: Einfache Zufallsstichprobe (X 1,,
Die Familie der χ 2 (n)-verteilungen
 Die Familie der χ (n)-verteilungen Sind Z 1,..., Z m für m 1 unabhängig identisch standardnormalverteilte Zufallsvariablen, so genügt die Summe der quadrierten Zufallsvariablen χ := m Z i = Z 1 +... +
Die Familie der χ (n)-verteilungen Sind Z 1,..., Z m für m 1 unabhängig identisch standardnormalverteilte Zufallsvariablen, so genügt die Summe der quadrierten Zufallsvariablen χ := m Z i = Z 1 +... +
Häufigkeiten. Verteilungen. Lageparameter Mittelwert. oder
 Formelsammlung Beschreibende Statistik Univariate Häufigkeitsverteilungen X ist ein diskretes Merkmal, mit k Ausprägungen TR: Mode 2 1 = AC absolute relative Häufigkeit Häufigkeiten Bivariate Häufigkeitsverteilungen
Formelsammlung Beschreibende Statistik Univariate Häufigkeitsverteilungen X ist ein diskretes Merkmal, mit k Ausprägungen TR: Mode 2 1 = AC absolute relative Häufigkeit Häufigkeiten Bivariate Häufigkeitsverteilungen
Einführung in die Statistik für Wirtschaftswissenschaftler für Betriebswirtschaft und Internationales Management
 Einführung in die Statistik für Wirtschaftswissenschaftler für Betriebswirtschaft und Internationales Management Sommersemester 2013 Hochschule Augsburg Lageparameter: Erwartungswert d) Erwartungswert
Einführung in die Statistik für Wirtschaftswissenschaftler für Betriebswirtschaft und Internationales Management Sommersemester 2013 Hochschule Augsburg Lageparameter: Erwartungswert d) Erwartungswert
Inhaltsverzeichnis. Robert Galata, Sandro Scheid. Deskriptive und Induktive Statistik für Studierende der BWL. Methoden - Beispiele - Anwendungen
 Inhaltsverzeichnis Robert Galata, Sandro Scheid Deskriptive und Induktive Statistik für Studierende der BWL Methoden - Beispiele - Anwendungen Herausgegeben von Robert Galata, Markus Wessler ISBN (Buch):
Inhaltsverzeichnis Robert Galata, Sandro Scheid Deskriptive und Induktive Statistik für Studierende der BWL Methoden - Beispiele - Anwendungen Herausgegeben von Robert Galata, Markus Wessler ISBN (Buch):
von x-würfeln bei wachsendem n? Zur Beantwortung führen wir ein Simulationsexperiment durch.
 Zentraler Grenzwertsatz Die Normalverteilung verdankt ihre universelle theoretische und praktische Bedeutung dem zentralen Grenzwertsatz. Unabhängig von der konkreten k Ausgangsverteilung konvergiert die
Zentraler Grenzwertsatz Die Normalverteilung verdankt ihre universelle theoretische und praktische Bedeutung dem zentralen Grenzwertsatz. Unabhängig von der konkreten k Ausgangsverteilung konvergiert die
Vorlesung: Statistik II für Wirtschaftswissenschaft
 Vorlesung: Statistik II für Wirtschaftswissenschaft Prof. Dr. Helmut Küchenhoff Institut für Statistik, LMU München Sommersemester 2017 Einführung 1 Wahrscheinlichkeit: Definition und Interpretation 2
Vorlesung: Statistik II für Wirtschaftswissenschaft Prof. Dr. Helmut Küchenhoff Institut für Statistik, LMU München Sommersemester 2017 Einführung 1 Wahrscheinlichkeit: Definition und Interpretation 2
Grundgesamtheit, Merkmale, Stichprobe. Eigenschaften der Stichprobe. Klasseneinteilung, Histogramm. Arithmetisches Mittel, empirische Varianz
 - 1 - Grundgesamtheit, Merkmale, Stichprobe Dimension, Umfang Skalierung Eigenschaften der Stichprobe kennzeichnende Größen Eigenschaften der Stichprobe kennzeichnende Größen Punktediagramm, Regressionsgerade,
- 1 - Grundgesamtheit, Merkmale, Stichprobe Dimension, Umfang Skalierung Eigenschaften der Stichprobe kennzeichnende Größen Eigenschaften der Stichprobe kennzeichnende Größen Punktediagramm, Regressionsgerade,
Klausur zur Vorlesung
 Institut für Mathematische Stochastik WS 2006/2007 Universität Karlsruhe 12. Februar 2007 Priv.-Doz. Dr. D. Kadelka Dipl.-Math. W. Lao Aufgabe 1 (15 Punkte) Klausur zur Vorlesung Statistik für Biologen
Institut für Mathematische Stochastik WS 2006/2007 Universität Karlsruhe 12. Februar 2007 Priv.-Doz. Dr. D. Kadelka Dipl.-Math. W. Lao Aufgabe 1 (15 Punkte) Klausur zur Vorlesung Statistik für Biologen
Einführung in die Statistik
 Einführung in die Statistik Analyse und Modellierung von Daten von Prof. Dr. Rainer Schlittgen Universität Hamburg 12., korrigierte Auflage Oldenbourg Verlag München Inhaltsverzeichnis 1 Statistische Daten
Einführung in die Statistik Analyse und Modellierung von Daten von Prof. Dr. Rainer Schlittgen Universität Hamburg 12., korrigierte Auflage Oldenbourg Verlag München Inhaltsverzeichnis 1 Statistische Daten
Statistik und Wahrscheinlichkeitsrechnung
 Statistik und Wahrscheinlichkeitsrechnung Dr. Jochen Köhler 1 Inhalt der heutigen Vorlesung Statistik und Wahrscheinlichkeitsrechnung Zusammenfassung der vorherigen Vorlesung Übersicht über Schätzung und
Statistik und Wahrscheinlichkeitsrechnung Dr. Jochen Köhler 1 Inhalt der heutigen Vorlesung Statistik und Wahrscheinlichkeitsrechnung Zusammenfassung der vorherigen Vorlesung Übersicht über Schätzung und
Teil VIII. Zentraler Grenzwertsatz und Vertrauensintervalle. Woche 6: Zentraler Grenzwertsatz und Vertrauensintervalle. Lernziele. Typische Situation
 Woche 6: Zentraler Grenzwertsatz und Vertrauensintervalle Patric Müller ETHZ Teil VIII Zentraler Grenzwertsatz und Vertrauensintervalle WBL 17/19, 29.05.2017 Wahrscheinlichkeit
Woche 6: Zentraler Grenzwertsatz und Vertrauensintervalle Patric Müller ETHZ Teil VIII Zentraler Grenzwertsatz und Vertrauensintervalle WBL 17/19, 29.05.2017 Wahrscheinlichkeit
Definition Sei X eine stetige Z.V. mit Verteilungsfunktion F und Dichte f. Dann heißt E(X) :=
 Definition 2.34. Sei X eine stetige Z.V. mit Verteilungsfunktion F und Dichte f. Dann heißt E(X) := x f(x)dx der Erwartungswert von X, sofern dieses Integral existiert. Entsprechend wird die Varianz V(X)
Definition 2.34. Sei X eine stetige Z.V. mit Verteilungsfunktion F und Dichte f. Dann heißt E(X) := x f(x)dx der Erwartungswert von X, sofern dieses Integral existiert. Entsprechend wird die Varianz V(X)
Statistik II. Weitere Statistische Tests. Statistik II
 Statistik II Weitere Statistische Tests Statistik II - 19.5.2006 1 Überblick Bisher wurden die Test immer anhand einer Stichprobe durchgeführt Jetzt wollen wir die statistischen Eigenschaften von zwei
Statistik II Weitere Statistische Tests Statistik II - 19.5.2006 1 Überblick Bisher wurden die Test immer anhand einer Stichprobe durchgeführt Jetzt wollen wir die statistischen Eigenschaften von zwei
Vorlesung: Statistik II für Wirtschaftswissenschaft
 Vorlesung: Statistik II für Wirtschaftswissenschaft Prof. Dr. Helmut Küchenhoff Institut für Statistik, LMU München Sommersemester 2017 Einführung 1 Wahrscheinlichkeit: Definition und Interpretation 2
Vorlesung: Statistik II für Wirtschaftswissenschaft Prof. Dr. Helmut Küchenhoff Institut für Statistik, LMU München Sommersemester 2017 Einführung 1 Wahrscheinlichkeit: Definition und Interpretation 2
1 Wahrscheinlichkeitsrechnung. 2 Zufallsvariablen und ihre Verteilung. 3 Statistische Inferenz. 4 Intervallschätzung
 0 Einführung 1 Wahrscheinlichkeitsrechnung Zufallsvariablen und ihre Verteilung 3 Statistische Inferenz 4 Intervallschätzung Motivation und Hinführung Der wahre Anteil der rot-grün Wähler 009 war genau
0 Einführung 1 Wahrscheinlichkeitsrechnung Zufallsvariablen und ihre Verteilung 3 Statistische Inferenz 4 Intervallschätzung Motivation und Hinführung Der wahre Anteil der rot-grün Wähler 009 war genau
2.3 Intervallschätzung
 2.3.1 Motivation und Hinführung Bsp. 2.11. [Wahlumfrage] Der wahre Anteil der rot-grün Wähler 2009 war genau 33.7%. Wie groß ist die Wahrscheinlichkeit, in einer Zufallsstichprobe von 1000 Personen genau
2.3.1 Motivation und Hinführung Bsp. 2.11. [Wahlumfrage] Der wahre Anteil der rot-grün Wähler 2009 war genau 33.7%. Wie groß ist die Wahrscheinlichkeit, in einer Zufallsstichprobe von 1000 Personen genau
1 EINLEITUNG Allgemeines Kapitelübersicht Gebrauch dieses Buches Verwenden zusätzlicher Literatur...
 Inhaltsverzeichnis 1 EINLEITUNG... 1 1.1 Allgemeines... 1 1.2 Kapitelübersicht... 2 1.3 Gebrauch dieses Buches... 3 1.4 Verwenden zusätzlicher Literatur... 4 DESKRIPTIVE STATISTIK 2 GRUNDLAGEN... 5 2.1
Inhaltsverzeichnis 1 EINLEITUNG... 1 1.1 Allgemeines... 1 1.2 Kapitelübersicht... 2 1.3 Gebrauch dieses Buches... 3 1.4 Verwenden zusätzlicher Literatur... 4 DESKRIPTIVE STATISTIK 2 GRUNDLAGEN... 5 2.1
Mathematische Statistik Aufgaben zum Üben. Schätzer
 Prof. Dr. Z. Kabluchko Wintersemester 2016/17 Philipp Godland 14. November 2016 Mathematische Statistik Aufgaben zum Üben Keine Abgabe Aufgabe 1 Schätzer Es seien X 1,..., X n unabhängige und identisch
Prof. Dr. Z. Kabluchko Wintersemester 2016/17 Philipp Godland 14. November 2016 Mathematische Statistik Aufgaben zum Üben Keine Abgabe Aufgabe 1 Schätzer Es seien X 1,..., X n unabhängige und identisch
Korollar 116 (Grenzwertsatz von de Moivre)
 Ein wichtiger Spezialfall das Zentralen Grenzwertsatzes besteht darin, dass die auftretenden Zufallsgrößen Bernoulli-verteilt sind. Korollar 116 (Grenzwertsatz von de Moivre) X 1,..., X n seien unabhängige
Ein wichtiger Spezialfall das Zentralen Grenzwertsatzes besteht darin, dass die auftretenden Zufallsgrößen Bernoulli-verteilt sind. Korollar 116 (Grenzwertsatz von de Moivre) X 1,..., X n seien unabhängige
Wahrscheinlichkeitsfunktion. Binomialverteilung. Binomialverteilung. Wahrscheinlichkeitshistogramme
 Binomialverteilung Wahrscheinlichkeitsfunktion Konstruktionsprinzip: Ein Zufallsexperiment wird n mal unabhängig durchgeführt. Wir interessieren uns jeweils nur, ob ein bestimmtes Ereignis A eintritt oder
Binomialverteilung Wahrscheinlichkeitsfunktion Konstruktionsprinzip: Ein Zufallsexperiment wird n mal unabhängig durchgeführt. Wir interessieren uns jeweils nur, ob ein bestimmtes Ereignis A eintritt oder
Zufallsvariablen [random variable]
![Zufallsvariablen [random variable] Zufallsvariablen [random variable]](/thumbs/52/29710821.jpg) Zufallsvariablen [random variable] Eine Zufallsvariable (Zufallsgröße) X beschreibt (kodiert) die Versuchsausgänge ω Ω mit Hilfe von Zahlen, d.h. X ist eine Funktion X : Ω R ω X(ω) Zufallsvariablen werden
Zufallsvariablen [random variable] Eine Zufallsvariable (Zufallsgröße) X beschreibt (kodiert) die Versuchsausgänge ω Ω mit Hilfe von Zahlen, d.h. X ist eine Funktion X : Ω R ω X(ω) Zufallsvariablen werden
Hans-Friedrich Eckey / Reinhold Kosfeld / Christian Dreger. Statistik. Grundlagen - Methoden - Beispiele GABLER
 Hans-Friedrich Eckey / Reinhold Kosfeld / Christian Dreger Statistik Grundlagen - Methoden - Beispiele GABLER INHALTSVERZEICHNIS TEIL I: DESKRIPTIVE STATISTIK 1. GEGENSTAND UND GRUNDBEGRIFFE DER STATISTIK
Hans-Friedrich Eckey / Reinhold Kosfeld / Christian Dreger Statistik Grundlagen - Methoden - Beispiele GABLER INHALTSVERZEICHNIS TEIL I: DESKRIPTIVE STATISTIK 1. GEGENSTAND UND GRUNDBEGRIFFE DER STATISTIK
Klausur zur Vorlesung
 Institut für Mathematische Stochastik WS 2004/2005 Universität Karlsruhe 14. Februar 2005 Dr. Bernhard Klar Sebastian Müller Aufgabe 1: (15 Punkte) Klausur zur Vorlesung Statistik für Biologen Musterlösungen
Institut für Mathematische Stochastik WS 2004/2005 Universität Karlsruhe 14. Februar 2005 Dr. Bernhard Klar Sebastian Müller Aufgabe 1: (15 Punkte) Klausur zur Vorlesung Statistik für Biologen Musterlösungen
Willkommen zur Vorlesung Statistik (Master)
 Willkommen zur Vorlesung Statistik (Master) Thema dieser Vorlesung: Verteilungen stetiger Zufallsvariablen Prof. Dr. Wolfgang Ludwig-Mayerhofer Universität Siegen Philosophische Fakultät, Seminar für Sozialwissenschaften
Willkommen zur Vorlesung Statistik (Master) Thema dieser Vorlesung: Verteilungen stetiger Zufallsvariablen Prof. Dr. Wolfgang Ludwig-Mayerhofer Universität Siegen Philosophische Fakultät, Seminar für Sozialwissenschaften
OLS-Schätzung: asymptotische Eigenschaften
 OLS-Schätzung: asymptotische Eigenschaften Stichwörter: Konvergenz in Wahrscheinlichkeit Konvergenz in Verteilung Konsistenz asymptotische Verteilungen nicht-normalverteilte Störgrößen zufällige Regressoren
OLS-Schätzung: asymptotische Eigenschaften Stichwörter: Konvergenz in Wahrscheinlichkeit Konvergenz in Verteilung Konsistenz asymptotische Verteilungen nicht-normalverteilte Störgrößen zufällige Regressoren
9 Die Normalverteilung
 9 Die Normalverteilung Dichte: f(x) = 1 2πσ e (x µ)2 /2σ 2, µ R,σ > 0 9.1 Standard-Normalverteilung µ = 0, σ 2 = 1 ϕ(x) = 1 2π e x2 /2 Dichte Φ(x) = 1 x 2π e t2 /2 dt Verteilungsfunktion 331 W.Kössler,
9 Die Normalverteilung Dichte: f(x) = 1 2πσ e (x µ)2 /2σ 2, µ R,σ > 0 9.1 Standard-Normalverteilung µ = 0, σ 2 = 1 ϕ(x) = 1 2π e x2 /2 Dichte Φ(x) = 1 x 2π e t2 /2 dt Verteilungsfunktion 331 W.Kössler,
Statistik. Andrej Depperschmidt. Sommersemester 2016
 Statistik Andrej Depperschmidt Sommersemester 2016 Schätzen der Varianz mit Stichprobenmittel Sei X = (X 1,..., X n ) eine Stichprobe u.i.v. ZV mit E[X i ] = µ R, Var[X i ] = σ 2 (0, ) und µ 4 = E[(X i
Statistik Andrej Depperschmidt Sommersemester 2016 Schätzen der Varianz mit Stichprobenmittel Sei X = (X 1,..., X n ) eine Stichprobe u.i.v. ZV mit E[X i ] = µ R, Var[X i ] = σ 2 (0, ) und µ 4 = E[(X i
Biostatistik, Winter 2011/12
 Biostatistik, Winter 2011/12 Wahrscheinlichkeitstheorie:, Kenngrößen Prof. Dr. Achim Klenke http://www.aklenke.de 7. Vorlesung: 09.12.2011 1/58 Inhalt 1 2 Kenngrößen von Lagemaße 2/58 mit Dichte Normalverteilung
Biostatistik, Winter 2011/12 Wahrscheinlichkeitstheorie:, Kenngrößen Prof. Dr. Achim Klenke http://www.aklenke.de 7. Vorlesung: 09.12.2011 1/58 Inhalt 1 2 Kenngrößen von Lagemaße 2/58 mit Dichte Normalverteilung
Schriftliche Prüfung (2 Stunden)
 Dr. L. Meier Statistik und Wahrscheinlichkeitsrechnung Sommer 2015 Schriftliche Prüfung (2 Stunden) Bemerkungen: Erlaubte Hilfsmittel: 10 hand- oder maschinengeschriebene A4 Seiten (=5 Blätter). Taschenrechner
Dr. L. Meier Statistik und Wahrscheinlichkeitsrechnung Sommer 2015 Schriftliche Prüfung (2 Stunden) Bemerkungen: Erlaubte Hilfsmittel: 10 hand- oder maschinengeschriebene A4 Seiten (=5 Blätter). Taschenrechner
4.1. Nullhypothese, Gegenhypothese und Entscheidung
 rof. Dr. Roland Füss Statistik II SS 8 4. Testtheorie 4.. Nullhypothese, Gegenhypothese und Entscheidung ypothesen Annahmen über die Verteilung oder über einzelne arameter der Verteilung eines Merkmals
rof. Dr. Roland Füss Statistik II SS 8 4. Testtheorie 4.. Nullhypothese, Gegenhypothese und Entscheidung ypothesen Annahmen über die Verteilung oder über einzelne arameter der Verteilung eines Merkmals
Chi-Quadrat-Verteilung
 Chi-Quadrat-Verteilung Wikipedia http://de.wikipedia.org/wiki/chi-quadrat-verteilung 1 von 7 6/18/2009 6:13 PM Chi-Quadrat-Verteilung aus Wikipedia, der freien Enzyklopädie Die Chi-Quadrat-Verteilung ist
Chi-Quadrat-Verteilung Wikipedia http://de.wikipedia.org/wiki/chi-quadrat-verteilung 1 von 7 6/18/2009 6:13 PM Chi-Quadrat-Verteilung aus Wikipedia, der freien Enzyklopädie Die Chi-Quadrat-Verteilung ist
3 Stetige Zufallsvariablen
 3 Stetige Zufallsvariablen Eine Zufallsvariable heißt stetig, falls zu je zwei Werten a < b auch jeder Zwischenwert im Intervall [a, b] möglich ist Beispiele: X = Alter, X = Körpergröße, X = Temperatur,
3 Stetige Zufallsvariablen Eine Zufallsvariable heißt stetig, falls zu je zwei Werten a < b auch jeder Zwischenwert im Intervall [a, b] möglich ist Beispiele: X = Alter, X = Körpergröße, X = Temperatur,
Hypothesentests für Erwartungswert und Median. Statistik (Biol./Pharm./HST) FS 2015
 Hypothesentests für Erwartungswert und Median Statistik (Biol./Pharm./HST) FS 2015 Normalverteilung X N μ, σ 2 X ist normalverteilt mit Erwartungswert μ und Varianz σ 2 pdf: pdf cdf:??? cdf 1 Zentraler
Hypothesentests für Erwartungswert und Median Statistik (Biol./Pharm./HST) FS 2015 Normalverteilung X N μ, σ 2 X ist normalverteilt mit Erwartungswert μ und Varianz σ 2 pdf: pdf cdf:??? cdf 1 Zentraler
Modellanpassung. Einführung in die induktive Statistik. Statistik. Statistik. Friedrich Leisch
 Modellanpassung Einführung in die induktive Statistik Friedrich Leisch Institut für Statistik Ludwig-Maximilians-Universität München SS 2009 Statistik Statistik Wahrscheinlichkeitsrechnung: Gesetze bekannt,
Modellanpassung Einführung in die induktive Statistik Friedrich Leisch Institut für Statistik Ludwig-Maximilians-Universität München SS 2009 Statistik Statistik Wahrscheinlichkeitsrechnung: Gesetze bekannt,
SozialwissenschaftlerInnen II
 Statistik für SozialwissenschaftlerInnen II Henning Best best@wiso.uni-koeln.de Universität zu Köln Forschungsinstitut für Soziologie Statistik für SozialwissenschaftlerInnen II p.1 Wahrscheinlichkeitsfunktionen
Statistik für SozialwissenschaftlerInnen II Henning Best best@wiso.uni-koeln.de Universität zu Köln Forschungsinstitut für Soziologie Statistik für SozialwissenschaftlerInnen II p.1 Wahrscheinlichkeitsfunktionen
Die Varianz (Streuung) Definition
 Die (Streuung) Definition Diskrete Stetige Ang., die betrachteten e existieren. var(x) = E(X EX) 2 heißt der Zufallsvariable X. σ = Var(X) heißt Standardabweichung der X. Bez.: var(x), Var(X), varx, σ
Die (Streuung) Definition Diskrete Stetige Ang., die betrachteten e existieren. var(x) = E(X EX) 2 heißt der Zufallsvariable X. σ = Var(X) heißt Standardabweichung der X. Bez.: var(x), Var(X), varx, σ
Einführung in einige Teilbereiche der Wirtschaftsmathematik für Studierende des Wirtschaftsingenieurwesens
 in einige Teilbereiche der für Studierende des Wirtschaftsingenieurwesens Sommersemester 2014 Hochschule Augsburg : Gliederung 1 Finanzmathematik 2 Lineare Programme 3 Differentialgleichungen 4 Statistik:
in einige Teilbereiche der für Studierende des Wirtschaftsingenieurwesens Sommersemester 2014 Hochschule Augsburg : Gliederung 1 Finanzmathematik 2 Lineare Programme 3 Differentialgleichungen 4 Statistik:
Kapitel 3 Schließende Statistik
 Bemerkung 3.34: Die hier betrachteten Konfidenzintervalle für unbekannte Erwartungswerte sind umso schmaler, je größer der Stichprobenumfang n ist, je kleiner die (geschätzte) Standardabweichung σ (bzw.
Bemerkung 3.34: Die hier betrachteten Konfidenzintervalle für unbekannte Erwartungswerte sind umso schmaler, je größer der Stichprobenumfang n ist, je kleiner die (geschätzte) Standardabweichung σ (bzw.
Theorie - Statistik und Wahrscheinlichkeitstheorie. 27. Mai 2008
 Theorie - Statistik und Wahrscheinlichkeitstheorie 27. Mai 2008 Inhaltsverzeichnis 1. Was ist eine Zufallsvariable?......................... 4 2. Wie ist Freiheitsgrad definiert?.......................
Theorie - Statistik und Wahrscheinlichkeitstheorie 27. Mai 2008 Inhaltsverzeichnis 1. Was ist eine Zufallsvariable?......................... 4 2. Wie ist Freiheitsgrad definiert?.......................
Diskrete Wahrscheinlichkeitstheorie
 SS 2013 Diskrete Wahrscheinlichkeitstheorie Javier Esparza Fakultät für Informatik TU München http://www7.in.tum.de/um/courses/dwt/ss13 Sommersemester 2013 Teil V Induktive Statistik Induktive Statistik
SS 2013 Diskrete Wahrscheinlichkeitstheorie Javier Esparza Fakultät für Informatik TU München http://www7.in.tum.de/um/courses/dwt/ss13 Sommersemester 2013 Teil V Induktive Statistik Induktive Statistik
2.2 Punktschätzung. Gegeben sei die in Kapitel 2.1 beschriebene Situation, also eine i.i.d. Stichprobe X 1,...,X n eines Merkmales X.
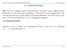 Ziel: Finde ein möglichst gutes Schätzverfahren und damit einen möglichst guten Schätzwert für eine bestimmte Kenngröße ϑ (Parameter) der Grundgesamtheit, z.b. den wahren Anteil der rot/grün-wähler, den
Ziel: Finde ein möglichst gutes Schätzverfahren und damit einen möglichst guten Schätzwert für eine bestimmte Kenngröße ϑ (Parameter) der Grundgesamtheit, z.b. den wahren Anteil der rot/grün-wähler, den
Hypothesentests für Erwartungswert und Median. für D-UWIS, D-ERDW, D-USYS und D-HEST SS15
 Hypothesentests für Erwartungswert und Median für D-UWIS, D-ERDW, D-USYS und D-HEST SS15 Normalverteilung X N(μ, σ 2 ) : «X ist normalverteilt mit Erwartungswert μ und Varianz σ 2» pdf: f x = 1 2 x μ exp
Hypothesentests für Erwartungswert und Median für D-UWIS, D-ERDW, D-USYS und D-HEST SS15 Normalverteilung X N(μ, σ 2 ) : «X ist normalverteilt mit Erwartungswert μ und Varianz σ 2» pdf: f x = 1 2 x μ exp
Klausur zu Statistik II
 Goethe-Universität Frankfurt Prof. Dr. Uwe Hassler FB Wirtschaftswissenschaften Sommersemester 2005 Klausur zu Statistik II Version B Bitte tragen Sie hier und auf den Lösungsblättern (oben links) Ihre
Goethe-Universität Frankfurt Prof. Dr. Uwe Hassler FB Wirtschaftswissenschaften Sommersemester 2005 Klausur zu Statistik II Version B Bitte tragen Sie hier und auf den Lösungsblättern (oben links) Ihre
k np g(n, p) = Pr p [T K] = Pr p [T k] Φ. np(1 p) DWT 4.1 Einführung 359/467 Ernst W. Mayr
![k np g(n, p) = Pr p [T K] = Pr p [T k] Φ. np(1 p) DWT 4.1 Einführung 359/467 Ernst W. Mayr k np g(n, p) = Pr p [T K] = Pr p [T k] Φ. np(1 p) DWT 4.1 Einführung 359/467 Ernst W. Mayr](/thumbs/52/28946049.jpg) Die so genannte Gütefunktion g gibt allgemein die Wahrscheinlichkeit an, mit der ein Test die Nullhypothese verwirft. Für unser hier entworfenes Testverfahren gilt ( ) k np g(n, p) = Pr p [T K] = Pr p
Die so genannte Gütefunktion g gibt allgemein die Wahrscheinlichkeit an, mit der ein Test die Nullhypothese verwirft. Für unser hier entworfenes Testverfahren gilt ( ) k np g(n, p) = Pr p [T K] = Pr p
Vorlesung: Statistik II für Wirtschaftswissenschaft
 Vorlesung: Statistik II für Wirtschaftswissenschaft Prof. Dr. Helmut Küchenhoff Institut für Statistik, LMU München Sommersemester 017 4 Spezielle Zufallsgrößen Einführung 1 Wahrscheinlichkeit: Definition
Vorlesung: Statistik II für Wirtschaftswissenschaft Prof. Dr. Helmut Küchenhoff Institut für Statistik, LMU München Sommersemester 017 4 Spezielle Zufallsgrößen Einführung 1 Wahrscheinlichkeit: Definition
Modellanpassung und Parameterschätzung. A: Übungsaufgaben
 7 Modellanpassung und Parameterschätzung 1 Kapitel 7: Modellanpassung und Parameterschätzung A: Übungsaufgaben [ 1 ] Bei n unabhängigen Wiederholungen eines Bernoulli-Experiments sei π die Wahrscheinlichkeit
7 Modellanpassung und Parameterschätzung 1 Kapitel 7: Modellanpassung und Parameterschätzung A: Übungsaufgaben [ 1 ] Bei n unabhängigen Wiederholungen eines Bernoulli-Experiments sei π die Wahrscheinlichkeit
Biostatistik, Sommer 2017
 1/39 Biostatistik, Sommer 2017 Wahrscheinlichkeitstheorie: Gesetz der großen Zahl, Zentraler Grenzwertsatz Schließende Statistik: Grundlagen Prof. Dr. Achim Klenke http://www.aklenke.de 9. Vorlesung: 16.06.2017
1/39 Biostatistik, Sommer 2017 Wahrscheinlichkeitstheorie: Gesetz der großen Zahl, Zentraler Grenzwertsatz Schließende Statistik: Grundlagen Prof. Dr. Achim Klenke http://www.aklenke.de 9. Vorlesung: 16.06.2017
Statistik Testverfahren. Heinz Holling Günther Gediga. Bachelorstudium Psychologie. hogrefe.de
 rbu leh ch s plu psych Heinz Holling Günther Gediga hogrefe.de Bachelorstudium Psychologie Statistik Testverfahren 18 Kapitel 2 i.i.d.-annahme dem unabhängig. Es gilt also die i.i.d.-annahme (i.i.d = independent
rbu leh ch s plu psych Heinz Holling Günther Gediga hogrefe.de Bachelorstudium Psychologie Statistik Testverfahren 18 Kapitel 2 i.i.d.-annahme dem unabhängig. Es gilt also die i.i.d.-annahme (i.i.d = independent
Anhang: Statistische Tafeln und Funktionen
 A1 Anhang: Statistische Tafeln und Funktionen Verteilungsfunktion Φ(z) der Standardnormalverteilung Die Tabelle gibt die Werte Φ(z) der Verteilungsfunktion zu vorgegebenem Wert z 0 an; ferner gilt Φ( z)
A1 Anhang: Statistische Tafeln und Funktionen Verteilungsfunktion Φ(z) der Standardnormalverteilung Die Tabelle gibt die Werte Φ(z) der Verteilungsfunktion zu vorgegebenem Wert z 0 an; ferner gilt Φ( z)
4.1. Verteilungsannahmen des Fehlers. 4. Statistik im multiplen Regressionsmodell Verteilungsannahmen des Fehlers
 4. Statistik im multiplen Regressionsmodell In diesem Kapitel wird im Abschnitt 4.1 zusätzlich zu den schon bekannten Standardannahmen noch die Annahme von normalverteilten Residuen hinzugefügt. Auf Basis
4. Statistik im multiplen Regressionsmodell In diesem Kapitel wird im Abschnitt 4.1 zusätzlich zu den schon bekannten Standardannahmen noch die Annahme von normalverteilten Residuen hinzugefügt. Auf Basis
Kapitel 7. Regression und Korrelation. 7.1 Das Regressionsproblem
 Kapitel 7 Regression und Korrelation Ein Regressionsproblem behandelt die Verteilung einer Variablen, wenn mindestens eine andere gewisse Werte in nicht zufälliger Art annimmt. Ein Korrelationsproblem
Kapitel 7 Regression und Korrelation Ein Regressionsproblem behandelt die Verteilung einer Variablen, wenn mindestens eine andere gewisse Werte in nicht zufälliger Art annimmt. Ein Korrelationsproblem
Statistik II. Regressionsanalyse. Statistik II
 Statistik II Regressionsanalyse Statistik II - 23.06.2006 1 Einfachregression Annahmen an die Störterme : 1. sind unabhängige Realisationen der Zufallsvariable, d.h. i.i.d. (unabh.-identisch verteilt)
Statistik II Regressionsanalyse Statistik II - 23.06.2006 1 Einfachregression Annahmen an die Störterme : 1. sind unabhängige Realisationen der Zufallsvariable, d.h. i.i.d. (unabh.-identisch verteilt)
Statistik im iadhetocr-studi der BWL und VWl
 Max C. Wewel Statistik im iadhetocr-studi der BWL und VWl Methoden, Anwendung, Interpretation 2., erweiterte Auflage Mit herausnehmbarer Formelsammlung ein Imprint von Pearson Education München Boston
Max C. Wewel Statistik im iadhetocr-studi der BWL und VWl Methoden, Anwendung, Interpretation 2., erweiterte Auflage Mit herausnehmbarer Formelsammlung ein Imprint von Pearson Education München Boston
Einführung in die Induktive Statistik: Schätzen von Parametern und Verteilungen
 Einführung in die Induktive Statistik: Schätzen von Parametern und Verteilungen Jan Gertheiss LMU München Sommersemester 2011 Vielen Dank an Christian Heumann für das Überlassen von TEX-Code! Inhalt Stichproben
Einführung in die Induktive Statistik: Schätzen von Parametern und Verteilungen Jan Gertheiss LMU München Sommersemester 2011 Vielen Dank an Christian Heumann für das Überlassen von TEX-Code! Inhalt Stichproben
Kapitel 9. Schätzverfahren und Konfidenzintervalle. 9.1 Grundlagen zu Schätzverfahren
 Kapitel 9 Schätzverfahren und Konfidenzintervalle 9.1 Grundlagen zu Schätzverfahren Für eine Messreihe x 1,...,x n wird im Folgenden angenommen, dass sie durch n gleiche Zufallsexperimente unabhängig voneinander
Kapitel 9 Schätzverfahren und Konfidenzintervalle 9.1 Grundlagen zu Schätzverfahren Für eine Messreihe x 1,...,x n wird im Folgenden angenommen, dass sie durch n gleiche Zufallsexperimente unabhängig voneinander
Statistik. Ludwig Fahrmeir Rita Künstler Iris Pigeot Gerhard Tutz. Der Weg zur Datenanalyse. Springer. Zweite, verbesserte Auflage
 Ludwig Fahrmeir Rita Künstler Iris Pigeot Gerhard Tutz Statistik Der Weg zur Datenanalyse Zweite, verbesserte Auflage Mit 165 Abbildungen und 34 Tabellen Springer Inhaltsverzeichnis Vorwort v 1 Einführung
Ludwig Fahrmeir Rita Künstler Iris Pigeot Gerhard Tutz Statistik Der Weg zur Datenanalyse Zweite, verbesserte Auflage Mit 165 Abbildungen und 34 Tabellen Springer Inhaltsverzeichnis Vorwort v 1 Einführung
Aufgabe 1 (8= Punkte) 13 Studenten haben die folgenden Noten (ganze Zahl) in der Statistikklausur erhalten:
 Aufgabe 1 (8=2+2+2+2 Punkte) 13 Studenten haben die folgenden Noten (ganze Zahl) in der Statistikklausur erhalten: Die Zufallsvariable X bezeichne die Note. 1443533523253. a) Wie groß ist h(x 5)? Kreuzen
Aufgabe 1 (8=2+2+2+2 Punkte) 13 Studenten haben die folgenden Noten (ganze Zahl) in der Statistikklausur erhalten: Die Zufallsvariable X bezeichne die Note. 1443533523253. a) Wie groß ist h(x 5)? Kreuzen
WS 2014/15. (d) Bestimmen Sie die Wahrscheinlichkeitsfunktion von X. (e) Bestimmen Sie nun den Erwartungswert und die Varianz von X.
 Fragenkatalog zur Übung Methoden der empirischen Sozialforschung WS 2014/15 Hier finden Sie die denkbaren Fragen zum ersten Teil der Übung. Das bedeutet, dass Sie zu diesem Teil keine anderen Fragen im
Fragenkatalog zur Übung Methoden der empirischen Sozialforschung WS 2014/15 Hier finden Sie die denkbaren Fragen zum ersten Teil der Übung. Das bedeutet, dass Sie zu diesem Teil keine anderen Fragen im
Kapitel 12 Stetige Zufallsvariablen Dichtefunktion und Verteilungsfunktion. stetig. Verteilungsfunktion
 Kapitel 1 Stetige Zufallsvariablen 1.1. Dichtefunktion und Verteilungsfunktion stetig Verteilungsfunktion Trägermenge T, also die Menge der möglichen Realisationen, ist durch ein Intervall gegeben Häufig
Kapitel 1 Stetige Zufallsvariablen 1.1. Dichtefunktion und Verteilungsfunktion stetig Verteilungsfunktion Trägermenge T, also die Menge der möglichen Realisationen, ist durch ein Intervall gegeben Häufig
1 Dichte- und Verteilungsfunktion
 Tutorium Yannick Schrör Klausurvorbereitungsaufgaben Statistik Lösungen Yannick.Schroer@rub.de 9.2.26 ID /455 Dichte- und Verteilungsfunktion Ein tüchtiger Professor lässt jährlich 2 Bücher drucken. Die
Tutorium Yannick Schrör Klausurvorbereitungsaufgaben Statistik Lösungen Yannick.Schroer@rub.de 9.2.26 ID /455 Dichte- und Verteilungsfunktion Ein tüchtiger Professor lässt jährlich 2 Bücher drucken. Die
Beziehungen zwischen Verteilungen
 Kapitel 5 Beziehungen zwischen Verteilungen In diesem Kapitel wollen wir Beziehungen zwischen Verteilungen betrachten, die wir z.t. schon bei den einzelnen Verteilungen betrachtet haben. So wissen Sie
Kapitel 5 Beziehungen zwischen Verteilungen In diesem Kapitel wollen wir Beziehungen zwischen Verteilungen betrachten, die wir z.t. schon bei den einzelnen Verteilungen betrachtet haben. So wissen Sie
Häufigkeitsverteilungen
 Häufigkeitsverteilungen Eine Häufigkeitsverteilung gibt die Verteilung eines erhobenen Merkmals an und ordnet jeder Ausprägung die jeweilige Häufigkeit zu. Bsp.: 100 Studenten werden gefragt, was sie studieren.
Häufigkeitsverteilungen Eine Häufigkeitsverteilung gibt die Verteilung eines erhobenen Merkmals an und ordnet jeder Ausprägung die jeweilige Häufigkeit zu. Bsp.: 100 Studenten werden gefragt, was sie studieren.
Wahrscheinlichkeitsrechnung und Statistik für Biologen Wiederholung: Verteilungen
 Wahrscheinlichkeitsrechnung und Statistik für Biologen Wiederholung: Verteilungen Noémie Becker & Dirk Metzler 31. Mai 2016 Inhaltsverzeichnis 1 Binomialverteilung 1 2 Normalverteilung 2 3 T-Verteilung
Wahrscheinlichkeitsrechnung und Statistik für Biologen Wiederholung: Verteilungen Noémie Becker & Dirk Metzler 31. Mai 2016 Inhaltsverzeichnis 1 Binomialverteilung 1 2 Normalverteilung 2 3 T-Verteilung
Einführung in die Maximum Likelihood Methodik
 in die Maximum Likelihood Methodik Thushyanthan Baskaran thushyanthan.baskaran@awi.uni-heidelberg.de Alfred Weber Institut Ruprecht Karls Universität Heidelberg Gliederung 1 2 3 4 2 / 31 Maximum Likelihood
in die Maximum Likelihood Methodik Thushyanthan Baskaran thushyanthan.baskaran@awi.uni-heidelberg.de Alfred Weber Institut Ruprecht Karls Universität Heidelberg Gliederung 1 2 3 4 2 / 31 Maximum Likelihood
7. Hypothesentests. Ausgangssituation erneut: ZV X repräsentiere einen Zufallsvorgang. X habe die unbekannte VF F X (x)
 7. Hypothesentests Ausgangssituation erneut: ZV X repräsentiere einen Zufallsvorgang X habe die unbekannte VF F X (x) Interessieren uns für einen unbekannten Parameter θ der Verteilung von X 350 Bisher:
7. Hypothesentests Ausgangssituation erneut: ZV X repräsentiere einen Zufallsvorgang X habe die unbekannte VF F X (x) Interessieren uns für einen unbekannten Parameter θ der Verteilung von X 350 Bisher:
Wahrscheinlichkeitsrechnung und Statistik
 10. Vorlesung - 017 Quantil der Ordnung α für die Verteilung des beobachteten Merkmals X ist der Wert z α R für welchen gilt z 1 heißt Median. P(X < z α ) α P(X z α ). Falls X stetige zufällige Variable
10. Vorlesung - 017 Quantil der Ordnung α für die Verteilung des beobachteten Merkmals X ist der Wert z α R für welchen gilt z 1 heißt Median. P(X < z α ) α P(X z α ). Falls X stetige zufällige Variable
Regression und Korrelation
 Kapitel 7 Regression und Korrelation Ein Regressionsproblem behandeltdie VerteilungeinerVariablen, wenn mindestens eine andere gewisse Werte in nicht zufälliger Art annimmt. Ein Korrelationsproblem dagegen
Kapitel 7 Regression und Korrelation Ein Regressionsproblem behandeltdie VerteilungeinerVariablen, wenn mindestens eine andere gewisse Werte in nicht zufälliger Art annimmt. Ein Korrelationsproblem dagegen
Parameterschätzung. Kapitel 14. Modell Es sei {P θ θ Θ}, Θ R m eine Familie von Verteilungen auf χ (sog. Stichprobenraum),
 Kapitel 14 Parameterschätzung Modell Es sei {P θ θ Θ}, Θ R m eine Familie von Verteilungen auf χ (sog. Stichprobenraum), = ( 1,..., n ) sei eine Realisierung der Zufallsstichprobe X = (X 1,..., X n ) zu
Kapitel 14 Parameterschätzung Modell Es sei {P θ θ Θ}, Θ R m eine Familie von Verteilungen auf χ (sog. Stichprobenraum), = ( 1,..., n ) sei eine Realisierung der Zufallsstichprobe X = (X 1,..., X n ) zu
