Informatik I Modul 2: Rechnerarithmetik (1)
|
|
|
- Heike Martin
- vor 6 Jahren
- Abrufe
Transkript
1 Herbstsemester 2011, Institut für Informatik IFI, UZH, Schweiz Informatik I Modul 2: Rechnerarithmetik (1) 2011 Burkhard Stiller M2 1 Modul 2: Rechnerarithmetik (1) Zahlensysteme Zahlendarstellung Zeichendarstellung 2011 Burkhard Stiller M2 2
2 Rechnerarithmetik Rechnerarithmetik soll als Beispiel vorbereitet werden, wie größere Informationseinheiten verarbeitet werden. Hierzu werden zunächst die formalen Grundlagen erarbeitet: Zahlensysteme Zahlendarstellungen Zeichendarstellungen Boole sche Algebra (Modul 3) bis Dann werden Schaltnetze und werke behandelt (Modul 3, 4). Danach werden Verfahren und Schaltungen zur Implementierung der vier Grundrechenarten in einem Rechner vorgestellt (Modul 5). Abschließend wird die Funktion einer arithmetisch logischen Einheit (ALU) eines Rechners besprochen (Modul 5) Burkhard Stiller M2 3 ab Zahlensysteme Römische Zahlen 2011 Burkhard Stiller M2 4
3 Zahlensysteme Leibniz sche Dualzahlen Leibniz-Traktat aus dem Jahre 1679 Vermutlich kommen Ideen zum Dualzahlensystem aus China 2011 Burkhard Stiller M2 5 Formale Grundlagen Menschen rechnen gewöhnlich im Dezimalzahlensystem. Rechner rechnen gewöhnlich im Dualzahlensystem. Eine Konvertierung ist erforderlich Daneben werden weitere Zahlensysteme wie Oktalzahlensystem oder Hexadezimalzahlensystem (eigentlich: Sedezimal) zur kompakteren Darstellung der sehr langen Dualzahlen verwendet. Es ist notwendig, die Zusammenhänge und mathematischen Grundlagen dieser Zahlensysteme zu verstehen Burkhard Stiller M2 6
4 Zahlensysteme (1) Gängigste Form: Stellenwertsysteme Zahlendarstellung in Form einer Reihe von Ziffern z i, wobei das Dezimalkomma (-punkt) rechts von z 0 plaziert sei: z n z n-1... z 1 z 0, z -1 z -2...z -m z.b. 1234,567 Jeder Position i der Ziffernreihe ist ein Stellenwert zugeordnet, der eine Potenz b i der Basis b des Zahlensystems ist. Der Wert X b der Zahl ergibt sich dann als Summe der Werte aller Einzelstellen z i b i : X b = z n b n + z n-1 b n z 1 b + z 0 + z -1 b z -m b -m = z i b 2011 Burkhard Stiller M2 7 n i= m i Zahlensysteme (2) Interessante Zahlensysteme in der Informatik b Zahlensystem Zahlenbezeichnung Dualsystem Oktalsystem Dezimalsystem Hexadezimalsystem (Sedezimalsystem) Dualzahl Oktalzahl Dezimalzahl Hexadezimalzahl (Sedezimalzahl) Hexadezimalsystem: Die Ziffern 10 bis 15 werden mit den Buchstaben A bis F dargestellt. Dualsystem: Wichtigstes Zahlensystem im Rechner Oktal- und Hexadezimalsystem: Leicht ins Dualsystem umwandelbar, besser zu verstehen als lange 0-1-Kolonnen Burkhard Stiller M2 8
5 Zahlensysteme (3) 2011 Burkhard Stiller M2 9 Der Euklidische Algorithmus Umwandlung vom Dezimalsystem in ein System zur Basis b 1. Methode: Euklidischer Algorithmus: Z = z n 10 n + z n-1 10 n z z 0 +z z -m 10 -m = y p b p + y p-1 b p y 1 b + y 0 + y -1 b y -q b -q Die Ziffern werden sukzessive, beginnend mit der höchstwertigen Ziffer, berechnet. 1. Schritt: Berechne p gemäß der Ungleichung b p Z < b p+1 (setze i = p) 2. Schritt: Ermittle y i und den Rest R i durch Division von Z i durch b i : y i = Z i div b i ; R i = Z i mod b i ; 3. Schritt: Wiederhole 2. Schritt für i = p-1, und ersetze dabei nach jedem Schritt Z durch R i, bis R i = 0 oder bis b i (und damit der Umrechnungsfehler) gering genug ist Burkhard Stiller M2 10
6 Beispiel Umwandlung von 15741, ins Hexadezimalsystem: 1. Schritt: ,233 < 16 4 höchste Potenz Schritt: 15741,233 : 16 3 = 3 Rest 3453, Schritt: 3453,233 : 16 2 = D Rest 125, Schritt: 125,233 : 16 = 7 Rest 13, Schritt: 13,233 : 1 = D Rest 0, Schritt: 0,233 : 16-1 = 3 Rest 0, Schritt: 0,0455 : 16-2 = B Rest 0, Schritt: 0,00253 : 16-3 = A Rest 0, Schritt: 0, : 16-4 = 5 Rest 0, ( Fehler) 15741, D7D,3BA Burkhard Stiller M2 11 Horner Schema Umwandlung vom Dezimalsystem in ein Zahlensystem zur Basis b 2. Methode: Abwandlung des Horner Schemas Hierbei müssen der ganzzahlige und der gebrochene Anteil getrennt betrachtet werden: Umwandlung des ganzzahligen Anteils: n i Eine ganze Zahl X b = z i b kann durch fortgesetztes i= 0 Ausklammern auch in folgender Form geschrieben werden: X b = ((...(((y n b + y n-1 ) b + y n-2 ) b + y n-3 ) b... ) b + y 1 ) b + y Burkhard Stiller M2 12
7 Horner Schema: Beispiel Die gegebene Dezimalzahl wird sukzessive durch die Basis b dividiert. Die jeweiligen ganzzahligen Reste ergeben die Ziffern der Zahl X b in der Reihenfolge von der niedrigstwertigen zur höchstwertigen Stelle. Wandle ins Hexadezimalsystem um: : 16 = 983 Rest 13 (D 16 ) : 16 = 61 Rest 7 (7 16 ) : 16 = 3 Rest 13 (D 16 ) 3 10 : 16 = 0 Rest 3 (3 16 ) = 3D7D Burkhard Stiller M2 13 Umwandlung: Basis b Dezimalsystem Die Werte der einzelnen Stellen der umzuwandelnden Zahl werden in dem Zahlensystem, in das umgewandelt werden soll, dargestellt und nach der Stellenwertgleichung aufsummiert. Der Wert X b der Zahl ergibt sich dann als Summe der Werte aller Einzelstellen z i b i : X b = z n b n + z n-1 b n z 1 b + z 0 + z -1 b z -m b -m = n z i b i= m i 2011 Burkhard Stiller M2 14
8 Beispiel Konvertiere , ins Dezimalsystem , * 2 = 0, * 2 = 0, * 2 = 0,5 0 1 * 2 = * 2 = 4 1 * 2 3 = * 2 = 32 45, Burkhard Stiller M2 15 Umwandlung beliebiger Stellenwertsysteme Man wandelt die Zahl ins Dezimalsystem um und führt danach mit Methode 1 oder 2 die Wandlung ins Zielsystem durch. Spezialfall: Ist eine Basis eine Potenz der anderen Basis, können einfach mehrere Stellen zu einer Ziffer zusammengefasst werden oder eine Stelle kann durch eine Folge von Ziffern ersetzt werden. Wandlung von , ins Hexadezimalsystem 2 4 = 16 4 Dualstellen 1 Hexadezimalstelle dual , , } } } } Ergänzen von Nullen zur Auffüllung auf Vierergruppen hexadezimal 3 4, D Burkhard Stiller M2 16
9 Modul 2: Rechnerarithmetik (1) Zahlensysteme Zahlendarstellung Zeichendarstellung 2011 Burkhard Stiller M2 17 Darstellung negativer Zahlen Für die Darstellung negativer Zahlen in Rechnern werden vier verschiedene Formate benutzt : Darstellung mit Betrag und Vorzeichen Stellenkomplement-Darstellung (Einerkomplement-Darstellung) Zweierkomplement-Darstellung Offset-Dual-Darstellung / Exzeß-Darstellung 2011 Burkhard Stiller M2 18
10 Darstellung mit Betrag und Vorzeichen Eine Stelle wird als Vorzeichenbit benutzt. Ist das am weitesten links stehende Bit (MSB, most significant bit): MSB = 0 positive Zahl MSB = 1 negative Zahl Beispiel: = = -18 Nachteile: Bei Addition und Subtraktion müssen die Vorzeichen der Operanden gesondert betrachtet werden. Es gibt zwei Repräsentationen der Zahl 0 (mit positivem und mit negativem Vorzeichen) 2011 Burkhard Stiller M2 19 Stellenkomplement / Einerkomplement Stellenkomplement der entsprechenden positiven Zahl. Um eine Zahl zu negieren, wird jedes Bit der Zahl komplementiert. Dies entspricht dem Einerkomplement: Komplementbildung z ek = (2 n -1) z Bsp: 4 = = 1011 ek -4 = = = Negative Zahlen sind wiederum durch ein gesetztes Bit in der ersten Stelle charakterisiert. Vorteil gegenüber der Darstellung mit Vorzeichenbit: Erste Stelle bei Addition und Subtraktion muß nicht gesondert betrachtet werden. Aber: Es gibt weiterhin zwei Darstellungen der Null 2011 Burkhard Stiller M2 20
11 Zweierkomplement-Darstellung (1) Man addiert nach der Stellenkomplementierung noch eine 1 Man erhält so das Zweierkomplement: z zk = 2 n -z Einerkomplement Zweierkomplement Nachteil: Unsymmetrischer Zahlenbereich. Die kleinste negative Zahl ist betragsmäßig um 1 größer als die größte positive Zahl Bit-Zweierkomplementzahlen (Beispiel): Burkhard Stiller M2 21 Zweierkomplement-Darstellung (2) Alle anderen negativen Zahlen werden um 1 verschoben, das MSB bleibt aber gleich 1. Aus der ersten Stelle kann das Vorzeichen der Zahl abgelesen werden Aus dieser Konstruktion ergibt sich der Stellenwert des MSB einer Zweierkomplementzahl mit n+1 Bit zu 2 n : z n z n-1... z 0 hat den Wert: Z = - z n 2 n + z n-1 2 n z Burkhard Stiller M2 22
12 Beispiel Die Zahl soll mit 8 Bit dargestellt werden = Bitweise komplementieren Mit Vorzeichenbit : -77= Einerkomplement : -77= Addition von 1 Zweierkomplement : -77= Burkhard Stiller M2 23 Offset-Dual- (Exzeß-)Darstellung Wird hauptsächlich bei der Exponenten-Darstellung von Gleitkommazahlen benutzt. Die Darstellung einer Zahl erfolgt in Form ihrer Charakteristik (bias). Der gesamte Zahlenbereich wird durch Addition einer Konstanten (Exzeß, Offset) so nach oben verschoben, daß die kleinste (negative) Zahl die Darstellung 0 0 erhält. Bei n Stellen ist der Offset 2 n-1 Der Zahlenbereich ist hier auch asymmetrisch Burkhard Stiller M2 24
13 Zusammenfassung der Möglichkeiten Darstellung mit Dezimalzahl Betrag + Vorzeichen Zweierkomplement Einerkomplement Charakteristik , , Burkhard Stiller M2 25 Fest- und Gleitkommazahlen Zahlendarstellung auf dem Papier: Ziffern Vorzeichen + - Komma (Punkt),. Zahlendarstellung im Rechner: Binärziffern 0, 1 spezielle Vereinbarungen für die Darstellung von Vorzeichen und Komma/Punkt im Rechner sind erforderlich Darstellung des Vorzeichens: Wurde im vorigen Abschnitt behandelt Darstellung des Kommas mit zwei Möglichkeiten: Festkommadarstellung Gleitkommadarstellung 2011 Burkhard Stiller M2 26
14 Festkomma-Zahlen (1) Vereinbarung: Das Komma sitzt innerhalb des Maschinenwortes, das eine Dualzahl enthalten soll, an einer festen Stelle. Meist setzt man das Komma hinter die letzte Stelle. Andere Zahlen können durch entsprechende Maßstabsfaktoren in die gewählte Darstellungsform überführt werden. Negative Zahlen: Meist Zweierkomplement-Darstellung. Festkomma-Darstellungen werden heute hardwareseitig nicht mehr verwendet, jedoch bei der Ein- oder Ausgabe! 2011 Burkhard Stiller M2 27 Festkomma-Zahlen (2) Datentyp "integer" (Ganzzahlen) ist ein spezielles Festkommaformat. Manche Programmiersprachen erlauben die Definition von Ganzzahlen unterschiedlicher Länge. Beispiel "C": "short int", "int", "long int", "unsigned" Datentyp short int int long int DEC-VAX (einer der Urahnen) Anzahl der Bits Zahlenbereich IBM-PC, Apple Macintosh Anzahl der Bits Zahlenbereich Burkhard Stiller M2 28
15 Gleitkomma-Darstellung (1) Zur Darstellung von Zahlen, die betragsmäßig sehr groß oder sehr klein sind, verwendet man die Gleitkommadarstellung. Sie entspricht einer halblogarithmischen Form X = ± Mantisse b Exponent Die Basis b ist für eine bestimmte Gleitkomma-Darstellung fest (meist 2 oder 16) und braucht damit nicht mehr explizit repräsentiert zu werden. Gleitkommazahlen werden meist nicht im Zweierkomplement, sondern mit Betrag und Vorzeichen dargestellt Burkhard Stiller M2 29 Gleitkomma-Darstellung (2) Bei der Mantisse ist die Lage des Kommas wieder durch Vereinbarung festgelegt (meist links vom MSB). Der Exponent ist eine ganze Zahl, die in Form ihrer Charakteristik dargestellt wird. Für die Charakteristik und die Mantisse wird im Rechner ein feste Anzahl von Speicherstellen festgelegt. Die Länge der Charakteristik y-x bestimmt die Größe des Zahlenbereichs. Die Länge der Mantisse x legt die Genauigkeit der Darstellung fest. y y-1 x x-1 0 Vz Charakteristik Mantisse Dezimalzahl = (-1) Vz * (0,Mantisse) * b Exponent Exponent = Charakteristik b (y 1) - x 2011 Burkhard Stiller M2 30
16 Normalisierung Legt man für die Zahl 0 ein spezielles Bitmuster fest, ist die erste Stelle der Mantisse in normalisierter Form immer gleich 1. Die erste Stelle der Mantisse braucht im Maschinenformat gar nicht erst dargestellt zu werden, d.h. (0,1.....) Man spart ein Bit bei der Speicherung oder gewinnt bei gleichem Speicherbedarf ein Bit an Genauigkeit. Bei arithmetischen Operationen und bei der Konversion in andere Darstellungen darf diese Stelle natürlich nicht vergessen werden Burkhard Stiller M2 31 Beispiel (1) 3 verschiedene Maschinenformate mit je 32 Bit und b = 2. Die Zahl wird in jedem dieser Formate dargestellt. a) Festkommadarstellung mit Zweierkomplement Vz = BDF Burkhard Stiller M2 32
17 Beispiel (2) b) Gleitkommadarstellung, normalisiert: Vz Charakteristik Mantisse = 46EF 7C00 16 c) Gleitkommadarstellung, normalisiert, erste "1" implizit: Vz Charakteristik Rest-Mantisse = 46DE F Burkhard Stiller M2 33 Darstellbarer Zahlenbereich (1) Die Anzahl darstellbarer Zahlen (Bitkombinationen) ist zwar in allen drei Fällen gleich (2 32 ) Der Bereich und damit die Dichte darstellbarer Zahlen auf dem Zahlenstrahl ist aber sehr unterschiedlich Burkhard Stiller M2 34
18 Darstellbarer Zahlenbereich (2) Format a: Zahlen zwischen und Vz Format b: Vz Charakteristik Mantisse negative Zahlen: -( ) , , positive Zahlen 0, ( ) 2 127, und Null 2011 Burkhard Stiller M2 35 Darstellbarer Zahlenbereich (3) Format c: normalisierte Gleitkommadarstellung Vz Charakteristik Rest-Mantisse negative Zahlen: -( ) , positive Zahlen 0, ( ) Die Null kann nicht dargestellt werden! 2011 Burkhard Stiller M2 36
19 Darstellbarer Zahlenbereich (4) 0 a) b) -( ) , , ( ) overflow underflow overflow c) -( ) , , ( ) Burkhard Stiller M2 37 Charakteristische Zahlen Um verschiedene Gleitkommadarstellungen miteinander vergleichen zu können, definiert man drei charakteristische Zahlen: maxreal ist die größte darstellbare normalisierte positive Zahl minreal ist die kleinste darstellbare normalisierte positive Zahl smallreal ist die kleinste Zahl, die man zu 1 addieren kann, um einen von 1 verschiedenen Wert zu erhalten Burkhard Stiller M2 38
20 Beispiel In Format b) im letzten Beispiel Vz Charakteristik Mantisse maxreal = ( ) minreal = 0, Die Zahl 1 wird normalisiert als 0,5 2 1 dargestellt. Die nächstgrößere darstellbare Zahl hat in der Mantisse zusätzlich zur 1 in Bit 22 eine 1 in Bit 0. smallreal = 0, , also smallreal = = Burkhard Stiller M2 39 Ungenauigkeiten Die Differenz zwischen zwei aufeinanderfolgenden Zahlen wächst bei Gleitkomma-Zahlen exponentiell mit der Größe der Zahlen, während sie bei Festkomma-Zahlen konstant ist. Bei der Darstellung großer Zahlen ergibt sich damit auch eine hohe Ungenauigkeit. Die Gesetzmäßigkeiten, die für reelle Zahlen gelten, werden für Maschinendarstellungen verletzt! Dies gilt insbesondere auch wenn diese Zahlen in einer höheren Programmiersprache oft real heißen Burkhard Stiller M2 40
21 Beispiel Das Assoziativgesetz (x + y) + z = x + (y + z) gilt selbst dann nicht unbedingt, wenn kein overflow oder underflow auftritt. z.b.: x = 1; y = z = smallreal/2 (x + y) + z = (1 + smallreal/2) + smallreal/2 = 1 + smallreal/2 = 1 x + (y + z) = 1 + (smallreal/2 + smallreal/2) = 1 + smallreal 1 Hinweis: smallreal ist die kleinste Zahl, die man zu 1 addieren kann, um einen von 1 verschiedenen Wert zu erhalten! 2011 Burkhard Stiller M2 41 Problematik unterschiedlicher Definitionen Es existieren beliebig viele Möglichkeiten, selbst mit einer festen Wortbreite unterschiedliche Gleitkommaformate zu definieren (unterschiedliche Basis b, Darstellung der Null, Anzahl der Stellen für Charakteristik und Mantisse). Es existierten (bis Mitte der 80er Jahre) viele verschiedene, herstellerabhängige Formate Man konnte mit dem gleichen Programm auf unterschiedlichen Rechnern sehr unterschiedliche Ergebnisse erhalten! Normierung erforderlich 2011 Burkhard Stiller M2 42
22 Normierung: IEEE-Standard (1) IEEE-P 754-Floating-Point-Standard In vielen Programmiersprachen lassen sich Gleitkomma-Zahlen mit verschiedener Genauigkeit darstellen z.b. in C: float, double, long double Der IEEE Standard definiert mehrere Darstellungsformen IEEE single: IEEE double: IEEE extended: Bit 64 Bit 80 Bit Vz Charakteristik Mantisse 8 Bit 23 Bit Vz Charakteristik Mantisse 11 Bit 52 Bit 2011 Burkhard Stiller M2 43 Normierung: IEEE-Standard (2) 2011 Burkhard Stiller M2 44
23 Modul 2: Rechnerarithmetik (1) Zahlensysteme Zahlendarstellung Zeichendarstellung 2011 Burkhard Stiller M2 45 ASCII Code zur Darstellung von Zeichen (1) ASCII-Code (American Standard for Coded Information Interchange) ist eine festgelegte Abbildungsvorschrift (Norm) zur binären Kodierung von Zeichen. Der ASCII-Code umfasst Klein-/Großbuchstaben des lateinischen Alphabets, (arabische) Ziffern und viele Sonderzeichen. Die Kodierung erfolgt in einem Byte (8 Bits), so daß mit dem ASCII-Code 256 verschiedene Zeichen dargestellt werden können. Da das erste Bit nicht vom Standard-ASCII-Code genutzt wird, können im Standard-ASCII-Code nur 128 Zeichen dargestellt werden. Unterschiedliche, speziell normierte, ASCII-Code-Erweiterungen nutzen das erste Bit, um weitere 128 Zeichen darstellen zu können Burkhard Stiller M2 46
24 ASCII Code zur Darstellung von Zeichen (2) 2011 Burkhard Stiller M2 47 ASCII Code zur Darstellung von Zeichen (3) Zur Speicherung von Texten werden einzelne Bytes, die jeweils immer ein Zeichen kodieren, einfach hintereinander abgespeichert, so daß man eine Zeichenkette (String) erhält. Um das Ende der Zeichenkette zu identifizieren, werden (in den Programmiersprachen) unterschiedliche Verfahren verwendet. Die Länge der Zeichenkette wird im ersten bzw. in den ersten Bytes vor der eigentlichen Zeichenkette gespeichert. Dieses Verfahren benutzt z. B. die Programmiersprache PASCAL. Das Ende der Zeichenkette wird durch ein besonderes, nicht darzustellendes Zeichen gekennzeichnet. So verwendet z.b. die Programmiersprache C/C++ ein 0-Byte (Byte, in dem alle Bits 0 sind), um das Ende einer Zeichenkette zu kennzeichnen Burkhard Stiller M2 48
25 Unterscheidung von Ziffern und Zeichen 2011 Burkhard Stiller M2 49 Beispiel: Speicherung von Ziffern und Zeichen 2011 Burkhard Stiller M2 50
26 UniCode zur Darstellung von Zeichen (1) Der ASCII-Code mit 256 Zeichen ist sehr begrenzt. Unicode für Zeichen oder Elemente praktisch aller bekannten Schriftkulturen und Zeichensysteme kodierbar. Zeichenwerte der Zeichen bis Unicode Version 3.0 (September 1999) wurden ausschließlich durch eine zwei Byte lange Zahl ausgedrückt. Auf diese Weise lassen sich bis zu verschiedene Zeichen unterbringen (2 Byte = 16 Bit = 2 16 Kombinationsmöglichkeiten). Bezeichnung des Zwei-Byte-Schemas: Basic Multilingual Plane (BMP) In Version 3.1 (März 2001) sind Zeichen aufgenommen, wobei die Zwei-Byte-Grenze durchbrochen wurde. Das Zwei-Byte-Schema wird deshalb von einem Vier-Byte-Schema abgelöst Burkhard Stiller M2 51 UniCode zur Darstellung von Zeichen (2) In Version 6.0 (Oktober 2010) sind Zeichen enthalten. Unicode in 17 Bereiche (planes) gegliedert, jeweils á Zeichen Basic Multilingual Plane: hauptsächliche Schriftsysteme Supplementary Multilingual Plane: historische Schriftsysteme Supplementary Ideographic Plane: Chinesische, Japanische und Koreanische Schrift Supplementary Special-purpose Plane: Supplementary Private Use Area-A und -B 2011 Burkhard Stiller M2 52
27 UniCode zur Darstellung von Zeichen (3) Die Notation lautet � für dezimale Notation bzw. � für die hexadezimale Notation, wobei das 0000 die Unicode-Nummer des Zeichens darstellt. Formate für Speicherung und Übertragung unterschiedlich: UTF-8 (Unicode Transformation Format) Internet und in Betriebssystemen UTF-16 Zeichencodierung in Java Unicode wird in ostasiatischen Ländern kritisiert. Schriftzeichen verschiedener nicht verwandter Sprachen sind vereinigt Vor allem in Japan konnte sich der Unicode kaum durchsetzen Japan mit zahlreichen Alternativen zu Unicode wie etwa der Mojiky-Standard Antike Texte in Unicode aufgrund der Vereinheitlichung ähnlicher CJK- Schriftzeichen (chinesisch, japanisch, koreanisch) nicht originalgetreu wiederzugeben 2011 Burkhard Stiller M2 53 BCD-Code zur Darstellung von Zeichen BCD (Binary Coded Decimals) kodieren binär Zahlen Ziffern. Für jede Dezimalziffer werden mindestens vier, manchmal auch acht Bits verwendet. Die Ziffern werden nacheinander immer durch ihren Dualwert angegeben. Diese speicherplatzverschwendende Art der Speicherung von Dezimalzahlen erleichert aber manche Anwendungen. Anwendungsbereiche: Rechnen im Dezimalsystem Speichern von Dezimalzahlen (Telefonnummern u.ä.) Ansteuerung von LCD-Anzeigen, um Dezimalziffern einzeln anzuzeigen Burkhard Stiller M2 54
28 Duale Größenangaben (1) 2011 Burkhard Stiller M2 55 Duale Größenangaben (2) Kilo entspricht dem Faktor 2 10 = 1024 Mega entspricht dem Faktor 2 10 * 2 10 = 1024 * 1024 = Giga entspricht dem Faktor 2 10 * 2 10 * 2 10 = 2 30 Beispiel Festplattenherstellerangaben zur Speicherkapazität MB MByte Faktor hier 10 3 = 1000 Folge: 1 GB Byte sondern Byte D.h., es fehlen real 73 MegaByte! 200 GB entsprechen damit nur 186 Gbyte! 2011 Burkhard Stiller M2 56
Repräsentation von Daten Binärcodierung von rationalen Zahlen und Zeichen
 Kapitel 4: Repräsentation von Daten Binärcodierung von rationalen Zahlen und Zeichen Einführung in die Informatik Wintersemester 2007/08 Prof. Bernhard Jung Übersicht Codierung von rationalen Zahlen Konvertierung
Kapitel 4: Repräsentation von Daten Binärcodierung von rationalen Zahlen und Zeichen Einführung in die Informatik Wintersemester 2007/08 Prof. Bernhard Jung Übersicht Codierung von rationalen Zahlen Konvertierung
Zahlensysteme Römische Zahlen
 Modul 2: Rechnerarithmetik (1) Informatik I Modul 2: Rechnerarithmetik Zahlensysteme Zahlendarstellung Grundrechenarten Zeichendarstellung 212 Burkhard Stiller M2 1 212 Burkhard Stiller M2 2 Rechnerarithmetik
Modul 2: Rechnerarithmetik (1) Informatik I Modul 2: Rechnerarithmetik Zahlensysteme Zahlendarstellung Grundrechenarten Zeichendarstellung 212 Burkhard Stiller M2 1 212 Burkhard Stiller M2 2 Rechnerarithmetik
Grundlagen der Informatik
 Grundlagen der Informatik Teil II Speicherung und Interpretation von Information Seite 1 Speicherung und Interpretation von Information Beginn der Datenverarbeitung => Erfindung von Zahlensystemen Quantifizierung
Grundlagen der Informatik Teil II Speicherung und Interpretation von Information Seite 1 Speicherung und Interpretation von Information Beginn der Datenverarbeitung => Erfindung von Zahlensystemen Quantifizierung
Informationsmenge. Maßeinheit: 1 Bit. 1 Byte. Umrechnungen: Informationsmenge zur Beantwortung einer Binärfrage kleinstmögliche Informationseinheit
 Informationsmenge Maßeinheit: 1 Bit Informationsmenge zur Beantwortung einer Binärfrage kleinstmögliche Informationseinheit 1 Byte Zusammenfassung von 8 Bit, kleinste Speichereinheit im Computer, liefert
Informationsmenge Maßeinheit: 1 Bit Informationsmenge zur Beantwortung einer Binärfrage kleinstmögliche Informationseinheit 1 Byte Zusammenfassung von 8 Bit, kleinste Speichereinheit im Computer, liefert
Kapitel 2. Zahlensysteme, Darstellung von Informationen
 Kapitel 2 Zahlensysteme, Darstellung von Informationen 1 , Darstellung von Informationen Ein Computer speichert und verarbeitet mehr oder weniger große Informationsmengen, je nach Anwendung und Leistungsfähigkeit.
Kapitel 2 Zahlensysteme, Darstellung von Informationen 1 , Darstellung von Informationen Ein Computer speichert und verarbeitet mehr oder weniger große Informationsmengen, je nach Anwendung und Leistungsfähigkeit.
Zahlen in Binärdarstellung
 Zahlen in Binärdarstellung 1 Zahlensysteme Das Dezimalsystem Das Dezimalsystem ist ein Stellenwertsystem (Posititionssystem) zur Basis 10. Das bedeutet, dass eine Ziffer neben ihrem eigenen Wert noch einen
Zahlen in Binärdarstellung 1 Zahlensysteme Das Dezimalsystem Das Dezimalsystem ist ein Stellenwertsystem (Posititionssystem) zur Basis 10. Das bedeutet, dass eine Ziffer neben ihrem eigenen Wert noch einen
Zahlensysteme. Digitale Rechner speichern Daten im Dualsystem 435 dez = 1100110011 binär
 Zahlensysteme Menschen nutzen zur Angabe von Werten und zum Rechnen vorzugsweise das Dezimalsystem Beispiel 435 Fische aus dem Teich gefischt, d.h. 4 10 2 + 3 10 1 +5 10 0 Digitale Rechner speichern Daten
Zahlensysteme Menschen nutzen zur Angabe von Werten und zum Rechnen vorzugsweise das Dezimalsystem Beispiel 435 Fische aus dem Teich gefischt, d.h. 4 10 2 + 3 10 1 +5 10 0 Digitale Rechner speichern Daten
Leseprobe. Taschenbuch Mikroprozessortechnik. Herausgegeben von Thomas Beierlein, Olaf Hagenbruch ISBN: 978-3-446-42331-2
 Leseprobe Taschenbuch Mikroprozessortechnik Herausgegeben von Thomas Beierlein, Olaf Hagenbruch ISBN: 978-3-446-4331- Weitere Informationen oder Bestellungen unter http://www.hanser.de/978-3-446-4331-
Leseprobe Taschenbuch Mikroprozessortechnik Herausgegeben von Thomas Beierlein, Olaf Hagenbruch ISBN: 978-3-446-4331- Weitere Informationen oder Bestellungen unter http://www.hanser.de/978-3-446-4331-
2 Repräsentation von elementaren Daten
 2 Repräsentation von elementaren Daten Alle (elemtaren) Daten wie Zeichen und Zahlen werden im Dualsystem repräsentiert. Das Dualsystem ist ein spezielles B-adisches Zahlensystem, nämlich mit der Basis
2 Repräsentation von elementaren Daten Alle (elemtaren) Daten wie Zeichen und Zahlen werden im Dualsystem repräsentiert. Das Dualsystem ist ein spezielles B-adisches Zahlensystem, nämlich mit der Basis
Grundlagen der Informatik 2 Grundlagen der Digitaltechnik. 1. Zahlensysteme
 Grundlagen der Informatik 2 Grundlagen der Digitaltechnik 1. Zahlensysteme Prof. Dr.-Ing. Jürgen Teich Dr.-Ing. Christian Haubelt Lehrstuhl für Hardware-Software Software-Co-Design Grundlagen der Digitaltechnik
Grundlagen der Informatik 2 Grundlagen der Digitaltechnik 1. Zahlensysteme Prof. Dr.-Ing. Jürgen Teich Dr.-Ing. Christian Haubelt Lehrstuhl für Hardware-Software Software-Co-Design Grundlagen der Digitaltechnik
Rechnerorganisation. IHS 2015/2016 H.-D. Wuttke, K. Henke
 Rechnerorganisation Mathematische Grundlagen (1) Boolesche Algebren: BMA, BAA (2,3) Kombinatorische Schaltungen (4,5) Automaten (6,7) Sequentielle Schaltungen (8) Programmierbare Strukturen (9) Rechneraufbau
Rechnerorganisation Mathematische Grundlagen (1) Boolesche Algebren: BMA, BAA (2,3) Kombinatorische Schaltungen (4,5) Automaten (6,7) Sequentielle Schaltungen (8) Programmierbare Strukturen (9) Rechneraufbau
Das Rechnermodell - Funktion
 Darstellung von Zahlen und Zeichen im Rechner Darstellung von Zeichen ASCII-Kodierung Zahlensysteme Dezimalsystem, Dualsystem, Hexadezimalsystem Darstellung von Zahlen im Rechner Natürliche Zahlen Ganze
Darstellung von Zahlen und Zeichen im Rechner Darstellung von Zeichen ASCII-Kodierung Zahlensysteme Dezimalsystem, Dualsystem, Hexadezimalsystem Darstellung von Zahlen im Rechner Natürliche Zahlen Ganze
TOTAL DIGITAL - Wie Computer Daten darstellen
 TOTAL DIGITAL - Wie Computer Daten darstellen Computer verarbeiten Daten unter der Steuerung eines Programmes, das aus einzelnen Befehlen besteht. Diese Daten stellen Informationen dar und können sein:
TOTAL DIGITAL - Wie Computer Daten darstellen Computer verarbeiten Daten unter der Steuerung eines Programmes, das aus einzelnen Befehlen besteht. Diese Daten stellen Informationen dar und können sein:
Kapitel 2 Grundlegende Konzepte. Xiaoyi Jiang Informatik I Grundlagen der Programmierung
 Kapitel 2 Grundlegende Konzepte 1 2.1 Zahlensysteme Römisches System Grundziffern I 1 erhobener Zeigefinger V 5 Hand mit 5 Fingern X 10 steht für zwei Hände L 50 C 100 Centum heißt Hundert D 500 M 1000
Kapitel 2 Grundlegende Konzepte 1 2.1 Zahlensysteme Römisches System Grundziffern I 1 erhobener Zeigefinger V 5 Hand mit 5 Fingern X 10 steht für zwei Hände L 50 C 100 Centum heißt Hundert D 500 M 1000
Technische Informatik I
 Technische Informatik I Vorlesung 2: Zahldarstellung Joachim Schmidt jschmidt@techfak.uni-bielefeld.de Übersicht Geschichte der Zahlen Zahlensysteme Basis / Basis-Umwandlung Zahlsysteme im Computer Binärsystem,
Technische Informatik I Vorlesung 2: Zahldarstellung Joachim Schmidt jschmidt@techfak.uni-bielefeld.de Übersicht Geschichte der Zahlen Zahlensysteme Basis / Basis-Umwandlung Zahlsysteme im Computer Binärsystem,
Prof. Dr. Oliver Haase Karl Martin Kern Achim Bitzer. Programmiertechnik Zahlensysteme und Datendarstellung
 Prof. Dr. Oliver Haase Karl Martin Kern Achim Bitzer Programmiertechnik Zahlensysteme und Datendarstellung Zahlensysteme Problem: Wie stellt man (große) Zahlen einfach, platzsparend und rechnergeeignet
Prof. Dr. Oliver Haase Karl Martin Kern Achim Bitzer Programmiertechnik Zahlensysteme und Datendarstellung Zahlensysteme Problem: Wie stellt man (große) Zahlen einfach, platzsparend und rechnergeeignet
Repräsentation von Daten: Binär-, Oktal- u. Hexadezimalcodierung von ganzen und rationalen Zahlen
 Großübung 1: Zahlensysteme Repräsentation von Daten: Binär-, Oktal- u. Hexadezimalcodierung von ganzen und rationalen Zahlen Lehrender: Dr. Klaus Richter, Institut für Informatik; E-Mail: richter@informatik.tu-freiberg.de
Großübung 1: Zahlensysteme Repräsentation von Daten: Binär-, Oktal- u. Hexadezimalcodierung von ganzen und rationalen Zahlen Lehrender: Dr. Klaus Richter, Institut für Informatik; E-Mail: richter@informatik.tu-freiberg.de
3. Datentypen, Ausdrücke und Operatoren
 3. Datentypen, Ausdrücke und Operatoren Programm muß i.a. Daten zwischenspeichern Speicherplatz muß bereitgestellt werden, der ansprechbar, reserviert ist Ablegen & Wiederfinden in höheren Programmiersprachen
3. Datentypen, Ausdrücke und Operatoren Programm muß i.a. Daten zwischenspeichern Speicherplatz muß bereitgestellt werden, der ansprechbar, reserviert ist Ablegen & Wiederfinden in höheren Programmiersprachen
Kapitel 2. Zahlensysteme
 Kapitel 2 Zahlensysteme 13.08.12 K.Kraft D:\MCT_Vorlesung\Folien2013\Zahlensysteme_2\Zahlensysteme.odt 2-1 Zahlensysteme Definitionen Ziffern : Zeichen zur Darstellung von Zahlen Zahl : Eine Folge von
Kapitel 2 Zahlensysteme 13.08.12 K.Kraft D:\MCT_Vorlesung\Folien2013\Zahlensysteme_2\Zahlensysteme.odt 2-1 Zahlensysteme Definitionen Ziffern : Zeichen zur Darstellung von Zahlen Zahl : Eine Folge von
1. Grundlagen der Informatik Zahlensysteme und interne Informationsdarstellung
 1. Grundlagen der Informatik Zahlensysteme und interne Informationsdarstellung Inhalt Grundlagen digitaler Systeme Boolesche Algebra / Aussagenlogik Organisation und Architektur von Rechnern Algorithmen,
1. Grundlagen der Informatik Zahlensysteme und interne Informationsdarstellung Inhalt Grundlagen digitaler Systeme Boolesche Algebra / Aussagenlogik Organisation und Architektur von Rechnern Algorithmen,
Prinzip 8 der von-neumann Architektur: (8) Alle Daten werden binär kodiert
 Binäre Repräsentation von Information Bits und Bytes Binärzahlen ASCII Ganze Zahlen Rationale Zahlen Gleitkommazahlen Motivation Prinzip 8 der von-neumann Architektur: (8) Alle Daten werden binär kodiert
Binäre Repräsentation von Information Bits und Bytes Binärzahlen ASCII Ganze Zahlen Rationale Zahlen Gleitkommazahlen Motivation Prinzip 8 der von-neumann Architektur: (8) Alle Daten werden binär kodiert
Lektion 1: Von Nullen und Einsen _ Die binäre Welt der Informatik
 Lektion 1: Von Nullen und Einsen _ Die binäre Welt der Informatik Helmar Burkhart Departement Informatik Universität Basel Helmar.Burkhart@unibas.ch Helmar Burkhart Werkzeuge der Informatik Lektion 1:
Lektion 1: Von Nullen und Einsen _ Die binäre Welt der Informatik Helmar Burkhart Departement Informatik Universität Basel Helmar.Burkhart@unibas.ch Helmar Burkhart Werkzeuge der Informatik Lektion 1:
Informationsdarstellung im Rechner
 Informationsdarstellung im Rechner Dr. Christian Herta 15. Oktober 2005 Einführung in die Informatik - Darstellung von Information im Computer Dr. Christian Herta Darstellung von Information im Computer
Informationsdarstellung im Rechner Dr. Christian Herta 15. Oktober 2005 Einführung in die Informatik - Darstellung von Information im Computer Dr. Christian Herta Darstellung von Information im Computer
Rechnergrundlagen SS Vorlesung
 Rechnergrundlagen SS 2007 3. Vorlesung Inhalt Zahlensysteme Binäre Darstellung von Integer-Zahlen Vorzeichen-Betrag Binary Offset 1er-Komplement 2er-Komplement Addition und Subtraktion binär dargestellter
Rechnergrundlagen SS 2007 3. Vorlesung Inhalt Zahlensysteme Binäre Darstellung von Integer-Zahlen Vorzeichen-Betrag Binary Offset 1er-Komplement 2er-Komplement Addition und Subtraktion binär dargestellter
1 Dualsystem Dualzahlen mit Vorzeichen 4. 2 Hexadezimalsystem Hexadezimalzahlen mit Vorzeichen Oktalsystem 13 4 Zahlenring 14
 Zahlensysteme Inhalt: 1 Dualsystem 1 1.1 Dualzahlen mit Vorzeichen 4 2 Hexadezimalsystem 8 2.1 Hexadezimalzahlen mit Vorzeichen 10 3 Oktalsystem 13 4 Zahlenring 14 Definition: Ein polyadisches Zahlensystem
Zahlensysteme Inhalt: 1 Dualsystem 1 1.1 Dualzahlen mit Vorzeichen 4 2 Hexadezimalsystem 8 2.1 Hexadezimalzahlen mit Vorzeichen 10 3 Oktalsystem 13 4 Zahlenring 14 Definition: Ein polyadisches Zahlensystem
2.1.2 Gleitkommazahlen
 .1. Gleitkommazahlen Überblick: Gleitkommazahlen Gleitkommadarstellung Arithmetische Operationen auf Gleitkommazahlen mit fester Anzahl von Mantissen- und Exponentenbits Insbesondere Rundungsproblematik:
.1. Gleitkommazahlen Überblick: Gleitkommazahlen Gleitkommadarstellung Arithmetische Operationen auf Gleitkommazahlen mit fester Anzahl von Mantissen- und Exponentenbits Insbesondere Rundungsproblematik:
Skript Zahlensysteme
 Skript Zahlensysteme Dieses Skript enthält die Themen meiner Unterrichtseinheit Zahlensysteme. Hier sollen die Grundlagen für das Verständnis der darauf folgenden Inhalte zu den Abläufen innerhalb des
Skript Zahlensysteme Dieses Skript enthält die Themen meiner Unterrichtseinheit Zahlensysteme. Hier sollen die Grundlagen für das Verständnis der darauf folgenden Inhalte zu den Abläufen innerhalb des
Das Maschinenmodell Datenrepräsentation
 Das Maschinenmodell Datenrepräsentation Darstellung von Zahlen/Zeichen in der Maschine Bit (0/1) ist die kleinste Informationseinheit Größere Einheiten durch Zusammenfassen mehrerer Bits, z.b. 8 Bit =
Das Maschinenmodell Datenrepräsentation Darstellung von Zahlen/Zeichen in der Maschine Bit (0/1) ist die kleinste Informationseinheit Größere Einheiten durch Zusammenfassen mehrerer Bits, z.b. 8 Bit =
Grundstrukturen: Speicherorganisation und Zahlenmengen
 Zahlendarstellung Zahlen und ihre Darstellung in Digitalrechnern Grundstrukturen: Speicherorganisation und Zahlenmengen Linear organisierter Speicher zu einer Adresse gehört ein Speicher mit 3 Bit-Zellen
Zahlendarstellung Zahlen und ihre Darstellung in Digitalrechnern Grundstrukturen: Speicherorganisation und Zahlenmengen Linear organisierter Speicher zu einer Adresse gehört ein Speicher mit 3 Bit-Zellen
Ein polyadisches Zahlensystem mit der Basis B ist ein Zahlensystem, in dem eine Zahl x nach Potenzen von B zerlegt wird.
 Zahlensysteme Definition: Ein polyadisches Zahlensystem mit der Basis B ist ein Zahlensystem, in dem eine Zahl x nach Potenzen von B zerlegt wird. In der Informatik spricht man auch von Stellenwertsystem,
Zahlensysteme Definition: Ein polyadisches Zahlensystem mit der Basis B ist ein Zahlensystem, in dem eine Zahl x nach Potenzen von B zerlegt wird. In der Informatik spricht man auch von Stellenwertsystem,
Musterlösung 1. Mikroprozessortechnik und Eingebettete Systeme 1 WS2015/2016
 Musterlösung 1 Mikroprozessortechnik und Eingebettete Systeme 1 WS2015/2016 Hinweis: Die folgenden Aufgaben erheben nicht den Anspruch, eine tiefergehende Kenntnis zu vermitteln; sie sollen lediglich den
Musterlösung 1 Mikroprozessortechnik und Eingebettete Systeme 1 WS2015/2016 Hinweis: Die folgenden Aufgaben erheben nicht den Anspruch, eine tiefergehende Kenntnis zu vermitteln; sie sollen lediglich den
Einführung in die Informatik I
 Einführung in die Informatik I Das Rechnen in Zahlensystemen zur Basis b=2, 8, 10 und 16 Prof. Dr. Nikolaus Wulff Zahlensysteme Neben dem üblichen dezimalen Zahlensystem zur Basis 10 sind in der Informatik
Einführung in die Informatik I Das Rechnen in Zahlensystemen zur Basis b=2, 8, 10 und 16 Prof. Dr. Nikolaus Wulff Zahlensysteme Neben dem üblichen dezimalen Zahlensystem zur Basis 10 sind in der Informatik
Dipl.-Ing. Halit Ünver Datenbanken/Künstliche Intelligenz FAW/n. Zahlensysteme
 Dipl.-Ing. Halit Ünver 7.. Datenbanken/Künstliche Intelligenz FAW/n Zahlensysteme Seite Zahlensysteme Dipl.-Ing. Halit Ünver 7.. Inhalt I. Informatik und Zahlen für Wirtschaftswissenschaftler? II. III.
Dipl.-Ing. Halit Ünver 7.. Datenbanken/Künstliche Intelligenz FAW/n Zahlensysteme Seite Zahlensysteme Dipl.-Ing. Halit Ünver 7.. Inhalt I. Informatik und Zahlen für Wirtschaftswissenschaftler? II. III.
Tutorium Rechnerorganisation
 Woche 1 Tutorien 3 und 4 zur Vorlesung Rechnerorganisation 1 Christian A. Mandery: KIT Universität des Landes Baden-Württemberg und nationales Grossforschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu
Woche 1 Tutorien 3 und 4 zur Vorlesung Rechnerorganisation 1 Christian A. Mandery: KIT Universität des Landes Baden-Württemberg und nationales Grossforschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu
Darstellung von Informationen
 Darstellung von Informationen Bit, Byte, Speicherzelle und rbeitsspeicher Boolesche Operationen, Gatter, Schaltkreis Bit Speicher (Flipflop) Binär- Hexadezimal und Dezimalzahlensystem, Umrechnungen Zweierkomplement
Darstellung von Informationen Bit, Byte, Speicherzelle und rbeitsspeicher Boolesche Operationen, Gatter, Schaltkreis Bit Speicher (Flipflop) Binär- Hexadezimal und Dezimalzahlensystem, Umrechnungen Zweierkomplement
Computergrundlagen Zahlensysteme
 Computergrundlagen Zahlensysteme Institut für Computerphysik Universität Stuttgart Wintersemester 2012/13 Wie rechnet ein Computer? Ein Mikroprozessor ist ein Netz von Transistoren, Widerständen und Kondensatoren
Computergrundlagen Zahlensysteme Institut für Computerphysik Universität Stuttgart Wintersemester 2012/13 Wie rechnet ein Computer? Ein Mikroprozessor ist ein Netz von Transistoren, Widerständen und Kondensatoren
Kapitel 1. Zahlendarstellung. Prof. Dr. Dirk W. Hoffmann. Hochschule Karlsruhe w University of Applied Sciences w Fakultät für Informatik
 Kapitel 1 Zahlendarstellung Prof. Dr. Dirk W. Hoffmann Hochschule Karlsruhe w University of Applied Sciences w Fakultät für Informatik Zahlensystemkonvertierung Motivation Jede nichtnegative Zahl z lässt
Kapitel 1 Zahlendarstellung Prof. Dr. Dirk W. Hoffmann Hochschule Karlsruhe w University of Applied Sciences w Fakultät für Informatik Zahlensystemkonvertierung Motivation Jede nichtnegative Zahl z lässt
1. Das dekadische Ziffernsystem (Dezimalsystem) Eine ganze Zahl z kann man als Summe von Potenzen zur Basis 10 darstellen:
 Zahlensysteme. Das dekadische Ziffernsystem (Dezimalsystem) Eine ganze Zahl z kann man als Summe von Potenzen zur Basis darstellen: n n n n z a a... a a a Dabei sind die Koeffizienten a, a, a,... aus der
Zahlensysteme. Das dekadische Ziffernsystem (Dezimalsystem) Eine ganze Zahl z kann man als Summe von Potenzen zur Basis darstellen: n n n n z a a... a a a Dabei sind die Koeffizienten a, a, a,... aus der
Lektion 1: Zahlensysteme und Binärdarstellung. Übersicht Lektion 1
 Lektion 1: Zahlensysteme und Binärdarstellung Helmar Burkhart Departement Informatik Universität Basel Helmar.Burkhart@unibas.ch Helmar Burkhart Werkzeuge der Informatik Lektion 1: Zahlensysteme 1-1 Übersicht
Lektion 1: Zahlensysteme und Binärdarstellung Helmar Burkhart Departement Informatik Universität Basel Helmar.Burkhart@unibas.ch Helmar Burkhart Werkzeuge der Informatik Lektion 1: Zahlensysteme 1-1 Übersicht
Rechnerarithmetik Ganzzahlen und Gleitkommazahlen Ac 2013
 Rechnerarithmetik Ganzzahlen und Gleitkommazahlen Ac 2013 Im folgenden soll ein Überblick über die in Computersystemen bzw. Programmiersprachen verwendeten Zahlen inklusive ausgewählter Algorithmen (in
Rechnerarithmetik Ganzzahlen und Gleitkommazahlen Ac 2013 Im folgenden soll ein Überblick über die in Computersystemen bzw. Programmiersprachen verwendeten Zahlen inklusive ausgewählter Algorithmen (in
Zahlendarstellungen und Rechnerarithmetik*
 Zahlendarstellungen und Rechnerarithmetik* 1. Darstellung positiver ganzer Zahlen 2. Darstellung negativer ganzer Zahlen 3. Brüche und Festkommazahlen 4. binäre Addition 5. binäre Subtraktion *Die Folien
Zahlendarstellungen und Rechnerarithmetik* 1. Darstellung positiver ganzer Zahlen 2. Darstellung negativer ganzer Zahlen 3. Brüche und Festkommazahlen 4. binäre Addition 5. binäre Subtraktion *Die Folien
Arithmetik: Vorzeichenregeln und Überlauf, Exponenten & Normalisierung, Umrechnungen. Architektur: - Rechnerarchitektur, Instruktionssatz, Assembler
 F. Zahlendarstellung und Rechnerarithmetik F.1. Einordnung & Inhalte Zahlendarstellungen: binär, BCD oder als ASCII-Text, Einer- und Zweierkomplement, Gleit- & Festkommazahlen. Arithmetik: Vorzeichenregeln
F. Zahlendarstellung und Rechnerarithmetik F.1. Einordnung & Inhalte Zahlendarstellungen: binär, BCD oder als ASCII-Text, Einer- und Zweierkomplement, Gleit- & Festkommazahlen. Arithmetik: Vorzeichenregeln
Technische Grundlagen der Informatik Kapitel 8. Prof. Dr. Sorin A. Huss Fachbereich Informatik TU Darmstadt
 Technische Grundlagen der Informatik Kapitel 8 Prof. Dr. Sorin A. Huss Fachbereich Informatik TU Darmstadt Kapitel 8: Themen Zahlensysteme - Dezimal - Binär Vorzeichen und Betrag Zweierkomplement Zahlen
Technische Grundlagen der Informatik Kapitel 8 Prof. Dr. Sorin A. Huss Fachbereich Informatik TU Darmstadt Kapitel 8: Themen Zahlensysteme - Dezimal - Binär Vorzeichen und Betrag Zweierkomplement Zahlen
Grundlagen der Informatik I. Übung
 Grundlagen der Informatik I Übung Studiengang Wirtschaftsingenieurwesen Wintersemester 2013/2014 Autor: Prof. Dr.-Ing. habil. Hans-Joachim Böhme HTW Dresden, Fachbereich Informatik/Mathematik Friedrich-List-Platz
Grundlagen der Informatik I Übung Studiengang Wirtschaftsingenieurwesen Wintersemester 2013/2014 Autor: Prof. Dr.-Ing. habil. Hans-Joachim Böhme HTW Dresden, Fachbereich Informatik/Mathematik Friedrich-List-Platz
Thema 1 -- Fortsetzung. Computersystem, Informationsdarstellung
 Thema 1 -- Fortsetzung Computersystem, Informationsdarstellung Codierung! Bei der Codierung erfolgt eine eindeutige Zuordnung der Zeichen eines Zeichenvorrates (Urmenge, Quellalphabet) zu denjenigen eines
Thema 1 -- Fortsetzung Computersystem, Informationsdarstellung Codierung! Bei der Codierung erfolgt eine eindeutige Zuordnung der Zeichen eines Zeichenvorrates (Urmenge, Quellalphabet) zu denjenigen eines
21.10.2013. Vorlesung Programmieren. Agenda. Dezimalsystem. Zahlendarstellung. Zahlendarstellung. Oder: wie rechnen Computer?
 Vorlesung Programmieren Zahlendarstellung Prof. Dr. Stefan Fischer Institut für Telematik, Universität zu Lübeck http://www.itm.uni-luebeck.de/people/pfisterer Agenda Zahlendarstellung Oder: wie rechnen
Vorlesung Programmieren Zahlendarstellung Prof. Dr. Stefan Fischer Institut für Telematik, Universität zu Lübeck http://www.itm.uni-luebeck.de/people/pfisterer Agenda Zahlendarstellung Oder: wie rechnen
2.5. Gleitkommaarithmetik
 2.5. Gleitkommaarithmetik Bei vorgegebener Länge m des Kodeworts (der rechnerinternen Darstellung) lassen sich nur 2 m verschiedene Werte darstellen. In der Mehrzahl der Fälle ist das zu wenig. Ein Ausweg
2.5. Gleitkommaarithmetik Bei vorgegebener Länge m des Kodeworts (der rechnerinternen Darstellung) lassen sich nur 2 m verschiedene Werte darstellen. In der Mehrzahl der Fälle ist das zu wenig. Ein Ausweg
2.0 Zahlendarstellung, Konvertierungsalgorithmen und arithmetische Algorithmen
 2.0 Zahlendarstellung, Konvertierungsalgorithmen und arithmetische Algorithmen Ziele dieses Kapitels Kennenlernen wesentlicher Zahlensysteme und die Konvertierung von Zahlen zwischen unterschiedlichen
2.0 Zahlendarstellung, Konvertierungsalgorithmen und arithmetische Algorithmen Ziele dieses Kapitels Kennenlernen wesentlicher Zahlensysteme und die Konvertierung von Zahlen zwischen unterschiedlichen
1. Vorzeichen und Betrag (engl. Sign-/Magnitude) 2. Stellenkomplement 3. Basiskomplement
 3 Darstellungsformen für Zahlen Informatik II SS 24 Dipl.-Inform. Michael Ebner. Vorzeichen und Betrag (engl. Sign-/Magnitude) 2. Stellenkomplement 3. Basiskomplement Warum 3 Darstellungsformen? Ziel:
3 Darstellungsformen für Zahlen Informatik II SS 24 Dipl.-Inform. Michael Ebner. Vorzeichen und Betrag (engl. Sign-/Magnitude) 2. Stellenkomplement 3. Basiskomplement Warum 3 Darstellungsformen? Ziel:
7. Übung zur Vorlesung Grundlagen der Informatik
 7. Übung zur Vorlesung Grundlagen der Informatik 13.Interne Darstellung von Daten In der Vorlesung wurde bereits darauf hingewiesen, dass ein Rechner intern lediglich die Zustände 0 (kein Signal liegt
7. Übung zur Vorlesung Grundlagen der Informatik 13.Interne Darstellung von Daten In der Vorlesung wurde bereits darauf hingewiesen, dass ein Rechner intern lediglich die Zustände 0 (kein Signal liegt
Daten, Informationen, Kodierung. Binärkodierung
 Binärkodierung Besondere Bedeutung der Binärkodierung in der Informatik Abbildung auf Alphabet mit zwei Zeichen, in der Regel B = {0, 1} Entspricht den zwei möglichen Schaltzuständen in der Elektronik:
Binärkodierung Besondere Bedeutung der Binärkodierung in der Informatik Abbildung auf Alphabet mit zwei Zeichen, in der Regel B = {0, 1} Entspricht den zwei möglichen Schaltzuständen in der Elektronik:
2 ARITHM. UND LOG. AUSDRÜCKE ZAHLEN
 2 ARITHM. UND LOG. AUSDRÜCKE ZAHLEN Leitidee: Die Darstellung von Zahlen durch eine feste Zahl von Bits erfordert eine Reihe von Kompromissen Ganzzahl- oder Gleitpunktarithmetik? Dual- und Hexadezimalzahlsystem
2 ARITHM. UND LOG. AUSDRÜCKE ZAHLEN Leitidee: Die Darstellung von Zahlen durch eine feste Zahl von Bits erfordert eine Reihe von Kompromissen Ganzzahl- oder Gleitpunktarithmetik? Dual- und Hexadezimalzahlsystem
Rechnergrundlagen SS Vorlesung
 Rechnergrundlagen SS 27 5. Vorlesung Inhalt Interpretation hexadezimal dargestellter Integer-Zahlen Little Endian / Big Endian Umrechnung in eine binäre Darstellung Ausführung von Additionen Optimierte
Rechnergrundlagen SS 27 5. Vorlesung Inhalt Interpretation hexadezimal dargestellter Integer-Zahlen Little Endian / Big Endian Umrechnung in eine binäre Darstellung Ausführung von Additionen Optimierte
Grundlagen der Datenverarbeitung - Zahlensysteme
 1. Zahlensysteme 1.1.Dezimalsystem Das Dezimalsystem ist das System, in dem wir gewohnt sind zu zählen und zu rechnen. Zahlen werden durch die Ziffern 0,1,2,...,9 dargestellt. Die Zahl 7243 wird als Siebentausendzweihundertdreiundvierzig
1. Zahlensysteme 1.1.Dezimalsystem Das Dezimalsystem ist das System, in dem wir gewohnt sind zu zählen und zu rechnen. Zahlen werden durch die Ziffern 0,1,2,...,9 dargestellt. Die Zahl 7243 wird als Siebentausendzweihundertdreiundvierzig
Informationssysteme Gleitkommazahlen nach dem IEEE-Standard 754. Berechnung von Gleitkommazahlen aus Dezimalzahlen. HSLU T&A Informatik HS10
 Informationssysteme Gleitkommazahlen nach dem IEEE-Standard 754 Berechnung von Gleitkommazahlen aus Dezimalzahlen Die wissenschaftliche Darstellung einer Zahl ist wie folgt definiert: n = f * 10 e. f ist
Informationssysteme Gleitkommazahlen nach dem IEEE-Standard 754 Berechnung von Gleitkommazahlen aus Dezimalzahlen Die wissenschaftliche Darstellung einer Zahl ist wie folgt definiert: n = f * 10 e. f ist
Lösungen: zu 1. a.) 0 0 1 1 b.) 1 1 1 1 c.) 0 1 1 0 + 1 1 0 0 + 0 0 1 1 + 0 1 1 1 1 1 1 1 1 0 0 1 0 1 1 0 1
 Lösungen: zu 1. a.) 0 0 1 1 b.) 1 1 1 1 c.) 0 1 1 0 + 1 1 0 0 + 0 0 1 1 + 0 1 1 1 1 1 1 1 1 0 0 1 0 1 1 0 1 vorzeichenlose Zahl: 15 vorzeichenlose Zahl: 18 vorzeichenlose Zahl: 13 Zweierkomplement: - 1
Lösungen: zu 1. a.) 0 0 1 1 b.) 1 1 1 1 c.) 0 1 1 0 + 1 1 0 0 + 0 0 1 1 + 0 1 1 1 1 1 1 1 1 0 0 1 0 1 1 0 1 vorzeichenlose Zahl: 15 vorzeichenlose Zahl: 18 vorzeichenlose Zahl: 13 Zweierkomplement: - 1
Grundlagen der Informatik I. Übung
 Grundlagen der Informatik I Übung Studiengang Wirtschaftsingenieurwesen Wintersemester 1/13 Autor: Prof. Dr.-Ing. habil. Hans-Joachim Böhme HTW Dresden, Fachbereich Informatik/Mathematik Friedrich-List-Platz
Grundlagen der Informatik I Übung Studiengang Wirtschaftsingenieurwesen Wintersemester 1/13 Autor: Prof. Dr.-Ing. habil. Hans-Joachim Böhme HTW Dresden, Fachbereich Informatik/Mathematik Friedrich-List-Platz
Technische Informatik - Eine Einführung
 Martin-Luther-Universität Halle-Wittenberg Fachbereich Mathematik und Informatik Lehrstuhl für Technische Informatik Prof. P. Molitor Ausgabe: 2005-02-21 Abgabe: 2005-02-21 Technische Informatik - Eine
Martin-Luther-Universität Halle-Wittenberg Fachbereich Mathematik und Informatik Lehrstuhl für Technische Informatik Prof. P. Molitor Ausgabe: 2005-02-21 Abgabe: 2005-02-21 Technische Informatik - Eine
Repräsentation von Daten Binärcodierung ganzer Zahlen
 Kapitel 3: Repräsentation von Daten Binärcodierung ganzer Zahlen Einführung in die Informatik Wintersemester 2007/08 Prof. Bernhard Jung Übersicht Repräsentation von Daten im Computer (dieses und nächstes
Kapitel 3: Repräsentation von Daten Binärcodierung ganzer Zahlen Einführung in die Informatik Wintersemester 2007/08 Prof. Bernhard Jung Übersicht Repräsentation von Daten im Computer (dieses und nächstes
1. Stellenwerte im Dualsystem
 1. a) Definitionen Stellenwertsystem Ein Zahlensystem bei dem der Wert einer Ziffer innerhalb einer Ziffernfolge von ihrer Stelle abhängt, wird Stellenwertsystem genannt. Die Stellenwerte sind also ganzzahlige
1. a) Definitionen Stellenwertsystem Ein Zahlensystem bei dem der Wert einer Ziffer innerhalb einer Ziffernfolge von ihrer Stelle abhängt, wird Stellenwertsystem genannt. Die Stellenwerte sind also ganzzahlige
D A T E N... 1 Daten Micheuz Peter
 D A T E N.....! Symbole, Alphabete, Codierung! Universalität binärcodierter Daten! Elementare Datentypen! Speicherung binärcodierter Daten! Befehle und Programme! Form und Bedeutung 1 Daten Micheuz Peter
D A T E N.....! Symbole, Alphabete, Codierung! Universalität binärcodierter Daten! Elementare Datentypen! Speicherung binärcodierter Daten! Befehle und Programme! Form und Bedeutung 1 Daten Micheuz Peter
2 Darstellung von Zahlen und Zeichen
 2.1 Analoge und digitale Darstellung von Werten 79 2 Darstellung von Zahlen und Zeichen Computer- bzw. Prozessorsysteme führen Transformationen durch, die Eingaben X auf Ausgaben Y abbilden, d.h. Y = f
2.1 Analoge und digitale Darstellung von Werten 79 2 Darstellung von Zahlen und Zeichen Computer- bzw. Prozessorsysteme führen Transformationen durch, die Eingaben X auf Ausgaben Y abbilden, d.h. Y = f
BSZ für Elektrotechnik Dresden. Zahlenformate. Dr.-Ing. Uwe Heiner Leichsenring www.leichsenring-homepage.de
 BSZ für Elektrotechnik Dresden Zahlenformate Dr.-Ing. Uwe Heiner Leichsenring www.leichsenring-homepage.de Gliederung 1 Überblick 2 Grundaufbau der Zahlensysteme 2.1 Dezimalzahlen 2.2 Binärzahlen = Dualzahlen
BSZ für Elektrotechnik Dresden Zahlenformate Dr.-Ing. Uwe Heiner Leichsenring www.leichsenring-homepage.de Gliederung 1 Überblick 2 Grundaufbau der Zahlensysteme 2.1 Dezimalzahlen 2.2 Binärzahlen = Dualzahlen
Modul 114. Zahlensysteme
 Modul 114 Modulbezeichnung: Modul 114 Kompetenzfeld: Codierungs-, Kompressions- und Verschlüsselungsverfahren einsetzen 1. Codierungen von Daten situationsbezogen auswählen und einsetzen. Aufzeigen, welche
Modul 114 Modulbezeichnung: Modul 114 Kompetenzfeld: Codierungs-, Kompressions- und Verschlüsselungsverfahren einsetzen 1. Codierungen von Daten situationsbezogen auswählen und einsetzen. Aufzeigen, welche
II. Grundlagen der Programmierung
 II. Grundlagen der Programmierung II.1. Zahlenssteme und elementare Logik 1.1. Zahlenssteme 1.1.1. Ganze Zahlen Ganze Zahlen werden im Dezimalsstem als Folge von Ziffern 0, 1,..., 9 dargestellt, z.b. 123
II. Grundlagen der Programmierung II.1. Zahlenssteme und elementare Logik 1.1. Zahlenssteme 1.1.1. Ganze Zahlen Ganze Zahlen werden im Dezimalsstem als Folge von Ziffern 0, 1,..., 9 dargestellt, z.b. 123
, 2015S Übungstermin: Mi.,
 VU Grundlagen digitaler Systeme Übung 1: Zahlendarstellungen, Numerik 183.580, 2015S Übungstermin: Mi., 18.03.2015 Allgemeine Hinweise: Versuchen Sie beim Lösen der Beispiele keine elektronischen Hilfsmittel
VU Grundlagen digitaler Systeme Übung 1: Zahlendarstellungen, Numerik 183.580, 2015S Übungstermin: Mi., 18.03.2015 Allgemeine Hinweise: Versuchen Sie beim Lösen der Beispiele keine elektronischen Hilfsmittel
Grundlagen der Informatik
 Mag. Christian Gürtler Programmierung Grundlagen der Informatik 2011 Inhaltsverzeichnis I. Allgemeines 3 1. Zahlensysteme 4 1.1. ganze Zahlen...................................... 4 1.1.1. Umrechnungen.................................
Mag. Christian Gürtler Programmierung Grundlagen der Informatik 2011 Inhaltsverzeichnis I. Allgemeines 3 1. Zahlensysteme 4 1.1. ganze Zahlen...................................... 4 1.1.1. Umrechnungen.................................
Vertiefungsstoff zum Thema Darstellung von Zahlen
 Vertiefungsstoff zum Thema Darstellung von Zahlen Addition von Zahlen in BCD-Kodierung Einerkomplementdarstellung von ganzen Zahlen Gleitpunktdarstellung nach dem IEEE-754-Standard 1 Rechnen mit BCD-codierten
Vertiefungsstoff zum Thema Darstellung von Zahlen Addition von Zahlen in BCD-Kodierung Einerkomplementdarstellung von ganzen Zahlen Gleitpunktdarstellung nach dem IEEE-754-Standard 1 Rechnen mit BCD-codierten
Rechnerstrukturen WS 2012/13
 Rechnerstrukturen WS 2012/13 Repräsentation von Daten Repräsentation natürlicher Zahlen (Wiederholung) Repräsentation von Texten Repräsentation ganzer Zahlen Repräsentation rationaler Zahlen Repräsentation
Rechnerstrukturen WS 2012/13 Repräsentation von Daten Repräsentation natürlicher Zahlen (Wiederholung) Repräsentation von Texten Repräsentation ganzer Zahlen Repräsentation rationaler Zahlen Repräsentation
EIN NEUES KAPITEL: SPEICHERUNG UND INTERPRETATION VON INFORMATION
 Auf diesem Computerschirm sieht man verschiedene Arten von Information dargestellt. Wie wird sie eigentlich im Computer abgespeichert. Was man sieht, ist nur eine Graphik! EIN NEUES KAPITEL EIN NEUES KAPITEL:
Auf diesem Computerschirm sieht man verschiedene Arten von Information dargestellt. Wie wird sie eigentlich im Computer abgespeichert. Was man sieht, ist nur eine Graphik! EIN NEUES KAPITEL EIN NEUES KAPITEL:
Digitaltechnik FHDW 1.Q 2007
 Digitaltechnik FHDW 1.Q 2007 1 Übersicht 1-3 1 Einführung 1.1 Begriffsdefinition: Analog / Digital 2 Zahlensysteme 2.1 Grundlagen 2.2 Darstellung und Umwandlung 3 Logische Verknüpfungen 3.1 Grundfunktionen
Digitaltechnik FHDW 1.Q 2007 1 Übersicht 1-3 1 Einführung 1.1 Begriffsdefinition: Analog / Digital 2 Zahlensysteme 2.1 Grundlagen 2.2 Darstellung und Umwandlung 3 Logische Verknüpfungen 3.1 Grundfunktionen
DIGITALTECHNIK 02 ZAHLENSYSTEME
 Seite 1 von 15 DIGITALTECHNIK 02 ZAHLENSYSTEME Inhalt Seite 2 von 15 1 ALLGEMEINES ZU ZAHLENSYSTEMEN... 3 1.1 ZAHLENSYSTEME... 3 1.2 KENNZEICHEN VON ZAHLENSYSTEMEN... 4 1.3 BILDUNGSGESETZE... 4 1.4 STELLENWERTSYSTEM...
Seite 1 von 15 DIGITALTECHNIK 02 ZAHLENSYSTEME Inhalt Seite 2 von 15 1 ALLGEMEINES ZU ZAHLENSYSTEMEN... 3 1.1 ZAHLENSYSTEME... 3 1.2 KENNZEICHEN VON ZAHLENSYSTEMEN... 4 1.3 BILDUNGSGESETZE... 4 1.4 STELLENWERTSYSTEM...
Einführung in die Programmiertechnik
 Einführung in die Programmiertechnik Darstellung von Zahlen Natürliche Zahlen: Darstellungsvarianten Darstellung als Text Üblich, wenn keine Berechnung stattfinden soll z.b. Die Regionalbahn 28023 fährt
Einführung in die Programmiertechnik Darstellung von Zahlen Natürliche Zahlen: Darstellungsvarianten Darstellung als Text Üblich, wenn keine Berechnung stattfinden soll z.b. Die Regionalbahn 28023 fährt
2.5 Primitive Datentypen
 2.5 Primitive Datentypen Wir unterscheiden 5 primitive Datentypen: ganze Zahlen -2, -1, -0, -1, -2,... reelle Zahlen 0.3, 0.3333..., π, 2.7 10 4 Zeichen a, b, c,... Zeichenreihen "Hello World", "TIFI",
2.5 Primitive Datentypen Wir unterscheiden 5 primitive Datentypen: ganze Zahlen -2, -1, -0, -1, -2,... reelle Zahlen 0.3, 0.3333..., π, 2.7 10 4 Zeichen a, b, c,... Zeichenreihen "Hello World", "TIFI",
Numerische Datentypen. Simon Weidmann
 Numerische Datentypen Simon Weidmann 08.05.2014 1 Ganzzahlige Typen 1.1 Generelles Bei Datentypen muss man immer zwei elementare Eigenschaften unterscheiden: Zuerst gibt es den Wertebereich, zweitens die
Numerische Datentypen Simon Weidmann 08.05.2014 1 Ganzzahlige Typen 1.1 Generelles Bei Datentypen muss man immer zwei elementare Eigenschaften unterscheiden: Zuerst gibt es den Wertebereich, zweitens die
Zur Universalität der Informatik. Gott ist ein Informatiker. Die Grundordnung der Welt läßt sich mathematisch formulieren:
 Daten und ihre Codierung Seite: 1 Zur Universalität der Informatik Gott ist ein Informatiker Die Grundordnung der Welt läßt sich mathematisch formulieren: Naturgesetze, wie wir sie in der Physik, Chemie
Daten und ihre Codierung Seite: 1 Zur Universalität der Informatik Gott ist ein Informatiker Die Grundordnung der Welt läßt sich mathematisch formulieren: Naturgesetze, wie wir sie in der Physik, Chemie
Zahlensysteme: Oktal- und Hexadezimalsystem
 20 Brückenkurs Die gebräuchlichste Bitfolge umfasst 8 Bits, sie deckt also 2 8 =256 Möglichkeiten ab, und wird ein Byte genannt. Zwei Bytes, also 16 Bits, bilden ein Wort, und 4 Bytes, also 32 Bits, formen
20 Brückenkurs Die gebräuchlichste Bitfolge umfasst 8 Bits, sie deckt also 2 8 =256 Möglichkeiten ab, und wird ein Byte genannt. Zwei Bytes, also 16 Bits, bilden ein Wort, und 4 Bytes, also 32 Bits, formen
Binäre Gleitkommazahlen
 Binäre Gleitkommazahlen Was ist die wissenschaftliche, normalisierte Darstellung der binären Gleitkommazahl zur dezimalen Gleitkommazahl 0,625? Grundlagen der Rechnerarchitektur Logik und Arithmetik 72
Binäre Gleitkommazahlen Was ist die wissenschaftliche, normalisierte Darstellung der binären Gleitkommazahl zur dezimalen Gleitkommazahl 0,625? Grundlagen der Rechnerarchitektur Logik und Arithmetik 72
Musterlösung 2. Mikroprozessor & Eingebettete Systeme 1
 Musterlösung 2 Mikroprozessor & Eingebettete Systeme 1 WS2014/2015 Hinweis: Die folgenden Aufgaben erheben nicht den Anspruch, eine tiefergehende Kenntnis zu vermitteln; sie sollen lediglich den Einstieg
Musterlösung 2 Mikroprozessor & Eingebettete Systeme 1 WS2014/2015 Hinweis: Die folgenden Aufgaben erheben nicht den Anspruch, eine tiefergehende Kenntnis zu vermitteln; sie sollen lediglich den Einstieg
Dualzahlen
 Dualzahlen Ein Schüler soll sich eine Zahl zwischen und 6 denken. Nun soll der Schüler seinen Zahl in folgenden Tabellen suchen und die Nummer der Tabelle nennen in welcher sich seine Zahl befindet. 7
Dualzahlen Ein Schüler soll sich eine Zahl zwischen und 6 denken. Nun soll der Schüler seinen Zahl in folgenden Tabellen suchen und die Nummer der Tabelle nennen in welcher sich seine Zahl befindet. 7
Unterstützte Datentypen
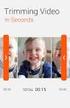 Unterstützte Datentypen Die folgende Tabelle zeigt die unterstützten Datentypen für die Triggervariable: Speicherbedarf und Format der Zahl 1-Byte 8-Bit-Ganzzahlen 16-Bit-Ganzzahlen 32-Bit-Ganzzahlen 64-Bit-Ganzzahlen
Unterstützte Datentypen Die folgende Tabelle zeigt die unterstützten Datentypen für die Triggervariable: Speicherbedarf und Format der Zahl 1-Byte 8-Bit-Ganzzahlen 16-Bit-Ganzzahlen 32-Bit-Ganzzahlen 64-Bit-Ganzzahlen
Informatik I: Abschnitt 7
 Informatik I: Abschnitt 7 Inhalt: 7. Interne Informationsdarstellung 7.1 Ganzzahlige Datentypen 7.2 Gleitkomma-Datentypen Die Folien basieren zum Teil auf einen Foliensatz von R. Großmann und T. Wiedemann
Informatik I: Abschnitt 7 Inhalt: 7. Interne Informationsdarstellung 7.1 Ganzzahlige Datentypen 7.2 Gleitkomma-Datentypen Die Folien basieren zum Teil auf einen Foliensatz von R. Großmann und T. Wiedemann
Zahlensysteme. Formale Methoden der Informatik WiSe 2008/2009 Folie 1 (von 54)
 Zahlensysteme Formale Methoden der Informatik WiSe 28/29 Folie (von 54) Teil I: Zahlensysteme. Einführung und Zahlensysteme 2. Zahlensysteme / Algorithmik 3. Zahlendarstellung im Rechner Franz-Josef Radermacher,
Zahlensysteme Formale Methoden der Informatik WiSe 28/29 Folie (von 54) Teil I: Zahlensysteme. Einführung und Zahlensysteme 2. Zahlensysteme / Algorithmik 3. Zahlendarstellung im Rechner Franz-Josef Radermacher,
Java Einführung VARIABLEN und DATENTYPEN Kapitel 2
 Java Einführung VARIABLEN und DATENTYPEN Kapitel 2 Inhalt dieser Einheit Variablen (Sinn und Aufgabe) Bezeichner Datentypen, Deklaration und Operationen Typenumwandlung (implizit/explizit) 2 Variablen
Java Einführung VARIABLEN und DATENTYPEN Kapitel 2 Inhalt dieser Einheit Variablen (Sinn und Aufgabe) Bezeichner Datentypen, Deklaration und Operationen Typenumwandlung (implizit/explizit) 2 Variablen
1. 4-Bit Binärzahlen ohne Vorzeichen 2. 4-Bit Binärzahlen mit Vorzeichen 3. 4-Bit Binärzahlen im 2er Komplement 4. Rechnen im 2er Komplement
 Kx Binäre Zahlen Kx Binäre Zahlen Inhalt. Dezimalzahlen. Hexadezimalzahlen. Binärzahlen. -Bit Binärzahlen ohne Vorzeichen. -Bit Binärzahlen mit Vorzeichen. -Bit Binärzahlen im er Komplement. Rechnen im
Kx Binäre Zahlen Kx Binäre Zahlen Inhalt. Dezimalzahlen. Hexadezimalzahlen. Binärzahlen. -Bit Binärzahlen ohne Vorzeichen. -Bit Binärzahlen mit Vorzeichen. -Bit Binärzahlen im er Komplement. Rechnen im
Computergrundlagen Boolesche Logik, Zahlensysteme und Arithmetik
 Computergrundlagen Boolesche Logik, Zahlensysteme und Arithmetik Institut für Computerphysik Universität Stuttgart Wintersemester 2012/13 Wie rechnet ein Computer? Ein Mikroprozessor ist ein Netz von Transistoren,
Computergrundlagen Boolesche Logik, Zahlensysteme und Arithmetik Institut für Computerphysik Universität Stuttgart Wintersemester 2012/13 Wie rechnet ein Computer? Ein Mikroprozessor ist ein Netz von Transistoren,
Teil II. Schaltfunktionen
 Teil II Schaltfunktionen 1 Teil II.1 Zahlendarstellung 2 b-adische Systeme Sei b IN mit b > 1 und E b = {0, 1,..., b 1} (Alphabet). Dann ist jede Fixpunktzahl z (mit n Vorkomma und k Nachkommastellen)
Teil II Schaltfunktionen 1 Teil II.1 Zahlendarstellung 2 b-adische Systeme Sei b IN mit b > 1 und E b = {0, 1,..., b 1} (Alphabet). Dann ist jede Fixpunktzahl z (mit n Vorkomma und k Nachkommastellen)
Algorithmen & Programmierung. Zahlensysteme Bits und Bytes
 Algorithmen & Programmierung Zahlensysteme Bits und Bytes Zahlensysteme Positionssystem Bei sogenannten Positionssystemen bestimmt (im Gegensatz zu additiven Systemen wie dem römischen Zahlensystem) die
Algorithmen & Programmierung Zahlensysteme Bits und Bytes Zahlensysteme Positionssystem Bei sogenannten Positionssystemen bestimmt (im Gegensatz zu additiven Systemen wie dem römischen Zahlensystem) die
Lösung 1. Übungsblatt
 Fakultät Informatik, Technische Informatik, Professur für Mikrorechner Lösung 1. Übungsblatt Konvertierung von Zahlendarstellungen verschiedener Alphabete und Darstellung negativer Zahlen Stoffverteilung
Fakultät Informatik, Technische Informatik, Professur für Mikrorechner Lösung 1. Übungsblatt Konvertierung von Zahlendarstellungen verschiedener Alphabete und Darstellung negativer Zahlen Stoffverteilung
Einstieg in die Informatik mit Java
 1 / 34 Einstieg in die Informatik mit Java Zahldarstellung und Rundungsfehler Gerd Bohlender Institut für Angewandte und Numerische Mathematik Gliederung 2 / 34 1 Überblick 2 Darstellung ganzer Zahlen,
1 / 34 Einstieg in die Informatik mit Java Zahldarstellung und Rundungsfehler Gerd Bohlender Institut für Angewandte und Numerische Mathematik Gliederung 2 / 34 1 Überblick 2 Darstellung ganzer Zahlen,
Grundlagen der Informatik
 Helmut Herold Bruno Lurz Jürgen Wohlrab Grundlagen der Informatik Praktisch Technisch Theoretisch ein Imprint von Pearson Education München Boston San Francisco Harlow, England Don Mills, Ontario Sydney
Helmut Herold Bruno Lurz Jürgen Wohlrab Grundlagen der Informatik Praktisch Technisch Theoretisch ein Imprint von Pearson Education München Boston San Francisco Harlow, England Don Mills, Ontario Sydney
2 Rechnen auf einem Computer
 2 Rechnen auf einem Computer 2.1 Binär, Dezimal und Hexadezimaldarstellung reeller Zahlen Jede positive reelle Zahl r besitzt eine Darstellung der Gestalt r = r n r n 1... r 1 r 0. r 1 r 2... (1) := (
2 Rechnen auf einem Computer 2.1 Binär, Dezimal und Hexadezimaldarstellung reeller Zahlen Jede positive reelle Zahl r besitzt eine Darstellung der Gestalt r = r n r n 1... r 1 r 0. r 1 r 2... (1) := (
Information in einem Computer ist ein
 4 Arithmetik Die in den vorhergehenden Kapiteln vorgestellten Schaltungen haben ausschließlich einfache, Boole sche Signale verarbeitet. In diesem Kapitel wird nun erklärt, wie Prozessoren mit Zahlen umgehen.
4 Arithmetik Die in den vorhergehenden Kapiteln vorgestellten Schaltungen haben ausschließlich einfache, Boole sche Signale verarbeitet. In diesem Kapitel wird nun erklärt, wie Prozessoren mit Zahlen umgehen.
Zahlensysteme Dezimal-System
 Zahlensysteme Dezimal-System Zahlenvorrat: 0,1,2,3,4,5,6,7,8,9 Mögliche unterschiedliche Zeichen pro Stelle:10 Basis: 10 Kennzeichnung: Index 10 oder D (dezimal) Wertigkeit 10 5 10 4 10 3 10 2 10 1 10
Zahlensysteme Dezimal-System Zahlenvorrat: 0,1,2,3,4,5,6,7,8,9 Mögliche unterschiedliche Zeichen pro Stelle:10 Basis: 10 Kennzeichnung: Index 10 oder D (dezimal) Wertigkeit 10 5 10 4 10 3 10 2 10 1 10
Alexander Halles. Zahlensysteme
 Stand: 26.01.2004 - Inhalt - 1. Die verschiedenen und Umwandlungen zwischen diesen 3 1.1 Dezimalzahlensystem 3 1.2 Das Dualzahlensystem 4 1.2.1 Umwandlung einer Dezimalzahl in eine Dualzahl 4 1.2.2 Umwandlung
Stand: 26.01.2004 - Inhalt - 1. Die verschiedenen und Umwandlungen zwischen diesen 3 1.1 Dezimalzahlensystem 3 1.2 Das Dualzahlensystem 4 1.2.1 Umwandlung einer Dezimalzahl in eine Dualzahl 4 1.2.2 Umwandlung
Einführung in die Computerorientierte Mathematik
 Einführung in die Computerorientierte Mathematik Wintersemester 2014/15 Thomas Gerstner Institut für Mathematik Goethe-Universität Frankfurt 28. Oktober 2014 Inhaltsverzeichnis Inhaltsverzeichnis ii 1
Einführung in die Computerorientierte Mathematik Wintersemester 2014/15 Thomas Gerstner Institut für Mathematik Goethe-Universität Frankfurt 28. Oktober 2014 Inhaltsverzeichnis Inhaltsverzeichnis ii 1
Übungen zu Informatik 1
 Communication Systems Group (CSG) Prof. Dr. Burkhard Stiller, Universität Zürich, Binzmühlestrasse 14, CH-8050 Zürich Telefon: +41 44 635 6710, Fax: +41 44 635 6809, stiller@ifi.uzh.ch Fabio Hecht, Telefon:
Communication Systems Group (CSG) Prof. Dr. Burkhard Stiller, Universität Zürich, Binzmühlestrasse 14, CH-8050 Zürich Telefon: +41 44 635 6710, Fax: +41 44 635 6809, stiller@ifi.uzh.ch Fabio Hecht, Telefon:
Programmieren. Kapitel 3: Wie funktioniert ein moderner Computer? Wintersemester 2008/2009. Prof. Dr. Christian Werner
 Institut für Telematik Universität zu Lübeck Programmieren Kapitel 3: Wie funktioniert ein moderner Computer? Wintersemester 8/9 Prof. Dr. Christian Werner 3- Überblick Typische Merkmale moderner Computer
Institut für Telematik Universität zu Lübeck Programmieren Kapitel 3: Wie funktioniert ein moderner Computer? Wintersemester 8/9 Prof. Dr. Christian Werner 3- Überblick Typische Merkmale moderner Computer
