DIMENSIONIERUNG 27 H A N D B U C H Ü B E R F I N N I S C H E S S P E R R H O L Z. = 1.35F k,perm F k,var. F d F k,var. 4.
|
|
|
- Kerstin Heinrich
- vor 6 Jahren
- Abrufe
Transkript
1 DIMENSIONIERUNG Allgemeines Die Dimensionierung eruht uf den Bemessungsprinzipien für Holzkonstruktionen gemäß der europäischen Norm Eurocode 5 (ENV ). Bei der Berechnung der Belstungstellen wurden die Teilsicherheitseiwerte gemäß Eurocode 5 sowie Koeffizienten enutzt, die den Einfluss der Lsteinwirkungsduer und des Feuchtigkeitsgehlts uf die Festigkeits- und Elstizitätseigenschften der Sperrhölzer erücksichtigen. Außerdem sind Gleichungen ngegeen, mit denen die Tellenwerte für weitere Annhmen umgerechnet werden können. Die Gleichungen ermöglichen somit die Anwendung dieses Hnduchs für ein reites Spektrum verschiedener Dimensionierungserechnungen und eziehen sich nicht nur uf die ngegeenen Tellenwerte. Mit der Grenzzustndserechnung werden die Sicherheit und die Geruchstuglichkeit der Konstruktion im Bruch- und Geruchstuglichkeitsgrenzzustnd erücksichtigt. Unter Bruchzustnd ist die extreme Trgfähigkeit der Konstruktion und unter Geruchstuglichkeitsgrenzzustnd die normle Geruchstuglichkeit der Konstruktion zu verstehen. Mit der Bruchzustndserechnung wird sichergestellt, dss die Bemessungsspnnung σ d die Bemessungsfestigkeit f d nicht üerschreitet. σ d < f d (4-1) Die Bemessungsspnnung σ d wird unter Einstz des Bemessungslstwertes F d erechnet. Für Bemessungssitutionen mit nur einer vrilen Lst wie z.b. Schnee- oder Nutzlst, ist der Bemessungswert der Belstung erhältlich us der Formel F d 5F k,perm + 1.5F k,vr (4-2) in der F k,perm der chrkteristische Wert der ständigen Lst und F k,vr der chrkteristische Wert der vrilen Lst ist. Für Bemessungssitutionen mit zwei oder mehr vrilen Lsten wird die Bemessungslst us folgender Formel erechnet F d 5F k,perm F k,vr (4-3) Die ungünstigste Bemessungslst ist zu wählen. Die in den Gleichungen (4-2) und (4-3) vorkommenden Teilsicherheitseiwerte für die Lsten können ei einstöckigen Geäuden mit geringen n, in denen sich nur gelegentlich Menschen ufhlten, mit 1.35 is 1.20 zw. 1.5 is 1.35 reduziert werden. 27 H A N D B U C H Ü B E R F I N N I S C H E S S P E R R H O L Z
2 Die Bemessungsfestigkeit f d wird erechnet us der Formel f d = f k (4-4) in der f k der chrkteristische Festigkeitswert und der Teilsicherheitseiwert für den Werkstoff ist. Für Sperrholz wie uch für ndere Werkstoffe uf Holzsis ist der Teilsicherheitseiwert. Der Beiwert erücksichtigt den Einfluss der Lsteinwirkungsduer und der Feuchtigkeit (Nutzungsklsse). Die Werte für sind in Telle 4-1 ngegeen. lsteinwirkungsklssen Ständig 10 Jhre Lng 6 Monte is 10 Jhre Mittel eine Woche is 6 Monte Kurz unter einer Woche Sehr kurz einige Minuten nutzungsklassen : Kennzeichnend für diese Klsse sind der Feuchtigkeitsgehlt der Werkstoffe, der einer Tempertur von 20 C entspricht, sowie die nur für die Duer von einigen Wochen pro Jhr 65% üerschreitende reltive Luftfeuchte. In ist die Gleichgewichtsfeuchte von Sperrholz 12 %. Nutzungsklsse 2: Kennzeichnend für diese Klsse sind der Feuchtigkeitsgehlt der Werkstoffe, der einer Tempertur von 20 C entspricht, sowie die nur für die Duer von einigen Wochen pro Jhr 85% üerschreitende reltive Luftfeuchte. In Nutzungsklsse 2 ist die Gleichgewichtsfeuchte von Sperrholz 18 %. Nutzungsklsse 3: Bedingungen, die zur Üerschreitung der Feuchtigkeitsgehlte nch Nutzungsklsse 2 führen. In Nutzungsklsse 3 ist die Gleichgewichtsfeuchte von Sperrholz >18 %. Mit der Betrieszustndserechnung wird sichergestellt, dss die Bemessungsdurchiegung u d kleiner ist ls die zulässige Durchiegung u preset u d < u preset (4-5) Die Bemessungsdurchiegung u d wird erechnet us der Formel u d = (1 + ) u inst (4-6) in der ein Beiwert ist, der den Einfluss der Lsteinwirkungsduer und der Feuchtigkeit erücksichtigt. Die Werte für sind in Telle 4-2 ngegeen. Die vorüergehende Durchiegung u inst wird unter Einstz der Bemessungslst F d erechnet, die us der Formel F d = F k,perm + F k,vr (4-7) erechnet wird. Als Bemessungswerte der Elstizitäts- und Schumodule werden ei den Durchiegungsrechnungen die Mittelwerte enutzt. Der zulässige Durchiegungswert hängt von der Konstruktion und wird im Allgemeinen im Verhältnis zur (L) ngegeen wie z.b. L spn /300 oder L spn /200. Auch solute Werte der zulässigen Durchiegung können enutzt werden. 28 H A N D B U C H Ü B E R F I N N I S C H E S S P E R R H O L Z
3 Telle Beiwerte Nutzungsklsse Ständig Lng Mittel Kurz Sehr kurz Telle Beiwerte Nutzungsklsse Ständig Lng Mittel Kurz Sehr kurz Geäudedächer Dächer werden im Allgemeinen nch Nutzungsklsse 2 und dimensioniert. Dher können für Dchpltten die Lstwerte für Fußöden gemäß den Tellen 4-3 is 4-32 eingesetzt werden. Zusätzlich sind die Durchiegungswerte der Tellen 4-3 is 4-32 mit dem Beiwert zu multiplizieren., corr = = 1.04 (4-8) H A N D B U C H Ü B E R F I N N I S C H E S S P E R R H O L Z
4 4.3 Geäudefußöden Im Folgenden sind nch llgemeinen Dimensionierungsgrundsätzen erechnete Bemessungswerte für Geäudefußöden und die entsprechenden Durchiegungen für verschiedene n und Plttendicken zusmmengestellt. Weiter ist den Tellen uch der für die Dimensionierung der Konstruktion mßgeende Fktor, Biege- zw. Schufestigkeit, zu entnehmen. Außerdem ist die durch die Lst verurschte Durchiegung ngegeen. Die Tellen wurden für folgende Auflge- und Lstfälle erechnet: Gleichmäßig verteilte Lst uf durchlufendem Plttenstreifen, ls Einfeldstreifen und mit zwei Feldern gleicher, Tellen 4-3, 4-4, 4-9, 4-10, 4-15, 4-16, 4-21, 4-22, 4-27 und Einzellst uf einer Fläche von 50 x 50 mm in der Mitte eines durchlufenden Plttenstreifens, ls Einfeldstreifen und mit zwei Feldern gleicher, Tellen 4-6, 4-7, 4-12, 4-13, 4-18, 4-19, 4-24, 4-25, 4-30 und Gleichmäßig verteilte Lst uf frei drehr gelgerter Einfeldpltte, Tellen 4-5, 4-11, 4-17, 4-23 und Einzellst uf einer Fläche von 50 x 50 mm in der Mitte einer frei drehr gelgerten Einfeldpltte, Tellen 4-8, 4-14, 4-20, 4-26 und Die emessungs- und Durchiegungswerte wurden unter folgenden Annhmen erechnet:, Teilsicherheitseiwert der Lst, Teilsicherheitseiwert des Werkstoffs = 0.8, Beiwert, der den Einfluss der Lsteinwirkungsduer und der Feuchtigkeit erücksichtigt, Beiwert, der den Einfluss der Lsteinwirkungsduer und der Feuchtigkeit erücksichtigt Die Bemessungs- und Durchiegungswerte gelten für und. Für ndere Annhmen sind die Tellenwerte mit dem Korrekturfktor k lod, corr zu multiplizieren, der us folgender Formel erechnet wird k k lod, corr = mod ,80 (4-9) Dementsprechend sind die Durchiegungswerte mit dem Korrektureiwert, corr zu multiplizieren, der us folgender Formel erechnet wird, corr = k lod, corr (4-10) ANMERKUNG Bei großen Lsten uf kleiner Auflgefläche knn die Druckspnnung senkrecht zur Sperrholzoerfläche kritisch werden. In den meisten Fällen der Prxis können folgende Mittelwerte in eingesetzt werden. Stempeldruck: Birkensperrholz 9 N/mm 2 Comi-Sperrholz 5 N/mm 2 Fichtensperrholz 4 N/mm 2 30 H A N D B U C H Ü B E R F I N N I S C H E S S P E R R H O L Z
5 emessungswerte q [kn/m 2 ] ODER F [kn] UND ENTSPRECHENDE DURCHBIEGUNGEN u [mm] FÜR GEBÄUDEFUSSBÖDEN us FINNISCHEM SPERRHOLZ Telle 4-3. Birkensperrholz Gleichmäßig verteilte Lst uf frei drehr gelgertem Einfeldstreifen M/M mm q u q u q u q u q u q u s s M/M mm q u q u q u q u q u q u s s s s s s s s s s s s s s s s s Telle 4-4. Birkensperrholz Gleichmäßig verteilte Lst uf durchlufendem Plttenstreifen mit zwei Feldern M/M mm q u q u q u q u q u q u s s s s M/M mm q u q u q u q u q u q u s s s s s s s s s s s s s s s s s s s s s s s = Begrenzung hinsichtlich Biegefestigkeit s = Begrenzung hinsichtlich Rollenschufestigkeit 31 H A N D B U C H Ü B E R F I N N I S C H E S S P E R R H O L Z
6 Telle 4-5. Birkensperrholz Gleichmäßig verteilte Lst uf frei drehr gelgerter Rechteckpltte mm x q u q u q u q u q u q u 300x s s s s x s s x s s x s s x x x x x x x x x x x x x x x x x x mm x q u q u q u q u q u q u 300x s s s s s s x s s s s s s x 122 s s s s s s x s s s s s s x s s s s s s x s s s s s x s s s s s s x s s s s x s s s s x s s s s x s s s x s s x s s s x x x x x x x x x Uniformly Gleichmäßig distriuted lod verteilte Lst = Begrenzung hinsichtlich Biegefestigkeit s = Begrenzung hinsichtlich Rollenschufestigkeit 32 H A N D B U C H Ü B E R F I N N I S C H E S S P E R R H O L Z
7 Telle 4-6. Birkensperrholz Einzellst uf einer Fläche von 50 x 50 mm in der Mitte eines Einfeldplttenstreifens M/M mm F u F u F u F u F u F u s M/M mm F u F u F u F u F u F u s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s 6.1 Telle 4-7. Birkensperrholz Einzellst uf einer Fläche von 50 x 50 mm eines Zweifeldplttenstreifens in der Mitte eines Feldes M/M mm F u F u F u F u F u F u s s s s s s s M/M mm F u F u F u F u F u F u s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s 4.7 = Begrenzung hinsichtlich Biegefestigkeit s = Begrenzung hinsichtlich Rollenschufestigkeit 33 H A N D B U C H Ü B E R F I N N I S C H E S S P E R R H O L Z
8 Telle 4-8. Birkensperrholz Einzellst uf einer Fläche von 50 x 50 mm in der Mitte einer frei drehr gelgerten Rechteckpltte mm x F u F u F u F u F u F u 300x s s s x s x s x s s x x x s x x x s x x x x x x x x x x x x mm x F u F u F u F u F u F u 300x s s s s s s x s s s s s s x 5.8 s s s s s s x s s s s s s x s s s s s s x 5.8 s s s s s s x s s s s s s x s s s s s s x 5.9 s s s s s s x s s s s s s x s s s s s x s s s s s x s s s s s s x s s s s s x s s s s s x s s s s s x s s s s x s s s s x s s s s s x s s s s x s s s s x s s s s 6.0 = Begrenzung hinsichtlich Biegefestigkeit s = Begrenzung hinsichtlich Rollenschufestigkeit 34 H A N D B U C H Ü B E R F I N N I S C H E S S P E R R H O L Z
9 Telle 4-9. Comi-Sperrholz Gleichmäßig verteilte Lst uf frei drehr gelgertem Einfeldstreifen mm q u q u q u q u q u q u q u q u s s Telle Comi-Sperrholz Gleichmäßig verteilte Lst uf durchlufendem Plttenstreifen mit zwei Feldern mm q u q u q u q u q u q u q u q u s s s s s = Begrenzung hinsichtlich Biegefestigkeit s = Begrenzung hinsichtlich Rollenschufestigkeit 35 H A N D B U C H Ü B E R F I N N I S C H E S S P E R R H O L Z
10 Telle Comi-Sperrholz Telle A3. Gleichmäßig verteilte Lst uf frei drehr gelgerter Rechteckpltte mm x q u q u q u q u q u q u q u q u 300x s s s s s s s x s s x s s x s s s s s s x x x s s s s s x x x s s s x x x s x x x x x x x x x Uniformly Gleichmäßig distriuted lod verteilte Lst Telle Comi-Sperrholz Einzellst uf einer Fläche von 50 x 50 mm in der Mitte eines Einfeldplttenstreifens mm F u F u F u F u F u F u F u F u s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s 9.4 = Begrenzung hinsichtlich Biegefestigkeit s = Begrenzung hinsichtlich Rollenschufestigkeit 36 H A N D B U C H Ü B E R F I N N I S C H E S S P E R R H O L Z
11 Telle Comi-Sperrholz Einzellst uf einer Fläche von 50 x 50 mm eines Zweifeldplttenstreifens in der Mitte eines Feldes mm F u F u F u F u F u F u F u F u s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s 8.8 Telle Comi-Sperrholz Einzellst uf einer Fläche von 50 x 50 mm in der Mitte einer frei drehr gelgerten Rechteckpltte mm x F u F u F u F u F u F u F u F u 300x s s s s s s s s x s s s s s s s x s s s s s s s x s s s s s s s x s s s s s s s x s s s s s s s x s s s s s s s x s s s s s s s x s s s s s s s x s s s s s s s x s s s s s s s x s s s s s s s x s s s s s s s x s s s s s s x s s s s s s x s s s s s s x s s s s s x s s s s s x s s s s s s x s s s s s x s s s s s x s s s s s 9.0 = Begrenzung hinsichtlich Biegefestigkeit s = Begrenzung hinsichtlich Rollenschufestigkeit 37 H A N D B U C H Ü B E R F I N N I S C H E S S P E R R H O L Z
12 Telle Comi Mirror -Sperrholz Gleichmäßig verteilte Lst uf frei drehr gelgertem Einfeldstreifen mm q u q u q u q u q u q u q u q u s s s s s s s s s s s s s s s s Telle Comi Mirror -Sperrholz Telle A2. Gleichmäßig verteilte Lst uf durchlufendem Plttenstreifen mit zwei Feldern mm q u q u q u q u q u q u q u q u s s s s s s s s s s s s s s s s s s s s s s s s s = Begrenzung hinsichtlich Biegefestigkeit s = Begrenzung hinsichtlich Rollenschufestigkeit 38 H A N D B U C H Ü B E R F I N N I S C H E S S P E R R H O L Z
13 Telle Comi Mirror -Sperrholz Gleichmäßig verteilte Lst uf frei drehr gelgerter Rechteckpltte mm x q u q u q u q u q u q u q u q u 300x s s s s s s x s s s s s s x s s s s s s x s s s s s x s s s s s x s s s s s x s s s s x s s s s x s s s x s s x s s x s s x x x x x x x x x x Uniformly Gleichmäßig distriuted lod verteilte Lst Telle Comi Mirror -Sperrholz Einzellst uf einer Fläche von 50 x 50 mm in der Mitte eines Einfeldplttenstreifens mm F u F u F u F u F u F u F u F u s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s 8.1 = Begrenzung hinsichtlich Biegefestigkeit s = Begrenzung hinsichtlich Rollenschufestigkeit 39 H A N D B U C H Ü B E R F I N N I S C H E S S P E R R H O L Z
14 Telle Comi Mirror -Sperrholz Einzellst uf einer Fläche von 50 x 50 mm eines Zweifeldplttenstreifens in der Mitte eines Feldes mm F u F u F u F u F u F u F u F u s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s 6.3 Telle Comi Mirror -Sperrholz Einzellst uf einer Fläche von 50 x 50 mm in der Mitte einer frei drehr gelgerten Rechteckpltte mm x F u F u F u F u F u F u F u F u 300x s s s s s s x s s s s s s s x s s s s s s s x s s s s s s x s s s s s s x s s s s s s x s s s s s x s s s s s s x s s s s s s x s s s s s x s s s s s x s s s s s s x s s s s s x s s s s s x s s s s s x s s s s x s s s s x s s s s x s s s s x s s s s x s s s x s s s s 8.1 = Begrenzung hinsichtlich Biegefestigkeit s = Begrenzung hinsichtlich Rollenschufestigkeit 40 H A N D B U C H Ü B E R F I N N I S C H E S S P E R R H O L Z
15 Telle Ndelholzsperrholz, dünne Furniere Gleichmäßig verteilte Lst uf frei drehr gelgertem Einfeldstreifen mm q u q u q u q u q u q u q u q u s s s Telle Ndelholzsperrholz, dünne Furniere Gleichmäßig verteilte Lst uf durchlufendem Plttenstreifen mit zwei Feldern mm q u q u q u q u q u q u q u q u s s s s s s = Begrenzung hinsichtlich Biegefestigkeit s = Begrenzung hinsichtlich Rollenschufestigkeit 41 H A N D B U C H Ü B E R F I N N I S C H E S S P E R R H O L Z
16 Telle Ndelholzsperrholz, dünne Furniere Gleichmäßig verteilte Lst uf frei drehr gelgerter Rechteckpltte mm x q u q u q u q u q u q u q u q u 300x s s s s s x s s s x s s s x s s s x x x s x x x x x x x x x x x x x x x Uniformly Gleichmäßig distriuted lod verteilte Lst Telle Ndelholzsperrholz, dünne Furniere Einzellst uf einer Fläche von 50 x 50 mm in der Mitte eines Einfeldplttenstreifens mm F u F u F u F u F u F u F u F u s s s s s s s s s s s s s s s s s s s s s s s s 10.6 = Begrenzung hinsichtlich Biegefestigkeit s = Begrenzung hinsichtlich Rollenschufestigkeit 42 H A N D B U C H Ü B E R F I N N I S C H E S S P E R R H O L Z
17 Telle Ndelholzsperrholz, dünne Furniere Einzellst uf einer Fläche von 50 x 50 mm eines Zweifeldplttenstreifens in der Mitte eines Feldes mm F u F u F u F u F u F u F u F u s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s 8.2 Telle Ndelholzsperrholz, dünne Furniere Einzellst uf einer Fläche von 50 x 50 mm in der Mitte einer frei drehr gelgerten Rechteckpltte mm x F u F u F u F u F u F u F u F u 300x s s s s s s x s s s s s x s s s s s x s s s s s x s s s s x s s s s x s s s s s x s s s s x s s s s x s s s s x s s s x s s s x s s s s x s s s x s s s x s s s x s s x s s x s s s x s s x s s x s 10.4 = Begrenzung hinsichtlich Biegefestigkeit s = Begrenzung hinsichtlich Rollenschufestigkeit 43 H A N D B U C H Ü B E R F I N N I S C H E S S P E R R H O L Z
18 Telle Ndelholzsperrholz, dicke Furniere Gleichmäßig verteilte Lst uf frei drehr gelgertem Einfeldstreifen M/M 9/3 fch 12/4 fch 12/5 fch 15/5 fch 18/6 fch 18/7 fch mm q u q u q u q u q u q u s s M/M 21/7 fch 24/8 fch 24/9 fch 27/9 fch 27/11 fch 30/10 fch 30/13 fch mm q u q u q u q u q u q u q u s s s s s s s s s s s s s s s Telle Ndelholzsperrholz, dicke Furniere Gleichmäßig verteilte Lst uf durchlufendem Plttenstreifen mit zwei Feldern M/M 9/3 fch 12/4 fch 12/5 fch 15/5 fch 18/6 fch 18/7 fch mm q u q u q u q u q u q u s s s s s s s M/M 21/7 fch 24/8 fch 24/9 fch 27/9 fch 27/11 fch 30/10 fch 30/13 fch mm q u q u q u q u q u q u q u s s s s s s s s s s s s s s s s s s s s s s = Begrenzung hinsichtlich Biegefestigkeit s = Begrenzung hinsichtlich Rollenschufestigkeit 44 H A N D B U C H Ü B E R F I N N I S C H E S S P E R R H O L Z
19 Telle Ndelholzsperrholz, dicke Furniere Gleichmäßig verteilte Lst uf frei drehr gelgerter Rechteckpltte mm 12/5 fch 15/5 fch 18/6 fch 18/7 fch 21/7 fch 24/8 fch x q u q u q u q u q u q u 300x s s s s s x s s s s x s s s s x s s s s x s s x s s x s s x s x s x s x s x s x s x s x s x s x s x s x s x s x s x s 32.1 mm 24/9 fch 27/9 fch 27/11 fch 30/10 fch 30/13 fch x q u q u q u q u q u 300x s s s s s x s s s s s x 42 s s s s s x s s s s s x s s s s s x 31 s s s s s x s s s s s x s s s x s s x s s s s x x x x x x x x x x x x Uniformly Gleichmäßig distriuted lod verteilte Lst = Begrenzung hinsichtlich Biegefestigkeit s = Begrenzung hinsichtlich Rollenschufestigkeit 45 H A N D B U C H Ü B E R F I N N I S C H E S S P E R R H O L Z
20 Telle Ndelholzsperrholz, dicke Furniere Einzellst uf einer Fläche von 50 x 50 mm in der Mitte eines Einfeldplttenstreifens M/M 12/5 fch 15/5 fch 18/6 fch 18/7 fch 21/7 fch 24/8 fch mm F u F u F u F u F u F u s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s 6.0 M/M 24/9 fch 27/9 fch 27/11 fch 30/10 fch 30/13 fch mm F u F u F u F u F u s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s 6.0 Telle Ndelholzsperrholz, dicke Furniere Einzellst uf einer Fläche von 50 x 50 mm eines Zweifeldplttenstreifens in der Mitte eines Feldes M/M 12/5 fch 15/5 fch 18/6 fch 18/7 fch 21/7 fch 24/8 fch mm F u F u F u F u F u F u s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s 5.4 M/M 24/9 fch 27/9 fch 27/11 fch 30/10 fch 30/13 fch mm F u F u F u F u F u s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s s 4.6 = Begrenzung hinsichtlich Biegefestigkeit s = Begrenzung hinsichtlich Rollenschufestigkeit 46 H A N D B U C H Ü B E R F I N N I S C H E S S P E R R H O L Z
21 Telle Ndelholzsperrholz, dicke Furniere Einzellst uf einer Fläche von 50 x 50 mm in der Mitte einer frei drehr gelgerten Rechteckpltte mm 12/5 fch 15/5 fch 18/6 fch 18/7 fch 21/7 fch 24/8 fch x F u F u F u F u F u F u 300x s s s s s s x s s s s s s x 0.6 s s s s s s x s s s s s s x s s s s s s x 0.6 s s s s s s x s s s s s s x s s s s s s x 0.6 s s s s s s x s s s s s x s s s s s x s s s s s x s s s s s x s s s s s x s s s s s x s s s s x s s s s x s s s s x s s s s x s s s s x s s s x s s s 5.8 mm 24/9 fch 27/9 fch 27/11 fch 30/10 fch 30/13 fch x F u F u F u F u F u 300x s s s s s x s s s s s x 1.3 s s s s s x s s s s s x s s s s s x 1.3 s s s s s x s s s s s x s s s s s x 1.3 s s s s s x s s s s s x s s s s s x 1.3 s s s s s x s s s s s x s s s s s x 1.3 s s s s s x s s s s s x s s s s s x 1.3 s s s s s x s s s s s x s s s s s x s s s s s x s s s s s 5.9 = Begrenzung hinsichtlich Biegefestigkeit s = Begrenzung hinsichtlich Rollenschufestigkeit 47 H A N D B U C H Ü B E R F I N N I S C H E S S P E R R H O L Z
Nullstellen quadratischer Gleichungen
Nullstellen qudrtischer Gleichungen Rolnd Heynkes 5.11.005, Achen Nch y ufgelöst hen qudrtische Gleichungen die Form y = x +x+c. Zeichnet mn für jedes x uf der rechten Seite und ds drus resultierende y
Bestimmtes (Riemannsches) Integral / Integral als Grenzwert einer Summe : Bedeutung: Fläche unter einer Funktion innerhalb bestimmter Grenzen
III. Integrlrechnung : Bestimmtes (Riemnnsches Integrl / Integrl ls Grenzwert einer Summe : Bedeutung: Fläche unter einer Funktion innerhl estimmter Grenzen yf( y n y n ( Δ Berechnung der Fläche A unter
Bestimmung der Adsorptionsisotherme von Essigsäure an Aktivkohle
S2-Adsorptionsisothermen_UWW rstelldtum 28.3.214 7:41: Üungen in physiklischer Chemie für Studierende der Umweltwissenschften Versuch Nr.: S2 Version 214 Kurzezeichnung: Adsorptionsisotherme estimmung
Definition: Eine Folge, bei welcher der Quotient zweier aufeinanderfolgender Glieder immer gleich gross ist, heisst geometrische Folge (GF).
7. Geometrische Folgen (exponentielles Wchstum) Beispiele: 2, 6, 8, 54, 62,... = 6= 2 8 8, -4, 2, -,,,... =, ds Vorzeichen wechselt b (lternierende Folge), -,, -,... = Definition: Eine Folge, bei welcher
Teilbarkeitsregeln. 6.1 Grundwissen Mathematik Algebra Klasse 6. Teilbarkeit durch 2: Eine Zahl ist durch 2 teilbar, wenn die Endziffer gerade ist.
6.1 Grundwissen Mthemtik Algebr Klsse 6 Teilbrkeitsregeln Definition und Regeln Teilbrkeit durch 2: Eine Zhl ist durch 2 teilbr, wenn die Endziffer gerde ist. Teilbrkeit durch 3: Eine Zhl ist durch 3 teilbr,
Multiplikative Inverse
Multipliktive Inverse Ein Streifzug durch ds Bruchrechnen in Restklssen von Yimin Ge, Jänner 2006 Viele Leute hben Probleme dbei, Brüche und Restklssen unter einen Hut zu bringen. Dieser kurze Aufstz soll
1.7 Inneres Produkt (Skalarprodukt)
Inneres Produkt (Sklrprodukt) 17 1.7 Inneres Produkt (Sklrprodukt) Montg, 27. Okt. 2003 7.1 Wir erinnern zunächst n die Winkelfunktionen sin und cos, deren Wirkung wir m Einheitskreis vernschulichen: ϕ
5. Vektor- und Matrizenrechnung
Ü F-Studiengng Angewndte lektronik, SS 6 Üungsufgen zur Lineren Alger und Anlysis II Vektor- und Mtrizenrechnung Für die Vektoren = (,,,) und = (,,,) erechne mn die Linerkomintion ( ) + ( + ), die Längen,
Aufgaben zu Brechung - Lösungen:
Aufgen zu Brechung - Lösungen: Aufg. 2 (mit Berechnung von n) ) 1 = 1,8 cm; = / n' mit n' = 1/1,5 ==> 1 = 1,8 cm. 1,5 = 2,7 cm r = 2,1cm; d 1 > r ==> Totlreflexion 2 = 0,9 cm; 2 = 0,9 cm. 1,5 = 1,35 cm
ARBEITSBLATT 5L-6 FLÄCHENBERECHNUNG MITTELS INTEGRALRECHNUNG
Mthemtik: Mg. Schmid WolfgngLehrerInnentem RBEITSBLTT 5L-6 FLÄHENBEREHNUNG MITTELS INTEGRLREHNUNG Geschichtlich entwickelte sich die Integrlrechnug us folgender Frgestellung: Wie knn mn den Flächeninhlt
Lösung zur Klausur. Grundlagen der Theoretischen Informatik. 1. Zeigen Sie, dass die folgende Sprache regulär ist: w {a, b} w a w b 0 (mod 3) }.
Lösung zur Klusur Grundlgen der Theoretischen Informtik 1. Zeigen Sie, dss die folgende Sprche regulär ist: { w {, } w w 0 (mod 3) }. Lösung: Wir nennen die Sprche L. Eine Sprche ist genu dnn regulär,
12 Schweißnahtberechnung
225 12 Schweißnherechnung 12 Schweißnherechnung Die Berechnung der ufreenden Spnnungen in Schweißnähen erfolg im Regelfll mi Hilfe der elemenren Gleichungen der esigkeislehre. Auf weierführende Berechnungsverfhren,
ARBEITSBLATT 14 ARBEITSBLATT 14
Mthemtik: Mg. Schmid Wolfgng reitsltt. Semester RBEITSBLTT RBEITSBLTT RBEITSBLTT RBEITSBLTT DS VEKTORPRODUKT Definition: Ds vektorielle Produkt (oder Kreuprodukt) weier Vektoren und ist ein Vektor mit
Spiele und logische Komplexitätsklassen
Spiele und logische Komplexitätsklssen Mrtin Horsch 26. Jnur 2006 Inhlt des Seminrvortrges Ehrenfeucht-Frïssé-Spiel mit k Mrken Formeln mit k Vrilen und logische Komplexitätsklssen k-vrileneigenschft logischer
DISC. Verdeckter Scheibenverbinder Dreidimensionales Lochblech aus Kohlenstoffstahl mit galvanischer Verzinkung DISC - 01 VERPACKUNG
DISC Verdeckter Scheibenverbinder Dreidimensionales Lochblech aus Kohlenstoffstahl mit galvanischer Verzinkung VERPACKUNG Montageschrauben und TX-Einsatz im Lieferumfang enthalten ANWENDUNGSBEREICHE Scherverbindungen
Grundwissen. Die Menge der reellen Zahlen 0 =0. Beispiele
Grundwissen Klsse 9 Die Menge der reellen Zhlen Die Umkehrung des Qudrierens wird für nicht negtive Zhlen ls Ziehen der Wurzel oder Rdizieren ezeichnet. Die Qudrtwurzel us (kurz: Wurzel us ) ist dei die
WARMDACH/KALTDACH. Wärmedämmplatten für den Einsatz am Flachdach» STEINBACHER. ENERGIESPAREN IST ZUKUNFT. «
WARMDACH/KALTDACH Wärmedämmpltten für den Einstz m Flchdch» STEINBACHER. ENERGIESPAREN IST ZUKUNFT. « SPEZIFIKUM steinothn 104 MV/steinothn FD steinothn 104 MV und steinothn FD sind Wärmedämmpltten us
Grenzwerte von Funktionen
Grenzwert und Stetigkeit von Funktionen Methodische Bemerkungen H Hinweise und didktisch-methodische Anmerkungen zum Einstz der Areitslätter und Folien für den Themenkreis Grenzwert und Stetigkeit von
JUSTUS-LIEBIG-UNIVERSITÄT GIESSEN
JUSTUS-LIEBIG-UNIVERSITÄT GIESSEN Professur für VWL II Wolfgng Scherf Die Exmensklusur us der Volkswirtschftslehre Erschienen in: WISU 8-9/2000, S. 1163 1166. Fchbereich Wirtschftswissenschften Prof. Dr.
Ergänzung Forschungsvorhaben DIN EN 1995 - Eurocode 5 - Holzbauten Untersuchung verschiedener Trägerformen
1 Vorbemerkungen Begründung und Ziel des Forschungsvorhabens Die Berechnungsgrundsätze für Pultdachträger, Satteldachträger mit geradem oder gekrümmtem Untergurt sowie gekrümmte Träger sind nach DIN EN
Die Keplersche Fassregel
Die Keplersche Fssregel K. Gerer Bei vielen Aufgen, z.b. ei der Lösung von Differentilgleichungen, tucht die Schwierigkeit uf, dss Integrtionen nicht durchgeführt werden können. So können z.b. die folgenden
Die Regelungen zu den Einsendeaufgaben (Einsendeschluss, Klausurzulassung) finden Sie in den Studien- und Prüfungsinformationen Heft Nr. 1.
Modul : Grundlgen der Wirtschftsmthemtik und Sttistik Kurs 46, Einheit, Einsendeufge Die Regelungen zu den Einsendeufgen (Einsendeschluss, Klusurzulssung) finden Sie in den Studien- und Prüfungsinformtionen
5.5. Integralrechnung
.. Integrlrechnung... Berechnung von Integrlen mit der Streifenmethode Definition: Gegeen seien, R mit < und eine uf [; ] stetige Funktion f. Der orientierte Inhlt der Fläche, die durch die -Achse, ds
Eufic Guide Enfant ALL 14/12/04 15:44 Page 1 10 Tipps für Kids Spiel mit uns! Zur gesundenernährung
Kids Ernährung für Tipps 10 Spiel mit uns! gesunden Zur Weißt du noch, wie du Rd fhren lerntest? Ds Wichtigste dei wr zu lernen ds Gleichgewicht zu hlten. Sold es gefunden wr, konntest du die Pedle gleichmäßig
Quadratische Funktionen
Qudrtische Funktionen Die Scheitelpunktform ist eine spezielle Drstellungsform von qudrtischen Funktionen, nhnd der viele geometrische Eigenschften des Funktionsgrphen bgelesen werden können. Abbildung
Tag der Mathematik 2011
Zentrum für Mthemtik Tg der Mthemtik 0 Gruppenwettbewerb Einzelwettbewerb Mthemtische Hürden Lösungen Allgemeine Hinweise: Als Hilfsmittel dürfen nur Schreibzeug, Geodreieck und Zirkel benutzt werden.
Einführung in die Festkörperphysik I Prof. Peter Böni, E21
Einführung in die Festkörperphsik I Prof. Peter Böni, E21 Lösung zum 2. Übungsbltt (Besprechung: 0. - 1. Oktober 2006) P. Niklowitz, E21 Aufgbe 2.1: Zweidimensionle Wigner-Seitz-Zellen Vernschulichen Sie,
Organisationsformen für den naturwissenschaftlichen Unterricht
Orgnistionsformen für den nturwissenschftlichen Unterricht Der nturwissenschftliche Unterricht wird in den Jhrgängen 5-7 integriert unterrichtet. Für die Jhrgänge 8-10 git es drei verschiedene Konzepte
Kegelschnitte. Geschichte der Kegelschnitte
Kegelschnitte Kegelschnitte ds sind geometrische Figuren, die sich ergeen, wenn mn einen Kegel und eine Eene einnder schneiden lässt. Wir unterscheiden 3 Tpen von Kegelschnitten: Prel, Ellipse und Hperel.
Einführung in die Schaltalgebra
Einführung in die chltlger GUNDBEGIFFE: - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 2 ECHENEGELN - - - - - - - - - - - - - - - - - - - - - - - -
Nutzung der Abwärme aus Erneuerbare-Energie-Anlagen
5 2014 Sonderdruck us BWK 5-2014 Wichtige Kennzhlen und effiziente Plnung für die dezentrle Wärmewende Nutzung der Abwärme us Erneuerbre-Energie-Anlgen Wichtige Kennzhlen und effiziente Plnung für die
Personal und Finanzen der öffentlich bestimmten Fonds, Einrichtungen, Betriebe und Unternehmen (FEU) in privater Rechtsform im Jahr 2003
Personl und Finnzen der öffentlich estimmten Fonds, Einrichtungen, Betriee und Unternehmen (FEU) in privter Rechtsform im Jhr 003 Dipl.-Volkswirt Peter Emmerich A Mitte der 980er-Jhre ist eine Zunhme von
Dreiecke als Bausteine
e ls usteine Jedes Viereck lässt sich in zwei e zerlegen. Wirklich jedes? Konstruktion eines s bei drei beknnten Seiten bmessen einer Strecke mit dem Geodreieck. Zirkelschlg um einen Punkt mit der zweiten
10 Anwendungen der Integralrechnung
9 nwendungen der Integrlrechnung Der Inhlt von 9 wren die verschiedenen Verfhren zur Berechnung eines Integrls Der Inhlt von sind die verschiedenen Bedeutungen, die ein Integrl hen knn Die Integrlrechnung
Marktnachfrage. Robert Stehrer, wiiw. The Vienna Institute for International Economic Studies - wiiw. 12. März 2015
Linere Iso-elstische Robert Stehrer The Vienn Institute for Interntionl Economic Studies - wiiw 12. März 2015 Linere Iso-elstische Linere Linere Elstizität Aggregtion 1 Nchgefrge Menge ist eine Funktion
STRATEGIEPAPIER für Abschlussprüfungen
.) Gleichungen: STRATEGIEPAPIER für Aschlussprüfungen.) normle Gleichungen : Auflösen nch (oder einer nderen Vrilen) Bestimmen der Lösungsmenge (L). Beispiel: + + / Zusmmenfssen + / + + / 9 / : { } L.)
a) Potenzieren ausgesprochen als Beispiel a b = c a = Basis a hoch b = c 4 3 = 64 b = Exponent c = Potenzwert
8. Potenzen 8. Einführung in Potenzen / Wurzeln / Logrithmen Neen den klssischen Grundrechenopertionen git es weitere Opertionen, welche Beziehungen zwischen Zhlen schffen: Potenzieren Rdizieren Wurzelziehen)
Grundlagen in Mathematik für die 1. Klassen der HMS und der FMS
Grundlgen in Mthemtik für die. Klssen der HMS und der FMS Einleitung In der Mthemtik wird häufig uf bereits Gelerntem und Beknntem ufgebut. Wer die Grundlgen nicht beherrscht, ht deshlb oft Mühe und Schwierigkeiten,
Das Rechnen mit Logarithmen
Ds Rechnen mit Logrithmen Etw in der 0. Klssenstufe kommt mn in Kontkt mit Logrithmen. Für die, die noch nicht so weit sind oder die, die schon zu weit dvon entfernt sind, hier noch einml ein kleiner Einblick:
Erweitern. a b. bd + bc. bd = ad+bc. bei ganzzahligem Nenner: Hauptnenner (= kgv der Nenner), z.b. 4 6 + 3 4 = 8 12 + 9. a d = ac
F FORMELSAMMLUNG Bruchrechnung Erweitern = Kürzen c c Addition Nenner gleichnmig mchen! + c d = d d + c d = d+c d, speziell + c = +c ei gnzzhligem Nenner: Huptnenner (= kgv der Nenner), zb 4 6 + 3 4 =
2.2. Aufgaben zu Figuren
2.2. Aufgen zu Figuren Aufge 1 Zeichne ds Dreieck ABC in ein Koordintensystem. Bestimme die Innenwinkel, und und erechne ihre Summe. Ws stellst Du fest? ) A(1 2), B(8 3) und C(3 7) ) A(0 3), B(10 1) und
Orientierungstest Mathematische Grundlagen
Orientierungstest Mthemtische Grundlgen Lösungen:. Welche Zhlenmengen git es? Beispiele? Menge der ntürlichen Zhlen N {,,, } Menge der gnzen Zhlen Z {,, 0,,, } Menge der rtionlen Zhlen Q Menge ller ls
Übungsblatt 1 zum Propädeutikum
Üungsltt zum Propädeutium. Gegeen seien die Mengen A = {,,,}, B = {,,} und C = {,,,}. Bilden Sie die Mengen A B, A C, (A B) C, (A C) B und geen Sie diese in ufzählender Form n.. Geen Sie lle Teilmengen
5 Gleichungen (1. Grades)
Mthemtik PM Gleichungen (. Grdes) Gleichungen (. Grdes). Einführung Betrchtet mn und (, Q) und vergleicht sie miteinnder, so git es Möglichkeiten:. > ist grösser ls. = ist gleich gross wie. < ist kleiner
Grundsätzliche Voraussetzungen für die Fachoberschule ab Klasse 11 im Fach Mathematik
Grundsätzliche Vorussetzungen für die Fchoberschule b Klsse im Fch Mthemtik Zum Eintritt in die Fchoberschule ist der mittlere Bildungsbschluss Vorussetzung. Ds heißt, im Fch Mthemtik werden die, bis zur
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 3 5. Semester ARBEITSBLATT 3 PARAMETERDARSTELLUNG EINER GERADEN
Mthemtik: Mg. Schmid Wolfgng Areitsltt 3 5. Semester ARBEITSBLATT 3 PARAMETERDARSTELLUNG EINER GERADEN Wir wollen eine Gerde drstellen, welche durch die Punkte A(/) und B(5/) verläuft. Die Idee ist folgende:
Für den Mathe GK, Henß. - Lineare Algebra und analytische Geometrie -
Für den Mthe GK, Henß - Linere Alger und nlytische Geometrie - Bis uf die Astände ist jetzt lles drin.. Ich h noch ne tolle Seite entdeckt mit vielen Beispielen und vor llem Aufgen zum Üen mit Lösungen..
Grundwissen Mathematik 8
Grundwissen Mthemtik 8 Proportionle Zuordnung Gehört bei einer Zuordnung zweier Größen zu einem Vielfchen der einen Größe ds gleiche Vielfche der nderen Größe, so heißt sie proportionle Zuordnung. Die
Quadratische Funktionen
Qudrtische Funktionen Definition: Eine Funktion mit der Gleichung y = c (,, c R; 0) heißt qudrtische Funktion oder Funktion. Grdes. qudrtisches Glied;...lineres Glied; c...solutes Glied Der Grph einer
Rechnen mit Termen. 1. Berechne das Volumen und die Oberfläche. 4. Löse die Klammern auf und fasse zusammen: a) 2x(3x 1) x(2 5x) b) 7a(1 b)+5b(2 a)
Rechnen mit Termen 1. Berechne ds Volumen und die Oberfläche. 2. 3 3 7 2 4b 3. 5 4 8 b 4. Löse die Klmmern uf und fsse zusmmen: ) 2x(3x 1) x(2 5x) b) 7(1 b)+5b(2 ) c) 4b( 3b) 4b( 2 3) 5. Löse die Gleichungen:
Vektorrechnung im R 3 mit dem Voyage 200:
Wir legen einen neuen Folder n: VAR-LINK F, 5 (CREATE FOLDER) Nme: vektor3 Wechseln in den Folder: MODE Current Folder vektor3 uswählen Vektorrechnung im R 3 mit dem Voge 00: Punkte und Vektoren werden
Monte-Carlo-Integration
Monte-Crlo-Integrtion von Dietmr Herrmnn, Anzing Kurzfssung: An Hnd eines einfchen Beispiels wird gezeigt, dß jedes Integrl ls Erwrtungswert einer reellen Zufllsgröße ufgefßt werden knn. een einer symptotischen
Grundwissen Mathematik 7I
Winkel m Kreis Grundwissen themtik 7I Rndwinkelstz Der Winkel heißt ittelpunktswinkel über der Sehne []. Die Winkel n sind die Rndwinkel über der Sehne []. lle Rndwinkel über einer Sehne eines Kreises
- 1 - VB Inhaltsverzeichnis
- - VB Inhltsverzeichnis Inhltsverzeichnis... Die Inverse einer Mtrix.... Definition der Einheitsmtrix.... Bedingung für die inverse Mtrix.... Berechnung der Inversen Mtrix..... Ds Verfhren nch Guß mit
1.2 Der goldene Schnitt
Goldener Schnitt Psclsches Dreieck 8. Der goldene Schnitt Beim Begriff Goldener Schnitt denken viele Menschen n Kunst oder künstlerische Gestltung. Ds künstlerische Problem ist, wie ein Bild wohlproportioniert
Klaus Palme Tel. +49 (0) Fax Nr. +49 (0)
Datum 06.12.2011 Bericht Auftraggeber 2011/016-B-5 / Kurzbericht Palme Solar GmbH Klaus Palme Tel. +49 (0) 73 24-98 96-433 Fax Nr. +49 (0) 73 24-98 96-435 info@palme-solar.de Bestellungsnummer 7 Auftragnehmer
Wie muss x gewählt werden, so dass K 1 anschließend einen geraden Stoß mit K 3 ausführt?
ZÜ 2.1 Aufgbe 2.1 Drei Kugeln K 1, K 2 und K 3 Mssen, m 2 und m 3 befinden sich in einer Rille und berühren sich nicht. Die erste Kugel gleitet mit der Geschwindigkeit v1 und stößt vollkommen elstisch
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2012. Sprachen. Grammatiken (Einführung)
Wörter, Grmmtiken und die Chomsky-Hierrchie Sprchen und Grmmtiken Wörter Automten und Formle Sprchen lis Theoretische Informtik Sommersemester 2012 Dr. Snder Bruggink Üungsleitung: Jn Stückrth Alphet Ein
2. Klausur in K2 am
Nme: Punkte: Note: Ø: Profilfch Physik Azüge für Drstellung: Rundung:. Klusur in K m.. 04 Achte uf die Drstellung und vergiss nicht Geg., Ges., Formeln, Einheiten, Rundung...! Aufge ) (8 Punkte) In drei
Die Brückenlappentechnik zum sicheren Verschluss von Nasenseptumdefekten
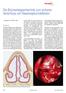Die Brückenlppentechnik zum sicheren Verschluss von Nsenseptumdefekten T. Stnge, H.-J. Schultz-Coulon Einleitung Die Rekonstruktion eines defekten Nsenseptums zählt zu den schwierigsten rhinochirurgischen
Wurzeln. bestimmen. Dann braucht man Wurzeln. Treffender müsste man von Quadratwurzeln sprechen. 1. Bei Quadraten, deren Fläche eine Quadratzahl ist,
Seitenlängen von Qudrten lssen sich mnchml sehr leicht und mnchml etws schwerer Wurzeln bestimmen. Dnn brucht mn Wurzeln. Treffender müsste mn von Qudrtwurzeln sprechen. Sie stehen in enger Beziehung zu
Grundwissen l Klasse 5
Grundwissen l Klsse 5 1 Zhlenmengen und Punktmengen {1; 2; 3; 4; 5; 6;... } Die Menge der ntürlichen Zhlen. 0 {0; 1; 2; 3; 4; 5;... } Die Menge der ntürlichen Zhlen mit Null. M {; ; C;... } Die Menge der
v P Vektorrechnung k 1
Vektorrechnung () Vektorielle Größen in der hysik: Sklren Größen wie Zeit, Msse, Energie oder Tempertur werden in der hysik mit einer Mßzhl und einer Mßeinheit ngegeen: 7 sec, 4.5 kg. Wichtige physiklische
Quadratische Gleichungen und Funktionen
Qudrtische Gleichungen und Funktionen Bei einer udrtischen Gleichung kommt die Unbeknnte Vrible mindestens einml in der.potenz vor, ber in keiner höheren Potenz. b c udrtischer Anteil linerer Anteil konstnter
Kurvenintegrale. 17. Juli 2006 (Korrigierte 2. Version) 1 Kurvenintegrale 1. Art (d.h. f ist Zahl, kein Vektor)
Kurvenintegrle Christin Mosch, Theoretische Chemie, Universität Ulm, christin.mosch@uni-ulm.de 7. Juli 26 (Korrigierte 2. Version Kurvenintegrle. Art (d.h. f ist Zhl, kein Vektor Bei Kurvenintegrlen. Art
Für den erforderlichen Wellendurchmesser bei Torsionsbeanspruchung gilt:
Dimensionierung einer Passfederverbindung Zu dimensionieren ist die unten dargestellte Passfederverbindung. Das schwellend zu übertragende Drehmoment beträgt. Die Nabe sei aus EN-GJL-200, die Welle aus
(Analog nennt man a die und b die des Winkels β.)
Mthemtik Einführung Ws edeutet ds Wort und mit ws eschäftigt sich die? Eine kleine Wortkunde: tri edeutet 'drei' Beispiel: Trithlon,... gon edeutet 'Winkel'/'Eck' Beispiel: Pentgon ds Fünfeck mit 5 Winkeln
Volumina der 8 konvexen Deltaeder
Arno Fehringer, Gymnsillehrer für Mthemtik und Physik, Wilhelm-Bläsig-Schule, Hegu-Jugendwerk, 78262 Gilingen, Kpellenstr. 31-1 - Volumin der 8 konvexen Delteder Arno Fehringer Juli 2007 Die Bestimmung
Erkundungen. Terme vergleichen. Rechteck Fläche als Produkt der Seitenlängen Fläche als Summe der Teilflächen A B
Erkundungen Terme vergleihen Forshungsuftrg : Fläheninhlte von Rehteken uf vershiedene Arten erehnen Die Terme () is (6) eshreien jeweils den Fläheninhlt von einem der drei Rehteke. Ordnet die Terme den
NCCI: Elastisches kritisches Biegedrillknickmoment
Dieses NCCI Dokument enthält die Gleichung ur Ermittlung des elastischen kritischen Biegedrillknickmomentes für doppelt symmetrische Querschnitte. Für die Berechnung werden Parameter für häufig auftretende
Der Gauß - Algorithmus
R Brinkmnn http://brinkmnn-du.de Seite 7..9 Der Guß - Algorithmus Der Algorithmus von Guss ist ds universelle Verfhren zur Lösung beliebiger linerer Gleichungssysteme. Einführungsbeispiel: 7x+ x 5x = Drei
über der Strangbreite 2. Zugleich vermindert Einschlüssen, wodurch sich die Qualität des gegossenen Stahls verbessert.
S T R N G G I E S S E N Elektromgnetisches remsen veressert die Sthlqulität eim Strnggießen Ds elektromgnetische remsen der Sthlströmung in der Kokille von Strnggießnlgen veressert die Qulität des gegossenen
5.3 Dynamisches Sitzen und Stehen
Dynmisches Sitzen und Stehen 5.3 Dynmisches Sitzen und Stehen Test Bewegen Sie sich eim Sitzen und Stehen kontinuierlich um den Mittelpunkt der senkrechten Oerkörperhltung (S. 39) mit neutrler Wirelsäulenschwingung
Aufgabe 5 (Lineare Nachfragefunktion): Gegeben sei die (aggregierte) Nachfragefunktion des Gutes x durch:
LÖSUNG AUFGABE 5 ZUR INDUSTRIEÖKONOMIK SEITE VON 5 Aufgbe 5 (Linere Nchfrgefunktion): Gegeben sei die (ggregierte) Nchfrgefunktion des Gutes durch: ( = b, > 0, b > 0. Dbei bezeichnen den Preis des Gutes
Biegefestigkeit parallel 40 N/mm² 38 N/mm² (F 25) 3) Biegefestigkeit quer 15 N/mm² 15 N/mm² (F 10) 3) ± 0,06 t 1) + (0,8 + 0,03 t) mm.
Europäische Normen für Sperrholz (1. Teil) Bereits seit dem 1. April 2004 gelten für Sperrholz die Euro-Normen. Die altvertrauten Begriffe wie z. B. BFU 100 (sollten) verschwinden und werden durch neue,
Werben mit Knauf Insulation Supafil. Einfach gestalten, professionell auftreten, erfolgreich kommunizieren.
Schüttdämmstoffe 07/2014 Werben mit Knuf Insultion Supfil. Einfch gestlten, professionell uftreten, erfolgreich kommunizieren. Inhltsverzeichnis Einleitung Erfolgreiche Kommuniktion beginnt bei der richtigen
8 Integralrechnung. 8.1 Das Riemann-Integral
8 Integrlrechnung Der Integrlbegriff ist wie der Ableitungsbegriff motiviert durch die physiklische Beschreibung von Bewegungsbläufen (Geschwindigkeit, Beschleunigung). Er ist u.. uch von Bedeutung bei
Vorkurs Mathematik DIFFERENTIATION
Vorkurs Mthemtik 6 DIFFERENTIATION Beispiel (Ableitung von sin( )). Es seien f() = sin g() = h() =f(g()) = sin. (f () =cos) (g () =) Also ist die Ableitung von h: h () =f (g())g () =cos = cos. Mn nennt
6.5 Bemessung einer Deckenschalung. b) Bemessung mit zulässigen Traglasten F N,zul der Baustützen. Grundriss-Entwurf der Schalung
6.5 Bemessung einer Deckenschalung 153 A R 7,4 kn B, E, B 3,6 m E 0 7,58 kn/m Die Stellfristen für iese Baustützen als Hilfsstützen wuren in Übungsbeispiel 6.1 ermittelt. b) Bemessung mit zulässigen Traglasten
Ungleichungen. Jan Pöschko. 28. Mai Einführung
Ungleichungen Jn Pöschko 8. Mi 009 Inhltsverzeichnis Einführung. Ws sind Ungleichungen?................................. Äquivlenzumformungen..................................3 Rechnen mit Ungleichungen...............................
Brückenkurs Lineare Gleichungssysteme und Vektoren
Brückenkurs Linere Gleichungssysteme und Vektoren Dr Alessndro Cobbe 30 September 06 Linere Gleichungssyteme Ws ist eine linere Gleichung? Es ist eine lgebrische Gleichung, in der lle Vriblen nur mit dem
Berufsmaturitätsprüfung 2012 Mathematik
GIBB Gewerblich-Industrielle Berufsschule Bern Berufsmturitätsschule Berufsmturitätsprüfung 2012 Mthemtik Zeit: Hilfsmittel: Hinweise: Punkte: 180 Minuten Formel- und Tbellensmmlung ohne gelöste Beispiele,
Das kleine 9er-Einmaleins mit den 10 Fingern lernen.
Ws? Multiplizieren 9er-Finger-Einmleins Wozu? Ds kleine 9er-Einmleins mit den 10 Fingern lernen. 1. Beide Hände mit usgestrekten Fingern zeigen nh oen. 2. Die Dumen zeigen nh ußen (Hndflähen zum Gesiht).
Internationale Ökonomie I Vorlesung 3: Das Riccardo-Modell: Komparative Vorteile und Produktivität (Master)
Interntionle Ökonomie I Vorlesung 3: Ds Riccrdo-Modell: Komprtive Vorteile und Produktivität (Mster) Dr. Dominik Mltritz Vorlesungsgliederung 1. Einführung 2. Der Welthndel: Ein Überblick 3. Ds Riccrdo-Modell:
von f im Punkt P ( 2 4) x x x Hilfsmittelfreier Teil. Beispielaufgabe 1 zur Analysis Gegeben ist die Funktion f mit der Gleichung
Hilfsmittelfreier Teil. Beispielufgbe zur Anlysis Gegeben ist die Funktion f mit der Gleichung f ( x ) = x + x x. Die zeigt den Grphen der Funktion f. () Berechnen ie lle Nullstellen der Funktion f. ()
Umwandlung von endlichen Automaten in reguläre Ausdrücke
Umwndlung von endlichen Automten in reguläre Ausdrücke Wir werden sehen, wie mn us einem endlichen Automten M einen regulären Ausdruck γ konstruieren knn, der genu die von M kzeptierte Sprche erzeugt.
1 Folgen von Funktionen
Folgen von Funktionen Wir etrchten Folgen von reell-wertigen Funktionen f n U R mit Definitionsereicht U R und interessieren uns für ntürliche Konvergenzegriffe. Genuer setzen wir uns mit folgenden Frgen
Umstellen von Formeln und Gleichungen
Umstellen von Formeln und Gleihungen. Ds Zusmmenfssen von Termen edeutet grundsätzlih ein Ausklmmern, uh wenn mn den Zwishenshritt niht immer ufshreit. 4 6 = (4 6) =. Steht eine Vrile, nh der ufgelöst
Kappa. Jahre Garantie
Kpp Flexible Anwendung Mit dem Kpp können rhmenlose Photovoltik-Module leicht in Dächer von Alt- und Neubuten mit beliebiger 1 Eindeckung integriert werden. Ds System wird uf die vorhndene Lttung montiert
- 1 - A H A V M A. Bild 5.17 Einfach statisch unbestimmtes System; a) Systemskizze; b) Schnittbild F 1 F 3 B C F 2 2 F 3
- - Lgerrektionen können nur mit Hilfe der Elstizitätstheorie bestimmt werden. Technische Mechnik II Elstosttik werden ein- und mehrfch "sttisch unbestimmt" gelgerte Trgwerke vorgestellt. ) b) M H V ild
Berechnungen am Prisma. Das Netz (Abwicklung) eines Prismas
Berechnungen m Prism Einführung des Prisms: Schüler ringen verschiedene Verpckungen mit in den Unterricht Klssifizierung der Verpckungen in Prismen und ndere Körper Erreitung der Eigenschften eines Prisms:
17 Doppelbündel-Rekonstruktion mit Semitendinosussehne
Kpitel 17 143 17 Doppelündel-Rekonstruktion mit Semitendinosussehne Wolf Petersen 17.1 Einleitung Ds vordere Kreuznd (VKB) esteht us 2 funktionellen Bündeln: einem nteromedilen (AM) und einem posterolterlen
2. Klausur zur Vorlesung Informatik III Wintersemester 2003/2004
Universität Krlsruhe Theoretische Informtik Fkultät für Informtik WS 2003/04 ILKD Prof. Dr. D. Wgner 14. April 2004 2. Klusur zur Vorlesung Informtik III Wintersemester 2003/2004 Lösung! Bechten Sie: Bringen
Kapitel IV Euklidische Vektorräume. γ b
Kpitel IV Euklidische Vektorräume 1 Elementrgeometrie in der Eene Sei E die Zeicheneene In der Schule lernt mn: (11) Stz des Pythgors: Sei E ein Dreieck mit den Seiten, und c, und sei γ der c gegenüerliegende
Kleine Algebra-Formelsammlung
Immnuel-Knt-Gymnsium Heiligenhus Gierhrt Kleine Alger-Formelsmmlung Mittelstufe (is Klsse 0) Drgestellt sin ie wichtigsten Fkten un Gesetze, woei iverse Ausnhmeregeln wie z.b. s Verot er Division urch
Vorkurs Mathematik Fachhochschule Frankfurt, Fachbereich 2. Fachhochschule Frankfurt am Main Fachbereich Informatik und Ingenieurwissenschaften
Vorkurs Mthemtik Fchhochschule Frnkfurt, Fchereich Fchhochschule Frnkfurt m Min Fchereich Informtik und Ingenieurwissenschften Vorkurs Mthemtik Sie finden lle Mterilien sowie ergänzende Informtionen unter
2. Das Rechnen mit ganzen Zahlen (Rechnen in )
. Ds Rechnen mit gnzen Zhlen (Rechnen in ).1 Addition und Subtrktion 5 + = 7 Summnd Summnd Summe 5 - = 3 Minuend Subtrhend Differenz In Aussgen mit Vriblen lssen sich nur gleiche Vriblen ddieren bzw. subtrhieren.
Mathematik Bruchrechnung Grundwissen und Übungen
Mthemtik Bruchrechnung Grundwissen und Übungen von Stefn Gärtner (Gr) Stefn Gärtner -00 Gr Mthemtik Bruchrechnung Seite Inhlt Inhltsverzeichnis Seite Grundwissen Ws ist ein Bruch? Rtionle Zhlen Q Erweitern
Vorbereitung auf die Mathematik Schularbeit
Vorbereitung uf die Mthemtik Schulrbeit 7. März 0 Alles Gute ll deinen Bemühungen, KL, KV Viel Erfolg! . Schulrbeit: MATHEMATIK KL.: M3b/I. - S. Mi, 7.03.0 ) Zeichne ds Prllelogrmm us den Bestimmungsstücken