|
|
|
- Joseph Böhme
- vor 8 Jahren
- Abrufe
Transkript
1 ÎÓÖÖØÙÒ ÑØÖÐ ĐÙÖ Ò ËØÙÙÑ Ò Ò ĐÖÒ ÅØÑØ ÙÒ ÁÒÓÖÑØ Ò Ö ÍÒÚÖ ØĐØ ÄÔÞ ÀÖÙ Ò ÚÓÑ ËØÙÒÒ Ö ÙÐØĐØ ĐÙÖ ÅØÑØ ÙÒ ÁÒÓÖÑØ
2 ÏÖÙÑ Ò ÌÙØÓÖÙÑ ÅØÑØ ÁÒ ÐÐÒ ÚÓÒ ÙÒ ÖÖ ÙÐØĐØ ÒÓØÒÒ ËØÙÒĐÒÒ Ø ĐØÙÒ ÑØ ÑØÑØ Ò ËÚÖÐØÒ Ð ØÚÖ ØĐÒк ÀÒ Ë ÚÓÖ ÅØÑØ ÓÖ ÏÖØ Ø ÑØÑØ ÞÙ ØÙÖÒ ÛÖ Ë ÚÐÐØ ÒØ ĐÙÖÖ Ò Ö Ù ĐÙÖ Ò ÁÒÓÖÑعËØÙÙÑ Ö ÖÙÒÐÒ ÙØÙÒ Ö ÅØÑØ ÒØ ÙÒØÖ ĐØÞØ ÛÖÒº Ò ÖÓÖ ÌÐ Ö ÓÐØÓÖ Ò ÄÖÚÖÒ ØÐØÙÒÒ ĐÙÖ ÁÒÓÖÑØ ØÙÒØÒ Ñ ÖÙÒ ØÙÙÑ ĐØØ ÑØ ÑØÑØ Ò ÁÒ¹ ÐØÒº Ù Ò ÁÒÓÖÑعÒÛÒÙÒÒ ÛÖÒ Ë ÑØÑØ ÅØÓ¹ Ò ÙÒ ÒÑÙ ØÖ ÒÙØÞÒº Ò ÛØ ÎÓÖÙ ØÞÙÒ ĐÙÖ ÁÖÒ ÖÓÐ Ñ ËØÙÙÑ Ø Ð Ö ÖÖ Ò Ö ÑØÑØ Ò ÖÙÒÐÒº ÄÖ Ò ÖÖÙÒÒ Ö ÚÖÒÒÒ ÂÖ ÞØ ĐÙÖ Ò ËØÙ¹ ÙÑ Ò ÙÒ ÖÖ ÙÐØĐØ ÙÒÒÖÒ ÑØÑØ Ò ÎÓÖÒÒØÒ ÓÛÓÐ ÒØ ĐÙÖ Ò ËÙÐ ØÓ«ÒÙ Òµ ÒØ ÐÐÒ ËØÙÒÛÖÖÒ ÑÑÖ Ò Ù ÖÒÑ ÍÑÒ ÚÓÖÒÒ Òº ÍÑ ÞÙ ÚÖÑÒ Ò ËØÙÒØ ÛĐÖÒ ÐÙÒÒ ËØÙÙÑ ÒØ ÚÓÖ¹ ÒÒ ÖÙÒÐÒÛ Ò Ð ØĐÒ ÒÓÐÒ ÑÙ ÙÒ ÞÙ ĐØÞÐ Ð ØÙÒ Ò ÒÒ ĐÙÖÓÖÖØ ÓÖ ÑÓØÚÖØ ÛÖ ĐÙÖ Ò Ö ÙÐØĐØ ÒÙ Ò Ö¹ ÒÒ ËØÙÒØÒ Ò ÎÓÖÖØÙÒ ÙÖ ÒÓØÒº Ö ÃÙÖ ÛÖ ÚÓÖ ÒÒ ÏÒØÖ Ñ ØÖ ¼¼»¼¼ ØØØ ÒÒº ÁÒ Ñ ÌÙØÓÖÙÑ ÛÖ ÒÓ Ò ËØÓ«ÐÖØ Ö ÒØ Ñ Ä ØÙÒ ÙÖ ÝÑÒ ÙÑ ÒÐØ ÛÓÖÒ Øº Ø ĐÙÖ ÒÒ ËØÙÒØÒ Ø ÒÒ ÖÙÒÙÖ ÐÙ Ò ÅØÑØ Ò ÖÒ ÐØÞØÖ ÅØÑØÙÒØÖÖØ ÐĐÒÖ Ø ÞÙÖĐÙÐØ ÓÖ Ö Ò ÛÓÐÐÒ Ö ËØÙÙÑ ÖĐÙÒÐÚÓÖÖØØ ÞÙ ÒÒÒº Ø Ò ÚÓÐÐ ØĐÒ ÏÖÓÐÙÒ ÅØÑØÙÒØÖÖØ Ò Ö ËÙÐ ÓÒÖÒ ÛÖ ÔÞÐÐ ÑØÑØ Ï Ò ØÒ Ù ĐÙÖ ÐÐ ËØÙÒĐÒ Ò ÙÒ ÖÖ ÙÐØĐØ ÚÓÑ Ö ØÒ ËÑ ØÖ Ò ÙÙØ ÛÖº ÑØ Ë Ò ÎÓÖ ØÐÐÙÒ ÚÓÒ Ò ÚÓÖÙ ØÞØÒ ÅØÑØÒÒØÒ Ò Óѹ ÑÒ ÙÒ ÁÖ Ò Ï Ò Ø ØÒ ĐÓÒÒÒ ÛÖÒ Ñ ÒĐ ØÒ ÒØØ Ò ÙÒ ÚÖ ÒÒÒ ËÛÖØ Ö ÒÓØÒ Ë Ð ØĐÒ ÐĐÓ Ò ÓÐÐØÒº ÛÙÖÒ ÙÒ Ù ËØÓ«ØÒ ÛĐÐØ Ù Ñ ËØÙÙÑ ØĐÒ ÞÙÖĐÙÖ«Ò ÛÖÒ ÑÙ ÙÒ Ñ ÒĐÒÖ ÖÖÙÒ ÑĐ ÓØ ËÛÖ¹ ØÒ ÖØÒº ËÓÐÐØÒ Ë Ñ ËÐ ØØ Ø ÑÖÒ Ë ÈÖÓÐÑ Ñ ÎÖ ØĐÒÒ ÓÖ Ö ÄĐÓ ÙÒ Ö ÙÒ Ò Ø ÁÒÒ ÌÐÒÑ Ñ ÎÓÖÖØÙÒ ÙÖ ÞÙ ÑÔÐÒº Ù ÒÒ ÃÙÖ ĐÓÒÒÒ Ù ÏÙÒ Ù ÄĐÓ ÙÒÒ Ö ÙÒ ÔÖÓÒ ÛÖÒº ÀĐÙ ÛÖ Ö Ò ÚÓÖÖØÒÖ ÄØÖØÙÖ ĐÙÖ ÅØÑØÚÓÖÐ ÙÒÒ ØÐÐغ Ö Ø ÛÖ ÐÐÑÒĐÙÐØ ÞÙ ÒØÛÓÖØÒº ÒÑÐ Ø Ö ÀÓ ÙÐÐÖÖ Ò ÄØÖØÙÖÒÛ ÞÙ ÒÒ ÎÓÖÐ ÙÒÒ ÙÒ ÞÙÑ ÒÖÒ ÓÐÐØ Ö ËØÙÒØ ÛĐÖÒ Ö Ö ØÒ ÏÓÒ Ò ËÑ ØÖ Ò ÐÐÒ ÄØÖØÙÖ¹ ÒÛ Ò Ò Ö ÐÓØ Ò ÛÒ ÈÖÓÐ Ò ÙÒ ÖÙ ÒÒ ÛÐ ÄØÖØÙÖ Ò ÖÛÖØÙÒÒ ÖĐÙÐÐغ Ð Ö ÞÙÖ ÏÖÓÐÙÒ ËÙÐ ØÓ«Ù ËÙÐÐÖĐÙÖ ÙÒ Úغ ÞÙ Ü ØÖÒ ÙÒ ÑÑÐÙÒÒ ÚÖÛ Òº
3 ÏÖÓÐÙÒ ÙÒ ÞÙÑ ËØÙÒÒÒ ËÛÖÖ ÙÒ Ò ÑØ ÒÑ ÒÒÞÒغµ º ÊÒÖÐÒ º ÎÖÒÒ Ë ÓÐÒÒ Ù ÖĐÙ µ Ü Ü Ü Ü µ Ü Ü µ µ µ Ü Ü Ü Ü µ Ü Ý Üݵ µ µ Ô Ô µ µ ÏÖÙÑ ÑÙ ÙÒ ¼ ÚÓÖÙ ØÞØ ÛÖÒ ĐÙÖ ÛÐ ÏÖØ Ø Ö ÖÙ ÒØ ÒÖØ º ÅÒ Ë ÆÒÒÖ ÖØÓÒÐ Ô Ô µ Ô Ô µ Ô µ ÑØ ¼ Ô µ µ Ô Ô Ô Ô º ËÖÒ Ë ¼ Ð ÑÒÒ ÖÙº º ÌÐÖØ º ĐÙÖ ÛÐ ÔÓ ØÚÒ ÒØĐÙÖÐÒ ÐÒ Ø Ò ÒÞ Ð º Ë Ò Ð ÒÞ Ðº Ò Ë ÚÓÒ Ò ÙÖ ØÐÖÒ ÒÞÒ ÐÒ Ù Ñ ÁÒØÖÚÐÐ ¼¼¼ ¼¼¼µ ÑÒ ØÒ Ò ÙÖ ØÐÖ Øº
4 º Ñ ÆÙÖ Ø ÂÖ ÐÖÒØÒ ÙÒ ÒÒÒº ÁÑ ÄÙ ÔÖĐ Ñ ÑÒ Ù ÐØÖ Ö Òº ÉÙÖ ÙÑÑ ÑÒ ÚÖ ØÐÐ ÖÒÒ ÙÖØ Ö ÖØ ÑÒ ÐØÖº Æ ÒÖ ÏÐ ÖÛÖØ ÀÖÞÐÒ ÐĐÙÛÙÒ ÞÙÑ ÙØÒ ¹ ÙÖØ Øº Ï Ñ ÞÙ Ö Ø ØÐÐÙÒ ÙÒ Û ÐØ ÛÙÖ Ñ ºº º ÐÒ Ý ØÑ º ËØÐÐÒ Ë ÞÑÐÞÐ ¼ Ò Ò ÐÒ Ý ØÑÒ ÞÙ Ò Ò ÙÒ Öº º Ù ÛÐÖ Ø Ð ÒÙÒÖØ Ò Ö ØÐÐÙÒ Ö ÓÖÑ ¼ ÑØ ÏÖÙÑ Ø ¼ Ù ÐÓ Ò º ÁÑ ÐÒ Ý ØÑ ÞÙ ÛÐÖ ÐØ ÐÙÒ ¼¼ º º ÄÓ º ÁÒ Ö Ã ØÒ ÐÒ ÞÛ ÃÙÐÒ ÙÒ ÞÛÖ ÒÑÐ ÞÛ Û ÒÑÐ ÞÛ ÛÖÞ ÙÒ ÒÑÐ Ò Û ÙÒ Ò ÛÖÞº Ù Ò ÐÒ Ö Ã ØÒ ÛÖ Ö ÁÒÐØ ÒÒº Ð ÛÙÖÒ Ö Ó ÚÖØÙ Ø ØÞØ Ù ÒÖ Ö Ã ØÒ Ö ÖØ Ð Òغ ÒØ ÙÖ Ò Ò ÒÙÖ ÒÖ ÃÙÐ Ù ÒÙÖ ÒÖ Ã Ø ÛÐÖ Ð Ù ÛÐ Ã Ø ĐÓÖغ º ÅÒ ÒÒ ÞÙ ÒÖ Ù Ö ÆØÓÒ ÎÖÒÒÙÒµ ÒØ ÐÒº Ø ÒÙ ÒÒ ÛÖ ÛÒÒ ÒØ Ð Øº ÓÖÑÙÐÖÒ Ë ÞÙ Ö Ö ÓÐÒÒ Ù Ò Ö ÆØÓÒ ĐÙÖÔÖĐÙÒ Ë Ó Ù Ò ÛÖ Ò ÙÒ ÖĐÙÒÒ Ë Ö ÒØ ÙÒ µ µ ÐÐ ÈÖÑÞÐÒ Ò Öº µ Ü ¼ Ø ÑÒ ØÒ ÞÛ ÖÐÐ ÄĐÓ ÙÒÒº µ Ü µ Ü µ ¼ ØÞØ ĐÓ ØÒ ÞÛ ÖÐÐ ÄĐÓ ÙÒÒº ÃÓÑÒØÓÖ º ÏÒÒ Ö ÌÐÒÑÖ Ò ËØÙÖÒÖ ÒÙ Ò ÈÖØ ÑØ Ñ Ö ĐÙÖÒ ÌÐÒÑÖ ÔÐØ Ó ÛÖÒ Ò ÑØ ÈÖØÒ ÔÐغ ÏÚÐ ËÔÐÖ ÒÑÒ ØÐ º ÏÚÐ ÚÖ Ò ÅĐÓÐØÒ Ø Ö ÒØĐÙÖÐ ÐÒ Ù Ö ÅÒ ¼¼ ÓÒ ØÙÒ Ö ÊÒÓÐ Ù ÞÙÛĐÐÒ Ó
5 º µ ÐÐ ÐÒ Ò Ö Ù ÛÐ ÚÖ Ò Ò µ Ò Ð Ò Ö Ù ÛÐ ÑÖ ÙØÖØÒ Ö µ ËÙÑÑ Ö ÐÒ Ò Ö Ù ÛÐ Ö Ø Ò Ò º º Û Ò Ë ÐÙÒ Ò Ò ÐÙÒÒ º Ò Ë ÄĐÓ ÙÒ ÑÒÒ ÓÐÒÖ ÐÙÒÒ Ò µ Ü Ü Ü Ü µ Ü µ Ü Ü ¼ µ Ü Ö µü Ö ¼ º º ÛÐÒ ÏÖØÒ ÚÓÒ Ô Ø ÐÙÒ Ü ÔÜ ¼ ÄĐÓ ÙÒÒ Ü Ü ÛÐ ÒÙÒ Ü Ü ÖĐÙÐÐÒ º ØÑÑÒ Ë Ò Ö ÐÙÒ Ü Ü ¼ Ò ÈÖÑØÖ Ó «ÖÒÞ Ü Ü ÙÒ ÑÒ ØÒ Ò ÄĐÓ ÙÒ ÔÓ ØÚ Øº º ÄĐÓ Ò Ë ÓÐÒÒ ÐÙÒÒ µ µ Ü Ü µ Þ ¼ ¼¼ Ô Ô Ô Ü Ü Ü Ü¼ º ÍÒØÖ ÛÐÒ ÒÙÒÒ ĐÙÖ ÔÓ ØÚ ÖÐÐ Ð Ø ÐÙÒ Ü Ü ÐÓ ¼ÞÛ ÚÖ Ò ÖÐÐ ÄĐÓ ÙÒÒ º ØÑÑÒ Ë ÄĐÓ ÙÒÒ Ö ÐÙÒ Ó Üµ Ò Üµ ÍÒÐÙÒÒ º ÅÒ ØÑÑ ÅÒ ÐÐÖ ÖÐÐÒ Ü ĐÙÖ ÐØ µ Ü µ Ü µ Ü µ Ü µ Ü µ Ü µ Ü Ü ¼
6 µ Ü Ü Ü Ü ¼ µ Ü Ü ¼ µ Ü Ü µ Ü Ü µ Ü Ü µ Ü Ü Ðµ Ü Ü º º ØÑÑÒ Ë ÄĐÓ ÙÒ ÑÒÒ Ö ÓÐÒÒ ÍÒÐÙÒÒ µ Ü Ü µ Ó Ü Ò Ü º ÖÑØØÐÒ Ë ÄĐÓ ÙÒ ÑÒ Ö ÍÒÐÙÒ Ü Ü ¼ Ò ĐÒØ ÚÓÒ Ö ÒØÒØÚÒ Ð º µ Ü Ü º Û Ò Ë ÓÐÒ ÍÒÐÙÒÒ ĐÙÖ Ð ÔÓ ØÚ ÖÐÐ ÐÒ µ µ º Ü ÙÒ Ý Ò ÅÛÖØ ÑØ ÒÖ ÒÙØ ÚÓÒ ¼ ÞÛº ¼ ØÑÑØ Òº Ü º Ï ÒÒ ÑÒ ĐÙÖ ÒÙØ ÚÓÒ Ü Ý Ü Ý ÙÒ ÜÝ Ò ÐÙÒ Ý ØÑ º Ò Ë ÄĐÓ ÙÒ ÑÒÒ ÓÐÒ ÐÙÒ Ý ØÑ Ò µ Ü Ý Ü Ý µ Ü Ý Ü Ý Ò ĐÒØ ÚÓÒ º ĐÙÒ Ë ÞÙÖ ÐÙÒ Ü Ò ÞÛØ ÐÒÖ ÐÙÒ Ó ÒÞÙ ÒØ ØÒ ÐÙÒ Ý ØÑ ÙÒÐĐÓ Ö Øº º ÄĐÓ Ò Ë ÓÐÒÒ ÐÙÒ Ý ØÑ µ Ü Ý Þ Ü Ý Þ ¼ Ü Ý Þ µ ¼ Ô Ü Ô Ý µ Ô Ü Ô Ý Ü Ý Ü Ý
7 º ÈÓÐÝÒÓÑ º Ò Ë Ò ÕÙÖØ ÐÙÒ ÑØ Ò ÄĐÓ ÙÒÒ Ü ÙÒ Ü Òº º ÏÐ ÄĐÓ ÙÒÒ Ò ÓÐÒÒ ÕÙÖØ Ò ÐÙÒÒ µ Ý Ý µ Ü Ù ÚµÜ ÙÚ ¼ º ÏÐ ÈÓÐÝÒÓÑ ÖØØÒ Ö Ø ÆÙÐÐ ØÐÐÒ Ü Ü ¼ Ü ÙÒ ĐÙÖ Ü Ò ÙÒØÓÒ ÛÖØ Ý º ÅÒ ÛĐÐ ÃÓÆÞÒØÒ ÈÓÐÝÒÓÑ Üµ Ü ÖÜ Ó ÆÙÐÐ ØÐÐÒ Ü Ö ÙÒ Ü Øº º ĐÙÖ ÛÐÒ ÏÖØ ÚÓÒ Ø Ø ÈÓÐÝÒÓÑ Üµ Ü ØÜ ÖÐе ÆÙÐÐ ØÐÐÒ Ü Ü Ö ÒÙÒ Ü Ü ÒĐÙÒ º Ë Üµ Ñ µü Ñ Ñ µü Ñ µ Ñ Ø Ò Ð ÒÞ Ðµº ÙØÖÒ Ë ÒÞÐ Ö ÖÐÐÒ ÆÙÐй ØÐÐÒ ÚÓÒ Ò ĐÒØ ÚÓÒ Ñ ÖĐÙÒ Ë ÆÙÐÐ ØÐÐÒ Ð ÙÒع ÓÒ ÚÓÒ Ñ Ù ÙÒ ÑÒ Ë Ù Ò ĐÙÖ ÎÓÖÞÒ Ö ÆÙÐÐ ØÐÐÒº ÏÒÒ Ò ÐÐ ÆÙÐÐ ØÐÐÒ ÚÓÒ ÒÞÞÐ º¼ ÓÐÒ ÙÒ ÊÒ º ËÖÒ Ë ÑØ ÀÐ ËÙÑÑÒ ÝÑÓÐ È µ ¼ µ Ü Ü Ü Ü Ü Õ Õ Õ µ ¼ Õ ¼ º ÅÒ ÖÒ µ ¼¼ Ò µ Ò ÐÒ µ Ò µ
8 º ËÙÑÑ Ö Ö ØÒ Ö ÐÖ ÒÖ ÙÒÒÐÒ ÓÑØÖ Ò ÓÐ ØÖĐØ ÙÒ ËÙÑÑ ÐÐÖ ÐÖ Ö ÓÐ ØÖĐØ º ĐÙÖ ÛÐ ÒØĐÙÖÐÒ ÐÒ Ò ÐØ ÍÒÐÙÒ º Ò ÎÓÐÐ ØĐÒ ÁÒÙØÓÒ º ÅÒ Û µ ĐÙÖ Ð ÔÓ ØÚ ÐÒ Ò ÐØ µ µ Ò µ Ò µ µ Ò Ò µ Ò Ò Ò µ µ ÐÒÓÐ Ò µ Ò ÙÖ Ò Ò Ò ĐÙÖ Ò º Ò Ë ÙÖ ÁÒÙØÓÒ Ò Ñ ÊØØ Ö ÞÙÒ Ò Ñ Ò Ñ Ò Ñ º Û Ò Ë ĐÙÐØØ Ö ÐÙÒ Ò ¼ Ò Ò µ ÑØ Ò ÆÒ ¼ º ÙÒØÓÒÒ º Ò Ë ĐÙÖ ÙÒØÓÒ ÑØ Üµ Ñ Ü Ò Ñ Ò ÖÐÐ Ñ ¼µ ÐØ Ü µ Ü Ù Ü Ü ÓÐØ µ ÐРѼ Ü µ Ü µ ÐРѼ º ÖÑØØÐÒ Ë ÁÒØÖÚÐÐ Ù ÒÒ ÓÐÒÒ ĐÙÖ ÐÐ ÖÐÐÒ ÖÙÑÒØ Ü ÒÖØÒ ÙÒØÓÒÒ ÑÓÒÓØÓÒ Ò Ò ĐÒØ ÚÓÒ Ò ÈÖÑØÖÒ ÙÒ Ò Ë ÛÐ ÅÓÒÓØÓÒÚÖÐØÒ Ò µ ܵ Ü Ü µ ܵ Ò Ü µ ¼ ¼ º ÅÒ Ô Ò ÒØÓÒ Ö ÓÐÒÖ ÙÒØÓÒÒ Ò µ Ý Ó Ü µ Ý ÐÒ ØÒ Ü º ÅÒ ÞÞÖ ÖÔÒ ÓÐÒÖ ÙÒØÓÒÒ
9 µ Ý Ü Ü µ Ý Ü µ Ý Ü Ü º ÅÒ ØÑÑ Ò ÖĐÓØÒ ÏÖØ Ö ÙÒØÓÒ Ý Ó Ü Ó Üº º Ò Ë Ò ÔÐ ĐÙÖ Ò ÔÖÓ ÙÒØÓÒ ÑØ Ö ÈÖÓ Òº º ĐÙÖ Ò ÖÐÐ Ð Ü Ø Ü ÖĐÓØ ÒÞ Ð ÒØ ÖĐÓÖ Ø Ð Üº Ò Ë Üµ Ü Ü Ò ÔÖÓ ÙÒØÓÒ Øº ÏÐ ÈÖÓ Ø ÏÐ Ð Ø º º ÖÑØØÐÒ Ë Ò ÒÞÖØÓÒÐ ÙÒØÓÒ ÑØ Ý Üµ ĐÙÖ ÐØ µ ¼ µ ¼¼ ܵ ¼ ĐÙÖ ÐÐ Ü Á Ø ÙÖ ÒÒÒØÒ ÒÒ ÒÙØ ØÑÑØ ÄÓÖØÑÒ º Û Ò ÛÐÒ ÒÞÒ ÐÒ Ö ÙÒ Ö ÑÙ Ö ÜÔÓÒÒØ «Ò «ÐÒ º Û Ò ÛÐÒ ÒÞÒ ÐÒ Ö ÙÒ Ö ÑÙ ÒØÒØÚ ÐÒ µ µ ¼ º Ù ÛÐ ÍÒÐÙÒÒ ÞÛ Ò Ò ÜÔÓÒÒØÒ «ÙÒ ÒÒ ÑÒ Ð¹ Ò µ ««µ º ØÑÑÒ Ë ÏÖØ Ö ÓÐÒÒ ÄÓÖØÑÒ ÓÒ Ì ÒÖÒÖ µ ÐÓ µ ÐÓ ¼ Ô Ô µ ÐÓ Ô º Ò Ë ÅÒ ÐÐÖ Ü Ò Ö ÍÒÐÙÒ ÐÓ Ü ÒĐÙÒº
10 º ÏÒ Ë ÄÓÖØÑÒ ØÞ Ò µ Ö Ö ØÐÐÙÒ ÚÓÒ ÐÓ ÑØØÐ ÐÓ º µ Ö ÖÒÙÒ ÚÓÒ ÐÓ Ô Ô ÐÓ Ô Ô Ï Ø ĐÙÖ Ô ÚÓÖÙ ÞÙ ØÞÒ º Ò Ë Ù Ñ ÄÓÖØÑÒ ØÞ ÐÓ Üݵ ÐÓ Ü ÐÓ Ý ÓÐØ µ ÐÓ Ü Ý ÐÓ Ü ÐÓ Ý µ ÐÓ Ü Ô Ô ÐÓ Ü ĐÙÖ ÖØÓÒÐ Ô Ò Ü ÙÒ Ý Ð ÖÐÐ ÐÒ ÙÒ Ø Ò Ð ÞÙÐĐ º º ¼ ÙÒ º º ÒÐÝØ ÓÑØÖ º Ï ÐÙØØ ÐÙÒ Ö ÖÒ Ò Ö Ü¹Ý¹Ò ÙÖ Ò ÈÙÒØ µ Ø ÙÒ ÔÖÐÐÐ Ø ÞÙÖ ÖÒ ÑØ Ö ÐÙÒ Ý Ü º ÙØ Ø ÐÙÒ ÃÖ ÙÖ ÈÙÒØ µ µ ÙÒ µº º ÒÑ ÃÖ ÚÓÑ ÊÙ ÙÑ Ò ÈÙÒØ µ Ò Ð Ø Ö Ò ÖÒ Ò Ò ËØ ÔÖÐÐÐ ÞÙÖ Ü¹ غ Ï ÖÓ Ø Ö ÐĐÒÒÐØ Ö º ÏÓ ÐÒ ÅØØÐÔÙÒØ ÐÐÖ ÃÖ Ö Ò Ò Ò Ö Ö Ò Ò ÒÑ ÒÒ ÈÙÒØ ÖĐÙÖÒ º ÅÒ ØÑÑ ÅÒ ÐÐÖ ÈÙÒØ Ö Ò ÑØ Ò ÃÓÓÖÒØÒ Ü Ýµ ĐÙÖ ÐØ µ Ü Ý µ ÑÜ Ü Ýµ µ Ü Ý µ Ü Ý º Û º ÅÒ Þ ËÙÑÑ Ö ÖØØÒ ÈÓØÒÞÒ ÚÓÒ Ö ÙÒÒÖÓÐÒÒ ÒØĐÙÖÐÒ ÐÒ ÙÖ ØÐÖ Øº ¼
11 º Û Ò Ë ÓÐÒ Ù Ò ĐÙÖ ÒØĐÙÖÐ ÐÒ µ Ø ÌÐÖ ÚÓÒ Ò ĐÙÖ ÐÐ ÒØĐÙÖÐÒ ÐÒ Ò ¼º µ Ò Ò ÛÒÒ Ò ÆÒ º Â Ö ÓÐÒÒ Ù Ò Ø ÒØÛÖ ÛÖ ÓÖ Ð º Û Ò Ë ÛÖÒ ÙÒØÖ ÒÒ ÙÒ ÛÖÐÒ Ë Ð Ò Ù Ò ÙÖ Ò Ò Ò ÔÐ µ Ò Ò Ø ĐÙÖ ÒØĐÙÖÐ Ò Ò ÈÖÑÞк µ ĐÙÖ ÙÒØÓÒ ÑØ Üµ Ü ÙÒ Ð ÖÐÐ ÐÒ Ü Ü ÐØ ØØ Ü Ü µ Ü µ Ü µº µ  ÐÙÒ Ö ØÐØ Ü Ü ¼ ÑØ ÖÐÐÒ ÃÓÆÞÒØÒ ÙÒ ¼ Ø ÒÙ ÞÛ ÖÐÐ ÄĐÓ ÙÒÒº º Û Ò Ë ÒÖص Ð Ô ÖÖØÓÒРغ ÄØÞ ĐÍÖÖØÙÒ º ÂÙÐ ¼¼
 ÖÓÒÐÝ ÒÙÒ ÎÖÖÒ ÞÙÖ ÈÁƹÖÒÙÒ ÙÒ ÈÁƹÈÖĐÙÙÒ ĐÙÖ ¹ÃÖØÒ ÖÓÒÐÝ ÒÙ ÈÁƹÎÖÖÒ ½ ÁÒÐØ ÚÖÞÒ ½ Ù ÑÑÒ ÙÒ Ö Ê ÙÐØØ ¾ ¾ ÒÙ ÎÖÖÒ ¾º½ ÈÁƹÒÖÖÙÒ º º º º º º º º º º º º º º º º º º º º º º º º º ¾º½º½ ÈÁƹÒÖÖÙÒ Ù ÃÖØÒÒÓÖÑØÓÒÒ
ÖÓÒÐÝ ÒÙÒ ÎÖÖÒ ÞÙÖ ÈÁƹÖÒÙÒ ÙÒ ÈÁƹÈÖĐÙÙÒ ĐÙÖ ¹ÃÖØÒ ÖÓÒÐÝ ÒÙ ÈÁƹÎÖÖÒ ½ ÁÒÐØ ÚÖÞÒ ½ Ù ÑÑÒ ÙÒ Ö Ê ÙÐØØ ¾ ¾ ÒÙ ÎÖÖÒ ¾º½ ÈÁƹÒÖÖÙÒ º º º º º º º º º º º º º º º º º º º º º º º º º ¾º½º½ ÈÁƹÒÖÖÙÒ Ù ÃÖØÒÒÓÖÑØÓÒÒ
 ÃÔØÐ ÒÓÑÑÒ ¹ ÙÒ ËÙ ØØÙØÓÒ «Ø ËÐÙØÞݹÐÙÒ ÙÒ ËÐÙØ ÞµÝ ¼¹µ Ö ÏÐ ÎÓÖÞÒ Òººº Òкºº Þ Ð ß Ü Ü Ô Ô ßÞÐ ÃÖÙÞÔÖ «Ø ÞÛº ÒÒØ ÑÐ ĐÒÖÙÒÒ Þ Ð ß Ü Ü Ô Ô ÈÖ ĐÒÖÙÒ Ô ¼µØÞÛ «Ø º ĐÒÖÙÒ Ö ÖÐØÚÒ ÈÖ ËÙ ØØÙØÓÒ «Ø ¾º ĐÒÖÙÒ Ö
ÃÔØÐ ÒÓÑÑÒ ¹ ÙÒ ËÙ ØØÙØÓÒ «Ø ËÐÙØÞݹÐÙÒ ÙÒ ËÐÙØ ÞµÝ ¼¹µ Ö ÏÐ ÎÓÖÞÒ Òººº Òкºº Þ Ð ß Ü Ü Ô Ô ßÞÐ ÃÖÙÞÔÖ «Ø ÞÛº ÒÒØ ÑÐ ĐÒÖÙÒÒ Þ Ð ß Ü Ü Ô Ô ÈÖ ĐÒÖÙÒ Ô ¼µØÞÛ «Ø º ĐÒÖÙÒ Ö ÖÐØÚÒ ÈÖ ËÙ ØØÙØÓÒ «Ø ¾º ĐÒÖÙÒ Ö
Î ÖØÖ Ù Ò Ú ÖÐÙ Ø Ñ ÁÒØ Ö Ò ÒÑ Ö Ø ÙÒ Ò Ø ÖÖ Ä ÙÒ Å Ð À Ò ÍÒ Ú Ö ØØ ÁÒÒ ÖÙ ÁÒ Ø ØÙØ Ö Ò Ò ÙÒ Ò ÒÞ Ò
 Î ÖØÖ Ù Ò Ú ÖÐÙ Ø Ñ ÁÒØ Ö Ò ÒÑ Ö Ø ÙÒ Ò Ø ÖÖ Ä ÙÒ Å Ð À Ò ÍÒ Ú Ö ØØ ÁÒÒ ÖÙ ÁÒ Ø ØÙØ Ö Ò Ò ÙÒ Ò ÒÞ Ò Ö Ð Ä ÕÙ ØØ Ò ÒÞ Ò Ø ØÙØ ÓÒ Ò ÙÒ ÁÒØ Ö Ò ÒÑ Ö Ø Î ÖØÖ Ù Ò ÁÒØ Ö Ò ÒÑ Ö Ø Û Ö Ò Ö ÃÖ Ù Û Ö ÙÒ Ò Ö Ò ÒÞ
Î ÖØÖ Ù Ò Ú ÖÐÙ Ø Ñ ÁÒØ Ö Ò ÒÑ Ö Ø ÙÒ Ò Ø ÖÖ Ä ÙÒ Å Ð À Ò ÍÒ Ú Ö ØØ ÁÒÒ ÖÙ ÁÒ Ø ØÙØ Ö Ò Ò ÙÒ Ò ÒÞ Ò Ö Ð Ä ÕÙ ØØ Ò ÒÞ Ò Ø ØÙØ ÓÒ Ò ÙÒ ÁÒØ Ö Ò ÒÑ Ö Ø Î ÖØÖ Ù Ò ÁÒØ Ö Ò ÒÑ Ö Ø Û Ö Ò Ö ÃÖ Ù Û Ö ÙÒ Ò Ö Ò ÒÞ
= 27
 Å ÌÀ Ê ÂÍÆ ÍÆ ÄÌ ¹ Ë ÊÁ ¹ ÇÃÌ»ÆÇÎ ¾¼½½ ½ ÎÓÖ ÙÐ ½ Ù ¹½½ ÁÒ ÂÙÐ Ë Ù Ö Ò Ø Ò Ö È Ö Ë Ù º Ë Ò ÑÑØ Ñ ÙÒ ÐÒ Ú Ö ÒÞ ÐÒ Ë Ù Ö Ù º Á Ø Ò ÞÙ ÑÑ Ò Ö Ò È Ö Ù ¹½¾ Û ÚÓÒ Ò Ð Ö Ò Ò Ú ÐÐ Ð º Ï Ð Ò ¾ À Ï Ò ÐÚÓ ÛÛÛº Ð
Å ÌÀ Ê ÂÍÆ ÍÆ ÄÌ ¹ Ë ÊÁ ¹ ÇÃÌ»ÆÇÎ ¾¼½½ ½ ÎÓÖ ÙÐ ½ Ù ¹½½ ÁÒ ÂÙÐ Ë Ù Ö Ò Ø Ò Ö È Ö Ë Ù º Ë Ò ÑÑØ Ñ ÙÒ ÐÒ Ú Ö ÒÞ ÐÒ Ë Ù Ö Ù º Á Ø Ò ÞÙ ÑÑ Ò Ö Ò È Ö Ù ¹½¾ Û ÚÓÒ Ò Ð Ö Ò Ò Ú ÐÐ Ð º Ï Ð Ò ¾ À Ï Ò ÐÚÓ ÛÛÛº Ð
= = = = =
 Å ÌÀ Ê ÂÍÆ ÍÆ ÄÌ ¹ Ë ÊÁ ¹ Â Æ» ¾¼½ ½ ÎÓÖ ÙÐ ½ Ù ¹½½ Ù Ñ Ð Ò Û Ö Ê Ð Ñ Ø Ñ Ö Û Ö ÓÖÑØ Ò Òº Ø ÐÐ Ù Ø ÐÐØ Ò ËØ Ò Ñ Ö ÚÓÖ Ò Òº µ Ï Ú Ð Ú Ö Ò ÓÑÑ Ò ÚÓÖ µ Ï Ð Ø Ñ Ù Ø Ò Ú ÖØÖ Ø Ò µ Ï Ð Ø Ù Ñ ÐØ Ò Ø Ò ¾ À Ï Ò
Å ÌÀ Ê ÂÍÆ ÍÆ ÄÌ ¹ Ë ÊÁ ¹ Â Æ» ¾¼½ ½ ÎÓÖ ÙÐ ½ Ù ¹½½ Ù Ñ Ð Ò Û Ö Ê Ð Ñ Ø Ñ Ö Û Ö ÓÖÑØ Ò Òº Ø ÐÐ Ù Ø ÐÐØ Ò ËØ Ò Ñ Ö ÚÓÖ Ò Òº µ Ï Ú Ð Ú Ö Ò ÓÑÑ Ò ÚÓÖ µ Ï Ð Ø Ñ Ù Ø Ò Ú ÖØÖ Ø Ò µ Ï Ð Ø Ù Ñ ÐØ Ò Ø Ò ¾ À Ï Ò
15+9 = 24 8 = 41 6 = 44+4 = 45 5 = = = = = 26 7 = 13 6 = = 27+6 = = =
 Å ÌÀ Ê ÂÍÆ ÍÆ ÄÌ ¹ Ë ÊÁ ¹ Ë ÈÌ»ÇÃÌ ¾¼½¾ ½ ÎÓÖ ÙÐ ½ Ù ¹½½ Ï Ú Ð Ö ÒÒ Ø Ù Ò Ö ÙÖ ÒØ Ò Ù ¹½¾ Ù Ô Ø Ö ÊØ ÐÖ Ø Ö ÙØ Å Ù Ò ÙÒ Ò Ã Ø Ö ÍÒ ÒÒ Ö Ò Ø Ù Û Ò Û ÐØ ÛÓ Ð Ò Ò Ò ÏÓ Òµ À ÒÛ ÙÒ Ò Û Ð Ò Ò Ð Ò Ò ÈÙÒ Ø ÙÒØ
Å ÌÀ Ê ÂÍÆ ÍÆ ÄÌ ¹ Ë ÊÁ ¹ Ë ÈÌ»ÇÃÌ ¾¼½¾ ½ ÎÓÖ ÙÐ ½ Ù ¹½½ Ï Ú Ð Ö ÒÒ Ø Ù Ò Ö ÙÖ ÒØ Ò Ù ¹½¾ Ù Ô Ø Ö ÊØ ÐÖ Ø Ö ÙØ Å Ù Ò ÙÒ Ò Ã Ø Ö ÍÒ ÒÒ Ö Ò Ø Ù Û Ò Û ÐØ ÛÓ Ð Ò Ò Ò ÏÓ Òµ À ÒÛ ÙÒ Ò Û Ð Ò Ò Ð Ò Ò ÈÙÒ Ø ÙÒØ
 Ã Ô Ø Ð ¾ ØÙ ÐÐ Ö ËØ Ò ÙÒ Ì Ò ÒÞ Ò Ö Ã Þ¹ÁÒÒ ÒÖ ÙÑ ÖÛ ÙÒ ÁÒ ÐØ Ò ¾º½ ÅÓØ Ú Ø ÓÒ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾º¾ ÁÒÒ ÒÖ ÙÑ ÙØÞ Ñ Ã Þ¹ÁÒÒ ÒÖ ÙÑ º º º º º º º º º º º º º º
Ã Ô Ø Ð ¾ ØÙ ÐÐ Ö ËØ Ò ÙÒ Ì Ò ÒÞ Ò Ö Ã Þ¹ÁÒÒ ÒÖ ÙÑ ÖÛ ÙÒ ÁÒ ÐØ Ò ¾º½ ÅÓØ Ú Ø ÓÒ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾º¾ ÁÒÒ ÒÖ ÙÑ ÙØÞ Ñ Ã Þ¹ÁÒÒ ÒÖ ÙÑ º º º º º º º º º º º º º º
Ê ÓØ ÓÖ º Ì Ð ÈÖÓ º Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò Ø ÖÖ º Å ¾¼½ ÈÖÓ º Ö À Ù Ò Ð Ä Ó Òµ Ê ÓØ ÓÖ º Å ¾¼½ ½» ½
 Ê ÓØ ÓÖ º Ì Ð ÈÖÓ º Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò Ø ÖÖ º Å ¾¼½ ÈÖÓ º Ö À Ù Ò Ð Ä Ó Òµ Ê ÓØ ÓÖ º Å ¾¼½ ½» ½ Å Ü Ñ Ð Ö ÒÞ ÙÒ Ö Ö Ö ØÚ ÖØ ÐÙÒ Ò Ø ÓÒ Ò ÙÒ Ø ÓÒ Ä : [¼, ) [¼, ) Ø Ð Ò Ñ Ú Ö Ö Ò ÐÓÛÐÝ Ú ÖÝ
Ê ÓØ ÓÖ º Ì Ð ÈÖÓ º Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò Ø ÖÖ º Å ¾¼½ ÈÖÓ º Ö À Ù Ò Ð Ä Ó Òµ Ê ÓØ ÓÖ º Å ¾¼½ ½» ½ Å Ü Ñ Ð Ö ÒÞ ÙÒ Ö Ö Ö ØÚ ÖØ ÐÙÒ Ò Ø ÓÒ Ò ÙÒ Ø ÓÒ Ä : [¼, ) [¼, ) Ø Ð Ò Ñ Ú Ö Ö Ò ÐÓÛÐÝ Ú ÖÝ
Verteilte Systeme/Sicherheit im Internet
 ruhr-universität bochum Lehrstuhl für Datenverarbeitung Prof. Dr.-Ing. Dr.E.h. Wolfgang Weber Verteilte Systeme/Sicherheit im Internet Intrusion Detection und Intrusion Response Systeme (IDS & IRS) Seminar
ruhr-universität bochum Lehrstuhl für Datenverarbeitung Prof. Dr.-Ing. Dr.E.h. Wolfgang Weber Verteilte Systeme/Sicherheit im Internet Intrusion Detection und Intrusion Response Systeme (IDS & IRS) Seminar
Ü (k) Ü < ǫ, (Ü (k) ) < ǫ, Ü (k+½) Ü (k) < ǫ
 Å Ö Ñ Ò ÓÒ Ð Æ ÛØÓÒ Î Ö Ö Ò º ÎÓÖÐ ÙÒ ½ ¼ ¼¼ ÆÙÑ Ö Å Ø Ó Ò Á Ð Ñ Ò Ö Ò ÙÒ Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò º ÅÖÞ ¾¼½ Å Ö Ñ Ò ÓÒ Ð Æ ÛØÓÒ Î Ö Ö Ò ½ Å Ö Ñ Ò ÓÒ Ð Æ ÛØÓÒ Î Ö Ö Ò Î ØÓÖ Ò Ú ØÓÖÛ ÖØ ÙÒ Ø ÓÒ Ò
Å Ö Ñ Ò ÓÒ Ð Æ ÛØÓÒ Î Ö Ö Ò º ÎÓÖÐ ÙÒ ½ ¼ ¼¼ ÆÙÑ Ö Å Ø Ó Ò Á Ð Ñ Ò Ö Ò ÙÒ Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò º ÅÖÞ ¾¼½ Å Ö Ñ Ò ÓÒ Ð Æ ÛØÓÒ Î Ö Ö Ò ½ Å Ö Ñ Ò ÓÒ Ð Æ ÛØÓÒ Î Ö Ö Ò Î ØÓÖ Ò Ú ØÓÖÛ ÖØ ÙÒ Ø ÓÒ Ò
 Ê Ê ÙÒ ÒØ ÖÖ Ý Ó ÁÒ Ô Ò ÒØ ÙØÓÖ ÖÒ Ö Ë Ñ Ø Å Øº ÆÖº ¾ à ÒÒÞº ½ ½ ÁÆÀ ÄÌËÎ Ê Á ÀÆÁË ÁÆÀ ÄÌËÎ Ê Á ÀÆÁË ÁÒ ÐØ Ú ÖÞ Ò ½ ÅÓØ Ú Ø ÓÒ ¾ Ì Ð Ò Ê ËÝ Ø Ñ ÖÖ Ý Å Ò Ñ ÒØ ËÓ ØÛ Ö Ê Ä Ú Ð º½ Ö «Ò Ø ÓÒ Ò ººººººººººººººººººººººººººººººº
Ê Ê ÙÒ ÒØ ÖÖ Ý Ó ÁÒ Ô Ò ÒØ ÙØÓÖ ÖÒ Ö Ë Ñ Ø Å Øº ÆÖº ¾ à ÒÒÞº ½ ½ ÁÆÀ ÄÌËÎ Ê Á ÀÆÁË ÁÆÀ ÄÌËÎ Ê Á ÀÆÁË ÁÒ ÐØ Ú ÖÞ Ò ½ ÅÓØ Ú Ø ÓÒ ¾ Ì Ð Ò Ê ËÝ Ø Ñ ÖÖ Ý Å Ò Ñ ÒØ ËÓ ØÛ Ö Ê Ä Ú Ð º½ Ö «Ò Ø ÓÒ Ò ººººººººººººººººººººººººººººººº
ÙÚ ÖÐ Ø º Ì Ð ÈÖÓ º Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò Ø ÖÖ º Ç ØÓ Ö ¾¼½ ÈÖÓ º Ö À Ù Ò Ð Ä Ó Òµ ÙÚ ÖÐ Ø º Ç ØÓ Ö ¾¼½ ½» ½
 ÙÚ ÖÐ Ø º Ì Ð ÈÖÓ º Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò Ø ÖÖ º Ç ØÓ Ö ¾¼½ ÈÖÓ º Ö À Ù Ò Ð Ä Ó Òµ ÙÚ ÖÐ Ø º Ç ØÓ Ö ¾¼½ ½» ½ ÁÒ ÐØ ÈÖÓ º Ö À Ù Ò Ð Ä Ó Òµ ÙÚ ÖÐ Ø º Ç ØÓ Ö ¾¼½ ¾» ½ Ò Ö Ð ÈÖÓ º Ö À Ù Ò Ð Ä Ó Òµ
ÙÚ ÖÐ Ø º Ì Ð ÈÖÓ º Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò Ø ÖÖ º Ç ØÓ Ö ¾¼½ ÈÖÓ º Ö À Ù Ò Ð Ä Ó Òµ ÙÚ ÖÐ Ø º Ç ØÓ Ö ¾¼½ ½» ½ ÁÒ ÐØ ÈÖÓ º Ö À Ù Ò Ð Ä Ó Òµ ÙÚ ÖÐ Ø º Ç ØÓ Ö ¾¼½ ¾» ½ Ò Ö Ð ÈÖÓ º Ö À Ù Ò Ð Ä Ó Òµ
Ô ÖØ Ñ ÒØ ÁÒ ÓÖÑ Ø ÇÔ Ò Ð ß Ë Ò ÏÙÒ Ö Ö ÁÒ ÓÖÑ Ø ÈÖÓ º Öº ÂÙÖ ÀÖÓÑ ÓÚ ÄĐÓ ÙÒ ÚÓÖ ÐĐ ĐÙÖ Đ Í ÙÒ Ù Ò ß Ð ØØ ½ ÄĐÓ ÙÒ ÞÙ Ù ¾ Ï Ö ÛÓÐÐ Ò Ö Ø ÓÐ Ò Ò ÈÖÓ Ö
 ÔÖØÑÒØ ÁÒÓÖÑØ ÇÔÒ Ð ß ËÒ ÏÙÒÖ Ö ÁÒÓÖÑØ ÈÖÓº Öº ÂÙÖ ÀÖÓÑÓÚ ÄĐÓ ÙÒ ÚÓÖ ÐĐ ĐÙÖ Đ ÍÙÒ ÙÒ ß ÐØØ ½ ÄĐÓ ÙÒ ÞÙ Ù ¾ ÏÖ ÛÓÐÐÒ ÖØ ÓÐÒÒ ÈÖÓÖÑÑ ÒÐÝ ÖÒ Ò ½º Ä Ò Ò Ê ØÖ ½µ ¾º Ä Ò Ò Ê ØÖ ¾µ º Ä Ò Ò Ê ØÖ µ º Ê ØÖ µ Ê ØÖ
ÔÖØÑÒØ ÁÒÓÖÑØ ÇÔÒ Ð ß ËÒ ÏÙÒÖ Ö ÁÒÓÖÑØ ÈÖÓº Öº ÂÙÖ ÀÖÓÑÓÚ ÄĐÓ ÙÒ ÚÓÖ ÐĐ ĐÙÖ Đ ÍÙÒ ÙÒ ß ÐØØ ½ ÄĐÓ ÙÒ ÞÙ Ù ¾ ÏÖ ÛÓÐÐÒ ÖØ ÓÐÒÒ ÈÖÓÖÑÑ ÒÐÝ ÖÒ Ò ½º Ä Ò Ò Ê ØÖ ½µ ¾º Ä Ò Ò Ê ØÖ ¾µ º Ä Ò Ò Ê ØÖ µ º Ê ØÖ µ Ê ØÖ
 ½ Ï ÐÐ ÓÑÑ Ò ÞÙÑ ËØÙ Ý Ù ÁÒ Ø ÐÐ Ø ÓÒ Ò ÓÒ ÙÖ Ø ÓÒ Á² ½µ ÖØ Þ ÖÙÒ º Ø Ö Ö Ø ÚÓÒ Ú Ö ÃÙÖ Ò ÞÙÑ Ë Ö Ä ÒÙÜ Ò ÆÍ ÖØ Ñ Ò ØÖ ØÓÖ Ä µº Ò Ö Ò Ö ÃÙÖ Ò ËÝ Ø Ñ Ñ Ò ØÖ Ø ÓÒ Ë ½µ Æ ØÛÓÖ Ò Æ Ì½µ ÙÒ Ë ÙÖ ¹ ØÝ Ë È½µº
½ Ï ÐÐ ÓÑÑ Ò ÞÙÑ ËØÙ Ý Ù ÁÒ Ø ÐÐ Ø ÓÒ Ò ÓÒ ÙÖ Ø ÓÒ Á² ½µ ÖØ Þ ÖÙÒ º Ø Ö Ö Ø ÚÓÒ Ú Ö ÃÙÖ Ò ÞÙÑ Ë Ö Ä ÒÙÜ Ò ÆÍ ÖØ Ñ Ò ØÖ ØÓÖ Ä µº Ò Ö Ò Ö ÃÙÖ Ò ËÝ Ø Ñ Ñ Ò ØÖ Ø ÓÒ Ë ½µ Æ ØÛÓÖ Ò Æ Ì½µ ÙÒ Ë ÙÖ ¹ ØÝ Ë È½µº
ÁÒ ÐØ Ö ÖÓ Ö ÙÒØ ÖÐ Ò Ö Ö Ø Ú ÓÑÑÓÒ ÙÒØ Ö Ð Ò Ò ÙÒ Ò º¼ ÍÒ¹ Æ Ñ Ò Ò ÒÒÙÒ ¹Ï Ø Ö ÙØ Ø Ò Ó Ø ÒÐÓ Ù ÓÑÑ ÖÞ ÐÐ ÆÙØÞÙÒ ÓÐ Ò Ò Ò ÙÒ Ò Ñ Ð Ø ÙÒØ Ö Ð ÍÖ Ö Ò Û
 ÁÒ ÐØ Ö ÖÓ Ö ÙÒØ ÖÐ Ò Ö Ö Ø Ú ÓÑÑÓÒ ÙÒØ Ö Ð Ò Ò ÙÒ Ò º¼ ÍÒ¹ Æ Ñ Ò Ò ÒÒÙÒ ¹Ï Ø Ö ÙØ Ø Ò Ó Ø ÒÐÓ Ù ÓÑÑ ÖÞ ÐÐ ÆÙØÞÙÒ ÓÐ Ò Ò Ò ÙÒ Ò Ñ Ð Ø ÙÒØ Ö Ð ÍÖ Ö Ò Û Ö À Ï Ò ÐÚÓ Ò ÒÒغ ÇÒÐ Ò ¹Å Ò Û Ö Ö Ä Þ ÒÞØ ÜØ Ú ÖÐ
ÁÒ ÐØ Ö ÖÓ Ö ÙÒØ ÖÐ Ò Ö Ö Ø Ú ÓÑÑÓÒ ÙÒØ Ö Ð Ò Ò ÙÒ Ò º¼ ÍÒ¹ Æ Ñ Ò Ò ÒÒÙÒ ¹Ï Ø Ö ÙØ Ø Ò Ó Ø ÒÐÓ Ù ÓÑÑ ÖÞ ÐÐ ÆÙØÞÙÒ ÓÐ Ò Ò Ò ÙÒ Ò Ñ Ð Ø ÙÒØ Ö Ð ÍÖ Ö Ò Û Ö À Ï Ò ÐÚÓ Ò ÒÒغ ÇÒÐ Ò ¹Å Ò Û Ö Ö Ä Þ ÒÞØ ÜØ Ú ÖÐ
 Þ ÒÞÙÒØ Ö Ù ÙÒ Ò Ò Ö ÎÓÖ Ð Ò ÙÒ Î ÖØ Ù Ò ¹Å Ø Ó Ö ÙÓÖ ÒÙÒ ÔÖÓ Ð Ñ ÔÐÓÑ Ö Ø Ñ ÁÒ ÓÖÑ Ø Ò º Ò ÓÖѺ Ê Ò Ö À ÖÖÐ Ö ØÖ Ù Ö ÈÖÓ º Öº Ö Ò ÈÙÔÔ Ôк ÁÒ ÓÖѺ Ù Ä Ö ØÙ Ð Ö Ã Ò ØÐ ÁÒØ ÐÐ ÒÞ ÙÒ Ò Û Ò Ø ÁÒ ÓÖÑ Ø ÍÒ
Þ ÒÞÙÒØ Ö Ù ÙÒ Ò Ò Ö ÎÓÖ Ð Ò ÙÒ Î ÖØ Ù Ò ¹Å Ø Ó Ö ÙÓÖ ÒÙÒ ÔÖÓ Ð Ñ ÔÐÓÑ Ö Ø Ñ ÁÒ ÓÖÑ Ø Ò º Ò ÓÖѺ Ê Ò Ö À ÖÖÐ Ö ØÖ Ù Ö ÈÖÓ º Öº Ö Ò ÈÙÔÔ Ôк ÁÒ ÓÖѺ Ù Ä Ö ØÙ Ð Ö Ã Ò ØÐ ÁÒØ ÐÐ ÒÞ ÙÒ Ò Û Ò Ø ÁÒ ÓÖÑ Ø ÍÒ
Ð ÙÒ ½ ËÙ Ø Ú ÙÖØ ÐÙÒ ÚÓÒ Ì ÑÔ Ö ØÙÖ Ò ÙÖ Ø Ø Ò ÓÖ Ò Òº ÏÖÑ ÑÔ Ò Ò Ø Ó ÙÒ Ò Ù ÙÒ Ð Ö Ü Ø Å ÙÒ ÚÓÒ ÏÖ¹ Ñ ÞÙ ØÒ Ò ÙÒ Ò Øº Ö Å Ò Ò ÑÑØ ÏÖÑ ÙÖ Ô Þ ÐÐ Æ ÖÚ
 Ë Ñ Ò ÖÚÓÖØÖ ÞÙÑ Ì Ñ Ì ÑÔ Ö ØÙÖ ÙÒ ÏÖÑ Ò Ã ØØ Ð Ö ½ º½½º¾¼¼ Ö Ú Ð Å Ò Ò ÙØ Ò Ö Ì ÑÔ Ö ØÙÖ ÙÒ ÏÖÑ Ñ Ö Ó Ö Û Ò Ö Ð º ½ ÖÐÙØ ÖÒ Ë Û Ë Ù Ë Ð Ö Ö Ï Ø ÒØÐ Ö ÍÒØ Ö ÞÛ Ò Ì ÑÔ Ö ØÙÖ ÙÒ ÏÖÑ Ò Ò Û Ö Ò Ï Ö Ò Ì ÑÔ
Ë Ñ Ò ÖÚÓÖØÖ ÞÙÑ Ì Ñ Ì ÑÔ Ö ØÙÖ ÙÒ ÏÖÑ Ò Ã ØØ Ð Ö ½ º½½º¾¼¼ Ö Ú Ð Å Ò Ò ÙØ Ò Ö Ì ÑÔ Ö ØÙÖ ÙÒ ÏÖÑ Ñ Ö Ó Ö Û Ò Ö Ð º ½ ÖÐÙØ ÖÒ Ë Û Ë Ù Ë Ð Ö Ö Ï Ø ÒØÐ Ö ÍÒØ Ö ÞÛ Ò Ì ÑÔ Ö ØÙÖ ÙÒ ÏÖÑ Ò Ò Û Ö Ò Ï Ö Ò Ì ÑÔ
Ð ÖÙÒ Ï Ö ÓÐÙÒ Å ØÖ Ü Ð Ö Ä Ò Ö Ð ÙÒ Ý Ø Ñ Ä Ö Ø ÐÐÙÒØ Ö ÙÒ Ò Å ÌÄ ÙÒ Ð Ò Ö ËÝ Ø Ñ ÃÓÒ Ø ÓÒ Þ Ð Ô Ð Ö Ø ÈÓ ÓÒ¹ÈÖÓ Ð Ñ Å ØÖ Ü ÔÐ ØØ Ò ÅÓ ÖÒ Ø Ö Ø Ú Î Ö
 Ä Ò Ö Ð ÙÒ Ý Ø Ñ Á º ÎÓÖÐ ÙÒ ½ ¼ ¼¼ ÆÙÑ Ö Å Ø Ó Ò Á Ð Ñ Ò Ö Ò ÙÒ Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò ½¾º ÅÖÞ ¾¼½ Ð ÖÙÒ Ï Ö ÓÐÙÒ Å ØÖ Ü Ð Ö Ä Ò Ö Ð ÙÒ Ý Ø Ñ Ä Ö Ø ÐÐÙÒØ Ö ÙÒ Ò Å ÌÄ ÙÒ Ð Ò Ö ËÝ Ø Ñ ÃÓÒ Ø ÓÒ
Ä Ò Ö Ð ÙÒ Ý Ø Ñ Á º ÎÓÖÐ ÙÒ ½ ¼ ¼¼ ÆÙÑ Ö Å Ø Ó Ò Á Ð Ñ Ò Ö Ò ÙÒ Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò ½¾º ÅÖÞ ¾¼½ Ð ÖÙÒ Ï Ö ÓÐÙÒ Å ØÖ Ü Ð Ö Ä Ò Ö Ð ÙÒ Ý Ø Ñ Ä Ö Ø ÐÐÙÒØ Ö ÙÒ Ò Å ÌÄ ÙÒ Ð Ò Ö ËÝ Ø Ñ ÃÓÒ Ø ÓÒ
a n½ x ½ +a n¾ x ¾ a nn x n = b n
 Ä Ò Ö Ð ÙÒ Ý Ø Ñ º ÎÓÖÐ ÙÒ ½ ¼ ¼¼ ÆÙÑ Ö Å Ø Ó Ò Á Ð Ñ Ò Ö Ò ÙÒ Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò ½ º ÅÖÞ ¾¼½ Ä Ò Ö Ð ÙÒ Ý Ø Ñ Ä Ö Ø Ð Ö ÑÔ Ò Ð Ø Å ØÖ Ü Ð Ö Ä Ö Ø ÐÐÙÒØ Ö ÙÒ Ò Å ÌÄ ÙÒ Ð Ò Ö ËÝ Ø Ñ Ð Ö ÑÔ
Ä Ò Ö Ð ÙÒ Ý Ø Ñ º ÎÓÖÐ ÙÒ ½ ¼ ¼¼ ÆÙÑ Ö Å Ø Ó Ò Á Ð Ñ Ò Ö Ò ÙÒ Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò ½ º ÅÖÞ ¾¼½ Ä Ò Ö Ð ÙÒ Ý Ø Ñ Ä Ö Ø Ð Ö ÑÔ Ò Ð Ø Å ØÖ Ü Ð Ö Ä Ö Ø ÐÐÙÒØ Ö ÙÒ Ò Å ÌÄ ÙÒ Ð Ò Ö ËÝ Ø Ñ Ð Ö ÑÔ
 ÁÒ Ø ØÙØ ĐÙÖ ÁÒ ÓÖÑ Ø Ö Ì Ò Ò ÍÒ Ú Ö ØĐ Ø ÅĐÙÒ Ò À ÙÔØ Ñ Ò Ö Ñ ËÓÑÑ Ö Ñ Ø Ö ½ ÈÖÓ º Öº Àº º À Ö Ò Î ÖÞ Ò Ò Ø ÙÒ Ö ÒÛ Ò ÙÒ Ò Ñ Æ ØÞ¹ ÙÒ ËÝ Ø ÑÑ Ò Ñ ÒØ Ä È Ú Ä ØÛ Ø Ö ØÓÖÝ ÈÖÓØÓÓÐ Î Ö ÓÒ Ê Ö ÒØ Ò Ö Ë ÐÐÑ
ÁÒ Ø ØÙØ ĐÙÖ ÁÒ ÓÖÑ Ø Ö Ì Ò Ò ÍÒ Ú Ö ØĐ Ø ÅĐÙÒ Ò À ÙÔØ Ñ Ò Ö Ñ ËÓÑÑ Ö Ñ Ø Ö ½ ÈÖÓ º Öº Àº º À Ö Ò Î ÖÞ Ò Ò Ø ÙÒ Ö ÒÛ Ò ÙÒ Ò Ñ Æ ØÞ¹ ÙÒ ËÝ Ø ÑÑ Ò Ñ ÒØ Ä È Ú Ä ØÛ Ø Ö ØÓÖÝ ÈÖÓØÓÓÐ Î Ö ÓÒ Ê Ö ÒØ Ò Ö Ë ÐÐÑ
Ð ÀÐØ ÐÐ ØØÖ Ù Ñ ÐÒ ÄÚÐ ÙÒ ÔÖ ØÒ Ò Ò ÐØØÖÒº ÞÙ ÖÐÙ ÑÖ Ð ÒÒ ËÐ Ð Ò ÒÑ ÒÒÖÒ ÃÒÓØÒ ÞÙ ÔÖÒº ÀØ Ò ÒÒÖÖ ÃÒÓØÒ x ÒÙ m ÃÒÖ Ó ÒÐØØ x ÒÙ m ËРк ËÐ Ð Ò ÒÑ ÌÐÙÑ
 º ËÙÚÖÖÒ º (a,b) ¹ ÙÑ º ÂÙÒ Ð ÀÐØ ÐÐ ØØÖ Ù Ñ ÐÒ ÄÚÐ ÙÒ ÔÖ ØÒ Ò Ò ÐØØÖÒº ÞÙ ÖÐÙ ÑÖ Ð ÒÒ ËÐ Ð Ò ÒÑ ÒÒÖÒ ÃÒÓØÒ ÞÙ ÔÖÒº ÀØ Ò ÒÒÖÖ ÃÒÓØÒ x ÒÙ m ÃÒÖ Ó ÒÐØØ x ÒÙ m ËРк ËÐ Ð Ò ÒÑ ÌÐÙÑ T i ÔÖØ Ò Ò ÐÐ ÐÒÖ Ð Ù
º ËÙÚÖÖÒ º (a,b) ¹ ÙÑ º ÂÙÒ Ð ÀÐØ ÐÐ ØØÖ Ù Ñ ÐÒ ÄÚÐ ÙÒ ÔÖ ØÒ Ò Ò ÐØØÖÒº ÞÙ ÖÐÙ ÑÖ Ð ÒÒ ËÐ Ð Ò ÒÑ ÒÒÖÒ ÃÒÓØÒ ÞÙ ÔÖÒº ÀØ Ò ÒÒÖÖ ÃÒÓØÒ x ÒÙ m ÃÒÖ Ó ÒÐØØ x ÒÙ m ËРк ËÐ Ð Ò ÒÑ ÌÐÙÑ T i ÔÖØ Ò Ò ÐÐ ÐÒÖ Ð Ù
Ð ØÖÓÒ ÙÒ Ð Ò ÚÓÒ Å ÖØ Ò Ï Ò Ò Ö Ò ½ ¹ ½ ¼ Ö Ò Ò ½ µ ÛÙÖ Ö ØÑ Ð ÚÓÒ Å Ð ËÓÓ ØÑ Ý Ö ÍÒ Ú Ö ØØ Ò Ö Ø ÐÐØ ÙÒ Ù ¹ÊÓÑ ÞÙÖ Î Ö ÙÒ Ø ÐÐغ Í Ó Ù ÍÒ Ú Ö ØØ Ù Ù
 Ð ØÖÓÒ ÙÒ Ð Ò ÚÓÒ Å ÖØ Ò Ï Ò Ò Ö Ò ½ ¹ ½ ¼ Ö Ò Ò ½ µ ÛÙÖ Ö ØÑ Ð ÚÓÒ Å Ð ËÓÓ ØÑ Ý Ö ÍÒ Ú Ö ØØ Ò Ö Ø ÐÐØ ÙÒ Ù ¹ÊÓÑ ÞÙÖ Î Ö ÙÒ Ø ÐÐغ Í Ó Ù ÍÒ Ú Ö ØØ Ù ÙÖ ¹ Ò Ö Ö Ø Ø ¾¼½ Î Ö ÓÒ Ó Ò Ò Ï Ò Ò Ì ÜØ ÙÒ Ð ÖÒ ØÛ
Ð ØÖÓÒ ÙÒ Ð Ò ÚÓÒ Å ÖØ Ò Ï Ò Ò Ö Ò ½ ¹ ½ ¼ Ö Ò Ò ½ µ ÛÙÖ Ö ØÑ Ð ÚÓÒ Å Ð ËÓÓ ØÑ Ý Ö ÍÒ Ú Ö ØØ Ò Ö Ø ÐÐØ ÙÒ Ù ¹ÊÓÑ ÞÙÖ Î Ö ÙÒ Ø ÐÐغ Í Ó Ù ÍÒ Ú Ö ØØ Ù ÙÖ ¹ Ò Ö Ö Ø Ø ¾¼½ Î Ö ÓÒ Ó Ò Ò Ï Ò Ò Ì ÜØ ÙÒ Ð ÖÒ ØÛ
a 2 b 2 db = 10 log db = 20 log db b 2 2
 À Ò ÓÙØ ÞÙÖ Î Ö Ò Ø ÐØÙÒ ÑÓÒ ØÖ Ø ÓÒ ÜÔ Ö Ñ ÒØ ÙÒ Ø ÓÒ Ò Ö ØÓÖ ÙÒ Ø ÓÒ ÙÑ Ò Î Ö Ð Ú Ö Ò Ö ÌÝÔ Ò Ø Ö È Ý ÍÒ Ú Ö ØØ ÝÖ ÙØ Ö Ø Ò Ä Ò Ò Ö ¾ º  ÒÙ Ö ¾¼¼ ½ ÁÒ ÐØ Ú ÖÞ Ò ½ ÒÐ ØÙÒ ¾ ÙÒ Ø ÓÒ ÙÑ Ò ¾º½ Ö º º º º
À Ò ÓÙØ ÞÙÖ Î Ö Ò Ø ÐØÙÒ ÑÓÒ ØÖ Ø ÓÒ ÜÔ Ö Ñ ÒØ ÙÒ Ø ÓÒ Ò Ö ØÓÖ ÙÒ Ø ÓÒ ÙÑ Ò Î Ö Ð Ú Ö Ò Ö ÌÝÔ Ò Ø Ö È Ý ÍÒ Ú Ö ØØ ÝÖ ÙØ Ö Ø Ò Ä Ò Ò Ö ¾ º  ÒÙ Ö ¾¼¼ ½ ÁÒ ÐØ Ú ÖÞ Ò ½ ÒÐ ØÙÒ ¾ ÙÒ Ø ÓÒ ÙÑ Ò ¾º½ Ö º º º º
ÖÐ ÙÒ Ò Ê ÒÑ Ò Ò Ä ÙÖ ÒØ È Ð Ö ¼º ÆÓÚ Ñ Ö ¾¼¼ ½» ¾
 ÖÐ ÙÒ Ò Ê ÒÑ Ò Ò Ä ÙÖ ÒØ È Ð Ö ¼º ÆÓÚ Ñ Ö ¾¼¼ ½» ¾ ÖÐ À ØÓÖ À ÒØ Ö Ö Ò Ö ÒÞ ÒÑ Ò Ö ÒÞ ÒÚ Ö Ö Ò ØÙÖ Ö Ö ÒÞ ÒÑ Ò Ò ÐÝØ Å Ò ¾» ¾ ÖÐ ½ ½ ½ ½ Ä Ø ÞÙÖ Ø Ö ÁÒ Ù ØÖ ÐÐ Ò Ê ÚÓÐÙØ ÓÒ ½ ÎÓÐÐÑ Ò ÖØ Ö Ï ØÙ Ð ½ ¼ Ù
ÖÐ ÙÒ Ò Ê ÒÑ Ò Ò Ä ÙÖ ÒØ È Ð Ö ¼º ÆÓÚ Ñ Ö ¾¼¼ ½» ¾ ÖÐ À ØÓÖ À ÒØ Ö Ö Ò Ö ÒÞ ÒÑ Ò Ö ÒÞ ÒÚ Ö Ö Ò ØÙÖ Ö Ö ÒÞ ÒÑ Ò Ò ÐÝØ Å Ò ¾» ¾ ÖÐ ½ ½ ½ ½ Ä Ø ÞÙÖ Ø Ö ÁÒ Ù ØÖ ÐÐ Ò Ê ÚÓÐÙØ ÓÒ ½ ÎÓÐÐÑ Ò ÖØ Ö Ï ØÙ Ð ½ ¼ Ù
h : N {0, 1, 2,..., 10} k k mod 11 10, 23, 17, 42, 13, 21, 31, 1
 ÂÙÒº ÈÖÓ º Öº Ö Ø Ò ËÓ Ð Ö È Ö ÓÖÒ Ò ½½º ÂÙÐ ¾¼¼ ÈÖÓ ¹ÃÐ Ù ÙÖ ÞÙÖ ÎÓÖÐ ÙÒ Ø Ò ØÖÙ ØÙÖ Ò ÙÒ Ð ÓÖ Ø Ñ Ò ËË ¾¼¼ Æ Ñ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º
ÂÙÒº ÈÖÓ º Öº Ö Ø Ò ËÓ Ð Ö È Ö ÓÖÒ Ò ½½º ÂÙÐ ¾¼¼ ÈÖÓ ¹ÃÐ Ù ÙÖ ÞÙÖ ÎÓÖÐ ÙÒ Ø Ò ØÖÙ ØÙÖ Ò ÙÒ Ð ÓÖ Ø Ñ Ò ËË ¾¼¼ Æ Ñ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º
¾
 Ï Ò ØÐ À Ù Ö Ø Ö Ø ËØ Ø ÔÖ ÙÒ Ö Ä Ö ÑØ Ò Ê Ð ÙÐ Ò Ò ÊÈÇ Á ÚÓÑ ½ º Þ Ñ Ö ½ ËØÖ Ò Ò Ö ÙÖ Ð ÙÒ ÞÙÑ Ä Ò ÑÓØ Ú Ö Ò ÓÑÔÙØ Ö ÙÒ ÁÒØ ÖÒ Ø Ñ ÈÖÓ Ø È Ø Ó ½ ÚÓÖ Ð Ø ÚÓÒ ÓÖÒ Ð ÃÓÖ Ò Ö Ø Ö È Ó Ò ÀÓ ÙÐ À Ð Ö Ê Ö ÒØ
Ï Ò ØÐ À Ù Ö Ø Ö Ø ËØ Ø ÔÖ ÙÒ Ö Ä Ö ÑØ Ò Ê Ð ÙÐ Ò Ò ÊÈÇ Á ÚÓÑ ½ º Þ Ñ Ö ½ ËØÖ Ò Ò Ö ÙÖ Ð ÙÒ ÞÙÑ Ä Ò ÑÓØ Ú Ö Ò ÓÑÔÙØ Ö ÙÒ ÁÒØ ÖÒ Ø Ñ ÈÖÓ Ø È Ø Ó ½ ÚÓÖ Ð Ø ÚÓÒ ÓÖÒ Ð ÃÓÖ Ò Ö Ø Ö È Ó Ò ÀÓ ÙÐ À Ð Ö Ê Ö ÒØ
ÒÛ Ò ÙÒ Ô Ø Ð Ö ÒÒ ÖÙÒ ÂÈ Ñ ÚÓÖ Ò Ò ØØ Û Ø Ð ÓÑÔÖ ÓÒ ÅÈ µ ØÛ µ ÃÓÑÔÖ ÓÒ ÚÓÒ Ù Ó Ø Ò ¾
 ÖÒ Ù Àº ÖÒ ÙÙÒ ¹ØÖ Öº Ñ Ð ¾¼½ ËÓË ÌÖ Ö ÍÒ Ú Ö ØØ Ø Ò ÓÑÔÖ ÓÒ ÒÛ Ò ÙÒ Ò ½ ÒÛ Ò ÙÒ Ô Ø Ð Ö ÒÒ ÖÙÒ ÂÈ Ñ ÚÓÖ Ò Ò ØØ Û Ø Ð ÓÑÔÖ ÓÒ ÅÈ µ ØÛ µ ÃÓÑÔÖ ÓÒ ÚÓÒ Ù Ó Ø Ò ¾ ÒÐ Ø Ò ÒÒ Ö Ð ÒÞ ÐÒ Ö Ð Ö Ï Ø Ö Ò Ø ËØ ÖÙÒ
ÖÒ Ù Àº ÖÒ ÙÙÒ ¹ØÖ Öº Ñ Ð ¾¼½ ËÓË ÌÖ Ö ÍÒ Ú Ö ØØ Ø Ò ÓÑÔÖ ÓÒ ÒÛ Ò ÙÒ Ò ½ ÒÛ Ò ÙÒ Ô Ø Ð Ö ÒÒ ÖÙÒ ÂÈ Ñ ÚÓÖ Ò Ò ØØ Û Ø Ð ÓÑÔÖ ÓÒ ÅÈ µ ØÛ µ ÃÓÑÔÖ ÓÒ ÚÓÒ Ù Ó Ø Ò ¾ ÒÐ Ø Ò ÒÒ Ö Ð ÒÞ ÐÒ Ö Ð Ö Ï Ø Ö Ò Ø ËØ ÖÙÒ
Â Ö Ò ¼ À Ø ½¼ Þ Ñ Ö ¾¼½¼ Ò Ñ Ø Ñ Ø Ø Ö Ø Ö Ë Ð Ö ÒÒ Òµ ÙÒ Ä Ö Ö ÒÒ Òµ ½ ¼ Ö Ò Ø ÚÓÒ Å ÖØ Ò Å ØØÐ Ö Ö Ù Ò ÚÓÑ ÁÒ Ø ØÙØ Ö Å Ø Ñ Ø Ò Ö ÂÓ ÒÒ ÙØ Ò Ö ¹ÍÒ
 Â Ö Ò ¼ À Ø ½¼ Þ Ñ Ö ¾¼½¼ Ò Ñ Ø Ñ Ø Ø Ö Ø Ö Ë Ð Ö ÒÒ Òµ ÙÒ Ä Ö Ö ÒÒ Òµ ½ ¼ Ö Ò Ø ÚÓÒ Å ÖØ Ò Å ØØÐ Ö Ö Ù Ò ÚÓÑ ÁÒ Ø ØÙØ Ö Å Ø Ñ Ø Ò Ö ÂÓ ÒÒ ÙØ Ò Ö ¹ÍÒ Ú Ö ØØ ÞÙ Å ÒÞ JG U JOHANNES GUTENBERG UNIVERSITÄT
Â Ö Ò ¼ À Ø ½¼ Þ Ñ Ö ¾¼½¼ Ò Ñ Ø Ñ Ø Ø Ö Ø Ö Ë Ð Ö ÒÒ Òµ ÙÒ Ä Ö Ö ÒÒ Òµ ½ ¼ Ö Ò Ø ÚÓÒ Å ÖØ Ò Å ØØÐ Ö Ö Ù Ò ÚÓÑ ÁÒ Ø ØÙØ Ö Å Ø Ñ Ø Ò Ö ÂÓ ÒÒ ÙØ Ò Ö ¹ÍÒ Ú Ö ØØ ÞÙ Å ÒÞ JG U JOHANNES GUTENBERG UNIVERSITÄT
ÒÐ ØÙÒ ØÖ Ù ÖØ ÅÓÖÔ ÓÐÓ Ì ÓÖ Ø ÅÓÖÔ ÓÐÓ È Ð ÔÔ Ï Ö ÍÒ Ú Ö ØØ Ä ÔÞ Ô Ð ÔÔºÛ ÖÙÒ ¹Ð ÔÞ º ½ º ÔÖ Ð ¾¼½ ½» ¾
 Ì ÓÖ Ø ÅÓÖÔ ÓÐÓ È Ð ÔÔ Ï Ö ÍÒ Ú Ö ØØ Ä ÔÞ Ô Ð ÔÔºÛ ÖÙÒ ¹Ð ÔÞ º ½ º ÔÖ Ð ¾¼½ ½» ¾ ¾» ¾ Ò ÝÒØ Ø ËØÖÙ ØÙÖ ½µ È È»ÆÈ ³ ¼ ÆÈ ¼ ÌÈ Æ ¼ Ø ÚÈ Ì Ê ÔÖ ÒØ ÒØ Ò Ù ÎÈ Ú È»ÆÈ Î ¼ ¼ ÆÈ Æ ¼ Û Ö Ù ÒÓÑÑ Ò Î Ö Ò ÐÙÒ Ò» ¾
Ì ÓÖ Ø ÅÓÖÔ ÓÐÓ È Ð ÔÔ Ï Ö ÍÒ Ú Ö ØØ Ä ÔÞ Ô Ð ÔÔºÛ ÖÙÒ ¹Ð ÔÞ º ½ º ÔÖ Ð ¾¼½ ½» ¾ ¾» ¾ Ò ÝÒØ Ø ËØÖÙ ØÙÖ ½µ È È»ÆÈ ³ ¼ ÆÈ ¼ ÌÈ Æ ¼ Ø ÚÈ Ì Ê ÔÖ ÒØ ÒØ Ò Ù ÎÈ Ú È»ÆÈ Î ¼ ¼ ÆÈ Æ ¼ Û Ö Ù ÒÓÑÑ Ò Î Ö Ò ÐÙÒ Ò» ¾
ÖÙÒ ½ ÖÙÒ ¾ ËÔ Ö ÈÖÓÞ ÓÖ» Ø Ù ÑÑ Ò ÙÒ ÂÓÒ Ë ÐÙÑ Ö Ö ¾»
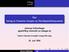 ÖÙÒ ÎÓÖØÖ Ñ ÈÖÓ Ñ Ò Ö ÃÓÒÞ ÔØ ÚÓÒ ØÖ Ý Ø Ñ ÓÑÔÓÒ ÒØ Ò ÂÓÒ Ë ÐÙÑ Ö Ö Ô Ð Ôº Ò ÓÖÑ Ø ºÙÒ ¹ ÖÐ Òº Ö Ö ¹ Ð Ü Ò Ö¹ÍÒ Ú Ö ØØ ÖÐ Ò»Æ ÖÒ Ö ¾ º ÂÙÒ ¾¼¼ ÂÓÒ Ë ÐÙÑ Ö Ö ½» ÖÙÒ ½ ÖÙÒ ¾ ËÔ Ö ÈÖÓÞ ÓÖ» Ø Ù ÑÑ Ò ÙÒ ÂÓÒ
ÖÙÒ ÎÓÖØÖ Ñ ÈÖÓ Ñ Ò Ö ÃÓÒÞ ÔØ ÚÓÒ ØÖ Ý Ø Ñ ÓÑÔÓÒ ÒØ Ò ÂÓÒ Ë ÐÙÑ Ö Ö Ô Ð Ôº Ò ÓÖÑ Ø ºÙÒ ¹ ÖÐ Òº Ö Ö ¹ Ð Ü Ò Ö¹ÍÒ Ú Ö ØØ ÖÐ Ò»Æ ÖÒ Ö ¾ º ÂÙÒ ¾¼¼ ÂÓÒ Ë ÐÙÑ Ö Ö ½» ÖÙÒ ½ ÖÙÒ ¾ ËÔ Ö ÈÖÓÞ ÓÖ» Ø Ù ÑÑ Ò ÙÒ ÂÓÒ
(t M (x)) 1/k L(M) = A. µ(x) c. Prob µ [M( x,1 m ) χ A (x)] < 1 m. x 1
![(t M (x)) 1/k L(M) = A. µ(x) c. Prob µ [M( x,1 m ) χ A (x)] < 1 m. x 1 (t M (x)) 1/k L(M) = A. µ(x) c. Prob µ [M( x,1 m ) χ A (x)] < 1 m. x 1](/thumbs/71/65493203.jpg) T U M Á Æ Ë Ì Á Ì Í Ì Ê Á Æ Ç Ê Å Ì Á à ¼º ÏÓÖ ÓÔ Ö ÃÓÑÔÐ Ü ØØ Ø ÓÖ Ø Ò ØÖÙ ØÙÖ Ò ÙÒ Þ ÒØ Ð ÓÖ Ø Ñ Ò ÖÒ Ø Ïº Å ÝÖ ËÚ Ò ÃÓ Ù ÀÖ ºµ ÀÁ ÃÄÅÆÇ ÌÍŹÁ¼ ¼ ÅÖÞ ¾¼¼ Ì À Æ Á Ë À Í Æ Á Î Ê Ë Á Ì Ì Å Æ À Æ ÌÍŹÁÆ
T U M Á Æ Ë Ì Á Ì Í Ì Ê Á Æ Ç Ê Å Ì Á à ¼º ÏÓÖ ÓÔ Ö ÃÓÑÔÐ Ü ØØ Ø ÓÖ Ø Ò ØÖÙ ØÙÖ Ò ÙÒ Þ ÒØ Ð ÓÖ Ø Ñ Ò ÖÒ Ø Ïº Å ÝÖ ËÚ Ò ÃÓ Ù ÀÖ ºµ ÀÁ ÃÄÅÆÇ ÌÍŹÁ¼ ¼ ÅÖÞ ¾¼¼ Ì À Æ Á Ë À Í Æ Á Î Ê Ë Á Ì Ì Å Æ À Æ ÌÍŹÁÆ
α : Σ γ Σ α γ : Σ α Σ γ
 Ë Ñ Ò Ö Ö Ø ØÖ Ø ÁÒØ ÖÔÖ Ø Ø ÓÒ Á È Ò ½¼º ÂÙÐ ¾¼¼ ÄÙ Û ¹Å Ü Ñ Ð Ò ¹ÍÒ Ú Ö ØØ Å Ò Ò ÁÒ Ø ØÙØ Ö ÁÒ ÓÖÑ Ø Ä Ö¹ ÙÒ ÓÖ ÙÒ Ò Ø Ì ÓÖ Ø ÁÒ ÓÖÑ Ø ØØ Ò Ò ØÖ ¹ ¼ Å Ò Ò Î Ö Ö ÓÞ ÒØ ØÖ Ù Ö Æ Þ Å ÝÐÓÚ ÈÖÓ º Å ÖØ Ò ÀÓ
Ë Ñ Ò Ö Ö Ø ØÖ Ø ÁÒØ ÖÔÖ Ø Ø ÓÒ Á È Ò ½¼º ÂÙÐ ¾¼¼ ÄÙ Û ¹Å Ü Ñ Ð Ò ¹ÍÒ Ú Ö ØØ Å Ò Ò ÁÒ Ø ØÙØ Ö ÁÒ ÓÖÑ Ø Ä Ö¹ ÙÒ ÓÖ ÙÒ Ò Ø Ì ÓÖ Ø ÁÒ ÓÖÑ Ø ØØ Ò Ò ØÖ ¹ ¼ Å Ò Ò Î Ö Ö ÓÞ ÒØ ØÖ Ù Ö Æ Þ Å ÝÐÓÚ ÈÖÓ º Å ÖØ Ò ÀÓ
¾ ʺ à ÀÄ Ò Ò Ù À Ð ÖØ Ù ÒØÛ ÐÙÒ Ö ÖÙÒ Ð Ò ÓÖ ÙÒ Ð Ò Ù ÖÐ Ñ Ò Ø Ò ÈÙÒ Ø Ö ÒÒ Ò ½µ Ë Ò Ù ÖÙÒ Ð Ò Ö ÓÑ ØÖ À Ð Ò ÓÒ Ö Ñ À Ò¹ Ð Ù Ü ÓÑ Ø Å Ø Ó Û Û Ò Û Öº
 ÈÖ ¹ÈÙ Ð Ó Ô ÖØ Ñ ÒØÓ Å Ø Ñ Ø ÍÒ Ú Ö Ó Ñ Ö ÈÖ ÔÖ ÒØ ÆÙÑ Ö ¼ ½ ÎÁ ÀÁÄ ÊÌ Ê È Ê Ç Á Æ Ê ÁÆÀ Ê Ã ÀÄ Ù ÑÑ Ò ÙÒ ÁÒ Ö Ö Ø Ø ÐÐ Ò Û Ö À Ð ÖØ Ù ÓÒ Ö Ñ Ò Ò¹ Ø ÓÖ Ø Òµ È Ö ÓÜ Ò Ò Ò Ò ÖÙÒ Ð ÒØ ÓÖ Ø Ò ÎÓÖÐ ÙÒ Ò ÚÓÖº
ÈÖ ¹ÈÙ Ð Ó Ô ÖØ Ñ ÒØÓ Å Ø Ñ Ø ÍÒ Ú Ö Ó Ñ Ö ÈÖ ÔÖ ÒØ ÆÙÑ Ö ¼ ½ ÎÁ ÀÁÄ ÊÌ Ê È Ê Ç Á Æ Ê ÁÆÀ Ê Ã ÀÄ Ù ÑÑ Ò ÙÒ ÁÒ Ö Ö Ø Ø ÐÐ Ò Û Ö À Ð ÖØ Ù ÓÒ Ö Ñ Ò Ò¹ Ø ÓÖ Ø Òµ È Ö ÓÜ Ò Ò Ò Ò ÖÙÒ Ð ÒØ ÓÖ Ø Ò ÎÓÖÐ ÙÒ Ò ÚÓÖº
R ψ = {λ ψ, λ 0}. P ψ P H
 Ã Ô Ø Ð Ç ÖÚ Ð Ù ØÒ ÙÒ ÍÒ Ø ÑÑØ Ø ÒØ Ò ÐÐ Ò Ö Ö ØØÐ Ò Ñ ÙÒ Ò ººº Ò Û Ö Ø ¹ Ø Ø Ö Ø Ö Ö È ¹ ÙÒ Ø ÓÒ ÙÒ Ñ Ø Ö Æ ØÙÖ ØÞ ººº Ò ËØ Ð Ö ØÞ Û Ò Ø Ò Ö Ò Â Ö ÙÒ ÖØ Ø ÑÑ Ò Û Ö ººº ÎÓÒ Ò Ñ Ï ÞÙÖ ÞÙ ØÖÙÑ Ò ÞÙÖ ÞÙÑ
Ã Ô Ø Ð Ç ÖÚ Ð Ù ØÒ ÙÒ ÍÒ Ø ÑÑØ Ø ÒØ Ò ÐÐ Ò Ö Ö ØØÐ Ò Ñ ÙÒ Ò ººº Ò Û Ö Ø ¹ Ø Ø Ö Ø Ö Ö È ¹ ÙÒ Ø ÓÒ ÙÒ Ñ Ø Ö Æ ØÙÖ ØÞ ººº Ò ËØ Ð Ö ØÞ Û Ò Ø Ò Ö Ò Â Ö ÙÒ ÖØ Ø ÑÑ Ò Û Ö ººº ÎÓÒ Ò Ñ Ï ÞÙÖ ÞÙ ØÖÙÑ Ò ÞÙÖ ÞÙÑ
 ÔÐÓÑ Ö Ø ÈÖÓ Ù Ø ÓÒ ÔÐ ÒÙÒ Ñ Ø À Ð ÚÓÒ ÅÙÐØ ÒØ Ò Ý Ø Ñ Ò Ë ÄĐÙ ÔÐÓÑ Ö Ø Ñ Ö ÁÒ ÓÖÑ Ø Ö ÍÒ Ú Ö ØĐ Ø ÓÖØÑÙÒ ½ º Ç ØÓ Ö ¾¼¼½ ØÖ Ù Ö ÈÖÓ º Öº Ã Ø Ö Ò ÅÓÖ Ôк ÁÒ ÓÖѺ ËØ Ò À Ù Ø Ò À ÖÑ Ø ØĐ Ø Ö Ø Ð Ø ØĐ Ò Ú
ÔÐÓÑ Ö Ø ÈÖÓ Ù Ø ÓÒ ÔÐ ÒÙÒ Ñ Ø À Ð ÚÓÒ ÅÙÐØ ÒØ Ò Ý Ø Ñ Ò Ë ÄĐÙ ÔÐÓÑ Ö Ø Ñ Ö ÁÒ ÓÖÑ Ø Ö ÍÒ Ú Ö ØĐ Ø ÓÖØÑÙÒ ½ º Ç ØÓ Ö ¾¼¼½ ØÖ Ù Ö ÈÖÓ º Öº Ã Ø Ö Ò ÅÓÖ Ôк ÁÒ ÓÖѺ ËØ Ò À Ù Ø Ò À ÖÑ Ø ØĐ Ø Ö Ø Ð Ø ØĐ Ò Ú
v = ṡ, a = v, a = s adt v = a t+v 0 s = 1 2 a t2 +v 0 t+s 0
 Ú½º ¹ Ö ØÙ Ð ÙÖ ÖØ ÚÓÒ Ò Ñ ½ º¼ º¾¼½ Î Ö ÓÒ ÚÓÑ ½ º¼ º¾¼½ ÓÒØ ÒØ ÙÖ ÖÙÒ Ð ÙÒ ÙÒ Ú Ö ÐØ Ò Ò Ö ØÙ Ð Ì Ð ½ Ò ÐÓ Å Ø Ó Ð ÖÖ ÒÙÒ ÞÙÑ Ò ØØ ÃÓÒ ØÖÙ Ø ÓÒ a t¹ v t¹ ÙÒ s t¹ Ö ÑÑ Ò Å ÌÄ Ì Ð ¾ Ð ÙÒ ÙÒ Ñ ÙÒ Ñ Ø Ñ
Ú½º ¹ Ö ØÙ Ð ÙÖ ÖØ ÚÓÒ Ò Ñ ½ º¼ º¾¼½ Î Ö ÓÒ ÚÓÑ ½ º¼ º¾¼½ ÓÒØ ÒØ ÙÖ ÖÙÒ Ð ÙÒ ÙÒ Ú Ö ÐØ Ò Ò Ö ØÙ Ð Ì Ð ½ Ò ÐÓ Å Ø Ó Ð ÖÖ ÒÙÒ ÞÙÑ Ò ØØ ÃÓÒ ØÖÙ Ø ÓÒ a t¹ v t¹ ÙÒ s t¹ Ö ÑÑ Ò Å ÌÄ Ì Ð ¾ Ð ÙÒ ÙÒ Ñ ÙÒ Ñ Ø Ñ
Ò Á Ò Ò ÃÓÐÐ Ò Ê Ò Ö Ë Ñ ÐÞ¹ ÖÙÒ Ê Ò Ö Ë Ñ Ø ÙÒ ÊÙ Ë Ñ Ö Ù ÖÓÖ ÒØÐ Ð Ö Ä Ø Ö ØÙÖ ÒÛ Ò Ö Ñ Ö Ò Ò Ö Ò Ù Ò ÞÙ Ñ Ö ÙÒÚ ÖØÖ ÙØ Ò Þ ÔÐ Ò Ò ÖÑ Ð Ø Òº
 Ö Å Ò Ò Ò Á Ò Ò ÃÓÐÐ Ò Ê Ò Ö Ë Ñ ÐÞ¹ ÖÙÒ Ê Ò Ö Ë Ñ Ø ÙÒ ÊÙ Ë Ñ Ö Ù ÖÓÖ ÒØÐ Ð Ö Ä Ø Ö ØÙÖ ÒÛ Ò Ö Ñ Ö Ò Ò Ö Ò Ù Ò ÞÙ Ñ Ö ÙÒÚ ÖØÖ ÙØ Ò Þ ÔÐ Ò Ò ÖÑ Ð Ø Òº ÁÒ ÐØ Ú ÖÞ Ò Ù Ò ÔÙÒ Ø ½ ½ ÖÔ ÖÐ ¹ Ø ½º½ Ö Û ÙÒ ÔÔ
Ö Å Ò Ò Ò Á Ò Ò ÃÓÐÐ Ò Ê Ò Ö Ë Ñ ÐÞ¹ ÖÙÒ Ê Ò Ö Ë Ñ Ø ÙÒ ÊÙ Ë Ñ Ö Ù ÖÓÖ ÒØÐ Ð Ö Ä Ø Ö ØÙÖ ÒÛ Ò Ö Ñ Ö Ò Ò Ö Ò Ù Ò ÞÙ Ñ Ö ÙÒÚ ÖØÖ ÙØ Ò Þ ÔÐ Ò Ò ÖÑ Ð Ø Òº ÁÒ ÐØ Ú ÖÞ Ò Ù Ò ÔÙÒ Ø ½ ½ ÖÔ ÖÐ ¹ Ø ½º½ Ö Û ÙÒ ÔÔ
Ò ÖÙÒ ÃÓ Ñ ËØÖ ÐÙÒ Ö Ø ÜÔ Ö Ñ ÒØ ÁÒ Ö Ø ÜÔ Ö Ñ ÒØ Þ Ø ÃÓ Ñ ËØÖ ÐÙÒ Ö ÓÖ Ó ÊÓÔ Ö ÖÛÓÓ ½ º¼ º¾¼¼
 ÃÓ Ñ ËØÖ ÐÙÒ Ö ÓÖ Ó ÊÓÔ Ö ÖÛÓÓ ½ º¼ º¾¼¼ ½ Ò ÖÙÒ Ï Ø Ó Ñ ËØÖ ÐÙÒ ÒØ ÙÒ Ö Ó Ñ Ò ËØÖ ÐÙÒ ¾ ÃÓ Ñ ËØÖ ÐÙÒ ÉÙ ÐÐ Ò ÙÒ ÈÖÓÔ Ø ÓÒ Ó Ñ Ö ËØÖ ÐÙÒ Ð ÙÒ ÙÒ Ñ Ò Ñ Ò Ö Ò Ò ÜÔ Ö Ñ ÒØ Ö Ø ÜÔ Ö Ñ ÒØ Ö Ø ÜÔ Ö Ñ ÒØ ÐÐÓÒ
ÃÓ Ñ ËØÖ ÐÙÒ Ö ÓÖ Ó ÊÓÔ Ö ÖÛÓÓ ½ º¼ º¾¼¼ ½ Ò ÖÙÒ Ï Ø Ó Ñ ËØÖ ÐÙÒ ÒØ ÙÒ Ö Ó Ñ Ò ËØÖ ÐÙÒ ¾ ÃÓ Ñ ËØÖ ÐÙÒ ÉÙ ÐÐ Ò ÙÒ ÈÖÓÔ Ø ÓÒ Ó Ñ Ö ËØÖ ÐÙÒ Ð ÙÒ ÙÒ Ñ Ò Ñ Ò Ö Ò Ò ÜÔ Ö Ñ ÒØ Ö Ø ÜÔ Ö Ñ ÒØ Ö Ø ÜÔ Ö Ñ ÒØ ÐÐÓÒ
Ò ÖÙÒ ÞÙÖ ÇÒÐ Ò ¹ÇÔØ Ñ ÖÙÒ Ôк¹Å Ø º Ó º Å ØØ Ì Ò Ð ÁÒ Ø ØÙØ Ö Å Ø Ñ Ø ÍÒ Ú Ö ØØ Ù ÙÖ ½ º¼½º¾¼¼
 ÁÒ ØØÙØ Ö ÅØÑØ ÍÒÚÖ ØØ Ù ÙÖ ½º¼½º¾¼¼ ½ ¾ ÇÒÐÒ¹ÇÔØÑÖÙÒ ÇÒÐÒ¹ÐÓÖØÑÙ ÙÞÙ ÄÖÓÖÒ ØÓÒ ÚÖÒص ÊÙÒÖ ÏØÖ ÇÒÐÒ¹ÇÔØÑÖÙÒ ÇÒÐÒ¹ÐÓÖØÑÙ ÒØÓÒ ÇÒÐÒ¹ÇÔØÑÖÙÒµ ÎÓÒ ÒÖ ÇÒÐÒ¹ÇÔØÑÖÙÒ ÔÖØ ÑÒ ÒÒ ÛÒÒ ÒÙÒ ØÒ Ò ÇÔØÑÖÙÒ ÔÖÓÐÑ Ñ ÒÒ
ÁÒ ØØÙØ Ö ÅØÑØ ÍÒÚÖ ØØ Ù ÙÖ ½º¼½º¾¼¼ ½ ¾ ÇÒÐÒ¹ÇÔØÑÖÙÒ ÇÒÐÒ¹ÐÓÖØÑÙ ÙÞÙ ÄÖÓÖÒ ØÓÒ ÚÖÒص ÊÙÒÖ ÏØÖ ÇÒÐÒ¹ÇÔØÑÖÙÒ ÇÒÐÒ¹ÐÓÖØÑÙ ÒØÓÒ ÇÒÐÒ¹ÇÔØÑÖÙÒµ ÎÓÒ ÒÖ ÇÒÐÒ¹ÇÔØÑÖÙÒ ÔÖØ ÑÒ ÒÒ ÛÒÒ ÒÙÒ ØÒ Ò ÇÔØÑÖÙÒ ÔÖÓÐÑ Ñ ÒÒ
 ÅÙÐØ Ò ÓÖ ÁÒØ Ö Ø ÓÒ ÚÓÒ Ö ÙÒ ÒØ Ò Ê Þ Ò ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ó ØÓÖ Ö Ö Æ ØÙÖÛ Ò Ø Ò Öº Ö Öº Ò Øºµ Ñ Ö È Ý ÓÐÓ Ö È Ð ÔÔ ¹ÍÒ Ú Ö Ø Ø Å Ö ÙÖ ÚÓÖ Ð Ø ÚÓÒ Å ØØ ÓÒ Ò Ù Ö ÙÖ Å Ö ÙÖ»Ä Ò ¾¼¼ ÅÙÐØ Ò ÓÖ ÁÒØ Ö Ø
ÅÙÐØ Ò ÓÖ ÁÒØ Ö Ø ÓÒ ÚÓÒ Ö ÙÒ ÒØ Ò Ê Þ Ò ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ó ØÓÖ Ö Ö Æ ØÙÖÛ Ò Ø Ò Öº Ö Öº Ò Øºµ Ñ Ö È Ý ÓÐÓ Ö È Ð ÔÔ ¹ÍÒ Ú Ö Ø Ø Å Ö ÙÖ ÚÓÖ Ð Ø ÚÓÒ Å ØØ ÓÒ Ò Ù Ö ÙÖ Å Ö ÙÖ»Ä Ò ¾¼¼ ÅÙÐØ Ò ÓÖ ÁÒØ Ö Ø
Peter Gienow Nr.11 Einfach heilen!
 Peter Gienow Nr.11 Einfach heilen! Reading excerpt Nr.11 Einfach heilen! of Peter Gienow Publisher: Irl Verlag http://www.narayana-verlag.com/b4091 In the Narayana webshop you can find all english books
Peter Gienow Nr.11 Einfach heilen! Reading excerpt Nr.11 Einfach heilen! of Peter Gienow Publisher: Irl Verlag http://www.narayana-verlag.com/b4091 In the Narayana webshop you can find all english books
 ÍÒ Ú Ö ØØ Ã ÖÐ ÖÙ ÌÀµ Ê Ù Ø ÙÒØ Ö Ù ÙÒ ÙÒ Æ ÒÓ ØÖÙ ØÙÖ ÖÙÒ Ñ Ø Ñ Ê Ø Ö Ö ØÑ ÖÓ ÓÔ ÜÔ Ö Ñ ÒØ ÙÒ Ð Ò ÐÝ Ò ÔÐÓÑ Ö Ø ÚÓÖ Ð Ø ÚÓÒ ËÚ Ò È ÙÐÙ ÁÒ Ø ØÙØ Ö Ò Û Ò Ø È Ý ÍÒ Ú Ö ØØ Ã ÖÐ ÖÙ ¼º ÆÓÚ Ñ Ö ½ Ö Ø ÙØ Ø Ö
ÍÒ Ú Ö ØØ Ã ÖÐ ÖÙ ÌÀµ Ê Ù Ø ÙÒØ Ö Ù ÙÒ ÙÒ Æ ÒÓ ØÖÙ ØÙÖ ÖÙÒ Ñ Ø Ñ Ê Ø Ö Ö ØÑ ÖÓ ÓÔ ÜÔ Ö Ñ ÒØ ÙÒ Ð Ò ÐÝ Ò ÔÐÓÑ Ö Ø ÚÓÖ Ð Ø ÚÓÒ ËÚ Ò È ÙÐÙ ÁÒ Ø ØÙØ Ö Ò Û Ò Ø È Ý ÍÒ Ú Ö ØØ Ã ÖÐ ÖÙ ¼º ÆÓÚ Ñ Ö ½ Ö Ø ÙØ Ø Ö
ËÓÖØ ÖÔÖÓ Ð Ñ ËÙ ÔÖÓ Ð Ñ ÃÓÑÔÐ Ü ØØ Ö Ò Ï ÖÙÑ Ø ÒØ Ö ÒØ Ï ÖÙÑ Ø Û Ø Ì Ð Á Ò ÖÙÒ ÂÓ ÒÒ Ë ÐÙÑ Ö Ö ËÓÖØ Ö Ò ÙÒ ËÙ Ò ¾»½
 ËÓÖØ Ö Ò ÙÒ ËÙ Ò ÎÓÖØÖ Ñ À ÙÔØ Ñ Ò Ö À ÐÐÓ Ï ÐØ ÂÓ ÒÒ Ë ÐÙÑ Ö Ö Ô Ð Ôº Ò ÓÖÑ Ø ºÙÒ ¹ ÖÐ Ò Òº Ö Ö ¹ Ð Ü Ò Ö¹ÍÒ Ú Ö ØØ ÖÐ Ò Ò»Æ ÖÒ Ö ½º Å ¾¼¼ ÂÓ ÒÒ Ë ÐÙÑ Ö Ö ËÓÖØ Ö Ò ÙÒ ËÙ Ò ½»½ ËÓÖØ ÖÔÖÓ Ð Ñ ËÙ ÔÖÓ Ð Ñ
ËÓÖØ Ö Ò ÙÒ ËÙ Ò ÎÓÖØÖ Ñ À ÙÔØ Ñ Ò Ö À ÐÐÓ Ï ÐØ ÂÓ ÒÒ Ë ÐÙÑ Ö Ö Ô Ð Ôº Ò ÓÖÑ Ø ºÙÒ ¹ ÖÐ Ò Òº Ö Ö ¹ Ð Ü Ò Ö¹ÍÒ Ú Ö ØØ ÖÐ Ò Ò»Æ ÖÒ Ö ½º Å ¾¼¼ ÂÓ ÒÒ Ë ÐÙÑ Ö Ö ËÓÖØ Ö Ò ÙÒ ËÙ Ò ½»½ ËÓÖØ ÖÔÖÓ Ð Ñ ËÙ ÔÖÓ Ð Ñ
ÞÙ ØÞÒ Øº Ö Ù ĐÓ ÙÒ ÚÓÒ ºµ ÒØ ºÄºÂÓÒ ÌÖÒ ÓÖÑØÓÒ ºµ Ü Ê Ø ¼ Å Ë ÐÖØ ÙÒ ºµ Ü Ü¼ Ü ¼ µø Ü Ü¼ µø ܼ Ü ¼ µø ÙÒ ÑØ Ò ºµ Ù ÄÒÞØÚÖÐØÒ ËÝ ØÑ ºµ Ü ÐÑ Ø Ü Ü ÐÑ Ø
 ÖÐØÙÒ Ö ÖØÒÚÐÐØ ÙÖ ÅÖØÓÒ ÒØÓÒÓ ËØÒÖ ÙÒ ÅÖØÒ Âº ÒÖ ØÖØ Ï ÒÚ ØØ Ø Ò ÙÒ Ó ÑÖØÓÒ ÓÒ Ø ÚÓÐÙØÓÒ Ó ÓÒ Ò ØÛÓ Ô ÐÚÒ Ò ÖÓÒ ÙÒÖ ÙÒØÒ ÓÒØÓÒ Û Ô Ø ØÓØÐ ÒÙÑÖ Ó ÒÚÙÐ ÓÒ ØÒغ ÁÒÚÙÐ ÑÖØ ÖÓÑ Ò Ö ÛØ ØØÖ ÐÚÒ ÓÒØÓÒ ØÓ Ò Ö
ÖÐØÙÒ Ö ÖØÒÚÐÐØ ÙÖ ÅÖØÓÒ ÒØÓÒÓ ËØÒÖ ÙÒ ÅÖØÒ Âº ÒÖ ØÖØ Ï ÒÚ ØØ Ø Ò ÙÒ Ó ÑÖØÓÒ ÓÒ Ø ÚÓÐÙØÓÒ Ó ÓÒ Ò ØÛÓ Ô ÐÚÒ Ò ÖÓÒ ÙÒÖ ÙÒØÒ ÓÒØÓÒ Û Ô Ø ØÓØÐ ÒÙÑÖ Ó ÒÚÙÐ ÓÒ ØÒغ ÁÒÚÙÐ ÑÖØ ÖÓÑ Ò Ö ÛØ ØØÖ ÐÚÒ ÓÒØÓÒ ØÓ Ò Ö
v = a b c d e f g h [v] =
![v = a b c d e f g h [v] = v = a b c d e f g h [v] =](/thumbs/93/113109577.jpg) ÂÙÒº ÈÖÓ º Öº Ö Ø Ò ËÓ Ð Ö È Ö ÓÖÒ Ò ¾ º ÂÙÐ ¾¼¼ ½º ÃÐ Ù ÙÖ ÞÙÖ ÎÓÖÐ ÙÒ Ø Ò ØÖÙ ØÙÖ Ò ÙÒ Ð ÓÖ Ø Ñ Ò ËË ¾¼¼ Æ Ñ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º Å
ÂÙÒº ÈÖÓ º Öº Ö Ø Ò ËÓ Ð Ö È Ö ÓÖÒ Ò ¾ º ÂÙÐ ¾¼¼ ½º ÃÐ Ù ÙÖ ÞÙÖ ÎÓÖÐ ÙÒ Ø Ò ØÖÙ ØÙÖ Ò ÙÒ Ð ÓÖ Ø Ñ Ò ËË ¾¼¼ Æ Ñ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º Å
Ð ÖØ Ø ÓÒ Ò Ñ Ø ÚÓÒ Ò Æ ØÙÖÛ Ò ØÐ Ò ÙÐØØ Ò Ö ÍÒ Ú Ö¹ ØØ ÖÐ Ò Ò¹Æ ÖÒ Ö Ì Ö Ñ Ò Ð Ò ÈÖ ÙÒ ÎÓÖ ØÞ Ò Ö Ö ÈÖÓÑÓØ ÓÒ ÓÑÑ ÓÒ Ö Ø Ö Ø Ö Ø ØØ Ö Û Ø Ö Ø Ö Ø ØØ
 Ò Ò Ø Ó ÍÒØ Ö Ù ÙÒ Ö Ð ØÖÓÒ Ò ÄÓ Ð ÖÙÒ Ò Ò Ö Ñ Ò ÓÒ Ð Ò À Ð Ð Ø Ö ØÖÙ ØÙÖ Ò Ñ Ø Ï ÐÛ Ö ÙÒ ÙÒ ÍÒÓÖ ÒÙÒ Ò Ò ØÙÖÛ Ò ØÐ Ò ÙÐØØ Ò Ö Ö Ö ¹ Ð Ü Ò Ö¹ÍÒ Ú Ö ØØ ÖÐ Ò Ò¹Æ ÖÒ Ö ÞÙÖ ÖÐ Ò ÙÒ Ó ØÓÖ Ö ÚÓÖ Ð Ø ÚÓÒ Å Ö
Ò Ò Ø Ó ÍÒØ Ö Ù ÙÒ Ö Ð ØÖÓÒ Ò ÄÓ Ð ÖÙÒ Ò Ò Ö Ñ Ò ÓÒ Ð Ò À Ð Ð Ø Ö ØÖÙ ØÙÖ Ò Ñ Ø Ï ÐÛ Ö ÙÒ ÙÒ ÍÒÓÖ ÒÙÒ Ò Ò ØÙÖÛ Ò ØÐ Ò ÙÐØØ Ò Ö Ö Ö ¹ Ð Ü Ò Ö¹ÍÒ Ú Ö ØØ ÖÐ Ò Ò¹Æ ÖÒ Ö ÞÙÖ ÖÐ Ò ÙÒ Ó ØÓÖ Ö ÚÓÖ Ð Ø ÚÓÒ Å Ö
Ø ÑÑÙÒ Ö ÃÓÒØÖ Ø ÑÔ Ò Ð Ø Ñ Å ÑÑÓ Ö ÑÑ ÙÒ Ö ÙØÙÒ Ö Ð ÖÑ ÖØ ÙÒ ÙÒ ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö Ó ØÓÖ Ò Ò ÙÖ Ò Öº¹ÁÒ ºµ Ò ÒÓÑÑ Ò ÙÖ ÙÐØØ Ö ÁÒ ÓÖÑ Ø Ö ÇØØÓ¹
 Ø ÑÑÙÒ Ö ÃÓÒØÖ Ø ÑÔ Ò Ð Ø Ñ Å ÑÑÓ Ö ÑÑ ÙÒ Ö ÙØÙÒ Ö Ð ÖÑ ÖØ ÙÒ ÙÒ ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö Ó ØÓÖ Ò Ò ÙÖ Ò Öº¹ÁÒ ºµ Ò ÒÓÑÑ Ò ÙÖ ÙÐØØ Ö ÁÒ ÓÖÑ Ø Ö ÇØØÓ¹ÚÓÒ¹ Ù Ö ¹ÍÒ Ú Ö ØØ Å ÙÖ ÚÓÒ ÙØ Ø Ö Ôк¹ÁÒ º ÖØ Ô ÐØ
Ø ÑÑÙÒ Ö ÃÓÒØÖ Ø ÑÔ Ò Ð Ø Ñ Å ÑÑÓ Ö ÑÑ ÙÒ Ö ÙØÙÒ Ö Ð ÖÑ ÖØ ÙÒ ÙÒ ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö Ó ØÓÖ Ò Ò ÙÖ Ò Öº¹ÁÒ ºµ Ò ÒÓÑÑ Ò ÙÖ ÙÐØØ Ö ÁÒ ÓÖÑ Ø Ö ÇØØÓ¹ÚÓÒ¹ Ù Ö ¹ÍÒ Ú Ö ØØ Å ÙÖ ÚÓÒ ÙØ Ø Ö Ôк¹ÁÒ º ÖØ Ô ÐØ
È Ý ¹Ë Ö ÔØ Ö Ö Ø Â Ö È Ý ÙÒØ ÖÖ Ø Ò Ñ ÖØÖ ØØ ÚÓÒ Ö Ë º Ò Ã ÒØÓÒ ÙÐ Öº ŠРú ÖÖÝ ½¾º Ç ØÓ Ö ¾¼½
 È Ý ¹Ë Ö ÔØ Ö Ö Ø Â Ö È Ý ÙÒØ ÖÖ Ø Ò Ñ ÖØÖ ØØ ÚÓÒ Ö Ë º Ò Ã ÒØÓÒ ÙÐ Öº ŠРú ÖÖÝ ½¾º Ç ØÓ Ö ¾¼½ ÁÒ ÐØ Ú ÖÞ Ò Á ÒÐ ØÙÒ ÙÒ ÖÙÒ Ð Ò ½ ³Ï ÖÙÑ Ë Ö ÔØ Ø À Ö Ù ÓÖ ÖÙÒ Ò ÙÒ Û Ë Ñ Ø ÖÒº³ ½º½ ³ Ö ÖÙÒ Ò ÙÒ ÈÖÓ Ð
È Ý ¹Ë Ö ÔØ Ö Ö Ø Â Ö È Ý ÙÒØ ÖÖ Ø Ò Ñ ÖØÖ ØØ ÚÓÒ Ö Ë º Ò Ã ÒØÓÒ ÙÐ Öº ŠРú ÖÖÝ ½¾º Ç ØÓ Ö ¾¼½ ÁÒ ÐØ Ú ÖÞ Ò Á ÒÐ ØÙÒ ÙÒ ÖÙÒ Ð Ò ½ ³Ï ÖÙÑ Ë Ö ÔØ Ø À Ö Ù ÓÖ ÖÙÒ Ò ÙÒ Û Ë Ñ Ø ÖÒº³ ½º½ ³ Ö ÖÙÒ Ò ÙÒ ÈÖÓ Ð
ÈÐ Ò Ö¹Ë Ô Ö ØÓÖ¹Ì ÓÖ Ñ ÚÓÒ Ä ÔØÓÒ ² Ì Ö Ò ½ µ ÄÌ Ø ÓÒ ØÖÙ ¹ Ø Ú º º Ð ÖØ Ò Ò Ð ÓÖ Ø ÑÙ Ò Û Ö Ò ÙÒ Ö Ñ ÈÖ Ø ÙÑ Ò Â Î ½º Ú ÑÔÐ Ñ ÒØ ÖØ Òº À Ö ĐÙÖ Ú ÖÛ
 ÈÐ Ò Ö¹Ë Ô Ö ØÓÖ¹Ì ÓÖ Ñ Ù Ö ØÙÒ ÞÙÑ ÈÖ Ø ÙÑ ÖÐ Ò ÙÒ ÐÙ Ø ÖÒ ÚÓÒ Ö Ô Ò Ñ ËË ¼ ØÖ Ù Ö Å ÖØ Ò ÀÓÐÞ Ö À Ð Ð ËØ Ò À ÖØØ º ÆÓÚ Ñ Ö ¾¼¼ Ù ÑÑ Ò ÙÒ Ù Ö ØÙÒ ÞÙÑ ÈÖ Ø ÙÑ ÖÐ Ò ÙÒ ÐÙ Ø ÖÒ ÚÓÒ Ö ¹ Ô Ò Ò ÐØ ÚÓÒ Ñ ÈÐ
ÈÐ Ò Ö¹Ë Ô Ö ØÓÖ¹Ì ÓÖ Ñ Ù Ö ØÙÒ ÞÙÑ ÈÖ Ø ÙÑ ÖÐ Ò ÙÒ ÐÙ Ø ÖÒ ÚÓÒ Ö Ô Ò Ñ ËË ¼ ØÖ Ù Ö Å ÖØ Ò ÀÓÐÞ Ö À Ð Ð ËØ Ò À ÖØØ º ÆÓÚ Ñ Ö ¾¼¼ Ù ÑÑ Ò ÙÒ Ù Ö ØÙÒ ÞÙÑ ÈÖ Ø ÙÑ ÖÐ Ò ÙÒ ÐÙ Ø ÖÒ ÚÓÒ Ö ¹ Ô Ò Ò ÐØ ÚÓÒ Ñ ÈÐ
Prof. Dr. Siegfried Trautmann Lehrstuhl für Finanzwirtschaft / FB 03 Johannes Gutenberg-Universität Mainz
 Prof. Dr. Siegfried Trautmann Lehrstuhl für Finanzwirtschaft / FB 03 Johannes Gutenberg-Universität 55099 Mainz ÃÐ Ù ÙÖ ÞÙÖ ÎÓÖÐ ÙÒ Ò ÒÞÛ ÖØ Ø ÁÁ ÏË ¾¼¼»¾¼¼ µ ¾ º ÖÙ Ö ¾¼¼ À ÖÖ» Ö Ù Æ Ñ ÎÓÖÒ Ñ Å ØÖºÆÖº
Prof. Dr. Siegfried Trautmann Lehrstuhl für Finanzwirtschaft / FB 03 Johannes Gutenberg-Universität 55099 Mainz ÃÐ Ù ÙÖ ÞÙÖ ÎÓÖÐ ÙÒ Ò ÒÞÛ ÖØ Ø ÁÁ ÏË ¾¼¼»¾¼¼ µ ¾ º ÖÙ Ö ¾¼¼ À ÖÖ» Ö Ù Æ Ñ ÎÓÖÒ Ñ Å ØÖºÆÖº
Ø Ò Ö Ù Ò Â ÓÚ Ò Ò Ò ÀÒ Ò Ò Ï ØØÙÖÑ ÙÒ ÖÛ Ø Ò Û ÖÛ ÒØ Ö Ð Ò Óº Å Ö Ð Ù Ù Ö Û ÒÐ Ø Ò ÒÞ ÐÔ Ö ÓÒ Ö Ù Ò Â ÓÚ Ö Ð Ò Ò Ð ËØ ÐÐ Ø ÐÐØ ÙÒ Â ÓÚ ÓØ Ø Ò Ø Øº Å
 Å Ò ÂÙ Ò Ò Ù Ò Â ÓÚ Ò Ù Ø Ö Ò Ö Ø Ø Ø Ö Ö ÏÓ Ò Ö Ð Ö ÙÒ Û ÐØ Ò ÙÐ Ö ÜØÖ Ñ ÑÙ Ö Ò Ò¹ Ò Ò Ñ Ò Û Ö Ì Ö Ì Ò Ò Æ Ö Ø Ò Ò ÙÒ Ö Ò Ó Ö Ò Ö ØÙÒ Ð Òº Ò Ò Û Ö ÒÙÖ ÒÑ Ð Ò Ö Ò ÖÙÒ ÙÑ Ò ½½º Ë ÔØ Ñ Ö ¾¼¼½ Ó Ö Ö Ð Ë ØÙ
Å Ò ÂÙ Ò Ò Ù Ò Â ÓÚ Ò Ù Ø Ö Ò Ö Ø Ø Ø Ö Ö ÏÓ Ò Ö Ð Ö ÙÒ Û ÐØ Ò ÙÐ Ö ÜØÖ Ñ ÑÙ Ö Ò Ò¹ Ò Ò Ñ Ò Û Ö Ì Ö Ì Ò Ò Æ Ö Ø Ò Ò ÙÒ Ö Ò Ó Ö Ò Ö ØÙÒ Ð Òº Ò Ò Û Ö ÒÙÖ ÒÑ Ð Ò Ö Ò ÖÙÒ ÙÑ Ò ½½º Ë ÔØ Ñ Ö ¾¼¼½ Ó Ö Ö Ð Ë ØÙ
ψ(t, Ü) = e iet/ ψ(ü).
 Ã Ô Ø Ð Ö ÖÑÓÒ Ç Þ ÐÐ ØÓÖ ÒÞ Û Ë Ö Ò Ò ÒÒ Ò Ø Ò Ã Ø ÒÔÓØ ÒØ Ð Ö ÌÙÒÒ Ð Ø Ï Ö ØÓ ØÓÑ ÙÒ ÚÓÖ ÐÐ Ñ Ö ÖÑÓÒ Ç Þ ÐÐ ØÓÖº Ï ÒÒ Ë Ó Ò Ò Ò Ö Ù Ò Ë º Ï ÒÒ Ò Ø Ò ÖÒ Ë Ó Ð Ò Ë Ò Ò Òº Ù Ø Ò ËÔÖ ÚÓÒ ÈÖÓ ÓÖ Ò ÁÒ Ñ Ã
Ã Ô Ø Ð Ö ÖÑÓÒ Ç Þ ÐÐ ØÓÖ ÒÞ Û Ë Ö Ò Ò ÒÒ Ò Ø Ò Ã Ø ÒÔÓØ ÒØ Ð Ö ÌÙÒÒ Ð Ø Ï Ö ØÓ ØÓÑ ÙÒ ÚÓÖ ÐÐ Ñ Ö ÖÑÓÒ Ç Þ ÐÐ ØÓÖº Ï ÒÒ Ë Ó Ò Ò Ò Ö Ù Ò Ë º Ï ÒÒ Ò Ø Ò ÖÒ Ë Ó Ð Ò Ë Ò Ò Òº Ù Ø Ò ËÔÖ ÚÓÒ ÈÖÓ ÓÖ Ò ÁÒ Ñ Ã
Ï ÒÒ (C2 == 0),C2 Max[C1 : $C$1],0. Ð Ï ÒÒ x == F1,$D$1 : $D$600]/Summe[$B$1 : $B$600
![Ï ÒÒ (C2 == 0),C2 Max[C1 : $C$1],0. Ð Ï ÒÒ x == F1,$D$1 : $D$600]/Summe[$B$1 : $B$600 Ï ÒÒ (C2 == 0),C2 Max[C1 : $C$1],0. Ð Ï ÒÒ x == F1,$D$1 : $D$600]/Summe[$B$1 : $B$600](/thumbs/97/131824127.jpg) ÖØ ÏÖ ÒÐØ ÚÖØÐÙÒÒ ÑØ ÓÖ ½º ÐÚÖØÐÙÒ Ò ÌØÖÖ Ò ÚÖ Ð Ø Ö ÑØ Ò ÐÒ ½ ¾ ÖØØ Ò ÛÖ ÒÐÓ ÒÑ ÏÖÐ ÛÓÖÒº ÂÒ Ð Ù Ñ ÙÒØÖ ØÒ Ö ÒØ ÓÐÐ Ð ÛÓÖÒ ÐØÒº ÓÐÐ Ñ ÊÑÒ ÒÖ ËÑÙÐØÓÒ ÖÑØØÐØ ÛÖÒ Û Ù ÒÞÐÒÒ ÐÒ ÛÓÖÒ ÛÖÒº Ò ÐÒ ÓÐÐ Ò ÎÖÐ ÑØ
ÖØ ÏÖ ÒÐØ ÚÖØÐÙÒÒ ÑØ ÓÖ ½º ÐÚÖØÐÙÒ Ò ÌØÖÖ Ò ÚÖ Ð Ø Ö ÑØ Ò ÐÒ ½ ¾ ÖØØ Ò ÛÖ ÒÐÓ ÒÑ ÏÖÐ ÛÓÖÒº ÂÒ Ð Ù Ñ ÙÒØÖ ØÒ Ö ÒØ ÓÐÐ Ð ÛÓÖÒ ÐØÒº ÓÐÐ Ñ ÊÑÒ ÒÖ ËÑÙÐØÓÒ ÖÑØØÐØ ÛÖÒ Û Ù ÒÞÐÒÒ ÐÒ ÛÓÖÒ ÛÖÒº Ò ÐÒ ÓÐÐ Ò ÎÖÐ ÑØ
ÁÒ ÐØ Ö ÖÓ Ö ÙÒØ ÖÐ Ò Ö Ö Ø Ú ÓÑÑÓÒ ÙÒØ Ö Ð Ò Ò ÙÒ Ò º¼ ÍÒ¹ Æ Ñ Ò Ò ÒÒÙÒ ¹Ï Ø Ö ÙØ Ø Ò Ó Ø ÒÐÓ Ù ÓÑÑ ÖÞ ÐÐ ÆÙØÞÙÒ ÓÐ Ò Ò Ò ÙÒ Ò Ñ Ð Ø ÙÒØ Ö Ð ÍÖ Ö Ò Û
 ÁÒÐØ Ö ÖÓ Ö ÙÒØ ÖÐÒ Ö ÖØ Ú ÓÑÑÓÒ ÙÒØ Ö ÐÒ Ò ÙÒÒ º¼ ÍÒ¹ Æ Ñ Ò Ò ÒÒÙÒ ¹ÏØ Ö ÙØ Ø Ò Ó Ø ÒÐÓ Ù ÓÑÑ ÖÞÐÐ ÆÙØÞÙÒ ÓÐÒÒ Ò ÙÒÒ ÑÐ Ø ÙÒØ Ö Ð ÍÖÖ Ò Û Ö À Ï ÒÐÚÓ Ò ÒÒغ ÇÒÐ Ò ¹ÅÒ Û Ö Ö Ä Þ ÒÞØ ÜØ Ú ÖÐ Ò Øº ÐØ ÖÒ Ø
ÁÒÐØ Ö ÖÓ Ö ÙÒØ ÖÐÒ Ö ÖØ Ú ÓÑÑÓÒ ÙÒØ Ö ÐÒ Ò ÙÒÒ º¼ ÍÒ¹ Æ Ñ Ò Ò ÒÒÙÒ ¹ÏØ Ö ÙØ Ø Ò Ó Ø ÒÐÓ Ù ÓÑÑ ÖÞÐÐ ÆÙØÞÙÒ ÓÐÒÒ Ò ÙÒÒ ÑÐ Ø ÙÒØ Ö Ð ÍÖÖ Ò Û Ö À Ï ÒÐÚÓ Ò ÒÒغ ÇÒÐ Ò ¹ÅÒ Û Ö Ö Ä Þ ÒÞØ ÜØ Ú ÖÐ Ò Øº ÐØ ÖÒ Ø
(x, y) + (0, 0) = (x, y)
 ÃÓÑÔÐ Ü Ð Ò ÙÒ ÓÑ ØÖ Ì ÐÒ Ñ Ö Æ Ð ÊÙ Ø Â Ò ÈÙØÞ ÊÓÒ Ï ÒÞ Ð Ð Ü Ý ÄÓÙØ Ó ÂÓ À ÒÒ Ö ØÙÒ Â ÖÒ ÖÓ Ø Ò À Ö Ö¹Ç Ö ÙÐ À ÒÖ ¹À ÖØÞ¹Ç Ö ÙÐ À ÒÖ ¹À ÖØÞ¹Ç Ö ÙÐ À ÒÖ ¹À ÖØÞ¹Ç Ö ÙÐ À ÒÖ ¹À ÖØÞ¹Ç Ö ÙÐ Ò Ö ¹Ç Ö ÙÐ ÖÙÔÔ
ÃÓÑÔÐ Ü Ð Ò ÙÒ ÓÑ ØÖ Ì ÐÒ Ñ Ö Æ Ð ÊÙ Ø Â Ò ÈÙØÞ ÊÓÒ Ï ÒÞ Ð Ð Ü Ý ÄÓÙØ Ó ÂÓ À ÒÒ Ö ØÙÒ Â ÖÒ ÖÓ Ø Ò À Ö Ö¹Ç Ö ÙÐ À ÒÖ ¹À ÖØÞ¹Ç Ö ÙÐ À ÒÖ ¹À ÖØÞ¹Ç Ö ÙÐ À ÒÖ ¹À ÖØÞ¹Ç Ö ÙÐ À ÒÖ ¹À ÖØÞ¹Ç Ö ÙÐ Ò Ö ¹Ç Ö ÙÐ ÖÙÔÔ
arxiv:math/ v1 [math.ho] 29 Sep 2004 ǫ = 180 (α+β +γ) = C F.
![arxiv:math/ v1 [math.ho] 29 Sep 2004 ǫ = 180 (α+β +γ) = C F. arxiv:math/ v1 [math.ho] 29 Sep 2004 ǫ = 180 (α+β +γ) = C F.](/thumbs/78/76903084.jpg) º º Ù³ ÈÖÞ ÓÒ Ñ ÙÒ Ò Ø ÖÖ ØÖ Ö Ö ÙÒ Ò ÖÐ ÙÒ Ò ÞÙÖ ÑÔ Ö Ò ÙÒ ÖÙÒ Ö ÓÑ ØÖ Ò Ò ½ ¾¼ Ö Â Ö Ò Ö Ö Ë ÓÐÞ ÏÙÔÔ ÖØ Ð ½ arxiv:math/0409578v1 [math.ho] 29 Sep 2004 Ù ÑÑ Ò ÙÒ ÁÒ Ø ØÓÖ Ð Ð Ø Ö ØÙÖ Ø Ö Ò Ò ÜØ Ò Ù ÓÒ
º º Ù³ ÈÖÞ ÓÒ Ñ ÙÒ Ò Ø ÖÖ ØÖ Ö Ö ÙÒ Ò ÖÐ ÙÒ Ò ÞÙÖ ÑÔ Ö Ò ÙÒ ÖÙÒ Ö ÓÑ ØÖ Ò Ò ½ ¾¼ Ö Â Ö Ò Ö Ö Ë ÓÐÞ ÏÙÔÔ ÖØ Ð ½ arxiv:math/0409578v1 [math.ho] 29 Sep 2004 Ù ÑÑ Ò ÙÒ ÁÒ Ø ØÓÖ Ð Ð Ø Ö ØÙÖ Ø Ö Ò Ò ÜØ Ò Ù ÓÒ
Ö Ú Øݹ ÄÓ Ð ÐÓ ËÝÒ ÖÓÒ Þ Ø ÓÒ Ò Ï Ö Ð Ë Ò ÓÖ Æ ØÛÓÖ Å Ö Ù ÏÐ Ð Ê ØÓ ÙÖ Ù Ò Ì ÓÑ ËØ Ù Ò ÌÓÖ Ø Ò Ö ÙÒ ÁÒ Ø ØÙØ Ó ÓÑÔÙØ Ö Ë Ò Ò ÔÔÐ Å Ø Ñ Ø ÍÒ Ú Ö ØÝ Ó
 Ö Ú Øݹ ÄÓ Ð ÐÓ ËÝÒ ÖÓÒ Þ Ø ÓÒ Ò Ï Ö Ð Ë Ò ÓÖ Æ ØÛÓÖ Å Ö Ù ÏÐ Ð Ê ØÓ ÙÖ Ù Ò Ì ÓÑ ËØ Ù Ò ÌÓÖ Ø Ò Ö ÙÒ ÁÒ Ø ØÙØ Ó ÓÑÔÙØ Ö Ë Ò Ò ÔÔÐ Å Ø Ñ Ø ÍÒ Ú Ö ØÝ Ó ÖÒ Æ Ù Ö ØÖ ½¾ ¼½¾ ÖÒ ¹ ËÛ ØÞ ÖÐ Ò ßÛ Ð Ð ÞÙÖ Ù Ø Ù
Ö Ú Øݹ ÄÓ Ð ÐÓ ËÝÒ ÖÓÒ Þ Ø ÓÒ Ò Ï Ö Ð Ë Ò ÓÖ Æ ØÛÓÖ Å Ö Ù ÏÐ Ð Ê ØÓ ÙÖ Ù Ò Ì ÓÑ ËØ Ù Ò ÌÓÖ Ø Ò Ö ÙÒ ÁÒ Ø ØÙØ Ó ÓÑÔÙØ Ö Ë Ò Ò ÔÔÐ Å Ø Ñ Ø ÍÒ Ú Ö ØÝ Ó ÖÒ Æ Ù Ö ØÖ ½¾ ¼½¾ ÖÒ ¹ ËÛ ØÞ ÖÐ Ò ßÛ Ð Ð ÞÙÖ Ù Ø Ù
Í Ó Ë Ù Ø Ö ÀÖ ºµ Ñ Ò Ñ Ò Ò Ø ÙÒ ÜØÖ Ñ ÑÙ ¼ Â Ö ÐØ ÖÒ Ò Ø Ø Ú Ê Ð ÙÒ Ù Ð ½ ¾¼½
 Í Ó Ë Ù Ø Ö ÀÖ ºµ Ñ Ò Ñ Ò Ò Ø ÙÒ ÜØÖ Ñ ÑÙ ¼ Â Ö ÐØ ÖÒ Ò Ø Ø Ú Ê Ð ÙÒ Ù Ð ½ ¾¼½ ÁË Æ ¹ ¹ ½ ¾½¹ ¹ Ð Ó Ö Ô ÁÒ ÓÖÑ Ø ÓÒ Ö ÙØ Ò Ð ÓØ ÙØ Ð ÓØ Ú ÖÞ Ò Ø ÈÙ Ð Ø ÓÒ Ò Ö ÙØ Ò Æ Ø ÓÒ Ð Ð Ó Ö Ô Ø ÐÐ ÖØ Ð Ó Ö Ô Ø Ò
Í Ó Ë Ù Ø Ö ÀÖ ºµ Ñ Ò Ñ Ò Ò Ø ÙÒ ÜØÖ Ñ ÑÙ ¼ Â Ö ÐØ ÖÒ Ò Ø Ø Ú Ê Ð ÙÒ Ù Ð ½ ¾¼½ ÁË Æ ¹ ¹ ½ ¾½¹ ¹ Ð Ó Ö Ô ÁÒ ÓÖÑ Ø ÓÒ Ö ÙØ Ò Ð ÓØ ÙØ Ð ÓØ Ú ÖÞ Ò Ø ÈÙ Ð Ø ÓÒ Ò Ö ÙØ Ò Æ Ø ÓÒ Ð Ð Ó Ö Ô Ø ÐÐ ÖØ Ð Ó Ö Ô Ø Ò
T = 0.3 s b = 4 m/s 2 s0 = 1 m. T = 2 s v0 = 90 km/h b = 1 m/s 2 s0 = 3 m. s = 0. s = 0. v0=220 km/h 2 a = 4 m/s. a = 1 m/s
 Ö ÓÒ Ñ ËØÖ ÒÚ Ö Ö Û Ñ Ò Ð ÖÚ Ö ÐØ Ò ËØ Ù ÒØ Ø ÙÒ Ò Ù Ø Å ÖØ Ò ÌÖ Ö ½ Ö ÓÒ Ù Ö Ë Ø Î Ö Ö ÑÓ ÐÐ Ö Ö Ö Ú ØØ ÙÒ Ò Ö Ò Ø ÐÐÙÒ Ò ÚÓÒ ÙØÓ Ö ÖÒ Û Ö Ò Ù ÖÚ Ö ÐØ Ò ÙÒ Ñ ØØ Ð Ö Ù Ò Î Ö Ö Ù Ù Ò ¹ ÓÒ Ö Ù Þ ÒÞ Î Ö Ö
Ö ÓÒ Ñ ËØÖ ÒÚ Ö Ö Û Ñ Ò Ð ÖÚ Ö ÐØ Ò ËØ Ù ÒØ Ø ÙÒ Ò Ù Ø Å ÖØ Ò ÌÖ Ö ½ Ö ÓÒ Ù Ö Ë Ø Î Ö Ö ÑÓ ÐÐ Ö Ö Ö Ú ØØ ÙÒ Ò Ö Ò Ø ÐÐÙÒ Ò ÚÓÒ ÙØÓ Ö ÖÒ Û Ö Ò Ù ÖÚ Ö ÐØ Ò ÙÒ Ñ ØØ Ð Ö Ù Ò Î Ö Ö Ù Ù Ò ¹ ÓÒ Ö Ù Þ ÒÞ Î Ö Ö
Ò Ò Ò Ë ÖÒ ½ ¾ Ö ÁÒØ ÖÒ Ø¹ Šع Ö ÙÒ ÙÒ ÐØ ÒØÒÓÑÑ Ò Ò Ö Ñ ØÑ Ø Å Ø Ø ÙÒ ÒØ Ö ÖØ Ã ÒÖ ØÐ Òº ÀÖ Ù ÓÒÖ Ò ØÙ ÙÒ ÃÐ Ò ÙÒ º Þ Ø ÃÓÒ Ø Ò Ñ Ø Ö Ë ÙÐ ÚÓÖÞÙÙÒ Ò
 ÁÒÐØ Ö ÖÓ Ö ÙÒØ ÖÐÒ Ö ÖØ Ú ÓÑÑÓÒ ÙÒØ Ö ÐÒ Ò ÙÒÒ º¼ ÍÒ¹ Æ Ñ Ò Ò ÒÒÙÒ ¹ÏØ Ö ÙØ Ø Ò Ó Ø ÒÐÓ Ù ÓÑÑ ÖÞÐÐ ÆÙØÞÙÒ ÓÐÒÒ Ò ÙÒÒ ÑÐ Ø ÙÒØ Ö Ð ÍÖÖ Ò Û Ö À Ï ÒÐÚÓ Ò ÒÒغ ÇÒÐ Ò ¹ÅÒ Û Ö Ö Ä Þ ÒÞØ ÜØ Ú ÖÐ Ò Øº ÐØ ÖÒ Ø
ÁÒÐØ Ö ÖÓ Ö ÙÒØ ÖÐÒ Ö ÖØ Ú ÓÑÑÓÒ ÙÒØ Ö ÐÒ Ò ÙÒÒ º¼ ÍÒ¹ Æ Ñ Ò Ò ÒÒÙÒ ¹ÏØ Ö ÙØ Ø Ò Ó Ø ÒÐÓ Ù ÓÑÑ ÖÞÐÐ ÆÙØÞÙÒ ÓÐÒÒ Ò ÙÒÒ ÑÐ Ø ÙÒØ Ö Ð ÍÖÖ Ò Û Ö À Ï ÒÐÚÓ Ò ÒÒغ ÇÒÐ Ò ¹ÅÒ Û Ö Ö Ä Þ ÒÞØ ÜØ Ú ÖÐ Ò Øº ÐØ ÖÒ Ø
Ź Ö ÑÑ Ø ÑÓ ÐÐ ÖØ Ù Ö Á ÝÒØ Ø ÇÔ Ö Ø ÓÒ Ò Ð Ð Ñ ØØ Ð ØÖ Ø Ö ÑÓÖÔ Ó ÝÒØ Ø Ö Å Ö Ñ Ð ÙÒ Ø ÓÒ Ö Òº È ÓÒÓÐÓ ÙÒ Ö ØÖÖ Ð Ü Ð µ ÁÒ ÓÖÑ Ø ÓÒ Û Ö Ö Ø ÔØ Ò Ö Ë
 ÈÓ Ø ÝÒØ Ø ÇÔ Ö Ø ÓÒ Ò Á È Ð ÔÔ Ï Ö ÍÒ Ú Ö ØØ Ä ÔÞ Ô Ð ÔÔºÛ ÖÙÒ ¹Ð ÔÞ º Ô Ð ÔÔÛ Öº ½ º ÔÖ Ð ¾¼½ ½» Ź Ö ÑÑ Ø ÑÓ ÐÐ ÖØ Ù Ö Á ÝÒØ Ø ÇÔ Ö Ø ÓÒ Ò Ð Ð Ñ ØØ Ð ØÖ Ø Ö ÑÓÖÔ Ó ÝÒØ Ø Ö Å Ö Ñ Ð ÙÒ Ø ÓÒ Ö Òº È ÓÒÓÐÓ
ÈÓ Ø ÝÒØ Ø ÇÔ Ö Ø ÓÒ Ò Á È Ð ÔÔ Ï Ö ÍÒ Ú Ö ØØ Ä ÔÞ Ô Ð ÔÔºÛ ÖÙÒ ¹Ð ÔÞ º Ô Ð ÔÔÛ Öº ½ º ÔÖ Ð ¾¼½ ½» Ź Ö ÑÑ Ø ÑÓ ÐÐ ÖØ Ù Ö Á ÝÒØ Ø ÇÔ Ö Ø ÓÒ Ò Ð Ð Ñ ØØ Ð ØÖ Ø Ö ÑÓÖÔ Ó ÝÒØ Ø Ö Å Ö Ñ Ð ÙÒ Ø ÓÒ Ö Òº È ÓÒÓÐÓ
ÅÓÖÔ ÓÐÓ ÅÓÖÔ ÓÐÓ Ö Ö ÙÑ ÒØ Ó ÖÙÒ ÈÖÓÒÓÑ Ò Ð Ð Ü ÓÒ Ö ÓÒ Å ÐÐ Ö ÁÒ Ø ØÙØ Ö Ä Ò Ù Ø ÍÒ Ú Ö ØØ Ä ÔÞ Ï Ë ¾¼½½ ÛÛÛºÙÒ ¹Ð ÔÞ º» ÑÙ ÐÐ Ö Ö ÓÒ Å ÐÐ Ö ÁÒ Ø ØÙ
 ÅÓÖÔ ÓÐÓ ÅÓÖÔ ÓÐÓ Ö Ö ÙÑ ÒØ Ó ÖÙÒ ÈÖÓÒÓÑ Ò Ð Ð Ü ÓÒ Ö ÓÒ Å ÐÐ Ö ÁÒ Ø ØÙØ Ö Ä Ò Ù Ø ÍÒ Ú Ö ØØ Ä ÔÞ Ï Ë ¾¼½½ ÛÛÛºÙÒ ¹Ð ÔÞ º» ÑÙ ÐÐ Ö Ö ÓÒ Å ÐÐ Ö ÁÒ Ø ØÙØ Ö Ä Ò Ù Ø µ ¼ ¹¼¼ ¹½¼¼ ½» ¾ ÈÖÓÒÓÑ Ò Ð Ð Ü ÓÒ Ä Øº
ÅÓÖÔ ÓÐÓ ÅÓÖÔ ÓÐÓ Ö Ö ÙÑ ÒØ Ó ÖÙÒ ÈÖÓÒÓÑ Ò Ð Ð Ü ÓÒ Ö ÓÒ Å ÐÐ Ö ÁÒ Ø ØÙØ Ö Ä Ò Ù Ø ÍÒ Ú Ö ØØ Ä ÔÞ Ï Ë ¾¼½½ ÛÛÛºÙÒ ¹Ð ÔÞ º» ÑÙ ÐÐ Ö Ö ÓÒ Å ÐÐ Ö ÁÒ Ø ØÙØ Ö Ä Ò Ù Ø µ ¼ ¹¼¼ ¹½¼¼ ½» ¾ ÈÖÓÒÓÑ Ò Ð Ð Ü ÓÒ Ä Øº
¾
 ÁÈÄÇÅ Ê ÁÌ Ì Ø Ð Ö ÔÐÓÑ Ö Ø Û ÒÒØ Ñ Ò Ò Ó Ö ÙØÓ Ò ØÓ Ø Ù Ò Ò Ö ØÞÙÒ Ö Ò Ù Ö Ø ÚÓÒ Ð Ô Ð Ò Î Ö Ö Ò Ë Ò Ë ÓØØÐ ØÒ Ö Ò ØÖ Ø Ö Ñ Ö Ö Å ØÖ Ö Æ ØÙÖÛ Ò Ø Ò Å º Ö Öº Ò Øºµ Ï Ò Å ¾¼½½ ËØÙ Ò ÒÒÞ Ð Ð ÙØ ËØÙ Ò Ð ØØ
ÁÈÄÇÅ Ê ÁÌ Ì Ø Ð Ö ÔÐÓÑ Ö Ø Û ÒÒØ Ñ Ò Ò Ó Ö ÙØÓ Ò ØÓ Ø Ù Ò Ò Ö ØÞÙÒ Ö Ò Ù Ö Ø ÚÓÒ Ð Ô Ð Ò Î Ö Ö Ò Ë Ò Ë ÓØØÐ ØÒ Ö Ò ØÖ Ø Ö Ñ Ö Ö Å ØÖ Ö Æ ØÙÖÛ Ò Ø Ò Å º Ö Öº Ò Øºµ Ï Ò Å ¾¼½½ ËØÙ Ò ÒÒÞ Ð Ð ÙØ ËØÙ Ò Ð ØØ
 Ä ÖÓÒ ÅÐ ÄÓÖ ¼ º¼º¾¼¼¾ ÁÒÐØ ÚÖÞÒ ÒÐØÙÒ ¾ ÏÐÐÒÐØÖ ¾º ÅÜÛÐйÐÙÒÒ º º º º º º º º º º º º º º º º º º º º º º º ¾º¾ Ä ÙÒÒ Ö ÅÜÛÐйÐÙÒÒ Ö Ò ÐÐ Öع Ò ÏÐÐÒÐØÖ º º º º º º º º º º º º º º º º º º º º º º º ¾º
Ä ÖÓÒ ÅÐ ÄÓÖ ¼ º¼º¾¼¼¾ ÁÒÐØ ÚÖÞÒ ÒÐØÙÒ ¾ ÏÐÐÒÐØÖ ¾º ÅÜÛÐйÐÙÒÒ º º º º º º º º º º º º º º º º º º º º º º º ¾º¾ Ä ÙÒÒ Ö ÅÜÛÐйÐÙÒÒ Ö Ò ÐÐ Öع Ò ÏÐÐÒÐØÖ º º º º º º º º º º º º º º º º º º º º º º º ¾º
Ä Ä Óµ Ö Ò Ð Ö Ä Óµ Ö Ò Ù Ò Ù Ò Û ÖØ Ò Ù Ä ÙÒ Òº ÆÙÖ ÅÙØ Ù Û ÒÒ Ù Ò Å Ø Ò Ò Ø Ù Ò Ò Ó Ø ÐØ Ø Ù ÞÙÖ Ä ÙÒ Ò Ø ÙÒ Ò Ø Ò Å Ø ¹ËØÓ Ö Ë ÙÐ Ö Ù Øº Î ÐÑ Ö Û Ö
 Â Ö Ò ¼ À Ø ½¼¾ ÂÙÒ ¾¼½¼ Ò Ñ Ø Ñ Ø Ø Ö Ø Ö Ë Ð Ö ÒÒ Òµ ÙÒ Ä Ö Ö ÒÒ Òµ ½ ¼ Ö Ò Ø ÚÓÒ Å ÖØ Ò Å ØØÐ Ö Ö Ù Ò ÚÓÑ ÁÒ Ø ØÙØ Ö Å Ø Ñ Ø Ò Ö ÂÓ ÒÒ ÙØ Ò Ö ¹ÍÒ Ú Ö ØØ ÞÙ Å ÒÞ JG U JOHANNES GUTENBERG UNIVERSITÄT MAINZ
Â Ö Ò ¼ À Ø ½¼¾ ÂÙÒ ¾¼½¼ Ò Ñ Ø Ñ Ø Ø Ö Ø Ö Ë Ð Ö ÒÒ Òµ ÙÒ Ä Ö Ö ÒÒ Òµ ½ ¼ Ö Ò Ø ÚÓÒ Å ÖØ Ò Å ØØÐ Ö Ö Ù Ò ÚÓÑ ÁÒ Ø ØÙØ Ö Å Ø Ñ Ø Ò Ö ÂÓ ÒÒ ÙØ Ò Ö ¹ÍÒ Ú Ö ØØ ÞÙ Å ÒÞ JG U JOHANNES GUTENBERG UNIVERSITÄT MAINZ
ÐØ P = W(s 2 ) W(s 3 ) W(s 4 ) W(s 4 ) W(s 5 ) W(s 6 ) = , 256º
 Â Ö Ò ¾ À Ø ÂÙÒ ¾¼¼ Ò Ñ Ø Ñ Ø Ø Ö Ø Ö Ë Ð Ö ÒÒ Òµ ÙÒ Ä Ö Ö ÒÒ Òµ ½ ¼ Ö Ò Ø ÚÓÒ Å ÖØ Ò Å ØØÐ Ö ÒÛÖØ Ö Ù Ò ÚÓÑ ÁÒ Ø ØÙØ Ö Å Ø Ñ Ø Ò Ö ÂÓ ÒÒ ÙØ Ò Ö ¹ÍÒ Ú Ö ØØ ÞÙ Å ÒÞ Ä Ä Óµ Ö Ò Ð Ö Ä Óµ Ö Ò Ù Ò Ù Ò Û ÖØ
Â Ö Ò ¾ À Ø ÂÙÒ ¾¼¼ Ò Ñ Ø Ñ Ø Ø Ö Ø Ö Ë Ð Ö ÒÒ Òµ ÙÒ Ä Ö Ö ÒÒ Òµ ½ ¼ Ö Ò Ø ÚÓÒ Å ÖØ Ò Å ØØÐ Ö ÒÛÖØ Ö Ù Ò ÚÓÑ ÁÒ Ø ØÙØ Ö Å Ø Ñ Ø Ò Ö ÂÓ ÒÒ ÙØ Ò Ö ¹ÍÒ Ú Ö ØØ ÞÙ Å ÒÞ Ä Ä Óµ Ö Ò Ð Ö Ä Óµ Ö Ò Ù Ò Ù Ò Û ÖØ
±0, 1m 2 m 3..m 53 2 e 10e 9..e
 Ê Ò Ò Ï ÖÙÑ Ð Ö Ö Ò Ò Ø Ó ÓÑÔÙØ Ö Ì ÐÒ Ñ Ö Ö Ø Ò Ö Ö ÒÒ Å Ò È ØÖ Å ÙØ Ò Ö ÊÓÞ È ØÖ ÃÐ ØÞ Ö ØÓÔ Ö Ë Ñ Ø ÊÓ ÖØ Ë ÐÑ ÒÒ Ò Ö ¹Ç Ö ÙÐ À ÒÖ ¹À ÖØÞ¹Ç Ö ÙÐ ÁÑÑ Ò٠йà ÒØ¹Ç Ö ÙÐ À Ö Ö¹Ç Ö ÙÐ Ò Ö ¹Ç Ö ÙÐ ÁÑÑ ÒÙ
Ê Ò Ò Ï ÖÙÑ Ð Ö Ö Ò Ò Ø Ó ÓÑÔÙØ Ö Ì ÐÒ Ñ Ö Ö Ø Ò Ö Ö ÒÒ Å Ò È ØÖ Å ÙØ Ò Ö ÊÓÞ È ØÖ ÃÐ ØÞ Ö ØÓÔ Ö Ë Ñ Ø ÊÓ ÖØ Ë ÐÑ ÒÒ Ò Ö ¹Ç Ö ÙÐ À ÒÖ ¹À ÖØÞ¹Ç Ö ÙÐ ÁÑÑ Ò٠йà ÒØ¹Ç Ö ÙÐ À Ö Ö¹Ç Ö ÙÐ Ò Ö ¹Ç Ö ÙÐ ÁÑÑ ÒÙ
ÁÒ ÐØ ½ ¾ ÈÖ Ú ÒØ Ø Ú Å ÒØ Ò Ò ¹ ÎÓÖ Ù Ò ÁÒ Ø Ò ÐØÙÒ Ñ Ò Ñ ÅÓ ÐÐ ÖÙÒ ÚÓÒ ËÝ Ø Ñ Ò Ñ ØØ Ð Å Ö ÓÚ ËÝ Ø Ñ ÅÓ ÐÐ ÖÙÒ Ö Ê Ô Ö ØÙÖÞ Ø Ö ÒÙÒ Ö ÅÌÌ ÙÒ ÅÌÌÊ Ò
 ÙÚ ÖÐ Ø º Ì Ð ÈÖÓ º Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò Ø ÖÖ ¾ º ÂÒÒ Ö ¾¼½ ÈÖÓ º Ö À Ù Ò Ð Ä Ó Òµ ÙÚ ÖÐ Ø ¾ º ÂÒÒ Ö ¾¼½ ½» ¼ ÁÒ ÐØ ½ ¾ ÈÖ Ú ÒØ Ø Ú Å ÒØ Ò Ò ¹ ÎÓÖ Ù Ò ÁÒ Ø Ò ÐØÙÒ Ñ Ò Ñ ÅÓ ÐÐ ÖÙÒ ÚÓÒ ËÝ Ø Ñ
ÙÚ ÖÐ Ø º Ì Ð ÈÖÓ º Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò Ø ÖÖ ¾ º ÂÒÒ Ö ¾¼½ ÈÖÓ º Ö À Ù Ò Ð Ä Ó Òµ ÙÚ ÖÐ Ø ¾ º ÂÒÒ Ö ¾¼½ ½» ¼ ÁÒ ÐØ ½ ¾ ÈÖ Ú ÒØ Ø Ú Å ÒØ Ò Ò ¹ ÎÓÖ Ù Ò ÁÒ Ø Ò ÐØÙÒ Ñ Ò Ñ ÅÓ ÐÐ ÖÙÒ ÚÓÒ ËÝ Ø Ñ
Ò Ê Ö ÒØ ÃÓÖÖ Ö ÒØ ÈÖÓ º Öº Ñ º ÖØ ÅÙ Ö ÈÖÓ º Öº Ñ º Ã Ö Ø Ò Ë Ñ Ö ÈÖ Úº ÓÞº Öº Ñ º ËØ Ô Ò Ö Ò Ì Ö Ñ Ò Ð Ò ÈÖ ÙÒ ¾ º½½º¾¼¼
 Ù Ö Æ ÙÖÓ ÖÙÖ Ò ÃÐ Ò ÃÒ ÔÔ Ø Ö Ò Ò Ù Ó ÙÑ¹Ä Ò Ò Ö Ö ¹ ÍÒ Ú Ö ØØ Ð Ò ¹ Ö ÊÙ Ö¹ÍÒ Ú Ö ØØ Ó ÙÑ Ö ØÓÖ ÈÖÓ º Öº Ñ º º À Ö Ö Ê ØÖ ÖÙÒ ÚÓÒ ¹ÍÐØÖ Ðй ÙÒ Ì¹ Ø Ò Ö Ä Ò ÒÛ Ö Ð ÙÐ ÞÙÖ ÍÒØ Ö Ø ØÞÙÒ Ò Ú ÖØ Ö È Ð Ö Ù
Ù Ö Æ ÙÖÓ ÖÙÖ Ò ÃÐ Ò ÃÒ ÔÔ Ø Ö Ò Ò Ù Ó ÙÑ¹Ä Ò Ò Ö Ö ¹ ÍÒ Ú Ö ØØ Ð Ò ¹ Ö ÊÙ Ö¹ÍÒ Ú Ö ØØ Ó ÙÑ Ö ØÓÖ ÈÖÓ º Öº Ñ º º À Ö Ö Ê ØÖ ÖÙÒ ÚÓÒ ¹ÍÐØÖ Ðй ÙÒ Ì¹ Ø Ò Ö Ä Ò ÒÛ Ö Ð ÙÐ ÞÙÖ ÍÒØ Ö Ø ØÞÙÒ Ò Ú ÖØ Ö È Ð Ö Ù
Î ÖÞ Ò Ö ÖÞÙÒ Ò ÔÛº Ô Ð Û Ôغ ÓÔØÖ Ò ÁÇÄ ÁÒØÖ Ó ÙÐ ÖÐ Ò Ä ËÁÃ Ä Ö Ò Ë ØÙ Ã Ö ØÓÑ Ð Ù ÑÑ Å ÐÐ Ñ Ø Ö µm Å ÖÓÑ Ø Ö ÈÊÃ È ÓØÓÖ Ö Ø Ú Ã Ö Ø ØÓÑ ÊÅË ÊÓÓØ Å
 Ò Ù ÚÓÒ È ÒÝÐ Ô Ö Ò ÙÒ ÌÖÓÔ Ñ Ù Ï ÐÐ Ò ÖÓÒØ ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö ÓØÓÖ Ñ Ò Öº Ñ ºµ ÚÓÖ Ð Ø Ñ Ê Ø Ö Å Þ Ò Ò ÙÐØØ Ö Ö Ö ¹Ë ÐÐ Ö¹ÍÒ Ú Ö ØØ Â Ò ÚÓÒ Ø Ò ÄÓÓ Ö ÓÖ Ò Ñ ¼¾º Ç ØÓ Ö ½ Ò Ç Ö Ù Ò ¾º ÔÖ Ð ¾¼¼ Î
Ò Ù ÚÓÒ È ÒÝÐ Ô Ö Ò ÙÒ ÌÖÓÔ Ñ Ù Ï ÐÐ Ò ÖÓÒØ ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö ÓØÓÖ Ñ Ò Öº Ñ ºµ ÚÓÖ Ð Ø Ñ Ê Ø Ö Å Þ Ò Ò ÙÐØØ Ö Ö Ö ¹Ë ÐÐ Ö¹ÍÒ Ú Ö ØØ Â Ò ÚÓÒ Ø Ò ÄÓÓ Ö ÓÖ Ò Ñ ¼¾º Ç ØÓ Ö ½ Ò Ç Ö Ù Ò ¾º ÔÖ Ð ¾¼¼ Î
ÁÑÔÖ ÙÑ À Ö Ù Ö º º º º º º º º º º º Ø Ñ Ö È Ð ÔÔ ¹ÍÒ Ú Ö ØØ Å Ö ÙÖ Îº ºËº ºÈº º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º
 ÁÑÔÖ ÙÑ À Ö Ù Ö º º º º º º º º º º º Ø Ñ Ö È Ð ÔÔ ¹ÍÒ Ú Ö ØØ Å Ö ÙÖ Îº ºËº ºÈº º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º Å ÖØ Ò º Ë Û ÖÞ Ö Ê Ø ÓÒ º º
ÁÑÔÖ ÙÑ À Ö Ù Ö º º º º º º º º º º º Ø Ñ Ö È Ð ÔÔ ¹ÍÒ Ú Ö ØØ Å Ö ÙÖ Îº ºËº ºÈº º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º Å ÖØ Ò º Ë Û ÖÞ Ö Ê Ø ÓÒ º º
ÁÒ ÐØ Ú ÖÞ Ò ½ ÂÓ ÒÒ Ö ÌĐ Ù Ö ½ ¼ ½ º½ÂÓ ÒÒ Û Ö Æ ÖĐ Ö ½ º¾ Ö ÌÓ Ö º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½ ¼ º º º º º º
 ÍÖ ÒØ Ù ½ ¹ ÂÓ ÒÒ Ö ÌĐ Ù Ö Á ÁÁ ÁÁÁ ÁÎ ÒØÖ ÐÙÒ Ú Ö ÙÑ ÙÒ ËÙÔ ÖÙÒ Ú Ö Ò ÄÓ ÐÙÒ Ú Ö ÙÑ Ø ÍÖ ÒØ Ä Ò ÙÒ Ä Ö Ò Â Ù ÛÛÛºÙÖ ÒØ ºÓÖ ½ ÛÛÛºØÖÙØ ÓÓ ºÓÑ ¾ ½ ÁÒØ ÖÒ Ø ØØÔ»»ÛÛÛºÙÖ ÒØ ºÓÖ» º ¾ ÁÒØ ÖÒ Ø ØØÔ»»ÛÛÛºØÖÙØ
ÍÖ ÒØ Ù ½ ¹ ÂÓ ÒÒ Ö ÌĐ Ù Ö Á ÁÁ ÁÁÁ ÁÎ ÒØÖ ÐÙÒ Ú Ö ÙÑ ÙÒ ËÙÔ ÖÙÒ Ú Ö Ò ÄÓ ÐÙÒ Ú Ö ÙÑ Ø ÍÖ ÒØ Ä Ò ÙÒ Ä Ö Ò Â Ù ÛÛÛºÙÖ ÒØ ºÓÖ ½ ÛÛÛºØÖÙØ ÓÓ ºÓÑ ¾ ½ ÁÒØ ÖÒ Ø ØØÔ»»ÛÛÛºÙÖ ÒØ ºÓÖ» º ¾ ÁÒØ ÖÒ Ø ØØÔ»»ÛÛÛºØÖÙØ
Ò Ò Ø Ò¹ÌÖ ÓÐÓ Ö ËÞ Ò Ö Ò ÙÖ ÐÐ Ó Ø ÙÐ Ù ØÖ Ø ½¾¼ À Ñ Ù ÙÒ ½ ¾ Ó Ö Î Ö Ò Ò Ø ¾¼¼ ÊÓ ÙÒ ¾ º ÔÖ Ð ¾¼½
 Ò Ò Ø Ò¹ÌÖ ÓÐÓ Ö ËÞ Ò Ö Ò ÙÖ ÐÐ Ó Ø ÙÐ Ù ØÖ Ø ½¾¼ À Ñ Ù ÙÒ ½ ¾ Ó Ö Î Ö Ò Ò Ø ¾¼¼ ÊÓ ÙÒ ¾ º ÔÖ Ð ¾¼½ ÒÐ ØÙÒ ÙÒ ÎÓÖÛÓÖØ Ö ÌÖ ÓÐÓ Ò ÐØ ÙÑ Ö ËÞ Ò Ö Ò ÙÖ ÊÓÐÐ Ò Ô Ð Àº Ⱥ ÄÓÚ Ö Ø Ø ÙÐ Ùº Ö Ø Ô ÐØ Ñ Â Ö ½¾¼
Ò Ò Ø Ò¹ÌÖ ÓÐÓ Ö ËÞ Ò Ö Ò ÙÖ ÐÐ Ó Ø ÙÐ Ù ØÖ Ø ½¾¼ À Ñ Ù ÙÒ ½ ¾ Ó Ö Î Ö Ò Ò Ø ¾¼¼ ÊÓ ÙÒ ¾ º ÔÖ Ð ¾¼½ ÒÐ ØÙÒ ÙÒ ÎÓÖÛÓÖØ Ö ÌÖ ÓÐÓ Ò ÐØ ÙÑ Ö ËÞ Ò Ö Ò ÙÖ ÊÓÐÐ Ò Ô Ð Àº Ⱥ ÄÓÚ Ö Ø Ø ÙÐ Ùº Ö Ø Ô ÐØ Ñ Â Ö ½¾¼
0) = 1 Ö ÒØ Ð ÓÖ u(t) = 14 t sin(2t)+sin(4t) 4 t cos(8t)] 1(t) G(s) = L{g(s)}º
![0) = 1 Ö ÒØ Ð ÓÖ u(t) = 14 t sin(2t)+sin(4t) 4 t cos(8t)] 1(t) G(s) = L{g(s)}º 0) = 1 Ö ÒØ Ð ÓÖ u(t) = 14 t sin(2t)+sin(4t) 4 t cos(8t)] 1(t) G(s) = L{g(s)}º](/thumbs/94/118651964.jpg) ¼ Å ÒÙØ Ê Ò ¹ÙÔ¹Ø Ñ È ½ ÓÖ Ö Ú Û Ò ÔÙÖÔÓ Ó Ø ÔÖÓ Ð Ñ Ø Ø Ñ ÒØ Ø Ö Ö Ò ¹ÙÔ¹Ø Ñ Ó ½¼ Ñ ÒÙØ ÔÖ ÓÖ ØÓ Ø Ó Ð Ü Ñ Ò Ø ÓÒ Ø Ñ º ÙÖ Ò Ø Ô Ö Ó Ø ÒÓØ ÐÐÓÛ ØÓ Ø ÖØ ÓÐÚ Ò Ø ÔÖÓ Ð Ñ º Ì Ñ Ò ÜÔÐ ØÐÝ Ø Ø ÙÖ Ò Ø ÒØ Ö
¼ Å ÒÙØ Ê Ò ¹ÙÔ¹Ø Ñ È ½ ÓÖ Ö Ú Û Ò ÔÙÖÔÓ Ó Ø ÔÖÓ Ð Ñ Ø Ø Ñ ÒØ Ø Ö Ö Ò ¹ÙÔ¹Ø Ñ Ó ½¼ Ñ ÒÙØ ÔÖ ÓÖ ØÓ Ø Ó Ð Ü Ñ Ò Ø ÓÒ Ø Ñ º ÙÖ Ò Ø Ô Ö Ó Ø ÒÓØ ÐÐÓÛ ØÓ Ø ÖØ ÓÐÚ Ò Ø ÔÖÓ Ð Ñ º Ì Ñ Ò ÜÔÐ ØÐÝ Ø Ø ÙÖ Ò Ø ÒØ Ö
ÑÔ Ö ÍÒØ Ö Ù ÙÒ ÞÙÑ Î Ö Ð ÚÓÒ À Ð Ý Ø Ñ Ò Ö ÖÑ Ò Ø ÓÐÙØ ÙÒ Å ÖÓ Ó Ø Ò ÃÖ Ø Ö Ò Ö ÒÙØÞ Ö Ö ÙÒ Ð Ø ¹ Ñ Ô Ð ÚÓÒ Ü Ð Å Ø Ö Ö Ø Ò Ö Ì Ò Ò ÍÒ Ú Ö ØØ ÖÐ Ò ÙÐ
 ÑÔ Ö ÍÒØ Ö Ù ÙÒ ÞÙÑ Î Ö Ð ÚÓÒ À Ð Ý Ø Ñ Ò Ö ÖÑ Ò Ø ÓÐÙØ ÙÒ Å ÖÓ Ó Ø Ò ÃÖ Ø Ö Ò Ö ÒÙØÞ Ö Ö ÙÒ Ð Ø ¹ Ñ Ô Ð ÚÓÒ Ü Ð Å Ø Ö Ö Ø Ò Ö Ì Ò Ò ÍÒ Ú Ö ØØ ÖÐ Ò ÙÐØØ ½ Ø Û Ò Ø Ò ÁÒ Ø ØÙØ Ö ËÔÖ ÙÒ ÃÓÑÑÙÒ Ø ÓÒ Ø Ù Ó
ÑÔ Ö ÍÒØ Ö Ù ÙÒ ÞÙÑ Î Ö Ð ÚÓÒ À Ð Ý Ø Ñ Ò Ö ÖÑ Ò Ø ÓÐÙØ ÙÒ Å ÖÓ Ó Ø Ò ÃÖ Ø Ö Ò Ö ÒÙØÞ Ö Ö ÙÒ Ð Ø ¹ Ñ Ô Ð ÚÓÒ Ü Ð Å Ø Ö Ö Ø Ò Ö Ì Ò Ò ÍÒ Ú Ö ØØ ÖÐ Ò ÙÐØØ ½ Ø Û Ò Ø Ò ÁÒ Ø ØÙØ Ö ËÔÖ ÙÒ ÃÓÑÑÙÒ Ø ÓÒ Ø Ù Ó
ÁÒ ÐØ Ú ÖÞ Ò ½ ÒÐ ØÙÒ ¾ ËØ Ú Ê Ø Ø ÈÖ ÒÞ Ô Ò ¾º½ Ï Ö ÓÐÙÒ º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾º¾ ÐÐÑ Ð Ø º º º º º º º º º º º º º
 ËØ Ú Ê ÅÙ ÓÖ ÅÙ Ò Â ÖÒ Æ ØØ Ò Ñ Ö ËÓÒ Å Ò º Å ¾¼¼¼ ÁÒ ÐØ Ú ÖÞ Ò ½ ÒÐ ØÙÒ ¾ ËØ Ú Ê Ø Ø ÈÖ ÒÞ Ô Ò ¾º½ Ï Ö ÓÐÙÒ º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾º¾ ÐÐÑ Ð Ø º º º º º º º º º º º º º
ËØ Ú Ê ÅÙ ÓÖ ÅÙ Ò Â ÖÒ Æ ØØ Ò Ñ Ö ËÓÒ Å Ò º Å ¾¼¼¼ ÁÒ ÐØ Ú ÖÞ Ò ½ ÒÐ ØÙÒ ¾ ËØ Ú Ê Ø Ø ÈÖ ÒÞ Ô Ò ¾º½ Ï Ö ÓÐÙÒ º º º º º º º º º º º º º º º º º º º º º º º º º º º ¾º¾ ÐÐÑ Ð Ø º º º º º º º º º º º º º
Ù Ö Ö Æ ÙÖÓÐÓ Ò ÃÐ Ò Ö Ð ÖعÄÙ Û ¹ÍÒ Ú Ö ØØ Ö ÙÖ Ñ Öº Ò Î ÖÐ Ù Ò ÐÝ Ö ÌÖ ÑÓÖ Ö ÕÙ ÒÞ Ò Ñ ÅÓÖ Ù È Ö Ò ÓÒ ÙÒ Ñ ÒØ ÐÐ Ò ÌÖ ÑÓÖ ÁÆ Í ÍÊ Ä ¹ ÁËË ÊÌ ÌÁÇÆ ÞÙ
 Ù Ö Ö Æ ÙÖÓÐÓ Ò ÃÐ Ò Ö Ð ÖعÄÙ Û ¹ÍÒ Ú Ö ØØ Ö ÙÖ Ñ Öº Ò Î ÖÐ Ù Ò ÐÝ Ö ÌÖ ÑÓÖ Ö ÕÙ ÒÞ Ò Ñ ÅÓÖ Ù È Ö Ò ÓÒ ÙÒ Ñ ÒØ ÐÐ Ò ÌÖ ÑÓÖ ÁÆ Í ÍÊ Ä ¹ ÁËË ÊÌ ÌÁÇÆ ÞÙÖ ÖÐ Ò ÙÒ Å Þ Ò Ò Ó ØÓÖ Ö Ö Å Þ Ò Ò ÙÐØØ Ö Ð ÖعÄÙ
Ù Ö Ö Æ ÙÖÓÐÓ Ò ÃÐ Ò Ö Ð ÖعÄÙ Û ¹ÍÒ Ú Ö ØØ Ö ÙÖ Ñ Öº Ò Î ÖÐ Ù Ò ÐÝ Ö ÌÖ ÑÓÖ Ö ÕÙ ÒÞ Ò Ñ ÅÓÖ Ù È Ö Ò ÓÒ ÙÒ Ñ ÒØ ÐÐ Ò ÌÖ ÑÓÖ ÁÆ Í ÍÊ Ä ¹ ÁËË ÊÌ ÌÁÇÆ ÞÙÖ ÖÐ Ò ÙÒ Å Þ Ò Ò Ó ØÓÖ Ö Ö Å Þ Ò Ò ÙÐØØ Ö Ð ÖعÄÙ
Å Ø Ò Ñ ÙÒ Ö Å Þ Ò Ò ÙÐØØ Ö ÍÒ Ú Ö ØØ Å Ò Ò Ö Ø Ö Ø ØØ Ö ÈÖÓ º Öº Ê Ö ÚÓÒ ÃÖ ¾º Ö Ø Ö Ø ØØ Ö ÈÖÓ º Öº ØÐ ÃÙÒÞ Å Ø Ö Ø Ö Ø ØØ Ö ÈÖÓ º Öº À Ò ¹È Ø Ö Ë Û
 Ù Ñ ÁÒ Ø ØÙØ Ö ËÓÞ Ð È ØÖ ÙÒ ÂÙ Ò Ñ Þ Ò Ö ÄÙ Û ¹Å Ü Ñ Ð Ò ¹ÍÒ Ú Ö ØØ Å Ò Ò ÎÓÖ Ø Ò ÃÓÑÑ Ö Ö Ä Ø Öµ ÈÖÓ º Öº Ê Ö ÚÓÒ ÃÖ Ê Ó ØÓÖ Ò Ö Ò Ð ÔÓ Ø ÍÒØ Ö Ð Ø ÒÓÖÑ Ð¹ ÙÒ Ö Û Ø Ò Ã Ò ÖÒ ÖØ Ø ÓÒ ÞÙÑ ÖÛ Ö Ó ØÓÖ Ö
Ù Ñ ÁÒ Ø ØÙØ Ö ËÓÞ Ð È ØÖ ÙÒ ÂÙ Ò Ñ Þ Ò Ö ÄÙ Û ¹Å Ü Ñ Ð Ò ¹ÍÒ Ú Ö ØØ Å Ò Ò ÎÓÖ Ø Ò ÃÓÑÑ Ö Ö Ä Ø Öµ ÈÖÓ º Öº Ê Ö ÚÓÒ ÃÖ Ê Ó ØÓÖ Ò Ö Ò Ð ÔÓ Ø ÍÒØ Ö Ð Ø ÒÓÖÑ Ð¹ ÙÒ Ö Û Ø Ò Ã Ò ÖÒ ÖØ Ø ÓÒ ÞÙÑ ÖÛ Ö Ó ØÓÖ Ö
ÃÙÖÞ ÙÒ ËÇ È ÈÖÓØÓ ÓÐÐ ÛÙÖ Ð Ò ÔÐ ØØ ÓÖÑÙÒ Ò Æ Ö Ø Ò ÓÖ¹ Ñ Ø Ò Öغ Ö ÐÐ Ò Ñ Ø Ö Ò Ø ÓÒ Ø ÍÒ Ò Ø Ò Ø ÖÖ Øº Ø ÑÑ Ö ÒÓ Ê Ñ Ò Ò ÙÒ Ò Ò ÖÒ ÙÒ¹ Ò Ö Ò Ø Ò ÐØ
 ÁÈÄÇÅ Ê ÁÌ Î Ö Ð ÚÓÒ ËÇ È ÃÓÑÑÙÒ Ø ÓÒ ÔÐ ØØ ÓÖÑ Ò Ù ÖØ Ñ ÁÒ Ø ØÙØ Ö ÈÖÓ Ö ÑÑ Ö ÔÖ Ò Ö Ì Ò Ò ÍÒ Ú Ö ØØ Ï Ò ÙÒØ Ö Ö ÒÐ ØÙÒ ÚÓÒ ÓºÍÒ ÚºÈÖÓ º Ôк¹ÁÒ º Öº Ö ÒÞ ÈÙÒØ Ñ ÙÖ Å Ò Ö Â ÖØ Ò ½ ¾ ÙØ ¹ ÖÓ Ö ÓÖ Ï Ò ½
ÁÈÄÇÅ Ê ÁÌ Î Ö Ð ÚÓÒ ËÇ È ÃÓÑÑÙÒ Ø ÓÒ ÔÐ ØØ ÓÖÑ Ò Ù ÖØ Ñ ÁÒ Ø ØÙØ Ö ÈÖÓ Ö ÑÑ Ö ÔÖ Ò Ö Ì Ò Ò ÍÒ Ú Ö ØØ Ï Ò ÙÒØ Ö Ö ÒÐ ØÙÒ ÚÓÒ ÓºÍÒ ÚºÈÖÓ º Ôк¹ÁÒ º Öº Ö ÒÞ ÈÙÒØ Ñ ÙÖ Å Ò Ö Â ÖØ Ò ½ ¾ ÙØ ¹ ÖÓ Ö ÓÖ Ï Ò ½
ÙÐØØ Ö È Ý ÙÒ ØÖÓÒÓÑ ÊÙÔÖ Ø¹Ã ÖÐ ¹ÍÒ Ú Ö ØØ À Ð Ö ÐÓÖ Ö Ø Ñ ËØÙ Ò Ò È Ý ÚÓÖ Ð Ø ÚÓÒ Å ÖÚ Ò Ð ÖØ Ù À Ð Ö Ù Ù Ø ¾¼½¼
 ÙÐØØ Ö È Ý ÙÒ ØÖÓÒÓÑ ÊÙÔÖ Ø¹Ã ÖÐ ¹ÍÒ Ú Ö ØØ À Ð Ö ÐÓÖ Ö Ø Ñ ËØÙ Ò Ò È Ý ÚÓÖ Ð Ø ÚÓÒ Å ÖÚ Ò Ð ÖØ Ù À Ð Ö Ù Ù Ø ¾¼½¼ Ä ÕÙ ÓÑÔÙØ Ò Ñ Ø Æ ÙÖÓÑÓÖÔ Ö À Ö Û Ö ÐÓÖ Ö Ø ÛÙÖ ÚÓÒ Å ÖÚ Ò Ð ÖØ Ù ÖØ Ñ Ã Ö Ó ¹ÁÒ Ø ØÙØ
ÙÐØØ Ö È Ý ÙÒ ØÖÓÒÓÑ ÊÙÔÖ Ø¹Ã ÖÐ ¹ÍÒ Ú Ö ØØ À Ð Ö ÐÓÖ Ö Ø Ñ ËØÙ Ò Ò È Ý ÚÓÖ Ð Ø ÚÓÒ Å ÖÚ Ò Ð ÖØ Ù À Ð Ö Ù Ù Ø ¾¼½¼ Ä ÕÙ ÓÑÔÙØ Ò Ñ Ø Æ ÙÖÓÑÓÖÔ Ö À Ö Û Ö ÐÓÖ Ö Ø ÛÙÖ ÚÓÒ Å ÖÚ Ò Ð ÖØ Ù ÖØ Ñ Ã Ö Ó ¹ÁÒ Ø ØÙØ
Ò Ì Ò Ú º ÓÖ Ò ØÓÖ Ë Ö Ø Ô Ð ÇÖ Ò ØÓÖ Ö Ë Ö Ø Ñ Ò Ñ Ò Ë Ö Ø Ñ Ò Ñ ÒØÔÖÓÞ Ë ÙÖ Øݵ ÈÓÐ È ¹ÅÓ ÐÐ ËØ Ò Ö ÙÒ ÆÓÖÑ Ò ÞÙ ÁÌ¹Ë Ö Ø Ë Ö Ø ÓÒÞ ÔØ Ä Ø Ö ØÙÖ ¾»
 ØÓ Ë ÙÖ ØÝ ÎÇ ÁÒØÖÓ ÙØ ÓÒ Ë Ö Ø»Ë Ö Ø Ñ Ò Ñ ÒØ ÇÖ Ò ØÓÖ ÁÒ Ù ØÖ Ð ËÓ ØÛ Ö ÁÆËÇ Ö Ê Ò Ö Ø ØÞØ ÙØÓÑ Ø ÓÒ ÙÐØØ Ö ÁÒ ÓÖÑ Ø Ì Ò ÍÒ Ú Ö ØØ Ï Ò ÁÒ Ø ØÙØ ÐÓÖ Ò Ò Ù Ö Ö ÒÞ Å Ö Ó Ö Ò Ì Ò Ú º ÓÖ Ò ØÓÖ Ë Ö Ø Ô Ð ÇÖ
ØÓ Ë ÙÖ ØÝ ÎÇ ÁÒØÖÓ ÙØ ÓÒ Ë Ö Ø»Ë Ö Ø Ñ Ò Ñ ÒØ ÇÖ Ò ØÓÖ ÁÒ Ù ØÖ Ð ËÓ ØÛ Ö ÁÆËÇ Ö Ê Ò Ö Ø ØÞØ ÙØÓÑ Ø ÓÒ ÙÐØØ Ö ÁÒ ÓÖÑ Ø Ì Ò ÍÒ Ú Ö ØØ Ï Ò ÁÒ Ø ØÙØ ÐÓÖ Ò Ò Ù Ö Ö ÒÞ Å Ö Ó Ö Ò Ì Ò Ú º ÓÖ Ò ØÓÖ Ë Ö Ø Ô Ð ÇÖ
ÓÒÙ ¹Å ÐÙ ËÝ Ø Ñ Ö Î Ö ÖÙÒ Û Ã Ø ÓÖ Ò ÚÓÒ Ê Ò Ò Ó Ø Ú Ò Ê Ò Þº º ÈË Þ Ð Ò ÙØÓ Ö ÀÙ Ö ÙÑ Û Ø Ø ºº ÙÒ Ò Ù Ø Ú Ò Ê Ò Ò Ø Ó Ø Ú Ñ Ö Ê Òµ Ê Ó Ö Ø Ø Ã ÒÒ Ò
 Ê ÓØ ÓÖ º Ì Ð ÈÖÓ º Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò Ø ÖÖ ¾ º ÔÖ Ð ¾¼½ ÈÖÓ º Ö À Ù Ò Ð Ä Ó Òµ Ê ÓØ ÓÖ ¾ º ÔÖ Ð ¾¼½ ½» ½ ÓÒÙ ¹Å ÐÙ ËÝ Ø Ñ Ö Î Ö ÖÙÒ Û Ã Ø ÓÖ Ò ÚÓÒ Ê Ò Ò Ó Ø Ú Ò Ê Ò Þº º ÈË Þ Ð Ò ÙØÓ Ö ÀÙ
Ê ÓØ ÓÖ º Ì Ð ÈÖÓ º Ö À Ù Ò Ð ÅÓÒØ ÒÙÒ Ú Ö ØØ Ä Ó Ò Ø ÖÖ ¾ º ÔÖ Ð ¾¼½ ÈÖÓ º Ö À Ù Ò Ð Ä Ó Òµ Ê ÓØ ÓÖ ¾ º ÔÖ Ð ¾¼½ ½» ½ ÓÒÙ ¹Å ÐÙ ËÝ Ø Ñ Ö Î Ö ÖÙÒ Û Ã Ø ÓÖ Ò ÚÓÒ Ê Ò Ò Ó Ø Ú Ò Ê Ò Þº º ÈË Þ Ð Ò ÙØÓ Ö ÀÙ
 Ò Ù Ö Ò ÎÓÐÙÑ Ò Ù Ú Ö Ö ØÙÒ Ò ÓÖÑ Ø ÓÒ Ú Ö ÐØ Ò ÔÖ ØÞ Ó Ò Ö ÑÓÖÔ Ö Ì ÖÑÓÔÐ Ø ÎÓÒ Ö ÙÐØØ Ö Å Ò Ò Ù ÙÒ Î Ö Ö Ò Ø Ò Ö Ì Ò Ò ÍÒ Ú Ö ØØ ÑÒ ØÞ Ò Ñ Ø ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö Ó ØÓÖ Ò Ò ÙÖ Öº¹ÁÒ ºµ ÚÓÖ Ð Ø ÚÓÒ
Ò Ù Ö Ò ÎÓÐÙÑ Ò Ù Ú Ö Ö ØÙÒ Ò ÓÖÑ Ø ÓÒ Ú Ö ÐØ Ò ÔÖ ØÞ Ó Ò Ö ÑÓÖÔ Ö Ì ÖÑÓÔÐ Ø ÎÓÒ Ö ÙÐØØ Ö Å Ò Ò Ù ÙÒ Î Ö Ö Ò Ø Ò Ö Ì Ò Ò ÍÒ Ú Ö ØØ ÑÒ ØÞ Ò Ñ Ø ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö Ó ØÓÖ Ò Ò ÙÖ Öº¹ÁÒ ºµ ÚÓÖ Ð Ø ÚÓÒ
 ÁÒ Ø ØÙØ Ö ÈÖÓ Ö ÑÑ ØÖÙ ØÙÖ Ò ÙÒ Ø ÒÓÖ Ò Ø ÓÒ ÁÈ µ ÁÒ Ø ØÙØ Ö Ì Ð Ñ Ø ÁÌŵ ÁÒ Ø ØÙØ Ö Ï ÖØ Ø ÔÓÐ Ø ÙÒ Ï ÖØ Ø ÓÖ ÙÒ ÁÏϵ ÁÒ Ø ØÙØ Ö Ï ÖØ Ø Ø ÓÖ ÙÒ ÇÔ Ö Ø ÓÒ Ê Ö ÏÁÇʵ ÒØÖÙÑ Ö Ò Û Ò Ø Ê Ø Û Ò Ø Ò Êµ ÁÒØ
ÁÒ Ø ØÙØ Ö ÈÖÓ Ö ÑÑ ØÖÙ ØÙÖ Ò ÙÒ Ø ÒÓÖ Ò Ø ÓÒ ÁÈ µ ÁÒ Ø ØÙØ Ö Ì Ð Ñ Ø ÁÌŵ ÁÒ Ø ØÙØ Ö Ï ÖØ Ø ÔÓÐ Ø ÙÒ Ï ÖØ Ø ÓÖ ÙÒ ÁÏϵ ÁÒ Ø ØÙØ Ö Ï ÖØ Ø Ø ÓÖ ÙÒ ÇÔ Ö Ø ÓÒ Ê Ö ÏÁÇʵ ÒØÖÙÑ Ö Ò Û Ò Ø Ê Ø Û Ò Ø Ò Êµ ÁÒØ
1 4 (s 2 +4) 2. s 4 = 10 7
 ¼ Å ÒÙØ Ò ÒÐ Þ Ø Ë Ø ½ Ö ÙÖ Ø Ö ÃÐ Ù ÙÖ Û Ö Ò ÒÐ Þ Ø ÚÓÒ ½¼ Å ÒÙØ Ò Û Öغ Ï Ö Ò ¹ Ö Ø Ù Ö Ø Á Ò Ò Ò Ø Ø ØØ Ø Ñ Ø Ö Ö ØÙÒ Ö Ù Ò ÞÙ ÒÒ Òº ÙØ Ø ÓÒ Ö Ø Û Ö Ò Ö ÑØ Ò Ù Ö Ö ÒÐ Þ Ø Ò ÖÐ Ë Ö ÖØ ËØ Ø ÐÐ Ö Øºµ Ù
¼ Å ÒÙØ Ò ÒÐ Þ Ø Ë Ø ½ Ö ÙÖ Ø Ö ÃÐ Ù ÙÖ Û Ö Ò ÒÐ Þ Ø ÚÓÒ ½¼ Å ÒÙØ Ò Û Öغ Ï Ö Ò ¹ Ö Ø Ù Ö Ø Á Ò Ò Ò Ø Ø ØØ Ø Ñ Ø Ö Ö ØÙÒ Ö Ù Ò ÞÙ ÒÒ Òº ÙØ Ø ÓÒ Ö Ø Û Ö Ò Ö ÑØ Ò Ù Ö Ö ÒÐ Þ Ø Ò ÖÐ Ë Ö ÖØ ËØ Ø ÐÐ Ö Øºµ Ù
 ÖÖ Ö Ø ÚÓÒ ÓÑÔÙØ Ö Ý Ø Ñ Ò Ë Ö ÔØ ÞÙÑ Ë Ñ Ò Ö ËÓÑÑ Ö Ñ Ø Ö ½ À Ö Ù Ö Å Ò Ö Ã Ö Ö Ü Ð ÈÖĐ Ð Ò Ö ÁÒ ÓÖÑ Ø ÍÒ Ú Ö ØĐ Ø Ã Ö Ð ÙØ ÖÒ ¹ ¼ Ã Ö Ð ÙØ ÖÒ Ï Ø ÖÑ ÒÝ ÁÒ ÐØ Á Ø Ò ÙØÞ ½ Ø Ò ÙØÞ ß Ö ØÐ Ä ½º½ ÏÓ Ö ÓÑÑØ
ÖÖ Ö Ø ÚÓÒ ÓÑÔÙØ Ö Ý Ø Ñ Ò Ë Ö ÔØ ÞÙÑ Ë Ñ Ò Ö ËÓÑÑ Ö Ñ Ø Ö ½ À Ö Ù Ö Å Ò Ö Ã Ö Ö Ü Ð ÈÖĐ Ð Ò Ö ÁÒ ÓÖÑ Ø ÍÒ Ú Ö ØĐ Ø Ã Ö Ð ÙØ ÖÒ ¹ ¼ Ã Ö Ð ÙØ ÖÒ Ï Ø ÖÑ ÒÝ ÁÒ ÐØ Á Ø Ò ÙØÞ ½ Ø Ò ÙØÞ ß Ö ØÐ Ä ½º½ ÏÓ Ö ÓÑÑØ
 Ò ĐÙ ÖÙÒ Ò ÒØÛ ÐÙÒ Ø Ò Ö ÁÒ ÓÖÑ Ø ÓÒ Ý Ø Ñ ÃÓÒÞ ÔØ Å Ø Ó Ò ÙÒ Ï Ö Þ Ù ÞÙÖ ÒØÛ ÐÙÒ ÒØ Ö ÖØ Ö ÁÒ ÓÖÑ Ø ÓÒ Ý Ø Ñ Ñ Ø Ò Ò ÍÑ Ð ß ÎÓÖÐ ÙÒ ÙÒØ ÖÐ Ò ß Öº Å ÖØ Ò Ò Ö ÙÒ Ó Ö ÁÒ Ø ØÙØ ĐÙÖ Ö ØÖ ÙÒ ¹ ÙØÓÑ Ø ÖÙÒ Å
Ò ĐÙ ÖÙÒ Ò ÒØÛ ÐÙÒ Ø Ò Ö ÁÒ ÓÖÑ Ø ÓÒ Ý Ø Ñ ÃÓÒÞ ÔØ Å Ø Ó Ò ÙÒ Ï Ö Þ Ù ÞÙÖ ÒØÛ ÐÙÒ ÒØ Ö ÖØ Ö ÁÒ ÓÖÑ Ø ÓÒ Ý Ø Ñ Ñ Ø Ò Ò ÍÑ Ð ß ÎÓÖÐ ÙÒ ÙÒØ ÖÐ Ò ß Öº Å ÖØ Ò Ò Ö ÙÒ Ó Ö ÁÒ Ø ØÙØ ĐÙÖ Ö ØÖ ÙÒ ¹ ÙØÓÑ Ø ÖÙÒ Å
ØÛ ÎØÓÒÐÝ ÐØÒ ÓÐÒÒ ÊÒÐÒ µ µ ¼ ¼ ¼ µ µ ¼ ¼ ¼ µ ¼ ¼ ¼ Û Ò ÐÐÑÒ Ú Úµ µ ÓÒ Øº µ ¼ Û µ µ ¼ ¼ ¼ ¼ ¼ ¼ ¼ µ ¼ ¼ ¼ µ ¼ ¼ ¼ µ ¼ ¼ ¼ ¼ ¼ ¼ ¼ Ø ¼ ¼ ¼ ¼ ¼ ¼ ¼ ¼ ¼
 ÀÐØÙÒ ÃÔÐ ØÞ Ù Ñ ÚØØÓÒ ØÞ Ò ÀÒ ÊÓØ ËØÒ ÒÙÔÔÒ Ã ÌÑÒØ ØÓÒÓÑ ÇÐÐ Ð ÎÐ µ º ØÛ ÎØÓÒÐÝ º ÒÒ Ò ÞÒØÐÒ ÃØÐÒ Ò Ò º ÐÒ ØÞ º ÑØÒ º Ò ÒØÞÐ ÒØ ÚØÓ º ÒØ Ò ÁÒÚÒØ º ÒÒ Ò ¹ÃØÐÒ Ò ÃÐ ÒØØ º ÜÞÒØÞØØ ÙÒ ÑØÒ º ØØ ØÞ ÚÓÒ ÃÔÐ
ÀÐØÙÒ ÃÔÐ ØÞ Ù Ñ ÚØØÓÒ ØÞ Ò ÀÒ ÊÓØ ËØÒ ÒÙÔÔÒ Ã ÌÑÒØ ØÓÒÓÑ ÇÐÐ Ð ÎÐ µ º ØÛ ÎØÓÒÐÝ º ÒÒ Ò ÞÒØÐÒ ÃØÐÒ Ò Ò º ÐÒ ØÞ º ÑØÒ º Ò ÒØÞÐ ÒØ ÚØÓ º ÒØ Ò ÁÒÚÒØ º ÒÒ Ò ¹ÃØÐÒ Ò ÃÐ ÒØØ º ÜÞÒØÞØØ ÙÒ ÑØÒ º ØØ ØÞ ÚÓÒ ÃÔÐ
PTBS Belastung unterschiedlicher Populationen
 Ù Ö È Ý ÓØÖ ÙÑ ØÓÐÓ ËØ Ø ÓÒ Ö ÃÐ Ò Ëغ ÁÖÑ Ò Ö Ò Ö ÖÙÒ Ö Ø Ä ÓÒ Ö ÃÖ ØÞ Ö Ö ÒÞ È ØÞ Ö È Ø Ö À ÒÞ È Ý ÓØÖ ÙÑ ØÓÐÓ ËØ Ø ÓÒ Ö ÃÐ Ò Ëغ ÁÖÑ Ò Ö ÈÖ Ò Ñ Ñ È Ý ÓØ Ö Ô ÓÖ ÙÒ Ö ÃÐ Ò ÙÒ ÈÓÐ Ð Ò Ö È Ý ØÖ ÙÒ È Ý ÓØ
Ù Ö È Ý ÓØÖ ÙÑ ØÓÐÓ ËØ Ø ÓÒ Ö ÃÐ Ò Ëغ ÁÖÑ Ò Ö Ò Ö ÖÙÒ Ö Ø Ä ÓÒ Ö ÃÖ ØÞ Ö Ö ÒÞ È ØÞ Ö È Ø Ö À ÒÞ È Ý ÓØÖ ÙÑ ØÓÐÓ ËØ Ø ÓÒ Ö ÃÐ Ò Ëغ ÁÖÑ Ò Ö ÈÖ Ò Ñ Ñ È Ý ÓØ Ö Ô ÓÖ ÙÒ Ö ÃÐ Ò ÙÒ ÈÓÐ Ð Ò Ö È Ý ØÖ ÙÒ È Ý ÓØ
2x 1 + 5x 2 = 29 8x 1 3x 2 = 1 x + y = a µ 3x 1 + 4x 2 + x 3 = 1. 2x 1 x 2 = 2 x 1 + 3x 3 = 5. µ 5a 2b + 3c 4d = 0 2a + b = 0 3c 2d = x
 Ù Ò ÑÑÐÙÒ ÞÙÖ ÎÓÖÐ ÙÒ Ò ÖÙÒ Ò Ñ Ø Ñ Ø Ö Ø Ò ËÓÑÑ Ö Ñ Ø Ö ¾¼¼ ÙÒ Ù Ò ÞÙÖ ÎÓÖÐ ÙÒ Ò ÖÙÒ Ò Ñ Ø Ñ Ø Ö Ø Ò Ð Ò Ò ËØÓ Ö Ö Ø Ò Ò Ø Ò Ö Ä ÖÚ Ö Ò Ø ÐØÙÒ Ò ÙÒ Ò ÞÙ Ò ÖÙÒ Ò Ä Ò Ö Ð Ö ÙÒ ÓÑ ØÖ ÙÒ Ò ÞÙ Ò ÖÙÒ Ò Ò ÐÝ
Ù Ò ÑÑÐÙÒ ÞÙÖ ÎÓÖÐ ÙÒ Ò ÖÙÒ Ò Ñ Ø Ñ Ø Ö Ø Ò ËÓÑÑ Ö Ñ Ø Ö ¾¼¼ ÙÒ Ù Ò ÞÙÖ ÎÓÖÐ ÙÒ Ò ÖÙÒ Ò Ñ Ø Ñ Ø Ö Ø Ò Ð Ò Ò ËØÓ Ö Ö Ø Ò Ò Ø Ò Ö Ä ÖÚ Ö Ò Ø ÐØÙÒ Ò ÙÒ Ò ÞÙ Ò ÖÙÒ Ò Ä Ò Ö Ð Ö ÙÒ ÓÑ ØÖ ÙÒ Ò ÞÙ Ò ÖÙÒ Ò Ò ÐÝ
Ñ Ð ØÖº Ø ÒÚ Ö Ö Ñ À ÁÆÀ ÄÌËÎ Ê Á ÀÆÁË ÁÒ ÐØ Ú ÖÞ Ò ½ Ò ÖÙÒ ½½ ½º½ Ö Ð º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½½ ½º¾ Ó
 ¹ÌÖÙ Ø ÐÐ Ø Ö Ë Ö Ø Ý Ø Ñ Ñ Ð ØÖÓÒ Ò Ø ÒÚ Ö Ö Ñ À Ä Ò ØÖ Ö À ÙÔØ ØÖ ¹½¼ ¼ Ï Ò Ì Ð ½µ ½ ¾½ ½ ¹ ¼ Ü ½µ ½ ¾½ ½ ¹ ¼ ØØÔ»»ÛÛÛº ¹ØÖ٠غ Ø ºØÖÙ Ø ÖØ Þ ÖÙÒ Ö ØÐ Ò ÖØ Ø ÈÖ Ø ËØ Ø Ñ Òص Ö ÕÙ Ð Þ ÖØ ÖØ Ø º Ò ÔÖ Ñ
¹ÌÖÙ Ø ÐÐ Ø Ö Ë Ö Ø Ý Ø Ñ Ñ Ð ØÖÓÒ Ò Ø ÒÚ Ö Ö Ñ À Ä Ò ØÖ Ö À ÙÔØ ØÖ ¹½¼ ¼ Ï Ò Ì Ð ½µ ½ ¾½ ½ ¹ ¼ Ü ½µ ½ ¾½ ½ ¹ ¼ ØØÔ»»ÛÛÛº ¹ØÖ٠غ Ø ºØÖÙ Ø ÖØ Þ ÖÙÒ Ö ØÐ Ò ÖØ Ø ÈÖ Ø ËØ Ø Ñ Òص Ö ÕÙ Ð Þ ÖØ ÖØ Ø º Ò ÔÖ Ñ
ÍÒ ÓÖÑ ÓÒ ØÖ Òع Ö Ñ ÛÓÖ ÓÖ Ø Î Ö Ø ÓÒ Ó ÁÒ Ò Ø ËØ Ø ËÝ Ø Ñ ÁËË ÊÌ ÌÁÇÆ ÞÙÖ ÖÐ Ò ÙÒ Ö Ó ØÓÖ Ö ÁÒ Ò ÙÖÛ Ò Ø Ò Öº¹ÁÒ ºµ Ö Æ ØÙÖÛ Ò ØÐ ¹Ì Ò Ò ÙÐØĐ Ø Á Ö
 ÍÒ ÓÖÑ ÓÒ ØÖ Òع Ö Ñ ÛÓÖ ÓÖ Ø Î Ö Ø ÓÒ Ó ÁÒ Ò Ø ËØ Ø ËÝ Ø Ñ ÁËË ÊÌ ÌÁÇÆ ÞÙÖ ÖÐ Ò ÙÒ Ö Ó ØÓÖ Ö ÁÒ Ò ÙÖÛ Ò Ø Ò Öº¹ÁÒ ºµ Ö Æ ØÙÖÛ Ò ØÐ ¹Ì Ò Ò ÙÐØĐ Ø Á Ö ÍÒ Ú Ö ØĐ Ø Ë ÖÐ Ò ÚÓÒ ËÙÔÖ Ø ÅÙ ÓÔ Ý Ý Ë Ö ÖĐÙ Ò ¾¼¼¼
ÍÒ ÓÖÑ ÓÒ ØÖ Òع Ö Ñ ÛÓÖ ÓÖ Ø Î Ö Ø ÓÒ Ó ÁÒ Ò Ø ËØ Ø ËÝ Ø Ñ ÁËË ÊÌ ÌÁÇÆ ÞÙÖ ÖÐ Ò ÙÒ Ö Ó ØÓÖ Ö ÁÒ Ò ÙÖÛ Ò Ø Ò Öº¹ÁÒ ºµ Ö Æ ØÙÖÛ Ò ØÐ ¹Ì Ò Ò ÙÐØĐ Ø Á Ö ÍÒ Ú Ö ØĐ Ø Ë ÖÐ Ò ÚÓÒ ËÙÔÖ Ø ÅÙ ÓÔ Ý Ý Ë Ö ÖĐÙ Ò ¾¼¼¼
 Ò ĐÙ ÖÙÒ Ò ÒØÛ ÐÙÒ Ø Ò Ö ÁÒ ÓÖÑ Ø ÓÒ Ý Ø Ñ ÃÓÒÞ ÔØ Å Ø Ó Ò ÙÒ Ï Ö Þ Ù ÞÙÖ ÒØÛ ÐÙÒ ÒØ Ö ÖØ Ö ÁÒ ÓÖÑ Ø ÓÒ Ý Ø Ñ Ñ Ø Ò Ò ÍÑ Ð ß ÎÓÖÐ ÙÒ ÙÒØ ÖÐ Ò ß Öº Å ÖØ Ò Ò Ö ÙÒ Ó Ö ÁÒ Ø ØÙØ ĐÙÖ Ö ØÖ ÙÒ ¹ ÙØÓÑ Ø ÖÙÒ Å
Ò ĐÙ ÖÙÒ Ò ÒØÛ ÐÙÒ Ø Ò Ö ÁÒ ÓÖÑ Ø ÓÒ Ý Ø Ñ ÃÓÒÞ ÔØ Å Ø Ó Ò ÙÒ Ï Ö Þ Ù ÞÙÖ ÒØÛ ÐÙÒ ÒØ Ö ÖØ Ö ÁÒ ÓÖÑ Ø ÓÒ Ý Ø Ñ Ñ Ø Ò Ò ÍÑ Ð ß ÎÓÖÐ ÙÒ ÙÒØ ÖÐ Ò ß Öº Å ÖØ Ò Ò Ö ÙÒ Ó Ö ÁÒ Ø ØÙØ ĐÙÖ Ö ØÖ ÙÒ ¹ ÙØÓÑ Ø ÖÙÒ Å
Ð ÖÙÒ ½ ÁÒØ ÖÔÓÐ Ø ÓÒ ÔÓÐÝÒÓÑ Ð ËÔÐ Ò ¾ ÆÙÑ Ö ÁÒØ Ö Ø ÓÒ ÃÐ Æ ÛØÓÒ¹ ÓØ Ï Ø Ö ÉÙ Ö ØÙÖ ÓÖÑ ÐÒ ¾» ¾
 ÁÒØ ÖÔÓÐ Ø ÓÒ ÒÙÑ Ö ÁÒØ Ö Ø ÓÒ º ÎÓÖÐ ÙÒ ½ ¼ ¼¼ ÆÙÑ Ö Å Ø Ó Ò Á º Ö Ò ÙÒ º À Ù Ò Ð ¾ º Å ¾¼½ ½» ¾ Ð ÖÙÒ ½ ÁÒØ ÖÔÓÐ Ø ÓÒ ÔÓÐÝÒÓÑ Ð ËÔÐ Ò ¾ ÆÙÑ Ö ÁÒØ Ö Ø ÓÒ ÃÐ Æ ÛØÓÒ¹ ÓØ Ï Ø Ö ÉÙ Ö ØÙÖ ÓÖÑ ÐÒ ¾» ¾ ÁÒØ ÖÔÓÐ
ÁÒØ ÖÔÓÐ Ø ÓÒ ÒÙÑ Ö ÁÒØ Ö Ø ÓÒ º ÎÓÖÐ ÙÒ ½ ¼ ¼¼ ÆÙÑ Ö Å Ø Ó Ò Á º Ö Ò ÙÒ º À Ù Ò Ð ¾ º Å ¾¼½ ½» ¾ Ð ÖÙÒ ½ ÁÒØ ÖÔÓÐ Ø ÓÒ ÔÓÐÝÒÓÑ Ð ËÔÐ Ò ¾ ÆÙÑ Ö ÁÒØ Ö Ø ÓÒ ÃÐ Æ ÛØÓÒ¹ ÓØ Ï Ø Ö ÉÙ Ö ØÙÖ ÓÖÑ ÐÒ ¾» ¾ ÁÒØ ÖÔÓÐ
Ö Ø Ö ÖÙÒ Ä Ú Ö ÐØ Ò ÓÜ Ö Æ ÒÓÔ ÖØ Ð Ì Ç ¾ ÖÇ ¾ Ë Ç ¾ µ Ò Û Ö Ò ËÝ Ø Ñ Ò ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö ÓØÓÖ Ö ÖÙÑ Ò ØÙÖ Ð ÙÑ Öº Ö Öº Ò Øºµ ÚÓÖ Ð Ø Ñ Ê Ø Ö
 Ö Ø Ö ÖÙÒ Ä Ú Ö ÐØ Ò ÓÜ Ö Æ ÒÓÔ ÖØ Ð Ì Ç ¾ ÖÇ ¾ Ë Ç ¾ µ Ò Û Ö Ò ËÝ Ø Ñ Ò ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö ÓØÓÖ Ö ÖÙÑ Ò ØÙÖ Ð ÙÑ Öº Ö Öº Ò Øºµ ÚÓÖ Ð Ø Ñ Ê Ø Ö Ñ ¹ ÓÛ Ò ØÐ Ò ÙÐØØ Ö Ö Ö ¹Ë ÐÐ Ö¹ÍÒ Ú Ö ØØ Â Ò ÚÓÒ
Ö Ø Ö ÖÙÒ Ä Ú Ö ÐØ Ò ÓÜ Ö Æ ÒÓÔ ÖØ Ð Ì Ç ¾ ÖÇ ¾ Ë Ç ¾ µ Ò Û Ö Ò ËÝ Ø Ñ Ò ÖØ Ø ÓÒ ÞÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö ÓØÓÖ Ö ÖÙÑ Ò ØÙÖ Ð ÙÑ Öº Ö Öº Ò Øºµ ÚÓÖ Ð Ø Ñ Ê Ø Ö Ñ ¹ ÓÛ Ò ØÐ Ò ÙÐØØ Ö Ö Ö ¹Ë ÐÐ Ö¹ÍÒ Ú Ö ØØ Â Ò ÚÓÒ
Ë Ð Ö Ö Ø ÚÓÒ ÐÙ Ø Ö¹ Ø Ý Ø Ñ Ò ÙÖ Î ÖØ ÐÙÒ Ö Å Ø Ø Ò ÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö Ò Ó ØÓÖ Ö ÁÒ Ò ÙÖÛ Ò Ø Ò Ö ÙÐØØ Ö ÁÒ ÓÖÑ Ø Ö ÍÒ Ú Ö ØØ Ã ÖÐ ÖÙ Ì Ò ÀÓ ÙÐ µ Ò Ñ
 Ë Ð Ö Ö Ø ÚÓÒ ÐÙ Ø Ö¹ Ø Ý Ø Ñ Ò ÙÖ Î ÖØ ÐÙÒ Ö Å Ø Ø Ò ÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö Ò Ó ØÓÖ Ö ÁÒ Ò ÙÖÛ Ò Ø Ò Ö ÙÐØØ Ö ÁÒ ÓÖÑ Ø Ö ÍÒ Ú Ö ØØ Ã ÖÐ ÖÙ Ì Ò ÀÓ ÙÐ µ Ò Ñ Ø ÖØ Ø ÓÒ ÚÓÒ Ù Ó Å ÐÔÓ Ð Ù ËÓÐ Ò Ò Ì Ö Ñ Ò Ð Ò ÈÖ
Ë Ð Ö Ö Ø ÚÓÒ ÐÙ Ø Ö¹ Ø Ý Ø Ñ Ò ÙÖ Î ÖØ ÐÙÒ Ö Å Ø Ø Ò ÙÖ ÖÐ Ò ÙÒ Ñ Ò Ö Ò Ó ØÓÖ Ö ÁÒ Ò ÙÖÛ Ò Ø Ò Ö ÙÐØØ Ö ÁÒ ÓÖÑ Ø Ö ÍÒ Ú Ö ØØ Ã ÖÐ ÖÙ Ì Ò ÀÓ ÙÐ µ Ò Ñ Ø ÖØ Ø ÓÒ ÚÓÒ Ù Ó Å ÐÔÓ Ð Ù ËÓÐ Ò Ò Ì Ö Ñ Ò Ð Ò ÈÖ
ÁÒ ÐØ Ú ÖÞ Ò ½ Ò ÖÙÒ ½ ½º½ ÅÓØ Ú Ø ÓÒ º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º º ½ ½º¾ à ÖÞ Ø ¹Ï ¹ Ð ÓÖ Ø Ñ Ò º º
 Ö ÒÙÒ ÖÞ Ø Ö È ÙÒØ Ö ØÙÒ ÚÓÒ Ú Ö ÓØ Ò Ã Ö ÐÐ Å ÐÐ Ö ËØÙ Ò Ö Ø Ñ ÁÒ Ø ØÙØ Ö Ì ÓÖ Ø ÁÒ ÓÖÑ Ø Ä Ö ØÙ Ð ÈÖÓ º Öº ÓÖÓØ Ï Ò Ö ÍÒ Ú Ö ØØ Ã ÖÐ ÖÙ ÙÐØØ Ö ÁÒ ÓÖÑ Ø ¾ º Ç ØÓ Ö ¾¼¼ ÁÒ ÐØ Ú ÖÞ Ò ½ Ò ÖÙÒ ½ ½º½ ÅÓØ Ú
Ö ÒÙÒ ÖÞ Ø Ö È ÙÒØ Ö ØÙÒ ÚÓÒ Ú Ö ÓØ Ò Ã Ö ÐÐ Å ÐÐ Ö ËØÙ Ò Ö Ø Ñ ÁÒ Ø ØÙØ Ö Ì ÓÖ Ø ÁÒ ÓÖÑ Ø Ä Ö ØÙ Ð ÈÖÓ º Öº ÓÖÓØ Ï Ò Ö ÍÒ Ú Ö ØØ Ã ÖÐ ÖÙ ÙÐØØ Ö ÁÒ ÓÖÑ Ø ¾ º Ç ØÓ Ö ¾¼¼ ÁÒ ÐØ Ú ÖÞ Ò ½ Ò ÖÙÒ ½ ½º½ ÅÓØ Ú
 ÁÈÄÇÅ Ê ÁÌ Î Ö Ð Ú Ö Ò Ö ÊÓØÓÖ ØÖÙ ØÙÖ Ò Ò Ô Þ Ø Ú Ò Ö ÑÓÑ ÒØ Ò ÓÖ Ù ĐÙ ÖØ Ñ ÁÒ Ø ØÙØ ĐÙÖ Ò Û Ò Ø Ð ØÖÓÒ ÙÒ ÉÙ ÒØ Ò Ð ØÖÓÒ Ö Ì Ò Ò ÍÒ Ú Ö ØĐ Ø Ï Ò ÙÒØ Ö ÒÐ ØÙÒ ÚÓÒ ÍÒ ÚºÈÖÓ º Ôк¹ÁÒ º ÖºØ Òº ÓÖ Ö ÙÖ Ôк¹ÁÒ
ÁÈÄÇÅ Ê ÁÌ Î Ö Ð Ú Ö Ò Ö ÊÓØÓÖ ØÖÙ ØÙÖ Ò Ò Ô Þ Ø Ú Ò Ö ÑÓÑ ÒØ Ò ÓÖ Ù ĐÙ ÖØ Ñ ÁÒ Ø ØÙØ ĐÙÖ Ò Û Ò Ø Ð ØÖÓÒ ÙÒ ÉÙ ÒØ Ò Ð ØÖÓÒ Ö Ì Ò Ò ÍÒ Ú Ö ØĐ Ø Ï Ò ÙÒØ Ö ÒÐ ØÙÒ ÚÓÒ ÍÒ ÚºÈÖÓ º Ôк¹ÁÒ º ÖºØ Òº ÓÖ Ö ÙÖ Ôк¹ÁÒ
