Lebensversicherungsmathematik Vorlesung am Institut für Mathematische Stochastik der Universität Hannover
|
|
|
- Rudolf Adler
- vor 8 Jahren
- Abrufe
Transkript
1 Lebensversicherungsmathematik Vorlesung am Institut für Mathematische Stochastik der Universität Hannover von Dr. Matthias Brake Sommersemester
2 INHALTSVERZEICHNIS 2 Inhaltsverzeichnis 1 Einleitung Was ist eine Versicherung? Einteilungsprinzipien für Versicherungsformen Aufgaben der Versicherungsmathematik Deterministische Modelle Lebensversicherung Elementare Finanzmathematik Die diskontinuierliche Methode Beispiele für Verzinsung kontinuierliche Methode Beispiele für Verzinsung Effektiver und nomineller Zinssatz Zeitrenten und ihre Barwerte von zinsbehafteten Zahlungen Zukünftige Lebenserwartung eines x-jährigen Einleitung vollständige Restlebenserwartung eines x-jährigen Sterbeintensität Stationaritätsbedingung Diskretisierung: ganzzahlig gestutzte zukünftige Verweildauern Sterbetafeln Arten von Sterbetafeln Vorgehensweise beim Herleiten einer Sterbetafel In der Praxis verwendete Sterbetafeln Leistungen und Barwerte Einleitung, Definition und Beispiele Berechnung von erwarteten Barwerten bei unterjährlicher Zahlungsweise Kommutationszahlen Einleitung und Definition Versicherungen mit ausschließlich Erlebensfallcharakter Versicherungen mit ausschließlich Todesfallcharakter Prämien Modellvoraussetzungen der klassischen LV Nettoprämie = Nettobeiträge Jahresnettoprämien Unterjährliche Renten und unterjährliche Beiträge Gebräuchliche Näherungsverfahren zur Berechnung unterjährlicher Beiträge (nicht in der Vorlesung behandelt) Kosten und Bruttobeiträge Kostenschlüsselung Allgemeine Berechnung der ausreichenden Prämie
3 INHALTSVERZEICHNIS Tarif- und Bruttoprämie Der Gleichbehandlungsgrundsatz 63 8 Der Verantwortliche Aktuar 65 9 Deckungsrückstellungen in der LV Einleitung Das prospektive Deckungskapital Klassische Lebensversicherung Rekursionsformel und retrospektive Darstellung Zerlegung der Nettoprämie in Spar- und Risikoanteil Gezillmerte und ausreichende Deckungsrückstellung Formeln für das gezillmerte und ausreichende Deckungskapital Bilanzdeckungsrückstellung Überschussbeteiligung in der Lebensversicherung Bilanz und GuV: Bilanz Die Gewinn- und Verlustrechnung (GuV) eines Lebensversicherers Überschussentstehung: Die Ursachen des Überschusses und seine Quellen. Kontributionsgleichung Kontributionsgleichung Überschussverteilungssystem Natürliche Dividendensysteme Mechanische Dividendensystem Überschussverwendungsarten Schlussüberschussbeteiligung Finanzierbarkeit der Überschussbeteiligung, Profit-Testing Varianten des Finanzierbarkeitsnachweises Rechtliche Rahmenbedingungen Rechtliche Rahmenbedingungen der Prämienkalkulation und der Wahl der Rechnungsgrundlagen Gesetzliche Vorgaben zur Berechnung von Deckungsrückstellungen Garantiewerte Aktuarverordnung, Erläuterungsbericht 109
4 1 EINLEITUNG 4 1 Einleitung 1.1 Was ist eine Versicherung? Aus Sicht des Versicherungsnehmers (VN): Mittel seiner individuellen Risikopolitik Aus Sicht des Versicherers (VR): Schutzversprechen als produziertes Wirtschaftsgut. Aus gemeinsamer Sicht: Finanzieller Risikotransfer vom VN auf den VR gegen Entgeltzahlung. Es sind mehrere Teilgebiete betroffen: 1. ökonomisches Phänomen 2. juristisches Phänomen 3. mathematisches Phänomen 4. medizinisches und technisches Phänomen etc. Die Versicherungswissenschaft ist somit interdisziplinär. Definition (Farny, 1988, S. 870) Versicherung ist die Deckung eines im einzelnen ungewissen, insgesamt geschätzten Mittelbedarfs auf der Grundlage des Risikoausgleichs im Kollektiv und in der Zeit. Es gibt drei Hauptmerkmale des Versicherungsgeschäftes: 1. Finanzierung aus den Entgelten, 2. Unsicherheit hinsichtlich des versicherten Ereignisses, 3. Risikokalkulation und Risikoausgleich. Der letzte Punkt stellt die Abgrenzung zum Bankgeschäft dar. Bei diesen Hauptmerkmalen bleibt die Unsicherheit bei den Prämienzahlungen zunächst unberücksichtigt. Die Unsicherheit bezieht sich hier nur auf das Risiko. Dabei besteht die Unsicherheit in Bezug auf: Tatsache des Eintritts des Risikos (Eintritt ja oder nein?), Zeitpunkt des Eintritts, Qualität des Eintrittes des Risikos (Art und Ausmaß). Bei der Modellierung der Unsicherheit sind zufällige Momente von Bedeutung. Hier kommt die Stochastik (Wahrscheinlichkeitstheorie und Statistik) ins Spiel.
5 1 EINLEITUNG 5 Fazit: Die Stochastik ist Basis der Versicherungsmathematik! 1.2 Einteilungsprinzipien für Versicherungsformen Die folgenden Einteilungsprinzipien für Versicherungsformen sind praxisorientiert und historisch gewachsen. Sie sind nicht disjunkt. Eine Einteilung kann beispielsweise erfolgen nach Art des versicherten Gegenstandes Personenversicherung Sachversicherung Vermögensversicherung (z.b. Haftpflicht) nach Art der Versicherungsleistung (s. VVG) Summenversicherung (fester Geldbetrag nach Eintritt des Versicherungsfalles ohne Nachweis eines konkreten Schadens) Schadenversicherung (vertragsmäßiger Ersatz des eingetretenen Schadens nach Art der versicherten Gefahr (Risikoart) Einbruchdiebstahlversicherung Feuerversicherung Glasbruchversicherung etc. Diese Einteilungsprinzipien ziehen eine Bildung von Versicherungszweigen und -sparten nach sich, welche wichtig sind für: die Kalkulation einer risikogerechten Prämie, die Vertragsverwaltung und die Ergebnisermittelung im Rahmen der Rechnungslegung. In dieser Vorlesung befassen wir uns mit der Personenversicherung und hier vorwiegend mit der Lebensversicherung (LV). 1.3 Aufgaben der Versicherungsmathematik Bereitstellung von mathematischen Modellen und Methoden, die die quantifizierbaren Sachverhalte des Versicherungswesens beschreiben oder erklären oder
6 1 EINLEITUNG 6 mit deren Hilfe Entscheidungproblem der Versicherungswirtschaft gelöst werden. Anmerkung: Recht abstrakte Umschreibung der Aufgaben der Versicherungsmathematik. Man unterscheidet zunächst zwischen drei (nicht disjunkten) Zweigen der Versicherungsmathematik: Personenversicherungsmathematik Schadenversicherungsmathematik Finanzmathematik Die Protagonisten in der Versicherungsmathematik sind die Versicherungsmathematiker und Aktuare (Begriffe häufig synonym verwendet). Die Hauptaufgaben der Versicherungsmathematik bestehen aus: mathematische Beschreibung des versicherten Risikos bis hin zur Erstellung von statistisch gesicherten Rechnungsgrundlagen (LV: Schätzung und Vertafelung von Ausscheide- und Überlebenswahrscheinlichkeiten) Tarifierung und Prämienkalkulation (LV: Berechnung von Barwerten, Nettoprämien, Kosten, Deckungskapitalien etc.) versicherungstechnische Analysen (LV: Überschussermittelung, Überschusszerlegung nach Gewinnquellen, Renditeberechnungen etc.) Risikoteilung VN - VR - Rückversicherer (hier: nicht behandelt) Berechnung von Rückstellungen für die Schadenabwicklung, von Schwankungsrückstellungen und Sicherheitsreserven (Solvabilitätsüberlegungen) (hier: nicht behandelt) Überlegungen zur Beschreibung des Zinsrisikos und zur Steuerung von Kapitalanlagen (hier: nur am Rande behandelt) In diese Probleme spielen häufig außermathematische Überlegungen, zum Beispiel betriebswirtschaftlicher oder steuerlicher Natur, hinein. Fazit: Ein Versicherungsmathematiker bzw. Aktuar ist folglich nicht nur ein Produktentwickler im Versicherungswesen, sondern (mit-)verantwortlich für viele Belange des VR. 1.4 Deterministische Modelle In der Praxis der Personenversicherung werden in der Regel deterministische Modelle und Methoden verwendet. Aus wissenschaftstheoretischer Sicht sind
7 1 EINLEITUNG 7 dies Erklärungsmodelle: Deterministische Modelle: Eingangs- und Zielgrößen werden als deterministisch angesehen (LV: Zins, Kosten etc.) oder durch ihre Erwartungswerte ersetzt (rechnungsmäßige = erwartete Anzahl von Leistungsfällen, erwartete Schadenhöhen) Eingangsgrößen bestimmen / erklären Zielgrößen im Ergebnis reines Mittelwertkalkül Nachteile deterministischer Modelle: Modell ungeeignet, wenn Zufallsschwankungen um den Mittelwert von Bedeutung sind (z.b. bei der Betrachtung von Großschäden in der Schadenversicherungsmathematik) keine fundierte Risikobewertung möglich keine Berechnung von Sicherheitszuschlägen möglich. Man unterscheidet bei der deterministischen Methode zwischen der kontinuierlichen Methode und der diskontinuierlichen Methode: diskontinuierlich = diskret höchstens abzählbare Menge von Zeitpunkten (meistens äquidistant), zu denen die relevanten Ereignisse auftreten oder registriert werden (ggf. Diskretisierung erforderlich) kontinuierlich = stetig Verteilung der Zufallsvariablen, die Zeiten modellieren, besitzen (Lesbuege-) Dichten. In der Praxis treten häufig gemischte Modelle auf: Zeitvariablen, die Gegenstand vertraglicher Regelungen und Einschränkungen sind (z.b. Prämienzahlungen, Leistungszeiten, Stornozeiten etc.) sind in der Regel diskret. biometrische Variablen (z.b. Todesfallzeitpunkt, Individualisierungszeitpunkt etc.) sind in der Regel kontinuierlich. Die Unterscheidung zwischen diskontinuierlichen und kontinuierlichen Modellen ist historisch gewachsen. In der Praxis wird häufig die diskontinuierliche Methode, in der Theorie wird häufig die kontinuierliche Methode verwendet. In dieser Vorlesung wird vorwiegend die diskontinuierliche Methode angewendet! 1.5 Lebensversicherung Charakter einer Lebensversicherung: Langfristiges Versicherungsverhältnis!
8 1 EINLEITUNG 8 Folgerung: Der Preis der Versicherung muss sorgfältig und vorausschauend bestimmt werden. Die verschiedenen Lebensversicherungsverträge kann man nach unterschiedlichen Kriterien einteilen: 1. Unterscheidung nach dem versicherten Ereignis Versicherungen auf das Leben oder den Tod Erwerbsunfähigkeitsversicherungen Krankenversicherungen (hier nicht behandelt) 2. Unterscheidung nach Erbringung der Leistung Versicherung auf das Leben oder den Tod Altersrente (mit Garantiezeit) Erlebensfallversicherung (lebenslängliche) Todesfallversicherung gemischte Versicherung (klassisches Beispiel!) Witwen- / Witwerrente Waisenrente Versicherung auf zwei Leben Rückgewähr (Zusatzversicherung, Todesfallversicherung in Höhe der bezahlten Beiträge) Erwerbsunfähigkeitsversicherung Invalidenrente Invaliditätskapital Prämienbefreiung Invalidenkinderrente 3. Unterscheidung nach versicherbaren Risiken Todesfallrisiko Unfalltodrisiko Erlebensfallrisiko Berufsunfähigkeitsrisiko, Erwerbsunfähigkeitsrisik, Arbeitsunfähigkeitsrisik Pflegebedürftigkeitsrisiko
9 2 ELEMENTARE FINANZMATHEMATIK 9 Heiratsrisiko Arbeitslosigkeitsrisiko Finanzierungsarten: Die Finanzierung in der Lebensversicherung erfolgt in der Regel die laufende Prämienzahlung oder gegen Zahlung eines Einmalbeitrages. Das Hauptprinzip bei der Berechnung der Versicherungsprämien ist das Äquivalenzprinzip. Es besagt, dass der Wert der Leistungen des Versicherers dem Wert der Leistungen des Versicherungsnehmers entsprechen muss. 2 Klassische oder elementare Finanzmathematik: Der Zins als Rechnungsgrundlage Neben der Wahrscheinlichkeitstheorie (Sterbewahrscheinlichkeit, Ausscheideordnung etc.) spielt der Zins als weitere Rechnungsgrundlage eine entscheidende Rolle in der Lebensversicherungsmathematik. Man unterscheidet wie in der Versicherungsmathematik üblich zwischen der diskontinuierlichen Methode und der kontinuierlichen Methode. Dies bezieht sich auf die Änderung des Kapitals bzw. auf den Zeitpunkt der Zinsgutschrift. Während der gesamten Vorlesung gehen wir davon aus, dass der Zins nicht stochastisch, sondern deterministisch ist. Ein stochastischer Zins ist Gegenstand der Finanzmathematik (stochastische Prozesse, Brownsche Bewegung). 2.1 Die diskontinuierliche Methode Der Zinssatz wird für einen Basiszeitraum festgelegt. Der Zins wird immer nur am Ende einer bestimmten Periode gutgeschrieben. Das Kapital ändert sich in diesen Punkten sprunghaft. Dabei sind nicht Gründe für die Zinszahlungen interessant, sondern nur die Auswirkungen der Zinszahlbuchungen auf die Änderung des Kapital (Zinstheorie ist Gegenstand der Wirtschaftswissenschaften). Einige wichtige Begriffe: Konversionsperiode: Zeitraum, an dessen Ende die Zinsen gutgeschrieben werden. Oft beträgt die Länge einer Konversionsperiode ein Jahr.
10 2 ELEMENTARE FINANZMATHEMATIK 10 Die Zinszuschreibung erfolgt nur zu bestimmten festen Zeiten, oft in gleichlangen Konversionsperioden. Am Ende dieser Konversionsperiode steigt das Kapital sprunghaft. effektiver Zins: Wenn die Konversionsperiode mit der Basiszeiteinheit übereinstimmt, dann heisst der Zins, der in dieser Zeiteinheit auf das Kapital 1 gezahlt wird, effektiver Zins. Die Angabe der Basiszeiteinheit, auf die sich der effektive Zins bezieht, ist somit immer erforderlich Beispiele für Verzinsung Sei i ein effektiver jährlicher Zinssatz. Zur Vereinfachung sei angenommen, dass i für alle Jahre identisch ist. Wir betrachten ein Bankkonto oder einen Fonds und ein Anfangskapital F 0, das investiert wird. Am Ende des Jahres k wird ein zusätzlicher Betrag r k investiert, k = 1,..., n. Frage: Wie sieht das Guthaben am Ende des n-ten Jahres aus? Sei F k das Guthaben am Ende des Jahres k, einschließlich der Zahlung r k. Dann gilt: F k = F k 1 + if k 1 + r k, k = 1,..., n F k (1 + i)f k 1 = r k, k = 1,..., n Multipliziert man die untere Gleichung mit (1 + i) n k und summiert über alle k, ergibt sich: n F n = (1 + i) n F 0 + (1 + i) n k r k. (1) k=1 Zusammengesetzte Verzinsung (Zinseszins) Interpretation: Das Kapital am Ende eines Zeitintervalls ist der verzinste Wert des Anfangskapitals plus der Summe der verzinsten Zwischenzahlungen. Vielfach ist man auch an dem umgekehrten Vorgang interessiert. Wir definieren r := 1 + i (2) v := i. (3) r nennt man Aufzinsungsfaktor und v den Diskontierungsfaktor. Dann gilt:
11 2 ELEMENTARE FINANZMATHEMATIK 11 n (1) v n F n = F 0 + v k r k. Der Zuwachs des Kapitals ergibt sich aus F k F k 1 = if k 1 + r k zu k=1 n F n F 0 = if k 1 + n k=1 k=1 als Summe der gutgeschriebenen Zinsen und der Gesamteinzahlung. r k Wir definieren weiter: d := 1 v. (4) d nennt man den jährlichen Diskont oder Vorauszins. Bemerkung Es gelten folgende Beziehungen: a) iv = d (5) b) dr = i. (6) Beweis: siehe Übung. Als weiteres Beispiel betrachten wir die einfach Verzinsung: Sei dazu die Konversionsperiode ein Jahr, i der verwendete Zinssatz und F 0 das Anfangskapital. Es werden am Ende jeder Konversionsperiode nur die Zinsen auf das Anfangskapital gezahlt. Am Ende des n-ten Versicherungsjahres liegt dann folgendes Kapital vor: F n = F 0 + if 0... if } {{ } 0 = F 0 (1 + ni) Aufzinsung. n mal Analog erhält man für die Abzinsung bei der einfachen Verzinsung: F 0 = F n 1 + ni. 2.2 kontinuierliche Methode Das Kapital wächst nicht sprunghaft zu gewissen Zeitpunkten, sondern stetig in jedem Zeitpunkt.
12 2 ELEMENTARE FINANZMATHEMATIK Beispiele für Verzinsung i) Einfache Verzinsung: Sei K(t) das Kapital zum Zeitpunkt t und K(0) das Startkapital. Dann gilt: K(t) = K(0)(1 + ti) K(0) = K(t) 1+ti Aufzinsung Abzinsung ii) zusammengesetzte Verzinsung (auch geometrische oder mathematische Verzinsung): K(t) = K(0)(1 + i) t = K(0)r t Aufzinsung K(0) = K(t) (1+i) t = K(t)v t Abzinsung Neben der reinen diskontinuierlichen Methode und der reinen kontinuierliche Methoden betrachtet man auch die sogenannte iii) gemischte Verzinsung: Sei n t < n + 1. Dann gilt mit s = t n: K(t) := K(0)(1 + i) n (1 + s i). Die gemischte Verzinsung gehört zu den kontinuierlichen Methoden. Es handelt sich hier um die zusammengesetzte Verzinsung für die vollendeten Konversionsperioden und um die einfache Verzinsung für die angebrochene Konversionsperiode. iv) kaufmännische Verzinsung: Sei n t < n + 1. Dann gilt mit s = t n: K(t) = r n i(1 s). Die kaufmännischen Verzinsung gehört zu den kontinuierlichen Methoden. Es handelt sich hier um die zusammengesetzte Verzinsung bis zum Ende der laufenden Konversionsperioden und um die einfache Abzinsung auf den Zeitpunkt t. Allgemein lassen sich die Verzinsungen durch folgendes Modell zusammenfassen:
13 2 ELEMENTARE FINANZMATHEMATIK 13 Definition Sei B R + der Anfangswert und K : [0; ) [1; ) eine monoton nicht fallende, rechtsseitig stetige Funktion mit K(0) = 1. Dann heißt K Kapitalfunktion oder Aufzinsungsfunktion. Die Größe S := B K(t) ist der Endwert des Startkapitals B zum Zeitpunkt t 0. r = K(1) heißt Aufzinsungsfaktor für das erste Jahr. i = r 1 heißt Zinssatz, v := 1 r heißt Abzinsungs- oder Diskontierungsfaktor und d := 1 v heißt der jährliche Diskont (Vorauszins). Bemerkung i) K ist eine endliche Verteilungsfunktion. ii) Geht man von einer Konversionsperiode von einem Jahr aus, so lassen sich die bisher genannten Verzinsungen wie folgt darstellen: a) einfach / lineare Verzinsung: K(t) = K E (t) = 1 + [t]i diskontinuierlich K(t) = K E (t) = 1 + ti kontinuierlich b) zusammengesetzte (geometrische) Verzinsung: K(t) = K Z (t) = r [t] diskontinuierlich K(t) = K Z (t) = r t kontinuierlich c) gemischte Verzinsung: K(t) = K G (t) = r [t] (1 + i(t [t])) kontinuierlich d) kaufmännische Verzinsung: K(t) = K K (t) = r [t]+1 1+i(1 (t [t])) kontinuierlich Lemma Bei kontinuierlicher Verzinsung gelten: a) K Z (t) K G (t) K Z ([t] + 1) b) K G (t) K Z (t) = (i δ)t + O(t 2 ) (t 0) mit K Z (0) = δ. c) K Z ([t]) K K (t) K Z (t) d) K Z (t) K K (t) = (δ d)t + O(t 2 ) (t 0). Beweis: Siehe Übung. 2.3 Effektiver und nomineller Zinssatz Eingangs haben wir schon von dem effektiven Zins für eine Konversionsperiode gesprochen. Ein Zins für eine Basisperiode heißt effektiv, wenn die Konversionsperiode mit der Basisperiode übereinstimmt. Ist dies nicht der Fall, so
14 2 ELEMENTARE FINANZMATHEMATIK 14 kommen wir zu dem Begriff nomineller Zinssatz oder nominelle Zinsrate. Sei dazu I D := der tatsächliche Gesamtzins, der in einem Zeitintervall der Länge (0; 1] auf das Kapital 1 gezahlt wird. I = 1 1, Diskont zu I. 1 + I 1 + I Dann heißt NI := I die nominelle jährliche Zinsrate und ND := D die nominelle jährliche Diskontrate. Der nomminelle Zins ist somit der Jahreszins, der sich bei kontinuierlicher einfacher Verzinsung aus I berechnet. Für = 1/k schreiben wir auch NI := i (k) := ki 1/k und ND := d (k) := k D 1/k. Analog: Der effektive Jahreszins i ist der Zins, der bei kontinuierlicher zusammengesetzter Verzinsung zum Zins I für die Dauer t = führt: I = (1 + i) 1. Der effektive Jahresdiskont ist definiert als d := Bemerkung Offensichtlich gelten: i 1 + i. D = 1 (1 d), (7) i (k) = k((1 + i) 1/k 1), (8) d (k) = k(1 (1 d) 1/k ), (9) d (k) = i (k) v 1/k, (10) i = (1 + I ) 1/ 1, (11) d = (1 (1 D ) 1/ ). (12) Satz Der effektive Jahreszins ist stets höher als der nominelle Jahreszins: Es gelten i > I D, > d ( (0; 1), I > 0), (13) I lim D 0 = lim 0 = δ. (14) Beweis: Der erste Teil folgt gemäß Übung. Die zweite Zeile ergibt sich wie folgt: I lim 0 = lim r 1 0 = d dt t=0r t = log r,
15 2 ELEMENTARE FINANZMATHEMATIK 15 und gemäß Definition von D D lim 0 = lim I = log r. 0 (1 + I ) 2.4 Zeitrenten und ihre Barwerte von zinsbehafteten Zahlungen Definition a) Eine Zeitrente ist ein vertraglich fixiertes System von zeitdiskreten Zahlungen an einen Vertragspartner, bei dem die Beträge und die Zahlungszeitpunkte, insbesondere also auch die Dauer, bei Vertragsabschluss festliegen. b) Vorschüssige Zahlungsweise: Die Zahlungen erfolgen zu Beginn des jeweiligen Rentenintervalls. Nachschüssige Zahlungsweise: Die Zahlungen erfolgen am Ende des Rentenintervalls. c) Der Barwert (Anfangswert) einer Zeitrente ist die Summe aller auf den Vertragsbeginn abgezinsten Zahlungen. d) Der Endwert einer Zeitrente ist die Summe aller auf das Vertragsende aufgezinsten Zahlungen. Schreibweise: Barwerte: ä a vorschüssige Zahlungsweise, nachschüssige Zahlungsweise. Endwerte: s s vorschüssige Zahlungsweise, nachschüssige Zahlungsweise. Im folgenden wird die Jahresrente auf 1 normiert. Wird der Betrag 1 in k gleich großen Teilen innerhalb eines Jahres jeweils zum Beginn oder zum Ende eines Zeitintervalls der Länge 1/k gezahlt, so sprechen wir von einer k-tel-jährlich n k-mal vorschüssig bzw. nachschüssig zahlbaren Rente. Bemerkung a) Im Gegensatz zu Leibrenten (etwa Alters- und Invalidenrenten), deren Zahlungen vom Leben bzw. allgemeinem Status einer Person abhängen, spielt bei Zeitrenten der Zufall keine Rolle! b) Im Folgenden ist das Rentenintervall in der Regel ein Jahr und die Verzinsung zusammengesetzt.
16 2 ELEMENTARE FINANZMATHEMATIK 16 c) Bei vorschüssigen Zahlungen ist das Rentenende verschieden vom Zeitpunkt der letzten Zahlung. Bei nachschüssigen Zahlungen ist der Rentenbeginn verschieden vom Zeitpunkt der ersten Zahlung. Lemma a) Der Barwert einer Zahlung vom Betrag 1 zu Beginn des k-ten Versicherungsjahres ist v k 1. b) Barwerte und Endwerte von n Jahre lang jährlich vorschüssig bzw. nachschüssig zahlbaren Zeitrenten: ä n = a n = n 1 v k = 1 vn 1 v = 1 vn, (15) d n n 1 v k = v k+1 = v ä n = 1 vn, (16) i k=1 c) Barwerte ewiger Zeitrenten: s n = ä n r n = rn 1, d (17) s n = a n r n = rn 1. i (18) ä = lim n ä n = 1 d, (19) a = lim n a n = 1 i, (20) Beispiel: Eine Erbschaft von e soll bei 7%-iger Verzinsung in einer 12- mal nachschüssig jährlich zahlbaren Zeitrente von x Geldeinheiten umgewandelt werden. 1 1, = x a 12 = x 0, 07 x = , 60. Lemma Barwerte m Jahre aufgeschobener, n Jahre jährlich zahlbarer Zeitrenten: m ä n = v m ä n = v m 1 1 vn i, (21) m a n = v m a n = v m 1 vn i. (22) Satz Seien B bzw. B der Barwert einer jährlich vorschüssig bzw. nachschüssig zahlbaren Zeitrente und B (k) bzw. B (k) der Barwert der k-tel-jährlich vorschüssig bzw. nachschüssig zahlbaren Zeitrente mit denselben Jahresgesamtbeiträgen. Dann gilt: a) zusammengesetzte Verzinsung: B (k) = d d (k) B, B (k) = i B, (23) i (k)
17 2 ELEMENTARE FINANZMATHEMATIK 17 b) kaufmännische Verzinsung: B (k) = (1 k 1 2k d) B, B (k) = (1 + k 1 i) B (24) 2k Beweis: Der Beweis erfolgt nur für die vorschüssigen Zahlungen. Der Beweis für die nachschüssigen Zahlungen erfolgt analog. a) Die k-tel-jährlich vorschüssige Zahlung des Betrages 1 im ν-ten Versicherungsjahr bei zusammengesetzter Verzinsung hat den Barwert ν 1 ä (k) 1 = 1 k 1 k vν 1 j=0 v j/k = vν 1 k 1 v d = vν 1 1 v1/k d (k). Summation über die einzelnen Versicherungsjahren liefert a). b) Die k-tel-jährlich vorschüssige Zahlung des Betrages 1 im ν-ten Versicherungsjahr bei kaufmännischer Verzinsung hat den Barwert ν 1 ä (k) 1 = vν k = vν k (1 + i(1 j/n)) k j=0 (1 + i)k i k 1 j k j=0 ( (1 + i)k i ) (k 1)k k 2 ) = vν k 1 ( = v ν (1 + i) i k 1 2k = ( 1 d k 1 2k ) v ν 1 wegen v = (1 + i) 1, d = i/(i + 1). Summation über die einzelnen Versicherungsjahre liefert b). Folgerung: Barwerte k-tel-jährlich nk-mal vor- bzw. nachschüssig zahlbare Zeitrenten bei a) zusammengesetzter Verzinsung ä (k) n = d d (k) ä n = a (k) n = i i (k) a n = 1 1 v n, k 1 v1/k (25) 1 1 v n k v 1/k 1. (26) b) kaufmännischer Verzinsung ä (k) n = (1 k 1 2k d)ä n = a (k) n = (1 + k 1 2k i)a n = 1 vn 1 v k 1 2k (1 vn ), (27) 1 vn v k 1 2k (1 vn ). (28)
18 3 ZUKÜNFTIGE LEBENSERWARTUNG EINES X-JÄHRIGEN 18 3 Zukünftige Lebenserwartung eines x-jährigen 3.1 Einleitung Gegenstand dieses Abschnittes ist die Modellierung des biometrischen Risikos. Da die Verzinsung deterministisch gewählt wurde, kommt hier erstmalig der Zufall und damit die Stochastik ins Spiel. Unter Risiko ist in der Lebensversicherung das Todesfallrisiko, aber auch das Invaliditätsrisiko zu verstehen. Dabei wird sowohl die Todesursache eines Einzelnen oder auch einer Gruppe von Leben betrachtet. Ebenso können auch mehrere Todesursachen berücksichtigt werden. Gibt es nur eine Ausscheideursache (z.b. nur Tod), so spricht man von einfacher Ausscheideordnung. Bei mehreren Ausscheideursachen spricht man von zusammengesetzter Ausscheideordnung. Einfache Ausscheideordnungen können ausschließlich mittels Zufallsvariablen modelliert werden (Lebensdauer und Ausscheideursachen), da die betrachtete Person nur einmal ihren Zustand ändert. Das allgemeine Geschehen in der Personenversicherungsmathematik ist dadurch gekennzeichnet, dass mehrere Personen zwischen endlich vielen Zuständen zu zufälligen Zeitpunkten wechseln. Dies kann nur mit Hilfe von stochastischen Prozessen beschrieben werden und ist nicht Gegenstand dieser Vorlesung. Wenn möglich sollen wie bei der Verzinsung auch hier die stetige Methode und die diskrete Methode einheitlich betrachtet werden. Dies geschieht dadurch, dass man nicht das Geschehen zu einen Zeitpunkt, sondern bis zu einem Zeitpunkt betrachtet. Bei der Gewinnung von biometrischen Rechnungsgrundlagen insbesondere bei der Herleitung von Sterbetafeln aus geeigneten Beobachtungen werden statistische Fragestellungen behandelt. Im folgenden bezeichnen wir mit (x) einen x-jährigen Mann bzw. eine x-jährige Frau. Mit T (genauer T x ) bezeichne man die restliche Lebenserwartung eines x-jährigen. Zum Zeitpunkt des Todes einer Person beträgt das Alter somit x + T = x + T x. Die zukünftige Lebenserwartung T x ist eine Zufallsgröße mit Verteilungsfunktion G x (t) = P (T x t), t 0. G x (t) ist somit die Wahrscheinlichkeit, dass die x-jährige Person innerhalb der nächsten t Jahre stirbt, t 0. Voraussetzung/Annahme: i) Die Wahrscheinlichkeitsverteilung von T x, G x, ist bekannt. ii) G x sei stetig und besitzt eine Dichte g(t) = G x(t) (Bemerkung: Die Existenz einer Dichte ist nicht zwingend erforderlich, s. Milbrodt/Helbig)
19 3 ZUKÜNFTIGE LEBENSERWARTUNG EINES X-JÄHRIGEN 19 g(t)dt = P (t < T x < t + dt) bezeichnet die Wahrscheinlichkeit, dass der Tod innerhalb eines infenitesimalen Zeitintervalls von t nach t + dt eintritt. Notationen in der IAA: tq x := G x (t), tp x := 1 G x (t) =: S x (t), (29) s tq x := P (s < T x s + t) = G x (s + t) G x (s) = s+t q x s q x. (30) Dabei ist t p x die Wahrscheinlichkeit, das eine x-jährige Person mindestens t Jahre überlebt. s tq x ist die Wahrscheinlichkeit, dass eine x-jährige Person s Jahre überlebt und innerhalb weiterer t Jahre stirbt. Außerdem sei tp x+s := P (T x > s + t T x > s) = P (Tx>s+t) 1 G x(s) tq x+s := P (T x s + t T x > s) = P (s<tx s+t) P (T x>s) und = G(s+t) G(s) 1 G(s). tp x+s ist die bedingte Wahrscheinlichkeit, dass eine Person noch mindestens weitere t Jahre überlebt, wenn sie das Alter x+s erreicht hat. (Dies ist per se nicht gleich P (T x+s > t), wie die Notation vermuten lässt. Hier benötigt man eine Zusatzbedingung, die sog. Stationaritätsbedingung.) tq x+s ist die bedingte Wahrscheinlichkeit, dass eine Person innerhalb der nächsten t Jahre stirbt gegeben das Ereignis, dass sie das Alter x + s erreicht hat. Es gelten folgende Beziehungen: s+tp x = 1 G x (s + t) = (1 G x (s)) 1 G x(s + t) 1 G x (s) = s p x t p x+s und s tq x = (G x (s + t) G x (s)) = (1 G x (s)) G x(s + t) G x (s) 1 G x (s) = s p x t q x+s. Die Interpretation dieser Beziehungen ist offensichtlich. Konvention: Für t = 1 wird der Index t in der Regel weggelassen: q x = 1 q x und s q x = s 1 q x.
20 3 ZUKÜNFTIGE LEBENSERWARTUNG EINES X-JÄHRIGEN vollständige Restlebenserwartung eines x-jährigen Die vollständige Restlebenserwartung eines x-jährigen ist der Erwartungswert E(T ) von T und wird mit e x bezeichnet. e x := E(T x ) = 0 t g(t)dt. Mit Hilfe der partiellen Integration mittels des Satzes von Fubini (vgl. evtl. Aufgabe) gilt: e x = 0 (1 G x(t))dt = 0 tp x dt. (31) 3.3 Sterbeintensität Definition Betrachte einen x-jährigen (x). Sei G x die Verteilungsfunktion der zukünftigen Restlebensdauer eines x-jährigen. G x sei stetig differenzierbar und besitze die (Riemann-) Dichte g(t). Dann heißt µ x (t) = g(t) 1 G x (t) = d dt ln(1 G x(t)) (32) mit 0/0 := 0 die Sterbeintensität eines x-jährigen im Alter x + t. (Die Annahme, dass G stetig differenzierbar ist, wird nur getroffen, um die Betrachtungen von technischem Ballast frei zu halten. Tatsächlich genügt es vorauszusetzen, dass G stetig ist und eine Lebesgue-Dichte besitzt. Dann muss man allerdings mit Nullmengen operieren. Sogar die Existenz einer Dichte kann man fallenlassen. Dann arbeitet man mit sog. kumulierten Sterbeintensitäten.) Da nach Annahme T = T x eine absolut stetige Verteilung mit Dichte g besitzt, gilt: t s g(τ)dτ = G x (t) G x (s) = P (s < T x t) = s t s q x. Die Sterbeintensität µ x läßt sich dann schreiben als Interpretation: µ x = g S x (0/0 := 0). P (t < T x t + δ T x > t) δ = t+δ t g(τ)dτ δ S x (t) δ 0 g(t) S x (t) = µ x(t) (λ f. ü.) µ x (t) beschreibt somit die Momentansterblichkeit zur Zeit t. für δ klein. µ x (t)δ P (t < T x t + δ T x > t) = S x(t + δ) S x (t) S x (t)
21 3 ZUKÜNFTIGE LEBENSERWARTUNG EINES X-JÄHRIGEN 21 Mit dem verallgemeinerten Hauptsatz der Differential und Integralrechnung folgt dann: µ x (t) = d dt log S x(t) = d dt log t p x ( t ) S x (t) = exp µ x (τ)dτ, t 0. Dabei gilt die erste Beziehung nur λ- fast überall auf [0; G 1 x (1)], falls G nicht stetig differenzierbar. Bemerkung: Wichtige versicherungsmathematische Größen: 0 a) w x := x + G 1 x (1) mit G 1 x (1) = inf{y : G x (y) 1} rechnerisches Höchstalter eines x-jährigen, b) med(t x ) := G 1 x (0, 5) (vollständige) mittlere Restlebensdauer von x, c) e x := E(T x ) = 0 S x (t)dt = 0 tp x dt (vollständige) Restlebenserwartung von (x), 3.4 Stationaritätsbedingung Für praktische Zwecke möchte man zumindestens für ganzzahlige Alter x und für ganzzahlige zukünftige Verweildauern n die Werte n p x, n, x N vertafeln. Dazu müsste man allerdings eine Vielzahl von Wahrscheinlichkeiten abspeichern, was äußerst unpraktisch ist. Wünschenswert ist es daher, nur die einjährigen Überlebenswahrscheinlichkeiten 1 p x, x N, abzuspeichern und die n-jährigen Überlebenswahrscheinlichkeiten aus diesen abzuleiten. Dadurch könnte man die Zahl der abzuspeichernden Wahrscheinlichkeiten um eine ganze Dimension blackuzieren. Im folgenden wird daher stets die Stationaritätsbedingung (Verträglichkeitsbedingung) gefordert, die diese Blackuktion ermöglicht: P (T x+s > t) = P (T x > s + t T x > s) = t p x+s, s, t, x 0 (33) Falls die Stationaritätsbedingung gilt, kann die bedingte Wahrscheinlichkeit in der Definition von t p x+s ersetzt werden durch die unbedingte Wahrscheinlichkeit P (T x+s > t). Die Schreibweise t p x+s ist somit konform mit der allgemeinen Definition von t p x. Interpretation: Die Verteilung der zukünftigen Lebenserwartung eines s-jährigen ergibt sich aus der Verteilung der Lebensdauer eines Neugeborenen (x = 0) ausschließlich durch die Berücksichtigung der Zusatzinformation, dass inzwischen das Alter s erreicht wurde. Andere Zusatzinformationen (etwa das Ergebnis einer Risikoprüfung) spielen keine Rolle.
Zinseszins- und Rentenrechnung
 Zinseszins- und Rentenrechnung 1 Berechnen Sie den Zeitpunkt, an dem sich das Einlagekapital K bei a) jährlicher b) monatlicher c) stetiger Verzinsung verdoppelt hat, wobei i der jährliche nominelle Zinssatz
Zinseszins- und Rentenrechnung 1 Berechnen Sie den Zeitpunkt, an dem sich das Einlagekapital K bei a) jährlicher b) monatlicher c) stetiger Verzinsung verdoppelt hat, wobei i der jährliche nominelle Zinssatz
Im weiteren werden die folgenden Bezeichnungen benutzt: Zinsrechnung
 4.2 Grundbegriffe der Finanzmathematik Im weiteren werden die folgenden Bezeichnungen benutzt: K 0 Anfangskapital p Zinsfuß pro Zeiteinheit (in %) d = p Zinssatz pro Zeiteinheit 100 q = 1+d Aufzinsungsfaktor
4.2 Grundbegriffe der Finanzmathematik Im weiteren werden die folgenden Bezeichnungen benutzt: K 0 Anfangskapital p Zinsfuß pro Zeiteinheit (in %) d = p Zinssatz pro Zeiteinheit 100 q = 1+d Aufzinsungsfaktor
Deckungskapital. Proseminar Versicherungsmathematik. TU Graz. 11. Dezember 2007
 Deckungskapital Gülnur Adanç Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 1 Inhaltsverzeichnis 1 Deckungskapital 2 1.1 Prospektive und Retrospektive Methode.................... 3 1.1.1
Deckungskapital Gülnur Adanç Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 1 Inhaltsverzeichnis 1 Deckungskapital 2 1.1 Prospektive und Retrospektive Methode.................... 3 1.1.1
Rente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren Rentenperiode = Zeitabstand zwischen zwei Rentenzahlungen
 1 3.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind
1 3.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind
Kapitalversicherungen
 Kapitalversicherungen Birgit Scharwitzl 10. Dezember 2008 Inhaltsverzeichnis 1 Begriffe und wichtige Definitionen 2 1.1 Prämie................................................... 2 1.2 Gewinnbeteiligung............................................
Kapitalversicherungen Birgit Scharwitzl 10. Dezember 2008 Inhaltsverzeichnis 1 Begriffe und wichtige Definitionen 2 1.1 Prämie................................................... 2 1.2 Gewinnbeteiligung............................................
Lebensdauer eines x-jährigen
 Lebensdauer eines x-jährigen Sabrina Scheriau 20. November 2007, Graz 1 INHALTSVERZEICHNIS 2 Inhaltsverzeichnis 1 Einleitung 3 2 Sterbewahrscheinlichkeiten 4 2.1 Definition und Ermittlung....................
Lebensdauer eines x-jährigen Sabrina Scheriau 20. November 2007, Graz 1 INHALTSVERZEICHNIS 2 Inhaltsverzeichnis 1 Einleitung 3 2 Sterbewahrscheinlichkeiten 4 2.1 Definition und Ermittlung....................
SS 2014 Torsten Schreiber
 SS 2014 Torsten Schreiber 204 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Bei der Rentenrechnung geht es um aus einem angesparten Kapital bzw. um um das Kapital aufzubauen, die innerhalb
SS 2014 Torsten Schreiber 204 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Bei der Rentenrechnung geht es um aus einem angesparten Kapital bzw. um um das Kapital aufzubauen, die innerhalb
Rente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren Rentenperiode = Zeitabstand zwischen zwei Rentenzahlungen
 5.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind zwei
5.2. entenrechnung Definition: ente = laufende Zahlungen, die in regelmäßigen Zeitabschnitten (periodisch) wiederkehren entenperiode = Zeitabstand zwischen zwei entenzahlungen Finanzmathematisch sind zwei
Mathematik 1 für Wirtschaftsinformatik
 Mathematik 1 für Wirtschaftsinformatik Wintersemester 2012/13 Hochschule Augsburg Äquivalenzprinzip der Finanzmathematik Das Äquivalenzprinzip der Finanzmathematik für Vergleich von Zahlungen, welche
Mathematik 1 für Wirtschaftsinformatik Wintersemester 2012/13 Hochschule Augsburg Äquivalenzprinzip der Finanzmathematik Das Äquivalenzprinzip der Finanzmathematik für Vergleich von Zahlungen, welche
Finanzmathematik. Wirtschaftswissenschaftliches Zentrum Universität Basel. Mathematik für Ökonomen 1 Dr. Thomas Zehrt
 Wirtschaftswissenschaftliches Zentrum Universität Basel Mathematik für Ökonomen 1 Dr. Thomas Zehrt Finanzmathematik Literatur Gauglhofer, M. und Müller, H.: Mathematik für Ökonomen, Band 1, 17. Auflage,
Wirtschaftswissenschaftliches Zentrum Universität Basel Mathematik für Ökonomen 1 Dr. Thomas Zehrt Finanzmathematik Literatur Gauglhofer, M. und Müller, H.: Mathematik für Ökonomen, Band 1, 17. Auflage,
n... Laufzeit der Kapitalanlage = Zeit, während der Zinsen zu zahlen sind (oder gezahlt werden) in Zinsperioden (z.b. Jahre)
 3. Finanzmathematik 3.1. Zinsrechnung 3.1.1. Grundbegriffe K... Kapital (caput - das Haupt) = Betrag, der der Verzinsung unterworfen ist; Geldbetrag (Währung) z... Zinsen = Vergütung (Preis) für das Überlassen
3. Finanzmathematik 3.1. Zinsrechnung 3.1.1. Grundbegriffe K... Kapital (caput - das Haupt) = Betrag, der der Verzinsung unterworfen ist; Geldbetrag (Währung) z... Zinsen = Vergütung (Preis) für das Überlassen
Krankenversicherungsmathematik
 Krankenversicherungsmathematik Florian Peycha 8. Januar 2008 Inhaltsverzeichnis 1 Kopfschaden 1 1.1 Die Methode von Rusam..................... 2 1.2 Altersgruppenbildung....................... 3 1.3 Die
Krankenversicherungsmathematik Florian Peycha 8. Januar 2008 Inhaltsverzeichnis 1 Kopfschaden 1 1.1 Die Methode von Rusam..................... 2 1.2 Altersgruppenbildung....................... 3 1.3 Die
Kalkulation versicherungstechnischer Risiken
 Kalkulation versicherungstechnischer Risiken mit Beispielen aus den Sparten Dr. Arnd Grimmer DBV-Winterthur Lebensversicherung AG Wiesbaden Begriff des Risikos Definition: Risiko bedeutet die Möglichkeit
Kalkulation versicherungstechnischer Risiken mit Beispielen aus den Sparten Dr. Arnd Grimmer DBV-Winterthur Lebensversicherung AG Wiesbaden Begriff des Risikos Definition: Risiko bedeutet die Möglichkeit
Verteilungsmodelle. Verteilungsfunktion und Dichte von T
 Verteilungsmodelle Verteilungsfunktion und Dichte von T Survivalfunktion von T Hazardrate von T Beziehungen zwischen F(t), S(t), f(t) und h(t) Vorüberlegung zu Lebensdauerverteilungen Die Exponentialverteilung
Verteilungsmodelle Verteilungsfunktion und Dichte von T Survivalfunktion von T Hazardrate von T Beziehungen zwischen F(t), S(t), f(t) und h(t) Vorüberlegung zu Lebensdauerverteilungen Die Exponentialverteilung
Anhand des bereits hergeleiteten Models erstellen wir nun mit der Formel
 Ausarbeitung zum Proseminar Finanzmathematische Modelle und Simulationen bei Raphael Kruse und Prof. Dr. Wolf-Jürgen Beyn zum Thema Simulation des Anlagenpreismodels von Simon Uphus im WS 09/10 Zusammenfassung
Ausarbeitung zum Proseminar Finanzmathematische Modelle und Simulationen bei Raphael Kruse und Prof. Dr. Wolf-Jürgen Beyn zum Thema Simulation des Anlagenpreismodels von Simon Uphus im WS 09/10 Zusammenfassung
III. Grundlagen der Lebensversicherungsmathematik III.5. Deckungskapital für Lebensversicherungsprodukte
 III. Grundlagen der Lebensversicherungsmathematik III.5. Deckungskapital für Lebensversicherungsprodukte Universität Basel Herbstsemester 2015 Dr. Ruprecht Witzel ruprecht.witzel@aktuariat-witzel.ch www.aktuariat-witzel.ch
III. Grundlagen der Lebensversicherungsmathematik III.5. Deckungskapital für Lebensversicherungsprodukte Universität Basel Herbstsemester 2015 Dr. Ruprecht Witzel ruprecht.witzel@aktuariat-witzel.ch www.aktuariat-witzel.ch
Kapitalversicherungen
 Kapitalversicherungen Sanela Omerovic Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 Inhaltsverzeichnis 1 Einführung 1 2 Einfache Versicherungsformen 3 2.1 Todesfallversicherungen (Life Insurance)....................
Kapitalversicherungen Sanela Omerovic Proseminar Versicherungsmathematik TU Graz 11. Dezember 2007 Inhaltsverzeichnis 1 Einführung 1 2 Einfache Versicherungsformen 3 2.1 Todesfallversicherungen (Life Insurance)....................
SS 2014 Torsten Schreiber
 SS 2014 Torsten Schreiber 221 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Wird im Bereich der Rentenrechnung die zugehörige zu Beginn eines Jahres / einer Zeitperiode eingezahlt, so spricht
SS 2014 Torsten Schreiber 221 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Wird im Bereich der Rentenrechnung die zugehörige zu Beginn eines Jahres / einer Zeitperiode eingezahlt, so spricht
Statistische Thermodynamik I Lösungen zur Serie 1
 Statistische Thermodynamik I Lösungen zur Serie Zufallsvariablen, Wahrscheinlichkeitsverteilungen 4. März 2. Zwei Lektoren lesen ein Buch. Lektor A findet 2 Druckfehler, Lektor B nur 5. Von den gefundenen
Statistische Thermodynamik I Lösungen zur Serie Zufallsvariablen, Wahrscheinlichkeitsverteilungen 4. März 2. Zwei Lektoren lesen ein Buch. Lektor A findet 2 Druckfehler, Lektor B nur 5. Von den gefundenen
Tutorium zur Mathematik (WS 2004/2005) - Finanzmathematik Seite 1
 Tutorium zur Mathematik WS 2004/2005) - Finanzmathematik Seite 1 Finanzmathematik 1.1 Prozentrechnung K Grundwert Basis, Bezugsgröße) p Prozentfuß i Prozentsatz i = p 100 ) Z Prozentwert Z = K i bzw. Z
Tutorium zur Mathematik WS 2004/2005) - Finanzmathematik Seite 1 Finanzmathematik 1.1 Prozentrechnung K Grundwert Basis, Bezugsgröße) p Prozentfuß i Prozentsatz i = p 100 ) Z Prozentwert Z = K i bzw. Z
Wirtschaftsmathematik für International Management (BA)
 Wirtschaftsmathematik für International Management (BA) Wintersemester 2012/13 Hochschule Augsburg : Gliederung 1 Grundlegende 2 Grundlegende 3 Lineare Algebra 4 Lineare Programme 5 Folgen und Reihen 6
Wirtschaftsmathematik für International Management (BA) Wintersemester 2012/13 Hochschule Augsburg : Gliederung 1 Grundlegende 2 Grundlegende 3 Lineare Algebra 4 Lineare Programme 5 Folgen und Reihen 6
Rekursionen. Georg Anegg 25. November 2009. Methoden und Techniken an Beispielen erklärt
 Methoden und Techniken an Beispielen erklärt Georg Anegg 5. November 009 Beispiel. Die Folge {a n } sei wie folgt definiert (a, d, q R, q ): a 0 a, a n+ a n q + d (n 0) Man bestimme eine explizite Darstellung
Methoden und Techniken an Beispielen erklärt Georg Anegg 5. November 009 Beispiel. Die Folge {a n } sei wie folgt definiert (a, d, q R, q ): a 0 a, a n+ a n q + d (n 0) Man bestimme eine explizite Darstellung
9.2. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83
 9.. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83 Die Grundfrage bei der Anwendung des Satzes über implizite Funktionen betrifft immer die folgende Situation: Wir haben eine Funktion f : V W und eine Stelle x
9.. DER SATZ ÜBER IMPLIZITE FUNKTIONEN 83 Die Grundfrage bei der Anwendung des Satzes über implizite Funktionen betrifft immer die folgende Situation: Wir haben eine Funktion f : V W und eine Stelle x
Wichtiges Thema: Ihre private Rente und der viel zu wenig beachtete - Rentenfaktor
 Wichtiges Thema: Ihre private Rente und der viel zu wenig beachtete - Rentenfaktor Ihre private Gesamtrente setzt sich zusammen aus der garantierten Rente und der Rente, die sich aus den über die Garantieverzinsung
Wichtiges Thema: Ihre private Rente und der viel zu wenig beachtete - Rentenfaktor Ihre private Gesamtrente setzt sich zusammen aus der garantierten Rente und der Rente, die sich aus den über die Garantieverzinsung
Anwendungen in der elementaren Zinsrechnung. Kapitalwert zum Zeitpunkt j (nach j Zinsperioden) Bsp. 1. 0 1 2 3 4 Zeitpunkte
 Anwendungen in der elementaren Zinsrechnung Zinssatz (Rendite) je Zinsperiode i = p% p= Prozentpunkte Zinsfaktor (Aufzinsungsfaktor) q =1+i Diskontfaktor (Abzinsungsfaktor) v =1/(1 + i) =q 1 Laufzeit n
Anwendungen in der elementaren Zinsrechnung Zinssatz (Rendite) je Zinsperiode i = p% p= Prozentpunkte Zinsfaktor (Aufzinsungsfaktor) q =1+i Diskontfaktor (Abzinsungsfaktor) v =1/(1 + i) =q 1 Laufzeit n
Arbeitskreis 1 Lebenserwartung und private Rentenversicherung Sterbetafeln und ihre Anwendung in der privaten Rentenversicherung
 Arbeitskreis 1 Lebenserwartung und private Rentenversicherung Sterbetafeln und ihre Anwendung in der privaten Rentenversicherung Dr. Johannes Lörper, Vorsitzender des Mathematikausschusses des Gesamtverbandes
Arbeitskreis 1 Lebenserwartung und private Rentenversicherung Sterbetafeln und ihre Anwendung in der privaten Rentenversicherung Dr. Johannes Lörper, Vorsitzender des Mathematikausschusses des Gesamtverbandes
SS 2014 Torsten Schreiber
 SS 2014 Torsten Schreiber 193 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Bei einer Abschreibung werden eines Gutes während der Nutzungsdauer festgehalten. Diese Beträge stellen dar und dadurch
SS 2014 Torsten Schreiber 193 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Bei einer Abschreibung werden eines Gutes während der Nutzungsdauer festgehalten. Diese Beträge stellen dar und dadurch
4.3 Bevölkerungsprozessstatistik: Raten und Tafeln
 Dynamik der Bevölkerungsstruktur ergibt sich aus Zugängen (Geburt, Zuwanderung) Abgängen (Tod, Abwanderung) Bewegungen zwischen Sektoren (ledig verheiratet, erwerbstätig nicht erwerbstätig, verschiedene
Dynamik der Bevölkerungsstruktur ergibt sich aus Zugängen (Geburt, Zuwanderung) Abgängen (Tod, Abwanderung) Bewegungen zwischen Sektoren (ledig verheiratet, erwerbstätig nicht erwerbstätig, verschiedene
Data Mining: Einige Grundlagen aus der Stochastik
 Data Mining: Einige Grundlagen aus der Stochastik Hagen Knaf Studiengang Angewandte Mathematik Hochschule RheinMain 21. Oktober 2015 Vorwort Das vorliegende Skript enthält eine Zusammenfassung verschiedener
Data Mining: Einige Grundlagen aus der Stochastik Hagen Knaf Studiengang Angewandte Mathematik Hochschule RheinMain 21. Oktober 2015 Vorwort Das vorliegende Skript enthält eine Zusammenfassung verschiedener
BONUS MALUS SYSTEME UND MARKOV KETTEN
 Fakultät Mathematik und Naturwissenschaften, Fachrichtung Mathematik, Institut für Mathematische Stochastik BONUS MALUS SYSTEME UND MARKOV KETTEN Klaus D. Schmidt Ringvorlesung TU Dresden Fakultät MN,
Fakultät Mathematik und Naturwissenschaften, Fachrichtung Mathematik, Institut für Mathematische Stochastik BONUS MALUS SYSTEME UND MARKOV KETTEN Klaus D. Schmidt Ringvorlesung TU Dresden Fakultät MN,
Rekursionen (Teschl/Teschl 8.1-8.2)
 Rekursionen (Teschl/Teschl 8.1-8.2) Eine Rekursion kter Ordnung für k N ist eine Folge x 1, x 2, x 3,... deniert durch eine Rekursionsvorschrift x n = f n (x n 1,..., x n k ) für n > k, d. h. jedes Folgenglied
Rekursionen (Teschl/Teschl 8.1-8.2) Eine Rekursion kter Ordnung für k N ist eine Folge x 1, x 2, x 3,... deniert durch eine Rekursionsvorschrift x n = f n (x n 1,..., x n k ) für n > k, d. h. jedes Folgenglied
Korrelation (II) Korrelation und Kausalität
 Korrelation (II) Korrelation und Kausalität Situation: Seien X, Y zwei metrisch skalierte Merkmale mit Ausprägungen (x 1, x 2,..., x n ) bzw. (y 1, y 2,..., y n ). D.h. für jede i = 1, 2,..., n bezeichnen
Korrelation (II) Korrelation und Kausalität Situation: Seien X, Y zwei metrisch skalierte Merkmale mit Ausprägungen (x 1, x 2,..., x n ) bzw. (y 1, y 2,..., y n ). D.h. für jede i = 1, 2,..., n bezeichnen
Beispiel 48. 4.3.2 Zusammengesetzte Zufallsvariablen
 4.3.2 Zusammengesetzte Zufallsvariablen Beispiel 48 Ein Würfel werde zweimal geworfen. X bzw. Y bezeichne die Augenzahl im ersten bzw. zweiten Wurf. Sei Z := X + Y die Summe der gewürfelten Augenzahlen.
4.3.2 Zusammengesetzte Zufallsvariablen Beispiel 48 Ein Würfel werde zweimal geworfen. X bzw. Y bezeichne die Augenzahl im ersten bzw. zweiten Wurf. Sei Z := X + Y die Summe der gewürfelten Augenzahlen.
Bericht zur Prüfung im Oktober 2003 über Mathematik der Lebensversicherung (Grundwissen)
 Bericht zur Prüfung im Oktober 2003 über Mathematik der Lebensversicherung Grundwissen) Jürgen Strobel Köln) und Hans-Jochen Bartels Mannheim) Am 04.10.2003 wurde in Köln die zehnte Prüfung über Mathematik
Bericht zur Prüfung im Oktober 2003 über Mathematik der Lebensversicherung Grundwissen) Jürgen Strobel Köln) und Hans-Jochen Bartels Mannheim) Am 04.10.2003 wurde in Köln die zehnte Prüfung über Mathematik
16 Risiko und Versicherungsmärkte
 16 Risiko und Versicherungsmärkte Entscheidungen bei Unsicherheit sind Entscheidungen, die mehrere mögliche Auswirkungen haben. Kauf eines Lotterieloses Kauf einer Aktie Mitnahme eines Regenschirms Abschluss
16 Risiko und Versicherungsmärkte Entscheidungen bei Unsicherheit sind Entscheidungen, die mehrere mögliche Auswirkungen haben. Kauf eines Lotterieloses Kauf einer Aktie Mitnahme eines Regenschirms Abschluss
50. Mathematik-Olympiade 2. Stufe (Regionalrunde) Klasse 11 13. 501322 Lösung 10 Punkte
 50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
50. Mathematik-Olympiade. Stufe (Regionalrunde) Klasse 3 Lösungen c 00 Aufgabenausschuss des Mathematik-Olympiaden e.v. www.mathematik-olympiaden.de. Alle Rechte vorbehalten. 503 Lösung 0 Punkte Es seien
ETWR TEIL B ÜBUNGSBLATT 4 WS14/15
 ETWR TEIL B ÜBUNGSBLATT 4 WS14/15 OTTO-VON-GUERICKE-UNIVERSITÄT MAGDEBURG F A K U L T Ä T F Ü R W I R T S C H A F T S W I S S E N S C H A FT LEHRSTUHL FÜR EMPIRISCHE WIRTSCHAFTSFORSCHUNG & GESUNDHEITSÖKONOMIE,
ETWR TEIL B ÜBUNGSBLATT 4 WS14/15 OTTO-VON-GUERICKE-UNIVERSITÄT MAGDEBURG F A K U L T Ä T F Ü R W I R T S C H A F T S W I S S E N S C H A FT LEHRSTUHL FÜR EMPIRISCHE WIRTSCHAFTSFORSCHUNG & GESUNDHEITSÖKONOMIE,
Unterrichtsmaterialien in digitaler und in gedruckter Form. Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis
 Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis Das komplette Material finden Sie hier: Download bei School-Scout.de
Unterrichtsmaterialien in digitaler und in gedruckter Form Auszug aus: Übungsbuch für den Grundkurs mit Tipps und Lösungen: Analysis Das komplette Material finden Sie hier: Download bei School-Scout.de
1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage:
 Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Zählen und Zahlbereiche Übungsblatt 1 1. Man schreibe die folgenden Aussagen jeweils in einen normalen Satz um. Zum Beispiel kann man die Aussage: Für alle m, n N gilt m + n = n + m. in den Satz umschreiben:
Mathematik-Klausur vom 4.2.2004
 Mathematik-Klausur vom 4.2.2004 Aufgabe 1 Ein Klein-Sparer verfügt über 2 000, die er möglichst hoch verzinst anlegen möchte. a) Eine Anlage-Alternative besteht im Kauf von Bundesschatzbriefen vom Typ
Mathematik-Klausur vom 4.2.2004 Aufgabe 1 Ein Klein-Sparer verfügt über 2 000, die er möglichst hoch verzinst anlegen möchte. a) Eine Anlage-Alternative besteht im Kauf von Bundesschatzbriefen vom Typ
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Gehen wir einmal davon aus, dass die von uns angenommenen
 geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
geben. Die Wahrscheinlichkeit von 100% ist hier demnach nur der Vollständigkeit halber aufgeführt. Gehen wir einmal davon aus, dass die von uns angenommenen 70% im Beispiel exakt berechnet sind. Was würde
Vorsorgestiftung für Gesundheit und Soziales. Reglement über die Bildung und Auflösung von technischen Rückstellungen
 Vorsorgestiftung für Gesundheit und Soziales Reglement über die Bildung und Auflösung von technischen Rückstellungen Sarnen, 1. Januar 2006 Inhaltsverzeichnis 1. Grundsätze und Ziele 1 1.1 Einleitung 1
Vorsorgestiftung für Gesundheit und Soziales Reglement über die Bildung und Auflösung von technischen Rückstellungen Sarnen, 1. Januar 2006 Inhaltsverzeichnis 1. Grundsätze und Ziele 1 1.1 Einleitung 1
Kommutationszahlen und Versicherungsbarwerte für Leibrenten 2001/2003
 Kommutationszahlen und Versicherungsbarwerte für Leibrenten 2001/2003 Tabellen zur jährlich und monatlich vorschüssigen Zahlungsweise Statistisches Bundesamt Impressum Herausgeber: Statistisches Bundesamt
Kommutationszahlen und Versicherungsbarwerte für Leibrenten 2001/2003 Tabellen zur jährlich und monatlich vorschüssigen Zahlungsweise Statistisches Bundesamt Impressum Herausgeber: Statistisches Bundesamt
Finanzwirtschaft. Teil II: Bewertung
 Sparpläne und Kreditverträge 1 Finanzwirtschaft Teil II: Bewertung Sparpläne und Kreditverträge Agenda Sparpläne und Kreditverträge 2 Endliche Laufzeit Unendliche Laufzeit Zusammenfassung Sparpläne und
Sparpläne und Kreditverträge 1 Finanzwirtschaft Teil II: Bewertung Sparpläne und Kreditverträge Agenda Sparpläne und Kreditverträge 2 Endliche Laufzeit Unendliche Laufzeit Zusammenfassung Sparpläne und
Professionelle Seminare im Bereich MS-Office
 Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Der Name BEREICH.VERSCHIEBEN() ist etwas unglücklich gewählt. Man kann mit der Funktion Bereiche zwar verschieben, man kann Bereiche aber auch verkleinern oder vergrößern. Besser wäre es, die Funktion
Austausch- bzw. Übergangsprozesse und Gleichgewichtsverteilungen
 Austausch- bzw. Übergangsrozesse und Gleichgewichtsverteilungen Wir betrachten ein System mit verschiedenen Zuständen, zwischen denen ein Austausch stattfinden kann. Etwa soziale Schichten in einer Gesellschaft:
Austausch- bzw. Übergangsrozesse und Gleichgewichtsverteilungen Wir betrachten ein System mit verschiedenen Zuständen, zwischen denen ein Austausch stattfinden kann. Etwa soziale Schichten in einer Gesellschaft:
Mathematik 1. Inhaltsverzeichnis. Prof. Dr. K. Melzer. karin.melzer@hs-esslingen.de http://www.hs-esslingen.de/de/mitarbeiter/karin-melzer.
 Mathematik 1 Prof Dr K Melzer karinmelzer@hs-esslingende http://wwwhs-esslingende/de/mitarbeiter/karin-melzerhtml Inhaltsverzeichnis 1 Finanzmathematik 1 11 Folgen und Reihen 1 111 Folgen allgemein 1 112
Mathematik 1 Prof Dr K Melzer karinmelzer@hs-esslingende http://wwwhs-esslingende/de/mitarbeiter/karin-melzerhtml Inhaltsverzeichnis 1 Finanzmathematik 1 11 Folgen und Reihen 1 111 Folgen allgemein 1 112
Im Jahr t = 0 hat eine Stadt 10.000 Einwohner. Nach 15 Jahren hat sich die Einwohnerzahl verdoppelt. z(t) = at + b
 Aufgabe 1: Im Jahr t = 0 hat eine Stadt 10.000 Einwohner. Nach 15 Jahren hat sich die Einwohnerzahl verdoppelt. (a) Nehmen Sie lineares Wachstum gemäß z(t) = at + b an, wobei z die Einwohnerzahl ist und
Aufgabe 1: Im Jahr t = 0 hat eine Stadt 10.000 Einwohner. Nach 15 Jahren hat sich die Einwohnerzahl verdoppelt. (a) Nehmen Sie lineares Wachstum gemäß z(t) = at + b an, wobei z die Einwohnerzahl ist und
4. Versicherungsangebot
 4. Versicherungsangebot Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie (FS 11) Versicherungsangebot 1 / 13 1. Einleitung 1.1 Hintergrund In einem grossen Teil
4. Versicherungsangebot Georg Nöldeke Wirtschaftswissenschaftliche Fakultät, Universität Basel Versicherungsökonomie (FS 11) Versicherungsangebot 1 / 13 1. Einleitung 1.1 Hintergrund In einem grossen Teil
Beurteilung der biometrischen Verhältnisse in einem Bestand. Dr. Richard Herrmann, Köln
 Beurteilung der biometrischen Verhältnisse in einem Bestand Dr. Richard Herrmann, Köln Beurteilung der biometrischen Verhältnisse in einem Bestand 1 Fragestellung Methoden.1 Vergleich der Anzahlen. Vergleich
Beurteilung der biometrischen Verhältnisse in einem Bestand Dr. Richard Herrmann, Köln Beurteilung der biometrischen Verhältnisse in einem Bestand 1 Fragestellung Methoden.1 Vergleich der Anzahlen. Vergleich
Swiss Life Vorsorge-Know-how
 Swiss Life Vorsorge-Know-how Thema des Monats: Sofortrente Inhalt: Sofortrente, Ansparrente Gemeinsamkeiten und Unterschiede. Sofortrente nach Maß Verschiedene Gestaltungsmöglichkeiten. Sofortrente und
Swiss Life Vorsorge-Know-how Thema des Monats: Sofortrente Inhalt: Sofortrente, Ansparrente Gemeinsamkeiten und Unterschiede. Sofortrente nach Maß Verschiedene Gestaltungsmöglichkeiten. Sofortrente und
Einführung in die Algebra
 Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
Prof. Dr. H. Brenner Osnabrück SS 2009 Einführung in die Algebra Vorlesung 13 Einheiten Definition 13.1. Ein Element u in einem Ring R heißt Einheit, wenn es ein Element v R gibt mit uv = vu = 1. DasElementv
2. Gesundheitsfinanzierung
 2. Gesundheitsfinanzierung Inhalte dieses Abschnitts 2.1 Grundmodell der Versicherung Versicherungsmotiv Optimale Versicherungsnachfrage Aktuarisch faire und unfaire Prämien 145 2.1 Grundmodell der Versicherung
2. Gesundheitsfinanzierung Inhalte dieses Abschnitts 2.1 Grundmodell der Versicherung Versicherungsmotiv Optimale Versicherungsnachfrage Aktuarisch faire und unfaire Prämien 145 2.1 Grundmodell der Versicherung
Sofort-Rente. Mit Sicherheit ein Leben lang
 Sofort-Rente Mit Sicherheit ein Leben lang Warum ist die lebenslange Absicherung so wichtig? Wir werden immer älter. Das heißt aber auch, der Ruhestand wird immer teuerer. Wer das Ziel kennt kann entscheiden,
Sofort-Rente Mit Sicherheit ein Leben lang Warum ist die lebenslange Absicherung so wichtig? Wir werden immer älter. Das heißt aber auch, der Ruhestand wird immer teuerer. Wer das Ziel kennt kann entscheiden,
SS 2014 Torsten Schreiber
 SS 2014 Torsten Schreiber 239 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Durch die wird ein Zahlungsstrom beschrieben, der zur Rückführung eines geliehenen Geldbetrags dient. Der zu zahlende
SS 2014 Torsten Schreiber 239 Diese Lücken sollten nicht auch bei Ihnen vorhanden sein: Durch die wird ein Zahlungsstrom beschrieben, der zur Rückführung eines geliehenen Geldbetrags dient. Der zu zahlende
Übungsklausur. Bitte wählen Sie fünf Aufgaben aus! Aufgabe 1. Übungsklausur zu Mathematik I für BWL und VWL (WS 2008/09) PD Dr.
 Übungsklausur zu Mathematik I für BWL und VWL (WS 2008/09) PD Dr. Gert Zöller Übungsklausur Hilfsmittel: Taschenrechner, Formblatt mit Formeln. Lösungswege sind stets anzugeben. Die alleinige Angabe eines
Übungsklausur zu Mathematik I für BWL und VWL (WS 2008/09) PD Dr. Gert Zöller Übungsklausur Hilfsmittel: Taschenrechner, Formblatt mit Formeln. Lösungswege sind stets anzugeben. Die alleinige Angabe eines
Überschussbeteiligung der Versicherungsnehmer
 Überschussbeteiligung der Versicherungsnehmer Die Sicherung der dauernden Erfüllbarkeit der Verträge mit garantierten Leistungen machen vorsichtige Annahmen bezüglich der versicherten Risiken und der Zinserwartung
Überschussbeteiligung der Versicherungsnehmer Die Sicherung der dauernden Erfüllbarkeit der Verträge mit garantierten Leistungen machen vorsichtige Annahmen bezüglich der versicherten Risiken und der Zinserwartung
Senkung des technischen Zinssatzes und des Umwandlungssatzes
 Senkung des technischen Zinssatzes und des Umwandlungssatzes Was ist ein Umwandlungssatz? Die PKE führt für jede versicherte Person ein individuelles Konto. Diesem werden die Beiträge, allfällige Einlagen
Senkung des technischen Zinssatzes und des Umwandlungssatzes Was ist ein Umwandlungssatz? Die PKE führt für jede versicherte Person ein individuelles Konto. Diesem werden die Beiträge, allfällige Einlagen
Regelaltersgrenze der gesetzlichen Rentenversicherung ersetzt vertragliche Altersgrenze 65
 Regelaltersgrenze der gesetzlichen Rentenversicherung ersetzt vertragliche Altersgrenze 65 Ernst Ludwig, Dipl. Math., BAV-Ludwig Wie bereits in unserem Newsletter IV/2012 berichtet, hat das BAG mit seinem
Regelaltersgrenze der gesetzlichen Rentenversicherung ersetzt vertragliche Altersgrenze 65 Ernst Ludwig, Dipl. Math., BAV-Ludwig Wie bereits in unserem Newsletter IV/2012 berichtet, hat das BAG mit seinem
Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR)
 Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR) Eine Firma stellt USB-Sticks her. Sie werden in der Fabrik ungeprüft in Packungen zu je 20 Stück verpackt und an Händler ausgeliefert. 1 Ein Händler
Abituraufgabe zur Stochastik, Hessen 2009, Grundkurs (TR) Eine Firma stellt USB-Sticks her. Sie werden in der Fabrik ungeprüft in Packungen zu je 20 Stück verpackt und an Händler ausgeliefert. 1 Ein Händler
Analysis I für Studierende der Ingenieurwissenschaften
 Fachbereich Mathematik der Universität Hamburg WiSe 2015/16 Prof. Dr. M. Hinze Dr. P. Kiani Analysis I für Studierende der Ingenieurwissenschaften Lösungshinweise zu Blatt 2 Aufgabe 1: (12 Punkte) a) Beweisen
Fachbereich Mathematik der Universität Hamburg WiSe 2015/16 Prof. Dr. M. Hinze Dr. P. Kiani Analysis I für Studierende der Ingenieurwissenschaften Lösungshinweise zu Blatt 2 Aufgabe 1: (12 Punkte) a) Beweisen
Ausarbeitung des Seminarvortrags zum Thema
 Ausarbeitung des Seminarvortrags zum Thema Anlagepreisbewegung zum Seminar Finanzmathematische Modelle und Simulationen bei Raphael Kruse und Prof. Dr. Wolf-Jürgen Beyn von Imke Meyer im W9/10 Anlagepreisbewegung
Ausarbeitung des Seminarvortrags zum Thema Anlagepreisbewegung zum Seminar Finanzmathematische Modelle und Simulationen bei Raphael Kruse und Prof. Dr. Wolf-Jürgen Beyn von Imke Meyer im W9/10 Anlagepreisbewegung
Stochastische Eingangsprüfung, 17.05.2008
 Stochastische Eingangsprüfung, 17.5.8 Wir gehen stets von einem Wahrscheinlichkeitsraum (Ω, A, P) aus. Aufgabe 1 ( Punkte) Sei X : Ω [, ) eine integrierbare Zufallsvariable mit XdP = 1. Sei Q : A R, Q(A)
Stochastische Eingangsprüfung, 17.5.8 Wir gehen stets von einem Wahrscheinlichkeitsraum (Ω, A, P) aus. Aufgabe 1 ( Punkte) Sei X : Ω [, ) eine integrierbare Zufallsvariable mit XdP = 1. Sei Q : A R, Q(A)
Behörde für Bildung und Sport Abitur 2008 Lehrermaterialien zum Leistungskurs Mathematik
 Abitur 8 II. Insektenpopulation LA/AG In den Tropen legen die Weibchen einer in Deutschland unbekannten Insektenpopulation jedes Jahr kurz vor Beginn der Regenzeit jeweils 9 Eier und sterben bald darauf.
Abitur 8 II. Insektenpopulation LA/AG In den Tropen legen die Weibchen einer in Deutschland unbekannten Insektenpopulation jedes Jahr kurz vor Beginn der Regenzeit jeweils 9 Eier und sterben bald darauf.
GEGENÜBERSTELLUNG PRODUKTINFORMATIONSBLATT
 GEGENÜBERSTELLUNG PRODUKTINFORMATIONSBLATT Gesamtverband der Deutschen Versicherungswirtschaft (GDV) / Prof. Hans-Peter SCHWINTOWSKI, Humboldt-Universität (beide Berlin) Produktinformationsblatt GDV Formulierungsvorschlag
GEGENÜBERSTELLUNG PRODUKTINFORMATIONSBLATT Gesamtverband der Deutschen Versicherungswirtschaft (GDV) / Prof. Hans-Peter SCHWINTOWSKI, Humboldt-Universität (beide Berlin) Produktinformationsblatt GDV Formulierungsvorschlag
vorschüssige, lebenslängliche Leibrente (whole life annuity-due) Vorschüssige jährliche Zahlungen von 1, solange die versicherte Person am Leben ist.
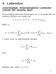 4. Leibrenten vorschüssige, lebenslängliche Leibrente (whole life annuity-due) Vorschüssige jährliche Zahlungen von 1, solange die versicherte Person am Leben ist. NEP ä x : Y = 1 + v + v 2 + + v K = ä
4. Leibrenten vorschüssige, lebenslängliche Leibrente (whole life annuity-due) Vorschüssige jährliche Zahlungen von 1, solange die versicherte Person am Leben ist. NEP ä x : Y = 1 + v + v 2 + + v K = ä
ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN
 ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN CHRISTIAN HARTFELDT. Zweiter Mittelwertsatz Der Mittelwertsatz Satz VI.3.4) lässt sich verallgemeinern zu Satz.. Seien f, g : [a, b] R auf [a,
ERGÄNZUNGEN ZUR ANALYSIS II MITTELWERTSATZ UND ANWENDUNGEN CHRISTIAN HARTFELDT. Zweiter Mittelwertsatz Der Mittelwertsatz Satz VI.3.4) lässt sich verallgemeinern zu Satz.. Seien f, g : [a, b] R auf [a,
Finanzierung: Übungsserie III Innenfinanzierung
 Thema Dokumentart Finanzierung: Übungsserie III Innenfinanzierung Lösungen Theorie im Buch "Integrale Betriebswirtschaftslehre" Teil: Kapitel: D1 Finanzmanagement 2.3 Innenfinanzierung Finanzierung: Übungsserie
Thema Dokumentart Finanzierung: Übungsserie III Innenfinanzierung Lösungen Theorie im Buch "Integrale Betriebswirtschaftslehre" Teil: Kapitel: D1 Finanzmanagement 2.3 Innenfinanzierung Finanzierung: Übungsserie
Würfelt man dabei je genau 10 - mal eine 1, 2, 3, 4, 5 und 6, so beträgt die Anzahl. der verschiedenen Reihenfolgen, in denen man dies tun kann, 60!.
 040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
Tarifarten im Rahmen der Tarifoptimierung
 Tarifarten im Rahmen der Tarifoptimierung BA510_201601 txt 2 3 Wir unterscheiden im Rahmen der Tarifoptimierung folgende Tarifarten Konventionell Konzeptversicherungen Dax-Rente Fondsgebunden OptimumGarant
Tarifarten im Rahmen der Tarifoptimierung BA510_201601 txt 2 3 Wir unterscheiden im Rahmen der Tarifoptimierung folgende Tarifarten Konventionell Konzeptversicherungen Dax-Rente Fondsgebunden OptimumGarant
Praktische Lebensversicheru ngsmathematik
 Karl MichaelOrtmann Praktische Lebensversicheru ngsmathematik Mit zahlreichen Beispielen, Abbildungen und Anwendungen STUDIUM 11 VIEWEG+ TEUBNER Inhaltsverzeichnis 1 Einleitung 1 1.1 Wesen der Versicherung
Karl MichaelOrtmann Praktische Lebensversicheru ngsmathematik Mit zahlreichen Beispielen, Abbildungen und Anwendungen STUDIUM 11 VIEWEG+ TEUBNER Inhaltsverzeichnis 1 Einleitung 1 1.1 Wesen der Versicherung
Finanzwirtschaft. Teil II: Bewertung. Zinssätze und Renten
 Zinssätze und Renten 1 Finanzwirtschaft Teil II: Bewertung Zinssätze und Renten Agenda Zinssätze und Renten 2 Effektivzinsen Spot-Zinsen Forward-Zinsen Bewertung Kennziffern Zusammenfassung Zinssätze und
Zinssätze und Renten 1 Finanzwirtschaft Teil II: Bewertung Zinssätze und Renten Agenda Zinssätze und Renten 2 Effektivzinsen Spot-Zinsen Forward-Zinsen Bewertung Kennziffern Zusammenfassung Zinssätze und
Lineare Funktionen. 1 Proportionale Funktionen 3 1.1 Definition... 3 1.2 Eigenschaften... 3. 2 Steigungsdreieck 3
 Lineare Funktionen Inhaltsverzeichnis 1 Proportionale Funktionen 3 1.1 Definition............................... 3 1.2 Eigenschaften............................. 3 2 Steigungsdreieck 3 3 Lineare Funktionen
Lineare Funktionen Inhaltsverzeichnis 1 Proportionale Funktionen 3 1.1 Definition............................... 3 1.2 Eigenschaften............................. 3 2 Steigungsdreieck 3 3 Lineare Funktionen
Klassische Finanzmathematik (Abschnitt KF.1 )
 Die Finanzatheatik ist eine Disziplin der angewandten Matheatik, die sich insbesondere it der Analyse und de Vergleich von Zahlungsströen und die theoretisch Erittlung des Geldwertes von Finanzprodukten.
Die Finanzatheatik ist eine Disziplin der angewandten Matheatik, die sich insbesondere it der Analyse und de Vergleich von Zahlungsströen und die theoretisch Erittlung des Geldwertes von Finanzprodukten.
OECD Programme for International Student Assessment PISA 2000. Lösungen der Beispielaufgaben aus dem Mathematiktest. Deutschland
 OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen
 Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen 1. Quadratische Gleichungen Quadratische Gleichungen lassen sich immer auf die sog. normierte Form x 2 + px + = 0 bringen, in
Grundlagen der höheren Mathematik Einige Hinweise zum Lösen von Gleichungen 1. Quadratische Gleichungen Quadratische Gleichungen lassen sich immer auf die sog. normierte Form x 2 + px + = 0 bringen, in
Informationsblatt Induktionsbeweis
 Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
Sommer 015 Informationsblatt Induktionsbeweis 31. März 015 Motivation Die vollständige Induktion ist ein wichtiges Beweisverfahren in der Informatik. Sie wird häufig dazu gebraucht, um mathematische Formeln
PKV-Info. Lohnt der Wechsel innerhalb der PKV?
 PKV-Info Lohnt der Wechsel innerhalb der PKV? 2 Die Unternehmen der privaten Krankenversicherung (PKV) stehen miteinander im Wettbewerb. Das ist so gewollt, zum Nutzen der Versicherten. Denn jeder Wettbewerb
PKV-Info Lohnt der Wechsel innerhalb der PKV? 2 Die Unternehmen der privaten Krankenversicherung (PKV) stehen miteinander im Wettbewerb. Das ist so gewollt, zum Nutzen der Versicherten. Denn jeder Wettbewerb
Die Renteninformation Alles klar! Oder doch nicht?
 Die Renteninformation Alles klar! Oder doch nicht? Veröffentlichung von Ulrich Watermann Schmitzbüchel 32a D 51491 Overath Tel: 02204 / 768733 Fax: 02204 / 768845 Mail: uw@watermann vorsorgekonzepte.de
Die Renteninformation Alles klar! Oder doch nicht? Veröffentlichung von Ulrich Watermann Schmitzbüchel 32a D 51491 Overath Tel: 02204 / 768733 Fax: 02204 / 768845 Mail: uw@watermann vorsorgekonzepte.de
Finanzmathematik. Dr. Bommhardt. Das Vervielfältigen dieses Arbeitsmaterials zu nicht kommerziellen Zwecken ist gestattet. www.bommi2000.
 Finanzmathematik Dr. Bommhardt. Das Vervielfältigen dieses Arbeitsmaterials zu nicht kommerziellen Zwecken ist gestattet. www.bommi2000.de Das Tilgungsrechnen Für Kredite gibt es drei unterschiedliche
Finanzmathematik Dr. Bommhardt. Das Vervielfältigen dieses Arbeitsmaterials zu nicht kommerziellen Zwecken ist gestattet. www.bommi2000.de Das Tilgungsrechnen Für Kredite gibt es drei unterschiedliche
8. Berechnung der kalkulatorischen Zinsen
 8. Berechnung der kalkulatorischen Zinsen 8.1. Allgemeines In der laufenden Rechnung werden im Konto 322.00 Zinsen nur die ermittelten Fremdkapitalzinsen erfasst. Sobald aber eine Betriebsabrechnung erstellt
8. Berechnung der kalkulatorischen Zinsen 8.1. Allgemeines In der laufenden Rechnung werden im Konto 322.00 Zinsen nur die ermittelten Fremdkapitalzinsen erfasst. Sobald aber eine Betriebsabrechnung erstellt
Einführung. Vorlesungen zur Komplexitätstheorie: Reduktion und Vollständigkeit (3) Vorlesungen zur Komplexitätstheorie. K-Vollständigkeit (1/5)
 Einführung 3 Vorlesungen zur Komplexitätstheorie: Reduktion und Vollständigkeit (3) Univ.-Prof. Dr. Christoph Meinel Hasso-Plattner-Institut Universität Potsdam, Deutschland Hatten den Reduktionsbegriff
Einführung 3 Vorlesungen zur Komplexitätstheorie: Reduktion und Vollständigkeit (3) Univ.-Prof. Dr. Christoph Meinel Hasso-Plattner-Institut Universität Potsdam, Deutschland Hatten den Reduktionsbegriff
6 Berechnung der Kapitalentwicklung auf der Basis der Zinseszinsrechnung
 6 Berechnung der Kaitalentwicklung auf der Basis der Zinseszinsrechnung 61 Wertentwicklung ohne Gut- oder Lastschrift von Zinsen Beisiele: 1 Konstante Produktionszunahme Produktion im 1 Jahr: P 1 Produktion
6 Berechnung der Kaitalentwicklung auf der Basis der Zinseszinsrechnung 61 Wertentwicklung ohne Gut- oder Lastschrift von Zinsen Beisiele: 1 Konstante Produktionszunahme Produktion im 1 Jahr: P 1 Produktion
7 Rechnen mit Polynomen
 7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
7 Rechnen mit Polynomen Zu Polynomfunktionen Satz. Zwei Polynomfunktionen und f : R R, x a n x n + a n 1 x n 1 + a 1 x + a 0 g : R R, x b n x n + b n 1 x n 1 + b 1 x + b 0 sind genau dann gleich, wenn
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA)
 Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2015/16 Hochschule Augsburg Rentenrechnung Definition Rente: Zahlungsstrom mit Zahlungen in gleichen
Wirtschaftsmathematik für International Management (BA) und Betriebswirtschaft (BA) Wintersemester 2015/16 Hochschule Augsburg Rentenrechnung Definition Rente: Zahlungsstrom mit Zahlungen in gleichen
Ab 2012 wird das Rentenalter schrittweise von 65 auf 67 Jahre steigen. Die Deutsche Rentenversicherung erklärt, was Ruheständler erwartet.
 Rente mit 67 was sich ändert Fragen und Antworten Ab 2012 wird das Rentenalter schrittweise von 65 auf 67 Jahre steigen. Die Deutsche Rentenversicherung erklärt, was Ruheständler erwartet. Wann kann ich
Rente mit 67 was sich ändert Fragen und Antworten Ab 2012 wird das Rentenalter schrittweise von 65 auf 67 Jahre steigen. Die Deutsche Rentenversicherung erklärt, was Ruheständler erwartet. Wann kann ich
Ein möglicher Unterrichtsgang
 Ein möglicher Unterrichtsgang. Wiederholung: Bernoulli Experiment und Binomialverteilung Da der sichere Umgang mit der Binomialverteilung, auch der Umgang mit dem GTR und den Diagrammen, eine notwendige
Ein möglicher Unterrichtsgang. Wiederholung: Bernoulli Experiment und Binomialverteilung Da der sichere Umgang mit der Binomialverteilung, auch der Umgang mit dem GTR und den Diagrammen, eine notwendige
Themenschwerpunkt Sofortrente
 Themenschwerpunkt Sofortrente Inhalt: Sofortrente, Ansparrente Gemeinsamkeiten und Unterschiede. Sofortrente nach Maß Verschiedene Gestaltungsmöglichkeiten. Sofortrente und Steuern Über die Besteuerung
Themenschwerpunkt Sofortrente Inhalt: Sofortrente, Ansparrente Gemeinsamkeiten und Unterschiede. Sofortrente nach Maß Verschiedene Gestaltungsmöglichkeiten. Sofortrente und Steuern Über die Besteuerung
Lineare Gleichungssysteme
 Brückenkurs Mathematik TU Dresden 2015 Lineare Gleichungssysteme Schwerpunkte: Modellbildung geometrische Interpretation Lösungsmethoden Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik auf der
Brückenkurs Mathematik TU Dresden 2015 Lineare Gleichungssysteme Schwerpunkte: Modellbildung geometrische Interpretation Lösungsmethoden Prof. Dr. F. Schuricht TU Dresden, Fachbereich Mathematik auf der
Berechnung der Erhöhung der Durchschnittsprämien
 Wolfram Fischer Berechnung der Erhöhung der Durchschnittsprämien Oktober 2004 1 Zusammenfassung Zur Berechnung der Durchschnittsprämien wird das gesamte gemeldete Prämienvolumen Zusammenfassung durch die
Wolfram Fischer Berechnung der Erhöhung der Durchschnittsprämien Oktober 2004 1 Zusammenfassung Zur Berechnung der Durchschnittsprämien wird das gesamte gemeldete Prämienvolumen Zusammenfassung durch die
Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema
 Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema 2x 4 + x 3 + x + 3 div x 2 + x 1 = 2x 2 x + 3 (2x 4 + 2x 3 2x 2 ) x 3 + 2x 2 + x + 3 ( x
Division Für diesen Abschnitt setzen wir voraus, dass der Koeffizientenring ein Körper ist. Betrachte das Schema 2x 4 + x 3 + x + 3 div x 2 + x 1 = 2x 2 x + 3 (2x 4 + 2x 3 2x 2 ) x 3 + 2x 2 + x + 3 ( x
Wirtschaftsmathematik-Klausur vom 04.02.2015 und Finanzmathematik-Klausur vom 27.01.2015
 Wirtschaftsmathematik-Klausur vom 04.0.015 und Finanzmathematik-Klausur vom 7.01.015 Bearbeitungszeit: W-Mathe 60 Minuten und F-Mathe 45 Min Aufgabe 1 a) Für die Absatzmenge x in ME) und den Verkaufspreis
Wirtschaftsmathematik-Klausur vom 04.0.015 und Finanzmathematik-Klausur vom 7.01.015 Bearbeitungszeit: W-Mathe 60 Minuten und F-Mathe 45 Min Aufgabe 1 a) Für die Absatzmenge x in ME) und den Verkaufspreis
Tangentengleichung. Wie lautet die Geradengleichung für die Tangente, y T =? Antwort:
 Tangentengleichung Wie Sie wissen, gibt die erste Ableitung einer Funktion deren Steigung an. Betrachtet man eine fest vorgegebene Stelle, gibt f ( ) also die Steigung der Kurve und somit auch die Steigung
Tangentengleichung Wie Sie wissen, gibt die erste Ableitung einer Funktion deren Steigung an. Betrachtet man eine fest vorgegebene Stelle, gibt f ( ) also die Steigung der Kurve und somit auch die Steigung
4.2.5 Wie berücksichtigt man den Einsatz und die Abnutzung der Anlagen?
 Seite 1 4.2.5 4.2.5 den Einsatz und die Bei der Erzeugung von Produkten bzw. der Erbringung von Leistungen sind in der Regel Anlagen (wie zum Beispiel Gebäude, Maschinen, Betriebs- und Geschäftsausstattung)
Seite 1 4.2.5 4.2.5 den Einsatz und die Bei der Erzeugung von Produkten bzw. der Erbringung von Leistungen sind in der Regel Anlagen (wie zum Beispiel Gebäude, Maschinen, Betriebs- und Geschäftsausstattung)
Beitragsfreiheit bei der Kalkulation von Pflegetagegeldtarifen in der KV
 Beitragsfreiheit bei der Kalkulation von Pflegetagegeldtarifen in der KV 1 Beitragsfreiheit bei der Kalkulation von Pflegetagegeldtarifen in der KV Gliederung: 1. Grundlagen der Beitragskalkulation in
Beitragsfreiheit bei der Kalkulation von Pflegetagegeldtarifen in der KV 1 Beitragsfreiheit bei der Kalkulation von Pflegetagegeldtarifen in der KV Gliederung: 1. Grundlagen der Beitragskalkulation in
Die Pareto Verteilung wird benutzt, um Einkommensverteilungen zu modellieren. Die Verteilungsfunktion ist
 Frage Die Pareto Verteilung wird benutzt, um Einkommensverteilungen zu modellieren. Die Verteilungsfunktion ist k a F (x) =1 k>0,x k x Finden Sie den Erwartungswert und den Median der Dichte für a>1. (Bei
Frage Die Pareto Verteilung wird benutzt, um Einkommensverteilungen zu modellieren. Die Verteilungsfunktion ist k a F (x) =1 k>0,x k x Finden Sie den Erwartungswert und den Median der Dichte für a>1. (Bei
 Name:... Matrikel-Nr.:... 3 Aufgabe Handyklingeln in der Vorlesung (9 Punkte) Angenommen, ein Student führt ein Handy mit sich, das mit einer Wahrscheinlichkeit von p während einer Vorlesung zumindest
Name:... Matrikel-Nr.:... 3 Aufgabe Handyklingeln in der Vorlesung (9 Punkte) Angenommen, ein Student führt ein Handy mit sich, das mit einer Wahrscheinlichkeit von p während einer Vorlesung zumindest
Absolute Stetigkeit von Maßen
 Absolute Stetigkeit von Maßen Definition. Seien µ und ν Maße auf (X, Ω). Dann heißt ν absolut stetig bezüglich µ (kurz ν µ ), wenn für alle A Ω mit µ(a) = 0 auch gilt dass ν(a) = 0. Lemma. Sei ν ein endliches
Absolute Stetigkeit von Maßen Definition. Seien µ und ν Maße auf (X, Ω). Dann heißt ν absolut stetig bezüglich µ (kurz ν µ ), wenn für alle A Ω mit µ(a) = 0 auch gilt dass ν(a) = 0. Lemma. Sei ν ein endliches
Merkblatt Rentenversicherung
 Merkblatt Rentenversicherung Von einer privaten Rentenversicherung ist besonders jungen Leuten abzuraten. Allenfalls für Ältere um die 60 Jahre kann sich eine Rentenversicherung per Einmalzahlung lohnen,
Merkblatt Rentenversicherung Von einer privaten Rentenversicherung ist besonders jungen Leuten abzuraten. Allenfalls für Ältere um die 60 Jahre kann sich eine Rentenversicherung per Einmalzahlung lohnen,
Rückstellungsreglement der Pensionskasse der ISS Schweiz, Zürich. Gültig ab 15.5.2013
 der Pensionskasse der ISS Schweiz, Zürich Gültig ab 15.5.2013 INHALT 1. Ziel 3 2. Definitionen 3 3. Versicherungstechnische Grundlagen 3 4. Zuständigkeiten 4 5. Rückstellungsarten 4 6. Vorsorgekapitalien
der Pensionskasse der ISS Schweiz, Zürich Gültig ab 15.5.2013 INHALT 1. Ziel 3 2. Definitionen 3 3. Versicherungstechnische Grundlagen 3 4. Zuständigkeiten 4 5. Rückstellungsarten 4 6. Vorsorgekapitalien
