Satz von Rademacher und weiterführende Resultate
|
|
|
- Lisa Holst
- vor 5 Jahren
- Abrufe
Transkript
1 S E M I N R R B E I T Saz von Rademacher und weierführende Resulae ausgeführ am Insiu für nalysis und Scienific Compuing TU Wien uner der nleiung von o.univ.prof. Dipl.-Ing. Dr.echn. Michael Kalenbäck durch Kaerina Uncovska Marikelnummer: Wien, am 27. Juni 2018
2 Inhalsverzeichnis 1 Einleiung 1 2 Saz von Rademacher Relevane Definiionen Funkionen auf R Saz von Rademacher Weierführende Resulae Differenzierbarkei in Räumen mi RNP i
3 1 Einleiung Zenral in dieser rbei is der Saz von Rademacher, der eine wichige ussage über Differenzierbarkei in endlichdimensionalen Banachräumen liefer. Sie orienier sich vor allem an den Ergebnissen in [DiB02] und [EG15]. Nach dem Einführen des relevanen Werkzeugs wird zunächs der eindimensionale, dann der allgemeine Fall berache. Schließlich wird ein kleiner Einblick in Räume mi Radon Nikodým Eigenschaf, vor allem Ergebnisse aus [BL00], in denen ähnliche, wenn auch schwächere ussagen über Differenzierbarkei geroffen werden können, geboen. 2 Saz von Rademacher 2.1 Relevane Definiionen Bevor wir zur ussage und zum Beweis des Sazes von Rademacher kommen, müssen zunächs einige Begriffe eingeführ werden. Im Folgenden werden alle Definiionen und Säze für auf R, beziehungsweise auf R N, mi N N definiere Funkionen formulier. nalog sind diese auch für offene Teilmengen von R (bzw. R n ) gülig. Mi bezeichnen wir die Zweinorm 2 = auf R n. Da alle Normen auf R n äquivalen sind, gelen alle Resulae analog für andere Normen. Definiion Eine Funkion f : R n R heiß Lipschiz-seig, wenn es eine Konsane L gib, sodass f(x) f(y) L x y für alle x, y R n. Definiion Eine Funkion f : R n R heiß demensprechend lokal Lipschizseig, wenn es für jede kompake Teilmenge K von R n eine Konsane L K gib, sodass die Lipschiz-Bedingung auf K erfüll is. Jede Lipschiz-seige Funkion is auch gleichmäßig seig. Die Umkehrung gil nich, wie man im folgenden Beispiel sieh. Beispiel Man berache die Wurzelfunkion, definier auf [0, ). Wäre diese Lipschiz seig, so gäbe es nun ein L > 0, sodass x y L x y auf ganz [0, ). Erweier man die linke Seie mi x+ y x+ y, so ergib sich 1 x+ 1 L. Für x =, y = 0 y 4L 2 erhalen wir einen Widerspruch. Wähl man δ = ε 2 zu ε > 0, dann folg, mi o.b.d.. y x, dass y x + ε 2 ( x + ε) 2 und somi x y ε. Dami is gleichmäßige Seigkei gezeig. Definiion Sei f : R n R. Für beliebiges v R n bezeichne man mi f(x + v) f(x) D v f(x) := lim, x R n, 0 1
4 die Richungsbleiung von f an der Selle x nach v, falls dieser Grenzwer exisier. Die Richungsableiungen nach den Einheisvekoren e 1,.., e n R n werden auch mi f x1 (x),.., f xn (x) bezeichne, der Gradien von f is f(x) = (f x1 (x),.., f xn (x)) T. Weiers is f pariell differenzierbar bei x R n, wenn die Richungsableiung D v (x) für v = e 1,..., e n exisier. Sind diese darüber hinaus seig, heiß f seig pariell differenzierbar. In dem Fall schreiben schreiben wir f C 1 (R n ). Nich mi diesen usdrücken zu verwechseln is der Begriff der Differenzierbarkei, der in der Lieraur auch als Fréche-Differenzierbarkei oder oale Differenzierbarkei bezeichne wird. Definiion Eine Funkion f : R n R is differenzierbar bei x R n, wenn es ein Df(x) R 1 n gib, sodass f(y) = f(x) + Df(x)(y x) + ε(x y), für y U ρ (x), erfüll is. Hierbei is ρ > 0 und ε: U ρ (0)\0 R derar, dass lim y x ε(x y) x y = 0. Elemenar zeig man: Gib es ein solches Df(x), so simm dieses mi f(x) überein. lso folg Parielle Differenzierbarkei aus der Differenzierbarkei. Umgekehr läss sich jedoch nich von der Exisenz von f(x) auf die Differenzierbarkei bei x schließen. us der seigen pariellen Differenzierbarkei folg aber sehr wohl die Differenzierbarkei. 2.2 Funkionen auf R Für den Beweis des Sazes von Rademacher is noch eine ussage zur Differenzierbarkei für Funkionen auf R nöig. Definiion Eine Funkion f : R R heiß absolu seig, falls es für jedes ε > 0 ein δ > 0 gib, sodass für jede endliche Menge paarweise disjunker Inervalle {(x k, y k )} n k=1 mi Gesamlänge n k=1 (y k x k ) < δ gil. f(y k ) f(x k ) < ε k=1 Ein wichiges Resula is, dass Lipschiz-seige Funkionen auf R absolu seig sind. Lemma Eine Lipschiz-seige Funkion f : R R is absolu seig. 2
5 Beweis. Für ε > 0 wähle δ := ε. Dann folg für alle {(x L k, y k )} n k=1 mi Gesamlänge n k=1 (y k x k ) < δ f(y k ) f(x k ) k=1 L (y k x k ) = L (y k x k ) < L δ = L ε L = ε. k=1 k=1 Definiion Eine Funkion f : [a, b] R heiß von beschränker Variaion (f BV ([a, b])), falls V b a (f) < +, wobei V b a (f) := sup { f(x i ) f(x i 1 ) : a = x 0 < x 1 <.. < x n = b, n N}. i=1 Ein bekannes Ergebnis aus der Maßheorie is, dass absolu seige Funkionen auf jedem Inervall [a, b] von beschränker Variaion sind [Kus14, Kapiel 12.2/3]. Der Saz von Lebesgue - siehe [Kus14, Kapiel 12.2/3] - liefer dann die Differenzierbarkei fas überall auf genannem Inervall; also is f außerhalb einer Lebesgue-Nullmenge differenzierbar. Da Differenzierbarkei eine lokale Eigenschaf is, läss sich dieses Resula dann für absolu seige Funkionen auf ganz R überragen. Wir erhalen also: Lemma Eine absolu seige Funkion f : R R is f.ü. differenzierbar. Dieses Ergebnis läss sich mi Lemma für lokal Lipschiz seige Funkionen kombinieren. Wir erhalen eine ussage, die wir für den Beweis vom Saz von Rademacher benöigen werden. Korollar Sei f : R R eine lokal Lipschiz-seige Funkion. Dann is f f.ü. differenzierbar. 2.3 Saz von Rademacher Wir kommen zur Haupaussage dieser rbei. Saz (Saz von Rademacher). Sei f : R n R eine lokal Lipschiz-seige Funkion. Dann is f f.ü. differenzierbar. Beweis. Der Beweis wird in drei Schrien erfolgen. Für den ersen und zweien Teil berache Richungsableiungen D v f(x) für v = Behaupung: D v f(x) exisier für fas alle x R n. 3
6 Wie definieren D v f(x) = lim sup 0 D v f(x) = lim inf 0 f(x + v) f(x), f(x + v) f(x). Bezeichne mi E v die Menge, auf der D v f nich definier is, genauer E v = {x R n D v f(x) < D v f(x)}. Da f seig is, kann der Grenzwer D v f(x) bzw. D v f(x) für ( 1, 1) Q gebilde werden. Es folg, dass D v f(x) und D v f(x) messbar sind und demensprechend auch E v messbar is [Kus14, Kapiel 7.2]. Mi f is auch φ: R R, f(x + v) für jedes x R n lokal Lipschiz-seig, da φ() φ(s) = f(x + v) f(x + sv) L x + v x sv = L s v = L s. us Korollar folg dami für φ die Differenzierbarkei fas überall auf R. Wegen φ () = D v f(x + v) ha der Schni von E v mi jeder zu v parallelen Linie L eindimensionales Lebesgue-Maß null. Mi dem Saz von Fubini [Kus14] folg λ n (E v ) = λ(e v L) dλ n 1 = 0. v 2. Behaupung: D v f(x) = f(x) v für fas alle x. uf der Menge = R n \(E v n j=1 E e j ) exisieren alle Richungsableiungen von f nach v sowie der Gradien. Berache ( 1, 1) Q und bezeichne mi e j, j = 1,..., n, die Einheisvekoren von R n. Da f lokal Lipschiz-seig is, gil für alle beliebig of differenzierbaren Funkionen mi kompakem Träger ζ C0 (R n ), f(x + v) f(x) ζ(x) L ζ ζ(x), wobei L ζ die Lipschiz Konsane von f auf einer hinreichend großen, den Träger von ζ enhalenden Kugel is. Somi sind die Bedingungen für den Saz von dominierer Konvergenz [Kus14] erfüll. Inegrier man auf der Menge, so folg f(x + v) f(x) D v f(x)ζ(x) dx = lim ζ(x) dx 0 = lim 0 ( f(x + v) ζ(x) dx Subsiuier man im linken Inegral mi x v, so erhäl man f(x) f(x) = lim( ζ(x v) dx ζ(x) dx) 0 ζ(x) ζ(x v) = lim f(x) dx. 0 4 f(x) ζ(x) dx)
7 Mi dem selben rgumen wie zuvor, kann man jez mi dominierer Konvergenz den Limes und das Inegral verauschen. Da ζ aus C 0 (R N ) gewähl wurde, ergib das v j j=1 f(x)ζ xj (x) dx = j=1 v j lim f(x) 0 ζ(x) ζ(x e j) Nun wird, ähnlich wie zuvor, mi v + e j subsiuier und dominiere Konvergenz angewende. lso simm obiger usdruck überein mi j=1 = v j lim 0 f(x + e j ) f(x) ζ(x) dx v f(x)ζ(x) dx dx. Das implizier (D v f(x) f(x) v)ζ(x) dx = 0 für alle ζ C0 (R n ). Nach [Kus14] folg daraus D v (x)f = f(x) v fas überall auf. Da nach dem ersen Teil E v n j=1 E e j Lebesgue-Maß Null ha, erhalen wir D v (x)f = v f(x) fas überall auf R n. Sei nun B = {u k k N} eine abzählbare diche Teilmenge auf dem Rand der Einheiskugel B 1, sodass alle Einheisvekoren e j darin enhalen sind. Berache F uk := {x R n D uk f(x) exisier und D uk f(x) = f(x) u k }. Nach dem bereis Gezeigen ha R n \ F uk k N Lebesgue-Maß Null. Um das Theorem zu beweisen, genüg es nun die Differenzierbarkei von f auf F = zu zeigen. F uk k N 3. Behaupung: f is differenzierbar auf F. Für x F, u B 1 und [ 1, 1]\{0} definieren wir Q(x, u, ) := f(x + u) f(x) f(x) u. Sei weiers L die Lipschizkonsane von f auf K 1 (x). Für beliebeige v B 1 gil Q(x, u, ) Q(x, v, ) f(x + u) f(x + v) + f(x) (u v) L u v + f(x) u v 5
8 L( n + 1) u v. (1) f(x+e Die leze Ungleichung gil, da f xj = lim j ) f(x) 0 L x+ x = L und somi f n L. Für ε > 0 wähle N(ε) N groß genug, sodass sup u =1 min u u k k=1,...,n(ε) ε 2L( n + 1). (2) Wegen der Dicheeigenschaf der Menge B und der Kompakhei von B gib es ein solches N(ε). Weiers gil nach Definiion der Menge F lim Q(x, u k, ) = 0 0 für k {1,..., N(ε)}. Es folg die Exisenz eines δ > 0 mi o.b.d.. δ 1, sodass Q(x, u k, ) < ɛ 2 für alle 0 < < δ und k = 1,..., N(ε). (3) Zusammen folg aus den Gleichungen (1)-(3) für alle u B 1 Q(x, u, ) Q(x,, u k ) + Q(x, u, ) Q(x, u k, ) < ε für 0 < < δ, wobei k so gewähl wird, dass u u k = min j=1,...,n(ε) u u j. Wähle y x aus R n und seze u := y x und = y x. Offensichlich is dann y x y = x + u. Es folg mi f(y) f(x) f(x) (y x) = f(x + u) f(x) f(x) u y x = Q(x,, y x ) y x, y x Q(x, y x, y x ) y x < ε für 0 < y x < δ. Somi is f bei x differenzierbar, wobei Df(x) = f(x). 3 Weierführende Resulae Der Saz von Rademacher is eine sehr schöne und sarke ussage auf endlichdimensionalen Vekorräumen. ber wie sieh das mi unendlichdimensionalen Räumen aus? Es lassen sich asächlich ähnliche Resulae finden. Eines davon berache Räume mi der Radon-Nikodým Eigenschaf. Da es vom Inhal dieser rbei zu sark abweich, werden usdrücke wie Radon-Nikodým bleiung, absolue Seigkei von Maßen und dami verbundene Eigenschafen vorausgesez. Die zuvor verwendeen Definiionen für absolue Seigkei und beschränke Variaion sind hier analog, mi der Norm sa dem Berag auf die Funkionswere angewand, zu verwenden. 6
9 3.1 Differenzierbarkei in Räumen mi RNP Definiion Sei E ein Banachraum, C E abgeschlossen, konvex und beschränk. Man sag, C habe RNP (Radon Nikodým Propery), wenn die folgene Eigenschaf erfüll is: Is (Ω, ) ein Maßraum, τ ein E-weriges Maß und µ ein skalares Wahrscheinlichkeismaß auf (Ω, ), sodass τ() C für alle mi µ() 0, dann exisier ein f µ() L1 (µ, E), sodass τ() = f(ω) dµ(ω) für alle. Dieses Inegral exisier im Sinne von Bochner. Man sag E habe RNP, wenn die Einheiskugel RNP ha. Offenbar ha eine abgeschlossene, konvexe, beschränke Teilmenge eines Banachraumes E RNP, falls E selbs RNP ha. Diese Definiion mag zunächs ein wenig absrak wirken. Zum besseren Versändnis is die folgende charakerisische Eigenschaf hilfreich. Lemma Der Banachraum E ha genau dann RNP, wenn jede absolu seige Funkion f : R E differenzierbar f.ü. is. Den Beweis kann man bei Theorem 5.21, [BL00, Kapiel 5.3] nachlesen. uf unendlichdimensionalen Räumen müssen wir zudem die Begriffe der Differenzierbarkei einführen. Differenzierbarkei (Fréche Differenzierbarkei) läss sich genau wie auf R N auch auf beliebigen Banachräumen definieren. Um ein nalogon zur pariellen Differenzierbarkei zu erhalen, muss aber noch weier ausgehol werden. Definiion Seien E und F Banachräume. Eine Funkion f : E F is Gâeaux differenzierbar bei x E, wenn für jedes v E die Richungsableiung D v f(x) exisier und v D v f(x) eine lineare, seige Funkion is. Kommen wir nun zu dem zu Beginn angesprochenen Resula über Differenzierbarkei in Räumen mi RNP. Saz Sei F ein Banachraum mi RNP und f : R n F lokal Lipschiz-seig. Dann is f fas überall Gâeaux differenzierbar auf R n. Für den Beweis des Sazes wird noch ein echnisches Lemma benöig. Lemma Seien E, F Banachräume über R, U E offen und f : U F eine Lipschiz seige Funkion. Sei weiers G E eine diche, abzählbare Unergruppe von (E, +). ngenommen, es gib ein x 0 E, sodass für alle u G die Richungsableiungen D u f(x 0 ) exisieren und die Funkion u D u f(x 0 ) addiiv is. Dann is f Gâeaux differenzierbar bei x 0. 7
10 Beweis. Berache Funkionen h (u) := f(x 0+u) f(x 0 ), 0. Dabei gil h (u) L u. ußerdem gil h (u) h (v) = f(x 0 + u) f(x 0 + v) L u v. lso gib es zu einem gegebenen ɛ > 0 und v E ein δ > 0, sodass für alle u G mi u v < δ die Ungleichung h (v) h (u) ɛ für alle R, 0, gil. Für solche u 3 exisier lim 0 h (u), wodurch h (v) h s (v) h (v) h (u) + h (u) h s (u) + h s (u) h s (v) < ɛ für und s klein genug, sodass h (u) h s (u) < ɛ. lso exisier lim 3 0 h (v) für alle v E. Die ddiiviä des Grenzweres auf G ha auch die ddiiviä auf E zu Folge und per Definiion gil lim 0 h (α u) = α lim 0 h (u). lso is lim 0 h ( ) ein linearer Operaor, der mi h (u) L u durch die Lipschizkonsane beschränk is. Ein weierer Begriff, der im Beweis wichig is, is der von Lebesgue-Punken einer Funkion. Definiion Sei f : R n R eine lokal Lebesgue inegrierbare Funkion. Dann heiß x R n ein Lebesgue-Punk von f, wenn 1 lim r 0 r f(x y) f(x) dy = 0. y <r Nach Theorem 1.37 [EG15, Kapiel 1.7.2] sind für lokal inegrierbare Funkionen fas alle x R Lebesgue-Punke. Beweis. [von Saz ] Sei G R n eine abzählbare, diche addiive Unergruppe. Eine solche is zum Beispiel Q n. Sei φ: R F, f(x + v). Nach Lemma is φ differenzierbar fas überall mi φ () = D v f(x + v). Bezeichne weiers mi E v die Menge, auf der die Richungsableiung nach einem v G nich exisier. nalog zum Beweis des Sazes von Rademacher läss sich der Saz von Fubini anwenden, um zu zeigen, dass E v eine Lebesgue-Nullmenge is. Da G abzählbar is, folg die Exisenz der Richungsableiungen nach allen v G von f fas überall. Nach Lemma genüg es zu zeigen, dass diese Richungsableiungen nach v G fas überall addiiv sind. Hierzu werden Falungen verwende. Berache eine seig differenzierbare Funkion ψ : R n [0, + ) mi kompakem Träger und ψ(x)dx = 1. Dann is auch R n g := f ψ = ψ(x y)f(y) dy R n seig differenzierbar. lso is für jedes x R n D u g(x) = D u ψ(x y)f(y) dy = (f D u ψ)(x) R n 8
11 linear in u R n. ndererseis folg für fas alle x und für alle u G mi dominierer Konvergenz g(x + u) g(x) f(x y + u) f(x y) D u g(x) = lim = ψ(y) lim dy. 0 R n 0 lso gil D u g(x) = (ψ h u )(x) mi der beschränken, messbaren Funkion f(x+u) f(x) h u (x) = lim 0. Es folg 0 = f (D u+v ψ D u ψ D v ψ) = D u+v g(x) D u g(x) D v g(x) = ψ (h u+v h u h v ) für alle u, v G. Diese rgumenaion funkionier ebenso für ψ k := k n ψ(kx), mi einer beliebigen naürlichen Zahl k, und somi auch für den Grenzwer lim k ψ k h u. Um diesen zu berechnen, berache lim k ψ k T h u (x) mi einem linearen und beschränken Funkional T : F R. Es ergib sich lim ψ k T h u (x) T h u (x) = lim k n ψ(ky) T h u (x y) dy T h u (x) k k R n = lim ψ(y) (T h u (x y k R k ) T h u(x)) dy. (4) n ls Grenzwer messbarer Funkionen is h u und somi auch die Zusammensezung T h u messbar. Weiers is T h u durch T h u (x) T L x beschränk, also lokal inegrierbar und beseh demensprechend f.ü. aus Lebesgue-Punken. Das Inegral in (4) is kleiner als ψ(y) (T h u (x y y <1 k ) T h u(x)) dy + ψ(y) (T h u (x y y 1 k ) T h u(x)) dy sup ψ(y) (T h u (x y) T h u (x)) dy + T L 1 ψ(y) y dy. (5) k y < 1 k Für den linken Teil von (5) finde sich nun auf allen Lebesgue-Punken von T h u für jedes ε > 0 ein K N groß genug, sodass (T h u (x y) T h u (x)) dy 1 k ε y < 1 k y 1 für alle k K. Für den rechen Teil von (5) gib es, da ψ einen kompaken Träger ha, ein R R, sodass supp ψ B R (0) gil. Es folg ψ(y) y dy = ψ(y) y dy R 2 sup ψ(y). y 1 1 y R Fass man nun alle Konsanen zu einer Konsane C zusammen, läss sich (5) durch 1 C(ε + 1) k 9
12 für alle k K abschäzen. Für k + konvergier der usdruck gegen Null und es folg fas überall lim k ψ k T h u (x) = T h u (x). Weiers is lim k ψ k T h u (x) = T lim k ψ k h u (x) für alle x R n. Da F punkerennend auf F operier (vgl. [WKB, Kapiel 5.2]), folg daraus lim k ψ k h u (x) = h u (x) fas überall. Da G abzählbar is, folg für alle u, v G : h u+v = h u + h v fas überall auf R n. 10
13 Lieraur [BL00] Yoav Benyamini and Joram Lindensrauss. Geomeric nonlinear funcional analysis. Vol. 1, volume 48 of merican Mahemaical Sociey Colloquium Publicaions. merican Mahemaical Sociey, Providence, RI, [DiB02] Emmanuele DiBenedeo. Real analysis. Birkhäuser dvanced Texs: Basler Lehrbücher. [Birkhäuser dvanced Texs: Basel Texbooks]. Birkhäuser Boson, Inc., Boson, M, [EG15] Lawrence C. Evans and Ronald F. Gariepy. Measure heory and fine properies of funcions. Texbooks in Mahemaics. CRC Press, Boca Raon, FL, revised ediion, [Kal14] Michael Kalenbäck. Fundamen nalysis, volume 26 of Berliner Sudienreihe zur Mahemaik [Berlin Sudy Series on Mahemaics]. Heldermann Verlag, Lemgo, [Kus14] Norber Kusolisch. Maß- und Wahrscheinlichkeisheorie. Springer-Lehrbuch. [Springer Texbook]. Springer Spekrum, Berlin Heidelberg, expanded ediion, Eine Einführung. [n inroducion]. [WKB] Harald Woracek, Michael Kalenbäck, and Marin Blümlinger. Funkionalanalysis. Vorlesungsskripum Version SS 2016 (11. uflage). 11
Differenzieren von Funktionen zwischen Banachräumen
 Differenzieren von Funkionen zwischen Banachräumen Ingmar Gezner In dieser Seminararbei wollen wir das Differenzieren auf Funkionen zwischen Banachräume verallgemeinern. In unendlichdimensionalen Räumen
Differenzieren von Funkionen zwischen Banachräumen Ingmar Gezner In dieser Seminararbei wollen wir das Differenzieren auf Funkionen zwischen Banachräume verallgemeinern. In unendlichdimensionalen Räumen
7 Das lokale Ito-Integral
 7 Das lokale Io-Inegral 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal 7.5 Seige, lokale Maringale
7 Das lokale Io-Inegral 7.3 Ein lokales L p -Maringal is uner einer gleichgradigen Inegrierbarkeisbedingung ein L p -Maringal 7.4 Rechsseiig seiges (seiges), lokales L p -Maringal 7.5 Seige, lokale Maringale
existiert. In der Regel wird zusätzlich zum oben gegebenen System von Differentialgleichungen noch eine Anfangsbedingung
 0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
0 Eine Anwendung der Jordan-Normalform in der Analysis In vielen physikalischen Anwendungen is es nowendig, Syseme von Differenialgleichungen der Form: y ( = b y ( + b 2 y 2 ( + + b n y n ( + f ( y 2(
Höhere Mathematik II für die Fachrichtung Physik
 Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Michael Ho, M. Sc. M. Sc. SS 6 9.7.6 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zur Übungsklausur Aufgabe
Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Michael Ho, M. Sc. M. Sc. SS 6 9.7.6 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zur Übungsklausur Aufgabe
Zwischenwerteigenschaft
 Zwischenwereigenschaf Markus Berberich Ausarbeiung zum Vorrag im Proseminar Überraschungen und Gegenbeispiele in der Analysis (Sommersemeser 2009, Leiung PD Dr. Gudrun Thäer) Zusammenfassung: In dieser
Zwischenwereigenschaf Markus Berberich Ausarbeiung zum Vorrag im Proseminar Überraschungen und Gegenbeispiele in der Analysis (Sommersemeser 2009, Leiung PD Dr. Gudrun Thäer) Zusammenfassung: In dieser
Definition Ein Homomorphismus von Lie-Algebren. Für uns ist vor allem die im folgenden Satz eingeführte Darstellung von Bedeutung.
 1 Lie-Gruppen 1. Lie-Algebren Im lezen Vorrag haben wir bereis das Konzep der Lie-Algebren kennengelern. Zunächs werde ich noch einige weiere grundlegende Definiionen dazu angeben. In diesem Kapiel sei
1 Lie-Gruppen 1. Lie-Algebren Im lezen Vorrag haben wir bereis das Konzep der Lie-Algebren kennengelern. Zunächs werde ich noch einige weiere grundlegende Definiionen dazu angeben. In diesem Kapiel sei
Einführung in gewöhnliche Differentialgleichungen
 Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
Einführung in gewöhnliche Differenialgleichungen Jonahan Zinsl 25. Mai 202 Definiionen Definiion.(Gewöhnliche Differenialgleichung. Ordnung) Uner einer gewöhnlichen Differenialgleichung. Ordnung verseh
7.3. Partielle Ableitungen und Richtungsableitungen
 7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
7.3. Parielle Ableiungen und Richungsableiungen Generell vorgegeben sei eine Funkion f von einer Teilmenge A der Ebene R oder allgemeiner des n-dimensionalen Raumes R n nach R. Für x [x 1,..., x n ] aus
2.2 Rechnen mit Fourierreihen
 2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
2.2 Rechnen mi Fourierreihen In diesem Abschni sollen alle Funkionen als sückweise seig und -periodisch vorausgesez werden. Ses sei ω 2π/. Wir sezen jez aus Funkionen neue Funkionen zusammen und schauen,
Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkeit Seminararbeit aus Numerik von Differentialgleichungen
 Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkei Seminararbei aus Numerik von Differenialgleichungen Michael Hubner, Sefan Wurm 8. Juli 22 Inhalsverzeichnis. Problemdefiniion 2 2. Einführende
Thema: Singuläres, skalares Problem 2. Ordnung - Lösbarkei Seminararbei aus Numerik von Differenialgleichungen Michael Hubner, Sefan Wurm 8. Juli 22 Inhalsverzeichnis. Problemdefiniion 2 2. Einführende
5. Übungsblatt zur Differentialgeometrie
 Insiu für Mahemaik Prof. Dr. Helge Glöckner Dipl. Mah. Rafael Dahmen 5. Übungsbla zur Differenialgeomerie (Aufgaben und Lösungen) SoSe 3.05.0 Gruppenübung Aufgabe G9 (Submersionen und Unermannigfaligkei)
Insiu für Mahemaik Prof. Dr. Helge Glöckner Dipl. Mah. Rafael Dahmen 5. Übungsbla zur Differenialgeomerie (Aufgaben und Lösungen) SoSe 3.05.0 Gruppenübung Aufgabe G9 (Submersionen und Unermannigfaligkei)
Probeklausur 1. Thema Nr. 1 (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeiten!
 Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
Universiä Regensburg, Winersemeser 3/4 Examenskurs Analysis (LGy) Dr. Farid Madani Probeklausur Thema Nr. (Aufgabengruppe) Es sind alle Aufgaben dieser Aufgabengruppe zu bearbeien! Aufgabe (5 Punke). Man
Lösungen zu Übungsblatt 4
 Fakulä für Mahemaik, Technische Universiä Dormund Vorlesung Geomerie für Lehram Gymnasium, Winersemeser 24/5 Dipl-Mah Aranç Kayaçelebi Lösungen zu Übungsbla 4 Aufgabe 2 Punke a Geben Sie eine Funkion f
Fakulä für Mahemaik, Technische Universiä Dormund Vorlesung Geomerie für Lehram Gymnasium, Winersemeser 24/5 Dipl-Mah Aranç Kayaçelebi Lösungen zu Übungsbla 4 Aufgabe 2 Punke a Geben Sie eine Funkion f
Stochastische Differentialgleichungen
 INSTITUT FÜR STOCHASTIK SS 2007/08 UNIVRSITÄT KARLSRUH Bla 9 Priv.-Doz. Dr. D. Kadelka Übungen zur Vorleung Sochaiche Differenialgleichungen Muerlöungen Aufgabe 21: Definieren Sie analog zur d-dimenionalen
INSTITUT FÜR STOCHASTIK SS 2007/08 UNIVRSITÄT KARLSRUH Bla 9 Priv.-Doz. Dr. D. Kadelka Übungen zur Vorleung Sochaiche Differenialgleichungen Muerlöungen Aufgabe 21: Definieren Sie analog zur d-dimenionalen
Karlsruher Institut für Technologie (KIT) Institut für Analysis Dr. A. Müller-Rettkowski Dipl.-Math. M. Uhl. Sommersemester 2011
 Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
Karlsruher Insiu für Technologie KIT) Insiu für Analysis Dr. A. Müller-Rekowski Dipl.-Mah. M. Uhl Sommersemeser Höhere Mahemaik II für die Fachrichungen Elekroingenieurwesen und Physik inklusive Komplee
Lösung zur Hausaufgabe in Topologie und Differentialrechnung mehrerer Variablen SS x 1. x 2. x 1+x 2+x 3
 Bl Nr. 11 Simon Reisser Lösung zur Husufgbe in Topologie und Differenilrechnung mehrerer Vriblen SS 17 Aufgbe () Sei f(x 1, x, x 3 ) = (y 1, y, y 3 ) = (e x1x x3, e x1x+x3, e xx3 ) und dg(y 1, y, y 3 )
Bl Nr. 11 Simon Reisser Lösung zur Husufgbe in Topologie und Differenilrechnung mehrerer Vriblen SS 17 Aufgbe () Sei f(x 1, x, x 3 ) = (y 1, y, y 3 ) = (e x1x x3, e x1x+x3, e xx3 ) und dg(y 1, y, y 3 )
Höhere Mathematik II für die Fachrichtung Physik
 Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Dipl.-Mah. Sebasian Schwarz SS 015 17.05.015 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zum 6. Übungsbla
Karlsruher Insiu für Technologie Insiu für Analysis Dr. Chrisoph Schmoeger Dipl.-Mah. Sebasian Schwarz SS 015 17.05.015 Höhere Mahemaik II für die Fachrichung Physik Lösungsvorschläge zum 6. Übungsbla
Der Raum C liegt dicht in L p
 Universiä Posdam Vorlesung Funkionalanalysis, SS 2009. (Dr. Seen Frölic Maias Ludewig Marikelnummer 73580 Daum: 8.05.2009 Der Raum C lieg dic in L p Überblick Aus der Vorlesung is bekann, dass der Raum
Universiä Posdam Vorlesung Funkionalanalysis, SS 2009. (Dr. Seen Frölic Maias Ludewig Marikelnummer 73580 Daum: 8.05.2009 Der Raum C lieg dic in L p Überblick Aus der Vorlesung is bekann, dass der Raum
Gewöhnliche Differentialgleichungen (DGL)
 Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
Gewöhnliche Differenialgleichungen (DGL) Einführende Beispiele und Definiion einer DGL Beispiel 1: 1. Die lineare Pendelbewegung eines Federschwingers führ uner Zuhilfenahme des Newonschen Krafgesezes
3.4 Systeme linearer Differentialgleichungen
 58 Kapiel 3 Invarianen linearer Transformaionen 34 Syseme linearer Differenialgleichungen Die Unersuchung der Normalformen von Marizen soll nun auf die Lösung von Differenialgleichungssysemen angewende
58 Kapiel 3 Invarianen linearer Transformaionen 34 Syseme linearer Differenialgleichungen Die Unersuchung der Normalformen von Marizen soll nun auf die Lösung von Differenialgleichungssysemen angewende
Universität Ulm Samstag,
 Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Universiä Ulm Samsag, 5.6. Prof. Dr. W. Arend Robin Nika Sommersemeser Punkzahl: Lösungen Gewöhnliche Differenialgleichungen: Klausur. Besimmen Sie die Lösung (in möglichs einfacher Darsellung) folgender
Lineare Algebra I - Lösungshinweise zur Klausur
 Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
Insiu für Mahemaik Winersemeser 0/3 Universiä Würzburg 0 Februar 03 Prof Dr Jörn Seuding Dr Anna von Heusinger Frederike Rüppel Lineare Algebra I - Lösungshinweise zur Klausur Aufgabe : (0 Punke) Zeigen
Technische Universität München. Lösung Montag SS 2012
 Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
Technische Universiä München Andreas Wörfel Ferienkurs Analysis für Physiker Lösung Monag SS 0 Aufgabe Gradien und Tangene ( ) Besimmen Sie zur Funkion f(x, y) = x y + xy + y die pariellen Ableiungen,
8.5 Uneigentliche Integrale Integrale über unbeschränkte Bereiche. f(x) dx. Integrale über unbeschränkte Funktionen mit Singularitäten am Rand
 8.5 Uneigenliche Inegrle Inegrle über unbeschränke Bereiche,, Inegrle über unbeschränke Funkionen mi Singulriäen m Rnd, f : (, b] R seig, f : [, b) R seig Lokle Inegrierbrkei: Definiion: Eine Funkion f
8.5 Uneigenliche Inegrle Inegrle über unbeschränke Bereiche,, Inegrle über unbeschränke Funkionen mi Singulriäen m Rnd, f : (, b] R seig, f : [, b) R seig Lokle Inegrierbrkei: Definiion: Eine Funkion f
Typ A: Separierbare Differentialgleichungen I. Separierbare Differentialgleichungen II. Beispiel einer separierbaren Dgl
 Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
Typ A: Separierbare Differenialgleichungen I Gegeben sei die Differenialgleichung y () = f () g(y) in einem Bereich D der (, y) Ebene. Gil g(y) 0, so lassen sich die Variablen und y rennen: y () g(y) =
DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN
 Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
Skrium zum Fach Mechanik 5Jahrgang HTL-Eisensad DIE LINEARE DIFFERENTIALGLEICHUNG ZWEITER ORDNUNG MIT KONSTANTEN KOEF- FIZIENTEN DilIngDrGüner Hackmüller 5 DilIngDrGüner Hackmüller Alle Reche vorbehalen
7. Funktionalgleichung der Zeta-Funktion
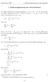 Oo Forser: RZF 7 Funkionalgleichung der Zea-Funkion 7 Funkionalgleichung der Zea-Funkion 7 Saz (Poissonsche Summaionsformel Sei f : R C eine seig differenzierbare Funkion mi f(x O ( x für x Sei ˆf : R
Oo Forser: RZF 7 Funkionalgleichung der Zea-Funkion 7 Funkionalgleichung der Zea-Funkion 7 Saz (Poissonsche Summaionsformel Sei f : R C eine seig differenzierbare Funkion mi f(x O ( x für x Sei ˆf : R
Ferienkurs Analysis I für Physiker WS 15/16 Aufgaben Tag 3. Aufgaben Tag 3
 für Physier WS 5/6 Reihen Zeigen Sie, dass die folgenden Reihen onvergieren und die angegebenen Summen haben. Dabei is f die -e Fibonacci-Zahl a + = 4 Wir fassen die gegebene Reihe als Grenzwer der Folge
für Physier WS 5/6 Reihen Zeigen Sie, dass die folgenden Reihen onvergieren und die angegebenen Summen haben. Dabei is f die -e Fibonacci-Zahl a + = 4 Wir fassen die gegebene Reihe als Grenzwer der Folge
Lösungshinweise zu den Hausaufgaben:
 P. Engel, T. Pfrommer S. Poppiz, Dr. I. Rbak 8. Gruppenübung zur Vorlesung Höhere Mahemaik Sommersemeser 9 Prof. Dr. M. Sroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe H. Konvergenzverhalen
P. Engel, T. Pfrommer S. Poppiz, Dr. I. Rbak 8. Gruppenübung zur Vorlesung Höhere Mahemaik Sommersemeser 9 Prof. Dr. M. Sroppel Prof. Dr. N. Knarr Lösungshinweise zu den Hausaufgaben: Aufgabe H. Konvergenzverhalen
14 Kurven in Parameterdarstellung, Tangentenvektor und Bogenlänge
 Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Dr. Dirk Windelberg Leibniz Universiä Hannover Mahemaik für Ingenieure Mahemaik hp://www.windelberg.de/agq 14 Kurven in Parameerdarsellung, Tangenenvekor und Bogenlänge Aufgabe 14.1 (Tangenenvekor und
Stochastische Analysis
 Sochasische Analysis Maringale und sochasisches Inegral Franz Hofbauer Einleiung Sei (Ω, A, P ) ein Maßraum mi P (Ω) = 1. Die messbaren Mengen, das sind die Mengen in der σ-algebra A, werden als Ereignisse
Sochasische Analysis Maringale und sochasisches Inegral Franz Hofbauer Einleiung Sei (Ω, A, P ) ein Maßraum mi P (Ω) = 1. Die messbaren Mengen, das sind die Mengen in der σ-algebra A, werden als Ereignisse
1 Integrale von Funktionen in mehreren Variablen
 $Id: inegral.ex,v 1.12 2015/10/26 13:46:09 hk Exp $ 1 Inegrale von Funkionen in mehreren Variablen 1.1 Das Rieman Inegral im R n Im lezen Semeser wurde die Differenialrechnung auf Funkionen f(x 1,...,
$Id: inegral.ex,v 1.12 2015/10/26 13:46:09 hk Exp $ 1 Inegrale von Funkionen in mehreren Variablen 1.1 Das Rieman Inegral im R n Im lezen Semeser wurde die Differenialrechnung auf Funkionen f(x 1,...,
Integralrechnung. Grundidee der Integralrechnung. Einführung des Riemann- Integrals
 1/8 Grundidee der Inegralrechnung Inegralrechnung Die Inegralrechnung is neben der Differenialrechnung der wichigse Zweig der Analysis. Sie is aus dem Problem der Flächen- und Volumenberechnung ensanden.
1/8 Grundidee der Inegralrechnung Inegralrechnung Die Inegralrechnung is neben der Differenialrechnung der wichigse Zweig der Analysis. Sie is aus dem Problem der Flächen- und Volumenberechnung ensanden.
Charakterisierung des Systems R C. Faltungsintegral. Faltungsintegral (anschaulich) Faltungsintegral (anschaulich) 1. Übertragungsfunktion zb
 Charakerisierung des Sysems. Überragungsfunkion zb Falungsinegral 2. Impulsanwor (Anwor auf δ()) δ() R C h() Gleiche Ergebnis wie Spannungseiler! Impulsanwor: Inverse Fourierransformaion Falung_4_2_5.pp
Charakerisierung des Sysems. Überragungsfunkion zb Falungsinegral 2. Impulsanwor (Anwor auf δ()) δ() R C h() Gleiche Ergebnis wie Spannungseiler! Impulsanwor: Inverse Fourierransformaion Falung_4_2_5.pp
Abiturprüfung Mathematik 2009 (Baden-Württemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe 1
 www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
www.mahe-aufgaben.com Abiurprüfung Mahemaik 009 (Baden-Würemberg) Berufliche Gymnasien ohne TG Analysis, Aufgabe. (7 Punke) Das Schaubild P einer Polynomfunkion drien Grades ha den Wendepunk W(-/-) und
Kurven in der Ebene und im Raum
 Kapiel 9 Kurven in der Ebene und im Raum 9. Parameerdarsellung von Kurven Aufgabe 9. : Skizzieren Sie die folgenden Mengen und beureilen Sie jeweils, ob es sich um eine abgeschlossene oder offene Menge
Kapiel 9 Kurven in der Ebene und im Raum 9. Parameerdarsellung von Kurven Aufgabe 9. : Skizzieren Sie die folgenden Mengen und beureilen Sie jeweils, ob es sich um eine abgeschlossene oder offene Menge
Kapitel 7. Exponentialfamilien. 7.1 Wahrscheinlichkeitsverteilungen
 Kapiel 7 Exponenialfamilien Exponenialfamilien sind dominiere saisische Räume, deren Likelihoodfunkion eine besonders einfache Srukur besiz, ihr Logarihmus is von affiner Gesal. Neben der daraus resulierenden
Kapiel 7 Exponenialfamilien Exponenialfamilien sind dominiere saisische Räume, deren Likelihoodfunkion eine besonders einfache Srukur besiz, ihr Logarihmus is von affiner Gesal. Neben der daraus resulierenden
5. Übungsblatt zur Linearen Algebra II
 Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
Fachbereich Mahemaik Prof. J. Bokowski Dennis Frisch, Nicole Nowak Sommersemeser 27 5., 8. und 2. Mai 5. Übungsbla zur Linearen Algebra II Gruppenübung Aufgabe G (Hüllen) In dieser Aufgabe soll es darum
Diese 3 Signale haben als Anregungssignale am Eingang eines Systems besondere Bedeutung für die lineare Systemtheorie erlangt.
 16 2.3 Sprungfunkion, Rampenfunkion Delafunkion Diese 3 Signale haben als Anregungssignale am Eingang eines Sysems besondere Bedeuung für die lineare Sysemheorie erlang. Sprungfunkion: ( σ ( ), 1( ) )
16 2.3 Sprungfunkion, Rampenfunkion Delafunkion Diese 3 Signale haben als Anregungssignale am Eingang eines Sysems besondere Bedeuung für die lineare Sysemheorie erlang. Sprungfunkion: ( σ ( ), 1( ) )
Analysis 3.
 Analysis 3 www.schulmahe.npage.de Aufgaben. Ermieln Sie die erse Ableiung. Vereinfachen Sie. a) fx) = e x x 3) b) fx) = ln x x + 4. Ermieln Sie die folgenden unbesimmen Inegrale. e x 5 a) e x dx b) dx
Analysis 3 www.schulmahe.npage.de Aufgaben. Ermieln Sie die erse Ableiung. Vereinfachen Sie. a) fx) = e x x 3) b) fx) = ln x x + 4. Ermieln Sie die folgenden unbesimmen Inegrale. e x 5 a) e x dx b) dx
10 Der Satz von Radon-Nikodym
 uch im Sinne einer Vorabinformation vor der Stochastik-Vorlesung wollen wir abschließend kurz absolut stetige Maße und den Satz von Radon-Nikodym streifen. Definition 10.1. Seien (, M) ein messbarer Raum
uch im Sinne einer Vorabinformation vor der Stochastik-Vorlesung wollen wir abschließend kurz absolut stetige Maße und den Satz von Radon-Nikodym streifen. Definition 10.1. Seien (, M) ein messbarer Raum
Hauptachsentransformation
 Haupachsenransformaion Erinnerung: A M n is genau ann nich inverierbar, wenn es ein x R n, x gib, mi A x. Definiion. Sei A M n eine Marix. Ein Vekor v R n, v heiß Eigenvekor von A zum Eigenwer λ R, wenn
Haupachsenransformaion Erinnerung: A M n is genau ann nich inverierbar, wenn es ein x R n, x gib, mi A x. Definiion. Sei A M n eine Marix. Ein Vekor v R n, v heiß Eigenvekor von A zum Eigenwer λ R, wenn
Kapitel : Exponentiell-beschränktes Wachstum
 Wachsumsprozesse Kapiel : Exponeniell-beschränkes Wachsum Die Grundbegriffe aus wachsum.xmcd werden auch hier verwende! Wir verwenden nun eine Angabe aus der Biologie und in einem weieren Beispiel eines
Wachsumsprozesse Kapiel : Exponeniell-beschränkes Wachsum Die Grundbegriffe aus wachsum.xmcd werden auch hier verwende! Wir verwenden nun eine Angabe aus der Biologie und in einem weieren Beispiel eines
MATLAB: Kapitel 4 Gewöhnliche Differentialgleichungen
 4. Einleiung Eine der herausragenden Särken von MATLAB is das numerische (näherungsweise) Auflösen von Differenialgleichungen. In diesem kurzen Kapiel werden wir uns mi einigen Funkionen zum Lösen von
4. Einleiung Eine der herausragenden Särken von MATLAB is das numerische (näherungsweise) Auflösen von Differenialgleichungen. In diesem kurzen Kapiel werden wir uns mi einigen Funkionen zum Lösen von
Mathematik III DGL der Technik
 Mahemaik III DGL der Technik Grundbegriffe: Differenialgleichung: Bedingung in der Form einer Gleichung in der Ableiungen der zu suchenden Funkion bis zu einer endlichen Ordnung aufreen. Funkions- und
Mahemaik III DGL der Technik Grundbegriffe: Differenialgleichung: Bedingung in der Form einer Gleichung in der Ableiungen der zu suchenden Funkion bis zu einer endlichen Ordnung aufreen. Funkions- und
Elementare Lösungsmethoden für gewöhnliche Differentialgleichungen
 454 Erforderliche Kennnisse: Höhere Analysis Elemenare Lösungsmehoden für gewöhnliche Differenialgleichungen Was is eigenlich eine Differenialgleichung? Eine Differenialgleichung is eine Gleichung, in
454 Erforderliche Kennnisse: Höhere Analysis Elemenare Lösungsmehoden für gewöhnliche Differenialgleichungen Was is eigenlich eine Differenialgleichung? Eine Differenialgleichung is eine Gleichung, in
Lösungen zu Übungsblatt 9
 Analysis : Camillo de Lellis HS 007 Lösungen zu Übungsblatt 9 Lösung zu Aufgabe 1. Wir müssen einfach das Integral 16 (x + y d(x, y x +y 4 ausrechnen. Dies kann man einfach mittels Polarkoordinaten, da
Analysis : Camillo de Lellis HS 007 Lösungen zu Übungsblatt 9 Lösung zu Aufgabe 1. Wir müssen einfach das Integral 16 (x + y d(x, y x +y 4 ausrechnen. Dies kann man einfach mittels Polarkoordinaten, da
Die Lösungen der Übungsaufgaben werden durch folgendes Lemma etwas vereinfacht:
 Prof. Dr. D. Kuske, M.Sc. M. Huschenbe Fachgebie Theoreische Informaik, TU Ilmenau Muserlösung zum 2. Übungsbla Auomaenheorie Die Lösungen der Übungsaufgaben werden durch folgendes Lemma ewas vereinfach:
Prof. Dr. D. Kuske, M.Sc. M. Huschenbe Fachgebie Theoreische Informaik, TU Ilmenau Muserlösung zum 2. Übungsbla Auomaenheorie Die Lösungen der Übungsaufgaben werden durch folgendes Lemma ewas vereinfach:
Mathematische Methoden der klassischen Physik Zusammenfassung Differentialgleichungen
 Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Dr. G. Lechner Mahemaische Mehoden der klassischen Physik Zusammenfassung Differenialgleichungen In der Vorlesung wurden drei unerschiedliche Typen von Differenialgleichungen (DGL) besprochen, die jeweils
Der Primzahlsatz, Teil 1. 1 Erste Abschätzungen zum Primzahlsatz
 Der Primzahlsaz, Teil Vorrag zum Seminar zur Funionenheorie, 07.05.0 Raffaela Biesenbach Diese Arbei beschäfig sich mi der Herleiung des Primzahlsazes. Dazu werden Definiionen und Säze aus dem Sri zur
Der Primzahlsaz, Teil Vorrag zum Seminar zur Funionenheorie, 07.05.0 Raffaela Biesenbach Diese Arbei beschäfig sich mi der Herleiung des Primzahlsazes. Dazu werden Definiionen und Säze aus dem Sri zur
8 1. GEOMETRIE DIFFERENZIERBARER MANNIGFALTIGKEITEN
 8 1. GEOMETRIE DIFFERENZIERBARER MANNIGFALTIGKEITEN (vi) Konvergenz von Folgen ist in topologischen Räumen folgendermaßen definiert: Ist (a n ) M eine Folge, so heißt sie konvergent gegen a M, wenn es
8 1. GEOMETRIE DIFFERENZIERBARER MANNIGFALTIGKEITEN (vi) Konvergenz von Folgen ist in topologischen Räumen folgendermaßen definiert: Ist (a n ) M eine Folge, so heißt sie konvergent gegen a M, wenn es
Stochastische Analysis und Finanzmathematik
 Sochasische Analysis und Finanzmahemaik Vorlesung im Winersemeser 211/212 von Dr. Markus Schulz Inhalsverzeichnis 1 Sochasische Prozesse 1 1.1 Grundlagen................................ 1 1.2 Die Brownsche
Sochasische Analysis und Finanzmahemaik Vorlesung im Winersemeser 211/212 von Dr. Markus Schulz Inhalsverzeichnis 1 Sochasische Prozesse 1 1.1 Grundlagen................................ 1 1.2 Die Brownsche
Differentialgleichungen
 Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
Ein einfaches Modell (Domar) Im Domar Wachsumsmodell reffen wir die folgenden Annahmen: Kapiel Differenialgleichungen () Erhöhung der Invesiionsrae I() erhöh das Einkommen Y(): dy d = s di (s = konsan)
Eigenwerte und Eigenvektoren
 Eigenwere un Eigenvekoren Vorbemerkung: Is ie n n Marix inverierbar, so ha as lineare Gleichungssysem A x b für jees b genau eine Lösung, nämlich x A b. Grun: i A x A A b b, ii Is y eine weiere Lösung,
Eigenwere un Eigenvekoren Vorbemerkung: Is ie n n Marix inverierbar, so ha as lineare Gleichungssysem A x b für jees b genau eine Lösung, nämlich x A b. Grun: i A x A A b b, ii Is y eine weiere Lösung,
Motivation: Sampling. (14) Sampling. Motivation: Sampling. Beispiele. Beispiel Kreisscheibe. Beispiel: Kreisscheibe
 Moivaion: Sampling (4) Sampling Vorlesung Phoorealisische Compuergraphik S. Müller Ein naiver (und sehr eurer) Ansaz, die Rendering Equaion mi Hilfe eines Rayracing-Ansazes zu lösen, wäre wird eine diffuse
Moivaion: Sampling (4) Sampling Vorlesung Phoorealisische Compuergraphik S. Müller Ein naiver (und sehr eurer) Ansaz, die Rendering Equaion mi Hilfe eines Rayracing-Ansazes zu lösen, wäre wird eine diffuse
Gewöhnliche Differentialgleichungen
 Prof. Dr. Guido Sweers WS 08/09 Jan Gerdung, M.Sc. Gewöhnliche Differenialgleichungen Übungsbla Die Lösungen müssen in den Übungsbriefkasen Gewöhnliche Differenialgleichungen (Raum 0 im MI) geworfen werden.
Prof. Dr. Guido Sweers WS 08/09 Jan Gerdung, M.Sc. Gewöhnliche Differenialgleichungen Übungsbla Die Lösungen müssen in den Übungsbriefkasen Gewöhnliche Differenialgleichungen (Raum 0 im MI) geworfen werden.
Abiturprüfung Mathematik 2012 (Baden-Württemberg) Berufliche Gymnasien Analysis, Aufgabe 1
 Abiurprüfung Mahemaik 0 (Baden-Würemberg) Berufliche Gymnasien Analysis, Aufgabe. (8 Punke) Die Abbildung zeig das Schaubild einer Funkion h mi der Definiionsmenge [-7 ; 4]. Die Funkion H is eine Sammfunkion
Abiurprüfung Mahemaik 0 (Baden-Würemberg) Berufliche Gymnasien Analysis, Aufgabe. (8 Punke) Die Abbildung zeig das Schaubild einer Funkion h mi der Definiionsmenge [-7 ; 4]. Die Funkion H is eine Sammfunkion
Analysis II Musterlösung 12. für t [ 0, 2π). y
 .. Saz von Green Die Randkurve des, in unensehender Figur dargesellen, umerangs kann paramerisier werden durch 4 cos ( + cos( sin( für, π..75.5.5 -.5 3 4 5 6 -.5 -.75 - Zur erechnung des Flächeninhales
.. Saz von Green Die Randkurve des, in unensehender Figur dargesellen, umerangs kann paramerisier werden durch 4 cos ( + cos( sin( für, π..75.5.5 -.5 3 4 5 6 -.5 -.75 - Zur erechnung des Flächeninhales
Analysis I. 14. Übungsstunde. Steven Battilana. battilana.uk/teaching
 Anlysis I 4. Übungssunde Seven Biln sevenb@suden.ehz.ch biln.uk/eching June 6, 07 Erinnerung Sz. (Prielle Inegrion) f (x) g(x)dx = [ ] b f(x)g(x) f(x) g (x)dx. Sz 6..5 (Subsiuion) Sei f : [, b] R seig,
Anlysis I 4. Übungssunde Seven Biln sevenb@suden.ehz.ch biln.uk/eching June 6, 07 Erinnerung Sz. (Prielle Inegrion) f (x) g(x)dx = [ ] b f(x)g(x) f(x) g (x)dx. Sz 6..5 (Subsiuion) Sei f : [, b] R seig,
Zusammenfassung der Lebesgue-Integrationstheorie
 Zusammenfassung der Lebesgue-Integrationstheorie Das Lebesguesche Integral verallgemeinert das Riemannsche Integral. Seine Vorteile liegen für unsere Anwendungen vor allem bei den wichtigen Konvergenzsätzen,
Zusammenfassung der Lebesgue-Integrationstheorie Das Lebesguesche Integral verallgemeinert das Riemannsche Integral. Seine Vorteile liegen für unsere Anwendungen vor allem bei den wichtigen Konvergenzsätzen,
Inhaltsverzeichnis. 4 Gleichgewichte Der Fluss einer Differentialgleichung... 97
 Inhalsverzeichnis Differenialgleichungen erser Ordnung 5. Allgemeine Definiion und Beispiele... 5.2 Lineare Differenialgleichungen......3 Lösungsmehoden für spezielle Typen von Dgln..Ordnung... 3.3. Die
Inhalsverzeichnis Differenialgleichungen erser Ordnung 5. Allgemeine Definiion und Beispiele... 5.2 Lineare Differenialgleichungen......3 Lösungsmehoden für spezielle Typen von Dgln..Ordnung... 3.3. Die
Übungsblatt 4 Lösungsvorschläge
 Insiu für Theoreische Informaik Lehrsuhl Prof. Dr. D. Wagner Übungsbla 4 Lösungsvorschläge Vorlesung Algorihmenechnik im WS 09/10 Problem 1: Flüsse [vgl. Kapiel 4.1 im Skrip] ** Gegeben sei ein Nezwerk
Insiu für Theoreische Informaik Lehrsuhl Prof. Dr. D. Wagner Übungsbla 4 Lösungsvorschläge Vorlesung Algorihmenechnik im WS 09/10 Problem 1: Flüsse [vgl. Kapiel 4.1 im Skrip] ** Gegeben sei ein Nezwerk
Grenzwertsätze für Zeitreihen
 KAPIEL 6 Grenzwersäze für Zeireihen In diesem Kapiel sellen wir wichige Grenzwersäze für saionäre Zeireihen {X n } in diskreer Zei zusammen. Sei µ = E(X ) und ρ(k) = E(X 1 µ)(x 1+k µ) = Cov (X 1, X 1+k
KAPIEL 6 Grenzwersäze für Zeireihen In diesem Kapiel sellen wir wichige Grenzwersäze für saionäre Zeireihen {X n } in diskreer Zei zusammen. Sei µ = E(X ) und ρ(k) = E(X 1 µ)(x 1+k µ) = Cov (X 1, X 1+k
Diplomarbeit. second sound
 Universiä Konsanz Diplomarbei Nichlineare Wärmeleiung mi second sound Verfasser: Naalie Indlekofer eingereich am: 5. Dezember 7 Bereuer: Prof. Dr. Reinhard Racke Guacher: Prof. Dr. Reinhard Racke Prof.
Universiä Konsanz Diplomarbei Nichlineare Wärmeleiung mi second sound Verfasser: Naalie Indlekofer eingereich am: 5. Dezember 7 Bereuer: Prof. Dr. Reinhard Racke Guacher: Prof. Dr. Reinhard Racke Prof.
Übungsblatt 8 Musterlösung
 Numerik gewöhnlicher Differenialgleichungen MA - SS6 Übungsbla 8 Muserlösung Aufgabe 7 Schriweienseuerung) Im Folgenden soll die Differenzialgleichung y ) = f,y)) = sign)y, y ) = e, im Zeiinervall [, ]
Numerik gewöhnlicher Differenialgleichungen MA - SS6 Übungsbla 8 Muserlösung Aufgabe 7 Schriweienseuerung) Im Folgenden soll die Differenzialgleichung y ) = f,y)) = sign)y, y ) = e, im Zeiinervall [, ]
Beweis. Bauer (4. Auflage, 1991), S , Hoffmann-Jørgensen, Vol. I, S. 457.
 Exkurs A: Bedingte Erwartungswerte, bedingte Verteilungen (Ω, A, P ) sei W-Raum, X : Ω IR P-quasiintegrierbar, F A Unter - σ- Algebra. E(X F) = E P (X F) (Version des) bedingter Erwartungswert von X unterf
Exkurs A: Bedingte Erwartungswerte, bedingte Verteilungen (Ω, A, P ) sei W-Raum, X : Ω IR P-quasiintegrierbar, F A Unter - σ- Algebra. E(X F) = E P (X F) (Version des) bedingter Erwartungswert von X unterf
Analysis 3. Weihnachtsblatt Prof. Dr. H. Koch Dr. F. Gmeineder Besprechung: TBC, Januar Aufgabe 1: (Besonders prüfungsrelevant)
 Analysis 3 04.12.2018 Prof. Dr. H. och Dr. F. Gmeineder Besprechung: TBC, Januar 2019 Weihnachtsblatt Aufgabe 1: (Besonders prüfungsrelevant) Aufgabe 2: Sei Ω eine Menge und Σ eine σ-algebra auf Ω. Seien
Analysis 3 04.12.2018 Prof. Dr. H. och Dr. F. Gmeineder Besprechung: TBC, Januar 2019 Weihnachtsblatt Aufgabe 1: (Besonders prüfungsrelevant) Aufgabe 2: Sei Ω eine Menge und Σ eine σ-algebra auf Ω. Seien
TECHNISCHE UNIVERSITÄT MÜNCHEN
 Prof. Dr. D. Casrigiano Dr. M. Prähofer Zenralübung TECHNISCHE UNIVERSITÄT MÜNCHEN Zenrum Mahemaik Mahemaik 3 für Physik (Analysis ) hp://www-hm.ma.um.de/ss/ph/ 49. Eine reguläre Kurve ha keinen Knick
Prof. Dr. D. Casrigiano Dr. M. Prähofer Zenralübung TECHNISCHE UNIVERSITÄT MÜNCHEN Zenrum Mahemaik Mahemaik 3 für Physik (Analysis ) hp://www-hm.ma.um.de/ss/ph/ 49. Eine reguläre Kurve ha keinen Knick
III.2 Radioaktive Zerfallsreihen
 N.BORGHINI Version vom 5. November 14, 13:57 Kernphysik III. Radioakive Zerfallsreihen Das Produk eines radioakiven Zerfalls kann selbs insabil sein und späer zerfallen, und so weier, sodass ganze Zerfallsreihen
N.BORGHINI Version vom 5. November 14, 13:57 Kernphysik III. Radioakive Zerfallsreihen Das Produk eines radioakiven Zerfalls kann selbs insabil sein und späer zerfallen, und so weier, sodass ganze Zerfallsreihen
4 Fehlerabschätzungen und Konvergenz der FEM
 4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
4. Fortsetzung auf R N.
 4. Fortsetzung auf R N. Frage: Wann kann man Funktionen u W (Ω) zu ũ W (RN ) fortsetzen? Hier wird i.a. eine Fortsetzung durch 0 in R N \ Ω nicht zum Erfolg führen, da man die schwachen Ableitungen über
4. Fortsetzung auf R N. Frage: Wann kann man Funktionen u W (Ω) zu ũ W (RN ) fortsetzen? Hier wird i.a. eine Fortsetzung durch 0 in R N \ Ω nicht zum Erfolg führen, da man die schwachen Ableitungen über
Scheinklausur zur Vorlesung Stochastik II
 Institut für Mathematische Stochastik WS 2007/2008 Universität Karlsruhe 25. 02. 2008 Dr. B. Klar Scheinklausur zur Vorlesung Stochastik II Muster-Lösung Dauer: 90 Minuten Name: Vorname: Matrikelnummer:
Institut für Mathematische Stochastik WS 2007/2008 Universität Karlsruhe 25. 02. 2008 Dr. B. Klar Scheinklausur zur Vorlesung Stochastik II Muster-Lösung Dauer: 90 Minuten Name: Vorname: Matrikelnummer:
Schwartz-Raum (Teil 1)
 Schwartz-Raum (Teil 1) Federico Remonda, Robin Krom 10. Januar 2008 Zusammenfassung Der Schwartz-Raum ist ein Funktionenraum, der besondere Regularitätseigenschaften besitzt, die uns bei der Fouriertransformation
Schwartz-Raum (Teil 1) Federico Remonda, Robin Krom 10. Januar 2008 Zusammenfassung Der Schwartz-Raum ist ein Funktionenraum, der besondere Regularitätseigenschaften besitzt, die uns bei der Fouriertransformation
Schlanke Baumzerlegungen von Graphen
 Parick Bellenbaum Schlanke Baumzerlegungen von Graphen 12. Dezember 2000 Diplomarbei am Mahemaischen Seminar der Universiä Hamburg Zusammenfassung Berache man zwei Teile einer Baumzerlegung eines endlichen
Parick Bellenbaum Schlanke Baumzerlegungen von Graphen 12. Dezember 2000 Diplomarbei am Mahemaischen Seminar der Universiä Hamburg Zusammenfassung Berache man zwei Teile einer Baumzerlegung eines endlichen
ist ein n-dimensionaler, reeller Vektorraum (vgl. Lineare Algebra). Wir definieren auf diesem VR ein Skalarprodukt durch i y i i=1
 24 14 Metrische Räume 14.1 R n als euklidischer Vektorraum Die Menge R n = {(x 1,..., x n ) x i R} versehen mit der Addition und der skalaren Multiplikation x + y = (x 1 + y 1,..., x n + y n ) λx = (λx
24 14 Metrische Räume 14.1 R n als euklidischer Vektorraum Die Menge R n = {(x 1,..., x n ) x i R} versehen mit der Addition und der skalaren Multiplikation x + y = (x 1 + y 1,..., x n + y n ) λx = (λx
Systemtheorie Teil A. - Zeitkontinuierliche Signale und Systeme - Musterlösungen. Manfred Strohrmann Urban Brunner
 Sysemheorie eil A - Zeikoninuierliche Signale und Syseme - Muserlösungen Manfred Srohrmann Urban Brunner Inhal 3 Muserlösungen - Zeikoninuierliche Syseme im Zeibereich 3 3. Nachweis der ineariä... 3 3.
Sysemheorie eil A - Zeikoninuierliche Signale und Syseme - Muserlösungen Manfred Srohrmann Urban Brunner Inhal 3 Muserlösungen - Zeikoninuierliche Syseme im Zeibereich 3 3. Nachweis der ineariä... 3 3.
4 Fehlerabschätzungen und Konvergenz der FEM
 4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
4 Fehlerabschätzungen und Konvergenz der FEM 4 Fehlerabschätzungen und Konvergenz der FEM 153 Es sei V der Lösungsraum und V N V ein endlich dimensionaler Unterraum. Weiters sei u V die exakte Lösung und
Das lineare H-unendlich Problem
 Das lineare H-unendlich Problem Salah-Eddine Sessou Seminarvorrag vom. Juli 6. Problemsellung Bild z P x u K Der Regler (Konroller)K ha zei Eingänge, x und den exogenen Eingang. Das H-unendlich Problem
Das lineare H-unendlich Problem Salah-Eddine Sessou Seminarvorrag vom. Juli 6. Problemsellung Bild z P x u K Der Regler (Konroller)K ha zei Eingänge, x und den exogenen Eingang. Das H-unendlich Problem
7. Vorlesung Wintersemester
 7. Vorlesung Winersemeser Der ungedämpfe Oszillaor mi komplexem Lösungsansaz Wie gezeig, wird die DGL des ungedämpfen Oszillaors mẍ() + kx() = 0 () im Komplexen von den Funkionen x () = e iω und x 2 ()
7. Vorlesung Winersemeser Der ungedämpfe Oszillaor mi komplexem Lösungsansaz Wie gezeig, wird die DGL des ungedämpfen Oszillaors mẍ() + kx() = 0 () im Komplexen von den Funkionen x () = e iω und x 2 ()
Abiturprüfung Baden-Württemberg 1986
 c 001 by Rainer Müller - www.emah.de 1 Lösng Abirprüfng Baden-Würemberg 1986 Leisngskrs Mahemaik - Analysis Z jedem > 0 is eine Fnkion f gegeben drch f x x x e x ; x IR a Asympoen Senkreche Asympoen Es
c 001 by Rainer Müller - www.emah.de 1 Lösng Abirprüfng Baden-Würemberg 1986 Leisngskrs Mahemaik - Analysis Z jedem > 0 is eine Fnkion f gegeben drch f x x x e x ; x IR a Asympoen Senkreche Asympoen Es
5.10 Der Hamilton-Jacobi-Formalismus
 5.10 Der Hamilon-Jacobi-Formalismus 183 5.10 Der Hamilon-Jacobi-Formalismus 5.10.1 Welle-Teilchen Dualismus Wir berachen die Ausbreiung von Lich in einem Medium mi veränderlicher Lichgeschwindigkei. Es
5.10 Der Hamilon-Jacobi-Formalismus 183 5.10 Der Hamilon-Jacobi-Formalismus 5.10.1 Welle-Teilchen Dualismus Wir berachen die Ausbreiung von Lich in einem Medium mi veränderlicher Lichgeschwindigkei. Es
Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie. Tobias Ried
 Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie Tobias Ried. März 2 2 Aufgabe (Messbarkeit der Komposition zweier Abbildungen). Seien (X, A), (Y, B) und (Z, C) Messräume und f : (X,
Lösung zu den Übungsaufgaben zur Lebesgueschen Integrationstheorie Tobias Ried. März 2 2 Aufgabe (Messbarkeit der Komposition zweier Abbildungen). Seien (X, A), (Y, B) und (Z, C) Messräume und f : (X,
Höhere Mathematik I für die Fachrichtung Physik
 Isiu für Aalysis SS7 Arbeisgruppe Agewade Aalysis 997 PD Dr Peer Chrisia Kusma Höhere Mahemaik I für die Fachrichug Physik Lösugsvorschläge zur Bachelor-Modulprüfug Aufgabe : (a) (i) Kurze Rechug liefer
Isiu für Aalysis SS7 Arbeisgruppe Agewade Aalysis 997 PD Dr Peer Chrisia Kusma Höhere Mahemaik I für die Fachrichug Physik Lösugsvorschläge zur Bachelor-Modulprüfug Aufgabe : (a) (i) Kurze Rechug liefer
3.2 Autoregressive Prozesse (AR-Modelle) AR(p)-Prozesse
 3. Auoregressive Prozesse (AR-Modelle 3.. AR(-Prozesse Definiion: Ein sochasischer Prozess ( heiß auoregressiver Prozess der Ordnung [AR(-Prozess], wenn er der Beziehung (3.. genüg. ( is darin ein reiner
3. Auoregressive Prozesse (AR-Modelle 3.. AR(-Prozesse Definiion: Ein sochasischer Prozess ( heiß auoregressiver Prozess der Ordnung [AR(-Prozess], wenn er der Beziehung (3.. genüg. ( is darin ein reiner
2.6 Der Satz von Fubini
 1 2.6 Der Satz von Fubini Unser Ziel ist der Beweis des folgenden Ergebnisses. 6.1. Satz von Fubini Sei f : R n+m R integrierbar. Dann gibt es eine Nullmenge N R m, so dass gilt: 1. Für alle y R m \ N
1 2.6 Der Satz von Fubini Unser Ziel ist der Beweis des folgenden Ergebnisses. 6.1. Satz von Fubini Sei f : R n+m R integrierbar. Dann gibt es eine Nullmenge N R m, so dass gilt: 1. Für alle y R m \ N
Lösung Klausur. p(t) = (M + dm)v p(t + dt) = M(v + dv) + dm(v + dv u) Wir behalten nur die Terme der ersten Ordnung und erhalten.
 T1 I. Theorieeil a) Zur Zei wird ein Pake der Masse dm mi der Geschwindigkei aus der Rakee ausgesoÿen. Newon's zweies Gesez läss sich schreiben als dp d = F p( + ) p() = F d = Av2 d Der Impuls des Sysems
T1 I. Theorieeil a) Zur Zei wird ein Pake der Masse dm mi der Geschwindigkei aus der Rakee ausgesoÿen. Newon's zweies Gesez läss sich schreiben als dp d = F p( + ) p() = F d = Av2 d Der Impuls des Sysems
22 Charakteristische Funktionen und Verteilungskonvergenz
 22 Charakteristische Funktionen und Verteilungskonvergenz Charakteristische Funktionen (Fourier-Transformierte liefern ein starkes analytisches Hilfsmittel zur Untersuchung von W-Verteilungen und deren
22 Charakteristische Funktionen und Verteilungskonvergenz Charakteristische Funktionen (Fourier-Transformierte liefern ein starkes analytisches Hilfsmittel zur Untersuchung von W-Verteilungen und deren
UNIVERSITÄT POTSDAM Institut für Mathematik
 UNIVERSITÄT POTSDAM Insiu für Mahemaik Harness-Prozesse Diplomarbei von Carola Regine Voss Mahemaische Saisik und Wahrscheinlichkeisheorie Universiä Posdam Insiu für Mahemaik Mahemaische Saisik und Wahrscheinlichkeisheorie
UNIVERSITÄT POTSDAM Insiu für Mahemaik Harness-Prozesse Diplomarbei von Carola Regine Voss Mahemaische Saisik und Wahrscheinlichkeisheorie Universiä Posdam Insiu für Mahemaik Mahemaische Saisik und Wahrscheinlichkeisheorie
3 Produktmaße und Unabhängigkeit
 3 Produktmaße und Unabhängigkeit 3.1 Der allgemeine Fall Im Folgenden sei I eine beliebige Indexmenge. i I sei (Ω i, A i ein messbarer Raum. Weiter sei Ω : i I Ω i ein neuer Ergebnisraum. Wir definieren
3 Produktmaße und Unabhängigkeit 3.1 Der allgemeine Fall Im Folgenden sei I eine beliebige Indexmenge. i I sei (Ω i, A i ein messbarer Raum. Weiter sei Ω : i I Ω i ein neuer Ergebnisraum. Wir definieren
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt Semester ARBEITSBLATT 11 LAGEBEZIEHUNG DREIER EBENEN
 Mahemaik Mag. Schmid Wolfgang Arbeisbla. Semeser ARBEITSBLATT LAGEBEZIEHUNG DREIER EBENEN Nachdem wir die Lage weier Ebenen unersuch haben, wollen wir uns nun mi der Lage von drei Ebenen beschäfigen. Anders
Mahemaik Mag. Schmid Wolfgang Arbeisbla. Semeser ARBEITSBLATT LAGEBEZIEHUNG DREIER EBENEN Nachdem wir die Lage weier Ebenen unersuch haben, wollen wir uns nun mi der Lage von drei Ebenen beschäfigen. Anders
Hörsaalübung 3 Differentialgleichungen I für Studierende der Ingenieurwissenschaften
 Fachbereich Mahemaik der Universiä Hamburg WiSe 26/27 Dr. Hanna Peywand Kiani Hörsaalübung 3 Differenialgleichungen I für Sudierende der Ingenieurwissenschafen Lineare Differenialgleichungssyseme Die ins
Fachbereich Mahemaik der Universiä Hamburg WiSe 26/27 Dr. Hanna Peywand Kiani Hörsaalübung 3 Differenialgleichungen I für Sudierende der Ingenieurwissenschafen Lineare Differenialgleichungssyseme Die ins
Extremalpunkte und der Satz von Krein-Milman. 1 Lokalkonvexe topologische Vektorräume
 Extremalpunkte und der Satz von Krein-Milman Seminar zu ausgewählten Kapiteln der Banachraumtheorie Vortrag von Michael Hoffmann 1 Lokalkonvexe topologische Vektorräume Im folgenden betrachten wir stets
Extremalpunkte und der Satz von Krein-Milman Seminar zu ausgewählten Kapiteln der Banachraumtheorie Vortrag von Michael Hoffmann 1 Lokalkonvexe topologische Vektorräume Im folgenden betrachten wir stets
Mathematik III. Vorlesung 74. Folgerungen aus dem Satz von Fubini. (( 1 3 x3 1 2 x2 y +2y 3 x) 1 2)dy. ( y +2y y +4y3 )dy
 Prof. Dr. H. Brenner Osnabrück WS 2010/2011 Mathematik III Vorlesung 74 Folgerungen aus dem Satz von Fubini Beispiel 74.1. Wir wollen das Integral der Funktion f :R 2 R, (x,y) x 2 xy +2y 3, über dem Rechteck
Prof. Dr. H. Brenner Osnabrück WS 2010/2011 Mathematik III Vorlesung 74 Folgerungen aus dem Satz von Fubini Beispiel 74.1. Wir wollen das Integral der Funktion f :R 2 R, (x,y) x 2 xy +2y 3, über dem Rechteck
Merkmale flexibler Fertigung
 FFS.41 PROF.DR.-ING. K.RALL TUHH 2-295 - 1 FFS.42 Die Aufgabe des Bedieners wurde anspruchsvoller (wenige psychische und physische Belasung, dafür mehr Warung, Überwachung, Sörungsbeseiigung). Die Ferigung
FFS.41 PROF.DR.-ING. K.RALL TUHH 2-295 - 1 FFS.42 Die Aufgabe des Bedieners wurde anspruchsvoller (wenige psychische und physische Belasung, dafür mehr Warung, Überwachung, Sörungsbeseiigung). Die Ferigung
4 Messbare Funktionen
 4 Messbare Funktionen 4.1 Definitionen und Eigenschaften Definition 4.1. Seien X eine beliebige nichtleere Menge, M P(X) eine σ-algebra in X und µ ein Maß auf M. Das Paar (X, M) heißt messbarer Raum und
4 Messbare Funktionen 4.1 Definitionen und Eigenschaften Definition 4.1. Seien X eine beliebige nichtleere Menge, M P(X) eine σ-algebra in X und µ ein Maß auf M. Das Paar (X, M) heißt messbarer Raum und
Stochastische Analysis
 Skrip Sochasische Analysis Seffen Schwarz 17. April 216 Dozen: PD Dr. Volker Paulsen Fakulä für Mahemaik Wesfälische Wilhelms-Universiä Münser Inhalsverzeichnis Einleiung 1 I Sochasische Inegraion 1 1
Skrip Sochasische Analysis Seffen Schwarz 17. April 216 Dozen: PD Dr. Volker Paulsen Fakulä für Mahemaik Wesfälische Wilhelms-Universiä Münser Inhalsverzeichnis Einleiung 1 I Sochasische Inegraion 1 1
MATHEMATIK 3 FÜR EI - ÜBUNGSBLATT 13 Wintersemester 2011/2012
 Prof Dr O Junge, A Biracher Zenrum Mahemaik - M3 Technische Universiä München MATHEMATIK 3 FÜR EI - ÜBUNGSBLATT 3 Winersemeser 2/22 Tuorübungsaufgaben (3-3222) Aufgabe T Berachen Sie das Anfangswerproblem
Prof Dr O Junge, A Biracher Zenrum Mahemaik - M3 Technische Universiä München MATHEMATIK 3 FÜR EI - ÜBUNGSBLATT 3 Winersemeser 2/22 Tuorübungsaufgaben (3-3222) Aufgabe T Berachen Sie das Anfangswerproblem
Mathematik: Mag. Schmid Wolfgang Arbeitsblatt 6 5. Semester ARBEITSBLATT 6 PARAMETERDARSTELLUNG EINER GERADEN
 ARBEITSBLATT PARAMETERDARSTELLUNG EINER GERADEN Eine Gerade sell man im R ensprechend zum R auf, nur daß eine z-koordinae hinzukomm: Definiion: Parameerdarsellung einer Gerade durch die Punke A und B:
ARBEITSBLATT PARAMETERDARSTELLUNG EINER GERADEN Eine Gerade sell man im R ensprechend zum R auf, nur daß eine z-koordinae hinzukomm: Definiion: Parameerdarsellung einer Gerade durch die Punke A und B:
Abituraufgaben Grundkurs 2009 Bayern Analysis I. dt mit D F = R.
 Abiuraufgaben Grundkurs 9 Bayern Analysis I I.). Die Abbildung zeig den Graphen G f einer ganzraionalen Funkion f drien Grades mi dem Definiionsbereich D f R. Die in der Abbildung angegebenen Punke P(
Abiuraufgaben Grundkurs 9 Bayern Analysis I I.). Die Abbildung zeig den Graphen G f einer ganzraionalen Funkion f drien Grades mi dem Definiionsbereich D f R. Die in der Abbildung angegebenen Punke P(
7 Der Gaußsche Integralsatz
 7 Der Gaußsche Integralsatz Im Folgenden sei eine k-dimensionale Untermannigfaltigkeit des R n und a. 7.1 Tangentialvektoren. Ein Vektor v R n heißt Tangentialvektor an in a, falls es eine stetig differenzierbare
7 Der Gaußsche Integralsatz Im Folgenden sei eine k-dimensionale Untermannigfaltigkeit des R n und a. 7.1 Tangentialvektoren. Ein Vektor v R n heißt Tangentialvektor an in a, falls es eine stetig differenzierbare
