Quantitative Entscheidungsmethoden Teil 1 Prof. Dr. Heinrich Paessens. Studiengang Business Management (Master) 1. Semester WS 2009/10
|
|
|
- Gregor Armbruster
- vor 8 Jahren
- Abrufe
Transkript
1 Quantitative Entscheidungsmethoden Teil 1 Prof. Dr. Heinrich Paessens Studiengang Business Management (Master) 1. Semester WS 2009/10 1. Durchführung eines Planungsprozesses Graphentheoretische Grundlagen.. 4 o Grundlegende Definitionen und Begriffe o Speicherung von Graphen o Bäume o Flüsse in Graphen 3. Algorithmen in Graphen 15 o Bestimmung der Nachfolger o Kürzester Weg o Minimalgerüst o Maximaler Fluss 4. Netzplantechnikmethode CPM Routen- und Tourenplanung.. 22 o Problemtypen o Graphentheoretische Erfassung eines Straßennetzes o Routenplanung mit TourMaster, NetMaster, Map&Guide o Tourenplanung mit der Saving-Methode o Vergleich von Tourenplanungsverfahren o Savingmethode mit Tourenformfaktoren o manuelle Erstellung eines Tourenplanes o Tourenplanung mit TourMaster o Simulation Fuhrparkgröße, Depotstandorte o Anwendungsbeispiele zur Tourenplanung D:\QE\QE_ws09\qe_ws09.doc Mathematik WI Seite 1 von 40
2 Literatur: DOMSCHKE, W.: Logistik: Transport. Oldenbourg Verlag. DOMSCHKE, W.: Logistik: Rundreisen und Touren. Oldenbourg Verlag. DOMSCHKE, W.; DREXL, A.: Einführung in Operations Research. Springer Verlag GRÜNERT, T.; IRNICH, S.: Optimierung im Transport. Band 1: Grundlagen. Shaker Verlag GRÜNERT, T.; IRNICH, S.: Optimierung im Transport. Band 2: Wege und Touren. Shaker Verlag HERBST, P.; PAESSENS, H.: Tourenplanung mit TourMaster 4. Expert Verlag (erscheint Ende 2009) PAESSENS, H.: Tourenplanung mit TourMaster. Oldenbourg Verlag. (Wi Qb 41) VAHRENKAMP, R.: Quantitative Logistik für das Supply Chain Management. Oldenbourg Verlag D:\QE\QE_ws09\qe_ws09.doc Mathematik WI Seite 2 von 40
3 1. Durchführung eines Planungsprozesses Ein Planungsprozess kann in 7 Schritten dargestellt werden (siehe auch DOMSCHKE, DREXL): S1: Erkennen und Analysieren des Problems S2: Darstellung des Problems -> Beschreibung durch ein Modell (vereinfachtes Abbild des realen Problems) S3: Formulierung von Zielen und Handlungsmöglichkeiten S4: Formulierung eines mathematischen Modells S5: Datenbeschaffung S6: Lösungsfindung mit Hilfe von Algorithmen (manuell oder mit Software) S7: Bewertung der Lösung D:\QE\QE_ws09\qe_ws09.doc Mathematik WI Seite 3 von 40
4 2. Graphentheoretische Grundlagen 2.1 Grundlegende Definitionen und Begriffe DEFINITION 1: Ein ungerichteter Graph G = (V,E) besteht aus einer Menge von Knoten V={1,2,...,n} und Kanten E={e 1,e 2,...,e m }. Die Anzahl der Knoten wird mit n, die Anzahl der Kanten mit m bezeichnet. Die einer Kante e zugeordneten Knoten i, j werden Endknoten von e genannt. Man schreibt e = (i, j) oder e = (j, i) und sagt, daß die Kante e die Knoten i, j "verbindet". Knoten i heißt Nachbar des Knotens j und umgekehrt, falls e = (i, j) eine Kante in G ist. Ein gerichteter Graph G = [V,E] besteht aus einer Menge von Knoten V={1,2,...,n} und Pfeilen E={e 1,e 2,...,e m }. Die Anzahl der Knoten wird wiederum mit n, die Anzahl der Pfeile mit m bezeichnet. Ein gerichteter Graph G = [V,E] wird auch Digraph D = [V,E] genannt. Für einen Pfeil e wird e = [i, j] geschrieben; i heißt Anfangsknoten und j Endknoten des Pfeiles e. Man sagt auch, daß der Pfeil e "vom Knoten i ausgeht" und "in den Knoten j einmündet". Knoten j wird (unmittelbarer) Nachfolger von Knoten i, Knoten i (unmittelbarer) Vorgänger von Knoten j genannt. Die Menge aller Nachfolger eines Knotens i wird mit S i und die Menge aller Vorgänger eines Knotens i mit P i bezeichnet. Ein Graph G = (V,E), der sowohl Pfeile wie auch Kanten enthält, heißt gemischter Graph. DEFINITION 2: Ist jeder Kante e (jedem Pfeil e) eines Graphen G (Digraphen D) eine Bewertung c(e) zugeordnet, so wird G = (V,E,c) bewerteter Graph (D = [V,E,c] bewerteter Digraph) genannt. DEFINITION 3: Ein Weg w=(i,...,j) in einem ungerichteten Graphen G bzw. ein Weg w=[i,...,j] in einem Digraphen D ist eine Aufeinanderfolge von zusammenhängenden Kanten bzw. Pfeilen entsprechender Richtung mit Anfangsknoten i und Endknoten j. D:\QE\QE_ws09\qe_ws09.doc Mathematik WI Seite 4 von 40
5 Ein Knoten j heißt von einem Knoten i aus erreichbar,falls ein Weg von i nach j existiert. Ein Weg w mit unterschiedlichen Anfangsknoten i und Endknoten j (i j) wird als offener Weg bezeichnet. Ein Weg w, dessen Anfangs- und Endknoten identisch sind (i=j), wird als geschlossener Weg oder Rundreise oder Zyklus bezeichnet. Ein Weg w, der jede Kante bzw. jeden Pfeil eines Graphen G genau einmal enthält, wird Eulerlinie genannt. Ein Weg w, der jeden Knoten eines Graphen G genau einmal enthält, wird Hamiltonlinie genannt. (Ausnahme: bei einer geschlossenen Hamiltonlinie sind Anfangs- und Endknoten identisch). Weitere Typen von Wegen in Graphen sind von praktischer Bedeutung: (1) Ein Weg w, der jede Kante (bestimmte Kanten) bzw. jeden Pfeil (bestimmte Pfeile) eines Graphen G mindestens einmal enthält (2) Ein Weg w, der jeden (bestimmte) Knoten eines Graphen G mindestens einmal enthält DEFINITION 4: Die Länge eines Weges c(w) ergibt sich aus der Aufsummierung der Bewertungen der benutzten Kanten bzw. Pfeile des Weges w. Ein Weg w in einem Graphen G, der unter allen von Knoten i nach Knoten j führenden Wegen die geringste Länge besitzt, heißt kürzester Weg von i nach j. Entsprechend wird eine Rundreise mit geringster Länge kürzeste oder auch minimale Rundreise genannt. DEFINITION 5: Unter dem Grad eines Knotens i in einem ungerichteten Graphen G versteht man die Anzahl derjenigen Kanten, die diesen Knoten als Endknoten besitzen ("berühren"), in Zeichen δi. Unter dem positiven (negativen) Grad eines Knotens i in einem Digraphen D versteht man die Anzahl der Pfeile, die diesen Knoten als Anfangsknoten (Endknoten) besitzen, in Zeichen δ + i (δ - i). D:\QE\QE_ws09\qe_ws09.doc Mathematik WI Seite 5 von 40
6 WEG GESCHLOSSEN ZYKLUS RUNDREISE OFFEN KNOTEN KANTEN / PFEILE KNOTEN KANTEN / PFEILE JEDER KNOTEN GENAU 1X G. HAMIL- TON LINIE JEDER KNOTEN MIND. 1X BEST. KNOTEN JEDE KANTE/ PFEIL GENAU 1X G. EULER- LINIE JEDE KANTE/ PFEIL MIND. 1X BEST. KANTEN/ PFEILE JEDER KNOTEN GENAU 1X O. HAMIL- TON LINIE JEDER KNOTEN MIND. 1X BEST. KNOTEN JEDE KANTE/ PFEIL GENAU 1X O. EULER- LINIE JEDE KANTE/ PFEIL MIND. 1X BEST. KANTEN/ PFEILE TSP CPP BEI VORLIEGEN EINES BEWERTETEN GRAPHEN KÖNNEN MINIMALE / MAXIMALE WEGE (ZYKLEN, RUNDREISEN,...) BESTIMMT WERDEN. MÖGLICHE WEGE -TYPEN D:\QE\QE_ws09\qe_ws09.doc Mathematik WI Seite 6 von 40
7 ANMERKUNGEN ZU EULERLINIEN: Regeln in ungerichteten Graphen G: (1) Sind in einem Graphen G alle Knoten von geradem Grad, so existiert in G eine geschlossene Eulerlinie. (2) Sind in einem Graphen G genau 2 Knoten i und j von ungeradem Grad und alle anderen Knoten von geradem Grad, so existiert in G eine offene Eulerlinie. i und j sind Anfangs- bzw. Endknoten der offenen Eulerlinie. Regeln in Digraphen D: (1) Gilt für jeden Knoten i in D δ+ i = δ- i, so existiert eine geschlossene Eulerlinie in D. (2) Gilt für genau 2 Knoten i und j in D δ+ i = δ+ j +1 und δ- i = δ- j -1 sowie für alle anderen Knoten k δ+ k = δ- k, so existiert eine offene Eulerlinie in D. i ist der Anfangsknoten und j der Endknoten der offenen Eulerlinie. DEFINITION 6: (1) Ein Knoten i ohne Vorgänger, d.h. δ- i =0, mit δ+ i >0 wird Quelle, ein Knoten i ohne Nachfolger, d.h. δ+ i =0, mit δ- i >0 wird Senke genannt. (2) Ein Knoten i mit δi = 0 bzw. mit δ+ i = δ- i = 0 heißt isoliert. DEFINITION 7: (1) Existieren mehrere Kanten (Pfeile), die dieselben Endknoten (Anfangs- und Endknoten) besitzen, so nennt man diese Kanten (Pfeile) parallel. (2) Stimmen die beiden Endknoten einer Kante (Anfangs- und Endknoten eines Pfeiles) miteinander überein, dann bezeichnet man diese(n) Kante (Pfeil) als Schlinge. (3) Ungerichtete (gerichtete) Graphen, die sich in der Ebene ohne Überschneiden von Kanten (Pfeilen) zeichnen lassen, nennt man planar. D:\QE\QE_ws09\qe_ws09.doc Seite 7 von 40
8 DEFINITION 8: Ein Graph G heißt vollständig, wenn je zwei verschiedene Knoten i und j des Graphen G durch mindestens eine Kante (i, j) bzw. durch mindestens einen Pfeil [i, j] sowie einen entgegengesetzt gerichteten Pfeil [j, i] miteinander verbunden sind. Es gilt für die Anzahl der Kanten bzw. Pfeile ungerichteter Graph : m := n*(n-1)/2 gerichteter Graph (Digraph) : m := n*(n-1) DEFINITION 9: Ein gerichteter Graph D heißt symmetrisch, falls für alle Pfeile von D gilt [i, j] E [j, i] E. Definition 10: Eine Nummerierung der Knoten eines zyklenfreien Digraphen D = [V,E] mit j Si i < j ( 1 i,j n ) heißt Topologische Sortierung von D, d.h. die Knotennummer des Anfangsknotens eines jeden Pfeiles von D ist kleiner als die Knotennummer des Endknotens. Insbesondere ist in einem topologisch sortierten Digraphen Knoten 1 eine Quelle und Knoten n eine Senke. 2.2 Speicherung von Graphen Definition 11: Die Adjazenzmatrix A(D) eines Digraphen D = [V,E] (ohne Schlingen und parallele Pfeile) mit V = {1,..., n} ist eine n x n - Matrix mit den Elementen 1, falls [i,j] E aij := 0, sonst. D:\QE\QE_ws09\qe_ws09.doc Seite 8 von 40
9 DEFINITION 12: Die einem bewerteten Digraphen D = [V,E,c] (ohne Schlingen und parallele Pfeile) zugeordnete n x n - Matrix C(D) mit den Elementen heißt Bewertungsmatrix von D. 0, falls i = j cij := c ([i,j]), falls e=[i,j] E, sonst DEFINITION 13: Sei D = [V,E,c] ein bewerteter Digraph mit E = {e1,..., em}. Dann heißen die Vektoren anf1 end1 anf :=... end :=... anfm endm Anfangsknotennummernvektor bzw. Endknotennummernvektor, wobei anfi (endi) die Knotennummer des Anfangsknotens (Endknotens) des Pfeiles ei ist. Der Vektor c1 c :=... cm wird Bewertungsvektor genannt, wobei c i die Bewertung des Pfeiles e i ist. D:\QE\QE_ws09\qe_ws09.doc Seite 9 von 40
10 DEFINITION 14: Eine Nummerierung der Pfeile eu = [anfu, endu] (anfu, endu V), u = 1,..., m eines Digraphen D = [V,E] mit E = {e1,..., em}, für die u > w anfu anfw (1 w < u m) gilt, heißt Pfeilsortierung von D, d.h. der Anfangsknoten-nummernvektor ist aufsteigend sortiert. DEFINITION 15: Sei D = [V,E] ein pfeilsortierter Digraph mit V = {1,..., n} und E = {e1,..., em}. Dann wird der Vektor pn := pn1... pnn+1 Pfeilnummernvektor von D genannt, wobei pni die Pfeilnummer desjenigen Pfeiles ist, der unter allen von Knoten i ausgehenden Pfeilen die kleinste Pfeilnummer hat (i = 1,..., n). Ist ein Knoten j eine Senke oder ein isolierter Knoten, so wird pnj := pnj+1 gesetzt. Zweckmäßigerweise ist pnn+1 := m + 1 festgelegt. DEFINITION 16: Sei D = [V,E,c] ein bewerteter Digraph ohne Zyklen negativer Länge und c*(w) die Länge des kürzesten Weges w = [i,..., j] von i nach j, dann heißt die Größe 0, falls i = j kij := c*(w), w = [i,..., j], falls j von i aus nicht erreichbar Entfernung von i nach j und die n x n - Matrix K(D) mit den Elementen kij Entfernungsmatrix von D. D:\QE\QE_ws09\qe_ws09.doc Seite 10 von 40
11 DEFINITION 17: Sei D = [V,E] ein Digraph. Dann heißt die n x n - Matrix P(D) mit den Elementen i, falls i = j oder [i,j] E pij := Vorgängermatrix von D. 0, sonst Speicherbedarf Speicherform Anzahl Speicherelemente Beispiel vollständiger Digraph n=100 m=n*(n-1) = 9900 p=1.0 Beispiel Straßennetz SL FL n=800 m=2800 Beispiel Straßennetz BW n=8500 m=25000 p=0.004 p= Bewertungsmatrix C(D) n*n pfeilorientiert: Anfangsknotenvekt. Endknotenvektor Bewertungsvektor pfeilorientiert und pfeilsortiert: Endknotenvektor Bewertungsvektor Pfeilnummernvektor m m m =3*m m m n+1 =2*m +n n: Anzahl Knoten SL FL: Landkreis m: Anzahl Pfeile Schleswig-Flensburg p: Pfeildichte: m/(n*(n-1)) BW: Baden-Württemberg D:\QE\QE_ws09\qe_ws09.doc Seite 11 von 40
12 2.3 Bäume DEFINITION 18: Sei D=[V,E,c] ein bewerteter Digraph. Der Digraph D' = [V,E'] mit E' E heißt Wurzelbaum mit Wurzel r (r V), wenn r Quelle von D' und jeder andere von r aus erreichbare Knoten k in D durch genau einen von r nach k führenden kürzesten Weg in D von r aus in D' erreichbar ist, d.h. der Wurzelbaum D' gibt die Verläufe der kürzesten Wege von Knoten r zu allen anderen Knoten von D an. DEFINITION 19: Ein Graph G heißt zusammenhängend, wenn jeder Knoten in G von jedem anderen Knoten aus erreichbar ist. DEFINITION 20: Sei G = (V,E) ein zusammenhängender Graph. Der zusammenhängende Graph G' = (V,E') mit E' E heißt dann spannender Baum oder Gerüst von G, wenn G' keinen Zyklus enthält. Ein Gerüst enthält m = n-1 Kanten. DEFINITION 21: Sei G = (V,E,c) ein zusammenhängender, bewerteter Graph. Ein Gerüst G' = (V,E',c') mit c'(e) = c(e) für alle e E' heißt Minimalgerüst von G, wenn c'(e) MIN e E' gilt. D:\QE\QE_ws09\qe_ws09.doc Seite 12 von 40
13 2.4 Flüsse in Graphen DEFINITION 22: Sei D = [V,E] ein Digraph und existiert für jeden Pfeil e E eine Minimalkapazität u(e) sowie eine Maximalkapazität o(e) mit (1) u(e) o(e), (2) u(e), o(e) 0, dann heißt D = [V,E,u,o] ein Kapazitätendigraph. Ist der Digraph bewertet, so heißt D = [V,E,u,o,c] bewerteter Kapazitätendigraph. DEFINITION 23: Seien D = [V,E,u,o] ein Kapazitätendigraph sowie fq und fs zwei verschiedene Knoten in D. ϕ heißt Fluss in D von fq nach fs, wenn gilt (a) ϕ fq,i - ϕ i,fq = ϕ i,fs - ϕ fs,i i S fq i P fq i P fs i S fs (b) ϕ i,j - ϕ j,i = 0 i V\{fq, fs}, j S i j P i erfüllt der Fluss ϕ zusätzlich die Bedingung (c) u(e) ϕ(e) o(e) e E, so heißt ϕ zulässig. fq wird als Flussquelle, fs als Flusssenke des Flusses ϕ bezeichnet. Die Größe des Flusses ϕ von fq nach fs wird mit (d) ω(ϕ) := ϕ fq,i - ϕ i,fq i S fq i P fq angegeben. D:\QE\QE_ws09\qe_ws09.doc Seite 13 von 40
14 DEFINITION 24: Ein zulässiger Fluss ϕ von fq nach fs mit maximaler Größe ω(ϕ*) wird maximaler Fluss genannt. DEFINITION 25: Sei D = [V,E,u,o] ein Kapazitätendigraph. Ein Fluss ϕ Zirkulationsfluss in D, wenn (e) ϕ i,j - ϕ j,i = 0 i V j S i j P i heißt ist. ϕ heißt zulässiger Zirkulationsfluss, wenn außerdem Bedingung (c) aus Definition 23 erfüllt ist. DEFINITION 26: Ein Zirkulationsfluss in einem bewerteten Kapazitätendigraph D = [V,E,u,o,c] heißt kostenminimaler Fluss, wenn gilt: (f) ϕ ist ein zulässiger Zirkulationsfluss, (g) ϕ ij * c ij ist minimal. [i,j] E ϕ ij * c ij sind dabei die Kosten des Flusses ϕ. [i,j] E D:\QE\QE_ws09\qe_ws09.doc Seite 14 von 40
15 3. Algorithmen in Graphen Bestimmung der Nachfolger eines Knotens i bei vektororientierter Speicherung eines pfeilsortierten Digraphen D Algorithmus NACHFOLGER - PN_GEN Aufbau des Pfeilnummernvektors PN: S1: für k 1.. n führe aus: setze PN[k] 0 setze PN[n+1] m+1 S2: für alle Pfeile e p in der Reihenfolge p 1.. m führe aus: falls ein neuer Anfangsknoten k auftritt, setze PN[k] p S3: Überprüfung auf Senken und isolierte Knoten (alle Knoten k mit PN[k]=0 sind Senken oder isolierte Knoten): für alle PN[k] in der Reihenfolge k n,..., 1 (-1) führe aus: falls PN[k]=0, setze PN[k] PN[k+1] Bestimmung der Nachfolger eines Knoten i: für p PN[i].. PN[i+1] - 1 führe aus : der Endknoten des Pfeiles mit Pfeilnummer p ist Nachfolger von i D:\QE\QE_ws09\qe_ws09.doc Seite 15 von 40
16 Bestimmung eines kürzesten Weges (Länge und Verlauf) von einem Startknoten a zu allen anderen Knoten in einem bewerteten Digraphen D = [V,E,c] mit dem Algorithmus von DIJKSTRA Eingabe: a: Startknoten c[i,j]: Bewertung (Länge) des Pfeiles von i nach j Ausgabe: kw_dist[i]: kürzeste Wegelänge von Startknoten a nach i pre[i]: Vorgänger von i auf dem kürzesten Weg von Startknoten a nach i Voraussetzung: D darf keine negativen Bewertungen enthalten S1: Initialisierung: Markiere Startknoten a: sei R die Menge der markierten Knoten, dann gilt a R (R={a}). Setze für Knoten a: kw_dist[a] 0, pre[a] 0. Setze für alle anderen Knoten i ( i a): kw_dist[i], pre[i] 0. S2: Falls ein oder mehrere Knoten markiert sind (R ): wähle einen Knoten aus mit MIN kw_dist[j], j R dieser Knoten sei i; sonst (R = ): ENDE Dijkstra-Algorithmus. S3: Für alle Nachfolger j S i, die noch nicht aus der Markierung entfernt worden sind, führe aus: falls kw_dist[i] + c[i,j] < kw_dist[j]: (1) setze kw_dist[j] kw_dist[i] + c[i,j], (2) setze pre[j] i, (3) markiere j (j R). Entferne die Markierung bei i (i R). Gehe zu S2. D:\QE\QE_ws09\qe_ws09.doc Seite 16 von 40
17 Bestimmung eines Minimalgerüstes G' zu einem zusammenhängenden, bewerteten Graphen G = (V, E, c) Algorithmus MINGERÜST S1: Der Graph G' besteht aus der Knotenmenge V und der Kantenmenge E' = S2: Wähle die Kante in G mit der geringsten Bewertung aus und füge sie zu G' hinzu, wenn dadurch kein Zyklus in G' entsteht. Existiert keine Kante in G mehr -> ENDE S3: Entferne die in S2 ausgewählte Kante aus G. S4: Gehe zu S2. D:\QE\QE_ws09\qe_ws09.doc Seite 17 von 40
18 Bestimmung eines maximalen Flusses von einer Flussquelle fq zu einer Flusssenke fs in einem Kapazitätendigraphen D=[V,E,u,o] mit dem Algorithmus von FORD und FULKERSON (1962) Eingabe: fq: Flussquelle fs: Flusssenke u[i,j]: Minimalkapazität des Pfeiles [i,j] o[i,j]: Maximalkapazität des Pfeiles [i,j] ϕ[i,j]: Fluss auf dem Pfeil [i,j] bei einem zulässigen Ausgangsfluss von fq nach fs Ausgabe: ϕ[i,j]: Fluss auf dem Pfeil [i,j] beim maximalen Fluss von fq nach fs S1: Markiere die Flussquelle fq mit der Marke +fq / ε [fq] :=. Alle anderen Knoten i haben keine Marke. S2: Finde einen Weg von der Flussquelle fq zur Flusssenke fs: Versuche alle nicht markierten Knoten zu markieren: ein Knoten j kann von einem Knoten i aus markiert werden, wenn i markiert und j nicht markiert ist: Fall A: Vorwärtsmarkierung, falls (1) j ist Nachfolger von i (2) ϕ[i,j] < o[i,j] gilt, markiere j mit der Marke +i /ε[j] := MIN (ε[i], o[i,j]- ϕ[i,j]) Fall B: Rückwärtsmarkierung, falls (1) j ist Vorgänger von i (2) ϕ[j,i] > u[j,i] gilt, markiere j mit der Marke -i / ε[j] := MIN (ε[i], ϕ[j,i]-u[j,i]) falls fs markiert wurde, gehe zu S3 falls fs nicht markiert werden konnte: der vorliegende Fluss ϕ ist ein maximaler Fluss: ENDE des Ford-Fulkerson-Algorithmus. D:\QE\QE_ws09\qe_ws09.doc Seite 18 von 40
19 S3: Flussveränderung: Setze j := fs. Wiederhole falls Knoten j die Marke +i / ε[j] besitzt (Flussvergrößerung), setze ϕ[i,j] := ϕ[i,j] + ε[fs], falls Knoten j die Marke i / ε[j] besitzt (Flussverkleinerung), setze ϕ[j,i] := ϕ[j,i] - ε[fs]. Setze j := i bis j = fq gilt. Gehe zu S1. D:\QE\QE_ws09\qe_ws09.doc Seite 19 von 40
20 4. Netzplantechnikmethode CPM (Critical Path Method) Netzplantechnik (NPT) : beinhaltet Methoden zur optimalen Planung und Überwachung der Ausführung von (meist) umfangreichen Projekten. Das Projekt besteht aus vielen Teilarbeiten (Vorgänge), die in einer bestimmten Reihenfolge durchgeführt werden müssen. Netzwerk (Netzplan) : zyklenfreier Digraph ohne parallele Pfeile mit genau einer Quelle und genau einer Senke. Die Pfeile stellen die Vorgänge, die Bewertungen der Pfeile die entsprechenden Dauern der Vorgänge, die Knoten die Ereignisse (Zeitpunkt: Beginn/Ende eines Vorgangs) dar. Start-Ende-Beziehung Vorgang X - Vorgang Y: Vorgang Y kann erst begonnen werden, wenn Vorgang X beendet ist X Y Wichtige CPM-Größen: kürzeste Projektdauer : Länge des längsten Weges von der Quelle q zur Senke s ( = FZ s ). Projektendtermin: kürzeste Projektdauer FZ s oder Projektende T, falls T explizit vorgegeben kritische Wege : alle längsten Wege von q nach s. kritischer Vorgang : Vorgang auf dem kritischen Weg D:\QE\QE_ws09\qe_ws09.doc Seite 20 von 40
21 ereignisbezogene Größen: FZ i : SZ i : frühest möglicher Zeitpunkt für den Eintritt des Ereignisses i (= Länge des längsten Weges (LW) von q nach i ). FZ q := 0. FZ s := kürzeste Projektdauer spätest möglicher Zeitpunkt für den Eintritt des Ereignisses i bei Einhaltung des Projektendtermines. SZ i := SZ s - Länge LW von i nach s SZ s := FZ s (oder SZ s :=T, falls das Projektende T explizit vorgegeben) vorgangsbezogene Größen: GP ij : gesamte Pufferzeit, d.h. maximale Zeitspanne, um die der Beginn des Vorgangs [i,j] verschoben werden kann, ohne den Projektendtermin zu gefährden. GP ij = SZ j - FZ i - c ij D:\QE\QE_ws09\qe_ws09.doc Seite 21 von 40
22 5. Routen- und Tourenplanung Knotenorientierte Routen- und Tourenplanung Transportauftrag Anfahren von bestimmten Knoten im Verkehrsnetz Kantenorientierte Routen- und Tourenplanung Transportauftrag Durchfahren von bestimmten Straßenabschnitten des Verkehrsnetzes D:\QE\QE_ws09\qe_ws09.doc Seite 22 von 40
23 DISPOSITION IM FUHRPARK Problemtypen Ortssuche A Funktion Routen- Planung Problemtyp Touren- Planung Fahrzeugeinsatzplanung Entfernungsermittlung A B Reihenfolgeoptimierung A -x - y - z B Auftragszuordnung zu Fahrzeugen Berücksichtigung von Zeitschranken Fahrzeug-/Fahrerzuordnung D:\QE\QE_ws09\qe_ws09.doc Seite 23 von 40
24 D:\QE\QE_ws09\qe_ws09.doc Seite 24 von 40
25 Darstellung von Verkehrsknoten mit Fahrtrichtungsvorschriften: Straßenkreuzung als Digraph Kreuzung + 1 Schild Einführung von 5A, (geographisch identisch mit 5) A D:\QE\QE_ws09\qe_ws09.doc Seite 25 von 40
26 Beispiel Angeln D:\QE\QE_ws09\qe_ws09.doc Seite 26 von 40
27 Beispiel Landkreis SL-FL - Generalkarte D:\QE\QE_ws09\qe_ws09.doc Seite 27 von 40
28 ROUTENBERECHNUNG START 34 Hamburg 367 Rostock 56 Bremen 446 Berlin 86 Hannover 467 Magdeburg 107 Münster 489 Leipzig 136 Kassel 144 Köln 571 Erfurt 187 Frankfurt 228 Nürnberg 329 Stuttgart ZIEL 350 München D:\QE\QE_ws09\qe_ws09.doc Seite 28 von 40
29 TourMaster Manuelle Tourenplanung Allgemein <?> Hilfe (Befehle) <NUM> Ein-/Ausschalten Nummernblock Tastatur RTP Tourenplan laden STP Tourenplan speichern D nn Entfernung Knoten nn zum aktuellen Knoten Aktuelle Knotenzeile < > nächster Knoten < > vorheriger Knoten Aktuelle Tourenzeile - Tour bearbeiten <Einfg> aktuellen Knoten in aktuelle Tour an Position 'ins' einfügen <Entf> aktuellen Knoten aus aktueller Tour entfernen <F1> Reihenfolge der aktuellen Tour optimieren <F2> nächste Tour aktuelles Fahrzeug < +F2> 1. Tour neues Fahrzeug Touren anzeigen <F5> nächste Tour anzeigen < +F5> vorherige Tour anzeigen <F10> angezeigte Tour zur Bearbeitung in aktuelle Tourenzeile bringen D:\QE\QE_ws09\qe_ws09.doc Seite 29 von 40
30 DEFINITION EINDEPOT - TOURENPLANUNGPROBLEM (ETP) Gegeben: 1) anzufahrende Auftragsknoten 1 = 1,2,...,n 2) Depot (Start- und Rückkehrknoten einer Tour) 3) Symmetrisches Straßennetz mit räumlichen oder zeitlichen Entfernungen - zwischen den Auftragsknoten d ij und - Depotentfernungen der Auftragsknoten dp i 4) Liefer- und Sammelmengen q i 5) Standzeit t i 6) einheitliche Kapazität von Q Transporteinheiten (TE) 7) Maximale Tourenlänge T Gesucht: Menge von Touren (Tourenplan) minimaler Gesamtlänge unter Berücksichtigung: - Kapazität Q - Maximale Tourenlänge T - Jeder Auftragsknoten i wird in genau einer Tour angefahren D:\QE\QE_ws09\qe_ws09.doc Seite 30 von 40
31 METHODEN ZUR TOURENPLANUNG A) Manuell B) Manuell + Hilfsmittel - Kürzeste Wege - Wurzelbaum C) Computergestützt Informationen - Kürzeste Wege / Fahrzeiten - Mengen - Standzeiten - Fahrzeuggrößen - sonstige Randbedingungen... sind sinnvoll aufbereitet auf dem Computer gespeichert D) Computergestützte Tourenplanungverfahren (Automatische Tourenoptimierung) E) Wie D) mit Eingriffsmöglichkeiten des Disponenten (Interaktive Tourenplanung) D:\QE\QE_ws09\qe_ws09.doc Seite 31 von 40
32 ZIELE COMPUTERGESTÜTZTER TOURENPLANUNG Reduzierung der Transportzeiten Reduzierung des Fuhrparkbestandes Umfassende Analyse der Transportkosten Entlastung des Disponenten Simulation des Fuhrparks Simulation der Depotstandorte Informationen zur Angebotserstellung Eigen- oder Fremdtransport Verbesserung des Kundenservice D:\QE\QE_ws09\qe_ws09.doc Seite 32 von 40
33 TOURENPLANUNGSPROBLEMVARIANTEN MÖGLICHE RANDBEDINGUNGEN Depots: 1-Depot, mehrere Depots - geschlossene, offene Touren Auftragsart: Auslieferung, Sammlung Fuhrpark: homogen, inhomogen Zeitbeschränkung: Tour, Tag, Woche Fahrzeugeinsatz: einmal pro Tag, mehrfach pro Tag Standzeiten: fix, -abhängig von Lademenge, Fahrzeugtyp Zeitschranken: Kunden, Depots Zuordnung: Kunde-Fahrzeug, Kunde-Fahrzeugtyp, Kunde-Depot Anfahrhäufigkeit: einheitlich, unterschiedlich Tourenplan: täglich, Rahmentourenplan Hängereinsatz: feste, freie Abstellplätze Kundenaufträge: unabhängig,-abhängig voneinander D:\QE\QE_ws09\qe_ws09.doc Seite 33 von 40
34 Methoden zur Tourenplanung Computergestützte Tourenplanungsverfahren Heuristische Verfahren Einstufige Verfahren Saving-Verfahren Clarke, Wrigth (1964) Zweistufige Verfahren Zuordnungsproblem - Reihenfolgeproblem Gillet, Miller (Sweep-Verfahren, Koordinatenmethode, 1974) Christofides, Mingozzi, Toth (2-Phasen-Methode, 1979) Verbesserungsverfahren - klassische Verbesserungsverfahren Christofides, Eilon (1969) - Metaheuristiken - Tabu Search - Simulated Annealing - Genetische Verfahren Unvollständige exakte Verfahren Foster, Ryan (1976) D:\QE\QE_ws09\qe_ws09.doc Seite 34 von 40
35 SAVING-VERFAHREN (Clarke + Wright 1964) S1: Einzelanfahrten für alle Aufträge S2: Berechnung der SAVING-Werte S ij i j i dij j dpi dpj D dpi D dpj S ij = dp i + dp j - d ij für alle Auftragsknotenpaare ( n 1) n * 2 Möglichkeiten S3: Absteigende Sortierung der SAVING-Werte S4: Aufbau der Touren mit dem größten SAVING-Wert beginnend... Lege die Touren, in denen sich i und j befinden durch Verbindung von i und j zusammen, falls 1. Kapazität Q eingehalten wird 2. max. Tourenlänge T eingehalten wird 3. i und j in unterschiedlichen Touren 4. i und j Endknoten (erster oder letzter Auftragsknoten) einer Tour sind D:\QE\QE_ws09\qe_ws09.doc Seite 35 von 40
36 Beispiel Savingverfahren Menge Länge D Entfernungsmatrix (Entfernungstabelle) D D Savingmatrix D:\QE\QE_ws09\qe_ws09.doc Seite 36 von 40
37 S1: Ausgangslösung Menge Länge D D 7 76 D D 9 84 D D D D D D D D Summe: S2: Berechnung der SAVING-Werte: S ij = dp i + dp j - d ij S 12 = dp 1 + dp 2 - d 12 = = 45 S 46 = dp 4 + dp 6 - d 46 = = 122 S3: Absteigende Sortierung der Savingwerte S4: Aufbau der Touren Mit dem größten Savingwert beginnend... Lege die Touren, in denen sich i und j befinden durch Verbindung von i und j zusammen, falls 1. Kapazität Q eingehalten wird 2. max. Tourenlänge T eingehalten wird 3. i und j in unterschiedlichen Touren 4. i und j Endknoten einer Tour sind Saving-Wert bei (4/6) = Q = 18, erfüllt 2. T = oo, erfüllt 3. erfüllt 4. erfüllt ==> Menge Länge D D 7 76 D D 9 84 D D D D D D Summe: D:\QE\QE_ws09\qe_ws09.doc Seite 37 von 40
38 Saving-Wert bei (3/5) = Q erfüllt 2. T erfüllt 3. erfüllt 4. erfüllt ==> Menge Länge D D 7 76 D D 9 84 D D D D Summe: Saving-Wert bei (4/5) = Q nicht erfüllt Saving-Wert bei (5/6) = Q nicht erfüllt Saving-Wert bei (1/2) = Q erfüllt 2. T erfüllt 3. erfüllt 4. erfüllt ==> Menge Länge D D D D D D Summe: Für Q = 22 Saving-Wert bei (4/6) = Q erfüllt 2. T erfüllt 3. erfüllt 4. erfüllt D:\QE\QE_ws09\qe_ws09.doc Seite 38 von 40
39 ==> Menge Länge D D 7 76 D D 9 84 D D D D D D Summe: Saving-Wert bei (3/5) = Q erfüllt 2. T erfüllt 3. erfüllt 4. erfüllt ==> Menge Länge D D 7 76 D D 9 84 D D D D Summe: Saving-Wert bei (4/5) = Saving-Wert bei (5/6) = Q nicht erfüllt Q nicht erfüllt Saving-Wert bei (2/4) = Q erfüllt 2. T erfüllt 3. erfüllt 4. erfüllt ==> Menge Länge D D 7 76 D D D D Summe: D:\QE\QE_ws09\qe_ws09.doc Seite 39 von 40
40 Saving-Wert bei (1/5) = Q erfüllt 2. T erfüllt 3. erfüllt 4. erfüllt ==> Menge Länge D D D D Summe: D:\QE\QE_ws09\qe_ws09.doc Seite 40 von 40
Algorithmen und Datenstrukturen 2
 Algorithmen und Datenstrukturen 2 Sommersemester 2006 3. Vorlesung Peter F. Stadler Universität Leipzig Institut für Informatik studla@bioinf.uni-leipzig.de Algorithmen für Graphen Fragestellungen: Suche
Algorithmen und Datenstrukturen 2 Sommersemester 2006 3. Vorlesung Peter F. Stadler Universität Leipzig Institut für Informatik studla@bioinf.uni-leipzig.de Algorithmen für Graphen Fragestellungen: Suche
Anmerkungen zur Übergangsprüfung
 DM11 Slide 1 Anmerkungen zur Übergangsprüfung Aufgabeneingrenzung Aufgaben des folgenden Typs werden wegen ihres Schwierigkeitsgrads oder wegen eines ungeeigneten fachlichen Schwerpunkts in der Übergangsprüfung
DM11 Slide 1 Anmerkungen zur Übergangsprüfung Aufgabeneingrenzung Aufgaben des folgenden Typs werden wegen ihres Schwierigkeitsgrads oder wegen eines ungeeigneten fachlichen Schwerpunkts in der Übergangsprüfung
Zeichen bei Zahlen entschlüsseln
 Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
Zeichen bei Zahlen entschlüsseln In diesem Kapitel... Verwendung des Zahlenstrahls Absolut richtige Bestimmung von absoluten Werten Operationen bei Zahlen mit Vorzeichen: Addieren, Subtrahieren, Multiplizieren
WS 2009/10. Diskrete Strukturen
 WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
WS 2009/10 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws0910
1 topologisches Sortieren
 Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Wolfgang Hönig / Andreas Ecke WS 09/0 topologisches Sortieren. Überblick. Solange noch Knoten vorhanden: a) Suche Knoten v, zu dem keine Kante führt (Falls nicht vorhanden keine topologische Sortierung
Das Briefträgerproblem
 Das Briefträgerproblem Paul Tabatabai 30. Dezember 2011 Inhaltsverzeichnis 1 Problemstellung und Modellierung 2 1.1 Problem................................ 2 1.2 Modellierung.............................
Das Briefträgerproblem Paul Tabatabai 30. Dezember 2011 Inhaltsverzeichnis 1 Problemstellung und Modellierung 2 1.1 Problem................................ 2 1.2 Modellierung.............................
Konzepte der Informatik
 Konzepte der Informatik Vorkurs Informatik zum WS 2011/2012 26.09. - 30.09.2011 17.10. - 21.10.2011 Dr. Werner Struckmann / Christoph Peltz Stark angelehnt an Kapitel 1 aus "Abenteuer Informatik" von Jens
Konzepte der Informatik Vorkurs Informatik zum WS 2011/2012 26.09. - 30.09.2011 17.10. - 21.10.2011 Dr. Werner Struckmann / Christoph Peltz Stark angelehnt an Kapitel 1 aus "Abenteuer Informatik" von Jens
GRAPHENTHEORIE. Grundlagen für Routen- und Tourenplanung. Algorithmen Implementierungen - Anwendungen
 GRAPHENTHEORIE Grundlagen für Routen- und Tourenplanung Algorithmen Implementierungen - Anwendungen Prof. Dr. Heinrich Paessens Fachhochschule Flensburg IUT Strasbourg Sud 1. Grundlagen 1.1 Graphen-Definitionen
GRAPHENTHEORIE Grundlagen für Routen- und Tourenplanung Algorithmen Implementierungen - Anwendungen Prof. Dr. Heinrich Paessens Fachhochschule Flensburg IUT Strasbourg Sud 1. Grundlagen 1.1 Graphen-Definitionen
Algorithmen und Datenstrukturen
 Algorithmen und Datenstrukturen Dipl. Inform. Andreas Wilkens aw@awilkens.com Überblick Grundlagen Definitionen Elementare Datenstrukturen Rekursionen Bäume 2 1 Datenstruktur Baum Definition eines Baumes
Algorithmen und Datenstrukturen Dipl. Inform. Andreas Wilkens aw@awilkens.com Überblick Grundlagen Definitionen Elementare Datenstrukturen Rekursionen Bäume 2 1 Datenstruktur Baum Definition eines Baumes
Algorithmische Mathematik
 Algorithmische Mathematik Wintersemester 2013 Prof. Dr. Marc Alexander Schweitzer und Dr. Einar Smith Patrick Diehl und Daniel Wissel Übungsblatt 6. Abgabe am 02.12.2013. Aufgabe 1. (Netzwerke und Definitionen)
Algorithmische Mathematik Wintersemester 2013 Prof. Dr. Marc Alexander Schweitzer und Dr. Einar Smith Patrick Diehl und Daniel Wissel Übungsblatt 6. Abgabe am 02.12.2013. Aufgabe 1. (Netzwerke und Definitionen)
1. Einführung. 1.1 Tourenplanung als Teilbereich der Logistik
 1. Einführung 1.1 Tourenplanung als Teilbereich der Logistik Die Logistik steht heute nicht nur in der Wissenschaft, sondern auch in der unternehmerischen Praxis stärker im Mittelpunkt als in den früheren
1. Einführung 1.1 Tourenplanung als Teilbereich der Logistik Die Logistik steht heute nicht nur in der Wissenschaft, sondern auch in der unternehmerischen Praxis stärker im Mittelpunkt als in den früheren
1. Motivation / Grundlagen 2. Sortierverfahren 3. Elementare Datenstrukturen / Anwendungen 4. Bäume / Graphen 5. Hashing 6. Algorithmische Geometrie
 Gliederung 1. Motivation / Grundlagen 2. Sortierverfahren 3. Elementare Datenstrukturen / Anwendungen 4. äume / Graphen 5. Hashing 6. Algorithmische Geometrie 4/5, olie 1 2014 Prof. Steffen Lange - HDa/bI
Gliederung 1. Motivation / Grundlagen 2. Sortierverfahren 3. Elementare Datenstrukturen / Anwendungen 4. äume / Graphen 5. Hashing 6. Algorithmische Geometrie 4/5, olie 1 2014 Prof. Steffen Lange - HDa/bI
Software-Engineering SS03. Zustandsautomat
 Zustandsautomat Definition: Ein endlicher Automat oder Zustandsautomat besteht aus einer endlichen Zahl von internen Konfigurationen - Zustände genannt. Der Zustand eines Systems beinhaltet implizit die
Zustandsautomat Definition: Ein endlicher Automat oder Zustandsautomat besteht aus einer endlichen Zahl von internen Konfigurationen - Zustände genannt. Der Zustand eines Systems beinhaltet implizit die
Statistische Untersuchungen zu endlichen Funktionsgraphen
 C# Projekt 1 Name: Statistische Untersuchungen zu endlichen Funktionsgraphen Aufgabe: Basierend auf dem Abschnitt 2.1.6. Random mappings, Kap.2, S 54-55, in [1] sollen zunächst für eine beliebige Funktion
C# Projekt 1 Name: Statistische Untersuchungen zu endlichen Funktionsgraphen Aufgabe: Basierend auf dem Abschnitt 2.1.6. Random mappings, Kap.2, S 54-55, in [1] sollen zunächst für eine beliebige Funktion
Programmiersprachen und Übersetzer
 Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Programmiersprachen und Übersetzer Sommersemester 2010 19. April 2010 Theoretische Grundlagen Problem Wie kann man eine unendliche Menge von (syntaktisch) korrekten Programmen definieren? Lösung Wie auch
Algorithmentheorie. 13 - Maximale Flüsse
 Algorithmentheorie 3 - Maximale Flüsse Prof. Dr. S. Albers Prof. Dr. Th. Ottmann . Maximale Flüsse in Netzwerken 5 3 4 7 s 0 5 9 5 9 4 3 4 5 0 3 5 5 t 8 8 Netzwerke und Flüsse N = (V,E,c) gerichtetes Netzwerk
Algorithmentheorie 3 - Maximale Flüsse Prof. Dr. S. Albers Prof. Dr. Th. Ottmann . Maximale Flüsse in Netzwerken 5 3 4 7 s 0 5 9 5 9 4 3 4 5 0 3 5 5 t 8 8 Netzwerke und Flüsse N = (V,E,c) gerichtetes Netzwerk
Periodische Fahrpläne und Kreise in Graphen
 Periodische Fahrpläne und Kreise in Graphen Vorlesung Algorithmentechnik WS 2009/10 Dorothea Wagner Karlsruher Institut für Technologie Eisenbahnoptimierungsprozess 1 Anforderungserhebung Netzwerkentwurf
Periodische Fahrpläne und Kreise in Graphen Vorlesung Algorithmentechnik WS 2009/10 Dorothea Wagner Karlsruher Institut für Technologie Eisenbahnoptimierungsprozess 1 Anforderungserhebung Netzwerkentwurf
Theoretische Grundlagen der Informatik
 Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
Theoretische Grundlagen der Informatik Vorlesung am 12.01.2012 INSTITUT FÜR THEORETISCHE 0 KIT 12.01.2012 Universität des Dorothea Landes Baden-Württemberg Wagner - Theoretische und Grundlagen der Informatik
8 Diskrete Optimierung
 8 Diskrete Optimierung Definition 8.1. Ein Graph G ist ein Paar (V (G), E(G)) besteh aus einer lichen Menge V (G) von Knoten (oder Ecken) und einer Menge E(G) ( ) V (G) 2 von Kanten. Die Ordnung n(g) von
8 Diskrete Optimierung Definition 8.1. Ein Graph G ist ein Paar (V (G), E(G)) besteh aus einer lichen Menge V (G) von Knoten (oder Ecken) und einer Menge E(G) ( ) V (G) 2 von Kanten. Die Ordnung n(g) von
Datenstrukturen & Algorithmen
 Datenstrukturen & Algorithmen Matthias Zwicker Universität Bern Frühling 2010 Übersicht Binäre Suchbäume Einführung und Begriffe Binäre Suchbäume 2 Binäre Suchbäume Datenstruktur für dynamische Mengen
Datenstrukturen & Algorithmen Matthias Zwicker Universität Bern Frühling 2010 Übersicht Binäre Suchbäume Einführung und Begriffe Binäre Suchbäume 2 Binäre Suchbäume Datenstruktur für dynamische Mengen
Die Verbindung von Linearer Programmierung und Graphentheorie
 Die Verbindung von Linearer Programmierung und Graphentheorie Definition 5.9. Ein kombinatorisches Optimierungsproblem entspricht einem LP, bei dem statt der Vorzeichenbedingungen x i 0 Bedingungen der
Die Verbindung von Linearer Programmierung und Graphentheorie Definition 5.9. Ein kombinatorisches Optimierungsproblem entspricht einem LP, bei dem statt der Vorzeichenbedingungen x i 0 Bedingungen der
Datenaufbereitung in SPSS. Daten zusammenfügen
 Daten zusammenfügen I. Fälle hinzufügen Diese Schritte müssen Sie unternehmen, wenn die Daten in unterschiedlichen Dateien sind; wenn also die Daten von unterschiedlichen Personen in unterschiedlichen
Daten zusammenfügen I. Fälle hinzufügen Diese Schritte müssen Sie unternehmen, wenn die Daten in unterschiedlichen Dateien sind; wenn also die Daten von unterschiedlichen Personen in unterschiedlichen
Ablauf bei der Synchronisation und Sortierung von Dateien aus mehreren Kameras
 Ablauf bei der Synchronisation und Sortierung von Dateien aus mehreren Kameras Dieser Abgleich ist immer dann nötig, wenn mit verschiedenen Kameras fotografiert und vorab vergessen wurde, die Aufnahmezeit
Ablauf bei der Synchronisation und Sortierung von Dateien aus mehreren Kameras Dieser Abgleich ist immer dann nötig, wenn mit verschiedenen Kameras fotografiert und vorab vergessen wurde, die Aufnahmezeit
Kapitel 6: Graphalgorithmen Gliederung
 Gliederung 1. Grundlagen 2. Zahlentheoretische Algorithmen 3. Sortierverfahren 4. Ausgewählte Datenstrukturen 5. Dynamisches Programmieren 6. Graphalgorithmen 7. String-Matching 8. Kombinatorische Algorithmen
Gliederung 1. Grundlagen 2. Zahlentheoretische Algorithmen 3. Sortierverfahren 4. Ausgewählte Datenstrukturen 5. Dynamisches Programmieren 6. Graphalgorithmen 7. String-Matching 8. Kombinatorische Algorithmen
Graphen: Einführung. Vorlesung Mathematische Strukturen. Sommersemester 2011
 Graphen: Einführung Vorlesung Mathematische Strukturen Zum Ende der Vorlesung beschäftigen wir uns mit Graphen. Graphen sind netzartige Strukturen, bestehend aus Knoten und Kanten. Sommersemester 20 Prof.
Graphen: Einführung Vorlesung Mathematische Strukturen Zum Ende der Vorlesung beschäftigen wir uns mit Graphen. Graphen sind netzartige Strukturen, bestehend aus Knoten und Kanten. Sommersemester 20 Prof.
Guten Morgen und Willkommen zur Saalübung!
 Guten Morgen und Willkommen zur Saalübung! 1 Wie gewinnt man ein Spiel? Was ist ein Spiel? 2 Verschiedene Spiele Schach, Tic-Tac-Toe, Go Memory Backgammon Poker Nim, Käsekästchen... 3 Einschränkungen Zwei
Guten Morgen und Willkommen zur Saalübung! 1 Wie gewinnt man ein Spiel? Was ist ein Spiel? 2 Verschiedene Spiele Schach, Tic-Tac-Toe, Go Memory Backgammon Poker Nim, Käsekästchen... 3 Einschränkungen Zwei
OPERATIONS RESEARCH. Studiengang Wirtschaftsinformatik 4. Semester Teil 1. Prof. Dr. Heinrich Paessens SS EINFÜHRUNG 3 1.
 OPERATIONS RESEARCH Studiengang Wirtschaftsinformatik. Semester Teil Prof. Dr. Heinrich Paessens SS 00 0. EINFÜHRUNG. GRAPHENTHEORIE. DEFINITIONEN/BEGRIFFE DER GRAPHENTHEORIE Grundlegende Definitionen
OPERATIONS RESEARCH Studiengang Wirtschaftsinformatik. Semester Teil Prof. Dr. Heinrich Paessens SS 00 0. EINFÜHRUNG. GRAPHENTHEORIE. DEFINITIONEN/BEGRIFFE DER GRAPHENTHEORIE Grundlegende Definitionen
Datensicherung. Beschreibung der Datensicherung
 Datensicherung Mit dem Datensicherungsprogramm können Sie Ihre persönlichen Daten problemlos Sichern. Es ist möglich eine komplette Datensicherung durchzuführen, aber auch nur die neuen und geänderten
Datensicherung Mit dem Datensicherungsprogramm können Sie Ihre persönlichen Daten problemlos Sichern. Es ist möglich eine komplette Datensicherung durchzuführen, aber auch nur die neuen und geänderten
Informatik I WS 07/08 Tutorium 24
 Info I Tutorium 24 Informatik I WS 07/08 Tutorium 24 3.2.07 astian Molkenthin E-Mail: infotut@sunshine2k.de Web: http://infotut.sunshine2k.de Organisatorisches / Review is zum 2.2 müssen alle Praxisaufgaben
Info I Tutorium 24 Informatik I WS 07/08 Tutorium 24 3.2.07 astian Molkenthin E-Mail: infotut@sunshine2k.de Web: http://infotut.sunshine2k.de Organisatorisches / Review is zum 2.2 müssen alle Praxisaufgaben
Austausch- bzw. Übergangsprozesse und Gleichgewichtsverteilungen
 Austausch- bzw. Übergangsrozesse und Gleichgewichtsverteilungen Wir betrachten ein System mit verschiedenen Zuständen, zwischen denen ein Austausch stattfinden kann. Etwa soziale Schichten in einer Gesellschaft:
Austausch- bzw. Übergangsrozesse und Gleichgewichtsverteilungen Wir betrachten ein System mit verschiedenen Zuständen, zwischen denen ein Austausch stattfinden kann. Etwa soziale Schichten in einer Gesellschaft:
Babeș-Bolyai Universität Cluj Napoca Fakultät für Mathematik und Informatik Grundlagen der Programmierung MLG5005. Paradigmen im Algorithmenentwurf
 Babeș-Bolyai Universität Cluj Napoca Fakultät für Mathematik und Informatik Grundlagen der Programmierung MLG5005 Paradigmen im Algorithmenentwurf Problemlösen Problem definieren Algorithmus entwerfen
Babeș-Bolyai Universität Cluj Napoca Fakultät für Mathematik und Informatik Grundlagen der Programmierung MLG5005 Paradigmen im Algorithmenentwurf Problemlösen Problem definieren Algorithmus entwerfen
3.1 Konstruktion von minimalen Spannbäumen Es gibt zwei Prinzipien für die Konstruktion von minimalen Spannbäumen (Tarjan): blaue Regel rote Regel
 3.1 Konstruktion von minimalen Spannbäumen Es gibt zwei Prinzipien für die Konstruktion von minimalen Spannbäumen (Tarjan): blaue Regel rote Regel EADS 3.1 Konstruktion von minimalen Spannbäumen 16/36
3.1 Konstruktion von minimalen Spannbäumen Es gibt zwei Prinzipien für die Konstruktion von minimalen Spannbäumen (Tarjan): blaue Regel rote Regel EADS 3.1 Konstruktion von minimalen Spannbäumen 16/36
Entladen und Aufladen eines Kondensators über einen ohmschen Widerstand
 Entladen und Aufladen eines Kondensators über einen ohmschen Widerstand Vorüberlegung In einem seriellen Stromkreis addieren sich die Teilspannungen zur Gesamtspannung Bei einer Gesamtspannung U ges, der
Entladen und Aufladen eines Kondensators über einen ohmschen Widerstand Vorüberlegung In einem seriellen Stromkreis addieren sich die Teilspannungen zur Gesamtspannung Bei einer Gesamtspannung U ges, der
15 Optimales Kodieren
 15 Optimales Kodieren Es soll ein optimaler Kodierer C(T ) entworfen werden, welcher eine Information (z.b. Text T ) mit möglichst geringer Bitanzahl eindeutig überträgt. Die Anforderungen an den optimalen
15 Optimales Kodieren Es soll ein optimaler Kodierer C(T ) entworfen werden, welcher eine Information (z.b. Text T ) mit möglichst geringer Bitanzahl eindeutig überträgt. Die Anforderungen an den optimalen
Algorithmen und Datenstrukturen 2
 Algorithmen und Datenstrukturen 2 Sommersemester 2007 4. Vorlesung Peter F. Stadler Universität Leipzig Institut für Informatik studla@bioinf.uni-leipzig.de Traversierung Durchlaufen eines Graphen, bei
Algorithmen und Datenstrukturen 2 Sommersemester 2007 4. Vorlesung Peter F. Stadler Universität Leipzig Institut für Informatik studla@bioinf.uni-leipzig.de Traversierung Durchlaufen eines Graphen, bei
Dokumentation IBIS Monitor
 Dokumentation IBIS Monitor Seite 1 von 16 11.01.06 Inhaltsverzeichnis 1. Allgemein 2. Installation und Programm starten 3. Programmkonfiguration 4. Aufzeichnung 4.1 Aufzeichnung mitschneiden 4.1.1 Inhalt
Dokumentation IBIS Monitor Seite 1 von 16 11.01.06 Inhaltsverzeichnis 1. Allgemein 2. Installation und Programm starten 3. Programmkonfiguration 4. Aufzeichnung 4.1 Aufzeichnung mitschneiden 4.1.1 Inhalt
Einführung in Scheduling
 Einführung in Scheduling Dr. Julien Bidot Sommersemester 28 Institut für Künstliche Intelligenz Inhalt I. Definition und Formulierung des Scheduling- Problems II. Projektplanung III. Produktionsplanung
Einführung in Scheduling Dr. Julien Bidot Sommersemester 28 Institut für Künstliche Intelligenz Inhalt I. Definition und Formulierung des Scheduling- Problems II. Projektplanung III. Produktionsplanung
Handbuch B4000+ Preset Manager
 Handbuch B4000+ Preset Manager B4000+ authentic organ modeller Version 0.6 FERROFISH advanced audio applications Einleitung Mit der Software B4000+ Preset Manager können Sie Ihre in der B4000+ erstellten
Handbuch B4000+ Preset Manager B4000+ authentic organ modeller Version 0.6 FERROFISH advanced audio applications Einleitung Mit der Software B4000+ Preset Manager können Sie Ihre in der B4000+ erstellten
Algorithmen und Datenstrukturen. Große Übung vom 29.10.09 Nils Schweer
 Algorithmen und Datenstrukturen Große Übung vom 29.10.09 Nils Schweer Diese Folien Braucht man nicht abzuschreiben Stehen im Netz unter www.ibr.cs.tu-bs.de/courses/ws0910/aud/index.html Kleine Übungen
Algorithmen und Datenstrukturen Große Übung vom 29.10.09 Nils Schweer Diese Folien Braucht man nicht abzuschreiben Stehen im Netz unter www.ibr.cs.tu-bs.de/courses/ws0910/aud/index.html Kleine Übungen
Im Folgenden wird Ihnen an einem Beispiel erklärt, wie Sie Excel-Anlagen und Excel-Vorlagen erstellen können.
 Excel-Schnittstelle Im Folgenden wird Ihnen an einem Beispiel erklärt, wie Sie Excel-Anlagen und Excel-Vorlagen erstellen können. Voraussetzung: Microsoft Office Excel ab Version 2000 Zum verwendeten Beispiel:
Excel-Schnittstelle Im Folgenden wird Ihnen an einem Beispiel erklärt, wie Sie Excel-Anlagen und Excel-Vorlagen erstellen können. Voraussetzung: Microsoft Office Excel ab Version 2000 Zum verwendeten Beispiel:
Petri-Netze / Eine Einführung (Teil 2)
 Manuel Hertlein Seminar Systementwurf Lehrstuhl Theorie der Programmierung Wiederholung (1) Petri-Netz = bipartiter, gerichteter Graph Aufbau: Plätze (passive Komponenten) Transitionen (aktive Komponenten)
Manuel Hertlein Seminar Systementwurf Lehrstuhl Theorie der Programmierung Wiederholung (1) Petri-Netz = bipartiter, gerichteter Graph Aufbau: Plätze (passive Komponenten) Transitionen (aktive Komponenten)
BMW ConnectedDrive. www.bmw.com/ connecteddrive. Freude am Fahren BMW CONNECTED DRIVE. NEUERUNGEN FÜR PERSONALISIERTE BMW CONNECTED DRIVE DIENSTE.
 BMW ConnectedDrive www.bmw.com/ connecteddrive Freude am Fahren BMW CONNECTED DRIVE. NEUERUNGEN FÜR PERSONALISIERTE BMW CONNECTED DRIVE DIENSTE. 1 EINLEITUNG. Im Rahmen der Neuausrichtung von BMW ConnectedDrive
BMW ConnectedDrive www.bmw.com/ connecteddrive Freude am Fahren BMW CONNECTED DRIVE. NEUERUNGEN FÜR PERSONALISIERTE BMW CONNECTED DRIVE DIENSTE. 1 EINLEITUNG. Im Rahmen der Neuausrichtung von BMW ConnectedDrive
4. Relationen. Beschreibung einer binären Relation
 4. Relationen Relationen spielen bei Datenbanken eine wichtige Rolle. Die meisten Datenbanksysteme sind relational. 4.1 Binäre Relationen Eine binäre Relation (Beziehung) R zwischen zwei Mengen A und B
4. Relationen Relationen spielen bei Datenbanken eine wichtige Rolle. Die meisten Datenbanksysteme sind relational. 4.1 Binäre Relationen Eine binäre Relation (Beziehung) R zwischen zwei Mengen A und B
Kombinatorische Optimierung
 Juniorprof. Dr. Henning Meyerhenke 1 Henning Meyerhenke: KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Vorlesung 1 Programm des
Juniorprof. Dr. Henning Meyerhenke 1 Henning Meyerhenke: KIT Universität des Landes Baden-Württemberg und nationales Forschungszentrum in der Helmholtz-Gemeinschaft www.kit.edu Vorlesung 1 Programm des
Bearbeitungshinweise. (20 Punkte)
 Bearbeitungshinweise - Es sind alle Aufgaben zu bearbeiten. - Als Hilfsmittel sind lediglich nicht programmierbare Taschenrechner erlaubt. - Die Klausur darf nicht auseinander genommen werden. - Sämtliche
Bearbeitungshinweise - Es sind alle Aufgaben zu bearbeiten. - Als Hilfsmittel sind lediglich nicht programmierbare Taschenrechner erlaubt. - Die Klausur darf nicht auseinander genommen werden. - Sämtliche
FTV 1. Semester. Spalte A Spalte B Spalte C Spalte D. Zeile 1 Zelle A1 Zelle B1 Zelle C1 Zelle D1. Zeile 3 Zelle A3 Zelle B3 Zelle C3 Zelle D3
 Eine besteht aus Zeilen und spalten von Zellen, die mit Text oder Grafik gefüllt werden können. Die wird standardmäßig mit einfachen Rahmenlinien versehen, die verändert oder entfernt werden können. Spalte
Eine besteht aus Zeilen und spalten von Zellen, die mit Text oder Grafik gefüllt werden können. Die wird standardmäßig mit einfachen Rahmenlinien versehen, die verändert oder entfernt werden können. Spalte
Vorlesung Diskrete Strukturen Graphen: Wieviele Bäume?
 Vorlesung Diskrete Strukturen Graphen: Wieviele Bäume? Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de WS 2013/14 Isomorphie Zwei Graphen (V 1, E 1 ) und (V
Vorlesung Diskrete Strukturen Graphen: Wieviele Bäume? Bernhard Ganter Institut für Algebra TU Dresden D-01062 Dresden bernhard.ganter@tu-dresden.de WS 2013/14 Isomorphie Zwei Graphen (V 1, E 1 ) und (V
Seminarvortag zum Thema Virtual Private Network Design im Rahmen des Seminars Network Design an der Universität Paderborn
 Seminarvortag zum Thema Virtual Private Network Design im Rahmen des Seminars Network Design an der Universität Paderborn Ein 5.55-Approximationsalgorithmus für das VPND-Problem Lars Schäfers Inhalt Einführung:
Seminarvortag zum Thema Virtual Private Network Design im Rahmen des Seminars Network Design an der Universität Paderborn Ein 5.55-Approximationsalgorithmus für das VPND-Problem Lars Schäfers Inhalt Einführung:
Benutzerkonto unter Windows 2000
 Jeder Benutzer, der an einem Windows 2000 PC arbeiten möchte, braucht dazu ein Benutzerkonto. Je nach Organisation des Netzwerkes, existiert dieses Benutzerkonto auf der lokalen Workstation oder im Active
Jeder Benutzer, der an einem Windows 2000 PC arbeiten möchte, braucht dazu ein Benutzerkonto. Je nach Organisation des Netzwerkes, existiert dieses Benutzerkonto auf der lokalen Workstation oder im Active
Vorlesung Betriebstechnik/Netzplantechnik Operations Research
 Vorlesung Betriebstechnik/Netzplantechnik Operations Research Organisation Agenda Übungen Netzplantechnik GANTT-Diagramme Weitere Übungen 2 Übungen 3 weitere Übungen Nr. Vorgang Dauer AOB 1 Kickoff 2-2
Vorlesung Betriebstechnik/Netzplantechnik Operations Research Organisation Agenda Übungen Netzplantechnik GANTT-Diagramme Weitere Übungen 2 Übungen 3 weitere Übungen Nr. Vorgang Dauer AOB 1 Kickoff 2-2
Visio 2013. Grundlagen. Linda York. 1. Ausgabe, Oktober 2013
 Visio 2013 Linda York 1. Ausgabe, Oktober 2013 Grundlagen V2013 2 Visio 2013 - Grundlagen 2 Einfache Zeichnungen erstellen In diesem Kapitel erfahren Sie wie Sie Shapes einfügen, kopieren und löschen was
Visio 2013 Linda York 1. Ausgabe, Oktober 2013 Grundlagen V2013 2 Visio 2013 - Grundlagen 2 Einfache Zeichnungen erstellen In diesem Kapitel erfahren Sie wie Sie Shapes einfügen, kopieren und löschen was
3. Schulungsprojekt zur Einführung eines PM-Handbuchs
 Netzplantechnik (NPT) Aufgaben zur Berechnung von Netzplänen In der heutigen Betriebspraxis werden Netzpläne nicht mehr per Hand gerechnet. Für diese Aufgabe werden Projektmanagement- Software-Programme
Netzplantechnik (NPT) Aufgaben zur Berechnung von Netzplänen In der heutigen Betriebspraxis werden Netzpläne nicht mehr per Hand gerechnet. Für diese Aufgabe werden Projektmanagement- Software-Programme
Logistik: Rundreisen und Touren
 Logistik: Rundreisen und Touren 2008 AGI-Information Management Consultants May be used for personal purporses only or by libraries associated to dandelon.com network. Von Universitätsprofessor Dr. Wolfgang
Logistik: Rundreisen und Touren 2008 AGI-Information Management Consultants May be used for personal purporses only or by libraries associated to dandelon.com network. Von Universitätsprofessor Dr. Wolfgang
Teil III: Routing - Inhalt I. Literatur. Geometric Routing. Voraussetzungen. Unit Disk Graph (UDG) Geometric Routing 29
 1 29 Teil III: Routing - Inhalt I Literatur Compass & Face Routing Bounded & Adaptive Face Routing Nicht Ω(1) UDG E. Kranakis, H. Singh und Jorge Urrutia: Compass Routing on Geometric Networks. Canadian
1 29 Teil III: Routing - Inhalt I Literatur Compass & Face Routing Bounded & Adaptive Face Routing Nicht Ω(1) UDG E. Kranakis, H. Singh und Jorge Urrutia: Compass Routing on Geometric Networks. Canadian
Mathematik 1: (ohne Taschenrechner) Korrekturanleitung. Kanton St.Gallen Bildungsdepartement. BMS/FMS/WMS/WMI Aufnahmeprüfung Frühling 2015
 Kanton St.Gallen Bildungsdepartement BMS/FMS/WMS/WMI Aufnahmeprüfung Frühling 2015 Mathematik 1: (ohne Taschenrechner) Korrekturanleitung Die Korrekturanleitung legt die Verteilung der Punkte auf die einzelnen
Kanton St.Gallen Bildungsdepartement BMS/FMS/WMS/WMI Aufnahmeprüfung Frühling 2015 Mathematik 1: (ohne Taschenrechner) Korrekturanleitung Die Korrekturanleitung legt die Verteilung der Punkte auf die einzelnen
Formale Systeme. Binary Decision Diagrams. Prof. Dr. Bernhard Beckert WS 2010/2011 KIT INSTITUT FÜR THEORETISCHE INFORMATIK
 Formale Systeme Prof. Dr. Bernhard Beckert WS / KIT INSTITUT FÜR THEORETISCHE INFORMATIK KIT University of the State of Baden-Württemberg and National Large-scale Research Center of the Helmholtz Association
Formale Systeme Prof. Dr. Bernhard Beckert WS / KIT INSTITUT FÜR THEORETISCHE INFORMATIK KIT University of the State of Baden-Württemberg and National Large-scale Research Center of the Helmholtz Association
Einführung in Petri-Netze. Modellierung von Abläufen und Prozessen (1) Abhängigkeitsgraphen: Motivation. Petri-Netze
 Einführung in Petri-Netze Modellierung von Abläufen und Prozessen () Motivation Abhängigkeitsgraphen: A B 6 C 5 D Petri-Netze Markierungen Invarianten Credits: L. Priese, H. Wimmel: Petri-Netze, Theoretische
Einführung in Petri-Netze Modellierung von Abläufen und Prozessen () Motivation Abhängigkeitsgraphen: A B 6 C 5 D Petri-Netze Markierungen Invarianten Credits: L. Priese, H. Wimmel: Petri-Netze, Theoretische
Folgeanleitung für Klassenlehrer
 Folgeanleitung für Klassenlehrer 1. Das richtige Halbjahr einstellen Stellen sie bitte zunächst das richtige Schul- und Halbjahr ein. Ist das korrekte Schul- und Halbjahr eingestellt, leuchtet die Fläche
Folgeanleitung für Klassenlehrer 1. Das richtige Halbjahr einstellen Stellen sie bitte zunächst das richtige Schul- und Halbjahr ein. Ist das korrekte Schul- und Halbjahr eingestellt, leuchtet die Fläche
Programmierkurs Java
 Programmierkurs Java Dr. Dietrich Boles Aufgaben zu UE16-Rekursion (Stand 09.12.2011) Aufgabe 1: Implementieren Sie in Java ein Programm, das solange einzelne Zeichen vom Terminal einliest, bis ein #-Zeichen
Programmierkurs Java Dr. Dietrich Boles Aufgaben zu UE16-Rekursion (Stand 09.12.2011) Aufgabe 1: Implementieren Sie in Java ein Programm, das solange einzelne Zeichen vom Terminal einliest, bis ein #-Zeichen
einfach klar sicher intelligent Die besten Telematiklösungen... übersichtlich wirtschaftlich effizient
 einfach klar sicher intelligent Die besten Telematiklösungen... übersichtlich wirtschaftlich effizient maßgeschneidert schnell direkt gezielt... finden Sie bei uns. individuell kompetent zuverlässig akquinet
einfach klar sicher intelligent Die besten Telematiklösungen... übersichtlich wirtschaftlich effizient maßgeschneidert schnell direkt gezielt... finden Sie bei uns. individuell kompetent zuverlässig akquinet
Berechnungen in Access Teil I
 in Access Teil I Viele Daten müssen in eine Datenbank nicht eingetragen werden, weil sie sich aus anderen Daten berechnen lassen. Zum Beispiel lässt sich die Mehrwertsteuer oder der Bruttopreis in einer
in Access Teil I Viele Daten müssen in eine Datenbank nicht eingetragen werden, weil sie sich aus anderen Daten berechnen lassen. Zum Beispiel lässt sich die Mehrwertsteuer oder der Bruttopreis in einer
Folgeanleitung für Fachlehrer
 1. Das richtige Halbjahr einstellen Folgeanleitung für Fachlehrer Stellen sie bitte zunächst das richtige Schul- und Halbjahr ein. Ist das korrekte Schul- und Halbjahr eingestellt, leuchtet die Fläche
1. Das richtige Halbjahr einstellen Folgeanleitung für Fachlehrer Stellen sie bitte zunächst das richtige Schul- und Halbjahr ein. Ist das korrekte Schul- und Halbjahr eingestellt, leuchtet die Fläche
Lehrer: Einschreibemethoden
 Lehrer: Einschreibemethoden Einschreibemethoden Für die Einschreibung in Ihren Kurs gibt es unterschiedliche Methoden. Sie können die Schüler über die Liste eingeschriebene Nutzer Ihrem Kurs zuweisen oder
Lehrer: Einschreibemethoden Einschreibemethoden Für die Einschreibung in Ihren Kurs gibt es unterschiedliche Methoden. Sie können die Schüler über die Liste eingeschriebene Nutzer Ihrem Kurs zuweisen oder
16. All Pairs Shortest Path (ASPS)
 . All Pairs Shortest Path (ASPS) All Pairs Shortest Path (APSP): Eingabe: Gewichteter Graph G=(V,E) Ausgabe: Für jedes Paar von Knoten u,v V die Distanz von u nach v sowie einen kürzesten Weg a b c d e
. All Pairs Shortest Path (ASPS) All Pairs Shortest Path (APSP): Eingabe: Gewichteter Graph G=(V,E) Ausgabe: Für jedes Paar von Knoten u,v V die Distanz von u nach v sowie einen kürzesten Weg a b c d e
Kürzeste Wege in Graphen. Maurice Duvigneau Otto-von-Guericke Universität Fakultät für Informatik
 Kürzeste Wege in Graphen Maurice Duvigneau Otto-von-Guericke Universität Fakultät für Informatik Gliederung Einleitung Definitionen Algorithmus von Dijkstra Bellmann-Ford Algorithmus Floyd-Warshall Algorithmus
Kürzeste Wege in Graphen Maurice Duvigneau Otto-von-Guericke Universität Fakultät für Informatik Gliederung Einleitung Definitionen Algorithmus von Dijkstra Bellmann-Ford Algorithmus Floyd-Warshall Algorithmus
Wichtige Hinweise zu den neuen Orientierungshilfen der Architekten-/Objektplanerverträge
 Wichtige Hinweise zu den neuen Orientierungshilfen der Architekten-/Objektplanerverträge Ab der Version forma 5.5 handelt es sich bei den Orientierungshilfen der Architekten-/Objektplanerverträge nicht
Wichtige Hinweise zu den neuen Orientierungshilfen der Architekten-/Objektplanerverträge Ab der Version forma 5.5 handelt es sich bei den Orientierungshilfen der Architekten-/Objektplanerverträge nicht
OECD Programme for International Student Assessment PISA 2000. Lösungen der Beispielaufgaben aus dem Mathematiktest. Deutschland
 OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
OECD Programme for International Student Assessment Deutschland PISA 2000 Lösungen der Beispielaufgaben aus dem Mathematiktest Beispielaufgaben PISA-Hauptstudie 2000 Seite 3 UNIT ÄPFEL Beispielaufgaben
Excel Pivot-Tabellen 2010 effektiv
 7.2 Berechnete Felder Falls in der Datenquelle die Zahlen nicht in der Form vorliegen wie Sie diese benötigen, können Sie die gewünschten Ergebnisse mit Formeln berechnen. Dazu erzeugen Sie ein berechnetes
7.2 Berechnete Felder Falls in der Datenquelle die Zahlen nicht in der Form vorliegen wie Sie diese benötigen, können Sie die gewünschten Ergebnisse mit Formeln berechnen. Dazu erzeugen Sie ein berechnetes
tentoinfinity Apps 1.0 EINFÜHRUNG
 tentoinfinity Apps Una Hilfe Inhalt Copyright 2013-2015 von tentoinfinity Apps. Alle Rechte vorbehalten. Inhalt der online-hilfe wurde zuletzt aktualisiert am August 6, 2015. Zusätzlicher Support Ressourcen
tentoinfinity Apps Una Hilfe Inhalt Copyright 2013-2015 von tentoinfinity Apps. Alle Rechte vorbehalten. Inhalt der online-hilfe wurde zuletzt aktualisiert am August 6, 2015. Zusätzlicher Support Ressourcen
eduvote Ein Umfragesystem für Lehrveranstaltungen - PowerPoint Add-In -
 eduvote Ein Umfragesystem für Lehrveranstaltungen - PowerPoint Add-In - Übersicht: Nach dem Herunterladen und Ausführen des Installationsprogamms für das eduvote PowerPoint Add-In befindet sich rechts
eduvote Ein Umfragesystem für Lehrveranstaltungen - PowerPoint Add-In - Übersicht: Nach dem Herunterladen und Ausführen des Installationsprogamms für das eduvote PowerPoint Add-In befindet sich rechts
Karten-Freischaltung mit dem UNLOCK MANAGER
 Karten-Freischaltung mit dem UNLOCK MANAGER WICHTIGE INFORMATION 1. Anzahl der Freischaltungen Die Karten können zweimal freigeschaltet werden. (z. B. Map Manager auf PC plus Map Manager auf Laptop oder
Karten-Freischaltung mit dem UNLOCK MANAGER WICHTIGE INFORMATION 1. Anzahl der Freischaltungen Die Karten können zweimal freigeschaltet werden. (z. B. Map Manager auf PC plus Map Manager auf Laptop oder
Dialognetze. Ziel : Beschreibung von Methoden und Beschreibungstechniken für den Entwurf und die Dokumentation von Dialogabläufen
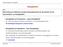 Dialognetze Ziel : Beschreibung von Methoden und Beschreibungstechniken für den Entwurf und die Dokumentation von Dialogabläufen Dialogabläufe auf Fensterebene "grobe Dialogabläufe" d.h. Wechsel zwischen
Dialognetze Ziel : Beschreibung von Methoden und Beschreibungstechniken für den Entwurf und die Dokumentation von Dialogabläufen Dialogabläufe auf Fensterebene "grobe Dialogabläufe" d.h. Wechsel zwischen
Wasserfall-Ansätze zur Bildsegmentierung
 Wasserfall-Ansätze zur Bildsegmentierung von Philipp Jester Seminar: Bildsegmentierung und Computer Vision 16.01.2006 Überblick 1. Problemstellung 2. Wiederholung: Wasserscheiden-Ansätze 3. Der Wasserfall-Ansatz
Wasserfall-Ansätze zur Bildsegmentierung von Philipp Jester Seminar: Bildsegmentierung und Computer Vision 16.01.2006 Überblick 1. Problemstellung 2. Wiederholung: Wasserscheiden-Ansätze 3. Der Wasserfall-Ansatz
Outlook. sysplus.ch outlook - mail-grundlagen Seite 1/8. Mail-Grundlagen. Posteingang
 sysplus.ch outlook - mail-grundlagen Seite 1/8 Outlook Mail-Grundlagen Posteingang Es gibt verschiedene Möglichkeiten, um zum Posteingang zu gelangen. Man kann links im Outlook-Fenster auf die Schaltfläche
sysplus.ch outlook - mail-grundlagen Seite 1/8 Outlook Mail-Grundlagen Posteingang Es gibt verschiedene Möglichkeiten, um zum Posteingang zu gelangen. Man kann links im Outlook-Fenster auf die Schaltfläche
Würfelt man dabei je genau 10 - mal eine 1, 2, 3, 4, 5 und 6, so beträgt die Anzahl. der verschiedenen Reihenfolgen, in denen man dies tun kann, 60!.
 040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
040304 Übung 9a Analysis, Abschnitt 4, Folie 8 Die Wahrscheinlichkeit, dass bei n - maliger Durchführung eines Zufallexperiments ein Ereignis A ( mit Wahrscheinlichkeit p p ( A ) ) für eine beliebige Anzahl
Graphentheorie Mathe-Club Klasse 5/6
 Graphentheorie Mathe-Club Klasse 5/6 Thomas Krakow Rostock, den 26. April 2006 Inhaltsverzeichnis 1 Einleitung 3 2 Grundbegriffe und einfache Sätze über Graphen 5 2.1 Der Knotengrad.................................
Graphentheorie Mathe-Club Klasse 5/6 Thomas Krakow Rostock, den 26. April 2006 Inhaltsverzeichnis 1 Einleitung 3 2 Grundbegriffe und einfache Sätze über Graphen 5 2.1 Der Knotengrad.................................
1 Mathematische Grundlagen
 Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Mathematische Grundlagen - 1-1 Mathematische Grundlagen Der Begriff der Menge ist einer der grundlegenden Begriffe in der Mathematik. Mengen dienen dazu, Dinge oder Objekte zu einer Einheit zusammenzufassen.
Fallbeispiel: Eintragen einer Behandlung
 Fallbeispiel: Eintragen einer Behandlung Im ersten Beispiel gelernt, wie man einen Patienten aus der Datenbank aussucht oder falls er noch nicht in der Datenbank ist neu anlegt. Im dritten Beispiel haben
Fallbeispiel: Eintragen einer Behandlung Im ersten Beispiel gelernt, wie man einen Patienten aus der Datenbank aussucht oder falls er noch nicht in der Datenbank ist neu anlegt. Im dritten Beispiel haben
Ohne Fehler geht es nicht Doch wie viele Fehler sind erlaubt?
 Ohne Fehler geht es nicht Doch wie viele Fehler sind erlaubt? Behandelte Fragestellungen Was besagt eine Fehlerquote? Welche Bezugsgröße ist geeignet? Welche Fehlerquote ist gerade noch zulässig? Wie stellt
Ohne Fehler geht es nicht Doch wie viele Fehler sind erlaubt? Behandelte Fragestellungen Was besagt eine Fehlerquote? Welche Bezugsgröße ist geeignet? Welche Fehlerquote ist gerade noch zulässig? Wie stellt
Lineare Funktionen. 1 Proportionale Funktionen 3 1.1 Definition... 3 1.2 Eigenschaften... 3. 2 Steigungsdreieck 3
 Lineare Funktionen Inhaltsverzeichnis 1 Proportionale Funktionen 3 1.1 Definition............................... 3 1.2 Eigenschaften............................. 3 2 Steigungsdreieck 3 3 Lineare Funktionen
Lineare Funktionen Inhaltsverzeichnis 1 Proportionale Funktionen 3 1.1 Definition............................... 3 1.2 Eigenschaften............................. 3 2 Steigungsdreieck 3 3 Lineare Funktionen
Lineare Gleichungssysteme
 Lineare Gleichungssysteme Eines der am häufigsten auftretenden Standardprobleme der angewandten Mathematik ist das Lösen linearer Gleichungssysteme, etwa zur Netzwerkberechnung in der Elektrotechnik oder
Lineare Gleichungssysteme Eines der am häufigsten auftretenden Standardprobleme der angewandten Mathematik ist das Lösen linearer Gleichungssysteme, etwa zur Netzwerkberechnung in der Elektrotechnik oder
Inventur. Bemerkung. / Inventur
 Inventur Die beliebige Aufteilung des Artikelstamms nach Artikeln, Lieferanten, Warengruppen, Lagerorten, etc. ermöglicht es Ihnen, Ihre Inventur in mehreren Abschnitten durchzuführen. Bemerkung Zwischen
Inventur Die beliebige Aufteilung des Artikelstamms nach Artikeln, Lieferanten, Warengruppen, Lagerorten, etc. ermöglicht es Ihnen, Ihre Inventur in mehreren Abschnitten durchzuführen. Bemerkung Zwischen
KONSTRUKTION VON ROT-SCHWARZ-BÄUMEN
 KONSTRUKTION VON ROT-SCHWARZ-BÄUMEN RALF HINZE Institut für Informatik III Universität Bonn Email: ralf@informatik.uni-bonn.de Homepage: http://www.informatik.uni-bonn.de/~ralf Februar, 2001 Binäre Suchbäume
KONSTRUKTION VON ROT-SCHWARZ-BÄUMEN RALF HINZE Institut für Informatik III Universität Bonn Email: ralf@informatik.uni-bonn.de Homepage: http://www.informatik.uni-bonn.de/~ralf Februar, 2001 Binäre Suchbäume
Hilfe zur Urlaubsplanung und Zeiterfassung
 Hilfe zur Urlaubsplanung und Zeiterfassung Urlaubs- und Arbeitsplanung: Mit der Urlaubs- und Arbeitsplanung kann jeder Mitarbeiter in Coffee seine Zeiten eintragen. Die Eintragung kann mit dem Status anfragen,
Hilfe zur Urlaubsplanung und Zeiterfassung Urlaubs- und Arbeitsplanung: Mit der Urlaubs- und Arbeitsplanung kann jeder Mitarbeiter in Coffee seine Zeiten eintragen. Die Eintragung kann mit dem Status anfragen,
Kurzanleitung fu r Clubbeauftragte zur Pflege der Mitgliederdaten im Mitgliederbereich
 Kurzanleitung fu r Clubbeauftragte zur Pflege der Mitgliederdaten im Mitgliederbereich Mitgliederbereich (Version 1.0) Bitte loggen Sie sich in den Mitgliederbereich mit den Ihnen bekannten Zugangsdaten
Kurzanleitung fu r Clubbeauftragte zur Pflege der Mitgliederdaten im Mitgliederbereich Mitgliederbereich (Version 1.0) Bitte loggen Sie sich in den Mitgliederbereich mit den Ihnen bekannten Zugangsdaten
WS 2013/14. Diskrete Strukturen
 WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
WS 2013/14 Diskrete Strukturen Prof. Dr. J. Esparza Lehrstuhl für Grundlagen der Softwarezuverlässigkeit und theoretische Informatik Fakultät für Informatik Technische Universität München http://www7.in.tum.de/um/courses/ds/ws1314
Primzahlen und RSA-Verschlüsselung
 Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Primzahlen und RSA-Verschlüsselung Michael Fütterer und Jonathan Zachhuber 1 Einiges zu Primzahlen Ein paar Definitionen: Wir bezeichnen mit Z die Menge der positiven und negativen ganzen Zahlen, also
Definition und Begriffe
 Merkblatt: Das Dreieck Definition und Begriffe Das Dreieck ist ein Vieleck. In der Ebene ist es die einfachste Figur, die von geraden Linien begrenzt wird. Ecken: Jedes Dreieck hat drei Ecken, die meist
Merkblatt: Das Dreieck Definition und Begriffe Das Dreieck ist ein Vieleck. In der Ebene ist es die einfachste Figur, die von geraden Linien begrenzt wird. Ecken: Jedes Dreieck hat drei Ecken, die meist
Idee: Wenn wir beim Kopfknoten zwei Referenzen verfolgen können, sind die Teillisten kürzer. kopf Eine Datenstruktur mit Schlüsselwerten 1 bis 10
 Binäre Bäume Bäume gehören zu den wichtigsten Datenstrukturen in der Informatik. Sie repräsentieren z.b. die Struktur eines arithmetischen Terms oder die Struktur eines Buchs. Bäume beschreiben Organisationshierarchien
Binäre Bäume Bäume gehören zu den wichtigsten Datenstrukturen in der Informatik. Sie repräsentieren z.b. die Struktur eines arithmetischen Terms oder die Struktur eines Buchs. Bäume beschreiben Organisationshierarchien
Datensicherung und Wiederherstellung
 Dokumentation Datensicherung und Wiederherstellung Versionsverzeichnis Version: Datum: Revisionsgrund: Version 1.0 Januar 2011 Erste Ausgabe www.babe-informatik.ch 1/7 Datensicherung von Voraussetzung
Dokumentation Datensicherung und Wiederherstellung Versionsverzeichnis Version: Datum: Revisionsgrund: Version 1.0 Januar 2011 Erste Ausgabe www.babe-informatik.ch 1/7 Datensicherung von Voraussetzung
Information Systems Engineering Seminar
 Information Systems Engineering Seminar Algorithmische Prüfung der Planarität eines Graphen Marcel Stüttgen, 22.10.2012 FH AACHEN UNIVERSITY OF APPLIED SCIENCES 1 Planarität - Definition Ein Graph heißt
Information Systems Engineering Seminar Algorithmische Prüfung der Planarität eines Graphen Marcel Stüttgen, 22.10.2012 FH AACHEN UNIVERSITY OF APPLIED SCIENCES 1 Planarität - Definition Ein Graph heißt
Wie Google Webseiten bewertet. François Bry
 Wie Google Webseiten bewertet François Bry Heu6ge Vorlesung 1. Einleitung 2. Graphen und Matrizen 3. Erste Idee: Ranking als Eigenvektor 4. Fragen: Exisi6ert der Eigenvektor? Usw. 5. Zweite Idee: Die Google
Wie Google Webseiten bewertet François Bry Heu6ge Vorlesung 1. Einleitung 2. Graphen und Matrizen 3. Erste Idee: Ranking als Eigenvektor 4. Fragen: Exisi6ert der Eigenvektor? Usw. 5. Zweite Idee: Die Google
Algorithmen & Datenstrukturen 1. Klausur
 Algorithmen & Datenstrukturen 1. Klausur 7. Juli 2010 Name Matrikelnummer Aufgabe mögliche Punkte erreichte Punkte 1 35 2 30 3 30 4 15 5 40 6 30 Gesamt 180 1 Seite 2 von 14 Aufgabe 1) Programm Analyse
Algorithmen & Datenstrukturen 1. Klausur 7. Juli 2010 Name Matrikelnummer Aufgabe mögliche Punkte erreichte Punkte 1 35 2 30 3 30 4 15 5 40 6 30 Gesamt 180 1 Seite 2 von 14 Aufgabe 1) Programm Analyse
FORUM HANDREICHUNG (STAND: AUGUST 2013)
 FORUM HANDREICHUNG (STAND: AUGUST 2013) Seite 2, Forum Inhalt Ein Forum anlegen... 3 Forumstypen... 4 Beiträge im Forum schreiben... 5 Beiträge im Forum beantworten... 6 Besondere Rechte der Leitung...
FORUM HANDREICHUNG (STAND: AUGUST 2013) Seite 2, Forum Inhalt Ein Forum anlegen... 3 Forumstypen... 4 Beiträge im Forum schreiben... 5 Beiträge im Forum beantworten... 6 Besondere Rechte der Leitung...
Die Komplexitätsklassen P und NP
 Die Komplexitätsklassen P und NP Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 3. Dezember 2009 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit und
Die Komplexitätsklassen P und NP Prof. Dr. Berthold Vöcking Lehrstuhl Informatik 1 Algorithmen und Komplexität RWTH Aachen 3. Dezember 2009 Berthold Vöcking, Informatik 1 () Vorlesung Berechenbarkeit und
PVS Grobkonzept: Strukturelle und funktionale Erweiterungen bei der Verwaltung der Arbeitszeit und der organisatorischen Zuordnung
 PVS Grobkonzept: Strukturelle und funktionale Erweiterungen bei der Verwaltung der Arbeitszeit und der organisatorischen Zuordnung Bearbeiter: Klopfer, Klopfer Software GmbH Version: 31.10.2010 Abkürzungen
PVS Grobkonzept: Strukturelle und funktionale Erweiterungen bei der Verwaltung der Arbeitszeit und der organisatorischen Zuordnung Bearbeiter: Klopfer, Klopfer Software GmbH Version: 31.10.2010 Abkürzungen
Online Schulung Anmerkungen zur Durchführung
 Online Schulung Anmerkungen zur Durchführung 1.0 Einleitung Vielen Dank, dass Sie sich für die Online Schulung von SoloProtect entschieden haben. Nachfolgend finden Sie Informationen für Identicomnutzer
Online Schulung Anmerkungen zur Durchführung 1.0 Einleitung Vielen Dank, dass Sie sich für die Online Schulung von SoloProtect entschieden haben. Nachfolgend finden Sie Informationen für Identicomnutzer
Ihr CMS für die eigene Facebook Page - 1
 Ihr CMS für die eigene Facebook Page Installation und Einrichten eines CMS für die Betreuung einer oder mehrer zusätzlichen Seiten auf Ihrer Facebook Page. Anpassen der "index.php" Installieren Sie das
Ihr CMS für die eigene Facebook Page Installation und Einrichten eines CMS für die Betreuung einer oder mehrer zusätzlichen Seiten auf Ihrer Facebook Page. Anpassen der "index.php" Installieren Sie das
MailUtilities: Remote Deployment - Einführung
 MailUtilities: Remote Deployment - Einführung Zielsetzung Die Aufgabe von Remote Deployment adressiert zwei Szenarien: 1. Konfiguration der MailUtilities von einer Workstation aus, damit man das Control
MailUtilities: Remote Deployment - Einführung Zielsetzung Die Aufgabe von Remote Deployment adressiert zwei Szenarien: 1. Konfiguration der MailUtilities von einer Workstation aus, damit man das Control
